2021年中考数学一轮专题汇编：平移与旋转(含答案)

合集下载

2021中考数学一轮知识点系统复习之图形的平移、旋转与轴对称能力达标测试题(附答案详解)

2021中考数学一轮知识点系统复习之图形的平移、旋转与轴对称能力达标测试题（附答案详解）1．在平行四边形ABCD 中，AB=6，AD=8，∠B 是锐角，将△ACD 沿对角线AC 折叠，点D 落在△ABC 所在平面内的点E 处．如果AE 过BC 的中点，则平行四边形ABCD 的面积等于（）A ．48 B ．106 C ．127 D ．242 2．如图，在直角坐标系中，△OBC 的顶点O （0，0），B （﹣6，0），且∠OCB=90°，OC=BC ，则点C 关于y 轴对称的点的坐标是（）A ．（3，3）B ．（﹣3，3）C ．（﹣3，﹣3）D ．（32，32） 3．下列各组图形，可以经过平移变换由一个图形得到另一个图形的是( )．A ．B ．C ．D ． 4．如图，COD 是AOB 绕点O 顺时针方向旋转38后所得的图形，点C 恰好在AB 上，AOD 90∠=，那么BOC ∠的度数为（）A ．12°B ．14°C ．24°D ．30°5．点P （﹣4，﹣3）关于原点对称的点的坐标是（）A ．（4，3）B ．（﹣4，3）C ．（﹣4，﹣3）D ．（4，﹣3）6．如图，将∠BAC 沿DE 向∠BAC 内折叠，使AD 与A′D 重合，A′E 与AE 重合，若∠A=30°，则∠1+∠2=（）A ．50°B ．60°C ．45°D ．以上都不对 7．图中由“○”和“□”组成轴对称图形，该图形的对称轴是直线（）8．下面的图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．9．下列分子结构模型平面图中，只有一条对称轴的是（）A．B．C．D．10．如图，ABCD和DCGH是两块全等的正方形铁皮，要使它们重合，则存在的旋转中心有（）A．1个B．2个C．3个D．4个11．如图，点P在等边△ABC的内部，且PC=6，PA=8，PB=10，将线段PC绕点C顺时针旋转60°得到P'C，连接AP'，则sin∠PAP'的值为________．12．如图，正方形ABCD的边长为4，E是边BC上的一点且BE＝1，P为对角线AC上的一动点，连接PB，PE，当点P在AC上运动时，△PBE周长的最小值是____．13．如图，把△ABC经过一定的变换得到△A′B′C′，如果图中△ABC上的点P的坐标为（a，b），那么它的对应点P′的坐标为________．14．如图，将△ABE向右平移3cm得到△DCF，如果△ABE的周长是12cm，那么四边形ABFD的周长是_____cm．15．将点P（﹣1，3）绕原点顺时针旋转180°后坐标变为_____．16．已知平面直角坐标系内点P的坐标为（-1,3），如果将平面直角坐标系．．．．．．．向左平移3个单位,再向下平移2个单位,那么平移后点P的坐标为___________17．在平面直角坐标系中，已知点P0的坐标为(1，0)，将P0绕原点O按逆时针方向旋转30°得点P1，延长OP1到P2，使OP2＝2OP1，再将点P2绕原点O按逆时针方向转动30°得到点P3，延长OP3到P4，使OP4＝2OP3，…，如果继续下去，点P2016的坐标为_________.18．如图，△ABC中，AC＝10，AB＝12，△ABC的面积为48，AD平分∠BAC，F，E分别为AC，AD上两动点，连接CE，EF，则CE+EF的最小值为______．19．在等腰三角形ABC中，∠C=90°，BC=2cm．如果以AC的中点O为旋转中心，将这个三角形旋转180°，点B落在点B′处，那么点B′与点B的原来位置相距_____cm．20．如图①，在平面直角坐标系中，等边△ABC的顶点A，B的坐标分别为（5，0），（9，0），点D是x轴正半轴上一个动点，连接CD，将△ACD绕点C逆时针旋转60°得到△BCE，连接DE．（1）直接写出点C的坐标，并判断△CDE的形状，说明理由；（2）如图②，当点D在线段AB上运动时，△BDE的周长是否存在最小值？若存在，求出△BDE的最小周长及此时点D的坐标；若不存在，说明理由；（3）当△BDE是直角三角形时，求点D的坐标．（直接写出结果即可）21．三角形右边的是由左边的怎样平移得到的？22．如图，已知在△ABC中，AB=AC，AD⊥BC于D，且AD=BC=4，若将三角形沿AD剪开成为两个三角形，在平面上把这两个三角形拼成一个四边形，你能拼出所有的不同形状的四边形吗？画出所拼四边形的示意图（标出图中的直角），并分别写出所拼四边形的对角线的长．（只需写出结果即可）23．如图，正方形ABCD和正方形A1B1C1D1的对角线(正方形相对顶点之间所连的线段)BD，B1D1都在x轴上，O，O1分别为正方形ABCD和正方形A1B1C1D1的中心(正方形对角线的交点称为正方形的中心)，O为平面直角坐标系的原点．OD＝3，O1D1＝2.(1)如果O1在x轴上平移时，正方形A1B1C1D1也随之平移，其形状、大小没有改变，当中心O1在x轴上平移到两个正方形只有一个公共点时，求此时正方形A1B1C1D1各顶点的坐标；(2)如果O在x轴上平移时，正方形ABCD也随之平移，其形状、大小没有改变，当中心O在x轴上平移到两个正方形公共部分的面积为2个平方单位时，求此时正方形ABCD 各顶点的坐标．24．如图，正方形网格中的△ABC，若小方格边长为1，格点三角形（顶点是网格线交点的三角形）ABC的顶点A，C的坐标分别为（﹣1，1），（0，﹣2），请你根据所学的知识．（1）在如图所示的网格平面内作出平面直角坐标系；（2）作出三角形ABC关于y轴对称的三角形A1B1C1；（3）判断△ABC的形状，并求出△ABC的面积．25．在平面直角坐标系中，△ABC的三个顶点坐标分别为A（2，﹣1），B（3，﹣3），C（0，﹣4）（1）画出△ABC关于原点O成中心对称的△A1B1C1；（2）画出△A1B1C1关于y轴对称的△A2B2C2．26．如图，在正方形网格中，每个小正方形的边长为1，格点△ABC（顶点在网格线的交点上）的顶点A、C的坐标分别为A（﹣3，4）C（0，2）（1）请在网格所在的平面内建立平面直角坐标系，并写出点B的坐标；（2）画出△ABC关于原点对称的图形△A1B1C1；（3）求△ABC的面积；（4）在x轴上存在一点P，使PA+PB的值最小，请直接写出点P的坐标．27．已知：如图，在△ABC中，∠BAC=120°，以BC为边向形外作等边三角形BCD，把△ABD绕着点D按顺时针方向旋转60°后得到△ECD，若AB=5，AC=3，求∠BAD 的度数与AD的长．28．将△ABC的∠C折起，翻折后角的顶点位置记作C′，当C′落在AC上时（如图1），易证：∠1=2∠2．当C′点落在CA和CB之间（如图2）时，或当C′落在CB、CA的同旁（如图3）时，∠1、∠2、∠3关系又如何，请写出你的猜想，并就其中一种情况给出证明．图1 图2 图329．已知，△AOB中，AB=BC=2,∠ABC=90°，点O是线段AC的中点，连接OB，将△AOB 绕点A逆时针旋转α度得到△ANM，连接CM，点P是线段CM的中点，连接PN、PB．（1）如图1，当α=180°时，直接写出线段PN和PB之间的位置关系和数量关系；（2）如图2，当α=90°时，探究线段PN和PB之间的位置关系和数量关系，并给出完整的证明过程；（3）如图3，直接写出当△AOB在绕点A逆时针旋转的过程中，线段PN的最大值和最小值．参考答案1．C【解析】设AE 与BC 交于O 点，O 点是BC 的中点．∵四边形ABCD 是平行四边形，∴∠B =∠D ．AB ∥CD ，又由折叠的性质推知∠D =∠E ，CE =CD∴∠B =∠E ．CE =AB∴△ABO 和△ECO 中，所以△ABO ≌△CEO （AAS ），所以AO =CO =4，OE =OB =4．∴AE =AD =8．∴△AED 为等腰三角形，又C 为底边中点，故三线合一可知∠ACE =90°，从而由勾股定理求得AC =．平行四边形ABCD 的面积=AC ×CD =12．故选：C ．2．A【解析】试题解析：已知90,OCB OC BC ∠=︒=，∴OBC 为等腰直角三角形，又因为顶点()()00,60,O B -，，过点C 作CD OB ⊥于点D ，则 3.OD DC ==所以C 点坐标为()33-，，点C 关于y 轴对称的点的坐标是()33.，故选A ．点睛：关于y轴对称的点的坐标特征：纵坐标不变，横坐标互为相反数. 3．A【解析】试题分析：根据平移的性质，结合图形对选项进行一一分析，选出正确答案．解：A、图形的形状和大小没有变化，符合平移的性质，属于平移得到；B、图形的大小发生变化，不符合平移的性质，不属于平移得到；C、图形的方向发生变化，不符合平移的性质，不属于平移得到；D、图形由轴对称得到，不属于平移得到．故选A．考点：生活中的平移现象．4．B【解析】【分析】直接利用旋转的性质得出∠AOC=∠BOD=38°，进而得出∠BOC的度数．【详解】∵△COD是△AOB绕点O顺时针方向旋转38°后所得的图形，∴∠AOC=∠BOD=38°，∵∠AOD=90°，∴∠BOC=90°-38°-38°=14°．故选：B．【点睛】此题主要考查了旋转的性质，正确得出∠AOC=∠BOD是解题关键．5．A【解析】解：点P(-4，-3)关于原点对称的点的坐标是（4，3）．故选A．6．B【解析】试题解析：∵∠1=180﹣2∠ADE；∠2=180﹣2∠AED．∴∠1+∠2=360°﹣2（∠ADE+∠AED）=360°﹣2（180°﹣30°）=60°．故选B．7．C【解析】【分析】根据轴对称图形的定义进行判断即可得到对称轴.【详解】解:观察可知沿l1折叠时，直线两旁的部分不能够完全重合，故l1不是对称轴；沿l2折叠时，直线两旁的部分不能够完全重合，故l2不是对称轴；沿l3折叠时，直线两旁的部分能够完全重合，故l3是对称轴，所以该图形的对称轴是直线l3，故选C．【点睛】本题主要考查了轴对称图形，关键是掌握轴对称图形的定义．根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴．8．B【解析】分析：根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．详解：A．该图形是是轴对称图形不是中心对称图形，故本选项错误；B．该图形既是轴对称图形，又是中心对称图形，故本选项正确；C．该图形不是轴对称图形，是中心对称图形，故本选项错误；D．该图形是是轴对称图形，不是中心对称图形，故本选项错误．故选B．点睛：本题主要考查了中心对称图形与轴对称的定义，根据定义得出图形形状是解决问题的关键．9．A【解析】根据图形可得：选项A有1条对称轴，选项B、C各有2条对称轴，选项D有6条对称轴，故选A.【点睛】本题主要考查了轴对称图形的定义，关键是正确找出每个图形的对称轴．10．C【解析】分析：旋转中心即是对应点连线的垂直平分线的交点.详解：根据旋转中心即是对应点连线的垂直平分线的交点，可得要使正方形ABCD和DCGH重合，有3种方法，可以分别绕D，C或CD的中点旋转，即旋转中心有3个．故选C．点睛：本题考查了旋转的性质旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等，旋转中心即是对应点连线的垂直平分线的交点.11．35．【解析】解：连接PP′．如图，∵线段PC绕点C顺时针旋转60°得到P'C，∴CP=CP′=6，∠PCP′=60°，∴△CPP′为等边三角形，∴PP′=PC=6．∵△ABC为等边三角形，∴CB=CA，∠ACB=60°，∴∠PCB=∠P′CA．在△PCB和△P′CA中，∵PC=P′C，∠PCB=∠P′CA，CB=CA，∴△PCB≌△P′CA，∴PB=P′A=10．∵62+82=102，∴PP′2+AP2=P′A2，∴△APP′为直角三角形，∠APP′=90°，∴sin∠P AP′='6'10PPP A=35．故答案为35．12．6【解析】连接DE于AC交于点P′，连接BP′，则此时△BP′E的周长就是△PBE周长的最小值，∵BE=1，BC=CD=4，∴CE=3，DE=5，∴BP′+P′E=DE=5，∴△PBE周长的最小值是5+1=6，故答案为6．13．（﹣a﹣2，﹣b）【解析】由图可知，△ABC关于点（﹣1，0）对称变换得到△A′B′C′，∵△ABC上的点P的坐标为（a，b），∴它的对应点P′的坐标为（﹣a﹣2，﹣b），故答案为：（﹣a﹣2，﹣b）．14．18．【解析】【分析】根据平移的性质可得DF=AE，然后判断出四边形ABFD的周长=△ABE的周长+AD+EF，然后代入数据计算即可得解．【详解】∵△ABE向右平移3cm得到△DCF，∴DF=AE，∴四边形ABFD的周长=AB+BE+DF+AD+EF，=AB+BE+AE+AD+EF，=△ABE的周长+AD+EF，∵平移距离为3cm，∴AD=EF=3cm，∵△ABE的周长是12cm，∴四边形ABFD的周长=12+3+3=18cm.故答案为18cm.【点睛】本题考查了平移的性质，解题的关键是熟练的掌握平移的性质.15．（1，﹣3）【解析】【分析】画出平面直角坐标系，然后作出点P绕原点O顺时针旋转180°的点P′的位置，再根据平面直角坐标系写出坐标即可．【详解】如图所示：点P（-1，3）绕原点O顺时针旋转180°后的对应点P′的坐标为（1，-3）．故答案是：（1，-3）．【点睛】考查了坐标与图形变化-旋转，作出图形，利用数形结合的思想求解更简便，形象直观．16．（2,5）【解析】【分析】平面直角坐标系．．．．．．．向左平移3个单位,再向下平移2个单位,相当于将点(-1,3)向右平移3个单位,再向上平移2个单位.应用点的平移与坐标关系便可得出答案.【详解】因为将平面直角坐标系．．．．．．．向左平移3个单位,再向下平移2个单位,相当于将点(-1,3)向右平移3个单位,再向上平移2个单位，此时得到对应点的坐标是(-1+3,3+2),即(2,5).故正确答案为: (2,5).【点睛】此题考核知识点：点的平移和坐标.关键要弄清点移动的方向和距离，特别要注意此题是移动平面直角坐标系．．．．．．．.17．(21008,0)【解析】∵点P0的坐标为(1,0)，∴OP0=1，∴OP2=2OP1=2，OP3=OP2=2，OP4=2OP3=2×2=22，…，OP2016=21008，∵2016÷24=84，∴点P2016是第84循环组的最后一个点，在x轴正半轴，∴点P2016的坐标为(21008,0).故答案为：(21008,0).点睛：本田考查了坐标与图形的变化-旋转，点的坐标变化规律，读懂题目信息，理解点的规律变化是解题的关键.18．8【解析】【分析】根据题意画出符合条件的图形，作F关于AD的对称点为M，作AB边上的高CP，求出EM+EC=MC，根据垂线段最短得出EM+EC=MC≥PC，求出PC即可得出CE+EF的最小值．【详解】试题分析：作F关于AD的对称点为M，作AB边上的高CP，∵AD平分∠CAB，△ABC为锐角三角形，∴M必在AC上，∵F关于AD的对称点为M，∴ME＝EF，∴EF＋EC＝EM＋EC，即EM＋EC＝MC≥PC（垂线段最短），∵△ABC的面积是48，AB＝12，∴12×12×PC＝48，∴PC＝8，即CE＋EF的最小值为8．故答案为8．点睛：本题考查了最短路线问题，关键是画出符合条件的图形，题目具有一定的代表性，是一道比较好的题目．19．．【解析】分析：由中心对称的性质得OA＝OC，OB＝OB′，用勾股定理求出OB即可.详解：根据中心对称的性质得，OB＝OB′，OC＝1，又BC＝2，由勾股定理得BO BB′＝2OB＝故答案为点睛：中心对称的性质有：①关于中心对称的两个图形是全等形；②关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分；③关于中心对称的两个图形，对应线段平行(或在同一直线上)且相等.20．（Ⅰ）C(7，△CDE是等边三角形；（Ⅱ）存在；4 ；D（7，0）；（Ⅲ）D（1，0）或（13，0）．【解析】分析：（1）如图1，过点C作CH⊥x轴于点H，由△ABC是等边三角形易得AH=12AB=2，结合AC=AB=4、OA=5，可得CH=OH=7，由此即可得到点C的坐标；由旋转的性质可知CE=CD，结合旋转角∠DCE=60°可知△CDE是等边三角形；（2）如图2，由（1）可知△CDE是等边三角形，由此可得DE=CD，由△CDE是由△CAD绕点C旋转得到的，由此可得BE=AD，从而可得△BDE的周长=BD+BE+DE=BD+AD+CD=AB+CD=4+CD，由此可知，当CD⊥AB时，CD最小，此时△BDE 的周长最小，由（1）可知，此时CD=23，OD=7，即当点D的坐标为（7，0）时，△BDE 的周长最小，最小值为423+；（3）如图3，由∠CBE=∠CAD=120°可得∠ABC=60°，由此可得∠DBE=60°≠90°，结合△BDE是直角三角形，可知：存在①∠BED=90°；②∠BDE=90°（如图3，∠BD'E'=90°）两种情况，分两种情况画出符合要求的图形，并结合已知条件进行分析计算即可.详解：（Ⅰ）如图1，过点C作CH⊥AB于H，∵△ABC是等边三角形，CH⊥AB于点H，∴∠AHC=90°，AH=12AB=12（9﹣5）=2，∴OH=OA+AH=7，∵AC=AB=4，∴在Rt△ACH中，224223-=∴ C(723)，；∵△CBE是由△CAD绕点C逆时针旋转60°得到的，∴∠DCE=60°，DC=EC，∴△CDE是等边三角形；（Ⅱ）存在，理由如下：如图2，由（Ⅰ）知，△CDE是等边三角形，∴DE=CD，由旋转知，BE=AD，∴C△DBE=BE+DB+DE=AB+DE=4+DE=4+CD，由垂线段最短可知，CD⊥AB于D时，△BDE的周长最小，此时，由（1）可知CD=23，OD=7，∴△BDE的周长最小值为4+23，点D（7，0）；（Ⅲ）如图3，∵由旋转知，∠CBE=∠CAD=120°，∵∠ABC=60°，∴∠DBE=60°≠90°，∵△BDE是直角三角形，∴存在∠BED=90°或∠BDE=90°（如图3，∠BD'E'=90°）两种情况，①当∠BED=90°时，∵△CDE是等边三角形，∴∠CED=60°，∴∠BEC=30°，∵∠CBE=∠CAD=120°，∴∠BCE=30°，∴BE=BC=AB=4，在Rt△BDE中，∠DBE=∠CBE﹣∠ABC=60°，∴BD=2BE=8，∵OB=9，∴OD=OB﹣BD=1，∴D（1，0），②当∠BD'E'=90°时，∵△CD'E'是等边三角形，∴∠CD'E'=60°，∴∠BD'C=30°，∵∠ABC=60°，∴∠BCD'=30°=∠BD'E，∴BD'=BC=6，∵OB=9，∴OD'=OB+BD'=13，∴D'（13，0），即：存在点D使△BDE是直角三角形，此时点D的坐标分别为：（1，0）或（13，0）．点睛：（1）解第1小题的关键是：作出如图1所示的辅助线，利用等边三角形的性质和直角三角形的性质求得AH和CH的长；（2）解第2小题的关键是：利用旋转的性质得到BE=AD，从而把△BDE的周长转化为为：(4+CD)来表达，这样当CD⊥x轴时，CD最短，则△BDE 的周长就最小，由此即可使问题得到解决；（3）解第3小题的要点是：根据已知条件分析存在∠BED=90°或∠BDE=90°两种情况，然后画出符合题意的图形，再进行分析计算即可得到所求结果.21．向右平移7个单位.【解析】试题分析:观察图形中对应点的变化，即可得出图形的变化规律.试题解析：找出对应点来后会发现右边的图形是由左边的向右平移7个单位长度得到的.22．略【解析】可让两斜边重合，得到一个矩形和一个一般的四边形，根据勾股定理和三角形的面积公式可求得对角线长；让两长直角边重合或两短直角边重合，可得到一个平行四边形，利用勾股定理求得一对角线的长．图1是矩形，两条对角线长相等，均为2；图2是平行四边形，两条对角线长4和4；图3是平行四边形，两条对角线长2和2；图4是一般的四边形，两条对角线长2和．23．（1）A1(5，2)，B1(3，0)，C1(5，－2)，D1(7，0)；（2）A(11，3)，B(8，0)，C(11，－3)，D(14，0)．【解析】【分析】（1）两个正方形只有一个公共点时，分D和B1为公共点，B和D1为公共点两种情况，结合平移的性质写出各点的坐标；（2）根据两个正方形的位置可知公共部分肯定是个正方形，面积是2，可以算出它的对角线长为2，所以有两种情况：点D和O1重合，点B和O1重合，据此解答.【详解】解：(1)当点B1与点D重合时，两个正方形只有一个公共点，此时A1(5，2)，B1(3，0)，C1(5，－2)，D1(7，0)；当点B与D1重合时，两个正方形只有一个公共点，此时A1(－5，2)，B1(－7，0)，C1(－5，－2)，D1(－3，0)．(2)当点D与O1重合时，两个正方形公共部分的面积为2个平方单位，此时A(5，3)，B(2，0)，C (5，－3)，D (8，0)；当点B 与O 1重合时，两个正方形公共部分的面积为2个平方单位，此时A (11，3)，B (8，0)，C (11，－3)，D (14，0)．【点睛】本题考查了坐标与图形变化-平移，解题的关键是熟练的掌握平移的相关知识点. 24．（1）见解析；（2）见解析；（3）直角三角形，2．【解析】【分析】（1）根据点A 和点C 的坐标即可作出坐标系；（2）分别作出三角形的三顶点关于y 轴的对称点，顺次连接可得；（3）根据勾股定理的逆定理可得．【详解】解：（1）如图所示：（2）如图所示，△A 1B 1C 1即为所求；（3）∵正方形小方格边长为1，∴AB 2211+2，BC 2222+2，AC 2213+10，∴AB 2+BC 2=AC 2，∴网格中的△ABC 是直角三角形．△ABC 的面积为122×2=2．【点睛】本题考查的是作图﹣轴对称变换，熟知关于y 轴对称的点的坐标特点是解答此题的关键． 25．（1）答案见解析；（2）答案见解析．【解析】试题分析：（1）根据网格结构找出点A 、B 、C 关于原点对称的点A 1、B 1、C 1的位置，然后顺次连接即可；（2）根据网格结构找出点A1、B1、C1关于y轴对称的点A2、B2、C2的位置，然后顺次连接即可．试题解析：（1）△A1B1C1如图所示；（2）△A2B2C2如图所示．考点：（1）作图-旋转变换；（2）作图-轴对称变换26．（1）坐标系详见解析，点B的坐标（﹣2，0）；（2）详见解析；（3）5；（4）点P 的坐标（﹣2，0）．【解析】【分析】（1）根据A、C点坐标，作出的平面直角坐标系即可，根据作出的平面直角坐标系写出B 点的坐标即可；（2）根据原点对称的特点画出图形即可；（3）利用矩形面积减去周围三角形面积得出即可；（4）根据轴对称的性质解答即可．【详解】解：（1）如图所示：点B的坐标（-2，0）；（2）如图所示，△A1B1C1即为所求；（3）△ABC的面积111 34222314222=⨯-⨯⨯-⨯⨯-⨯⨯=5；（4）点P的坐标（-2，0）．【点睛】本题考查的知识点是平移变换以及三角形面积求法和坐标轴确定方法，解题关键是正确平移顶点．27．∠BAD=60°，AD=8．【解析】【分析】根据旋转的性质先证明△ADE是等边三角形，由相似三角形的性质可得∠EAD=60°，AD=AE，即可得到∠BAD=∠BAC﹣∠CAD=60°，AD=AE=AC+CE=AC+AB=3+5=8．【详解】∵△ABD≌△ECD，∴AD=DE，∠BDA=∠DCE，∴∠BDC=∠ADE=60°，∠ABD=∠ECD，∵∠BAC=120°，∠BDC=60°，∴∠BAC+∠BDC=180°，∴∠ABD+∠ACD=180°，∴∠ACD+∠ECD=180°，∴A、C、E共线，∴△ADE是等边三角形，∴∠EAD=60°，AD=AE，∴∠BAD=∠BAC﹣∠CAD=60°，∴AD=AE=AC+CE=AC+AB=3+5=8．【点睛】本题考查了旋转的性质、等边三角形的判定与性质，证明△AED是等边三角形是解决问题的关键．28．∠1－∠3=2∠2，证明见解析．【解析】【分析】利用轴对称的知识找出等解即可进行推理判断．【详解】解：当C′点落在CA和CB之间（如图2）时，∠1+∠3=2∠2；当C′落在CB、CA的同旁（如图3）时，∠1－∠3=2∠2；对于图2证明如下：连结CC’，如图4所示，∵⊿EC’D是由⊿ECD翻折得到的，∴⊿EC’D≌⊿ECD，由此得EC=EC’，DC=DC’，∠EC’D=∠ECD，∴∠EC’C=∠ECC；∠DC’C=∠DCC，∵∠1=∠DC’C+∠DCC’ ，∠3=∠EC’C+∠ECC’ ，∴∠1+∠3=∠DC’C+∠DCC’ +∠EC’C+∠ECC’=2∠D C’C+2∠ EC’C =2(∠DC’C+∠EC’C)= 2∠2；∴∠1+∠3=2∠2；对于图3证明如下：设AC与DC’在⊿ABC内部所夹角为∠4，如图5所示，则有∠1=∠C +∠4，∠4=∠3+∠2，又由翻折得：∠2=∠C ，∴∠1=∠2+∠3+∠2=∠3+2∠2，∴∠1－∠3=2∠2．【点睛】本题主要考查了轴对称的性质.找准对称轴是解题的关键．29．(1)PN=PB ，PN⊥PB；(2)略；221-【解析】（1）由旋转的性质可得△ABC ≌△ANM ,再由直角三角形斜边的中线等于斜边的一半，得到PN 和PB 之间的位置关系和数量关系；（2）结论一样，证明的方法与（1）一样；（3）连接OP ，利用勾股定理可得出线段PN 的最大值和最小值.解：（1）PN PB ⊥，PN PB =．（2）连接PO ，∵90α=︒，∴90MAB ∠=︒．∵90ABC ∠=︒，∴//AM BC ． ∵AMN ≌ABO ，∴AB AM =，OB MN =，∴//AM BC ，=AM BC ,又∵90ABC ∠=︒,∴四边形ABCM 为正方形．∵P 为CM 中点，O 为AC 中点，∴12OP AM ， ∴OP PM =，45POC MAC ∠=∠=︒， ∴135BOP BOC POC ∠=∠+∠=︒． ∵9045135PMN ∠=︒+︒=︒， ∴PMN POB ∠=∠． PMN ≌POB ， ∴PN PB =，MPN OPB ∠=∠． ∵90MPO ∠=︒， ∴90NPB ∠=︒， ∴PN PB ⊥．（3）连接OP ． ∵P ，O 为AC ，MC 中点， ∴11122OP AM AB ===．在Rt AOB 中， ∵OA OB =，2AB =，∴OB =PO OP PB BO PO -≤≤+． ∵PB PN =，11PN ≤≤．PN ∴11．。

2020-2021学年中考数学平移与旋转专题训练(含答案)

2021中考数学平移与旋转专题训练一、选择题（本大题共10道小题）1. 如图，在平面直角坐标系xOy中，将四边形ABCD先向下平移，再向右平移，得到四边形A1B1C1D1，已知A(-3，5)，B(-4，3)，A1(3，3)，则B1的坐标为()A.(1，2)B.(2，1)C.(1，4)D.(4，1)2. 如图，将△OAB绕点O逆时针旋转得到△OA′B′，使点B恰好落在边A′B′上．已知AB＝4 cm，OB＝1 cm，∠B′＝60°，那么A′B的长是()A．4 cm B．3 cmC．2 3 cm D．(4－3)cm3. 如图，在Rt△ABC中，∠ABC＝90°，AB＝2，BC＝1.把△ABC分别绕直线AB 和BC旋转一周，所得几何体的底面圆的周长分别记作l1，l2，侧面积分别记作S1，S2，则()A. l1∶l2＝1∶2，S1∶S2＝1∶2B. l1∶l2＝1∶4，S1∶S2＝1∶2C. l1∶l2＝1∶2，S1∶S2＝1∶4D. l1∶l2＝1∶4，S1∶S2＝1∶44. 如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB上，点B的对应点为E，连接BE，下列结论一定正确的是()A.AC=ADB.AB⊥EBC.BC=DED.∠A=∠EBC5. 如图，四边形ABCD是边长为5的正方形，E是DC上一点，DE=1，将△ADE 绕着点A顺时针旋转到与△ABF重合，则EF=()A.B.C.5D.26. 如图，将线段AB先向右平移5个单位长度，再将所得线段绕原点顺时针旋转90°，得到线段A′B′，则点B的对应点B′的坐标是()A．(－4，1) B．(－1，2)C．(4，－1) D．(1，－2)7. 如图，Rt△OCB的斜边在y轴上，OC＝3，含30°角的顶点与原点重合，直角顶点C在第二象限，将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′，则点B的对应点B′的坐标是()A．(3，－1) B．(1，－3)C．(2，0) D．(3，0)8. 如图，在平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2，将△AOB绕点O逆时针旋转90°，点B的对应点B′的坐标是()图7－ZT－1A．(－1，2＋3) B．(－3，3)C．(－3，2＋3) D．(－3，3)9. 如图，在正方形ABCD中，边长AB=1，将正方形ABCD绕点A逆时针方向旋转180°至正方形AB1C1D1，则线段CD扫过的面积为()A.B.C.πD.2π10. 如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A′B′C，M是BC的中点，P是A′B′的中点，连接PM.若BC＝2，∠A＝30°，则线段PM的最大值是()A．4 B．3 C．2 D．1二、填空题（本大题共8道小题）11. 在如图所示的方格纸(1格长为1个单位长度)中，△ABC的顶点都在格点上，将△ABC绕点O按顺时针方向旋转得到△A'B'C'，各顶点仍在格点上，则其旋转角的度数是.12. 如图，在△ABC中，∠BAC=90°，AB=AC=10 cm，点D为△ABC内一点，∠BAD=15°，AD=6 cm，连接BD，将△ABD绕点A按逆时针方向旋转，使AB 与AC重合，点D的对应点为点E，连接DE，DE交AC于点F，则CF的长为cm.13. 如图，△ABC，△BDE都是等腰直角三角形，BA＝BC，BD＝BE，AC＝4，DE＝2 2.将△BDE绕点B逆时针旋转后得△BD′E′，当点E′恰好落在线段AD′上时，CE′＝________．14. 在如图所示的方格纸(1格长为1个单位长度)中，△ABC的顶点都在格点上，将△ABC绕点O按顺时针方向旋转得到△A′B′C′，使各顶点仍在格点上，则其旋转角的度数是________．15. 把二次函数y＝(x－1)2＋2的图象绕原点旋转180°后得到的图象的解析式为_______．16. 如图，将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE，直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF，连接EF，若AB＝3，AC＝2，且α＋β＝∠B，则EF＝________.17. 如图，在四边形ABCD中，AB＝AD，∠BAD＝∠BCD＝90°，连接AC.若AC＝6，则四边形ABCD的面积为________．18. 如图，AB⊥y轴，将△ABO绕点A逆时针旋转到△AB1O1的位置，使点B的对应点B1落在直线y＝－33x上，再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置，使点O1的对应点O2落在直线y＝－33x上，依次进行下去……若点B的坐标是(0，1)，则点O12的纵坐标为________．三、解答题（本大题共5道小题）19. 如图①，等腰直角三角形OEF的直角顶点O为正方形ABCD的中心，点C，D分别在OE和OF上，现将△OEF绕点O逆时针旋转角α(0°<α<90°)，连接AF，DE(如图K32-②).(1)在图②中，∠AOF=;(用含α的式子表示)(2)在图②中，猜想AF与DE的数量关系，并证明你的结论.①②20. 已知∠AOB=30°，H为射线OA上一定点，OH=+1，P为射线OB上一点，M为线段OH上一动点，连接PM，满足∠OMP为钝角，以点P为中心，将线段PM顺时针旋转150°，得到线段PN，连接ON.(1)依题意补全图;(2)求证:∠OMP=∠OPN;(3)点M关于点H的对称点为Q，连接QP.写出一个OP的值，使得对于任意的点M总有ON=QP，并证明.21. 如图①，在Rt△ABC中，∠A＝90°，AB＝AC，点D，E分别在边AB，AC 上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点．(1)观察猜想图①中，线段PM与PN的数量关系是________，位置关系是________；(2)探究证明把△ADE绕点A逆时针方向旋转到图②的位置，连接MN，BD，CE，判断△PMN 的形状，并说明理由；(3)拓展延伸把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝10，请直接写出△PMN面积的最大值．22. (1)如图(a)，在△ABC中，D是BC边的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF.①求证：BE＋CF＞EF；②若∠A＝90°，探索线段BE，CF，EF之间的数量关系，并加以证明．(2)如图(b)，在四边形ABDC中，∠B＋∠C＝180°，BD＝CD，∠BDC＝120°，以D为顶点作一个60°的角，角的两边分别交AB，AC于E，F两点，连接EF，探索线段BE，CF，EF之间的数量关系，并加以证明．23. △ABC和△DEF是两个全等的等腰直角三角形，∠BAC＝∠EDF＝90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q.(1)如图①，当点Q在线段AC上，且AP＝AQ时，求证：△BPE≌△CQE；(2)如图②，当点Q在线段CA的延长线上时，①求证：△BPE∽△CEQ；②当BP＝2，CQ＝9时，求BC的长．2021中考数学平移与旋转专题训练-答案一、选择题（本大题共10道小题）1. 【答案】B[解析]由A(-3，5)，A1(3，3)可知四边形ABCD先向下平移2个单位，再向右平移6个单位得到四边形A1B1C1D1，∵B(-4，3)，∴B1的坐标为(2，1).2. 【答案】B[解析] ∵旋转前、后的两个图形是全等图形，AB＝4 cm，OB＝1 cm，∴A′B′＝AB＝4 cm，OB′＝OB＝1 cm.在△OB′B中，∵∠B′＝60°，OB′＝OB，∴△OB′B是等边三角形，∴BB′＝OB＝1 cm，∴A′B＝A′B′－BB′＝4－1＝3(cm)．3. 【答案】A【解析】∵∠ABC＝90°，AB＝2，BC＝1，∴勾股定理得，AC＝ 5.①当△ABC绕AB旋转时，则底面周长l1＝2π×BC＝2π，侧面积为S1＝π×BC×AC ＝5π；②当△ABC绕BC旋转时，则底面周长l2＝2π×AB＝4π，侧面积为S2＝π×AB×AC＝25π，∴l1∶l2＝2π∶4π＝1∶2，S1∶S2＝5π∶25π＝1∶2.4. 【答案】D[解析]由旋转的性质可知，AC=CD，但∠A不一定是60°，所以不能证明AC=AD，所以选项A错误;由于旋转角度不确定，所以选项B不能确定;因为AB=DE，不确定AB和BC的数量关系，所以BC和DE的数量关系不能确定;由旋转的性质可知∠ACD=∠BCE，AC=DC，BC=EC，所以2∠A=180°-∠ACD，2∠EBC=180°-∠BCE，从而可证选项D是正确的.5. 【答案】D[解析]由旋转的性质可知，△ADE≌△ABF，∴BF=DE=1，∴FC=6，∵CE=4，∴EF===2.故选:D .6. 【答案】D7. 【答案】A8. 【答案】B[解析] 如图，过点B′作B′H ⊥y 轴于点H.由题意得，OA′＝A′B′＝2，∠B′A′H ＝60°， ∴∠A′B′H ＝30°，∴AH′＝12A′B′＝1，B′H ＝3， ∴OH ＝3，∴B′(－3，3)．9. 【答案】B【解析】如图，作出C ，D 点的运动路径，连接CC 1，S 线段CD 扫过的阴影部分=+S △ABC +-S正方形ABCD -=.因为AB=1，所以AC=，所以S 线段CD 扫过的阴影部分=π·AC 2-π·AD 2=，故选B .10. 【答案】B[解析] 连接PC.在Rt △ABC 中，∵∠A ＝30°，BC ＝2， ∴AB ＝4.根据旋转的性质可知，∠A′CB′＝90°，A′B′＝AB ＝4. ∵P 是A′B′的中点，∴PC ＝12A′B′＝2. ∵M 是BC 的中点，∴CM ＝12BC ＝1. 又∵PM≤PC ＋CM ，即PM≤3，∴PM的最大值为3(此时点P，C，M共线)．故选B.二、填空题（本大题共8道小题）11. 【答案】90°【解析】找到一组对应点A，A'，分别与旋转中心连接起来，则∠AOA'为旋转角，为90°.12. 【答案】(10-2)[解析]∵∠BAC=90°，∠BAD=15°，∴∠DAF=75°.由旋转可知，△ADE为等腰直角三角形，∠ADF=45°，过点A作AM⊥DF于点M，∠F AM=∠DAF-∠DAM=75°-45°=30°，∴AM=AD=3，∴AF=AM=2.∵AC=AB=10，∴FC=AC-AF=10-2.13. 【答案】2＋6[解析] 如图，连接CE′，∵△ABC，△BDE都是等腰直角三角形，BA＝BC，BD＝BE，AC＝4，DE＝2 2，∴AB＝BC＝2 2，BD＝BE＝2.∵将△BDE绕点B逆时针旋转后得△BD′E′，∴D′B＝BE′＝BD＝2，∠D′BE′＝90°，∠D′BD＝∠ABE′，∴∠ABD′＝∠CBE′，∴△ABD′≌△CBE′(SAS)，∴∠D ′＝∠CE′B ＝45°.过点B 作BH ⊥CE′于点H ，在Rt △BHE′中，BH ＝E′H ＝22BE′＝2，在Rt △BCH 中，CH ＝BC 2－BH 2＝6，∴CE′＝2＋ 6.故答案为2＋ 6.14. 【答案】90° [解析] 找到一组对应点A ，A′，并将其与旋转中心连接起来，确定旋转角，进而得到旋转角的度数为90°.15. 【答案】y ＝－x 2－2x －3 [解析] 旋转前二次项的系数a ＝1，抛物线的顶点坐标是(1，2)，旋转后二次项的系数a ＝－1，抛物线的顶点坐标是(－1，－2)，∴新抛物线的解析式为y ＝－(x ＋1)2－2，即y ＝－x 2－2x －3.16. 【答案】13 [解析] ∵α＋β＝∠B ，∴∠EAF ＝∠BAC ＋∠B ＝90°，∴△AEF 是直角三角形，且AE ＝AB ＝3，AF ＝AC ＝2，∴EF ＝AE 2＋AF 2＝13.17. 【答案】18 [解析] 如图．∵∠BAD ＝∠BCD ＝90°，∴∠B ＋∠ADC ＝180°.又∵AB ＝AD ，∴将△ABC 绕点A 逆时针旋转90°后点B 与点D 重合，点C 的对应点E 落在CD 的延长线上，∴AE ＝AC ＝6，∠CAE ＝90°，∴S 四边形ABCD ＝S △ACE ＝12AC·AE ＝12×6×6＝18.18. 【答案】9＋3 3 [解析] 将y ＝1代入y ＝－33x ，解得x ＝－ 3.∴AB ＝3，OA ＝2，且直线y ＝－33x 与x 轴所夹的锐角是30°.由图可知，在旋转过程中每3次一循环，其中OO 2＝O 2O 4＝O 4O 6＝O 6O 8＝O 8O 10＝O 10O 12＝2＋3＋1＝3＋ 3.∴OO 12＝6×(3＋3)＝18＋6 3.∴点O 12的纵坐标＝12OO 12＝9＋3 3.三、解答题（本大题共5道小题）19. 【答案】解:(1)90°-α [解析]∵△OEF 绕点O 逆时针旋转角α，∴∠DOF=∠COE=α，∵四边形ABCD 为正方形，∴∠AOD=90°，∴∠AOF=90°-α.故答案为90°-α.(2)AF=DE.证明:∵四边形ABCD 为正方形，∴∠AOD=∠COD=90°，OA=OD ，∵∠DOF=∠COE=α，∴∠AOF=∠DOE.∵△OEF 为等腰直角三角形，∴OF=OE.在△AOF 和△DOE 中，∴△AOF ≌△DOE (SAS)，∴AF=DE.20. 【答案】解:(1)如图所示:(2)证明:在△OPM 中，∠OMP=180°-∠POM -∠OPM=150°-∠OPM ，∠OPN=∠MPN -∠OPM=150°-∠OPM ，∴∠OMP=∠OPN.(3)过点P 作PK ⊥OA 于点K ，过点N 作NF ⊥OB 于点F .∵∠OMP=∠OPN，∴∠PMK=∠NPF.在△NPF和△PMK中，∴△NPF≌△PMK(AAS)，∴PF=MK，∠PNF=∠MPK，NF=PK.在Rt△NFO和Rt△PKQ中，∴Rt△NFO≌Rt△PKQ(HL)，∴KQ=OF.设MK=y，PK=x，∵∠POA=30°，PK⊥OQ，∴OP=2x，∴OK=x，OM=x-y，∴OF=OP+PF=2x+y，MH=OH-OM=+1-(x-y)，KH=OH-OK=+1-x，∵M与Q关于点H对称，∴MH=HQ，∴KQ=KH+HQ=+1-x++1-x+y=2+2-2x+y，∵KQ=OF，∴2 +2-2x+y=2x+y，整理得2+2=x(2+2)，∴x=1，即PK=1，∴OP=2.21. 【答案】(1)PM＝PN，PM⊥PN；【解法提示】∵AB＝AC，AD＝AE，∴BD＝CE，∵M，P，N分别为DE，DC，BC的中点，∴PM//CE且PM=12CE，PN∥BD且PN=12BD，∴PM＝PN，∠DPM＝∠DCE，∠CNP＝∠B，∴∠DPN＝∠PNC＋∠PCN＝∠B＋∠PCN，∵∠A＝90°，∴∠B＋∠ACB＝90°，∴∠MPN＝∠MPD＋∠DPN＝∠ACD＋∠PCN＋∠B＝∠ACB＋∠B＝90°，∴PM⊥PN；(2)△PMN为等腰直角三角形．理由如下：由题可知△ABC和△ADE均为等腰直角三角形，∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°，∴∠BAD＋∠DAC＝∠DAC＋∠CAE，∴∠BAD＝∠CAE，∴△BAD≌△CAE(SAS)，∴∠ABD＝∠ACE，BD＝CE，又∵M，P，N分别是DE，CD，BC的中点，∴PM是△CDE的中位线，∴PM∥CE且PM=12 CE，同理PN∥BD且PN=12 BD，∴PM＝PN，∴∠MPD＝∠ECD＝∠ACD＋∠ACE＝∠ACD＋∠ABD，∠DPN＝∠PNC＋∠PCN＝∠DBC＋∠PCN，∴∠MPN＝∠MPD＋∠DPN＝∠ACD＋∠ABD＋∠DBC＋∠PCN＝∠ABC＋∠ACB＝90°，∴△PMN为等腰直角三角形；(3)49 2.【解法提示】∵△PMN为等腰直角三角形，∴S△PMN ＝12PM2，要使△PMN的面积最大，即PM最大，由(2)得，PM＝12CE，即当CE最大时，PM最大．如解图，当点C、E在点A异侧，且在同一条直线上时，CE最大，此时CE＝AE ＋AC＝AD＋AB＝14，解图∴PM＝12CE＝12×14＝7，故△PMN 的最大面积为S △PMN ＝12×7×7＝492.22. 【答案】解：(1)①证明：如图(a)，将△DBE 绕点D 旋转180°得到△DCG ，连接FG ，则△DCG ≌△DBE.∴DG ＝DE ，CG ＝BE.又∵DE ⊥DF ，∴DF 垂直平分线段EG ，∴FG ＝EF.∵在△CFG 中，CG ＋CF ＞FG ，∴BE ＋CF ＞EF.②BE 2＋CF 2＝EF 2.证明：∵∠A ＝90°，∴∠B ＋∠ACD ＝90°.由①得，∠FCG ＝∠FCD ＋∠DCG ＝∠FCD ＋∠B ＝90°，∴在Rt △CFG 中，由勾股定理，得CG 2＋CF 2＝FG 2，∴BE 2＋CF 2＝EF 2.(2)EF ＝BE ＋CF.证明：如图(b)．∵CD ＝BD ，∠BDC ＝120°，∴将△CDF 绕点D 逆时针旋转120°得到△BDM ，∴△BDM ≌△CDF ，∴DM ＝DF ，BM ＝CF ，∠BDM ＝∠CDF ，∠DBM ＝∠C.∵∠ABD ＋∠C ＝180°，∴∠ABD ＋∠DBM ＝180°，∴点A ，B ，M 共线，∴∠EDM ＝∠EDB ＋∠BDM ＝∠EDB ＋∠CDF ＝∠BDC －∠EDF ＝120°－60°＝60°＝∠EDF.在△DEM 和△DEF 中，⎩⎨⎧DE ＝DE ，∠EDM ＝∠EDF ，DM ＝DF ，∴△DEM ≌△DEF ，∴EF ＝EM ＝BE ＋BM ＝BE ＋CF.23. 【答案】(1)证明：∵△ABC 是等腰直角三角形，∴AB ＝AC ，∠B ＝∠C ＝45°，又∵AP ＝AQ ，∴BP ＝CQ ，∵E 是BC 的中点，∴BE ＝EC .∴在△BPE 与△CQE 中，∠∠BP CQ B C BE CE =⎧⎪=⎨⎪=⎩，∴△BPE ≌△CQE (SAS)；(2)①证明：∵∠BEF ＝∠C ＋∠CQE ，∠BEF ＝∠BEP ＋∠DEF ， ∠C ＝∠DEF ＝45°，∴∠CQE ＝∠BEP ，∵∠B ＝∠C ，∴△BPE ∽△CEQ ；②解：由①知△BPE ∽△CEQ ， ∴BE BP CQ CE=， ∴BE ·CE ＝BP ·CQ ，又∵BE ＝EC ，∴BE 2＝BP ·CQ ，∵BP ＝2，CQ ＝9，∴BE 2＝2×9＝18，∴BE ＝32，∴BC ＝2BE ＝6 2.。

中考数学一轮复习专题过关检测卷—轴对称、平移、旋转(含答案解析)

中考数学一轮复习专题过关检测卷—轴对称、平移、旋转（含答案解析）（考试时间：90分钟，试卷满分：100分）一、选择题（本题共10小题，每小题3分，共30分）。

1．下列图形中，对称轴最多的图形是（）A．B．C．D．【答案】A【解答】解：A．该图有无数条对称轴；B．该图有一条对称轴；C．该图有两条对称轴；D．该图有三条对称轴．所以对称轴最多的图形是选项A．故选：A．2．如图，将△ABC沿直线DE折叠，使点C与点A重合，已知AB＝7，BC＝6，则△BCD的周长为（）A．12B．13C．19D．20【答案】B【解答】解：由折叠可知，AD＝CD，∵AB＝7，BC＝6，∴△BCD的周长＝BC+BD+CD＝BC+BD+AD＝BC+AB＝7+6＝13．故选：B．3．在平面直角坐标系中，点（3，2）关于x轴对称的点是（）A．（﹣3，2）B．（3，﹣2）C．（﹣3，﹣2）D．（﹣2，3）【答案】B【解答】解在平面直角坐标系中，点（3，2）关于x轴对称的点是（3，﹣2）．故选：B．4．在平面直角坐标系中，将点A（﹣3，﹣2）向右平移5个单位长度得到的点坐标为（）A．（2，2）B．（﹣2，2）C．（﹣2，﹣2）D．（2，﹣2）【答案】D【解答】解：将点A（﹣3，﹣2）向右平移5个单位长度得到的点坐标为（﹣3+5，﹣2），即（2，﹣2），故选：D．5．“方胜”是中国古代妇女的一种发饰，其图案由两个全等正方形相叠组成，寓意是同心吉祥．如图，将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′，形成一个“方胜”图案，则重叠部分的小正方形边长为（）A．1cm B．2cm C．D．【答案】C【解答】解：∵四边形ABCD是正方形，∵AB＝AD＝2cm，∠A＝90°，∴BD＝AB＝2（cm），由平移变换的性质可知BB′＝1cm，∴DB′＝BD﹣BB﹣1）cm，∴小正方形的边长＝DB′＝×（2﹣1）＝（2﹣）cm，故选：C．6．如图，把三角形ABC沿BC方向平移1个单位长度得到三角形DEF，若四边形ABFD的周长为10，则三角形ABC的周长为（）A．8B．10C．12D．14【答案】A【解答】解：∵把三角形ABC沿BC方向平移1个单位长度得到三角形DEF，∴AD＝BE＝1，△ABC≌△DEF，∵四边形ABFD的周长为10，∴AD+BF+AB+DF＝10，∵BF＝BE+EF＝1+EF，∴1+1+EF+AB+DF＝10，即EF+AB+DF＝8，又∵DF＝AC，EF＝BC，∴AB+AC+BC＝8，∴三角形ABC的周长为：8．故选：A．7．如图，将△ABC绕点C逆时针旋转一定的角度得到△A′B′C′，此点A在边B′C上，若BC＝5，AC ＝3，则AB′的长为（）A．5B．4C．3D．2【答案】D【解答】解：∵△ABC绕点C逆时针旋转一定的角度得到△A′B′C′，点A在边B′C上，∴CB′＝CB＝5，∴AB′＝CB′﹣CA＝5﹣3＝2．故选：D．8．已知点A（a，1）与点B（﹣4，b）关于原点对称，则a﹣b的值为（）A．﹣5B．5C．3D．﹣3【答案】B【解答】解：∵点A（a，1）与点B（﹣4，b）关于原点对称，∴a＝4，b＝﹣1．∴a﹣b＝4﹣（﹣1）＝5．故选：B．9．如图，在方格纸上建立的平面直角坐标系中，将△ABO绕点O按顺时针方向旋转90°，得△A′B′O′，则点A′的坐标为（）A．（3，1）B．（3，2）C．（2，3）D．（1，3）【答案】D【解答】解：如图，点A′的坐标为（1，3）．故选D．10．如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（）A．6B．8C．10D．12【答案】C【解答】解：连接AD，∵△ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，＝BC•AD＝×4×AD＝16，解得AD＝8，∴S△ABC∵EF是线段AC的垂直平分线，∴点C关于直线EF的对称点为点A，∴AD的长为CM+MD的最小值，∴△CDM的周长最短＝CM+MD+CD＝AD+BC＝8+×4＝8+2＝10．故选：C．二、填空题(本题共6题，每小题2分，共12分）。

河北省2021年中考数学一轮复习训练：第七章第四节图形的平移与旋转附答案

第四节图形的平移与旋转基础分点练（建议用时：20分钟）考点1图形的平移1.[2020浙江台州]如图,把△ABC先向右平移3个单位长度,再向上平移2个单位长度得到△DEF,则顶点C(0,-1)对应点的坐标为()A.(0,0)B.(1,2)C.(1,3)D.(3,1)2.[2020上海]如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形,下列图形中,是平移重合图形的是()A.平行四边形B.等腰梯形C.正六边形D.圆3.[2020甘肃金昌]如图,在平面直角坐标系中,△OAB的顶点A,B的坐标分别为(3,),(4,0).把△OAB沿x轴向右平移得到△CDE,如果点D的坐标为(6,),则点E的坐标为.考点2图形的旋转4.[2020天津]如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B 的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是()A.AC=DEB.BC=EFC.∠AEF=∠DD.AB⊥DF5.[2020唐山路南区二模]如图,在△ABC中,AB=6,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1,连接AA1,则图中阴影部分的面积为()A.8B.9C.16D.186.[2020江苏苏州]如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB'=CB',则∠C'的度数为()A.18°B.20°C.24°D.28°7.[2020山东烟台]如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为.综合提升练（建议用时：25分钟）1.[2020石家庄四区联考]下列各图中,既可经过平移,又可经过旋转,由图形①得到图形②的是()2.[2020河南]如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(-2,6)和(7,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为()A.(,2)B.(2,2)C.(,2)D.(4,2)3.[2020浙江绍兴]如图,等腰直角三角形ABC中,∠ABC=90°,BA=BC,将BC绕点B顺时针旋转θ(0°<θ<90°),得到BP,连接CP,过点A作AH⊥CP交CP的延长线于点H,连接AP,则∠PAH 的度数()A.随着θ的增大而增大B.随着θ的增大而减小C.不变D.随着θ的增大,先增大后减小4.[2019秦皇岛海港区二模]已知正方形MNKL和正六边形ABCDEF的边长均为1,把正方形放在正六边形外边,使LK边与AB边重合,如图所示.按下列步骤操作:将正方形在正六边形外绕点B顺时针旋转,使KN边与BC边重合,完成第1次旋转;再绕点C 顺时针旋转,使NM边与CD边重合,完成第2次旋转……在这样连续6次旋转的过程中,点M 在图中直角坐标系中的纵坐标可能是()A.2.2B.-2.2C.2.3D.-2.35.[2020石家庄新华区一模]如图,在等腰三角形ABC中,AB=BC,∠BAC=α.将△ABC绕点A 逆时针旋转2α,得到△ADE,连接BE.(1)求证:BE=BC.(2)判断四边形ABED是什么形状的四边形,并说明理由.(3)请直接写出当α分别是多少度时,下列情况成立.①BE⊥AC;②BE∥AC.(1)证明:根据旋转的性质,得AE=AC,∠EAC=2α.6.[2020湖北孝感]如图,在平面直角坐标系中,已知点A(-1,5),B(-3,1)和C(4,0),请按下列要求画图并填空.(1)平移线段AB,使点A平移到点C,画出平移后所得的线段CD,并直接写出点D的坐标:;(2)将线段AB绕点A逆时针旋转90°,画出旋转后所得的线段AE,并直接写出cos∠BCE的值:;(3)在y轴上找出点F,使△ABF的周长最小,并直接写出点F的坐标:.解:(1)如图,线段CD即为所求.答案第四节图形的平移与旋转基础分点练（建议用时：20分钟）考点1图形的平移1.[2020浙江台州]如图,把△ABC先向右平移3个单位长度,再向上平移2个单位长度得到△DEF,则顶点C(0,-1)对应点的坐标为( D )A.(0,0)B.(1,2)C.(1,3)D.(3,1)2.[2020上海]如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形,下列图形中,是平移重合图形的是( A )A.平行四边形B.等腰梯形C.正六边形D.圆3.[2020甘肃金昌]如图,在平面直角坐标系中,△OAB的顶点A,B的坐标分别为(3,),(4,0).把△OAB沿x轴向右平移得到△CDE,如果点D的坐标为(6,),则点E的坐标为(7,0).考点2图形的旋转4.[2020天津]如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B 的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是( D )A.AC=DEB.BC=EFC.∠AEF=∠DD.AB⊥DF5.[2020唐山路南区二模]如图,在△ABC中,AB=6,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1,连接AA1,则图中阴影部分的面积为( B )A.8B.9C.16D.186.[2020江苏苏州]如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB'=CB',则∠C'的度数为( C )A.18°B.20°C.24°D.28°7.[2020山东烟台]如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为(4,2).综合提升练（建议用时：25分钟）1.[2020石家庄四区联考]下列各图中,既可经过平移,又可经过旋转,由图形①得到图形②的是( D )2.[2020河南]如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(-2,6)和(7,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为( B )A.(,2)B.(2,2)C.(,2)D.(4,2)3.[2020浙江绍兴]如图,等腰直角三角形ABC中,∠ABC=90°,BA=BC,将BC绕点B顺时针旋转θ(0°<θ<90°),得到BP,连接CP,过点A作AH⊥CP交CP的延长线于点H,连接AP,则∠PAH 的度数( C )A.随着θ的增大而增大B.随着θ的增大而减小C.不变D.随着θ的增大,先增大后减小4.[2019秦皇岛海港区二模]已知正方形MNKL和正六边形ABCDEF的边长均为1,把正方形放在正六边形外边,使LK边与AB边重合,如图所示.按下列步骤操作:将正方形在正六边形外绕点B顺时针旋转,使KN边与BC边重合,完成第1次旋转;再绕点C 顺时针旋转,使NM边与CD边重合,完成第2次旋转……在这样连续6次旋转的过程中,点M 在图中直角坐标系中的纵坐标可能是( A )A.2.2B.-2.2C.2.3D.-2.35.[2020石家庄新华区一模]如图,在等腰三角形ABC中,AB=BC,∠BAC=α.将△ABC绕点A 逆时针旋转2α,得到△ADE,连接BE.(1)求证:BE=BC.(2)判断四边形ABED是什么形状的四边形,并说明理由.(3)请直接写出当α分别是多少度时,下列情况成立.①BE⊥AC;②BE∥AC.(1)证明:根据旋转的性质,得AE=AC,∠EAC=2α.又∵∠BAC=α,∴∠BAE=∠EAC-∠BAC=2α-α=α,∴∠BAE=∠BAC.又∵AE=AC,AB=AB,∴△ABE≌△ABC,∴BE=BC.(2)四边形ABED是菱形.理由:根据旋转的性质得AD=AB,DE=BC.又∵AB=BC,BE=BC,∴AD=AB=BE=DE,∴四边形ABED是菱形.(3)①α=30°.②α=60°.解法提示:①∵四边形ABED是菱形,∴AD∥BE.又BE⊥AC,∴AD⊥AC,即∠DAC=90°.又∵∠DAE=∠BAE=∠BAC,∴∠BAC=∠DAC=30°,即α=30°.②∵BE∥AC,∴∠ABE=∠BAC.又∵∠BAE=∠BAC,∴∠ABE=∠BAE.∵AB=BE,∴∠BEA=∠BAE,∴∠ABE=∠BAE=∠BEA,∴∠EAB==60°,即α=60°.6.[2020湖北孝感]如图,在平面直角坐标系中,已知点A(-1,5),B(-3,1)和C(4,0),请按下列要求画图并填空.(1)平移线段AB,使点A平移到点C,画出平移后所得的线段CD,并直接写出点D的坐标: (2,-4);(2)将线段AB绕点A逆时针旋转90°,画出旋转后所得的线段AE,并直接写出cos∠BCE的值:;(3)在y轴上找出点F,使△ABF的周长最小,并直接写出点F的坐标:(0,4).解:(1)如图,线段CD即为所求.(2,-4)(2)如图,线段AE即为所求.55(3)如图,作点A关于y轴的对称点A',连接A'B,A'B与y轴的交点即为所求点F. (0,4)。

备战2021年中考数学精品系列-专题26 平移、旋转与对称(解析版)

备战2021年中考数学精品系列-专题26 平移、旋转与对称（解析版）☞解读考点知识点名师点晴图形的平移1.平移的概念知道什么是图形的平移。

2.平移的性质掌握平移的性质。

3.平移的条件了解平移条件。

4.平移作图能准确利用平移作图。

图形的旋转 5.旋转的定义知道什么是旋转。

6.旋转的性质掌握旋转的性质。

7.中心对称及中心对称图形了解中心对称和中心对称图形概念，能区分两个概念。

8.中心对称的性质能掌握中心对称的性质，能正确作图。

图形的轴对称 9.轴对称、轴对称图形的定义能区别两个概念。

10.轴对称的性质能正确应用性质。

11.轴对称作图会正确作出一个图形关于某直线的轴对称图形。

☞2年中考[2020年题组]1. （2020年广西来宾）将点P（﹣2，3）向右平移3个单位得到点P1，点P2与点P1关于原点对称，则P2的坐标是【】A．（﹣5，﹣3）B．（1，﹣3）C．（﹣1，﹣3）D．（5，﹣3）【答案】C．【考点】1.坐标与图形的平移变化；2. 关于原点对称的点的坐标特征.2. （2020年广西玉林、防城港）如图，边长分别为1和2的两个等边三角形，开始它们在左边重合，大三角形固定不动，然后把小三角形自左向右平移直至移出大三角形外停止．设小三角形移动的距离为x ，两个三角形重叠面积为y ，则y 关于x 的函数图象是【】A ．B ．C ．D ．【答案】B ．【分析】根据题目提供的条件可以求出函数的解析式，根据解析式应用排它法判断函数的图象的形状：①当t≤1时，两个三角形重叠面积为小三角形的面积， ∴133y 1224=⋅⋅=.故可排除选项D. ②当1＜x≤2时，重叠三角形的边长为2﹣x ，高为()322x -，∴()()()232x 13y 2x x 2224-=⋅-⋅=-，它的图象是开口向上，顶点为()2,0 的抛物线在1＜x≤2的部分. 故可排除选项A ，C.故选B ．【考点】1.面动平移问题的函数图象问题；2.由实际问题列函数关系式；3.二次函数的性质和图象；4.分类思想和排它法的应用．3. （2020年贵州遵义）如图，已知△ABC 中，∠C=90°，AC=BC=，将△ABC 绕点A 顺时针方向旋转60°到△AB′C′的位置，连接C′B ，则C′B 的长为【】A ．22-B ．32C ．31-D ．1 【答案】C ．如答图，连接BB′，延长BC′交AB′于D ，∵△ABC 绕点A 顺时针方向旋转60°得到△AB′C′，∴AB=AB′，∠BAB′=60°.∴△ABB′是等边三角形. ∴AB=BB′，在△ABC′和△B′BC′中，∵AB BB 'AC ' B 'C 'BC 'BC '=⎧⎪=⎨⎪=⎩，∴△ABC′≌△B′BC′（SSS ）. ∴∠ABC′=∠B′BC′. ∴BD ⊥AB′.∵∠C=90°，2，∴()()22222+=.∴BD=3232⨯=，C′D=12×2=1. ∴BC′=BD ﹣C′D=31-．故选C ．【考点】1.旋转的性质；2. 等边三角形的判定和性质；3.全等三角形的判定和性质；4.勾股定理．4. （2020年江苏苏州）如图，△AOB 为等腰三角形，顶点A 的坐标为（2，5），底边OB 在x 轴上．将△AOB 绕点B 按顺时针方向旋转一定角度后得△A'O'B ，点A 的对应点A'在x 轴上，则点O'的坐标为【】A ．（203，103） B ．（163，453） C ．（203，453） D ．（163，43）【答案】C.【分析】利用等面积法求O'的纵坐标，再利用勾股定理或三角函数求其横坐标：如答图，过O’作O’F ⊥x 轴于点F ，过A 作AE ⊥x 轴于点E ，∵A 的坐标为（2，5），∴AE=5，OE=2.学科网由等腰三角形底边上的三线合一得OB=2OE=4，在Rt △ABE 中，由勾股定理可求AB=3，则A’B=3，由旋转前后三角形面积相等得OB AE A'B O'F22⋅⋅=，453O'F2⋅⋅=，∴45·在Rt △O’FB 中，由勾股定理可求BF=22458433⎛⎫-= ⎪ ⎪⎝⎭，∴OF=820433+=. ∴O’的坐标为（2045,33）. 故选C.【考点】1.坐标与图形的旋转变化；2.勾股定理；3. 等腰三角形的性质；4.三角形面积公式．5.（2020年贵州黔东南）如图，在矩形ABCD 中，AB=8，BC=16，将矩形ABCD 沿EF 折叠，使点C 与点A 重合，则折痕EF 的长为【】A ．6B ．12C ．25D ．45【答案】D ．【分析】设BE=x ，则CE=BC ﹣BE=16﹣x ，∵沿EF 翻折后点C 与点A 重合，∴AE=CE=16﹣x.在Rt △ABE 中，AB 2+BE 2=AE 2，即82+x 2=（16﹣x ）2，解得x=6.∴AE=16﹣6=10.学科网由翻折的性质得，∠AEF=∠CEF ，∵矩形ABCD 的对边AD ∥BC ，∴∠AFE=∠CEF.∴∠AEF=∠AFE. ∴AE=AF=10.如答图，过点E 作EH ⊥AD 于H ，则四边形ABEH 是矩形，∴EH=AB=8，AH=BE=6.∴FH=AF ﹣AH=10﹣6=4.在Rt △EFH 中，2222EF EH FH 8445=+=+=故选D．【考点】1.翻折变换（折叠问题）；2.翻折对称的性质；3.矩形的判定和性质；4.勾股定理；5.方程思想的应用．6.（2020年湖南邵阳）如图，A点的初始位置位于数轴上的原点，现对A点做如下移动：第1次从原点向右移动1个单位长度至B点，第2次从B点向左移动3个单位长度至C点，第3次从C点向右移动6个单位长度至D点，第4次从D点向左移动9个单位长度至E点，…，依此类推，这样至少移动▲ 次后该点到原点的距离不小于41．【答案】28．【分析】根据数轴上点的坐标变化和平移规律（左减右加），分别求出点所对应的数，进而求出点到原点的距离；然后对奇数项、偶数项分别探究，找出其中的规律（相邻两数都相差3），写出表达式；然后根据点到原点的距离不小于41建立不等式，就可解决问题：由题意可得：移动1次后该点对应的数为0+1=1，到原点的距离为1；移动2次后该点对应的数为1﹣3=﹣2，到原点的距离为2；移动3次后该点对应的数为﹣2+6=4，到原点的距离为4；移动4次后该点对应的数为4﹣9=﹣5，到原点的距离为5；移动5次后该点对应的数为﹣5+12=7，到原点的距离为7；移动6次后该点对应的数为7﹣15=﹣8，到原点的距离为8；…∴移动（2n﹣1）次后该点到原点的距离为3n﹣2；移动2n次后该点到原点的距离为3n﹣1．①当3n﹣2≥41时，学科网解得：n≥433．∵n是正整数，∴n最小值为15，此时移动了29次．②当3n﹣1≥41时，解得：n≥14．∵n是正整数，∴n最小值为14，此时移动了28次．综上所述：至少移动28次后该点到原点的距离不小于41．【考点】1.探索规律题（图形的变化类）；2.数轴；3.不等式的应用；4.分类思想的应用.7.（2020年黑龙江齐齐哈尔、大兴安岭地区、黑河）如图，在在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB=90°，直角边AO在x轴上，且AO=1．将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1，且A1O=2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2，且A2O=2A1O…，依此规律，得到等腰直角三角形A2020OB2020，则点A2020的坐标为▲ ．【答案】（﹣22020，0）．【分析】根据题意得出A点坐标变化规律，得出点A2020的坐标位置，进而得出答案：∵将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1，且A1O=2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2，且A2O=2A1O…，依此规律，∴每4次循环一周，A1（0，﹣2），A2（﹣4，0），A3（0，8），A4（16，0），∵2020÷4=503…2，∴点A2020的坐标与A2所在同一象限．∵﹣4=﹣22，8=23，16=24，∴点A2020（﹣22020，0）．【考点】1.探索规律题（图形的变化类型----循环问题）；2.点的坐标．8.（2020年湖南张家界）如图，AB、CD是⊙O两条弦，AB=8，CD=6，MN是直径，AB⊥MN于E,CD⊥MN 于点F,P为EF上任意一点,，则PA+PC的最小值为▲ ．【答案】72【分析】由于A、B两点关于MN对称，因而PA+PC=PB+PC，即当B、C、P在一条直线上时，PA+PC的最小，即BC的值就是PA+PC的最小值．学科网因此，如答图，连接BC，OB，OC，过点C作CH垂直于AB于H．∵AB=8，CD=6，MN 是直径，AB ⊥MN 于点E ，CD ⊥MN 于点F ，∴BE=12AB=4，CF=12CD=3. ∴22222222OE OB BE 543OF OC CF 534=-=-==-=-=，.∴CH=OE+OF=3+4=7，BH=BE+EH=BE+CF=4+3=7.在Rt △BCH 中根据勾股定理得到2222BC BH CH 7772=+=+=，即PA+PC 的最小值为72．【考点】1.轴对称的应用（最短路线问题）；2.勾股定理；3.垂径定理．9. （2020年江苏连云港）如图1，将正方形纸片ABCD 对折，使AB 与CD 重合，折痕为EF ，如图2，展开再折叠一次，使点C 与点E 重合，折痕为GH ，点B 的对应点为M ，EM 交AB 于N ，则tan ∠ANE= ▲ .【答案】34. 【分析】设正方形的边长为2，DH=x ，则CH=2x -，由翻折的性质，11DE AD 2122==⨯=，EH CH 2x ==-，学科网在Rt △DEH 中，DE 2+DH 2=EH 2，即()2221x 2x +=-，解得x=34. ∵∠MEH=∠C=90°，∴∠AEN+∠DEH=90°.∵∠ANE+∠AEN=90°，∴∠ANE=∠DEH.∴tan∠ANE=tan∠DEH=3DH 34DE14==．【考点】1. 翻折变换（折叠问题）；2.正方形的性质；3.勾股定理；4.锐角三角函数定义；5.方程思想、转换思想和特殊元素法的应用．10.（2020年辽宁本溪）如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC+∠EAD=180°，△ABC 不动，△ADE绕点A旋转，连接BE、CD，F为BE的中点，连接AF．（1）如图①，当∠BAE=90°时，求证：CD=2AF；（2）当∠BAE≠90°时，（1）的结论是否成立？请结合图②说明理由．【答案】解：（1）证明：如图①，∵∠BAC+∠EAD=180°，∠BAE=90°，∴∠DAC=90°．在△ABE与△ACD中，∵AE=AD，∠BAE=∠CAD=90°，AB=AC，∴△ABE≌△ACD（SAS）．∴CD=BE．∵在Rt△ABE中，F为BE的中点，∴BE=2AF．∴CD=2AF．（2）成立，证明如下：如答图，延长EA交BC于G，在AG上截取AH=AD，∵∠BAC+∠EAD=180°，∴∠EAB+∠DAC=180°．∵∠EAB+∠BAH=180°，在△ABH与△ACD中，∵AH=AD，∠BAH=∠CAD，AB=AC，∴△ABH≌△ACD（SAS）．∴BH=DC．∵AD=AE，AH=AD，∴AE=AH．∵EF=FB，∴BH=2AF．∴CD=2AF．【分析】（1）因为AF是直角三角形ABE的中线，所以BE=2AF，学科网然后通过△ABE≌△ACD即可求得．（2）延长EA交BC于G，在AG上截取AH=AD，证出△ABH≌△ACD从而证得BH=CD，然后根据三角形的中位线等于底边的一半，求得BH=2AF，即可求得．【考点】1.面动旋转问题；2.全等三角形的判定和性质；3.等腰三角形的性质；4.三角形中位线定理；5.旋转的性质．[2020年题组]1. （2020年湖北荆门）如下图所示，已知等腰梯形ABCD，AD∥BC，若动直线l垂直于BC，且向右平移，设扫过的阴影部分的面积为S，BP为x，则S关于x的函数图象大致是【】A．B．C．D．【答案】A。

2021年全国各地中考数学试卷分类汇编平移旋转与对称

平移旋转与对称一．选择题1．〔2021贵州省六盘水，4，3分〕以下图形中，是轴对称图形的是〔〕A．B．C．D．考点：轴对称图形．分析：根据正多边形的性质和轴对称图形的定义解答即可．解答：解：根据轴对称图形的概念可直接得到A是轴对称图形，应选：A．点评：此题主要考查了轴对称图形，关键是掌握轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的局部能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴．2．〔2021贵州省黔西南州，8，4分〕在平行四边形、等腰梯形、等腰三角形、矩形、菱形五个图形中，既是中心对称图形又是轴对称图形的有〔〕A．1个B．2个C．3个D．4个3．〔2021河北省，3，2分〕以下图形中，既是轴对称图形又是中心对称图形的是4．〔2021河南省，2，3分〕以下图形中，既是轴对称图形又是中心对称图形的是〔〕【解析】轴对称是指在平面内，如果一个图形沿一条直线折叠，直线两旁的局部能够完全重合，这样的图形叫做轴对称图形。

中心对称图形是指平面内，如果把一个图形绕某个点旋转180°后，能与自身重合，那么就说这两个图形关于这个点成中心对称。

结合定义可知，答案是D【答案】D5．〔2021黑龙江省哈尔滨市，3〕以下图形中，既是轴对称图形又是中心对称图形的是( )．考点：轴对称图形与中心对称图形．分析：题考查了中心对称图形．掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两局部折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两局部重合．解答：A.是轴对称图形，不是中心对称图形；B. 是中心对称图形，不是轴对称图形．；C.是轴对称图形，不是中心对称图形；D. 是轴对称图形，又是中心对称图形；应选D．6．〔2021湖北省鄂州市，10，3分〕如图，直线a∥b，且a与b之间的距离为4，点A到直线a的距离为2，点B到直线b的距离为3，AB=．试在直线a上找一点M，在直线b上找一点N，满足MN⊥a且AM+MN+NB的长度和最短，那么此时AM+NB=〔〕A．6B．8C．10 D．12:// qiujieda /exercise/math/262714/?mty点评：此题考查了勾股定理的应用、平行线之间的距离，解答此题的关键是找到点M、点N 的位置，难度较大，注意掌握两点之间线段最短．7．〔2021湖北省十堰市，1，3分〕如图，将△ABC沿直线DE折叠后，使得点B与点A重合．AC=5cm，△ADC的周长为17cm，那么BC的长为〔〕A．7cm B．10cm C．12cm D．22cm8．〔2021湖北省咸宁市，1，3分〕以下学习用具中，不是轴对称图形的是〔〕A．B．C．D．9．〔2021湖北省咸宁市，1，3分〕如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧在第二象限交于点P．假设点P的坐标为〔2a，b+1〕，那么a与b的数量关系为〔〕A．a=b B．2a+b=﹣1 C．2a﹣b=1 D．2a+b=110．〔3分〕〔2021•桂林〕以下图形分别是桂林、湖南、甘肃、佛山电视台的台徽，其中为中心对称图形的是〔〕A．B．C．D．11．〔2021贵州毕节，8，3分〕在以下图形中既是轴对称图形又是中心对称图形的是〔〕①线段，②角，③等边三角形，④圆，⑤平行四边形，⑥矩形．A．③④⑥B．①③⑥C．④⑤⑥D．①④⑥12.〔2021湖南长沙，9，3分〕在以下某品牌T恤的四个洗涤说明图案的设计中，没有．．运用旋转或轴对称知识的是〔A B C D 13．〔2021湖南郴州，3，3分〕以下图案中，不是中心对称图形的是〔〕A．B．C．D．考点：中心对称图形．分析：根据中心对称图形的概念求解．解答：解：A、是中心对称图形，故本选项错误；B、不是中心对称图形，故本选项正确；C、是中心对称图形，故本选项错误；D、是中心对称图形，故本选项错误；应选B．点评：此题考查了中心对称图形的知识，解题的关键是掌握中心对称图形的概念．中心对称图形是要寻找对称中心，旋转180度后重合．14. ．〔2021湖南娄底，9，3分〕以下图形中是中心对称图形的是〔〕A．B．C．D．考点：中心对称图形．分析：根据中心对称的定义，结合所给图形即可作出判断．解答：解：A、不是中心对称图形，故本选项错误；B、是中心对称图形，故本选项正确；C、不是中心对称图形，故本选项错误；D、不是中心对称图形，故本选项错误；应选：B．点评：此题考查了中心对称图形的特点，属于根底题，判断中心对称图形的关键是旋转180°后能够重合．15 ．[2021湖南邵阳，2，3分]以下四个图形中，不是轴对称图形的是〔〕知识考点：轴对称图形、图形的旋转.审题要津：此题考查轴对称图形的概念.如果一个图形沿一条直线折叠，直线两旁的局部可以互相重合，那么这个图形就叫做轴对称图形.总分值解答：解：由图可知A、C、D都是轴对称图形，唯独B是由图形的旋转得到的.应选B.名师点评：此题主要考查轴对称图形的概念，解答此类题目还应注意中心对称图形、图形的旋转与平移与轴对称图形的区别.16．〔2021·泰安，11，3分〕在如下图的单位正方形网格中，△ABC经过平移后得到△A1B1C1，在AC上一点P〔2.4，2〕平移后的对应点为P1，点P1绕点O逆时针旋转180°，得到对应点P2，那么P2点的坐标为〔〕A．〔1.4，－1〕B．〔1.5，2〕C．〔1.6，1〕D．〔2.4，1〕17．〔2021·泰安，4，3分〕以下图形：其中所有轴对称图形的对称轴条数之和为〔〕A．13 B．11 C．10 D．819．〔2021·济宁，8，3分〕如图，在直角坐标系中，点A、B的坐标分别为〔1，4〕和〔3，0〕，点C是y轴上的一个动点，且A、B、C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是〔〕A．〔0，0〕B．〔0，1〕C．〔0，2〕D．〔0，3〕20．〔2021·济宁，12，3分〕如图，△ABC和△A′B′C是两个完全重合的直角三角板，∠B=30°，斜边长为10cm．三角板A′B′C绕直角顶点C顺时针旋转，当点A′落在AB边上时，CA′旋转所构成的扇形的弧长为cm．21.〔2021杭州3分〕以下“表情图〞中，属于轴对称图形的是〔〕A．B．C．D．【方法指导】此题考查了轴对称图形的知识，判断轴对称的关键寻找对称轴，属于根底题22. 〔2021•宁波3分〕以下电视台的台标，是中心对称图形的是〔〕A．B．C．D．23.〔2021山西，8，2分〕如图，正方形地砖的图案是轴对称图形，该图形的对称轴有〔〕A．1条B．2条C．4条D．8条【答案】C【解析】这是一个正八边形，对称轴有4条。

2021年中考数学真题汇编—旋转(含解析)

2021年中考数学真题汇编—旋转一．选择题（共23小题）1．（2021•西宁）下列图形中，既是轴对称图形又是中心对称图形的是（）A．三角形B．等边三角形C．平行四边形D．菱形2．（2021•青岛）如图，将线段AB先绕原点O按逆时针方向旋转90°，再向下平移4个单位，得到线段A'B'，则点A的对应点A'的坐标是（）A．（1，﹣6）B．（﹣1，6）C．（1，﹣2）D．（﹣1，﹣2）3．（2021•济南）以下是我国部分博物馆标志的图案，其中既是轴对称图形又是中心对称图形的是（）A．B．C．D．4．（2021•河池）下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．5．（2021•鞍山）下列四幅图片上呈现的是垃圾类型及标识图案，其中标识图案是中心对称图形的是（）A．B．C．D．6．（2021•梧州）下列图形既是轴对称图形，也是中心对称图形的是（）A．B．C．D．7．（2021•毕节市）下列城市地铁标志图案中，既是中心对称图形又是轴对称图形的是（）A．B．C．D．8．（2021•大连）如图，在△ABC中，∠ACB＝90°，∠BAC＝α，将△ABC绕点C顺时针旋转90°得到△A'B'C，点B的对应点B'在边AC上（不与点A，C重合），则∠AA'B'的度数为（）A．αB．α﹣45°C．45°﹣αD．90°﹣α9．（2021•遵义）下列美术字中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．10．（2021•牡丹江）如图，△AOB中，OA＝4，OB＝6，AB＝2，将△AOB绕原点O旋转90°，则旋转后点A的对应点A′的坐标是（）A．（4，2）或（﹣4，2）B．（2，﹣4）或（﹣2，4）C．（﹣2，2）或（2，﹣2）D．（2，﹣2）或（﹣2，2）11．（2021•牡丹江）下列美术字中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．12．（2021•哈尔滨）下列图形中既是轴对称图形又是中心对称图形的是（）A．B．C．D．13．（2021•徐州）下列图形，是轴对称图形但不是中心对称图形的是（）A．B．C．D．14．（2021•黔东南州）如图，在边长为2的正方形ABCD中，若将AB绕点A逆时针旋转60°，使点B落在点B′的位置，连接BB′，过点D作DE⊥BB′，交BB′的延长线于点E，则B′E 的长为（）A．B．C．D．15．（2021•黑龙江）下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．16．（2021•营口）中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹，用于装点生活或配合其他民俗活动的民间艺术．下列四个剪纸图案中，是中心对称图形的是（）A．B．C．D．17．（2021•益阳）以下有关勾股定理证明的图形中，不是中心对称图形的是（）A．B．C．D．18．（2021•常州）观察如图所示脸谱图案，下列说法正确的是（）A．它是轴对称图形，不是中心对称图形B．它是中心对称图形，不是轴对称图形C．它既是轴对称图形，也是中心对称图形D．它既不是轴对称图形，也不是中心对称图形19．（2021•烟台）下列数学符号中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．20．（2021•本溪）下列漂亮的图案中似乎包含了一些曲线，其实它们这种神韵是由多条线段呈现出来的，这些图案中既是中心对称图形又是轴对称图形的是（）A．B．C．D．21．（2021•黄石）如图，△ABC的三个顶点都在方格纸的格点上，其中A点的坐标是（﹣1，0），现将△ABC绕A点按逆时针方向旋转90°，则旋转后点C的坐标是（）A．（2，﹣3）B．（﹣2，3）C．（﹣2，2）D．（﹣3，2）22．（2021•永州）如图，在平面内将五角星绕其中心旋转180°后所得到的图案是（）A．B．C．D．23．（2021•贺州）在平面直角坐标系中，点A（3，2）关于原点对称的点的坐标是（）A．（﹣3，2）B．（3，﹣2）C．（﹣2，﹣3）D．（﹣3，﹣2）二．填空题（共5小题）24．（2021•巴中）如图，把边长为3的正方形OABC绕点O逆时针旋转n°（0＜n＜90）得到正方形ODEF，DE与BC交于点P，ED的延长线交AB于点Q，交OA的延长线于点M．若BQ：AQ＝3：1，则AM＝．25．（2021•抚顺）在平面直角坐标系中，点M（﹣2，4）关于原点对称的点的坐标是．26．（2021•桂林）如图，正方形OABC的边长为2，将正方形OABC绕点O逆时针旋转角α（0°＜α＜180°）得到正方形OA′B′C′，连接BC′，当点A′恰好落在线段BC′上时，线段BC′的长度是．27．（2021•吉林）如图，在平面直角坐标系中，点A的坐标为（0，3），点B的坐标为（4，0），连接AB，若将△ABO绕点B顺时针旋转90°，得到△A′BO′，则点A′的坐标为．28．（2021•鄂州）如图，在平面直角坐标系中，点C的坐标为（﹣1，0），点A的坐标为（﹣3，3），将点A绕点C顺时针旋转90°得到点B，则点B的坐标为．三．解答题（共4小题）29．（2021•绵阳）如图，点M是∠ABC的边BA上的动点，BC＝6，连接MC，并将线段MC绕点M逆时针旋转90°得到线段MN．（1）作MH⊥BC，垂足H在线段BC上，当∠CMH＝∠B时，判断点N是否在直线AB 上，并说明理由；（2）若∠ABC＝30°，NC∥AB，求以MC、MN为邻边的正方形的面积S．30．（2021•淮安）如图，方格纸上每个小正方形的边长均为1个单位长度，△ABC的顶点A、B、C都在格点上（两条网格线的交点叫格点）．请仅用无刻度的直尺按下列要求画图，并保留画图痕迹（不要求写画法）．（1）将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B1，点C的对应点为C1，画出△AB1C1；（2）连接CC1，△ACC1的面积为；（3）在线段CC1上画一点D，使得△ACD的面积是△ACC1面积的．31．（2021•阜新）下面是小明关于“对称与旋转的关系”的探究过程，请你补充完整．（1）三角形在平面直角坐标系中的位置如图1所示，简称G，G关于y轴的对称图形为G1，关于x轴的对称图形为G2．则将图形G1绕点顺时针旋转度，可以得到图形G2．（2）在图2中分别画出G关于y轴和直线y＝x+1的对称图形G1，G2．将图形G1绕点（用坐标表示）顺时针旋转度，可以得到图形G2．（3）综上，如图3，直线l1：y＝﹣2x+2和l2：y＝x所夹锐角为α，如果图形G关于直线l1的对称图形为G1，关于直线l2的对称图形为G2，那么将图形G1绕点（用坐标表示）顺时针旋转度（用α表示），可以得到图形G2．32．（2021•桂林）如图，在平面直角坐标系中，线段AB的两个端点的坐标分别是A（﹣1，4），B（﹣3，1）．（1）画出线段AB向右平移4个单位后的线段A1B1；（2）画出线段AB绕原点O旋转180°后的线段A2B2．第23章旋转—2021年数学中考真题汇编参考答案与试题解析一．选择题（共23小题）1．（2021•西宁）下列图形中，既是轴对称图形又是中心对称图形的是（）A．三角形B．等边三角形C．平行四边形D．菱形【分析】根据轴对称图形和中心对称图形的概念，对各选项分析判断即可得解．把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．【解答】解：A．三角形不一定是轴对称图形，不是中心对称图形，故本选项不合题意；B．等边三角形是轴对称图形，不是中心对称图形，故本选项不合题意；C．平行四边形不是轴对称图形，是中心对称图形，故本选项不合题意；D．菱形既是轴对称图形，又是中心对称图形，故本选项符合题意．故选：D．【点评】本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．2．（2021•青岛）如图，将线段AB先绕原点O按逆时针方向旋转90°，再向下平移4个单位，得到线段A'B'，则点A的对应点A'的坐标是（）A．（1，﹣6）B．（﹣1，6）C．（1，﹣2）D．（﹣1，﹣2）【分析】先求出A点绕O点逆时针旋转90°后的坐标为（﹣1，2），再求向下平移4个单位后的点的坐标即可．【解答】解：A点绕O点逆时针旋转90°，得到点A''（﹣1，2），A''向下平移4个单位，得到A'（﹣1，﹣2），故选：D．【点评】本题考查坐标与图形变化，能够根据题意画出线段AB旋转、平移后的图形是解题的关键．3．（2021•济南）以下是我国部分博物馆标志的图案，其中既是轴对称图形又是中心对称图形的是（）A．B．C．D．【分析】中心对称图形是在平面内，把一个图形绕某一定点旋转180°，能够与自身重合的图形．轴对称图形是在平面内，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形．依据定义判断．【解答】解：A．是轴对称图形，又是中心对形，符合题意；B．是轴对称图形，不是中心对称图形，不符合题意；C．不是轴对称图形，是中心对称图形，不符合题意；D．不是轴对称图形，又不是中心对称图形，不符合题意．故选：A．【点评】本题考查了中心对称图形和轴对称图形的定义，能熟记中心对称图形和轴对称图形的定义是解此题的关键．4．（2021•河池）下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．【解答】解：A．是轴对称图形，不是中心对称图形，故本选项不符合题意；B．既是轴对称图形，又是中心对称图形，故本选项符合题意；C．不是轴对称图形，是中心对称图形，故本选项不符合题意；D．是轴对称图形，不是中心对称图形，故本选项不符合题意．故选：B．【点评】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与原图重合．5．（2021•鞍山）下列四幅图片上呈现的是垃圾类型及标识图案，其中标识图案是中心对称图形的是（）A．B．C．D．【分析】把一个图形绕某一点旋转180°后与自身重合，那么这个图形就叫做中心对称图形．据此判断即可．【解答】解：A．不是中心对称图形，故本选项不合题意；B．不是中心对称图形，故本选项不合题意；C．不是中心对称图形，故本选项不合题意；D．是中心对称图形，故本选项符合题意．故选：D．【点评】本题考查了中心对称图形的概念．中心对称图形是要寻找对称中心，旋转180度后与自身重合．6．（2021•梧州）下列图形既是轴对称图形，也是中心对称图形的是（）A．B．C．D．【分析】中心对称图形的定义：把一个图形绕某一点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形就叫做中心对称图形；轴对称图形的定义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形．【解答】解：A．不是轴对称图形，是中心对称图形，故此选项不合题意；B．是轴对称图形，不是中心对称图形，故此选项不合题意；C．是轴对称图形，不是中心对称图形，故此选项不合题意；D．既是轴对称图形又是中心对称图形，故此选项符合题意．故选：D．【点评】本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与自身重合．7．（2021•毕节市）下列城市地铁标志图案中，既是中心对称图形又是轴对称图形的是（）A．B．C．D．【分析】根据把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行解答．【解答】解：A．既不是轴对称图形，也不是中心对称图形，故此选项不合题意；B．不是轴对称图形，是中心对称图形，故此选项不合题意；C．是轴对称图形，不是中心对称图形，故此选项不合题意；D．既是轴对称图形，又是中心对称图形，故此选项符合题意；故选：D．【点评】此题主要考查了中心对称图形和轴对称图形，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与原图重合．8．（2021•大连）如图，在△ABC中，∠ACB＝90°，∠BAC＝α，将△ABC绕点C顺时针旋转90°得到△A'B'C，点B的对应点B'在边AC上（不与点A，C重合），则∠AA'B'的度数为（）A．αB．α﹣45°C．45°﹣αD．90°﹣α【分析】由旋转知AC＝A'C，∠BAC＝∠CA'B'，∠ACA'＝90°，从而得出△ACA'是等腰直角三角形，即可解决问题．【解答】解：∵将△ABC绕点C顺时针旋转90°得到△A'B'C，∴AC＝A'C，∠BAC＝∠CA'B'，∠ACA'＝90°，∴△ACA'是等腰直角三角形，∴∠CA'A＝45°，∵∠BAC＝α，∴∠CA'B'＝α，∴∠AA'B'＝45°﹣α．故选：C．【点评】本题主要考查了旋转的性质、等腰直角三角形的性质，明确旋转前后对应角相等、对应线段相等是解题的关键．9．（2021•遵义）下列美术字中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：A．是轴对称图形，不是中心对称图形．故本选项不合题意；B．是轴对称图形，不是中心对称图形．故本选项不合题意；C．是轴对称图形，不是中心对称图形．故本选项不合题意；D．既是轴对称图形又是中心对称图形．故本选项符合题意．故选：D．【点评】本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．10．（2021•牡丹江）如图，△AOB中，OA＝4，OB＝6，AB＝2，将△AOB绕原点O旋转90°，则旋转后点A的对应点A′的坐标是（）A．（4，2）或（﹣4，2）B．（2，﹣4）或（﹣2，4）C．（﹣2，2）或（2，﹣2）D．（2，﹣2）或（﹣2，2）【分析】如图，过点A作AH⊥OB于H，设OH＝m，则BH＝6﹣m，利用勾股定理构建方程求出m，再分两种情形求解即可．【解答】解：如图，过点A作AH⊥OB于H，设OH＝m，则BH＝6﹣m，∵AH2＝OA2﹣OH2＝AB2﹣BH2，∴42﹣m2＝（2）2﹣（6﹣m）2，∴m＝2，∴AH＝＝2，∴A（2，2），若将△AOB绕原点O顺时针旋转90°，则旋转后点A的对应点A′（2，﹣2），若将△AOB绕原点O逆时针旋转90°，则旋转后点A的对应点A′（﹣2，2），故选：C．【点评】本题考查坐标与图形变化﹣旋转，解直角三角形等知识，解题的关键是求出点A 的坐标，属于中考常考题型．11．（2021•牡丹江）下列美术字中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：A．是轴对称图形，不是中心对称图形．故本选项不合题意；B．不是轴对称图形，也不是中心对称图形．故本选项不合题意；C．既是轴对称图形又是中心对称图形．故本选项符合题意；D．是轴对称图形，不是中心对称图形．故本选项不合题意．故选：C．【点评】本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．12．（2021•哈尔滨）下列图形中既是轴对称图形又是中心对称图形的是（）A．B．C．D．【分析】根据把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行解答．【解答】解：A．既是轴对称图形，又是中心对称图形，故此选项符合题意；B．是轴对称图形，不是中心对称图形，故此选项不合题意；C．是轴对称图形，不是中心对称图形，故此选项不合题意；D．是轴对称图形，不是中心对称图形，故此选项不合题意；故选：A．【点评】此题主要考查了中心对称图形和轴对称图形，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与原图重合．13．（2021•徐州）下列图形，是轴对称图形但不是中心对称图形的是（）A．B．C．D．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：A．不是轴对称图形，也不是中心对称图形，故此选项不符合题意；B．是轴对称图形，也是中心对称图形，故此选项不符合题意；C．不是轴对称图形，是中心对称图形，故此选项不符合题意；D．是轴对称图形，不是中心对称图形，故此选项符合题意．故选：D．【点评】此题主要考查了中心对称图形与轴对称图形，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与原图重合．14．（2021•黔东南州）如图，在边长为2的正方形ABCD中，若将AB绕点A逆时针旋转60°，使点B落在点B′的位置，连接BB′，过点D作DE⊥BB′，交BB′的延长线于点E，则B′E 的长为（）A．B．C．D．【分析】分别延长AD和BE交于点F，利用特殊角三角函数求出EF的长，根据△ABB'是等边三角形，求出B'E＝BF﹣BB'﹣EF即可．【解答】解：分别延长AD和BE交于点F，由题知，AB＝2，∠ABF＝60°，∴BF＝AB÷cos60°＝2÷＝4，AF＝BF•sin60°＝4×＝2，∠F＝90°﹣∠ABF＝30°，∴DF＝AF﹣AD＝2﹣2，∴EF＝DF•cos∠F＝（2）×＝3﹣，由题知，△ABB'是等边三角形，∴B'E＝BF﹣BB'﹣EF＝4﹣2﹣（3﹣）＝﹣1，故选：A．【点评】本题主要考查旋转的性质，等边三角形的性质，正方形的性质等知识点，根据旋转判断△ABB'是等边三角形及特殊角三角函数的应用是解题的关键．15．（2021•黑龙江）下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．【分析】根据轴对称图形和中心对称图形的定义判断即可．【解答】解：A选项是轴对称图形，不是中心对称图形，不符合题意；B选项是轴对称图形，不是中心对称图形，不符合题意；C选项既是轴对称图形，又是中心对称图形，符合题意；D选项不是轴对称图形，是中心对称图形，不符合题意；故选：C．【点评】本题考查了轴对称图形和中心对称图形的定义，牢记轴对称图形和中心对称图形的定义是解题的关键．如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形．16．（2021•营口）中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹，用于装点生活或配合其他民俗活动的民间艺术．下列四个剪纸图案中，是中心对称图形的是（）A．B．C．D．【分析】一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形．根据中心对称图形的概念对各选项分析判断即可得解．【解答】解：A、不是中心对称图形，故本选项不合题意；B、不是中心对称图形，故本选项不合题意；C、不是中心对称图形，故本选项不合题意；D、是中心对称图形，故本选项符合题意；故选：D．【点评】本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后与原图重合．17．（2021•益阳）以下有关勾股定理证明的图形中，不是中心对称图形的是（）A．B．C．D．【分析】根据中心对称图形的概念求解．把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形．【解答】解：A．不是中心对称图形，符合题意；B．是中心对称图形，不符合题意；C．是中心对称图形，不符合题意；D．是中心对称图形，不符合题意．故选：A．【点评】此题考查了中心对称图形的概念．熟记定义是解答本题的关键．18．（2021•常州）观察如图所示脸谱图案，下列说法正确的是（）A．它是轴对称图形，不是中心对称图形B．它是中心对称图形，不是轴对称图形C．它既是轴对称图形，也是中心对称图形D．它既不是轴对称图形，也不是中心对称图形【分析】把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．据此判断即可．【解答】解：该图是轴对称图形，不是中心对称图形．故选：A．【点评】此题主要考查了中心对称图形和轴对称图形，熟记相关定义是解答本题的关键．19．（2021•烟台）下列数学符号中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【分析】根据轴对称图形与中心对称图形的定义进行判断，即可求出答案．【解答】解：A．是轴对称图形，不是中心对称图形，故本选项不合题意；B．不是轴对称图形，是中心对称图形，故本选项不合题意；C．是轴对称图形，不是中心对称图形，故本选项不合题意；D．既是轴对称图形，又是中心对称图形，故本选项符合题意．故选：D．【点评】本题考查了中心对称图形与轴对称图形的概念，判断轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，判断中心对称图形是要寻找对称中心，旋转180度后和原图形重合．20．（2021•本溪）下列漂亮的图案中似乎包含了一些曲线，其实它们这种神韵是由多条线段呈现出来的，这些图案中既是中心对称图形又是轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形和中心对称图形的概念，对各选项分析判断即可得解．【解答】解：A．既是轴对称图形，又是中心对称图形，故本选项符合题意；B．是轴对称图形，不是中心对称图形，故本选项不合题意；C．是轴对称图形，不是中心对称图形，故本选项不合题意；D．是轴对称图形，不是中心对称图形，故本选项不合题意．故选：A．【点评】本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．21．（2021•黄石）如图，△ABC的三个顶点都在方格纸的格点上，其中A点的坐标是（﹣1，0），现将△ABC绕A点按逆时针方向旋转90°，则旋转后点C的坐标是（）A．（2，﹣3）B．（﹣2，3）C．（﹣2，2）D．（﹣3，2）【分析】利用旋转变换的性质分别作出B，C的对应点B′，C′可得结论．【解答】解：观察图像，可知C′（﹣2，3），故选：B．【点评】本题考查坐标与图形变化﹣旋转，平移等知识，解题的关键是熟练掌握旋转变换的性质，属于中考常考题型．22．（2021•永州）如图，在平面内将五角星绕其中心旋转180°后所得到的图案是（）A．B．C．D．【分析】根据旋转的性质，旋转前后，各点的相对位置不变，得到的图形全等，找到关键点，分析选项可得答案．【解答】解：根据旋转的性质，旋转前后，各点的相对位置不变，得到的图形全等，五角星图案绕中心旋转180°后，阴影部分的等腰三角形的顶点向下，得到的图案是C．故选：C．【点评】本题考查了利用旋转设计图案的知识，图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动，其中对应点到旋转中心的距离相等，旋转前后图形的大小和形状没有改变．23．（2021•贺州）在平面直角坐标系中，点A（3，2）关于原点对称的点的坐标是（）A．（﹣3，2）B．（3，﹣2）C．（﹣2，﹣3）D．（﹣3，﹣2）【分析】两个点关于原点对称时，它们的坐标符号相反，即点P（x，y）关于原点O的对称点是P′（﹣x，﹣y）．【解答】解：点（3，2）关于原点对称的点的坐标是：（﹣3，﹣2）．故选：D．【点评】此题主要考查了关于原点对称点的性质，正确记忆横纵坐标的符号是解题关键．二．填空题（共5小题）24．（2021•巴中）如图，把边长为3的正方形OABC绕点O逆时针旋转n°（0＜n＜90）得到正方形ODEF，DE与BC交于点P，ED的延长线交AB于点Q，交OA的延长线于点M．若BQ：AQ＝3：1，则AM＝．【分析】连接OQ，OP，利用HL证明Rt△OAQ≌Rt△ODQ，得QA＝DQ，同理可证：CP＝DP，设CP＝x，则BP＝3﹣x，PQ＝x+，在Rt△BPQ中，利用勾股定理列出方程（3﹣x）2+（）2＝（x+）2，解方程得x＝，再利用△AQM∽△BQP可求解．【解答】解：连接OQ，OP，∵将正方形OABC绕点O逆时针旋转n°（0＜n＜90）得到正方形ODEF，∴OA＝OD，∠OAQ＝∠ODQ＝90°，在Rt△OAQ和Rt△ODQ中，，∴Rt△OAQ≌Rt△ODQ（HL），∴QA＝DQ，同理可证：CP＝DP，∵BQ：AQ＝3：1，AB＝3，∴BQ＝，AQ＝，设CP＝x，则BP＝3﹣x，PQ＝x+，在Rt△BPQ中，由勾股定理得：（3﹣x）2+（）2＝（x+）2，解得x＝，∴BP＝，∵∠AQM＝∠BQP，∠BAM＝∠B，∴△AQM∽△BQP，∴，∴，∴AM＝．故答案为：．【点评】本题主要考查了旋转的性质，全等三角形的判定与性质，勾股定理，相似三角形的判定与性质等知识，利用全等证明QA＝DQ，CP＝DP是解题的关键．25．（2021•抚顺）在平面直角坐标系中，点M（﹣2，4）关于原点对称的点的坐标是（2，﹣4）．【分析】根据关于原点对称的点，横坐标与纵坐标都互为相反数，可得答案．【解答】解：点（﹣2，4）关于原点对称的点的坐标为（2，﹣4）．故答案为：（2，﹣4）．【点评】本题考查了关于原点对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于原点对称的点，横坐标与纵坐标都互为相反数．26．（2021•桂林）如图，正方形OABC的边长为2，将正方形OABC绕点O逆时针旋转角α（0°＜α＜180°）得到正方形OA′B′C′，连接BC′，当点A′恰好落在线段BC′上时，线段BC′的长度是+．【分析】如图，作辅助线，构建直角三角形，利用勾股定理分别计算OB，OE，EC'和BE 的长，根据线段的和可得结论．【解答】解：如图，连接OB，过点O作OE⊥C'B于E，则∠OEC'＝∠OEB＝90°，∵将正方形OABC绕点O逆时针旋转角α（0°＜α＜180°）得到正方形OA′B′C′，点A′恰好落在线段BC′上，∴∠OC'E＝45°，OA＝OC'＝AB＝2，∠A＝90°，∴OB＝2，OE＝EC'＝，在Rt△OBE中，由勾股定理得：BE＝＝＝，∴BC'＝BE+EC'＝+．故答案为：+．【点评】本题考查了旋转的性质，勾股定理，正方形的性质，等腰直角三角形，解题的关键是：作辅助线，构建等腰直角三角形OEC'和直角三角形OEB．27．（2021•吉林）如图，在平面直角坐标系中，点A的坐标为（0，3），点B的坐标为（4，。

2021年全国中考数学真题分类汇编--图形与变换：平移与旋转(答案版 )

如此循环，每旋转 7 次，而 2021＝6×336+5， ∴A2021 在第四象限，且 OA2021＝42021，示意图如下：
OH＝ OA2021＝52020，A2021H＝ OH＝ 2020，
∴A2021（（42020，﹣ 故选：C．
×22020），
9. （2021•天津市）如图，在 V ABC 中， BAC 120 ，将 V ABC 绕点 C 逆时针旋转得到 VDEC ，点 A，B 的对应点分别为 D，E，连接 AD ．当点 A，D，E 在同一条直线上时，
∴AA'＝
＝＝．
故选：B．
4. （2021•长沙市）下列几何图形中，是中心对称图形的是（）
A.
B.
C.
D.
【答案】C
5. （2021•江苏省苏州市）．如图，在方格纸中，将 Rt△AOB 绕点 B 按顺时针方向旋转 90° 后得到 Rt△A′O′B（）
A．
B．
C．
D．
【分析】本题主要考查旋转的性质，旋转过程中图形和大小都不发生变化，根据旋转性
A．
B．
C．
D．
【分析】根据中心对称图形的概念对各选项分析判断即可得解．把一个图形绕某一点旋转 180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．【解答】解：A．不是中心对称图形，故本选项不合题意； B．不是中心对称图形，故本选项不合题意；
C．是中心对称图形，故本选项符合题意； D．不是中心对称图形，故本选项不合题意．故选：C．
D、是轴对称图形也是中心对称图形，故符合题意；
故选 D ．
19. （2021•辽宁省本溪市）下列漂亮的图案中似乎包含了一些曲线，其实它们这种神韵是由多条线段呈现出来的，这些图案中既是中心对称图形又是轴对称图形的是（）

2021年中考数学试卷解析分类汇编专题29-平移旋转与对称

2021年中考数学试卷解析分类汇编专题29-平移旋转与对称平移旋转与对称一. 选择题1,（2021?山东莱芜,第3题3分）在下列四个图案中既是轴对称图形，又是中心对称图形的是( )A．B．C． D．【答案】B因此：A、不是轴对称图形，是中心对称图形，不符合题意；B、是轴对称图形，也是中心对称图形，符合题意；C、不是轴对称图形，也不是中心对称图形，不符合题意；D、是轴对称图形，不是中心对称图形，不符合题意．故选B．考点：轴对称图形和中心对称图形2, (2021山东青岛，第3题,3分)下列四个图形中，既是轴对称图形又是中心对称图形的是1（）．【答案】B 【解析】试题分析：在一个平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形；在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形与另一个图形重合，这样的图形叫做中心对称图形.根据定义可以判定B既是轴对称图形，也是中心对称图形.考点：轴对称图形与中心对称图形.3, （2021?淄博第3题,4分）将图1围成图2的正方体，则图1中的红心“方形是正方体中的（）”标志所在的正面ABFGD．面ADHGA．面CDHEB．面BCEF C．考点：展开图折叠成几何体．.分析：由平面图形的折叠及正方体的展开图解题．注意找准红心“解答：解：由图1中的红心“”标志，”标志所在的相邻面．可知它与等边三角形相邻，折叠成正方体是正方体中的面CDHE．故选A．2点评：本题考查了正方体的展开图形，解题关键是从相邻面入手进行分析及解答问题．【答案】【解析】点P坐标为【备考指导】此题主要考查了关于原点对称点的坐标性质，这一类题目是需要识记的基础题，要熟悉关于原点对称点的横纵坐标变化规律．3)向右平移8个4．（2021・湖北省孝感市，第6题3分）在平面直角坐标系中，把点P(?5，单位得到点P1，再将点P1绕原点旋转90?得到点P2，则点P2的坐标是C．(3， 3)或(?3，?3)?3) A．(3，3) B．(?3，?3)或(?3， 3) D．(3，考点：坐标与图形变化－旋转；坐标与图形变化－平移．.专题：分类讨论．分析：首先利用平移的性质得出点P1的坐标，再利用旋转的性质得出符合题意的答案．解答：解：∵把点P（��5，3）向右平移8个单位得到点P1，∴点P1的坐标为：（3，3），如图所示：将点P1绕原点逆时针旋转90°得到点P2，则其坐标为：（��3，3），3将点P1绕原点顺时针旋转90°得到点P3，则其坐标为：（3，��3），故符合题意的点的坐标为：（3，��3）或（��3，3）．故选：D．点评：此题主要考查了坐标与图形的变化，正确利用图形分类讨论得出是解题关键．5．(2021?湖南株洲,第4题3分)下列几何图形中，既是轴对称图形，又是中心对称图形的是( )A．等腰三角形B．正三角形C．平行四边形 D．正方形【试题分析】本题考点为：轴对称图形与中心对称图形的理解答案为：D1．(2021?江苏无锡,第6题2分)下列图形，是轴对称图形但不是心对称图形的是（）D．圆A．等边三角形 B．平行四边形 C．矩形4考点：心对称图形；轴对称图形．分析：根据轴对称图形和心对称图形的概念以及等边三角形、平行四边形、矩形、圆的性质解答．解答：解：A、只是轴对称图形，不是心对称图形，符合题意； B．只是心对称图形，不合题意；C．D既是轴对称图形又是心对称图形，不合题意．故选A．点评：掌握好心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，两边图象折叠后可重合，心对称图形是要寻找对称心，旋转180度后重合．6.（2021?福建泉州第5题3分）如图，△ABC沿着由点B到点E的方向，平移到△DEF，已知BC=5．EC=3，那么平移的距离为（）B． 3C． 5D． 7A． 2解：根据平移的性质，易得平移的距离=BE=5��3=2，故选A．7．（2021?广东佛山,第2题3分）在下列四个图案中，不是中心对称图形的是（） A．B．C．5感谢您的阅读，祝您生活愉快。

2021年人教版中考数学专题《轴对称、平移与旋转》复习试卷含答案

2021年人教版中考数学专题《轴对称、平移与旋转》复习试卷含答案2021年中考数学专题复习卷: 轴对称、平移与旋转一、选择题1.下列图形中一定是轴对称图形的是（）A. B. C. D.【答案】D【解析】 A、40°的直角三角形不是轴对称图形，故不符合题意； B、两个角是直角的四边形不一定是轴对称图形，故不符合题意； C、平行四边形是中心对称图形不是轴对称图形，故不符合题意； D、矩形是轴对称图形，有两条对称轴，故符合题意，故答案为：D.【分析】把一个图形沿着一条直线折叠，直线两旁的部分能完全重合的图形就是轴对称图形；根据轴对称图形的定义，再一一判断即可。

2.下列图形中，是轴对称图形但不是中心对称图形的是（）A. 正三角形B. 菱形C. 直角梯形D. 正六边形【答案】C【解析】：A.正三角形是轴对称图形，不是中心对称图形，故正确，A符合题意；B.菱形既是轴对称图形，又是中心对称图形，故错误，B不符合题意；C.直角梯形既不是轴对称图形，也不是中心对称图形，故错误，C不符合题意；D.正六边形既是轴对称图形，又是中心对称图形，故错误，D不符合题意；故答案为：A.【分析】根据轴对称图形和中心对称图形定义一一判断对错即可得出答案.3.将抛物线y=-5x +l向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为（）. A. y=-5(x+1) -1 B. y=-5(x-1) -1 C. y=-5(x+1) +3 D. y=-5(x-1) +3 【答案】A【解析】：将抛物线y=-5x+l向左平移1个单位长度，得到的抛物线解析式为： y=-5（x+1）2+1再向下平移2个单位长度得到的抛物线为：y=-5(x-1)+1-2 即y=-5(x+1)-1 故答案为：A【分析】根据二次函数图像的平移规律：上加下减，左加右减，将抛物线y=ax 向上或向下平移m个单位，再向左或向右平移n个单位即得到y=a（x±n）2±m。

全国各地2021年中考数学试卷解析版分类汇编平移旋转与对称

平移旋转与对称一、选择题1. （2021•四川巴中，第7题3分）以下汽车标志中既是轴对称图形又是中心对称图形的是（）A．B． C．D．考点：轴对称图形和中心对称图形的识别．分析：依照轴对称图形与中心对称图形的概念求解．若是一个图形沿着一条直线对折后两部份完全重合，如此的图形叫做轴对称图形，这条直线叫做对称轴．若是一个图形绕某一点旋转180°后能够与自身重合，那么那个图形就叫做中心对称图形，那个点叫做对称中心．解答：A、是轴对称图形，不是中心对称图形．故本选项错误；B、不是轴对称图形，也不是中心对称图形．故本选项错误；C、是轴对称图形，也是中心对称图形．故本选项正确；D、是轴对称图形，不是中心对称图形．故本选项错误．应选C．点评：考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻觅对称轴，图形两部份沿对称轴折叠后可重合；中心对称图形是要寻觅对称中心，旋转180度后与原图重合．2. （2021•山东枣庄，第8题3分）将一次函数y=x的图象向上平移2个单位，平移后，假设y＞0，那么x 的取值范围是（）A．x＞4B．x＞﹣4C．x＞2D．x＞﹣2考点：一次函数图象与几何变换分析：利用一次函数平移规律得出平移后解析式，进而得出图象与坐标轴交点坐标，进而利用图象判断y＞0时，x的取值范围．解答：解：∵将一次函数y=x的图象向上平移2个单位，∴平移后解析式为：y=x+2，当y=0，则x=﹣4，x=0时，y=2，如图：∴y＞0，则x的取值范围是：x＞﹣4，故选：B．点评：此题主要考查了一次函数图象与几何变换以及图象画法，得出函数图象进而判断x的取值范围是解题关键．3. （2021•山东潍坊，第2题3分）以下标志中不是中心对称图形的是( )考点：中心对称图形．分析：依照中心对称图形的概念对各选项分析判定后利用排除法求解．解答：A、是中心对称图形，故本选项错误；B、是中心对称图形，故本选项错误；C、是不中心对称图形，故本选项正确；D、是中心对称图形，故本选项错误．应选：C．点评：此题考查了中心对称图形的概念：把一个图形绕某一点旋转180°，若是旋转后的图形能够与原先的图形重合，那么那个图形就叫做中心对称图形，那个点叫做对称中心．中心对称图形是要寻觅对称中心，旋转180度后两部份重合．4. （2021•山东烟台，第2题3分）以下电话软件图标中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．考点：轴对称图形和中心对称图形的识别．分析：依照中心对称图形的概念旋转180°后能够与原图形完全重合即是中心对称图形，和轴对称图形的概念即可判定出．解答：A、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项错误；B、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，也不是轴对称图形，故此选项错误；C、此图形旋转180°后不能与原图形重合，此图形不是中心对称图形，是轴对称图形，故此选项错误；D、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，也是轴对称图形，故此选项正确．应选：D．点评：此题要紧考查了中心对称图形与轴对称的概念，依照概念得出图形形状是解决问题的关键．5. （2021•山东烟台，第10题3分）如图，将△ABC绕点P顺时针旋转90°取得△A′B′C′，那么点P的坐标是（）A．（1，1）B．（1，2）C．（1，3）D．（1，4）考点：平面直角坐标系与旋转．分析：先依照旋转的性质取得点A的对应点为点A′，点B的对应点为点B′，再依照旋转的性质取得旋转中心在线段AA′的垂直平分线，也在线段BB′的垂直平分线，即两垂直平分线的交点为旋转中心．解答：∵将△ABC以某点为旋转中心，顺时针旋转90°取得△A′B′C′，∴点A的对应点为点A′，点B的对应点为点B′，作线段AA′和BB′的垂直平分线，它们的交点为P（1，2），∴旋转中心的坐标为（1，2）．应选B．点评：此题考查了坐标与图形转变﹣旋转：图形或点旋转以后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．6. （2021•江西抚州，第2题，3分）以下平安标志图中，是中心对称图形的是解析：选B. ∵A、C、D是轴对称图形.7. （2021山东济南，第5题，3分）以下图案既是轴对称图形又是中心对称图形的是【解析】图A为轴对称图但不是中心对称图形；图B为中心对称图但不是轴对称图形；图C既不是轴对称图也不是中心对称图形；图D既是轴对称图形又是中心对称图形．8．（2021•山东聊城，第11题，3分）如图，在平面直角坐标系中，将△ABC绕点P旋转180°，取得△A1B1C1，那么点A1，B1，C1的坐标别离为（）A．A1（﹣4，﹣6），B1（﹣3，﹣3），C1（﹣5，﹣1）B．A1（﹣6，﹣4），B1（﹣3，﹣3），C1（﹣5，﹣1）C．A1（﹣4，﹣6），B1（﹣3，﹣3），C1（﹣1，﹣5）D．A1（﹣6，﹣4），B1（﹣3，﹣3），C1（﹣1，﹣5）考点：坐标与图形变化-旋转分析：根据网格结构找出点A、B、C关于点P的对称点A1，B1，C1的位置，再根据平面直角坐标系写出坐标即可．解答：解：△A1B1C1如图所示，A1（﹣4，﹣6），B1（﹣3，﹣3），C1（﹣5，﹣1）．故选A．点评：本题考查了坐标与图形变化﹣旋转，熟练掌握网格结构准确找出对应点的位置是解题的关键．9. (2021年贵州黔东南5．（4分）)如图，将Rt△ABC绕点A按顺时针旋转必然角度取得Rt△ADE，点B的对应点D恰好落在BC边上．假设AC=，∠B=60°，那么CD的长为（）A．0.5 B． 1.5 C． D．1考点：旋转的性质分析：解直角三角形求出AB，再求出CD，然后根据旋转的性质可得AB=AD，然后判断出△ABD是等边三角形，根据等边三角形的三条边都相等可得BD=AB，然后根据CD=BC﹣BD计算即可得解．解答：解：∵∠B=60°，∴∠C=90°﹣60°=30°，∵AC=，∴AB=×=1，∴BC=2AB=2，由旋转的性质得，AB=AD，∴△ABD是等边三角形，∴BD=AB=1，∴CD=BC﹣BD=2﹣1=1．应选D．点评：本题考查了旋转的性质，等边三角形的判定与性质，解直角三角形，熟记性质并判断出△ABD是等边三角形是解题的关键．10.（2021•遵义2．（3分））观看以下图形，是中心对称图形的是（）A．B．C．D．中心对称图形考点：分根据中心对称图形的概念对各选项分析判断后利用排除法求解．析：解答：解：A、不是中心对称图形，故本选项错误；B、不是中心对称图形，故本选项错误；C、是中心对称图形，故本选项正确；D、不是中心对称图形，故本选项错误．故选：C．点评：本题考查了中心对称图形的概念：把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．中心对称图形是要寻找对称中心，旋转180度后两部分重合．11.（2021•遵义10．（3分））如图，已知△ABC中，∠C=90°，AC=BC=，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接C′B，那么C′B的长为（）A．2﹣B．C．﹣1D．1考点：旋转的性质．分析：连接BB′，根据旋转的性质可得AB=AB′，判断出△ABB′是等边三角形，根据等边三角形的三条边都相等可得AB=BB′，然后利用“边边边”证明△ABC′和△B′BC′全等，根据全等三角形对应角相等可得∠ABC′=∠B′BC′，延长BC′交AB′于D，根据等边三角形的性质可得BD⊥AB′，利用勾股定理列式求出AB，然后根据等边三角形的性质和等腰直角三角形的性质求出BD、C′D，然后根据BC′=BD﹣C′D计算即可得解．解答：解：如图，连接BB′，∵△ABC绕点A顺时针方向旋转60°得到△AB′C′，∴AB=AB′，∠BAB′=60°，∴△ABB′是等边三角形，∴AB=BB′，在△ABC′和△B′BC′中，，∴△ABC′≌△B′BC′（SSS），∴∠ABC′=∠B′BC′，延长BC′交AB′于D，则BD⊥AB′，∵∠C=90°，AC=BC=，∴AB==2，∴BD=2×=，C′D=×2=1，∴BC′=BD﹣C′D=﹣1．故选C．点评：本题考查了旋转的性质，全等三角形的判定与性质，等边三角形的判定与性质，等腰直角三角形的性质，作辅助线构造出全等三角形并求出BC′在等边三角形的高上是解题的关键，也是本题的难点．12.（2021•娄底5．（3分））以下图形既是轴对称图形又是中心对称图形的是（）A．B．C．D．考点：中心对称图形；轴对称图形分析：根据轴对称图形与中心对称图形的概念求解．解答：解：A、此图形是轴对称图形，不是中心对称图形，故此选项错误；B、此图形是轴对称图形，不是中心对称图形，故此选项错误；C、此图形不是轴对称图形，是中心对称图形，故此选项错误；D、此图形是轴对称图形，也是中心对称图形，故此选项正确；故选：D．点评：此题主要考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．13 (2021年湖北咸宁9．（3分）)点P（1，﹣2）关于y轴对称的点的坐标为（﹣1，﹣2）．考点：关于x轴、y轴对称的点的坐标．分析：根据“关于y轴对称的点，纵坐标相同，横坐标互为相反数”解答即可．解答：解：点P（1，﹣2）关于y轴对称的点的坐标为（﹣1，﹣2）．故答案为：（﹣1，﹣2）．点评：本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数．14. （2021•江苏苏州,第10题3分）如图，△AOB为等腰三角形，极点A的坐标（2，），底边OB在x轴上．将△AOB绕点B按顺时针方向旋转必然角度后得△A′O′B′，点A的对应点A′在x轴上，那么点O′的坐标为（）A．（，）B．（，）C．（，）D．（，4）考点：坐标与图形变化-旋转．分过点A作AC⊥OB于C，过点O′作O′D⊥A′B于D，根据点A的坐标求出OC、AC，再利用勾股定理列析：式计算求出OA，根据等腰三角形三线合一的性质求出OB，根据旋转的性质可得BO′=OB，∠A′BO′=∠ABO，然后解直角三角形求出O′D、BD，再求出OD，然后写出点O′的坐标即可．解答：解：如图，过点A作AC⊥OB于C，过点O′作O′D⊥A′B于D，∵A（2，），∴OC=2，AC=，由勾股定理得，OA===3，∵△AOB为等腰三角形，OB是底边，∴OB=2OC=2×2=4，由旋转的性质得，BO′=OB=4，∠A′BO′=∠ABO，∴O ′D=4×=，BD=4×=，∴OD=OB+BD=4+=，∴点O ′的坐标为（，）．故选C．点评：本题考查了坐标与图形变化﹣旋转，主要利用了勾股定理，等腰三角形的性质，解直角三角形，熟记性质并作辅助线构造出直角三角形是解题的关键．15. （2021•江苏徐州,第6题3分）按序连接正六边形的三个不相邻的极点．取得如图的图形，该图形（）A．既是轴对称图形也是中心对称图形B．是轴对称图形但并不是中心对称图形C．是中心对称图形但并不是轴对称图形D．既不是轴对称图形也不是中心对称图形考点：中心对称图形；轴对称图形．分析：根据正多边形的性质和轴对称图形与中心对称图形的定义解答．解答：解：此图形是轴对称图形但并不是中心对称图形，应选：B．点评：此题考查正多边形对称性．关键要记住偶数边的正多边形既是轴对称图形，又是中心对称图形，奇数边的正多边形只是轴对称图形．16. （2021•江苏徐州,第15题3分）在平面直角坐标系中，将点A（4，2）绕原点逆时针方向旋转90°后，其对应点A′的坐标为（﹣2，4）．考点：坐标与图形变化-旋转．分析：建立网格平面直角坐标系，然后确定出点A与A′的位置，再写出坐标即可．解答：解：如图A′的坐标为（﹣2，4）．故答案为：（﹣2，4）．点评：本题考查了坐标与图形变化﹣旋转，作出图形，利用数形结合的思想求解更形象直观．17．（2021•四川南充，第3题，3分）以下几何体的主视图既是中心对称图形又是轴对称图形的是（）A．B．C．D．分析：先判断主视图，再根据轴对称图形与中心对称图形的概念求解．解：A、主视图是扇形，扇形是轴对称图形，不是中心对称图形，故错误；B、主视图是等腰三角形，是轴对称图形，不是中心对称图形，故错误；C、主视图是等腰梯形，是轴对称图形，不是中心对称图形，故错误；D、主视图是矩形，是轴对称图形，也是中心对称图形，故正确．应选D．点评：把握中心对称图形与轴对称图形的概念：轴对称图形的关键是寻觅对称轴，图形两部份沿对称轴折叠后可重合；中心对称图形是要寻觅对称中心，旋转180度后与原图重合．18．（2021•四川遂宁，第10题，4分）如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕点C顺时针旋转至△A′B′C，使得点A′恰好落在AB上，那么旋转角度为（）A．30°B．60°C．90°D．150°考点：旋转的性质．分析：根据直角三角形两锐角互余求出∠A=60°，根据旋转的性质可得AC=A′C，然后判断出△A′AC是等边三角形，根据等边三角形的性质求出∠ACA′=60°，然后根据旋转角的定义解答即可．解答：解：∵∠ACB=90°，∠ABC=30°，∴∠A=90°﹣30°=60°，∵△ABC绕点C顺时针旋转至△A′B′C点A′恰好落在AB上，∴AC=A′C，∴△A′AC是等边三角形，∴∠ACA′=60°，∴旋转角为60°．故选B．点评：本题考查了旋转的性质，直角三角形两锐角互余，等边三角形的判定与性质，熟记各性质并准确识图是解题的关键．19.（2021•甘肃白银、临夏,第6题3分）以下图形中，是轴对称图形又是中心对称图形的是（）A．B．C．D．考点：中心对称图形；轴对称图形．分析：根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．解答：解：A、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项错误；B、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项错误；C、此图形旋转180°后能与原图形重合，此图形是中心对称图形，不是轴对称图形，故此选项错误；D、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，也是轴对称图形，故此选项正确．故选：D．点评：此题主要考查了中心对称图形与轴对称的定义，根据定义得出图形形状是解决问题的关键．20．（2021•甘肃兰州,第1题4分）在以下绿色食物、回收、节能、节水四个标志中，是轴对称图形的是（）A．B．C．D．考点：轴对称图形．分析：根据轴对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．解答：解：A、是轴对称图形，符合题意；B、不是轴对称图形，不符合题意；C、不是轴对称图形，不符合题意；D、不是轴对称图形，不符合题意．故选A．点本题主要考查轴对称图形的知识点．确定轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．评：21．（2021•广州,第2题3分）以下图形是中心对称图形的是（）．（A）（B）（C）（D）【考点】轴对称图形和中心对称图形．【分析】旋转180°后能与完全重合的图形为中心对称图形．【答案】D22．（2021•广东梅州,第3题3分）以下电视台的台标，是中心对称图形的是（）A．B．C．D．考点：中心对称图形．分析：根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，即可判断得出．解答：解：A、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，故此选项正确；B、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，故此选项错误；C、此图形旋转180°后不能与原图形重合，此图形不是中心对称图形，故此选项错误；D、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，故此选项错误．故选；A．点评：此题主要考查了中心对称图形的定义，根据定义得出图形形状是解决问题的关键．7.8.二、填空题1. （2021•四川巴中，第18题3分）如图，直线y=x+4与x轴、y轴别离交于A、B两点，把△A0B绕点A顺时针旋转90°后取得△AO′B′，那么点B′的坐标是．考点：一次函数的性质，旋转．分析：第一依照直线AB来求出点A和点B的坐标，B′的横坐标等于OA+OB，而纵坐标等于OA，进而得出B′的坐标．解答：直线y=﹣x+4与x轴，y轴别离交于A（3，0），B（0，4）两点．旋转前后三角形全等．由图易知点B′的纵坐标为OA长，即为3，即横坐标为OA+OB=OA+O′B′=3+4=7．故点B′的坐标是（7，3）．故答案为：（7，3）．点评：此题要紧考查了关于图形翻转的明白得，其中要考虑到点B和点B′位置的特殊性，和点B'的坐标与OA和OB的关系．2. （2021•山东枣庄，第13题4分）如图，在正方形方格中，阴影部份是涂黑7个小正方形所形成的图案，再将方格内空白的一个小正方形涂黑，使取得的新图案成为一个轴对称图形的涂法有3 种．考点：利用轴对称设计图案分析：根据轴对称图形的概念：把一个图形沿着某条直线折叠，直线两旁的部分能够完全重合及正方形的对称轴是两条对角线所在的直线和两组对边的垂直平分线，得出结果．解答：解：在1，2，3处分别涂黑都可得一个轴对称图形，故涂法有3种，故答案为：3．3. （2021•江西抚州，第14题，3分）如图，两块完全相同的含30°角的直角三角板ABC 和A'B'C'重合在一路，将三角板A'B'C'绕其极点C'按逆时针方向旋转角α（0°< α≤90°），有以下四个结论：①当α=30°时，A'C 与AB 的交点恰好为AB 的中点；②当α=60°时，A'B'恰好通过点B ；③在旋转进程中，存在某一时刻，使得AA'BB'=；④在旋转进程中，始终存在AA'BB'⊥，其中结论正确的序号是 ① ② ④ .(多填或填错得0分，少填酌情给分）解析：如图1，∵α=30°，∴∠ACA ′=∠A=30°,∠BCA ′=∠B=60°，∴DC=DA,DC=DB,∴DA=DB,∴D 是AB 的中点.正确如图2，当α=60°时，取A ′B ′的中点E,连接CE,那么∠B ′CE=∠B ′CB=60°,又CB=CB ′,∴E 、B 重合，∴A ′、B ′恰好通过点B.正确如图3，连接AA ′,BB ′,那么⊿CAA ′∽⊿CBB ′,∴AA AC BB BCtan '==︒='60∴AA ′′.错误如图4，∠A ′B ′D=∠CBB ′－60°,∠B ′A ′D=180°－(∠CA ′A+30°),∴∠A ′B ′D ＋∠B ′A ′D=90°＋∠CBB ′－∠CA ′A∵ ∠CBB ′=∠CA ′A ,∴∠A ′B ′D ＋∠B ′A ′D=90°,即∠D=90°,∴AA ′⊥BB ′.正确∴①，②，④正确.4. （2021山东济南，第20题，3分）如图，将边长为12的正方形ABCD 是沿其对角线AC 剪开，再把ABC ∆沿着AD 方向平移，取得C B A '''∆，当两个三角形重叠的面积为32时，它移动的距离A A '等于________.【解析】设m A A ='，那么222121264m (m )+-=-，解之m =4或8，应填4或8．5. （2021•山东聊城，第7题，3分）如图，点P 是∠AOB 外的一点，点M ，N 别离是∠AOB 两边上的点，点P 关于OA 的对称点Q 恰好落在线段MN 上，点P 关于OB 的对称点R 落在MN 的延长线上．假设PM=2.5cm ，PN=3cm ，MN=4cm ，那么线段QR 的长为（）A ． 4.5B ． 5.5C ． 6.5D ． 7考点：轴对称的性质分析：利用轴对称图形的性质得出PM=MQ ，PN=NR ，进而利用MN=4cm ，得出NQ 的长，即可得出QR 的长．解答：解：∵点P 关于OA 的对称点Q 恰好落在线段MN 上，点P 关于OB 的对称点R 落在MN 的延长线上， ∴PM=MQ ，PN=NR ，∵PM=2.5cm ，PN=3cm ，MN=4cm ，∴RN=3cm ，MQ=2.5cm ，NQ=MN ﹣MQ=4﹣2.5=1.5（cm ），则线段QR 的长为：RN+NQ=3+1.5=4.5（cm ）．故选：A ．点评：此题主要考查了轴对称图形的性质，得出PM=MQ ，PN=NR 是解题关键．6．（2021•四川宜宾，第14题，3分）如图，在Rt △ABC 中，∠B =90°，AB =3，BC =4，将△ABC 折叠，使点B 恰好落在边AC 上，与点B ′重合，AE 为折痕，那么EB ′= 1.5 ．A D C BC ’ 第20题图考点：翻折变换（折叠问题）分析：首先根据折叠可得BE=EB′，AB′=AB=3，然后设BE=EB′=x，则EC=4﹣x，在Rt△ABC中，由勾股定理求得AC的值，再在Rt△B′EC中，由勾股定理可得方程x2+22=（4﹣x）2，再解方程即可算出答案．解答：解：根据折叠可得BE=EB′，AB′=AB=3设BE=EB′=x，则EC=4﹣x，∵∠B=90°，AB=3，BC=4，∴在Rt△ABC中，由勾股定理得，，∴B′C=5﹣3=2，在Rt△B′EC中，由勾股定理得，x2+22=（4﹣x）2，解得x=1.5．故答案为：1.5．点评：此题主要考查了翻折变换，关键是分析清楚折叠以后哪些线段是相等的．7．（2021•四川宜宾，第13题，3分）在平面直角坐标系中，将点A（﹣1，2）向右平移3个单位长度取得点B，那么点B关于x轴的对称点C的坐标是（2，﹣2）．考点：坐标与图形变化－平移；关于x轴、y轴对称的点的坐标分析：首先根据横坐标，右移加，左移减可得B点坐标，然后再关于x轴对称点的坐标特点可得答案．解答：解：点A（﹣1，2）向右平移3个单位长度得到的B的坐标为（﹣1+3，2），即（2，2），则点B关于x轴的对称点C的坐标是（2，﹣2），故答案为：（2，﹣2）．点评：此题主要考查了坐标与图形变化﹣平移，以及关于x轴对称点的坐标，关键是掌握点的坐标变化规律．8．（2021•四川南充，第16题，3分）如图，有一矩形纸片ABCD，AB=8，AD=17，将此矩形纸片折叠，使极点A落在BC边的A′处，折痕所在直线同时通过边AB、AD（包括端点），设BA′=x，那么x的取值范围是．分析：作出图形，依照矩形的对边相等可得BC=AD，CD=AB，当折痕通过点D时，依照翻折的性质可得A′D=AD，利用勾股定理列式求出A′C，再求出BA′；当折痕通过点B时，依照翻折的性质可得BA′=AB，此两种情形为BA′的最小值与最大值的情形，然后写出x的取值范围即可．解：如图，∵四边形ABCD是矩形，AB=8，AD=17，∴BC=AD=17，CD=AB=8，①当折痕通过点D时，由翻折的性质得，A′D=AD=17，在Rt△A′CD中，A′C===15，∴BA′=BC﹣A′C=17﹣15=2；②当折痕通过点B时，由翻折的性质得，BA′=AB=8，∴x的取值范围是2≤x≤8．故答案为：2≤x≤8．点评：本题考查了翻折变换的性质，勾股定理的应用，难点在于判断出BA′的最小值与最大值时的情形，作出图形更形象直观．5．（2021•广东梅州,第11题3分）如图，把△ABC绕点C按顺时针方向旋转35°，取得△A′B′C，A′B′交AC于点D．假设∠A′DC=90°，那么∠A= ．考点：旋转的性质．分析：根据题意得出∠ACA′=35°，则∠A′=90°﹣35°=55°，即可得出∠A的度数．解答：解：∵把△ABC绕点C按顺时针方向旋转35°，得到△A′B′C，A′B′交AC于点D，∠A′DC=90°，∴∠ACA′=35°，则∠A′=90°﹣35°=55°，则∠A=∠A′=55°．故答案为：55°．点评：此题主要考查了旋转的性质以及三角形内角和定理等知识，得出∠A′的度数是解题关键．三、解答题1. （2021•四川巴中，第24题7分）如图，在平面直角坐标系xOy中，△ABC三个极点坐标别离为A（﹣2，4），B（﹣2，1），C（﹣5，2）．（1）请画出△ABC关于x轴对称的△A1B1C1．（2）将△A1B1C1的三个极点的横坐标与纵坐标同时乘以﹣2，取得对应的点A2，B2，C2，请画出△A2B2C2．（3）求△A1B1C1与△A2B2C2的面积比，即：= 1：4 （不写解答进程，直接写出结果）．考点：平面直角坐标系，相似三角形的面积比．分析：（1）依照关于x轴对称点的性质得出对应点位置进而得出答案；（2）依照将△A1B1C1的三个极点的横坐标与纵坐标同时乘以﹣2，得出各点坐标，进而得出答案；（3）利用位似图形的性质得出位似比，进而得出答案．解答：（1）如下图：△A1B1C1即为所求；（2）如下图：△A2B2C2即为所求；（3）∵将△A1B1C1的三个极点的横坐标与纵坐标同时乘以﹣2，取得对应的点A2，B2，C2，∴△A1B1C1与△A2B2C2的相似比为：1：2，∴：=1：4．故答案为：1：4．点评：此题要紧考查了位似变换和轴对对称变换，得出对应点位置是解题关键．2. （2021•山东潍坊，第22题12分）如图1，在正方形ABCD中，E、F别离为BC、CD的中点，连接AE、BF，交点为G．(1)求证：AE⊥BF；(2)将△BCF沿BF对折，取得△BPF（如图2），延长FP交BA的延长线于点Q，求sin∠BQP的值；(3)将△ABE绕点A逆时针方向旋转，使边AB正好落在AE上，取得△AHM（如图3），假设AM和BF相交于点N，当正方形ABCD的面积为4时，求四边形GHMN的面积．考点：相似三角形的判定与性质；全等三角形的判定与性质；正方形的性质；解直角三角形．分析：（1）由四边形ABCD是正方形，可得∠ABE=∠BCF=90°，AB=BC，又由BE=CF，即可证得△ABE≌△BCF,可得∠BAE =∠CBF ，由∠ABF +∠CBF =900可得∠ABF +∠BAE =900，即AE ⊥BF ；（2）由△BCF ≌△BPF , 可得CF =PF ,BC =BP ,∠BFE =∠BFP ，由CD ∥AB 得∠BFC =∠ABF ,从而QB =QF ，设PF 为x ,那么BP 为2x ,在Rt △QBF 中可求 QB 为25x ，即可求得答案；（3）由2)(AMAN AHM AGN =∆∆可求出△AGN 的面积，进一步可求出四边形GHMN 的面积．解答：(1)证明：∵E 、F 别离是正方形ABCD 边BC 、CD 的中点，∴CF =BE ，∴Rt △ABE ≌Rt △BCF ∴∠BAE =∠CBF 又∵∠BAE +∠BEA =900，∴∠CBF +∠BEA =900，∴∠BGE =900， ∴AE ⊥BF(2)依照题意得：FP =FC ，∠PFB =∠BFC ，∠FPB =900，∵CD ∥AB , ∴∠CFB =∠ABF ，∴∠ABF =∠PFB ．∴QF =QB令PF =k （k >O ），那么PB =2k ，在Rt △BPQ 中，设QB =x ， ∴x 2=(x －k )2+4k 2, ∴x =25k ，∴sin ∠BQP =54252==k k QP BP (3)由题意得：∠BAE =∠EAM ,又AE ⊥BF , ∴AN =AB =2,∵ ∠AHM =900, ∴GN //HM , ∴2)(AM AN AHM AGN =∆∆ ∴54)52(12==ΛAGN ∴ 四边形GHMN =SΔAHM － SΔAGN =1一54= 54 答：四边形GHMN 的面积是54. 点评：此题考查了相似三角形的判定与性质、正方形的性质、全等三角形的判定与性质和三角函数等知识．此题综合性较强，难度较大，注意把握旋转前后图形的对应关系，注意数形结合思想的应用．3.（2021•湖南张家界，第19题，6分）利用对称变换可设计出漂亮图案，如图，在方格纸中有一个极点都在格点上的四边形，且每一个小正方形的边长都为1，完成以下问题：（1）图案设计：先作出四边形关于直线l 成轴对称的图形，再将你所作的图形和原四边形绕0点按顺时针旋转90°；（2）完成上述图案设计后，可知那个图案的面积等于 20 ．考点：利用旋转设计图案；利用轴对称设计图案．分析：（1）首先找出对称点的坐标，然后画图即可；（2）首先利用割补法求出每一个小四边形的面积，再乘以4即可．解答：解：（1）如图所示：（2）面积：（5×2﹣2×1×﹣2×1×﹣3×1××2）×4=20，故答案为：20．点评：此题主要考查了利用轴对称和旋转作图，以及求不规则图形的面积，关键是在作图时，找出关键点的对称点．4．（2021•江西抚州，第15题，5分）如图，△ABC与△DEF关于直线对称，请用无刻度的直尺，在下面两个图中别离作出直线.解析：利用轴对称性质：对应线段（或延长线）的交于对称轴上一点.如图，直线l 确实是所求作的对称轴.5 (2021年湖北咸宁19．（8分）)如图，在Rt△ABC中，∠ACB=90°，∠B=30°，将△ABC绕点C按顺时针方向旋转n度后，取得△DEC，点D恰好落在AB边上．（1）求n的值；（2）假设F是DE的中点，判定四边形ACFD的形状，并说明理由．考点：旋转的性质；含30度角的直角三角形；直角三角形斜边上的中线；菱形的判定．分析：（1）利用旋转的性质得出AC=CD，进而得出△ADC是等边三角形，即可得出∠ACD的度数；（2）利用直角三角形的性质得出FC=DF，进而得出AD=AC=FC=DF，即可得出答案．。

湖南省2021年中考数学真题分项汇编—专题13 图形的相似、平移、对称与旋转(含答案解析)

专题13 图形的相似、平移、对称与旋转一、单选题1．（2021·湖南永州市·中考真题）如图，在平面内将五角星绕其中心旋转180︒后所得到的图案是（）A．B．C．D．【答案】C【分析】根据旋转的性质找出阴影部分三角形的位置即可得答案．【详解】∵将五角星绕其中心旋转180︒，∴图中阴影部分的三角形应竖直向下，故选：C．【点睛】本题考查旋转的性质，图形旋转前后，对应边相等，对应角相等，前后两个图形全等；熟练掌握旋转的性质是解题关键．2．（2021·湖南岳阳市·中考真题）下列品牌的标识中，是轴对称图形的是（）A．B．C．D．【答案】A【分析】根据轴对称图形的概念判断各项即可．【详解】A. 是轴对称图形，符合题意；B. 不是轴对称图形，不符合题意；C. 不是轴对称图形，不符合题意；D. 不是轴对称图形，不符合题意；故选：A．【点睛】本题考查的知识点是轴对称图形，解题的关键是熟练的掌握轴对称图形．3．（2021·湖南衡阳市·中考真题）在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（）A．B．C．D．【答案】D【分析】根据轴对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．【详解】A、不是轴对称图形，故A不符合题意；B、不是轴对称图形，故B不符合题意；C、不是轴对称图形，故C不符合题意；D、是轴对称图形，故D符合题意．故选D.【点睛】本题主要考查轴对称图形的知识点．确定轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．4．（2021·湖南中考真题）以下有关勾股定理证明的图形中，不是中心对称图形的是（）A．B．C．D．【答案】A【分析】根据中心对称图形的定义即可得．【详解】A、不是中心对称图形，此项符合题意；B、是中心对称图形，此项不符题意；C、是中心对称图形，此项不符题意；D、是中心对称图形，此项不符题意；故选：A．【点睛】本题考查了中心对称图形，熟记定义是解题关键．5．（2021·湖南长沙市·中考真题）下列几何图形中，是中心对称图形的是（）A．B．C．D．【答案】C【分析】根据中心对称图形的定义即可得．【详解】A、不是中心对称图形，此项不符题意；B、不是中心对称图形，此项不符题意；C、是中心对称图形，此项符合题意；D、不是中心对称图形，此项不符题意；故选：C．【点睛】本题考查了中心对称图形，熟记定义是解题关键．6．（2021·湖南邵阳市·中考真题）下列四个图形中，是中心对称图形的是（）A．B．C．D．【答案】C【分析】根据中心对称图形的定义就可以选出答案．【详解】解：A、不是中心对称图形，不符合题意；B、不是中心对称图形，不符合题意；C、是中心对称图形，符合题意；D、不是中心对称图形，不符合题意．故选：C．【点睛】本题考查中心对称图形的定义：把一个图形绕某个点旋转180︒，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形．7．（2021·湖南中考真题）下列垃圾分类标志分别是厨余垃圾、有害垃圾、其他垃圾和可回收物，其中既是轴对称图形又是中心对称图形的是（）A．B．C．D．【答案】B【分析】根据轴对称图形与中心对称图形的概念求解．【详解】解：A 、是轴对称图形，不是中心对称图形，故此选项不合题意；B 、既是轴对称图形，也是中心对称图形，故此选项符合题意；C 、是轴对称图形，不是中心对称图形，故此选项不合题意；D 、既不是轴对称图形，也不是中心对称图形，故此选项不符合题意；故选：B ．【点睛】此题主要考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与原图重合．8．（2021·湖南邵阳市·中考真题）如图，在AOB 中，1AO =，32BO AB ==．将AOB 绕点O 逆时针方向旋转90︒，得到A OB ''△，连接AA '．则线段AA '的长为（）A ．1B C ．32 D 【答案】B【分析】根据旋转性质可知=OA OA '，90AOA '∠=︒，再由勾股定理即可求出线段AA '的长．【详解】解：∵旋转性质可知==1OA OA '，90AOA '∠=︒，∴AA '=故选：B ．【点睛】此题主要考查旋转的性质和勾股定理求出直角三角形边长，解题关键是根据旋转性质得出OAA '是等腰直角三角形．9．（2021·湖南娄底市·中考真题）如图，直角坐标系中，以5为半径的动圆的圆心A 沿x 轴移动，当⊙A 与直线5:12l y x =只有一个公共点时，点A 的坐标为（）A ．(12,0)-B ．(13,0)-C ．(12,0)±D ．(13,0)± 【答案】D【分析】当⊙A 与直线5:12l y x =只有一个公共点时，则此时⊙A 与直线5:12l y x =相切，（需考虑左右两侧相切的情况）；设切点为B ，此时B 点同时在⊙A 与直线5:12l y x =上，故可以表示出B 点坐标，过B 点作//BC OA ，则此时AOB OBC △∽△，利用相似三角形的性质算出OA 长度，最终得出结论．【详解】如下图所示，连接AB ，过B 点作//BC OA ，此时B 点坐标可表示为512x,x ⎛⎫ ⎪⎝⎭， ∴512OC x =，BC x =，在Rt OBC中，1312OB x ===，又∵A 半径为5，∴5AB =，∵//BC OA ，∴AOB OBC △∽△，则OA AB OB BO OC BC==， ∴51351212OA =x x ， ∴13OA=，∵左右两侧都有相切的可能，∴A 点坐标为(13,0)±，故选：D ．【点睛】本题考查的是直线与圆的位置关系，熟知相似三角形的判定与性质是解答此题的关键．二、填空题10．（2021·湖南中考真题）下图是一架梯子的示意图，其中1111//////AA BB CC DD ，且AB BC CD ==．为使其更稳固，在A ，1D 间加绑一条安全绳（线段1AD ），量得0.4m AE =，则1AD =________m ．【答案】1.2【分析】根据平行线分线段成比例定理，可得1AE EF FD ==，进而即可求解．【详解】解：∵1111//////AA BB CC DD ，AB BC CD ==，∴1AE EF FD ==，∵0.4m AE =，∴1AD =3 1.2m AE =，故答案是：1.2．【点睛】本题主要考查平行线分线段成比例定理，掌握“平行线所截得的对应线段成比例”，是解题的关键．11．（2021·湖南怀化市·中考真题）如图，在平面直角坐标系中，已知(2,1)A -，(1,4)B -，(1,1)C -，将ABC先向右平移3个单位长度得到111A B C △，再绕1C 顺时针方向旋转90︒得到221A B C △，则2A 的坐标是____________．【答案】（2，2）．【分析】直接利用平移的性质和旋转的性质得出对应点位置，然后作图，进而得出答案．【详解】解：如图示：111A B C △，221A B C △为所求，根据图像可知，2A 的坐标是（2，2），故答案是：（2，2）．【点睛】本题主要考查了平移作图和旋转作图，熟悉相关性质是解题关键．12．（2021·湖南中考真题）如图，Rt ABC 中，390,tan 2BAC ABC ∠=︒∠=，将ABC 绕A 点顺时针方向旋转角9(0)0αα︒<<︒得到AB C ''△，连接BB '，CC '，则CAC '△与BAB '△的面积之比等于_______．【答案】9:4【分析】先根据正切三角函数的定义可得32AC AB =，再根据旋转的性质可得,,AB AB AC AC BAB CAC α''''==∠=∠=，从而可得1AC AB AC AB ==''，然后根据相似三角形的判定可得CAC BAB ''~，最后根据相似三角形的性质即可得．【详解】解：在Rt ABC 中，390,tan 2BAC ABC ∠=︒∠=， 32AC AB ∴=，由旋转的性质得：,,AB AB AC AC BAB CAC α''''==∠=∠=，1AC AB AC AB ∴==''，在CAC '△和BAB '△中，AC AB AC AB CAC BAB ''''⎧=⎪⎨⎪∠=∠⎩，CAC BAB ''~∴，294CAC BAB AC S AB S ''⎛⎫== ⎪⎝⎭∴，即CAC '△与BAB '△的面积之比等于9:4，故答案为：9:4．【点睛】本题考查了正切三角函数、旋转的性质、相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题关键．三、解答题13．（2021·湖南衡阳市·中考真题）如图，点E 为正方形ABCD 外一点，90AEB =︒∠，将Rt ABE △绕A 点逆时针方向旋转90︒得到,ADF DF 的延长线交BE 于H 点．（1）试判定四边形AFHE 的形状，并说明理由；（2）已知7,13BH BC ==，求DH 的长．【答案】（1）正方形，理由见解析；（2）17【分析】（1）由旋转的性质可得∠AEB ＝∠AFD ＝90°，AE ＝AF ，∠DAF ＝∠EAB ，由正方形的判定可证四边形BE 'FE（2）连接BD ，利用勾股定理可求BD ==，再利用勾股定理可求DH 的长．【详解】解：（1）四边形AFHE 是正方形，理由如下：根据旋转：90AEB AFD AE AF DAF EAB ∠∠︒∠∠＝＝，＝，＝，∵四边形ABCD 是正方形∴∠DAB=90°∴∠F AE ＝∠DAB=90°∴90AEB AFH FAE ∠∠∠=︒＝＝∴四边形AFHE 是矩形，又∵AE AF =∴矩形AFHE 是正方形．（2）连接BD∵13BC CD ==，在Rt BCD 中，BD ==∵四边形AFHE 是正方形∴90EHD ∠=︒在Rt DHB △中，DH =7BH =，故答案是17．【点睛】本题是四边形综合题，考查了正方形的判定和性质，旋转的性质，勾股定理，全等三角形的判定和性质，等腰三角形的性质等知识，灵活运用这些性质进行推理是本题的关键．14．（2021·湖南株洲市·中考真题）将一物体（视为边长为2π米的正方形ABCD ）从地面PQ 上挪到货车车厢内．如图所示，刚开始点B 与斜面EF 上的点E 重合，先将该物体绕点()B E 按逆时针方向旋转至正方形111A BC D 的位置，再将其沿EF 方向平移至正方形2222A B C D 的位置（此时点2B 与点G 重合），最后将物体移到车厢平台面MG 上．已知//MG PQ ，30FBP ∠=︒，过点F 作FH MG ⊥于点H ，13FH =米，4EF =米．（1）求线段FG 的长度；（2）求在此过程中点A 运动至点2A 所经过的路程．【答案】（1）23米；（2）4米．【分析】（1）利用直角三角形FGH 即可求解；（2）连接A 1A 2，则必过点D 1，分别求出A 1A 2和1A A 的长，即可求出点A 经过的路程．【详解】解：（1）∵MG ∥PQ ，∴∠FGM =∠FBP =30°．∴在Rt FGH △中， 122233FG FH ==⨯=（米）．（2）连接A 1A 2，则必过点D 1，且四边形A 1BGA 2是矩形．∴A 1A 2=BG =BF -GF =210433（米）． ∵四边形ABCD 和四边形A 1BC 1D 1都是正方形，∴AB =A 1B ，∠A 1BC 1=∠ABC =90°．∴∠ABA 1=180°-∠A 1BC 1-∠FBP =180°-90°-30°=60°．∴126021803AA l ππ⨯⨯==（米）． ∴在整个运动过程中，点A 运动至A 2的路程为：112210433AA l A A +=+=（米）．【点睛】本题考查了直角三角形的性质、矩形和正方形的性质、平移和旋转的性质等知识点，熟知旋转和平移的性质是解题的关键．15．（2021·湖南衡阳市·中考真题）如图，OAB 的顶点坐标分别为()()()0,0,3,4,6,0O A B ，动点P 、Q 同时从点O 出发，分别沿x 轴正方向和y 轴正方向运动，速度分别为每秒3个单位和每秒2个单位，点P 到达点B 时点P 、Q 同时停止运动．过点Q 作//MN OB 分别交AO 、AB 于点M 、N ，连接PM 、PN ．设运动时间为t （秒）．（1）求点M的坐标（用含t 的式子表示）；（2）求四边形MNBP 面积的最大值或最小值；（3）是否存在这样的直线l ，总能平分四边形MNBP 的面积？如果存在，请求出直线l 的解析式；如果不存在，请说明理由；（4）连接AP ，当OAP BPN ∠=∠时，求点N 到OA 的距离．【答案】（1）3,22M t t ⎛⎫ ⎪⎝⎭；（2）四边形MNBP 面积不存在最小值，存在最大值，最大值为6.（3）存在，443y x =-；（4）103或24.5【分析】（1）做适当的辅助线，过M 点作MG x ⊥轴于G 点．过A 点作AD x ⊥轴于D 点，利用三角形相似的判定定理证明两个三角形相似，根据对应边成比例，从而可得答案；（2）根据坐标先求解,,,OM OA OP OB 长度，再证明,MOP AOB ∽ 再利用相似三角形的性质证明//,MP AB 证明四边形MNBP 为平行四边形，再列面积函数关系式，利用二次函数的性质求解最大值即可；（3）先判断存在，通过观察图形知，当直线l 过MNBP 的对角线交点时，总能平分其面积；再利用平行四边形的性质求解对角线的中点坐标，从而可得答案；（4）当0t <＜2时，证明AOP PBN ∽，利用三角形相似，对应边成比例，求解时间,t 再利用等面积法求解点N 到直线OA 的距离即可．当0t =时，利用等面积法直接求解即可，当2t =不合题意，舍去．【详解】解：（1）过M 点作MG x ⊥轴于G 点．过A 点作AD x ⊥轴于D 点．则90,//,MGO MG AD ∠=︒90,//,QOB MN OB ∠=︒18090,OQM QOB ∴∠=︒-∠=︒ 四边形QOGM 为矩形，则2,MG OQ t ==()()()0,0,3,4,6,0O A B ，,AD OB ⊥()3,0D ∴，3,4,OD AD ==//,MQ ADMOG AOD ∴∽，∴OG MG OD AD =，即234OG t = ∴32OG t =∴3,22M t t ⎛⎫ ⎪⎝⎭（2）∵()32,,3,4,2OQ t QM t OG A ===5,5,2OM t OA ∴====()3,60,OP t B =，6,OB ∴=5132,526t OM t OP t OA OB∴==== ,MOP AOB ∠=∠,MOP AOB ∴∽,MPO ABO ∴∠=∠//,MP AB ∴//,MN OB∴四边形MNBP 为平行四边形∵2(63)26(1)6MNBP S BP OQ t t t =⋅=-⨯=--+，0＜t ＜2, （当0t =或2t =时，四边形不存在）而6a =-，∴当1t =时，S 取最大值6∴四边形MNBP 面积不存在最小值，存在最大值，最大值为6.（3）存在．理由如下：连接,BM 交PN 于,H由（2）得：四边形PBNM 为平行四边形，∴ 过H 的任意直线都平分MNBP 的面积，,MH BH =()3,2,6,0,2M t t B ⎛⎫ ⎪⎝⎭所以由中点坐标公式可得：33,4H t t ⎛⎫+ ⎪⎝⎭，即l 过点H ， 33,4x t y t⎧=+⎪∴⎨⎪=⎩ 33,4x y ∴=+∴4:43l y x =- （4）如图，当0t <＜2时，()()3,4,6,0,5,A B AO =5,AB ∴==5,AB AO ∴==,AOB ABO ∴∠=∠∵,OAP BPN ∠=∠∴AOP PBN ∽ ∴AO OP PB BN =，即5363BNt t =-， //,MN OB,,AMN AOB ANM ABO ∴∠=∠∠=∠,AMN ANM ∴∠=∠,AM AN ∴=5,2OM BN t ∴== 53,6352t t t ∴=- ∴1211,018t t ==，经检验；11118t =是原方程的根，20t =是增根，舍去，此时：2563,6MN PB t ==-= 112,9OQ t ==如图，过N 作NK AO ⊥于,K112,2ABC OBN AON S OB AD S S =⨯⨯==+11116512,292NK ∴⨯⨯+⨯⨯= 10.3NK ∴= 当0t =时，0,OAP BPN ∠=∠=︒ 此时N 到OA 的距离是B 到OA 的距离，设这个距离为,h 由等面积法可得：11,22OA h OB AD = 564,h ∴=⨯24.5h ∴= 当2t =时，不合题意，舍去．综上：N 到OA 的距离为：103或24.5 【点睛】本题考查了平面图形中动点的综合性问题，涉及动点的轨迹，相似三角形的判定与性质，等腰三角形的定义与性质，矩形的判定与性质，图形与坐标，列二次函数的关系式，二次函数的性质，解题的关键是：灵活应用基础知识；注意知识的系统化．16．（2021·湖南岳阳市·中考真题）如图，在Rt ABC 中，90ACB ∠=︒，60A ∠=︒，点D 为AB 的中点，连接CD ，将线段CD 绕点D 顺时针旋转()60120αα︒<<︒得到线段ED ，且ED 交线段BC 于点G ，CDE ∠的平分线DM 交BC 于点H ．（1）如图1，若90α=︒，则线段ED 与BD 的数量关系是________，GD CD=________；（2）如图2，在（1）的条件下，过点C 作//CF DE 交DM 于点F ，连接EF ，BE ．①试判断四边形CDEF 的形状，并说明理由；②求证：BE FH =；（3）如图3，若2AC =，()tan 60m α-︒=，过点C 作//CF DE 交DM 于点F ，连接EF ，BE ，请直接写出BE FH的值（用含m 的式子表示）．【答案】（1）ED BD =（2）①正方形，理由见解析；②见解析；（3）2m 【分析】（1）根据“斜中半”定理可得CD AD BD ==，然后根据旋转的性质可得CD ED =，从而得出ED BD =，再结合题意推出30B DCG ∠=∠=︒，从而根据正切函数的定义求出GD CD即可；（2）①通过证明CDF EDF △≌△，并综合条件//CF DE ，推出四边形CDEF 是正方形；②首先根据CFH DGH △△∽推出DH DG FH CD ==GBE GDH △≌△得到BE DH =，即可得出结论；（3）根据题意可首先证明四边形CDEF 是菱形，然后证明出EBG HFC △△∽，即可推出结论BE BG FH FC =，再作DK CG ⊥，通过解直角三角形，求出BG 的长度，从而得出结论．【详解】（1）∵点D 为Rt ABC 中斜边AB 的中点，∴CD AD BD ==，∵线段CD 绕点D 顺时针旋转得到线段ED ，∴CD ED =，∴ED BD =，∵Rt ABC 中，90ACB ∠=︒，60A ∠=︒，∴30B ∠=︒，∵CD BD =，∴30B DCG ∠=∠=︒，∴在Rt DCG 中，tan tan 30GD DCG CD =∠=︒=，故答案为：ED BD = （2）①正方形，理由如下：∵90α=︒，DM 平分CDE ∠，∴90CDE ∠=︒，CDF EDF ∠=∠，∵CD ED =，DF DF =，∴()CDF EDF SAS △≌△， ∴DCF DEF ∠=∠，∵//CF DE ，∴180FCD CDE ∠+∠=︒，∴90FCD ∠=︒，∴90DCF DEF CDE ∠=∠=∠=︒，∴四边形CDEF 为矩形，又∵CD ED =，∴四边形CDEF 为正方形；②显然，在正方形CDEF 中，CFH GDH △△∽， ∴DH DG FH CF=，又∵CD CF =，∴DH DG FH CD == 由（1）得：60,,A CD AD ∠=︒=则ACD △为等边三角形， ∴60ADC ∠=︒，∵90CDE ∠=︒，∴30GDB ∠=︒，∴GDB GBD ∠=∠，GD GB =，又∵DE DB =，∴()1180752DBE DEB GDB ∠=∠=︒-∠=︒， ∴753045GBE ∠=︒-︒=︒，∵45GDH ∠=︒，∴GBE GDH ∠=∠在GBE 与GDH 中，GDH GBE GD GBDGH BGE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()GBE GDH ASA △≌△， ∴BE DH =，∴BE DH DG FH FH CD ===；（3）同（2）中①理，CDF EDF △≌△，∴CDF EDF ∠=∠，CFD EFD ∠=∠，∵//CF DE ，∴CFD EDF ∠=∠，∴CFD CDF ∠=∠，EDF EFD ∠=∠，∴CF CD =，ED EF =，∴四边形CDEF 为菱形，∵ACD △为等边三角形，∴2AC CD AD BD ====，菱形的边长也为2，由题意，2HDG α∠=，13022DEB DBE ADE α∠=∠=∠=︒+， ∵30DBG ∠=︒， ∴2EBG α∠=，即：HDG EBG ∠=∠，∴EBG HDG △△∽，∵在菱形CDEF 中，HFC HDG △△∽，∴EBG HFC △△∽，∴BE BG FH FC=，如图，作DK CG ⊥，∵30DCK ∠=︒，∴60CDK ∠=︒，60KDG α∠=-︒，∵2CD =，∴1DK =，CK =在Rt KDG △中，()tan tan 60GK KDG m DK α=∠=-︒=， ∴GK m =，∴CG m ，在Rt ABC 中，BC ==∴BG BC CG m m =-==，∵2CF CD ==，∴2BE BG m FH FC ==．【点睛】本题考查相似三角形的判定与性质，特殊平行四边形的判定与性质，以及锐角三角函数等，综合性较强，掌握基本图形的性质，灵活运用相似三角形以及锐角三角函数是解题关键．17．（2021·湖南中考真题）如图1，在等腰直角三角形ABC 中，90BAC ∠=︒．点E ，F 分别为AB ，AC 的中点，H 为线段EF 上一动点（不与点E ，F 重合），将线段AH 绕点A 逆时针方向旋转90︒得到AG ，连接GC ，HB ．（1）证明：AHB AGC ≌；（2）如图2，连接GF ，HC ，AF 交AF 于点Q ．①证明：在点H 的运动过程中，总有90HFG ∠=︒；②若4AB AC ==，当EH 的长度为多少时，AQG 为等腰三角形？【答案】（1）见详解；（2）①见详解；②当EH 的长度为2AQG 为等腰三角形【分析】（1）由旋转的性质得AH =AG ，∠HAG =90°，从而得∠BAH =∠CAG ，进而即可得到结论；（2）①由AHB AGC ≌，得AH =AG ，再证明AEH AFG ≌，进而即可得到结论；②AQG 为等腰三角形，分3种情况：（a ）当∠QAG =∠QGA =45°时，（b ）当∠GAQ =∠GQA =67.5°时，（c ）当∠AQG =∠AGQ =45°时，分别画出图形求解，即可．【详解】解：（1）∵线段AH 绕点A 逆时针方向旋转90︒得到AG ，∴AH =AG ，∠HAG =90°，∵在等腰直角三角形ABC 中，90BAC ∠=︒，AB =AC ，∴∠BAH =90°-∠CAH =∠CAG ，∴AHB AGC ≌；（2）①∵在等腰直角三角形ABC 中，AB =AC ，点E ，F 分别为AB ，AC 的中点，∴AE =AF ，AEF 是等腰直角三角形，∵AH =AG ，∠BAH =∠CAG ，∴AEH AFG ≌，∴∠AEH =∠AFG =45°，∴∠HFG =∠AFG +∠AFE =45°+45°=90°，即：90HFG ∠=︒；②∵4AB AC ==，点E ，F 分别为AB ，AC 的中点，∴AE =AF =2，∵∠AGH =45°，AQG 为等腰三角形，分3种情况：（a ）当∠QAG =∠QGA =45°时，如图，则∠HAF =90°-45°=45°，∴AH 平分∠EAF ，∴点H 是EF 的中点，∴EH 12==（b ）当∠GAQ =∠GQA =（180°-45°）÷2=67.5°时，如图，则∠EAH =∠GAQ =67.5°，∴∠EHA =180°-45°-67.5°=67.5°，∴∠EHA =∠EAH ，∴EH =EA =2；（c ）当∠AQG =∠AGQ =45°时，点H 与点F 重合，不符合题意，舍去，综上所述：当EH 的长度为2AQG 为等腰三角形．【点睛】本题主要考查等腰直角三角形的性质，旋转的性质，全等三角形的判定和性质，勾股定理，熟练掌握全等三角形的判定定理，根据题意画出图形，进行分类讨论，是解题的关键．18．（2021·湖南娄底市·中考真题）如图①，E F 、是等腰Rt ABC 的斜边BC 上的两动点，45,EAF CD BC ∠=︒⊥且CD BE =．（1）求证：ABE ACD △≌△；（2）求证：222EF BE CF =+；（3）如图②，作AH BC ⊥，垂足为H ，设,EAH FAH αβ∠=∠=，不妨设AB =，请利用（2）的结论证明：当45αβ+=︒时，tan tan tan()1tan tan αβαβαβ++=-⋅成立．【答案】（1）证明见详解；（2）证明见详解；（3）证明见详解．【分析】（1）△ABC 是等腰直角三角形，AB =AC ，∠BAC =90°，由CD ⊥BC ，可求∠DCA =∠ABE 即可；（2）由△ABE ≌△ACD ，可得∠F AD =∠EAF ，可证△AEF ≌△ADF （SAS ），可得EF =DF ，在Rt △CDF 中，根据勾股定理，222DF CD CF =+即可；（3）将△ABE 逆时针绕点A 旋转90°到△ACD ，由△ABC 为等腰直角三角形，可求∠DCF =90°，由AB =，在Rt △ABC 中由勾股定理2BC =，由AH ⊥BC ，可求BH =CH =AH =1，可表示EF = tan α+ tan β,BE =1-tan α,CF = 1-tan β，可证△AEF ≌△ADF （SAS ），得到EF =DF ，由222EF BE CF =+可得()()()222tan tan 1tan +1tan αβαβ+=--，整理即得结论．【详解】（1）证明：∵△ABC 是等腰直角三角形，∴AB =AC ，∠BAC =90°，∴∠ABC =∠ACB =45°，∵CD ⊥BC ，∴∠DCB =90°，∴∠DCA =90°-∠ACB =90°-45°=45°=∠ABE ，在△ABE 和△ACD 中，AB AC ABE ACD BE CD =⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△ACD （SAS ），（2）证明∵△ABE ≌△ACD ，∴∠BAE =∠CAD ，AE =AD ，∵∠EAF =45°，∴∠BAE +∠F AC =90°-∠EAF =90°-45°=45°，∴∠F AD =∠F AC +∠CAD =∠F AC +∠BAE =45°=∠EAF ，在△AEF 和△ADF 中，AE AD EAF DAF AF AF =⎧⎪∠=∠⎨⎪=⎩，∴△AEF ≌△ADF （SAS ），∴EF =DF ，在Rt △CDF 中，根据勾股定理，222DF CD CF =+，即222EF BE CF =+；（3）证明：将△ABE 逆时针绕点A 旋转90°到△ACD ，连结FD ，∴∠BAE =∠CAD ，BE =CD ，AE =AD ，∵△ABC 为等腰直角三角形，∠ACB =∠B =∠ACD =45°，∠DCF =∠DCA +∠ACF =45°+45°=90°，∵AB =，∴AC= AB =，在Rt △ABC中由勾股定理2BC === ∵AH ⊥BC ，∴BH =CH =AH =112BC =， ∴EF =EH +FH =AH tan α+AH tan β= tan α+ tan β,BE =BH -EH =1-tan α,CF =CH -HF =1-tan β，∵∠EAF =45°，∴∠BAE +∠CAF =90°-∠EAF =45°，∴∠DAF =∠DAC +∠CAF =∠BAE +∠CAF =45°=∠EAF ，在△AEF 和△ADF 中，AE AD EAF DAF AF AF =⎧⎪∠=∠⎨⎪=⎩，∴△AEF ≌△ADF （SAS ），∴EF =DF ，在Rt △CDF 中，222DF CD CF =+即222EF BE CF =+，∴()()()222tan tan 1tan +1tan αβαβ+=--，整理得2tan tan 12tan +12tan αβαβ⋅=--，即tan tan 1tan tan αβαβ⋅=--，∴tan +tan 1tan tan αβαβ=-⋅， ∴()tan +tan 1=tan 45=tan +1tan tan αβαβαβ=︒-⋅， ∴()tan +tan tan +=1tan tan αβαβαβ-⋅．【点睛】本题考查等腰直角三角形的性质，三角形全等判定与性质，三角形旋转变换，勾股定理，锐角三角函数及其公式推导，掌握上述知识、灵活应用全等三角形的判定和性质是解题关键．19．（2021·湖南邵阳市·中考真题）如图，在Rt ABC △中，点P 为斜边BC 上一动点，将ABP △沿直线AP 折叠，使得点B 的对应点为B '，连接AB '，CB '，BB '，PB '．（1）如图①，若PB AC '⊥，证明：PB AB ''=．（2）如图②，若AB AC =，3BP PC =，求cos B AC '∠的值．（3）如图③，若30ACB ∠=︒，是否存在点P ，使得AB CB '=．若存在，求此时PC BC的值；若不存在，请说明理由．【答案】（1）证明见解析；（2）35；（3）存在，PC BC 的值为12或34．【分析】（1）先根据平行线的判定与性质可得CPB ABP '∠=∠，再根据折叠的性质可得,AB P ABP PB PB ''∠=∠=，从而可得CPB AB P ''∠=∠，然后根据平行线的判定可得//'AB BC ，最后根据菱形的判定与性质即可得证；（2）设AC 与PB '的交点为点O ，过点O 作OD AB '⊥于点D ，设4(0)AB AC a a ==>，从而可得BC =，先证出COP B OA '~，从而可得OC OP PC OB OA AB ===''，设,4(0)OC OB b b '=>，根据线段的和差可得4,4OP b OA a =-=，代入可求出b =，从而可得207OA a =，再在Rt B OD '中，解直角三角形可得167B D a '==，由此可得127AD a =，然后在Rt AOD △中，根据余弦三角函数的定义即可得；（3）如图（见解析），设2(0)AB CB m m '==>，从而可得4,,2BC m AC AB m '===，分①点B '在直线AC 的左侧；②点B '在直线AC 的右侧两种情况，再分别利用等边三角形的判定与性质、等腰三角形的性质求解即可得．【详解】（1）证明：PB AC '⊥，90BAC ∠=︒，//PB AB '∴，CPB ABP '∴∠=∠，由折叠的性质得：,AB P ABP PB PB ''∠=∠=，CPB AB P ''∴∠=∠，//AB BC '∴，∴四边形ABPB '是平行四边形，又PB PB '=，∴平行四边形ABPB '是菱形，PB AB ''∴=；（2）如图，设AC 与PB '的交点为点O ，过点O 作OD AB '⊥于点D ，AB AC =，Rt ABC ∴是等腰三角形，45ABC ACB ∠=∠=︒，设4(0)AB AC a a ==>，则BC =，3BP PC =，,BP PC ∴=，由折叠的性质得：45,,4AB P ABP PB PB AB AB a '''∠=∠=︒====，在COP 和B OA '中，45OCP OB A COP B OA ∠=∠=︒∠'∠='⎧⎨⎩， COP B OA '∴~，OC OP PC OB OA AB ∴====''设(0)OC b =>，则4,4,4OB b OP b OA a '==-=，4OP OA ∴==，解得7b a =，2047OA a a ∴=-=，在Rt B OD '中，16cos 7B D OB AB P a '''=⋅∠==， 127AD AB B D a ''∴=-=，则1237cos 2057a AD B AC OA a '∠===；（3）30,90ACB BAC ∠=︒∠=︒，60ABC ∴∠=︒，设2(0)AB CB m m '==>，则4,BC m AC ===，由折叠的性质得：60,2AB P ABP AB AB m ''∠=∠=︒==，2AB CB m ''∴==，由题意，分以下两种情况：①如图，当点B '在直线AC 的左侧时，过点B '作B E AC '⊥于点E ，12CE AC ∴==（等腰三角形的三线合一），12B E m BC ''∴===， ∴在Rt B CE '中，30B CE '∠=︒，303060B CP B CE ACB ''∴∠=∠+∠=︒+︒=︒，又AB CB ''=，30B AC B CE ''∴∠=∠=︒，180120AB C B AC B CE '''∴∠=︒-∠-∠=︒，1206060CB P AB C AB P '''∴∠=∠-∠=︒-︒=︒，CB P '∴是等边三角形，2PC CB m '∴==，2142PC m BC m ∴==； ②如图，当点B '在直线AC 的右侧时，过点B '作B F AC '⊥于点F ，同理可得：30B CF '∠=︒，B CF ACB '∴∠=∠，∴点B '在BC 上，由折叠的性质得：AP BB '⊥，在Rt ABP 中，cos BP AB ABC m =⋅∠=，3PC BC BP m ∴=-=，3344PC m BC m ∴==，综上，存在点P ，使得AB CB '=，此时PC BC 的值为12或34．【点睛】本题考查了菱形的判定与性质、相似三角形的判定与性质、解直角三角形、折叠的性质、等边三角形的判定与性质等知识点，较难的是题（3），正确分两种情况讨论是解题关键．。

中考数学试题分项解析专题51图形的平移对称与旋转含解析试题

专题5.1 图形的平移对称与旋转一、单项选择题1．点A〔2，﹣5〕关于x轴对称的点的坐标是〔〕A．〔2，5〕 B．〔﹣2，5〕 C．〔﹣2，﹣5〕 D．〔﹣5，2〕【来源】2021年中考数学试卷【答案】A【解析】【分析】根据“关于x轴对称的点，横坐标一样，纵坐标互为相反数〞进展解答即可.【详解】因为点〔m，n〕关于x轴的对称的点的坐标为〔m，-n〕，所以点A〔2，﹣5〕关于x轴的对称点B的坐标为〔2，5〕，应选A．【点睛】此题考察了关于x轴、y轴对称的点的坐标，解决此题的关键是掌握好对称点的坐标规律：〔1〕关于x轴对称的点，横坐标一样，纵坐标互为相反数；〔2〕关于y轴对称的点，纵坐标一样，横坐标互为相反数；〔3〕关于原点对称的点，横坐标与纵坐标都互为相反数．2．以下图形中，既是中心对称图形，又是轴对称图形的是〔〕A． B． C． D．【来源】2021年初中毕业学业考试数学试题【答案】C点睛：此题考察了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两局部折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两局部重合．3．如下字体的四个汉字中，是轴对称图形的是〔〕A． B． C． D．【来源】2021年中考数学试卷【答案】D点睛：此题考察了轴对称图形的定义，可以正确观察图形和理解轴对称图形的定义是解此题的关键．4．在以下图形中，既是轴对称图形又是中心对称图形的是〔〕A． B． C． D．【来源】州2021年中考数学试题【答案】D【解析】分析：根据轴对称图形与中心对称图形的概念求解．详解：A、不是轴对称图形，是中心对称图形，故此选项错误；B、是轴对称图形，不是中心对称图形，故此选项错误；C、不是轴对称图形，也不是中心对称图形，故此选项错误；D、是轴对称图形，也是中心对称图形，故此选项正确．应选：D．点睛：此题考察了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两局部沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．5．如图，在平面直角坐标系中，把△ABC绕原点O旋转180°得到△CDA，点A，B，C的坐标分别为〔﹣5，2〕，〔﹣2，﹣2〕，〔5，﹣2〕，那么点D的坐标为〔〕A．〔2，2〕 B．〔2，﹣2〕 C．〔2，5〕 D．〔﹣2，5〕【来源】2021年中考数学试卷【答案】A点睛：此题主要考察了坐标与图形变化，图形或者点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．6．如图，点P是边长为1的菱形ABCD对角线AC上的一个动点，点M，N分别是AB，BC边上的中点，那么MP+PN的最小值是〔〕A． B． 1 C． D． 2【来源】HY自治区2021年中考数学试题【答案】B【解析】分析：先作点M关于AC的对称点M′，连接M′N交AC于P，此时MP+NP有最小值．然后证明四边形ABNM′为平行四边形，即可求出MP+NP=M′N=AB=1．详解：如图，点睛：此题考察的是轴对称-最短道路问题及菱形的性质，熟知两点之间线段最短的知识是解答此题的关键．7．如图，在平面直角坐标系中，△ABC的顶点A在第一象限，点B，C的坐标分别为〔2，1〕，〔6，1〕，∠BAC=90°，AB=AC，直线AB交y轴于点P，假设△ABC与△A′B′C′关于点P 成中心对称，那么点A′的坐标为〔〕A．〔﹣4，﹣5〕 B．〔﹣5，﹣4〕 C．〔﹣3，﹣4〕 D．〔﹣4，﹣3〕【来源】2021年中考数学试题【答案】A【解析】分析：先求得直线AB解析式为y=x-1，即可得出P〔0，-1〕，再根据点A与点A'关于点P成中心对称，利用中点公式，即可得到点A′的坐标．令x=0，那么y=-1，∴P〔0，-1〕，又∵点A与点A'关于点P成中心对称，∴点P为AA'的中点，设A'〔m，n〕，那么=0，=-1，∴m=-4，n=-5，∴A'〔-4，-5〕，应选：A．点睛：此题考察了中心对称，等腰直角三角形的运用，利用待定系数法得出直线AB的解析式是解题的关键．8．如图，在平面直角坐标系xOy中，A〔4，0〕，B〔0，3〕，C〔4，3〕，I是△ABC的内心，将△ABC绕原点逆时针旋转90°后，I的对应点I'的坐标为〔〕A．〔﹣2，3〕 B．〔﹣3，2〕 C．〔3，﹣2〕 D．〔2，﹣3〕【来源】2021年中考数学试卷【答案】A【解析】【分析】直接利用直角三角形的性质得出其内切圆半径，进而得出I点坐标，再利用旋转的性质得出对应点坐标．那么I〔3，2〕，∵△ABC绕原点逆时针旋转90°，∴I的对应点I'的坐标为：〔﹣2，3〕，应选A．【点睛】此题考察了直角三角形的内心、旋转的性质，根据直角三角形内心的性质得出其内心I的坐标是解题的关键.9．以下图形中的五边形ABCDE都是正五边形，那么这些图形中的轴对称图形有〔〕A． 1个 B． 2个 C． 3个 D． 4个【来源】2021年中考数学试题【答案】D【解析】分析：直接利用轴对称图形的性质画出对称轴得出答案．详解：如下图：直线l即为各图形的对称轴．，应选：D．点睛：此题主要考察了轴对称图形，正确把握轴对称图形的定义是解题关键．10．如图直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=3，将腰CD以D为中心逆时针旋转90°至ED，连AE、CE，那么△ADE的面积是〔〕A． 1 B． 2 C． 3 D．不能确定【来源】临安2021年中考数学试卷【答案】A在△DCG与△DEF中，，∴△DCG≌△DEF〔AAS〕，∴EF=CG，∵AD=2，BC=3，∴CG=BC﹣AD=3﹣2=1，∴EF=1，∴△ADE的面积是：×AD×EF=×2×1=1，应选A．【点睛】此题考察梯形的性质和旋转的性质，熟知旋转变换前后，对应点到旋转中心的间隔相等、每一对对应点与旋转中心连线所构成的旋转角相等是解题的关键．同时要注意旋转的三要素：①定点为旋转中心；②旋转方向；③旋转角度．11．图中由“○〞和“□〞组成轴对称图形，该图形的对称轴是直线〔〕A． l1 B． l2 C． l3 D． l4【来源】2021年中考数学试卷【答案】C【点睛】此题主要考察了轴对称图形，关键是掌握轴对称图形的定义．根据假如一个图形沿一条直线折叠，直线两旁的局部可以互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴．12．如图，一段抛物线y=﹣x2+4〔﹣2≤x≤2〕为C1，与x轴交于A0，A1两点，顶点为D1；将C1绕点A1旋转180°得到C2，顶点为D2；C1与C2组成一个新的图象，垂直于y轴的直线l 与新图象交于点P1〔x1，y1〕，P2〔x2，y2〕，与线段D1D2交于点P3〔x3，y3〕，设x1，x2，x3均为正数，t=x1+x2+x3，那么t的取值范围是〔〕A． 6＜t≤8 B．6≤t≤8 C． 10＜t≤12 D．10≤t≤12【来源】2021年中考数学试卷【答案】D【点睛】此题考察二次函数与x轴的交点，二次函数的性质，抛物线的旋转等知识，纯熟掌握和灵敏应用二次函数的相关性质以及旋转的性质是解题的关键.二、填空题13．在平面直角坐标系中，将点A′〔﹣2，3〕向右平移3个单位长度，再向下平移2个单位长度，那么平移后对应的点A′的坐标是_____．【来源】2021年中考数学试题【答案】〔1，1〕【解析】分析：直接利用平移的性质分别得出平移后点的坐标得出答案．详解：∵将点A′〔-2，3〕向右平移3个单位长度，∴得到〔1，3〕，∵再向下平移2个单位长度，∴平移后对应的点A′的坐标是：〔1，1〕．故答案为：〔1，1〕．点睛：此题主要考察了平移，正确掌握平移规律：上加下减，左加右减，是解题关键．14．有五张卡片〔形状、大小、质地都一样〕，上面分别画有以下图形：①线段；②正三角形；③平行四边形；④等腰梯形；⑤圆．将卡片反面朝上洗匀，从中抽取一张，正面图形一定满足既是轴对称图形，又是中心对称图形的概率是__________．【来源】2021年中考数学试卷【答案】点睛：此题考察了概率公式的应用.注意用到的知识点为：概率=所求情况数与情况总数之比.15．如图，将绕点A逆时针旋转，得到，这时点恰好在同一直线上，那么的度数为______．【来源】2021年初中毕业学业考试数学试题【答案】15【解析】分析：先判断出∠BAD=150°，AD=AB，再判断出△BAD是等腰三角形，最后用三角形的内角和定理即可得出结论．详解：∵将△ABC绕点A逆时针旋转150°，得到△ADE，∴∠BAD=150°，AD=AB，∵点B，C，D恰好在同一直线上，∴△BAD是顶角为150°的等腰三角形，∴∠B=∠BDA，∴∠B=〔180°-∠BAD〕=15°，故答案为：15°．点睛：此题主要考察了旋转的性质，等腰三角形的断定和性质，三角形的内角和定理，判断出三角形ABD是等腰三角形是解此题的关键．16．如图，正方形ABCD的边长为1，点A与原点重合，点B在y轴的正半轴上，点D在x 轴的负半轴上，将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置，B'C′与CD相交于点M，那么点M的坐标为_____．【来源】2021年中考数学试卷【答案】〔﹣1，〕【详解】如图，连接AM，∵将边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB'C′D′，∴AD=AB′=1，∠BAB′=30°，∴∠B′AD=60°，在Rt△ADM和Rt△AB′M中，，∴Rt△ADM≌Rt△AB′M〔HL〕，∴∠DAM=∠B′AM=∠B′AD=30°，∴DM=AD•tan∠DAM=1×=，∴点M的坐标为〔﹣1，〕，故答案为：〔﹣1，〕．【点睛】此题主要考察旋转的性质、正方形的性质，解题的关键是掌握旋转变换的不变性与正方形的性质、全等三角形的断定与性质及三角函数的应用．17．点O是平行四边形ABCD的对称中心，AD＞AB，E、F分别是AB边上的点，且EF＝AB；G、H分别是BC边上的点，且GH＝BC；假设S1,S2分别表示∆EOF和∆GOH的面积，那么S1,S2之间的等量关系是______________【来源】2021年中考数学试题【答案】2S1＝3S2【详解】过点O分别作OM⊥BC，垂足为M，作ON⊥AB，垂足为N，∵点O是平行四边形ABCD的对称中心，∴S平行四边形ABCD=AB•2ON， S平行四边形ABCD=BC•2OM，∴AB•ON=BC•OM，∵S1=EF•ON，S2=GH•OM，EF＝AB，GH＝BC，∴S1=AB•ON，S2=BC•OM，∴2S1＝3S2，故答案为：2S1＝3S2.【点睛】此题考察了平行四边形的面积，中心对称的性质，正确添加辅助线、准确表示出图形面积是解题的关键.18．如图，平面直角坐标系中，矩形OABC的顶点A〔﹣6，0〕，C〔0，2〕．将矩形OABC 绕点O顺时针方向旋转，使点A恰好落在OB上的点A1处，那么点B的对应点B1的坐标为_____．【来源】2021年中考数学试题【答案】〔-2，6〕【解析】分析：连接OB1，作B1H⊥OA于H，证明△AOB≌△HB1O，得到B1H=OA=6，OH=AB=2，得到答案．详解：连接OB1，作B1H⊥OA于H，由题意得，OA=6，AB=OC-2，那么tan∠BOA=，∴∠BOA=30°，∴∠OBA=60°，由旋转的性质可知，∠B1OB=∠BOA=30°，∴∠B1OH=60°，在△AOB和△HB1O，，∴△AOB≌△HB1O，∴B1H=OA=6，OH=AB=2，∴点B1的坐标为〔-2，6〕，故答案为：〔-2，6〕．点睛：此题考察的是矩形的性质、旋转变换的性质，掌握矩形的性质、全等三角形的断定和性质定理是解题的关键．19．如图，在▱ABCD中，AD=7，AB=2，∠B=60°．E是边BC上任意一点，沿AE剪开，将△ABE沿BC方向平移到△DCF的位置，得到四边形AEFD，那么四边形AEFD周长的最小值为_____．【来源】2021年中考数学试卷【答案】20【点睛】此题考察平移的性质，解题的关键是确定出当AE⊥BC时，四边形AEFD的周长最小．20．如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE，点B经过的途径为弧BD，那么图中阴影局部的面积为_____．【来源】2021年中考数学试卷【答案】【解析】【分析】先根据勾股定理得到AB=2，再根据扇形的面积公式计算出S扇形ABD，由旋转的性质得到Rt△ADE≌Rt△ACB，于是S阴影局部=S△ADE+S扇形ABD﹣S△ABC=S扇形ABD．【点睛】此题考察了旋转的性质、扇形面积的计算，得到S阴影局部 =S扇形ABD是解题的关键.三、解答题21．【来源】2021年中考数学试卷图①、图②均是8×8的正方形网格，每个小正方形的顶点称为格点，线段OM、ON的端点均在格点上．在图①、图②给定的网格中以OM、ON为邻边各画一个四边形，使第四个顶点在格点上．要求：〔1〕所画的两个四边形均是轴对称图形．〔2〕所画的两个四边形不全等．【答案】作图见解析.【解析】【分析】结合网格特点以及轴对称图形的定义进展作图，然后用全等四边形的定义判断即可得符合题意的图形．【详解】如下图：【点睛】此题考察了作图﹣轴对称变换，以及全等形的断定，纯熟掌握各自的性质是解此题的关键．22．如图，在平面直角坐标系中，△ABC的三个顶点坐标分别是A〔1，1〕，B〔4，1〕，C〔3，3〕．〔1〕将△ABC向下平移5个单位后得到△A1B1C1，请画出△A1B1C1；〔2〕将△ABC绕原点O逆时针旋转90°后得到△A2B2C2，请画出△A2B2C2；〔3〕判断以O，A1，B为顶点的三角形的形状．〔无须说明理由〕【来源】广西2021年中考数学试卷【答案】〔1〕画图见解析；〔2〕画图见解析；〔3〕三角形的形状为等腰直角三角形．【详解】〔1〕如下图，△A1B1C1即为所求；【点睛】此题考察了作图﹣旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．23．在边长为1个单位长度的正方形网格中建立如下图的平面直角坐标系，△ABC的顶点都在格点上，请解答以下问题：〔1〕①作出△ABC向左平移4个单位长度后得到的△A1B1C1，并写出点C1的坐标；②作出△ABC关于原点O对称的△A2B2C2，并写出点C2的坐标；〔2〕△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为〔－4，－2〕，请直接写出直线l 的函数解析式.【来源】2021年中考数学试题【答案】(1)作图见解析，C1的坐标C1〔-1,2〕, C2的坐标C2〔-3,-2〕；〔2〕y=-x.详解：〔1〕如下图， C1的坐标C1〔-1,2〕, C2的坐标C2〔-3,-2〕〔2〕解：∵A〔2,4〕，A3〔-4，-2〕，∴直线l的函数解析式：y=-x.点睛：此题考察了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考察了轴对称变换和平移变换．24．如图，矩形ABCD中，AB=m，BC=n，将此矩形绕点B顺时针方向旋转θ〔0°＜θ＜90°〕得到矩形A1BC1D1，点A1在边CD上．〔1〕假设m=2，n=1，求在旋转过程中，点D到点D1所经过途径的长度；〔2〕将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2，点D2在BC的延长线上，设边A2B与CD交于点E，假设=﹣1，求的值．【来源】2021年中考数学试题【答案】〔1〕D到点D1所经过途径的长度为π；〔2〕〔负根已经舍弃〕．详解：〔1〕作A1H⊥AB于H，连接BD，BD1，那么四边形ADA1H是矩形．∴AD=HA1=n=1，在Rt△A1HB中，∵BA1=BA=m=2，∴BA1=2HA1，∴∠ABA1=30°，∴旋转角为30°，∵BD=，∴D到点D1所经过途径的长度=〔2〕∵△BCE∽△BA2D2，点睛：此题考察轨迹，旋转变换、解直角三角形、弧长公式等知识，解题的关键是理解题意，灵敏运用所学知识解决问题，属于中考常考题型．25．如图，在中，，，D是AB边上一点点D与A，B不重合，连结CD，将线段CD绕点C按逆时针方向旋转得到线段CE，连结DE交BC于点F，连接BE．求证：≌；当时，求的度数．【来源】2021年中考数学试卷【答案】证明见解析；.【解析】【分析】由题意可知：，，由于，从而可得，根据SAS即可证明≌；由≌可知：，，从而可求出的度数．【详解】由题意可知：，，，，，，在与中，，≌；【点睛】此题考察了旋转的性质、全等三角形的断定与性质，解题的关键是纯熟运用旋转的性质以及全等三角形的断定与性质．26．如图1，一副直角三角板满足AB=BC，AC=DE，∠ABC=∠DEF=90°，∠EDF=30°操作：将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板DEF绕点E 旋转，并使边DE与边AB交于点P，边EF与边BC于点Q．探究一：在旋转过程中，〔1〕如图2，当时，EP与EQ满足怎样的数量关系？并给出证明；〔2〕如图3，当时，EP与EQ满足怎样的数量关系？并说明理由；〔3〕根据你对〔1〕、〔2〕的探究结果，试写出当时，EP与EQ满足的数量关系式为，其中m的取值范围是．〔直接写出结论，不必证明〕探究二：假设且AC=30cm，连接PQ，设△EPQ的面积为S〔cm2〕，在旋转过程中：〔1〕S是否存在最大值或者最小值？假设存在，求出最大值或者最小值；假设不存在，说明理由．〔2〕随着S取不同的值，对应△EPQ的个数有哪些变化，求出相应S的值或者取值范围．【来源】巿2021年中考数学试卷【答案】探究一：〔1〕EP=EQ；证明见解析；〔2〕1:2，证明见解析；〔3〕EP：EQ=1：m，∴0＜m≤2+；探究二：〔1〕当x=10时，面积最小，是50cm2；当x=10时，面积最大，是75cm2时，这样的三角形有2个；当S=50或者62.5＜S≤75时，这样的三角形有一个．〔3〕根据〔2〕中求解的过程，可以直接写出结果；要求m的取值范围，根据交点的位置的限制进展分析；探究二：〔1〕设EQ=x，结合上述结论，用x表示出三角形的面积，根据x的最值求得面积的最值；〔2〕首先求得EQ和EB重合时的三角形的面积的值，再进一步分情况讨论．【详解】探究一：〔1〕连接BE，根据E是AC的中点和等腰直角三角形的性质，得BE=CE，∠PBE=∠C，又∠BEP=∠CEQ，那么△BEP≌△CEQ，得EP=EQ；〔2〕作EM⊥AB，EN⊥BC于M，N，∴∠EMP=∠ENC，∵∠MEP+∠PEN=∠PEN+∠NEF=90°，∴∠MEP=∠NEF，∴△MEP∽△NEQ，∴EP：EQ=EM：EN=AE：CE=1：2；〔3〕过E点作EM⊥AB于点M，作EN⊥BC于点N，∵在四边形PEQB中，∠B=∠PEQ=90°，∴∠EPB+∠EQB=180°〔四边形的内角和是360°〕，又∵∠EPB+∠MPE=180°〔平角是180°〕，∴∠MPE=∠EQN〔等量代换〕，∴Rt△MEP∽Rt△NEQ，∴，在Rt△AME∽Rt△ENC，∴，∴，EP与EQ满足的数量关系式为EP：EQ=1：m，∴0＜m≤2+；〔当m＞2+时，EF与BC不会相交〕．【点睛】此题考察了旋转的性质、等腰直角三角形的性质、全等三角形的断定与性质，相似三角形的断定与性质等，综合性较强，正确添加辅助线，纯熟运用等腰直角三角形的性质和相似三角形的断定和性质进展求解是关键．27．在平面直角坐标系中，四边形是矩形，点，点，点.以点为中心，顺时针旋转矩形，得到矩形，点，，的对应点分别为，，.〔Ⅰ〕如图①，当点落在边上时，求点的坐标；〔Ⅱ〕如图②，当点落在线段上时，与交于点.①求证；②求点的坐标.〔Ⅲ〕记为矩形对角线的交点，为的面积，求的取值范围〔直接写出结果即可〕.【来源】2021年中考数学试题【答案】〔Ⅰ〕点的坐标为.〔Ⅱ〕①证明见解析；②点的坐标为.〔Ⅲ〕.详解：〔Ⅰ〕∵点，点，∴，.∵四边形是矩形，∴，，.∵矩形是由矩形旋转得到的，∴.在中，有，∴. ∴.∴点的坐标为.〔Ⅲ〕.点睛：本大题主要考察了等腰三角形的断定和性质，勾股定理以及旋转变换的性质等知识，灵敏运用勾股定理求解是解决此题的关键.28．在中，，，，过点作直线，将绕点顺时针得到〔点，的对应点分别为，〕，射线，分别交直线于点，.〔1〕如图1，当与重合时，求的度数；〔2〕如图2，设与的交点为，当为的中点时，求线段的长；〔3〕在旋转过程时，当点分别在，的延长线上时，试探究四边形的面积是否存在最小值.假设存在，求出四边形的最小面积；假设不存在，请说明理由.【来源】2021年中考数学试题【答案】〔1〕60°；〔2〕；〔3〕详解：〔1〕由旋转可得：AC=A'C=2，∵∠ACB=90°，AB=，AC=2，∴BC=，∵∠ACB=90°，m∥AC，∴∠A'BC=90°，∴cos∠A'CB=，∴∠A'CB=30°，∴∠ACA'=60°；〔2〕∵M为A'B'的中点，∴∠A'CM=∠MA'C，由旋转可得，∠MA'C=∠A，∴∠A=∠A'CM，∴tan∠PCB=tan∠A=，∴PB=BC=，∵tan∠Q=tan∠A=，∴BQ=BC×=2，∴PQ=PB+BQ=；点睛：此题属于四边形综合题，主要考察了旋转的性质，解直角三角形以及直角三角形的性质的综合运用，解题时注意：旋转变换中，对应点到旋转中心的间隔相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．29．如图，在矩形ABCD中，AB═2，AD=，P是BC边上的一点，且BP=2CP．〔1〕用尺规在图①中作出CD边上的中点E，连接AE、BE〔保存作图痕迹，不写作法〕；〔2〕如图②，在〔1〕的条体下，判断EB是否平分∠AEC，并说明理由；〔3〕如图③，在〔2〕的条件下，连接EP并廷长交AB的廷长线于点F，连接AP，不添加辅助线，△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形？假如能，说明理由，并写出两种方法〔指出对称轴、旋转中心、旋转方向和平移间隔〕【来源】2021年中考数学试卷【答案】〔1〕作图见解析；〔2〕EB是平分∠AEC，理由见解析；〔3〕△PFB能由都经过P 点的两次变换与△PAE组成一个等腰三角形，变换的方法为：将△BPF绕点B顺时针旋转120°和△EPA重合，①沿PF折叠，②沿AE折叠．【详解】〔1〕依题意作出图形如图①所示；〔2〕EB是平分∠AEC，理由：∵四边形ABCD是矩形，∴∠C=∠D=90°，CD=AB=2，BC=AD=，∵点E是CD的中点，∴DE=CE=CD=1，在△ADE和△BCE中，，∴△ADE≌△BCE，∴∠AED=∠BEC，在Rt△ADE中，AD=，DE=1，∴tan∠AED==，∴∠AED=60°，∴∠BCE=∠AED=60°，∴∠AEB=180°﹣∠AED﹣∠BEC=60°=∠BEC，∴BE平分∠AEC；在Rt△ABP中，tan∠BAP==，∴∠PAB=30°，∴∠EAP=30°=∠F=∠PAB，∵CB⊥AF，∴AP=FP，∴△AEP≌△FBP，∴△PFB能由都经过P点的两次变换与△PAE组成一个等腰三角形，变换的方法为：将△BPF绕点B顺时针旋转120°和△EPA重合，①沿PF折叠，②沿AE折叠．【点睛】此题考察了矩形的性质，全等三角形的断定和性质，解直角三角形，图形的变换等，纯熟掌握和灵敏应用相关的性质与定理、判断出△AEP≌△△FBP是解此题的关键．30．Rt△OAB，∠OAB=90°，∠ABO=30°，斜边OB=4，将Rt△OAB绕点O顺时针旋转60°，如题图1，连接BC．〔1〕填空：∠OBC= °；〔2〕如图1，连接AC，作OP⊥AC，垂足为P，求OP的长度；〔3〕如图2，点M，N同时从点O出发，在△OCB边上运动，M沿O→C→B途径匀速运动，N 沿O→B→C途径匀速运动，当两点相遇时运动停顿，点M的运动速度为单位/秒，点N的运动速度为1单位/秒，设运动时间是为x秒，△OMN的面积为y，求当x为何值时y获得最大值？最大值为多少？【来源】2021年中考数学试题【答案】〔1〕60；〔2〕；〔3〕.【详解】〔1〕由旋转性质可知：OB=OC，∠BOC=60°，∴△OBC是等边三角形，∴∠OBC=60°，故答案为：60；〔3〕①当0＜x≤时，M在OC上运动，N在OB上运动，此时过点N作NE⊥OC且交OC于点E，如图，那么NE=ON•sin60°=x，∴S△OMN=•OM•NE=×1.5x×x，∴y=x2，∴x=时，y有最大值，最大值=；②当＜x≤4时，M在BC上运动，N在OB上运动，③当时，M、N都在BC上运动，作OG⊥BC于G，如图，MN=12﹣2.5x，OG=AB=2，∴y=•MN•OG=12﹣x，当x=4时，y有最大值，最大值=2，综上所述，y有最大值，最大值为．【点睛】此题考察了旋转变换综合题，涉及到二次函数的最值，30度的直角三角形的性质、等边三角形的断定和性质、三角形的面积等知识，仔细分析，正确添加辅助线，分类讨论的思想考虑问题是解题的关键.励志赠言经典语录精选句；挥动**，放飞梦想。

2021年九年级数学中考一轮复习知识点基础达标测评：平移旋转轴对称(附答案)

2021年九年级数学中考一轮复习知识点基础达标测评：平移旋转轴对称（附答案）1．如图，弹性小球从点P（0，1）出发，沿所示方向运动，每当小球碰到正方形OABC的边时反弹，反弹时反射角等于入射角，当小球第1次碰到正方形的边时的点为P1（﹣2，0），第2次碰到正方形的边时的点为P2，…，第n次碰到正方形的边时的点为P n，则点P2020的坐标是（）A．（0，1）B．（﹣2，4）C．（﹣2，0）D．（0，3）2．在△ABC中，AB＝AC，点D在边AC上，连接BD，点E在边AB上，△BCD和△BED 关于BD对称，若△ADE是等腰三角形，则∠BAC＝（）A．36°B．72°C．90°D．108°3．下列说法正确的是（）A．若两个三角形全等，则它们必关于某条直线成轴对称B．直角三角形是关于斜边上的中线成轴对称C．如果两个三角形关于某条直线成轴对称的图形，那么它们是全等三角形D．线段是关于经过该线段中点的直线成轴对称的图形4．室内墙壁上挂一平面镜，小明在平面镜内看到他背后墙上时钟的示数如图所示，则这时的实际时间应是（）A．3：20B．3：40C．4：40D．8：205．下列现象中是平移的是（）A．翻开书中的每一页纸张B．飞碟的快速转动C．将一张纸沿它的中线折叠D．电梯的上下移动6．如图，将三角形ABE向右平移1cm得到三角形DCF，如果三角形ABE的周长是10cm，那么四边形ABFD的周长是（）A．12cm B．16cm C．18cm D．20cm7．如图，已知在△AOB中A（0，4），B（﹣2，0），点M从点（4，1）出发向左平移，当点M平移到AB边上时，平移距离为（）A．4.5B．5C．5.5D．5.758．如图，表示直线a平移得到直线b的两种画法，下列关于三角板平移的方向和移动的距离说法正确的是（）A．方向相同，距离相同B．方向不同，距离不同C．方向相同，距离不同D．方向不同，距离相同9．在俄罗斯方块游戏中，已拼好的图案如图所示，现出现一小方格体正向下运动，你必须进行以下（）操作，才能拼成一个完整图案，使所有图案消失．A．顺时针旋转90°，向右平移B．逆时针旋转90°，向右平移C．顺时针旋转90°，向下平移D．逆时针旋转90°，向下平移10．如图，在△ABC中，AB＝3，AC＝2，∠BAC＝30°，将△ABC绕点A逆时针旋转60°得到△AB1C1，连接BC1，则BC1的长为（）A．B．C．4D．611．如图，是一个纸折的小风车模型，将它绕着旋转中心旋转下列哪个度数后不能与原图形重合（）A．90°B．135°C．180°D．270°12．如图，点O为矩形ABCD的对称中心，AD＞AB，点E从点B出发（不含点B）沿BC 向点C运动，移动到点C停止，延长EO交AD于点F，则四边形BEDF形状的变化依次为（）A．平行四边形→菱形→正方形→矩形B．平行四边形→正方形→菱形→矩形C．平行四边形→菱形→平行四边形→矩形D．平行四边形→正方形→平行四边形一矩形13．如图，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时反射角等于入射角，当小球第1次碰到矩形的边时的点为P1，第2次碰到矩形的边时的点为P2，…，第n次碰到矩形的边时的点为P n，点P2019的坐标是．14．如图，点P是∠AOB外一点，点M、N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在线段MN的延长线上．若PM ＝2.5cm，PN＝3cm，MN＝4cm，则线段QR的长为．15．如果一个三角形是轴对称图形，且有一个角为60°，那么这个三角形是，它有条对称轴．16．小明从镜子里看到对面电子钟的像如图所示，那么实际时间是．17．如图所示，在长为50m，宽为25m的草坪上修了一条恒为1m宽的弯曲小路，则余下草坪的面积为m2．18．如图，三角形ABC中，AB＝2cm，BC＝4cm，将三角形ABC沿BC方向平移2cm得到三角形A'B'C'，A'B'与AC交于点D，A'D＝1cm，则图中四边形DCC′A′的面积为．19．将点P（﹣3，1）向上平移2个单位长度得到点Q，则点Q的坐标为．20．时钟的时针在不停地转动，从上午6时到上午9时，时针旋转的旋转角为度，从上午9时到下午5时时针旋转的旋转角为度．21．如图，△ABC绕点A逆时针旋转30°后到△A′B′C′的位置，若∠B′＝45°，∠C′＝60°，则∠B′AC＝．22．如图，在正方形ABCD中，点M是边CD的中点，那么正方形ABCD绕点M至少旋转度与它本身重合．23．如图，长方形台球桌ABCD上有两个球P，Q．（1）请画出一条路径，使得球P撞击台球桌边AB反弹后，正好撞到球Q；（2）请画出一条路径，使得球P撞击台球桌边，经过两次反弹后，正好撞到球Q；24．在等边△ABC中，点D在BC边上，点E在AC的延长线上，DE＝DA（如图1）．（1）求证：∠BAD＝∠EDC；（2）若点E关于直线BC的对称点为M（如图2），连接DM，AM．求证：DA＝AM．25．已知点A（a﹣5，1﹣2a），解答下列问题：（1）若点A到x轴和y轴的距离相等，求点A的坐标；（2）若点A向右平移若干个单位后，与点B（﹣2，﹣3）关于x轴对称，求点A的坐标．26．如图，若将△ABC顶点横坐标增加4个单位，纵坐标不变，三角形将如何变化？若将△ABC顶点横坐标都乘以﹣1，纵坐标不变，三角形将如何变化？27．如图所示，一块长为18m，宽为12m的草地上有一条宽为2m的曲折的小路，求这块草地的绿地面积．28．小明同学在完成七年级下册数学第1章的线上学习后，遇到了一些问题，请你帮他解决一下．（1）如图1，已知AB∥CD，则∠AEC＝∠BAE+∠DCE成立吗？请说明理由．（2）如图2，已知AB∥CD，BE平分∠ABC，DE平分∠ADC．BE、DE所在直线交于点E，若∠F AD＝50°，∠ABC＝40°，求∠BED的度数．（3）将图2中的线段BC沿DC所在的直线平移，使得点B在点A的右侧，若∠F AD＝m°，∠ABC＝n°，其他条件不变，得到图3，请你求出∠BED的度数（用含m，n的式子表示）．29．已知：如图，把△ABC向上平移3个单位长度，再向右平移2个单位长度，得到△A′B′C′．（1）写出A′、B′，C′的坐标；（2）点P在y轴上，且△BCP与△ABC的面积相等，求点P的坐标．30．如图，点E是正方形ABCD的边BC上一点，连接AE，将线段AE绕点E顺时针旋转一定的角度得到EF，点C在EF上，连接AF交边CD于点G．（1）若AB＝4，BF＝8，求CE的长；（2）求证：AE＝BE+DG．31．如图，D是△ABC边BC的中点，连接AD并延长到点E，使DE＝AD，连接BE．（1）图中哪两个图形成中心对称？（2）若△ADC的面积为4，求△ABE的面积．参考答案1．解：如图，根据反射角等于入射角画图，可知光线从P2反射后到P3（0，3），再反射到P4（﹣2，4），再反射到P5（﹣4，3），再反射到P点（0，1）之后，再循环反射，每6次一循环，2020÷6＝336……4，即点P2020的坐标是（﹣2，4），故选：B．2．解：如图，设∠A＝x．∵EA＝ED，∴∠A＝∠ADE＝x，∵∠BED＝∠A+∠ADE＝2x，△BDE与△BDC关于BD对称，∴∠BED＝∠C＝2x，∵AB＝AC，∴∠ABC＝∠C＝2x，∵∠A+∠ABC+∠C＝180°，∴5x＝180°，∴x＝36°，∴∠A＝36°，故选：A．3．解：A、若两个三角形全等，则它们必关于某条直线成轴对称，错误．本选项不符合题意．B、直角三角形是关于斜边上的中线成轴对称，错误，本选项不符合题意．C、如果两个三角形关于某条直线成轴对称的图形，那么它们是全等三角形，正确，本选项符合题意．D、线段是关于经过该线段中点的直线成轴对称的图形，错误，本选项不符合题意．故选：C．4．解：根据镜面对称的性质，分析可得题中所显示的时刻与3：40成轴对称，所以此时实际时刻为3：40．故选：B．5．解：A不是沿某一直线方向移动，不属于平移．B不是沿某一直线方向移动，不属于平移．C新图形与原图形的形状和大小不同，不属于平移．因此C错误．故选：D．6．解：∵△ABE的周长＝AB+BE+AE＝10（cm），由平移的性质可知，BC＝AD＝EF＝1（cm），AE＝DF，∴四边形ABFD的周长＝AB+BE+EF+DF+AD＝10+1+1＝12（cm）．7．解：设直线AB解析式为y＝kx+b，将点A（0，4），B（﹣2，0）代入，得：，所以直线AB解析式为y＝2x+4，当y＝1时，2x+4＝1，解得：x＝﹣1.5，则当点M平移到AB边上时，平移距离为4﹣（﹣1.5）＝5.5，故选：C．8．解：由图和平移可得：三角板平移的方向不同，距离不同，故选：B．9．解：顺时针旋转90°，向右平移．故选：A．10．解：∵将△ABC绕点A逆时针旋转60°得到△AB1C1，∴AC＝AC1＝2，∠CAC1＝60°，∵AB＝3，AC＝2，∠BAC＝30°，∴∠BAC1＝90°，∴在Rt△BAC1中，BC1＝＝．故选：B．11．解：图案可以被平分成四部分，因而每部分被分成的圆心角是90°，并且圆具有旋转不变性，因而旋转90度的整数倍，就可以与自身重合，12．解：连接BD．∵点O为矩形ABCD的对称中心，∴BD经过点O，OD＝OB，∵AD∥BC，∴∠FDO＝∠EBO，在△DFO和△BEO中，，∴△DFO≌△BEO（ASA），∴DF＝BE，∵DF∥BE，∴四边形BEDF是平行四边形，观察图形可知，四边形AECF形状的变化依次为平行四边形→菱形→平行四边形→矩形．故选：C．13．解：如图，根据反射角与入射角的定义作出图形，根据图形可以得到：每6次反弹为一个循环组依次循环，经过6次反弹后动点回到出发点（0，3），∵2019÷6＝336…3，当点P第2019次碰到矩形的边时为第337个循环组的第3次反弹，点P的坐标为（8，3），故答案为：（8，3）．14．解：由轴对称的性质可知：PM＝MQ＝2.5cm，PN＝RN＝3cm，QN＝MN﹣QM＝4﹣2.5＝1.5cm，QR＝QN+NR＝1.5+3＝4.5cm．故答案为：4.5cm．15．解：∵该三角形是轴对称图形，∴该三角形是等腰三角形，又∵该三角形有一个角为60°，∴这个三角形是等边三角形，∴这个三角形有3条对称轴．故答案为：等边三角形，3．16．解：根据镜面对称的性质，题中所显示的时刻与21：05成轴对称，所以此时实际时刻为21：05．故答案为：21：0517．解：∵把宽度为1m的弯曲小路分割成若干个四边形，这些四边形等于一个宽度为1m 的矩形，如图矩形ABCD，∴小路为宽恒为1m的弯曲小路，∴面积为50×1＝50（m2），∴余下草坪的面积为50×25﹣50＝1200（m2），故答案为：1200．18．解：根据平移的性质知，AB＝A′B′，△ABC≌△A′B′C′，则S△ABC＝S△A′B′C′．∵将三角形ABC沿BC方向平移2cm得到三角形A'B'C'，∴BB′＝2cm．∵AB＝2cm，BC＝4cm，A'D＝1cm，∴B′C＝2cm，DB′＝1cm．∴S四边形DCC′A′＝S△ABC﹣S△B′CD＝﹣＝3（cm2）．故答案是：3cm2．19．解：将点P（﹣3，1）向上平移2个单位长度得到点Q，则点Q的坐标为（﹣3，1+2），即（﹣3，3），故答案为：（﹣3，3）．20．解：从上午6时到上午9时时针转过3个大格，所以，3×30°＝90°，上午9时到下午5时时针转过8个大格，所以，8×30°＝240°．故答案为：90；240．21．解：∵∠B′＝45°，∠C′＝60°，∴∠BAC＝∠B′A′C′＝180°﹣45°﹣60°＝75°，∵∠BAB′＝30°，∴∠B′AC＝75°﹣30°＝45°，故答案为：45°．22．解：在正方形ABCD中，点M是边CD的中点，∴正方形ABCD绕点M至少旋转360°与它本身重合．故答案为：360．23．解：（1）如图，运动路径：P→M→Q，点M即为所求．（2）如图，运动路径：P→E→F→Q，点E，点F即为所求．24．解：（1）如图1，∵△ABC是等边三角形，∴∠BAC＝∠ACB＝60°，∴∠BAD＝60°﹣∠DAE，∠EDC＝60°﹣∠E，又∵DE＝DA，∴∠E＝∠DAE，∴∠BAD＝∠EDC．（2）由轴对称可得，DM＝DE，∠EDC＝∠MDC，∵DE＝DA，∴DM＝DA，由（1）可得，∠BAD＝∠EDC，∴∠MDC＝∠BAD，∵△ABD中，∠BAD+∠ADB＝180°﹣∠B＝120°，∴∠MDC+∠ADB＝120°，∴∠ADM＝60°，∴△ADM是等边三角形，∴AD＝AM．25．解：（1）若点A在第一象限或第三象限，则a﹣5＝1﹣2a，解得：a＝2，则a﹣5＝1﹣2a＝﹣3，∴点A的坐标为（﹣3，﹣3），若点A在第二象限或第四象限，则a﹣5+1﹣2a＝0，解得a＝﹣4，则a﹣5＝﹣9，1﹣2a＝9，∴点A的坐标为（﹣9，9），综上所述，点A的坐标为（﹣3，﹣3）或（﹣9，9）；（2）∵若点A向右平移若干个单位，其纵坐标不变为（1﹣2a），又∵点A向右平移若干个单位后与点B（﹣2，﹣3）关于x轴对称，∴1﹣2a+（﹣3）＝0，a＝﹣1a﹣5＝﹣1﹣5＝﹣6，1﹣2a＝1﹣2×（﹣1）＝3，即点A的坐标为（﹣6，3）．26．解：横坐标增加4个单位，纵坐标不变，所得各顶点的坐标依次是A（1，3），B（1，1），C（3，1），连接AB、AC、BC，整个三角形向右平移4个单位；横坐标都乘以﹣1，纵坐标不变，所得各顶点的坐标依次是A（3，3），B（3，1），C（1，1），连接AB、AC、BC，所得到的三角形与原三角形关于y轴对称．27．解：绿地的面积为：（18﹣2）×（12﹣2）＝160（m2），答：这块草地的绿地面积是160m2．28．解：（1）如图1中，作EF∥AB，则有EF∥CD，∴∠1＝∠BAE，∠2＝∠DCE，∴∠AEC＝∠1+∠2＝∠BAE+∠DCE．（2）如图2，过点E作EH∥AB，∵AB∥CD，∠F AD＝50°，∴∠F AD＝∠ADC＝50°，∵DE平分∠ADC，∠ADC＝50°，．∴∠EDC＝∠ADC＝25°，∵BE平分∠ABC，∠ABC＝40°，∴∠ABE＝∠ABC＝20°，∵AB∥CD，∴AB∥CD∥EH，∴∠ABE＝∠BEH＝20°，∠CDE＝∠DEH＝25°，∴∠BED＝∠BEH+∠DEH＝45°．（3）∠BED的度数改变．过点E作EG∥AB，∵BE平分∠ABC，DE平分∠ADC，∠ABC＝n°，∠ADC＝∠F AD＝m°∴∠ABE＝∠ABC＝n°，∠CDE＝∠ADC＝m°∵AB∥CD，∴AB∥CD∥EG，∴∠BEG＝180°﹣∠ABE＝180°﹣n°，∠CDE＝∠DEG＝m°，∴∠BED＝∠BEG+∠DEG＝180°﹣n°+m°．29．解：（1）如图，△A′B′C′即为所求，A′（0，4），B′（﹣1，1），C′（3，1）．（2）设P（0，m），由题意：×4×|m+2|＝×4×3，解得m＝1或﹣5，∴P（0，1）或（0，﹣5）．30．（1）解：设AE＝EF＝x，∵四边形ABCD是正方形，∴∠ABE＝90°，AB＝BC＝4，∵BF＝8，∴CF＝8﹣4＝4，∵BE＝BF﹣EF＝8﹣x，AB＝4，AE＝x，∴x2＝42+（8﹣x）2，∴x＝5，∴EC＝EF﹣CF＝1．（2）证明：延长EB到H，使得BH＝DG，则△ADG≌△ABH（SAS），∴∠BAH＝∠DAG，∴∠HAF＝∠BAD＝90°，∵EF＝AE，∴∠EAF＝∠F，∵∠EAH+∠EAF＝90°，∠F+∠H＝90°，∴∠H＝∠EAH，∴EA＝EH，∵EH＝BE+BH＝BE+DG，∴AE＝BE+DG．31．解：（1）图中△ADC和三角形EDB成中心对称；（2）∵△ADC和三角形EDB成中心对称，△ADC的面积为4，∴△EDB的面积也为4，∵D为BC的中点，∴△ABD的面积也为4，所以△ABE的面积为8。

2021年中考数学一轮专题汇编：平移与旋转(含答案)

2021中考数学一轮专题汇编：平移与旋转一、选择题1 .如图，匚A3C 沿着点B 到点上的方向，平移到匚QEF,如果BC=5, EC=3,那么平移的距离为A.2C.5 2 .如图，在平面直角坐标系xQy 中，将四边形月38先向下平移，再向右平移, 5), 3(-4, 3), 41(3, 3),则 Bi 的坐标为A(l, 2)C.(l, 4)3 .如图，在 Rs ABC 中，ZABC=9009 AB=2, 8c= 1 ,把△ ABC 分别绕直线 A3 和8c 旋转一周，所得几何体的底面圆的周长分别记作八，/2,侧面积分别记作 5i ，S2，贝ij()h=\ ： 2, Si 12=1 ： 4, 51 h=l ： 2, S\ l 2=l : 4,Si4 .如图，四边形」38是边长为5的正方形，E 是。

上一点，DE=L 将匚立加绕着得到四边形/由iQQi ，已知以(-3, B.(2, 1) 0.(4, 1)A. l\ C. 52=1 ：252=1 ： 252=1 ： D.7点d顺时针旋转到与匚43厂重合，则EF=()B.AB±EBD. /A=/EBC Z 如图，在正方形.48中，边长43=1,将正方形48cZ ）绕点d 逆时针方向旋A 回C5也 B.闻 D.2V135 .如图，在平面直角坐标系中，边长为2的正方形的边在x 轴上，边的中点是坐标原点。

，将正方形绕点C 按逆时针方向旋转90。

后，点B 的对应点戌的坐标是（） >T A(-l, 2)B.(l, 4)C.(3, 2) 0)6 .如图，将二"。

绕点C 顺时针旋转得到匚QEG 使点4的对应点。

恰好落在边AS 上，点8的对应点为石，连接3石，下列结论一定正确的是（）人 AC = AD C.BC=DE转180。

至正方形481。

1», 则线段CQ 扫过的面积为nB ， D.2兀A D8.如图，将△48C绕点8逆时针旋转G,得到△EBO,若点A恰好在石。

2021年全国中考数学真题分类汇编：旋转专项复习含答案.docx

2021年全国中考数学真题分类汇编-一旋转一、选择题1. （2021,辽宁省营口）中国剪纸是一种用刀或刻刀在纸上剪刻花纹，用于装点生活或配合其他民俗活动的民间艺术。

下列四个剪纸图案中，是中心对称图形的是（）2. （2021,湖南省益阳市）以下有关勾股定理证明的图形中，不是中心对称图形的是（）3. （201.湖南长沙）下列几何图形中，是中心对称图形的是（）4. （2021,湖北恩施）下列图形中，既是轴对称图形又是中心对称图形的是（）5. （2021.辽宁省辽阳市）下列漂亮的图案中似乎包含了一些曲线，其实它们这种神韵是由多条线段呈现出来的，这些图案中既是中心对称图形又是轴对称图形的是（）6. （2021,黑龙江龙东地区）下列图形中，既是中心对称图形又是轴对称图形的是（）得到△ A'B'C'，点B 对应点B'在边AC 上（不与点A,C 重合），则ZAA'B'的度数为（） A. a B. a-45° C. 45°-a D. 90°-a310. （2021.湖南省邵阳市）如图，SAAOB 中，AO=1, BO=AB=-,将Z^AOB 绕点0逆时针 2方向旋转90°,得到△ A'OB',连接AA',则线段AA'的长为（）A.l Bo ^2 C. - D.-V2 2 211. （2021.湖北黄石）如图，ZkABC 的三个顶点都在方格纸的格点上，其中A 点的坐标是（-1, 0）.现将^ABC 绕点A 按逆时针方向旋转90。

，则旋转后点C 的坐标是（B ）A. （2, -3）B. （-2, 3）C. （-2, 2）D. （-3, 2）C.米7. （2021.齐齐哈尔市）下面四个图形中, 8. （2021,黑龙江省哈尔滨市）下列图形中既是轴对称图形又是中心对称图形的是（）9. （2021,大连）如图，在ZXABC 中，ZACB=90°, /BAC=a,将z^ABC 绕点C 顺时针旋转90°二、填空题12. （2021.吉林省）如图，在平面直角坐标系中，点A的坐标为（0, 3）,点B的坐标为（4, 0）,连接AB,若将绕点B顺时针旋转90。

2021年人教版数学中考一轮复习：平移与旋转专项练习题(含答案)

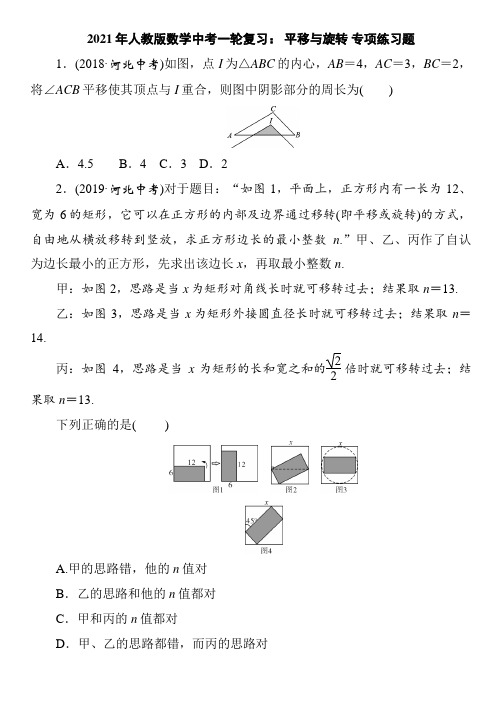
2021年人教版数学中考一轮复习：平移与旋转专项练习题1．(2018·河北中考)如图，点I为△ABC的内心，AB＝4，AC＝3，BC＝2，将∠ACB平移使其顶点与I重合，则图中阴影部分的周长为()A．4.5 B．4 C．3 D．22．(2019·河北中考)对于题目：“如图1，平面上，正方形内有一长为12、宽为6的矩形，它可以在正方形的内部及边界通过移转(即平移或旋转)的方式，自由地从横放移转到竖放，求正方形边长的最小整数n.”甲、乙、丙作了自认为边长最小的正方形，先求出该边长x，再取最小整数n.甲：如图2，思路是当x为矩形对角线长时就可移转过去；结果取n＝13.乙：如图3，思路是当x为矩形外接圆直径长时就可移转过去；结果取n＝14.丙：如图4，思路是当x为矩形的长和宽之和的22倍时就可移转过去；结果取n＝13.下列正确的是()A.甲的思路错，他的n值对B．乙的思路和他的n值都对C．甲和丙的n值都对D．甲、乙的思路都错，而丙的思路对3.如图，△ABC中，AC＝3 cm，将△ABC沿AC方向向右平移1 cm得到△DEF，则AF＝cm.第3题第4题4.如图，在△ABC中，AB＝4，BC＝6，∠B＝60°，将△ABC沿射线BC 方向平移2个单位后得到△DEF，连接DC，则DC的长为4．5.如图，在△AOB中，∠B＝30°.将△AOB绕点O顺时针旋转52°得到△A′OB′，边A′B′与边OB交于点C(A′不在OB上)，则∠A′CO等于() A．22° B．52° C．60° D．82°第5题第6题6.如图，将△ABC绕点A逆时针旋转90°得到△ADE，点C和点E是对应点，若AB＝1，则BD＝．7.如图，点A(－4，0)，B(－1，0)，将线段AB平移后得到线段CD，点A 的对应点C恰好落在y轴上，且四边形ABDC的面积为9，则点D的坐标为．8.如图，已知△ABC的面积为3，且AB＝AC，现将△ABC沿CA方向平移CA长度得到△EF A.(1)求四边形CEFB的面积；(2)试判断AF与BE的位置关系，并说明理由；(3)若∠BEC＝15°，求AC的长．9.．如图，在平面直角坐标系xOy中，将四边形ABCD先向下平移，再向右平移得到四边形A1B1C1D1，已知A(－3，5)，B(－4，3)，A1(3，3)，则点B1的坐标为()A．(1，2) B．(2，1) C．(1，4) D．(4，1)第9题第10题10．(2020·遵化市一模)如图，将△ABC沿BC边上的中线AD平移到△A′B′C′的位置，已知△ABC的面积为9，阴影部分三角形的面积为4.若AA′＝1，则A′D等于()A．2 B．3 C．23 D．3211．如图，在△ABC中，∠BAC＝90°，AB＝3，AC＝4，将△ABC沿直线。

2020-2021初中数学图形的平移,对称与旋转的全集汇编附答案

2020-2021初中数学图形的平移，对称与旋转的全集汇编附答案一、选择题1．如图，△ABC中，∠BAC＝45°，∠ACB＝30°，将△ABC绕点A顺时针旋转得到△AB1C1，当点C1、B1、C三点共线时，旋转角为α，连接BB1，交AC于点D．下列结论：①△AC1C 为等腰三角形；②△AB1D∽△BCD；③α＝75°；④CA＝CB1，其中正确的是（）A．①③④B．①②④C．②③④D．①②③④【答案】B【解析】【分析】将△ABC绕点A顺时针旋转得到△AB1C1，得到△ABC≌△AB1C1，根据全等三角形的性质得到AC1=AC，于是得到△AC1C为等腰三角形；故①正确；根据等腰三角形的性质得到∠C1=∠ACC1=30°，由三角形的内角和得到∠C1AC=120°，得到∠B1AB=120°，根据等腰三角形的性质得到∠AB1B=30°=∠ACB，于是得到△AB1D∽△BCD；故②正确；由旋转角α=120°，故③错误；根据旋转的性质得到∠C1AB1=∠BAC=45°，推出∠B1AC=∠AB1C，于是得到CA=CB1；故④正确．【详解】解：∵将△ABC绕点A顺时针旋转得到△AB1C1，∴△ABC≌△AB1C1，∴AC1＝AC，∴△AC1C为等腰三角形；故①正确；∴AC1＝AC，∴∠C1＝∠ACC1＝30°，∴∠C1AC＝120°，∴∠B1AB＝120°，∵AB1＝AB，∴∠AB1B＝30°＝∠ACB，∵∠ADB1＝∠BDC，∴△AB1D∽△BCD；故②正确；∵旋转角为α，∴α＝120°，故③错误；∵∠C1AB1＝∠BAC＝45°，∴∠B1AC＝75°，∵∠AB1C1＝∠BAC＝105°，∴∠AB1C＝75°，∴∠B 1AC ＝∠AB 1C ，∴CA ＝CB 1；故④正确．故选：B ．【点睛】本题考查了相似三角形的判定和性质，等腰三角形的判定和性质，旋转的性质，正确的识别图形是解题的关键．2．如图，ABC ∆是O e 的内接三角形，45A ∠=︒，1BC =，把ABC ∆绕圆心O 按逆时针方向旋转90︒得到DEB ∆，点A 的对应点为点D ，则点A ，D 之间的距离是（）A ．1B ．2C ．3D ．2【答案】A【解析】【分析】连接AD ，构造△ADB ，由同弧所对应的圆周角相等和旋转的性质，证△ADB 和△DBE 全等，从而得到AD=BE=BC=1.【详解】如图，连接AD ，AO ，DO∵ABC ∆绕圆心O 按逆时针方向旋转90︒得到DEB ∆，∴AB=DE ，90AOD ∠=︒，45CAB BDE ∠=∠=︒∴1452ABD AOD ∠=∠=︒（同弧所对应的圆周角等于圆心角的一半），即45ABD EDB ∠=∠=︒，又∵DB=BD ，∴DAB BED ∠=∠（同弧所对应的圆周角相等），在△ADB 和△DBE 中ABD EDB AB EDDAB BED ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADB ≌△EBD （ASA ）,∴AD=EB=BC=1.故答案为A.【点睛】本题主要考查圆周角、圆中的计算问题以及勾股定理的运用；顶点在圆上，两边都与圆相交的角角圆周角；掌握三角形全等的判定是解题的关键.3．如图，P 是等边三角形ABC 内一点，将线段AP 绕点A 顺时针旋转60︒得到线段AQ ，连接BQ ．若6PA =，8PB =，10PC =，则四边形APBQ 的面积为（）A ．2493+B ．483+C ．243+D ．48183+【答案】A【解析】【分析】连结PQ ，先根据等边三角形的性质和旋转的性质证明△APQ 为等边三角形，则P Q=AP=6，再证明△APC ≌△AQB,可得PC=QB=10，然后利用勾股定理的逆定理证明△PBQ 为直角三角形，再根据三角形面积公式求出面积，最后利用S 四边形APBQ =S △BPQ +S △APQ 即可解答．【详解】解：如图，连结PQ ，∵△ABC 为等边三角形，∴∠BAC=60°，AB=AC ，∵线段AP 绕点A 顺时针旋转60°得到线段AQ ，∴AP=PQ=6，∠PAQ=60°，∴△APQ 为等边三角形，∴PQ=AP=6，∵∠CAP+∠BAP=60°，∠BAP+∠BAQ=60°，∴∠CAP=∠BAQ ，∵在△APC 和△ABQ 中，AC=AB ，∠CAP=∠BAQ ，AP=AQ∴△APC ≌△AQB ，∴PC=QB=10，在△BPQ中， PB2=82=64，PQ2=62=36，BQ2=102=100，∴PB2+PQ2=BQ2，∴△PBQ为直角三角形，∴∠BPQ=90°，∴S四边形APBQ=S△BPQ+S△APQ=12×6×8+34×62=24+93故答案为A．.【点睛】本题考查了旋转的性质和勾股定理的逆定理，掌握旋转的定义、旋转角以及旋转前、后的图形全等是解答本题的关键．4．在平面直角坐标系中，一个图案上各个点的横坐标和纵坐标分别加正数(1)a a＞，那么所得的图案与原来图案相比()A．形状不变，大小扩大到原来的a倍B．图案向右平移了a个单位C．图案向上平移了a个单位D．图案向右平移了a个单位，并且向上平移了a个单位【答案】D【解析】【分析】直接利用平移中点的变化规律求解即可．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．【详解】在直角坐标系中，一个图案上各个点的横坐标和纵坐标分别加上正数a（a＞1），那么所得的图案与原图案相比，图案向右平移了a个单位长度，并且向上平移了a个单位长度．故选D．【点睛】本题考查了坐标系中点、图形的平移规律，在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．5．如图，在平面直角坐标系中，其中一个三角形是由另一个三角形绕某点旋转一定的角度得到的，则其旋转中心是（）A．（1，0）B．（0，0）C．（-1，2）D．（-1，1）【答案】C【解析】【分析】根据其中一个三角形是由另一个三角形绕着某点旋转一定的角度得到的，那么对应点到旋转中心的距离相等，找出这个点即可．【详解】解：如图所示，根据旋转的性质，对应点到旋转中心的距离相等，只有（-1，2）点到三角形的三顶点距离相等，故（-1，2）是图形的旋转中心，故选：C．【点睛】此题主要考查了旋转的性质，根据旋转中心到对应点的距离相等，是解决问题的关键．6．下列说法正确的是（）A．平移不改变图形的形状和大小，而旋转则改变图形的形状和大小B．在成中心对称的两个图形中，连结对称点的线段都被对称中心平分C．在平面直角坐标系中，一点向右平移2个单位，纵坐标加2D．在平移和旋转图形中，对应角相等，对应线段相等且平行【答案】B【解析】【分析】分别利用图形的平移以及中心对称图形的性质和旋转的性质分别判断得出即可．【详解】A、平移不改变图形的形状和大小，旋转也不改变图形的形状和大小，故此选项错误；B、在成中心对称的两个图形中，连结对称点的线段都被对称中心平分，此选项正确；C、在平面直角坐标系中，一点向右平移2个单位，横坐标加2，故此选项错误；D、在平移中，对应角相等，对应线段相等且平行，旋转则对应线段有可能不平行，故此选项错误．故选B．7．如图，在平面直角坐标系中，AOB ∆的顶点B 在第一象限，点A 在y 轴的正半轴上，2AO AB ==，120OAB ∠=o ，将AOB ∠绕点O 逆时针旋转90o ，点B 的对应点'B 的坐标是（）A ．3(2,3)--B ．33(2,2)---C ．3(3,2)--D ．(3,3)- 【答案】D【解析】【分析】过点'B 作x 轴的垂线，垂足为M ，通过条件求出'B M ，MO 的长即可得到'B 的坐标.【详解】解：过点'B 作x 轴的垂线，垂足为M ，∵2AO AB ==，120OAB ∠=︒，∴'''2A O A B ==，''120OA B ∠=︒，∴'0'6M B A ∠=︒，在直角△''A B M 中，3==2=B'M B'M 'sin B A M B '''A ∠ ， 1==22=A'M A'M 'cos B A M B '''A ∠， ∴'3B M ='1A M =，∴OM=2+1=3，∴'B 的坐标为(3)-.故选：D.【点睛】本题考查坐标与图形变化-旋转，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．8．在下列图案中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．【答案】A【解析】【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．【详解】A、既是轴对称图形，又是中心对称图形，故本选项正确；B、是轴对称图形，不是中心对称图形，故本选项错误；C、不是轴对称图形，是中心对称图形，故本选项错误；D、是轴对称图形，不是中心对称图形，故本选项错误．故选A．【点睛】本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．9．下列图形中，是轴对称图形但不是中心对称图形的是（）A．B．C．D．【答案】A【解析】A.是轴对称图形不是中心对称图形，正确；B.是轴对称图形也是中心对称图形，错误；C.是中心对称图形不是轴对称图形，错误；D. 是轴对称图形也是中心对称图形，错误，故选A.【点睛】本题考查轴对称图形与中心对称图形，正确地识别是解题的关键.10．下列图案中既是轴对称又是中心对称图形的是（）A．B．C．D．【答案】C【解析】【分析】根据轴对称图形与中心对称图形的概念判断即可．【详解】A、不是轴对称图形，是中心对称图形，故本选项错误；B、不是轴对称图形，也不是中心对称图形，故本选项错误；C、是轴对称图形，是中心对称图形，故本选项正确；D、是轴对称图形，不是中心对称图形，故本选项错误；故选C．【点睛】此题主要考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．11．下列图形中，不是轴对称图形的是（）A．有两个内角相等的三角形 B．有一个内角为45°的直角三角形C．有两个内角分别为50°和80°的三角形 D．有两个内角分别为55°和65°的三角形【答案】D【解析】A.有两个内角相等的三角形是等腰三角形，等腰三角形是轴对称图形；B.有一个内角为45度的直角三角形是等腰直角三角形，也是等腰三角形，是轴对称图形；C.有两个内角分别为50度和80度的三角形，第三个角是50度，故是等腰三角形，是轴对称图形；D.有两个内角分别为55度和65度的三角形,不是等腰三角形，不是轴对称图形.故选：D.12．如图所示的网格中各有不同的图案，不能通过平移得到的是（）A．B．C．D．【答案】C【解析】【分析】根据平移的定义：在平面内，把一个图形整体沿某一的方向移动，这种图形的平行移动，叫做平移变换，结合各选项所给的图形即可作出判断．【详解】A、可以通过平移得到，不符合题意；B、可以通过平移得到，不符合题意；C、不可以通过平移得到，符合题意；D、可以通过平移得到，不符合题意．故选C．【点睛】本题考查平移的性质，属于基础题，要掌握图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转．13．下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（）A ．B ．C ．D ．【答案】B【解析】由中心对称图形的定义：“把一个图形绕一个点旋转180°后，能够与自身完全重合，这样的图形叫做中心对称图形”分析可知，上述图形中，A 、C 、D 都不是中心对称图形，只有B 是中心对称图形.故选B.14．如图，一个长为2、宽为1的长方形以下面的“姿态”从直线l 的左侧水平平移至右侧（下图中的虚线是水平线），其中，平移的距离是（）A ．1B ．2C ．3D ．22【答案】C【解析】【分析】根据平移的性质即可解答.【详解】如图连接AA '，根据平行线的性质得到∠1=∠2，如图，平移的距离AA '=的长度123=+=故选C.【点睛】此题考查平移的性质，解题关键在于利用平移的性质求解.15．如图，已知点P(0，3) ，等腰直角△ABC中，∠BAC=90°，AB=AC，BC=2，BC边在x轴上滑动时，PA+PB的最小值是（）A．102+B．26C．5 D．26【答案】B【解析】【分析】过点P作PD∥x轴，做点A关于直线PD的对称点A´，延长A´ A交x轴于点E，则当A´、P、B三点共线时，PA+PB的值最小，根据勾股定理求出A B'的长即可.【详解】如图，过点P作PD∥x轴，做点A关于直线PD的对称点A´，延长A´ A交x轴于点E，则当A´、P、B三点共线时，PA+PB的值最小，∵等腰直角△ABC中，∠BAC=90°，AB=AC，BC=2，∴AE=BE=1，∵P(0，3) ，∴A A´=4， ∴A´E=5， ∴22221526A B BE A E ''=+=+=，故选B.【点睛】本题考查了勾股定理，轴对称-最短路线问题的应用，解此题的关键是作出点A 关于直线PD 的对称点，找出PA +PB 的值最小时三角形ABC 的位置．16．下列图形中，既是轴对称图形，又是中心对称图形的是（）A ．B ．C ．D ．【答案】C【解析】【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．【详解】A 、是轴对称图形，不是中心对称的图形，故本选项不符合题意；B 、不是轴对称图形，是中心对称的图形，故本选项不符合题意；C 、既是轴对称图形，又是中心对称的图形，故本选项符合题意；D 、是轴对称图形，不是中心对称的图形，故本选项不符合题意．故选：C ．【点睛】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合． 17．如图，在ABC ∆中，90,2,4C AC BC ∠=︒==，将ABC ∆绕点A 逆时针旋转90︒，使点C 落在点E 处，点B 落在点D 处，则B E 、两点间的距离为（）A 10B ．2C ．3D ．25【答案】B【解析】【分析】延长BE和CA交于点F，根据旋转的性质可知∠CAE=90︒，证明∠BAE=∠ABC，即可证得AE∥BC，得出2142EF AF AEFB FC BC====，即可求出BE．【详解】延长BE和CA交于点F∵ABC∆绕点A逆时针旋转90︒得到△AED ∴∠CAE=90︒∴∠CAB+∠BAE=90︒又∵∠CAB+∠ABC=90︒∴∠BAE=∠ABC∴AE∥BC∴2142 EF AF AEFB FC BC====∴AF=AC=2，FC=4∴BF=42∴BE=EF=12BF=22故选：B【点睛】本题考查了旋转的性质，平行线的判定和性质．18．如图，点E是正方形ABCD的边DC上一点，把ADE∆绕点A顺时针旋转90︒到ABF∆的位置．若四边形AECF的面积为20，DE=2，则AE的长为（）A．4 B．5C．6 D．26【答案】D【解析】【分析】利用旋转的性质得出四边形 AECF 的面积等于正方形 ABCD 的面积，进而可求出正方形的边长，再利用勾股定理得出答案．【详解】ADE ∆Q 绕点A 顺时针旋转90︒到ABF ∆的位置．∴四边形AECF 的面积等于正方形ABCD 的面积等于20， 25AD DC ∴==，2DE =Q ， Rt ADE ∴∆中，2226AE AD DE =+=故选：D ．【点睛】本题主要考查了旋转的性质以及正方形的性质，正确利用旋转的性质得出对应边关系是解题关键．19．已知互不平行的两条线段AB ，CD 关于直线l 对称，AB ，CD 所在直线交于点P ，下列结论中：①AB =CD ；②点P 在直线l 上； ③若A 、C 是对称点，则l 垂直平分线段AC ； ④若B 、D 是对称点，则PB =PD .其中正确的结论有( )A ．1个B ．2个C ．3个D ．4个【答案】D【解析】【分析】【详解】由轴对称的性质知，①②③④都正确.故选D.20．如图，将ABC V 绕点A 逆时针旋转90︒得到,ADE V 点,B C 的对应点分别为,,1,D E AB =则BD 的长为（）A ．1B 2C ．2D ．22【答案】B【解析】【分析】根据旋转的性质得到AD=AB=1，∠BAD=90°，即可根据勾股定理求出BD ．【详解】由旋转得到AD=AB=1，∠BAD=90°，∴，故选：B．【点睛】此题考查了旋转的性质，勾股定理，找到直角是解题的关键．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2021中考数学一轮专题汇编：平移与旋转一、选择题1. 如图，△ABC沿着点B到点E的方向，平移到△DEF，如果BC=5，EC=3，那么平移的距离为()A.2B.3C.5D.72. 如图，在平面直角坐标系xOy中，将四边形ABCD先向下平移，再向右平移，得到四边形A1B1C1D1，已知A(-3，5)，B(-4，3)，A1(3，3)，则B1的坐标为()A.(1，2)B.(2，1)C.(1，4)D.(4，1)3. 如图，在Rt△ABC中，∠ABC＝90°，AB＝2，BC＝1.把△ABC分别绕直线AB 和BC旋转一周，所得几何体的底面圆的周长分别记作l1，l2，侧面积分别记作S1，S2，则()A. l1∶l2＝1∶2，S1∶S2＝1∶2B. l1∶l2＝1∶4，S1∶S2＝1∶2C. l1∶l2＝1∶2，S1∶S2＝1∶4D. l1∶l2＝1∶4，S1∶S2＝1∶44. 如图，四边形ABCD是边长为5的正方形，E是DC上一点，DE=1，将△ADE 绕着点A顺时针旋转到与△ABF重合，则EF=()A.B.C.5D.25. 如图，在平面直角坐标系中，边长为2的正方形的边AB在x轴上，AB边的中点是坐标原点O，将正方形绕点C按逆时针方向旋转90°后，点B的对应点B'的坐标是()A.(-1，2)B.(1，4)C.(3，2)D.(-1，0)6. 如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB上，点B的对应点为E，连接BE，下列结论一定正确的是()A.AC=ADB.AB⊥EBC.BC=DED.∠A=∠EBC7. 如图，在正方形ABCD中，边长AB=1，将正方形ABCD绕点A逆时针方向旋转180°至正方形AB1C1D1，则线段CD扫过的面积为()A.B.C.πD.2π8. 如图，将△ABC绕点B逆时针旋转α，得到△EBD，若点A恰好在ED的延长线上，则∠CAD的度数为()A．90°－αB．αC．180°－αD．2α二、填空题9. 如图，在△ABC中，∠C=90°，AC=BC=，将△ABC绕点A按顺时针方向旋转60°到△AB'C'的位置，连接C'B，则C'B=.10. 一副三角板如图放置，将三角板ADE绕点A逆时针旋转α(0°<α<90°)，使得三角板ADE的一边所在的直线与BC垂直，则α的度数为.11. 如图，在矩形ABCD中，AD=3，将矩形ABCD绕点A逆时针旋转，得到矩形AEFG，点B的对应点E落在CD上，且DE=EF，则AB的长为.12. 把二次函数y＝(x－1)2＋2的图象绕原点旋转180°后得到的图象的解析式为_______．13. 在如图所示的方格纸(1格长为1个单位长度)中，△ABC的顶点都在格点上，将△ABC绕点O按顺时针方向旋转得到△A′B′C′，使各顶点仍在格点上，则其旋转角的度数是________．14. 如图，正方形ABCD和正方形CEFG的边长分别为a和b，正方形CEFG绕点C旋转，给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2.其中正确结论是(填序号).15. 如图，两块完全相同的含30°角的三角尺ABC和A′B′C′重合在一起，将三角尺A′B′C′绕其顶点C′逆时针旋转角α(0°<α≤90°)，有以下三个结论：①当α＝30°时，A′C与AB的交点恰好为AB的中点；②当α＝60°时，A′B′恰好经过点B；③在旋转过程中，始终存在AA′⊥BB′.其中正确结论的序号是__________．16. 如图，AB⊥y轴，将△ABO绕点A逆时针旋转到△AB1O1的位置，使点B的对应点B1落在直线y＝－33x上，再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置，使点O1的对应点O2落在直线y＝－33x上，依次进行下去……若点B的坐标是(0，1)，则点O12的纵坐标为________．三、解答题17. 如图，将一个钝角三角形ABC(其中∠ABC＝120°)绕点B顺时针旋转得到△A1BC1，使得点C落在AB的延长线上的点C1处，连接AA1.(1)写出旋转角的度数；(2)求证：∠A1AC＝∠C1.18. 如图，在△ABC中，∠BAC＝90°，AB＝AC，D，E是BC边上的点，将△ABD 绕点A逆时针旋转得到△ACD′.(1)求∠DAD′的度数；(2)当∠DAE＝45°时，求证：DE＝D′E.19. 如图，在等腰直角三角形ABC中，∠ACB＝90°，点D，E在边AB上，且∠DCE＝45°，BE＝2，AD＝3.将△BCE绕点C逆时针旋转90°，画出旋转后的图形，并求DE的长．20. △ABC和△DEF是两个全等的等腰直角三角形，∠BAC＝∠EDF＝90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q.(1)如图①，当点Q在线段AC上，且AP＝AQ时，求证：△BPE≌△CQE；(2)如图②，当点Q在线段CA的延长线上时，①求证：△BPE∽△CEQ；②当BP＝2，CQ＝9时，求BC的长．21. 已知：如图，在四边形ABCD中，∠ADC＝60°，∠ABC＝30°，AD＝CD. 求证：BD2＝AB2＋BC2.22. 将矩形ABCD绕点A顺时针旋转α(0°＜α＜360°)，得到矩形AEFG.(1)如图①，当点E在BD上时，求证：FD＝CD；(2)当α为何值时，GC＝GB？画出图形，并说明理由．2021中考数学一轮专题汇编：平移与旋转-答案一、选择题1. 【答案】A[解析]观察图形，发现平移前后B，E为对应点，C，F为对应点.根据平移的性质，易得平移的距离=BE=5-3=2.2. 【答案】B[解析]由A(-3，5)，A1(3，3)可知四边形ABCD先向下平移2个单位，再向右平移6个单位得到四边形A1B1C1D1，∵B(-4，3)，∴B1的坐标为(2，1).3. 【答案】A【解析】∵∠ABC＝90°，AB＝2，BC＝1，∴勾股定理得，AC＝ 5.①当△ABC绕AB旋转时，则底面周长l1＝2π×BC＝2π，侧面积为S1＝π×BC×AC ＝5π；②当△ABC绕BC旋转时，则底面周长l2＝2π×AB＝4π，侧面积为S2＝π×AB×AC＝25π，∴l1∶l2＝2π∶4π＝1∶2，S1∶S2＝5π∶25π＝1∶2.4. 【答案】D[解析]由旋转的性质可知，△ADE≌△ABF，∴BF=DE=1，∴FC=6，∵CE=4，∴EF===2.故选:D.5. 【答案】C[解析]如图，由旋转得:CB'=CB=2，∠BCB'=90°，D，C，B'三点共线.∵四边形ABCD是正方形，且O是AB的中点，∴OB=1，∴B'(2+1，2)，即B'(3，2)，故选C.6. 【答案】D[解析]由旋转的性质可知，AC=CD，但∠A不一定是60°，所以不能证明AC=AD，所以选项A错误;由于旋转角度不确定，所以选项B不能确定;因为AB=DE，不确定AB和BC的数量关系，所以BC和DE的数量关系不能确定;由旋转的性质可知∠ACD=∠BCE，AC=DC，BC=EC，所以2∠A=180°-∠ACD，2∠EBC=180°-∠BCE，从而可证选项D是正确的.7. 【答案】B【解析】如图，作出C，D点的运动路径，连接CC1，S线段CD扫过的阴=+S△ABC+-S正方形ABCD-=.因为影部分AB=1，所以AC=，所以S线段CD扫过的阴影部分=π·AC2-π·AD2=，故选B.8. 【答案】C[解析] 由题意可得∠CBD＝α，∠C＝∠EDB. ∵∠EDB＋∠ADB＝180°，∴∠C＋∠ADB＝180°.由四边形的内角和定理，得∠CAD＋∠CBD＝180°.∴∠CAD＝180°－∠CBD＝180°－α.故选C.二、填空题9. 【答案】-1[解析]如图，连接BB'，∵将△ABC绕点A按顺时针方向旋转60°得到△AB'C'，∴AB=AB'，∠BAB'=60°，∴△ABB'是等边三角形，∴AB=BB'.在△ABC'和△B'BC'中，∴△ABC'≌△B'BC'(SSS)，∴∠ABC'=∠B'BC'，延长BC'交AB'于D，则BD⊥AB'，∵AB==2，∴BD=2×=，C'D=×2=1，∴BC'=BD-C'D=-1.故答案为-1.10. 【答案】15°或60°11. 【答案】3[解析]∵DE=EF=AD=3，∠D=90°，∴AE2=AD2+DE2=18，∴AB=AE==3.12. 【答案】y＝－x2－2x－3[解析] 旋转前二次项的系数a＝1，抛物线的顶点坐标是(1，2)，旋转后二次项的系数a＝－1，抛物线的顶点坐标是(－1，－2)，∴新抛物线的解析式为y＝－(x＋1)2－2，即y＝－x2－2x－3.13. 【答案】90°[解析] 找到一组对应点A，A′，并将其与旋转中心连接起来，确定旋转角，进而得到旋转角的度数为90°.14. 【答案】①②③[解析]设BE，DG交于O，∵四边形ABCD和四边形EFGC都为正方形，∴BC=CD，CE=CG，∠BCD=∠ECG=90°，∴∠BCD+∠DCE=∠ECG+∠DCE，即∠BCE=∠DCG，∴△BCE≌△DCG(SAS)，∴BE=DG，∠1=∠2，∵∠1+∠4=∠3+∠1=90°，∴∠2+∠3=90°，∴∠BOD=90°，∴BE⊥DG.故①②正确.连接BD，EG，如图所示，∴DO2+BO2=BD2=BC2+CD2=2a2，EO2+OG2=EG2=CG2+CE2=2b2，则BG2+DE2=BO2+OG2+OE2+OD2=DO2+BO2+EO2+OG2=2a2+2b2，故③正确. 15. 【答案】①②③16. 【答案】9＋3 3 [解析] 将y ＝1代入y ＝－33x ，解得x ＝－ 3.∴AB ＝3，OA ＝2，且直线y ＝－33x 与x 轴所夹的锐角是30°.由图可知，在旋转过程中每3次一循环，其中OO 2＝O 2O 4＝O 4O 6＝O 6O 8＝O 8O 10＝O 10O 12＝2＋3＋1＝3＋ 3. ∴OO 12＝6×(3＋3)＝18＋6 3. ∴点O 12的纵坐标＝12OO 12＝9＋3 3.三、解答题17. 【答案】解：(1)旋转角的度数为60°.(2)证明：由旋转的性质知∠ABC ＝∠A 1BC 1＝120°，∠C ＝∠C 1，AB ＝A 1B.∵点A ，B ，C 1在同一直线上，∴∠ABC 1＝180°，∴∠ABA 1＝∠CBC 1＝60°，∴∠A 1BC ＝60°，∵AB ＝A 1B ，∴△ABA 1是等边三角形， ∴∠AA 1B ＝∠A 1BC ＝60°， ∴AA 1∥BC ，∴∠A 1AC ＝∠C. 又∵∠C ＝∠C 1，∴∠A 1AC ＝∠C 1.18. 【答案】解：(1)∵将△ABD 绕点A 逆时针旋转，得到△ACD′， ∴∠DAD′＝∠BAC.∵∠BAC ＝90°，∴∠DAD′＝90°.(2)证明：∵△ABD 绕点A 逆时针旋转得到△ACD′， ∴AD ＝AD′，∠DAD′＝∠BAC ＝90°. ∵∠DAE ＝45°，∴∠D′AE ＝∠DAD′－∠DAE ＝90°－45°＝45°， ∴∠D′AE ＝∠DAE.在△AED 与△AED′中，⎩⎨⎧AE ＝AE ，∠DAE ＝∠D′AE ，AD ＝AD′，∴△AED ≌△AED′(SAS)，∴DE ＝D′E.19. 【答案】解：如图，将△BCE 绕点C 逆时针旋转90°，得到△ACF ，连接DF.由旋转的性质，得CE ＝CF ，AF ＝BE ＝2，∠ACF ＝∠BCE ，∠CAF ＝∠B ＝45°.∵∠ACB ＝90°，∠DCE ＝45°，∴∠DCF ＝∠ACD ＋∠ACF ＝∠ACD ＋∠BCE ＝∠ACB －∠DCE ＝90°－45°＝45°，∴∠DCE ＝∠DCF.在△CDE 和△CDF 中，⎩⎨⎧CE ＝CF ，∠DCE ＝∠DCF ，CD ＝CD ，∴△CDE ≌△CDF(SAS)，∴DE ＝DF.∵∠DAF ＝∠BAC ＋∠CAF ＝45°＋45°＝90°，∴△ADF 是直角三角形，∴DF 2＝AD 2＋AF 2，∴DE 2＝AD 2＋BE 2＝32＋22＝13， ∴DE ＝13.20. 【答案】(1)证明：∵△ABC 是等腰直角三角形，∴AB ＝AC ，∠B ＝∠C ＝45°，又∵AP ＝AQ ，∴BP ＝CQ ，∵E 是BC 的中点，∴BE ＝EC .∴在△BPE 与△CQE 中，∠∠BP CQ B C BE CE =⎧⎪=⎨⎪=⎩，∴△BPE ≌△CQE (SAS)；(2)①证明：∵∠BEF ＝∠C ＋∠CQE ，∠BEF ＝∠BEP ＋∠DEF ，∠C ＝∠DEF ＝45°，∴∠CQE ＝∠BEP ，∵∠B ＝∠C ，∴△BPE ∽△CEQ ；②解：由①知△BPE∽△CEQ，∴BE BP，CQ CE∴BE·CE＝BP·CQ，又∵BE＝EC，∴BE2＝BP·CQ，∵BP＝2，CQ＝9，∴BE2＝2×9＝18，∴BE＝32，∴BC＝2BE＝6 2.21. 【答案】证明：如图，将△ADB绕点D顺时针旋转60°，得到△CDE，连接BE，则∠ADB＝∠CDE，∠A＝∠DCE，AB＝CE，BD＝DE.又∵∠ADC＝60°，∴∠BDE＝60°，∴△DBE是等边三角形，∴BD＝BE.又∵∠ECB＝360°－∠BCD－∠DCE＝360°－∠BCD－∠A＝360°－(360°－∠ADC－∠ABC)＝90°，∴△ECB是直角三角形，∴BE2＝CE2＋BC2，即BD2＝AB2＋BC2.22. 【答案】解：(1)证明：连接EG，AF，则EG＝AF.由旋转的性质可得EG＝BD，∴AF＝BD.又∵AD＝BC，∴Rt△ADF≌Rt△BCD.∴FD＝CD.(2)分两种情况：①若点G位于BC的垂直平分线上，且在BC的右边，如图(a)．∵GC＝GB，∴∠GCB＝∠GBC，∴∠GCD＝∠GBA.又CD＝BA，∴△GCD≌△GBA，∴DG＝AG.又∵AG＝AD，∴△ADG是等边三角形，∴∠DAG＝60°，∴α＝60°.②若点G位于BC的垂直平分线上，且在BC的左边，如图(b)．同理，△ADG是等边三角形，∴∠DAG＝60°.此时α＝300°.综上所述，当α为60°或300°时，GC＝GB.。

2021年中考数学 一轮专题汇编：平移与旋转(含答案)

2021中考数学一轮知识点系统复习之图形的平移、旋转与轴对称能力达标测试题(附答案详解)

2020-2021学年中考数学 平移与旋转 专题训练(含答案)

中考数学一轮复习专题过关检测卷—轴对称、平移、旋转(含答案解析)

河北省2021年中考数学一轮复习训练：第七章 第四节 图形的平移与旋转 附答案

备战2021年中考数学精品系列-专题26 平移、旋转与对称(解析版)

2021年全国各地中考数学试卷分类汇编平移旋转与对称

2021年中考数学真题汇编—旋转(含解析)

2021年全国中考数学真题分类汇编--图形与变换：平移与旋转(答案版 )

2021年中考数学试卷解析分类汇编专题29-平移旋转与对称

2021年人教版中考数学专题《轴对称、平移与旋转》复习试卷含答案

全国各地2021年中考数学试卷解析版分类汇编 平移旋转与对称

湖南省2021年中考数学真题分项汇编—专题13 图形的相似、平移、对称与旋转(含答案解析)

中考数学试题分项解析专题51图形的平移对称与旋转含解析试题

2021年九年级数学中考一轮复习知识点基础达标测评：平移旋转轴对称(附答案)

2021年中考数学一轮专题汇编：平移与旋转(含答案)

2021年全国中考数学真题分类汇编：旋转专项复习含答案.docx

2021年人教版数学中考一轮复习： 平移与旋转 专项练习题(含答案)

2020-2021初中数学图形的平移,对称与旋转的全集汇编附答案

2021年中考数学一轮专题汇编：平移与旋转(含答案)

2020-2021学年中考数学平移与旋转专题训练(含答案)

河北省2021年中考数学一轮复习训练：第七章第四节图形的平移与旋转附答案

全国各地2021年中考数学试卷解析版分类汇编平移旋转与对称

2021年人教版数学中考一轮复习：平移与旋转专项练习题(含答案)