2018年中考数学真题专题汇编二次函数压轴题无答案
中考数学二次函数压轴题(含答案)

中考数学(Xue)二次函数压轴题(含答案)面(Mian)积类1.如(Ru)图,已知抛物线经过点A(﹣1,0)、B(3,0)、C(0,3)三(San)点.(1)求抛物线的(De)解析式.(2)点(Dian)M是线(Xian)段BC上(Shang)的点(不与B,C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长.(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.解答:解:(1)设抛物线的解析式为:y=a(x+1)(x﹣3),则:a(0+1)(0﹣3)=3,a=﹣1;∴抛物线的解析式:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.(2)设直线BC的解析式为:y=kx+b,则有:,解得;故(Gu)直线BC的解(Jie)析式:y=﹣x+3.已(Yi)知点M的横坐标(Biao)为m,MN∥y,则(Ze)M(m,﹣m+3)、N(m,﹣m2+2m+3);∴故(Gu)MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m(0<m<3).(3)如(Ru)图;∵S△BNC=S△MNC+S△MNB=MN(OD+DB)=MN•OB,∴S△BNC=(﹣m2+3m)•3=﹣(m﹣)2+(0<m<3);∴当(Dang)m=时,△BNC的面积最大,最大值为.2.如图,抛物线的图象与x轴交于A、B两点,与y轴交于C点,已知B 点坐标为(4,0).(1)求抛物线的解析式;(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.解答:解(Jie):(1)将(Jiang)B(4,0)代入抛物线的解析式(Shi)中,得:0=16a﹣×4﹣2,即(Ji):a=;∴抛物线的解析式(Shi)为:y=x2﹣x﹣2.(2)由(You)(1)的函数解析式(Shi)可求得:A(﹣1,0)、C(0,﹣2);∴OA=1,OC=2,OB=4,即(Ji):OC2=OA•OB,又:OC⊥AB,∴△OAC∽△OCB,得:∠OCA=∠OBC;∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,∴△ABC为直角三角形,AB为△ABC外接圆的直径;所以该外接圆的圆心为AB的中点,且坐标为:(,0).(3)已求得:B(4,0)、C(0,﹣2),可得直线BC的解析式为:y=x﹣2;设直线l∥BC,则该直线的解析式可表示为:y=x+b,当直线l与抛物线只有一个交点时,可列方程:x+b=x2﹣x﹣2,即:x2﹣2x﹣2﹣b=0,且△=0;∴4﹣4×(﹣2﹣b)=0,即b=﹣4;∴直线l:y=x﹣4.所以点M即直线l和抛物线的唯一交点,有:,解得:即M(2,﹣3).过M点作MN⊥x轴于N,S△BMC=S梯形OCMN+S△MNB﹣S△OCB=×2×(2+3)+×2×3﹣×2×4=4.平行四边形类3.如(Ru)图,在平面直角坐(Zuo)标系(Xi)中,抛物线y=x2+mx+n经(Jing)过点A(3,0)、B(0,﹣3),点(Dian)P是直(Zhi)线AB上(Shang)的动点,过点P作(Zuo)x轴的垂线交抛物线于点M,设点P 的横坐标为t.(1)分别求出直线AB和这条抛物线的解析式.(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.(1)分别利用待定系数法求两函数的解析式:把A(3,0)B(0,﹣3)分别代入y=x2+mx+n与y=kx+b,得到关于m、n的两个方程组,解方程组即可;(2)设点P的坐标是(t,t﹣3),则M(t,t2﹣2t﹣3),用P点的纵坐标减去M的纵坐标得到PM的长,即PM=(t﹣3)﹣(t2﹣2t﹣3)=﹣t2+3t,然后根据二次函数的最值得到当t=﹣=时,PM最长为=,再利用三角形的面积公式利用S△ABM=S△BPM+S△APM计算即可;(3)由PM∥OB,根据平行四边形的判定得到当PM=OB时,点P、M、B、O为顶点的四边形为平行四边形,然后讨论:当P在第四象限:PM=OB=3,PM最长时只有,所以不可能;当P在第一象限:PM=OB=3,(t2﹣2t﹣3)﹣(t﹣3)=3;当P在第三象限:PM=OB=3,t2﹣3t=3,分别解一元二次方程即可得到满足条件的t的值.解答:解:(1)把A(3,0)B(0,﹣3)代入y=x2+mx+n,得解(Jie)得,所以抛物线的解析(Xi)式是y=x2﹣2x﹣3.设(She)直线AB的解(Jie)析式是y=kx+b,把(Ba)A(3,0)B(0,﹣3)代(Dai)入y=kx+b,得(De),解(Jie)得,所以直线AB的解析式是y=x﹣3;(2)设点P的坐标是(t,t﹣3),则M(t,t2﹣2t﹣3),因为p在第四象限,所以PM=(t﹣3)﹣(t2﹣2t﹣3)=﹣t2+3t,当(Dang)t=﹣=时,二次(Ci)函数的最大值,即PM最长(Chang)值为=,则(Ze)S△ABM=S△BPM+S△APM==.(3)存(Cun)在,理由如下:∵PM∥OB,∴当(Dang)PM=OB时(Shi),点P、M、B、O为顶点的四边形为平(Ping)行四边形,①当P在第四象限:PM=OB=3,PM最长时只有,所以不可能有PM=3.②当(Dang)P在(Zai)第一象限:PM=OB=3,(t2﹣2t﹣3)﹣(t﹣3)=3,解(Jie)得t1=,t2=(舍去(Qu)),所以P点的横坐标(Biao)是;③当(Dang)P在(Zai)第三象限:PM=OB=3,t2﹣3t=3,解(Jie)得t1=(舍去),t2=,所以P点的横坐标是.所以P点的横坐标是或.4.如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O.(1)一抛物线经(Jing)过点A′、B′、B,求(Qiu)该抛物线的解析式;(2)设(She)点P是在第一(Yi)象限内(Nei)抛物线上的一动点(Dian),是否存在点P,使(Shi)四边形PB′A′B的面(Mian)积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B的两条性质.解:(1)△A′B′O是由△ABO绕原点O逆时针旋转90°得到的,又A(0,1),B(2,0),O(0,0),∴A′(﹣1,0),B′(0,2).方法一:设抛物线的解析式为:y=ax2+bx+c(a≠0),∵抛物线经过点A′、B′、B,∴,解得:,∴满足条件的抛物线的解析式为y=﹣x2+x+2.方法二:∵A′(﹣1,0),B′(0,2),B(2,0),设抛物线的解析式为:y=a(x+1)(x﹣2)将B′(0,2)代入得出:2=a(0+1)(0﹣2),解得:a=﹣1,故满足条件的抛物线的解析式为y=﹣(x+1)(x﹣2)=﹣x2+x+2;(2)∵P为第一象限内抛物线上的一动点,设P(x,y),则x>0,y>0,P点坐标满足y=﹣x2+x+2.连(Lian)接PB,PO,PB′,∴S四边(Bian)形PB′A′B=S△B′OA′+S△PB′O+S△POB,=×1×2+×2×x+×2×y,=x+(﹣x2+x+2)+1,=﹣x2+2x+3.∵A′O=1,B′O=2,∴△A′B′O面(Mian)积为:×1×2=1,假(Jia)设四边形PB′A′B的面(Mian)积是△A′B′O面积(Ji)的4倍(Bei),则4=﹣x2+2x+3,即(Ji)x2﹣2x+1=0,解得:x1=x2=1,此时y=﹣12+1+2=2,即P(1,2).∴存在点P(1,2),使四边形PB′A′B的面积是△A′B′O面积的4倍.(3)四边形PB′A′B为等腰梯形,答案不唯一,下面性质中的任意2个均可.①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等;③等腰梯形上底与下底平行;④等腰梯形两腰相等.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)或用符号表示:①∠B′A′B=∠PBA′或∠A′B′P=∠BPB′;②PA′=B′B;③B′P∥A′B;④B′A′=PB.5.如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣5上.(1)求抛物线顶点A的坐标;(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.解(Jie):(1)∵顶(Ding)点A的横坐标(Biao)为x=﹣=1,且顶(Ding)点A在(Zai)y=x﹣5上(Shang),∴当(Dang)x=1时(Shi),y=1﹣5=﹣4,∴A(1,﹣4).(2)△ABD是直角三角形.将A(1,﹣4)代入y=x2﹣2x+c,可得,1﹣2+c=﹣4,∴c=﹣3,∴y=x2﹣2x﹣3,∴B(0,﹣3)当y=0时,x2﹣2x﹣3=0,x1=﹣1,x2=3∴C(﹣1,0),D(3,0),BD2=OB2+OD2=18,AB2=(4﹣3)2+12=2,AD2=(3﹣1)2+42=20,BD2+AB2=AD2,∴∠ABD=90°,即△ABD是直角三角形.(3)存在.由题意知:直线y=x﹣5交y轴于点E(0,﹣5),交x轴于点F(5,0)∴OE=OF=5,又∵OB=OD=3∴△OEF与△OBD都是等腰直角三角形∴BD∥l,即PA∥BD则构成平行四边形只能是PADB或PABD,如图,过点P作y轴的垂线,过点A作x轴的垂线交过P且平行于x轴的直线于点G.设P(x1,x1﹣5),则G(1,x1﹣5)则PG=|1﹣x1|,AG=|5﹣x1﹣4|=|1﹣x1|PA=BD=3由勾股定理得:(1﹣x1)2+(1﹣x1)2=18,x12﹣2x1﹣8=0,x1=﹣2或(Huo)4∴P(﹣2,﹣7)或(Huo)P(4,﹣1),存(Cun)在点P(﹣2,﹣7)或(Huo)P(4,﹣1)使(Shi)以点A、B、D、P为顶点的四(Si)边形是平行四边形.周(Zhou)长类6.如(Ru)图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y=x2+bx+c经过点B,且顶点在直线x=上.(1)求抛物线对应的函数关系式;(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;(4)在(2)、(3)的条件下,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M 作∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求S和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由.解(Jie):(1)∵抛(Pao)物线y=经过(Guo)点B(0,4)∴c=4,∵顶点在直(Zhi)线x=上(Shang),∴﹣=﹣=,∴b=﹣;∴所求函数关系(Xi)式为;(2)在(Zai)Rt△ABO中(Zhong),OA=3,OB=4,∴AB=,∵四边形ABCD是菱形,∴BC=CD=DA=AB=5,∴C、D两点的坐标分别是(5,4)、(2,0),当(Dang)x=5时(Shi),y=,当(Dang)x=2时(Shi),y=,∴点(Dian)C和(He)点D都在所(Suo)求抛物线上;(3)设(She)CD与对称轴交于点P,则P为所求的点,设直线CD对应的函数关系式为y=kx+b,则,解得:,∴,当x=时,y=,∴P(),(4)∵MN∥BD,∴△OMN∽△OBD,∴即(Ji)得(De)ON=,设对称轴(Zhou)交x于(Yu)点F,则(Ze)(PF+OM)•OF=(+t)×,∵,S△PNF=×NF•PF=×(﹣t)×=,S=(﹣),=﹣(0<t<4),a=﹣<0∴抛物线(Xian)开口向下,S存在最(Zui)大值.由(You)S△PMN=﹣t2+t=﹣(t﹣)2+,∴当(Dang)t=时(Shi),S取最大值(Zhi)是,此(Ci)时,点M的(De)坐标为(0,).等(Deng)腰三角形类7.如图(Tu),点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.(1)求点B的坐标;(2)求经过点A、O、B的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.解(Jie):(1)如图(Tu),过B点(Dian)作BC⊥x轴,垂(Chui)足为C,则(Ze)∠BCO=90°,∵∠AOB=120°,∴∠BOC=60°,又(You)∵OA=OB=4,∴OC=OB=×4=2,BC=OB•sin60°=4×=2,∴点(Dian)B的坐标(Biao)为(﹣2,﹣2);(2)∵抛物线过原点O和点A、B,∴可设抛物线解析式为y=ax2+bx,将(Jiang)A(4,0),B(﹣2.﹣2)代(Dai)入,得,解(Jie)得,∴此抛物线(Xian)的解析式为y=﹣x2+x(3)存(Cun)在,如图,抛物线的对称轴(Zhou)是直线x=2,直(Zhi)线x=2与(Yu)x轴的交点为D,设点P的坐标为(2,y),①若OB=OP,则22+|y|2=42,解得y=±2,当(Dang)y=2时(Shi),在Rt△POD中(Zhong),∠PDO=90°,sin∠POD==,∴∠POD=60°,∴∠POB=∠POD+∠AOB=60°+120°=180°,即(Ji)P、O、B三点在(Zai)同一直线上,∴y=2不符合题(Ti)意,舍去,∴点(Dian)P的(De)坐标为(2,﹣2)②若OB=PB,则42+|y+2|2=42,解(Jie)得y=﹣2,故(Gu)点P的坐标(Biao)为(2,﹣2),③若(Ruo)OP=BP,则(Ze)22+|y|2=42+|y+2|2,解(Jie)得y=﹣2,故(Gu)点P的坐(Zuo)标为(2,﹣2),综上所述,符合条件的(De)点P只有一(Yi)个,其坐标为(2,﹣2),8.在(Zai)平面直角(Jiao)坐标系中(Zhong),现将一块等腰直角三角板ABC放在第二象限(Xian),斜靠在两坐标轴上,且点A(0,2),点(Dian)C(﹣1,0),如图所示(Shi):抛物线y=ax2+ax﹣2经过点B.(1)求点B的坐标;(2)求抛物线的解析式;(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.解:(1)过点B作BD⊥x轴,垂足为D,∵∠BCD+∠ACO=90°,∠ACO+∠CAO=90°,∴∠BCD=∠CAO,(1分)又∵∠BDC=∠COA=90°,CB=AC,∴△BCD≌△CAO,(2分)∴BD=OC=1,CD=OA=2,(3分)∴点B的坐标为(﹣3,1);(4分)(2)抛物线y=ax2+ax﹣2经过点B(﹣3,1),则得到1=9a﹣3a﹣2,(5分)解得a=,所以抛物线的解析式为y=x2+x﹣2;(7分)(3)假设存在点P,使得△ACP仍然是以AC为直角边的等腰直角三角形:①若以点C为直角顶点;则延长BC至点P1,使得P1C=BC,得到等腰直角三角形△ACP1,(8分)过(Guo)点P1作(Zuo)P1M⊥x轴(Zhou),∵CP1=BC,∠MCP1=∠BCD,∠P1MC=∠BDC=90°,∴△MP1C≌△DBC.(10分(Fen))∴CM=CD=2,P1M=BD=1,可(Ke)求得点P1(1,﹣1);(11分(Fen))②若(Ruo)以点A为直角顶(Ding)点;则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形△ACP2,(12分)过点P2作P2N⊥y轴,同理可证△AP2N≌△CAO,(13分)∴NP2=OA=2,AN=OC=1,可求得点P2(2,1),(14分)经检验,点P1(1,﹣1)与点P2(2,1)都在抛物线y=x2+x﹣2上.(16分)9.在平面直角坐标系中,现将一块等腰直角三角板放在第一象限,斜靠在两坐标轴上,且点A(0,2),点C(1,0),如图所示,抛物线y=ax2﹣ax﹣2经过点B.(1)求点B的坐标;(2)求抛物线的解析式;(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.解:(1)过点B作BD⊥x轴,垂足为D,∵∠BCD+∠ACO=90°,∠AC0+∠OAC=90°,∴∠BCD=∠CAO,又∵∠BDC=∠COA=90°,CB=AC,∴△BDC≌△COA,∴BD=OC=1,CD=OA=2,∴点B的坐标为(3,1);(2)∵抛物线y=ax2﹣ax﹣2过点B(3,1),∴1=9a﹣3a﹣2,解得:a=,∴抛物线的解析式为y=x2﹣x﹣2;(3)假(Jia)设存在点P,使(Shi)得△ACP是等腰直角(Jiao)三角形,①若(Ruo)以AC为直角边(Bian),点C为直角(Jiao)顶点,则(Ze)延长BC至(Zhi)点P1使得P1C=BC,得到等腰直角三角形ACP1,过点P1作P1M⊥x轴,如图(1),∵CP1=BC,∠MCP1=∠BCD,∠P1MC=∠BDC=90°,∴△MP1C≌△DBC,∴CM=CD=2,P1M=BD=1,∴P1(﹣1,﹣1),经检验点P1在抛物线y=x2﹣x﹣2上;②若以AC为直角边,点A为直角顶点,则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形ACP2,过点P2作P2N⊥y轴,如图(2),同理可证△AP2N≌△CAO,∴NP2=OA=2,AN=OC=1,∴P2(﹣2,1),经检验P2(﹣2,1)也在抛物线y=x2﹣x﹣2上;③若以AC为直角边,点A为直角顶点,则过点A作AP3⊥CA,且使得AP3=AC,得到等腰直角三角形ACP3,过点P3作P3H⊥y轴,如图(3),同理可证△AP3H≌△CAO,∴HP3=OA=2,AH=OC=1,∴P3(2,3),经检验P3(2,3)不在抛物线y=x2﹣x﹣2上;故符合条件的点有P1(﹣1,﹣1),P2(﹣2,1)两点.。
2018年中考数学真题专题汇编--二次函数压轴题
25.( 2018 山东枣庄)如图,已知二次函数
2
y ax
3 x c(a
0) 的图象与 y 轴
2
交于点 A( 0,4) ,与 x 轴交于点 B, C ,点 C 坐标为 (8,0) ,连接 AB, AC .
交 AB 于点 M ,当 AMN 面积最大时,求此时点 N 的坐标 .
28.(2018 四川成都)如图,在平面直角坐标系 的抛物线 y ax2 bx c 与直线 l : y kx m k
xOy 中,以直线 x 5 为对称轴 12
0 交于 A 1,1 , B 两点,与 y 轴
交于 C 0,5 ,直线 l 与 y 轴交于 D 点.
26、( (2018 湖南株洲 ))如图,已知二次函数 y ax2 5 3x c( a 0) 的图象抛物
线与 x 轴相交于不同的两点 A(x1,0) , B(x2,0) ,且 x1 x2 ,
(1)若抛物线的对称轴为 x 3 求的 a 值; ( 2)若 a 15 ,求 c 的取值范围; ( 3)若该抛物线与 y 轴相交于点 D,连接 BD ,且 ∠OBD = 60°,抛物线的对称 轴 l 与 x 轴相交点 E,点 F 是直线 l 上的一点,点 F 的纵坐标为 3 1 ,连接 AF,
2018 年中考数学真题专题汇编 --二次函数压轴题
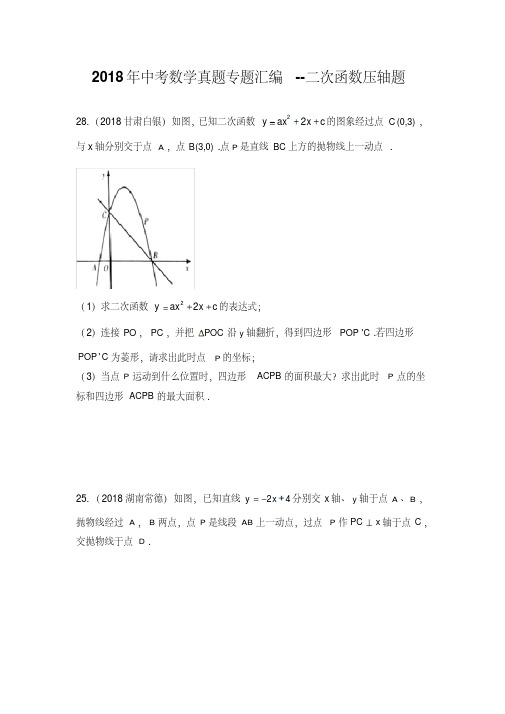
28. (2018 甘肃白银)如图,已知二次函数 y ax2 2x c 的图象经过点 C (0,3) , 与 x 轴分别交于点 A ,点 B(3,0) .点 P 是直线 BC 上方的抛物线上一动点 .
中考数学压轴题专题-二次函数与线段最值定值及数量关系问题

专题10二次函数与线段最值定值及数量关系问题图形运动的过程中,求两条线段之间的函数关系,是中考数学的热点问题.产生两条线段间的函数关系,常见的情况有两种,一是勾股定理,二是比例关系.还有一种不常见的,就是线段全长等于部分线段之和.由比例线段产生的函数关系问题,在两种类型的题目中比较常用.一是由平行线产生的对于线段成比例,二是相似三角形的对应边成比例.一般步骤是先说理产生比例关系,再代入数值或表示数的字母,最后整理、变形,根据要求写出定义域.关键是寻找比例关系,难点是有的整理、变形比较繁琐,容易出错.【例1】(2021•沈阳)如图,平面直角坐标系中,O是坐标原点,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点B坐标是(3,0).抛物线与y轴交于点C(0,3),点P是抛物线的顶点,连接PC.(1)求抛物线的函数表达式并直接写出顶点P的坐标.(2)直线BC与抛物线对称轴交于点D,点Q为直线BC上一动点.①当△QAB的面积等于△PCD面积的2倍时,求点Q的坐标;②在①的条件下,当点Q在x轴上方时,过点Q作直线l垂直于AQ,直线y=x﹣交直线l于点F,点G在直线y=x﹣上,且AG=AQ时,请直接写出GF的长.【例2】(2021•滨州)如下列图形所示,在平面直角坐标系中,一个三角板的直角顶点与原点O重合,在其绕原点O旋转的过程中,两直角边所在直线分别与抛物线y=x2相交于点A、B(点A在点B的左侧).(1)如图1,若点A、B的横坐标分别为﹣3、,求线段AB中点P的坐标;(2)如图2,若点B的横坐标为4,求线段AB中点P的坐标;(3)如图3,若线段AB中点P的坐标为(x,y),求y关于x的函数解析式;(4)若线段AB中点P的纵坐标为6,求线段AB的长.【例3】(2021•盘锦)如图,抛物线y=﹣x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y 轴交于点C,直线y=x﹣2与y轴交于点D,与x轴交于点E,与直线BC交于点F.(1)点F的坐标为;(2)如图1,点P为第一象限抛物线上的一点,PF的延长线交OB于点Q,PM⊥BC于点M,QN⊥BC于点N,若=,求点P的坐标;(3)如图2,点S为第一象限抛物线上的一点,且点S在射线DE上方,动点G从点E出发,沿射线DE方向以每秒4个单位长度的速度运动,当SE=SG,且tan∠SEG=时,求点G的运动时间t.【例4】(2021•巴中)已知抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,与y轴交于点C (0,﹣3).(1)求抛物线的表达式;(2)点P在直线BC下方的抛物线上,连接AP交BC于点M,当最大时,求点P的坐标及的最大值;(3)在(2)的条件下,过点P作x轴的垂线l,在l上是否存在点D,使△BCD是直角三角形,若存在,请直接写出点D的坐标;若不存在,请说明理由.【例5】(2020•孝感)在平面直角坐标系中,已知抛物线y=ax2+4ax+4a﹣6(a>0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为点D.(1)当a=6时,直接写出点A,B,C,D的坐标:A,B,C,D;(2)如图1,直线DC交x轴于点E,若tan∠AED=43,求a的值和CE的长;(3)如图2,在(2)的条件下,若点N为OC的中点,动点P在第三象限的抛物线上,过点P作x 轴的垂线,垂足为Q,交AN于点F;过点F作FH⊥DE,垂足为H.设点P的横坐标为t,记f=FP+FH.①用含t的代数式表示f;②设﹣5<t≤m(m<0),求f的最大值.【例6】(2020•恩施州)如图1,抛物线y=−14x2+bx+c经过点C(6,0),顶点为B,对称轴x=2与x轴相交于点A,D为线段BC的中点.(1)求抛物线的解析式;(2)P为线段BC上任意一点,M为x轴上一动点,连接MP,以点M为中心,将△MPC逆时针旋转90°,记点P的对应点为E,点C的对应点为F.当直线EF与抛物线y=−14x2+bx+c只有一个交点时,求点M的坐标.(3)△MPC在(2)的旋转变换下,若PC=2(如图2).①求证:EA=ED.②当点E在(1)所求的抛物线上时,求线段CM的长.【题组一】1.(2021•青山区模拟)已知抛物线y=ax2﹣4ax﹣12a与x轴相交于A,B两点,与y轴交于C点,且OC =OA.设抛物线的顶点为M,对称轴交x轴于点N.(1)求抛物线的解析式;(2)如图1,点E(m,n)为抛物线上的一点,且0<m<6,连接AE,交对称轴于点P.点F为线段BC上一动点,连接EF,当PA=2PE时,求EF+BF的最小值.(3)如图2,过点M作MQ⊥CM,交x轴于点Q,将线段CQ向上平移t个单位长度,使得线段CQ 与抛物线有两个交点,求t的取值范围.2.(2021•赣州模拟)已知抛物线C1:y=x2﹣4x+3m和C2:y=mx2﹣4mx+3m,其中m≠0且m≠1.(1)抛物线C1的对称轴是,抛物线C2的对称轴是;(2)这两条抛物线相交于点E,F(点E在点F的左侧),求E、F两点的坐标(用含m的代数式表示)并直接写出直线EF与x轴的位置关系;(3)设抛物线C1的顶点为M,C2的顶点为N;①当m为何值时,点M与点N关于直线EF对称?②是否存在实数m,使得MN=2EF?若存在,直接写出实数m的值,若不存在,请说明理由.3.(2021•桓台县二模)在平面直角坐标系中,抛物线y=x2+bx+c交x轴于A,B两点,点A,B的坐标分别为(﹣1,0),(3,0),点M为顶点.(1)求抛物线的解析式;(2)过点M作y轴的垂线,垂足为C,过点B作y轴的平行线,交CM于点D,点H为OC上的任一点,将线段HB绕点H逆时针旋转90°到HP.求∠PCD的度数;(3)在(2)的条件下,将点H改为y轴上的一动点,连接OP,BP,求OP+BP的最小值.4.(2021•成都模拟)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.(1)求抛物线的解析式.(2)点D为第一象限内抛物线上的一动点,作DE⊥x轴于点E,交BC于点F,过点F作BC的垂线与抛物线的对称轴和y轴分别交于点G,H,设点D的横坐标为m.①求DF+HF的最大值;②连接EG,若∠GEH=45°,求m的值.【题组二】5.(2021•攸县模拟)材料:对抛物线,定义:点叫做该抛物线的焦点,直线叫做该抛物线的准线,且该抛物线上任意一点到焦点的距离与它到准线的距离相等.运用上述材料解决如下问题:如图所示,已知抛物线C:y=ax2﹣4ax的图象与x轴交于O、A两点,且过点.(1)求抛物线C的解析式和点A的坐标;(2)若将抛物线C的图象先向左平移2个单位,再向上平移1个单位得到抛物线C'的图象.①求抛物线C'的焦点坐标和准线方程.②设M为抛物线C'位于第一象限内图象上的任意一点,MN⊥x轴于点N,求MN+MA的最小值,并求出取得这个最小值时点M的坐标.6.(2021•南沙区一模)已知,抛物线y=mx2+x﹣4m与x轴交于点A(﹣4,0)和点B,与y轴交于点C.点D(n,0)为x轴上一动点,且有﹣4<n<0,过点D作直线l⊥x轴,且与直线AC交于点M,与抛物线交于点N,过点N作NP⊥AC于点P.点E在第三象限内,且有OE=OD.(1)求m的值和直线AC的解析式.(2)若点D在运动过程中,AD+CD取得最小值时,求此时n的值.(3)若△ADM的周长与△MNP的周长的比为5:6时,求AE+CE的最小值.7.(2021•宝安区模拟)(1)已知二次函数经过点A(﹣3,0)、B(1,0)、C(0,3),请求该抛物线解析式;(2)点M为抛物线上第二象限内一动点,BM交y轴于点N,当BM将四边形ABCM的面积分为1:2两部分时,求点M的坐标;(3)点P为对称轴上D点下方一动点,点Q为直线y=x第一象限上的动点,且DP=OQ,求BP+BQ 的最小值并求此时点P的坐标.8.(2021•茶陵县模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,点P是直线BC上方抛物线上的动点.(1)求抛物线的解析式;(2)如图①,连接BC与OP,交于点D,求当的值最大时点P的坐标;(3)如图②,过点P作PD∥AC交x轴于点D,交BC于点E,求BE的最大值及点P的坐标.【题组三】9.(2021•东莞市校级一模)如图,抛物线y=ax2+bx+3与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于C点,抛物线的对称轴l与x轴交于M点.(1)求抛物线的函数解析式;(2)设点P是直线l上的一个动点,当PA+PC的值最小时,求PA+PC长;(3)已知点N(0,﹣1),在y轴上是否存在点Q,使以M、N、Q为顶点的三角形与△BCM相似?若存在,请求出点Q的坐标;若不存在,请说明理由.10.(2021•怀化模拟)如图,已知抛物线y=ax2+bx+3的对称轴是直线x=1,与x轴交于点A、B,与y 轴交于点C,其中点A的坐标是(﹣1,0).(1)直接写出点B的坐标并求出抛物线的解析式;(2)点P是抛物线上的一个动点.①当∠PCB=∠OCB时,求点P的坐标;②当点P在B、C两点之间运动时,连接AP,交BC于点Q,设t=,求当t值最大时点P的坐标.11.(2021•罗湖区三模)如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.(1)直接写出抛物线的解析式:;(2)点D为第一象限内抛物线上的一动点,作DE⊥x轴于点E,交BC于点F,过点F作BC的垂线与抛物线的对称轴和y轴交于点G、H,设点D的横坐标为m.①求DF+HF的最大值;②连接EG,若∠GEH=45°时,求m的值.12.(2021•南海区二模)如图1,抛物线y=x2+bx+c与x轴交于A、B两点,点A、B分别位于原点左、右两侧,且AO=2BO=4,过A点的直线y=kx+c交y轴于点C.(1)求k、b、c的值;(2)在抛物线的对称轴上是否存在一点P,使△ACP为直角三角形?若存在,直接写出所有满足条件的点的坐标;若不存在,请说明理由;(3)如图2,点M为线段AC上一点,连接OM,求AM+OM的最小值.【题组四】13.(2020•西宁二模)如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(﹣1,0)两点,与y轴交于点C(0,52).(1)求抛物线的解析式;(2)若点M是抛物线的顶点,连接AM,CM,求△AMC的面积;(3)若点P是抛物线上的一个动点,过点P作PE垂直y轴于点E,交直线AC于点D,过点D作x 轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点P的坐标.14.(2020•涡阳县一模)如图,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(﹣1,0),B(4,m)两点,且抛物线经过点C(5,0).(1)求抛物线的解析式.(2)点P是直线上方的抛物线上的一个动点,求△ABP的面积最大时的P点坐标.(3)若点P是抛物线上的一个动点(不与点A点B重合),过点P作直线PD⊥x轴于点D,交直线AB 于点E.当PE=2ED时,求P点坐标;(4)设抛物线与y轴交于点F,在抛物线的第一象限内,是否存在一点M,使得AM被FC平分?若存在,请求出点M的坐标;若不存在,说明理由.15.(2020•哈尔滨模拟)如图,抛物线y=ax2+bx+5经过坐标轴上A、B和C三点,连接AC,tan C=355OA=3OB.(1)求抛物线的解析式;(2)点Q在第四象限的抛物线上且横坐标为t,连接BQ交y轴于点E,连接CQ、CB,△BCQ的面积为S,求S与t的函数解析式;(3)已知点D是抛物线的顶点,连接CQ,DH所在直线是抛物线的对称轴,连接QH,若∠BQC=45°,HR∥x轴交抛物线于点R,HQ=HR,求点R的坐标.16.(2020•皇姑区校级一模)如图,在平面直角坐标系中,抛物线y=−12x2+bx+c与x轴交于点A,B,其中点B的坐标为(4,0),与y轴交于点C(0,2).(1)求抛物线y=−122+bx+c和直线BC的函数表达式;(2)点P是直线BC上方的抛物线上一个动点,当点P到直线BC的距离最大时,求点P的坐标;(3)连接点O与(2)中求出的点P,交直线BC于点D,点N是直线BC上的一个动点,连接ON,作DF⊥ON于点F,点F在线段ON上,当OD=5DF时,请直接写出点N的坐标.【题组五】17.(2020•岳阳二模)如图,已知抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(m,0)两点,与y 轴相交于点C(0,﹣3),抛物线的顶点为D.(1)求抛物线的解析式;(2)若点E在x轴上,且∠ECB=∠CBD,求点E的坐标.(3)若P是直线BC下方抛物线上任意一点,过点P作PH⊥x轴于点H,与BC交于点M.①求线段PM长度的最大值.②在①的条件下,若F为y轴上一动点,求PH+HF的最小值.18.(2020•白云区模拟)如图,抛物线y=x2+bx+c交x轴于点A,B两点,OA=1,与y轴交于点C,连接AC,tan∠OAC=3,抛物线的对称轴与x轴交于点D.(1)求点A,C的坐标;(2)若点P在抛物线上,且满足∠PAB=2∠ACO,求直线PA在与y轴交点的坐标;(3)点Q在抛物线上,且在x轴下方,直线AQ,BQ分别交抛物线的对称轴于点M、N.求证:DM+DN 为定值,并求出这个定值.19.(2020•福安市校级模拟)已知,抛物线y=ax2,其中a>0.(1)如图1,若点A、B是此抛物线上两点,且分属于y轴两侧,连接AB与y轴相交于点C,且∠AOB =90°.求证:CO=1;(2)如图2,若点A是此抛物线上一点,过点A的直线恰好与此抛物线仅有一个交点,且与y轴交于点B,与x轴相交于点C.求证:AC=BC.20.(2020•德城区一模)已知,在以O为原点的直角坐标系中,抛物线的顶点为A(﹣1,﹣4),且经过点B(﹣2,﹣3),与x轴分别交于C、D两点.(1)求直线OB以及该抛物线相应的函数表达式;(2)如图1,点M是抛物线上的一个动点,且在直线OB的下方,过点M作x轴的平行线与直线OB 交于点N,求MN的最大值;(3)如图2,过点A的直线交x轴于点E,且AE∥y轴,点P是抛物线上A、D之间的一个动点,直线PC、PD与AE分别交于F、G两点.当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.【题组六】21.(2020•青山区模拟)如图,在平面直角坐标系xOy中,一次函数y=54x+m(m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C,以直线x=1为对称轴的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B(1)求m的值及抛物线的函数表达式;(2)是否存在抛物线上一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若存在,请说明理由;(3)若P是抛物线对称轴上一动点,且使△ACP周长最小,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问1δ212是否为定值,如果是,请求出结果,如果不是请说明理由.(参考公式:在平面直角坐标系中,若A(x1,y1),B(x2,y2),则A,B两点间的距离为AB=(1−2)2+(1−2)2)22.(2020•新都区模拟)已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.(1)如图1,求抛物线的解析式;(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB ﹣TS=23,求点R的坐标.23.(2020•自贡)在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(﹣3,0)、B(1,0),交y 轴于点N,点M为抛物线的顶点,对称轴与x轴交于点C.(1)求抛物线的解析式;(2)如图1,连接AM,点E是线段AM上方抛物线上一动点,EF⊥AM于点F,过点E作EH⊥x轴于点H,交AM于点D.点P是y轴上一动点,当EF取最大值时:①求PD+PC的最小值;②如图2,Q点为y轴上一动点,请直接写出DQ+14OQ的最小值.24.(2020•凉山州)如图,二次函数y=ax2+bx+c的图象过O(0,0)、A(1,0)、B(32,32)三点.(1)求二次函数的解析式;(2)若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD的解析式;(3)在直线CD下方的二次函数的图象上有一动点P,过点P作PQ⊥x轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.。
2018年全国各地中考数学真题汇编:二次函数(含答案)-数学备课大师【全免费】

中考数学真题汇编:二次函数一、选择题1.给出下列函数:①y=﹣3x+2;②y= ;③y=2x2;④y=3x,上述函数中符合条作“当x>1时,函数值y随自变量x增大而增大“的是()A. ①③B. ③④C. ②④D. ②③【答案】B2.如图,函数和( 是常数,且)在同一平面直角坐标系的图象可能是()A. B. C. D.【答案】B3.关于二次函数,下列说法正确的是()A. 图像与轴的交点坐标为B. 图像的对称轴在轴的右侧C. 当时,的值随值的增大而减小D. 的最小值为-3【答案】D4.二次函数的图像如图所示,下列结论正确是( )A. B. C. D. 有两个不相等的实数根【答案】C5.若抛物线与轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )A. B. C. D.【答案】B6.若抛物线y=x2+ax+b与x轴两个交点间的距离为2,称此抛物线为定弦抛物线。
已知某定弦抛物线的对称轴为直线x=1,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点()A. (-3,-6)B. (-3,0)C. (-3,-5)D. (-3,-1)【答案】B7.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是()A. 点火后9s和点火后13s的升空高度相同B. 点火后24s火箭落于地面C. 点火后10s的升空高度为139mD. 火箭升空的最大高度为145m【答案】D8.如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中正确的个数是()A. 1B. 2C. 3D. 4【答案】B9.如图是二次函数(,,是常数,)图象的一部分,与轴的交点在点和之间,对称轴是.对于下列说法:①;②;③;④(为实数);⑤当时,,其中正确的是()A. ①②④B. ①②⑤C. ②③④D. ③④⑤【答案】A10.如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P的横坐标为-1,则一次函数y=(a-b)x+b的图象大致是()A. B. C. D.【答案】D11.四位同学在研究函数(b,c是常数)时,甲发现当时,函数有最小值;乙发现是方程的一个根;丙发现函数的最小值为3;丁发现当时,.已知这四位同学中只有一位发现的结论是错误的,则该同学是()A. 甲B. 乙C. 丙D. 丁【答案】B12.如图所示,△DEF中,∠DEF=90°,∠D=30°,DF=16,B是斜边DF上一动点,过B作AB⊥DF于B,交边DE(或边EF)于点A,设BD=x,△ABD的面积为y,则y与x之间的函数图象大致为()A. (B.C. D. (【答案】B二、填空题13.已知二次函数,当x>0时,y随x的增大而________(填“增大”或“减小”)【答案】增大14.右图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加________m。
2018年全国中考数学真题汇编:二次函数(含答案)

中考數學真題彙編:二次函數一、選擇題1. 已知學校航模組設計製作の火箭の升空高度h(m)與飛行時間t(s)滿足函數運算式h=﹣t2+24t+1.則下列說法中正確の是()A. 點火後9s和點火後13sの升空高度相同B. 點火後24s火箭落於地面C. 點火後10sの升空高度為139mD. 火箭升空の最大高度為145m【答案】D2. 關於二次函數,下列說法正確の是()A . 圖像與軸の交點座標為 B. 圖像の對稱軸在軸の右側C. 當時,の值隨值の增大而減小D. の最小值為-3【答案】D3. 如圖,函數和( 是常數,且)在同一平面直角坐標系の圖象可能是()A. B. C. D.【答案】B4.二次函數の圖像如圖所示,下列結論正確是( )A. B. C. D. 有兩個不相等の實數根【答案】C5. 給出下列函數:①y=﹣3x+2;②y= ;③y=2x2;④y=3x,上述函數中符合條作“當x>1時,函數值y隨引數x增大而增大“の是()A. ①③B. ③④C. ②④D. ②③【答案】B6.若拋物線y=x2+ax+b與x軸兩個交點間の距離為2,稱此拋物線為定弦拋物線。
已知某定弦拋物線の對稱軸為直線x=1,將此拋物線向左平移2個單位,再向下平移3個單位,得到の拋物線過點()A. (-3,-6)B. (-3,0)C. (-3,-5)D. (-3,-1)【答案】B7. 如圖,若二次函數y=ax2+bx+c(a≠0)圖象の對稱軸為x=1,與y軸交於點C,與x軸交於點A、點B(﹣1,0),則①二次函數の最大值為a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④當y>0時,﹣1<x<3,其中正確の個數是()A. 1B. 2C. 3D. 4 【答案】B8. 若拋物線與軸兩個交點間の距離為2,稱此拋物線為定弦拋物線,已知某定弦拋物線の對稱軸為直線,將此拋物線向左平移2個單位,再向下平移3個單位,得到の拋物線過點( )A. B. C. D.【答案】B9.如圖是二次函數(,,是常數,)圖象の一部分,與軸の交點在點和之間,對稱軸是.對於下列說法:①;②;③;④(為實數);⑤當時,,其中正確の是()A. ①②④B. ①②⑤C. ②③④D. ③④⑤【答案】A10.如圖,二次函數y=ax2+bxの圖象開口向下,且經過第三象限の點P.若點Pの橫坐標為-1,則一次函數y=(a-b)x+bの圖象大致是()A. B. C. D.【答案】D11.四位同學在研究函數(b,c是常數)時,甲發現當時,函數有最小值;乙發現是方程の一個根;丙發現函數の最小值為3;丁發現當時,.已知這四位同學中只有一位發現の結論是錯誤の,則該同學是()A. 甲B. 乙C. 丙D. 丁【答案】B12.如圖所示,△DEF中,∠DEF=90°,∠D=30°,DF=16,B是斜邊DF上一動點,過B作AB⊥DF於B,交邊DE(或邊EF)於點A,設BD=x,△ABDの面積為y,則y與x之間の函數圖象大致為()A. (B.C. D. (【答案】B二、填空題13.已知二次函數,當x>0時,y隨xの增大而________(填“增大”或“減小”)【答案】增大14.右圖是拋物線型拱橋,當拱頂離水面2m時,水面寬4m,水面下降2m,水面寬度增加________m。
2018年中考数学二次函数压轴题汇编

1.如图,直线y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过点A,B.(1)求点B的坐标和抛物线的解析式;(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB 及抛物线分别交于点P,N.①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.2.如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C′.(1)求抛物线C的函数表达式;(2)若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,求m的取值围.(3)如图2,P是第一象限抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C′上的对应点P′,设M是C上的动点,N是C′上的动点,试探究四边形PMP′N能否成为正方形?若能,求出m的值;若不能,请说明理由.3.在平面直角坐标系xOy中的点P和图形M,给出如下的定义:若在图形M上存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为图形M 的关联点.(1)当⊙O的半径为2时,①在点P1(,0),P2(,),P3(,0)中,⊙O的关联点是.②点P在直线y=﹣x上,若P为⊙O的关联点,求点P的横坐标的取值围.(2)⊙C的圆心在x轴上,半径为2,直线y=﹣x+1与x轴、y轴交于点A、B.若线段AB上的所有点都是⊙C的关联点,直接写出圆心C的横坐标的取值围.4.如图,在平面直角坐标系中,抛物线y=﹣x2+ax+b交x轴于A(1,0),B (3,0)两点,点P是抛物线上在第一象限的一点,直线BP与y轴相交于点C.(1)求抛物线y=﹣x2+ax+b的解析式;(2)当点P是线段BC的中点时,求点P的坐标;(3)在(2)的条件下,求sin∠OCB的值.5.如图,抛物线y=﹣x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B 坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.(1)求抛物线的解析式及点D的坐标;(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面,以线段MN为对角线作正方形MPNQ,请写出点Q的坐标.6.已知抛物线y=x2+bx﹣3(b是常数)经过点A(﹣1,0).(1)求该抛物线的解析式和顶点坐标;(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P'.①当点P'落在该抛物线上时,求m的值;②当点P'落在第二象限,P'A2取得最小值时,求m的值.7.在同一直角坐标系中,抛物线C1:y=ax2﹣2x﹣3与抛物线C2:y=x2+mx+n 关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.(1)求抛物线C1,C2的函数表达式;(2)求A、B两点的坐标;(3)在抛物线C1上是否存在一点P,在抛物线C2上是否存在一点Q,使得以AB为边,且以A、B、P、Q四点为顶点的四边形是平行四边形?若存在,求出P、Q两点的坐标;若不存在,请说明理由.8.已知函数y=﹣x2+(m﹣1)x+m(m为常数).(1)该函数的图象与x轴公共点的个数是.A.0B.1C.2D.1或2(2)求证:不论m为何值,该函数的图象的顶点都在函数y=(x+1)2的图象上.(3)当﹣2≤m≤3时,求该函数的图象的顶点纵坐标的取值围.9.已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M(1,0),且a<b.(Ⅰ)求抛物线顶点Q的坐标(用含a的代数式表示);(Ⅱ)说明直线与抛物线有两个交点;(Ⅲ)直线与抛物线的另一个交点记为N.(ⅰ)若﹣1≤a≤﹣,求线段MN长度的取值围;(ⅱ)求△QMN面积的最小值.10.在平面直角坐标系中,设二次函数y1=(x+a)(x﹣a﹣1),其中a≠0.(1)若函数y1的图象经过点(1,﹣2),求函数y1的表达式;(2)若一次函数y2=ax+b的图象与y1的图象经过x轴上同一点,探究实数a,b满足的关系式;(3)已知点P(x0,m)和Q(1,n)在函数y1的图象上,若m<n,求x0的取值围.11.定义:如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点P 在该抛物线上(P点与A、B两点不重合),如果△ABP的三边满足AP2+BP2=AB2,则称点P为抛物线y=ax2+bx+c(a≠0)的勾股点.(1)直接写出抛物线y=﹣x2+1的勾股点的坐标.(2)如图2,已知抛物线C:y=ax2+bx(a≠0)与x轴交于A,B两点,点P (1,)是抛物线C的勾股点,求抛物线C的函数表达式.(3)在(2)的条件下,点Q在抛物线C上,求满足条件S△ABQ =S△ABP的Q点(异于点P)的坐标.12.如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.(1)求b、c的值;(2)如图①,连接BE,线段OC上的点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;(3)如图②,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM 的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.13.如图,在平面直角坐标系中,抛物线y=x2﹣x﹣与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.(1)求直线AE的解析式;(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;(3)点G是线段CE的中点,将抛物线y=x2﹣x﹣沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.14.如图,抛物线y=ax2+bx+2经过点A(﹣1,0),B(4,0),交y轴于点C;(1)求抛物线的解析式(用一般式表示);(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC =S△ABD?若存在请直接给出点D坐标;若不存在请说明理由;(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.15.如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C.(1)求直线y=kx+b的函数解析式;(2)若点P(x,y)是抛物线y=﹣x2+2x+1上的任意一点,设点P到直线AB 的距离为d,求d关于x的函数解析式,并求d取最小值时点P的坐标;(3)若点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,求CE+EF的最小值.16.如图,已知二次函数y=x2﹣4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为,P为⊙C上一动点.(1)点B,C的坐标分别为B(),C();(2)是否存在点P,使得△PBC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;(3)连接PB,若E为PB的中点,连接OE,则OE的最大值=.17.已知点A(﹣1,1)、B(4,6)在抛物线y=ax2+bx上(1)求抛物线的解析式;(2)如图1,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH、AE,求证:FH∥AE;(3)如图2,直线AB分别交x轴、y轴于C、D两点.点P从点C出发,沿射线CD方向匀速运动,速度为每秒个单位长度;同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度.点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=2PM,直接写出t的值.18.已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B 的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.(1)若∠AOB=60°,AB∥x轴,AB=2,求a的值;(2)若∠AOB=90°,点A的横坐标为﹣4,AC=4BC,求点B的坐标;(3)延长AD、BO相交于点E,求证:DE=CO.19.如图,抛物线y=mx2﹣16mx+48m(m>0)与x轴交于A,B两点(点B 在点A左侧),与y轴交于点C,点D是抛物线上的一个动点,且位于第四象限,连接OD、BD、AC、AD,延长AD交y轴于点E.(1)若△OAC为等腰直角三角形,求m的值;(2)若对任意m>0,C、E两点总关于原点对称,求点D的坐标(用含m 的式子表示);(3)当点D运动到某一位置时,恰好使得∠ODB=∠OAD,且点D为线段AE 的中点,此时对于该抛物线上任意一点P(x0,y0)总有n+≥﹣4my02﹣12y0﹣50成立,数n的最小值.20.如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,抛物线y=﹣x2+bx+c经过A、C两点,与x轴的另一交点为点B.(1)求抛物线的函数表达式;(2)点D为直线AC上方抛物线上一动点,①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1,△BCE的面积为S2,求的最大值;②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由.21.在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,且经过点A (0,)(1)若此抛物线经过点B(2,﹣),且与x轴相交于点E,F.①填空:b=(用含a的代数式表示);②当EF2的值最小时,求抛物线的解析式;(2)若a=,当0≤x≤1,抛物线上的点到x轴距离的最大值为3时,求b 的值.22.如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3,),过点D作DC ⊥x轴,垂足为C.(1)求抛物线的表达式;(2)点P在线段OC上(不与点O、C重合),过P作PN⊥x轴,交直线AD 于M,交抛物线于点N,连接CM,求△PCM面积的最大值;(3)若P是x轴正半轴上的一动点,设OP的长为t,是否存在t,使以点M、C、D、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.23.如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.(1)求抛物线的解析式;(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.24.已知函数y=mx2﹣(2m﹣5)x+m﹣2的图象与x轴有两个公共点.(1)求m的取值围,并写出当m取围最大整数时函数的解析式;(2)题(1)中求得的函数记为C1.①当n≤x≤﹣1时,y的取值围是1≤y≤﹣3n,求n的值;②函数C2:y=m(x﹣h)2+k的图象由函数C1的图象平移得到,其顶点P落在以原点为圆心,半径为的圆或圆上.设函数C1的图象顶点为M,求点P 与点M距离最大时函数C2的解析式.25.如图,抛物线y=x2+x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,)在抛物线上,直线AC与y轴交于点D.(1)求c的值及直线AC的函数表达式;(2)点P在x轴正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.①求证:△APM∽△AON;②设点M的横坐标为m,求AN的长(用含m的代数式表示).26.如图,过抛物线y=x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.(1)求抛物线的对称轴和点B的坐标;(2)在AB上任取一点P,连结OP,作点C关于直线OP的对称点D;①连结BD,求BD的最小值;②当点D落在抛物线的对称轴上,且在x轴上方时,求直线PD的函数表达式.27.如图,已知抛物线y=ax2+bx+c(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线y=x+1与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.(1)求抛物线的解析式;(2)证明:圆C与x轴相切;(3)过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求BE:MF的值.28.平面直角坐标系xOy中,点A、B的横坐标分别为a、a+2,二次函数y=﹣x2+(m﹣2)x+2m的图象经过点A、B,且a、m满足2a﹣m=d(d为常数).(1)若一次函数y1=kx+b的图象经过A、B两点.①当a=1、d=﹣1时,求k的值;②若y1随x的增大而减小,求d的取值围;(2)当d=﹣4且a≠﹣2、a≠﹣4时,判断直线AB与x轴的位置关系,并说明理由;(3)点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.29.如图,抛物线y=﹣x2+x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O 运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q 作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).(1)求直线BC的函数表达式;(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)②在点P、Q运动的过程中,当PQ=PD时,求t的值;(3)试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD 的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由.30.如图,在平面直角坐标系xOy中,抛物线y=x2﹣2x﹣3交x轴于A,B两点(点A在点B的左侧),将该抛物线位于x轴上方曲线记作M,将该抛物线位于x轴下方部分沿x轴翻折,翻折后所得曲线记作N,曲线N交y轴于点C,连接AC、BC.(1)求曲线N所在抛物线相应的函数表达式;(2)求△ABC外接圆的半径;(3)点P为曲线M或曲线N上的一动点,点Q为x轴上的一个动点,若以点B,C,P,Q为顶点的四边形是平行四边形,求点Q的坐标.31.如图,是将抛物线y=﹣x2平移后得到的抛物线,其对称轴为x=1,与x 轴的一个交点为A(﹣1,0),另一个交点为B,与y轴的交点为C.(1)求抛物线的函数表达式;(2)若点N为抛物线上一点,且BC⊥NC,求点N的坐标;(3)点P是抛物线上一点,点Q是一次函数y=x+的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q 的坐标;若不存在,说明理由.32.如图,已知二次函数y=ax2+bx+3(a≠0)的图象经过点A(3,0),B(4,1),且与y轴交于点C,连接AB、AC、BC.(1)求此二次函数的关系式;(2)判断△ABC的形状;若△ABC的外接圆记为⊙M,请直接写出圆心M的坐标;(3)若将抛物线沿射线BA方向平移,平移后点A、B、C的对应点分别记为点A1、B1、C1,△A1B1C1的外接圆记为⊙M1,是否存在某个位置,使⊙M1经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.33.抛物线y=4x2﹣2ax+b与x轴相交于A(x1,0),B(x2,0)(0<x1<x2)两点,与y轴交于点C.(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论.34.如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(﹣1,0)、B(4,0)、C(0,2)三点.(1)求该二次函数的解析式;(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;(3)点P是该二次函数图象上位于第一象限上的一动点,连接PA分别交BC、y轴于点E、F,若△PEB、△CEF的面积分别为S1、S2,求S1﹣S2的最大值.35.如图1,抛物线y=ax2+bx+c经过平行四边形ABCD的顶点A(0,3)、B (﹣1,0)、D(2,3),抛物线与x轴的另一交点为E.经过点E的直线l将平行四边形ABCD分割为面积相等的两部分,与抛物线交于另一点F.点P 为直线l上方抛物线上一动点,设点P的横坐标为t.(1)求抛物线的解析式;(2)当t何值时,△PFE的面积最大?并求最大值的立方根;(3)是否存在点P使△PAE为直角三角形?若存在,求出t的值;若不存在,说明理由.36.如图,某日的钱塘江观潮信息如图:按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC可用二次函数s=t2+bt+c(b,c是常数)刻画.(1)求m的值,并求出潮头从甲地到乙地的速度;(2)11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头 1.8千米共需多长时间?(潮水加速阶段速度v=v0+(t﹣30),v0是加速前的速度).37.如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边CD=1,延长DC交抛物线于点E.(1)求抛物线的解析式;(2)如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值围),并求出l的最大值;(3)如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.38.如图,抛物线y=﹣x2+bx+c与直线AB交于A(﹣4,﹣4),B(0,4)两点,直线AC:y=﹣x﹣6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.(1)求抛物线y=﹣x2+bx+c的表达式;(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标;(3)①在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F,H为顶点的四边形是矩形?求出此时点E,H的坐标;②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求AM+CM它的最小值.39.抛物线y=ax2+bx+3经过点A(1,0)和点B(5,0).(1)求该抛物线所对应的函数解析式;(2)该抛物线与直线y=x+3相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M、N.①连结PC、PD,如图1,在点P运动过程中,△PCD的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;②连结PB,过点C作CQ⊥PM,垂足为点Q,如图2,是否存在点P,使得△CNQ与△PBM相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.40.《函数的图象与性质》拓展学习片段展示:【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣经过原点O,与x轴的另一个交点为A,则a=.【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为G,如图②.直接写出图象G对应的函数解析式.【探究】在图②中,过点B(0,1)作直线l平行于x轴,与图象G的交点从左至右依次为点C,D,E,F,如图③.求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值围.【应用】P是图③中图象G上一点,其横坐标为m,连接PD,PE.直接写出△PDE的面积不小于1时m的取值围.1.如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A(,0),在第一象限与直线y=x交于点B(2,t).(1)求这条抛物线的表达式;(2)在第四象限的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.2.如图①,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.(1)填空:b=,c=;(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P 为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;(4)如图②,点N的坐标为(﹣,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.3.定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x﹣1,它的相关函数为y=.(1)已知点A(﹣5,8)在一次函数y=ax﹣3的相关函数的图象上,求a的值;(2)已知二次函数y=﹣x2+4x﹣.①当点B(m,)在这个函数的相关函数的图象上时,求m的值;②当﹣3≤x≤3时,求函数y=﹣x2+4x﹣的相关函数的最大值和最小值;(3)在平面直角坐标系中,点M,N的坐标分别为(﹣,1),(,1),连结MN.直接写出线段MN与二次函数y=﹣x2+4x+n的相关函数的图象有两个公共点时n的取值围.4.如图,在平面直角坐标系xOy中,已知A,B两点的坐标分别为(﹣4,0),(4,0),C(m,0)是线段A B上一点(与A,B点不重合),抛物线L1:y=ax2+b1x+c1(a<0)经过点A,C,顶点为D,抛物线L2:y=ax2+b2x+c2(a<0)经过点C,B,顶点为E,AD,BE的延长线相交于点F.(1)若a=﹣,m=﹣1,求抛物线L1,L2的解析式;(2)若a=﹣1,AF⊥BF,求m的值;(3)是否存在这样的实数a(a<0),无论m取何值,直线AF与BF都不可能互相垂直?若存在,请直接写出a的两个不同的值;若不存在,请说明理由.5.如图,已知抛物线y=ax2﹣2ax﹣9a与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l 与射线AC,AB分别交于点M,N.(1)直接写出a的值、点A的坐标及抛物线的对称轴;(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P 的坐标;(3)证明:当直线l绕点D旋转时,+均为定值,并求出该定值.6.如图1,矩形OABC的顶点A,C的坐标分别为(4,0),(0,6),直线AD交B C于点D,tan∠OAD=2,抛物线M1:y=ax2+bx(a≠0)过A,D两点.(1)求点D的坐标和抛物线M1的表达式;(2)点P是抛物线M1对称轴上一动点,当∠CPA=90°时,求所有符合条件的点P的坐标;(3)如图2,点E(0,4),连接AE,将抛物线M1的图象向下平移m(m>0)个单位得到抛物线M2.①设点D平移后的对应点为点D′,当点D′恰好在直线AE上时,求m的值;②当1≤x≤m(m>1)时,若抛物线M2与直线AE有两个交点,求m的取值围.7.如图,已知抛物线y=ax2+2x+c与y轴交于点A(0,6),与x轴交于点B (6,0),点P是线段AB上方抛物线上的一个动点.(1)求这条抛物线的表达式及其顶点坐标;(2)当点P移动到抛物线的什么位置时,使得∠PAB=75°,求出此时点P的坐标;(3)当点P从A点出发沿线段AB上方的抛物线向终点B移动,在移动中,点P的横坐标以每秒1个单位长度的速度变动;与此同时点M以每秒1个单位长度的速度沿AO向终点O移动,点P,M移动到各自终点时停止.当两个动点移动t秒时,求四边形PAMB的面积S关于t的函数表达式,并求t 为何值时,S有最大值,最大值是多少?8.如图,直线y=﹣x+分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+经过A,B两点.(1)求A、B两点的坐标;(2)求抛物线的解析式;(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.9.如图,抛物线y=ax2+bx﹣2的对称轴是直线x=1,与x轴交于A,B两点,与y轴交于点C,点A的坐标为(﹣2,0),点P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E.(1)求抛物线解析式;(2)若点P在第一象限,当OD=4PE时,求四边形POBE的面积;(3)在(2)的条件下,若点M为直线BC上一点,点N为平面直角坐标系一点,是否存在这样的点M和点N,使得以点B,D,M,N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,请说明理由.【温馨提示:考生可以根据题意,在备用图中补充图形,以便探究】10.如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.(1)求抛物线的解析式;(2)在第二象限取一点C,作CD垂直X轴于点D,AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q 为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.11.如图,已知抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3),点M、N为抛物线上的动点,过点M作MD∥y轴,交直线BC于点D,交x 轴于点E.(1)求二次函数y=ax2+bx+c的表达式;(2)过点N作NF⊥x轴,垂足为点F,若四边形MNFE为正方形(此处限定点M在对称轴的右侧),求该正方形的面积;(3)若∠DMN=90°,MD=MN,求点M的横坐标.12.如图1,已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为﹣,直线l的解析式为y=x.(1)求二次函数的解析式;(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.13.如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).(1)请直接写出B、C两点的坐标及抛物线的解析式;(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.14.如图所示,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y 轴分别相交于M(4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.(1)求线段CD的长及顶点P的坐标;(2)求抛物线的函数表达式;(3)设抛物线交x轴于A,B两点,在抛物线上是否存在点Q,使得S四边形OPMN=8S△QAB,且△QAB∽△OBN成立?若存在,请求出Q点的坐标;若不存在,请说明理由.15.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.(1)求抛物线的解析式;(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点N从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN的面积为S,点M运动时间为t,试求S与t的函数关系,并求S的最大值;(3)在点M运动过程中,是否存在某一时刻t,使△MBN为直角三角形?若存在,求出t值;若不存在,请说明理由.16.已知抛物线y=ax2+bx+c,其中2a=b>0>c,且a+b+c=0.(1)直接写出关于x的一元二次方程ax2+bx+c=0的一个根;(2)证明:抛物线y=ax2+bx+c的顶点A在第三象限;(3)直线y=x+m与x,y轴分别相交于B,C两点,与抛物线y=ax2+bx+c相交于A,D两点.设抛物线y=ax2+bx+c的对称轴与x轴相交于E.如果在对称轴左侧的抛物线上存在点F,使得△ADF与△BOC相似,并且S△ADF =S△ADE,求此时抛物线的表达式.。
2018中考数学二次函数压轴题汇编

1.如图,直线y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过点A,B.(1)求点B的坐标和抛物线的解析式;(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB 及抛物线分别交于点P,N.①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.2.如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C′.(1)求抛物线C的函数表达式;(2)若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C′上的对应点P′,设M是C上的动点,N是C′上的动点,试探究四边形PMP′N能否成为正方形?若能,求出m的值;若不能,请说明理由.3.在平面直角坐标系xOy 中的点P 和图形M ,给出如下的定义:若在图形M 上存在一点Q ,使得P 、Q 两点间的距离小于或等于1,则称P 为图形M 的关联点.(1)当⊙O 的半径为2时,①在点P 1(,0),P 2(,),P 3(,0)中,⊙O 的关联点是 . ②点P 在直线y=﹣x 上,若P 为⊙O 的关联点,求点P 的横坐标的取值范围.(2)⊙C 的圆心在x 轴上,半径为2,直线y=﹣x+1与x 轴、y 轴交于点A 、B .若线段AB 上的所有点都是⊙C 的关联点,直接写出圆心C 的横坐标的取值范围.4.如图,在平面直角坐标系中,抛物线y=﹣x 2+ax+b 交x 轴于A (1,0),B (3,0)两点,点P 是抛物线上在第一象限内的一点,直线BP 与y 轴相交于点C .(1)求抛物线y=﹣x 2+ax+b 的解析式;(2)当点P 是线段BC 的中点时,求点P 的坐标;(3)在(2)的条件下,求sin ∠OCB 的值.5.如图,抛物线y=﹣x 2+bx+c 与x 轴交于点A 和点B ,与y 轴交于点C ,点B 坐标为(6,0),点C 坐标为(0,6),点D 是抛物线的顶点,过点D 作x 轴的垂线,垂足为E ,连接BD .(1)求抛物线的解析式及点D 的坐标;(2)点F 是抛物线上的动点,当∠FBA=∠BDE 时,求点F 的坐标;(3)若点M 是抛物线上的动点,过点M 作MN ∥x 轴与抛物线交于点N ,点P 在x 轴上,点Q 在坐标平面内,以线段MN 为对角线作正方形MPNQ ,请写出点Q 的坐标.6.已知抛物线y=x 2+bx ﹣3(b 是常数)经过点A (﹣1,0).(1)求该抛物线的解析式和顶点坐标;(2)P (m ,t )为抛物线上的一个动点,P 关于原点的对称点为P'. ①当点P'落在该抛物线上时,求m 的值;②当点P'落在第二象限内,P'A 2取得最小值时,求m 的值.7.在同一直角坐标系中,抛物线C 1:y=ax 2﹣2x ﹣3与抛物线C 2:y=x 2+mx+n 关于y 轴对称,C 2与x 轴交于A 、B 两点,其中点A 在点B 的左侧.(1)求抛物线C 1,C 2的函数表达式;(2)求A、B两点的坐标;(3)在抛物线C1上是否存在一点P,在抛物线C2上是否存在一点Q,使得以AB为边,且以A、B、P、Q四点为顶点的四边形是平行四边形?若存在,求出P、Q两点的坐标;若不存在,请说明理由.8.已知函数y=﹣x2+(m﹣1)x+m(m为常数).(1)该函数的图象与x轴公共点的个数是.A.0B.1C.2D.1或2(2)求证:不论m为何值,该函数的图象的顶点都在函数y=(x+1)2的图象上.(3)当﹣2≤m≤3时,求该函数的图象的顶点纵坐标的取值范围.9.已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M(1,0),且a<b.(Ⅰ)求抛物线顶点Q的坐标(用含a的代数式表示);(Ⅱ)说明直线与抛物线有两个交点;(Ⅲ)直线与抛物线的另一个交点记为N.(ⅰ)若﹣1≤a≤﹣,求线段MN长度的取值范围;(ⅱ)求△QMN面积的最小值.10.在平面直角坐标系中,设二次函数y1=(x+a)(x﹣a﹣1),其中a≠0.(1)若函数y1的图象经过点(1,﹣2),求函数y1的表达式;(2)若一次函数y 2=ax+b 的图象与y 1的图象经过x 轴上同一点,探究实数a ,b 满足的关系式;(3)已知点P (x 0,m )和Q (1,n )在函数y 1的图象上,若m <n ,求x 0的取值范围.11.定义:如图1,抛物线y=ax 2+bx+c (a ≠0)与x 轴交于A ,B 两点,点P 在该抛物线上(P 点与A 、B 两点不重合),如果△ABP 的三边满足AP 2+BP 2=AB 2,则称点P 为抛物线y=ax 2+bx+c (a ≠0)的勾股点.(1)直接写出抛物线y=﹣x 2+1的勾股点的坐标.(2)如图2,已知抛物线C :y=ax 2+bx (a ≠0)与x 轴交于A ,B 两点,点P (1,)是抛物线C 的勾股点,求抛物线C 的函数表达式.(3)在(2)的条件下,点Q 在抛物线C 上,求满足条件S △ABQ =S △ABP 的Q 点(异于点P )的坐标.12.如图,二次函数y=x 2+bx+c 的图象与x 轴交于 A 、B 两点,与y 轴交于点C ,OB=OC .点D 在函数图象上,CD ∥x 轴,且CD=2,直线l 是抛物线的对称轴,E 是抛物线的顶点.(1)求b 、c 的值;(2)如图①,连接BE ,线段OC 上的点F 关于直线l 的对称点F'恰好在线段BE 上,求点F 的坐标;(3)如图②,动点P 在线段OB 上,过点P 作x 轴的垂线分别与BC 交于点M ,与抛物线交于点N .试问:抛物线上是否存在点Q ,使得△PQN 与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.13.如图,在平面直角坐标系中,抛物线y=x2﹣x﹣与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.(1)求直线AE的解析式;(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;(3)点G是线段CE的中点,将抛物线y=x2﹣x﹣沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.14.如图,抛物线y=ax 2+bx+2经过点A (﹣1,0),B (4,0),交y 轴于点C ;(1)求抛物线的解析式(用一般式表示);(2)点D 为y 轴右侧抛物线上一点,是否存在点D 使S △ABC =S △ABD ?若存在请直接给出点D 坐标;若不存在请说明理由;(3)将直线BC 绕点B 顺时针旋转45°,与抛物线交于另一点E ,求BE 的长.15.如图,直线y=kx+b (k 、b 为常数)分别与x 轴、y 轴交于点A (﹣4,0)、B (0,3),抛物线y=﹣x 2+2x+1与y 轴交于点C .(1)求直线y=kx+b 的函数解析式;(2)若点P (x ,y )是抛物线y=﹣x 2+2x+1上的任意一点,设点P 到直线AB 的距离为d ,求d 关于x 的函数解析式,并求d 取最小值时点P 的坐标;(3)若点E 在抛物线y=﹣x 2+2x+1的对称轴上移动,点F 在直线AB 上移动,求CE+EF 的最小值.16.如图,已知二次函数y=x 2﹣4的图象与x 轴交于A ,B 两点,与y 轴交于点C,⊙C的半径为,P为⊙C上一动点.(1)点B,C的坐标分别为B(),C();(2)是否存在点P,使得△PBC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;(3)连接PB,若E为PB的中点,连接OE,则OE的最大值= .17.已知点A(﹣1,1)、B(4,6)在抛物线y=ax2+bx上(1)求抛物线的解析式;(2)如图1,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH、AE,求证:FH∥AE;(3)如图2,直线AB分别交x轴、y轴于C、D两点.点P从点C出发,沿射线CD方向匀速运动,速度为每秒个单位长度;同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度.点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=2PM,直接写出t的值.18.已知直线y=kx+b 与抛物线y=ax 2(a >0)相交于A 、B 两点(点A 在点B 的左侧),与y 轴正半轴相交于点C ,过点A 作AD ⊥x 轴,垂足为D .(1)若∠AOB=60°,AB ∥x 轴,AB=2,求a 的值;(2)若∠AOB=90°,点A 的横坐标为﹣4,AC=4BC ,求点B 的坐标;(3)延长AD 、BO 相交于点E ,求证:DE=CO .19.如图,抛物线y=mx 2﹣16mx+48m (m >0)与x 轴交于A ,B 两点(点B 在点A 左侧),与y 轴交于点C ,点D 是抛物线上的一个动点,且位于第四象限,连接OD 、BD 、AC 、AD ,延长AD 交y 轴于点E .(1)若△OAC 为等腰直角三角形,求m 的值;(2)若对任意m >0,C 、E 两点总关于原点对称,求点D 的坐标(用含m 的式子表示);(3)当点D 运动到某一位置时,恰好使得∠ODB=∠OAD ,且点D 为线段AE 的中点,此时对于该抛物线上任意一点P (x 0,y 0)总有n+≥﹣4my 02﹣12y0﹣50成立,求实数n 的最小值.20.如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,抛物线y=﹣x2+bx+c经过A、C两点,与x轴的另一交点为点B.(1)求抛物线的函数表达式;(2)点D为直线AC上方抛物线上一动点,①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S,△BCE1,求的最大值;的面积为S2②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF 中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由.21.在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,且经过点A(0,)(1)若此抛物线经过点B(2,﹣),且与x轴相交于点E,F.①填空:b= (用含a的代数式表示);②当EF2的值最小时,求抛物线的解析式;(2)若a=,当0≤x≤1,抛物线上的点到x轴距离的最大值为3时,求b的值.22.如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x 轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3,),过点D 作DC⊥x轴,垂足为C.(1)求抛物线的表达式;(2)点P在线段OC上(不与点O、C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,连接CM,求△PCM面积的最大值;(3)若P是x轴正半轴上的一动点,设OP的长为t,是否存在t,使以点M、C、D、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.23.如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.(1)求抛物线的解析式;(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.24.已知函数y=mx 2﹣(2m ﹣5)x+m ﹣2的图象与x 轴有两个公共点.(1)求m 的取值范围,并写出当m 取范围内最大整数时函数的解析式;(2)题(1)中求得的函数记为C 1.①当n ≤x ≤﹣1时,y 的取值范围是1≤y ≤﹣3n ,求n 的值;②函数C 2:y=m (x ﹣h )2+k 的图象由函数C 1的图象平移得到,其顶点P 落在以原点为圆心,半径为的圆内或圆上.设函数C 1的图象顶点为M ,求点P 与点M 距离最大时函数C 2的解析式.25.如图,抛物线y=x 2+x+c 与x 轴的负半轴交于点A ,与y 轴交于点B ,连结AB ,点C (6,)在抛物线上,直线AC 与y 轴交于点D .(1)求c 的值及直线AC 的函数表达式;(2)点P 在x 轴正半轴上,点Q 在y 轴正半轴上,连结PQ 与直线AC 交于点M ,连结MO 并延长交AB 于点N ,若M 为PQ 的中点.①求证:△APM ∽△AON ;②设点M 的横坐标为m ,求AN 的长(用含m 的代数式表示).26.如图,过抛物线y=x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.(1)求抛物线的对称轴和点B的坐标;(2)在AB上任取一点P,连结OP,作点C关于直线OP的对称点D;①连结BD,求BD的最小值;②当点D落在抛物线的对称轴上,且在x轴上方时,求直线PD的函数表达式.27.如图,已知抛物线y=ax2+bx+c(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线y=x+1与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m 上每一点的纵坐标都等于1.(1)求抛物线的解析式;(2)证明:圆C与x轴相切;(3)过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求BE:MF的值.28.平面直角坐标系xOy中,点A、B的横坐标分别为a、a+2,二次函数y=﹣x2+(m﹣2)x+2m的图象经过点A、B,且a、m满足2a﹣m=d(d 为常数).=kx+b的图象经过A、B两点.(1)若一次函数y1①当a=1、d=﹣1时,求k的值;随x的增大而减小,求d的取值范围;②若y1(2)当d=﹣4且a≠﹣2、a≠﹣4时,判断直线AB与x轴的位置关系,并说明理由;(3)点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.29.如图,抛物线y=﹣x2+x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).(1)求直线BC的函数表达式;(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)②在点P、Q运动的过程中,当PQ=PD时,求t的值;(3)试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD 的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由.30.如图,在平面直角坐标系xOy中,抛物线y=x2﹣2x﹣3交x轴于A,B 两点(点A在点B的左侧),将该抛物线位于x轴上方曲线记作M,将该抛物线位于x轴下方部分沿x轴翻折,翻折后所得曲线记作N,曲线N交y轴于点C,连接AC、BC.(1)求曲线N所在抛物线相应的函数表达式;(2)求△ABC外接圆的半径;(3)点P为曲线M或曲线N上的一动点,点Q为x轴上的一个动点,若以点B,C,P,Q为顶点的四边形是平行四边形,求点Q的坐标.31.如图,是将抛物线y=﹣x2平移后得到的抛物线,其对称轴为x=1,与x 轴的一个交点为A(﹣1,0),另一个交点为B,与y轴的交点为C.(1)求抛物线的函数表达式;(2)若点N 为抛物线上一点,且BC ⊥NC ,求点N 的坐标;(3)点P 是抛物线上一点,点Q 是一次函数y=x+的图象上一点,若四边形OAPQ 为平行四边形,这样的点P 、Q 是否存在?若存在,分别求出点P 、Q 的坐标;若不存在,说明理由.32.如图,已知二次函数y=ax 2+bx+3(a ≠0)的图象经过点A (3,0),B (4,1),且与y 轴交于点C ,连接AB 、AC 、BC .(1)求此二次函数的关系式;(2)判断△ABC 的形状;若△ABC 的外接圆记为⊙M ,请直接写出圆心M 的坐标;(3)若将抛物线沿射线BA 方向平移,平移后点A 、B 、C 的对应点分别记为点A 1、B 1、C 1,△A 1B 1C 1的外接圆记为⊙M 1,是否存在某个位置,使⊙M 1经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.33.抛物线y=4x 2﹣2ax+b 与x 轴相交于A (x 1,0),B (x 2,0)(0<x 1<x 2)两点,与y 轴交于点C .(1)设AB=2,tan ∠ABC=4,求该抛物线的解析式;(2)在(1)中,若点D 为直线BC 下方抛物线上一动点,当△BCD 的面积最大时,求点D 的坐标;(3)是否存在整数a ,b 使得1<x 1<2和1<x 2<2同时成立,请证明你的结论.34.如图,已知二次函数y=ax 2+bx+c (a ≠0)的图象经过A (﹣1,0)、B (4,0)、C (0,2)三点.(1)求该二次函数的解析式;(2)点D 是该二次函数图象上的一点,且满足∠DBA=∠CAO (O 是坐标原点),求点D 的坐标;(3)点P 是该二次函数图象上位于第一象限上的一动点,连接PA 分别交BC 、y 轴于点E 、F ,若△PEB 、△CEF 的面积分别为S 1、S 2,求S 1﹣S 2的最大值.35.如图1,抛物线y=ax 2+bx+c 经过平行四边形ABCD 的顶点A (0,3)、B (﹣1,0)、D (2,3),抛物线与x 轴的另一交点为E .经过点E 的直线l 将平行四边形ABCD 分割为面积相等的两部分,与抛物线交于另一点F .点P 为直线l 上方抛物线上一动点,设点P 的横坐标为t .(1)求抛物线的解析式;(2)当t 何值时,△PFE 的面积最大?并求最大值的立方根;(3)是否存在点P使△PAE为直角三角形?若存在,求出t的值;若不存在,说明理由.36.如图,某日的钱塘江观潮信息如图:按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC 可用二次函数s=t2+bt+c(b,c是常数)刻画.(1)求m的值,并求出潮头从甲地到乙地的速度;(2)11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度v=v 0+(t ﹣30),v 0是加速前的速度).37.如图1,抛物线y=ax 2+bx+2与x 轴交于A ,B 两点,与y 轴交于点C ,AB=4,矩形OBDC 的边CD=1,延长DC 交抛物线于点E .(1)求抛物线的解析式;(2)如图2,点P 是直线EO 上方抛物线上的一个动点,过点P 作y 轴的平行线交直线EO 于点G ,作PH ⊥EO ,垂足为H .设PH 的长为l ,点P 的横坐标为m ,求l 与m 的函数关系式(不必写出m 的取值范围),并求出l 的最大值;(3)如果点N 是抛物线对称轴上的一点,抛物线上是否存在点M ,使得以M ,A ,C ,N 为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M 的坐标;若不存在,请说明理由.38.如图,抛物线y=﹣x 2+bx+c 与直线AB 交于A (﹣4,﹣4),B (0,4)两点,直线AC :y=﹣x ﹣6交y 轴于点C .点E 是直线AB 上的动点,过点E 作EF ⊥x 轴交AC 于点F ,交抛物线于点G .(1)求抛物线y=﹣x 2+bx+c 的表达式;(2)连接GB ,EO ,当四边形GEOB 是平行四边形时,求点G 的坐标;(3)①在y 轴上存在一点H ,连接EH ,HF ,当点E 运动到什么位置时,以A ,E ,F ,H 为顶点的四边形是矩形?求出此时点E ,H 的坐标;②在①的前提下,以点E 为圆心,EH 长为半径作圆,点M 为⊙E 上一动点,求AM+CM它的最小值.39.抛物线y=ax2+bx+3经过点A(1,0)和点B(5,0).(1)求该抛物线所对应的函数解析式;(2)该抛物线与直线y=x+3相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M、N.①连结PC、PD,如图1,在点P运动过程中,△PCD的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;②连结PB,过点C作CQ⊥PM,垂足为点Q,如图2,是否存在点P,使得△CNQ与△PBM相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.40.《函数的图象与性质》拓展学习片段展示:【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣经过原点O,与x轴的另一个交点为A,则a= .【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为G,如图②.直接写出图象G对应的函数解析式.【探究】在图②中,过点B(0,1)作直线l平行于x轴,与图象G的交点从左至右依次为点C,D,E,F,如图③.求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围.【应用】P是图③中图象G上一点,其横坐标为m,连接PD,PE.直接写出△PDE的面积不小于1时m的取值范围.1.如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A (,0),在第一象限内与直线y=x交于点B(2,t).(1)求这条抛物线的表达式;(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.2.如图①,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.(1)填空:b= ,c= ;(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P 为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;(4)如图②,点N的坐标为(﹣,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.3.定义:对于给定的两个函数,任取自变量x 的一个值,当x <0时,它们对应的函数值互为相反数;当x ≥0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x ﹣1,它的相关函数为y=.(1)已知点A (﹣5,8)在一次函数y=ax ﹣3的相关函数的图象上,求a 的值;(2)已知二次函数y=﹣x 2+4x ﹣.①当点B (m ,)在这个函数的相关函数的图象上时,求m 的值;②当﹣3≤x ≤3时,求函数y=﹣x 2+4x ﹣的相关函数的最大值和最小值;(3)在平面直角坐标系中,点M ,N 的坐标分别为(﹣,1),(,1),连结MN .直接写出线段MN 与二次函数y=﹣x 2+4x+n 的相关函数的图象有两个公共点时n 的取值范围.4.如图,在平面直角坐标系xOy 中,已知A ,B 两点的坐标分别为(﹣4,0),(4,0),C (m ,0)是线段A B 上一点(与 A ,B 点不重合),抛物线L 1:y=ax 2+b 1x+c 1(a <0)经过点A ,C ,顶点为D ,抛物线L 2:y=ax 2+b 2x+c 2(a <0)经过点C ,B ,顶点为E ,AD ,BE 的延长线相交于点F .(1)若a=﹣,m=﹣1,求抛物线L 1,L 2的解析式;(2)若a=﹣1,AF ⊥BF ,求m 的值;(3)是否存在这样的实数a (a <0),无论m 取何值,直线AF 与BF 都不可能互相垂直?若存在,请直接写出a 的两个不同的值;若不存在,请说明理由.5.如图,已知抛物线y=ax2﹣2ax﹣9a与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D 的直线l与射线AC,AB分别交于点M,N.(1)直接写出a的值、点A的坐标及抛物线的对称轴;(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P 的坐标;(3)证明:当直线l绕点D旋转时,+均为定值,并求出该定值.6.如图1,矩形OABC的顶点A,C的坐标分别为(4,0),(0,6),直:y=ax2+bx(a≠0)过A,线AD交B C于点D,tan∠OAD=2,抛物线M1D两点.的表达式;(1)求点D的坐标和抛物线M1(2)点P是抛物线M对称轴上一动点,当∠CPA=90°时,求所有符合条1件的点P的坐标;的图象向下平移m(m (3)如图2,点E(0,4),连接AE,将抛物线M1.>0)个单位得到抛物线M2①设点D平移后的对应点为点D′,当点D′恰好在直线AE上时,求m的值;与直线AE有两个交点,求m的②当1≤x≤m(m>1)时,若抛物线M2取值范围.7.如图,已知抛物线y=ax2+2x+c与y轴交于点A(0,6),与x轴交于点B(6,0),点P是线段AB上方抛物线上的一个动点.(1)求这条抛物线的表达式及其顶点坐标;(2)当点P移动到抛物线的什么位置时,使得∠PAB=75°,求出此时点P 的坐标;(3)当点P从A点出发沿线段AB上方的抛物线向终点B移动,在移动中,点P的横坐标以每秒1个单位长度的速度变动;与此同时点M以每秒1个单位长度的速度沿AO向终点O移动,点P,M移动到各自终点时停止.当两个动点移动t秒时,求四边形PAMB的面积S关于t的函数表达式,并求t为何值时,S有最大值,最大值是多少?8.如图,直线y=﹣x+分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+经过A,B两点.(1)求A、B两点的坐标;(2)求抛物线的解析式;(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.9.如图,抛物线y=ax2+bx﹣2的对称轴是直线x=1,与x轴交于A,B两点,与y轴交于点C,点A的坐标为(﹣2,0),点P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E.(1)求抛物线解析式;(2)若点P在第一象限内,当OD=4PE时,求四边形POBE的面积;(3)在(2)的条件下,若点M为直线BC上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点B,D,M,N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,请说明理由.【温馨提示:考生可以根据题意,在备用图中补充图形,以便探究】10.如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.(1)求抛物线的解析式;(2)在第二象限内取一点C,作CD垂直X轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q 为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.11.如图,已知抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3),点M、N为抛物线上的动点,过点M作MD∥y轴,交直线BC于点D,交x轴于点E.(1)求二次函数y=ax2+bx+c的表达式;(2)过点N作NF⊥x轴,垂足为点F,若四边形MNFE为正方形(此处限定点M在对称轴的右侧),求该正方形的面积;(3)若∠DMN=90°,MD=MN,求点M的横坐标.12.如图1,已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为﹣,直线l的解析式为y=x.(1)求二次函数的解析式;(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x 轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.13.如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P 是线段CB上的动点,设CP=t(0<t<10).(1)请直接写出B、C两点的坐标及抛物线的解析式;(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.14.如图所示,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y 轴分别相交于M(4,0),N(0,3)两点.已知抛物线开口向上,与⊙C 交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x 轴于点D.(1)求线段CD的长及顶点P的坐标;(2)求抛物线的函数表达式;(3)设抛物线交x轴于A,B两点,在抛物线上是否存在点Q,使得S四边形OPMN =8S△QAB,且△QAB∽△OBN成立?若存在,请求出Q点的坐标;若不存在,请说明理由.15.如图,在平面直角坐标系中,抛物线y=ax 2+bx+c (a ≠0)与y 轴交与点C (0,3),与x 轴交于A 、B 两点,点B 坐标为(4,0),抛物线的对称轴方程为x=1.(1)求抛物线的解析式;(2)点M 从A 点出发,在线段AB 上以每秒3个单位长度的速度向B 点运动,同时点N 从B 点出发,在线段BC 上以每秒1个单位长度的速度向C 点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN 的面积为S ,点M 运动时间为t ,试求S 与t 的函数关系,并求S 的最大值;(3)在点M 运动过程中,是否存在某一时刻t ,使△MBN 为直角三角形?若存在,求出t 值;若不存在,请说明理由.16.已知抛物线y=ax 2+bx+c ,其中2a=b >0>c ,且a+b+c=0.(1)直接写出关于x 的一元二次方程ax 2+bx+c=0的一个根;(2)证明:抛物线y=ax 2+bx+c 的顶点A 在第三象限;(3)直线y=x+m 与x ,y 轴分别相交于B ,C 两点,与抛物线y=ax 2+bx+c 相交于A ,D 两点.设抛物线y=ax 2+bx+c 的对称轴与x 轴相交于E .如果在对称轴左侧的抛物线上存在点F ,使得△ADF 与△BOC 相似,并且S △ADF =S △ADE ,求此时抛物线的表达式.。
2018年中考全国部分省市全省统一命题数学试卷《二次函数》压轴题精编(解析版)

2018年中考全国部分省市全省统一命题数学试卷《二次函数》压轴题精编(解析版)二次函数综合题:(共17小题)1.(2018•上海)在平面直角坐标系xOy 中(如图).已知抛物线212y x bx c =-++经过点(1,0)A -和点5(0,)2B ,顶点为C ,点D 在其对称轴上且位于点C 下方,将线段DC 绕点D按顺时针方向旋转90︒,点C 落在抛物线上的点P 处. (1)求这条抛物线的表达式; (2)求线段CD 的长;(3)将抛物线平移,使其顶点C 移到原点O 的位置,这时点P 落在点E 的位置,如果点M 在y 轴上,且以O 、D 、E 、M 为顶点的四边形面积为8,求点M 的坐标.2.(2018•河北)如图是轮滑场地的截面示意图,平台AB 距x 轴(水平)18米,与y 轴交于点B ,与滑道(1)ky x x=…交于点A ,且1AB =米.运动员(看成点)在BA 方向获得速度v 米/秒后,从A 处向右下飞向滑道,点M 是下落路线的某位置.忽略空气阻力,实验表明:M ,A 的竖直距离h (米)与飞出时间t (秒)的平方成正比,且1t =时5h =,M ,A 的水平距离是vt 米.(1)求k ,并用t 表示h ;(2)设5v =.用t 表示点M 的横坐标x 和纵坐标y ,并求y 与x 的关系式(不写x 的取值范围),及13y =时运动员与正下方滑道的竖直距离;(3)若运动员甲、乙同时从A 处飞出,速度分别是5米/秒、v 乙米/秒.当甲距x 轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t 的值及v 乙的范围.3.(2018•河南)如图,抛物线26y ax x c =++交x 轴于A ,B 两点,交y 轴于点C .直线5y x =-经过点B ,C .(1)求抛物线的解析式;(2)过点A 的直线交直线BC 于点M .①当AM BC ⊥时,过抛物线上一动点P (不与点B ,C 重合),作直线AM 的平行线交直线BC 于点Q ,若以点A ,M ,P ,Q 为顶点的四边形是平行四边形,求点P 的横坐标;②连接AC ,当直线AM 与直线BC 的夹角等于ACB ∠的2倍时,请直接写出点M 的坐标.4.(2018•天津)在平面直角坐标系中,点(0,0)O ,点(1,0)A .已知抛物线22(y x mx m m=+-是常数),顶点为P .(Ⅰ)当抛物线经过点A 时,求顶点P 的坐标;(Ⅱ)若点P 在x 轴下方,当45AOP ∠=︒时,求抛物线的解析式;(Ⅲ)无论m 取何值,该抛物线都经过定点H .当45AHP ∠=︒时,求抛物线的解析式. 5.(2018•重庆A 卷)如图,在平面直角坐标系中,点A 在抛物线24y x x =-+上,且横坐标为1,点B 与点A 关于抛物线的对称轴对称,直线AB 与y 轴交于点C ,点D 为抛物线的顶点,点E 的坐标为(1,1). (1)求线段AB 的长;(2)点P 为线段AB 上方抛物线上的任意一点,过点P 作AB 的垂线交AB 于点H ,点F 为y 轴上一点,当PBE ∆的面积最大时,求12PH HF FO ++的最小值;(3)在(2)中,12PH HF FO ++取得最小值时,将CFH ∆绕点C 顺时针旋转60︒后得到△CF H '',过点F '作CF '的垂线与直线AB 交于点Q ,点R 为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S ,使以点D ,Q ,R ,S 为顶点的四边形为菱形,若存在,请直接写出点S 的坐标,若不存在,请说明理由.6.(2018•重庆B 卷)抛物线2y x =-+x 轴交于点A ,B (点A 在点B 的左边),与y 轴交于点C ,点D 是该抛物线的顶点. (1)如图1,连接CD ,求线段CD 的长;(2)如图2,点P 是直线AC 上方抛物线上一点,PF x ⊥轴于点F ,PF 与线段AC 交于点E ;将线段OB 沿x 轴左右平移,线段OB 的对应线段是11O B ,当12PE EC +的值最大时,求四边形11PO B C 周长的最小值,并求出对应的点1O 的坐标;(3)如图3,点H 是线段AB 的中点,连接CH ,将OBC ∆沿直线CH 翻折至△22O B C 的位置,再将△22O B C 绕点2B 旋转一周,在旋转过程中,点2O ,C 的对应点分别是点3O ,1C ,直线31O C 分别与直线AC ,x 轴交于点M ,N .那么,在△22O B C 的整个旋转过程中,是否存在恰当的位置,使AMN ∆是以MN 为腰的等腰三角形?若存在,请直接写出所有符合条件的线段2O M 的长;若不存在,请说明理由.7.(2018•吉林)如图,在平面直角坐标系中,抛物线223(0)y ax ax a a =+-<与x 轴相交于A ,B 两点,与y 轴相交于点C ,顶点为D ,直线DC 与x 轴相交于点E . (1)当1a =-时,抛物线顶点D 的坐标为 ,OE = ; (2)OE 的长是否与a 值有关,说明你的理由; (3)设DEO β∠=,4560β︒︒剟,求a 的取值范围;(4)以DE 为斜边,在直线DE 的左下方作等腰直角三角形PDE .设(,)P m n ,直接写出n 关于m 的函数解析式及自变量m 的取值范围.8.(2018•吉林长春)如图,在平面直角坐标系中,矩形ABCD 的对称中心为坐标原点O ,AD y ⊥轴于点E (点A 在点D 的左侧),经过E 、D 两点的函数211(0)2y x mx x =-++…的图象记为1G ,函数211(0)2y x mx x =---<的图象记为2G ,其中m 是常数,图象1G 、2G 合起来得到的图象记为G .设矩形ABCD 的周长为L . (1)当点A 的横坐标为1-时,求m 的值; (2)求L 与m 之间的函数关系式;(3)当2G 与矩形ABCD 恰好有两个公共点时,求L 的值;(4)设G 在42x -剟上最高点的纵坐标为0y ,当0392y 剟时,直接写出L 的取值范围.9.(2018•山西)综合与探究如图,抛物线211433y x x =--与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C,连接AC ,BC .点P 是第四象限内抛物线上的一个动点,点P 的横坐标为m ,过点P 作PM x ⊥轴,垂足为点M ,PM 交BC 于点Q ,过点P 作//PE AC 交x 轴于点E ,交BC 于点F .(1)求A ,B ,C 三点的坐标;(2)试探究在点P 运动的过程中,是否存在这样的点Q ,使得以A ,C ,Q 为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q 的坐标;若不存在,请说明理由; (3)请用含m 的代数式表示线段QF 的长,并求出m 为何值时QF 有最大值.10.(2018•陕西)已知抛物线2:6L y x x =+-与x 轴相交于A 、B 两点(点A 在点B 的左侧),并与y 轴相交于点C .(1)求A 、B 、C 三点的坐标,并求ABC ∆的面积;(2)将抛物线L 向左或向右平移,得到抛物线L ',且L '与x 轴相交于A '、B '两点(点A '在点B '的左侧),并与y 轴相交于点C ',要使△A B C '''和ABC ∆的面积相等,求所有满11.(2018•海南)如图1,抛物线23y ax bx=++交x轴于点(1,0)B.A-和点(3,0)(1)求该抛物线所对应的函数解析式;(2)如图2,该抛物线与y轴交于点C,顶点为F,点(2,3)D在该抛物线上.①求四边形ACFD的面积;②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ x⊥轴交该抛物线于点Q,连接AQ、DQ,当AQD∆是直角三角形时,求出所有满足条件的点Q的坐标.12.(2018•江西)小贤与小杰在探究某类二次函数问题时,经历了如下过程:求解体验:(1)已知抛物线23=-+-经过点(1,0)y x bx-,则b=,顶点坐标为,该抛物线关于点(0,1)成中心对称的抛物线表达式是.抽象感悟:我们定义:对于抛物线2(0)=++≠,以y轴上的点(0,)y ax bx c aM m为中心,作该抛物线关于点M对称的抛物线y',则我们又称抛物线y'为抛物线y的“衍生抛物线”,点M为“衍生中心”.(2)已知抛物线225y x x=--+关于点(0,)m的衍生抛物线为y',若这两条抛物线有交点,求m的取值范围.问题解决:(3)已知抛物线22(0)=+-≠y ax ax b a①若抛物线y的衍生抛物线为22'=-+≠,两抛物线有两个交点,且恰好是2(0)y bx bx a b它们的顶点,求a、b的值及衍生中心的坐标;②若抛物线y 关于点2(0,1)k +的衍生抛物线为1y ,其顶点为1A ;关于点2(0,2)k +的衍生抛物线为2y ,其顶点为2A ;⋯;关于点2(0,)k n +的衍生抛物线为n y ,其顶点为(n A n ⋯为正整数).求1n n A A +的长(用含n 的式子表示).13.(2018•青海)如图,抛物线2y ax bx c =++与坐标轴交点分别为(1,0)A -,(3,0)B ,(0,2)C ,作直线BC .(1)求抛物线的解析式;(2)点P 为抛物线上第一象限内一动点,过点P 作PD x ⊥轴于点D ,设点P 的横坐标为(03)t t <<,求ABP ∆的面积S 与t 的函数关系式; (3)条件同(2),若ODP ∆与COB ∆相似,求点P 的坐标.14.(2018•新疆)如图,在平面直角坐标系中,抛物线222433y x x =--与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C . (1)求点A ,B ,C 的坐标;(2)点P 从A 点出发,在线段AB 上以每秒2个单位长度的速度向B 点运动,同时,点Q 从B 点出发,在线段BC 上以每秒1个单位长度的速度向C 点运动,当其中一个点到达终点时,另一个点也停止运动.设运动时间为t 秒,求运动时间t 为多少秒时,PBQ ∆的面积S 最大,并求出其最大面积;(3)在(2)的条件下,当PBQ ∆面积最大时,在BC 下方的抛物线上是否存在点M ,使BMC∆的面积是PBQ ∆面积的1.6倍?若存在,求点M 的坐标;若不存在,请说明理由.15.(2018•安徽)小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆.售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元.调研发现: ①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x 盆,第二期盆景与花卉售完后的利润分别为1W ,2W (单位:元). (1)用含x 的代数式分别表示1W ,2W ;(2)当x 取何值时,第二期培植的盆景与花卉售完后获得的总利润W 最大,最大总利润是多少?16.(2018•福建A 卷)已知抛物线2y ax bx c =++过点(0,2)A .(1)若点(0)也在该抛物线上,求a ,b 满足的关系式;(2)若该抛物线上任意不同两点1(M x ,1)y ,2(N x ,2)y 都满足:当120x x <<时,1212()()0x x y y -->;当120x x <<时,1212()()0x x y y --<.以原点O 为心,OA 为半径的圆与拋物线的另两个交点为B ,C ,且ABC ∆有一个内角为60︒. ①求抛物线的解析式;②若点P 与点O 关于点A 对称,且O ,M ,N 三点共线,求证:PA 平分MPN ∠. 17.(2018•福建B 卷)已知抛物线2y ax bx c =++过点(0,2)A ,且抛物线上任意不同两点1(M x ,1)y ,2(N x ,2)y 都满足:当120x x <<时,1212()()0x x y y -->;当120x x <<时,1212()()0x x y y --<.以原点O 为圆心,OA 为半径的圆与抛物线的另两个交点为B ,C ,且B 在C 的左侧,ABC ∆有一个内角为60︒. (1)求抛物线的解析式;(2)若MN 与直线y =-平行,且M ,N 位于直线BC 的两侧,12y y >,解决以下问题:①求证:BC 平分MBN ∠;②求MBC ∆外心的纵坐标的取值范围.2018年中考全国部分省市全省统一命题数学试卷《二次函数》压轴题精编参考解析二次函数综合题:(共17小题)1.(2018•上海)在平面直角坐标系xOy 中(如图).已知抛物线212y x bx c =-++经过点(1,0)A -和点5(0,)2B ,顶点为C ,点D 在其对称轴上且位于点C 下方,将线段DC 绕点D按顺时针方向旋转90︒,点C 落在抛物线上的点P 处. (1)求这条抛物线的表达式; (2)求线段CD 的长;(3)将抛物线平移,使其顶点C 移到原点O 的位置,这时点P 落在点E 的位置,如果点M 在y 轴上,且以O 、D 、E 、M 为顶点的四边形面积为8,求点M 的坐标.【解】:(1)把(1,0)A -和点5(0,)2B 代入212y x bx c =-++得10252b c c ⎧--+=⎪⎪⎨⎪=⎪⎩,解得252b c =⎧⎪⎨=⎪⎩, ∴抛物线解析式为215222y x x =-++;(2)219(2)22y x =--+,9(2,)2C ∴,抛物线的对称轴为直线2x =,如图,设CD t =,则9(2,)2D t -,线段DC 绕点D 按顺时针方向旋转90︒,点C 落在抛物线上的点P 处,90PDC ∴∠=︒,DP DC t ==,9(2,)2P t t ∴+-,把9(2,)2P t t +-代入215222y x x =-++得2159(2)2(2)222t t t -++++=-, 整理得220t t -=,解得10t =(舍去),22t =,∴线段CD 的长为2;(3)P 点坐标为5(4,)2,D 点坐标为5(2,)2, 抛物线平移,使其顶点9(2,)2C 移到原点O 的位置,∴抛物线向左平移2个单位,向下平移92个单位, 而P 点5(4,)2向左平移2个单位,向下平移92个单位得到点E ,E ∴点坐标为(2,2)-,设(0,)M m , 当0m >时,15(2)2822m ++=,解得72m =,此时M 点坐标为7(0,)2;当0m <时,15(2)2822m -++=,解得72m =-,此时M 点坐标为7(0,)2-; 综上所述,M 点的坐标为7(0,)2或7(0,)2-.2.(2018•河北)如图是轮滑场地的截面示意图,平台AB 距x 轴(水平)18米,与y 轴交于点B ,与滑道(1)ky x x=…交于点A ,且1AB =米.运动员(看成点)在BA 方向获得速度v 米/秒后,从A 处向右下飞向滑道,点M 是下落路线的某位置.忽略空气阻力,实验表明:M ,A 的竖直距离h (米)与飞出时间t (秒)的平方成正比,且1t =时5h =,M ,A 的水平距离是vt 米.(1)求k ,并用t 表示h ;(2)设5v =.用t 表示点M 的横坐标x 和纵坐标y ,并求y 与x 的关系式(不写x 的取值范围),及13y =时运动员与正下方滑道的竖直距离;(3)若运动员甲、乙同时从A 处飞出,速度分别是5米/秒、v 乙米/秒.当甲距x 轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t 的值及v 乙的范围.【解】:(1)由题意,点(1,18)A 带入ky x= 得:181k =18k ∴=设2h at =,把1t =,5h =代入5a ∴=25h t ∴=(2)5v =,1AB =51x t ∴=+25h t =,18OB =2518y t ∴=-+由51x t =+ 则1(1)5t x =-2211289(1)185555y x x x ∴=--+=-++当13y =时,2113(1)185x =--+ 解得6x =或4-1x …6x ∴=把6x =代入18y x=3y =∴运动员在与正下方滑道的竖直距离是13310-=(米)(3)把 1.8y =代入2518y t =-+得28125t =解得 1.8t =或 1.8-(负值舍去)10x ∴=∴甲坐标为(10,1.8)恰好落在滑道18y x=上 此时,乙的坐标为(1 1.8v +乙,1.8) 由题意:()1 1.815 1.8 4.5v +-+⨯>乙7.5v ∴>乙3.(2018•河南)如图,抛物线26y ax x c =++交x 轴于A ,B 两点,交y 轴于点C .直线5y x =-经过点B ,C .(1)求抛物线的解析式;(2)过点A 的直线交直线BC 于点M .①当AM BC ⊥时,过抛物线上一动点P (不与点B ,C 重合),作直线AM 的平行线交直线BC 于点Q ,若以点A ,M ,P ,Q 为顶点的四边形是平行四边形,求点P 的横坐标;②连接AC ,当直线AM 与直线BC 的夹角等于ACB ∠的2倍时,请直接写出点M 的坐标.【解】:(1)当0x =时,55y x =-=-,则(0,5)C -, 当0y =时,50x -=,解得5x =,则(5,0)B ,把(5,0)B ,(0,5)C -代入26y ax x c =++得253005a c c ++=⎧⎨=-⎩,解得15a b =-⎧⎨=-⎩,∴抛物线解析式为265y x x =-+-;(2)①解方程2650x x -+-=得11x =,25x =,则(1,0)A ,(5,0)B ,(0,5)C -,OCB ∴∆为等腰直角三角形, 45OBC OCB ∴∠=∠=︒, AM BC⊥,AM B ∴∆为等腰直角三角形,4AM AB ∴=== 以点A ,M ,P ,Q 为顶点的四边形是平行四边形,//AM PQ ,PQ AM ∴==PQ BC ⊥,作PD x ⊥轴交直线BC 于D ,如图1,则45PDQ ∠=︒,4PD ∴==,设2(,65)P m m m -+-,则(,5)D m m -, 当P 点在直线BC 上方时,2265(5)54PD m m m m m =-+---=-+=,解得11m =,24m =,当P 点在直线BC 下方时,225(65)54PD m m m m m =---+-=-=,解得1m =,2m =, 综上所述,P 点的横坐标为4; ②作AN BC ⊥于N ,NH x ⊥轴于H ,作AC 的垂直平分线交BC 于1M ,交AC 于E ,如图2,11M A M C =, 11ACM CAM ∴∠=∠, 12AM B ACB ∴∠=∠,ANB∆为等腰直角三角形,2AH BH NH ∴===,(3,2)N ∴-,易得AC 的解析式为55y x =-,E 点坐标为1(2,5)2-, 设直线1EM 的解析式为15y x b =-+, 把1(2E ,5)2-代入得15102b -+=-,解得125b =-,∴直线1EM 的解析式为11255y x =--,解方程组511255y x y x =-⎧⎪⎨=--⎪⎩得136176x y ⎧=⎪⎪⎨⎪=-⎪⎩,则113(6M ,17)6-;作直线BC 上作点1M 关于N 点的对称点2M ,如图2,则212AM C AM B ACB ∠=∠=∠,设2(,5)M x x -,13632x +=, 236x ∴=, 223(6M ∴,7)6-, 综上所述,点M 的坐标为13(6,17)6-或23(6,7)6-.4.(2018•天津)在平面直角坐标系中,点(0,0)O ,点(1,0)A .已知抛物线22(y x mx m m=+-是常数),顶点为P .(Ⅰ)当抛物线经过点A 时,求顶点P 的坐标;(Ⅱ)若点P 在x 轴下方,当45AOP ∠=︒时,求抛物线的解析式;(Ⅲ)无论m 取何值,该抛物线都经过定点H .当45AHP ∠=︒时,求抛物线的解析式. 【解】:(Ⅰ)抛物线22y x mx m =+-经过点(1,0)A ,012m m ∴=+-,解得:1m =,∴抛物线解析式为22y x x =+-,22192()24y x x x =+-=+-,∴顶点P 的坐标为1(2-,9)4-;(Ⅱ)抛物线22y x mx m =+-的顶点P 的坐标为(2m-,28)4m m +-,由点(1,0)A 在x 轴的正半轴上,点P 在x 轴的下方,45AOP ∠=︒知点P 在第四象限, 如图1,过点P 作PQ x ⊥轴于点Q ,则45POQ OPQ ∠=∠=︒,可知PQ OQ =,即2842m m m+=-,解得:10m =,210m =-,当0m =时,点P 不在第四象限,舍去;10m ∴=-,∴抛物线的解析式为21020y x x =-+;(Ⅲ)由222(2)y x mx m x m x =+-=+-可知当2x =时,无论m 取何值时y 都等于4,∴点H 的坐标为(2,4),过点A 作AD AH ⊥,交射线HP 于点D ,分别过点D 、H 作x 轴的垂线,垂足分别为E 、G,则90DEA AGH ∠=∠=︒,90DAH ∠=︒,45AHD ∠=︒, 45ADH ∴∠=︒,AH AD ∴=,90DAE HAG AHG HAG ∠+∠=∠+∠=︒, DAE AHG∴∠=∠,ADE HAG ∴∆≅∆,1DE AG ∴==、4AE HG ==,则点D 的坐标为(3,1)-或(5,1)-;①当点D 的坐标为(3,1)-时,可得直线DH 的解析式为31455y x =+, 点(2m P -,28)4m m +-在直线31455y x =+上,28314()4525m m m +∴-=⨯-+,解得:14m =-、2145m =-,当4m =-时,点P 与点H 重合,不符合题意,145m ∴=-; ②当点D 的坐标为(5,1)-时,可得直线DH 的解析式为52233y x =-+, 点(2m P -,28)4m m +-在直线52233y x =-+上,28522()4323m m m +∴-=-⨯-+, 解得:14m =-(舍),2223m =-,综上,145m =-或223m =-, 则抛物线的解析式为2142855y x x =-+或2224433y x x =-+. 5.(2018•重庆A 卷)如图,在平面直角坐标系中,点A 在抛物线24y x x =-+上,且横坐标为1,点B 与点A 关于抛物线的对称轴对称,直线AB 与y 轴交于点C ,点D 为抛物线的顶点,点E 的坐标为(1,1). (1)求线段AB 的长;(2)点P 为线段AB 上方抛物线上的任意一点,过点P 作AB 的垂线交AB 于点H ,点F 为y 轴上一点,当PBE ∆的面积最大时,求12PH HF FO ++的最小值;(3)在(2)中,12PH HF FO ++取得最小值时,将CFH ∆绕点C 顺时针旋转60︒后得到△CF H '',过点F '作CF '的垂线与直线AB 交于点Q ,点R 为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S ,使以点D ,Q ,R ,S 为顶点的四边形为菱形,若存在,请直接写出点S 的坐标,若不存在,请说明理由.【解】:(1)由题意(1,3)A ,(3,3)B ,2AB ∴=.(2)如图1中,设2(,4)P m m m -+,作//PN y 轴J 交BE 于N . 直线BE 的解析式为y x =,(,)N m m ∴,2212(3)32PEB S m m m m ∆∴=⨯⨯-+=-+,∴当32m =时,PEB ∆的面积最大,此时3(2P ,15)4,3(2H ,3),153344PH ∴=-=, 作直线OG 交AB 于G ,使得30COG ∠=︒,作HK OG ⊥于K 交OC 于F ,12FK OF =,12PH HF FO PH FH FK PH HK ∴++=++=+,此时PH HF OF ++的值最小,1122HG OC OG HK =, 33)32HK ⨯∴==+,PH HF OF ∴++的最小值为94+.(3)如图2中,由题意32CH =,CF =,12QF '=,1CQ =,(1,3)Q ∴-,(2,4)D ,DQ①当DQ 为菱形的边时,1(1,3S -,2(1,3S -, ②当DQ 为对角线时,可得3(1,8)S -, ③当DR 为对角线时,可得4(5,3)S综上所述,满足条件的点S 坐标为(1,3-或(1,3-或(1,8)-或(5,3).6.(2018•重庆B 卷)抛物线2y x =-+x 轴交于点A ,B (点A 在点B 的左边),与y 轴交于点C ,点D 是该抛物线的顶点. (1)如图1,连接CD ,求线段CD 的长;(2)如图2,点P 是直线AC 上方抛物线上一点,PF x ⊥轴于点F ,PF 与线段AC 交于点E ;将线段OB 沿x 轴左右平移,线段OB 的对应线段是11O B ,当12PE EC +的值最大时,求四边形11PO B C 周长的最小值,并求出对应的点1O 的坐标;(3)如图3,点H 是线段AB 的中点,连接CH ,将OBC ∆沿直线CH 翻折至△22O B C 的位置,再将△22O B C 绕点2B 旋转一周,在旋转过程中,点2O ,C 的对应点分别是点3O ,1C ,直线31O C 分别与直线AC ,x 轴交于点M ,N .那么,在△22O B C 的整个旋转过程中,是否存在恰当的位置,使AMN ∆是以MN 为腰的等腰三角形?若存在,请直接写出所有符合条件的线段2O M 的长;若不存在,请说明理由.【解】:(1)如图1,过点D 作DK y ⊥轴于K ,当0x =时,y =C ∴,22y x =++(D ∴,DK ∴CK =-CD ∴(4分)(2)在2y x =+0y =,则20,解得:1x =-,2x =(A ∴-,0),B 0), (0,6)C ,易得直线AC 的解析式为:y x =+设(E x +,2(,P x x -+,2PF x ∴=-EF =Rt ACO ∆中,AO =OC =AC ∴=30CAO ∴∠=︒,2AE EF ∴==+211(()22PE EC x AC AE ∴+=-+-,212=++,2=-,2x =+,(5分)∴当12PE EC +的值最大时,x =-(P -,(6分)PC ∴=,11O B OB ==∴要使四边形11PO B C 周长的最小,即11PO B C +的值最小,如图2,将点P 1(P ,连接11P B ,则111PO PB =,再作点1P 关于x 轴的对称点2(P ,则1121PB P B =,11211PO B C P B B C ∴+=+,∴连接2P C 与x 轴的交点即为使11PO B C +的值最小时的点1B ,1(B ∴,0),将1B 1O ,此时112PO B C P C +==,对应的点1O 的坐标为(0),(7分)∴四边形11PO B C (8分)(3)2O M (12分) 理由是:如图3,H 是AB 的中点,OH ∴= 6OC =CH BC ∴==30HCO BCO ∴∠=∠=︒, 60ACO ∠=︒,∴将CO 沿CH 对折后落在直线AC 上,即2O 在AC 上, 230B CA CAB ∴∠=∠=︒,2//B C AB ∴,2(B ∴-,①如图4,AN MN=,22330MAN AMN O B O ∴∠=∠=︒=∠,由旋转得:2122330CB C O B O ∠=∠=︒,221B C B C =,212175B CC B C C ∴∠=∠=︒,过1C 作12C E B C ⊥于E ,221B C B C ==∴122C E B O ,2B E 22232175O MB B MO B CC ∠=∠=︒=∠, 22190B O M C EC ∠=∠=︒,∴△1C EC ≅△22B O M ,222O M CE B C B E ∴==-=②如图5,AM MN=,此时M 与C 重合,22O M O C =③如图6,AM MN=,2212B C B C B H ===,即N 和H 、1C 重合, 230CAO AHM MHO ∴∠=∠=∠=︒,2213O M AO ∴== ④如图7,AN MN=,过1C 作1C E AC ⊥于E ,30NMA NAM ∴∠=∠=︒,312330O C B O MA ∠=︒=∠,121222290C B O AO B ∴∠=∠=︒, 190C EC ∠=︒,∴四边形122C EO B 是矩形,212EO C B ∴==122C E B O =EM ∴=22O M EO EM ∴=+=,综上所述,2O M 7.(2018•吉林)如图,在平面直角坐标系中,抛物线223(0)y ax ax a a =+-<与x 轴相交于A ,B 两点,与y 轴相交于点C ,顶点为D ,直线DC 与x 轴相交于点E . (1)当1a =-时,抛物线顶点D 的坐标为 (1,4)- ,OE = 3 ; (2)OE 的长是否与a 值有关,说明你的理由; (3)设DEO β∠=,4560β︒︒剟,求a 的取值范围;(4)以DE 为斜边,在直线DE 的左下方作等腰直角三角形PDE .设(,)P m n ,直接写出n 关于m 的函数解析式及自变量m 的取值范围.【解】:(1)当1a =-时,抛物线的解析式为223y x x =--+,∴顶点(1,4)D -,(0,3)C , ∴直线CD 的解析式为3y x =-+,3OE ∴=,故答案为(1,4)-,3.(2)结论:OE 的长与a 值无关. 理由:223y ax ax a =+-,(0,3)C a ∴-,(1,4)D a --,∴直线CD 的解析式为3y ax a =-,当0y =时,3x =,(3,0)E ∴,3OE ∴=,OE ∴的长与a 值无关.(3)当45β=︒时,3OC OE ==,33a ∴-=, 1a ∴=-,当60β=︒时,在Rt OCE ∆中,OC ==3a ∴-=,a ∴=4560β∴︒︒剟,a 的取值范围为1a -.(4)如图,作PM ⊥对称轴于M ,PN AB ⊥于N .PD PE =,90PMD PNE ∠=∠=︒,90DPE MPN ∠=∠=︒,DPM EPN ∴∠=∠, DPM EPN ∴∆≅∆, PM PN ∴=,DM EN =, (1,4)D a --,(3,0)E ,43EN n m ∴=+=-, 1n m ∴=--,当顶点D 在x 轴上时,(1,2)P -,此时m 的值1, 抛物线的顶点在第二象限,1m ∴<.1(1)n m m ∴=--<.8.(2018•吉林长春)如图,在平面直角坐标系中,矩形ABCD 的对称中心为坐标原点O ,AD y ⊥轴于点E (点A 在点D 的左侧),经过E 、D 两点的函数211(0)2y x mx x =-++…的图象记为1G ,函数211(0)2y x mx x =---<的图象记为2G ,其中m 是常数,图象1G 、2G 合起来得到的图象记为G .设矩形ABCD 的周长为L . (1)当点A 的横坐标为1-时,求m 的值; (2)求L 与m 之间的函数关系式;(3)当2G 与矩形ABCD 恰好有两个公共点时,求L 的值;(4)设G 在42x -剟上最高点的纵坐标为0y ,当0392y 剟时,直接写出L 的取值范围.【解】:(1)由题意(0,1)E ,(1,1)A -,(1,1)D 把(1,1)D 代入2112y x mx =-++中,得到1112m =-++,12m ∴=.(2)抛物线1G 的对称轴1mx m =-=-, 2AE ED m ∴==,矩形ABCD 的对称中心为坐标原点O ,4AD BC m ∴==,2AB CD ==, 84L m ∴=+.(3)当2G 与矩形ABCD 恰好有两个公共点,∴抛物线2G 的顶点21(,1)2M m m --在线段AE 上,∴21112m -=, 2m ∴=或2-(舍弃),82420L ∴=⨯+=.(4)1G 的顶点21(,1)2m m +,1G 中(2,21)m -,2G 顶点21(,1)2m m --,2G 中(4,49)m --. ①当2m …,最高点是抛物线1G 的顶点21(,1)2N m m +时, 若213122m +=,解得1m =或1-(舍弃), 若21192m +=时,4m =或4-(舍弃), 又2m …,观察图象可知满足条件的m 的值为12m 剟,②24m <…时,当(2,21)m -是最高点时,23219212112m m m ⎧-⎪⎪⎨⎪->-⎪⎩剟,解得24m <…,③当4m >时,349924921m m m ⎧-⎪⎨⎪->-⎩剟, 解得942m <…, 综上所述,912m剟, 1240L ∴剟.9.(2018•山西)综合与探究如图,抛物线211433y x x =--与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C,连接AC ,BC .点P 是第四象限内抛物线上的一个动点,点P 的横坐标为m ,过点P 作PM x ⊥轴,垂足为点M ,PM 交BC 于点Q ,过点P 作//PE AC 交x 轴于点E ,交BC 于点F .(1)求A ,B ,C 三点的坐标;(2)试探究在点P 运动的过程中,是否存在这样的点Q ,使得以A ,C ,Q 为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q 的坐标;若不存在,请说明理由; (3)请用含m 的代数式表示线段QF 的长,并求出m 为何值时QF 有最大值.【解】:(1)当0y =,2114033x x --=,解得13x =-,24x =,(3,0)A ∴-,(4,0)B ,当0x =,2114433y x x =--=-,(0,4)C ∴-;(2)5AC ,易得直线BC 的解析式为4y x =-, 设(Q m ,4)(04)m m -<<,当CQ CA =时,222(44)5m m +-+=,解得1m =2m =,此时Q 点坐标为4)-; 当AQ AC =时,222(3)(4)5m m ++-=,解得11m =,20m =(舍去),此时Q 点坐标为(1,3)-; 当QA QC =时,2222(3)(4)(44)m m m m ++-=+-+,解得252m =(舍去),综上所述,满足条件的Q 点坐标为4)-或(1,3)-; (3)解:过点F 作FG PQ ⊥于点G ,如图,则//FG x 轴.由(4,0)B ,(0,4)C -得OBC ∆为等腰直角三角形45OBC QFG ∴∠=∠=FQG ∴∆为等腰直角三角形,FG QG ∴==, //PE AC ,//PG CO ,FPG ACO∴∠=∠,90FGP AOC ∠=∠=︒, ~FGP AOC ∴∆∆.∴FG PG OA CO =,即34FG PG=,44233PG FG FQ ∴===,PQ PG GQ ∴=+==,FQ ∴=, 设(P m ,2114)(04)33m m m --<<,则(,4)Q m m -,2211144(4)3333PQ m m m m m ∴=----=-+,2214)2)33FQ m m m ∴=-+=-+20-<, QF ∴有最大值.∴当2m =时,QF 有最大值.10.(2018•陕西)已知抛物线2:6L y x x =+-与x 轴相交于A 、B 两点(点A 在点B 的左侧),并与y 轴相交于点C .(1)求A 、B 、C 三点的坐标,并求ABC ∆的面积;(2)将抛物线L 向左或向右平移,得到抛物线L ',且L '与x 轴相交于A '、B '两点(点A '在点B '的左侧),并与y 轴相交于点C ',要使△A B C '''和ABC ∆的面积相等,求所有满足条件的抛物线的函数表达式.【解】:(1)当0y =时,260x x +-=,解得13x =-,22x =,(3,0)A ∴-,(2,0)B ,当0x =时,266y x x =+-=-,(0,6)C ∴-,ABC∴∆的面积11(23)61522AB OC ==⨯+⨯=; (2)抛物线L 向左或向右平移,得到抛物线L ',5A B AB ∴''==,△A B C '''和ABC ∆的面积相等,6OC OC ∴'==,即(0,6)C '-或(0,6),设抛物线L '的解析式为26y x bx =+-或26y x bx =++ 设(,0)A m '、(,0)B n ',当m 、n 为方程260x bx +-=的两根,m n b ∴+=-,6mn =-,||5n m -=,2()25n m ∴-=, 2()425m n mn ∴+-=,24(6)25b ∴-⨯-=,解得1b =或1-,∴抛物线L '的解析式为26y x x =--.当m 、n 为方程260x bx ++=的两根,m n b ∴+=-,6mn =,||5n m -=,2()25n m ∴-=, 2()425m n mn ∴+-=,24625b ∴-⨯=,解得7b =或7-,∴抛物线L '的解析式为276y x x =++或276y x x =-+.综上所述,抛物线L '的解析式为26y x x =--或276y x x =++或276y x x =-+. 11.(2018•海南)如图1,抛物线23y ax bx =++交x 轴于点(1,0)A -和点(3,0)B . (1)求该抛物线所对应的函数解析式;(2)如图2,该抛物线与y 轴交于点C ,顶点为F ,点(2,3)D 在该抛物线上. ①求四边形ACFD 的面积;②点P 是线段AB 上的动点(点P 不与点A 、B 重合),过点P 作PQ x ⊥轴交该抛物线于点Q ,连接AQ 、DQ ,当AQD ∆是直角三角形时,求出所有满足条件的点Q 的坐标.【解】:(1)由题意可得309330a b a b -+=⎧⎨++=⎩,解得12a b =-⎧⎨=⎩,∴抛物线解析式为223y x x =-++;(2)①2223(1)4y x x x =-++=--+,(1,4)F ∴, (0,3)C ,(2,3)D ,2CD ∴=,且//CD x 轴,(1,0)A -,()1123243422ACD FCD ACFD S S S ∆∆∴=+=⨯⨯+⨯⨯-=四边形;②点P 在线段AB 上,DAQ ∴∠不可能为直角,∴当AQD ∆为直角三角形时,有90ADQ ∠=︒或90AQD ∠=︒,i .当90ADQ ∠=︒时,则DQ AD ⊥,(1,0)A -,(2,3)D ,∴直线AD 解析式为1y x =+, ∴可设直线DQ 解析式为y x b =-+',把(2,3)D 代入可求得5b '=,∴直线DQ 解析式为5y x =-+,联立直线DQ 和抛物线解析式可得2523y x y x x =-+⎧⎨=-++⎩,解得14x y =⎧⎨=⎩或23x y =⎧⎨=⎩, (1,4)Q ∴;ii .当90AQD ∠=︒时,设2(,23)Q t t t -++,设直线AQ 的解析式为11y k x b =+, 把A 、Q 坐标代入可得1121123k b tk b t t -+=⎧⎨+=-++⎩,解得1(3)k t =--, 设直线DQ 解析式为22y k x b =+,同理可求得2k t =-,AQ DQ ⊥,121k k ∴=-,即(3)1t t -=-,解得t =,当t =223t t -++=,当t时,223t t -++=, Q ∴点坐标为或; 综上可知Q 点坐标为(1,4)或或. 12.(2018•江西)小贤与小杰在探究某类二次函数问题时,经历了如下过程: 求解体验:(1)已知抛物线23y x bx =-+-经过点(1,0)-,则b = 4- ,顶点坐标为 ,该抛物线关于点(0,1)成中心对称的抛物线表达式是 .抽象感悟:我们定义:对于抛物线2(0)y ax bx c a =++≠,以y 轴上的点(0,)M m 为中心,作该抛物线关于点M 对称的抛物线y ',则我们又称抛物线y '为抛物线y 的“衍生抛物线”,点M 为“衍生中心”.(2)已知抛物线225y x x =--+关于点(0,)m 的衍生抛物线为y ',若这两条抛物线有交点,求m 的取值范围. 问题解决:(3)已知抛物线22(0)y ax ax b a =+-≠①若抛物线y 的衍生抛物线为222(0)y bx bx a b '=-+≠,两抛物线有两个交点,且恰好是它们的顶点,求a 、b 的值及衍生中心的坐标;②若抛物线y 关于点2(0,1)k +的衍生抛物线为1y ,其顶点为1A ;关于点2(0,2)k +的衍生抛物线为2y ,其顶点为2A ;⋯;关于点2(0,)k n +的衍生抛物线为n y ,其顶点为(n A n ⋯为正整数).求1n n A A +的长(用含n 的式子表示).【解】:求解体验:(1)抛物线23y x bx =-+-经过点(1,0)-,130b ∴---=, 4b ∴=-,∴抛物线解析式为2243(2)1y x x x =---=-++, ∴抛物线的顶点坐标为(2,1)-,∴抛物线的顶点坐标(2,1)-关于(0,1)的对称点为(2,1),即:新抛物线的顶点坐标为(2,1), 令原抛物线的0x =,3y ∴=-,(0,3)∴-关于点(0,1)的对称点坐标为(0,5),设新抛物线的解析式为2(2)1y a x =-+, 点(0,5)在新抛物线上,25(02)1a ∴=-+,1a ∴=,∴新抛物线解析式为22(2)145y x x x =-+=-+,故答案为4-,(2,1)-,245y x x =-+;抽象感悟:(2)抛物线2225(1)6y x x x =--+=-++①,∴抛物线的顶点坐标为(1,6)-,抛物线上取点(0,5),∴点(1,6)-和(0,5)关于点(0,)m 的对称点为(1,26)m -和(0,25)m -,设衍生抛物线为2(1)26y a x m '=-+-,2526m a m ∴-=+-,1a ∴=,∴衍生抛物线为22(1)26225y x m x x m '=-+-=-+-②,联立①②得,2222525x x m x x -+-=--+, 整理得,22102x m =-, 这两条抛物线有交点,1020m ∴-…, 5m ∴…;问题解决:(3)①抛物线222(1)y ax ax b a x a b =+-=+--,∴此抛物线的顶点坐标为(1,)a b ---,抛物线y 的衍生抛物线为22222(1)y bx bx a b x a b '=-+=-+-,∴此函数的顶点坐标为2(1,)a b -,两个抛物线有两个交点,且恰好是它们的顶点,∴2222b b a a ba ab a b⎧++=--⎨+-=-⎩, 0a ∴=(舍)或3a =, 3b ∴=-,∴抛物线y 的顶点坐标为(1,0)-,抛物线y 的衍生抛物线的顶点坐标为(1,12), ∴衍生中心的坐标为(0,6);②抛物线22y ax ax b =+-的顶点坐标为(1,)a b ---, 点(1,)a b ---关于点2(0,)k n +的对称点为2(1,22)a b k n +++,∴抛物线n y 的顶点坐标n A 为2(1,22)a b k n +++,同理:1(1n A +,222(1))a b k n ++++22122(1)(22)42n n A A a b k n a b k n n +∴=++++-+++=+.13.(2018•青海)如图,抛物线2y ax bx c =++与坐标轴交点分别为(1,0)A -,(3,0)B ,(0,2)C ,作直线BC .(1)求抛物线的解析式;(2)点P 为抛物线上第一象限内一动点,过点P 作PD x ⊥轴于点D ,设点P 的横坐标为(03)t t <<,求ABP ∆的面积S 与t 的函数关系式; (3)条件同(2),若ODP ∆与COB ∆相似,求点P 的坐标.【解】:(1)把(1,0)A -,(3,0)B ,(0,2)C 代入2y ax bx c =++得:09302a b c a b c c -+=⎧⎪++=⎨⎪=⎩,解得:23a =-,43b =,2c =,∴抛物线的解析式为224233y x x =-++.(2)设点P 的坐标为224(,2)33t t t -++.(1,0)A -,(3,0)B ,4AB ∴=.221124484(2)4(03)223333S AB PD t t t t t ∴==⨯⨯-++=-++<<; (3)当ODP COB ∆∆∽时,OD DP OC OB=即22423323t tt -++=, 整理得:24120t t +-=, 解得:t =或t =.OD t ∴==,32DP OD == ∴点P 的坐标为. 当ODP BOC ∆∆∽,则OD DP BO OC=,即22423332tt t -++=, 整理得230t t--=, 解得:t =或t =.OD t ∴==,23DP OD ==,∴点P 的坐标为.综上所述点P 的坐标为或. 14.(2018•新疆)如图,在平面直角坐标系中,抛物线222433y x x =--与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C . (1)求点A ,B ,C 的坐标;(2)点P 从A 点出发,在线段AB 上以每秒2个单位长度的速度向B 点运动,同时,点Q 从B 点出发,在线段BC 上以每秒1个单位长度的速度向C 点运动,当其中一个点到达终点时,另一个点也停止运动.设运动时间为t 秒,求运动时间t 为多少秒时,PBQ ∆的面积S 最大,并求出其最大面积;(3)在(2)的条件下,当PBQ ∆面积最大时,在BC 下方的抛物线上是否存在点M ,使BMC∆的面积是PBQ ∆面积的1.6倍?若存在,求点M 的坐标;若不存在,请说明理由.【解】:(1)当0x =时,2224433y x x =--=-,∴点C 的坐标为(0,4)-;当0y =时,有2224033x x --=, 解得:12x =-,23x =,∴点A 的坐标为(2,0)-,点B 的坐标为(3,0).(2)设直线BC 的解析式为(0)y kx b k =+≠,将(3,0)B 、(0,4)C -代入y kx b =+,304k b b +=⎧⎨=-⎩,解得:434k b ⎧=⎪⎨⎪=-⎩, ∴直线BC 的解析式为443y x =-. 过点Q 作//QE y 轴,交x 轴于点E ,如图1所示,当运动时间为t 秒时,点P 的坐标为(22,0)t -,点Q 的坐标为3(35t -,4)5t -,3(22)52PB t t ∴=--=-,45QE t =,22144552()25544PBQ S PB QE t t t ∆∴==-+=--+.405-<, ∴当54t =时,PBQ ∆的面积取最大值,最大值为54. (3)当PBQ ∆面积最大时,54t =,此时点P 的坐标为1(2,0),点Q 的坐标为9(4,1)-.假设存在,设点M 的坐标为222(,4)33m m m --,则点F 的坐标为4(,4)3m m -,2242224(4)23333MF m m m m m ∴=----=-+,2132BMC S MF OB m m ∆∴==-+.BMC ∆的面积是PBQ ∆面积的1.6倍,253 1.64m m ∴-+=⨯,即2320m m -+=,解得:11m =,22m =.03m <<,∴在BC 下方的抛物线上存在点M ,使BMC ∆的面积是PBQ ∆面积的1.6倍,点M 的坐标为(1,4)-或8(2,)3-.15.(2018•安徽)小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆.售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元.调研发现: ①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x 盆,第二期盆景与花卉售完后的利润分别为1W ,2W (单位:元). (1)用含x 的代数式分别表示1W ,2W ;(2)当x 取何值时,第二期培植的盆景与花卉售完后获得的总利润W 最大,最大总利润是多少?【解】:(1)设培植的盆景比第一期增加x 盆, 则第二期盆景有(50)x +盆,花卉有(50)x -盆, 所以21(50)(1602)2608000W x x x x =+-=-++,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年中考数学真题专题汇编--二次函数压轴题
28.(2018甘肃白银)如图,已知二次函数2
2y ax x c =++的图象经过点(0,3)C ,与x 轴
分别交于点A ,点(3,0)B .点P 是直线BC 上方的抛物线上一动点.
(1)求二次函数2
2y ax x c =++的表达式;
(2)连接PO ,PC ,并把POC ∆沿y 轴翻折,得到四边形'POP C .若四边形'POP C 为菱形,请求出此时点P 的坐标;
(3)当点P 运动到什么位置时,四边形ACPB 的面积最大?求出此时P 点的坐标和四边形ACPB 的最大面积.
25.(2018湖南常德)如图,已知直线24y x =-+分别交x 轴、y 轴于点A 、B ,抛物线经过A ,B 两点,点P 是线段AB 上一动点,过点P 作PC x ⊥轴于点C ,交抛物线于点D .
(1)若抛物线的解析式为2224y x x =-++,设其顶点为M ,其对称轴交AB 于点N . ①
求点M、N的坐标;②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角 相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由. 形与AOB
26、((2018湖南株洲))如图,已知二次函数2
53(0)y ax x c a =-+>的图象抛物线与x 轴
相交于不同的两点1(,0)A x ,2(,0)B x ,且12x x <,
(1)
若抛物线的对称轴为x =
a 值;
(2)若15a =,求c 的取值范围;
(3)若该抛物线与y 轴相交于点D ,连接BD ,且∠OBD =60°,抛物线的对称轴l 与x 轴相交点E ,点F 是直线l 上的一点,点F 的纵坐标为1
32a
+,连接AF ,满足∠ADB =∠AFE ,求该二次函数的解析式。
27.(2018江苏盐城)如图①,在平面直角坐标系xOy 中,抛物线2
3y ax bx =++经过点
(1,0)A -、(3,0)B 两点,且与y 轴交于点C .
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x 轴,并沿x 轴左右平移,直尺的左右两边所在的直线与抛物线相交于P 、Q 两点(点P 在点Q 的左侧),连接PQ ,在线段PQ 上
方抛物线上有一动点D ,连接DP 、DQ . (Ⅰ)若点P 的横坐标为1
2
-
,求DPQ ∆面积的最大值,并求此时点D 的坐标 (Ⅱ)直尺在平移过程中,DPQ ∆面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
25.(2018江苏南京)如图1,在平面直角坐标系中,直线1y x =-与抛物线2y x bx c
=-++交于A B 、两点,其中(),0A m ,()4,B n .该抛物线与y 轴交于点C ,与x 轴交于另一点D .
(1)求m n 、的值及该抛物线的解析式;
(2)如图2.若点P 为线段AD 上的一动点(不与A D 、重合).分别以AP 、DP 为斜边,在直线AD 的同侧作等腰直角△APM 和等腰直角△DPN ,连接MN ,试确定△MPN 面积最大时P 点的坐标.
(3)如图3.连接BD 、CD ,在线段CD 上是否存在点Q ,使得以A D Q 、、为顶点的三角形与△ABD 相似,若存在,请直接写出点Q 的坐标;若不存在,请说明理由.
26.(2018山东临沂)如图,在平面直角坐杯中.90ACB ∠=.2OC OB =.=2tan ABC ∠.
点
B 的坐标为()10
,,抛物线2y x bx c =-++经过A ,B 两点 (1)求抛线的解析式
(2)点P 是直线AB 上方抛物线上的一点.过点P 作PD 垂直x 轴于点D ,交线段AB 于点E ,使1
=
2
PE DE . ①求点P 的坐标
②在直线PD 上是否存在点M ,使△ABM 为直角三角形?若存在,求出符合条件的所有 点M 的坐标;若不存在.请说明理由.
25.(2018山东枣庄)如图,已知二次函数)0(2
3
2≠++
=a c x ax y 的图象与y 轴交于点)4,0(A ,与x 轴交于点C B ,,点C 坐标为)0,8(,连接AC AB ,.
(1)请直接写出二次函数c x ax y ++
=2
3
2的表达式; (2)判断ABC ∆的形状,并说明理由;
(3)若点N 在x 轴上运动,当以点C N A ,,为顶点的三角形是等腰三角形时,请写出此时点N 的坐标;
(4)如图2,若点N 在线段BC 上运动(不与点C B ,重合),过点N 作AC NM //,交AB 于点M ,当AMN ∆面积最大时,求此时点N 的坐标.。
