参数的矩估计及评价标准
矩法估计PPT课件

点 估 计 问 题 就 是 要 构 造 一 个 适 当 的 统 计 量
ˆ(1,2,L,n),用 它 的 观 察 值 ˆ(x1,x2,L,xn) 来 估 计 未 知 参 数 .
ˆ(1 ,2 ,L ,n )称 为 的 估 计 量 . 通 称 估 计 ,
ˆ ( x 1 ,x 2 ,L ,x n ) 称 为 的 估 计 值 . 简 记 为 ˆ.
.
5
二、估计量的求法
由于估计量是样本的函数, 是随机变量, 故 对不同的样本值, 得到的参数值往往不同, 求估 计量的问题是关键问题.
点估计的求法: (两种) 矩估计法和极大似然估计法.
.
6
一、 矩估计法 它是基于一种简单的“替换” 思想建立起来的一种估计方法 . 是英国统计学家K.皮尔逊最早提出的 . 其基本思想是用样本矩估计总体矩 .
.
19
例 6 .设 X 在 [ 0 , ] 上 均 匀 分 布 , 求 的 矩 法 估 计 量 并 确 定
是 否 为 无 偏 估 计 量 ?
1
解 : f(x,)
0x, 0
( 列 1) 方矩 程法 :2 估 =0计 X : E X 0 x 1 其 dx 它 2 解 方 程 : ˆ = 2 X 即 为 的 矩 法 估 计 量 。
112X312X7
2 13X232X5
都是EX的无偏估计,并问哪一个比较有效?
解 E 1 E ( 1 2 X 3 1 2 X 7 ) 1 2 E X 3 1 2 E X 7 E X
E 2 E ( 1 3 X 2 2 3 X 5 ) 1 3 E X 3 2 3 E X 5 E X
参数的矩估计及评价标准PPT课件

2.有效性(不作要求)
设 ˆ1 ˆ1( X1, X与2,, X n ) ˆ2 都ˆ2是( X1, X 2,, X n ) 参数 的无偏估计量,如果
D(ˆ1) D(ˆ2), 则称 ˆ1 比 ˆ2 有效.
如果对于给定的样本容量 , 的方差 n 最小ˆ , 称 是ˆ 的有效估计量.
D(ˆ)
则
第15页/共25页
3.一致性(不作要求)
如果 n 时, 按概率收ˆn敛于 , 的正数 ,有
即对于任意给定
lim
n
P(
ˆn
) 1,
则称 是ˆn 的一致估计量.
n 第16页/共25页
小结
未知参数的估计量的三个评选标准:无偏性,有效性
和一致性. 评价估计量,不能从一个估计量的某次具体表现上
去衡量好坏,而应看其整体性质.
i
X )2
,
则
(A)
S 是 的无偏估计量.
(B) (C) (D)
S 是 的最大似然估计. S 是 的相合估计量(即一致估计量). S 与 相X互独立.
[1992 数学四]
第18页/共25页
分析:
对于任何总体,
虽然有 E(S 2 ) 2 , 即 S是2 2
的无偏估计量,
但是未必有 E(S) , 即 S未必是
Xi)
1 n
n i1
E(
X
i
)
1 n
n
.
X 是 的无偏估计量:
ˆ X .
第12页/共25页
(2)
S2
1 n 1
n i1
(Xi
X
)2
1
n
(
n 1 i1
X
2 i
第16次课——矩估计讲解
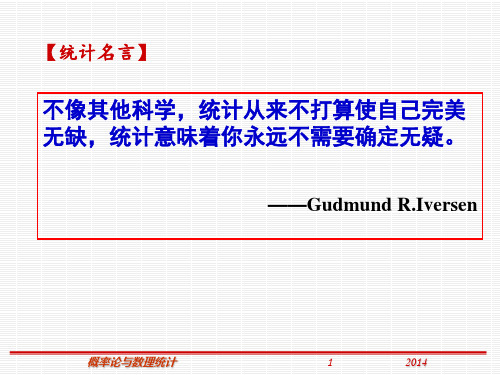
k k (1,2,L ,l ), (1 k l)
(2)设来自总体X样本的k阶矩
Ak
1 n
n i 1
X
k i
其中1 k l.
(3)令总体的k阶矩分别与样本的k阶矩相等,即
概率论与数理统计
6
2014
1(1,2 ,L ,l ) A1,
令
2
(1
,2,L ,l
LLLL
)
A2 ,
l (1,2,L ,l ) Al .
这是含待估参数1
,2
,,l
的联立方程组,其解
1(X1,, Xn ),2(X1,, Xn ),,l (X1,, Xn )
将样本观测值 (x1, x2 ,, xn ) 代入估计量ˆ(X1, X2,, Xn ) ,就得到 它的一个具体数值ˆ(x1, x2 ,, xn ) ,这个数值称为θ 的点估计值.
点估计的方法有很多,本节主要介绍:矩法和极大似然估计法.
概率论与数理统计
4
2014
二、矩法
它是基于一种简单的“替换”思想建立起来的一种估计方法 . 是英国统计学家K.皮尔逊最早提出的 . 其基本思想是用样本矩估计总体矩 . 理论依据: 大数定律
p=0.1,0. 3 或 0.6 若在一次观测中,事件A竟然发生了,
试让你推想一下 p应取何值?
你自然会认为事件A发生的概率是0.6,而 非其他数值。 【极大似然原理】
概率大的事件在一次观测中更容易发生。
由上述两例可知,极大似然估计法是要选取这样的
)
,当它
作为估计值时,使观测结果出现的可能性最大,即概率最大.
参数的矩估计及评价标准
概率论与数理统计(第三版)龙永红
目录
上一页
下一页
返回
结束
衡量点估计量好坏的标准
概率论与数理统计(第三版)龙永红
目录
上一页
下一页
返回
结束
1.无偏性
ˆ ˆ( X1, X 2 ,, X n ) 的数学期望 设参数 的估计量 存在且等于 ,即 ˆ) , E (
则称 ˆ 是 的无偏估计量.
目录 上一页 下一页 返回 结束
概率论与数理统计(第三版)龙永红
复习知识点
1. 事件间的关系与运算,概率的公理化定义, 概率的性质,古典概率,条件概率,乘法公式, 全概率公式、贝叶斯公式,事件的独立性; 书上相关内容,例题1.9,1.11,1.15, 1.16, 1.20 , 1.23, 1.25, 1.26及课后练习P14 4、5, P20 3, P29 9,P35 习题一 7.
ˆ2 有效. ˆ1 比 则称
ˆ) 最小, 则 如果对于给定的样本容量n ,ˆ 的方差 D( 称 ˆ 是 的有效估计量.
概率论与数理统计(第三版)龙永红
目录
上一页
下一页
返回
结束
3.一致性(不作要求)
如果 n 时,ˆn 按概率收敛于 , 即对于任意给定 的正数 ,有
n
ˆn ) 1, lim P(
ˆ( X1 , X 2 ,, X n ) 作为未知参数的估计量; 选择适当的统计量
ˆ( x1 , x2 ,, xn ) 作为未知参数 的估计值. 相应的观测值
概率论与数理统计(第三版)龙永红
目录
上一页
下一页
返回
结束
1.矩估计法
设总体 X 的分布中含有未知参数 1 , 2 ,, m , 假定 总体X 的 1 ,2 , ,m 阶原点矩都存在,
参数估计

一、参数估计(一)参数估计内涵参数估计(parameter estimation )是根据从总体中抽取的样本估计总体分布中包含的未知参数的方法。
它是统计推断的一种基本形式,是数理统计学的一个重要分支,分为点估计和区间估计两部分。
(二)估计量的评价准则对于同一参数,用不同方法来估计,结果是不一样的。
例1 设总体X 服从参数为λ的泊松分布,即,2,1,0,!}{===-k k ek X P kλλ则易知λλ==)(,)(X D X E ,分别用样本均值和样本方差取代)(X E 和)(X D ,于是得到λ的两个矩估计量21ˆ,ˆS X ==λλ. 既然估计的结果往往不是唯一的,那么究竟孰优孰劣?这里首先就有一个标准的问题。
1、 无偏性(Unbiased)定义1 设),,,(ˆˆ21nX X X θθ=是θ的一个估计量,若对任意的Θ∈θ,都有θθθ=)ˆ(E ,则称θˆ是θ的无偏估计量(Unbiased estimator),如果 0)(lim )),,,((lim 21=∆-∞→∧∞→θθθδn n n n b X X X E则称θˆ是θ的渐近无偏估计量(Approximation unbiased estimator),其中)(θn b 称为是θˆ的偏差(affect)。
无偏性反映了估计量的取值在真值θ周围摆动,显然,我们希望一个量具有无偏性。
例2 X 是总体期望值μ=)(X E 的无偏估计,因为μμ===⎪⎭⎫ ⎝⎛=∑∑==n n X E n X n E X E ni i n i i 1)(11)(112、 最小方差性和有效性(Minimum Variance and efficiency) 前面已经说过,无偏估计量只说明估计量的取值在真值周围摆动,但这个“周围”究竟有多大?我们自然希望摆动范围越小越好,即估计量的取值的集中程度要尽可能的高,这在统计上就引出最小方差无偏估计的概念。
定义2 对于固定的样本容量n ,设),,,(21n X X X T T =是参数函数)(θg 的无偏估计量,若对)(θg 的任一个无偏估计量),,,(21n X X X T T '='有Θ∈≤θθθ对一切),'()(T D T D则称),,,(21n X X X T 为)(θg 的(一致)最小方差无偏估计量,简记为UMVUE(Uniformly Minimum Variance Unbiased Estimation)或者称为最优无偏估计量。
应用数理统计——参数估计

这就是矩法估计的理论依据。
三、正态总体参数的区间估计 前面讨论了未知参数的点估计问题,它是用估计
量 θ 的值作为未知参数θ的估计。然而不管θ 是一 个怎样优良的估计量,它也只是一定程度的精确, 至于如何反映精确度,参数的点估计并没有回答。 由于θ 是一随机变量,需说明用θ 去估计θ的精度, 也就是要说明在一定概率意义下, 与θ的误差有 θ 多大。即确定具有特定概率意义的区间,使它以 相当大的概率包含未知参数的真值,以表明总体 参数真值所处的范围。
α
α
α
2
− uα
σ
n } = 1−α ) = 1−α
2
2
2
uα
2
σ
n
< µ < X + uα 2 < µ < x − uα 2
于是P{x − uα 2
σ
n
σ
n
例6:见教材82页例1。
(2)总体方差σ 2未知时,正态总体均值µ的区间估计
X −µ 因为若X服从N ( µ , σ ),则T = 服从t (n − 1) S n
2 2
小结:学习了
1、点估计法——矩法 2、评价估计量优劣的标准——无偏性、有效性 和一致性 3、正态总体的区间估计——均数和方差的区间估计 作业:教材98页第4题。 教材99页第10、13题。 教材100页第17、18题。
3、正态总体方差σ 的区间估计
2
因为若X服从N ( µ , σ 2 ),则χ 2 = 由附表4知P{χ12−α 2 < (n − 1) S 2
(n − 1) S 2
σ2
服从χ 2 (n − 1)
σ2
2 < χα 2 } = 1 − α
参数估计

(2)再用样本k阶矩代替相应的总体k阶矩
上一页
下一页
返回
设 总 体X ~ N ( , 2 ), , 2 未 知 , 设 例1: ( X 1 , X 2 ,..., X n )为 来 自 总 体 的 样 本 , 求 X 与 2的 矩 估 计 量 。
解:先建立待估参数与总体矩的关系
维随机变量,样本的联合概率密度为:
f ( x1 , x2 ,, xn ) f X 1 ( x1 ) f X 2 ( x2 ) f X n ( xn )
f ( x1 , ) f ( x2 , ) f ( xn , ) f ( xi , )
i 1
n
显然上式也为θ的函数,记作 L( ),即
L( ) f ( xi , )
i 1 n
我们称 L( ) 为似然函数。
小结:
似然函数
n p( x i ; ) i 1 L( ) n f ( x i ; ) i 1
由上可知,求极大似然估计值就是求使 L( ) 取最大的θ值。 下面我们用例子来说明求解极大似然估计值的步骤。
6
3
[ x dx x dx]
2 3 0 0
2
用样本k阶矩代替相应的总体k阶矩,得θ的矩估计量:
ˆ 2X
2)将数据代入,得θ的矩估计值为:
ˆ 2x 2 1 xi 8.9 8 i 1
8
计 算 器 的 使 用
例3:设总体X在区间[a,b]上服从均匀分布, a , b
实为 发生的概率。
根据极大似然原理,
概率大的事件在一次观测中更容易发生。
现在只做一次抽样, 事件 { X 1 x1 , X 2 x2 ,, X n xn } 故 认为其概率较大。 认为其概率较大。 也即我们应选择 使 L( ) 取最大值。 我们把使 L( ) 取最大值的 值称为 的极大 竟然发生了,
矩估计法的公式

矩估计法的公式摘要:一、矩估计法简介1.矩估计法的概念2.矩估计法在统计学中的应用二、矩估计法公式1.矩的定义2.矩估计法的推导过程3.常见矩估计量及其公式三、矩估计法的性质与特点1.矩估计量的性质2.矩估计法的优点与局限性四、矩估计法在实际问题中的应用1.参数估计问题2.假设检验问题正文:一、矩估计法简介矩估计法是一种常用的参数估计方法,它基于样本数据对未知参数进行估计。
矩估计法的核心思想是通过样本数据的矩(如均值、方差等)来估计总体的矩,从而得到参数的估计值。
矩估计法在统计学中有着广泛的应用,例如在区间估计、假设检验等问题中都有涉及。
二、矩估计法公式1.矩的定义矩是描述数据分布特征的一个量,它反映了数据围绕均值分布的情况。
对于连续型随机变量,其矩的定义如下:μk = E(X^k) = ∫x^kf(x)dx,k∈N其中,E(X^k) 表示随机变量X 的k 阶矩,f(x) 表示X 的概率密度函数,∫表示积分。
2.矩估计法的推导过程设总体分布为F(x),参数为θ,根据矩的定义,我们有:E(X) = ∫xf(x;θ)dx = μθ其中,μθ表示总体均值,μ表示样本均值,θ表示参数。
根据样本数据,我们可以得到n 个样本观测值x1, x2, ..., xn,对应的样本矩为:S_n = (x1^2 + x2^2 + ...+ xn^2) / n对S_n 求导,可得:dS_n/dθ = 2(x1 + x2 + ...+ xn) / n令dS_n/dθ = 0,解得:θ= μ = (x1 + x2 + ...+ xn) / n因此,我们可以用样本均值μ作为参数θ的估计值。
3.常见矩估计量及其公式除了均值,还有其他一些常见的矩估计量,如方差、协方差等。
这里列举一些常见的矩估计量及其公式:- 样本均值:μ = (x1 + x2 + ...+ xn) / n- 样本方差:s^2 = (Σ(xi - μ)^2) / (n - 1)- 样本标准差:s = √s^2- 样本相关系数:r = Σ(xi - μ)(yi - μ) / (s * s")三、矩估计法的性质与特点1.矩估计量的性质矩估计量具有良好的性质,如无偏性、有效性、一致性等。
第二章参数估计

第二章 参数估计【学习目标】1、掌握矩估计的替代原则;会求已知分布中未知参数的矩估计(值)2、熟练掌握极大似然估计的思想及求法3、估计量的评价标准:无偏性、有效性、相合性的定义4、统计量的无偏性的判断;两个无偏估计的有效性判断;会用Fisher 信息量及c-R 下界进行统计量的UMVUE 充分性判断5、掌握区间估计的定义6、单个正态总体均值的区间估计(包括方差已知、方差未知);单个正态总体方差的区间估计(包括均值已知、均值未知)7、两个正态总体均值差的区间估计(方差未知);两个正态总体方差比的区间估计 8、单侧置信区间的求法 【典型例题讲解】例1、设1,,n X X 是来自均匀分布(,1)U θθ+的总体的容量为n 的样本,其中θ-∞<<+∞为未知参数,试证:θ的极大似然估计量不止一个,例如1(1)ˆXθ=,2()ˆ1n X θ=-,3(1)()11ˆ()22n XXθ=+-都是θ的极大似然估计。
解:(,1)U θθ+分布的密度函数为11()0x f x θθ≤≤+⎧=⎨⎩其他似然函数(1)()11()0n x x L θθθ≤≤≤+⎧=⎨⎩其他由于在(1)()1n x x θθ≤≤≤+上()L θ为常数,所以凡是满足:(1)()ˆˆ1n x x θθ≤≤≤+的ˆθ均为θ的极大似然估计。
从而(1)1(1)ˆX θ=满足此条件,故1(1)ˆX θ=是θ的极大似然估计;(2)由于()(1)1n X X -≤,故2()(1)()2ˆˆ11n n X X X θθ=-≤≤=+,所以2()ˆ1n Xθ=-为θ的极大似然估计;(3)由于()(1)1n X X -≤,故(1)()(1)12n X X X +-≤,(1)()()12n n X X X ++≥,从而有3(1)()(1)()(1)()31111ˆˆ()()12222n n n XXXXXXθθ=+-≤≤≤++=+,故3ˆθ也为θ的极大似然估计。
参数估计之矩估计

第七章: 参数估计
7.1 矩估计
7.2 极大似然估计
7.3 估计量的优良性准则
7.4 正态总体的区间估计(一) *7.5 正态总体的区间估计(二) *7.6 非正态总体的区间估计
第七章: 参数估计
数理统计的任务:
●总体分布类型的判断;
● 总体分布中未知参数的推断(参数估计与
假设检验)。
参数估计问题的一般提法
设总体 X 的分布函数为 F ( x , θ ),其中θ 为未知参数或参数向量,现从该总体中抽样,得到样本
X 1, X 2 , … , X n .
依样本对参数θ 做出估计,或估计参数 θ 的某个已知函数 g (θ ) 。
这类问题称为参数估计。
参数估计包括:点估计和区间估计。
称该计算值为θ的一个点估计。
为估计参数θ,需要构造适当的统计量 T ( X 1, X 2 , … , X n ),
一旦当有了样本值,就将样本值代入到该统计量中,算出一个值作为θ的估计,点估计:
θ
θˆ的点估计常用符号为
寻求估计量的方法
1. 矩估计法
2. 极大似然法
3. 最小二乘法
4. 贝叶斯方法…
我们仅介绍前面的两种参数估计法。
提出。
矩估计的优点是:简单易行, 不需要事先知道总体是什么分布。
缺点是:当总体的分布类型已知时,未充分利用分布所提供的信息;此外,一般情形下,矩估计不具有唯一性 。
矩估计和极大似然估计分析解析

14
注:
总体均值方差的矩估计量与总体分布无关。
做矩估计时,也可用中心矩建立关于未知参数的 方程组, 因而矩估计不唯一。
例3
解:
λ未知,求参数λ的矩估计。
15
例4 不合格品率 p 的矩法估计 设某车间生产一批产品,为估计该批产品不合格品 率,抽取了n 件产品进行检查. 分析 设总体X 为抽的不合格产品数,相当于抽取了 一组样本X1,X2,… ,Xn , 且
中出现的概率最大。 极大似然估计就是在一次抽样中,若得到观测值
则选取
使得当
作为θ的估计值。 时,样本出现的概率最大。
24
极大似然估计法:
定义7.1 设 是
的一个样本值
形式已知
(如离散型) X的分布列为 的联合分布列为:
事件 为
发生的概率为 的函数,
25
为样本的似然函数。
样本的似然函数
现从中挑选使概率
θ
1 0 ( y )2 e θ dy 2θ 2 2 2
x μ 2 x θ e dx μ θ y
=θ2+(θ+μ)2
注意到 令 θ μ X , 2 θ M 2 . DX = E ( X2 )-( EX )2=θ2
2 1 ˆ M2 (Xi X ) , n i 1 ˆ X M . μ n
(b a ) ( a b) 1 A2 12 4 n
2 2
i 1
n
2 Xi
2 1
即 a b 2 A1 , b a 12( A2 A )
n 3 2 2 ˆ 解得: a A2 3( A2 A1 ) X ( X i X ) 17 n i 1
参数的矩法估计

第七章 参数估计
引 言
例:
的指数分布, 设总体 X 是服从参数为 λ 的指数分布,其中参数 λ 未知, λ > 0 . X 1 , L , X n 是总体 X 的一个样本, 未知, 的一个样本,
的取值, 我们的任务是根据样本 ,来估计 λ 的取值,从 而估计总体的分布. 而估计总体的分布.
第二十一讲2 第七章 参数估计(第二十一讲2)
引
言
在数理统计学中,总体的分布是未知的。 在数理统计学中,总体的分布是未知的。它包括 两种情形: 两种情形: 1)总体分布的类型是已知的,但其中包含未知参数。 )总体分布的类型是已知的,但其中包含未知参数。 我们的任务就是通过样本来估计这些未知参数。这就 我们的任务就是通过样本来估计这些未知参数。 是参数估计问题。 是参数估计问题。 2) 总体分布的类型是未知的。我们的任务就是通过 ) 总体分布的类型是未知的。 样本来估计总体的分布。这就是非参数估计问题。 样本来估计总体的分布。这就是非参数估计问题。 我们这里只讨论参数估计问题。 我们这里只讨论参数估计问题。
∑ = 250
解: µ 1 = EX = λ ,
令 X = λ,
1 n A1 = ∑ X i = X n i =1
ˆ = x = 1 ( 0 × 75 + 1 × 90 + L + 6 × 1) = 1.22 则λ 250
ˆ 所以估计值 λ = 1 . 22。
目 录
前一页
后一页
退 出
第七章 参数估计
n
1 l 令 Al = µl , l = 1,L, k, 其中 Al = ∑ X i n i =1
目 录 前一页 后一页 退 出
参数的点估计、估计量的评价标准以及参数的区间估计讲义

第七章参数估计内容介绍本章主要内容是参数的点估计、估计量的评价标准以及参数的区间估计等.内容讲解引言:本章将讨论统计推断,所谓统计推断就是由样本来推断总体. 当总体的某个参数未知时,用样本来对它进行估计,就是参数估计. 至于参数,目前没有准确的定义,只有一些具体的参数,本书指出三类参数:①分布中含有的未知参数θ;②θ的函数;③分布的各种特证数。
§ 7.1点估计1.点估计定义:设x1,x2,…x n是总体X的一个样本,θ是它的未知参数,用一个关于x1,x2,…x n的统计量的取值作为θ的估计值,称为θ的点估计.2.点估计的两种常用方法(1)替换原理和矩法估计① 替换原理:替换原理常指如下两句话:一是:用样本矩替换总体矩;二是:用样本矩的函数替换相应的总体矩的函数.② 矩估计的方法:根据替换原理,用样本矩或样本矩的函数对总体的矩或矩的函数进行估计。
例如:用样本均值估计总体均值E(X),即;用样本二阶中心矩估计总体方差,即;用事件A的频率估计事件A的概率等.例题1. P146【例7-1】对某型号的20辆汽车记录其每5L汽油的行驶里程(km),观测数据如下:29.8 27.6 28.3 27.9 30.1 28.7 29.9 28.0 27.9 28.728.4 27.2 29.5 28.5 28.0 30.0 29.1 29.8 29.6 26.9【答疑编号12070101】(2)概率函数p(x;θ)已知时未知参数的矩法估计设总体具有已知的概率函数p(x;θ1,…,θk),(θ1,…,θk)是未知参数或参数向量,x1,…,x n是样本,假定总体的k阶原点矩μk存在,则对所有的j(0<j<k),μj都存在。
(3)若假设θ1,…,θk能够表示成μ1,…,μk的函数θj=θj(μ1,…,μk),则可给出诸θj的矩法估计。
例题2. P146【例7-2】设总体为指数分布,其密度函数为【答疑编号12070102】这说明矩估计可能是不惟一的,这是矩法估计的一个缺点,此时通常应该尽量采用低阶矩给出未知参数的估计。
6.1矩估计
有两种,一种是对未知参数作出点估计,另一种是
对未知参数作出区间估计,以下分别讨论
5
假如我们要估计某队男生的平均身高.
2 N ( , 0 . 1 ) (假定身高服从正态分布 )
是要根据选出的样本(5个数)求出总体均值 的 估计. 而全部信息就由这5个数组成 .
现从该总体选取容量为5的样本,我们的任务
ˆ h ( A , , A ) j j 1 k
j=1,2,…,k
15
例 设总体X的概率密度为
X1,X2,…,Xn是取自X的样本,求参数 的矩估计.
数学期望 是一阶 原点矩
( 1) x , 0 x 1 f ( x) 其它 0,
其中
1
是未知参数,
解: 1 E ( X ) x( 1) x dx
23
矩法估计的缺点:(1)矩法估计有时会得到不合理的解;
(2)求矩法估计时,不同的做法会得到不同的解;
(通常规定,在求矩法估计时,要尽量使用低阶矩)
例 设总体X~P(λ),求 λ的矩估计。 n
解
若上例中,不是用1阶矩,而是用2阶矩 n 1 E ( X 2 ) D( X ) ( EX ) 2 ( X ) 2 X i2 n i 1 n n 1 1 2 2 2 ˆ ˆ X 不同 X X ( X X ) 与 i i n i 1 n i 1
14
设总体的分布函数中含有k个未知参数
1 , , k
,那么它的前k阶矩
1 ,, k
一般
都是这k个参数的函数,记为:
i gi (1,, k )
从这k个方程中解出
i=1,2,…,k
j h j ( 1 ,, k )
应用数理统计(武汉理工大)2-参数估计

1
D(S 2 )nI (
2)
n 1 n
1,
n
故S 2是渐进有效的。
第二章 参数估计
例: 设总体X (), X1, X 2 , , X n是X的一个样本, 讨论的无偏估计X的有效性。
解:lnp( X
,)
ln
X e
X!
X
ln
ln( X
!)
区间估计的关键: 用合适的方法确定两个统计量
1(X1, X2 , , Xn), 2(X1, X2 , , Xn)
第二章 参数估计
1.区间估计的定义及计算步骤
3) 区间估计的例子
例1 设总体X~N(μ , σ2), σ2已知,μ未知,设X1,…,Xn是X的样本, 求μ的置信度为1-α的置信区间。
)
2
n
,
D(ˆ2 )
D(nZ )
n2D(Z )
n2
n
2
2
当n 1时,显然D(ˆ1) D(ˆ2 ),故ˆ1比ˆ2有效。
第二章 参数估计
最小方差无偏估计问题 设 若 及T对 任(g意X(1, , X)的2都,任有一 , XD无n()T是 偏) g估(D计()T的量')一, T '个 ( X无1, X偏2估 , 计, X量n ), 则 无称 偏T估(计X1,, X或2 ,者,称X为n )是最g优(无)的偏一估致计最。小方差
其它类型的估计,如 贝叶斯估计…
第二章 参数估计
2.1参数的点估计
1. 矩估计 2. 极大似然估计 3. 点估计量的评价
7.2参数点估计的评价标准

都是 的无偏估计量
ˆ 3 最有效. 由例6(2) 知
Ch7-59
罗—克拉美(Rao – Cramer)不等式 若 ˆ 是参数 的无偏估计量, 则
D (ˆ) 1 nE ln p ( X , )
2
D0 ( )
其中 p ( x , ) 是 总体 X 的概率分布或密 度函数,称 D0 ( )为方差的下界.
ˆ 为达到方差下界的 当 D (ˆ) D0 ( ) 时, 称 无偏估计量, 此时称 ˆ 为最有效的估计量, 简称有效估计量.
定义
一致性(相合性) 设 ˆ ˆ( X 1 , X 2 , , X n ) 是总体参数
Ch7-60
的估计量. 若对于任意的 , 当n 时,
ˆ 依概率收敛于 , 即 0, ˆ ) ) 0 lim P (
n
ˆ 是总体参数 的一致(或相合)估计量. 则称
1 P( X 1 z)P( X 2 z) P( X n z)
Ch7-54
有效性
定义 设 ˆ1 1 ( X 1 , X 2 , , X n )
ˆ2 2 ( X 1 , X 2 , , X n )
都是总体参数 的无偏估计量, 且
D (ˆ1 ) D (ˆ2 )
Ch7-64
智商
组别
人数
智商平均数
样本标准差
甲组
乙组
n 6
46
x 78
99
s
19 16
由此结果推断母亲嗜酒是否影响下一 代的智力?若有影响,推断其影响程度有 多大? 提示 前一问题属假设检验问题 后一问题属区间估计问题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
1 n
n i1
Xi
,
2
2
1 n
n i1
X
2 i
.
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
于是解得 及 2的矩估计量为
ˆ
1 n
n
i 1
X
i
X
,
ˆ 2
1 X n
2
i
n i1
X
2
1 n
n
i 1
(
X
i
X )2
S2 0
.
而 及 2的矩估计值就是
ˆ
ˆ
1 n
n i1
xi
21 n ( n i1
设 X ~ N(70, 2),且P(X 90) 0.0228, ?
分析: X 70 ~ N (0,1) P( X 70 20) 0.0228.
即
1
Φ(20
)
查表
0.0228
20
2.0.由此确定
10.
以上是通过已知条件来确定参数,不是参数估计.
点估计:通过抽样估计未知参数的具体值.
ˆm ˆm ( X1, X 2, , X n ).
分别是未知参数 1,2, ,m的估计量,称为矩估计量.
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
如果已知样本观测值为 x1 , x2 , , xn , 则
ˆ1 ˆ1(x1 , x2 , , xn ), ˆ2 ˆ2 (x1 , x2 , , xn ),
Xi)
2
1 n2
n i1
D(Xi )
2
1 n2
n
2
2
2 2.
n
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
由此得
[ ] E(S2) E
1( n 1
n i1
X
2 i
nX
2)
1 [n( 2 2 ) n( 2 2 )]
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
点估计 设总体 X 的分布中含有未知参数 ;
从总体 X 中抽取样本 X1 , X 2 , , X n;
选择适当的统计量ˆ( X1 , X2 , , Xn )作为未知参数的估计量;
相应的观测值ˆ(x1 , x2 , , xn )作为未知参数 的估计值.
ˆk ( X )
Ak
1 X n
k
i
n i1
,
k 1, 2 , , m.
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
( , , k 12
, ) m
1 X n
k
i
n i1
,
k 1, 2 , , m.
解这个方程组,得
ˆ1 ˆ1( X1, X 2, , X n ), ˆ2 ˆ2 ( X1, X 2, , X n ),
xi
x
, x)2
~2 .
书上P158
例题5.9
Eˆ ( X
)
1n
n i1
Xi
X,
Dˆ ( X
)
1 n
n
(Xi
i 1
X
)2
S02 .
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
2.最大似然估计法
(不作要求,考研出现过)
直观思想:一次抽样就出现的一组观测值可能性最大. 例如 有两件相同的零件箱,各装1000个零件. 一箱有 950个正品,50个次品;另一箱50个正品, 950个次品.现 任取一件,任取一个零件,发现取得正品.问,所取零件 来自哪一件?
E( Xi ) , D( Xi ) 2 , i 1 ,2 , ,n.
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
由数学期望与方差的性质可知
E(X
)
E(1 n
n i1
Xi)
1 n
E(
n i1
Xi)
1 n
n i1
E(Xi
)
1 n
n
.
所以, X 是 的无偏估计量:
ˆ X .
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
1.矩估计法
设总体 X 的分布中含有未知参数 1,2, ,m , 假定 总体X的 1 ,2 , ,m 阶原点矩都存在,
k ( X ) E( X k ) k (1,2 , ,m ) , k 1, 2 , , m. 从总体 X中抽取样本 X1 , X 2 , , X n,用样本各阶原点矩 作为总体X 的各阶原点矩的估计量
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
[例1] 设总体X 的均值 E(X ) , 方差 D(X ) 2,证明:
(1)样本均值 X
1 n
n i1
Xi
是总体均值
的无偏估计量;
(2)样本方差 S
无偏估计量.
2
1 n 1
n i1
(Xi
X
)2
是总体方差
2
的
证: 因为样本 X1 , X 2 , , X n 相互独立,且与总体 X 服从相同分布,所以有
求 及 2的矩估计值.
解: 因为总体 X 的分布有两个未知参数,所以应考虑
一、二阶原点矩, 1(X ) E(X ) ,
2( X ) E(X 2) D(X ) [E( X )]2 2 2 .
于是,按矩估计法
得方程组
ˆ1( X
)
1 n
n
i 1
Xi
,
ˆ2 ( X
)
1 n
n
i 1
X
2 i
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
衡量点估计量好坏的标准
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
1.无偏性
设参数 的估计量 ˆ ˆ( X1, X2, , Xn ) 的数学期望 存在且等于 ,即
E(ˆ) , 则称 ˆ 是 的无偏估计量.
如果样本观测值为 x1 , x2 , , xn ,则称 ˆ(x1 , x2 , , xn ) 是 的无偏估计值.
答:来自第一件.
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
小结
求未知参数估计量的常用方法是矩估计法和最大 似然估计法. 矩估计法: 以样本矩作为总体的相应矩的估计, 以样本 矩的函数作为总体的相应矩的函数的估计. 最大似然估计法: 使似然函数达到最大值. 似然函数对 离散情形考虑概率,连续情形考虑概率密度.
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
(2)
S2
1 n 1
n i1
(Xi
X
)2
1( n 1
n i1
X
2 i
nX
2).
而
E(
X
2 i
)
D(Βιβλιοθήκη Xi) [E( Xi )]2 2 2
,
i 1,2 ,
,n.
E( X 2) D( X ) [E( X )]2
D(1 n
n i1
ˆm ˆm (x1 , x2 , , xn ).
分别是未知参数 1,2, ,m 的估计值,称为矩估计值.
概率论与数理统计(第三版)龙永红
目录
上一页 下一页
返回
结束
[例] 设总体 X 服从正态分布 N( , 2) , 其中 及 2
都是未知参数,如果取得样本观测值为 x1 , x2 , , xn ,
