高等数学中特殊符号的读法及功能
高等数学中符号的读法及功能 (挺全的)之欧阳与创编

大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米伽符号表符号含义i-1的平方根f(x)函数f在自变量x处的值sin(x)在自变量x处的正弦函数值exp(x)在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax同a^xlogba以b为底a的对数;blogba = acos x在自变量x处余弦函数的值tan x其值等于sin x/cos xcot x余切函数的值或cos x/sin xsec x正割含数的值,其值等于1/cos xcsc x余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin y acos x y,余弦函数反函数在x处的值,即x = cos y atan x y,正切函数反函数在x处的值,即x = tan y acot x y,余切函数反函数在x处的值,即x = cot y asec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a?b a、b向量的点积(a?b)a、b向量的点积|v|向量v的模|x|数x的绝对值Σ表示求和,通常是某项指数。
高等数学中符号的读法及功能 (挺全的)之欧阳科创编

大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米伽符号表符号含义i-1的平方根f(x)函数f在自变量x处的值sin(x)在自变量x处的正弦函数值符号含义exp(x)在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax同a^xlogba以b为底a的对数;blogba = acos x在自变量x处余弦函数的值tan x其值等于sin x/cos xcot x余切函数的值或cos x/sin xsec x正割含数的值,其值等于1/cos xcsc x余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin y acos x y,余弦函数反函数在x处的值,即x = cos y atan x y,正切函数反函数在x处的值,即x = tan y acot x y,余切函数反函数在x处的值,即x = cot y asec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a?b a、b向量的点积(a?b)a、b向量的点积|v|向量v的模|x|数x的绝对值Σ表示求和,通常是某项指数。
高等数学中符号的读法及功能 (挺全的)之欧阳物创编

大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米伽符号表符号含义i-1的平方根符号含义f(x)函数f在自变量x处的值sin(x)在自变量x处的正弦函数值exp(x)在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax同a^xlogba以b为底a的对数;blogba = acos x在自变量x处余弦函数的值tan x其值等于sin x/cos xcot x余切函数的值或cos x/sin xsec x正割含数的值,其值等于1/cos xcsc x余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin y acos x y,余弦函数反函数在x处的值,即x = cos y atan x y,正切函数反函数在x处的值,即x = tan y acot x y,余切函数反函数在x处的值,即x = cot y asec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a?b a、b向量的点积(a?b)a、b向量的点积|v|向量v的模|x|数x的绝对值Σ表示求和,通常是某项指数。
高等数学中符号的读法及功能 (挺全的)之欧阳理创编

大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米伽符号表符号含义i-1的平方根f(x)函数f在自变量x处的值符号表符号含义sin(x)在自变量x处的正弦函数值exp(x)在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax同a^xlogba以b为底a的对数;blogba = acos x在自变量x处余弦函数的值tan x其值等于sin x/cos xcot x余切函数的值或cos x/sin xsec x正割含数的值,其值等于1/cos xcsc x余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin y acos x y,余弦函数反函数在x处的值,即x = cos y atan x y,正切函数反函数在x处的值,即x = tan y acot x y,余切函数反函数在x处的值,即x = cot y asec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a?b a、b向量的点积(a?b)a、b向量的点积|v|向量v的模|x|数x的绝对值Σ表示求和,通常是某项指数。
高等数学中符号的读法及功能(挺全的)之欧阳引擎创编

大写小写英文注音国际音标注音中文注音欧阳引擎(2021.01.01)Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米伽符号表符号含义i-1的平方根f(x)函数f在自变量x处的值sin(x)在自变量x处的正弦函数值符号含义exp(x)在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax同a^xlogba以b为底a的对数;blogba = acos x在自变量x处余弦函数的值tan x其值等于sin x/cos xcot x余切函数的值或cos x/sin xsec x正割含数的值,其值等于1/cos xcsc x余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin y acos x y,余弦函数反函数在x处的值,即x = cos y atan x y,正切函数反函数在x处的值,即x = tan y acot x y,余切函数反函数在x处的值,即x = cot y asec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z 用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a?b a、b向量的点积(a?b)a、b向量的点积|v|向量v的模|x|数x的绝对值Σ表示求和,通常是某项指数。
高等数学中符号的读法及功能 (挺全的)之欧阳索引创编

大写小写英文注音国际音标注音中文注音欧阳家百(2021.03.07)Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米伽符号表符号含义i-1的平方根f(x)函数f在自变量x处的值sin(x)在自变量x处的正弦函数值符号含义exp(x)在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax同a^xlogba以b为底a的对数;blogba = acos x在自变量x处余弦函数的值tan x其值等于sin x/cos xcot x余切函数的值或cos x/sin xsec x正割含数的值,其值等于1/cos xcsc x余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin y acos x y,余弦函数反函数在x处的值,即x = cos y atan x y,正切函数反函数在x处的值,即x = tan y acot x y,余切函数反函数在x处的值,即x = cot y asec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a?b a、b向量的点积(a?b)a、b向量的点积|v|向量v的模|x|数x的绝对值Σ表示求和,通常是某项指数。
高等数学中特殊符号的读法及功能

常用高等数学符号的读法及含义表一、常用符号读法大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Γδdeta delta 德耳塔Δεepsilon epsilon 艾普西隆Εδzeta zeta 截塔Ζεeta eta 艾塔Θζtheta ζita西塔Ηηiota iota 约塔Κθkappa kappa 卡帕∧ιlambda lambda 兰姆达Μκmu miu 缪Νλnu niu 纽Ξμxi ksi 可塞Ονomicron omikron 奥密可戎∏πpi pai 派Ρξrho rou 柔∑ζsigma sigma 西格马Τηtau tau 套Υυupsilon jupsilon 衣普西隆Φθphi fai 斐Φχchi khai 喜Χψpsi psai 普西Ψωomega omiga 欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax 同a^xlogba 以b为底a的对数;blogba = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值,其值等于1/cos xcsc x 余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin y acos x y,余弦函数反函数在x处的值,即x = cos y atan x y,正切函数反函数在x处的值,即x = tan y acot x y,余切函数反函数在x处的值,即x = cot y asec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc yζ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模符号含义|x| 数x的绝对值Σ表示求和,通常是某项指数。
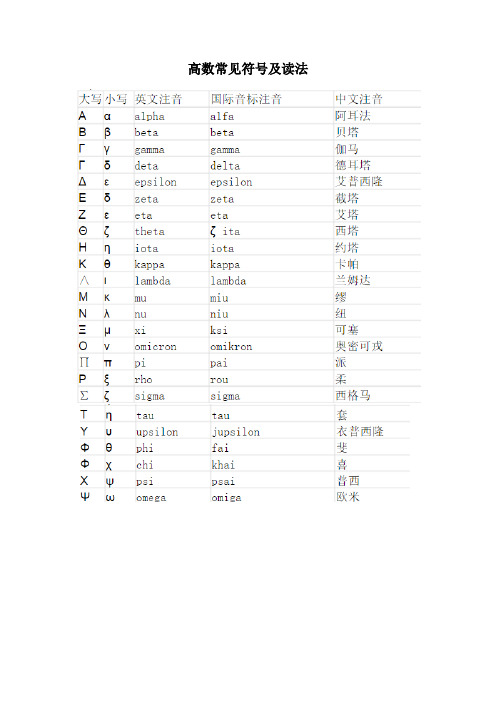
高数常见符号及读法
y,正切函数反函数在x处的值,即x = tan y
acot x
y,余切函数反函数在x处的值,即x = cot y
asec x
y,正割函数反函数在x处的值,即x = sec y
acsc x
y,余割函数反函数在x处的值,即x = csc y
θ
角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时
M
表示一个矩阵或数列或其它
|v>
列向量,即元素被写成列或可被看成k×1阶矩阵的向量
<v|
被写成行或可被看成从1×k阶矩阵的向量
dx
变量x的一个无穷小变化,dy, dz, dr等类似
ds
长度的微小变化
ρ
变量(x2 + y2 + z2)1/2或球面坐标系中到原点的距离
r
变量(x2 + y2)1/2或三维空间或极坐标中到z轴的距离
i, j, k
分别表示x、y、z方向上的单位向量
(a, b, c)
以a、b、c为元素的向量
(a, b)
以a、b为元素的向量
(a, b)
a、b向量的点积
a•b
a、b向量的点积
(a•b)
a、b向量的点积
|v|
向量v的模
|x|
数x的绝对值
Σ
表示求和,通常是某项指数。下边界值写在其下部,上边界值写在其上部。如j从1到100的和可以表示成:数学常用符号。这表示1 + 2 +…+ n
ds
沿曲线方向距离的导数
κ
曲线的曲率,单位切线向量相对曲线距离的导数的值:|dT/ds|
N
高等数学符号读法大全

高等数学符号读法大全一、算术运算符号:1. 加号 (+):读作“加”。
2. 减号 (-):读作“减”。
3. 乘号(×):读作“乘”、“乘以”、“乘号”,或“乘积”。
4. 除号(÷):读作“除”、“除以”、“除号”,或“商”。
5. 等号 (=):读作“等于”、“等于号”。
6. 小于 (<):读作“小于”、“小于号”,或“不大于”。
7. 大于 (>):读作“大于”、“大于号”,或“不小于”。
二、集合运算符号:1. 并集(∪):读作“并集”。
2. 交集(∩):读作“交集”。
3. 补集 (-):读作“补集”、“减去”、“不属于”。
三、数学函数符号:1. 求和(∑):读作“求和”、“总和”的符号。
2. 积分(∫):读作“积分”、“定积分”。
3. 极限 (lim):读作“极限”。
4. 求导(∂):读作“求导”、“导数”、“偏微分”。
5. 阶乘 (x!):读作“阶乘”、“x的阶乘”。
四、常用数学符号:1. 无限(∞):读作“无穷大”。
2. 正无穷(+∞):读作“正无穷大”。
3. 负无穷 (-∞):读作“负无穷大”。
4. 接近(∝):读作“接近于”、“趋向于”。
5. 不等于(≠):读作“不等于”、“不等于号”。
6. 大约(≈):读作“大约”、“约等于”。
7. 因果关系(∴):读作“因此”、“所以”。
五、概率与统计符号:1. 平均值 (x̄x̄):读作“x bar”、“x平均值”。
2. 标准差 (x̄):读作“sigma”、“标准差”。
3. 方差 (x̄²):读作“sigma squared”、“方差”。
4. 期望值 (x̄):读作“期望值”、“期望”、“mean”。
5. 随机变量 (x̄):读作“X”、“随机变量”。
6. 概率 (x̄):读作“P”、“概率”。
六、三角函数符号:1. 正弦 (sin):读作“正弦”。
2. 余弦 (cos):读作“余弦”。
3. 正切 (tan):读作“正切”。
大学数学符号的读法

大学数学符号的读法数学作为一门抽象的学科,充斥着各种符号和公式。
对于初学者来说,正确地理解和读取这些数学符号是十分重要的。
本文将为大家介绍一些常见的大学数学符号的读法。
1. 希腊字母希腊字母在数学中被广泛使用,以下是一些常见的希腊字母及其读法:- α(alpha): 读作“阿尔法”,表示角度、系数等;- β(beta): 读作“贝塔”,表示角度、系数等;- γ(gamma): 读作“伽马”,表示角度、系数等;- δ(delta): 读作“德尔塔”,表示变量的增量、差分等;- θ(theta): 读作“西塔”,表示角度;- λ(lambda): 读作“兰姆达”,表示波长、特征值等;- μ(mu): 读作“缪”,表示平均值、系数等;- π(pi): 读作“派”,表示圆周率;- σ(sigma): 读作“西格玛”,表示标准差、总和等;- ω(omega): 读作“欧米伽”,表示角速度、角频率等。
这些希腊字母在数学和物理等领域中都有广泛的应用,熟悉它们的读法能够帮助我们更好地理解和表达数学知识。
2. 数学运算符号数学运算符号是数学中常用的符号,正确地读取这些符号对于解题和理解概念至关重要。
以下是一些常见的数学运算符号及其读法:- +(plus): 读作“加”,表示两个数的和;- -(minus): 读作“减”,表示两个数的差;- ×(times): 读作“乘”,表示两个数的积;- ÷(divide): 读作“除”,表示两个数的商;- =(equal): 读作“等于”,表示两个数或表达式相等;- ≠(not equal): 读作“不等于”,表示两个数或表达式不相等;- <(less than): 读作“小于”,表示一个数小于另一个数;- >(greater than): 读作“大于”,表示一个数大于另一个数;- ≤(less than or equal to): 读作“小于等于”,表示一个数小于等于另一个数;- ≥(greater than or equal to): 读作“大于等于”,表示一个数大于等于另一个数。
高等数学所有符号的写法与读法

高等数学所有符号的写法与读法 ̄连字符' 省略号;所有格符号—破折号‘’单引号“”双引号( ) 圆括号[ ] 方括号{}《》法文引号;书名号... 省略号¨双点号" 同上‖双线号/斜线号&=~代字号§ ; 分节号→箭号;参见号+加号;正号-减号;负号±正负号×乘号÷除号=等于号≠不等于号≡全等于号≌等于或约等于号≈约等于号<小于号>大于号≮不小于号≯不大于号≤小于或等于号≥大于或等于号%百分之…‰千分之…∞无限大号∝与…成比例√ () 平方根∵ ; 因为∴所以∷ , () 等于,成比例∠角⌒半圆⊙圆○圆周π圆周率△三角形⊥垂直于∪并,合集∩交,通集∫…的积分∑ () 总和°度′分〃秒#…号℃摄氏度@单价x'是x (比如转置矩阵)x"是x常用数学符号读法大全以及主要数学符号含义-转载数学符号:(1)数量符号:如:i,2,a,x,自然对数底e,圆周率π。
(2)运算符号:如加号(+),减号(-),乘号(×或·),除号(÷或/),两个集合的并集(∪),交集(∩),根号(√),对数(,,),比(:),微分(),积分(∫)等。
(3)关系符号:如“=”是等号,“≈”是近似符号,“≠”是不等号,“>”是大于符号,“<”是小于符号,“→”表示变量变化的趋势,“∽”是相似符号,“≌”是全等号,“∥”是平行符号,“⊥”是垂直符号,“∝”是反比例符号,“∈”是属于符号,“C”或“C下面加一横”是“包含”符号等。
(4)结合符号:如圆括号“()”方括号“[]”,花括号“{}”括线“—”(5)性质符号:如正号“+”,负号“-”,绝对值符号“‖”(6)省略符号:如三角形(△),正弦(),余弦(),x的函数(f(x)),极限(),因为(∵),所以(∴),总和(∑),连乘(∏),从n个元素中每次取出r个元素所有不同的组合数(C(r)(n) ),幂(A,,,x^n),阶乘(!)等。
高等数学中符号的读法及功能 (挺全的)之欧阳语创编

大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米伽符号表符号含义i-1的平方根f(x)函数f在自变量x处的值sin(x)在自变量x处的正弦函数值exp(x)在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax同a^xlogba以b为底a的对数;blogba = acos x在自变量x处余弦函数的值tan x其值等于sin x/cos xcot x余切函数的值或cos x/sin xsec x正割含数的值,其值等于1/cos xcsc x余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin y acos x y,余弦函数反函数在x处的值,即x = cos y atan x y,正切函数反函数在x处的值,即x = tan y acot x y,余切函数反函数在x处的值,即x = cot y asec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a?b a、b向量的点积(a?b)a、b向量的点积|v|向量v的模|x|数x的绝对值Σ表示求和,通常是某项指数。
常用数学符号读法大全以及主要数学符号含义

高等数学常用数学符号读法大全以及主要数学符号含义-转载大写小写英文注音国际音标注音中文注音Α α alpha alfa阿耳法Β β beta beta贝塔Γ γ gamma gamma伽马Γ δ deta delta德耳塔Δ ε epsilon epsilon艾普西隆Ε δ zeta zeta截塔Ζ ε eta eta艾塔Θ ζ theta ζita西塔Η η iota iota约塔Κ θ kappa kappa卡帕∧ι lambda lambda兰姆达Μ κmu miu缪Ν λ nu niu纽Ξ μ xi ksi可塞Ο ν omicro n omikron奥密可戎∏ π pi pai派Ρ ξ rho rou柔∑ ζ sigma sigma西格马Τ η tau tau套Υ υ upsilon jupsilon衣普西隆Φ θ phi fai斐Φ χ chi khai喜Χ ψ psi psai普西Ψ ω omega omiga欧米伽数学符号:(1)数量符号:如:i,2+i,a,x,自然对数底e,圆周率π。
(2)运算符号:如加号(+),减号(-),乘号(×或·),除号(÷或/),两个集合的并集(∪),交集(∩),根号(√),对数(log,lg,ln),比(:),微分(dx),积分(∫)等。
(3)关系符号:如“=”是等号,“≈”是近似符号,“≠”是不等号,“>”是大于符号,“<”是小于符号,“→ ”表示变量变化的趋势,“∽”是相似符号,“≌”是全等号,“∥”是平行符号,“⊥”是垂直符号,“∝”是反比例符号,“∈”是属于符号,“C”或“C下面加一横”是“包含”符号等。
(4)结合符号:如圆括号“()”方括号“[]”,花括号“{}”括线“—”(5)性质符号:如正号“+”,负号“-”,绝对值符号“‖”(6)省略符号:如三角形(△),正弦(sin),余弦(cos),x的函数(f(x)),极限(lim),因为(∵),所以(∴),总和(∑),连乘(∏),从n个元素中每次取出r个元素所有不同的组合数(C(r)(n) ),幂(A,Ac,Aq,x^n),阶乘(!)等。
高等数学中符号的读法及功能 (挺全的)之欧阳育创编

大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米伽符号表符号含义i-1的平方根f(x)函数f在自变量x处的值sin(x)在自变量x处的正弦函数值符号含义exp(x)在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax同a^xlogba以b为底a的对数;blogba = acos x在自变量x处余弦函数的值tan x其值等于sin x/cos xcot x余切函数的值或cos x/sin xsec x正割含数的值,其值等于1/cos xcsc x余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin y acos x y,余弦函数反函数在x处的值,即x = cos y atan x y,正切函数反函数在x处的值,即x = tan y acot x y,余切函数反函数在x处的值,即x = cot y asec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a?b a、b向量的点积(a?b)a、b向量的点积|v|向量v的模|x|数x的绝对值Σ表示求和,通常是某项指数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔
Γγgamma gamma 伽马
Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔
Ηηeta eta 艾塔
Θθtheta θita西塔
Ιιiota iota 约塔
Κκkappa kappa 卡帕
∧λlambda lambda 兰姆达Μμmu miu 缪
Ννnu niu 纽
Ξξxi ksi 可塞
Οοomicron omikron 奥密可戎∏πpi pai 派
Ρρrho rou 柔
∑σsigma sigma 西格马
Ττtau tau 套
Υυupsilon jupsilon 衣普西隆Φφphi fai 斐
Χχchi khai 喜
Ψψpsi psai 普西
Ωωomega omiga 欧米伽
符号表符号含义i -1的平方根
f(x) 函数f在自变量x处的值
sin(x) 在自变量x处的正弦函数值
exp(x) 在自变量x处的指数函数值,常被写作ex
a^x a的x次方;有理数x由反函数定义
ln x exp x 的反函数
ax 同a^x
logba 以b为底a的对数;blogba = a
cos x 在自变量x处余弦函数的值
tan x 其值等于sin x/cos x
cot x 余切函数的值或cos x/sin x
sec x 正割含数的值,其值等于1/cos x
csc x 余割函数的值,其值等于1/sin x
asin x y,正弦函数反函数在x处的值,即x = sin y acos x y,余弦函数反函数在x处的值,即x = cos y atan x y,正切函数反函数在x处的值,即x = tan y acot x y,余切函数反函数在x处的值,即x = cot y asec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc y
θ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时
i, j, k 分别表示x、y、z方向上的单位向量
(a, b, c) 以a、b、c为元素的向量
(a, b) 以a、b为元素的向量
(a, b) a、b向量的点积
a?b a、b向量的点积
(a?b) a、b向量的点积
|v| 向量v的模
|x| 数x的绝对值
Σ
表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在其上部。
如j从1到100的
和可以表示成:。
这表示 1 + 2 + … + n
M 表示一个矩阵或数列或其它
符号含义
|v> 列向量,即元素被写成列或可被看成k×1阶矩阵的向量
<v| 被写成行或可被看成从1×k阶矩阵的向量
dx 变量x的一个无穷小变化,dy, dz, dr等类似
ds 长度的微小变化
ρ变量(x2 + y2 + z2)1/2 或球面坐标系中到原点的距离
r 变量(x2 + y2)1/2 或三维空间或极坐标中到z轴的距离
|M| 矩阵M的行列式,其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值,为一个面积、体积或超体积
det M M的行列式
M-1 矩阵M的逆矩阵
v×w 向量v和w的向量积或叉积
θvw向量v和w之间的夹角
A?B×C 标量三重积,以A、B、C为列的矩阵的行列式
uw 在向量w方向上的单位向量,即w/|w|
df 函数f的微小变化,足够小以至适合于所有相关函数的线性近似
df/dx f关于x的导数,同时也是f的线性近似斜率
f ' 函数f关于相应自变量的导数,自变量通常为x
f/x y、z固定时f关于x的偏导数。
通常f关于某变量q的偏导数为当其它几个变量固定时df与dq的比值。
任何可能导致变量混淆的地方都应明确地表述
(?f/?x)|r,z 保持r和z不变时,f关于x的偏导数
grad f 元素分别为f关于x、y、z偏导数[(?f/?x), (?f/?y), (?f/?z)] 或(?f/?x)i + (?f/?y)j + (?f/?z)k; 的向量场,称为f的梯度
向量算子(?/?x)i + (?/?x)j + (?/?x)k, 读作"del"
f f的梯度;它和uw 的点积为f在w方向上的方向导数
w 向量场w的散度,为向量算子? 同向量w的点积, 或(?wx /?x) + (?wy /?y) + (?wz /?z) curl w 向量算子? 同向量w 的叉积
×w w的旋度,其元素为[(?fz /?y) - (?fy /?z), (?fx /?z) - (?fz /?x), (?fy /?x) - (?fx /?y)] 拉普拉斯微分算子:(?2/?x2) + (?/?y2) + (?/?z2)
f "(x) f关于x的二阶导数,f '(x)的导数
d2f/dx2 f关于x的二阶导数
f(2)(x) 同样也是f关于x的二阶导数
f(k)(x) f关于x的第k阶导数,f(k-1) (x)的导数
T 曲线切线方向上的单位向量,如果曲线可以描述成r(t), 则T = (dr/dt)/|dr/dt|
ds 沿曲线方向距离的导数
κ曲线的曲率,单位切线向量相对曲线距离的导数的值:|dT/ds|
符号含义
N dT/ds投影方向单位向量,垂直于T
B 平面T和N的单位法向量,即曲率的平面
τ曲线的扭率:|dB/ds|
g 重力常数
F 力学中力的标准符号
k 弹簧的弹簧常数
pi 第i个物体的动量
H 物理系统的哈密尔敦函数,即位置和动量表示的能量
{Q, H} Q, H的泊松括号
以一个关于x的函数的形式表达的f(x)的积分
函数f 从a到b的定积分。
当f是正的且 a < b 时表示由x轴和直线y = a, y = b 及在这些直
线之间的函数曲线所围起来图形的面积
L(d) 相等子区间大小为d,每个子区间左端点的值为f的黎曼和
R(d) 相等子区间大小为d,每个子区间右端点的值为f的黎曼和
M(d) 相等子区间大小为d,每个子区间上的最大值为f的黎曼和
m(d) 相等子区间大小为d,每个子区间上的最小值为f的黎曼和。
