动目标检测器(MTD)
雷达系统中的信号处理技术
雷达系统中的信号处理技术摘要本文介绍了雷达系统及雷达系统信号处理的主要内容,着重介绍与分析了雷达系统信号处理的正交采样、脉冲压缩、MTD和恒虚警检测几种现代雷达技术,雷达系统通过脉冲压缩解决解决雷达作用距离和距离分辨力之间的矛盾,通过MTD来探测动目标,通过恒虚警〔CFAR〕来实现整个系统对目标的检测。
关键词雷达系统正交采样脉冲压缩MTD 恒虚警检测1雷达系统概述雷达是Radar〔Radio Detection And Ranging〕的音译词,意为“无线电检测和测距”,即利用无线电波来检测目标并测定目标的位置,这也是雷达设备在最初阶段的功能。
雷达的任务就是测量目标的距离、方位和仰角,还包括目标的速度,以及从目标回波中获取更多有关目标的信息。
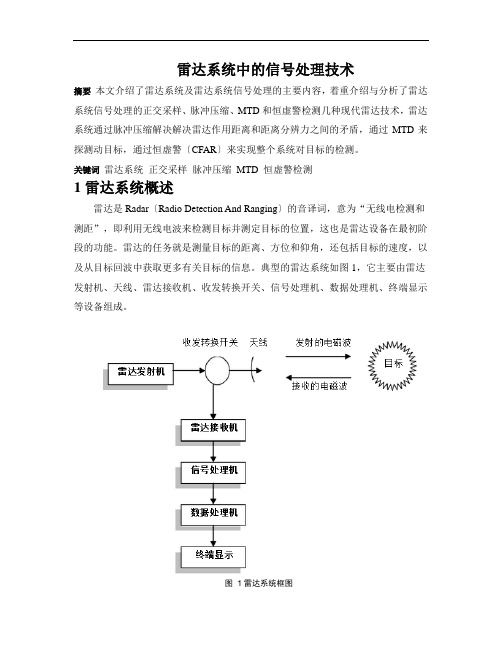
典型的雷达系统如图1,它主要由雷达发射机、天线、雷达接收机、收发转换开关、信号处理机、数据处理机、终端显示等设备组成。
图1雷达系统框图随着现代电子技术的不断发展,特别是数字信号处理技术、超大规模集成数字电路技术、电脑技术和通信技术的告诉发展,现代雷达信号处理技术正在向着算法更先进、更快速、处理容量更大和算法硬件化方向飞速发展,可以对目标回波与各种干扰、噪声的混叠信号进行有效的加工处理,最大程度低剔除无用信号,而且在一定的条件下,保证以最大发现概率发现目标和提取目标的有用信息。
雷达发射机产生符合要求的雷达波形,然后经馈线和收发开关由发射天线辐射出去,遇到目标后,电磁波一部分反射,经接收天线和收发开关由雷达接收机接收,然后对雷达回波信号依次进行信号处理、数据处理,就可以获知目标的相关信息。
雷达信号处理的流程如下:图 2 雷达信号处理流程2雷达信号处理的主要内容雷达信号处理是雷达系统的主要组成部分。
信号处理消除不需要的杂波,通过所需要的目标信号,并提取目标信息。
内容包括雷达信号处理的几个主要部分:正交采样、脉冲压缩、MTD和恒虚警检测。
正交采样是信号处理的第一步,担负着为后续处理提供高质量数据的任务。
航管一次雷达抗风电场干扰目标检测方法

杂波的方法对消 目标回波 , 而具有较 宽频谱宽度的风 电场杂波经对消后仍有大部分 的能量剩余 。 然后采用恒虚警率
f C o n s t a n t F a l s e A l a r m R a t e , C F A R ) 检测确定杂波所在的距离单元,并剔除待检测数据中所有杂波单元,解决了
D e t e c t o r , MT D ) 技术无法抑制具有非零频成分的风电场杂波,可能导致 目 标遮蔽和虚警率上升。针对此问题,该
文提 出了一种在 风电场杂波下航管一次雷达的 目标检测方法 。 该方法在 MTD前端设置风 电场杂波抑制器 。在该抑 制 器中首先估计雷达 回波 每个距离单元的谱中心 , 并把所有距离单元的谱 中心移到零频 。 其次利用类似 于对 消固定
Ab s t r a c t :I n r e c e n t y e a r s ,t h e g l o b a l wi n d p o we r i n s t a l l e d c a p a c i t y i s g r o wi n g e xp o n e n t i a l l y .Ho we v e r ,c u r r e n t
第3 5 卷第 3 期
2 0 1 3年 3月
电
子
与
信
息
学
报
Vl 0 1 . 3 5 NO . 3 Ma r . 2 0 1 3
动目标检测器MTD-PPT精选
Sc(f)
1
2c
exp2fc22
计算列表如下:
σc T
0.07 0.08 0.10 0.12 0.14 0.20
CAV(dB) 85.2 61.0 33.5 19.4 11.6 2.8
而 (IS) Im R a C x A(d V) B 1l0 o 1N 0 g (d)B
Ps为每个信号回波的功率,这里假设天线波瓣形状为矩形,所以 每个Ps相等。 Φ 为信号的随机相位。
2fdTr ,是脉冲——脉冲间的相移
2. 杂波回波是:
C TC 1,C 2,.C .M .,
这里: 3. 热噪声:
PcECi 2 是杂波功率
nTn 1,n2,..nM .,
2. 25dB 旁瓣 Chebyshev 加权
c 0.006 0.05 0.07 0.08 0.1 I SIR 93 51.3 43.8 40 32.8 可见,比理想性能相差较大, Chebyshev 加权副瓣越低,则 I SIR
这是系统改善因子上界;当非矩形窗加权时会有 S/N 损失,当 fd 不处于滤波器中央时,应算平均相参积累增益,也会有损失。
三. 实际 MTD 系统的改善因子
非理想白化 非矩形窗加权
实际 ISIR < 理想 ISIR
实际系统为一个 2 脉冲或 3 脉冲 MTI 级联加权滤波器组。 令:对消器传递函数和第 i 个滤波器传递函数的合成为:
具有复加权 W 的多普勒滤波器的噪声增益为
G nP P n n0 i W TP P nnIW *W TW *iN 1W i2
当信号的 fd 从 0PRF均匀分布时,信号平均增益
N
Gs Gn Wi 2 i1
输出信干比为:
MTI动目标显示雷达

样,取样后的波形和频谱均将发生变化。
动目标显示雷达的工作原理及主要组成
当用多普勒效应来鉴别运动目标回波和固定目标回波时, 与普通脉冲雷 达的差别是必须在相位检波器的输入端加上基准电压(或称相参电压) ,该 电压应和发射信号频率相参并保存发射信号的初相, 且在整个接收信号期间 连续存在。 工程上,基准电压的频率常选在中频(相位检波器的相位基准) 。各种 回波信号均与基准电压比较相位。从相位检波器输出的视频脉冲,有固定目 标的等幅脉冲串和运动目标的调幅脉冲串。通常在送到终端(显示器或数据 处理系统)去之前要将固定杂波消去,故要采用相消设备或杂波滤波器,滤 去杂波干扰而保存运动目标信息。 下面着重讨论相参电压的获取和固定杂波 消除这两个特殊问题。
脉冲工作状态时的多普勒效应 盲速和频闪
盲速:是指目标虽然有一定的径向速度������������ ,但若其回波信号经过相位检 波器后,输出为一串等幅脉冲,与固定目标的回波相同,此时的运动速度称 为盲速。 (������������ 等于脉冲重复频率������������ 的整数倍) 频闪: 频闪效应是指当脉冲工作状态时,相位检波器输出端回波脉冲信 号的包络调制频率������������ ,与目标运动的径向速度������������ 不再保持正比关系。此时如 用包络调制频率测速时将产生测速模糊。 (即������������ 超过重复频率������������ 的一半) 产生盲速和频闪效应的基本原因在于, 脉冲工作状态是对连续发射的取
2.消除固定目标回波
在相位检波器输出端, 固定目标的回波是一串振幅不变的脉冲,而运动 目标的回波是一串振幅调制的脉冲。将它们加到偏转调制显示器上,固定目 标的回波是振幅稳定的脉冲,而运动目标的回波呈现上下“跳动”的“蝴蝶 效应” 。 可以根据这种波形特点, 在偏转显示器上区分固定目标与运动目标。 如果要把回波信号加到亮度调制显示器或终端数据处理设备, 则必须先消除 固定目标回波。 最直观的一种办法是将相邻重复周期的信号相减,使固定目 标回波由于振幅不变而相互抵消; 运动目标回波相减后剩下相邻重复周期振 幅变化的部分输出。 A. 相消设备特性 相消设备等效于一个梳齿形滤波器,其频率特性在������ = ������������ ������ 各点均为零。 固定目标频谱的特点是,谱线位于������������������ 点上,因而在理想情况下,通过相消 器这样的梳齿滤波器后输出为零。 但当目标的多普勒频率为重复频率整数倍 时,其频谱结构也有相同的特点,故通过上述梳状滤波器后无输出。 B. 数字相消器 相消器需要迟延线将信号迟延一个脉冲重复周期并和未迟延的信号相 减。 现代大规模的集成电路的迅猛发展,可完全用数字技术来实现信号的存 储、延时和各种实时运算。 首先把从相位检波器输出的模拟信号变为数字信号。 以时钟脉冲控制取 样保持电路对输入相参视频信号取样, 被时间量化的取样保持信号送到模数 转换电路(A/D 变换器)进行幅度分层,转为数字信号输出。数字信号的延 迟可用存储器完成, 将数字信号按取样顺序写入存储器内,当下一个重复周 期的数字信号到来时, 由存储器中都会出同一距离单元的信号进行相减运算, 在输出端得到跨周期相消的数字信号。 一般取样间隔应小于脉冲宽度的一半, 即在一个脉冲宽度以内取样两次 以上。A/D 变换器的量化位数 N 应选到 N≥7 后,量化损失低于 0.08dB,可 以忽略其影响。N 的选择还对系统改善因子有影响。
雷达原理笔记之动目标检测及测速技术

1.1.3 二次杂波对消器
滤波器频率特性:
其中通常取接近2但小于2的常数。
目的同样是在保证尽可能多地滤除杂波的
同时,处在零多普勒点的运动目标不被抑制完全。
对比见下图:
二次杂波对消器是工程中应用最多的杂波处理滤波器。
对于低速的杂波消除,频响特性可以向右平移一定的区间,平移的量是杂波运动速度对应的多普勒频移。
因此对于低速运动杂波对消的滤波特性为:
其中为杂波速度对应的多普勒频移。
利用二次杂波对消器处理杂波时,选取相参积累脉冲个数为。
1.2 多普勒滤波器组处理
一般,将MTI处理后输出的信号进行MTD处理,即窄带滤波处理,得到运动目标的速度信息。
1.2.1 窄带多普勒滤波器组实现
利用有N个输出的横向滤波器,经过各脉冲的加权求和实现。
频响幅度为:。
动目标检测器(MTD)
2)多普勒滤波器组的实现方法
1. FFT算法: 当 M=2T(T=整数)时,可用基 2FFT,并采用加权来 减小旁瓣,降低杂波通过旁瓣的泄漏,提高改善因子。 一般采用:Hamming 或 Chebyshev 加权效果较好。
于前面讲过的平均改善因子。
可见MTD可以看成白化滤波器(具有平均改善因子IMTI) 和相干积累器(多普勒滤波器组)的级联。
白化滤波 IMTI
多普勒滤 波器组GC
由文献知,最佳 W OPT 应为: 干扰协方差阵的逆
* W OPT ( f d ) P R P I S ( f ) c c n d 1
4 ×M2 例:M = 16,则 4×(16)2 :运算量大,复杂
§3. MTD 系统的改善因子
一. 最佳多普勒滤波器组构成的 MTD 系统的改善因子 所谓最佳多普勒滤波器组,即每个滤波器的权函数 Wi 都是 最优权函数。这里最优是相对于一定的杂波模型和信号假设而言 的。 1. CPI 中M个信号回波可用一复矢量表示:
所以 BMTD 的定义为:将一个 CPI 中的回波结合为一 组,来进行 MTD 处理。 波束中的回波应分为 2 个CPI,才能保证至少一个CPI
中包含了全部目标信息,否则会导致 S/N 下降,降低
检测性能。
CPI2 CPI1 ¿ ± Ä ê
例:击中数 H=32 时, m=16 (个), 这是最大值
1
2
这里: Sc(f) 是杂波功率谱 (采样前,f 是从 0 内扩展的)
rep 1 SC ( f ) SC ( f j ) T T j
mtd动目标检测原理

mtd动目标检测原理
MTD动目标检测原理是一种用于实时视频监控和检测的技术,它能够通过对视频帧进行分析,准确地检测出移动物体。
该原理基于视频中移动目标的像素值变化,通过比较相邻帧的像素值差异来确定是否存在移动目标。
在检测的过程中,MTD会将每帧图像分成多个区域,并计算每个区域的像素变化值。
首先,MTD采集两个连续帧的图像,并将它们转换为灰度图像。
然后,它计算每个像素的绝对差值。
接下来,MTD将所有像素的差值相加,得到某个区域的总像素差值。
在确定移动目标的位置时,MTD通过设置一个动态阈值来筛选出像素差值大于阈值的区域。
这些区域被认为是可能存在移动目标的部分。
为了减少误检测和提高检测的准确性,MTD还可以通过应用一些滤波算法来排除噪声。
同时,MTD还会采用多帧图像的平均像素值来对比判断移动目标。
MTD动目标检测原理具有实时性强、准确性高的特点。
它可以应用于各种实时监控系统中,如交通监控、安防监控、智能家居等领域,为人们提供更安全、便捷的生活环境。
总之,MTD动目标检测原理是一种基于像素变化的实时视频监控技术。
通过计算像素差值和设定动态阈值,它能够快速、准确地检测出移动目标,为各种实时监控系统提供支持。
RSP_MTI & MTD

2005.07
MTD 与 MTI 的比较
早期的MTI雷达改善因子一般在20dB左右,而雷达的实际杂波强 度可能达到50dB甚至更强。MTI雷达性能不高是多方面原因造成的: 如锁相相参系统的高频稳定性不够,采用模拟延迟线通常只能做一次 相消且性能不稳定,不能实现最佳滤波,等等。 动目标检测(MTD)是在MTI基础上发展起来的一项更有效的 频域滤波技术。与MTI相比,MTD主要在三个方面作了改进: 1. 增加一个多普勒滤波器组,使之更接近于最佳(匹配)线性滤 波,在抑制固定杂波的同时,也能抑制气象、鸟群等慢动杂波,有效 地提高改善因子。这是MTD不同于MTI的核心区别; 2. 增加一个或多个杂波图,使之能够检测切向飞行的大目标; 3. 利用数字信号处理实现长时间的存储与延迟,并增大信号处理 的线性动态范围。
SCV(dB) I(dB)-V0 dB) = (
CA、CR、I和SCV只要知道其中一个就能推算其它三个。 其它指标:杂波间可见度、滤波器失配损耗、杂波可见度 因子可参见《雷达手册》。
参考文献:马晓岩,向家彬等,《雷达信号处理》,湖南科学技术出版社,第5章
盲相及其消除方法
相参MTI通过相邻回波脉冲的相位相减提取动目标回波,当 相邻脉冲间动目标回波的相位差正好为π 的整数倍时,MTI滤波 器将无输出(推导过程见参考书),出现“盲相”。
参考文献:《雷达手册》(第二版),第15章,电子工业出版社,2003
MTI 原理
对非相参雷达,实现MTI则需要对回波包络进行对 消,其原理可见参考书。 MTI实际上是一种频域滤波器。用数字器件实现的 一次对消MTI滤波器结构图如下:
参考文献:马晓岩,向家彬等,《雷达信号处理》,湖南科学技术出版社,第5章
雷达信号处理

雷达信号处理技术与系统设计第一章绪论1.1 论文的背景及其意义近年来,随着电子器件技术与计算机技术的迅速发展,各种雷达信号处理技术的理论与应用研究成为一大热门领域。
雷达信号的动目标检测(MAD)是利用动目标、地杂波、箔条和气象干扰在频谱上的差别,抑制来自建筑物、山、树、海和雨之类的固定或低速杂波信号。
区分运动目标和杂波的基础是它们在运动速度上的差别,运动速度不同会引起回波信号频率产生的多普勒频移不相等,这就可以从频率上区分不同速度目标的回波。
固定杂波的中心频率位于零频,很容易设计滤波器将其消除。
但对于运动杂波,由于其多普勒频移未知,不能像消除固定杂波那样很容易地设计滤波器,其抑制就变得困难了从本质上来讲,雷达信号的检测问题就是对某一坐标位置上目标信号“有”或“无”的判断问题。
最初,这一任务由雷达操作员根据雷达屏幕上的目标回波信号进行人工判断来完成。
后来,出现了自动检测技术,一开始为固定或半固定门限检测,这种体制下当干扰和杂波功率水平增加几分贝,虚警概率将急剧增加,以至于显示器画面饱和或数据处理过载,这时即使信噪比很大,也不能作出正确的判断。
为克服这些问题进而发展了自适应恒虚警(Constant FalseAlarm Rate,CFAR)检测。
CFAR 检测使得雷达在多变的背景信号中能够维持虚警概率的相对稳定,这种虚警概率的稳定性对于大多数的雷达,如搜索警戒雷达、跟踪雷达、火控雷达等。
第二章 雷达信号数字脉冲压缩技术2.1 引言雷达脉冲压缩器的设计实际上就是匹配滤波器的设计。
根据脉冲压缩系统实 现时的器件不同,通常脉冲压缩的实现方法分为两类,一类是用模拟器件实现的 模拟方式,另一类是数字方式实现的,主要采用数字器件实现。
脉冲压缩处理时必须解决降低距离旁瓣的问题,否则强信号脉冲压缩的旁瓣 会掩盖或干扰附近的弱信号的反射回波。
这种情况在实际工作中是不允许的。
采 用加权的方法可以降低旁瓣,理论设计旁瓣可以达到小于-40dB 的量级。
动目标显示与动目标检测
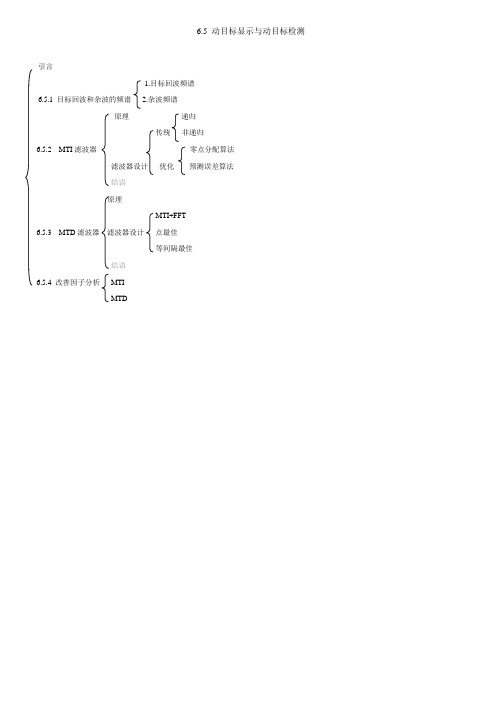
6.5 动目标显示与动目标检测引言1.目标回波频谱6.5.1 目标回波和杂波的频谱 2.杂波频谱原理递归传统非递归6.5.2 MTI滤波器零点分配算法滤波器设计优化预测误差算法结语原理MTI+FFT6.5.3 MTD滤波器滤波器设计点最佳等间隔最佳结语6.5.4 改善因子分析MTIMTD6.5 动目标显示与动目标检测雷达探测的运动目标如飞机,导弹,舰艇,车辆等周围存在各种背景,包括不动的地物和运动着的云雨,海浪或金属丝干扰等。
动目标显示(Moving Target Indicator :MTI )与动目标检测(Moving Target Detection: MTD )就是使用各种滤波器,滤去这些背景产生的杂波而取出运动目标的回波。
此外也可以通过把雷达安装在山上、增加雷达天线的倾角、安装防杂波网来阻止杂波进入天线;或通过调整雷达天线的波束形式、采用极化技术、降低雷达的分辨单元、在时域采用CFAR 检测、自适应门限、杂波图来抑制杂波。
在频域上应用MTI 与MTD 技术可以提高信杂比,改善杂波背景下检测运动目标的能力。
本节首先分析目标回波和杂波的频谱特性;然后分别讨论MTI 与MTD 原理及滤波器设计方法;最后分析MTI 与MTD 对改善因子的提高。
6.5.1 目标回波和杂波的频谱运动目标回波和杂波在频谱结构上有所差别,运动目标检测就是利用这种差别,从频率上将它们区分,以达到抑制杂波而显示目标回波的目的。
为此,应首先弄清楚目标和杂波的回波的特性。
(1) 目标回波的频谱雷达发射相参脉冲串,其脉冲宽度为e T ,脉冲重复频率为r f 。
当天线不扫描而对准目标时,所得脉冲为无限脉冲串。
调制信号)(1t u 及其频谱)(1f U 分别为∑∞-∞=⎪⎪⎭⎫⎝⎛-=n e rTnT t rect A t u )(1 (6.5.1)∑∞-∞=-=n r e e r e f n f T f T f T AT f U )()sin()(1δππ (6.5.2)A 为信号振幅。
mtd多普勒维fft的点数_径向速度_解释说明

mtd多普勒维fft的点数径向速度解释说明1. 引言1.1 概述本文主要研究关于MTD(多普勒维)FFT(快速傅里叶变换)的点数以及径向速度的解释说明。
MTD在雷达系统中广泛应用,可以实时检测目标物体的动态信息。
而FFT作为一种常用的信号处理方法,被广泛应用于雷达信号处理中。
1.2 文章结构本文共分为四个部分进行讨论。
首先是引言部分,概述了文章的背景和研究内容。
其次是第2部分,探讨了MTD多普勒维FFT的点数选择问题,包括相关概念、选择因素以及选择方法和准则。
第3部分则着重介绍了径向速度的概念、测量方法和原理以及相关技术应用场景。
最后,在第4部分中对研究内容和结果进行总结,并指出当前研究不足之处,并展望未来的发展方向。
1.3 目的本文旨在通过对MTD多普勒维FFT点数选择和径向速度解释说明的深入研究,提供对于雷达信号处理相关领域从业人员更加全面详尽的知识体系。
通过阐明点数选择的理论依据和方法,以及径向速度的测量原理和应用场景,有助于读者深入了解相关技术背后的原理,并为实际项目中的应用提供参考和指导。
2. MTD多普勒维FFT的点数2.1 MTD多普勒维FFT的概念MTD(Moving Target Detection)多普勒维FFT(Fast Fourier Transform)是一种信号处理技术,用于探测和分析移动目标在雷达回波中引起的频率变化。
通过将雷达接收到的信号进行FFT计算,可以得到不同速度下目标回波的频谱信息,进而实现对移动目标的检测和定位。
2.2 FFT的点数选择因素在进行MTD多普勒维FFT分析时,选择适当的FFT点数非常重要。
FFT点数决定了频率分辨率以及所能覆盖的最高和最低频率范围。
点数越大,频率分辨率越高,但计算复杂度也会增加。
选择FFT点数需要考虑以下因素:- 目标速度范围:目标速度范围较大时,需要选择更高的FFT点数来保证对所有速度区间进行准确检测。
- 必要平滑度:如果需要更平滑且精确的速度谱估计结果,则需要使用较大的FFT点数。
MTI和MTD解读

Wik e
j[ 2ik / N ]
,i 0,1,2...N 1
i表示第几个滤波器的抽头,k表示从0到N-1的标记,每一个k值对应一组 不同的加权值,即对应于不同的多普勒滤波器,每一个k值决定了一个独 立的滤波器的响应。
窄带滤波器组的每个抽头有N个输出,并且对应N个加权值,输入信号x(i) 与滤波器组Y(k)关系为
FFT实现
FFT将N个脉冲分成N个频段(对应N个窄带滤波器)做FFT运算,每个 频段分别积累N个脉冲时长的数据,每个点的运算相当于是一个带通滤 波器,每个滤波器都有一定的副瓣,可考虑使用窗函数加权抑制杂波。
但FFT滤波器在零频和脉冲重复频率整数倍处没有凹陷,所以无 法抑制静态杂波,需要考虑其他方式帮助解决。可以考虑添加MTI对消 器,或者将静态杂波对应的滤波器通道的输出去除。 此外,FFT需要回波脉冲串个数为2的整数次幂,同时如果想要 达到比较高的检测精度,FFT变换的点数不能太少,也就是需要更多的 回波脉冲串。但是在实际情况中,雷达的回波脉冲串个数是受多方面影 响,不可能随意变更的。这会使FFT滤波器组的应用受到一定的限制。
h1 (t ) (t ) (t T )
傅里叶变换为 H1 (w) 1 e jwt,w 2f
功率增益为 H1 ( w) H1 ( w) (1 e jwT )(1 e jwT )
* 2(1 cos wT Nhomakorabea) 4 sin 2 (
wT ) 2
双延迟线对消器:
零号滤波器,也就是K=0的滤波器,其通带中心位置分别是0,1/T,2/T.... 即零频和雷达重复频率的整数倍处,以雷达脉冲重复周期为周期,通带 正是静态杂波的频谱集中的位置,所以可以把此滤波器的输出看成是静 态杂波的输出。同理,K=n时的滤波器,其通带中心分别位于 n/NT,n/NT+1/T,n/NT+1/T....。 一般情况下,不同的滤波器对信噪比的改善不相同,如果几个滤波器的 通带靠近杂波频率谱的中心位置,那么他们的改善就相对差一些。因此, 如果杂波谱比较集中,采用MTD窄带滤波器可以得到较好的滤波性能。 但是,如果杂波的频谱分布比较宽,那么与MTI相比,窄带滤波器的改 善也就没那么明显。 此外,窄带滤波器对滤除低速运动杂波也有优势。因为低速目标杂波可 能只出现在滤波器组的某一个滤波器中,根据实际情况,如果此滤波器 频带内的噪声和杂波较强,则可适当提高此滤波器的门限电压,这样可 以很好的减小低速杂波的影响,同时又不影响其他滤波器的输出。
雷达习题

2试推导用最小可检电平表示的雷达距离方程,说明方程中各参数的意义以及提高雷达作用距离的可能途径。
六、公式解析题
雷达基本方程之一 ,
1)给出上述方程中各参量Pt、、Ar、L的名称及其量纲单位(国际单位制);
2)列举通过提高Pt来增加Rmax的缺点(至少2条);
4)假设雷达接收信号中地杂波功率随斜距的变化规律为Pc(R) = 16dB-30lgR,其中Pc(R)和R的量纲单位分别为dBW和m,目标回波功率函数同第3)小题,试推导R0= 50km处的信杂比SCR(目标信号功率与杂波功率之比)表达式(dB)?
八、某-100dBmW,雷达波长为=3cm,带宽为Bn= 150kHz。单个脉冲检测非起伏目标的检测因子与发现概率(检测概率)的关系曲线如下图所示。
11.某车载全相参脉冲雷达的峰值发射功率为Pt,脉冲重复频率为fr,工作频率为f0,雷达车以速度vr直线行进,在雷达车正侧方某处有一巨石,测得该巨石的脉冲回波延时为,则对雷达接收机来说,该巨石的距离为。若该雷达采用N个等幅脉冲进行多普勒滤波处理,则该雷达的多普勒分辨力为。
12.根据最优滤波理论,匹配滤波器应位于白化滤波器(之前/之后/都可以)。
3)根据上述方程,某甲得出结论“雷达工程师可通过增加值来提高Rmax”。请判断该结论是否正确,并简要说明理由。
4)某搜索雷达沿方位向360o匀速旋转扫描,某乙根据上述方程得出结论“雷达工程师可通过提高Ar来增加该雷达的Rmax”。试分析该结论可能会面临的缺点。
七、综合题某雷达发射等幅相参脉冲串,脉冲重复频率为fr= 10kHz,脉冲宽度为= 2s,对于=2m2的目标,在发现概率与虚警概率分别为Pd和Pfa的条件下,由雷达方程算得的雷达最大作用距离为Ru= 40km,
基于GPU的MTD性能优化

火控雷达技术Fie Control Radar Technology第50卷第1期(总第195期)2021年3月Vol. 50 Na 1( Series 195)Mar. 2021基于GPU 的MTD 性能优化杨千禾袁子乔扈月松(西安电子工程研究所 西安 710100)摘 要:为了解决传统雷达信号处理机在研发阶段面临的调试困难,计算能力受硬件限制及程序复用性差等问题,本文提出了使用GPU 作为雷达计算核心的方案。
在使用GPU 实现雷达信号处理算法的过程中,动目标检测(MTD )部分的优化效果远低于脉冲压缩和恒虚警检测。
经过分析, MTD 过程中的矩阵转置与向量点乘占据了算法的大量时间。
本文从GPU 的数据读取方式和CU-DA 函数特性入手,优化快速傅里叶变换实现MTD 的过程,并在GPU 上使用CUBLAS 矩阵运算实现有限脉冲响应滤波器组对脉冲压缩之后数据的滤波,实现了更具灵活性的MTD 。
最终得到的 GPU 计算结果与CPU 平台实现的结果相比,误差不超过0.05%,同时实现了相比CPU 平台优化实现最多200余倍的性能提升。
关键词:动目标检测;GPU ;异构处理平台;CUBLAS中图分类号:TN95 文献标志码:A 文章编号:1008 -8652(2021)01 -086 -08引用格式:杨千禾,袁子乔,扈月松.基于GPU 的MTD 性能优化[J ].火控雷达技术,2021,50 (1):86 -93.DOI :10.19472/j. oki. 1008 -8652.2021.01.016Performance Optimization of MTD Basee on GPUYANG Qianhe $ YUAN Ziqiao $ HU Yuesong(Xiin Electronic Engineering Research Institute $ Xiin 710100 )Abstract : In order to solve the problems of adjustwent , hardware limitation and program reusability of traditional ra dar signal processor in the research and development stage , this paper proposes a scheme of using GPU as the compu ting core of radar. In the process of using GPU to realize radar signal processing algorithms , the improvement in mov ing target detection ( MTD ) is far les s than that in PC and CFAR. Our anCysis reveals that the matne transpose and vector point multiplication occupy a lot of time in the MTD process. This paper starts with the data reading mode ofGPU and the characteristics of CUD A function , optimizes the process of fast Fourier transform based MTD, and uses CUBLAS matne opvation on GPU to enable data filteUng after pulse ompnsion by finite impulse response filter bank , so as to realize more flexible MTD. Compared with the results of a CPU plaVorm , the error of the final GPU cal culation results is less than 0.05% , and the performance improvement is 200 times of that of the CPU platform.Keyworit : MTD ; GPU ; heterogeneous computing platform ; CUBLAS节。
MTI和MTD的区别

MTI和MTD的区别MTI是一种频域滤波器(radar主席的ppt中说到),它是对多组脉冲回波的同一个距离单元加权求和,得到一个结果;也就是多个输入一个输出;相当于一个高通滤波器,用来抑制固定目标和慢速杂波。
就一次对消MTI滤波器来说,就是将第一个发射脉冲的回波与第二个发射脉冲的回波相减,除去固定目标和慢速杂波,而保留了运动目标的信息,通过视频显示器可以看到幅度上下振动的波形,这也是为什么叫动目标显示;MTD是带通滤波器组,也就是多个输入多个输出,可以用FIR组实现,但是一般用FFT实现,即对不同脉冲组回波信号的相同距离单元做FFT处理,N 个输入得到N个输出,CACFAR既是对这N个输出进行检测和判断目标!若存在目标,这N个输出中比出现一个峰值最大的数,则这个可能就是目标的位置信息,根据位置信息,即可以得到运动目标的多普勒值!上面的理解基本正确,但不仅有些说法不准确,而且整体上也不全面。
说MTI是多个输入一个输出,而MTD是多个输入多个输出就有点狭隘,实际上他们的输出都是同一个距离单元多个回波的频谱,只不过MTI的输出是抑制了0频率附近频谱后的高通滤波连续频谱,频谱范围为fa~PRF,fa为高通滤波器左端的截止频率;而MTD的输出则是将位于0~PRF的频谱分割成N(N为一次处理的脉冲数目,大小由波束宽度、天线扫描速度等因素决定)个等间隔的离散谱线0,PRF/N,2*PRF/N,…,(N-1)*PRF/N,其目的是便于抑制位置不在0频率附近的运动平台地杂波。
这是从滤波器的侠义角度理解的,也是MTI和MTD的最本质区别。
除此之外,MTD在实现上还增加了一个或多个运动杂波图,使雷达能够在平台运动时检测切向飞行的大目标;而且MTD还通过采用数字信号处理实现了长时间的存储与延迟,相比MTI大大增加了信号处理的线性动态范围。
两者在实现上是完全不一样的。
可以说MTD是比MTI更先进的一种动目标检测技术,完全可以替代MTI,但由于MTI实现简单,在现有地面雷达中仍大量使用。
机载雷达系统的信号处理技术

机载雷达系统的信号处理技术在现代航空领域中,机载雷达系统扮演着至关重要的角色。
它就像是飞机的“眼睛”,能够帮助飞行员在复杂的环境中探测目标、获取信息,保障飞行的安全与高效。
而在机载雷达系统中,信号处理技术则是核心关键,它决定了雷达性能的优劣。
机载雷达系统所接收到的信号通常是极其微弱且混杂在各种噪声中的。
这就好比在一个嘈杂的集市中,要从众多的声音中分辨出特定的一个人的讲话。
为了能从这些复杂的信号中提取出有用的信息,先进的信号处理技术应运而生。
首先,我们来谈谈脉冲压缩技术。
脉冲压缩可以理解为一种在保持雷达发射功率不变的情况下,通过对发射脉冲进行特殊编码,使其在接收端经过匹配滤波处理后,能同时获得大的探测距离和高的距离分辨率。
简单来说,就是让雷达在看得远的同时,也能看得清楚。
在实际应用中,常见的脉冲压缩技术包括线性调频、相位编码等。
线性调频就像是一个逐渐升高或降低的音调,通过对接收信号的处理,可以将这个“音调”压缩成一个很窄的脉冲,从而提高距离分辨率。
相位编码则是给发射脉冲赋予特定的相位模式,接收端根据这个模式进行解码和处理。
接下来是动目标显示(MTI)和动目标检测(MTD)技术。
在充满各种运动目标的环境中,如何有效地检测出那些相对于背景有相对运动的目标是个关键问题。
MTI 技术通过对相邻脉冲回波的相减,来抑制固定杂波,突出运动目标。
而 MTD 技术则是在 MTI 的基础上发展而来,通过更复杂的滤波器组,进一步提高了对运动目标的检测性能。
机载雷达在工作时,往往会受到各种干扰,比如敌方的电子干扰、自然环境中的电磁干扰等。
这时候,抗干扰技术就显得尤为重要。
频率捷变技术通过快速改变雷达的工作频率,让敌方难以跟踪和干扰。
而自适应波束形成技术则能够根据干扰的方向,自动调整雷达波束的形状和指向,降低干扰的影响。
在信号处理中,数字滤波技术也是不可或缺的一部分。
它就像是一个筛子,能够把我们不需要的噪声和干扰滤除掉,只留下有用的信号。
MTD雷达信号处理实现过程简析

MTD雷达信号处理实现过程简析作者:徐卫合赵咏梅来源:《无线互联科技》2014年第05期摘要:动目标检测(MTD,Moving target detection)是现代雷达系统中重要的信号处理技术,采用MTD技术的雷达在当前得到了越来越广泛的应用。
文中介绍了MTI/MTD技术的基本原理,对MTD雷达信号处理的实现方法和一般过程进行了简要的分析,并对某些关键部分的多种实现方法进行了一些比较。
关键词:MTI;MTD;动目标;多普勒滤波器组雷达在探测各种运动目标时几乎都会受到杂波的干扰。
由于运动目标和固定目标、一些缓慢运动的目标如气象杂波,敌方施放的铝箔干扰条、鸟群等产生的回波信号的多普勒频移是不同的,针对此区别采用MTI/MTD技术就可以获得所需的目标信息。
1 MTI/MTD的简介动目标显示(MTI)简单理解就是一种抑制固定杂波或缓慢运动杂波的频域滤波器。
它利用运动目标回波和固定杂波及慢速杂波在频域上的不同,有效抑制杂波而获取目标回波信号。
MTD是为了弥补MTI某些情况下检测能力不够的缺陷,提高在强杂波、弱目标时,依据最佳滤波器理论使用的一种信号处理技术。
在信号处理方面MTD比MTI从下面三个方面进行了改进:⑴采用了更多的数字信号处理技术,改善了滤波器频率特性,更接近于最佳滤波,提高了改善因子;⑵能够检测到强地物杂波中低速运动的目标甚至是处于切向方向飞行的大目标;⑶能够同时抑制平均多普勒频移等于零的固定目标杂波和诸如气象、鸟群等产生的慢动杂波。
2 MTD雷达信号处理系统MTD雷达信号处理系统,简单的说就是在MTI的基础上增加了一组覆盖目标回波多普勒频率的所有可能范围的窄带滤波器。
其基本框图如图1所示。
2.1 MTI的信号处理MTI是基于多普勒频率来区分运动目标回波和地物杂波及慢速杂波干扰的,因而MTI一般包括含有多普勒信息的回波信号的相参处理和进行目标区分时的对消处理这两个基本部分。
⑴多普勒信息的获取是使用I、Q正交双通道相干检波器来实现的。
采用单片CPLD实现雷达动目标检测处理

导 航与 雷达动 态
20 0 2年第 4期
其传递函数为 Hz= .Z z ()1 ’ 一。本电路中 K值取 2 K + 。其实际构
成框 图如 图 3所示。 由双端 口存储器 D R M 构成数字延迟线。输 PA 入信 号经过延迟线延迟一个重复周期后 ,与下 一个周期 的输入信 号相
减后输出。由两级相同的一次对消器电路级联构成二次对消器。
处理电路一共需要七级延迟 线来存储前七个周期的回波数据。在 F T F
蝶 型运 算 网络 电路之前 串接 时域 加权 电路 来降低 输 出信 号 的副瓣 电
平。经过 F T 蝶型运算网络的运算产生八个窄带子滤波器输出。其 F
中零号滤波器 中的是固定杂波,故零号滤 波器将不被输 出。其余七个
是处理速度快、集成度高,电路体积小。MT D原理框图如图 1 所示。
输出
图 1 动 目标 检 测 ( : MTD )原 理 框 图
来 自 A, 转换器的 1 D 0位 I 、Q 双通道数字化回波信 号先经过 二 次对消器 ,对消掉大部分静止 杂波。再经过 由 8点 F T 处理 电路所 F
3用 C L 实现动 目标检 测的原理及工程实现 PD
在动 目标检 测雷达 中,动 目标检测 ( D)主要 由二次对消器 、 MT
多卜 勒滤 波器组 、求模 以及恒虚警 处理等 电路组成 。本设 计使用一片
ATR L E A公 司的 A E 2 K 0 E C L P X 0 4 0 P D芯 片来实现上述 电路。其特 点
窄带子滤波器输 出运动 目标信 息。其输 出的 I 、Q 两路信 号经求模 电
路求模后输 出模值到恒虚警处理电路。
由于 F T蝶形运算网络采用并行运算结构,所以运算速度很快。 F
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可见MTD可以看成白化滤波器(具有平均改善因子IMTI) 和相干积累器(多普勒滤波器组)的级联。
白化滤波 IMTI
多普勒滤 波器组GC
由文献知,最佳 W OPT 应为: 干扰协方差阵的逆
W OPT ( f d ) Pc R c Pn I S ( f d )*
2
n
(这里假设 s,c,n 为统计独立的)
5. 改善因子:
输入信干比为:
Ps ( SIR) in Pc Pn
令多普勒滤波器组有复加权 W
W w1 , w2 ,..., wN
T
, wi 为每一个滤波器通道的权值
则滤波器的输出为: 相应的输出功率为:
YX W
T
*
PY E Y
T
所以 BMTD 的定义为:将一个 CPI 中的回波结合为一 组,来进行 MTD 处理。 波束中的回波应分为 2 个CPI,才能保证至少一个CPI
中包含了全部目标信息,否则会导致 S/N 下降,降低
检测性能。
CPI2 CPI1 ¿ ê Ä ±
例:击中数 H=32 时, m=16 (个), 这是最大值
二. 乒乓存储器:
为了实时进行成组处理,必须首先将一个 CPI 中的全
部回波数据存储起来,当该 CPI 数据全部存完后(乒 存储器存满后),则取出来沿距离间隔顺序处理,与此 同时,对下一个 CPI 的回波数据进行存储(存入乓存 储器)
乒乓存储器容量: 设:CPI = m 距离间隔 = n A/D字长 = b bits
PCi
PRF
0 PRF
rep1 Sc ( f )df Sc ( f )df
T
PC0
Pni 1
0
rep1 Sc ( f ) H iw ( f ) df
T
2
Pn0
则:
PRF
0
H iw ( f ) df
2
C AVi
PRF 0
PRF0reFra bibliotek 1 S c ( f )df
Pn0
T
*
2
当信号的 f d 从 0 PRF 均匀分布时,信号平均增益
G s Gn Wi
i 1
N
2
输出信干比为:
( SIR) out
Ps W R s ( f d )W Pc0 Pn0 Pc W T R c W * PnGn
Ps0
T
*
则改善因子:
输入(杂波+噪声)功率 信号功率增益
MTD 输出值
F1 F2
. . .
CFAR CFAR
¡ ó Ñ ´
FN
CFAR
§2. 成组处理MTD——BMTD
一. CPI:
天线扫过一个点目标时在方位上的相继回波数,称为
击中数 H。 CPI —— 相参处理间隔是BMTD中组的大小。若一个 CPI内的回波数为 m,应保证:
H m n
这里
n 2(整数)
T 2 T
rep 1 S c ( f ) H iw ( f ) df
xi
加权
FFT
滤波器组的FFT实现
优点:运算量少,设备简单;
M 运算量为: log 2 M 次蝶形运算。 2 M 采用四周蝶形算法,故乘法次数为 4 log 2 M 2
16 例:M=16,乘法次数为 4 log 2 16 4 32 128 次乘加。 2
缺点:每个滤波器形状完全一致,不灵活。
1
2
这里: Sc(f) 是杂波功率谱 (采样前,f 是从 0 内扩展的)
rep 1 SC ( f ) SC ( f j ) T T j
0 f PRF 1 T PRF
,j 取整数
相当于把杂波功率折叠到
0 PRF 内
白化滤波器平均归一化对消比:
C AV
3) 匹配滤波器
目标 fd 从 0-fr 均匀分布,所以设置多普勒滤波器组
来近似实现匹配滤波;可用 FIR 或 FFT 来实现。
ä ö Ë ² ÷ Ê ³  ¨Æ
fd ¿ ± Ä ê
fr
f
4) 频域CFAR和选大
在每一多普勒滤波器通道输出设置CFAR电路;各通
道过 CFAR 门限的信号相互比大,取最大值作为
实际系统为一个 2 脉冲或 3 脉冲 MTI 级联加权滤波器组。 令:对消器传递函数和第 i 个滤波器传递函数的合成为:
H iw ( f ) H1 ( f ) H i ( f )
对
H iw ( f ) 而言,归一化对消比为:
C AVi PCi Pn0 (杂波抑制比)×(噪声增益) PC0 Pni
T *
输出(杂波+噪声)功率
Pc Pn I SIR ( f d ) W R s ( f d )W T * W ( Pc R c Pn I )W W R s ( f d )W W W ( Pc Pn ) T T * * W W W ( Pc R c Pn I )W
T * T *
又:
PCi Pn0 (杂波抑制比)×(噪声增益) PC0 Pni
PRF 0 PRF
PCi
rep1 Sc ( f )df Sc ( f )df
T
PC0
令
0
rep1 Sc ( f ) H w ( f ) df PRF
T
PRF 0
2
Pni 1,
Pn0
f d 2 f c ( f d ) k exp 2 c
可用数值计算出不同
c
和 N 时的
I SIR
当:
c
fr
I SIR
0.09, N 9 时
6 4 N=2 8
I SIR 55 dB
c
fr
0.11
2 3 14 4 18 6 25 9 32.5 16 40
2. FIR算法
a) 权系数设计:窗函数法 ……任意窗函数 Remez多重变换算法……旁瓣约束等波纹设计法
权系数 hi(n), ( i=1,2,……,M), (n=1,2,……,M)
b) 具体算法: yi
x h (M n 1),
n 1 n i
M
i=1,2,……,M
这里 yi 和 xn 为复数, 于是有:
T
C C1 , C2 ,..., CM
这里:
3. 热噪声:
T
Pc E C i
2
是杂波功率
n n1 , n2 ,..., nM
这里: 4. 总输入为:
PN E n i
2 S C
为噪声功率
X S ( fd ) C n
PX E X i
P P P
I SIR ( f d ) Gc I MTI
W R s ( f d )W Gc T * W W
T *
T
*
为信号功率增益对噪声功率增 益之比,即为相干积累增益
I MTI
W W ( Pc Pn ) 为归一化的干扰抑制比,即干 T * W ( Pc R c Pn I )W 扰抑制比乘噪声增益。这相当
E( X W )
2 T
* T*
其中,E X X
*
W E X X W
* T
T
(X W )
T
*
*
代表输入回波的协方差矩阵,用 R X 表示
R X PS R S ( f d ) PC R C Pn R n
(因S,C,n相互统计独立)
1 这里, R s ( f d ) E S ( f d )* S ( f d )T Ps 1 * T Rc E C C Pc
其中,
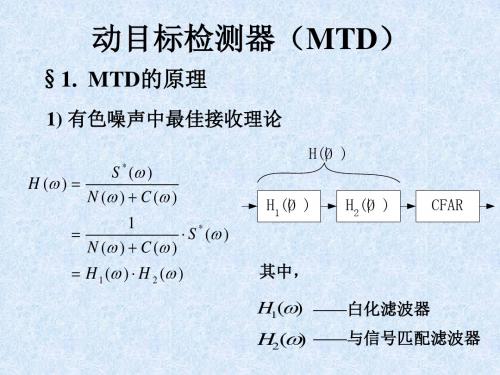
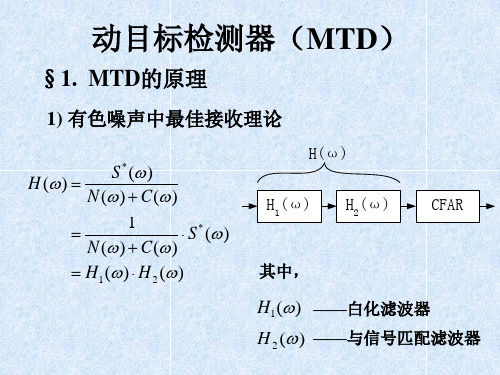
H1 ( ) ——白化滤波器
H 2 ( ) ——与信号匹配滤波器
2) 白化滤波器的实现
白化滤波器频率特性应为有色杂波加噪声谱的倒 数,在实现上有几种近似方法: A) MTI 对地杂波近似白化 B) 速度自适应 MTI,对运动杂波近似白化 C) MTI + 速度自适应 MTI,对地杂波和运动杂 波同时实现近似白化 D) 最大熵谱估计 AMTI,理想白化
1
信号的复共轭
具有最佳加权的MTD就是有色噪声中的最佳检测器。 由于 W OPT ( f d ) 和 I SIR ( f d ) 都是 f d 的函数,当 f d 在 0 PRF 中均匀分布时,该最佳处理器的平均改善因 子为:
I SIR
1 fr
fr
0
I SIR ( f d )dfd
例:杂波谱为高斯形
4 ×M2 例:M = 16,则 4×(16)2 = 1024 (复乘)
优点:灵活,性能好 缺点:运算量大,复杂
§3. MTD 系统的改善因子
一. 最佳多普勒滤波器组构成的 MTD 系统的改善因子 所谓最佳多普勒滤波器组,即每个滤波器的权函数 Wi 都是 最优权函数。这里最优是相对于一定的杂波模型和信号假设而言 的。 1. CPI 中M个信号回波可用一复矢量表示:
动目标检测器(MTD)
§1. MTD的原理
1) 有色噪声中最佳接收理论
S * ( ) H ( ) N ( ) C ( ) 1 S * ( ) N ( ) C ( ) H 1 ( ) H 2 ( )
H(¦ ) Ø H1(¦ ) Ø H2(¦ ) Ø CFAR
¸ æ ¢ ÷ Æ ´ ´ Æ Ò æ ¢ ÷ Å ´ ´ Æ
则:Z = 2 × m × n × b × 2 = 4mnb | | 乒乓 I, Q
