(word完整版)四年级奥数专题09:格点与面积.docx
四年级奥数专题 格点与面积(学生版)

学科培优数学“格点与面积”学生姓名授课日期教师姓名授课时长知识定位本讲知识点比较简单,首次引入面积这个概念,主要是培养学生对图形面积的感觉与认识。
【授课批注】在开始讲解面积这个概念之前可适当复习有关图形周长的概念,帮助学生区分周长和面积。
知识梳理格点图形的概念在一张纸上,先画出一些水平直线和一些竖直直线,并使任意两条相邻的平行线的距离都相等(通常规定是1个单位),这样在纸上就形成了一个方格网,其中的每个交点就叫做一个格点.在方格网中,以格点为顶点画出的多边形叫做格点多边形。
a)正方形格点正方形格点问题就是它的格点都是由两组互相垂直相交的平行线的交点构成的.每一个小方格都是一个小正方形b)三角形格点所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.【授课批注】讲解格点图形概念的时候最好能借助诸如钉子板之类的道具,提高教学的形象性,更容易让学生理解,加深印象。
【重点难点解析】1.方形格点与三角形格点面积的特点2.格点图形的分割与拼补【竞赛考点挖掘】1.两种格点图形的基本面积计算2.格点图形面积的等量变形例题精讲【试题来源】【题目】判断下列图形哪些是格点多边形?【试题来源】【题目】如右图,计算各个格点多边形的面积.【试题来源】【题目】如右图(a),计算这个格点多边形的面积.【试题来源】【题目】右图是一个方格网,计算阴影部分的面积.【试题来源】【题目】分别计算右图中两个格点多边形的面积。
【试题来源】【题目】如图“乡村小屋”的面积是多少?【试题来源】【题目】第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一个小方格的面积是1,那么7、2、1三个数字所占的面积之和是多少?习题演练【试题来源】【题目】右图中每个小正方形的面积都是1,那么图中这只“狗”所占的面积是多少?【试题来源】【题目】用9个钉子钉成相互间隔为1厘米的正方阵(如右图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形的个数有多少? 面积等于2平方厘米的三角形有多少个?【试题来源】【题目】在4×7的方格纸板上面有如阴影所示的“6”字,阴影边缘是线段或圆弧.问阴影面积占纸板面积的几分之几?【试题来源】【题目】右图是5×5的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么,所围图形的面积是______平方厘米.【试题来源】【题目】如图,每一个小方格的面积都是l平方厘米,那么用粗线围成的图形的面积是多少平方厘米?【试题来源】【题目】如图(a),有21个点,每相邻三个点成“∵”或“∴”,所形成的三角形都是等边三角形.计算三角形ABC的面积.【试题来源】【题目】如右图,每相邻三个点所形成的三角形都是面积为1的等边三角形,计算△ABC的面积.【试题来源】【题目】如右图,每相邻三个点所形成的三角形都是面积为1的正三角形,计算四边形ABCD 的面积.【试题来源】【题目】把大正三角形每边八等份,组成如右图所示的三角形网.如果大三角形的面积是128,求图中粗线所围成的三角形的面积.【试题来源】【题目】如图涂阴影部分的小正六角星形面积是16平方厘米,问:大正六角星形面积是多少平方厘米?【试题来源】【题目】如果下图中任意相邻的三个点构成的三角形面积都是2平方厘米.那么,三角形ABC 的面积是_____平方厘米【试题来源】【题目】把同一个三角形的三条边分别5等分、7等分(如图l图2),然后适当连接这些等分点,便得到了若干个面积相等的小三角形.已知图1中阴影部分面积是294平方分米,那么图2中阴影部分的面积是______平方分米.【试题来源】【题目】如图,如果每一个小三角形的面积是1平方厘米,那么四边形ABCD的面积是多少平方厘米?【试题来源】【题目】求下列各个格点多边形的面积【试题来源】【题目】右图是一个8 12面积单位的图形.求矩形内的箭形ABCDEFGH的面积.【试题来源】【题目】求下列格点多边形的面积(每相邻三个点“∵”或“∴”成面积为1的等边三角形).【试题来源】【题目】右图有12个点,相邻两个点之间的距离是1厘米,这些点可以连成多少个面积为2平方厘米的三角形?【试题来源】【题目】将图中的图形分割成面积相等的三块.。
小学四年级奥数:《格点与面积》试题及解析

小学四年级奥数:《格点与面积》试题及解析.DOC如下图;在一张由一组水平线和一组垂直线组成方格纸上;如果任意相邻平行线之间的距离都相等;我们就把这样两组平行线的交点称为格点(如下图中的红点);把图中相邻两个格点的距离看着一个单位长度;把每个小正方形的面积看作一个面积单位(如图中带阴影的方格)。
一个多边形的顶点如果全是格点;这个多边形就叫做格点多边形;本讲就;学习求格点多边形的面积问题。
这种格点多边形的面积计算起来很方便;一般有三种方法:①规则的格点多边形;可以运用多边形的面积公式求出面积;②一些简单而又特殊的格点多边形;可以通过数格子求出面积;③较复杂的不规则图形;一般用皮克公式计算。
其中数格子的方法比较原始;很少用。
任意格点多边形;只要数出多边形周界上的格点的个数及图内格点的个数;就可用下面的皮克公式算出面积:格点多边形面积=内格点个数+ 边格点数÷2-1这个公式是皮克(Pick)在1899年给出的;被称为“皮克定理”;这是一个实用而有趣的定理。
例1:求下面各图形的面积。
【解析】:图①是个平行四边形;周界上有10个格点;图内有4个格点;根据格点面积公式;图①的面积为:4+10÷2-1=8;图②是个梯形;周界上有8个格点;图内有2个格点;根据格点面积公式;图②的面积为:2+8÷2-1=5;图③是个三角形;周界上有6个格点;图内有4个格点;根据格点面积公式;图③的面积为:4+6÷2-1=6;以上3个图形都是规则图形;但四年级学生还没有学过这3种图形的面积计算;不能用面积公式计算。
图④是个六边形;周界上有8个格点;图内有9个格点;根据格点面积公式;图④的面积为:9+8÷2-1=12。
这四个图形也可以用数格子的方法计算面积。
例2:下图中喇叭、小猫、小狗的面积各是多少?【解析】:这三个图形都适合用格点面积公式计算面积。
喇叭周界上有8个格点;图内没有格点;面积为:0+8÷2-1=3;小猫周界上有20个格点;图内有2个格点;面积为:2+20÷2-1=11;小狗图案可以看着是两个格点多边形组成;先分别求出每个格点多边形的面积;再求出总面积。
(完整版)小学奥数:格点型面积(毕克定理)

小学奥数:格点型面积(毕克定理)板块一 正方形格点问题在一张纸上,先画出一些水平直线和一些竖直直线,并使任意两条相邻的平行线的距离都相等(通常规定是1个单位),这样在纸上就形成了一个方格网,其中的每个交点就叫做一个格点.在方格网中,以格点为顶点画出的多边形叫做格点多边形,例如,右图中的乡村小屋图形就是一个格点多边形.那么,格点多边形的面积如何计算?它与格点数目有没有关系?如果有,这两者之间的关系能否用计算公式来表达?下面就让我们一起来探讨这些问题吧!用N 表示多边形内部格点,L 表示多边形周界上的格点,S 表示多边形面积,请同学们分析前几个例题的格点数.我们能发现如下规律:12LS N =+-.这个规律就是毕克定理.【例 1】 用9个钉子钉成相互间隔为1厘米的正方阵(如右图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形的个数有多少? 面积等于2平方厘米的三角形有多少个?【例 2】 如图,44⨯的方格纸上放了16枚棋子,以棋子为顶点的正方形有 个.【例 3】 判断下列图形哪些是格点多边形?⑴⑵⑶【例 4】 如图,计算各个格点多边形的面积.⑹⑸⑷【巩固】如果两格点之间的距离是2,能利用刚计算的结果说出相应面积么?(教师总结:面积数值均扩大4倍.)毕克定理若一个格点多边形内部有N 个格点,它的边界上有L 个格点, 则它的面积为12LS N =+-.【例 5】如图(a),计算这个格点多边形的面积.【例 6】(“新加坡小学数学奥林匹克”竞赛试题)右图是一个方格网,计算阴影部分的面积.【例 7】分别计算图中两个格点多边形的面积.⑴⑵【巩固】求下列各个格点多边形的面积.⑵⑴⑷⑶【例 8】我们开始提到的“乡村小屋”的面积是多少?【例 9】右图是一个812面积单位的图形.求矩形内的箭形ABCDEFGH的面积.HGFAEDCB【例 10】右图中每个小正方形的面积都是1,那么图中这只“狗”所占的面积是多少?【巩固】如图,每一个小方格的面积都是1平方厘米,那么用粗线围成的图形的面积是多少平方厘米?【例 11】(“小学数学奥林匹克”竞赛试题)55的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么,所围图形的面积是平方厘米.【例 12】(“保良局亚洲区城市小学数学”竞赛试题)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一个小方格的面积是1,那么7、2、1三个数字所占的面积之和是多少?【例 13】(第六届“从小爱数学”邀请赛试题)两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来,若左上角的阴影部分(块状)面积为25.12cm,右下角的阴影部分(线状)面积为27.4cm,求大正方形的面积.【例 14】(第六届“华杯赛”试题)图中正六边形ABCDEF的面积是54,AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.B PQFEDCB A板块二 三角形格点问题所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.关于三角形格点多边形的面积同样有它的计算公式:如果用S 表示面积,N 表示图形内包含的格点数,L 表示图形周界上的格点数,那么有22S N L =⨯+-,就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2.【例 15】 如图(a ),有21个点,每相邻三个点成“∵”或“∴”,所形成的三角形都是等边三角形.计算三角形ABC 的面积.A B CD F E(b )(a )【巩固】如图,每相邻三个点所形成的三角形都是面积为1的等边三角形,计算ABC 的面积.【例 16】求下列格点多边形的面积(每相邻三个点“∵”或“∴”成面积为1的等边三角形).⑴⑵⑶⑷【例 17】 把大正三角形每边八等分,组成如右图所示的三角形网.如果大三角形的面积是128,求图中粗线所围成的三角形的面积.【例 18】如图,如果每一个小三角形的面积是1平方厘米,那么四边形ABCD 的面积是多少平方厘米?【例 19】把同一个三角形的三条边分别5等分、7等分(如图1,图2),然后适当连接这些等分点,便得到了若干个面积相等的小三角形.已知图1中阴影部分面积是294平方分米,那么图2中阴影部分的面积是______平方分米.【例 20】将图中的图形分割成面积相等的三块.【例 21】如图涂阴影部分的小正六角星形面积是16平方厘米,问:大正六角星形面积是多少平方厘米?【例 22】 (第五届“华杯赛”试题)正六边形ABCDEF 的面积是6平方厘米.M 是AB 中点,N 是CD 中点,P 是EF 中点.问:三角形MNP 的面积是多少平方厘米?SRQAB CD EF NM P P M F EDCBA【例 23】如果下图中任意相邻的三个点构成的三角形面积都是2平方厘米.那么,三角形ABC 的面积是_____平方厘米.。
奥数格点与面积

.. .......... 名师点拨 --- -------- --- 学科:学科:奥数** 教学内容:第六讲格点与面积开始学习生活中我们常借助一些工具来迅速简便的解决一些问题,如为了能捕到鱼,人们制作了鱼钩和网。
同样在数学的学习中,为了更好的解决问题聪明的人类也创造了一些“工具”。
这一讲我们主要介绍利用格点求几何图形的面积。
先来介绍什么是“格点”。
见下图:这是一张由水平线和垂直线组成的方格纸,我们把水平线和垂直线的交点称为“格点”,水平线和垂直线围成的每个小正方形称为“面积单位”。
图中带阴影的小方格就是一个面积单位。
借助格点图,我们可以很快的比较或计算图形的面积大小。
利用格点求图形的面积通常有两种思路,一是直接将图形分成若干个面积单位,然后通过计算有多少个面积单位来求图形面积;二是将某些图形转化成长方形的面积来求。
当然还可以将这两种方法结合起来,求出某些较复杂图形的面积。
例1 计算下图中各图形的面积:分析:先仔细观察图中的每个图形,选择方法。
显然第一、三、六图可以直接数出包含多少个面积单位即可。
而二、四、五图显然不适合用数单位面积的方法来求面积,可以采用虚线把这些图形扩展或割补成长方形,通过求长方形面积来求这些图形面积。
解答:(1)图中长方形包括3X2=6 (个)面积单位,所以它的面积为6。
(2)将图中平行四边形割补成一个长方形,长方形的面积为3X2=6,而平行四边形的面积等于长方形面积,所以平行四边形的面积为3X2=6。
(3)将图中三角形用虚线分成3块,它包含有1个面积单位和2个面积单位的一半,合起来有2个面积单位,所以它的面积为2。
(4)图中将三角形扩展成一个长方形,长方形的面积为3X2=6,而三角形面积为长方形面积的一半,则三角形面积为3。
(5)将图中梯形的互相平行的一组对边延长,补出一个和原来梯形方向颠倒,但面积一样的梯形,形成一个大的长方形。
长方形的面积为2+4)X3=18,而梯形的面积为长方形的面积的一半。
小学四年级奥数专题训练AB卷九:格点与面积(附答案)
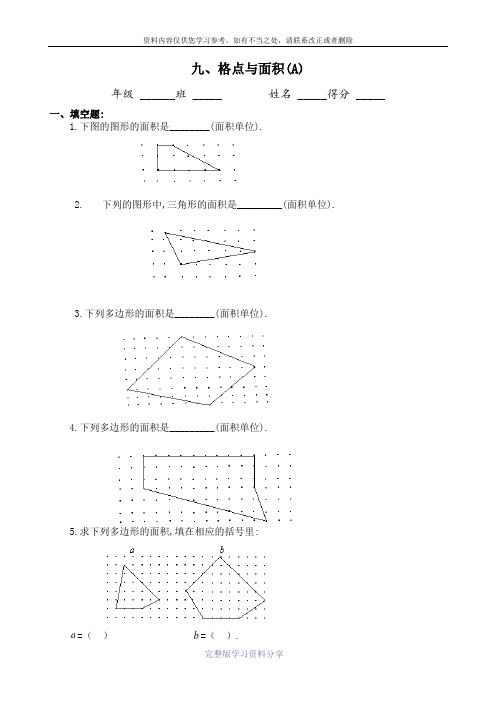
九、格点与面积(A)年级______班_____ 姓名 _____得分_____一、填空题:1.下图的图形的面积是________(面积单位).2. 下列的图形中,三角形的面积是_________(面积单位).3.下列多边形的面积是________(面积单位).4.下列多边形的面积是_________(面积单位).5.求下列多边形的面积,填在相应的括号里:a=()b=().6.用9个钉子钉成相互间隔为1厘米的正方阵(如右图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形的个数有多少?7.在右图中,如果钉与钉之间距离为1厘米,用橡皮筋将适当的三个钉子连结起来就得到一个三角形.在这些三角形中,面积等于2平方厘米的三角形有多少个?8.右图有12个点,相邻两个点之间的距离是1厘米,这些点可以连成多少个面积为2平方厘米的三角形?9.12个钉钉成右图那样的一个矩形钉阵,相邻两钉间的距离都是13平方厘米的三角形有多少个?10.右图是由8个钉组成的不规则钉阵,我们依次给它们编号,分别为1,2,3,4,5,6,7,8.这1,3,5;2,3,4;6,7,8分别在一条直线上,用皮筋去套这些钉,一共可以套出多少个三角形?二、解答题:1.右图中的正方形被分成9个相同的小正方形,它们一共有16个顶点(共同的顶点算一个),以其中不在一条直线上的3个点为顶点,可以构成三角形.在这些三角形中,与阴影三角形有同样大小面积的有多少个?2.右图中有A 1 A 2 ,…,A 10共10个点,以这些点为顶点,可以画多少个不同的三角形?6个点,在圆内再选4个点,使得以这10个点为顶点构成尽可能多的彼此不重叠的三角形.这些三角形最多有多少个?4.右图是一个相邻横竖两排距离都相等的4 6矩形钉阵,你能套出多少个不同的正方形来?九、格点与面积(B)年级______班_____ 姓名 _____得分_____一、填空题:1.右图是用皮筋在钉板上围成的一个三角形,计算它的面积是多少.(每相邻两个小钉之间的距离都等于1个长度单位).2.右图是一根用皮筋在钉板上围成的一个四边形,计算它的面积是多少.(每相邻两个小钉之间的距离都等于1个长度单位).3.在一个9⨯6的长方形内,有一个凸四边形ABCD(如右图).用毕克定理先求出它的面积来,再用拼割方法计算它的面积,看两者是否一致.4.右图中每个小正方形的面积都是4平方厘米,求图中阴影部分的面积.5.右图是一个10⨯10的正方形,求正方形内的四边形ABCD的面积.6.右图是一个8⨯12ABCDEFGH的面积.1,那么图中这只“狗”所占的面积是多少?8.右图是一个5⨯5的方格纸,小方格的面积是17个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用线段连结所围成的面积尽可能大,那么,所用图形的面积1是多少平方厘米?9.右图中每个小正方形的面积为1平方分米,那么阴影部分的面积是多少平方分米?10.右图中每个小平行四边形的面积是1个面积单位,求阴影部分的面积.二、解答题:1.右图中有21个点,其中每相邻的三点“∴”或“∵”所形成的三角形都是面积为1的等边的面积.三角形,试计算ABC2.右图中有21个点,其中每相邻的三点“∴”或“∵”所形成的三角形都是面积为1的等边三角形,试计算四边形DEFG的面积.3.把等边三角形ABC12cm,试求图中三角形DEF的面积.4.1,求图中粗线所围成的三角形的面积.—————————————————————A卷答案—————————————————————一、填空题:1. 5.2. 8. 点金术:设图形内的点为V,图形边上的点为L,则面积为L÷2-1+V.3. 14÷2-1+35=41.4. 36. 点金术:可以分成一个长方形和三角形.5. a=10+9÷2-1 b=30+15÷2-1=13.5 =36.56. 共有32个.解:分类统计如下:①②③底为2,高为1 底为2,高为1 底为1,高为23⨯2=6(个) 3⨯2=6(个) 3⨯2=6(个)④⑤⑥底为1,高为2 底为2,高为1 底为1,高为23⨯2=6(个) 2⨯2=4(个) 2⨯2=4(个)所以,面积等于1平方厘米的三角形的个数有:6+6+6+6+4+4=32(个).7. 答:面积等于2平方厘米的三角形有8个.8. 共有54个.解:分类如下:①②③底为2,高为2 底为2,高为2 底为2,高为25⨯3=15(个) 5⨯3=15(个) 2(个)④⑤⑥底为4,高为1 底为4,高为1 底为1,高为45⨯2=10(个) 2⨯2=4(个) 4(个)它的面积为⑦ 4⨯2-1⨯3÷2-1⨯1÷2-(1+3)⨯2÷24个 =2(平方厘米)所以,面积为2平方厘米的三角形有:15+15+2+10+4+4+4=54(个).9. 答:面积为3平方厘米的三角形有26个.10. 解:由于“不在一条直线上的三点可确定一个三角形”,根据排列组合知识得,一共可套出三角形:8⨯7⨯6÷(3⨯2⨯1)-1-1-1=56-3=53(个).这里减去的31,3,5;2,3,4;6,7,8分别在一条直线上.二、解答题:1. 解: ①设每个小正方形的边长为1个长度单位,则阴影三角形面积为:2⨯3÷2=3(面积单位).②分类统计如下:①②③底为2,高为3 底为2,高为3 底为3,高为24⨯2=8(个) 4⨯2=8(个) 4⨯2=8(个)④⑤⑥底为3,高为2 底为2,高为3 底为3,高为24⨯2=8(个) 2⨯2⨯2=8(个) 2⨯2⨯2=8(个)③与阴影三角形面积相同的三角形有:8+8+8+8+8+8=48(个).2. 答:可画100个.提示:将所有的三角形按有一个顶点在直径上和两个顶点在直径上及三个顶点都不在直径上的三类.3. 答:12 个.提示:对任意给定的6 个点可以构成4个互不重叠的三角形(图①),下图②中如果选取A点只能增加一个互不重叠的三角形,如果选取B点可以增加两个互不重叠的三角形,所以只要在图①的4个三角形内各取一点,就得到12个互不重叠的三角形.4.一共能套出40个正方形.———————————————————B卷答案——————————————————————一、填空题:面积单位.分析:解答这类问题可直接套用毕克定理:格点面积=内部格点数+周界上格点数÷2-1.注意:一是毕克定理只对格点凸多边形适用,二是在数格点时要细心.解: 5+3÷2-1=5.5(面积单位).2. 5+5÷2-1=6.5(面积单位).面积单位.解: ①由毕克定理得:25+7÷2-1=27.5(面积单位).②用拼割方法得:ABCD的面积=长方形EFGH的面积-四角上的四个三角形的面积 =9⨯6-(6⨯2÷2+3⨯3÷2+4⨯3÷2+4⨯5÷2)=54-(6+4.5+6+10)=27.5(面积单位).4. 48平方厘米.解: ①内部格点数为: 9个;②周界上格点数为: 8个;③阴影部分的面积是: 4⨯(9+8÷2-1)=48(平方厘米).5. 30面积单位.解: 因为ABCD不是凸四边形,所以如在原题图上取格点E,则三角形BCE及四边形AECD都是凸的图形,故:S=(4+6÷2-1)+(21+8÷2-1)ABCD=6+24=30(面积单位).6. 46面积单位.解: 因为ABCDEFGH不是凸多边形,所以,连结GC、MN,则ABH∆、矩形GCNM、三角形MFE、EDN都是凸的图形.故箭形ABCDEFGH的面积=(8+10÷2-1)+4⨯8+(4÷2-1)⨯2=12+32+2=46(面积单位).7. 面积单位.解: 图形内部格点数为59,图形周界上格点数为19.所以图形的面积为:59+19÷2-1=67.5(面积单位).(平方厘米).分析与解: 这是一个5⨯5的方格纸,共有25个格点.现在要围成一个面积最大的图形,根据格点面积公式,要使图形面积最大,必须使图形包含的内部格点数和周界上格点数尽可能多.由方格纸可知,内部格点数最多为4⨯4=16,周界上格点数最多为5⨯4=20.但是,当周界上格点数为最多时,不符合题中“任意3个格点不在一条直线上”的条件,因此,适当调整图上7个格点的位置,如右上图所示,就得到了面积最大的图形.所围成图形的最大面积为: 16+17÷2-1=23.5(平方厘米).9. 平方分米.解:图形内部格点数为7,图形周界上格点数为5.阴影部分的面积为:7+5÷2-1=8.5(平方分米).面积单位.解: 图形内部格点数为16,图形周界上格点数为7.图形的面积为: 16+7÷2-1=18.5(面积单位).二、解答题:1. 10面积单位.分析: 由“∵”和“∴”重合两点可拼为平行四边形 ,可以推出如下计算这类格点面积的公式:图形面积=(内部格点数+周界上格点数÷2-1)⨯2.解: 图形内部格点数为4,图形周界上格点数为4.ABC S ∆=(4+4÷2-1)⨯2=10(面积单位).2. 12面积单位.解: DEFG S 四边形=(5+4÷2-1)⨯2=12(面积单位).3. 11面积单位.解: 图形内部格点数为5,图形周界上格点数为3.DEF S ∆=(5+3÷2-1)⨯2=11(2cm ).4. 26面积单位.解: 图形内部格点数为12,图形周界上格点数为4.图形的面积为: (12+4÷2-1)⨯2=26(面积单位).。
四年级上册奥数知识点专讲第9课《格点与面积》试题附答案

被你默诵过,懂了
被你翻开又合起
被你动了奶酪和心思
不舍你的过往
和过往的你
记挂你的现今
和现今的你
遐想你的将来
和将来的你
难了难了
相思可以这一世
---------------------谢谢喜欢------Байду номын сангаас-------------
小学四年级上册数学奥数知识点讲解第9课《格点与面积》试题附答案
答案
四年级奥数上册:第十一讲格点与面积习题解答
---------------------赠予---------------------
【幸遇•书屋】
你来,或者不来
我都在这里,等你、盼你
等你婉转而至
盼你邂逅而遇
你想,或者不想
我都在这里,忆你、惜你
忆你来时莞尔
惜你别时依依
你忘,或者不忘
我都在这里,念你、羡你
念你袅娜身姿
羡你悠然书气
人生若只如初见
任你方便时来
随你心性而去
却为何,有人
为一眼而愁肠百转
为一见而不远千里
晨起凭栏眺
但见云卷云舒
风月乍起
春寒已淡忘
如今秋凉甚好
几度眼迷离
感谢喧嚣
把你高高卷起
砸向这一处静逸
惊翻了我的万卷
和其中的一字一句
幸遇只因这一次
小学奥数格点型面积毕克定理

小学奥数:格点型面积(毕克定理)板块一正方形格点问题在一张纸上,先画出一些水平直线和一些竖直直线,并使任意两条相邻的平行线的距离都相等(通常规定是1个单位),这样在纸上就形成了一个方格网,其中的每个交点就叫做一个格点.在方格网中,以格点为顶点画出的多边形叫做格点多边形,例如,右图中的乡村小屋图形就是一个格点多边形.那么,格点多边形的面积如何计算?它与格点数目有没有关系?如果有,这两者之间的关系能否用计算公式来表达?下面就让我们一起来探讨这些问题吧!用N表示多边形内部格点,L表示多边形周界上的格点,S表示多边形面积,请同学们分析前几个例题的格点数.我们能发现如下规律:12LS N=+-.这个规律就是毕克定理.【例1】用9个钉子钉成相互间隔为1厘米的正方阵(如右图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形的个数有多少?面积等于2平方厘米的三角形有多少个?【例2】如图,44⨯的方格纸上放了16枚棋子,以棋子为顶点的正方形有个.【例3】判断下列图形哪些是格点多边形?⑴⑵⑶【例4】如图,计算各个格点多边形的面积.【巩固】如果两格点之间的距离是2,能利用刚计算的结果说出相应面积么?(教师总结:面积数值均扩大4倍.)毕克定理若一个格点多边形内部有N个格点,它的边界上有L个格点,则它的面积为12LS N=+-.【例5】如图(a),计算这个格点多边形的面积.【例6】(“新加坡小学数学奥林匹克”竞赛试题)右图是一个方格网,计算阴影部分的面积.【例7】分别计算图中两个格点多边形的面积.⑴⑵【巩固】求下列各个格点多边形的面积.⑵⑴⑷⑶【例8】我们开始提到的“乡村小屋”的面积是多少?【例9】右图是一个812面积单位的图形.求矩形内的箭形ABCDEFGH的面积.HGFAEDCB【例10】右图中每个小正方形的面积都是1,那么图中这只“狗”所占的面积是多少?1平方厘米,那么用粗线围成的图形的面积是多少平方厘米?【例11】(“小学数学奥林匹克”竞赛试题)55的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么,所围图形的面积是平方厘米.【例12】(“保良局亚洲区城市小学数学”竞赛试题)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一个小方格的面积是1,那么7、2、1三个数字所占的面积之和是多少?【例13】(第六届“从小爱数学”邀请赛试题)两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来,若左上角的阴影部分(块状)面积为25.12cm,右下角的阴影部分(线状)面积为27.4cm,求大正方形的面积.【例14】(第六届“华杯赛”试题)图中正六边形ABCDEF的面积是54,AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.B PQFEDCB A板块二 三角形格点问题所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.关于三角形格点多边形的面积同样有它的计算公式:如果用S 表示面积,N 表示图形内包含的格点数,L 表示图形周界上的格点数,那么有22S N L =⨯+-,就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2.【例 15】 如图(a ),有21个点,每相邻三个点成“∵”或“∴”,所形成的三角形都是等边三角形.计算三角形ABC 的面积.A B CD F E(b )(a )【巩固】如图,每相邻三个点所形成的三角形都是面积为1的等边三角形,计算ABC的面积.【例 16】 求下列格点多边形的面积(每相邻三个点“∵”或“∴”成面积为1的等边三角形).⑴⑵⑶⑷【例 17】 把大正三角形每边八等分,组成如右图所示的三角形网.如果大三角形的面积是128,求图中粗线所围成的三角形的面积.【例 18】 如图,如果每一个小三角形的面积是1平方厘米,那么四边形ABCD 的面积是多少平方厘米?【例19】把同一个三角形的三条边分别5等分、7等分(如图1,图2),然后适当连接这些等分点,便得到了若干个面积相等的小三角形.已知图1中阴影部分面积是294平方分米,那么图2中阴影部分的面积是______平方分米.【例20】将图中的图形分割成面积相等的三块.【例21】如图涂阴影部分的小正六角星形面积是16平方厘米,问:大正六角星形面积是多少平方厘米?【例22】(第五届“华杯赛”试题)正六边形ABCDEF的面积是6平方厘米.M是AB中点,N是CD中点,P是EF中点.问:三角形MNP的面积是多少平方厘米?SRQABC DEFNM PEB【例23】如果下图中任意相邻的三个点构成的三角形面积都是2平方厘米.那么,三角形ABC的面积是_____平方厘米.。
小学奥数格点型面积毕克定理

小学奥数:格点型面积(毕克定理)板块一正方形格点问题在一张纸上,先画出一些水平直线和一些竖直直线,并使任意两条相邻的平行线的距离都相等(通常规定是1个单位),这样在纸上就形成了一个方格网,其中的每个交点就叫做一个格点.在方格网中,以格点为顶点画出的多边形叫做格点多边形,例如,右图中的乡村小屋图形就是一个格点多边形.那么,格点多边形的面积如何计算?它与格点数目有没有关系?如果有,这两者之间的关系能否用计算公式来表达?下面就让我们一起来探讨这些问题吧!用N表示多边形内部格点,L表示多边形周界上的格点,S表示多边形面积,请同学们分析前几个例题的格点数.我们能发现如下规律:12LS N=+-.这个规律就是毕克定理.【例1】用9个钉子钉成相互间隔为1厘米的正方阵(如右图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形的个数有多少?面积等于2平方厘米的三角形有多少个?【例2】如图,44⨯的方格纸上放了16枚棋子,以棋子为顶点的正方形有个.【例3】判断下列图形哪些是格点多边形?⑴⑵⑶【例4】如图,计算各个格点多边形的面积.【巩固】如果两格点之间的距离是2,能利用刚计算的结果说出相应面积么?(教师总结:面积数值均扩大4倍.)毕克定理若一个格点多边形内部有N个格点,它的边界上有L个格点,则它的面积为12LS N=+-.【例5】如图(a),计算这个格点多边形的面积.【例6】(“新加坡小学数学奥林匹克”竞赛试题)右图是一个方格网,计算阴影部分的面积.【例7】分别计算图中两个格点多边形的面积.⑴⑵【巩固】求下列各个格点多边形的面积.⑵⑴⑷⑶【例8】我们开始提到的“乡村小屋”的面积是多少?【例9】右图是一个812面积单位的图形.求矩形内的箭形ABCDEFGH的面积.HGFAEDCB【例10】右图中每个小正方形的面积都是1,那么图中这只“狗”所占的面积是多少?1平方厘米,那么用粗线围成的图形的面积是多少平方厘米?【例11】(“小学数学奥林匹克”竞赛试题)55的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么,所围图形的面积是平方厘米.【例12】(“保良局亚洲区城市小学数学”竞赛试题)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一个小方格的面积是1,那么7、2、1三个数字所占的面积之和是多少?【例13】(第六届“从小爱数学”邀请赛试题)两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来,若左上角的阴影部分(块状)面积为25.12cm,右下角的阴影部分(线状)面积为27.4cm,求大正方形的面积.【例14】(第六届“华杯赛”试题)图中正六边形ABCDEF的面积是54,AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.B PQFEDCB A板块二 三角形格点问题所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.关于三角形格点多边形的面积同样有它的计算公式:如果用S 表示面积,N 表示图形内包含的格点数,L 表示图形周界上的格点数,那么有22S N L =⨯+-,就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2.【例 15】 如图(a ),有21个点,每相邻三个点成“∵”或“∴”,所形成的三角形都是等边三角形.计算三角形ABC 的面积.A B CD F E(b )(a )【巩固】如图,每相邻三个点所形成的三角形都是面积为1的等边三角形,计算ABC的面积.【例 16】 求下列格点多边形的面积(每相邻三个点“∵”或“∴”成面积为1的等边三角形).⑴⑵⑶⑷【例 17】 把大正三角形每边八等分,组成如右图所示的三角形网.如果大三角形的面积是128,求图中粗线所围成的三角形的面积.【例 18】 如图,如果每一个小三角形的面积是1平方厘米,那么四边形ABCD 的面积是多少平方厘米?【例19】把同一个三角形的三条边分别5等分、7等分(如图1,图2),然后适当连接这些等分点,便得到了若干个面积相等的小三角形.已知图1中阴影部分面积是294平方分米,那么图2中阴影部分的面积是______平方分米.【例20】将图中的图形分割成面积相等的三块.【例21】如图涂阴影部分的小正六角星形面积是16平方厘米,问:大正六角星形面积是多少平方厘米?【例22】(第五届“华杯赛”试题)正六边形ABCDEF的面积是6平方厘米.M是AB中点,N是CD中点,P是EF中点.问:三角形MNP的面积是多少平方厘米?SRQABC DEFNM PEB【例23】如果下图中任意相邻的三个点构成的三角形面积都是2平方厘米.那么,三角形ABC的面积是_____平方厘米.。
奥数——格点与面积

格点与面积
例1 下图是一个格点图。
图中有长方形、三角形、平行四边形和梯形各一个。
请你利用方格网计算出它们的面积各是多少?(每个小正方形的面积是1平方厘米)
例2 在图中正方形格点中,这个宝塔图形的面积是多少?
例3 下图是一个四角形,每个小正方形的面积均为1平方厘米。
求图中阴影部分的面积。
例4、求下列图形的面积。
例5、如图,每个小正方形的面积都是1平方厘米。
则在此图中最多可以画出多少个面积是2平方厘米的格点正方形?
课堂练习
1、求下面各图形的面积。
2、求下图中各图形的面积。
3、求下图中各图形的面积。
4、下面是一个5*5的方格图,求出图中阴影部分面积的和(每小格的面积是1平方厘米)。
5、图中每个小正方形的边长都是1厘米,则在图中最多可以画出面积是3平方厘米的格点三角形多少个?
课后作业
1、计算所给图形的面积。
2、求出下面格点图形的面积。
3、在下面5*10的方格图中,连接格点,画出4个面积为7的图形,要求每个图形形状都不相同(每个小方格的面积是1)。
4、下图是由8个边长为1厘米的正方形所组成的一个图形,共有15个格点。
请以15个格点中的3个为顶点作一个面积为3.5平方厘米的三角形。
四年级奥数---格点与面积 (学生版)

格点与面积一、知识要点(1)基本概念1、格点:在方格纸(平面)上,纵横两组平行线垂直相交的交点称为格点。
2、格点与多边形:以格点为顶点画出的多边形称为格点多边形。
3、面积单位:以格点为顶点围成的小正方形称为面积单位。
(格点多边形面积的大小,与格点数有关,格点越多,面积越大。
)(2)常用技巧利用格点求图形的面积。
一是,直接将图形分成若干个面积单位,再通过计算有多少个面积单位求图形的面积。
二是,将复杂的图形转化成长、正方形来求。
(3) 格点图形面积的计算方法1、格点多边形的面积=图内格点数+周界上的格点数的一半-112L S N =+- 2、三角形格点多边形面积=图内格点数的2倍+周界上格点数-222S N L =+-二、例题精讲【例1】根据下组图填表(1) (2) (3)图形号 1 2 3周界格点数图内格点数面积(单位)【例2】求下图格点多边形的面积。
(每相邻三个点“∵”或“∴”成面积为1 的等边三角形)【例3】下图中每一个小方格的面积都是1平方厘米,那么用粗线围成的图形的面积是多少平方厘米?【例4】如下图所示,在圆周上有5个钉,在这5个钉中,任取三个钉用皮筋可套出一个三角形,问以钉1为顶点的三角形有多少个?【例5】如图ABFE和CDEF都是长方形,AB的长是4厘米,BC长3厘米,图中阴影部分的面积是多少平方厘米?【例6】如下图中小猫图的面积是多少?••••••••••••••••••••••••••••••••••••【例7】下图中有21个点,其中相邻的三点所形成的等边三角形的面积是1,试计算四边形的面积。
•••••••••••••••••••••【例8】思考题小刚和小强比赛,用一条长36米的绳子在格点上看谁围出的面积最大,你知道他们是怎样围的吗?(每块土地的长宽均为1米)三、课后作业【作业1】右图是用皮筋在钉板上围成的一个三角形,计算它的面积是多少。
(每相邻两个小钉之间的距离都等于1个长度单位)。
奥数 格点与面积精编版

学科:奥数教学内容:第六讲格点与面积生活中我们常借助一些工具来迅速简便的解决一些问题,如为了能捕到鱼,人们制作了鱼钩和网。
同样在数学的学习中,为了更好的解决问题聪明的人类也创造了一些“工具”。
这一讲我们主要介绍利用格点求几何图形的面积。
先来介绍什么是“格点”。
见下图:这是一张由水平线和垂直线组成的方格纸,我们把水平线和垂直线的交点称为“格点”,水平线和垂直线围成的每个小正方形称为“面积单位”。
图中带阴影的小方格就是一个面积单位。
借助格点图,我们可以很快的比较或计算图形的面积大小。
利用格点求图形的面积通常有两种思路,一是直接将图形分成若干个面积单位,然后通过计算有多少个面积单位来求图形面积;二是将某些图形转化成长方形的面积来求。
当然还可以将这两种方法结合起来,求出某些较复杂图形的面积。
例1 计算下图中各图形的面积:分析:先仔细观察图中的每个图形,选择方法。
显然第一、三、六图可以直接数出包含多少个面积单位即可。
而二、四、五图显然不适合用数单位面积的方法来求面积,可以采用虚线把这些图形扩展或割补成长方形,通过求长方形面积来求这些图形面积。
解答:(1)图中长方形包括3×2=6(个)面积单位,所以它的面积为6。
(2)将图中平行四边形割补成一个长方形,长方形的面积为3×2=6,而平行四边形的面积等于长方形面积,所以平行四边形的面积为3×2=6。
(3)将图中三角形用虚线分成3块,它包含有1个面积单位和2个面积单位的一半,合起来有2个面积单位,所以它的面积为2。
(4)图中将三角形扩展成一个长方形,长方形的面积为3×2=6,而三角形面积为长方形面积的一半,则三角形面积为3。
(5)将图中梯形的互相平行的一组对边延长,补出一个和原来梯形方向颠倒,但面积一样的梯形,形成一个大的长方形。
长方形的面积为(2+4)×3=18,而梯形的面积为长方形的面积的一半。
所以梯形的面积为:(2+4)×3÷2=9。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九、格点与面积(A)年级 ______班 _____姓名_____得分_____一、填空题 :1.下图的图形的面积是 ________(面积单位 ).2.下列的图形中 ,三角形的面积是 _________(面积单位 ).3.下列多边形的面积是 ________(面积单位 ).4.下列多边形的面积是 _________(面积单位 ).5.求下列多边形的面积 ,填在相应的括号里 :a =()b =().6.用 9 个钉子钉成相互间隔为 1 厘米的正方阵 (如右图 ).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形 ,这样得到的三角形中,面积等于 1 平方厘米的三角形的个数有多少 ?7.在右图中,如果钉与钉之间距离为1 厘米,用橡皮筋将适当的三个钉子连结起来就得到一个三角形 .在这些三角形中,面积等于2 平方厘米的三角形有多少个?8.右图有 12 个点 ,相邻两个点之间的距离是 1 厘米 ,这些点可以连成多少个面积为 2 平方厘米的三角形 ?9.12 个钉钉成右图那样的一个矩形钉阵,相邻两钉间的距离都是1 厘米 .以这些钉为顶点用皮筋去套 ,可以得到不少三角形 .问这些三角形中面积为 3 平方厘米的三角形有多少个 ?10.右图是由8 个钉组成的不规则钉阵,我们依次给它们编号, 分别为1,2,3,4,5,6,7,8.这1,3,5;2,3,4;6,7,8分别在一条直线上,用皮筋去套这些钉 ,一共可以套出多少个三角形 ?二、解答题 :1.右图中的正方形被分成 9 个相同的小正方形 ,它们一共有 16 个顶点(共同的顶点算一个 ),以其中不在一条直线上的 3 个点为顶点 ,可以构成三角形 .在这些三角形中 ,与阴影三角形有同样大小面积的有多少个?2.右图中有 A 1 A 2 ,⋯,A 10共 10 个点 ,以这些点为顶点 ,可以画多少个不同的三角形 ?3.在圆周上任意给定 6 个点 ,在圆内再选 4 个点 ,使得以这 10 个点为顶点构成尽可能多的彼此不重叠的三角形 .这些三角形最多有多少个 ?4.右图是一个相邻横竖两排距离都相等的 4 6 矩形钉阵 ,你能套出多少个不同的正方形来 ?九、格点与面积(B)年级 ______班 _____姓名_____得分_____一、填空题 :1. 右图是用皮筋在钉板上围成的一个三角形 , 计算它的面积是多少.(每相邻两个小钉之间的距离都等于 1 个长度单位 ).2.右图是一根用皮筋在钉板上围成的一个四边形 ,计算它的面积是多少.(每相邻两个小钉之间的距离都等于 1 个长度单位 ).3.在一个 9 6 的长方形内 ,有一个凸四边形 ABCD (如右图 ).用毕克定理先求出它的面积来 ,再用拼割方法计算它的面积 ,看两者是否一致 .4.右图中每个小正方形的面积都是 4 平方厘米 ,求图中阴影部分的面积 .5.右图是一个 10 10 的正方形 ,求正方形内的四边形ABCD 的面积 .6.右图是一个 8 12 面积单位的图形 .求矩形内的箭形 ABCDEFGH 的面积 .7.右图中每个小正方形的面积都是 1,那么图中这只“狗”所占的面积是多少 ?8.右图是一个 5 5 的方格纸 ,小方格的面积是 1 平方厘米 ,小方格的顶点为格点 .请你在图上选 7 个格点 ,要求其中任意 3 个格点都不在一条直线上 ,并且使这 7 个点用线段连结所围成的面积尽可能大 ,那么 ,所用图形的面积 1 是多少平方厘米?9.右图中每个小正方形的面积为 1 平方分米 ,那么阴影部分的面积是多少平方分米 ?10.右图中每个小平行四边形的面积是 1 个面积单位 ,求阴影部分的面积 .二、解答题 :1.右图中有 21 个点 ,其中每相邻的三点“∴”或“∵”所形成的三角形都是面积为 1 的等边三角形 ,试计算 ABC 的面积 .2.右图中有 21 个点 ,其中每相邻的三点“∴ ”或“∵”所形成的三角形都是面积为 1 的等边三角形 ,试计算四边形 DEFG 的面积 .3.把等边三角形ABC 每边六等分 ,组成如右图的三角形网.若图中每个小三角形的面积均为 1 cm2 ,试求图中三角形DEF的面积 .4.把大正三角形每边八等份 ,组成如右图所示的三角形网 .如果每个小三角形的面积都是 1, 求图中粗线所围成的三角形的面积 .———————————————答案——————————————————————一、填空题 :1. 5.2.8. 点金术 : 设图形内的点为 V,图形边上的点为 L,则面积为 L 2-1+V.3.14 2-1+35=41.4.36. 点金术 :可以分成一个长方形和三角形 .5. a =10+92-1 b =30+152-1=13.5=36.56.共有 32 个.解 :分类统计如下 :①底为 2,高为3 2=6(个)1②底为 2,高为3 2=6(个)1③底为 1,高为3 2=6(个)2④底为 1,高为3 2=6(个)2⑤底为 2,高为2 2=4(个)1⑥底为 1,高为2 2=4(个)2所以 ,面积等于 1 平方厘米的三角形的个数有:6+6+6+6+4+4=32(个).7.答:面积等于 2 平方厘米的三角形有 8 个.8.共有 54 个.解 :分类如下 :①底为 2,高为5 3=15( )2②底为 2,高为 25 3=15( )③底为 2,高为2( )2④⑤⑥底为 4,高为 1底为4,高为1底为1,高为45 2=10(个) 2 2=4(个)4(个 )它的面积为⑦ 4 2-1 3 2-1 1 2-(1+3) 224 个=2(平方厘米 )所以 ,面积为 2 平方厘米的三角形有 :15+15+2+10+4+4+4=54(个).9.答:面积为 3 平方厘米的三角形有 26 个 .10.解 :由于“不在一条直线上的三点可确定一个三角形”,根据排列组合知识得 ,一共可套出三角形 :8 7 6 (3 2 1)-1-1-1=56-3=53(个).这里减去的 3 个三角形 ,实际上是不能构成的 .因为 1,3,5;2,3,4;6,7,8 分别在一条直线上 .二、解答题 :1.解: ①设每个小正方形的边长为 1 个长度单位 ,则阴影三角形面积为 :2 3 2=3(面积单位 ).②分类统计如下 :①②③底为 2,高为 3底为2,高为3底为3,高为24 2=8(个) 4 2=8(个) 4 2=8(个)④⑤⑥底为 3,高为 2底为2,高为3底为3,高为24 2=8(个) 2 2 2=8(个) 2 2 2=8(个)③与阴影三角形面积相同的三角形有:8+8+8+8+8+8=48(个).2.答:可画 100 个 .提示 :将所有的三角形按有一个顶点在直径上和两个顶点在直径上及三个顶点都不在直径上的三类 .3.答:12 个 .提示 :对任意给定的 6 个点可以构成 4 个互不重叠的三角形(图① ),下图②中如果选取 A 点只能增加一个互不重叠的三角形,如果选取 B 点可以增加两个互不重叠的三角形 ,所以只要在图①的 4 个三角形内各取一点 ,就得到 12 个互不重叠的三角形 .4.一共能套出 40 个正方形 .———————————————答案——————————————————————一、填空题 :1. 5.5 面积单位 .分析 :解答这类问题可直接套用毕克定理:格点面积 =内部格点数 +周界上格点数2-1.注意 :一是毕克定理只对格点凸多边形适用,二是在数格点时要细心 .解 : 5+32-1=5.5(面积单位 ).2. 5+52-1=6.5(面积单位 ).3. 27.5 面积单位 .解 : ①由毕克定理得 :25+72-1=27.5(面积单位 ).②用拼割方法得 :ABCD 的面积 =长方形 EFGH 的面积 -四角上的四个三角形的面积=9 6-(6 2 2+3 3 2+4 3 2+4 52)=54-(6+4.5+6+10)=27.5(面积单位 ).4.48 平方厘米 .解: ①内部格点数为 : 9 个 ; ②周界上格点数为 : 8 个;③阴影部分的面积是 : 4 (9+8 2-1)=48(平方厘米 ).5.30 面积单位 .解 : 因为 ABCD 不是凸四边形 ,所以如在原题图上取格点 E ,则三角形BCE及四边形AECD 都是凸的图形 ,故:S ABCD=(4+62-1)+(21+82-1)=6+24=30(面积单位 ).6.46 面积单位 .解: 因为 ABCDEFGH 不是凸多边形 ,所以 ,连结 GC 、 MN ,则ABH、矩形 GCNM 、三角形MFE 、EDN都是凸的图形.故箭形 ABCDEFGH 的面积 =(8+102-1)+4 8+(4 2-1) 2=12+32+2=46(面积单位 ).7.67.5 面积单位 .解: 图形内部格点数为 59,图形周界上格点数为 19.所以图形的面积为 :59+19 2-1=67.5(面积单位 ).8.23.5(平方厘米 ).分析与解 : 这是一个 5 5 的方格纸 ,共有 25 个格点 .现在要围成一个面积最大的图形,根据格点面积公式 ,要使图形面积最大 ,必须使图形包含的内部格点数和周界上格点数尽可能多 .由方格纸可知 ,内部格点数最多为 4 4=16,周界上格点数最多为 5 4=20.但是 ,当周界上格点数为最多时 ,不符合题中“任意 3 个格点不在一条直线上”的条件 ,因此 ,适当调整图上 7个格点的位置 , 如右上图所示 ,就得到了面积最大的图形 .所围成图形的最大面积为: 16+172-1=23.5(平方厘米 ).9.8.5 平方分米 .解 :图形内部格点数为7,图形周界上格点数为 5.阴影部分的面积为 :7+52-1=8.5(平方分米).10.18.5 面积单位 .解 : 图形内部格点数为16,图形周界上格点数为7.图形的面积为 : 16+72-1=18.5(面积单位 ).二、解答题 :1.10 面积单位 .,可以推出如下计算这类格点面积分析 : 由“∵”和“∴”重合两点可拼为平行四边形的公式 :图形面积 =( 内部格点数 +周界上格点数2-1) 2.解 : 图形内部格点数为4,图形周界上格点数为 4.S ABC=(4+42-1)2=10(面积单位 ).2. 12 面积单位 .=(5+42-1)2=12(面积单位 ).解 :S四边形DEFG3.11 面积单位 .解: 图形内部格点数为 5,图形周界上格点数为 3. SDEF =(5+3 2-1) 2=11(cm2 ).4.26 面积单位 .解: 图形内部格点数为 12,图形周界上格点数为 4.图形的面积为 : (12+4 2-1) 2=26(面积单位 ).。
