[整理]matlab实现矩形孔衍射.

衍射的Matlab 模拟

10
二、菲涅耳－基尔霍夫衍射公式（确定了C、K()) 基尔霍夫 (Kirchhoff) 从波动方程出发，用场论得出了比较严格的衍射公式。
A expik l expik r cosn, r cosn, l E P ＝ d i l r 2
菲涅尔假设：当 = 0 时，K()=Max, p/ 时，K()=0.
（实验证明是不对的）若S发出的光源振幅为A（单位距离处）,整个波面’的贡献
CA expikr ~ E P expikR K d R r
求解此公式主要问题：C、K()没有确切的表达式。
设
l
x sin x , f
a b
m
y sin y f
~ E x, y C 2a 2b exp ik lx1 my1 dx1 dy1
2 2
28
~ E x, y C 2a 2b exp ik lx1 my1 dx1 dy1
2 2
P0 E
17
r z1
2 2 x x1 y y1
2 z1
称为菲涅耳近似。
得到菲涅耳衍射：
e ikz1 ~ E x, y iz1

k ~ 2 2 E x1 , y1 exp i x x1 y y1 2 z1 y y
~ 和E0 abC
则
~ ~ sin sin E x, y E0
子波的复振幅与 cosn, r cosn, l 2 成正比，与波长成反比。 K ( )
1 p i exp[ i ] i 2 表示子波的振动位相超前于入射波90。
12
当光线接近于正入射时

基于MATLAB的矩孔夫琅和费衍射场模拟计算

第29卷　第3期2009年　5月河北大学学报(自然科学版)Journal of Hebei University(Nat ural Science Edition)Vol.29No.3May2009基于MA TL AB的矩孔夫琅和费衍射场模拟计算郝忠秀,赵亚军,李立功,丁文革(河北大学物理科学与技术学院,河北保定　071002) 摘　要:利用MA TL AB软件对夫琅和费矩孔衍射场进行模拟,得到了不同参数下各种衍射场的三维分布图样,并且采用彩色网格图的形式输出,可以方便地观察衍射图样的细节.模拟结果与实验观测的结果非常吻合.这种方法作为辅助教学手段,不仅可以观察夫琅和费矩孔衍射完整、清晰的立体图像,而且可以很容易地调节参数,观察不同的衍射现象,有助于学生更加深刻地理解夫琅和费矩孔衍射的特征和规律,提高教学质量.关键词:夫琅和费衍射;矩孔;MA TL AB中图分类号:O436.1 文献标识码:A 文章编号:1000-1565(2009)03-0266-04On Simulated C alculation of Fraunhofer Diffractionfrom R ectangular Aperture B ased on MAT LABH AO Zhong2xiu,ZH AO Y a2jun,LI Li2gong,DI NG Wen2ge(College of Physics Science and Technology,Hebei U niversity,Baoding071002,China)Abstract:Based on MA TL AB software,t he Fraunhofer diffraction field of rectangular apert ure was simulated and t he t hree2dimensional dist ributions of Fraunhofer diff raction wit h different parameters were obtained.The simulatio n result s were outp ut in t he form of color grid,which helped us to observe t he de2 tails of t he diffraction patterns.Our result s were consistent wit h t he experimental result s.As an auxiliary teaching means,t he met hod p rovids us complete and clear t hree2dimensional grap h of Fraunhofer diff rac2 tion from a rectangular apert ure,and help s us to p rofoundly understood t he diffraction p henomenon and characteristic.K ey w ords:Fraunhofer diff raction;rectangular apert ure;MA TLAB光的衍射现象是光的波动性的重要表现.所有光学系统,特别是成像光学系统,一般都将光波限制在一个特定的空间区域内,这种光波传播过程实际上是一种衍射过程.所以对光的衍射现象的研究,不仅具有重要的理论意义,而且在光学仪器研制和成像分析等诸多实际应用方面均具有重要价值.衍射现象可以利用菲涅耳2基尔霍夫衍射公式来讨论,但由于这些数学公式的复杂性,在解决具体问题时,实际的计算工作很繁杂[1].在教学过程中,为建立清晰的物理图像,加深对各种现象的理解,通常利用演示实验辅助课堂教学,但是由于衍射实验需要较复杂的演示仪器和较苛刻的实验条件,在课堂上常常难以进行,而在实验室中一般也　收稿日期:2008-11-18　基金项目:河北省自然科学基金资助项目(E2007000197)　第一作者:郝忠秀(1949-),女,河北藁城人,河北大学副教授,主要从事基础物理方面研究.第3期郝忠秀等:基于MA TL AB 的矩孔夫琅和费衍射场模拟计算只能对矩孔夫琅和费衍射结果进行定性观察.因此在分析衍射问题时,为突出物理图像,避免复杂的数学计算,利用计算机对光的衍射图像进行模拟,是一种很好的解决方法[2-4].1　矩孔夫琅和费衍射场的理论分析矩孔夫琅和费衍射是二维衍射,一般利用菲涅耳2基尔霍夫衍射公式对衍射屏上通光的矩孔面积进行双重积分得到其衍射场的分布.为突出衍射的物理实质,简化运算,将二维的矩孔衍射转化为一维微缝衍射的叠加来处理,即把矩孔划分为无限多很窄的微缝,先求出微缝的衍射场,再将所有微缝的衍射场叠加,得到矩孔的衍射场.由这种运算过程可以看到,单缝衍射场是矩孔的衍射场的一个特例.矩孔夫琅和费衍射实验装置如图1所示,设矩孔沿x ,y 轴方向的边长分别为a 和b ,透镜L 的焦距为f ,在接收屏E 上任意点P 会聚的衍射光,其方向由二维衍射角(θ1,θ2)表示.在矩孔上任取一平行于y 轴宽为d x 的微缝b dx.图1　矩孔夫琅和费衍射实验装置Fig.1　F raunhofer diffraction setup设光波在矩孔面上的初位相为零,在微缝b d x 上任取面元d x d y ,到P 点的光程为r ,该面元上的次波在P 点的振动为d E 1,根据惠更斯2菲涅耳原理[5],在傍轴条件下,该面元上的次波在P 点的振动为d E 1=C 1d x d y co s (ωt -2πλr ),(1)式中C 1为常数,和λ分别为入射光的圆频率和波长.设微缝中点(x ,0)到P 点的光程为r ′0,考虑到图中几何关系r =r ′0+y sin θ2,则微缝上所有次波在P 点的合振动为d E =C 1d x ∫b 2-b 2co s [ωt -2πλ(r ′0+y sin θ2)]d y =C 1b sin πb sin θ2λπb sin θ2λco s (ωt -2πλr ′0)d x.(2)设矩孔中心O 到P 点的光程为r 0,有r ′0=r 0+x sin θ1,则矩孔上所有次波在P 点的合振动为E =C 1b sin πb sin θ2λπb sin θ2λ∫a 2-a 2cos [ωt -2πλ(r 0+x sin θ1)]d x =C 1ab sin ααsin ββco s (ωt -2πλr 0),(3)式中,α=πa sin θ1λ,β=πb sin θ2λ.由(5)式可知,P 点的光强为I =I 0(sin αα)2(sin ββ)2,(4)其中I 0=(ab λfC 1)2为衍射场的中心强度.(3)式即为矩孔夫琅和费衍射场光场分布公式,(4)式为相应的光・762・河北大学学报(自然科学版)2009年强分布公式.2　矩孔夫琅和费衍射场的MA TL AB 模拟及分析利用MA TLAB 软件,对矩孔夫琅和费衍射场分布进行模拟.为了获得矩孔夫琅和费衍射场分布的各种特征,分别对入射光的波长λ、矩孔的边长a 和b 、会聚透镜的焦距f 对衍射场的影响进行了分析.由于MA TL AB 允许用不同格式输出图形,采用彩色网格图的形式输出了矩孔夫琅和费衍射光强分布的立体图,同时为便于和实验结果比较,还输出了矩孔夫琅和费衍射光强分布的平面图.2.1　矩孔夫琅和费衍射场分布当矩孔的边长a =b =1mm ,入射光的波长λ=500nm ,会聚透镜的焦距f =2.5m 时,衍射场分布的模拟结果如图2所示.由于光波在矩孔x ,y 轴方向上受到的限制程度相同,则接收平面上衍射图样在x ,y 轴方向的扩展情况相同.由图2可以很清晰地观察到这一衍射特征.a.光场分布;b.光强分布;c.衍射图样图2　矩孔夫琅和费衍射场Fig.2　Fraunhofer diffraction from the rectangular aperture2.2　矩孔线度对衍射场的影响保持入射光的波长与会聚透镜的焦距保持不变,当方孔的边长a =b =1.5mm 时,衍射场的光强分布模拟结果如图3所示.由图3可见,当矩孔的线度变大时,衍射图样的扩展范围变小,衍射现象不明显.同时整图3　a =b =1.5mm 时的夫琅和费衍射场Fig.3　Fraunhofer diffraction for a =b =1.5mm 图4　b =10a =5mm 时的夫琅和费衍射场Fig.4　Fraunhofer diffraction for b =10a =5mm・862・第3期郝忠秀等:基于MA TL AB 的矩孔夫琅和费衍射场模拟计算体衍射场的光强增加,而零级衍射斑的面积显著减小.若继续增大矩孔的线度,则衍射效应越来越弱,这就说明,当光孔线度远大于光波的波长时,衍射的散射角Δθ→0,衍射场基本上集中在沿直线传播的原方向上,在透镜焦面上衍射斑收缩为几何光学像点.当矩孔的边长b =10a =5mm 时,衍射场的光强分布模拟结果如图4所示.由图可见,由于a 很小,光波在x 方向上受到的限制很大,所以光波在x 轴方向上的衍射很明显;同时,由于b 比较大,光在y 方向上受到的限制很小,y 轴方向上的衍射较弱.若继续增加b 的量值,则在y 轴方向上的衍射将越来越弱,矩孔夫琅和费衍射场过渡到单缝夫琅和费衍射场.2.3　透镜焦距对衍射场的影响当矩孔的边长与入射光的波长保持不变,而会聚透镜的焦距f =5m 时,衍射场的振幅和光强分布模拟结果如图5所示.比较图5与图2a 可见,当透镜的焦距变大时,整体衍射场的光强减小,而零级衍射斑的面积增大.实际上衍射图样的形状和零级衍射斑的半角宽度都不变,但透镜的焦距增加使得各级亮斑的面积及其间距同时被放大.图5　f =5m 时的夫琅和费衍射场Fig.5　F raunhofer diffraction for f =5m 图6　λ=800nm 时的夫琅和费衍射场Fig.6　F raunhofer diffraction for λ=800nm2.4　入射光波长对衍射场的影响当矩孔的边长与会聚透镜的焦距保持不变,而入射光的波长λ=800nm 时,衍射场的光强分布模拟结果如图6所示.比较图6与图2a 可见,当光波波长增大时,衍射图样的扩展范围变大,衍射现象更加明显.同时整体衍射场的光强减小,而零级衍射斑的面积增大.显然波长越长,衍射效应越显著;波长越短,衍射效应越可忽略,所以通常说,几何光学是短波(λ→0)极限.利用MA TLAB 软件对不同参数下的矩孔夫琅和费衍射场分布进行了大量模拟,经过比较,这些计算机模拟结果与实验观测[1,6-7]的结果非常吻合.参　考　文　献:[1]赵凯华.光学:新概念物理教程[M ].北京:高等教育出版社,2004:183-184.[2]谢嘉宁,赵建林,陈伟成,等.夫琅禾费衍射的计算机仿真[J ].大学物理,2004,23(3):51-54.[3]谢嘉宁,赵建林.光学空间滤波过程的计算机仿真[J ].光子学报,2002,31(7):847-850.[4]飞思科技产品研发中心.MA TL AB7基础与提高[M ].北京:电子工业出版社,2005:166-174.[5]梁绍荣.普通物理学:光学[M ].北京:高等教育出版社,1988:160-202.[6]章志鸣,沈元华,陈惠芬.光学[M ].北京:高等教育出版社,2000:91-101.[7]H ECH T E.Optics[M ].4th ed.New Y ork :Addision 2wesley Publishing Company ,2002:453-466.(责任编辑:孟素兰)・962・。

圆孔矩孔的菲涅尔衍射模拟(matlab实现)-工程光学

工程光学综合练习-----圆孔、矩孔的菲涅尔衍射模拟圆孔和矩孔的菲涅尔衍射模拟一、原理由惠更斯-菲涅尔原理可知接收屏上的P点的复振幅可以表示为其中为衍射屏上的复振幅分布，为倾斜因子。

根据基尔霍夫对此公式的完善，有设衍射屏上点的坐标为（x1, y1），接收屏上点的坐标为（x, y），衍射屏与接收屏间距离为z1，当满足菲涅尔近似条件时，即此时可得到菲涅尔衍射的计算公式把上式指数项中的二次项展开，并改写成傅里叶变换的形式，可以写成上式为菲涅尔衍射的傅里叶变换表达式，它表明除了积分号前面的一个与x1、y1无关的振幅和相位因子外，菲涅尔衍射的复振幅分布是孔径平面的复振幅分布和一个二次相位因子乘积的傅里叶变换。

相对于夫琅和费衍射而言，菲涅尔衍射的观察屏距衍射屏不太远。

在菲涅尔衍射中，输入变量和输出变量分别为衍射孔径平面的光场分布和观察平面的光场以及光强分布，考虑到这三个量都是二维分布,而且Matlab主要应用于矩阵数值运算,所以本程序选择用二维矩阵来存储衍射孔径平面和观察平面的场分布,并分别以矩阵的列数和行数来对应平面的直角坐标值(x, y)以及(x1, y1)。

二、圆孔菲涅尔衍射用MATLAB分别构造表示衍射屏和接收屏的二维矩阵。

注意使两矩阵阶次相同，考虑到运算量的要求，采样点数不能过多，所以每个屏的x和y方向各取200到300点进行运算。

根据式（4），选取合适的衍射屏和接收屏尺寸和相距的距离，模拟结果如下：取典型的He-Ne激光器波长λ=632.8nm，固定衍射屏和接收屏尺寸和相距的距离，分别取不同的圆孔半径，得到以下三组衍射图样，其圆孔半径分别为12mm，20mm，50mm图1（r=12mm）图2（r=20mm）图3(r=50mm) 三、矩孔的菲涅尔衍射步骤与上述相同，仅需改变与衍射屏形状对应的矩阵。

这里选择矩孔的长宽相等，分别为15mm，20mm，30mm，其衍射图样及强度分布如图4、5、6图4（a=b=15mm）图5(a=b=20mm)图 6(a=b=30mm)四、MATLAB 程序%所有长度单位为毫米lamda=632.8e-6; k=2*pi/lamda;z=1000000;%先确定衍射屏N=300; %圆屏采样点数a=15;b=15;[m,n]=meshgrid(linspace(-N/2,N/2-1,N));I=rect(m/(2*a)).*rect(n/(2*b));q=exp(j*k*(m.^2+n.^2)/2/z);subplot(2,2,1); %圆孔图像画在2行2列的第一个位置 imagesc(I) %画衍射屏的形状colormap([0 0 0; 1 1 1]) %颜色以黑白区分axis imagetitle('衍射屏形状')L=300;M=300; %取相同点数用于矩阵运算若为圆孔，方框内替换为以下程序 r=12;a=1;b=1; I=zeros(N,N); [m,n]=meshgrid(linspace(-N/2,N/2-1,N)); D=((m-a).^2+(n-b).^2).^(1/2); i=find(D<=r); I(i)=1; %孔半径范围内透射系数为1[x,y]=meshgrid(linspace(-L/2,L/2,M));h=exp(j*k*z)*exp((j*k*(x.^2+y.^2))/(2*z))/(j*lamda*z);%接收屏H =fftshift(fft2(h));B=fftshift(fft2(I)); %圆孔频谱G=H.*B; %公式中为卷积，空间域中相卷相当于频域中相乘U= fftshift(ifft2(G)); %求逆变换，得到复振幅分布矩阵Br=(U/max(U)); %归一化subplot(2,2,2);imshow(abs(U));axis image;colormap(hot)% figure,imshow(C);title('衍射后的图样');subplot(2,2,3);mesh(x,y,abs(U)); %画三维图形subplot(2,2,4);plot(abs(Br))。

matlab实现夫朗和费矩形和圆孔衍射

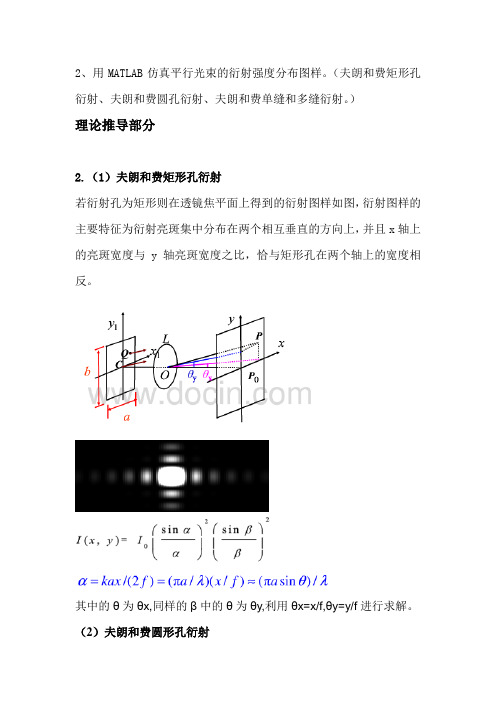
2、用MATLAB仿真平行光束的衍射强度分布图样。

（夫朗和费矩形孔衍射、夫朗和费圆孔衍射、夫朗和费单缝和多缝衍射。

）理论推导部分2.（1）夫朗和费矩形孔衍射若衍射孔为矩形则在透镜焦平面上得到的衍射图样如图，衍射图样的主要特征为衍射亮斑集中分布在两个相互垂直的方向上，并且x轴上的亮斑宽度与y轴亮斑宽度之比，恰与矩形孔在两个轴上的宽度相反。

其中的θ为θx,同样的β中的θ为θy,利用θx=x/f,θy=y/f进行求解。

（2）夫朗和费圆形孔衍射夫朗和费圆孔衍射的讨论方法和矩形孔衍射的讨论方法相同，只是由于圆孔的几何对称性，采用极坐标更为方便。

Ф=kaθ2.（1）夫朗和费矩形孔衍射clear all;lamda=500e-9;a=1e-3;b=1e-3;f=1;m=500;ym=8000*lamda*f;ys=linspace(-ym,ym,m)xs=ys;n=255;for i=1:msinth2=ys./sqrt(ys.^2+f^2);%相当于x/fsinth1=xs(i)/sqrt(xs(i).^2+f^2);%xs(i）作用每给一个ys值，要遍历到所有的x值angleA=pi*a*sinth1/lamda;%相当于书上的alfa=kax/2f k=2*pi/lamdaangleB=pi*b*sinth2./lamda;B(:,i)=(sin(angleA).^2.*sin(angleB).^2.*5000./(angleA.^2.*a ngleB.^2));%光强度公式endsubplot(1,2,1)image(xs,ys,B)colormap(gray(n))subplot(1,2,2)plot(B(m/2,:),ys)（2）夫朗和费圆孔衍射clearlam=500e-9a=1e-3f=1m=300;ym=5*0.61*lam*f/a;%取爱里光斑半径的5倍ys=linspace(-ym,ym,m);xs=ys;n=200;for i=1:mr=xs(i)^2+ys.^2;%相当于r的平方sinth=sqrt(r./(r+f^2));%角度fai=2*pi*a*sinth./lam;%fai=k*a*sinthhh=(2*BESSELJ(1,fai)).^2./fai.^2;%贝塞尔函数 b(:,i)=hh.*5000;endsubplot(1,2,1)image(xs,ys,b)colormap(gray(n))subplot(1,2,2)b(:,m/2)plot(ys,b(:,m/2))。

写平行光束分别通过圆孔和矩形孔的菲涅尔衍射的matlab代码

写平行光束分别通过圆孔和矩形孔的菲涅尔衍射的matlab代码1. 引言1.1 概述在光学领域中，菲涅尔衍射是一种常见的现象，它描述了当平行光束通过孔洞或物体边缘时所产生的衍射效应。

这个现象在很多应用中都具有重要意义，例如光学仪器的设计、天文学以及激光技术等领域。

理解和研究菲涅尔衍射现象对于深入探究光的波动性质以及相干光的传播具有重要意义。

1.2 文章结构本文将从以下几个方面进行讨论：首先介绍菲涅尔衍射理论中与本文相关的基本概念和原理；其次详细阐述使用MATLAB代码实现菲涅尔衍射的方法和步骤；然后，通过对圆孔和矩形孔两种情况下的菲涅尔衍射结果进行分析和讨论；最后给出文章总结，并提出进一步研究方向。

1.3 目的本文旨在通过编写MATLAB代码来模拟实现平行光束通过圆孔和矩形孔时的菲涅尔衍射现象，并利用结果分析和比较两种情况下的衍射效应。

通过这样的研究，可以加深对菲涅尔衍射原理的理解，并为后续相关研究提供参考和借鉴。

同时，通过MATLAB代码实现，读者也可以根据自己的需求进行扩展和修改，从而进一步探索不同形状孔洞的菲涅尔衍射特性。

2. 菲涅尔衍射理论2.1 光的波动特性菲涅尔衍射是一种描述光波传播和衍射现象的理论。

根据光的波动特性，当光通过一个孔径较小的障碍物时，它会弯曲并发生衍射现象。

在菲涅尔衍射中，平行光束通过圆孔或矩形孔后，在进入屏幕上的观察点处产生干涉图样。

2.2 菲涅尔近似理论菲涅尔近似理论是在进一步简化计算过程中使用的近似方法。

它假设观察点距离光源和障碍物足够远，使得远场近似成立。

2.3 圆孔和矩形孔的描述圆孔和矩形孔是两种常见形状的障碍物，用于描述光线传播时发生的菲涅尔衍射效应。

- 圆孔: 圆孔通常由一个具有确定半径大小的圆形开口组成。

当平行光束通过圆孔时，它会扩散并形成一系列同心环状条纹。

- 矩形孔: 矩形孔是由一个具有确定边长的矩形开口组成。

当平行光束通过矩形孔时，它会扩散并在屏幕上生成一系列矩形衍射图样。

[整理]matlab实现矩形孔衍射.

【四】实验结果及分析单缝
z1=0.1时
z1=1时
z1=2时
Z1=3时
Z1=4时
Z1=5时
Z1=6时
仿真图像分析：
当矩形孔的长宽比例接近于单峰时，为单缝衍射，衍射条纹的各级明纹的光强随着级数K的增加而减少
近场远场衍射图样的特点及近场远场的判断：随着z1的不断增大衍射图形
上中心亮斑发生变化时，此时为近场，近似为菲涅尔；当随着z1的不断增大中心亮斑没有明显变化时，此时在远场。

对一定波长的光来说，衍射孔径越大，相应的近场与远场的距离也越远。

随着光屏距离的增大，光斑范围不断扩大，光屏上矩形光斑的数量逐渐增多，中心光斑的亮度逐渐减弱，最后近似保持不变。

中央亮斑的面积与矩形孔面积成反比，衍射孔愈小，中央亮斑愈大。

衍射亮斑集中分布在两相互垂直的方向上，并且x轴上的亮斑与y轴上亮斑宽度之比，恰与矩形孔在两个轴上的宽度关系相反。

用Matlab GUI模拟圆环和矩形环夫琅禾费衍射

用Matlab GUI模拟圆环和矩形环夫琅禾费衍射李继军;徐大海;田永红【摘要】为动态反映圆环和矩形环夫琅禾费衍射光强随波长、衍射屏的几何特征等重要参数的变化。

利用Matlab图形用户界面的设计和开发功能，结合真实的可见光谱，制作了圆环和矩形环夫琅禾费衍射的交互式图形仿真界面．仿真结果细致逼真，使该过程的物理规律直观形象，有助于学生理解衍射过程中的物理规律．%In order to simulate the fraunhofer diffraction pattern of circular ring and rectangular ring with the change of lambda and geometric parameter of the ring and take advantage of the design and development function of Matlab graphic user interface by combining a visible optical spectrogram, an interactive simulation graphical user interface for fraunhofer diffraction of circular ring and rectangular ring was created. The result of simulation is the same as the experiment. The GUI makes it easy for students to understand the diffraction.【期刊名称】《常熟理工学院学报》【年(卷),期】2011(025)008【总页数】4页(P111-114)【关键词】物理光学;Matlab;仿真;夫琅禾费衍射【作者】李继军;徐大海;田永红【作者单位】长江大学物理科学与技术学院,湖北荆州434023;长江大学物理科学与技术学院,湖北荆州434023;长江大学物理科学与技术学院,湖北荆州434023【正文语种】中文【中图分类】O436.1在当前的光学衍射教学中，教师在黑板上推导出光强度公式后，根据该公式在黑板上画出光强分布曲线，或利用PPT将预先准备好的光强分布图片投影在屏幕上.经验表明，并不是所有的学生都能通过这种静态的结果理解衍射的物理规律.随着计算机性能的提高及模拟仿真技术的发展，在课堂上利用计算机软件对光学过程进行仿真已经成为一种可能.MATLAB软件是当今最优秀的科技应用软件和开发环境之一[1]，它以强大的科学计算与可视化功能、简单易用、可开放式、可扩展环境等特点在许多科学领域中成为计算机辅助设计和分析、算法研究和应用开发的基本工具和首选平台.已有的使用Matlab软件模拟光学现象的文献中[2-5]，只是对单一波长进行模拟，模拟结果为该波长下光强分布的灰度图，无法体现可见光波段波长连续变化时的光学现象，而且没有使用Matlab图形用户界面（Graphical User Interfaces，GUI），无法实现交互式模拟.本文利用可见光的光谱图，采用Matlab GUI对圆环和矩形环的夫琅禾费衍射在可见光波段进行仿真，仿真结果与实验结果一致.GUI中采用交互式滚动条动态的展现各物理量对衍射结果的影响，有利于加深学生对物理规律的理解和认识.1 圆环衍射的光强公式图1 圆环衍射屏如图1所示，衍射屏上有一个内外半径分别为R1和R2的圆环区域，设该衍射屏的透射率为：本文模拟将单位振幅的平面波入射到衍射屏上的情况，根据标量衍射理论[6]，通过圆环的光在观察平面上的夫琅禾费衍射强度分布为：式中λ是入射光波长，z是观察平面与衍射屏的距离.根据远场近似的要求，本文中z取50米，观察区域是一个0.2米×0.2米的正方形.r是观察平面上的观察点到该平面坐标原点的距离，J1()表示一阶贝塞尔函数.2 矩形环衍射的光强公式如图2所示，衍射屏上有一个内外边长分别为d和D的矩形环区域，该衍射屏的透射率为：当单位振幅的平面波透射过该衍射屏，在远离该屏的观察平面上产生的夫琅禾费衍射光强分布为：图2 矩形环衍射屏式中x，y是观察点在观察面中的坐标.3 Matlab GUI模拟3.1 界面的设计本程序将实现两个不同衍射屏下的仿真，为了编程的方便和界面的简洁，我们使用了matlab的容器控件——面板（Panel），加上初始界面，总共使用了三个面板.当其中一个界面出现时，另外两个界面是隐藏的.图3所示为程序执行后的初始界面.为实现仿真对象的转换，在界面中使用了两个按钮（Push Button），“Circle with Obscuration”实现圆环的仿真，“Rectangle with Obscuration”实现矩形环的仿真，界面上还有一个标示为“Exit”的按钮用于程序的退出.3.2 颜色的仿真我们用imread命令读入图4所示的可见光谱，并将光谱保存在color_spectrum 这个变量中，该变量是一个三维数组，前面二维对应着空间的行、列坐标，第三维对应该坐标下像素点的红、绿、蓝颜色值.每个像素点的颜色是由这三个值混合而成[7].为仿真不同波长所对应的色彩，我们先将该波长的衍射光强与该波长所对应的红、绿、蓝的颜色值分别相乘，然后再将结果混合起来，最后用imagesc命令即可得到与该波长相对应颜色的光强分布图.处理光谱的代码如下：3.3 回调的处理图5为圆环的仿真界面，界面右边自上而下的三个滚动条分别控制入射光波长，圆环外径和内径，因此涉及到三个回调函数.第一个回调函数是对波长改变的响应.代码如下：图3 初始界面图4 可见光谱图5 圆环的仿真后面两个回调函数是对外径改变的响应，颜色信息以及调用fraun_obscuration 计算光强与上面的callback_slider_wavelength函数一样.不同的是这两个回调函数获取的是内外径的当前值.具体代码是：4 结论图6是矩形环夫琅禾费衍射的仿真界面，回调函数的处本文利用Matlab图形用户界面的开发功能对圆环和矩形环的夫琅禾费衍射进行了仿真.仿真界面是交互式的，光强分布图可随入射波长以及衍射屏几何参数的改变而变化，仿真结果与实验观测结果一致，但清晰度更高.本程序可以对不同参数条件下的实验结果进行动态对比，从理方法与圆环的方法相同，由于篇幅的限制，本文不给出具体的代码.图6 矩形环的仿真以上两个模拟在内径为零时，可分别仿真圆孔和矩形孔的夫琅禾费衍射光强分布.结果如图7、图8所示.而将抽象的物理规律直观地展现在学生面前，加深学生对此类光学问题的理解.图7 圆孔的仿真图8 矩形孔的仿真参考文献：[1]Marchand P，Thomas Holland O.Graphics and GUIs withMATLAB[M].third edition.New York：CRC Press，2003.[2]崔祥霞，杨兆华，陈君.基于MATLAB的光学衍射与干涉实验仿真[J].泰山学院学报，2009，31（3）:109-113.[3]王惠临，赵俊卿.Matlab在大学物理教学中的应用[J].山东建筑大学学报，2009，24（3）:279-281.[4]吕波.基于Matlab的光学衍射仿真[J].东华理工大学学报（自然科学版），2010，33（4）：363-368.[5]华晋，尹金花.基于GUI的干涉衍射的实验教学研究[J].大学物理实验，2011，24（1）:79-82.[6]Joseph W Goodman.Introduction to Fourier Optics[M].third edition.New York:Roberts&Company Publishers，2004.[7]Roy s Berns.颜色技术原理[M].李小梅，译.北京：化学工业出版社，2002.。

基于Matlab的光学衍射实验仿真

基于Matlab的光学衍射实验仿真（）摘要通过Matlab软件编程，实现对矩孔夫琅和费衍射的计算机仿真，结果表明：该方法直观正确的展示了衍射这一光学现象，操作性强，仿真度高，取得了较好的仿真效果。

关键词夫琅和费衍射；Matlab；仿真1引言物理光学是高校物理学专业的必修课，其中，光的衍射既是该门课程的重点内容，也是人们研究的热点。

然而由于光学衍射部分公式繁多，规律抽象，学生对相应的光学图像和物理过程的理解有一定的困难，大大影响了教学效果。

当然，在实际中可以通过加强实验教学来改善教学效果，但是光学实验对仪器设备和人员掌握的技术水平要求都较高，同时实验中物理现象容易受外界因素的影响，这给光学教学带来了较大的困难1【-5】。

随着计算机技术的迅速发展，现代化的教育模式走进了课堂，利用计算机对光学现象进行仿真也成为一种可能。

Matlab是一款集数值分析、符号运算、图形处理、系统仿真等功能于一体的科学与工程计算软件，它具有编程效率高、简单易学、人机交互好、可视化功能、拓展性强等优点[6-8]，利用Matlab编程仿真光学现象只需改变程序中的参数，就可以生成不同实验条件下的光学图像，使实验效果更为形象逼真。

在课堂教学中，能快速的验证实验理论，使学生更直观的理解理论知识，接受科学事实。

本文以矩孔夫琅和费衍射为例，介绍了Matlab在光学衍射实验仿真中的应用。

2 衍射基本原理衍射是光波在空间或物质中传播的基本方式。

实际上，光波在传播的过程中，只要光波波面受到某种限制，光波会绕过障碍物偏离直线传播而进入几何阴影，并在屏幕上出现光强分布不均匀的现象，称为光的衍射。

根据障碍物到光源和考察点的距离，把衍射现象分为两类：菲涅尔衍射和夫琅和费衍射。

研究不同孔径在不同实验条件下的光学衍射特性，对现代光学有重要的意义。

如图1所示，衍射规律可用菲涅尔衍射积分表示，其合振幅为[9]：(1)其中，K是孔径平面，E是观察平面，r是衍射孔径平面Q到观察平面P的距离，d是衍射孔径平面O到观察平面P0的距离，cosθ是倾斜因子，k=2π／λ是光波波数，λ是光波波长，x1，y1和x，y分别是孔径平面和观察平面的坐标。

基于MATLAB衍射的矩形孔实验模拟

基于MATLAB衍射的矩形孔实验模拟[摘要] 根据物理光学中光的矩形孔衍射理论，利用MATLAB工具编写程序进行实验模拟，绘出矩形孔衍射图样和光强分布曲线，直观的展现了矩孔衍射的物理现象，并考虑到实际衍射的情况，对非单色光进行了讨论，结果与理论计算符合。

[关键词] MATLAB 矩形孔衍射MATLAB是一种主要用于数值计算即可视化图形处理的工程语言和应用软件。

它将数值分析、矩阵计算、图形图像处理、信号处理和仿真等诸多强大的功能集成在较易使用的交互式计算机环境中，为科学研究，工程应用提供了一种功能强、效率高的编程工具。

光的衍射是光的波动性的主要标志之一。

利用MATLAB模拟实验可以形象直观的演示实验现象，探究光的衍射问题，而且不受实验仪器和实验场所的限制，可以通过改变模拟参数获得不同的仿真结果，并在显示屏上直接显示出来，动态直观地展现各种物理量之间的关系，对于理解光学理论具有积极的作用。

1、夫琅禾费衍射实验的理论夫琅禾费衍射装置的光路图如下，其中分别在孔径平面和透镜建立坐标系和，两坐标原点和在透镜光轴上。

假设光在衍射屏Σ面上某一波前点Q和观察屏P点的坐标分别是（x1,y1）和（x，y）。

在远场条件下满足夫琅禾费近似，即：则：其中：为的距离；为的距离；为波矢量。

图1: 夫琅禾费衍射装置的光路图Fig1: Diagram of Fraunhofer diffraction equipment并假定的是衍射孔受平面波垂直照射，即是常数设为，则光强复振幅的分布满足以下夫琅禾费衍射公式：（1）式中因此，观察屏上的任意一点的光强分为：（2）对于不同的情况的衍射屏，只要对衍射孔积分，理论上是可以求出观察屏上任意一点的的光强分布I。

2、夫琅禾费矩孔的衍射模拟当衍射孔是长宽分别为a，b，的矩孔时，其主要特征是：衍射亮斑集中分布在相互垂直的两个轴（x轴和y轴）上，并且短边的亮斑的宽度比长边的宽度大，这一点与矩形在两个轴上的宽度关系这好相反。

矩孔菲涅而衍射MATLAB模拟

基于Matlab的矩孔菲涅尔衍射仿真摘要光学试验中衍射实验是非常重要的实验. 光的衍射是指光在传播过程中遇到障碍物时能够绕过障碍物的边缘前进的现象, 光的衍射现象为光的波动说提供了有力的证据. 衍射系统一般有光源、衍射屏和接受屏组成, 按照它们相互距离的大小可将衍射分为两大类, 一类是衍射屏与光源和接受屏的距离都是无穷远时的衍射, 称为夫琅禾费衍射, 一类是衍射屏与光源或接受屏的距离为有限远时的衍射称为菲涅尔衍射。

本文用Matlab软件主要针对矩孔菲涅尔衍射现象建立了数学模型，对衍射光强分布进行了编程运算，对衍射实验进行了仿真。

关键字：Matlab；矩孔菲涅尔衍射；仿真;光学实验AbstractOptical diffraction experiment is a very important experiment. is the diffraction of light propagation of light in the obstacles encountered in the process to bypass the obstacles when the forward edge of the phenomenon of light diffraction phenomenon of the wave theory of light provides a strong Evidence. diffraction systems generally have light, diffraction screen and accept the screen composition, size according to their distance from eachother diffraction can be divided into two categories, one is the diffraction screen and the light source and the receiving screen is infinity when the distance between the diffraction Known as Fraunhofer diffraction, one is diffraction screen and the light source or accept a limited away from the screen when the diffraction is called Fresnel diffraction.In this paper, Matlab software on a typical phenomenon of a mathematical model of single slit Fresnel diffraction, the diffraction intensity distribution of the programming operation, the diffraction experiment is simulated.Key word: matlab；single slit Fresnel diffraction; simulation; optical experiment一、菲涅尔衍射原理由惠更斯-菲涅尔原理可知接收屏上的P点的复振幅可以表示为其中为衍射屏上的复振幅分布，为倾斜因子。

圆孔矩孔的菲涅尔衍射模拟(matlab实现)-工程光学

圆孔矩孔的菲涅尔衍射模拟(m a t l a b实现)-工程光学-标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII工程光学综合练习-----圆孔、矩孔的菲涅尔衍射模拟圆孔和矩孔的菲涅尔衍射模拟一、原理由惠更斯-菲涅尔原理可知接收屏上的P点的复振幅可以表示为其中为衍射屏上的复振幅分布，为倾斜因子。

根据基尔霍夫对此公式的完善，有设衍射屏上点的坐标为（x1, y1），接收屏上点的坐标为（x, y），衍射屏与接收屏间距离为z1，当满足菲涅尔近似条件时，即此时可得到菲涅尔衍射的计算公式把上式指数项中的二次项展开，并改写成傅里叶变换的形式，可以写成上式为菲涅尔衍射的傅里叶变换表达式，它表明除了积分号前面的一个与x1、y1无关的振幅和相位因子外，菲涅尔衍射的复振幅分布是孔径平面的复振幅分布和一个二次相位因子乘积的傅里叶变换。

相对于夫琅和费衍射而言，菲涅尔衍射的观察屏距衍射屏不太远。

在菲涅尔衍射中，输入变量和输出变量分别为衍射孔径平面的光场分布和观察平面的光场以及光强分布，考虑到这三个量都是二维分布,而且Matlab主要应用于矩阵数值运算,所以本程序选择用二维矩阵来存储衍射孔径平面和观察平面的场分布,并分别以矩阵的列数和行数来对应平面的直角坐标值(x, y)以及(x1, y1)。

二、圆孔菲涅尔衍射用MATLAB分别构造表示衍射屏和接收屏的二维矩阵。

注意使两矩阵阶次相同，考虑到运算量的要求，采样点数不能过多，所以每个屏的x和y方向各取200到300点进行运算。

根据式（4），选取合适的衍射屏和接收屏尺寸和相距的距离，模拟结果如下：取典型的He-Ne激光器波长λ=，固定衍射屏和接收屏尺寸和相距的距离，分别取不同的圆孔半径，得到以下三组衍射图样，其圆孔半径分别为12mm，20mm，50mm图 1（r=12mm）图 2（r=20mm）图 3(r=50mm)三、矩孔的菲涅尔衍射步骤与上述相同，仅需改变与衍射屏形状对应的矩阵。

基于MATLAB光学衍射之矩形孔的夫琅禾费衍射

MATLAB的课程报告项目名称：基于MATLAB光学衍射之矩型孔的夫琅和费衍射一，MATLAB 基础：MatlaB是功能强大的科学及工程计算软件，它不但表现具有以矩阵计算为基础的强大数学计算和分析功能，而且还具有丰富的可视化图形表现功能和方便的程序设计能力。

Matlab是一款集数值分析、符号运算、图形处理、系统仿真等功能于一体的科学与工程计算软件，它具有编程效率高、简单易学、人机交互好、可视化功能、拓展性强等优点。

MatlAB是面向21世纪的计算机程序设计及科学计算语言。

MatlAB系统包括5个部分：开发环境，MAtlAB数学函数库，MAtlAB语言，图形功能，应用程序接口。

二，光的衍射的原理：光的衍射是光波在物质或空间里传播的基本发式，实际上，光波在传播的过程中，只要光波波面受到某种限制，光波会绕过障碍物偏离直线传播而进入几何阴影，并在屏幕上出现光强分布不均匀的现象，称为光的衍射。

根据障碍物到光源和考察点的距离，把衍射现象分为两类：菲涅尔衍射和夫琅和费衍射。

此次课程报告主要是围绕夫琅和费衍射展开的。

在光学上，夫琅和费衍射在场波通过圆孔或狭缝时发生，导致观测到的成像大小有所改变，成因是观测点的远场位置，及通过圆孔向外的衍射波有渐趋平面波的性质。

1，惠更斯原理：根据惠更斯-菲涅耳原理，单缝后面空间任一点P 的光振动是单缝处波阵面上所有子波波源发出的子波传到P 点的振动的相干叠加。

2. 菲涅耳-基尔霍夫衍射公式：由于菲涅耳理论本身的缺陷，所以从波动微分方程出发，利用场论中的Green 定理及电磁场的边值条件，其中倾斜因子为()k θ和常数C 均在下面所设。

~exp()exp()cos(,)cos(,)()[]2A ikl ikr n r n l E P d i l r σλ-=∑⎰⎰ 若设 1C i λ=； ~exp()()A ikl E Q l= ；cos(,)cos(,)()2n r n l K θ-= 则上式可化为：~~exp ikr E()()()P C E Q K d θσ=∑⎰⎰（）r3. 基尔霍夫衍射公式的近似菲涅耳衍射近似满足：2222221111111121111()()11[]222x x y y xx yy x y x y r z z z z z z ⎧⎫-+-+++=+=+-+⎨⎬⎩⎭ 当上式中1z 很大而使得第四项相对相位的贡献远小于π时，即满足：221()2x y k z π+<< 随着1z 的逐渐增大，从而可推得夫琅和费衍射公式如下: ~~2211,1111111exp()(,)exp[()]()exp[()]2ikz ik ik E x y x y E x y xx yy dx dy i z z z λ=+-+∑⎰⎰以上是矩孔的矩孔夫琅和费衍射复振幅计算公式的推导过程。

用MATLAB语言模拟光衍射实验

第14卷第4期大　学　物　理　实　验　V ol.14N o.42001年12月出版PHY SIC A L EXPERI ME NT OF C O LLEGE Dec.2001收稿日期:2001-07-30文章编号:1007-2934(2001)04-0047-02用MAT LAB 语言模拟光衍射实验周　忆(安徽省科学技术培训中心,合肥,230031)　梁　齐(合肥工业大学,合肥,230009)摘　要:用M AT LAB 语言模拟编写了光衍射的模拟实验程度,给出了五种元件的夫琅和费衍射图。

关键词:衍射;模拟;M AT LAB 语言中图分类号:O4-39 文献标识码:A光的衍射现象是光具有波动性的重要特征,衍射无论在理论研究还是在大学物理教学中都占有较重要的地位。

笔者利用MAT LAB 较强的绘图和图像功能,针对多种衍射元件(单缝、双缝、光栅、矩孔、圆孔)编写了光衍射的模拟实验程序。

在计算机的模拟光的衍射,条件限制较少,对于衍射的实验教学是一种较好的补充。

程序首先根据衍射强度分布的理论公式及实验参数建立衍射相对强度的数据矩阵B (x ,y )然后利用image (B )和colormap (gray )命令绘出衍射图样。

同时,也绘制了衍射光强分布的二维或三维图。

单缝夫琅和费衍射的模拟结果见图1。

衍射光强公式为I =I 0(sin u/u )2,u =(πa sin θ/λ),a 是缝宽,λ是入射光的波长,θ是衍射角。

设观察屏位于单缝后正透镜的焦平面上,f 为透镜的焦距,x 为屏上横向坐标。

θ=arctan (x/f )。

模拟分成三组:第一组,λ=600nm ,f =600mm ,(a )a =0.20mm ;(b )a =0.10mm ;(c )a =0.05mm 第二组,a =0.10mm ,f =600mm ,(d )λ=500nm ;(e )a =600nm ;(f )λ=700nm第三组,a =0.10mm ,λ=600nm ,(g )f =300mm ;(h )f =600mm ;(i )f =900mm以下内容中,取λ=600nm ,f =600mm ,衍射图样横坐标x 和纵坐标y 的范围均为[-20,20]mm 。

matlab计算衍射

matlab计算衍射【原创实用版】目录1.引言2.MATLAB 计算衍射的原理3.MATLAB 计算衍射的实践应用4.MATLAB 计算衍射的优点与局限性5.结论正文1.引言衍射是光学中的一个重要现象，它揭示了光的波动性。

在光学研究中，衍射的分析与计算具有重要的意义。

MATLAB 作为一种强大的光学仿真软件，可以方便地用于计算衍射。

本文将从 MATLAB 计算衍射的原理、实践应用、优点与局限性等方面进行介绍。

2.MATLAB 计算衍射的原理MATLAB 计算衍射主要基于光学的物理原理和数学方法。

其中，菲涅尔 - 基尔霍夫衍射积分公式是计算光波场和光强度分布的常用方法。

此外，MATLAB 提供了丰富的光学元件库和函数，如透镜、光栅、单缝等，可以方便地构建光学系统并进行仿真计算。

3.MATLAB 计算衍射的实践应用MATLAB 在衍射计算方面的应用非常广泛，包括夫琅禾费衍射、双缝干涉、平面光栅衍射、单缝衍射等。

通过 MATLAB 仿真计算，可以直观地观察到各种衍射现象，有助于深入理解光的波动性。

同时，MATLAB 还可以计算衍射的光强度分布，为光学设计和实验提供参考数据。

4.MATLAB 计算衍射的优点与局限性MATLAB 计算衍射具有以下优点：（1）MATLAB 易于学习和使用，方便进行衍射计算；（2）MATLAB 提供了丰富的光学元件库和函数，可以方便地构建光学系统；（3）MATLAB 计算衍射的结果可视化程度高，便于观察和分析。

然而，MATLAB 计算衍射也存在一定的局限性：（1）需要对光学原理有一定了解才能进行有效计算；（2）计算过程中可能涉及到复杂的数学运算，需要具备一定的数学基础；（3）MATLAB 计算衍射的结果受计算机性能和仿真参数设置等因素影响，可能存在一定误差。

5.结论MATLAB 作为一种强大的光学仿真软件，可以方便地用于计算衍射。

通过 MATLAB 计算衍射，可以深入了解光的波动性，并为光学设计和实验提供参考数据。

圆孔和矩形孔夫琅禾费衍射的MATLAB仿真对比研究

>,?7(06.!^=8A-:>F;=B/FF=8,9/>-*M5IN5OD/6A@89/>-*,/=,A@8=:>@;*J;,98-7A@8=:>@;
!概述
状&孔径大小的关系" 因此需要借助计算机来对衍射图样
光绕过障碍物偏离直线继续向前传播而进入几何阴进行仿真模拟"达到对衍射现象的直接观察和理解的目
@?
电子信息
科技风 ABAA 年 C 月
4 4 8 正方形孔衍射图样44 ? 正方形孔光强三维图像图 0 边长 9 UL!!EUL66的正方形孔夫琅禾费衍射图样
(&( 圆孔与矩孔夫琅禾费衍射的 M89@8? 仿真对比圆孔与矩形( 正方形) 孔对比"当 )CU9 UE时"即圆孔大小为方形孔的内接圆的衍射图样如表 $ 所示"比较表 $ 中 5组和 O组"圆孔的衍射图样为明暗相间的同心
射光斑的尺寸越大%
8 圆孔衍射光强曲线444 ? 圆孔衍射图样4 图 ) 半径 JU%&$66的圆孔夫琅禾费衍射图样
8 圆孔衍射光强曲线444 ? 圆孔衍射图样4 图 ( 圆孔 JU%&%$66的圆孔夫琅禾费衍射图样 (&) 夫琅禾费矩孔衍射的 M89@8? 仿真根据公式(3) "利用 M89@8? 软件进行编程运算"在入射光波长保持不变的情况下"如 $U0()F_>!"当矩孔边长 9 U$!!"EUL66时"衍射图样如图 3 所示"衍射亮斑集中分布在 ,轴和 0轴上"呈+ 十, 字状"且 ,方向衍射比 0方向的衍射更加明显*随着 9 的变大"0方向的衍射变得越来越明显"如 9 U(!!"EUL66时"衍射图样如图 L 所示*当 9 U L!!"EUL!!时的衍射图样如图 0 所示"即当 9 UE时",方向的衍射和 0方向的衍射一样"所以"衍射扩展与矩孔的宽度成反比"在哪个方向上限制"就在该方向上扩展% 通过图 3 l0 的三维图还可以发现"衍射孔由长方形变化到正方形的过程中"三维图样从扁平逐渐变为立体%

衍射的Matlab 模拟

( n,l ) ( n,r )
r
P
则 K
1 1 cos 2
13
将近似条件代入得到：菲涅耳－基尔霍夫衍射近似公式
exp ikR i ~ E P A 2 R

exp ikr 1 cos d r
( n,l ) ( n,r )
2
2
x1 x y1 y x 2 y 2 取上式前三项 r z1＋ z1 2 z1
x2 y2 exp[ ik ( z1 )] 2 z1 ~ E x, y iz1 ~ k i xx1 yy1 dx1dy1 E x1 , y1 exp z1
y1 x1
进一步的计算需要将exp( ikr )中的r表示成(x,y,z)的函数。
Q C z1 K
r
P
x
P0 E
孔径的衍射
16
2.菲涅耳近似（对位相项的近似）
r z1 ( x x1 ) 2 y y1 z1 1
2 2
x x1 2 y y1 2
非平行光衍射光源面和接收面非物象共扼面源点和场点均满足远场近似源点和场点均在无限远处平行光衍射光源面和接收面物菲涅耳衍射夫琅和费衍射121
衍射的MATLAB模拟
刘雁三峡大学理学院 2013.4
内容提要
衍射的基本理论
单缝衍射的Matlab模拟
一衍射的基本原理
光的衍射现象：光波在空间传播遇到障碍时，其传播方
2 2 夫琅合费衍射对z的要求 =600nm, x1 y1
x z
2
1
y1
2

max
2cm2

基于Matlab的光学衍射实验仿真

基于Matlab的光学衍射实验仿真（）摘要通过Matlab软件编程，实现对矩孔夫琅和费衍射的计算机仿真，结果表明：该方法直观正确的展示了衍射这一光学现象，操作性强，仿真度高，取得了较好的仿真效果。

关键词夫琅和费衍射；Matlab；仿真1引言物理光学是高校物理学专业的必修课，其中，光的衍射既是该门课程的重点内容，也是人们研究的热点。

然而由于光学衍射部分公式繁多，规律抽象，学生对相应的光学图像和物理过程的理解有一定的困难，大大影响了教学效果。

当然，在实际中可以通过加强实验教学来改善教学效果，但是光学实验对仪器设备和人员掌握的技术水平要求都较高，同时实验中物理现象容易受外界因素的影响，这给光学教学带来了较大的困难1【-5】。

随着计算机技术的迅速发展，现代化的教育模式走进了课堂，利用计算机对光学现象进行仿真也成为一种可能。

Matlab是一款集数值分析、符号运算、图形处理、系统仿真等功能于一体的科学与工程计算软件，它具有编程效率高、简单易学、人机交互好、可视化功能、拓展性强等优点[6-8]，利用Matlab编程仿真光学现象只需改变程序中的参数，就可以生成不同实验条件下的光学图像，使实验效果更为形象逼真。

在课堂教学中，能快速的验证实验理论，使学生更直观的理解理论知识，接受科学事实。

本文以矩孔夫琅和费衍射为例，介绍了Matlab在光学衍射实验仿真中的应用。

2 衍射基本原理衍射是光波在空间或物质中传播的基本方式。

实际上，光波在传播的过程中，只要光波波面受到某种限制，光波会绕过障碍物偏离直线传播而进入几何阴影，并在屏幕上出现光强分布不均匀的现象，称为光的衍射。

根据障碍物到光源和考察点的距离，把衍射现象分为两类：菲涅尔衍射和夫琅和费衍射。

研究不同孔径在不同实验条件下的光学衍射特性，对现代光学有重要的意义。

如图1所示，衍射规律可用菲涅尔衍射积分表示，其合振幅为[9]：(1)其中，K是孔径平面，E是观察平面，r是衍射孔径平面Q到观察平面P的距离，d是衍射孔径平面O到观察平面P0的距离，cosθ是倾斜因子，k=2π／λ是光波波数，λ是光波波长，x1，y1和x，y分别是孔径平面和观察平面的坐标。

模拟夫琅禾费衍射的matlab源代码(精.选)

源代码：N=512;disp('衍射孔径类型 1.圆孔 2.单缝 3.方孔')kind=input('please input 衍射孔径类型：');% 输入衍射孔径类型while kind~=1&kind~=2&kind~=3disp('超出选择范围，请重新输入衍射孔径类型');kind=input('please input 衍射孔径类型：');% 输入衍射孔径类型endswitch(kind)case 1r=input('please input 衍射圆孔半径(mm)：');% 输入衍射圆孔的半径I=zeros(N,N);[m,n]=meshgrid(linspace(-N/16,N/16-1,N));D=(m.^2+n.^2).^(1/2);I(find(D<=r))=1;subplot(1,2,1),imshow(I);title('生成的衍射圆孔');case 2a=input('please input 衍射缝宽：');% 输入衍射单缝的宽度b=1000;% 单缝的长度I=zeros(N,N);[m,n]=meshgrid(linspace(-N/4,N/4,N));I(-a<m&m<a&-b<n&n<b)=1;subplot(1,2,1);imshow(I);title('生成的衍射单缝');case 3a=input('please input 方孔边长：');% 输入方孔边长I=zeros(N,N);[m,n]=meshgrid(linspace(-N/4,N/4,N));I(-a/2<m&m<a/2&-a/2<n&n<a/2)=1;subplot(1,2,1),imshow(I);title('生成的方孔');otherwise kind=input('please input 衍射孔径类型：');% 输入衍射孔径类型end% 夫琅禾费衍射的实现过程L=500;[x,y]=meshgrid(linspace(-L/2,L/2,N));lamda_1=input('please input 衍射波长(nm)：');% 输入衍射波长;lamda=lamda_1/1e6k=2*pi/lamda;z=input('please input 衍射屏距离衍射孔的距离(mm)：');% 衍射屏距离衍射孔的距离h=exp(1j*k*z)*exp((1j*k*(x.^2+y.^2))/(2*z))/(1j*lamda*z);%脉冲相应H =fftshift(fft2(h));%传递函数B=fftshift(fft2(I));%孔频谱G=fftshift(ifft2(H.*B));subplot(1,2,2),imshow(log(1+abs(G)),[]);title('衍射后的图样');figuremeshz(x,y,abs(G));title('夫琅禾费衍射强度分布')实验输入：衍射孔径类型1.圆孔 2.单缝3.方孔please input 衍射孔径类型：1please input 衍射圆孔半径(mm)：3please input 衍射波长(nm)：632lamda =6.3200e-04please input 衍射屏距离衍射孔的距离(mm)：1000000实验结果：程序说明：本实验可以选择孔径类型、孔径半径、输入波长、衍射屏和衍射孔的距离等。

3_衍射的MATLAB计算[1]

三(2)衍射的MATLAB 计算•一、狭缝衍射的Fresnel积分计算(直接)•二、远场衍射计算(FT)•三、近场衍射计算(看做卷积，先求FT，再X，再IFFT)•四、直接卷积核(看做卷积，直接计算)•五、园域函数•六、FT平面位移与干涉2006-3-10衍射的MATLAB计算比较1近场衍射2 1.5 1 0.5 0 -2 1.5 irradiance 1 0.5 0 -2 1.5 1 0.5 0 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2Nf =1subplot(3,1,1); slit(1); subplot(3,1,2); slit(8); ylabel('irradiance'); 8 N f =subplot(3,1,3); slit(16); xlabel('x/w');-1.5-1-0.500.511.52N f = 16-1.5 -1 -0.5 0 x/w 0.5 1 1.5 22006-3-10衍射的MATLAB计算比较11极近场衍射1.5 1 0.5 0 -2 1.5 irradiance 1 0.5 0 -2 1.5 1 0.5 0 -2N f = 10-1.5 -1 -0.5 0 0.5 1 2 subplot(3,1,1); slit(10); subplot(3,1,2); slit(100); N f = 100ylabel('irradiance') subplot(3,1,3); slit(1000); xlabel('x/w'); 1.5 2 1.5-1.5-1-0.500.51N f = 1000-1.5 -1 -0.5 0 x/w 0.5 1 1.5 22006-3-10衍射的MATLAB计算比较12衍射区域w2 Nf = Fresnel 数 λz w2 w = 1; ⇒ = 1 N f =1 ⇒ N f = λz bb=wb=λzw=λww Nf衍射扩散(b)几何阴影区(w)2wzNf >1“近” 场2006-3-10Nf <1“远”场衍射的MATLAB计算比较夫琅和费Nf ≈013Fresnel 区域2π 1 (x 2 + y 2 )2 << 1 3 λ 8 z12 2π 1 4 w << 1 3 λ 8 z12展开中忽略的第一项在 “近场” Nf >13w2 Nf = λ z12π4 ≈12π 1 ⎛ λ N f ⎞ 4 ⎜ ⎟ w << 1 λ 8 ⎜ w2 ⎟ ⎝ ⎠⎛w⎞ N f << ⎜ ⎟ ⎝λ⎠2 3令 λ = 0.5 µm 以及 w = 1 mm, 那么 Nf << 160 令 l = 0.5 mm,当w = 10 mm, 那么 Nf << 7402006-3-10 衍射的MATLAB计算比较 14二、远场衍射的计算⎡e ⎤ ⎛x 2π ⎞ ⎛ ⎞ N f ⎥ q⎜ ; N f ⎟ ∫ u1 (α )q(α ; N f )exp⎜ − j α x ⎟dα u2 ( x ) = ⎢ b ⎝ ⎠ ⎠ ⎣ j ⎦ ⎝wjkz12 1 2w2 Nf = λ z12b=⎛α ⎞ u1 (α ) = rect ⎜ ⎟ ⎝2⎠归一化坐标中狭缝宽度＝2wλ z12wU1 (ξ ) = 2 sinc(2ξ )2 ⎛ x⎞ u2 = 4 N f sinc 2 ⎜ 2 ⎟ ⎝ b⎠ξ=x b将峰值归一化: 将irradiance 乘以0.25，2006-3-10 衍射的MATLAB计算比较并且不考虑 Nf.15远场例子N=1024; D=32; k=-N/2:N/2-1; x = (D/N)*k; dx = x(2)-x(1); f = rect(x/2); z = fftshift(fft(fftshift(f)))*dx; fx = (1/D)*k; fy = z.*conj(z)/4; frange=2; idx = find(abs(fx)<frange); plot(fx(idx),fy(idx),'k'); xlabel('x/b'); ylabel('normalized irradiance');1 0.9 0.8 normalized irradiance 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 -2 -1.5 -1 -0.5 0 x/b 0.5 1 1.5 22006-3-10衍射的MATLAB计算比较16远场衍射的Matlab 代码function [fy, fx] = fslit(a) N=1024; D=32; k=-N/2:N/2-1; x = (D/N)*k; dx = x(2)-x(1); f = qchirp(x,a).*rect(x/2); xrange = 2; idx=find(abs(x)<xrange); subplot(2,1,1); plot(x(idx),real(f(idx)),'k',x(idx),imag(f(idx)),'b'); axis([-xrange xrange -1.5 1.5]); xlabel('x/w'); ylabel('f(x)'); z = fftshift(fft(fftshift(f)))*dx; fx = (1/D)*k; fy = z.*conj(z); if (a<1) fy = 0.25*fy; else fy = fy*a; fx = fx/a; end frange=2; idx = find(abs(fx)<frange); subplot(2,1,2); plot(fx(idx),fy(idx),'k'); %axis([-frange frange 0 1.0]); if (a<1) xlabel('x/b'); else xlabel('x/w'); end ylabel('|F|^2');2006-3-10衍射的MATLAB计算比较171.5 1 0.5 f(x) 0 -0.5 -1 -1.5 -2 -1.5 -1远场计算Nf = 1黒色为实数部分, 兰色为虚部部分tu1 (α )q(α ; N f )-0.50 x/w0.511.5221.5 |F|210.50 -2-1.5-1-0.5⎡e ⎤ ⎛x 2π ⎞ ⎛ ⎞ α x ⎟ dα N f ⎥ q⎜ ; N f ⎟ ∫ u1 (α )q(α ; N f )exp⎜ − j u2 ( x ) = ⎢ b ⎠ ⎝ ⎠ ⎣ j ⎦ ⎝wjkz121 20 x/w0.511.522006-3-10 fslit(1);衍射的MATLAB计算比较18远场计算 Nf = 81.5 1 0.5 f(x) 0 -0.5 -1 -1.5 -2 -1.5 -1 -0.5 0 x/w 0.5 1 1.5 2黒色为实数部分, 兰色为虚部部分t1.4 1.2 1 |F|2 0.8 0.6 0.4 0.2 0 -2 -1.5 -1 -0.5 0 x/w 0.5 1 1.5 22006-3-10 fslit(8);衍射的MATLAB计算比较19同直接计算的比较1.6 1.4 1.2 irradiance 1 0.8 0.6 0.4 0.2 0 -2 -1.5 -1 -0.5 0 x/w 0.5 1 1.5 2Nf =1function compare(a)Blue：远场计算, Black：直接计算.compare(1); 2006-3-10[fy fx] = fslit(a); [y x] = slit(a); idx = find(abs(fx)<2.0); subplot(1,1,1); plot(fx(idx),fy(idx),'b',x,y,'k'); if (a<1) xlabel('x/b'); ylabel('normalized irradiance'); else xlabel('x/w'); ylabel('irradiance'); 衍射的MATLAB计算比较 20 endb b远场衍射的Matlab代码function [outp, inp] = fourier(fcn),N=1024;D=sqrt(N);k = -N/2:N/2-1;[xs,ys] = meshgrid(k*D/N);dx= D/N;;dy= D/N;f = feval(fcn,xs,ys);A = sum(sum(f))*dx*dy;subplot(1,2,1);range = 4;xr= k/D;idx= find( (-range <= xr) & (xr<range) );inp= f(idx,idx);imshow(inp);x = xs(idx,idx);y = ys(idx,idx);z = fftshift(fft2(fftshift(f)))*(dx*dy/A);fy= z.*conj(z);subplot(1,2,2);frange= 4;idx= find( (-frange<= xr) & (xr<frange) );outp= fy(idx,idx);logim(outp,3);2006-3-10衍射的MATLAB计算比较45。