第二十三章旋转知识点总结-经典例题-单元测试
旋转单元测试试题及答案

第13题.如图,已知四边形 ,是关于点 成中心对称图形,试判定四边形 的形状.并说明理由.
答案:解:是平行四边形,理由如下:
四边形 是关于点 成中心对称图形.
.
四边形 是平行四边形.
第14题. 在等边三角形、平行四边形、矩形和圆这四个图形中,即是轴对称图形,又是中心对称图形的有( )
A.1个B.2个C.3个D.4个
A.矩形、菱形、正方形都是中心对称图形,对角线的交点是对称中心
B.中心对称的对称中心只有一个,而轴对称图形的对称轴可能不只一条
C.中心对称图形一定是轴对称图形
D.正方形有4条对称轴,一个对称中心
答案:C.
第20题.把图中的各三角形绕 边中点 ,旋转 ,画出得到的图形,并说明拼成了一个什么图形?分析它的对称性.
答案:B.
第32题. 下列文字中属于中心对称图形的有( )
A.干B.中C.我D.甲
答案:B.
第33题. 下图中是中心对称图形的是( )
A.A和BB.B和CC.C和DD.都是
答案:B.
第34题.如图 与 关于 点成中心对称.则 _______ , ______, ________.
答案:=, , .
第35题.已知四边形 和点 ,作四边形 使四边形 和四边形 交于点 成中心对称.
A.只能作一个B.能作三个C.能作无数个D.不存在
答案:A.
第24题. 已知 及边 上一点 ,画出 以点 为对称中心的对称图形.
答案:略.
第25题. 等边三角形、正方形、菱形和等腰梯形这四个图形中,是中心对称图形的有( )
A.1个B.2个C.3个D.4个
答案:B.
第26题. 下列各图中,不是中心对称图形的是( )
九年级数学上册第二十三章旋转总结(重点)超详细(带答案)

九年级数学上册第二十三章旋转总结(重点)超详细单选题1、在平面直角坐标系中,点A(a,1)与点B(−2,b)关于原点成中心对称,则a+b的值为()A.−3B.−1C.1D.3答案:C分析:根据关于原点对称的两个点,横坐标、纵坐标分别互为相反数,求得a,b的值即可求解.解:∵点A(a,1)与点B(−2,b)关于原点成中心对称,∴a=2,b=−1,∴a+b=2−1=1,故选C.小提示:本题考查了关于原点对称的两个点,横坐标、纵坐标分别互为相反数,代数式求值,掌握关于原点对称的两个点,横坐标、纵坐标分别互为相反数是解题的关键.2、将如图的七巧板的其中几块,拼成一个多边形,为中心对称图形的是()A.B.C.D.答案:D分析:根据中心对称的定义,结合所给图形即可作出判断.A、不是中心对称图形,故本选项不符合题意;B、不是中心对称图形,故本选项不符合题意;C、不是中心对称图形,故本选项不符合题意;D、是中心对称图形,故本选项符合题意.故选:D.小提示:此题主要考查了中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后两部分能够完全重合.3、下列图形中,是中心对称图形但不是轴对称图形的是()A.B.C.D.答案:B分析:根据中心对称图形和轴对称图形的定义判断即可.解:∵A中的图形旋转180°后不能与原图形重合,∴A中的图象不是中心对称图形,∴选项A不正确;∵B中的图形旋转180°后能与原图形重合,∴B中的图形是中心对称图形,但不是轴对称图形,∴选项B正确;∵C中的图形旋转180°后能与原图形重合,∴C中的图形是中心对称图形,也是轴对称图形,∴选项C不正确;∵D中的图形旋转180°后不能与原图形重合,∴D中的图形不是中心对称图形,∴选项D不正确;故选:B.小提示:本题考查了轴对称图形和中心对称图形的定义,熟练掌握轴对称图形和中心对称图形的定义是解题的关键.4、有一个正n边形旋转90∘后与自身重合,则n为()A.6B.9C.12D.15答案:C分析:根据选项求出每个选项对应的正多边形的中心角度数,与90∘一致或有倍数关系的则符合题意.如图所示,计算出每个正多边形的中心角,90∘是30∘的3倍,则可以旋转得到.A.B.C.D.观察四个正多边形的中心角,可以发现正12边形旋转90°后能与自身重合故选C.小提示:本题考查正多边形中心角与旋转的知识,解决本题的关键是求出中心角的度数并与旋转度数建立关系.5、在平面直角坐标系中,点P(−3,−5)关于原点对称的点的坐标是()A.(3,−5)B.(−3,5)C.(3,5)D.(−3,−5)答案:C分析:根据关于原点对称的点的坐标特点解答.解:点P(-3,-5)关于原点对称的点的坐标是(3,5),故选:C.小提示:本题考查的是关于原点的对称的点的坐标,平面直角坐标系中任意一点P(x,y),关于原点的对称点是(-x,-y),即关于原点的对称点,横纵坐标都变成相反数.6、以原点为中心,将点P(4,5)按逆时针方向旋转90°,得到的点Q所在的象限为()A.第一象限B.第二象限C.第三象限D.第四象限答案:B分析:根据旋转的性质,以原点为中心,将点P(4,5)按逆时针方向旋转90°,即可得到点Q所在的象限.解:如图,∵点P(4,5)按逆时针方向旋转90°,得点Q所在的象限为第二象限.故选:B.小提示:本题考查了坐标与图形变化-旋转,解决本题的关键是掌握旋转的性质.7、将△AOB绕点O旋转180∘得到△DOE,则下列作图正确的是()A.B.C.D.答案:D分析:把一个图形绕某一点O转动一个角度的图形变换叫做旋转.解:观察选项中的图形,只有D选项为△ABO绕O点旋转了180°.小提示:本题考察了旋转的定义.8、如图,在方格纸中,将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B,则下列四个图形中正确的是()A.B.C.D.答案:B分析:根据绕点B按顺时针方向旋转90°逐项分析即可.A、Rt△A′O′B是由Rt△AOB关于过B点与OB垂直的直线对称得到,故A选项不符合题意;B、Rt△A′O′B是由Rt△AOB绕点B按顺时针方向旋转90°后得到,故B选项符合题意;C、Rt△A′O′B与Rt△AOB对应点发生了变化,故C选项不符合题意;D、Rt△AOB是由Rt△AOB绕点B按逆时针方向旋转90°后得到,故D选项不符合题意.故选:B.小提示:本题考查旋转变换.解题的关键是弄清旋转的方向和旋转的度数.9、如图,先将该图沿着它自己的右边缘翻折,再绕着右下角的一个端点按顺时针方向旋转180°,之后所得到的图形是()A.B.C.D.答案:A分析:将图沿着它自己的右边缘翻折,则圆在正方形图形的右上角,然后绕着右下角的一个端点按顺时针方向旋转180°,则圆在正方形的左下角,利用此特征可对四个选项进行判断.先将图沿着它自己的右边缘翻折,得到,再绕着右下角的一个端点按顺时针方向旋转180°,之后所得到的图形为.故选:A小提示:本题考查了利用旋转设计图案:由一个基本图案可以通过平移、旋转和轴对称以及中心对称等方法变换一些复合图案.10、如图,将△AOB绕着点O顺时针旋转,得到△COD(点C落在△AOB外),若∠AOB=30°,∠BOC=10°,则最小旋转角度是()A.20°B.30°C.40°D.50°答案:C分析:直接利用已知得出∠AOC的度数,再利用旋转的性质得出对应边之间夹角,得出答案即可.∵∠AOB= 30°,∠BOC = 10°,∴∠AOC=∠AOB+∠COB = 30°+ 10°= 40°∵将△AOB绕着点O顺时针旋转,得到△COD,∴最小旋转角为∠AOC = 40°.故选: C.小提示:此题主要考查了旋转的性质,正确得出∠AOC的度数是解题关键.填空题11、如图,在△ABC中,∠C=90°,点D、E分别在AC、BC上,∠CDE=45°,△ECD绕点D顺时针旋转x度(45<x<180)到△E1C1D,则∠BEE1等于______度.(用含x的代数式表示)答案:(45+x)2分析:根据旋转的性质可得DE=DE1,∠EDE1=x,利用等腰三角形的性质和三角形内角和定理求出∠E1ED 和∠CED即可解决问题.解:如图,由旋转的性质可得:DE=DE1,∠EDE1=x,∴∠E1ED=180°−x2=90°−x2,∵∠C=90°,∠CDE=45°,∴∠CED=45°,∴∠BEE1=180°−∠E1ED−∠CED=180°−(90°−x2)−45°=(45+x2)°,所以答案是:(45+x2).小提示:本题考查了旋转的性质,等腰三角形的性质以及三角形内角和定理,灵活运用各性质进行推理计算是解题的关键.12、如图,△ABC绕点A按逆时针方向旋转50°后的图形为△AB1C1,则∠ABB1=_______.答案:65°分析:根据旋转的性质知AB=AB1,∠BAB1=50°,然后利用三角形内角和定理进行求解.解:∵△ABC绕点A按逆时针方向旋转50°后的图形为△AB1C1,,∴AB=AB1,∠BAB1=50°,∴∠ABB1=12(180°−50°)=65°.所以答案是:65°.小提示:本题考查了旋转的性质,三角形内角和定理,熟知旋转角的定义与旋转后对应边相等是解题的关键.13、在平面直角坐标系内,点P(−3,2)关于原点的对称点Q的坐标为______.答案:(3,−2)分析:根据平面直角坐标系中任意一点P(x,y),关于原点的对称点是(−x,−y),即可直接作答.根据中心对称性质可知:点P(−3,2)关于原点的对称点Q的坐标为(3,−2),故答案为(3,−2).小提示:本题考查了关于原点对称点的坐标,属于基础问题,熟记知识点是解题关键.14、已知点A(1,m)与A′(n,−3)关于原点对称,则mn=___________.答案:-3分析:直接利用关于原点对称点的性质得出m,n的值,即可求解.解:∵点A(1,m)与点A′(n,−3)关于坐标原点对称,∴n=−1,m=3,∴mn=−3所以答案是:-3.小提示:此题主要考查了关于原点对称点的特征,关于原点对称的点横纵坐标都变为原来的相反数.15、如图,矩形ABCD中,AB=2,BC=1,将矩形ABCD绕顶点C顺时针旋转90°,得到矩形EFCG,连接AE,取AE的中点H,连接DH,则DH=_______.答案:√22分析:根据题意构造并证明ΔDAH≅ΔKEH(ASA),通过全等得到KE=AD,DH=HK,再结合矩形的性质、旋转的性质,及可求解;如图,延长DH交EF于点k,∵H是AE的中点∴AH=HE又∵AD//FE∴∠DAH=∠KEH∴ΔDAH≅ΔKEH(ASA)∴KE=AD,DH=HK∵EF=AB=CD=2,AD=FC=1∴DF=FK=KE=AD=1则DK=√DF2+FK2=√2∴DH=12DK=√22所以答案是:√22小提示:本题主要考查了矩形的性质、三角形的全等证明,掌握相关知识并结合旋转的性质正确构造全等三角形是解题的关键.解答题16、如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.(1)求证:EF=BC;(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.答案:(1)见解析(2)78°分析:(1)只需要证明△ABC≌△AEF即可得到答案;(2)先求出∠FAG=∠BAE=50°,然后根据全等三角形的性质得到∠F=∠C=28°,再利用三角形外角的性质求解即可.(1)解:∵∠CAF=∠BAE,∴∠BAC=∠EAF.∵将线段AC绕A点旋转到AF的位置,∴AC=AF.在△ABC与△AEF中,{AB=AE∠BAC=∠EAF AC=AF∴△ABC≌△AEF(SAS),∴EF=BC;(2)∵AB=AE,∠ABC=65°,∴∠ABC=∠AEB=65°∴∠BAE=180°−65°×2=50°,∴∠FAG=∠BAE=50°.∵△ABC≌△AEF,∴∠F=∠C=28°,∴∠FGC=∠FAG+∠F=50°+28°=78°.小提示:本题主要考查了旋转的性质,全等三角形的性质与判定,三角形内角和定理,等腰三角形的性质,三角形外角的性质,解题的关键在于能够熟练掌握相关知识进行求解.17、如图1,二次函数y=a(x+3)(x﹣4)的图象交坐标轴于点A,B(0,﹣2),点P为x轴上一动点.(1)求该二次函数的解析式;(2)过点P作PQ⊥x轴,分别交线段AB、抛物线于点Q,C,连接AC.若OP=1,求△ACQ的面积;(3)如图2,连接PB,将线段PB绕点P逆时针旋转90°得到线段PD.当点D在抛物线上时,求点D的坐标.答案:(1)y=16x2−16x−2;(2)SΔACQ=34;(3)D(3,−1)或D(−8,10)分析:(1)将B(0,−2)代入y=a(x+3)(x−4),即可求解;(2)先求直线AB的解析式为y=12x−2,则Q(1,−32),C(1,−2),可求SΔACQ=SΔACP−SΔAPQ=34;(3)设P(t,0),过点D作x轴垂线交于点N,可证明ΔPND≅ΔBOP(AAS),则D(t+2,−t),将D点代入抛物线解析式得−t=16(t+2+3)(t+2−4),求得D(3,−1)或D(−8,10).解:(1)将B(0,−2)代入y=a(x+3)(x−4),∴a=16,∴y=16(x+3)(x−4)=16x2−16x−2;(2)令y=0,则16(x+3)(x−4)=0,∴x=−3或x=4,∴A(4,0),设直线AB的解析式为y=kx+b,∴{b=−24k+b=0,∴{k=1 2b=−2,∴y=12x−2,∵OP=1,∴P(1,0),∵PQ⊥x轴,∴Q(1,−32),C(1,−2),∴AP=3,∴SΔACQ=SΔACP−SΔAPQ=12×3×2−12×3×32=34;(3)设P(t,0),如图2,过点D作x轴垂线交于点N,∵∠BPD=90°,∴∠OPB+∠NPD=90°,∠OPB+∠OBP=90°,∴∠NPD=∠OBP,∵BP=PD,∴ΔPND≅ΔBOP(AAS),∴OP=ND,BO=PN,∴D(t+2,−t),∴−t=16(t+2+3)(t+2−4),解得t=1或t=−10,∴D(3,−1)或D(−8,10).小提示:本题是二次函数综合题,考查了二次函数图象和性质,待定系数法求抛物线解析式,三角形面积,全等三角形判定和性质,旋转的性质等,解题的关键是熟练掌握二次函数的图象及性质,分类讨论,数形结合.18、如图1,正方形ABCD的边长为4,点P在边AD上(P不与A,D重合),连接PB,PC.将线段PB绕点P顺时针旋转90°得到PE,将线段PC绕点P逆时针旋转90°得到PF.连接EF,EA,FD.(1)求证:PD2;①ΔPDF的面积S=12②EA=FD;(2)如图2,EA.FD的延长线交于点M,取EF的中点N,连接MN,求MN的取值范围.答案:(1)①见详解;②见详解;(2)4≤MN<2√5分析:(1)①过点F作FG⊥AD交AD的延长线于点G,证明△PFG≌△CPD,即可得到结论;②过点E作EH⊥DA交DA的延长线于点H,证明△PEH≌△BPA,结合△PFG≌△CPD,可得GD=EH,同理:FG=AH,从而得△AHE≌△FGD,进而即可得到结论;(2)过点F作FG⊥AD交AD的延长线于点G,过点E作EH⊥DA交DA的延长线于点H,可得∠AMD=90°,EF,HG= 2AD=8,EH+FG=AD=4,然后求出当点P与点D重合时,EF最大值=4√5,当点P与AD的中点重合MN=12时,EF最小值= HG=8,进而即可得到答案.(1)①证明:过点F作FG⊥AD交AD的延长线于点G,∵∠FPG+∠PFG=90°,∠FPG+∠CPD=90°,∴∠FPG=∠CPD,又∵∠PGF=∠CDP=90°,PC=PF,∴△PFG≌△CPD(AAS),∴FG=PD,∴ΔPDF的面积S=12PD⋅FG=12PD2;②过点E作EH⊥DA交DA的延长线于点H,∵∠EPH+∠PEH=90°,∠EPH +∠BPA=90°,∴∠PEH =∠BPA,又∵∠PHE=∠BAP=90°,PB=PE,∴△PEH≌△BPA(AAS),∴EH=PA,由①得:FG=PD,∴EH+FG=PA+PD=AD=CD,由①得:△PFG≌△CPD,∴PG=CD,∴PD+GD= CD= EH+FG,∴FG+GD= EH+FG,∴GD=EH,同理:FG=AH,又∵∠AHE=∠FGD,∴△AHE≌△FGD,∴EA=FD;(2)过点F作FG⊥AD交AD的延长线于点G,过点E作EH⊥DA交DA的延长线于点H,由(1)得:△AHE≌△FGD,∴∠HAE=∠GFD,∵∠GFD+∠GDF=90°,∴∠HAE+∠GDF=90°,∵∠HAE=∠MAD,∠GDF=∠MDA,∴∠MAD+∠MDA=90°,∴∠AMD=90°,∵点N是EF的中点,∴MN=1EF,2∵EH=DG=AP,AH=FG=PD,∴HG=AH+DG+AD=PD+AP+AD=2AD=8,EH+FG=AP+PD=AD=4,当点P与点D重合时,FG=0,EH=4,HG=8,此时EF最大值=√42+82=4√5,当点P与AD的中点重合时,FG=2,EH=2,HG=8,此时EF最小值= HG=8,∴MN的取值范围是:4≤MN<2√5.小提示:本题主要考查全等三角形的判定和性质,正方形的性质,勾股定理,旋转的性质,添加辅助线,构造直角全等的直角三角形,是解题的关键.。
第二十三章旋转知识点总结,经典例题,单元测试

e an dAl l t h i ng si nt he i rb ei n gare go od fo r第二十三章旋转知识点总结,经典例题,单元测试:1.旋转:把一个平面图形绕着平面内某一点0转动一个角度,就叫做图形的旋转。
点0叫做旋转中心,旋动的角叫做旋转角。
旋转方向:顺时针和逆时针。
2.旋转的特征:(旋转不改变图形的大小和方向)(1)对应点到旋转中心的距离相等。
(2)对应点与旋转中心所连线段的夹角都等于旋转角。
(3)旋转前、后的图形全等。
3.旋转对称图形:一个图形绕着某一动点转动一定的角度后能与自身完全重合,这种图形称为旋转对称图形,绕着转动的这一点,称为旋转中心。
注:结合旋转对称图形的定义知:正三角形绕其中心旋转1200后能与自身完全重合,故正三角形是旋转对称图形;正方形绕其对角线的交点(旋转中心)旋转900后能与自身完全重合,故正方形是旋转对称图形。
一般的正n (n ≥3)变形是旋转对称图形,那么最少旋转时,能与自身完全重合。
4.设计旋转对称图形:(1)确定旋转中心、旋转角度和旋转方向;这是旋转的三要素。
(2)确定图形中的关键点;(3)将这些关键点绕旋转中心绕指定方向旋转指定的角度。
(4)顺次连接新关键点,得到所求图形。
旋转的定义:【例1】如图,如果把钟表的指针看做三角形OAB ,它绕O 点按顺时针方向旋转得到△OEF,在这个旋转过程中: 1.旋转中心是什么?旋转角是什么?2.经过旋转,点A 、B 分别移动到什么位置?【例2】如图所示,⊿ABC 和⊿ADE 都是等腰直角三角形,∠ACB 和∠AED 都是旋转对称图形:【例1】如图所示,它由哪个旋转得到的?旋转中心是哪里?旋转了多少度?旋转作图:【例1】请画出⊿ABCA.旋转角不变,改变旋转中心以下所示图形,四边形ABCD分别为O、O为中心,旋转角都为at i t he i rb ei n ga re go 因此,从以上的画图中,我们可以得到旋转中心不变,改变旋转角与旋转角不变,改变旋转中心会产生不同的效果,所以,我们可以经过旋转设计出美2】如图,正方形网格中,△ABC 为格点三角形(顶点都是格点)11AB C △.(1)在正方形网格中,作出11AB C ;(不要求写作法)dooge.如图,以点为为旋转中心,将∠1nisgnihfo rs o m ABC ∆A 050'''C B A ∆0'33=∠B。
最新人教版数学九年级上册第二十三章—旋转知识点总结及其练习

第二十三章—旋转一、旋转变换1、旋转的定义把一个图形绕着某一点O转动一个角度的图形变换叫做旋转。
点O叫做旋转中心,转动的角叫做旋转角,如果图形上的点P经过旋转变为点P',那么这两个点叫做这个旋转的对应点。
2、旋转的性质(1)对应点到旋转中心的距离相等。
(旋转中心就是各对应点所连线段的垂直平分线的交点。
)(2)对应点与旋转中心所连线段的夹角等于旋转角。
(3)旋转前、后的图形全等。
3、作旋转后的图形的一般步骤(1)明确三个条件:旋转中心,旋转方向,旋转角度;(2)确定关键点,作出关键点旋转后的对应点;(3)顺次连结。
4、欣赏较复杂旋转图形图形是由什么基本图形,以哪个点为中心,按哪个方向(顺时针或逆时针)旋转多少度,连续旋转几次,便得到美丽的图案。
5、有关图形旋转的一些计算题和证明题例题练习1.将叶片图案旋转180°后,得到的图形是( )2.如图,在等腰直角△ABC中,B=90°,将△ABC绕顶点A逆时针方向旋转60°后得到△AB′C′,则等于()A.60°B.105°C.120°D.135°3.如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在位置,A点落在位置,若,则的度数是()A.50°B.60°C.70°D.80°4.数学来源于生活,下列生活中的运动属于旋转的是 ( )A.国旗上升的过程B.球场上滚动的足球C.工作中的风力发电机叶片D.传输带运输东西5.如图,将方格纸中的图形绕点O逆时针旋转90°后得到的图形是 ( )6.如图,在△ABC中,AB=AC,∠ABC=30°,点D、E分别为AB、AC上的点,且DE∥BC.将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,连接BD、EC.下列结论:①△ADE的旋转角为120°;②BD=EC;③BE=AD+AC;④DE⊥AC.其中正确的为( )A.②③B.②③④C.①②③D.①②③④7.如图,将△ABC绕点A顺时针旋转得到△ADE,且点D恰好在AC上,∠BAE=∠CDE=136°,则∠C的度数是()8.如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.(1)求证:△FAC≌△BAE;(2)图中可以通过旋转△BAE而得到△FAC,请你说出旋转中心、旋转方向和旋转角的度数.9.如图,四边形ABCD是正方形,点E是边BC上的动点(不与B,C重合),将线段AE 绕点E顺时针旋转90°得到线段EF,连接AF,EF、AF分别与CD交于点M、N,连接EN,作FG⊥BC交BC的延长线于点G.(1)求证:BE=CG;(2)若BE=2,DN=3,求EN的长.二、中心对称图形1、中心对称的定义把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点。
第二十三章旋转单元测试题
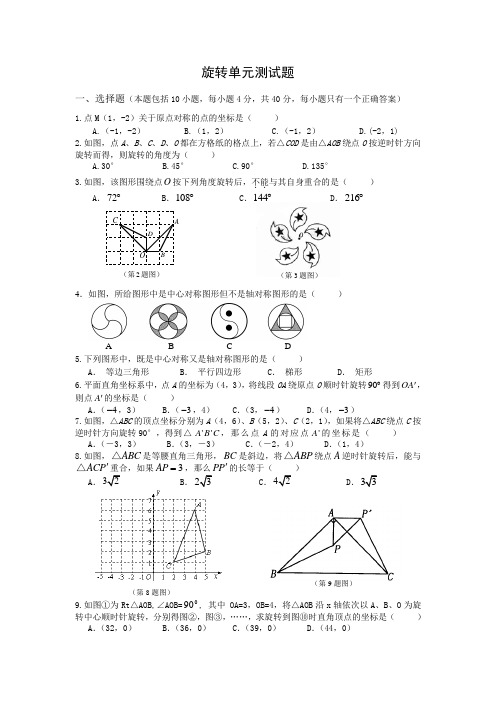
旋转单元测试题一、选择题(本题包括10小题,每小题4分,共40分,每小题只有一个正确答案)1.点M (1,-2)关于原点对称的点的坐标是( )A.(-1,-2)B.(1,2)C.(-1,2)D.(-2,1)2.如图,点A 、B 、C 、D 、O 都在方格纸的格点上,若△COD 是由△AOB 绕点O 按逆时针方向旋转而得,则旋转的角度为( )A.30°B.45°C.90°D.135°3.如图,该图形围绕点O 按下列角度旋转后,不能..与其自身重合的是( ) A .72︒ B .108︒ C .144︒ D .216︒4.如图,所给图形中是中心对称图形但不是轴对称图形的是( )A B C D5.下列图形中,既是中心对称又是轴对称图形的是( )A . 等边三角形B . 平行四边形C . 梯形D . 矩形6.平面直角坐标系中,点A 的坐标为(4,3),将线段OA 绕原点O 顺时针旋转90︒得到OA ',则点A '的坐标是( )A .(4-,3)B .(3-,4)C .(3,4-)D .(4,3-)7.如图,△ABC 的顶点坐标分别为A (4,6)、B (5,2)、C (2,1),如果将△ABC 绕点C 按逆时针方向旋转90°,得到△''A B C ,那么点A 的对应点'A 的坐标是( )A .(-3,3)B .(3,-3)C .(-2,4)D .(1,4)8.如图,ABC △是等腰直角三角形,BC 是斜边,将ABP △绕点A 逆时针旋转后,能与 ACP '△重合,如果3AP =,那么PP '的长等于( )A .32B .23C .42D .339.如图①为Rt △AOB,∠AOB=090, 其中 OA=3,OB=4,将△AOB 沿x 轴依次以A 、B 、O 为旋转中心顺时针旋转,分别得图②,图③,……,求旋转到图⑩时直角顶点的坐标是( )A .(32,0)B .(36,0)C .(39,0)D .(44,0)(第3题图)图 A B O C D (第2题图) (第9题图)(第8题图)10.如图,P 是等腰直角△ABC 外一点,把BP 绕点B 顺时针旋转90o 到BP ',已知 ∠AP 'B=135o , P 'A:P 'C=1:3,则P 'A:PB=( ) A.1:2 B.1:2 C.3:2 D.1: 3二、填空题(每小题4分,共20分)11.如图,△ABC 中,∠C =30°.将△ABC 绕点A 顺时针旋转60°得△ADE ,AE 与BC 交于F ,则∠AFB = °.12.如图,PQR ∆是ABC ∆经过某种变换后得到的图形.如果ABC ∆中任意一点M 的坐标为(a ,b ),那么它的对应点N 的坐标为 .13.如图, 在平面直角坐标系中, 若△ABC 与△A 1B 1C 1关于E 点成中心对称, 则对称中心E 点的坐标是 .14.如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是_________点.15.Rt △ABC 中,已知∠C =90°,∠B =50°,点D 在边BC 上,BD =2CD .把△ABC 绕着点D 逆时针旋转m (0<m <180)度后,如果点B 恰好落在初始Rt △ABC 的边上,那么m =_________.A O x y1 2 -1 -2 -3 -11 2 3 4 -4 B C A 1C 1 B 15 (第12题图) D C B A (第9题图) (第10题图)(第11题图) (第14题图) (第15题图)(第13题图)如图,若将△ABC 的绕点C 顺时针旋转90°后得到△DEC ,则A 点的对应点D 的坐标是 ,B 点的对应点E 的坐标是 ,请画出旋转后的△DEC(不要求写画法)17.( 10分 )如图,在正方形网络中,△ABC 的三个顶点都在格点上,点A 、B 、C 的坐标分别为(-2,4)、(-2,0)、(-4,1),结合所给的平面直角坐标系解答下列问题:(1)画出△ABC 关于原点O 对称的△111A B C .(2)平移△ABC ,使点A 移动到点2A (0,2),画出平移后的△222A B C 并写出点2B 、2C 的坐标.(3)在△ABC 、△111ABC 、△222A B C 中,△222A B C 与 成中心对称,其对称中心的坐标为 .0 1 2 3 4 -1 -2 -3 -4 2 1 4 3-1 -2 -3-4ABC x y一副直角三角板叠放如图所示,现将含45°角的三角板ADE 固定不动,把含30°角的三角板ABC 绕顶点A 顺时针...旋转∠α(α=∠BAD 且0°<α<180°),使两块三角板至少有一组边平行.(1)如图①,α=______°时,BC ∥DE ;(2)请你分别在图②、图③的指定框内,各画一种符合要求的图形,标出α,并完成各项填空:图②中α=______°时,______∥______;图③中α=______°时,______∥______.19.( 10分 )如图,在平面直角坐标系中,有一Rt △ABC ,且A (-1,3),B (-3,-1),C (-3,3),已知△A 1AC 1是由△ABC 旋转得到的.(1)请写出旋转中心的坐标是 ,旋转角是 度;(2)以(1)中的旋转中心为中心,分别画出△A 1AC 1顺时针旋转90°、180°的三角形;(3)设Rt △ABC 两直角边BC =a 、AC =b 、斜边AB =c ,利用变换前后所形成的图案证明勾股定理.A D EBC α图①图②图③ADE A D E A B C D E (第22题图)。
2024九年级数学上册“第二十三章 旋转”必背知识点

2024九年级数学上册“第二十三章旋转”必背知识点一、旋转的基本概念定义:将一个图形绕着某点O转动一个角度的变换叫做旋转。
其中,O叫做旋转中心,转动的角度叫做旋转角。
旋转三要素:旋转中心、旋转角度、旋转方向。
二、旋转的性质旋转后的图形与原图形的关系:旋转后的图形与原图形全等。
对应点与旋转中心的距离:对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角:对应点与旋转中心所连线段的夹角等于旋转角。
图形变化:图形的大小和形状都没有发生改变,只改变了图形的位置。
三、中心对称定义:若一个图形绕着某个点O旋转180°,能够与另一个图形完全重合,则这两个图形关于这个点对称或中心对称。
这个点叫做对称中心。
中心对称图形:若一个图形绕着某个点O旋转180°,能够与原来的图形完全重合,则这个图形叫做中心对称图形。
这个点叫做该图形的对称中心。
性质:1. 关于中心对称的两个图形上的对应点的连线都经过对称中心,并且都被对称中心平分。
2. 关于中心对称的两个图形能够互相重合,是全等形。
3. 关于中心对称的两个图形,对应线段平行(或共线)且相等。
四、关于原点对称的点的坐标在平面直角坐标系中,如果两个点关于原点对称,它们的坐标符号相反。
即点P(x,y)关于原点对称的点的坐标为P'(-x,-y)。
五、作图与应用利用旋转性质作图:关键是连接图形中的每一个关键点与旋转中心,并按要求绕旋转中心转过一定角度,然后在新的位置上截取与原来等长的线段,连接各点得到新的图形。
旋转的应用:旋转在几何图形的变换、证明以及解决实际问题中都有广泛的应用,如通过旋转构造全等图形、证明角相等或线段相等。
六、例题与练习为了加深对旋转知识点的理解和记忆,可以通过做一些相关的例题和练习题来巩固所学内容。
这些题目通常会涉及到旋转的基本概念、性质以及应用等方面的知识点。
综上所述,九年级数学上册 “第二十三章 旋转”的必背知识点主要包括旋转的基本概念、性质、中心对称及其性质、关于原点对称的点的坐标以及作图与应用等方面。
九年级数学上册第二十三章旋转知识汇总笔记(带答案)

九年级数学上册第二十三章旋转知识汇总笔记单选题1、如图,菱形ABCD的对角线AC、BD交于点O,将△BOC绕着点C旋转180°得到△B′O′C,若AC=2,AB′=5,则菱形ABCD的边长是()A.3B.4C.√15D.√17答案:D分析:连接AB′,根据菱形的性质、旋转的性质,得到OA=OC=O′C=1,OB△OC,O′B′△O′C、BC=B′C,根据AB′=5,利用勾股定理计算O′B′,再次利用勾股定理计算B′C即可.解:连接AB′,如图:∵四边形ABCD是菱形,且△BOC绕着点C旋转180°得到△B′O′C,且AC=2,∴OA=OC=O′C=1,OB△OC,BC=B′C∴O′B′△O′C,O′A=AC+O′C=2+1=3,∵AB′=5,∴O′B′=√AB′2-O′A2=√5-32=4,∴B′C=√O′B′2+O′C2=√42+12=√17,∴BC=B′C=√17,即菱形ABCD的边长是√17,故选:D.小提示:本题考查了菱形的性质、旋转的性质以及勾股定理等知识,熟练掌握菱形的基本形式并灵活运用勾股定理是解决本题的关键.2、如图,将一个正方形纸片沿图中虚线剪开,能拼成下列四个图形,其中是中心对称图形的是()A.B.C.D.答案:B分析:根据拼成的四个图形是否存在中心对称点,即可判断图形是否为中心对称图形.解:依照中心对称图形的特征:若图形存在中心对称点,沿中心对称点旋转180°后可与原图形重合.选项A图形无中心对称点,故不是中心对称图形,不符合题意;选项B图形有中心对称点,故是中心对称图形,符合题意;选项C图形无中心对称点,故不是中心对称图形,不符合题意;选项D图形无中心对称点,故不是中心对称图形,不符合题意;故选:B.小提示:本题考查中心对称图形的性质特征,熟练掌握相关知识是解题的关键.3、下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是()A.B.C.D.答案:C分析:根据轴对称图形和中心对称图形的概念逐项判断即可.A.不是轴对称图形,也不是中心对称图形,故此选项不符合题意;B.是轴对称图形,不是中心对称图形,故此选项不符合题意;C.是轴对称图形,也是中心对称图形,故此选项符合题意;D.不是轴对称图形,也不是中心对称图形,故此选项不符合题意,故选:C.小提示:本题考查轴对称图形、中心对称图形,理解轴对称图形和中心对称图形是解答的关键.4、把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为()A.30°B.90°C.120°D.180°答案:C分析:根据图形的对称性,用360°除以3计算即可得解.解:∵360°÷3=120°,∴旋转的角度是120°的整数倍,∴旋转的角度至少是120°.故选C.小提示:本题考查了旋转对称图形,仔细观察图形求出旋转角是120°的整数倍是解题的关键.5、连接正八边形的三个顶点,得到如图所示的图形,下列说法不正确的是()A.四边形ABCH与四边形EFGH的周长相等B.连接HD,则HD平分∠CHEC.整个图形不是中心对称图形D.△CEH是等边三角形答案:D分析:根据正八边形和圆的性质进行解答即可.解:A.∵根据正八边形的性质,四边形ABCH与四边形EFGH能够完全重合,即四边形ABCH与四边形EFGH 全等∴四边形ABCH与四边形EFGH的周长相等,故选项正确,不符合题意;B.连接DH,如图1,∵正八边形是轴对称图形,直线HD是对称轴,∴HD平分∠CHE故选项正确,不符合题意;C.整个图形是轴对称图形,但不是中心对称图形,故选项正确,不符合题意;D.∵八边形ABCDEFGH是正八边形,∴B=BC=CD=DE=EF=FG=GH,CH=EH,设正八边形的中心是O,连接EO、DH,如图2,∠DOE=360°=45°8∵OE=OH∴∠OEH =∠OHE =12∠DOE =22.5° ∴∠CHE =2∠OHE =45°∴∠HCE =∠HEC =12(180°-∠CHE )=67.5° ∴△CEH 不是等边三角形,故选项错误,符合题意.故选:D .小提示:本题考查了正多边形和圆,熟记正八边形与等腰三角形的性质是解题的关键.6、如图,射线OM,ON 互相垂直,OA =8,点B 位于射线OM 的上方,且在线段OA 的垂直平分线l 上,连接AB ,AB =5.将线段AB 绕点O 按逆时针方向旋转得到对应线段A ′B ′,若点B ′恰好落在射线ON 上,则点A ′到射线ON 的距离是( )A .245B .133C .4D .√17 答案:A分析:添加辅助线,连接OA ′,OB ,过A ′点作A ′P ⊥ON 交ON 与点P .根据旋转的性质,得到△A ′B ′O ≌△ABO ,在Rt △A ′PO 和中,∠B ′OA =∠BOA ,根据三角函数和已知线段的长度求出点A ′到射线ON 的距离d =A ′P .解:如图所示,连接OA ′,OB ,过A ′点作A ′P ⊥ON 交ON 与点P .∵线段AB绕点O按逆时针方向旋转得到对应线段A′B′,∴OA′=OA=8,∠B′OB=∠A′OA,∴∠B′OB−∠BOA′=∠A′OA−∠BOA′,即∠B′OA′=∠BOA,∵点B在线段OA的垂直平分线l上,∴OC=12OA=12×8=4,OB=AB=5,BC=√OB2−OC2=√52−42=3,∵∠B′OA′=∠BOA,∴sin∠B′OA′=A′PA′O =sin∠BOA=BCOB,∴A′P8=35,∴d=A′P=245,故选:A小提示:本题主要考查旋转的性质和三角函数.对应点到旋转中心的距离相等,对应点与旋转中心所连的线段的夹角等于旋转角,旋转前、后的图形全等.7、如图,在矩形ABCD中,AB=4,BC=6,O是矩形的对称中心,点E、F分别在边AD、BC上,连接OE、OF,若AE=BF=2,则OE+OF的值为()A.2√2B.5√2C.√5D.2√5答案:D分析:连接AC,BD,过点O作OM⊥AD于点M,交BC于点N,利用勾股定理求得OE的长即可解题.解:如图,连接AC,BD,过点O作OM⊥AD于点M,交BC于点N,∵四边形ABCD是矩形,∴OA=OD=OB∵OM⊥AD∴AM=DM=3∴OM=12AB=2∵AE=2∴EM=AM−AE=1∴OE=√EM2+OM2=√12+22=√5同理可得OF=√5∴OE+OF=2√5故选:D.小提示:本题考查中心对称、矩形的性质、勾股定理等知识,学会添加辅助线,构造直角三角形是解题关键.8、如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为()A.90°﹣αB.αC.180°﹣αD.2α答案:C分析:根据旋转的性质和四边形的内角和是360°,可以求得∠CAD的度数,本题得以解决.解:由题意可得,∠CBD=α,∠ACB=∠EDB,∵∠EDB+∠ADB=180°,∴∠ADB+∠ACB=180°,∵∠ADB+∠DBC+∠BCA+∠CAD=360°,∠CBD=α,∴∠CAD=180°−α,故选C.小提示:本题考查旋转的性质,解答本题的关键是明确题意,利用数形结合的思想解答.9、如图,△ABC是等边三角形,D为BC边上的点,△ABD经旋转后到达△ACE的位置,那么旋转角为()A.75°B.60°C.45°D.15°答案:B分析:根据题意可知旋转角为∠BAC,根据等边三角形的性质即可求解.解:∵△ABD经旋转后到达△ACE的位置,△ABC是等边三角形,∴旋转角为∠BAC=60°,故选B小提示:本题考查了等边三角形的性质,找旋转角,找到旋转前后对应的线段所产生的夹角即为旋转是解题的关键.10、将矩形ABCD绕点A顺时针旋转α(0°<α<360°),得到矩形AEFG.当GC=GB时,下列针对α值的说法正确的是()A.60°或300°B.60°或330°C.30°D.60°答案:A分析:当GB=GC时,点G在BC的垂直平分线上,分两种情况讨论,依据∠DAG=60°,即可得到旋转角α的度数.如图,当GB=GC时,点G在BC的垂直平分线上,分两种情况讨论:①当点G在AD右侧时,取BC的中点H,连接GH交AD于M,∵GC=GB,∴GH⊥BC,∴四边形ABHM是矩形,∴AM=BH=1AD,2∴GM垂直平分AD,∴GD=GA=DA,∴△ADG是等边三角形,∴∠DAG=60°,∴旋转角α=60°;②当点G在AD左侧时,同理可得△ADG是等边三角形,∴∠DAG=60°,∴旋转角α=360°-60°=300°,故选:A.小提示:本题主要考查了旋转的性质,全等三角形的判定与性质的运用,解题时注意:对应点与旋转中心所连线段的夹角等于旋转角.填空题11、如图,在△ABC中,∠ACB=90°,AC=√2,BC=2√2,将△ABC绕点C按逆时针方向旋转得到△DEC,连接AD,BE,直线AD,BE相交于点F,连接CF,在旋转过程中,线段CF的最大值为__________.答案:√10分析:取AB的中点H,连接CH、FH,设EC,DF交于点G,在△ABC中,由勾股定理得到AB=√10,由旋转可知:△DCE≌△ACB,从而∠DCA=∠BCE,∠ADC=∠BEC,由∠DGC=∠EGF,可得∠AFB=90º,由直角三角形斜边上的中线等于斜边的一半,可得FH =CH =12AB =√102,在△FCH 中,当F 、C 、H 在一条直线上时,CF 有最大值为√10.解:取AB 的中点H ,连接CH 、FH ,设EC ,DF 交于点G ,在△ABC 中,∠ACB =90º,∵AC =√2,BC =2√2,∴AB =√AC 2+BC 2=√10,由旋转可知:△DCE ≌△ACB ,∴∠DCE =∠ACB ,DC =AC ,CE =CB ,∴∠DCA =∠BCE ,∵∠ADC =12(180º-∠ACD ) ,∠BEC =12 (180º-∠BCE ), ∴∠ADC =∠BEC ,∵∠DGC =∠EGF ,∴∠DCG =∠EFG =90º,∴∠AFB =90º,∵H 是AB 的中点,∴FH =12AB , ∵∠ACB =90º,∴CH =12AB ,∴FH =CH =12AB =√102,在△FCH中,FH+CH>CF,当F、C、H在一条直线上时,CF有最大值√102+√102=√10,∴线段CF的最大值为√10.所以答案是:√10小提示:本题考查了旋转的性质、勾股定理,解决本题的关键是掌握全等的性质.12、如图,在平面直角坐标系中,已知A(−2,1),B(−1,4),C(−1,1),将△ABC先向右平移3个单位长度得到△A1B1C1,再绕C1顺时针方向旋转90°得到△A2B2C1,则A2的坐标是____________.答案:(2,2).分析:直接利用平移的性质和旋转的性质得出对应点位置,然后作图,进而得出答案.解:如图示:△A1B1C1,△A2B2C1为所求,根据图像可知,A2的坐标是(2,2),故答案是:(2,2).小提示:本题主要考查了平移作图和旋转作图,熟悉相关性质是解题关键.13、在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab=_____.答案:12分析:直接利用关于原点对称点的性质得出a,b的值,进而得出答案.∵点A的坐标为(a,3),点B的坐标是(4,b),点A与点B关于原点O对称,∴a=﹣4,b=﹣3,则ab=12,所以答案是:12.小提示:本题考查了关于原点对称的点的坐标,熟知关于原点对称的两点的横、纵坐标互为相反数是解题的关键.14、以水平数轴的原点O为圆心过正半轴Ox上的每一刻度点画同心圆,将Ox逆时针依次旋转30°、60°、90°、⋯、330°得到11条射线,构成如图所示的“圆”坐标系,点A、B的坐标分别表示为(5,0°)、(4,300°),则点C的坐标表示为_______.答案:(3,240°)分析:根据同心圆的个数以及每条射线所形成的角度,以及A,B点坐标特征找到规律,即可求得C点坐标.解:图中为5个同心圆,且每条射线与x轴所形成的角度已知,A、B的坐标分别表示为(5,0°)、(4,300°),根据点的特征,所以点C的坐标表示为(3,240°);所以答案是:(3,240°).小提示:本题考查坐标与旋转的规律性问题,熟练掌握旋转性质,并找到规律是解题的关键.15、如图,在△ABC中,AB=3,AC=2,∠BAC=60°,P为△ABC内一点,则PA+PB+PC的最小值为__________.答案:√19分析:将△APB绕点A顺时针旋转60°,得到△AP′B′,连接PP′、CB′,作CN⊥B′A交B′A的延长线于点N,则△AP′B′≌△APB,由题意可证△P′AP是等边三角形,所以PA+PB+PC=PC+PP′+P′B′,所以当B′、P′、P、C共线时,PA+PB+PC=B′C最小,求出B′C=√B′N2+CN2=√19即可;将△APB绕点A顺时针旋转60°,得到△AP′B′,连接PP′、CB′,作CN⊥B′A交B′A的延长线于点N,则△AP′B′≌△APB,∴∠BAP=∠B′AP′,∴AB′=AB=3,AP′=AP,∠B′AB=∠P′AP=60°,∴△P′AP是等边三角形,∴AP′=AP=PP′,∴PA+PB+PC=PC+PP′+P′B′,∴当B′、P′、P、C共线时,PA+PB+PC=B′C最小,∴∠CAN=180°-∠BAB′−∠BAC=60°,CN⊥AN,∴∠ACN=30°,∴AN=1AC=1,CN=√3AN=√3,2∴B′N=AB′+AN=3+1=4,∴B′C=√B′N2+CN2=√19,∴PA+PB+PC=B′C=√19;所以答案是:√19.小提示:本题考查了全等三角形判定与性质,旋转的性质,以及等边三角形的性质和求线段最值的问题,掌握做辅助线是解题的关键.解答题16、如图是在北京举办的世界数学家大会的会标“弦图”.请将“弦图”中的四个直角三角形通过你所学过的图形变换,在以下方格纸中设计另外两个不同的图案.画图要求:①每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠;②所设计的图案(不含方格纸)必须是中心对称图形或轴对称图形.答案:解:如下图所示,答案不唯一.易错:容易把三角形画成重叠的.错因:没有看清题目要求.满分备考:由“基本图形”经过旋转、轴对称、平移等可以得到美丽而丰富的图案,而图案涉及的关键是确定基本图形,制定图形变换的具体操作程序.注意应用几种常见的图形变换.解析:运用基本图,按照轴对称和中心对称的特点以及画图规律直接绘制图形即可.17、[问题提出](1)如图①,△ABC、△ADE均为等边三角形,点D、E分别在边AB、AC上.将△ADE绕点A沿顺时针方向旋转,连结BD、CE.在图②中证明△ADB≌△AEC.[学以致用](2)在(1)的条件下,当点D、E、C在同一条直线上时,∠EDB的大小为度.[拓展延伸](3)在(1)的条件下,连结CD.若BC=6,AD=4,直接写出△DBC的面积S的取值范围.答案:(1)见解析;(2)60或120;(3)9√3−12≤S≤9√3+12分析:(1)运用SAS证明△ADB≌△AEC即可;(2)分“当点E在线段CD上”和“当点E在线段CD的延长线上”两种情况求出∠EDB的大小即可;(3)分别求出△DBC的面积最大值和最小值即可得到结论(1)∵△ABC,△ADE均为等边三角形,∴AD=AE,AB=AC,∴∠DAE−∠BAE=∠BAC−∠BAE,即∠BAD=∠CAE在△ADB和△AEC中{AD=AE∠BAD=∠CAE AB=AC∴△ABD≅△ACE(SAS);(2)当D,E,C在同一条直线上时,分两种情况:①当点E在线段CD上时,如图,∵△ADE是等边三角形,∴∠ADE=∠AED=60°,∴∠AEC=180°−∠AED=120°,由(1)可知,△ADB≅△AEC,∴∠ADB=∠AEC=120°,∴∠EDB=∠ADB−∠ADE=120°−60°=60°②当点E在线段CD的延长线上时,如图,∵△ADE是等边三角形,∴∠ADE=∠AED=60°∴∠ADC=180°−∠ADE=120°,由(1)可知,△ADB≅△AEC∴∠ADB=∠AEC=60°,∴∠EDB=∠ADB+∠ADE=60°+60°=120°综上所述,∠EDB的大小为60°或120°(3)过点A作AF⊥BC于点F,当点D在线段AF上时,点D到BC的距离最短,此时,点D到BC的距离为线段DF的长,如图:∵△ABC是等边三角形,AF⊥BC,BC=6∴AB=BC=6,BF=12BC=3∴AF=√AB2−BF2=√62−32=3√3∴DF=3√3−4此时S△DBC=12BC⋅DF=12×6×(3√3−4)=9√3−12;当D在线段FA的延长线上时,点D到BC的距离最大,此时点D到BC的距离为线段DF的长,如图,∵△ABC是等边三角形,AF⊥BC,BC=6∴AB=BC=6,BF=12BC=3,∴AF=√AB2−BF2=√62−32=3√3∵AD=4∴DF=AF+AD=3√3+4此时,S△DBC=12BC⋅DF=12×6×(3√3+4)=9√3+12;综上所述,△DBC的面积S 取值是9√3−12≤S≤9√3+12小提示:此题是几何变换综合题,主要考查了旋转和全等三角形的性质和判定,旋转过程中面积变化分析,解本题的关键是三角形全等的判定.18、如图,点M,N分别在正方形ABCD的边BC,CD上,且∠MAN=45°,把△ADN绕点A顺时针旋转90°得到△ABE.(1)求证:△AEM≌△ANM.(2)若BM=3,DN=2,求正方形ABCD的边长.答案:(1)证明见解析;(2)正方形ABCD的边长为6.分析:(1)先根据旋转的性质可得AE=AN,∠BAE=∠DAN,再根据正方形的性质、角的和差可得∠MAE= 45°,然后根据三角形全等的判定定理即可得证;(2)设正方形ABCD的边长为x,从而可得CM=x−3,CN=x−2,再根据旋转的性质可得BE=DN=2,从而可得ME=5,然后根据三角形全等的性质可得MN=ME=5,最后在Rt△CMN中,利用勾股定理即可得.(1)由旋转的性质得:AE=AN,∠BAE=∠DAN∵四边形ABCD是正方形∴∠BAD=90°,即∠BAN+∠DAN=90°∴∠BAN+∠BAE=90°,即∠EAN=90°∵∠MAN=45°∴∠MAE=∠EAN−∠MAN=90°−45°=45°在△AEM和△ANM中,{AE=AN∠MAE=∠MAN=45°AM=AM∴△AEM≅△ANM(SAS);(2)设正方形ABCD的边长为x,则BC=CD=x∵BM=3,DN=2∴CM=BC−BM=x−3,CN=CD−DN=x−2由旋转的性质得:BE=DN=2∴ME=BE+BM=2+3=5由(1)已证:△AEM≅△ANM∴MN=ME=5又∵四边形ABCD是正方形∴∠C=90°则在Rt△CMN中,CM2+CN2=MN2,即(x−3)2+(x−2)2=52解得x=6或x=−1(不符题意,舍去)故正方形ABCD的边长为6.小提示:本题考查了正方形的性质、旋转的性质、三角形全等的判定定理与性质、勾股定理等知识点,较难的是题(2),熟练掌握旋转的性质与正方形的性质是解题关键.。
第二十三章旋转知识点总结,经典例题,单元测试

第二十三章旋转知识点总结,经典例题,单元测试:1.旋转:把一个平面图形绕着平面内某一点0转动一个角度,就叫做图形的旋转。
点0叫做旋转中心,旋动的角叫做旋转角。
旋转方向:顺时针和逆时针。
2.旋转的特征:(旋转不改变图形的大小和方向)(1)对应点到旋转中心的距离相等。
(2)对应点与旋转中心所连线段的夹角都等于旋转角。
(3)旋转前、后的图形全等。
3.旋转对称图形:一个图形绕着某一动点转动一定的角度后能与自身完全重合,这种图形称为旋转对称图形,绕着转动的这一点,称为旋转中心。
注:结合旋转对称图形的定义知:正三角形绕其中心旋转1200后能与自身完全重合,故正三角形是旋转对称图形;正方形绕其对角线的交点(旋转中心)旋转900后能与自身完全重合,故正方形是旋转对称图形。
一般的正n(n≥3)变形是旋转对称图形,那么最少旋转时,能与自身完全重合。
4.设计旋转对称图形:(1)确定旋转中心、旋转角度和旋转方向;这是旋转的三要素。
(2)确定图形中的关键点;(3)将这些关键点绕旋转中心绕指定方向旋转指定的角度。
(4)顺次连接新关键点,得到所求图形。
旋转的定义:【例1】如图,如果把钟表的指针看做三角形OAB,它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中:1.旋转中心是什么?旋转角是什么?2.经过旋转,点A、B分别移动到什么位置?【例2】如图所示,⊿ABC 和⊿ADE 都是等腰直角三角形,∠ACB 和∠AED 都是直角,点C 在AD 上,如果⊿ABC 经旋转后能与⊿ADE 重合,那么哪一点是旋转中心?旋转角度是多少?并指出对应点。
CBDEAM DBC EAN练一练:如图所示,⊿ABC 是等腰三角形,∠ACB=900,D 是AB 边上一点,⊿CBD 经逆时针旋转后到达⊿CAE 的位置,则旋转中心是 ,旋转角度是 ,点B 的对应点是 ,点D 的对应点是 ,线段CB 的对应线段是 ,线段CD 的对应线段是 ,∠CBD 的对应角是 ,如果点M 是线段BC 的中点,点N 是线段AC 的中点,那么经过上述旋转之后,点M 旋转到了 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十三章
旋转知识点总结,经典例题,单元测试
:
1.旋转:把一个平面图形绕着平面内某一点0转动一个角度,就叫做图形的旋转。
点0叫做旋转中心,旋动的角叫做旋转角。
旋转方向:顺时针和逆时针。
2.旋转的特征:(旋转不改变图形的大小和方向)
(1)对应点到旋转中心的距离相等。
(2)对应点与旋转中心所连线段的夹角都等于旋转角。
(3)旋转前、后的图形全等。
3.旋转对称图形:一个图形绕着某一动点转动一定的角度后能与自身完全重合,这种图形称为旋转对称图形,绕着转动的这一点,称为旋转中心。
注:结合旋转对称图形的定义知:正三角形绕其中心旋转1200后能与自身完全重合,故正三角形是旋转对称图形;正方形绕其对角线的交点(旋转中心)旋转900后能与自身完全重合,故正方形是旋转对称图形。
一般的正n(n≥3)变形是旋转对称图形,那么最少旋转时,能与自身完全重合。
4.设计旋转对称图形:
(1)确定旋转中心、旋转角度和旋转方向;这是旋转的三要素。
(2)确定图形中的关键点;
(3)将这些关键点绕旋转中心绕指定方向旋转指定的角度。
(4)顺次连接新关键点,得到所求图形。
旋转的定义:
【例1】如图,如果把钟表的指针看做三角形OAB,它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中:
1.旋转中心是什么?旋转角是什么?
2.经过旋转,点A、B分别移动到什么位置?
【例2】如图所示,⊿ABC 和⊿ADE 都是等腰直角三角形,∠ACB 和∠AED 都是直角,点C 在AD 上,如果⊿ABC 经旋转后能与⊿ADE 重合,那么哪一点是旋转中心?旋转角度是多少?并指出对应点。
C
B
D
E
A
M D
B
C E
A
N
练一练:如图所示,⊿ABC 是等腰三角形,∠ACB=900
,D 是AB 边上一点,⊿CBD 经逆时针旋转后到达⊿CAE 的位置,则旋转中心是 ,旋转角度是 ,点B 的对应点是 ,点D 的对应点是 ,线段CB 的对应线段是 ,线段CD 的对应线段是 ,∠CBD 的对应角是 ,如果点M 是线段BC 的中点,点N 是线段AC 的中点,那么经过上述旋转之后,点M 旋转到了 。
如果连接DE ,则⊿ECD 是什么三角形? 【例3】 根据图回答下面问题。
1.线段OA 与OA ′,OB 与OB ′,OC 与OC ′有什么关系? 2.∠AOA ′,∠BOB ′,∠COC ′有什么关系? 3.△ABC 与△A ′B ′C ′形状和大小有什么关系? 综合以上得出:
(1)对应点到旋转中心的距离相等;
(2)对应点与旋转中心所连线段的夹角等于旋转角; (3)旋转前、后的图形全等.
旋转对称图形:
【例1】如图所示,它由哪个“基本图形”旋转得到的?旋转中心是哪里?旋转了多少度?
j
D
E
F
C
G
H
F
G
A
B
D
C
E
H
【例2】如图,四边形ABCD 、四边形EFGH 都是边长为1的正方形. 1.这个图案可以看做是哪个“基本图案”通过旋转得到的?
2.请画出旋转中心和旋转角.
3.指出,经过旋转,点A、B、C、D分别移到什么位置?
旋转作图:
【例1】请画出⊿ABC绕点0顺时针旋转450,后的图形。
C
A
0O
C
B
A 0
C
B
A
练一练:请画出四边形ABCD绕点0逆时针旋转600后的图形。
请画出⊿ABC绕点0顺时针旋转900,后的图形。
从上面的作图题中,我们知道,作图应满足三要素:旋转中心、旋转角、对应点,而旋转中心、旋转角固定下来,对应点就自然而然地固定下来.因此,下面就选择不同的旋转中心、不同的旋转角来进行研究.
1.旋转中心不变,改变旋转角
下图所示的四边形ABCD以O点为中心,旋转角分别为30°、60°的旋转图形.
2.旋转角不变,改变旋转中心
以下所示图形,四边形ABCD分别为O、O为中心,旋转角都为30•°的旋转
图形.
因此,从以上的画图中,我们可以得到旋转中心不变,改变旋转角与旋转角不变,改变旋转中心会产生不同的效果,所以,我们可以经过旋转设计出美丽的图案.
【例2】如图,正方形网格中,△ABC 为格点三角形(顶点都是格点),将△ABC
绕点A 按逆时针方向旋转90°得到11AB C △.(1)在正方形网格中,作出11AB C △;(不要求写作法)
【例3】如图所示,每个小方格都是边长为1的正方形,以O 点为坐标原点建立平面直角
坐标系.
1.画出四边形OABC 关于y 轴对称的四边形OA 1B 1C 1,并写出点B 1的坐标是 .
2.画出四边形OABC 绕点O 顺时针方向旋转90°后得到的四边形OA 2B 2C 2。
练一练:如图,四边形ABCD 是边长为1的正方形,且DE=1
4
,△ABF 是△ADE
的旋转图形.
1.旋转中心是哪一点?
2.旋转了多少度?
3.AF 的长度是多少?
4.如果连结EF ,那么△AEF 是怎样的三角形?
1.在平面直角坐标系中,点A 的坐标为(1,4),将线段O A 绕点O 顺时针旋转90°得到线段OA′,则点A′的坐标是 .
2.如图所示,图①沿逆时针方向旋转90°可得到图________;图①按顺时针方向至少旋转______________度可得图③.
3.如图,在正方形ABCD 中,E 是AD 的中点,F 是BA 延长线上的一点,若AF=0.5AB,则可通过 (填“平移”、“旋转”、“轴对称”)变换,使三角形ABE 变换到三角形ADF 的位置;且线段BE 、DF 的数量关系是 .
4.如图,以点
为为旋转中心,将∠1按顺时
针方向旋转100°,得到∠2.若∠1=40°, 则∠2= 度.
5.如图,将左边的矩形绕点B 旋转一定角度后,位置如右边的矩形,则∠ABC= . 6. 如图,一块等边三角形木板ABC 的边长为1,现将木板沿水平线翻转(绕一个点旋转), 那么A 点从开始到结束所走的路径长度为 .
7. 如图,在△ABC 中,AB =AC ,若将△ABC 绕点C 顺时针旋转180°得到△FEC .则 AE 与BF 的关系是____________;若△ABC 的面积为3cm 2,则四边形ABFE 的面积是 ___________;当∠ACB 为______________度时,四边形ABFE 为矩形。
8.如图,四边形EFGH 是由四边形ABCD 经过旋转得到的.如果用有序数对(2,1)表示 方格纸上A 点的位置,用(1,2)表示B 点的位置,那么四边形ABCD 旋转得到四边形EFGH
时的旋转中心用有序数对表示是 .
9.如图,四边形ABCD 是正方形,△ADE 旋转后能与△ABF 重合.则旋转中心是 ,旋转角
等于 度,如果连接EF ,那么△AEF 是 三角形。
10.如图,P 是等边三角形ABC 内的一点,且68PA PB ==,,10PC =.
若将PAC △ 绕点A 逆时针旋转后,得到P AB '△,则点P 与点P '之间的距离为 .
11.如图所示,ABC ∆绕点A 旋转了050后到了'''C B A ∆的位置,
若0'33=∠B ,0
56=∠C , 则________'
=∠AC B .
12.如图,画出已知图形关于点O 的对称图形.
13.如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角
坐标系后,
△ABC 的顶点均在格点上.
(1)把△ABC 向上平移5个单位后得到对应的△A 1B 1C 1,画出△A 1B 1C 1, (2)以原点O 为对称中心,再画出与△A 1B 1C 1关于原点O 对称的△A 2B 2C 2,。
A
C D
O
A B
C
O
x
y。
