8 金属的固态扩散
金属学与热处理 第八章 扩散
二.
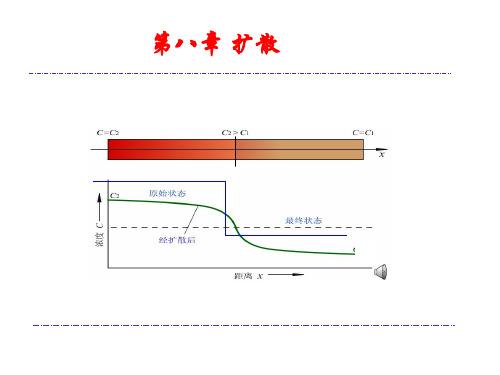
菲克第二定律
适用范围: 非稳态扩散(扩散过程中, 合金各处的浓度和浓度梯度随距离和时间变化.)
设:I, II 为垂直的单位平面;J1,J2为进出两平面的扩散流量;浓度 随时间的变化率为 ; 则单元dx内溶质的积累速率为:
菲克第二定律数学表达式:
若扩散系数D为常数,则: 扩散第二定律是由第一定律推导出来, 它适用于一般的扩散过程. 方程的解具有C=f (x, t )关系.
举例: AL-C合金棒弹性弯曲,并在一定温度下加热, 发生扩散. 大的铝原子向受拉伸的一边扩散, 小的铜原子小受压缩 的一边扩散.
四. 固态扩散的分类
(一) 根据扩散过程中是否发生浓度变化分类 •自扩散: •互扩散: (二) 根据扩散方向是否与浓度梯度的方向相同进行分类 •下坡扩散: •上坡扩散: (三) 根据扩散过程中是否出现新相进行分类 •原子扩散 •反应扩散
间隙原子扩散速度 > 置换原子扩散速度 例如:
四.晶体缺陷
原因:缺陷处原子排列不整齐, 晶格畸变大,能量较高,所以 原子扩散的激活能小,原子容 易扩散。
表面
晶界
亚晶界
晶体内部
晶体内部位错、空位处
扩散速度由快到慢
晶体内部完整部分
五.化学成分 1.加入的合金元素影响合金的熔点时 提高熔点的合金元素, 降低原子扩散系数; 反之, 降低熔点的元素, 提高扩散系数.
二.扩散机理
扩散的条件: 热振动 + 一定的晶体结构 间隙固溶体中绝大部分都Βιβλιοθήκη 着.(一). 间隙扩散机理
置换固溶体
固溶体中的间隙扩散方式
间隙固溶体中
顶替式(a)
挤列式(b)
(二).换位扩散机理
直接换位扩散机制
8.金属学热处理 扩散
第八章 扩散
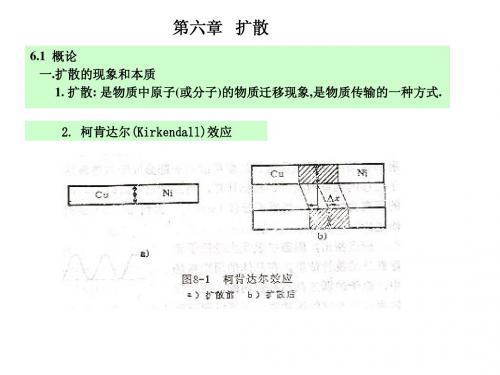
§8-1 概述 一、扩散现象和本质 柯肯达尔效应 柯肯达尔(Kirkendall)于1947年首先用实验验证了置换 型原子的互扩散过程。
实验结果发现,随着保温时间的延长,即界面位置向内发 生了微量漂移。
第八章 扩散
如果铜和锌的扩散系数相同,由于锌原子尺寸大于铜原子, 扩散以后界面外侧的铜晶格膨胀,内部的黄铜晶格收缩, 这种因为原子尺寸不同也会引起界面向内漂移,但位移量 只有实验值的十分之一左右。
位机制。
图 直接换位扩散模型
第八章 扩散
图 面心立方晶体的空位扩散机制 图 环形换位扩散模型
第八章 扩散
扩散激活能 晶体点阵中的原子进行扩散时,均需具有一定的超 额能量方可克服周围原子的能垒而实现迁移,该能量 称为扩散激活能。它在数值上等于势垒的高度Q。
第八章 扩散
三、固态金属扩散的条件
(一)、温度要足够高 温度越高,原子的热振动越激烈,原子被激活而进行 迁移的几率就越大。 固态扩散必须在足够高的温度以上才能进行。例如碳 原子在室温下的扩散过程极其微弱,在100℃以上时 才较为显著,而铁原子必须在500℃以上时才能有效 地进行扩散。 (二)、时间要足够长 扩散原子在晶体中每跃迁一次最多也只能移动0.3~ 0.5nm的距离,要扩散1 mm的距离,必须跃迁亿万次 才行。
第八章 扩散
前面讨论的是单相固溶体中的扩散,其特点是溶质原子的 浓度未超过固溶体的溶解度。
在许多的实际相图中,不仅包含一种固溶体,有可能出现 几种固溶体或者中间相。如果由构成这样相图的两个组元 制成扩散偶,或者在一种组元的表面渗入另一种组元,并 且在温度适宜保温时间足够的情况下,就会由于作为基体 的组元过饱和而反应生成一种或者几种新的合金相(中间 相或者固溶体)。
固体金属的扩散课件

REPORT
THANKS
感谢观看
CATALOG
DATE
ANALYSIS
SUMMAR Y
REPORT
CATALOG
DAห้องสมุดไป่ตู้E
ANALYSIS
SUMMAR Y
04
固体金属扩散的实验研 究方法
实验研究方法概述
• 实验研究方法是通过观察和实验来研究固体金属扩散现象的一 种方法。这种方法可以提供直接、客观的数据,帮助我们深入 了解固体金属扩散的规律和机制。
实验研究方法分类
直接观察法
通过显微镜等设备直接观察固体 金属在扩散过程中的变化,记录 相关数据。这种方法可以提供直 观的证据,但实验条件要求较高
SUMMAR Y
06
固体金属扩散的前沿研 究进展
前沿研究进展概述
固体金属扩散是材料科学领域的重要研究内容,涉及到金属材料的制备、加工、 性能优化等方面。近年来,随着科技的不断进步,固体金属扩散的研究取得了显 著的进展。
新的实验技术和计算模拟方法的出现,为研究固体金属扩散提供了更深入、更全 面的认识。同时,随着新材料、新工艺的不断涌现,固体金属扩散的应用前景也 越来越广泛。
。
物理模拟法
通过模拟实际环境中的温度、压 力等条件,研究固体金属在模拟 环境下的扩散行为。这种方法可 以模拟实际工况,但实验条件难
以完全控制。
化学分析法
通过化学分析手段,测定固体金 属在扩散过程中的成分变化,从 而推断扩散行为。这种方法可以 提供较为准确的数据,但实验过
程较为繁琐。
实验研究方法应用实例
前沿研究进展分类
实验研究
利用先进的实验设备和技术,如原子力显微镜、X射线衍 射、中子散射等,对固体金属扩散进行微观观测和表征, 揭示扩散机制和扩散行为。
金属扩散

稳定态扩散:单位时间内通过单位垂直截面的扩散物 质的量(扩散通量)J对于各处都相等,即每一时刻从 左边扩散来多少原子,就向右边扩散走多少原子,没 有盈亏,浓度不随时间变化。
J D dC dx dC 式中,D为扩散系数; 为体积浓度梯度; dx 负号表示物质的扩散方向与浓度梯度的方向相反。
间隙扩散机制
当间隙原子存在晶体结构中,可从一个间 隙位置移动到另一个间隙位置。 间隙原子尺寸越小,扩散越快。 由于间隙位置比空位位置多,间隙扩散比 空位扩散更容易发生。
三、固态金属扩散的条件
扩散要有驱动力:化学位梯度 扩散原子要固溶 温度要足够高 时间要足够长
四、固态扩散的分类
第八章 扩散
本章重点
扩散的微观机理 扩散的宏观规律 影响扩散的因素
§8-1 概述
一、扩散现象和本质
在气体和液体中的传质过程主要通过对流形成, 在固体中基本不发生对流,物质的传输只能靠原 子或粒子的扩散来进行。 扩散的本质:原子的热运动
柯肯达尔效应
左侧Ni的浓度高于右侧Cu的浓度,使左侧点阵 膨胀,最终导致界面向右漂移。
二、菲克第二定律
非稳定态扩散:在扩散过程中,各处的浓度不 仅随距离变化,而且还随时间发生变化。
C t C t x (D C x )
如果扩散系数D与浓度C、距离x无关,则 D C
2
x
2
三、扩散应用举例
铸锭间的均匀化退火 金属的粘接 钎焊 镀锌
§8-3 影响扩散的因素
根据扩散过程是否发生浓度变化分类 自扩散 互(异)扩散 根据扩散方向是否与浓度梯度的方向相同进行分类 下坡扩散 上坡扩散 根据扩散过程是否出现新相进行分类 原子扩散 反应扩散
金属学与热处理第八章_扩散

• 1885年,菲克进行了固态原子从高浓度向低浓度的扩 散实验,表明:单位时间内通过垂直于扩散方向的单 位截面积的扩散流量与该截面处的浓度梯度成正比。 • 称菲克第一定律,其数学表达式称扩散第一方程:
J D dC dx
• J:扩散流量,扩散物质流过单位截面速度; • D:扩散系数,反映扩散速度的物理量,是单位浓度梯 度时的扩散流量,D值越大,扩散越快。 • dC :体积浓度梯度,
r应用举例
u铸造合金消除枝晶偏析的均匀化退火
u钢在加热和冷却时的一些相变
u变形金属的回复与再结晶
u钢的化学热处理
第一节
概述
一、扩散现象 气体和液体中的扩散现象 • 例如:鲜花的芬芳,糖水的甜味 • 由物质的原子或分子迁移造成,是物质传输的结果。扩 散方向是自浓度高的方向向浓度低的方向进行,直至 各处浓度均匀为止. 固态物质中的扩散现象 • 金属结晶时,液态金属原子向固态晶核的迁移,再结晶 晶粒长大,钢的渗碳,金属的焊接等 • 固体中的扩散速率十分缓慢,但确实存在。
C(1/2 ,t)= Cp+
r因为A0= Cmax- Cp,所以有
:为偏析峰值衰减程度 r实际上,想达到完全均匀化( C=Cp)和偏析峰 值衰减程度0,是不可能的。
设铸锭经均匀化退火后,成分偏析的振幅要求降到 立,得到 t x
将
(4)
J DdC/dx
代入(4)式,
即为菲克第二定律.若扩散系数 D与浓度无关,为常数,则 写为: C 2C D 2 t x
(6)
三、扩散应用举例
r扩散第二定律普遍适用于一般的扩散过程。 r扩散方程是偏微分方程,不能直接应用,必须 结合实际的扩散过程,运用具体的起始条件和 边界条件,求解后才能应用。 r从 C 2C 式可知,扩散第 D 2 (6) t x 二定律是以浓度C为因变量,以距离x和时间t 为自变量得偏微分方程,方程的解由解析式 C=f(x,t) 给出.
材料科学基础—张代东—chap8 金属的固态扩散

一般仅为间隙扩散机制和空位扩散机制的补充
FMS
8.1.2 扩散的微观机制
间隙扩散机制 是否证实 实验证实 空位扩散机制 实验证实 纯金属 置换固溶体(溶 质原子较大) 间隙扩散和 空位扩散的 补充 换位机制 环形换位 直接换位 未得实验 证实 可能性不 大 协同跳动, 能垒太高
间隙固溶体(溶 适用对象 质原子较小) 条件 原子自由能>扩 散自由能
x C Cs (C s C0 )erf 2 Dt
若C为定值,渗入距离与时 间关系 x K Dt
C0 0
x C Cs 1 erf 2 Dt
FMS
半无限长物体的扩散
渗碳 C0=0.1%C(钢件原始浓度),CS =1%(钢件渗碳
空位激活能(空位形成能+跃迁能)比间隙扩散激活能大得
面心立方空位扩散
多
FMS
8.1.2 扩散的微观机制
„ 换位机制
分类 ‡
直接换位机制(2-换位) ‡
能垒太高(无实验证实)
环形换位机制 (n-换位)
能垒有所降低 ‡
扩散需要两个或两个以上的原子协同跳动,所
需能量较高,垂直于扩散方向平面的净通量等
旁边有空位 原子具有可以越 过能垒的自由焓
能垒较直接 换位有所降 低
图例
FMS
固态金属扩散的条件
前提条件 扩散原子与基体有固溶性 热力学条件 扩散要有驱动力
梯度——化学位、温度、应力、电场、磁场等
动力学条件
足够高温度
足够长时间
FMS
8.2 固态扩散定律
„ 扩散第一定律 扩散理论的基础 反映扩散物质量与浓度梯度间的关系J = -D(dc/dx)
金属学第四章固体中的扩散

3. 扩散分类
根据C/t是否随时间变化分类 稳态扩散和非稳态扩散
根据C/x分类 C/x=0 自扩散,在纯金属和均匀合金中进行 C/x0 互扩散,上坡扩散和下坡扩散
根据扩散途径分类 体扩散、晶界扩散、表面扩散、短程扩散(沿位错进行的扩散)
根据合金组织分类 单相扩散、多相扩散
6
4.1 扩散的宏观规律
不仅适用于扩散系统的任何位置,而且适合于扩散过程的 任一时刻。其中J、D、 C/x可以是常量(稳态扩散),也可 以是变量(非稳态扩散)。
9
Fick第一定律的应用 - 扩散系数的测定
方法:通过C原子在-Fe中的扩散来测定D 选择一纯Fe的空心圆筒,内部通过含碳性的气氛,外部
则为脱碳气氛。在一定温度下,经过一定的时间后,C原子从 Fe筒的内壁渗入,外壁渗出。
①x=0.05cm 浓度为0.45%所需要的时间t:
②在同一温度下两个不同距离x1和x2所对应的时间t1和t2为:
25
举例3:均匀化退火过程
设溶质沿x轴为正弦曲线分布。式中,C0- 平均浓度;Cmax-最大浓度
26
四、互扩散 (Kirkendall效应)
概念
在置换式固溶体中,由于两种原子以不同的速度相对扩 散而造成标记面漂移的现象被称之为Kirkendall效应。
11
二、Fick第二扩散定律
Fick第一定律只适用于浓度梯度C/x不随时 间变化的稳态扩散。
实际上在扩散过程中,扩散方向上各处的扩散 物质的浓度梯度是随时间而变化的,即为非稳态扩 散,因此必须在扩散方程中引入时间参数。
12
1. Fick第二定律公式的推导
一维扩散 流入体积元的物质量J1-流出体积元的物质量J2 =体积元中物质的积累量m
第八章 扩散(金属学与热处理)

菲克第一定律
扩散系数D是描述扩散速度的重要物理量。从式 中可以看出,它相当于浓度梯度为1时的扩散通量。 D值越大,则扩散越快。第一定律仅适用于稳定态扩 散,即在扩散过程中合金各处的浓度及浓度梯度都 不随时间改变的情况,实际上稳定态扩散的情况是 很少的,大部分属于非稳定态扩散,这就需要应用 菲克第二定律。
第二节 扩 散 定 律
一、菲克第一定律
将两根不同溶质浓 度的固溶体合金棒料对 焊起来,加热到高温, 则溶质原子将从浓度较 高的一端向浓度较低的 一端扩散,并沿长度方 向形成一浓度梯度,如 图8-10所示。
图8-10 扩散对溶质原子分布的影响
菲克第一定律
如若在扩散过程中各处的体积浓度C只随距离x 变化,不随时间t变化,那么,单位时间通过单位垂 直截面的扩散物质的量(扩散通量)J对于各处都相 等,即每一时刻从左边扩散来多少原子,就向右边 扩散走多少原子,没有盈亏,所以浓度不随时间变 化。这种扩散称为稳定态扩散。气体通过金属薄膜 且不与金属发生反应时就会发生稳定态扩散。
图8-13 钎焊示意图 a)钎料安置 b)钎缝 c)熔蚀缺陷
扩散应用举例
(二)金属的粘接 2.镀锌 钢板在镀锌时会发生 反应扩散,除了锌通过扩 散形成锌在铁中的固溶体 外,还会形成脆性的金属 化合物,如果控制不当, 则镀层便易于剥落。镀锌 的一般工艺过程是,在镀 锌之前,先将钢板表面清 洗干净,然后浸入450℃熔 融锌槽中若干分钟,就可 在钢板表面镀上一层锌。 图8-17
扩散现象和本质
图8-3 对称和倾斜的势能曲线
扩散现象和本质
图8-4 纯金属中的扩散过程
二、扩 散 机 制
(1)空位扩散机制 在自扩散和涉及置换原子的扩散过程中,原 子可离开其点阵位置,跳入邻近的空位,这样就 会在原来的点阵位置产生一个新的空位。当扩散 继续,就产生原子与空位两个相反的迁移流向, 称为空位扩散。自扩散和置换原子的扩散程度取 决于空位的数目。温度越高,空位浓度越大,金 属中原子的扩散越容易。
8 金属的固态扩散

7
= 1× 1019 原子 / m3
位置
X
(3) 正弦解
边界条件:C ( x = 0, t ) = C p dC λ (x = , t) = 0 dx 2 求解Fick第二定律 ∂C = ∂ ( D ∂C ) ∂t ∂x ∂x 2 解为 C ( x, t ) = C p + A0 sin( π x ) exp(− π Dt ) λ λ2 πx π 2 Dt 即 C ( x, t ) − C p = A0 sin( ) exp(− 2 ) λ λ
J1 A − J 2 A = −
∂C ∂J =− ∂t ∂x
∂J Adx ∂x
∂ (CAdx) ∂C = Adx ∂t ∂t J = −D dC dx
∂C ∂ ∂C = (D ) ∂t ∂x ∂x
∂C ∂C =D 2 ∂t ∂x
2
(1) 误差函数解
适用条件:无限长棒或半无限长棒的扩散 问题。
1) 无限长扩散偶的扩散
扩散对于材料的加工过程具有重要影响。
Furnace for heat treating steel using the carburization process
8.1.1 固态扩散的分类
(1) 根据扩散方向是否与浓度的方向相同进 行分类 1) 上坡扩散:原子由低浓度处向高浓度处进 行的扩散。(如液态合金的共晶转变、固 溶体的共析转变;固溶体中新相析出及新 相长大)
8.3.2 扩散激活能
(3) 空位扩散的激活能 D=D0exp[-(∆Ev+∆E)/kT] 空位扩散激活能包括原子迁移能和空位形 成能。 Q空位>Q间隙 lnD=lnD0-Q/kT,lnD与1/T呈直线关系。
8.3.3 柯肯达尔效应与扩散驱动力
金属学与热处理第八章扩散ppt课件.ppt

固态扩散是依靠原子热激活能进行的过程,必须在足 够高的温度才能进行。当温度低于某一温度时,原子被激 活的几率很低,扩散几乎不能进行即被“冻结”。C被冻 结的温度为100℃ ,Fe被冻结的温度为500℃。
(三)时间足够长。 扩散原子在晶体中每跃迁一次最多也只能移动0.3~
不同的金属或合金,其扩散机制是不同的。目前,被 大家所公认的扩散机制由如下几种:间隙扩散机制;换位 扩散机制;空位扩散机制等。
(一)间隙扩散 1)在间隙固溶体中,溶质原子由一个间隙位置跳到其
相邻的另一间隙位置,即为间隙扩散。
这种方式进行扩散的可能性很大,因为在间隙固溶体 中,溶质原子只占据少量间隙位置,即每个间隙原子周围 都有较多的间隙位置是空着的,故供其跃迁的位置很多。
在微小体积Adx内的物资积存速率为:
(CAdx) C Adx (2)
t
t
式(1)与式(2)相等,则可得
C Adx J Adx
t
x
即: C J (3)
t
x
将扩散第一定律代入(3)有:
C C
(D ) t x x
(4)
式(4)即为菲克第二定律,如果扩散系数 是 D与浓度无 关的常数,则式(4)可写为:
0.5nm的距离,经过相当长的时间才能造成物质的宏观定 向迁移。
由这一原理人们设计了固溶处理,如:铝合 金的固溶处理,不锈钢的固溶处理等。
此外,在热加工刚完成时迅速将金属材料冷却到室温, 抑制扩散过程,避免发生静态再结晶,可把动态回复或动 态再结晶的组织保留下来,以达到提高金属材料性能的目 的。
(四)扩散原子要有固溶。 扩散原子在基体金属中必须有一定的固溶度,能够溶入
C t
固态金属间的扩散课件

2019/11/4
Introduction to Material Science
第七章-15
一、扩散驱动力
Material Science
基本概念
Material
• 下坡扩散 ( 顺扩散): 从高浓度向低浓度扩散。 • 上坡扩散 (逆扩散):从低浓度向高浓度扩散。
产生原因
Material
•
产生上坡扩散的原因:扩散的真正驱动力时化学位梯度
Q , 原子越容易实现扩散。
2019/11/4
Introduction to Material Science
第七章-12
三、扩散系数(D)
Material Science
1. 微观物理量的表达式
• 设单位面积晶面I、II相距d,晶面上每个原子任意跳动到对面 的几率为P,原子跳动频率为 ,则
D Pd2
2019/11/4
Introduction to Material Science
第七章-9
一、扩散的微观机理
Material Science
1. 间隙微观机制
•
间隙固溶体中溶质原子的扩散一般采用间隙机制进行。
•
扩散原子由所在间隙位置跳跃至另一相邻的间隙中。
间隙扩散机制示意图
2019/11/4
Introduction to Material Science
实例
Material
• ①化学热处理,如渗碳、渗氮、渗金属等; • ②纯Fe的氧化
2019/11/4
Introduction to Material Science
第七章-17
讨论:
① : 与原子本性和温度有关。温度 , ,则 D ,扩散越容易;
关于影响金属材料固态扩散的因素与控制

关于影响金属材料固态扩散的因素与控制影响金属材料固态扩散的因素与控制摘要:由扩散第一定律可知,在浓度梯度一定时,原子扩散仅取决于扩散系数D。
对于典型的原子扩散过程,D符合Arrhenius公式,。
因此,D仅取决于D0、Q和T,凡是能改变这三个参数的因素都将影响扩散过程。
关键词:温度,因素,扩散,组元,系数一,温度由扩散系数表达式看出,温度越高,原子动能越大,扩散系数呈指数增加。
以C 在γ-Fe中扩散为例,已知D0=2.0×10-5m2/s,Q=140×103J/mol,计算出927℃和1027℃时C的扩散系数分别为1.76×10-11m2/s,5.15×10-11m2/s。
温度升高100℃,扩散系数增加三倍多。
这说明对于在高温下发生的与扩散有关的过程,温度是最重要的影响因素。
应该注意,有些材料在不同温度范围内的扩散机制可能不同,那么每种机制对应的D和Q不同,D便不同。
在这种情况下,~并不是一条直线,而是由若干条直线组成的折线。
例如,许多卤化物和氧化物等离子化合物的扩散系数在某一温度会发生突变,反映了在这一温度以上和以下受到两种不同的机制控制。
图3.15表示出Na+离子在NaCl晶体中扩散系数的实验值。
其中,高温区发生的是以点缺陷扩散为主的本征扩散,低温区发生的是以夹杂产生或控制的缺陷扩散为主的非本征扩散。
二,成分1,组元性质原子在晶体结构中跳动时必须要挣脱其周围原子对它的束缚才能实现跃迁,这就要部分地破坏原子结合键,因此扩散激活能Q和扩散系数D必然与表征原子结合键大小的宏观或者微观参量有关。
无论是在纯金属还是在合金中,原子结合键越弱,Q越小,D越大。
合金中的情况也一样。
考虑A、B组成的二元合金,若B组元的加入能使合金的熔点降低,则合金的互扩散系数增加;反之,若能使合金的熔点升高,则合金的互扩散系数减小,在微观参量上,凡是能使固溶体溶解度减小的因素,都会降低溶质原子的扩散激活能,扩散系数增大。
金属学与热处理第八章扩散

2.3 1011 m2 / s 2.11017 m2 / s
Ni D1200
1 106
间隙原子碳的扩散系数比置换 原子镍大的多
(CAdx ) C Adx t t
(2)
式(1)与式(2)相等,则可得
C J Adx Adx t x
即:
C J t x
(3)
将扩散第一定律代入(3)有:
C C (D ) t x x
(4)
式(4)即为菲克第二定律,如果扩散系数 是 D与浓度无 关的常数,则式(4)可写为:
和均匀固溶体中,例如晶粒长大,驱动力是表面能的降
低;
2)互扩散,伴随有浓度变化的扩散,与浓度梯度有关, 这类扩散又称为“化学扩散”或者“异扩散”。 (二)按扩散方向与浓度梯度的方向的关系分为: 1)下坡扩散:下坡扩散是沿着浓度降低的方向扩散, 如渗碳、均匀化退火; 2)上坡扩散:沿着浓度升高的方向进行的扩散,如珠
光体形成时,碳原子由浓度低的A向碳浓度高的Fe3C的扩
散。
又如图所示,Si提 高了C的化学位,使碳 向着无硅一侧扩散。
此外,弹性应力梯度如图所
示的电位梯度。此外,温度梯度
等作用下也可发生上坡扩散。
(三)按扩散过程是否出现新相分为: 1)原子扩散:在扩散过程中基体晶格始终不变,无
新相产生;
2)反应扩散:通过扩 散使固溶体的溶质组元浓 度超过固溶极限后形成新 相的扩散称为反应扩散,
第八章
扩散
§8-1概 述
一. 扩散的现象和本质
人们对气体和液体中的 扩散现象并不陌生,虽然扩 散现象在固态物质中不易察
觉,但确实存在的...
(一) 柯肯达尔效应
扩散前:Zn-Cu
固体金属中的扩散

其中一种方法可通过碳在γ-Fe中的扩散来测定纯 Fe的空心园筒,心部通渗碳气氛,外部为脱碳气氛, 在一定温度下经过一定时间后,碳原子从内壁渗入, 外壁渗出。
稳态扩散下的菲克第一定律的应用--扩散系数的测定:
碳原子从内壁渗入,外壁渗出达到平衡时,则为稳态扩散 单位面积中碳流量: J=q/(At)=q/(2πrLt) A:圆筒总面积,r及L:园筒半径及长度,q:通过圆筒的碳量 则 J=q/(At)=q/(2πrLt)=-D(dc/dx) =-D( dc/dr) 即-D= [q/(2πrLt)]×1/ ( dc/dr) = [q(dlnr)]/[( 2πLt ) dc] q可通过炉内脱碳气体的增碳求得,再通过剥层法测出不同 r处的碳含量,作出C-lnr曲线可求得D。 第一定律可用来处理扩散中浓度不因时间变化的问题,如 有些气体在金属中的扩散。
Fick第二定律的解无限大物体中扩散应用
Fick第二定律 的解无限 大物体中 扩散应用
如一根长的 纯铁一端 放在碳浓 度Co不变 的气氛中, 铁棒端部 碳原子达 到Co后, 同时向右 经铁棒中 扩散的情 形
试验结果与计算 结果符合很好
二、固溶体合金中的扩散
自扩固态金属中,溶剂原子偏离平衡位臵,发
c 2c 令 t ,代入 t D x 2 则 c dc dc x / 2 t d dt d 2t 3 2 2c d 2 c d 2c 1 D 2 D 2 D 2 x d x d t dc x d 2c 1 D 则菲克第二定律为 3/2 2 d 2t t d
i n 等温等压下i组元化学位 i n
G
j
G:系统自由能,nj为除i组元外j组元的摩尔数
代入ni ,则 i M C i ,对距离x取偏导,则
固体在金属中的扩散

第三章固体金属中的扩散物质的迁移可通过对流可扩散两种方式进行。
在气体和液体中物质的迁移一般是通过对流和扩散来实现的。
但在固体中不发生对流,扩散是唯一的物质迁移方式,其原子或分子由于热运动不断地从一个位置迁移到另一个位置。
扩散是固体材料中的一个重要现象,诸如金属铸件的凝固及均匀化退火,冷变形金属的回复和再结晶,陶瓷或粉末冶金的烧结,材料的固态相变,高温蠕变,以及各种表面处理等等,都与扩散密切相关。
要深入地了解和控制这些过程,就必须先掌握有关扩散的基本规律。
研究扩散一般有两种方法:①表象理论——根据所测量的参数描述物质传输的速率和数量等;②原子理论——扩散过程中原子时如何迁移的。
本章主要讨论固体材料中扩散的一般规律、扩散的影响因素和扩散机制等内容。
固体材料设计金属、陶瓷和高分子化合物三类;金属中的原子结合是以金属键方式;陶瓷中的原子结合主要是以离子键方式为主;而高分子化合物中的原子结合方式是共价键或氢键结合,并形成长链结构,这就导致了三种类型固体中原子或分子扩散的方式不同,描述它们各自运动方式的特征也是本章的主要目的之一。
3.1扩散定律及其应用3.1.1菲克第一定律当固体中存在着成分差异时,原子将从浓度高处向浓度低处扩散。
如何描述原子的迁移速率,阿道夫•菲克(Adolf Fick)对此进行了研究,并在1855年久得出:扩散中原子的通量与质量浓度梯度成正比,即该方程称为菲克第一定律或扩散第一定律。
其中,J为扩散通量,表示单位时间内通过垂直于扩散方向x的单位面积的扩散物质质量,其单位为kg∕(㎡·s);D为扩散系数,其单位为㎡∕s;而ρ是扩散物质的质量浓度,其单位为kg∕m³。
式中的负号表示物质的扩散方向与质量浓度梯度dρ∕dx方向相反,即表示物质从高的质量浓度区向低的质量浓度区方向迁移。
菲克第一定律描述了一种稳态扩散,即质量浓度不随时间而变化。
史密斯(R.P.Smith)在1953年发表了运用菲克第一定律测定碳在у-Fe中的扩散系数的论文,他将一个半径为r,长度为l的纯铁空心圆筒置于1000℃高温中渗碳,即筒内和筒外分别渗碳和脱碳气氛,经过一定时间后,筒壁内各点的浓度不再随时间面变化,满足稳态扩散的条件,此时,单位时间内通过管壁的碳量q∕t为常数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3) 正弦解
适用于铸造合金中晶内 偏析的均匀化退火问题。 溶质原子沿距离x方向 的分布,用正弦方程表 示: πx Cx = C p + A0 sin λ 振幅 A = C −C
0 max p
A 2λ
B
(a)
溶质浓度(℃)
Cmax Cp Cmin
0
C=
9.43 ×1019
π × 4 ×10 × 7 × 10
8.2.2 扩散第二定律(Fick’s second law) Fick第二定律描述非稳态扩散(nonsteady state diffusion)。在扩散过程中各 处的浓度都随时间变化而变化,因而通过 各处的扩散流量不再相等而随距离和时间 发生变化。
4
8.2.2 扩散第二定律
J 2 = J1 + ∂J ∂x
−7
7
= 1× 1019 原子 / m3
位置
X
(3) 正弦解
边界条件:C ( x = 0, t ) = C p dC λ (x = , t) = 0 dx 2 求解Fick第二定律 ∂C = ∂ ( D ∂C ) ∂t ∂x ∂x 2 解为 C ( x, t ) = C p + A0 sin( π x ) exp(− π Dt ) λ λ2 πx π 2 Dt 即 C ( x, t ) − C p = A0 sin( ) exp(− 2 ) λ λ
当x =
铸锭(件)的均匀化退火
λ
2时Leabharlann sin(πx λ π 2 Dt ) = 1 ∴ C ( , t ) − C p = A0 exp(− 2 ) λ 2 λ
∵ A0 = Cmax − C p
λ π 2 Dt C ( 2 , t ) − C p ∴ exp(− 2 ) = λ Cmax − C p
本章主要内容
第8章 金属的固态扩散
扩散机制、扩散分类以及固态金属扩散的 条件 扩散第一定律、扩散第二定律的表达式及 意义 影响扩散的因素
8.1 扩散概述
8.1 扩散概述
气体、液体——对流、扩散(具有很大扩 散速率和完全各向同性) 固体——扩散——唯一机制(具有低扩散 速率和各向异性) 扩散:由于热运动而导致原子(或分子)在 介质中迁移的现象。 材料工程中:烧结、渗碳、均匀化、析出、 相变、腐蚀…
8.3.4 影响扩散的因素
(3) 晶体结构 1) 固溶体类型 间隙固溶体间隙原子的扩散激活能比置换 固溶体中置换原子的扩散激活能小得多, 扩散速度也快得多。 钢件表面热处理在获得同样渗层浓度时, 渗C,N比渗Cr或Al等金属的周期短。
9
8.3.4 影响扩散的因素
(3) 晶体结构 2) 晶体结构类型 在温度及成分一定的条件下任一原子在密 堆点阵中的扩散要比在非密堆点阵中的扩 散慢。 3) 晶体的各向异性 因晶体中晶面间距的不同,不同方向上原 子的扩散系数也有所不同。
8.3.2 扩散激活能
(1) 原子的激活概率 间隙原子总数为N;G≥G1的原子总数为 n1;G≥G2的原子总数为n2。
n1 −G = exp( 1 ) N kT n2 −G2 = exp( ) N kT
n2 −ΔG = exp( ) n1 kT
−ΔG n2 = exp( ) N kT
G1为平衡态能量,n1(G≥G1)≈N 满足能量条件的原子分数:
8
8.3.3 柯肯达尔效应与扩散驱动力
(2) 扩散的驱动力 对于多元体系,设n为组元i的原子数,则 在等温等压条件下,组元i原子的自由能 可用化学位表示:μi=∂G/∂ni 扩散的驱动力为化学位梯度,即: F=-∂μi /∂x 负号表示扩散驱动力指向化学位降低的方 向。 (1) 温度
8.3.4 影响扩散的因素
c=
c1 + c2 c1 − c2 + erf ( β ) 2 2
5
2) 半无限长物体的扩散
这种情况相当于无限大情况下半边的扩散 情况。 初始条件:t=0时,x≥0,C=0; 边界条件:t>0时,x=0,C=C0,x=∞, C=0。
(2) 高斯函数解
适用条件:扩散过程中扩散元素质量保持 不变,其值为M;扩散开始时扩散元素集 中在表面,好像一层薄膜。 衰减薄膜源—表面沉积过程。 初始条件:t=0,C=0 边界条件:x=∞,C=0
1
(1) 根据扩散方向是否与浓度的方向相同 进行分类
其它引起上坡扩散的因素:
弹性应力的作用:大直径原子跑向点阵的受 拉部分,小直径原子跑向点阵的受压部分。 晶界的内吸附:某些原子易富集在晶界上。 电场作用:大电场作用可使原子按一定方向 扩散。
8.1.1 固态扩散的分类
(2) 根据扩散过程是否发生浓度变化分类 1) 自扩散:原子经由自身元素的晶体点阵而 迁移的扩散。(无浓度变化,如纯金属和 均匀固溶体的晶粒长大) 2) 互扩散:原子通过进入对方元素晶体点阵 而导致的扩散。(有浓度变化,如化学热 处理、材料成分均匀化)
相对于原子扩散区长度而言,只要扩散物质 长度比扩散区长得多,可认为物体是无限的。 条件 1) 两根无限长A、B合金,截面浓度均匀,浓度 C2>C1; 2) 两合金棒对焊,扩散方向为x方向; 3) 合金棒无限长,棒的两端浓度不受扩散影响。
1) 无限长扩散偶的扩散
初始条件:t=0时,C=C1,(x>0), C=C2,(x<0); 边界条件:t≥0时,C=C1,(x=∞), C=C2,(x=-∞)。 采用变量代换法求解,结果如下:
7
8.3.2 扩散激活能
(2) 间隙扩散的激活能 跳动频率:Γ=vZn2/N=vZexp(-∆G/kT); v为振动频率,Z为最近邻间隙数。 D=PΓd2;D=d2vPZexp(-∆G/kT) D=[d2vPZexp(∆S/k)]exp(-∆H/kT) D=D0exp(-∆E/kT) D0为扩散常数,∆E扩散激活能,常用Q 表示。
Cs − C x x ) = erf ( Cs − C0 2 Dt
∫
∞
0
Adx = M
C=
⎛ x2 ⎞ M exp ⎜ − ⎟ πDt ⎝ 4Dt ⎠
(2) 高斯函数解
例:半导体Si中B的掺杂。 测得1100℃硼在硅中的扩散系数D为 4×10-7m2/s,硼薄膜质量M=9.43×1019 原子,由高斯解求扩散7×107s后,表面 (x=0)硼浓度为:
固态金属扩散的条件
1、扩散要有驱动力——热力学条件 梯度:化学位、温度、应力、电场、磁场 等 2、扩散原子与基体有固溶性——前提条件 3、足够高温度——动力学条件 4、足够长时间——宏观迁移的动力学条件
3
8.2 固态扩散定律
8.2.1 扩散第一定律(Fick’s first law) Fick第一定律描述在稳态条件下的扩散 (steady state diffusion),即各处浓度不随 时间变化,只随距离变化而变化。
8.2.3 扩散第二定律的解及其应用
第一定律—求解一阶微分方程 第二定律—设置中间变量求通解 误差函数解(error function solution)—无限长棒、半无限长棒 高斯函数解(Gauss solution) 正弦解(sinusoidal solution) 解微分方程初始条件,边界条件求方程式。
J1 A − J 2 A = −
∂C ∂J =− ∂t ∂x
∂J Adx ∂x
∂ (CAdx) ∂C = Adx ∂t ∂t J = −D dC dx
∂C ∂ ∂C = (D ) ∂t ∂x ∂x
∂C ∂C =D 2 ∂t ∂x
2
(1) 误差函数解
适用条件:无限长棒或半无限长棒的扩散 问题。
1) 无限长扩散偶的扩散
2
(2) 间隙扩散机制
间隙固溶体中间隙原子的扩散机制。 间隙固溶体中,小尺寸的溶质原子(如C、 N、H、B、O)可由一个间隙位置跳到另 一个间隙位置。 扩散激活能:原子跃迁时所需克服周围原 子对其束缚的势垒。
(3) 空位扩散机制——主要机制
纯金属的自扩散和置换固溶体中原子的扩 散机制。 方式:原子迁移到邻近的空位,即原子与 空位交换位置实现扩散。 条件:扩散原子近旁存在空位;邻近空位 的原子具有可以越过能垒的自由焓。
8.2.1 扩散第一定律
内容:在单位时间内通过垂直扩散方向的 单位截面积上的扩散物质通量(diffusion fluxes)与该截面处的浓度梯度成正比. 表达式:J=-D(dc/dx)(D为扩散系数; dc/dx为体积浓度梯度,负号表示物质的 扩散方向与浓度梯度的方向相反。) 扩散系数D:描述扩散速度的物理量。D 越大,则扩散越快。
设铸锭经均匀化退火后,成分偏析的振幅 降低到原来的1%,此时 λ C( , t) − Cp 1 2 = Cmax − C p 100
A0
(b)
6
铸锭(件)的均匀化退火
则
exp(− exp(
8.3 扩散系数及影响扩散的因素
8.3.1 原子跳动和扩散系数 从1晶面跳到2晶面的溶质原子数为 N1=n1PΓ∆t。其中n1为溶质原子总数;P为成 功跳动几率;Γ为跳动频率;∆t为时间间隔。 从2晶面跳到1晶面的溶质原子数为 N2=n2PΓ∆t。 2晶面的净增溶质原子数为J∆t=(n1-n2)PΓ∆t 则,J=(n1-n2)PΓ(J的单位为原子个数/(m2s)) 原子浓度:C1=n1/d,C2=n2/d=C1+d∂C/∂x
π 2 Dt 1 )= λ2 100
2
π Dt ) = 100 λ2
取对数,可算出要使枝晶中心成分偏析的 振幅降低到1%所需的退火时间t为:
t = 0.467
λ
2
D
8.3.1 原子跳动和扩散系数
即,n1-n2=-d2∂C/∂x 则 J=-d2PΓ∂C/∂x D=d2PΓ 表明扩散系数与原子的跃迁频率Г成正比。 Γ是温度的强函数,所以D必是强烈依赖于 温度的。P与扩散机制和点阵类型有关,对 于立方结构晶体P=1/6;d为晶面间距,取决 于固溶体的结构,不同晶向上的扩散系数不 同。
