圆切割线定理与相交弦定理练习题

合集下载

2021年中考数学必考点培优系列 18 圆与相似：相交线定理、切割线定理(有答案)

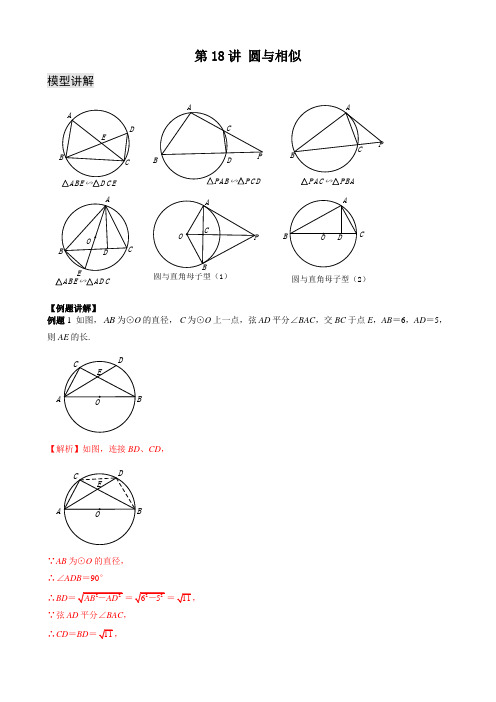
第18讲圆与相似模型讲解圆与直角母子型（1）圆与直角母子型（2）ABE ∽AD CPAC ∽PBAPAB ∽PC DABE ∽D C EBCDPABCAB CEPDC BA【例题讲解】例题1 如图，AB 为⊙O 的直径， C 为⊙O上一点，弦AD 平分∠BAC ，交BC 于点E ，AB ＝6，AD ＝5，则AE 的长.A【解析】如图，连接BD 、CD ，A∵AB 为⊙O 的直径， ∴∠ADB＝90°∴BD＝ ∵弦AD 平分∠BAC ， ∴CD ＝BD∴∠CBD ＝∠DAB ，在△ABD 和△BED 中， BAD EBD ADB BDE⎧⎨⎩∠＝∠∠＝∠∴△ABD ∽△BED ， ∴DE DB ＝DBAD解得DE ＝115． ∴AE ＝AD －DE ＝5－115＝145. 例题2 如图，在△ABC 中，以AC 边为直径的⊙O 交BC 于点D ，过点B 作BG ⊥AC 交⊙O 于点E 、H ，连AD 、ED 、EC ．若BD ＝8，DC ＝6，求CE 的长．B【解析】∵AC 为⊙O 的直径， ∴∠ADC ＝90°， ∵BG ⊥AC ，∴∠BGC ＝∠ADC ＝90°， ∵∠BCD ＝∠ACD , ∴△ADC ∽△BGC ， ∴DC CG＝ACBC ， ∴CG ·AC ＝DC ·BC ＝6×14＝84，连接AE ，∵AC 为⊙O 的直径， ∴∠AEC ＝90°， ∴∠AEC ＝∠EGC ＝90°， ∵∠ACE ＝∠ECG ， ∴△CEG ∽△CAE ， ∴CG CE ＝CE AC，∴CE＝．B【巩固练习】1.如图，已知D D为等腰三角形ABC的底边BC上的任意一点，AD的延长线交△ABC的外接圆于点E，连接BE、CE，则图中相似三角形共有()A．8对B．6对C．4对D．2对2．如图，AB为⊙O的直径，C是⊙O上一点，连接AC，过点C作直线CD⊥AB交AB于点D，E是OB上一点，直线CE与⊙O交于点F，连接AF交直线CD于点G．若AC＝AG·AF＝.BA3、如图，已知半圆的直径AB＝10，点C在半圆上，CB＝6，O为AB的中点，OD⊥AB交AC于点D，则OD＝.4.如图，⊙O是△ABC的外接圆，BC是⊙O的直径，D是劣弧AC的中点，BD交AC于点E，若BC＝52，CD，则DE ＝．B5、如图，已知△ABC 内接于⊙0，且AB ＝AC ，直径AD 交BC 于点E ，F 是OE 的中点，如果BD ∥CF ，BC ＝，则CD ＝ .BDA（第5题）（第6题）（第7题）6、如图，已知⊙0的半径为4，AB ＝6，锐角△ABC 内接于⊙0，BD ⊥AC 于点D ，OE ⊥AB于点M ，则sin ∠CBD 的值等于 .7、如图，AD 是圆内接△ABC 的高，AE 是OO 的直径，AB ，AC AE ·AD ＝ .8、如图，△ABC 是⊙0的内接三角形，AB ＝AC ，BD 平分∠ABC 交⊙0于点D ，连接AD 、C D .作AE ⊥BD 于点E ，若AE ＝3，DE ＝1，则△ACD 的面积是 .A9、如图：M 、N 分别为直角坐标系x 、y 正半轴上两点，过M 、N 和原点0三点的圆和直线y ＝x 交于点P ，（1）试判断△PMN 的形状；（2）连接MN ，设直线y ＝x 交MN 于点G ，若PG :PN ＝3：4，△PGN 的周长为6，求△PON 的周长.10、如图，PB 为⊙O 0的切线，B 为切点，直线PO 交⊙O 于点E ，F ，过点B 作PO 的垂线BA ，垂足为点D ，交⊙O 于点A ，延长AO 与⊙O 交于点C ，连接BC 、AF 。

相交弦.切割线练习题汇编

相交弦、切割线定理练习题一、填空：1.圆内两弦相交，一弦长8cm 且被交点平分，另一弦被交点分为1：4，则另一弦长为（）3.如图:已知同心圆⊙O,AB 是大圆的直径,交小圆于C,D,EC⊥AB 交大圆于E,连接ED 交小圆4.自圆外一点所作过圆心的割线长是12cm ，圆的半径为4cm ，则过此点所引的切线长为（）5.如图1，⊙O 的半径为6，PQ ＝6，AR ＝8则QR 的长为（）6.如图2，CD 为⊙O 直径，弦AB 垂直CD 于P,AP ＝4， PD ＝2，则PO ＝___.7.⊙O 中直径CD ⊥弦AB 于E ，AB ＝6，DE ∶CE ＝1∶3，则DE 的长为（）8.由圆外一点作圆的切线长为6，过这点作过圆心的割线长为12，则此圆半径长为（）9．如图，PAB 为⊙O 的割线，PO 交⊙O 于C ，OP ＝13，PA ＝9， AB ＝7，求⊙O 直径的长.10．如图2，△ABC 中∠A ＝90°，AC ＝3，AB ＝4，半圆圆心在BC 上，与AB,AC 切于D,E ，则⊙O 半径为（）11．⊙O 中直径CD 垂直弦AB 于E ，AB ＝8，DE ∶CE ＝3∶1，则DE 的长为（） 11、（2002•南京）如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足是G ，F 是CG 的中点，延长AF 交⊙O 于E ，CF=2，AF=3，则EF 的长是 _________ ．1、如图：⊙O 1和⊙O2相交于A 、B 两点， P 是AB 上任一点过P 点分别作直线C D 和E F ，分别交⊙O1于C 、D ，交⊙O2于E 、F ，求证：PC·PD=PE·PFRQA OP 1ABO CDP2r ABCOPÍ¼22.如图，圆o1和圆o2相交于A 和 B 两点，点P 在BA 的延长线上。

过点P 作圆O1的割线PMN 交圆O1于M .N ，作圆O2的切线PC 切圆O2于C 。

切线长定理、弦切角定理、切割线定理、相交弦定理

切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段［学习目标］1.切线长概念切线长是在经过圆外一点的圆的切线上，这点和切点之间的线段的长度，“切线长”是切线上一条线段的长，具有数量的特征，而“切线”是一条直线，它不可以度量长度。

（PA长）2.切线长定理对于切线长定理，应明确（1）若已知圆的两条切线相交，则切线长相等；（2）若已知两条切线平行，则圆上两个切点的连线为直径；（3）经过圆外一点引圆的两条切线，连结两个切点可得到一个等腰三角形；（4）经过圆外一点引圆的两条切线，切线的夹角与过切点的两个半径的夹角互补；（5）圆外一点与圆心的连线，平分过这点向圆引的两条切线所夹的角。

3.弦切角：顶点在圆上，一边和圆相交，另一边和圆相切的角。

直线AB切⊙O于P，PC、PD为弦，图中几个弦切角呢？（四个）4.弦切角定理：弦切角等于其所夹的弧所对的圆周角。

5.弄清和圆有关的角：圆周角，圆心角，弦切角，圆内角，圆外角。

6.遇到圆的切线，可联想“角”弦切角，“线”切线的性质定理及切线长定理。

7.与圆有关的比例线段定理图形已知结论证法相交弦定理⊙O中，AB、CD为弦，交于P.PA·PB＝PC·PD. 连结AC、BD，证：△APC∽△DPB.相交弦定理的推论⊙O中，AB为直径，CD⊥AB于P.PC2＝PA·PB.（特殊情况）用相交弦定理.切割线定理⊙O中，PT切⊙O于T，割线PB交⊙O于APT2＝PA·PB连结TA、TB，证：△PTB∽△PAT切割线定理推论PB、PD为⊙O的两条割线，交⊙O于A、CPA·PB＝PC·PD过P作PT切⊙O于T，用两次切割线定理（记忆的方法方法）圆幂定理⊙O中，割线PB交⊙O于A，CD为弦P'C·P'D＝r2－OP'2PA·PB＝OP2－r2r为⊙O的半径延长P'O交⊙O于M，延长OP'交⊙O于N，用相交弦定理证；过P作切线用切割线定理勾股定理证8.圆幂定理：过一定点P向⊙O作任一直线，交⊙O于两点，则自定点P到两交点的两条线段之积为常数||（R为圆半径），因为叫做点对于⊙O的幂，所以将上述定理统称为圆幂定理。

切线长定理、弦切角定理、切割线定理、相交弦定理93336

切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段［学习目标］ 1.切线长概念切线长是在经过圆外一点的圆的切线上，这点和切点之间的线段的长度，“切线长”是切线上一条线段的长，具有数量的特征，而“切线”是一条直线，它不可以度量长度。

2.切线长定理对于切线长定理，应明确（1）若已知圆的两条切线相交，则切线长相等；（2）若已知两条切线平行，则圆上两个切点的连线为直径；（3）经过圆外一点引圆的两条切线，连结两个切点可得到一个等腰三角形；（4）经过圆外一点引圆的两条切线，切线的夹角与过切点的两个半径的夹角互补；（5）圆外一点与圆心的连线，平分过这点向圆引的两条切线所夹的角。

3.弦切角：顶点在圆上，一边和圆相交，另一边和圆相切的角。

直线AB 切⊙O 于P ，PC 、PD 为弦，图中几个弦切角呢？（四个） 4.弦切角定理：弦切角等于其所夹的弧所对的圆周角。

5.弄清和圆有关的角：圆周角，圆心角，弦切角，圆内角，圆外角。

6.遇到圆的切线，可联想“角”弦切角，“线”切线的性质定理及切线长定理。

7.与圆有关的比例线段定理图形已知结论证法相交弦定理⊙O 中，AB 、CD 为弦，交于P. PA ·PB ＝PC ·PD. 连结AC 、BD ，证：△APC ∽△DPB.相交弦定理的推论⊙O 中，AB 为直径，CD ⊥AB 于P.PC 2＝PA ·PB. 用相交弦定理.切割线定理⊙O 中，PT 切⊙O 于T ，割线PB 交⊙O 于APT 2＝PA ·PB 连结TA 、TB ，证：△PTB ∽△PAT切割线定理推论PB 、PD 为⊙O 的两条割线，交⊙O 于A 、CPA ·PB ＝PC ·PD 过P 作PT 切⊙O 于T ，用两次切割线定理圆幂定理⊙O 中，割线PB 交⊙O 于A ，CD 为弦 P'C ·P'D ＝r 2－OP'2PA ·PB ＝OP 2－r 2r 为⊙O 的半径延长P'O 交⊙O 于M ，延长OP'交⊙O 于N ，用相交弦定理证；过P 作切线用切割线定理勾股定理证8.圆幂定理：过一定点P 向⊙O 作任一直线，交⊙O 于两点，则自定点P 到两交点的两条线段之积为常数||（R 为圆半径），因为叫做点对于⊙O 的幂，所以将上述定理统称为圆幂定理。

相交弦定理、切割线定理、割线定理综合训练(最新整理)

6．如图， ⊙ O的直径AB与弦CD相交于点E，若AE = 7，BE = 1，cos∠AED = 23，则CD = ________．
7．如图，PA切 ⊙ O于A，PBC是 ⊙ O的割线，如果PB = 2，PC = 4，则PA的长为________．
试卷第 1 页，总 3 页
8．如图，PAB、PCD是 ⊙ O的割线，PA = 3，PB = 6，PC = 2，则PD = ________． 9．如图，PT是 ⊙ O的切线，T为切点，PAB是 ⊙ O的割线，PA = 5cm，AB = 4cm，则 PT = ________cm．
三、解答题 10．如图，在半径为5cm的 ⊙ O中，直径AB与弦CD相交于点P，∠CAB = 50 ∘ ，∠APD = 80 ∘ ． (1)求∠ABD的大小； (2)求弦BD的长．
11．如图，⊙O 直径 AB 和弦 CD 相交于点 E，AE=4，EB=8，∠DEB=30°，求弦 CD 长．
12．如图，弦 AB 和弦 CD 相交于⊙O 内一点 E，AD=CB，求证：AB=CD．
相交弦定理、切割线定理、割线定理
一、单选题 1．如图，PA与 ⊙ O切于点A，PBC是 ⊙ O的割线，如果PB = BC = 2，那么PA 的长为（）
A．2 B．2 2 C．4 D．8
2．P是 ⊙ O外一点，PA切 ⊙ O于A，割线PBC交 ⊙ O于点B、C，若PB = BC = 3，则PA的长
是（
）
A．9 B．3 C．3 2 D．18
二、填空题
3．如图，半圆
O
的直径
AB=7，两弦
AC、BD
相交于点
E，弦
CD=7，且
2
BD=5，
则 DE=_____．

切割线定理习题

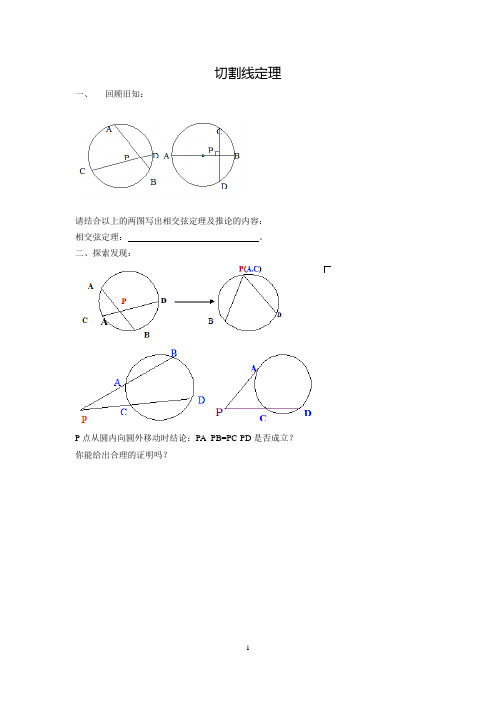
切割线定理一、回顾旧知：请结合以上的两图写出相交弦定理及推论的内容：相交弦定理：。

二、探索发现：AP点从圆内向圆外移动时结论：PA ·PB=PC·PD是否成立？你能给出合理的证明吗？三、练习：（1）已知PAB 、PCD 是圆O 的割线，PA=5 ， AB=3 ，CD=3，则PC ＝（2）已知PT 是圆O 的切线，PA=4， PT=6 ，则圆O 的面积＝（3）已知：圆1O 、2O 圆相交于A 、B ， P 是BA 延长线上的一点，PCD 是圆1O 的割线，PEF 是圆2O 的割线，求证：PC •PD=PE• PF巩固加深一、选择题（共15小题）1．如图，PAB为割线且PA=AB，PO交⊙O于C，若OC=3，OP=5，则AB的长为（）A. B. C. D.第1题第2题第3题2．如图，⊙O的割线PAB交⊙O于点A，B，PA=14cm，AB=10cm，PO=20cm，则⊙O的半径是（）A. 8cmB. 10cmC. 12cmD. 14cm3．如图，已知⊙O的弦AB、CD相交于点P，PA=4cm，PB=3cm，PC=6cm，EA切⊙O于点A，AE与CD的延长线交于点E，若AE=cm，则PE的长为（）A. 4cmB. 3cmC. 5cmD.cm4．如图，⊙O1与⊙O2相交于A、B两点，PQ切⊙O1于点P，交⊙O2于点Q、M，交AB 的延长线于点N．若MN=1，MQ=3，则NP等于（）A. 1B.C. 2D.3第4题第5题第7题5．如图，PAB、PCD是⊙O的两条割线，PA=3，AB=5，PC=4，则CD等于（）A.6B. 3C.D.6．已知PA是⊙O的切线，A为切点，PBC是过点O的割线，PA=10cm，PB=5cm，则⊙O 的半径长为（）A. 15cmB. 10cmC. 7.5cmD. 5cm 7．（2004•锦州）如图，⊙O和⊙O′都经过点A和点B，点P在BA的延长线上，过P作⊙O 的割线PCD交⊙O于C、D，作⊙O′的切线PE切⊙O′于E，若PC=4，CD=5，则PE等于（）A. 6B. 2C. 20D.368．如图⊙O的两条弦AB、CD相交于点E，AC与DB的延长线交于点P，下列结论中成立的是（）A. CE•CD=BE•BAB. CE•AE=BE•DEC. PC•CA=PB•BDD. PC•PA=PB•PD第8题第10题第11题9．已知AB为⊙O的直径，C为AB的延长线上一点，过C的直线与相切于点D，若BC=2，CD=4，则⊙O的半径长是（）A.3B.6C.8D. 无法计算10．如图，已知⊙O1、⊙O2相交于A、B两点，且点O1在⊙O2上，过A作⊙O1的切线AC交BO1的延长线于点P，交⊙O2于点C，BP交⊙O1于点D，若PD=1，PA=，则AC 的长为（）A. B. C. D.11．如图，PT是外切两圆的公切线，T为切点，PAB，PCD分别为这两圆的割线．若PA=3，PB=6，PC=2，则PD等于（）A.12B.9C. 8D.412．如图，在Rt△ABC中，AC=5，BC=12，⊙O分别与边AB，AC相切，切点分别为E，C，则⊙O的半径是（）A. B. C. D.第12题第13题第14题13．如图，已知PAC为⊙O的割线，连接PO交⊙O于B，PB=2，OP=7，PA=AC，则PA 的长为（）A. B. 2 C. D. 314．如图，PA，PB为⊙O的切线，A，B分别为切点，∠APB=60°，点P到圆心O的距离OP=2，则⊙O的半径为（）A. B.1 C. D.215．（2007•双柏县）如图，已知PA是⊙O的切线，A为切点，PC与⊙O相交于B、C两点，PB=2cm，BC=8cm，则PA的长等于（）A. 4cmB. 16cmC. 20cmD. 2cm二、填空题（共15小题）（除非特别说明，请填准确值）16．（2003•泸州）如图，⊙O1与⊙O2相交于C、D两点，⊙O1的割线PAB与DC的延长线交于点P，PN与⊙O2相切于点N，若PB=10，AB=6，则PN=_________．第16题第17题第18题17．如图，PA切⊙O于点A，割线PBC交⊙O于点B、C，若PA=6，PB=4，弧AB的度数为60°，则BC=_________，∠PCA=_________度，∠PAB=_________度．18．如图，ABCD是边长为2 a的正方形，AB为半圆O的直径，CE切⊙O于E，与BA的延长线交于F，EF的长_________．19．如图，已知⊙O的割线PAB交⊙O于点A和B，PA=6cm，AB=8cm，PO交⊙O于点C，且PO=10cm，则⊙O的半径为_________cm．第19题第20题第21题20．如图，PA、PB与⊙O分别相切于点A、点B，AC是⊙O的直径，PC交⊙O于点D，已知∠APB=60°，AC=2，那么CD的长为_________．21．如图，在△ABC中，∠C=90度．以BC为直径作⊙O与斜边AB交于点D，且AD=3.2cm，BD=1.8cm，则AC=_________cm．22．如图，PT是半径为4的⊙O的一条切线，切点为T，PBA是经过圆心的一条割线，若B是OP的中点，则PT的长是_________．第22题第23题第24题23．如图，已知⊙O的弦AB、CD相交于点P，PA=4，PB=3，PC=6，EA切⊙O于点A，AE与CD的延长线交于点E，AE=2，那么PE的长_________．24．如图，⊙O的割线PAB交⊙O于点A、B，PA=7cm，AB=5cm，PO=10cm，则⊙O的半径为_________．25．如图，已知两圆相交于CD两点，AB为两圆的外公切线，A、B为切点，CD的延长线交AB于M，若MD=3，CD=9，则AB的长等于_________．第25题第26题第27题26．如图，PT是⊙O的切线，切点是T，M是⊙O内一点，PM及PM的延长线交⊙O于B，C，BM=BP=2，PT=，OM=3，那么⊙O的半径为_________．27．如图，已知AB是⊙O的直径，BC是和⊙O相切于点B的切线，⊙O的弦AD平行于OC，若OA=2，且AD+OC=6，则CD=_________．28．如图，已知PA为⊙O的切线，PBC为⊙O的割线，PA=，PB=BC，⊙O的半径OC=5，那么弦BC的弦心距OM=_________．第28题第29题第30题29．如图，已知Rt△ABC的两条直角边AC，BC的长分别为3，4，以AC为直径作圆与斜边AB交于点D，则AD=_________．30．如图，PT切⊙O于点T，直径BA的延长线交PT于点P，若PT=4，PA=2，则⊙O的半径长是_________．31．如图，AB是⊙O的直径，CB、CE分别切⊙O于点B、D，CE与BA的延长线交于点E，连接OC、OD．（1）△OBC与△ODC是否全等？_________（填“是”或“否”）；（2）已知DE=a，AE=b，BC=c，请你思考后，选用以上适当的数，设计出计算⊙O半径r 的一种方案：①你选用的已知数是_________；②写出求解过程．（结果用字母表示）【单点训练】切割线定理参考答案与试题解析一、选择题（共15小题）1．（2004•呼和浩特）如图，PAB为割线且PA=AB，PO交⊙O于C，若OC=3，OP=5，则AB的长为（）A．B．C．D．考点：切割线定理．专题：计算题．分析：延长PO到E，延长线与圆O交于点E，连接EB，AC，由半径OC的长，得到半径OE的长，再由OE+OP得出EP的长，OP﹣OC得出CP的长，由PA=AB，设出PA=AB=x，则BP=2x，根据四边形ACEB为圆O的内接四边形，利用圆内接四边形的外角等于它的内对角得到一对角相等，再由公共角相等，利用两对对应角相等的两三角形相似，可得出三角形ACP与三角形EBP相似，由相似得比例，将各自的长代入列出关于x 的方程，求出方程的解得到x的值，即为AB的长．解答：解：延长PO到E，延长线与圆O交于点E，连接EB，AC，∵OC=3，OP=5，∴OE=OC=3，∴EP=OE+OP=3+5=8，CP=OP﹣OC=5﹣3=2，设PA=AB=x，则BP=2x，∵四边形ACEB为圆O的内接四边形，∴∠ACP=∠E，又∠P=∠P，∴△ACP∽△EBP，∴=，即=，解得：x=2或x=﹣2（舍去），则AB=2．故选B点评：此题考查了圆内接四边形的性质，相似三角形的判定与性质，利用了转化及方程的思想，其中作出如图所示的辅助线是解本题的关键．2．（2006•泰安）如图，⊙O的割线PAB交⊙O于点A，B，PA=14cm，AB=10cm，PO=20cm，则⊙O的半径是（）A．8cm B．10cm C．12cm D．14cm考点：切割线定理．分析：根据切割线定理代入公式即可求解．解答：解：设圆O的半径是x，则PA•PB=（PO﹣r）（PO+r），∴14×（14+10）=（20﹣x）（20+x），解得x=8．故选A．点评：本题的关键是利用割线定理求线段的长．3．（2004•镇江）如图，已知⊙O的弦AB、CD相交于点P，PA=4cm，PB=3cm，PC=6cm，EA切⊙O于点A，AE与CD的延长线交于点E，若AE=cm，则PE的长为（）A．4cm B．3cm C．5cm D．cm考点：切割线定理；相交弦定理．分析：首先根据相交弦定理得PA•PB=PC•PD，得PD=2．设DE=x，再根据切割线定理得AE2=ED•EC，即x（x+8）=20，x=2或x=﹣10（负值舍去），则PE=2+2=4．解答：解：∵PA•PB=PC•PD，PA=4cm，PB=3cm，PC=6cm，∴PD=2；设DE=x，∵AE2=ED•EC，∴x（x+8）=20，∴x=2或x=﹣10（负值舍去），∴PE=2+2=4．故选A．点评：此题综合运用了相交弦定理和切割线定理．4．（2004•淮安）如图，⊙O1与⊙O2相交于A、B两点，PQ切⊙O1于点P，交⊙O2于点Q、M，交AB的延长线于点N．若MN=1，MQ=3，则NP等于（）A．1B．C．2D．3考点：切割线定理；切线长定理．分析：根据切线长定理得PN2=NB•NA，根据割线定理得NB•NA=NM•NQ，所以PN2=NM•NQ即可求得PN的长．解答：解：∵PN2=NB•NA，NB•NA=NM•NQ，∴PN2=NM•NQ=4，∴PN=2．故选C．点评：此题能够有机地把切割线定理和割线定理相结合，把要求的线段和已知的线段联系到一起．5．（2004•三明）如图，PAB、PCD是⊙O的两条割线，PA=3，AB=5，PC=4，则CD等于（）A．6B．2C．D．考点：切割线定理．分析：首先求得PB的长，再根据割线定理得PC•PD=PA•PB即可求得PD及CD的长．解答：解：∵PA=3，AB=5，PC=4，∴PB=8，∵PC•PD=PA•PB，∴PD=6，∴CD=6﹣4=2．故选B．点评：此题主要是运用了割线定理．6．（2005•荆门）已知PA是⊙O的切线，A为切点，PBC是过点O的割线，PA=10cm，PB=5cm，则⊙O的半径长为（）A．15cm B．10cm C．7.5cm D．5cm考点：切割线定理．分析：根据切割线定理分析解答．解答：解：根据切割线定理的PA2=PO•PC，所以100=5×PC，PC=20cm，BC=20﹣5=15cm．因为PBC是过点O的割线，所以⊙O的半径长为15×=7.5cm．故选C．点评：利用切割线解题时要注意BC是直径，而求得是半径，不要误选A．7．（2004•锦州）如图，⊙O和⊙O′都经过点A和点B，点P在BA的延长线上，过P作⊙O 的割线PCD交⊙O于C、D，作⊙O′的切线PE切⊙O′于E，若PC=4，CD=5，则PE等于（）A．6B．2C．20 D．36考点：切割线定理．分析：根据割线定理得PA•PB=PC•PD，根据切割线定理得PE2=PA•PB，所以PE2=PC•PD，从而可求得PE的长．解答：解：∵PA•PB=PC•PD，PE2=PA•PB，PC=4，CD=5，∴PE2=PC•PD=36，∴PE=6．故选A．点评：注意：割线定理和切割线定理的运用必须在同一个圆中．这里借助割线PAB，把要求的线段和已知线段建立了关系．8．（2004•天津）如图⊙O的两条弦AB、CD相交于点E，AC与DB的延长线交于点P，下列结论中成立的是（）A．C E•CD=BE•BA B．C E•AE=BE•DE C．P C•CA=PB•BD D．P C•PA=PB•PD考点：切割线定理；相交弦定理．分析：根据相交弦定理的割线定理即可求解．解答：解：由相交弦定理知，CE•ED=BE•AE，由割线定理知，PC•PA=PB•PD，只有D正确．故选D．点评：本题利用了相交弦定理和割线定理．9．（2003•资阳）已知AB为⊙O的直径，C为AB的延长线上一点，过C的直线与相切于点D，若BC=2，CD=4，则⊙O的半径长是（）A．3B．6C．8D．无法计算考点：切割线定理．分析：设圆的半径是x，根据切割线定理得CD2=CB•AC，可求得CA与AB的长，从而可得到圆的半径．解答：解：设圆的半径是x；∵CD2=CB•AC，BC=2，CD=4，∴CA=8，∴AB=6，∴圆的半径是3．故选A．点评：此题主要是运用了切割线定理．10．（2003•武汉）如图，已知⊙O1、⊙O2相交于A、B两点，且点O1在⊙O2上，过A作⊙O1的切线AC交BO1的延长线于点P，交⊙O2于点C，BP交⊙O1于点D，若PD=1，PA=，则AC的长为（）A．B．C．D．考点：切线的性质；勾股定理；切割线定理．专题：综合题．分析：根据PA2=PD•PB，作为相等关系可求得PB=5，BD=4，O1D=O1B=2，再根据割线定理PA•PC=PO1•PB，可求得PC=3，从而求得AC=2．解答：解：∵PA2=PD•PB，即（）2=1×PB，解得PB=5，∴BD=BP﹣PD=5﹣1=4，O1D=O1B=4÷2=2，∵PA•PC=PO1•PB，∴×PC=3×5，即PC=3，∴AC=PC﹣AP=3﹣=2．故选B．点评：根据切割线定理和割线定理解答．此题要关注两个关键点：A为两圆交点，PB过点O1．11．（2004•温州）如图，PT是外切两圆的公切线，T为切点，PAB，PCD分别为这两圆的割线．若PA=3，PB=6，PC=2，则PD等于（）A．12 B．9C．8D．4考点：切割线定理．分析：根据切割线定理得PT2=PA•PB，PT2=PC•PD，所以PA•PB=PC•PD，从而可求得PD 的长．解答：解：∵PT2=PA•PB，PT2=PC•PD，∴PA•PB=PC•PD，∵PA=3，PB=6，PC=2，∴PD=9．故选B．点评：注意：切割线定理和割线定理都是在同一个圆中运用的．此题借助切线把要求的线段和已知线段联系到了一起．12．（2006•临沂）如图，在Rt△ABC中，AC=5，BC=12，⊙O分别与边AB，AC相切，切点分别为E，C，则⊙O的半径是（）A．B．C．D．考点：切割线定理；切线长定理．分析：根据切线长定理得AE=AC，根据勾股定理得AB的长，从而得到BE的长，再利用切割线定理得BE2=BD•BC，从而可求得BD的长，也就得到了半径的长．解答：解：∵AE=AC=5，AC=5，BC=12，∴AB=13，∴BE=8；∵BE2=BD•BC，∴BD=，∴CD=，∴圆的半径是，故选A．点评：此题综合运用了切线长定理、勾股定理和切割线定理．13．（2004•沈阳）如图，已知PAC为⊙O的割线，连接PO交⊙O于B，PB=2，OP=7，PA=AC，则PA的长为（）A．B．2C．D．3考点：切割线定理．分析：设PA=x，延长PO交圆于D，根据割线定理得PA•PC=PB•PD即可求得PA的长，也就求得了AC的长．解答：解：设PA=x，延长PO交圆于D，∵PA•PC=PB•PD，PB=2，OP=7，PA=AC，∴x•2x=24，∴x=2．故选B．点评：此题通过作辅助线构造割线定理列方程求解．14．（2006•永州）如图，PA，PB为⊙O的切线，A，B分别为切点，∠APB=60°，点P到圆心O的距离OP=2，则⊙O的半径为（）A．B．1C．D．2考点：切割线定理；等边三角形的性质；勾股定理．分析：根据切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线，平分两条切线的夹角，可知∠APO的度数，连接OA，可知OA⊥AP，故在Rt△AOP中，根据三角函数公式，可将半径求出．解答：解：连接OA∵PA为⊙O的切线∴PA⊥OA∵∠APO=∠APB=30°∴OA=OP×sin∠APO=2×=1∴⊙O的半径为1故选B．点评：本题主要考查圆的切线长定理．15．（2007•双柏县）如图，已知PA是⊙O的切线，A为切点，PC与⊙O相交于B、C两点，PB=2cm，BC=8cm，则PA的长等于（）A．4cm B．16cm C．20cm D．2cm考点：切割线定理．分析：根据已知得到PC的长，再根据切割线定理即可求得PA的长．解答：解：∵PB=2cm，BC=8cm，∴PC=10cm，∵PA2=PB•PC=20，∴PA=2，故选D．点评：此题主要是运用了切割线定理．注意：切线长的平方应是PB和PC的乘积．二、填空题（共15小题）（除非特别说明，请填准确值）16．（2003•泸州）如图，⊙O1与⊙O2相交于C、D两点，⊙O1的割线PAB与DC的延长线交于点P，PN与⊙O2相切于点N，若PB=10，AB=6，则PN=2．考点：切割线定理．分析：根据割线定理和切割线定理，可以证明PA•PB=PC•PD=PN2，从而求得PN的值．解答：解：根据割线定理，得PA•PB=PC•PD=（10﹣6）×10=40，根据切割线定理，得PN2=PC•PD=40，则PN=2．故答案为：2．点评：此题综合运用了割线定理和切割线定理进行计算．17．（2003•常州）如图，PA切⊙O于点A，割线PBC交⊙O于点B、C，若PA=6，PB=4，弧AB的度数为60°，则BC=5，∠PCA=30度，∠PAB=30度．考点：切割线定理；圆心角、弧、弦的关系；圆周角定理．分析：根据切割线定理得PA2=PB•PC可求得PC与BC的长，根据圆周角定理知：圆周角的度数等于它所对的弧的度数的一半，即∠PCA=30°，最后根据弦切角定理得∠PAB=30°．解答：解：∵PA2=PB•PC，PA=6，PB=4；∴PC=9，∴BC=5；∵弧AB的度数为60°，∴∠PCA=30°，∴∠PAB=30°．点评：此题综合运用了切割线定理和圆周角、弦切角与弧的度数的关系．18．（2001•内江）如图，ABCD是边长为2 a的正方形，AB为半圆O的直径，CE切⊙O 于E，与BA的延长线交于F，求EF的长．答：EF=a．考点：切割线定理；圆周角定理．分析：本题利用切线的性质，割线定理，及圆周角定理，结合相似三角形的性质解答．解答：解：连接OE；∵CE切⊙O于E，∴OE⊥CF，∴△EFO∽△BFC，∴=；又∵OE=AB=BC，∴EF=FB；设EF=x，则FB=2x，FA=2x﹣2a；∵FE切⊙O于E，∴FE2=FA•FB，∴x2=（2x﹣2a）•2x，解得x=a，∴EF=a．点评：本题考查切线的性质、切割线定理、相似三角形性质、以及正方形有关性质．解答此题的关键是连接OE，构造出相似三角形，再解答．19．（1999•贵阳）如图，已知⊙O的割线PAB交⊙O于点A和B，PA=6cm，AB=8cm，PO 交⊙O于点C，且PO=10cm，则⊙O的半径为4cm．考点：切割线定理．分析：延长PO交⊙O于D，设⊙O的半径是xcm．根据割线定理列方程求解．解答：解：延长PO交⊙O于D，设⊙O的半径是xcm．根据割线定理，得PA•PB=PC•PD．即（10﹣x）（10+x）=6×（6+8），100﹣x2=84，x2=16，x=±4（负值舍去）．即圆的半径是4cm．点评：此题主要是通过作辅助线，构造割线，熟练运用割线定理列方程求解．20．（2002•四川）如图，PA、PB与⊙O分别相切于点A、点B，AC是⊙O的直径，PC交⊙O于点D，已知∠APB=60°，AC=2，那么CD的长为．考点：切割线定理；切线的性质．分析：连接AD，OB，OP，根据已知可求得AP，PC的长，再根据切割线定理得，PA2=PD•PC，从而可求得PD与CD的长．解答：解：连接AD，OB，OP；∵PA、PB与⊙O分别相切于点A、点B，∴∠OAP=∠OBP=90°，∠AOB=180°﹣∠P=120°，∴∠AOP=60°，AP=AOtan60°=，∴PC=；∵PA2=PD•PC，∴PD=，∴CD=．点评：本题考查切线的性质，勾股定理，四边形的内角和为360°，切割线定理等的综合运用．21．（2004•泸州）如图，在△ABC中，∠C=90度．以BC为直径作⊙O与斜边AB交于点D，且AD=3.2cm，BD=1.8cm，则AC=4cm．考点：切割线定理；切线的判定．分析：先根据已知条件，证得AC是⊙O的切线；然后运用切割线定理求出AC的长．解答：解：∵BC是⊙O的直径，AC⊥BC，∴AC是⊙O的切线，且切点为C；由切割线定理，得：AC2=AD•AB，∵AD=3.2cm，BD=1.8cm，AB=5cm，∴AC2=3.2×5=16，即AC=4cm．故答案为：4．点评：解决此题的关键是能够发现AC是圆的切线，再熟练运用切割线定理求解．22．（2002•丽水）如图，PT是半径为4的⊙O的一条切线，切点为T，PBA是经过圆心的一条割线，若B是OP的中点，则PT的长是4．考点：切割线定理．分析：根据题意，得PB=4，PA=12；再根据切割线定理得PT2=PB•PA，即可求得PT的值．解答：解：∵半径为4，B是OP的中点，∴PB=4，PA=12，∵PT2=PB•PA，∴PT=4．点评：此题主要是考查了切割线定理的运用．23．（1999•成都）如图，已知⊙O的弦AB、CD相交于点P，PA=4，PB=3，PC=6，EA切⊙O于点A，AE与CD的延长线交于点E，AE=2，那么PE的长4．考点：切割线定理；相交弦定理．分析：首先根据相交弦定理求得PD的长，再根据切割线定理求得DE的长，进而可求出PE 的长．解答：解：∵PA=4，PB=3，PC=6，∴PD==2．设DE=x．∵EA切⊙O于点A，∴EA2=ED•EC，即x（x+8）=20，x2+8x﹣20=0，x=2，x=﹣10（负值舍去）．则PE=DE+PD=4．点评：此题综合运用了相交弦定理和切割线定理．24．（2006•余姚市）如图，⊙O的割线PAB交⊙O于点A、B，PA=7cm，AB=5cm，PO=10cm，则⊙O的半径为4．考点：切割线定理．分析：根据割线定理求解．解答：解：延长PO交圆于点D，由割线定理知，PA•PB=PC•PD=（PO﹣CO）（PO+CD），代入数据解得，CO=4．点评：本题利用了割线定理：从圆外一点P引两条割线与圆分别交于A、B、C、D，则有PA•PB=PC•PD．25．（2001•湖州）如图，已知两圆相交于CD两点，AB为两圆的外公切线，A、B为切点，CD的延长线交AB于M，若MD=3，CD=9，则AB的长等于12．考点：切割线定理．分析：根据切割线定理得AM2=MD•MC=36，BM2=MD•MC，从而可求得AM=BM=6，即得到了AB的长．解答：解：∵AM2=MD•MC=36，BM2=MD•MC，MD=3，CD=9；∴AM=BM=6，∴AB=12．点评：此题主要是运用切割线定理进行计算．26．（2000•金华）如图，PT是⊙O的切线，切点是T，M是⊙O内一点，PM及PM的延长线交⊙O于B，C，BM=BP=2，PT=，OM=3，那么⊙O的半径为．考点：切割线定理；勾股定理；垂径定理．分析：已知了PT、BP的长，根据切割线定理易求得BC的长；在线段OM的基础上作⊙O 的直径，根据相交弦定理即可求出⊙O的半径．解答：解：∵PT是⊙O的切线，由切割线定理，得：PT2=PB•PC；∵PT=2，BP=2；∴PC=PT2÷PC=10；∴BC=8，CM=6；过O、M作⊙O的直径，交⊙O于E、F；设⊙O的半径为R，则EM=R+3，MF=R﹣3；由相交弦定理，得：（R+3）（R﹣3）=BM•MC；R2﹣9=2×6，即R=．故⊙O的半径为．点评：此题综合考查了切割线定理和相交弦定理．27．（2000•台州）如图，已知AB是⊙O的直径，BC是和⊙O相切于点B的切线，⊙O的弦AD平行于OC，若OA=2，且AD+OC=6，则CD=．考点：切割线定理；平行线的性质；圆周角定理．专题：计算题．分析：连接BD，根据AD∥OC，易证得OC⊥BD，根据垂径定理知：OC垂直平分BD，可得CD=CB，因此只需求出CB的长即可；延长AD，交BC的延长线于E，则OC是△ABC的中位线；设未知数，表示出OC、AD、AE的长，然后在Rt△ABE中，表示出BE的长；最后根据切割线定理即可求出未知数的值，进而可在Rt△CBO中求出CB的长，即CD的长．解答：解：连接BD，则∠ADB=90°；∵AD∥OC，∴OC⊥BD；根据垂径定理，得OC是BD的垂直平分线，即CD=BC；延长AD交BC的延长线于E；∵O是AB的中点，且AD∥OC；∴OC是△ABE的中位线；设OC=x，则AD=6﹣x，AE=2x，DE=3x﹣6；Rt△ABE中，根据勾股定理，得：BE2=4x2﹣16；由切割线定理，得BE2=ED•AE=2x（3x﹣6）；∴4x2﹣16=2x（3x﹣6），解得x=2，x=4；当x=2时，OC=OB=2，由于OC是Rt△OBC的斜边，显然x=2不合题意，舍去；当x=4时，OC=4，OB=2；在Rt△OBC中，CB==2．∴CD=CB=2．点评：本题主要考查了圆周角定理、平行线的性质、切割线定理、中位线定理等知识，综合性强，难度较大．28．（2005•河南）如图，已知PA为⊙O的切线，PBC为⊙O的割线，PA=，PB=BC，⊙O的半径OC=5，那么弦BC的弦心距OM=4．考点：切割线定理．分析：根据切割线定理得到PA2=PB•PC，设BC=x，则PB=x，PC=2x，因而得到2x2=72，解得x=6；OM⊥BC，则满足垂径定理，在直角△OMC中，根据勾股定理可得到OM=4．解答：解：∵PA为⊙O的切线，PBC为⊙O的割线，∴PA2=PB•PC；设BC=x，则PB=x，PC=2x，∴2x2=72，解得x=6；∵OM⊥BC，在直角△OMC中，∵OC=5，CM=3，∴OM=4．点评：本题解决的关键是正确理解记忆切割线定理，以及垂径定理．29．（2007•包头）如图，已知Rt△ABC的两条直角边AC，BC的长分别为3，4，以AC为直径作圆与斜边AB交于点D，则AD=．考点：切割线定理；勾股定理．分析：根据勾股定理求得AB的长，再根据切割线定理解答．解答：解：∵AC=3，BC=4，∴AB===5；∵BC2=BD•BA，∴42=BD•5，∴BD=，∴AD=AB﹣BD=5﹣=．点评：此题主要考查切割线定理的运用．30．（2003•江西）如图，PT切⊙O于点T，直径BA的延长线交PT于点P，若PT=4，PA=2，则⊙O的半径长是3．考点：切割线定理．专题：计算题．分析：根据切割线定理得PT2=PA•PB从而可求得PB的长，也可得到AB的长，即不难求得圆的半径．解答：解：∵PT2=PA•PB，PT=4，PA=2，∴PB=8，∴AB=6，∴圆的半径是3．点评：考查了圆的性质，切线的性质及切割线定理及其的运用．三、解答题（共1小题）（选答题，不自动判卷）31．（2006•双柏县）如图，AB是⊙O的直径，CB、CE分别切⊙O于点B、D，CE与BA 的延长线交于点E，连接OC、OD．（1）△OBC与△ODC是否全等？是（填“是”或“否”）；（2）已知DE=a，AE=b，BC=c，请你思考后，选用以上适当的数，设计出计算⊙O半径r 的一种方案：①你选用的已知数是a、b、c，或其中2个；②写出求解过程．（结果用字母表示）考点：切割线定理；全等三角形的判定与性质；勾股定理；切线的性质．专题：方案型．分析：（1）由切线和切线长定理可知，∠ODC=∠OBC=90°，OD=OB，OC=OC从而得到△OBC≌△ODC（HL）；（2）可选择a，b，c或其中的两个．求由勾股定理求解或切割线定理求解．解答：解：（1）△OBC与△ODC全等．证明：∵CD、CB是⊙O的切线∴∠ODC=∠OBC=90°∵OD=OB，OC=OC∴△OBC≌△ODC（HL）；（2）①选择a、b、c，或其中2个；②若选择a、b：由切割线定理：a2=b（b+2r），得r=若选择a、b、c：方法一：在Rt△EBC中，由勾股定理：（b+2r）2+c2=（a+c）2，得r=方法二：Rt△ODE∽Rt△CBE，，得r=方法三：连接AD，可证：AD∥OC，，得r=若选择a、c：需综合运用以上的多种方法，得r=若选择b、c，则有关系式2r3+br2﹣bc2=0．点评：本题考查了切线的概念，切线长定理，勾股定理及全等三角形的判定等知识点的综合运用．。

中考数学复习相交弦定理切割线定理2课件

复习之五
相交弦定理
一.复习目标:
1.熟练掌握相交弦定理及其应用.
2.熟练掌握切割线定理及其应用.
3.掌握与其它知识的联系,综合应用.
二,检测题:
1.已知⊙O的半径为4,过
一点P作⊙O的割线PAB,
若PA=4,PB=2,则OP的距
离2.如为图:已知同心.
圆⊙O,AB是大圆的
E G
直径,交小圆于
B
M
5.已知如图, ⊙O的直径
AB的延长线与弦CD的延
长线相交于P,E为⊙o上
一点, AE=AC,DE交AB于
点F,求 E
证:PF×PO=PA×PB
A
FB O
P
D C
D
C,D,EC⊥AB交大圆 A C O B
于E,连接ED交小圆
于G,设大圆半径为
3.如图:⊿ABC是⊙O的内接
正三角形,弦PQ过AB,AC的中点D,E,求PQ:BC的值. A
4.如图:已知
ቤተ መጻሕፍቲ ባይዱ
AD切⊙O于D,
割线ACB交
⊙O于点C,B,
线段
A
AP=AD,PC交
⊙O于N,PB交
P
Q DE
B
C
D
C N
O•

九年级数学相交弦定理和切割线定理知识精讲四年制试题

九年级数学相交弦定理和切割线定理知识精讲一. 本周教学内容：相交弦定理和切割线定理二. 重点、难点：1. 相交弦定理的使用特征。

2. 切割线定理的使用特征。

[例1] 如图，AC=BD ，CE 、DF 切⊙O 于E 、F 两点，连EF ，求证：CM=MD 。

证明：作DN ∥EC ，交MF 于N ，那么∠1=∠2，∠C=∠4 由弦切角定理得：∠3=∠1 ∴ ∠2=∠3 ∴ DN=DF由切割线定理，CB CA CE ⋅=2DA DB DF ⋅=2∵ AC=DB ∴ CB=DA ∴ 22DF CE = CE=DF∴ CE=DN 又 ∵ ∠5=∠6 ∴ DNM CEM ∆≅∆〔AAS 〕 ∴ CM=MD[例2] PT 切⊙O 于T ，PBA 为割线，交OC 于D ，CT 为直径，假设OC=BD=4cm ，AD=3cm ，求PB 长。

解：设即3由切割线定理，BP AP PT ⋅=2 由勾股定理，222TD PT PD +=∴ 22TD BP AP PD +⋅= ∴ )7(6)4(22++=+y y y∴ cm y 20=[例3]假设BC=9，解：连AB ，∴ ∠1=∴EF CE =由相交弦定理得26⨯=ab ② 由①、②解得：4=b ，3=a 由切割线定理得：1441692=⨯=⋅=CF CB AC ∴ AC=12[例4] P 为弦AB 上一点，C 在圆O 上，OP ⊥PC ，求证：〔1〕PB PA PC ⋅=2〔2〕假设证明：〔1〕延长CP 解：〔2〕易知PM 由相交弦定理，MN CM MB AM ⋅=⋅，即27)63(3)3(=+⨯=+y x ① 由垂径定理，CP=PD ，故在CPO Rt ∆中有2046222=-=PC ∴ 由〔1〕结论，20)3(=+y x ② 由①—②得：37+=x y 代②得，0203162=-+x x ∴ 0601632=-+x x ，36128±-=x 〔舍负〕∴ AP 长为36128+-[例5] 如图，AB 切⊙O 于B ，OB 交割线ACD 于E ，AC=CE=3，OE=25，求AB 长。

切割线定理

B A O C P
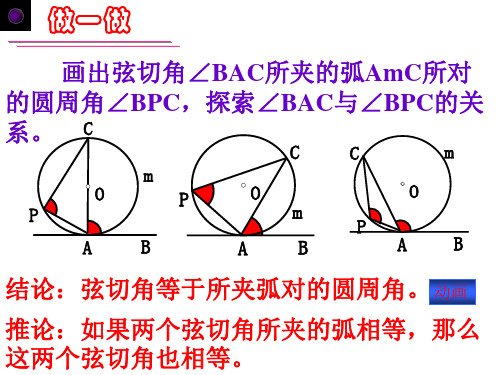
推论：从圆外一点引圆的两条割线，这点到每条割线与圆的交点的两条线段长的积相等。
A B O C D P
PA· PB=PC· PD
切割线定理的应用
例1 、填空
B
（1）已知PAB、PCD是圆O的割线， PA=3 ， AB=5 CD=2，则PC＝（2）已知：PAB是圆O的割线， PA=6 ，AB=4 ，PO=10 ，则PC＝；
.
16
A
相交弦定理：PA· PB=PC· PD
P C
D B
探索：如果把两弦相交点P移到圆外，并且有一条线段是切线，会产生什么现象，得出什么比例关系？ A
O B C
P
切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。
A
O
B
C
PA2=PB· PC
P
例1、已知:如图,⊙O的割线PAB交⊙O于点A 和B，PA=6,AB=8,PO=10.9,求⊙O的半径。
做一做
画出弦切角∠BAC所夹的弧AmC所对的圆周角∠BPC，探索∠BAC与∠BPC的关系。 C
C
C
m m O P A B
P A
O
O
m
B
P
A
B
结论：弦切角等于所夹弧对的圆周角。动画推论：如果两个弦切角所夹的弧相等，那么这两个弦切角也相等。
相交弦定理
一1、定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。 2、弦AB和CD交与O内一点P，那么 PA PB=PC PD
B
F
A B
图3
D
P A
图7
C
例4、如图，已知 PAB、PCD是⊙O的割线,PE 切⊙O于点E，PE=6cm，PC=3cm，PA=4cm， AC=2cm求BD的长 E P C D

《弦切角定理》《圆幂定理》练习题及答案

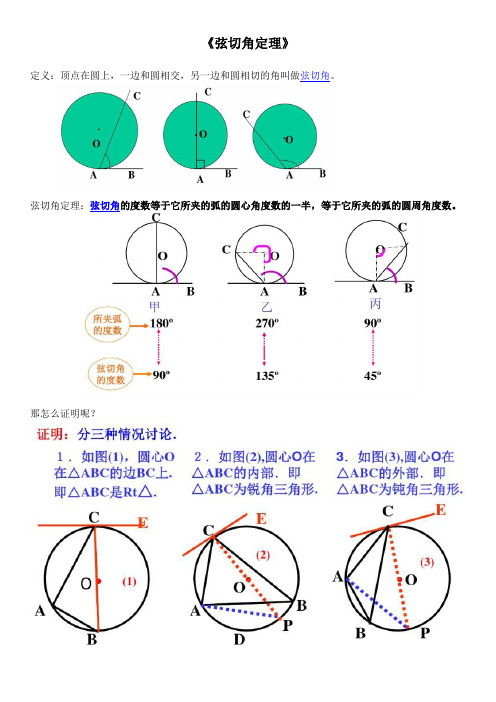
《弦切角定理》定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。

弦切角定理：弦切角的度数等于它所夹的弧的圆心角度数的一半，等于它所夹的弧的圆周角度数。

那怎么证明呢？《圆幂定理》（1）相交弦定理：圆内两弦相交，交点分得的两条线段的乘积相等。

即：在⊙O 中，∵弦AB 、CD 相交于点P ，∴PA PB PC PD ⋅=⋅（2）推论：如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项。

即：在⊙O 中，∵直径AB CD ⊥， ∴2CE AE BE =⋅（3）切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

即：在⊙O 中，∵PA 是切线，PB 是割线∴ 2PA PC PB =⋅（4）割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等（如上图）。

即：在⊙O 中，∵PB 、PE 是割线 ∴PC PB PD PE ⋅=⋅【精典例题】1、如图，PA 、PB 是⊙O 的切线，AC 是⊙O 的直径，∠P=50°，则∠BOC 的度数为（） A ．50°B ．25°C ．40°D ．60°2、如图，BD 为圆O 的直径，直线ED 为圆O 的切线，A ．C 两点在圆上，AC 平分∠BAD 且交BD 于F 点．若∠ADE ＝19°，则∠AFB 的度数为何？（） A ．97°B ．104°C ．116°D ．142°解答：解：∵PA 、PB 是⊙O 的切线， ∴∠OAP =∠OBP =90°，而∠P =50°，∴∠AOB =360°﹣90°﹣90°﹣50°= 130°，又∵AC 是⊙O 的直径，∴∠BOC =180°﹣130°=50°．故选A ．BADB3、如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，交AB 的延长线于D ，且CO=CD ，则∠PCA=（）A 、30°B 、45°C 、60°D 、67.5°4、已知⊙O 的半径为1，圆心O 到直线l 的距离为2，过l 上任一点A 作⊙O 的切线，切点为B ，则线段AB 长度的最小值为（）A 、1B 、2C 、3D 、2解答：如右图所示，OA ⊥l ，AB 是切线，连接OB ， ∵OA ⊥l ，∴OA=2，又∵AB 是切线， ∴OB ⊥AB ，在Rt △AOB 中，AB =22OB OA -=2212-=3．故选C ．5、如图是油路管道的一部分，延伸外围的支路恰好构成一个直角三角形，两直角边分别为6m 和8m.按照输油中心O 到三条支路的距离相等来连接管道，则O 到三条支路的管道总长（计算时视管道为线，中心O 为点）是（）A.2mB.3mC.6mD.9m解答：在Rt △ABC 中，BC =8m,AC =6m,AB =22BC AC +=2286+=10． ∵中心O 到三条支路的距离相等，设距离是r ．△ABC 的面积=△AOB 的面积+△BOC 的面积+△AOC 的面积即：12AC •BC =12AB •r+12BC •r+12AC •r 即：6×8=10r+8r+6r ∴r=4824=2．故O 到三条支路的管道总长是2×3=6m ．故选C ．解答：解：∵BD 是圆O 的直径， ∴∠BAD ＝90°，又∵AC 平分∠BAD ，∴∠BAF ＝∠DAF ＝45°， ∵直线ED 为圆O 的切线， ∴∠ADE ＝∠ABD ＝19°，∴∠AFB ＝180°－∠BAF －∠ABD ＝180°－45°－19°＝116°．故选C ．解答：解：如图：∵PD 切⊙O 于点C ， ∴OC ⊥PD ，又∵OC=CD ， ∴∠COD=45°，连接AC ，∵AO=CO ， ∴∠ACO=22.5°，∴∠PCA=90°-22.5°=67.5°．故选D ．O（第5题图）6、如图，AB 是⊙O 的直径，BC 交⊙O 于点D ，DE ⊥AC 于点E ，要使DE 是⊙O 的切线，还需补充一个条件，则补充的条件不正确．．．的是（） A. DE ＝DO B. AB ＝AC C. CD ＝DB D. AC ∥OD7、已知AB 是⊙O 的直径，点P 是AB 延长线上的一个动点，过P 作⊙O 的切线，切点为C ，∠APC 的平分线交AC 于点D ，则∠CDP 等于（）A 、30°B 、60°C 、45°D 、50°解答：连接OC ，∵OC=OA ，，PD 平分∠APC ，∴∠CPD=∠DPA ，∠A=∠ACO ， ∵PC 为⊙O 的切线，∴OC ⊥PC ，∵∠CPD+∠DPA+∠A+∠ACO=90°，∴∠DPA+∠A=45°，即∠CDP=45°．故选C ．8、如图，CB 切⊙O 于点B ，CA 交⊙O 于点D 且AB 为⊙O 的直径，点E 是ABD 上异于点A 、D 的一点．若∠C =40°，则∠E 的度数为．9、已知：如图，三个半圆以此相外切，它们的圆心都在x 轴的正半轴上并与直线y ＝x 相切，设半圆C 1、半圆C 2、半圆C 3的半径分别是r 1、r 2、r 3，则当r 1＝1时，r 3＝解答：由三个半圆依次与直线y ＝x 相切并且圆心都在x 轴上，∴y ＝x 倾斜角是30°，∴得，OO 1=2r 1，OO 1=2r 2，001=2r 3，r 1＝1，∴r3=9．故答案为9．333333解答：当AB=AC 时，连接AD ，∵AB 是⊙O 的直径，∴AD ⊥BC ，∴CD=BD ， ∵AO=BO ，∴OD 是△ABC 的中位线，∴OD ∥AC ，∵DE ⊥AC ，∴DE ⊥OD ，∴DE 是⊙O 的切线．所以B 正确．当CD=BD 时，AO=BO ，∴OD 是△ABC 的中位线，∴OD ∥AC ∵DE ⊥AC ∴DE ⊥OD ∴DE 是⊙O 的切线．所以C 正确．当AC ∥OD 时，∵DE ⊥AC ，∴DE ⊥OD ．∴DE 是⊙O 的切线．所以D 正确．故选A ．ABCD P· OE解答：如图：连接BD ，∵AB 是直径，∴∠ADB =90°，∵BC 切⊙O 于点B ，∴∠ABC =90°， ∵∠C =40°，∴∠BAC =50°，∴∠ABD =40°，∴∠E =∠ABD =40°．故答案为：40°．10、如图，在Rt △ABC 中，∠ABC 是直角，AB=3，BC=4，P 是BC 边上的动点，设BP=x ，若能在AC 边上找到一点Q ，使∠BQP=90°，则x 的取值范围是．解答：解：过BP 中点以BP 为直径作圆，连接QO ，当QO ⊥AC 时，QO 最短，即BP 最短， ∵∠OQC=∠ABC=90°，∠C=∠C ，∴△ABC ∽△OQC ，∴=，∵AB=3，BC=4，∴AC=5， ∵BP=x ，∴QO=x ，CO=4﹣x ，∴=，解得：x=3，当P 与C 重合时，BP=4，∴BP=x 的取值范围是：3≤x ≤4，故答案为：3≤x ≤4．11、如图，AD 是⊙O 的弦，AB 经过圆心O ，交⊙O 于点C ，∠DAB=∠B=30°. (1)直线BD 是否与⊙O 相切？为什么？ (2)连接CD ，若CD=5，求AB 的长.解答：（1）直线BD 与⊙O 相切．如图连接OD ，CD ， ∵∠DAB=∠B=30°，∴∠ADB=120°， ∵OA=OD ，∴∠ODA=∠OAD=30°，∴∠ODB=∠ADB ﹣∠ODA=120°﹣30°=90°．所以直线BD 与⊙O 相切．（2）连接CD ，∠COD=∠OAD+∠ODA=30°+30°=60°，又OC=OD ，∴△OCD 是等边三角形，即：OC=OD=CD=5=OA ，∵∠ODB=90°，∠B=30°，∴OB=10，∴AB=AO+OB=5+10=15．12、已知：如图，AB 为⊙O 的直径，⊙O 过AC 的中点D ，DE ⊥BC 于点E ．（1）求证：DE 为⊙O 的切线；（2）若DE =2，tan C =12，求⊙O 的直径．【解析】（1）证明：联结OD ． ∵ D 为AC 中点， O 为AB 中点，∴ OD 为△ABC 的中位线． ∴OD ∥BC ． ∵ DE ⊥BC ， ∴∠DEC=90°.∴∠ODE=∠DEC=90°. ∴OD ⊥DE 于点D. ∴ DE 为⊙O 的切线．（2）解：联结DB ． ∵AB 为⊙O 的直径， ∴∠ADB=90°． ∴DB ⊥AC ． ∴∠CDB=90°. ∵ D 为AC 中点， ∴AB=AC ．在Rt △DEC 中，∵DE=2 ，tanC=12， ∴EC=4tan DEC=. 由勾股定理得：DC=在Rt △DCB 中， BD=tan DC C ⋅ BC=5. ∴AB=BC=5. ∴⊙O 的直径为5.【巩固练习】1．已知⊙O 的半径为10cm ，如果一条直线和圆心O 的距离为10cm ，那么这条直线和这个圆的位置关系为（）A. 相离B. 相切C. 相交D. 相交或相离2．如右图，A 、B 是⊙O 上的两点，AC 是⊙O 的切线，∠B=70°，则∠BAC 等于（）A. 70°B. 35°C. 20°D. 10°（第2题）（第3题）（第4题）（第5题）3．如图，PA 切⊙O 于A ，PB 切⊙O 于B ，OP 交⊙O 于C ，下列结论中，错误的是（）A. ∠1=∠2B. PA=PBC. AB ⊥OPD. 2PA PC ·PO4．如图，已知⊙O 的直径AB 与弦AC 的夹角为30°，过C 点的切线PC 与AB 的延长线交于P ，PC=5，则⊙O 的半径为（）A.335 B. 635 C. 10 D. 55．如图已知AB 是⊙O 的直径，弦AD 、BC 相交于点P ，那么AB ︰CD 等于∠BPD 的（）A. 正弦B. 余弦C. 正切D. 余切6．如图A 、B 、C 是⊙O 上三点，AB ⌒的度数是50°，∠OBC=40°，则∠OAC 等于（）A. 15°B. 25°C. 30°D. 40°（第6题）（第7题）（第8题）（第9题）7．如图AB 为⊙O 的一条固定直径，它把⊙O 分成上、下两个半圆，自上半圆上一点C ，作弦CD ⊥AB ，∠OCD 的平分线交⊙O 于点P ，当C 点在半圆（不包括A 、B 两点）上移动时，点P （）A. 到CD 的距离不变B. 位置不变C. 等分DB ⌒D. 随C 点的移动而移动8．如图AD 、AE 和BC 分别切⊙O 于D 、E 、F ，如果AD=20，则△ABC 的周长为（） A. 20 B. 30 C. 40 D. 21359．如图在⊙O 中，直径AB 、CD 互相垂直，BE 切⊙O 于B ，且BE=BC ，CE 交AB 于F ，交⊙O 于M ，连结MO 并延长，交⊙O 于N ，则下列结论中，正确的是（）A. CF=FMB. OF=FBC. BM⌒的度数是22.5° D. BC ∥MN 10．如图⊙O 的两条弦AB 、CD 相交于点P ，已知AP=2cm ，BP=6cm ，CP ︰PD =1︰3，则DP=_________．（第10题）（第11题）（第12题）（第13题）11．如图AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，P 是BA 的延长线上的点，连结PC ，交⊙O 于F ，如果PF=7，FC=13，且PA ︰AE ︰EB = 2︰4︰1，则CD =_________．12．从圆外一点P 引圆的切线PA ，点A 为切点，割线PDB 交⊙O 于点D 、B ，已知PA=12，PD=8，则=∆∆DAP ABP S S :__________．13．⊙O 的直径AB=10cm ，C 是⊙O 上的一点，点D 平分BC ⌒，DE=2cm ，则AC=_____． 14．如图，AB 是⊙O 的直径，∠E=25°，∠DBC=50°，则∠CBE=________．（第14题）（第15题）（第17题）（第18题）15．点A 、B 、C 、D 在同一圆上，AD 、BC 延长线相交于点Q ，AB 、DC 延长线相交于点P ，若∠A=50°，∠P=35°，则∠Q=________．16.在Rt △ABC 中,∠C=90°，AC=12cm ，BC=5cm ，以点C 为圆心，6cm 的长为半径的圆与直线AB 的位置关系是________.17.如图,在△ABC 中,AB=AC,∠BAC=120°,⊙A 与BC 相切于点D,与AB 相交于点E,则∠ADE 等于___度. 18.如图,PA 、PB 是⊙O 的两条切线,A 、B 为切点,直线OP 交⊙A 于点D 、E,交AB 于C.图中互相垂直的线段有_________(只要写出一对线段即可).19.已知⊙O 的半径为4cm,直线L 与⊙O 相交,则圆心O 到直线L 的距离d 的取值范围是____.E A PO EC D BA20.如图,PA 、PB 是⊙O 的切线,切点分别为A 、B,且∠APB=50°,点C 是优弧AB 上的一点,则∠ACB 的度数为________.（第20题）（第21题）（第22题）（第23题）21.如图,⊙O 为△ABC 的内切圆,D 、E 、F 为切点,∠DOB=73°,∠DOE=120°, 则∠DOF=_______度,∠C=______度,∠A=_______度.22.如图,AB 、AC 为⊙O 的切线,B 、C 是切点,延长OB 到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ ADO 等于_______23.如图AB 是⊙O 的直径，AC 是⊙O 的切线，，A 为切点，连结BC 交圆0于点D,连结AD,若∠ABC ＝45°,则下列结论正确的是（）A.AD ＝BCB.AD ＝ACC.AC ＞ABD.AD ＞DC24.如图，在平面直角坐标系中，⊙P 与x 轴相切于原点O ，平行于y 轴的直线交⊙P 于M,N 两点．若点M 的坐标是(2,-1)，则点N 的坐标是（）A ．(2,-4) B. (2,-4.5) C.(2,-5) D.(2,-5.5)（第24题）（第25题）（第26题）（第27题）25、如图，AB 是⊙O 的直径，AD 是⊙O 的切线，点C 在⊙O 上，BC ∥OD ，AB ＝2,OD ＝3,则BC 的长为（）A ．B ． CD26、已知圆O 的半径为R ，AB是圆O 的直径，D 是AB 延长线上一点，DC是圆O 的切线，C 是切点，连结AC ，若∠CAB ＝30°，则BD 的长为（）A ．BC ．D 27、如图，在平面直角坐标系中，⊙A 与y 轴相切于原点O ，平行于x 轴的直线交⊙A 于M 、M 两点，若点M 的坐标是（-4,-2），则点N 的坐标为（）A ．（-1,-2）B ．（1,2）C ．（-1.5,-2）D ．（1.5,-2）PO C BA212123322R R R28、如图，AB 是圆O 的直径，AC 是圆O 的切线，A 为切点，连结BC 交圆于点D ，连结AD ，若∠ABC ＝45°，则下列结论正确的是（）A ．B ．C ．D ．（第28题）（第29题）（第30题）（第31题）29、如图，AB 是⊙O 的直径，⊙O 交BC 的中点于D,DE ⊥AC 于E,连接AD,则下列结论正确的个数是( ）①AD ⊥BC ②∠EDA ＝∠B ③OA ＝AC ④DE 是⊙O 的切线A ．1 个B ．2个C ．3 个D ．4个30、一个钢管放在V 形架内，右图是其截面图，O 为钢管的圆心．如果钢管的半径为25 cm ，∠MPN ＝60︒，则OP ＝( )A ．50 cmB ．25cm C ．cm D ．50cm 31、如图，DB 为半圆的直径，A 为BD 延长线上一点，AC 切半圆于点E ，BC ⊥AC 于点C ，交半圆于点 F ．已知BD ＝2，设AD ＝x ，CF ＝y ，则y 关于x 的函数解析式是．32、如图， AB 与⊙O 相切于点B ，线段OA 与弦BC 垂直于点D ，∠AOB ＝60°，BC ＝4cm ，则切线AB ＝ cm.（第32题）（第33题）（第34题）（第35题）33、如图，直线AB 切⊙O 于C 点，D 是⊙O 上一点，∠EDC ＝30º，弦EF ∥AB ，连结OC 交EF 于H 点，连结CF ，且CF ＝2，则HE 的长为_________．34、如图，点A 、B 、C 在⊙O 上，切线CD 与OB 的延长线交于点D ，若∠A ＝30°，CD ＝，则⊙O 的半径长为．35、如图，在中，，与相切于点，且交于两点，则图中阴影部分的面积是（保留）．O 12AD BC =12AD AC =AC AB >AD DC >12333503第19题图ABC DO32ABC △120AB AC A BC =∠==，°，A ⊙BC D AB AC 、M N 、π36、如图，⊙O 内切于△ABC ，切点分别为D ，E ，F .∠B ＝50°，∠C ＝60°，连结OE ，OF ，DE ，DF ，则∠EDF 等于( )A ．40°B ．55°C ．65°D ．70°（第36题）（第73题）（第38题）37、如图，一个边长为4 cm 的等边三角形ABC 的高与⊙O 的直径相等．⊙O 与BC 相切于点C ，与AC 相交于点E ，则CE 的长为________cm.38、如图，直线l 与半径为4的⊙O 相切于点A ，P 是⊙O 上的一个动点(不与点A 重合)，过点P 作PB ⊥l ，垂足为B ，连结PA .设PA ＝x ，PB ＝y ，则x －y 的最大值是________．39、如图，AB 是半圆O 的直径，C 为半圆上一点，过C 作半圆的切线，连接AC, 作直线AD ，使∠DAC=∠CAB ，AD 交半圆于E,交过C 点的切线于点D. (1)试判断AD 与CD 有何位置关系,并说明理由; (2)若AB=10,AD=8,求AC 的长.40、如图，点A ，B ，C 在半径为8的⊙O 上，过点B 作BD ∥AC ，交OA 延长线于点D ，连结BC ，且∠BCA ＝∠OAC ＝30°.(1)求证：BD 是⊙O 的切线； (2)求图中阴影部分的面积．答案：8、据切线长定理有AD=AE，BE=BF，CD=CF；则△ABC的周长=AB+BC+AC=AB+BF+CF+AC=AB+BE+AC+CD=AD+AE=2AD=40．故选C．9、解：A错，F显然不是弦的平分点；B错，F不是半径的中点；C错，M点平分应为45°；D对，∵BE为圆O的切线，∴BE⊥AB，∵CD⊥AB，∴BE∥CD，∴∠BEF=∠DCF，∵BC=BE，∴∠BCE=∠BEF，∴∠BCE=∠DCF，∵OC=OM，∴∠DCF=∠CMN，∴∠BCE=∠CMN，∴BC∥MN．故选D．10、解：如图利用相交弦定理可知：11、根据割线定理，PF*PC=PA*PB，设EB=X则PA=2X，AE=4X，PB=7X7*（7+13）=2X*7X，X2=10在三角形PCE中，CE2=PC2-PE2=400-360=40，CD=2CE=10412、由切割线定理可得PA2=PD×PB，∵PA=12，PD=8 ∴PB=18．由弦切角和公共角易知△PAD∽△PBA．∴S△PAD：S△PBA=PA2：PB2=4：9．⌒，∴OD平分BC，∴OE为△ABC的中位线，13、∵点D平分BC又∵⊙O的直径AB=10cm，∴OD=5cm，DE=2cm，∴0E=3cm，则弦AC=6cm．故答案为6cm．14、连接AC，∵∠DBA和∠DCA都为AD所对的圆周角，∴∠DBA=∠DCA，∵AB为⊙O的直径，∴∠BCA=90°，∴∠CBA+∠CAB=90°，∵∠CAB=∠E+∠DCA，∴∠CBD+∠DBA+∠E+∠DBA=90°，∵∠E=25°，∠DBC=50°，∴∠DBA=7.5°，∴∠CBE=∠DBA+∠DBC=57.5°15、∠A=50°,故∠BCD=130°（因为是圆,同弧的角互补)，由P=35°计得∠CDQ=85°,故可以计出∠Q=45°.16.相交 17.60 18.如OA⊥PA,OB⊥PB,AB⊥OP等. 19.0≤d<4. 20.65°21. 146°,60°,86° 22.64°23、【答案】Ａ 24、【答案】A 25、【答案】A 26、【答案】C27、【答案】C 28、【答案】A 29、【答案】D 30、【答案】A31、 32、【答案】433、【答案】34、【答案】2．3536、B 由∠B ＝50°，∠C ＝60°可求出∠A ＝70°，则易求得∠EOF ＝110°，∴∠EDF ＝12∠EOF ＝55°.37、过O 作OF ⊥AC 于F ，连结OC ，如图．则CE ＝2CF .根据△ABC 为等边三角形，且边长为4 cm ，易求得它的高为2 3 cm ，即OC ＝ 3 cm.∵BC 与⊙O 相切，∴∠OCB ＝90°.又∠ACB ＝60°，∴∠OCF ＝30°.3π3在Rt△OFC中，可得CF＝OC·cos 30°＝3×32＝32(cm)，故CE＝2CF＝3 cm.38、如图，连结OA，过点O作OC⊥AP于点C，所以∠ACO＝90°，AC＝12AP.易证△OAC∽△APB，所以OA AP ＝ACPB，即4x＝x2y，所以y＝x28.所以x－y＝x－x28＝－18(x－4)2＋2，所以x－y的最大值是2.39.(1)AD⊥CD.理由:连接OC,则OC⊥CD.∵OA=OC,∴∠OAC=∠OCA,又∠OAC= ∠DAC,∴∠DAC=∠OCA,∴AD∥OC,∴AD⊥CD.(2)连接BC,则∠ACB=90°由(1)得∠ADC=∠ACB,又∠DAC=∠CAB.∴△ACD∽△ABC,∴AC ADAB AC=,即AC2=AD·AB=80,故40、22．(1)证明：如图，连结OB，交CA于点E.∵∠C＝30°，∠C＝12∠BOA，∴∠BOA＝60°.∵∠OAC＝30°，∴∠AEO＝90°.∵BD∥AC，∴∠DBE＝∠AEO＝90°.∴OB⊥BD.∴BD是⊙O的切线．(2)解：∵AC∥BD，∴∠D＝∠OAC＝30°.∵∠OBD＝90°，OB＝8，∴BD＝3OB＝8 3.∴S阴影＝S△BDO－S扇形AOB＝12×8×83－60·π×82360＝323－32π3.。

九年级数学切割线定理

C A P •O D B A O P D C
B
推论: 如果弦与直径垂直相交，那么弦的一半
是它分直径所成的两条线段的比例中项． PC2=PA· PB
• 练习 : ⊙o的弦 CD平分AB于P, 且AB=12cm,CD=13cm • 试求: PC 和 PD 的长.
A
C P •O
B
D
A
D P • C
PA · PB = PD · PC
切割线定理
加油！
D
已知：线段a，b．求作：线段c，使c2＝ab．
A
c
a B b C
反思：这个作图题是作两
已知线段的比例中项的问题，可以当作基本作图加以应用．请同学们想一想，这到题还有别的作法吗？
C
c
A
O
a
D
b
B
相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等． PA· PB = PD· PC
B
T(C , D)
C
D
P C D • A
P•BA源自BPA•PB=PC•PD 吗?
PT2 =PA· PB 吗?
已知：如下图，点P是⊙o外一点，PT是切线，T是切点， PA是割线 , 点A和B是它与⊙o的交点。求证：PT2 =PA · PB 切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。即 PT2 =PA· PB T 证明: 连结TA，TB P 1 ∠ 1= ∠ B ∠ P= ∠ P A △PTA∽ △PBT PA:PT=PT:PB B
BC2=BD•BA
Rt△ABC中 AC=3; BC=4. BD=3.2 (cm) AB=5 BC=4
B

相交弦.切割线练习题

相交弦、切割线定理练习题一、填空：1.圆内两弦相交，一弦长8cm 且被交点平分，另一弦被交点分为1：4，则另一弦长为（）3.如图:已知同心圆⊙O,AB 是大圆的直径,交小圆于C,D,EC⊥AB 交大圆于E,连接ED 交小圆4.自圆外一点所作过圆心的割线长是12cm ，圆的半径为4cm ，则过此点所引的切线长为（）5.如图1，⊙O 的半径为6，PQ ＝6，AR ＝8则QR 的长为（）6.如图2，CD 为⊙O 直径，弦AB 垂直CD 于P,AP ＝4， PD ＝2，则PO ＝___.7.⊙O 中直径CD ⊥弦AB 于E ，AB ＝6，DE ∶CE ＝1∶3，则DE 的长为（）8.由圆外一点作圆的切线长为6，过这点作过圆心的割线长为12，则此圆半径长为（）9．如图，PAB 为⊙O 的割线，PO 交⊙O 于C ，OP ＝13，PA ＝9， AB ＝7，求⊙O 直径的长.10．如图2，△ABC 中∠A ＝90°，AC ＝3，AB ＝4，半圆圆心在BC 上，与AB,AC 切于D,E ，则⊙O 半径为（）11．⊙O 中直径CD 垂直弦AB 于E ，AB ＝8，DE ∶CE ＝3∶1，则DE 的长为（） 11、（2002•南京）如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足是G ，F 是CG 的中点，延长AF 交⊙O 于E ，CF=2，AF=3，则EF 的长是 _________ ．1、如图：⊙O 1和⊙O2相交于A 、B 两点， P 是AB 上任一点过P 点分别作直线C D 和E F ，分别交⊙O1于C 、D ，交⊙O2于E 、F ，求证：PC·PD=PE·PFRQA OP 1ABO CD P2r ABCOPÍ¼22.如图，圆o1和圆o2相交于A 和 B 两点，点P 在BA 的延长线上。

过点P 作圆O1的割线PMN 交圆O1于M .N ，作圆O2的切线PC 切圆O2于C 。

九年级数学切割线定理

切割线定理
加油！
D
已知：线段a，b．求作：线段c，使c2＝ab．
A
c
a B b C
反思：这个作图题是作两
已知线段的比例中项的问题，可以当作基本作图加以应用．请同学们想一想，这到题还有别的作法吗？
C
c
A
O
a
D
b
B
相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等． PA· PB = PD· PC
PT2 =PA· PB
问题：如下图，点P是⊙o外一点，过P点向圆作两条直线与圆相交得四条线段 PA与PB及PC与PD 它们有等积关系 PA•PB=PC•PD 吗?
切割线定理从圆外一点引圆的两条割线，从这一点到每条割线与圆的交点的两条线段长的积推论相等. 即 PA· ：如图，圆o1，圆o2，圆o3…都经过点A和 B，点P
提示：PC = PD = PE …
B o1• C A o2 • o3• D
E
P
练习六 P114 2.
•
提示：法一：BC是为圆O 的切线解： Rt△ABC中，AC⊥BC AC为圆O的直径 BC切圆O于C BDA为圆O的割线
法二：连接CD ,射影定理。 A D •O
T
练习一: 如下图,圆o的两条弦AB和CD相交于点E,AC和DB 的延长线交于P,下列结论成立的是( D ). (A) PC • CA=PB • BD (B) CE • AE=BE • ED (C) CE • CD=BE • BA (D) PB • PD=PC • PA
PA· PB = PD· PC
Ｂ
PD=10.9+r
Ｐ
６ＡＣ
Ｏ

切割线定理

3
.
A
由推论得 PB•PA=PD•PC
例1 如图过圆外一点P作两条割线,分别交圆O于A、B和C、D.
再作圆O切线PE,E为切点,连结CE、DE.已知 AB=3cm, PA=2cm,CD=4cm。 (1) 求PC,PE的长
3
B
A 2 C
x
4
解: 设PC=x ∵CD=4cm, ∴PD=PC+CD=x+4 P ∵AB=3cm, PA=2cm ∴ PB=AB+PA=5(cm) 由切割线定理,得PE2=PA•PB ∴PE2= 2×5=10 ∴PE= 10 (cm). 由切割线定理推论得，PC•PD=PA•PB ∴x(x+4)=2×5 化简,整理得 x2+4x－10=0 解得 x= － 2 ± 14 (负数不合题意,舍去) ∴ x= ( 14 －2)(cm) 答:PC长是PC=( 14－ 2)cm
1。若过圆外一点P的切线与⊙O相切于T点，P与圆心O的
P A T
连线与圆交于A点，若PO=5，半径是4，求切线长PT。
O
B
2。如图，过点A作圆的两条割线分别交⊙O于B，C
和D，E。已知AD=4cm，DE=2cm，CE=5cm， AB=BC，求AB,BD。
E
D
A
B
C
1.切割线定理及其推论
2.切割线定理及其推论和相交线定理一样是相似三角形对应边成比例的另一种形
式。
3. 应用切割线定理和推论可以运用其乘积式和比例式关系进行问题的转化。
（1）如图⊙O1与⊙O2相交于A、B两点，P是
AB的延长线上的一点，过P点的割线分
P
别与⊙O1、⊙O2交于D、C；E，F。试判断PD•PC是否和PF•PE相等。为什么？

九年级数学相交弦定理和切割线定理知识精讲四年制试题

九年级数学相交弦定理和切割线定理知识精讲本卷贰O 贰贰年贰月捌日编写；出题人：令狐学复；欧阳化语；令狐理总。

一. 本周教学内容：相交弦定理和切割线定理二. 重点、难点：1. 相交弦定理的使用特征。

2. 切割线定理的使用特征。

[例1] 如图，AC=BD ，CE 、DF 切⊙O 于E 、F 两点，连EF ，求证：CM=MD 。

解：设TD=x ，即(43=⨯由切割线定理，BP AP PT ⋅=2 由勾股定理，222TD PT PD += ∴ 22TD BP AP PD +⋅= ∴ )7(6)4(22++=+y y y ∴ cm y 20=[例3] 两圆交于A 、AE=6，DE=2，求AC 解：连AB ，DF ∴ ∠1=∠C ∴ED AE EF CE =由相交弦定理得26⨯=ab ② 由①、②解得：4=b ，3=a 由切割线定理得：1441692=⨯=⋅=CF CB AC ∴ AC=12[例4] P 为弦AB 上一点，C 在圆O 上，OP ⊥PC ，求证：〔1〕PB PA PC ⋅=2〔2〕假设CM=MO=3，证明：〔1〕延长CP 交⊙O 于由相交弦定理，解：〔2〕易知21=PM 由相交弦定理，MN CM MB AM ⋅=⋅，即27)63(3)3(=+⨯=+y x ① 由垂径定理，CP=PD ，故在CPO Rt ∆中有2046222=-=PC ∴ 由〔1〕结论，20)3(=+y x ② 由①—②得：37+=x y 代②得，0203162=-+x x ∴ 0601632=-+x x ，6128±-=x 〔舍负〕[例5]解：设⊙O 半径为r ，DE=a ，延长BO 交⊙O 于K由相交弦定理，ED CE BE EK ⋅=⋅，故a r r 3)25)(25(=-+ ① 由AB 切⊙O 于B 知BE AB ⊥，故AD AC EB AE AB ⋅=-=222∴ )6(3)25(622a r +=-- ② 由②—①得：018522=--r r ，291=r ，22-=r 〔舍〕 ∴ 32)2529(6222=--=AB ，AB=24一. 选择题：1. 如图，PTA. PB ⋅C.PC PA =2. PA 切⊙O A. 223. PAB 为⊙ A. 324. 如图，PA 、PB 切⊙O 于A 、B ，AO 延长线与PB 延长线相交于C ，假设⊙O 半径为3，BC=4，那么=∠P cos 〔〕A.53 B. 43 C. 32 D. 21CP= cm2. 半径为5的⊙O内有点A，OA=2，过A点的弦CD恰被A点平分，那么AC= 。

切割线定理证明及例题

切割线定理定理切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

是圆幂定理的一种。

几何语言：∵PT切⊙O于点T，PBA是⊙O的割线∴PT的平方=PA·PB（切割线定理）推论：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等几何语言：∵PBA，PDC是⊙O的割线∴PD·PC=PA·PB（切割线定理推论）(割线定理）由上可知:PT的平方=PA·PB=PC·PD编辑本段证明切割线定理证明:设ABP是⊙O的一条割线，PT是⊙O的一条切线，切点为T，则PT²=PA·PB证明：连接AT, BT∵∠PTB=∠P AT(弦切角定理)∠P=∠P(公共角)∴△PBT∽△PTA(两角对应相等,两三角形相似)则PB：PT=PT：AP即：PT²=PB·PA编辑本段比较切割线定理与割线定理，相交弦定理统称为圆幂定理一. 教学内容：相交弦定理和切割线定理二. 重点、难点：1. 相交弦定理的使用特征。

2. 切割线定理的使用特征。

【典型例题】[例1] 已知P为⊙O内一点，，⊙O半径为，过P任作一弦AB，设，，则关于的函数关系式为。

解：由相交弦定理得，即，其中[例2] 如图，AC=BD，CE、DF切⊙O于E、F两点，连EF，求证：CM=MD。

证明：作DN∥EC，交MF于N，则∠1=∠2，∠C=∠4由弦切角定理得：∠3=∠1 ∴∠2=∠3 ∴DN=DF由切割线定理，∵AC=DB ∴CB=DA ∴ CE=DF∴CE=DN 又∵∠5=∠6 ∴（AAS）∴CM=MD[例3] 已知PT切⊙O于T，PBA为割线，交OC于D，CT为直径，若OC=BD=4cm，AD=3cm，求PB长。

解：设TD=，BP=，由相交弦定理得：即，（舍）由切割线定理，由勾股定理，∴∴∴[例4] 两圆交于A、B，AC、AD切两圆于A，交两圆于C、D，连CB，延长交AD于E，圆于F，若BC=9，AE=6，DE=2，求AC长。

相交弦定理、切割线定理、割线定理综合训练

12．如图，弦 AB 和弦 CD 相交于⊙O 内一点 E，AD=CB，求证：AB=CD．
13．如图，⊙O 直径 AB 和弦 CD 相交于点 E，AE=2，EB=6，∠DEB=30°，求弦 CD 长．
14．如图，中，弦与弦相交于点，且
．求证：
．
15．如图，⊙O 与割线 AC 交于点 B，C，割线 AD 过圆心 O，且∠DAC=30°．若⊙O 的半径 OB=5，AD=13，求弦 BC 的长．
8．如图，、是的割线，
，ห้องสมุดไป่ตู้
，
，则 ________．
9．如图，是的切线，为切点，是的割线，
，
，
则 ________ ．
三、解答题
10．如图，在半径为的中，直径与弦相交于点，
，
．
求的大小；
求弦的长．
11．如图，⊙O 直径 AB 和弦 CD 相交于点 E，AE=4，EB=8，∠DEB=30°，求弦 CD 长．
1．B 2．C 3．． 4．75°． 5． 6． 7． 8．9
9． 3 5
10．(1)
；(2)
11． CD 2 35
12．详见解析.
13． 2 15
14．详见解析. 15．6．
参考答案 .
相交弦定理、切割线定理、割线定理
一、单选题
1．如图，与的长为（）
切于点，是
的割线，如果
，那么
A． B．
C． D．
2．是长是（
外一点，切）
于，割线交
于点、，若
，则的
A． B． C．
D．
二、填空题
3．如图，半圆 O 的直径 AB=7，两弦 AC、BD 相交于点 E，弦 CD= ，且 BD=5，则 DE=_____．

切割线定理习题

切割线定理习题切割线定理回顾旧知：相交弦定理：对于一个圆，两条相交的弦，它们各自的线段长度的乘积相等。

探索发现：A。

当点P从圆内向圆外移动时，PA·PB=PC·PD不成立。

证明：考虑当P在圆上时，PA·PB=PC·PD成立，但当P向圆外移动时，___增大而PB减小，PC减小而PD增大，因此PA·PB和PC·PD不再相等。

练：1.PC=4解析：根据相交弦定理，PA·PB=PC·PD，代入已知量得5×3=4×PD，解得PD=15/4，因此PC=PD+DC=15/4+3=27/4.2.圆O的面积=48π解析：根据切线长度公式，PT^2=PA·PB，代入已知量得PT=2√15，因此圆O的半径r=PA+PT=4+2√15，面积S=πr^2=48π。

3.证明PC·PD=PE·PF解析：根据相交弦定理，PA·PB=PC·PD，PE·PF=PA·PB，因此PC·PD=PE·PF。

巩固加深：1.C解析：根据相交弦定理，PA·PB=PC·PD，代入已知量得AB=15/4.2.A解析：根据相交弦定理，PA·PB=PC·PD，代入已知量得⊙O的半径r=8.3.C解析：根据相交弦定理，PA·PB=PC·PD，代入已知量得AE=5，因此PE=PA+AE=9.4.C解析：根据相交弦定理，AN·NB=QN·NM，代入已知量得AN=1/4，NP=1-AN=3/4.5.A解析：根据相交弦定理，PA·PB=PC·PD，代入已知量得CD=6.6.B解析：根据切线长度公式，PA^2=PO·PB，代入已知量得⊙O的半径r=10.7.A解析：根据相交弦定理，PC·PD=PE^2，代入已知量得PE=6.8.B解析：根据相交弦定理，CE·AE=BE·DE。

培训学习资料-切割线定理-2023年学习资料

例2如图，A是圆O上的一点，过点A的切线交直径-CB的延长线于点P,AD⊥BC,D为垂足。-求证：-PB O-PD PC-证明：-连结OA-PA切圆O于A->-OA⊥PA-≥-PD.PO=PA2-0-ADLPCA切圆O于APBPC=PA2-今>-PB.PC=PD.PO
1。若过圆外一点P的切线与⊙0相切于T点，P与圆心0的-连线与圆交于A点，若P0=5,半径是4，求切线长P 。-B-综用
例1如图过圆外一点P作两条割线，分别交⊙O于A、B和C、D.再作⊙O-切线PE,E为切点，连结CE、DE. 知AB=3cm,PA=2cm,CD=4cm-2设CE=a,试用含a的代数式表示DE-解：-由弦切角定理，得 CEP=∠D-又.∠CPE=∠EPD,∴.△CPE△EPD-DE PD-10-,PD=Pc+cD=V14+42+V14m-DE2+V14V10+V35-/10-DB=号0+v35
从圆外一点引圆的切线和割线，切线长-切割线定理-是这点到割线与圆的交点的两条线段-长的比例中项-PT切⊙O TPT2=PBPA-由切割线定理-PT2=PDPC;-从而得到-PBPA=PD+PC-从圆外一点引圆的两条 -推论-线，这一点到每条割线与圆-0-的交点的两条线段长的积-相等.
想-你能想出其它的办法来证-明切割线定理的推论吗？-B-D-C-A
判断题-如图所示，PT切⊙0于T。下面的判断是否正确-1PT2=PE.PD-A/C-2PA.PB=PE.P -3PAAB=PE·EDX-4PT2=PC.PO
在上题中，若PO=5,r=2,你能求出-PA和PB的积吗？-分析：-延长PO交⊙O于D-A/-C-PC=P -C0=5-2=3-PD=PO+OD=5+2=7-PA.PB=PC.PD=21-尽专

圆切割线定理与相交弦定理练习题

2021年中考数学必考点培优系列 18 圆与相似：相交线定理、切割线定理(有答案)

相交弦.切割线练习题汇编

切线长定理、弦切角定理、切割线定理、相交弦定理

切线长定理、弦切角定理、切割线定理、相交弦定理93336

相交弦定理、切割线定理、割线定理综合训练(最新整理)

切割线定理习题

中考数学复习相交弦定理切割线定理2课件

九年级数学相交弦定理和切割线定理知识精讲 四年制 试题

切割线定理

《弦切角定理》《圆幂定理》练习题及答案

九年级数学切割线定理

相交弦.切割线练习题

九年级数学切割线定理

切割线定理

九年级数学相交弦定理和切割线定理知识精讲 四年制 试题

切割线定理证明及例题

相交弦定理、切割线定理、割线定理综合训练

切割线定理习题

培训学习资料-切割线定理-2023年学习资料

九年级数学相交弦定理和切割线定理知识精讲四年制试题

九年级数学相交弦定理和切割线定理知识精讲四年制试题