大地坐标与空间直角坐标转换_C程序
坐标转换从经纬度坐标到大地坐标及源码

坐标转换从经纬度坐标到大地坐标及源码坐标转换是指将一个坐标系下的点的坐标转换为另一个坐标系下的点的坐标。
在地理空间领域,经纬度坐标(也称为地理坐标)和大地坐标是两个常用的坐标系。
经纬度坐标是地理坐标系中用来表示地球表面上其中一点位置的一种方式。
它使用经度和纬度两个数值来确定一个点的位置。
经度表示点与地球质心之间的角度差,范围为-180°到180°,其中0°表示位于本初子午线上,东经为正,西经为负。
纬度表示点与地球赤道间的角度差,范围为-90°到90°,南纬为负,北纬为正。
大地坐标(也称为投影坐标)是将地球表面的球面坐标映射到平面上的坐标系。
大地坐标系使用X、Y坐标来表示一个点的位置,其中X轴通常表示东西方向,Y轴通常表示南北方向。
接下来,我们将提供一种经纬度坐标到大地坐标的转换方法以及相关源码。
方法一:使用Python编程语言在Python中,我们可以使用Pyproj库来进行经纬度坐标到大地坐标的转换。
下面是一个示例代码,展示了如何使用该库进行转换:```pythonimport pyprojdef latlon_to_utm(lat, lon):#定义转换器utm_x, utm_y = transformer.transform(lon, lat)return utm_x, utm_y#测试lat = 39.9087 # 纬度值lon = 116.3975 # 经度值utm_x, utm_y = latlon_to_utm(lat, lon)print("UTM坐标: X =", utm_x, "Y =", utm_y)```方法二:使用JavaScript编程语言在JavaScript中,我们可以使用proj4js库来进行经纬度坐标到大地坐标的转换。
下面是一个示例代码,展示了如何使用该库进行转换:```javascriptvar proj4 = require('proj4');function latlon_to_utm(lat, lon)//定义转换器var source = '+proj=longlat +datum=WGS84 +no_defs';var target = '+proj=utm +zone=50 +datum=WGS84 +units=m+no_defs';var utm = proj4(source, target, [lon, lat]);return {x: utm[0], y: utm[1]};//测试var lat = 39.9087; // 纬度值var lon = 116.3975; // 经度值var utm = latlon_to_utm(lat, lon);console.log("UTM坐标: X =", utm.x, "Y =", utm.y);```在上述代码中,我们使用proj4库来定义转换器并进行转换。
大地坐标及直角空间坐标转换计算公式

大地坐标与直角空间坐标转换计算公式一、参心大地坐标与参心空间直角坐标转换1名词解释:A :参心空间直角坐标系:a) 以参心0为坐标原点;b) Z 轴与参考椭球的短轴(旋转轴)相重合;c) X 轴与起始子午面和赤道的交线重合;d) Y 轴在赤道面上与X 轴垂直.构成右手直角坐标系0-XYZ ;e) 地面点P 的点位用(X.Y.Z )表示;B :参心大地坐标系:a) 以参考椭球的中心为坐标原点.椭球的短轴与参考椭球旋转轴重合;b) 大地纬度B :以过地面点的椭球法线与椭球赤道面的夹角为大地纬度B ;c) 大地经度L :以过地面点的椭球子午面与起始子午面之间的夹角为大地经度L ;d) 大地高H :地面点沿椭球法线至椭球面的距离为大地高H ;e) 地面点的点位用(B.L.H )表示。
2 参心大地坐标转换为参心空间直角坐标:⎪⎭⎪⎬⎫+-=+=+=B H e N Z L B H N Y L B H N X sin *])1(*[sin *cos *)(cos *cos *)(2公式中.N 为椭球面卯酉圈的曲率半径.e 为椭球的第一偏心率.a 、b 椭球的长短半径.f 椭球扁率.W 为第一辅助系数ab a e 22-= 或 ff e 1*2-= Wa N B W e =-=22sin *1( XX80椭球参数:长半轴a=6378140±5(m )短半轴b=6356755.2882m扁 率α=1/298.2573 参心空间直角坐标转换参心大地坐标 []N BY X H H e N Y X H N Z B XY L -+=+-++==cos ))1(**)()(*arctan()arctan(22222 二 高斯投影及高斯直角坐标系1、高斯投影概述高斯-克吕格投影的条件:1. 是正形投影;2. 中央子午线不变形高斯投影的性质:1. 投影后角度不变;2. 长度比与点位有关.与方向无关;3. 离中央子午线越远变形越大为控制投影后的长度变形.采用分带投影的方法。
大地测量控制点坐标转换技术规程

近似表示地球的形状和大小,并且其表面为等位面的旋 转椭球。 3.3 参考椭球 reference ellipsoid 最符合一定区域的大地水准面,具有一定大小和定位参 数的旋转地球椭球。 3.4 国 际 地 球 参 考 系 统 Reference System,ITRS 由国际地球自转服务(IERS)给出的地球 International Terrestrial Reference Frame,ITRF 国际地球参考系统(ITRS)的实现。由国际地球自转服 务局(IERS)根据空间大地测量技术,包括甚长基线干涉测 量(VLBI) 、卫星激光测距(SLR) 、多里斯系统(DORIS) 、 全球定位系统(GPS)等,所确定的地面点的坐标所构成的 集合。 3.6 大地坐标系 geodetic coordinate system 以地球椭球中心为原点、起始子午面和赤道面为基准面 的地球坐标系。 3.7 1954 年 北 京 坐 标 系 Beijing Geodetic Coordinate System 1954 将我国大地控制网与苏联 1942 普尔科沃大地坐标系联 结后建立的我国过渡性大地坐标系。 International Terrestrial
大地测量控制点坐标转换技术规程
1 范围
本规程规定了各种坐标系控制点坐标转换到 2000 国家 大地坐标系时控制点选取、坐标转换模型、转换方法、精度 评价等方面应遵循的原则、适用范围和精度要求。 本规程适用于大地测量控制点坐标转换过程中的重合 点选取、模型选择和转换方法。 2 规范性引用文件 下列文件对于本文件的应用是必不可少的。凡是注日期 的引用文件,仅注日期的版本适用于本文件。凡是不注日期 的引用文件,其最新版本(包括所有的修改单)适用于本文 件。 GB/T 17159-2009 GB/T 18314-2009 GB/T 19391-2003 GB/T 22021-2008 GB/T 28588 - 2012 站网技术规范 CH/T 1004-2005 2010(第三版) 3 术语和定义 下列术语和定义适用于本文件。 3.1 控制点 control point 以一定精度测定其位置为其他测绘工作提供依据的固 定点。 3.2 地球椭球 earth ellipsoid 测绘技术设计规定 测绘学名词 大地测量术语 全球定位系统(GPS)测量规范 全球定位系统(GPS)术语及定义 国家大地测量基本技术规定 全球导航卫星系统连续运行基准
坐标转换中的大地坐标系与空间直角坐标系转换公式

坐标转换中的大地坐标系与空间直角坐标系转换公式在测量与地理信息领域,坐标转换是一个非常重要的概念。
它涉及将不同坐标系下的位置互相转换,使得地理空间信息能够得到准确而一致地表达。
而在坐标转换的过程中,大地坐标系与空间直角坐标系的相互转换公式则是至关重要的工具。
大地坐标系是一种常用的坐标系,在地理测量和导航等领域广泛应用。
它采用了经纬度和大地高作为坐标参数,可以精确地描述地球上任意一点的位置。
经度表示东西方向上的位置,纬度表示南北方向上的位置,而大地高则表示相对于海平面的高度。
在大地坐标系下,地球被近似看作一个椭球体,因此大地坐标系也被称为椭球坐标系。
然而,由于大地坐标系的曲线性质,它并不适合直接参与复杂三维计算,尤其是在工程测量中需要使用的情况。
因此,我们需要将大地坐标系转换为空间直角坐标系,以便进行进一步的计算和分析。
空间直角坐标系采用了直角坐标的表示方式,其坐标参数分别为X、Y、Z,可以方便地进行几何运算。
在进行坐标转换时,我们需要采用适当的公式来实现大地坐标系到空间直角坐标系的转换。
下面将介绍两种常用的转换公式。
1. 大地坐标系到空间直角坐标系的转换公式大地坐标系到空间直角坐标系的转换公式可以通过三个连续的旋转和平移变换来实现。
具体而言,我们首先将大地坐标系的原点O与空间直角坐标系原点重合,然后进行三次坐标轴的旋转,使得大地坐标系的纬度线与空间直角坐标系的Z轴重合。
接着,我们对大地坐标系进行一个小角度的旋转,使得大地纬线与空间直角坐标系的Y轴重合。
最后,再进行一个小角度的旋转,将大地经线与空间直角坐标系的X轴重合。
通过以上步骤,即可完成大地坐标系到空间直角坐标系的转换。
2. 空间直角坐标系到大地坐标系的转换公式与大地坐标系到空间直角坐标系的转换相反,空间直角坐标系到大地坐标系的转换需要进行三次逆变换。
即首先将空间直角坐标系的原点与大地坐标系原点重合,然后进行三次逆变换,回到大地坐标系。
为了实现空间直角坐标系到大地坐标系的转换,我们需要利用解析几何的知识。
坐标转换源代码--GPS定位程序(C--)

坐标转换源代码--GPS定位程序(C++)GPS数据处理中为了满足不同的需要,处理的数据要进行坐标转换,得到在不同坐标系统下的结果,下面是笛卡尔坐标系,大地坐标系,站心地平坐标系(线型和极坐标形式)之间的转换源代码:头文件:#ifndef _COORDCOVERT_H#define _COORDCOVERT_H#include "stdlib.h"//WGS-84椭球体参数const double a=6378137.0;//长半轴const double flattening=1/298.257223563;//扁率const double delta=0.0000001;typedef struct tagCRDCARTESIAN{double x;double y;double z;}CRDCARTESIAN;typedef CRDCARTESIAN *PCRDCARTESIAN;//笛卡尔坐标系typedef struct tagCRDGEODETIC{double longitude;double latitude;double height;}CRDGEODETIC;typedef CRDGEODETIC *PCRDGEODETIC;//大地坐标系typedef struct tagCRDTOPOCENTRIC{double northing;double easting;double upping;}CRDTOPOCENTRIC;typedef CRDTOPOCENTRIC *PCRDTOPOCENTRIC; //站心地平坐标系(线坐标形式)typedef struct tagCRDTOPOCENTRICPOLAR{ double range;double azimuth;double elevation;}CRDTOPOCENTRICPOLAR;typedef CRDTOPOCENTRICPOLAR *PCRDTOPOCENTRICPOLAR;//站心地平坐标系(极坐标形式)//由笛卡尔坐标转换为大地坐标void CartesianToGeodetic (PCRDGEODETIC pcg, PCRDCARTESIAN pcc, double dSemiMajorAxis, double dFlattening);//pcg:指向所转换出的大地坐标的指针;//pcc:指向待转换的笛卡尔坐标的指针;//dSemiMajorAxis:参考椭球的长半轴;//dFlattening:参考椭球的扁率。
大地坐标转换c代码

以下是一个大地坐标转换的C代码示例,它可以将经度、纬度和高程转换为笛卡尔坐标系中的x、y和z坐标。
```c#include <stdio.h>#include <math.h>#define RADIUS_EARTH 6371000.0 // 地球半径,单位为米void cartesian_coords(double longitude, double latitude, double height, double *x, double *y, double *z) {double r = RADIUS_EARTH + height; // 计算半径double sin_lat = sin(latitude * M_PI / 180.0);double cos_lat = cos(latitude * M_PI / 180.0);double sin_lon = sin(longitude * M_PI / 180.0);double cos_lon = cos(longitude * M_PI / 180.0);*x = r * cos_lon * cos_lat;*y = r * sin_lon * cos_lat;*z = r * sin_lat;}int main() {double longitude = 120.0; // 经度double latitude = 30.0; // 纬度double height = 0.0; // 高程,单位为米double x, y, z; // 笛卡尔坐标系中的x、y和z坐标cartesian_coords(longitude, latitude, height, &x, &y, &z);printf("经度:%lf\n", longitude);printf("纬度:%lf\n", latitude);printf("高程:%lf\n", height);printf("x坐标:%lf\n", x);printf("y坐标:%lf\n", y);printf("z坐标:%lf\n", z);return 0;}```该代码使用了地球半径和球面三角学公式将大地坐标转换为笛卡尔坐标系中的x、y和z坐标。
大地测量问答1111

⼤地测量问答1111考试题⽬类型名词解释简答题问答题计算题计算题内容1、ITRF框架转换2、⾼斯投影(换带计算,中央⼦午线计算)3、⽔准,⽅向观测的记录与计算4、概略⾼程计算(P324)1、⼤地测量学?答:在⼀定的时间与空姐参考系中,测量喝描绘地球形状及其重⼒场并监测其变化,为⼈类活动提供关于地球的空间信息的⼀门学科。
2、⼤地测量分类?答:分为常规(经典)⼤地测量和现代⼤地测量。
常规⼤地测量:应⽤⼤地测量学;椭球⼤地测量学;天⽂⼤地测量学;重⼒⼤地测量学;测量平差。
现代⼤地测量:⼏何⼤地测量学;物理⼤地测量学;空间⼤地测量学。
3、⼤地测量的发展经历了哪⼏个阶段?答:第⼀阶段:地球圆球阶段;主要是弧度测量第⼆阶段:地球椭球阶段;⾸创三⾓测量法;创⽴⽇⼼说;开普勒发表⾏星三⼤定律;伽利略进⾏第⼀次重⼒测量,⽜顿提出地球特征:两极扁平的旋转椭球,重⼒加速度由⾚道向两极成⽐例增加。
长度单位的建⽴;最⼩⼆乘法的提出;椭球⼤地测量学的形成解决了椭球数学性质,椭球⾯上测量计算,以及将椭球⾯投影到平⾯的正投影法;弧度测量⼤规模展开;推算了不同的地球椭球参数;第三阶段:⼤地⽔准⾯阶段;天⽂⼤地⽹的布设有了重⼤发展;铟⽡基线尺出现;提出新的椭球参数第四阶段:现代⼤地测量新时期;各国各⾃的⼤规模⽔准⽹建⽴;有些国家建⽴⾃⼰的⾼精度重⼒⽹,⼤地控制⽹优化设计理论和最⼩⼆乘配置法的提出和应⽤。
4、主要的空间⼤地测量技术包括哪些?5、天球?春分点?⼦午⾯?⼦午圈?岁差?章动?极移?答:天球:以地球质⼼为中⼼,半径为⽆穷⼤的假想球体。
春分点:当太阳在黄道上从天球南半球向北半球运⾏时,黄道与天球⾚道的交点。
⼦午⾯:包含天轴并通过地球上任意⼀点的平⾯⼦午圈:⼦午⾯与天球相交的⼤圆岁差:由于⽇⽉等天体的影响,地球的旋转轴在空间围绕黄极发⽣缓慢旋转,其锥⾓等于黄⾚交⾓23.5°,旋转周期为26000年,这种运动叫岁差。
章动:由于⽉球轨道相对于黄道有倾斜,使得⽉球引⼒产⽣的转矩的⼤⼩和⽅向不断变化,导致地球旋转轴在岁差的基础上叠加18.6年的短周期圆周运动,振幅为9.21″极移:地球⾃转轴存在着相对于地球体⾃⾝内部结构的相对位置变化,导致极点在地球表⾯的位置随时间⽽变化,这种现象叫极移6、恒星时?平太阳时?世界时?真太阳时?回归年?原⼦时?协调世界时?答:恒星时:以春分点作为基本参考点,由春分点周⽇视运动确定的时间叫恒星时。
高斯正反算及空间直角坐标与大地地理坐标转换

高斯正反算及空间直角坐标与大地地理坐标转换一、实验目的与要求1.对以上理论内容的验证与应用。
2.通过学习掌握测绘软件开发过程与方法,初步具备测绘软件开发基本技能。
3.熟练掌握Visual C++编程环境的使用,了解其特点与程序开发过程,掌软件调试、测试的技术方法。
4.分析测绘程序设计技术课程中相关软件的结构和模块功能,掌握结构化程序设计方法和技术,掌握测绘数据处理问题的基本特点。
5.开发相关程序功能模块,独立完成相关问题概念结构分析、程序结构设计、模块设计、代码编写、调试、测试等工作。
二、实验安排1.实验时数12学时。
2.每实验小组可以由3~4人组成,或独立完成。
若由几个人完成程序设计,应进行合理的分工。
三、实验步骤和要点1.熟悉程序设计任务书的基本内容,调查了解软件需求状况,进行需求分析;2.进行总体设计。
根据所调查收集的资料和任务书的要求,对系统的硬件资源进行初步设计,提出硬件配置计划;进行软件总体设计,设计出软件程序功能的模块;3.根据总体设计的结果,进行详细设计,进行数据存储格式设计、算法等,写出逻辑代码;4.编写程序代码,调试运行;5.程序试运行。
最后同学们可根据自己的选题,写出软件开发设计书一份,打印程序代码和运行结果。
四实验原理高斯正反算:高斯正反算包括两部分内容:高斯正算和高斯反算。
简单的说就是大地地理坐标系坐标(B,L)与其对应的高斯平面直角坐标系坐标(x,y)之间的转换。
若已知大地地理坐标系坐标(B,L)解求对应的高斯平面直角坐标系坐标(x,y)称为高斯正算;反之,则为高斯反算。
空间直角坐标与大地地理坐标转换:地球表面可用一个椭球面表示。
设空间直角坐标系为OXYZ,当椭球的中心与空间直角坐标系原点重合,空间坐标系Z 轴与地球旋转重合(北极方向为正),X 轴正向经度为零时,就可以确定空间直角坐标系与大地地理坐标系的数学关系。
⎪⎩⎪⎨⎧+-=+=+=B H e N Z LB H N Y L B H N X sin ])1([sin cos )(cos cos )(2 式中 N 为卯酉圈曲率半径,B e a N 22sin 1-=; e 为椭球偏心率,222a b a e -=(a ,b 为椭球长半轴和短半轴)。
大地坐标与空间直角坐标的转换程序代码

#include "stdio、h"#include "math、h"#include "stdlib、h"#include "iostream"#define PI 3、14323double a,b,c,e2,ep2;int main(){int m,n,t;double RAD(double d,double f,double m);void RBD(double hd);void BLH_XYZ();void XYZ_BLH();void B_ZS();void B_FS();void GUS_ZS();void GUS_FS();printf(" 大地测量学\n");sp1:printf("请选择功能:\n");printf("1、大地坐标系到大地空间直角坐标的转换\n");printf("2、大地空间直角坐标到大地坐标系的转换\n");printf("3、贝塞尔大地问题正算\n");printf("4、贝塞尔大地问题反算\n");printf("5、高斯投影正算\n");printf("6、高斯投影反算\n");printf("0、退出程序\n");scanf("%d",&m);if(m==0)exit(0);sp2:printf("请选择椭球参数(输入椭球序号):\n");printf("1、克拉索夫斯基椭球参数\n");printf("2、IUGG_1975椭球参数\n");printf("3、CGCS_2000椭球参数\n");printf("0、其她椭球参数(自行输入)\n");scanf("%d",&n);switch(n){case 1:a=6378245、0;b=6356863、0188;c=6399698、9018;e2=0、297;ep2=0、468;break;case 2:a=6378140、0;b=6356755、2882;c=6399596、6520;e2=0、959;ep2=0、947;break;case 3:a=6378137、0;b=6356752、3141;c=6399593、6259;e2=0、290;ep2=0、547;break;case 0:{printf("请输入椭球参数:\n");printf("长半径a=");scanf("%lf",&a);printf("短半径b=");scanf("%lf",&b);c=a*a/b;ep2=(a*a-b*b)/(b*b);e2=(a*a-b*b)/(a*a);break;}default:printf("\n\n输入错误!\n请重新输入!\n\n");goto sp2 ;}while(1){switch(m){case 1:BLH_XYZ();break;case 2:XYZ_BLH();break;case 3:B_ZS();break;case 4:B_FS();break;case 5:GUS_ZS();break;case 6:GUS_FS();break;default:printf("\n\n输入错误!\n请重新输入!\n\n");goto sp1 ;}printf("就是否继续进行此功能计算? \n\n");printf("( 若继续进行此功能计算,则输入1;\n 若选择其她功能进行计算,则输入2;\n 若退出, 则输入0、)\n");scanf("%d",&t);switch(t){case 1:break;case 2:goto sp1;case 0:exit(0);}}}double RAD(double d,double f,double m) {double e;double sign=(d<0、0)?-1、0:1、0;if(d==0){sign=(f<0、0)?-1、0:1、0;if(f==0){sign=(m<0、0)?-1、0:1、0;}}if(d<0)d=d*(-1、0);if(f<0)f=f*(-1、0);if(m<0)m=m*(-1、0);e=sign*(d*3600+f*60+m)*PI/(3600*180);return e;}void RBD(double hd){int t;int d,f;double m;double sign=(hd<0、0)?-1、0:1、0;if(hd<0)hd=fabs(hd);hd=hd*3600*180/PI;t=int(hd/3600);d=sign*t;hd=hd-t*3600;f=int(hd/60);m=hd-f*60;printf("%d'%d'%lf'\n",d,f,m);}void BLH_XYZ(){double B,L,H,N,W;double d,f,m;double X,Y,Z;printf(" 请输入大地坐标(输入格式为角度(例如:30'40'50')):\n");printf(" 大地经度L=");scanf("%lf'%lf'%lf'",&d,&f,&m);L=RAD(d,f,m);printf(" 大地纬度B=");scanf("%lf'%lf'%lf'",&d,&f,&m);B=RAD(d,f,m);printf(" 大地高H=");scanf("%lf",&H);W=sqrt(1-e2*sin(B)*sin(B));N=a/W;X=(N+H)*cos(B)*cos(L);Y=(N+H)*cos(B)*sin(L);Z=(N*(1-e2)+H)*sin(B);printf("\n\n 转换后得到大地空间直角坐标为:\n\n");printf("X=%lf\nY=%lf\nZ=%lf\n\n",X,Y,Z);}void XYZ_BLH(){double B,L,H,N,W;double X,Y,Z;double tgB0,tgB1;printf(" 请输入大地空间直角坐标:\n");printf(" X=");scanf("%lf",&X);printf(" Y=");scanf("%lf",&Y);printf(" Z=");scanf("%lf",&Z);printf("\n\n 转换后得到大地坐标为:\n\n");L=atan(Y/X);printf(" 大地经度为: L=");RBD(L);printf("\n");tgB0=Z/sqrt(X*X+Y*Y);tgB1=(1/sqrt(X*X+Y*Y))*(Z+a*e2*tgB0/sqrt(1+tgB0*tgB0-e2*tgB0*tgB0));while(fabs(tgB0-tgB1)>5*pow(10,-10)){tgB0=tgB1;tgB1=(1/sqrt(X*X+Y*Y))*(Z+a*e2*tgB0/sqrt(1+tgB0*tgB0-e2*tgB0*tgB0));}B=atan(tgB1);printf(" 大地纬度为:B=");RBD(B);printf("\n");W=sqrt(1-e2*sin(B)*sin(B));N=a/W;H=sqrt(X*X+Y*Y)/cos(B)-N;printf(" 大地高为:H=%lf\n\n",H);}void B_ZS(){double L1,B1,A1,s,d,f,mi;double u1,u2,m,M,k2,alfa,bt,r,kp2,alfap,btp,rp;double sgm0,sgm1,lmd,lmd1,lmd2,A2,B2,l,L2;printf("请输入已知点的大地坐标(输入格式为角度(例如:30'40'50'),下同):\nL1=");scanf("%lf'%lf'%lf'",&d,&f,&mi);L1=RAD(d,f,mi);printf("\nB1=");scanf("%lf'%lf'%lf'",&d,&f,&mi);B1=RAD(d,f,mi);printf("请输入大地方位角:\nA1=");scanf("%lf'%lf'%lf'",&d,&f,&mi);A1=RAD(d,f,mi);printf("请输入该点至另一点的大地线长:\ns=");scanf("%lf",&s);u1=atan(sqrt(1-e2)*tan(B1));m=asin(cos(u1)*sin(A1));M=atan(tan(u1)/cos(A1));m=(m>0)?m:m+2*PI;M=(M>0)?M:M+PI;k2=ep2*cos(m)*cos(m);alfa=(1-k2/4+7*k2*k2/64-15*k2*k2*k2/256)/b;bt=k2/4-k2*k2/8+37*k2*k2*k2/512;r=k2*k2/128-k2*k2*k2/128;sgm0=alfa*s;sgm1=alfa*s+bt*sin(sgm0)*cos(2*M+sgm0)+r*sin(2*sgm0)*cos(4*M+2*sgm0); while(fabs(sgm0-sgm1)>2、8*PI/180*pow(10,-7)){sgm0=sgm1;sgm1=alfa*s+bt*sin(sgm0)*cos(2*M+sgm0)+r*sin(2*sgm0)*cos(4*M+2*sgm0); }sgm0=sgm1;A2=atan(tan(m)/cos(M+sgm0));A2=(A2>0)?A2:A2+PI;A2=(A1>PI)?A2:A2+PI;u2=atan(-cos(A2)*tan(M+sgm0));lmd1=atan(sin(u1)*tan(A1));lmd1=(lmd1>0)?lmd1:lmd1+PI;lmd1=(m<PI)?lmd1:lmd1+PI;lmd2=atan(sin(u2)*tan(A2));lmd2=(lmd2>0)?lmd2:lmd2+PI;lmd2=(m<PI)?(((M+sgm0)<PI)?lmd2:lmd2+PI):(((M+sgm0)>PI)?lmd2:lmd2+PI);lmd=lmd2-lmd1;B2=atan(sqrt(1+ep2)*tan(u2));kp2=e2*cos(m)*cos(m);alfap=(e2/2+e2*e2/8+e2*e2*e2/16)-e2/16*(1+e2)*kp2+3*e2*kp2*kp2/128;btp=e2*(1+e2)*kp2/16-e2*kp2*kp2/32;rp=e2*kp2*kp2/256;l=lmd-sin(m)*(alfap*sgm0+btp*sin(sgm0)*cos(2*M+sgm0)+rp*sin(2*sgm0)*cos(4*M+2*sg m0));L2=L1+l;printf("\n\n得到另一点的大地坐标与大地线在该点的大地方位角为:\n\n");printf("L2=");RBD(L2);printf("\n");printf("B2=");RBD(B2);printf("\n");printf("A2=");RBD(A2);printf("\n");}void B_FS(){double L1,B1,L2,B2,s,A1,A2,du,f,mi,m0,m,M;double l,u1,u2,alfa,bt,r,lmd0,dit_lmd,lmd,sgm,dit_sgm,sgm0,sgm1,alfap,btp,rp,k2,kp2;printf("请输入第一个点大地坐标(输入格式为角度(例如:30'40'50'),下同):\n大地经度L1=");scanf("%lf'%lf'%lf'",&du,&f,&mi);L1=RAD(du,f,mi);printf("大地纬度B1=");scanf("%lf'%lf'%lf'",&du,&f,&mi);B1=RAD(du,f,mi);printf("\n请输入第二个点大地坐标:\n大地经度:L2=");scanf("%lf'%lf'%lf'",&du,&f,&mi);L2=RAD(du,f,mi);printf("大地纬度:B2=");scanf("%lf'%lf'%lf'",&du,&f,&mi);B2=RAD(du,f,mi);l=L2-L1;u1=atan(sqrt(1-e2)*tan(B1));u2=atan(sqrt(1-e2)*tan(B2));sgm0=acos(sin(u1)*sin(u2)+cos(u1)*cos(u2)*cos(l));m0=asin(cos(u1)*cos(u2)*sin(l)/sin(sgm0));dit_lmd=0、003351831*sgm0*sin(m0);lmd0=l+dit_lmd;dit_sgm=sin(m0)*dit_lmd;sgm1=sgm0+dit_sgm;m=asin(cos(u1)*cos(u2)*sin(lmd0)/sin(sgm1));A1=atan(sin(lmd0)/(cos(u1)*tan(u2)-sin(u1)*cos(lmd0)));A1=(A1>0)?A1:A1+PI;A1=(m>0)?A1:A1+PI;M=atan(sin(u1)*tan(A1)/sin(m));M=(M>0)?M:M+PI;k2=ep2*cos(m)*cos(m);alfa=(1-k2/4+7*k2*k2/64-15*k2*k2*k2/256)/b;bt=k2/4-k2*k2/8+37*k2*k2*k2/512;r=k2*k2/128-k2*k2*k2/128;kp2=e2*cos(m)*cos(m);alfap=(e2/2+e2*e2/8+e2*e2*e2/16)-e2/16*(1+e2)*kp2+3*e2*kp2*kp2/128;btp=e2*(1+e2)*kp2/16-e2*kp2*kp2/32;rp=e2*kp2*kp2/256;sgm0=acos(sin(u1)*sin(u2)+cos(u1)*cos(u2)*cos(l));sgm1=acos(sin(u1)*sin(u2)+cos(u1)*cos(u2)*cos(l+sin(m)*(alfap*sgm0+btp*sin(sgm0)*cos( 2*M+sgm0))));while(fabs(sgm0-sgm1)>1*PI/180*pow(10,-8)){sgm0=sgm1;sgm1=acos(sin(u1)*sin(u2)+cos(u1)*cos(u2)*cos(l+sin(m)*(alfap*sgm0+btp*sin(sgm0)*cos( 2*M+sgm0))));}sgm=sgm1;lmd=l+sin(m)*(alfap*sgm+btp*sin(sgm)*cos(2*M+sgm));s=(sgm-bt*sin(sgm)*cos(2*M+sgm)-r*sin(2*sgm)*cos(4*M+2*sgm))/alfa;A1=atan(sin(lmd)/(cos(u1)*tan(u2)-sin(u1)*cos(lmd)));A1=(A1>0)?A1:A1+PI;A1=(m>0)?A1:A1+PI;A2=atan(sin(lmd)/(sin(u2)*cos(lmd)-tan(u1)*cos(u2)));A2=(A2>0)?A2:A2+PI;A2=(m<0)?A2:A2+PI;printf("\n\n得到两点间大地线长S与大地正反方位角A1、A2如下:\n\n");printf("s=%lf\n",s);printf("A1=");RBD(A1);printf("\n");printf("A2=");RBD(A2);printf("\n");}void GUS_ZS(){double B,L,x3,x6,y3,y6,Y3,Y6,du,f,mi,X,N,n,t;double At,Bt,Ct,Dt,m3,m6,l3,l6,W,L03,L06;int DH3,DH6;printf("请输入大地坐标(输入格式为角度(例如:30'40'50')):\n大地经度L=");scanf("%lf'%lf'%lf'",&du,&f,&mi);L=RAD(du,f,mi);printf("\n大地纬度B=");scanf("%lf'%lf'%lf'",&du,&f,&mi);B=RAD(du,f,mi);At=1+3*e2/4+45*e2*e2/64+175*e2*e2*e2/256;Bt=3*e2/4+15*e2*e2/16+525*e2*e2*e2/512;Ct=15*e2*e2/64+105*e2*e2*e2/256;Dt=35*e2*e2*e2/512;X=a*(1-e2)*(At*B-Bt*sin(2*B)/2+Ct*sin(4*B)/4-Dt*sin(6*B)/6);W=sqrt(1-e2*sin(B)*sin(B));N=a/W;n=sqrt(ep2)*cos(B);t=tan(B);DH3=(L-(1、5*PI/180))/(3*PI/180)+1;DH6=L/(6*PI/180)+1;L03=DH3*(3*PI/180);L06=DH6*(6*PI/180)-(3*PI/180);l3=L-L03;l6=L-L06;m3=cos(B)*l3;m6=cos(B)*l6;x3=X+N*t*(m3*m3/2+(5-t*t+9*n*n+4*n*n*n*n)*m3*m3*m3*m3/24+(61-58*t*t+t*t*t*t)* m3*m3*m3*m3*m3*m3/720);x6=X+N*t*(m6*m6/2+(5-t*t+9*n*n+4*n*n*n*n)*m6*m6*m6*m6/24+(61-58*t*t+t*t*t*t)* m6*m6*m6*m6*m6*m6/720);y3=N*(m3+(1-t*t+n*n)*m3*m3*m3/6+(5-18*t*t+t*t*t*t+14*n*n-58*n*n*t*t)*m3*m3*m3 *m3*m3/120);y6=N*(m6+(1-t*t+n*n)*m6*m6*m6/6+(5-18*t*t+t*t*t*t+14*n*n-58*n*n*t*t)*m6*m6*m6 *m6*m6/120);Y3=DH3*1000000+500000+y3;Y6=DH6*1000000+500000+y6;printf("\n\n 得到的高斯平面坐标为:\n\n");printf(" 对于3度带:\n 纵坐标x=%、3lf\n 横坐标y=%、3lf(通用坐标Y=%、3lf)\n\n",x3,y3,Y3);printf(" 对于6度带:\n 纵坐标x=%、3lf\n 横坐标y=%、3lf(通用坐标Y=%、3lf)\n\n",x6,y6,Y6);}void GUS_FS(){double x,y,Y,B,B0,B1,Bf,Vf,tf,Nf,nf,L,At,Bt,Ct,Dt,L3,L6;long DH;printf(" 请输入高斯平面坐标:\n\n");printf(" 纵坐标X=");scanf("%lf",&x);printf("\n");printf(" 自然坐标y=");scanf("%lf",&y);printf("\n");printf(" 通用坐标Y=");scanf("%lf",&Y);printf("\n");At=1+3*e2/4+45*e2*e2/64+175*e2*e2*e2/256;Bt=3*e2/4+15*e2*e2/16+525*e2*e2*e2/512;Ct=15*e2*e2/64+105*e2*e2*e2/256;Dt=35*e2*e2*e2/512;B0=x/(a*(1-e2)*At);B1=(x-a*(1-e2)*(-Bt*sin(2*B0)/2+Ct*sin(4*B0)/4-Dt*sin(6*B0)/6))/(a*(1-e2)*At);while(fabs(B1-B0)>1*pow(10,-8)){B0=B1;B1=(x-a*(1-e2)*(-Bt*sin(2*B0)/2+Ct*sin(4*B0)/4-Dt*sin(6*B0)/6))/(a*(1-e2)*At);}Bf=B1;nf=sqrt(ep2)*cos(Bf);tf=tan(Bf);Vf=sqrt(1+ep2*cos(Bf)*cos(Bf));Nf=c/Vf;B=Bf-Vf*Vf*tf/2*((y/Nf)*(y/Nf)-(5+3*tf*tf+nf*nf-9*nf*nf*tf*tf)*pow((y/Nf),4)/12+(61+90*tf *tf+45*tf*tf)*pow((y/Nf),6)/360);L=((y/Nf)-(1+2*tf*tf+nf*nf)*(y/Nf)*(y/Nf)*(y/Nf)/6+(5+28*tf*tf+24*pow(tf,4)+6*nf*nf+8*nf *nf*tf*tf)*pow((y/Nf),5)/120)/cos(Bf);DH=Y/1000000;L3=3*PI/180*double(DH)+L;L6=6*PI/180*double(DH)-3*PI/180+L;printf("\n\n 得到的大地坐标为:\n\n");printf(" 大地纬度B=");RBD(B);printf("\n");printf(" 若为6度带,大地经度L=");RBD(L6);printf("\n");printf(" 若为3度带,大地经度L=");RBD(L3);printf("\n"); }。
空间大地坐标系与平面直角坐标系转换公式

§坐标系的分类正如前方所说起的 ,所谓坐标系指的是描绘空间地点的表达形式 ,即采纳什么方法来表示空间地点。
人们为了描绘空间地点,采纳了多种方法,进而也产生了不一样的坐标系,如直角坐标系、极坐标系等。
在丈量中常用的坐标系有以下几种:一、空间直角坐标系空间直角坐标系的坐标系原点位于参照椭球的中心,Z 轴指向参照椭球的北极,X 轴指向开端子午面与赤道的交点,Y 轴位于赤道面上且按右手系与X 轴呈 90°夹角。
某点在空间中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
空间直角坐标系可用图2-3来表示:图 2-3 空间直角坐标系二、空间大地坐标系空间大地坐标系是采纳大地经、纬度和大地高来描绘空间地点的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角;经度是空间中的点与参照椭球的自转轴所在的面与参照椭球的开端子午面的夹角;大地高是空间点沿参照椭球的法线方向到参照椭球面的距离。
空间大地坐标系可用图2-4 来表示:图 2-4 空间大地坐标系三、平面直角坐标系平面直角坐标系是利用投影变换,将空间坐标空间直角坐标或空间大地坐标经过某种数学变换映照到平面上,这类变换又称为投影变换。
投影变换的方法有好多,如横轴墨卡托投影、 UTM 投影、兰勃特投影等。
在我国采纳的是高斯-克吕格投影也称为高斯投影。
UTM 投影和高斯投影都是横轴墨卡托投影的特例,不过投影的个别参数不一样而已。
高斯投影是一种横轴、椭圆柱面、等角投影。
从几何意义上讲,是一种横轴椭圆柱正切投影。
如图左边所示,假想有一个椭圆柱面横套在椭球外面,并与某一子午线相切(此子午线称为中央子午线或轴子午线),椭球轴的中心轴CC’经过椭球中心而与地轴垂直。
高斯投影知足以下两个条件:1、它是正形投影;2、中央子午线投影后应为x 轴,且长度保持不变。
将中央子午线东西各必定经差(一般为 6 度或 3 度)范围内的地域投影到椭圆柱面上,再将此柱面沿某一棱线睁开,便组成了高斯平面直角坐标系,以以下图2-5右边所示。
CGCS2000国家大地坐标系换算程序的设计

季刊
第 1 4卷
21 0 2年第 2期
技术 交流 5 3
C C 20 G S 0 0国家大地 坐标 系换算程序 的设计
杨 战辉 ’ 蒙晓 锋 ’ 刘念 (. 1国家 测绘 地理 信 息局 第一 航测 遥 感 院 陕西 西安
2 国家 测绘 地理 信 息局第 一 地 形测量 队 陕西 西安 .
( B 1 9 9 9 )中没 有规 定 ,程序 中定义 ,1: 0 0 G/ 3 8— 2 2 0
比例 尺 图是 1: 00地 形 图为 基础 , 50 按经 差 3 . 、 75 按纬 差 2 分幅 ,图幅编 号 以 l: 0 0地形 图编 号 5 50
● - 。_ 逝
I ’膏熄
害
害
嘉
嘉
芸
未
鑫
I l
盏
害
1 1 ● ●● 。
霉
I I H m
譬
-
兽
| I
算
"
8
”
-
蚕 夏 至 耍 i 至 至 重 量 i 夏 至
[】 江宽 ,龚小鹏 . o g e A I开发 详解 :G o l a s与 G o i a t 5 G o l P ogeMp o g e E rh双剑合璧 【】 北 京:电子工业 出版 社,2 0 ,1 M. 08 .
【 oge 6 o 官方 h : Q . g !Q 旦 ]G l 望 g 塑
在 我 国 国 民经 济 、社 会 发 展和 科 学 研 究 中 发挥 了重 的图采 用 3 。分 带 。 要 作用 。但 由于采 用 这 些 坐标 系得 到 的成 果精 度 偏 从格 林 尼 治 0起 ,每 隔 3或 6 划 一 带 ,按 高斯 。 。 。
大地坐标与空间直角坐标转换

大地坐标与空间直角坐标转换在地理空间相关的领域中,大地坐标和空间直角坐标是两种常用的坐标系统。
大地坐标通常用经度和纬度表示,是为了描述地球表面上的点的位置而设计的坐标系统;而空间直角坐标则是一种常用的三维笛卡尔坐标系,用来描述平面内的点的位置。
在实际应用中,有时候我们需要将一个点从大地坐标系转换到空间直角坐标系,或者反过来进行转换,这就需要进行一定的坐标转换计算。
大地坐标的表示大地坐标通常是以经度(Longitude)和纬度(Latitude)表示的。
经度表示东西方向,是一个0到360度的值,通常以东经为正值,西经为负值。
纬度表示南北方向,是一个-90到90度的值,赤道为0度,南纬为负值,北纬为正值。
空间直角坐标的表示空间直角坐标是以直角坐标系表示的,通常是三维笛卡尔坐标系,包括X、Y和Z三个坐标轴。
X轴和Y轴在平面内垂直,Z轴垂直于平面,组成一个右手坐标系。
一个点在空间直角坐标系中的位置可以由其X、Y和Z坐标值表示。
大地坐标与空间直角坐标的转换大地坐标和空间直角坐标之间的转换涉及到地球的椭球面和大地水准面的关系,通常需要考虑椭球体参数、大地水准面的高度等因素。
实际转换过程中可能涉及到大圆距离、球面三角计算等复杂的数学运算。
结论大地坐标与空间直角坐标之间的转换是地理信息处理中一个重要的问题,通常需要借助专业的地理信息系统软件或者编程语言进行计算。
在进行坐标转换时,需要考虑到地球的椭球体特征以及大地水准面的高度影响,以确保转换的准确性。
对于从事地理测绘、地图制作、地理信息系统等领域的人员,熟练掌握大地坐标与空间直角坐标之间的转换方法是非常重要的。
以上就是关于大地坐标与空间直角坐标转换的一些内容,希望对您有所帮助。
BJS54测绘成果到CGCS2000的转换方法应用

汉),长期从事空间数据处理工作。
・38・
万方数据
ConVersion
Method
and Application from BJS54 SurVeying and Results to CGCS2000
Mapping
TAN Qing-hua,ZENG Xiang-xin,ZHANG Ren (j、k行行i,lg E|户ZDrnfiD甩&S“,一z,ey J疗sf础“£F,N口砣行i以g
引
言
1954北京坐标系(BJS54)在我国经济和国防 建设中发挥了重要作用,但随着时代的进步,它们 已不能适应测绘以及相关产业发展的需要。根据 《中华人民共和国测绘法》,我国自2008年7月1 日起,启用2000国家大地坐标系。如何充分利用 已有的基于BJS54的测绘成果,保持BJS54与 CGCS2000的前后兼容,是测绘工作者要经常面对 的一个问题。分析讨论了一种将已有BJS54测绘 成果转换到CGCS2000的方法。
O.053744458127766848一O.15943147148936987 0.094216924393549562—0.10488546098349616
从以上数据可以看出,在BJS54下大地高初 值为O或100时,内外中误差均在6 cm左右,完全 能满足精度要求。
[3]刘基余.GPs卫星导航定位原理与方法[M].北京;科 学出版社,2003,374—421. [4]柳光魁,赵永强,张守忱,杜明成.北京54和西安80 坐标系转换方法及精度分析口].测绘与空间地理信
BJS54测绘成果到CGCS2000的 转换方法应用
谭清华,曾祥新,张任
(南宁市勘测院,广西南宁530000)
摘
要:2000中国大地坐标系(CGCS2000)是我国新启用的地心坐标系。讨论了如何将
利用EXCEL实现空间直角坐标与大地坐标间的转换
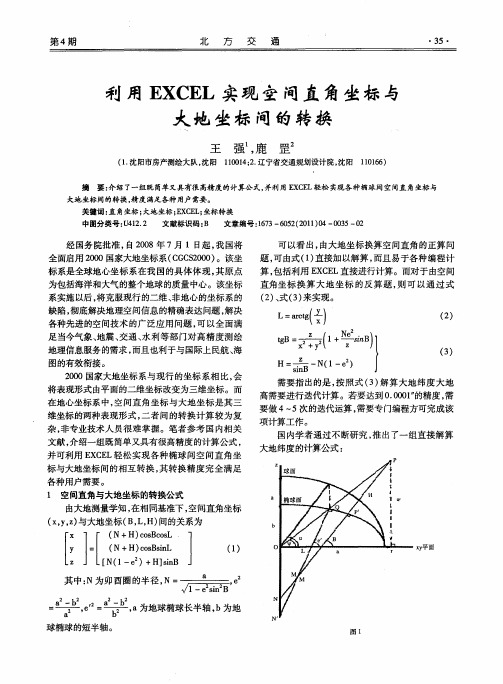
大地纬度 B 转换度分秒方法与 L 同, 相 在此不 做累述。表 1 为空间直角坐标与大地坐标的正反算 ( 反算) 有关参数 , 2为某两点的具体计算示例。 表
表 1 空间直角坐标 与大地坐标 的正反算 ( 反算 ) 有关参数
点名 x
已知数 据空 间直角坐标 Y z 经度 L ” ( )
u与 B 的转换 关 系 , 得到 Байду номын сангаас. 为 的更
需要指 出的是 , 出的 L和 B均为 度 的十进 求 制, 通常使用度分秒形式来表示经纬度 , 以需要将 所 十进制度的形式转换 为度分秒形式 , L为例 , 以 其 转换 过程 为 : 利用 E C L中的 T U C函数 , XE RN 首先将度 的整 数部分求 出: 在相应的单元格 内用 T U C L 算 0 R N ( 计 ,) 表示 即可 完成 。 然后 将 不 足整 数 的十进 制 度 化 为分 的形 式 , 同 样在 相应 的单元 格 内用 【 计 L 算一T U C( 计 0 ]X R N L 算,) 6 将计算结果对应 的单元格记为 L 。 O, 进一步将不足分 的部分化为秒 , 在相应 的单元 格内用【 T U C L ,) × 0 , L 一 R N ( 】 6” 0 将计算结果对应 的单 元格 记为 L, , 。 最终将三部分合并起来 , 即在相应 的单 元格 内
rM = e2acos3U
P ,
M= 一e b i P 2 sn U ,
rM
= e =e
2acos3u
() 7
Q
即可求 出大 地经度 L 并 保证 其为正 值 。利 用式 , (O , 1 ) 可首先计算出辅助角 , 然后利用式 ( ) 8 或式( ) 9 即可求出大地纬度 B 通过 B进而求出大地高 H。 , 大地高除可利用式 ( ) 3 求得 以外 , 可通过严 还 密公式 ( 1 求得 。 1)
MATLAB实验大地坐标与空间直角坐标的换算程序设计(经典)

min=fix((du-degree)*60); second=(((du-degree)*60-min)*60); B=degree+min/100+second/10000; end
3、实例计算验证 首先将文件 data1.txt 中大地坐标转换为空间直角坐标, 并将转换后的数据按照格 式存贮在文件 data2.txt 中, data1.txt 格式为: data2.txt 格式为: x test 程序如下:
function [x, y, z] = geo2xyz (L, B, h) a=6378137; %椭球长半轴 f=1/298.257223563; %椭球扁率 b=a*(1-f); %求椭球短半轴 e=sqrt(a^2-b^2)/a; %椭球第一偏心率 N=a./sqrt(1-(e^2)*(sin(B)).^2); % 卯酉圈曲率半径 %大地坐标换算为空间直角坐标 x、 y、z x=(N+h).*cos(B).*cos(L); y=(N+h).*cos(B).*sin(L); z=[N.*(1-e^2)+h].*sin(B); end 度分秒转化为弧度函数如下: function azimuth=dms2rad(dms)%度分秒转弧度函数
大地坐标系与空间直角坐标系的相互转换公式

大地坐标系与空间直角坐标系的相互转换公式概述大地坐标系和空间直角坐标系是地理信息系统中两种常用的坐标系。
大地坐标系主要用于描述地球上点的位置,而空间直角坐标系则是使用笛卡尔坐标系的三维空间中的坐标来表示点的位置。
在地理信息系统中,需要经常进行大地坐标系和空间直角坐标系之间的转换,以便在不同的坐标系统之间进行数据交互和分析。
大地坐标系大地坐标系是一种基于地球椭球体的坐标系统,常用来描述地球上点的位置。
一般采用经度(longitude)、纬度(latitude)和高程(elevation)来表示点在地球表面的位置。
经度表示点在东经或西经的位置,纬度表示点在北纬或南纬的位置,高程表示点相对于海平面的高度。
大地坐标系中经度的表示方式有多种,常见的有度分秒制和十进制制。
而纬度则一般用度制表示。
对于高程的表示方式,通常使用米作为单位。
空间直角坐标系空间直角坐标系是使用笛卡尔坐标系的三维空间中的坐标来表示点的位置。
在空间直角坐标系中,每个点的位置由三个数值组成,分别表示点在X轴、Y轴和Z轴方向上的位置。
这三个数值通常以米为单位。
空间直角坐标系中的原点可以选择任意位置,常见的有地心、地心地固、地心地独立三种坐标系。
地心坐标系以地球质心为原点,地心地固坐标系以地球上某一固定点为原点,地心地独立坐标系则是相对于地轴的一个旋转坐标系。
大地坐标系到空间直角坐标系的转换将大地坐标系中的点转换为空间直角坐标系中的点需要使用转换公式。
常用的转换方法有大地测量学和地心测量学两种。
### 大地测量学方法大地测量学方法中,将地球近似为椭球体,利用椭球体的形状参数和点的大地坐标来进行转换。
该方法的核心思想是通过计算点在曲线面上的法线方向,将大地坐标系的点转换为空间直角坐标系的点。
### 地心测量学方法地心测量学方法中,将地球近似为球体,并以地球质心或地球上某一固定点为原点。
该方法利用球面三角学的原理,根据点的经纬度和高程来进行转换。
北京54坐标与WGS84坐标转换说明

坐标转换程序说明COOD坐标转换4.2版,无需安装,直接运行即可使用,可以实现、空间直角坐标、大地坐标、平面坐标的七参数或四参数转换。
下面以北京1954坐标系(中央子午线经度123°)平面坐标转换为施工工程坐标系(GWS84椭球,中央子午线经度121-44-05,投影大地高40m)坐标为例,说明四参数平面坐标转换的具体步骤。
1、运行COOD坐标转换程序,程序界面如下图所示:2、计算转换参数单击“坐标转换”下拉菜单,单击“计算四参数”或者在键盘上直接输入字母“C”,进入参数计算,如图2所示:输入坐标转换重合点的源坐标和目标坐标,输入一个点的源坐标和目标坐标后,单击“增加”,然后依次输入下一个重合点的源坐标和目标坐标,一般四参数转换应输入至少3个重合点的坐标,以便对检核参数计算的正确性,也可提高转换精度,最后单击“计算”。
则显示计算结果如下图:随后弹出地方坐标转换参数,如下图:单击“确定”,此时四参数计算完成,软件自动将计算的参数作为当前值,并将参数计算结果保存在名为FourResult的文本文件中,查看COOD坐标转换程序的当前目录,找到FourResult文本文件查看转换误差,该例计算结果如下图:若转换后中误差过大,说明输入的重合点有误,或者重合点误差较大,应重新选择合适的重合点计算转换参数。
确认转换参数无误后,然后单击文件菜单,保存转换项目,例如保存为“54北京坐标系与84施工坐标系转换”。
2、坐标转换首先设置坐标类型和转换参数的类型,源坐标坐标类型为平面坐标,椭球基准为北京-54坐标系,目标坐标类型为平面坐标,椭球基准为WGS-84坐标系,坐标转换参数勾选“四参数转换”如下图所示:(1)单点坐标转换设置好坐标类型和转换参数的类型后,直接在对话框中输入一个控制点的源坐标,单击右侧的“转换坐标”按纽,则在右侧“输出目标坐标”框内显示转换后的坐标值,如下图所示:(2)文件转换对于少量的坐标可以通过单点转换来实现,但是对于批量坐标的转换就应采用文件转换实现比较方便。
空间直角坐标系与大地坐标系转换程序

空间直角坐标系与大地坐标系转换程序#include<iostream>#include<cmath>#include<iomanip>using namespace std;#define PI (2.0*asin(1.0))void main(){ double a,b,c,d1,d2,f1,f2,m1,m2,B,L,H,X,Y,Z,W,N,e;//cout<<"请分别输入椭球的长半轴、短半轴(国际单位)"<<endl;//cin>>a>>b;a=6378137; //以WGS84为例b=6356752.3142;e=sqrt(a*a-b*b)/a;c=a*a/b;int x;cout<<"请输入0或1,0:大地坐标系到空间直角坐标系;1:空间直角坐标系到大地坐标系"<<endl;cin>>x;switch(x){case 0:{cout<<"请分别输入该点大地纬度、经度、大地高(国际单位,纬度经度请按度分秒,分别输入)"<<endl;cin>>d1>>f1>>m1>>d2>>f2>>m2>>H;B=PI*(d1+f1/60+m1/3600)/180;L=PI*(d2+f2/60+m2/3600)/180;W=sqrt(1-e*e*sin(B)*sin(B));N=a/W;X=(N+H)*cos(B)*cos(L);Y=(N+H)*cos(B)*sin(L);Z=(N*(1-e*e)+H)*sin(B);cout<<"空间直角坐标系中X,Y,Z,坐标值(国际单位)分别为"<<fixed<<setprecision(6)<<X<<" "<<fixed<<setprecision(6)<<Y<<" "<<fixed<<setprecision(6)<<Z<<endl;break;}case 1:{cout<<"请分别输入空间直角坐标系中X,Y,Z的值(国际单位)"<<endl;cin>>X>>Y>>Z;double t,m,n, P,k,B0;m=Z/sqrt(X*X+Y*Y); //t0B0=atan(m); //初值n=Z/sqrt(X*X+Y*Y);P=c*e*e/sqrt(X*X+Y*Y);k=1+(a*a-b*b)/(b*b);t=m+P*n/sqrt(k+n*n); //现在为t1,之后代替t2,t3...B=atan(t);W=sqrt(1-e*e*sin(B)*sin(B));N=a/W;H=Z/sin(B) - N*(1-e*e);int i;for(i=1;fabs(B-B0)>10E-10;i++)//每一次新的B与上一次计算的B比较,误差小于10E-10 rad {B0=B;n=t;t=m+P*n/sqrt(k+n*n);//迭代B=atan(t);}W=sqrt(1-e*e*sin(B)*sin(B));N=a/W;//if((X<0)&(Y>0))//L=atan(Y/X)+PI;//if((X<0)&(Y<0))// L=atan(Y/X)+PI;// if((X>0)&(Y<0))//L=2*PI-atan(Y/X);L=atan2(Y,X);H=sqrt(X*X+Y*Y)/cos(B)-N;int Bd,Bf,Ld,Lf;double Bm,Lm;B=180*B/PI;//B转化为度做单位Bd=B;Bf=(B-Bd)*60;Bm=((B-Bd)*60-Bf)*60;L=180*L/PI;//L转化为度做单位Ld=L;Lf=(L-Ld)*60;Lm=((L-Ld)*60-Lf)*60;cout<<"大地坐标系中纬度,经度,大地高(国际单位)分别为"<<Bd<<" "<<Bf<<" "<<fixed<<setprecision(6)<<Bm<<endl<<Ld<<" "<<Lf<<" "<<fixed<<setprecision(6)<<Lm<<endl<<fixed<<setprecision(6)<<H<<endl;break;}}}运行结果。
《GPS原理及其应用》习题集a答案

《GPS原理及其应用》习题集a答案子午卫星系统的缺点该系统卫星数目少,运行高度低,从地面站观测到卫星的时间间隔长,因而不能进行三维连续导航。
加之获得一次导航所需要的时间较长,所以难以充分满足军事导航的要求,从大地测量的角度来看,由于它的定位速度慢,精度较低,因此,该系统在大地测量学和动力学研究方面受到了极大限制。
GPS的基本组成卫星星座,地面控制与监控站,用户设备3个部分什么是标准定位服务?提供C/A码(又称粗码)民用SPS定位服务GPS信号接收机主要组成主要由接收机硬件、数据处理软件以及微处理机及其终端设备组成(硬件包括主机、天线、电源。
软件部分主要是对数据处理的软件)子午卫星系统与GPS定位原理有何区别?子午卫星系统是根据多普勒效应原理进行接收定位的,而GPS定位则是以后方交汇原理进行测量。
名词解释:天球:是指以地球质心为中心、以无穷大为半径的一个假象球体。
赤经:含天轴和春分点r的天球子午面与过空间点s的天球子午面之间的夹角。
赤纬:为原点O至空间点S与天球赤道面之间的夹角。
黄道:地球绕太阳公转的轨道面与天球相交的平面称为黄道面,相交的大圆称为黄道。
春分点:黄道与天球赤道有两个交点,其中太阳的视位置由南向北通过赤道的交点为春分点。
岁差:地球在太阳、月亮的万有引力和其他天体引力对地球隆起的部分的作用,地球自转轴方向不再保持不变,这使得春分点在黄道上产生缓慢的西移现象,这种现象称为岁差。
章动:由于月球轨道和月地距离不断变化,地球自转轴所产生的一系列短周期变化被统称为章动极移:由于地球内部质量不均匀的影响,地球自转轴相对于地球体位置随时间而变化的现象世界时:以平子夜为零时起算的格林尼治平太阳时。
原子时:原子时秒长:位于海平面上的C133原子基态有2个超精细能级,在零磁场中跃迁辐射振荡9192631770周所持续的时间为1原子时秒。
而原子时的原点由式AT=UT2-0.0039()来确定,UT2为经过改正的世界时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
scanf("%lf",&y);
printf("请输入Z:\n");
scanf("%lf",&z);
l=atan2(y,x);
do{m=(z+a1*e*e*g/sqrt(1+g*g-e*e*g*g))/sqrt(x*x+y*y);
m1=atan(m);
b=HD(a,b1,c);
printf("请输入H:\n");
scanf("%lf",&h);
w=sqrt((1-e*e*sin(b)*sin(b)));
n=a1/w;
x=(n+h)*cos(b)*cos(l);
y=(n+h)*cos(b)*sin(l);
z=(n*(1-e*e)+h)*sin(b);
void lbhxyz(double a1,double e)
{double l,b,h,x,y,z,a,b1,c,n,w;
printf("请输入L:\n");
scanf("%lf%lf%lf",&a,&b1,&c);
l=HD(a,b1,c);
printf("请输入B:\n");
scanf("%lf%lf%lf",&a,&b1,&c);
e=sqrt(e2);
if (b==1)lbhxyz(a1,e);
else if(b==2)xyzlbh(a1,e);}
main()
{int a=1;
do{DY(a);
printf("继续使用请按1,结束使用请按0\n");
scanf("%d",&a);}
while(a);
}
b=atan(m);
w=sqrt(1-e*e*sin(b)*sin(b));
n=a1/w;
h=sqrt(x*x+y*y)/cos(b)-n;
JD(l,&l1,&l2,&l3);
JD(b,&b1,&b2,&b3);
printf("L=%d°%d'%2.6f''\nB=%d°%d'%2.6f''\nH=%5.6fm\n",l1,l2,l3,b1,b2,b3,h);}
scanf("%d",&c);
if (c==1){a1=6378245.0000,e2=0.00669342162297;}
else if (c==2){a1=6378140.0000,e2=0.00669438499959;}
else if (c==3){a1=6378137.0000,e2=0.00669438002290;};
void DY(int a)
{double a1,e,e2;int b,c;
printf("请选择:L,B,H→X,Y,Z(请输入1) 或 X,Y,Z→L,B,H(请输入2)\n");
scanf("%d",&b);
printf("请选择参考椭球面:\n克拉索夫斯基椭球(请输入1) \n或 IUGG 1975椭球(请输入2) \n或 CGCS 2000椭球(请输入3)\n");
printf("X=%f\nY=%f\nZ=%f\n",x,y,z);}
void xyzlbh(double a1,double e)
{double l,b,h,x,y,z,n,w,m,g,m1,g1,l3,b3;int l1,l2,b1,b2;
printf("请输入X:\n");
scanf("%lf& d,int *d1,int *d2,double *d3)
{d=d/3.1415926535897932384626433832795*180;
*d1=(int)d;
*d2=(int)((d-*d1)*60);
*d3=((d-*d1)*60-*d2)*60;}
#include <stdio.h>
#include <math.h>
double HD(double a,double b,double c)
{b=b+c/60;
a=a+b/60;
a=a/180*3.1415926535897932384626433832795;
return a;}
g1=atan(g);
m1=m1/3.1415926535897932384626433832795*180*3600;
g1=g1/3.1415926535897932384626433832795*180*3600;
g=m;}
while(sqrt((m1-g1)*(m1-g1))>0.0001);
