空间大地直角坐标系及其转换模型
大地坐标及直角空间坐标转换计算公式
大地坐标与直角空间坐标转换计算公式一、参心大地坐标与参心空间直角坐标转换1名词解释：A ：参心空间直角坐标系：a) 以参心0为坐标原点；b) Z 轴与参考椭球的短轴（旋转轴）相重合；c) X 轴与起始子午面和赤道的交线重合；d) Y 轴在赤道面上与X 轴垂直.构成右手直角坐标系0-XYZ ；e) 地面点P 的点位用（X.Y.Z ）表示；B ：参心大地坐标系：a) 以参考椭球的中心为坐标原点.椭球的短轴与参考椭球旋转轴重合；b) 大地纬度B ：以过地面点的椭球法线与椭球赤道面的夹角为大地纬度B ；c) 大地经度L ：以过地面点的椭球子午面与起始子午面之间的夹角为大地经度L ；d) 大地高H ：地面点沿椭球法线至椭球面的距离为大地高H ；e) 地面点的点位用（B.L.H ）表示。
2 参心大地坐标转换为参心空间直角坐标：⎪⎭⎪⎬⎫+-=+=+=B H e N Z L B H N Y L B H N X sin *])1(*[sin *cos *)(cos *cos *)(2公式中.N 为椭球面卯酉圈的曲率半径.e 为椭球的第一偏心率.a 、b 椭球的长短半径.f 椭球扁率.W 为第一辅助系数ab a e 22-= 或 ff e 1*2-= Wa N B W e =-=22sin *1( XX80椭球参数：长半轴a=6378140±5（m ）短半轴b=6356755.2882m扁 率α=1/298.2573 参心空间直角坐标转换参心大地坐标 []N BY X H H e N Y X H N Z B XY L -+=+-++==cos ))1(**)()(*arctan()arctan(22222 二 高斯投影及高斯直角坐标系1、高斯投影概述高斯-克吕格投影的条件：1. 是正形投影；2. 中央子午线不变形高斯投影的性质：1. 投影后角度不变；2. 长度比与点位有关.与方向无关；3. 离中央子午线越远变形越大为控制投影后的长度变形.采用分带投影的方法。
坐标转换中的大地坐标系与空间直角坐标系转换公式
坐标转换中的大地坐标系与空间直角坐标系转换公式在测量与地理信息领域，坐标转换是一个非常重要的概念。
它涉及将不同坐标系下的位置互相转换，使得地理空间信息能够得到准确而一致地表达。
而在坐标转换的过程中，大地坐标系与空间直角坐标系的相互转换公式则是至关重要的工具。
大地坐标系是一种常用的坐标系，在地理测量和导航等领域广泛应用。
它采用了经纬度和大地高作为坐标参数，可以精确地描述地球上任意一点的位置。
经度表示东西方向上的位置，纬度表示南北方向上的位置，而大地高则表示相对于海平面的高度。
在大地坐标系下，地球被近似看作一个椭球体，因此大地坐标系也被称为椭球坐标系。
然而，由于大地坐标系的曲线性质，它并不适合直接参与复杂三维计算，尤其是在工程测量中需要使用的情况。
因此，我们需要将大地坐标系转换为空间直角坐标系，以便进行进一步的计算和分析。
空间直角坐标系采用了直角坐标的表示方式，其坐标参数分别为X、Y、Z，可以方便地进行几何运算。
在进行坐标转换时，我们需要采用适当的公式来实现大地坐标系到空间直角坐标系的转换。
下面将介绍两种常用的转换公式。
1. 大地坐标系到空间直角坐标系的转换公式大地坐标系到空间直角坐标系的转换公式可以通过三个连续的旋转和平移变换来实现。
具体而言，我们首先将大地坐标系的原点O与空间直角坐标系原点重合，然后进行三次坐标轴的旋转，使得大地坐标系的纬度线与空间直角坐标系的Z轴重合。
接着，我们对大地坐标系进行一个小角度的旋转，使得大地纬线与空间直角坐标系的Y轴重合。
最后，再进行一个小角度的旋转，将大地经线与空间直角坐标系的X轴重合。
通过以上步骤，即可完成大地坐标系到空间直角坐标系的转换。
2. 空间直角坐标系到大地坐标系的转换公式与大地坐标系到空间直角坐标系的转换相反，空间直角坐标系到大地坐标系的转换需要进行三次逆变换。
即首先将空间直角坐标系的原点与大地坐标系原点重合，然后进行三次逆变换，回到大地坐标系。
为了实现空间直角坐标系到大地坐标系的转换，我们需要利用解析几何的知识。
空间大地坐标系与平面直角坐标系转换公式
空间大地坐标系与平面直角坐标系转换公式空间大地坐标系和平面直角坐标系是两种不同的坐标系统，用于描述地球上的点的位置。
在进行空间大地坐标系与平面直角坐标系之间的转换时，需要考虑到地球的椭球体形状和投影方式。
下面将详细介绍空间大地坐标系与平面直角坐标系的转换方法。
1.空间大地坐标系经度：经度是指地球上特定点与本初子午线之间的角度差，用度、分、秒的形式表示。
纬度：纬度是指地球上特定点距离赤道的角度，用度、分、秒的形式表示。
大地高：大地高是指地球表面特定点到参考椭球体上其中一参考面的高度差，可分为正高和负高。
2.平面直角坐标系平面直角坐标系是以地球上一些基准点为原点建立的二维坐标系。
在平面直角坐标系下，点的位置通常用东方向坐标值X和北方向坐标值Y来表示。
3.空间大地坐标系到平面直角坐标系的转换公式3.1平面直角投影平面直角投影是将地球表面上的点投影到一个水平的平面上。
其转换公式为：X = k₀ + R * cosL * sin(λ - λ₀)Y = k₀ + R * (cosφ₀ * sinL - sinφ₀ * cosL * cos(λ - λ₀))其中，X和Y为平面直角坐标系下的坐标值，L为参考点与待转换点的经度差，λ为待转换点的经度，φ₀为参考点的纬度，λ₀为参考点的经度，k₀为常数，R为参考点到地心的距离。
3.2高斯投影高斯投影是将地球上的点投影到一个平面上，使得该平面上的距离尽可能与大地距离一致。
其转换公式为：X = X₀ + N * cosB * (λ - L₀)Y = Y₀ + N * (tanB * cos(λ - L₀) - sinB * (B - B₀))其中，X和Y为平面直角坐标系下的坐标值，X₀和Y₀为参考点的平面坐标，N为法向子午线长度，B为待转换点的纬度，λ为待转换点的经度，L₀为参考点的经度，B₀为参考点的纬度。
4.平面直角坐标系到空间大地坐标系的转换公式平面直角坐标系到空间大地坐标系的转换公式为空间大地坐标系到平面直角坐标系的逆运算，可以通过解方程组或迭代法来进行计算。
空间大地坐标系及平面直角坐标系转换公式
§2.3.1 坐标系的分类正如前面所提及的,所谓坐标系指的是描述空间位置的表达形式,即采用什么方法来表示空间位置。
人们为了描述空间位置，采用了多种方法，从而也产生了不同的坐标系，如直角坐标系、极坐标系等。
在测量中常用的坐标系有以下几种：一、空间直角坐标系空间直角坐标系的坐标系原点位于参考椭球的中心，Z 轴指向参考椭球的北极，X 轴指向起始子午面与赤道的交点，Y 轴位于赤道面上且按右手系与X 轴呈90°夹角。
某点在空间中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
空间直角坐标系可用图2-3来表示：图2-3 空间直角坐标系二、空间大地坐标系空间大地坐标系是采用大地经、纬度和大地高来描述空间位置的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角；经度是空间中的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角；大地高是空间点沿参考椭球的法线方向到参考椭球面的距离。
空间大地坐标系可用图2-4来表示：图2-4空间大地坐标系三、平面直角坐标系平面直角坐标系是利用投影变换，将空间坐标空间直角坐标或空间大地坐标通过某种数学变换映射到平面上，这种变换又称为投影变换。
投影变换的方法有很多，如横轴墨卡托投影、UTM 投影、兰勃特投影等。
在我XX 用的是高斯-克吕格投影也称为高斯投影。
UTM 投影和高斯投影都是横轴墨卡托投影的特例，只是投影的个别参数不同而已。
高斯投影是一种横轴、椭圆柱面、等角投影。
从几何意义上讲，是一种横轴椭圆柱正切投影。
如图左侧所示，设想有一个椭圆柱面横套在椭球外面，并与某一子午线相切〔此子午线称为中央子午线或轴子午线〕，椭球轴的中心轴CC ’通过椭球中心而与地轴垂直。
高斯投影满足以下两个条件：1、 它是正形投影；2、 中央子午线投影后应为x 轴，且长度保持不变。
将中央子午线东西各一定经差〔一般为6度或3度〕X 围内的地区投影到椭圆柱面上，再将此柱面沿某一棱线展开，便构成了高斯平面直角坐标系，如以下图２－５右侧所示。
常用坐标系之间的关系与转换
7.5 常用坐标系之间的关系与转换一、大地坐标系和空间大地直角坐标系及其关系大地坐标系用大地纬度企丈地经度L 和丈地髙H 来表示点的位置°这种坐标系是经 典大地测量甬:両用座标紊7屜据地图投影的理论,大地坐标系可以通过一定的投影转 化为投影平面上的直角坐标系，为地形测图和工程测量提供控制基础。
同时，这种坐标系 还是研究地球形状和大小的 种有用坐标系°所以大地坐标系在大地测量中始终有着重要 的作用.空间大地直角坐标系是-种以地球质心为原点购亘墮®坐标系，一般用X 、化Z 表 示点BSSTSTT 逐碇SS 範菇飞両H 绕禎扭转冻其轨道平面随时通过 地球质心。
对它们的跟踪观测也以地球质心为坐标原点，所以空间大地直角坐标系是卫星 大地测量中一种常用的基本坐标系。
现今，利用卫星大地测量的手段*可以迅速地测定点的空间大地直角坐拯，广泛应用于导航定位等空间技术。
同时经过数学变换，还可求岀点 的大地坐标I 用以加强和扩展地面大地网，进行岛屿和洲际联测，使传统的大地测量方法 发生了深刻的变化，所以空间大地宜角坐标系对现今大地测量的发展’具有重要的意义。
、大地坐标系和空间大地直角坐标系的转换如图7- 23所示’尸点的位置用空间 大地直角坐标〔X, Y, Z)表示，其相应 的大地坐标为(E, L)a 将该图与图？一5上式表明了 2种基本坐标系之间的关系。
加以比较可见，图7-5中的子午椭圆平面 相当于图7-23中的OJVP 平面.其中 PPz=Z.相当于图7-5中的j7；OP 3相当 丫于图7-5中的仏两平面的经度乙可视为相同，等于"叽 于是可以直接写岀X=jrcQsi f Y=jrsinL, Z=y将式(7-21).式(7-20)分别代入上式, 井考虑式(7-26)得X=Ncos^cosZr ”Y =NcQsBsinL > (7—78)Z=N (1—护〉sin^ ；BB 7-231.由大地坐标求空间大地直角坐标当已知椭球面上任一点P 的大地坐标(B, L)时，可以按式(7-78)直接求该点的 空间大地直角坐标(X, Y, Z)。
不同空间直角坐标系的转换
不同空间直角坐标系的转换
欧勒角
不同空间直角坐标系的转换，包括三个坐标轴的平移和坐标轴的旋转，以及两个坐标系的尺度比参数，坐标轴之间的三个旋转角叫欧勒角。
三参数法
三参数坐标转换公式是在假设两坐标系间各坐标轴相互平行，轴系间不存在欧勒角的条件下得出的。
实际应用中，因为欧勒角不大，可以用三参数公式近似地进行空间直角坐标系统的转换。
公共点只有一个时,采用三参数公式进行转换。
七参数法
用七参数进行空间直角坐标转换有布尔莎公式，莫洛琴斯基公式和范氏公式等。
下面给出布尔莎七参数公式：
坐标转换多项式回归模型
坐标转换七参数公式属于相似变换模型。
大地控制网中的系统误差一般呈区域性，当区域较小时，区域性的系统误差被相似变换参数拟合，故局部区域的坐标转换采用七参数公式模型是比较适宜的。
但对全国或一个省区范围内的坐标转换，可以采用多项式回归模型，将各区域的系统偏差拟合到回归参数中，从而提高坐标转换精度。
两种不同空间直角坐标系转换时，坐标转换的精度取决于坐标转换的数学模型和求解转换系数的公共点坐标精度，此外，还与公共点的分布有关。
鉴于地面控制网系统误差在⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000111222Z Y X Z Y X Z Y X ⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000111111222000)1(Z Y X Z Y X Z Y X m Z Y X X Y X Z Y Z εεεεεε
不同区域并非是一个常数，所以采用分区进行坐标转换能更好地反映实际情况，提高坐标转换的精度。
不同坐标系统间的转换和精度平差
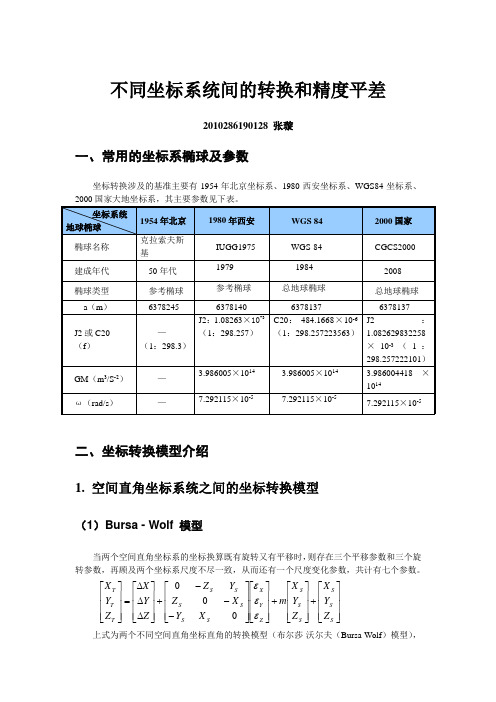
不同坐标系统间的转换和精度平差2010286190128 张璇一、常用的坐标系椭球及参数坐标转换涉及的基准主要有1954年北京坐标系、1980西安坐标系、WGS84坐标系、二、坐标转换模型介绍1. 空间直角坐标系统之间的坐标转换模型（1）Bursa - Wolf 模型当两个空间直角坐标系的坐标换算既有旋转又有平移时，则存在三个平移参数和三个旋转参数，再顾及两个坐标系尺度不尽一致，从而还有一个尺度变化参数，共计有七个参数。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∆∆∆=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡S S S S S S Z Y X SSS S S S T T T Z Y X Z Y X m X Y X Z Y Z Z Y X Z Y X εεε000上式为两个不同空间直角坐标直角的转换模型（布尔莎-沃尔夫（Bursa-Wolf ）模型），也称默特（Helmert ）模型，其转换参数分别是3个平移参数（Δx ，Δy ，Δz ），三个旋转参数（εx ，εy ，εz ）和一个尺度参数m 。
为了求得这7个转换参数，至少需要3个公共点，当多于3个公共点时，可按最小二乘法求得7个参数的最或是值。
（2）Molodensky 模型如果旋转与尺度是相对于参考点P K ，即以参考点P K 作变换中心。
则有Molodensky 模型。
()()⎪⎪⎪⎭⎫ ⎝⎛'-''-''-'++⎪⎪⎪⎭⎫ ⎝⎛'''+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛K iK i Ki Z Y X K K K i i i Z Z Y Y X X Z Y X Z Y X Z Y X εεεδμ,,1000R旋转角为小角度时，上式可简化为：δμεεεεεε⎪⎪⎪⎭⎫⎝⎛'-''-''-'+⎪⎪⎪⎭⎫ ⎝⎛'-''-''-'⎪⎪⎪⎭⎫ ⎝⎛---+⎪⎪⎪⎭⎫ ⎝⎛'-''-''-'+⎪⎪⎪⎭⎫ ⎝⎛'''+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛Ki K i K i K i K i Ki XY X Z Y ZK i K i K iK K Ki i i Z Z Y Y X X Z Z Y Y X X Z Z Y Y X X Z Y X Z Y X Z Y X 000000 上式同样可以简化为求解转换参数的形式如下：δμεεε⎪⎪⎪⎭⎫⎝⎛'∆'∆'∆+⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛'∆'∆-'∆'∆'∆'∆-+⎪⎪⎪⎭⎫ ⎝⎛'''+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛iKiK iK Z Y X iKiK iKikiKiK i i i i i i Z Y X X Y X Z Y Z Z Y X Z Y X Z Y X 000000 其中，⎪⎪⎪⎭⎫ ⎝⎛'-''-''-'=⎪⎪⎪⎭⎫⎝⎛'∆'∆'∆K iK i Ki iK iKiKZ Z Y Y X X Z Y X相应于Molodensky 模型的坐标差的转换模型与Bursa-Wolf 模型相同。
测量学中的坐标系和他们之间相互转换
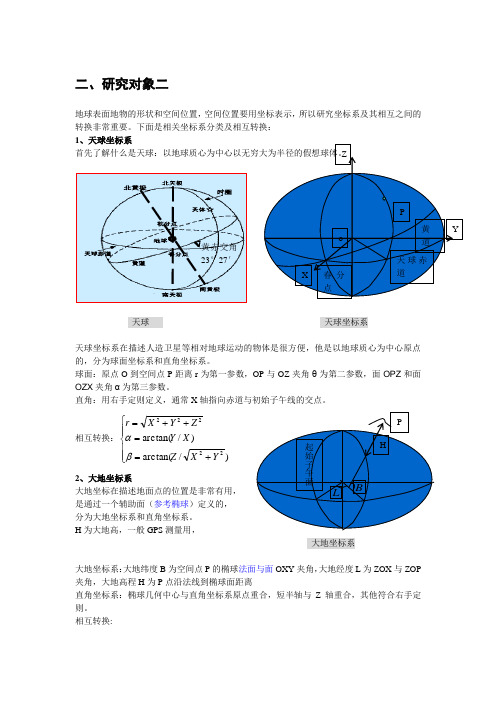
二、研究对象二地球表面地物的形状和空间位置，空间位置要用坐标表示，所以研究坐标系及其相互之间的转换非常重要。
下面是相关坐标系分类及相互转换： 1、天球坐标系首先了解什么是天球：以地球质心为中心以无穷大为半径的假想球体。
天球 天球坐标系天球坐标系在描述人造卫星等相对地球运动的物体是很方便，他是以地球质心为中心原点的，分为球面坐标系和直角坐标系。
球面：原点O 到空间点P 距离r 为第一参数，OP 与OZ 夹角θ为第二参数，面OPZ 和面OZX 夹角α为第三参数。
直角：用右手定则定义，通常X 轴指向赤道与初始子午线的交点。
相互转换：⎪⎪⎩⎪⎪⎨⎧+==++=)/arctan()/arctan(22222Y X Z X Y Z Y X r βα 2、大地坐标系大地坐标在描述地面点的位置是非常有用， 是通过一个辅助面（参考椭球）定义的， 分为大地坐标系和直角坐标系。
H 为大地高，一般GPS 测量用，大地坐标系大地坐标系：大地纬度B 为空间点P 的椭球法面与面OXY 夹角，大地经度L 为ZOX 与ZOP 夹角，大地高程H 为P 点沿法线到椭球面距离直角坐标系：椭球几何中心与直角坐标系原点重合，短半轴与Z 轴重合，其他符合右手定则。
相互转换:黄赤交角23°27′X YZ oP春分点黄道 天球赤道 起始子午面L B PH[]⎪⎩⎪⎨⎧+=+=-=+-=L B H N X L B H N Y B e a N B H e N Z cos cos )(sin cos )(e ,2sin 21/ sin )21(为第一扁率卯酉全曲率半径，其中3、惯性坐标系（CIS ）与协议天球坐标系① 惯性坐标系（CIS ）:在空间不动或做匀速直线运动的坐标系.② 协议天球坐标系：以某一约定时刻t0作为参考历元，把该时刻对应的瞬时自转轴经岁差和章动改正后作为Z 轴，以对应的春分点为X 轴的指向点，以XOZ 的垂直方向为Y 轴方向建立的天球坐标系。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
N cos B cos L a N sin 2 B cos B cos L 2W 2 2 2 其中： B = N cos B sin L a N sin B cos B sin L 2W N 1 − e 2 sin B a − N cos 2 B + W 2 cos B 2W 2
§2.4 空间大地直角坐标系及其转换模型
2.4.1 空间直角坐标系与相应大地坐标系的关系
1、X、Y、Z与B、L、H间的关系 、 、 、 与 、 、 间的关系 空间坐标系的定义： 空间坐标系的定义：Z//自转轴，X位于赤道面，指格林 尼治天文台，Y指东，构成右手系。 大地坐标系的定义： 大地坐标系的定义：B为过坐标点椭球面的法线与赤道面 交角、L为过坐标点的子午线与起始子午线的夹角，H Z 为点沿法线到椭球面的距离。 大地高与正高、正常高之间的关系： 大地高与正高、正常高之间的关系： P L
1
( (
)
)
2.4.1 空间直角坐标系与相应大地坐标系的关系
2、由X、Y、Z计算 、L、H的迭代解法 、 计算B、 、 的迭代解法 、 、 计算 计算L：
Y L = tan = sin 迭代计算B：
B
(i +1)
= tan
−1
Z + N (i )e 2 sin B (i ) X 2 +Y 2
Z X 2 +Y 2
迭代初值为： B
(0 )
= tan
−1
最后计算H： H = Z csc B − N (1 − e 2 ) = X 2 + Y 2 sec B − N
2.4.1 空间直角坐标系与相应大地坐标系的关系
3、X、Y、Z与B、L、H间的微分关系 、 、 、 与 、 、 间的微分关系 由前面 1 式微分得；
L P′
O
B
Z
P
(
)
rP′P
H cos B cos L = Hn = H cos B sin L H sin B
Y
Q
KP
X
X ( N + H ) cos B cos L Y = rOP = rOP′ + rP′P = ( N + H ) cos B sin L Z N 1 − e 2 + H sin B
Z Z ′′ Z′
εY ε X
Y
O
εY
εX
εZ
Y ′′ Y′
εZ
X ′′
X
2.4.2 空间直角坐标系之间的旋转变换
坐标变换公式为：
X X ′ Y = R Z (ε Z )R Y ′′ (ε Y )R X ′ (ε X ) Y ′ Z Z′
Z Z ′′ Z′
εY ε X
Y
O
其中，旋转矩阵：
R = R Z (ε Z )R Y ′′ (ε Y )R X ′ (ε X ) X ′
εY
εX
εZ
Y ′′ Y′
εZ
是正交矩阵。
X ′′
X
2.4.2 空间直角坐标系之间的旋转变换
若α、β、 γ分别表示X与X’、Y与Y’和Z与Z’之 间的夹角，则有：
dX − (M + H )sin B cos L − ( N + H ) cos B sin L cos B cos L dB dY = − (M + H )sin B sin L ( N + H ) cos B cos L cos B sin L dL dZ (M + H ) cos B 0 sin B dH dB = AJ dL dH
O
Y ′′′ Y ′′ Y
旋转矩阵：
R = R Z − ε Z 2 R X ′′ (ε X )R Z ′ ε Z1
(
)
( )
X′ X X ′′
Y′
是正交矩阵。
2.4.2 空间直角坐标系之间的旋转变换
若γ表示Z与Z’之间的夹角，则有：
cos γ = cos ε X
若α、β分别表示X与X’和Y与Y’之间的夹角，则有：
cos β = sin ε Z1 sin ε Z 2 + cos ε Z1 cos ε Z 2 cos ε X cos α = cos ε Z1 cos ε Z 2 + sin ε Z1 sin ε Z 2 cos ε X
2.4.2 空间直角坐标系之间的旋转变换
方法二： 方法二： 转换到X、 将X’、Y’、Z’转换到 、 、 、 转换到 Y 、 Z 坐 标 系 ： 先绕X’将Y’旋转到YOZ 平面与Y’OZ’平面的交线 Y” ，再绕Y” 轴将Z ”旋 转到Z轴，最后再绕Z轴， 将X” 旋转到X轴方向。 X ′ 由于 三 坐 标 轴的正 交关 系， 经 最 后 一次旋 转的 Y”必位于Y轴上。
1 旋转矩阵简化为： R = − ε Z ε Y
εZ
1 −εX
− εY εX 1
坐标转换模型简化为：
X 1 Y = −εZ Z ε Y
εZ
1 −εX
− ε Y X ′ ε X Y ′ 1 Z ′
N cos B sin B 2 − e 2 sin 2 B 2 2W (M + H ) da 0 de 2 2 N sin B 2
(
)
2.4.2 空间直角坐标系之间的旋转变换
两个右手旋转坐标系之间的旋转角，取逆时针旋 转为正，顺时针旋转为负，旋转矩阵为正交阵，可表 示为：
Z′
Y ′′′
O
Y ′′ Y
X′ X X ′′
Y′
2.4.2 空间直角坐标系之间的旋转变换
坐标变换公式为：
X Y = R Z − ε Z 2 R X ′′ (ε X )R Z ′ ε Z1 Z
Z Z′
(
)
( )
X ′ Y′ Z′
2.4.1 空间直角坐标系与相应大地坐标系的关系
顾及A是正交阵，J是对角阵，得：
dB dX dX −1 −1 T dL = (AJ ) dY = J A dY dH dZ dZ sin B cos L − M +H sin L − = ( N + H ) cos B cos B cos L sin B sin L M +H cos L (N + H ) cos B − cos B sin L cos B M + H dX dY 0 dZ sin B
0 1 R X (ε X ) = 0 cos ε X 0 − sin ε X sin ε X cos ε X 0
cos ε Y R Y (ε Y ) = 0 sin ε Y
sin ε Z cos ε Z 0 0 0 1
0 − sin ε Y 1 0 0 cos ε Y
(
)
(
)
2.4.1 空间直角坐标系与相应大地坐标系的关系
由上式可得：
dB dX −1 T da −1 T dL = J A dY − J A B 2 de dH dZ
若空间坐标系的原点和坐标轴指向保持 不变，即椭球的定位与定向不变，则：
M + H 其中： J = 0 0 0 0 (N + H ) cos B 0 0 1
− sin B cos L − sin L cos B cos L A = − sin B sin L cos L cos B sin L cos B 0 sin B
r11r31 + r12 r32 + r13r33 = 0 r21r31 + r22 r32 + r23r33 = 0
2 2 2 r11 + r12 + r13 = 1 2 2 2 r21 + r22 + r23 = 1 2 2 2 r31 + r32 + r33 = 1
2.4.2 空间直角坐标系之间的旋转变换
H = H N + N = Hζ + ζ
X
P′
O
B Y
KP
Q
2.4.1 空间直角坐标系与相应大地坐标系的关系
如图所示：
rOP′ X N cos B cos L = Y = N cos B sin L Z N 1 − e 2 sin B P′
dX dY = 0 dZ
2.4.1 空间直角坐标系与相应大地坐标系的关系
上式简化成大地坐标与椭球间的微分关系：
dB −1 T da dL = −J A B 2 de dH e 2 cos B sin B W (M + H ) 0 = −W
2.4.2 空间直角坐标系之间的旋转变换
旋转矩阵是正交阵，满足条件：
r11 R = r21 r 31 r12 r22 r32 r13 r23 r33
RR T = I
若：
则根据正交条件，得： r r + r r + r r = 0 11 21 12 22 13 23
cos α = cos ε Y cos ε Z cos β = cos ε X cos ε Z + sin ε X sin ε Y cos ε Z cos γ = cos ε X cos ε Y