平行四边形中面积问题
平行四边形的面积_《平行四边形的面积》典型例题
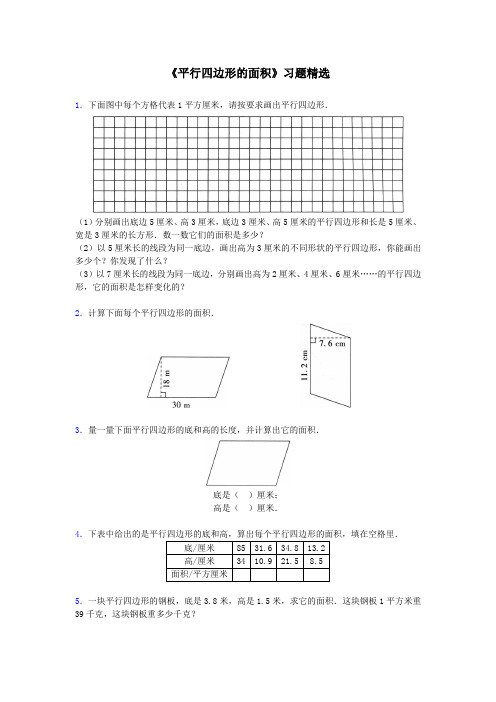
《平行四边形的面积》习题精选1.下面图中每个方格代表1平方厘米,请按要求画出平行四边形.(1)分别画出底边5厘米、高3厘米,底边3厘米、高5厘米的平行四边形和长是5厘米、宽是3厘米的长方形.数一数它们的面积是多少?(2)以5厘米长的线段为同一底边,画出高为3厘米的不同形状的平行四边形,你能画出多少个?你发现了什么?(3)以7厘米长的线段为同一底边,分别画出高为2厘米、4厘米、6厘米……的平行四边形,它的面积是怎样变化的?2.计算下面每个平行四边形的面积.3.量一量下面平行四边形的底和高的长度,并计算出它的面积.底是()厘米;高是()厘米.4.底/厘米85 31.6 34.8 13.2高/厘米34 10.9 21.5 8.5面积/平方厘米5.一块平行四边形的钢板,底是3.8米,高是1.5米,求它的面积.这块钢板1平方米重39千克,这块钢板重多少千克?6.一块平行四边形菜地,底是18.4米,高是9.2米.在这块地种茄子,每棵苗占地0.18平方米,这块地可种茄子多少棵?(得数保留整数)7.一块六边形水泥砖(如图),由三个面积相同的平行四边形组成.要铺300平方米地面大约需要多少块这样的水泥砖?参考答案1.(1)15平方厘米 15平方厘米 15平方厘米(2)无数个它们面积都相等(3)14平方厘米 28平方厘米 42平方厘米2.540m2 85.12cm23.略4.2890 344.44 748.2 112.25.5.7平方米 222.3千克6.169.28 ≈940棵7.≈2858块《平行四边形的面积》习题精选一、填空.1.4.5平方米=()平方分米 2400平方厘米=()平方分米2.一个平行四边形的底是9分米,高是底的2倍,它的面积是()平方分米.3.一个平行四边形的底是12厘米,面积是156平方厘米,高是()厘米.4.一块平行四边形钢板,底是1.5米,高是1.2米,如果每平方米钢板重23.5千克,这块钢板重()千克.二、判断题.1.平行四边形的面积等于长方形面积.()2.一个平行四边形的底是5分米,高是20厘米,面积是100平方分米.()3.一个平行四边形面积是42平方米,高是6米,底是7米.()三、选择题.1.下面的长方形和平行四边形面积()a.相等b.不相等2.用木条钉成的长方形拉成一个平行四边形,它的高和面积()a.都比原来大b.都比原来小c.都与原来相等3.平行四边形的底扩大3倍,高缩小3倍,面积()a.扩大3倍b.缩小3倍c.不变d.不好判断四、评议.下面是四个平行四边形,小红认为它们的面积都是6平方厘米,你认为对吗?(单位:厘米)23323232五、已知下图中正方形的周长为36厘米,求平行四边形的面积.参考答案一、填空1.450 24 2.162 3.13 4.42.3二、判断题.1.(×) 2.(×) 3.(√)三、选择题.1.a 2.b 3.c四、评议.2332(√)(×)3232(√)(×)五、已知下图中正方形的周长为36厘米,求平行四边形的面积.36÷4=9(厘米) 9×9=81(平方厘米)《平行四边形的面积》典型例题例.求下面平行四边形的面积.分析:图中给出的两个已知条件并不是一组相对应的底和高,要根据平行四边形“对边相等”的特性可以得出和高(6厘米)相对应的底也是4厘米,利用平行四边形的面积公式可以求出它的面积.解:2464=⨯(平方厘米)答:这个平行四边形的面积是24平方厘米.《平行四边形的面积》典型例题例.在两条平行线间画出两个平行四边形(如下图),试判断甲和乙谁的面积大?乙甲CB EFDA分析:平行四边形ABCD 和BCEF 是画在两条平行线之间,那么这两个平行四边形的高相等,因为两条平行线间的距离处处相等.这两个平行四边形都是以BC 为底,所以说这两个平行四边形的底也相等的.4厘米6厘米底和高都分别相等,那么底和高的乘积(面积)也相等,从两个面积相等的平行四边形中减去同样的一个三角形,剩下的面积也相等,所以甲和乙的面积是一样大的.解答:一样大.《平行四边形的面积》典型例题例.如图,正方形BDEC 周长是24厘米,平行四边形ADEB 面积是多少平方厘米?分析:从图上可以看出,平行四边形的底和高,都与正方形的边长相等.而正方形的边长是 (24÷4)厘米,所以平行四边形ADEB 的面积就是(24÷4)×(24÷4)=6×6=36(平方厘米)答:平行四边形ADEB 面积是36平方厘米.《平行四边形的面积》典型例题例.求下面平行四边形的周长(单位:分米)1267分析:已知平行四边形的一组底和高分别是12分米和7分米,可以求出它的面积是84712=⨯(平方分米),通过“平行四边形面积=底×高”,可以逆推出:底=平行四边形面积÷高,已知面积是84平方分米,高是6分米,可以求出和6分米相对应的底,用14684=÷(分米),平行四边形对边相等,已知平行四边形相邻的两条边分别是12分米和14分米,就可以求出它的周长.解:5221412=⨯+)((分米)答:这个平行四边形的周长是52分米.《平行四边形的面积》典型例题例.一个平行四边形,若底增加2厘米,高不变,则面积增加6平方厘米;若高增加1厘米,底不变,则面积增加4平方厘米,原平行四边形的面积是多少?分析:要求原平行四边形的面积,必须知道原平行四边形的底和高.根据第一组条件,增加部分是一个底是2厘米,面积是6平方厘米的平行四边形,根据平行四边形的面积公式可以求出这个平行四边形的高,即求出原平行四边形的高.根据第二组条件,,增加部分是一个高为1厘米,面积为4平方厘米的平行四边形,由此可以求出增加部分的底,即求出原平行四边形的底.解:12)14()26(=÷⨯÷(平方厘米)答:原平行四边形的面积是12平方厘米.《平行四边形的面积》典型例题例.在一块长80米,宽35米的长方形地上,修了两条宽分别为3米和2米的通道,其余的地方铺上草皮(如图).问:应铺多少平方米的草皮?分析:很显然,铺草皮的面积等于长方形的面积减去两条通道的面积,问题的关键是这两条 通道是什么图形?因为两条通道都是四边形,且两组对边分别平行,所以两条通道都是平行四边形.要求出这两个平行四边形的面积,底边分别是3米和2米,高是多少呢?这恐怕是个难点,你发现了吗?它们的高就是长方形的宽35米,问题得解.解:80×35-(3×35+2×35) =2800-175=2625(平方米)答:应铺2625平方米的草皮.《平行四边形的面积》典型例题例.如图,平行四边形的面积是150平方米,它的阴影部分的面积是多少平方米?分析:平行四边形的面积为已知,底边长已知,所以平行四边形的高可求出,由观察知阴影部分是一个直角梯形,这个直角梯形的上底为15米,下底为15-4=11(米),高就是平行四边形的高,问题得解.解:[15+(15-4)]×(150÷15)÷2=26×10÷2=130(平方米)答:阴影部分的面积是130平方米.。
平行四边形中与面积有关的问题
变式:若将例2中“扩大后的池塘是平行四 边形”,这个条件去掉,其他条件不变, 能否实现?能的话,说明理由。
六、小结
本节课你的收获是什么?
七、布置作业
1. 平行四边形ABCD中,点E 为外部一点,过 点E,作直线EF,把平行四边形ABCD 的面积 平分,如何做?
2.AB∥CD∥FE,AF∥BC∥DE,∠B=∠E=90°。 把这个图形的面积平分,如何做?
3.正方形ABCD中,剪掉一个平行四边形 AGFE,剩下的图形中,把面积平分,如何做 ?
4.请你设计一个将平行四边形面积缩小为原 来一半的题,画出图形, 并、O、C为顶
点的平行四边形的面积,若平行四边形有两 个顶点的坐标为A(1,4),B(5,0),求 直线L的表达式为。
五、拓展提升
1..某村有一个四边形的池塘,一个人准备将 这个四边形面积扩大为原来的2倍,并且扩大后的 池塘是平行四边形,能否实现?能的话, 画出图形,并说明理由。
一、复习巩固
能否添加一条线段,把△ABC的面积平分? 并说明理由。
二、探究新知
1.在□ ABCD中,能否添加一条线段, 把□ ABCD分成面积相等的两个三角形?
说明理由。
结论1:平行四边形的对角线能把平行 四边形的面积平分
2. 在1题的基础上,你能提出什么问题?
结论2:过对角线交点的任意一条直线都将 平行四边形分成面积相等的两部分
三、典例分析
例1. 小明家有一块平行四边形菜地,菜地中间有一 口井,为了浇水的方便,小明建议妈妈经过水井修一条
路,可以把菜地分成面积相等的两部分. 同学们,你知
道聪明的小明是怎么帮妈妈分的吗?
A
D
●
OM
B
C
四、巩固练习
平行四边形面积的计算练习题

平行四边形面积的计算练习题一、填空(1)4.5平方米()平方分米2400平方厘米()平方分米(2)一个平行四边形的底是9分米,高是底的2倍,它的面积是()平方分米。
(3)一个平行四边形的底是12厘米,面积是156平方厘米,高是()厘米。
(4)一块平行四边形钢板,底是1.5米,高是1.2米,如果每平方米钢板重23.5千克,这块钢板重()千克。
二、判断题。
(1)平行四边形的面积等于长方形面积。
()(2)一个平行四边形的底是5分米,高是20厘米,面积是100平方分米。
()(3)一个平行四边形面积是42平方米,高是6米,底是7米。
()三、选择题。
(1)下面的长方形和平行四边形面积()a.相等b.不相等(2)用木条钉成的长方形拉成一个平行四边形,它的高和面积()a.都比原来大b.都比原来小c.都与原来相等(3)平行四边形的底扩大3倍,高缩小3倍,面积()扩大3倍b.缩小3倍c.不变d.不好判断2. 一块平行四边形木板, 它的底是12分米, 高是8分米, 这块木板的面积是多少平方分米?3. 一块平行四边形的草坪, 已知它的面积是1050平方米, 高是25米, 这块草坪的底边长是多少米?4. 一块平行四边形地, 底23米, 高15米, 如果每平方米栽瓜秧9棵, 共栽多少棵?5. 平行四边形的高是70.2厘米, 是底的2倍, 平行四边形的面积是多少?2. 一个平行四边形, 底是1.2米, 高是底的1.5倍, 求它的面积.3. 一块平行四边形钢板, 底5米, 高3米, 如果1平方米钢重39千克, 这块钢板重多少千克?4. 下图中的正方形周长为28厘米, 求平行四边形的面积.5. 一个平行四边形的底是9.6分米, 高2.5分米, 它的面积是多少平方分米?1、填空:(1)把一个平行四边形转化成一个(),它的面积和原来的平行四边形(),平行四边形的底是长方形的(),长方形的宽和平行四边形的()相等。
(2)平行四边形面积的计算公式是(),用含有字母的式子表示是()。
数学五年级上册平行四边形的面积解决问题复习题(含答案)

6.1平行四边形的面积1.王老伯家一块平行四边形菜地,底边长8米,高6米,已知平均每平方米可收青菜15千克,这块菜地可以收青菜多少千克?2.用一根铁丝折成一个长方形,这个长方形的长是12厘米、宽是8厘米.如果把它拉成一个平行四边形(如图),面积就减少了6平方厘米.平行四边形12厘米的底边上的高是多少厘米?3.用一根铁丝围成一个边长是8分米的正方形,如果把它拉成平行四边形,面积减少了16平方分米,这个平行四边形的高是多少分米?4.有一块平行四边形菜地,底40米,高25米,如果每平方米能收获7千克青菜.这块地一共可以收获多少千克青菜?5.一个平行四边形的果园内栽了1800棵果树,平均每棵果树占地10平方米,这个平行四边形果园的底是360米,高是多少米?6.一块平行四边形的土地,底是10.5米,高是6.4米.用这块地种辣椒,每棵辣椒占地0.2平方米,这块地一共可以种多少棵辣椒?7.植物是制造氧气的“工厂”,根据有关测算,1平方米的草坪,每天能够释放0.03千克的氧气.下图这块近似于平行四边形的草坪一周(按7天算)大约能释放氧气多少千克?8.一个平行四边形的菜地,高6米,底是高的3倍还多2米,这块地有多大?如果每平方米收菜5.5千克,一共收多少千克的菜?9.画出下面图形的高,并量出有用的数据标在图上,再计算图形的面积.10.一块平行四边形的麦地底是48米,高50米,如果每平方米收小麦4千克,这块地一共收小麦多少千克?11.如图是用1:400的比例尺画出的图形.先作出平行四边形的高,并量出有关的数据,(取整厘米数),再计算出这个平行四边形的实际面积是多少平方米?每平方米收小麦0.5千克,这块地可收小麦多少千克.12.干强胜老师准备在自家的空地开辟一块平行四边形的菜地,底是12米,比高长4米,这块菜地平均每平方米种3棵白菜,这块菜地一共可以种植多少棵白菜?13.在一块平行四边形地里共收稻谷32400千克.已知平行四边行地的底450米,高120米,平均每公顷产稻谷多少千克?14.一块平行四边形小麦地,底长80米,高是底的一半,平均每平方米可收小麦6.4千克.这块小麦地可收小麦多少千克?15.看图填表.(每个小方格的边长表示1cm.)平行四边形的面积a/cm h/cm S/cm2①②③16.一块平行四边形的麦地底是48米,高50米,如果每平方米收小麦4千克,这块地一共收小麦多少千克?17.有一条水渠穿过一块菜地(如图),这块菜地的面积是多少?18.如图中长方形的周长是20cm,计算平行四边形的面积.19.一块平行四边地,底长150m,高80m,这块地有多少公顷?在这块地里共收小麦7680千克,平均每公顷收小麦多少千克?20.计算如图所示每个平行四边形的面积,你发现了什么?21.如图,大平行四边形的面积是72cm2,图中小平行四边形(阴影部分)的面积是多少?22.如下图,一块近似平行四边形的草坪中间有条石子小路.如果铺好1平方米草坪需要12元,铺好这块草坪大约需要多少元?23.平行四边形的底扩大4倍,高扩大2倍,它的面积有什么变化?24.一块平行四边形的地,底边长1200米,高约为600米,在这块地里种小麦,平均每平方米可收小麦0.56千克,这块地共收割小麦多少千克?合多少吨?25.一块平行四边形的草地中有一条长8米、宽1米的小路,求草地的面积.参考答案1.8×6×15=48×15,=720(千克).答:这块菜地可以收青菜720千克.2.(12×8﹣6)÷12,=(96﹣6)÷12,=90÷12,=7.5(厘米).答:平行四边形12厘米的底边上的高是7.5厘米.3.(8×8﹣16)÷8,=(64﹣16)÷8,=48÷8,=6(分米).答:这个平行四边形的高是6分米.4.7×(40×25),=7×1000,=7000(千克);答:这块地一共可以收获7000千克青菜.5.1800×10÷360,=18000÷360,=50(米).答:高是50米.6.5×6.4÷0.2,=67.2÷0.2,=336(棵),答:这块地一共可以种336棵辣椒.7.(20﹣1)×9×(0.03×7),=19×9×0.21,=171×0.21,=35.91(千克);答:大约能释放氧气35.91千克.8.(6×3+2)×6,=20×6,=120(平方米),120×5.5=660(千克),答:这块地的面积是120平方米,可以收菜660千克.9.6×2.5,=15(平方分米).答:平行四边形的面积是15平方分米.10.48×50×4,=2400×4,=9600(千克).答:这块地一共收小麦9600千克.11.(1)实际的底为:3÷=1200(厘米),1200厘米=12米;实际的高为:2=800(厘米),800厘米=8米;平行四边形的实际面积是:12×8=96(平方米);(2)0.5×96=48(千克),答:这个平行四边形的实际面积是96平方米;这块地可收小麦48千克.12.平行四边形的面积:12×(12﹣4),=12×8,=96(平方米);一共种多少棵白菜:96×3=288(棵).答:这块菜地一共可以种288棵白菜.13.450×120=54000(平方米)54000平方米=5.4公顷32400÷5.4=6000(千克)答:平均每公顷的稻谷产量是6000千克.14.80×(80÷2)×6.4=80×40×6.4,=3200×6.4,=20480(千克);答:这块小麦地可收小麦20480千克.15.①3×3=9(平方厘米);②2×4=8(平方厘米);③4×3=12(平方厘米).故答案为16.48×50×4,=2400×4,=9600(千克).答:这块地一共收小麦9600千克.17.解:(40﹣5)×25,=35×25,=875(平方米);答:这块菜地的面积是875平方米.18.解:(20÷2﹣4)×4,=6×4,=24(平方厘米),答:这个平行四边形的面积是24平方厘米.19.150×80=12000(平方米)12000平方米=1.2公顷7680÷1.2=6400(千克)答:这块地有1.2公顷,平均每公顷收小麦6400千克.20.(1)S=ah,=2×3,=6(平方分米).(2)S=ah,=2×3,=6(平方分米).(3)S=ah,=2×3,=6(平方分米).我发现它们的面积都相等,它们的形状虽然不同,但是它们的高和底都相同.所以等底等高的平行四边形的面积相同.答:我发现等底等高的平行四边形的面积相同.21.解:72÷12×4,=6×4,=24(平方厘米),答:阴影部分的面积是24平方厘米.22.20×9-1×9=171(平方米)171×12=2052(元)23.解:因为平行四边形面积=底×高,底扩大4倍,高扩大2倍,则面积扩大了4×2=8倍,答:平行四边形的面积扩大8倍.24.56×(1200×600),=0.56×720000,=403200(千克),=403.2吨.答:这块地共收割小麦403200千克,合403.2吨.25.(20﹣1)×8=19×8,=152(平方米);答:草地的面积为152平方米.。
五年级上册平行四边形面积易错题

五年级上册平行四边形面积易错题一、计算平行四边形面积公式1. 问题:平行四边形ABCD的底边长为8厘米,高为5厘米,求其面积。
解答:根据平行四边形的面积公式,面积等于底边长乘以高,所以平行四边形ABCD的面积为8厘米乘以5厘米,即40平方厘米。
2. 问题:平行四边形EFGH的底边长为12厘米,高为4厘米,求其面积。
解答:同样根据平行四边形的面积公式,面积等于底边长乘以高,所以平行四边形EFGH的面积为12厘米乘以4厘米,即48平方厘米。
二、平行四边形面积的应用1. 问题:一个平行四边形的面积为30平方米,其中底边长为6米,求其高。
解答:根据平行四边形的面积公式,面积等于底边长乘以高,已知底边长为6米,所以30平方米等于6米乘以高,解方程得到高为5米。
2. 问题:一个平行四边形的面积为18平方米,其中高为3米,求其底边长。
解答:同样根据平行四边形的面积公式,面积等于底边长乘以高,已知高为3米,所以18平方米等于底边长乘以3米,解方程得到底边长为6米。
三、综合运用1. 问题:一个平行四边形的面积是24平方厘米,如果将其底边长扩大到原来的2倍,面积会发生什么变化?解答:根据平行四边形的面积公式,面积等于底边长乘以高,已知面积为24平方厘米,所以24平方厘米等于底边长乘以高。
当底边长扩大为原来的2倍时,那么高也需要扩大为原来的1/2,这样才能保持面积不变。
所以面积不会发生变化。
2. 问题:一个平行四边形的面积是36平方米,如果将其高减少为原来的1/3,面积会发生什么变化?解答:同样根据平行四边形的面积公式,面积等于底边长乘以高,已知面积为36平方米,所以36平方米等于底边长乘以高。
当高减少为原来的1/3时,底边长需要增加为原来的3倍,这样才能保持面积不变。
所以面积不会发生变化。
以上是五年级上册平行四边形面积易错题的相关内容,希望对您有所帮助。
平行四边形 面积练习题

平行四边形面积练习题平行四边形是初中数学中重要的几何概念之一,它具有特殊的性质和计算方法,本文将通过一些面积练习题来帮助读者更好地理解和掌握平行四边形的面积计算。
1. 问题描述:已知平行四边形ABCD的底边AB为8cm,高为5cm,求其面积。
解答:根据平行四边形的面积公式,可以得到面积S = 底边 ×高。
将已知数据代入公式,可得S = 8cm × 5cm = 40cm²。
因此,该平行四边形的面积为40平方厘米。
2. 问题描述:已知平行四边形EFGH的底边EF为12cm,高为9cm,求其面积。
解答:同样地,利用平行四边形的面积公式,可得S = 12cm × 9cm= 108cm²。
因此,该平行四边形的面积为108平方厘米。
3. 问题描述:已知平行四边形IJKL的底边IJ为15cm,高为6cm,求其面积。
解答:根据面积公式,S = 底边 ×高,代入已知数据可得S = 15cm× 6cm = 90cm²。
因此,该平行四边形的面积为90平方厘米。
通过以上三道练习题,我们熟悉了平行四边形的面积计算方法。
不过,有时候给出的数据不直接给出底边和高,需要我们通过其他已知条件求解。
4. 问题描述:已知平行四边形MNOP的对角线MO为12cm,对角线NP为9cm,求其面积。
解答:对角线MO和NP将平行四边形分成两个全等的三角形。
我们可以利用三角形的面积公式,再将两个三角形的面积相加,来求解平行四边形的面积。
首先,利用三角形面积公式,三角形MON的面积可以表示为S₁ = (1/2) × MO × ON。
其中ON为平行四边形的高。
根据毕达哥拉斯定理,我们可以求得ON = √(MO² - NP²) = √(12cm)² - (9cm)² = √144cm² - 81cm² = √63cm² ≈ 7.94cm。
平行四边形面积问题模型结论

平行四边形面积问题模型结论
平行四边形面积问题模型结论:
在平行四边形ABCD中,已知点O为任意一点。
过点O作BC的平行线分别交AB、CD于E、F,四边形AEFD和四边形BEFC都是平行四边形。
由于△OBC与▱BEFC等底等高,所以有:
S△OBC=1/2S▱BEFC
同理,S△ADO=1/2S▱AEFD。
因此,S△CBO+S△ADO=1/2(S▱BEFC+S▱AEFD)=1/2S▱ABCD。
同理,S△ABO+S△DCO=1/2S▱ABCD。
所以,S△ABO+S△DCO=S△BCO+S△ADO=1/2S▱ABCD。
此外,由于四边形ABCD是平行四边形,所以AD=BC。
因此,
△BCE≌△ADF(SAS)。
过点E作平行四边形ABCD的高HG,则△AED的面积=AD×HE÷2,△BCE的面积=BC×GE÷2。
因此,△AED的面积+△AED
的面积=AD×HE÷2+BC×GE÷2=BC×HG÷2。
由于S=BC×HG,所以△AED的面积+△AED的面积=S/2。
又因为△BCE≌△ADF,所以△BCE与△ADF的面积相等。
因此,T=△AFD的面积+△AE D的面积=△BCE的面积+△AED的面积=S/2,即S:T=2。
五年级数学 平行四边形的面积 练习题(含答案)

人教版数学五年级上册6.1 平行四边形面积练习卷一、选择题1.将一个长方形拉成平行四边形,它的面积().A.不变B.变大C.变小2.下列说法正确的是()。
A.平行四边形是特殊的长方形B.平行四边形易变形C.梯形两组对边分别平行3.如图,已知“4,7,20,35”(单位:厘米)是一个平行四边形的两条底和两条高的长度,这个平行四边形的面积是()平方厘米。
A.245B.140C.80D.284.把一个长方形拉成一个平行四边形(如图),拉成后的平行四边形与长方形相比,它的周长(),面积()。
A.变小;变小B.变大;变大C.不变;变小二、图形计算5.求图中阴影部分的面积(单位:cm)三、填空题6.一块平行四边形草地,底是3.6米,对应的高是2米,它的面积是( )平方米。
7.如图,M、N分别是平行四边形ABCD两边上的中点,三角形AMN的面积是7.2平方厘米,平行四边形ABCD的面积是平方厘米.8.一个平行四边形相邻的两条边分别是4厘米和6厘米,如果较长边上的高是2厘米,那么这个平行四边形的面积是( ).9.如图,正方形ABCD的边长为4厘米,EF和BC平行,ECH的面积是7平方厘米,EG的长为( )。
10.把一个木条做成的长方形框架沿着对角拉成一个平行四边形,拉成后的平行四边形与原长方形比较,周长( )。
11.一个边长5厘米的正方形木框,拉成一个平行四边形后,面积减少了5平方厘米.拉成的平行四边形的高是厘米.四、判断题12.在平行四边形内画一个最大的三角形,三角形的面积一定等于平行四边形面积的一半。
( )13.两个平行四边形的面积相等,这两个平行四边形的形状也一定相同._____.(判断对错)14.计算组合图形面积时,常用的方法有分割法和添补法..15.一个平行四边形的高和底都扩大到原数的4倍,那么这个平行四边形的面积也要扩大到原数的4倍。
( )16.把平行四边形割补成一个长方形后,面积变小。
( )五、解答题17.植物园里有一个平行四边形的玫瑰园,玫瑰园的底是120m,高是60m,如果每平方米种8株玫瑰,这个玫瑰园一共能种多少株玫瑰?18.河西村有一块平行四边形的实验田,底长600米,高250米.平均每公顷收稻谷1.2吨,这块田可收稻谷多少吨?19.一个平行四边形,若底增加2厘米,高不变,则面积增加6平方厘米;若高增加1厘米,底不变,则面积增加4平方厘米,原平行四边形的面积是多少?参考答案:1.C【详解】2.B(1)平行四边形的两组对边平行且相等,长方形不仅两组对边平行且相等,四个角均为直角。
平行四边形的面积计算方法

平行四边形的面积计算方法平行四边形是一种特殊的四边形,它具有两对平行边,对边的长度相等,对角线彼此相等。
在几何学中,计算平行四边形的面积是一项基本技能。
本文将介绍两种常见的计算平行四边形面积的方法。
方法一:基于底边长度和高的公式计算平行四边形面积的一种常见方法是使用底边长度和高的公式。
底边指的是平行四边形的其中一条边,而高则是从底边垂直下降到另一条平行边的长度。
步骤一:确定底边长度和高的数值。
根据题目或给定图形,确定底边的长度和垂直于底边的高的数值。
确保这两个数值的单位相同,比如都是以厘米或者米为单位。
步骤二:使用公式计算面积。
使用公式:面积 = 底边长度 ×高,将步骤一中得到的数值代入公式中进行计算。
最终得到的结果即为平行四边形的面积。
方法二:基于对角线长度的公式除了使用底边长度和高的公式,还可以使用平行四边形的对角线长度来计算面积。
步骤一:确定对角线的长度。
根据题目或给定图形,确定平行四边形的两条对角线的长度。
同样,确保对角线长度的单位相同。
步骤二:使用公式计算面积。
使用公式:面积 = 0.5 ×对角线1长度 ×对角线2长度 × sin(∠对角线1对角线2的夹角),其中sin代表正弦函数,∠对角线1对角线2的夹角指的是两条对角线之间的夹角(通常使用角度制)。
将步骤一中得到的数值代入公式中进行计算,得到的结果即为平行四边形的面积。
总结计算平行四边形的面积可以使用不同的方法,根据已知条件和题目要求选择合适的公式。
如果已知底边长度和高,可以直接使用底边长度乘以高的公式进行计算。
如果已知对角线的长度,可以使用对角线长度的公式进行计算。
无论使用哪种方法,注意单位的一致性,确保计算结果的准确性。
平行四边形的面积计算方法可以应用在日常生活中的各种情景,比如建筑设计、地理测量、图形绘制等。
通过掌握这些计算方法,我们可以更好地理解和应用平行四边形的概念。
同时,这也为进一步学习和探索几何学奠定了基础。
数学五年级上册平行四边形的面积解决问题练习题(含答案)

6.1平行四边形的面积1.一个平行四边形果园,底长150米,高40米.如果这个果园一共种了1000棵果树,那么每棵果树平均占地多少平方米?2.一块平行四边形形稻田,底是90米,高60米,如果每平方米施肥0.2千克,这块稻田需施肥多少千克?3.一个平行四边形的面积是90平方厘米.它的底是15厘米,高是多少厘米?(列方程解)4.有一块平行四边形的菜地,底和高都是12米,它的面积是多少平方米?如果每平方米种10颗白菜,那么这块菜地一共可以种多少棵白菜?5.李大伯家有一块平行四边形的稻田,底是110m,是高的0.25倍.他今年计划每公顷稻田需施肥45kg,那么这块稻田共要施肥多少千克?6.有一块平行四边形的瓜地,底是6.8m,是高的2倍,如果每平方米栽瓜苗5棵,大约可栽多少棵瓜苗?7.如图,红星广告公司要将一块平行四边形的铁板的一面刷上油漆,如果每千克油漆能刷1.2平方米,这块铁板共需多少千克油漆?8.(如图)请回忆老师引导你推导平行四边形面积公式进的情境,给(1)、(2)填空;(3)计算.(1)以将平行四边形转化为长方形来推导平行四边形的面积公式.把平行四边形转化成长方形采用的方法是:(2)观察转化前的平行四边形与转化后的长方形,你发现了什么?(请写在下面的横线上,至少写三条)(3)计算上面平行四边形的面积.(先动手在图中量出计算时需要的数据,再算出它的面积)9.自己测量需要的数据,并求出图中草地的总面积.(测量数据以厘米为单位四舍五入到整数)10.张大爷有一块平行四边形的地,底长175米,高80米,今年共收绿豆2856千克,平均每公顷收绿豆多少千克?这块平行四边形的面积是多少平方米?合多少公顷呢?11.一块底长1.5米,高1.2米的平行四边形铁板.现在要油漆它的两面,每平方米用油漆0.3千克,一共要油漆多少千克?12.学校要制作一块平行四边形宣传牌,底长4米,高2米,如果广告公司制作广告牌每平方米收费30元,那么学校应支付给这个广告公司多少元?13.一块平行四边形的地,底边长250m,高84m,在这块地里种小麦,共收小麦14.7吨,平均每公顷收小麦多少吨?14.在一块底50m,高30m的平行四边形地里栽桃树,平均每6m2栽一棵,这块地能栽多少棵桃树?如果每棵收4.5kg桃子,这块土地共收桃子多少千克?15.有一块平行四边形的菜地,底长48米,高是底的一半,这块地的面积是多少平方米?16.画出下面图形的高,并量出有用的数据标在图上,再计算图形的面积.17.有一块平行四边形的麦田,底225米,高60米,共收小麦10.8吨,这块麦田有多少公顷?平均每公顷收小麦多少吨?18.一块平行四边形的花生地,底长45米,高18米,每平方米种花生6棵,每棵花生的产量约是0.8千克,这块花生地共收花生多少千克?19.一块平行四边形的地共收油菜籽3400kg,它的底长250m,高68m.平均每公顷收油菜籽多少千克?20.某乡镇中学开垦了一块平行四边形荒地种油菜,这块平行四边形地的底是32米,高是35米.如果平均每平方米收油菜1.5千克.这块地一共收油菜多少千克?21.如图,一块长方形草地,长方形的长是16米,宽是10米,中间铺了一条石子路.那么草地部分面积有多大?22.如图是一块长方形草地,长是20米,宽是12米,中间有两条石子路,一条是底是2米的平行四边形,一条是2米的长方形.求草地的面积.23.一块平行四边形钢板,底是3.8m,高是1.5m,求它的面积.这块钢板每平方米重39kg,整块钢板重多少千克?24.一个平行四边形的底边长6分米,高40厘米,面积是多少?25.某工人师傅要将两根长15厘米的钢条都按3:2的长度折弯,然后摆成一个首尾相连的平行四边形,这个平行四边形的面积能不能是36平方厘米?如果能那么平行四边形的高是多少?如果不能,为什么?参考答案1.150×40÷1000=6000÷1000,=6(平方米),答:每棵果树平均占地6平方米.2.2×(90×60)=0.2×5400,=1080(千克);答:这块稻田需施肥1080千克.3.设高为x厘米,15x=90,x=90÷15,x=6.答:高是6厘米.4.平行四边形的面:12×12=144(平方米);一共种多少棵白菜:10×144=1440(棵).答:它的面积是144平方米这块菜地一共可以种1440棵白菜.5.110÷0.25×110,=440×110,=48400(平方米),=4.84(公顷); 4.84×45=217.8(千克);答:这块稻田共要施肥217.8千克.6.平行四边形的高是:6.8÷2=3.4(米),6.8×3.4×5,=23.12×5,≈116(棵);答:大约可载116棵瓜苗.7.(4.2×3.5)÷1.2,=14.7÷1.2,=12.25(千克);答:这块铁板共需12.25千克油漆.8.(1)从左边沿平行四边形的高剪下一个直角三角形,拼到平行四边形的右侧,就形成了一个长方形,把平行四边形转化成长方形采用的方法是:剪拼法;(2)观察转化前的平行四边形与转化后的长方形,发现:长方形的长就是平行四边形的底、长方形的高就是平行四边形的高、长方形的面积等于平行四边形的面积;(3)平行四边形的底是2厘米,高是1厘米,平行四边形的面积=2×1=2(平方厘米);答:平行四边形的面积是2平方厘米.故答案为剪拼法、长方形的长就是平行四边形的底、长方形的高就是平行四边形的高、长方形的面积等于平行四边形的面积.9.经测量知:平行四边形的底是3厘米,高是2.5≈3厘米,通道的长就等于平行四边形的高,宽为0.5≈1厘米,则草地的面积:3×3﹣3×1,=9﹣3,=6(平方厘米);答:草地的总面积是6平方厘米.10.175×80=14000(平方米)=1.4(公顷);2856÷1.4=2040(千克);答:平均每公顷收绿豆2040千克,这块平行四边形的面积是14000平方米,合1.4公顷.11.5×1.2×0.3,=1.8×0.3,=0.54(千克);答:一共要油漆0.54千克.12.4×2×30=8×30=240(元)答:学校应支付给这个广告公司240元.13.250×84=21000(平方米)=2.1(公顷);14.7÷2.1=7(吨);答:平均每公顷收小麦7吨.14.(1)50×30÷6,=1500÷6,=250(棵),(2)250×4.5=1125(千克),答:这块地能栽250棵桃树;这块土地共收桃子1125千克.15.48×(48÷2),=48×24,=1152(平方米);答:这块地的面积是1152平方米.16.6×2.5,=15(平方分米).答:平行四边形的面积是15平方分米.17.225×60=13500(平方米)=1.35(公顷);10.8÷1.35=8(吨);答:这块麦田有135公顷,平均每公顷收小麦8吨.18.(45×18)×6×0.8,=810×6×0.8,=3888(千克);答:这块花生地共收花生3888千克.19.400×68÷10000,=27200÷1000,=2.72(公倾);3400÷2.72=1250(千克);答:平均每公顷收油菜籽1250千克.20.32×35×1.5,=1120×1.5,=1680(千克);答:这块地一共收油菜1680千克.21.16×10-16×2=16×(10-2)=16×8=128(平方米)答:草地面积有128平方米.22.解:(20﹣2)×(12﹣2),=18×10,=180(平方米).答:草地的面积是180平方米.23.解:3.8×1.5=5.7(平方米),5.7×39=222.3(千克);答:它的面积是5.7平方米,整块钢板重222.3千克.24.6分米=60厘米,60×40=2400(平方厘米);答:它的面积是2400平方厘米.25.按照3:2折可得到一条边为9厘米,另一条边为6厘米,折成直角时的面积为:9×6=54(平方厘米),如果继续拉,几乎成为直线,那么此时的面积最小,几乎为0,36平方厘米的面积在0到54之间,所以能折成36平方厘米的平行四边形,高为:36÷9=4(厘米);答:能折成面积为36平方厘米的平行四边形,高为4厘米.。
平行四边形的面积计算

平行四边形的面积计算平行四边形是一种特殊的四边形,它的两对边分别平行。
计算平行四边形的面积可以使用多种方法,下面将介绍两种常用的计算方法。
方法一:基于底边和高的计算公式计算平行四边形面积最直接的方法是使用底边和高的计算公式。
首先,我们需要确定底边和高的长度。
假设底边的长度为b,高的长度为h。
那么平行四边形的面积可以按照以下公式进行计算:面积 = 底边 ×高通过测量或已知条件,我们可以得到底边和高的具体数值,然后将其代入公式进行计算即可得到平行四边形的面积。
方法二:基于两对边的计算公式除了使用底边和高进行计算外,我们还可以使用平行四边形的两对边的长度来计算面积。
假设平行四边形的两对边的长度分别为a和b,两对边之间的夹角为θ。
那么平行四边形的面积可以按照以下公式进行计算:面积= a × b × sin(θ)这里的sin(θ)表示夹角θ的正弦值。
通过测量或已知条件,我们可以得到两对边和夹角的具体数值,然后将其代入公式进行计算即可得到平行四边形的面积。
两种方法的优缺点使用底边和高的计算公式简单直观,仅需要直接测量或已知条件的两个数值,计算过程相对简单。
然而,当我们无法直接测量或已知底边和高时,这种方法就不适用了。
相比之下,使用两对边和夹角的计算公式能够更加灵活地计算平行四边形的面积。
这种方法相对复杂一些,需要测量或已知两对边的长度和夹角的数值,以及计算夹角的正弦值。
然而,通过这种方法,我们可以在对平行四边形的不同部分进行测量后,通过组合计算得到整个平行四边形的面积。
总结无论是使用底边和高的计算公式,还是使用两对边和夹角的计算公式,都能够准确计算平行四边形的面积。
在实际应用中,我们可以根据具体情况选择适用的计算方法。
无论选择哪种方法,我们都应该确保测量准确、计算正确,以得到准确的平行四边形面积。
平行四边形的面积计算是数学中的基础知识点,掌握这个计算方法对于解决与平行四边形相关的问题非常重要。
平行四边形与面积问题-八年级数学课件

B
F
G
3.若池塘BC边有一房屋建筑M,因此扩建时BC 保持不动,扩建时应满足上述条件,请你再设计一 个开挖方案,画出设计图纸。
D EGCA源自·BM F
4、张大爷十年前承包的一块五边形土地,经过多年的 开垦荒地,现已变成如图所示的形状,但承包地与开垦 荒地的分界小路(即折线CDE)还留着,张大爷想过E 点修一条直路,直路修好后要保持直路左边的土地与承 包时的一样多,右边的土地与开垦的荒地面积一样多, 请你按张大爷要求设计方案(不计分界小路与直路占地 E 面积)。
G E B
·
F
SΔABF= SΔADE
C 方法小结: 平行四边形一边的两端点与对边
上的一点构成的三角形面积等于平行四边形 面积的一半 。
应用(二)
若张大爷家的菜地的形状如图所示,AB∥ EF∥ CD, AF∥ ED∥ BC,请你用一条直线将其分为面积相等的两 部分。(不写作法,保留作图痕迹)
A
F
两平行线间的距离处处相等。
2.如何计算三角形的面积?
1 S = 底 x高 2
3.如何计算平行四边形的面积?
S =底x高
探究(一)
如图:已知任意直线l把平行四边形ABCD分成 两部分,要使这两部分的面积相等,直线l所在的 位置满足的条件是 过AC,BD的交点O的任意一条直线
A A D D E
O
B B
A
C B
D
应用(三)
如图,某村口有一口呈三角形的池塘,在它的三个顶点 A,B,C处均有一棵大核桃树,该村现准备开挖池塘建养 鱼塘,要求池塘的面积扩大一倍,且核桃树不动,且扩建 后的池塘呈平行四边形形状,请你设计一个开挖方案, 并画出设计图纸。
人教版八年级数学下册_平行四边形中的特殊面积关系知识点讲解

平行四边形中的特殊面积关系1.问题引入平行四边形中涉及到很多面积计算问题,根据平行四边形的性质,可以得到一些特殊面积之间的规律性关系,掌握这些结论将有助于问题的求解。
下面是一个我们都很熟悉的结论:如图1,□ABCD 中对角线AC (或BD )将平行四边形分成的两个三角形全等,因此有S △ABC =S △ADC =21S □ABCD (或S △ABD =S △CBD =21S □ABCD )。
引例:如图,某村有一个呈四边形的池塘,在它的四个角的顶点A 、B 、C 、D 处均种有一棵大核桃树,该村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又不想移动核桃树,并要求扩建后的池塘成平行四边形形状,该村能否实现这一设想?若能,请你设计并画出图形;若不能,请你说明理由。
(画图要保留痕迹,不写画法)分析:连接对角线AC 、BD ,分别过点A ,B ,C ,D 作对角线的平行线,相交于点E 、F 、G 、H ,则□EFGH 即为所求。
2.问题拓展2.1.平行四边形对角线将平行四边形分成的四个三角形间的面积关系。
如图2,□ABCD 中对角线互相平分,OA=OC ,OB=OD ,易证△AOB ≌△COD ,△BOC≌△DOA ,所以S △AOB =S △COD ,S △BOC =S △DOA又由同底等高的三角形面积相等,可知:S △AOB = S △BOC故有:S △AOB =S △COD =S △BOC =S △DOA =41S □ABCD 拓展结论1:在平行四边形中,两条对角线将平行四边形分成的四个部分面积相等,且都等于平行四边形面积的四分之一。
例1.如图2,□ABCD 的对角线相交于O ,S △AOB =4cm 2,S □ABCD = 。
分析:由拓展结论1,S □ABCD =4 S △AOB =4×4=16(cm 2)2.2.平行四边形一条边上的点与其对边端点所连接的线段将平行四边形分成三个三角形间的面积关系。
平行四边形的面积计算与问题解析

平行四边形的面积计算与问题解析平行四边形是几何学中的一个常见形状,它具有特殊的性质和应用。
本文将介绍平行四边形的面积计算方法,并探讨一些与平行四边形面积相关的问题。
一、平行四边形的面积计算方法平行四边形的面积计算方法有几种,下面将介绍两种常用的方法。
方法一:基于底边和高的计算公式设平行四边形的底边长为a,高为h,则平行四边形的面积S可以通过以下公式计算:S = a * h方法二:基于两边长度和夹角的计算公式设平行四边形的两个相邻边长分别为a和b,它们之间的夹角为θ,则平行四边形的面积S可以通过以下公式计算:S = a * b * sin(θ)需要注意的是,使用这个公式时,夹角θ的取值应为其对应锐角的度数。
二、平行四边形面积的问题解析1. 如何确定平行四边形的底边和高?平行四边形的底边可以通过两个任意相邻边之一确定,高则是垂直于底边的线段。
根据给定的信息,我们可以通过测量或已知条件进行判断。
2. 如何确定平行四边形的两个相邻边和夹角?平行四边形的两个相邻边可以通过测量或已知条件确定。
夹角可以通过测量两边之间的角度得出。
3. 平行四边形与其他几何形状的关系平行四边形是梯形和矩形的特殊情况。
当一个四边形的对边平行且相等时,它就是一个平行四边形。
当四边形的所有角均为直角时,它就是一个矩形。
4. 如何计算由多个平行四边形组成的复杂图形的面积?当复杂图形由多个平行四边形组成时,可以通过将其分解为若干个平行四边形,计算每个平行四边形的面积,再将它们相加得到整个图形的面积。
5. 平行四边形面积计算的应用举例平行四边形的面积计算在实际中有广泛的应用。
例如,在建筑和土木工程中,可以通过计算平行四边形面积来确定场地的面积或物体的表面积。
在日常生活中,可以利用平行四边形面积计算来规划家具摆放或装修空间。
总结:本文介绍了平行四边形的面积计算方法,包括基于底边和高以及基于两边长度和夹角的计算公式。
同时,讨论了一些与平行四边形面积相关的问题,包括如何确定底边、高、相邻边和夹角,平行四边形与其他几何形状的关系,以及复杂图形的面积计算等。
第六单元平行四边形面积的实际应用“拓展型”专项练习-五年级数学(解析版)人教版

2023-2024学年五年级数学上册典型例题系列第六单元:平行四边形面积的实际应用“拓展型”专项练习1.下图中两个平行四边形的面积相等吗?它们的面积各是多少?【答案】相等;4.2平方厘米【分析】观察图形可知,两个平行四边形的底都是2.8厘米,高都是1.5厘米,根据平行四边形的面积公式:S=ah,据此代入数值进行计算即可。
【详解】2.8×1.5=4.2(平方厘米)答:图中两个平行四边形的面积相等,它们的面积都是4.2平方厘米。
【点睛】本题考查平行四边形的面积,熟记公式是解题的关键。
2.下面4个平行四边形的面积一样大吗,你发现了什么规律?(单位:cm)【答案】一样大不管平行四边形的形状如何,只要底和高分别相等,面积就相等。
【分析】观察题图可知,4个平行四边形在一组平行线内,说明它们的高相等;它们的底都是1cm,说明底也相等。
平行四边形的面积=底×高,它们四个等底等高,所以面积相等,与它们的形状无关。
【详解】4个平行四边形的面积一样大。
发现:不管平行四边形的形状如何,只要底和高分别相等,面积就相等。
【点睛】明确4个平行四边形等底等高是解答本题的关键。
3.李伯伯积极响应社会主义新农村建设的号召,准备将一块周长为480米的直角梯土地分割成一块三角形和一块平行四边形菜地,计划利用平行四边形菜地种植花菜,请你帮李伯伯在图上分一分,并计算出花菜的种植面积。
【答案】作图见详解;7200平方米【分析】是在同一个平面内,由两组平行线段组成的闭合图形是平行四边形;由三条线段首尾相连围成的封闭图形是三角形,据此将梯形分割成一个三角形和一个平行四边形;梯形周长减去已知的3条边的长度是梯形的高,即平行四边形的高,平行四边形的底=梯形的上底,根据平行四边形面积=底×高,列式解答即可。
【详解】120×(480-120-100-200)=120×60=7200(平方米)答:花菜的种植面积是7200平方米。
14 平行四边形中的周长和面积问题-【初中数学】120个题型大招!冲刺满分秘籍!

平行四边形中的周长和面积问题题型一平行四边形中的周长问题1.如图,在ABCD 中,AE BC ⊥于点E ,AF CD ⊥交DC 于DC 的延长线于点F ,3AB cm =,7AF cm =,30EAF ∠=︒,求B ∠的度数和ABCD 周长.【解答】解: 在ABCD 中,AF CD ⊥,BA AF ∴⊥,90BAF ∴∠=︒,30EAF ∠=︒ ,60BAE ∴∠=︒,AE BC ⊥ ,30B ∴∠=︒;3AB cm = ,1.5AE cm ∴=,故AE BC AF CD ⨯=⨯,则1.573BC ⨯=⨯,解得:14BC =,故14AD cm =,则ABCD 周长为:(143)234()cm +⨯=.2.如图,在ABC ∆中,5AB AC ==,D 是BC 边上的点,//DE AB 交AC 于点E ,//DF AC 交AB 于点F ,那么四边形AFDE 的周长是10.【解答】解:5AB AC == ,B C ∴∠=∠,由//DF AC ,得FDB C B ∠=∠=∠,FD FB ∴=,同理,得DE EC =.∴四边形AFDE 的周长AF AE FD DE=+++AF FB AE EC=+++AB AC=+5510=+=.故答案为10.3.如图,在ABCD 中,AE BC ⊥于点E ,AF CD ⊥于点F ,45EAF ∠=︒,且22AE AF +=,则ABCD 的周长为8.【解答】解:45EAF ∠=︒ ,360135C AEC AFC EAF ∴∠=︒-∠-∠-∠=︒,18045B D C ∴∠=∠=︒-∠=︒,则AE BE =,AF DF =,设AE x =,则22AF x =-,在Rt ABE ∆中,根据勾股定理可得,2AB x=同理可得2(22)AD x =-则平行四边形ABCD 的周长是2()2[22(22)]8AB AD x x +=+-=故答案为8.4.如图,平行四边形ABCD 的周长为20,对角线AC 、BD 交于点O ,E 为CD 的中点,6BD =,则DOE ∆的周长为()A .5B .8C .10D .12【解答】解:ABCD 的周长为20,2()20BC CD ∴+=,则10BC CD +=.四边形ABCD 是平行四边形,对角线AC ,BD 相交于点O ,6BD =,132OD OB BD ∴===.又 点E 是CD 的中点,OE ∴是BCD ∆的中位线,12DE CD =,12OE BC ∴=,DOE ∴∆的周长11()53822OD OE DE BD BC CD =++=++=+=,即DOE ∆的周长为8.故选:B .5.如图,在平行四边形ABCD 中,AE 平分BAD ∠交BC 边于点E ,若平行四边形ABCD 的周长是24,2EC =,则AB 的长为()A .4B .5C .5.5D .6【解答】解: 四边形ABCD 是平行四边形,//AD BC ∴,AB CD =,AD BC =,DAE AEB ∴∠=∠,AE 平分DAB ∠,DAE EAB ∴∠=∠,AEB EAB ∴∠=∠,BE AB ∴=,BC BE EC -= ,2BC AB ∴-=①,平行四边形ABCD 的周长是24,12AB BC ∴+=②,①+②得:214BC =,7BC ∴=,5AB ∴=,故选:B .6.如图,四边形ABCD 中,点E ,F 分别在边AD ,BC 上,线段EF 与AC 交于点O 且互相平分,若10AD BC ==,6EF AB ==,则四边形EFCD 的周长是()A.16B.20C.22D.26【解答】解:线段EF与AC交于点O且互相平分,得OA OC=,=,OE OF又AOE COF,∠=∠AOE COF ASA∴∆≅∆,()∴∠=∠,EAO FCO∴,AD BC//,=AD BC∴四边形ABCD是平行四边形,∴=,CD AB∴四边形CDEF的周长=+++=+++=++=++=;CD DE EF CF CD AB DE AE CD AB AD661022故选:C.7.如图,平行四边形ABCD的周长为32cm,AC,BD相交于点O,OE AC⊥交AD于点E,则DCE∆的周长为()A.8cm B.24cm C.10cm D.16cm【解答】解:ABCD的周长为32cm,∴+=,OA OC=,AD CD cm16⊥,OE AC∴=,AE CE++=++=+=.CD DE CE CD DE AE CD AD cmDCE∴∆的周长为:16故选:D.8.如图,ABCD∠=︒,1CF=,4CE=,⊥于点F,若60EAF中,AE BC⊥于点E,AF CD则ABCD的周长为()A .20B .24C .26D .28【解答】解:AE BC ⊥ ,AF CD ⊥,60EAF ∠=︒,360909060120C ∴∠=︒-︒-︒-︒=︒,四边形ABCD 是平行四边形,//AB CD ∴,//AD BC ,18060B D C ∴∠=∠=︒-∠=︒,∴在Rt BAE ∆中,30BAE ∠=︒,2AB BE ∴=,设BE x =,则2AB CD x ==,4BC BE CE x =+=+,3AE x ,21DF CD CF x ∴=-=-,在Rt ADF ∆中,30DAF ∠=︒,242AD DF x ∴==-,BC AD = ,424x x ∴-=+,解得:2x =,4AB CD ∴==,6BC AD ==,∴平行四边形ABCD 周长2(46)20=⨯+=.故选:A .9.如图,ABC ∆的周长为19,点D ,E 在边BC 上,ABC ∠的平分线垂直于AE ,垂足为N ,ACB ∠的平分线垂直于AD ,垂足为M ,若7BC =,则MN 的长度为52.【解答】解:BN 平分ABC ∠,BN AE ⊥,NBA NBE ∴∠=∠,BNA BNE ∠=∠,在BNA ∆和BNE ∆中,ABN EBN BN BN ANB ENB ∠=∠⎧⎪=⎨⎪∠=∠⎩.()BNA BNE ASA ∴∆≅∆,BA BE ∴=,BAE ∴∆是等腰三角形,同理CAD ∆是等腰三角形,∴点N 是AE 中点,点M 是AD 中点(三线合一),MN ∴是ADE ∆的中位线,1919712BE CD AB AC BC +=+=-=-= ,5DE BE CD BC ∴=+-=,1522MN DE ∴==.故答案是:52.10.在平行四边形ABCD 中,BC 边上的高为4,5AB =,AC =,则平行四边形ABCD 周长等于20或12.【解答】解:①如图1所示:在ABCD 中,BC 边上的高为4,5AB =,AC =2EC ∴==,5AB CD ==,3BE =,5AD BC ∴==,ABCD ∴ 的周长等于:20,②如图2所示:在ABCD 中,BC 边上的高为4,5AB =,AC =2EC ∴==,5AB CD ==,3BE =,321BC ∴=-=,ABCD ∴ 的周长等于:115512+++=,则ABCD 的周长等于20或12,故答案为:20或12.11.在平行四边形ABCD 中,A ∠的平分线分对边BC 为3和4两部分,求平行四边形的周长.【解答】解:在平行四边形ABCD 中,//AD BC ,则DAE AEB ∠=∠.AE 平分BAD ∠,BAE DAE ∴∠=∠,BAE BEA ∴∠=∠,AB BE ∴=,BC BE EC =+,①当3BE =,4EC =时,平行四边形ABCD 的周长为:2()2(334)20AB AD +=++=.②当4BE =,3EC =时,平行四边形ABCD 的周长为:2()2(443)22AB AD +=++=.综上所述,平行四边形的周长是20或22.题型二平行四边形中的面积问题12.如图,在平行四边形ABCD 中,AC ,BD 为对角线,6BC =,BC 边上的高为4,则图中阴影部分的面积为()A .3B .6C .12D .24【解答】解:通过观察结合平行四边形性质得:164122S =⨯⨯=阴影.故选:C .13.如图,在平行四边形ABCD 中,//AB EF ,//AD GH ,EF 与GH 交于点O ,分成的4个小平行四边形的面积分别为1S ,2S ,3S ,4S ,若18S =,210S =,330S =,则4S =24.【解答】解: 四边形ABCD 是平行四边形,//AB EF ,//AD GH ,////AB EF CD ∴,////AD GH BC ,∴12S EO S OF =,43S EO S OF=,∴1423S S S S =,∴481030S =,424S =.14.如图,在ABCD 中,3AB =,4AD =,60ABC ∠=︒,过BC 的中点E 作EF AB ⊥,垂足为点F ,与DC 的延长线相交于点H ,则DEF ∆的面积是()A .23B .43C .33D .623+【解答】解: 四边形ABCD 是平行四边形,4AD BC ∴==,//AB CD ,3AB CD ==,E 为BC 中点,2BE CE ∴==,60B ∠=︒ ,EF AB ⊥,30FEB ∴∠=︒,1BF ∴=,由勾股定理得:3EF =,//AB CD ,B ECH ∴∠=∠,在BFE ∆和CHE ∆中,B ECH BE CE BEF CEH ∠=∠⎧⎪=⎨⎪∠=∠⎩,()BFE CHE ASA ∴∆≅∆,3EF EH ∴==,1CH BF ==,1432DHF S DH FH ∆== ,1232DEF DHF S S ∆∆∴==.故选:A .15.如图,在平行四边形ABCD 中,点1A ,2A ,3A ,4A 和1C ,2C ,3C ,4C 分别是ABCD 的五等分点,点1B ,2B 和1D ,2D 分别是BC 和DA 的三等分点,已知四边形4242A B C D 的面积为2,则平行四边形ABCD 的面积为()A .4B .310C .103D .30【解答】解:设平行四边形ABCD 的面积是s ,设5AB a =,3BC b =.AB 边上的高是3x ,BC 边上的高是5y .则5335s a x b y =⋅=⋅.即15s ax by ==.△42AA D 与△24B CC 全等,213B C BC b ==,2B C 边上的高是4545y y ⋅=.则△42AA D 与△24B CC 的面积是2215by s =.同理△24D C D 与△42A BB 的面积是15s .则四边形4242A B C D 的面积是223151515155s s s s s s ----=,即325s =,解得103s =.解法2:如图所示:设42A BB S a = ,则242B C P S a = ,42C D Q S a = ,242D A M S a = ,42A B N S a = ,2232a a a a a ∴++++=,即92a =,解得:29a =,∴平行四边形ABCD 的面积210922151593a a a a a a =++++==⨯=;故选:C .16.如图,P 是平行四边形ABCD 内一点,且5PAB S ∆=,2PAD S ∆=,则阴影部分的面积为3.【解答】解:12PAB PCD ABCD ACD S S S S ∆∆∆+== ,ACD PCD PAB S S S ∆∆∆∴-=,则PAC ACD PCD PAD S S S S ∆∆∆∆=--,PAB PAD S S ∆∆=-,52=-,3=.故答案为:3.17.如图,在ABCD 中,点E 、F 分别在AD 和AB 上,依次连接EB 、EC 、FC 、FD ,阴影部分面积分别为1S ,2S ,3S ,4S ,已知13S =,215S =,34S =,则4S 的值是()A .8B .14C .16D .22【解答】解:设平行四边形的面积为S ,则12CBE CDF S S S ∆∆==,由图形可知,CDF ∆面积CBE +∆面积1432()S S S S +++-=平行四边形ABCD 的面积,43415CBE CDF S S S S ∆∆∴=++++-,即411341522S S S S =++++-,解得48S =,故选:A .18.如图,在边长为1的正方形网格中,平行四边形ABCD 的顶点在格点上,平行四边形EFGH 的顶点E 、F 在边CD 上,且//AD EH ,AD EH =,AG 交CD 于点O ,则S 阴影为()A .7平方单位B .8平方单位C .14平方单位D .无法确定【解答】解: 四边形ABCD 是平行四边形,7214ABCD S ∴=⨯=平行四边形(平方单位), 四边形EFGH 是平行四边形,EH GF ∴=,//EH GF ,//AD EH ,AD EH =,//AD GF ∴,AD GF =,DAO FGO ∴∠=∠,在AOD ∆和GOF ∆中,DAO FGO AOD GOF AD GF ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AOD GOF AAS ∴∆≅∆,AOD GOF S S ∆∆∴=,172ADC ABCD S S S ∆∴===阴影平行四边形(平方单位),故选:A .19.如图,平行四边形ABCD 中,对角线AC 、BD 交于点E ,90CBD ∠=︒,4BC =,10AC =,则这个平行四边形面积为()A .24B .40C .20D .12【解答】解: 四边形ABCD 是平行四边形,10AC =,152AE CE AC ∴===,12BE DE BD ==,90CBD ∠=︒ ,4BC =,2222543BE CE BC ∴=-=-=,26BD BE ∴==,则这个平行四边形面积为6424BD BC ⋅=⨯=,故选:A .20.如图,ABCD 中,60B ∠=︒,4AB =,5BC =,P 是对角线AC 上任一点(点P 不与点A 、C 重合),且//PE BC 交AB 于E ,//PF CD 交AD 于F ,则阴影部分的面积为()A .5B .53C .10D .103【解答】解: 四边形ABCD 是平行四边形,//AB CD ∴,//AD BC//PE BC ,//PE AD∴//PF CD ,//PF AB ∴,∴四边形AEPF 为 .设AEPF 的对角线AP 、EF 相交于O ,则AO PO =,EO FO =,AOE POF ∠=∠()POF AOE SAS ∴∆≅∆,∴图中阴影部分的面积等于ABC ∆的面积,过A 作AM BC ⊥交BC 于M ,60B ∠=︒ ,4AB =,23AM ∴=,1523532ABC S ∆=⨯⨯=,即阴影部分的面积等于53.故选:B .21.如图,在平行四边形ABCD 中,E ,F 分别是边BC ,CD 的中点,AE ,AF 分别交BD 于点G ,H ,则图中阴影部分图形的面积之和与平行四边形ABCD 的面积之比为()A .712B .724C .1336D .1372【解答】解://BE AD ,E 是BC 的中点,BEG DAG ∴∆∆∽,∴12BG BE DG DA ==,即13BG BD =,同理可得,13DH BD =,13GH BD ∴=,1136AGH ABD ABCD S S S ∆∆∴==四边形,E 、F 分别是边BC 、CD 的中点,//EF BD ∴,12EF BD =,CEF CBD ∴∆∆∽,∴211()24CEF CBD S S ∆∆==,1148CEF BCD ABCD S S S ∆∆∴==四边形,,∴图中阴影部分图形的面积1176824ABCD ABCD S S ⎛⎫=+= ⎪⎝⎭四边形四边形,即图中阴影部分图形的面积与ABCD 的面积之比为7:24=,故选:B .22.如图,ABCD 的面积为S ,点P 是它内部任意一点,PAD ∆的面积为1S ,PBC ∆的面积为2S ,则S ,1S ,2S 之间满足的关系是()A .1212S S S +>B .1212S S S +<C .1212S S S +=D .无法判定【解答】解:过点P 作EF AD ⊥交AD 于点E ,交BC 的延长线于点F , 四边形ABCD 是平行四边形,AD BC ∴=,S BC EF ∴=⋅,12AD PE S ⋅=,22BC PF S ⋅=,EF PE PF =+ ,AD BC =,122S S S ∴+=,故选:C .23.如图,平行四边形ABCD 的对角线AC 和BD 相交于点O ,过点O 的直线分别交AD 和BC 于点F ,E ,若设该平行四边形的面积为2,则图中阴影部分的面积为()A .4B .1C .12D .无法确定【解答】解: 四边形ABCD 是平行四边形,AB CD ∴=,OA OC =,OB OD =,在AOB ∆和COD ∆中,AB CD OA OC OB OD =⎧⎪=⎨⎪=⎩,()AOB COD SSS ∴∆≅∆,AOB COD S S ∆∆∴=,同理可证:()AFO CEO ASA ∆≅∆,()BOE DOF ASA ∆≅∆,AFO CEO S S ∆∆∴=,BOE DOF S S ∆∆=,∴阴影部分的面积112ABEF ABCD S S ===四边形平行四边形.故选:B .24.如图,平行四边形ABCD 中,点E 、F 分别在AD 、AB 上,依次连接EB 、EC 、FC 、FD ,图中阴影部分的面积分别为1S 、2S 、3S 、4S ,已知12S =、212S =、33S =,则4S 的值是7.【解答】解:设平行四边形的面积为S ,则12CBE CDF S S S ∆∆==,由图形可知,CDF ∆面积CBE +∆面积1432()S S S S +++-=平行四边形ABCD 的面积42312CBE CDF S S S S ∆∆∴=++++-,即411231222S S S S =++++-,解得47S =,故答案为:7.25.如图,过ABCD 的对角线BD 上一点M 分别作平行四边形两边的平行线EF 与GH ,那么图中的AEMG 的面积1S 与HCFM 的面积2S 的大小关系是相等.【解答】解: 四边形ABCD 是平行四边形,//GH AB ,//EF AD ,AD BC ∴=,AB CD =,////AB GH CD ,////AD EF BC ,∴四边形HBEM 、GMFD 是平行四边形,在ABD ∆和CDB ∆中,AB CD BD DB DA CB =⎧⎪=⎨⎪=⎩,()ABD CDB SSS ∴∆≅∆,即ABD ∆和CDB ∆的面积相等;同理BEM ∆和MHB ∆的面积相等,GMD ∆和FDM ∆的面积相等,故四边形AEMG 和四边形HCFM 的面积相等,即12S S =.故答案为:相等.26.如图,在ABCD 中,BE CD ⊥,BF AD ⊥,45EBF ∠=︒,3CE =,1DF =,则ABCD 的面积是()A .1832-B .1532+C .1532-D .1832+【解答】解:BE CD ⊥ ,BF AD ⊥,90BEC ∴∠=︒,90BED BFD ∠=∠=︒,45EBF ∠=︒ ,360909045135D ∴∠=︒-︒-︒-︒=︒,四边形ABCD 是平行四边形,//BC AD ∴,18045C D ∴∠=︒-∠=︒,45A C ∴∠=∠=︒,3CE = ,3BE EC ∴==,BC ∴=,1DF = ,1AF BF ∴==-,ABCD ∴ 的面积是1)18AD BF ⨯=-=-故选:A .27.如图,在ABCD 中,BE 平分ABC ∠交AD 于点E ,过点A 作AF DC ⊥,交DC 的延长线于点F ,分别交BE ,BC 于点G ,H ,若AH =,CD =,则ABE ∆的面积是【解答】解:如图,过A 点作AM BC ⊥交BC 于点M ,过B 点作BN EN ⊥交EA 的延长线点N ,四边形ABCD 是平行四边形,//AB CD ∴,//AD BC ,AB CD ==,AM BN =,AF DC ⊥ ,//AB CD ,90ABH ∴∠=︒,3BH ∴==,1122ABH S AB AH BH AM ∆=⨯⋅=⨯⋅ ,AM ∴=,BN AM ∴==,BE 平分ABC ∠交AD 于点E ,//AD BC ,ABE CBE AEB ∴∠=∠=∠,AE AB ∴==,1122ABE S AE BN ∆∴=⨯⋅==28.如图,在ABCD 中,P 为AB 上的一点,E 、F 分别是DP 、CP 的中点,G 、H 为CD 上的点,连接EG 、FH ,若ABCD 的面积为224cm ,12GH AB =,则图中阴影部分的面积为26cm .【解答】解:如图,设EG ,FH 交于点O ,四边形ABCD 为平行四边形,且ABCD 的面积为224cm ,21122PCD ABCD S S cm ∆∴== ,AB CD =,//AB CD ,E 、F 分别是DP 、CP 的中点,EF ∴为PCD ∆的中位线,2CD EF ∴=,////EF CD AB ,:1:4PEF PCD S S ∆∆∴=,3PEF S ∆∴=,12GH AB = ,EF GH ∴=,//EF GH ,21 1.52OEF OGH PEF S S S cm ∆∆∆∴===,232 1.56S cm ∴=+⨯=阴影,故答案为26cm .29.如图,平行四边形ABCD 的顶点A 是等边EFG ∆边FG 的中点,60B ∠=︒,4EF =,则阴影部分的面积为【解答】解:如图,过A 作AM EF ⊥于E ,AN EG ⊥于N ,连接AE .ABC ∆ 是等边三角形,AF AG =,AEF AEN ∴∠=∠,AM EF ⊥ ,AN EG ⊥,AM AN ∴=,60MEN ∠=︒ ,90EMA ENA ∠=∠=︒,120MAN ∴∠=︒,四边形ABCD 是平行四边形,//BC AD ∴,180120DAB B ∴∠=︒-∠=︒,MAN DAB ∴∠=∠,MAH NAL ∴∠=∠,()AMH ANL ASA ∴∆≅∆,AMEN S S ∴=阴四边形,4EF = ,2AF =,AE ∴=,AM =,3EM =,1232AMEN S ∴=⨯⨯=四边形,AMEN S S ∴==阴四边形.故答案为:.30.如图,在ABCD 中,3AB =,4AD =,60ABC ∠=︒,过BC 的中点E 作EF AB ⊥,垂足为点F ,与DC 的延长线相交于点H ,则DEF ∆的面积是23.【解答】解: 四边形ABCD 是平行四边形,4AD BC ∴==,//AB CD ,3AB CD ==,E 为BC 中点,2BE CE ∴==,60B ∠=︒ ,EF AB ⊥,30FEB ∴∠=︒,1BF ∴=,由勾股定理得:3EF =,//AB CD ,HCE B ∴∠=∠,在BFE ∆和CHE ∆中B HCE BE CE BEF CEH ∠=∠⎧⎪=⎨⎪∠=∠⎩()BFE CHE ASA ∴∆≅∆,3EF EH ∴==,1BF CH ==,即134HD =+=,1134322DEF S EF DH ∆∴=⨯=⨯=故答案为:23.31.如图所示,点O 为ABCD 内一点,连接BD ,OA ,OB ,OC ,OD ,已知BCO ∆的面积为3,ABO ∆的面积为3,则阴影部分的面积是533-.【解答】解:ABCD 的面积2()2AOB COD BCD S S S ∆∆∆=+=,设COD ∆的面积为x ,ABCD 的面积()()25323BOD x S x ∆=+=++阴影,∴阴影部分BOD ∆的面积533x x =+--,533=-,故答案为:533-.32.如图在ABCD 中,60ABC ∠=︒,28BC AB ==,点C 关于AD 的对称点为E ,连接BE 交AD 于点F ,点G 为CD 的中点,连接EG ,BG .则BEG ∆的面积为()A .3B .3C .83D .3【解答】解:如图,取BC 中点H ,连接AH ,连接EC 交AD 于N ,作EM CD ⊥交CD 的延长线于M .2BC AB = ,BH CH =,60ABC ∠=︒,BA BH CH ∴==,ABH ∴∆是等边三角形,HA HB HC ∴==,90BAC ∴∠=︒,30ACB ∴∠=︒,EC BC ⊥ ,180120BCD ABC ∠=︒-∠=︒,60ACE ∴∠=︒,30ECM ∠=︒,28BC AB == ,4CD ∴=,CN EN ==,EC ∴=,EM =,BEG BCE ECG BCGS S S S ∆∆∆∴=+-11182224ABCD S =⨯⨯⨯⨯平行四边形=-=故选:B .题型三与函数结合求点的坐标、求面积33.如图,在平面直角坐标系中,已知O 为原点,四边形ABCD 为平行四边形,A 、B 、C的坐标分别是(A -,(2B -,,(2C ,,点D 在第一象限.(1)求D 点的坐标;(2)将平行四边形ABCD 个单位长度所得的四边形1111A B C D 四个顶点的坐标是多少?(3)求平行四边形ABCD 与四边形1111A B C D 重叠部分的面积?【解答】解:(1)由B 、C 的坐标可知,4AD BC ==,则可得点D 的横坐标为1,点D 的纵坐标与点A 的纵坐标相等,为,可得点D 的坐标为.(2)依题意得1A 、1B 、1C 、1D 的坐标分别为(3A -0),(2B -,(2C +,,(1D +0).(3)如图,平行四边形ABCD 与四边形1111A B C D 重叠部分的面积为平行四边形1DEB G 的面积,由题意直线11A B 的解析式为3y x =+-,当y =时,52x =,52G ∴-,174(22GD AD AG ∴=-=-+=-平行四边形1DEB G 的高为-=∴重叠部分的面积为7(222-.34.在平面直角坐标系中,O 是坐标原点,平行四边形ABCD 的顶点A 的坐标为(2,0)-,点D 的坐标为(0,,且:3:2AB AD =,点B 在x 轴的正半轴上,点E 为线段AD 的中点,过点E 的直线与x 轴交于点(4,0)F -,与DC 交于点G .(1)求ABCD 的面积;(2)求点G 的坐标;(3)若过点F 的直线l 平分ABCD 的面积,求直线l 的解析式.【解答】解:(1) 点(2,0)A -,点(0D ,,90AOD ∠=︒,2OA ∴=,OD =4AD ∴=,:3:2AB AD = ,6AB ∴=,6ABCD S AB OD ∴=⋅=⨯ ;(2) 点E 是线段AD 的中点,∴点(E -,设点G 的坐标为(,)x y ,//DG AB ,DGE AFE ∴∠=∠,在DGE ∆和AFE ∆中,DGE AFE AEF DEG ED EA ∠=∠⎧⎪∠=∠⎨⎪=⎩,()DGE AFE AAS ∴∆≅∆,FE EG ∴=,即点E 为线段FG 的中点, 点(4,0)F -,点(,)G x y,点(E -,∴412x -+=-,02y +=,解得,2x =,y =G 的坐标是(2,;(3) 过点F 的直线l 平分ABCD 的面积,∴直线l 过平行四边形的中心点H ,如右图所示, 点(0D,,点(4,0)B ,∴点H ,设过点(4,0)F -,点H 的直线l 的解析式为y kx b =+,402k b k b -+=⎧⎪⎨+=⎪⎩解得,36233k b ⎧=⎪⎪⎨⎪=⎪⎩即直线l的解析式为63y x =+.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
过AC,BD的交点O的任意一条直线
目 录 首 页 上一页 下一页 末 页
宇轩图书
应用
1.如图,张大爷家有一块平行四边形菜地,在其内部
有一平行四边形的水池,张大爷想引一条笔直的水渠,
且这条笔直的水渠将平行四边形菜地和水池分成面积
相等的两部分,请你为他设计一种引水渠方案,画出
图形,并说明理由。
2、在平行四边形ABCD中,已知AB、
BC、CD三条边的长度分别为(x+3),
(x-4)和16,则这个四边形的周长
是
。
目 录 首 页 上一页 下一页 末 页
宇轩图书
3、一个平行四边形的一边长为10,一 条对角线的长为7,则它的另一条对角
线x的取值范围是_________.
4、若平行四边形的一边长为5,则它的两条 对角线长可以是( D ) A.12和2 B.3和4 C.4和6 D.4和8
目 录 首 页 上一页 下一页 末 页
宇轩图书
(P80) 目 录 首 页 上一页 下一页 末 页
宇轩图书
ABCD中,E是CD上一点,若S AED:S BCE =4:1,
则S AED:S BCE=
。
目 录 首 页 上一页 下一页 末 页
宇轩图书
在 ABCD中,E、F分别是AD、BC上任意
两点,S APB=20,S CDQ=30, 则S阴影
=
。
目 录 首 页 上一页 下一页 末 页
宇轩图书
ABCD中,EF∥BD,S BEC=2,则
S CFD=
.
目 录 首 页 上一页 下一页 末 页
宇轩图书
张大爷承包的一块五边形土地,如图所示的形状, 承包地与开垦荒地的分界小路是折线CDE,张大爷 想过E点修一条直路,修好后要保持左边和右边的土
地面积不变,请你按要求设计方案。
A B
E G
N D
M
C
H
目 录 首 页 上一页 下一页 末 页
宇轩图书
拓展延伸
已知:如图a,平行四边形ABCD的对角 线AC、BD相交于点O,EF过点O与AB、 CD分别相交于点E、F. (1)求证:OE=OF
A
D
E B
O
F
C
目 录 首 页 上一页 下一页 末 页
宇轩图书
探究
如图:已知任意直线l把平行四边形ABCD分成两部 分,要使这两部分的面积相等,直线l所在的位置满
宇轩图书
平行四边形中的面积问题
目 录 首 页 上一页 下一页 末 页
宇轩图书
平行四边形的性质
目 录 首 页 上一页 下一页 末 页
宇轩图书
平行四边形的周长与面积
目 录 首 页 上一页 下一页 末 页
宇轩图书
达 标 练习
1、平行四边形的周长为36cm,相邻两
边的比为1:2,则它的两邻边长分别是
图,某村口有一口呈四边形的池塘,在它的四个顶 点A,B,C,D处均有一棵大核桃树,该村现准备开挖池塘 建养鱼塘,要求池塘的面积扩大一倍,且核桃树不动,且 扩建后的池塘呈平行四边形形状,请你设计一个开挖方
案,并画出设计图纸。
D
E
H
C A
F
G
B
目 录 首 页 上一页 下一页 末 页
A
M D
O
E
H
O’
F
G
B
N
C
目 录 首 页 上一页 下一页 末 页
宇轩图书
2.若张大爷家的菜地的形状如图所示,AB∥ EF∥ CD, AF∥ ED∥ BC,请你用一条直线将其分为面积相等的两部
分。(不写作法,保留作图痕迹)
A
F
下一题
按钮一
E D
B C
按钮二
按钮三
目 录 首 页 上一页 下一页 末 页
