中考：数学锐角三角函数专题

合集下载

专题28.17 锐角三角函数(中考常考考点专题)(基础篇)(专项练习)-2022-2023学年九年级

专题28.17 锐角三角函数（中考常考考点专题）（基础篇）（专项练习）一、单选题【类型一】锐角三角函数【考点一】（正弦✮✮余弦✮✮正切）概念➽➸辨析1．（2022·吉林长春·中考真题）如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图，该起重机的变幅索顶端记为点A ，变幅索的底端记为点B ，AD 垂直地面，垂足为点D ，BC AD ⊥，垂足为点C ．设ABC α∠=，下列关系式正确的是（）A ．sin AB BC α= B ．sin BC AB α= C ．sin AB AC α=D ．sin AC AB α= 2．（2022·湖北湖北·模拟预测）如图，在Rt ABC △中，BD 是斜边AC 上的高，AB BC ≠，则下列比值中等于sin A 的是（）．A ．AD AB B ．BD ADC ．BD BC D ．DC BC【考点二】角➽➸（正弦✮✮余弦✮✮正切）函数值3．（2022·浙江宁波·三模）如图，将ABC 放在每个小正方形的边长为1的网格中，点A ，B ，C 均在格点上，则tan A 的值是（）A B C ．2 D ．124．（2022·福建省厦门第二中学模拟预测）如图，在Rt ABC 中，90,2C BC AC ∠=︒=，则sin B =（）A ．12 B ．2 C D 【考点三】（正弦✮✮余弦✮✮正切）函数值➽➸求边长5．（2020·四川雅安·中考真题）如图，在Rt ACB 中，900.5C sinB ∠=︒=，，若6AC =，则BC 的长为（）A ．8B ．12C ．D ．6．（2022·吉林·长春市赫行实验学校一模）如图要测量小河两岸相对的两点P 、A 的距离，可以在小河边取PA 的垂线PB 上的一点C ，测得50PC =米，44PCA ∠=︒，则小河宽PA 为（）米A ．50sin44︒B ．50cos44︒C ．50tan 44︒D ．50tan46︒【类型二】特殊锐角三角函数【考点一】特殊锐角➽➸函数值7．（2016·江苏无锡·中考真题）sin30°的值为（）A ．12 B C ．2 D 8．（2021·广东深圳·中考真题）计算|1tan 60|-︒的值为（）A ．1B ．0C 1D ．1【考点二】函数值➽➸特殊锐角9．（2022·河南焦作·()101α+︒=，则锐角α的度数为（）A ．40°B ．30°C ．20°D ．10°10．（2021·江苏无锡·一模）已知cos A A =∠是锐角，则A ∠的度数为（） A ．30︒ B ．45︒ C ．60︒ D ．90︒【考点三】混合运算➽➸特殊锐角✮✮二次根式11．（2021·山东泰安·模拟预测）计算：202122sin 60|1(1)2-︒----的结果是（）A ．74B ．4C ．14D ．1412．（2021·山东省日照市实验中学二模）计算（tan30°）﹣1﹣2|）0的结果是（）A ．6B ．12C ．2D ．2＋【考点四】特殊锐角值➽➸判断三角形形状13．（2021·贵州黔西·模拟预测）在ABC 中，若A ∠，B ∠都是锐角，且1sin 2A =，1cos 2B =，则ABC 的形状是（） A ．钝角三角形 B ．等腰三角形C ．锐角三角形D ．直角三角形14．（2020·山东德州·二模）如果△ABC 中，sin A =cos B 2，则下列最确切的结论是（） A ．△ABC 是直角三角形B ．△ABC 是等腰三角形 C ．△ABC 是等腰直角三角形D ．△ABC 是锐角三角形【类型三】解直角三角形【考点一】解直角三角形➽➸直接解直角三角形15．（2022·陕西·中考真题）如图，AD 是ABC 的高，若26BD CD ==，tan 2C ∠=，则边AB 的长为（）A ．B ．C ．D ．16．（2022·四川广元·中考真题）如图，在△ABC 中，BC ＝6，AC ＝8，△C ＝90°，以点B 为圆心，BC 长为半径画弧，与AB 交于点D ，再分别以A 、D 为圆心，大于12AD 的长为半径画弧，两弧交于点M 、N ，作直线MN ，分别交AC 、AB 于点E 、F ，则AE 的长度为（）A ．52B ．3C ．D ．103【考点二】解非直角三角形➽➸转化为直角三角形并解之17．（2019·河北石家庄·二模）在东西方向的海岸线上有A ，B 两个港口，甲货船从A 港沿东北方向以5海里/时的速度出发，同时乙货船从B 港口沿北偏西60︒方向出发，2h 后相遇在点P 处，如图所示．问A 港与B 港相距（）海里．A．B ． C ．10+D ．2018．（2019·重庆·一模）缙云山是国家级自然风景名胜区，上周周末，小明和妈妈到缙云山游玩，登上了香炉峰观景塔，从观景塔底中心D 处水平向前走14米到A 点处，再沿着坡度为0.75的斜坡AB 走一段距离到达B 点，此时回望观景塔，更显气势宏伟，在B 点观察到观景塔顶端的仰角为45︒再往前沿水平方向走27米到C 处，观察到观景塔顶端的仰角是22︒，则观景塔的高度DE 为（）（tan22°≈0.4）A ．21米B ．24米C ．36米D ．45米【考点三】解不规则图形➽➸构造直角三角形并解之19．（2019·重庆九龙坡·模拟预测）如图是重庆轻轨10号线龙头寺公园站入口扶梯建设示意图．起初工程师计划修建一段坡度为3:2的扶梯AB ，扶梯总长为度大陡，扶梯太长容易引发安全事故．工程师修改方案：修建AC 、DE 两段扶梯，并减缓各扶梯的坡度，其中扶梯AC 和平台CD 形成的ACD ∠为135°，从E 点看D 点的仰角为36.5°，AC 段扶梯长则DE 段扶梯长度约为（）米（参考数据：3sin 36.55︒≈，4cos36.55︒≈，3tan 36.54︒≈）A ．43B ．45C ．47D ．4920．（2018·河北·模拟预测）如图（1）是一个六角星的纸板，其中六个锐角都为60°，六个钝角都为120°，每条边都相等，现将该纸板按图（2）切割，并无缝隙无重叠地拼成矩形ABCD ．若六角星纸板的面积为2，则矩形ABCD 的周长为（）A ．18cmB ．C ．（）cmD ．（）cm【类型四】解直角三角形的应用【考点一】解直角三角形➽➸仰角✮✮俯角21．（2022·广西贵港·中考真题）如图，某数学兴趣小组测量一棵树CD 的高度，在点A 处测得树顶C 的仰角为45︒，在点B 处测得树顶C 的仰角为60︒，且A ，B ，D 三点在同一直线上，若16m AB =，则这棵树CD 的高度是（）A ．8(3B ．8(3+C ．6(3D ．6(3+22．（2021·山东济南·中考真题）无人机低空遥感技术已广泛应用于农作物监测．如图，某农业特色品牌示范基地用无人机对一块试验田进行监测作业时，在距地面高度为135m 的A 处测得试验田右侧出界N 处俯角为43︒，无人机垂直下降40m 至B 处，又测得试验田左侧边界M 处俯角为35︒，则M ，N 之间的距离为（参考数据：tan 430.9︒≈，sin 430.7︒≈，cos350.8︒≈，tan350.7︒≈，结果保留整数）（）A ．188mB ．269mC ．286mD ．312m【考点二】解直角三角形➽➸方位角23．（2022·河北·模拟预测）从观测点A 测得海岛B 在其北偏东60°方向上，测得海岛C 在其北偏东80°方向上，若一艘小船从海岛B 出发沿南偏西40°方向以每小时40海里的速度，行驶2小时到C 海岛，则C 海岛到观测点A 的距离是（）A．20海里B．40海里C．60海里D．80海里24．（2022·山东·济南市市中区泉秀学校一模）如图，一艘测量船在A处测得灯塔S在它的南偏东60°方向，测量船继续向正东航行30海里后到达B处，这时测得灯塔S在它的南偏西75°方向，则灯塔S离观测点A的距离是（）B．（15）海里A．C．（）海里D．【考点三】解直角三角形➽➸坡度坡比25．（2022·贵州毕节·中考真题）如图，某地修建一座高5mBC=的天桥，已知天桥斜面AB的坡度为AB的长度为（）A．10m B．C．5m D．26．（2021·湖南衡阳·中考真题）如图是某商场营业大厅自动扶梯的示意图．自动扶梯AB 的倾斜角为37︒，大厅两层之间的距离BC为6米，则自动扶梯AB的长约为︒≈︒≈︒≈）（）．（sin370.6,cos370.8,tan370.75A ．7.5米B ．8米C ．9米D ．10米【考点四】解直角三角形➽➸其他问题27．（2022·广西·中考真题）如图，某博物馆大厅电梯的截面图中，AB 的长为12米，AB 与AC 的夹角为α，则高BC 是（）A ．12sin α米B ．12cos α米C ．12sin α米D ．12cos α米 28．（2022·湖北十堰·中考真题）如图，坡角为α的斜坡上有一棵垂直于水平地面的大树AB ，当太阳光线与水平线成45°角沿斜坡照下，在斜坡上的树影BC 长为m ，则大树AB 的高为（）A ．()cos sin m αα-B ．()sin cos m αα-C ．()cos tan m αα-D ．sin cos m m αα- 二、填空题【类型一】锐角三角函数【考点一】（正弦✮✮余弦✮✮正切）概念➽➸辨析29．（2022·上海市青浦区教育局二模）小明要测量公园里一棵古树的高，被一条小溪挡住去路，采用计算方法，在A 点测得古树顶的仰角为α，向前走了100米到B 点，测得古树顶的仰角为β，则古树的高度为________米．30．（2021·福建厦门·一模）在Rt△ABC中，△C＝90°，AC＝AB＝10，则△B＝_____．【考点二】角➽➸（正弦✮✮余弦✮✮正切）函数值31．（2021·四川乐山·三模）如图，在3×3的正方形网格中，A、B均为格点，以点A为圆心，AB长为半径画弧，图中的点C是该弧与网格线的交点．则sin△BAC的值等于_____．32．（2022·湖南益阳·中考真题）如图，在Rt△ABC中，△C＝90°，若sin A＝45，则cos B＝_____．【考点三】（正弦✮✮余弦✮✮正切）函数值➽➸求边长33．（2022·广东深圳·二模）如图，直角ABC中，90C∠=︒，根据作图痕迹，若3cmCA=，3tan4B=，则DE=________cm．34．（2021·湖南邵阳·中考真题）如图，在矩形ABCD 中，DE AC ⊥，垂足为点E ．若4sin 5ADE ∠=，4=AD ，则AB 的长为______．【类型二】特殊锐角三角函数【考点一】特殊锐角➽➸函数值35．（2021·西藏·中考真题）计算：（π﹣3）0＋（﹣12）﹣2﹣4sin30°＝___． 36．（2020·湖南湘潭·中考真题）计算：sin 45︒=________．【考点二】函数值➽➸特殊锐角37．（2022·陕西·西安辅轮中学三模）若sin(α+15°)=1，则△α等于_____________度． 38．（2020·湖北·武汉二中广雅中学三模）若sin A ＝12，则tan A ＝_____．【考点三】混合运算➽➸特殊锐角✮✮二次根式39．（2022·重庆·模拟预测）计算：sin45°+212-⎛⎫- ⎪⎝⎭＝_____．40．（2022·湖北荆门·一模）计算：)02112sin 45()2-+-︒--=________．【考点四】特殊锐角值➽➸判断三角形形状41．（2020·江苏淮安·三模）在ABC ∆中,若21 02sinA tanB -+⎛ ⎝⎭= ，则ABC ∆是_____三角形．42．（2019·四川自贡·一模）在△ABC 中，（cos A ﹣12）2+|tan B ﹣1|＝0，则△C ＝_____．【类型三】解直角三角形【考点一】解直角三角形➽➸直接解直角三角形43．（2019·辽宁大连·中考真题）如图，ABC ∆是等边三角形，延长BC 到点D ，使CD AC =，连接AD．若2AB=，则AD的长为_____．44．（2015·广西玉林·中考真题）如图，等腰直角△ABC中，AC=BC，△ACB=90°，点△BOC绕C点顺时针方向旋转到△AQC的位置，则O分斜边AB为BO：OA=1△AQC=___________．【考点二】解非直角三角形➽➸转化为直角三角形并解之45．（2021·湖北武汉·模拟预测）如图是某商场自动扶梯的示意图，自动扶梯AB的倾斜角是30°，在自动扶梯下方地面C处测得扶梯顶端B的仰角是60°，则自动扶梯的垂直高度BD=___________m． 1.732，结果精确到0.1米）46．（2020·安徽阜阳·二模）如图，在一条东西方向笔直的沿湖道路l上有A、B两个游船码头，观光岛屿C在码头A的北偏东60°方向、在码头B的北偏西45°方向，AC＝4千米．那么码头A、B之间的距离等于_____千米．（结果保留根号）【考点三】解不规则图形➽➸构造直角三角形并解之47．（2021·湖北湖北·中考真题）如图，某活动小组利用无人机航拍校园，已知无人机的飞行速度为3m/s，从A处沿水平方向飞行至B处需10s，同时在地面C处分别测得A处的仰角为75︒，B处的仰角为30︒．则这架无人机的飞行高度大约是_______m 1.732≈，结果保留整数）48．（2019·辽宁辽阳·中考真题）某数学小组三名同学运用自己所学的知识检测车速，他们将观测点设在一段笔直的公路旁且距公路100米的点A处，如图所示，直线l表示公路，一辆小汽车由公路上的B处向C处匀速行驶，用时5秒，经测量，点B在点A北偏东45°方向上，点C在点A北偏东60°方向上，这段公路最高限速60千米/小时，此车_____（填“超速”或“没有超速”） 1.732）【类型四】解直角三角形的应用【考点一】解直角三角形➽➸仰角✮✮俯角49．（2021·山东烟台·中考真题）数学兴趣小组利用无人机测量学校旗杆高度，已知无人机的飞行高度为40米，当无人机与旗杆的水平距离是45米时，观测旗杆顶部的俯角为30°，则旗杆的高度约为______________米．（结果精确到1米， 1.41≈ 1.73）50．（2021·四川乐山·中考真题）如图，为了测量“四川大渡河峡谷”石碑的高度，佳佳在点C 处测得石碑顶A 点的仰角为30︒，她朝石碑前行5米到达点D 处，又测得石顶A 点的仰角为60︒，那么石碑的高度AB 的长=________米．（结果保留根号）【考点二】解直角三角形➽➸方位角51．（2022·四川·巴中市教育科学研究所中考真题）一艘轮船位于灯塔P 的南偏东60︒方向，距离灯塔30海里的A 处，它沿北偏东30︒方向航行一段时间后，到达位于灯塔P 的北偏东67︒方向上的B 处，此时与灯塔P 的距离约为________海里．（参考数据：3sin 375︒≈，4cos375≈︒，3tan 374︒≈）52．（2022·辽宁沈阳·二模）如图，我国的一艘海监船在钓鱼岛A 附近沿正东方向航行，船在B 点时测得钓鱼岛A 在船的北偏东60°方向，船以50海里/时的速度继续航行2小时后到达C 点，此时钓鱼岛A 在船的北偏东30°方向．请问船继续航行______海里与钓鱼岛A 的距离最近．【考点三】解直角三角形➽➸坡度坡比53．（2022·广西柳州·中考真题）如图，某水库堤坝横断面迎水坡的坡角为α，sin α＝35，堤坝高BC ＝30m ，则迎水坡面AB 的长度为 ____m ．54．（2021·江苏无锡·中考真题）一条上山直道的坡度为1：7，沿这条直道上山，则前进100米所上升的高度为________米．【考点四】解直角三角形➽➸其他问题55．（2022·山东泰安·中考真题）如图，某一时刻太阳光从窗户射入房间内，与地面的夹角30DPC ∠=︒，已知窗户的高度2m AF =，窗台的高度1m CF =，窗外水平遮阳篷的宽0.8m AD =，则CP 的长度为______（结果精确到0.1m ）．56．（2021·广西梧州·中考真题）某市跨江大桥即将竣工，某学生做了一个平面示意图（如图），点A 到桥的距离是40米，测得△A ＝83°，则大桥BC 的长度是 ___米．（结果精确到1米）（参考数据：sin83°≈0.99，cos83°≈0.12，tan83°≈8.14）参考答案1．D【分析】根据正弦三角函数的定义判断即可．解：△BC△AC，△△ABC 是直角三角形， △△ABC =α， △sin ACABα=，故选：D ．【点拨】本题考查了正弦三角函数的定义．在直角三角形中任意锐角△A 的对边与斜边之比叫做△A 的正弦，记作sin△A ．掌握正弦三角函数的定义是解答本题的关键．2．D【分析】由同角的余角相等求得△A =△DBC ，根据正弦三角函数的定义判断即可；解：△△ABD +△A =90°，△ABD +△DBC =90°， △△A =△DBC ， A ．ADAB=cos A ，不符合题意； B ．BDAD=tan A ，不符合题意； C ．BDBC=cos△DBC =cos A ，不符合题意； D ．DCBC=sin△DBC =sin A ，符合题意；故选： D ．【点拨】本题考查了三角函数的概念，掌握直角三角形中锐角的正弦为对边比斜边是解题关键．3．D【分析】首先构造以△A 为锐角的直角三角形，然后利用正切的定义即可求解．解：连接BD ，如图所示：根据网格特点可知，BD AC ⊥， △90ADB ∠=︒，△BD AD =△在Rt△ABD 中，tan A ＝BD AD 12=，故D 正确．故选：D ．【点拨】本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边，构造直角三角形是本题的关键．4．C【分析】根据勾股定理，可得AB 与BC 的关系，根据正弦函数的定义，可得答案．解：△△C =90°，2BC AC =，△AB ，sinAC B AB ==C 正确．故选：C ．【点拨】本题考查了锐角三角函数的定义，先利用勾股定理得出AB 与AC 的关系，再利用正弦函数的定义．5．C【分析】利用正弦的定义得出AB 的长，再用勾股定理求出BC. 解：△sinB=ACAB=0.5， △AB=2AC ， △AC=6， △AB=12，故选C.【点拨】本题考查了正弦的定义，以及勾股定理，解题的关键是先求出AB 的长. 6．C【分析】在直角三角形APC 中根据△PCA 的正切函数可求小河宽P A 的长度．解：△P A △PB ， △△APC =90°，△PC =50米，△PCA =44°，△tan44°=PA PC，△小河宽P A=PCtan△PCA=50•tan44°米．故选：C．【点拨】本题考查了解直角三角形的应用，解直角三角形的一般过程是：△将实际问题抽象为数学问题（画出平面图形，构造出直角三角形转化为解直角三角形问题）．△根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形，得到数学问题的答案，再转化得到实际问题的答案．7．A【分析】根据特殊角的三角函数值求解即可．解：sin30°=12故答案为：A．【点拨】本题考查了锐角三角函数的问题，掌握特殊角的三角函数值是解题的关键．8．C【分析】直接利用特殊角的三角函数值、绝对值的性质分别化简得出答案．解：|1tan60||11-︒==故选C．【点拨】此题主要考查了特殊角的三角函数值，绝对值的性质等知识，正确化简各数是解题关键．9．C【分析】根据特殊角的三角函数值求解即可．解：（α+10°）=1，△tan（α+10°）△α为锐角，△α+10°=30°，α=20°．故选C．【点拨】熟记特殊角的三角函数值是解答此题的关键．10．A【分析】根据特殊角的三角函数值以及三角函数的定义，即可得到答案．解：△cos A A =∠是锐角， △A ∠=30°，故选A ．【点拨】本题主要考查锐角三角函数，掌握特殊角三角函数值是解题的关键． 11．A【分析】原式利用特殊角的三角函数值，绝对值的代数意义，乘方的意义，以及负整数指数幂法则计算即可得到结果．解：原式121)(1)4=--- 1114=+-74=．故选：A ．【点拨】本题考查实数的运算，掌握运算顺序是解决为题的关键，先乘方、再乘除、最后加减，注意牢记特殊角的三角函数值．12．D【分析】原式利用特殊角的三角函数值，零指数幂、负整数指数幂法则，绝对值的代数意义，以及立方根定义计算即可求出值．解：原式＝1-⎝⎭﹣（2+3+1＝．故选：D ．【点拨】本题考查实数的运算，掌握正确的运算顺序是解决问题的关键. 13．D【分析】根据特殊角的三角函数值可判断30A ∠=︒，=60B ∠︒，从而可求出90C ∠=︒，即证明ABC 的形状是直角三角形．解：△A ∠，B ∠都是锐角，且1sin 2A =，1cos 2B =， △30A ∠=︒，=60B ∠︒，△180180306090C A B ∠=︒-∠-∠=︒-︒-︒=︒，△ABC 的形状是直角三角形．故选D ．【点拨】本题考查由特殊角的三角函数值判断三角形形状，三角形内角和定理．熟记特殊角的三角函数值是解题关键．14．C解：△sin A =cos B ， △△A =△B =45°，△△ABC 是等腰直角三角形．故选：C ． 15．D【分析】先解直角ABC 求出AD ，再在直角ABD △中应用勾股定理即可求出AB ．解：△26BD CD ==， △3CD =，△直角ADC 中，tan 2C ∠=， △tan 326AD CD C =⋅∠=⨯=，△直角ABD △中，由勾股定理可得，AB = 故选D ．【点拨】本题考查利用锐角函数解直角三角形和勾股定理，难度较小，熟练掌握三角函数的意义是解题的关键．16．A【分析】由题意易得MN 垂直平分AD ，AB =10，则有AD =4，AF =2，然后可得4cos 5AC A AB ∠==，进而问题可求解．解：由题意得：MN 垂直平分AD ，6BD BC ==， △1,902AF AD AFE =∠=︒， △BC ＝6，AC ＝8，△C ＝90°，△10AB =，△AD =4，AF =2，4cos 5AC AF A AB AE ∠===， △5cos 2AF AE A ==∠；故选A ．【点拨】本题主要考查勾股定理、垂直平分线的性质及三角函数，熟练掌握勾股定理、垂直平分线的性质及三角函数是解题的关键．17．B【分析】先作PC AB ⊥于点C ，根据甲货船从A 港沿东北的方向以5海里/小时的速度出发，求出PAC ∠和AP ，从而得出PC 的值，得出BC 的值，即可求出答案．解：作PC AB ⊥于点C ，甲货船从A 港沿东北的方向以5海里/小时的速度出发，45PAC ∴∠=︒，5210AP =⨯=，PC AC ∴==乙货船从B 港沿西北方向出发，60PBC ∴∠=︒，BC ∴=AB AC BC ∴=+=，答：A 港与B 港相距海里，故选：B ．【点拨】本题考查了解直角三角形的应用-方向角问题，解题的关键是从实际问题中整理出直角三角形并利用解直角三角形的知识求解．本题要注意关键词：在东西方向的海岸线上有A ，B 两个港口.18．A【分析】作BN DA ⊥交DA 的延长线于N ，延长CB 交DE 于M ，则四边形DMBN 是矩形,根据AB 的坡度，设3,4,BN k AN k ==表示出144,3,MB DN k DM BN k ==+==414,CM k =+在Rt EBM 中，144,EM BM k ==+ 在Rt ECM 中，根据tan 0.4,EM C CM == 列出式子，求出k 的值，即可求解.解：如图，作BN DA ⊥交DA 的延长线于N ，延长CB 交DE 于M ，则四边形DMBN 是矩形,:3:4,BN AN =可以假设3,4,BN k AN k ==则，144,3,MB DN k DM BN k ==+== 414,CM k =+在Rt EBM 中， 90,45,EMB EBM ∠=∠=144,EM BM k ∴==+在Rt ECM 中， tan 0.4,EM C CM== 1440.4,414k k +∴=+ 解得：1,k =3,18,DM EM ∴==21.DE DM EM =+=答：观景塔的高度DE 为21米.故选A.【点拨】考查解直角三角形，坡度问题，熟练掌握锐角三角函数是解题的关键.19．B【分析】首先构建直角三角形，然后利用三角函数值得出DG ，即可得解.解：作AH△EB 于H ，延长DC 交AH 于N ，作DG△EB 于G ，如图所示：△△ACD=135°△△ACN=45°在Rt△ACN 中，AC=△ACN=45°△AN=CN=18在Rt△ABH 中，AB=AH ：BH=3:2，设3,2AH k BH k ==△()()(22232k k +=解得15k =或15k =-（不符合题意，舍去）△AH=45△HN=AH -AN=45-18=27△四边形DGHN 是矩形△DG=HN=27在Rt△DEG 中，sin sin 36.5DG DEB DE ︒==∠ △274535DE ≈≈故选：B.【点拨】此题主要考查锐角三角函数的实际应用，熟练掌握，即可解题.20．D【分析】过点E 作EF△AB 于点F ，设AE=x cm ，则AD=3x ,则=AB ,然后利用AB•AD=x 的值，即可得到AD,AB 的长度，则周长可求．解：如图，过点E 作EF△AB 于点F ，△六个锐角都为60°，六个钝角都为120°，△设AE=x cm ，则AD=3x ，△△AEB=120°，△△EAB=30°，△AB=2AF=2cos30x︒，△六角星纸板的面积为2，△AB•AD=3393x x=解得x△AD=AB=3，△矩形ABCD的周长=3)26)⨯=cm．故选:D．【点拨】本题主要考查解直角三角形和一元二次方程的应用，掌握特殊角的三角函数值，利用方程的思想是解题的关键．21．A【分析】设CD=x，在Rt△ADC中，△A=45°，可得CD=AD=x，BD=16-x，在Rt△BCD 中，用△B的正切函数值即可求解．解：设CD=x，在Rt△ADC中，△A=45°，△CD=AD=x，△BD=16-x，在Rt△BCD中，△B=60°，△tanCDBBD =，即：16xx= -解得8(3x=，故选A．【点拨】本题考查三角函数，根据直角三角形的边的关系，建立三角函数模型是解题的关键．22．C【分析】根据题意易得OA△MN，△N=43°，△M=35°，OA=135m，AB=40m，然后根据三角函数可进行求解．解：由题意得：OA△MN，△N=43°，△M=35°，OA=135m，AB=40m，△95mOB OA AB=-=，△135==150mtan0.9OAONN=∠，95=136mtan0.7OBOMM=≈∠，△286mMN OM ON=+=；故选C．【点拨】本题主要考查解直角三角形的应用，熟练掌握三角函数是解题的关键．23．D【分析】利用平行线性质得出：△ABD=△EAB=60°，进而得出△ABC=△BAC=20°，得出BC=AC，进而得出答案．解：由题意可得出：△EAC=80°，△EAB=60°，△DBC=40°，BC=40×2=80（海里），△△BAC=80°-60°=20°，△BCA=60°，△AE△BD，△△ABD=△EAB=60°，△△DBC=40°，△△ABC=60°-40°=20°，△△ABC=△BAC=20°，△BC=AC=80（海里）．△C海岛到观测点A的距离是80海里．故选D.【点拨】本题主要考查了解直角三角形的应用，利用方向角得出BC=AC是解题的关键．24．B【分析】题中利用特殊角度，做辅助线过S作SC△AB于C，在AB上截取CD＝AC，设CS＝x+2x＝AB，可得：x，可知AS＝（15）海里．解：过S作SC△AB于C，在AB上截取CD＝AC，△AS ＝DS ，△△CDS ＝△CAS ＝30°，△△ABS ＝15°，△△DSB ＝15°，△SD ＝BD ，设CS ＝x 海里，在Rt △ASC 中，△CAS ＝30°，△AC（海里），AS ＝DS ＝BD ＝2x （海里），△AB ＝30海里，+2x ＝30，解得：x △AS ＝（15）海里．故选：B ．【点拨】本题主要考查方位角问题，熟练运用特殊角三角函数是解题的关键．25．A【分析】直接利用坡度的定义得出AC 的长，再利用勾股定理得出AB 的长．解：△i =5BC m =， △5BC AC AC ==解得：AC =，则10AB m =．故选：A ．【点拨】本题考查解直角三角形和勾股定理的实际应用．由坡度的定义得出AC 的长是解答本题的关键． 26．D【分析】结合题意，根据三角函数的性质计算，即可得到答案．解：根据题意，得：sin 370.6BC AB ︒=≈ △6BC =米 △6100.60.6BC AB ===米故选：D ．【点拨】本题考查了三角函数的知识；解题的关键是熟练掌握三角函数的性质，从而完成求解．27．A【分析】在Rt △ACB 中，利用正弦定义，sin α=BC AB ，代入AB 值即可求解．解：在Rt △ACB 中，△ACB =90°，△sin α=BC AB， △BC = sin α⋅AB =12 sin α（米），故选：A ．【点拨】本题考查解直角三角形的应用，熟练掌握直角三角形边角关系是解题的关键．28．A【分析】应充分利用所给的α和45°在树的位置构造直角三角形，进而利用三角函数求解．解：如图，过点C 作水平线与AB 的延长线交于点D ，则AD △CD ，△△BCD =α，△ACD =45°．在Rt △CDB 中，CD =m cos α，BD =m sin α，在Rt △CDA 中，AD =CD ×tan45°=m ×cos α×tan45°=m cos α，△AB =AD -BD=（m cos α-m sin α）=m （cosα-sin α）．故选：A ．【点拨】本题考查锐角三角函数的应用．需注意构造直角三角形是常用的辅助线方法，另外，利用三角函数时要注意各边相对．29．100tan tan tan tan αββα- 【分析】由正切的定义分别确定tan ,tan αβ的表达式，进而联立成方程组，求解方程组即可得到答案．解：如图，CD 为树高，点C 为树顶，则,CAD CBD αβ∠=∠=，BD =AD -100△依题意，有tan tan 100CD AD CD AD αβ⎧=⎪⎪⎨⎪=⎪-⎩①② 由△得tan CDAD α=③将△代入△，解得100tan tan =tan tan CD αββα- 故答案为：100tan tan tan tan αββα-．【点拨】本题考查正切的定义，二元一次方程组得应用，能依题意根据正切的定义列出方程组是解题的关键．30．60°【分析】利用正弦定义计算即可．解：如图，△sinB ＝AC AB == △△B ＝60°，故答案为：60°．【点拨】此题主要考查了解直角三角形，关键是掌握正弦定义．31．23【分析】利用CD ∥AB ，得到△BAC =△DCA ，根据同圆的半径相等，AC =AB =3，可得sin△ACD =AD AC =23，从而可得答案．解：如图：△CD ∥AB ，△△BAC ＝△DCA ．△同圆的半径相等，△AC ＝AB ＝3．在Rt ACD △中，sin△ACD ＝23AD AC ． △sin△BAC ＝sin△ACD ＝23．故答案为：23．【点拨】此题考查了解直角三角形的应用，解题的关键是利用图形的性质进行角的等量代换．32．45【分析】根据三角函数的定义即可得到cos B ＝sin A ＝45．解：在Rt△ABC 中，△C ＝90°，△sin A ＝BC AB ＝45， △cos B ＝BC AB ＝45．故答案为：45．【点拨】本题考查了三角函数的定义，由定义可推出互余两角的三角函数的关系：若△A +△B ＝90°，则sin A ＝cos B ，cos A ＝sin B ．熟知相关定义是解题关键．33．158【分析】先解直角三角形ABC 求出BC 的长，从而求出AB 的长，再由作图方法可知DE 是线段AB 的垂直平分线，即可得到BE 的长，再解直角△BED 即可得到答案．解：△△C =90°，AC =3cm ，3tan =4B ， △3tan ==4AC B BC ， △BC =4cm ，△AB ，由作图方法可知DE 是线段AB 的垂直平分线，△DE △AB ，522AB AE BE cm ===， △3tan =4DE B BE =， △31548DE BE cm ==，故答案为：158．【点拨】本题主要考查了锐角三角函数，勾股定理，线段垂直平分线的性质，线段垂直平分线的尺规作图，正确理解DE 是线段AB 的垂直平分线是解题的关键．34．3【分析】在Rt ADE △中，由正弦定义解得165AE =，再由勾股定理解得DE 的长，根据同角的余角相等，得到sin sin ADE ECD ∠=∠，最后根据正弦定义解得CD 的长即可解题．解：在Rt ADE △中，4sin 5AE ADE AD ∠==165AE ∴=125DE ∴=== DE AC ⊥90ADE EDC EDC ECD ∴∠+∠=∠+∠=︒ADE ECD ∴∠=∠4sin sin 5DE ADE ECD CD ∴∠=∠== 534CD DE ∴=⋅= 在矩形ABCD 中，3AB CD ==故答案为：3．【点拨】本题考查矩形的性质、正弦、勾股定理等知识，是重要考点，难度较易，掌握相关知识是解题关键．35．3【分析】直接利用零指数幂的性质以及负整数指数幂的性质、特殊角的三角函数值分别化简得出答案．解：原式＝1＋4﹣4×12＝1＋4﹣2＝3．故答案为：3．【点拨】此题主要考查了负整数指数幂的性质、特殊角的三角函数值、零指数幂的性质，正确化简各数是解题关键．36【分析】根据特殊角的三角函数值直接书写即可．解：sin 45︒=．【点拨】本题考查了特殊角的三角函数值，牢固记忆是解题的关键．【分析】直接利用特殊角的三角函数值即可求解．解：△sin （α+15°）=1，△α+15°=90°，△α=75°，故答案为：75．【点拨】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键．38 【分析】先根据特殊角的三角函数值求出△A 的度数，然后求出tanA 的值．解：△sinA ＝12，△△A ＝30°，则tanA【点拨】本题考查了对特殊角的三角函数值的应用，解题的关键是检查学生能否熟练地运用进行计算．394##42+ 【分析】根据特殊角的三角函数值和负整数指数幂的运算法则进行计算即可．解：sin45°+2142-⎛⎫-= ⎪⎝⎭，+4．【点拨】本题考查了特殊角的三角函数值和负整数指数幂，相关公式有：sin 452=°，()10p pa a a -=≠． 403【分析】根据绝对值的性质、零指数幂的性质、特殊角的三角函数值、负指数幂的性质即可求解．解：原式124=-14=3=．3．【点拨】本题主要考查了绝对值的性质、零指数幂的性质、特殊角的三角函数值、负指数幂的性质．41．等腰【分析】根据绝对值和平方的非负性求出sinA和tanB的值，再根据锐角三角函数的特殊值求出△A和△B的角度，即可得出答案.解：△210 2sinA tanB-+⎛⎝⎭=△12sinA=，tanB=△△A=30°，△B=30°△△ABC是等腰三角形故答案为等腰.【点拨】本题考查的是特殊三角函数值，比较简单，需要牢记特殊三角函数值. 42．75°．【分析】先根据非负数的性质确定cosA=12，tanB=1，再根据特殊角的三角函数解答．解：△（cos A﹣12）2+|tan B﹣1|＝0，△cos A﹣12＝0，tan B﹣1＝0，则cos A＝12，tan B＝1，△△A＝60°，△B＝45°，△△C＝180°﹣60°﹣45°＝75°．故答案为75°．【点拨】熟记特殊角的三角函数值是解题的关键，同时还考查了三角形内角和定理43．【分析】AB=AC=BC=CD，即可求出△BAD=90°，△D=30°，解直角三角形即可求得．解：△ABC∆是等边三角形，△60B BAC ACB︒∠=∠=∠=，△CD AC=，。

中考数学-锐角三角函数(解析版)

专题 28 锐角三角函数
知识点一：锐角三角函数 1．三角函数定义在 Rt△ABC 中，若∠C=90°
sin A A的对边 a
斜边
c
A的邻边
b
cos A
斜边
c
A的对边
a
tan A A的邻边 b
A的邻边
b
cot A A的对边 a
2.同角三角函数的关系
（1）平方关系： sin2 Acos2 A1
（1）三边之间的关系为 a2 b2 c2 （勾股定理）
（2）锐角之间的关系为∠A+∠B=90°
（3）30°角所对直角边等于斜边的一半。
（4）直角三角形斜边上的中线等于斜边的一半。
（5）边角之间的关系为：（三角函数定义）
2.其他有关公式
（1）
S
1 2
ab sin C
=
1 2
bc sin
A
=
1 2
ac sin
B
（2）Rt△面积公式：
S
1 2
ab
1 2
ch
（3）直角三角形外接圆的半径
R c 2
，内切圆半径
r abc 2
结论：直角三角形斜边上的高 h ab c
3.实际问题中术语的含义
(1)仰角与俯角
在视线与水平线所成的角中，视线在水平线上方的角叫做仰角，在水平线下方的角叫做俯角。
(2)坡度：如图，我们通常把坡面的铅直高度和水平宽度的比叫做坡度（或坡比），用字母 i 表示，即 i h . l
见问题，这也是以后中考命题的趋势。 5.解决实际问题的关键在于建立数学模型，要善于把实际问题的数量关系转化为解直角三角形的问题．在解直角三角形的过程中，常会遇到近似计算，应根据题目要求的精确度定答案．

2024陕西中考数学二轮重点专题研究微专题常考锐角三角函数测量问题(课件)

地之间的距离．(结果精确到1海里，参考数据：sin65°≈0.91，
cos65°≈0.42，tan65°≈2.14， 2 ≈1.41)
第2题图
解：如图，过点C作CD⊥AB于点D，
由题意可知∠BCD＝65°，∠ACD＝45°，
在Rt△BCD中，∵∠BCD＝65°，
∴
BD BC
＝sin65°，CBDC
解题思路：通过在三角形内部作高CP，构造出Rt△ACP， Rt△BCP和矩形CPAD，其中公共边CP为解题的关键
考向三母子型
4. 如图，某建筑物AB顶部有一信号塔BC，且点A、B、C在一条直线上，某同学为了测量建筑物的高度，在地面的D处测得信号塔下端B的仰角为30°，然后他正对塔的方向前进了8米到达地面的E处，又测得信号塔顶端C的仰角为45°，已知AC⊥AD，信号塔BC的高度为6米，求建筑物AB的高度．(结果精确到1米，参考数据：3 ≈1.73)
＝cos65°，
∴BD＝BC·sin65°，CD＝BC·cos65°，
在Rt△ACD中，∵∠ACD＝45°，
∴AD＝CD，
∴AB＝AD＋BD＝15·cos65°＋15·sin65°≈20.
答：A，B两地之间的距离约为20海里．
D
第2题图
3. (2023陕师大附中模拟)如图，图②是图①秋千的侧面示意图，秋千的静止状态为OC.已知AB与地面平行，OD、OE是其在摆动过程中的两个位置，其中∠AOD＝65°，∠BOE＝40°，点E相对于点D秋千升高了 30 cm(即EN－DM＝30 cm，其中DM⊥MN于点M，EN⊥MN于点N)，求该秋千摆绳OC的长度．(结果精确到0.1 cm.参考数据：sin25°≈0.42， cos25°≈0.91，sin65°≈0.91，cos65°≈0.42， sin50°≈0.77，cos50°≈0.64，sin40°≈0.64， cos40°≈0.77)

中考数学锐角三角函数(共56张PPT)

二、填空题
(1)求旋转木马E处到出口B处的距离； (2)求海洋球D处到出口B处的距离.(结果保留整数)
解：(1) ∵AE=80，∠BAE=30°，∠ABE =90°, ∴BE=AEsin30°=80× =40(m). 答：旋转木马E处到出口B处的距离为40 m.
(2) ∵∠CED=∠AEB，∠DCE=∠ABE =90°,
∴∠D=∠BAE=30°.
∵CD=34 m,
∴DE=
=
=
(m).
∴DB=BE+DE=
≈40+
≈79(m).
答：海洋球D处到出口B处的距离为79 m.
二、填空题
11. 小明在某次作业中得到如下结果： sin27°+ sin283°≈0．122+0．992=0．9945; sin222°+ sin268°≈0．372+0932=1．0018; sin229°+ sin261°≈0．482+0．872=0．9873; sin237°+ sin253°≈0．602+0．802=1．0000;
二、填空题
9. (2017北京)计算：4cos30°+
原式=4× +1-
+2
=
+1- +2=3.
-
+
.
10.(2017湘潭)某游乐场部分平面图如图Z2816所示，点C,E,A在同一直线上，点D,E,B在同一直线上，测得A处与E处的距离为80 m， C处与D处的距离为34 m，∠C=90°，∠ABE =90°，∠BAE=30°. (2≈1．4，3≈1．7)
图Z28-7
A.
m
B.
m

中考数学锐角三角函数综合经典题含答案

中考数学锐角三角函数综合经典题含答案一、锐角三角函数1．图1是一种折叠式晾衣架．晾衣时，该晾衣架左右晾衣臂张开后示意图如图2所示，两支脚OC＝OD＝10分米，展开角∠COD＝60°，晾衣臂OA＝OB＝10分米，晾衣臂支架HG ＝FE＝6分米，且HO＝FO＝4分米．当∠AOC＝90°时，点A离地面的距离AM为_______分米；当OB从水平状态旋转到OB′（在CO延长线上）时，点E绕点F随之旋转至OB′上的点E′处，则B′E′﹣BE为_________分米．【答案】553【解析】【分析】如图，作OP⊥CD于P，OQ⊥AM于Q，FK⊥OB于K，FJ⊥OC于J．解直角三角形求出MQ，AQ即可求出AM，再分别求出BE，B′E′即可．【详解】解：如图，作OP⊥CD于P，OQ⊥AM于Q，FK⊥OB于K，FJ⊥OC于J．∵AM⊥CD，∴∠QMP＝∠MPO＝∠OQM＝90°，∴四边形OQMP是矩形，∴QM＝OP，∵OC＝OD＝10，∠COD＝60°，∴△COD是等边三角形，∵OP⊥CD，∠COD＝30°，∴∠COP＝12∴QM＝OP＝OC•cos30°＝3∵∠AOC＝∠QOP＝90°，∴∠AOQ＝∠COP＝30°，∴AQ＝1OA＝5（分米），2∴AM＝AQ＋MQ＝5＋3∵OB∥CD，∴∠BOD＝∠ODC＝60°在Rt△OFK中，KO＝OF•cos60°＝2（分米），FK＝OF•sin60°＝23（分米），在Rt△PKE中，EK＝22-＝26（分米），EF FK∴BE＝10−2−26＝（8−26）（分米），在Rt△OFJ中，OJ＝OF•cos60°＝2（分米），FJ＝23（分米），在Rt△FJE′中，E′J＝22-（2）＝26，63∴B′E′＝10−（26−2）＝12−26，∴B′E′−BE＝4．故答案为：5＋53，4．【点睛】本题考查解直角三角形的应用，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．2．（6分）某海域有A，B两个港口，B港口在A港口北偏西30°方向上，距A港口60海里，有一艘船从A港口出发，沿东北方向行驶一段距离后，到达位于B港口南偏东75°方向的C处，求该船与B港口之间的距离即CB的长（结果保留根号）．【答案】．【解析】试题分析：作AD⊥BC于D，于是有∠ABD=45°，得到AD=BD=，求出∠C=60°，根据正切的定义求出CD的长，得到答案．试题解析：作AD⊥BC于D，∵∠EAB=30°，AE∥BF，∴∠FBA=30°，又∠FBC=75°，∴∠ABD=45°，又AB=60，∴AD=BD=，∵∠BAC=∠BAE+∠CAE=75°，∠ABC=45°，∴∠C=60°，在Rt △ACD 中，∠C=60°，AD=，则tanC=，∴CD==，∴BC=．故该船与B 港口之间的距离CB 的长为海里．考点：解直角三角形的应用-方向角问题．3．如图（9）所示（左图为实景侧视图，右图为安装示意图），在屋顶的斜坡面上安装太阳能热水器：先安装支架AB 和CD （均与水平面垂直），再将集热板安装在AD 上.为使集热板吸热率更高，公司规定：AD 与水平面夹角为1θ，且在水平线上的射影AF 为1.4m .现已测量出屋顶斜面与水平面夹角为2θ，并已知1tan 1.082θ=，2tan 0.412θ=．如果安装工人确定支架AB 高为25cm ，求支架CD 的高（结果精确到1cm ）？【答案】【解析】过A 作AF CD ⊥于F ，根据锐角三角函数的定义用θ1、θ2表示出DF 、EF 的值，又可证四边形ABCE为平行四边形，故有EC=AB=25cm，再再根据DC=DE+EC进行解答即可．4．如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP．（1）求证：直线CP是⊙O的切线．（2）若BC=2，sin∠BCP=，求点B到AC的距离．（3）在第（2）的条件下，求△ACP的周长．【答案】（1）证明见解析（2）4（3）20【解析】试题分析：（1）利用直径所对的圆周角为直角，2∠CAN=∠CAB，∠CAB=2∠BCP判断出∠ACP=90°即可；（2）利用锐角三角函数，即勾股定理即可．试题解析：（1）∵∠ABC=∠ACB，∴AB=AC，∵AC为⊙O的直径，∴∠ANC=90°，∴∠CAN+∠ACN=90°，2∠BAN=2∠CAN=∠CAB，∵∠CAB=2∠BCP，∴∠BCP=∠CAN，∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°，∵点D在⊙O上，∴直线CP是⊙O的切线；（2）如图，作BF⊥AC∵AB=AC，∠ANC=90°，∴CN=CB=，∵∠BCP=∠CAN，sin∠BCP=，∴sin∠CAN=，∴∴AC=5，∴AB=AC=5，设AF=x，则CF=5﹣x，在Rt△ABF中，BF2=AB2﹣AF2=25﹣x2，在Rt△CBF中，BF2=BC2﹣CF2=2O﹣（5﹣x）2，∴25﹣x2=2O﹣（5﹣x）2，∴x=3，∴BF2=25﹣32=16，∴BF=4，即点B到AC的距离为4．考点：切线的判定5．如图，在⊙O的内接三角形ABC中，∠ACB＝90°，AC＝2BC，过C作AB的垂线l交⊙O于另一点D，垂足为E.设P是上异于A，C的一个动点，射线AP交l于点F，连接PC与PD，PD交AB于点G.(1)求证：△PAC∽△PDF；(2)若AB＝5，，求PD的长；(3)在点P运动过程中，设＝x，tan∠AFD＝y，求y与x之间的函数关系式．(不要求写出x的取值范围)【答案】（1）证明见解析；（2）；（3）.【解析】试题分析：（1）应用圆周角定理证明∠APD＝∠FPC，得到∠APC＝∠FPD，又由∠PAC＝∠PDC，即可证明结论.（2）由AC=2BC，设，应用勾股定理即可求得BC，AC的长，则由AC=2BC得，由△ACE∽△ABC可求得AE，CE的长，由可知△APB是等腰直角三角形，从而可求得PA的长，由△AEF是等腰直角三角形求得EF=AE=4，从而求得DF的长，由（1）△PAC∽△PDF得，即可求得PD的长.（3）连接BP，BD，AD，根据圆的对称性，可得，由角的转换可得，由△AGP∽△DGB可得，由△AGD∽△PGB可得，两式相乘可得结果.试题解析：（1）由APCB内接于圆O，得∠FPC＝∠B，又∵∠B＝∠ACE＝90°－∠BCE，∠ACE＝∠APD，∴∠APD＝∠FPC.∴∠APD＋∠DPC＝∠FPC＋∠DPC，即∠APC＝∠FPD.又∵∠PAC＝∠PDC，∴△PAC∽△PDF.（2）连接BP，设，∵∠ACB=90°，AB=5，∴.∴.∵△ACE∽△ABC，∴，即. ∴.∵AB⊥CD，∴.如图，连接BP，∵，∴△APB是等腰直角三角形. ∴∠PAB＝45°，.∴△AEF是等腰直角三角形. ∴EF=AE=4. ∴DF=6.由（1）△PAC∽△PDF得，即.∴PD的长为.（3）如图，连接BP，BD，AD，∵AC=2BC，∴根据圆的对称性，得AD=2DB，即.∵AB⊥CD，BP⊥AE，∴∠ABP＝∠AFD.∵，∴.∵△AGP∽△DGB，∴.∵△AGD∽△PGB，∴.∴，即.∵，∴.∴与之间的函数关系式为.考点：1.单动点问题；2.圆周角定理；3.相似三角形的判定和性质；4.勾股定理；5.等腰直角三角形的判定和性质；6.垂径定理；7.锐角三角函数定义；8.由实际问题列函数关系式.6．如图，抛物线y=﹣x2+3x+4与x轴交于A、B两点，与y轴交于C点，点D在抛物线上且横坐标为3．（1）求tan∠DBC的值；（2）点P为抛物线上一点，且∠DBP=45°，求点P的坐标．【答案】（1）tan∠DBC=；（2）P（﹣，）．【解析】试题分析：（1）连接CD，过点D作DE⊥BC于点E．利用抛物线解析式可以求得点A、B、C、D的坐标，则可得CD//AB，OB=OC，所以∠BCO=∠BCD=∠ABC=45°．由直角三角形的性质、勾股定理和图中相关线段间的关系可得BC=4，BE=BC﹣DE=．由此可知tan∠DBC=；（2）过点P作PF⊥x轴于点F．由∠DBP=45°及∠ABC=45°可得∠PBF=∠DBC，利用（1）中的结果得到：tan∠PBF=．设P（x，﹣x2+3x+4），则利用锐角三角函数定义推知=，通过解方程求得点P的坐标为（﹣，）．试题解析：（1）令y=0，则﹣x2+3x+4=﹣（x+1）（x﹣4）=0，解得 x1=﹣1，x2=4．∴A（﹣1，0），B（4，0）．当x=3时，y=﹣32+3×3+4=4，∴D（3，4）．如图，连接CD，过点D作DE⊥BC于点E．∵C（0，4），∴CD//AB，∴∠BCD=∠ABC=45°．在直角△OBC中，∵OC=OB=4，∴BC=4．在直角△CDE中，CD=3．∴CE=ED=，∴BE=BC﹣DE=．∴tan∠DBC=；（2）过点P作PF⊥x轴于点F．∵∠CBF=∠DBP=45°，∴∠PBF=∠DBC，∴tan∠PBF=．设P（x，﹣x2+3x+4），则=，解得 x1=﹣，x2=4（舍去），∴P（﹣，）．考点：1、二次函数；2、勾股定理；3、三角函数7．如图，已知点从出发，以1个单位长度/秒的速度沿轴向正方向运动，以为顶点作菱形，使点在第一象限内，且；以为圆心，为半径作圆．设点运动了秒，求：（1）点的坐标（用含的代数式表示）；（2）当点在运动过程中，所有使与菱形的边所在直线相切的的值．【答案】解：（1）过作轴于，，，，，点的坐标为．（2）①当与相切时（如图1），切点为，此时，，，．②当与，即与轴相切时（如图2），则切点为，，过作于，则，，．③当与所在直线相切时（如图3），设切点为，交于，则，，．过作轴于，则，，化简，得，解得，，．所求的值是，和．【解析】（1）过作轴于,利用三角函数求得OD、DC的长，从而求得点的坐标⊙P 与菱形OABC 的边所在直线相切，则可与OC 相切；或与OA 相切；或与AB 相切，应分三种情况探讨：①当圆P 与OC 相切时，如图1所示，由切线的性质得到PC 垂直于OC ，再由OA=+t ，根据菱形的边长相等得到OC=1+t ，由∠AOC 的度数求出∠POC 为30°，在直角三角形POC 中，利用锐角三角函数定义表示出cos30°=oc/op ，表示出OC ，等于1+t 列出关于t 的方程，求出方程的解即可得到t 的值；②当圆P 与OA ，即与x 轴相切时，过P 作PE 垂直于OC ，又PC=PO ，利用三线合一得到E 为OC 的中点，OE 为OC 的一半，而OE=OPcos30°，列出关于t 的方程，求出方程的解即可得到t 的值；③当圆P 与AB 所在的直线相切时，设切点为F ，PF 与OC 交于点G ，由切线的性质得到PF 垂直于AB ，则PF 垂直于OC ，由CD=FG ，在直角三角形OCD 中，利用锐角三角函数定义由OC 表示出CD ，即为FG ，在直角三角形OPG 中，利用OP 表示出PG ，用PG+GF 表示出PF ，根据PF=PC ，表示出PC ，过C 作CH 垂直于y 轴，在直角三角形PHC 中，利用勾股定理列出关于t 的方程，求出方程的解即可得到t 的值，综上，得到所有满足题意的t 的值．8．在平面直角坐标系中，四边形OABC 是矩形，点()0,0O ，点()3,0A ，点()0,4C ，连接OB ，以点A 为中心，顺时针旋转矩形AOCB ，旋转角为()0360αα︒<<︒，得到矩形ADEF ，点,,O C B 的对应点分别为,,D E F .(Ⅰ)如图，当点D 落在对角线OB 上时，求点D 的坐标；(Ⅱ)在(Ⅰ)的情况下，AB 与DE 交于点H .①求证BDE DBA ∆≅∆；②求点H 的坐标.(Ⅲ)α为何值时，FB FA =.(直接写出结果即可).【答案】(Ⅰ)点D 的坐标为5472(,)2525；(Ⅱ)①证明见解析；②点H 的坐标为(3，258)；(Ⅲ)60α=︒或300︒.【解析】【分析】 (Ⅰ) 过A D 、分别作,AM OB DN OA ⊥⊥，根据点A 、点C 的坐标可得出OA 、OC 的长，根据矩形的性质可得AB 、OB 的长，在Rt △OAM 中，利用∠BOA 的余弦求出OM 的长，由旋转的性质可得OA=AD ，利用等腰三角形的性质可得OD=2OM ，在Rt △ODN 中，利用∠BOA 的正弦和余弦可求出DN 和ON 的长，即可得答案；(Ⅱ)①由等腰三角形性质可得∠DOA=∠ODA ，根据锐角互余的关系可得ABD BDE ∠∠=，利用SAS 即可证明△DBA ≌△BDE ；②根据△DBA ≌△BDE 可得∠BEH=∠DAH ，BE=AD ，即可证明△BHE ≌△DHA ，可得DH=BH ，设AH=x ，在Rt △ADH 中，利用勾股定理求出x 的值即可得答案；（Ⅲ）如图，过F 作FO ⊥AB ，由性质性质可得∠BAF=α，分别讨论0<α≤180°时和180°<α<360°时两种情况，根据FB=FA 可得OA=OB ，利用勾股定理求出FO 的长，由余弦的定义即可求出∠BAF 的度数.【详解】(Ⅰ)∵点()30A ，，点()04C ，， ∴3,4OA OC ==.∵四边形OABC 是矩形，∴AB=OC=4，∵矩形DAFE 是由矩形AOBC 旋转得到的∴3AD AO ==.在Rt OAB ∆中，225OB OA AB =+=，过A D 、分别作B,DN OA AM O ⊥⊥在Rt ΔOAM 中，OM OA 3cos BOA OA OB 5∠===， ∴9OM 5= ∵AD=OA ，AM ⊥OB ， ∴18OD 2OM 5==. 在Rt ΔODN 中：DN 4sin BOA OD 5∠==，cos ∠BOA=ON OD =35， ∴72DN 25=，54ON 25=. ∴点D 的坐标为5472,2525⎛⎫⎪⎝⎭.(Ⅱ)①∵矩形DAFE 是由矩形AOBC 旋转得到的，∴OA AD 3,ADE 90,DE AB 4∠===︒==.∴OD AD =.∴DOA ODA ∠∠=.又∵DOA OBA 90∠∠+=︒，BDH ADO 90∠∠+=︒∴ABD BDE ∠∠=. 又∵BD BD =，∴ΔBDE ΔDBA ≅.②由ΔBDE ΔDBA ≅，得BEH DAH ∠∠=，BE AD 3==，又∵BHE DHA ∠∠=，∴ΔBHE ΔDHA ≅.∴DH=BH ，设AH x =，则DH BH 4x ==-，在Rt ΔADH 中，222AH AD DH =+，即()222x 34x =+-，得25x 8=， ∴25AH 8=. ∴点H 的坐标为253,8⎛⎫ ⎪⎝⎭. (Ⅲ)如图，过F 作FO ⊥AB ，当0<α≤180°时，∵点B 与点F 是对应点，A 为旋转中心，∴∠BAF 为旋转角，即∠BAF=α，AB=AF=4，∵FA=FB ，FO ⊥AB ，∴OA=12AB=2， ∴cos ∠BAF=OA AF =12， ∴∠BAF=60°，即α=60°，当180°<α<360°时，同理解得：∠BAF′=60°，∴旋转角α=360°-60°=300°.综上所述：α60=︒或300︒.【点睛】本题考查矩形的性质、旋转变换、全等三角形的判定与性质、锐角三角函数的定义等知识，正确找出对应边与旋转角并熟记特殊角的三角函数值是解题关键.9．如图，在⊙O 的内接三角形ABC 中，∠ACB ＝90°，AC ＝2BC ，过C 作AB 的垂线l 交⊙O 于另一点D ，垂足为E ．设P 是»AC 上异于A ，C 的一个动点，射线AP 交l 于点F ，连接PC 与PD ，PD 交AB 于点G ．（1）求证：△PAC ∽△PDF ；（2）若AB ＝5，¼¼AP BP=，求PD 的长．【答案】(1)证明见解析；（2310 【解析】【分析】（1）根据AB ⊥CD ，AB 是⊙O 的直径，得到¶¶ADAC =，∠ACD ＝∠B ，由∠FPC ＝∠B ，得到∠ACD ＝∠FPC ，可得结论；（2）连接OP ，由¶¶APBP =，得到OP ⊥AB ，∠OPG ＝∠PDC ，根据AB 是⊙O 的直径，得到∠ACB ＝90°，由于AC ＝2BC ，于是得到tan ∠CAB ＝tan ∠DCB ＝BC AC ，得到12CE BE AE CE ==，求得AE ＝4BE ，通过△OPG ∽△EDG ，得到OG OP GE ED=，然后根据勾股定理即可得到结果．【详解】（1）证明：连接AD，∵AB⊥CD，AB是⊙O的直径，∴¶¶AD AC=，∴∠ACD＝∠B＝∠ADC，∵∠FPC＝∠B，∴∠ACD＝∠FPC，∴∠APC＝∠ACF，∵∠FAC＝∠CAF，∴△PAC∽△CAF；（2）连接OP，则OA＝OB＝OP＝15 22 AB=，∵¶¶AP BP=，∴OP⊥AB，∠OPG＝∠PDC，∵AB是⊙O的直径，∴∠ACB＝90°，∵AC＝2BC，∴tan∠CAB＝tan∠DCB＝BCAC，∴12 CE BEAE CE==，∴AE＝4BE，∵AE+BE＝AB＝5，∴AE＝4，BE＝1，CE＝2，∴OE＝OB﹣BE＝2.5﹣1＝1.5，∵∠OPG＝∠PDC，∠OGP＝∠DGE，∴△OPG∽△EDG，∴OG OP GE ED=，∴2.52 OE GE OPGE CE-==，∴GE＝23，OG＝56，∴PG5 6 =，GD23 =，∴PD＝PG+GD【点睛】本题考查了相似三角形的判定和性质，垂径定理，勾股定理，圆周角定理，证得△OPG ∽△EDG 是解题的关键．10．阅读下面材料：观察与思考：阅读下列材料，并解决后面的问题．在锐角△ABC 中，∠A 、∠B 、∠C 的对边分别是a 、b 、c ，过A 作AD ⊥BC 于D （如图），则sin B ＝AD c ，sin C ＝AD b ，即AD ＝c sin B ，AD ＝b sin C ，于是c sin B ＝b sin C ，即sin sin b c B C = ．同理有：sin sin c a C A =，sin sin a b A B=，所以sin sin sin a b c A B C ==．即：在一个三角形中，各边和它所对角的正弦的比相等．在锐角三角形中，若已知三个元素（至少有一条边），运用上述结论和有关定理就可以求出其余三个未知元素．根据上述材料，完成下列各题．（1）如图，△ABC 中，∠B ＝75°，∠C ＝45°，BC ＝60，则AB ＝；（2）如图，一货轮在C 处测得灯塔A 在货轮的北偏西30°的方向上，随后货轮以60海里/时的速度按北偏东30°的方向航行，半小时后到达B 处，此时又测得灯塔A 在货轮的北偏西75°的方向上（如图），求此时货轮距灯塔A 的距离AB ．（3）在（2）的条件下，试求75°的正弦值．（结果保留根号）【答案】（1）6；（2）6海里；（36+2 【解析】【分析】（1）根据材料：在一个三角形中，各边和它所对角的正弦的比相等，写出比例关系，代入数值即可求得AB的值.（2）此题可先由速度和时间求出BC的距离，再由各方向角得出∠A的角度，过B作BM⊥AC于M，求出∠MBC=30°，求出MC，由勾股定理求出BM，求出AM、BM的长，由勾股定理求出AB即可；（3）在三角形ABC中，∠A=45，∠ABC=75，∠ACB=60，过点C作AC的垂线BD，构造直角三角形ABD，BCD，在直角三角形ABD中可求出AD的长，进而可求出sin75°的值．【详解】解：（1）在△ABC中，∠B=75°，∠C=45°，BC=60，则∠A=60°，∵ABsinC =sinBCA，∴45ABsin o=60sin60o，即2 =3，解得：AB=206.（2）如图，依题意：BC=60×0.5=30（海里）∵CD∥BE，∴∠DCB+∠CBE=180°∵∠DCB=30°，∴∠CBE=150°∵∠ABE=75°．∴∠ABC=75°，∴∠A=45°，在△ABC中，sin AB ACB∠=BCsin A∠即60?ABsin=3045?sin，解之得：AB=156．答：货轮距灯塔的距离AB=156海里．（3）过点B作AC的垂线BM，垂足为M.在直角三角形ABM中，∠A=45°，6，所以3BDC中，∠BCM=60°，BC=30°，可求得CM=15，所以3，15315+156sin75°6+2．【点睛】本题考查方向角的含义，三角形的内角和定理，含30度角的直角三角形，等腰三角形的性质和判定等知识点，解题关键是熟练掌握解直角三角形方法．11．如图，A（0，2），B（6，2），C（0，c）（c＞0），以A为圆心AB长为半径的¶BD 交y轴正半轴于点D，¶BD与BC有交点时，交点为E，P为¶BD上一点．（1）若c＝3，①BC＝，¶DE的长为；②当CP＝2时，判断CP与⊙A的位置关系，井加以证明；（2）若c＝10，求点P与BC距离的最大值；（3）分别直接写出当c＝1，c＝6，c＝9，c＝11时，点P与BC的最大距离（结果无需化简）【答案】（1）①12，π；②详见解析；（2）①65；②65（3）答案见详解【解析】【分析】（1）①先求出AB ，AC ，进而求出BC 和∠ABC ，最后用弧长公式即可得出结论；②判断出△APC 是直角三角形，即可得出结论；（2）分两种情况，利用三角形的面积或锐角三角函数即可得出结论；（3）画图图形，同（2）的方法即可得出结论．【详解】（1）①如图1，∵c ＝3+2，∴OC ＝3，∴AC ＝3﹣2＝3∵AB ＝6，在Rt △BAC 中，根据勾股定理得，BC ＝12，tan ∠ABC ＝AC AB3 ∴∠ABC ＝60°，∵AE ＝AB ，∴△ABE 是等边三角形，∴∠BAE ＝60°，∴∠DAE ＝30°， ∴»DE的长为306180π⨯＝π，故答案为12，π；②CP 与⊙A 相切．证明：∵AP ＝AB ＝6，AC ＝OC ﹣OA ＝63， ∴AP 2+CP 2＝108，又AC 2＝（63）2＝108，∴AP 2+PC 2＝AC 2．∴∠APC ＝90°，即：CP ⊥AP ．而AP 是半径，∴CP 与⊙A 相切．（2）若c ＝10，即AC ＝10﹣2＝8，则BC ＝10．①若点P 在»BE上，AP ⊥BE 时，点P 与BC 的距离最大，设垂足为F ，则PF 的长就是最大距离，如图2，S △ABC ＝12AB ×AC ＝12BC ×AF ， ∴AF ＝AB AC BC ⋅＝245， ∴PF ＝AP ﹣AF ＝65； ②如图3，若点P 在»DE 上，作PG ⊥BC 于点G ，当点P 与点D 重合时，PG 最大．此时，sin ∠ACB ＝PG AB CP BC =，即PG ＝AB CP BC ⋅＝65∴若c ＝10，点P 与BC 距离的最大值是65；（3）当c ＝1时，如图4，过点P 作PM ⊥BC ，sin ∠BCP ＝AB PMBC CD= ∴PM ＝67423737AB CD BC ⋅⨯===423737；当c ＝6时，如图5，同c ＝10的①情况，PF ＝6﹣1213=1213613-，当c ＝9时，如图6，同c ＝10的①情况，PF ＝4285685-，当c ＝11时，如图7，点P 和点D 重合时，点P 到BC 的距离最大，同c ＝10时②情况，DG 18117．【点睛】此题是圆的综合题，主要考查了弧长公式，勾股定理和逆定理，三角形的面积公式，锐角三角函数，熟练掌握锐角三角函数是解本题的关键．12．如图，AB 为O e 的直径，C 、D 为O e 上异于A 、B 的两点，连接CD ，过点C作CE DB ⊥，交CD 的延长线于点E ，垂足为点E ，直径AB 与CE 的延长线相交于点F .（1）连接AC 、AD ，求证：180DAC ACF ∠+∠=︒. （2）若2ABD BDC ∠=∠. ①求证：CF 是O e 的切线. ②当6BD =，3tan 4F =时，求CF 的长. 【答案】（1）详见解析；（2）①详见解析；② 203CF =. 【解析】【分析】（1）根据圆周角定理证得∠ADB=90°，即AD ⊥BD ，由CE ⊥DB 证得AD ∥CF ，根据平行线的性质即可证得结论；（2）①连接OC ．先根据等边对等角及三角形外角的性质得出∠3=2∠1，由已知∠4=2∠1，得到∠4=∠3，则OC ∥DB ，再由CE ⊥DB ，得到OC ⊥CF ，根据切线的判定即可证明CF 为⊙O 的切线；②由CF ∥AD ，证出∠BAD=∠F ，得出tan ∠BAD=tan ∠F=BD AD =34，求出AD=43BD=8，利用勾股定理求得AB=10，得出OB=OC=，5，再由tanF=OC CF =34，即可求出CF ．【详解】解：（1）AB 是O e 的直径，且D 为O e 上一点，90ADB ∴∠=︒， CE DB ⊥Q ， 90DEC ∴∠=︒， //CF AD ∴，180DAC ACF ∴∠+∠=︒. （2）①如图，连接OC . OA OC =Q ，12∴∠=∠. 312∠=∠+∠Q ， 321∴∠=∠.42BDC Q ∠=∠，1BDC ∠=∠， 421∴∠=∠， 43∴∠=∠，//OC DB ∴. CE DB ⊥Q ， OC CF ∴⊥.又OC Q 为O e 的半径， CF ∴为O e 的切线.②由（1）知//CF AD ，BAD F ∴∠=∠，3tan tan 4BAD F ∴∠==， 34BD AD ∴=. 6BD =Q483AD BD ∴==， 226810AB ∴=+=，5OB OC ==. OC CF Q ⊥， 90OCF ∴∠=︒，3tan 4OC F CF ∴==，解得203CF =. 【点睛】本题考查了切线的判定、解直角三角形、圆周角定理等知识；本题综合性强，有一定难度，特别是（2）中，需要运用三角函数、勾股定理和由平行线得出比例式才能得出结果．13．如图，在平面直角坐标系xOy 中，抛物线y ＝﹣14x 2+bx +c 与直线y ＝12x ﹣3分别交x 轴、y 轴上的B 、C 两点，设该抛物线与x 轴的另一个交点为点A ，顶点为点D ，连接CD 交x 轴于点E ．（1）求该抛物线的表达式及点D 的坐标；（2）求∠DCB 的正切值；（3）如果点F 在y 轴上，且∠FBC ＝∠DBA +∠DCB ，求点F 的坐标．【答案】（1）21y 234x x =-+-，D （4，1）；（2）13；（3）点F 坐标为（0，1）或（0，﹣18）．【解析】【分析】（1）y ＝12x ﹣3，令y ＝0，则x ＝6，令x ＝0，则y ＝﹣3，求出点B 、C 的坐标，将点B 、C 坐标代入抛物线y ＝﹣14x 2+bx+c ，即可求解；（2）求出则点E （3，0），EH ＝EB•sin ∠OBC ＝5，CE ＝32，则CH ＝5，即可求解；（3）分点F 在y 轴负半轴和在y 轴正半轴两种情况，分别求解即可．【详解】（1）y ＝12x ﹣3，令y ＝0，则x ＝6，令x ＝0，则y ＝﹣3，则点B 、C 的坐标分别为（6，0）、（0，﹣3），则c ＝﹣3，将点B 坐标代入抛物线y ＝﹣14x 2+bx ﹣3得：0＝﹣14×36+6b ﹣3，解得：b ＝2，故抛物线的表达式为：y ＝﹣14x 2+2x ﹣3，令y ＝0，则x ＝6或2，即点A （2，0），则点D （4，1）；（2）过点E 作EH ⊥BC 交于点H ，C 、D 的坐标分别为：（0，﹣3）、（4，1），直线CD 的表达式为：y ＝x ﹣3，则点E （3，0）， tan ∠OBC ＝3162OC OB ==，则sin ∠OBC 5，则EH＝EB•sin∠OBC＝5，CE＝32，则CH＝5，则tan∠DCB＝13 EHCH=；（3）点A、B、C、D、E的坐标分别为（2，0）、（6，0）、（0，﹣3）、（4，1）、（3，0），则BC＝35，∵OE＝OC，∴∠AEC＝45°，tan∠DBE＝164-＝12，故：∠DBE＝∠OBC，则∠FBC＝∠DBA+∠DCB＝∠AEC＝45°，①当点F在y轴负半轴时，过点F作FG⊥BG交BC的延长线与点G，则∠GFC＝∠OBC＝α，设：GF＝2m，则CG＝GFtanα＝m，∵∠CBF＝45°，∴BG＝GF，即：5＝2m，解得：m＝5CF22GF CG+5＝15，故点F（0，﹣18）；②当点F在y轴正半轴时，同理可得：点F（0，1）；故：点F坐标为（0，1）或（0，﹣18）．【点睛】本题考查的是二次函数综合运用，涉及到一次函数、解直角三角形等相关知识，其中（3），确定∠FBC ＝∠DBA+∠DCB ＝∠AEC ＝45°，是本题的突破口．14．如图，在ABC △中，10AC BC ==，3cos5C =,点P 是BC 边上一动点（不与点,A C 重合），以PA 长为半径的P e 与边AB 的另一个交点为D ，过点D 作DE CB ⊥于点E .()1当P e 与边BC 相切时，求P e 的半径；()2联结BP 交DE 于点F ，设AP 的长为x ，PF 的长为y ，求y 关于x 的函数解析式，并直接写出x 的取值范围；()3在()2的条件下，当以PE 长为直径的Q e 与P e 相交于AC 边上的点G 时，求相交所得的公共弦的长.【答案】（1）409；（2）)25880010x x x y x -+=<<；（3）105- 【解析】【分析】（1）设⊙P 与边BC 相切的切点为H ，圆的半径为R ，连接HP ，则HP ⊥BC ，cosC=35，则sinC=45，sinC=HP CP =R 10R -=45，即可求解；（2）PD ∥BE ，则EB PD ＝BFPF，即：2248805x x x y xy--+=，即可求解；（3）证明四边形PDBE 为平行四边形，则AG=GP=BD ，即：5求解．【详解】（1）设⊙P 与边BC 相切的切点为H ，圆的半径为R ，连接HP ，则HP ⊥BC ，cosC=35，则sinC=35， sinC=HP CP =R 10R -=45，解得：R=409；（2）在△ABC 中，AC=BC=10，cosC=35，设AP=PD=x ，∠A=∠ABC=β，过点B 作BH ⊥AC ，则BH=ACsinC=8，同理可得：CH=6，HA=4，AB=45，则：tan ∠CAB=2BP=()2284x +-=2880x x -+， DA=25x ，则BD=45-25x ，如下图所示，PA=PD ，∴∠PAD=∠CAB=∠CBA=β，tanβ=2，则cosβ=5，sinβ=5，EB=BDcosβ=（45-25x）×5=4-25x，∴PD∥BE，∴EBPD＝BFPF，即：2248805x x x yx y--+-=，整理得：y=()25x x8x800x10-+<<；（3）以EP为直径作圆Q如下图所示，两个圆交于点G，则PG=PQ，即两个圆的半径相等，则两圆另外一个交点为D，GD为相交所得的公共弦，∵点Q时弧GD的中点，∴DG⊥EP，∵AG是圆P的直径，∴∠GDA=90°，∴EP∥BD，由（2）知，PD∥BC，∴四边形PDBE为平行四边形，∴AG=EP=BD，∴5设圆的半径为r，在△ADG中，55AG=2r，5551+，则：55相交所得的公共弦的长为5【点睛】本题考查的是圆知识的综合运用，涉及到解直角三角形、勾股定理等知识，其中（3），要关键是根据题意正确画图，此题用大量的解直角三角形的内容，综合难度很大．15．已知AB 是⊙O 的直径，弦CD ⊥AB 于H ，过CD 延长线上一点E 作⊙O 的切线交AB 的延长线于F ，切点为G ，连接AG 交CD 于K ．（1）如图1，求证：KE ＝GE ；（2）如图2，连接CABG ，若∠FGB ＝12∠ACH ，求证：CA ∥FE ；（3）如图3，在（2）的条件下，连接CG 交AB 于点N ，若sin E ＝35，AK ＝10，求CN 的长．【答案】（1）证明见解析；（2）△EAD 是等腰三角形．证明见解析；（3201013【解析】试题分析：（1）连接OG ，则由已知易得∠OGE=∠AHK=90°，由OG=OA 可得∠AGO=∠OAG ，从而可得∠KGE=∠AKH=∠EKG ，这样即可得到KE=GE ；（2）设∠FGB=α，由AB 是直径可得∠AGB=90°，从而可得∠KGE=90°-α，结合GE=KE 可得∠EKG=90°-α，这样在△GKE 中可得∠E=2α，由∠FGB=12∠ACH 可得∠ACH=2α，这样可得∠E=∠ACH ，由此即可得到CA ∥EF ；（3）如下图2，作NP ⊥AC 于P ，由（2）可知∠ACH=∠E ，由此可得sinE=sin ∠ACH=35AH AC =，设AH=3a ，可得AC=5a ，CH=4a ，则tan ∠CAH=43CH AH =，由（2）中结论易得∠CAK=∠EGK=∠EKG=∠AKC ，从而可得CK=AC=5a ，由此可得HK=a ，tan ∠AKH=3AHHK=，10a ，结合10可得a=1，则AC=5；在四边形BGKH 中，由∠BHK=∠BKG=90°，可得∠ABG+∠HKG=180°，结合∠AKH+∠GKG=180°，∠ACG=∠ABG 可得∠ACG=∠AKH ，在Rt △APN 中，由tan ∠CAH=43PN AP=，可设PN=12b ，AP=9b ，由tan ∠ACG=PN CP =tan ∠AKH=3可得CP=4b ，由此可得AC=AP+CP=13b =5，则可得b=513，由此即可在Rt △CPN 中由勾股定理解出CN 的长. 试题解析：（1）如图1，连接OG ．∵EF 切⊙O 于G ， ∴OG ⊥EF ，∴∠AGO+∠AGE=90°， ∵CD ⊥AB 于H ， ∴∠AHD=90°， ∴∠OAG=∠AKH=90°， ∵OA=OG ， ∴∠AGO=∠OAG ， ∴∠AGE=∠AKH ， ∵∠EKG=∠AKH ， ∴∠EKG=∠AGE ， ∴KE=GE ．（2）设∠FGB=α， ∵AB 是直径， ∴∠AGB=90°，∴∠AGE =∠EKG=90°﹣α， ∴∠E=180°﹣∠AGE ﹣∠EKG=2α，∵∠FGB=12∠ACH ， ∴∠ACH=2α， ∴∠ACH=∠E ， ∴CA ∥FE ．（3）作NP ⊥AC 于P ． ∵∠ACH=∠E ， ∴sin ∠E=sin ∠ACH=35AH AC =，设AH=3a ，AC=5a ，则224AC CH a -=，tan ∠CAH=43CH AH =， ∵CA ∥FE ，∴∠CAK=∠AGE，∵∠AGE=∠AKH，∴∠CAK=∠AKH，∴AC=CK=5a，HK=CK﹣CH=4a，tan∠AKH=AHHK =3，AK=2210AH HK a+=，∵AK=10，∴1010a=，∴a=1．AC=5，∵∠BHD=∠AGB=90°，∴∠BHD+∠AGB=180°，在四边形BGKH中，∠BHD+∠HKG+∠AGB+∠ABG=360°，∴∠ABG+∠HKG=180°，∵∠AKH+∠HKG=180°，∴∠AKH=∠ABG，∵∠ACN=∠ABG，∴∠AKH=∠ACN，∴tan∠AKH=tan∠ACN=3，∵NP⊥AC于P，∴∠APN=∠CPN=90°，在Rt△APN中，tan∠CAH=43PNAP=，设PN=12b，则AP=9b，在Rt△CPN中，tan∠ACN=PNCP=3，∴CP=4b，∴AC=AP+CP=13b，∵AC=5，∴13b=5，∴b=513，∴CN=22PN CP+=410b⋅=2010 13．。

锐角三角函数及其应用(共60题)(学生版)

锐角三角函数及其应用(60题)一、解答题1(2023·河南·统考中考真题)综合实践活动中，某小组用木板自制了一个测高仪测量树高，测高仪ABCD为正方形，AB=30cm，顶点A处挂了一个铅锤M．如图是测量树高的示意图，测高仪上的点D，A与树顶E在一条直线上，铅垂线AM交BC于点H．经测量，点A距地面1.8m，到树EG的距离AF= 11m，BH=20cm．求树EG的高度(结果精确到0.1m)．2(2023·四川宜宾·统考中考真题)渝昆高速铁路的建成，将会显著提升宜宾的交通地位．渝昆高速铁路宜宾临港长江公铁两用大桥(如图1)，桥面采用国内首创的公铁平层设计．为测量左桥墩底到桥面的距离CD，如图2．在桥面上点A处，测得A到左桥墩D的距离AD=200米，左桥墩所在塔顶B的仰角∠BAD=45°，左桥墩底C的俯角∠CAD=15°，求CD的长度．(结果精确到1米．参考数据：2≈1.41，3≈1.73)3(2023·辽宁·统考中考真题)暑假期间，小明与小亮相约到某旅游风景区登山，需要登顶600m高的山峰，由山底A处先步行300m到达B处，再由B处乘坐登山缆车到达山顶D处．已知点A，B．D，E，F在同一平面内，山坡AB的坡角为30°，缆车行驶路线BD与水平面的夹角为53°(换乘登山缆车的时间忽略不计)(1)求登山缆车上升的高度DE；(2)若步行速度为30m/min，登山缆车的速度为60m/min，求从山底A处到达山顶D处大约需要多少分钟(结果精确到0.1min)(参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33)4(2023·甘肃兰州·统考中考真题)如图1是我国第一个以“龙”为主题的主题公园--“兰州龙源”．“兰州龙源”的“龙”字主题雕塑以紫铜铸造，如巨龙腾空，气势如虹，屹立在黄河北岸．某数学兴趣小组开展了测量“龙”字雕塑CD高度的实践活动．具体过程如下：如图2，“龙”字雕塑CD位于垂直地面的基座BC上，在平行于水平地面的A处测得∠BAC=38°、∠BAD=53°，AB=18m．求“龙”字雕塑CD的高度．(B，C，D三点共线，BD⊥AB．结果精确到0.1m)(参考数据：sin38°≈0.62，cos38°≈0.79，tan38°≈0.78，sin53°≈0.80，cos53°≈0.60，tan53°≈1.33)5(2023·内蒙古通辽·统考中考真题)如图，一艘海轮位于灯塔P的北偏东72°方向，距离灯塔100nmile的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东40°方向上的B处．这时，B 处距离灯塔P有多远(结果取整数)？(参考数据：sin72°≈0.95,cos72°≈0.31,tan72°≈3.08,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84．)6(2023·湖北·统考中考真题)为了防洪需要，某地决定新建一座拦水坝，如图，拦水坝的横断面为梯形ABCD，斜面坡度i=3:4是指坡面的铅直高度AF与水平宽度BF的比．已知斜坡CD长度为20米，∠C=18°，求斜坡AB的长．(结果精确到米)(参考数据：sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)7(2023·湖南张家界·统考中考真题)“游张家界山水，逛七十二奇楼”成为今年旅游新特色．某数学兴趣小组用无人机测量奇楼AB的高度，测量方案如图：先将无人机垂直上升至距水平地面225m的P 点，测得奇楼顶端A的俯角为15°，再将无人机沿水平方向飞行200m到达点Q，测得奇楼底端B的俯角为45°，求奇楼AB的高度．(结果精确到1m，参考数据：sin15°≈0.26，cos15°≈0.97，tan15°≈0.27)8(2023·辽宁大连·统考中考真题)如图所示是消防员攀爬云梯到小明家的场景．已知AE⊥BE,BC ⊥BE,CD∥BE，AC=10.4m,BC=1.26m，点A关于点C的仰角为70°，则楼AE的高度为多少m？(结果保留整数．参考数据：sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)9(2023·广东·统考中考真题)2023年5月30日，神舟十六号载人飞船发射取得圆满成功，3名航天员顺利进驻中国空间站，如图中的照片展示了中国空间站上机械臂的一种工作状态，当两臂AC=BC= 10m，两臂夹角∠ACB=100°时，求A，B两点间的距离．(结果精确到0.1m，参考数据sin50°≈0.766，cos50°≈0.643，tan50°≈1.192)10(2023·湖南·统考中考真题)我国航天事业捷报频传，2023年5月30日，被誉为“神箭”的长征二号F运载火箭托举神舟十六号载人飞船跃入苍穹中国空间站应用与发展阶段首次载人发射任务取得圆满成功，如图(九)，有一枚运载火箭从地面O处发射，当火箭到达P处时，地面A处的雷达站测得AP距离是5000m，仰角为23°．9s，火箭直线到达Q处，此时地面A处雷达站测得Q处的仰角为45°．求火箭从P 到Q处的平均速度(结果精确到1m/s)．(参考数据：sin23°≈0.39,cos23°≈0.92,tan23°≈0.42)11(2023·浙江绍兴·统考中考真题)图1是某款篮球架，图2是其示意图，立柱OA垂直地面OB，支架CD与OA交于点A，支架CG⊥CD交OA于点G，支架DE平行地面OB，篮筺EF与支架DE在同一直线上，OA=2.5米，AD=0.8米，∠AGC=32°．(1)求∠GAC的度数．(2)某运动员准备给篮筐挂上篮网，如果他站在発子上，最高可以把篮网挂到离地面3米处，那么他能挂上篮网吗？请通过计算说明理由．(参考数据：sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)12(2023·浙江台州·统考中考真题)教室里的投影仪投影时，可以把投影光线CA，CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC，∠BAC=90°．黑板上投影图像的高度AB=120cm，CB 与AB的夹角∠B=33.7°，求AC的长．(结果精确到1cm．参考数据：sin33.7°≈0.55，cos33.7°≈0.83，tan33.7°≈0.67)13(2023·湖南怀化·统考中考真题)为弘扬革命传统精神，清明期间，某校组织学生前往怀化市烈士陵园缅怀革命先烈．大家被革命烈士纪念碑的雄伟壮观震撼，想知道纪念碑的通高CD(碑顶到水平地面的距离)，于是师生组成综合实践小组进行测量．他们在地面的A点用测角仪测得碑顶D的仰角为30°，在B点处测得碑顶D的仰角为60°，已知AB=35m，测角仪的高度是1.5m(A、B、C在同一直线上)，根据以上数据求烈士纪念碑的通高CD．(3≈1.732，结果保留一位小数)14(2023·新疆·统考中考真题)烽燧即烽火台，是古代军情报警的一种措施，史册记载，夜间举火称“烽”，白天放烟称“燧”．克孜尔尕哈烽燧是古丝绸之路北道上新疆境内时代最早、保存最完好、规模最大的古代烽燧(如图1)．某数学兴趣小组利用无人机测量该烽燧的高度，如图2，无人机飞至距地面高度31.5米的A处，测得烽燧BC的顶部C处的俯角为50°，测得烽燧BC的底部B处的俯角为65°，试根据提供的数据计算烽燧BC的高度．(参数据：sin50°≈0.8，cos50°≈0.6，tan50≈1.2，sin65°≈0.9，cos65°≈0.4，tan65°≈2.1)15(2023·四川遂宁·统考中考真题)某实践探究小组想测得湖边两处的距离，数据勘测组通过勘测，得到了如下记录表：实践探究活动记录表活动内容测量湖边A、B两处的距离成员组长：××× 组员：××××××××××××测量工具测角仪，皮尺等测量示意图说明：因为湖边A、B两处的距离无法直接测量，数据勘测组在湖边找了一处位置C．可测量C处到A、B两处的距离．通过测角仪可测得∠A、∠B、∠C的度数．测量数据角的度数∠A=30°∠B=45°∠C=105°边的长度BC=40.0米AC=56.4米数据处理组得到上面数据以后做了认真分析．他们发现不需要勘测组的全部数据就可以计算出A、B之间的距离．于是数据处理组写出了以下过程，请补全内容．已知：如图，在△ABC中，∠A=30°，∠B=45°．．(从记录表中再选一个条件填入横线)求：线段AB的长．(为减小结果的误差，若有需要，2取1.41，3取1.73，6取2.45进行计算，最后结果保留整数．)16(2023·四川成都·统考中考真题)为建设美好公园社区，增强民众生活幸福感，某社区服务中心在文化活动室墙外安装避阳篷，便于社区居民休憩．如图，在侧面示意图中，遮阳篷AB长为5米，与水平面的夹角为16°，且靠墙端离地高BC为4米，当太阳光线AD与地面CE的夹角为45°时，求阴影CD的长．(结果精确到0.1米；参考数据：sin16°≈0.28,cos16°≈0.96,tan16°≈0.29)17(2023·贵州·统考中考真题)贵州旅游资源丰富．某景区为给游客提供更好的游览体验，拟在如图①景区内修建观光索道．设计示意图如图②所示，以山脚A为起点，沿途修建AB、CD两段长度相等的观光索道，最终到达山顶D处，中途设计了一段与AF平行的观光平台BC为50m．索道AB与AF的夹角为15°，CD与水平线夹角为45°，A、B两处的水平距离AE为576m，DF⊥AF，垂足为点F．(图中所有点都在同一平面内，点A、E、F在同一水平线上)(1)求索道AB的长(结果精确到1m)；(2)求水平距离AF的长(结果精确到1m)．(参考数据：sin15°≈0.25，cos15°≈0.96，tan15°≈0.26，2≈1.41)18(2023·湖北鄂州·统考中考真题)鄂州市莲花山是国家4A级风景区，元明塔造型独特，是莲花山风景区的核心景点，深受全国各地旅游爱好者的青睐．今年端午节，景区将举行大型包粽子等节日庆祝活动．如图2，景区工作人员小明准备从元明塔的点G处挂一条大型竖直条幅到点E处，挂好后，小明进行实地测量，从元明塔底部F点沿水平方向步行30米到达自动扶梯底端A点，在A点用仪器测得条幅下端E的仰角为30°；接着他沿自动扶梯AD到达扶梯顶端D点，测得点A和点D的水平距离为15米，且tan∠DAB=43；然后他从D点又沿水平方向行走了45米到达C点，在C点测得条幅上端G的仰角为45°．(图上各点均在同一个平面内，且G，C，B共线，F，A，B共线，G、E、F共线，CD∥AB，GF⊥FB)．(1)求自动扶梯AD的长度；(2)求大型条幅GE的长度．(结果保留根号)19(2023·山东东营·统考中考真题)一艘船由A港沿北偏东60°方向航行30km至B港，然后再沿北偏西30°方向航行40km至C港，则A，C两港之间的距离为多少km？20(2023·四川凉山·统考中考真题)超速容易造成交通事故．高速公路管理部门在某隧道内的C、E 两处安装了测速仪，该段隧道的截面示意图如图所示，图中所有点都在同一平面内，且A、D、B、F在同一直线上．点C、点E到AB的距离分别为CD、EF，且CD=EF=7m,CE=895m，在C处测得A点的俯角为30°，在E处测得B点的俯角为45°，小型汽车从点A行驶到点B所用时间为45s．(1)求A,B两点之间的距离(结果精确到1m)；(2)若该隧道限速80千米/小时，判断小型汽车从点A行驶到点B是否超速？并通过计算说明理由．(参考数据：2≈1.4,3≈1.7)21(2023·内蒙古·统考中考真题)为了增强学生体质、锤炼学生意志，某校组织一次定向越野拉练活动．如图，A点为出发点，途中设置两个检查点，分别为B点和C点，行进路线为A→B→C→A．B点在A点的南偏东25°方向32km处，C点在A点的北偏东80°方向，行进路线AB和BC所在直线的夹角∠ABC为45°．(1)求行进路线BC和CA所在直线的夹角∠BCA的度数；(2)求检查点B和C之间的距离(结果保留根号)．22(2023·湖南常德·统考中考真题)今年“五一”长假期间，小陈、小余同学和家长去沙滩公园游玩，坐在如图的椅子上休息时，小陈感觉很舒服，激发了她对这把椅子的好奇心，就想出个问题考考同学小余，小陈同学先测量，根据测量结果画出了图1的示意图(图2)．在图2中，已知四边形ABCD是平行四边形，座板CD与地面MN平行，△EBC是等腰三角形且BC=CE，∠FBA=114.2°，靠背FC=57cm，支架AN=43cm，扶手的一部分BE=16.4cm．这时她问小余同学，你能算出靠背顶端F点距地面(MN)的高度是多少吗？请你帮小余同学算出结果(最后结果保留一位小数)．(参考数据：sin65.8°=0.91，cos65.8°=0.41，tan65.8°=2.23)23(2023·山东·统考中考真题)无人机在实际生活中的应用广泛，如图所示，某人利用无人机测最大楼的高度BC，无人机在空中点P处，测得点P距地面上A点80米，点A处俯角为60°，楼顶C点处的俯角为30°，已知点A与大楼的距离AB为70米(点A，B，C，P在同一平面内)，求大楼的高度BC(结果保留根号)24(2023·重庆·统考中考真题)人工海产养殖合作社安排甲、乙两组人员分别前往海面A，B养殖场捕捞海产品，经测量，A在灯塔C的南偏西60°方向，B在灯塔C的南偏东45°方向，且在A的正东方向，AC=3600米．(1)求B养殖场与灯塔C的距离(结果精确到个位)；(2)甲组完成捕捞后，乙组还未完成捕捞，甲组决定前往B处协助捕捞，若甲组航行的平均速度为600米/每分钟，请计算说明甲组能否在9分钟内到达B处？(参考数据：2≈1.414，3≈1.732)25(2023·山东聊城·统考中考真题)东昌湖西岸的明珠大剧院，隔湖与远处的角楼、城门楼、龙堤、南关桥等景观遥相呼应．如图所示，城门楼B在角楼A的正东方向520m处，南关桥C在城门楼B的正南方向1200m处．在明珠大剧院P测得角楼A在北偏东68.2°方向，南关桥C在南偏东56.31°方向(点A，B，C，P四点在同一平面内)．求明珠大剧院到龙堤BC的距离(结果精确到1m)．(参考数据：sin68.2°≈0.928，cos68.2°≈0.371，tan68.2°≈2.50，sin56.31°≈0.832，cos56.31°≈0.555，tan56.31°≈1.50)26(2023·四川·统考中考真题)“一缕清风银叶转”，某市20台风机依次矗立在云遮雾绕的山脊之上，风叶转动，风能就能转换成电能，造福千家万户．某中学初三数学兴趣小组，为测量风叶的长度进行了实地测量．如图，三片风叶两两所成的角为120°，当其中一片风叶OB 与塔干OD 叠合时，在与塔底D 水平距离为60米的E 处，测得塔顶部O 的仰角∠OED =45°，风叶OA 的视角∠OEA =30°．(1)已知α，β两角和的余弦公式为：cos α+β =cos αcos β-sin αsin β，请利用公式计算cos75°；(2)求风叶OA 的长度．27(2023·湖北宜昌·统考中考真题)2023年5月30日，“神舟十六号”航天飞船成功发射．如图，飞船在离地球大约330km 的圆形轨道上，当运行到地球表面P 点的正上方F 点时，从中直接看到地球表面一个最远的点是点Q ．在Rt △OQF 中，OP =OQ ≈6400km ．(参考数据：cos16°≈0.96，cos18°≈0.95，cos20°≈0.94，cos22°≈0.93，π≈3.14)(1)求cos α的值(精确到0.01)；(2)在⊙O 中，求PQ的长(结果取整数)．28(2023·四川泸州·统考中考真题)如图，某数学兴趣小组为了测量古树DE的高度，采用了如下的方法：先从与古树底端D在同一水平线上的点A出发，沿斜面坡度为i=2:3的斜坡AB前进207m到达点B，再沿水平方向继续前进一段距离后到达点C．在点C处测得古树DE的顶端E的俯角为37°，底部D的俯角为60°，求古树DE的高度(参考数据：sin37°≈35，cos37°≈45，tan37°≈34，计算结果用根号表示，不取近似值)．29(2023·山西·统考中考真题)2023年3月，水利部印发《母亲河复苏行动河湖名单(2022-2025年)》，我省境内有汾河、桑干河、洋河、清漳河、浊漳河、沁河六条河流入选．在推进实施母亲河复苏行动中，需要砌筑各种驳岸(也叫护坡)．某校“综合与实践”小组的同学把“母亲河驳岸的调研与计算”作为一项课题活动，利用课余时间完成了实践调查，并形成了如下活动报告．请根据活动报告计算BC 和AB 的长度(结果精确到0.1m ．参考数据：3≈1.73，2≈1.41)．课题母亲河驳岸的调研与计算调查方式资料查阅、水利部门走访、实地查看了解功能驳岸是用来保护河岸，阻止河岸崩塌或冲刷的构筑物驳岸剖面图相关数据及说明，图中，点A ，B ，C ，D ，E 在同一竖直平面内，AE 与CD 均与地面平行，岸墙AB ⊥AE 于点A ，∠BCD =135°，∠EDC =60°，ED =6m ，AE =1.5m ，CD =3.5m计算结果交流展示30(2023·湖南·统考中考真题)如图所示，在某交叉路口，一货车在道路①上点A处等候“绿灯”一辆车从被山峰POQ遮挡的道路②上的点B处由南向北行驶．已知∠POQ=30°，BC∥OQ，OC⊥OQ，AO⊥OP，线段AO的延长线交直线BC于点D．(1)求∠COD的大小；(2)若在点B处测得点O在北偏西α方向上，其中tanα=35，OD=12米．问该轿车至少行驶多少米才能发现点A处的货车？(当该轿车行驶至点D处时，正好发现点A处的货车)31(2023·四川内江·统考中考真题)某中学依山而建，校门A处有一坡角α=30°的斜坡AB，长度为30米，在坡顶B处测得教学楼CF的楼顶C的仰角∠CBF=45°，离B点4米远的E处有一个花台，在E 处测得C的仰角∠CEF=60°，CF的延长线交水平线AM于点D，求DC的长(结果保留根号)．32(2023·湖北随州·统考中考真题)某校学生开展综合实践活动，测量某建筑物的高度AB，在建筑物附近有一斜坡，坡长CD=10米，坡角α=30°，小华在C处测得建筑物顶端A的仰角为60°，在D处测得建筑物顶端A的仰角为30°．(已知点A，B，C，D在同一平面内，B，C在同一水平线上)(1)求点D到地面BC的距离；(2)求该建筑物的高度AB．33(2023·天津·统考中考真题)综合与实践活动中，要利用测角仪测量塔的高度．如图，塔AB前有一座高为DE的观景台，已知CD=6m,∠DCE=30°，点E，C，A在同一条水平直线上．某学习小组在观景台C处测得塔顶部B的仰角为45°，在观景台D处测得塔顶部B的仰角为27°．(1)求DE的长；(2)设塔AB的高度为h(单位：m)．①用含有h的式子表示线段EA的长(结果保留根号)；②求塔AB的高度(tan27°取0.5，3取1.7，结果取整数)．34(2023·山东临沂·统考中考真题)如图，灯塔A周围9海里内有暗礁．一渔船由东向西航行至B 处，测得灯塔A在北偏西58°方向上，继续航行6海里后到达C处，测得灯塔A在西北方向上．如果渔船不改变航线继续向西航行，有没有触礁的危险？(参考数据：sin32°≈0.530,cos32°≈0.848,tan32°≈0.625;sin58°≈0.848,cos58°≈0.530，tan58°≈1.6)35(2023·湖南永州·统考中考真题)永州市道县陈树湘纪念馆中陈列的陈树湘雕像高2.9米(如图1所示)，寓意陈树湘为中国革命“断肠明志”牺牲时的年龄为29岁．如图2，以线段AB代表陈树湘雕像，一参观者在水平地面BN上D处为陈树湘雕拍照，相机支架CD高0.9米，在相机C处观测雕像顶端A的仰角为45°，然后将相机架移到MN处拍照，在相机M处观测雕像顶端A的仰角为30°，求D、N两点间的距离(结果精确到0.1米，参考数据：3≈1.732)36(2023·重庆·统考中考真题)为了满足市民的需求，我市在一条小河AB两侧开辟了两条长跑锻炼线路，如图；①A-D-C-B；②A-E-B．经勘测，点B在点A的正东方，点C在点B的正北方10千米处，点D在点C的正西方14千米处，点D在点A的北偏东45°方向，点E在点A的正南方，点E在点B 的南偏西60°方向．(参考数据：2≈1.41,3≈1.73)(1)求AD的长度．(结果精确到1千米)(2)由于时间原因，小明决定选择一条较短线路进行锻炼，请计算说明他应该选择线路①还是线路②？37(2023·江苏苏州·统考中考真题)四边形不具有稳定性，工程上可利用这一性质解决问题．如图是某篮球架的侧面示意图，BE,CD,GF为长度固定的支架，支架在A,D,G处与立柱AH连接(AH垂直于MN，垂足为H)，在B,C处与篮板连接(BC所在直线垂直于MN)，EF是可以调节长度的伸缩臂(旋转点F处的螺栓改变EF的长度，使得支架BE绕点A旋转，从而改变四边形ABCD的形状，以此调节篮板的高度)．已知AD=BC,DH=208cm，测得∠GAE=60°时，点C离地面的高度为288cm．调节伸缩臂EF，将∠GAE由60°调节为54°，判断点C离地面的高度升高还是降低了？升高(或降低)了多少？(参考数据：sin54°≈0.8,cos54°≈0.6)38(2023·湖南·统考中考真题)随着科技的发展，无人机已广泛应用于生产生活，如代替人们在高空测量距离和高度．圆圆要测量教学楼AB的高度，借助无人机设计了如下测量方案：如图，圆圆在离教学楼底部243米的C处，遥控无人机旋停在点C的正上方的点D处，测得教学楼AB的顶部B处的俯角为30°，CD长为49.6米．已知目高CE为1.6米．(1)求教学楼AB的高度．(2)若无人机保持现有高度沿平行于CA的方向，以43米/秒的速度继续向前匀速飞行，求经过多少秒时，无人机刚好离开圆圆的视线EB．39(2023·山东烟台·统考中考真题)风电项目对于调整能源结构和转变经济发展方式具有重要意义．某电力部门在一处坡角为30°的坡地新安装了一架风力发电机，如图1．某校实践活动小组对该坡地上的这架风力发电机的塔杆高度进行了测量，图2为测量示意图．已知斜坡CD长16米，在地面点A处测得风力发电机塔杆顶端P点的仰角为45°，利用无人机在点A的正上方53米的点B处测得P点的俯角为18°，求该风力发电机塔杆PD的高度．(参考数据：sin18°≈0.309，cos18°≈0.951，tan18°≈0.325)40(2023·甘肃武威·统考中考真题)如图1，某人的一器官后面A处长了一个新生物，现需检测到皮肤的距离(图1)．为避免伤害器官，可利用一种新型检测技术，检测射线可避开器官从侧面测量．某医疗小组制定方案，通过医疗仪器的测量获得相关数据，并利用数据计算出新生物到皮肤的距离．方案如下：课题检测新生物到皮肤的距离工具医疗仪器等示意图说明如图2，新生物在A处，先在皮肤上选择最大限度地避开器官的B处照射新生物，检测射线与皮肤MN的夹角为∠DBN；再在皮肤上选择距离B处9cm的C处照射新生物，检测射线与皮肤MN的夹角为∠ECN．测量数据∠DBN=35°，∠ECN=22°，BC=9cm请你根据上表中的测量数据，计算新生物A处到皮肤的距离．(结果精确到0.1cm)(参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70，sin22°≈0.37，cos22°≈0.93，tan22°≈0.40)41(2023·四川达州·统考中考真题)莲花湖湿地公园是当地人民喜爱的休闲景区之一，里面的秋千深受孩子们喜爱．如图所示，秋千链子的长度为3m，当摆角∠BOC恰为26°时，座板离地面的高度BM为0.9m，当摆动至最高位置时，摆角∠AOC为50°，求座板距地面的最大高度为多少m？(结果精确到0.1m；参考数据：sin26°≈0.44，cos26°≈0.9，tan26°≈0.49，sin50°≈0.77，cos50°≈0.64，tan50°≈1.2)42(2023·江西·统考中考真题)如图1是某红色文化主题公园内的雕塑，将其抽象成加如图2所示的示意图，已知点B，A，D，E均在同一直线上，AB=AC=AD，测得∠B=55°，BC=1.8m，DE=2m．(结果保小数点后一位)(1)连接CD，求证：DC⊥BC；(2)求雕塑的高(即点E到直线BC的距离)．(参考数据：sin55°≈0.82，cos55°≈0.57，tan55°≈1.43)43(2023·浙江宁波·统考中考真题)某综合实践研究小组为了测量观察目标时的仰角和俯角，利用量角器和铅锤自制了一个简易测角仪，如图1所示．(1)如图2，在P点观察所测物体最高点C，当量角器零刻度线上A，B两点均在视线PC上时，测得视线与铅垂线所夹的锐角为α，设仰角为β，请直接用含α的代数式示β．(2)如图3，为了测量广场上空气球A离地面的高度，该小组利用自制简易测角仪在点B，C分别测得气球A的仰角∠ABD为37°，∠ACD为45°，地面上点B，C，D在同一水平直线上，BC=20m，求气球A离地面的高度AD．(参考数据：sin37°≈0.60,cos37°≈0.80，tan37°≈0.75)44(2023·江苏连云港·统考中考真题)渔湾是国家“AAAA”级风景区，图1是景区游览的部分示意图．如图2，小卓从九孔桥A处出发，沿着坡角为48°的山坡向上走了92m到达B处的三龙潭瀑布，再沿坡角为37°的山坡向上走了30m到达C处的二龙潭瀑布．求小卓从A处的九孔桥到C处的二龙潭瀑布上升的高度DC为多少米？(结果精确到0.1m)(参考数据：sin48°≈0.74，cos48°≈0.67，sin37°≈0.60，cos37°≈0.80)45(2023·四川广安·统考中考真题)为了美化环境，提高民众的生活质量，市政府在三角形花园ABC 边上修建一个四边形人工湖泊ABDE，并沿湖泊修建了人行步道．如图，点C在点A的正东方向170米处，点E在点A的正北方向，点B、D都在点C的正北方向，BD长为100米，点B在点A的北偏东30°方向，点D在点E的北偏东58°方向．(1)求步道DE的长度．(2)点D处有一个小商店，某人从点A出发沿人行步道去商店购物，可以经点B到达点D，也可以经点E到达点D，请通过计算说明他走哪条路较近．结果精确到个位)(参考数据：sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,3≈1.73)46(2023·浙江嘉兴·统考中考真题)图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角围内才能被识别)，其示意图如图2，摄像头A的仰角、俯角均为15°，摄像头高度OA=160cm，识别的最远水平距离OB=150cm．(1)身高208cm的小杜，头部高度为26cm，他站在离摄像头水平距离130cm的点C处，请问小杜最少需要下蹲多少厘米才能被识别．(2)身高120cm的小若，头部高度为15cm，踮起脚尖可以增高3cm，但仍无法被识别．社区及时将摄像头的仰角、俯角都调整为20°(如图3)，此时小若能被识别吗？请计算说明．(精确到0.1cm，参考数据sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)47(2023·安徽·统考中考真题)如图，O,R是同一水平线上的两点，无人机从O点竖直上升到A点时，测得A到R点的距离为40m,R点的俯角为24.2°，无人机继续竖直上升到B点，测得R点的俯角为36.9°．求无人机从A点到B点的上升高度AB(精确到0.1m)．参考数据：sin24.2°≈0.41,cos24.2°≈0.91,tan24.2°≈0.45，sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75．48(2023·浙江·统考中考真题)如图，某工厂为了提升生产过程中所产生废气的净化效率，需在气体净化设备上增加一条管道A -D -C ，已知DC ⊥BC ，AB ⊥BC ,∠A =60°,AB =11m ,CD =4m ，求管道A -D -C的总长．49(2023·浙江温州·统考中考真题)根据背景素材，探索解决问题．测算发射塔的高度背景素材某兴趣小组在一幢楼房窗口测算远处小山坡上发射塔的高度MN (如图1)．他们通过自制的测倾仪(如图2)在A ，B ，C 三个位置观测，测倾仪上的示数如图3所示．经讨论，只需选择其中两个合适的位置，通过测量、换算就能计算发射塔的高度．问题解决任务1分析规划选择两个观测位置：点_________和点_________获取数据写出所选位置观测角的正切值，并量出观测点之间的图上距离．任务2推理计算计算发射塔的图上高度MN．任务3换算高度楼房实际宽度DE为12米，请通过测量换算发射塔的实际高度．注：测量时，以答题纸上的图上距离为准，并精确到1mm．50(2023·四川自贡·统考中考真题)为测量学校后山高度，数学兴趣小组活动过程如下：(1)测量坡角如图1，后山一侧有三段相对平直的山坡AB，BC，CD，山的高度即为三段坡面的铅直高度BH，CQ，DR之和，坡面的长度可以直接测量得到，要求山坡高度还需要知道坡角大小．如图2，同学们将两根直杆MN，MP的一端放在坡面起始端A处，直杆MP沿坡面AB方向放置，在直杆MN另一端N用细线系小重物G，当直杆MN与铅垂线NG重合时，测得两杆夹角α的度数，由此可得山坡AB坡角β的度数．请直接写出α，β之间的数量关系．(2)测量山高同学们测得山坡AB，BC，CD的坡长依次为40米，50米，40米，坡角依次为24°，30°，45°；为求BH，小熠同学在作业本上画了一个含24°角的Rt△TKS(如图3)，量得KT≈5cm，TS≈2cm．求山高DF．(2≈1.41，结果精确到1米)(3)测量改进由于测量工作量较大，同学们围绕如何优化测量进行了深入探究，有了以下新的测量方法．如图4，5，在学校操场上，将直杆NP置于MN的顶端，当MN与铅垂线NG重合时，转动直杆NP，使点N，P，D共线，测得∠MNP的度数，从而得到山顶仰角β1，向后山方向前进40米，采用相同方式，测得山顶仰角β2；画一个含β1的直角三角形，量得该角对边和另一直角边分别为a1厘米，b1厘米，再画一个含β2的直角三角形，量得该角对边和另一直角边分别为a2厘米，b2厘米．已知杆高MN为1.6米，求山高DF．(结果用不含β1，β2的字母表示)。

专题4.5锐角三角函数中考数学第一轮总复习课件

锐角α的正切值随着α的增大而增大.
(3)sinA+cosA_＞___1；sin2A+cos2A_＝___1, sinα=cos(_9_0_º_-_α_)；cosα=sin(_9_0_º_-_α_)；
典例精讲
锐角三角函数
知识点一
【例1】(1)式子2cos30º-tan45º- （1 tan 60 )2 的值是__0__.
5.已知△ABC中,AB=10,AC= 2 7,∠B=30º,则△ABC的面积等于_1_5__3_或__1_0__3_.
6.四边形ABCD中,BD是对角线,∠ABC=90º,tan∠ABD=
3 4
,AB=20，
BC=10,AD=13,则线段CD=1_7__或___8_9__.
A
A A
E F
B
DC
B
C´
02
解直角三角形
精讲精练
03 解直角三角形应用
考点聚焦
解直角三角形的应用
知识点三
1.视角,2.方向角(方位角),3.坡度(坡比),坡角:i=tanα=h:l.
在测量高度,宽度,距离等问题中,常见的构造的基本图形如下：
③利用反射构造相似. ②同一地点看不同点 ①不同地点看同一点
典例精讲
直角三角形应用
A
K
I
H
N
M
D
A
K
I
NH M
D
A
K
I
H N
M
D
E
O
B 图1 G
FE O
CB 图2 G
FE
O
C B 图3 G
F C
B. 1
c os2
1
C.sin2α+1 D.cos2α+1

中考数学专题复习之锐角三角函数(共20题)

中考数学专题复习之锐角三角函数（共20题）一．选择题（共10小题）1．如图，一个长方体木箱沿斜面滑至如图位置时，AB＝2m，木箱高BE＝1m，斜面坡角为α，则木箱端点E距地面AC的高度表示为（）m．A．+2sinαB．2cosα+sinαC．cosα+2sinαD．tanα+2sinα2．为了疫情防控工作的需要，某学校在学校门口的大门上方安装了一个人体体外测温摄像头，学校大门高ME＝7.5米，学生身高BD＝1.5米，当学生准备进入识别区域时，在点B时测得摄像头M的仰角为30°，当学生刚好离开识别区域时，在点A时测得摄像头M 的仰角为60°，则体温监测有效识别区域AB的长（）A．米B．米C．5米D．6米3．某网红地惊现震撼的裸眼3D超清LED巨幕，成功吸引了广大游客前来打卡．小丽想了解该LED屏AB的高度，进行了实地测量，她从大楼底部C点沿水平直线步行30米到达台阶底端D点，在D点测得屏幕下端点B的仰角为27°，然后她再沿着i＝4：3长度为35米的自动扶梯到达扶梯顶端E点，又沿水平直线行走了45米到达F点，在F点测得屏幕上端点A的仰角为50°（A，B，C，D，E，F，G在同一个平面内，且E、F和C、D、G分别在同一水平线上），则该LED屏AB的高度约为（）（结果精确到0.1，参考数据sin27°≈0.45，cos27°≈0.89，tan27°≈0.51，sin50°≈0.77，tan50°≈1.19）A．86.2米B．114.2米C．126.9米D．142.2米4．如图，旗杆AB竖立在斜坡CB的顶端，斜坡CB长为65米，坡度为i＝．小明从与点C相距115米的点D处向上爬12米到达建筑物DE的顶端点E，在此测得旗杆顶端点A的仰角为39°，则旗杆的高度AB约为（）米．（参考数据：sin39°≈0.63，cos39°≈0.78，tan39°≈0.81）A．12.9B．22.2C．24.9D．63.15．我校小伟同学酷爱健身，一天去爬山锻炼，在出发点C处测得山顶部A的仰角为30度，在爬山过程中，每一段平路（CD、EF、GH）与水平线平行，每一段上坡路（DE、FG、HA）与水平线的夹角都是45度，在山的另一边有一点B（B、C、D同一水平线上），斜坡AB的坡度为2：1，且AB长为900，其中小伟走平路的速度为65.7米/分，走上坡路的速度为42.3米/分．则小伟从C出发到坡顶A的时间为（）（图中所有点在同一平面内≈1.41，≈1.73）A．60分钟B．70分钟C．80分钟D．90分钟6．李白笔下“孤帆一片日边来”描述了在喷薄而出的红日映衬下，远远望见一叶帆船驶来的壮美河山之境．聪明的小芬同学利用几何图形，构造出了此意境！如图，半径为5的⊙O在线段AB上方，且圆心O在线段AB的中垂线上，到AB的距离为，AB＝20，线段PQ在边AB上（AP＜AQ），PQ＝6，以PQ中点C为顶点向上作Rt△CDE，其中∠D＝90°，CD＝3，sin∠DCE＝sin∠DCQ＝，设AP＝m，当边DE与⊙O有交点时，m的取值范围是（）A．B．C．D．7．勾股定理有着悠久的历史，它曾引起很多人的兴趣．英国佩里加（H．Perigal，1801﹣1898）用“水车翼轮法”（图1）证明了勾股定理．该证法是用线段QX，ST，将正方形BIJC分割成四个全等的四边形，再将这四个四边形和正方形ACYZ拼成大正方形AEFB （图2）．若AD＝，tan∠AON＝，则正方形MNUV的周长为（）A．B．18C．16D．8．如图，在Rt△ABC中，∠ACB＝90°，CE是斜边AB上的中线，过点E作EF⊥AB交AC于点F．若BC＝4，△AEF的面积为5，则sin∠CEF的值为（）A．B．C．D．9．已知α，β均为锐角，若tanα＝，tanβ＝，则α+β＝（）A．45°B．30°C．60°D．90°10．如图，已知A、B两点的坐标分别为（8，0）、（0，8），点C、F分别是直线x＝﹣5和x轴上的动点，CF＝10，点D是线段CF的中点，连接AD交y轴于点E，当△ABE面积取得最小值时，tan∠BAD的值是（）A．B．C．D．二．填空题（共5小题）11．如图1是一张双挡位可调节靠背椅，挡位调节示意图如图2．两脚AB，AC以及靠背DE，座位FG，其中D，F分别为AC，DE上固定连接点，GF在点A上移动实现靠背的调节，DC＝4AD，EF＝4DF，已知AB＝AC＝DE＝50分米，tan∠ABC＝2．（1）当GF∥BC时，点E离水平地面BC的高度为分米．（2）当靠背DE′⊥AC时，有G′E′∥BC，则GF的长为分米．12．如图1为温州乐园的游乐设施一摩天轮与飞天梭．当摩天轮一座舱A与飞天梭高度相同时（如图2），另一座舱B恰好位于摩天轮最低点；当座舱A顺时针旋转至与飞天梭相同高度的A′点时，座舱B旋转至点B'．此时地面某观测点P与点A'，圆心O恰好在同一条直线上，且sin∠A'PC＝，已知摩天轮的半径为32米，则点B，B'间的距离为米；现又测得∠APC＝∠B'PC，则点B'距离地面的高度为米．13．如图，已知A、B两点的坐标分别为（﹣8，0）、（0，8），点C、F分别是直线x＝5和x轴上的动点，CF＝10，点D是线段CF的中点，连接AD交y轴于点E，当△ABE的面积取得最小值时，tan∠BAD＝．14．如图是一款利用杠杆原理设计的平衡灯，灯管AB与支架AD，砝码杆AC均成120°角，且AB＝40cm，AC＝18cm，AD＝6cm，底座是半径为2cm的圆柱体，点P是杠杆的支点．如图1，若砝码E在端点C时，当杠杆平衡时，支架AD垂直于桌面，则此时垂直光线照射到最远点M到支点P的距离PM为cm．由于特殊设计，灯管的重力集中在端点B，砝码杆重力集中在砝码E上，支架AD的重力忽略不计，由杠杆原理可知，平衡时重力保持垂直水平桌面向下，且G1•h2＝G2•h1，如图2．为了使得平衡时砝码杆与桌面平行，则砝码E到离A点的距离为cm．15．小君家购入如图1的划船机一台，如图2是划船机的部分示意图．阻尼轮⊙O由支架AD和AC支撑，点A处于点O的正下方，AD与⊙O相切，脚踏板点E和圆心O在连杆CE上，CD部分隐藏在阻尼轮内部，测量发现点E到地面的高度EF为35cm，E、A两点间的水平距离AF为72cm，tan∠DAC＝，则CD的长为cm．三．解答题（共5小题）16．某海域有一小岛P，在以P为圆心，半径r为10（3+）海里的圆形海域内有暗礁．一海监船自西向东航行，它在A处测得小岛P位于北偏东60°的方向上，当海监船行驶20海里后到达B处，此时观测小岛P位于B处北偏东45°方向上．（1）求A，P之间的距离AP；（2）若海监船由B处继续向东航行是否有触礁危险？请说明理由．如果有触礁危险，那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域？17．如图，一艘货船在灯塔C的正南方向，距离灯塔257海里的A处遇险，发出求救信号．一艘救生船位于灯塔C的南偏东40°方向上，同时位于A处的北偏东60°方向上的B处，救生船接到求救信号后，立即前往救援．求AB的长．（结果取整数）参考数据：tan40°≈0.84，取1.73．18．脱贫攻坚工作让老百姓过上了幸福的生活．如图①是政府给贫困户新建的房屋，如图②是房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高AB所在的直线，为了测量房屋的高度，在地面上C点测得屋顶A的仰角为35°，此时地面上C点、屋檐上E 点、屋顶上A点三点恰好共线，继续向房屋方向走8m到达点D时，又测得屋檐E点的仰角为60°，房屋的顶层横梁EF＝12m，EF∥CB，AB交EF于点G（点C，D，B在同一水平线上）．（参考数据：sin35°≈0.6，cos35°≈0.8，tan35°≈0.7，≈1.7）（1）求屋顶到横梁的距离AG；（2）求房屋的高AB（结果精确到1m）．19．【材料阅读】2020年5月27日，2020珠峰高程测量登山队成功登顶珠穆朗玛峰，将用中国科技“定义”世界新高度．其基本原理之一是三角高程测量法，在山顶上立一个觇标，找到2个以上测量点，分段测量山的高度，再进行累加．因为地球面并不是水平的，光线在空气中会发生折射，所以当两个测量点的水平距离大于300m时，还要考虑球气差，球气差计算公式为f＝（其中d为两点间的水平距离，R为地球的半径，R取6400000m），即：山的海拔高度＝测量点测得山的高度+测量点的海拔高度+球气差．【问题解决】某校科技小组的同学参加了一项野外测量某座山的海拔高度活动．如图，点A，B的水平距离d＝800m，测量仪AC＝1.5m，觇标DE＝2m，点E，D，B在垂直于地面的一条直线上，在测量点A处用测量仪测得山顶觇标顶端E的仰角为37°，测量点A处的海拔高度为1800m．（1）数据6400000用科学记数法表示为；（2）请你计算该山的海拔高度．（要计算球气差，结果精确到0.01m）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）20．筒车是我国古代利用水力驱动的灌溉工具，唐代陈廷章在《水轮赋》中写道：“水能利物，轮乃曲成”．如图，半径为3m的筒车⊙O按逆时针方向每分钟转圈，筒车与水面分别交于点A、B，筒车的轴心O距离水面的高度OC长为2.2m，筒车上均匀分布着若干个盛水筒．若以某个盛水筒P刚浮出水面时开始计算时间．（1）经过多长时间，盛水筒P首次到达最高点？（2）浮出水面3.4秒后，盛水筒P距离水面多高？（3）若接水槽MN所在直线是⊙O的切线，且与直线AB交于点M，MO＝8m．求盛水筒P从最高点开始，至少经过多长时间恰好在直线MN上．（参考数据：cos43°＝sin47°≈，sin16°＝cos74°≈，sin22°＝cos68°≈）。

中考数学—锐角三角函数的综合压轴题专题复习附答案

一、锐角三角函数真题与模拟题分类汇编（难题易错题）1．如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走6m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．（1）求∠BPQ的度数；（2）求该电线杆PQ的高度（结果精确到1m）．备用数据：，【答案】（1）∠BPQ=30°；（2）该电线杆PQ的高度约为9m．【解析】试题分析：（1）延长PQ交直线AB于点E，根据直角三角形两锐角互余求得即可；（2）设PE=x米，在直角△APE和直角△BPE中，根据三角函数利用x表示出AE和BE，根据AB=AE-BE即可列出方程求得x的值，再在直角△BQE中利用三角函数求得QE的长，则PQ的长度即可求解．试题解析：延长PQ交直线AB于点E，（1）∠BPQ=90°-60°=30°；（2）设PE=x米．在直角△APE中，∠A=45°，则AE=PE=x米；∵∠PBE=60°∴∠BPE=30°在直角△BPE中，BE=33PE=33x米，∵AB=AE-BE=6米，则3，解得：3则BE=（33+3）米．在直角△BEQ中，QE=33BE=33（33+3）=（3+3）米．∴PQ=PE-QE=9+33-（3+3）=6+23≈9（米）．答：电线杆PQ的高度约9米．考点：解直角三角形的应用-仰角俯角问题．2．如图，在△ABC中，∠ABC＝90°，以AB的中点O为圆心，OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE．（1）判断DE与⊙O的位置关系，并说明理由；（2）求证：BC2＝2CD•OE；（3）若314cos,53BAD BE∠==，求OE的长．【答案】（1）DE为⊙O的切线，理由见解析；（2）证明见解析；（3）OE =356．【解析】试题分析：（1）连接OD，BD，由直径所对的圆周角是直角得到∠ADB为直角，可得出△BCD为直角三角形，E为斜边BC的中点，由直角三角形斜边上的中线等于斜边的一半，得到CE=DE，从而得∠C=∠CDE，再由OA=OD，得∠A=∠ADO，由Rt△ABC中两锐角互余，从而可得∠ADO与∠CDE互余，可得出∠ODE为直角，即DE垂直于半径OD，可得出DE为⊙O的切线；（2）由已知可得OE是△ABC的中位线，从而有AC=2OE，再由∠C=∠C，∠ABC=∠BDC，可得△ABC∽△BDC，根据相似三角形的对应边的比相等，即可证得；（3）在直角△ABC中，利用勾股定理求得AC的长，根据三角形中位线定理OE的长即可求得．试题解析：（1）DE为⊙O的切线，理由如下：连接OD，BD，∵AB为⊙O的直径，∴∠ADB=90°，在Rt△BDC中，E为斜边BC的中点，∴CE=DE=BE=BC，∴∠C=∠CDE，∵OA=OD，∴∠A=∠ADO，∵∠ABC=90°，∴∠C+∠A=90°，∴∠ADO+∠CDE=90°，∴∠ODE=90°，∴DE⊥OD，又OD为圆的半径，∴DE为⊙O的切线；（2）∵E是BC的中点，O点是AB的中点，∴OE是△ABC的中位线，∴AC=2OE，∵∠C=∠C，∠ABC=∠BDC，∴△ABC∽△BDC，∴，即BC2=AC•CD．∴BC2=2CD•OE；（3）解：∵cos∠BAD=，∴sin∠BAC=，又∵BE=，E是BC的中点，即BC=，∴AC=．又∵AC=2OE，∴OE=AC=．考点：1、切线的判定；2、相似三角形的判定与性质；3、三角函数3．如图13，矩形的对角线，相交于点，关于的对称图形为．（1）求证：四边形是菱形；（2）连接，若，．①求的值；②若点为线段上一动点（不与点重合），连接，一动点从点出发，以的速度沿线段匀速运动到点，再以的速度沿线段匀速运动到点，到达点后停止运动．当点沿上述路线运动到点所需要的时间最短时，求的长和点走完全程所需的时间．【答案】（1）详见解析；（2）①②和走完全程所需时间为【解析】试题分析：（1）利用四边相等的四边形是菱形；（2）①构造直角三角形求；②先确定点沿上述路线运动到点所需要的时间最短时的位置，再计算运到的时间.试题解析：解：（1）证明：四边形是矩形.与交于点O,且关于对称四边形是菱形.（2）①连接,直线分别交于点,交于点关于的对称图形为在矩形中，为的中点，且O为AC的中点为的中位线同理可得：为的中点，②过点P作交于点由运动到所需的时间为3s由①可得，点O以的速度从P到A所需的时间等于以从M运动到A即：由O运动到P所需的时间就是OP+MA和最小.如下图，当P运动到,即时，所用时间最短.在中，设解得：和走完全程所需时间为考点：菱形的判定方法；构造直角三角形求三角函数值；确定极值时动点的特殊位置4．如图，抛物线y=﹣x2+3x+4与x轴交于A、B两点，与y轴交于C点，点D在抛物线上且横坐标为3．（1）求tan∠DBC的值；（2）点P为抛物线上一点，且∠DBP=45°，求点P的坐标．【答案】（1）tan∠DBC=；（2）P（﹣，）．【解析】试题分析：（1）连接CD，过点D作DE⊥BC于点E．利用抛物线解析式可以求得点A、B、C、D的坐标，则可得CD//AB，OB=OC，所以∠BCO=∠BCD=∠ABC=45°．由直角三角形的性质、勾股定理和图中相关线段间的关系可得BC=4，BE=BC﹣DE=．由此可知tan∠DBC=；（2）过点P作PF⊥x轴于点F．由∠DBP=45°及∠ABC=45°可得∠PBF=∠DBC，利用（1）中的结果得到：tan∠PBF=．设P（x，﹣x2+3x+4），则利用锐角三角函数定义推知=，通过解方程求得点P的坐标为（﹣，）．试题解析：（1）令y=0，则﹣x2+3x+4=﹣（x+1）（x﹣4）=0，解得 x1=﹣1，x2=4．∴A（﹣1，0），B（4，0）．当x=3时，y=﹣32+3×3+4=4，∴D（3，4）．如图，连接CD，过点D作DE⊥BC于点E．∵C（0，4），∴CD//AB，∴∠BCD=∠ABC=45°．在直角△OBC中，∵OC=OB=4，∴BC=4．在直角△CDE中，CD=3．∴CE=ED=，∴BE=BC﹣DE=．∴tan∠DBC=；（2）过点P作PF⊥x轴于点F．∵∠CBF=∠DBP=45°，∴∠PBF=∠DBC，∴tan∠PBF=．设P（x，﹣x2+3x+4），则=，解得 x1=﹣，x2=4（舍去），∴P（﹣，）．考点：1、二次函数；2、勾股定理；3、三角函数5．如图，矩形OABC中，A(6，0)、C(0，23)、D(0，33)，射线l过点D且与x轴平行，点P、Q分别是l和x轴的正半轴上的动点，满足∠PQO＝60º．(1)点B的坐标是，∠CAO＝ º，当点Q与点A重合时，点P的坐标为；(2)设点P的横坐标为x，△OPQ与矩形OABC重叠部分的面积为S，试求S与x的函数关系式和相应的自变量x的取值范围．【答案】（1）（6，3）． 30．（3，3）（2）()()()()243x 430x 3331333x x 3x 5232S {23x 1235x 93543x 9x +≤≤-+-<≤=-+<≤>【解析】解：（1）（6，23）． 30．（3，33）．（2）当0≤x≤3时，如图1，OI=x ，IQ=PI•tan60°=3，OQ=OI+IQ=3+x ；由题意可知直线l ∥BC ∥OA ，可得EF PE DC 31==OQ PO DO 333==，∴EF=13（3+x ），此时重叠部分是梯形，其面积为：EFQO 14343S S EF OQ OC 3x x 43233==+⋅=+=+梯形（）（）当3＜x≤5时，如图2，)HAQ EFQO EFQO 221S S S S AH AQ243331333 3x 3=∆=-=-⋅⋅=+---梯形梯形当5＜x≤9时，如图3，12S BE OAOC 312x 2323 =x 1233=+⋅=--+（）（）。

2023年中考数学专题汇编：锐角三角函数应用、解直角三角形

2023年中考数学专题汇编：锐角三角函数应用、解直角三角形一．解答题（共60小题）1．校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载．某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道l上确定点D，使CD与l垂直，测得CD的长等于21米，在l上点D的同侧取点A、B，使∠CAD＝30°，∠CBD＝60°．（1）求AB的长（精确到0.1米，参考数据：＝1.73，＝1.41）；（2）已知本路段对校车限速为40千米/小时，若测得某辆校车从A到B用时2秒，这辆校车是否超速？说明理由．2．如图，从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度．如果这时气球的高度CD为90米．且点A、D、B在同一直线上，求建筑物A、B间的距离．3．如图，在电线杆上的C处引拉线CE、CF固定电线杆，拉线CE和地面成60°角，在离电线杆6米的B 处安置测角仪，在A处测得电线杆上C处的仰角为30°，已知测角仪高AB为1.5米，求拉线CE的长（结果保留根号）．4．如图，某大楼的顶部树有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底部D的仰角为60°．沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度i＝1：，AB＝10米，AE＝15米．（i＝1：是指坡面的铅直高度BH与水平宽度AH的比）（1）求点B距水平面AE的高度BH；（2）求广告牌CD的高度．（测角器的高度忽略不计，结果精确到0.1米．参考数据： 1.414， 1.732）5．如图，某防洪指挥部发现长江边一处长500米，高10米，背水坡的坡角为45°的防洪大堤（横断面为梯形ABCD）急需加固．经调查论证，防洪指挥部专家组制定的加固方案是：背水坡面用土石进行加固，并使上底加宽3米，加固后背水坡EF的坡比i＝1：．（1）求加固后坝底增加的宽度AF；（2）求完成这项工程需要土石多少立方米？（结果保留根号）6．如图所示，A、B两城市相距100km，现计划在这两座城市间修建一条高速公路（即线段AB），经测量，森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上，已知森林保护区的范围在以P 点为圆心，50km为半径的圆形区域内，请问计划修建的这条高速公路会不会穿越保护区，为什么？（参考数据：≈1.732，≈1.414）7．如图，AD是△ABC的中线，tan B＝，cos C＝，AC＝．求：（1）BC的长；（2）sin∠ADC的值．8．一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援，求海警船到达事故船C处所需的大约时间．（温馨提示：sin53°≈0.8，cos53°≈0.6）9．如图，放置在水平桌面上的台灯的灯臂AB长为40cm，灯罩BC长为30cm，底座厚度为2cm，灯臂与底座构成的∠BAD＝60°．使用发现，光线最佳时灯罩BC与水平线所成的角为30°，此时灯罩顶端C到桌面的高度CE是多少cm？（结果精确到0.1cm，参考数据：≈1.732）10．如图，我国的一艘海监船在钓鱼岛A附近沿正东方向航行，船在B点时测得钓鱼岛A在船的北偏东60°方向，船以50海里/时的速度继续航行2小时后到达C点，此时钓鱼岛A在船的北偏东30°方向．请问船继续航行多少海里与钓鱼岛A的距离最近？11．高考英语听力测试期间，需要杜绝考点周围的噪音．如图，点A是某市一高考考点，在位于A考点南偏西15°方向距离125米的C处有一消防队．在听力考试期间，消防队突然接到报警电话，告知在位于C点北偏东75°方向的F点处突发火灾，消防队必须立即赶往救火．已知消防车的警报声传播半径为100米，若消防车的警报声对听力测试造成影响，则消防车必须改进行驶，试问：消防车是否需要改道行驶？请说明理由．（取1.732）12．如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°，若坡角∠F AE＝30°，求大树的高度（结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，≈1.73）13．如图，小山顶上有一信号塔AB，山坡BC的倾角为30°，现为了测量塔高AB，测量人员选择山脚C 处为一测量点，测得塔顶仰角为45°，然后顺山坡向上行走100米到达E处，再测得塔顶仰角为60°，求塔高AB（结果保留整数，≈1.73，≈1.41）14．某海域有A，B两个港口，B港口在A港口北偏西30°方向上，距A港口60海里，有一艘船从A港口出发，沿东北方向行驶一段距离后，到达位于B港口南偏东75°方向的C处，求该船与B港口之间的距离即CB的长（结果保留根号）．15．如图，在坡角为30°的山坡上有一铁塔AB，其正前方矗立着一大型广告牌，当阳光与水平线成45°角时，测得铁塔AB落在斜坡上的影子BD的长为6米，落在广告牌上的影子CD的长为4米，求铁塔AB的高（AB，CD均与水平面垂直，结果保留根号）．16．如图，在电线杆CD上的C处引拉线CE、CF固定电线杆，拉线CE和地面所成的角∠CED＝60°，在离电线杆6米的B处安置高为1.5米的测角仪AB，在A处测得电线杆上C处的仰角为30°，求拉线CE 的长（结果保留小数点后一位，参考数据：≈1.41，≈1.73）．17．天塔是天津市的标志性建筑之一，某校数学兴趣小组要测量天塔的高度，如图，他们在点A处测得天塔最高点C的仰角为45°，再往天塔方向前进至点B处测得最高点C的仰角为54°，AB＝112m，根据这个兴趣小组测得的数据，计算天塔的高度CD（tan36°≈0.73，结果保留整数）．18．如图，一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处，渔船从A处沿正南方向航行一段距离后，到达位于小岛南偏东60°方向的B处．（1）求渔船从A到B的航行过程中与小岛M之间的最小距离（结果用根号表示）；（2）若渔船以20海里/小时的速度从B沿BM方向行驶，求渔船从B到达小岛M的航行时间（结果精确到0.1小时）．（参考数据：≈1.41，≈1.73，≈2.45）19．如图，已知Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线，过点A作AE⊥CD，AE分别与CD、CB相交于点H、E，AH＝2CH．（1）求sin B的值；（2）如果CD＝，求BE的值．20．如图，大楼AN上悬挂一条幅AB，小颖在坡面D处测得条幅顶部A的仰角为30°，沿坡面向下走到坡脚E处，然后向大楼方向继续行走10米来到C处，测得条幅的底部B的仰角为45°，此时小颖距大楼底端N处20米．已知坡面DE＝20米，山坡的坡度i＝1：（即tan∠DEM＝1：），且D、M、E、C、N、B、A在同一平面内，E、C、N在同一条直线上，求条幅的长度（结果精确到1米）（参考数据：≈1.73，≈1.41）21．如图所示，一幢楼房AB背后有一台阶CD，台阶每层高0.2米，且AC＝17.2米，设太阳光线与水平地面的夹角为α，当α＝60°时，测得楼房在地面上的影长AE＝10米，现有一只小猫睡在台阶的MN这层上晒太阳．（取1.73）（1）求楼房的高度约为多少米？（2）过了一会儿，当α＝45°时，问小猫能否还晒到太阳？请说明理由．22．如图，在一个18米高的楼顶上有一信号塔DC，李明同学为了测量信号塔的高度，在地面的A处测的信号塔下端D的仰角为30°，然后他正对塔的方向前进了18米到达地面的B处，又测得信号塔顶端C 的仰角为60°，CD⊥AB于点E，E、B、A在一条直线上．请你帮李明同学计算出信号塔CD的高度（结果保留整数，≈1.7，≈1.4）23．如图，某数学兴趣小组在活动课上测量学校旗杆的高度．已知小亮站着测量，眼睛与地面的距离（AB）是1.7米，看旗杆顶部E的仰角为30°；小敏蹲着测量，眼睛与地面的距离（CD）是0.7米，看旗杆顶部E的仰角为45°．两人相距5米且位于旗杆同侧（点B、D、F在同一直线上）．（1）求小敏到旗杆的距离DF．（结果保留根号）（2）求旗杆EF的高度．（结果保留整数，参考数据：≈1.4，≈1.7）24．如图所示，某工程队准备在山坡（山坡视为直线l）上修一条路，需要测量山坡的坡度，即tanα的值．测量员在山坡P处（不计此人身高）观察对面山顶上的一座铁塔，测得塔尖C的仰角为37°，塔底B的仰角为26.6°．已知塔高BC＝80米，塔所在的山高OB＝220米，OA＝200米，图中的点O、B、C、A、P在同一平面内，求山坡的坡度．（参考数据sin26.6°≈0.45，tan26.6°≈0.50；sin37°≈0.60，tan37°≈0.75）25．我市准备在相距2千米的M，N两工厂间修一条笔直的公路，但在M地北偏东45°方向、N地北偏西60°方向的P处，有一个半径为0.6千米的住宅小区（如图），问修筑公路时，这个小区是否有居民需要搬迁？（参考数据：≈1.41，≈1.73）26．如图，轮船从点A处出发，先航行至位于点A的南偏西15°且与点A相距100km的点B处，再航行至位于点B的北偏东75°且与点B相距200km的点C处．（1）求点C与点A的距离（精确到1km）；（2）确定点C相对于点A的方向．（参考数据：≈1.414，≈1.732）27．一测量爱好者，在海边测量位于正东方向的小岛高度AC，如图所示，他先在点B测得山顶点A的仰角为30°，然后向正东方向前行62米，到达D点，在测得山顶点A的仰角为60°（B、C、D三点在同一水平面上，且测量仪的高度忽略不计）．求小岛高度AC（结果精确的1米，参考数值：）28．如图，在一次军事演习中，蓝方在一条东西走向的公路上的A处朝正南方向撤退，红方在公路上的B 处沿南偏西60°方向前进实施拦截，红方行驶1000米到达C处后，因前方无法通行，红方决定调整方向，再朝南偏西45°方向前进了相同的距离，刚好在D处成功拦截蓝方，求拦截点D处到公路的距离（结果不取近似值）．29．如图，某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造．供水站M在笔直公路AD 上，测得供水站M在小区A的南偏东60°方向，在小区B的西南方向，小区A、B之间的距离为300（+1）米，求供水站M分别到小区A、B的距离．（结果可保留根号）30．如图，热气球的探测器显示，从热气球看一栋高楼顶部的仰角为30°，看这栋高楼底部的俯角为60°，热气球与高楼的水平距离为66m，这栋高楼有多高？（结果精确到0.1m，参考数据：≈1.73）31．阅读材料：在一个三角形中，各边和它所对角的正弦的比相等，＝＝，利用上述结论可以求解如下题目：在△ABC中，∠A、∠B、∠C的对边分别为a，b，c．若∠A＝45°，∠B＝30°，a＝6，求b．解：在△ABC中，∵＝∴b＝＝＝＝3．理解应用：如图，甲船以每小时30海里的速度向正北方向航行，当甲船位于A1处时，乙船位于甲船的北偏西105°方向的B1处，且乙船从B1处按北偏东15°方向匀速直线航行，当甲船航行20分钟到达A2时，乙船航行到甲船的北偏西120°方向的B2处，此时两船相距10海里．（1）判断△A1A2B2的形状，并给出证明；（2）求乙船每小时航行多少海里？32．如图，在一笔直的海岸线l上有A、B两个码头，A在B的正东方向，一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处，此时从B码头测得小船在它的北偏东45°的方向．求此时小船到B码头的距离（即BP的长）和A、B两个码头间的距离（结果都保留根号）．33．如图，防洪大堤的横截面是梯形ABCD，其中AD∥BC，α＝60°，汛期来临前对其进行了加固，改造后的背水面坡角β＝45°．若原坡长AB＝20m，求改造后的坡长AE．（结果保留根号）34．某水库大坝的横截面是如图所示的四边形ABCD，其中AB∥CD，大坝顶上有一瞭望台PC，PC正前方有两艘渔船M，N．观察员在瞭望台顶端P处观测到渔船M的俯角α为31°，渔船N的俯角β为45°．已知MN所在直线与PC所在直线垂直，垂足为E，且PE长为30米．（1）求两渔船M，N之间的距离（结果精确到1米）；（2）已知坝高24米，坝长100米，背水坡AD的坡度i＝1：0.25，为提高大坝防洪能力，请施工队将大坝的背水坡通过填筑土石方进行加固，坝底BA加宽后变为BH，加固后背水坡DH的坡度i＝1：1.75，施工队施工10天后，为尽快完成加固任务，施工队增加了机械设备，工作效率提高到原来的2倍，结果比原计划提前20天完成加固任务，施工队原计划平均每天填筑土石方多少立方米？（参考数据：tan31°≈0.60，sin31°≈0.52）35．在△ABC中，AD是BC边上的高，∠C＝45°，sin B＝，AD＝1．求BC的长．36．我们把“按照某种理想化的要求（或实际可能应用的标准）来反映或概括的表现某一类或一种事物关系结构的数学形式”看作是一个数学中的一个“模式”（我国著名数学家徐利治）．如图是一个典型的图形模式，用它可测底部可能达不到的建筑物的高度，用它可测河宽，用它可解决数学中的一些问题．等等．（1）如图，若B1B＝30米，∠B1＝22°，∠ABC＝30°，求AC（精确到1）；（参考数据：sin22°≈0.37，cos22°≈0.92，tan22°≈0.40，≈1.73）（2）如图2，若∠ABC＝30°，B1B＝AB，计算tan15°的值（保留准确值）；（3）直接写出tan7.5°的值．（注：若出现双重根式，则无需化简）37．已知：如图，在△ABC中，AD是边BC上的高，E为边AC的中点，BC＝14，AD＝12，sin B＝．求：（1）线段DC的长；（2）tan∠EDC的值．38．如图，某人在山坡坡脚A处测得电视塔尖点C的仰角为60°，沿山坡向上走到P处再测得点C的仰角为45°，已知OA＝100米，山坡坡度为（即tan∠P AB＝），且O，A，B在同一条直线上．求电视塔OC的高度以及此人所在位置点P的铅直高度．（测倾器的高度忽略不计，结果保留根号形式）39．如图，兰兰站在河岸上的G点，看见河里有一只小船沿垂直于岸边的方向划过来，此时，测得小船C 的俯角是∠FDC＝30°，若兰兰的眼睛与地面的距离是1.5米，BG＝1米，BG平行于AC所在的直线，迎水坡的坡度i＝4：3，坡长AB＝10米，求小船C到岸边的距离CA的长？（参考数据：，结果保留两位有效数字）40．如图，某广场一灯柱AB被一钢缆CD固定，CD与地面成40°夹角，且CB＝5米．（1）求钢缆CD的长度；（精确到0.1米）（2）若AD＝2米，灯的顶端E距离A处1.6米，且∠EAB＝120°，则灯的顶端E距离地面多少米？（参考数据：tan40°＝0.84，sin40°＝0.64，cos40°＝）41．如图，某高速公路建设中需要确定隧道AB的长度．已知在离地面1500m高度C处的飞机上，测量人员测得正前方A、B两点处的俯角分别为60°和45°，求隧道AB的长．42．如图某幢大楼顶部有广告牌CD．张老师目高MA为1.60米，他站立在离大楼45米的A处测得大楼顶端点D的仰角为30°；接着他向大楼前进14米、站在点B处，测得广告牌顶端点C的仰角为45°．（取，计算结果保留一位小数）（1）求这幢大楼的高DH；（2）求这块广告牌CD的高度．43．图1是疫情期间测温员用“额温枪”对小红测温时的实景图，图2是其侧面示意图，其中枪柄BC与手臂MC始终在同一直线上，枪身BA与额头保持垂直．量得胳膊MN＝28cm，MB＝42cm，肘关节M与枪身端点A之间的水平宽度为25.3cm（即MP的长度），枪身BA＝8.5cm．（1）求∠ABC的度数；（2）测温时规定枪身端点A与额头距离范围为3～5cm．在图2中，若测得∠BMN＝68.6°，小红与测温员之间距离为50cm．问此时枪身端点A与小红额头的距离是否在规定范围内？并说明理由．（结果保留小数点后一位）（参考数据：sin66.4°≈0.92，cos66.4°≈0.40，sin23.6°≈0.40，≈1.414）44．图1是某小型汽车的侧面示意图，其中矩形ABCD表示该车的后备箱，在打开后备箱的过程中，箱盖ADE可以绕点A逆时针方向旋转，当旋转角为60°时，箱盖ADE落在AD′E′的位置（如图2所示）．已知AD＝90厘米，DE＝30厘米，EC＝40厘米．（1）求点D′到BC的距离；（2）求E、E′两点的距离．45．一架无人机沿水平直线飞行进行测绘工作，在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°，面向AB方向继续飞行5米，测得该建筑物底端B的俯角为45°，已知建筑物AB的高为3米，求无人机飞行的高度（结果精确到1米，参考数据：≈1.414，≈1.732）．46．如图，在港口A处的正东方向有两个相距6km的观测点B、C．一艘轮船从A处出发，沿北偏东26°方向航行至D处，在B、C处分别测得∠ABD＝45°、∠C＝37°．求轮船航行的距离AD．（参考数据：sin26°≈0.44，cos26°≈0.90，tan26°≈0.49，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75．）47．风电已成为我国继煤电、水电之后的第三大电源，风电机组主要由塔杆和叶片组成（如图1），图2是从图1引出的平面图．假设你站在A处测得塔杆顶端C的仰角是55°，沿HA方向水平前进43米到达山底G处，在山顶B处发现正好一叶片到达最高位置，此时测得叶片的顶端D（D、C、H在同一直线上）的仰角是45°．已知叶片的长度为35米（塔杆与叶片连接处的长度忽略不计），山高BG为10米，BG⊥HG，CH⊥AH，求塔杆CH的高．（参考数据：tan55°≈1.4，tan35°≈0.7，sin55°≈0.8，sin35°≈0.6）48．如图，某学校体育场看台的顶端C到地面的垂直距离CD为2m，看台所在斜坡CM的坡比i＝1：3，在点C处测得旗杆顶点A的仰角为30°，在点M处测得旗杆顶点A的仰角为60°，且B，M，D三点在同一水平线上，求旗杆AB的高度．（结果精确到0.1m，参考数据：≈1.41，＝1.73）49．如图，一艘船由A港沿北偏东65°方向航行30km至B港，然后再沿北偏西40°方向航行至C港，C港在A港北偏东20°方向，求（1）∠C的度数．（2）A，C两港之间的距离为多少km．50．数学兴趣小组到黄河风景名胜区测量炎帝塑像（塑像中高者）的高度．如图所示，炎帝塑像DE在高55m的小山EC上，在A处测得塑像底部E的仰角为34°，再沿AC方向前进21m到达B处，测得塑像顶部D的仰角为60°，求炎帝塑像DE的高度．（精确到1m．参考数据：sin34°≈0.56，cos34°≈0.83，tan34°≈0.67，≈1.73）51．为践行“绿水青山就是金山银山”的重要思想，某森林保护区开展了寻找古树活动．如图，在一个坡度（或坡比）i＝1：2.4的山坡AB上发现有一棵古树CD．测得古树底端C到山脚点A的距离AC＝26米，在距山脚点A水平距离6米的点E处，测得古树顶端D的仰角∠AED＝48°（古树CD与山坡AB 的剖面、点E在同一平面上，古树CD与直线AE垂直），则古树CD的高度约为多少米？（参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11）52．如图（1）是一种简易台灯，在其结构图（2）中灯座为△ABC（BC伸出部分不计），A、C、D在同一直线上．量得∠ACB＝90°，∠A＝60°，AB＝16cm，∠ADE＝135°，灯杆CD长为40cm，灯管DE长为15cm．（1）求DE与水平桌面（AB所在直线）所成的角；（2）求台灯的高（点E到桌面的距离，结果精确到0.1cm）．（参考数据：sin15°＝0.26，cos15°＝0.97，tan15°＝0.27，sin30°＝0.5，cos30°＝0.87，tan30°＝0.58．）53．如图，某中学数学活动小组在学习了“利用三角函数测高”后，选定测量小河对岸一幢建筑物BC的高度，他们先在斜坡上的D处，测得建筑物顶端B的仰角为30°．且D离地面的高度DE＝5m．坡底EA ＝30m，然后在A处测得建筑物顶端B的仰角是60°，点E，A，C在同一水平线上，求建筑物BC的高．（结果用含有根号的式子表示）54．已知如图，斜坡AP的坡度为1：2.4，斜坡AP的水平长度为24米在坡顶A处的同一水平面上有一座古塔BC在斜坡底P处测得该塔的塔顶B的仰角为45°，在坡顶A处测得该塔的塔顶B的仰角为60°．求：（1）坡顶A到地面PQ的距离；（2）古塔BC的高度（结果保留根号）．55．如图，山顶有一塔AB，塔高33m．计划在塔的正下方沿直线CD开通穿山隧道EF．从与E点相距80m 的C处测得A、B的仰角分别为27°、22°，从与F点相距50m的D处测得A的仰角为45°．求隧道EF的长度．（参考数据：tan22°≈0.40，tan27°≈0.51．）56．求下列各式的值：（1）2sin30°+3cos60°﹣4tan45°；（2）tan60°﹣（4﹣π）0+2cos30°+（）﹣1．57．计算：．58．如图，港口B位于港口A的南偏东37°方向，灯塔C恰好在AB的中点处．一艘海轮位于港口A的正南方向，港口B的正西方向的D处，它沿正北方向航行5km到达E处，测得灯塔C在北偏东45°方向上，这时，E处距离港口A有多远？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）59．王刚同学在学习了解直角三角形及其应用的知识后，尝试利用所学知识测量河对岸大树AB的高度，他在点C处测得大树顶端A的仰角为45°，再从C点出发沿斜坡走2米到达斜坡上D点，在点D处测得树顶端A的仰角为30°，若斜坡CF的坡比为i＝1：3（点E、C、B在同一水平线上）．（1）求王刚同学从点C到点D的过程中上升的高度；（2）求大树AB的高度（结果保留根号）．60．计算：（1）2sin30°+3cos60°﹣4tan45°（2）+tan260°。

中考专项复习锐角三角函数

与几何图形有关的锐角三角函数问题
总结词
理解几何图形中的角度关系与边长关系，掌握三角函数的定义及使用。
详细描述
在几何图形中，锐角三角函数通常被用于求解角度、边长等问题。例如，在直角三角形中，可以用正弦、余弦、正切等函数来描述各边与斜边的关系。
与实际生活有关的锐角三角函数问题
总结词
将实际问题转化为数学问题，通过锐角三角函数求解。
余弦函数的图像与性质
图像描述
余弦函数图像也是周期性的，但其波形与正弦函数相反，波峰和波谷随着x的增大而交替出现，且函数值先正后负，周期为2π。
性质总结
余弦函数具有对称性和周期性，其对称轴为y轴，对称中心为 (kπ+π/2,0)，其中k为整数。此外，余弦函数在区间[0,π/2] 上为增函数，在区间[π/2,π]上为减函数。
中考专项复习锐角三角函
数
汇报人：
2023-12-11
• 锐角三角函数概述 • 锐角三角函数的图像与性质 • 锐角三角函数的应用题解析 • 锐角三角函数的实际应用 • 中考中锐角三角函数的常见考点与题
型 • 中考真题解析与备考策略01锐角三角函数概述
锐角三角函数的定义
正弦函数（sine function）：锐角α的正弦值与直角三角形斜边长度的比值，记作sin α。
总结
中考中锐角三角函数一般以填空题和选择题的形式出现，主要考察的是锐角三角函数的定义以及运用。题目会设定一个或者几个锐角，然后利用锐角三角函数的定义，求出这个锐角的三角函数值。
例子
例如，如果一个锐角A的对边长度为4，邻边长度为3，那么我们可以使用锐角三角函数的定义来求出这个锐角的正弦值和余弦值。根据定义，正弦值=对边长度/斜边长度

中考数学复习《锐角三角函数》专项练习题-附带有答案

中考数学复习《锐角三角函数》专项练习题-附带有答案一、选择题1．已知α是锐角，若sinα=12，则α的度数是（）A．30°B．45°C．60°D．75°2．如图，在Rt△ABC中，BC＝3，斜边AC＝5，则下列等式正确的是（）A．sinC＝35B．cosC＝43C．tanA＝34D．sinA＝453．在Rt△ABC中，∠C=90°，sinA= 513，则tanB的值为（）A．1213B．512C．1312D．1254．如图所示，河堤横断面迎水坡AB的坡比是1：2，堤高BC=4m，则坡面AB的长度是（）mA．8 B．16 C．4√5D．4√35．如图所示，△ABC的顶点是正方形网格的格点，则sin∠A的值为（）A．12B．√1010C．√55D．2√556．如图，点A到点C的距离为100米，要测量河对岸B点到河岸AD的距离.小明在A点测得B在北偏东60°的方向上，在C点测得B在北偏东30°的方向上，则B点到河岸AD的距离为（）A．100米B．50米C．200√33米D．50√3米7．图1是第七届国际数学教育大会（ICME）的会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图2所示的四边形OABC .若 AB=BC=1，∠AOB=α，则 OC2的值为（）A．sin2α+1B．1sin2α+1C．cos2α+1D．1cos2α+18．如图所示，正方形ABCD中AB=4，点E为BC中点，BF⊥AE于点G，交CD边于点F，连接DG，则DG长为（）A．95√5B．4 C．165D．85√5二、填空题9．已知∠A是锐角tanA=√32，则sinA=.10．平放在地面上的直角三角形铁板ABC的一部分被沙堆掩埋，其示意图如图所示，量得∠A为54°，∠B 为36°，边AB的长为2m，BC边上露出部分BD的长为0.9m，则铁板BC边被掩埋部分CD的长是m.（参考数据：sin54°≈0.8，cos54°≈0.6，tan54°≈1.4）.11．如图，在⊙O中，弦AB的长为12√3，圆心到弦AB的距离为6，则∠BOC的度数为.12．如图，△ABC的顶点B、C的坐标分别是(1，0)、(0，√3)，且∠ABC=90°，∠A=30°，则顶点A的坐标是.13．如图，正方形AFEB和正方形BEDC的边长相等，点A、B、C在同一条直线上．连接AD、BD，那么cos ∠ADB的值为．三、解答题14．计算：2sin30°+cos30°•tan60°.15．先化简，再求值：xx2−1÷(1−1x+1)，其中x=√2sin45°+2tan60°.16．为践行“绿水青山就是金山银山”的重要思想，某森林保护区开展了寻找古树活动.如图，在一个坡度（或坡比）i＝1：2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC＝26米，在距山脚点A水平距离6米的点E处，测得古树顶端D的仰角∠AED＝48°（古树CD与山坡AB的剖面、点E在同一平面上，古树CD与直线AE垂直），则古树CD的高度约为多少米？（参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11）17．今年第6号台风“烟花”登录我国沿海地区，风力强，累计降雨量大，影响范围大，有极强的破坏力.如图，台风“烟花”中心沿东西方向AB 由A 向B 移动，已知点C 为一海港，在A 处测得C 港在北偏东45°方向上，在B 处测得C 港在北偏西60°方向上，且 AB =400+400√3 千米，以台风中心为圆心，周围600千米以内为受影响区域.（1）海港C 受台风影响吗？为什么？（2）若台风中心的移动速度为20千米/时，则台风影响该海港持续的时间有多长？（结果保留整数，参考数据 √2≈1.41 √3≈1.73 √5≈2.24 ）18．如图所示，已知BC 是⊙O 的直径，A 、D 是⊙O 上的两点，连接AD 、AC 、CD ，线段AD 与直径BC 相交于点E.（1）若∠ACB ＝60°，求sin∠ADC 的值.（2）当CD ⌢=12AC ⌢时 ①若CE =√2，BC⋅CE AB =2求∠COD 的度数.②若CD ＝1，CB ＝4求线段CE 的长.参考答案1．A2．C3．D4．C5．C6．D7．B8．B9．√217 10．0.711．60°12．(4，√3)13．3√101014．解：原式＝2× 12 + √32× √3 ＝1+ 32＝ 5215．解： x x 2−1÷(1−1x+1)=x (x+1)(x−1)÷x+1−1x+1 =x (x+1)(x−1)⋅x+1x=1x −1 当x =√2sin45°+2tan60°=√2×√22+2×√3=1+2√3时 1x −1=11+2√3−1=12√3=√36原式=√36. 16．解：延长DC 交EA 的延长线于点F ，则CF ⊥EF∵山坡AC上坡度i＝1：2.4∴令CF＝km，则AF＝2.4km在Rt△ACF中，由勾股定理得CF2+AF2＝AC2∴k2+（2.4k）2＝262解得k＝10∴AF＝24m，CF＝10m∴EF＝30m在Rt△DEF中，tanE＝DFEF∴DF＝EF•tanE＝30×tan48°＝30×1.11＝33.3（m）∴CD＝DF﹣CF＝23.3m因此，古树CD的高度约为23.3m.17．（1）解：如下图，过点C作CH⊥AB交AB于点H设CH=x在Rt△ACH中在Rt△BCH中∴AB=(√3+1)x=400+400√3∴x=400，∴CH=400∵400<600，海港C受台风影响（2）解：如下图，以CP=600千米为半径画弧交AB于P、Q两点，此时台风在PQ之间时，海港受到影响在 Rt △PCH 中∴PH =√CP 2−CH 2=200√5∴PQ =2PH =400√5则时间： t =400√520=20√5≈45 （小时）答：台风影响该海港持续的时间有45小时.18．（1）解：∵BC 是⊙O 的直径∴∠BAC ＝90°∵∠ACB ＝60°∴∠B ＝30°∵AC ⌢＝AC ⌢∴∠ADC ＝∠B ＝30°∴sin∠ADC ＝sin30°=12所以sin∠ADC 的值为12；（2）解：①∵CE =√2 BC⋅CE AB =2∴BC AB =√2∵∠BAC ＝90°∴cos∠B ＝AB BC =√22∴∠B ＝45°∵CD ⌢＝12AC ⌢∴∠CAD ＝12∠B ＝22.5°∴∠COD ＝2∠CAD ＝45°即∠COD 的度数为45°；②∵CD ⌢＝12AC ⌢∵∠ADC＝∠COD，∠OCD＝∠DCE ∴△OCD∽△DCE∴CDOC =CECD∵BC＝4∴OC＝2∴12=CE1∴CE＝12∴线段CE的长为12.。

2023年中考九年级数学高频考点专题训练--锐角三角函数

2023年中考九年级数学高频考点专题训练--锐角三角函数一、综合题1．如图，以AB为直径作半圆O，点C是半圆上一点，∠ABC的平分线交∠O于E，D为BE延长线上一点，且∠DAE＝∠FAE.（1）求证：AD为∠O切线；（2）若sin∠BAC＝35，求tan∠AFO的值.2．如图，一个正方体木箱沿斜面下滑，正方体木箱的边长BE为2m，斜面AB的坡角为∠BAC，且tan∠BAC= 3 4．（1）当木箱滑到如图所示的位置时，AB=3m，求此时点B离开地面AC的距离；（2）当点E离开地面AC的距离是3.1m时，求AB的长．3．如图，在∠ABC中，∠A＝30°，∠C＝90°，AB＝12，四边形EFPQ是矩形，点P与点C重合，点Q、E、F分别在BC、AB、AC上（点E与点A、点B均不重合）．（1）当AE＝8时，求EF的长；（2）设AE＝x，矩形EFPQ的面积为y．①求y与x的函数关系式；②当x为何值时，y有最大值，最大值是多少？（3）当矩形EFPQ的面积最大时，将矩形EFPQ以每秒1个单位的速度沿射线CB匀速向右运动（当点P到达点B时停止运动），设运动时间为t秒，矩形EFPQ与∠ABC重叠部分的面积为S，求S与t的函数关系式，并写出t的取值范围．4．如图，以∠ABC的一边AB为直径的半圆O与边AC，BC的交点分别为点E，点D，且D是BE⌢的中点．（1）若∠A＝80°，求∠DBE的度数．（2）求证：AB＝AC．（3）若∠O 的半径为5cm，BC＝12cm，求线段BE的长．5．如图，抛物线y=﹣x2+bx+c过点B（3，0），C（0，3），D为抛物线的顶点．（1）求抛物线的解析式以及顶点坐标；（2）如果点C关于抛物线y=﹣x2+bx+c对称轴的对称点为E点，连接BC，BE，求tan∠CBE的值；（3）点M是抛物线对称轴上一点，且∠DAM和∠BCE相似，求点M坐标．6．如图，已知tan∠EOF=2，点C在射线OF上，OC=12．点M是∠EOF内一点，MC∠OF于点C，MC=4．在射线CF上取一点A，连结AM并延长交射线OE于点B，作BD∠OF于点D．（1）当AC的长度为多少时，∠AMC和∠BOD相似；（2）当点M恰好是线段AB中点时，试判断∠AOB的形状，并说明理由；（3）连结BC．当S∠AMC=S∠BOC时，求AC的长．7．如图1，在∠ABC中，∠ACB=90°，AC=BC，∠EAC=90°，点M为射线AE上任意一点(不与A 重合)，连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，直线NB分别交直线CM，射线AE于点F，D．（1）直接写出∠NDE的度数；（2）如图2、图3，当∠EAC为锐角或钝角时，其他条件不变，(1)中的结论是否发生变化?如果不变，选取其中一种情况加以证明；如果变化，请说明理由；，其他条件不（3）如图4，若∠EAC=15°，∠ACM=60°，直线CM与AB交于G，BD= √6+√22变，求线段AM的长．8．（1）【基础巩固】如图1，在∠ABC中，D，E，F分别为AB，AC，BC上的点，DE∠BC，BF=CF，AF交DE于点G，求证：DG= EG．（2）【尝试应用】如图2，在(1)的条件下，连结CD，CG．若CG∠DE，CD=6，AE=3，求DEBC的值．（3）【拓展提高】如图3，在∠ABCD中，∠ADC=45°，AC与BD交于点O，E为AO上一点，EG∠BD交AD于点G，EF∠EG交BC于点F．若∠EGF=40°，FG平分∠EFC，FG=10，求BF的长．9．在锐角∠ABC中，AB=4，BC=5，∠ACB=45°，将∠ABC绕点B按逆时针方向旋转，得到∠DBE．（1）当旋转成如图①，点E在线段CA的延长线上时，则∠CED的度数是度；（2）当旋转成如图②，连接AD、CE，若∠ABD的面积为4，求∠CBE的面积；（3）点M为线段AB的中点，点P是线段AC上一动点，在∠ABC绕点B按逆时针方向旋转过程中，点P的对应点P′，连接MP′，如图③，直接写出线段MP′长度的最大值和最小值．10．如图，在矩形ABCD中，AB＝8，BC＝6，点E，F分别从点B，D同时出发沿AB延长线和射线DA以相同的速度运动，连结EF，交射线DB于点G.连结CG.（1）当BE＝2时，求BD，EG的长.（2）当点F在线段AD上时，记∠DCG为∠1，∠AFE为∠2，那么tan∠1tan∠2的值是否会变化？若不变，求出该比值；若变化，请说明理由.（3）在整个运动过程中，当∠DCG为等腰三角形时，求BE长.11．我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．（1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A＝75°，∠D＝85°，则∠C ＝．（2）已知：在“等对角四边形”ABCD中，∠DAB＝60°，∠ABC＝90°，AB＝4，AD＝3．求对角线AC的长．（3）已知：如图2，在平面直角坐标系xOy中，四边形ABCD是“等对角四边形”，其中A（﹣2，0）、C（2，0）、B（﹣1，﹣√3），点D在y轴上，抛物线y＝ax2+bx+c（a＜0）过点A、D，且当﹣2≤x≤2时，函数y＝ax2+bx+c取最大值为3，求二次项系数a的值．12．如图，已知BC为∠O的直径，点D为CE⌢的中点，过点D作DG∠CE，交BC的延长线于点A，连接BD，交CE于点F．（1）求证：AD是∠O的切线；（2）若EF＝3，CF＝5，tan∠GDB＝2，求AC的长．13．已知：如图，AB为∠O的直径，C是BA延长线上一点，CP切∠O于P，弦PD∠AB于E，过点B作BQ∠CP于Q，交∠O于H，（1）如图1，求证：PQ＝PE；（2）如图2，G是圆上一点，∠GAB＝30°，连接AG交PD于F，连接BF，若tan∠BFE＝3√3，求∠C的度数；（3）如图3，在（2）的条件下，PD＝6 √3，连接QC交BC于点M，求QM的长．14．定义：一边上的中线与另一边的夹角为30°的三角形称作美妙三角形。

锐角三角函数中考专题讲评(教案)

还有，学生在小组讨论中表现出较强的合作意识，但部分学生在思考问题时仍显得有些局限。为了激发学生的创新思维，我在今后的教学中，可以尝试设置一些更具挑战性的问题，引导学生从多角度、多维度去思考问题。
最后，总结回顾环节，学生能够较好地掌握本节课的知识点，但仍有个别学生对某些细节问题存在疑问。这说明在后续的教学中，我需要更加关注学生的个体差异，及时解答他们的疑问，确保每位学生都能跟上教学进度。
3.重点难点解析：在讲授过程中，我会特别强调正弦、余弦、正切函数的定义和应用这两个重点。对于难点部分，如函数性质的理解，我会通过具体角度的计算和图像分析来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与锐角三角函数相关的实际问题。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作，如使用三角板和量角器来测量并计算物体的高度。
其次，教学难点部分，如函数性质的推导和应用，学生掌握起来相对困难。在讲解这一部分时，我应该更加注重引导学生通过观察、实验、归纳等方法，逐步发现并理解函数的性质。此外，运用一些形象生动的比喻或实物演示，可能有助于学生更好地理解和记忆。
此外，实践活动环节，学生分组讨论和实验操作的积极性较高，但个别小组在成果展示时表达不够清晰。针对这一点，我考虑在以后的课堂上，多给予学生一些表达和交流的机会，培养他们的语言组织和表达能力。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解锐角三角函数的基本概念。锐角三角函数是描述直角三角形中角度与边长比例关系的数学工具。它们在解决实际问题，如测量、建筑等领域发挥着重要作用。
2.案例分析：接下来，我们来看一个具体的案例。通过测量角度和已知边长，如何计算未知边长，这个案例将展示锐角三角函数在实 Nhomakorabea中的应用。

中考数学专项复习《锐角三角函数》练习题(附答案)

中考数学专项复习《锐角三角函数》练习题(附答案)一、单选题1．如图，在△ABC中CA＝CB＝4，cosC＝14，则sinB的值为（）A．√102B．√153C．√64D．√1042．在Rt△ABC中,△C=90°,cosA=35,那么tanB=()A．35B．45C．43D．34 3．如图，在Rt△ABC中∠ACB=90°，BC=1，AB=2则下列结论正确的是（）A．sinA=√32B．tanA=12C．cosB=√32 D．tanB=√34．如图，已知△ABC内接于△O，△BAC=120°，AB=AC，BD为△O的直径，AD=6，则BC的长为（）A．2√3B．6C．2√6D．3√3 5．如图，一艘海轮位于灯塔P的北偏东55°方向，距离灯塔2海里的点A处，如果海轮沿正南方向航行到灯塔的正东方向，海轮航行的距离AB长是（）A．2海里B．2sin55°海里C．2cos55°海里D．2tan55°海里6．在矩形ABCD中AD=2,AB=1,G为AD的中点，一块足够大的三角板的直角顶点与点G重合，将三角板绕点G旋转，三角板的两直角边分别交AB、BC(或它们的延长线)于点E、F设∠AGE=α(0°<α<90°)，下列四个结论：①AE= CF；②∠AEG=∠BFG；③AE+CF=1；④S△GEF=1cos2α，正确的个数是（）A．1B．2C．3D．4 7．小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．如图，旗杆PA的高度与拉绳PB的长度相等．小明将PB拉到PB′的位置，测得△PB′C=α（B′C为水平线），测角仪B′D的高度为1米，则旗杆PA的高度为（）A．11−sinαB．11+sinαC．11−cosαD．11+cosα8．如图，方格纸中小正方形的边长为1，△ABC的三个顶点都在小正方形的格点上，下列结论：①△ABC的形状是等腰三角形；②△ABC的周长是2√10+√2；③点C到AB边的距离是38√10；④tan∠ACB的值为2，正确的个数为（）A ．0个B ．1个C ．2个D ．3个9．在Rt△ABC 中△ACB=90°，BC=1，AB=2，则下列结论正确的是（）A ．sinA=√32B ．cosA=√32C ．tanA=12D ．cotA=√3310．已知：如图，正方形网格中∠AOB 如图放置，则cos∠AOB 的值为（）A ．2√55B ．2C ．12D ．√5511．如图，菱形ABCD 的周长为20cm ，DE△AB ，垂足为E ，cosA=45，则下列结论中正确的个数为（）①DE=3cm ；②EB=1cm ；③S 菱形ABCD =15cm 2A ．3个B ．2个C ．1个D ．0个12．如图，在Rt △ABC 中 ∠ABC =90°，以其三边为边向外作正方形，连接EH ，交AC 于点P ，过点P 作PR ⊥FG 于点R.若tan∠AHE =12，EH =8√5，则PR 的值为（）A．10B．11C．4√5D．5√5二、填空题13．如图，在RtΔABC中∠B=90°，AB=3 ，BC=4 ，点M、N分别在AC、AB两边上，将ΔAMN沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当ΔDCM是直角三角形时，则tan∠AMN的值为.14．如图，在△ABC中∠ABC=60°，AB=6，BC=10将△ABC绕点B顺时针旋转得到△A1BC1（点A的对应点是点A1，点C的对应点是点C1，A1落在边BC上，连接AC1，则AC1的长为．15．如图，在P处利用测角仪测得某建筑物AB的顶端B点的仰角为60°，点C 的仰角为45°，点P到建筑物的距离为PD=20米，则BC=米.16．如图，正六边形A1B1C1D1E1F1的边长为1，它的六条对角线又围成一个正六边形A2B2C2D2E2F2，如此继续下去，则正六边形A4B4C4D4E4F4的面积是．17．如图，某高为60米的大楼AB旁边的山坡上有一个“5G”基站DE，从大楼顶端A 测得基站顶端E的俯角为45°，山坡坡长CD＝10米，坡度i＝1：√3，大楼底端B 到山坡底端C的距离BC＝30米，则该基站的高度DE＝米．18．在数学实践与综合课上，某兴趣小组同学用航拍无人机对某居民小区的1，2号楼进行测高实践，测得1号楼顶部E的俯角为67°，测得2号楼顶部F的俯角为40°，此时航拍无人机的高度为60米，已知1号楼的高度为20米，且EC和FD分别垂直地面于点C和D，点B为CD的中点，则2号楼的高度为（结果精确到0.1）（参考数据sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin67°≈0.92，cos67°≈0.39，tan67°≈2.36）三、综合题19．（1）已知Rt△ABC中△C=90°，△A=30°，BC= √3，解直角三角形.（2）已知△ABC中△A=45°，AB=4，BC=3，求AC的长.20．如图1，已知∠PAQ=60°．请阅读下列作图过程，并解答所提出的问题．△如图2，以点A为圆心，任意长为半径画弧，分别与AP，AQ交于B，C两点；△如图3，分别以B，C两点为圆心，以大于12BC的长为半径画弧，两弧交于点D；△如图4，作射线AD，连接BC，与AD交于点E．问题：（1）∠ABC的度数为．（2）若AB=4，求AE的长．21．如图，在△ABC中△C=60°，△O是△ABC的外接圆，点P在直径BD的延长线上，且AB=AP．（1）求证：PA是△O的切线；（2）若AB=2 √3，求图中阴影部分的面积．（结果保留π和根号）22．如图，物理教师为同学们演示单摆运动，单摆左右摆动中在OA的位置时俯角△EOA=30°，在OB的位置时俯角△FOB=60°，若OC△EF，点A比点B高7cm．求：（1）单摆的长度（√3≈1.7）；（2）从点A摆动到点B经过的路径长（π≈3.1）．23．已知：如图，AB是△O的直径，C是△O上一点，OD△BC于点D，过点C作△O 的切线，交OD的延长线于点E，连接BE．（1）求证：BE与△O相切；（2）连接AD并延长交BE于点F，若OB=9，sin△ABC= 23，求BF的长．24．如图，AB是△O的直径，OE垂直于弦BC，垂足为F，OE交△O于点D，且△CBE=2△C.（1）求证：BE与△O相切；（2）若DF=9，tanC= 34，求直径AB的长.参考答案1．【答案】D2．【答案】D3．【答案】D4．【答案】B5．【答案】C6．【答案】A7．【答案】A8．【答案】C9．【答案】B10．【答案】D11．【答案】A12．【答案】B13．【答案】1或214．【答案】1415．【答案】(20√3−20)16．【答案】√31817．【答案】（25﹣5 √3）18．【答案】45.8米19．【答案】（1）解：在Rt△ABC中△C=90°，△A=30°∴△B=90°-△A=60°，AB=2BC=2 √3∴AC= √AB2−BC2=√(2√3)2−(√3)2=3；（2）解：如图，过点B作BD△AC于D∵△A=45°∴△ABD=△A=45°∴AD=BD∵AB=4，AD2+BD2=AB2∴AD=BD= 2√2在Rt△BCD中BC=3∴CD=√BC2−BD2=1∴AC=AD+CD= 2√2+1.20．【答案】（1）60°（2）由作图可知AB=AC，AD平分∠PAQ∴AE⊥BC．∵∠PAQ=60°∴∠BAE=30°．在Rt△ABC中AE=AB⋅cos30°=4×√32=2√3．答：AE的长为2√3．21．【答案】（1）解：如图，连接OA；∵△C=60°∴△AOB=120°；而OA=OB∴△OAB=△OBA=30°；而AB=AP∴△P=△ABO=30°；∵△AOB=△OAP+△P∴△OAP=120°﹣30°=90°∴PA是△O的切线．（2）解：如图，过点O作OM△AB，则AM=BM= √3∵tan30°= OMAM sin30°=OMAO∴OM=1，OA=2；∴S△AOB=12·AB·OM= 12× 2√3×1= √3S扇形OAB =120π⋅22360= 4π3∴图中阴影部分的面积= 4π3−√3．22．【答案】（1）解：如图，过点A作AP△OC于点P，过点B作BQ△OC于点Q∵△EOA=30°、△FOB=60°，且OC△EF∴△AOP=60°、△BOQ=30°设OA=OB=x则在Rt△AOP中OP=OAcos△AOP= 1 2x在Rt△BOQ中OQ=OBcos△BOQ= √32x由PQ=OQ﹣OP可得√32x﹣12x=7解得：x=7+7 √3≈18.9（cm）答：单摆的长度约为18.9cm（2）解：由（1）知，△AOP=60°、△BOQ=30°，且OA=OB=7+7 √3∴△AOB=90°则从点A摆动到点B经过的路径长为90⋅π⋅(7+7√3)180≈29.295答：从点A摆动到点B经过的路径长为29.295cm 23．【答案】（1）证明：连接OC∵OD△BC∴△COE=△BOE在△OCE和△OBE中∵{OC=OB∠COE=∠BOEOE=OE∴△OCE△△OBE∴△OBE=△OCE=90°，即OB△BE∵OB 是△O 半径∴BE 与△O 相切．（2）解：过点D 作DH△AB ，连接AD 并延长交BE 于点F∵△DOH=△BOD ，△DHO=△BDO=90°∴△ODH△△OBD∴OD OB =OH OD =DH BD又∵sin△ABC= 23，OB=9 ∴OD=6易得△ABC=△ODH∴sin△ODH= 23 ，即 OH OD = 23∴OH=4∴DH= √OD 2−OH 2 =2 √5又∵△ADH△△AFB∴AH AB = DH FB 1318 = 2√5FB∴FB= 36√51324．【答案】（1）证明：∵OE 垂直于弦BC∴△BOE+△OBF=90°∵△CBE=2△C ， △BOE=2△C∴△CBE=△BOE∴△CBE+△OBF=90°∴△OBE=90°∴BE 与△O 相切；（2）解：∵OE 垂直于弦BC∴△CFD=△BFO=90°，CF=BF.∵DF=9，tanC= 34∴CF=BF=12.设半径长是x，则OF=x-9在Rt△BOF中∵x2=(x-9)2+122∴x= 25 2∴直径AB=25.。

中考数学复习《锐角三角函数和解直角三角形》经典题型及测试题(含答案)

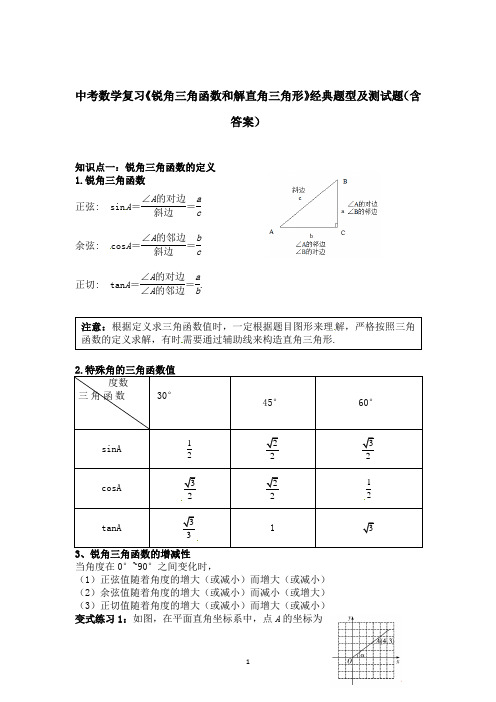
中考数学复习《锐角三角函数和解直角三角形》经典题型及测试题（含答案）知识点一：锐角三角函数的定义 1.锐角三角函数正弦: sin A ＝∠A 的对边斜边＝ac余弦: cos A ＝∠A 的邻边斜边＝bc正切: tan A ＝∠A 的对边∠A 的邻边＝ab.来源:学&科&网]2.特殊角的三角函数值[来度数三角函数[来源:Z 。

xx 。

]30°[来源:学#科#网] 45° 60°sinA1222 32 cosA32 2212tanA 331 33、锐角三角函数的增减性当角度在0°~90°之间变化时，（1）正弦值随着角度的增大（或减小）而增大（或减小）（2）余弦值随着角度的增大（或减小）而减小（或增大）（3）正切值随着角度的增大（或减小）而增大（或减小）变式练习1：如图，在平面直角坐标系中，点A 的坐标为注意：根据定义求三角函数值时，一定根据题目图形来理解，严格按照三角函数的定义求解，有时需要通过辅助线来构造直角三角形.[(4，3)，那么cos α的值是( ) A. 34 B. 43 C. 35 D. 45【解析】D 如解图，过点A 作AB ⊥x 轴于点B ，∵A (4，3)，∴OB ＝4，AB ＝3，∴OA ＝32＋42＝5，∴cos α＝OB OA ＝45.变式练习2：在Rt △ABC 中，∠ABC ＝90°，AB ＝3，BC ＝4，则sinA ＝________．【解析】∵在Rt △ABC 中，由勾股定理得AC ＝22AB BC +＝32＋42＝5，∴sin A ＝BC AC ＝45. 变式练习3：在Rt △ABC 中，∠C ＝90°，sin A ＝35，BC ＝6，则AB ＝( D )A ．4B ．6C ．8D ．10变式练习4：如图，若点A 的坐标为(1，3)，则sin ∠1＝__32__. ,知识点二：解直角三角形 1.解直角三角形的概念在直角三角形中，除直角外，一共有五个元素，即三条边和两个锐角，由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形． 2.解直角三角形的常用关系在Rt △ABC 中，∠C=90°，∠A ，∠B ，∠C 所对的边分别为a ，b ，c (1)三边之间的关系：a 2＋b 2＝c 2；(2)锐角之间的关系：∠A ＋∠B ＝90°； (3)边角之间的关系：,tan ,cos ,sin ;,tan ,cos ,sin abB c a B c b B b a A c b A c a A ======（sinA＝=cosB=ac，c osA＝sinB=bc，tanA＝ab.）变式练习1：在Rt△ABC中，已知a=5,sinA=30°，则c=10,b=5.变式练习2：如图，Rt△ACB中，∠B＝30°，∠ACB＝90°，CD⊥AB交AB于D.以CD为较短的直角边向△CDB的同侧作Rt△DEC，满足∠E＝30°，∠DCE＝90°，再用同样的方法作Rt△FGC，∠FCG＝90°，继续用同样的方法作Rt△HIC，∠HCI ＝90°.若AC＝a，求CI的长．解：在Rt△ABC中，∠B＝30°，∠ACB＝90°，CD⊥AB，∴∠A＝60°，∵AC＝a，∴CD＝AC·sin60°＝32a，依此类推CH＝(32)3a＝338a，在Rt△CHI中，∵∠CHI＝60°，∴CI＝CH·tan60°＝338a×3＝98a.变式练习3：如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝8，则BC的长是( D )A.433B．4 C．8 3 D．4 3,灵活选择解直角三角形的方法顺口溜：已知斜边求直边，正弦、余弦很方便；已知直边求直边，理所当然用正切；已知两边求一边，勾股定理最方便；已知两边求一角，函数关系要记牢；已知锐角求锐角，互余关系不能少；已知直边求斜边，用除还需正余弦.变式练习4：如图，一山坡的坡度为i＝1∶3，小辰从山脚A出发，沿山坡向上走了200米到达点B，则小辰上升了__100__米．, ,变式练习5：一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处，沿正西方向航行3小时后到达小岛的北偏西45°的C处，则该船行驶的速度为___40＋4033___海里/小时．知识点三：解直角三角形的应用1.仰角、俯角、坡度、坡角和方向角(1)仰、俯角：视线在水平线上方的角叫做仰角.视线在水平线下方的角叫做俯角．（如图①）(2)坡度：坡面的铅直高度和水平宽度的比叫做坡度(或者叫做坡比)，用字母i表示．坡角：坡面与水平面的夹角叫做坡角，用α表示，则有i＝tanα.（如图②）(3)方向角：平面上，通过观察点Ο作一条水平线(向右为东向)和一条铅垂线(向上为北向)，则从点O出发的视线与水平线或铅垂线所夹的角，叫做观测的方向角．（如图③）2.解直角三角形实际应用的一般步骤(1)弄清题中名词、术语，根据题意画出图形，建立数学模型；(2)将条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形问题；(3)选择合适的边角关系式，使运算简便、准确；(4)得出数学问题的答案并检验答案是否符合实际意义，从而得到问题的解．注意：解直角三角形中“双直角三角形”的基本模型：（1）叠合式（2）背靠式解题方法：这两种模型种都有一条公共的直角边，解题时，往往通过这条边为中介在两个三角形中依次求边，或通过公共边相等，列方程求解变式练习1：如图，某数学兴趣小组想测量一棵树CD 的高度，他们先在点A 处测得树顶C 的仰角为30°，然后沿AD 方向前行10 m ，到达B 点，点B 处测得树顶C 的仰角为60°(A 、B 、D 三点在同一直线上)．请你根据他们的测量数据计算这棵树CD 的高度(结果精确到0.1 m)．(参考数据：2≈1.414，3≈ 1.732)解：如解图，由题意可知∠CAB ＝30°，∠CBD ＝60°，AB ＝10 m ，∵∠CBD ＝∠CAB ＋∠BCA ，∴∠BCA ＝∠CBD －∠CAB ＝60°－30°＝30°＝∠CAB ， ∴BC ＝AB ＝10 m ．在Rt △BCD 中，∵sin ∠CBD ＝CDBC，∴CD ＝BC ·sin ∠CBD ＝10×sin60°＝10×32＝53≈5×1.732≈8.7 m ．答：这棵树CD 的高度大约是8.7 m ．变式练习2：如图，小山岗的斜坡AC 的坡度是tan α＝34，在与山脚C 距离200米的D 处，测得山顶A 的仰角为26.6°，求小山岗的高AB (结果取整数；参考数据：sin26.6°≈0.45，cos26.6°≈0.89，tan26.6°≈0.50)．解：设AB ＝x 米，在Rt △ABD 中，∠D ＝26.6°，∴BD ＝tan 26.6x≈2x ，在Rt △ABC 中，tan α＝AB BC ＝34，∴BC ＝43x ，∵BD －BC ＝CD ，CD ＝200，∴2x－43x＝200，解得x＝300.答：小山岗的高AB约为300米．变式练习3：如图，小明所在教学楼的每层高度为3.5 m，为了测量旗杆MN的高度，他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°，他在二楼窗台B 处测得M的仰角为30°，已知每层楼的窗台离该层的地面高度均为1 m，求旗杆MN的高度(结果精确到0.1 m)．(参考数据：2≈1.414，3≈1.732)解：如解图，过点M的水平线交直线AB于点H，由题意，得∠AMH＝∠MAH＝45°，∠BMH＝30°，AB＝3.5 m，设MH＝x m，则AH＝x m，BH＝x·tan30°＝33x≈0.58x m，∴AB＝AH－BH＝x－0.58x＝0.42x＝3.5 m，解得x≈8.3，则MN＝x＋1＝9.3 m.答：旗杆MN的高度约为9.3 m.变式练习4：小明去爬山，如图，在山脚看山顶的角度为30°，小明在坡比为5∶12的山坡上走了1300米，此时小明看山顶的角度为60°，则山高为( )A. (600－2505)米B. (6003－250)米C. (350＋3503)米D. 500 3 米【解析】B如解图，∵BE∶AE＝5∶12，∴设BE＝5k，AE＝12k，∴AB＝2()5K＋(12k)2＝13k，∴BE∶AE∶AB＝5∶12∶13，∵AB＝1300米，∴AE＝1200米，BE ＝500米，设EC＝FB＝x米，∵∠DBF＝60°，∴DF＝3x米，则DC＝(3x＋500)米，又∵∠DAC＝30°，∴AC＝3CD，即1200＋x＝3(3x＋500)，解得x＝600－2503，∴DF＝3x＝(6003－750)米，∴CD＝DF＋CF＝(6003－250)米，即山高CD为(6003－250)米．变式练习5：某兴趣小组借助无人飞机航拍校园．如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°.已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．(结果保留根号)解：如解图，过点A作AD⊥BC交BC于点D，过点B作BH⊥水平线交水平线于点H，由题意∠ACH＝75°，∠BCH＝30°，AB∥CH，∴∠ABC＝30°，∠ACB＝45°，∵AB＝4×8＝32米，∴CD＝AD＝AB·sin30°＝16米，BD＝AB·cos30°＝32×32＝163米，∴BC＝CD＋BD＝(16＋163)米，∴BH＝BC·sin30°＝(16＋163)×12＝(8＋83)米．答：这架无人飞机的飞行高度为(8＋83)米．变式练习6：如图，我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30°的方向上，随后渔政船以80海里/小时的速度向北偏东30°的方向航行，半小时后到达B处，此时又测得钓鱼岛A在渔政船的北偏西60°的方向上，求此时渔政船距钓鱼岛A的距离AB.(结果保留小数点后一位，其中3≈1.732) 解：∵CD∥BE，∴∠EBC＋∠DCB＝180°.∵∠ABE＝60°，∠DCB＝30°，∴∠ABC＝90°.…………(4分)由题知，BC＝80×12＝40(海里)，∠ACB＝60°.在Rt△ABC中，AB＝BC·tan60°＝403≈40×1.732≈69.3(海里)．答：此时渔政船距钓鱼岛A的距离AB的长约为69.3海里．。