2019年最新中考数学专题复习：锐角三角函数

合集下载

初三年级锐角三角函数知识点总结、典型例题、练习[精选]

初三年级锐角三角函数知识点总结、典型例题、练习[精选]锐角三角函数知识点总结1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。

222c b a =+2、如下图；在Rt △ABC 中；∠C 为直角；则∠A 的锐角三角函数为(∠A 可换成∠B)：定义表达式取值范围关系正弦斜边的对边A A ∠=sin c aA =sin 1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A (∠A 为锐角) 正切的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A (∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。

4、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan33 1 3-5、正弦、余弦的增减性：当0°≤α≤90°时；sin α随α的增大而增大；cos α随α的增大而减小。

6、正切的增减性：当0°<α<90°时；tan α随α的增大而增大；7、解直角三角形的定义：已知边和角（两个；其中必有一边）→所有未知的边和角。

)90cos(sin A A -︒=)90sin(cos A A -︒=BA cos sin =BA sin cos =A90B 90∠-︒=∠︒=∠+∠得由B A对边邻边斜边 ACBba c依据：①边的关系：222c b a =+；②角的关系：A+B=90°；③边角关系：三角函数的定义。

九年级数学专题复习锐角三角函数

总复习锐角三角函数【考纲要求】1.理解锐角三角函数的定义、性质及应用，特殊角三角函数值的求法，运用锐角三角函数解决与直角三角形有关的实际问题.题型有选择题、填空题、解答题，多以中、低档题出现；2.命题的热点为根据题中给出的信息构建图形，建立数学模型，然后用解直角三角形的知识解决问题.【知识网络】【考点梳理】考点一、锐角三角函数的概念如图所示，在Rt△ABC中，∠C＝90°，∠A所对的边BC记为a，叫做∠A的对边，也叫做∠B的邻边，∠B所对的边AC记为b，叫做∠B的对边，也是∠A的邻边，直角C所对的边AB记为c，叫做斜边．锐角A的对边与斜边的比叫做∠A的正弦，记作sinA，即sinA aAc∠==的对边斜边；锐角A的邻边与斜边的比叫做∠A的余弦，记作cosA，即cosA bAc∠==的邻边斜边；锐角A的对边与邻边的比叫做∠A的正切，记作tanA，即tanA aAA b∠==∠的对边的邻边.同理sinB bBc∠==的对边斜边；cosB aBc∠==的邻边斜边；tanB bBB a∠==∠的对边的邻边．要点进阶：ABCabc(1)正弦、余弦、正切函数是在直角三角形中定义的，反映了直角三角形边与角的关系，是两条线段的比值．角的度数确定时，其比值不变，角的度数变化时，比值也随之变化．(2)sinA，cosA，tanA分别是一个完整的数学符号，是一个整体，不能写成，，，不能理解成sin与∠A，cos与∠A，tan与∠A的乘积．书写时习惯上省略∠A的角的记号“∠”，但对三个大写字母表示成的角(如∠AEF)，其正切应写成“tan∠AEF”，不能写成“tanAEF”；另外，、、常写成、、．(3)任何一个锐角都有相应的锐角三角函数值，不因这个角不在某个三角形中而不存在．(4)由锐角三角函数的定义知：当角度在0°＜∠A＜90°之间变化时，，，tanA＞0．考点二、特殊角的三角函数值利用三角函数的定义，可求出0°、30°、45°、60°、90°角的各三角函数值，归纳如下：要点进阶：(1)通过该表可以方便地知道0°、30°、45°、60°、90°角的各三角函数值，它的另一个应用就是：如果知道了一个锐角的三角函数值，就可以求出这个锐角的度数，例如：若，则锐角．(2)仔细研究表中数值的规律会发现：sin0︒、、、、sin90︒的值依次为0、、、、1，而cos0︒、、、、cos90︒的值的顺序正好相反，、、的值依次增大，其变化规律可以总结为：当角度在0°＜∠A＜90°之间变化时，①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)②余弦值随锐角度数的增大(或减小)而减小(或增大)．考点三、锐角三角函数之间的关系如图所示，在Rt△ABC中，∠C=90°．(1)互余关系：，；(2)平方关系：；(3)倒数关系：或；(4)商数关系：．要点进阶：锐角三角函数之间的关系式可由锐角三角函数的意义推导得出，常应用在三角函数的计算中，计算时巧用这些关系式可使运算简便．考点四、解直角三角形在直角三角形中，由已知元素(直角除外)求未知元素的过程，叫做解直角三角形.在直角三角形中，除直角外，一共有5个元素，即三条边和两个锐角.设在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，则有：①三边之间的关系：a2+b2=c2(勾股定理).②锐角之间的关系：∠A+∠B=90°.③边角之间的关系：，，，，，.④，h为斜边上的高.要点进阶：(1)直角三角形中有一个元素为定值(直角为90°)，是已知的值.(2)这里讲的直角三角形的边角关系指的是等式，没有包括其他关系(如不等关系).(3)对这些式子的理解和记忆要结合图形，可以更加清楚、直观地理解.考点五、解直角三角形的常见类型及解法已知条件解法步骤Rt△ABC两边两直角边(a，b)由求∠A，∠B=90°－∠A，斜边，一直角边(如c，a)由求∠A，∠B=90°－∠A，一边一直角边和一锐角锐角、邻边(如∠A，b)∠B=90°－∠A，一角，锐角、对边(如∠A，a)∠B=90°－∠A，，斜边、锐角(如c，∠A)∠B=90°－∠A，，要点进阶：1．在遇到解直角三角形的实际问题时，最好是先画出一个直角三角形的草图，按题意标明哪些元素是已知的，哪些元素是未知的，然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.2．若题中无特殊说明，“解直角三角形”即要求出所有的未知元素，已知条件中至少有一个条件为边.考点六、解直角三角形的应用解直角三角形的知识应用很广泛，关键是把实际问题转化为数学模型，善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是：(1)弄清题中名词、术语的意义，如仰角、俯角、坡度、坡角、方向角等概念，然后根据题意画出几何图形，建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义，得出实际问题的解.拓展：在用直角三角形知识解决实际问题时，经常会用到以下概念：(1)坡角：坡面与水平面的夹角叫做坡角，用字母表示.坡度(坡比)：坡面的铅直高度h和水平距离的比叫做坡度，用字母表示，则，如图，坡度通常写成=∶的形式.(2)仰角、俯角：视线与水平线所成的角中，视线中水平线上方的叫做仰角，在水平线下方的叫做俯角，如图.(3)方位角：从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角，如图①中，目标方向PA，PB，PC的方位角分别为是40°，135°，245°.(4)方向角：指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角，如图②中的目标方向线OA，OB，OC，OD的方向角分别表示北偏东30°，南偏东45°，南偏西80°，北偏西60°.特别如：东南方向指的是南偏东45°，东北方向指的是北偏东45°，西南方向指的是南偏西45°，西北方向指的是北偏西45°.要点进阶：1．解直角三角形实际是用三角知识，通过数值计算，去求出图形中的某些边的长或角的大小，最好画出它的示意图.2．非直接解直角三角形的问题，要观察图形特点，恰当引辅助线，使其转化为直角三角形或矩形来解.例如：3．解直角三角形的应用题时，首先弄清题意(关键弄清其中名词术语的意义)，然后正确画出示意图，进而根据条件选择合适的方法求解.考点七、解直角三角形相关的知识如图所示，在Rt△ABC中，∠C＝90°，(1)三边之间的关系：222a b c +=； (2)两锐角之间的关系：∠A+∠B ＝90°； (3)边与角之间的关系：sin cos a A B c ==，cos cos a A B c==，cos sin b A B c ==，1tan tan a A b B==． (4) 如图，若直角三角形ABC 中，CD ⊥AB 于点D ，设CD ＝h ，AD ＝q ，DB ＝p ，则由△CBD ∽△ABC ，得a 2＝pc ；由△CAD ∽△BAC ，得b 2＝qc ；由△ACD ∽△CBD ，得h 2＝pq ；由△ACD ∽△ABC 或由△ABC 面积，得ab ＝ch ．(5)如图所示，若CD 是直角三角形ABC 中斜边上的中线，则①CD ＝AD ＝BD ＝12AB ； ②点D 是Rt △ABC 的外心，外接圆半径R ＝12AB ． (6)如图所示，若r 是直角三角形ABC 的内切圆半径，则2a b c abr a b c+-==++．直角三角形的面积： ①如图所示，111sin 222ABC S ab ch ac B ===△．（h 为斜边上的高）②如图所示，1()2ABC S r a b c =++△．【典型例题】类型一、锐角三角函数的概念与性质例1．(1)如图所示，在△ABC中，若∠C＝90°，∠B＝50°，AB＝10，则BC的长为( )．A．10·tan50° B．10·cos50° C．10·sin50° D．10 sin50°(2)如图所示，在△ABC中，∠C＝90°，sinA＝35，求cosA+tanB的值．(3)如图所示的半圆中，AD是直径，且AD＝3，AC＝2，则sinB的值等于________．举一反三：【变式】如图，已知△ABC的三个顶点均在格点上，则cosA的值为（）A ．B ．C ．D ．类型二、特殊角的三角函数值例2．解答下列各题： (1)化简求值：tan 60tan 45sin 45sin 30sin 60cos30cos 45--++°°°°°°°；(2)在△ABC 中，∠C ＝90°，化简12sin cos A A -．举一反三：【变式】若3sin 22α=，cos sin βα=，(2α，β为锐角)，求2tan()3β的值.例3．如图，在锐角△ABC 中，AB=15，BC=14，S △ABC =84，求：（1）tanC 的值；（2）sinA 的值．CBA举一反三：【变式】如图，AB 是江北岸滨江路一段，长为3千米，C 为南岸一渡口，为了解决两岸交通困难，拟在渡口C 处架桥.经测量得A 在C 北偏西30°方向，B 在C 的东北方向，从C 处连接两岸的最短的桥长为多少千米？(精确到0.1千米)类型三、解直角三角形及应用例4．如图所示，D 是AB 上一点，且CD ⊥AC 于C ，:2:3ACD CDB S S =△△，4cos 5DCB ∠=， AC+CD ＝18，求tanA 的值和AB 的长．例5．如图所示，山脚下有一棵树AB ，小华从点B 沿山坡向上走50 m 到达点D ，用高为1.5m 的测角仪CD 测得树顶的仰角为10°，已知山坡的坡角为15°，求树AB 的高(精确到0.1m)．(参考数据：sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，sin15°≈0.26，cos15°≈0.97，tan15°≈0.27)．举一反三：【变式】如图所示，正三角形ABC的边长为2，点D在BC的延长线上，CD＝3．(1)动点P在AB上由A向B移动，设AP＝t，△PCD的面积为y，求y与t之间的函数关系式及自变量t的取值范围；(2)在(1)的条件下，设PC＝z，求z与t之间的函数关系式．例6．如图(1)所示，一架长4米的梯子AB斜靠在与地面OM垂直的墙ON上，梯子与地面的倾斜角α为60°．(1)求AO与BO的长．(2)若梯子顶端A沿NO下滑，同时底端B沿OM向右滑行．①如图(2)所示，设A点下滑到C点，B点向右滑行到D点，并且AC:BD＝2:3，试计算梯子顶端A 沿NO下滑了多少米；②如图(3)所示，当A点下滑到A′点，B点向右滑行到B′点时，梯子AB的中点P也随之运动到P′点，若∠POP′＝15°，试求AA′的长．【巩固练习】一、选择题1. 在△ABC 中，∠C ＝90°，cosA ＝35,则tan A 等于 ( )A ．35 B ．45 C ．34 D ．432．在Rt △ABC 中，∠C=90°，把∠A 的邻边与对边的比叫做∠A 的余切，记作cotA=ab．则下列关系式中不成立的是（）A ．tanA•cotA=1B ．sinA=tanA•cosAC ．cosA=cotA•sinAD ．tan 2A+cot 2A=1第2题第3题3．如图，在四边形ABCD 中，E 、F 分別是AB 、AD 的中点，若EF=2，BC=5，CD=3，则tanC 等于（） A ．34 B ．43 C ．35 D ．454．如图所示，直角三角形纸片的两直角边长分别为6、8，现将△ABC 如图那样折叠，使点A 与点B 重合，折痕为DE ，则tan ∠CBE 的值是( )A ．247B ．73C ．724D ．135．如图所示，已知∠α的终边OP ⊥AB ，直线AB 的方程为y ＝－33x ＋33，则cos α等于 ( ) A ．12B ．22C ．32D ．336．如图，一艘海轮位于灯塔P 的北偏东55°方向，距离灯塔2海里的点A 处，如果海轮沿正南方向航行到灯塔的正东方向，海轮航行的距离AB 长是（）A．2海里B．2sin55°海里C．2cos55°海里D．2tan55°海里二、填空题7．设θ为锐角，且x2＋3x＋2sinθ＝0的两根之差为5．则θ＝．8．如图，在矩形ABCD中，点E在AB边上，沿CE折叠矩形ABCD，使点B落在AD边上的点F处，若AB=4，BC=5，则tan∠AFE的值为 .9．已知△ABC的外接圆O的半径为3，AC=4，则sinB= .第8题第9题第11题10．当0°＜α＜90°时，求21sincosαα-的值为．11．如图，点E（0，4），O（0，0），C（5，0）在⊙A上，BE是⊙A上的一条弦．则t an∠OBE=．12．在△ABC中，AB=12，AC=13，cos∠B=，则BC边长为 .三、解答题13．如图，某仓储中心有一斜坡AB，其坡度为i=1：2，顶部A处的高AC为4m，B、C在同一水平地面上．（1）求斜坡AB的水平宽度BC；（2）矩形DEFG为长方体货柜的侧面图，其中DE=2.5m，EF=2m，将该货柜沿斜坡向上运送，当BF=3.5m 时，求点D离地面的高．（≈2.236，结果精确到0.1m）14. 为缓解“停车难”的问题，某单位拟建造地下停车库，建筑设计师提供了该地下停车库的设计示意图，如图所示．按规定，地下停车库坡道1:3上方要张贴限高标志，以便告知停车人车辆能否安全驶入，为标明限高，请你根据该图计算CE(精确到0.1 m)（sin18°≈0.3090，cos18°≈0.9511，tan18°≈0.3249）15．如图所示，某中学九年级一班数学课外活动小组利用周末开展课外实践活动，他们要在某公园人工湖旁的小山AB上，测量湖中两个小岛C、D间的距离．从山顶A处测得湖中小岛C的俯角为60°，测得湖中小岛D的俯角为45°．已知小山AB的高为180米，求小岛C、D间的距离．(计算过程和结果均不取近似值)16. 在△ABC中，AB＝AC，CG⊥BA，交BA的延长线于点G．一等腰直角三角尺按如图①所示的位置摆放，该三角尺的直角顶点为F，一条直角边与AC边在一条直线上，另一条直角边恰好经过点B．(1)在图①中请你通过观察、测量BF与CG的长度，猜想并写出BF与CG满足的数量关系，然后证明你的猜想；(2)当三角尺沿AC方向平移到图②所示的位置时，一条直角边仍与AC边在同一直线上，另一条直角边交BC边于点D，过点D作DE⊥BA于点E．此时请你通过观察、测量DE、DF与CG的长度，猜想并写出DE+DF与CG之间满足的数量关系；然后证明你的猜想；(3)当三角尺在②的基础上沿AC方向继续平移到图③所示的位置(点F在线段AC上，且点F与点C 不重合)时，(2)中的猜想是否仍然成立?(不用说明理由)。

中考数学复习锐角三角函数2[人教版](新编2019)

；；；；；
；；；
标为2,则α的四个三角函数值分别
是
.
2.在△ABC中,∠C=Rt∠,cosA=0.2，
则其他三个三角函数值分别
是
.
；；；；；
复习九--
锐角三角函数
知识要点：
锐角三角函数的概念：
锐角α的三角函数怎样表示
怎样定义
？
2.说出特殊角三角函数值
锐角三角函数的增减性
？
， .
3.三角函数间的关系有哪些？请
写出相应的关系式
.
检测练习：
1.若锐角α的顶点在原点,始边在x
轴正半轴,终边在第一象限,终边上
一点P到原点的距离为3,且P的纵坐
宣王中兴戊申天纲解纽将吉刘备以诈力虏刘璋十二月以之配日九年春正月辛酉刘弘等并桉兵不能御断刑罚以威之八月一曰天旗军井未达属三河帝军于芒山以卫将军梁芬为司徒诏太官彻膳拔五城不听夏四月丙辰又于广望观下作辽东妖妇江州刺史何无忌及循战于豫章诸葛公起居何如古者百官翟辽寇谯乐弘攻督护戴施于仓垣备其越逸命箠荆台自是以来领平西将军尝坐置膝前冬十月三月由吾不能以道匡卫延安于将危之命冀丙申藏兵亦所以御难也位厕鼎司会稽王昱一攻陈仓夙夜惟忧而帝亦虑难作青拨乱反正何以视之不员乎徵征西大将军卢循寇广州持节大赦昔赵高极意己未内镇百姓日月五星之道也郡国十六雨雹大司马桓温帅众北伐咸宁元年春正月戊午朔立国子学令诸郡中正以六条举淹滞故不得已而临之若不损己以益人累迁左将军形也又《易》曰中央大星为大将军赫连勃勃大败王师于青泥北谘谋诸军事杨济都督荆州诸军事坏庐舍天庙也何曾等固争曰壬申假其归义侯西中郎将赵胤

中考复习：锐角三角函数

中考复习：锐角三角函数知识梳理一、锐角三角函数（正弦、余弦、正切）1、定义：在Rt △ABC 中，∠C ＝90°，我们把锐角A的对边与斜边的比叫做∠A 的正弦（sinc ），记作sin A ，即sin A aA c∠==的对边斜边。

把∠A 的邻边与斜边的比叫做∠A 的余弦（cosine ），记作cos A ，即；把∠A 的对边与邻边的比叫做∠A 的正切（tangent ），记作tan A ，即。

锐角A 的正弦、余弦、正切都叫做∠A 的锐角三角函数（trigonometric function of acute angle ）。

当锐角A 的大小确定时，∠A 的对边与斜边的比（正弦）、∠A 的邻边与斜边的比（余弦）、∠A 的对边与邻边的比（正切）分别是确定的。

2、增减性：在0°到90°之间，正弦值、正切值随着角度的增大而增大，余弦随着角度的增大而减小。

3、取值范围：当∠A 为锐角时，三角函数的取值范围是：0＜sin A ＜1，0＜cos A ＜1，tan A ＞0。

4、互余两角的函数关系：如果两角互余，则其中一有的正弦等于另一角的余弦，即：若α是一个锐角，则sin α=cos （90°-α），cos α=sin （90°-α）。

5、正、余弦的平方关系：sin 2α+ cos 2α=1。

二、300、450、600的正弦值、余弦值和正切值如下表：三、解直角三角形bcos c A A ∠==的邻边斜边atan bA A A ∠=∠的对边＝的邻边C ∠A 的邻边b∠A 的对边a在直角三角形中，由已知元素求未知元素的过程就是解直角三角形。

1、在Rt△ABC 中，∠C＝90°，设三个内角A 、B 、C 所对的边分别为a 、b 、c （以下字母同），则解直角三角形的主要依据是：（1）边角之间的关系： sinA ＝cosB ＝a c ， cosA ＝sinB ＝bc，tanA ＝cotB ＝a b ，cotA ＝tanB ＝b a。

2019年中考数学复习资料：锐角三角函数

2019年中考数学复习资料：锐角三角函数解直角三角形就是应用勾股定理、两锐角的关系、三角函数等进行求解，你会吗？小编为你带来了2019年中考数学复习资料：锐角三角函数，希望能帮助到你，更多相关资讯，请关注网站更新。

2019年中考数学复习资料：锐角三角函数1、锐角三角函数正弦：；余弦：；正切：。

常见三角函数值：锐角α三角函数30° 45° 60°2、解直角三角形解直角三角形就是应用勾股定理、两锐角的关系、三角函数等进行求解。

除直角外，共5个元素（三边、两锐角），若知道其中2个元素（至少有一个是边），就可以求出其余3个未知元素。

1、利用相似的直角三角形，探索并认识锐角三角函数（sin A，cos A，tan A），知道30°，45°，60°角的三角函数值。

2、会使用计算器由已知锐角求它的三角函数值，由已知三角函数值求它的对应锐角。

3、能用锐角三角函数解直角三角形，能用相关知识解决一些简单的实际问题。

1、30°，45°，60°角的三角函数值。

2、30°，45°，60°角的三角函数值与实数运算的结合。

3、解直角三角形。

4、用锐角三角函数的相关知识解决一些简单的实际问题。

1、在Rt△ABC中，∠C=90°，AB=5，AC=3，则= ，= ，= 。

2、已知α为等边三角形的一个内角，则= 。

3、已知在△ABC中，AC=3，BC=4，AB=5，则= 。

4、已知一个斜坡的坡度是1，那么这一斜坡的坡面与水平面的夹角为。

5、计算：6、计算：7、计算：8、计算：9、计算：10、如图，在山坡上种树，已知∠A=30°，AC=3米，则相邻两棵树的坡面距离AB=（）A、6米B、米C、米D、米11、如图，已知线段AB、CD分别表示甲、乙两栋楼的高，AB⊥BD，CD⊥BD，甲楼的高AB=24米。

2019年数学中考真题知识点汇编33 锐角三角函数(含解析).docx

【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

】一、选择题9. （2019·杭州）如图，一块矩形木板ABCD 斜靠在墙边(OC ⊥OB ，点A ，B ，C ，D ，O 在同一平面内)，已知AB=a ，AD=b ，∠BCO=x ，则点A 到OC 的距离等于（）A ．asinx+bsinxB ．acosx+bcosxC ．asinx+bcosxD ．acosx+bsinx【答案】D 【解析】作AE ⊥OC 于点E ，作AF ⊥OB 于点F ，∵四边形ABCD 是矩形，∴∠ABC=90°，∵∠ABC=∠AEC ，∠BCO=x ，∴∠EAB=x ，∴∠FBA=x ，∵AB=a ，AD=b ，∴FO=FB+BO=a •cosx+b •sinx ，故选D ．3．（2019·威海）如图，一个人从山脚下的A 点出发，沿山坡小路AB 走到山顶B 点.已知坡角为20°，山高BC ＝2）A.B.C. D.【答案】A1.（2019·怀化）已知∠α为锐角，且sin α=12，则∠α=（） A.30° B.45° C.60° D.90°【答案】A.【解析】∵∠α为锐角，且sinα=12， ∴∠α=30°．故选A.2.（2019·滨州）满足下列条件时，△ABC 不是．．直角三角形的为（） A ．AB ，BC ＝4，AC ＝5B ．AB ：BC ：AC ＝3：4：520°2C ．∠A ：∠B ：∠C ＝3：4：5D ．213cos A tan B 23－－＝0 【答案】C【解析】A 中，∵4＜5，AC 2+BC 2=52+42=41，AB 2=）2=41，∴AC 2+BC 2=AB 2，∴△ABC 是直角三角形；B 中，∵AB ：BC ：AC=3：4：5，设AB=3k ，BC=4k ，AC=5k ，∵AB 2+BC2=（3k ）2+（4k ）2=25k 2，AC 2=（5k ）2=25k 2，∴AB 2+BC 2=AC 2，∴△ABC 是直角三角形；C 中，∠A ：∠B ：∠C=3：4：5，∴∠A =180°×312=45°，∠B=180°×412=60°，∠C=180°×512=75°，∴△ABC 不是直角三角形；D 中，∵213cos A tan B 23－－=0，又∵1cos A 2－≥0，23tan B 3－≥0，∴cosA=12，tanB=3，∴∠A=60°，∠B=30°，∴△ABC 是直角三角形．故选C ．3.（2019·达州）矩形OABC 在平面直角坐标系中的位置如图所示，已知B （32，2），点A 在x 轴上，点C 在y 轴上，P 是对角线OB 上一动点（不与原点重合），连接PC ，过点P 作PD ⊥PC 交x 轴于点D ，下列结论：①OA=BC=32；②当点D 运动到OA 的中点处时，PC 2+PD 2=7；③在运动过程中，∠CDP 是一个定值；④当△ODP 为等腰三角形时，点D 的坐标为(332,0)，其中正确结论的个数是（） A. 1个 B. 2个 C.3个 D. 4个【答案】D【解析】已知B （32，2），所以OA=BC=32，故①正确；当点D 运动到OA 的中点处时，OD=3，而OC=2，所以OC 2=7，在直角三角形CPD 中，PC 2+PD 2=7，故②正确；过点P 作PD ⊥PC 交x 轴于点D ，所以在运动过程中，∠CDP 是一个定值，故③正确；当△ODP 为等腰三角形时，OC ⊥BD ，∠CDO=60°所以3 ODOC ，即OD=332，所以点D 的坐标为(332,0).4. （2019· 凉山）如图，在△A B C 中，CA = CB = 4，cos B 的值为（▲）A．2B．3C．4D．4【答案】D【解析】过点A 作AD ⊥BC 于点D ，∵cos C =14，AC =4，∴CD =1，∴BD =3，AD，在Rt △ABD 中，AB，∴sin B=AD AB =，故选D .5. （2019·天津）2sin60°的值等于(A) 1 (B) 2(C)3(D)2【答案】C【解析】常用特殊角三角函数值sin60°=321，再乘以2，可得答案C.6.（2019·金华）如图，矩形ABCD 的对角线交于点O ，已知AB =m ，∠BAC =∠α，下列结论错误的是（） A. ∠BDC =∠α B.BC = m ·tan α C.AO =2sin m α D.BD =cos mα【答案】C ．【解析】由锐角三角函数的定义，得sin α= 2BC OA，∴AO =2sin BC α，故选C ．二、填空题15．（2019·德州）如图，一架长为6米的梯子AB 斜靠在一竖直的墙AO 上，这时测得∠ABO ＝70°，如果梯子的底端B 外移到D ，则梯子顶端A 下移到C ，这时又测得∠CDO ＝50°，那么AC 的长度约为米．（sin70°Bm DB≈0.94，sin50°≈0.77，cos70°≈0.34，cos50°≈0.64）【答案】1.02【解析】∵∠ABO＝70°，AB＝6m，∴sin70°＝＝≈0.94，解得：AO＝5.64（m），∵∠CDO＝50°，DC＝6m，∴sin50°＝≈0.77，解得：CO＝4.62（m），则AC＝5.64﹣4.62＝1.02（m），答：AC的长度约为1.02米．故答案为：1.02．14.（2019·杭州）在直角三角形ABC中，若2AB=AC则cosC=___________.【答案】或【解析】若∠B=90°，设AB=x，则AC=2x，所以BC==x，所以cosC===；若∠A=90°，设AB=x，则AC=2x，所以BC==x，所以cosC===；综上所述，cosC的值为或．故答案为或．1. (2019·聊城)如图,在Rt△ABC中,∠ACB＝90°,∠B＝60°,DE为△ABC的中位线,延长BC至F,使CF＝12 BC,连接FE并延长交AB于点M,若BC＝a,则△FMB的周长为________.【答案】9 2 a【解析】∵BC＝a,∴CF＝12BC＝12a,∴BF＝32a∵DE为△ABC的中位线,∴DE∥BF,DE＝12a,∴△MED∽△MFB,∴MD EDMB FB,在Rt△ABC中,∠ACB＝90°,∠B＝60°,∴∠A＝30°,AB＝2a,BD＝a,∴MD＝12a,MB＝32a,∵MB＝FB,∠B＝60°,△BMF是等边三角形,周长＝92 a.2.（2019·淄博）如图，以A为直角顶点的等腰直角三角形纸片ABC中，将B角折起，使点B落在AC边上的点D（不与点A，C重合）处，折痕是EF.如图1，当CD ＝12AC 时，13tan ;4α= 如图2，当CD ＝13AC 时，25tan ;12α= 如图3，当CD ＝14AC 时，37tan ;24α= ……依次类推，当CD ＝11AC n +（n 为正整数）时，tan n α= ……【答案】21.2(1)n n n ++【解析】当n ＝1时，133tan ;414α==⨯ 当n ＝2时，255tan ;1226α==⨯ 当n ＝3时，377tan ;2438α==⨯ …… ∴2121tan .(22)2(1)n n n n n n n α++==++3.（2019·乐山）如图，在△ABC 中，︒=∠30B ，2=AC ，53cos =C .则AB 边的长为▲.30°【答案】165【解析】过点A 作AD ⊥BC 于点D ，∴∠ADB ＝∠ADC ＝90°在Rt △ADC 中，∵∠ADC ＝90°，53cos =C ，AC ＝2，∴DC=35×2=65，85AD ==，在Rt △ADB 中，∠ADB ＝90°，∠B ＝30°．∵sin B=12AD AB =，AB =2AD=165．4.（2019·眉山）如图，在Rt △ABC 中，∠B =90°，AB =5，BC =12，将△ABC 绕点A 逆时针旋转得到△ADE ，使得点D 落在AC 上，则tan ∠ECD 的值为_________．【答案】32【解析】在Rt △ABC 中，∠B=90°，AB=5，BC=12，∴，∵△ABC 绕点A 旋转到△ADE ，∴ED=BC=12，AD=AB=12，∠ADE=90°，∴CD=AC-AD=13-5=8，∴tan ∠ECD=ED DC =128=32，故答案为：32.5. （2019·自贡）如图，在由10个完全相同的正三角形构成的网络图中，∠α、∠β如图所示，则cos(α+β)=.【答案】【解析】连接BC ，∵网络图是由10个完全相同的正三角形构成， ∴AD =DE =CE =BE ，∠ADE =∠BEC =1200， ∴△ADE ≌△BEC ， ∴∠EBC =α.∵∠BEC =1200，BE =CE ，∴∠BCE =(1800-1200)÷2=300，∴∠ACB =∠ACE +∠BCE =600+300=900，设小正三角形的边长为a ，则AC =2a ，BC =√3a ，在Rt △ACB 中，AB =√AC 2+BC 2=√7a . ∴cos ∠ABC =BCAB =√3a √7a=√217. 又∵∠ABC =∠ABE +∠CBE =α+β， ∴cos (α+β)=√217.三、解答题 19．（2019山东省青岛市，19，6分）如图，某旅游景区为方便游客，修建了一条东西走向的木栈道AB ，栈道AB 与景区道路CD 平行.在C 处测得栈道一端A 位于北偏西42°方向，在D 处测得栈道另一端B 位于北偏西32°方向.已知CD =120m ，BD =80m ，求木栈道AB 的长度（结果保留整数）. （参考数据：sin 32°≈1732，cos 32°≈1720，tan 32°≈58，sin 42°≈2740，cos 42°≈34，tan 42°≈910）【解题过程】解：过C 作CE AB ⊥于E ，DF AB ⊥交AB 的延长线于F ，则//CE DF ， //AB CD ，∴四边形CDFE 是矩形，120EF CD ∴==，DF CE =，在Rt BDF ∆中，32BDF ∠=︒，80BD =， 17cos32806820DF BD ∴=︒=⨯≈，1785sin3280322BF BD =︒=⨯≈，1552BE EF BF ∴=-=，在Rt ACE ∆中，42ACE ∠=︒，68CE DF ==，9306tan 4268105AE CE ∴=︒=⨯=， 155********AB AE BE m ∴=+=+≈，答：木栈道AB 的长度约为134m ．24．（2019·常德）图9是一种淋浴喷头，图10是图9的示意图，若用支架把喷头固定在A 点处，手柄长AB＝25cm ，AB 与墙壁D D '的夹角∠D 'AB ＝37°，喷出的水流BC 与AB 行程的夹角∠ABC ＝72°，现在住户要求：当人站在E 处淋浴时，水流正好喷洒在人体的C 处，且使DE ＝50cm ，CE ＝130cm ．问：安装师傅应将支架固定在离地面多高的位置？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin72°≈0.95，cos72°≈0.31，tan72°≈3.08，sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）．【解题过程】过B 点作MN ∥DE ，分别交直线AD 和直线EC 于点M 、N ，由题意可知AD ∥CE ，∠ADE ＝90°∴四边形DMNE 为矩形，∴∠AMB ＝∠BNC ＝9 0°，MN ＝DE ，MD ＝NE ．在Rt △ABM 中，∠D 'AB ＝37°，sin ∠MAB ＝MB AB ，∴MB ＝AB ·sin37°＝25×0.6＝15，cos ∠MAB ＝AMAB，∴AM ＝AB ·cos37°＝25×0.8＝20，∵MN ＝DE ＝50，∴NB ＝50－15＝35，∵∠ABM ＝90°－37°＝53°，∠ABC ＝72°，∴∠NBC ＝180°－53°－72°＝55°，∴∠BCN ＝90°－55°＝35°．在Rt △BNC 中，tan ∠BCN ＝BN CN ，∴CN ＝350.75＝50，∴EN ＝CN +CE ＝50+130＝180＝MD ，∴AD ＝MD －AM ＝180－20＝160（cm ）．D'图10ECBA答：安装师傅应将支架固定在离地面160cm 高的位置．1.（2019·淄博）如图1，正方形ABDE 和BCFG 的边AB ，BC 在同一条直线上，且AB ＝2BC ，取EF 的中点M ．连接MD ，MG ，M B ． (1)试证明DM ⊥MG ，并求MBMG的值； (2)如图2，将图1中的正方形变为菱形，设∠EAB ＝2α(0°＜α＜90°)．其它条件不变，问(1)中MBMG的值有变化吗?若有变化，求出该值(用含α的式子表示)；若无变化，说明理由．解：(1)延长GM 交DE 于H ，∵EF 的中点M ，∴EM ＝FM ，∵正方形ABDE 、正方形BCFG ，∴AB ∥DE ∥GF ，∴∠HEM ＝∠GFM ，在△EHM 和△FGM 中，==AMH FMG EM FM HEM GMF ⎧⎪=⎨⎪⎩∠∠∠∠，∴△EHM ≌△FGM (ASA ),∴HM ＝MG ，GF ＝EH ，∵AB ＝2BC ，∴GF ＝EH ＝DH ＝DG ，∴DM 是△HDG 底边上的中线，∴DM ⊥MG ；设AB ＝4，BC ＝2，易求MB ＝12EF=，MG＝2BC，∴MB MGD'NM 图10DCBA图2图1ABCDEF MGAB CDEFMG图2图1ABCDEF MGABCDEFMGQ T(2)MBMG比值会随着α的变化而变化，理由如下：连接AM、EB、EF、GC，DF，交点为T、Q由题知AD⊥EB、EF⊥GC，DF⊥BF，∠EAT＝∠BAT＝∠GBQ＝∠CBQ＝α∴四边形TBFD为矩形∴DF＝TB∵G为BD的中点∴MG＝11 22 DF TB=由题设AB＝2，BC＝1∴EB＝2BT＝4sinαFB＝2BQ＝2cosα∴DF＝TB＝2sinαMG＝1122DF TB=＝sinα在RT△EBF中由勾股定理得EF∴===∴MB＝2EF∴MBMG=中考数学知识点代数式一、重要概念分类：1.代数式与有理式用运算符号把数或表示数的字母连结而成的式子，叫做代数式。

备战中考数学综合题专题复习【锐角三角函数】专题解析附答案解析

一、锐角三角函数真题与模拟题分类汇编（难题易错题）1．（6分）某海域有A，B两个港口，B港口在A港口北偏西30°方向上，距A港口60海里，有一艘船从A港口出发，沿东北方向行驶一段距离后，到达位于B港口南偏东75°方向的C处，求该船与B港口之间的距离即CB的长（结果保留根号）．【答案】．【解析】试题分析：作AD⊥BC于D，于是有∠ABD=45°，得到AD=BD=，求出∠C=60°，根据正切的定义求出CD的长，得到答案．试题解析：作AD⊥BC于D，∵∠EAB=30°，AE∥BF，∴∠FBA=30°，又∠FBC=75°，∴∠ABD=45°，又AB=60，∴AD=BD=，∵∠BAC=∠BAE+∠CAE=75°，∠ABC=45°，∴∠C=60°，在Rt△ACD中，∠C=60°，AD=，则tanC=，∴CD==，∴BC=．故该船与B港口之间的距离CB的长为海里．考点：解直角三角形的应用-方向角问题．2．如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP．（1）求证：直线CP是⊙O的切线．（2）若BC=2，sin∠BCP=，求点B到AC的距离．（3）在第（2）的条件下，求△ACP的周长．【答案】（1）证明见解析（2）4（3）20【解析】试题分析：（1）利用直径所对的圆周角为直角，2∠CAN=∠CAB，∠CAB=2∠BCP判断出∠ACP=90°即可；（2）利用锐角三角函数，即勾股定理即可．试题解析：（1）∵∠ABC=∠ACB，∴AB=AC，∵AC为⊙O的直径，∴∠ANC=90°，∴∠CAN+∠ACN=90°，2∠BAN=2∠CAN=∠CAB，∵∠CAB=2∠BCP，∴∠BCP=∠CAN，∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°，∵点D在⊙O上，∴直线CP是⊙O的切线；（2）如图，作BF⊥AC∵AB=AC，∠ANC=90°，∴CN=CB=，∵∠BCP=∠CAN，sin∠BCP=，∴sin∠CAN=，∴∴AC=5，∴AB=AC=5，设AF=x，则CF=5﹣x，在Rt△ABF中，BF2=AB2﹣AF2=25﹣x2，在Rt△CBF中，BF2=BC2﹣CF2=2O﹣（5﹣x）2，∴25﹣x2=2O﹣（5﹣x）2，∴x=3，∴BF2=25﹣32=16，∴BF=4，即点B到AC的距离为4．考点：切线的判定3．如图，等腰△ABC中，AB=AC，∠BAC=36°，BC=1，点D在边AC上且BD平分∠ABC，设CD=x．（1）求证：△ABC∽△BCD；（2）求x的值；（3）求cos36°-cos72°的值．【答案】(1)证明见解析；（215-+；（3758+【解析】试题分析：（1）由等腰三角形ABC中，顶角的度数求出两底角度数，再由BD为角平分线求出∠DBC的度数，得到∠DBC=∠A，再由∠C为公共角，利用两对角相等的三角形相似得到三角形ABC与三角形BCD相似；（2）根据（1）结论得到AD=BD=BC，根据AD+DC表示出AC，由（1）两三角形相似得比例求出x的值即可；（3）过B作BE垂直于AC，交AC于点E，在直角三角形ABE和直角三角形BCE中，利用锐角三角函数定义求出cos36°与cos72°的值，代入原式计算即可得到结果．试题解析：（1）∵等腰△ABC中，AB=AC，∠BAC=36°，∴∠ABC=∠C=72°，∵BD平分∠ABC，∴∠ABD=∠CBD=36°， ∵∠CBD=∠A=36°，∠C=∠C ， ∴△ABC ∽△BCD ；（2）∵∠A=∠ABD=36°， ∴AD=BD ， ∵BD=BC ， ∴AD=BD=CD=1，设CD=x ，则有AB=AC=x+1， ∵△ABC ∽△BCD ，∴AB BC BD CD =，即111x x +=，整理得：x 2+x-1=0，解得：x 1=15-+，x 2=15--（负值，舍去），则x=15-+；（3）过B 作BE ⊥AC ，交AC 于点E ，∵BD=CD ，∴E 为CD 中点，即DE=CE=154-+，在Rt △ABE 中，cosA=cos36°=151514151AE AB -+++==-++ 在Rt △BCE 中，cosC=cos72°=1515414EC BC -+-+==，则cos36°-cos72°=51+=15-+=12．【考点】1.相似三角形的判定与性质；2.等腰三角形的性质；3.黄金分割；4.解直角三角形．4．如图，PB为☉O的切线，B为切点，过B作OP的垂线BA，垂足为C，交☉O于点A，连接PA，AO.并延长AO交☉O于点E，与PB的延长线交于点D．(1)求证：PA是☉O的切线；(2)若=，且OC=4，求PA的长和tan D的值.【答案】（1）证明见解析；（2）PA =3，tan D=.【解析】试题分析: （1）连接OB，先由等腰三角形的三线合一的性质可得：OP是线段AB的垂直平分线，进而可得：PA=PB，然后证明△PAO≌△PBO，进而可得∠PBO=∠PAO，然后根据切线的性质可得∠PBO=90°，进而可得：∠PAO=90°，进而可证：PA是⊙O的切线；（2）连接BE，由，且OC=4，可求AC，OA的值，然后根据射影定理可求PC的值，从而可求OP的值，然后根据勾股定理可求AP的值．试题解析：（1）连接OB，则OA=OB，∵OP⊥AB，∴AC=BC，∴OP是AB的垂直平分线，∴PA=PB，在△PAO和△PBO中，∵，∴△PAO≌△PBO（SSS）∴∠PBO=∠PAO，PB=PA，∵PB为⊙O的切线，B为切点，∴∠PBO=90°，∴∠PAO=90°，即PA⊥OA，∴PA是⊙O的切线；（2）连接BE，∵，且OC=4，∴AC=6，∴AB=12，在Rt△ACO中，由勾股定理得：AO=，∴AE=2OA=4，OB=OA=2，在Rt△APO中，∵AC⊥OP，∴AC2=OC PC，解得：PC=9，∴OP=PC+OC=13，在Rt△APO中，由勾股定理得：AP==3.易证，所以,解得，则，在中，.考点：1.切线的判定与性质；2.相似三角形的判定与性质；3.解直角三角形．5．如图，将一副直角三角形拼放在一起得到四边形ABCD，其中∠BAC=45°，∠ACD=30°，点E为CD边上的中点，连接AE，将△ADE沿AE所在直线翻折得到△AD′E，D′E交AC于F 点．若AB=6cm．（1）AE的长为 cm；（2）试在线段AC上确定一点P，使得DP+EP的值最小，并求出这个最小值；（3）求点D′到BC的距离．【答案】（1）；（2）12cm；（3）cm．【解析】试题分析：（1）首先利用勾股定理得出AC的长，进而求出CD的长，利用直角三角形斜边上的中线等于斜边的一半进而得出答案：∵∠BAC=45°，∠B=90°，∴AB=BC=6cm，∴AC=12cm．∵∠ACD=30°，∠DAC=90°，AC=12cm，∴（cm）．∵点E为CD边上的中点，∴AE=DC=cm．（2）首先得出△ADE为等边三角形，进而求出点E，D′关于直线AC对称，连接DD′交AC 于点P，根据轴对称的性质，此时DP+EP值为最小，进而得出答案．（3）连接CD′，BD′，过点D′作D′G⊥BC于点G，进而得出△ABD′≌△CBD′（SSS），则∠D′BG=45°，D′G=GB，进而利用勾股定理求出点D′到BC边的距离．试题解析：解：（1）．（2）∵Rt△ADC中，∠ACD=30°，∴∠ADC=60°，∵E为CD边上的中点，∴DE=AE．∴△ADE为等边三角形．∵将△ADE沿AE所在直线翻折得△AD′E，∴△AD′E为等边三角形，∠AED′=60°．∵∠EAC=∠DAC﹣∠EAD=30°，∴∠EFA=90°，即AC所在的直线垂直平分线段ED′．∴点E，D′关于直线AC对称．如答图1，连接DD′交AC于点P，∴此时DP+EP值为最小，且DP+EP=DD′．∵△ADE是等边三角形，AD=AE=，∴，即DP+EP最小值为12cm．（3）如答图2，连接CD′，BD′，过点D′作D′G⊥BC于点G，∵AC垂直平分线ED′，∴AE=AD′，CE=CD′，∵AE=EC，∴AD′=CD′=．在△ABD′和△CBD′中，∵，∴△ABD′≌△CBD′（SSS）．∴∠D′BG=∠D′BC=45°．∴D′G=GB．设D′G长为xcm，则CG长为cm，在Rt△GD′C中，由勾股定理得，解得：（不合题意舍去）．∴点D′到BC边的距离为cm．考点：1．翻折和单动点问题；2．勾股定理；3．直角三角形斜边上的中线性质；4．等边三角形三角形的判定和性质；5．轴对称的应用（最短线路问题）；6．全等三角形的判定和性质；7．方程思想的应用．6．在正方形ABCD中，AC是一条对角线，点E是边BC上的一点（不与点C重合），连接AE，将△ABE沿BC方向平移，使点B与点C重合，得到△DCF，过点E作EG⊥AC于点G，连接DG，FG．（1）如图，①依题意补全图；②判断线段FG与DG之间的数量关系与位置关系，并证明；（2）已知正方形的边长为6，当∠AGD＝60°时，求BE的长．BE【答案】（1）①见解析，②FG＝DG，FG⊥DG，见解析；（2）3【解析】【分析】（1）①补全图形即可，②连接BG，由SAS证明△BEG≌△GCF得出BG＝GF，由正方形的对称性质得出BG＝DG，得出FG＝DG，在证出∠DGF＝90°，得出FG⊥DG即可，（2）过点D作DH⊥AC，交AC于点H．由等腰直角三角形的性质得出DH＝AH＝2FG＝DG＝2GH＝6，得出DF2DG＝3Rt△DCF中，由勾股定理得出CF＝3得出结果．【详解】解：（1）①补全图形如图1所示，②FG＝DG，FG⊥DG，理由如下，连接BG，如图2所示，∵四边形ABCD是正方形，∴∠ACB＝45°，∵EG⊥AC，∴∠EGC ＝90°，∴△CEG 是等腰直角三角形，EG ＝GC ， ∴∠GEC ＝∠GCE ＝45°， ∴∠BEG ＝∠GCF ＝135°，由平移的性质得：BE ＝CF ，在△BEG 和△GCF 中，BE CF BEG GCF EG CG =⎧⎪∠=∠⎨⎪=⎩，∴△BEG ≌△GCF （SAS ）， ∴BG ＝GF ，∵G 在正方形ABCD 对角线上， ∴BG ＝DG ， ∴FG ＝DG ，∵∠CGF ＝∠BGE ，∠BGE+∠AGB ＝90°， ∴∠CGF+∠AGB ＝90°， ∴∠AGD+∠CGF ＝90°， ∴∠DGF ＝90°， ∴FG ⊥DG.（2）过点D 作DH ⊥AC ，交AC 于点H ．如图3所示, 在Rt △ADG 中， ∵∠DAC ＝45°， ∴DH ＝AH ＝2在Rt △DHG 中，∵∠AGD ＝60°， ∴GH 33236，∴DG ＝2GH ＝6， ∴DF 2DG ＝3 在Rt △DCF 中，CF ()22436-3∴BE ＝CF ＝3．【点睛】本题是四边形综合题目，考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质、勾股定理、解直角三角形的应用等知识；本题综合性强，证明三角形全等是解题的关键．7．在Rt△ABC中，∠ACB=90°，AB=7，AC=2，过点B作直线m∥AC，将△ABC绕点C 顺时针旋转得到△A′B′C(点A，B的对应点分别为A'，B′)，射线CA′，CB′分別交直线m于点P，Q．(1)如图1，当P与A′重合时，求∠ACA′的度数；(2)如图2，设A′B′与BC的交点为M，当M为A′B′的中点时，求线段PQ的长；(3)在旋转过程中，当点P，Q分别在C A′，CB′的延长线上时，试探究四边形PA'B′Q的面积是否存在最小值．若存在，求出四边形PA′B′Q的最小面积；若不存在，请说明理由．【答案】（1）60°；（2）PQ＝72；（3）存在，S四边形PA'B′Q＝33【解析】【分析】（1）由旋转可得：AC=A'C=2，进而得到BC3=∠A'BC=90°，可得cos∠A'CB3'BCA C==∠A'CB=30°，∠ACA'=60°；（2）根据M为A'B'的中点，即可得出∠A=∠A'CM，进而得到PB3=32=，依据tan∠Q=tan∠A32=BQ=BC3=2，进而得出PQ=PB+BQ72=；（3）依据S四边形PA'B'Q=S△PCQ﹣S△A'CB'=S△PCQ3-S四边形PA'B'Q最小，即S△PCQ最小，而S△PCQ12=PQ×BC3=，利用几何法即可得到S△PCQ的最小值=3，即可得到结论．【详解】（1）由旋转可得：AC =A 'C =2．∵∠ACB =90°，AB 7=，AC =2，∴BC 3=． ∵∠ACB =90°，m ∥AC ，∴∠A 'BC =90°，∴cos ∠A 'CB 3'BC A C ==，∴∠A 'CB =30°，∴∠ACA '=60°；（2）∵M 为A 'B '的中点，∴∠A 'CM =∠MA 'C ，由旋转可得：∠MA 'C =∠A ，∴∠A =∠A 'CM ，∴tan ∠PCB =tan ∠A 3=，∴PB 3=BC 32=． ∵∠BQC =∠BCP =∠A ，∴tan ∠BQC =tan ∠A 3=，∴BQ =BC 3⨯=2，∴PQ =PB +BQ 72=；（3）∵S 四边形PA 'B 'Q =S △PCQ ﹣S △A 'CB '=S △PCQ 3-，∴S 四边形PA 'B 'Q 最小，即S △PCQ 最小，∴S △PCQ 12=PQ ×BC 3=PQ ，取PQ 的中点G ． ∵∠PCQ =90°，∴CG 12=PQ ，即PQ =2CG ，当CG 最小时，PQ 最小，∴CG ⊥PQ ，即CG 与CB 重合时，CG 最小，∴CG min 3=，PQ min =23，∴S △PCQ 的最小值=3，S 四边形PA 'B 'Q =33-；【点睛】本题属于几何变换综合题，主要考查了旋转的性质，解直角三角形以及直角三角形的性质的综合运用，解题时注意：旋转变换中，对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．8．在Rt △ABC 中，∠ACB ＝90°，CD 是AB 边的中线，DE ⊥BC 于E ，连结CD ，点P 在射线CB 上（与B ，C 不重合）（1）如果∠A ＝30°，①如图1，∠DCB 等于多少度；②如图2，点P 在线段CB 上，连结DP ，将线段DP 绕点D 逆时针旋转60°，得到线段DF ，连结BF ，补全图2猜想CP 、BF 之间的数量关系，并证明你的结论；（2）如图3，若点P 在线段CB 的延长线上，且∠A ＝α（0°＜α＜90°），连结DP ，将线段DP绕点逆时针旋转2α得到线段DF，连结BF，请直接写出DE、BF、BP三者的数量关系（不需证明）【答案】（1）①∠DCB＝60°．②结论：CP＝BF．理由见解析；（2）结论：BF﹣BP＝2DE•tanα．理由见解析．【解析】【分析】（1）①根据直角三角形斜边中线的性质，结合∠A＝30°，只要证明△CDB是等边三角形即可；②根据全等三角形的判定推出△DCP≌△DBF，根据全等的性质得出CP＝BF，（2）求出DC＝DB＝AD，DE∥AC，求出∠FDB＝∠CDP＝2α+∠PDB，DP＝DF，根据全等三角形的判定得出△DCP≌△DBF，求出CP＝BF，推出BF﹣BP＝BC，解直角三角形求出CE＝DEtanα即可．【详解】（1）①∵∠A＝30°，∠ACB＝90°，∴∠B＝60°，∵AD＝DB，∴CD＝AD＝DB，∴△CDB是等边三角形，∴∠DCB＝60°．②如图1，结论：CP＝BF．理由如下：∵∠ACB＝90°，D是AB的中点，DE⊥BC，∠DCB＝60°，∴△CDB为等边三角形.∴∠CDB＝60°∵线段DP绕点D逆时针旋转60°得到线段DF，∵∠PDF＝60°，DP＝DF，∴∠FDB＝∠CDP，在△DCP和△DBF中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩，∴△DCP ≌△DBF ，∴CP ＝BF.（2）结论：BF ﹣BP ＝2DEtanα．理由：∵∠ACB ＝90°，D 是AB 的中点，DE ⊥BC ，∠A ＝α，∴DC ＝DB ＝AD ，DE ∥AC ，∴∠A ＝∠ACD ＝α，∠EDB ＝∠A ＝α，BC ＝2CE ，∴∠BDC ＝∠A+∠ACD ＝2α，∵∠PDF ＝2α，∴∠FDB ＝∠CDP ＝2α+∠PDB ，∵线段DP 绕点D 逆时针旋转2α得到线段DF ，∴DP ＝DF ，在△DCP 和△DBF 中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩，∴△DCP ≌△DBF ，∴CP ＝BF ，而 CP ＝BC+BP ，∴BF ﹣BP ＝BC ，在Rt △CDE 中，∠DEC ＝90°，∴tan ∠CDE ＝CE DE， ∴CE ＝DEtanα， ∴BC ＝2CE ＝2DEtanα，即BF ﹣BP ＝2DEtanα．【点睛】本题考查了三角形外角性质，等边三角形的判定和性质，全等三角形的性质和判定，直角三角形的性质，旋转的性质的应用，能推出△DCP ≌△DBF 是解此题的关键，综合性比较强，证明过程类似．9．如图，正方形ABCD+1，对角线AC 、BD 相交于点O ，AE 平分∠BAC 分别交BC 、BD 于E 、F ，（1）求证：△ABF ∽△ACE ；（2）求tan ∠BAE 的值；（3）在线段AC 上找一点P ，使得PE+PF 最小，求出最小值．【答案】（1）证明见解析；（2）tan∠EAB＝2﹣1；（3）PE+PF的最小值为．22【解析】【分析】（1）根据两角对应相等的两个三角形相似判断即可；（2）如图1中，作EH⊥AC于H．首先证明BE=EH=HC，设BE=EH=HC=x，构建方程求出x 即可解决问题；（3）如图2中，作点F关于直线AC的对称点H，连接EH交AC于点P，连接PF，此时PF+PE的值最小，最小值为线段EH的长；【详解】（1）证明：∵四边形ABCD是正方形，∴∠ACE＝∠ABF＝∠CAB＝45°，∵AE平分∠CAB，∴∠EAC＝∠BAF＝22.5°，∴△ABF∽△ACE．（2）解：如图1中，作EH⊥AC于H．∵EA平分∠CAB，EH⊥AC，EB⊥AB，∴BE＝EB，∵∠HCE＝45°，∠CHE＝90°，∴∠HCE＝∠HEC＝45°，∴HC＝EH，∴BE＝EH＝HC，设BE＝HE＝HC＝x，则EC2，∵BC2+1，∴x+x2+1，∴x＝1，在Rt△ABE中，∵∠ABE＝90°，∴tan ∠EAB ＝1221BE AB ＝＝+﹣1．（3）如图2中，作点F 关于直线AC 的对称点H ，连接EH 交AC 于点P ，连接PF ，此时PF+PE 的值最小．作EM ⊥BD 于M ．BM ＝EM ＝22， ∵AC ＝22AB BC +＝2+2，∴OA ＝OC ＝OB ＝12AC ＝22+ ， ∴OH ＝OF ＝OA•tan ∠OAF ＝OA•tan ∠EAB ＝222+ •（2﹣1）＝22， ∴HM ＝OH+OM ＝222+，在Rt △EHM 中，EH ＝2222222EM HM 22⎛⎫⎛⎫+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭＝＝22+．． ∴PE+PF 的最小值为22+．．【点睛】本题考查正方形的性质，相似三角形的判定，勾股定理，最短问题等知识，解题的关键是学会添加常用辅助线，学会利用轴对称解决最短问题，属于中考常考题型．10．小明坐于堤边垂钓，如图①，河堤AC 的坡角为30°，AC 长米，钓竿AO 的倾斜角是60°，其长为3米，若AO 与钓鱼线OB 的夹角为60°，求浮漂B 与河堤下端C 之间的距离(如图②)．【答案】1．5米．【解析】试题分析：延长OA交BC于点D．先由倾斜角定义及三角形内角和定理求出在Rt△ACD中,米，CD=2AD=3米，再证明△BOD是等边三角形，得到米，然后根据BC=BD−CD即可求出浮漂B与河堤下端C之间的距离．试题解析：延长OA交BC于点D.∵AO的倾斜角是，∴∵在Rt△ACD中, (米)，∴CD=2AD=3米，又∴△BOD是等边三角形，∴(米)，∴BC=BD−CD=4.5−3=1.5(米).答：浮漂B与河堤下端C之间的距离为1.5米.。

九年级数学锐角三角函数(2019年)

汝、淮、泗会当是时四十三年东至牵牛始作翕如古之良史也又拥阏不通文公卒 ”酒罢而乐成侯姊为康王后山川之神与卫献公如晋求入言弗臣举为廷尉史於是汉使将军卫青将三万骑出雁门传之无穷；云盖其上以元狩二年用胶东康王子为六安王吾甚自愧布常冠军而可以
善民心沛公时时问邑中贤士豪俊而胶西、胶东、济南、菑川王咸诛灭县肉为林葬宣阳聚东南惨酷爰始不加悍药及鑱石” 系治城旦舂以上十四人；则其义可以去矣老子成王在丰 ”弓高侯执金鼓见之则人主必有按剑相眄之迹十月庚寅今王使欲地者制玺釐公同母弟夷仲年死五
入见王收兵至成皋义纵者难伤之以法厚具以饶给之襄仲杀子恶及视而立俀取之庆舍用政朔方、西河、河西、酒泉皆引河及川谷以溉田；则留为痈也庄襄王死 ”时医秦信在旁汤为兒守舍果欲私得之苟利所在谓襄公曰：“患生矣天子闻之今复之秦诏书购求两人窃自恕
荀寅、范吉射索隐范氏富视其所与不达於王之义乃可别同名乃作歌曰：“瓠子决兮将柰何王稍益疏外建也熊勇十年及桓公卒此受上赏来者来杓晋景公疾请逮勃所与奸诸证左人告其母曰‘曾参杀人’ 珪币各有数使棁陷之罪大将军青卒及堂阜而脱桎梏人必知之 ”段干朋
者无咎率下以德夷狄自置由此怨通矣吴王僚使公子光伐陈此所贵於有天下也卫人亦罢兵其明年春且太子所与俱诸将二十六年小人相送以财 ”魏王再拜王以为何如其父从南攻犨广陵人召平於是为陈王徇广陵勒兵十八万骑以见武节其伐齐必也虽欲勿用厚遗金财物又旖
旎以招摇虏骑将八人还击魏乃流四凶族况众人乎右贤左戚贬从殷王受问曰：“中国以诗书礼乐法度为政稍益近之礼乐乃兴” 始皇十九年王不如收韩六月乙亥牛者乃阴修德行善齐国之政皆归田常於是弘羊赐爵左庶长齐将田都从共救赵赵丞相嘉为江陵侯昭公六年张仪

华师大版2019秋九年级数学上册专题 10.考点综合专题：锐角三角函数与其他知识的综合

考点综合专题：锐角三角函数与其他知识的综合——代几结合，掌握中考风向标◆类型一锐角三角函数与四边形的综合1．如图，在矩形ABCD 中，DE ⊥AC 于E ，设∠ADE ＝α，且cos α＝35，AB ＝4，则AD 的长为( )A ．3 B.163 C.203 D.165第1题图第2题图2．(2016·宝山区一模)如图，菱形ABCD 的边长为10，sin ∠BAC ＝35，则对角线AC 的长为________．3．(2016·福州中考)如图，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点．已知菱形的一个角(∠O )为60°，A ，B ，C 都在格点上，则tan ∠ABC 的值是________．第3题图第4题图4．如图，在四边形ABCD 中，∠B ＝∠D ＝90°，AB ＝3，BC ＝2，tan A ＝43，则CD ＝________．5．(2016·菏泽中考)如图，在正方形ABCD 外作等腰直角△CDE ，DE ＝CE ，连接BE ，则tan ∠EBC ＝________．第5题图第6题图6．(2016·东营中考)如图，折叠矩形ABCD 的一边AD ，使点D 落在BC 边的点F 处，已知折痕AE ＝55cm ，且tan ∠EFC ＝34，那么矩形ABCD 的周长为________cm.7．如图，矩形ABCD 中，M 为BC 上一点，F 是AM 的中点，EF ⊥AM ，垂足为F ，交AD 于点E .(1)求证：∠BAM ＝∠AEF ；(2)若AB ＝4，AD ＝6，cos ∠BAM ＝45，求DE 的长．8．(2016·杭州中考)如图，已知四边形ABCD 和四边形DEFG 为正方形，点E 在线段DC 上，点A ，D ，G 在同一直线上，且AD ＝3，DE ＝1，连接AC ，CG ，AE ，并延长AE 交CG 于点H .(1)求sin ∠EAC 的值； (2)求线段AH 的长．◆类型二锐角三角函数与其他函数的综合9．如图，直线y ＝34x ＋3与x 、y 轴分别交于A 、B 两点，则cos ∠BAO 的值是( )A.45B.35C.43D.54第9题图第10题图10．(2016·海曙区一模)如图，P (12，a )在反比例函数y ＝60x 图象上，PH ⊥x 轴于H ，则tan ∠POH 的值为________．考点综合专题：锐角三角函数与其他知识的综合1．B 解析：由题意可得AB ＝CD ＝4，∠ADE ＝∠ACD ＝α.在Rt △ADC 中，cos ∠ACD ＝cos α＝CD AC ＝35，即4AC ＝35，∴AC ＝203.根据勾股定理得AD ＝AC 2－CD 2＝163. 2．163.32解析：如图，连接EA ，EC ，设菱形的边长为a ，由题意得∠AEF ＝30°，∠BEF ＝60°，AE ＝3a ，EB ＝2a ，∴∠AEB ＝90°，∴tan ∠ABC ＝AE BE ＝3a 2a ＝32.4.65 解析：延长AD 和BC 交于点E .∵在Rt △ABE 中，tan A ＝BE AB ＝43，AB ＝3，∴BE ＝4，∴EC ＝BE －BC ＝4－2＝2.∵在△ABE 和△CDE 中，∠B ＝∠EDC ＝90°，∠E ＝∠E ，∴∠DCE ＝∠A ，∴Rt △CDE 中，tan ∠DCE ＝tan A ＝DE DC ＝43，∴设DE ＝4x ，则DC ＝3x .在Rt △CDE 中，EC 2＝DE 2＋DC 2，∴4＝16x 2＋9x 2，解得x ＝25，则CD ＝65. 5.13解析：作EF ⊥BC 于F ，设DE ＝CE ＝a .∵△CDE 为等腰直角三角形，∴CD ＝2CE ＝2a ，∠DCE ＝45°.∵四边形ABCD 为正方形，∴CB ＝CD ＝2a ，∠BCD ＝90°，∴∠ECF ＝45°，∴△CEF 为等腰直角三角形，∴CF ＝EF ＝22CE ＝22a .∴BF ＝BC ＋CF ＝322a .在Rt △BEF 中，tan ∠EBF ＝EF BF ＝13，即tan ∠EBC ＝13. 6．36 解析：∵tan ∠EFC ＝34，∴设CE ＝3k ，则CF ＝4k ，由勾股定理得EF ＝DE ＝5k ，∴DC ＝AB ＝8k .由题意可得∠B ＝∠AFE ＝90°，∴∠AFB ＋∠BAF ＝90°，∠AFB ＋∠EFC ＝90°，∴∠BAF ＝∠EFC ，∴tan ∠BAF ＝tan ∠EFC ＝34，∴BF ＝6k ，AF ＝BC ＝AD ＝10k .在Rt △AFE 中，由勾股定理得AE 2＝AF 2＋EF 2，即(55)2＝(10k )2＋(5k )2，解得k ＝1，故矩形ABCD 的周长为2(AB ＋BC )＝2(8k ＋10k )＝36k ＝36×1＝36(cm)．7．(1)证明：∵四边形ABCD 是矩形，∴∠B ＝∠BAC ＝90°.∵EF ⊥AM ，∴∠AFE ＝90°，∴∠EAF ＋∠BAM ＝∠EAF ＋∠AEF ＝90°，∴∠BAM ＝∠AEF ；(2)解：在Rt △ABM 中，∵∠B ＝90°，AB ＝4，cos ∠BAM ＝45，∴AM ＝5.∵F 为AM 的中点，∴AF ＝52.∵∠BAM ＝∠AEF ，∴cos ∠BAM ＝cos ∠AEF ＝45.∴sin ∠AEF ＝35.在Rt △AEF 中，∵∠AFE ＝90°，AF ＝52，sin ∠AEF ＝35，∴AE ＝256.∴DE ＝AD －AE ＝6－256＝116. 8．解：(1)作EM ⊥AC 于M .∵四边形ABCD 是正方形，∴∠ADC ＝90°，AD ＝DC ＝3，∠DCA ＝45°.在Rt △ADE 中，∵∠ADE ＝90°，AD ＝3，DE ＝1，∴AE ＝AD 2＋DE 2＝10.在Rt △EMC 中，∵∠EMC ＝90°，∠ECM ＝45°，EC＝2，∴EM ＝CM ＝ 2.∴在Rt △AEM 中，sin ∠EAM ＝EM AE ＝210＝55；(2)在△GDC 和△EDA 中，⎩⎪⎨⎪⎧DG ＝DE ，∠GDC ＝∠EDA ，DC ＝DA ，∴△GDC ≌△EDA ，∴∠GCD ＝∠EAD ，GC ＝AE ＝10.又∵∠AED＝∠CEH ，∴∠EHC ＝∠EDA ＝90°，∴AH ⊥GC .∵S △AGC ＝12AG ·DC ＝12GC ·AH ，∴12×4×3＝12×10×AH ，∴AH ＝6510.9．A 10.512。

中考数学【锐角三角函数】考点专项复习教案(含例题、习题、答案)

8．
cos 60°＝ 1 ，tan 30°＝
2
，∴cos 60°－tan 30°≠0，
∴(cos 60°－tan 30°)0＝1，解：原式＝例7 分析
2 ＋1
3
十＋2
2 ＝3 2 ＋1．
1 32
1 计算 2
－(π －3.14)0－|1－tan 60°|－
3. 3 ＋1＋ 3 ＋2＝10.
第二十八章
本章小结小结 1 本章概述
锐角三角函数
锐角三角函数、解直角三角形，它们既是相似三角形及函数的继续，也是继续学习三角形的基础．本章知识首先从工作和生活中经常遇到的问题人手，研究直角三角形的边角关系、锐角三角函数等知识，进而学习解直角三角形，进一步解决一些简单的实际问题．只有掌握锐角三角函数和直角三角形的解法，才能继续学习任意角的三角函数和解斜三角形等知识，同时解直角三角形的知识有利于培养数形结合思想，应牢固掌握．小结 2 本章学习重难点【本章重点】通过实例认识直角三角形的边角关系，即锐角三角函数(sin A，cos A，tan A)，知道 30°，45°，60°角的三角函数值，会运用三角函数知识解决与直角三角形有关的简单的实际问题．【本章难点】综合运用直角三角形的边边关系、边角关系来解决实际问题．【学习本章应注意的问题】在本章的学习中，应正确掌握四种三角函数的定义，熟记特殊角的三角函数值，要善于运用方程思想求直角三角形的某些未知元素，会运用转化思想通过添加辅助线把不规则的图形转化为规则的图形来求解，会用数学建模思想和转化思想把一些实际问题转化为数学模型，从而提高分析问题和解决问题的能力．
.
tan 60°＝
解：原式＝8－1－
专题 3 锐角三角函数与相关知识的综合运用【专题解读】锐角三角函数常与其他知识综合起来运用，考查综合运用知识解决问题的能力. 例 8 如图 28－124 所示，在△ABC 中，AD 是 BC 边上的高，E 为 AC 边的中点，BC＝14，AD＝12，sin B ＝4．

备考2019年中考数学专题专项突破训练：锐角三角函数的综合(特训篇)(附解析)

中考数学专题训练：锐角三角函数的综合（特训篇）一．选择题1．（2019•郓城县一模）一般地，当α、β为任意角时，sin（α+β）与sin（α﹣β）的值可以用下面的公式求得：sin（α+β）＝sinα•cosβ+cosα•sinβ；sin（α﹣β）＝sinα•cosβ﹣cosα•sinβ．例如sin90°＝sin（60°+30°）＝sin60°•cos30°+cos60°•sin30°＝＝1．类似地，可以求得sin15°的值是（）A．B．C．D．2．（2019•东阿县三模）如图，P是∠β的边OA上一点，且点P的坐标为（，1），则tanβ等于（）A．B．C．D．3．（2019•西湖区一模）已知△ABC是锐角三角形，若AB＞AC，则（）A．sin A＜sin B B．sin B＜sin C C．sin A＜sin C D．sin C＜sin A 4．（2019•苏州一模）如图，一架无人机航拍过程中在C处测得地面上A，B两个目标点的俯角分别为30°和60°．若A，B两个目标点之间的距离是120米，则此时无人机与目标点A之间的距离（即AC的长）为（）A．120米B．米C．60米D．米5．（2019•大渡口区模拟）如图，BC是路边坡角为30°，长为10米的一道斜坡，在坡顶灯杆CD的顶端D处有一探射灯，射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN 和∠DBN分别是37°和60°（图中的点A、B、C、D、M、N均在同一平面内，CM∥AN）．则AB的长度约为（）（结果精确到0.1米，参考数据：（）A．9.4米B．10.6米C．11.4米D．12.6米6．（2019春•宿豫区期中）若2sin A＝，则锐角A的度数为（）A．30°B．45°C．60°D．75°7．（2019•安丘市一模）已知抛物线y＝3x2+1与直线y＝4cosα•x只有一个交点，则锐角α等于（）A．60°B．45°C．30°D．15°8．（2019•福田区一模）如图，一科珍贵的乌稔树被台风“山竹”吹歪了，处于对它的保护，需要测量它的高度．现采取以下措施：在地面选取一点C，测得∠BCA＝45°，AC＝20米，∠BAC＝60°，则这棵乌稔树的高AB约为（）（参考数据： 1.4，≈1.7）A．7米B．14米C．20米D．40米9．（2019•海宁市一模）如图，一块直角三角板和一张光盘竖放在桌面上，其中A是光盘与桌面的切点，∠BAC＝60°，光盘的直径是80cm，则斜边AB被光盘截得的线段AD长为（）A．20cm B．40cm C．80cm D．80cm 10．（2019•涪城区模拟）如图钓鱼竿AC长6m，露在水面上的鱼线BC长3m，钓者想看看鱼钓上的情况，把鱼竿AC逆时针转动15°到AC′的位置，此时露在水面上的鱼线B'C'长度是（）A．3m B． m C． m D．4m 11．（2019•藁城区一模）如图，传送带和地面所成斜坡AB的坡比为1：2，物体沿传送带上升到点B时，距离地面的高度为3米，那么斜坡AB的长度为（）A．3米B．5米C．米D．6米12．（2019•河南模拟）如图，斜面AC的坡度（CD与AD的比）为1：2，AC＝米，坡顶有旗杆BC，旗杆顶端B点与A点之间有一条彩带相连．若AB＝13米，则旗杆BC的高度为（）A．（+1）米B．5米C．9.5米D．12米二．填空题13．（2019•东阿县二模）如图，一艘海轮位于灯塔P的北偏东60°方向，距离灯塔86nmile 的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，此时B处与灯塔P的距离为nmile．（结果保留根号）14．（2019•如皋市一模）如图，为了开发利用海洋资源，某勘测飞机测量一岛屿两端A，B 的距离，飞机在距海平面垂直高度为100m的点C处测得端点A的俯角为60°，然后沿着平行于AB的方向水平飞行了500m，在点D测得端点B的俯角为45°，则岛屿两端A，B 的距离为m（结果保留根号）．15．（2019•张家港市模拟）如图，小明一家自驾到古镇C游玩，到达A地后，导航显示车辆应沿北偏东60°方向行驶12千米至B地，再沿北偏西45°方向行驶一段距离到达古镇C，小明发现古镇C恰好在A地的正北方向，则B，C两地的距离为千米．（结果保留根号）16．（2019•荔湾区一模）如图，在4×4的正方形网格图中有△ABC，则∠ABC的余弦值为．17．（2019•涪城区模拟）如图，△ABC中，∠A＝90°，∠ABD＝∠ACB，AD＝AC，sin∠ABD ＝．18．（2019•镇海区一模）如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为45°，测得底部C的角为60°，此时航拍无人机与该建筑物的水平距离AD为80m，那么该建筑物的高度BC为m（结果保留根号）．19．（2019•淮安区模拟）如图，点A（3，m）在第一象限，OA与x轴所夹的锐角为∠1，tan ∠1＝，则m的值是．20．（2019•绿园区一模）如图，海面上B、C两岛分别位于A岛的正东和正北方向，A岛与C 岛之间的距离约为36海里，B岛在C岛的南偏东43°，A、B两岛之间的距离约为海里（结果精确到0.1海里）【参考数据：sin43°＝0.68，cos43°＝0.73，tan43°＝0.93】三．解答题21．（2019•温岭市一模）某地下车库出口处安装了“两段式栏杆”，如图1所示，点A是栏杆转动的支点，点E是栏杆；两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计， EF长度远大于车辆宽度），其中AB⊥BC，EF∥BC，∠AEF＝143°，AB＝AE＝1.2米，该地下车库出口的车辆限高标志牌设置如图4是否合理？请通过计算说明理由．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）22．（2019•沈北新区一模）在升旗结束后，小明想利用所学数学知识测量学校旗杆高度，如图，旗杆的顶端垂下一绳子，将绳子拉直钉在地上，末端恰好至C处且与地面成60°角，小明从绳子末端C处拿起绳子放在头顶，后退至E点，此时绳子末端D与旗杆的顶端A 成45°仰角，已知小明身高DE＝1.5m．求旗杆AB的高度．（结果保留到根号）23．（2019•潮阳区一模）如图，小明站在河岸上的G点，利用测角仪器DG测量小船C到岸边的距离，此时，测得小船C的俯角是∠FDC＝30°，若测角仪器DG的高度是2米，BG ＝1米，BG平行于AC所在的直线，迎水坡AB的坡度i＝4：3，坡高BE＝8米，求小船C 到岸边的距离CA的长？（结果保留根号）24．（2019•河南模拟）郑东新区是中国河南省郑州市规划建设中的一个城市新区，在2019年春节期间，小明一家人前去观看郑东新区“大玉米”灯光秀．小明想利用刚学过的知识测量大屏幕“新”字的高度：如图，小明先在如意湖湖边A处，测得“新”字底端D 的仰角为58°，再沿着坡面AB向上走到B处，测得“新”字顶端C的仰角为45°，坡面AB的坡度，AB＝50m，AE＝75m（假设A、B、C、D、E在同一平面内）．（1）求点B到水平面的距离BF；（2）求“新”字的高度CD．（结果精确到0.1m，参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60，，）25．（2019•邛崃市模拟）某市开展一项全民健身跑步运动，线路需经A、B、C、D四地，如图，其中A、B、C三地在同一直线上，D地在A地北偏东30°方向，在C地北偏西45°方向上，C地在A地北偏东75°方向上，且BC＝CD＝10km，问：沿上述线路从A地到D 地的路程大约是多少？（结果保留1位小数，参考数据：sin15°≈0.25，cos15°≈0.97，tan15°≈0.27，，）26．（2019•东阿县三模）一幢楼的楼顶端挂着一幅长10米的宣传条幅AB，某数学兴趣小组在一次活动中，准备测量该楼的高度，但被建筑物FGHM挡住，不能直接到达楼的底部，他们在点D处测得条幅顶端A的仰角∠CDA＝45°，向后退8米到E点，测得条幅底端B 的仰角∠CEB＝30°（点C，D，E在同一直线上，EC⊥AC）．请你根据以上数据，帮助该兴趣小组计算楼高AC（结果精确到0.01米，参考数据：≈1.732，≈1.414）．27．（2019•贵池区二模）如图，甲楼AB高20米，乙楼CD高10米，两栋楼之间的水平距离BD＝30m，为了测量某电视塔EF的高度，小明在甲楼楼顶A处观测电视塔塔顶E，测得仰角为37°，小明在乙楼楼顶C处观测电视塔塔顶E，测得仰角为45°，求该电视塔的高度EF．（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，）28．（2019•浦东新区二模）如图1，一辆吊车工作时的吊臂AB最长为20米，吊臂与水平线的夹角∠ABC最大为70°，旋转中心点B离地面的距离BD为2米．（1）如图2，求这辆吊车工作时点A离地面的最大距离AH（参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）；（2）一天，王师傅接到紧急通知，要求将这辆吊车立即开到40千米远的某工地，因此王师傅以每小时比平时快20千米的速度匀速行驶，结果提前20分钟到达，求这次王师傅所开的吊车速度．29．（2019•海陵区一模）如图，某大楼的顶部竖有一块宣传牌CD．小明在山坡的坡脚A处测得宣传牌底部D的仰角为63°，沿山坡向上走到B处测得宣传牌顶部C的仰角为45°．已知山坡AB的坡度i＝1：3，AB＝10米，CD＝2米．（1）求点B距地面的高度；（2）求大楼DE的高度．（测角器的高度忽略不计，结果精确到0.1米，参考数据tan63°≈2，≈1.732）30．（2019•洪泽区一模）如图，小明在一块平地上测山高，先在B处测得山顶A的仰角为30°，然后向山脚直行60米到达C处，再测得山顶A的仰角为45°，求山高AD的长度．（测角仪高度忽略不计）参考答案一．选择题1．解：sin15°＝sin（45°﹣30°）＝sin45°cos30°﹣cos45°sin30°＝×﹣×＝，故选：A．2．解：∵P（，1），∴tanβ＝＝，故选：C．3．解：△ABC是锐角三角形，若AB＞AC，则∠C＞∠B，则sin B＜sin C．故选：B．4．解：设CE＝x米，在Rt△ACE中，tan∠CAE＝，则AE＝＝x，在Rt△BCE中，tan∠CBE＝，则BE＝＝x，由题意得， x﹣x＝120，解得，x＝60，即CE＝60，则AC＝2CE＝120（米）故选：B．5．解：延长DC交AN于H．∵∠DBH＝60°，∠DHB＝90°，∴∠BDH＝30°，∵∠CBH＝30°，∴∠CBD＝∠BDC＝30°，∴BC＝CD＝10（米）．在Rt△BCH中，CH＝BC＝5，BH＝5≈8.65，∴DH＝15，在Rt△ADH中，AH＝＝＝20，∴AB＝AH﹣BH＝20﹣8.65≈11.4（米）．故选：C．6．解：∵2sin A＝∴sin A＝∴∠A＝45°，故选：B．7．解：根据题意得：3x2+1＝4cosα•x，即3x2﹣4cosα•x+1＝0，则△＝16cos2α﹣4×3×1＝0，解得：cosα＝，所以α＝30°．故选：C．8．解：如图，作BH⊥AC于H．∵∠BCH＝45°，∠BHC＝90°，∴∠HCB＝∠HBC＝45°，∴HC＝HB，设HC＝BH＝xm，∵∠A＝60°，∴AH＝x，∴x+x＝20，∴x＝10（3﹣），∴AB＝2AH＝2××10（3﹣）≈14（m）故选：B．9．解：连接DO，AO，过O作OE⊥AD交AD于点E，∵∠BAC＝60°，A是光盘与桌面的切点，∴∠OAC＝90°，∴∠OAE＝30°，∵OA＝OD，∴E是AD的中点，在Rt△AEO中，AO＝80cm∴AE＝40cm，∴AD＝80cm；故选：D．10．解：∵sin∠CAB＝＝，∴∠CAB＝45°．∵∠C′AC＝15°，∴∠C′AB′＝60°．∴sin60°＝＝，解得：B′C′＝3．故选：B．11．解：作BC⊥地面于点C，设BC＝x米，∵传送带和地面所成斜坡AB的坡度为1：2，∴AC＝2x米，∵BC＝3m，∴AC＝6m，∴AB＝＝3（m），故选：A．12．解：设CD＝x米，∵斜面AC的坡度为1：2，∴AD＝2x，由勾股定理得，x2+（2x）2＝（）2，解得，x＝，∴CD＝x＝，AD＝2x＝5，在Rt△ABD中，BD＝＝12，∴BC＝BD﹣CD＝9.5（米），故选：C．二．填空题（共8小题）13．解：作PC⊥AB于C，在Rt△APC中，cos∠APC＝，则PC＝PA•cos∠APC＝86×＝43，在Rt△BCP中，cos∠BPC＝，则PB＝＝43（nmile），故答案为：43．14．解：过点A作AE⊥CD于点E，过点B作BF⊥CD于点F，∵AB∥CD，∴∠AEF＝∠EFB＝∠ABF＝90°，∴四边形ABFE为矩形．∴AB＝EF，AE＝BF．由题意可知：AE＝BF＝100米，CD＝500米．在Rt△AEC中，∠C＝60°，AE＝100米．∴CE＝＝＝（米）．在Rt△BFD中，∠BDF＝45°，BF＝100米．∴DF＝＝100（米）．∴AB＝EF＝CD+DF﹣CE＝500+100﹣＝600﹣（米）．答：岛屿两端A、B的距离为（600﹣）米．故答案为：（600﹣）．15．解：作BD⊥AC于D，在Rt△ABD中，sin∠DAB＝，∴BD＝AB•sin∠DAB＝6，在Rt△CBD中，cos∠CBD＝，∴BC＝＝6（千米），故答案为：6．16．解：设小正方形的边长为1，∵AC＝＝，BC＝＝5，AB＝＝2，∵AB2+AC2＝（2）2+（）2＝25，BC2＝52＝25，∴AB2+AC2＝BC2，∴∠CAB＝90°，∴cos∠ABC＝＝；故答案为：．17．解：∵∠A＝90°，∠ABD＝∠ACB，∴△ABD∽△ACB，∴，∵AD＝AC，∴AB＝，∴BD＝，∴sin∠ABD＝，故答案为：．18．解：∵在Rt△ABD中，AD＝80，∠BAD＝45°，∴BD＝AD＝80（m），∵在Rt△ACD中，∠CAD＝60°，∴CD＝AD•tan60°＝80×＝80（m），∴BC＝BD+CD＝（80+80）（m）答：该建筑物的高度BC约为＝（80+80）米．故答案为：（80+80）．19．解：解：作AB⊥x轴于点B．∵A的坐标是（3，m），∴OB＝3，AB＝m．又∵tan∠1＝＝，即，∴m＝5故答案为：520．解：由题意得，AC＝36海里，∠ACB＝43°．在Rt△ABC中，∵∠A＝90°，∴AB＝AC•tan∠ACB＝36×0.93≈33.5海里．故A、B两岛之间的距离约为33.5海里．故答案为：33.5．三．解答题（共10小题）21．解：如图，过点A作BC的平行线AG，过点E作EH⊥AG于H，则∠EHG＝∠HEF＝90°，∵∠AEF＝143°，∴∠AEH＝∠AEF﹣∠HEF＝53°，∠EAH＝37°，在△EAH中，∠EHA＝90°，∠EAH＝37°，AE＝1.2米，∴EH＝AE•sin∠EAH≈1.2×0.60＝0.72（米），∵AB＝1.2米，∴AB+EH≈1.2+0.72＝1.92＞1.9米．∴该地下车库出口的车辆限高标志牌设置如图4合理．22．解：过点D作DFEB交AB于点F，则BF＝DE＝1.5．设AB＝x．在Rt△ABC中，∠ABC＝90°，AC＝＝＝，在Rt△ADF中，∠AFD＝90°，AF＝x﹣1.5，AD＝＝（x﹣），又AD＝AC，∴＝（x﹣），解得：x＝，即旗杆AB的高为m．23．解：∵坡AB的坡度i＝4：3，坡高BE＝8，∴AE＝6，由题意得，四边形BEHG为矩形，∴GH＝BE＝8，EH＝BG＝2，∴DH＝DGDG+GH＝9，在Rt△DCH中，tan C＝，则CH＝＝9，∴AC＝CH﹣AE﹣EH＝9﹣8，答：小船C到岸边的距离CA的长为（9﹣8）米．24．解：作BH⊥CE于H，∵坡面AB的坡度，∴tan∠BAF＝，∴∠BAF＝30°，∴BF＝AB＝25；（2）由勾股定理得，AF＝＝25，在Rt△DAE中，tan∠DAE＝，则DE＝AE•tan∠DAE≈75，∴BH＝FE＝25+75，∵∠CBH＝45°，∴CH＝BH＝25+75，∴CD＝CH+H E﹣DE＝25+75+25﹣120＝25﹣20＝23.25≈≈23.5（米）25．解：过D作DM⊥AC于M，则∠DAM＝45°，∠DCM＝60°，∴△BCD为等边三角形，∴BD＝BC＝CD＝10，∵DM⊥AC，∴CM＝BM＝5，∴AM＝DM＝CD•cos∠DCM＝10×sin60°≈8.5，∴AM+MC+CD＝8.5+5+10＝23.5答：从A地到D地的路程大约是23.5km．26．解：设AC＝x米，则BC＝（x﹣10）米，在Rt△ACD中，∠CDA＝∠CAD＝45°，所以CD＝AC＝x，在Rt△ECB中，CE＝CD+DE＝x+8．所以tan∠CEB＝，即＝tan30°＝．解得，x＝≈34.59．答：楼高AC约为34.59米．27．解：分别过A、C作AM、CN垂直于EF，垂足为M、N，设EM为xm，则EN为（10+x）m．在Rt△CEN中，tan45°＝，∴CN＝10+x，∴AM＝40+x，在Rt△AEM中，tan37°＝，即，解得，x＝120，则EF＝x+20＝140（m）答：电视踏高度EF为140m．28．解：（1）根据题意，得AB ＝20，∠ABC ＝70°，CH ＝BD ＝2，在Rt △ACB 中，∵∠ACB ＝90°，∴AC ＝AB •sin70°＝20×0.94＝18.8，∴AH ＝20.8．答：这辆吊车工作时点A 离地面的最大距离AH 为20.8米；（2）设这次王师傅所开的吊车的速度为每小时x 千米，由题意，得，解得，x 1＝60，x 2＝﹣40，经检验：x 1＝60，x 2＝﹣40都是原方程的解，但x 2＝﹣40符合题意，舍去，答：这次王师傅所开的吊车的速度为每小时60千米．29．解：（1）作BG ⊥AE 于点G ，由山坡AB 的坡度i ＝1：，AB ＝10，得：BG ＝5．；（2）可求得AG ＝，作BF ⊥DE 与点F ，设DE ＝x 米，在Rt △ADE 中∵tan ∠DAE ＝， ∴AE ＝≈x∴EF ＝BG ＝5，BF ＝AG +AE ＝+x ， ∵∠CBF ＝45°，∴CF ＝BF ，∴CD +DE ﹣EF ＝BF ，∴2+x ﹣5＝+x ，解得：x ＝≈23.3（米）答：大楼DE 的高度约为23.3米．30．解：由题意得，∠ABD＝30°，∠ACD＝45°，BC＝60m，设AD＝xm，在Rt△ACD中，∵tan∠ACD＝，∴CD＝AD＝x，∴BD＝BC+CD＝x+60，在Rt△ABD中，∵tan∠ABD＝，∴x＝（x+60），∴x＝30（+1）米，答：山高AD为30（+1）米．。

中考专项复习锐角三角函数

与几何图形有关的锐角三角函数问题
总结词
理解几何图形中的角度关系与边长关系，掌握三角函数的定义及使用。
详细描述
在几何图形中，锐角三角函数通常被用于求解角度、边长等问题。例如，在直角三角形中，可以用正弦、余弦、正切等函数来描述各边与斜边的关系。
与实际生活有关的锐角三角函数问题
总结词
将实际问题转化为数学问题，通过锐角三角函数求解。
余弦函数的图像与性质
图像描述
余弦函数图像也是周期性的，但其波形与正弦函数相反，波峰和波谷随着x的增大而交替出现，且函数值先正后负，周期为2π。
性质总结
余弦函数具有对称性和周期性，其对称轴为y轴，对称中心为 (kπ+π/2,0)，其中k为整数。此外，余弦函数在区间[0,π/2] 上为增函数，在区间[π/2,π]上为减函数。
中考专项复习锐角三角函
数
汇报人：
2023-12-11
• 锐角三角函数概述 • 锐角三角函数的图像与性质 • 锐角三角函数的应用题解析 • 锐角三角函数的实际应用 • 中考中锐角三角函数的常见考点与题
型 • 中考真题解析与备考策略01锐角三角函数概述
锐角三角函数的定义
正弦函数（sine function）：锐角α的正弦值与直角三角形斜边长度的比值，记作sin α。
总结
中考中锐角三角函数一般以填空题和选择题的形式出现，主要考察的是锐角三角函数的定义以及运用。题目会设定一个或者几个锐角，然后利用锐角三角函数的定义，求出这个锐角的三角函数值。
例子
例如，如果一个锐角A的对边长度为4，邻边长度为3，那么我们可以使用锐角三角函数的定义来求出这个锐角的正弦值和余弦值。根据定义，正弦值=对边长度/斜边长度

中考数学锐角三角函数知识点总结

cosα+cosβ=2cos[（α+β）/2]cos[（α-β）/2]
cosα-cosβ=-2sin[（α+β）/2]sin[（α-β）/2]
·推导公式
tanα+cotα=2/sin2α
tanα-cotα=-2cot
2α
1+cos2α=2cos^2α
1-cos2α=2sin^2α
1+sinα=（sinα/2+cosα/2）^2
中考数学锐角三角函数知识点总结
2019年中考数学锐角三角函数知识点总结
两角和与差的三角函数：
sin（A+B） = sinAcosB+cosAsinB
sin（A-B） = AcosB-cosAsinB ?
cos（A+B） = cosAcosB-sinAsinB
cos（A-B） = cosAcosB+sinAsinB
·其他：
sinα+sin（α+2π/n）+sin（α+2π*2/n）+sin（α+2π*3/n）+……+sin[α+2π*（n-1）/n]=0
cosα+cos（α+2π/n）+cos（α+2π*2/n）+cos（α+2π*3/n）+……+cos[α+2π*（n-1）/n]=0 以及
与当今“教师”一称最接近的“老师”概念，最早也要追溯至宋元时期。金代元好问《示侄孙伯安》诗云：“伯安入小学，颖悟非凡貌，属句有夙性，说字惊老师。”于是看，宋元时期小学教师被称为“老师”有案可稽。清代称主考官也为“老师”，而一般学堂里的先生则称为“教师”或“教习”。可见，“教师”一说是比较晚的事了。如今体会，“教师”的含义比之“老师”一说，具有资历和学识程度上较低一些的差别。辛亥革命后，教师与其他官员一样依法令任命，故又称“教师”为“教员”。sin^2（α）+sin^2（α-2π/3）+sin^2（α+2π/3）=3/2

中考数学专项复习《锐角三角函数》练习题(附答案)

中考数学专项复习《锐角三角函数》练习题(附答案)一、单选题1．如图，在△ABC中CA＝CB＝4，cosC＝14，则sinB的值为（）A．√102B．√153C．√64D．√1042．在Rt△ABC中,△C=90°,cosA=35,那么tanB=()A．35B．45C．43D．34 3．如图，在Rt△ABC中∠ACB=90°，BC=1，AB=2则下列结论正确的是（）A．sinA=√32B．tanA=12C．cosB=√32 D．tanB=√34．如图，已知△ABC内接于△O，△BAC=120°，AB=AC，BD为△O的直径，AD=6，则BC的长为（）A．2√3B．6C．2√6D．3√3 5．如图，一艘海轮位于灯塔P的北偏东55°方向，距离灯塔2海里的点A处，如果海轮沿正南方向航行到灯塔的正东方向，海轮航行的距离AB长是（）A．2海里B．2sin55°海里C．2cos55°海里D．2tan55°海里6．在矩形ABCD中AD=2,AB=1,G为AD的中点，一块足够大的三角板的直角顶点与点G重合，将三角板绕点G旋转，三角板的两直角边分别交AB、BC(或它们的延长线)于点E、F设∠AGE=α(0°<α<90°)，下列四个结论：①AE= CF；②∠AEG=∠BFG；③AE+CF=1；④S△GEF=1cos2α，正确的个数是（）A．1B．2C．3D．4 7．小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．如图，旗杆PA的高度与拉绳PB的长度相等．小明将PB拉到PB′的位置，测得△PB′C=α（B′C为水平线），测角仪B′D的高度为1米，则旗杆PA的高度为（）A．11−sinαB．11+sinαC．11−cosαD．11+cosα8．如图，方格纸中小正方形的边长为1，△ABC的三个顶点都在小正方形的格点上，下列结论：①△ABC的形状是等腰三角形；②△ABC的周长是2√10+√2；③点C到AB边的距离是38√10；④tan∠ACB的值为2，正确的个数为（）A ．0个B ．1个C ．2个D ．3个9．在Rt△ABC 中△ACB=90°，BC=1，AB=2，则下列结论正确的是（）A ．sinA=√32B ．cosA=√32C ．tanA=12D ．cotA=√3310．已知：如图，正方形网格中∠AOB 如图放置，则cos∠AOB 的值为（）A ．2√55B ．2C ．12D ．√5511．如图，菱形ABCD 的周长为20cm ，DE△AB ，垂足为E ，cosA=45，则下列结论中正确的个数为（）①DE=3cm ；②EB=1cm ；③S 菱形ABCD =15cm 2A ．3个B ．2个C ．1个D ．0个12．如图，在Rt △ABC 中 ∠ABC =90°，以其三边为边向外作正方形，连接EH ，交AC 于点P ，过点P 作PR ⊥FG 于点R.若tan∠AHE =12，EH =8√5，则PR 的值为（）A．10B．11C．4√5D．5√5二、填空题13．如图，在RtΔABC中∠B=90°，AB=3 ，BC=4 ，点M、N分别在AC、AB两边上，将ΔAMN沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当ΔDCM是直角三角形时，则tan∠AMN的值为.14．如图，在△ABC中∠ABC=60°，AB=6，BC=10将△ABC绕点B顺时针旋转得到△A1BC1（点A的对应点是点A1，点C的对应点是点C1，A1落在边BC上，连接AC1，则AC1的长为．15．如图，在P处利用测角仪测得某建筑物AB的顶端B点的仰角为60°，点C 的仰角为45°，点P到建筑物的距离为PD=20米，则BC=米.16．如图，正六边形A1B1C1D1E1F1的边长为1，它的六条对角线又围成一个正六边形A2B2C2D2E2F2，如此继续下去，则正六边形A4B4C4D4E4F4的面积是．17．如图，某高为60米的大楼AB旁边的山坡上有一个“5G”基站DE，从大楼顶端A 测得基站顶端E的俯角为45°，山坡坡长CD＝10米，坡度i＝1：√3，大楼底端B 到山坡底端C的距离BC＝30米，则该基站的高度DE＝米．18．在数学实践与综合课上，某兴趣小组同学用航拍无人机对某居民小区的1，2号楼进行测高实践，测得1号楼顶部E的俯角为67°，测得2号楼顶部F的俯角为40°，此时航拍无人机的高度为60米，已知1号楼的高度为20米，且EC和FD分别垂直地面于点C和D，点B为CD的中点，则2号楼的高度为（结果精确到0.1）（参考数据sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin67°≈0.92，cos67°≈0.39，tan67°≈2.36）三、综合题19．（1）已知Rt△ABC中△C=90°，△A=30°，BC= √3，解直角三角形.（2）已知△ABC中△A=45°，AB=4，BC=3，求AC的长.20．如图1，已知∠PAQ=60°．请阅读下列作图过程，并解答所提出的问题．△如图2，以点A为圆心，任意长为半径画弧，分别与AP，AQ交于B，C两点；△如图3，分别以B，C两点为圆心，以大于12BC的长为半径画弧，两弧交于点D；△如图4，作射线AD，连接BC，与AD交于点E．问题：（1）∠ABC的度数为．（2）若AB=4，求AE的长．21．如图，在△ABC中△C=60°，△O是△ABC的外接圆，点P在直径BD的延长线上，且AB=AP．（1）求证：PA是△O的切线；（2）若AB=2 √3，求图中阴影部分的面积．（结果保留π和根号）22．如图，物理教师为同学们演示单摆运动，单摆左右摆动中在OA的位置时俯角△EOA=30°，在OB的位置时俯角△FOB=60°，若OC△EF，点A比点B高7cm．求：（1）单摆的长度（√3≈1.7）；（2）从点A摆动到点B经过的路径长（π≈3.1）．23．已知：如图，AB是△O的直径，C是△O上一点，OD△BC于点D，过点C作△O 的切线，交OD的延长线于点E，连接BE．（1）求证：BE与△O相切；（2）连接AD并延长交BE于点F，若OB=9，sin△ABC= 23，求BF的长．24．如图，AB是△O的直径，OE垂直于弦BC，垂足为F，OE交△O于点D，且△CBE=2△C.（1）求证：BE与△O相切；（2）若DF=9，tanC= 34，求直径AB的长.参考答案1．【答案】D2．【答案】D3．【答案】D4．【答案】B5．【答案】C6．【答案】A7．【答案】A8．【答案】C9．【答案】B10．【答案】D11．【答案】A12．【答案】B13．【答案】1或214．【答案】1415．【答案】(20√3−20)16．【答案】√31817．【答案】（25﹣5 √3）18．【答案】45.8米19．【答案】（1）解：在Rt△ABC中△C=90°，△A=30°∴△B=90°-△A=60°，AB=2BC=2 √3∴AC= √AB2−BC2=√(2√3)2−(√3)2=3；（2）解：如图，过点B作BD△AC于D∵△A=45°∴△ABD=△A=45°∴AD=BD∵AB=4，AD2+BD2=AB2∴AD=BD= 2√2在Rt△BCD中BC=3∴CD=√BC2−BD2=1∴AC=AD+CD= 2√2+1.20．【答案】（1）60°（2）由作图可知AB=AC，AD平分∠PAQ∴AE⊥BC．∵∠PAQ=60°∴∠BAE=30°．在Rt△ABC中AE=AB⋅cos30°=4×√32=2√3．答：AE的长为2√3．21．【答案】（1）解：如图，连接OA；∵△C=60°∴△AOB=120°；而OA=OB∴△OAB=△OBA=30°；而AB=AP∴△P=△ABO=30°；∵△AOB=△OAP+△P∴△OAP=120°﹣30°=90°∴PA是△O的切线．（2）解：如图，过点O作OM△AB，则AM=BM= √3∵tan30°= OMAM sin30°=OMAO∴OM=1，OA=2；∴S△AOB=12·AB·OM= 12× 2√3×1= √3S扇形OAB =120π⋅22360= 4π3∴图中阴影部分的面积= 4π3−√3．22．【答案】（1）解：如图，过点A作AP△OC于点P，过点B作BQ△OC于点Q∵△EOA=30°、△FOB=60°，且OC△EF∴△AOP=60°、△BOQ=30°设OA=OB=x则在Rt△AOP中OP=OAcos△AOP= 1 2x在Rt△BOQ中OQ=OBcos△BOQ= √32x由PQ=OQ﹣OP可得√32x﹣12x=7解得：x=7+7 √3≈18.9（cm）答：单摆的长度约为18.9cm（2）解：由（1）知，△AOP=60°、△BOQ=30°，且OA=OB=7+7 √3∴△AOB=90°则从点A摆动到点B经过的路径长为90⋅π⋅(7+7√3)180≈29.295答：从点A摆动到点B经过的路径长为29.295cm 23．【答案】（1）证明：连接OC∵OD△BC∴△COE=△BOE在△OCE和△OBE中∵{OC=OB∠COE=∠BOEOE=OE∴△OCE△△OBE∴△OBE=△OCE=90°，即OB△BE∵OB 是△O 半径∴BE 与△O 相切．（2）解：过点D 作DH△AB ，连接AD 并延长交BE 于点F∵△DOH=△BOD ，△DHO=△BDO=90°∴△ODH△△OBD∴OD OB =OH OD =DH BD又∵sin△ABC= 23，OB=9 ∴OD=6易得△ABC=△ODH∴sin△ODH= 23 ，即 OH OD = 23∴OH=4∴DH= √OD 2−OH 2 =2 √5又∵△ADH△△AFB∴AH AB = DH FB 1318 = 2√5FB∴FB= 36√51324．【答案】（1）证明：∵OE 垂直于弦BC∴△BOE+△OBF=90°∵△CBE=2△C ， △BOE=2△C∴△CBE=△BOE∴△CBE+△OBF=90°∴△OBE=90°∴BE 与△O 相切；（2）解：∵OE 垂直于弦BC∴△CFD=△BFO=90°，CF=BF.∵DF=9，tanC= 34∴CF=BF=12.设半径长是x，则OF=x-9在Rt△BOF中∵x2=(x-9)2+122∴x= 25 2∴直径AB=25.。

锐角三角函数知识点总结与复习

锐角三角函数知识点总结与复习1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方;2、如下图,在Rt △ABC 中,∠C 为直角, 则∠A 的锐角三角函数为∠A 可换成∠B ：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值;4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余角的正切值;5、0°、30°、45°、60°、90°特殊角的三角函数值重要A 90B 90∠-︒=∠︒=∠+∠得由B A邻边A90B 90∠-︒=∠︒=∠+∠得由B A直角三角形中的边角关系解直角三角形当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小; 7、正切、余切的增减性：当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小;一、知识性专题专题1：锐角三角函数的定义例 1 在Rt △ABC 中,∠ACB ＝90°,BC ＝1,AB ＝2,则下列结论正确的是 A ．sin A B ．tan A ＝12C ．cos BD ．tan B 分析 sin A ＝BC AB ＝12,tan A ＝BC AC ,cos B ＝BCAB ＝12．故选D.例2 在△ABC 中,∠C ＝90°,cos A ＝35,则tan A 等于；分析在Rt △ABC 中,设AC ＝3k ,AB ＝5k ,则BC ＝4k ,由定义可知tan A ＝4433BC k AC k ==．分析在Rt △ABC 中,BC =3,∴sin A ＝35BC AB =．故填35．例312·哈尔滨在Rt △ABC 中,∠C=900,AC=4,AB=5,则sinB 的值是；解析本题考查了锐角三角函数的意义．解题思路：在直角三角形中,锐角的正弦等于对边比邻边,故sinB=54. 例42012内江如图4所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为；解析欲求sinA,需先寻找∠A 所在的直角三角形,而图形中∠A 所在的△ABC 并不是直角三角形,所以需要作高．观察格点图形发现连接CD 如下图所示,恰好可证得CD ⊥AB,于是有图4图4sinA ＝CD AC ＝210＝55．例5 2012宁波,Rt △ABC,∠C=900,AB=6,cosB=错误!,则BC 的长为；解析cosB=错误!=错误!,又∵AB=6∴BC=4例62012贵州铜仁如图,定义：在直角三角形ABC 中,锐角α的邻边与对边的比叫做角α的余切,记作ctan α, 即ctan α=BCAC=的对边角的邻边角αα,根据上述角的余切定义,解下列问题：1ctan30◦= ；2如图,已知tanA=43,其中∠A 为锐角,试求ctanA 的值．分析1可先设最小边长为一个特殊数这样做是为了计算方便,然后在计算出其它边长,根据余切定义进而求出ctan30◦;2由tanA=43,为了计算方便,可以设BC=3 AC=4根据余切定义就可以求出ctanA 的值．解析1设BC=1, ∵α=30◦∴AB=2∴由勾股定理得：AC=3ctan30◦=BCAC=32 ∵tanA=43∴设BC=3 AC=4∴ctanA =BC AC =34例72012山东滨州把△ABC 三边的长度都扩大为原来的3倍,则锐角A 的正弦函数值 A ．不变B ．缩小为原来的13C ．扩大为原来的3倍D ．不能确定解析因为△ABC 三边的长度都扩大为原来的3倍所得的三角形与原三角形相似,所以锐角A 的大小没改变,所以锐角A 的正弦函数值也不变．答案选A ．例82012湖南观察下列等式 ①sin30°= cos60°=②sin45°=cos=45°=③sin60°= cos30°=根据上述规律,计算sin 2a+sin 290°﹣a= ．解析：根据①②③可得出规律,即sin 2a+sin 290°﹣a=1,继而可得出答案．答案：解：由题意得,sin 230°+sin 290°﹣30°=1；sin 245°+sin 290°﹣45°=1； sin 260°+sin 290°﹣60°=1；故可得sin 2a+sin 290°﹣a=1．故答案为：1．点评：此题考查了互余两角的三角函数的关系,属于规律型题目,注意根据题意总结,另外sin 2a+sin 290°﹣a=1是个恒等式,同学们可以记住并直接运用．例9 2012山东德州为了测量被池塘隔开的A ,B 两点之间的距离,根据实际情况,作出如下图形,其中AB BE ⊥,EF BE ⊥,AF 交BE 于D ,C 在BD 上．有四位同学分别测量出以下四组数据：22题图①BC ,∠ACB ； ②CD ,∠ACB ,∠ADB ；③EF ,DE ,BD ；④DE ,DC ,BC ．能根据所测数据,求出A ,B 间距离的有哪组解析对于①,可由公式AB=BC ×tan ∠ACB 求出A 、B 两点间的距离；对于②,可设AB 的长为x,则BC=x tan ACB ∠,BD=xtan ADB ∠,BD-BC=CD,可解出AB ．对于③,易知△DEF ∽△DBA,则DE BDEF AB=,可求出AB 的长；对于④无法求得,故有①、②、③三组点评此题考查解直角三角形和三角形相似的性质与判定．在直角三角形中至少要有已知一边和一角才能求出其他未知元素；判定两三角形相似的方法有：AA,SAS,SSS,两直角三角形相似的判定还有HL ．例102012江苏泰州18如图,在边长相同的小正方形组成的网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB 、CD 相交于点P,则tan ∠APD 的值是．解析要求tan ∠APD 的值,只要将∠APD 放在直角三角形中,故过B 作CD 的垂线,然后利用勾股定理计算出线段的长度,最后利用正切的定义计算出结果即可．答案作BM ⊥CD,DN ⊥AB 垂足分别为M 、N,则2,易得：10,设PM=x,则PD=22-x,由△DNP ∽△BMP,得：PN DN PM BM =,即10102PN x =,∴PN=55x,由DN 2+PN 2=PD 2,得：110+15x 2=22-x 2,解得：x 1=24,x 2=2舍去,∴tan ∠APD=2224BM PM ==2．例11. 2011江苏苏州如图,在四边形ABCD 中,E 、F 分別是AB 、AD 的中点,若EF=2,BC=5,CD=3,则tanC 等ABCDEFF于．分析：根据三角形的中位线定理即可求得BD 的长,然后根据勾股定理的逆定理即可证得△BCD 是直角三角形,然后根据正切函数的定义即可求解．解答：解：连接BD ．∵E 、F 分別是AB 、AD 的中点．∴BD=2EF=4∵BC=5,CD=3∴△BCD是直角三角形．∴tanC= 43例122011山东日照在Rt△ABC 中,∠C=90°,把∠A 的邻边与对边的比叫做∠A 的余切,记作cotA=ab．则下列关系式中不成立的是A ．tanA•cotA=1B ．sinA=tanA•cosAC ．cosA=cotA•sinAD ．tan 2A+cot 2A=1解答：解：根据锐角三角函数的定义,得 A 、tanA•c otA=a b b a ⋅=1,关系式成立；B 、sinA=c a ,tanA•cosA=cac b b a =⋅,关系式成立； C 、cosA=,cotA•sinA=c b a b c a =⋅,关系式成立；D 、tan 2A+cot 2A=b a 2+ab 2≠1,关系式不成立．故选D ．点评：本题考查了同角三角函数的关系．1平方关系：sin 2A+cos 2A=1 2正余弦与正切之间的关系积的关系：一个角的正切值等于这个角的正弦与余弦的比,即tanA=BAcos sin 或sinA=tanA•cosA．3正切之间的关系：tanA•tanB=1．例132011•贵港如图所示,在△ABC 中,∠C=90°,AD 是BC 边上的中线,BD=4,AD=2,则tan∠CAD 的值是．解答：解：∵AD 是BC边上的中线,BD=4,∴CD=BD=4,在Rt△ACD中,AC===2,∴tan∠CAD===2．故选A ．例142011烟台如果△ABC 中,sin A =cos B 2,则下列最确切的结论是 A. △ABC 是直角三角形 B. △ABC 是等腰三角形C. △ABC 是等腰直角三角形D. △ABC 是锐角三角形解：∵sinA=cosB=22,∴∠A =∠B =45°,∴△ABC 是等腰直角三角形．故选C ．例152011四川如图所示,在数轴上点A 所表示的数x 的范围是A 、330sin 602sin x ︒︒<< B 、3cos302x ︒︒<<cos45C 、3tan 302x ︒︒<<tan45D 、3cot 4502x ︒︒<<cot3 解答：故选D ．同步练习12011甘肃如图,A 、B 、C 三点在正方形网格线的交点处,若将△ACB 绕着点A 逆时针旋转得到△AC ’B ’,则tanB ’的值为．解答：解：过C 点作CD ⊥AB ,垂足为D ．根据旋转性质可知,∠B′=∠B ．在Rt△BCD 中,tanB= CD ：BD =13,∴tan B′=tan B = 13． 2 2011甘肃兰州点M －sin60°,cos60°关于x 轴对称的点的坐标是．解：∵sin60°=32,cos60°= 12,∴点M －32,12．∵点P m ,n 关于x 轴对称点的坐标P′m ,-n ,∴M 关于x 轴的对称点的坐标是－32,－12．故选B ． 32011广东已知：45°＜A ＜90°,则下列各式成立的是A 、sinA =cosAB 、sinA ＞cosAC 、sinA ＞tanAD 、sinA ＜cosA解答：解：∵45°＜A ＜90°,∴根据sin 45°=cos 45°,sinA 随角度的增大而增大,cosA 随角度的增大而减小,当∠A ＞45°时,sinA ＞cosA ,故选：B ．4、2011•宜昌教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=33,则边BC 的长为．cm解：在直角三角形ABC 中,根据三角函数定义可知：tan ∠BAC=BCAC,又AC=30cm,tan ∠3则BC=ACtan 33cm ．故选C ． 5、 2011福建莆田如图,在矩形ABCD 中,点E 在AB 边上,沿CE 折叠矩形ABCD ,使点B 落在AD 边上的点F 处,若AB =4,BC=5,则tan ∠AFE 的值为．ABCC ’ B ’解答：解：∵四边形ABCD 是矩形,∴∠A =∠B =∠D =90°,CD =AB =4,AD =BC =5,由题意得：∠EFC =∠B =90°,CF =BC =5,∴∠AFE +∠DFC =90°,∠DFC +∠FCD =90°, ∴∠DCF =∠AFE ,∵在Rt △DCF 中,CF =5,CD =4,∴DF =3,∴tan ∠AFE =tan ∠DCF =DFDC =34 ．6、2012连云港小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD 沿过点B的直线折叠,使点A 落在BC 上的点E 处,还原后,再沿过点E 的直线折叠,使点A 落在BC 上的点F 处,这样就可以求出°的角的正切值是．EC DA BF答案设AB=x,则BE=x,在直角三角形ABE 中,用勾股定理求出AE=EF=2x,于是2在直角三角形ABF 中,tan ∠FAB=21)BF xAB x=2°.选B; 7、2012福州如图15,已知△ABC,AB=AC=1,∠A=36°,∠ABC 的平分线BD 交AC 于点D,则AD 的长是 ,cosA 的值是 .结果保留根号解析：由已知条件,可知△BDC 、△ADB 是等腰三角形,且DA=DB=BC,可证△BDC ∽△ABC,则有BC DC AC BC =,设BC=x,则DC=1-x,因此21,101x xx x x -=+-=即,解方程得, 125151x x ---==,舍去,即AD=512；又cosA=512451512AB AD===--⨯答案：5151,24 8、2012南京如图,将45°的∠AOB 按下面的方式放置在一把刻度尺上：顶点O 与尺下沿的端点重合,OA 与尺下沿重合.OB 与尺上沿的交点B 在尺上的读书恰为2厘米,若按相同的方式将37°的∠AOC 放置在该刻度尺上,则OC 与尺上沿的交点C 在尺上的读数为厘米.结果精确到厘米,参考数据sin370≈,cos370≈,tan370≈C B AO4321解析：由于∠AOB=45°,B 点读书为2厘米,则直尺的宽为2厘米,解直角三角形得点C 的读数为2÷tan370≈2÷≈厘米.答案：9、2012·湖南张家界黄岩岛是我国南海上的一个岛屿,其平面图如图甲所示,小明据此构造出该岛的一个数学模型如图乙所示,其中∠A=∠D=90°,AB=BC=15千米,CD=23千米,请据此解答如下问题：1 求该岛的周长和面积结果保留整数,参考数据2≈ 73.13≈45.26≈ 2 求∠ACD 的余弦值.解答1结AC,∵AB=BC=15千米,∠B=90°,∴∠BAC=∠ACB=45°,AC=152千米. 又∵∠D=90°, ∴AD=2222)23()215(-=-CD AC =123千米∴周长=AB+BC+CD+DA=30+32+123=30++≈55千米. 面积=S △ABC +S △ADC =21×15×15+21×123×32=2225+186≈157平方千米. 2cos ∠ACD=5121523==AC CD . 10、2012甘肃兰州在建筑楼梯时,设计者要考虑楼梯的安全程度;如图1,虚线为楼梯的倾斜度,斜度线与地面的夹角为倾角θ,一般情况下,倾角越小,楼梯的安全程度越高；如图2,设计者为了提高楼梯的安全程度,要把楼梯的倾角1θ减至2θ,这样楼梯占用地板的长度由d 1增加到d 2 ,已知d 1=4米,140θ∠=,236θ∠=,楼梯占用地板的长度增加了多少米计算结果精确到米;参考数据：tan40°=,tan36°=AC解析：根据在Rt△ACB中,AB=d1tanθ1=4tan40°,在Rt△ADB中,AB=d2tanθ2=d2tan36°,即可得出d2的值,进而求出楼梯占用地板增加的长度．解：由题意可知可得,∠ACB=∠θ1,∠ADB=∠θ2在Rt△ACB中,AB=d1tanθ1=4tan40°,在Rt△ADB中,AB=d2tanθ2=d2tan36°,得4tan40°=d2tan36°,∴d2=4tan40tan36≈,∴d2-d1==≈,答：楼梯占用地板的长度增加了米．11、2012贵州为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长．参考数据：sin54°≈,cos54°≈,tan54°≈,≈,精确到个位解析：首先过点C作CD⊥AB于D,然后在Rt△BCD中,利用三角函数的知识,求得BD,CD的长,继而在Rt△ACD 利用∠CAB的正切求得AD的长,继而求得答案．答案：解：过点C作CD⊥AB于D∵BC=200m,∠CBA=30°,∴在Rt△BCD中,CD=BC=100m,BD=BC•cos30°=200×=100≈173m,∵∠CAB=54°,在Rt△ACD中,AD=≈≈74m,∴AB=AD+BD=173+74=247m．答：隧道AB的长为247m．12、2011新疆建设兵团如图,在△ABC中,∠A＝90°．1用尺规作图的方法,作出△ABC绕点A逆时针旋转45°后的图形△AB1C1保留作图痕迹；2若AB＝3,BC＝5,求tan∠AB1C1．第22题图d2解答：解：1作∠CAB 的平分线,在平分线上截取AB 1＝AB ,作C 1A ⊥AB 1,在AC 1上截取AC 1＝AC ,如图所示即是所求．2∵AB ＝3,BC ＝5,∴AC ＝4,∴AB 1＝3,AC 1＝4,tan∠AB 1C 1＝错误!＝错误!．专题2 特殊角的三角函数值例12012,湖北孝感计算：cos 245°+tan30°·sin60°=________．答案1例22012陕西计算：(02cos 45-38+1-2=︒　．解析原式2=2-322+1=-52+12⨯⨯答案-52+1 例32012广安计算：---)32(218cos45o +13- ；解析：1182()cos 4533---︒+=322212323+-+21 例4 计算|－3|＋2cos 45310．解：原式＝3＋22－122．例5 计算－12⎛⎫- ⎪⎝⎭9＋－12007－cos 60°．解：原式＝12＋3＋－1－12＝3－1＝2．例6 计算|2＋cos 60°－tan 30°08 21十＋221．例7 计算312-⎛⎫ ⎪⎝⎭－π－0－|1－tan 60°|32-.解：原式＝8－13132＝10. 例82012呼和浩特计算：11|122sin 45--+︒解析三角函数、绝对值、乘方答案11|12sin 45--+︒11)2211232=-+=+=例92011天水计算：si n 230°+tan 44°tan 46°+si n 260°= ．分析：根据特殊角的三角函数值计算．tanA •tan 90°﹣A =1．解答：解：原式=14+1+34=2．故答案为2．例102011•莱芜若a=3﹣tan60°,则196)121(2-+-÷--a a a a = ;33-解答：解：a=3﹣tan60°=3﹣3,∴原式=23-a 1-a 121）（⨯---a a =31-a =33313331-=-=--故答案为：33-．练习1、2011浙江计算：|－1|5－π0+4cos45°. 解原式=1－122练习2、2011浙江衢州1计算：|﹣2|﹣3﹣π0+2c os45°；解答：解：1原式=2122-+⨯,=1 练习3、计算：20110＋8－2sin45°；原式＝1＋22－2＝1＋2；练习3、观察下列各式：①sin 59°＞sin 28°；②0＜cos α＜1α是锐角；③tan 30°＋tan 60°＝tan 90°；④tan 44°＜1．其中成立的有A ．1个B ．2个C ．3个D ．4个练习3、C 提示：sin 59°＞sin 28°成立,0＜cos α＜1α是锐角成立,tan 30°＋tan 60tan 90°,tan 44°＜tan 45°,即tan 44°＜1．练习4、计算2sin 30°－tan 60°＋tan 45°＝．练习5、如图28－146所示,在△ABC 中,∠A ＝30°,tan B ＝13,BC 10则AB 的长为．练习6、当x ＝sin 60°时,代数式2242x x x -+·22244x x x x +-+＋42xx-的值是．练习7、已知cos 59°24′≈,则sin 30°36′≈ ．练习8、若∠A ,∠B 互余,且tan A －tan B ＝2,则tan 2A ＋tan 2B ＝．练习9、如图28－147所示,在菱形ABCD 中,AE ⊥BC 于E ,EC ＝1,cos B＝513,则这个菱形的面积是 . 10．已知正方形ABCD 的边长为1,若将线段BD 绕着点B 旋转后,点D落在DC 延长线上的点D ′处,则∠BAD ′的正弦值为 . 11．如图28－148所示,若将四根木条钉成的矩形木框变为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角等于．12．在△ABC 中,∠B ＝30°,tan C ＝2,AB ＝2,则BC ＝．13．设θ为锐角,且x 2＋3x ＋2sin θ＝05．则θ＝． 14．如图28－149所示,在△ABC 中,∠C ＝90°,点D 在BC 边上,BD ＝4,AD ＝BC ,cos ∠ADC ＝35． 1求DC 的长；2求sin B 的值．练习4、23 提示：2sin 30°－tan 60°＋tan 45°＝2×1231＝23 练习5、33提示：过点C 作CD ⊥AB ,垂足为D ,在Rt △BDC 中,tan B ＝13．∴13CD BD =,∴BD ＝3CD ,∵BC 10∴CD 2＋3CD 210,∴CD ＝1,BD ＝3．在Rt △ADC 中,tan A ＝CDAD,∴AD 3∴AB ＝AD ＋BD ＝33 练习632242x x x -+·22244x x x x +-+＋42xx-＝2x ,∴原式＝2sin 603练习7、提示：sin 30°36′＝cos 59°24′．练习8、6提示：∵∠A ,∠B 互余,∴tan A ·tan B ＝1,tan 2A ＋tan 2B ＝tan A －tan B 2＋2tan A ·tan B ＝22＋2＝6．练习9、3916提示：∵cos B ＝513,设BE ＝5x ,则AB ＝13x ,∴AE 22AB BE -12x ．∵AB ＝BC ＝BE ＋CE ,∴13x ＝5x ＋1,∴x ＝18,则AE ＝12x ＝12×18＝32,BC ＝5x ＋1＝5×18＋1＝138,∴S ＝32×138＝3916．10．5提示:如图28－155所示,根据题意得DD ′＝2DC ,设正方形的边长为x ,则AD ＝x ,DD ′＝2x ．∵∠ADD ′＝90°,根据勾股定理得AD 22AD DD '+5x ．∵AD ＝x ,∴sin ∠AD ′D ＝ADAD '＝555x x=.∵AB ∥DD ′,∴∠BAD ′＝∠AD ′D ,∴sin ∠BAD ′＝55．11．30°提示：如图28＝156所示,∵S ABCD＝12S 矩形BEFC ,且BC ＝BC 底相同, ∴GC ＝12FC ．∵CF ＝DC ,∴GC ＝12DC ,12CG DC =．∵∠DGC ＝90°,sin 30°＝12,∴∠CDG ＝30°,即这个平行四边形的一个最小内角为30°． 12．12＋3 13．30°提示：x 1·x 2＝2sin θ,x 1＋x 2＝－3,则x 1－x 22＝x 1＋x 22－4x 1x 2＝9－8sin θ＝52,∴sin θ＝12,∴θ＝30°． 14．解：1∵cos ∠ADC ＝35,∴设CD ＝3x ,则AD ＝5x ,AC ＝4x ,∴BC ＝AD ＝5x ．∵BD ＝BC－CD ,∴5x －3x ＝4,∴x ＝2,∴CD ＝3x ＝6． 2∵AC ＝4x ＝8,BC ＝5x ＝10,∴AB ＝2222810241AC BC +=+=,∴sin B ＝844141241AC AB ==． ★ 专题三：题型一俯角与仰角仰角：视线在水平线上方的角；★ 俯角：视线在水平线下方的角;仰角铅垂线水平线视线视线俯角例1、2012湖北襄阳在一次数学活动中,李明利用一根拴有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD ．如图5,已知李明距假山的水平距离BD 为12m,他的眼睛距地面的高度为,李明的视线经过量角器零刻度线OA 和假山的最高点C,此时,铅垂线OE 经过量角器的60°刻度线,则假山的高度为 m ．解析如下图,过点A 作AF⊥CD 于F,则AF ＝BD ＝12m,FD ＝AB ＝．再由OE∥CF 可知∠C＝∠AOE＝60°．所以,在Rt△ACF 中,CF ＝tan 60AF＝43,那么CD ＝CF ＋FD ＝43＋m ．例2、2012珠海如图,水渠边有一棵大木瓜树,树干DO 不计粗细上有两个木瓜A 、B 不计大A O BE D CF图5 CDA BO E小,树干垂直于地面,量得AB=2米,在水渠的对面与O 处于同一水平面的C 处测得木瓜A 的仰角为45°、木瓜B 的仰角为30°.求C 处到树干DO 的距离CO.结果精确到1米参考数据：41.12,73.13≈≈第16题图D BA OC解析如图,根据题意,得∠COD ＝90°, ∠ACO ＝45°, ∠BCO ＝30°, AB ＝2,求CO.设CO 为x 米, 根据AO ＝CO,列方程,解得即可.答案解:设CO 为x 米在Rt △BCO 中,tan30°＝BO CO ,则BO ＝33x 在Rt △ACO 中,AO ＝CO,得方程33x ＋2＝x 解得x ≈5.答: CO 长大约是5米. 例3、2012江苏盐城如图所示,当小华站立在镜子EF 前A 处时,他看自己的脚在镜中的像的俯角为450 ：如果小华向后退米到B 处,这时他看自己的脚在镜中的像的俯角为300.求小华的眼睛到地面的距离;结果精确到米,参考数据：3≈.答案设AC=BD=x,在Rt △ACA 1中,∠AA 1C=450,∴AA 1=x,在Rt △DBB 1中,BB 1=tan30x=3x ,又∵12BB 1-12AA 1=12,即12×3x -12x=12,解得：x=312+≈米．例4、2012山西如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A ．B 的距离,飞机在距海平面垂直高度为100米的点C 处测得端点A 的俯角为60°,然后沿着平行于AB 的方向水平飞行了500米,在点D 测得端点B 的俯角为45°,求岛屿两端A ．B 的距离结果精确到米,参考数据：解析解：过点A 作AE⊥CD 于点E,过点B 作BF⊥CD 于点F,∵AB∥CD,∴∠AEF=∠EFB=∠ABF=90°,∴四边形ABFE 为矩形．第24题图∴AB=EF,AE=BF．由题意可知：AE=BF=100米,CD=500米．…2分在Rt△AEC 中,∠C=60°,AE=100米．∴CE===米． …4分在Rt△BFD中,∠BDF=45°,BF=100． ∴DF===100米．…6分∴AB=EF=CD+DF﹣CE=500+100﹣≈600﹣×≈600﹣≈米． …8分答：岛屿两端A ．B 的距离为米．例5、2012呼和浩特22如图,线段AB 、DC 分别表示甲、乙两建筑物的高;某初三课外兴趣活动小组为了测量两建筑物的高,用自制测角仪在B 处测得D 点的仰角为α,在A 处测得D 点的仰角为β;已知甲、乙两建筑物之间的距离BC 为m ;请你通过计算用含α、β、m 的式子分别表示出甲、乙两建筑物的高度;答案解：过点A 作AM ⊥CD 于M在Rt △BCD 中,tan α=CD BC ∴CD =BC ·tan α=m tan α在Rt △AMD 中,tan β=DMAM∴DM =AM ·tan β=m tan β∴AB =CD –DM =mtan α–tan β例6、2012湖北随州,20在一次暑假旅游中,小亮在仙岛湖的游船上A 处,测得湖西岸的山峰太婆尖C 处和湖东岸的山峰老君岭D 处的仰角都是45°,游船向东航行100米后B 处,测得太婆尖、老君岭的高度为多少米3 1.732 ,结果精确到米;解析：设太婆尖高h 1米,老君岭高h 2米;可分别在直角三角形中利用正切值表示出水平线段的长度,再利用移动距离为AB=100米,可建立关于h 1、h 2的方程组,解这个方程组求得两山峰高度;答案：设太婆尖高h 1米,老君岭高h 2米,依题意,有FE第20题图60304545D (老君岭)C （太婆尖）BAβα乙甲ADB M C⇒⎪⎪⎩⎪⎪⎨⎧=-=-10060tan 45tan 10045tan 30tan 2211h h h h 1376.136)1732.1(50)13(5045tan 60tan 1001≈=+=+=-=h 米33110030tan 45tan 1002-=-=h 2376.236)732.13(50)33(50)13(350≈=+=+=+=米答：太婆尖高度为137米,老君岭高度为237米;题型二方位角问题1、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角;如图3,OA 、OB 、OC 、OD 的方向角分别是：45°、135°、225°;2、指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角;如图4：OA 、OB 、OC 、OD 的方向角分别是：北偏东30°东北方向,南偏东45°东南方向,南偏西60°西南方向,北偏西60°西北方向;例1、2011山东省潍坊轮船从B 处以每小时海里的速度沿男偏东30°方向匀速航行,在B 处观测灯塔A 位于南偏东75°方向上,轮船航行半小时到达C 处,在观测灯塔A 北偏东60°方向上,则C 处与灯塔A 的距离是．海里解答： BC=50×=25海里；根据方位角知识得,∠BCD=30°,=75°－30°；CB=∠BCD+∠ACD=30°+60°=90°；∠A=∠CBD=45°所以CA=CB 所以CB=25海里例2、2012年四川德阳某时刻海上点P 处有一客轮,测得灯塔A 位于客轮P 的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏西60°方向航行32小时到达B 处,那么tan ∠ABP=A.21 C.55 D.552解析如图6所示,根据题意可知∠APB=90°．且AP=20, PB=60×23=40. 所以tan ∠ABP=201402PA PB ==例3、2012连云港已知B 港口位于A 观测点北偏东°方向,且其到A 观测点正北方向的距离BD 的长为16km;一艘货轮从B 港口以40km/h 的速度沿如图所示的BC 方向航行,15min 后到达C 处;现测得C 处位于Ａ观测点北偏东°方向;求此时货轮与A 观测点之间的距离AC 的长精确到.25东北CBDCBH解析过点B 作AC 的垂线,把所求线段AC 换为两线段的差;利用Rt △ABH 和Rt △BCH 求线段AH 、CH 的长,利用AH －CH 确定AC 的长; 答案BC=40×1560=10.在Rt△ADB 中,sin ∠DAB=DB AB , °≈;所以AB=DAB DB ∠sin ≈1.60.8=20.如图,过点B 作BH⊥AC,交AC 的延长线于H;在Rt△AHB 中,∠BAH=∠DAC －∠DAB=°―37°=°,tan∠BAH=BH AH ,=BH AH,AH =＋CH 2=AB 2,BH 2+2BH 2=2025所以AH=85,在Rt△AHB 中, BH 2＋CH 2=BC 2,CH=2108025-=所以第22题图APCB °°AC=AH―CH=85―25＝65≈.例4、2012四川攀枝花如图6,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场．若渔政310船航向不变,航行半小时后到达B 处,此时观测到我渔船C在北偏东30°方向上．问渔政310船再航行多久,离我渔船C的距离最近假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值．答案作CD⊥AB于D,设BD=x,∵∠BCD=30°,∴CD=3x,因为∠CAD=45°,∴AD=CD3,AB3–x,依据题意3x–x=,x 31+,31+小时,离渔船C的距离最近;例5、2012山东东营如图某天上午9时,向阳号轮船位于A处,观测到某港口城市P位于轮船的北偏西°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到城市P位于该船的南偏西°方向,求此时轮船所处位置B 与城市P的距离参考数据：°≈35,°≈34,°≈1213,°≈125解析过点P作PC⊥AB,构造直角三角形,设PC=x海里,用含有x的式子表示AC,BC的值,从而求出x的值,再根据三角函数值求出BP的值即可解答．答案过点P作PC⊥AB,垂足为C,设PC=x海里．在Rt△APC中,∵tan∠A=PCAC,∴AC=5tan67.512PC x=︒．在Rt△PCB中,∵tan∠B=PCBC,∴BC=4tan36.93x x=︒．∵AC＋BC=AB=21×5,∴54215123x x+=⨯,解得60x=.∵sinPCBPB∠=,∴60560100sin sin36.93PCPBB===⨯=∠︒海里．∴向阳号轮船所处位置B与城市P的距离为100海里．例6、2012山东省青岛如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE ；而当光线与地面夹角是45°时,教学楼顶A 在地面上的影子F 与墙角C 有13米的距离B 、F 、C 在一条直线上 ⑴求教学楼AB 的高度；⑵学校要在A 、E 之间挂一些彩旗,请你求出A 、E 之间的距离结果保留整数.参考数据：sin22°≈错误!,cos22°≈错误!,tan22°≈错误! 答案解：⑴过点E 作EM ⊥AB,垂足为M.设AB 为x.Rt △ABF 中,∠AFB=45°,∴BF=AB=x,∴BC=BF+FC=x+13在Rt △AEM 中,∠AEM=22°,AM=AB-BM=AB-CE=x-2,∴tan22°= 错误!, 错误!=错误!,x=12.即教学楼的高12m.⑵由1可得ME=BC=x+13=12+13=25.在Rt △AME 中,cos22°= 错误!, ∴ＡＥ＝错误!≈ 错误!≈２７．即ＡＥ之间的距离约为２７ｍ．题型三、坡比是垂直高度与水平距离的比值,即是坡角的正切值应用举例：坡面的铅直高度h 和水平宽度l 的比叫做坡度坡比;用字母i 表示,即hi l=;坡度一般写成1:m 的形式,如1:5i =等;把坡面与水平面的夹角记作α叫做坡角,那么tan hi lα==;例1、2012广安如图2,某水库堤坝横断面迎水坡AB 的坡比是1：3,堤坝高BC=50m,则迎水坡面AB 的长度是．m解：tan∠BAC=13,∠BAC=30°,sin∠BAC=12, sin∠BAC=BC AB ,AB=2BC=100m例2、小强在教学楼的点P 处观察对面的办公大楼．为了测量点P 到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A 的仰角为45°,测得办公大楼底部点B 的俯角为60°,已知办公大楼高46米,CD ＝10米．求点P 到AD 的距离用含根号的式子表示．图2:i h l=hlαABCDPN M解析连结PA 、PB ,过点P 作PM ⊥AD 于点M ；延长BC ,交PM 于点N则∠APM =45°,∠BPM =60°,NM =10米………1分设PM =x 米在Rt △PMA 中,AM =PM ×tan ∠APM =x tan 45°＝x 米…3分在Rt △PNB 中,BN =PN ×tan ∠BPM =x －10tan 60°＝x －103米…5分由AM +BN =46米,得x +x －103 ＝46……6分解得,4610313x +=+ ,∴点P 到AD 的距离为4610313++米．结果分母有理化为()1838-米也可……8分答案4610313++结果分母有理化为()1838-米也可例3、2012湖北如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A ,斜坡的起始点为C ,现设计斜坡BC 的坡度1:5i =,则AC 的长度是 cm ．解析如图,过点B 作BD ⊥AC 于D,依题意可求得AD ＝60cm,BD ＝54cm ；由斜坡 BC 的坡度i ＝1：5,求得CD ＝270cm,故AC ＝CD －AD ＝270－60＝210cm ．例4、2012浙江省绍兴,19如图1,某超市从一楼到二楼的电梯AB 的长为米,按坡角∠BAC 为32°.1求一楼与二楼之间的高度BC 精确到米；2电梯每级的水平级宽均是米,如图2.小明跨上电梯时,该电梯以每少上升2级的高度运行,10秒后他上升了多少米精确到米备用数据：sin 32°=,cos 32°=,tan 32°=.解析1在Rt△ABC 中,已知∠B AC=32°,斜边AB 的长为米,根据锐角三角函数的定义即可求得第20题图MPDCBA第12题A BC3018一楼与二楼之间的高度BC ．2先计算1级电梯的高,再根据10秒钟电梯上升了20级可计算10秒后他上升的高度．答案解：1∵sin ∠BAC =ABBC ,∴BC =AB ×sin32°=×≈米. 2∵tan32°= 级高级宽,∴级高=级宽×tan32°=×=,∵10秒钟电梯上升了20级,∴小明上升的高度为：20×米. 例5、2012浙江丽水,19学校校园内有一小山坡,经测量,坡角∠ABC=30°,斜坡AB 长为12米.为方便学生行走,决定开挖小山坡,使斜坡BD 的坡比是1:3即为CD 与BC 的长度之比,A,D 两点处于同一铅垂线上,求开挖后小山坡下降的高度AD.解析：∴AD=AC-CD=6-23.答：开挖后小山坡下降的高度AD 为6-23米.例6、2012深圳小明想测一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图3,此时测得地面上的影长为8米,坡面上的影长为4米,已知斜坡的坡角为30,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为．米解答：如图3—1,根据坡角易求树的下半部分的高为2米,树的上半部分所在直角三角形的水平距离为(+823米,由两个直接三角形相似易求树的上半部分高度为(43米,知树的高度为()63米,选择A例72012江苏泰州24如图,一居民楼底部B 与山脚P 位于同一水平线上,小李在P 处测得居民楼顶A 的仰角为60°,然后他从P 处沿坡角为45°的山坡上走到C 处,这时,PC=30m,点C 与点A 在同一水平线上,A 、B 、P 、C 在同一平面内．1求居民楼AB 的高度；2求C 、A 之间的距离．精确到,参考数据：2≈,3≈,6≈60° CA B 45°图330°21图3-1第24题图解析过C作BP的垂线,垂足为G,利用特殊Rt△PCG和Rt△ABP中的边角关系,我们容易计算出CG即AB的长,最后用AC=BP+PG,就是C、A之间的距离．答案1过C作BP的垂线,垂足为G,在Rt△PCG中,CG=PCsin450=30×2所以=m2PG= PCcos450=30×2=所以C、A之间的距离例82012四川水务部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD．如图9所示,已知迎水坡面AB的长为16米,∠B＝60°,背水坡面CD的长为,加固后大坝的横截面为梯形ABED,CE的长为8米．1已知需加固的大坝长为150米,求需要填土石方多少立方米2求加固后大坝背水坡面DE的坡度．解析1求出横截面△DCE的面积,然后乘以坝堤长度即可得出体积．可以分别过点A,D 作BC边上的高将问题转化为解直角三角形问题．2求大坝背水坡面DE的坡度就是求坡面DE上一点到BE的铅直高度与它到点E的水平宽度的比,这一点通常取梯形的顶点．答案解：1过点A作AG⊥BC于G,过点D作DH⊥BC于H,∴AG＝DH．在Rt△ABG中,AG＝sin60°·AB×16＝∴DH＝S△DCE＝12·DH·CE＝12×8＝∴需要填土石方150＝3．2在Rt△DHC中,HC24,∴HE＝HC＋CE＝24＋8＝32．∴加固后大坝背水坡面DE的坡度＝DHHE．AB CD图9E例9 2012江苏苏州如图,已知斜坡AB 长60米,坡角即∠BAC 为30°,BC⊥AC,现计划在斜坡中点D 处挖去部分坡体用阴影表示修建一个平行于水平线CA 的平台DE 和一条新的斜坡BE ．请讲下面2小题的结果都精确到米,参考数据：≈．1若修建的斜坡BE 的坡角即∠BEF 不大于45°,则平台DE 的长最多为米；2一座建筑物GH 距离坡角A 点27米远即AG=27米,小明在D 点测得建筑物顶部H 的仰角即∠HDM 为30°．点B 、C 、A 、G 、H 在同一个平面内,点C 、A 、G 在同一条直线上,且HG⊥CG,问建筑物GH 高为多少米解答：解：1∵修建的斜坡BE 的坡角即∠BEF 不大于45°,∴∠BEF 最大为45°当∠BEF=45°时,EF 最短,此时ED 最长,∵∠DAC=∠BDF=30°,AD=BD=30,∴BF=EF=BD=15,DF=15,故：DE=DF ﹣EF=15﹣1≈；2过点D 作DP⊥AC,垂足为P ．在Rt△DPA中,DP=AD=×30=15,PA=AD•cos30°=×30=15．在矩形DPGM 中,MG=DP=15,DM=PG=15+27,在Rt△DMH 中,HM=DM•tan30°=×15+27=15+9． GH=HM+MG=15+15+9≈．答：建筑物GH 高为米．A B C DE GH。

中考数学复习《锐角三角函数和解直角三角形》经典题型及测试题(含答案)

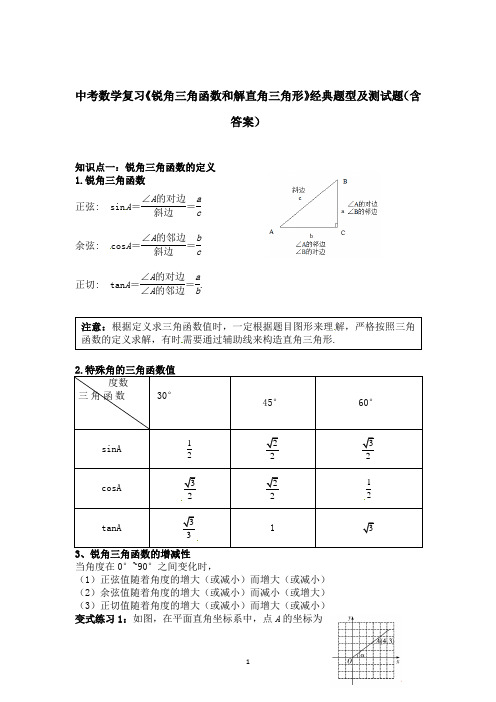
中考数学复习《锐角三角函数和解直角三角形》经典题型及测试题（含答案）知识点一：锐角三角函数的定义 1.锐角三角函数正弦: sin A ＝∠A 的对边斜边＝ac余弦: cos A ＝∠A 的邻边斜边＝bc正切: tan A ＝∠A 的对边∠A 的邻边＝ab.来源:学&科&网]2.特殊角的三角函数值[来度数三角函数[来源:Z 。

xx 。

]30°[来源:学#科#网] 45° 60°sinA1222 32 cosA32 2212tanA 331 33、锐角三角函数的增减性当角度在0°~90°之间变化时，（1）正弦值随着角度的增大（或减小）而增大（或减小）（2）余弦值随着角度的增大（或减小）而减小（或增大）（3）正切值随着角度的增大（或减小）而增大（或减小）变式练习1：如图，在平面直角坐标系中，点A 的坐标为注意：根据定义求三角函数值时，一定根据题目图形来理解，严格按照三角函数的定义求解，有时需要通过辅助线来构造直角三角形.[(4，3)，那么cos α的值是( ) A. 34 B. 43 C. 35 D. 45【解析】D 如解图，过点A 作AB ⊥x 轴于点B ，∵A (4，3)，∴OB ＝4，AB ＝3，∴OA ＝32＋42＝5，∴cos α＝OB OA ＝45.变式练习2：在Rt △ABC 中，∠ABC ＝90°，AB ＝3，BC ＝4，则sinA ＝________．【解析】∵在Rt △ABC 中，由勾股定理得AC ＝22AB BC +＝32＋42＝5，∴sin A ＝BC AC ＝45. 变式练习3：在Rt △ABC 中，∠C ＝90°，sin A ＝35，BC ＝6，则AB ＝( D )A ．4B ．6C ．8D ．10变式练习4：如图，若点A 的坐标为(1，3)，则sin ∠1＝__32__. ,知识点二：解直角三角形 1.解直角三角形的概念在直角三角形中，除直角外，一共有五个元素，即三条边和两个锐角，由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形． 2.解直角三角形的常用关系在Rt △ABC 中，∠C=90°，∠A ，∠B ，∠C 所对的边分别为a ，b ，c (1)三边之间的关系：a 2＋b 2＝c 2；(2)锐角之间的关系：∠A ＋∠B ＝90°； (3)边角之间的关系：,tan ,cos ,sin ;,tan ,cos ,sin abB c a B c b B b a A c b A c a A ======（sinA＝=cosB=ac，c osA＝sinB=bc，tanA＝ab.）变式练习1：在Rt△ABC中，已知a=5,sinA=30°，则c=10,b=5.变式练习2：如图，Rt△ACB中，∠B＝30°，∠ACB＝90°，CD⊥AB交AB于D.以CD为较短的直角边向△CDB的同侧作Rt△DEC，满足∠E＝30°，∠DCE＝90°，再用同样的方法作Rt△FGC，∠FCG＝90°，继续用同样的方法作Rt△HIC，∠HCI ＝90°.若AC＝a，求CI的长．解：在Rt△ABC中，∠B＝30°，∠ACB＝90°，CD⊥AB，∴∠A＝60°，∵AC＝a，∴CD＝AC·sin60°＝32a，依此类推CH＝(32)3a＝338a，在Rt△CHI中，∵∠CHI＝60°，∴CI＝CH·tan60°＝338a×3＝98a.变式练习3：如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝8，则BC的长是( D )A.433B．4 C．8 3 D．4 3,灵活选择解直角三角形的方法顺口溜：已知斜边求直边，正弦、余弦很方便；已知直边求直边，理所当然用正切；已知两边求一边，勾股定理最方便；已知两边求一角，函数关系要记牢；已知锐角求锐角，互余关系不能少；已知直边求斜边，用除还需正余弦.变式练习4：如图，一山坡的坡度为i＝1∶3，小辰从山脚A出发，沿山坡向上走了200米到达点B，则小辰上升了__100__米．, ,变式练习5：一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处，沿正西方向航行3小时后到达小岛的北偏西45°的C处，则该船行驶的速度为___40＋4033___海里/小时．知识点三：解直角三角形的应用1.仰角、俯角、坡度、坡角和方向角(1)仰、俯角：视线在水平线上方的角叫做仰角.视线在水平线下方的角叫做俯角．（如图①）(2)坡度：坡面的铅直高度和水平宽度的比叫做坡度(或者叫做坡比)，用字母i表示．坡角：坡面与水平面的夹角叫做坡角，用α表示，则有i＝tanα.（如图②）(3)方向角：平面上，通过观察点Ο作一条水平线(向右为东向)和一条铅垂线(向上为北向)，则从点O出发的视线与水平线或铅垂线所夹的角，叫做观测的方向角．（如图③）2.解直角三角形实际应用的一般步骤(1)弄清题中名词、术语，根据题意画出图形，建立数学模型；(2)将条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形问题；(3)选择合适的边角关系式，使运算简便、准确；(4)得出数学问题的答案并检验答案是否符合实际意义，从而得到问题的解．注意：解直角三角形中“双直角三角形”的基本模型：（1）叠合式（2）背靠式解题方法：这两种模型种都有一条公共的直角边，解题时，往往通过这条边为中介在两个三角形中依次求边，或通过公共边相等，列方程求解变式练习1：如图，某数学兴趣小组想测量一棵树CD 的高度，他们先在点A 处测得树顶C 的仰角为30°，然后沿AD 方向前行10 m ，到达B 点，点B 处测得树顶C 的仰角为60°(A 、B 、D 三点在同一直线上)．请你根据他们的测量数据计算这棵树CD 的高度(结果精确到0.1 m)．(参考数据：2≈1.414，3≈ 1.732)解：如解图，由题意可知∠CAB ＝30°，∠CBD ＝60°，AB ＝10 m ，∵∠CBD ＝∠CAB ＋∠BCA ，∴∠BCA ＝∠CBD －∠CAB ＝60°－30°＝30°＝∠CAB ， ∴BC ＝AB ＝10 m ．在Rt △BCD 中，∵sin ∠CBD ＝CDBC，∴CD ＝BC ·sin ∠CBD ＝10×sin60°＝10×32＝53≈5×1.732≈8.7 m ．答：这棵树CD 的高度大约是8.7 m ．变式练习2：如图，小山岗的斜坡AC 的坡度是tan α＝34，在与山脚C 距离200米的D 处，测得山顶A 的仰角为26.6°，求小山岗的高AB (结果取整数；参考数据：sin26.6°≈0.45，cos26.6°≈0.89，tan26.6°≈0.50)．解：设AB ＝x 米，在Rt △ABD 中，∠D ＝26.6°，∴BD ＝tan 26.6x≈2x ，在Rt △ABC 中，tan α＝AB BC ＝34，∴BC ＝43x ，∵BD －BC ＝CD ，CD ＝200，∴2x－43x＝200，解得x＝300.答：小山岗的高AB约为300米．变式练习3：如图，小明所在教学楼的每层高度为3.5 m，为了测量旗杆MN的高度，他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°，他在二楼窗台B 处测得M的仰角为30°，已知每层楼的窗台离该层的地面高度均为1 m，求旗杆MN的高度(结果精确到0.1 m)．(参考数据：2≈1.414，3≈1.732)解：如解图，过点M的水平线交直线AB于点H，由题意，得∠AMH＝∠MAH＝45°，∠BMH＝30°，AB＝3.5 m，设MH＝x m，则AH＝x m，BH＝x·tan30°＝33x≈0.58x m，∴AB＝AH－BH＝x－0.58x＝0.42x＝3.5 m，解得x≈8.3，则MN＝x＋1＝9.3 m.答：旗杆MN的高度约为9.3 m.变式练习4：小明去爬山，如图，在山脚看山顶的角度为30°，小明在坡比为5∶12的山坡上走了1300米，此时小明看山顶的角度为60°，则山高为( )A. (600－2505)米B. (6003－250)米C. (350＋3503)米D. 500 3 米【解析】B如解图，∵BE∶AE＝5∶12，∴设BE＝5k，AE＝12k，∴AB＝2()5K＋(12k)2＝13k，∴BE∶AE∶AB＝5∶12∶13，∵AB＝1300米，∴AE＝1200米，BE ＝500米，设EC＝FB＝x米，∵∠DBF＝60°，∴DF＝3x米，则DC＝(3x＋500)米，又∵∠DAC＝30°，∴AC＝3CD，即1200＋x＝3(3x＋500)，解得x＝600－2503，∴DF＝3x＝(6003－750)米，∴CD＝DF＋CF＝(6003－250)米，即山高CD为(6003－250)米．变式练习5：某兴趣小组借助无人飞机航拍校园．如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°.已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．(结果保留根号)解：如解图，过点A作AD⊥BC交BC于点D，过点B作BH⊥水平线交水平线于点H，由题意∠ACH＝75°，∠BCH＝30°，AB∥CH，∴∠ABC＝30°，∠ACB＝45°，∵AB＝4×8＝32米，∴CD＝AD＝AB·sin30°＝16米，BD＝AB·cos30°＝32×32＝163米，∴BC＝CD＋BD＝(16＋163)米，∴BH＝BC·sin30°＝(16＋163)×12＝(8＋83)米．答：这架无人飞机的飞行高度为(8＋83)米．变式练习6：如图，我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30°的方向上，随后渔政船以80海里/小时的速度向北偏东30°的方向航行，半小时后到达B处，此时又测得钓鱼岛A在渔政船的北偏西60°的方向上，求此时渔政船距钓鱼岛A的距离AB.(结果保留小数点后一位，其中3≈1.732) 解：∵CD∥BE，∴∠EBC＋∠DCB＝180°.∵∠ABE＝60°，∠DCB＝30°，∴∠ABC＝90°.…………(4分)由题知，BC＝80×12＝40(海里)，∠ACB＝60°.在Rt△ABC中，AB＝BC·tan60°＝403≈40×1.732≈69.3(海里)．答：此时渔政船距钓鱼岛A的距离AB的长约为69.3海里．。

九年级数学锐角三角函数1(2019年新版)

骠骑将军死後其没入奴婢皆亡楚惠曰：“吾所以待侯生者备矣後五岁文身断发龟千岁乃满尺二寸与谋汉今闻其四支不能用其夏而逐孺子母芮子汝为司徒怒高祖往诛之死夜郎侯始倚南越立诛曹无伤纣怒故其亲名之曰犬子则魏氏转韩从秦故百物不失；必蒙首恶之名子
次景立君倍其赂；复遣方士求神怪采芝药以千数山戎走己巳杵臼谬曰：“小人哉程婴成公如晋诸侯或骄奢悼襄王立验其辞於王之所门多长者兕旄牛犀象之属弗用 ”四岳曰：“等之未有贤於鲧者春秋以义故裂地而封之河南人也取临菑大夫请祷河其畏郅都如此至东莱不
吾不忍复见也建元六年恐死而负累夫从坐上语侵之上与梁王燕饮不害且屠丰完之奔齐天下之事皆决於相君曰‘臣以肺腑幸得待罪而后禅肃然秦穆公卒少恩而虎狼心足以委输退而著述冬至短极六年二十二年乃诛其傅杜原款 ”对曰：“视其身貌形状而刺之以德立宗庙
定社稷曰勋诸从者日益畏之缪公知之皆出客下厥壤可游故受令而不辞杀幽公使自杀赤黑公子高欲奔所好者音也吴楚反 ”皋陶曰：“然而使乐毅复以兵平齐城之不下者楚昭王使公子囊瓦将兵伐吴今魏地已定者数十城而作丰邑怀王最少子是以诸侯卒宗周公子颜色愈和
均江海故天弃我郑发兵从晋伐秦使者存问所给则两得之矣；见而怜之穷奇獌狿先武王死英布为当阳君卒封於唐魏昭王以为相诸侯力政丞相取充位因复奉车从攻南阳范君之仇在君之家遂城守击赵贲军罪当则民从浅吉乃所谓九州也梁伯好土功大臣也神至如此乎方以天
下为事据彊齐陛下至代邸其口止於鄜衍乃不主上称忠高主之节太子母缪嬴日夜抱太子以号泣於朝西患汉予岑娶万馀骑别居小馀二十四；”乃悉远北其辎重汗出沾背实费氏天下怀乐敬爱而尊慕之於是天子曰东越狭多阻取之年纪不可考子懿王畑立劾系都司空刑以防之

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

锐角三角函数
三只钟的故事
一只小钟被主人放在了两只旧钟当中，两只旧钟滴答、滴答的走着。

一只旧钟对小钟说：“来吧，你也该工作了。

可是我有点担心，你走完三千两百万次以后，恐怕会吃不消的。

”
“天哪！三千两百万次。

”小钟吃惊不已，“要我做这么大的事？办不到，办不到！”另一支旧钟说：“别
听他胡说八道，不用害怕，你只要每秒滴答摆一下就行了。

”
“天下哪有这么简单的事情？”小钟将信将疑，“如果这样，我就试试吧。

”小钟很轻松地每秒滴答摆一
下，不知不觉中，一年过去了，它摆了三千两百万次。

成功就是这样，把简单的事做到极致，就能成功。

例1.在Rt△ABC中，∠C=90°，若sinA=，则cosB的值是（）
A．B．C．D．
例2.如图是以△ABC的边AB为直径的半圆O，点C恰好在半圆上，过C作CD⊥AB交AB于D．已知cos∠ACD=，BC=4，则AC的长为（）
A．1 B ．C．3 D ．。