2018年中考数学《锐角三角函数》专题练习含答案
普通中学2018届初三中考数学复习锐角三角函数专题综合练习含答案

天津市和平区普通中学2018届初三中考数学复习锐角三角函数专题综合练习 1. 计算4sin60°-3tan30°的值为( ) A.3 B .23 C .33 D .0 2.计算sin 245°+cos 245°的值为( ) A .2 B .1 C .0 D .33. 为测量如图所示的上山坡道的倾斜度,小明测得数据如图所示,则该坡道倾斜角α的正切值是( )A.117B .4 C.14 D.4174. sin α=0.231 6,cos β=0.231 6,则锐角α与锐角β之间的关系是( ) A .α=β B .α+β=180° C .α+β=90° D .α-β=90°5. 在△ABC 中,∠C =90°,下列各式中不正确的是( )A .b =a ·tanB B .a =b ·cosAC .c =b sinBD .c =acosB6. 如图,小雅家(图中点O 处)门前有一条东西走向的公路,现测得有一水塔(图中点A 处)在她家北偏东60°方向500 m 处,那么水塔所在的位置到公路的距离AB 长是( )A .250 mB .250 3 m C.500 33m D .250 2 m7.王师傅在楼顶上的点A 处测得楼前一棵树CD 的顶端C 的俯角为60°,已知水平距离BD =10 m ,楼高AB =24 m ,则树CD 的高度为( )A .(24-1033)m B .(24-103) m C .(24-53) m D .9 m8. 使用计算器计算:sin 52°18′≈________.(精确到0.001)9.已知cos β=0.741 6,利用计算器求出β的值约为________.(精确到1°) 10. 在Rt △ABC 中,∠C =90°,c =10,b =53,则∠A =________,S △ABC =________. 11. 如图,在Rt △ABC 中,∠C =90°,求sinA 和sinB 的值.12. 如图,在Rt △ABC 中,∠C =90°,AB =10,BC =6,求sinA ,cosA ,tanA 的值.13. 如图(1),在Rt △ABC 中,∠C =90°,AB =6,BC =3,求∠A 的度数;14. 如图(2),AO是圆锥的高,OB是底面半径,AO=3OB,求α的度数.15. 如图,在Rt△ABC中,∠C=90°,AC=2,BC=6,解这个直角三角形.16. 如图,在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形.(结果保留小数点后一位)。
【精品】2018版中考数学:6.4-锐角三角函数(含答案)

§6.4锐角三角函数
A 组2018年全国中考题组
一、选择题
1.(2018·浙江丽水,8,3分)如图,点A 为∠α边上任意一点,作AC ⊥BC 于点C ,CD ⊥AB 于点D ,下列用线段比表示cos α的值,错误的是()
A.BD BC
B.BC AB
C.AD AC
D.CD AC
解析∵AC ⊥BC ,CD ⊥AB ,
∴∠α+∠BCD =∠ACD +∠BCD ,
∴∠α=∠ACD ,
∴cos α=cos ∠ACD =BD BC =BC AB =DC AC ,
只有选项C 错误,符合题意.
答案C
2.(2018·浙江衢州,9,3分)如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm 长的绑绳EF ,tan α=5
2,则“人字梯”的顶端离地
面的高度AD 是()
A .144cm
B .180cm
C .240cm
D .360cm
解析由题意得EF BC =2.56,∴BC =144,∴CD =72.
又∵tan α=AD CD =52,所以AD =180cm.
答案B
3.(2018·山东威海,7,3分)如图,在△ABC 中,∠ACB =90°,∠
ABC =26°,BC =5.若用科学计算器求边AC 的长,则下列按键顺序正确的是()A.5÷tan 26=B C.5×cos 26= D.5×tan 26=。
备考2019届中考:2018年数学中考真题演练(锐角三角函数)(附解析)

2018年数学中考真题演练(锐角三角函数)一.选择题1.(2018•巴彦淖尔)南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向10(1+)海里的C处,为了防止某国海巡警干扰,请求我A处的渔监船前往C处护航.如图,已知C位于A处的东北方向上,A位于B的北偏西30°方向上,则A和C之间的距离为()A.10海里B.20海里C.20海里D.10海里2.(2018•益阳)如图,小刚从山脚A出发,沿坡角为α的山坡向上走了300米到达B点,则小刚上升了()A.300sinα米B.300cosα米C.300tanα米D.米3.(2018•凉山州)无人机在A处测得正前方河流两岸B、C的俯角分别为α=70°、β=40°,此时无人机的高度是h,则河流的宽度BC为()A.h(tan50°﹣tan20°)B.h(tan50°+tan20°)C.D.4.(2018•苏州)如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为()A.40海里B.60海里C.20海里D.40海里5.(2018•贵阳)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为()A.B.1 C.D.6.(2018•云南)在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为()A.3 B.C.D.7.(2018•孝感)如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sin A等于()A.B.C.D.8.(2018•宜昌)如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于()A.100sin35°米B.100sin55°米C.100tan35°米D.100tan55°米9.(2018•重庆)如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角∠AED=58°,升旗台底部到教学楼底部的距离DE=7米,升旗台坡面CD的坡度i=1:0.75,坡长CD=2米,若旗杆底部到坡面CD的水平距离BC=1米,则旗杆AB的高度约为()(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6)A.12.6米B.13.1米C.14.7米D.16.3米10.(2018•重庆)如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)()A.21.7米B.22.4米C.27.4米D.28.8米11.(2018•绵阳)一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是()(结果保留小数点后两位)(参考数据:≈1.732,≈1.414)A.4.64海里B.5.49海里C.6.12海里D.6.21海里12.(2018•金华)如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A.B.C.D.二.填空题13.(2018•辽阳)如图,一艘轮船自西向东航行,航行到A 处测得小岛C 位于北偏东60°方向上,继续向东航行10海里到达点B 处,测得小岛C 在轮船的北偏东15°方向上,此时轮船与小岛C 的距离为 海里.(结果保留根号)14.(2018•德阳)如图,点D 为△ABC 的AB 边上的中点,点E 为AD 的中点,△ADC 为正三角形,给出下列结论,①CB =2CE ,②tan ∠B =,③∠ECD =∠DCB ,④若AC =2,点P 是AB 上一动点,点P 到AC 、BC 边的距离分别为d 1,d 2,则d 12+d 22的最小值是3.其中正确的结论是 (填写正确结论的序号).15.(2018•荆州)荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A 处测得塔顶的仰角为30°,再向古塔方向行进a 米后到达B 处,在B 处测得塔顶的仰角为45°(如图所示),那么a 的值约为 米(≈1.73,结果精确到0.1).16.(2018•葫芦岛)如图,某景区的两个景点A 、B 处于同一水平地面上、一架无人机在空中沿MN 方向水平飞行进行航拍作业,MN 与AB 在同一铅直平面内,当无人机飞行至C 处时、测得景点A 的俯角为45°,景点B 的俯角为30°,此时C 到地面的距离CD 为100米,则两景点A 、B 间的距离为 米(结果保留根号).17.(2018•湖北)我国海域辽阔,渔业资源丰富.如图,现有渔船B在海岛A,C附近捕鱼作业,已知海岛C位于海岛A的北偏东45°方向上.在渔船B上测得海岛A位于渔船B的北偏西30°的方向上,此时海岛C恰好位于渔船B的正北方向18(1+)nmile处,则海岛A,C之间的距离为nmile.18.(2018•广西)如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B 处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是m (结果保留根号)19.(2018•泰安)如图,在△ABC中,AC=6,BC=10,tan C=,点D是AC边上的动点(不与点C重合),过D作D E⊥BC,垂足为E,点F是BD的中点,连接EF,设CD=x,△DEF 的面积为S,则S与x之间的函数关系式为.20.(2018•宁波)如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45°和30°.若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为米(结果保留根号).21.(2018•济宁)如图,在一笔直的海岸线l上有相距2km的A,B两个观测站,B站在A 站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离是km.三.解答题22.(2018•梧州)随着人们生活水平的不断提高,旅游已成为人们的一种生活时尚.为开发新的旅游项目,我市对某山区进行调查,发现一瀑布.为测量它的高度,测量人员在瀑布的对面山上D点处测得瀑布顶端A点的仰角是30°,测得瀑布底端B点的俯角是10°,AB与水平面垂直.又在瀑布下的水平面测得CG=27m,GF=17.6m(注:C、G、F三点在同一直线上,CF⊥AB于点F).斜坡CD=20m,坡角∠ECD=40°.求瀑布AB的高度.(参考数据:≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)23.(2018•常州)京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).24.(2018•莱芜)在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC 是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C、E、D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)25.(2018•贺州)如图,一艘游轮在A处测得北偏东45°的方向上有一灯塔B.游轮以20海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:≈1.41,≈1.73)26.(2018•资阳)如图是小红在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA表示小红身高1.5米.1(1)当风筝的水平距离AC=18米时,求此时风筝线AD的长度;(2)当她从点A跑动9米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10米,这一过程中风筝线的长度保持不变,求风D.筝原来的高度C127.(2018•贵阳)如图①,在Rt△ABC中,以下是小亮探究与之间关系的方法:∵sin A=,sin B=∴c=,c=∴=根据你掌握的三角函数知识.在图②的锐角△ABC中,探究、、之间的关系,并写出探究过程.28.(2018•湘西州)如图,某市郊外景区内一条笔直的公路l经过A、B两个景点,景区管委会又开发了风景优美的景点C.经测量,C位于A的北偏东60°的方向上,C位于B的北偏东30°的方向上,且AB=10km.(1)求景点B与C的距离;(2)为了方便游客到景点C游玩,景区管委会准备由景点C向公路l修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)29.(2018•通辽)我市304国道通辽至霍林郭勒段在修建过程中经过一座山峰,如图所示,其中山脚A、C两地海拔高度约为1000米,山顶B处的海拔高度约为1400米,由B处望山脚A处的俯角为30°,由B处望山脚C处的俯角为45°,若在A、C两地间打通一隧道,求隧道最短为多少米(结果取整数,参考数据≈1.732)30.(2018•桂林)如图所示,在某海域,一艘指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A 的救援?(参考数据:≈1.41,≈1.73,≈2.45,结果精确到0.1小时)31.(2018•吉林)数学活动小组的同学为测量旗杆高度,先制定了如下测量方案,使用工具是测角仪和皮尺,请帮助组长林平完成方案内容,用含a,b,α的代数式表示旗杆AB 的高度.数学活动方案活动时间:2018年4月2日活动地点:学校操场填表人:林平32.(2018•烟台)汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速.如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时.数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°.上午9时测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)33.(2018•河南)“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)参考答案一.选择题1.解:过点A作AD⊥BC于点D,如图所示.设AD=x,则CD=x,AC=x,BD=x.∵BC=BD+CD=(+1)x=10(1+),∴x=10,∴AC=10.故选:A.2.解:在Rt△AOB中,∠AOB=90°,AB=300米,BO=AB•sinα=300sinα米.故选:A.3.解:过A作CB延长线的高,垂足为D,由题意可知∠ABD=α,∠ACB=β,AD=h,∴BD=h•tan20°,CD=h•tan50°,∴BC=CD﹣BD=h(tan50°﹣tan20°).故选:A.4.解:在Rt△PAB中,∵∠APB=30°,∴PB=2AB,由题意BC=2AB,∴PB=BC,∴∠C=∠CPB,∵∠ABP=∠C+∠CPB=60°,∴∠C=30°,∴PC=2PA,∵PA=AB•tan60°,∴PC=2×20×=40(海里),故选:D.5.解:连接BC,由网格可得AB=BC=,AC=,即AB2+BC2=AC2,∴△ABC为等腰直角三角形,∴∠BAC=45°,则tan∠BAC=1,故选:B.6.解:∵在Rt△ABC中,∠C=90°,AC=1,BC=3,∴∠A的正切值为==3,故选:A.7.解:在Rt△ABC中,∵AB=10、AC=8,∴BC===6,∴sin A===,故选:A.8.解:∵PA⊥PB,PC=100米,∠PCA=35°,∴小河宽PA=PC tan∠PCA=100tan35°米.故选:C.9.解:如图延长AB交ED的延长线于M,作CJ⊥DM于J.则四边形BMJC是矩形.在Rt△CJD中,==,设CJ=4k,DJ=3k,则有9k2+16k2=4,∴k=,∴BM=CJ=,BC=MJ=1,DJ=,EM=MJ+DJ+DE=,在Rt△AEM中,tan∠AEM=,∴1.6=,解得AB≈13.1(米),故选:B.10.解:作BM⊥ED交ED的延长线于M,CN⊥DM于N.在Rt△CDN中,∵==,设CN=4k,DN=3k,∴CD=10,∴(3k)2+(4k)2=100,∴k=2,∴CN=8,DN=6,∵四边形BMNC是矩形,∴BM=CN=8,BC=MN=20,EM=MN+DN+DE=66,在Rt△AEM中,tan24°=,∴0.45=,∴AB=21.7(米),故选:A.11.解:如图所示,由题意知,∠BAC=30°、∠ACB=15°,作BD⊥AC于点D,以点B为顶点、BC为边,在△ABC内部作∠CBE=∠ACB=15°,则∠BED=30°,BE=CE,设BD=x,则AB=BE=CE=2x,AD=DE=x,∴AC=AD+DE+CE=2x+2x,∵AC=30,∴2x+2x=30,解得:x=≈5.49,故选:B.12.解:在Rt△ABC中,AB=,在Rt△ACD中,AD=,∴AB:AD=:=,故选:B.二.填空题(共9小题)13.解:如图,作BH⊥AC于H.在Rt△ABH中,∵AB=10海里,∠BAH=30°,∴∠ABH=60°,BH=AB=5(海里),在Rt△BCH中,∵∠CB H=∠C=45°,BH=5(海里),∴BH=CH=5海里,∴CB=5(海里).故答案为5.14.解:∵D是AB中点∴AD=BD∵△ACD是等边三角形,E是AD中点∴AD=CD,∠ADC=60°=∠ACD,CE⊥AB,∠DCE=30°∴CD=BD∴∠B=∠DCB=30°,且∠DCE=30°,CE⊥AB∴∠ECD=∠DCB,BC=2CE,tan∠B=故①③正确,②错误∵∠DCB=30°,∠ACD=60°∴∠ACB=90°若AC=2,点P是AB上一动点,点P到AC、BC边的距离分别为d1,d2,∴四边形PMCN是矩形∴MN=CP∵d12+d22=MN2=CP2∴当CP为最小值,d12+d22的值最小∴根据垂线段最短,则当CP⊥AB时,d12+d22的值最小此时:∠CAB=60°,AC=2,CP⊥AB∴CP=∴d12+d22=MN2=CP2=3即d12+d22的最小值为3故④正确故答案为①③④15.解:如图,设CD为塔身的高,延长AB交CD于E,则CD=40,DE=7,∴CE=33,∵∠CBE=45°=∠BCE,∠CAE=30°,∴BE=CE=33,∴AE=a+33,∵tan A=,∴tan30°=,即33=a+33,解得a=33(﹣1)≈24.1,∴a的值约为24.1米,故答案为:24.1.16.解:∵∠MCA=45°,∠NCB=30°,∴∠ACD=45°,∠DCB=60°,∠B=30°,∵CD=100米,∴AD=CD=100米,DB=米,∴AB=AD+DB=100+100(米),故答案为:100+10017.解:作AD⊥BC于D,设AC=x海里,在Rt△ACD中,AD=AC×sin∠ACD=x,则CD=x,在Rt△ABD中,BD=x,则x+x=18(1+),解得,x=18,答:A,C之间的距离为18海里.故答案为:1818.解:由题意可得:∠BDA=45°,则AB=AD=120m,又∵∠CAD=30°,∴在Rt△ADC中,tan∠CDA=tan30°==,解得:CD=40(m),故答案为:40.19.解:在Rt△CDE中,tan C=,CD=x∴DE=x,CE=x,∴BE=10﹣x,=×(10﹣x)•x=﹣x2+3x.∴S△BED∵DF=BF,=x2,∴S=S△BED故答案为S =x 2.20.解:由于CD ∥HB ,∴∠CAH =∠ACD =45°,∠B =∠BCD =30°在Rt △ACH 中,∵∴∠CAH =45°∴AH =CH =1200米,在Rt △HCB ,∵tan ∠B =∴H B ====1200(米).∴AB =HB ﹣HA=1200﹣1200 =1200(﹣1)米故答案为:1200(﹣1)21.解:过点C 作CD ⊥AB 于点D ,根据题意得:∠CAD =90°﹣60°=30°,∠CBD =90°﹣30°=60°, ∴∠ACB =∠CBD ﹣∠CAD =30°,∴∠CAB =∠ACB ,∴BC =AB =2km ,在Rt △CBD 中,CD =BC •sin60°=2×=(km ).故答案为:.三.解答题(共12小题)22.解:过点D作DM⊥CE,交CE于点M,作DN⊥AB,交AB于点N,如图所示.在Rt△CMD中,CD=20m,∠DCM=40°,∠CMD=90°,∴CM=CD•cos40°≈15.4m,DM=CD•sin40°≈12.8m,∴DN=MF=CM+CG+GF=60m.在Rt△BDN中,∠BDN=10°,∠BND=90°,DN=60m,∴BN=DN•tan10°≈10.8m.在Rt△ADN中,∠ADN=30°,∠AND=90°,DN=60m,∴AN=DN•tan30°≈34.6m.∴AB=AN+BN=45.4m.答:瀑布AB的高度约为45.4米.23.解:过D作DE⊥AB,可得四边形CHED为矩形,∴HE=CD=40m,设CH=DE=xm,在Rt△BDE中,∠DBA=60°,∴BE=xm,在Rt△ACH中,∠BAC=30°,∴AH=xm,由AH+HE+EB=AB=160m,得到x+40+x=160,解得:x=30,即CH=30m,则该段运河的河宽为30m.24.解:过点B作BF⊥AC于F,BG⊥CD于G,在Rt△BAF中,∠BAF=65°,BF=AB•sin∠BAF=0.8×0.9=0.72,AF=AB•cos∠BAF=0.8×0.4=0.32,∴FC=AF+AC=4.32,∵四边形FCGB是矩形,∴BG=FC=4.32,CG=BF=0.72,∵∠BDG=45°,∴∠BDG=∠GBD,∴GD=GB=4.32,∴CD=CG+GD=5.04,在Rt△ACE中,∠AEC=50°,CE=,∴DE=CD﹣CE=5.04﹣3.33=1.71≈1.7,答:小水池的宽DE为1.7米.25.解:过点C作CM⊥AB,垂足为M,在Rt△ACM中,∠MAC=90°﹣45°=45°,则∠MCA=45°,∴AM=MC,由勾股定理得:AM2+MC2=AC2=(20×2)2,解得:AM=CM=40,∵∠ECB=15°,∴∠BCF=90°﹣15°=75°,∴∠B=∠BCF﹣∠MAC=75°﹣45°=30°,在Rt △BCM 中,tan B =tan30°=,即=,∴BM =40,∴AB =AM +BM =40+40≈40+40×1.73≈109(海里),答:A 处与灯塔B 相距109海里.26.解:(1)∵在Rt △ACD 中,cos ∠CAD =,AC =18、∠CAD =30°,∴AD ====12(米),答:此时风筝线AD 的长度为12米;(2)设AF =x 米,则BF =AB +AF =9+x (米),在Rt △BEF 中,BE ===18+x (米),由题意知AD =BE =18+x (米), ∵CF =10,∴AC =AF +CF =10+x ,由cos ∠CAD =可得=,解得:x =3+2,则AD =18+(3+2)=24+2,∴CD =AD sin ∠CAD =(24+2)×=12+,则C 1D =CD +C 1C =12++=+; 方法二:设CD =x ,∵∠CAD =30°,∴BE =AD =2CD =2x ,AC ===x ,∵CF =10,∴AF =AC ﹣CF =x ﹣10,∵AB =9,∴BF =AB +AF =9+x ﹣10, ∵∠EBF =45°,∴由cos ∠EBF =可得=,解得:x =12+,即CD =12+,则C 1D =CD +C 1C =12++=+.答:风筝原来的高度C 1D 为(+)米.27.解:==,理由为:过A 作AD ⊥BC ,BE ⊥AC ,在Rt △ABD 中,sin B =,即AD =c sin B ,在Rt △ADC 中,sin C =,即AD =b sin C ,∴c sin B =b sin C ,即=,同理可得=,则==.28.解:(1)如图,由题意得∠CAB =30°,∠ABC =90°+30°=120°,∴∠C =180°﹣∠CAB ﹣∠ABC =30°,∴∠CAB =∠C =30°,∴BC =AB =10km ,即景点B 、C 相距的路程为10km .(2)过点C作CE⊥AB于点E,∵BC=10km,C位于B的北偏东30°的方向上,∴∠CBE=60°,在Rt△CBE中,CE=km.29.解:如图,作BD⊥AC于D,由题意可得:BD=1400﹣1000=400(米),∠BAC=30°,∠BCA=45°,在Rt△ABD中,∵,即,∴AD=400(米),在Rt△BCD中,∵,即,∴CD=400(米),∴AC=AD+CD=400+400≈1092.8≈1093(米),答:隧道最短为1093米.30.解:因为A在B的正西方,延长AB交南北轴于点D,则AB⊥CD于点D∵∠BCD=45°,BD⊥CD∴BD=CD在Rt△BDC中,∵cos∠BCD=,BC=60海里即cos45°=,解得CD=海里∴BD=CD=海里在Rt△ADC中,∵tan∠ACD=即 tan60°==,解得AD=海里∵AB=AD﹣BD∴AB=﹣=30()海里∵海监船A的航行速度为30海里/小时则渔船在B处需要等待的时间为==≈2.45﹣1.41=1.04≈1.0小时∴渔船在B处需要等待1.0小时31.解:(1)用测角仪测得∠ADE=α;(2)用皮尺测得BC=a米,CD=b米.(3)计算过程:∵四边形BCDE是矩形,∴DE=BC=a,BE=CD=b,在Rt△ADE中,AE=ED•tanα=a•tanα,∴AB=AE+EB=a•tanα+b.32.解:在Rt△APC中,AC=PC tan∠APC=30tan71°≈30×2.90=87,在Rt△BPC中,BC=PC tan∠BPC=30tan35°≈30×0.70=21,则AB=AC﹣BC=87﹣21=66,∴该汽车的实际速度为=11m/s,又∵40km/h≈11.1m/s,∴该车没有超速.33.解:在Rt△ACE中,∵tan∠CAE=,∴AE==≈≈21(cm)在Rt△DBF中,∵tan∠DBF=,∴BF==≈=40(cm)∵EF=EA+AB+BF≈21+90+40=151(cm)∵CE⊥EF,CH⊥DF,DF⊥EF∴四边形CEFH是矩形,∴CH=EF=151cm答:高、低杠间的水平距离CH的长为151cm.。
2018年全国各地中考数学真题汇编:锐角三角函数

中考数学真题汇编:锐角三角函数一、选择题1.的值等于()A. B. C. 1 D.【答案】B2.如图,过点,,,点是轴下方上的一点,连接,,则的度数是()A. B. C. D.【答案】B3.如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是( )A.3B.C.D.【答案】D4.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为()(参考数据:,,)A. 12.6米B. 13.1米C. 14.7米D. 16.3米【答案】B5.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:)()A. 4.64海里B. 5.49海里C. 6.12海里D. 6.21海里【答案】B6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A. B. C. D.【答案】B7. 如图,已知在中,,,,则的值是()A. B. C. D.【答案】A8. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B 在同一条直线上)()A. B. C. D. h•cosα【答案】B二、填空题9.如图.一-艘渔船正以60海里/小时的速度向正东方向航行,在处测得岛礁在东北方向上,继续航行1.5小时后到达处此时测得岛礁在北偏东方向,同时测得岛礁正东方向上的避风港在北偏东方向为了在台风到来之前用最短时间到达处,渔船立刻加速以75海里/小时的速度继续航行________小时即可到达(结果保留根号)【答案】10.如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=________。
2018年全国各地中考数学真题汇编:锐角三角函数(及答案)

中考数学真题汇编:锐角三角函数一、选择题1.的值等于()A. B. C. 1 D.【答案】B2.如图,过点,,,点是轴下方上的一点,连接,,则的度数是()A. B. C. D.【答案】B3.如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是( )A.3B.C.D.【答案】D4.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为()(参考数据:,,)A. 12.6米B. 13.1米C. 14.7米D. 16.3米【答案】B5.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:)()A. 4.64海里B. 5.49海里C. 6.12海里D. 6.21海里【答案】B6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A. B. C. D.【答案】B7. 如图,已知在中,,,,则的值是()A. B. C. D.【答案】A8. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B 在同一条直线上)()A. B. C. D. h•cosα【答案】B二、填空题9.如图.一-艘渔船正以60海里/小时的速度向正东方向航行,在处测得岛礁在东北方向上,继续航行1.5小时后到达处此时测得岛礁在北偏东方向,同时测得岛礁正东方向上的避风港在北偏东方向为了在台风到来之前用最短时间到达处,渔船立刻加速以75海里/小时的速度继续航行________小时即可到达(结果保留根号)【答案】10.如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=________。
2018年中考数学真题分类汇编第三期专题27锐角三角函数与特殊角试题含解

锐角三角函数与特殊角一.选择题1.(2018·云南省·4分)在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为()A.3 B.C.D.【分析】根据锐角三角函数的定义求出即可.【解答】解:∵在Rt△ABC中,∠C=90°,AC=1,BC=3,∴∠A的正切值为==3,故选:A.【点评】本题考查了锐角三角函数的定义,能熟记锐角三角函数的定义的内容是解此题的关键.2. (2018•陕西•3分)如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为A. B. 2 C. D. 3【答案】C【分析】由已知可知△ADC是等腰直角三角形,根据斜边AC=8可得AD=4,在Rt△ABD 【解析】中,由∠B=60°,可得BD==,再由BE平分∠ABC,可得∠EBD=30°,从而可求得DE长,再根据AE=AD-DE即可【详解】∵AD⊥BC,∴△ADC是直角三角形,∵∠C=45°,∴∠DAC=45°,∴AD=DC,∵AC=8,∴AD=4,在Rt△ABD中,∠B=60°,∴BD===,∵BE平分∠ABC,∴∠EBD=30°,∴DE=BD•tan30°==,∴AE=AD-DE=,故选C.【点睛】本题考查了解直角三角形的应用,熟练掌握直角三角形中边角之间的关系是解题的关键.二.填空题1.(2018·辽宁省阜新市)如图,在点B处测得塔顶A的仰角为30°,点B到塔底C的水平距离BC是30m,那么塔AC的高度为10m(结果保留根号).【解答】解:∵在点B处测得塔顶A的仰角为30°,∴∠B=30°.∵BC=30m,∴AC=m.故答案为:10.2. (2018•莱芜•4分)计算:(π﹣3.14)0+2cos60°= 2 .【分析】原式利用零指数幂法则,特殊角的三角函数值计算即可求出值.【解答】解:原式=1+2×=1+1=2,故答案为:2【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.三.解答题1. (2018·湖北荆州·10分)问题:已知α、β均为锐角,tanα=,tanβ=,求α+β的度数.探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;延伸:(2)设经过图中M、P、H三点的圆弧与AH交于R,求的弧长.【解答】解:(1)连结AM、MH,则∠MHP=∠α.∵AD=MC,∠D=∠C,MD=HC,∴△ADM≌△MCH.∴AM=MH,∠DAM=∠HMC.∵∠AMD+∠DAM=90°,∴∠AMD+∠HMC=90°,∴∠AMH=90°,∴∠MHA=45°,即α+β=45°.(2)由勾股定理可知MH==.∵∠MHR=45°,∴==.2.(2018·辽宁省阜新市)(1)计算:()﹣2+﹣2co s45°;【解答】解:(1)原式=4+3﹣2×=4+3﹣=4+23. (2018•广安•9分)如图,已知AB是⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.(1)求证:∠PCA=∠ABC.(2)过点A作AE∥PC交⊙O于点E,交CD于点F,连接BE,若cos∠P=,CF=10,求BE 的长【分析】(1)连接半径OC,根据切线的性质得:OC⊥PC,由圆周角定理得:∠ACB=90°,所以∠PCA=∠OCB,再由同圆的半径相等可得:∠OCB=∠ABC,从而得结论;(2)本题介绍两种解法:方法一:先证明∠CAF=∠ACF,则AF=CF=10,根据cos∠P=cos∠FAD=,可得AD=8,FD=6,得CD=CF+FD=16,设OC=r,OD=r﹣8,根据勾股定理列方程可得r的值,再由三角函数cos ∠EAB=,可得AE的长,从而计算BE的长;方法二:根据平行线的性质得:OC⊥AE,∠P=∠EAO,由垂直的定义得:∠OCD=∠EAO=∠P,同理利用三角函数求得:CH=8,并设AO=5x,AH=4x,表示OH=3x,OC=3x﹣8,由OC=OA列式可得x的值,最后同理得结论.【解答】证明:(1)连接OC,交AE于H,∵PC是⊙O的切线,∴OC⊥PC,∴∠PCO=90°,∴∠PCA+∠ACO=90°,(1分)∵AB是⊙O的直径,∴∠ACB=90°,(2分)∴∠ACO+∠OCB=90°,∴∠PCA=∠OCB,(3分)∵OC=OB,∴∠OCB=∠ABC,∴∠PCA=∠ABC;(4分)(2)方法一:∵AE∥PC,∴∠CAF=∠PCA,∵AB⊥CG,∴,∴∠ACF=∠ABC,(5分)∵∠ABC=∠PCA,∴∠CAF=∠ACF,∴AF=CF=10,(6分)∵AE∥PC,∴∠P=∠FAD,∴cos∠P=cos∠FAD=,在Rt△AFD中,cos∠FAD=,AF=10,∴AD=8,(7分)∴FD==6,∴CD=CF+FD=16,在Rt△OCD中,设OC=r,OD=r﹣8,r2=(r﹣8)2+162,r=20,∴AB=2r=40,(8分)∵AB是直径,∴∠AEB=90°,在Rt△AEB中,cos∠EAB=,AB=40,∴AE=32,∴BE==24.(9分)方法二:∵AE∥PC,OC⊥PC,∴OC⊥AE,∠P=∠EAO,(5分),∴∠EAO+∠COA=90°,∵AB⊥CG,∴∠OCD+∠COA=90°,∴∠OCD=∠EAO=∠P,(6分)在Rt△CFH中,cos∠HCF=,CF=10,∴CH=8,(7分)在Rt△OHA中,cos∠OAH=,设AO=5x,AH=4x,∴OH=3x,OC=3x+8,由OC=OA得:3x+8=5x,x=4,∴AO=20,∴AB=40,(8分)在Rt△ABE中,cos∠EAB=,AB=40,∴AE=32,∴BE==24.(9分)【点评】本题考查了切线的性质,锐角三角函数,圆周角定理,等腰三角形的性质,连接OC构造直角三角形是解题的关键.4.(2018·江苏常州·6分)计算:|﹣1|﹣﹣(1﹣)0+4sin30°.【分析】直接利用特殊角的三角函数值以及绝对值的性质、零指数幂的性质分别化简得出答案.【解答】解:原式=1﹣2﹣1+4×=1﹣2﹣1+2=0.【点评】此题主要考查了实数运算,正确化简各数是解题关键.5.(2018·江苏镇江·4分)(1)计算:2﹣1+(2018﹣π)0﹣sin30°【解答】解:(1)原式=+1﹣=1;。
2018年中考数学真题汇编 锐角三角函数

中考数学真题汇编:锐角三角函数一、选择题1.的值等于()A. B.C.1 D.【答案】B2.如图,过点,,,点是轴下方上的一点,连接,,则的度数是()A. B.C.D.【答案】B3.如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是( )A.3B.C.D.【答案】D4.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为()(参考数据:,,)A. 12.6米B. 13.1米 C. 14.7米 D. 16.3米【答案】B5.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:)()A. 4.64海里B. 5.49海里 C. 6.12海里 D. 6.21海里【答案】B6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A. B.C.D.【答案】B7. 如图,已知在中,,,,则的值是()A.B.C.D.【答案】A8. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B 在同一条直线上)()A. B.C.D. h•cosα【答案】B二、填空题9.如图.一-艘渔船正以60海里/小时的速度向正东方向航行,在处测得岛礁在东北方向上,继续航行1.5小时后到达处此时测得岛礁在北偏东方向,同时测得岛礁正东方向上的避风港在北偏东方向为了在台风到来之前用最短时间到达处,渔船立刻加速以75海里/小时的速度继续航行________小时即可到达 (结果保留根号)【答案】10.如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=________。
2018年中考数学真题分类汇编第二期专题27锐角三角函数与特殊角试题含解析

锐角三角函数与特殊角一.选择题1.2018•山东烟台市•3分)利用计算器求值时,小明将按键顺序为显示结果记为a,的显示结果记为b.则a,b的大小关系为()A.a<b B.a>b C.a=b D.不能比较【分析】由计算器的使用得出A.b的值即可.【解答】解:由计算器知a=(sin30°)﹣4=16.b==12,∴a>b,故选:B.【点评】本题主要考查计算器﹣基础知识,解题的关键是掌握计算器的使用.. 2(2018•金华、丽水•3分)如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A.B.C.D.【解析】【解答】解:设AC=x,在Rt△ABC中,AB= .在Rt△ACD中,AD= ,则,故答案为:B。
【分析】求AB与AD的比,就不必就求AB和AD的具体的长度,不妨设AB=x,用含x的代数式分别表示出AB,AD的长,再求比。
3. (2018·黑龙江大庆·3分)2cos60°=()A.1 B.C.D.【分析】直接利用特殊角的三角函数值进而计算得出答案.【解答】解:2cos60°=2×=1.二.填空题1. (2018·湖北江汉油田、潜江市、天门市、仙桃市·3分)我国海域辽阔,渔业资源丰富.如图,现有渔船B在海岛A,C附近捕鱼作业,已知海岛C位于海岛A的北偏东45°方向上.在渔船B上测得海岛A位于渔船B的北偏西30°的方向上,此时海岛C恰好位于渔船B的正北方向18(1+)n mile处,则海岛A,C之间的距离为18n mile.【分析】作AD⊥BC于D,根据正弦的定义、正切的定义分别求出BD.CD,根据题意列式计算即可.【解答】解:作AD⊥BC于D,设AC=x海里,在Rt△ACD中,AD=AC×sin∠ACD=x,则CD=x,在Rt△ABD中,BD=x,则x+x=18(1+),解得,x=18,答:A,C之间的距离为18海里.故答案为:18【点评】本题考查的是解直角三角形的应用,掌握方向角的概念、锐角三角函数的定义是解题的关键.2.(2018•江苏宿迁•3分)如图,将含有30°角的直角三角板ABC放入平面直角坐标系,顶点A,B分别落在x、y轴的正半轴上,∠OAB=60°,点A的坐标为(1,0),将三角板ABC 沿x轴向右作无滑动的滚动(先绕点A按顺时针方向旋转60°,再绕点C按顺时针方向旋转90°,…)当点B第一次落在x轴上时,则点B运动的路径与坐标轴围成的图形面积是________.【答案】+π【分析】在Rt△AOB中,由A点坐标得OA=1,根据锐角三角形函数可得AB=2,OB=,在旋转过程中,三角板的角度和边的长度不变,所以点B运动的路径与坐标轴围成的图形面积:S=,计算即可得出答案.【详解】在Rt△AOB中,∵A(1,0),∴OA=1,又∵∠OAB=60°,∴cos60°=,∴AB=2,OB=,∵在旋转过程中,三角板的角度和边的长度不变,∴点B运动的路径与坐标轴围成的图形面积:S==π,故答案为:π.【点睛】本题考查了扇形面积的计算,锐角三角函数的定义,旋转的性质等,根据题意正确画出图形是解题的关键.3. (2018•广西北海•3分)如图,从甲楼底部A 处测得乙楼顶部 C 处的仰角是 30°,从甲楼顶部B 处测得乙楼底部D 处的俯角是 45°.已知甲楼的高 AB 是 120m ,则乙楼的高 CD 是 m (结果保留根号)。
各地2018年中考数学试卷精选汇编 锐角三角函数与特殊角(含解析).-2019-11-12-20-48-24-653

锐角三角函数与特殊角一、选择题1.(2018•山东枣庄•3分)如图,在矩形 ABCD 中,点 E 是边 BC 的中点,AE⊥BD,垂足为 F,则 tan∠BDE 的值是()A.B.C.D.【分析】证明△BEF∽△DAF,得出EF=AF,EF= AE,由矩形的对称性得:AE=DE,得出 EF=DE,设 EF=x,则 DE=3x,由勾股定理求出 DF==2x,再由三角函数定义即可得出答案.【解答】解:∵四边形ABCD是矩形,∴AD=BC,AD∥BC,∵点E是边BC的中点,∴BE=BC=AD,∴△BEF∽△DAF,∴=,∴EF=AF,∴EF=AE,∵点E是边BC的中点,∴由矩形的对称性得:AE=DE,∴EF=DE,设 EF=x,则 DE=3x,∴DF==2x,∴tan∠BDE===;故选:A.【点评】本题考查了相似三角形的判定和性质,矩形的性质,三角函数等知识;熟练掌握矩形的性质,证明三角形相似是解决问题的关键.2.(2018•山东淄博•4 分)一辆小车沿着如图所示的斜坡向上行驶了100米,其铅直高度上升了15米.在用科学计算器求坡角α 的度数时,具体按键顺序是()A.B.C.D.【考点】T9:解直角三角形的应用﹣坡度坡角问题;T6:计算器—三角函数.【分析】先利用正弦的定义得到sinA=0.15,然后利用计算器求锐角α .【解答】解:sinA===0.15,所以用科学计算器求这条斜道倾斜角的度数时,按键顺序为故选:A.【点评】本题考查了计算器﹣三角函数:正确使用计算器,一般情况下,三角函数值直接可以求出,已知三角函数值求角需要用第二功能键.3.(2018·湖北省孝感·3分)如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA等于()A.B.C.D.【分析】先根据勾股定理求得BC=6,再由正弦函数的定义求解可得.【解答】解:在Rt△ABC中,∵AB=10、AC=8,∴BC===6,∴sinA== =,故选:A.【点评】本题主要考查锐角三角函数的定义,解题的关键是掌握勾股定理及正弦函数的定义.4(2018·山东青岛·3分)计算:2﹣1×+2cos30°=2.【分析】根据特殊角的三角函数值和有理数的乘法和加法可以解答本题.【解答】解:2﹣1×+2cos30°===2,故答案为:2.【点评】本题考查实数的运算、负整数指数幂、特殊角的三角函数值,解答本题的关键是明确它们各自的计算方法.5(2018·天津·3分)的值等于()A. B. C. 1 D.【答案】B【解析】分析:根据特殊角的三角函数值直接求解即可.详解:cos30°=.故选:B.点睛:本题考查特殊角的三角函数值的记忆情况.特殊角三角函数值计算在中考中经常出现,要熟练掌握.6(2018·重庆(A)·4分)如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角∠AED =58︒,升旗台底部到教学楼底部的距离 DE =7米,升旗台坡面CD的坡度 i =1: 0.75,坡长 CD =2米,若旗杆底部到坡面CD的水平距离 BC =1米,则旗杆AB的高度约为(参考数据: sin 58︒ ≈ 0.85 , cos 58︒ ≈ 0.53 , tan 58︒ ≈ 1.6 )A.12.6 米B.13.1 米C.14.7 米D.16.3 米【考点】三角函数的综合运用【解析】延长AB交地面与点H.作CM⊥DE.易得AH AHCM =1.6. DM =1.2,, = tan58︒ ∴ =1.6 ∴AH=14.72,∴AB=14.72 -1.6 ≈13.1HE 1 + 1.2 + 7【点评】此题考查三角函数的综合运用,解题关键是从图中提取相关信息,特别是直角三角形的三边关系,属于中等题7(2018·广东深圳·3 分)如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是()A.3B.C.D.【答案】D【考点】切线的性质,锐角三角函数的定义,切线长定理【解析】【解答】解:设光盘切直角三角形斜边于点 C ,连接OC 、OB 、 OA (如图),∵∠DAC=60°,∴∠BAC=120°.又∵AB、AC 为圆 O 的切线,∴AC=AB,∠BAO=∠CAO=60°,在 Rt△AOB 中,∵AB=3,∴tan∠BAO= ,∴OB=AB×tan∠60°=3 ,∴光盘的直径为6 .故答案为:D.【分析】设光盘切直角三角形斜边于点C,连接OC、OB、OA(如图),根据邻补角定义得∠BAC=120°,又由切线长定理AC=AB,∠BAO=∠CAO=60°;在Rt△AOB中,根据正切定义得tan∠BAO= ,代入数值即可得半径 OB 长,由直径是半径的 2 倍即可得出答案.二.填空题1.(2018·广东广州·3分)如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=________。
2018年全国各地中考数学真题汇编:锐角三角函数(含答案)-数学备课大师【全免费】

中考数学真题汇编:锐角三角函数一、选择题1.的值等于()A. B. C. 1 D.【答案】B2.如图,过点,,,点是轴下方上的一点,连接,,则的度数是()A. B. C. D.【答案】B3.如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是( )A.3B.C.D.【答案】D4.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为()(参考数据:,,)A. 12.6米B. 13.1米C. 14.7米D. 16.3米【答案】B5.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:)()A. 4.64海里B. 5.49海里C. 6.12海里D. 6.21海里【答案】B6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A. B. C. D.【答案】B7. 如图,已知在中,,,,则的值是()A. B. C. D.【答案】A8. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B 在同一条直线上)()A. B. C. D. h•cosα【答案】B二、填空题9.如图.一-艘渔船正以60海里/小时的速度向正东方向航行,在处测得岛礁在东北方向上,继续航行1.5小时后到达处此时测得岛礁在北偏东方向,同时测得岛礁正东方向上的避风港在北偏东方向为了在台风到来之前用最短时间到达处,渔船立刻加速以75海里/小时的速度继续航行________小时即可到达(结果保留根号)【答案】10.如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=________。
2018年中考数学《锐角三角函数》回归考点练习试卷含答案

锐角三角函数练习卷1.tan 60︒的值等于( )(A )1(B 2(C 3(D )22.Rt △ABC 中,∠C=90°,AC ∶BC=1∶3,则cosA=_______,tanA=_________.3.设α、β为锐角,若sin α=23,则α=________;若tan β=33,则β=_________. 4.已知α是锐角,且sin α=54,则cos(90°-α)=( ) A.54 B.43 C.53 D.51 5.三角形在正方形网格纸中的位置如图所示,则sin α的值是( ) A.43 B.34 C.53 D.546.如图,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,连接CD ,若⊙O 的半径23=r ,AC=2,则cosB 的值是( )A.23 B.35 C.25 D.327.如图,若∠A =60°,AC =20m ,则BC 大约是(结果精确到0.1m)( ) A .34.64m B .34.6m C .28.3m D .17.3m8.在△ABC 中,∠C=90°,AB=15,sinA=31,则BC=() BA.45B.5C.51 D.451 9.如图,CD 是Rt △ABC 斜边上的高,AC=4,BC=3,则cos ∠BCD=( ) A.53 B.43 C.34 D.5410.计算:(02cos 45-38+2=︒ .11.计算:()102 3.142sin 6012133.3π-︒⎛⎫+--+- ⎪⎝⎭12.已知:如图,△ABC 内接于⊙O ,点D 在OC 的延长线上,sinB=21,∠CAD=30°. (1)求证:AD 是⊙O 的切线; (2)若OD ⊥AB ,BC=5,求AD 的长.13.计算:2sin60º+12--02008–|1–3|14.计算:101(2013)832452-⎛⎫--+ ⎪⎝⎭15.如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD = 24 m,OE⊥CD于点E.已测得sin∠DOE =.(1)求半径OD;(2)根据需要,水面要以每小时0.5 m的速度下降,则经过多长时间才能将水排干?O16.如图,在△中,∠=90°,sin=,=15,求△的周长和tan的值.参考答案 1 .C 2 .21,3 3 .60°,30° 4 . A 5. C 6. B 7. B 8 . B 9 .D 10. 521-+ 11 .3212答案思路解析:圆的切线问题跟过切点的半径有关,连接OA ,证∠OAD=90°.由sinB=21可以得到∠B=30°,由此得到圆心角∠AOD=60°,从而得到△ACO 是等边三角形,由此∠OAD=90°.AD 是Rt △OAD 的边,有三角函数可以求出其长度.(1)证明:如图,连接OA. ∵sinB=21,∴∠B=30°.∴∠AOD=60°. ∵OA=OC ,∴△ACO 是等边三角形. ∴∠OAC=60°.∴∠OAD=90°.∴AD 是⊙O 的切线. (2)解:∵OD ⊥AB ∴ OC 垂直平分AB. ∴ AC=BC=5.∴OA=5.在Rt △OAD 中,由正切定义,有tan ∠AOD=OAAD. ∴ AD=35. 13.2114. 2 15.(1)∵OE ⊥CD 于点E ,CD =24(m ),∴ED ==12(m).在Rt△DOE中,∵sin∠DOE = =,∴OD =13(m).(2)OE== (m)∴将水排干需:5÷0.5=10(小时).16.在中, ∠=90°, =15==, ∴∴周长为36,BC124 tan A.AC93===。
2018年中考数学《锐角三角函数》专题练习含答案

2018中考数学专题练习《锐角三角函数》(时间:100分钟 满分:120分)一、选择题(本大题共10小题,每小题3分,共30分)1.下列各数是有理数的是( )A. B. 4πC. sin 45︒D.1cos60︒ 2一个公共房门前的台阶高出地面1.2米,台阶拆除并改造成供轮椅行走的斜坡,数据如图1所示,则下列关系或说法正确的是( )A.斜坡AB 的坡度是10ºB.斜坡AB 的坡度是tan10︒C. 1.2tan10AC =︒米D. 1.2cos10AB =︒米3.在ABC ∆中,A ∠,B ∠都是锐角,且1sin 2A =,cos 2B =,则ABC ∆三个角的大小关系是( )A. C A B ∠>∠>∠B. B C A ∠>∠>∠C. A B C ∠>∠>∠D. C B A ∠>∠>∠4.如图2,在R t A B C ∆中,90A ∠=︒,AD BC ⊥于点D ,:3:2BD CD =,则t a n B 的值是( )A. 32B. 23C. D. 5.如图3,AB 是⊙O 的直径,C 是⊙O 上的点,过点C 作⊙O 的切线,交AB 的延长线于点E ,30A ∠=︒,则s sin E 的值为( )A. 12B. 2C.D.6.数学社团的同学们对某塔的高度进行了测量,如图4,他们在A 处仰望塔顶,测得仰角为30º,再往楼的方向前进60 m 至B 处,测得仰角为60º,若学生的身高忽略不计,1.7≈,结果精确到1m ,则该楼的高度CD 为( )A.47 mB.51 mC.53 mD.54 m7.如图5,点O 是摩天轮的圆心,长为110米的AB 是其垂直地面的直径,小莹在地面C 点处利用测角仪测得摩天轮的最高点A 的仰角为33º,测得圆心O 的仰角为21º,则小莹所在C 点到直径AB 所在直线的距离约为(参考数据:tan330.65︒≈,tan 210.38︒≈)( )图 5A.169米B.204米C.240米D.407米8.如图6,在ABC ∆中,已知90ABC ∠=︒,点D 沿BC 自B 向C 运动(点D 与点B , C 不重合),作BE AD ⊥于E ,CF AD ⊥交AD 的延长线于F ,则BE CF +的值( )A.不变B.增大C.减小D.先变大,再变小9.如图7,轮船从B 处以每小时50海里的速度沿南偏东30º方向匀速航行,在B 处观测灯塔A 位于南偏东75º的方向上,轮船航行半小时到达C 处,在C 处观测灯塔A 位于北偏东60º的方向上,则C 处与灯塔A 的距离是( )A. B.C. 50海里D. 25海里10.某数学兴趣小组的同学进行测量大树CD 高度的综合实践活动,如图8,在点A 处测得直立于地面的大树顶端C 的仰角为36º,然后沿在同一剖面的斜坡AB 行走13米至坡顶B 处,然后沿水平方向行走6米至大树脚底点D 处,斜面AB 的坡度(或坡比)1:2.4i =,那么大树CD 的高度约为(参考数据:sin360.59︒≈,cos360.81︒≈,tan360.73︒≈)( )A.8.1米B.17.2米C.19.7米D.25.5米二、填空题(本大题共8小题,每小题3分,共24分)11.若θ为三角形的一个锐角,且2sin 0θ=,则tan θ= .12.在Rt ABC ∆中,90C ∠=︒,4tan 3A =,8BC =,则ABC ∆的面积为 . 13.在平面直角坐标系中,已知点P 在第一象限内,点P 与原点O 的距离2OP =,点P 与原点O 的连线与x 轴的正半轴的夹角为60º,则点P 的坐标是 .14.如图9,某景区从游客中心A 处修建通往百米观景长廊BC 的两条栈道AB ,AC .若56B ∠=︒,45C ∠=︒,则游客中心A 到观景长廊BC 的距离AD 的长度约为 米.(参考数据:sin560.8︒≈,tan56 1.5︒≈ )15.如图10,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱的一个角(O ∠)为60º,A ,B ,C 都在格点上,则tan ABC ∠的值是 .16.如图11,一艘渔船位于灯塔P 的北偏东30º方向,距离灯塔18海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东55º方向上的B 处,此时渔船与灯塔P 的距离约为 海里.(结果取整数,参考数据:sin550.8︒≈,cos550.6︒≈,tan55 1.4︒≈)17.如图12,以边长为20 cm 的正三角形纸板的各顶点为端点,在各边上分别截取4 cm 长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形,把它们沿图中的虚线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为 cm 3.18.图13是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD 的面积是小正方形EFGH 面积的13倍,那么tan ADE ∠的值为 .三、解答题(本大题共6小题,共66分)19. ( 8分)计算2145cos 302sin 602tan 60︒+︒-+︒︒.20.(10分)在Rt ABC ∆中,90C ∠=︒,30A B ∠-∠=︒,2a b -=,试解该直角三角形.21. (10分)如图14,物理实验室有一个单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C 处测得E ,F 两点的俯角分别为60ACE ∠=︒,45BCF ∠=︒,这时点F 相对于点E 升高了3cm ,求该摆绳CD 的长度.(参考数据 1.7≈ 1.4≈)22. (12分)太阳能光伏发电因其清洁、安全、便利、高效等特点。
2018-2019学年初三中考数学专题复习锐角三角函数(含答案)
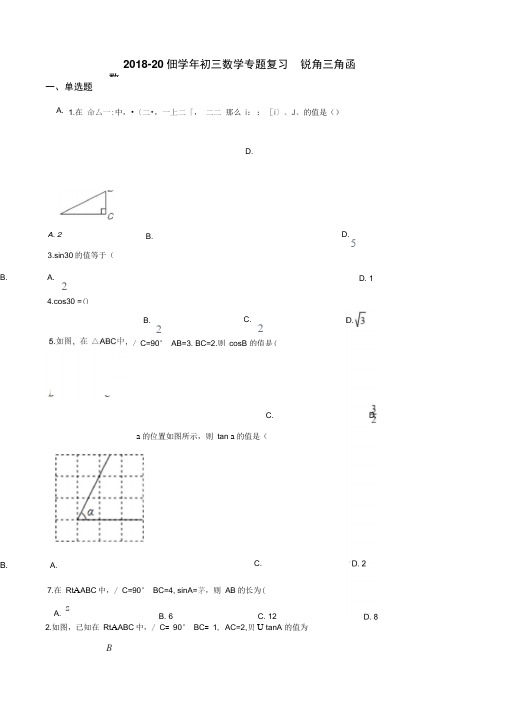
2018-20佃学年初三数学专题复习 锐角三角函数一、单选题1.在 命厶一:中,•〔二•,一上二「, 二二 那么 i ::[i 〕、J 、的值是()D.2.如图,已知在 Rt A ABC 中,/ C = 90° BC = 1, AC=2,贝U tanA 的值为A. A. 2B.3.sin30的值等于(A.24.cos30 =()B.D.5D. 1C.2B.2/ C=90° AB=3, BC=2,则 cosB 的值是(C.a 的位置如图所示,则 tan a 的值是(A.B.C.7.在 Rt A ABC 中,/ C=90° BC=4, sinA=茅,则 AB 的长为(s A.B. 6C. 12 B8.如图,铁路路基横断面为一个等腰梯形,若腰的坡度为下i=3:2,顶宽是7米,路基高是6米,则路基的底宽是()14•如图,钓鱼竿 AC 长6m ,露在水面上的鱼线 BC 长3 m ,某钓者想看看鱼钓上的情况,把鱼竿 AC 转动到AC'的位置,此时露在水面上的鱼线B'为3 m ,则鱼竿转过的角度是()A. 7米B. 1米 9.三角形在正方形网格纸中的位置如图所示,则C. 1米 sin a 的值是(D. 1米 B.C.D.10.在三角形ABC 中,/ C 为直角,sinA=,则tanB 的值为(B.C.11.游客上歌乐山山有两种方式:一种是如图,先从 是沿着盘山公路开车上山到C,已知在A 处观铡到A 沿登山步道走到B ,再沿索道乘座缆车到C ,另一种C ,得仰角/ CAD=3°,且A 、B 的水平距离 AE=430米,A 、B 的竖直距离 BE=210米,索道 BC 的坡度i=1: 米;(参考数据:tan310.6cos3l °~).91.5, CD 丄AD 于D , BF 丄CD 于F ,则山篙 CD 为() C. 686D. 69312.在 Rt A ABC 中,/ C=90° 如果/ A=a, BC=a,那么AC 等于()A. a • tan aB. a • cot aC. 13.化简等于( A. sin28 — °cos28 °B. 0C. cos28— sin28D.以上都不对A. 60 °B. 45 °C.15 °D. 9015.如图在 Rt A ABC 中,/ C=90° AB=15,sinA=g ,贝U BC 等于()16•如图1,是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货 物通过斜坡进行搬运•根据经验,木板与地面的夹角为20° (即图2中/ ACB=20 )时最为合适,已知货车车厢底部到地面的距离 AB=1.5m ,木板超出车厢部分 AD=0.5m ,则木板CD 的长度为 ____________ •(参考数据:sin20 °~ 0.34,2Gbos20°~ 0.9397精确到 0.1m ).17. 已知 cosB=』(,则/ B=18. 如图,在一次数学课外实践活动中,小聪在距离旗杆 10m 的A 处测得旗杆顶端 B 的仰角为60 °测角仪高AD 为1m ,则旗杆高BC 为 __________ m (结果保留根号).■rf|FJ 1 f J 1 f *c fA. 45B. 5二、填空题C.D.A f:侧....lw ___ _ __ CD <io?«—M19. 一山坡的坡比为3: 4,一人沿山坡向上走了_ 20米,那么这人垂直高度上升了米.20•如图,如果在坡度i=1: 2.4的斜坡上两棵树间的水平距离AC 为3米,那么两树间的坡面距离 AB 是21•如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口 C 测得教学楼顶中D 的仰角为18°教学楼底部B 的俯角为20°量得实验楼与教学楼之间的距离 AB=30m.(结果精确到 0.1m 。
2018年中考数学真题汇编 锐角三角函数-精选

中考数学真题汇编:锐角三角函数一、选择题1.的值等于()A. B.C. 1D.【答案】B2.如图,过点,,,点是轴下方上的一点,连接,,则的度数是()A. B.C.D.【答案】B3.如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是( )A.3B.C.D.【答案】D4.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为()(参考数据:,,)A. 12.6米B. 13.1米 C. 14.7米 D. 16.3米【答案】B5.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:)()A. 4.64海里B. 5.49海里 C. 6.12海里 D. 6.21海里【答案】B6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A. B.C.D.【答案】B7. 如图,已知在中,,,,则的值是()A. B. C.D.【答案】A8. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B 在同一条直线上)()A. B.C.D. h•cosα【答案】B二、填空题9.如图.一-艘渔船正以60海里/小时的速度向正东方向航行,在处测得岛礁在东北方向上,继续航行1.5小时后到达处此时测得岛礁在北偏东方向,同时测得岛礁正东方向上的避风港在北偏东方向为了在台风到来之前用最短时间到达处,渔船立刻加速以75海里/小时的速度继续航行________小时即可到达 (结果保留根号)【答案】10.如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=________。
【精编】2018年中考数学真题汇编 锐角三角函数

中考数学真题汇编:锐角三角函数一、选择题1.的值等于()A. B. C. 1 D.【答案】B2.如图,过点,,,点是轴下方上的一点,连接,,则的度数是()A. B. C. D.【答案】B3.如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是( )A.3B.C.D.【答案】D4.如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角,升旗台底部到教学楼底部的距离米,升旗台坡面CD的坡度,坡长米,若旗杆底部到坡面CD的水平距离米,则旗杆AB的高度约为()(参考数据:,,)A. 12.6米B. 13.1米C. 14.7米D. 16.3米【答案】B5.一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位)(参考数据:)()A. 4.64海里B. 5.49海里C. 6.12海里D. 6.21海里【答案】B6.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A. B. C. D.【答案】B7. 如图,已知在中,,,,则的值是()A. B. C. D.【答案】A8. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)()A. B. C. D. h•cosα【答案】B二、填空题9.如图.一-艘渔船正以60海里/小时的速度向正东方向航行,在处测得岛礁在东北方向上,继续航行1.5小时后到达处此时测得岛礁在北偏东方向,同时测得岛礁正东方向上的避风港在北偏东方向为了在台风到来之前用最短时间到达处,渔船立刻加速以75海里/小时的速度继续航行________小时即可到达(结果保留根号)【答案】10.如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018中考数学专题练习《锐角三角函数》(时间:100分钟 满分:120分)一、选择题(本大题共10小题,每小题3分,共30分) 1.下列各数是有理数的是( )A.B. 4πC. sin 45︒D.1cos60︒2一个公共房门前的台阶高出地面1.2米,台阶拆除并改造成供轮椅行走的斜坡,数据如图1所示,则下列关系或说法正确的是( ) A.斜坡AB 的坡度是10º B.斜坡AB 的坡度是tan10︒ C. 1.2tan10AC =︒米D. 1.2cos10AB =︒米3.在ABC ∆中,A ∠,B ∠都是锐角,且1sin 2A =,cos 2B =,则ABC ∆三个角的大小关系是( )A. C A B ∠>∠>∠B. B C A ∠>∠>∠C. A B C ∠>∠>∠D. C B A ∠>∠>∠ 4.如图2,在R t A B C ∆中,90A ∠=︒,AD BC ⊥于点D ,:3:2BD CD =,则t a n B 的值是( )A.32 B. 23C. D.5.如图3,AB 是⊙O 的直径,C 是⊙O 上的点,过点C 作⊙O 的切线,交AB 的延长线于点E ,30A ∠=︒,则s sin E 的值为( )A.12B. 2C.D.6.数学社团的同学们对某塔的高度进行了测量,如图4,他们在A 处仰望塔顶,测得仰角为30º,再往楼的方向前进60 m 至B 处,测得仰角为60º,若学生的身高忽略不计,1.7≈,结果精确到1m ,则该楼的高度CD 为( )A.47 mB.51 mC.53 mD.54 m 7.如图5,点O 是摩天轮的圆心,长为110米的AB 是其垂直地面的直径,小莹在地面C 点处利用测角仪测得摩天轮的最高点A 的仰角为33º,测得圆心O 的仰角为21º,则小莹所在C 点到直径AB 所在直线的距离约为(参考数据:tan330.65︒≈,tan 210.38︒≈)( )图 5A.169米B.204米C.240米D.407米8.如图6,在ABC ∆中,已知90ABC ∠=︒,点D 沿BC 自B 向C 运动(点D 与点B , C 不重合),作BE AD ⊥于E ,CF AD ⊥交AD 的延长线于F ,则BE CF +的值( )A.不变B.增大C.减小D.先变大,再变小 9.如图7,轮船从B 处以每小时50海里的速度沿南偏东30º方向匀速航行,在B 处观测灯塔A 位于南偏东75º的方向上,轮船航行半小时到达C 处,在C 处观测灯塔A 位于北偏东60º的方向上,则C 处与灯塔A 的距离是( )A. B.C. 50海里D. 25海里10.某数学兴趣小组的同学进行测量大树CD 高度的综合实践活动,如图8,在点A 处测得直立于地面的大树顶端C 的仰角为36º,然后沿在同一剖面的斜坡AB 行走13米至坡顶B 处,然后沿水平方向行走6米至大树脚底点D 处,斜面AB 的坡度(或坡比)1:2.4i =,那么大树CD 的高度约为(参考数据:sin360.59︒≈,cos360.81︒≈,tan360.73︒≈)( )A.8.1米B.17.2米C.19.7米D.25.5米 二、填空题(本大题共8小题,每小题3分,共24分)11.若θ为三角形的一个锐角,且2sin 0θ=,则tan θ= .12.在Rt ABC ∆中,90C ∠=︒,4tan 3A =,8BC =,则ABC ∆的面积为 . 13.在平面直角坐标系中,已知点P 在第一象限内,点P 与原点O 的距离2OP =,点P 与原点O 的连线与x 轴的正半轴的夹角为60º,则点P 的坐标是 .14.如图9,某景区从游客中心A 处修建通往百米观景长廊BC 的两条栈道AB ,AC .若56B ∠=︒,45C ∠=︒,则游客中心A 到观景长廊BC 的距离AD 的长度约为 米.(参考数据:sin560.8︒≈,tan56 1.5︒≈ )15.如图10,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱的一个角(O ∠)为60º,A ,B ,C 都在格点上,则tan ABC ∠的值是 .16.如图11,一艘渔船位于灯塔P 的北偏东30º方向,距离灯塔18海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东55º方向上的B 处,此时渔船与灯塔P 的距离约为 海里.(结果取整数,参考数据:sin550.8︒≈,cos550.6︒≈,tan55 1.4︒≈)17.如图12,以边长为20 cm 的正三角形纸板的各顶点为端点,在各边上分别截取4 cm 长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形,把它们沿图中的虚线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为 cm 3.18.图13是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD 的面积是小正方形EFGH 面积的13倍,那么tan ADE ∠的值为 .三、解答题(本大题共6小题,共66分)19. ( 8分)计算2145cos 302sin 602tan 60︒+︒-+︒︒.20.(10分)在Rt ABC ∆中,90C ∠=︒,30A B ∠-∠=︒,2a b -=,试解该直角三角形.21. (10分)如图14,物理实验室有一个单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C 处测得E ,F 两点的俯角分别为60ACE ∠=︒,45BCF ∠=︒,这时点F 相对于点E 升高了3cm ,求该摆绳CD 的长度.(参考数据 1.7≈ 1.4≈)22. (12分)太阳能光伏发电因其清洁、安全、便利、高效等特点。
已成为世界各国普遍关注和重点发展的新兴产业,图15是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,均为300 cm,AB的倾斜角为30º,50BE AC==cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,FE AB⊥于点E,两个底座地基的高度相同(即点D,F到地面的垂直距离相同),均为30 cm,点A到地面的垂直距离为50 cm,求支撑角钢CD和EF的长度各是多少.(结果保留根号)23. (12分)如图16,为了测量出楼房AC的高度,从距离楼底C处D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=DB前进30米到达点B.在点B处测得楼顶A的仰角为53º,求楼房AC的高度.(参考数据:sin530.8︒≈,cos530.6︒≈,4tan533︒≈,计算结果用根号表示)24. (14分)如图17,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处按到指挥部通知,在他们的东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75º方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.参考答案1. D2. B3. D4. D5. A6. B7. B8. C9. D 10. A11.12. 2413. 14. 6015.16. 11 17. 144 18.2319.原式2(24222=++⨯1344=+1=+20. 在Rt ABC ∆中,∵9030A B A B ∠+∠=︒⎧⎨∠-∠=︒⎩,∴6030A B ∠=︒⎧⎨∠=︒⎩.∴tan tan 60a b A b =∠=︒=.由2a ab ⎧=⎪⎨-=⎪⎩,解得31a b ⎧=+⎪⎨=⎪⎩又∵30B ∠=︒,∴22c b ==.21.分别过E ,F 作EG CD ⊥于G ,FH CD ⊥与H ,则3HG =cm.∵CD AB ⊥,60ECA ∠=︒,45FCB ∠=︒, ∴30ECD ∠=︒,45FCH ∠=︒. 设CE FC CD x ===,则,cos 452CH x x =︒=g .∴32CG CH x x -=-=,即6x =,解得20x ≈cm.∴该摆绳CD 的长度为20cm.22.如图8,过A 作AG CD ⊥于G , 则30CAG ∠=︒.在Rt ACG ∆中,1sin 3050252CG AC =︒=⨯=(cm). ∵503020CG =-=(cm).∴252045CD CG GD =+=+=(cm).连接FD 并延长与BA 的延长线交于H ,则30H ∠=︒.在Rt CDH ∆中,290sin 30CDCH CD ===︒(cm).∴300505090290EH EC CH AB BE AC CH =+=--+=--+=(cm).在Rt EFH ∆中,tan 30290EF EH =︒==g (cm).∴支撑角钢CD 和EF 的长度分别是45cm 23.如图9,作BN CD ⊥于N ,BM AC ⊥于M .在Rt BDN ∆中,30BD =米,:BN ND =∴15BN =米,DN =. ∵90C CMB CNB ∠=∠=∠=︒, ∴四边形CMBN 是矩形.∴15CM BN ==(米),BM CN ===(米). 在Rt ABM ∆中,4tan 3AM ABM BM ∠=≈,∴AM =.∴(15AC AM CM =+=+米.24.设巡逻船从出发到成功拦截所用时间为x 小时,如图10.由题意,得4575120ABC ∠=︒+︒=︒,12AB =海里,10BC x =,14AC x =. 过点A 作AD CB ⊥的延长线于点D .在Rt ABD ∆中,12AB =海里,60ABD ∠=︒,∴1cos6062BD AB AB =︒==g 海里,sin 60AD AB =︒=. ∴(106)CD x =+海里.在Rt ACD ∆中,由勾股定理,得222(14)(106)x x =++.解得1232,4x x ==- (舍去). ∴巡逻船从出发到成功拦截所用时间为2小时.。
