圆周率π的计算方法
计算圆周率公式

计算圆周率公式
圆周率是一个数学常数,通常用希腊字母π表示,它是圆的周长与直径的比值,也可以通过各种公式来计算。
其中最著名的是由数学家Gregory和Leibniz发现的级数公式,以及数学家Ramanujan 发现的无穷级数公式。
Gregory-Leibniz公式是由数学家James Gregory和Gottfried Leibniz在17世纪发现的。
这个公式通过级数的形式来计算圆周率。
它的公式为:
π = 4 × (1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + …)
这个公式的原理是通过不断地加上和减去分数项来逼近圆周率。
这个级数的收敛速度比较慢,需要加上很多项才能得到较为准确的结果。
但它的优点是容易理解,可以用来介绍数学级数的概念。
Ramanujan公式是由印度数学家Srinivasa Ramanujan在20世纪初发现的,它的公式为:
1/π = 2√2/9801 × ∑(n=0)∞(4n)!(1103+26390n)/(n!)^4 × 396^4n
这个公式的收敛速度非常快,只需要加上几项就可以得到非常精确的结果。
但由于公式比较复杂,不太容易理解,也不容易推导得出。
除了这两个公式,还有其他的方法来计算圆周率,比如Monte
Carlo方法、Bailey-Borwein-Plouffe公式等。
这些方法各有优缺点,适用于不同的场合。
计算圆周率是数学研究的一个重要课题,也是计算机科学中的一个重要问题。
通过不断地探索和研究,我们可以发现越来越多的方法来计算圆周率,也可以更好地理解数学和计算机科学的基础知识。
推导过程圆周率的计算方法

推导过程圆周率的计算方法圆周率,又称π,是数学中一个非常重要的数。
它的计算一直以来都备受关注和探索。
本文将介绍三种经典的计算圆周率的方法,分别是蒙特卡洛方法、无穷级数法和中学几何法。
一、蒙特卡洛方法蒙特卡洛方法是一种基于随机抽样的计算方法,其原理是通过随机点在一个区域内的分布状况来估计该区域的属性。
这个方法也可以被用于计算圆周率。
假设我们有一个边长为2的正方形,围绕它画一个内切圆。
通过随机投点,我们可以计算正方形内与圆相交的点和总点数的比例,从而估算圆周率。
通过重复进行投点实验,随着实验次数的增加,计算结果会逐渐逼近真实值。
这是因为随机点的分布越来越接近整个区域的均匀分布。
二、无穷级数法无穷级数法是一种通过无穷级数进行逼近计算的方法,其中一个著名的无穷级数就是莱布尼茨级数。
莱布尼茨级数的公式是:π/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ...我们可以通过将级数的前n项相加来逼近π的值。
随着级数项数的增加,逼近结果会越来越接近π。
此外,还有其他一些无穷级数,如马青公式和阿基米德公式等,它们也可以被用于计算圆周率。
三、中学几何法中学几何法是一种通过几何形状和关系计算圆周率的方法。
一个著名的中学几何法是通过正多边形的内接和外接圆来逼近圆周率。
首先,我们可以构建一个正多边形,然后通过计算多边形的周长和直径的比例来逼近圆周率。
当多边形的边数不断增加时,逼近结果会越来越接近π。
此外,还有其他形状和关系,如圆的面积和周长的关系等,也可以被用于计算圆周率。
综上所述,我们介绍了三种经典的计算圆周率的方法,包括蒙特卡洛方法、无穷级数法和中学几何法。
这些方法都是基于不同原理和数学概念的,并且在实际应用中具有一定的价值。
无论是使用蒙特卡洛方法的随机模拟,还是通过无穷级数的逼近计算,或者是通过几何形状的关系,计算圆周率的方法都追溯到了数学领域的深入探索和发展。
它们的推导过程和运用都有着独特的数学魅力,能够帮助我们更好地理解和应用圆周率的概念。
圆周率计算方法

圆周率计算方法圆周率,又称π,是数学中一个十分重要的常数,它代表了圆的周长与直径的比值。
圆周率的精确值是一个无限不循环小数,最常见的近似值是3.14159。
在数学、物理、工程等领域,圆周率都有着广泛的应用。
因此,研究圆周率的计算方法对于我们深入理解数学规律和解决实际问题具有重要意义。
圆周率的计算方法有很多种,下面我们将介绍几种常见的计算方法。
首先,最简单直观的计算方法是利用圆的周长与直径的关系进行计算。
根据定义,圆的周长C等于π乘以直径d,即C=πd。
因此,我们可以通过测量圆的周长和直径,然后利用这个关系式来计算圆周率的近似值。
其次,我们还可以利用圆的面积与半径的关系来计算圆周率。
根据定义,圆的面积A等于π乘以半径r的平方,即A=πr^2。
因此,我们可以通过测量圆的面积和半径,然后利用这个关系式来计算圆周率的近似值。
除了利用圆的几何特性进行计算外,还可以利用级数、积分、连分数等数学方法来计算圆周率。
其中,著名的皮亚诺级数和莱布尼兹级数都可以用来计算圆周率的近似值。
此外,利用积分和连分数也可以得到圆周率的近似值,这些方法在数值计算和数学研究中都有着重要的应用。
需要注意的是,圆周率的计算是一个充满挑战性的问题,因为它是一个无理数,无法用有限的小数或分数来表示。
因此,我们通常只能得到它的近似值。
随着计算机技术的发展,人们可以利用计算机来进行圆周率的计算,得到更精确的近似值。
目前,圆周率的计算已经超过了数万亿位小数,但仍然有许多数学家和计算机科学家在不断努力,希望能够得到更多的圆周率的小数位数。
综上所述,圆周率的计算方法有很多种,可以利用几何特性、级数、积分、连分数等数学方法来进行计算。
圆周率的计算是一个重要而又具有挑战性的问题,它对于我们深入理解数学规律和解决实际问题具有重要意义。
希望通过不断的努力和研究,我们能够更深入地理解圆周率,并得到更精确的近似值。
圆周率π的近似计算方法

圆周率π的近似计算方法圆周率π是一个无理数,精确值是无法完全计算的,然而可以使用不同的方法来近似计算π。
下面将介绍一些常见的计算π的方法。
1.随机投掷法(蒙特卡洛法):该方法通过随机投掷点在一个正方形区域内,然后计算落在正方形内且在一个给定圆形内的点的比例。
根据几何原理,圆的面积与正方形的面积之比等于π/4、通过对大量的随机点进行投掷和计数,可以估计π的值。
2.利用级数公式:许多级数公式都可以用来计算π的近似值。
其中最知名的是勾股定理的泰勒级数展开式:π/4=1-1/3+1/5-1/7+1/9-...通过计算级数中的前n项和,可以获得π的近似值。
然而,这种方法需要计算大量的级数项才能获得较高的精确度。
3.利用几何图形:利用几何图形的特性,可以近似计算π的值。
例如,可以使用正多边形逼近圆,然后通过对正多边形的边数进行增加,计算出逼近圆的周长。
随着边数的增加,逼近圆周长的值将越来越接近π的值。
4.首位公式:首位公式是由印度数学家 Srinivasa Ramanujan 提出的方法,通过将π 表示为一个无穷级数来计算。
该方法利用一种连分数的性质,可以将π 的近似值计算到高精度。
5.利用计算机算法:随着计算机性能的提升,可以使用各种数值计算算法来计算π 的近似值。
其中最有名的算法是Bailey-Borwein-Plouffe算法(BBP算法),它可以通过级数计算出π 的各个十六进制位数。
虽然上面提到了一些常见的方法,但是计算π的精确值仍然是一个开放的问题。
现代数学家不断提出新的计算方法和算法,以改进π的计算精度。
总之,圆周率π的近似计算方法有很多种,每种方法都有不同的优缺点和适用场景。
无论哪种方法,都需要通过对数学公式和几何特性的推导,以及大量的计算和迭代,来获得更精确的π近似值。
圆周率的推导过程

圆周率的推导过程圆周率(π)是一个基本的数学常数,它表示圆的周长与直径的比值。
它的值大约为3.14159,但实际上无限不循环小数。
圆周率的推导过程可以从不同的角度来看。
以下是几种常见的推导方法:1.通过圆的面积推导假设有一个半径为r的圆,那么它的周长C和面积S分别为:C = 2πrS = πr^2将周长公式代入面积公式,得到:S = πr^2 = (2πr)(r/2) = πr^2/4因此,圆周率π的值为4。
2.通过圆的周长推导假设有一个半径为1的圆,那么它的周长C为:C = 2π。
而这个圆的直径D为2。
因此,圆周率π的值为C/D=2π/2=π。
3.通过三角函数推导假设有一个半径为1的圆,那么它的周长C为:C = 2π将圆拆分成若干个扇形,再将扇形拆分成若干个三角形,则每个三角形的底为1,高为r,即为半径。
这样的话,每个三角形的面积就是1/2(底*高)=1/2。
将圆拆分成足够多的三角形,则圆的面积就是若干个三角形的面积之和,即S = n/2。
其中n表示圆被拆分成的三角形的个数。
同时,由于圆的周长C=2π,所以π的值为C/2=2π/2=π。
4.通过高斯-莫比乌斯函数推导高斯-莫比乌斯函数(G-M函数)是一种常用的数学函数,它与圆周率有着密不可分的关系。
G-M函数可以表示为:G(x) = ∑(n=-∞)^∞(exp(-πn^2x))。
其中x为一个实数,n为整数。
当x=1时,G(1)=∑(n=-∞)^∞(exp(-πn^2)),即圆周率的值。
因此,可以通过计算G(1)的值来推导出圆周率π的值。
这些方法都可以用来推导出圆周率的值,但在实际应用中,通常采用精确的数值近似值来代替无限不循环小数的真实值。
有关圆周率的计算公式

有关圆周率的计算公式圆周率是数学中一个常数,通常用希腊字母π表示。
它代表了一个圆的周长与直径之比,在几何学、物理学和工程学等领域中有广泛应用。
圆周率的计算公式有多种,下面将介绍几种常见的计算方法。
1. 随机投点法随机投点法是一种通过随机生成点的方法来估计圆周率的值。
假设有一个边长为1的正方形,将这个正方形放置在一个坐标系中,以正方形的中心为原点。
然后,随机生成一系列坐标为(x,y)的点,这些点均匀分布在正方形内部。
通过统计这些点中落入正方形内的点与落入正方形内并且在半径为0.5的圆内的点的比例,可以估计圆周率的值。
当生成的点足够多时,估计的值将趋近于真实值。
2. 蒙特卡洛方法蒙特卡洛方法是一种基于随机抽样的统计方法,也可以用来估计圆周率的值。
这种方法与随机投点法类似,不同之处在于它通过在正方形内随机生成大量的点,并计算这些点与圆心的距离来估计圆周率。
具体而言,假设正方形的边长为2,圆的半径为1,将正方形内随机生成的点(x,y)代入圆的方程x^2 + y^2 = 1,统计落在圆内的点的数量,并将这个数量与总点数的比例乘以4,就可以得到一个近似的圆周率值。
3. 雷马努金公式雷马努金公式是一种用级数表示圆周率的公式,它由印度数学家拉马努金在20世纪初提出。
这个公式的形式较为复杂,其中涉及到无穷级数和多项式的运算。
雷马努金公式的一个简化形式为:1/π = 2√2/99^2 * (1 + 1/3*2^1 + 1/3*2^2 + 1/3*2^3 + ...)这个公式的特点是收敛速度较慢,但每一项都可以通过简单的运算得到,因此可以用来计算圆周率的近似值。
4. 高斯-勒让德公式高斯-勒让德公式是一种基于连分数的方法,可以用来计算圆周率的近似值。
这个公式的形式为:1/π = 1 + a1/(1 + a2/(1 + a3/(1 + a4/(1 + ...))))其中ai是一个正整数序列,可以通过递推关系得到。
这个公式的特点是每一项的计算都相对简单,并且收敛速度较快,因此可以用来计算圆周率的高精度近似值。
圆周率是几除以几

圆周率是几除以几圆周率=周长除以直径=面积除以(半径的平方)3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172...圆周率,一般以π来表示,是一个在数学及物理学普遍存在的数学常数。
它定义为圆形之周长与直径之比值。
它也等于圆形之面积与半径平方之比值。
是精确计算圆周长、圆面积、球体积等几何形状的关键值。
在分析学上,π可以严格地定义为满足sin(x) = 0的最小正实数x。
2011年6月部分学者认为圆周率定义不合理,要求改为6.28。
π是第十六个希腊字母,本来它是和圆周率没有关系的,但大数学家欧拉从一七三六年开始,在书信和论文中都用π来表示圆周率。
因为他是大数学家,所以人们也有样学样地用π来表示圆周率了。
但π除了表示圆周率外,也可以用来表示其他事物,在统计学中也能看到它的出现。
π=Pai(π=Pi)古希腊欧几里德《几何原本》(约公元前3世纪初)中提到圆周率是常数,中国古算书《周髀算经》(约公元前2世纪)中有“径一而周三”的记载,也认为圆周率是常数[1]。
历史上曾采用过圆周率的多种近似值,早期大都是通过实验而得到的结果,如古埃及纸草书(约公元前1700)中取pi=(4/3)^4≒3.1604 。
第一个用科学方法寻求圆周率数值的人是阿基米德,他在《圆的度量》(公元前3世纪)中用圆内接和外切正多边形的周长确定圆周长的上下界,从正六边形开始,逐次加倍计算到正96边形,得到(3+(10/71))<π<(3+(1/7)),开创了圆周率计算的几何方法(亦称古典方法,或阿基米德方法),得出精确到小数点后两位的π值。
中国数学家刘徽在注释《九章算术》(263年)时只用圆内接正多边形就求得π的近似值,也得出精确到两位小数的π值,他的方法被后人称为割圆术。
推算圆周率的六种方法

推算圆周率的六种方法一、欧几里得算法欧几里得算法是一种基于辗转相除法的算法,用于计算两个整数的最大公约数。
同时,它也可以用于计算圆周率π。
欧几里得算法的基本思想是通过不断减去大数和小数的差值,最终得到一个0,此时的除数即为最大公约数。
利用这个思想,我们可以构造一个序列,其中每个数是前两个数的差值,当序列中出现0时,此时的非零数就是π的值。
二、祖暅恒等式祖暅恒等式是数学中一个重要的恒等式,它可以用来计算π的值。
祖暅恒等式是由南北朝时期的数学家祖暅提出的,它表达了π与正多边形的边数之间的关系。
通过选取适当的正多边形边数,可以使得正多边形的周长与圆的周长相等,从而利用祖暅恒等式计算出π的值。
三、圆内接正多边形法圆内接正多边形法是一种古老的推算π的方法。
它的基本思想是通过构造一个圆内接正多边形,使得多边形的周长与圆的周长相等,从而计算出π的值。
具体来说,可以不断增加正多边形的边数,使得多边形的周长逐渐逼近圆的周长,当多边形的周长与圆的周长相等时,此时的边数即为π的近似值。
四、阿基米德方法阿基米德方法是由古希腊数学家阿基米德提出的一种计算π的方法。
它的基本思想是通过构造一个正多边形和一个圆的内切正多边形,使得它们的面积相等,从而利用正多边形的面积计算出π的值。
具体来说,可以先计算正多边形的面积,再利用圆的半径和面积公式计算出圆的半径,从而得到π的值。
五、蒙特卡洛方法蒙特卡洛方法是一种基于概率统计的方法,它可以用来计算π的值。
蒙特卡洛方法的基本思想是通过构造一个概率模型,模拟随机抽样过程,然后根据概率分布计算出π的值。
具体来说,可以构造一个正方形和两个相切的正方形,其中大正方形的面积是4个小正方形的面积之和,然后通过随机抽样计算出落在小正方形内的点数与总点数之比,从而得到π的近似值。
六、格里戈里-莱布尼茨级数格里戈里-莱布尼茨级数是一种无穷级数,它可以用来计算π的值。
格里戈里-莱布尼茨级数的基本思想是通过不断将级数的项进行求和,最终得到π的值。
π的计算方法有哪些
圆周率π的计算方法圆周率π的计算方法,是一个饶有趣味,值得探讨的问题。
最直观的计算方法自然是从几何上着手,历史上也正是如此,这便是割圆法。
设一半径为1的圆,作这个圆的内接正n边形,用此正n边形的周长去近似圆的周长。
显然当n→∞时,正n边形的周长就无限趋近于圆周长,求得正n边形周长后除以直径便求出了圆周率。
I.从几何上观察,可知:正n边形周长随n递增而递增,但始终是个有限值。
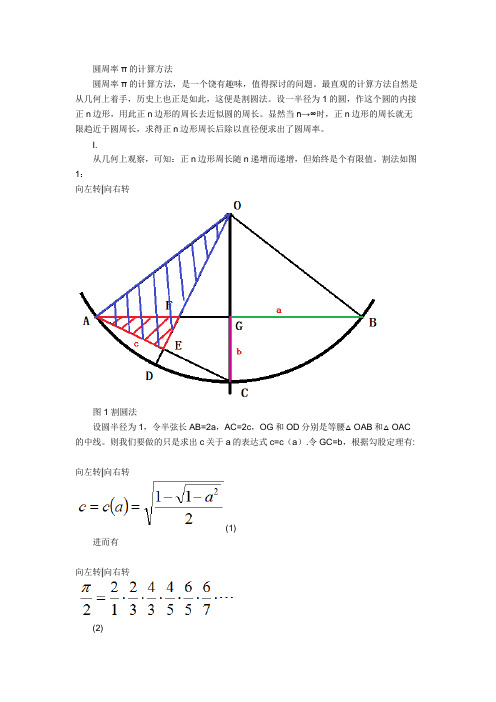
割法如图1:向左转|向右转图1 割圆法设圆半径为1,令半弦长AB=2a,AC=2c,OG和OD分别是等腰△OAB和△OAC 的中线。
则我们要做的只是求出c关于a的表达式c=c(a).令GC=b,根据勾股定理有:向左转|向右转(1)进而有向左转|向右转(2)得到此式后,编写计算机程序就很容易了,C语言程序如下:#include <stdio.h>#include <math.h>main(){double a,b,c,d,pi;double sqrt(double);int i,j,n;a=0.5;b=0;c=0;d=0.5;scanf("%d",&n);for(i=1;i<=n;i++){b=sqrt(1-a*a);c=(1-b)*0.5;d=sqrt(c);a=d;}j=pow(2,n)*3;pi=2*d*j;printf("%d\n",j);printf("%f\n",pi)}这里有一个问题就是a的初值如何选择?显然越简单直观越好,而已知对于圆内接正六边形的每一条边长等于圆的半径。
所以取a=0.5,程序中参数n是对正六边形分割的次数,d的作用是当输入n=0(正六边形)的时候,得到π=3,此所谓的“径圆一三”。
将这个文件保存为文本,在linux下用“gcc -lm”命令编译后,打开编译后得到的文件就能执行。
在古代可没有电子计算机,而祖冲之利用割圆法算得圆周率介于3.1415926和3.1415927之间,可见古人之伟大!II.上面的方法简单直观,但是缺点也很明显。
π的计算方式

π的计算方式π,又称圆周率,是一个数学常数,代表圆的周长与直径之比。
在数学中,π是一个非常重要的数,它出现在许多数学公式和计算中。
本文将围绕π的计算方式展开,介绍一些有趣的计算方法和应用。
一、π的历史与发现π的历史可以追溯到古代文明。
早在公元前2000年左右,古代埃及人就已经开始使用近似值3.16来计算圆周。
而希腊数学家阿基米德则在公元前250年左右,通过逐步逼近法,将π的值计算到了3.14。
二、π的几种计算方法1. 蒙特卡洛方法蒙特卡洛方法是一种基于概率统计的数值计算方法,可以用来估算π的值。
该方法的基本思想是在一个正方形内随机散布大量点,并计算落在内切圆内的点的比例。
通过统计实验次数与落在圆内的点数的比例,可以得到π的近似值。
2. 随机行走方法随机行走方法是一种通过模拟随机路径来计算π的方法。
可以想象一个人在一个无限大的平面上进行随机行走,每次行走的方向是随机选择的,但步长保持不变。
当进行大量次数的随机行走后,可以通过统计所到达的点与原点的距离与步长的比例,估算出π的值。
3. 调和级数方法调和级数方法是一种通过级数求和来计算π的方法。
这种方法的基本思想是利用调和级数的性质,将π表达为一个级数的和。
通过不断增加级数的项数,可以逐渐接近π的真实值。
三、π的应用领域1. 几何学π在几何学中有着广泛的应用。
例如,计算圆的面积和体积时,都需要使用π。
另外,π还可以用来计算弧长、球体积等。
2. 物理学在物理学中,π的应用也非常重要。
例如,计算圆周运动的周期和频率时,需要使用π。
此外,π还出现在很多物理公式中,如牛顿第二定律、万有引力定律等。
3. 计算机科学在计算机科学中,π也有着广泛的应用。
例如,π可以用来生成随机数,进行密码学算法设计,以及在图形学、计算机视觉等领域进行图像处理和分析。
四、π的奇特性质1. 无理数π是一个无理数,即它不能被表示为两个整数的比值。
这意味着π的小数部分是无限不循环的,没有规律可循。
圆周率周长计算公式

圆周率周长计算公式圆周率是数学中一个非常重要的常数,用希腊字母π表示。
它的值约等于 3.14159,是一个无理数,无限不循环小数。
圆周率的定义是,任何一个圆的周长与其直径的比值都是圆周率。
圆周率周长计算公式是用来计算圆的周长的公式,它可以通过直径或者半径来计算。
圆的周长是圆上所有点到圆心的距离之和,也可以理解为圆的一周的长度。
以直径计算圆的周长,公式为:周长= π * 直径以半径计算圆的周长,公式为:周长= 2 * π * 半径这两个公式的推导过程相对简单,直接使用了圆周率π。
对于直径计算公式,直径是圆的最长直线段,而周长就是这个直线段上的所有点到圆心的距离之和。
因此,周长等于圆周率π乘以直径。
对于半径计算公式,半径是直径的一半,所以周长等于圆周率π乘以直径的两倍,即2πr。
圆周率周长计算公式的应用非常广泛。
在几何学中,通过圆周率周长计算公式可以计算圆的周长,从而求解圆的面积、体积等相关问题。
在工程学中,圆的周长计算公式可以用来计算圆形管道的长度,以便进行材料的选择和规划。
在物理学中,圆的周长计算公式可以用来计算运动物体的轨迹长度,例如行星绕太阳的轨道长度等。
除了圆周率周长计算公式,还有许多与圆相关的公式和定理。
例如,圆的面积计算公式是通过圆周率π来计算的,公式为:面积= π * 半径的平方。
圆的体积计算公式是通过圆周率π和高度来计算的,公式为:体积= π * 半径的平方 * 高度。
圆周率的计算历史可以追溯到古代。
在古希腊时期,人们已经开始研究圆的性质和计算圆的周长。
最早对圆周率的估算可以追溯到公元前250年左右的古希腊数学家阿基米德,他使用了一个逼近圆周率的方法。
随着数学的发展,人们不断改进了对圆周率的计算方法,到现在已经计算到了数十亿位的小数。
虽然圆周率周长计算公式非常简单,但其应用却非常广泛,涉及到了许多不同领域的问题。
无论是在几何学、工程学还是物理学等领域,圆周率周长计算公式都起着重要的作用。
圆周率兀的计算过程

圆周率兀的计算过程
计算圆周率的方法有很多种,以下是其中一种常见的方法:
1. 画一个正方形,内切一个圆形。
2. 在正方形内随机生成很多个点。
3. 统计这些点中有多少个落在圆内,以及有多少个落在正方形内但不在圆内。
4. 计算圆的面积与正方形的面积之比,即可得到圆周率的近似值。
具体计算方法如下:
设正方形边长为2r,则正方形面积为(2r)²=4r²,圆的半径为r,则圆面积为πr²r²。
假设在正方形内随机生成了N个点,其中有M个点落在圆内,则圆的面积与正方形的面积之比为:
M/N ≈ πr²r²/4r² = πr²/4
因此,圆周率πr²的近似值为4M/N。
随着N的增加,圆周率的近似值会越来越精确。
但是,这种方法的计算量很大,需要生成大量的随机点才能得到较为精确的结果。
圆周率的算法公式

圆周率的算法公式
圆周率是一个数学常数,通常用希腊字母π表示,它表示一个圆的周长与直径之比。
精确的圆周率是一个无限不循环小数,但我们可以使用不同的算法来近似计算它。
以下是一些与圆周率计算相关的算法公式。
1. 马青公式(Leibniz公式):
马青公式是一种最简单的计算圆周率的公式之一,它基于泰勒级数展开式:
π/4=1-1/3+1/5-1/7+1/9-1/11+...
这个公式对于计算π的近似值非常慢收敛,但是使用这个公式可以得到π的前几位小数。
2.欧拉公式:
欧拉公式是另一种计算圆周率的公式,它基于欧拉级数展开式:
π^2/6=1/1^2+1/2^2+1/3^2+1/4^2+...
利用这个公式可以计算π的精确值。
3.级数求和法:
这个方法使用泰勒级数展开式等级数求和来逼近π的值。
例如,可以使用以下公式:
π=4x(1-1/3+1/5-1/7+1/9-1/11+...)
这个公式可以使用不断增加级数的方式逼近π的值。
4.蒙特卡洛方法:
蒙特卡洛方法是一种基于随机数的概率统计方法。
通过使用蒙特卡洛方法,可以通过在一个正方形内随机选择点,并计算其与圆心的距离来近似计算圆周率。
例如,如果我们在单位正方形内随机选择足够多的点,并计算这些点与圆心的距离,那么圆内的点的数量与正方形中的总点数的比例应该接近π/4
这些是一些常见的圆周率计算算法公式,每个算法都有其优缺点。
根据所需的精确度和计算效率,我们可以选择适合的算法来计算圆周率。
圆周率的计算及简单应用

圆周率的计算及简单应用圆周率(π)是数学中一个重要的无理数,常用来表示圆的周长和面积的关系。
它可以近似地计算,也可以通过一些数学方法推导得到。
本文将介绍圆周率的计算方法以及一些简单的应用。
1.随机法:随机法是基于蒙特卡洛方法的一种计算圆周率的方法。
通过在一个正方形中随机生成大量的点,并统计落在圆内的点的比例,然后用这个比例乘以4,就可以得到一个近似的圆周率值。
2.数列法:数列法是一种通过无限级数来逼近圆周率的方法。
其中最著名的数列是莱布尼兹级数和无穷乘积级数。
莱布尼兹级数公式为π/4=1-1/3+1/5-1/7+1/9-1/11+...,通过不断累加这个级数,可以得到一个越来越接近圆周率的值。
3.迭代法:迭代法是通过不断迭代计算,逐步逼近圆周率的方法。
其中最著名的是马刁尼方法,其公式为π/4=1-1/3+1/5-1/7+1/9-1/11+...,每迭代一次,将结果乘以4,就可以得到一个更接近圆周率的值。
除了以上的计算方法,还有许多其他的计算圆周率的方法,如连分数法、遍历法、插值法等。
这些方法的精度和效率不同,可以根据实际需求选择合适的方法。
圆周率在科学、工程和日常生活中有许多应用。
1.几何学:圆周率是计算圆的面积和周长的基本参数。
根据公式:周长=2πr,面积=πr²,可以使用圆周率来计算圆的周长和面积。
2.物理学:圆周率在物理学中有着广泛的应用。
例如,在电学中,圆周率出现在计算电容和电感的公式中;在力学中,圆周率出现在计算圆周运动的速度和加速度的公式中。
3.计算机图形学:计算机图形学中常常需要绘制圆和圆弧,这时就需要使用到圆周率。
通过圆周率的值来计算圆上的点的坐标,就可以绘制出精确的圆形图形。
4.概率统计:圆周率在概率统计中也有一些应用。
例如,在蒙特卡洛方法中,可以使用圆周率来模拟随机事件的概率分布。
5.数学研究:圆周率是数学研究中一个重要的无理数,由于它的无限不循环小数性质,一直以来都吸引着数学家们的研究。
圆周率公式简单计算方法

圆周率公式简单计算方法圆周率,通常用希腊字母π表示,是数学中的一个重要常数,用于计算表示圆周长度(周长)与其直径(直径)的比值。
计算圆周率的方法有很多,其中最经典的方法是使用圆的面积公式和周长公式进行简单的求解。
以下是详细的计算方法,供大家参考。
计算圆的面积圆的面积公式是πr²,其中r是圆的半径。
因此,计算圆的面积的方法是将圆的半径平方,然后用π乘以该值。
例如,如果一个圆的半径为5厘米,那么它的面积为π×5²=78.5平方厘米。
要注意的是,圆的面积通常以平方单位表示,比如平方米、平方毫米或平方英寸等等。
计算圆的周长圆的周长公式是2πr,其中r是圆的半径。
因此,计算圆的周长的方法是将圆的直径乘以π。
圆的直径是通过圆心的任意两个点之间的距离得到的。
例如,如果一个圆的半径为5厘米,那么它的周长为2×π×5=31.4厘米。
要注意的是,圆的周长通常以长度单位表示,比如米、厘米或英寸等等。
使用图形计算圆周率另一种计算圆周率的方法是使用图形,具体方法如下:1. 首先,画一个正方形,边长为2个单位。
2. 在正方形内画一个圆,直径等于正方形的边长(即2个单位),如下图所示。
____/ \| || ● || |\____/3. 确定圆的面积。
由于圆的直径等于正方形的边长,那么圆的半径r就是正方形边长的一半,即r=1个单位。
因此,圆的面积就是π×r²=π×1²=π平方单位。
4. 确定正方形的面积。
由于正方形的边长为2个单位,那么正方形的面积就是2²=4平方单位。
5. 用圆的面积除以正方形的面积,得到圆在正方形内的面积占比。
即π平方单位÷4平方单位=π/4。
6. 使用占比的反函数,即4/π,得出圆周率的近似值。
即4/π≈1.273。
这种方法称为蒙特卡罗方法,它是计算圆周率的一种估算方法。
方法的原理是,如果在正方形内随机投放大量的点,并计算有多少点落在圆内,那么圆的面积与正方形的面积之比就可以用在圆内落点的数量与总投放点数之比来估算。
圆周率计算方法

圆周率计算方法圆周率,简称π,是数学中一个重要的常数,它代表了圆的周长与直径的比值。
圆周率的精确值是一个无限不循环小数,最常见的近似值是3.14159。
在数学和工程领域,计算圆周率是一个重要且有趣的问题。
本文将介绍一些常见的圆周率计算方法。
首先,最简单直观的圆周率计算方法之一是利用圆的周长公式。
根据圆的定义,周长C等于直径D乘以π,即C=πD。
因此,我们可以通过测量圆的直径,然后用周长除以直径的方法来计算π的近似值。
这种方法简单易行,但精度较低。
其次,利用圆的面积公式也可以计算圆周率。
圆的面积A等于π乘以半径的平方,即A=πr^2。
因此,我们可以通过测量圆的半径,然后用面积除以半径平方的方法来计算π的近似值。
这种方法同样简单易行,但精度较低。
除了利用圆的基本公式,还可以通过一些数学方法来计算圆周率的近似值。
例如,利用无穷级数公式来计算π。
著名的莱布尼兹级数和欧拉级数都可以用来计算π的近似值,它们是通过对无穷级数进行逐项相加得到π的近似值。
虽然这些方法需要进行大量的计算,但可以得到较高精度的π的近似值。
此外,利用蒙特卡洛方法也可以计算圆周率。
蒙特卡洛方法是一种基于随机抽样的数值计算方法,通过在一个正方形内随机投点,然后统计落在圆内的点的比例来估算圆的面积,从而计算π的近似值。
这种方法虽然需要大量的随机抽样,但可以得到较为精确的π的近似值。
综上所述,计算圆周率是一个重要且有趣的数学问题,我们可以通过多种方法来得到π的近似值。
无论是利用基本的圆的公式,还是通过数学方法或者随机方法,都可以得到不同精度的π的近似值。
在实际应用中,我们可以根据需求和计算资源的限制选择合适的方法来计算π的近似值。
希望本文介绍的方法能够对圆周率的计算有所帮助。
多种解法计算圆周率π

多种解法计算圆周率π计算圆周率π一直以来都是一个数学问题中的难题。
虽然我们通常将π的近似值记作3.14,但是π的真实值是一个无限不循环的十进制小数。
因此,数学家们一直致力于发展出更加精确的π的计算方法。
在以下文字中,我将介绍一些现代和传统的π计算方法,并解释它们的原理和应用。
1.随机法随机法是一种通过随机抽样来估计π值的方法。
一种常见的随机法是蒙特卡洛方法。
在蒙特卡洛方法中,我们在一个边长为2的正方形内随机生成大量的点,并统计落在半径为1的圆内的点的数量。
根据概率统计的原理,圆内的点占所有点的比例应该接近于π/4、通过计算这个比例,我们可以估计π的近似值。
2.数学级数法数学级数法利用级数展开的思想来计算π值。
其中一种著名的级数就是莱布尼茨级数。
莱布尼茨级数是一个无限级数,通过不断计算级数的部分和,可以逐渐接近π/4、另一种著名的级数是Nilakantha级数,通过计算级数的部分和,也可以估计π的值。
3.数值积分法数值积分法通过将圆的面积转化为定积分,并利用数值积分的近似方法来计算π值。
一种常见的数值积分方法是辛普森法则。
辛普森法则将定积分近似为一系列小矩形和小梯形的面积之和,进而计算出圆的面积。
通过对圆的面积进行计算,我们可以估计π的值。
4.数值计算法数值计算法是一种根据数值计算的方法来计算π值的方法。
其中一种常见的数值计算方法是连分数法。
连分数法通过将π表示为一个无限连分数的形式,并利用连分数的递推关系来逐步计算π的近似值。
5.贝尔项级数法贝尔项级数法是一种利用贝尔项级数来计算π值的方法。
贝尔项级数是一个无限级数,通过计算级数的部分和,可以逐渐逼近π的值。
贝尔项级数法在计算机科学和数学研究中得到广泛应用。
以上只是几种常见的π计算方法,实际上还有很多其他方法。
随着数学和计算机科学的发展,人们不断提出新的π计算方法,以提高π的精确度和计算效率。
总结起来,计算圆周率π是一个复杂而有趣的问题。
无论是传统的方法还是现代的方法,都需要借助数学知识和计算工具来进行计算。
圆周率如何计算

圆周率如何计算
圆周率是用圆的周长除以它的直径计算出来的。
“圆周率”即圆的周长与其直径之间的比率。
1.圆周率是一个超越数,它不但是无理数,而且比无理数还要无理。
2.阿基米德是最早得出圆周率大约等于
3.14的人。
3.以前的人计算圆周率,是要探究圆周率是否循环小数。
圆周率(Pi)是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。
π也等于圆形之面积与半径平方之比,是精确计算圆周长、圆面积、球体积等几何形状的关键值。
在分析学里,π可以严格地定义为满足sin x=0的最小正数x。
圆周率用希腊字母π(读作[paɪ])表示,是一个常数(约等于
3.141592654),是代表圆周长和直径的比值。
它是一个无理数,即无限不循环小数。
在日常生活中,通常都用3.14代表圆周率去进行近似计算。
而用九位小数3.141592654便足以应付一般计算。
即使是工程师或物理学家要进行较精密的计算,充其量也只需取值至小数点后几百个位。
圆周率π等于多少

圆周率π等于多少圆周率(π)简介圆周率是一个数学常数,为一个圆的周长和其直径的比率,近似值约等于3.,常用符号π (读作pài)来表示。
圆周率(π)是一个无理数,它不能用分数完全表示出来(即它的小数部分是一个无限不循环小数)。
π 的数字序列被认为是随机分布的,有一种统计上特别的随机性,但至今未能证明。
此外,π 还是一个超越数——它不是任何有理数系数多项式的根。
在日常生活中,通常都用3.14代表圆周率去进行近似计算。
圆周率的定义π 常用定义为圆的周长c与直径d的比值:π=c/d无论圆的大小如何,比值c/d为恒值。
如果一个圆的直径变为原先的二倍,它的周长也将变为二倍,比值c/d不变。
圆周率的近似值圆周率近似等于以下几个分数的值(依准确度顺序排列):22/7、333/106、355/113、52163/16604、103993/33102、/圆周率怎么算圆周率计算方法1:通过测量圆的周长和直径来计算 pi 值1.找到标准的圆形物体。
2.尽量精确地测量圆的周长。
3. 尽量精确地测量圆的直径。
4. 用周长除以直径,就可以得到圆周率的近似值。
并且周长和直径测量得越精确,圆周率的计算值就越精确。
圆周率计算方法2:通过无穷级数来计算 pi 值 1. 使用格雷戈里 - 莱布尼茨无穷级数进行计算,公式如下:π = (4/1) - (4/3) + (4/5) - (4/7) + (4/9) - (4/11) + (4/13) - (4/15) ...2. 使用尼拉坎特级数进行计算,公式如下:π = 3 +4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11*12) - (4/(12*13*14) ...圆周率计算方法3:通过反正弦函数来计算 pi 值 1. 选一个介于-1和1之间的数。
因为反正弦函数不能用于大于1或小于-1的参数。
2. 将选好的数字代入以下公式,其结果将约等于pi 值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆周率π的计算方法
圆周率的计算方法
古人计算圆周率,一般是用割圆法。
即用圆的内接或外切正多边形来逼近圆的周长。
Archimedes用正96边形得到圆周率小数点后3位的精度;刘徽用正3072边形得到5位精度;Ludolph Van Ceulen 用正262边形得到了35位精度。
这种基于几何的算法计算量大,速度慢,吃力不讨好。
随着数学的发展,数学家们在进行数学研究时有意无意地发现了许多计算圆周率的公式。
1、Machin公式
这个公式由英国天文学教授John Machin于1706年发现。
他利用这个公式计算到了100位的圆周率。
Machin公式每计算一项可以得到1.4位的十进制精度。
因为它的计算过程中被乘数和被除数都不大于长整数,所以可以很容易地在计算机上编程实现。
用马青公式计算Pi至小数点后100位程序
program Pi_Value;
{$APPTYPE CONSOLE}
//将Pi计算精确小数点后100位
//Machin公式
//Pi=16arctan(1/5)-4arctan(1/239)
uses
SysUtils;
const
N=100;
S=2*N+50;
aNum=5;
bNum=239;
type
Num=array [1..S] of byte;
//初始化数组
procedure AZero(var arr:Num);
var
i:smallint;
begin
for i:=1 to S do
arr:=0;
end;
//除法
procedure Division(var arr:Num;const b:smallint); var
c,y,i:smallint;
begin
c:=0;
for i:=1 to S do
begin
y:=arr+c*10;
c:=y mod b;
arr:=y div b;
end;
end;
//加法
procedure Addition(var arr:Num;const b:Num);
var
i,y,c:smallint;
begin
c:=0;
for i:=S downto 1 do
begin
y:=arr+b+c;
if y>=10 then
begin
c:=1;
arr:=y-10;
end
else
begin
c:=0;
arr:=y;
end;
end;
end;
//减法
procedure Minus(var arr:Num;const b:Num); var
i,y,c:smallint;
begin
c:=0;
for i:=S downto 1 do
begin
y:=arr-b-c;
if y<0 then
begin
c:=1;
arr:=10+y;
end
else
begin
c:=0;
arr:=y;
end;
end;
end;
var
tag:boolean;
a,b,Ra,Rb,t:Num;
i,j:smallint;
begin
AZero(t);
Ra:=t;Rb:=t;
tag:=true;
writeln('计算中,请等待......'); for i:=1 to N do
begin
a:=t;b:=t;
a[1]:=16;b[1]:=4;
for j:=1 to i*2-1 do
begin
Division(a,aNum);
DiVision(b,bNum);
end;
Division(a,i*2-1);
Division(b,i*2-1);
if tag then
begin
tag:=false;
Addition(Ra,a);
Addition(Rb,b);
end
else
begin
tag:=true;
Minus(Ra,a);
Minus(Rb,b);
end;
end;
Minus(Ra,Rb);
writeln('计算结果如下:'); writeln(Ra[1],'.');
for i:=2 to N+1 do
write(Ra);
readln;
End.
还有很多类似于Machin公式的反正切公式。
在所有这些公式中,Machin公式似乎是最快的了。
虽然如此,如果要计算更多的位数,比如几千万位,Machin公式就力不从心了。
下面介绍的算法,在PC 机上计算大约一天时间,就可以得到圆周率的过亿位的精度。
这些算法用程序实现起来比较复杂。
因为计算过程中涉及两个大数的乘除运算,要用FFT(Fast Fourier Transform)算法。
FFT可以将两个大数的乘除运算时间由O(n2)缩短为O(nlog(n))。
2、Ramanujan公式
1914年,印度数学家Srinivasa Ramanujan在他的论文里发表了一系列共14条圆周率的计算公式,这是其中之一。
这个公式每计算一项可以得到8位的十进制精度。
1985年Gosper用这个公式计算到了圆周率的17,500,000位。
1989年,David & Gregory Chudnovsky兄弟将Ramanujan公式改良成为:
这个公式被称为Chudnovsky公式,每计算一项可以得到15位的十进制精度。
1994年Chudnovsky兄弟利用这个公式计算到了
4,044,000,000位。
Chudnovsky公式的另一个更方便于计算机编程的形式是:
3、AGM(Arithmetic-Geometric Mean)算法
Gauss-Legendre公式:
初值:
重复计算:
最后计算:
这个公式每迭代一次将得到双倍的十进制精度,比如要计算100万位,迭代20次就够了。
1999年9月Takahashi和Kanada用这个算法计算到了圆周率的206,158,430,000位,创出新的世界纪录。
4、Borwein四次迭代式:
初值:
重复计算:
最后计算:
这个公式由Jonathan Borwein和Peter Borwein于1985年发表,它四次收敛于圆周率。
5、Bailey-Borwein-Plouffe算法
这个公式简称BBP公式,由David Bailey, Peter Borwein和Simon Plouffe于1995年共同发表。
它打破了传统的圆周率的算法,可以计算圆周率的任意第n位,而不用计算前面的n-1位。
这为圆周率的分布式计算提供了可行性。
1997年,Fabrice Bellard找到了一个比BBP快40%的公式:
参考百度文库、人民网-数学故事欣赏。
