化工热力学 第3章例题
化工热力学 第三章(魏顺安课后习题)

实际态 T、p
真实气体 H、S
1
理想气体 H 、S 基准态 T0、p 0
* 0
3
* 0
2
理想气体 H*、S* 实际态 T、p
1 2 3 因 p 0 1atm, 所 1 0 为 以 2 3
• 气体在基准态下的 H0和S0 是相对值:
e 0.78785 f P 1.5962 MPa
0.23845
普遍化方程
BPc P r Z 1 RTc Tr BPc B 0 B1 RTc
成于勤,毁于惰, 荒于嬉,败于奢
pr 0 1 ln i B B Tr
铁可磨,石可穿, 攻必克,胜必谦
H0 0
S0 0
id R
• 从设计过程可知:
H H0 H H2 H3 nH nH
id
S S0 S S2 S3 nS nS
1cal( 热力学 ) 4.184J
R
• 为方便后面求解,现将摩尔等压热容进行单位换算。
Cp (0.886 5.602 102 T 2.771 105 T 2 5.266 109 T 3 ) 4.184 3.707 0.2344 1.159 10 4 T 2 2.203 10 8 T 3 ( J .mol1 . K 1 ) T
ZRT 0.65500 8.314 410 Vm 0.40806 10 3 m 3 .mol1 p 5471.55 103
V nVm 1 0.40806 103 4.0806 104 m 3
• (2) 求H、S
设计如下热力学过程:
化工热力学
化工热力学一、是否题1. 纯物质由蒸汽变成固体,必须通过液相。
〔错。
能够直截了当变成固体。
〕2. 纯物质由蒸汽变成液体,必须通过冷凝的相变化过程。
〔错。
能够通过超临界流体区。
〕3. 当压力大于临界压力时,纯物质就以液态存在。
〔错。
假设温度也大于临界温度时,那么是超临界流体。
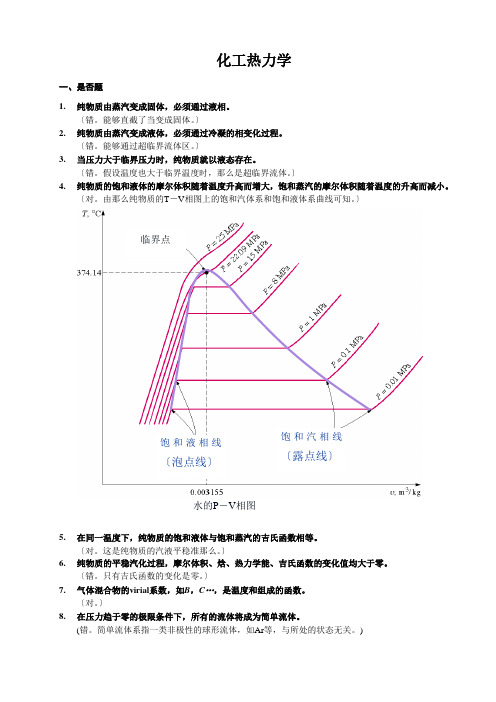
〕4. 纯物质的饱和液体的摩尔体积随着温度升高而增大,饱和蒸汽的摩尔体积随着温度的升高而减小。
〔对。
由那么纯物质的T -V 相图上的饱和汽体系和饱和液体系曲线可知。
〕5. 在同一温度下,纯物质的饱和液体与饱和蒸汽的吉氏函数相等。
〔对。
这是纯物质的汽液平稳准那么。
〕6. 纯物质的平稳汽化过程,摩尔体积、焓、热力学能、吉氏函数的变化值均大于零。
〔错。
只有吉氏函数的变化是零。
〕 7. 气体混合物的virial 系数,如B ,C …,是温度和组成的函数。
〔对。
〕8. 在压力趋于零的极限条件下,所有的流体将成为简单流体。
(错。
简单流体系指一类非极性的球形流体,如Ar 等,与所处的状态无关。
)饱和液相线〔泡点线〕饱和汽相线〔露点线〕水的P -V 相图 临界点二、选择题1. 指定温度下的纯物质,当压力低于该温度下的饱和蒸汽压时,那么气体的状态为〔 〕(C 。
参考P -V 图上的亚临界等温线。
)A. 饱和蒸汽B. 超临界流体C. 过热蒸汽2. T 温度下的过冷纯液体的压力P〔A 。
参考P -V 图上的亚临界等温线。
〕 3. T 温度下的过热纯蒸汽的压力P〔B 。
参考P -V 图上的亚临界等温线。
〕 4. 纯物质的第二virial 系数B〔A 。
virial 系数表示了分子间的相互作用,仅是温度的函数。
〕5. 能表达流体在临界点的P-V 等温线的正确趋势的virial 方程,必须至少用到〔A 。
要表示出等温线在临界点的拐点特点,要求关于V 的立方型方程〕 6. 关于纯物质,一定温度下的泡点压力与露点压力是 (A) A 相同的 B 不同的7. 关于纯物质,一定温度下泡点与露点,在P -T 图上是 (A) A 重叠的 B 分开的8. 关于纯物质,一定温度下泡点与露点,在P-V 图上是 (B) A 重叠的 B 分开的 9. 泡点的轨迹称为 (A) A 饱和液相线 B 饱和汽相线 10. 露点的轨迹称为 (B) A 饱和液相线 B 饱和汽相线 11. 关于混合物,PR 方程常数a 的表达式∑∑==-=3131)1(i j ij jj ii jik a a yy a 中的相互作用参数k ij ,i =j 时,其值 (A)A 为1B 为0C 从实验数据拟合得到,在没有实验数据时,近似作零处理A. >()T P sB. <()T P sC. =()T P sA. >()T P sB. <()T P sC. =()T P sA 仅是T 的函数B 是T 和P 的函数C 是T 和V 的函数D 是任何两强度性质的函数A. 第三virial 系数B. 第二virial 系数C. 无穷项D. 只需要理想气体方程纯物质的P -V 相图P C V C12. 关于混合物,PR 方程常数a 的表达式∑∑==-=3131)1(i j ij jj ii jik a a yy a 中的相互作用参数k ij ,i ≠j 时,其值 ( C )A 为1B 为0C 从实验数据拟合得到,在没有实验数据时,近似作零处理 三、运算题1. 由饱和蒸汽压方程,在合适的假设下估算水在25℃时的汽化焓。
化工热力学课后答案

化工热力学课后答案(填空、判断、画图)第1章 绪言一、是否题1. 封闭体系的体积为一常数。
(错)2. 封闭体系中有两个相βα,。
在尚未达到平衡时,βα,两个相都是均相敞开体系;达到平衡时,则βα,两个相都等价于均相封闭体系。
(对) 3. 理想气体的焓和热容仅是温度的函数。
(对)4. 理想气体的熵和吉氏函数仅是温度的函数。
(错。
还与压力或摩尔体积有关。
)5. 封闭体系的1mol 气体进行了某一过程,其体积总是变化着的,但是初态和终态的体积相等,初态和终态的温度分别为T 1和T 2,则该过程的⎰=21T T V dT C U ∆;同样,对于初、终态压力相等的过程有⎰=21T T P dT C H ∆。
(对。
状态函数的变化仅决定于初、终态与途径无关。
)二、填空题1. 状态函数的特点是:状态函数的变化与途径无关,仅决定于初、终态 。
2. 封闭体系中,温度是T 的1mol 理想气体从(P i ,V i )等温可逆地膨胀到(P f ,V f ),则所做的功为()f i rev V V RT W ln =(以V 表示)或()i f rev P P RT W ln = (以P 表示)。
3. 封闭体系中的1mol 理想气体(已知igP C ),按下列途径由T 1、P 1和V 1可逆地变化至P 2,则A 等容过程的 W = 0 ,Q =()1121T P P R C igP⎪⎪⎭⎫ ⎝⎛--,U =()1121T PP R C igP⎪⎪⎭⎫⎝⎛--,H =1121T P P C ig P ⎪⎪⎭⎫ ⎝⎛-。
B 等温过程的 W =21lnP P RT -,Q =21ln P PRT ,U = 0 ,H = 0 。
第2章P-V-T关系和状态方程一、是否题1. 纯物质由蒸汽变成液体,必须经过冷凝的相变化过程。
(错。
可以通过超临界流体区。
)2. 当压力大于临界压力时,纯物质就以液态存在。
(错。
若温度也大于临界温度时,则是超临界流体。
化工热力学第三版(完全版)课后习题答案解析

化工热力学课后答案第1章 绪言一、是否题1. 封闭体系的体积为一常数。
(错)2. 封闭体系中有两个相βα,。
在尚未达到平衡时,βα,两个相都是均相敞开体系;达到平衡时,则βα,两个相都等价于均相封闭体系。
(对)3. 理想气体的焓和热容仅是温度的函数。
(对)4. 理想气体的熵和吉氏函数仅是温度的函数。
(错。
还与压力或摩尔体积有关。
)5. 封闭体系的1mol 气体进行了某一过程,其体积总是变化着的,但是初态和终态的体积相等,初态和终态的温度分别为T 1和T 2,则该过程的⎰=21T T V dT C U ∆;同样,对于初、终态压力相等的过程有⎰=21T T P dT C H ∆。
(对。
状态函数的变化仅决定于初、终态与途径无关。
)二、填空题1. 状态函数的特点是:状态函数的变化与途径无关,仅决定于初、终态 。
2. 封闭体系中,温度是T 的1mol 理想气体从(P i ,V i )等温可逆地膨胀到(P f ,V f ),则所做的功为()f i rev V V RT W ln =(以V 表示)或()i f rev P P RT W ln = (以P 表示)。
3. 封闭体系中的1mol 理想气体(已知igP C ),按下列途径由T 1、P 1和V 1可逆地变化至P 2,则A 等容过程的 W = 0 ,Q =()1121T P P R C igP⎪⎪⎭⎫ ⎝⎛--,错误!未找到引用源。
U =()1121T PP R C igP⎪⎪⎭⎫⎝⎛--,错误!未找到引用源。
H = 1121T P P C ig P ⎪⎪⎭⎫ ⎝⎛-。
B 等温过程的 W =21lnP P RT -,Q =21ln P PRT ,错误!未找到引用源。
U = 0 ,错误!未找到引用源。
H = 0 。
C 绝热过程的 W =()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛--11211igPC RigPP P R V P R C ,Q = 0 ,错误!未找到引用源。
化工热力学第三版课后习题答案(1)

化工热力学课后答案第1章绪言—、是否题1. 封闭体系的体积为一常数。
(错)2. 封闭体系中有两个相, 。
在尚未达到平衡时,, 两个相都是均相敞开体系;达到平衡时,则,两个相都等价于均相封闭体系。
(对)3. 理想气体的焓和热容仅是温度的函数。
(对)4. 理想气体的熵和吉氏函数仅是温度的函数。
(错。
还与压力或摩尔体积有关。
)5. 封闭体系的1mol 气体进行了某一过程, 其体积总是变化着的, 但是初态和终态的体积相T 2等,初态和终态的温度分别为 T [和丁2,则该过程的 UC V dT ;同样,对于初、终态T iT 2压力相等的过程有 HC p dT 。
(对。
状态函数的变化仅决定于初、 终态与途径无关。
)T 1二、填空题状态函数的特点是: ________ 。
封闭体系中,温度是 T 的1mol 理想气体从(P , V )等温可逆地膨胀到(P ,V f ),则所做的 功为 W revRTl nV i V f (以 V 表示)或 W rev RT l nP f P (以 P 表示)。
C PP T1T 1。
1.3. 封闭体系中的imol 理想气体(已知C pg ),按下列途径由T 、P i 和V 可逆地变化至P 2,则A 等容过程的 W = _,Q= Cp 1RP 2 P 2P i/C Pg RP 1 1 T 1 , H=B等温过程的RTln l,^RTln t,U= 0 ,H=_0 ___ 。
解:EOSW revV 2 b RTl n丄 V 1 bRTln 纟V 1999In 2 1.0007222. 对于c P为常数的理想气体经过一绝热可逆过程,状态变化符合下列方程解: 3. 解: T 1 P 1(1),其式又是如何?以上a 、b 、 理想气体的绝热可逆过程,C ;gRdTT 22a Rb TT 1aln 旦 b T 2T1RT dV V cT dTCigC !,试问,对于C P a bTcT 2的理想气体,上述关系c 为常数。
化工热力学第三章习题答案

2013年3月28日
§第二题
2013年3月28日
§第二题
始态水为液体,V1 =Vf·m =1.0435× 10-3× 10=0.010435m3 终态水为蒸汽,V2 =Vg·m =1673.0× 10-3× 10=16.730m3 故△V= V2-V1=16.720m3 将△V代入△U=T△S-P△V,得 △U=373.15× 60.485 × 103-0.10113× 106 × 16.720 =20879084J≈20879kJ
2013年3月28日
§第二题
解法二 思路:查出水的汽化潜热Hfg,根据热力学基 本关系式依次求出△H,△S, △A,△U,△G
• 热力学基本关系式:
dH=TdS+Vdp dA=-SdT-pdV dU=TdS-pdV dG=-SdT+Vdp
T,p不变,V变 dH=TdS+Vdp=TdS dA=-SdT-pdV=-pdV dU=TdS-pdV dG=-SdT+Vdp=0
2013年3月28日
§第二题
由dA=-SdT-pdV,且dT=0,得 △A= -p△V= -0.10113× 106 × 16.720J =-1690.9kJ 由dG=-SdT+Vdp,且dT=0,dp=0,得 △G=0
《化工热力学章节习题及解答》第三章 例题

另外,还需要理想气体等压热容的数据,查附录A-4得到,得到异丁烷的理想气体等压热容是
(J mol-1K-1)
初态是T0=300K,P0=0.1MPa的理想气体;终态是T=360K的饱和蒸汽,饱和蒸汽压可以从Antoine方程计算,查附录A-2,得
性质
沸点或蒸汽压
U/Jg-1
H/Jg-1
S/Jg-1K-1
饱和蒸汽
340℃或14.59MPa
2464.5
2622.0
5.3359
总性质
2464500(J)
2622000(J)
5335.9(JK-1)
所以, J; J; JK-1。
又因为,是一个等容过程,故需要吸收的热为 J
7. 压力是3MPa的饱和蒸汽置于1000cm3的容器中,需要导出多少热量方可使一半的蒸汽冷凝?(可忽视液体水的体积)
解:以1g为基准来计算。
(1)对于绝热可逆膨胀,Q=0,W=-1000ΔU,S2=S1,
从 Pa,查附录C-1,得到 , 940.87Jg-1, ,
则 和
由于可确定膨胀后仍处于汽液两相区内,终态压力就是饱和蒸汽压,从 Pa查 , ; ,
从
则W=-1000(U2-U1)=278.45(kJ)
(2)再恒容加热成饱和蒸汽,W=0,
解:由Maxwell关系式
左边= ;
又因为 ,右边= ,由此可以得到
(这种体积关系一般能成立,故方程有一定的可靠性)。
5.试证明 ,并说明 。
解:由定义 ;
右边= =左边。
代入理想气体状态方程, 可以得到
6.证明(a)在汽液两相区的湿蒸汽有 。(b)在临界点有 。
化工热力学 例题 与解答(9).

第 3章均相封闭体系热力学原理及其应用一、是否题1. 体系经过一绝热可逆过程,其熵没有变化。
2. 吸热过程一定使体系熵增,反之,熵增过程也是吸热的。
3. 热力学基本关系式 dH=TdS+VdP只适用于可逆过程。
4. 象 dU=TdS-PdV等热力学基本方程只能用于气体,而不能用于液体或固相。
5. 当压力趋于零时, ((0, , ≡-P T M P T M ig (M 是摩尔性质。
6.[](0ln , P PR P T S S ig+-与参考态的压力 P 0无关。
纯物质逸度的完整定义是,在等温条件下, f RTd dG ln =。
7. 理想气体的状态方程是 PV=RT, 若其中的压力 P 用逸度 f 代替后就成为了真实流体状态方程。
8. 当0→P 时, ∞→P f 。
9. 因为⎰⎪⎭⎫⎝⎛-=PdP P RT V RT 01ln ϕ,当0→P 时, 1=ϕ,所以, 0=-P RT V 。
10. 逸度与压力的单位是相同的。
11. 吉氏函数与逸度系数的关系是 ((ϕln 1, , RT P T G P T G ig ==-。
12. 由于偏离函数是两个等温状态的性质之差, 故不可能用偏离函数来计算性质随着温度的变化。
13. 由于偏离函数是在均相体系中引出的概念, 故我们不能用偏离函数来计算汽化过程的热力学性质的变化。
14. 由一个优秀的状态方程,就可以计算所有的均相热力学性质随着状态的变化。
二、选择题1. 对于一均匀的物质,其 H 和 U 的关系为(B 。
因 H =U +PVA. H ≤UB. H>UC. H=UD. 不能确定2. 一气体符合 P=RT/(V-b 的状态方程从 V 1等温可逆膨胀至 V 2,则体系的∆S 为(C 。
b V b V R b V R dV T P dV V S S V V V V V V V T --=-=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫⎝⎛∂∂=⎰⎰⎰12ln 212121∆ A. bV bV RT --12lnB. 0C. bV bV R --12lnD. 12lnV V R 3. 对于一均相体系, VP T S T T S T ⎪⎭⎫⎝⎛-⎪⎭⎫⎝⎛∂∂∂∂等于(D 。
化工热力学答案(3章)

化⼯热⼒学答案(3章)3-1. 物质的体积膨胀系数β和等温压缩系数k 的定义分别为:1P V V T β=,1TV k V P =- ?。
试导出服从Vander Waals 状态⽅程的β和k 的表达式。
解:Van der waals ⽅程2 RT a P V b V=--由Z=f(x,y)的性质1y x z z x y x y z =- ? ?得 1T P VP V T V T P=- ? ? ???? ⼜ ()232TP a RTV VV b =-- VP R T V b= ?-所以 ()2321P a RT V V b V T RV b -??-??=-??-()()3232P RV V b V T RTV a V b -= ?-- 故 ()()22312PRV V b V V T RTV a V b β-==--()()222312T V V b V k V P RTV a V b -=-= ?-- 3-2. 某理想⽓体借活塞之助装于钢瓶中,压⼒为,温度为93℃,反抗⼀恒定的外压⼒ MPa ⽽等温膨胀,直到两倍于其初始容积为⽌,试计算此过程之U ?、H ?、S ?、A ?、G ?、TdS ?、pdV ?、Q和W 。
解:理想⽓体等温过程,U ?=0、H ?=0∴ Q =-W =21112ln 2V V V V RTpdV pdV dV RT V==== J/mol ∴ W = J/mol⼜ PP dT V dSC dP T T=- ?理想⽓体等温膨胀过程dT =0、P V R T P= ? ∴ R dS dP P=-∴ 222111ln ln ln2S P P P S P SdS R d P R PR ?==-=-=??=(mol·K)A U T S ?=?-?=-366×= J/(mol·K)G H T S A ?=?-?=?= J/(mol·K)TdS T S A =?=??= J/(mol·K)21112ln 2V V V V RTpdV pdV dV RT V==== J/mol 3-3. 试求算1kmol 氮⽓在压⼒为、温度为773K 下的内能、焓、熵、V C 、p C 和⾃由焓之值。
化工热力学课后习题答案

sv sl sv sl 1、表达纯物质的汽平衡的准则有 G (T ) = G (T )或G T ,V = G T ,V (吉氏函数) 、 dT
V sv
(
)
(
)
∆H vap T∆V vap
(Claperyon
(Maxwell 等面积规则) 。它们能(能/不能)推广到其它类型的相平衡。 方程) 、V 2、对于纯物质,一定温度下的泡点压力与露点压力相同的(相同/不同) ;一定温度下的泡点与露点,在 P -T 图上是重叠的(重叠/分开),而在 P-V 图上是分开的(重叠/分开),泡点的轨迹称为饱和液相线,露点 的轨迹称为饱和汽相线,饱和汽、液相线与三相线所包围的区域称为汽液共存区。纯物质汽液平衡时,压 力称为蒸汽压,温度称为沸点。
s 汽化曲线方程是 P = 610.62 + 2.4688(T − 273.15)
2508 = 2.4688 8.314 × 273.15 273.15 × -1 610.62 PaK
解两直线的交点,得三相点的数据是: Pt = 615.09 Pa, Tt = 273.1575 K 2. 试由饱和蒸汽压方程(见附录 A-2) ,在合适的假设下估算水在 25℃时的汽化焓。
T2 T 终态的温度分别为 T1 和 T2,则该过程的 ;同样,对于初、终态压力相等的过程有 (对。状态函数的变化仅决定于初、终态与途径无关。 )
1
∆U = CV dT
∫
T2
∆H = C P dT
T1
∫
。
二、填空题 1. 状态函数的特点是:状态函数的变化与途径无关,仅决定于初、终态 。 2. 封闭体系中,温度是 T 的 1mol 理想气体从 (Pi , Vi) 等温可逆地膨胀到 (Pf , Vf) ,则所做的功为 W = RT ln Pf Pi Wrev = RT ln Vi V f (以 V 表示)或 rev (以 P 表示)。
《化工热力学》综合复习资料.

《化工热力学》综合复习资料第2章 流体的p-V-T 关系一、试用Pitzer 三参数普遍化方法计算水蒸汽在107.9×105Pa 、593K 下的比容。
第3章 流体的热力学性质一、丙烷气体的始态为1.013×105Pa 、400K(可以视为理想气体),终态为3.013×105Pa 、500K 。
已知丙烷在理想气体状态下的摩尔热容为:T C ig p 1775.099.22+= (J/mol.K)试采用三参数普遍化关系式计算始态至终态的焓变与熵变。
二、用三参数普遍化方法计算1kmol 的1,3-丁二烯,从25atm 及130℃压缩至125atm 和280℃时的ΔH 、ΔS 、ΔU 和ΔV 。
已知理想气体状态下的定压热容(cal/mol.K)与温度(K)的函数关系为: 26310649.1710224.53432.5T T C ig p--⨯-⨯+=第5章 化工过程的能量分析一、1.57MPa 、484℃的过热水蒸气推动透平作功,并在0.0687MPa 下排出。
此透平既不绝热也不可逆,输出的轴功相当于可逆绝热膨胀功的85%。
由于隔热不好,每kg 的蒸汽有7.12kJ 的热量散失于20℃的环境中。
求此过程的理想功、损失功及热力学效率。
二、某炼厂有一台蒸汽透平,已知水蒸汽入口的温度为440℃,压力为40×105Pa ,流率为4000kg/h ,蒸汽排出的压力为7.0×105Pa 。
(1) 假定透平绝热可逆操作,试计算透平的功率;(2) 若透平绝热操作,输出的轴功等于绝热可逆轴功的82.65%。
则蒸汽的出口温度为多少?并计算过程的有效能(火用 )损失。
三、有一逆流式换热器,利用废气加热空气,空气由0.1MPa ,293K 被加热到398K ,空气流量为1.5kg.s –1;而废气从0.13MPa 、523K 冷却到368K 。
空气的等压热容为1.04kJ.kg –1.K –1,而废气的等压热容为0.84 kJ.kg –1.K –1,假定空气与废气通过换热器的压力与动能变化可忽略不计,而且换热器与环境无热量交换,环境状态为0.1MPa 、293K 。
化工热力学第3章 流体的PVT关系

纯物质的P-T图
P
Pc
固 相
1
3
密
流
A
区
C
液
相
2 B 气相
1-2线 汽固平衡线(升华线) 2-c线 汽液平衡线(汽化线) 2-3线 液固平衡线(熔化线)
C点临界点,2点三相点
P=Pc,T=Tc的区域, 两相性质相同
Tc
T
P>Pc,T>Tc的区域,压缩流体区(密流区,超临界流体区)
2021/2/22
3
Shanghai university
Shanghai university
Shanghai university
2021/2/22
三维相图2
液 临界点
固 气
汽
汽液混合物 饱和汽
p=0.2MPa
过热蒸汽
恒温(150o C )下,水的体积随压力变化的示意图
2021/2/22
12
Shanghai university
纯物质的P-V图
T2 T1 T3
Tc
气
T4
C
P
T5
汽 液
汽液两相区
V
特性:
在单相区,等温线为 光滑的曲线或直线; 高于Tc的的等温线 光滑,无转折点,低 于Tc的的等温线有 折点,由三部分组成。
PVRbTVVbabVb
a
acT
0.45724R2Tc2 Pc
T
b 0.07780RTc
Pc
T 1 0 . 3 7 1 . 54 4 0 . 2 6 2 6 2 4 1 2 T r 0 9 . 5 2 6
2021/2/22
41
4 Peng - Robinson ( PR )方程
化工热力学答案(3章).

3-1. 物质的体积膨胀系数β和等温压缩系数k 的定义分别为:1PV V T β∂⎛⎫=⎪∂⎝⎭,1TV k V P ∂⎛⎫=- ⎪∂⎝⎭。
试导出服从 状态方程的β和k 的表达式。
解: 方程2RT aP V b V=-- 由()的性质1y xz z x y x y z ⎛⎫∂∂∂⎛⎫⎛⎫⋅⋅=- ⎪⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭得 1T P VP V T V T P ∂∂∂⎛⎫⎛⎫⎛⎫⋅⋅=- ⎪⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ 又 ()232TP a RTV V V b ∂⎛⎫=-⎪∂⎝⎭- VP R T V b∂⎛⎫=⎪∂-⎝⎭所以 ()2321P a RTV V b VT R V b ⎡⎤∂-⎛⎫-⋅⋅=-⎢⎥⎪∂⎝⎭-⎢⎥⎣⎦()()3232P RV V b V T RTV a V b -∂⎛⎫= ⎪∂⎝⎭-- 故 ()()22312PRV V b V V T RTV a V b β-∂⎛⎫==⎪∂⎝⎭--()()222312T V V b V k V P RTV a V b -∂⎛⎫=-= ⎪∂⎝⎭-- 3-2. 某理想气体借活塞之助装于钢瓶中,压力为34.45,温度为93℃,反抗一恒定的外压力3.45 而等温膨胀,直到两倍于其初始容积为止,试计算此过程之U ∆、H ∆、S ∆、A ∆、G ∆、TdS ⎰、pdV ⎰、Q 和W 。
解:理想气体等温过程,U ∆=0、H ∆=0 ∴ 21112ln 2V V V VRTpdV pdV dV RT V===⎰⎰⎰2109.2 ∴ 2109.2 又 P PdTV dS C dP T T ∂⎛⎫=- ⎪∂⎝⎭ 理想气体等温膨胀过程0、P V R T P∂⎛⎫= ⎪∂⎝⎭∴ R dS dP P=-∴ 222111ln ln ln2S P P P SP S dS R d P R PR ∆==-=-=⎰⎰=5.763(·K)A U T S ∆=∆-∆366×5.7632109.26 (·K)G H T S A ∆=∆-∆=∆2109.26 (·K)TdS T S A =∆=∆⎰2109.26 (·K)21112ln 2V V V V RTpdV pdV dV RT V===⎰⎰⎰=2109.2 3-3. 试求算1氮气在压力为10.13、温度为773K 下的内能、焓、熵、V C 、p C 和自由焓之值。
化工热力学第一,二三章完整!!!答案

第二章 流体的压力、体积、浓度关系:状态方程式2-1 试分别用下述方法求出400℃、4.053MPa 下甲烷气体的摩尔体积。
(1) 理想气体方程;(2) RK 方程;(3)PR 方程;(4) 维里截断式(2-7)。
其中B 用Pitzer 的普遍化关联法计算。
[解] (1) 根据理想气体状态方程,可求出甲烷气体在理想情况下的摩尔体积idV 为33168.314(400273.15)1.381104.05310id RT V m mol p --⨯+===⨯⋅⨯ (2) 用RK 方程求摩尔体积将RK 方程稍加变形,可写为0.5()()RT a V b V b p T pV V b -=+-+ (E1)其中2 2.50.427480.08664c c c cR T a p RT b p ==从附表1查得甲烷的临界温度和压力分别为c T =190.6K, c p =4.60MPa ,将它们代入a, b 表达式得2 2.56-20.560.427488.314190.6 3.2217m Pa mol K 4.6010a ⨯⨯==⋅⋅⋅⨯ 53160.086648.314190.6 2.9846104.6010b m mol --⨯⨯==⨯⋅⨯ 以理想气体状态方程求得的idV 为初值,代入式(E1)中迭代求解,第一次迭代得到1V 值为5168.314673.152.9846104.05310V -⨯=+⨯⨯ 350.563353.2217(1.38110 2.984610)673.15 4.05310 1.38110(1.38110 2.984610)-----⨯⨯-⨯-⨯⨯⨯⨯⨯⨯+⨯ 3553311.381102.984610 2.1246101.389610m mol -----=⨯+⨯-⨯=⨯⋅ 第二次迭代得2V 为353520.563353553313.2217(1.389610 2.984610)1.381102.984610673.154.05310 1.389610(1.389610 2.984610)1.381102.984610 2.1120101.389710V m mol ------------⨯⨯-⨯=⨯+⨯-⨯⨯⨯⨯⨯⨯+⨯=⨯+⨯-⨯=⨯⋅1V 和2V 已经相差很小,可终止迭代。
《化工热力学》详细课后习题答案解析(陈新志)

2习题第1章 绪言一、是否题1. 孤立体系的热力学能和熵都是一定值。
(错。
和,如一体积等于2V 的绝热刚性容器,被一理想的隔板一分为二,左侧状态是T ,P 的理想气体,右侧是T 温度的真空。
当隔板抽去后,由于Q =W =0,,,,故体系将在T ,2V ,0.5P 状态下达到平衡,,,)2. 封闭体系的体积为一常数。
(错)3. 封闭体系中有两个相。
在尚未达到平衡时,两个相都是均相敞开体系;达到平衡时,则两个相都等价于均相封闭体系。
(对)4. 理想气体的焓和热容仅是温度的函数。
(对)5. 理想气体的熵和吉氏函数仅是温度的函数。
(错。
还与压力或摩尔体积有关。
)6. 要确定物质在单相区的状态需要指定两个强度性质,但是状态方程 P=P (T ,V )的自变量中只有一个强度性质,所以,这与相律有矛盾。
(错。
V 也是强度性质)7. 封闭体系的1mol 气体进行了某一过程,其体积总是变化着的,但是初态和终态的体积相等,初态和终态的温度分别为T 1和T 2,则该过程的;同样,对于初、终态压力相等的过程有。
(对。
状态函数的变化仅决定于初、终态与途径无关。
)8. 描述封闭体系中理想气体绝热可逆途径的方程是(其中),而一位学生认为这是状态函数间的关系,与途径无关,所以不需要可逆的条件。
(错。
) 9. 自变量与独立变量是一致的,从属变量与函数是一致的。
(错。
有时可能不一致)10. 自变量与独立变量是不可能相同的。
(错。
有时可以一致)三、填空题1. 状态函数的特点是:状态函数的变化与途径无关,仅决定于初、终态 。
2. 单相区的纯物质和定组成混合物的自由度数目分别是 2 和 2 。
3. 封闭体系中,温度是T 的1mol 理想气体从(P ,V )等温可逆地膨胀到(P ,V ),则所做的功为i i f f(以V 表示)或 (以P 表示)。
4. 封闭体系中的1mol 理想气体(已知),按下列途径由T 1、P 1和V 1可逆地变化至P,则mol ,温度为 和水 。
化工热力学第三章2

(1)T-S图
(2)lnp-H图
3.11.1 T-S图和lnp-H图的一般形式
C点是临界点,饱和液体 线AC,饱和蒸气线BC。 线段B-A-D是气-液-固三相 平衡线。
(1)T-S图
3.11.1 T-S图和lnp-H图的一般形式
气、液共存区内的任一点可以视为是该点所对应的 饱和蒸气与饱和液体的混合物(也称为湿蒸气),其摩
3.7 逸度和逸度系数
对于T=303.15K的等温线有
fl 8.314 303.15 ln 0.00001808 ( p 4246)
4246
由此可计算不同压力下的逸度。
(b)当p=lMPa时
f l 4276.44Pa
(c)当p=10MPa时
f l 4561.64Pa
3.8 均相热力学性质计算
3.7 逸度和逸度系数
解:(a)由于在低压力下,水蒸气可作为理想气体, 从汽-液平衡准则知
f sv f sl p s 4246 Pa
ln f p
T
V RT
若忽视Vsl 随压力的变化,沿等温线从饱和液体至
压缩液体区积分
RT ln f l V sl ( p p s ) f sl
3.11.2 热力学性质图、表的制作原理
任意状态的焓和熵可以这样来计算,如
H(T , p) H(T , p) H(T0 , p0 )
模型,还能计算
性质随温度和压力的变化。
状态方程在流体物性的研究中有着特别重要的意义,结
合一定的混合法则,状态方程还可以计算非均相混合物的性
质(相平衡、各相的热力学性质)。
3.10.2 饱和热力学性质计算
(5)对于混合物,在单相区,定组成混合物的性质计
化工热力学第三版(完全版)课后习题答案

(a)由软件计算可知
(b)
3.试由饱和液体水的性质估算(a)100℃,2.5MPa和(b)100℃,20MPa下水的焓和熵,已知100℃下水的有关性质如下
MPa, Jg-1, J g-1K-1, cm3g-1,
cm3g-1K-1
化工热力学课后答案
第1章 绪言
一、是否题
1.封闭体系的体积为一常数。(错)
2.封闭体系中有两个相 。在尚未达到平衡时, 两个相都是均相敞开体系;达到平衡时,则 两个相都等价于均相封闭体系。(对)
3.理想气体的焓和热容仅是温度的函数。(对)
4.理想气体的熵和吉氏函数仅是温度的函数。(错。还与压力或摩尔体积有关。)
2.对于混合物体系,偏离函数中参考态是与研究态同温.同组成的理想气体混合物。
四、计算题
1.试计算液态水从2.5MPa和20℃变化到30MPa和300℃的焓变化和熵变化,既可查水的性质表,也可以用状态方程计算。
解:用PR方程计算。查附录A-1得水的临界参数Tc=647.30K;Pc=22.064MPa;ω=0.344
A.
B.0
C.
D.
3. 等于(D。因为 )
A.
B.
C.
D.
4.吉氏函数变化与P-V-T关系为 ,则 的状态应该为(C。因为 )
A.T和P下纯理想气体
B.T和零压的纯理想气体
C.T和单位压力的纯理想气体
三、填空题
1.状态方程 的偏离焓和偏离熵分别是 和 ;若要计算 和 还需要什么性质? ;其计算式分别是 和 。
四、计算题
1.某一服从P(V-b)=RT状态方程(b是正常数)的气体,在从1000b等温可逆膨胀至2000b,所做的功应是理想气体经过相同过程所做功的多少倍?
化工热力学课后习题答案

第1章绪言一、是否题3. 封闭体系中有两个相。
在尚未达到平衡时,两个相都是均相敞开体系;达到平衡时,则两个相都等价于均相封闭体系。
(对)4. 理想气体的焓和热容仅是温度的函数。
(对)5. 理想气体的熵和吉氏函数仅是温度的函数。
(错。
还与压力或摩尔体积有关。
)第2章P-V-T关系和状态方程一、是否题2. 纯物质由蒸汽变成液体,必须经过冷凝的相变化过程。
(错。
可以通过超临界流体区。
)3. 当压力大于临界压力时,纯物质就以液态存在。
(错。
若温度也大于临界温度时,则是超临界流体。
)4. 由于分子间相互作用力的存在,实际气体的摩尔体积一定小于同温同压下的理想气体的摩尔体积,所以,理想气体的压缩因子Z=1,实际气体的压缩因子Z<1。
(错。
如温度大于Boyle温度时,Z>1。
)7. 纯物质的三相点随着所处的压力或温度的不同而改变。
(错。
纯物质的三相平衡时,体系自由度是零,体系的状态已经确定。
)8. 在同一温度下,纯物质的饱和液体与饱和蒸汽的热力学能相等。
(错。
它们相差一个汽化热力学能,当在临界状态时,两者相等,但此时已是汽液不分)9. 在同一温度下,纯物质的饱和液体与饱和蒸汽的吉氏函数相等。
(对。
这是纯物质的汽液平衡准则。
)10. 若一个状态方程能给出纯流体正确的临界压缩因子,那么它就是一个优秀的状态方程。
(错。
)11. 纯物质的平衡汽化过程,摩尔体积、焓、热力学能、吉氏函数的变化值均大于零。
(错。
只有吉氏函数的变化是零。
)12. 气体混合物的virial系数,如B,C…,是温度和组成的函数。
(对。
)13. 三参数的对应态原理较两参数优秀,因为前者适合于任何流体。
(错。
三对数对应态原理不能适用于任何流体,一般能用于正常流体normal fluid)14. 在压力趋于零的极限条件下,所有的流体将成为简单流体。
(错。
简单流体系指一类非极性的球形流,如Ar等,与所处的状态无关。
)二、选择题1. 指定温度下的纯物质,当压力低于该温度下的饱和蒸汽压时,则气体的状态为(C。
第三章 化工热力学习题解答

第三章 纯流体的热力学性质计算思考题3-1气体热容,热力学能和焓与哪些因素有关?由热力学能和温度两个状态参数能否确定气体的状态?答:气体热容,热力学能和焓与温度压力有关,由热力学能和温度两个状态参数能够确定气体的状态。
3-2 理想气体的内能的基准点是以压力还是温度或是两者同时为基准规定的? 答:理想气体的内能的基准点是以温度为基准规定的。
3-3 理想气体热容差R p v c c -=是否也适用于理想气体混合物?答:理想气体热容差R p v c c -=不适用于理想气体混合物,因为混合物的组成对此有关。
3-4 热力学基本关系式d d d H T S V p =+是否只适用于可逆过程? 答:否。
热力学基本关系式d d d H T S V p =+不受过程是否可逆的限制3-5 有人说:“由于剩余函数是两个等温状态的性质之差,故不能用剩余函数来计算性质随着温度的变化”,这种说法是否正确?答:不正确。
剩余函数是针对于状态点而言的;性质变化是指一个过程的变化,对应有两个状态。
3-6 水蒸气定温过程中,热力学内能和焓的变化是否为零?答:不是。
只有理想气体在定温过程中的热力学内能和焓的变化为零。
3-7 用不同来源的某纯物质的蒸气表或图查得的焓值或熵值有时相差很多,为什么?能否交叉使用这些图表求解蒸气的热力过程?答:因为做表或图时选择的基准可能不一样,所以用不同来源的某纯物质的蒸气表或图查得的焓值或熵值有时相差很多。
不能够交叉使用这些图表求解蒸气的热力过程。
3-8 氨蒸气在进入绝热透平机前,压力为2.0 MPa ,温度为150℃,今要求绝热透平膨胀机出口液氨不得大于5%,某人提出只要控制出口压力就可以了。
你认为这意见对吗?为什么?请画出T -S 图示意说明。
答:可以。
因为出口状态是湿蒸汽,确定了出口的压力或温度,其状态点也就确定了。
3-9 很纯的液态水,在大气压力下,可以过冷到比0℃低得多的温度。
假设1kg 已被冷至-5℃的液体。
化工热力学习题-041111-第3章参考答案
U 1.015 10 4 J / mol
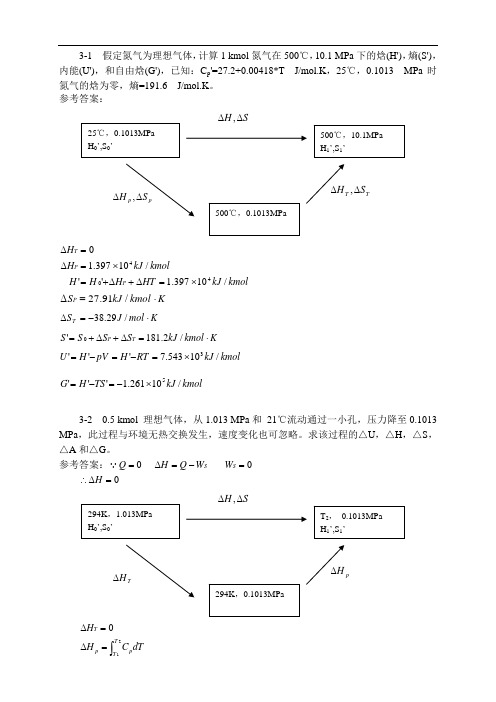
V 7.518 10 4 m 3 / mol 对于 0.45kmol
H 总 1.064 10 4 450 4.788 10 6 J S 总 13.66 450 6.147 10 3 J / K V总 7.518 10 4 450 0.338m 3 U 总 1.015 10 4 450 4.568 10 6 J
pV RT 2 RT 1 0
U 0 S ST SP 19.14 J / mol
A U TS 5628J / mol
G H TS 5628 J / mol 对 0.5kmol: H 总 0 U 总 0 S总 9.571kJ / K A总 2814kJ G总 2814 kJ
3
3-5 已知 350℃,0.1013 MPa 时水蒸汽的焓为 3192 kJ/kg,用通用关系式求 10.1 MPa, 360℃时水蒸汽的焓。已知水的 Cp’=29.16 + 14.49*10-3T – 2.022*10-6T2 J/mol.K 。 参考答案:
H
623K,0.1013MPa,R.g. 633K, 10.1 MPa,R.g.
H , S
25℃,0.1013MPa H0’,S0’ 500℃,10.1MPa H1’,S1’
H p , S p
500℃,0.1013MPa
H T , S T
H T 0 HP 1.397 10 4 kJ / kmol H ' H 0' HP HT 1.397 10 4 kJ / kmol
