第五章 晶体结构1教材
合集下载
化学优质课公开课课件晶体结构
第一讲 晶体结构
晶体：是质点（分子、离子、原子）在空间有规 则的排列，是具有规则的多面体固体物质。
结晶晶格：以确定位置的点在空间作有规则的 排列所得到的具有一定几何外形的物质，称为 结晶晶格。每个质点在晶格中所占的位置称为 晶体的点阵点。
问题1：为什么晶胞是指大立方体，而不 是小立方体呢？
晶胞特性之-----------晶胞均等性
的金属钠是体心晶胞，而氯化铯则不是体心晶胞而是素晶胞。 考察某晶胞是否面心晶胞最简单的方法是：晶胞内所有原子可作在其［原子
坐标+（ ½ ，½ ，0） （0 ，½ ，½） （ ½ ，0 ，½）］的平移而得到
周围环境完全相同的原子。如金刚石是面心晶胞而干冰是素晶胞，因为干冰 晶胞中处于面心位置的二氧化碳分子与处于顶角位置的二氧化碳分子的取向 互不相同，框架移动后得到的新晶胞中原子的位置不同于原晶胞中原子的位 置了。底心晶胞在中学课本中未涉及，不再赘述。
8
2
即晶体中每个小正方体中平均含有 1 个
2
NiO.其质量为:
74.7g × 1
8
6.02×1023 2
而此小正方体体积为(a×10-8㎝)3
74.7g 6.02×1023
×
1 2
(a×10-8㎝)3
=
62. 0 a3
，故NiO晶体密度为： g. ㎝-3
3
4
8
7
1
2
5
6
(2)天然的和绝大多数人工制备的晶体都存在着各种缺陷，例 如在某种NiO晶体中就存在着缺陷：一个Ni2+被两个Ni3+所取 代，其结果是晶体仍呈电中性，但化合物中Ni 和O的比值发生 了变化，某种氧化镍样品组成为Ni0.97O，试计算该晶体中Ni3+ 与Ni2+的离子个数之比。
晶体：是质点（分子、离子、原子）在空间有规 则的排列，是具有规则的多面体固体物质。
结晶晶格：以确定位置的点在空间作有规则的 排列所得到的具有一定几何外形的物质，称为 结晶晶格。每个质点在晶格中所占的位置称为 晶体的点阵点。
问题1：为什么晶胞是指大立方体，而不 是小立方体呢？
晶胞特性之-----------晶胞均等性
的金属钠是体心晶胞，而氯化铯则不是体心晶胞而是素晶胞。 考察某晶胞是否面心晶胞最简单的方法是：晶胞内所有原子可作在其［原子
坐标+（ ½ ，½ ，0） （0 ，½ ，½） （ ½ ，0 ，½）］的平移而得到
周围环境完全相同的原子。如金刚石是面心晶胞而干冰是素晶胞，因为干冰 晶胞中处于面心位置的二氧化碳分子与处于顶角位置的二氧化碳分子的取向 互不相同，框架移动后得到的新晶胞中原子的位置不同于原晶胞中原子的位 置了。底心晶胞在中学课本中未涉及，不再赘述。
8
2
即晶体中每个小正方体中平均含有 1 个
2
NiO.其质量为:
74.7g × 1
8
6.02×1023 2
而此小正方体体积为(a×10-8㎝)3
74.7g 6.02×1023
×
1 2
(a×10-8㎝)3
=
62. 0 a3
，故NiO晶体密度为： g. ㎝-3
3
4
8
7
1
2
5
6
(2)天然的和绝大多数人工制备的晶体都存在着各种缺陷，例 如在某种NiO晶体中就存在着缺陷：一个Ni2+被两个Ni3+所取 代，其结果是晶体仍呈电中性，但化合物中Ni 和O的比值发生 了变化，某种氧化镍样品组成为Ni0.97O，试计算该晶体中Ni3+ 与Ni2+的离子个数之比。
新人教版版高考化学总复习第五章晶体结构与性质教案
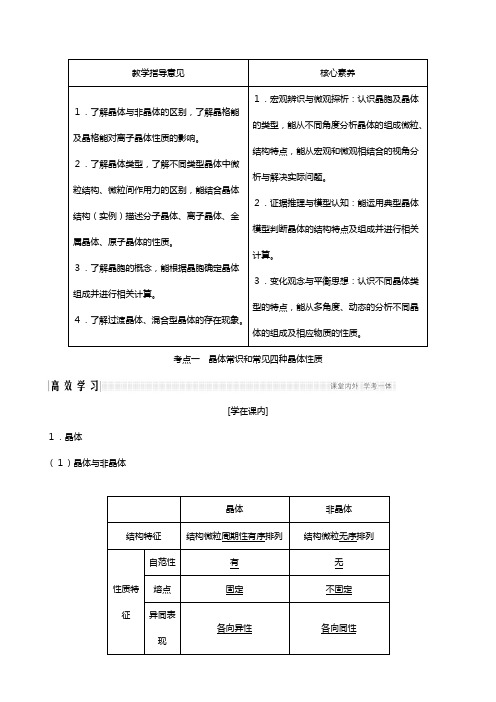
教学指导意见核心素养１．了解晶体与非晶体的区别，了解晶格能及晶格能对离子晶体性质的影响。
２．了解晶体类型，了解不同类型晶体中微粒结构、微粒间作用力的区别，能结合晶体结构（实例）描述分子晶体、离子晶体、金属晶体、原子晶体的性质。
３．了解晶胞的概念，能根据晶胞确定晶体组成并进行相关计算。
４．了解过渡晶体、混合型晶体的存在现象。
１．宏观辨识与微观探析：认识晶胞及晶体的类型，能从不同角度分析晶体的组成微粒、结构特点，能从宏观和微观相结合的视角分析与解决实际问题。
２．证据推理与模型认知：能运用典型晶体模型判断晶体的结构特点及组成并进行相关计算。
３．变化观念与平衡思想：认识不同晶体类型的特点，能从多角度、动态的分析不同晶体的组成及相应物质的性质。
考点一晶体常识和常见四种晶体性质[学在课内]１．晶体（１）晶体与非晶体晶体非晶体结构特征结构微粒周期性有序排列结构微粒无序排列性质特征自范性有无熔点固定不固定异同表现各向异性各向同性对固体进行X射线衍射实验（２）得到晶体的途径１熔融态物质凝固。
２气态物质冷却不经液态直接凝固（凝华）。
３溶质从溶液中析出。
（３）晶胞１概念：描述晶体结构的基本单元。
２晶体中晶胞的排列——无隙并置Ａ．无隙：相邻晶胞之间没有任何间隙。
Ｂ．并置：所有晶胞平行排列、取向相同。
（４）晶格能１定义：气态离子形成１摩尔离子晶体释放的能量，通常取正值，单位：kJ·mol—１。
２影响因素Ａ．离子所带电荷数：离子所带电荷数越多，晶格能越大。
Ｂ．离子的半径：离子的半径越小，晶格能越大。
３与离子晶体性质的关系晶格能越大，形成的离子晶体越稳定，且熔点越高，硬度越大。
[名师点拨]（１）具有规则几何外形的固体不一定是晶体，如玻璃。
（２）晶胞是从晶体中“截取”出来具有代表性的“平行六面体”，但不一定是最小的“平行六面体”。
２．四种晶体类型的比较[考在课外]教材延伸判断正误（１）晶体和非晶体的本质区别是晶体中粒子在微观空间里呈周期性的有序排列。
晶体结构.ppt最新版最新版
乐清市二中 翁旦临
教案 讲解 练习 退出
退出
晶 体 类 型
离子晶体 分子晶体 原子晶体 石墨晶体 金属晶体 退出
氯化钠晶体
离 子 晶 体
氯化铯晶体
晶体形成 氯化钠晶胞 质点分析
氯化铯晶胞 质点分析
退出
氯化钠晶体的形成：
Na+ Cl- Na+ Cl- Na+ ClNa+ Cl- Na+
返回
氯 化 钠
返回
氯 化 铯
返回
干 冰
质点 返回
金刚石
硅晶体
原
子
晶
碳化硅
体
二氧化硅
退出
质点分析 质点分析
金 刚 石
返回
质点
习题
晶 体 硅
返回
碳 化 硅
返回
二氧化硅
返回
石 墨
返回
金 属 钠
返回
氯 化 钠
每个NaCl晶胞中有 4 个Cl -，有 4 个Na+。
返回
氯化铯
每个CSCl晶胞中有 1 个CS+，有 1 个Cl -。
向；我们习惯了飞翔，却成了无脚的鸟。年轻时我们并不了解自己，不知道自己需要什么。不知道什么才是自己最想要的，什么才是最适合自己的，自己又是怎么样的一个 人。”时光叠加，沧桑有痕，终究懂得，漫漫人生路，得失爱恨别离，不过是生命的常态。原来，人生最曼妙的风景，就是那颗没被俗世河流污染的初心。大千世界，有很多 的东西可以去热爱，或许一株风中摇曳的小草，一朵迎风招展的小花，一条弯弯曲曲的小河，都足够让我们触摸迷失的初心。紫陌红尘，芸芸众生，皆是过客。若时光允许， 我愿意一生柔软，爱了樱桃，爱芭蕉，静守于轮回的渡口，揣一颗云水禅心，将寂寞坐断，将孤独守成一帧最美的山水画卷。一直渴盼着，与心悦的人相守于古朴的小院，守 着老旧的光阴，只闻花香，不谈悲喜，读书喝茶，不争朝夕。阳光暖一点，再暖一点，日子慢一些，再慢一些，从容而优雅地老去。浮生荡荡，阳春白雪，触目横斜千万朵， 赏心不过两三枝；任凭弱水三千，只取一瓢饮。有梦的季节，有爱的润泽，走过的日子，都会成为笔尖温润如玉的诗篇。相信越是走到最后，剩下的唯有一颗向真向善向美的 初心。似水流年，如花美眷，春潮带雨晚来急，野渡无人舟自横朝花夕拾，当回望过往，你是此生无憾，还是满心懊悔呢？随着芳华的流逝，我们终究会明白：任何的财富都 比不上精神上的愉悦，任何的快感都不及对初心的执着。愿你不趋炎附势，不阿谀奉迎，不苟且偷生，不虚掷有限的年华，活出属于自己的风采，活在每一个当下，不忘初心，
教案 讲解 练习 退出
退出
晶 体 类 型
离子晶体 分子晶体 原子晶体 石墨晶体 金属晶体 退出
氯化钠晶体
离 子 晶 体
氯化铯晶体
晶体形成 氯化钠晶胞 质点分析
氯化铯晶胞 质点分析
退出
氯化钠晶体的形成：
Na+ Cl- Na+ Cl- Na+ ClNa+ Cl- Na+
返回
氯 化 钠
返回
氯 化 铯
返回
干 冰
质点 返回
金刚石
硅晶体
原
子
晶
碳化硅
体
二氧化硅
退出
质点分析 质点分析
金 刚 石
返回
质点
习题
晶 体 硅
返回
碳 化 硅
返回
二氧化硅
返回
石 墨
返回
金 属 钠
返回
氯 化 钠
每个NaCl晶胞中有 4 个Cl -，有 4 个Na+。
返回
氯化铯
每个CSCl晶胞中有 1 个CS+，有 1 个Cl -。
向；我们习惯了飞翔，却成了无脚的鸟。年轻时我们并不了解自己，不知道自己需要什么。不知道什么才是自己最想要的，什么才是最适合自己的，自己又是怎么样的一个 人。”时光叠加，沧桑有痕，终究懂得，漫漫人生路，得失爱恨别离，不过是生命的常态。原来，人生最曼妙的风景，就是那颗没被俗世河流污染的初心。大千世界，有很多 的东西可以去热爱，或许一株风中摇曳的小草，一朵迎风招展的小花，一条弯弯曲曲的小河，都足够让我们触摸迷失的初心。紫陌红尘，芸芸众生，皆是过客。若时光允许， 我愿意一生柔软，爱了樱桃，爱芭蕉，静守于轮回的渡口，揣一颗云水禅心，将寂寞坐断，将孤独守成一帧最美的山水画卷。一直渴盼着，与心悦的人相守于古朴的小院，守 着老旧的光阴，只闻花香，不谈悲喜，读书喝茶，不争朝夕。阳光暖一点，再暖一点，日子慢一些，再慢一些，从容而优雅地老去。浮生荡荡，阳春白雪，触目横斜千万朵， 赏心不过两三枝；任凭弱水三千，只取一瓢饮。有梦的季节，有爱的润泽，走过的日子，都会成为笔尖温润如玉的诗篇。相信越是走到最后，剩下的唯有一颗向真向善向美的 初心。似水流年，如花美眷，春潮带雨晚来急，野渡无人舟自横朝花夕拾，当回望过往，你是此生无憾，还是满心懊悔呢？随着芳华的流逝，我们终究会明白：任何的财富都 比不上精神上的愉悦，任何的快感都不及对初心的执着。愿你不趋炎附势，不阿谀奉迎，不苟且偷生，不虚掷有限的年华，活出属于自己的风采，活在每一个当下，不忘初心，
结构化学第5章--晶体结构-5-04
结构 类型
点阵型 式
caesium chloride
CsCl
sodium chloride NaCl
立方P
立方 F
Zine blende structure
wurtzide structure
立方 ZnS
六方 ZnS
立方F 六方
calsium fluoride CaF2
rutile structቤተ መጻሕፍቲ ባይዱre TiO2
NaCl rNa+/rCl-=959pm/181pm=0.525 Na+填在Cl-堆积的八面体空隙中. CsCl rCs+/rCl-=169pm/181pm=0.934 Cs+填在Cl-堆积的正方体空隙中。
⑵正、负离子的配位数和离子晶体结构参数 对于简单的二元离子晶体来说，除正负离子半径比决定离 子晶体的结构类型外，离子晶体堆积的紧密程度(负离子 堆积产生的空隙是否被正离子填充满等)也影响着晶体的 结构型式。若Z+、Z-分别为正负离子的电荷数，n+、n-分 别为正负离子数，CN+、 CN-分别为正负离子的配位数， 有
电负性较大的非金属元素和电负性较小的金属元 素生成的化合物一般都是离子化合物。在离子化合物 中，金属元素将价电子转移给非金属，形成具有较稳 定电子结构的正、负离子。正、负离子由于静电力互 相吸引靠近，当它们充分靠近时又会因电子云重叠而 相互排斥。当吸引和排斥相平衡时，形成稳定的离子 化合物。由此可知，离子化合物中存在的结合力是以 正、负离子间静电力为基础的离子键。正、负离子具 有球对称的电子云(Unsöld定理)，所以离子键也和金属 键一样没有饱和性和方向性。离子键向空间各个方向 发展，即形成了离子晶体。
立方F 四方P
晶体结构
第五章 晶体结构安徽师范大学化学与材料科学学院§51晶体的点阵理论晶体具有按一定几何规律排列的内部结构，即晶 体由原子(离子、原子团或离子团)近似无限地、在三 维空间周期性地呈重复排列而成。
这种结构上的长 程有序，是晶体与气体、液体以及非晶态固体的本 质区别。
晶体的内部结构称为晶体结构。
1. 晶体的结构特征(1)均匀性(2) 各向异性(3) 自发形成多面体外形(4) 具有确定的熔点(5) 对称性(6) X射线衍射2.周期性下面两个图形均表现出周期性：沿直线方向，每 隔相同的距离，就会出现相同的图案。
如果在图形 中划出一个最小的重复单位（阴影部分所示），通 过平移，将该单位沿直线向两端周期性重复排列， 就构成了上面的图形。
最小重复单位的选择不是唯一的，例如，在图(a) 中，下面任何一个图案都可以作为最小的重复单位。
点的位置可以任意指定，可以在单位中或边缘的任 何位置，但一旦指定后，每个单位中的点的位置必须 相同。
如，不论点的位置如何选取，最后得到的一组点在空间 的取向以及相邻点的间距不会发生变化。
3.结构基元在晶体中，原子(离子、原子团或离子团)周期性地重 复排列。
上面我们在图形找出了最小的重复单位，类似 的，可以在晶体中划出结构基元。
结构基元是指晶体中 能够通过平移在空间重复排列的基本结构单位。
【例1】一维实例：在直线上等间距排列的原子。
一个原子组成一个结构基元，它同时也是基本的化学组成单位。
结构基元必须满足如下四个条件：化学组成相同；空间结构相 同；排列取向相同；周围环境相同。
【例2】一维实例：在伸展的聚乙烯链中，CH2CH2组成一个 结构基元，而不是CH2。
【例3】二维实例：层状石墨分子，其结构基元由两个C原子组 成(相邻的2个C原子的周围环境不同)。
结构基元可以有不同的选法，但其中的原子种类和数目应保 持不变。
《晶体结构与性质》课件
总结词
密排六方结构是一种晶体结构，其特点是原子或分子的排列具有高度的六方对称性，且每个原子或分子的周围都有相同数量的最近邻。
详细描述
密排六方结构是一种晶体结构，其原子或分子在晶格中以密排六方的形式排列。这种结构的六方对称性使得原子或分子的排列非常紧密。由于每个原子或分子周围都有相同数量的最近邻，这种结构也具有高度的稳定性。密排六方结构在金属材料中较为常见，如镁、锌、镉等。
总结词
金属材料在晶体结构与性质方面具有广泛的应用，其性能受到晶体结构的影响。
详细描述
金属材料的物理和化学性质，如导电性、导热性、耐腐蚀性等，都与其晶体结构密切相关。通过了解金属材料的晶体结构，可以预测其在不同环境下的性能表现，从而优化材料的选择和应用。
陶瓷材料的晶体结构对其硬度、耐磨性和耐高温性能具有重要影响。
分子晶体结构是一种由分子通过范德华力结合形成的晶体结构。
总结词
分子晶体结构是一种由分子通过范德华力结合形成的晶体结构。范德华力是一种较弱的作用力，因此分子晶体通常具有较低的熔点和硬度。常见的分子晶体有冰、干冰等。分子晶体在材料科学和工程中也有一定的应用，如某些塑料和橡胶材料。
详细描述
晶体结构与材料性能的应用
总结词
硬度是衡量晶体抵抗被划痕或刻入的能力的物理量。硬度通常与晶体中原子的排列方式和相互间的作用力有关。例如，金刚石是自然界中硬度最高的物质，这归功于其独特的碳原子排列方式。
详细描述
VS
晶体的光学性质主要取决于其内部结构和对称性。
详细描述
当光照射到晶体上时，会发生折射、反射、双折射等光学现象。这些现象的产生与晶体内原子或分子的振动和排列方式有关。例如，某些晶体具有特殊的颜色，这是由于它们对不同波长的光有不同的折射率。
【免费下载】第五章晶体结构
① 用平移群中任何一个向量，作用于任一阵点进行平移，向量终端必指
向 另一阵点。
② 点阵中任一两点间相联的向量必为平移群中的元素。
这两点可作为是否是点阵的判据，如果一组点不满足这两条，就可判断这
3
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根保通据护过生高管产中线工资敷艺料设高试技中卷术资配0料不置试仅技卷可术要以是求解指，决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高高与中中带资资负料料荷试试下卷卷高问总中题体资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下，安与要全过加，度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高；试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中，核资或对料者定试对值卷某，弯些审扁异核度常与固高校定中对盒资图位料纸置试，.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置，弯高尤曲中其半资要径料避标试免高卷错等调误，试高要方中求案资技，料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高，术料课中并中3试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术，管以术来架及避等系免多统不项启必方动要式方高，案中为；资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资，管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装，工置合作调理并试利且技用进术管行，线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确：指灵在导活分。。线对对盒于于处调差，试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷，术调应问试采题技用，术金作是属为指隔调发板试电进人机行员一隔，变开需压处要器理在组；事在同前发一掌生线握内槽图部内纸故，资障强料时电、，回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资，料料线试试缆卷卷敷试切设验除完报从毕告而，与采要相用进关高行技中检术资查资料和料试检，卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。
晶体结构PPT教学课件
(b)
a2 a1
a4 a3
a6
a5
固体物理学原胞
a8 a7
维格纳--塞茨单胞
(3)三维
立方晶系 ab bc ca a b c
取 i , j ,k为坐标轴的单位矢量,
设晶格常量(布拉维原胞棱边的长度)为a,
即立方体边长为a, a ai ,b a j,c ak
布拉维原胞的体积: V a3
布拉维晶格(简单格)
第二节 晶体结构
本节主要内容: 1.2.1 晶体结构的周期性 1.2.2 原胞 1.2.3 密堆积、配位数和致密度
§1.2 晶体结构
(a)
(b)
(c)
(a)、(b)、(c)为二维晶体结构示意图，它们有何异同?
(a)
(b)
(c)
1.2.1 晶体结构的周期性
一个理想的晶体是由完全相同的结构单元在空间周期性重
垂面(或中垂线)，由这些中垂面(或中垂线)所围成的最小体积 (或面积)即为W--S原胞。
特点：它是晶体体积的最小重复单元，每个原胞只包含1 个格点。其体积与固体物理学原胞体积相同。
2.几种晶格的实例 (1)一维原子链 一维单原子链
a
x na x 0 x a
一维双原子链
b a
(2)二维
(a)
(a)简立方
c b a
a1 ai a2 a j a3 ak
每个布拉维原胞包含1个格点。
固体物理学原胞的体积 Ω a3
(b)面心立方
ak
a1
a2 a j a3
ai
a
a1 j k 2
a 2 a i k 2 a a3 i j
2
平均每个布拉维原胞包含4个格点。
固体物理学原胞的体积 Ω a1 a2 a3 1 a3 4
典型晶体结构
一个球体积：4/3πr3=4/3π×( 2/4 a )3=
3 4/3π× 2 2/64 a =
2 /24 πa 3
立方最密堆积一个单胞中球的数目： 8×1/8+6×1/2= 4个 球体积= 4× 2/24 πa 3 = 2 /6 πa 3 空间利用率= 2 a 3 / a 3 2 / 6 74.05% 6
(3) 体心立方bcc
密排面和密排方向： 密排面为{110}，密排方向<111>
体心立方密排面
原子半径:
bcc的晶胞体积为a3，晶胞内含2个原子。 原子体积
空间利用率
＝
单胞体积
4 æ 3 ö 2´ pç a÷ 3 è 4 ø a3
3
＝
3 ＝ p = 68.02% 8
空间利用率：68.02%
(4) 金刚石型堆积(A4) 在这种堆积方式中，等径圆球的排布与金刚石中 碳原子排布类似，所以称为金刚石型堆积。从金刚 石型堆积中可抽出面心立方晶胞，如下图所示
所以密堆积结构至少具有3m1点群对称性
其最低空间群对称性为P3m1和R3m1
密堆结构共有8个空间群：
P3m1, P3m1, P 6m2, P63 mc, P 63 mc m
R3m1, R3m1, Fm3m
能容纳3次旋转对称的点阵只有： 菱面体点阵 R 3层为周期密堆积结构的 六角点阵 H R点阵等价于cF（立方面 心）点阵
A
C A B
A
表示：方法一：四层：…ABAC ABAC… 五层：…ABCAB ABCAB… 六层： …ABCACB ABCACB ABCACB… …h c c h c c h c c h c c … 方法二 …ABABAC ABABAC ABABAC… …c h h h c h c h h h c h …
高分子物理——第五章 聚合物的结晶态ppt课件
a=b=c
a=b=c
a=b=c
a=b=c
其中，
高分子结晶中正交晶系和单斜晶系占了60%左右。
高聚物有各向异性，合成完高整编聚辑pp物t 的晶格中无立方晶系33。
(二)、高分子晶体的特征 1、高分子晶体本质上是分子晶体 2、具各向异性 3、无立方晶系 4、晶体结构具有多重性 5、高分子结晶的不完全性
Seven crystalline morphologies of polymer
完整编辑ppt
9
（一）、单晶（体）
形成条件－－极稀溶液中缓慢结晶 具有规则的几何外形 内部在三维空间的排列具有高度的规整性 晶片厚度为100Å，基本单元是折叠链晶片 不同聚合物的单晶形状不同 不仅能形成单层片晶，还能形成多层晶体 凡能结晶的高分子在适当条件下都可以形成单晶。
（2）螺旋型构象 带有较大侧基的高分子，为减少空间位阻，降低 位能，通常采用螺旋构象。
HPq
H—螺旋构象
P—每个等同周期重复单元的数目
等同周期：在高分子链上具有相同结构的两 点间的最小距离。
q—每个等同周期中螺旋的数目
完整编辑ppt
36
PTFE 晶体中分子链构象呈螺旋型构象 H136
因为PTFE的螺旋构象，使碳原子被F所包围，F原 子相互排斥，有自润滑性，因此具有冷流性。又由于它 的螺旋硬棒状结构，因此熔点高，可耐三酸两碱。
1、刚柔性适当结晶能力强
PE>PET>PC
天然橡胶柔性很好，但结晶能力很弱。
2、分子间作用力使分子链柔性↓ ，结晶能力 ↓ 适当的分子间作用力，有利于巩固已形成的结晶结构
3、支化使分子对称性↓，结晶能力↓ 4、交联限制了链段运动，减弱或失去结晶能力
晶体结构
q q f R2
没有方向性和饱和性（库仑引力的性质所决定）
NaCl
CsCl
人们习惯上将正离子周围直接接触的负离子数称为正离 子的配位数，并将周围的负离子原子核的连线形成的多 面体称之为配位多面体。
90
2.
14种布拉维点阵形式
布拉维系有7种不同几何特征的晶胞。晶胞又有素晶胞、 体心晶胞、面心晶胞和底心晶胞之分。所以，7种不同 的晶胞在保持α、β、γ、a、b、c不变的情况下，又可 素复结合，变异为14种晶胞，如表3-1和图3-20所示。 在晶体学中称为布拉维点阵形式，也叫14种晶格。表 3-1给出了这14种晶胞的符号。 小写字母：为晶族代号：c（立方）、t（四方）、o （正交）、m（单斜）、a（三斜）、h（六方）。 大写字母：P 、I、 F分别素晶胞、体心晶胞、面心晶 胞； A、B、C代表底心晶胞；R只代表菱方晶胞。
例如： 金属锂的能带结构
Metal lithium
由于每个锂原子只有1个价
电子，该离域轨道应处于 半满状态。电子成对地处 于能带内部能级最低的轨
道上，使能级较高的一半
轨道空置。 在充满了的那一半能带的
最高能级上,电子靠近能
量较低的空能级,从而很 容易离开原来能级,进入 能量略高的空能级。
能带理论中的一些重要概念 能带理论中的一些重要概念
小写字母与大写字母结合，是一种既涉及： 布拉维系又涉及素复的晶胞代号。
例如:cP是素立方晶胞，cI是体心立方晶 胞，mP是单斜素晶胞，等等。这些符号 是国际晶体学会组织编写的重要工具书 晶体学国际表（1983）推荐的，已广泛 应用。
3-3 点阵· 晶系（选学内容，不 作要求，可作为课外阅读内容）
晶体学基础第五章-晶面间距与晶格常数
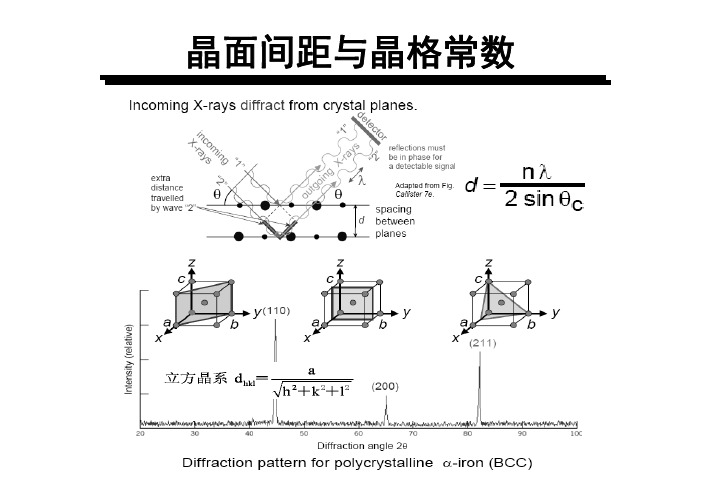
晶面间距与晶格常数第五章 晶体的质点堆积与缺陷¾ 密堆积原理 ¾ 配位数和配位多面体 ¾ 化学键和晶格类型¾ 晶体的缺陷晶体化学晶体化学：研究晶体结构和晶体化学组成与其性质之间的关系和规律性的分支学科。
材料科学：晶体结构=空间点阵+基元Na+Cl-•晶体结构中的质点（阵点或基元）可以是原子、离子 或分子。
•晶体化学主要阐述这些质点的特性：离子类型、离子 和原子半径等； •讨论质点在组成晶体结构时的相互作用和规律：离子 或原子相互结合时的堆积方式和配位形式、键和晶格 类型。
z 理论半径：将原子或离子的电子云分布视为球形，其半 径为原子或离子的理论半径。
• 原子在形成化学键时，总要有一定程度的轨道重叠，而且 与不同的原子分别成化学键时，原子轨道重叠的程度又各 有不同，因此单纯地把原子半径理解成原子最外层电子到 原子核的距离是不严格的。
z 有效半径：以键长数据为基础，由实验方法得到的原子或 离子的半径，称为原子或离子的有效半径。
共价半径、金 属半径、范德华半径。
• 原子或离子半径的影响因素：价态、配位数、电子自旋态• 原子和离子半径的大小，特别是相对大小对晶体结构中的质 点的排列方式影响很大。
其对理解和阐明晶体结构类型的变化、 晶体化学组成的变异以及有关物理性质的变化都是非常重要的。
元素的原子半径和共价半径原子或离子半径的基本规律原子或离子半径的影响因素：价态、配位数、电子自旋态z 同种元素原子半径: 共价半径 < 金属原子半径 z 同种元素离子半径:阳离子半径小于原子半径，价态高半径小； 阴离子半径大于原子半径，负价高半径大； 氧化态相同，配位数高半径大； z 同族元素: 原子和离子半径随周期数增加而增大 z 同周期元素: 原子和离子半径随Z的增加而减小 z 从周期表左上到右下对角线上，阳离子半径近于相等 z 镧系和锕系:阳离子半径随Z增加而略有减小 z 通常, 阳离子半径都小于阴离子半径。
结构化学教案 第五章
二、晶胞及晶胞的二个基本要素 空间点阵是晶体结构的数学抽象，晶体具 有点阵结构。空间点阵中可以划分出一个个的 平行六面体一空间格子，空间格子在实际晶体 中可以切出一个个平行六面体的实体，这些包 括了实际内容的实体，叫晶胞，即晶胞是晶体 结构中的基本重复单位。 晶胞一定是平行六面体，它们堆积起来就 能构成晶体。晶胞也有素晶胞，复晶胞和正当 晶胞之分，素晶胞只含一个结构基元。
的状态； （长程有序） 非晶态材料则象液体那样，只有在几个 原子间距量级的短程范围内具有原子有序的 状态。（短程有序）
晶体的原子呈周期性排列
非晶体的原子不呈周期性排列
§5-1、晶体的点阵理论
一个理想晶体是由全同的称作基元的结构 单元在空间作无限的重复排列而构成的；基元 可以是原子、离子、原子团或者分子；晶体中 所有的基元都是等同的，也就是说它们的组 成、位形和取向都是相同的。因此，晶体的内 部结构可以抽象为在空间作周期性的无限分布 的一些相同的几何点，这些几何点（点阵点） 代表了基元的某个相同位臵，而这些几何点的 集合就称作空间点阵，简称点阵。
2a
倒易截数之比：1/2：1/3：1/4 = 6：4：3 ， 为整数。
1、当一个晶面与某一个晶面平行时，可认 为晶面在这个晶轴上的截数为无穷大∞，而 其倒易截数为0。 2、由于采用了互质整数比，所以一个晶面 指标（ h*:k*:l*）代表了一组晶面，只有同 一个方向的晶面均可用一个h*:k*:l*表示。 3、晶面指标的数值反应了这组晶面之间的 间距跟阵点的疏密。 4、已知一组晶面的晶面指标可求得这组晶 面在三个晶轴上的截数与截长。
a
b
a 方向生长LBGM晶体
b 方向生长LBGM晶体
c 方向生长LBGM晶体
2、晶体缺陷：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 多晶体：由小晶粒组成 • 非晶体：与晶体有本质区别，各向同性，无点阵结构 • 液晶：各向异性，无点阵结构 • 介于“晶体 液晶 非晶体”之间 • 因此液晶原则上不能称为晶体，但有些性质其应用价值超过了晶体 • 准晶： （非传统意义上的晶体）准晶是具有长程准周期性平移序和非晶体
• 同一种晶体在本质上具有相同的点阵结构，故其外形上也 必服从同一规律。 石英晶体的不同外形及其相应晶面
• ◆→
石英晶体（外形）的晶面、晶棱与其平面点 阵，直线点阵对应关系示意图
• 。←◆
石英晶体的不同外形及其相应晶面
∠ab=141°47‘， ∠bc=120°00’， ∠ac=113°08‘
4.2.1晶面、晶棱定律与晶面夹角守恒定律
单位，称正当单位（可以是素单位，也可以是复 单位
平面点阵的素单位、 复单位
5.1.2晶体的点阵结构
• c．三维点阵，也叫密置堆 • 或空间点阵 • Tmnp = ma + nb + pc (m、n、p = 0、±1、
±2……)
5.1.2晶体的点阵结构
• 2．）点阵结构与晶体 • 能为某一点阵相应的平移群所复原的任何结构，
• 晶体物理学是研究晶体结构与某些物理性 能关系的学科。
• 晶体学是基础（最基础）
5.2.1晶面、晶棱定律与晶面夹角守 恒定律
• 晶面、晶棱定律：指晶体在形成过程中会自发生长出具有 晶面、晶棱及顶点的多面体外形（也叫晶体的自范性）→
• 晶面夹角守恒定律：同一品种晶体的每两个相应晶面的夹 角不受外界条件影响，保持恒定不变的数值，若对各相应 晶面引法线，则每两条法线间的夹角为一常数，此规律称 晶面夹角守恒定律
5.1.2晶体的点阵结构
• a．一维点阵（one-dimen sional lattice） • 等径圆球密置列
• 所谓平移：指将图形中所有的点（称点阵点，简称阵 点lattice points）在同一方向上移动同一距离的操作。
• “a”为表示移动方向和距离的向量叫平移向量 a为素 向量，其他为复向量，组成一个群，此称平移群，用 Tm表示。
5. 晶体结构
5.1 晶体的特性与点阵结构 晶体状态，简称“晶态”（crystalline state） 晶体的定义：由原子、分子、离子等微粒在空间有规则地排列 而成的固体
5.1.1晶体的特性 1．）晶体均匀性和各向异性 a．晶体均匀性 b. 各向异性 2．）晶体的对称性和对X射线的衍射性质
有对称的外形，如雪花等 晶体能对X-射线发生衍射（非晶体不具有此功能）
• 其原因是密勒在1839年建议使用的，为纪念此人 而叫“密勒（Miller）指数”。
• 晶体学中将晶体的每个晶面在三个晶轴上的倒易 截数的值都成互质的整数比的这一规律叫有理指 数定律（定理），此规律是郝蔚（R.T.Hauy） 1802年提出的。◆→
倒易截数
ቤተ መጻሕፍቲ ባይዱ
• 设在晶体中选取规定晶胞的三个平移向量a、 b、c的方向作为坐标轴，则某一平面点阵
• Tm=ma (m = 0±1、±2……)
5.1.2晶体的点阵结构
• b．二维点阵（由一维点阵平移得到） • Tmn= ma + nb (m ，n = 0、±1、±2……) • 也叫平面点阵。见下图，a叫蜜置层、c叫平面格
子。
5.1.2晶体的点阵结构
• 平面点阵的素单位和复单位见下图2-3 • I II 素单位，个阵点 • III VI为复单位 ：阵点 • 应尽量选取具有较规则形状的较小的平行四边形
5.2.2晶面符号与有理指数定律
• 晶面符号（也叫晶面指标）:用于表示晶体的不同 晶面的不同平面点阵组 ◆→
•
1 : 1 : 1 h* : k* : l*
h k l
也可记为h*k*l*或hkl
• 用三个数表示某一晶面（或平面点阵），称其为 晶面符号[也叫晶面指标或叫密勒（Miller）指数]
1 0
举例
立方晶体的几组晶面指标
举例
铜单晶晶面指标
236晶面截数示意图
平面点阵间距及阵点密度与晶面指 数关系图
5.3理想晶体、实际晶体、准晶与非晶体
• 理想晶体：按照点阵的周期性在空间可以无限伸展的晶体可称其为理想晶 体，相反为实际晶体。而实际晶体只能无限趋近
• 微晶体：每颗晶粒只有几千或几万个晶胞，晶棱只能重复几十个或十几个 周期，目前研究的纳米晶等
空间点阵
晶体
素晶胞 复晶胞 正当晶胞 晶棱 晶面 晶体
例Cu、晶 体
1mm长的晶粒有2.8百 万个Cu晶胞
5.2 晶体学的基本规律和点阵理论
• 晶体学是研究晶体规律性的科学。 • 与其相关的结晶学是研究物质结晶状态和
过程的科学，在晶体学与结晶学基础上建 立起结晶化学,结晶化学——主要研究晶体 的化学组成与其内部结构的关系以及晶体 结构与其化学性能联系的科学。
组（晶面）在三个轴上的截长分别为h＇a 、
k＇b及l＇c，根据平移群的概念，h＇，k＇ 及l＇应为有理数，称其为晶面在三个轴上
的截数。其倒数
• 1 ，1 • 。h k
，1
l
也应为有理数，叫
倒易截数
选用倒易截数的由来
• 晶体的晶面必平行于相应平面点阵，晶体 的棱必与相应的直线点阵平行，但无论是 平面点阵还是直线点阵都必须通过阵点。 所以其与晶棱或坐标轴相交时，截长应为 素向量的整数倍。为防止出现无穷大，故 采用倒易截数表示。←◆
3．）晶体的其它特性 有固定的熔点，自发长出晶面、晶棱及顶点而构成多面体外形。
各种形状的钙轴云母图片
X-射线衍射图
非晶态
晶态
非晶铝合金图
淡水珍珠粉的x衍射图
5.1.2晶体的点阵结构(本章的重点)
• 1．）周期性与点阵 • 周期性是晶体内部结构的本质特征，也既晶胞的
重复排列，晶体内部的微粒（原子、分子、离子 或原子团等）在空间排列上按照一定的方式，每 隔一定距离地重复出现 • 将这些微粒抽象成几何学上的点，就称为点阵 • 点阵是微粒有规则排列的具体方式，也是反映结 构周期性的几何形式， • 点阵——按连接其中任意两点的向量进行平移后 能复原的一组点。
称为“点阵结构” • 空间、平面、直线等对应的点阵结构 • 晶体为空间点阵。 • a．点阵中的阵点， • 在点阵结构中叫“结构基元” • 在晶体中叫物质微粒（原子、分子、离子）
5.1.2晶体的点阵结构
• b．晶体 空间点阵
中的点相
应于点阵 素单位
中的基本 单位
复单位
• 见图
正当单位
直线点阵
平面点阵
• 同一种晶体在本质上具有相同的点阵结构，故其外形上也 必服从同一规律。 石英晶体的不同外形及其相应晶面
• ◆→
石英晶体（外形）的晶面、晶棱与其平面点 阵，直线点阵对应关系示意图
• 。←◆
石英晶体的不同外形及其相应晶面
∠ab=141°47‘， ∠bc=120°00’， ∠ac=113°08‘
4.2.1晶面、晶棱定律与晶面夹角守恒定律
单位，称正当单位（可以是素单位，也可以是复 单位
平面点阵的素单位、 复单位
5.1.2晶体的点阵结构
• c．三维点阵，也叫密置堆 • 或空间点阵 • Tmnp = ma + nb + pc (m、n、p = 0、±1、
±2……)
5.1.2晶体的点阵结构
• 2．）点阵结构与晶体 • 能为某一点阵相应的平移群所复原的任何结构，
• 晶体物理学是研究晶体结构与某些物理性 能关系的学科。
• 晶体学是基础（最基础）
5.2.1晶面、晶棱定律与晶面夹角守 恒定律
• 晶面、晶棱定律：指晶体在形成过程中会自发生长出具有 晶面、晶棱及顶点的多面体外形（也叫晶体的自范性）→
• 晶面夹角守恒定律：同一品种晶体的每两个相应晶面的夹 角不受外界条件影响，保持恒定不变的数值，若对各相应 晶面引法线，则每两条法线间的夹角为一常数，此规律称 晶面夹角守恒定律
5.1.2晶体的点阵结构
• a．一维点阵（one-dimen sional lattice） • 等径圆球密置列
• 所谓平移：指将图形中所有的点（称点阵点，简称阵 点lattice points）在同一方向上移动同一距离的操作。
• “a”为表示移动方向和距离的向量叫平移向量 a为素 向量，其他为复向量，组成一个群，此称平移群，用 Tm表示。
5. 晶体结构
5.1 晶体的特性与点阵结构 晶体状态，简称“晶态”（crystalline state） 晶体的定义：由原子、分子、离子等微粒在空间有规则地排列 而成的固体
5.1.1晶体的特性 1．）晶体均匀性和各向异性 a．晶体均匀性 b. 各向异性 2．）晶体的对称性和对X射线的衍射性质
有对称的外形，如雪花等 晶体能对X-射线发生衍射（非晶体不具有此功能）
• 其原因是密勒在1839年建议使用的，为纪念此人 而叫“密勒（Miller）指数”。
• 晶体学中将晶体的每个晶面在三个晶轴上的倒易 截数的值都成互质的整数比的这一规律叫有理指 数定律（定理），此规律是郝蔚（R.T.Hauy） 1802年提出的。◆→
倒易截数
ቤተ መጻሕፍቲ ባይዱ
• 设在晶体中选取规定晶胞的三个平移向量a、 b、c的方向作为坐标轴，则某一平面点阵
• Tm=ma (m = 0±1、±2……)
5.1.2晶体的点阵结构
• b．二维点阵（由一维点阵平移得到） • Tmn= ma + nb (m ，n = 0、±1、±2……) • 也叫平面点阵。见下图，a叫蜜置层、c叫平面格
子。
5.1.2晶体的点阵结构
• 平面点阵的素单位和复单位见下图2-3 • I II 素单位，个阵点 • III VI为复单位 ：阵点 • 应尽量选取具有较规则形状的较小的平行四边形
5.2.2晶面符号与有理指数定律
• 晶面符号（也叫晶面指标）:用于表示晶体的不同 晶面的不同平面点阵组 ◆→
•
1 : 1 : 1 h* : k* : l*
h k l
也可记为h*k*l*或hkl
• 用三个数表示某一晶面（或平面点阵），称其为 晶面符号[也叫晶面指标或叫密勒（Miller）指数]
1 0
举例
立方晶体的几组晶面指标
举例
铜单晶晶面指标
236晶面截数示意图
平面点阵间距及阵点密度与晶面指 数关系图
5.3理想晶体、实际晶体、准晶与非晶体
• 理想晶体：按照点阵的周期性在空间可以无限伸展的晶体可称其为理想晶 体，相反为实际晶体。而实际晶体只能无限趋近
• 微晶体：每颗晶粒只有几千或几万个晶胞，晶棱只能重复几十个或十几个 周期，目前研究的纳米晶等
空间点阵
晶体
素晶胞 复晶胞 正当晶胞 晶棱 晶面 晶体
例Cu、晶 体
1mm长的晶粒有2.8百 万个Cu晶胞
5.2 晶体学的基本规律和点阵理论
• 晶体学是研究晶体规律性的科学。 • 与其相关的结晶学是研究物质结晶状态和
过程的科学，在晶体学与结晶学基础上建 立起结晶化学,结晶化学——主要研究晶体 的化学组成与其内部结构的关系以及晶体 结构与其化学性能联系的科学。
组（晶面）在三个轴上的截长分别为h＇a 、
k＇b及l＇c，根据平移群的概念，h＇，k＇ 及l＇应为有理数，称其为晶面在三个轴上
的截数。其倒数
• 1 ，1 • 。h k
，1
l
也应为有理数，叫
倒易截数
选用倒易截数的由来
• 晶体的晶面必平行于相应平面点阵，晶体 的棱必与相应的直线点阵平行，但无论是 平面点阵还是直线点阵都必须通过阵点。 所以其与晶棱或坐标轴相交时，截长应为 素向量的整数倍。为防止出现无穷大，故 采用倒易截数表示。←◆
3．）晶体的其它特性 有固定的熔点，自发长出晶面、晶棱及顶点而构成多面体外形。
各种形状的钙轴云母图片
X-射线衍射图
非晶态
晶态
非晶铝合金图
淡水珍珠粉的x衍射图
5.1.2晶体的点阵结构(本章的重点)
• 1．）周期性与点阵 • 周期性是晶体内部结构的本质特征，也既晶胞的
重复排列，晶体内部的微粒（原子、分子、离子 或原子团等）在空间排列上按照一定的方式，每 隔一定距离地重复出现 • 将这些微粒抽象成几何学上的点，就称为点阵 • 点阵是微粒有规则排列的具体方式，也是反映结 构周期性的几何形式， • 点阵——按连接其中任意两点的向量进行平移后 能复原的一组点。
称为“点阵结构” • 空间、平面、直线等对应的点阵结构 • 晶体为空间点阵。 • a．点阵中的阵点， • 在点阵结构中叫“结构基元” • 在晶体中叫物质微粒（原子、分子、离子）
5.1.2晶体的点阵结构
• b．晶体 空间点阵
中的点相
应于点阵 素单位
中的基本 单位
复单位
• 见图
正当单位
直线点阵
平面点阵