数电1-6_公式化简法
数电1-6_公式化简法

阎石主编(第五版)
信息科学与工程学院基础部
标准与或式和标准或与式之间的关系
【 】
内容 回顾
k
若Y
mi,
则Y
k i
m k
M
k i
如果已知逻辑函数Y=∑mi时,定能将Y 化成编号i以外的那些最大项的乘积。
1
2.6 逻辑函数的化简方法
逻辑函数的最简形式
常见逻辑函数的几种形式
5
【例3】 Y AB AC BC AB ( A B)C
AB ( AB )C
AB C
6
5. 配项法 利用公式 A A A 和 A A 1 先配项 或添加多余项,然后再逐步化简。 【例1】 Y A BC ABC ABC
15
一.卡诺图
1. 定义:将逻辑函数的真值表图形化,把真值表中 的变量分成两组分别排列在行和列的方格中,就构成 二维图表,即为卡诺图,它是由卡诺(Karnaugh) 和范奇(Veich)提出的。 2. 卡诺图的构成:将最小项按相邻性排列成矩阵,就 构成卡诺图。实质是将逻辑函数的最小项之和以图形 的方式表示出来。最小项的相邻性就是它们中变量 只有一个是不同的。
(AB AB) (BC BC)
AB AB(C C) BC( A A) BC
配项
被吸收
AB ABC A BC ABC A BC BC
被吸收
AB AC(B B) BC
AB AC BC
整体提公因子A 只有一个变量不同的 两个最大项的乘积等 于各相同变量之和
(A+C)
10
解:
1.Y AB B AB
数电总结以及要点.

1 逻辑代数基础一、 数制和码制1.二进制和十进制、十六进制的相互转换 2.补码的表示和计算 3.8421码表示 二、 逻辑代数的运算规则1.逻辑代数的三种基本运算:与、或、非 2.逻辑代数的基本公式和常用公式 逻辑代数的基本公式(P10) 逻辑代数常用公式:吸收律:A AB A =+消去律:AB B A A =+ A B A AB =+ 多余项定律:C A AB BC C A AB +=++ 反演定律:B A AB += B A B A ∙=+ B A AB B A B A +=+ 三、 逻辑函数的三种表示方法及其互相转换 ★逻辑函数的三种表示方法为:真值表、函数式、逻辑图 会从这三种中任一种推出其它二种,详见例1-6、例1-7 逻辑函数的最小项表示法 四、 逻辑函数的化简: ★1、 利用公式法对逻辑函数进行化简2、 利用卡诺图队逻辑函数化简3、 具有约束条件的逻辑函数化简 例1.1利用公式法化简 BD C D A B A C B A ABCD F ++++=)(解:BD C D A B A C B A ABCD F ++++=)(BD C D A B A B A ++++= )(C B A C C B A +=+ BD C D A B +++= )(B B A B A =+C D A D B +++= )(D B BD B +=+ C D B ++= )(D D A D =+ 例1.2 利用卡诺图化简逻辑函数 ∑=)107653()(、、、、m ABCD Y 约束条件为∑8)4210(、、、、m 解:函数Y 的卡诺图如下:00 01 11 1000011110AB CD111×11××××D B A Y +=第2章 集成门电路一、 三极管如开、关状态 1、饱和、截止条件:截止:be T V V < 饱和:CSBS B Ii I β>=2、反相器饱和、截止判断 二、基本门电路及其逻辑符号 ★与门、或非门、非门、与非门、OC 门、三态门、异或、传输门 (详见附表:电气图用图形符号 P321 ) 二、 门电路的外特性★1、电阻特性:对TTL 门电路而言,输入端接电阻时,由于输入电流流过该电阻,会在电阻上产生压降,当电阻大于开门电阻时,相当于逻辑高电平。
常用的代数化简方法_数字电子技术(第2版)_[共2页]
![常用的代数化简方法_数字电子技术(第2版)_[共2页]](https://img.taocdn.com/s3/m/bb3d10ddbb68a98270fefa9c.png)
第1章 数字电路基础– 19 – 简的形式,因此,经常需要通过化简的手段找出逻辑函数的最简形式。
因为与或表达式是比较常见的,同时与或表达式可以容易同其他形式的表达式相互转换,所以本节所谓化简,一般是指化为最简的与或表达式。
最简与或表达式的标准是:首先应是乘积项的数目最少,其次是每个乘积项中的变量个数最少。
因为乘积项的数目最少,对应的逻辑电路所用的与门个数就最少;乘积项中变量的个数最少,对应逻辑电路所用的与门输入端个数就最少。
所以如果逻辑函数表达式是最简的,则实现它所用的电路也是最简的,即经济又可靠。
1.5.2 常用的代数化简方法代数化简法又称公式化简法,它是直接运用基本定律及规则化简逻辑函数,常用的方法有下述几种。
1.并项法利用基本公式A + A =1将两项合并为一项,并消去一个变量。
A 可以是任何一个复杂的逻辑式。
例如1Y ABC ABC =+()AC B B AC =+=2Y ABC AB AC =++ ()A BC B C =++ ()A BC BC A =+=2.吸收法利用公式A +AB=A 消去多余的乘积项。
A 、B 可以是任何一个复杂的逻辑式。
例如1Y B ABD B =+= 2()[1()]Y AB ABC D E AB C D E AB=++=++=3.消去法(消因子法) 利用A+AB =A+B 消去多余的因子。
A 、B 也可以是任何一个复杂的逻辑式。
例如1Y B ABC B AC =+=+ 2()Y AB AC BCAB A B C AB ABCAB C=++=++=+=+4.消项法 利用AB AC BC AB AC AB +AC BCD AB +AC ++=++及=将BC 或BCD 消去。
其中A 、B 、。
精选数字电路逻辑函数的化简方法讲解讲义

000 001 010 011 100 101 110 111
0
1
2
3
4
5
6
7
m0
m1
m2
m3 m4
m5
m6
m7
第四页,共28页。
4. 最小项是组成逻辑函数的基本单元
任何逻辑函数都是由其变量的若干个最小项构成,都 可以表示成为最小项之和的形式。
[例] 写出下列函数的标准与或式:
Y F ( A ,B ,C ) AB AC [解] Y AB(C C ) AC(B B)
核心
Y AB AC BC 最简与或式
最简
与非-与非式
AB AC
AB AC
最简或与非式 ( A B)( A C )
最简与或非式
AB AC BC
最简或与式 ( A B) ( A C )
A B AC
最简或非-或式
最简或非-或非式
AB AC
第七页,共28页。
1. 2. 2 逻辑函数的公式化简法
Y F ( A ,B ,C ,D ) ( 4 变量共有 16 个最小项) ABC D ABCD ABC D … … ABC D ABCD
( n 变量共有 2n 个最小项)
第二页,共28页。
2. 最小项的性质:
ABC
000 001 010 011 100 101 110 111
ABC ABC ABC ABC ABC ABC ABC ABC
(1) 两个相邻最小项合并可以消去一个因子
BC
A 00 01 11 10
00
32
CD AB 00 01 11 10
00
1
01 4
6
14
数字电子电路卡诺图法化简

图1 二极管的伏安特性曲线
理想化 伏安特 性曲线
图2 二极管的开关等效电路 (a) 导通时 (b) 截止时
1. 电路
2. 工作原理
A、B为输入信号 (+3V或0V)
F 为输出信号 VCC=+12V
表1 电路输入与输出电压的关系
A
B
F
0V
0V 0.7V
0V
3V 0.7V
3V
0V 0.7V
3V
3V 3.7V
《数字电子电路设计与制作》
逻辑函数卡诺图化简
课前回顾
逻辑函数化简的意义:逻辑表达式越简单,实现 它的电路越简单,电路工作越稳定可靠。
最简与或表达式为: ① 与项(乘积项)的个数最少; ② 每个与项中的变量最少。
公式化简法
返回
反复利用逻辑代数的基本公式、常用公式和运算规则进 行化简,又称为代数化简法。
与
Y=A·B
全1出1 见0出0
或
Y=A+B
全0出0 见1出1
非
YA
见0出1 见1出0
四、集电极开路门(OC门) 1.集电极开路门的电路结构
(1)电路结构:输出级是集电极开路的。
(2)逻辑符号:用“◇”表示集电极开路。 集电极 开路
集电极开路的TTL与非门 (a)电路 (b)逻辑符号
注意: OC门电路必须外接电源和负载电阻, 才能提供高电平输出信号。
例1-7 将Y=AB+BC展开成最小项表达式。
解:YA B B C A(C B C ) (A A )BC
AC B AB A B CC 或:Y(A ,B,C)m 3m 6m 7
m (3,6,7)
2.卡诺图及其画法
数字电路与系统-逻辑运算与简化(常用三个公式)

数字电路与系统-逻辑运算与简化(常⽤三个公式)
常⽤公式
这些个公式实际上就是教⼈如何利⽤前⾯所述的定律,规则来进⾏简化或论证逻辑函数。
1.并项公式
从名字可以看出,⽅便逻辑运算时简化式⼦。
AB+A'B=B, (A+A'=1,A'是A变量的反变量,逻辑变量是⼆值逻辑,只能是0或者1),此处这种等式还可以进⾏对偶的扩展,
(A+B)(A'+B)=B,这样也侧⾯说明对偶对于公式的论证是有帮助的。
并项顾名思义,并的各部分先得有相同的因⼦,然后合并的部分互成反量即可。
并项也能反应出吸收率A+AB=A(1+B)=A
2.销冗余因⼦公式
消除冗余因⼦定义中主要有两部分组成,从两项到三项。
A+A'B=A+B,从公式看确实是消除了左式中的⼀项的因⼦,证明过程:(A+A')(A+B)=A+B,这步是⽤了分配律的知识,逻辑运算中的分配律挺奇怪,尤其是本式中出现的分配律,⼀个变量“或”两个变量就是可以采⽤逻辑运算中的分配律来进⾏,“或”的这种分配律是貌似算术运算中的分配律。
数电 第二章 逻辑代数基础(3)

3、将合并后的各个乘积项进行逻辑相加。
数字电子技术
16
•
注意:
• 每一个1必须被圈,不能遗漏。
• 某一个1可以多次被圈,但每个圈至少包含一个新的1。
• 圈越大,则消去的变量越多,合并项越简单。圈内1 的个数应是2n(n=0,1,2…)。
• 合并时应检查是否最简。 • 有时用圈0的方法更简便,但得到的化简结果是原函 数的反函数。
在存在约束项的情况下,由于约束项的值始终等于0, 所以既可以将约束项写进逻辑函数式中,也可以将 约束项从函数式中删掉,而不影响函数值。
数字电子技术
21
二.任意项
在输入变量的某些取值下函数值是1 还是 0皆可,并不影响电路的功能。
由于任意项的取值不影响电路的功能。所 以既可以把任意项写入函数式中,也可以不 写进去。
数字电子技术
28
例: 例1 Y
ABC D ABCD ABC D
给定约束条件为: ABCD+ABC D+ABC D+AB C D+ABCD+ABCD+ABCD=0
AB
00 00 0 01 0
CD
01 1 x 0 x
AD
AD
Y BC 00 A 0 0 1 1
数字电子技术
01 1 1 1
11 1 0
10 1 1
13
二、用卡诺图化简函数
例1: 将 Y ( A, B, C ) AC AC BC BC 化简为最简与或式。 Y BC 00 A 0 0 1 1
01 1 1
11 1 0
10 1 1
Y BC 00 A 0 0 1 1
ABC D ABCD ABC D
数字电路复习例题

数电例题:一、公式化简法1、化简函数L=EAB++ABD解:先用摩根定理展开:AB=BA+再用吸收法L=D++=E++BA+ABD=)++((D+)=)A++D+A1()1(EBB=BA+2、化简函数L=ABCA++B+BBAEA解:L=ABCA+++BBEABA=)B+E++(ABC()=)A+B+E+BA)((BCB=)BCBA+B++++))(A)((BBB(C=)BA+++CBA)(C(=AC+B++=CA+B+BA3、化简函数L=B A++A+BBCBC解:L=BBA+++CACBB=)+A++BB⋅⋅+C+C(C)(BAABCA=CA+CB+++⋅+⋅BABCBACABBCA=)++⋅⋅A+++)(()(BCBBA=)()1()1(B B C A A C B C B A +++++⋅ =C A C B B A ++⋅4、将下列函数化简成最简的与-或表达式 1)L=A D DCE BD B A +++ 2) L=AC C B B A ++ 3) L=ABCD B AB +++ 解:1)L=A D DCE BD B A +++ =DCE A B D B A +++)( =DCE A B D B A ++ =DCE B A D B A ++ =DCE D +++))(( =DCE D B A ++ =D B A + 2) L=AC C B B A ++ =AC C B C C B A +++)( =AC A A +++ =)1()1(A C B B AC +++ =C B AC +3) L=ABCD C B C A AB +++=ABCD A A C B C A AB ++++)( =ABCD AB ++++ =)()(ABCD AB ++++=)+++AB+1()1(BCD=CAB+A二、逻辑函数的化简—卡诺图化简法:卡诺图是由真值表转换而来的,在变量卡诺图中,变量的取值顺序是按循环码进行排列的,在与—或表达式的基础上,画卡诺图的步骤是:1.画出给定逻辑函数的卡诺图,若给定函数有n个变量,表示卡诺图矩形小方块有n2个。
数字电子技术基础逻辑代数和逻辑函数化简ppt课件

• 把对应函数值为“1”的变量组合挑出 (即第1、4)组合,写成一个乘积项; •凡取值为“1”的写成原变量 A,取值为 “0”的写成反变量 A ; •最后,将上述乘积项相或,即为所求函数:
L A B AB
ab
A
B
~
cd
220
ABL
0 01 01 0 10 0 11 1
(5) AB AB A B AB
AB A B
A B AB
左 AB AB ( A B) ( A B)
A A A B AB B B A B AB 即 A B = A⊙B 同理可证 A⊙B A B
六、关于异或运算的一些公式
异或 A B AB AB 同或 A⊙B AB A B
0 0 0 1 11 1 0 1 1
0 1 0 1 10 1 1 0 0
1 0 0 1 01 1 1 0 0
1 1 1 0 00 0 1 0 0
相等
相等
还原律 A A
五、若干常用公式
(1) AB AB A(B B) A (2) A AB A(1 B) A 推广 A A( ) A
开关A 开关B
电源
灯Y
与逻辑关系
功能表
AB Y 断断 灭 断合 灭 合断 灭 合合 亮
与逻辑的表示方法:
真值表 (Truth table) 功能表
AB Y 00 0 01 0 10 0 11 1
AB Y 断断 灭 断合 灭
合断 灭 合合 亮
开关断用0表示, 开关闭合用1表示 灯亮用1表示, 灭用0表示
AB AB AB AB
Y F ( A ,B ,C ) ( 3 变量共有 8 个最小项)
ABC ABC ABC ABC ABC ABC ABC ABC
(完整版)数电1-10章自测题及答案(2)

第一章绪论一、填空题1、根据集成度的不同,数字集成电路分位以下四类:小规模集成电路、中规模集成电路、大规模集成电路、超大规模集成电路。
2、二进制数是以2为基数的计数体制,十六体制数是以16为基数的计数体制。
3、二进制数只有0和1两个数码,其计数的基数是2,加法运算的进位规则为逢二进一。
4、十进制数转换为二进制数的方法是:整数部分用除2取余法,小数部分用乘2取整法,十进制数23.75对应的二进制数为10111.11。
5、二进制数转换为十进制数的方法是各位加权系数之和,二进制数10110011对应的十进制数为179。
6、用8421BCD码表示十进制时,则每位十进制数可用四位二进制代码表示,其位权值从高位到低位依次为8、4、2、1。
7、十进制数25的二进制数是11001,其对应的8421BCD码是00100101。
8、负数补码和反码的关系式是:补码=反码+1。
9、二进制数+1100101的原码为01100101,反码为01100101,补码为01100101。
-1100101的原码为11100101,反码为10011010,补码为10011011。
10、负数-35的二进制数是-100011,反码是1011100,补码是1011101。
二、判断题1、二进制数有0~9是个数码,进位关系为逢十进一。
()2、格雷码为无权码,8421BCD码为有权码。
(√)3、一个n位的二进制数,最高位的权值是2^n+1。
(√)4、十进制数证书转换为二进制数的方法是采用“除2取余法”。
(√)5、二进制数转换为十进制数的方法是各位加权系之和。
(√)6、对于二进制数负数,补码和反码相同。
()7、有时也将模拟电路称为逻辑电路。
()8、对于二进制数正数,原码、反码和补码都相同。
(√)9、十进制数45的8421BCD码是101101。
()10、余3BCD码是用3位二进制数表示一位十进制数。
()三、选择题1、在二进制技术系统中,每个变量的取值为(A)A、0和1B、0~7C、0~10D、0~F2、二进制权值为(B )A、10的幂B、2的幂C、8的幂D、16的幂3、连续变化的量称为(B )A、数字量B、模拟量C、二进制量D、16进制量4、十进制数386的8421BCD码为(B)A、0011 0111 0110B、0011 1000 0110C、1000 1000 0110D、0100 1000 01105、在下列数中,不是余3BCD码的是(C )A、1011B、0111C、0010D、10016、十进制数的权值为(D )A、2的幂B、8的幂C、16的幂D、10的幂7、负二进制数的补码等于(D )A、原码B、反码C、原码加1D、反码加18、算术运算的基础是 ( A )A 、加法运算B 、减法运算C 、乘法运算D 、除法运算9、二进制数-1011的补码是 ( D )A 、00100B 、00101C 、10100D 、1010110、二进制数最高有效位(MSB )的含义是 ( A )A 、最大权值B 、最小权值C 、主要有效位D 、中间权值第二章 逻辑代数基础一、填空题1、逻辑代数中三种最基本的逻辑运算是与运算、或运算、非运算。
数字电路逻辑函数的化简方法ppt

四变量 得卡诺图: 十六个最小项
CD
AB 00 01 11 10
00 m0 m1 m3 m2
几
01 m4 m5 m7 m6
何
11 m12 m13 m15 m14
相 邻
10 m8 m9 m11 m10
五变量 得卡诺图: CDE
三十二个最小项
AB 00
000 m0
001 m1
01几1 何01相0 邻110 m3 m2 m6
AB AB C
四、配项消项法:
[例] Y BC AC AC BC AB
BC AC AB 或 BC AC AC BC AB
冗余项
AB AC BC
[例 1、 2、 Y AB AC BC AB AC BC 15]
AB AC BC 或 AB AC BC AB AC BC
AB AC BC
综合练习:
Y ACE ABE BC D BEC DEC AE E ( AC AB BC DC A ) BC D E ( C B D A ) BC D
CE BE DE AE BC D E (B C D) AE BC D
E BC D AE BC D E AE BC D E BC D
核心
Y AB AC BC 最简与或式
最简 与非-与非式
AB AC
AB AC
最简或与非式 ( A B)( A C )
最简与或非式 AB AC BC 最简或与式 ( A B) ( A C )
A B AC
最简或非-或式
最简或非-或非式
AB AC
1、 2、 2 逻辑函数得公式化简法 (与或式 公式 最简与或式)
CD AB 00 01 11 10
00 0
《数电》教材习题答案 第1章习题答案
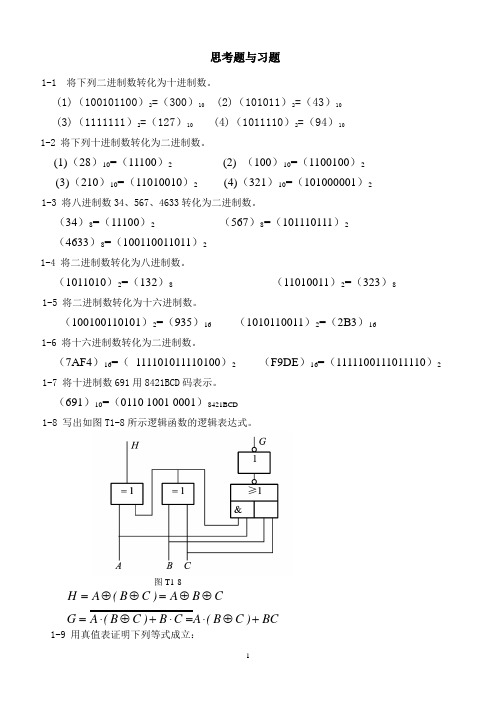
思考题与习题1-1 将下列二进制数转化为十进制数。
(1)(100101100)2=(300)10 (2)(101011)2=(43)10(3)(1111111)2=(127)10 (4)(1011110)2=(94)101-2 将下列十进制数转化为二进制数。
(1)(28)10=(11100)2 (2) (100)10=(1100100)2(3)(210)10=(11010010)2 (4)(321)10=(101000001)2 1-3 将八进制数34、567、4633转化为二进制数。
(34)8=(11100)2 (567)8=(101110111)2(4633)8=(100110011011)21-4 将二进制数转化为八进制数。
(1011010)2=(132)8 (11010011)2=(323)8 1-5 将二进制数转化为十六进制数。
(100100110101)2=(935)16 (1010110011)2=(2B3)16 1-6 将十六进制数转化为二进制数。
(7AF4)16=( 111101*********)2 (F9DE )16=(1111100111011110)2 1-7 将十进制数691用8421BCD 码表示。
(691)10=(0110 1001 0001)8421BCD1-8 写出如图T1-8所示逻辑函数的逻辑表达式。
图T1-8BC)C B (A C B )C B (A G CB A )C B (A H +⊕⋅=⋅+⊕⋅=⊕⊕=⊕⊕= 1-9 用真值表证明下列等式成立:(1)A B + A B = (A +B )(A+B)可见,左式=右式,得证。
(2)A ⊕B =A ⊕B可见,左=右,得证。
(3)A ⊕0 = A可见,左式=右式,得证。
(4)A ⊕1 = A可见,左式=右式,得证。
1-10 利用公式和运算规则证明下列等式:(1)ABC + A BC + A B C = BC + AC证明:左=(ABC + A BC ) +( A B C +ABC )= BC + AC =右(2)C AB = AB + C证明:左=C AB C AB +=+=右(3)(A +B)(A + C)(B + C + D) = (A + B)(A + C)证明:将以上等式两边作对偶变换,可得到以下公式:AB +A C +BCD =AB +A C由常用公式四可知该式是成立的,则由对偶定理可知,对偶等式成立,则原等式也成立。
数字电路第3章 布尔代数与逻辑函数化简

Y f ( A, B, C,)
注意:与普通代数不同的是,在逻辑代数中,不管是变 量还是函数,其取值都只能是0或1,并且这里的0和1只表示两 种不同的状态,没有数量的含义。
(3)逻辑函数相等的概念:设有两个逻辑函数
Y1 f ( A, B, C,)
Y2 g ( A, B, C,)
它们的变量都是A、B、C、…,如果对应于变量A、B、 C、…的任何一组变量取值,Y1和Y2的值都相同,则称Y1和Y2 是相等的,记为Y1=Y2。 若两个逻辑函数相等,则它们的真值表一定相同;反之, 若两个函数的真值表完全相同,则这两个函数一定相等。 证明等式:
第 3章
学习要点:
基本定理和化简方法
掌握布尔(逻辑)代数的基本运算法则、基本公式、
了解不同类型逻辑表达式的相互转换以及最简与或
表达式。
能够熟练地运用真值表、逻辑表达式、卡诺图、波
形图和逻辑图表示逻辑函数。
3.1 基本公式
和规则
逻辑代数是按一定的逻辑关系进行运算的代数,是分 析和设计数字电路的数学工具。在逻辑代数,只有0和1 两种逻辑值,有与、或、非三种基本逻辑运算,还有与或、 与非、与或非、异或几种导出逻辑运算。
A A 0
等幂律: A A A
A A A
双重否定律: A A
分别令A=0及 A=1代入这些 公式,即可证 明它们的正确 性。
A B B A 交换律: A B B A
利用真值表很容易证 明这些公式的正确性。 如证明A· B=B· A:
( A B) C A ( B C ) 结合律: ( A B) C A ( B C )
证明分配率:A+BC=(A+B)(A+C) 证明:
数字电路3(函数表达式的化简)

Y = ABC + ABC + ABC = ABC + ABC + ABC + ABC = BC + C =C
广东科贸职业学院信息工程系
2. 卡诺图化简法
卡诺图是由真值表演变成的方格图,可以把逻辑 函数中的化简关系直观地表现出来.图形化简具有 直观,简便,彻底三大优点. (1)卡诺图的构成 构成:把真值表中对应各组变量组合的逻辑值排成 方格矩阵,把变量的取值分成行,列两部分,作为 方格矩阵的行,列标识,并把变量取值顺序作特殊 排列,真值表就变成了卡诺图.
广东科贸职业学院信息工程系
1. 代数化简法
3,消去法 , 利用公式A+AB=A+B,消去多余的因子.
Y = AB + A C + B C = AB + ( A + B ) C = AB + AB C = AB + C
广东科贸职业学院信息工程系
1. 代数化简法
4,配项法 利用重叠律A+A =A来配项,以获得更加简单的化简结果, 例如:
(1)Y=∑m(0,1,3,4,5,7) (2)Y= ∑m(0,2,8,10) (3) Y = ABC + A + B + C (4) Y = AB + ABD + AC + BCD (5) Y = ∑ m(0,1,2,3,6,8) + ∑ d (10,11,12,13,14,15)
广东科贸职业学院信息工程系
广东科贸职业学院信息工程系
(2)卡诺图的特点
①卡诺图跟逻辑函数的标准与或表达式之间有对应关系,卡 诺图的各个方格,即对应全部变量的各个组合以及相对应 的逻辑值,以对应各个全变量乘积项. ②我们把只在一个变量互反(又称做互补)的两个乘积项互 称为"逻辑相邻项",一对相邻项相或,可消去其中的互 补变量,合并为一个新的乘积项. 卡诺图利用它的特殊结构,把所有具有逻辑相邻关系的全 变量乘积项都给以相邻 使具有可以化简关系的全变量乘 积项以特殊的位置关系直观地显示出来.
数字电子技术- 逻辑函数的化简(卡诺图化简)

CD AB 00 01 11 10
00 0
2
01 4 5 7 6
11 12 13 15 14
10 8
10
C
B
D
总结: 2n 个相邻最小项合并可以消去 n 个取值不同因子。
2. 用卡诺图化简逻辑函数的基本步骤
(1)首先将逻辑函数变换为最小项之和表达式。 (2)画出逻辑函数的卡诺图。 (3)将卡诺图中按照矩形排列的相邻1画圈为若干个相邻组。 (4)合并最小项。 (5)将合并后的乘积项加起来就是最简与或表达式。
② 约束项: 不会出现的变量取值所对应的最小项。 ③ 约束条件: 由约束项相加所构成的值为 0 的逻辑表达式。
例如,上例中 ABC 的不可能取值为 000 011 101 110 111
约束项: ABC ABC ABC ABC ABC
约束条件:A B C ABC ABC ABC ABC 0
01 1
11
11
10 1
11
Y A B AC A C D B D
[例4] 用卡诺图法求反函数的最简与或表达式
Y AB BC AC
[解] ① 画函数的卡诺图
② 合并函数值为 0 的最小项
③ 写出 Y 的反函数的 最简与或表达式
BC A 00 01 11 10
00 010
10 111
Y AB BC AC
(3)化简举例 [例] 化简逻辑函数
F(A,B,C,D )
m( 1 , 7 , 8 ) d( 3 , 5 , 9 , 10 , 12 , 14 , 15 )
[解] 化简步骤:
① 画函数的卡诺图,顺序 为:先填 1 ╳ 0
② 合并最小项,画圈时 ╳ 既可以当 1 ,又可以当 0
数字电路第4章逻辑函数及化简

1
1
1
1
4.3逻辑函数公式化简法 一、逻辑函数化间的意义 用最少门和输入端来实现函数的功能
P81
二 、化简标准
经济、可靠、品种单一
三、化简的方法
1、代数法化简
利用公式、定律、对逻辑函数化简
2、卡诺图化简
四. 逻辑函数的代数化简 逻辑函数的公式化简法就是运用逻辑代数 的基本公式、定理和规则来化简逻辑函数。 1、并项法
A
;
A A
反演律: A B A B ; A B A B (靡根定理)
摩根定理 A•B =A+B
证明: 用真值表证明
A B 0
0 1 1
A+B = A•B
A B 0 0 0 1 A+B A • B 1 0 1 0
A•B A+B 1
1 1 0
0
1 0 1
1
1 1 0
1
1
0
1
Y ABC ABC ABC ABC ABC
=AB(C+C)+ABC+AB(C+C)
=AB+ABC+AB
=(A+A)B+ABC
利用C+C=1
=B+BAC
=B+AC
利用A+AB=A+B
例2 将Y化简为最简与或式。
Y =AB+(A+B)CD
解:Y =AB+(A+B)CD ;A=A
= AB+(A+B)CD
0
0
0
0
m0
0
0 0 1 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(A+C)
10
解:
1.Y AB B AB
A B AB
消因子法
A B
2.Y ABC A B C
看作整体运用还原 律和德摩根定律
ABC (( A B C))
16
卡诺图的构成原则
构成卡诺图的原则是: ① N变量的卡诺图有2N个小方块(最小项); ② 最小项排列规则:几何相邻的必须逻辑相邻。 逻辑相邻:两个最小项,只有一个变量的 形式不同,其余的都相同。逻辑相邻的最小项可以合 并。 几何相邻的含义: 一是相邻——紧挨的; 二是相对——任一行或一列的两头; 在五变量和六变量的卡诺图中,用相重来判断 三是相重——对折起来后位置相重。 某些最小项的几何相邻性,其优点是十分突出的。
Y ( A, B, C) AB(C C) A(B B)C ABC
ABC ABC ABC ABC
m7 m6 m5 m1
A BC 00 0 m0 0 m4 01 1 m1 1 m5 11 0 m3 1 m7 10 0 m2 1 m6
0
1
0
1 1 1
32
Y2 ( A, B, C, D) m(0,1,2,3,4,6,7,8,9,11 ,15)
1 1 0 1
1 0 0 1
1 1 1 1
1 1 0 0
33
Y3 A B C ABCD
1 1 1 1
1 1 1 1
1 1 1 1
22
二、 用卡诺图表示逻辑函数
(1)从真值表画卡诺图 根据变量个数画出卡诺图,再按真值表填写每一个小方 块的值(0或1)即可。需注意二者顺序不同。 例1: 已知Y的真值表,要求画Y的卡诺图。 逻辑函数Y的真值表 A B C Y 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 卡诺图
ABC ( ABC)
1
11
解: 3.Y A (B C)( A B C)( A B C)
A BC( A C)
A ABC BC
A BC
只有一个变量不同的 两个最大项的乘积等 于各相同变量之和
(A+C)
整体提公因子A
AB AC C D ADE AB AC C D
4
4. 消因子法
★
利用公式 A A B A B 消去多余的因 子。
【例1】
Y B ABC
B AC
【例2】
Y AB B A B
A B A B
A B
26
卡诺图如表
Y m(0,1,2,3,5,7,9,10)
Y CD AB 00 00 01 11 10 1 的卡诺图 01 1 1 11 10 1
1
1
1
1
27
(3)观察法
采用观察法不需要前两种方法需要将逻辑函数 转换成最小项,而是采用观察逻辑函数,将应为“ 1” 的项填到卡诺图中
Y的卡诺图
例5 用卡诺图表示下面的 逻辑函数
15
一.卡诺图
1. 定义:将逻辑函数的真值表图形化,把真值表中 的变量分成两组分别排列在行和列的方格中,就构成 二维图表,即为卡诺图,它是由卡诺(Karnaugh) 和范奇(Veich)提出的。 2. 卡诺图的构成:将最小项按相邻性排列成矩阵,就 构成卡诺图。实质是将逻辑函数的最小项之和以图形 的方式表示出来。最小项的相邻性就是它们中变量 只有一个是不同的。
1
2
0
0
0
1
1 A B C (m 1) 0 A BC (m2 ) 1 A BC (m3 ) 1 AB C (m5 )
0 ABC (m6 )
三变量的卡诺图 BC A 00 01 11 10
3
4
0
1
1
0
0 AB C ( m4 )
0
1
m0 m1 m3 m2
5
6
1
1
0
1
m4 m5 m7 m6
数字电子技术基础
阎石主编(第五版)
信息科学与工程学院基础部
标准与或式和标准或与式之间的关系
【 】
内容 回顾
k
若Y
mi,
则Y
k i
m k
M
k i
如果已知逻辑函数Y=∑mi时,定能将Y 化成编号i以外的那些最大项的乘积。
1
2.6 逻辑函数的化简方法
逻辑函数的最简形式
常见逻辑函数的几种形式
AC ABC AC CD
A(C BC C) CD A CD
13
公式化简法评价: 特点:目前尚无一套完整的方法,能否以最快 的速度进行化简,与我们的经验和对公式掌握及运 用的熟练程度有关。 优点:变量个数不受限制。 缺点:结果是否最简有时不易判断。
14
2.6.2 逻辑函数的卡诺图化简法
【 】
内容 回顾
与或非式 摩 根 展 定 开 ★ 理 或非-或非式
2
与或式、与非-与非式、与或非式、或非-或非式
与非-与非式 与或式 摩根定理展开 ★ 两次取反 摩根定理 展开 ★
2.6.1 公式化简法
1. 并项法
★
【 】
内容 回顾
利用公式 AB AB A将两项合并成一项, 并消去互补因子。
2. 吸收法 利用公式A+AB=A消去多余的乘积项。
3
3. 消项法
★
利用公式 AB A C BC AB A C 消 去多余的乘积项。
【例1】 Y AC AB ( B C ) AC AB BC
AC BC
【例2】 Y AB AC ADE C D
Y A' B' C ' D A' BD' ACD AB'
CD AB 00
01
11
10
00
A
1 1 1 1 1 1 1
28
01 11 10
1
解:其卡诺图如右表所示
A
观察法:
首先分别将每个与项的原变量用1表示, 反变量对应的变量用0表示,在卡诺图上找出交叉点, 在其方格上填上1;其没有交叉点的方格上填上0。
m4
m1
m5 m9
m3
m7 m11
m2
m6
m12
m8
m13 m15
m14
m10
相邻
20
五变量的卡诺图
21
① n变量的卡诺图有2n个方格,对应表示2n 个最小项。每当变量数增加一个,卡诺图的 方格数就扩大一倍。 ②卡诺图中任何几何位臵相邻的两个最小 项,在逻辑上都是相邻的。 ③ 5变量卡诺图相邻项不直观,因此它只适 于表示5变量以下的逻辑函数。
25
例4 画出下面逻辑函数的卡诺图
Y ABD BD ABD
解: Y A' BD B' D' A' B' D
A' B(C C ' ) D ( A A' ) B' (C C ' ) D' A' B' (C C ' ) D A' BCD A' BC' D AB' CD ' AB' C ' D' A' B' CD ' A' B' C ' D' A' B' CD A' B' C ' D m7 m5 m10 m9 m2 m0 m3 m1 m(0,1,2,3,5,7,9,10)
30
练习:画出下列函数的卡诺图
Y1 AB B BCD
Y2 ( A, B, C, D) m(0,1,2,3,4,6,7,8,9,11 ,15)
Y3 A B C ABCD
31
Y1 AB B BCD
10XX
0
1 1 1
0 1 1 1
0
1 1 1
19
7
1
1
1 ABC(m7 )
BC A 00 01 11 10 正确认识卡诺图的“逻辑相邻”:是指除了一个变量不同外 三变量ABC C ABC ABC ABC AB其余变量都相同的两个与项。 的卡诺图: 0 相邻 m0 m1 m3 m2 上下相邻,左右相邻,并呈现“循环相邻”的特性, BC ABC ABC ABC 它类似于一个封闭的球面,如同展开了的世界地图一样。 1 Am m m m 4 5 7 6 对角线上不相邻。 相邻 CD AB 00 01 11 10 不 相邻 01 四变量ABCD 11 的卡诺图: 相邻 10 00 m0
17
二变量的卡诺图
二变量
十进 制数
A 0 0 1 1
B
mi
A
二变量的卡诺图
B
0 1 2 3
0 A B (m0 ) 1 A B ( m1 ) 0 AB ( m2 ) 1 AB( m3 )
0
1
0
m0 m2
m1 m3
18
1
三变量的卡诺图
三变量
十进 制数
A 0
B 0
C
mi
0
0 A B C (m0 )
23
(2)化为标准与或型
Y mi
把标准与或表达式中所有的最小项在对应的 小方块中填入1,其余的小方块中填入0。 例2:画出函数Y(A、B、C、D)= ∑m(0,3,5,7,9,12,15) 的卡诺图。
