浙江大学计算方法大作业第八题
计算方法课后习题答案

计算方法课后习题答案计算方法课后习题答案计算方法是一门重要的学科,它为我们提供了解决数学问题的方法和工具。
在学习这门课程时,我们经常会遇到一些习题,这些习题旨在帮助我们巩固所学的知识并提高我们的计算能力。
然而,习题的解答并非总是容易的,有时候我们可能会遇到困难。
因此,我将在本文中为大家提供一些计算方法课后习题的答案,希望能够帮助大家更好地理解和掌握这门学科。
1. 线性方程组的解法线性方程组是计算方法中的一个重要概念。
解决线性方程组的方法有很多种,其中最常用的方法是高斯消元法。
这种方法通过行变换将线性方程组转化为简化的行阶梯形矩阵,从而求得方程组的解。
下面是一个例子:2x + 3y = 84x - 5y = -7通过高斯消元法,我们可以得到方程组的解为x = 1,y = 2。
2. 数值积分的计算数值积分是计算方法中的另一个重要概念。
它可以用来计算曲线下的面积或者求解定积分。
常用的数值积分方法有梯形法则、辛普森法则等。
下面是一个例子:计算定积分∫[0, 1] (x^2 + 2x)dx。
通过梯形法则,我们可以得到定积分的近似值为1.5。
3. 插值和拟合插值和拟合是计算方法中的重要概念,它们可以用来估计未知数据点的值。
插值是通过已知数据点之间的连线或曲线来估计未知点的值,而拟合是通过已知数据点的函数来估计未知点的值。
下面是一个例子:已知数据点 (1, 3), (2, 5), (3, 8),通过插值和拟合方法来估计点 (4, ?) 的值。
通过线性插值,我们可以得到点 (4, 11) 的值。
通过多项式拟合,我们可以得到点 (4, 10.5) 的值。
4. 数值微分的计算数值微分是计算方法中的另一个重要概念,它可以用来估计函数在某一点的导数值。
常用的数值微分方法有前向差分法、后向差分法和中心差分法。
下面是一个例子:计算函数 f(x) = x^2 在点 x = 2 处的导数值。
通过中心差分法,我们可以得到导数的近似值为 4。
大学计算机基础(浙江大学)题库

浙江大学大学计算机基础题库测试试卷:计科教材练习【01】--------------------------------------------------------------------------------一、判断题,共10题, 总分:10分。
请直接点击选择True or False.1.计算机文化是指能够理解计算机是什么以及它是如何作为资源被使用的。
( T ) True False2.计算思维的本质是对求解问题的抽象和实现问题处理的自动化。
如果说,数学思维是“抽象和关系”,那么计算思维则是“状态和过程”。
( T ) True False3.我们可以定义计算机系统是指计算机的所有资源。
它包括了计算机硬件和软件。
( T ) True False4.计算机系统结构是研究计算机的硬件互联使得计算机更有效、更高速和更可靠。
( T ) True False5.应用软件是管理计算机所需要的那些软件。
( F ) True False6.程序设计主要有面向文本设计技术和面向对象设计技术。
( F ) True False7.程序是算法的具体实现。
( T ) True False8.计算机被加电后进入工作状态,就开始执行程序,直到关机为止。
( T ) True False9.因特网的开放结构,主要表现在进入网络的机器,属于企业、机构、政府甚至个人的,它们之间的关系是平等地位,没有权限的定义。
( T ) True False10.因特网是一个庞大的计算机互联形成的网络,构建因特网的主要目的是实现各种通信。
( F ) True False--------------------------------------------------------------------------------二、单选题,共11题, 总分:11分。
请四个中选择一个是正确的答案。
1.半导体技术是按一个较高的指数规律发展的。
根据摩尔定律,当价格不变时,集成电路上可容纳的晶体管数目,约每隔( D )个月便会增加一倍,性能也将提升一倍。
计算方法大作业(第二次)

计算方法大作业(第二次)数值计算第二次大作业1.给定插值条件如下:i01234567xi8.1258.49.09.4859.69.95910.16610.2yi0.07740.0990.2800.600.7081.2001 .8002.177作三次样条函数插值,挑第一类边界条件y0’=0.01087y7’=100根据题目要求,首先要构造三次样条函数,三次样条函数的构造过程如下:建有x0<x1<…<xn共n个插值节点,任一取值一组常数y0,y1,…,yn,建议结构一个插值三次样条函数s(x),使如下插值条件以求满足用户:s(xi)?yi,i=0,1,…,n经过插值点的三次样条函数就是一组三次多项式,即为存有:23?s1(x)?a1?b1(x?x1)?c1(x?x1)?d1(x?x1),x?[x1,x2],?23s2(x)?a2?b2(x?x2)?c2(x?x2) d2(xx2),x[x2,x3],s(x)ab(xx)c(xx)2d(xx)3,x[x,x]n1n1n1n1n1n 1n1n1nn1由节点处的连续性可知:si(xi)?yi,si(xi?1)?yi?1,i?1,2,?n?1.ai?yi,i?1,2,?n?1,??23y2?y1?b1(x2?x1)?c1(x2?x1)?d1(x2?x1)y?y?b(x?x)?c(x?x) 2?d(x?x)3n?1n?1nn?1n?1nn?1n?1nn?1?n由节点处的一阶与二阶光滑性可知:si?1(xi)?si(xi),si?1(xi)?si(xi),i?1,2,?,n''''''又设cn?sn?1(xn)/2,记?i?xi?1?xi,?i?yi?1?yi,i?1,2,?,n?1,则di?ci?1?ci3?i,i?1,2,?,n?1。
再根据边界条件,从而可以相继求出bi,ci''用matlab编程,编写三次样条函数(见附录),对第一题求解:>>formatshortg;>>x1=[8.125,8.4,9.0,9.485,9.6,9.959,10.166,10.2]';>>y1=[0.0774,0.099,0.280,0.60,0.708,1.200,1.800,2.177]';>>u1=0.01087;un=10 0;>>xx1=[x1(1):0.001:x1(end)]';>>[yy1b1c1d1]=spline3(x1,y1,xx1,1,u1,un);>>fprintf('\\t\\tb1\\t\\tc1\\t\\td1\\n');b1c1d1>>disp([b1c1(1:end-1,1)d1]);0.010870.144890.3680.174050.4485-0.3930.2878-0.258912.11531.52942.8188-69.141-0.56548-21.03573.61412.79458.247-512.32-28.949-259.942279>>plot(x1,y1,'bo',xx1,yy1,'r-');>>gridon画出插值曲线的图像。
2020吉大网络教育(直属)计算方法大作业解答

2020吉大网络教育(直属)计算方法大作业解答
计算题
1. 证明下列差分格式是二阶的
是二阶方法,并求出误差首项。
2. 用梯形方法解初值问题证明其近似解为
证明当时,其原初值问题的准确解3. 方程将其改写为
4. 用尤拉法解初值问题取步长计算。
5. 给定常微分初值问题试构造求解常微分初值问题的梯形差分格式。
6. 试证明显格式是一阶方法。
7. 方程将其改写为
8. 证明对于任意的参数,下列龙格—库塔公式是二阶的:
9. 利用改进的方法求解初值问题(取)
10. 就初值问题导出改进尤拉方法的近似解的表达式,并与准确解相比较。
答案完整解答部分:
计算题
1. 答:
2. 答:
3. 答:
4. 答:
5. 答:
6. 答:
7. 答:
8. 答:
9. 答:
10. 答:。
计算方法大作业

计算方法大作业学院:电子工程姓名:班级:学号:大作业选题:分析方程求根问题中牛顿法的性能,包括收敛性等,并用该方法求解一个问题,给出过程和结果。
一、牛顿迭代法介绍:用迭代法求方程0)(=x f 的根时,首先要构造一个迭代函数,迭代函数构造的好坏,不仅影响收敛速度,而且有可能使迭代序列发散,构造迭代函数的一条重要途径,是用近似方程代替原方程去求根,因此如果能将非线性方程0)(=x f 用线性方程来近似代替,那么求近似根问题就容易得到解决,而且十分方便。
牛顿法就是把非线性方程线性化的一种方法。
二、牛顿迭代法原理设已知方程0)(=x f 的近似根0x ,则在0x 附近)(x f 可用一阶泰勒多项式))((')()(000x x x f x f x p -+=近似代替.因此, 方程0)(=x f 可近似地表示为0)(=x p .用1x 表示0)(=x p 的根,它与0)(=x f 的根差异不大.设0)('0≠x f ,由于1x 满足,0))((')(0100=-+x x x f x f 解得)(')(0001x f x f x x -= 重复这一过程,得到迭代公式)(')(1n n n n x f x f x x -=+ 这就是著名的牛顿迭代公式,它相应的不动点方程为)(')()(x f x f x x g -=.用牛顿迭代公式求方程根的方法称为牛顿迭代法,简称牛顿法。
三、牛顿迭代法的几何解析在0x 处作曲线的切线,切线方程为))((')(000x x x f x f y -+=。
令0=y ,可得切线与x 轴的交点坐标)(')(0001x f x f x x -=,这就是牛顿法的迭代公式。
因此,牛顿法又称“切线法”,其几何意义即为0x 点处的切线方程。
四、牛顿迭代法的收敛性 计算可得2)]('[)(")()('x f x f x f x g -=,设*x 是0)(=x f 的单根,有0)(',0)(**≠=x f x f ,则0)]('[)(")()('2****=-=x f x f x f x g , 故在*x 附近,有1)('<x g .根据不动点原理知牛顿迭代法对单根收敛.同理可知当*x 是0)(=x f 的重根时也收敛,则可分析出牛顿法不论对单根还是重根均是局部收敛的,只要初值足够靠近*x ,牛顿迭代序列均收敛于*x 。
计算方法的课后答案
《计算方法》习题答案第一章 数值计算中的误差1.什么是计算方法?(狭义解释)答:计算方法就是将所求的的数学问题简化为一系列的算术运算和逻辑运算,以便在计算机上编程上机,求出问题的数值解,并对算法的收敛性、稳定性和误差进行分析、计算。
2.一个实际问题利用计算机解决所采取的五个步骤是什么?答:一个实际问题当利用计算机来解决时,应采取以下五个步骤: 实际问题→建立数学模型→构造数值算法→编程上机→获得近似结果 4.利用秦九韶算法计算多项式4)(53-+-=x x x x P 在3-=x 处的值,并编程获得解。
解:400)(2345-+⋅+-⋅+=x x x x x x P ,从而所以,多项式4)(53-+-=x x x x P 在3-=x 处的值223)3(-=-P 。
5.叙述误差的种类及来源。
答:误差的种类及来源有如下四个方面:(1)模型误差:数学模型是对实际问题进行抽象,忽略一些次要因素简化得到的,它是原始问题的近似,即使数学模型能求出准确解,也与实际问题的真解不同,我们把数学模型与实际问题之间存在的误差称为模型误差。
(2)观测误差:在建模和具体运算过程中所用的一些原始数据往往都是通过观测、实验得来的,由于仪器的精密性,实验手段的局限性,周围环境的变化以及人们的工作态度和能力等因素,而使数据必然带有误差,这种误差称为观测误差。
(3)截断误差:理论上的精确值往往要求用无限次的运算才能得到,而实际运算时只能用有限次运算的结果来近似,这样引起的误差称为截断误差(或方法误差)。
(4)舍入误差:在数值计算过程中还会用到一些无穷小数,而计算机受机器字长的限制,它所能表示的数据只能是一定的有限数位,需要把数据按四舍五入成一定位数的近似的有理数来代替。
这样引起的误差称为舍入误差。
6.掌握绝对误差(限)和相对误差(限)的定义公式。
答:设*x 是某个量的精确值,x 是其近似值,则称差x x e -=*为近似值x 的绝对误差(简称误差)。
浙大计算方法上机报告.

学号:3100300038 姓名: 专业:作业1:用列主元高斯消去法和列主元三角分解法解P227页第3题1. 列主元高斯消去法目的:用高斯消去法解Ax=b 时,其中设A 为非奇异矩阵,可能出现a kk =0 情况,这时必须进行带行交换的高斯消去法。
但在实际计算中即使0)( k kk a 但其绝对值很小时,用)(k kk a 作除数,会导致中间结果矩阵A(k)元素数量级严重增长和舍入误差的扩散,使得最后的计算结果不可靠。
列主元高斯消去法可以难过一般高斯法的这些缺点。
一、列主元高斯消去法解方程的Matlab 程序如下:function a=columneli(a) %对矩阵a 进行列主元消去 [m n]=size(a); %求取a 的行数m 和列数n for i=1:m-1[maxEle,pos]=max(abs(a(i:end,i)));maxRow=pos+i-1; %在每次变换前寻找绝对值最大主所在列maxRow if a(maxRow,i)==0disp('矩阵为奇异矩阵')return %对于非奇异矩阵,在程序中给予提示,结束程序 end if(maxRow~=i)temp=a(maxRow,:);a(maxRow,:)=a(i,:);a(i,:)=temp;end %与列主元绝对值最大的行进行行交换 for j=i+1:ma(j,i)=a(j,i)/a(i,i); %求取第j 列主元 for k=i+1:na(j,k)=a(j,k)-a(j,i)*a(i,k); %对第j 列主元进行行变换 end end endfunction x=elisolve(a) %利用列主元消去的结果求方程的解,a 为方程组的增广矩阵 a=columneli(a); [m,n]=size(a);x=zeros(m,1); for i=m:-1:1x(i)=(a(i,n)-a(i,i:m)*x(i:m))/a(i,i); end二、列主元高斯消去法解P227页第3题:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-321321212111430x x x 答案:x=[7/6 -1/3 1/2]T三、程序流程图如下:条件图框里面没有条件式,因为i 是从m 到1,所以i=1后运行下面的命令,直接输出结果。
计算方法智慧树知到答案章节测试2023年浙江大学

绪论单元测试1.工科人认知世界的时候,需要认可误差的存在。
A:对B:错答案:A2.不需要掌握很多很好的计算方法,单单凭借计算机强大的能力就可以解决大部分实际问题。
A:错B:对答案:A3.计算方法是一门理论数学课,可以获得寻求数学问题的精确解析解的知识A:错B:对答案:A4.解决某些实际问题时,选择不合适的计算方法有可能无法得到满意的结果。
A:对B:错答案:A5.求解高阶线性方程组(比如,大于150阶),用克莱姆法则来直接求解也是可以接受的。
A:对B:错答案:B第一章测试1.计算机进行乘除运算时按照先舍入后运算的原则。
()A:错B:对答案:A2.相对误差是个无名数,没有量纲。
()A:错B:对答案:B3.两近似值之商的相对误差等于被除数的相对误差与除数的相对误差之差。
()A:错B:对答案:B4.用 1+x近似表示所产生的误差是( )A:模型误差B:截断误差C:舍入误差D:观测误差答案:B5.设某数x,那么x的有四位有效数字且绝对误差限是的近似值是()A:0.006930B:0.6930C:0.06930D:0.693答案:B第二章测试1.若f(a)f(b)<0 ,则f(x)在(a,b)内一定有根。
()A:对B:错答案:B2.如果迭代格式在根的附近导数值的模大于1,则迭代发散。
()A:对B:错答案:A3.若x*是f(x)=0的重根,则牛顿不收敛。
()A:对B:错答案:B4.非线性方程的求根方法中,正割法收敛速度比Newton迭代法快。
()A:对B:错答案:B5.用牛顿迭代法求方程f(x)=在附近的根,第一次迭代值()A:3B:2C:0D:1答案:B6.用简单迭代法求方程f(x)=0的实根,把方程f(x)=0表示成x=g(x),则f(x)=0的根是()A:y=x与x轴交点的横坐标B:y=g(x)与x轴交点的横坐标C:y=x与y=g(x)的交点D:y=x与y=g(x)交点的横坐标答案:D7.以下对非线性方程的求根方法中哪些是线性收敛的?()A:不动点迭代法B:二分法C:牛顿迭代法在重根的情况下D:牛顿迭代法在单根的情况下答案:AC第三章测试1.上面式子,用高斯消去法计算,解为()。
计算方法实验报告习题2(浙大版)

计算方法实验报告实验名称: 实验2 列主元素消去法解方程组 1 引言工程实际问题中,线型方程的系数矩阵一般为低阶稠密矩阵和大型稀疏矩阵。
用高斯消去法解Ax =b 时,可能出现)(k kk a 很小,用作除数会导致中间结果矩阵元素数量级严重增长和舍入误差的扩散,使结果不可靠;采用选主元素的三角分解法可以避免此类问题。
高斯消去法的消去过程,实质上是将A 分解为两个三角矩阵的乘积A =LU ,并求解Ly =b 的过程。
回带过程就是求解上三角方程组Ux =y 。
所以在实际的运算中,矩阵L 和U 可以直接计算出,而不需要任何中间步骤,从而在计算过程中将高斯消去法的步骤进行了进一步的简略,大大提高了运算速度,这就是三角分解法。
采用选主元的方式与列主元高斯消去法一样,也是为了避免除数过小,从而保证了计算的精确度。
2 实验目的和要求通过列主元素消去法求解线性方程组,实现P A =LU 。
要求计算解x ,L ,U ,整形数组IP (i ),(i =1,2,…,)(记录主行信息)。
3 算法原理与流程图(1)原理将A 分解为两个三角矩阵的乘积A =LU 。
对方程组的增广矩阵[]b A A ,=经过k-1步分解后,可变成如下形式:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡→-------------n nnnjnkk n n n i in ij ik k i i i k kn kj kk k k k k k n k j k k k k k k k n j k k n j k k b a a a l l l b a a a l l l b a a a l l l y u u u u l l y u u u u u l y u u u u u u A1,211,211,211,1,1,11,12,11,122221,2222111,1,11,11211第k 步分解,为了避免用绝对值很小的数kku 作除数,引进量1111 (,1,,;1,2,,) ()/ (1,2,,;1,2,,)k kj kj km mj m k ik ik im mk kk m u a l u j k k n k n l a l u u i k k n k n -=-=⎧=-=+=⎪⎪⎨⎪=-=++=⎪⎩∑∑11(,1,,)k i ik im mkm s a l u i k k n -==-=+∑,于是有kk u =ks 。
【浙江大学】大学计算机基础教程——习题与参考答案

4. 频率
5. 读数据包并解包、打包并发送
6. 易失性、RAM、被读出
7. FAT
8. 150K
9. RAM
10.用户、计算机
11.通用串行总线
选择题:
1、B 2、C 3、C 4、BCDEF 5、C 6、B 7、D 8、D 9、D 10、A
6.多媒体信息交互处理所需的硬件设备是在普通PC机的基础上,再包括:高性能的CPU(带有多媒体扩展指令MMX);快速、大容量的内存;声卡;显卡;视频卡和质量较高的显示器;CD-ROM或DVD-ROM驱动器;扫描仪;数码相机;数字摄像机等外围设备。多媒体信息处理所需的软件有:多媒体操作系统;多媒体创作软件和应用软件,如图像处理、音乐处理、演示文稿制作、动画制作、视频处理等。
11、D 12、B 13、D 14、B 15、B
第4章 核心:操作系统
简答题:
1.系统软件是指管理、监控和维护计算机软、硬件资源,起到为用户提供友好的交互界面、支持用户运行应用软件、提高计算机的使用效率等的软件。应用软件是人们为了解决某些特定的具体问题而设计开发的各种程序。
选择题:
1、E 2、C 3、B 4、BDFJLE 5、C 6、ABEFH
7、B 8、D 9、A 10、C 11、A 12、B
第2章 信息表示和逻辑基础
简答题:
1.数制又称为“计数(或记数)体制”,一般把多位数码中每一位的构成方法以及实现从低位到高位的进位规则叫做数制。数制的3个基本特点为:(1)一个R进制的数制有R-1个数码;(2)最大的数码为R-1;(3)计数规则为“逢R进一”。
12.一个正数的原码和它的真值相同,负数的原码为这个数真值的绝对值,符号位为1。反码的定义是:一个正数的反码等于它的原码;一个负数的反码,最高位(符号位)为1,其余各位按位求反。补码的定义是:一个正数的补码等于它的原码;一个负数的补码等于它的反码加上1(从最低位上加1,并考虑进位,但进位不改变符号位)。
2019-2020学年第一学期期末考试《计算方法》大作业答案

吉林大学网络教育学院2019-2020学年第一学期期末考试《计算方法》大作业答案学生姓名专业层次年级学号学习中心成绩年月日作业完成要求:大作业要求学生手写,提供手写文档的清晰扫描图片,并将图片添加到word文档内,最终wod文档上传平台,不允许学生提交其他格式文件(如JPG,RAR等非word文档格式),如有雷同、抄袭成绩按不及格处理。
一、解线性方程(每小题8分,共80分)1、用矩阵的LU分解算法求解线性方程组X1+2X2+3X3= 02X1+2X2+8X3= -4-3X1-10X2-2X3= -11答:2、用矩阵的Doolittle分解算法求解线性方程组X1+2X2+3X3= 12X1– X2+9X3= 0-3X1+ 4X2+9X3= 1答:3、用矩阵的Doolittle分解算法求解线性方程组2X1+X2+X3= 46X1+4X2+5X3=154X1+3X2+6X3= 13答:4、用高斯消去法求解线性方程组2X1- X2+3X3= 24X1+2X2+5X3= 4-3X1+4X2-3X3= -3答:5、用无回代过程消元法求解线性方程组2X1- X2+3X3= 24X1+2X2+5X3= 4-3X1+4X2-3X3= -3答:6、用主元素消元法求解线性方程组2X1- X2+3X3= 24X1+2X2+5X3= 4-3X1+4X2-3X3= -3答:7、用高斯消去法求解线性方程组1231231232344272266x x x x x x x x x -+=++=-++=答:8、利用Doolittle 分解法解方程组Ax=b ,即解方程组12341231521917334319174262113x x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦ 答:9、利用Doolittle 分解法解方程组Ax=b ,即解方程组123421111443306776081011112x x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦ 答:10、用高斯消元法解方程组1237811351341231x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦答案:二、计算(每小题10分,共20分)1、已知节点x1,x2及节点处函数值f(x1),f(x2),构造线性插值多项式p1(x). 答:2、设f(xi)=i(i=0,1,2),构造二次式p2(x),使满足: p2(xi)=f(xi)(i=0,1,2)答:。
计算方法考试题及答案

计算方法考试题及答案一、选择题(每题3分,共30分)1. 以下哪个算法是用于求解线性方程组的?A. 快速傅里叶变换B. 高斯消元法C. 牛顿迭代法D. 蒙特卡洛方法答案:B2. 在数值分析中,插值和逼近的主要区别是什么?A. 插值通过已知点,逼近不一定通过B. 逼近通过已知点,插值不一定通过C. 插值和逼近都必须通过所有已知点D. 插值和逼近没有区别答案:A3. 以下哪个方法不是数值积分的方法?A. 梯形法则B. 辛普森法则C. 牛顿迭代法D. 龙格-库塔方法答案:C4. 对于非线性方程的求解,以下哪个方法是基于迭代的?A. 二分法B. 牛顿迭代法C. 高斯消元法D. 蒙特卡洛方法答案:B5. 在数值分析中,以下哪个方法用于求解微分方程?A. 插值法B. 逼近法C. 欧拉方法D. 傅里叶变换答案:C6. 以下哪个算法是用于求解非线性方程的?A. 高斯消元法B. 牛顿迭代法C. 梯形法则D. 蒙特卡洛方法答案:B7. 在数值分析中,以下哪个方法用于求解线性方程组的?A. 牛顿迭代法B. 高斯消元法C. 梯形法则D. 蒙特卡洛方法答案:B8. 以下哪个方法不是数值积分的方法?A. 梯形法则B. 辛普森法则C. 高斯消元法D. 龙格-库塔方法答案:C9. 对于非线性方程的求解,以下哪个方法是基于迭代的?A. 二分法B. 高斯消元法C. 梯形法则D. 蒙特卡洛方法答案:A10. 在数值分析中,以下哪个方法用于求解微分方程?A. 插值法B. 逼近法C. 欧拉方法D. 傅里叶变换答案:C二、填空题(每题2分,共20分)1. 插值法中,拉格朗日插值多项式的最高次数是______。
答案:n2. 在数值积分中,梯形法则的误差与步长的______次幂成正比。
答案:23. 牛顿迭代法中,每次迭代的公式为______。
答案:x_{n+1} = x_n - f(x_n) / f'(x_n)4. 高斯消元法中,主元的选择是为了______。
2018-2019学年第二学期期末考试《计算方法》大作业参考答案

吉林大学网络教育学院2018-2019学年第二学期期末考试《计算方法》大作业学生姓名专业层次年级学号学习中心成绩年月日一、构造次数不超过三次的多项式P3(X),使满足:(10分)P3(0)= 1;P3(1)=0;P3′(0)=P3′(1)=0。
二、设f(x i)=i(i=0,1,2),构造二次式p2(x),使满足:(10分) p2(x i)=f(x i)(i=0,1,2)三、设节点x i=i(i=0,1,2,3),f(0)=1,f(1)=0,f(2)=-7,f(3)=26,构造次数不超过3次的多项式p3(x),满足p3(x i)=f(x i),i=0,1,2,3 (10分)四、对于上题的问题,构造Newton插值多项式。
(10分)五、构造三次多项式P 3(X )满足:P 3(0)= P 3(1)=0,P 3′(0)=P 3′(1)=1。
(10分)六、利用Doolittle 分解法解方程组Ax=b 即解方程组 (15分) 12341231521917334319174262113x x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦解:用公式七、基于迭代原理证明(10分)+++=22 (22)八、构造二次多项式2()x p 满足: (10分)'010222()1;()0;()1p p p x x x ===九、构造一个收敛的迭代法求解方程3210x x --=在[1.3,1.6]内的实根。
合理选择一个初值,迭代一步,求出1x 。
(15分)作业完成要求:大作业要求学生手写,提供手写文档的清晰扫描图片,并将图片添加到word 文档内,最终word文档上传平台,不允许学生提交其他格式文件(如JPG,RAR等非word 文档格式),如有雷同、抄袭成绩按不及格处理。
计算方法及答案.docx

A. det A = 0B.detA k = 0(1 乞 k n)c. detA 0D. det A :: 0《计算方法》练习题一一、填空题1.理=3.14159…的近似值3.1428 ,准确数位是()。
2 .满足 f(a) = C, f(b) = d 的插值余项 R(X)=()。
3 .设{P k (x)}为勒让德多项式,则(F 2(χ), P 2(x)) - ( )o4 •乘幕法是求实方阵()特征值与特征向量的迭代法。
5 .欧拉法的绝对稳定实区间是()o6. e =2.71828…具有3位有效数字的近似值是( )。
7 .用辛卜生公式计算积分[fc ( ) oVHx8 .设A (kJ0 =(a (Z )第k 列主兀为a Pk J),则a (Pk A) =()10 •已知迭代法:X n 1 =(X n ), (n=0,1,…)收敛,则:(x)满足条件()。
、单选题1•已知近似数a,b,的误差限;(a), ;(b),则;(ab)=()。
A. E(a)E(b)B. E(a)+^(b)c. ag(a)+∣bw(b) D . a E (b)+'b w(a)2 .设 f(x) =X 2 X ,则 f[1,2,3]=()。
A.lB. 2C. 3D .4 3 . 设A =们 ,则化A 为对角阵的平面旋转 Q =().:1 3一ππππ A.—B .—C .—D .—23 464 . 若双点弦法收敛, 则双点弦法具有()敛速.A.线性B.超线性C.平方D .三次5 .改进欧拉法的局部截断误差阶是().A. o(h)Bo(h 2)C.o(h 3)D.o(h 4)6 .近似数 a = 20.47820 "0的误差限是()o1 一 c -51 _ -4 1__3 1 _ _2A. ×10B.×10 C.×10D . × 1022229 .已知贝TtJ 1 25 4_-7 .矩阵A满足(),则存在三角分解A=LR)&已知 X =(—1,3,-5)T ,则 X 1 =()。
浙江大学08计算机上机题(含答案)

浙江大学08计算机上机题(含答案)一、又一版A+B题目描述:输入两个不超过整型定义的非负10进制整数A和B(<=231-1),输出A+B的m (1 < m<10)进制数。
输入:输入格式:测试输入包含若干测试用例。
每个测试用例占一行,给出m和A,B的值。
当m为0时输入结束。
输出:输出格式:每个测试用例的输出占一行,输出A+B的m进制数。
样例输入:8 1300 482 1 7样例输出:25041000答案:想偷个懒,用C自带的函数过,但是CE了,估计后台禁止这个函数了,1.#include2.#include3.int main()4.{5. unsigned a,b,m;6. char z[35];7. while(scanf("%u",&m),m)8. {9. scanf("%u%u",&a,&b);10. itoa(a+b,z,m);11. printf("%s\n",z);12. }13. return 0;14.}另:1.#include/doc/1c18388767.html,ing namespace std;3.4.void Function(long long lRadix, long long lNumber);5.int main()6.{7.long long lRadix, lNumA, lNumB;8.while(cin>>lRadix && lRadix &&cin>>lNumA>>lNumB)9.{10. Function(lRadix, lNumA+ lNumB);11. cout<<endl;< bdsfid="109" p=""></endl;<>12.}13.}14.void Function(long long lRadix, long long lNumber)15.{16.if(lNumber/lRadix)17.{18. Function(lRadix, lNumber/lRadix);19.}20.cout<<lnumber%lradix;< bdsfid="119" p=""></lnumber%lradix;<>21.}22.23.呵呵,我的代码,可以AC的哦另:已经ac过了:#includeint main(){unsigned int a,b,sum,shang,yu;//必须无符号数,否则溢出int m,s[100];while(scanf("%d",&m),m){int i=0,j=0;scanf("%d%d",&a,&b);sum=a+b;do//模除取余,并存入数组s{shang=sum/m;yu=sum%m;s[i]=yu;sum=shang;i++;}while(shang);for(j=i-1;j>=0;j--)//将数组s倒序输出printf("%d",s[j]);putchar('\n');}return 0;}二、欧拉回路题目描述:欧拉回路是指不令笔离开纸面,可画过图中每条边仅一次,且可以回到起点的一条回路。
计算方法实验报告习题1(浙大版)

计算方法实验报告实验名称: 实验1 从函数表出发进行插值 1 引言某个实际问题中,函数f (x)在区间[a,b]上存在且连续,但难以找到其表达式,只能通过实验和观测得到有限点上的函数表。
有些情况虽然可以写出表达式,但结构复杂,使用不方便。
所以希望构造简单函数P (x)作为f (x)的近似值。
插值法是解决此类问题的一种方法。
设函数y=在插值区间[a,b]上连续,且在n+1个不同的插值节点a≤x 0,x 1,…,x n ≤b 上分别取值y 0,y 1,…,y n 。
目的是要在一个性质优良、便于计算的插值函数类Φ中,求一简单函数P (x),满足插值条件P (x i )=y i (i=0,1,…,n),而在其他点x≠x i 上,作为f (x)近似值。
求插值函数P (x)的方法称为插值法[1]。
2 实验目的和要求运用Matlab 编写m 文件,定义三种插值函数,要求一次性输入整张函数表,并利用计算机选择在插值计算中所需的节点。
分别通过分段线性插值、分段二次插值和全区间上拉格朗日插值计算f (0.15),f (0.31),f (0.47)的近似值。
3 算法原理与流程图(1)原理 1.线性插值当给定了n+1个点x 0<x 1<…<x n 上的函数值y 0,y 1,…,y n 后,若要计算x≠x i 处函数值f (x)的近似值,可先选取两个节点x i-1与x i 使x ∈[x i-1,x i ],然后在小区间[x i-1,x i ]上作线性插值,即得11111)()(------+--=≈i i i i i i i i x x x x y x x x x y x P x f这种分段低次插值叫分段线性插值。
2.分段二次插值当给定了n+1个点x 0<x 1<…<x n 上的函数值y 0,y 1,…,y n 后,若要计算x≠x i 处函数值f (x)的近似值,可先选取距离x 最近的三个节点x i-1,x i 与x i+1,然后进行二次插值,即得专业:电气工程及其自动化 姓名: 李X∑∏+-=+≠-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛--=≈11112)()(i i k i k j i j j k j k x x x x y x P x f 这种分段低次插值叫分段二次插值。
浙江大学计算方法大作业第十二题

exp(2*b0*x[i])*a0 + y[i]*exp(b0*x[i]) - a0*exp(2*b0*x[i]); A[1][0] = A[1][0] + 2*a0*x[i]*exp(2*b0*x[i]) - x[i]*y[i]*exp(b0*x[i]); A[1][1] = A[1][1] + 2*a0*a0*x[i]*x[i]*exp(2*b0*x[i]) - a0*x[i]*x[i]*y[i]*exp(b0*x[i]); B[1] = B[1] + (2*a0*x[i]*exp(2*b0*x[i]) - x[i]*y[i]*exp(b0*x[i]))*a0 +
浙大-计算方法作业

来自14 级机械专业的《计算方法》课程课本为黄皮小书只有当年作业布置的部分题目 2.4.7.8.10.13.17第2题二分法#include<iostream>#include<math.h>double calculate_y(double n){using namespace std;return exp(n)+10*n-2;}int main(){using namespace std;int k;double a,b,c1;double y1,y2,x,y;cout<<"请依次输入a (左端点),b (右端点),c (控制精度),中间用enter隔开"<<endl;cin>>a>>b>>c1;y1 = calculate_y(a);y2 = calculate_y(b);if(y1*y2<=0);else{do{cout<<"["<<y1<<","<<y2<<"]"<<endl;cout<<" 实根不再此范围内,请重新输入!" <<endl;cin>>a>>b>>c1;y1 = calculate_y(a);y2 = calculate_y(b);}while(y1*y2>0);}k=0;do{k=k+1; x=(a+b)/2; y=calculate_y(x);if(y1*y<0) b=x;else {a=x;y1=y;}}while(b-a>=c1);cout<<"k="<<k<<" x="<<x<<" y="<<y<<endl; cout<<"["<<y1<<","<<y2<<"]"<<" "<<y<<endl<<""<<endl;结果如上,感谢使用!cin.get();cin.get();}迭代法#include<iostream> #include<cmath>int main(){using namespace std;int k=1,N;double x0,c,x1;cout<<"请依次输入N, xO, c"<<endl;cin>>N>>x0>>c;do{k=k+1;x1=(2-exp(xO))/1O; if(fabs(x1-xO)<c){cout<<"k="<<k<<" x"<<k<<"="<<x1<<endl;break;}else{ cout<<"x"<<k<<"="<<x1<<endl; xO=x1;}}while(k<N);if(k<N);elsecout<<" 失败!迭代次数太少,未达到精度要求"<<endl;cin.get();cin.get();return 0;}牛顿法#include<iostream> #include<cmath>double fx(double n1){using namespace std; return exp(n1)+10*n1-2;}double f1x(double n2){using namespace std; return exp(n2)+10;}int main(){using namespace std;int N,k=0,I;double x0,x1,c,f_x0,f1_x0;cout<<"请依次输入x0 (迭代初值),c (精度),N (最大允许迭代次数)"<<endl;cin>>x0>>c>>N;do{k++;f_x0=fx(x0); f1_x0=f1x(x0);if(f1_x0==0){I=-1;break;}elsex1=x0-f_x0/f1_x0;} if(fabs(x1-x0)<c){I=0;cout<<"x"<<k<<"="<<x1<<" k="<<k<<endl;break;}f(x"<<k<<")="<<fx(x1)<<"else x0=x1;}while(k<N); if(k>=N)I=1; cout<<"I="<<I<<endl;cin.get();cin.get();return 0; }第4题顺序消元法#include<iostream> using namespace std;#define N 4int main() {double a[N][N]={{1.1348,3.8326,1.1651,3.4017}, {0.5301,1.7875,2.5330,1.5435},{3.4129,4.9317,8.7643,1.3142},{1.2371,4.9998,10.6721,0.0147}};double b[N]={9.5342,6.3941,18.4231,16.9237}; double m[N][N];double x[N];int k,i,j;for(k=0;k<=N;k++) {for(i=k+1;i<N;i++){m[i][k]=a[i][k]/a[k][k]; for(j=k+1;j<N;j++) {a[i][j]-=m[i][k]*a[k][j];}b[i]-=m[i][k]*b[k];}}for(i=0;i<N;i++){for(j=0;j<N;j++){cout<<a[i][j]<<" ";}cout<<endl;}for(i=0;i<N;i++)cout<<b[i]<<endl;double t=0.0;x[N-1]=b[N-1]/a[N-1][N-1];for(i=N-2;i>=0;i--){x[i]=b[i];for(j=i+1;j<N;j++){x[i]-=a[i][j]*x[j];}x[i]/=a[i][i];}cout<<" 方程的解依次为"<<endl; for(i=0;i<N;i++){ cout<<"x["<<i+1<<"]="<<x[i]<<endl;}}列主元消元法#include<iostream> #include<cmath> using namespace std;#define N 4 void display(double (*a)[N],double *b){for(int i=0;i<N;i++){for(int j=0;j<N;j++){cout<<a[i][j]<<" ";}cout<<b[i]<<endl;}}int main(){double a[N][N]={{1.1348,3.8326,1.1651,3.4017}, {0.5301,1.7875,2.5330,1.5435},{3.4129,4.9317,8.7643,1.3142},{1.2371,4.9998,10.6721,0.0147}};double b[N]={9.5342,6.3941,18.4231,16.9237};double m[N][N];double x[N];int k,i,j,l;double max;double p;for(k=0;k<N-1;k++){max=a[k][k];l=k;for(i=k+1;i<N;i++){if(fabs(a[i][k])>fabs(max)){max=a[i][k];l=i;}}if(fabs(max)*100000<1)cout<<"det A=0"<<endl;else{if(l!=k){p=b[l];b[l]=b[k];b[k]=p;for(j=0;j<N;j++){p=a[l][j];a[l][j]=a[k][j];a[k][j]=p;}display(a,b); cout<<endl;} for(i=k+1;i<N;i++){m[i][k]=a[i][k]/a[k][k];for(j=k+1;j<N;j++){a[i][j]-=m[i][k]*a[k][j];}b[i]-=m[i][k]*b[k];}display(a,b);cout<<endl;}}if(fabs(a[N-1][N-1])*100000<1)cout<<"det A=0"<<endl;else{x[N-1]=b[N-1]/a[N-1][N-1];for(i=N-2;i>=0;i--){x[i]=b[i];for(j=i+1;j<N;j++){x[i]-=a[i][j]*x[j];}x[i]/=a[i][i];}}cout<<" 方程的解依次为"<<endl;for(i=0;i<N;i++){cout<<"x["<<i+1<<"]="<<x[i]<<endl;第7题雅可比迭代法#include<iostream>#include<math.h>#include <iomanip> using namespace std;int main(){double s=0;double max(double array[6]); double a[6][6]={{4,-1,0,-1,0,0},{-1,4,-1,0,-1,0},{0,-1,4,-1,0,-1},{-1,0,-1,4,-1,0},{0,-1,0,-1,4,-1},{0,0,-1,0,-1,4,},};double b[6]={0,5,-2,5,-2,6};double c[6]={0,0,0,0,0,0};double x[6]={0,0,0,0,0,0};double x0[6]={0,0,0,0,0,0};int i,k,j;double r,sum=0;cout<<" 输入精度:"<<endl;cin>>s;for(k=1;;k++){for(i=0;i<6;i++){for(j=0;j<6;j++){sum=a[i][j]*x0[j]+sum;}x[i]=x0[i]+((b[i]-sum)/a[i][i]);c[i]=fabs(x[i]-x0[i]);sum=0;r=max(c);if(r<s){for(i=0;i<6;i++)cout<<"x"<<i<<" = "<<x[i]<<setprecision(6)<<endl;cout<<" 迭代次数:"<<k<<endl;return 0;}elsefor(i=0;i<6;i++)x0[i]=x[i];}}double max(double array[6]){double a=array[0];int i;for(i=1;i<6;i++){if(a<array[i])a=array[i];}return a;}高斯-赛德尔迭代法#include<iostream> #include<math.h> #include <iomanip> using namespace std;int main(){double s=0;double max(double array[3]);double a[6][6]={{4,-1,0,-1,0,0},{-1,4,-1,0,-1,0}, {0,-1,4,-1,0,-1},{-1,0,-1,4,-1,0}, {0,-1,0,-1,4,-1},{0,0,-1,0,-1,4},};double b[6]={0,5,-2,5,-2,6};double c[6]={0,0,0,0,0,0};double x[6]={0,0,0,0,0,0};double x0[10]={0,0,0,0,0,0};int i,k,j;double r,sum=0;cout<<" 输入精度:"<<endl;cin>>s;for(k=1;;k++){for(i=0;i<6;i++){for(j=0;j<6;j++){sum=a[i][j]*x0[j]+sum;}x[i]=x0[i]+((b[i]-sum)/a[i][i]);c[i]=x[i]-x0[i];if(c[i]<0)c[i]=-c[i];x0[i]=x[i];sum=0;}r=max(c);if(r<s){for(i=0;i<6;i++)cout<<"x"<<i<<" = "<<x[i]<<setprecision(6)<<endl; cout<<" 迭代次数:"<<k<<endl;return 0;}}}double max(double array[6]) {double a=array[0]; int i; for(i=1;i<6;i++) {if(a<array[i])a=array[i];return a; }SOR迭代法#include<iostream>#include<math.h>#include <iomanip> using namespace std;int main(){double s=0,w=0;double max(double array[3]); double a[6][6]={{4,-1,0,-1,0,0},{-1,4,-1,0,-1,0},{0,-1,4,-1,0,-1},{-1,0,-1,4,-1,0},{0,-1,0,-1,4,-1},{0,0,-1,0,-1,4}};double b[6]={0,5,-2,5,-2,6}; double c[6]={0,0,0};double x[6]={0,0,0,0,0,0};double x0[6]={0,0,0,0,0,0};int i,k,j;double r,sum=0;cout<<" 输入精度:"<<endl; cin>>s;cout<<" 松弛因子:"<<endl; cin>>w;for(k=1;;k++){ for(i=0;i<6;i++) {for(j=0;j<6;j++){ sum=a[i][j]*x0[j]+sum;} x[i]=x0[i]+(w*(b[i]-sum)/a[i][i]);c[i]=x[i]-x0[i];if(c[i]<0)c[i]=-c[i];x0[i]=x[i];sum=0;}r=max(c);if(r<s){for(i=0;i<6;i++)cout<<"x"<<i<<" = "<<x[i]<<setprecision(6)<<endl;cout<<"迭代次数:"<<k<<endl;return 0;}}}double max(double array[6]){double a=array[0];int i; for(i=1;i<6;i++) {if(a<array[i])a=array[i];} return a;}第8题分段线性插值#include<stdio.h>int main(void){int i,j; double a[6],b[6],x,y;printf("Enter x:"); for(i=0;i<6;i++) scanf("%lf",&a[i]); printf("Enter f(x):");for(i=0;i<6;i++) scanf("%lf",&b[i]);for(j=0;j<3;j++){printf("Enter x:");scanf("%lf",&x);for(i=0;x>a[i];i++);y=b[i-1]*(x-a[i])/(a[i-1]-a[i])+b[i]*(x-a[i-1])/(a[i]-a[i-1]); printf("x=%lf , ",x);printf("y=%lf\n",y);}return 0;}分段二次插值#include<stdio.h>int main(void){int i,j;double a[6],b[6],x,y;printf("Enter x:");for(i=0;i<6;i++) scanf("%lf",&a[i]);printf("Enter f(x):");for(i=0;i<6;i++) scanf("%lf",&b[i]);for(j=0;j<3;j++){printf("Enter x:");scanf("%lf",&x);for(i=0;x>a[i];i++);if((a[i+1]-x)<(x-a[i-2])){ y=b[i-1]*(x-a[i])/(a[i-1]-a[i])*(x-a[i+1])/(a[i-1]-a[i+1]); y=y+b[i]*(x-a[i-1])/(a[i]-a[i-1])*(x-a[i+1])/(a[i]-a[i+1]); y=y+b[i+1]*(x-a[i-1])/(a[i+1]-a[i-1])*(x-a[i])/(a[i+1]-a[i]); printf("x=%lf , ",x);printf("y=%lf\n",y);}else{y=b[i-2]*(x-a[i-1])/(a[i-2]-a[i-1])*(x-a[i])/(a[i-2]-a[i]); y=y+b[i-1]*(x-a[i-2])/(a[i-1]-a[i-2])*(x-a[i])/(a[i-1]-a[i]); y=y+b[i]*(x-a[i-2])/(a[i]-a[i-2])*(x-a[i-1])/(a[i]-a[i-1]); printf("x=%lf , ",x);printf("y=%lf\n",y);}}return 0;}全区间上拉格朗日插值#include<stdio.h>int main(void){int i,j,k; double a[6],b[6],x,y,p;printf("Enter x:"); for(i=0;i<6;i++)scanf("%lf",&a[i]); printf("Enter f(x):");for(i=0;i<6;i++) scanf("%lf",&b[i]);for(j=0;j<3;j++) {y=0; printf("Enter x:"); scanf("%lf",&x); for(i=0;i<6;i++){p=1;for(k=0;k<6;k++){ if(k!=i) p=p*(x-a[k])/(a[i]-a[k]);} y=y+p*b[i];}printf("x=%lf , ",x); printf("y=%lf\n",y);} return 0;}第10 题最小二乘法二次回归#include<stdio.h>#include<math.h>#include<conio.h>float cf(int i,float f){ float g=1.0;while(i--)g*=f;return g;}void ColPivot(float a[99][99], int n, float b[99][1],float x[99]){float max,m,temp;int k,q=0,i,j,I;for(k=0;k<n && q==0;k++){ max=a[k][k];for(i=k+1;i<n;i++)if(fabs(max)<fabs(a[i][k])){max=a[i][k];I=i;}if(max==0)q=1;else{ if(I!=k){temp=b[I][0]; b[I][0]=b[k][0]; b[k][0]=temp;for(j=k;j<n;j++){temp=a[I][j]; a[I][j]=a[k][j]; a[k][j]=temp;}} for(i=k+1;i<n;i++){m=a[i][k]/a[k][k];b[i][0]=b[i][0]-b[k][0]*m;for(j=0;j<n;j++)a[i][j]=a[i][j]-a[k][j]*m;}}}for(i=n-1;i>=0;i--){for(j=n-1;j>=i+1;j--) b[i][0]=b[i][0]-a[i][j]*x[j]; x[i]=b[i][0]/a[i][i];}float x0,y0;x0=-x[1]/(2*x[2]);y0=x[0]-x[1]*x[1]/(4*x[2]);printf("\nx0=%f",x0);printf("\ny0=%f",y0);}int main(){float x[99],y[99],z[99],s[99][99],t[99][1]; int n,m,i,j,k;printf("n( 变量数)="); scanf("%d",&n);printf("m (拟合阶数) ="); scanf("%d",&m);printf("x[%]=",n);for(i=0;i<n;i++)scanf("%f",&y[i]); printf("y[%d]=",n);for(i=0;i<n;i++)scanf("%f",&z[i]);for(i=0;i<=m;i++){ for(j=0;j<=m;j++) {s[i][j]=0.0;for(k=0;k<=n-1;k++)s[i][j]+=cf(i+j,y[k]);t[i][0]=0.0;for(j=0;j<=n-1;j++)t[i][0]+=z[j]*cf(i,y[j]);}for(i=0;i<=m;i++)s[i][m+1]=t[i][0];for(i=0;i<=m;i++){for(j=0;j<=m+1;j++) printf("%f\t",s[i][j]); printf("\n");}ColPivot(s,m+1,t,x);printf("\n\n");for(i=0;i<=m;i++) printf("\na[%d]=%f",i,x[i]); printf("\n\n");}第13 题复合梯形递推算法#include<cmath> #include<iostream>/*************** 计算函数值**************/double f(double x)//{using namespace std;double s,e=exp(1);s=sqrt((1-pow(e,-x)))/x;// 预先输入的待积分函数return(s);}************************************************ 算 2八k ***************/double power(int K)//{using namespace std;double P;P=pow(2.0,double(K)); return P;}伴************************************************ 复化梯形公式的递推过程***************/double DTGCH(double a,double b,double precision)// {using namespace std;int i,k;double fa,fb,t1,p,S,X,t;fa=1;fb=f(b);k=1;//h=b-a;t1=(b-a)/2*(fa+fb);// 公式T1=(b-a)/2[f(a)+f(b)] p=precision+1;// 误差值初始化while(p>=precision) {double n;S=0;for(i=1;i<=power(k-1);i++)〃计算公式中:刀(2A(k-1),i=1 ) f[a+(2i-1)(b-a)/2A k]{X=a+(2*i-1)*((b-a)/power(k));S=S+f(X);}t=(t1)/2+(b-a)/power(k)*S;p=fabs(t1-t);// 误差值n=power(k-1);cout<<"步长2A(k-1)为"<<*<"时的"<<"T2A(k-1)="<<t1<<'\t'<<"T2Ak="<<t<<'\t'<<" 差值:"<<p<<endl;t1=t;k++;return(t);}/**************************************************/int main(){using namespace std;double result,a,b,precision;//result 为计算出的积分值、a 为积分下限、b 为积分上限、precision 为要求的精确度cout<<" 需要求解的积分式为f(x)=(1-e(-x))(1/2)/x"<<endl<<" 括号表示次数,因e 取的14 位有效数字,故结果略有偏差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
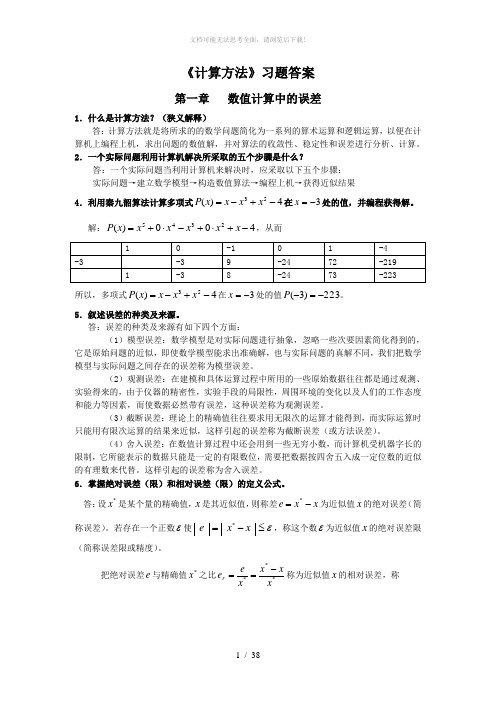
x f(x) 0.0 0.39894 0.1 0.39695 0.195 0.39142 0.3 0.38138 0.401 0.36812 0.5 0.35206
出发,用下列方法计算 f(0.15),f(0.31),及 f(0.47)的近似值: (1)分段线性插值; (2)分段二次插值; (3)全区间上拉格朗日插值
结果分析:很漂亮的结果,本题基本上完全套书里面的公式,只有第二小问稍麻烦点。
结果很精确,并且可以很明显的看到,三个结果越来越精确。
源程序:
(1) #include<stdio.h> int main(void) { printf("输入表格:\n"); double a[2][6]; int i,j,b; double y,x,x1,x0,y0,y1; for(i=0;i<2;i++) for(j=0;j<6;j++) scanf("%lf",&a[i][j]); for(b=1;b<=3;b++) { printf("x=") ; scanf("%lf",&x); for(j=1;j<6;j++) { if(x<a[0][j])break; } x0=a[0][j-1]; x1=a[0][j]; y0=a[1][j-1]; y1=a[1][j]; y=y0+(y1-y0)*(x-x0)/(x1-x0); printf("f(%.2f)=%.5f\n",x,y); } return 0; } (2) #include<stdio.h> int main(void) { printf("表格就不用输入了,已经初始化了(嘿嘿! )直接输入 x 就好了\n"); double a[2][6]={{0.0,0.1,0.195,0.3,0.401,0.5}, {0.39894,0.39695,0.39142,0.38138,0.36812,0.35206}}; int i,j,b,n; double y,x,x0,x1,x2,y1,y2,y0,o,p,q; for(b=1;b<=3;b++) { printf("x=") ; scanf("%lf",&x);
k 0 n
( x x 0 ) * ... * ( x x k 1 )( x x k 1 ) * ... * ( x x n ) ( x k x 0 ) * ... * ( x k x k 1 )( x k x k 1 ) * ... * ( x k x n )
} (3) #include<stdio.h> int main(void) { printf("表格就不用输入了,已经初始化了(嘿嘿! )直接输入 x 就好了\n"); double a[2][6]={{0.0,0.1,0.195,0.3,0.401,0.5}, {0.39894,0.39695,0.39142,0.38138,0.36812,0.35206}}; int i,j,k; double y,x,o,p,q,b,c; for(b=1;b<=3;b++) { printf("x=") ; y=0; scanf("%lf",&x); for(k=0;k<6;k++) { c=1; b=a[1][k]; for(i=0;i<6;i++) { if(i!=k) { c=c*(a[0][k]-a[0][i]) ; b=b*(x-a[0][i]); continue; } } y=y+b/c; } printf("f(%.2f)=%.5f\n",x,y); } }
思路步Байду номын сангаас:
(1)利用公式 l ( x)
y0
( y1 y0 )( x x0 ) 就可以求得结果 ( x1 x0 )
(2)利用公式 l ( x)
y0
( x x0 )( x x2 ) ( x x0 )( x x1 ) ( x x1 )( x x2 ) y1 y2 ( x0 x1 )( x0 x2 ) ( x1 x0 )( x1 x2 ) ( x2 x0 )( x2 x1 )
最开始一个三个输入的循环,然后是加法公式的六个循环,除法式子上下都要用到循环, 每 个里面要判断 x 取的值不能取到 k,这里需要一个判断。很简单。
计算结果:
(输入省略) (1)f(0.15)=0.39404 f(0.31)=0.38007 f(0.47)=0.35693 (2)表格就不用输入了,已经初始化了(嘿嘿! ) f(0.15)=0.39446 f(0.31)=0.38022 f(0.47)=0.35725 (3)表格就不用输入了,已经初始化了(嘿嘿! ) f(0.15)=0.39447 f(0.31)=0.38022 f(0.47)=0.35722
for(j=1;j<6;j++) { if(x<a[0][j])break; } if((j!=1)&&(j!=5)) { if((a[0][j]-x)>(x-a[0][j-1])) { x0=a[0][j-2]; x1=a[0][j-1]; x2=a[0][j]; n=j-2; }else{ x0=a[0][j-1]; x1=a[0][j]; x2=a[0][j+1]; n=j-1; } }else{ if(j==1) { x0=a[0][0]; x1=a[0][1]; x2=a[0][2]; n=0; }else{ x0=a[0][3]; x1=a[0][4]; x2=a[0][5]; n=3; } } y0=a[1][n]; y1=a[1][n+1]; y2=a[1][n+2]; o=(x0-x1)*(x0-x2); p=(x1-x0)*(x1-x2); q=(x2-x0)*(x2-x1); y0=y0*(x-x1)*(x-x2)/o; y1=y1*(x-x0)*(x-x2)/p; y2=y2*(x-x0)*(x-x1)/q; y=y0+y1+y2; printf("f(%.2f)=%.5f\n",x,y); }
中间有一点麻烦的可能就是要分几种情况,因为如果 x 在最左端或最右端的区间,都很肯 x0,x1,x2。如果 x 在其他,x< xh 要判断 x xh 2 与 xh 1 x 哪个更大,也就是判断 x 离哪一 边更近,然后就去那边的三个点,然后套公式。 (3)利用公式 l n ( x ) y k
