多叉树的设计、建立、层次优先遍历和深度优先遍历
算法设计:深度优先遍历和广度优先遍历

算法设计:深度优先遍历和广度优先遍历实现深度优先遍历过程1、图的遍历和树的遍历类似,图的遍历也是从某个顶点出发,沿着某条搜索路径对图中每个顶点各做一次且仅做一次访问。
它是许多图的算法的基础。
深度优先遍历和广度优先遍历是最为重要的两种遍历图的方法。
它们对无向图和有向图均适用。
以下假定遍历过程中访问顶点的操作是简单地输出顶点。
2、布尔向量visited[0 ..n-1] 的设置图中任一顶点都可能和其它顶点相邻接。
在访问了某顶点之后,又可能顺着某条回路又回到了该顶点。
为了避免重复访问同一个顶点,必须记住每个已访问的顶点。
为此,可设一布尔向量visited[0 ..n-1] ,其初值为假,一旦访问了顶点Vi 之后,便将visited[i] 置为真。
深度优先遍历(Depth-First Traversal)1.图的深度优先遍历的递归定义假设给定图G的初态是所有顶点均未曾访问过。
在G中任选一顶点V为初始出发点(源点),则深度优先遍历可定义如下:首先访问出发点V ,并将其标记为已访问过;然后依次从V出发搜索V的每个邻接点W。
若W未曾访问过,则以W为新的出发点继续进行深度优先遍历,直至图中所有和源点V 有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。
若此时图中仍有未访问的顶点,则另选一个尚未访问的顶点作为新的源点重复上述过程,直至图中所有顶点均已被访问为止。
图的深度优先遍历类似于树的前序遍历。
采用的搜索方法的特点是尽可能先对纵深方向进行搜索。
这种搜索方法称为深度优先搜索(Depth-First Search) 。
相应地,用此方法遍历图就很自然地称之为图的深度优先遍历。
2、深度优先搜索的过程设x 是当前被访问顶点,在对x 做过访问标记后,选择一条从x 出发的未检测过的边(X , y)。
若发现顶点y已访问过,则重新选择另一条从X出发的未检测过的边,否则沿边(X,y)到达未曾访问过的y ,对y访问并将其标记为已访问过;然后从y开始搜索, 直到搜索完从y出发的所有路径,即访问完所有从y出发可达的顶点之后,才回溯到顶点X,并且再选择一条从X出发的未检测过的边。
多叉树讲解版课件

多叉树的节点表示数据元素,每个节点包含数据元素和指向其子节点的指针。
多叉树的分支由节点和子节点之间的关系表示,分支可以继续向下延伸,形成更多的子节点。
分支
节点
多叉树的深度是指从根节点到最远叶子节点的最长路径上的节点数。
深度
多叉树的高度是指从根节点到叶子节点的最长路径上的节点数。
高度
02
多叉树的种类与特性
06
多叉树的常见问题与解决方案
Chapter
多叉树在插入或删除节点后,可能会导致树的结构失衡,影响搜索效率。
为了维护树的平衡,可以采用自平衡二叉查找树(如AVL树和红黑树)等数据结构,它们在插入或删除节点时会进行旋转等操作来调整树的结构,保持树的平衡。
总结词
详细描述
总结词
多叉树结构的存储需要占用一定的空间,如何优化存储空间是值得关注的问题。
完全多叉树
满多叉树
平衡多叉树
平衡多叉树是一种特殊的自平衡二叉查找树,它通过旋转操作保持平衡状态。平衡多叉树的查找、插入和删除操作的时间复杂度为O(log n)。
AVL树
AVL树是最早的平衡二叉查找树,它通过旋转操作保持平衡状态。AVL树的查找、插入和删除操作的时间复杂度为O(log n)。
03
多叉树的遍历方法
详细描述
可以采用压缩存储、前缀编码等方法来减少存储空间占用。对于非常大的多叉树,可以考虑使用散列存储、分块存储等策略来提高存储效率。此外,还可以使用编码技术对节点信息进行压缩,减少存储空间占用。
感谢观看
THANKS
05
多叉树的应用场景
Chapter
数据结构中的多叉树是一种常见的数据结构,用于存储具有多于两个子节点的节点。多叉树具有广泛的用途,包括搜索、排序、数据压缩等。
深度优先遍历的算法

深度优先遍历的算法
深度优先遍历(Depth-FirstSearch,简称DFS)是一种常见的图遍历算法。
该算法以深度为优先级,先访问一个结点的所有子结点,再依次访问每个子结点的所有子结点,直到遍历完整个图。
DFS算法通常使用递归实现,在访问一个结点时,先将该结点标记为已访问,并对其所有未访问过的子结点进行深度优先遍历。
这一过程会一直持续下去,直到所有结点都被遍历过。
在实际应用中,DFS算法常用于解决以下问题:
1. 图的连通性问题:使用DFS算法可以判断一个图是否为连通图。
2. 寻找图中能够到达某一个结点的所有路径:在DFS算法的递归过程中,可以记录下所有访问过的结点,从而得到到达目标结点的所有路径。
3. 拓扑排序:DFS算法可以实现拓扑排序,即对图中的所有结点进行排序,使得对于任意的有向边(u, v),u在排序结果中都排在v的前面。
4. 最短路径问题:DFS算法可以用于解决最短路径问题,例如在无权图中,可以通过DFS算法找到从起点到目标结点的最短路径。
总之,DFS算法是一种非常重要的图遍历算法,在各种实际应用中都具有广泛的运用价值。
- 1 -。
深度优先遍历 总结

深度优先遍历是一种常用的图遍历算法,用于遍历和搜索图结构。
其主要思想是从一个顶点开始,尽可能地往下搜索,直到不能搜索为止,然后回溯到前面的顶点继续搜索。
这个过程类似于一条路走到底,然后返回原路,继续走其他路。
深度优先遍历通常采用递归实现,也可以使用栈实现。
深度优先遍历的优点在于能够更深入地搜索图结构,对于深度优先遍历搜索过的节点可以通过回溯的方式遍历其它节点。
但是其缺点在于可能会搜索到无用的节点或进入死循环,因此在实现时需要注意控制搜索深度和避免重复搜索。
深度优先遍历常用于图的遍历、拓扑排序、连通性检查、最短路径等问题中,也可以用于解决一些搜索问题,例如八皇后问题、迷宫问题等。
算法设计:深度优先遍历和广度优先遍历

算法设计:深度优先遍历和广度优先遍历实现深度优先遍历过程1、图的遍历和树的遍历类似,图的遍历也是从某个顶点出发,沿着某条搜索路径对图中每个顶点各做一次且仅做一次访问。
它是许多图的算法的基础。
深度优先遍历和广度优先遍历是最为重要的两种遍历图的方法。
它们对无向图和有向图均适用。
注意:以下假定遍历过程中访问顶点的操作是简单地输出顶点。
2、布尔向量visited[0..n-1]的设置图中任一顶点都可能和其它顶点相邻接。
在访问了某顶点之后,又可能顺着某条回路又回到了该顶点。
为了避免重复访问同一个顶点,必须记住每个已访问的顶点。
为此,可设一布尔向量visited[0..n-1],其初值为假,一旦访问了顶点Vi之后,便将visited[i]置为真。
--------------------------深度优先遍历(Depth-First Traversal)1.图的深度优先遍历的递归定义假设给定图G的初态是所有顶点均未曾访问过。
在G中任选一顶点v为初始出发点(源点),则深度优先遍历可定义如下:首先访问出发点v,并将其标记为已访问过;然后依次从v出发搜索v的每个邻接点w。
若w未曾访问过,则以w为新的出发点继续进行深度优先遍历,直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。
若此时图中仍有未访问的顶点,则另选一个尚未访问的顶点作为新的源点重复上述过程,直至图中所有顶点均已被访问为止。
图的深度优先遍历类似于树的前序遍历。
采用的搜索方法的特点是尽可能先对纵深方向进行搜索。
这种搜索方法称为深度优先搜索(Depth-First Search)。
相应地,用此方法遍历图就很自然地称之为图的深度优先遍历。
2、深度优先搜索的过程设x是当前被访问顶点,在对x做过访问标记后,选择一条从x出发的未检测过的边(x,y)。
若发现顶点y已访问过,则重新选择另一条从x出发的未检测过的边,否则沿边(x,y)到达未曾访问过的y,对y访问并将其标记为已访问过;然后从y开始搜索,直到搜索完从y出发的所有路径,即访问完所有从y出发可达的顶点之后,才回溯到顶点x,并且再选择一条从x出发的未检测过的边。
叉树的建立与基本操作

范围较大,而B+树的子节点数范围较小。
03
插入操作
在B树或B+树中插入一个新元素时,需要从根节点开始向下查找合适的
位置来插入新元素。如果当前节点的子节点数超过了限制范围,则需要
分裂或合并节点来保持平衡。
B树和B+树
查找操作
从根节点开始向下查找要查找的元素所在的区间或叶子节点,然后进行比较查找具体元 素。
左子节点入队
03
if (node->right != NULL) q.push(node->right);
//将右子节点入队
层次遍历
} } ```
PART 04
叉树的算法应用
REPORTING
WENKU DESIGN
二叉搜索树
定义
二叉搜索树是一种特殊的二叉树,其中每个节点的左子树上的所有元 素都小于该节点,右子树上的所有元素都大于该节点。
平衡性
在删除过程中,也需要保持二叉搜索树的平 衡性,以避免出现高度过大的情况。可以通 过旋转等操作来平衡树的结构。
THANKS
感谢观看
REPORTING
https://
删除操作
在B树或B+树中删除一个元素时,需要从根节点开始向下查找要删除的元素所在区间或 叶子节点,然后进行删除操作。如果当前节点的子节点数低于限制范围,则需要合并或
分裂节点来保持平衡。
PART 05
案例分析
REPORTING
WENKU DESIGN
二叉搜索树的插入操作
定义二叉搜索树
二叉搜索树是一种特殊的二叉树,每 个节点的左子树上的所有元素都小于 该节点,右子树上的所有元素都大于 该节点。
叉树的建立与基本操 作
多叉树的层次遍历算法

{ p_childList = list<TreeNode*>; } p_childList->push_back((TreeNode*)treeNode); } /*遍历树层次遍历*/ void TreeNode::LevelTraverse { queue<TreeNode*> queue ; queue.push((TreeNode*)this); TreeNode *p = NULL; while (!queue.empty) { p = queue.front; queue.pop; cout<<"treenode is: "<<p->getSelfId<<endl; (NULL!= p->getChildList) { list<TreeNode*>::iterator it = (p->getChildList)->begin; while(it!= (p->getChildList)->end) { queue.push((*it)); it; } } } } 测试代码: # "stdafx.h" # "TreeNode.h" ( argc, char* argv) { TreeNode root;
其中10是故意用来测试这个只是简单测试大家可以用模板来实现
多叉树的层次遍历算法
疯狂代码 / ĵ:http://Arithmetic/Article33649.html 最近学习c,越看越觉得以前所学只是皮毛.这几天正好有空闲就写点小算法玩玩. 多叉树层次遍历 这个在网上有完整好像不多.这次我就把写贴出来, 有兴趣朋友起来研究下. TreeNode.h 文件 #ndef __TREENODE_ # __TREENODE_ # "StdAfx.h" # <> # <list> # <iostream> # <queue> using std; TreeNode { private: long selfID; nodeName; list<TreeNode*> *p_childList; public: TreeNode; ~TreeNode; /*向当前节点中插入个子节点*/ void insertChildNode(TreeNode *treeNode); /*遍历树层次遍历*/ void LevelTraverse ; //判断某个节点是否为叶子节点 bool isLeaf; //返回当前节点孩子集合 list <TreeNode*>* getChildList;
深度优先遍历实现策略概述

深度优先遍历实现策略概述深度优先遍历(Depth First Search,简称DFS)是图和树算法中常用的一种遍历策略。
该策略在解决很多问题中都起到了重要的作用。
本文将会概述深度优先遍历的实现策略。
一、深度优先遍历的基本原理深度优先遍历是一种先序遍历算法,它从根节点开始遍历,然后沿着树的深度访问节点,直到遍历到没有子节点的节点,然后回溯到前一个节点,继续遍历其它未被访问过的节点。
二、深度优先遍历的实现思路1. 递归实现:深度优先遍历可以通过递归实现。
递归过程分为三步:1.1 访问当前节点;1.2 递归遍历当前节点的子节点;1.3 深度优先遍历当前节点的兄弟节点。
2. 栈实现:深度优先遍历也可以通过栈来实现。
首先将根节点压入栈中,然后进入循环,直到栈为空为止。
每次循环中,弹出栈顶节点,并访问它,然后将其子节点按照倒序压入栈中。
三、深度优先遍历的应用场景深度优先遍历广泛应用于图算法和树算法中,例如:1. 图的连通性分析:通过深度优先遍历可以判断两个节点之间是否有路径相连,常用于寻找连通分量。
2. 拓扑排序:通过深度优先遍历可以对有向无环图进行拓扑排序,得到一种节点的线性排序。
3. 寻找路径:通过深度优先遍历可以寻找图中两个节点之间的路径。
四、深度优先遍历的复杂度分析对于含有n个节点和m条边的图,深度优先遍历的时间复杂度为O(n+m)。
空间复杂度为O(n),其中n为节点数量,m为边的数量。
五、总结深度优先遍历是一种重要的算法策略,通过递归或者栈实现,可以应用于图和树的遍历、连通性分析、拓扑排序、路径寻找等多个问题中。
在实际应用中,我们可以根据具体问题的特点选择适合的深度优先遍历的实现方式。
深度优先遍历迭代法

深度优先遍历迭代法深度优先遍历(Depth-First Search ,简称 DFS )是一种用于图和树的遍历算法,它从起始节点开始,沿着路径尽可能深地访问节点,直到无法继续或达到目标节点。
如果遇到无法继续的节点,则回溯到上一个未完全探索的节点,并继续深入搜索。
以下是使用迭代法实现深度优先遍历的示例代码:```javaclass Graph {int V; // 图的顶点数List<List<Integer>> adjList; // 邻接表表示图Graph(int vertices) {V = vertices;adjList = new ArrayList<>(vertices);for (int i = 0; i < vertices; i++) {adjList.add(new ArrayList<>());}}void addEdge(int u, int v) {adjList.get(u).add(v);adjList.get(v).add(u); // 假设图是无向图}}class DFSIterator {boolean[] visited;Stack<Integer> stack;DFSIterator(Graph graph, int startVertex) {visited = new boolean[graph.V];stack = new Stack<>();visited[startVertex] = true;stack.push(startVertex);}int next() {if (stack.empty()) {return -1;}int vertex = stack.peek();for (int neighbor : graph.adjList.get(vertex)) { if (!visited[neighbor]) {visited[neighbor] = true;stack.push(neighbor);return neighbor;}}// 没有未访问的邻接节点,弹出当前顶点并返回stack.pop();return vertex;}}public class DFS {public static void main(String[] args) {Graph graph = new Graph(9);graph.addEdge(0, 1);graph.addEdge(0, 2);graph.addEdge(1, 2);graph.addEdge(2, 3);graph.addEdge(3, 4);graph.addEdge(4, 5);graph.addEdge(5, 6);graph.addEdge(6, 7);graph.addEdge(7, 8);DFSIterator iterator = new DFSIterator(graph, 0);while (iterator.next() != -1) {System.out.print(iterator.next() + " ");}}}```上述代码实现了一个深度优先遍历的迭代器 `DFSIterator`,它通过维护一个栈来记录已访问的节点,并按照深度优先的顺序遍历图。
PHP实现二叉树深度优先遍历(前序、中序、后序)和广度优先遍历(层次)实例详解

PHP实现⼆叉树深度优先遍历(前序、中序、后序)和⼴度优先遍历(层次)实例详解本⽂实例讲述了PHP实现⼆叉树深度优先遍历(前序、中序、后序)和⼴度优先遍历(层次)。
分享给⼤家供⼤家参考,具体如下:前⾔:深度优先遍历:对每⼀个可能的分⽀路径深⼊到不能再深⼊为⽌,⽽且每个结点只能访问⼀次。
要特别注意的是,⼆叉树的深度优先遍历⽐较特殊,可以细分为先序遍历、中序遍历、后序遍历。
具体说明如下:前序遍历:根节点->左⼦树->右⼦树中序遍历:左⼦树->根节点->右⼦树后序遍历:左⼦树->右⼦树->根节点⼴度优先遍历:⼜叫层次遍历,从上往下对每⼀层依次访问,在每⼀层中,从左往右(也可以从右往左)访问结点,访问完⼀层就进⼊下⼀层,直到没有结点可以访问为⽌。
例如对于⼀下这棵树:深度优先遍历:前序遍历:10 8 7 9 12 11 13中序遍历:7 8 9 10 11 12 13后序遍历:7 9 8 11 13 12 10⼴度优先遍历:层次遍历:10 8 12 7 9 11 13⼆叉树的深度优先遍历的⾮递归的通⽤做法是采⽤栈,⼴度优先遍历的⾮递归的通⽤做法是采⽤队列。
深度优先遍历:1、前序遍历:/*** 前序遍历(递归⽅法)*/private function pre_order1($root){if (!is_null($root)) {//这⾥⽤到常量__FUNCTION__,获取当前函数名,好处是假如修改函数名的时候,⾥⾯的实现不⽤修改$function = __FUNCTION__;echo $root->key . " ";$this->$function($root->left);$this->$function($root->right);}}/*** 前序遍历(⾮递归⽅法)* 因为当遍历过根节点之后还要回来,所以必须将其存起来。
多叉树的遍历算法

多叉树的遍历算法
1. 广度优先遍历:先访问根节点,然后顺序访问同一层的其他
节点;
2. 深度优先遍历:从根节点开始,沿着一条路径一直访问到某一个节点,然后回溯到上一节点,再去访问它的另一个相邻节点;
3. 子树:从某一节点开始,往下连着所有的节点,形成一棵子树,如
果节点有多个子节点,就有多棵子树;
4. 前序遍历:先访问根节点,再访问子节点,最后访问它的同级节点;
5. 中序遍历:先访问根节点的左子节点,然后是它自己,最后访
问右子节点;
6. 后序遍历:先访问根节点的左子节点和右子节点,然后是它自己。
数据结构-树以及深度、广度优先遍历(递归和非递归,python实现)

数据结构-树以及深度、⼴度优先遍历(递归和⾮递归,python实现)前⾯我们介绍了队列、堆栈、链表,你亲⾃动⼿实践了吗?今天我们来到了树的部分,树在数据结构中是⾮常重要的⼀部分,树的应⽤有很多很多,树的种类也有很多很多,今天我们就先来创建⼀个普通的树。
其他各种各样的树将来我将会⼀⼀为⼤家介绍,记得关注我的⽂章哦~⾸先,树的形状就是类似这个样⼦的:它最顶上⾯的点叫做树的根节点,⼀棵树也只能有⼀个根节点,在节点下⾯可以有多个⼦节点,⼦节点的数量,我们这⾥不做要求,⽽没有⼦节点的节点叫做叶⼦节点。
好,关于树的基本概念就介绍到这⾥了,话多千遍不如动⼿做⼀遍,接下来我们边做边学,我们来创建⼀棵树:树# 定义⼀个普通的树类class Tree:def __init__(self, data):self.data = dataself.children = []def get(self):return self.datadef set(self):return self.datadef addChild(self, child):self.children.append(child)def getChildren(self):return self.children这就是我们定义好的树类了,并给树添加了三个⽅法,分别是获取节点数据、设置节点数据、添加⼦节点、获取⼦节点。
这⾥的树类其实是⼀个节点类,很多个这样的节点可以构成⼀棵树,⽽我们就⽤根节点来代表这颗树。
接下来我们实例化⼀棵树:# 初始化⼀个树tree = Tree(0)# 添加三个⼦节点tree.addChild(Tree(1))tree.addChild(Tree(2))tree.addChild(Tree(3))children = tree.getChildren()# 每个⼦节点添加两个⼦节点children[0].addChild(Tree(4))children[0].addChild(Tree(5))children[1].addChild(Tree(6))children[1].addChild(Tree(7))children[2].addChild(Tree(8))children[2].addChild(Tree(9))我们实例化好的树⼤概是这个样⼦的:OK,我们的树已经实例化好了,我们先来对它分别采⽤递归和⾮递归的⽅式进⾏⼴度优先遍历:⼴度优先遍历⼴度优先遍历,就是从上往下,⼀层⼀层从左到右对树进⾏遍历。
二叉树遍历(前序、中序、后序、层次、深度优先、广度优先遍历)java实现

⼆叉树遍历(前序、中序、后序、层次、深度优先、⼴度优先遍历)java实现⼆叉树是⼀种⾮常重要的数据结构,⾮常多其他数据结构都是基于⼆叉树的基础演变⽽来的。
对于⼆叉树,有深度遍历和⼴度遍历,深度遍历有前序、中序以及后序三种遍历⽅法,⼴度遍历即我们寻常所说的层次遍历。
由于树的定义本⾝就是递归定义,因此採⽤递归的⽅法去实现树的三种遍历不仅easy理解并且代码⾮常简洁,⽽对于⼴度遍历来说,须要其他数据结构的⽀撑。
⽐⽅堆了。
所以。
对于⼀段代码来说,可读性有时候要⽐代码本⾝的效率要重要的多。
四种基本的遍历思想为:前序遍历:根结点 —> 左⼦树 —> 右⼦树中序遍历:左⼦树—> 根结点 —> 右⼦树后序遍历:左⼦树 —> 右⼦树 —> 根结点层次遍历:仅仅需按层次遍历就可以⽐如。
求以下⼆叉树的各种遍历1/ \2 3/ \ /4 5 6/ \7 8前序遍历:1 2 4 5 7 8 3 6中序遍历:4 2 7 5 8 1 3 6后序遍历:4 7 8 5 2 6 3 1层次遍历:1 2 3 4 5 6 7 8⼀、前序遍历1)依据上⽂提到的遍历思路:根结点 —> 左⼦树 —> 右⼦树,⾮常easy写出递归版本号:public void preOrderTraverse1(TreeNode root) {if (root != null) {System.out.print(root.val+" ");preOrderTraverse1(root.left);preOrderTraverse1(root.right);}}2)如今讨论⾮递归的版本号:依据前序遍历的顺序,优先訪问根结点。
然后在訪问左⼦树和右⼦树。
所以。
对于随意结点node。
第⼀部分即直接訪问之,之后在推断左⼦树是否为空,不为空时即反复上⾯的步骤,直到其为空。
若为空。
则须要訪问右⼦树。
注意。
多叉树的设计、建立、层次优先遍历和深度优先遍历.docx
多叉树的设计、建立、层次优先遍历和深度优先遍历早起曾实现过一个简单的多义树《实现一个多义树》。
其实现原理是多叉树中的节点有两个域,分别表示节点名以及一个数组,该数组存储其子节点的地址。
实现了一个多义树建立函数,用于输入格式为A Bo A表示节点的名字,B表示节点的子节点个数。
建立函数根据用户的输入,首先建立一个新的节点,然后根据B的值进行深度递归调用。
用户输入节点的顺庁就是按照深度递归的顺序。
另外,我们实现了一个层次优先遍历函数。
该函数用一个队列实现该多义树的层次优先遍历。
首先将根节点入队列,然后检测队列是否为空,如果不为空,将队列出队列,访问出队列的节点,然后将该节点的子节点指针入队列,依次循环下去,直至队列为空,终止循环,从而完成整个多叉树的层次优先遍历。
本文我们将还是介绍一个多义树,其内容和之前的实现差不多。
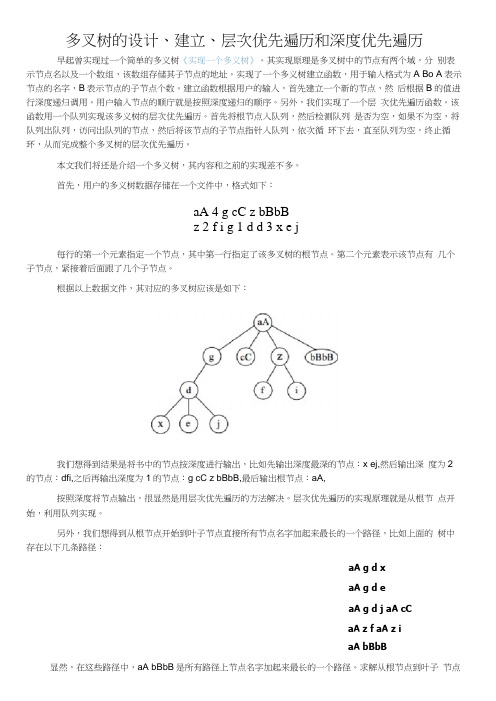
首先,用户的多义树数据存储在一个文件中,格式如下:aA 4 g cC z bBbBz 2 f i g 1 d d 3 x e j每行的第一个元素指定一个节点,其中第一行指定了该多叉树的根节点。
第二个元素表示该节点有几个子节点,紧接着后面跟了几个子节点。
根据以上数据文件,其对应的多叉树应该是如下:我们想得到结果是将书中的节点按深度进行输出,比如先输出深度最深的节点:x ej,然后输出深度为2的节点:dfi,之后再输出深度为1的节点:g cC z bBbB,最后输出根节点:aA,按照深度将节点输出,很显然是用层次优先遍历的方法解决。
层次优先遍历的实现原理就是从根节点开始,利用队列实现。
另外,我们想得到从根节点开始到叶子节点直接所有节点名字加起来最长的一个路径,比如上面的树中存在以下几条路径:aA g d xaA g d eaA g d j aA cCaA z f aA z iaA bBbB显然,在这些路径中,aA bBbB是所有路径上节点名字加起来最长的一个路径。
求解从根节点到叶子节点上的所有路径,利用深度优先遍历更为合适。
深度优先遍历(DFS)(转)

深度优先遍历(DFS)(转)优先搜索(DFS, Depth First Search)是⼀个针对图和树的遍历算法。
早在19世纪就被⽤于解决迷宫问题。
对于下⾯的树⽽⾔,DFS⽅法⾸先从根节点1开始,其搜索节点顺序是1,2,3,4,5,6,7,8(假定左分枝和右分枝中优先选择左分枝)。
DFS的实现⽅式相⽐于BFS应该说⼤同⼩异,只是把queue换成了stack⽽已,stack具有后进先出LIFO(Last Input First Output)的特性,DFS的操作步骤如下:1、把起始点放⼊stack;2、重复下述3步骤,直到stack为空为⽌:a、从stack中访问栈顶的点;b、找出与此点邻接的且尚未遍历的点,进⾏标记,然后全部放⼊stack中;c、如果此点没有尚未遍历的邻接点,则将此点从stack中弹出。
下⾯结合⼀个图(graph)的实例,说明DFS的⼯作过程和原理:(1)将起始节点1放⼊栈stack中,标记为已遍历。
(2)从stack中访问栈顶的节点1,找出与节点1邻接的节点,有2,9两个节点,我们可以选择其中任何⼀个,选择规则可以⼈为设定,这⾥假设按照节点数字顺序由⼩到⼤选择,选中的是2,标记为已遍历,然后放⼊stack中。
(3)从stack中取出栈顶的节点2,找出与节点2邻接的节点,有1,3,5三个节点,节点1已遍历过,排除;3,5中按照预定的规则选中的是3,标记为已遍历,然后放⼊stack中。
(4)从stack中取出栈顶的节点3,找出与节点3邻接的节点,有2,4两个节点,节点2已遍历过,排除;选中的是节点4,标记为已遍历,然后放⼊stack中。
(5)从stack中取出栈顶的节点4,找出与节点4邻接的节点,有3,5,6三个节点,节点3已遍历过,排除;选中的是节点5,标记为已遍历,然后放⼊stack中。
(6)从stack中取出栈顶的节点5,找出与节点5邻接的节点,有2,4两个节点,节点2,4都已遍历过,因此节点5没有尚未遍历的邻接点,则将此点从stack中弹出。
深度优先遍历 总结

深度优先遍历总结
深度优先遍历是一种常见的图遍历算法。
其基本思想是从图的某个顶点出发,沿着一条路径一直走到不能走为止,然后回溯到前一个节点,继续走下一个路径,直到遍历完整个图。
深度优先遍历可以用递归或者栈来实现。
递归实现方法比较简单,栈实现方法需要手动维护一个栈。
深度优先遍历的时间复杂度为O(V+E),其中V为顶点数,E为边数。
空间复杂度为O(V),即需要开辟一个visited数组来记录每个
顶点是否被访问过。
深度优先遍历可以用来解决一些图论问题,例如判断图是否连通,找到图中的所有连通分量,求解最短路径等。
需要注意的是,深度优先遍历不一定能够找到最优解,因为它只考虑了当前路径,而没有考虑其他路径的可能性。
因此,在实际应用中,需要根据具体问题来选择合适的算法。
- 1 -。
树的先序、中序、后序遍历及其代码、层序遍历

树的先序、中序、后序遍历及其代码、层序遍历树是一种重要的数据结构,在计算机科学领域中有广泛的应用。
树的遍历是一种对树进行访问节点的方式,其中包括先序遍历、中序遍历、后序遍历以及层序遍历。
本文将详细介绍这四种遍历方式,并给出相应的代码示例,以帮助读者理解和使用。
首先,我们来了解一下树的基本概念。
树是由节点和边组成的一种非线性数据结构,其中一个节点充当树的根节点,其他节点通过边连接在一起。
每个节点可以有零个或多个子节点,而子节点又可以有自己的子节点,这样就形成了树的层级结构。
树的先序遍历是指首先访问根节点,然后按照先序遍历的方式依次访问左子树和右子树。
具体代码如下:```class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef preorderTraversal(root):if root is None:return []result = []result.append(root.val)result += preorderTraversal(root.left)result += preorderTraversal(root.right)return result```树的中序遍历是指按照先序遍历的方式访问左子树,然后访问根节点,最后访问右子树。
具体代码如下:```def inorderTraversal(root):if root is None:return []result = []result += inorderTraversal(root.left)result.append(root.val)result += inorderTraversal(root.right)return result```树的后序遍历是指按照先序遍历的方式依次访问左子树和右子树,最后访问根节点。
Python实现二叉树的前序、中序、后序、层次遍历

Python实现⼆叉树的前序、中序、后序、层次遍历 有关树的理论部分描述:; 下⾯代码均基于python实现,包含:⼆叉树的前序、中序、后序遍历的递归算法和⾮递归算法;层次遍历;由前序序列、中序序列重构⼆叉树;由后序序列、中序序列重构⼆叉树;# -*- coding: utf-8 -*-# @Time: 2019-04-15 18:35# @Author: chenclass NodeTree:def __init__(self, root=None, lchild=None, rchild=None):"""创建⼆叉树Argument:lchild: BinTree左⼦树rchild: BinTree右⼦树Return:Tree"""self.root = rootself.lchild = lchildself.rchild = rchildclass BinTree:# -----------前序遍历 ------------# 递归算法def pre_order_recursive(self, T):if T == None:returnprint(T.root, end=' ')self.pre_order_recursive(T.lchild)self.pre_order_recursive(T.rchild)# ⾮递归算法def pre_order_non_recursive(self, T):"""借助栈实现前驱遍历"""if T == None:returnstack = []while T or len(stack) > 0:if T:stack.append(T)print(T.root, end=' ')T = T.lchildelse:T = stack[-1]stack.pop()T = T.rchild# -----------中序遍历 ------------# 递归算法def mid_order_recursive(self, T):if T == None:returnself.mid_order_recursive(T.lchild)print(T.root, end=' ')self.mid_order_recursive(T.rchild)# ⾮递归算法def mid_order_non_recursive(self, T):"""借助栈实现中序遍历"""if T == None:returnstack = []while T or len(stack) > 0:if T:stack.append(T)T = T.lchildelse:T = stack.pop()print(T.root, end=' ')T = T.rchild# -----------后序遍历 ------------# 递归算法def post_order_recursive(self, T):if T == None:returnself.post_order_recursive(T.lchild)self.post_order_recursive(T.rchild)print(T.root, end=' ')# ⾮递归算法def post_order_non_recursive(self, T):"""借助两个栈实现后序遍历"""if T == None:returnstack1 = []stack2 = []stack1.append(T)while stack1:node = stack1.pop()if node.lchild:stack1.append(node.lchild)if node.rchild:stack1.append(node.rchild)stack2.append(node)while stack2:print(stack2.pop().root, end=' ')return# -----------层次遍历 ------------def level_order(self, T):"""借助队列(其实还是⼀个栈)实现层次遍历"""if T == None:returnstack = []stack.append(T)while stack:node = stack.pop(0) # 实现先进先出print(node.root, end=' ')if node.lchild:stack.append(node.lchild)if node.rchild:stack.append(node.rchild)# ----------- 前序遍历序列、中序遍历序列 —> 重构⼆叉树 ------------ def tree_by_pre_mid(self, pre, mid):if len(pre) != len(mid) or len(pre) == 0 or len(mid) == 0:returnT = NodeTree(pre[0])index = mid.index(pre[0])T.lchild = self.tree_by_pre_mid(pre[1:index+1], mid[:index])T.rchild = self.tree_by_pre_mid(pre[index+1:], mid[index+1:]) return T# ----------- 后序遍历序列、中序遍历序列 —> 重构⼆叉树 ------------ def tree_by_post_mid(self, post, mid):if len(post) != len(mid) or len(post) == 0 or len(mid) == 0:returnT = NodeTree(post[-1])index = mid.index(post[-1])T.lchild = self.tree_by_post_mid(post[:index], mid[:index])T.rchild = self.tree_by_post_mid(post[index:-1], mid[index+1:]) return Tif __name__ == '__main__':# ----------- 测试:前序、中序、后序、层次遍历 -----------# 创建⼆叉树nodeTree = NodeTree(1,lchild=NodeTree(2,lchild=NodeTree(4,rchild=NodeTree(7))),rchild=NodeTree(3,lchild=NodeTree(5),rchild=NodeTree(6)))T = BinTree()T.pre_order_recursive(nodeTree) # 前序遍历-递归print('\n')T.pre_order_non_recursive(nodeTree) # 前序遍历-⾮递归print('\n')T.mid_order_recursive(nodeTree) # 中序遍历-递归print('\n')T.mid_order_non_recursive(nodeTree) # 前序遍历-⾮递归print('\n')T.post_order_recursive(nodeTree) # 后序遍历-递归print('\n')T.post_order_non_recursive(nodeTree) # 前序遍历-⾮递归print('\n')T.level_order(nodeTree) # 层次遍历print('\n')print('==========================================================================') # ----------- 测试:由遍历序列构造⼆叉树 -----------T = BinTree()pre = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']mid = ['B', 'C', 'A', 'E', 'D', 'G', 'H', 'F', 'I']post = ['C', 'B', 'E', 'H', 'G', 'I', 'F', 'D', 'A']newT_pre_mid = T.tree_by_pre_mid(pre, mid) # 由前序序列、中序序列构造⼆叉树T.post_order_recursive(newT_pre_mid) # 获取后序序列print('\n')newT_post_mid = T.tree_by_post_mid(post, mid) # 由后序序列、中序序列构造⼆叉树T.pre_order_recursive(newT_post_mid) # 获取前序序列 测试⽤的两个⼆叉树:。
java实现二叉树的创建及5种遍历方法(总结)

java实现⼆叉树的创建及5种遍历⽅法(总结)⽤java实现的数组创建⼆叉树以及递归先序遍历,递归中序遍历,递归后序遍历,⾮递归前序遍历,⾮递归中序遍历,⾮递归后序遍历,深度优先遍历,⼴度优先遍历8种遍历⽅式:package myTest;import java.util.ArrayList;import java.util.LinkedList;import java.util.List;import java.util.Stack;public class myClass {public static void main(String[] args) {// TODO Auto-generated method stubmyClass tree = new myClass();int[] datas = new int[]{1,2,3,4,5,6,7,8,9};List<Node> nodelist = new LinkedList<>();tree.creatBinaryTree(datas, nodelist);Node root = nodelist.get(0);System.out.println("递归先序遍历:");tree.preOrderTraversal(root);System.out.println();System.out.println("⾮递归先序遍历:");tree.preOrderTraversalbyLoop(root);System.out.println();System.out.println("递归中序遍历:");tree.inOrderTraversal(root);System.out.println();System.out.println("⾮递归中序遍历:");tree.inOrderTraversalbyLoop(root);System.out.println();System.out.println("递归后序遍历:");tree.postOrderTraversal(root);System.out.println();System.out.println("⾮递归后序遍历:");tree.postOrderTraversalbyLoop(root);System.out.println();System.out.println("⼴度优先遍历:");tree.bfs(root);System.out.println();System.out.println("深度优先遍历:");List<List<Integer>> rst = new ArrayList<>();List<Integer> list = new ArrayList<>();tree.dfs(root,rst,list);System.out.println(rst);}/**** @param datas 实现⼆叉树各节点值的数组* @param nodelist ⼆叉树list*/private void creatBinaryTree(int[] datas,List<Node> nodelist){//将数组变成node节点for(int nodeindex=0;nodeindex<datas.length;nodeindex++){Node node = new Node(datas[nodeindex]);nodelist.add(node);}//给所有⽗节点设定⼦节点for(int index=0;index<nodelist.size()/2-1;index++){//编号为n的节点他的左⼦节点编号为2*n 右⼦节点编号为2*n+1 但是因为list从0开始编号,所以还要+1//这⾥⽗节点有1(2,3),2(4,5),3(6,7),4(8,9)但是最后⼀个⽗节点有可能没有右⼦节点需要单独处理nodelist.get(index).setLeft(nodelist.get(index*2+1));nodelist.get(index).setRight(nodelist.get(index*2+2));}//单独处理最后⼀个⽗节点因为它有可能没有右⼦节点int index = nodelist.size()/2-1;nodelist.get(index).setLeft(nodelist.get(index*2+1)); //先设置左⼦节点if(nodelist.size() % 2 == 1){ //如果有奇数个节点,最后⼀个⽗节点才有右⼦节点nodelist.get(index).setRight(nodelist.get(index*2+2));}}/*** 遍历当前节点的值* @param nodelist* @param node*/public void checkCurrentNode(Node node){System.out.print(node.getVar()+" ");}/*** 先序遍历⼆叉树* @param root ⼆叉树根节点*/public void preOrderTraversal(Node node){if (node == null) //很重要,必须加上当遇到叶⼦节点⽤来停⽌向下遍历return;checkCurrentNode(node);preOrderTraversal(node.getLeft());preOrderTraversal(node.getRight());}/*** 中序遍历⼆叉树* @param root 根节点*/public void inOrderTraversal(Node node){if (node == null) //很重要,必须加上return;inOrderTraversal(node.getLeft());checkCurrentNode(node);inOrderTraversal(node.getRight());}/*** 后序遍历⼆叉树* @param root 根节点*/public void postOrderTraversal(Node node){if (node == null) //很重要,必须加上return;postOrderTraversal(node.getLeft());postOrderTraversal(node.getRight());checkCurrentNode(node);}/*** ⾮递归前序遍历* @param node*/public void preOrderTraversalbyLoop(Node node){Stack<Node> stack = new Stack();Node p = node;while(p!=null || !stack.isEmpty()){while(p!=null){ //当p不为空时,就读取p的值,并不断更新p为其左⼦节点,即不断读取左⼦节点 checkCurrentNode(p);stack.push(p); //将p⼊栈p = p.getLeft();}if(!stack.isEmpty()){p = stack.pop();p = p.getRight();}}}/*** ⾮递归中序遍历* @param node*/public void inOrderTraversalbyLoop(Node node){Stack<Node> stack = new Stack();Node p = node;while(p!=null || !stack.isEmpty()){while(p!=null){stack.push(p);p = p.getLeft();}if(!stack.isEmpty()){p = stack.pop();checkCurrentNode(p);p = p.getRight();}}}/*** ⾮递归后序遍历* @param node*/public void postOrderTraversalbyLoop(Node node){Stack<Node> stack = new Stack<>();Node p = node,prev = node;while(p!=null || !stack.isEmpty()){while(p!=null){stack.push(p);p = p.getLeft();}if(!stack.isEmpty()){Node temp = stack.peek().getRight();if(temp == null||temp == prev){p = stack.pop();checkCurrentNode(p);prev = p;p = null;}else{p = temp;}}}}/*** ⼴度优先遍历(从上到下遍历⼆叉树)* @param root*/public void bfs(Node root){if(root == null) return;LinkedList<Node> queue = new LinkedList<Node>();queue.offer(root); //⾸先将根节点存⼊队列//当队列⾥有值时,每次取出队⾸的node打印,打印之后判断node是否有⼦节点,若有,则将⼦节点加⼊队列 while(queue.size() > 0){Node node = queue.peek();queue.poll(); //取出队⾸元素并打印System.out.print(node.var+" ");if(node.left != null){ //如果有左⼦节点,则将其存⼊队列queue.offer(node.left);}if(node.right != null){ //如果有右⼦节点,则将其存⼊队列queue.offer(node.right);}}}/*** 深度优先遍历* @param node* @param rst* @param list*/public void dfs(Node node,List<List<Integer>> rst,List<Integer> list){if(node == null) return;if(node.left == null && node.right == null){list.add(node.var);/* 这⾥将list存⼊rst中时,不能直接将list存⼊,⽽是通过新建⼀个list来实现,* 因为如果直接⽤list的话,后⾯remove的时候也会将其最后⼀个存的节点删掉*/rst.add(new ArrayList<>(list));list.remove(list.size()-1);}list.add(node.var);dfs(node.left,rst,list);dfs(node.right,rst,list);list.remove(list.size()-1);}/*** 节点类* var 节点值* left 节点左⼦节点* right 右⼦节点*/class Node{int var;Node left;Node right;public Node(int var){this.var = var;this.left = null;this.right = null;}public void setLeft(Node left) {this.left = left;}public void setRight(Node right) {this.right = right;}public int getVar() {return var;}public void setVar(int var) {this.var = var;}public Node getLeft() {return left;}public Node getRight() {return right;}}}运⾏结果:递归先序遍历:1 2 4 8 9 5 3 6 7⾮递归先序遍历:1 2 4 8 9 5 3 6 7递归中序遍历:8 4 9 2 5 1 6 3 7⾮递归中序遍历:8 4 9 2 5 1 6 3 7递归后序遍历:8 9 4 5 2 6 7 3 1⾮递归后序遍历:8 9 4 5 2 6 7 3 1⼴度优先遍历:1 2 3 4 5 6 7 8 9深度优先遍历:[[1, 2, 4, 8], [1, 2, 4, 9], [1, 2, 5], [1, 3, 6], [1, 3, 7]]以上这篇java实现⼆叉树的创建及5种遍历⽅法(总结)就是⼩编分享给⼤家的全部内容了,希望能给⼤家⼀个参考,也希望⼤家多多⽀持。
二叉树、前序遍历、中序遍历、后序遍历

⼆叉树、前序遍历、中序遍历、后序遍历⼀、树在谈⼆叉树前先谈下树和图的概念树:不包含回路的连通⽆向图(树是⼀种简单的⾮线性结构)树有着不包含回路这个特点,所以树就被赋予了很多特性1、⼀棵树中任意两个结点有且仅有唯⼀的⼀条路径连通2、⼀棵树如果有n个结点,那它⼀定恰好有n-1条边3、在⼀棵树中加⼀条边将会构成⼀个回路4、树中有且仅有⼀个没有前驱的结点称为根结点在对树进⾏讨论的时候将树中的每个点称为结点,根结点:没有⽗结点的结点叶结点:没有⼦结点的结点内部结点:⼀个结点既不是根结点也不是叶结点每个结点还有深度,⽐如上图左边的树的4号结点深度是3(深度是指从根结点到这个结点的层数,根结点为第⼀层)⼆、⼆叉树基本概念:⼆叉树是⼀种⾮线性结构,⼆叉树是递归定义的,其结点有左右⼦树之分⼆叉树的存储结构:⼆叉树通常采⽤链式存储结构,存储结点由数据域和指针域(指针域:左指针域和右指针域)组成,⼆叉树的链式存储结构也称为⼆叉链表,对满⼆叉树和完全⼆叉树可按层次进⾏顺序存储特点:1、每个结点最多有两颗⼦树2、左⼦树和右⼦树是有顺序的,次序不能颠倒3、即使某结点只有⼀个⼦树,也要区分左右⼦树4、⼆叉树可为空,空的⼆叉树没有结点,⾮空⼆叉树有且仅有⼀个根节点⼆叉树中有两种特殊的⼆叉树:满⼆叉树、完全⼆叉树满⼆叉树:⼆叉树中每个内部结点都有存在左⼦树和右⼦树(或者说满⼆叉树所有的叶结点都有同样的深度)满⼆叉树⼀定是完全⼆叉树,但完全⼆叉树不⼀定是满⼆叉树(满⼆叉树的严格的定义是:⼀颗深度为h且有2h-1个结点的⼆叉树)(图⽚来源:https:///polly333/p/4740355.html)完全⼆叉树:第⼀种解释:如果⼀颗⼆叉树除最右边位置上有⼀个或⼏个叶结点缺少外,其他是丰满的那么这样的⼆叉树就是完全⼆叉树(这句话不太好理解),看下⾯第⼆种解释第⼆种解释:除第h层外,其他各层(1到h-1)的结点数都达到最⼤个数,第h层从右向左连续缺若⼲结点,则这个⼆叉树就是完全⼆叉树也就是说如果⼀个结点有右⼦结点,那么它⼀定也有左⼦结点第三种解释:除最后⼀层外,每⼀层上的节点数均达到最⼤值,在最后⼀层上只缺少右边的若⼲结点完全⼆叉树的形状类似于下图为了⽅便理解请看下图(个⼈理解:完全⼆叉树就是从上往下填结点,从左往右填,填满了⼀层再填下⼀层)(图⽚来源:)⼆叉树相关词语解释:结点的度:结点拥有的⼦树的数⽬叶⼦结点:度为0的结点(tips:在任意⼀个⼆叉树中,度为0的叶⼦结点总是⽐度为2的结点多⼀个)分⽀结点:度不为0的结点树的度:树中结点的最⼤的度层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1树的⾼度:树中结点的最⼤层次⼆叉树基本性质:性质1:在⼆叉树的第k层上⾄多有2k-1个结点(k>=1)性质2:在深度为m的⼆叉树⾄多有2m-1个结点性质3:对任意⼀颗⼆叉树,度为0的结点(即叶⼦结点)总是⽐度为2的结点多⼀个性质4:具有n个结点的完全⼆叉树的深度⾄少为[log2n]+1,其中[log2n]表⽰log2n的整数部分存储⽅式存储的⽅式和图⼀样,有链表和数组两种,⽤数组存访问速度快,但插⼊、删除节点操作就⽐较费时了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
// 节点名
int n_children;
// 子节点个数
int level;
// 记录该节点在多叉树中的层数
struct node_t** children; // 指向其自身的子节点,children一个数组,该数组中的元素时node_t*指针
} NODE; // 对结构体重命名
// 实现一个栈,用于后续操作 typedef struct stack_t {
if (sp == NULL || sp->index >= sp->size) // sp没有被初始化,或者已满 {
return 0; // 压栈失败 }
sp->array[sp->index++] = data; // 压栈 return 1; }
// 弹栈操作 int STACKpop(STACK* sp, NODE** data_ptr) {
return sp; }
// 检测栈是否为空 // 如果为空返回1,否则返回0 int STACKempty(STACK* sp) {
if (sp == NULL || sp->index <= 0) // 空 {
return 1; } return 0; }
// 压栈操作 int STACKpush(STACK* sp, NODE* data) {
return qp; }
// 入队列 int QUEUEenqueue(QUEUE* qp, NODE* data) {
if (qp == NULL || qp->num >= qp->size) // qp未初始化或已满 {
return 0; // 入队失败 }
qp->array[qp->tail] = data; // 入队,tail一直指向最后一个元素的下一个位置 qp->tail = (qp->tail + 1) % (qp->size); // 循环队列 ++qp->num; return 1;
NODE** array; // array是个数组,其元素为NODE*型指针 int index; // 指示栈顶元素 int size; // 栈的大小 } STACK; // 重命名
// 实现一个队列,用于后续操作 typedef struct queue_t {
NODE** array; // array是个数组,其内部元素为NODE*型指针 int head; // 队列的头 int tail; // 队列的尾 int num; // 队列中元素的个数 int size; // 队列的大小 } QUEUE;
NODE* temp = NULL; int i = 0;
if (head != NULL) {
if (strcmp(name, head->name) == 0) // 如果名字匹配 {
temp = head; } else // 如果不匹配,则查找其子节点 {
for (i = 0; i < head->n_children && temp == NULL/*如果temp不为空,则结束查找*/; ++i)
// 实现一些栈操作
// 栈的初始化 STACK* STACKinit(int size) // 初始化栈大小为size {
STACK* sp;
sp = (STACK*)util_malloc(sizeof (STACK)); sp->size = size; sp->index = 0; sp->array = (NODE**)util_malloc(size * sizeof (NODE*));
if (sp == NULL || sp->index <= 0) // sp为初始化,或者为空没有元素 {
return 0; }
*data_ptr = sp->array[--sp->index]; // 弹栈 return 1; }
// 将栈消毁 void STACKdestroy(STACK* sp) {
// 生成多叉树节点 NODE* create_node() {
NODE* q;
q = (NODE*)util_malloc(sizeof (NODE));
q->n_children = 0;
q->level
= -1;
q->children = NULL;
return q; }
// 按节点名字查找 NODE* search_node_r(char name[M], NODE* head) {
return 1; }
// 检测队列是否为空 int QUEUEempty(QUEUE* qp) {
if (qp == NULL || qp->num <= 0) {
return 1; }
return 0; }
// 销毁队列 void QUEUEdestroy(QUEUE* qp) {
free(qp->array); free(qp); } // 以上是队列的有关操作实现
}
// 出队列 int QUEUEdequeue(QUEUE* qp, NODE** data_ptr) {
if (qp == NULL || qp->num <= 0) // qp未初始化或队列内无元素 {
return 0; }
*data_ptr = qp->array[qp->head]; // 出队 qp->head = (qp->head + 1) % (qp->size); // 循环队列 --qp->num;
// 多叉树的建立、层次遍历、深度遍历 #include <stdio.h> #include <stdlib.h> #include <string.h>
#define M 100+1 // 宏定义,定义最大名字字母长度
// 定义多叉树的节点结构体
typedef struct node_t
{
char* name;
// 这里的栈和队列,都是用动态数组实现的,另一种实现方式是用链表
// 内存分配函数 void* util_malloc(int size) {
void* ptr = malloc(size);
if (ptr == NULL) // 如果分配失败,则终止程序 {
printf("Mem;); exit(EXIT_FAILURE); }
FILE* fp = fopen(name, access);
if (fp == NULL) // 如果打开文件失败,终止程序 {
printf("Error opening file %s!\n", name); exit(EXIT_FAILURE); }
// 打开成功,返回 return fp; }
free(sp->array); free(sp); } // 以上是栈的操作
// 实现队列的操作 QUEUE* QUEUEinit(int size) {
QUEUE* qp;
qp = (QUEUE*)util_malloc(sizeof (QUEUE)); qp->size = size; qp->head = qp->tail = qp->num = 0; qp->array = (NODE**)util_malloc(size * sizeof (NODE*));
// 分配成功,则返回 return ptr; }
// 字符串赋值函数 // 对strdup函数的封装,strdup函数直接进行字符串赋值,不用对被赋值指针分配空间 // 比strcpy用起来方便,但其不是标准库里面的函数 // 用strdup函数赋值的指针,在最后也是需要free掉的 char* util_strdup(char* src) {
char* dst = strdup(src);
if (dst == NULL) // 如果赋值失败,则终止程序 {
printf ("Memroy allocation error!\n"); exit(EXIT_FAILURE); }
// 赋值成功,返回 return dst; }
// 对fopen函数封装 FILE* util_fopen(char* name, char* access) {
本文我们将还是介绍一个多叉树,其内容和之前的实现差不多。 首先,用户的多叉树数据存储在一个文件中,格式如下:
每行的第一个元素指定一个节点,其中第一行指定了该多叉树的根节点。第二个元素表示该节点有 几个子节点,紧接着后面跟了几个子节点。
根据以上数据文件,其对应的多叉树应该是如下:
我们想得到结果是将书中的节点按深度进行输出,比如先输出深度最深的节点:x e j,然后输出深 度为2的节点:d f i,之后再输出深度为1的节点:g cC z bBbB,最后输出根节点:aA。
按照深度将节点输出,很显然是用层次优先遍历的方法解决。层次优先遍历的实现原理就是从根节 点开始,利用队列实现。
另外,我们想得到从根节点开始到叶子节点直接所有节点名字加起来最长的一个路径,比如上面的 树中存在以下几条路径:
aA g d x aA g d e aA g d j aA cC
aA z f aA z i aA bBbB 显然,在这些路径中,aA bBbB是所有路径上节点名字加起来最长的一个路径。求解从根节点到叶子 节点上的所有路径,利用深度优先遍历更为合适。 下面我们讨论一下多叉树节点应该如何建立。首先多叉树的节点应该如何定义,节点除了有自身的 名字外,还要记录其子节点有多少个,每个子节点在哪里,所以我们需要增加一个记录子节点个数的域, 还要增加一个数组,用来记录子节点的指针。另外,还要记录多叉树中每个节点的深度值。 在读取数据文件的过程中,我们顺序扫描整个文件,根据第一个名字,建立新的节点,或者从多叉 树中找到已经有的节点地址,将后续的子节点生成,并归属于该父节点,直至扫描完整个数据文件。 读取完整个文件后,也就建立了多叉树,之后,我们利用队列对多叉树进行广度优先遍历,记录各 个节点的深度值。并将其按照深度进行输出。 获取从根节点到子节点路径上所有节点名字最长的路径,我们利用深度优先遍历,递归调用深度优 先遍历函数,找到最长的那个路径。 初次之外,还需定义队列结构体,这里使用的队列是循环队列,实现相关的队列操作函数。还有定 义栈的结构体,实现栈的相关操作函数。另外对几个内存分配函数、字符串拷贝函数、文件打开函数进行 了封装。需要注意的一点就是当操作完成后,需要对已经建立的任何东西都要销毁掉,比如中途建立的队 列、栈、多叉树等,其中还包含各个结构体中的指针域。 另外,函数测试是用户在命令行模式下输入程序名字后面紧跟数据文件的形式。 该程序的主要部分有如下几点: 1.多叉树节点的定义和生成一个新节点 2.数据文件的读取以及多叉树的建立 3.根据节点名字在多叉树中查找节点的位置 4.多叉树的层次优先遍历 5.多叉树的深度优先遍历 6.队列的定义以及相关操作函数实现 7.栈的定义以及相关操作函数实现 8.消毁相关已经建立好的队列、栈、多叉树等 9.测试模块 下面我们给出相关的程序实现,具体细节可以查看代码和注释说明。
