加法器ppt课件

合集下载

数字逻辑第三章加法器.ppt

四位二进制并行加法器
三、四位二进制并加法器的外部特性和逻辑符号 1．外部特性
图中，A4、A3、A2、A1 ------- 二进制被加数； B4、B3、 B2、B1 ------- 二进制加数； F4、 F3、 F2、 F1 ------相加产生的和数； C0 --------------------来自低位的进位输入； FC4 -------------------向高位的进位输出。
a3b1
+) 乘积 Z5 a3b2 Z4 a2b2 Z3
a2b1
a1b2 Z2
a1b1
Z1
因为： ☆1位二进制数乘法法则和逻辑“与”运算法则相同，“积”项aibj(i =1，2，3；j=1，2)可用两输入与门实现。 ☆对部分积求和可用并行加法器实现。所以：该乘法运算电路可由6个两输入与门和1 b2 个4位二进制并行加法器构成。逻辑电路图如右图所示。
四位二进制并行加法器
实现给定功能的逻辑电路图如下图所示。 1) 输入端A4、A3、A2、 A1输入8421码；
2) 而从另一输入端B4、 B3、B2、B1输入二进制数0011； 3) 进位输入端C0接上“0”；
4) 可从输出端F4、F3、F2、 F1得到与输入8421码对
应的余3码。
四位二进制并行加法器
Z5 Z4 Z3 Z 2 Z1
F4 F3 F2 F 1 FC4 T 693 C0
0
A4 A3 A2 A1
B4 B 3 B2 B1
＆
＆
＆
＆
＆
＆
b1
a3
a2
a1 0 a 3
a2
a1
FA4
F3 C3
FA3
F2

第4章应用VHDL语言方法设计八位二进制加法器《EDA技术》PPT 教学课件

五、检查
对所设计的八位二进制加法器的各个底层模块和顶层模块进行编译仿真，以验证所设计电路否符合设计的要求。
上一页下一页
§2 完成工作任务的引导
六、评估
应用第一种方案设计八位二进制加法器在编译后，可以看到它的延时情况，如图4-1所示。
第一种设计方案占用资源的情况如图4-2所示。应用第一种方案设计八位二进制加法器在编译后，可以看到它的延时情况，如图4-3所示。第一种设计方案占用资源的情况如图4-4所示。所以，无论从输出信号对输入信号的延迟时间或占用资源的情况来看，第一种方案性能都好一些。
返回
§4.2 完成工作任务的引导
第三种方案在设计上不是很简单，但性能好，在加法器的位数比较大时应采用此法。可在学习第5章时再做练习。
四、实施
在应用第一种方案设计时，请参考下一节例4.1或例4.2。先设计底层模块全加器，再在顶层文件中调用全加器元件，构成八位二进制加法器。在应用第一种方案设计时，请参考下一节例4.3。
上一页下一页
§4.3 相关技术基础知识与基本技能
对于弹出的选择其他EDA工具的对话框，由于我们使用 Quartus且的集成环境进行开发，因此不需做任何改动。单击Next 按钮进入如图4-11所示工程的信息总概对话框。
在图4-11中单击Finish按钮就建立了一个空的工程项目。 2.建立VHDL文件
如图4-12所示，执行File=>New命令，弹出如图4-13所示的新建文件对话框。
在新建文件对话框中选择“VHDL File”，单击OK按钮即建立一个空的文件。执行File=>SaVe as命令，把它另存为文件名是 fulladd 的 VHDL文件，文件后缀为.vhd。
上一页下一页

定点加法减法运算(共10张PPT)

[例11] ｘ＝＋0.1101,ｙ＝＋0.0110,求ｘ－ｙ。
[解:] [ｘ]补＝0.1101 [ｙ]补＝0.0110,
[ｘ]补
0.1101
＋[－ｙ]补
1.1010
[ｘ－ｙ]补 10.0111
所以ｘ－ｙ＝＋0.0111
[－ｙ]补＝1.1010
在定点小数机器中,数的表示范围为|ｘ|<1. 在运算过程中如出现大
数用补码表示时,减法运算的公式为
[ｘ－ｙ]补＝[ｘ]补－[ｙ]补＝[ｘ]补＋[－ｙ]补 (2.18)
只要证明[－ｙ]补＝－[ｙ]补,上式即得证。现证明如下：
∵
[ｘ＋ｙ]补＝[ｘ]补＋[ｙ]补
(mod 2)
∴
[ｙ]补＝[ｘ＋ｙ]补－[ｘ]补
(2.19a)
又∵
[ｘ－ｙ]补＝[ｘ＋(－ｙ)]补＝[ｘ]补＋[－ｙ]补
对[ｙ]补包括符号位“求反且最末位加1”,即可得到[－ｙ]补。写成运算表
达式，则为 [－ｙ]补＝﹁[ｙ]补＋2－n
(2.21)
[例10]
已知ｘ1＝－0.1110,ｘ2＝＋0.1101, 求：[ｘ1]补,[－ｘ1]补,[ｘ2]补,[－ｘ2]补。 [解:]
[ｘ1]补＝1.0010
[－ｘ1]补＝﹁[ｘ1]补＋2-4＝0.1101＋0.0001＝0.1110 [ｘ2]补＝0.1101 [－ｘ2]补＝﹁[ｘ2]补＋2-4＝1.0010＋0.0001＝1.0011
又因(ｘ＋ｙ)<0, 所以 0110, [－ｙ]补＝1.
大一倍。变形补码定义为么(2＋ｘ＋ｙ)就一定是小于2而大于1的数,进位”2”必丢失. x 2＞ｘ≥0 数用补码表示时,减法运算的公式为
故溢出逻辑表达式为V＝Cf ⊕Co,其中Cf为符号位产生的进位,Co为最高有效位产生的进位。

第2章加法器

3.5 定点运算器的组成 1）定点运算器的基本结构 • 不同的计算机其运算器的组成结构是不同的，但一般都包含以下几部分。 1．算术逻辑运算单元ALU • 在计算机中，通常具体实现算术运算和逻辑运算的部件称为算术逻辑运算单元（Arithmetic and Logic Unit），简称ALU，它是加法器、乘法器和逻辑运算器的集成，是运算器的核心。ALU通常表示为两个输入端，一个输出端和多个功能控制信号端的一个逻辑符号。加法器是ALU的核心，是决定 ALU运算速度的主要因素。
第2 章加法器
• 计算机要对各种信息进行加工和处理。 • 如对数值数据进行加、减、乘、除的数值运算，对非数值数据进行与、或、非的逻辑运算。 • 在计算机中必须有对数据进行处理的部件，这个部件就是运算器。 • 目前，大多数计算机都将运算器和控制器集成在一个芯片上，也就是我们常说的CPU。
二进制加法器 1.半加器 • 两个一位二进制数相加（不考虑低位的进位），称为半加。实现半加操作的电路称为半加器。 • 半加器的真值表、逻辑图和逻辑符号。 2.全加器 • 在实现多位二进制数相加时，不仅考虑本位，还要考虑低位来的进位，这种考虑低位的进位加法运算就是全加运算， • 实现全加运算的电路称为全加器。
A8 A7A6A5 B8B7B6B5
A4 A3A2A1B4B3B2B1
16位行波进位加法器
• 在这种结构中，由于组间进位C4、C8、 C12、C16仍然是串行产生的，最高进位的产生时间为4×（2.5ty）=10ty。 • 采用这种结构，在大大地缩短了进位延迟时间的同时兼顾了电路设计的复杂性。 • 如果还需要进一步提高速度，可以采用两级先行进位结构。
• 4）附加的控制线路运算器要求运算速度快，运算精度高。为了达到这一目的，通常还在运算器中附加一些控制线路。 i -i • 如：运算器中的乘2 或乘2 运算和某些逻辑运算是通过移位操作来实现的。这通常是在ALU的输出端设置移位线路来实现。移位包括左移，右移和直送。移位线路也是一个多路选择器。 • 定点运算器的组成

组合逻辑电路(加法器)

Ci m3 m5 Ai Bi ( Ai Bi )Ci 1 Ai Bi
全加器的逻辑图和逻辑符号
Si m1 m2 m4 m7 Ai BiCi 1 Ai BiCi 1 Ai BiCi 1 Ai BiCi 1 Ai ( BiCi 1 BiCi 1 ) Ai ( BiCi 1 BiCi 1 ) Ai ( Bi Ci 1 ) Ai ( Bi Ci 1 ) Ai Bi Ci 1
加法器
半加器和全加器
1、半加器
能对两个1位二进制数进行相加而求得和及进位的逻辑电路称为半加器.
半加器真值表 Ai Bi 0 1 0 1 Si 0 1 1 0 Ci 0 0 0 1
本位的和向高位的进位
Ai Bi
=1
Si Ci
加数
0 0 1 1
&
半加器电路图 Ai Bi ∑
CO
Si Ci
Si Ai Bi Ai Bi Ai Bi Ci Ai Bi
0
0
1
1
被加数/被减数
加数/减数
加减控制
BCD码+0011=余3码
C0-1＝0时，B0=B，电路执行A+B运算；当C0-1＝1 时，B1=B，电路执行A －B=A+B运算。
3、二-十进制加法器
修正条件 C C3 S3S2 S3S1
8421 BCD 输出 S3 ' S2 ' S1 ' S0' 4 位二进制加法器 C0-1 A1 A0 B3 B2 B1 B0
4位超前进位加法器递推公式
S 2 P2 C1 1G0 P 2P 1P 0C0 1 C2 G2 P2C1 G2 P2G1 P2 P S3 P3 C2 1G0 P 3P 2P 1P 0C0 1 C3 G3 P3C2 G3 P3G2 P3 P2G1 P3 P2 P

十进制加法器(8421余3码)-PPT课件

不校正
+6校正
校正举例
0101 + 1000 1101 + 0110 1 0011 5 8 6 13
1001 + 1000 1 0001 + 0110 1 0111
9 8
6 17
2.余3码加法运算余3 ⑴两个十进制数的余3码相加，按 “逢二进一” ⑵若其和没有进位，则减3（即+1101） ⑶若其和有进位，则加3（即+0011）校正。
一位余3码加法器
A4B4 C4
1
A3 B3 FA S3'
A2 B2 FA S2'
A1 B1 FA S1'
C0
FA C4' S4'
FA 忽略 S4
FA S3
FA S2
Fig. 一位余3码加法器
1
S1
三、多位十进制法
对于多位十进制数加法可采用多个 BCD 码加法器，每个 BCD 码加法器就是前述的一个一位十进制加法器，可执行两个一位BCD数的加法。若n位BCD数相加，由从低位至高位采用行波式串行进位的n 位十进制加法器完成。
余3码的校正关系
十进制数
0 1 ｜ 8 9
余3码 C4S4S3S2S1
0 0011 0 0100 ｜ 0 1011 0 1100
校正前的二进制数 C4’S4’S3’S2’S1’
0 0110 0 0111 ｜ 0 1110 0 1111
校正与否
-3校正
10 11 ｜ 18 19
1 0011 1 0100 ｜ 1 1011 1 1100
1 0000 1 0001 ｜ 1 1000 1 1001
+3校正

组合逻辑电路—加法器(电子技术课件)

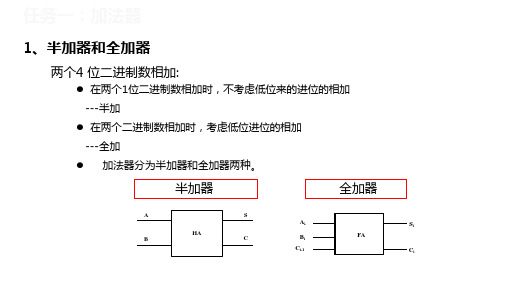
例. 用74283构成将8421BCD码转换为余3码的码制转换电路。
8421码
0000 0001 0010
+0011 +0011 +0011
余3码
0011 0100 0101
8421码输入 0011
A3 A2 A1 A0 B3 B2 B1 B0
CCO
O
S3
74283 S2 S1 S0
C–1 0
余3码输出
A B Ci Co AB + ABCi + ABCi
AB + (A B)Ci
A
A B A B Ci S
B
AB CO
CO ( A B)Ci
Ci
≥1 Co
A S B Ci C I C O CO
任务一：加法器
加法器的应用
全加器真值表
AB C SC 0 0 00 0 0 0 11 0 0 1 01 0 0 1 101 1 0 01 0 1 0 10 1 1 1 00 1 1 1 11 1
➢ 不考虑低位进位，将两个1位二进制数A、B相加的器件。
• 半加器的真值表 • 逻辑表达式
S AB+ AB C = AB
如用与非门实现最少要几个门?
A
半加器的真值表
=1
S
A
B
BA
B
S
C
0000
1010
& C=AB
0110
1101
• 逻辑图
任务一：加法器
（2）全加器（Full Adder）
全加器能进行加数、被加数和低位来的进位信号相加，并根据求和结果给出
余 3 码输出
A3 B3 A2 B2 A1 B1 A0 B0

加法器(Adder) 数电课件

2. 分析
半加器有两个输入：加数、被加数Ai ；两个输出：B和i 输出、进位输出。
Si
Ci
3. 真值表
半加器的真值表如表4.2.1—1所示。
表4.2.1—1
4. 逻辑函数表达式
半加器的逻辑函数表达式为
Si Ai Bi Ai Bi Ai Bi Ci Ai Bi
5. 逻辑电路图
定
。
An1 An、2 L A2 A1 A0 Cn1Cn2 L C2C1C0
B和n1Bn给2出L，B便2可B1以B直0 接C确01
方法二
C0 P0C01 G0
C1 P1C0 G1
P1 P0C01 G0 G1
C2 P2C1 G2
P2 P1 P0C01 G0 G1 G2
图4.2.5—3 Ⅰ. 加减控制输入为0时，该电路实现加法运算； Ⅱ. 加减控制输入为1时，该电路实现减法运算（补码加法）。
返回
半加器的逻辑函数表达式为
Si Ai Bi Ai Bi Ai Bi Ci Ai Bi
5. 逻辑电路图
半加器的逻辑电路图如图4.2.1—1所示。
（公式4.2.1）（公式4.2.2）
图4.2.1—1
6. 逻辑符号
半加器的逻辑符号如图4.2.1—2所示。
图4.2.1—2
二、全加器（Full Adder）
依次递推可知，只要
定
。
An1 An、2 L A2 A1 A0 Cn1Cn2 L C2C1C0
B和n1Bn给2出L，B便2可B1以B直0 接C确01
四位超前进位加法器的逻辑电路图如图4.2.3—2所示。图4.2.3—2
四、中规模集成加法器

数字逻辑课件——加法器

31
综上所述，接法如图3-3-23(b)所示。与方法1比较，多用了一个与非门，却省去两个“四选一” 选择器。“选择输入”端A1，A0，可接C，D，也可接A，B或A，C或B，D或A，D或B，C，相应的卡诺图略加变动，所得的D0，D1， D2， D3的表达式各不相同。经过各种方案的比较，可得最佳的简化结构。
例3-6 用74153实现逻辑函数Z F (A, B) m(1, 3)
解：由最小项表达式得该函数的真值表，如表 3-3-12所示，用半片74153即可实现该逻辑函数，接法如图3-3-20。
输入变量A，B分别送选择输入端A1，A0选通输入，ST 应接0，数据输入D0，D1，D2，D3根据真值表分别接0，1，0，1。这样，74153的输出端Y 即逻辑函数Z。
逻辑图可以看出，数据输出Y 的逻辑表达式为
Y ST[D0 ( A1 A0 ) D1( A1 A0 ) D2 ( A1 A0 ) D3 ( A1 A0 )]
即当选通输入 ST 0 时，若将选择输入A1，
A0分别为00，01，10，11则相应地把D0，D1，
D2，D3送到数据输出端Y去，当
图3-3-21 例3-7图
25
①B当C BC =00时，Z = D0 ；由卡诺图可见，Z 此时不②不A管管当01 AAB0000等等C 于于=01110001或或时111011，，，Z1ZZ001 =都都D等等1 于于；01由，，卡因因B0C 诺此此图以以S可AAT0110 输输见D012入入，7DY411DD此53D012。。时D3
从图3-3-22可以发现，下层的片0和片3，输出分别恒为0和1，故可省去片0和片3，同时，片4的D0和D3分别改接0和1。因此，在用74153实现逻辑函数时，必须根据具体情况考虑简化结构的可能性。

4.3 加法器解析

功能：实现两个四位二进制数相加。特点：电路结构简单，但运算速度慢。
2.超前进位加法器
第四章组合逻辑电路
通过逻辑电路事先得出每一位全加器的进位输入信号。 C3
超前进位电路
A3 B3 A2 B2 A1 B1 A0 B0 C0-1
CI
Σ
S3 S2 S1 S0
CI Σ
Σ CI
CI Σ
超前进位电路图
特点：运算速度快，电路比较复杂。
S i Ai Bi Ci 1 Ai Bi Ci 1 Ai Bi Ci 1 Ai Bi Ci 1
( Ai Bi )Ci 1 ( Ai Bi )Ci 1 Ai Bi Ci 1
Ci Ai Bi Ci 1 Ai Bi Ci 1 Ai Bi Ci 1 Ai Bi Ci 1
第四章组合逻辑电路
4.3 加法器
• 定义
能够实现二进制加法运算的逻辑电路称为加法器。
• 分类
加法器一位加法器
多位加法器
半加器全加器
第四章组合逻辑电路
4.3.1 半加器和全加器
• 定义半加器：只能进行本位加数、被加数的加法运算而不考虑相邻低位进位的逻辑部件。全加器：能同时进行本位加数、被加数和相邻低位的进位信号的加法运算的逻辑部件。
4.多位加法器的应用举例
例4.3.1 设计一个代码转换电路，将8421BCD码转换为余3码，用74HC283实现。解：（1）依据逻辑功能，确定输入、输出变量输入变量：8421BCD码DCBA 输出变量：余3码Y3Y2Y1Y0
第四章组合逻辑电路
（2）真值表
例4.3.1的逻辑真值表输入8421BCD码输出余3码
Ai Bi ( Ai Bi )Ci-1

逻辑电路设计加法器64页PPT

▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
64
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
逻辑电路设计加法器
1、合法而稳定的权力在使用得当时很少遇到抵抗。 ——塞 ·约翰逊 2、权力会使人渐渐失去温厚善良的美德。— —伯克
3、最大限度地行使权力总是令人反感；权力不易确定之处始终存在着危险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊，可是金子可以拉着它的鼻子走。— —莎士比

multisim仿真教程.加法器.ppt

2. 全加器真值表如表8.5.1所示
表8.5.1全加器真值表
3. 全加器逻辑表达式:
S CO ( A B)
C CO ( A B) AB
4. 全加器逻辑电路
8.5.2 全加器电路
电路仿真，双击逻辑转换仪图标, 如图8.5.3 逻辑转换仪面板。逻辑转换仪的使用方法请看 1.5节中的1.5.9小节（逻辑转换仪）。图中测出的是和S的结果，若要测出向高位进位的结果，
半加器。
按照二进制加法运算规则可以列出如表
8.5.1所示的半加器真值表。其中A、B是两个加数，
s是相加的和，CO是向高位的进位。将S、CO和A、 B的关系写成逻辑表达式则得到.
S A B AB A B
C AB
8.5.1半加器真值表
因此半加器是由一个异或门和一个与
门组成的，如图8.5.1所示。
实际又是种最本的制算术算器件实际的加法运算必须同时考虑由低位来的进位这种由被加数加数和一个来自低位的进位数三者相加的运算称为全加运算
8.5. 加法器
两个二进制数之间的算术运算无论是加、减、乘、除，目前在数字计算机中都是化做若干步加法运算进行的。因此，加法器是构成算术运算器的基本单元。
8.5.1 半加器如果不考虑有来自低位的进位将两个1位二进制数相加，称为半加。实现半加运算的电路叫做
8.5.2 全加器
全加器是一种广义名称．就其电路结构而言，
它是一种二进制运算的单元电路。从器件角度看，
它又是一种最基本的二进制算术运算器件。实际
的加法运算，必须同时考虑由低位来的进位，这种由被加数、加数和一个来自低位的进位数三者
相加的运算称为全加运算。执行这种运算的器件
称为全加器。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A
0 0 1 1
B
0 1 0 1
S
0 1 1 0
C
0 0 0 1
思考：如何在只能用与非门的情况下做出半加器？
三丶全加器
全加器的特点：全加器与半加器的不同是它的求和运算考虑了低位
来的进位信号的影响。它能进行加数（A）、被加数（B）和低位的进位（Cn-1）相加，并根据求和（S）结果给出该位的进位（Cn）信号。
பைடு நூலகம்
思考：如何用两个半加器构成一个一位全加器？
A
0 0
B
0 0
Cn-1
S
0 1
Cn
0 0
ABCn - 1
0 1
0
0 1 1
1
1 0 0
0
1 0 1
1
0 1 0
0
1 0 1
ABCn - 1
ABCn - 1 ABCn -1
ABCn - 1
ABCn - 1
1
1
1
1
0
1
0
1
1
1
AB Cn - 1
Si Ai BiCi1 Ai BiCi1 Ai BiCi1 Ai BiCi1
Ci1(Ai Bi ) Ci1(Ai Bi )
Ai Bi Ci1
Ci Ai BiCi1 Ai BiCi1 Ai BiCi1 Ai BiCi1
Ai Bi Bi Ci-1 Ai Ci-1
S = Cn-1 (A B) C n = AnBn+Cn-1(An Bn) = AnBn Cn-1(An Bn)
加法器
工学院应用电子05班罗坤
一丶知识回顾
• 逻辑函数的三种基本运算
与、或、非
• 逻辑函数的几种基本复合逻辑运算与或、与非、或非、与或非、同或、异或 • 组合逻辑电路的设计
二丶半加器
半加器的特点：半加器是只考虑本位二进制数相加，而不考虑从低位
向本位进位的加法运算的电路。它只进行加数（A）和被加数（B）相加，并根据求和（S）结果给出该位的进位（C）信号。