卧式容器液位体积计算
卧式储罐不同液位下地容积(高质量)计算
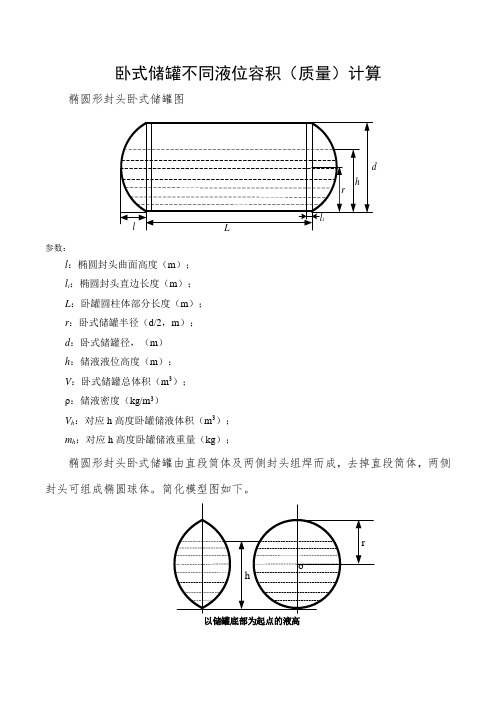
卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐储液体积(m3);m h:对应h高度卧罐储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式油罐液位体积的计算

卧式油罐液位体积的计算
设卧式油罐截面半径为R,液面高度为h,油罐长为L.则液位为h时所盛液体的体积
V=[R²arccos(1-h/R)-(R-h)√()]L
求法:
作出卧式油罐的一个截面圆O,作出液面AB(假设AB低于圆心O),过O作AB的垂线交AB于D,交圆周于C.DC=h
则由弦AB和弧ACB围成的面积为
S=S扇形OACB-S三角形OAB
=R²arccos(1-h/R)-(R-h)√(2Rh-h²)
液体的体积V=液体的底面积S*液体的长度L
得V=[R²arccos(1-h/R)-(R-h)√(2Rh-h²)]L
注:上式虽然是在液面低于圆心的情况下推导出的,但也适用于液面于圆心相平以及液面高于圆心的情况
卧式椭圆封头容器不同液位的体积计算

符号
L(m)R t(m)h(m)hi(m)(E3-D3)/D3Vt(m3)Vf(m3)V(m 3)数值2100.0001000.0001000.000500.0000.0003298672230.000523598766.6673822270996.667卧式椭圆形封头容器不同液位的体积计算
Dt ——筒体内径,m Rt——筒体或球形封头内半径,m h ——液面高度,m V——卧式容器体积,m3hi ——封头曲面深度,m (标准型:hi=1/2Rt ) Vt——筒体部分体积,m3
L ——筒体长度(含封头直边高度),m Vf——封头部分体积,m3
1、 筒体内液体体积计算(如上图):
筒体的截面积方程:X 2+Y 2=Rt 2 故:X=(Rt 2-Y 2)1/2
因此:液面高度为h 时筒体内液体的体积:
2、椭圆封头内液体体积计算(如上图):
椭圆封头的椭球面方程:
]2
arcsin 2)^(1[2^2^2^2π+-+--∙-∙=-=⎰--Rt Rt h Rt Rt h Rt Rt h Rt L dy
y Rt L Vt Rt
h Rt 2^2^2^)/(12
^2^2^2^2^y x Rt Rt hi z hi z Rt y x --=∴=++
因此:当容器内的液面高度为h 时,封头内液体的体积:
]33^233)^()(2^[22^2^2^22^2^0Rt Rt h Rt h Rt Rt hi dx y x Rt dy Rt hi zdxdy
Vf y Rt Rt h Rt
f ----=--==⎰⎰⎰⎰---π。
卧式容器液位体积计算

卧式容器液位体积计算
液位的测量方式有很多种,常用的液位传感器包括浮子式液位计、压力式液位计、雷达液位计、超声波液位计等。
这些液位传感器可以精确地测量液位并将其转换为相应的电信号。
液位体积计算的原理是根据容器的几何形状和液位的高度来计算液体的体积。
在卧式容器中,通常采用水平切面积乘以液位高度的方法进行计算。
卧式圆柱形容器的液位体积计算可以使用以下公式:
V=π*R^2*H
如果容器的底部是平的,液体的高度可以通过测量液体表面到容器底部的垂直距离来确定。
对于容器的底部是圆锥形的情况,液位体积计算的公式略有不同。
在这种情况下,可以使用以下公式进行计算:
V=(1/3)*π*(R1^2+R2^2+R1*R2)*H
其中,V表示液体的体积,π表示圆周率,R1表示底部较小半径(圆锥顶部半径),R2表示底部较大半径(圆锥底部半径),H表示液位的高度。
卧式容器的液位体积计算涉及到容器的几何形状和液体的液位测量,因此在进行计算时需要准确地测量液位和容器的尺寸。
此外,还需要注意单位的一致性,在计算中使用相同的单位。
液位体积计算在工业生产中非常重要,可以帮助企业准确掌握液体的储存量、流量和消耗情况,从而进行生产计划和资源调配。
此外,液位体
积计算还可以用于监测液体储罐的安全性能,确保液位不超过容器的额定容积,避免溢出和泄露。
总之,卧式容器液位体积计算是一项重要的工程计算,涉及到液位测量和容器几何形状分析。
通过准确地测量液位和应用相应的公式,可以计算出容器中液体的体积,为工业生产提供准确的数据支持。
卧式储罐液位体积计算

卧式储罐液位体积计算在咱们的日常生活和工业生产中,卧式储罐那可是相当常见的。
比如说,在一些化工厂里,储存着各种化学原料的大罐子;又或者在加油站,储存燃油的大储罐。
那您有没有想过,怎么才能知道这些卧式储罐里的液体到底有多少体积呢?这可不像咱们用个量杯那么简单!我还记得有一次,我去一家小工厂参观。
那工厂主要生产一些小型的机械零件,在角落里就有一个卧式储罐。
当时负责管理这个储罐的师傅正愁眉苦脸的,我就好奇上去问了问。
原来啊,他要给客户提供准确的储罐内液体量,可这储罐的液位测量让他犯了难。
咱们先来说说这卧式储罐的形状。
它就像一个长长的圆柱体,被放倒在地上。
想象一下,一个大香肠平躺着,差不多就是那个样子。
要计算它里面液位对应的体积,咱们得先搞清楚几个关键的参数。
首先就是储罐的长度,这就好比香肠的长度。
然后是储罐的直径,这相当于香肠的粗细。
还有就是液位的高度,也就是液体在储罐里达到的高度。
那具体怎么算呢?假设这储罐的长度是 L,直径是 D,液位高度是h。
咱们先把这个问题简化一下。
如果液位高度正好是储罐直径的一半,那计算就相对简单些,就是半个圆柱体的体积。
但通常情况下,液位高度可没那么凑巧。
这时候,咱们就得用到一些数学知识啦。
把储罐沿着液位高度分成两部分,上面一部分是空的,下面一部分是有液体的。
对于有液体的这部分,我们可以把它想象成是由一个矩形和两个半圆组成的图形旋转得到的。
具体来说,矩形的长度就是储罐的长度 L,宽度就是液位高度 h。
两个半圆的半径就是储罐半径,也就是 D/2。
然后通过一些复杂的数学公式和计算,就能得出这部分的体积。
可别觉得这太复杂啦,其实只要掌握了方法,也不难的。
就像咱们学骑自行车,一开始觉得晃晃悠悠掌握不好平衡,多练几次不就顺溜了嘛!再回到那个小工厂,我给师傅大概讲了讲计算的方法,他虽然听得有点迷糊,但还是很感激。
后来听说他专门找了个懂行的人帮忙算清楚了,顺利给客户交了差。
总之啊,卧式储罐液位体积的计算虽然有点麻烦,但只要咱们用心去琢磨,多练习练习,也能轻松搞定。
卧式储罐不同液位下的容积(质量)计算精选全文

可编辑修改精选全文完整版卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部份长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐整体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及双侧封头组焊而成,去掉直段筒体,双侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液整体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h 假设密度为ρ,那么卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导进程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及双侧封头组焊而成,去掉直段筒体,双侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部份该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,那么有222221x y z a c++= 垂直于y 轴分成无穷小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部份:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 那么筒体部份容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液整体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液整体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h假设液位高度h 以卧罐底部为起点,如以下图那么卧式储罐内储液整体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h 假设密度为ρ,那么卧式储罐内储液总重量为:hh V m ρ=其它方式如下:第一种方式卧式储罐不同液位下的容积简化计算公卧式储罐内储液整体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π假设密度为ρ,那么卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐体积与液位关系计算工具
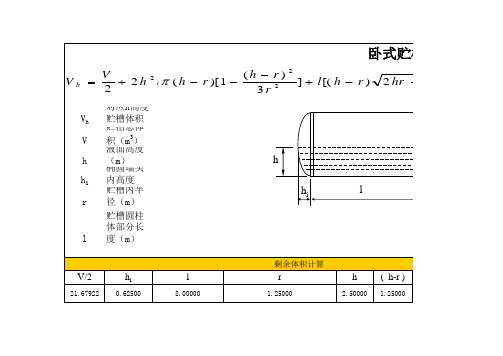
卧式贮槽体积计算公式
Vh V 2h 2
Vh [( h r ) i ( h r )[ 1 2 3r
2.50000
( h-r )
1.25000
卧式贮槽体积计算公式
2 hr h
2
r
2
arcsin(
h r )] r
剩余体积(M3) 43.35948
液位百分数
100.00000
注:设置好罐的参数,更改液位百分数即可计算出剩余体积,适合各种卧式罐
,适合各种卧式罐
2 hr h
2
r
2
arcsin
对应h高度贮槽体积(m3) 贮槽总体积(m3)=43.35844m³ 液面高度(m)
h hi
l
椭圆墙头内高度(不包括直边高度)(m) 贮槽内半径(m) 贮槽圆柱体部分长度(m)
剩余体积计算
V/2
21.67922
hi
0.62500
l
8.00000
r
1.25000
h
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐不同液位下的容积计算

卧式储罐不同液位下的容积计算卧式储罐是一种常见的储存液体的设备,通常用于存储液态化学品、石油产品、水等。
在工业和民用领域中广泛应用。
对于卧式储罐来说,液位的高低与储罐内的容积有着密切的关系。
在储罐内液位不同的情况下,其容积计算也会有所不同。
本文将详细介绍卧式储罐在不同液位下的容积计算方法。
首先,我们需要了解卧式储罐的结构和常见参数。
卧式储罐通常为圆柱形,由罐体、进出口、排放口、液位计、压力表等组成。
在容积计算中,我们通常会用到储罐内径、长度、液位高度、横截面积等参数。
其次,对于卧式储罐在不同液位下的容积计算,我们可以根据液位高度来进行分析。
一般来说,液位高度越高,储罐内的容积就越大。
容积计算的基本原理是利用几何体积公式,通过求解被液体填充后的几何体积来确定储罐内的液体容积。
接下来,我们以一个实际案例来说明卧式储罐在不同液位下的容积计算方法。
假设我们有一个直径为2米,长度为5米的卧式储罐,液位高度分别为1米、2米、3米、4米和5米。
我们将逐一计算不同液位下的储罐容积。
1.当液位高度为1米时,我们可以先计算液位1米以下的圆柱体积,然后再计算液位为1米处的部分体积。
首先求出液位1米以下的部分体积,即整个圆柱的体积减去1米高度的部分的体积。
计算公式为V1=π*r²*h1,其中r为半径,h1为液体高度,代入数据可得V1=π*1²*1=3.14立方米。
接着计算液位1米处的部分体积,即液位高为1米的沟槽体积。
计算公式为V2=π*r²*(h2-r),其中r为半径,h2为液体高度,代入数据可得V2=π*1²*(1-1/π)=0.283立方米。
因此,液位高度为1米时,储罐容积为V=V1+V2=3.423立方米。
2.当液位高度为2米时,沟槽部分可以按照液位高度为1米时的方式计算,然后再加上液位高度为2米的圆柱体积。
继续使用上述的计算方法,可得液位高度为2米时的储罐容积为V=V1+V2+V3=9.696立方米。
