高三文科数学小题模拟练

合集下载

高三文科数学模拟题八

高三数学模拟试题（八）一、选择题（5×10=50分）1．设}35|),{(},64|),{(-==+-==x y y x B x y y x A ，则B A 等于（）A ．}2,1{B ．}1,2{C ．)}2,1{(D ．)}1,2{( 2．函数22()log (1)f x x x =+-的零点个数为（）A ．0B ．1C ．2D ．33 “1x ≥”是“2x >”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．双曲线2213y x -=的一个焦点到它的渐近线的距离为（） ABC ．1D ．25．下列命题中正确的是（）A ．如果两条直线都平行于同一个平面，那么这两条直线互相平行B ．过一条直线有且只有一个平面与已知平面垂直C ．如果一条直线平行于一个平面内的一条直线，那么这条直线平行于这个平面D ．如果两条直线都垂直于同一平面，那么这两条直线共面 6．等比数列{}n a 的前n 项和为n S ，11a =，若1234,2,a a a 成等差数列，则4S =（）A ．7B ．8C ．6D ．157．已知()y x P ,的坐标满足：⎪⎩⎪⎨⎧≥-+≤≤02221y x y x ，那么22y x +的取值范围是（）A ．[]4,1B ．[]5,1C ．⎥⎦⎤⎢⎣⎡4,54D ．⎥⎦⎤⎢⎣⎡5,548．点()2,1P -为圆()22125x y -+=内弦AB 的中点，则直线AB 的方程为（）A ．30x y --=B ．230x y +-=C ．10x y +-=D ．250x y --=9．一个几何体的三视图如右图所示，则该几何体的体积为：（）AB ．CD10．已知函数sin()y x ωϕ=+（0,||2πωϕ><）的部分图象如图所示，则（）A ．6,1πϕω== B ．6,2πϕω-== C ．6,1πϕω-== D ．6,2πϕω==二、填空题（5×5=25分）11．某校高三有1000个学生，高二有1200个学生，高一有1500个学生，现按年级分层抽样，调查学生的视力情况，若高一抽取了75人，则全校共抽取了人12．从1,2,3,4这四个数中一次随机取两个数，则其中一个数是另一个的两倍的概率是_____ 13．已知函数()*,y f x x N =∈，任取*,m n N ∈，均有()()()()42f m n f m f n m n +=+++-成立，且()11f =，若()2p tp f x -≤对任意的[][)2,3,3,p x ∈∈+∞恒成立，则t 的最小值为14．设e 1，e 2是不共线向量，e 1－4e 2与k e 1＋e 2共线，则实数k 的值为____15．若直线y x b =+与曲线y =b 的取值范围是三、解答题（75分）16．（本小题满分13分）已知函数2()sin cos f x x x x =+，π[,π]2x ∈. （1）求2π()3f 的值；（2）求()f x 的最大值和最小值.E P D CBA17．（本小题满分13分）设函数d cx bx ax x f y +++==23)(的图象在0=x 处的切线方程为01224=-+y x .（1）求c ，d ；（2）若函数在2=x 处取得极值16-，试求函数解析式并确定函数的单调区间. 18．（本小题满分13分）以下茎叶图记录了甲、乙两组各四名同学在某次数学测验中的成绩，甲组记录中有一个数据模糊，无法确认，在图中以X 表示. 甲组乙组 6 x 8 7 4 1 9 0 0 3（1）如果甲组同学与乙组同学的平均成绩一样，求x 及甲组同学数学成绩的方差；（2）如果x =7，分别从甲、乙两组同学中各随机选取一名，求这两名同学的数学成绩之和大于180的概率.（注：方差2222121=[()()...()],n s x x x x x x n-+-++-其中12,,...,.n x x x x 为的平均数） 19．（本小题满分12分）已知等比数列{}n a 中，142,16a a ==。

高三文科数学小综合专题练习--应用问题

高三文科数学小综合专题练习——应用问题一、选择题1. 某种细菌经60分钟培养，可繁殖为原来的2倍.10个细菌经过7小时培养，细菌能达到的个数是A.640B.1280C.2560D.51202. 台风中心从A 地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B 在A 的正东40千米处，B 城市处于危险区的时间为A.5.0小时B.1小时C.5.1小时D.2小时 3. 客车从甲地以h km 60的速度行驶1小时到达乙地，在乙地停留了半小时，然后以h km 80的速度行驶1小时到达丙地，下列描述客车从甲地出发，经过乙地，最后到达丙地所经过的路程s 与时间t 之间的关系图象中，正确的是4. 已知甲、乙两车由同一起点同时出发,并沿同一路线（假定为直线）行驶．甲车、乙车的速度曲线分别为v v 乙甲和（如图2所示）．那么对于图中给定的01t t 和，下列判断中一定正确的是A. 在1t 时刻，甲车在乙车前面B. 1t 时刻后，甲车在乙车后面C. 在0t 时刻，两车的位置相同D. 0t 时刻后，乙车在甲车前面5. 某电信公司推出两种手机收费方式：A 种方式是月租20元，B 种方式是月租0元.一个月的本地网内打出电话时间t （分钟）与打出电话费s （元）的函数关系如图，当打出电话150分钟时，这两种方式电话费相差A.10B.20C.30D.340二、填空题6. 某人向东走了x 千米，然后向右转0120，再朝新方向走了3千米，结果他离出发点恰好tOB As 50 100 15013千米，那么x 的值是___________.7. 里氏震级M 的计算公式为：0lg lg A A M -=,其中A 是测震仪记录的地震曲线的最大振幅，0A 是相应的标准地震的振幅.假设在一次地震中，测震仪记录的最大振幅是1000，此时标准地震的振幅是001.0，则此次地震的震级为_________;9级地震的最大振幅是5级地震最大振幅的______倍.8. 某地区居民生活用电分为高峰和低谷两个时间段进行分时计价．该地区的电网销售电价表如下：高峰时间段用电价格表低谷时间段用电价格表高峰月用电量（单位：千瓦时）高峰电价（单位：元/千瓦时）低谷月用电量（单位：千瓦时）低谷电价（单位：元/千瓦时）50及以下的部分 568.0 50及以下的部分 288.0 超过50至200的部分 598.0 超过50至200的部分318.0超过200的部分 668.0 超过200的部分 388.0若某家庭5月份的高峰时间段用电量为200千瓦时，低谷时间段用电量为100千瓦时，则按这种计费方式该家庭本月应付的电费为元（用数字作答）．w.w.w.k.s.5.u.c.o.m9．有一批材料可以建成m 200的围墙，如果用此材料在一边靠墙的地方围成一块矩形场地，中间用同样的材料隔成三个面积相等的矩形(如图所示)，则围成的矩形最大面积为________．(围墙厚度不计)10．某商家一月份至五月份累计销售额达3860万元，预测六月份销售额为500万元，七月份销售额比六月份递增00x ，八月份销售额比七月份递增00x ，九、十月份销售总额与七、八月份销售总额相等，若一月份至十月份销售总额至少达7000万元，则x 的最小值是________．三、解答题11. 如图，为了解某海域海底构造，在海平面内一条直线上的C B A ,,三点进行测量，已知50AB m =，120BC m =，于A 处测得水深80AD m =，于B 处测得水深200BE m =，于C 处测得水深110CF m =，求DEF ∠的余弦值。

高三文科数学模拟试题含答案

高三文科数学模拟试题含答案高三文科数学模拟试题本试卷共150分，考试时间120分钟。

第Ⅰ卷（选择题，共50分）一、选择题（共10小题，每小题5分，共50分。

在每小题中，只有一项是符合题目要求的）1.复数3+ i的虚部是（）。

A。

2.B。

-1.C。

2i。

D。

-i2.已知集合A={-3,-2,0,1,2}，集合B={x|x+2<0}，则A∩(CRB) =（）。

A。

{-3,-2,0}。

B。

{0,1,2}。

C。

{-2,0,1,2}。

D。

{-3,-2,0,1,2}3.已知向量a=(2,1)，b=(1,x)，若2a-b与a+3b共线，则x=（）。

A。

2.B。

11/22.C。

-1.D。

-24.如图所示，一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的表面积为（）。

A。

4π/3.B。

π。

C。

3π/2.D。

2π5.将函数f(x)=sin2x的图像向右平移π/6个单位，得到函数g(x)的图像，则它的一个对称中心是（）。

A。

(π/6,0)。

B。

(π/3,0)。

C。

(π/2,0)。

D。

(π,0)6.执行如图所示的程序框图，输出的s值为（）。

开始是否输出结束A。

-10.B。

-3.C。

4.D。

57.已知圆C:x^2+2x+y^2=1的一条斜率为1的切线l1，若与l1垂直的直线l2平分该圆，则直线l2的方程为（）。

A。

x-y+1=0.B。

x-y-1=0.C。

x+y-1=0.D。

x+y+1=08.在等差数列{an}中，an>0，且a1+a2+⋯+a10=30，则a5⋅a6的最大值是（）。

A。

4.B。

6.C。

9.D。

369.已知变量x,y满足约束条件2x-y≤2，x-y+1≥0，设z=x^2+y^2，则z的最小值是（）。

A。

1.B。

2.C。

11.D。

3210.定义在R上的奇函数f(x)，当x≥0时，f(x)=2，当x<0时，f(x)=1-|x-3|，则函数F(x)=f(x)-a(0<a<1)的所有零点之和为（）。

高三文科数学第二学期综合模拟题

高三文科数学第二学期综合模拟题一、本大题共8小题，每小题5分，共40分。

（1）若a ，b ∈R ，i 是虚数单位，且(2)i 1i b a +-=+，则a b +的值为（A ）1 （B ）2 （C ）3 （D ）4（2）若集合},0{2m A =，}2,1{=B ，则“1=m ”是“}2,1,0{=B A ”的（A ）充分不必要条件（B ）必要不充分条件（C ）充分必要条件（D ）既不充分也不必要条件（3）若点(,)P x y 在不等式组,,2y x y x x ≤⎧⎪≥-⎨⎪≤⎩表示的平面区域内，则2z x y =+的最大值为（A ）0 （B ）2 （C ） 4 （D ）6（4）已知x ，y ，z ∈R ，若1-，x ，y ，z ，3-成等差数列，则x y z ++的值为（A ）2-（B ）4-（C ）6-（D ）8-（5）右图给出的是计算1001...81614121+++++的值的一个程序框图，其中判断框内应填入的条件是（A ） 50>i （B ） 25>i （C ）50<i （D ） 25<i（6）已知2sin(45)10α-=-，且090<<α，则cos α的值为（A ）513 （B ）1213（C ） 35 （D ）45（7）已知函数()()()f x x a x b =--(其中)a b >的图象如右图所示，则函数()xg x a b =+的图象大致为（A ）（B ）（C ）（D ）（8）设集合1[0,)2A =，1[,1]2B =，函数1,,()22(1),.x x A f x x x B ⎧+∈⎪=⎨⎪-∈⎩若0x A ∈，且0[()]f f x A ∈，则0x 的取值范围是（A ）(41,0] （B ） (21,41] （C ）(21,41) （D ） [0，83]俯视图左视图主视图21122二、填空题：本大题共6小题，每小题5分，共30分。

江西省宜春市2023届高三高考模拟文科数学试题(含解析)

江西省宜春市2023届高三高考模拟文科数学试题一、单选题1．（2023·江西宜春·统考模拟预测）设全集U =R ，{1A x x =<-或}2x ≥，{}2,1,0,1,2B =--，则()U B A ⋂=ð（）A ．{}0,1B ．{}1,0-C ．{}0,1,2D ．{}1,0,1-2．（2023·江西宜春·统考模拟预测）已知复数z 满足()1i 2z +=-，则z 等于（）A ．1i--B ．1i-C ．1i+D ．1i-+3．（2023·江西宜春·统考模拟预测）非零向量a r ，b r ，c r 满足()a cb ⊥-r r r ，a r 与b r 的夹角为π3，2b =r ，则c r 在a r 上的投影为（）A ．－1B．C ．1D4．（2023·江西宜春·统考模拟预测）已知实数,x y 满足约束条件0,30,1,x y x y y -≥⎧⎪+-≤⎨⎪≥⎩则23x yz -+=的最大值是（）A ．3B ．13CD ．1275．（2023·江西宜春·统考模拟预测）从棱长为2的正方体内随机取一点，则取到的点到中心的距离不小于1的概率为（）A ．π6B ．π4C ．π16-D ．π14-6．（2023·江西宜春·统考模拟预测）若30.04,ln1.04,log 1.04a b c ===则（）A ．c b a <<B ．b a c <<C ．c a b<<D ．b<c<a7．（2023·江西宜春·统考模拟预测）在数学和许多分支中都能见到很多以瑞士数学家欧拉命名的常数，公式和定理，若正整数,m n 只有1为公约数，则称,m n 互质，对于正整数(),n n ϕ是小于或等于n 的正整数中与n 互质的数的个数，函数()n ϕ以其首名研究者欧拉命名，称为欧拉函数，例如：()()32,76ϕϕ==，()96ϕ=.记n S 为数列(){}3nϕ的前n 项和，则10S =（）A ．9312-B ．931-C ．10312-D ．1031-8．（2023·江西宜春·统考模拟预测）函数()πsin 6f x x ω⎛⎫=+ ⎪⎝⎭的图象(04)ω<<关于直线π6x =对称，将()f x 的图象向左平移π4个单位长度后与函数()y g x =图象重合，下列说法正确的是（）A ．函数()g x 图象关于直线π6x =对称B ．函数()g x 图象关于点π,06⎛⎫- ⎪⎝⎭对称C ．函数()g x 在π0,3⎛⎫⎪⎝⎭单调递减D ．函数()g x 最小正周期为π29．（2023·江西宜春·统考模拟预测）在Rt ABC V 中，1,2CA CB ==.以斜边AB 为旋转轴旋转一周得到一个几何体，则该几何体的内切球的体积为（）ABC ．32π81D ．4π8110．（2023·江西宜春·统考模拟预测）如图，设1F ，2F 是双曲线2222:1(0,0)x y C a b a b -=>>的左右焦点，点A ，B 分别在两条渐近线上，且满足22133OA OF OB =+u u u r u u u u r u u u r ，20OA BF ⋅=u u u r u u u u r，则双曲线C 的离心率为（）A ．B ．2CD11．（2023·江西宜春·统考模拟预测）已知数列{}n a 满足1321223n n a a a a n+++++=L ，若数列()21n n n a ⎧⎫+⎪⎪⎨⎬+⎪⎪⎩⎭的前n 项和n S ，对任意*N n ∈不等式n S λ<恒成立，则实数λ的取值范围是（）A ．1λ>B ．1λ≥C ．58λ≥D ．58λ>12．（2023·江西宜春·统考模拟预测）已知函数()()()ln 1,ln (0)1m xf x xg x x m x m =+-=+>+，且()()120f x g x ==，则()2111em xx -+的最大值为（）A ．1B ．eC ．2eD ．1e二、填空题13．（2023·江西宜春·统考模拟预测）已知)114d πa x x -=+⎰，则到点(),0M a 的距离为2的点的坐标可以是___________.（写出一个满足条件的点就可以）14．（2023·江西宜春·统考模拟预测）已知点()()1,1,1,1A B ---，若圆22()(24)1x a y a -+-+=上存在点M 满足3MA MB ⋅=u u u r u u u r，则实数a 的取值的范围是___________.15．（2023·江西宜春·统考模拟预测）已知某线路公交车从6:30首发，每5分钟一班，甲、乙两同学都从起点站坐车去学校，若甲每天到起点站的时间是在6:30--7:00任意时刻随机到达，乙每天到起点站的时间是在6:45-7:15任意时刻随机到达，那么甲、乙两人搭乘同一辆公交车的概率是___________________16．（2023·江西宜春·统考模拟预测）如图，多面体ABCDEF 中，面ABCD 为正方形，DE ⊥平面,ABCD CF DE ∥，且2,1,AB DE CF G ===为棱BC 的中点，H 为棱DE 上的动点，有下列结论：①当H 为DE 的中点时，GH P 平面ABE ；②存在点H ，使得GH AC ⊥；③直线GH 与BE ④三棱锥A BCF -的外接球的表面积为9π.其中正确的结论序号为___________.（填写所有正确结论的序号）三、解答题17．（2023·江西宜春·统考模拟预测）在ABC V 中，角,,A B C 所对的边分别为,,a b c ，且2cos a b c B +=.(1)求证：2C B =；(2)求3cos a bb B+的最小值.18．（2023·江西宜春·统考模拟预测）如图1，在直角梯形ABCD 中，//,90,224AB CD DAB CD AB AD ∠====o ，点E ，F 分别是边,BC CD 的中点，现将CEF △沿EF 边折起，使点C 到达点P 的位置（如图2所示），且2BP =.(1)求证：平面APE ⊥平面ABD ；(2)求点B 到平面ADP 的距离.19．（2023·江西宜春·统考模拟预测）为了缓解日益拥堵的交通状况，不少城市实施车牌竞价策略，以控制车辆数量.某地车牌竞价的基本规则是：①“盲拍”，即所有参与竞拍的人都是网络报价，每个人不知晓其他人的报价，也不知道参与当期竞拍的总人数；②竞价时间截止后，系统根据当期车牌配额，按照竞拍人的出价从高到低分配名额.某人拟参加2023年5月份的车牌竞拍，他为了预测最低成交价，根据竞拍网站的公告，统计了最近5个月参与竞拍的人数（见表）：月份2022.122023.12023.22023.32023.4月份编号t12345竞拍人数y （万人）1.72.12.52.83.4(1)由收集数据的散点图发现可用线性回归模型拟合竞拍人数y （万人）与月份编号t 之间的相关关系.请用最小二乘法求y 关于t 的线性回归方程：ˆˆˆy bt a =+，并预测2023年5月份参与竞拍的人数.(2)某市场调研机构对200位拟参加2023年5月份车牌竞拍人员的报价进行抽样调查，得到如下一份频数表：报价区间（万元）[)1,2[)2,3[)3,4[)4,5[)5,6[]6,7频数206060302010（i ）求这200位竞拍人员报价X 的平均数x 和样本方差2s （同一区间的报价可用该价格区间的中点值代替）；（ii ）假设所有参与竞价人员的报价X 可视为服从正态分布()2,N μσ，且μ与2σ可分别由（i ）中所求的样本平均数x 及方差2s 估值.若2023年5月份实际发放车牌数是5000，请你合理预测（需说明理由）竞拍的最低成交价.附：()()()121ˆ 1.3niii nii x x y y bx x ==--=≈-∑∑，若()0,1Y N :，则( 1.11)0.8660<=P Y ，( 1.12)0.8686P Y <=.20．（2023·江西宜春·统考模拟预测）已知函数()ln 2f x x x =--.(1)求函数的最小值；(2)若方程()f x a =有两个不同的实数根1x ，2x 且12x x <，证明：1223x x +>.21．（2023·江西宜春·统考模拟预测）在平面直角坐标系xoy 中，已知椭圆2222:1(0)x y C a b a b+=>>的离心率为12，左､右焦点分别是12,F F ，以1F 为圆心，6为半径的圆与以2F 为圆心，2为半径的圆相交，且交点在椭圆C 上.(1)求椭圆C 的方程；(2)设过椭圆C 的右焦点2F 的直线12,l l 的斜率分别为12,k k ，且122k k =-，直线1l 交椭圆C 于,M N 两点，直线2l 交椭圆C 于,G H 两点，线段,MN GH 的中点分别为,R S ，直线RS 与椭圆C 交于,P Q 两点，,A B 是椭圆C 的左､右顶点，记PQA △与PQB △的面积分别为12,S S ，证明：12S S 为定值.22．（2023·江西宜春·统考模拟预测）在平面直角坐标系xoy 中，曲线C 的参数方程11222122t t t t x y ⎧⎛⎫=+ ⎪⎪⎪⎝⎭⎨⎪=-⎪⎩（t 为参数），以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程cos 2sin 10m ρθρθ+-=.(1)求曲线C 的普通方程；(2)若直线l 与曲线C 有两个不同公共点，求m 的取值范围.23．（2023·江西宜春·统考模拟预测）已知函数()244f x x x =++-.(1)求不等式24410x x ++-≥的解集；(2)若()f x 的最小值为m ，正实数a ，b ，c 满足a b c m ++=，求证：11192a b b c c a m++≥+++.参考答案：1．D【分析】先计算得到U A ð，进而求出交集.【详解】{}12U A x x =-≤<ð，故(){}1,0,1U B A =-I ð故选：D 2．A【分析】利用复数的除法运算和共轭复数的定义求解.【详解】由题可得2(1i)1i 1iz -==--=-++，所以1i z =--，故选:A.3．C【分析】根据投影公式计算出正确答案.【详解】由于()a c b ⊥-r r r，所以()0,a c a b a c a a b b c ⋅-=⋅-⋅=⋅=⋅r r r r r r r r r r r ，由于a r 与b r 的夹角为π3，所以πcos 3a c a b a b a ⋅=⋅=⋅⋅=r r r r r r r，c r 在a r 上的投影为1a a c a a⋅==rr r r r .故选：C 4．B【分析】画出可行域，向上平移基准直线20x y -+=到可行域边界位置，由此求得23x y z -+=的最大值.【详解】画出可行域如下图所示，向上平移基准直线20x y -+=到可行域边界点()1,1B 的位置，此时z 取得最大值为1max 12111,3z z --⨯+=-==，.故选：B.5．C【分析】根据几何概型概率问题的计算公式求得正确答案.【详解】点到中心距离小于等于1的几何体是以中心为球心，1为半径的球体.所以，取到的点到中心的距离不小于1的概率为334π1π31126⨯-=-.故选：C 6．A【分析】构造函数()()ln 1f x x x =+-，利用导数判断函数单调性，再结合对数的性质即可判断大小关系.【详解】因为0.04a =，ln1.04b =，3log 1.04c =，当()0,1x ∈时，设()()ln 1f x x x =+-，则()11011xf x x x -'=-=<++，所以()f x 在()0,1上单调递减且()00f =，所以()()()0.04ln 10.040.0400f f =+-<=，即()0.04ln 10.04>+，所以a b >；又因为3e >，所以ln 3ln e 1>=，3ln1.04log 1.03ln1.04ln 3=<，即b c >，所以c b a <<.故选：A.7．D【分析】根据题意分析可得()1323nn ϕ-=⋅，结合等比数列求和公式运算求解.【详解】由题意可知：若正整数3nm ≤与3n不互质，则m 为3的倍数，共有1333n n -=个，故()1133332n n n n ϕ---=⋅=，∵()()113233233n n n n ϕϕ+-⋅==⋅，即数列(){}3n ϕ是以首项()32ϕ=，公比3q =的等比数列，故()1010102133113S -==--.故选：D.8．C【分析】由对称性求得ω，由图象平移变换求得()g x ，然后结合正弦函数的对称性，单调性，周期判断各选项．【详解】由已知ππππ662k ω+=+，62k ω=+，Z k ∈，又04ω<<，∴2ω=，ππ2π()sin[2()sin(2463g x x x =++=+，π2ππ2ππ,Z 632k k ⨯+=≠+∈，A 错；π2ππ2()π,Z 633k k ⨯-+=≠∈，B 错；π(0,3x ∈时，2π2π4ππ3π2(,)(,)33322x +∈⊆，C 正确；()g x 的最小正周期是2ππ2T ==，D 错．故选：C ．9．C【分析】根据旋转体的概念得出该旋转体是两个共底面的圆锥的组合体，作出轴截面，得出内切球于心O 位于对称轴AB 上，由平行线性质求得球半径r 后可得球体积．【详解】由题意该几何体是两个共底面的圆锥的组合体，如图是其轴截面，由对称性知其内切球球心O 在AB 上，O 到,CA CB 的距离,OE OF 相等为球的半径，设其为r ，因为C 是直角，所以OECF 是正方形，即CF CE r ==，由//OF CA 得OF BF CA BC =，即212r r -=，解得23r =，球体积为3344232ππ(π33381V r ==⨯=．故选：C ．10．C【分析】先求出AB 所在的直线方程，分别与两条渐近线联立方程组，求出,A B 两点的坐标，再根据22133OA OF OB =+u u u r u u u u r u u u r，求出,a c 之间的关系，从而可得双曲线的离心率【详解】由题意：OA b k a = ，20OA BF =u u u r u u u u r Q g ,2OA BF ∴⊥ ,2BF ak b ∴=-所以直线2BF 的方程为：()ay x c b=-- ①直线OA 的方程为：by x a =②直线OB 的方程为：by x a=-③联立①②可得：2a x cab y c⎧=⎪⎪⎨⎪=⎪⎩ ，即2(,)a ab A c c 联立①③可得22222a c x a babcy a b ⎧=⎪⎪-⎨-⎪=⎪-⎩，即22222(,a c abc B a b a b ---又22133OA OF OB =+u u u r u u u u r u u u r Q 22222221(,)(,0)(,)33a ab a c abcc c c a b a b-∴=+--可得222222233()3()a a c c c a b ab abcc a b ⎧=+⎪-⎪⎨-⎪=⎪-⎩ ，化简可得223a c = ，即2e 3=，e ∴= 故选：C 11．C【分析】根据1321223n n a a a a n+++++=L 求得 n a ,再因为对任意*N n ∈不等式n S λ<恒成立，()max n S λ>，求出实数λ的取值范围.【详解】1321223n n a a a a n+++++=L ①,31212231n n a a a a n -++++=-L ②,由①-②可得，当 2n ≥ 时,2n na n=,当211,2n a ==,当2n ≥,()()()122211222111n n n n n n n a n n n n +⎛⎫++==- ⎪ ⎪++⨯⨯+⨯⎝⎭,当1,n =()2318n n n a +=+，所以()()2312131111311228223221282212n n n n S n n n ++⎡⎤⎛⎫⎛⎫⎛⎫=+-++-=+-⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⨯⨯⨯+⨯⨯+⨯⎝⎭⎢⎥⎝⎭⎝⎭⎣⎦L ,对任意*N n ∈不等式n S λ<恒成立,所以 ()max n S λ>,()21332528882221181n n S n +⎛⎫=+<+=⎪ ⎪-⨯+⎝⎭⨯.所以58λ≥.故选:C.12．A【分析】根据题意表示出()()21121ln 1e ,x x x x m ++==从而推导出21e 1,xx =+将问题转化为()21111e em m x x m--+=，利用导数求得函数的最值.【详解】()()()()()ln 10,ln 10,1ln 1,11m mf x x x m x x x x =+-=+-==++++()ln0,e ,x xg x x m x m=+==由题意知，()()21121ln 1e ,x x x x m ++==即()()2221121ln 1e e ln e ,x x xx x x m ++===因为0m >，所以21e 1,11xx >+>，设()ln ,1p x x x x =>，则()1ln 0p x x '=+>，()()211e ,xp x p m +==所以211e x x +=，所以()22121111e e e e x m m m x x x m---+==，1(),0e m m t m m -=>，则11(),em mt m --'=当01m <<时，()0;t m '>当1m >时，()0;t m '<所以()t m 在()0,1时单调递增，在()1,+∞时单调递减，所以max ()(1)1,t m t ==故选：A.13．22(2)4x y -+=上的任意一点都可以【分析】根据定积分的几何意义先求出a ，再写出到点(),0M a 的距离为2的点表示一个圆.【详解】由于11d x -⎰表示以()0,0为圆心，1为半径且在第一、二象限的圆弧与坐标轴围成的面积，其面积是半径为1的圆的面积的一半，即为π2.所以)111144π4d d 202ππ2πa x x x x --==⨯+=+=⎰⎰,到点()2,0M 的距离为2的点是圆22(2)4x y -+=上的点.故答案为：22(2)4x y -+=上的任意一点.14．120,5⎡⎤⎢⎥⎣⎦【分析】设(,)M x y ，由数量积的坐标表示求得M 点轨迹是一个圆，然后由圆与圆的位置关系可得a 的范围．【详解】设(,)M x y ，则(1,1),(1,1)MA x y MB x y =----=---u u u r u u u r，2(1)(1)(1)3MA MB x x y ⋅=---+--=u u u r u u u r，即22(1)4x y ++=，M 在以(0,1)-为圆心，2为半径的圆上，由题意该圆与圆22()(24)1x a y a -+-+=有公共点，所以2121-≤≤+，解得1205a ≤≤．故答案为：12[0,]5．15．112【分析】由题意知本题是一个几何概型，设甲和乙到达的分别为6时x +分、6时y +分，则3060x ……，4575y ……，他们能搭乘同一班公交车，则4560x ……，4560y ……．试验包含的所有区域是{(,)|3060x y x Ω=……，4575}y ……，他们能搭乘同一班公交车所表示的区域为A ，由此能求出结果．【详解】解：由题意知本题是一个几何概型，设甲和乙到达的分别为6时x +分、6时y +分，则3060x ……，4575y ……，则试验包含的所有区域是{(,)|3060x y x Ω=……，4575}y ……，他们能搭乘同一班公交车所表示的区域为4550{(,)|4550x A x y y ⎧=⎨⎩…………或50555055x y ⎧⎨⎩…………或5560}5560x y ⎧⎨⎩…………，则他们能搭乘同一班公交车的概率5531303012P ⨯⨯==⨯．故答案为：11216．①④【分析】根据线面平行的判定定理，以及线线垂直的判定，结合异面直线所成角，以及棱锥外接球半径的求解，对每一项进行逐一求解和分析即可.【详解】对①：当H 为DE 的中点时，取EA 中点为M ，连接,MH MB ，因为,H M 分别为,ED EA 的中点，故可得MH //AD ，12MH AD =，根据已知条件可知：BG //1,2AD BG AD =，故MH //,BG MH BG =，故四边形HMBG 为平行四边形，则H G //MB ，又MB ⊂平面,ABE HG ⊄平面ABE ，故H G //面ABE ，故①正确；对②：因为ED ⊥平面ABCD ，,⊂DA DC 平面ABCD ，故,DE DA DE DC ⊥⊥，又四边形ABCD 为矩形，故DA DC ⊥，则,,DE DA DC 两两垂直，以D 为坐标原点，建立空间直角坐标系如图所示：则()()()()()2,0,0,0,2,0,2,2,0,0,0,2,1,2,0A C B E G ，设()0,0,H m ，[]0,2m ∈，若GH AC ⊥，则()()1,2,2,2,020GH AC m ⋅=--⋅-=-≠u u u r u u u r，不满足题意，故②错误；对③：()1,2,GH m =--u u u r，()2,2,2BE =--u u u r ，()()()()1222262GH BE m m ⋅=-⨯-+-⨯-+=+u u u r u u u r，GH ==u u u r，BE =u u u r []0,2m ∈，,cos GH =u u u r u=[]0,2m ∈，令2325m y m +=+，设32t m =+，[]2,4t ∈，23t m -=，则29492453ty t t t==-⎛⎫+-+ ⎪⎝⎭，当[]2,4t ∈时，根据对勾函数的性质得4949454,42t t ⎡⎤+-∈⎢⎥⎣⎦，则236,549y ⎡⎤∈⎢⎥⎣⎦，当25y =时，cos ,GH BE u u u r u u u r有最小值，最小值为，故③错误；对④：由题可得CF ⊥平面ABCD ，又面ABCD 为正方形，∴,,AB BC CF AB BC CF C ⊥⊥⋂=，∴AB ⊥平面BCF ，则AB ，BC ，CF 两两垂直，∴AF 为三棱锥A BCF -的外接球的直径，又22222212219AF AB BC CF =++=++=，∴三棱锥A BCF -的外接球表面积为9π，故④正确.故答案为：①④.17．(1)证明见解析(2)最小值为【分析】（1）根据正弦定理边角互化和两角和差正弦化简即可证明.（2）将问题转化32cos 2cos cos a b c B b b B b B++=24cos cos B B =+，根据第一问解得π10,,cos ,132B B ⎛⎫⎛⎫∈∈ ⎪ ⎪⎝⎭⎝⎭，然后结合不等式求解.【详解】（1）在ABC V 中，2cos a b c B +=，由正弦定理得sin sin 2sin cos A B C B +=，又()πA B C =-+，因为()sin sin 2sin cos B C B C B ++=⋅,所以sin cos sin cos sin C B B C B ⋅-⋅=,所以()sin sin C B B -=,又sin 0B >,所以0πC B C <-<<，且πB C B C +-=<,所以B C B =-，故2C B =.（2）由（1）2C B =得()30,πB C B +=∈，所以π10,,cos ,132B B ⎛⎫⎛⎫∈∈ ⎪ ⎪⎝⎭⎝⎭，因为2cos ,2a b c B C B +==，所以32cos 2cos cos a b c B b b B b B++=2sin cos 2sin 2sin2cos 2sin sin cos sin cos C B B B B BB B B B⋅+⋅+==⋅⋅24cos cos B B=+≥当且仅当24cos cos B B =即cos B =π0,3B ⎛⎫∈ ⎪⎝⎭，即当且仅当π4B =时等号成立，所以当π4B =时，3cos a bb B +的最小值为18．(1)证明见解析【分析】（1）连接,BD BF ，由等腰三角形的性质和勾股定理，证明PE EF ⊥，PE BE ⊥，可证得PE ⊥平面ABD ，即可证得平面APE ⊥平面ABD .（2）取AD 的中点O ，连接,,OE DE PO ，由勾股定理求,,PD PA PO ，又B PAD P ABD V V --=，利用体积法求点B 到平面ADP 的距离.【详解】（1）证明：由题意，连接,BD BF ，因为224CD AB AD ===，//AB CD ，90,DAB F ∠=o 是边CD 的中点，所以2BF CF ==，则BC =又E 是边BC 的中点，则EF BC ⊥，在折起中PE EF ⊥.又222224BE PE BP +=+==，所以PE BE ⊥，又BE EF E =I ，BE ⊂平面ABD ，EF ⊂平面ABD ，故PE ⊥平面ABD ，又PE ⊂平面APE ，所以平面APE ⊥平面ABD .（2）由（1）中取AD 的中点O ，连接,,OE DE PO ，由（1）可知，PE ⊥平面ABD ，所以,,PE DE PE AE PE OE ⊥⊥⊥，而()132OE AB DC =+=，112OD AD ==，所以DE =同理AE =所以PD PA PO ======所以PAD V 是等腰三角形，所以1122PAD S AD PO =⋅=⨯=V 又B PAD P ABD V V --=，即1133PAD ABD S h S PE ⋅=⋅V V ，所以ABD PADS PE h S ⋅==VV =，即点B 到平面ADP19．(1)0.41.7ˆ12=+yt ，预测2023年5月份参与竞拍的人数为3.73万人(2)（i ） 3.5x =，2 1.7s =；（ii ）预测竞拍的最低成交价为4.943万元【分析】（1）由已知公式求得线性回归方程，6t =代入回归方程可得预测值；（2）（i ）由均值与方差公式计算出均值与方差；（ii ）由预测值求得报价在最低成交价以上人数占总人数比例，然后由正态分布的性质求得预测竞拍的最低成交价．【详解】（1）11(12345)3,(1.7 2.1 2.5 2.8 3.4) 2.555t y =++++==++++=，55211149162555, 1.7 4.27.511.21741.6,ii i i i tt y ===++++==++++=∑∑，241.653 2.5ˆˆ0.41, 2.50.413 1.275553ba -⨯⨯∴===-⨯=-⨯，y 关于t 的线性回归方程0.41.7ˆ12=+y t 2023年5月份对应6t =，所以0.416 1.27 3.73ˆ=⨯+=y所以预测2023年5月份参与竞拍的人数为3.73万人.（2）（i ）由题意可得：1.50.12.50.33.50.34.50.155.50.16.50.05 3.5x =⨯+⨯+⨯+⨯+⨯+⨯=22222(1.5 3.5)0.1(2.5 3.5)0.3(3.5 3.5)0.3(4.5 3.5)0.15s =-⨯+-⨯+-⨯+-⨯22(5.5 3.5)0.1(6.5 3.5)0.05 1.7+-⨯+-⨯=（ii ）2023年5月份实际发放车牌数是5000，设预测竞拍的最低成交价为a 万元，根据竞价规则，报价在最低成交价以上人数占总人数比例为5000100%13.40%37300⨯≈根据假设报价X 可视为服从正态分布()22,, 3.5, 1.7, 1.3===≈N μσμσσ，令 3.51.3--==X X Y μσ，由于( 1.11)0.8660<=P Y ，1( 1.11)0.1340P Y ∴-<=，3.5() 1.110.86601.3a P Y a P Y -⎛⎫∴<=<== ⎪⎝⎭，所以 3.5 1.111.3a -=得 4.943=a ，所以预测竞拍的最低成交价为4.943万元．20．(1)1-(2)证明见解析【分析】(1)利用导数法求函数最值的步骤解求解；(2)根据题意构造函数()()()2F x f x f x =--，()0,1x ∈.对函数求导，利用导函数的正负判断函数的单调性，进而利用函数的最值得出()()212f x f x >-，再结合（1）中函数的单调性即可得证.【详解】（1）由题意可知：函数()ln 2f x x x =--的定义域为：()0,∞+.则()11f x x'=-，令()0f x '=，解得1x =.当()0,1x ∈，()0f x '<，函数()f x 单调递减；当()1,x ∈+∞，()0f x ¢>，函数()f x 单调递增.所以1x =为极小值点，且()()min 11f x f ==-.所以函数()f x 的最小值为1-.（2）根据题意可知：()()12f x f x =，根据（1）设101x <<，21x >，构造函数()()()2F x f x f x =--，()0,1x ∈.()()()()()221202x F x f x f x x x -'''=+-=<-，所以()F x 在()0,1上单调递减.则有()()10F x F <=，也即()()1120f x f x -->.因为()()12f x f x =，所以()()2120f x f x -->，也即()()212f x f x >-因为121x ->，21x >，由（1）可知()f x 在()1,+∞上单调递增，所以212x x >-，也即122x x +>.由已知21x >，所以1223x x +>.21．(1)2211612x y +=；(2)证明见解析．【分析】（1）根据离心率的定义和椭圆定义求得,a c ，再计算出b 后得椭圆方程；（2）设()()1122,,,M x y N x y ，直线方程代入椭圆方程，利用韦达定理求得中点,R S 的坐标，当直线PQ 斜率存在时，设直线:PQ y mx n =+，点,R S 在直线PQ 上，代入整理得12,k k 是一个一元二次方程的根，由韦达定理得12k k ，从而得出,m n 关系，得出直线PQ 过定点E ，再确定直线PQ 斜率不存在时也过这个定点E ，然后结合该定点得出三角形面积比．【详解】（1）依题意得12622c a a⎧=⎪⎨⎪+=⎩，则4,2,a c =⎧⎨=⎩则22212b a c =-=，所以椭圆C 的方程为2211612x y +=；（2）直线()11:2l y k x =-，设()()1122,,,M x y N x y ，由122(2)11612y k x x y =-⎧⎪⎨+=⎪⎩得()2222111341616480k x k x k +-+-=，所以2112211634k x x k +=+，211221164834k x x k -=+，且0∆>，则中点211221186,3434k k R k k ⎛⎫- ⎪++⎝⎭，同理可算222222286,3434k k S k k ⎛⎫- ⎪++⎝⎭①当直线斜率存在时，设直线:PQ y mx n =+，点,R S 在直线PQ 上，点,R S 坐标代入整理得()()21122284630,84630,m n k k n m n k k n ⎧+++=⎪⎨+++=⎪⎩易知12,k k 为方程()284630m n k k n +++=的两个根，则123284n k k m n==-+，所以1611n m =-，所以直线16:11PQ y mx m =-，则直线恒过点16,011E ⎛⎫⎪⎝⎭②当直线的斜率不存在时，由对称性可知12k k =-，由122k k =-，不妨设12k k ==，所以221222128816343411k k k k ==++，直线16:11PQ x =过16,011⎛⎫⎪⎝⎭，根据①②可知，直线PQ 恒过点16,011E ⎛⎫⎪⎝⎭，因为PQA △的面积11212S AE y y =⋅-，PQB △的面积21212S BE y y =⋅-，所以121641511167411AE S S BE +===-.【点睛】方法点睛：椭圆中的直线过定点问题的解决方法：斜率存在时，设出直线方程为y mx n =+，根据已知条件确定,m n 的关系后，由直线方程得出定点坐标．本题中，动直线PQ 是由点,R S 确定的，因此可由已知直线12,l l 确定,R S 的坐标，再把坐标代入所设直线方程，发现12,k k 是一个一元二次的两根，这样可由韦达定理求得,m n 的关系，得出结论．22．(1)()22441x y x -=≥(2)4m <<【分析】（1）在曲线C 的参数方程中消去参数t ，可得出曲线C 的普通方程，利用基本不等式求出x 的取值范围，即可得解；（2）求出直线l 的普通方程，分析可知直线l 与双曲线2214y x -=的右支有两个交点，将直线l 与双曲线2214y x -=方程联立，利用直线与双曲线的位置关系可得出关于m 的不等式组，即可解得实数m 的取值范围.【详解】（1）因为112122t t x ⎛⎫=+≥ ⎪⎝⎭()222222221422,2441122,2t t t t x x y x y ⎧=++⎪⎪-=≥⎨⎪=+-⎪⎩则则曲线的普通方程为()22441x y x -=≥（2）cos 2sin 10m ρθρθ+-=则210mx y +-=由得()22210,1,14mx y y x x +-=⎧⎪⎨-=≥⎪⎩得()22162170m x mx -+-=有两个不等正根()22222160,Δ468160,20,1617016m m m m m m ⎧-≠⎪=+->⎪⎪⎨->⎪-⎪⎪->-⎩则4m <<23．(1)[)10,2,3∞∞⎛⎤--⋃+ ⎥⎝⎦(2)证明见解析【分析】（1）利用零点分段法分类讨论，分别求出不等式的解集，即可得解；（2）利用绝对值三角不等式求出()f x 的最小值，即m 的值，再利用柯西不等式证明即可.【详解】（1）不等式24410x x ++-≥，所以224410x x x ≤-⎧⎨---+≥⎩，解得103x ≤-，或2424410x x x -<<⎧⎨+-+≥⎩，解得24x ≤<，或424410x x x ≥⎧⎨++-≥⎩，解得4x ≥，所以原不等式解集为[)10,2,3∞∞⎛⎤--⋃+ ⎥⎝⎦.（2）()244242f x x x x x x =++-=++-++()2406x x ≥+--+=，当且仅当2x =-时取得，即min ()6f x =，所以6a b c m ++==，因为()1112a b c a b b c a c ⎛⎫++⨯++ ⎪+++⎝⎭()111a b b c c a a b b c c a ⎛⎫=+++++++ ⎪+++⎝⎭()()()111a b b c c a a b b c c a ⎛⎫=+++++++⎡⎤ ⎪⎣⎦+++⎝⎭222222⎡⎤⎡⎤⎢⎥=++++⎢⎥⎣⎦⎢⎥⎣⎦2≥()21119=++=，当且仅当12a b c ===时取等号，所以()1119922a b b c c a a b c m ++≥=+++++成立.。

(完整版)高三数学文科模拟试题.doc

数学（文）模拟试卷1.复数 z2i （ i 为虚数单位）在复平面内对应的点所在象限为（） i 1第二象限B.第一象限C.第四象限D.第三象限2.已知命题 p ： x 0 ，总有 ( x1)e x 1，则 p 为（）A ． x 0 0 ，使得 (x 0 1)e x 01B ． x 0 ，总有 ( x x1 1)e C ． x 00 ，使得 (x 0 1)e x 01D ． x0 ，总有 ( x 1)e x 13.已知集合 A 1,0,1,2,3 , Bx x 2 2x0 , 则 A I B（）A ． {3}=B.{2,3}C.{ － 1,3}D.{1,2,3}4.如下图所示是一个几何体的三视图，则这个几何体外接球的表面积为（）A ． 8πB ． 16π C. 32 π D ． 64π5.秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法，即使在现代，它依然是利用计算机解决多项式问题的最优算法．如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例，若输入 n,x 的值分别为 3,4 则输出 v 的值为（）A ． 399B ． 100C ． 25D ． 66.要得到函数 f (x)2sin x cos x 的图象，只需将函数 g (x)cos 2 x sin 2 x 的图象（）A ．向左平移π个单位B ．向右平移π个单位 C ．向左平移π个单位 D ．向右平移 π个单位2244第 1 页，总 9 页x y 1 07.若变量 x ， y 满足约束条件 2 x y1 0 ，则目标函数 z2 x y 的最小值为（）x y1 0A ． 4B ．－ 1C. － 2 D ．－ 38.在正方形内任取一点，则该点在此正方形的内切圆外的概率为（）4 B ．C ．3 ． 2A ．4 D 4449.三棱锥 P ABC 中， PA 面 ABC ， ACBC ， AC BC1, PA3 ，则该三棱锥外接球的表面积为A ． 5B ．2C ． 20D ．7210.已知是等比数列 ,若,数列的前项和为 ,则为（）A ．B ．C ．D ．log 2 x, x 0, 11.已知函数 f (x)( 1 )x, x则 f ( f ( 2)) 等于（）0,2A ． 2B ．－ 21D ．－ 1C ．22412.设双曲线x y1( a 0，b 0) 的左、右焦点分别为 F 1 、F 2，离心率为 e ，过 F 2 的直线与双曲线的2b 2a右支交于 A 、 B 两点，若 △F 1AB 是以 A 为直角顶点的等腰直角三角形，则2（）e A ． 3 2 2 B ． 5 2 2 C ． 1 2 2 D ． 4 2 2 二．填空题13.已知平面向量 a , b 的夹角为2，且 | a | 1 , | b | 2 ，若 ( a b) (a 2b) ，则_____．314.曲线 y=2ln x 在点 (1,0)处的切线方程为 __________．x 22315.已知椭圆y1(a b 0) 的左、右焦点为 F 1，F 2，离心率为，过 F 2 的直线 l 交椭圆 C 于 A ， C ：2b 23aB 两点．若 AF 1 B 的周长为 4 3 ，则椭圆C 的标准方程为.16.以 A 表示值域为R 的函数组成的集合，B 表示具有如下性质的函数( x) 组成的集合：对于函数(x) ，存在一个正数M ，使得函数(x) 的值域包含于区间[ M , M ] 。

高三文科数学模拟题二十

高三数学模拟试题（二十）一、选择题（5×10=50分）1．已知0,0a b >>，且12(2)y a b x =+为幂函数，则ab 的最大值为( )A ．18 B ．14 C ．12 D ．342．有60件产品，编号为01至60，现从中抽取5件检验，用系统抽样的方法所确定的抽样编号是（）A ．5,10,15,20,25B ．5,12,31,39,57C ．5,15,25,35,45D ．5,17,29,41,53 3．已知复数1i z =-，z 为z 的共轭复数，则下列结论正确的是（）A ．1i z =--B ．1+i z =-C ．2z =D．z =4．已知向量()2,1p =-,(),4q x =,且p q ⊥，则p q +的值为（）AB ．5 CD ．135．已知()⎪⎭⎫ ⎝⎛+=32sin πx x f ，为了得到()x x g 2sin =的图象，则只要将()x f 的图象（）A ．向右平移6π个单位长度 B ．向右平移12π个单位长度C ．向左平移6π个单位长度 D ．向左平移12π 个单位长度6．如图，正方体1111ABCD A BC D -中，E 是棱11B C 的中点，动点P 在底面ABCD 内，且11PA A E =，则点P 运动形成的图形是（）A ．线段B ．圆弧C ．椭圆的一部分D ．抛物线的一部分7．已知x 、y 满足约束条件2010220x y x y -≤⎧⎪-≤⎨⎪+-≥⎩，则z x y =-的取值范围为( )A ．[]2,1--B ．[]2,1-C ．[]1,2-D ．[]1,28．直线022=+-y x 经过椭圆(a by a x 12222=+＞b ＞)0的一个焦点和一个顶点，则该椭圆的离心率为（）A ．552 B ．21 C ．55 D ．329．已知数列{}n a 的前n 项和为n S ，22-=n n a S ，则4a =（）A ．64B ．32C ．16D ．8 10．设函数3x y =与2)21(-=x y 的图像的交点为),(00y x ，则0x 所在的区间是（）A ．)1,0(B ．)2,1(C ．)3,2(D ．)4,3(（选做）已知S n 是等差数列{a n }(n ∈N *)的前n 项和，且S 6>S 7>S 5，有下列四个命题，假命题．．．的是( ) A ．公差d <0 B ．在所有S n <0中，S 13最大 C ．满足S n >0的n 的个数有11个 D ．a 6>a 7 二、填空题（5×5=25分）12．已知函数()f x 是以5为周期的奇函数，且(3)2f -=，则(2)f -=13．执行框图，会打印出一列数，这个数列的第3项是 .14．已知ABC ∆的内角C B A 、、所对的边分别为,,a b c ，且2a =，3b =，4cos 5B =．则sin A 的值为 15．观察下列等式：12133+=； 781011123333+++=； 16171920222339333333+++++=； …则当m n <且,m n ∈N 表示最后结果.313232313333n n m m ++--++++= （最后结果用,m n 表示最后结果）三、解答题（75分）16．（本题满分13分）已知向量)0)(1,cos sin 3(),1,cos 2(>+=-=ωωωωx x x ，函数x f ⋅=)(的最小正周期为π．（1）求函数)(x f 的表达式及最大值；（2）若在0,2x π⎡⎤∈⎢⎥⎣⎦上a x f ≥)(恒成立，求实数a 的取值范围17．（本小题满分13分）设等差数列{}n a 满足246=S ，109a =-。

高三文科数学模拟题七

高三数学模拟试题（七）一、选择题（5×10=50分）1．已知a ＋2ii＝b ＋i(a ，b ∈R )，则a ＋b ＝（）A ．－1B ．1C ．2D ．32．如果命题“非p 或非q ”是假命题，则在下列各结论中正确的是（） ① 命题“p 且q ”是真命题； ② 命题“p 且q ”是假命题；③ 命题“p 或q ”是真命题； ④ 命题“p 或q ”是假命题；A ．① ③B ．② ④C ．② ③D ．① ④3．在等比数列{}n a 中，5113133,4a a a a ⋅=+=，则155aa =（）A ．3B ．13C ．3或13D ．133--或4．若椭圆)0(12222>>=+b a b y a x 的离心率为23，则双曲线12222=-by a x 的渐近线方程为（） A ．x y 2±= B ．x y 41±= C ．x y 4±= D ． x y 21±=5．若⎪⎭⎫ ⎝⎛∈20πα，，且412cos sin 2=+αα，则αtan 的值等于（）A ．22 B ．33 C ．2 D ．36．已知a ，b ，c 满足c ＜b ＜a ，且ac ＜0.那么下列选项中一定成立的是（） A ．cb 2＜ab 2 B ．c (b －a )＜0 C ．ab ＞ac D ．ac (a －c )＞07．函数⎪⎭⎫⎝⎛+=34cos πx y 的图象的两条相邻对称轴间的距离为（） A ．8π B ．4π C ．2πD ．π 8．直线1y kx =+与曲线3y x ax b =++相切于点(1,3),A 则b 的值为（）A ．3B ．3-C ．5D ．5-9．在正方体1111ABCD A BC D -中，1A B 与平面11BB D D 所成的角的大小是（）A ．90°B ．30°C ．45°D ．60°10．已知y x 、满足约束条件500,3x y x y x -+≥⎧⎪+≥⎨⎪≤⎩则23x y z x ++=+的最小值为（）A ．13 B ．136 C ．4 D ．23- 二、填空题（5×5=25分）11．已知平面向量(1,2),(1,)//,23a b m a b a b ==-+=且则 12．已知()x f 是定义在[]2,2-上的函数，且对任意实数)(,2121x x x x ≠，恒有1212()()0f x f x x x -<-，且()x f 的最大值为1，则满足()1log 2<x f 的解集为 13．若某程序框图如图所示，则该程序运行后输出的值是 14．已知直线:30l x y +-=与圆22:(1)(2)2,C x y -++= 则圆C 上各点到l 距离的最大值为____ 15．设562)(sin ),2,0(+-=∈x xy θπθ且函数的最大值为16,则=θ三、解答题（75分）16．（本题满分13分）春节期间，小乐对家庭中的六个成员收到的祝福短信数量进行了统计：（1）若,138=x 求a（2）在六位家庭成员中任取两位，收到的短信数均超过100的概率为多少？(第13题图)17．（本小题满分13分）已知三次函数()c bx ax x x f +++=23在1=x 和1-=x 时取极值，且()42-=-f（1）求函数()x f y =的表达式（2）求函数()x f y =的单调区间和极值18．（本小题满分13分）在ABC ∆中，已知点(5,2),(7,3)A B -，且边AC 的中点M 在y 轴上，边BC 的中点N 在x 轴上．（1）求点C 的坐标；（2）求直线MN 的方程．19．（本小题满分12分）已知等差数列}{n a 的前n 项和为n S ，且.62,546-=-=S a（1）求}{n a 通项公式；（2）求数列|}{|n a 的前n 项和.n T20．（本小题满分12分）已知四边形ABCD 为直角梯形，090,//,2,1ABC AD BC AD AB BC ∠====．沿AC 将ABC ∆折起，使点B 到点P 的位置，且平面PAC ⊥平面ACD ．（1）证明：DC ⊥平面APC ；（2）求棱锥A PBC -的高．21．（本小题满分12分）已知椭圆C ：22221(0)x y a b a b+=>>1F ，2F 是它的左，右焦点．（1）若P C ∈，且021=⋅PF PF ，12||||4PFPF ⋅=，求1F 、2F 的坐标；（2）在（1）的条件下，过动点Q 作以2F 为圆心、以1为半径的圆的切线QM （M 是切点），且使1QF =，求动点Q 的轨迹方程高三数学模拟试题（七）参考答案BACDD CBABA 11．(1,2)-- 12．⎥⎦⎤⎝⎛4,41 13．910 14．15．6π16．(1)60 (2)1517．（1）()232--=x x x f （2）增区间：(]1,-∞-，[)+∞,1；减区间：[]1,1-。

高三文科数学模拟题十五

高三数学模拟试题（十五）一、选择题（5×10=50分）1．若全集{1,2,3,4}U =且{2}U C A =，则集合A 的真子集共有（）A ．3个B ．5个C ．7个D ．8个2．在平面直角坐标系中，已知向量)1,2(),1,3(=-=，且7=n ，那么⋅等于（）A ．2或2-B ．2C ．2-D ．03．过圆()()22125x y -++=上一点()3,1M -的切线方程是（）A ．250x y +-=B ．270x y +-=C ．210x y +-=D ．250x y --=4．已知等差数列{}n a 中, 315,a a 是方程2610x x --=的两根, 则7891011a a a a a ++++等于（）A ．18B ．18-C ．15D ．125．已知,x y R ∈，i 为虚数单位，且1xi y i -=-+，则(1)x yi ++的值为（）A ．2B ．2i -C ．4-D ．2i6．已知一工厂生产某原料的生产成本y （万元）为产量x （千吨）之间的关系为1400++=x x y ,则生产成本最少时该工厂的产量x 为 ( )A ．17千吨B ．18千吨C ．19千吨D ．20千吨7．—空间几何体的三视图如图所示，则此空间几何体的直观图为（）8．对任意实数θ，则方程22sin 4x y θ+=所表示的曲线不可能是( )A ．抛物线B ．双曲线C ．椭圆D ．圆9．已知,x y 满足不等式组242y x x y y ≤⎧⎪+≤⎨⎪≥-⎩，则22222z x y x y =++-+的最小值为（）A ．95B ．2C ．3 D10．已知函数()2,f x x bx c =++其中04,04b c ≤≤≤≤.记函数满足()()21213f f ≤⎧⎪⎨-≤⎪⎩的事件为A ，则事件A 的概率为（）A ．58 B ．12 C ．38 D ．14二、填空题（5×5=25分）11．某大学对1000名学生的自主招生水平测试成绩进行统计，得到样本频率分布直方图如图所示，现规定不低于70分为合格，则合格人数是12．若函数a x x x f +-=3)(3有三个不同的零点，则实数a 的取值范围是 13．如果函数2()3f x x bx c =++是偶函数，则b =14．已知直线0ax by c ++=与圆22:1O x y +=相交于B A 、两点，且AB = 则OA OB ⋅=15．点P 在正方体1111D C B A ABCD -的面对角线1BC 上运动，给出下列四个命题： ①三棱锥PC D A 1-的体积不变；②P A 1 //平面1ACD ；③1DP BC ⊥；④平面1PDB ⊥平面1ACD 。

高三文科数学模拟题一

高三数学模拟试题（一）一、选择题（5×10=50分）1. 设集合{}2|230A x x x =--<，{}|14B x x =≤≤,则AB =（）A ．{}|13x x ≤<B ．{}|13x x ≤≤C ．{}|34x x <≤D ． {}|34x x ≤≤ 2．若命题:|1|4p x +≤，命题2:56q x x <-，则p q ⌝⌝是的（）A ．必要不充分条件B ．充分不必要条件C ．充要条件D ．既不充分也不必要条件 3．已知向量(1,),(1,),a n b n a b b ==--若2与垂直，则||a =（） A ．1B ．2C ．2D ．44．过点)2,1(与圆221x y +=相切的直线方程是（） A ．1x =B ．3450x y -+=C ．34501x y x -+==或D ．54301x y x -+==或5．已知函数⎩⎨⎧=x x x f 3log )(2 00≤>x x ，则))41((f f = ( )A ．9B ．19C ．9-D ．91-6．ABC ∆中,三边之比4:3:2::=c b a ，则最大角的余弦值等于（） A ．41 B ．87 C ．21- D ．41-7．已知焦点在x 轴上的椭圆22219x y a +=的离心率是12e =，则a 的值为（） A ．23 B ．3 C ．32 D ．12 8．若不等式4)2(2)2(2<-+-x a x a 的解集为R ,则实数a 的取值范围是( ) A ．)2,2(- B ．]2,2(- C ．),2()2,(+∞--∞ D ．)2,(-∞9．函数236()(04)1x x f x x x ++=≤≤+的最小值为（） A ．2 B ．1 C ．6 D ．510．已知函数()2sin()f x x ωϕ=+(0,0π)ωϕ><<的图象如图所示，则ω等于( )A ．13 B ．1 C ．32D ．2二、填空题（5×5=25分）11．若点(),9a 在函数3xy =的图象上，则tan6a π= 12．经过圆2220x x y ++=的圆心C ，且与直线0x y +=垂直的直线方程是13．设y x ,满足约束条件⎪⎩⎪⎨⎧≤-≥-≥+,1,1,1x y x y x 则y x z 2-=的最小值是_______14．已知数列{}n a 为等差数列，且28143,a a a ++=则()2313log a a +=_______ 15．若扇形的面积和弧长都是10，则这个扇形中心角的弧度数是____三、解答题（75分）16．（本题满分13分）已知集合{}|||2A x x a =-<，26|12x B x x +⎧⎫=>⎨⎬+⎩⎭. （1）求集合A 和集合B（2）若A B R =，求a 的取值范围17．（本小题满分13分）等比数列{}n a 中，已知142,16a a == （1）求数列{}n a 的通项公式（2）若35,a a 分别为等差数列{}n b 的第3项和第5项，试求数列{}n b 的通项公式及前n 项和n S18．（本小题满分12分）已知向量a =(sin ,cos())x x π-，b =(2cos ,2cos )x x ，函数()1f x =⋅a b+.（1）求π()4f -的值；（2）求()f x 在π0,2⎡⎤⎢⎥⎣⎦上的最大值和最小值，并求出相应的x 的值.19．（本小题满分13分）如图所示，已知三棱锥BPC A -中，,,AP PC AC BC M ⊥⊥为AB 中点D 为PB 中点，且PMB ∆为正三角形。

高三数学试卷模拟题文科版

一、选择题（本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1. 已知函数f(x) = x^2 - 2ax + 1，若f(x)的图像关于x=a对称，则a的值为（）A. 0B. 1C. -1D. 22. 下列各式中，绝对值最小的是（）A. |2x-3|B. |3x-2|C. |x-2|D. |x+2|3. 若复数z满足|z+2i|=|z-1|，则z的实部为（）A. 1B. -1C. 2D. -24. 已知数列{an}的通项公式为an = 3n - 2，则数列{an}的前n项和S_n为（）A. n(n+1)B. n(n-1)C. 3n(n+1)D. 3n(n-1)5. 已知向量a = (2, 3)，向量b = (-1, 2)，则向量a·b的值为（）A. -1B. 1C. 0D. 56. 若等差数列{an}的首项为2，公差为3，则第10项a_10为（）A. 25B. 28C. 31D. 347. 已知函数f(x) = log2(x+1)，若f(2x-1) = 3，则x的值为（）A. 3B. 4C. 5D. 68. 在△ABC中，若∠A = 60°，∠B = 45°，则∠C的度数为（）A. 75°B. 90°C. 105°D. 120°9. 已知等比数列{bn}的首项为b_1，公比为q，若b_3 = 8，b_6 = 32，则b_1的值为（）A. 1B. 2C. 4D. 810. 若函数f(x) = x^3 - 3x + 2在x=1处取得极值，则该极值为（）A. 0B. -1C. 1D. 2二、填空题（本大题共5小题，每小题5分，共25分。

）11. 若复数z满足|z+1|=|z-1|，则z在复平面上的几何意义是______。

12. 数列{an}的前n项和S_n = n^2 + n，则数列{an}的通项公式an = ______。

高三文科数学模拟题二十一

AB D C高三数学模拟试题（21）一、选择题（5×10=50分）1．已知集合{0,1}A=,{1,0,3}B a=-+，且A B⊆，则a等于（）A．1 B．0 C．2-D．3-2．已知z是复数，i是虚数单位，()z i-1在复平面中对应的点为P，若P对应的复数是模等于2的负实数，那么=z( )A．i--1B．i+-1C．i-1D．i-3．已知2sin cos9,tansin3cosααααα+=-则等于( )A．4-B．41-C．14D．44．下列命题的否定为假命题的是（）A．22,sin cos1x R x x∀∈+=B．任意一个四边形的四个顶点共圆C．所有能被3整除的整数都是奇数D．2,220x R x x∃∈++≤5．某雷达测速区规定：凡车速大于或等于hkm/70的汽车视为“超速”，并将受到惩罚。

如图是某路段的一个检测点对200辆汽车的车速进行检测所得的结果的频率分布直方图，则从图中可以看出将被处罚的汽车大约有（）A．30辆B．40辆C．60辆D．80辆6．曲线xxy2313-=在1=x处的切线的倾斜角是（）A．43πB．6πC．4πD．3π7．已知m，n为两条不同的直线，α、β为两个不同的平面，则下列命题中正确的是A．若l m⊥,l n⊥,且,m nα⊂,则lα⊥. B．若α⊥nnm,//，则α⊥mC．若平面α内有不共线的三点到平面β的距离相等，则βα//.D．若nmm⊥⊥,α，则α//n8．已知数列{}n a为等差数列，若2163,12a a a=+=，则789a a a++= （）A．27 B．36C．45 D．639．设函数3()f x x x=+，x R∈. 若当02πθ<<时，不等式0)1()sin(>-+mfmfθ恒成立，则实数m的取值范围是（）.A．(,1]-∞B．[1,)+∞C．1(,1)2D．1(,1]210．若某程序框图如图所示，则该程序运行后输出的值是（）A．2 B．3 C．4D．5（选做）已知O是△ABC外接圆的圆心，A、B、C为△ABC的内角，若mBCCB⋅=+2sincossincos，则m的值为( )A．1 B．sin A C．cos A D．tan A二、填空题（5×5=25分）11．函数)2sin(sin)(xxxf-=π的最小正周期为12．2012年黄冈中学春季球类运动会的篮球决赛需要两名学生裁判，经过两轮筛选后有来自高二的3名同学和高三的3名同学入围。

高三数学假期作业-文科模拟测试题2

阳历2010年月日星期当你感到悲哀痛苦时，最好是去学些什么东西。

学习会使你永远立于不败之地。

寒假作业基础自测1. 复数21i+的虚部是A . 1B . i -C . iD . -12. 若全集U R =，集合M ={x |-2≤x ≤2}，N ={x |23x x -≤0}，则M ∩(U C N )＝A . [-2，0]B . [-2,0)C . [0，2]D .（0，2］ 3. 下列函数，在其定义域内既是奇函数又是增函数的是 A . 3y x x =+ (x ∈R ) B . 3x y = (x ∈R ) C . 2log y x =- (x ＞0, x ∈R ) D . 1y x=-(x ∈R ,x ≠0) 4. 设0,0a b >>,则以下不等式中不一定成立的是A .a bb a+≥2 B . ln(1)ab +≥0 C . 222a b ++≥22a b + D . 33a b +≥22ab 5. 已知一空间几何体的三视图如右图所示，它的表面积是A . 4+B . 2C . 3D . 3 6. 若3sin 5α=, (,)22ππα∈-,则5cos()4πα+=A . 10-B . 10-C . 10D . 10第5题图能力提升1.已知点A (2,1),B (0,2),C (-2,1), O (0,0).给出下面的结论：① OC ∥BA；② OA ⊥AB；③ OA OC + = OB ；④ 2AC OB OA =- .其中正确结论的个数是A . 0个B . 1个C . 2个D . 3个 2. 函数||xx y a x=⋅ (1a >)的图象的基本形状是3. 设,a b 是两条不同的直线，,αβ是两个不同的平面，则能得出a ⊥b 的是 A . a ⊥α，b ∥β，α⊥β B . a ⊥α，b ⊥β，α∥β C . a ∥α，b ⊥β，α∥β D . a ∥α，b ∥β，α⊥β4. 抛物线24y x =上一点A 的横坐标为4，则点A 与抛物线焦点的距离为 .5. 等差数列{n a }中，若1479a a a ++=，3693a a a ++=，则{n a }的前9项的和9S = .拓展演练1.过椭圆22221x y a b += (0a b >>)的焦点垂直于x 轴的弦长为2a ，则双曲线22221x y a b-=的离心率e 的值是A B C D . 542. 观察图中各正方形图案，每条边上有n (n ≥2)个圆点，第n个图案中圆点的个数是n a ，按此规律推断出所有圆点总和n S 与n 的关系式为 A .222n S n n =- B .22n S n = C .243n S n n =- D .222n S n n =+3. 图1是某市参加2008年高考的学生身高条形统计图，从左到右的各条形图表示学生人数依次记为A 1、A 2、…，A 10[如A 2表示身高（单位：cm ）在[150，155)内的人数]。

高三文科数学模拟题二

高三数学模拟试题（二）一、选择题（5×10=50分）1．在等差数列{}n a 中，,2,41==d a 则=3a （）A ．4B ．6C ．8D ．102．函数lg y x = ）A ．{|0}x x >B ．{|01}x x <≤C ．{|1}x x >D ．{|1}x x ≥3．要得到x x y 2cos 2sin +=的图象，只需将x y 2sin 2=的图象（）A ．向左移4π个单位B ．向左平移8π个单位C ．右平移4π个单位D ．向右平移8π个单位4．两平行平面之间的距离等于12，一直线与它们相交且夹在两平面间的线段长等于24，则该直线与这两个平行平面所成角等于（）A ．060 B ．090 C ．030 D ．045 5．设1.52.42.46.0,7.0,6.0===c b a ，则c b a ,,大小关系正确的是（）A ．c b a >>B ．a b c >>C ．a c b >>D ．c a b >>6．过抛弧线24y x =的焦点作直线l 交抛物线于A B 、两点，若线段AB 中点的横坐标为3，则AB 等于（）A ．10B ．8C ．6D ．47．已知(1,3)a =-，OA a b =-，OB a b =+，若△AOB 是以O 为直角顶点的等腰直角三角形，则△AOB 的面积为（）A ．4B ．2C ．D 8．函数()sin(2)f x x =-的一个单调增区间是（）A ．⎥⎦⎤⎢⎣⎡-4,4ππ B ．⎥⎦⎤⎢⎣⎡-2,2ππ C ．⎥⎦⎤⎢⎣⎡--2,23ππ D ．⎥⎦⎤⎢⎣⎡--4,43ππ9．函数x y cos =在点)23,6(π处的切线斜率为（） A ．21-B ．23 C ．22-D ．23-10．数列{}n a 定义如下：*12211,3,22()n n n a a a a a n N ++===-+∈，则11a =( )A ．91B ．110C ．111D ．133二、填空题（5×5=25分）11．已知向量(3,1)a =，(1,3)b =，(,7)c k =，若()a c -//b ，则k =12．若函数2()(1)f x x a x a a =+-+=为偶函数，则_____13．双曲线的中心在坐标原点，离心率等于2，一个焦点的坐标为()0,2，则此双曲线的方程是14．一直线l 被两直线0653:064:21=--=++y x l y x l 和截得的线段MN 的中点P 恰好是坐标原点，则直线l 的方程为15．函数)(x f 对于任意实数x 满足条件)(1)2(x f x f =+,若5)1(-=f ，则[])5(f f =___ 三、解答题（75分）16．（本小题满分13分）已知函数2()sin(2)cos .6f x x x π=-+（1）若()1,f θ=求θθcos sin 的值；（2）求函数()f x 的单调区间17．（本小题满分13分）已知{}n a 是等差数列，首项31=a ，公差为整数，前n 项和为n S ，数列{}n b 是等比数列，首项.20,12,123221=+==b S b a b 且（1）求{}n a 和{}n b 的通项公式.（2）令(),n n c n b n N +=⋅∈求{}n c 的前n 项和nTF E DB A P C18．（本小题满分12分）如图，在四棱锥ABCD P -中，底面ABCD 是正方形，PA ⊥平面ABCD ， E 是PC 中点，F 为线段AC 上一点. （1）求证：EF BD ⊥；（2）试确定点F 在线段AC 上的位置，使EF //平面PBD ，并说明理由.19．（本小题满分12分）设圆C 与两圆((22224,4x y x y ++=+=中的一个内切，另一个外切（1）求C 的圆心轨迹L 的方程（2）已知点),55M F ⎛ ⎝⎭，且P 为L 上动点，求||||||PF PM -的最大值及此时点P的坐标20．（本小题满分13分）设函数)()(23R x cx bx x x f ∈++=，已知)()()(x f x f x g '-=是奇函数．（1）求c b 、的值；（2）求)(x g 的单调区间与极值21．（本小题满分12分）为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层。

高三文科数学模拟题三

高三数学模拟试题（三）一、选择题（5×10=50分）1．设全集{}{}{}2,1,0,1,2,2,1,0,0,1,2U A B =--=--=则=B A C U )(( )A ．{}0B ．{}2,1--C ．{}0,1,2D ．{}1,22．等差数列}{n a 中，若39741=++a a a ，27963=++a a a ，则前9项的和9S 等于（） A ．99 B ．66 C ．144 D ．297 3．已知:1231,:(3)0p x q x x -<-<-<, 则p 是q 的什么条件（）A ．必要不充分B ．充分不必要C ．充要D ．既不充分也不必要4．已知函数)(x f y =是R 上的偶函数，且在(]0,∞-上是减函数，若)2()(f b f ≥，则实数b 的取值范围是（）A ．2≤bB ．2-≤b 或2≥bC ．2-≥b bD ．22≤≤-b 5．已知4sin ,sin cos 0,5θθθ=<则θ2sin 的值为（）A ．2524-B ．2512-C ．54- D ．25246．函数)1()1(2-+=x x y 在1=x 处的导数等于 ( )A ．1B ．2C ．3D ．47．已知点A （3,1）和B )6,4(-在直线023=+-a y x 的两侧，则的a 取值范围是（）A ．a ＜－7或 a ＞24B ．a ＜－24或 a ＞7C ．－7＜a ＜24D ．－24＜a ＜78．已知i 为虚数单位，复数121iz i +=-，则复数z 的虚部是（）A ．i 23B ．23C ．i 21-D ．21-9．在ABC ∆中，c b a 、、分别为角C B A 、、的对边，若2cos ,a b C =则此三角形一定是（）A ．等腰直角三角形B ．直角三角形C ．等腰三角形D ．等腰或直角三角形10．圆心在曲线2(0)y x x=>上，且与直线210x y ++=相切的面积最小的圆的方程为（） A ．22(1)(2)5x y -+-= B ．22(2)(1)5x y -+-= C ．22(1)(2)25x y -+-= D ．22(2)(1)25x y -+-=二、填空题（5×5=25分）11．函数322-+=x x y 的单调减区间为12．某个容量为100的样本的频率分布直方图见右图，则在区间[4,5)上的数据的频数．．为．13．如图，P 是椭圆192522=+y x 上的一点，F 是椭圆的左焦点，且)(21OF OP OQ +=，4||=则点P 到该椭圆左准线的距离为14．在ABC ∆中，角,,A B C 所对的边分别为,,,6a b c AB AC ⋅=，向量(cos ,sin )m A A =与向量(4,3)n =-相互垂直。

高三数学文科模拟考试 (含答案)

高三数学文科模拟考试 (含答案)高三模拟考试数学（文科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题），共4页，满分150分，考试时间120分钟。

考生作答时，请将答案涂在答题卡上，不要在试题卷和草稿纸上作答。

考试结束后，请将答题卡交回。

第Ⅰ卷（选择题，共60分）注意事项：请使用2B铅笔在答题卡上涂黑所选答案对应的标号。

第Ⅰ卷共12小题。

1.设集合A={x∈Z|x+1<4}，集合B={2,3,4}，则A∩B的值为A.{2,4}。

B.{2,3}。

C.{3}。

D.空集2.已知x>y，且x+y=2，则下列不等式成立的是A.x1.D.y<-113.已知向量a=(x-1,2)，b=(x,1)，且a∥b，则x的值为A.-1.B.0.C.1.D.24.若___(π/2-θ)=2，则tan2θ的值为A.-3.B.3.C.-3/3.D.3/35.某单位规定，每位职工每月用水不超过10立方米的，按每立方米3元收费；用水超过10立方米的，超过的部分按每立方米5元收费。

某职工某月缴水费55元，则该职工这个月实际用水为（）立方米。

A.13.B.14.C.15.D.166.已知命题p：“存在实数x使得e^x=1”，命题q：“对于任意实数a和b，如果a-1=b-2，则a-b=-1”，下列命题为真的是A.p。

B.非q。

C.p或q。

D.p且q7.函数f(x)满足f(x+2)=f(x)，且当-1≤x≤1时，f(x)=|x|。

若函数y=f(x)的图象与函数y=log_a(x)（a>0且a≠1）的图象有且仅有4个交点，则a的取值集合为A.(4,5)。

B.(4,6)。

C.{5}。

D.{6}8.已知函数f(x)=sin(θx)+3cos(θx)（θ>0），函数y=f(x)的最高点与相邻最低点的距离是17.若将y=f(x)的图象向右平移1个单位得到y=g(x)的图象，则函数y=g(x)图象的一条对称轴方程是A.x=1.B.x=2.C.x=5.D.x=6删除了格式错误的部分，对每段话进行了简单的改写，使其更流畅易懂。

高三文科数学第二次月考模拟训练(6)

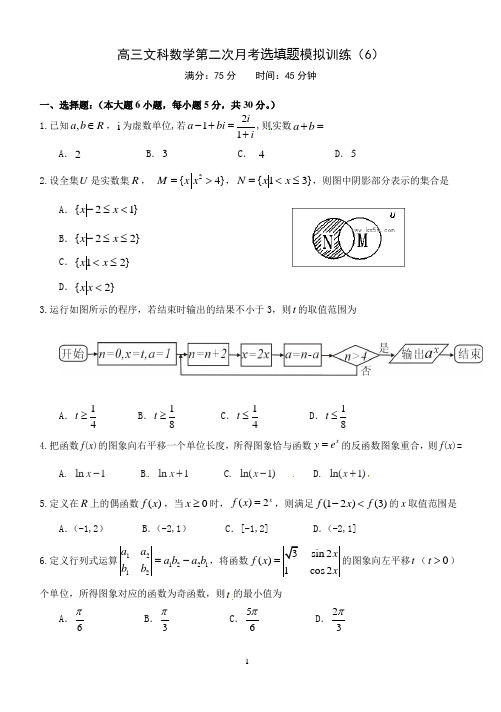
高三文科数学第二次月考选填题模拟训练（6）满分：75分时间：45分钟一、选择题：（本大题6小题，每小题5分，共30分。

） 1.已知,a b R ∈，i 为虚数单位,若211ia bi i-+=+,则实数a b += A ．2 B ．3 C ． 4 D ．52.设全集U 是实数集R ， 2{4}M x x =>，}31{≤<=x x N ，则图中阴影部分表示的集合是A ．}12{<≤-x xB ．}22{≤≤-x xC ．}21{≤<x xD ．}2{<x x3.运行如图所示的程序，若结束时输出的结果不小于3，则t 的取值范围为A ．14t ≥B ．18t ≥C ．14t ≤D ．18t ≤ 4.把函数f (x )的图象向右平移一个单位长度，所得图象恰与函数xy e =的反函数图象重合，则f (x )=A. ln 1x -B. ln 1x +C. ln(1)x -D. ln(1)x +5.定义在R 上的偶函数)(x f ，当0x ≥时，()2xf x =，则满足(12)(3)f x f -<的x 取值范围是A ．（-1,2）B ．（-2,1）C ．[-1,2]D ．（-2,1]6.定义行列式运算12122112a a a b a b b b =-，将函数sin 2()cos 2x f x x=的图象向左平移t （0t >）个单位，所得图象对应的函数为奇函数，则t 的最小值为 A ．6π B ．3π C ．56π D ．23π二、填空题：（本大题共5小题，每小题5分，满分25分） 7.方程 2cos()4x π-=在区间()0,π内的解为8.曲线sin y x x =+在点()0,0处的切线方程是 .9.计算：013ln 8lg 2lg5e ⎛+++ ⎝=10.在锐角ABC V 中,4,3AC BC ==，三角形的面积等于AB 的长为___________. 11.如果x x cos sin +>λ对一切R x ∈都成立，则实数λ的取值范围是． 12.不透明的袋子中装有除颜色不同其它完全一样的黑、白小球共10只，从中任意摸出一只小球得到是黑球的概率为25．则从中任意摸出2只小球，至少得到一只白球的概率为． 13.已知x 是7,6,5,,3,2,1x 这7个数据的中位数，且y x -,,2,12这四个数据的平均数为1，则xy 1-的最小值为． 14.设ω>0，若函数)(x f =sin 2x ωcos 2x ω在区间[－3π，4π]上单调递增，则ω的范围是________． 15.下列四个命题：①11(0,),()()23xxx ∃∈+∞>； ②23(0,),log log x x x ∃∈+∞<； ③121(0,),()log 2xx x ∀∈+∞>； ④1311(0,),()log 32xx x ∀∈<．其中正确命题的序号是．。

高三文科数学模拟题十三

高三数学模拟试题（十三）一、选择题（5×10=50分）1．设全集{}{}{}2,1,0,1,2,2,1,0,0,1,2U A B =--=--=则)U C A B （=（ )A ．{}B ．{}2,1--C ．{}0,1,2D ．{}1,22．已知正数m 是2，8的等比中项，则圆锥曲线122=+myx 的离心率是（） A ．23 B ．25C ．5D ．33．已知函数()f x =是奇函数，则实数a 的值为（）A ．1-B ．0C ．1D ．2 4．复数22i z i-=+（i为虚数单位）在复平面内对应的点所在象限为（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限5．连续掷两次骰子分别得到点数m 、n ，则向量(,)a m n =与向量(1,1)b =-的夹角2πθ>的概率是（）A ．12B ．13C ．712D ．5126．角α的终边经过点A ()a ，且点A 在抛物线214y x =-的准线上，则sin α=（）A ．12-B ．12 C．2- D．27．已知变量x y ，满足条件10290x x y x y ≥⎧⎪-≤⎨⎪+-≤⎩，，，则x y +的最大值是( )A ．2B ．5C ．6D ．8 8．下列命题中正确的个数为（）①三点确定一个平面；②若一条直线垂直于平面内的无数条直线，则该直线与平面垂直；③同时垂直于一条直线的两条直线平行；④底面边长为2，侧棱长为5的正四棱锥的表面积为12。

A ．0B ．1C ．2D ．3 9．函数x xy sin 3+=的图象大致是（）10．在ABC ∆中，角A B C 、、所对边的长分别为a b c 、、，若60=∠A ,2=a ,则ABC ∆面积的最大值为 ( )A ．1B ．3C ．2D ．23二、填空题（5×5=25分）11．某市有大型超市200家、中型超市400家、小型超市1400家。

为掌握各类超市的营业情况，现按分层抽样方法抽取一个容量为100的样本，应抽取中型超市_______家 12．设直线过点(0,),a 其斜率为1，且与圆222x y +=相切，则a 的值为13．已知函数322()3(1)1(0)f x kx k x k k =+--+>的单调递减区间是(0,4)，则k 的值是14．数列{}n a 满足*11()2n n a a n N ++=∈，且112a =-，n S 是数列{}n a 的前n 项和，则2011S =15．若函数2()4f x x x a =--的有3个零点，则a =（选做）若)0,3(-C 、)0,3(D ，M 是椭圆1242=+y x 上的动点，则11+的最小值为 . 三、解答题（75分）16．（本题满分13分）在ABC ∆中，角A 、B 、C 所对的边分别是a 、b 、c ，且83ABC AB AC S ∆⋅=（其中ABC S ∆为ABC ∆的面积）。