实验任务书(随机)
第九届力学竞赛实验团体赛综合实验任务书

第九届全国周培源大学生力学竞赛“基础力学实验”团体赛综合实验任务书实验时间 5小时一、实验任务如图1所示,被测实验件为一铝制直杆,两端装有L 形钢制连接件。
铝杆实验段GH 为等截面段,横截面为阶梯形(见I-I 剖面图)。
铝杆两端面上各分布有3个加载螺孔A ()、B (A 'B ')、C (C )和一个加载槽E ('E '),两端的L 形钢制连接件上各有一个加载螺孔D (),见A 向视图和B 向视图,各孔的位置可能有微小加工误差。
D '请用电阻应变测量方法完成下列工作:1、确定阶梯形截面的形心位置并与理论值进行对比分析。
(30分)说明:(1)只能利用三对加载螺孔A (A ')、B (B ')、C (C ')进行拉伸加载。
(2)载荷最大值为1000N。
2、实现在单向拉伸加载,并确定此状态下应变为零0αε=的方位角α。
(20分) 说明:载荷最大值为1000N。
3、使用L 形钢制连接件上的加载螺孔D 和D '进行加载,确定当载荷为400N 时, I -I 截面上的内力x F 、z M 、y M 和截面上K'-K 位置的扭转切应力K τ(见I-I 剖面图)。
材料的弹性模量E =74GPa ,泊松比μ =0.31。
(35分) 说明:载荷最大值为500N。
4、使用L 形钢制连接件上的加载螺孔D 和D '进行加载,确定加载点的连线与铝杆横向对称面II 的交点位置。
(15分)说明:(1)数据保留到整数位。
(2)载荷最大值为500N。
图 1 实验件二、实验要求1、完成实验报告;2、报告中必须有较详细的实验方案;3、有完整的原始数据记录;4、实验过程中所有粘贴的应变片均需要保留,试件随实验报告一起上交。
三、实验装置与配件1、综合实验架中的拉伸实验部分,见图2。
2、电阻应变片 35片3、接线端子 35对4、M4螺栓 4个5、M4螺帽 4个6、其他辅助材料 酒精棉、丙酮棉、502胶、导线等。
实验实训任务书

一、实验实训主要内容
通过手感目测来判断纤维的大类,而后通过显微镜来观察纤维的纵向结构进一步来判断纤维的种类。
二、实验实训方法、过程步骤
A、试样准备(纵向结构)
取试样一小束,手扯整理平直,用右手拇指和食指夹取20-30根纤维,将纤维放在载玻片上,滴上蒸馏水,将盖玻片从一侧慢慢压下,即制备好玻片试样。
B、显微镜的认识和调节
(1)取镜和放置:显微镜平时存放在柜或箱中,用时从柜中取出,右手紧握镜臂,左一手托住镜座,将显微镜放在自己左肩前方的实验台上,镜座后端距桌边1-2寸为宜,便于坐着操作。
(2)对光:用拇指和中指移动旋转器(切忌手持物镜移动),使低倍镜对准镜台的通光孔(当转动听到碰叩声时,说明物镜光轴已对准镜筒中心)。
打开光圈,上升集光器,并将反光镜转向光源,以左眼在目镜上观察(右眼睁开),同时调节反光镜方向,直到视野内的光线均匀明亮为止。
(3)放置玻片试样:取一玻片试样放在镜台上,一定使有盖玻片的一面朝上,切不可放反,用推片器弹簧夹夹住,然后旋转推片器螺旋,将所要观察的部位调到通光孔的正中。
(4)调节焦距:以左手按逆时针方向转动粗调节器,使镜台缓慢地上升至物镜距试样片约5毫米处,应注意在上升镜台时,切勿在目镜上观察。
一定要从右侧看着镜台上升,以免上升过多,造成镜头或试样片的损坏。
然后,两眼同时睁开,用左眼在目镜上观察,左手顺时针方向缓慢转动粗调节器,使镜台缓慢下降,直到视野中出现清晰的物象为止。
(5)如果采用高倍物镜,一般先用低倍物镜,然后转动物镜转换器,使高倍物镜代替低倍物镜。
三、实验实训结果与分析
四、讨论与小结
自己写。
实验报告、任务书模板

(5)α=60°时正常情况下的ud、uVT1及id波形如图5所示。
图5α=60°时正常情况下的ud、uVT1及id波形
4.分析与讨论:
(1)三相桥式全控整流电路对触发脉冲的具体要求。
(2)对典型实验数据进行理论验证,说明误差原因。(指由实验得到的移相特性曲线与由公式计算出的移相特性曲线的区别)
(2)测取三相桥式全控整流电路带阻感负载时的移相特性。
(3)测取α=30°时正常及VT1脉冲丢失情况下的ud、uVT1及id波形。
(4)测取α=60°时正常情况下的ud、uVT1及id波形。
3.实验原理图:
实验原理图如图1所示(仅要求按教材画出实验电路主接线并标明有关电压、电流正方向)。
4.实验记录:
1.实验目的:
(1)熟悉三相桥式全控整流电路的接线及工作原理。
(2)掌握双踪示波器的调整及使用方法(特别是如何灵活解决双踪共地的两条曲线测量问题)。
(3)掌握三相桥式全控整流电路对触发脉冲的具体要求。
(4)观察并分析三相桥式全控整流电路带阻感负载时电压、电流波形。
2.实验内容:
(1)观察触发脉冲的形状、相序、相差及移相调节。
(3)对比分析α=30°时正常及VT1脉冲丢失情况下的ud、uVT1及id波形。
(1)不同α角时的Ud、U2测量数值如表1所示。
表1不同α角时的Ud、U2测量值α15°30°45°
60°
75°
Ud
U2
(2)由表1做出移相特性Ud=f(α)曲线如图2所示(要求用坐标纸画出)。
(3)α=30°时正常情况下的ud、uVT1及id波形如图3所示。
(4)α=30°时VT1脉冲丢失情况下的ud及uVT1波形如图4所示。
钢筋工实训任务书、指导书

钢筋工实训任务书一、目的通过该实习过程,提高学生对钢筋工程的认识和了解,并学会和基本掌握一两门钢筋加工技术。
二、要求1.严格按指导人员的要求进行实训作业;2.遵守纪律,注意安全;3.学会正确使用钢筋机械;4.基本掌握钢筋加工制作的工艺方法。
三、任务书(一)实训任务1.钢筋加工制作①钢筋机械调直②钢筋下料(断钢机、切割机)③手工弯制箍筋④粗箍筋弯曲成型2.钢筋绑扎3.钢筋连接①双面搭接焊②竖向电渣压力焊③窄间隙焊4.观摩机械连接工艺及试作①套筒挤压连接技术②滚轧直螺纹连接技术5.观摩钢筋接头力学实验(二)任务量1.钢筋调直和断料按个人完成的加工需求量进行;2.手工弯制箍筋每人数10个;3.粗钢筋弯曲成型在指导师傅的协助下完成;4.钢筋绑扎以组为单位完成数个构件;5.构件连接的三种方法,每人完成一个成品焊件。
四、组织管理及工作秩序安排(一)组织与管理1.由实训中心方面负责任务及技术安排;2.由相关工种指导人员组成实训指导小组,分工合作指导各组学生相关内容实训;3.由实训中心安排专人员负责安全管理;4.每班以8人一组,共分五个组,轮流进行各项内容的训练;5.严格考勤制度,每天由指导师傅负责每组的考勤。
(二)工作秩序安排每班自行安排流到秩序。
集中拉力试验,由各组完成试件后利用7~8节课到实验室去观摩试验过程及结果。
钢筋工实训指导书一、钢筋放样在钢筋师傅的指导下,完成一根构件的放样任务,并填写成钢筋大样表,完成后交给实训中心,作为评定成绩的依据。
二、钢筋机械的使用1.调直机打开护盖,观看内部构造;2.开机调直断料,按加工的箍筋下料尺寸断料;3.断钢机在师傅的指导下,完成粗钢筋下料工作;4.弯钢机的使用,由师傅指导确定好弯心直径大小,弯折移动量大小,弯折角度控制,试弯,最后弯曲成型。
三、焊接1.选定焊件的钢筋尺寸Ф12~22(一、二级钢均可)电渣压力焊800mm两根2.焊件长窄间隙焊350mm两根搭接焊(双面)300mm两根注明:电渣压力焊和窄间隙焊的焊件可反复割断,重复使用,直到满足基本试件长度为止。
XX大学大学生创新性实验项目计划任务书【模板】

大学生创新性实验项目
计划任务书
项目编号
项目名称
项目负责人
指导教师
填报日期
XX大学教务处
一、项目基本情况
项目基本情况
项目名称
是否有依托项目
依托项目名称
项目负责人基本情况
姓名
性别
出生年月
学院
班级
电子信箱
联系电话
项目组成员基本情况
姓名
学院
出生年月
班级
联系方式
二、项目内容与预期成果
内容描述(500字以内)
实用价值与创新点
预期效果与具体成果
三、计划进度安排及审批意见
Hale Waihona Puke 1.计划进度安排2.审批意见
教务处意见
处长(签字)(公章)
年月日
实验任务书、指导书

《工程施工试验与检测》课程实训任务书一、课程实训目的工程施工试验检测技术,将工程试验检测的基本理论和测试操作技能及建设工程相关科学基础知识融为一体,是工程中确定设计参数、质量控制、验收评定、养护管理等的主要依据。
工程试验检测工作对于提高工程质量、加快工程进度、降低工程造价、推广新材料、新技术和新工艺、保证人民生命财产和安全,推动工程施工技术进步等方面均起到极为重要的作用。
随着铁路客运专线、高速公路技术等级的提高,铁道、交通行业各级建设主管部门和施工单位对加强工程质量检测与施工质量控制及验收工作给予高度重视。
通过本次实训,使学生熟悉和掌握试验检测各项常规检测的步骤和方法,巩固和扩大专业知识,并进一步学会综合运用已学到的理论知识与现场实践相结合。
通过查阅有关的资料,提高学生独立分析和解决处理工程施工试验与检测复杂问题的能力,为今后从事工程施工试验与检测工作奠定坚实的基础。
二、课程实训基础资料1.《公路桥涵施工技术规范》(JTJ 041-2000)2.《公路土程水泥混凝土试验规程》(JTJ 053-94)3.《公路工程集料试验规程》(JTGE42-2005)4. 《公路土工试验规程》(JTG E40-2007)5.《公路工程质量检验评定标准》(JTJ F80/1-2004)6.《工程施工试验与检测》教材三、课程实训内容(一)开工前试验室筹建内容设计(二)案例分析及计算1.普通混凝土配合比设计案例(质量法)K70+100匝道桥钢筋混凝土盖梁,设计强度等级为C30,要求坍落度50~70mm。
材料:葛洲坝股份有限公司水泥厂(三峡牌普通硅酸盐42.5)硅酸盐水泥,砂为唐白河黄砂(中砂),襄南粘土矿碎石Dmax=40mm;采用假定容重法每立方混凝土2450kg计算。
要求:计算并优选混凝土配合比(必须采用三个水灰比)。
2.普通混凝土配合比设计案例(体积法)K70+100匝道桥钢筋混凝土墩身,设计强度等级为C25,要求坍落度30~50mm。
实验毕业论文任务书模板范文

学生姓名xxx院系、专业xxxx院xxxx专业指导教师xxx选题目的和意义:少数民族语言文字及其所承载的民族文化是中华民族大家庭文化的重要组成部分,同时又与世界民族文化有着千丝万缕的联系。
面对各民族间政治、经济和文化交流日趋密切的社会发展现实,面对开放的世界,少数民族语言文字信息化,特别是跨境民族语言文字信息化对提高我国国际地位,扩大国际影响力有不可忽视的积极作用。
少数民族语言信息化理论的研究、少数民族语言的资源与信息处理技术的开发和利用等工作,关系到少数民族语言政策的贯彻和落实,关系到少数民族语言文字的学习、使用和发展,关系到少数民族语言文字信息技术的科学化,关系到民族文化兴衰,促进各民族共同繁荣与发展,并涉及国家稳定与安全以及国际影响的重要社会问题。
因此,加速少数民族语言文字信息化进程,具有重要的社会意义和科学意义。
本课题在国内外的研究状况及发展趋势:
从网络检索的资料看,藏文编码的国家标准和国际标准于20世纪90年代初开始正式启动实施。
通过西藏自治区和国内相关研究机构和大专院校专家们精诚合作和艰辛努力,最终使藏文编码字符集国际标准成为我国少数民族文字中的第一个国际标准。
藏文编码方案在传统藏文字素的认知和计算机字符代码处理上做到了合理的继承和创新,体现了藏文应用开发的本土化和国际化的有机结合。
藏文编码标准在各种藏文信息处理领域的正式启用,将带动藏语文在信息技术发展和国际化交流方面发挥更加广泛和积极的社会作用,推动藏语文的使用和发展上一个新的台阶,为少数民族地区的物质文明建设和精神文明建设服务。
肖攸安武汉理工大学实验室课外开放实验项目任务书

目录实验选题:密码学实验⑴ (1)学生姓名:孙瑞、张淼森、王婷婷、顾舰灵、孙世敏1实验选题:密码学实验⑵ (2)学生姓名:姜海霞、陈佳、何仕秋、杜芬、张成刚2实验选题:密码学实验⑶ (3)学生姓名:涂一霜、陈云飞、陈雅倩、李俊峰、王洪兵3实验选题:密码学实验⑷ (4)学生姓名:杨柳、李立、惠祥、武岳、程慧平4实验选题:网络与通信安全实验⑴ (5)学生姓名:戴晓云、杨浩、吕义斌、杜冠军、库琪琪5实验选题:网络与通信安全实验⑵ (6)学生姓名:郑宗清、俞鹰、支领、陈明、杨飞、陈晨6实验选题:网络与通信安全实验⑶ (7)学生姓名:张建朋、林茂福、徐磊、刘欢、刘珍、刘苗、朱邦培7实验选题:数字水印实验⑴ (8)学生姓名:叶鑫、夏雨晴、卢立梓、王鸿传8实验选题:数字水印实验⑵ (9)学生姓名:张少宾、张雪雷、张凡、顾晨曦9实验选题:数字水印实验⑶ (10)学生姓名:朱东莱、彭俊杰、焦瑾、张光亚、岳雯珏实验选题:信息隐藏实验⑴ (11)学生姓名:王扬、朱亮、巩志彬、文青松、魏体鉴实验选题:信息隐藏实验⑵ (12)学生姓名:邓先雨、赵永新、李高阳、章帆实验选题:信息隐藏实验⑶ (13)学生姓名:杜浩然、龙腾、刘冬、尹龙剑、陈赟实验选题:密码学实验⑴学生姓名:孙瑞、张淼森、王婷婷、顾舰灵、孙世敏实验内容:密码学是信息安全研究领域最重要的基础研究课题之一,本实验要求在学习信息安全知识的基础上,完成古典密码学、对称密码学、公钥密码学和密钥密码学的学习,包括:加解密算法的工作原理、工作过程和算法特点的理解,主要算法包括:Hill算法、Enigma密码、DES密码、AES密码、RSA密码和ECC密码。
在此基础上,开发小型文件加密应用系统。
主要任务指标:1、学习信息安全和密码学基础知识,完成古典密码学、对称密码学、公钥密码学和密钥密码学的学习。
2、研究Hill算法、Enigma密码、DES密码、AES密码、RSA密码和ECC密码等密码算法的工作原理、工作过程和算法特点,以及算法的评估方法。
实验任务书(通用)

2. 试验项目名称:
3. 试验性质(在相应的性质上打√) □入厂检验 □型式检验 □送样检验 □委托检验 4. 试验的其他附加要求:
□产品开发 □认证检验
□抽样检验 □其他
送样人签字:
时间:
联系方式:
注:此任务书一式两联,白联留底,蓝联交给试验申请人。
ቤተ መጻሕፍቲ ባይዱ
表号:SYR WS-
XINGBANG
试品名称: 要 求 试 验 部 门: 试 验 下 达 日 期: 批准试验 (签字): 被 被 试 品 型 号: 试 品 编 号:
试验任务书
生效日: 共 页,第 页
试验编号: 被试品提供者: 申请完成日期: 批准完成日期: 试 试 品 数 量: 品 产 地:
以下由申请试验部门填写
薄层鉴别实验任务书

薄层鉴别实验任务书薄层鉴别实验任务书一、实验目的本实验旨在通过薄层鉴别技术,掌握有机化合物的初步鉴别方法,培养学生观察、分析和判断的能力,并提高其实验操作技巧。
二、实验原理薄层鉴别是一种常用的有机化合物初步鉴定方法。
其原理基于各种有机化合物在不同溶剂中的溶解性、色谱性质以及在薄层上的吸附行为不同,从而通过对比样品与已知标准品的色谱行为差异来进行鉴别。
三、实验仪器与药品1. 实验仪器:薄层色谱仪、显微镜。
2. 实验药品:苯酚、甲苯、苯甲酸、乙基乙酸乙烯酯等有机化合物。
四、实验步骤1. 准备样品:将待测有机化合物溶解于适当溶剂中,制备浓度适宜的样品溶液。
2. 准备薄层板:取一块无菌玻璃板,在其上均匀涂布薄层剂,待干燥后即可使用。
3. 上样:将样品溶液用毛细管或微量注射器在薄层板上均匀地滴上一条直径约0.5cm的样斑。
4. 开展薄层色谱:将涂有样斑的薄层板放入薄层色谱仪中,加入适当的溶剂系统,待溶剂前进到合适位置时取出。
5. 显色观察:将薄层板置于显微镜下观察,并记录各样品的显色情况和Rf值。
五、实验结果与分析根据实验步骤所得到的结果,可以通过比对已知标准品的Rf值和显色情况来对待测有机化合物进行初步鉴别。
根据Rf值的大小以及显色情况,可以判断出化合物在不同溶剂系统中的迁移性质,并与已知标准品进行对比。
六、实验注意事项1. 实验操作过程中要注意安全,避免有机化合物接触皮肤和吸入。
2. 严格控制实验条件,保证实验结果的准确性。
3. 操作时要轻拿轻放,避免划伤薄层板。
4. 注意观察显色情况和Rf值的变化,及时记录并进行分析。
七、实验总结通过本次实验,我对薄层鉴别技术有了更深入的了解,并掌握了有机化合物初步鉴别的方法。
在实验过程中,我注意到样品的溶解性、色谱行为以及显色情况对于鉴别结果的影响。
同时,实验还提高了我的观察、分析和判断能力,并加强了我的实验操作技巧。
薄层鉴别实验是一种常用的有机化合物初步鉴定方法,通过比对样品与已知标准品的色谱行为差异来进行鉴别。
实验报告任务书

实验报告任务书实验目的:本实验旨在通过提供详细的任务要求和实验要求,指导学生完成实验过程,并培养学生动手能力、实验设计能力、数据处理能力及科学思维能力。
实验项目及内容:本实验包括以下项目:1. 实验准备:a. 列出实验所需材料和器材清单;b. 准备实验所需的试剂和溶液;c. 设计实验流程和步骤。
2. 实验操作:a. 按照实验流程和步骤,进行实验操作;b. 注意实验操作的安全性和准确性;c. 记录实验过程中的观察、数据、测量值等。
3. 数据处理:a. 对实验数据进行收集和整理;b. 进行数据分析,包括计算、统计和图表制作;c. 对结果进行合理解释和推理。
4. 结果与讨论:a. 撰写实验报告,包括实验目的、实验原理、实验步骤和结果分析;b. 对实验结果进行讨论,并提出不足之处和改进意见;c. 总结实验的重要发现和对相关领域的意义。
要求:1. 遵守实验室的安全规定,正确使用实验器材和试剂;2. 严格按照实验要求进行实验操作,注意记录实验过程和数据;3. 对实验数据进行合理处理和分析,确保结果的准确性和可靠性;4. 实验报告要有明确的结构,清晰的逻辑,语言准确简练;5. 实验报告要包括必要的图表和数据分析,且结果与讨论相结合;6. 实验报告要注重实验的可重复性和推广性,结果能够得到验证和应用。
参考资料:学生可参考教材、期刊论文、相关实验指导书等资料进行实验设计、数据处理和结果分析。
可以使用国内外通用的引文格式,如APA、MLA等。
截止日期:学生需按时完成实验报告并交至指定邮箱或实验室办公室。
逾期不交或考核不合格者,成绩将受到相应扣分或不予批阅。
备注:学生在实验过程中如遇到实验器材缺失、操作不当等问题,请立即向实验室管理员或实验指导教师反馈,以便及时解决。
希望同学们能够认真准备实验,并按照要求完成实验报告。
通过实验的开展,巩固理论知识,培养实验技能,提高动手实践能力,更好地理解和掌握实验所涉及的科学原理和方法。
试验任务书

(二)实验项目二
实验名称:渗透实验
实验性质:验证性实验
实验学时:2学时
实验目的:掌握渗透仪的操作方法。
设备名称型号:90渗透仪
实验内容:测定土体渗透系数,为渗透指标计算提供依据。
(三)实验项目三
实验项目:固结实验
实验性质:验证性实验
实验学时:2学时
实验目的:掌握高、中、低压固结仪的操作方法。
3.通过实验,巩固并加强学生对土工实验基本理论的理解,激发学生的创新思维。
4.通过实验培养学生的安全意识、团队精神和撰写报告的能力。
主要内容:
(一)实验项目一
实验名称:液限塑限联合测定实验
实验性质:验证性实验
实验学时:2学时
实验目的:掌握联合测定仪的使用方法。
设备名称型号:光电式液限塑限联合测。
注:表格大小根据实际填写内容可调整
指导教师:教研室主任:
年月日
3.中等(70-79):能够完成实验;能独立完成报告,报告内容较完整,表达较好。
4.及格(60-69):基本能够完成实验;能基本完成实验报告,报告内容基本满足要求。
5.不及格(60以下):未能完成规定的实验,未能完成实验报告。
参考文献
1.苏栋主编,《土力学》,清华大学出版社。2019年第2版。
2.张克恭,刘松玉主编,《土力学》,中国建筑工业出版社,2016年第4版。
4.测定土的内摩擦角和黏聚力。
成绩评定
要素及权重
成绩的评定依据实验现场表现和实验报告成绩两方面来评定,实验现场表现占总评成绩的30%,实验报告占总成绩的70%,最终成绩按百分制等级评定。
1.优秀(90-100):能够出色地完成实验;能独立完成报告,报告内容充实,论述清楚,表达准确。
实验教学任务书

成都信息工程大学实验教学任务书
(201 -201 学年第学期)
教学单位教研室行课实验室实验课程名称实验学时__ ___
注:1.此表一式三份,由教研室主任负责按教学大纲组织拟订与核对,经系部审核及教务处审核后,实验室主任负责组织实施,教务处、教研室、实验室各留一份存档。
2.实验室名称填建制实验室名称,实验类型请填写演示、验证、综合、设计,实验要求请填写必修或选修。
3.如有新增和改进实验及实验项目名称有误,请在备注栏内注明,如不够请在空白表内填写。
教研室主任签字(单位盖章) 教务处审核(单位盖章) ______________。
实验报告任务书

硬件课程设计指导书一、课程性质与目的《硬件课程设计》是计算机科学与技术专业的专业必修核心课程。
适用于计算机科学与技术专业。
是计算机科学与技术专业重要的实践环节。
通过本课程的学习,使学生基本掌握硬件编程语言VHDL ,并熟悉FPGA 设计的实验和使用方法。
通过设计、编程、调试过程,培养学生的设计和实验动手能力。
二、教学基本内容及基本要求1、学习现代硬件系统设计基本方法。
2、学习使用硬件描述语言VHDL。
3、学会使用图形方式和文本方式设计逻辑与时序电路。
4、学会分层次设计方法。
5、学会FPGA编程和应用。
6、详细的设计任务要求见附件1。
三、时间安排课程设计教学时间共5周。
结合实际情况,本次安排时间跨度为第19周~第20周,第26~第28周,共计5周,从7月5日开始,到9月10日结束。
第19周~第20周:理论教学第26周~第28周:实验调试四、参考书目1. 邹彦,庄严等.EDA技术与数字系统设计.电子工业出版社.2007,42. 薛宏熙,胡秀珠.计算机组成与设计.清华大学出版社.2007,13. 潘松,黄继业. EDA技术与VHDL. 清华大学出版社. 2007.1五、成绩评定设计成绩由平时听课状况、设计结果、设计报告三部分构成。
平时成绩占20%,实验与设计调试占50%,设计报告占30%。
考核依据:(1)平时听课/实验。
由值班教师负责考核,记录出勤状况、听课过程中回答问题状况等。
(2)实验与设计结果。
该部分由学生独立完成具体的设计项目,完成后由教师验收,根据验收情况和设计结果给出相应的成绩。
(3)设计报告。
在实验部分完成的基础上,学生根据自己设计的实验与调试过程,每人写出自己的设计报告,根据设计报告的情况由指导老师评定并给出得分。
六、要求在课程设计阶段,严格考勤,根据题目要求认真独立完成设计,要求学生全程参与课程设计过程,完成理论到实践的全过程训练。
在实验过程中,独立完成设计任务并调试,根据设计结果和设计过程中的努力程度,由指导教师给出设计成绩。
电机电气控制综合实验任务书

《电机与电气控制综合实验》任务书指导教师:周伟、田林红一、电机与电气控制综合实验的性质、目的和任务1.通过综合实验,对电气控制原理知识进行深入认识,掌握常用低压电器元件的结构及工作原理;2.通过实验掌握由电气原理图变换成安装接线图并进行相应操作的能力;3.通过实验,掌握电气控制线路的设计方法、电气安装接线图的绘制方法;4.常用的故障检测及维修方法;5.通过综合实验,使学生具有独立进行电气控制系统设计的能力。
二、电机与电气控制综合实验的内容1.对学生进行安全教育;2.由学生随机选择设计题目,然后在限定时间内完成相关任务;3.选择拖动方案与控制方式;4.确定电动机的类型、容量、转速,并选择具体型号(根据实际情况也可忽略此步操作过程,但要让学生明白此步操作的关键性及其重要性);5.设计电气控制原理框图,确定各部分之间的联系,拟定部分技术要求;6.设计并绘制电气原理图,并根据要求计算主要技术参数;7.选择电气元件,制定元器件目录清单;8.根据题目要求绘出元件分布图;9.绘出安装接线图(根据情况也可忽略此步操作);10.编写设计说明书;11.进行安装调试并验收。
三、电机与电气控制综合实验的基本要求1.必需对学生进行安全操作培训2.学生必须遵守安全操作规程,确保人身及设备的安全3.学生必需学会实践操作3.电气控制信号测量必须注意安全,测量时必须由老师指导4.学生不允许拆卸及人为损坏元器件5.学生必须撰写出符合要求的综合实验报告6.教学过程中,注重师生互动、沟通,及时解决学生的疑惑,培养学生主动获取知识的能力。
四、综合实验实践环节所选用组件1.三相鼠笼异步电动机一台UN=220V(△接法)及双速电动机一台。
2.常用电器元件(如接触器KM、热继电器FR、时间继电器KT、万能转换开关SA、按钮SB、行程开关SQ等)。
3.万用表、电笔等。
4. 常用电工工具及导线若干。
五、综合实验(时间分配)六、综合实验配套教材及参考资料建议使用教材:电气控制技术相关的各种技术资料建议参考书目及资料:1.《电机与电气控制》机械工业出版社许翏2.《电机及电气控制实验指导书》郑州大学出版社史增芳3.《维修电工技能训练》高等教育出版社王廷才4. 网络上相关资料七、考核方式与评分办法按考核标准,评定成绩等级为优、良、中、及格、不及格1.综合实验的态度,安全文明情况(30%)2.综合实验报告(30%)3.面试答辩。
单片机课程设计任务书

单片机课程设计任务书1、选题:(随机抽题)⑴液晶屏+DS18B20;⑵288YJ48步进电机控制;⑶16X16LED点阵显示;⑷超声波测距;⑸液晶屏+直流电机调速;2、命题说明:⑴液晶屏+DS18B20;液晶屏推荐使用型号为:LCD1602 温度传感器推荐型号:DS18B20;实现功能:通过键盘设定温度控制上线和温度控制下线,当温度在下线以下时继电器吸合,温度达到上线时继电器释放;温度下降到下线之后继电器吸合,重复上述工程;液晶屏实时显示当前温度和上下线温度值。
⑵288YJ48步进电机控制;步进电机推荐使用型号为:288YJ48; 驱动电路器推荐型号:2803;实现功能:通过键盘设定步进电机运行速度,行走步数,通过键盘发布运行指令;步进电机按设定值运行到位,停止;能够重复上述工程;LED数码管显示设定值。
⑶16X16LED点阵显示;16X16LED点阵推荐使用8X8点阵4块拼接; 驱动电路器推荐型号:2803或自选;实现功能:在屏幕上显示:常州工学院电气工程学院08自名字学号显示方式:滚动显示和单字显示交替;⑷超声波测距;器件推荐使用为:超声波发送接收一体模块;实现功能:通过超声波模块测试距离在LED数码管实时显示;⑸直流电机调速;驱动电路推荐使用型号为:LM298 直流电机:自选;实现功能:使用CPU自带的PWM硬件模块实现调速功能;通过键盘设定起始速度,通过键盘驱动电机,通过键盘加1或减1控制电机加速或减速;LED数码管实时显示当前PWM值及电机旋转方向。
3、设计报告要求:(打印并提交报告,图纸,程序电子文档)封面:名称单片机课程设计;班级;学号;姓名;等信息⑴硬件原理图;⑵元件位置图;⑶程序框图;⑷源程序清单⑸报告,图纸,程序电子文档提交4、成绩构成:作品60%,报告30%,考勤10%。
白盒测试任务书
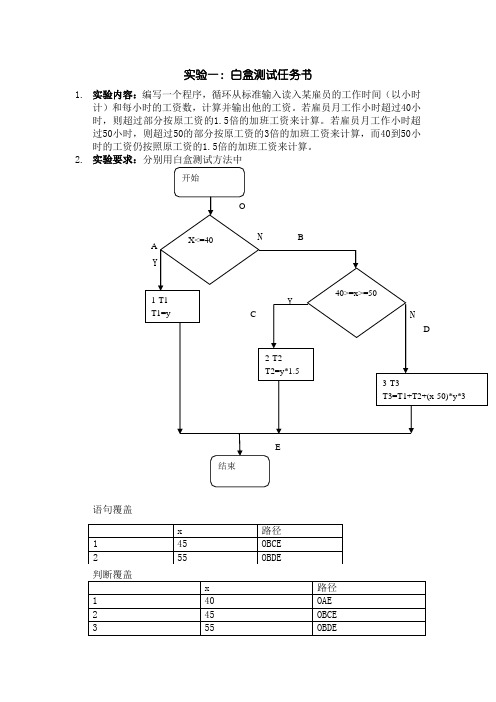
实验一:白盒测试任务书1.实验内容:编写一个程序,循环从标准输入读入某雇员的工作时间(以小时计)和每小时的工资数,计算并输出他的工资。
若雇员月工作小时超过40小时,则超过部分按原工资的1.5倍的加班工资来计算。
若雇员月工作小时超过50小时,则超过50的部分按原工资的3倍的加班工资来计算,而40到50小时的工资仍按照原工资的1.5倍的加班工资来计算。
2.实验要求:分别用白盒测试方法中语句覆盖条件覆盖X<=40为真记为T1x>40为假记为-T1x>50为真记为T2X<=40为真记为T1x>40为假记为-T1x>50为真记为T23.程序参考:#include <iostream.h>double main(){int hours;double payment,wage;cout<<"please input hours and per hour pay:";cin>>hours>>wage;if (hours<40)payment=hours*wage ;else if ((hours>40) && (hours<=50))payment=40*wage+(hours-40)*1.5*wage;else if (hours>50)payment=40*wage+10*1.5*wage+(hours-50)*3*wage;cout<<"The final payment are:"<<payment;return payment;}提交作业命名格式:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机过程的模拟与特征估计
一、实验目的
了解随机过程特征估计的基本概念和方法,学会运用MATLAB 软件产生各种随机过程,对随机过程的特征进行估计,并通过实验了解不同估计方法所估计出来的结果之间的差异。
二、实验原理
(1)高斯白噪声的产生
提示:利用MA TLAB 函数randn 产生
(2)自相关函数的估计
||10
1ˆ()()()||N m x n R m x n m x n N m --==+-∑ 提示:MA TLAB 自带的函数为xcorr
(3)功率谱的估计
先估计自相关函数ˆ()x
R m ,再利用维纳-辛钦定理,功率谱为自相关函数的傅立叶变换:1(1)()()N jm x x m N G R m e ωω+-=--=
∑
提示:MA TLAB 自带的函数为pyulear
(4)均值的估计
1
11ˆ()N x n m x n N -==∑
提示:MA TLAB 自带的函数为mean
(5)方差的估计
12
211ˆˆ[()]N x x
n x n m N σ-==-∑
提示:MA TLAB 自带的函数为var
(6) AR(1)模型的理论自相关函数和理论功率谱
对于AR(1)模型()(1)()X n aX n W n =-+ 自相关函数22()1m X a R m a σ=-,0m ≥
功率谱为2
2()(1)X j G ae ωσω-=-
(7) ARMA(N,N)模型的理论自相关函数和理论功率谱
对于ARMA(N,N)模型12()(1)(2)()()N X n a X n a X n a X n N W n =-+-++-+ 功率谱为221
1()N j k k k X N
j k k
k b e G a e
ωωωσ-=-==∑∑ 三、实验内容(带*为选作)
1. 相关高斯随机序列的产生
按如下模型产生一组随机序列()(1)()x n ax n w n =-+,其中()w n 为均值为1,方差为4的正态分布白噪声序列。
(1)产生并画出a=0.8和a=0.2的x(n)的波形;
(2)估计x(n)的均值和方差;
(3)估计x(n)的自相关函数。
2. 两个具有不同频率的正弦信号的识别
设信号为12()sin(2)2cos(2)()x n f n f n w n ππ=++,1,2,,n N = ,其中()w n 为正态白噪声,方差为2
σ。
(1)假定21σ=,针对10.05f =,20.08f =和10.05f =, 20.20f =两种情况,使用周期图periodogram()的方法估计功率谱。
(2)假定10.05f =,20.08f =,针对21σ=和2
4σ=两种情况,用周期图periodogram()的方法估计功率谱
*(3) 假定10.05f =,20.08f =,24σ=, 分别用pyulear()、periodogram() 和pburg()估计功率谱。
3. 理论值与估计值的对比分析
设有AR(1)模型,
()0.8(1)()X n X n W n =--+,
W(n)是零均值正态白噪声,方差为4。
●用MA TLAB模拟产生X(n)的500个样本,并估计它的均值和方差;
●画出X(n)的理论的自相关函数和功率谱;
●估计X(n)的自相关函数和功率谱。
四、预习思考题
(1)按照公式
1
22
1
1
ˆ[()]
N
x x
n
x n m
N
σ
-
=
=-
∑对方差的估计是有偏估计还是无偏估计?为什
么?
(2)函数rand和randn的区别?
(3)rand(10) ,rand(10,1),rand(1,10),rand(10,10)产生的随机数序列的形式如何?即它们到底是列向量,行向量,标量,还是矩阵?
(4)如何产生均值为m,方差为2
σ的高斯白噪声序列?
(5)subplot,plot和stem等3个函数在MATLAB绘图中非常有用,请务必掌握。
五、实验思考题
(1)自相关函数R(m)最大值应该在n=0,用MATLAB估计得到的结果与理论的结果相同吗?为什么?
(2)随机序列的功率谱是以2π为周期的周期函数,功率谱的周期性在MA TLAB估计得到的结果中是如何体现的?
六、实验要求
(1)一人一组完成实验,切勿抄袭;
(2)用MATLAB完成所有要求的实验内容;
(3)撰写详细的实验报告,实验报告中应该包括以下內容:
●实验内容和原理的简单阐述,分析;
●得到的实验结果图形及简要分析,比较;
●对“实验思考题”的详细分析和回答;
●自己的实验心得(评判实验报告水平高低的重要因素)。
