线路坐标计算(交点法)
全线三维坐标计算(交点法)

请输入线路起点桩号:K00+000.0000
(输入交点及起终点点号时,交点编号只要输入数字即可,起点输为0,终点输为一个"-"数),请在蓝格子里(第1~6、23、24列)输入曲线数据
请输入线路起点桩号:K00+000.0000
(输入交点及起终点点号时,交点编号只要输入数字即可,起点输为0,终点输为一个"-"数),请在蓝格子里(第1~6、23、24列)输入曲线数据
线路曲线要素请输入线路起点桩号:K00+000.0000
(输入交点及起终点点号时,交点编号只要输入数字即可,起点输为0,终点输为一个"-"数),请在蓝格子里(第1~6、23、24列)输入曲线数据
路曲线要素。
交点计算线路坐标(全线断链)

中线坐标 桩 号 切线方位角
左 边 桩 坐 标
右 边 桩 坐 标
中线坐标 桩 号 切线方位角
左 边 桩 坐 标
右 边 桩 坐 标
中线坐标 桩 号 切线方位角
左 边 桩 坐 标
右 边 桩 坐 标
中线坐标 桩 号 切线方位角
左 边 桩 坐 标
右 边 桩 坐 标
中线坐标 桩 号 切线方位角
左 边 桩 坐 标
右 边 桩 坐 标
中线坐标 桩 号 切线方位角
左 边 桩 坐 标
右 边 桩 坐 标
中线坐标 桩 号 切线方位角
左 边 桩 坐 标
右 边 桩 坐 标
中线坐标 桩 号 切线方位角
左 边 桩 坐 标
右 边 桩 坐 标
中线坐标 桩 号 切线方位角
左 边 桩 坐 标
右 边 桩 坐 标
中线坐标 桩 号 切线方位角
CAD线
, , , , , , , , , , , , , , , , , , , , , , , , ,
CAD线
, , , , , , , , , , , , , , , , , , , , , , , , ,
CAD线
, , , , , , , , , , , , , , , , , , , , , , , , ,
CAD线
, , , , , , , , , , , , , , , , , , , , , , , , ,
CAD线
, , , , , , , , , , , , , , , , , , , , , , , , ,
CAD线
, , , , , , , , , , , , , , , , , , , , , , , , ,
交点法线路平曲线坐标计算 [新方法]
![交点法线路平曲线坐标计算 [新方法]](https://img.taocdn.com/s3/m/4eaa9513964bcf84b9d57bf7.png)
线路线路工程工程工程[[交点法交点法]]平曲线坐标计算[新方法]作者作者::刘宗远 联系方式QQ :63453673 2013年10月[简述]:在网上看了很多网友的线路交点法计算程序,平曲线小坐标大多采用的是切线支距法切线支距法切线支距法。
经本人结合线路工程的施工特点和相关资料,总结归纳出一套全新的全新的全新的线路坐标编程线路坐标编程线路坐标编程解算方法解算方法解算方法(弦线偏弦线偏角支距法角支距法——————也叫极坐标法也叫极坐标法也叫极坐标法)。
计算精度满足线路主线要求。
第一部分第一部分::基本公式基本公式一、圆曲线圆曲线::1、偏角:2、弦长:式中: —偏角—弧长所对应的圆心角—待求点到zy 点的距离 二、缓和曲线缓和曲线:: 1、切线角:(1)缓和曲线上任意一点切线角:(2)曲线上任一点偏角:(3)弦切角:(hy(yh)点处弦线与切线的交角)2、弦长:22590Lsr l l c i ××−= 式中:zh ki l −= 缓和曲线一点到zh 点的距离 —前(或后)缓和曲线总长第二部分第二部分::程序分步公式程序分步公式一、交点参数计算:(非对称缓和曲线型)1、内移值P :前缓和曲线内移值:341212688241R L R L P S s −= 后缓和曲线内移值:342222688242RL R L P S S −= 2、切线增长值q :前缓和曲线切增值:231124021R L L q s s −=后缓和曲线切增值:232224022RL L q s s −= 3、切线角β:前缓和曲线切线角: R L S 1901=β 后缓和曲线切线角: RL s 2902=β 4、切线长T :前切线长:ααsin 2112tan)1(1p p q P R T −−++=后切线长:ααsin 2122tan )2(2p p q P R T −+++=5、曲线总长:)(5.018021S S L L RL +×+=πα二、主点计算主点计算::1、桩号计算桩号计算::ZH=交点桩号-T1 HZ=ZH+L HY=ZH+L S1 YH=HZ-L S22、坐标计算坐标计算::1)ZH 点坐标点坐标:: 方位角:F 前=前直线方位角前直线方位角(或前切线方位角) X zh =X J D -T 1×cosF 前 Y zh =Y J D -T 1×sinF 前2)HZ 点坐标点坐标::方位角:F 后=F 前+ξα(交点转角) 注:ξ—交点转角偏向符,左偏-1 右偏+1 X hz =X J D +T 2×cosF 后 Y hz =Y J D +T 2×sinF 后3)HY 点坐标点坐标::前缓曲线终点偏角:前缓曲线终点弦长:212511901S S S L r L L C ××−=方位角:F=F 前+ξδ0 (缓曲线终点偏角) X hy =X zh +C 1×cosF Y hy =Y zh +C 1×sinF 4)HY 点坐标点坐标::后缓曲线终点偏角:后缓曲线终点弦长:222522902S S S L r L L C ××−=方位角:F=F 后+180-ξδ0 (缓曲线终点偏角) X yh =X hz +C 2×cosF Y yh =Y hz +C 2×sinF三、各线元段坐标计算 1、前直线段 Ki<ZH待求点到ZH 点的距离:Li=Ki-ZH方位角:F 前=前直线方位角(或前切线方位角) X=X ZH +Li ×cosF 前 Y=Y ZH +Li ×sinF 前2、前缓曲线段前缓曲线段 ZH ZH ≤Ki ≤HY HY待求点到ZH 点的距离:Li=Ki-ZH前缓曲线任意点偏角:1230S L R Li ××=πδ前缓曲线任意点弦长:212590S ii L r L L Ci ××−=中桩弦线弦线弦线方位角:F 中=F 前+ξδ 注:ξ—交点转角偏向符,左偏-1 右偏+1 中桩切线切线切线方位角:F 切=F 中+2 δ—缓曲线偏角 X=X zh +C i ×cosF 中+B×cos(F 切+θ) 注:θ—中线与中桩至边桩连线的夹角 Y=Y zh +C i ×sinF 中+B×sin(F 切+θ) B—中桩至边桩的距离3、圆曲线段HY HY<Ki<<Ki<<Ki<YH YH YH待求点到HY 点的距离:Li=Ki-HY 圆曲线任意点弦长:2243rL L Ci i i ×−= 前缓曲终点切线角:RL S 1901=β 圆曲线偏角RLi×=πδ90 中桩弦线弦线弦线方位角:F 中=F 前+ξ(+)中桩切线切线切线方位角:F 切= F 前+ξ(+2) 注:圆曲线偏角为圆心角的一半X=X HY +C i ×cosF 中+B×cos(F 切+θ) 注:θ—中线与中桩至边桩连线的夹角 Y=Y HY +C i ×sinF 中+B×sin(F 切+θ) B—中桩至边桩的距离 4、后缓曲线段后缓曲线段 YH YH ≤Ki ≤HZ待求点到HZ 点的距离:Li= ZH -Ki 后缓曲线任意点偏角:2230S L R Li ××=πδ后缓曲线任意点弦长:222590S ii L r L L Ci ××−=中桩弦线弦线弦线方位角:F 中=F 后+180-ξδ 注: ξ—交点转角偏向符,左偏-1 右偏+1 中桩切线切线切线方位角:F 切=F 中-2 δ—缓曲线偏角 X=X HZ +C i ×cosF 中-B×cos(F 切+θ) 注:θ—中线与中桩至边桩连线的夹角 Y=Y HZ +C i ×sinF 中-B×sin(F 切+θ) B—中桩至边桩的距离 5、后直线段后直线段 Ki>HZ Ki>HZ Ki>HZ待求点到HZ 点的距离:Li=H Z-Ki 方位角:F 后= F 前+ξα(交点转角) 注:ξ—交点转角偏向符,左偏-1 右偏+1 X=X HZ +Li ×cosF 后 Y=Y HZ +Li ×sinF 后工程实例工程实例表一表一 直曲表直曲表逐桩坐标表桩坐标表第三部分第三部分 [TI [TI 计算器计算器]]线路综合线路综合程序代码程序代码程序代码((坐标计算部分坐标计算部分))程序显示界面:一、主程序代码程序子程序二、坐标正算坐标正算子交点数据库子程序三、交点数据库子程序数据库子程序四、桩号桩位显示字符转换子程序 线元段、、桩位显示字符转换子程序桩号、、线元段。
交点法、线元法坐标计算

3、交点法、线元法坐标计算坐标计算是根据图纸中“直线及曲线转角一览表”提供的数据计算道路中桩坐标,然后和图纸提供的“逐桩坐标表”比对,如果一样则说明输入平曲线参数输入正确,可以计算边桩坐标和其他结构物坐标了;如果中桩坐标不一样,一般是平曲线参数输入有误,需要重新检查输入,另一种结果是图纸有错,这种情况少见,但不代表没有。
“直线及曲线转角一览表”和“逐桩坐标表”见附件1、附件2。
线元法是以路线的起点坐标、方位角、起终点桩号等节点元素来计算出要求的坐标;交点法是以路线的交点要素和路线的主要要素来求得坐标。
①交点法交点:路线的转折点,路线改变方向是相邻两直线的延长线相交的点。
用JD表示,有些图纸上用IP 表示。
看下图:交点是针对曲线的(包含圆曲线和缓和曲线),一段曲线就有一个交点。
交点参数有:坐标(X,Y)、交点桩号、转角值、圆曲线半径R、缓和曲线长度。
教学提供软件(轻松测量、双心软件、测量工具)交点法曲线要素输入说明:1、QD起点坐标:起点坐标必须在直线段上,或填写前一交点的坐标。
2、JD交点曲线要素:(1)交点桩号(2)交点坐标(X,Y)(3)曲线半径R(4)第一缓和曲线长度LS1,若为0,输入0,不能为空。
(5)第二缓和曲线长度LS2,若为0,输入0,不能为空。
3、ZD终点坐标:终点坐标也必须在直线段上,或填写后一交点的坐标。
检核数据是否输入正确的方法:软件生成的圆曲线要素中切线长、外距、交点里程:注意校正起点里程、等与设计图纸是否一致。
如果上述数据和图纸不一样,请认真检查有错误的交点处的数据输入是否正确,如果输入没有错误,请考虑是否包含不完整缓和曲线,使用公式A2=R*Ls检查是否包含不完整缓和曲线。
如果包含不完整缓和曲线,那就需要用线元法也叫积木法计算了。
有的设计院给出的直曲表是整条设计线路的直曲表的一部分,以其中某个交点作为起始点的话,起始里程有时候需要校正,当然,并不是每个图纸给出的起点里程都需要校正,大多数图纸的起点里程已经被设计院校正过,我们输入平曲线的时候需要验证一下。
交点法原理

交点法原理交点法是一种用来求解两条直线交点坐标的数学方法,它在计算机图形学、几何学和工程学等领域有着广泛的应用。
在实际应用中,我们常常需要求解两条直线的交点坐标,这时候交点法就能派上用场。
首先,我们来看一下两条直线的一般方程。
一条直线的一般方程可以表示为Ax + By = C,其中A、B、C为常数。
当然,这里有一个前提条件,就是A和B不能同时为0。
如果A和B同时为0,那这条直线就不存在了。
假设我们有两条直线,它们的一般方程分别为A1x + B1y = C1和A2x + B2y =C2,我们需要求解它们的交点坐标。
我们可以通过联立这两个方程,得到一个二元一次方程组。
这个方程组的解就是两条直线的交点坐标。
一般来说,我们会选择使用消元法或者代入法来解决这个方程组。
但是,交点法提供了另外一种更加简洁和直接的解决方案。
我们可以通过一些简单的数学推导,得到两条直线交点坐标的表达式。
假设我们有两条直线的一般方程为A1x + B1y = C1和A2x + B2y = C2,它们的交点坐标为(x, y)。
我们可以利用克莱姆法则来求解这个交点坐标。
克莱姆法则告诉我们,如果一个二元一次方程组的系数行列式不为0,那么这个方程组有唯一解,且这个解可以通过系数行列式的比值来求得。
对于两条直线的交点坐标,我们可以利用克莱姆法则得到如下的表达式:x = (C1B2 C2B1) / (A1B2 A2B1)。
y = (A1C2 A2C1) / (A1B2 A2B1)。
通过这个表达式,我们就可以直接计算出两条直线的交点坐标。
这种方法不需要进行繁琐的消元和代入运算,能够更加高效地求解交点坐标。
除了利用克莱姆法则,我们还可以通过向量的方法来求解两条直线的交点坐标。
我们可以将两条直线表示为参数方程的形式,然后通过向量的叉乘运算来求解它们的交点坐标。
这种方法也能够得到同样的结果,而且在一些情况下更加直观和易于理解。
总的来说,交点法是一种简洁而高效的求解两条直线交点坐标的方法。
两直线交点坐标的公式

两直线交点坐标的公式
直线,这是我们学数学和物理时最熟悉的图形了,在图形中,直
线有着广泛的使用。
这也是有关直线交点坐标的计算公式,一般用来
求出两条直线交点的坐标位置。
直线的表示方式有两种:一种是直角坐标系的标准形式:
ax+by+c=0,一种是斜率形式的y=k*x+b (k为斜率,b为直线的截距)。
两一条直线相交,需要满足其系数相同,即其系数取值都一样,就可
以计算出交点的坐标位置。
两条直线的交点坐标计算公式可以表示为:X=(c2-b2)/(a2-b2),Y=(a1*X+c1)/(-b1)。
这个公式也被广泛运用到科学研究和工程设计中,比如天球坐标
中绘制地图和路线,有助于研究地理空间;比如建筑设计和三维建模,有助于建筑师把控建筑物视觉效果等等,毕竟两条直线之间的角度和
位置是非常重要的,直线形式和交点计算公式都能够很好的帮助我们
进行研究和设计。
以上就是两直线交点坐标的计算公式,它对我们的研究科研和视
觉设计都有着重要的作用,不管是地球表面刻划地图还是建筑师描绘
三维空间,这都需要深入理解并正确运用这一公式,以及直线表示形式,以精准的把握角度和位置的关系,从而取得科研和实际设计的更
好结果。
线路坐标计算公式(带偏移)

1.直线坐标计算直线上一点坐标公式如下:COS αl X X A ⨯+=SIN αl Y Y A ⨯+=X A :直线上一点A 的X 坐标(待求点里程-A 点里程必须大于零) Y A :直线上一点A 的Y 坐标(待求点里程-A 点里程必须大于零) l : 待求点里程-A 点里程α:直线方位角(A 点至待求点的方位角) 2.圆曲线坐标计算圆曲线上一点坐标计算公式如下:)90K πR 180lK COS(αR )90K COS(αR X X 起起起︒⨯-⨯+⨯+︒⨯+⨯+= )90K πR180l K SIN(αR )90K SIN(αR Y Y 起起起︒⨯-⨯+⨯+︒⨯+⨯+=切线方位角πR180lK α起⨯+=,起始方位角β+=ZH 起αα X 起:圆曲线起点处的X 坐标 Y 起:圆曲线起点处的Y 坐标α起:圆曲线起点处的切线方位角 R :圆曲线半径l :待求点里程-圆曲线起点里程 K :右转取1,左转取-1 偏移:K1:右转取1,左转取-1,K2:右转取-1,左转取+1,3.带有圆曲线的缓和曲线(缓和曲线为完整缓和曲线)坐标计算:(1)曲线要素的计算:①切线角:π1802Rl β11︒⨯=,π1802Rl β22︒⨯=②内移值:24R l p 211=,24Rl p 222= ③切线增值:23111240R l 2l m -=,23222240R l 2l m -= ④切线长:sin αp p m 2αtan )p (R T 21111--+⨯+=sin αp p m 2αtan)p (R T 21222-++⨯+= ⑤曲线长:2121l l 180πR )ββ(αL ++︒⨯⨯--=⑥外矢距:R OS E -+=1112α)/C p (R)90K2πR 180l K1COS(αE)-R ()90K COS(αR X X 起起起︒⨯+⨯+⨯+︒⨯+⨯+=⑦缓和曲线总偏角:/310βδ= 其中:β1:前缓和曲线切线角 β2:后缓和曲线切线角 p 1:前缓和曲线内移值 p 2:后缓和曲线内移值 m 1:前缓和曲线切线增值 m 2:后缓和曲线切线增值 T 1:前切线长 T 2:后切线长 l 1:前缓和曲线长 l 2:后缓和曲线长 R :为圆曲线半径 E :外矢距0δ:缓和曲线总偏角(2)前缓和曲线一点坐标计算公式如下:)πRl 30l K COS(α)90Rl (l X X s12ZHs1225ZH l⨯+⨯-+=)πRl 30l K SIN(α)90Rl (l Y Y s12ZHs1225ZH l⨯+⨯-+=切线方位角=s12ZHπRl 90l K α⨯+X ZH :ZH 点X 坐标 Y ZH :ZH 点Y 坐标K:右转取1,左转取-1 R :圆曲线半径l :待求点里程-ZH 点里程 l s1:前缓和曲线长度偏移:(3)后缓和曲线一点坐标计算公式如下:)πRl 30l K 180COS(α)90R l (l X X s22HZs2225HZ l ⨯-︒+⨯-+=)πRl 30l K 180SIN(α)90Rl (l Y Y s22HZs2225HZ l⨯-︒+⨯-+=切线方位角=s22HZπRl 90l K α⨯- )90K πRl 90l K COS(α)E l (X 偏X s12ZH s1l ︒⨯+⨯+⨯⨯+=X:HZ点X坐标HZY:HZ点Y坐标HZK:右转取1,左转取-1R:圆曲线半径l: HZ点里程- 待求点里程l s2:后缓和曲线长度。
两直线交点坐标怎么求

两直线交点坐标怎么求引言在几何学中,直线是一种基本的图形元素,往往与其他直线或者曲线相交。
当两条直线相交时,我们往往希望能够求得它们的交点坐标,因为交点的坐标可以帮助我们解决很多与直线相关的问题。
本文将介绍两种常见的方法来求解两直线的交点坐标。
方法一:解方程法步骤1.确定两条直线的方程:通过确定直线上的两个点或者直线的斜率和截距,我们可以得到两条直线的方程。
2.将两条直线的方程联立:将两条直线的方程联立,构成一个方程组。
3.解方程组:通过解方程组,求解出交点的坐标。
示例假设有直线L1和直线L2,它们的方程分别为:L1: 2x + 3y = 8 L2: -4x + y = 5将这两条直线的方程联立,得到方程组:2x + 3y = 8 -4x + y = 5我们可以通过消元或代入等方法解方程组,求解出交点的坐标。
结果通过解方程组,我们可以求解出交点的坐标为(1,2)。
方法二:向量叉积法步骤1.确定两条直线上的两个点:分别从每条直线上选取两个点,记为A、B和C、D。
2.计算向量:根据选取的点,计算向量AB和向量CD。
3.计算向量叉积:计算向量AB和向量CD的叉积,得到向量E。
4.计算交点坐标:利用向量叉积的性质,可以得到交点的坐标。
示例假设有直线L1和直线L2,它们通过如下两个点确定:L1: A(1,2) B(3,4) L2: C(5,6) D(7,8)通过计算向量AB和向量CD的叉积,得到向量E的数值为(-4,4)。
根据向量叉积的性质,我们可以得到交点的坐标为(1,2)。
结果通过计算向量叉积,我们可以求解出交点的坐标为(1,2)。
总结本文介绍了两种常见的方法来求解两直线的交点坐标:解方程法和向量叉积法。
解方程法通过联立方程组,通过求解方程组的方法来求得交点的坐标。
向量叉积法则是通过计算向量的叉积,并利用叉积的性质来求得交点的坐标。
两种方法都可以有效地求解两直线的交点,选择哪种方法取决于问题的具体情况。
直曲表1:常规交点法路线(坐标简单型)计算程序

48.043
35.000 45.000
41.006 46.497
12.454
10.469
K0+658.889
55°06′32.1″ (Z)
60.000
35
45.826 49.200 92.710 8.633 5.689 K0+757.890
56°24′47.4″ (Y)
0.000
110.710
252°23′01.5 ″
0.000
105.905
182°01′09.9 ″
0.000
97.926
126°54′37.8 ″
57.896
132.582
183°19′25.3 ″
16.459
65.185
228°22′32.4 ″
备注 21
编制:
复核:
审核:
图号:S2-4-1
83°41′31.1″ (Y)
35.000
31.344 51.125 11.984 11.564
20°23′37.7″ (Z)
199.358
35.000 45.000
83.532 94.716
53.880 57.946
110.959
3.545
0.867
K0+547.930
70°21′51.5″ (Z)
计算方位角
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
BP 3560468.929 421168.528
K0+000
JD1 3560034.969 421099.131 K0+439.474 JD2 3560043.396 420925.435 K0+601.810 JD3 3560009.891 420819.917 K0+711.653 JD4 3559904.051 420816.185 K0+807.090 JD5 3559845.240 420894.484 K0+899.326
交点法坐标计算程序

1.主程序 JDFZBZFS17→DimZ: Norm 2:1→ A " XY=1,FS=2,GC=3,LJKD=4,BPFY=5,BZFY=6”?A:A=1=>Goto1:A=2=>Goto 2: A=3=>Goto 3:A=4=>Goto 4: A=5=>Goto 5: A=6=>Goto 6LbI 1:Prog "DX":LbI A:Prog"QX": 90→B: "PJ1"?B:B →C: "PJ2"?C:B→Z[1]:C→Z[8]:LbI B:1→F: "KM"?Z: Prog"X1":?D:Prog"THB":O→L: Z[2]+Z[1]-Z[8] →E:X+L cos(E) →X:Y+Lsin(E) →Y:Prog"XY":Prog"JS":Goto B LbI 2:2→F:90→Z[1] :Prog"QX":LbI C: "KM"?Z:Prog"X 1": "XO"?X: "Y0"?Y:Prog"THB":Fix 5:Prog"ZD":G oto CLbI 3:Prog"QX": 0→B: "H-B"?B:B→Z[9]:LbI D: "KM"? Z:?D:Prog"H":Fix 5: "H=": H-Z[9] →H◢"I=":I◢Goto DLbI 4:Prog"QX":LbI E: "KM"?Z:?D:Prog"GD":Fix 5:" SJGD=": Locate 6,4,L:Goto ELbI 5:Prog"QX":0.5→B:"TH-GD"?B:B→Z[19]:LbI F:2→F: 90→Z[1]:"KM"?Z:Prog "X1":"X0"?X: "Y0"?Y: "SJ GC"?H: 0→M: "M0(YDMGC) "?M: Prog"BP FY":Fix 3:S→O: "L0=":Locate 6,4,O:Prog"ZD":H-M→G:"TW=": Lcoate 6,4,G: Goto FLbI 6:Prog"DX":LbI G:Prog"QX":LbI H:1→F:90→Z[1]:"KM"?Z: Goto G:Prog"X1":?D:Prog"THB":Prog"XY":Prog"JS":Prog"H":0→M:"M0"?M:Fix 2:H-M→T:"TW=": 6,4,T◢ Goto H2. 坐标计算次程序(THB)LbI J: If F=1:Then Prog "Z":Goto 1:Else Prog "ZX":Goto 2: IfEnd: LbI 1:I+D×COS(Z[2]+Z[1]) →X: J+D×Sin(Z[2]+Z[1]) →Y: LbI 23.路基开挖边线及填方坡脚线放样程序程序名:BP FYLbI H: 13→L:H-M→G: Prog “W1”:If G <0:Then –G →G:G oto W:Else G →G:Goto TLbI W:Z[8]+Z[9]→A: If G >A:Then Goto 1:Else If G >Z[8]: Then Goto 2:Else Goto 3:IfEndLbI 1: L+Z[10]+Z[11]+Z[12]+( G -A-( Z[11]+Z[12])×0.03)×Z[7]+Z[9]×Z[6]+Z[8]×Z[5] →S:Goto ZLbI 2: L+Z[10]+Z[11]+( G -Z[8]- Z[11]×0.03)×Z[6]+Z[8]×Z[5] →S:Goto ZLbI 3: L+ G×Z[5]→S:Goto ZLbI T:Z[16]+Z[17] →B:If G >B:Then Goto 4:Else If G >Z [16]:Then Goto 5:Else Goto 6:IfEndLbI 4: L+Z[18] ×2+ (G -B-2×Z[18]×0.03)×Z[15]+ Z[17]×Z[14]+ Z[16]×Z[13]→S:Goto ZLbI 5: L+Z[18]+( G -Z[16]- Z[18]×0.03)×Z[14]+Z[16]×Z [13]→S:Goto ZLbI 6: L+ G×Z[13]→S:Goto ZLbI Z4.极坐放样计算程序(计算放样点至置仪点方位角及距离)程序名:JSX:Y:Z[11]→K:Z[12]→L:Pol(X-K, Y-L):IF J<0:Then J+360→J:IfEnd:Fix 4:” FWJ=”: J◢DMS◢Fix 5:” S=”: I◢程序名:ZDFix 3:"KM=":Locate 6,4,Z:"D=":Locate 6,4,D5.交点法正算子程序(Z)程序名:ZH2÷R÷24-H∧(4) ÷2688÷R∧(3)→A(圆曲线内移量H表示缓和曲线长)H÷2-H∧(3) ÷240÷R2→B(切垂距)((H2-N2)÷24÷R)÷Sin(Abs(P))-((H∧(4)-N∧(4))/2688/R∧(3)) ÷Sin(Abs(P))→E(R+A)tan(Abs(P) ÷2)+B-E→T:P÷Abs(P) →W0→M:H→CIf Z≤O-T:Then Z-O→S:G→Z[2]:Goto 2: IfEndIf Z≤O-T+H:Then Z-O+T→S:Prog “HX”:G+WK→Z[2]:Goto 4:IfEndIf Z≤O-T+ΠR×Abs(P) ÷180+H÷2-N÷2: Then 180(Z-O+T-0.5H) ÷R÷Π→S: A+R(1-Cos(S))→B H÷2-H∧(3) ÷240÷R2+Rsin(S)→A:R→M:G+WS→Z[2]:Goto 4: IfEnd:O-T+ΠR×Abs(P)÷180+H÷2+N÷2-Z→S:(R+N2÷R÷24-N∧(4)÷2688÷R∧(3))tan(Abs(P) ÷2)+N÷2-N∧(3) ÷240÷R2+E→T :N→H:Prog “HX”:G+P →S:S-WK→Z[2]:U+(T-A)Cos(S)-WBSin(S)→I:V+(T-A)Sin(S)+WBcos(S)→J:Goto 3:LbI 4:U+(A-T)cos(G)-WBsin(G)→I:V+(A-T)Sin(G)+WBcos(G) →J: Goto 3: LbI 2:U+Scos(Z[2])→I:V+Ssin(Z[2]) →J: LbI 3:C→H6. 交点法缓和段转化子程序(HX)程序名:HXS-S∧(5) ÷40÷R2÷H2+S∧(9)÷3456÷R∧(4) ÷H∧(4)→A:S∧(3) ÷6÷R÷H-S∧(7) ÷336÷R∧(3) ÷H∧(3)+S∧(11) ÷42240÷R∧(5) ÷H∧(5)→B:90S2÷Π÷R÷H→K:RS÷H→M7. 交点法反算子程序(ZX)程序名:ZXZ:0→D:LbI 0:Prog “Z”:Pol(X-I,Y-J):J-Z[2] →J:Isin(J) →S:Icos(J) →I:If Abs(I)<0.1:Then Z+I→Z:S→D:Goto 2:Else Goto 1: LbI 1:If M=0:Then Z+I→Z:Goto 0:Eles Pol(M-WS,I):(JMΠ)/180→I:Z+I→Z:Goto 0:IfEndLbI 28.路基标准半幅宽度计算程序程序名GD1→S: Prog “G1”:Z-C→E:(B-A)*E/S+A→L:9. 导线点子程序(DX)程序名:DX“X Z”?K:”YZ”?L:K→Z[11]:L→Z[12]10.高程计算子程序(H)程序名:HP rog “S1”:C-T→F:Z-F→S:C+T→E:G-TI→Q:If T=O:Then Q+SI→H:Goto 0:Else If Z<F:Then Q+SI→H:Goto 0:Else If Z≤E:Then Q+SI+S2÷2÷R→H:Goto 0:LbI 0:H:If D=0:Then Goto I:Else Prog “I”:H+V→H:Goto ILbI I11.高程超高计算程序(I)程序名:IIf Z[3]=1:Then Prog “I1”:Goto 1: IfEndLbI 1: If W=1:Then Goto Z:Else Goto X: IfEndLbI Z:If S=0:Then Abs(D)×M→V:Goto 2:Else Abs(D)×((N-M)×(Z-C)÷S+M)→V:Goto 2:IfEnd:LbI X:If S=0:Then Abs(D)×M→V:Goto 2:Else Abs(D)×(((3((Z-C)÷S)2-2((Z-C)÷S)∧(3))×(N-M))+M)→V:Goto 2:IfEndLbI 2:Abs(D)→E:V÷E→I:I(E-K)→V15.线路选择子程序(线路选择输0时。
交点法坐标计算

本程序由一个主程序JD和三个子程序(JDA、JDB、JDC)构成,运行时只需运行主程序即可!本程序适用于单交点对称型、不对称型、无缓和曲线单圆曲线型一个交点范围内(含交点前后有直线段时)的曲线要素核对和坐标计算,手工输入要素,对设计图纸的“直线、曲线转角表”中交点数据进行复核验证,并为线元法程序提供起点坐标起点切线方位角等数据!当然本程序也可单独逐交点输入进行放样计算用!鉴于5800计算器的空间和以上所述本程序的主要目的,故此程序不修改为数据库版本!需要的自行修改结合XY框架自己修改为数据库反算程序等!主程序名:JD24→Dimz↙Cls :"XC"?U :"YC"?V :"K(JD)"?K :"X(JD)"?X :"Y(JD)"?Y :"LS1"?B :"LS2"?C : ?R :"(ZH)FWJ°"?M : "α(Z-,Y+)°"?O : M+O→N :Prog "JDA"↙Cls :"T1=":"T2=":"L=":"LY=": Locate 4,1,S : Locate 4,2,T : Locate 4,3,L : Locate 4,4,Q◢Cls :"E=":"K(ZH)=": Locate 7,1,E : Locate 7,2,Z[1]◢Cls : "K(HY)=":"K(QZ)=":"K(YH)=":"K(HZ)=": Locate 7,1, Z[2] : Locate 7,2, Z[3] : Locate 7,3, Z[4] : Locate 7,4, Z[5]◢LbI 0 : "K×+×××"?P : "Z"?D : If D≠0 :Then "RJ"?H : IfEnd : Prog "JDB"↙If D<0 :Then Cls : "X(L)=":"Y(L)=": Locate 6,1,F : Locate 6,2,G◢Pol(F-U,G-V : Cls : "S(L)=": Locate 6,1,I : "F(L)=":360Frac((J+360)÷360▼DMS◢Goto 0 : IfEnd↙If D=0 :Then Cls : "X(Z)=":"Y(Z)=": Locate 6,1,F : Locate 6,2,G : "QXFWJ(Z)=": Z▼DMS◢Pol(F-U,G-V : Cls : "S(Z)=": Locate 6,1,I : "F(Z)=":360Frac((J+360)÷360▼DMS◢Goto 0 : IfEnd↙If D>0 :Then Cls : "X(R)=":"Y(R)=": Locate 6,1,F : Locate 6,2,G◢Pol(F-U,G-V : Cls : "S(R)=": Locate 6,1,I : "F(R)=":360Frac((J+360)÷360▼DMS◢Goto 0 : IfEnd↙子程序1名: JDAIf O<0 :Then -1→W : Else 1→W : IfEnd : WO→A ↙B2 ÷24÷R-B^(4)÷2688÷R ^(3) →Z[6] ↙C2 ÷24÷R-C^(4)÷2688÷R ^(3) →Z[7] ↙B÷2-B^(3)÷240÷R2 →Z[8] ↙C÷2-C^(3)÷240÷R2 →Z[9] ↙Z[8]+((R+Z[7]-(R+Z[6])cos(A))÷sin(A))→S↙Z[9]+((R+Z[6]-(R+Z[7])cos(A))÷sin(A))→T↙RAπ÷180+(B+C) ÷2→L↙RAπ÷180-(B+C) ÷2→Q↙(R+(Z[6]+Z[7])÷2)÷cos(A÷2)-R→E↙K-S→Z[1] ↙↙Z[1]+B→Z[2] ↙↙Z[2]+Q÷2→Z[3]↙Z[1]+L-C→Z[4]↙Z[4]+C→Z[5]↙子程序2名: JDBX-Scos(M)→Z[19]:Y-Ssin(M)→Z[20]↙X+Tcos(N)→Z[21]:Y+Tsin(N)→Z[22]↙If P>Z[1]:Then Goto 1 :IfEnd↙Z[1]-P→L↙X-(S+L)cos(M)+Dcos(Z+H)→F↙Y-(S+L)s in(M)+Dsin(Z+H)→G↙M→Z : Goto 5↙LbI 1 : If P>Z[2]:Then Goto 2 :IfEnd↙P-Z[1]→L→Z[12]:B→Z[13]rog"JDC"↙Z[19]+Z[14]cos(M)-WZ[15]sin(M)+Dcos(Z+H)→F↙Z[20]+Z[14]sin(M)+WZ[15]cos(M)+Dsin(Z+H)→G↙M+90WL2 ÷(BRπ)→Z↙Goto 5↙LbI 2 : If P>Z[4]:Then Goto 3 :IfEnd↙P-Z[1]→L:90(2L-B)÷R÷π→Z[11]↙Rsin(Z[11])+Z[8]→Z[14]:R(1-cos(Z[11]))+Z[6]→Z[15]↙Z[19]+Z[14]cos(M)-WZ[15]sin(M)+Dcos(Z+H)→F↙Z[20]+Z[14]sin(M)+WZ[15]cos(M)+Dsin(Z+H)→G↙M+WZ[11]→Z↙Goto 5↙LbI 3 : If P>Z[5]:Then Goto 4 :IfEnd↙Z[5]-P→L→Z[12]:C→Z[13]rog"JDC"↙Z[21]-Z[14]cos(N)-WZ[15]sin(N)+Dcos(Z+H)→F↙Z[22]-Z[14]sin(N)+WZ[15]cos(N)+Dsin(Z+H)→G↙N-90WL2 ÷(CRπ)→Z↙Goto 5↙LbI 4 : P-Z[5]→L↙X+(T+L)cos(N)+Dcos(Z+H)→F↙Y+(T+L)sin(N)+Dsin(Z+H)→G↙N→Z↙Goto 5↙LbI 5 : 360Frac((Z+360)÷360→Z↙子程序3名: JDCIf Z[12]=0 :T hen 0→Z[14]: 0→Z[15]:Else↙Z[12]- Z[12]^(5)÷40÷(RZ[13])2+ Z[12]^(9)÷3456÷(RZ[13])^(4)→Z[14]↙Z[12]^(3)÷6÷(RZ[13])-Z[12]^(7)÷336÷(RZ[13])^(3)+ Z[12]^(11) ÷42240÷(RZ[13])^(5)→Z[15] ↙IfEnd↙程序说明:已知数据输入:XC ? 测站X坐标YC ? 测站Y坐标K(JD)?交点桩号X(JD)?交点X坐标交点法线路坐标计算Y(JD)?交点Y坐标LS1 ?第一缓和曲线长度LS2 ?第二缓和曲线长度R ? 圆曲线半径(ZH)FWJ°?交点前(即前交点至本交点也即ZH点)的正切线方位角α(Z-,Y+)?本交点处线路转角(左转为负,右转为正,度分秒输入)K×+×××? 待求桩号Z ?待求桩号距中距离(左负值,右正值,中为0)RJ ?斜交右角(线路切线前进方向与边桩右侧夹角)计算结果显示:T1=第一切线长T2=第二切线长L=曲线总长LY=圆曲线长E=曲线外距K(ZH)=直缓点桩号K(HY)=缓圆点桩号K(QZ)=曲中点桩号K(YH)=圆缓点桩号K(HZ)=缓直点桩号X= Y=待求点的坐标(其中:L-左 Z-中 R-右)QXFWJ(Z)=待求点的中桩切线方位角(当求中桩坐标时显示)S= F=测站至待求点的水平距离、方位角(其中L-左 Z-中 R-右)。
交点法、线元法坐标计算精编版

3、交点法、线元法坐标计算坐标计算是根据图纸中“直线及曲线转角一览表”提供的数据计算道路中桩坐标,然后和图纸提供的“逐桩坐标表”比对,如果一样则说明输入平曲线参数输入正确,可以计算边桩坐标和其他结构物坐标了;如果中桩坐标不一样,一般是平曲线参数输入有误,需要重新检查输入,另一种结果是图纸有错,这种情况少见,但不代表没有。
“直线及曲线转角一览表”和“逐桩坐标表”见附件1、附件2。
线元法是以路线的起点坐标、方位角、起终点桩号等节点元素来计算出要求的坐标;交点法是以路线的交点要素和路线的主要要素来求得坐标。
①交点法交点:路线的转折点,路线改变方向是相邻两直线的延长线相交的点。
用JD表示,有些图纸上用IP表示。
看下图:交点是针对曲线的(包含圆曲线和缓和曲线),一段曲线就有一个交点。
交点参数有:坐标(X,Y)、交点桩号、转角值、圆曲线半径R、缓和曲线长度。
教学提供软件(轻松测量、双心软件、测量工具)交点法曲线要素输入说明:1、QD起点坐标:起点坐标必须在直线段上,或填写前一交点的坐标。
2、JD交点曲线要素:(1)交点桩号(2)交点坐标(X,Y)(3)曲线半径R(4)第一缓和曲线长度LS1,若为0,输入0,不能为空。
(5)第二缓和曲线长度LS2,若为0,输入0,不能为空。
3、ZD终点坐标:终点坐标也必须在直线段上,或填写后一交点的坐标。
检核数据是否输入正确的方法:软件生成的圆曲线要素中切线长、外距、交点里程:注意校正起点里程、等与设计图纸是否一致。
如果上述数据和图纸不一样,请认真检查有错误的交点处的数据输入是否正确,如果输入没有错误,请考虑是否包含不完整缓和曲线,使用公式A²=R*Ls检查是否包含不完整缓和曲线。
如果包含不完整缓和曲线,那就需要用线元法也叫积木法计算了。
有的设计院给出的直曲表是整条设计线路的直曲表的一部分,以其中某个交点作为起始点的话,起始里程有时候需要校正,当然,并不是每个图纸给出的起点里程都需要校正,大多数图纸的起点里程已经被设计院校正过,我们输入平曲线的时候需要验证一下。
道路测量坐标计算系统交点法简介

⑴采用资源管理器界面类型进行设计,数据按照“工程、曲线、计算表”三级进行组织。
可以建立数个工程,每个工程包含数个曲线,每个曲线又包含若干计算表。
结构清晰,便于测量资料的计算、存储、管理。
⑵对于一个曲线,可以根据不同需要,计算不同的点位坐标(如中桩、边桩),产生一个相对独立的计算表,而不需重复输入曲线交点坐标、半径、缓和曲线长等资料。
⑶能够计算出中桩、边桩任意点的坐标。
软件提供中桩、中桩+左右边桩、中桩+左边桩、中桩+右边桩四种计算表类型,可以根据实际需要进行选择。
⑷能够计算法线方向及任意方向边桩的坐标。
⑸计算出中桩的切线方位角,便于您进行其他的计算。
⑹可以利用“坐标查询”窗口针对一个曲线或一项工程进行某一桩号的坐标查询,而不需建立计算表,灵活方便。
⑺已知一点的坐标,可以利用“桩号查询”窗口进行桩号查询。
利用此窗口可以计算出此点对应中桩的里程以及到中桩的距离,这样可以用于高边坡、挡土墙、隧道净空的检查。
⑻计算坐标时,桩号输入提供手动输入和自动输入两种方式。
自动输入方式能够自动产生整桩号以及固定距离的左右边桩;自动输入后还可以进入手动输入状态进行更改,以适合您的特殊需要。
⑼可以对桩号自动输入的起讫点进行设置。
⑽计算表产生后,可以输入置镜点、后视点坐标,能够计算出现场放样数据。
置镜点、后视点也可以从控制桩表中进行选择。
⑾每一项工程都有一个独立的控制桩表。
打开控制桩表后可以进行控制桩的添加、删除等操作。
⑿具有极强的纠错能力,能够对您输入的数据进行自动检查,对错误数据给出提示。
⒀计算结果可以导出,可以用Excel软件进行编辑或用于往测量仪器的传输;也可以自动生成精美报表,并能够进行打印预览或打印输出。
⑴软件采用Windows 界面风格进行设计,界面友好,易于理解。
软件提供下拉菜单、快捷键、工具栏三种操作方式,操作方便、快捷;⑵能够进行标准曲线、C型、S型、卵型曲线等任意复杂形式的线形坐标计算;⑶不仅能够计算任意点的平面坐标,而且还能够计算其标高;⑷通过设置可以自动计算全线任意区段的整桩号或固定间距的中桩及边桩坐标;⑸能够计算法线方向及任意方向边桩的坐标;⑹软件自动处理竖曲线及路面横坡,能够计算任一桩号的标高及路面横坡;⑺通过设置,可以计算出路基顶面、底基层、基层、路面等各施工层的标高,并能打印出标高计算表,可以直接用于路基、路面施工中的标高控制;⑻可以根据实测坐标反算出该点对应的桩号及与中桩的距离,也可以计算出该点的设计标高及实际与设计的高差,用于施工过程中的检查;⑼自动进行路面加宽数据的计算。
直线方程求交点坐标

直线方程求交点坐标介绍直线是解析几何中最基本的图形之一,在实际问题中经常需要求解直线的交点坐标。
直线方程是求解直线问题的重要工具,通过直线方程,我们可以简洁地确定直线的位置和性质。
本文将介绍如何通过直线方程求解直线的交点坐标。
直线方程的一般形式一般来说,直线方程可以用以下一般形式表示:ax + by + c = 0其中,a、b、c是常数,x和y是直线上的任意一点的坐标。
这种形式被称为一般方程或一般式。
直线方程的斜截式直线方程的另一种常见形式是斜截式,可以表示为:y = mx + b其中,m表示直线的斜率,b表示直线与y轴的截距。
求解直线交点的方法要求解两条直线的交点坐标,可以采用以下步骤:1.将两条直线的方程表示成一般形式或斜截式。
2.将两个方程中的x、y系数相等的项相减,得到一个关于x的方程。
3.解这个关于x的方程,得到x的值。
4.将x的值代入其中一个原始方程中,求解y的值。
5.得到交点坐标。
示例为了更好地理解如何求解直线交点的坐标,我们来看一个示例。
假设有两条直线,直线1的方程为:2x + 3y = 7,直线2的方程为:5x - 4y = 8。
我们将按照上述步骤来求解它们的交点坐标。
1.将直线1的方程写成斜截式。
通过移项可得:y = (-2/3)x + 7/3。
直线1的斜率为-2/3,截距为7/3。
2.将直线2的方程写成斜截式。
通过移项可得:y = (5/4)x - 2。
直线2的斜率为5/4,截距为-2。
3.求解交点的x坐标。
将直线1和直线2的x系数相减得:(5/4)x - (-2/3)x = 8 - 7/3。
化简得:(7/12)x = 17/3。
解得:x = (17/3) / (7/12) = 68/21。
4.求解交点的y坐标。
将x = 68/21 代入直线1的斜截式可得:y = (-2/3) * (68/21) + 7/3。
化简得:y = 50/21。
5.得到交点坐标。
交点的坐标为 (68/21, 50/21)。
5800交点法全线坐标计算程序

我自用的5800交点法全线坐标计算程序,适用于主线(等长完整缓和曲线)全线任意中边桩坐标计算。
特点是输入参数少,方便,一般设计图纸上都有。
一、主程序 ZB1、Lbl 02、”ZHANGHAO”?Z3、Prog ”SJ”(交点参数子程序)4、”BZ”?M5、I-D→Q: J-F→P6、tan-1(P÷Q)→A7、If Q<0:Then A+180→A:IfEnd8、If A<0:Then A+360→A:IfEnd9、H-I→Q:V-J→P10、tan-1(P÷Q)→B11、If Q<0:Then B+180→B:IfEnd12、If B<0:Then B+360→B:IfEnd13、A-B+180→E:1→U14、If E>360:Then E-360→E:IfEnd15、If E<0:Then 360+E→E:IfEnd16、If E<180:Then 180-E→○:IfEnd17、If E>180:Then E-180→○:-1→U:IfEnd18、L÷2-L3÷240÷R2→Q19、L2÷24÷R-L3÷2688÷R3→P20、(R+P)tan(○÷2)+Q→T21、R○∏÷180+L→G22、C-T→N23、Z-N→S24、If S>G:Then Z-N-G+T→S:I+ScosB→X: J+SsinB→Y: B→W:Else If S>G-L:Then G-S→S: S-S5÷40÷R2÷L2→E: S3÷6÷R÷L→K: I+TcosB+Ecos(B+1 80)+UKcos(90+B)→X: J+TsinB+Esin(180+B)+UKsin(90+B)→Y: B-180U S2÷2÷R÷L÷∏→W: Else If S>L:Then Rsin(180(2S-L)÷2÷R÷∏)+Q →E: R(1-cos(180(2S-L)÷2÷R÷∏))+P→K:I-TcosA+EcosA-UKsinA→X: J-TsinA+EsinA+UKcosA→Y: A+180U(S-L)÷R÷∏+180UL÷2÷∏÷R→W: Els e If S>0:Then S-S5÷40÷R2÷L2→E:S3÷6÷R÷L→K:I-TcosA+EcosA-UKsinA →X: J-TsinA+EsinA+UKcosA→Y:A+180US2÷2÷R÷L÷∏→W: Else If S<0:T hen I-(T-S)cosA→X: J-(T-S)sinA→Y: A→W: IfEnd: IfEnd: IfEnd: If End: IfEnd29、X+Mcos(90+W)→X:Y+Msin(90+W)→Y”X”:X◢”Y”:Y◢30、Goto 0二、数据库子程序:SJIf Z<本曲线HZ(或YZ)桩号:Then 本曲线前一交点X坐标→D:本曲线前一交点Y坐标→F:本曲线交点X坐标→I: 本曲线交点Y坐标→J:本曲线后一交点X 坐标→H:本曲线后一交点Y坐标→V:本曲线交点桩号→C:本曲线曲线半径→R:本曲线缓和曲线长度→L:Else If Z<二曲线HZ(或YZ)桩号:Then二曲线前一交点X坐标→D:二曲线前一交点Y坐标→F:二曲线交点X坐标→I:二曲线交点Y 坐标→J:二曲线后一交点X坐标→H:二曲线后一交点Y坐标→V:二曲线交点桩号→C:R=二曲线曲线半径:二曲线缓和曲线长度→L:Else If ………… IfEnd:说明:变量输入:Z=计算点桩号:M=计算桩号边桩距离(左负右正)。
线路坐标计算公式
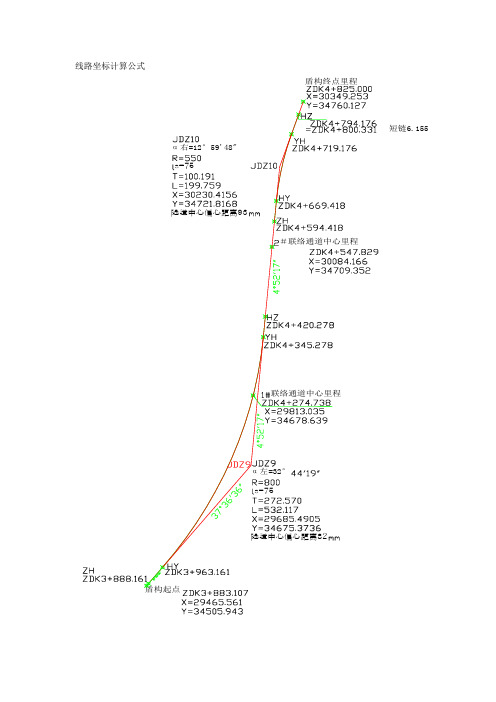
线路坐标计算公式α左=32°s=75隧道中心偏心距离82α右=12°59'48"s=75隧道中心偏心距离93盾构终点里程短链6.155#联络通道中心里程联络通道中心里程盾构起点一、线路中心线坐标计算公式:1、3+883.107—3+888.161直线段计算公式X=X0+L*cosα1Y=Y0+L*sinα1(X0,Y0为直线段起点坐标,α1为直线方位角,L为待求点到起点的距离) 2、ZH—HY段计算公式(缓和曲线计算公式)X=X ZH+(L-L5/(40*R2*ls2))÷cos(30*L2/(π*R *ls))*cos(α1±30*L2/(π*R*ls))Y=Y ZH+(L-L5/(40*R2*ls2))÷cos(30*L2/(π*R *ls))*sin(α1±30*L2/(π*R*ls)) (X ZH, Y ZH为缓和曲线起点坐标,α1为方位角,R为圆曲线半径,L 为待求点到起点的距离,ls为缓和曲线长,±曲线左偏为-,右偏为+)3、HY—YH段计算公式(圆曲线计算公式)X=X HY+2R*sin(90*L/π/R)*cos(α1±90*(L+ls)/ π/R )Y=Y HY+2R*sin(90*L/π/R)*sin(α1±90*(L+ls)/ π/R )(X HY, Y HY为圆曲线起点坐标,α1为方位角,R为圆曲线半径,L为待求点到起点的距离,ls为缓和曲线长,±曲线左偏为-,右偏为+)4、YH-HZ段计算公式X=X HZ+(L-L5/(40*R2*ls2))÷cos(30*L2/(π*R *ls))*cos(α2+180±30*L2/(π*R*ls)) Y=Y HZ+(L-L5/(40*R2*ls2))÷cos(30*L2/(π*R *ls))*sin(α2+180±30*L2/(π*R*ls))(X HZ, Y HZ为圆曲线起点坐标,α2为方位角,R为圆曲线半径,L为待求点到起点的距离,ls为缓和曲线长,±曲线左偏为-,右偏为+)二、隧道中心线坐标计算公式:1、直线段中线路中心线与隧道中线重合。
卡西欧5800交点法坐标计算程序

交点法坐标计算JDFZBJS第一种:单一交点法计算任意里程位的坐标。
程序如下:待求段的交点X坐标→V:待求段的交点Y坐标→W:前一段的交点X坐标→M:前一段的交点Y坐标→N:直缓点ZH的里程→Q:缓直点HZ的里程→Z:待求段圆曲线半径→R:待求段缓和曲线长度→U:待求段的切线长度→T:待求段转向方向(左转取-1,右转取+1)→P:待求段转向偏角→A:10→DimZ:Cls:“KM=”?L: 待求点里程“L-1,R+1”?K: 待求点位于前进方向左侧为-1,右侧为+1“PJ=”?S: 待求点到线路设计中心的平距Lbl 0:Pol(V-M,W-N):J→Z[1]:Rec(T,Z[1]+180):V+I→Z[2]:W+J→Z[3]:Lbl 1:If L≤Q:Then Rec(Q-L,Z[1]+180):Else Goto 2:IfEnd:Z[2]+I→Z[4]:Z[3]+J→Z[5]:If K=1:Then Rec(S,Z[1]+90):Else Rec(S,Z[1]+270):IfEnd:Goto 6:Lbl 2:Abs(Q-L)→Z[6]:If U≥Z[6]:Then Pol(Z[6]-Z[6]ˆ(5)÷(40R2U2)+Z[6]^(9)÷(3456(RU)^(4)),Z[6]^(3)÷(6RU)-Z[6]^(7)÷(336(RU)^(3))+Z[6]^(11)÷(42240(RU)^(5))):Else Goto 3:IfEnd:J→Z[7]:Rec(I,Z[1]+Z[7]P):Z[2]+I→Z[4]:Z[3]+J→Z[5]:Z[1]+Z[7]P+60PZ[6]2÷(RUπ)+90→Z[10]:If K=1:Then Rec(S,Z[10]):Else Rec(S,Z[10]+180):IfEnd:Goto 6:Lbl 3:Abs(Q-L)→Z[6]:If L≤Z-U:Then Pol(Rsin(90(2Z[6]-U)÷(Rπ))+U-Rsin(90U÷(Rπ))-U^(3)÷(40R2),R-Rcos(90(2Z[6]-U)÷(Rπ))+U2÷(24R)):Else Goto 4:IfEnd:J→Z[7]:Rec(I,Z[1]+Z[7]P):Z[2]+I→Z[4]:Z[3]+J→Z[5]:Z[1]+90P(2Z[6]-U)÷(Rπ)+90→Z[10]:If K=1:Then Rec(S,Z[10]):Else Rec(S,Z[10]+180):IfEnd:Goto 6:Lbl 4:If L≥Z-U And L≤Z:Then Z[1]+AP→Z[1]:Else Goto 5:IfEnd:Rec(T,Z[1]):V+I→Z[2]:W+J→Z[3]:Z→Q:-P→P:-K→K:Z[1]+180→Z[1]:Goto 2:Lbl 5:If L≥Z:Then Z[1]+AP→Z[1]:IfEnd:Rec(T,Z[1]):V+I→Z[2]:W+J→Z[3]:Rec(L-Z,Z[1]):Z[2]+I→Z[4]:Z[3]+J→Z[5]:If K=1:Then Rec(S,Z[1]+90):Else Rec(S,Z[1]+270):IfEnd:Goto 6:Lbi 6:Z[4]+I→Z[8]:Z[5]+J→Z[9]:Cls:Fix 3:“Xp=”: 计算的X坐标“Yp=”: 计算的Y坐标Locate 7,1,Z[8]: X坐标显示在第一行Locate 7,2,Z[9]◢Y坐标显示在第二行Stop注解:在本程序中考虑了ZH点前和HZ点后的直线情况。
