第八讲 动态规划与最短路径(3)_538106033
动态规划求最短路径的两种方法
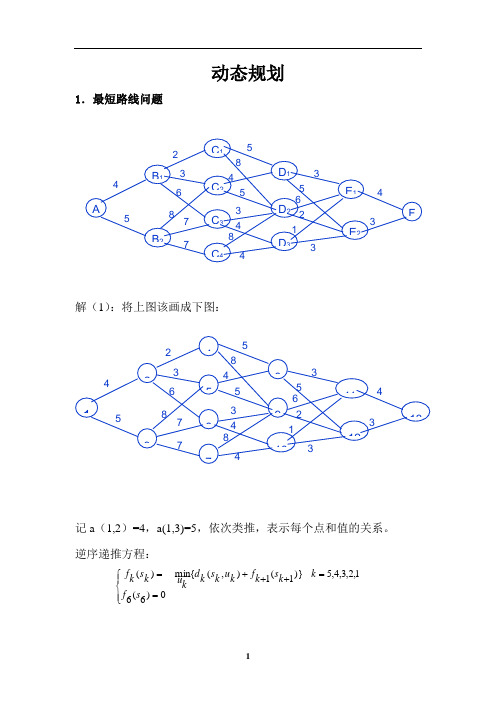
动态规划1.最短路线问题解(1):将上图该画成下图:记a (1,2)=4,a(1,3)=5,依次类推,表示每个点和值的关系。
逆序递推方程:⎪⎩⎪⎨⎧==+++=0)6(61,2,3,4,5)}1(1),({min )(s f k k s k f k u k s k d k uk s k fAB 1B 2C 1 C 2C 3 C 4D 1D 2 D 3E 1 E 2F4523 6 8 7 75845348435 6 2 314 31234 5 6 789 101112134523 6 8 7 7584534 8435 6 2 314 3如图各状态:逆序递推,找出上一个状态到下一阶段的最小路径值。
例如,当K=4时,状态 它们到F 点需经过中途 点E ,需一一分析从E 到 F 的最短路:先说从D1到F 的最短路 有两种选择:经过 E1, E2, 比较最短。
这说明由 D1 到F 的最短距离为7,其路径为AB 1B 2C 1 C 2C 3 C 4D 1 D 2 D 3E 1 E 2F4523 6 87 75845348435 62 31 4 3第1阶段 第2阶段 第3阶段 第4阶段 第5阶段状态 1状态 2状态3状态 4状态 5状态 6)}(),(),(),(m in{)(252141511414E f E D d E f E D d D f ++=.7}35,43min{=++=.11F E D →→},,{3214D D D S =a=[0,4,5,inf,inf,inf,inf,inf,inf,inf,inf,inf,inf 4,0,inf,2,3,6,inf,inf,inf,inf,inf,inf,inf 5,inf,0,inf,8,7,7,inf,inf,inf,inf,inf,inf inf,2,inf,0,inf,inf,inf,5,8,inf,inf,inf,inf inf,3,8,inf,0,inf,inf,4,5,inf,inf,inf,inf inf,6,7,inf,inf,0,inf,inf,3,4,inf,inf,inf inf,inf,7,inf,inf,inf,0,inf,8,4,inf,inf,inf inf,inf,5,4,inf,inf,inf,0,inf,inf,3,5,inf inf,inf,inf,8,5,3,8,inf,0,inf,6,2,inf inf,inf,inf,inf,inf,4,4,inf,inf,0,1,3,inf inf,inf,inf,inf,inf,inf,inf,3,6,1,0,inf,4 inf,inf,inf,inf,inf,inf,inf,5,2,3,inf,0,3 inf,inf,inf,inf,inf,inf,inf,inf,inf,inf,4,3,0]; s8=min(a(8,11)+a(11,13),a(8,12)+a(12,13)); s9=min(a(9,11)+a(11,13),a(9,12)+a(12,13)); s10=min(a(10,11)+a(11,13),a(10,12)+a(12,13)); s4=min(a(4,8)+s8,a(4,9)+s9); s5=min(a(5,8)+s8,a(5,9)+s9); s6=min(a(6,9)+s9,a(6,10)+s10); s7=min(a(7,9)+s9,a(7,10)+s10); s2=[a(2,4)+s4,a(2,5)+s5,a(2,6)+s6]; s2=min(s2);s3=[a(3,5)+s5,a(3,6)+s6,a(3,7)+s7]; s3=min(s3);s1=min(a(1,2)+s2,a(1,3)+s3)运行结果为:s8 = 7 s9 = 5 s10 = 5 s4 = 12 s5 = 10 s6 = 8 s7 = 9 s2 =13s3 = 15 s1 = 17结果分析:s 表示每个点到终点的最短距离,那么最短路程为17。
《最短路径算法》课件

探索最短路径算法的奥秘,了解其在各领域中的应用,以及选择最佳算法的 依据,展望最短路径算法的未来。
最短路径算法简介
最短路径问题的定义和最短路径算法的广泛应用。
单源最短路径算法
1
贝尔曼-福德算法2 Nhomakorabea算法思想:通过利用松弛操作,逐步更新节 点之间的最短路径。
算法步骤:进行N-1次松弛操作,其中N为节 点数,再进行一次检查负权边。
电路板布线
通过最短路径算法规划电路板 上元件的布线路径,减小电路 的延迟,提高性能。
应用最短路径算法的问题探讨
1 负权边问题
2 负环问题
遇到边权值为负数的情况,部分最短路径算法需 要特殊处理。
当图中存在负权环时,部分最短路径算法无法得 到准确的最短路径。
最短路径算法总结
1 各种算法的优劣
不同最短路径算法在不同场景下有不同的优劣,需要根据具体情况进行选择。
算法复杂度分析:时间复杂度为O(V*E),V 为节点数,E为边数。
迪杰斯特拉算法
算法思想:通过记录已知最短路径和待确认 节点,逐步更新最短路径。
算法步骤:从起点出发,不断更新最短路径, 直到所有节点都被确认为最短路径。
算法复杂度分析:时间复杂度为O(V^2),V 为节点数。
多源最短路径算法
1
弗洛伊德算法
算法思想:通过动态规划,逐步更新节点间 的最短路径。
算法步骤:利用矩阵记录节点间最短路径, 逐步更新矩阵,得到所有节点的最短路径。
算法复杂度分析:时间复杂度为O(V^3),V为 节点数。
最短路径算法的应用实例
地图导航
使用最短路径算法规划最佳行 驶路线,提供准确的导航指引。
网络路由
应用数学之动态规划 最短路径;单调递增最长子序列

最优化计算方法中的动态规划算法电子科技大学微固学院[摘要]本文首先介绍了动态规划的原理思想,然后给出了利用动态规划解决问题的基本步骤,最后文中给出两个例子,利用动态规划算法和matlab软件解决了图论中的最短路径问题和单调递增最长子序列问题。
[关键词]动态规划最短路径递增最长子序列一.引言动态规划算法大约产生于50年代,1951年由美国数学家R.贝尔曼首先提出动态规划的概念,是用来解决多阶段决策过程最优化的一种数学方法。
我们知道,在计算机算法中,当处理的问题规模比较大时,可以利用分治法将大问题分为若干独立子问题,再利用递归法解决这些子问题,最后将子问题合并得到原问题的解。
但是当子问题之间不独立时,分治法将失效,而应当用动态规划算法来解决。
动态规划属于运筹学的分支,也属于最优计算方法的一种。
图论中的最短路径问题可以利用Dijkstra算法来解决,计算出起点到各个点的最短路径以及如何找到最短路径,本文中应用动态规划算法结合matlab软件,同样找到从起点到各个点的最短路径,以及起点到终点的最短搜索路径,并动态表示出来。
在实际生活中,有一些问题可以化归为最短路径问题,如排队买票问题,假设第i位歌迷买一张票需要时间T[i](1<=i<=n),队伍中相邻的两位歌迷(第j 个人和第j+1个人)也可以由其中一个人买两张票,而另一个人就可以不用排队了,则这两位歌迷买两张票的时间变为R[j],且有R[j]<T[j]+T[j+1],这样做就可以缩短后面歌迷的等待时间,加快整个售票的进程。
现在给出 n ,T[j]和R[j],求使每个人都买到票的最短时间和算法。
这可以化归为图1所示最短路径问题:图1第一个人为N,最后一个人为S相当于求出S到N的最短路径,两点之间的连线的权重相当于每个人的买票时间,如D和N之间的连线用来表示N买票的时间,点N和点C之间的连线表示点N这个人买两张票,所以用不着点D买票了,直接就到点C了,依此类推,相当于求点N到点S的最短路径,即动态规划方程,min{DN+min{SD},CN+min{SC}}。
动态规划实现最短路径问题

动态规划实现最短路径问题⼀、设计最短路径的动态规划算法 <算法导论>中⼀般将设计动态规划算法归纳为下⾯⼏个步骤: 1)分析最优解的结构 2)递归定义最优解的值 3)⾃底向上计算最优解的值 4)从计算的最优解的值上⾯构建出最优解⼆、最短路径的结构 从最优解的结构开始分析(我们假设没有权值为负的路径),对于图G<V,E>的所有结点对最短路径的问题,我们能知道⼀条最短路径的⼦路径都是最短路径。
假设⽤邻接矩阵W=w(ij)来表⽰输⼊带权图,考虑从结点i到结点j的⼀条最短路径p,如果p最多有m(m为有限值)条边。
若i=j,则p的权值为0⽽且不包含其他边。
若i ≠ j,可以将i到j的路径转换为i -> k、k->j。
三、⼀个给定的图 1)给定⼀个有向图 2)我们可以给出这个有向图的邻接矩阵四、C++实现1 #include <iostream>2 #include<fstream>3 #include<sstream>4 #include<vector>5 #include<string>6using namespace std;7const int Max_Num = 100;89 typedef struct Point {10int n; //点的个数11double p[Max_Num];12double q[Max_Num];13int root[Max_Num][Max_Num];14double w[Max_Num][Max_Num];15double e[Max_Num][Max_Num];16 }Point;1718 vector<Point> points;19 vector<string> res;20 vector<int> num;2122void file_read();23void createPoint();24void optimalBST();25void printRoot(Point P);26void printOptimalBST(int i, int j, int r, Point P, ofstream &fileWrite);27 template <class Type>28 Type stringToNum(const string& str) {29 istringstream iss(str);30 Type num;31 iss >> num;32 iss.str("");33return num;34 }3536void file_read() {37string str2, str1 = "", result;38 ifstream fileRead("in.dat");39if (fileRead.is_open()) {40while (getline(fileRead, str2, '\n')) {41if (str2.find("") != -1) {42 str1.append(str2 + "");43 }44else {45 num.push_back(stringToNum<int>(str2));46if (str1 != "") {47 res.push_back(str1);48 }49 str1 = "";50 }51 }52 res.push_back(str1);53 fileRead.close();54 }55 }5657void createPoint() {58string temp;59 Point P;60for (int i = 0; i < res.size(); i++) {61 vector<string> temp_str; //存放按照空格分开后的数字62int n = num[i];63 stringstream input(res[i]);64while (input >> temp) {65 temp_str.push_back(temp);66 }67 P.n = n;68for(int k = 0; k<=n; k++) P.p[k] = stringToNum<double>(temp_str[k]);69for(int k = n + 1; k<temp_str.size(); k++) P.q[k-(n+1)] = stringToNum<double>(temp_str[k]);70 points.push_back(P);71 }72 }7374//根据书上的伪代码:接收概率列表p1....pn和q0.....qn以及规模n作为输⼊计算出e和root75void optimalBST(){76 Point P;77for(int i = 0; i<res.size(); i++) {78 vector<string> temp_str; //存放按照空格分开后的数字79int n = num[i];80string temp;81 stringstream input(res[i]);82while (input >> temp) {83 temp_str.push_back(temp);84 }85 P.n = n;8687for(int k = 0; k<=n; k++) P.p[k] = stringToNum<double>(temp_str[k]);88for(int k = n + 1; k<temp_str.size(); k++) P.q[k-(n+1)] = stringToNum<double>(temp_str[k]); 8990//初始化只包括虚拟键的⼦树91for (int i = 1;i <= P.n + 1;++i){92 P.w[i][i-1] = P.q[i-1];93 P.e[i][i-1] = P.q[i-1];94 }95//由下到上,由左到右逐步计算96for (int len = 1;len <= P.n;++len){97for (int i = 1;i <= P.n - len + 1;++i){98int j = i + len - 1;99 P.e[i][j] = Max_Num;100 P.w[i][j] = P.w[i][j-1] + P.p[j] + P.q[j];101//求取最⼩代价的⼦树的根102for (int r = i;r <= j;++r)103 {104double temp = P.e[i][r-1] + P.e[r+1][j] + P.w[i][j];105if (temp < P.e[i][j])106 {107 P.e[i][j] = temp;108 P.root[i][j] = r;109 }110 }111 }112 }113 points.push_back(P);114 }115 }116117void printOptimalBST(int i, int j, int r, Point P, ofstream &fileWrite){118int root_node = P.root[i][j];//⼦树根节点119if (root_node == P.root[1][P.n]){120//输出整棵树的根121 fileWrite << "k" << root_node << "是根" << endl;122 printOptimalBST(i, root_node - 1, root_node, P, fileWrite);123 printOptimalBST(root_node +1 , j, root_node, P, fileWrite);124return;125 }126127if (j < i - 1){128return;129 }else if (j == i - 1){//遇到虚拟键130if (j < r)131 fileWrite << "d" << j << "是" << "k" << r << "的左孩⼦" << endl;132else133 fileWrite << "d" << j << "是" << "k" << r << "的右孩⼦" << endl;134return;135 }136else{//遇到内部结点137if (root_node < r)138 fileWrite << "k" << root_node << "是" << "k" << r << "的左孩⼦" << endl; 139else140 fileWrite << "k" << root_node << "是" << "k" << r << "的右孩⼦" << endl; 141 }142 printOptimalBST(i, root_node - 1, root_node, P, fileWrite);143 printOptimalBST(root_node + 1, j, root_node, P, fileWrite);144 }145146//输出最优⼆叉查找树所有⼦树的根147void printRoot(Point P){148 cout << "各⼦树的根:" << endl;149for (int i = 1;i <= P.n;++i){150for (int j = 1;j <= P.n;++j){151 cout << P.root[i][j] << "";152 }153 cout << endl;154 }155 cout << endl;156 }157158int main(){159 file_read();160 optimalBST();161 ofstream fileWrite("out.dat");162 Point P ;163for(int i = 0; i<points.size(); i++) {164 P = points[i];165 printRoot(P);166 printOptimalBST(1,P.n,-1, P, fileWrite);167 }168 fileWrite.clear();169return0;170 } 上述代码是将给定的邻接矩阵从⽂件中读取 然后根据输⼊的邻接矩阵求出最短路径。
动态规划在最短路径问题中的应用

动态规划在最短路径问题中的应用动态规划是一种解决复杂问题的方法,它将问题分解成更小的子问题,并通过保存子问题的解来避免重复计算,从而提高解决问题的效率。
最短路径问题是在图或者网络中找到从起点到终点的最短路径的问题,可以使用动态规划算法来解决。
本文将介绍动态规划在最短路径问题中的应用及其算法实现。
一、最短路径问题在最短路径问题中,我们需要在图或网络中找到从一个节点到另一个节点的最短路径。
最短路径可以通过边的权重来衡量,权重可以表示距离、时间、代价等。
最短路径问题有多种变体,其中最常见的是单源最短路径和全源最短路径。
单源最短路径问题是在给定一个起点的情况下,找到该起点到其他所有节点的最短路径。
最常用的算法是Dijkstra算法和Bellman-Ford算法。
二、动态规划原理动态规划通过保存子问题的解来避免重复计算,从而提高算法的效率。
它将问题分解成更小的子问题,并使用递推关系来计算子问题的解。
在最短路径问题中,我们可以使用动态规划来计算从起点到每个节点的最短路径。
首先,我们定义一个一维数组dist[]来保存从起点到每个节点的最短路径长度。
初始化时,dist[]的值为无穷大,表示路径长度未知。
然后,我们从起点开始逐步计算每个节点的最短路径长度。
具体的动态规划算法如下:1. 初始化dist[]为无穷大,起点的dist[]为0。
2. 对于每个节点v,按照拓扑顺序进行如下操作:2.1. 对于节点v的所有邻接节点u,如果dist[v] + weight(v, u) < dist[u],则更新dist[u]。
2.2. 拓扑顺序可以根据节点的拓扑顺序进行计算或者使用深度优先搜索(DFS)算法。
三、算法实现下面是使用动态规划算法解决最短路径问题的示例代码:```// 定义图的邻接矩阵和节点个数int graph[MAX][MAX];int numNodes;// 定义dist[]数组来保存最短路径长度int dist[MAX];// 定义拓扑排序和DFS算法需要的变量bool visited[MAX];stack<int> s;// 动态规划算法求解最短路径void shortestPath(int startNode) {// 初始化dist[]数组为无穷大for (int i = 0; i < numNodes; i++) {dist[i] = INT_MAX;}dist[startNode] = 0;// 拓扑排序或DFS计算每个节点的最短路径长度 for (int i = 0; i < numNodes; i++) {if (!visited[i]) {DFS(i);}}// 输出最短路径长度for (int i = 0; i < numNodes; i++) {cout << "Node " << i << ": " << dist[i] << endl; }}// 深度优先搜索void DFS(int node) {visited[node] = true;for (int i = 0; i < numNodes; i++) {if (graph[node][i] != 0 && !visited[i]) {DFS(i);}}s.push(node);}```以上示例代码演示了使用动态规划算法求解最短路径问题的基本原理和步骤。
动态规划所有点对的最短距离课件

• 最小的子问题D0:从顶点i (不得经过任 何其他顶点)到顶点j的距离;
• 子问题D1:从顶点i(可以经过顶点1, 不得经过其他任何其他顶点)到顶点j的 距离。
动态规划所有点对的最短距离课件
• 子问题Dk:从顶点i(可以经过顶点1、 顶点2、……顶点k,不得经过任何其他 顶点)到顶点j的距离。
动态规划所有点对的最短距离课件
8.3 单源最短路径
Dijkstra算法的迭代过程:
迭代
S
u dist[2] dist[3] dist[4] dist[5]
初始
{1}
-
10 maxint 30
100
1
{1,2}
2
10
60
2
{1,2,4}
4
10
50
3
{1,2,4,3} 3
10
50
4
{1,2,4,3,5} 5
• 用动态规划来解决
动态规划所有点对的最短距离课件
选做题
1、设A和B是两个字符串。我们要用最少的字符 操作将字符串A转换为字符串B。这里所说的字 符串操作包括:
(1) 删除一个字符; (2) 插入一个字符; (3) 将一个字符改为另一个字符; 将字符串A变换为字符串B所用的最少字符操作成
为字符串A到字符串B的编辑距离,记为d(A,B)。 试设计一个有效算法,对任给的两个字符串A和 B,求他们的编辑距离d(A,B) A=“abcde”,B=“acdefa”
计算过程
• 例:考虑下图所示的带权有向图,求所 有顶点之间的最短距离。
1
2
1
89
1
V= 2
029
最短路径问题的动态规划算法

最短路径问题的动态规划算法动态规划是一种解决复杂问题的有效算法。
最短路径问题是指在给定的图中找到从起点到终点路径中距离最短的路径。
本文将介绍动态规划算法在解决最短路径问题中的应用。
1. 最短路径问题简介最短路径问题是图论中的经典问题之一,旨在找到从图中一点到另一点的最短路径。
通常使用距离或权重来衡量路径的长度。
最短路径问题有多种算法可以解决,其中动态规划算法是一种常用且高效的方法。
2. 动态规划算法原理动态规划算法的核心思想是将原问题分解为更小的子问题,并存储已解决子问题的结果,以供后续使用。
通过逐步解决子问题,最终得到原问题的解。
在最短路径问题中,动态规划算法将路径分解为多个子路径,并计算每个子路径的最短距离。
3. 动态规划算法步骤(1)定义状态:将问题转化为一个状态集合,每个状态表示一个子问题。
(2)确定状态转移方程:通过递推或计算得到子问题之间的关系,得到状态转移方程。
(3)确定初始状态:设置与最小子问题相关的初始状态。
(4)递推求解:根据状态转移方程,逐步计算中间状态,直到得到最终解。
(5)回溯路径:根据存储的中间状态,找到最短路径。
4. 动态规划算法示例以经典的Dijkstra算法为例,演示动态规划算法在解决最短路径问题中的应用。
假设有带权重的有向图G,其中节点数为n,边数为m。
算法步骤如下:(1)定义状态:对于图G中的每个节点v,定义状态d[v]代表从起点到节点v的最短距离。
(2)确定状态转移方程:d[v] = min(d[u]+w[u,v]),其中u为节点v 的直接前驱节点,w[u,v]为边(u,v)的权重。
(3)确定初始状态:设置起点s的最短距离d[s]为0,其他节点的最短距离d[v]为无穷大。
(4)递推求解:根据状态转移方程逐步计算中间状态d[v],更新最短距离。
(5)回溯路径:根据存储的前驱节点,从终点t开始回溯,得到最短路径。
5. 动态规划算法的优缺点优点:(1)求解速度快,适用于大规模问题。
最短路径问题的求解PPT精选文档

.
3
最短路径问题的求解
三、等代价搜索法 等代价搜索法也是在宽度优先搜索的基础上进行了部分优化的一种算法,它与
启发式搜索的相似之处都是每次只展开某一个结点(不是展开所有结点),不同之 处在于:它不需要去另找专门的估价函数,而是以该结点到A点的距离作为估价值, 也就是说,等代价搜索法是启发式搜索的一种简化版本。它的大体思路是:
.
2
最短路径问题的求解
二、 启发式搜索 在宽度优先搜索算法的基础上,每次并不是把所有可展开的结点展开,
而是对所有没有展开的结点,利用一个自己确定的估价函数对所有没展开 的结点进行估价,从而找出最应该被展开的结点(也就是说我们要找的答 案最有可能是从该结点展开),而把该结点展开,直到找到目标结点为止。
.
12
最短路径问题的求解
八、Dijkstra算法(从一个顶点到其余各顶点的最短路径,单源最短路径) 例3、如下图,假设C1,C2,C3,C4,C5,C6是六座城市,他们之间的连线表示两 城市间有道路相通,连线旁的数字表示路程。请编写一程序,找出C1到Ci 的最短路径(2≤i≤6),输出路径序列及最短路径的路程长度。
3、由数轴可见,A与A'点相比,A点离原点近,因而保留A点,删除A'点,相应的,B、B'点保留B点, D、D'保留D',E、E'保留E',得到下图:
.
11
最短路径问题的求解
4、此时再以离原点最近的未展开的点B联接的所有点,处理后,再展开离原点最近未展开的D点, 处理后得到如下图的最终结果:
最短路径问题 ppt课件

12
图论及其应用 作业 用Dijkstra算法求出下图中从顶点a到其它所有 顶点的最短路径及及长度。
13
图论及其应用
有向图中求最短路径的Dijkstra算法
设Sj是带权有向图G中自顶点1到顶点j的最短有向路的长度 步骤1:置P={1},T={2,3,…,n}且S1=0,Sj=w1j, j=2,3,…,n 。 步骤2:在T中寻找一点k,使得Sk=min{Sj},置P=P{k}, T=T- {k}。若T=,终止;否则,转向步骤3。 步骤3:对T中每一点j,置Sj=min {Sj ,Sk+ wkj},然后转向步 骤2。 算法经过n-1 次循环结束。
6
1-6-8-B
6-8-B
13
10
5
图论及其应用
指定点到其它所有点的最短路径
解决这一问题最著名的方法是 Dijkstra算法,这个算法是由荷 兰计算机科学教授Edsger W.Dijkstra在1959年提出的。 他在1972年获得美国计算机协 会授予的图灵奖,这是计算机 科学中最具声望的奖项之一。
最终,起点上方的最短路线及权值即为起点到终点的最 短路线及长度。
3
图论及其应用
例 使用回溯法求下图中结点1到结点10的最短路径
2-6-9-10 600
1-4-6-9-10 650
4-6-9-10 500
6-9-10
300
9-10
100 5-8-10
400
8-10
150
3-5-8-10 600
7-8-10 275
定义2 已知矩阵A=(aij)m n ,B =(bij)mn,规定C=AB=(dij)mn,
其中dij=min(aij, bij)
最短路径问题的动态规划算法

最短路径问题的动态规划算法最短路径问题的动态规划算法是一种常用的解决路径优化的方法。
动态规划算法的核心思想是将原问题拆分成若干个子问题,通过递推关系找到最优解。
在最短路径问题中,我们通常希望找到从起点到终点的最短路径。
首先,我们需要定义一个二维数组dp,其中dp[i][j]表示从起点到达坐标(i, j)的最短路径长度。
初始化dp数组,将起点的值设为0,其他位置的值设为无穷大(即表示不可达)。
接下来,我们需要确定动态规划的状态转移方程。
对于任意一个坐标(i, j),它可以从上方的坐标(i-1, j)、左方的坐标(i, j-1)、右方的坐标(i, j+1)、下方的坐标(i+1, j)四个位置中的某一个到达。
因此,可以得到状态转移方程如下:
dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i][j+1], dp[i+1][j]) + 1
其中,min表示取其中的最小值。
通过以上状态转移方程,我们可以逐步更新dp数组,直到最终得到终点的最短路径长度。
需要注意的是,动态规划算法的时间复杂度通常是O(n^2),其中n 表示问题规模。
因此,在处理大规模最短路径问题时,需要考虑算法的效率,可能需要进行剪枝等优化操作。
总的来说,最短路径问题的动态规划算法在路径优化领域有着重要的应用价值,通过合理定义状态转移方程和优化算法效率,可以找到从起点到终点的最短路径长度,为路径规划提供有效的解决方案。
动态规划(完整)ppt课件

3
• Ⅲ --Ⅳ :
B1—C1—T
4
• Ⅱ--Ⅲ--Ⅳ :A2—B1—C1—T
7
• Ⅰ--Ⅱ--Ⅲ --Ⅳ:
•
Q—A2—B1—C1—T
11
•
Q--A3—B1—C1—T
11
•
Q--A3—B2—C2—T
11
最新版整理ppt
3
最短路径
11
4
7
A1
4
2
6
11
47
3 2
Q
A2
4
B1
1
4 76
3
C1
3
B2 3
最新版整理ppt
16
(4)策略和允许策略集合
策略(Policy)也叫决策序列.策略有全过程 策略和 k 部子策略之分,全过程策略是指具 有n 个阶段的全部过程,由依次进行的 n 个 阶段决策构成的决策序列,简称策略,表示
为 p1,n{x1,x2, ,xn}。从 k 阶段到第 n 阶段,
依次进行的阶段决策构成的决策序列称为 k
新分支的创立。
最新版整理ppt
6
• 动态规划将复杂的多阶段决策问题分解为 一系列简单的、离散的单阶段决策问题, 采用顺序求解方法, 通过解一系列小问题 达到求解整个问题目的;
• 动态规划的各个决策阶段不但要考虑本阶 段的决策目标, 还要兼顾整个决策过程的 整体目标, 从而实现整体最优决策.
最新版整理ppt
第七章 动态规划
主要内容:
§7.1多阶段决策问题 §7.2 动态规划的基本概念和基本原理 §7.3 动态规划应用举例
最新版整理ppt
1
例 求解最短路问题
2
Q
4
最短路径算法讲义

如 果 T (v ji ) < +∞ , 则 把 v ji 的 标 号 变 为 P 标 号 P ( v ji ) = T (v ji ) , 令
S i +1 = Si ∪ {v ji } ,k=ji,i=i+1,转①,否则终止,这时对每一个 v∈Si,d(vs,v)=P(v),而
对每一个 v ∉ S i , d (v s v) = T (v) 。 算法实现: 1、 数据结构 用邻接矩阵表示图 G 用一维数组 D[I]存放从源点到 I 点的最短路径长度或其上界。 (上面算法中的 P 标 号与 T 标号实际上存放着源点到某点的最短路径长度或其上界, 因此我们可以统一 用 D 数组来表示) 。 用一维数组 P,其中 P[I]记录到 I 点的最短路径中前一个顶点的序号。 {$R+} 2、源程序 Program Min_Road_Dijkstra; Const MaxN=100; Type GraphType=Array[1..MaxN,1..MaxN]of integer; {有向图邻接矩阵}
该回路上的结点就不存在最短路径。当有向图中出现负权时,则 Dijkstra 算法失效。当不 存在源 s 可达的负回路时,我们可用 Bellman-Ford 算法实现。 下面我们介绍有向图中,存在具有负权的弧时,求最短路的方法。 为了方便起见,不妨设从任一点 vi 到任一点 vj 都有一条弧(如果在 Gk ,(vi,vj)不存在, 。 则添加(vi,vj)且令 wij=+∝) 显然,从 vs 到 vj 的最短路总是从 vs 出发,沿着一条路到某个点 vi,再沿(vi,vj)到 vj 的 ,由本章开始时介绍的一个结论可知,从 vs 到 vi 的这条路必定是 (这里 vi 可以是 vs 本身) 从 vs 到 vi 的最短路,所以 d(vs,vi)必满足如下方程:
动态规划专题完整ppt

s[c[k,i]]:=m; { S[c[k,j] ] 记录第K个阶段的第J个结点到 终点的最短距离}
h[c[k,i]]:=d;{h[j]记录第j阶段最优路径经过的编号} end; end; writeln(s[n]);
三、动态规划中的几个概念
1、阶段
把解题的次序称为规划方向,把地位相同的结点称为一个 阶段。
2、状态
每一阶段的一个结点称为这个阶段的一个状态。如例1 中的第3阶段,有3个结点C1、C2、C3,称第3阶段有4种 状态,分别是C1、C2、C3。
3、状态转移方程 除边界外的任一阶段都得由其前面的阶段递推得到,这递
如:输入数据: N=7 4 3 2 1 4 4 t[i] 3 4 2 2 4 r[i] 输出 14 1 2+3 4+5 6+7
分析:
设F[i] 表示第i个人到第N个人买票所要的最小 时间。
F[i]=min{t[i]+f[i+1],r[i]+f[i+2] } (i=1,2,…,n-1)
F[n]=t[n] 目标是求f[1], 即所有歌迷总的买票时间的最小 值。
推的过程就表现出了阶段的动态演变。这种根据已有状态求得
未知状态的过程,我们称之为状态转移,状态转移的规则用数 学语言来描述,就称为状态转移方程。状态转移方程的形式多 样,如例1中的形式为G[i]=min{G[j]+ei,j},ei,j∈E。
例题2:排队买票问题
一场演唱会即将举行。现有N(0〈N<=200〉个歌迷 排队买票,一个人买一张,而售票处规定,一个人每次最 多只能买两张票。假设第i位歌迷买一张票需要时间Ti(1 〈=I〈=n〉,队伍中相邻的两位歌迷(第j个人和第j+1个 人)也可以由其中一个人买两张票,而另一位就可以不用 排队了,则这两位歌迷买两张票的时间变为Rj,假如 Rj<T(j)+T(j+1),则这样做就可以缩短后面歌迷等待的时间, 加快整个售票的进程。现给出N,Tj和Rj,求使每个人都买 到票的最短时间和方法。
动态规划及其在求最短路径问题中的应用

计算机算法设计与分析论文名:动态规划及其在求最短路径问题中的应用班级:12医软一班学号:姓名:张健<日期:2015年6月动态规划及其在求最短路径问题中的应用摘要:在概述动态规划原理的基础上,提出了动态规划数学模型建模主要步骤,并运用动态规划思想对最短路径进行求解,最后总结出动态规划在此类问题中的优越性。
关键字:动态规划;最短路径;多阶段决策。
在实践中有许多决策问题与时间有关系,决策过程分成若干阶段,各阶段的决策相互关联,共同决定最终的目标,这样的问题称之为多阶段决策问题。
动态规划方法是解决多阶段决策过程最优化的一种方法。
这一方法最初是由美国数学家等人在20世纪50年代提出的,实践证明许多问题用动态规划建模求解比用线性规划或非线性规划更加有效,特别是对离散性问题,运用解析数学无法解决,而动态规划就成为得力的工具。
动态规划方法把一个比较复杂的问题分析为一系列同一类型的更容易求解的子问题先按照整体最优思想逆序求出各个可能状态的最优策略,然后顺序求出整个问题的最优策略和最优路径。
由于将动态规划思想应用到求解运输问题的最短路径中,计算过程单一化便于应用于计算机,求解结果清晰明了,在实践应用中获得显著效果。
1 动态规划原理概述动态规划最优化原理可以这样阐述:一个最优化策略不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸多策略必须构成最优策略,即其子策略总是最优的。
任何思想方法都有一定的局限性,动态规划也有其适应的条件。
如果某阶段的状态给定后,则在这阶段以后过程的发展不受这阶段以前各段状态的影响,这个性质称为无后效性,适用动态规划的问题必须满足这个性质;其次还须满足上述最优化原理。
动态规划基本思想一是正确的写出基本的递推关系式和恰当的边界条件;二是在多阶段决策过程中,动态规划方法是即把当前一段和后来各阶段分开,又把当前效益和未来效益结合起来考虑的一种多阶段决策的最优化方法,每阶段决策和选取是从全局来考虑,与该段的最优选择的答案一般是不同的;三是在求整个问题的最优策略时,由于初始状态是已知的,儿每阶段的决策又都是该阶段状态的函数,因而最优策略所经过的各阶段状态便可逐次变换得到,从而确定最优路线。
动态规划之最短路问题、背包问题、排序问题

3. 航天飞机飞行控制问题:由于航天飞机的 运动的环境是不断变化的,因此就要根据航天飞机 飞行在不同环境中的情况,不断地决定航天飞机的 飞行方向和速度(状态),使之能最省燃料和实现 目的(如软着落问题)。
不包含时间因素的静态决策问题(本质上是一 次决策问题)也可以适当地引入阶段的概念,作为 多阶段的决策问题用动态规划方法来解决。 4 . 线性规划、非线性规划等静态的规划问题也 可以通过适当地引入阶段的概念,应用动态规划方 法加以解决。
变量称为状态变量。 状态变量的取值有一定的允许集合或范围,此集合 称为状态允许集合。
3、决策:表示当过程处于某一阶段的某个状态时, 可以作出不同的决定,从而确定下一阶段的状态,这 种决定称为决策。
描述决策的变量,称为决策变量。决策变量是状态 变量的函数。可用一个数、一组数或一向量(多维情 形)来描述。 在实际问题中决策变量的取值往往在某一范围之内, 此范围称为允许决策集合。 4、多阶段决策过程 可以在各个阶段进行决策,去控制过程发展的多段过 其发展是通过一系列的状态转移来实现的; 程; 系统在某一阶段的状态转移不但与系统的当前的状态 和决策有关,而且还与系统过去的历史状态和决策有 关。
这时,机器的年完好率为a,即如果年初完好机 器的数量为u,到年终完好的机器就为au, 0<a<1。
在低负荷下生产时,产品的年产量h和投入生产 的机器数量u2的关系为 h=h(u2)
相应的机器年完好率b, 0< b<1。
假定开始生产时完好的机器数量为s1。要求制 定一个五年计划,在每年开始时,决定如何重新 分配完好的机器在两种不同的负荷下生产的数量, 使在五年内产品的总产量达到最高。
3 2 A 4 B2 B1 2 3 1 3 1
动态规划在最短路径问题中的应用

动态规划在最短路径问题中的应用最短路径问题是计算两个给定节点之间的最短路径的问题。
在现实生活和计算机科学中,这个问题经常出现。
一种常用的解决方法是动态规划。
本文将介绍动态规划在最短路径问题中的应用。
动态规划是一种用于解决优化问题的算法思想。
它通常用于寻找最优解,避免重复计算。
在最短路径问题中,动态规划可以帮助我们找到从起点到终点的最短路径。
为了更好地理解动态规划在最短路径问题中的应用,我们先来介绍一下最短路径问题的定义。
最短路径问题可以建模成一个图的问题,其中节点表示位置,边表示路径。
每条边都有一个相关的权重,表示从一个节点到另一个节点的代价或距离。
目标是找到从起点到终点的最短路径。
现在,我们来看一下动态规划如何解决最短路径问题。
首先,我们定义一个二维数组dp,其中dp[i][j]表示从起点到节点i的最短路径的权重。
我们将所有的dp[i][j]初始值设为无穷大,表示路径不存在。
接下来,我们需要定义一些转移方程来更新dp数组的值。
对于节点i和节点j之间存在一条边的情况,我们可以使用如下的转移方程来更新dp[i][j]:dp[i][j] = min(dp[i][j], dp[i][k]+dp[k][j]+w[i][j])其中,k是一个介于i和j之间的节点,w[i][j]是从节点i到节点j的边的权重。
这个转移方程表示,如果从起点到节点k的路径加上从节点k到终点的路径再加上边的权重,比当前的dp[i][j]的值小,那么我们更新dp[i][j]的值。
通过不断更新dp数组的值,我们最终可以得到从起点到终点的最短路径的权重。
同时,我们还可以通过修改转移方程来记录路径上的节点,从而得到最短路径。
在实际应用中,动态规划在最短路径问题中有着广泛的应用。
例如,在导航系统中,我们可以使用动态规划算法来计算从当前位置到目的地的最短路径。
在网络路由中,动态规划可以帮助我们找到从源节点到目标节点的最短路径。
总结一下,动态规划是一种解决优化问题的算法思想,在最短路径问题中有着重要的应用。
最短路径算法PPT课件

初始时,S中仅含有源。设u是G的某一个顶点,把从源 到u且中间只经过S中顶点的路称为从源到u的特殊路径,并 用数组dist记录当前每个顶点所对应的最短特殊路径长度。 Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点 u,将u添加到S中,同时对数组dist作必要的修改。一旦S 包含了所有V中顶点,dist就记录了从源到所有其它顶点之 间的最短路径长度。
2取最6小值83
91∞
130
0
在说D(D(1D11[D从1[3)22)]1=][顶不[2中不3]]:点经从:,经从08过1顶过第顶到顶02点顶点1顶点行3点268到点到1和1:顶:顶j第或点仍点仍一顶2是3是的的列点DD距距0D是0[j[33到离2离]=不][([顶2(3]变]=可点=可07∞6以的以;1;20:经,经过允过因86顶许顶为点点经11)) 过((2顶2))点过过1顶顶是1点点没131:有:0D意D00[义[32]][的[11]]++DD00[[11]][[23]]==118++293==3170
计算过程
§ 例:考虑下图所示的带权有向图,求所有顶 点之间的最短距离。
1
2
1
89
2
3
6
(a)
1
V= 2
3
029
L= 8 0 6
91∞ 0
(b)
Di,jk:从顶点i(可以经过顶点1、顶点
2、……顶点k)到顶点j的距离。
D( (2212[1))]8[1不过3]9:经 顶从1过 点顶顶2点:D点10到D=21:顶[1]点仍08[23是]+的20DD距11[[9621离]][[(33]]==也29D+可;16=以=8经08过顶20 点962)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6
25.1 每对顶点间最短路径问题的一 个递归解
现在设 l(m)ij 是从顶点i到顶点j的至多包含m条边的 任何路径的权值最小值。
当m=0时,从i到j存在一条不包含边的最短路径当且 仅当i=j。因此 0 若i j
l(0)ij 若 i j (m -1) 对m ≥ 1,先计算 l ij (从i到j的最短路径的权至多包
d ij
(k )
wij ( k 1) ( k 1) ( k 1) min d , d d ij ik kj
如果k 0 如果k 1
下图显示了一个图,以及由过程SLOW-ALLPAIRS-SHORTEST-PATHS计算出的矩阵L(m)
15
25.1 自底向上计算最短路径的权值
16
25.1 改进运行时间
我们的目标并不是计算出全部的L(m)矩阵,我们 仅仅需要矩阵L(n-1)。 等式25.3蕴含着对所有整数m≥n-1,有L(m) = L(n-1)。如同传统的矩阵乘法满足结合律,由 EXTEND-SHORTEST-PATHS定义的矩阵乘法 也是一样。因此,通过计算下列矩阵序列,只 需计算⌈lg(n - 1)⌉个矩阵乘积就能计算出L(n-1)
4
动态规划
设计一个动态程序算法的过程为:
刻划最优解的结构(最优子结构) 递归定义最优解的值(动态规划设计) 按自底向上的方式计算最优解的值(重叠?) 由计算出的结果构造一个最优解(可省略)
用循环填表:
表中的项:子问题的最优解 循环嵌套的层数=表格的维度(子问题分解的维度)+1( 如果做选择时需要) 循环的初始值:平凡子问题之外的最小子问题(需用递归 求解的最小子问题)。 循环增量方向:例如从左上向右下方填表,保证计算某个 子问题最优解时需要的表中的项都已求解。
18
25.1 改进运行时间
在第4-6行while循环的每一次迭代中,从m=1开始 计算L(2m) = (L(m))2。在每次迭代的最后,m乘以2。 最后一次迭代实际通过对某个n-1≤2m<2n-2计算 L(2m),然后计算出L(n-1) 。根据等式25.3,有L(2m) = L(n-1)。下一次执行第4行中的测试语句时,由于m 已被乘以2,所以m≥n-1,测试失败,过程返回它 计算出的最后一个矩阵。 因为⌈lg(n - 1)⌉个矩阵乘积中的每一个都需要Θ(n3) 时间,因此FASTER-ALL-PAIRS-SHORTESTPATHS的运行时间为Θ(n3lgn)。算法中不包含复 杂数据结构,因此隐含于Θ中的常数很小
9
25.1 自底向上计算最短路径的权值
EXTEND-SHORTEST-PATHS(L, W) 1 n ← rows[L] 2 let be an n × n matrix 3 for i ← 1 to n 4 do for j ← to n 5 do lij ' 6 for k ← 1 to n 7 do lij ' min lij ' , lik wkj 8 return L′
21
25.2 最短路径的结构
如果k不是路径p的中间顶点,则p的所有中间顶点皆在 集合{1,2,...,k-1}中。因此从顶点i到顶点j且满足所有中 间顶点皆属于集合{1,2,...,k-1}的一条最短路径,也同样 是从i到j且满足所有中间顶点皆属于集合{1,2,...k}的一条 最短路径。 如果k是路径p的中间顶点,那么可将p分解为 p1 p2 i k j 。由引理24.1可知,p1是从i到k的一条 最短路径,且其所有中间顶点均属于集合{1,2,...,k}。因 为顶点k不是路径p1上的一个中间顶点,所以p1是从i到k 的一条最短路径,且其所有中间顶点皆属于集合 {1,2,...,k-1}。类似的, p2以是从k到j的一条最短路径, 且其所有中间顶点皆属于集合{1,2,...,k-1}
19
ቤተ መጻሕፍቲ ባይዱ
25.2 Floyd-Warshall算法
本节要介绍另一个动态规划算法,用来解决有 向图G=(V,E)上每对顶点间的最短路径问题。算 法称为Floyd-Warshall算法,运行时间为Θ(V3)。 算法允许存在负值的边,但我们假设没有权值 为负的回路。
20
25.2 最短路径的结构
在Floyd-Warshall算法中,我们利用最短路径结构 中的另一个特征:该算法考虑最短路径上的中间顶 点,其中简单路径p=<v1, v2,..., vl>上的中间顶点是 除了v1和vl 以外p上的任何一个顶点,即任何属于集 合{v2, v3,..., vl-1}的顶点。 Floyd-Warshall算法主要基于以下观察:设G的顶点 为V={1, 2,..., n},对某个k考虑顶点的一个子集{1, 2,..., k}。对任意一对顶点i, j∈V,考虑从i到j且中间 顶点皆属于集合{1, 2,..., k}的所有路径。设p是其中 的一条最小权值路径。Floyd-Warshall算法利用了 路径p与i到j之间的最短路径之间的联系。这一联系 依赖于k是否是路径p的一个中间顶点:
10
25.1 自底向上计算最短路径的权值
该过程计算出矩阵L'=(lij ' )作为返回值。对所有 的i和j计算等式25.2,用L代表L(m-1),用L'代表 L(m)算,来计算这个返回值。由于算法中存在三 个嵌套的for循环,因此运行时间为Θ(n3)。 算法和矩阵乘法运算的关系:假定我们希望计 算两个n×n的矩阵A和B的矩阵乘积C = A· B。 于是对i,j=1,2,...,n ,计算 n
cij aik bkj
k 1
如果对等式25.2做如下的替换
11
25.1 自底向上计算最短路径的权值
l(m-1) → w → l(m) → min → + → 则得到等式矩阵乘法运算:
a, b, c, +, ·
cij aik bkj
k 1 n
因此,如果对过程EXTEND-SHORTESTPATHS进行这样的变换,并用0(表示+)替换∞(表 示min),得到一个直接的Θ(n3)的矩阵乘法过程
第八讲:动态规划与最短路径(3)
《算法与算法复杂性》2011年春季 赵颖
第十五章 动态规划
本章主要内容:
动态规划介绍 装配线调度问题 矩阵链相乘问题 动态规划问题关键特征 背包问题(补充) 最长公共子序列 最优二叉查找树
每对顶点间的最短路径(第25章)
2
比较
分治 把问题转化为子问题 本质是递归的 子问题是否重叠 子问题的数目 预处理 运行时间 解决最优化问题 最优子结构 贪心选择 动态规划 贪心
13
25.1 自底向上计算最短路径的权值
回到顶点最短路径问题,我们是通过把最短路径 逐边延长,最终计算出最短路径权值的。设A· B 代表过程EXTEND-SHORTEST-PATHS(A, B)返 回的矩阵乘积,我们计算n-1个矩阵的序列:
L(1)
L(2) L(3)
=
= =
L(0) ·W
L(1) ·W L(2) ·W ⋮
(i, j ) lij
( n 1)
lij
(n)
lij
( n 1)
... (25.3)
8
25.1 自底向上计算最短路径的权值
把矩阵W= (wij)作为输入,来计算一组矩阵L(1), (m) (2) ( n -1) (m) l L ,..., L ,其中对m = 1, 2,..., n - 1,有L = ij 最后矩阵L(n-1) 包含实际的最短路径权值。注意 对所有的顶点i, j∈V, l(1)ij = wij,因此L(1)=W。 算法如下页所示,给定矩阵L(m-1)和W,返回矩 阵L(m) ,也就是它把已经计算出来的最短路径 延长一条边。
22
25.2 最短路径的结构
23
25.2 最短路径的结构
我们定义一个最短路径估计的递归公式。令dij ( k ) 为从顶点i到顶点j、且满足所有中间顶点皆属于 集合{1,2,...,k}的一条最短路径的权值。当k=0时, 从顶点i到顶点j的路径中,没有编号大于0的中 间顶点;亦即,根本不存在中间顶点。这样的 (k ) 路径至多包含一条边因此 d ij =wij。根据上述讨 论,我们用下式给出一个递归式
1 k n 1 k n
7
25.1 每对顶点间最短路径问题的一 个递归解
实际的最短路径权值:如果图中不包含权值为 负的回路,那么对于所有的顶点对i和j,当δ(i, j) < ∞时,存在一条从i到j的最短路径,它是简单 路径,从而至多包含n-1条边。从顶点i到顶点j 的多于n-1条边的路径其权值不可能小于从i到j 的最短路径的权值。因此,实际的最短路径权 值由下式给出:
等于L(n-1) 因为2 下面过程利用重复平方技术计算上述矩阵序列
lg(n 1)
lg( n1)
2 n 1 ,最终乘积 L
FASTER-ALL-PAIRS-SHORTEST-PATHS(W) 1 n ← rows[W] 2 L(1) ← W 3m←1 4 while m < n - 1 5 do L(2m) ← EXTEND-SHORTEST-PATHS(L(m), L(m)) 6 m ← 2m 7 return L(m)
5
25.1 最短路径的结构
假设图以邻接矩阵W=(wij)来表示 考察从顶点i到顶点j的一条最短路径p,假设p至多 包含m条边。假设途中不存在权值为负的回路,则 m必是有限值。
如果i=j,则路径p权值为0而且没有边。 p' k , j 若顶点i和顶点j是不同顶点,则把路径p分解为i 其中路径p'至多包含m-1条边。由引理24.1,p'是从i到k 的一条最短路径,因而δ(i, j) = δ(i, k) + wkj
