数学专业英语外文翻译
微积分英文词汇,高数名词中英文对照,高等数学术语英语翻译一览

微积分英文词汇,高数名词中英文对照,高等数学术语英语翻译一览V、X、Z:Value of function :函数值Variable :变数Vector :向量Velocity :速度Vertical asymptote :垂直渐近线Volume :体积X-axis :x轴x-coordinate :x坐标x-intercept :x截距Zero vector :函数的零点Zeros of a polynomial :多项式的零点T:Tangent function :正切函数Tangent line :切线Tangent plane :切平面Tangent vector :切向量Total differential :全微分Trigonometric function :三角函数Trigonometric integrals :三角积分Trigonometric substitutions :三角代换法Tripe integrals :三重积分S:Saddle point :鞍点Scalar :纯量Secant line :割线Second derivative :二阶导数Second Derivative Test :二阶导数试验法Second partial derivative :二阶偏导数Sector :扇形Sequence :数列Series :级数Set :集合Shell method :剥壳法Sine function :正弦函数Singularity :奇点Slant asymptote :斜渐近线Slope :斜率Slope-intercept equation of a line :直线的斜截式Smooth curve :平滑曲线Smooth surface :平滑曲面Solid of revolution :旋转体Space :空间Speed :速率Spherical coordinates :球面坐标Squeeze Theorem :夹挤定理Step function :阶梯函数Strictly decreasing :严格递减Strictly increasing :严格递增Sum :和Surface :曲面Surface integral :面积分Surface of revolution :旋转曲面Symmetry :对称R:Radius of convergence :收敛半径Range of a function :函数的值域Rate of change :变化率Rational function :有理函数Rationalizing substitution :有理代换法Rational number :有理数Real number :实数Rectangular coordinates :直角坐标Rectangular coordinate system :直角坐标系Relative maximum and minimum :相对极大值与极小值Revenue function :收入函数Revolution , solid of :旋转体Revolution , surface of :旋转曲面Riemann Sum :黎曼和Riemannian geometry :黎曼几何Right-hand derivative :右导数Right-hand limit :右极限Root :根P、Q:Parabola :拋物线Parabolic cylinder :抛物柱面Paraboloid :抛物面Parallelepiped :平行六面体Parallel lines :并行线Parameter :参数Partial derivative :偏导数Partial differential equation :偏微分方程Partial fractions :部分分式Partial integration :部分积分Partiton :分割Period :周期Periodic function :周期函数Perpendicular lines :垂直线Piecewise defined function :分段定义函数Plane :平面Point of inflection :反曲点Polar axis :极轴Polar coordinate :极坐标Polar equation :极方程式Pole :极点Polynomial :多项式Positive angle :正角Point-slope form :点斜式Power function :幂函数Product :积Quadrant :象限Quotient Law of limit :极限的商定律Quotient Rule :商定律M、N、O:Maximum and minimum values :极大与极小值Mean Value Theorem :均值定理Multiple integrals :重积分Multiplier :乘子Natural exponential function :自然指数函数Natural logarithm function :自然对数函数Natural number :自然数Normal line :法线Normal vector :法向量Number :数Octant :卦限Odd function :奇函数One-sided limit :单边极限Open interval :开区间Optimization problems :最佳化问题Order :阶Ordinary differential equation :常微分方程Origin :原点Orthogonal :正交的L:Laplace transform :Leplace 变换Law of Cosines :余弦定理Least upper bound :最小上界Left-hand derivative :左导数Left-hand limit :左极限Lemniscate :双钮线Length :长度Level curve :等高线L'Hospital's rule :洛必达法则Limacon :蚶线Limit :极限Linear approximation:线性近似Linear equation :线性方程式Linear function :线性函数Linearity :线性Linearization :线性化Line in the plane :平面上之直线Line in space :空间之直线Lobachevski geometry :罗巴切夫斯基几何Local extremum :局部极值Local maximum and minimum :局部极大值与极小值Logarithm :对数Logarithmic function :对数函数I:Implicit differentiation :隐求导法Implicit function :隐函数Improper integral :瑕积分Increasing/Decreasing Test :递增或递减试验法Increment :增量Increasing Function :增函数Indefinite integral :不定积分Independent variable :自变数Indeterminate from :不定型Inequality :不等式Infinite point :无穷极限Infinite series :无穷级数Inflection point :反曲点Instantaneous velocity :瞬时速度Integer :整数Integral :积分Integrand :被积分式Integration :积分Integration by part :分部积分法Intercepts :截距Intermediate value of Theorem :中间值定理Interval :区间Inverse function :反函数Inverse trigonometric function :反三角函数Iterated integral :逐次积分H:Higher mathematics 高等数学/高数E、F、G、H:Ellipse :椭圆Ellipsoid :椭圆体Epicycloid :外摆线Equation :方程式Even function :偶函数Expected Valued :期望值Exponential Function :指数函数Exponents , laws of :指数率Extreme value :极值Extreme Value Theorem :极值定理Factorial :阶乘First Derivative Test :一阶导数试验法First octant :第一卦限Focus :焦点Fractions :分式Function :函数Fundamental Theorem of Calculus :微积分基本定理Geometric series :几何级数Gradient :梯度Graph :图形Green Formula :格林公式Half-angle formulas :半角公式Harmonic series :调和级数Helix :螺旋线Higher Derivative :高阶导数Horizontal asymptote :水平渐近线Horizontal line :水平线Hyperbola :双曲线Hyper boloid :双曲面D:Decreasing function :递减函数Decreasing sequence :递减数列Definite integral :定积分Degree of a polynomial :多项式之次数Density :密度Derivative :导数of a composite function :复合函数之导数of a constant function :常数函数之导数directional :方向导数domain of :导数之定义域of exponential function :指数函数之导数higher :高阶导数partial :偏导数of a power function :幂函数之导数of a power series :羃级数之导数of a product :积之导数of a quotient :商之导数as a rate of change :导数当作变率right-hand :右导数second :二阶导数as the slope of a tangent :导数看成切线之斜率Determinant :行列式Differentiable function :可导函数Differential :微分Differential equation :微分方程partial :偏微分方程Differentiation :求导法implicit :隐求导法partial :偏微分法term by term :逐项求导法Directional derivatives :方向导数Discontinuity :不连续性Disk method :圆盘法Distance :距离Divergence :发散Domain :定义域Dot product :点积Double integral :二重积分change of variable in :二重积分之变数变换in polar coordinates :极坐标二重积分C:Calculus :微积分differential :微分学integral :积分学Cartesian coordinates :笛卡儿坐标一般指直角坐标Cartesian coordinates system :笛卡儿坐标系Cauch’s Mean Value Theorem :柯西均值定理Chain Rule :连锁律Change of variables :变数变换Circle :圆Circular cylinder :圆柱Closed interval :封闭区间Coefficient :系数Composition of function :函数之合成Compound interest :复利Concavity :凹性Conchoid :蚌线Cone :圆锥Constant function :常数函数Constant of integration :积分常数Continuity :连续性at a point :在一点处之连续性of a function :函数之连续性on an interval :在区间之连续性from the left :左连续from the right :右连续Continuous function :连续函数Convergence :收敛interval of :收敛区间radius of :收敛半径Convergent sequence :收敛数列series :收敛级数Coordinate:s:坐标Cartesian :笛卡儿坐标cylindrical :柱面坐标polar :极坐标rectangular :直角坐标spherical :球面坐标Coordinate axes :坐标轴Coordinate planes :坐标平面Cosine function :余弦函数Critical point :临界点Cubic function :三次函数Curve :曲线Cylinder:圆柱Cylindrical Coordinates :圆柱坐标A、B:Absolute convergence :绝对收敛Absolute extreme values :绝对极值Absolute maximum and minimum :绝对极大与极小Absolute value :绝对值Absolute value function :绝对值函数Acceleration :加速度Antiderivative :反导数Approximate integration :近似积分Approximation :逼近法by differentials :用微分逼近linear :线性逼近法by Simpson’s Rule :Simpson法则逼近法by the Trapezoidal Rule :梯形法则逼近法Arbitrary constant :任意常数Arc length :弧长Area :面积under a curve :曲线下方之面积between curves :曲线间之面积in polar coordinates :极坐标表示之面积of a sector of a circle :扇形之面积of a surface of a revolution :旋转曲面之面积Asymptote :渐近线horizontal :水平渐近线slant :斜渐近线vertical :垂直渐近线Average speed :平均速率Average velocity :平均速度Axes, coordinate :坐标轴Axes of ellipse :椭圆之轴Binomial series :二项级数。
数学专业英语翻译2-4

Let P denote the set of all positive integers. Then P is itself an inductive set because (a) it contains 1, and (b) it contains x+1 whenever it contains x. Since the members of P belong to every inductive set, we refer to P as the smallest inductive set. 表示所有正整数的集合。 用 P表示所有正整数的集合。那么 本身是一个归纳 表示所有正整数的集合 那么P本身是一个归纳 集 , 因为其中含1, 满足(a); 只要包含x就包含 因为其中含 , 满足 ; 只要包含 就包含x+1, 就包含 满足(b)。由于P中的元素属于每一个归纳集 因此P 中的元素属于每一个归纳集, 满足 。由于 中的元素属于每一个归纳集,因此 是最小的归纳集。 是最小的归纳集。
Quotients of integers a/b (where b≠0) are called rational numbers. The set of rational numbers, denoted by Q, contains Z as a subset. The reader should realize that all the field axioms and the order axioms are satisfied by Q. For this reason, we say that the set of rational numbers is an ordered field. Real numbers that are not in Q are called irrational. 整数a与 的商被叫做有理数 有理数集用Q表示 的商被叫做有理数, 表示, 整数 与b的商被叫做有理数,有理数集用 表示,Z 的子集。 是Q的子集。读者应该认识到 满足所有的域公理和 的子集 读者应该认识到Q满足所有的域公理和 序公理。因此说有理数集是一个有序的域。 序公理 。 因此说有理数集是一个有序的域 。 不是有 理数的实数被称为无理数。 理数的实数被称为无理数。
数学专业英语翻译2-7

7-B The limit of a sequence
The main question we are concerned with here is to decide whether or not the terms f(n) tend to a finite limit as n increases infinitely. 这里我们关心的主要问题是当n无限增加时,项 f(n) 是否会趋于一个有限的极限。
如果对每一个正整数 n都有一个实数或复数an与之对 应, 则有序集a1 , a2, …, an ,… 称为一个无穷序列.
The important thing here is that each member of the set has been labeled with an integer so that we may speak of the first term a1, the second term a2, and, in general, the nth term an. 这里重要的是集合中的每一个元素都由一个整数标 记,因此我们可以说第一项 , 第二项, 一般的,第n项
This particular rule is known as a recursion formula and it defines a famous sequence whose terms are called Fibonacci numbers. The first few terms are 1,1,2,3,5,8,13,21,34. 这个特殊的规则就是常见的递推公式,它定义了一个 著名的序列,其中的项称为菲波那契数。前几项是…...
数学专业英语中英文对照翻译

2.5笛卡尔几何学的基本概念(basic concepts of Cartesian geometry)课文5-A the coordinate system of Cartesian geometryAs mentioned earlier, one of the applications of the integral is the calculation of area. Ordinarily , we do not talk about area by itself ,instead, we talk about the area of something . This means that we have certain objects (polygonal regions, circular regions, parabolic segments etc.) whose areas we wish to measure. If we hope to arrive at a treatment of area that will enable us to deal with many different kinds of objects, we must first find an effective way to describe these objects.The most primitive way of doing this is by drawing figures, as was done by the ancient Greeks. A much better way was suggested by Rene Descartes, who introduced the subject of analytic geometry (also known as Cartesian geometry). Descartes’ idea was to represent geometric points by numbers. The procedure for points in a plane is this :Two perpendicular reference lines (called coordinate axes) are chosen, one horizont al (called the “x-axis”), the other vertical (the “y-axis”). Their point of intersection denoted by O, is called theorigin. On the x-axis a convenient point is chosen to the right of O and its distance from O is called the unit distance. Vertical distances along the Y-axis are usually measured with the same unit distance ,although sometimes it is convenient to use a different scale on the y-axis. Now each point in the plane (sometimes called the xy-plane) is assigned a pair of numbers, called its coordinates. These numbers tell us how to locate the points.Figure 2-5-1 illustrates some examples.The point with coordinates (3,2) lies three units to the right of the y-axis and two units above the x-axis.The number 3 is called the x-coordinate of the point,2 its y-coordinate. Points to the left of the y-axis have a negative x-coordinate; those below the x-axis have a negtive y-coordinate. The x-coordinateof a point is sometimes called its abscissa and the y-coordinateis called its ordinate.When we write a pair of numberssuch as (a,b) to represent a point, we agree that the abscissa or x-coordinate,a is written first. For this reason, the pair(a,b) is often referred to as an ordered pair. It is clear that two ordered pairs (a,b) and (c,d) represent the same point if and only if we have a=c and b=d. Points (a,b) with both a and b positiveare said to lie in the first quadrant ,those with a<0 and b>0 are in the second quadrant ; and those with a<0 and b<0 are in the third quadrant ; and those with a>0 and b<0 are in the fourthquadrant. Figure 2-5-1 shows one point in each quadrant.The procedure for points in space is similar. We take three mutually perpendicular lines in space intersecting at a point (the origin) . These lines determine three mutually perpendicular planes ,and each point in space can be completely described by specifying , with appropriate regard for signs ,its distances from these planes. We shall discuee three-dimensional Cartesian geometry in more detail later on ; for the present we confine our attention to plane analytic geometry.课文5-A:笛卡尔几何坐标系正如前面所提到的,积分应用的一种是计算面积。
数学专业英语翻译
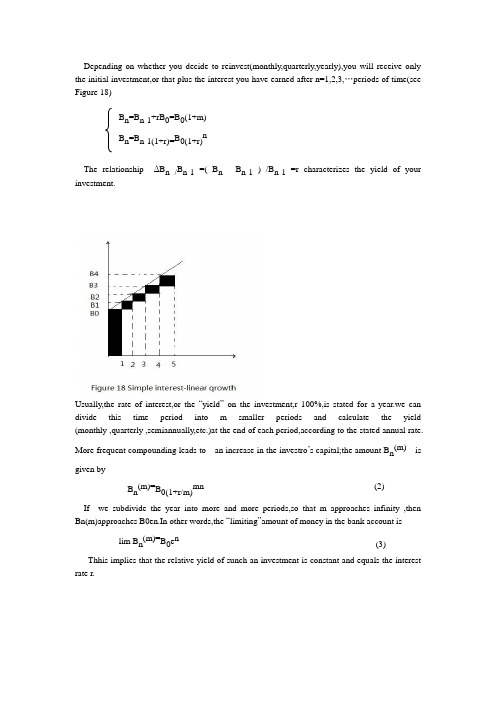
Depending on whether you decide to reinvest(monthly,quarterly,yearly),you will receive only the initial investment,or that plus the interest you have earned after n=1,2,3,…periods of time(see Figure 18)B n=B n-1+rB0=B0(1+m)B n=B n-1(1+r)=B0(1+r)nThe relationship ΔB n /B n-1 =( B n- B n-1 ) /B n-1 =r characterizes the yield of your investment.Usually,the rate of interest,or the “yield”on the investment,r 100%,is stated for a year.we can divide this time period into m smaller periods and calculate the yield (monthly ,quarterly ,semiannually,etc.)at the end of each period,according to the stated annual rate.More frequent compounding leads to an increase in the investro’s capital;the amount B n(m)is given byB n(m)=B0(1+r/m)mn (2)If we subdivide the year into more and more periods,so that m approaches infinity ,then Bn(m)approaches B0en.In other words,the “limiting”amount of money in the bank account islim B n(m)=B0e n(3)Thhis implies that the relative yield of sunch an investment is constant and equals the interest rate r.The three methods of calculating interest discussed above are called simple ,compound ,and continuous .Formulas (1),(2)and (3)provide ways to calculate the amount in the investor’s bank account and clearly show the dependence of the value of money on time.On the other hand,we have the bank’s interest rate R,s that if we invest the amount (1-R)B1,at time 1 ,say after one year,we will receive the amount B1.This is equivalent to the issuance of a bond with a nominal value B1(to be paid to the bond holder at the end of this year),but now the bond sells for a lower price(decreased by the amount of the lending rate R over one period ,that is m=1).So today’s price is determined by the formula(1-R)B1,which is equal to the discounted price B1/(1+r) .Therefore,we can view the bank account as a coupon-free bond in the sense of a risk-free asset of the financial market.The lack of ,or very small,changes in interest rates characterize the stability of financial and economic systems ,for which the corresponding bank acccount serves as the basic non-risky asset.Reality shows that such suggestions present limits in The idealization of mathematical models for financial markets.译文:依赖于你是否决定再投资(平稳的,按季度的,一年一次的),你将仅仅收到最初的投资,否则就会加上n=1,2,3…个时期后你所赚的利息。
数学专业英语(Doc版).14

数学专业英语-MathematicansLeonhard Euler was born on April 15,1707,in Basel, Switzerland, the son of a mathematician and Caivinist pastor who wanted his son to become a pastor a s well. Although Euler had different ideas, he entered the University of Basel to study Hebrew and theology, thus obeying his father. His hard work at the u niversity and remarkable ability brought him to the attention of the well-known mathematician Johann Bernoulli (1667—1748). Bernoulli, realizing Euler’s tal ents, persuaded Euler’s father to change his mind, and Euler pursued his studi es in mathematics.At the age of nineteen, Euler’s first original work appeared. His paper failed to win the Paris Academy Prize in 1727; however this loss was compensated f or later as he won the prize twelve times.At the age of 28, Euler competed for the Pairs prize for a problem in astrono my which several leading mathematicians had thought would take several mont hs to solve.To their great surprise, he solved it in three days! Unfortunately, th e considerable strain that he underwent in his relentless effort caused an illness that resulted in the loss of the sight of his right eye.At the age of 62, Euler lost the sight of his left eye and thus became totally blind. However this did not end his interest and work in mathematics; instead, his mathematical productivity increased considerably.On September 18, 1783, while playing with his grandson and drinking tea, Eul er suffered a fatal stroke.Euler was the most prolific mathematician the world has ever seen. He made s ignificant contributions to every branch of mathematics. He had phenomenal m emory: He could remember every important formula of his time. A genius, he could work anywhere and under any condition.George cantor (March 3, 1845—June 1,1918),the founder of set theory, was bo rn in St. Petersburg into a Jewish merchant family that settled in Germany in 1856.He studied mathematics, physics and philosophy in Zurich and at the University of Berlin. After receiving his degree in 1867 in Berlin, he became a lecturer at the university of Halle from 1879 to 1905. In 1884,under the stra in of opposition to his ideas and his efforts to prove the continuum hypothesis, he suffered the first of many attacks of depression which continued to hospita lize him from time to time until his death.The thesis he wrote for his degree concerned the theory of numbers; however, he arrived at set theory from his research concerning the uniqueness of trigon ometric series. In 1874, he introduced for the first time the concept of cardinalnumbers, with which he proved that there were “more”transcendental numb ers than algebraic numbers. This result caused a sensation in the mathematical world and became the subject of a great deal of controversy. Cantor was troub led by the opposition of L. Kronecker, but he was supported by J.W.R. Dedek ind and G. Mittagleffer. In his note on the history of the theory of probability, he recalled the period in which the theory was not generally accepted and cri ed out “the essence of mathematics lies in its freedom!”In addition to his work on the concept of cardinal numbers, he laid the basis for the concepts of order types, transfinite ordinals, and the theory of real numbers by means of fundamental sequences. He also studied general point sets in Euclidean space a nd defined the concepts of accumulation point, closed set and open set. He wa s a pioneer in dimension theory, which led to the development of topology.Kantorovich was born on January 19, 1912, in St. Petersburg, now called Leni ngrad. He graduated from the University of Leningrad in 1930 and became a f ull professor at the early age of 22.At the age of 27, his pioneering contributi ons in linear programming appeared in a paper entitled Mathematical Methods for the Organization and planning of production. In 1949, he was awarded a S talin Prize for his contributions in a branch of mathematics called functional a nalysis and in 1958, he became a member of the Russian Academy of Science s. Interestingly enough, in 1965,kantorovich won a Lenin Prize fo r the same o utstanding work in linear programming for which he was awarded the Nobel P rize. Since 1971, he has been the director of the Institute of Economics of Ma nagement in Moscow.Paul R. Halmos is a distinguished professor of Mathematics at Indiana Univers ity, and Editor-Elect of the American Mathematical Monthly. He received his P h.D. from the University of Illinois, and has held positions at Illinois, Syracuse, Chicago, Michigan, Hawaii, and Santa Barbara. He has published numerous b ooks and nearly 100 articles, and has been the editor of many journals and se veral book series. The Mathematical Association of America has given him the Chauvenet Prize and (twice) the Lester Ford award for mathematical expositio n. His main mathematical interests are in measure and ergodic theory, algebraic, and operators on Hilbert space.Vito Volterra, born in the year 1860 in Ancona, showed in his boyhood his e xceptional gifts for mathematical and physical thinking. At the age of thirteen, after reading Verne’s novel on the voyage from earth to moon, he devised hi s own method to compute the trajectory under the gravitational field of the ear th and the moon; the method was worth later development into a general proc edure for solving differential equations. He became a pupil of Dini at the Scu ola Normale Superiore in Pisa and published many important papers while still a student. He received his degree in Physics at the age of 22 and was made full professor of Rational Mechanics at the same University only one year lat er, as a successor of Betti.Volterra had many interests outside pure mathematics, ranging from history to poetry, to music. When he was called to join in 1900 the University of Rome from Turin, he was invited to give the opening speech of the academic year. Volterra was President of the Accademia dei Lincei in the years 1923-1926. H e was also the founder of the Italian Society for the Advancement of Science and of the National Council of Research. For many years he was one of the most productive scientists and a very influential personality in public life. Whe n Fascism took power in Italy, Volterra did not accept any compromise and pr eferred to leave his public and academic activities.Vocabularypastor 牧师 hospitalize 住进医院theology 神学 thesis 论文strain 紧张、疲惫transcendental number 超越数relentless 无情的sensation 感觉,引起兴趣的事prolific 多产的controversy 争论,辩论depression 抑郁;萧条,不景气essence 本质,要素transfinite 超限的Note0. 本课文由几篇介绍数学家生平的短文组成,属传记式体裁。
《数学专业英语》常用英文表达

7
max, min maximum value, minimum value Eample: max f ( x) Maximum value of f(x)
max(a1 ,an ) Maximum value of the series
a1 to an Powers and roots Example: x 2 x squared
10
Function f
2 Example: f ( x ) ax bx c , a 0. The function of x
equals a times the square of x plus b times x plus c, where a is not equal to zero.
Imaginary number and two common irrational numbers
, ratio of the circumference of a circle to its
diameter,approximate value 3.1415926
9
1 x i 1, e lim(1 ) x x
Example:
f ( x ) f double-prime x, f double-dashed x f ( x ) f triple-prime x, f triple-dashed x (4) f ( x ) f four x
8
xn x 1
Example:
3
x x
4 n
x x
fourth root (of) x
nth root (of) x
Example: 24 16 Two to the fourth power is sixteen
数学专业英语2.7-c翻译

Monotonic sequences of real numbersA sequences {f(n)} is said to be increasing iff(n)f(n+1) for all n 1≤≥We indicate this briefly by writeing(n)f . if, on the otherhand ,we have(n)f(n+1) for all n 1 f ≥≥ We call the sequences decreasing and write (n)f . .A sequences is called monotonic if it is increasing or if it is decreasing.Monotonic sequences are pleasant to work with because their convergence or divergence is particularly easy to determine. In fact ,we have the following simple criterion.Note:A sequences {f(n)} is called bounded if there exists a positive number M such that(n ) M f ≤ for all n. A sequences that is not bounded is called unbounded.It is clear that an unbounded sequence cannot converge. Therefore, all we need to prove is that a bounded monotonic sequences must converge.Assume (n)f and let L denote the least upper bound ofthe set of function values.then (n) f L ≤ for all n, and we shallprove that the sequence converges to L.Choose any poitive number ε.since0(n)L f ε≤-< cannot be an upper bound for all numbersf(n),we must have (N)L L f ε-≤ for some N.If n N ≥ we have(N)f(n)f ≥ since (n)f .Hence we have (N)L L f ε-≤ for all n N ≥, as illustrate inFigure 2-7-1. Form these inequalities we find that0(n)L f ε≤-< for all n N ≥And this means that the sequences converges to L,as asserted.If (n)f ,the proof is similar, the limit in this case being the greatest lower bound of the set of function values.单调的实数序列如果一个序列是增加≤≥f(n)f(n+1) for all n1我们指出这个简要写全方位。
数学专业英语翻译2-6

It may be done by a formula as the 18th century mathematics presumed but it can equally well be done by a tabulation such as a statistical chart, or by some other form of description.
EXAMPLE 1. The force F necessary to stretch a steel spring a distance x beyond its natural length is proportional to x. That is, F=cx, where c is a number independent of x called the spring constant.
这个公式是在17世纪中叶被胡克发现的,叫做胡克定 律,它用来表示力关于位移的函数。
EXAMPLE 2. The volume of a cube is a function of its edge-length. If the edges have length x, the volume V is given by the formula V=x3.
Today, the meaning of function is essentially this: Given two sets, say X and Y, a function is a correspondence which associates with each element of X one and one only element of Y.
数学专业英语翻译

第一段翻译(2):what is the exact value of the number pai?a mathematician made an experiment in order to find his own estimation of the number pai.in his experiment,he used an old bicycle wheel of diameter 63.7cm.he marked the point on the tire where the wheel was touching the ground and he rolled the wheel straight ahead by turning it 20 times.next,he measured the distance traveled by the wheel,which was 39.69 meters.he divided the number 3969 by 20*63.7 and obtained 3.115384615 as an approximation of the number pai.of course,this was just his estimate of the number pai and he was aware that it was not very accurate.数π的精确值是什么?一位数学家做了实验以便找到他自己对数π的估计。
在试验中,他用了一直径63.1厘米的旧自行车轮。
他在车轮接触地面的轮胎上做了标记,而且将车轮向前转动20次。
接下来,他测量了车轮经过的距离,是39.69米。
他用3969除20*63.7得到了数π的近似值3.115384615。
当然,这只是对数π的估计值,并且他也意识到不是很准确。
第二段翻译(5):one of the first articles which we included in the "History Topics" section archive was on the history of pai.it is a very popular article and has prompted many to ask for a similar article about the number e.there is a great contrast between the historical developments of these two numbers and in many ways writing a history of e is a much harder task than writing one of pai.the number e is,compared to pai,a relative newcomer on the mathematical scene.我们包括在“历史专题”部分档案中的第一篇文章就是历史上的π,这是一篇很流行的文章,也促使许多人想了解下一些有关数e的类似文章。
数学专业英语翻译

第一段翻译(2):what is the exact valueo f the number pai?a mathematici an made an experi mentin orderto find his own estima tionof the number pai.in his experi ment,he used an old bicycl e wheelof diamet er 63.7cm.he marked the pointon the tire wherethe wheelwas touchi ng the ground and he rolled the wheelstraig ht aheadby turnin g it 20 times.next,he measur ed the distan ce travel ed by the wheel,whichwas 39.69 meters.he divide d the number3969 by 20*63.7 and obtain ed 3.115384615 as an approx imati on of the number pai.of course,this was just his estima te of the number pai and he was awarethat it was not very accura te.数π的精确值是什么?一位数学家做了实验以便找到他自己对数π的估计。
在试验中,他用了一直径63.1厘米的旧自行车轮。
他在车轮接触地面的轮胎上做了标记,而且将车轮向前转动20次。
接下来,他测量了车轮经过的距离,是39.69米。
他用3969除20*63.7得到了数π的近似值3.115384615。
数学学科的英文翻译及相关术语解释和应用场景介绍

数学学科的英文翻译及相关术语解释和应用场景介绍Mathematics is a subject that is concerned with the study of numbers, quantities, and shapes. It is a fundamental discipline that has wide applications in science, engineering, economics, and other fields. In this article, we will explore the English translation of mathematical terms and their meanings, as well as the practical applications of mathematics.1. AlgebraAlgebra is a branch of mathematics that deals with the study of mathematical symbols and the rules for manipulating these symbols. It involves the use of variables, equations, and functions to solve problems. Algebra is used in many fields, including physics, engineering, and economics.代数是数学的一个分支,它涉及到数学符号的研究以及操作这些符号的规则。
它涉及到使用变量、方程和函数来解决问题。
代数在许多领域中得到了应用,包括物理学、工程学和经济学。
2. CalculusCalculus is a branch of mathematics that deals with the study of rates of change and slopes of curves. It involves the use of limits, derivatives, and integrals to solve problems related to motion, optimization, and other applications. Calculus is used in physics, engineering, and economics.微积分是数学的一个分支,它涉及到速率变化和曲线斜率的研究。
数学专业英语翻译

数学专业英语翻译IntroductionAs a field of study, mathematics has been around for over two thousand years, yet it remains a fundamental subject of study in today's society. It has applications in science, engineering, economics, and even in artistic works. However, understanding mathematical concepts can be challenging, as the subject includes a variety of topics ranging from algebra to geometry, calculus, and beyond. In this article, we will explore some common mathematical terminology and concepts, with the aim of helping students who are studying mathematics at a higher level.AlgebraAlgebra is a branch of mathematics that focuses on the manipulation of variables and symbols to solve equations and understand patterns. It covers a wide range of topics, including simplifying expressions, solving linear and nonlinear equations, and working with matrices. Some of the common terms in algebra include:- Variable: a symbol that represents a value that can change.- Coefficient: a numerical value that is multiplied by a variable in an expression.- Equation: a statement that shows the equality between two expressions.- System of equations: a set of equations withmultiple variables that are solved simultaneously.- Matrix: a rectangular array of numbers or variables.GeometryGeometry is a branch of mathematics that dealswith the study of shapes, sizes, and dimensions of objects in space. It includes the study of points, lines, planes, angles, curves, and surfaces amongother things. Some common terms in geometry include: - Point: an infinitesimally small location in space, represented by a dot.- Line: a straight, one-dimensional sequence of points. - Plane: a two-dimensional flat surface that extends infinitely in all directions.- Angle: the measure of the space between two intersecting lines or curves.- Circle: a two-dimensional shape consisting of a curved line that is equidistant from a central point. - Sphere: a three-dimensional shape consisting of a curved surface that is equidistant from a central point.CalculusCalculus is a branch of mathematics that dealswith the study of rates of change and motion of objects, with a focus on interpreting data and functions using derivatives and integrals. The subject is divided into two main branches; differential calculus, and integral calculus. Some common terms in calculus include:- Derivative: the rate of change of a function with respect to its variable.- Limit: the value that a function approaches as its input approaches a specified value.- Slope: the rate of change of a line, given by the ratio of the change in y over the change in x.- Integral: the sum of infinitely small parts of a whole.StatisticsStatistics is a branch of mathematics that focuses on the interpretation and analysis of data. It involves collecting, organizing, and analyzing data to make inferences and predictions about future events. Some common terms in statistics include:- Mean: the average value of a set of numbers.- Median: the middle value in a set of numbers.- Mode: the value that appears most frequently in a set of numbers.- Standard deviation: a measure of the amount of variation in a set of data.- Correlation: a measure of the relationship betweentwo or more variables.ConclusionIn conclusion, mathematics is a complex subject that requires an understanding of a wide range of topics and concepts. This article has explored some common mathematical terminology that is essential for anyone studying the subject at a higher level. Whileit can be a challenging subject to master, with dedication and practice, students can develop a deep understanding of the subject and apply it in real-life situations with confidence.。
数学专业英语翻译3.4.5

3.4数学的应用与应用数学3.4.5Construction of mathematical model(建立数学模型)In the preceding discussion we viewed modeling as a process and considered briefly the form of the model.Now let's focus attention on the construction of mathematical models.(在前面的讨论中,我们将建模视为一个过程,并简要地仔细思考了模型的形式。
现在让我们把注意力集中在数学模型的构建上。
)We begin by presenting an outline of a peocedure that is helpful in constructing models.In the next section,we illustrate the various steps in the procedure by discussing several real-world examples.(我们首先介绍一种有助于构建模型的概述。
在下一节中,我们通过讨论几个实际示例来说明过程中的各个步骤。
)STEP1Identify the problem(确定问题)What is the problem you would like to explore?Typically this is a difficult step because in real-life situations no one simply hands you a mathematical problem to solve.(你想探索的问题是什么?通常这是一个困难的步骤,因为在现实生活中,没有人只是给你一个数学问题来解决。
)Usually you have to sort through large amounts of data and identify some particular aspect of the situation to study.Moreover,it is imperative to be sufficiently precise(ultimately)in the formulation of the problem to allow for translation of the verbal statements describing the problem into mathematical symbology.(通常你必须对大量数据进行排序,并确定要研究的某些特定情况。
数学专业英语

数学专业英语(1)、Given ε>0,there exists a number N >0 such that ε<-a a n for all N n ≥ 译文:对给定的ε>0,存在一个数N >0使得不等式ε<-a a n 对所有的N n ≥都成立。
(2)、The function )(x f approaches infinity as x tends to zero.译文:当x 趋于0时,函数)(x f 趋于∞。
(3)、Suppose D is an open set with its closure in G .译文:假定D 是一个开区间,且其闭包在G 中。
(4)、Suppose )(x f is a function on domain D such that M x f <)( for all x ∈D ,where M is a constant .译文:假定)(x f 是区域D 上的一个函数,使得对所有x ∈D ,不等式M x f <)(成立,其中M 是一个常数。
(可用“satisfying ”代替上述“such that ”。
)(5)、表示推理的根据常用“by 短语”,有时也用“according to ”。
By Lemma 2 we have x y ≥.译文:根据引理2可推出x y ≥。
(6)、有时用现在分词表示“经过……而得到……”(推论)。
Integrating the above inequality twice,we see that . log )(0t t c t y ≥译文:将上一不等式两次积分得到. log )(0t t c t y ≥。
(7)、表示充分必要条件The sufficient and necessary condition for the equality isα>0 and ≥p 3. 译文:该等式成立的充分必要条件是α>0 且≥p 3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆理工大学数学专业英语学院学号姓名年月 2012年12月17日CONTROLLABILITY OF NEUTRAL FUNCTIONAL DIFFERENTIAL EQUATIONS WITH INFINITE DELA Y可控的无穷时滞中立型泛函微分方程In this article, we establish a result about controllability to the following class of partial neutral functional di fferential equations with infinite delay:0,),()(0≥⎪⎩⎪⎨⎧∈=++=∂∂t x xt t F t Cu ADxt Dxt t βφ (1)在这篇文章中,我们建立一个关于可控的结果偏中性与无限时滞泛函微分方程的下面的类: 0,),()(0≥⎪⎩⎪⎨⎧∈=++=∂∂t x xt t F t Cu ADxt Dxt tβφ (1) where the state variable (.)x takes values in a Banach space ).,(E and the control (.)u is given in[]0),,,0(2>T U T L ,the Banach space of admissible control functions with U a Banach space. C is abounded linear operator from U into E, A : D(A) ⊆ E → E is a linear operator on E, B is the phase space of functions mapping (−∞, 0] into E, which will be specified later, D is a bounded linear operator from B into E defined byB D D ∈-=ϕϕϕϕ,)0(0状态变量(.)x 在).,(E 空间值和控制用(.)u 受理控制范围[]0),,,0(2>T U T L 的Banach 空间,Banach 空间。
C 是一个有界的线性算子从U 到E ,A :A : D(A) ⊆ E → E 上的线性算子,B 是函数的映射相空间( - ∞,0]在E ,将在后面D 是有界的线性算子从B 到E 为B D D ∈-=ϕϕϕϕ,)0(00D is a bounded linear operator from B into E and for each x : (−∞, T ] → E, T > 0, and t ∈ [0, T ], xtrepresents, as usual, the mapping from (−∞, 0] into E defined by]0,(),()(-∞∈+=θθθt x xtF is an E-valued nonlinear continuous mapping on B ⨯ℜ+.0D 是从B 到E 的线性算子有界,每个x : (−∞, T ] → E, T > 0,,和t ∈[0,T],xt 表示为像往常一样,从(映射 - ∞,0]到由E 定义为]0,(),()(-∞∈+=θθθt x xtF 是一个E 值非线性连续映射在B ⨯ℜ+。
The probl em of controllability of linear and nonlinear systems represented by ODE in finitdimensional space was extensively studied. Many authors extended the controllability concept to infinite dimensional systems in Banach space with unbounded operators. Up to now, there are a lot of works on this topic, see, for example, [4, 7, 10, 21]. There are many systems that can be written as abstract neutral evolution equations with infinite delay to study [23]. In recent years, the theory of neutral functional di fferential e quations with infinite delay in infiniteODE 的代表在三维空间中的线性和非线性系统的可控性问题进行了广泛的研究。
许多作者延长无限维系统的可控性概念,在Banach 空间无限算子。
到现在,也有很多关于这一主题的作品,看到的,例如,[4,7,10,21]。
有许多方程可以无限延迟的研究[23]为抽象的中性演化方程的书面。
近年来,中立与无限时滞泛函微分方程理论在无限。
dimension was developed and it is still a field of rese arch (see, for instance, [2, 9, 14, 15] and the references therein). Meanwhile, the controllability problem of such systems was also discussed by many mathematicians, see, for example, [5, 8]. The objective of this article is to discuss the controllability for Eq. (1), where the linear part is supposed to be non-densely defined but satisfies the resolvent estimates of the Hille -Y osida theorem. We shall assume conditions that assure global existence and give the su fficient conditions for controllability of some partial neutral functional di fferential equations with infinite delay. The results are obtained using the integrated semigroups theory and Banach fixed point theorem. Besides, we make use of the notion of integral solution and we do not use the analytic semigroups theory.维度仍然是一个研究领域(见,例如,[2,9,14,15]和其中的参考文献)。
同时,这种系统的可控性问题也受到许多数学家讨论可以看到的,例如,[5,8]。
本文的目的是讨论方程的可控性。
(1),其中线性部分是应该被非密集的定义,但满足的Hille- Y osida 定理解估计。
我们应当保证全局存在的条件,并给一些偏中性无限时滞泛函微分方程的可控性的充分条件。
结果获得的积分半群理论和Banach 不动点定理。
此外,我们使用的整体解决方案的概念和我们不使用半群的理论分析。
Treatin g equations with infinite delay such as Eq. (1), we need to introduce the phase space B. To avoid repetitions and understand the interesting properties of the phase space, suppose that ).,(B B is a (semi)normed abstract linear space of funct ions mapping (−∞, 0] into E, and satisfies the following fundamental axioms that were first introduced in [13] and widely discussed in [16].方程式,如无限时滞方程。
(1),我们需要引入相空间B.为了避免重复和了解的相空间的有趣的性质,假设是(半)赋范抽象线性空间函数的映射( - ∞,0到E]满足首次在[13]介绍了以下的基本公理和广泛[16]进行了讨论。
(A )There exist a positive constant H and functions K(.), M(.):++ℜ→ℜ,with K continuous and M locally bounded, such that, for any ℜ∈σand 0>a ,if x : (−∞, σ + a] → E, B x ∈σ and (.)x is continuous on [σ, σ+a], then, for every t in [σ, σ+a], the following conditions hold:(i) B xt ∈,(ii) Bt x H t x ≤)(,which is equivalent to BH ϕϕ≤)0(or every B ∈ϕ(iii) Bσσσσx t M s x t K xtts B)()(sup )(-+-≤≤≤(A) For the function (.)x in (A), t → xt is a B -valued continuous function for t in [σ, σ + a].(一) 存在一个正的常数H 和功能K ,M :++ℜ→ℜ连续与K 和M ,局部有界,例如,对于任何ℜ∈σ,如果x : (−∞, σ + a] → E,,B x ∈σ和(.)x 是在 [σ,σ+ A] 连续的,那么,每一个在T[σ,σ+ A],下列条件成立: (i) B xt ∈,(ii) Btx H t x ≤)(,等同与 BH ϕϕ≤)0(或者对伊B ∈ϕ(iii) Bσσσσx t M s x t K xtts B)()(sup )(-+-≤≤≤(A )对于函数(.)x 在A 中,t → xt 是B 值连续函数在[σ, σ + a].(B )The space B is complete.Throughout this article, we also assume that the operator A satisfies the Hille -Y osida condition :(H1) There exist and ℜ∈ω,such that )(),(A ρω⊂+∞ and{}M N n A I n n ≤≥∈---ωλλωλ,:)()(sup (2)(B )空间B 是封闭的整篇文章中,我们还假定算子A 满足的Hille- Y osida 条件:(1) 在和ℜ∈ω,)(),(A ρω⊂+∞和 {}M N n A I n n ≤≥∈---ωλλωλ,:)()(sup (2)Let A0 be the part of operator A in )(A D defined by {}⎩⎨⎧∈=∈∈=)(,,)(:)()(000A D x f o r Ax x A A D Ax A D x A DIt is well known that )()(0A D A D =and the operator 0A generates a strongly continuous semigroup))((00≥t t T on )(A D .设A0是算子的部分一个由)(A D 定义为 {}⎩⎨⎧∈=∈∈=)(,,)(:)()(000A D x for Ax x A A D Ax A D x A D这是众所周知的,)()(0A D A D =和算子0A 对于)(A D 具有连续半群))((00≥t t T 。
