数学实验作业汇总
五下数学暑假实践作业清单

7月10日
7月11日
715日
7月16日
7月17日
7月18日
7月19日
7月20日
最高气温
最低气温
绘制统计图:
活动三:学习并研究本册数学课本中所有的“你知道吗”并写一份关于“你学到了什么的”200字小结。
活动四:从报纸、杂志或网上分别收集几条用分数或统计图表示的信息并摘抄。(至少10条)
五下数学暑假实践作业清单
暑假数学实践作业
班级:姓名:
活动一:请选择家里长方体、正方体物品,分别测量长、宽、高,然后计算棱长总和、表面积和体积。(如鞋盒、书本、冰箱等等)(别忘了单位呦!)
物品名称
长
宽
高
棱长总和
表面积
体积
活动二:记录2018年7月10日——7月20日每天的最高气温和最低气温,并记录如下表。再绘制出复式折线统计图表示7月10日——7月20日的最高气温和最低气温的温度变化情况。
50个简单的数学小实验

50个简单的数学小实验1. 滚动骰子,记录每个点数的数量,进行统计分析。
2. 观察不同颜色的薯片在水中的沉浮情况,研究密度与沉浮关系。
3. 使用不同比例的液体混合,观察颜色的变化。
4. 抛掷硬币,记录正反面的次数,进行概率分析。
5. 用尺子测量不同物品的长度、宽度和高度,并计算体积。
6. 研究太阳光的折射现象,观察镜面反射和散射。
7. 测量水的密度,并探究不同温度下密度的变化。
8. 按照不同比例混合物质制作彩色火焰,观察颜色的变化。
9. 观察火柴棒在水中的漂浮情况,探究密度与沉浮关系。
10. 测量不同颜色纸张的吸光度,并研究颜色与吸光度的关系。
11. 投掷骰子,计算点数之和的概率分布。
12. 测量不同材质的物体上的摩擦系数,并计算摩擦力。
13. 研究声音的传播和反射,观察声波在不同介质中的特性。
14. 制作简易水银温度计,测量温度的变化。
15. 用万能表测量不同电器的电阻、电流和电压。
16. 研究气体的扩散速率,观察气体分子在不同温度下的运动状态。
17. 测量不同颜色光线的波长和频率,并探究颜色与波长频率的关系。
18. 使用不同硬度的铅笔在不同纸张上写字,观察痕迹的深浅和清晰度。
19. 用扫描电镜观察不同物质的微观结构,并比较不同物质之间的差异。
20. 研究磁场的强度和方向,探究电流与磁场的相互作用关系。
21. 设计和制作简易的电磁铁,测量其磁场强度和电阻。
22. 投掷飞镖,研究飞行轨迹和命中准确度。
23. 测量不同物体的密度,计算质量和体积的比值。
24. 制作水晶,观察不同溶液的晶体形态和颜色。
25. 研究不同材质之间的传热过程,探究热传导和热辐射的特性。
26. 测量不同物体的电荷量,研究电荷与电力的相互作用关系。
27. 观察不同金属的折射率和反射率,研究光的特性在金属中的表现。
28. 测量不同水平面上的液体压力和重力,探究液体压力和重力的关系。
29. 研究不同状态的气体压强,探究气体压强与体积的关系。
三年级数学实践性作业

学校_____________班级_________姓名__________等级_________
同学们,三角形的三边有什么关系呢?用三根小棒来围三角形,研究一下吧!
思考:为什么有的能围成三角形,有的却不能呢?带着你的小棒,在小组内一起研究一下。并把结果记录在表格中。
《三角形特性及三边关系》实验记录单
试验次数Biblioteka 边的长度(cm)围的结果
较短的两条边的长度之和与第三条边的关系
一
二
三
能围成打√
不能围成打×
大于
等于
小于
1
2
3
4
说说你们组出现什么情况?告诉大家你们围成三角形了吗?
你得出什么结论?。
解决问题:小凌打算把一根60厘米长的小棒截成三段,围成一个三角形,请你提醒她,三根小棒在剪的时候要注意什么?你建议她各剪多长?
设计教师:赵霞(东新小学)
批阅教师————批阅时间—————
西南交通大学数学实验作业全面版

实验课题一基础编程第一大题:编程完成下列计算1. 当x = 3, x =2π 时,求1sin()xy x e =+ 的值。
%第一大题 %1x=[3,2*pi];y1=sin(x)+exp(x) %{ y1 =1517/75 31594/59 %}2. 用冒号法作等差数列x = 2,4,6,8,10求对应的函数22y x =+%2x=2:2:10;y2=x.^2+sqrt(2*x) %{ y2 =6 3841/204 7143/181 68 3761/36 %}3. 已知:22,35,a b c e π===计算:31sin cos();532tan()cot .3a y b c a y b ⎛⎫=+⨯ ⎪⎝⎭⎛⎫= ⎪⎝⎭%3a=2*pi,b=35,c=exp(2); y31=sin(a/5)+cos(b)*c y32=tan(b)*cot(a/3) %{ y31 =-4060/709y32 =-1019/3725 %}4. 将数据格式转换成有理格式后,清屏后重新输出a ,b ,c ,y 31,y 32(提示:参数选项或format rational ,清屏clc ) %4format rationalclc5.查看工作空间已有变量及信息。
(提示:打开变量信息窗口或whos)%5whos%{Name Size Bytes Class AttributesA 3x3 72 doubleA1 3x3 72 doubleA2 1x1 8 doubleA3 3x3 72 doubleS 21x2 336 doubleX 1x21 168 doubleY 1x21 168 doublea 1x1 8 doublea1 1x1 8 doublea11 1x1 8 doublea2 1x1 8 doublea21 1x1 8 doublea3 1x1 8 doublea31 1x1 8 doubleb 1x1 8 doublec 1x1 8 doubles 1x1 8 doublex 1x2 16 doubley1 1x2 16 doubley2 1x5 40 doubley31 1x1 8 doubley32 1x1 8 doubley71 1x1 8 doubley72 1x1 8 double%}6.a1=-6.28 a2=7.46 a3=5.37将a1,a2,a3分别向零取整后赋给a11,a21,a31。
数学实验之学生实验题目

数学实验之学生实验题目 MATLAB 简介实验一:数组操作及运算练习1.设有分块矩阵⎥⎦⎤⎢⎣⎡=⨯⨯⨯⨯22322333S O R E A ,其中E,R,O,S 分别为单位阵、随机阵、零阵和对角阵,试通过数值计算验证⎥⎦⎤⎢⎣⎡+=22S 0RS R EA 。
2.求如下非齐次线性方程组的通解,⎪⎩⎪⎨⎧=--+=+-+=+-+.12,2224,12w z y x w z y x w z y x3.某零售店有9种商品的单件进价(元)、售价(元)及一周的销量下表,问哪种商品的利润最大,哪种商品的利润最小;按收入由小到大,列出所有商品及其收入;求这一周该10种商品的总收入和总利润。
实验二:作图练习1. 用两种方法在同一个坐标下作出y 1= x 2,y 2= x 3,y 3= x 4 y 4= x 5这四条曲线的图形,并要求用两种方法在图上加各种标注。
2.用subplot 分别在不同的坐标系下作出下列四条曲线,为每幅图形加上标题, 1)概率曲线 2exy -=;2)四叶玫瑰线 r =sin2q ;3)叶形线 ⎪⎪⎩⎪⎪⎨⎧+=+=;13,13323t ty t t x 4)曳物线 22111lnyyy x --±= 。
3.作出下列曲面的3维图形,1))sin(22y x z +=π;2)环面:⎪⎩⎪⎨⎧=+=+=,sin ,sin )cos 1(,cos )cos 1(u z v u y v u x )2,0()2,0(ππ∈∈v u 。
实验三:编写M-文件1.建立一个命令M-文件:求所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其各位数字的立方和等于该数本身。
例如,153是一个水仙花数,因为153=13+53+33。
2.编写函数M-文件SQRT.m :用迭代法求a x =的值。
求平方根的迭代公式为迭代的终止条件为前后两次求出的x 的差的绝对值小于10-5。
〈返回〉方程求解实验一:油价与船速的优化问题油价的上涨,将影响大型海船确定合理的航行速度,以优化航行收入。
数学实验课习题总结(带答案)

第二次实验内容
1、求下列方程的根 1)ex-3x=0, 在[-1,1]上的近似解,使用 fzero,fsolve 分 别进行求解 2 )判定方程 x7+2x5+3x3+5x+7=0 有几个实根,并使用 roots,fzero,fsolve 分别进行求解,也使用牛顿法编程计算 问题的近似解。 2、求解线性方程组:
答案:
1. 程序设计: (1) fzero('exp(x)-3*x',[-1,1]) fsolve('exp(x)-3*x',[-1,1]) (2)函数 fun1: function ff=fun1(x) ff=(x^7+2*x^5+3*x^3+5*x+7)/(7*x^6+10*x^4+9*x^2+5); 程序: x=-1:0.01:1; y=x.^7+2*x.^5+3*x.^3+5*x+7; plot(x,y,'r-') gtext('零点') grid on 数 p=[1,0,2,0,3,0,5,7]; roots(p) fzero('x^7+2*x^5+3*x^3+5*x+7',0) fsolve('x^7+2*x^5+3*x^3+5*x+7',0) x0=1; x1=x0-fun1(x0); while abs(x1-x0)>=0.0001 x0=x1; x1=x0-fun1(x0); end x0 结果: (1) ans = 0.6191 0.6191 (2)有 1 个实根,如右图 ans = 1.0633 + 0.8552i 1.0633 - 0.8552i 0.1980 + 1.4799i 0.1980 - 1.4799i -0.8442 + 1.1442i -0.8442 - 1.1442i -0.8341 ans = -0.8341 %画图法判断实根个
初一至初三数学实践作业集锦
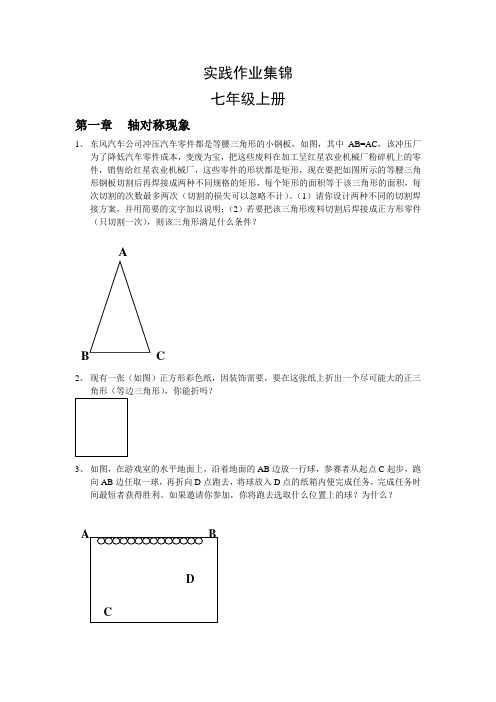
实践作业集锦七年级上册第一章轴对称现象1、东风汽车公司冲压汽车零件都是等腰三角形的小钢板,如图,其中AB=AC,该冲压厂为了降低汽车零件成本,变废为宝,把这些废料在加工呈红星农业机械厂粉碎机上的零件,销售给红星农业机械厂,这些零件的形状都是矩形,现在要把如图所示的等腰三角形钢板切割后再焊接成两种不同规格的矩形,每个矩形的面积等于该三角形的面积,每次切割的次数最多两次(切割的损失可以忽略不计)。
(1)请你设计两种不同的切割焊接方案,并用简要的文字加以说明;(2)若要把该三角形废料切割后焊接成正方形零件(只切割一次),则该三角形满足什么条件?2、现有一张(如图)正方形彩色纸,因装饰需要,要在这张纸上折出一个尽可能大的正三角形(等边三角形),你能折吗?3、如图,在游戏室的水平地面上,沿着地面的AB边放一行球,参赛者从起点C起步,跑向AB边任取一球,再折向D点跑去,将球放入D点的纸箱内便完成任务,完成任务时间最短者获得胜利。
如果邀请你参加,你将跑去选取什么位置上的球?为什么?D BAC AC4、(1)如图①,△ABC 中,∠C=900,请用直尺和圆规作一条直线,把△ABC 分割成两个等腰三角形(不写作法,但必须保留作图痕迹);(2)已知内角度数的两个三角形如图②、③所示,请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的度数。
① ② ③5、如图,电力工作人员栽完电线杆后,用两根等长的拉线把电线杆固定住了(AB=AC ),但有的工作人员说看上去电线杆有点倾斜,请你帮助工作人员测一下电线杆是否倾斜,简要说明理由。
6、张庄、李庄、马庄的位置如图,每两个村庄之间都有笔直的公路相连,他们计划共同投资打一眼机井,希望机井的位置到三庄的距离相同,试确定机井的位置。
7、如图,从A 村到B 村要修一条路,中间隔着一条河,河宽为d ,河两岸需架一座桥,桥与河两岸必须垂直,要使从A 村到B 村的总路程最短,聪明的你能确定桥应架的具体位置吗?AB 240C A 1040 520 A BC 张庄李庄 马庄8、图1是由5张大小相同的正方形纸片拼成的图形.现只移动1张纸片,使5张纸片组成轴对称图形,要求每张纸片至少有2个点与其余纸片相连,但纸片彼此不覆盖,请画出尽可能多的不同形状的图形. 9、由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑。
六年级数学寒假实践作业

六年级数学寒假实践作业一、寻找生活中的数学1. 请计算家中一年四季的温度差和湿度差。
你可以使用温度计和湿度计来测量每天的室内温度和湿度,然后记录下来。
最后,计算一年的温度差和湿度差。
2. 购物时,注意观察商品的价格标签,记录下你经常购买的商品的单价和数量。
计算一年中你在这些商品上花费了多少钱。
3. 测量你家的房屋面积和周长,计算出房屋的容积率和使用率。
二、制作数学模型1. 制作一个简单的几何模型,例如长方体、圆柱体或圆锥体。
使用纸板、胶水和剪刀等工具,按照你所选择的几何形状进行制作。
完成后,测量模型的各个维度,并验证其几何特性。
2. 设计一个简单的数学游戏,例如24点游戏或数独。
为游戏制定规则,并在纸上画出游戏板。
你可以与家人或朋友一起玩,看看谁的得分更高。
三、解决生活中的数学问题1. 制定一份家庭预算。
记录每月的收入和支出,计算每月的净收入和储蓄金额。
预测未来几个月的家庭开支,并制定相应的预算计划。
2. 如果你计划在寒假期间参加旅行,请计算旅行所需的总费用,包括交通费、住宿费、餐饮费和门票等。
制定一个合理的旅行预算,确保旅行不会超出你的经济能力。
3. 如果你有一笔存款,请计算在银行定期存款的利息下,存款到期时的总金额。
你可以选择不同的存款期限和利率进行比较,看看哪种存款方式更划算。
四、数学趣味活动1. 与家人或朋友一起观看一部与数学相关的电影或纪录片,例如《数列大作战》或《数学之美》。
讨论电影中的主题和情节,并分享你对数学的看法和感受。
2. 设计一个有趣的数学谜语或趣味数学题,与家人或朋友一起解答。
看看谁能够最快地找到答案,并分享解题思路和方法。
(整理)小学数学五年级上册数学实践作业
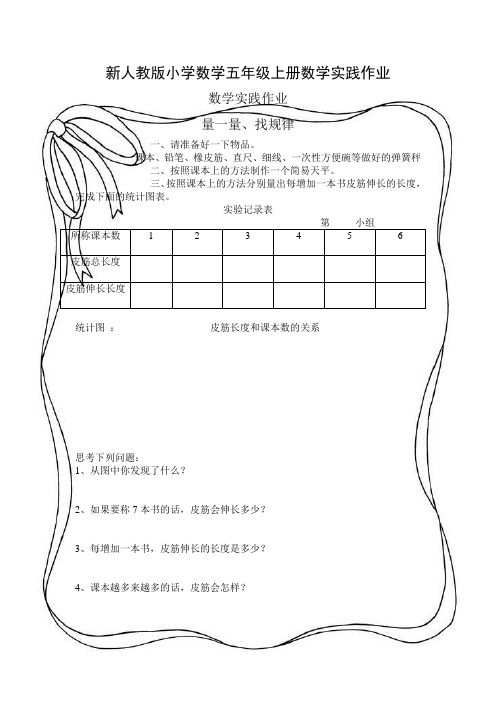
新人教版小学数学五年级上册数学实践作业
数学实践作业
量一量、找规律
一、请准备好一下物品。
课本、铅笔、橡皮筋、直尺、细线、一次性方便碗等做好的弹簧秤
二、按照课本上的方法制作一个简易天平。
三、按照课本上的方法分别量出每增加一本书皮筋伸长的长度,完成下面的统计图表。
实验记录表
第小组
所称课本数 1 2 3 4 5 6
皮筋总长度
皮筋伸长长度
统计图:皮筋长度和课本数的关系
思考下列问题:
1、从图中你发现了什么?
2、如果要称7本书的话,皮筋会伸长多少?
3、每增加一本书,皮筋伸长的长度是多少?
4、课本越多来越多的话,皮筋会怎样?
班级:姓名:
数学实践作业
铺一铺
你还记得密铺吗?请从书后的附页中剪下下面的图形分别铺一铺,看看哪些图形可以密铺,在它们的下面画“√”
()()()()()()
思考下列问题:
哪些图形不能密铺?
哪些图形可以密铺?剪下附页中的图形在下面铺一铺。
王小明家要铺地,下面有两组瓷砖,请你选用一组为他设计一个图案。
并在方格中试一试。
(课本P110页)
在你的设计的图案中,用了()块,所占面积是()平方厘米,用了()块,所占面积是()平方厘米,用了()块,所占面积是()平方厘米。
你还能用附页中的图形再进行一些设计吗?
班级:姓名:。
下学期数学实验作业

实验一图形的画法1. 做出下列函数的图像:(1) y(x)二x sin(x -X-2),一.2_x_2 (分别用plot、fplot )(2) X2/9 y2/25"(用参数方程)(3) 在同一图形窗口中,画出四幅不同图形(用subplot命令):比=cos(x) y2= sin(x_ pi /2) y3 = x2cos(x- pi) y4 = e sin(x)(x^[0,2兀])(2作出极坐标方程为r =2(1 _cost)的曲线的图形.3作出极坐标方程为r=e t/10的对数螺线的图形.‘X =4 cost,4绘制螺旋线《y =4sin t,在区间[0, 4江]上的图形.在上实验中,显示坐标轴名称.z =t5作出函数z=rye工工的图5形.2 2 26作出椭球面―七1的图形.4 9 1(该曲面的参数方程为x =2sin ucos v, y =3sin u sin v, z =cos u, ( 0 兰u 兰兀0 兰v 兰2兀).)2 2 27作双叶双曲面亠•差一二-_1的图形.1.521.421.32(曲面的参数方程是x =1.5cot u cosv, y =1.4 cot usin v, z =1.3cscu,其中参数0 ::: u ,-二:::v :::二时对应双叶双曲面的一叶,参数u :::0,-二:::v :::二时对应2 2 双叶双曲面的另一叶.)8作出圆环x=(8+3cosv)cosu,y=(8+3cosv)sinu,z=7sinv,( 0 勺兰3兀/2, Jl/2 <v <2兀) 的图形.9作出球面x2■ y2 -z2 =22和柱面(x_1)2,y2 =1相交的图形.10作出锥面x2y2 =z2和柱面(x-1)2• y21相交的图形.11用动画演示由曲线y =sin乙z • [0,二]绕z轴旋转产生旋转曲面的过程.(该曲线绕z轴旋转所得旋转曲面的方程为x2 -y^sin2 z,其参数方程为x =sinzcosu, y =sin zsinu,z =z, (z 三[0,c.],u 三[0,2二]))x12.画出变上限函数tsint2dt及其导函数的图形.・0实验二一元函数微分学_ 4 I4 2 x~ty在命令窗口中键入表达式^x y -x -e2. 已知多项式f(x)=6x52x3-5x21,g(x)(1) f(x)的根;(2)f(x)计x42x_3x 3,求:g(x)在闭区间[-1,2]上的最小值;3.(3)f(x) + g(x), f(x) g(x)和g(x);n n .(-1) +4n li^^ J 十i ■ n 十在MATLAB^求下列极限(1) ^-:-3 - 4f(X)的导数.(2)x + a xxim「)1. -2xy-y2 ,并求(1)>> sym n;>> limit(((-1)An+4.An)./(3.A(n+1)+4A(n+1)),n,inf); >> ans ans = 1/4(2) >> syms x a;>> limit(((x+a)./(x-a))4x,x,inf); >> ans ans = exp(2*a)5.根据要求在MATLAB^求下列函数的导数(1) >> syms a x;>> y=a. Aa+a. ^x+x. ^a+x.人(a*x); >> diff(y,x); >> ans ans =a A x*log(a)+x A a*a/x+x A (a*x)*(a*log(x)+a) (2) >> syms x>> y=asi n( (1-x.A2”(1+x.A2)); >> diff(y,x); >> ans ans =(-2*x/(1+xA2)-2*(1-xA2)/(1+xA2)A2*x)/(1-(1-xA2)A2/(1+xA2)A2)A(1/2) (3) >> syms a x;>> diff(log(x+sqrt(a.A2+x.A2)),x); >> ansans =(1+1/(aA2+xA2)A(1/2)*x)/(x+(aA2+xA2)A(1/2)) (4)>> diff(x.A2.*log(1+x),2);>> ansdy —?a 丄 x 丄 a 丄 ax—:⑴ y =a a x x ,求dx⑵f (x) = arcs in1-x 2、1 x 2(3)设AT n(X"a 2+X 2),求 dy丿,求厂⑴二?d 2yy =x 2ln( 1 x),求 dx 2ans =2*log(x+1)+4*x/(x+1)-xA2/(x+1)A2实验三一元函数积分学 一元函数积分学1.用MATLAB 十算下列不定积分. (1) x 2 1 dx (2)a xsin xcos 2xdxx(1) >> syms x; >> y=sqrt(x.A 2+1)./x.A 2; >> in t(y,x); >> ans ans =-1/x*(xA2+1)A(3/2)+x*(xA2+1)A(1/2)+asi nh(x) (2) >> syms a x;>> y=a.Ax.*si n(x).*(cos(x)).A2; >> in t(y,x);>> ans ans = (2*(log(a)A2+3)/(10*log(a)A2+9+log(a)A4)*log(a)*exp(x*log(a))*ta n(1/2*x)-4*log⑻ *(log (a) A2-1)/(10*log (a)A2+9+log(a)A4)*exp(x*log(a))*tan(1/2*x)A3-(log(a)A2 +3)/(10*log (a)A2+9+log (a)A4)*exp(x*log(a))-(11*log(a)A2+9)/(10*log(a) A2+9+log( a)A4)*exp(x*log(a))*tan(1/2*x)A4+(log(a)A2+3)/(10*log(a)A2+9+log(a)A4)*exp(x*l og(a))*ta n(1/2*x)A6+(11*log(a)A2+9)/(10*log(a)A2+9+log(a)A4)*exp(x*log(a))*tan (1/2*x)A2+2*(log(a)A2+3)/(10*log(a)A2+9+log(a)A4)*log(a)*exp(x*log(a))*ta n(1/2 *x)A5)/(1+ta n(1/2*x)A2)A3 2.用MATLAB 求解下列各积分(1)2二 2xoegdx(2) 0e 'sin 2tdt(3)设 f(xjO^x 汨,求1 x 乞22f(x)dx .>> y=exp(2*x).*cos(x);>> in t(y,x,0,2*pi);>> ansans =2/5*exp(pi)A4-2/5(2) >> syms t;>> in t(exp(-t).*si n(2*t),t,0,i nf);>> ansans =2/5(3) >> syms x;>> y=i nt(x.A2,x,0,1)+i nt(x,x,1,2);>> yy = 11/62 24•求由曲线x ,(y-5) -16绕x轴旋转所产生的旋转体的体积.>> syms x;>> y=pi*(5+sqrt(16-x.A2)).A2;>> in t(y,x,-4,4);>> ansans =856/3*pi+80*piA25•求下列曲线与所围成图形的面积:(1)y=^x2与x2y2=8 (两部分都要计算);(2)2sin^ 与r2二cos2二2(1) >> syms x;>> s1=i nt(sqrt(8-x.A2),x,-sqrt(2),sqrt(2))-i nt(0.5*x.A2,x,-sqrt(2),sqrt(2));>> s1s1 =2A(1/2)*6A(1/2)+4/3*pi-2/3*2A(1/2)>> s2=8*pi-s1;>> s2s2 =20/3*pi-2A(1/2)*6A(1/2)+2/3*2A(1/2)>>2 23 2 X6•计算半立方抛物线y (x-1)被抛物线y 截得的一段弧的长度.3 3实验四多元函数微积分求多元函数的偏导数与全微分1.1 设z =sin(xy) cos2(xy),求z,上,二,「三.2◎ ©乐(X d>> syms x y;>> z=si n(x.*y)+(cos(x.*y)).A2;>> y1=diff(z,x);>> y2=diff(z,y);>> y3=diff(z,x,2);>> y4=diff(y1,y);>> y1y1 =cos(x*y)*y-2*cos(x*y)*si n(x*y)*y>> y2y2 =cos(x*y)*x-2*cos(x*y)*s in (x*y)*x>> y3y3 = -si n(x*y)*yA2+2*si n( x*y)A2*yA2-2*cos(x*y)A2*yA2>> y4y4=-si n(xx*y)*x*y+cos(x*y)+2*si n(xx*yF2*x*y-2*cos(x*y)A2*x*y-2*cos(x*y)*s in (x*y)1.2 设x =e u u sin v,y =e u -Ucosv,求丄,丄,」,」.e x t y e x ty微分学的几何应用1.3求出曲面z =2x2y2在点(1,1)处的切平面、法线方程,并画出图形.1.4求曲面k(x,y)= 2 42在点丄,丄,聖处的切平面方程,并把曲面和它的切平面作x +y +1 <4 2 21 /在同一图形里.多元函数的极值1.5 求 f (x,y) =x3 _y3+3x2+3y2 _9x 的极值.1.6求函数z =x2■ y2在条件x2 y2 x y =0下的极值.实验2多元函数积分学(基础实验)计算重积分2.1计算xy2dxdy,其中D为由x ^2,^.<y, y =2所围成的有界区域.D2.2 计算ill (x2- y2- z)dxdydz,其中I 】由曲面z = 2 -x2 -y2与z=, x2- y2围成.h重积分的应用2.3 求由曲面f x,y =1 _x _y与g x, y [=2-x2-y2所围成的空间区域I】的体积.2.4在Oxz平面内有一个半径为2的圆,它与z轴在原点0相切,求它绕z轴旋转一周所得旋转体体积.计算曲线积分2.5 求[f(x,y,z)ds,其中f(x,y,z pj l +30x2甘Oy,积分路径为L : x =t, y =t2, z =3t2, 0 _y _2.(注意到,弧长微兀ds = . xj •y2• zj dt,将曲线积分化为定积分)2.6求L F.dr ,其中6 5F =xy i 3x(xy 2)j, r(t) =2costi sintj,0 咲岂2二.计算曲面积分2.7计算曲面积分y (xy亠yz亠zx)dS ,其中二为锥面z= x2亠y2被柱面x2亠y2 =2x所截得的有限部分.(注意到,面积微元dS = J +公+z:dxdy ,投影曲线x2+y2 =2x的极坐标方程为r =2cost,」^ <—,2 2将曲面积分化作二重积分,并采用极坐标计算重积分.)2.8计算曲面积分'i;ix3dydz y3dzdx - z3dxdy,其中二为球面x2y2a2的外侧.y实验六无穷级数及微分方程(基础实验)数项级数1.1 (1)观察级数7鸟的部分和序列的变化趋势.n±n(2)观察级数丄的部分和序列的变化趋势.n±n10n乂1.2 设an =——,求' a n .n! n壬求幕级数的收敛域2n n1.3求v 4 (x_3)的收敛域与和函数.n卫n也函数的幕级数展开1.4求cosx的6阶麦克劳林展开式.>> taylor(cos(x),7);>> ansans =1-1/2*x A2+1/24*x A4-1/720*x A61.5求arctanx的5阶泰勒展开式.>> taylor(ata n( x),6);>> ansans = x-1/3*xA3+1/5*xA51.6 求x 1$在x =1处的8阶泰勒展开,并通过作图比较函数和它的近似多>> y=exp(-((x-1).A2.*(x+1).A2));>> taylor(y,9,1);>> ans ans =1-4*(X -1)A 2-4*(X -1F3+7*(X -1)A 4+16*(X -1)A 5+4/3*(X -1F6-28*(X -1)A 7-173/6*(X -1)A求解微分方程22.1 求微分方程 y 2xy xe x 的通解 .2.2求微分方程xy y e x 0在初始条件y xi 2e 下的特解.但它的解却很有趣和耐人寻味 . 试求解洛伦兹方程组2.3 求解微分方程 xy 2x e ,并作出其积分曲线 .2.4 求微分方程组 dxx 2ydt dy xy dte t在初始条件 x t 0 1,y t 0 0下的特解2.5 求出初值问题y y sin 2 x y cos 2 x y(0) 1, y(0) 0的数值解, 并作出数值解的图形 .2.6 洛伦兹 (Lorenz) 方程组是由三个一阶微分方程组成的方程组3 2 1 3 3 设 M2 13 17512 3 ,求矩阵M 的秩. 8. 这三个方程看似简单也没有包含复杂的函数并画出解曲线的图形11x 1 x2 1 计算范德蒙行列式 2 x 1 2x 2 3 3x 1 x 44x 1x 237 2 679 4 22 设矩阵 A 115 6 92 78 357 9实验七 矩阵运算与方程组求解 11 1222 xxx .333x x x 4 444 已知矩阵 M6 求向量组x (t) i6y(t) i6x(t)y (t) x(t)z(t) 45x(t) y(t) z(t) x(t)y(t)4z(t) x(0) i2,y(0) 4, z(0) 0» ans ans = 1-4*(x-1 )A2-4*(x-1 )A3+7*(x-1 )A4+16*(x-1 )A5+4/3*(x-1 )A6-28*(x-1 )A7-173/6*(x-1 )A7/11求解微分方程2.1 2.2 2.3 求微分方程 y 求微分方程xy 求解微分方程 2xy y e 2.4 求微分方程组 y dx dt dy dt 2x 2.5 求出初值问题 2 xe x 的通解. 0在初始条件y- 2e 下的特解. e\并作出其积分曲线. 2y gt 在初始条件X to 1-yt o 0下的特解. o .2 y y sin x y y (o )i,y (o )o 2 COS X 的数值解,并作出数值解的图形• 方程组是由三个一阶微分方程组成的方程组 •这三个方程看似简单, 但它的解却很有趣和耐人寻味.试求解洛伦兹方程组 16y(t) 16x(t) x(t)z(t) 45x(t) y(t) x(t)y(t) 4z(t) ' 12,y(0) 4, z(0) 0 2.6 洛伦兹(Lorenz) 也没有包含复杂的函数, x(t) y (t) z(t) x(0) 并画出解曲线的图形•实验七 矩阵运算与方程组求解 1 1 1 1 1 Xi x 2 Xs X4 X5 计算范德蒙行列式 2 X1 2 x 2 2 x 4 2 X 5・ 3 33 3 3 X1 X2 X3 X4 X5 4 4 4 4 4 Xi X 2 X 3 X 4 X 5 3 7 26 47 9 4 2 0 设矩阵 A 11 5 6 9 3 , 求 I A|,tr(A),A 3. 2 78 3 7 5 79 0 63 2 1 3 2 设M 2 1 3 1 3 , 求矩阵 M 的秩. 7 0 5 1 8已知矩阵 3 1的秩等于2,求常数t 的值. 1 3 12 3 2 12 ,求矩阵A 的秩. 4 求向量组 (1,2, 1,1), 3 (0, 4,5, 2), 2 (2,0,3,0)的秩.。
高等数学(第三版)各章实验作业题答案

1. 作出函数[]53()3123,2,2f x x x x x =+-+∈-的图像.第1题图2. 求下列各极限.(1)1lim 1nn n →∞⎛⎫- ⎪⎝⎭; (2)sin lim x x x →∞;(3)0sin lim x x x →; (4)10lim x x e +→.解(1)11lim 1enn n →∞⎛⎫-= ⎪⎝⎭; (2)sin lim 0x x x →∞=;(3)0sin lim 1x xx →=; (4)12lim e x x e →3. 求方程20.2 1.70x x --=的近似解(精确到0.0001). 解 1 1.2077x ≈-,2 1.4077x ≈. 4. 探究高级计算器的其他功能.(略)1. 求函数3(21)y x x =-的导数; 操作:在命令窗口中输入:>> syms xy=x^3*(2*x -1); dy=diff(y) 按Enter 键,显示:dy = 3*x^2*(2*x -1)+2*x^3 继续输入:>> simplify(dy) % 将导数化简 按Enter 键,显示: ans =8*x^3-3*x^2即 3283y x x '=-. 2. 求函数()ln 1y x x =-+的二阶导数; 操作:在命令窗口中输入: >> syms xy=1-log(1+x); dy=diff(y,x,2) 按Enter 键,显示: dy = 1/(1+x)^2即 21(1)y x ''=+. 3.函数4322341y x x x x =-+-+在区间[-3,2]上的最小值. 操作:在命令窗口中输入:>>x=fminbnd('x^4-2*x^3+3*x^2-4*x+1',-3,2) y=x^4-2*x^3+3*x^2-4*x+1 按Enter 键,显示: x =1 y =-11.求下列不定积分(1)在命令窗口中输入: >> syms xint(x/(sqrt(x^2+1)),x)按键Enter 键,显示结果: ans = (x^2+1)^(1/2)即c +.(2)在命令窗口中输入: >> syms xint(x^3*cos(x))按键Enter 键,显示结果:ans =x^3*sin(x)+3*x^2*cos(x)-6*cos(x)-6*x*sin(x) 即332cos =sin 3cos 6cos 6sin x xdx x x x x x x x c +--+⎰. 2.求下列定积分(1)在命令窗口中输入: >> int((-3*x+2)^10,x,0,1) 点击Enter 键,显示结果: ans = 683/11 即1100683(-3+2)d =11x x ⎰. (2)在命令窗口中输入: >> int(x*sin(x),x,0,pi/2)点击Enter 键,显示结果: ans = 1 即 π20sin d =1x x x ⎰.3.求广义积分0e d x x x -∞⎰.操作:在命令窗口中输入: >>int(x*exp(x),x,-inf,0)按Enter 键,显示结果: ans =-1 即e d =1xx x -∞-⎰.1. 230y y y '''++=.操作:在命令窗口中输入: >> syms x y;y=dsolve('D2y -4*Dy -5*y=0','x') 显示:y =C1*exp(5*x)+C2*exp(-x)即满足所给初始条件的特解为:512xx y c e c e -=-.2. 232sin xy y e x '''-=.操作:在命令窗口中输入: >> syms x y;y=dsolve('D2y -3*Dy=2*exp(3*x)*sin(x)','x') 显示:y = -3/5*exp(3*x)*cos(x)-1/5*exp(3*x)*sin(x)+1/3*exp(x)^3*C1+C2即满足所给初始条件的特解为:33312311cos sin 553xxxy e x e x c e c =--++. 整理得:33213cos +sin 5xxy e x x ce c =-++()(令113c c =)3. +cos x y y y e x '''+=+,00x y ==,032x y ='=.操作:在命令窗口中输入: >> syms x y;y=dsolve('D2y+Dy+y=exp(x)+cos(x)','y(0)=0', 'Dy(0)=3/2', 'x') 显示:y = -1/3*exp(-1/2*x)*cos(1/2*3^(1/2)*x)+1/3*exp(x)+sin(x)即满足所给初始条件的特解为:211cos()sin 323x xy e e x -=-++.1. 绘制平面曲线ln y x =. 操作:在命令窗口中输入: >> x=1:0.02: exp(2); y=log(x); plot(x,y);按Enter 键,显示下图:2. 绘制空间曲面2232z x y =-. 操作:在命令窗口输入 >>[x,y]=meshgrid(-4:0.5:4); z=-3*x.^2-2*y.^2; surf(x,y,z)按Enter 键,显示下图:3. 绘制空间曲线23,23.t t t x e y e z e ---⎧=⎪⎪=⎨⎪=⎪⎩操作:在命令窗口输入>>t=0:0.01:1;x=exp(-t);y=exp(-2*t)/4;z=3*exp(-3*t)/9;plot3(x,y,z)按Enter键,显示下图:实验6作业题1. 求函数cos z xy =的偏导数. 操作:在命令窗口中输入:>> dz_dx=diff('cos(x*y)', 'x ') 显示dz_dx = -sin(x*y)*y 继续输入:>> dz_dy=diff('cos(x*y)', 'y ') 显示:dz_dy =-sin(x*y)*x即sin zx xy x∂=-∂, sin z x xy y ∂=-∂2. 计算函数23y x y =-的极值.操作:在matlab 中依次选择“File\New\M -File ”,在弹出的M 文件编辑窗口中在命令窗口中输入:clear all;clc syms x y;z=x^3-6*x-y^3+3*y;dz_dx=diff(z,x); %计算z 对x 的偏导数 dz_dy=diff(z,y); %计算z 对y 的偏导数 [x0,y0]=solve(dz_dx,dz_dy); %求驻点x0,y0A_=diff(z,x,2); %计算z 对x 的二阶偏导数B_=diff(diff(z,x),y); %计算z 对x,y 的二阶混合偏导数 C_=diff(z,y,2); %计算z 对y 的二阶偏导数 x0=double(x0); %数据转换 y0=double(y0);n=length(x0); %计算x0中元素的个数 for i=1:nA_x=subs(A_, x,x0(i)); %把x=x0(i)(即x0的第i 个元素值)代入z 对x 的二阶偏导数A=subs(A_x, y,y0(i)); %继续把y=y0(i)(即y0的第i 个元素值)代入z 对x 的二阶偏导数,得到AB_x=subs(B_, x,x0(i)); %把x=x0(i)代入z 对x 、y 的二阶混合偏导数 B=subs(B_x, y,y0(i)); %继续把y=y0(i)代入二阶混合偏导数,得到B C_x=subs(C_, x,x0(i)); %把x=x0(i)代入z 对y 的二阶偏导数C=subs(C_x, y,y0(i)); %继续把y=y0(i)代入z 对y 的二阶偏导数,得到C D=A*C-B^2;text=['原函数在(',num2str(x0(i)), ', ',num2str(y0(i)), ')处' ]; if D>0fm=subs(x^3-6*x-y^3+3*y,{x,y},{x0(i),y0(i)}); %求函数值 if A>0disp([text, '有极小值',num2str(fm)]) %在命令窗口中输出 elsedisp([text, '有极大值',num2str(fm)])end end if D==0disp([text, '的极值情况还不确定,还需另作讨论' ]) end end保存后,选择M 文件编辑窗口中的“Debug\run ”,显示如下结果: 原函数在(1.4142,-1)处有极小值-7.6569 原函数在(-1.4142,1)处有极大值7.65693. 计算(2)d d Dx y x y -⎰⎰,D :顶点分别为(0,0),(1,1)和(0,1)的三角形闭区域;操作:在命令窗口中输入: >>syms x y;S=int(int(2*x-y,y,0,1-x),x,0,1) 显示: S=1/6即:二重积分1(2)d d =6Dx y x y -⎰⎰.实验7作业题1. 将函数xx f -=11)(展开为幂级数,写出展开至6次幂项. 操作:在命令窗口中输入: >> clear;clc syms x; f=1/(1-2*x); taylor(f,7,x) 显示:ans = 1+2*x+4*x^2+8*x^3+16*x^4+32*x^5+64*x^6即65432643216842111x x x x x x x ++++++=-. 2. 求函数2()tf t e =的拉氏变换.操作:在命令窗口中输入: >> clear;clc syms x;laplace(exp(2*t)) 显示: ans = 1/(s -2)即 21)(2-=s e L t. 3.求函数22()56s F s s s +=-+的拉氏逆变换.操作:在命令窗口中输入: >>syms silaplace((s+2)/(s^2-5*s+6)) 显示:ans =-4*exp(2*t)+5*exp(3*t)即 12256s L s s -+⎡⎤⎢⎥-+⎣⎦234e 5e t t =-+.。
二上数学寒假实践作业

二上数学寒假实践作业
以下是一个适合二年级学生的数学寒假实践作业的例子:
题目:测量和计算
1. 测量你的房间或卧室的长、宽、高,计算其面积和体积。
记住,体积是长度、宽度和高度相乘的结果。
2. 使用家里常见的物品(如杯子、碗等),测量其容量(即可以容纳多少水或其他液体),并记录下来。
3. 测量你家中一些物品的周长,例如桌子、椅子、电视等。
周长是围绕物体边缘一圈的长度。
4. 尝试用不同的方法来测量同一个物品或距离,例如使用皮尺、步数等。
比较结果,看看哪种方法更准确。
5. 观察家中物品的形状,例如圆形、正方形、长方形等。
尝试计算每种形状的面积或周长。
这个实践作业旨在帮助学生了解测量和计算的原理,并锻炼他们的观察和解决问题的能力。
完成这个作业需要一些基本的数学知识和生活技能,例如使用测量工具、读懂测量单位等。
通过实践,学生可以更好地理解和应用数学知识,同时提高他们的动手能力和解决问题的能力。
数学实验作业汇总

(1)产生一个5阶魔方矩阵M:M=magic(5)(2)将矩阵M的第3行4列元素赋值给变量t:t=M(3,4)(3)将由矩阵M第2,3,4行第2,5列构成的子矩阵赋给变N:N=M(2:4,2:3:5)(4)将由矩阵M的前3行赋给变量N:N=M(1:3,:)(5)将由矩阵M的后3列赋给变量N:N=M(:,end:-1:end-2)(6)提取M的主对角线元素,并以这些对角线元素构成对角矩阵N:N=diag(diag(M))或N=tril(triu(M)) (7)随机产生1000个100以内的整数赋值给变量t:t=round(rand(1,1000)*100)(8)随机产生100*5个100以内的实数赋值给变量M:M=rand(100,5)*100(1)删除矩阵M的第7个元素M(7)=[](2)将含有12个元素的向量t转换成3*4的矩阵:reshape(t,3,4)(3)产生和M同样大小的单位矩阵:eye(size(M))(4)寻找向量t中非零元素的下标:find(t)(5)逆序显示向量t中的元素:t(end:-1:1)(6)显示向量t偶数位置上的元素:t(2:2:end)(7)利用find函数,将向量t中小于10的整数置为0:t(find(t<10&rem(t,1)==0))=0(8)不用find函数,将向量t中小于10的整数置为0:t(t<10&rem(t,1)==0)=0(9)将向量t中的0元素用机器0(realmin)来代替:t(find(t=0))=realmin(10)将矩阵M中小于10的整数置为0:M(find(M<10)&rem(M,1)==0)=02、写出完成下列操作的命令及结果。
(1)将1~50这50个整数按行优先存放到5*10的矩阵中,求该矩阵四周元素的和;>> t=[1:10];>> M=[t;t+10;t+20;t+30;t+40]M =1 2 3 4 5 6 7 8 9 1011 12 13 14 15 16 17 18 19 2 021 22 23 24 25 26 27 28 29 3 031 32 33 34 35 36 37 38 39 4 041 42 43 44 45 46 47 48 49 5 0>> N=M(2:4,2:9)N =12 13 14 15 16 17 18 1922 23 24 25 26 27 28 2932 33 34 35 36 37 38 39>> sum(sum(M))-sum(sum(n))ans =6632)n取100、1000、10000,求序列1、1/2、1/3……1/n的和。
【必刷题】2024八年级数学下册数学实验操作专项专题训练(含答案)

【必刷题】2024八年级数学下册数学实验操作专项专题训练(含答案)试题部分一、选择题:1. 在数学实验中,用刻度尺测量物体长度时,下列哪种做法是正确的?A. 将刻度尺与物体紧贴B. 将刻度尺与物体保持一定距离C. 观察刻度尺时眼睛要与尺面垂直D. 观察刻度尺时眼睛可以倾斜2. 下列哪个工具在数学实验中用于测量角度?A. 直尺B. 圆规C. 量角器D. 三角板3. 在进行数学实验时,下列哪个步骤不是数据处理的一般步骤?A. 收集数据B. 整理数据C. 分析数据D. 编写报告4. 下列哪个数学实验适合研究三角形内角和?A. 测量不同形状的三角形周长B. 测量等边三角形的高C. 测量三角形内角的度数D. 比较不同三角形的面积5. 在数学实验中,下列哪个量需要用天平来测量?A. 长度B. 重量C. 温度D. 速度6. 下列哪个数学实验方法可以用来探究平面几何图形的性质?A. 观察法B. 实验法C. 类比法D. 归纳法7. 在数学实验中,下列哪个步骤是数据收集的关键?A. 确定实验目的B. 设计实验方案C. 实施实验操作D. 记录实验数据8. 下列哪个数学实验适合研究平行线的性质?A. 制作三角形模型B. 观察长方形的对角线C. 画出一组平行线并探究其性质D. 比较不同角度的锐角9. 在数学实验中,下列哪个工具不是测量工具?A. 刻度尺B. 量角器C. 计算器D. 三角板10. 下列哪个数学实验方法可以用来验证勾股定理?A. 观察法B. 实验法C. 反证法D. 演绎法二、判断题:1. 在数学实验中,刻度尺可以弯曲测量曲线长度。
(错)3. 在数学实验中,天平可以用来测量长度。
(错)4. 数学实验方法中的归纳法可以用来探究几何图形的性质。
(对)5. 在数学实验中,观察法是一种有效的数据收集方法。
(对)三、计算题:1. 已知一个等腰三角形的底边长为10cm,腰长为13cm,求该三角形的周长。
2. 一个正方形的对角线长为10cm,求正方形的面积。
六年级数学实践作业

六年级数学实践作业
六年级数学实践作业示例:
题目:测量并计算家中常见物品的面积或体积
目标:通过实际操作,加深对面积和体积计算的理解,提高数学应用能力。
步骤:
1. 选择家中常见的物品,例如:餐桌、电视机、书柜、水桶等。
2. 使用测量工具(如卷尺)测量所选物品的长、宽、高。
3. 根据测量数据,使用面积和体积的计算公式(面积=长×宽,体积=长×宽×高),计算所选物品的面积和体积。
4. 将测量数据、计算过程和结果记录在实践作业表格中。
5. 分析测量和计算过程中的误差来源,讨论如何减小误差。
6. 将实践作业表格贴在数学实践作业本上,供老师检查。
注意事项:
1. 测量时要小心谨慎,避免损坏物品。
2. 记录数据时要准确无误,保证计算结果的准确性。
3. 在计算过程中,要注意单位的统一(如:长度单位为米或厘米,面积单位为平方米或平方厘米,体积单位为立方米或立方厘米)。
4. 分析误差时,可以从测量工具、测量方法、计算过程等方面进行考虑。
通过这样的实践作业,学生可以在实际操作中加深对面积和体积计算的理解,提高数学应用能力,同时也可以培养细心、耐心和观察力等素质。
数学实验作业

例题(2):假设某地区人口数量N(t)随时间t 连续增长,即dN(t)/dt=λN(t),其中λ是人口增长率.易得其解 N(t)=N o e λt ,N O 是该地区的初始人口。
如果考虑到移民以速度V 进入该地区,则dN(t )/dt=λN(t)+v微分方程的解为N(t)=N o e λt +v (e λt -1)/λ问题提出:假设该地区的初始人口有100万。
第一年内有43.5万移民迁入,第一年末总计人口156.4万,则43.5156.4100(1)λλλ=+-e e求该地区的人口增长率λ(一元方程求根)。
编程练习题1:对带有迁移的人口模型,试用几种非线性方程求根方法,确定模型公式中的人口增长率λ。
其满足:43.5156.4100(1)λλλ=+-e e设人口数量随着时间以固定的相对增长率变化。
领N(t)为t 食客的人口数量。
λ 为人口出生率。
1)人口数量的微分方程模型:dN(t)/dt=λN(t)2)指数模型: N(t)=N oe λt N O :初始时刻人口数量。
如果允许移民移入且移入速率v 为固定常数dN(t )/dt=λN(t)+v3)有移民移入的指数模型:N(t)=N o e λt +v (e λt -1)/λ假设:N o =1000000 (人) ,v=435000(人/年) ,N(t)=1564000(人) 通过求解方程:43.5156.4100(1)λλλ=+-e e 的该地区人口的出生率λ=0.1。
设方程f(λ)=0在区间[0,1]内有根,二分法就是逐步收缩有根区间,最后得出所求的根。
具体过程如下区有根区间[0,1]得重点,将它分为两半,分点λo =0+1/2=0.5 这样就可以缩少有根区间。
有三种情可以出现:1)若f(λ)f(0)﹤0,则f(λ)在区间[0,0.5)内有零点;2)若f(λ)f(1)﹤0,则f(λ)在区间(0.5,1]内有零点;3)若f(λo)=0,则λo 再区间[0,1]内的零点。
小学生数学实验100例

小学生数学实验100例实验一:糖果计数Obj:培养小学生的计数能力Materials:糖果Procedure:1. 给每个小学生发放相同数量的糖果。
2. 让小学生一边将手中的糖果一个一个取出,一边用口数数。
3. 让他们将自己数的结果告诉老师,老师确认无误后,鼓励他们继续进行下一轮的计数。
4. 重复以上步骤,直到小学生们计数无误。
实验二:数字拼图Obj:提高小学生的数字认知和逻辑思维能力Materials:数字卡片、拼图板Procedure:1. 将数字卡片打乱顺序放在桌上。
2. 让小学生们按照数字的顺序将卡片拼在拼图板上。
3. 鼓励小学生们在完成之后互相检查答案,找出错误并及时修改。
实验三:趣味运算Obj:强化小学生的运算能力Materials:纸、铅笔Procedure:1. 给每个小学生发放纸和铅笔。
2. 出题者可以随机给出一道加法、减法或乘法的算式。
3. 小学生们写下自己的答案,并在完成后把纸张交给出题者。
4. 出题者检查答案,将答对的小学生召集起来并鼓励他们。
实验四:图形分类Obj:提高小学生的图形识别和分类能力Materials:各种图形卡片(正方形、长方形、圆形、三角形等)Procedure:1. 将各种图形卡片打乱顺序放在桌上。
2. 让小学生们按照图形的特征将卡片分类。
3. 鼓励小学生们在完成之后互相检查分类结果,并讨论不同分类方式的合理性和差异。
实验五:分数比较Obj:加深小学生对分数大小关系的理解Materials:纸、铅笔Procedure:1. 准备一些简单的分数题目,例如1/2、1/4、1/8等。
2. 让小学生们通过比较分子和分母的大小,判断分数的大小关系。
3. 引导小学生们用纸和铅笔练习绘制简单的分数图形,加深对分数大小关系的理解。
实验六:时钟读表Obj:提高小学生的时间概念和读表能力Materials:模拟时钟、题目卡片Procedure:1. 准备一些时钟读表题目卡片,包括小时和分钟的各种组合。
数学实验作业8月10日第五组

实验七T7:取不同的初值计算下列平方和形式的非线性规划,尽可能求出所有局部极小点,进而找出全局极小点,并对不同算法(搜索方向、搜索步长、数值梯度与分析梯度等)的结果进行分析、比较。
2)min 22222121212(1211)(4949812324681)x x x x x x +-++++-4)min 100θ2221/222312123{[χ-10(χ,χ)]+[(χ+χ)-1]}+χ 其中1(), >0 2(,)11(), <0 22arctg arctg πθπ21112211⎧χχχ⎪⎪χχ=⎨⎪χχ+χ⎪⎩ 解:2)在matlab 中输入程序(exam0705grad.m ,exam0705grad_run.m ): function [f,g]=exam0705grad(x)f=(x(1)^2+12*x(2)-11)^2+(49*x(1)^2+49*x(2)^2+81*x(1)+2324*x(2)-681)^2;% compute the function value at xif nargout > 1 % fun called with 2 output argumentsg(1)=2*(98*x(1) + 81)*(49*x(1)^2 + 81*x(1) + 49*x(2)^2 + 2324*x(2) - 681) + 4*x(1)*(x(1)^2 + 12*x(2) - 11); % compute the gradient evaluated at xg(2)=288*x(2) + 2*(98*x(2) + 2324)*(49*x(1)^2 + 81*x(1) + 49*x(2)^2 + 2324*x(2) - 681) + 24*x(1)^2 - 264;endclear all ;clc;% comparing different algorithms: using gradient vectorformat short ex0=[-1.9,2];'---case1: bfgs, hybrid 2,3 poly-------'opt1=optimset('LargeScale','off', 'MaxFunEvals',1000,'GradObj','on');[x1,v1,exit1,out1]=fminunc(@exam0705grad,x0,opt1)pause'---case2: dfp, hybrid 2,3 poly-------'fopt=optimset(opt1,'HessUpdate','dfp');[x2,v2,exit2,out2]=fminunc(@exam0705grad,x0,fopt) pause'---case3: bfgs, hybrid 2,3 poly-------'fopt=optimset(opt1,'HessUpdate','bfgs');[x3,v3,exit3,out3]=fminunc(@exam0705grad,x0,fopt) pause'---case4: steep, hybrid 2,3 poly-------'fopt=optimset(opt1,'HessUpdate','steepdesc');[x4,v4,exit4,out4]=fminunc(@exam0705grad,x0,fopt) pause'---case5: bfgs, 3rd poly-------'opt2=optimset(opt1,'LineSearchType','cubicpoly'); [x5,v5,exit5,out5]=fminunc(@exam0705grad,x0,opt2) pause'---case6: dfp, 3rd poly-------'fopt=optimset(opt2,'HessUpdate','dfp');[x6,v6,exit6,out6]=fminunc(@exam0705grad,x0,fopt) pause'---case7:bfgs , 3rd poly-------'fopt=optimset(opt2,'HessUpdate','bfgs');[x7,v7,exit7,out7]=fminunc(@exam0705grad,x0,fopt) pause'---case8: steep, 3rd poly-------'fopt=optimset(opt2,'HessUpdate','steepdesc');[x8,v8,exit8,out8]=fminunc(@exam0705grad,x0,fopt)pause'++++ results of solutions ++++++'solutions=[x1;x2;x3;x4;x5;x6;x7;x8];funvalues=[v1;v2;v3;v4;v5;v6;v7;v8];iterations=[out1.funcCount;out2.funcCount;out3.funcCount;out4.funcCou nt;out5.funcCount;out6.funcCount;out7.funcCount;out8.funcCount]; [solutions,funvalues,iterations]则输出:x1 =-2.8997e+000 2.1583e-001v1 =3.2329e-006exit1 =1out1 =iterations: 32funcCount: 41stepsize: 1firstorderopt: 2.3873e+000algorithm: 'medium-scale: Quasi-Newton line search' message: [1x438 char]x2 =-2.3709e+000 2.5629e-001v2 =6.8300e+000exit2 =out2 =iterations: 401funcCount: 422stepsize: 1firstorderopt: 5.7455e+003algorithm: 'medium-scale: Quasi-Newton line search' message: [1x128 char]x3 =-2.8997e+000 2.1583e-001v3 =3.2329e-006exit3 =1out3 =iterations: 32funcCount: 41stepsize: 1firstorderopt: 2.3873e+000algorithm: 'medium-scale: Quasi-Newton line search' message: [1x438 char]x4 =-2.0594e+000 2.7379e-001v4 =1.2063e+001exit4 =out4 =iterations: 118funcCount: 1000stepsize: 4.7397e-006firstorderopt: 1.7291e+002algorithm: 'medium-scale: Quasi-Newton line search' message: [1x144 char]x5 =-2.8997e+000 2.1583e-001v5 =3.2329e-006exit5 =1out5 =iterations: 32funcCount: 41stepsize: 1firstorderopt: 2.3873e+000algorithm: 'medium-scale: Quasi-Newton line search' message: [1x438 char]x6 =-2.3709e+000 2.5629e-001v6 =6.8300e+000exit6 =out6 =iterations: 401funcCount: 422stepsize: 1firstorderopt: 5.7455e+003algorithm: 'medium-scale: Quasi-Newton line search'message: [1x128 char]x7 =-2.8997e+000 2.1583e-001v7 =3.2329e-006exit7 =1out7 =iterations: 32funcCount: 41stepsize: 1firstorderopt: 2.3873e+000algorithm: 'medium-scale: Quasi-Newton line search' message: [1x438 char]x8 =-2.0594e+000 2.7379e-001v8 =1.2063e+001exit8 =out8 =iterations: 118funcCount: 1000stepsize: 4.7397e-006firstorderopt: 1.7291e+002algorithm: 'medium-scale: Quasi-Newton line search' message: [1x144 char]ans =++++ results of solutions ++++++ans =-2.8997e+000 2.1583e-001 3.2329e-006 4.1000e+001-2.3709e+000 2.5629e-001 6.8300e+000 4.2200e+002-2.8997e+000 2.1583e-001 3.2329e-006 4.1000e+001-2.0594e+000 2.7379e-001 1.2063e+001 1.0000e+003-2.8997e+000 2.1583e-001 3.2329e-006 4.1000e+001-2.3709e+000 2.5629e-001 6.8300e+000 4.2200e+002-2.8997e+000 2.1583e-001 3.2329e-006 4.1000e+001-2.0594e+000 2.7379e-001 1.2063e+001 1.0000e+003改变x0,程序见附序(di1tix0.m),因太过繁琐,只输出最后x的值,输出:ans =-2.8956e+000 2.1618e-001 4.6001e-004 4.9000e+001-2.9377e+000 2.1295e-001 1.0877e+000 4.6600e+002-2.8956e+000 2.1618e-001 4.6001e-004 4.9000e+001-1.4106e+000 2.9837e-001 2.9482e+001 1.0000e+003-2.8956e+000 2.1618e-001 4.6001e-004 4.9000e+001-2.9377e+000 2.1295e-001 1.0877e+000 4.6600e+002-2.8956e+000 2.1618e-001 4.6001e-004 4.9000e+001-1.4106e+000 2.9837e-001 2.9482e+001 1.0000e+0034)程序见(exam07052grad.m, Untitled.m),输出结果:-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001改变初值x0后程序见Untitled1.m,输出结果:-1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001-1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001-1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001-1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001-1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001 -1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001 -1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001 -1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001 结论:从2)4)输出观察和比较数据可以看出改变x0,最优解随之改变,而bfgs 公式,混合2,3次插值,求得的局部最优解最接近全局最优解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)产生一个5阶魔方矩阵M:M=magic(5)(2)将矩阵M的第3行4列元素赋值给变量t:t=M(3,4)(3)将由矩阵M第2,3,4行第2,5列构成的子矩阵赋给变N:N=M(2:4,2:3:5)(4)将由矩阵M的前3行赋给变量N:N=M(1:3,:)(5)将由矩阵M的后3列赋给变量N:N=M(:,end:-1:end-2)(6)提取M的主对角线元素,并以这些对角线元素构成对角矩阵N:N=diag(diag(M))或N=tril(triu(M)) (7)随机产生1000个100以内的整数赋值给变量t:t=round(rand(1,1000)*100)(8)随机产生100*5个100以内的实数赋值给变量M:M=rand(100,5)*100(1)删除矩阵M的第7个元素M(7)=[](2)将含有12个元素的向量t转换成3*4的矩阵:reshape(t,3,4)(3)产生和M同样大小的单位矩阵:eye(size(M))(4)寻找向量t中非零元素的下标:find(t)(5)逆序显示向量t中的元素:t(end:-1:1)(6)显示向量t偶数位置上的元素:t(2:2:end)(7)利用find函数,将向量t中小于10的整数置为0:t(find(t<10&rem(t,1)==0))=0(8)不用find函数,将向量t中小于10的整数置为0:t(t<10&rem(t,1)==0)=0(9)将向量t中的0元素用机器0(realmin)来代替:t(find(t=0))=realmin(10)将矩阵M中小于10的整数置为0:M(find(M<10)&rem(M,1)==0)=02、写出完成下列操作的命令及结果。
(1)将1~50这50个整数按行优先存放到5*10的矩阵中,求该矩阵四周元素的和;>> t=[1:10];>> M=[t;t+10;t+20;t+30;t+40]M =1 2 3 4 5 6 7 8 9 1011 12 13 14 15 16 17 18 19 2021 22 23 24 25 26 27 28 29 3031 32 33 34 35 36 37 38 39 4041 42 43 44 45 46 47 48 49 50>> N=M(2:4,2:9)N =12 13 14 15 16 17 18 1922 23 24 25 26 27 28 2932 33 34 35 36 37 38 39>> sum(sum(M))-sum(sum(n))ans =6632)n取100、1000、10000,求序列1、1/2、1/3……1/n的和。
>> n=100;>> t=[1:n];>> format rat>> M=t.^-1;>> S=sum(M)S =2630/507>> n=1000;>> t=[1:n];>> format rat>> M=t.^-1;>> S=sum(M)S =1804/241>> n=10000;>> t=[1:n];>> format rat>> M=t.^-1;>> S=sum(M)S =1106/1131.在同一坐标系下绘制y1=sin(t),y2=sin(2t),y3=sin(3t),其中y1的数据点用星号,线形为黑色虚线,y2的数据点用方块,线形为红色实线,y3的数据点用小圆圈,线形为蓝色点线。
(要求采用一次绘出和逐次填加两种方式完成绘图)>> t=linspace(0,2*pi,100);>> y1=sin(t);>> y2=sin(2*t);>> y3=sin(3*t);>> plot(t,y1,’*k:’,t,y2,’sr-’,t,y3,’ob-.’)>> t=linspace(0,2*pi,100);>> y1=sin(t);>> plot(t,y1,’*k:’)>> hold on>> y2=sin(2*t);>> plot(t,y2,’sr-’)>> hold on>> y3=sin(3*t);>> plot(t,y3,’ob-.’)>> hold off2.分别用plot和fplot函数绘制y=sin(1/x)的曲线,分析两曲线的差别>> x=linspace(0,1/(2*pi),100);>> y=sin(x.^-1);>> plot(x,y,’*-’)>> fplot(’sin(x.^-1)’,[0,1/(2*pi)],’o-’)两曲线的差别:plot 曲线在确定自变量x 的取值间隔时采用平均间隔,图像不是十分准确;fplot 曲线自动取值,在函数值变化平稳时,它的数值点会自动相对稀疏一点,在函数值变化剧烈处,所取点会自动密集一点,所以曲线更加光滑准确。
6.已知曲面方程f (x,y )=,x ∈ [-1.5π,1.5π],y ∈ [-2.5π,2.5π],用建立子窗口的方法在同一图形窗口绘制出三维线图,网线图,曲面图。
>> x=-1.5*pi:pi/50:1.5*pi; >> y=-2.5*pi:pi/50:2.5*pi; >> [X,Y]=meshgrid(x,y);>> Z=sin(sqrt(X.^2+Y.^2))./sqrt(1+X.^2+Y.^2); >> subplot(1,3,1);plot3(X,Y,Z); >> subplot(1,3,2);mesh(X,Y,Z); >> subplot(1,3,3);surf(X,Y,Z);8.将peaks 函数生成的最高峰削去,并用色图矩阵“cool ”修饰。
>> [x,y,z]=peaks(30); >> x1=x(1,:);y1=y(:,1); >> i=find(y1>1&y1<3); >> j=find(x1>-1&x1<1); >> z(i,j)=NaN*z(i,j); >> surf(x,y,z) >> colormap(cool)3. 定义一个函数,函数的自变量为整数n ,函数的功能是:随机产生n 个三位整数,将其中小于平均值的数用0代替。
function [mean,x]=ff (n) x=floor (100+899*rand (1,n)); m=length (x); mean=sum (x)/m; x (x<mean)=0;4. 编写函数,用来求下列函数的和,并给出n 分别为100,1000,10000时,下列各式的值。
()()()()2n 2n 224466=1335572n-12n-12π⎛⎫⨯⨯⨯⨯⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪⎪⎪ ⎪ ⎪⨯⨯⨯⨯⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭…… function y=s(n) y=1; for i=1:1:nx=4*i^2/(4*i^2-1); y=y*x; end disp(y) s(100)=1.5669 s(1000)=1.5704 s(10000)=1.57085. 通过命令文件实现:随机产生20个数,输出其中的最大数和最小数。
通过函数文件实现:随机产生n个数,输出其中的最大最小数。
命令文件>> t=rand(1,20);>> disp('max=');disp(max(t))max=0.7942>> disp('min=');disp(min(t))min=0.0503函数文件function f3(n)t=rand(1,n);disp('max=');disp(max(t));disp('min=');disp(min(t));end3.求下列函数的一阶和二阶导数()() cos2y=tan3xx+>> syms x>> diff(2/tan(x)+cos(x)/3,’x’,1)ans =- sin(x)/3 - (2*(tan(x)^2 + 1))/tan(x)^2>> syms xdiff(2/tan(x)+cos(x)/3,’x’,2)4.求积分>> syms xint(sqrt(exp(x)+1),x)ans =2*(exp(x) + 1)^(1/2) + 2*atan((exp(x) + 1)^(1/2)*i)*i5.求下列级数的和>> syms n>> s=symsum((-1)^(n+1)*1/n,1,inf)s =log(2)6.求函数在x=0处的泰勒展开式>> syms x>> taylor((exp(x)+exp(-x))/2,x,5,0)ans =x^4/24 + x^2/2 + 11. 利用randn函数声称符合正态分布的10*5随机矩阵A,进行以下操作:(1).A的各列元素的均值和标准方差(2).A的最大元素及其所在位置(3).A的每行元素的和以及全部元素之和(4).分别对A的每行元素按升序排序(5).将A中的每行元素的总和按从大到小的顺序存入line_sum中,相应的行号存入line_num中>> A=randn(10,5);>> a1=mean(A)>> a2=std(A)>> AA=max(max(A))>> [i j]=find(A==AA)>> a3=sum(A,2)>> a4=sum(sum(A))>> a5=sort(A,2)>> [line_sum,line_num]=sort(sum(A,2),'descend')2、补充题:利用导入向导(或借助函数imread)导入一幅单色图片存入变量ima_data中,然后依次完成下列操作:(1)用imshow函数显示图片;(2)删除图片前若干行(例如前100行)再次显示该图片。
