2020年4月学考选考高2020届高2017级浙江省衢州湖州丽水三地市高三教学质量检测试卷数学试题参考答案
衢州、湖州、丽水2020年4 月三地市高三教学质量检测试卷答案

1分
3
v=0(x≥ 32 m) 3
22.(10 分)解:
A I d
(1)由图几何关系: d2来自L0.75L tan 370
L
1 分 1.5L
d 2R cos 530 L
R
m
v0 cos 370
1分
Bq
得: B 3mv0
1分
2qL
O
O1
O2
P
37º R
37º
53º
C
D
B
2L
2L
解图 1
0.75L 1 Uq ( 2L) 2 2 1.5Lm v0
衢州、丽水、湖州三地市教学质量检测
物理参考答案及评分标准
一、选择题 I(每题 3 分) 1.B 2.A 3.B 4.D 5.A 6.B 7.B 8.D 11.C 12.C 13.A
二、选择题Ⅱ(每题 2 分,选错、不选得 0 分,部分对得 1 分) 14.BD 15.CD 16.BC
三、非选择题(本题共 6 小题,共 55 分)
③h<0.15m 时,不满足条件。
21.(10 分) 解:
(1) U=BLv=kt=t
v U 2t BL
a=2m/s2
1分 1分 2分
由牛顿第二定律,有 F ma IBL IBL 2 1.2 t
1分
(2)由功能关系,有
W=Q+Wf+ΔEK=Q(1+μ) 得:Q=12J
2分
(3)
① t≤t1 时, v 2ax 2 x t=t1 时 v1=4m/s x1=4m
1分
② t>t1 时,由动量定理,有 (1 )BLq mv mv1
v
v1
衢州湖州丽水2020年4月三地市高三教学质量检测英语试卷及参考答案(17页)

衢州湖州丽水2020年4月三地市高三教学质量检测英语试卷英语试题本试卷分第I卷(选择题)和第II卷(非选择题)。
第I卷1至8页,第II 卷9至10页。
第1卷注意事项:1.答第I卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在本试卷上,否则无效。
第一部分:听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.Where does the conversation take place?A.In a shop.B.In a restaurant.C.In a supermarket.2.How did the man spend his free time with his friends'A.They played sports.B.They watched TV programs.C.They played computer games.3.What does the man think of the seats on the plane?A.Wide.fortable.C.Small.4.What are the speakers mainly talking about?A.The whales.B.The weather.C. A voyage.5.When was Tim born?A.On February 24.B.On February 28.C.On February29.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
浙江省衢州、丽水、湖州三地市2020届高三下学期数学4月教学质量检测试卷

浙江省衢州、丽水、湖州三地市2020届高三下学期数学4月教学质量检测试卷一、单选题 (共10题;共20分)1.(2分)已知集合A=[0,4],B={x∈R||x|≤1},则(∁R A)∩B=()A.[−1,0)B.[−1,0]C.[0,1]D.(1,4]2.(2分)椭圆x22+y2=1的离心率是()A.12B.13C.√23D.√223.(2分)已知某空间几何体的三视图如图所示,则该几何体的体积是()A.323B.4C.163D.84.(2分)明朝的程大位在《算法统宗》中(1592年),有这么个算法歌诀:三人同行七十稀,五树梅花廿一枝,七子团圆正半月,除百零五便得知.它的意思是说:求某个数(正整数)的最小正整数值,可以将某数除以3所得的余数乘以70,除以5所得的余数乘以21,除以7所得的余数乘以15,再将所得的三个积相加,并逐次减去105,减到差小于105为止,所得结果就是这个数的最小正整数值.《孙子算经》上有一道极其有名的“物不知数”问题:“今有物不知其数,三三数之余二,五五数之余三,七七数之余二,问物几何.”用上面的算法歌诀来算,该物品最少是几件()A.21B.22C.23D.245.(2分)函数f(x)=(e x+e−x)ln|x|的图象大致为()A .B .C .D .6.(2分)若实数x ,y 满足约束条件 {x −2y +3≥02x −y −3≤0x +y ≥0 ,则 2x +3y 的取值范围是( )A .[−1,15]B .[1,15]C .[−1,16]D .[1,16]7.(2分)若 a >,b >0 ,则“ ab ≤4 ”是“ ab a+b≤1 ”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件8.(2分)已知任意 a ∈[−1,2] ,若存在实数b 使不等式 |x 2−ax|≤b 对任意的 x ∈[0,2] 恒成立,则( ) A .b 的最小值为4 B .b 的最小值为6 C .b 的最小值为8D .b 的最小值为109.(2分)如图,正方形ABCD 的中心与圆O 的圆心重合,P 是圆O 上的动点,则下列叙述不正确的是( )A .PA ⃗⃗⃗⃗⃗ ⋅PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ ⋅PD⃗⃗⃗⃗⃗⃗ 是定值. B .PA ⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ ⋅PC ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ ⋅PD ⃗⃗⃗⃗⃗⃗ +PD ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗ 是定值.C .|PA⃗⃗⃗⃗⃗ |+|PB ⃗⃗⃗⃗⃗ |+|PC ⃗⃗⃗⃗⃗ |+|PD ⃗⃗⃗⃗⃗ | 是定值.D .PA ⃗⃗⃗⃗⃗ 2+PB ⃗⃗⃗⃗⃗ 2+PC ⃗⃗⃗⃗⃗ 2+PD⃗⃗⃗⃗⃗⃗ 2是定值. 10.(2分)对任意的实数 x >0 ,不等式 2ae 2x −lnx +lna ≥0 恒成立,则实数a 的最小值为( ) A .2√eB .12√eC .2eD .12e二、填空题 (共3题;共3分)11.(1分)若复数 z =21+i(i 为虚数单位),则 |z|= . 12.(1分)在平面直角坐标系 xOy 中,已知点M 是双曲线 x 2a 2−y 2b2=1(a >0,b >0) 上的异于顶点的任意一点,过点M 作双曲线的切线l ,若 k OM ⋅k l =13,则双曲线离心率 e 等于 .13.(1分)已知函数 f(x)=x 2+ax +a , A ={x ∈R|f(x)≤x} , B ={x ∈R|f[f(x)]≤f(x)} , A ≠∅,A ⊆B ,则实数a 的取值范围是 .三、双空题 (共4题;共8分)14.(2分)在数列 {a n } 中, S n 为它的前 n 项和,已知 a 2=1 , a 3=6 ,且数列 {a n +n} 是等比数列,则 a n = , S n = .15.(2分)二项式 (1x −x 2)6 的展开式的各项系数之和为 , x 4 的系数为 .16.(2分)已知直线 l:mx −y =1, 若直线 l 与直线 x −my −1=0 平行,则m 的值为 ,动直线 l 被圆 x 2+y 2−2y −8=0 截得的弦长最短为 .17.(2分)已知随机变量X 的分布列如下表:其中 a >0,b >0 .且 E(X)=2 ,则b= , D(2X −1) = .四、解答题 (共5题;共50分)18.(10分)在 △ABC 中,内角A ,B ,C 所对的边分别为 a,b,c 已知 tan(π4+A)=3 .(1)(5分)求 sin2A +cos 2A 的值;(2)(5分)若 △ABC 的面积 S =1 , c =2 ,求 a 的值.19.(10分)如图,已知四棱锥 A −BCDE ,正三角形ABC 与正三角形ABE 所在平面互相垂直,BC// 平面 ADE ,且 BC =2 , DE =1 .(1)(5分)求证: BC//DE ;(2)(5分)若 AF ⃗⃗⃗⃗⃗ =2FD ⃗⃗⃗⃗⃗⃗ ,求 CF 与平面 ABE 所成角的正弦值. 20.(10分)已知数列 {a n } 的前 n 项和 S n =a n 2+2a n 4,且 a n >0(n ∈N ∗) .(1)(5分)写出 a 1,a 2,a 3 的值,并求出数列 {a n } 的通项公式;(2)(5分)设 b n =√S n , T n 为数列 {b n } 的前n 项和;求证: n 2+n 2<T n <n 2+2n 2.21.(10分)如图,设抛物线方程为 x 2=2py (p >0),M 为直线 y =−2p 上任意一点,过M 引抛物线的切线,切点分别为A ,B.(1)(5分)求直线AB 与y 轴的交点坐标;(2)(5分)若E 为抛物线弧AB 上的动点,抛物线在E 点处的切线与三角形MAB 的边MA ,MB 分别交于点 C , D ,记 λ=S△EAB S △MCD,问 λ 是否为定值?若是求出该定值;若不是请说明理由.22.(10分)已知 f(x)=(x 2−a)e −x , g(x)=a(e −x +1)(1)(5分)当 a =1 时,判断函数 f(x) 的单调性;(2)(5分)当a>−1时,记f(x)的两个极值点为x1,x2(x1<x2),若不等式x2f(x1)≤λ[f′(x2)−g(x1)]恒成立,求实数λ的值.答案解析部分1.【答案】A【解析】【解答】由题意∁R A=(−∞,0)∪(4,+∞),B={x∈R||x|≤1}={x∈R|−1≤x≤1},则(∁RA)∩B=[−1,0).故答案为:A.【分析】先计算出集合∁RA与B,再利用集合交集的概念即可得解.2.【答案】D【解析】【解答】由题意该椭圆a2=2,b2=1,由椭圆性质可得c2=a2−b2=1,所以离心率e=√c2a2=√12=√22.故答案为:D.【分析】由椭圆的一般式求得a2=2、b2=1、c2=1,利用e=√c2a2即可得解.3.【答案】C【解析】【解答】解:根据几何体的三视图转换为几何体为:所以V=13×2×4×2=163.故答案为:C.【分析】首先把三视图转换为几何体,进一步求出几何体的体积.4.【答案】C【解析】【解答】由题意可得70×2+3×21+2×15=233,则233−105×2=23.故答案为:C.【分析】由题意先计算出70×2+3×21+2×15=233,再计算233−105×2=23即可得解.5.【答案】D【解析】【解答】根据题意,函数的定义域 {x|x ≠0} ,因为 f(x)=(e x +e −x )ln|x| ,所以 f(x) 为偶函数,图象关于 y 轴对称,排除B 项, 当 x >1 时, f(x)>0 ,当 0<x <1 时, f(x)<0 ,排除 A,C 选项, 当 x →0 时, f(x)→−∞ ,所以D 项是正确的, 故答案为:D.【分析】根据题意,求出函数的定义域 {x|x ≠0} ,分析可得 f(x) 为偶函数,进而分析可得当 x >1 时, f(x)>0 ,当 0<x <1 时, f(x)<0 ,当 x →0 时, f(x)→−∞ ,分析选项,从而选出正确的结果.6.【答案】A【解析】【解答】由题意画出可行域,如图所示,令 z =2x +3y ,转化可得 y =−23x +z 3,数形结合可得,当直线 y =−23x +z3分别过点 A 、点 B 时, z 取最小值和最大值,由 {2x −y −3=0x +y =0 可得点 A(1,−1) ,由 {2x −y −3=0x −2y +3=0 可得点 B(3,3) , 所以 z min =2−3=−1 , z max =2×3+3×3=15 . 所以 2x +3y 的取值范围是 [−1,15] . 故答案为:A.【分析】由题意画出可行域,设 z =2x +3y ,数形结合即可得解.7.【答案】A【解析】【解答】 ∵ a >0 , b >0 ,若 ab ≤4 ,则ab a+b ≤ab2ab =√ab 2≤1 ,当且仅当 a =b =2 时取等号,所以 ab a+b≤1 ; 当 a =1 , b =5 时, ab a+b =56≤1 ,但 ab =5>4 ; ∴ “ ab ≤4 ”是“aba+b≤1 ”充分不必要条件.故答案为:A.【分析】由基本不等式可得:若 ab ≤4 ,则aba+b ≤1 成立;举出反例可得若 ab a+b≤1 ,则 ab ≤4 不一定成立,由充分条件和必要条件的概念即可得解.8.【答案】B【解析】【解答】由题意 |x 2−ax|≤b ⇔−b ≤x 2−ax ≤b ,设 f(x)=x 2−ax , x ∈[0,2] ,其图象为开口向上,对称轴为 x =a2 的抛物线的一部分,当 a ∈[−1,0] 即 a 2∈[−12,0] 时, f(x)min =f(0)=0 , f(x)max =f(2)=4−2a ≤6 ;当 a ∈(0,2] 即 a2∈(0,1] 时, f(x)min =f(a 2)=−a 24≥−1 , f(x)max =f(2)=4−2a <4 ;若要 |x 2−ax|≤b 对于任意 a ∈[−1,2] , x ∈[0,2] 均成立, 则 {b ≥6−b ≤−1 即b ≥6 ,所以b 的最小值为6.故答案为:B.【分析】转化条件得 −b ≤x 2−ax ≤b ,设 f(x)=x 2−ax , x ∈[0,2] ,根据 a ∈[−1,0] 、 a ∈(0,2] 分类,分别求出函数 f(x) 的最值即可得解.9.【答案】C【解析】【解答】如图建立直角坐标系,设正方形边长为为 2a ,圆的半径为 r ,设点 P(x,y) ,则 A(a,a) , B(−a,a) , C(−a,−a) , D(a,−a) , x 2+y 2=r 2 ,则 PA ⃗⃗⃗⃗⃗ =(a −x,a −y) , PB ⃗⃗⃗⃗⃗ =(−a −x,a −y) , PC ⃗⃗⃗⃗⃗ =(−a −x,−a −y) , PD⃗⃗⃗⃗⃗⃗ =(a −x,−a −y) ,对于A , PA ⃗⃗⃗⃗⃗ ⋅PC ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ ⋅PD ⃗⃗⃗⃗⃗⃗ =2(x 2+y 2)−4a 2=2r 2−4a 2 ,A 正确,不符合题意; 对于B , PA ⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ ⋅PC ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ ⋅PD ⃗⃗⃗⃗⃗⃗ +PD ⃗⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗ =PB ⃗⃗⃗⃗⃗ ⋅(PA ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )+PD⃗⃗⃗⃗⃗⃗ ⋅(PA ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ ) =(PB ⃗⃗⃗⃗⃗ +PD ⃗⃗⃗⃗⃗ )⋅(PA ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )=4(x 2+y 2)=4r 2 ,B 正确,不符合题意; 对于C ,不妨令 a =1 , r =2 ,当点 P(0,2) , |PA ⃗⃗⃗⃗⃗ |+|PB ⃗⃗⃗⃗⃗ |+|PC ⃗⃗⃗⃗⃗ |+|PD ⃗⃗⃗⃗⃗ |=2√(2−1)2+12+2√(2+1)2+12 =2√2+2√10 ;当点 P(√2,√2) , |PA ⃗⃗⃗⃗⃗ |+|PB ⃗⃗⃗⃗⃗ |+|PC ⃗⃗⃗⃗⃗ |+|PD ⃗⃗⃗⃗⃗ |=2−√2+2+√2+2√2+22=4+2√6 ; C 错误,符合题意.对于D , PA ⃗⃗⃗⃗⃗ 2+PB ⃗⃗⃗⃗⃗ 2+PC ⃗⃗⃗⃗⃗ 2+PD ⃗⃗⃗⃗⃗⃗ 2=2(a −x)2+2(a +x)2+2(a −y)2+2(a +y)2 =8a 2+4(x 2+y 2)=8a 2+4r 2 ,D 正确,不符合题意. 故答案为:C.【分析】建立直角坐标系后,设正方形边长为2a ,圆的半径为r ,表示出各点坐标,利用坐标运算即可判断A 、B 、D ,举出反例即可判断C ,即可得解.10.【答案】D【解析】【解答】设 f(x)=2ae 2x −lnx +lna ,则 f′(x)=4ae 2x −1x.当 a ≤0 时, f′(x)<0 ,故 f(x) 单调递减,当 x →+∞ 时, f(x)→−∞ ,不成立; 当 a >0 时,取 f′(x)=4ae 2x −1x=0 ,根据图像知,方程有唯一解设为 x 0 ,则函数在 (0,x 0) 上单调递减,在 (x 0,+∞) 上单调递增,故 f(x)min =f(x 0)=2ae 2x 0−lnx 0+lna ≥0 ,且 4ae 2x 0−1x 0=0 ,代换得到: 12x 0−2lnx 0−2x 0−2ln2≥0 ,易知函数 g(x)=12x −2lnx −2x −2ln2 在 (0,+∞) 上单调递减,且 g(12)=0 ,故 x 0≤12 . a =14x 0⋅e2x 0≥12e ,故当 x 0=12 时,有最小值为 12e . 故答案为: D .【分析】排除 a ≤0 的情况,存在唯一解 x 0 ,使则函数在 (0,x 0) 上单调递减,在 (x 0,+∞) 上单调递增,故 f(x)min =f(x 0) , 4ae 2x 0−1x 0=0 ,代换得到 x 0≤12 ,代入计算得到答案.11.【答案】√2【解析】【解答】由题意 z =21+i =2(1−i)(1+i)(1−i)=1−i ,所以 |z|=√12+12=√2 . 故答案为: √2 .【分析】由复数的运算法则得 z =1−i ,由复数模的概念即可得解.12.【答案】2√33【解析】【解答】当 y >0 时,由 x 2a 2−y 2b2=1 可得 y =√(x 2a 2−1)⋅b 2 ,求导得y ′=12⋅b2a2⋅2x ⋅1√(x 2a2−1)⋅b =b 2x a 2⋅1√(x 2a2−1)⋅b =b 2x a 2y , 所以在双曲线上点 (x 0,y 0) 处的切线方程为 y −y 0=b 2x0a 2y 0⋅(x −x 0) ,化简得 x 0a 2x −y 0b2y =1 ,同理可得当 y ≤0 时依然成立;设点 M(m,n) ,则 k l =b 2m a 2n , k OM =n m , 由 k OM ⋅k l =13 得 b 2m a 2n ⋅n m =13 ,所以 b 2a 2=13 , 所以双曲线离心率 e =√1+b 2a 2=√1+13=2√33 .故答案为: 2√33.【分析】利用导数证明在双曲线上点 (x 0,y 0) 处的切线方程为 x 0a 2x −y 0b 2y =1 ,转化条件得 b 2m a 2n ⋅n m =13,再利用 e =√1+b 2a 2即可得解. 13.【答案】0≤a ≤3−2√2 或 3+2√2≤a ≤6【解析】【解答】由 A ≠∅ ,可设 x 1 , x 2(x 1≤x 2) 是方程 f(x)=x 即 x 2+(a −1)x +a =0的两个实根,则 A ={x ∈R|f(x)≤x}={x ∈R|x 1≤x ≤x 2} , f[f(x)]=f(x)⇔f(x)=x 1 或 x 2 , 则 f(x)−x =(x −x 1)(x −x 2) ,f[f(x)]−f(x)=[f(x)−x 1][f(x)−x 2] = [f(x)−x +x −x 1][f(x)−x +x −x 2]=[(x −x 1)(x −x 2)+(x −x 1)][(x −x 1)(x −x 2)+(x −x 2)]=(x −x 1)(x −x 2)(x −x 1+1)(x −x 2+1) .由 A ⊆B 可得对任意 x 1≤x ≤x 2 ,均有 f[f(x)]−f(x)≤0 ,即 (x −x 1)(x −x 2)(x −x 1+1)(x −x 2+1)≤0 对任意 x 1≤x ≤x 2 均成立,由 x −x 1≥0 , x −x 2≤0 , x −x 1+1>0 可得 x −x 2+1≥0 对任意 x 1≤x ≤x 2 均成立,所以 x 1−x 2+1≥0 ,所以 {Δ=(a −1)2−4a ≥0x 1−x 2+1=−√(x 1+x 2)2−4x 1x 2+1≥0 即 {(a −1)2−4a ≥0(a −1)2−4a ≤1 , 解得 0≤a ≤3−2√2 或 3+2√2≤a ≤6 . 故答案为: 0≤a ≤3−2√2 或 3+2√2≤a ≤6 .【分析】设 x 1 , x 2(x 1≤x 2) 是方程 f(x)=x 的两个实根,则可得 f[f(x)]=f(x)⇔f(x)=x 1 或 x 2 ,进而可得 f[f(x)]−f(x) =(x −x 1)(x −x 2)(x −x 1+1)(x −x 2+1) ,由 A ⊆B 可得对任意 x 1≤x ≤x 2 ,均有 f[f(x)]−f(x)≤0 ,即可得 x 1−x 2+1≥0 ,由韦达定理和根的判别式列出不等式组即可得解.14.【答案】3n−1−n ;3n2−n 2+n+12【解析】【解答】设 b n =a n +n ,数列 {b n } 的公比为 q ,则由题意 b 2=a 2+2=3 , b 3=a 3+3=9 ,∴ q =b 3b 2=3 , b 1=b 2q =1 , ∴ b n =b 1q n−1=3n−1 ,∴ a n =b n −n =3n−1−n ,∴ S n =1−1+3−2+32−3+⋅⋅⋅+3n−1−n =(1+3+32+⋅⋅⋅+3n−1)−(1+2+3+⋅⋅⋅+n)=1⋅(1−3n)1−3−(1+n)n 2=3n2−n 2+n+12. 故答案为: 3n−1−n , 3n2−n 2+n+12.【分析】设 b n =a n +n ,由等比数列的性质先求得 b n =3n−1 ,进而求得 a n =3n−1−n ;再利用分组求和法即可求得 S n .15.【答案】164;−316【解析】【解答】令 x =1 , (1x −x 2)6=(1−12)6=164,故该二项式的展开式的各项系数之和为 164;二项式 (1x −x 2)6的展开式的通项公式为 T r+1=C 6r ⋅(1x )6−r ⋅(−x 2)r =C 6r ⋅(−12)r ⋅x 2r−6 , 令 2r −6=4 即 r =5 , C 65⋅(−12)5=−316,故 x 4 的系数为 −316 . 故答案为:164 , −316.【分析】令 x =1 即可求得该二项式的展开式的各项系数之和;写出该二项式展开式的通项公式 T r+1=C 6r ⋅(−12)r ⋅x2r−6 ,令 2r −6=4 即可求得 x 4 的系数. 16.【答案】−1;2√5【解析】【解答】 ∵ 直线 l:mx −y =1 与直线 x −my −1=0 平行,∴m 1=−1−m ≠−1−1,解得 m =−1 ; 由题意可知直线 l:mx −y =1 恒过点 P(0,−1) ,圆 x 2+y 2−2y −8=0 的圆心 C(0,1) ,半径 r =3 , CP =2 , 易知当 CP ⊥l 时,直线被圆截得的弦长最短, 此时弦长为 2√r 2−CP 2=2√9−5=2√5 . 故答案为: −1 ; 2√5 .【分析】由直线平行的性质可得 m 1=−1−m ≠−1−1 ,解方程即可得 m =−1 ;由题意知直线 l 恒过点 P(0,−1) ,圆的圆心 C(0,1) ,半径 r =3 ,由圆的性质即可得所求弦长最小值为 2√r 2−CP ;即可得解.17.【答案】14;24 【解析】【解答】由题意 {12+b +14=1E(X)=0×12+2b +14a =2 ,解得 b =14, a =6 ; 所以 D(X)=(0−2)2×12+(2−2)2×14+(6−2)2×14=6 ,所以 D(2X −1)=22⋅D(X)=24 . 故答案为: 14, 24 .【分析】由概率和为1即可的 b =14,由题意结合期望公式可得 a =6 ,根据方差公式求得 D(X)后利用 D(2X −1)=22⋅D(X) 即可得解.18.【答案】(1)解:由题意 tanA =tan[(π4+A)−π4]=tan(π4+A)−tan π41+tan(π4+A)⋅tan π4=12 , 所以 sin2A +cos 2A =2sinAcosA+cos 2A sin 2A+cos 2A=2tanA+1tan 2A+1=85(2)解:由(1) tanA =12 可得: tanA =sinA cosA =12即 cosA =2sinA ,又 sin 2A +cos 2A =1 , A ∈(0,π) ,所以 sinA =√55 , cosA =2√55;又 S =12bcsinA =1 , c =2 可得 b =√5 ;a 2=b 2+c 2−2bccosA =5+4−8=1所以 a =1 .【解析】【分析】(1)由两角差的正切公式可得 tanA =12 ,转化条件 sin2A +cos 2A =2tanA+1tan 2A+1即可得解;(2)由同角三角函数的关系结合题意可得 sinA =√55 , cosA =2√55,由三角形面积公式S =12bcsinA 可得 b =√5 ,再由余弦定理即可得解.19.【答案】(1)证明:因为 BC// 平面 ADE , BC ⊂BCED ,且平面 BCED ∩ 平面 ADE =DE , 所以 BC//DE(2)解:取 AB 中点O ,连接EO ,CO ,由题意可得OC 、OB 、OE 两两垂直, 如图所示建立空间直角坐标系,各点的坐标分别为 A(−1,0,0) , B(1,0,0) , C(0,√3,0) , E(0,0,√3) ,..所以 BC ⃗⃗⃗⃗⃗ =(−1,√3,0) , ED ⃗⃗⃗⃗⃗⃗ =12BC ⃗⃗⃗⃗⃗ =(−12,√32,0) ,所以 D(−12,√32,√3) , AD⃗⃗⃗⃗⃗⃗ =(12,√32,√3) . 所以 AF ⃗⃗⃗⃗⃗ =23AD ⃗⃗⃗⃗⃗⃗ =(13,√33,2√33) ,所以 F(−23,√33,2√33). 所以 CF ⃗⃗⃗⃗⃗ =(−23,−2√33,2√33) , 因为平面 ABE 的一个法向量是 OC⃗⃗⃗⃗⃗ =(0,√3,0) 设CF 与平面ABE 所成的角为 θ ,则 sinθ=|cos〈OC ⃗⃗⃗⃗⃗ ,CF ⃗⃗⃗⃗⃗ 〉|=|OC ⃗⃗⃗⃗⃗⃗⃗ ⋅CF ⃗⃗⃗⃗⃗⃗⃗ ||OC ⃗⃗⃗⃗⃗⃗⃗ |⋅|CF ⃗⃗⃗⃗⃗⃗⃗ |=−23⋅2√73=√217 , 所以CF 与平面ABE 所成角的正弦值为 √217.【解析】【分析】(1)由线面平行的性质即可得证;(2)建立空间直角坐标系,求出各点坐标,进而可得平面 ABE 的一个法向量是 OC ⃗⃗⃗⃗⃗ 和直线 CF 的方向向量 CF ⃗⃗⃗⃗⃗ ,利用 sinθ=|cos〈OC ⃗⃗⃗⃗⃗ ,CF⃗⃗⃗⃗⃗ 〉| 即可得解.20.【答案】(1)解:因为 a n >0 ,当 n =1 时, a 1=S 1=a 12+2a 14 ,所以 a 1=2 ,当 n =2 时, S 2=a 1+a 2=a 22+2a 24 ,所以 a 2=4 ,当 n =3 时, S 3=a 1+a 2+a 3=a 32+2a 34 ,所以 a 3=6 ,当 n ≥2 时, a n =S n −S n−1=a n 2+2a n 4−a n−12+2a n−14 ,化简得 (a n +a n−1)(a n −a n−1−2)=0 , 因为 a n >0 ,所以 a n −a n−1−2=0 ; 所以数列 {a n } 是首项为2,公差为2的等差数列,a n =2+2(n −1)=2n(2)证明:由(1)可得 S n =2+2n2⋅n =n(n +1) , b n =√n(n +1) ;所以 b n >n ,所以 T n =b 1+b 2+⋅⋅⋅+b n >1+2+⋅⋅⋅+n =n 2+n 2;又 b n =√n(n +1)<n+(n+1)2=n +12;所以 T n =b 1+b 2+⋅⋅⋅+b n <(1+12)+(2+12)+⋅⋅⋅+(n +12)=n(n+1)2+n 2=n 2+2n 2 ;综上可得 n 2+n 2<T n <n 2+2n 2【解析】【分析】(1)分别令 n =1 、 n =2 、 n =3 即可得 a 1 、 a 2 、 a 3 的值;当 n ≥2时,利用 a n =S n −S n−1 可得 (a n +a n−1)(a n −a n−1−2)=0 ,则数列 {a n } 是首项为2,公差为2的等差数列,即可得解;(2)由等差数列前n 项和公式结合题意可得 b n =√n(n +1) ,根据b n >n 即可得 T n >n 2+n 2 ,根据 b n <n+(n+1)2 即可得 T n <n 2+2n 2,即可得证.21.【答案】(1)解:设 A(x 1,x 122p ) , B(x 2,x 222p) ,抛物线方程 x 2=2py(p >0) 可变为 y =x 22p ,所以 y ′=xp ,所以 k AM =x 1p, k BM =x 2p ,直线 AM 的方程为 y −x 122p =x 1p (x −x 1) ,直线 BM 方程为 y −x 222p =x2p (x −x 2) ,则 {y −x 122p =x 1p (x −x 1)y −x 222p =x 2p (x −x 2) 解得 x M =x 2+x 12 , y M =x 1x 22p , 又k AB=x 222p −x 122px 2−x 1=x 2+x 12p ,所以直线 AB 的方程为 y −x 122p =x 2+x 12p(x −x 1) ,化简得 (x 1+x 2)x −2py −x 1x 2=0 , 令 x =0 , y =−x 1x 22p , 又 y M =x 1x 22p=−2p , 所以 y =2p , 所以直线AB 与 y 轴的交点坐标为 (0,2p)(2)解:记 x M =x 1+x 22 ,设点 E(x 3,x 322p ) , 可得直线 CD 的方程为 y −x 322p =x3p(x −x 3) ,由 {y −x 122p =x 1p (x −x 1)y −x 322p =x 3p (x −x 3) 可得 x C =x 1+x 32 ,同理 x D =x 2+x 32 , 所以 |ACCM |=|x C −x 1x M −x C |=|x 1+x32−x 1||x 1+x 22−x 1+x 32|=|x 3−x 1x 2−x 3||CEED |=|x 3−x C x D −x 3|=|x 3−x 1+x32x 2+x 32−x3|=|x 3−x 1x 2−x 3| , 所以 |AC CM |=|CEED | ,同理 |MD DB |=|x 3−x 1x 2−x 3| , 所以 |AC CM |=|CE ED |=|MDDB| , 设 |AC CM |=|CE ED |=|MD DB |=t ,记 S △MCE =S ,则 S △ACE =tS , S △MDE =S t , S △BDE =S t2 , S △MAB S △MCD =|MA||MB||MC||MD|=t+11⋅t+1t =(t+1)2t, S △MCD =t+1t ⋅S , 于是 S △MAB=(t+1)2t S △MCD =(t+1)2t ⋅t+1t ⋅S =(t+1)3t2S ,所以 S △EAB =S △MAB −S △MCD −S △ACE −S △BDE=(t+1)3t 2S −t+1t ⋅S −tS −S t 2=2(t+1)t ⋅S ,所以 λ=S△EAB S △MCD=2【解析】【分析】(1)设 A(x 1,x 122p ) , B(x 2,x 222p) ,求导后可得直线AM 的方程与直线BM 方程,联立方程组可得yM =x1x22p,写出直线AB的方程为y−x122p=x2+x12p(x−x1),令x=0即可得解;(2)设点E(x3,y3),联立方程组可得x C=x1+x32,x D=x2+x32,进而可得|ACCM|=|CEED|=|MDDB|,设|ACCM|=|CEED|=|MDDB|=t,记S△MCE=S,表示出各三角形面积后,即可得解.22.【答案】(1)解:当a=1时,f(x)=(x2−1)e−x,所以f′(x)=(−x2+2x+1)e−x,令f′(x)=(−x2+2x+1)e−x=0,得−x2+2x+1=0,所以x1=1−√2,x2=1+√2,所以f(x)单调递减区间为(−∞,1−√2),(1+√2,+∞),单调递增区间为(1−√2,1+√2)(2)解:因为f′(x)=(−x2+2x+a)e−x,a>−1,所以−x2+2x+a=0有两个不等实根,由题意x1,x2为方程(−x2+2x+a)e−x=0即x2−2x−a=0的两相异根,则{x1+x2=2 x1x2=−a−x i2+2x i+a=0,所以f′(x2)−g(x1)=0−a(e−x1+1)=−a(e−x1+1),x2f(x1)=x2(x12−a)e−x1=x2⋅2x1e−x1=2x1x2e−x1=−2ae−x1所以x2f(x1)≤λ[f′(x2)−g(x1)]可以转化为−2ae−x1≤−aλ(e−x1+1),所以上式可化为(x12−2x1)[λ(e−x1+1)−2e−x1]≤0,则(x12−2x1)(λ−21+e x1)(e−x1+1)≤0即(x12−2x1)(λ−21+e x1)≤0,①当a∈(−1,0)时,由0<x1x2<1、x1+x2=2、x1<x2可得x1∈(0,1),所以x12−2x1<0,所以λ−21+e x1≥0恒成立,因为此时21+e x1∈(21+e,1)所以λ≥1;②当a=0时x1=0,x12−2x1=0,显然(x12−2x1)(λ−21+e x1)≤0恒成立,即λ∈R;③当a∈(0,+∞)时,由x1x2<0可得x1∈(−∞,0),x12−2x1>0,所以λ−21+e x1≤0恒成立,因为此时21+e x1∈(1,2),所以λ≤1;综上可知:λ=1【解析】【分析】(1)求出导函数后,找到f′(x)>0、f′(x)<0的解集即可得解;(2)由题意结合韦达定理可知{x1+x2=2 x1x2=−a−x i2+2x i+a=0,原条件可化为(x12−2x1)(λ−21+e x1)≤0,根据a∈(−1,0)、a=0、a∈(0,+∞)分类讨论,即可得解.。
浙江省衢州、湖州、丽水三地市2020届高三4月教学质量检测化学试题含解析

D.二氧化碳分子为直线型分子,碳原子半径大于氧原子半径,正确的比例模型为: ,故D错误;
答案选A.
7。下列说法正确的是( )
A. 同位素之间或同素异形体之间的相互转化均属于化学变化
B. 硬脂酸、软脂酸、油酸和亚油酸互为同系物
6。下列表示正确的是( )
A. 乙醚的分子式:C4H10OB. 二氧化硅的结构式:O=Si=O
C。 O2—的离子结构示意图: D。 二氧化碳分子的的比例模型:
【答案】A
【解析】
【详解】A.乙醚的结构式为CH3CH2OCH2CH3,分子式:C4H10O,故A正确;
B.由于二氧化硅为原子晶体,1个硅原子形成4个硅氧键,1个氧原子形成2个硅氧键,所以二氧化硅中不存在硅氧双键,故B错误;
1.括号内物质是消毒剂的有效成分,其中含离子键的化合物是( )
A。84消毒液(NaClO)B.福尔马林(HCHO)
C。医用酒精(CH3CH2OH)D。过氧乙酸(CH3COOOH)
【答案】A
【解析】
【详解】A.NaClO由钠离子和次氯酸根离子构成,含有离子键,是离子化合物,故A符合题意;
B.HCHO只含有共价键,属于共价化合物,故B不符合题意;
答案选A。
5。下列物质的名称正确的是( )
A。 2CaSO4·H2O:生石膏
B。 CO(NH2)2:尿素
C。 C6H10O5:纤维素
D. :2-乙基-1,4—丁二烯
【答案】B
【解析】
【详解】A.2CaSO4·H2O可写为CaSO4·0。5H2O,是熟石膏,CaSO4·2H2O是生石膏,故A错误;
B.尿素分子式为CH4N2O,化学式为CO(NH2)2,故B正确;
衢州、湖州、丽水2020年4月三地市高三年级教学质量检测试卷--地理答案

衢州、湖州、丽水2020年4月三地市高三年级教学质量检测联考试卷地理答案一、选择题(本大题共20小题,每小题2分,共40分。
)1-5:CCDDB6-10:BCACD11-15:CBDDB16-20:BADDC二、选择题Ⅱ(本大题共5小题,每小题3分,共15分)21-25:BDDDC三、非选择题(本大题共4小题,共45分)26.(10分)(1)该国为降雨量丰富,降雨强度大(1分),有利于快速排水(1分),防止城市内涝的发生(1分);本国国土面积狭小,水资源紧张(1分),收集雨水有利于缓解该国水资源紧张的状况(1分)。
(2)太阳能,风能,潮汐能(答任两项即可)(3)少占耕地,节地节水;治理盐碱地,重建良好的生态系统;治理污水,实现水资源的循环利用。
借鉴新加坡相关技术,实现生态禁地的生态改造。
(答任三项即可)27.(10分)(1)高(1分)。
山地多,平原面积少(1分),人口分布分散(1分);海岸线曲折,多优良港湾(1分);气候温和多雨,宜居范围广(1分)。
(2)植被覆盖率高(1分);较往年气温高,降水少,(1分)且持续时间较长(1分);处西风背风坡,气流下沉增温,多焚风(1分);风速大(1分),火灾蔓延速度快。
28.(12分)(1)下游河道宽阔;地势低平,河流流速慢;枯水期流量较小,水位低;河床泥沙淤积。
(答三点得3分)(2)流水量与水位关系:流量和位最高值均出现在7月份,最低值均出现在1月份;流量越大,水位越高(流量与水位正相关)。
(2分)最高潮位的原因:天文大潮潮水位高;台风导致风暴潮顶托;河流流量大,水位高;夏季风影响。
(答三点得3分)(3)丰水年份,地下水埋藏浅;春秋季节降水量小于蒸发量;蒸发导致盐分在地表累积;春秋季地下水位下降,海水易入侵。
(4分)29.(13分)(1)降水总量丰富;降水季节差异大(9月至次年1月降水最集中);(2分)雨季成因:位于东北季风迎风坡;台风带来丰富降水。
(2分)(2)山地高原为主,耕地面积小;位于热带,温带农作物种植面积小;自然灾害多发;人口众多,农产品需求量大;热带经济作物种植面积大。
2020届浙江省衢州、湖州、丽水三地市高三4月教学质量检测(含听力)英语试题(原卷版)

衢州、湖州、丽水2020年4月三地市高三教学质量检测试卷英语试题本试卷分第I卷(选择题)和第II卷(非选择题)。
第I卷1至8页,第II 卷9至10页。
第1卷注意事项:1.答第I卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在本试卷上,否则无效。
第一部分:听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.Where does the conversation take place?A.In a shop.B.In a restaurant.C.In a supermarket.2.How did the man spend his free time with his friends'A.They played sports.B.They watched TV programs.C.They played computer games.3.What does the man think of the seats on the plane?A.Wide.fortable.C.Small.4.What are the speakers mainly talking about?A.The whales.B.The weather.C. A voyage.5.When was Tim born?A.On February 24.B.On February 28.C.On February 29.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
浙江省衢州、湖州、丽水三地市高三4月教学质量检测语文试题【带答案】

衢州、湖州、丽水2020 年 4 月三地市高三教学质量检测试卷语文考生须知:1.全卷分试卷和答题卷,考试结束后,将答题卷上交。
2.试卷共 8 页,有四大题,24 小题。
满分 150 分,考试时间 150 分钟。
3.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
4.请将答案做在答题卷的相应位置上,写在试卷上无效。
一、语言文字运用(共 20 分)1.下列各句中,没有错别字且加点字的注音全都正确的一项是(3 分)A.在全球化和反全球化风起云涌、波谲.(jué)云诡的时代,技术的变革是大势所趋,不可避免,宜未雨绸缪,调.(tiáo)适出一个更佳的运行状态。
B.积多年之功撰成的《异闻集校证》,澄.(chénɡ)清了诸多谬识,是迄.(qì)今首部容辑佚、校勘、考辨、汇评于一炉的“唐人选唐传奇”整理本。
C.人头在大草坪上攒.(cuán)动,舞台灯光骤.(zòu)然亮起,犹如序幕般引发大家的呐喊,伴随着琴弦与鼓点,街舞摇滚轮番登场,高潮迭起。
D.一本简历在印制上要讲究细节,如前几页要用铜板纸彩色打印,封面要附上一层透明膜以防弄湿、折(zhé)页,整本简历要用铁圈装订(dìnɡ)。
阅读下面的文字,完成 2~3 题。
[甲]什么是基本功?画家李可染先生说得通.透.:“基本功是从艺术修炼的全过程中抽出最根本、最困难、最关键性的规律部分,只有这些最根本的规律被掌握被攻破了,以后在创作上遇到具体问题也就容易解决了。
”艺术创作规律如此,推及各个行业也大概不差,基本功是在技艺传承中沉淀下来的、带有一些规律性的内容,掌握了它,才可以谈登.堂.入.室.,谈推陈出新。
[乙]然而,在一些捷径的诱惑下,有些年轻人偏离了下笨功夫、练基本功的正途。
其实那些所谓捷径通往的注定不是成功的彼岸,而.且.可能是泥潭和陷阱,即使暂时有了获益,却可能形成路径依赖。
2020年4月学考选考高2020届高2017级浙江省衢州湖州丽水三地市高三教学质量检测试卷物理试题及参考答案

衢州、湖州、丽水2020年4月三地市高三教学质量检测试卷物理本试题卷分选择题和非选择题两部分,共6页,满分100分,考试时间90分钟。
考生注意:1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。
3.非选择题的答案必须使用黑色字迹的签字笔或钢笔写在答题纸上相应的区域内,作图时先使用2B 铅笔,确定后必须使用黑色字迹的签字笔或钢笔描黑。
4.可能用到的相关参数:重力加速度g 均取10m/s 2。
选择题部分一、选择题Ⅰ(本题共13小题,每小题3分,共39分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.下列物理量属于标量,且单位属于国际单位制导出单位的是A .位移、mB .电压、VC .电流、AD .力、N 2.在2020年的春节晚会上,杂技《绽放》表演了花样飞天,如图是女演员举起男演员的一个场景,两位杂技演员处于静止状态。
下列说法正确的是A .水平地面对女演员的支持力等于两演员的重力之和B .水平地面对女演员的摩擦力水平向右C .女演员对男演员的作用力大于男演员对女演员的作用力D .女演员对男演员的作用力小于男演员对女演员的作用力3.如图所示,甲、乙两车在水平面同心圆弧道路上转弯,甲行驶在内侧,乙行驶在外侧,它们转弯时线速度大小相等,则两车在转弯时,下列说法正确的是A .角速度:ω甲=ω乙B .向心加速度:a 甲>a 乙C .向心力F 甲<F 乙D .地面对车的摩擦力:F f 甲>F f 乙4.如图所示,网球发球机水平放置在距地面某处,正对着竖直墙面发射网球,两次发射网球分别在墙上留下A 、B 两点印迹。
测得OA AB 。
OP 为水平线,若忽略网球在空中受到的阻力,则下列说法正确的是A .两球发射的初速度:v OA :v OB =1∶2B .两球碰到墙面前运动的时间:t A :t B =1∶2C .两球碰到墙面时的动量可能相同D .两球碰到墙面时的动能可能相等O AB网球发球机网球出口孔P 墙水平地面P 第4题图第2题图衢州湖州丽水三地市5.北斗系统空间段由若干地球静止轨道卫星、倾斜地球同步轨道卫星和中圆地球轨道卫星组成。
2020届浙江省衢州、丽水、湖州三地市高三下学期4月教学质量检测数学试题(解析版)

根据题意,函数的定义域 ,
因为 ,所以 为偶函数,图象关于 轴对称,排除B项,
当 时, ,当 时, ,排除 选项,
当 时, ,所以D项是正确的,
故选D.
【点睛】
该题考查的是有关函数图象的选择问题,在选择的过程中,注意从函数的定义域,图象的对称性,函数值的符号,函数图象的变化趋势,属于简单题目.
故选:A.
【点睛】
本题考查了简单的线性规划,考查了数形结合思想,属于基础题.
7.若 ,则“ ”是“ ”的()
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
【答案】A
【解析】由基本不等式可得:若 ,则 成立;举出反例可得若 ,则 不一定成立,由充分条件和必要条件的概念即可得解.
则 , , , , ,
则 , , , ,
对于A, ,故A正确;
对于B,
,故B正确;
对于C,不妨令 , ,
当点 ,
;
当点 , ;
故C错误.
对于D,
,故D正确.
故选:C.
【点睛】
本题考查了平面向量的应用,考查了圆的方程的应用和运算能力,属于中档题.
10.对任意的实数 ,不等式 恒成立,则实数 的最小值为()
【详解】
由题意 ,解得 , ;
所以 ,
所以 .
故答案为: , .
【点睛】
本题考查了分布列的应用,考查了利用分布列进行期望和方差的相关计算,属于基础题.
四、解答题
18.在 中,内角A,B,C所对的边分别为 已知 .
(1)求 的值;
(2)若 的面积 , ,求 的值.
【答案】(1) (2)
【解析】(1)由两角差的正切公式可得 ,转化条件 即可得解;
衢州、湖州、丽水2020年4月三地市高三教学质量检测试卷 化学试题

规定的位置上。
4. 请将答案做在答题卷的相应位置上,写在试卷上无效。作图时先使用 2B 铅笔,确定
后必须使用黑色字迹的签字笔或钢笔描黑。
可能用到的相对原子质量:H 1 C 12 N 14 O 16 F 19 Mg 24 Al 27 S 32 Cl 35.5
Fe 56 Cu 64 Ba 137
选择题部分
+2HClO D.硫酸铜溶液中加入过量的氨水:Cu2++2NH3·H2O==Cu(OH)2↓+2NH+ 4
高三化学试卷 第 2页 共 8 页
14.下列说法不.正.确.的是 A.油脂皂化反应中加入乙醇的主要目的是增加反应物的接触面积,以加快反应速率 B.往皂化液中加入热的饱和食盐水,搅拌,发现固体硬脂酸钠沉积在容器底部 C.用酸性 KMnO4 溶液(必要时可加热)能鉴别苯、甲苯、乙醇 D.医用酒精可以消杀新冠病毒,因为它能使组成病毒的蛋白质变性
高三化学试卷 第 1页 共 8 页
8.下列说法不.正.确.的是 A.“水玻璃”是建筑行业常用的一种黏合剂 B.碘化银可用于人工降雨 C.海水中溴的含量很高,因此溴被称作“海洋元素” D.氧化镁具有很高的熔点,可作耐高温材料
9.工业上利用无机矿物资源生产部分材料的流程示意图如下:
下列说法不.正.确.的是 A.石灰石、纯碱、石英都属于盐,都能与盐酸反应 B.用铝土矿制备较高纯度 Al 的过程中常用到 NaOH 溶液、CO2、冰晶石等 C.在制粗硅时,被氧化的物质与被还原的物质的物质的量之比为 2∶1 D.黄铜矿(CuFeS2)与 O2 反应产生的 Cu2S、FeO 均是还原产物 10.下列说法不.正.确.的是 A.石油的裂解主要是为了得到乙烯、丙烯等短链气态不饱和烃 B.煤气化生成的 CO 和 H2 再经过催化合成得到液体燃料,属于煤的液化 C.利用化石燃料放出的热量使水分解产生氢气,是氢能开发的研究方向 D.捕获工业排放的 CO2,既能降低地球的温室效应,又能用来合成全降解塑料,实现
【语文试卷】20.04 湖丽衢三地(含答案)

衢州、湖州、丽水2020年4月三地市高三教学质量检测语文答案及评分标准选择题共9题,26分,其中第3题2分,其余3分。
题号123478141516答案A C B D C D C C D1.A(B.容-熔;C.骤zòu-zhòu;D.板-版)2.C(“而且”应改为“反而”)3.B(“捷径”应加引号)4.D(A.不合逻辑,“广大网友”与“游客”概念有交叉,不能并列;B.结构混乱,可在“成为”前加“使之”;C.主客体颠倒,应该是“部分驾乘人员对新的收费结算模式还需要一个适应期”。
)5.①政府教育投入不足;②能带来更好的教育;③人们所预期的巨大效应(1处1分,共3分)6.身体状况正常;来自重点疫情地区的经集中隔离后解除隔离;确诊(疑似)为新冠病毒感染的经收治并康复。
(每一点2分,共6分)7.C(第1版的编写情况)8.D(A.“词典的编写和修订属于汉语规范工作”,不合文意;B.“词语发展的规律”,不属作者要阐明的内容;C.仅有设备不足以“提高”)9.①落实国家语言文字方面的新规范;②反映现代汉语词汇新面貌;③体现有关科学研究的新成果;④有释义不精练、提示语不规范、举例不当等问题。
(4分)10.紧张;平静/坚定;专注/物我两忘11.①运用反复手法,重复了两遍喝水的动作,突出紧张的气氛;②多用动词,几乎每一句都用动词,有很强的画面感;③全用短句,有传统说书的意味,给人以紧张感。
(1点1分,2点3分,3点满分,答“多用口语”也可,如儿化音、拟声词、叠词等。
)12.①营造神秘气氛,起初老者的不出场,出场后又由旁人交代“世家后人”的身份,增添了小说的神秘气氛。
②衬托王一生的形象,由“冠军”兼“世家后人”的老者来评棋,凸显了王一生棋道高深。
③借老人之口深化小说主题,“中华棋道,毕竟不颓”。
(每点2分,言之成理即可)13.①体现了儒家的孝道。
②体现了儒家由器而见道的哲学思想。
老者称其棋技熔儒道佛于一炉,且上升到“中华棋道”的高度。
2020年4月浙江衢州、湖州、丽水三地市高三教学质量检测试卷物理和答案.pdf_1

衢州、湖州、丽水2020年4月三地市高三教学质量检测试卷本试题卷分选择题和非选择题两部分,共 6页,满分100分,考试时间90分钟。
考生注意:1 .答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题 卷和答题纸规定的位置上。
2 .答题时,请按照答题纸上 “注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。
3 .非选择题的答案必须使用黑色字迹的签字笔或钢笔写在答题纸上相应的区域内,作图 时先使用2B 铅笔,确定后必须使用黑色字迹的签字笔或钢笔描黑。
4 .可能用到的相关参数:重力加速度 g 均取10m/s 2。
选择题部分、选择题I (本题共13小题,每小题3分,共39分。
每小题列出的四个备选项中只有 个是符合题目要求的,不选、多选、错选均不得分)1.下列物理量属于标量,且单位属于国际单位制导出单位的是A.位移、mB.电压、VC.电流、AD.力、N在2020年的春节晚会上,杂技《绽放》表演了花样飞天,如图是女演员举起男演员的一个场景,两位杂技演员处于静止状态。
下列说法正 的是A .水平地面对女演员的支持力等于两演员的重力之和 B.水平地面对女演员的摩擦力水平向右C.女演员对男演员的作用力大于男演员对女演员的作用力D.女演员对男演员的作用力小于男演员对女演员的作用力如图所示,甲、乙两车在水平面同心圆弧道路上转弯,甲行驶在 侧,乙行驶在外侧,它们转弯时线速度大小相等,则两车在转 弯时,下列说法正确的是A.角速度:3甲=3乙B.向心加速度:a 甲〉a 乙C.向心力F 甲<F 乙D.地面对车的摩擦力:F f 甲〉F f 乙4.如图所示,网球发球机水平放置在距地面某处,正对着竖直墙面发射网球,两次发射网球分别在墙上留下 A 、B 两点印迹。
测得 向 ABT 的阻力,则下列说法正确的是A.两球发射的初速度:V OA :V OB =1 : 2B.两球碰到墙面前运动的时间:t A :t B =1 : 2C.两球碰到墙面时的动量可能相同D.两球碰到墙面时的动能可能相等2. 3. OP 为水平线,若忽略网球在空中受到北斗系统空间段由若干地球静止轨道卫星、倾斜地球同步轨道卫 星和中圆地球轨道卫星组成。
衢州、湖州、丽水2020 年4 月三地市高三教学质量检测试卷化学答案
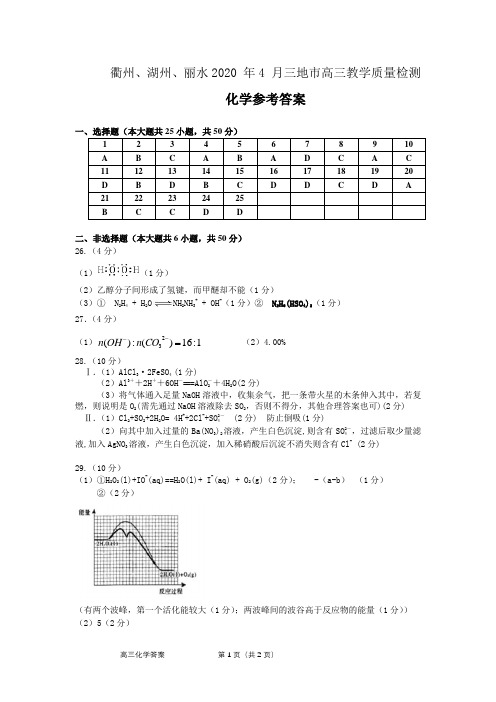
衢州、湖州、丽水2020 年4 月三地市高三教学质量检测化学参考答案一、选择题(本大题共25小题,共50分)二、非选择题(本大题共6小题,共50分) 26.(4分) (1)(1分)(2)乙醇分子间形成了氢键,而甲醚却不能(1分)(3)① N 2H 4 + H 2O NH 2NH 3+ + OH -(1分)② N 2H 6(HSO 4)2(1分) 27.(4分)(1)1:16)(:)(23=--CO n OH n (2)4.00%28.(10分)Ⅰ.(1)AlCl 3·2FeSO 4 (1分)(2)Al 3++2H ++6OH -===AlO -2+4H 2O(2分)(3)将气体通入足量NaOH 溶液中,收集余气,把一条带火星的木条伸入其中,若复燃,则说明是O 2(需先通过NaOH 溶液除去SO 2,否则不得分,其他合理答案也可)(2分)Ⅱ.(1)Cl 2+SO 2+2H 2O= 4H ++2Cl -+SO 2-4 (2分) 防止倒吸(1分)(2)向其中加入过量的Ba(NO 3)2溶液,产生白色沉淀,则含有SO 2-4,过滤后取少量滤液,加入AgNO 3溶液,产生白色沉淀,加入稀硝酸后沉淀不消失则含有Cl - (2分)29.(10分)(1)①H 2O 2(l)+IO -(aq)==H 2O(l)+ I -(aq) + O 2(g)(2分); -(a-b ) (1分)②(2分)(有两个波峰,第一个活化能较大(1分);两波峰间的波谷高于反应物的能量(1分)) (2)5(2分)(3)C (1分); 因该反应是不可逆反应,不考虑温度对平衡移动的影响。
温度升高反应速率加快,因而经过相同反应时间后测得的O 2体积随温度升高而增大(2分)30.(10分)Ⅰ.NaCl +H 2O=====通电NaClO +H 2↑(2分)Ⅱ.(1)过滤(1分) 冷凝管(1分) (2)B(1分)(3)Fe 会被过氧化氢氧化,且生成的Fe 3+会催化过氧化氢分解(1分)(4)①cdba(1分) ②A(1分) ③VW18920(2分) 31.(12分)(1)AD (2)(5)(CH 3)3C-CH 2-NH 2(CH 3)3C-NH-CH 3(CH 3)2CH-N(CH 3)2 (CH 3CH 2)2 N-CH 32NHCH 2CH(CH 3)2(3)CH 2CH(CH 3)2O O —C 2-CH CH-CH -N-CH -OH +NH 2OHCH 2CH(CH 3)22-CH - CH-CH 2-N-CH 2O O —C —O —N OO+ HO —NOOCH 2NHCH 3 CH=NCH CH 2OH Cu/O 2 △CHO(4)。
衢州、湖州、丽水2020 年4 月三地市高三教学质量检测试卷政治试题(含答案)

衢州、湖州、丽水2020年4月三地市高三教学质量检测试卷思想政治本试题卷分选择题和非选择题两部分,共6页,满分100分,考试时间90分钟。
考生注意:1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。
选择题部分一、判断题(本大题共10小题,每小题1分,共10分。
判断下列说法是否正确,正确的请将答题纸相应题号后的T涂黑,错误的请将答题纸相应题号后的F涂黑)1.一般来讲,当某种商品价格大幅度上升时,人们会大量减少对它的购买。
2.小华的爸爸购买了某公司的股票,这意味着他具有了参加该公司股东会的权利。
3.现阶段,推动我国经济持续健康发展必须以供给侧结构性改革为主线。
4.我国政府坚决反对任何外部势力干涉香港事务,这是我国行使主权的体现。
5.某市人大常委会决定罢免孙某的省人民代表大会代表职务,行使了决定权。
6.我们对待传统文化的正确态度是取其精华,去其糟粕,推陈出新,革故鼎新。
7.思想运动往往催生社会变革,大大促进文化自身的发展。
8.“真理只有一个”,所以“仁者见仁,智者见智”是不存在的。
9.划转部分国有资本充实社保基金的举措,遵循了上层建筑一定要适合经济基础状况的规律。
10.“越分享,越富有”的观点认识到了个人只能在社会中实现价值。
二、选择题I(本大题共21小题,每小题2分,共42分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)11.基于5G的低延时传输特性,以及数据采集、清洗和导出能力强的特点,很多传统工业企业纷纷“牵手”5G。
企业这样做主要是为了A.提升企业的盈利空间B.提高商品的价值量C.增加商品的科技含量D.增强品牌的竞争力12.受非洲猪瘟疫情与“猪周期”因素叠加影响,我国近年来的猪肉价格持续走高,为稳定猪肉价格,我国政府①限定猪肉价格,规范市场秩序②投放中央储备冻猪肉,增加市场供应量③实施政策支持,促进生猪生产④启动价格补贴联动机制,保障居民生活A.①③B.①④C.②③D.②④13.“今天,你家垃圾分类了吗?”已然成为中国很多地方居民的口头禅,垃圾分类也成了新时代的一种新时尚。
2020年4月学考选考高2020届高2017级浙江省选考科目考试绍兴市适应性试卷地理试题参考答案

26.(10 分)(1)冰雪融水和山地降水(1 分)(只答山地降水不给分) 淡水湖(1 分) 博
斯腾湖淡水补给量较大(1 分),有河流注入,也有河流流出,实现了水体更新(1 分)。
(2)原因:当地降水少,光照充足(1 分);生长期昼夜温差大,有利于糖分(有机物)积累(1
分);灌溉水源来自冰雪融水,水质好(1 分);无霜期长,平均气温较低,生长周期长(1 分)。
B
C
A
C
C
D
题号 11 12 13 14 15 16 17 18 19 20
答案 C
D
B
D
B
D
C
A
D
C
二、选择题Ⅱ(本大题共 5 小题,每小题 3 分,共 15 分。每小题列出的四个备选项中只有一个是符
合题目要求的,不选、多选、错选均不得分)
题号 21 22 23 24 25
答案 D
A
B
B
C
三、非选择题(本大题共 4 小题,共 45 分)
地理答案 第 2 页(共 2 页)
(3)地处多省交界处,位置偏僻,开发程度较低,对生态的破坏少;第二产业比重较低,对环 境的破坏和污染较少,水质较好;水电站的修建,增大了湿地面积,生物多样性增加;水电是清洁能 源,减少了碳的排放。(答出 3 方面得 6 分,需要答出因果关系)
29.(13 分)(1)树枝(1 分) 原因:流域内多山地,山与谷相间分布,易发育众多支流(1 分);热带季风气候区,降水量大, 地表水丰富,易汇聚成河(1 分)。 (2)热带季风气候区,雨季时间长,降水量大(1 分);位于湄南河入海口附近,众多支流水(潮汐)顶托,排水不畅(1 分)。 (3)城市内河道纵横,船只成为重要交通工具(1 分);沿河聚落(人口)密集、市场需求量大, 交易方便(1 分);河运成本较低(1 分);历史悠久,已成为传统习俗(1 分);城市基础设施不完 善,陆路交通拥堵(1 分);受旅游业刺激(1 分)等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a2 = b2 + c2 - 2bc cos A = 1 ;
所以 a = 1 ...................................................14 分
19.(本题满分 15 分)
解:(Ι)因为 BC / / 平面 ADE , BC �BCED ,且
平面B平C面ED I
l
恒成立,求实数
的值.
衢州、丽水、湖州三地市教学质量检测试卷
高三数学卷参考答案(2020.04)
一、选择题:本大题共 10 小题,每小题 4 分,共 40 分.
题号 1
2
3
4
5
6
7
8
9
10
答案 A
D
B
C
D
A
A
B
C
D
二、填空题:本大题共 7 小题,多空题每题 6 分,单空题每题 4 分,共 36 分.
( ) uuur
所以 BC = -1, 3, 0 ,
uuur ED
=
1 2
uuur BC
=
� � � �-
1 2
,
3 2
,
0
� � � �,
所以
D
� � � �-
1 2
,
3 2
,
3
� � � �,
uuur AD
=
�1 � � �2
,
3 2
,
3
� � � �.........9
分
高三数学试题卷(共四页)第 9 页
f ( f (x)) - f (x) = ( f (x) - x1)( f (x) - x2 ) = [ f (x) - x + x - x1][ f (x) - x + x - x1]
= (x - x1)(x - x2 )(x - x1 +1)(x - x2 +1) .
由题意,对任意 x1 x x2 时, f ( f (x)) - f (x) 0 即 x1 - x2 +1 0 ,即可解得.
f[
] fn-1(x) ,
f0(x) =
x
,由题意方程
f (x) =
x 的存在实根,且
(a -1)2 - 4a 0
都在函数
y
=
f
(x) 的对称轴右侧(含对称轴).因此有 -
a 2
2
+ (a -1).
a 2
+
a
0;
解得 0 a 3 - 2 2 或 3 + 2 2 a 6
方法二:设 x1, x2 ( x1 x2 )是方程 f (x) = x 的两个实根,则 f (x) - x = (x - x1)(x - x2 )
市 地 三 水 丽 州 湖 州
所以
uuur AF
=
2 3
uuur AD
=
�1 � � �3
,
3 3
,
2
3 3
� � � �,所以
F
� � � �-
2 3
,
3 3
,
2
3 3
� � � �.........11
分
( ) 所以
uuur CF
=
� � � �-
2 3
,
-2 3
3
,
23 3
� � � �,因为面
高三数学试题卷(共四页)第 7 页
市 地 三 水 丽 州 湖 州
11. √2
12. 3n−1−n
,
3n 2
−
n2
+n 2
+
1
13.
614 ,-
3 16
14. -1,
2 √5
15.
1 4
,
24
16.
2√3
3
17. 0 a 3 - 2 2 或 3 + 2 2 a 6
解析:方法一:设
fn (x) =
ABE
的一个法向量是
uuur OC
=
0,3, 0
.....13 分
CF
ABE
q
设 与平面
所成的角为 ,则
uuur uuur uuur uuur OC �CF sinq = cos OC, CF = uuur uuur
OC �CF
所以 sinq =
21 7 .........15 分
解法 2
如图所示,延长 CD, BE 交于 P ,连接 PA ,延长 CF 交 AP 于 G ,显然 G 为 PA 的中点, OC ^ 面ABE ,,.......7 分
A
=
2 tan A +1 tan2 A +1
=
8 5
.......7
分
高三数学试题卷(共四页)第 8 页
市 地 三 水 丽 州 湖 州
(Ⅱ)由(1)
tan
A
=
1 2
可得: sin
A
=
5 5
,
cos
A
=
2
5 5
;............9
分
又
S
=
1 2
bc
sin
A
=
1
,
c
=
2
可得 b
=
5 ;......................11 分
a1
an > 0
,又因为
,所以
a1= 2
,
a2=4 ,
a3=¿ 6--------------------------------------------------------------------- ---3 分
高三数学试题卷(共四页)第 10 页
所以 �CGO 即为设 CF 与平面 ABE 所成的角.......11 分 因为 OC = 3,OG = 2 ,所以 CG = 7 ,.........13 分
所以 sin �CGO =
21 7
.........15 分
20.(本题满分 15 分)
n =1
解:(I)当 时,
a1=
S
1=
a12
+2 4
ADE = DE ,..........3 分
所以 BC // DE ...................5 分
(Π)解法 1
如图所示建立空间直角坐标系,设 AB = 2
各点的坐标分别为 A( -1, 0, 0) , B ( 1, 0, 0) ,
( ) ( ) C 0, 3, 0 , E 0, 0, 3 ,..........7 分
三、解答题:本大题共 5 个题,共 74 分,解答应写出文字说明、证明过程或演算步 骤.
18.(本题满分 14 分)
解:(Ⅰ)
tan
A
=
tan(p4
+
A)
-
A
=
tan(p4 + 1+ tan(p4
A)
-
tan
p 4
+
A).
tan
p 4=1 2源自..........3分
sin
2A
+
cos2
A
=
2sin Acos A + cos2 sin2 A + cos2 A
市 地 三 水 丽 州 湖 州
已知 f ( x)
) ( ) -x , g ( x) = a e-x +1
(Ι)当 a = 1 时,判断函数 f ( x) 的单调性;
(Π)当 a > -1 时,记 f ( x) 的两个极值点为 x1, x2 ( x1 x2 ) ,若不等式 x2 f ( x1 ) �l ��f '( x2 ) - g ( x1 ) ��
