一元与多元数据分析实验报告
多元统计分析实验报告
第二部分:实验过程记录(可加页) (包括实验原始数据记录,实验现象记录,实验过程发现的问题
等) 操作步骤: 1、 执行“分析”—“比较均值”—“单因素方差分析” ; 2、 在弹出的单因素方差分析对话框中,将时期选为因子,将 X1、X2、X3、X4 选为因变量; 3、 单击“对比” ,选择“多项式” ,在后面的下拉菜单中选择“线性” ,然后继续; 4、 单击“两两比较” ,选择“LSD”和“S-N-K” ,显著性水平默认为 0.05,然后继续; 5、 单击“选项” ,选择“方差同质性检验”和“均值图” ,然后继续,点击“确定”后即可输出结果。
12
题目:研究者提出,随着时间的推移头骨尺寸会发生变化,这是外来移民与原住民人口民族融合的证据。表 6.13 是古埃及三个时期的男性头骨的四个观测值得观测数据,这是个观测变量是: X1=头骨最大的最大宽度 X2=头骨高度 X3=头骨底穴至齿槽的长度 X4=头骨鼻梁高度 对古埃及头骨数据构造单因子 MANOVA 表, a=0.05.并构造 95%联合置信区间来判断在三个时期中哪个分 令 量的均值发生了改变。同常的 MANOVA 假设对这些数据是不是合理的?请解释。 部分数据如下:
实验课程名称:多元统计分析-均值向量检验
实验项目名称 实 验 者 同 组 者
均值向量检验习题 均值向量检验习题 6.24
专业班级
实验成绩 实验成绩 组 别 年 月 日
实验日期
一部分:实验预习报告(包括实验目的、意义,实验基本原理与方法,主要仪器设备及耗材,实验
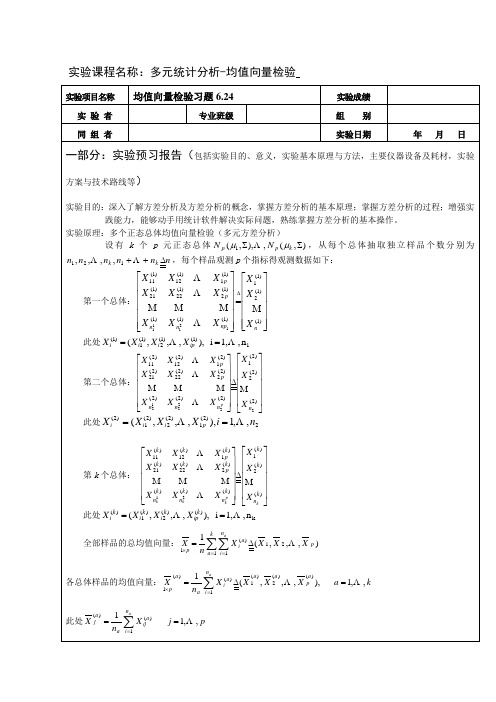
方案与技术路线等) 实验目的:深入了解方差分析及方差分析的概念,掌握方差分析的基本原理;掌握方差分析的过程;增强实 践能力,能够动手用统计软件解决实际问题,熟练掌握方差分析的基本操作。 实验原理:多个正态总体均值向量检验(多元方差分析) 设 有 k 个 p 元 正 态 总 体 N p ( µ1 , Σ), L , N p ( µ k , Σ) , 从 每 个 总 体 抽 取 独 立 样 品 个 数 分 别 为
多元统计数据分析报告(3篇)

第1篇一、引言随着大数据时代的到来,数据量急剧增加,传统的统计分析方法已无法满足复杂数据关系的挖掘需求。
多元统计分析作为一种处理多个变量之间关系的方法,在社会科学、自然科学、工程技术等领域得到了广泛应用。
本报告旨在通过对某研究项目的多元统计分析,揭示变量之间的关系,为决策提供科学依据。
二、研究背景与目的本研究以某企业员工绩效评估数据为研究对象,旨在通过多元统计分析方法,探究员工绩效与个人特质、工作环境等因素之间的关系,为企业人力资源管理部门提供决策支持。
三、数据与方法1. 数据来源本研究数据来源于某企业员工绩效评估系统,包括员工的基本信息、个人特质、工作环境、绩效评分等。
2. 研究方法本研究采用以下多元统计分析方法:(1)描述性统计分析:对员工绩效、个人特质、工作环境等变量进行描述性统计分析,了解数据的分布情况。
(2)相关分析:分析变量之间的线性关系,找出相关系数较大的变量对。
(3)因子分析:将多个变量归纳为少数几个因子,揭示变量之间的内在关系。
(4)聚类分析:将员工根据绩效、个人特质、工作环境等因素进行分类,分析不同类别员工的特点。
(5)回归分析:建立员工绩效与个人特质、工作环境等因素之间的回归模型,分析各因素对绩效的影响程度。
四、数据分析结果1. 描述性统计分析通过对员工绩效、个人特质、工作环境等变量的描述性统计分析,得出以下结论:(1)员工绩效评分呈正态分布,平均绩效评分为75分。
(2)个人特质得分集中在中等水平,其中创新能力得分最高,稳定性得分最低。
(3)工作环境得分普遍较高,其中工作压力得分最低。
2. 相关分析通过对员工绩效、个人特质、工作环境等变量进行相关分析,得出以下结论:(1)绩效与创新能力、稳定性、工作环境等因素呈正相关。
(2)创新能力与稳定性呈负相关。
3. 因子分析通过对员工绩效、个人特质、工作环境等变量进行因子分析,得出以下结论:(1)提取了3个因子,分别对应创新能力、稳定性、工作环境。
多元统计分析 实验报告

多元统计分析实验报告1. 引言多元统计分析是一种用于研究多个变量之间关系的统计方法。
在实验中,我们使用了多元统计分析方法来探索一组数据中的变量之间的关系。
本报告将介绍我们的实验设计、数据收集和分析方法以及结果和讨论。
2. 实验设计为了进行多元统计分析,我们设计了一个实验,收集了一组相关变量的数据。
我们选择了X、Y和Z这三个变量作为我们的研究对象。
为了获得准确的结果,我们采用了以下实验设计:1.确定研究目的:我们的目标是探索X、Y和Z之间的关系,并确定它们之间是否存在任何相关性。
2.数据收集:我们通过调查问卷的方式收集了一组数据。
我们请参与者回答与X、Y和Z相关的问题,以获得关于这些变量的定量数据。
3.数据整理:在收集完数据后,我们将数据进行整理,将其转化为适合多元统计分析的格式。
我们使用Excel等工具进行数据整理和清洗。
4.数据验证:为了确保数据的准确性,我们对数据进行验证。
我们检查数据的有效性,比较数据之间的一致性,并排除任何异常值。
3. 数据分析在数据收集和整理完毕后,我们使用了一些常见的多元统计分析方法来分析我们的数据。
以下是我们使用的方法和步骤:1.描述统计分析:我们首先对数据进行了描述性统计分析。
我们计算了X、Y和Z的均值、标准差、最大值和最小值等。
这些统计量帮助我们了解数据的基本特征。
2.相关性分析:接下来,我们进行了相关性分析,以确定X、Y和Z之间是否存在相关关系。
我们计算了变量之间的相关系数,并绘制了相关系数矩阵。
这帮助我们确定变量之间的线性关系。
3.回归分析:为了更进一步地研究X、Y和Z之间的关系,我们进行了回归分析。
我们建立了一个多元回归模型,通过回归方程来预测因变量。
同时,我们还计算了回归系数和R方值,以评估模型的拟合度和预测能力。
4. 结果和讨论根据我们的实验设计和数据分析,我们得出了以下结果和讨论:1.描述统计分析结果显示,X的平均值为x,标准差为s;Y的平均值为y,标准差为s;Z的平均值为z,标准差为s。
计量经济实验报告多元(3篇)

第1篇一、实验目的本次实验旨在通过多元线性回归模型,分析多个自变量与因变量之间的关系,掌握多元线性回归模型的基本原理、建模方法、参数估计以及模型检验等技能,提高运用计量经济学方法解决实际问题的能力。
二、实验背景随着经济的发展和社会的进步,影响一个变量的因素越来越多。
在经济学、管理学等领域,多元线性回归模型被广泛应用于分析多个变量之间的关系。
本实验以某地区居民消费支出为例,探讨影响居民消费支出的因素。
三、实验数据本实验数据来源于某地区统计局,包括以下变量:1. 消费支出(Y):表示居民年消费支出,单位为元;2. 家庭收入(X1):表示居民家庭年收入,单位为元;3. 房产价值(X2):表示居民家庭房产价值,单位为万元;4. 教育水平(X3):表示居民受教育程度,分为小学、初中、高中、大专及以上四个等级;5. 通货膨胀率(X4):表示居民消费价格指数,单位为百分比。
四、实验步骤1. 数据预处理:对数据进行清洗、缺失值处理和异常值处理,确保数据质量。
2. 模型设定:根据理论知识和实际情况,建立多元线性回归模型:Y = β0 + β1X1 + β2X2 + β3X3 + β4X4 + ε其中,Y为因变量,X1、X2、X3、X4为自变量,β0为截距项,β1、β2、β3、β4为回归系数,ε为误差项。
3. 模型估计:利用统计软件(如SPSS、R等)对模型进行参数估计,得到回归系数的估计值。
4. 模型检验:对估计得到的模型进行检验,包括以下内容:(1)拟合优度检验:通过计算R²、F统计量等指标,判断模型的整体拟合效果;(2)t检验:对回归系数进行显著性检验,判断各变量对因变量的影响是否显著;(3)方差膨胀因子(VIF)检验:检验模型是否存在多重共线性问题。
5. 结果分析:根据模型检验结果,分析各变量对因变量的影响程度和显著性,得出结论。
五、实验结果与分析1. 拟合优度检验:根据计算结果,R²为0.812,F统计量为30.456,P值为0.000,说明模型整体拟合效果较好。
多元统计课程实验报告

一、实验背景随着社会经济的发展和科学技术的进步,数据量日益庞大,如何从大量数据中提取有价值的信息,成为统计学研究的热点问题。
多元统计分析作为统计学的一个重要分支,通过对多个变量之间的关系进行分析,为决策者提供有力的数据支持。
本实验旨在通过实际操作,让学生熟练掌握多元统计分析方法,提高数据分析能力。
二、实验目的1. 掌握多元统计分析的基本概念和方法;2. 学会运用多元统计分析方法解决实际问题;3. 提高数据分析能力,为后续课程打下坚实基础。
三、实验内容本次实验以某城市居民消费数据为例,运用多元统计分析方法对其进行分析。
四、实验步骤1. 数据导入首先,将实验数据导入统计软件(如SPSS、R等)。
本实验采用SPSS软件,数据集包含以下变量:(1)收入(y):居民年收入;(2)教育程度(x1):居民最高学历;(3)年龄(x2):居民年龄;(4)家庭人口(x3):家庭人口数量;(5)住房面积(x4):家庭住房面积。
2. 描述性统计分析对数据集进行描述性统计分析,包括各变量的均值、标准差、最大值、最小值等。
3. 相关性分析运用皮尔逊相关系数、斯皮尔曼等级相关系数等方法,分析变量之间的相关关系。
4. 主成分分析运用主成分分析方法,提取主要成分,降低数据维度。
5. 聚类分析运用K-means聚类分析方法,将居民划分为不同的消费群体。
6. 随机森林回归分析运用随机森林回归分析方法,预测居民收入。
五、实验结果与分析1. 描述性统计分析根据描述性统计分析结果,可知居民年收入、教育程度、年龄、家庭人口、住房面积的平均值、标准差、最大值、最小值等。
2. 相关性分析通过相关性分析,发现收入与教育程度、年龄、家庭人口、住房面积之间存在显著的正相关关系。
3. 主成分分析根据主成分分析结果,提取出两个主成分,累计方差贡献率为84.95%,可以解释大部分的变量信息。
4. 聚类分析通过K-means聚类分析,将居民划分为3个消费群体。
实验报告 一元回归模型

图4
方差分析
由方差分析结果可知:
F F (1, n 2)
,拒绝零假设,y 与 x 存在线性关系,所求的线
多元计分析实验报告——刘晓丽
性回归方程有意义,故线性回归效果显著。 回归模型的回归诊断可以通过残差图和 Q-Q 图实现。下图为残差图和 Q-Q 图。
图5
残差图和 Q-Q 图
ˆ1 , ˆ2 ,, ˆn 相互独立且等方差。 由残差图可知:线性回归模型的假定成立,
Y 30477.01 33212 32055.99 32502.01 35450.01 38727.98 40731.02 37910.99 39150.99 40298.01 39408 40755 44624 43529.01 44265.79 45648.82 44510.09 46661.8 50453.5 49417.1 51229.5
实验目的:
学会利用 SAS 统计软件的“交互数据分析”窗口,建立一元回归模型,并通过决定系数 和方差分析实现回归模型的显著性检验,通过残差图和残差的 Q-Q 图实现回归诊断。
实验过程与结果分析:
资料:已知我国粮食生产量 Y(万吨) 、农业机械总动力 X(万千瓦)1978~1998 年的样 本观测值见表一。
多元统计分析实验报告——刘晓丽
实验五
实验要求:
建立一元回归模型
选取一组有意义的数据 ( x1 , y1 ),( x2 , y2 ), ,( xn , yn ) ,说明 x 与 y 之间具有较强的相关 性。利用 SAS 的“交互数据分析”建立回归方程,并进行如下说明: 1. 方程的显著性如何?哪些量能反映这一点? 2. 方程的前提假设是否满足?如何判定?
表一
年份 1978 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998
多元统计分析实验报告(精选多篇)

多元统计分析实验报告(精选多篇)第一篇:多元统计分析实验报告多元统计分析得实验报告院系:数学系班级:13级 B 班姓名:陈翔学号:20131611233 实验目得:比较三大行业得优劣性实验过程有如下得内容:(1)正态性检验;(2)主体间因子,多变量检验a;(3)主体间效应得检验;(4)对比结果(K 矩阵);(5)多变量检验结果;(6)单变量检验结果;(7)协方差矩阵等同性得Box 检验a,误差方差等同性得Levene 检验 a;(8)估计;(9)成对比较,多变量检验;(10)单变量检验。
实验结果:综上所述,我们对三个行业得运营能力进行了具体得比较分析,所得数据表明,从总体来瞧,信息技术业要稍好于电力、煤气及水得生产与供应业以及房地产业。
1。
正态性检验Kolmogorov-SmirnovaShapir o—Wilk 统计量 df Sig.统计量df Sig、净资产收益率。
113 35、200*。
978 35。
677 总资产报酬率。
121 35、200*。
964 35、298 资产负债率。
086 35。
200*.962 35、265 总资产周转率.180 35、006。
864 35。
000流动资产周转率、164 35、018.88535、002 已获利息倍数、28135.000。
55135、000 销售增长率.103 35、200*。
949 35、104 资本积累率。
251 35。
000、655 35。
000 *。
这就是真实显著水平得下限。
a。
Lilliefors显著水平修正此表给出了对每一个变量进行正态性检验得结果,因为该例中样本中n=35<2000,所以此处选用 Shapiro—W ilk 统计量。
由 Sig。
值可以瞧到,总资产周转率、流动资产周转率、已获利息倍数及资本积累率均明显不遵从正态分布,因此,在下面得分析中,我们只对净资产收益率、总资产报酬率、资产负债率及销售增长率这四个指标进行比较,并认为这四个变量组成得向量遵从正态分布(尽管事实上并非如此)。
数据结构实验报告-一元多项式

数据结构实验报告-一元多项式数据结构课程设计报告课题: 一元多项式姓名:XX学号:201417030218专业班级:XXXX指导教师:XXXX设计时间:2015年12月30日星期三评阅意见:评定成绩:指导老师签名:年月日目录一、任务目标 (3)二、概要设计 (4)三、详细设计 (6)四、调试分析 (8)五、源程序代码 (8)六、程序运行效果图与说明 (15)七、本次实验小结 (16)八、参考文献 (16)一丶任务目标分析 (1) a.能够按照指数降序排列建立并输出多项式b.能够完成两个多项式的相加,相减,并将结果输入要求:程序所能达到的功能:a.实现一元多项式的输入;b.实现一元多项式的输出;c.计算两个一元多项式的和并输出结果;d.计算两个一元多项式的差并输出结果;除任务要求外新增乘法:计算两个一元多项式的乘积并输出结果(2)输入的形式和输入值的范围:输入要求:分行输入,每行输入一项,先输入多项式的指数,再输入多项式的系数,以0 0为结束标志,结束一个多项式的输入。
输入形式:2 3-1 23 01 20 0输入值的范围:系数为int型,指数为float型(3)输出的形式:第一行输出多项式1;第二行输出多项式2;第三行输出多项式1与多项式2相加的结果多项式;第四行输出多项式1与多项式2相减的结果多项式;第五行输出多项式1与多项式2相乘的结果多项式二、概要设计程序实现a. 功能:将要进行运算的二项式输入输出;b. 数据流入:要输入的二项式的系数与指数;c. 数据流出:合并同类项后的二项式;d. 程序流程图:二项式输入流程图;e. 测试要点:输入的二项式是否正确,若输入错误则重新输入。
流程图:三、详细设计(1):存储结构一元多项式的表示在计算机内可以用链表来表示,为了节省存储空间,只存储多项式中系数非零的项。
链表中的每一个结点存放多项式的一个系数非零项,它包含三个域,分别存放该项的系数、指数以及指向下一个多项式项结点的指针。
多元统计分析 实验报告

多元统计分析实验报告多元统计分析实验报告一、引言多元统计分析是一种研究多个变量之间关系的统计方法,可以帮助我们更全面地了解数据集中的信息。
本实验旨在通过多元统计分析方法,探索不同变量之间的关系,并分析其对研究结果的影响。
二、数据收集与处理在本实验中,我们收集了一份关于学生学业成绩的数据集。
数据集包括学生的性别、年龄、家庭背景、学习时间、考试成绩等多个变量。
为了方便分析,我们对数据进行了清洗和预处理,包括删除缺失值、标准化处理等。
三、描述性统计分析在进行多元统计分析之前,我们首先对数据进行了描述性统计分析。
通过计算各变量的均值、标准差、最小值、最大值等统计量,我们对数据的整体情况有了初步的了解。
例如,我们发现男生和女生的平均成绩存在差异,家庭背景与学习时间之间存在一定的相关性等。
四、相关性分析为了探索不同变量之间的关系,我们进行了相关性分析。
通过计算各个变量之间的相关系数,我们可以了解它们之间的线性关系强弱。
通过绘制相关系数矩阵的热力图,我们可以直观地观察到各个变量之间的相关性。
例如,我们发现学习时间与考试成绩之间存在较强的正相关关系,而年龄与考试成绩之间的相关性较弱。
五、主成分分析主成分分析是一种常用的降维方法,可以将多个相关变量转化为少数几个无关的主成分。
在本实验中,我们应用主成分分析方法对数据进行了降维处理。
通过计算各个主成分的解释方差比例,我们可以确定保留的主成分个数。
通过绘制主成分得分图,我们可以观察到不同变量在主成分上的贡献程度。
例如,我们发现第一主成分主要与学习时间和考试成绩相关,而第二主成分主要与家庭背景和性别相关。
六、聚类分析聚类分析是一种将样本按照相似性进行分类的方法,可以帮助我们发现数据集中的潜在模式和群体。
在本实验中,我们应用聚类分析方法对学生进行了分类。
通过选择适当的聚类算法和距离度量,我们可以将学生分为不同的群体。
通过绘制聚类结果的散点图,我们可以观察到不同群体之间的差异。
(整理)excel一元及多元线性回归实例.

野外实习资料的数理统计分析一元线性回归分析一元回归处理的是两个变量之间的关系,即两个变量X和Y之间如果存在一定的关系,则通过观测所得数据,找出两者之间的关系式。
如果两个变量的关系大致是线性的,那就是一元线性回归问题。
对两个现象X和Y进行观察或实验,得到两组数值:X1,X2,…,Xn和Y1,Y2,…,Yn,假如要找出一个函数Y=f(X),使它在X=X1,X2, …,Xn时的数值f(X1),f(X2), …,f(Xn)与观察值Y1,Y2,…,Yn趋于接近。
在一个平面直角坐标XOY中找出(X1,Y1),(X2,Y2),…,(Xn,Yn)各点,将其各点分布状况进行察看,即可以清楚地看出其各点分布状况接近一条直线。
对于这种线性关系,可以用数学公式表示:Y = a + bX这条直线所表示的关系,叫做变量Y对X的回归直线,也叫Y对X 的回归方程。
其中a为常数,b为Y对于X的回归系数。
对于任何具有线性关系的两组变量Y与X,只要求解出a与b的值,即可以写出回归方程。
计算a与b值的公式为:式中:为变量X的均值,Xi为第i个自变量的样本值,为因变量的均值,Yi为第i个因变量Y的样本值。
n为样本数。
当前一般计算机的Microsoft Excel中都有现成的回归程序,只要将所获得的数据录入就可自动得到回归方程。
得到的回归方程是否有意义,其相关的程度有多大,可以根据相关系数的大小来决定。
通常用r来表示两个变量X和Y之间的直线相关程度,r为X和Y的相关系数。
r值的绝对值越大,两个变量之间的相关程度就越高。
当r为正值时,叫做正相关,r为负值时叫做负相关。
r 的计算公式如下:式中各符号的意义同上。
在求得了回归方程与两个变量之间的相关系数后,可以利用F检验法、t检验法或r检验法来检验两个变量是否显著相关。
具体的检验方法在后面介绍。
2.多元线性回归分析一元回归研究的是一个自变量和一个因变量的各种关系。
但是客观事物的变化往往受到多种因素的影响,即使其中有一个因素起着主导作用,但其它因素的作用也是不可忽视的。
多元统计分析实验报告)

. . .数学与计算科学学院实验报告实验项目名称相应与典型相关分析所属课程名称多元统计分析实验实验类型验证型实验日期2016年6月13日星期一班级学号姓名成绩因素B 具有对等性。
通过变换。
得c '=ΣZ Z ,r '=ΣZZ 。
(3)对因素B 进行因子分析。
计算出c '=ΣZ Z 的特征向量 及其相应的特征向量计算出因素B 的因子)(4)对因素A 进行因子分析。
计算出r '=ΣZZ 的特征向量 及其相应的特征向量计算出因素A 的因子(5)选取因素B 的第一、第二公因子 选取因素A 的第一、第二公因子将B 因素的c 个水平,,A 因素的r 个水平同时反应到相同坐标轴的因子平面上上(6)根据因素A 和因素B 各个水平在平面图上的分布,描述两因素及各个水平之间的相关关系。
1.3 在进行相应分析时,应注意的问题要注意通过独立性检验判定是否有必要进行相应分析。
因此在进行相应分析前应做独立性检验。
独立性检验中,0H :因素A 和因素B 是独立的;1H :因素A 和因素B 不独立 由上面的假设所构造的统计量为2211ˆ[()]ˆ()rcij ij i j ijk E k E k χ==-=∑∑211()r c ij i j k z ===∑∑ 其中....(/)/ij ij i j i j z k k k k k k =-,拒绝区域为221[(1)(1)]r c αχχ->--()(1)()(1)i i P Pa X '++a X ()(2)()(2)i i q qb X '++b X(2))1=X 的条件下,使得()(2)()(2)i i q qb X '+b X(2))1=X 的条件下,使得(1)、(2)X 的第一对典型相关变量。
1,2,,)r()p⎦()p ⎥⎦pU⎥⎥⎦p V⎥⎥⎦*(1)*== A X V Bˆˆr() ++b bz【实验过程】(实验步骤、记录、数据、分析)一.问题1的求解步骤:1. 将数据输入在SPSS后,在窗口中选择数据→加权个案,调出加权个案主界面,并将变量人数移入加权个案中的频率变量框中。
应用多元统计分析实验报告

应用多元统计分析实验报告一、引言多元统计分析是一种通过同时考虑多个自变量对因变量的影响来进行数据分析的方法。
它可以帮助研究人员了解不同自变量之间的关系,并预测因变量的表现。
本实验旨在应用多元统计分析方法,探索自变量对于因变量的影响。
二、实验设计在本次实验中,我们选择了一个具体的研究问题:探究学生的学习成绩在不同自变量下的表现。
我们收集了100名学生的数据,包括他们的性别(自变量1)、年龄(自变量2)、家庭背景(自变量3)以及他们的数学和语文成绩(因变量)。
三、数据收集与处理我们使用问卷调查的方式收集了学生的性别、年龄和家庭背景的数据,并从学校的成绩数据库中获取了他们的数学和语文成绩。
在处理数据之前,我们进行了数据清洗和缺失值处理。
四、数据分析步骤1.描述统计分析:首先,我们对数据进行了描述性统计分析,包括计算平均值、标准差、最小值、最大值等指标,以了解数据的基本情况。
2.相关性分析:接下来,我们进行了相关性分析,探索自变量与因变量之间的关系。
我们使用皮尔逊相关系数来衡量两个变量之间的线性相关性,并进行了显著性检验。
3.多元线性回归分析:为了探究多个自变量对因变量的综合影响,我们进行了多元线性回归分析。
我们选择了逐步回归的方法,逐步将自变量加入模型,并根据显著性检验的结果决定是否保留自变量。
4.方差分析:最后,我们进行了方差分析,检验不同自变量水平下因变量均值之间的差异是否显著。
我们使用了单因素方差分析和多重比较方法。
五、结果与讨论1.描述统计分析结果显示,学生平均年龄为18岁,数学平均成绩为80分,语文平均成绩为85分。
标准差较小,表明数据的波动较小。
2.相关性分析结果显示,学生的性别和家庭背景与他们的数学和语文成绩之间存在显著相关性(p < 0.05)。
而年龄与成绩之间的相关性不显著。
3.多元线性回归分析结果显示,性别和家庭背景对学生的成绩有显著影响(p < 0.05),而年龄的影响不显著。
数据结构实验报告数值转换和一元多项式

编号:江西理工大学数据结构课程设计报告班级:网络112班学号:09姓名:李秀光时间:2012年12月31日~2012年1月11日指导教师:涂燕琼井福荣2013年01月数制转换一、需求分析1、输入的形式和输入值的范围n和f的输入形式均为int型,n和f的输入范围均为1~327672、输出的形式十六进制10-15输出A-E,超过十六进制时按16以上数值按原值输出。
3、程序所能达到的功能把十进制数n转换成任意进制数f(对于输入的任意一个非负十进制整数,输出与其等值的任意进制数(如二,四,八,十六进制)。
4、测试数据n(十进制)f(进制)输出值22 2 10110354 4 112025376 8 1240032767 16 7FFF1、抽象数据类型的定义ADT Stack{基本操作:InitStack(&S)操作结果:构造一个空栈s。
Push(&S,e)初始条件:栈s已存在。
操作结果:插入元素e为新的栈顶元素。
Pop(SqStack &S)初始操作:栈s已存在且非空。
操作结果:删除s的栈顶元素,并用e返回其值。
StackEmpty(SqStack S)初始条件:栈s已存在。
操作结果:若栈为空则返回1,否则返回0。
}ADT Stack2、主程序的流程以及各程序模块之间的层次调用关系见(三、详细设计3、流程图)↓1、数据类型// = = = = = ADT Stack 的表示与实现= = = = = //// - - - - - 数制转换- - - - -//#define STACK_INIT_SIZE 100 //存储空间初始分配量#define STACKINCREMENT 10 //存储空间分配增量typedef struct {int *base;int *top;int stacksize;}SqStack;// - - - - - 基本操作的函数原型说明- - - - - //void InitStack(SqStack &S)//构造一个空栈svoid Push(SqStack &S,int e)//插入e为新的栈顶元素int Pop(SqStack &S)//删除s的栈顶元素,并用e返回其值int StackEmpty(SqStack S)//若栈为空则返回1,否则返回0void conversion(int n,int f)//对于输入的任意一个非负十进制整数,打印输出与其等值的八进制数2、伪码算法// - - - - - 基本操作的算法描述 - - - - - //void InitStack(SqStack &S){//构造一个空栈sS.base = (int *)malloc(STACK_INIT_SIZE * sizeof(int));if(!S.base) exit(-2);S.top = S.base;S.stacksize = STACK_INIT_SIZE;}// InitStackvoid Push(SqStack &S,int e){//插入元素e为新的栈顶元素if(S.top- S.base >= S.stacksize){S.base = (int *)realloc(S.base,(S.stacksize + STACKINCREMENT)*sizeof(int));if(!S.base) exit(-2);S.top = S.base + S.stacksize;S.stacksize += STACKINCREMENT;}*S.top++ = e;}// Pushint Pop(SqStack &S){//删除s的栈顶元素,并用e返回其值int e;if(S.top == S.base) return 0;e = *--S.top;return e;}//Popint StackEmpty(SqStack S){//若栈为空则返回1,否则返回0if(S.top == S.base) return 1;else return 0;}// StackEmpty//对于输入的任意一个非负十进制整数,打印输出与其等值的八进制数void conversion(int n,int f){InitStack(S);while(n){Push(S,n%f);n = n/f;}while(!StackEmpty(S)){Pop(S,e)printf("%d",e);}}// conversion3、流程图(1)调试过程中遇到的问题和解决方法在调试过程中主要遇到一些符号打错或输出、输出和函数之类的名称打错或漏打,根据第一行提示的错误然后进行修改,修改之后再运行调试,如此循环,直到彻底正常运行,后面就是优化见面的问题了。
一元与多元线性回归

实用回归分析实验报告一实验题目:一元线性回归与多元线性回归专业:经济统计学班级:学号:姓名:一实验目的:1、熟悉运用spss软件画散点图以及线性回归、估计、参数检验、残差分析2、熟悉运用spss软件解决一元线性回归的问题3、熟悉运用spss软件解决多元线性回归的问题二实验内容:步骤:一. P63---- 3.9(1)画出散点图分析→相关→双变量回归模型y=9.508+9.747x回归标准差为ô 4.70420β0(2.696 16.319)(6)计算x和y的决定系数;(7)对方程作方差分析(9)对回归方程作残差图分析水平为95%的置信区间当广告费用为4.2万元时,销售收入:46.9232.00 30.00 1.00 29.00159 0.99841 23.94274 34.060442.00 35.00 2.00 29.00159 5.99841 23.94274 34.060443.00 40.00 3.00 38.74856 1.25144 34.46648 43.030634.00 45.00 4.00 48.49552 -3.49552 44.86531 52.125745.00 50.00 5.00 58.24249 -8.24249 55.06149 61.423494.50 55.006.00 53.36901 1.63099 49.99464 56.743375.50 66.007.00 63.11597 2.88403 60.05400 66.177957.50 75.00 8.00 82.60991 -7.60991 79.19690 86.022918.00 85.00 9.00 87.48339 -2.48339 83.80533 91.161459.00 100.00 10.00 97.23036 2.76964 92.88747 101.5732410.00 110.00 11.00 106.97732 3.02268 101.84982 112.10483 二. P94----4.8研究货运总量y与工业总产量x1、农业总产量x2、居民非商品支出x3的关系,其数据见表4.15试完成:(1)计算y,x1,x2,x3的相关系数矩阵;分析→相关→偏变量(2)求y关于x1,x2,x3的三元线性回归模型;分析—》回归—》线性回归模型y=-348.280+3.754x1+7.101x2+12.447x3(3)对所求方程作拟合优度检验;分析—》回归—》线性分析—》回归—》线性(6)如果有回归系数没有通过显著性检验,将其剔除,重新建立回归方程,再作回归方程的显著性检验和回归系数的显著性检验X3没有通过显著性检验,P=0.284,显著,予以剔除。
多元统计分析实验报告

多元统计分析实验报告多元统计分析实验报告引言:多元统计分析是一种研究多个变量之间关系的方法,通过对多个变量进行综合分析,可以揭示出变量之间的相互作用和影响,帮助我们更好地理解数据背后的规律和现象。
本实验旨在通过对一组数据进行多元统计分析,探索变量之间的关系,并对实验结果进行解读。
实验设计:本实验选取了一组包含多个变量的数据集,其中包括性别、年龄、教育程度、收入水平、婚姻状况等变量。
通过对这些变量进行多元统计分析,我们希望了解这些变量之间是否存在相关性,并进一步探究各个变量对于整体数据集的影响。
数据收集与处理:首先,我们收集了一份包含上述变量的样本数据,共计1000个样本。
接下来,我们对数据进行了清洗和处理,包括去除异常值、缺失值的处理等。
经过处理后,我们得到了一份完整的数据集,可以进行后续的多元统计分析。
多元统计分析方法:在本实验中,我们使用了多元统计分析中的主成分分析和聚类分析两种方法。
主成分分析是一种通过将原始变量转化为一组新的综合变量,来降低数据维度并保留尽可能多的信息的方法。
聚类分析则是一种通过对样本进行分类,使得同一类别内的样本相似性较高,不同类别之间的差异性较大的方法。
实验结果与分析:经过主成分分析,我们得到了一组主成分,它们分别代表了原始变量的不同方面。
通过对主成分的解释,我们可以发现性别、年龄和教育程度等变量对于整体数据集的解释性较高,而收入水平和婚姻状况等变量的解释性较低。
这说明性别、年龄和教育程度等因素在整体数据中起着较为重要的作用。
接下来,我们进行了聚类分析,将样本分为若干个类别。
通过观察不同类别的样本特征,我们可以发现在同一类别内,样本的性别、年龄和教育程度等变量较为相似,而收入水平和婚姻状况等变量的差异较大。
这说明性别、年龄和教育程度等因素在样本分类中起到了重要的作用,而收入水平和婚姻状况等因素则对样本分类的影响较小。
结论与展望:通过本次实验的多元统计分析,我们可以得出以下结论:性别、年龄和教育程度等因素在整体数据集中起着较为重要的作用,并且对样本分类也具有一定的影响。
实验1-一元多项式实验报告

实验1-一元多项式实验报告数据结构实验报告实验名称:实验1——一元多项式Polynomial学生姓名:孙广东班级:2011211109班内序号:08学号:2011210251日期:2012年11月1日1.实验要求实验目的:1.熟悉C++语言的基本编程方法,掌握集成编译环境的调试方法2.学习指针、异常处理的使用3.掌握单链表的操作的实现方法4.学习使用线性表解决实际问题的能力实验内容:利用线性表实现一个一元多项式Polynomialf(x) = a0 + a1x + a2x2 + a3x3+ … + a n x n要求:1.能够实现一元多项式的输入和输出2.能够进行一元多项式相加3.能够进行一元多项式相减4.能够计算一元多项式在x处的值5.能够计算一元多项式的导数(选作)6.能够进行一元多项式相乘(选作)7.编写测试main()函数测试线性表的正确性2. 程序分析由于多项式是线性结构,故选择线性表来实现,在这个程序中我采用的是带头结点的单链表结构,每个结点代表一个项,多项式的每一项可以用其系数和指数唯一的表示。
如果采用顺序存储,那么对于结点的插入和删除的操作会比较麻烦,程序的时间空间复杂度增加,而且顺序表的结点个数动态增加不便,因为决定采用单链表的方式解决。
本程序完成的主要功能:1.输入和输出:需要输入的信息有多项式的系数和指数,用来向系统动态申请内存;系数和指数用来构造每个结点,形成链表。
在构造链表的时候我添加了出泡排序以及合并同类项的功能,因此输入时没有要求。
输出即是将多项式的内容向屏幕输出。
2.多项式相加与相减:多项式的加减要指数相同即是同类项才能实现,所以在运算时要注意判断指数出现的各种不同的情况,分别考虑可能出现的不同情况。
将每项运算得到的结果都插入到新的链表中,形成结果多项式。
多项式相减可视为加上第二个多项式的相反数。
3.多项式的求导运算:多项式的求导根据数学知识,就是将每项的系数乘以指数,将指数减1即可,将每项得到的结果更新到结果多项式的链表中。
多元数据的数学表达实验报告总结

多元数据的数学表达实验报告总结这个多元数据的表达方法在这篇论文中是非常重要的,对我们理解有关的概念和方法都有很大的帮助。
我用了大量时间去研究和分析实验结果,并且完成了一些简单的实际应用:(1)用自己手头的样本估计全国人口,假设参与观察的人口为总人口的40%;(2)得到了全部人群参与统计工作的平均人数为10人/年;(3)从样本的平均值上减掉2%左右的标准误差后发现,假如样本小于20,则总体的统计推断误差会增加30%左右,而其他两组实验,误差都比较接近于0.05;(4)一旦使用了这种统计技术,那么就不能再依赖于样本的统计数字进行判断,因此需要更严格地选择参与调查的人群。
从前面的实验可以看出,多元数据在研究中占有极大的优势。
首先,它给予了人们新的视野——从几个维度来认识事物;第二,它拓展了人类思考问题的深度,把问题从多层次的复杂性归纳为简单、易懂的模型;最后,它使得人们能够利用抽象的技巧处理过于精细的信息,便于整合;由于人脑具有惊人的适应性,通过观察他人,可以获取各种资源,丰富自身的知识。
而这些将为社会科学家所用,探索出很多“社会规律”,造福广大民众。
然而这种高效率、低成本的方式却只存在于统计学之内。
多元数据研究的确立无疑扩宽了其应用领域。
对我们生活中的方方面面也带来了巨大影响。
虽然很多专业人士对多元数据抱着怀疑的态度,但是我相信随着越来越多数据库的建立和多元数据的普及化,这种情况终将被改变。
对于社会科学的发展而言,我想再没有什么能比数据的积累更加困难,需要花费更多的精力去挖掘真正意义上的有价值的东西,从中找寻问题产生的根源。
即使每天都在重复做着同样的工作,你还是要用新的眼光审视周围,向别人虚心求教。
或许,对这个世界最好的报答就是努力工作吧!从经济学的角度来说,多元数据主要是指数据种类的多元化,数据采集方式的多元化,数据处理技术的多元化,这是多元数据研究的基础。
在多元数据中,数据特征往往决定着研究者采用何种策略去提取数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元与多元数据分析实验报告
一、研究目的
通货膨胀的日趋严重,失业率的日益增加,都严重影响着人们的生活水平,通过西方经济学的学习知道菲利普斯曲线是研究通货膨胀和失业率之间关系的曲线,是表明失业与通货膨胀存在一种交替关系的曲线,通货膨胀率高时,失业率低;通货膨胀率低时,失业率高。
但是由于预期通货膨胀率的出现,失业率与实际通货膨胀率的关系不能简单的用菲利普斯曲线来解释。
二、模型设定
为进一步分析通货膨胀率和失业率的关系,以及与预期通货膨胀率之间的关系,选择某国“际通货膨胀率”为被解释变量Y,失业率为解释变量X2,预期通货膨胀率为解释变量X3。
数据为书99页表3.8
1970到1982年某国实际通货膨胀率,失业率,和预期通货膨胀率(单位%)年份实际通货膨胀率Y 失业率X2 预期通货膨胀率X3
1970 5.92 4.90 4.78
1971 4.30 5.90 3.84
1972 3.30 5.60 3.31
1973 6.23 4.90 3.44
1974 10.97 5.60 6.84
1975 9.14 8.50 9.47
1976 5.77 7.70 6.51
1977 6.45 7.10 5.92
1978 7.60 6.10 6.08
1979 11.47 5.80 8.09
1980 13.46 7.10 10.01
1981 10.24 7.60 10.81
1982 5.99 9.70 8.00
以下是用EV软件分别对Y,X2,X3作的线形图
说明:实际通货膨胀率是与失业率满足交替变动的,实际通货膨胀率也是与预期通货膨胀率同向变动的
三参数估计
回归表的解读
一元回归Y X2的解读
Dependent Variable: Y
Method: Least Squares
Date: 09/28/11 Time: 08:47
Sample: 1970 1982
Included observations: 13
Variable Coefficient Std. Error t-Statistic Prob.
C 6.127172 4.285283 1.429817 0.1806
X2 0.244934 0.630456 0.388502 0.7051
R-squared 0.013536 Mean dependent var 7.756923 Adjusted R-squared -0.076143 S.D. dependent var 3.041892 S.E. of regression 3.155577 Akaike info criterion 5.276858 Sum squared resid 109.5343 Schwarz criterion 5.363773 Log likelihood -32.29958 F-statistic 0.150934 Durbin-Watson stat 0.969568 Prob(F-statistic) 0.705058
Y=6.127172+0.244934X2
系数6.127172 0.244934
标准差4.285283 0.630456
T统计量1.429817 0.388502
P值0.1806 0.7051
P值0.1806与0.05相比,P值较大,接受H0,没有显著水平
R^2为0.013536,可决系数小,拟合效果不明显
Dependent Variable: Y
Method: Least Squares
Date: 09/28/11 Time: 08:50
Sample: 1970 1982
Included observations: 13
Variable Coefficient Std. Error t-Statistic Prob.
C 1.323831 1.626284 0.814022 0.4329
X3 0.960163 0.228633 4.199588 0.0015
R-squared 0.615875 Mean dependent var 7.756923 Adjusted R-squared 0.580955 S.D. dependent var 3.041892 S.E. of regression 1.969129 Akaike info criterion 4.333698 Sum squared resid 42.65216 Schwarz criterion 4.420613 Log likelihood -26.16904 F-statistic 17.63654 Durbin-Watson stat 1.282331 Prob(F-statistic) 0.001487
系数1.323831 0.960163
标准差1.626284 0.228633
T统计量0.814022 4.199588
P值0.4329 0.0015
P值0.4329与0.05相比,P值较大,接受H0,没有显著水平
R^2为0.615875,可决系数较小,拟合效果不明显,但是X3的拟合效果比X2好
Y与X2,X3的拟合回归表
Dependent Variable: Y
Method: Least Squares
Date: 09/28/11 Time: 08:51
Sample: 1970 1982
Included observations: 13
Variable Coefficient Std. Error t-Statistic Prob.
C 7.105975 1.618555 4.390321 0.0014
X2 -1.393115 0.310050 -4.493196 0.0012
X3 1.480674 0.180185 8.217506 0.0000
R-squared 0.872759 Mean dependent var 7.756923
Adjusted R-squared 0.847311 S.D. dependent var 3.041892
S.E. of regression 1.188632 Akaike info criterion 3.382658
Sum squared resid 14.12846 Schwarz criterion 3.513031
Log likelihood -18.98728 F-statistic 34.29559
Durbin-Watson stat 2.254851 Prob(F-statistic) 0.000033
Y=7.105975-1.393115X2+1.480674X3
系数-1.393115 1.480674
标准差0.310050 0.180185
T统计量-4.493196 8.217506
P值0.0012 0.0000
P值0.0012与0.05相比,P值较小,拒绝H0,有显著水平
R^2为0.847311,可决系数较大,拟合效果明显,比X2和X3 单独拟合的效果都要显著
做出残差拟合值图表
实际值与拟合值重叠部分较多,说明有较好的拟合
四模型检验
1.经济意义
用实际通货膨胀率和失业率的一元关系来说明Y=6.127172+0.244934X2
系数为6.127172 0.244934
失业率每增加一个单位,通过膨胀率会增加0.244934个单位。
用实际通货膨胀率和预期通货膨胀率一员关系来说明Y=1.323831+0.960163X3
系数为1.323831 0.960163
预期通货膨胀率每增加一个单位,实际通货膨胀率会增加0.960163个单位。
用实际通货膨胀率和失业率、预期通货膨胀率的二元关系来说明
Y=7.105975-1.393115X2+1.480674X3
系数-1.393115 1.480674
在其他条件不变的情况下,失业率每增加1个单位,实际通货膨胀率会减少
1.393115个单位;在其他条件不变的情况下,预期通货膨胀率每增加一个单位,实际通货膨胀率会增加1.480674个单位。
满足实际通货膨胀率和失业率交替变动关系,同时也满足预期通货膨胀率与实际通货膨胀率同向变动的关系
2. 拟合优度和统计检验
(1)拟合优度
可决系数X2的R^2为0.013536,可决系数小,拟合效果不明显
X3的R^2为0.615875,可决系数较小,拟合效果不明显。
X2 X3的R^2为0.847311,可决系数较大,拟合效果明显,比X2和X3
单独拟合的效果都要显著
(2)统计检验
T检验Y与X2 一元方程中T统计量1.429817 0.388502
N=13 N-2=11 所以T0.025(11)=2.201
由于1.429817 和0.388502均小于2.201,均接受原假设,则说明Y与X2无显著关系。
T检验Y与X3 一元方程中T统计量0.814022 4.199588
0.814022小于2.201,接收原假设,无显著影响;
4.199588大于2.201,拒绝原假设,有显著影响
T检验Y与X2、X3 二元方程中T统计量-4.493196 8.217506
T0.025(9)=2.262
由于二元统计量中T值得绝对值大于2.262,所以均拒绝原假设,说明在其他条件不变的情况下,失业率和预期通货膨胀率对实际通货膨胀率有显著影响。
五回归预测。
