长沙理工大学结构力学考试
长沙理工结构力学期末考试题库和答案第二章静定梁与钢架 结构力学超静定

长沙理工结构力学期末考试题库和答案第二章静定梁与钢架结构力学超静定第二章静定梁及静定刚架一、判断题1.静定结构在荷载作用下产生的内力与杆件弹性常数、截面尺寸无关。
( O )2.计算位移时,对称的静定结构是指杆件几何尺寸、约束、刚度均对称的结构。
( O ) 3.静定结构在支座移动、变温及荷载分别作用下,均产生位移和内力。
( X )4.几何不变体系一定是静定结构。
( X )25.图示结构 MK = ql/2(内侧受拉)。
( X )q6.图示结构中 AB 杆弯矩为零。
( X ) q7.图示结构中 |MAC|=|MBD|。
( O )|8.图示结构中 |MAC|=|MBD。
( O )l9.图示结构 M 图的形状是正确的。
( X ) M 图 10.图示结构|MC|=0 。
( O)11.图示结构中 A、B 支座反力均为零。
d二、选择题12.静定结构有变温时:( C )A. 无变形,无位移,无内力;B. 有变形,有位移,有内力;C. 有变形,有位移,无内力;D. 无变形,有位移,无内力。
13.静定结构在支座移动时:( D )A. 无变形,无位移,无内力;B. 有变形,有位移,有内力;C. 有变形,有位移,无内力; D 无变形,有位移,无内力。
O )(14.静定结构的内力计算与( A )A. EI 无关;B. EI 相对值有关;C. EI 绝对值有关;D. E 无关, I 有关。
15.图示结构MA 、MC (设下面受拉为正)为:( C )A.MA =0 ,MC=Pa/2 ;B.MA =2Pa ,MC=2Pa ;C.MA =Pa ,MC=Pa ;D.MA =-Pa,MC=Pa 。
16.图示结构 MA、 MB (设以内侧受拉为正)为:( DA. MA=-Pa , MB =Pa;B. MA=0 , MB =-Pa ;C. MA=Pa ,MB =Pa ;D.MA=0 , MB =Pa 。
17.图示结构 B 点杆端弯矩(设内侧受拉为正)为:( C )A.MBA = Pa, MBC = -Pa ;B.MBA = MBC = 2Pa;C. MBA = MBC = Pa ;D.MBA = MBC = 0 。
长沙理工工程力学复习题及答案
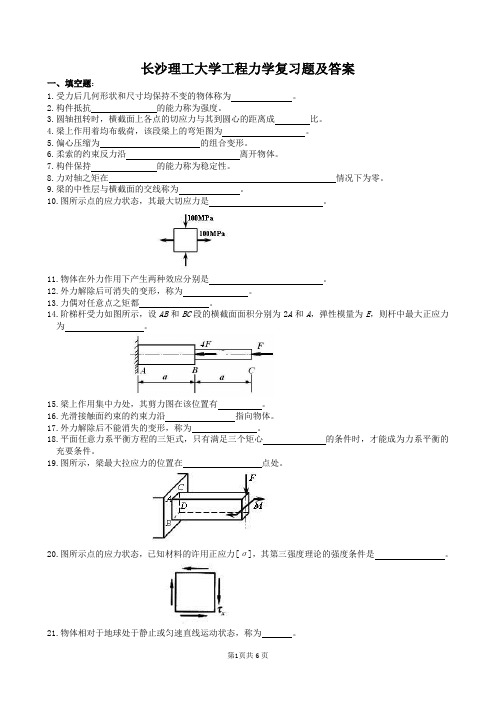
长沙理工大学工程力学复习题及答案一、填空题:1.受力后几何形状和尺寸均保持不变的物体称为。
2.构件抵抗的能力称为强度。
3.圆轴扭转时,横截面上各点的切应力与其到圆心的距离成比。
4.梁上作用着均布载荷,该段梁上的弯矩图为。
5.偏心压缩为的组合变形。
6.柔索的约束反力沿离开物体。
7.构件保持的能力称为稳定性。
8.力对轴之矩在情况下为零。
9.梁的中性层与横截面的交线称为。
10.图所示点的应力状态,其最大切应力是。
11.物体在外力作用下产生两种效应分别是。
12.外力解除后可消失的变形,称为。
13.力偶对任意点之矩都。
14.阶梯杆受力如图所示,设AB和BC段的横截面面积分别为2A和A,弹性模量为E,则杆中最大正应力为。
15.梁上作用集中力处,其剪力图在该位置有。
16.光滑接触面约束的约束力沿指向物体。
17.外力解除后不能消失的变形,称为。
18.平面任意力系平衡方程的三矩式,只有满足三个矩心的条件时,才能成为力系平衡的充要条件。
19.图所示,梁最大拉应力的位置在点处。
20.图所示点的应力状态,已知材料的许用正应力[σ],其第三强度理论的强度条件是。
21.物体相对于地球处于静止或匀速直线运动状态,称为。
22.在截面突变的位置存在集中现象。
23.梁上作用集中力偶位置处,其弯矩图在该位置有。
24.图所示点的应力状态,已知材料的许用正应力[σ],其第三强度理论的强度条件是。
25.临界应力的欧拉公式只适用于杆。
26.只受两个力作用而处于平衡状态的构件,称为。
27.作用力与反作用力的关系是。
28.平面任意力系向一点简化的结果的三种情形是。
29.阶梯杆受力如图所示,设AB和BC段的横截面面积分别为2A和A,弹性模量为E,则截面C的位移为。
30.若一段梁上作用着均布载荷,则这段梁上的剪力图为。
二、计算题:1.梁结构尺寸、受力如图所示,不计梁重,已知q=10kN/m,M=10kN·m,求A、B、C处的约束力。
2.铸铁T梁的载荷及横截面尺寸如图所示,C为截面形心。
长沙理工大学结构力学解答集(学生版)

第一章机动分析一、判断题1.( X ) 2.( X ) 3.( X ) 4.( O )二、选择题5.(B) 6.(D) 7.(C) 8.(A) 9.(A) 10.(A) 11.(C) 12.(B) 13.(A)三、填空题14.几何瞬变15. 或不定值16.两刚片用不完全相交及平行的三根链杆连接而的体系。
17.几何不变且无多余约束。
四、分析与计算题18.几何不变且无多余约束。
19.瞬变。
20.几何不变无多余约束。
21.几何不变无多余约束。
22.瞬变。
23.几何不变无多余约束。
24.可变。
25.几何不变无多余约束。
26.几何不变无多余约束。
27.几何不变,有两个多余约束。
28.几何不变无多余约束。
29.几何不变无多余约束。
30.几何不变无多余约束。
1第二章静定梁与静定刚架一、判断题1.(O)2.(O)3.(X)4.(X)5.(X)6.( X ) 7.( O ) 8.( O ) 9.( X ) 10.( O ) 11.( O )二、选择题12.(C)13.(D)14.(A)15.( C )16.( D )17.( C ) 18.( C )19.(C)20.(B)21.(C )三、填空题22.不变,零23.无关24.位移,变形,内力25.在任意荷载作用下,所有反力和内力都可由静力平衡条件求得确定的、有限的、唯一的解答。
26.0 ,027.20kN·m ,下28.75kN·m ,右29.2Pa,右30.0.5pa ,上31.Pa, 左四、分析与计算题32.33.20.5q lq l28M图PaPaPaPaPaPaPaM图2334. 35.图(k N m 1616M RA ql H 0M B B ql 0.5( )图M Bql 0.522______A36. 37.1050203050().图 M kN m DC BE Aql20.5ql 2ql20.5图M DC B A38. 39.图M m CA B().图 M kN m 2020AB 5DC40. 41.BCD40120图 M ()kN .m A 408040图M PlPl2Pl ABC D442. 43.().图 M kN m 4441535 图M ql 28ql 223ABDC44. 45.()图 M kN .m AB 151515151515C DE F 1515Pa 2/3图Pa 2/3Pa 2/3Pa 2/3M AB46. 47.Pa 2/3Pa /34AB图MPaPa0.5P a0.5P a图M48. 49.PaPaPaPa图M图M550. 51.ql20.5ql20.5ql20.5ql20.5图M图M mmm m52. 53.P aPa0.5P a0.5P a0.5M 图m0.5m54. 55.mmmmqPM 图56. 57.4040404020kN1k N 1k N3k N1k N Q 图 (3.5)N 图 (3.5)658.PPPQ 图N 图59.qaqa qa /2qaqa qa/2qa /232Q 图 N 图60. 61.PPa 图M ACDB图M qa 22qa 2262.ABC ED F Pa Pa 13237第三章 静 定 拱一、判断题1.(X ) 2.(O )3. ( O )二、选择题4.(C )5.(B ) 6.(D ) 7.(B ) 8.( B ) 9.( D )三、填空题10. 0 , 011. 7.5kN ·m , 下四、分析与计算题12. 00K K K M Q N qr ===-13. 20(13)5(31)5(31)K K K M kN m Q kNN kN =-⋅=-=-+14. 100105K K K M kN m Q N kN =-⋅==-8第四章 静定桁架一、判断题1.(O ) 2.(O ) 3.(X ) 4.(X ) 5.(X ) 6.(X )二、选择题7. ( D ) 8.( D ) 9.( D ) 10.(D ) 11.(D )三、填空题12. 0 , 013. BC , FG , ED , DB , DF 14. 1.414P , -2P 15. 0.5P ( 拉 ) 16. P四、分析与计算题17. 18.图M 2Pa2Pa 2Pa Pa6Pa 6ABC D E FG图M 2qa 22qa 22qa 22qa 2qa219.9ABDC806020M ()kN .m 图20. 14/3N P = 21. N 10= N P 22=22. N 1=PN P 22=-23. N 125kN =-N 2=44kNN 310kN =24. N 10= N P 2233=/ 25. N 10= N P 2= N P 322=/ 26. N P 12= N P 22=-27. N P 115=-. N P 2=28. N P 106=. N P 2=29. 1222N P N P =-=30. 1234101052102N N N N =-==-=-kN , kN , kN , kN 31. N P 1=-32.(kN)(kN)(kN)30280/3350/31404050140/3140/320M 图图图Q N 203033.10444().4图 M kN m 链 杆 轴 力, N = -2 kN34.Q 图(kN)1515().图 M kN m 555512.55157.512.52N 图(kN)1535.1502.5272.5452.52150100250250N 图 (kN)903015028026010100Q 图(kN )图 M (kN .m )11第五章 图 乘 法一、判断题1.( X ) 2.( X ) 3.( X ) 4.( X ) 5.( O )二、选择题6.( C ) 7.( C ) 8.( C ) 9.( C ) 10.( B ) 11.( A ) 12.( A ) 13.( C )三、填空题14.(////)ac ad bd bc l 3636+++⋅ 15.()ql EI 424/ ()→ 16.733ql EI /()17.5482Pa EI /() (逆 时 针) 18.4Pa/EA (↓) 19.qa EI qa EA 330625/./+四、分析与计算题20. ()()()C EI Pl h Plh EI ϕ=-⋅⋅⋅=-113322//// ()21. ()AVPl EIh l ∆=+22916// (↓)1222. ()AV Pl EI ∆=↓29243/ 23. ()BH EI ∆=-←11340/ 24. A φ=00016.rad ()25. ()CH Pl EI ∆=-←19483/() 26. ()DH ∆=→00084.m27. K D =4860/EI ()28. AB Pl EI ϕ=492/ ()29. AB Pl EI H ∆=35813/() ()30. BVE I 2M l2=∆(31. ()ϕD MlEI =632.ϕB = 15.625( )EI33. ∆AH = - 5 P a 3 / E I ( ← )34. ∆BH = - 8Pa 3/ E I ( ← ) 35. ϕD EI =835/ () 36.ϕD = /2()52P l E I37.3ϕC 左 =13 /162ql EI ()38. ()∆EV ql EI =-↑74324/()39. ϕAB EA =2414. ( )1340. ()∆CV Pa EA =↓2414.41. ϕC Pa EI P EA =+532752/./() 42. ∆AV EI EA =+3101875(↓)43. ()ϕC EI EI EI =++=301333408333..() 44. ∆C D H cm =0795.()45. ∆∆CH R =-⋅=∑--⋅=()1∆∆ (→)46. ()ϕB R l l =-⋅=--=∑∆∆∆0505././ ()14第六章 力 法一、判断题1.(X) 2.(X) 3.(X) 4.(X) 5.(X) 6.(X) 7.(X)二、选择题8.(B) 9.(D) 10.(A) 11.(C) 12.(C)三、填空题13.6次14. (2+1.414)Pl/EA 15. -256/EI , 0 16.l EA l EI //()+13123 17.l EA h EI //()+233 18.0 , 0 , 0四、分析与计算题20. δ1145=./EI ; ∆1405P EI =-/ 21. 111234/765/P E I E I δ=∆=- 22.152 /2Pl图M PPlPl /2Pl 基 本 体 系PX 123.X 1X 1基 本 体 系 8322432248图M ()kN .m ()分 2()分 324.X 1413431基本体系图 M ()kN .m kN .m4kN .m25.X 1X 14522.5X 2X 2基 本 体 系 图M ()kN .m ()分 2()分 326.16基本体系31.42222.89X 1图 M ()kN .m27.qa /2qa 2/242 /122 /242 /242 /242基本体系qa qa qa qa qa a /21X 图 M ()kN .m /122qa28.X 1X 2=0ql 2/4ql 2/2基本体系 M 图 X 1ql 2/2ql 2/4(2分 )(3分 )29.175050图 M ()kN .m30.q1EI =基 本 体 系X 432720图 M ()kN .m 504231.X 2X 1基 本 体 系图 M ()kN .m 17. 8231. 6826. 6432. 33.M 图1.77P1.77P3PPP3P1.23P 1.23P4.234.23-12.796-12.8-13.870.5340.5346.1337.20.534a-a a -bb c N (k N )a b c =-=-=0755********...34.120.4375 1.417N P N P =-=35.1810kNX 1基本体系( 2分 )3030M 图·()kN m ( 3分)36.X1图M X 2q基 本 体 系8.71 6.773.8716.52 1.87qqqqq37.EI/l X=X =1M 1图图M N 图 1lα1分 )(2分 )(7.521138.l图M X 11=()34EI l θ基 本 体 系39.1922.2X=图M R=kN .m-3.7kN X=1-1(2分 )(4分 )基 本 体 系40.()()()()()()()334164 24hA h EI Ph h EI h Ph h PhEI ∆=⋅⋅-⋅⋅⋅=第七章 位 移 法一、判断题:1.(X ) 2.(X ) 3.(O ) 4.(O ) 5.(O ) 6.(X )7.(O ) 8.(X ) 9.(X )二、选择题10.(B )三、填空题11. 0 12. 4 13. 273EI l / 14. 0 15. -6l 016. -Pl17. r 22 = 4.5 R P 1 = -8 18. r 11 = 13 R P 1 = 020四、分析与计算题19. r EI l 1110=/ R ql P 12316=-/ 20. r 22 = 3EI R P 2 = 021.ql /8ql 2/8M Z 12图22.Z 1101010101010(kN m).M 图23.Z 117.417.47.74(kN m).M 图24.Z 1M Pl/4Pl/4Pl/4Pl/4图25.21Z 1hhhha aM a= Pl/h= Pl/图12432717226.Z 12- Pl+ ql 192962Pl+ql Pl-ql 2192Pl/M 35315图827.P /23 图P /23P /23P /23M28.Z 1/9/9/9/9/9245图Pl Pl Pl Pl M Pl29.2210kN Z 1Z 2基 本 体 系20/320/320/310/3图 (kN m).M30.Z 110kN/m10.665.3320.1314.2111.25 5.33基 本 体 系图 (kN m)M .Z 231.Z 1基 本 体 系=10kN/m 80kNZ 248.648.68037.0362.8125.78图 M ()kN .m q32.Z 1基 本 体 系图(kN m)4kN/mZ 225/1450/775/14M .33.23140/13160/1310kN10kN/m320/1320Z 1Z 2基 本 体 系 M 图 (kN ·m ) 34.7101010M 图 ( 2332ql /) 35.Z 2图 (kN m).=10kN/m5.42.961.481.4811.8311.83简 化 图q M Z 136.2kN/mZ 1Z 2基 本 体 系图 ( N m).1.470.421.262.740.21M 4k37.24P /2P/2Z 1Z 2基 本 体 系5 /185 /18/6/62 /92 /9/18/18M 图Pl Pl PlPlPlPl Pl Pl简 化38.EI 1= 图=11/4 3 /420/320/37.540/3M EI3 3 /8EI3 /8EIZ ∞EI39.图M40.Z 1图 (kN m)1cm193.5918211.5.M第八章力矩分配法一、判断题1.( X ) 2.( O ) 3.( X ) 4.( X )二、选择题5.( B ) 6.( B ) 7.( C ) 8.( C ) 9.( D ) 10.( D )三、填空题11.012.0 , M AB2, MAB13.M/2 下14.8 kN·m15.1/3 ,1/3 ,1/316.0 ,1 ,0.2252617.i EI l =,()μBA i i i =+=34337,μBC =47,μBD =0四、分析与计算题18. μAD =19 , μAC =49 , μAB =49, μBA = 1 , μBE = 0M BE F = -160 kN ·m19. μμAB AC ==3812/,/, μμAD AE ==180/,M k N m M AB AC FF .,,=⋅=750 M M kN m AD AE FF ,==⋅02020. μμμμAD AC FD FG ====05. μμμDA DE DF ===13/,M kN m DF F,=-⋅375 MkN mFDF=-⋅37521. 14.7BC M kN m =-⋅ 22. 40AC M kN m =-⋅ 23. 0.3EB M kN m =⋅ 24. 2BA M kN m =⋅ 25.27MF2 分 ( )M 图 kN m .( )3 分( )2 分( )5 分( )1/21/2-1BA BCCB CD DC0.50.51/32/3-40-2013.3326.67-13.3313.33-6.67-6.67-3.331.111.112.22-1.11-0.56-0.56-7.217.2125.56-25.56-34.4434.44A B CD25.567.217.213.626.BDAC10.8430.8347.0830.83202023.5523.5510.845.425.42对 称 结 构 , 对 称 荷 载 , 取 一 半 结 构 计 算M 图 kN m .( )27.28M 图 kN m .( )CABDEBA BE EB μMFDA AD AC AB 11.54-1.62 -2.43 2.5 分 ( )2.5 分( )7 分( )6/133/134/1345-12012034.6217.3123.08-26.31-52.62-78.9212.14 6.078.14.0546.7668.38-115.1381.35-81.3581.3546.7668.38115.1323.3840.680.40.628.μM F5.126.6901234521 23-9090454.238.594.3 4.849.68-2.6-5.21-3.93-1.970.86 1.75+1.975.09-5.0926.5690-90( 2.5 分 )( 2.5 分 )( 7 分 )0.330.670.570.4310-12.83-25.65-19.35-9.68图 M ()kN .m -26.564345343229.7.4CB M kN m =-⋅30.29对 称 性 取 半 结 构1.891.055.712.86307.8722.138.66A D EFB CAD AB BA BC BEBF 301.5-7.5-22.5-11.251.492.983.980.99 1.79-0.37-1.12-0.560.170.230.060.1-7.87-22.13-8.66 5.71 1.051.89μ 3 分 ( )3 分( )8 分 ( )0.250.750.30610.4082 0.102 0.1837M 图 (kN.m)31. 16.85CB M kN m =⋅ 32.kN m .( )M 图 2.231.934.167.895AD μμAB i AD AB S AB i EI l=i/=i AC i ==6i ,,,,AC μ= 0.257,= 0.446 ,= - 7.5kN m .,DA M = - 3.75kN m .,= 4i 32i =0.297M AD FF,AC S =⨯3,AD S =6i ,1.123033.CD B A EF 56.8518.960图 M ()kN .m 对 称 性 取 半 刚 架 ,u MFCA AC AB BA BF BE EB 0.50.50.40.30.3-4040-60-604866-618189-1.8-3.6-2.7-2.72.70.90.918.9-18.953.43.3-56.7-63.3( 4 分 )( 3 分 ) ( 3 分 )(8 分 )53.7 3.1563.1518.934. 3.31DC M kN m =⋅31第九章 影响线及其应用一、判断题1. ( X ) 2.( O ) 3.( X ) 4.( X ) 5.( O ) 6.( X ) 7.( X )二、选择题8.( C ) 9.( B ) 10.( C ) 11.(C ) 12.(C ) 13.(D ) 14.(A )三、填空题15. 结 构 在 恒 载 及 活 载 作 用 下 , 各 截 面 内 力 最 大 最 小 值变 化 范 围 图 。
长沙理工大学结构力学考试题库及详细答案(适合本科期末和考研)力矩分配法

第八章 力矩分配法一、判断题1.力 矩 分 配 法 中 的 分 配 系 数 、传 递 系 数 与 外 来 因 素 ( 荷 载 、温 度 变 化 等 ) 有 关 。
( )2.力 矩 分 配 中 的 传 递 系 数 等 于 传 递 弯 矩 与 分 配 弯 矩 之 比 , 它 与 外 因 无 关 。
( )3. 图 示 结 构 用 力 矩 分 配 法 计 算 时 分 配 系 数 μBC 为 1 / 8 。
( )mmABCD II I4. 图 示 结 构 的 最 后 弯 矩 绝 对 值 关 系 有 M M CB BC =/2 。
(E I = 常 数) ( )q lll二、选择题5.力 矩 分 配 法 中 的 分 配 系 数 μ 、传 递 系 数 C , 与 外 来 因 素 ( 荷 载 、温 度 变 化 等 ) :( )A . 均 有 关 ;B . 均 无 关 ;C . μ 有 关 ,C 无 关 ;D . μ 无 关 ,C 有 关 。
6.力 矩 分 配 法 中 的 传 递 弯 矩 等 于 : ( )A . 固 端 弯 矩 ;B . 分 配 弯 矩 乘 以 传 递 系 数 ;C . 固 端 弯 矩 乘 以 传 递 系 数 ;D . 不 平 衡 力 矩 乘 以 传 递 系 数 。
7.力 矩 分 配 法 中 的 分 配 弯 矩 等 于 : ( )A . 固 端 弯 矩 ;B . 远 端 弯 矩 ;XOXXBBCC . 不 平 衡 力 矩 ( 即 约 束 力 矩 ) 乘 以 分 配 系 数 再 改变 符 号 ;D . 固 端 弯 矩 乘 以 分 配 系 数 。
8.图 示 结 构 用 力 矩 分 配 法 计 算 时 分 配 系 数 μAB , μAD 为 :( )A . μAB =12/ , μAD =16/ ; B .μAB =411/ , μAD =18/ ;C .μAB =12/ , μAD =18/ ; D . μAB =411/ , μAD =16/ 。
长沙理工大学研究生专业考试大纲

结构力学:1、了解:平面体系的自由度;几何构造与静定性的关系;静定结构的特性;三铰拱的计算;三铰拱的合理拱轴线;各式桁架比较;组合结构的计算;变形体系的虚功原理;单位荷载法;线弹性结构的互等定理;温度变化时超静定结构的计算;支座位移时超静定结构的计算;用弹性中心法计算无铰拱;两铰拱及系杆拱;超静定结构的特性;铁路和公路的标准荷载制;换算荷载;简支梁的包络图;超静定结构影响线作法;连续梁的均布活载最不利位置及包络图。
2、掌握:瞬变体系;三刚片体系中虚铰在无穷远处的情况;单跨静定梁的内力计算;多跨静定梁的内力计算;用结点法和截面法计算静定平面桁架;静定结构温度变化时的位移计算;静定结构支座移动时的位移计算;超静定次数的确定;力法的基本概念;力法的典型方程;力法中对称性的利用;超静定结构的位移计算;等截面直杆的转角位移方程;位移法的基本未知量和基本结构;直接由平衡条件建立位移法基本方程;位移法中对称性的利用;力矩分配法的基本原理;用力矩分配法计算连续梁和无侧移刚架;用静力法作单跨静定梁的影响线;间接荷载作用下的影响线;多跨静定梁的影响线;桁架的影响线;最不利荷载位置。
3、重点掌握:几何不变体系的基本组成规则;静定平面刚架的内力计算;静定平面桁架的内力计算;用图乘法计算静定刚架在荷载作用下的位移;用力法计算超静定结构的内力;超静定结构的位移计算;用位移法计算超静定结构的内力;用机动法作静定结构的影响线;利用影响线求量值。
桥梁工程:一、考试的总体要求要求掌握我国桥梁总体规划设计原则和作用;中、小型桥梁上部结构的构造、设计计算方法和施工方法;了解现代大跨度桥梁的构造、计算特点和施工方法;熟悉桥梁墩台的构造和设计计算方法;理解现代桥梁结构电算的相关理论和方法。
二、考试内容1、总论桥梁的组成、分类和名词术语;桥梁设计原则、平纵横断面设计和建设程序及方案比选;桥梁作用和作用组合;桥面布置与构造。
2、混凝土梁式桥和刚架桥混凝土梁式桥的构造;简支梁桥桥面板计算、荷载横向分布系数计算、主梁内力计算、横隔板内力计算、挠度和预拱度计算;箱梁剪力滞和有效宽度;超静定结构次内力计算;刚架桥的种类、构造和受力特点;支座构造、布置原则与设计计算方法;斜梁桥的基本概念、斜板桥的受力特点;弯梁桥的特点和构造。
长沙理工大学结构力学考试题库及详细答案(适合本科期末和考研)影响线
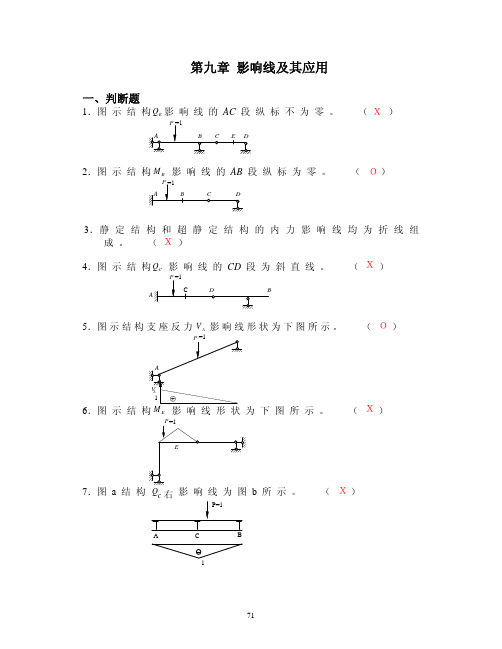
第九章 影响线及其应用一、判断题1.图 示 结 构影 响 线 的 AC 段 纵 标 不 为 零 。
( )Q E2.图 示 结 构 影 响 线 的 AB 段 纵 标 为 零 。
( )M B3.静 定 结 构 和 超 静 定 结 构 的 内 力 影 响 线 均 为 折 线 组成 。
( )4.图 示 结 构 影 响 线 的 CD 段 为 斜 直 线 。
( )Q C5.图 示 结 构 支 座 反 力 V 影 响 线 形 状 为 下 图 所 示 。
( )A 6.图 示 结 构 影 响 线 形 状 为 下 图 所 示 。
( )M E7.图 a 结 构右所示 。
( )c Q A C 1XOXXOXX二、选择题8.图 示 结 构 影 响 线 ( P = 1 在 BE 移 动 ) BC 、CD 段 纵 标为 :( )c Q A. BC 、CD 均 不 为 零 ; B. BC 、CD 均 为 零 ;C. BC 为 零, CD 不 为 零 ;D. BC 不 为 零,CD 为 零 。
9.图 示 结 构 影 响 线 ,其 中 ACD 部 分 为 :( )Q C A. AC 不 为 零 ,CD 为 斜 线 ; B. AC 为 零 ,CD 为 水 平 线 ; C. AC 为 零 ,CD 为 斜 线 ; D. AC 为 零 ,CD 为 零 。
10.单 位 荷 载 作 用 在 简 支 结 间 梁 上 , 通 过 结 点 传 递 的 主梁 影 响 线 , 在 各 结 点 之 间 ( ):A. 部 分 为 直 线 , 部 分 为 曲 线 ;B. 均 为 曲 线 ;C. 均 为 直 线 ;D. 竖 标 为 零 。
11.图 示 结 构 ,M 影 响 线 (下 侧 受 拉 为 正)D 处 的 纵 标 为 :( )A A . 0 ;B . l ;C . - l ; D. -2.236l /2 。
CBCC22l/212.图示结构影响线(P = 1在BE移动,右侧受拉为正)B、D 两点纵标(单位m)为:()MAA.4 ,4 ;B. B.-4 , -4 ;C.0 , -4;D.D. 0 , 4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、结构:建筑物和工程设施中承受、传递荷载而起骨架作用的部分称为工程结构,简称结构。
从几何角度来看,结构分为三类:1、杆件结构:这类结构由杆件组成,杆件的几何特征是横截面尺寸比长度小得多。
梁、拱、桁架、刚架是杆件结构的典型形式。
2、板壳结构,也称薄壁结构,它的厚度要比长度和宽度小得多,房屋中的楼板和壳体屋盖、水工结构中的拱坝都是。
3、实体结构,这类结构的长宽厚三个尺度大小相仿,水工结构中的重力坝属于。
2、结构力学的研究对象:结构力学以杆件结构为主要研究对象,它的任务是根据力学原理研究在外力和其他外界因素作用下结构的内力和变形,结构的强度、刚度、稳定性和动力反应,以及结构的组成规律和受力性能,包括以下方面1、讨论结构的组成规律、受力性能和合理形式,以及结构计算简图的合理选择。
2、讨论结构内力和变形的计算方法,进行结构的强度与刚度的验算。
3、讨论结构的稳定性以及在动力荷载作用下的结构反应。
研究手段包含理论分许、实验研究和数值计算三个方面。
在结构分析中首先把实际结构简化成计算模型,称为结构计算简图,然后再对计算简图进行计算。
计算方法考虑以下三类基本方程1、力系的平衡方程或运动方程2、变形与位移间的几何方程3、应力与变形间的物理方程(本构方程)以上称为”平衡-几何-本构解法或三基方程解法。
3、用一个简化的图形来代替实际结构,这种图形称为结构的计算简图。
4、支座分为1、滚轴支座,被支承的部分可以转动和水平移动,不能竖向移动,能提供的反力只有竖向反力,用一根竖向支杆表示。
2、较支座,被支承的部分可以转动,不能移动,能提供两个反力,用两根相交的支杆表示。
3、定向支座,被支承的部分不能转动,但可沿一个方向平行滑动,能提供反力矩和一个反力,用两根平行支杆表示。
4、固定支座,被支承的部分完全被固定,能提供三个反力。
5、杆件结构通常分为以下几类:1、梁,梁是一种受弯构件,其轴线通常为直线,可以是单跨的或多跨的。
2、拱,拱的轴线为曲线,其力学特点是在竖向荷载作用下有水平支座反力(推力)3、桁架,是由直杆组成,所有结点都为铰结点。
4、刚架,也由直杆组成,其结点通常为刚结点。
5、组合结构,是桁架和梁或刚架组合在一起形成的结构,其中含有组合结点。
6、静定结构,如果结构的杆件内力和支座反力可由平衡条件唯一确定。
超静定结构,如果杆件内力和支座反力由平衡条件还不能唯一确定,而必须同时考虑变形条件才能唯一确定。
对静定结构进行受力分析时,只需考虑平衡条件,而不需要考虑变形条件。
7、荷载分类,根据荷载作用时间的久暂分为恒载和活载,根据荷载作用的性质,可以分为静力荷载和动力荷载。
静力荷载的数量、方向和位置不随时间变化或变化极为缓慢,不使结构产生显著的加速度,因而惯性力的影响可以忽略。
动力荷载是随时间迅速变化或在短暂时段内突然作用或消失的荷载,使结构产生显著的加速度,因而惯性力的影响不能忽略。
结构的自重和其他恒载是静力荷载。
8、几何不变体系,在不考虑材料应变的条件下,体系的位置和形状是不能改变的,几何可变体系,反之即是9、自由度等于这个体系运动时可以独立改变的坐标的数目10、多余约束,如果在一个体系中增加一个约束,而体系的自由度并不因而减少,则此约束称为多余约束。
11、瞬变体系,这种本来是几何可变,经微小位移后又成为几何不变的体系称为瞬变体系常变体系,如果一个几何可变体系可以发生大位移,称为常变体系。
12、瞬铰,从瞬时微小运动来看,两根链杆所起的约束作用相当于在链杆交点处的一个铰所起的约束作用。
13、无穷远处的瞬铰,两根平行的链杆把刚片与基础相连接,则两根链杆的交点在无穷远处。
因此用两根链杆所起的约束作用相当于无穷远处的瞬铰所起的约束作用,射影几何中关于无穷点和无穷线的四点结论:1、每个方向有一个无穷点(即该方向各平行线的交点)2、不同的方向有不同的无穷点3、各无穷点都在同一直线上,此直线称为无穷线4、各有限点都不在无穷线上。
14、铰结三角形规律,1、三个点之间的连接方式,不共线的三个点用三个链杆两两相连,则所组成的铰结三角形体系是一个几何不变的整体,且没有多余约束。
2、一个刚片与一个点用两根链杆相连,且三个铰不在一直线上,则组成几何不变的整体,且没有多余约束。
3、两个刚片用一个铰和一根链杆相连接,且三个铰不在一直线上,则组成几何不变的整体,且没有多余约束。
4、三个刚片用三个铰两两相连,且三个铰不在一直线上,则组成几何不变的整体,且没有多余约束。
5、两个刚片用三根链杆相连,且三链杆不交于同一点,则组成几何不变的整体,且没有多余约束。
15、计算自由度,计算自由度数W、自由度数S、多余约束数N三者之间的关系:S-W=N,其中S>=W,N>=-W,也就是说,W是自由度S的下限,而-w则是多余约束数N的下限。
即可以得出如下定性结论:若W>0,则S>0,体系是几何可变的,若W=0,则S=N,如无多余约束则为几何不变,如有多余约束则为几何可变,若W<0,则N>0,体系有多余约束。
根据W的数值,可对体系的几何构造特性得出一些结论,若W>0,对象的自由度总数大于约束总数,体系为几何可变,不能用于结构。
若W=0,对象的自由度总数等于约束总数,如体系为几何可变,则无多余约束,体系为静定结构,如体系为几何可变,则有多余约束。
若W<0,对象的自由度总数小于约束总数,体系有多余约束,如体系为几何可变,则为超静定结构。
16、梁内力计算的截面法,计算指定截面内力的基本方法是截面法,即将杆件在制定截面切开,取左边部分(或右边部分)为隔离体,利用隔离体的平衡条件,确定此截面的三个内力分量。
1、轴力等于截面一边的所有外力沿杆轴切线方向的投影代数和,2、剪力等于截面一边的所有外力沿杆轴法线方向的投影代数和。
3、弯矩等于截面一边的所有外力对截面形心的力矩代数和。
画隔离体受力图时,要注意以下几点,1、隔离体与周围的约束要全部截断,而以相应的约束力代替2、约束力要符合约束的性质,截断链杆时,在截面上加轴力,截断受弯杆件时,在截面上加轴力、剪力和弯矩,去掉滚轴支座、铰支座、固定支座时分别加一个、二个、三个支座反力。
3、隔离体是应用平衡条件进行分析的对象,在受力图中只画隔离体本身所受到的力,不画隔离体施给周围的力。
4、不要遗漏力,受力图上的力包括两类:一类是荷载,一类是截断约束处的约束力。
5、未知力一般假设为正号方向,数值是代数值,已知力按实际方向画,数值是绝对值,未知力计算得到的正负号就是实际的正负号。
17、梁的弯矩图的一般作法归纳如下:1、选定外力的不连续点(如集中力作用点、集中力偶作用点、分布荷载的起点和终点等)为控制截面,求出控制截面的弯矩值2、分段画弯矩图,当控制截面间有荷载作用时,根据控制截面的弯矩值作出直线图形后,还应叠加这一段按简支梁求得的弯矩图。
18、从几何构造来看,静定多跨梁是由几根梁组成的,组成的次序是先固定基本部分,后固定附属部分,因而计算静定多跨梁时,要遵守的原则是先计算附属部分,再计算基本部分。
将附属部分的支座反力反其指向,就是加于基本部分的荷载,这样便把多跨梁拆成为单跨梁,各个解决,从而可避免解算联立方程,将各单跨梁的内力图连在一起,就是多跨梁的内力图。
19、桁架内力计算中的假定1,桁架的结点都是光滑的铰结点,2、各杆的轴线都是直线并通过铰的中心3,荷载和支座反力都作用在结点上。
结点法最适合于计算简单桁架,如果截取结点的次序与桁架组成时添加结点的次序相反,就可以顺利地求出全部轴力。
20、单杆,如果在同一结点的所有内力为未知的各杆中,除某一杆外,其余各杆都共线,则该杆称为此结点的单杆,关于结点单杆有下面两种情况1、结点只包含两个未知力杆,且此二杆不共线,则每杆都是单杆2、结点只包含三个未知力杆,其中有两杆共线,则第三杆是单杆。
单杆的性质,1、结点单杆的内力可由该结点的平衡条件直接求出,而非结点单杆的内力则不能由该结点的平衡条件直接求出2、当结点无荷载作用时,单杆的内力必为零(称为零杆)3、如果依靠拆除结点单杆的方法可将整个桁架拆完,则此桁架即可应用结点法按照每次只解一个未知力的方式将各杆内力求出21、截面单杆,如果某个截面所截的内力为未知的各杆中,除某一杆外其余各杆都交于一点(或彼此平行,交点在无穷远处)则此杆称为该截面的单杆,分两种情况1、截面只截断三个杆,且此三杆不交于一点(或不彼此平行),则其中每一杆都是截面单杆2、截面所截杆数大于3,但除某一杆外,其余各杆都交于一点(或都彼此平行),则此杆也是截面单杆。
截面单杆性质,截面单杆的内力可从本截面相应的隔离体的平衡条件直接求出。
22、刚架和桁架都是由直杆组成的结构,二者的区别是桁架中的结点全部都是铰结点,刚架中的结点全部或部分是刚结点。
静定平面刚架的受力分析中,通常是先求支座反力,再求控制截面的内力,最后作内力图。
刚架内力图的基本作法是把刚架拆成杆件,也就是说,先求各杆的杆端内力,然后利用杆端内力分别作各杆的内力图,各杆的内力图合在一起就是刚架的内力图。
23、组合结构,在有些由直杆组成的结构中,一部分杆件是链杆,只受轴力作用,另一部分杆件是梁式杆,除受轴力作用外,还受弯矩和剪力作用,这种由链杆和梁式杆组成的结构为组合结构。
24、三铰拱,是一种静定的拱式结构,在桥梁和屋盖中都得到应用,受力特点,1、在竖向荷载作用下,梁没有水平反力,而拱则有推力2、由于推力的存在,三铰拱截面上的弯矩比简支梁的弯矩小,弯矩的降低,使拱能更充分地发挥材料的作用3、在竖向荷载作用下,梁的截面内没有轴力,而拱的截面内轴力较大,且一般为压力。
25、三铰拱的压力作用线,各段中任一截面左边(或右边)所有外力的合力作用线,对拱来说,由于截面轴力一般都是压力,故称为压力多边形或三铰拱的压力线。
三铰拱的合理轴线,在固定荷载作用下使拱处于无弯矩状态的轴线称为合理轴线。
26、隔离体的形式,从结构中截取的隔离体有多种形式,结点(铰结点、刚结点、组合结点)、杆件、微段单元或有限单元。
桁架的结点法以结点为隔离体,桁架截面法截取的隔离体通常含多个结点,多跨静定梁以杆件为隔离体,在刚架分析中,常以杆件为隔离体计算杆端剪力,以结点为隔离体计算杆端轴力。
推导荷载与内力之间的微分关系时取杆件微段为隔离体。
27、约束力的类型,选取隔离体时,在截断约束处暴露出来的约束力成为隔离体的外力,这些约束力的个数和类型是由所截断的约束的性质决定的,列如,在平面结构中截断链杆有一个约束力,截断简单铰结,一般有两个约束力,截断简单刚结,一般有三个约束力,截断滚轴支座、铰支座、定向支座、嵌固支座分别有一个,二个,三个约束力28、隔离体的独立平衡方程个数,对隔离体建立平衡方程时,其独立平衡方程的个数等于隔离体的自由度的个数。
