《三角形的尺规作图》导学案2
八年级数学上册 1.3 尺规作图学案(无答案) (新版)青岛版

1.3《尺规作图(2)》导学案学习目标1、经历探索与实践的过程,会利用基本作图完成已知两边及夹角和已知三边作三角形.2、通过作图,培养学生的动手操作能力、逻辑思维能力、分析和解决问题的能力.3、通过作图训练学生的作图语言.学习过程:一、自主预习课本P21——P22内容,独立完成课后练习1、2后,与小组同学交流(课前完成)二、实验与探究1、思考:已知三角形的哪几个元素就可以作出这个三角形?与同学交流。
2、利用你学过的基本作图,已知三边分别为a,b,c,如何作三角形?已知::线段a,b,c a求作:△ABC,使BC=a,AC=b,AB=c bc3、图1-29是以B,C为圆心,c,b为半径作弧在B,C所在直线的上方相交的情况,是否可能在BC的下方相交?如果可能,所得到的三角形与△ABC全等吗?为什么?4、利用你学过的基本作图,已知两边及其夹角,例如已知a,c 和∠α,如何作△ABC,使∠B=∠α,AB=c,BC=a呢?与同学交流。
ac α5、在上面的作图步骤中,分别用到了哪些基本作图?挑战自我已知三条线段a,b,c,作△ABC,使AB=c,BC=a,AC=b时,对a,b,c三条线段的大小有没有限制?如果有,a,b,c的大小应当满足什么条件?三、巩固练习利用尺规作图:1、已知线段a,求作边长等于a的等边三角形。
a2、已知线段a,∠α,求作△ABC,使∠A=∠α,AB=AC=aaα四、学习小结:(回顾一下这一节所学的,你学会了吗?)五、达标检测1、已知线段a,b,求作:△ABC,使AB=AC=a,BC=b。
ab2.已知线段a、b,求作:△ABC,使AB=2a,BC=b,AC=a.(保留作图痕迹,不写作法)ab3、已知:∠1和线段a,求作:△ABC,使∠A=∠1,AB=AC=2a.a这节课我安排了三个尺规作图,第一个作图给出作法和示范,让学生进行模仿;第二个作图只给出作法,没有给出示范,让学生根据已知步骤独立作出图形;第三个作图让学生自己探索作法,并独立作出图形。
冀教版初二数学上册三角形的尺规作图教案

活动2SSS作图.
学习SSS作图.
活动3 ASA作图.
学习ASA作图.
活动4SAS作图.
学习SAS作图.
活动5回忆与反思.
总结三角形的作图,加深明白得三角形全等的判定方法.
课前预备
教具
学具
补充材料
电脑、投影仪
课件资源、投影片
教学过程设计
问题与情形
师生行为
设计意图
活动1认识直尺和圆规
3.你能够画一条长度为5cm的线段AB吗?
学生画图,教师指导并鼓舞.
感受直尺的作用.
通过上面的的作图,你认为画一条规定长度的线段需要用________(填“直尺”或“圆规”),找一个点到固定点A的距离为3cm需要用________(填“直尺”或“圆规”).
学生回答,教师鼓舞.
总结直尺和圆规的作用.
活动2 SSS作图
讨论:我们一定要先作AB=a吗?能够先作一个角等于∠α吗?
学生讨论,教师引导.
认识先作“夹边”的好处.
活动4 ASA作图
已知:
求作:,使.
学生填空,教师点评并给予鼓舞.
学习书写已知、求证.
请同学们设计作图的步骤,并进行交流.
学生讨论,教师点评.
训练SAS作图.
活动5回忆与反思
1.我们今天学习了用直尺和圆规作三角形,作三角形的关键是什么?
冀教版初二数学上册13
教学任务分析
教学
目标
知识与技能
1.明白圆规和直尺在作图中的作用;
2.会用直尺和圆规完成SSS、ASA、SAS作图;
过程与方法
经历探究三角形作图的过程,会用直尺和圆规作图.
情感态度与
八年级数学上册 第1章 全等三角形 1.3 探索三角形全等的条件 1.3.1 尺规作图导学案 苏科版

一、学习目标:1、要掌握尺规作图的方法及一般步骤。
2、通过“作图题〞练习,提高学生的几何语言表达能力。
3、通过画图,培养学生的作图能力及动手能力二、学习重难点:重点:会作一个角等于角难点:熟练掌握相等角的作图,作图时要做到标准使用尺规,标准使用作图语言,标准地按照步骤作出图形。
探究案三、合作探究学生阅读教材,并答复以下问题:〔1〕什么是尺规作图?〔2〕什么是根本作图?一些复杂的尺规作图,都是由根本作图组成的,前面我们学过的用尺规作一条线段等于线段,这是一种根本作图,下面我们将再学习一种新的根本作图。
议一议:如图,∠AOB,用直尺和圆规作∠A′O′B′,使∠A′O′B′=∠AOB。
作法:(1)作射线O′A′.(2)以点___为圆心,以____ 为半径画弧,交OA于点C,交OB于点D.(3)以点_____为圆心,以____长为半径画弧,交O′A′于点C′.(4)以点_____为圆心,以_____长为半径画弧,交前面的弧于点D′.(5)过点D′作射线______∠A′O′B′就是所求作的角.想一想:通过以上作图过程。
你能证明∠A′O′B′=∠AOB吗?如何验证?(小组交流)随堂检测1.尺规作图的画图工具是( )A.刻度尺、圆规B.三角板、量角器C.直尺和量角器D.无刻度的直尺和圆规2.以下各作图题中,可直接用“边边边〞条件作出三角形的是( )A.腰和底边,求作等腰三角形B.两条直角边,求作直角三角形C.高,求作等边三角形D.腰长,求作等腰三角形3.利用直尺和圆规作一个角等于角的示意图如图,那么说明∠A’O’B’=∠AOB的依据是。
4.如图,∠α和∠β(∠α>∠β).求作∠AOB,使∠AOB=2∠α-∠β课堂小结通过本节课的学习在小组内谈一谈你的收获,并记录下来:我的收获___________________________________________________________________________ ______________________________________________________________________________ _参考答案探究案〔1〕什么是尺规作图?在几何里,把限定用直尺和圆规来画图,称为尺规作图.〔2〕什么是根本作图?最根本,最常用的尺规作图,通常称根本作图.议一议:(2)O,任意长,(3)O’,OC,(4) C’,CD,(5)O’B’想一想:根据SSS判定全等,然后得出对应角相等.随堂检测1. D2.A3.SSS4.作法:(1)作∠COD=∠α(2)以射线OD为边,在∠COD外部作∠DOA=∠α(3)以射线OC为一边,在∠COD内部作∠BOC=∠β.那么∠AOB就是所求作的角.如图:如有侵权请联系告知删除,感谢你们的配合!。
八年级数学上册 13.4 三角形的尺规作图学案(无答案)(新版)冀教版

13.4 三角形的尺规作图学习目标:1.了解尺规作图的概念,会用尺规作图法作线段和角.2.熟悉尺规作图的步骤并能熟练运用作图语言.3.以三角形全等的判定方法为基础,利用尺规作三角形.(重点)学习重点:尺规作图的步骤.学习难点:利用尺规作三角形.一、知识链接1.如图,已知线段a,b.求作:线段c,使线段c的长度为线段a,b长度的和.2.如图,已知∠1.求作:∠2,使∠2=2∠1.二、新知预习3.只用直尺(没有刻度)和圆规也可以画出一些图形,这种画图方法被称为尺规作图.由三角形全等判定可以知道,每一种判定两个三角形全等的条件(_____,_____,_____,_____),都只能作出唯一的三角形.如图,已知线段a,b,c.求作:△ABC,使AB=c,BC=a,AC=b.自主学习分析:由作一条线段等于已知线段,能够作出边AB,即A,B两点确定,而BC=a,AC=b,故以点A 为圆心,b为半径画弧长,以点B为圆心,a为半径画弧,两弧的交点就是点C.作法:第一步:作线段AB等于c;第二步:以点A为圆心,以b为半径画弧长;第三步:一点B为圆心,以a为半径画弧,两弧交于点C;第四步:连接AC,BC,△ABC即为所求.三、自学自测1.如图,已知线段a,b.求作:△ABC,使得CB=a,AC=AB=b.2.如图,已知线段a,b,∠1.求作:△ABC,使得∠BAC=∠1.AB=a,AC=b.四、我的疑惑_____________________________________________________________________________ ___________________________________________________________________________ __________________________________________________________________________一、要点探究探究点:用尺规作三角形问题1:如图,已知线段a,b(a>b),∠α.求作:△ABC,使得∠A=∠α,AB=a,BC=b.合作探究【归纳总结】判定作出符合要求的三角形,关键是根据条件确定三角形的三个顶点的位置.解题时候要根据实际情况判断是否存在多个符合题设条件的△ABC.【针对训练】已知:线段a、b和∠α,如图所示.求作:△ABC,使AB=3a,AC=b,∠A=∠α.问题2:已知:线段a,b,c,如图所示.求作:△ABC,使得AB=a,AC=b且BC边上的中线AD=c.【归纳总结】判定作在作较复杂的三角形时,先画草图,从中找出一个较容易作出的三角形,然后以它为基础作所求作的三角形就比较方便了.【针对训练】已知:如图所示,已知线段a,b和m.求作:△ABC,使得BC=a,AC=b,AC上的中线BM=m.二、课堂小结类型三角形的尺规作图①已知三边作三角形②已知两边及其夹角作三角形③已知两角及其夹边作三角形④已知两角和其中一角的对边作三角形1.下列条件能作一个唯一三角形的是_________(填序号).①∠A=65°,∠B=45°,∠C=90°;②∠A=60°,∠B=60°,∠C=60°;③AB=4cm,BC=3cm,AC=5cm;④AB=2cm,BC=5cm,AC=3cm;2.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作三角形,使所作出的三角形与△ABC 全等,这样的三角形最多可以作出()A.2个B.4个C.6个D.1个3.已知线段b,∠β,如图所示.求作:△ABC,使得BC=b,∠B=∠C=∠β.当堂检测当堂检测参考答案:1.③2.B3.作法:(1)作线段BC=b;(2)以B为顶点,射线BC为一边,作∠MBC=∠β,(3)以C为顶点,射线CB为一边,在BC同侧作∠NCB=∠β;射线BM,CN交于点A,则△ABC就是所求作的△ABC.。
冀教版数学八上13.4《三角形的尺规作图》word学案

中考链接:
1.已知,△ABC ,求作△DBC ,使△DBC ≌△ABC (写出做法,保留作图痕迹) A
B
C
2.如图,己知,线段a,∠1,求作:△ABC ,使AB=AC=a ∠A=∠1
(写出作法,保留作图痕迹)
六、作业布置:
英 才 学 校 导 学 学 案
学科:八年级数学 执笔:魏静 审核:八年级数学组 课题:13.4三角形的 尺规作图 课型:新授 时间:
一、导入( 分钟)
二、学前准备:( 分钟)
学习目标:1.能根据作图的要求合理的运用三角形全等的条件进行尺规作图。
2.会写出作三角形的己知,求作和作法。
(2)知识链接:
(SSS ):
(SAS):
a 1
(AAS):
三、探究活动
(1)自主探究(分钟)
己知,线段a、b、c,求作△ABC使AB=c BC=a AC=b
1.作线段AB=c
2.以点A为圆心,以b为半径画弧
3.以点B为圆心,以a为半径画弧,两弧交于点C
4.连结AC,BC,得到△ABC
(二)师生合作探究( 分钟)
每个人按照上面的方法作出的三角形一定全等吗?为什么?
练一练:
己知三角形的两个角分别等于∠A,∠B,这两个角所夹的边等于a,按下列步骤作出这个三角形。
a b
c
a
A B
1.
2.
3.
四、学习体会(分钟)
1、你学会了什么?
2、你还有哪些疑惑?
五、课堂自测:(分钟)
己知一个三角形的两边长为a、b夹角为30°作出这个三角形。
a b
30°。
数学七上1.4《三角形的尺规作图》课件(2)

B
D
O
2、分别以___为圆心,_____的长为半径作弧,
两条圆弧交于∠AOB内一点____;
3、作射线___; _____就是所求作的射线。
朱 德
zhū
朱砂 姓朱
朱德(1886~1976)马克思主义 者,无产阶级革命家,军事家,政治 家;中国共产党、中国人民解放军和 中华人民共和国的主要领导人,中国 人民解放军和中华人民共和国的主要 缔造者之一;中华人民共和国元帅 (1959 ~ 1976)。
A′
B
B′
C
在△ABC和△ A'B'C'中
{∠A= ∠A' ∠B= ∠B'
BC= B'C' ∴ △ABC≌△ A'B'C'
C′
(AAS)
尺规作图:用直尺
(不带刻度)和圆规 作图
尺规作图:
1.做一条线段等于已知线段
a
步骤: 第一步:做射线AB
第二步:用圆规量出MN的长, 在射线AB上截取AC=MN
F
知识回顾: 三角形全等判定方法Ⅱ
如果两个三角形的两边和他们的夹角对应相等,
那么这两个三角形全等(可以简写为“边角边”或“SFra bibliotekS”)。A
用符号语言表达为:
在△ABC和△ DEF中
B
C
AB=DE
D
∠A= ∠D
CA=FD
∴ △ABC ≌△ DEF(SAS) E
F
三角形全等的判定方法Ⅲ:
如果两个三角形的两个角及其夹边对应相等,
(扁担)
齐读课题,有什么疑问想提呢?
1.“朱德的扁担”这个故事发生 在什么时候?
冀教版八年级数学上册13.4三角形的尺规作图学案(无答案)

13.4 三角形的尺规作图学习目标:知识与技能:1.了解尺规作图的含义及其历史背景;已知三边利用尺规作三角形.2.在给出两边及其夹角的条件下,能够利用尺规作三角形.3.在给出两角及其夹边的条件下,能够利用尺规作三角形.过程与方法:会画一个角等于已知角;作角平分线;给定边角条件下,求作三角形; 情感态度与价值观:培养学生作已知线段的垂直平分线;要了解作法的理由.重 点:尺规作给定边角条件下的三角形.难 点:探索作图过程.预习过程:1、如图,使用直尺作图,看图填空.① ② ③ ④① 过点____和_______作直线AB (2)连结线段___________;(3)以点_______为端点,过点_______作射线___________;(4)延长线段__________到_________,使得BC=2AB.2、如图,使用圆规作图,看图填空:在射线AM 上__________线段________=___________.① 以点______为圆心,以线段______为半径作弧交_________于点___________.以点______为圆心,以任意长为半径作弧,分别交∠AOB 两边,交_________于点___________, 交________于点__________.活动一 做一做已知线段c b a ,,,如何用直尺(没有刻度)和圆规作ABC ∆使得c AB b AC a BC ===,,(三边符合三角形的条件)a b c作法:展示过程:略.αα活动二做一做: 已知三角形的两边及其夹角,求作这个三角形.已知:线段a ,c ,∠α.求作:ΔABC ,使得BC= a ,AB=c ,∠ABC=∠α.作法与过程:展示过程:略活动三:做一做 已知三角形的两角及其夹边,求作这个三角形.已知:线段∠α,∠β,线段c .求作:ΔABC ,使得∠A=∠α,∠B=∠β,AB=c.作法:(1)作线段BC=(2) 在BC 的同旁,作∠ =∠α, 作∠______=∠β,________与_______交于 .ΔABC 就是所求作的三角形.∠α+∠β应满足什么条件,才能作出ΔABC ?[动脑筋]例:已知一直角边和它相邻的一个锐角,如何作出这个直角三角形呢?a已知:锐角∠α 和线段a 如图.求作:ABC Rt ∆,使∠BCA=90度,AC=a∠A=∠α展示过程:略反馈练习:选一选1、利用尺规不能唯一作出的三角形是()A、已知三边B、已知两边及夹角C、已知两角及夹边D、已知两边及其中一边的对角2、利用尺规不可作的直角三角形是()A、已知斜边及一条直角边B、已知两条直角边 C.已知两锐角 D.已知一锐角及一直角边3、以下列线段为边能作三角形的是()A、2厘米、3厘米、5厘米B、4厘米、4厘米、9厘米C、1厘米、2厘米、3厘米D、2厘米、3厘米、4厘米学后反思:。
初中数学 教学设计2:三角形的尺规作图

三角形的尺规作图教学设计思想:本课的主要学习利用尺规按要求做三角形,表面上看是操作的过程,但教科书中提出了有关探究性问题,目的是引导学生关注作图背后的数学思考,即用尺规作三角形用到了两个三角形全等的条件,因此本课教学应引导学生积极思考,使学生体会到,作图的每一步骤都是有根有据的。
教学目标:知识与技能:1.会利用尺规作三角形:已知三边作三角形,已知两角及夹边作三角形,已知两边及夹角作三角形。
2.会写出三角形的已知、求作和作法。
3.能对新作三角形给出合理的解释。
过程与方法:1.在用尺规作三角形与已知三角形的过程中,体会、思考作图的合理性及依据。
2.在作图中领会设计作图过程,大胆尝试,动手作图,提高有条理的叙述问题及解决问题的能力情感态度价值观:1.通过师生共同观察、探索、交流、操作,品尝成功的喜悦,形成良好的思维品质,养成科学严谨的学习态度。
2.体会数学作图语言和图形的和谐统一。
教学重点:熟练掌握五个基本作图,作图时要做到规范使用尺规,规范使用作图语言,规范地按照步骤作出图形。
教学难点:作图语言的准确应用,作图的规范与准确。
教学用具:直尺,圆规教学过程:一、复习知识,引入新课谁能画一条线段等于已知线段、画一个角等于已知角?有几种方法?你用到了几种作图工具?根据什么判断你画的线段等于已知线段、画的角等于已知角?师:刚才有同学只用圆规和没有刻度的直尺就能做出线段和角,这种作图方法就是尺规作图。
今天我们来研究用尺规作图画三角形。
二、讲授新课师:若已知三边,如何作出一个三角形?(教师在黑板上画出如图1(1)的三条线段a、b、c,然后请一名学生上黑板作图,布置其他学生在下面做.学生完成作图后,请他口述作图过程.)生:作一条直线,在直线上截取线段AB=c.分别以A、B为圆心,以线段b、a为半径作弧,两弧相交于点O,连结AC、BC,则△ABO就是所求作的三角形.(教师根据学生作图的情况予以讲评,提醒学生注意作图工具的正确使用和作图语言的准确表达.)师:每个人按照上面的方法作出的三角形是唯一的三角形吗?请你验证自己的结论。
13.4《尺规作图》导学案2

13.4 尺规作图(2)学习目标:1.掌握三种尺规作图的方法及一般步骤,并能熟练掌握基本作图语言。
2.通过动手操作、合作探究,培养学生的作图能力、语言表达能力、逻辑思维和推理能力。
3.激情投入,全力以赴,认识到尺规作图与实际生活的紧密联系,激发学生的学习兴趣重点:掌握经过一已知点作已知直线的垂线,作已知线段的垂直平分线 难点:尺规作图的理论依据 导学过程 预习88--90 一.复习已知如图,ΔABC ,求作ΔA'B'C',使ΔA'B'C'≌方法1: 方法2:二.新知探究(1)经过一已知点作已知直线的垂线 已知:直线l 及其外一点C . 求作:过C 点垂直于直线l 的直线.作法:①以 点为圆心,以大于C 点到直线L 的距 离为半经画弧,交直线于A 、B 两点;②分别以 、 两点为圆心,以大于1/2AB 的 长度为半径画弧,两弧相交于D 点;③过 、 两点作直线 ,即为所求作的垂线. 证明:AB ClCl如果过直线上一点作已知直线的垂线 能否利用画平角的平分线的方法解决呢? 试试看,自己完成整个作图. 作法:(2)画线段的垂直平分线已知:线段AB ,画出它的垂直平分线.作法:①分别以 、 两点为圆心,以大于AB 线段一半的长为半径画弧,两弧交于C 、D 两点; ②过C 、D 两点作直线,即为所求作线段AB 的 垂直平分线. 证明: 三.练习1.如图,过点P 画∠O 两边的垂线2.已知:线段a 和b ,求作:一个Rt △ABC,使它的两条直角边分别等于线段a 和b 。
作法:ABABCD。
冀教版数学八年级上册13.4《三角形的尺规作图》教学设计

冀教版数学八年级上册13.4《三角形的尺规作图》教学设计一. 教材分析冀教版数学八年级上册13.4《三角形的尺规作图》是学生在学习了三角形的基本概念、性质和三角形的全等、相似后的内容,是对学生尺规作图能力的进一步要求。
本节内容通过让学生亲手作图,培养学生的观察能力、动手能力、逻辑思维能力,让学生体会数学的严谨性,提高学生学习数学的兴趣。
二. 学情分析学生在之前的学习中已经掌握了尺规作图的基本方法,对三角形的基本概念、性质和全等、相似也有了一定的了解。
但部分学生在尺规作图时仍然存在操作不规范、观察不细致的问题,对于一些复杂图形的作图还缺乏思路。
三. 教学目标1.知识与技能:掌握三角形尺规作图的方法,能独立完成一些简单的三角形尺规作图题目。
2.过程与方法:通过动手实践,提高观察能力、动手能力和逻辑思维能力。
3.情感态度价值观:培养学生对数学的兴趣,体会数学的严谨性。
四. 教学重难点1.重点:三角形尺规作图的方法。
2.难点:对于一些复杂图形的作图思路。
五. 教学方法采用问题驱动法、分组合作法、师生互动法等,让学生在动手实践中掌握三角形尺规作图的方法。
六. 教学准备1.教具:尺规、直尺、圆规、三角板等。
2.教学素材:一些三角形尺规作图的题目。
七. 教学过程1.导入(5分钟)教师通过向学生展示一些生活中的三角形图形,引导学生思考如何用尺规作图来构造这些三角形。
让学生体会到数学与生活的紧密联系,激发学生的学习兴趣。
2.呈现(10分钟)教师向学生讲解三角形尺规作图的基本方法,并通过具体的例子进行演示。
学生在教师指导下,动手实践,尝试完成一些简单的三角形尺规作图题目。
3.操练(10分钟)学生分组合作,共同完成一些中等难度的三角形尺规作图题目。
教师巡回指导,解答学生的问题,纠正学生的错误操作。
4.巩固(10分钟)教师选取一些学生完成的题目,进行讲解和分析,让学生理解三角形尺规作图的原理和方法。
学生对照自己的作品,找出不足之处,进行改进。
华东师大版八年级数学上册13.4.2尺规作图(2)导学案

南城中学八年级数学导学案班级:编制:八年级数学备课组课题:13.4.2尺规作图(2) 课时:第课时学习目标:1.了解两种基本作图:经过一已知点作已知直线的垂线;作已知线段的垂直平分线.并能掌握基本步骤.2.会解尺规作图题,会写已知、求作和作法,能掌握准确的作图语言.重点:画图.难点:作图的主要画法及尺规作图的应用.预习案阅读教材P88-89内容,并解决下面问题.1.点和直线的位置关系有两种:⑴;⑵.2.“经过已知直线上一点作这条直线的垂线”的实质是作一个平角的并反向延长;“经过已知直线外一点作这条直线的垂线”实质是相当于作一个的角平分线.3.用尺规作线段AB的垂直平分线.(不写作法保留作图痕迹)探究案探究一按教材画法画过一点作已知点垂线3.过点C作直线AB的垂线的思想方法是把这个问题转化为作_________ 的方法来解决. 探究二过一点作直线的垂线的应用4.利用直尺和圆规作一个等于45°的角.探究三作已知线段的垂直平分线作线段AB的垂直平分线.练习案1.用尺规作图,不能作出唯一三角形的( )A.已知两角和夹边B.已知两边和其中一边的对角C.已知两边和夹角D.已知两角和其中一角的对边2.用尺规作图,不能作出唯一直角三角形的是( )A.已知两条直角边B.已知两个锐角C.已知一直角边和一锐角D.已知斜边和一直角边姓名:BA1.如图1经过已知直线AB和AB上一点C,求作出直线AB的垂线.2.如图2,经过已知直线AB和AB外一点C,求作出直线AB的垂线.BA A BB3.如图1,过点P 作∠O 两边的垂线.8.如图6,作△ABC 边BC 上的高和AB 边的垂直平分线.4.如图2,请把线段AB 四等分.5.如图3,已知∠AOB ,作∠AOB 的平分线OC ,并在OC 上取一点P ,过P 作∠AOB 的两条边的垂线,垂足为M 、N ,探究PM 与PN 有怎样的大小关系.6.画一个等腰△ABC ,使底边长BC=a ,底边上的高为h ,如图4,(要求:用尺规作图,保留作图痕迹,写出已知,求作,不写作法和证明).7.已知:如图5,线段a ,b ,a >b .求作:Rt △ABC ,使∠C=90°,AC=a ,BC=b .*9.如图⑴,已知直线l 及l 同旁的两点A 、B ,在直线l 上求作一点P ,使AP +PB 的值最小.变式:如图⑵,在直线l 上求作一点P ,使PB -AP 的值最大.变式:如图⑶,在直线l 上求作一点P ,使|PB -AP|的值最小(或距离相等).ah图4图1B O A 图5a b l ⑴ l ⑵ A B C图6l ⑶。
8三角形的尺规作图

α初二数学三角形的尺规作图导学案教学目标:1、在分别给出的两角夹边、两边夹角和三边的条件下,能够利用尺规作三角形。
2、能结合三角形全等的条件与同伴交流作图过程和结果的合理性。
准备活动:已知线段a ,求作线段AB ,使得AB=a 。
(1) 已知:∠α求作:∠AOB ,使∠AOB=∠α(3) 已知:线段a 求作线段AB=2a.教学过程:内容一 (作一个三角形与已知三角形全等)1、已知三角形的两边及其夹角,求作这个三角形.已知:线段a ,c ,∠α。
求作:ΔABC ,使得BC= a ,AB=c ,∠ABC=∠α。
作图:同桌互相说一说作法,对比一下,你们所做的三角形全等吗?为什么?跟踪练习:1、求作一直角三角形,使其两直角边分别等于如图所示的已知线段a,b2、已知三角形的两角及其夹边,求作这个三角形.已知:线段∠α,∠β,线段c 。
求作:ΔABC ,使得∠A=∠α,∠B=∠β,AB=c 。
作法:(1)作____________=∠α;(2) 在射线______上截取线段_________=c;(3) 以______为顶点,以_________为一边,α作∠______=∠β,________交_______于点_______.ΔABC 就是所求作的三角形.作图:跟踪练习::已知∠α和线段a ,用尺规作一个三角形,使其一个内角等于∠α,另一个内角等于2∠α,且这两个内角的夹边等于a3、已知三角形的三边,求作这个三角形.已知:线段a ,b ,c 。
求作:ΔABC ,使得AB=c ,AC=b ,BC=a 。
课堂测试:已知线段a,用尺规作ΔABC ,使得AB= a ,BC=AC=2a。
用尺规作三角形(七年级下册 思维可视化导学案)
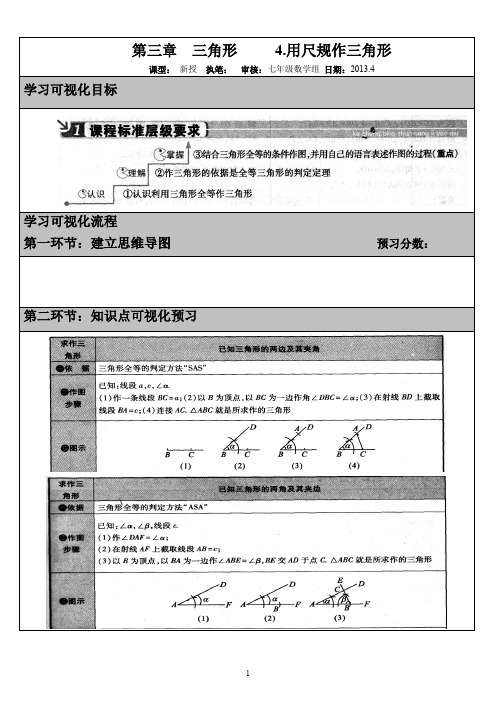
第三章 三角形 4.用尺规作三角形
课型: 新授 执笔: 审核:七年级数学组பைடு நூலகம்日期:2013.4
学习可视化流程 第一环节:建立思维导图
第二环节:知识点可视化预习
预习分数:
1
第三环节:探究可视化解题
第四环节:总结可视化解题规律
知识点
尺规作图
难点 分析
第四环节:总结可视化解题规律
知识点
尺规作图
难点 分析
2
第五环节:方法可视化巩固
同底数幂乘法
知识点
难点 分析
同底数幂乘法
知识点
难点 分析
3
第六环节:思维可视化检测
第七环节:课后可视化反思(请绘制本节课的“问题树”,有疑惑的地方,用红笔标注)
第八环节:今天你的学习真棒啊!明天你的“问题树”希望能结出更多的果实!
放学前将本节课“问题树”导学案全部完成后,上交给老师。
教师评语:
教师评分:
4
杨陵区第三中学八年级数学上册第13章全等三角形13.4尺规作图第2课时教案新版华东师大版

第2课时尺规作图(2)【基本目标】1.进一步掌握并熟练尺规作图的方法及一般步骤;2.介绍另两种基本作图,明确尺规作图的意义;3.熟练掌握基本作图语言.【教学重点】掌握过一点作已知直线的垂线,作线段的垂直平分线,掌握画一个角的角平分线.【教学难点】理解作图的理论依据以及利用基本作图画一些其他图形.一、创设情景,引入新课复习提问:(1)什么是尺规作图?基本作图?(2)我们已经学习了哪两种基本作图?(3)在练习本上画出这两个基本作图,并准确写出作法.圆规和直尺除了可以画出上述两个图形外,还可以画出哪些图形呢,这节课我们再介绍两个基本作图.二、师生互动,突破难点画线段的垂直平分线.分析:线段的垂直平分线上的点到线段两端点的距离相等;反过来,到线段两端点距离相等的点在线段的垂直平分线上.因此如果能找到两个到线段两端点的距离相等的点,那么过这两点就可以画出线段的垂直平分线.已知:线段AB.求作:线段AB的垂直平分线.作法:1.分别以点A和点B为圆心,大于12AB的长为半径画弧,两弧相交与点M和N.2.画直线MN.所以直线MN就是线段AB的垂直平分线.注:1.若半径等于或小于12AB,两弧就没有交点.2.直线MN与线段AB的交点,就是AB的中点,所以我们也可以用这种方法作线段的中点.引导学生思考:(1)已知直线上的一点作这条直线的垂线;(2)已知直线外的一点作这条直线的垂线.三、随堂练习,巩固新知完成练习册中本课时对应的课后作业部分,教师及时点评.四、典例精析,拓展新知例如图,过点P画∠O两边的垂线.【分析】角的两边可看作两条直线,点在直线外,故可归结为经过直线外一点作这条直线的垂线.解:【教学说明】通过本例旨在基本作图在几何作图题中的运用,注意先画草图,找出作图顺序再操作.五、运用新知,深化理解完成教材P91第4、5题.六、师生互动,课堂小结通过对基本作图的学习,掌握作图的一般步骤,熟练叙述一些作图的规范语句,主要有:(1)过点×、点×作直线××;或作直线××,或作射线××;(2)连结两点×、×;或连结××;(3)在××上截取××=××;(4)以点×为圆心,××为半径画弧(或圆);(5)以点×为圆心,××为半径画弧,交××于点×;(6)分别以点×、点×为圆心,以××、××为半径画弧,两弧相交于点×、×.完成练习册中本课时对应的课后作业部分.这节课内容较多,前三个基本作图较简单,主要是学生自学后独立操作,教师演示的目的是规范作图语言,搞清其中的几何道理.后两个作图实际上用到了转化思想,较为复杂,要让学生搞明白作图的原理,是掌握作图步骤的关键.运用基本作图解作图题时,应让学生先分析作图顺序后,再完成.对于作图语言应逐步规范.学习资料八年级数学下册第六章平行四边形 1 平行四边形的性质第1课时平行四边形的边角特征教案(新版)北师大版班级:科目:1 平行四边形的性质第1课时平行四边形的边角特征【知识与技能】探索并掌握平行四边形的性质,并能简单应用.【过程与方法】经历探索平行四边形有关概念和性质的过程,在活动中发展学生的探究意识和合作交流的习惯。
《三角形的尺规作图》教案 (同课异构)2022年冀教版
§27.3 过三点的圆一、课题 §27.3 过三点的圆 二、教学目标1.经历过一点、滦县第五中学八年级数学导学案 时间: 学案编号:设计人 :郑爱平 审核人: 审批人:班级: 姓名:附记 课题:课型: 新授课时:1附记教学目标 知识目标:会利用尺规作出:三边作三角形,两角及夹边作三角形,两边及夹角作三角形.会写出、求作和作法.2.能力目标:在用尺规作三角形与三角形的过程中,体会、思考作图的合理性及依据.领会设计作图过程,提高表达问题及解决问题的能力。
3.情感目标:品尝成功的喜悦,形成良好的思维品质. 重点:熟练掌握五个根本作图,作图时要做到标准使用尺规,标准使用作图语言,标准地按照步骤作出图形.难点:作图语言的准确应用,作图的标准与准确.教学方法 启发式谈话法学习方法:自主探究 合作交流 精讲点拨 反响纠正【教学过程】 一、预习导航:怎样作一条线段等于线段,怎样作一个角等于角?怎样用尺规作三角形呢? 活动1 认识直尺和圆规1、以点O 为圆心,以1为半径,画一条弧,请指出到O 点距离为1的点,这样的点有多少?2.分别以A ,B 为圆心,以1,1.5为半径,画出两条弧,图中到A 点距离为1的点有多少?到B 点距离为1.5的点有多少?到A 点距离为1并且到B 点距离为1.5的点有多少?什么是尺规作图?生: 。
二、合作探究、展示交流:活动2 假设三边,如何作出一个三角形?请看课本P52的作图过程,然后考虑,我们是如何确定△ABC 的三个顶点的?. (教师在黑板上画出如图1(1)的三条线段a 、b 、c ,然后请一名学生上黑板作图,布置其他学生在下面做.学生完成作图后,请他口述作图过程.)活动3 三角形的两个角分别等于∠a ,∠b ,这两角所夹的边等于a 如图,按以下步骤作出这个三角形.第一步:作一条线段AB ,使得AB=a 。
第二步:作∠BAD=∠a ,∠ABE=∠b 第三步:取AD,BE 的交点为C ,连结AC,BC ,得到△ABC.把自己作出的三角形和其他同学作出的三角形进行比拟,这些三角形全等吗?为什么?三、拓展提高,能力提升。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题 1.4三角形的尺规作图课型自学互学展示
学习目标1、能够利用尺规作三角形.
2、能结合三角形全等的条件与同伴交流作图过程和结果的合理性.
3、培养学生实际动手能力和合作、自主探究的能力.
重点根据题目的条件作三角形. 难点探索作图过程.
环节
预设
学法建议课堂设计
自学作三角形的几种方法和情形,然后尝试作三角形饼清楚必须的条件,练习后巩固作角及三角形.
自学课本一、前置作业
1、全等三角形的判定方法有:
2、你都学过哪些尺规作图?
3、
称为尺规作图.
4、作一条线段等于已知线段.
已知:线段AB.
求作:线段A′B′
,使A′B′=AB.
A B
5、作一个角等于已知角.
已知:∠AOB.
求作:∠A’O’B’
使∠A’O’B’=
∠AOB.
认真思考充分发挥小组作用
[做一做]:
已知三角形的两边及其夹角,求作这个三角形.
已知:线段a,c,∠α.
求作:ΔABC,使得BC= a,AB=c,∠ABC=∠α.
作法与过程:
[做一做] 已知三角形的两角及其夹边,求作这个三角形. 已知:线段∠α,∠β,线段c.
求作:ΔABC,使得∠A=∠α,∠B=∠β,AB=c.
已知线段c b a ,,,如何用直尺(没有刻度)和圆规作
ABC 使得c AB b AC a BC ,,(三边符合三角形的条件)
a
b c
作法:[动脑筋]
你能用尺规作一个等腰三角形,使它的底边长为a ,底边上的高为b 吗?
a
b
[选一选]
1、利用尺规不能唯一作出的三角形是(
)A 、已知三边
B 、已知两边及夹角
C 、已知两角及夹边
D 、已知两边及其中一边的对角
2、以下列线段为边能作三角形的是(
)A 、2厘米、3厘米、5厘米
B 、4厘米、4厘米、9厘米
C 、1厘米、2厘米、3厘米
D 、2厘米、3厘米、4厘米
课后检测
课后反思1、已知:M为∠AOB边上的一点,如图所示,过M作直线CD,使得CD//OA.。
