信息论与编码第5章 信源编码技术
信息论与编码Chapter 5

15
5.2 无失真信源编码
更一般的弱大数定理
C SWUST 2011 - All rights reserved
16
5.2 无失真信源编码
AEP( Asymptotic Equipartition Property) 渐进等同分割原理
n→∞
等同分割-> 等概率-> 最大熵定理-> 定长编码定理
C SWUST 2011 - All rights reserved
信源编码
source coding
C SWUST 2011 - All rights reserved
西南科大信息工程学院—马强
引子
信源熵:H∞ (X)是理论上传输信源所需的最少比 特数;实际中存在信息冗余,如何减少或消除这 些冗余? 信息率失真函数:在一定失真允许下,所需要的 传输信源的最小比特数;如何来实现这一过程? 信源编码:无失真信源编码(第一极限定理)、限 失真信源编码(第三极限定理)、信道编码定理(第 二极限定理)
C SWUST 2011 - All rights reserved
27
5.2 无失真信源编码
香农编码方法 Fano编码方法 Huffman编码方法
Huffman编码注意: Huffman编码注意:
1. 如何使得码方差变得很小? 1. 如何使得码方差变得很小? 2. 初始编码时,符号数目的个数应该满足什么条件? 2. 初始编码时,符号数目的个数应该满足什么条件? 28 3. 长序列编码,可以使平均码长降低 SWUST 2011 - All rights reserved 3. 长序列编码,可以使平均码长降低
17
5.2 无失真信源编码
AEP的另外一种描述
《信息论与编码》课件第5章 信源编码技术

❖ 例5.2对例5.1的信源进行费诺编码,具体编码过程如下
消息符 号
概率
a1
0.20
a2
0.19
a3
0.18
a4
0.17
编码效率为
H (X ) 2.61 0.953
L 2.74
➢ 显然,费诺码要比上述香农码的平均码长小,编码效率高。
➢ 从上面的例子可以看出,p(a4)<p(a2),而码长L4<L2,从 统计角度来看,平均码长一定不是最短的;
➢ 如果将两个符号对应的码字互换,这样编码得到的平均码长
肯定小于原来的平均码长。尽管如此,费诺码的平均码长仍
10 2
11 2 010 3
011 3
方法1 方法2
❖ 根据两种方法的编码结果,计算两种哈夫曼码的平 均码长,结果是两种编码方法的平均码长相等,即
7
L p(ai )li =2.2 码元/符号 i 1
编码效率也相等,都为 H (X ) =0.965
,L
但是两种码的质量不完全相同,编码质量可以用码方差衡量,即
a5
0.15
a6
0.10
a7
0.01
第一次 分组
0
1
第二次 分组
0 1 0
1
第三次 分组
0 1 0
1
第四次 分组
0 1
二元码字
00 010 011 10 110
1110
1111
码长
2 3 3 2 3
4
第5章:信源编码

可以看出,编码效率并不是很高。
4、费诺编码
将概率按从大到小的顺序排列,令:
p(x1)≥ p(x2)≥…≥ p(xn)
按编码进制数将概率分组,使每组概率尽可能接近或相
等。如编二进制码就分成两组,编 m 进制码就分成 m
组。
给每一组分配一位码元。 将每一分组再按同样原则划分,重复步骤 2 和 3,直 至概率不再可分为止。
麦克米伦不等式:设信源为 U u1 , u2 ,, un ,对其进行r 元信源编码,相应码字长度为 l1 , l2 ,, ln ,则唯一可译码 存在的充要条件是:
r
i 1
n
li
1
不同编码方式的衡量标准
平均码长:对离散无记忆信源进行信源编码,设编码后各个 码字的码长分别为
信源熵为:H(X)=2.75(比特/符号) 平均码长为:
K (0.25 0.25) 2 0.12 2 3 0.0625 4 4 2.75 (比特/符号)
编码效率为η=1。之所以如此,因为每次所分两组的 概率恰好相等。
5、哈弗曼编码 哈夫曼(Huffman) 编码是一种效率比较高的变长无失 真信源编码方法。
0 1
即时
s2
任何一个码字不是其它码字的延长或前缀
即 时 码
即时码的判决准则
克拉夫特不等式:设信源为 U u1 , u2 ,, un ,对其进行r 元信源编码,相应码字长度为 l1 , l2 ,, ln ,则即时码存在 的充要条件是:
r
i 1
n
li
1
唯一可译码的判决准则
2、编码的分类 信源编码可看成是从信源符号集到码符号集的一种映射,即将 信源符号集中的每个元素(可以是单符号,也可以是符号序列)映 射成一个长度为n的码字。对于同一个信源,编码方法是多种的。 【例5.1】 用{u1 ,u2 ,u3,u4, } 表示信源的四个消息,码符号集 为{0,1},表1列出了该信源的几种不同编码。 表1 同一信源的几种不同编码 信 源 消息 u1 u2 u3 各消息 概率 q(u1) q(u2) q(u3)
信息论与编码第5章限失真信源编码

第一节 失真测度
• 以上所举的三个例子说明了具体失真度的定义. 一般情况下根据实际信源的失真, 可以定义不同 的失真和误差的度量.
• 另外还可按照其他标准, 如引起的损失、风险、 主观感受上的差别大小等来定义失真度d(ui,vj).
• 从实用意义上说, 研究符号实际信源主观要求的、 合理的失真函数是很重要的.
第一节 失真测度
设信源变量为U={u1,…,ur}, 接收端变量为 V={v1,…,vs}, 对于每一对(u,v), 指定一个非负 函数
d(ui,vj)≥0 称为单个符号的失真度(或称失真函数). 失真函数用来表征信源发出符号ui, 而接收端再现 成符号vj所引起的误差或失真. d越小表示失真越小, 等于0表示没有失真.
➢ 应该指出, 研究R(D)时, 条件概率p(v|u)并没有 实际信道的含义. 只是为了求互信息的最小值而引 用的、假想的可变试验信道. ➢ 实际上这些信道反映的仅是不同的有失真信源编 码或信源压缩. 所以改变试验信道求平均互信息最 小值, 实质上是选择编码方式使信息传输率为最小.
率失真理论与信息传输理论的对偶关系
– 接收端获得的平均信息量可用平均互信息量I(U;V)表示;
– 这就变成了在满足保真度准则的条件下 D D 找平均互信息量I(U;V)的最小值.
,寻
– 因为BD是所有满足保真度准则的试验信道集合, 即可以 在D失真许可的试验信道集合BD中寻找某一个信道 p(vj|ui), 使I(U;V)取最小值.
本章所讨论的内容是量化、数模转换、频带 压缩和数据压缩的理论基础.
前言
本章主要介绍信息率失真理论的基本内容, 侧 重讨论离散无记忆信源.
首先给出信源的失真度和信息率失真函数的定 义与性质, 然后讨论离散信源的信息率失真函数计 算. 在这个基础上论述保真度准则下的信源编码定 理.
第五章信源编码(编码定义及定长编码)

所以送一个信源符号x需要的平均信息率为:
K KL logm L
信息率最小就是找到一种编码方式使
KL logm L
最小。
5.2.1定长编码定理
定义:各个码字码长都相等的码 定长码中每个码字长度相等,所以只要定长码是非奇异
码,则必为唯一可译码
非奇异码 唯一可译码
即时码
非奇异码 唯一可译码
即时码
变长码
等长码
消息
概率
C1
C2
C3
C4
C5
C6
u1
1/2
000
0
0
0
1
01
u2
1/4
001
01
10
10
000
001
u3
1/16
010
011
110
1101 001
100
u4
1/16
011
0111 1110 1100 010
101
u5
1/16
100
01111 11110 1001 110
110
u6
1/16
101
解码:按照码符号的顺序,从根节点依次查询到终端节点,就得到对应的 信源符号。再从根节点对剩下的码符号序列做相同的处理,直到处理完码 符号序列中所有的码符号
对应表中的码4分析
A01Fra bibliotek01
1
0
0
1
0
10 1
0
1
000
001 010
011 100 101 110
111
一阶节点 二阶节点 三阶节点
唯一可译码存在的充要条件
我们之后介绍的是二元信道中的编码。
第五章 信源编码

第五章信源编码信息论基础第五章信源编码 本章主要讨论的问题:5.1 离散信源编码5.1.1 编码器5.1.2分组码5.1.3定长码5.1.4 变长码5.2 连续信源编码5.3 相关信源编码简介信源编码:以提高通信有效性为目的的编码。
通常通过压缩信源的冗余度来实现。
采用的方法是压缩每个信源符号的平均比特数或信源的码率。
即同样多的信息用较少的码率传送,使单位时间内传送的平均信息量增加,从而提高通信的有效性。
信源编码理论是信息论的一个重要分支,其理论基础是信源编码的两个定理。
–无失真信源编码定理:是离散信源/数字信号编码的基础;–限失真信源编码定理:是连续信源/模拟信号编码的基础,如语音、图像等信号。
信源编码的分类:离散信源编码、连续信源编码和相关信源编码三类。
–离散信源编码:独立信源编码,可做到无失真编码;–连续信源编码:独立信源编码,只能做到限失真信源编码;–相关信源编码:非独立信源编码。
编码器编码器可以看作这样一个系统,它的输入端为原始信源S ,其符号集为;而信道所能传输的符号集为。
编码器的功能是用符号集X 中的元素,将原始信源的符号变换为相应的码字符号,所以编码器输出端的符号集为称为码字,为码字的码元个数,称为码字的码字长度,简称码长。
码字的集合C 称为码书。
称为码元。
12{,,...,}q S S S S =12{,,...,}r X x x x =12{,,...,}q S s s s =12{,,...,}r X x x x =编码器12:{,,...,}q C W W W 12:{,,...,}q C w w w i S i w i w i L i w i w i x例:二元信道的信源编码器:码符号集X={0,1},如果要将信源通过二元信道传输,必须将信源编成二元码,这也是最常用的一种码。
等长码非等长码非奇异码非奇异码 等长码与变长码码中各个码字都是由同样多个码元构成的,称为等长码,反之,称为变长码。
第5章信源编码(1)

2
第5章 信源编码 章
信源编码的基础是信息论中的两个编码定理: 信源编码的基础是信息论中的两个编码定理: 无失真编码定理 限失真编码定理 编码定理不但证明了必定存在一种编码方法,可使代码 编码定理不但证明了必定存在一种编码方法, 的平均长度可任意接近但不低于符号熵, 的平均长度可任意接近但不低于符号熵,而且还阐明了 达到这一目的,就要使概率与码长相匹配. 达到这一目的,就要使概率与码长相匹配.
2
+2
2
+2
3
9 = >1 8
因此不存在满足这种K 的唯一可译码. 因此不存在满足这种 i的唯一可译码.
普通高等教育"十五"国家级规划教材《信息论与编码》 曹雪虹等编著
17
5.1 编码的定义
{1,01,001,000} 惟一可译码 {1,01,101,000}不是惟一可译码 不是惟一可译码 均满足克劳夫特不等式
15
5.1 编码的定义
唯一可译码存在的充分和必要条件 唯一可译码存在的充分和必要条件 存在
m -K i ≤ 1 各码字的长度K 应符合克劳夫特不等式 克劳夫特不等式: 各码字的长度 i 应符合克劳夫特不等式: ∑
i =1 n
其中m是进制数; 是信源符号数 是信源符号数. 其中 是进制数;n是信源符号数. 是进制数 如果码是唯一可译码,则必满足该不等式; 如果码是唯一可译码,则必满足该不等式; 如果满足不等式,则这种码长的唯一可译码一定存在, 如果满足不等式,则这种码长的唯一可译码一定存在, 但并不表示所有满足不等式的码一定是唯一可译码; 但并不表示所有满足不等式的码一定是唯一可译码; 该不等式是唯一可译码存在的充要条件, 该不等式是唯一可译码存在的充要条件,而不是唯一可 存在的充要条件 译码的充要条件. 译码的充要条件.
第五章信源编码

(每个符号有m种可能值)进行定长编码。对任意的 0,0
只要
KLHL(X)ε L logm
,则:当L足够大时,必可使译码差
错小于 (几乎无失真编码);反之,当 KLHL(X)2ε L logm
时,译码差错一定是有限值,而当L足够大时,译码几乎必定 出错(译码错误概率接近于1)。
1、解释: KL/L-----编码时,每个信源符号输出的 码长。即每个信源符
其中:左边--KL长码字所能携带的最大信息量, 右边--L长信源序列携带的信息量。
定理表明,只要码字所能携带的信息量大于信源序列输出的信 息量,则可以实现几乎无失真编码,当然条件是L足够大。 反之,不可能实现无失真的编码,也就是不可能做一种编码 器,能使收端译码时差错概率趋于零。
2、举例: (1 单 ) 符号 X A 信 {a1,a源 2...8} ., .n,a 8 ,等,L 概 1 。 分 H 1(X )H (X )lb3 8b /信 it 源符号。 若进行二进B制 {0编 ,1}m ,码 2,据定理,只要 K LLKLH lo(X g)m 3码元 /信源符号,就 无可 失以 真实 编现 码 事实上 3位,二进制码确实示 可8种 以信 表源符号。
或映射规则 元 b 转 j,j换 1,2..m 成 .构由 成码 的码 (也元 称序 为列
y i,i1,2..n.L。
f:xiyi
码K 长 L, i i1,2..n.L .; 平 均_KL 码 nL长 KLPi(: yi)码/元 符 号 序
i1 _
定长编 KL1 码 KL: 2...K .L .L n.KL, KLKL
注:奇异码一定非惟一可译。(非奇异码则不一定)
4、即时码和非即时码:
收到一个完整的码字后能立即译码,或曰及时可译---即时码
信息论与编码第5章

信息论与编码第5章第五章信源编码(第⼗讲)(2课时)主要内容:(1)编码的定义(2)⽆失真信源编码重点:定长编码定理、变长编码定理、最佳变长编码。
难点:定长编码定理、哈夫曼编码⽅法。
作业:5。
2,5。
4,5。
6;说明:本堂课推导内容较多,枯燥平淡,不易激发学⽣兴趣,要注意多讨论⽤途。
另外,注意,解题⽅法。
多加⼀些内容丰富知识和理解。
通信的实质是信息的传输。
⽽⾼速度、⾼质量地传送信息是信息传输的基本问题。
将信源信息通过信道传送给信宿,怎样才能做到尽可能不失真⽽⼜快速呢?这就需要解决两个问题:第⼀,在不失真或允许⼀定失真的条件下,如何⽤尽可能少的符号来传送信源信息;第⼆,在信道受⼲扰的情况下,如何增加信号的抗⼲扰能⼒,同时⼜使得信息传输率最⼤。
为了解决这两个问题,就要引⼊信源编码和信道编码。
⼀般来说,提⾼抗⼲扰能⼒(降低失真或错误概率)往往是以降低信息传输率为代价的;反之,要提⾼信息传输率常常⼜会使抗⼲扰能⼒减弱。
⼆者是有⽭盾的。
然⽽在信息论的编码定理中,已从理论上证明,⾄少存在某种最佳的编码或信息处理⽅法,能够解决上述⽭盾,做到既可靠⼜有效地传输信息。
这些结论对各种通信系统的设计和估价具有重⼤的理论指导意义。
§3.1 编码的定义编码实质上是对信源的原始符号按⼀定的数学规则进⾏的⼀种变换。
讨论⽆失真信源编码,可以不考虑⼲扰问题,所以它的数学描述⽐较简单。
图 3.1是⼀个信源编码器,它的输⼊是信源符号},,, {21q s s s S =,同时存在另⼀符号},,,{21r x x x X =,⼀般来说,元素xj 是适合信道传输的,称为码符号(或者码元)。
编码器的功能就是将信源符号集中的符号s i (或者长为N 的信源符号序列)变换成由x j (j=1,2,3,…r)组成的长度为l i 的⼀⼀对应的序列。
输出的码符号序列称为码字,长度l i 称为码字长度或简称码长。
可见,编码就是从信源符号到码符号的⼀种映射。
信息论与编码chapter5

渐进均分特性
典型序列的概率估计
设 x G 1 ( 满 足 公 式 5 .3 )
log p ( x ) N H (X )
N [ H ( X ) ] log p ( x ) N [ H ( X ) ]
设取2为底 2 N [ H ( X ) ] p ( x ) 2 N [ H ( X ) ]
(适用于离散信源的编码)
限失真信源编码: 信源符号不能通过编码序列无 差错地恢复。
(可以把差错限制在某一个限度内)
信源编码的目的:提高传输有效性,即用尽可能短 的码符号序列来代表信源符号。
§5.1 信源编码的相关概念
本节主要内容
一、信源编码器 二、码的分类 三、分组码
§5.1.1 信源编码器
将信源符号集中的每一个符号固定映 射成一个码字的码 分组码单符号信源编码器
第五章 无失真信源编码
主要内容
本章主要介绍无失真信源编码定理与一 些重要的无失真信源编码方法
一、概述 二、定长码 三、变长码
四、哈夫曼编码
信源编码:将信源符号序列按一定的数学规律映射 成由码符号组成的码序列的过程。 信源译码: 根据码序列恢复信源序列的过程。 无失真信源编码: 即信源符号可以通过编码序列 无差错地恢复。
若不满足上式 =
H (X
N
l N
l l
log r H ( X )
;Y )
N
l
) H (X
N
/ Y ) H (Y ) lH (Y ) l log r
H (X
) NH ( X )
H (X
N
/ Y ) NH ( X ) l log r 0
第5章信源编码

• 平均码长:
二元码符号 / 信源符号
• 编码效率:
• 输出的信息传输率:
再对长度 L 为 2 的信源序列进行 变长编码,其即时码如表: • 码字平均长度:
• 单个符号的平均码长 • 编码效率 • 输出的信息传输率: R2 = 0.961bit/ 二元码符号
H ( X )H ( X )
log m
log m
+1
离散平稳无记忆序列变长编码定理 对于平均符号熵为 HL(X) 的离散平稳无记忆信
源,必存在一种无失真编码方法,使平均信息率R
满足不等式:
其中 ε 为任意小正数。
无失真变长信源编码定理(香农第一定理)
对于平均符号熵为 HL(X) 的离散平稳无记忆信源(离散 无记忆信源 X 的 L 次扩展信源
非即时码 唯一可译码
即时码
非即时码 接收端收到一个完整的码字后,不能立即译码,还需 等下一个码字开始接收后才能判断是否可以译码。 码 3
即时码 ( 非延长码 ) ( 异前缀码 )
在译码时无需参考后续的码符号就能立即作出判断,
译成对应的信源符号。
码4
任意一个码字都不是其它码字的前缀部分
ai
码1
码2
编码后码字 Y1 , Y 2 , ‥ , Y n 码长分别为 K 1 , K 2 , ‥ , K n
码的平均长度为:
编码后的信息传输率为:
对于某一信源和某一码符号集,若有一个唯一可译 码,其平均长度小于所有其他唯一可译码的平均长 度,则称该码为最佳码(紧致码)。
单个符号变长编码定理
若离散无记忆信源的符号熵为 H(X) ,每个信源符号 用 m 进制码元进行变长编码,一定存在一种无失真 编码方法,其码字平均长度 K 满足下列不等式:
(信息论)第5章无失真信源编码
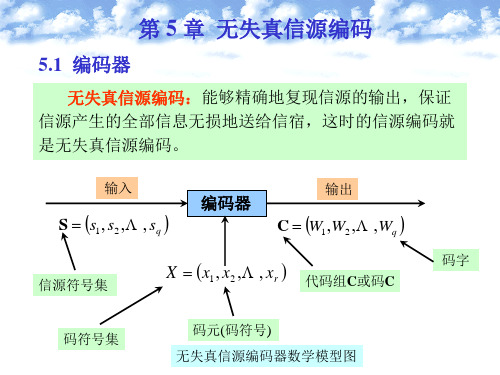
定长编码定理
定长信源编码定理讨论了编码的有关参数对译 码差错的限制关系
sq p s q
定理 5.3.1 设离散无记忆信源
S s1 P p s 1 p s 2 s2
的熵为H S ,其 N 次扩展信源为
S N 1 p 1 P
2 q p 2 p q
N N
现在用码符号集 X x1 , x2 ,, xr 对N次扩展信源 S N 进行长度为 l 的定长编码,对于 0, 0 ,只要满足
l H S N log r
则当 N 足够大时,译码错误概率为任意小,几乎可以实 现无失真编码。 反之,若满足
l H S 2 N log r
则不可能实现无失真编码。而当N足够大时,译码错误概 14 率近似等于1。
以上的定理5.3.1 和定理5.3.2实际上说明的是一个 问题,虽然该定理是在平稳无记忆离散信源的条件下 证明的,但它也同样适合于平稳有记忆信源,只要要 2 求有记忆信源的极限熵 H S 和极限方差 存在 即可。对于平稳有记忆信源,式(5.6)和式(5.7 ) 中 H S 应该为极限熵 H S 。
变长码(可变长度码)
2
奇异码:若码中所有码字都不相同,则称此码为非
奇异码。反之,称为奇异码。
同价码:每个码符号所占的传输时间都相同的码。定
长码中每个码字的传输时间相同。而变长码中的每个码 字的传输时间不一定相等。
表 5.1
信源符号si
信源符号出现概率 si p
第五章信源编码——信息论与编码

04:48
5
5.1 编码器及相关概念
为了分析方便和突出问题的重点,当研究信源 编码时,我们把信道编码和译码看成是信道的 一部分,从而突出信源编码。同样,在研究信 道编码时,可以将信源编码和译码看成是信源 和信宿的一部分,从而突出信道编码。
由码符号 xi 组成的输出序列 Wi 称为码字.
其长度 li称为码字长度或码长,全体码字 Wi 的 集合C称为码或码书 .
编码器将信源符号集中的信源符号 s(i 或长为N 的信源符号序列 i)变成由码符号组成的长为 的与信源符号一一对应的输出序列。即 :
si (i 1, 2, , q) Wi (i 1, 2, , q) ( xi1, xi2, , xili ), xij X
p(ai ) }
其中,
LN
p(i )li
为N次扩展信源的平均码长,
i 1
li 为信源符号扩展序列i 的码长.
LN N
为对扩展信源进行编码后,每个信源符号
编码所需的等效的平均码长。
04:48
33
要做到无失真的信源编码,平均每个信源符号 所需最少的r元码元数为信源的熵 Hr (S)。 即 它是无失真信源压缩的极限值。
04:48
3
信源编码的基本途径有两个:
一是编码后使序列中的各个符号之间尽可能地 互相独立,即解除相关性----方法包括预测编 码和变换编码.
二是使编码后各个符号出现的概率尽可能相等, 即均匀化分布----方法主要是统计编码.
04:48
4
信源编码常分为无失真信源编码和限失真信源 编码,前者主要用于文字、数据信源的压缩, 后者主要用于图像、语音信源的压缩。
信息论与编码技术第五章课后习题答案

码,并求出其编码效率。
解:
信源符号 概率 编码
码字 码长
X1
3/8 0
0
1
X2
1/6 1
0
10 2
X3
1/8
1
11 2
X4
1/8 2
0
20 2
X5
1/8
1
21 2
X6
1/12
2
22 2
H(X)=-((3/8)*log(3/8)+(1/6)*log(1/6)+(1/8)*log(1/8)+(1/8)*log(1/8)+(1/8)*log(1/8)+(1/12)*log(1/12))
=2.3852 (三进制单位/信源符号)
H3(X)= H(X)/ 1.5850=2.3852/1.5850= 1.5049(三进制单位/信源符号)
L =(3/8)*1+ (1/6)*2+ (1/8)*2+ (1/8)*2+ (1/8)*2+ (1/12)*2=1.625(码符号/信源符号)
η= H3(X)/ L =1.5049/1.625= 92.61 %
5.8 已知符号集合 {x1, x2 , x3,"} 为无限离散消息集合,它们出现的概率分别为 p(x1) = 1/ 2 , p(x2 ) = 1/ 4 , p(x3 ) = 1/ 8 , p(xi ) = 1/ 2i ,……。
(1) 用香农编码方法写出各个符号消息的码字。 (2) 计算码字的平均信息传输速率。
L =4*(1/4)*1=1(码符号/信源符号)
Rt= H(X)/(t* L )=1/(1*10*10-2)=10(比特/秒)
信息论与编码第5章

定长编码定理
• 定长编码定理:
• 由L个符号组成的、每个符号的熵为HL(X)的无记 忆平稳信源符号序列X1…Xl…XL,可用 K个符号 Y1…Yk…YK(每个符号有m种可能值)进行定长编 码。对任意ε>0,δ>0,只要
K L
log
m
H
L
(
X
)
则当L足够大时,必可使译码差错小于δ;反之,当
K L
L
log 2 n log 2 m
log 2
27
5
每个英文电报符号至少
要用5位二元符号编码 21
定长编码
• 实际英文电报符号信源,在考虑了符号出现的 概率以及符号之间的依赖性后,平均每个英文 电报符号所提供的信息量约等于1.4比特,大大 小于5比特。
• 编码后5个二元符号只携带约1.4比特信息量。 • 定长编码的信息传输效率极低。
X
Y
信源
信源编码器
信道
L长序列
码表
K长码字
20
定长编码
• 若对信源进行定长编码,必须满足:
nL mK 或 K log n L log m
• 只有当K长的码符号序列数 mK大于或等于信源的 符号数nL时,才可能存在定长非奇异码。
• 例如英文电报有27个符号,n=27,L=1,m=2(二元编码)
K
• 针对信源输出符号序列的统计特性,寻找一定的方 法把信源输出符号序列变换为最短的码字序列。
X
Y
信源
信源编码器
信道
码表
5
编码的定义
• 编码定理证明:
– 必存在一种编码方法,使代码的平均长度可任意 接近但不能低于符号熵;
– 达到这目标的途径就是使概率与码长匹配。 • 统计匹配编码:
第5章信源编码-信息论与编码(第3版)-曹雪虹-清华大学出版社

普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著
7
5.1 编码的概念
码可分为两类: 一、固定长度的码,码中所有码字的长度
都相同,如表5-1中的码1就是定长码 二、可变长度码,码中的码字长短不一,
如表中码2就是变长码。
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著
8
1
第5章 信源编码
信源编码的作用可归纳为:
(1) 符号变换:使信源的输出符号与信 道的输入符号相匹配;
(2)信息匹配:使信息传输率达到信道 容量;
(3) 冗余度压缩:使编码效率等于或接 近100%。
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著
2
第5章 信源编码
信源编码的基础是信息论中的两个编码定理:
每个符号序列xi依照固定码表映射成一个码字yi, yi=(yi1yi2…yil…yiL), yilB={b1,b2,…,bi,…,bm}
这样的码称为分组码,有时也叫块码。只有分组码才有对 应的码表,而非分组码中则不存在码表。
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著
6
5.1 编码的概念
9
5.1 编码的概念
(1)奇异码和非奇异码 若信源符号和码字是一一对应的,则该 码为非奇异码。反之为奇异码。 如表5-2中的码1是奇异码,码2是非奇异 码。
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著
10
5.1 编码的概念
(2)唯一可译码 任意有限长的码元序列,只能被唯一地 分割成一个个的码字,便称为唯一可译 码
如图5-1所示,如果信源输出符号序列长度L=1,
信源符号集A(a1,a2,…,an)
信息论与编码[第五章无失真信源编码定理与编码]山东大学期末考试知识点复习
![信息论与编码[第五章无失真信源编码定理与编码]山东大学期末考试知识点复习](https://img.taocdn.com/s3/m/80df4dc9b90d6c85ed3ac6c3.png)
第五章无失真信源编码定理与编码5.1.1 信源编码和码的类型1.信源编码2.码的类型若码符号集中符号数r=2称为二元码,r=3称为三元码,……,r元码。
若分组码中所有码字的码长都相同则称为等长码,否则称为变长码。
若分组码中所有码字都不相同则称为非奇异码,否则称为奇异码。
若每个码符号x i∈X的传输时间都相同则称为同价码,否则称为非同价码。
若分组码的任意一串有限长的码符号只能被唯一地译成所对应的信源符号序列则称为唯一可译码,否则称为非唯一可译码。
若分组码中,没有任何完整的码字是其他码字的前缀,则称为即时码(又称非延长码或前缀条件码),否则称为延长码。
本章主要研究的是同价唯一可译码.5.1.2 即时码及其树图构造法即时码(非延长码或前缀条件码)是唯一可译码的一类子码。
即时码可用树图法来构造。
构造的要点是:(1)最上端为树根A,从根出发向下伸出树枝,树枝总数等于r,树枝的尽头为节点。
(2)从每个节点再伸出r枝树枝,当某节点被安排为码字后,就不再伸枝,这节点为终端节点。
一直继续进行,直至都不能伸枝为止。
(3)每个节点所伸出的树枝标上码符号,从根出发到终端节点所走路径对应的码符号序列则为终端节点的码字。
即时码可用树图法来进行编码和译码。
从树图可知,即时码可以即时进行译码。
当码字长度给定,即时码不是唯一的。
可以认为等长唯一可译码是即时码的一类子码。
5.1.3 唯一可译码存在的充要条件(1)对含有q个信源符号的信源用含r个符号的码符号集进行编码,各码字的码长为l1,l2,…,l q的唯一可译码存在的充要条件是,满足Kraft不等式5.1.4 唯一可译码的判断法唯一可译码的判断步骤:首先,观察是否是非奇异码.若是奇异码则一定不是唯一可译码。
其次,计算是否满足Kraft不等式。
若不满足一定不是唯一可译码。
再次,将码画成一棵树图,观察是否满足即时码的树图的构造,若满足则是唯一可译码。
或用Sardinas和Patterson设计的判断方法:计算出分组码中所有可能的尾随后缀集合F,观察F中有没有包含任一码字,若无则为唯一可译码;若有则一定不是唯一可译码.上述判断步骤中Sardinas和Patterson设计的判断方法是能确切地判断出是否是唯一可译码的方法,所以可以跳过前三个步骤直接采用该判断法。
信息论与编码第五章

r
pE 1 pE s r r 1 s 1 p(ai b j ) log p(ai b j ) log p(ai b j ) log p(aibi ) log (r 1) p(ai | b j ) j 1 i * p ( ai | b j ) j 1 i 1 pE j 1 i * 1 pE j 1 i *
p ( ai b j )
pE (r 1)p(b1 ) p(b2 ) p(bs ) p E p E p E 0 r 1
第二项
s
1 pE 1 pE log 1 p ( ai | b j ) p ( ai | b j )
s
即
j 1 i *
第五章
有噪信道编码
无失真信源编码(无噪离散信道编码)的抗干扰能力很 脆弱,如把信源编码器的输出直接接入信道,必然会因干扰 造成错误,使通信不可靠,为了使通信既有效,又可靠,可 在以缩短平均码长、提高通信有效性为主要目标的信源编码 器的输出与信道的输入之间,对信源编码器输出的最佳码再 进行一次编码,以提高其抗干扰能力,称为信道编码。
1、输入端只有2个消息(符号)且等概出现,则每个消息携
带的信息量是 log M 1 bit / 符号 。 2、简单重复三次后,(三次无记忆扩展信道),入端有 2 3 8 个二进序列,但只选其中两个作为消息,M=2,每个消 1 息携带的信息量仍为 1bit ,但用三个符号,∴ R bit /符号。
p E min
1 8 1 p(b j | ai ) p 3 p p 2 p p 2 p p 2 p p 2 p p 2 p p 2 p 3 2 j 1 i * 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
哈夫曼码的主要特点 1、哈夫曼码的编码方法保证了概率大的符号对 应于短码,概率小的符号对应于长码,充分 利用了短码; 2、缩减信源的两个码字的最后一位总是不同, 可以保证构造的码字为即时码。 3、哈夫曼码的效率是相当高的,既可以使用单 个信源符号编码,也可以对信源序列编码。 4、要得到更高的编码效率,可以使用较长的序 列进行编码。
5.1.2费诺码
费诺码的基本思想: 1、按照累加概率尽可能相等的原则对信源符号 进行分组: 对于二元码,则每次分为两组; 对于d元码,则每次分为d个组。 并且给不同的组分配一个不同的码元符号。 2、对其中的每组按照累计概率尽可能相等的原 则再次进行分组,并指定码元符号,直到不能 再分类为止。 3、然后将每个符号指定的码元符号排列起来就 得到相应的码字。
算术编码
适用于JPEG2000,H.263等图像压缩标准。 特点: 1、随着序列的输入,就可对序列进行编码 2、平均符号码长 L 满足
1 H (X ) L H (X ) N
(最佳编码)
3、需要知道信源符号的概率 是对shanno-Fanno-Elias编码的改进。
累计分布函数的定义
H(X ) H(X ) L 1 log d log d
费诺码的最佳性
1、保证每个集合概率和近似相等,保证d个码元近 似等概率,每个码字承载的信息量最大,码长近似 最短。 2、是次最佳的编码方法,只在当信源符号概率满足:
p(ai ) d
时达最佳。
li
信源符号
a1 a2 a3 a4 a5 a6 a7 a8 a9
费诺二元码的编码步骤
1、将源消息符号按概率大小排序:
p1 p2 p3 pn
2、将依次排列的信源符号分为两大组,使每组的概 率和尽可能相等,且每组赋与二进制码元“0”和 “1”。 3、将每一大组的信源符号再分为两组,使每组的概 率和尽可能相等,且每组赋与二进制码元“0”和 “1”。 4、如此重复,直至每组只剩下一个符号。 信源符号所对应的码字即费诺码。
例5.2对例5.1的信源进行费诺编码,,具体编码过程参 见表5.2
根据每个信源符号的码长,得到每个符号的平均码长 7 为 L p(ai )li 2.74 码元/符号
i 1
用树码表示的费诺码编码过程
a1 , a2 ,, a7
0 1
a1 , a2 , a3
7
编码过程 0.4 0.4 0 0.2 1
码字 码长
Wi
0.6 0 0.4 1
li
2 2 2 3 3
}
0 1
}
}
}
1.0
00 10 11 010 011
方法2
合并后的 概率尽量 往上
根据两种方法的编码结果,计算两种哈夫曼码 的平均码长,相等,即
L p(ai )li =2.2 码元/符号
i 1 7
例5.4 设有离散无记忆信源的概率空间为
X a1 a2 a3 a4 a5 p 0.4 0.2 0.2 0.1 0.1
信源符号 概率
ai a1 a2 a3 a4 a5
p ( ai )
0.4 0.2 0.2 0.1 0.1 0.4 0.2 0.2 0 0.2 1
算术编码
对于长为n的符号序列 ( X 1 , X 2 ,...X n ) 序列个数共有 比如0,1) 分别是 对应概率
2
n
个(若每个符号可取2个值,
X1, X 2 ,..., X k ,....X 2n
p( X1 ), p( X 2 ),...p( X k ),...p( X 2n )
序列k的累计分布函数
5.1.1 香农码
香农码的根据:离散无记忆信源的自信息量 设离散无记忆信源所对应的概率空间为
X a1 p ( x) p (a ) 1 a2 p(a2 ) ar p(ar )
对应码字的长度Li应该满足下列关系
符号自信 息量
I ( xi ) li I ( xi ) 1
对信源
a1 X p1 a2 p2 ... ... aK pK
且假定 p1 p2 ... pK
对aK-1和aK的码字最后一位分别指定0、1,然后合并, 产生辅助符号a’k-1,做一辅助集 0 ' ' ' ‘ a a a a ... a k-1 k-1 ' 1 2 K 1 X ' ' ' ak 1 p1 p2 ... pK 1
H(X ) 编码效率也相等,都为 =0.965 L 两种码的质量不完全相同,用码方差衡量,即
,
2 2 l2 E ( l L ) p ( a )( l L ) i i i i 1
r
l12 1.36 l 22 0.16 由于方法2的码方差比方法1的码方差小许多, 所以方法2编码质量好。
0 1.0
0.39 1
信源符号 概率
0.26
0.26
a1 a2 a3 a4 a5 a6 a7
0.20 0.19 0.18 0.17 0.15 0.10 0.01
码字 码长li
0.19
0.18 0.17
10 11 000 001
2 2 3 3
0
010
3
0110 4
0111 4
平均码长
L p(ai )li 2.72 比特 / 符号
i
这样就可以保证对于每个信源符号而言,码字长度是 最佳的 。
香农码编码方法 (1)将信源消息符号按其出现的概率大小依次排列为
p1 p2 pn
(2)确定每个信源符号的码长,同时保证码长为满足下 列不等式的整数 lbp(ai ) li lbp(ai ) 1 (3)为了编成唯一可译码,计算第i个消息的累加概率
1
a1
00 0
a2 , a3
a4
0 110
a5 , a6 , a7
1
a2
010
a3
011
1
10
a5
0
a6 , a7
1
1110
a6
1111
a7
编码效率为
总结:
H ( X ) 2.61 0.953 2.74 L
1、费诺码要比上述香农码的平均码长小,编码 效率高。 2、从上面的例子可以看出,p(a4)<p(a2),而码 长L4<L2,从统计角度来看,平均码长一定不是 最短的; 如果将两个符号对应的码字互换,这样编码 得到的平均码长肯定小于原来的平均码长。 3、费诺码的平均码长满足
编码过程 0.4 0.4 0 0.2 1
码字 码长
Wi
0.6 0 0.4 1
li
1 2 3 4 4
方法1
}
0 1
}
}
}
1.0
1 01 000 0010 0011
信源符号 概率
ai a1 a2 a3 a4 a5
p ( ai )
0.4 0.2 0.2 0.1 0.1 0.4 0.2 0.2 0 0.2 1
第5章 信源编码技术
5.1 最佳变长编码
回顾: 1、根据信源编码理论,将能够荷载一定信息量, 且码字的平均长度最短,可分离的变长码字 集合称为最佳变长码。 2、最佳变长码编码的基本原则是:概率大的信 源符号分配短的码字,而概率小的信源符号 分配长码字,从而使得平均码长最短。 具有代表性变长编码方法有:香农码,费诺码 和哈夫曼码等。
' ' pk nk ( p K 1 p K )
K 1
n ' ( p K 1 p K )
辅助集平均码长
二元码的哈夫曼编码步骤
(1)将信源消息符号按其出现的概率大小依次排列为 p1 p2 pn (2)取两个概率最小的两个信源符号分别分配码元0和1, 并将这两个概率相加作为一个新符号的概率,与未 分配的二进符号的符号一起重新进行概率排序。 (3)对重排后的两个概率最小符号重复步骤(2)的 过程。 (4)不断继续上述过程,直到最后两个符号配以0和1 为止。 (5)从最后一级开始,反向搜索参与编码的符号,得 到各个信源符号所对应的码元序列,即相应的码 字。
F ( X k)
累计分布函数的计算
递推公式
F (ua) F (u ) p(u ) F (a) p(ua) p(u ) p(a)
u :已输入序列
a :当前输入符号
算术编码
将[0,1)分割成小区间,如长为n的二元序列,分为 2n个区间,用区间[F(u),F(u)+p(u))表示序列u, 实际取F(u)。将F(u)截短,截断长度为
i 1 7
编码效率
H ( X ) 2.61 0.96 L 2.72
关于哈夫曼编码的讨论 1、每次对信源缩减时,赋予信源最后两个概率 最小的符号,分配码元0和1是可以任意的, 即大概率符号或者合并后的符号集合可以分 配码元0也可以是1,这种选择任意性可以得 到不同的哈夫曼码,但不会影响码字的长度。 2、对信源进行缩减时,如果两个概率最小的符 号合并后的概率与其它信源符号的概率相同, 应当放在上面,以便减少更多符号分配更长 码的可能。
例5.3 对例5.1的信源符号进行哈夫曼编码, 给出编码过程,每个信源符号的码字,码 长,求平均码长、编码效率。
哈夫曼编码过程
0.39 0.35 0.35 0 0.26 1 0.20 0.19 0.18 0.17 0.15 0 0.11 1 1 0.20 0.20 0.19 0 1 0 1
0.61
概率
0 2
1
1/ 3 1/ 9 1/ 9 1/ 9 1/ 9 1/ 9 1 / 27 1 / 27 1 / 27
