风电场随机潮流计算共23页文档
含风电场电力系统的潮流计算方法综述

含风电场电力系统的潮流计算方法综述【摘要】含风电场电力系统的潮流计算对分析风电场并网后对电力系统稳定运行的影响具有十分重要的意义。
本文在介绍在风电场潮流计算模型的基础上,分析和总结了目前含风电场电力系统的确定性潮流计算方法和不确定性潮流计算方法的研究现状和特点。
【关键词】风电场;电力系统;确定性潮流;不确定性潮流0.引言随着能源结构的调整,风力发电的比重日益加大,我国政府一直积极支持风力发电的发展,制定了一系列鼓励风力发电的政策,支持风力发电的快速发展,使得风力发电的成本已大幅下降,成为了可再生能源中发展速度最快和最有前途的发电方式之一[1]。
但风能所具有的随机性和不可控性决定了风电机组的出力具有波动性和间歇性的特点。
与传统发电方式相比,风电场容量可信度较低,随着风电场规模的不断扩大和风力发电装置容量的显著增加,风电并网后对原有电力系统的影响也加大了,因此对其的研究也更加迫切。
当风电机组装机容量在电网总容量的比例较大时,风力发电将改变输电系统中的网损及其原有的潮流分布,输电网运行的安全性将受到较大的挑战,其运行的经济性也可能受到一定的影响[2-5]。
因此,为了研究风电机组接入电网以后对整个电力系统的影响,就必须对风电并网前后的系统潮流分布进行计算。
目前,对风电场潮流计算的研究已经具有一定的基础,风电场潮流计算主要包括含普通异步电机的风电场潮流计算和含双馈异步电机的风电场潮流计算[6]。
从上世纪80年代起,随着并网风电场的出现,人们就开始关注含风电场电力系统的潮流计算问题。
在电力系统潮流计算中,传统节点主要分为PV节点、PQ节点和平衡节点。
一般异步电机本身没有励磁调节装置,不能有效地调整节点电压,因此不能与常规的同步电机一样看作电压幅值恒定的PV节点。
异步电机向系统注入有功功率时也要从系统吸收一定的无功功率,吸收无功大小与发电机发出的有功功率、滑差率和机端电压等有着紧密的联系,因此不能简单的处理为恒功率的PQ节点[7]。
含风电场的电力系统潮流计算

含风电场的电力系统潮流计算一、本文概述随着全球能源结构的转型和可再生能源的大力发展,风电作为一种清洁、可再生的能源形式,其在电力系统中的比重日益增加。
风电场的大规模接入对电力系统的运行和控制带来了新的挑战,尤其是风电场出力的随机性和波动性对电力系统的潮流分布、电压稳定性以及保护控制等方面产生了显著影响。
因此,对含风电场的电力系统进行准确的潮流计算,对于电力系统的规划、设计、运行和控制具有重要的理论价值和现实意义。
本文旨在研究含风电场的电力系统潮流计算方法,分析风电场接入对电力系统潮流分布的影响,提出相应的潮流计算模型和算法。
文章首先介绍了风电场的基本特性及其在电力系统中的接入方式,然后详细阐述了含风电场的电力系统潮流计算的基本原理和方法,包括风电场出力模型的建立、潮流计算的基本方程和求解算法等。
在此基础上,文章进一步探讨了风电场接入对电力系统潮流分布的影响,包括风电场出力波动对电压稳定性、线路潮流和节点功率分布的影响等。
文章提出了针对含风电场的电力系统潮流计算的一些改进措施和优化策略,为提高电力系统的运行效率和稳定性提供参考。
通过本文的研究,可以为含风电场的电力系统潮流计算提供理论支持和实践指导,有助于更好地理解和解决风电场接入带来的电力系统运行问题,推动可再生能源在电力系统中的广泛应用和持续发展。
二、风电场特性及建模风电场作为可再生能源的重要组成部分,具有随机性、间歇性和不可预测性等特点。
这些特性使得风电场在电力系统中的建模和潮流计算变得复杂。
风电场的出力受到风速、风向、湍流等多种因素的影响,因此,准确描述风电场的特性并建立合适的模型是电力系统潮流计算的关键。
在风电场建模中,通常将风电场看作一个由多个风电机组组成的集合。
每个风电机组的出力取决于其装机容量、风速以及控制策略等因素。
为了简化计算,通常将风电场视为一个等效的电源,其出力等于所有风电机组出力的总和。
等效电源的出力特性可以通过统计方法得到,如威布尔分布、贝塔分布等。
(完整word版)电力系统潮流计算课程设计
一、问题重述课程设计要求1、在读懂程序的基础上画出潮流计算根本流程图2、经过输入数据,进行潮流计算输出结果3、对不同样的负荷变化,解析潮流分布,写出解析说明。
4、对不同样的负荷变化,进行潮流的调治控制,并说明调治控制的方法,并列表表示调治控制的参数变化。
5、打印利用 DDRTS 进行潮流解析绘制的系统图,以及潮流分布图。
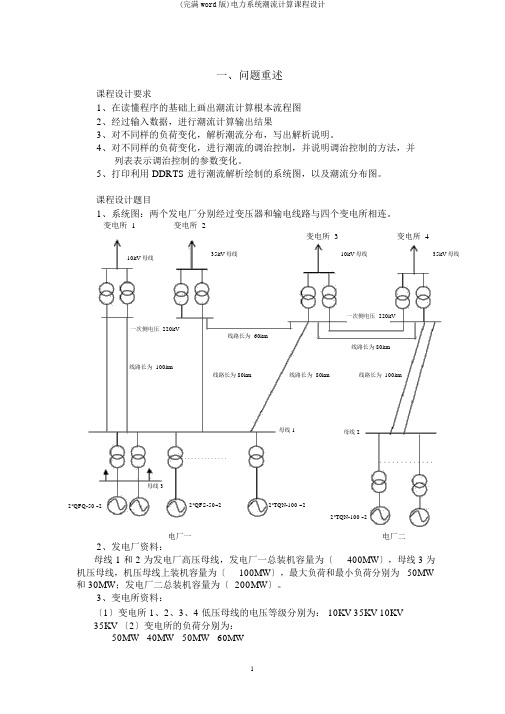
课程设计题目1、系统图:两个发电厂分别经过变压器和输电线路与四个变电所相连。
变电所 1变电所 2变电所 3变电所 435kV 母线10kV 母线35kV 母线10kV 母线一次侧电压 220kV一次侧电压 220kV线路长为 60km线路长为 80km线路长为 100km线路长为 80km线路长为 80km线路长为 100km母线 1母线 2。
母线 32*QFQ-50 -22*QFS-50-22*TQN-100 -22*TQN-100 -2电厂一电厂二2、发电厂资料:母线 1 和 2 为发电厂高压母线,发电厂一总装机容量为〔400MW〕,母线 3 为机压母线,机压母线上装机容量为〔100MW〕,最大负荷和最小负荷分别为 50MW和 30MW;发电厂二总装机容量为〔 200MW〕。
3、变电所资料:〔1〕变电所 1、2、3、4 低压母线的电压等级分别为: 10KV 35KV 10KV35KV 〔2〕变电所的负荷分别为:50MW 40MW 50MW60MW〔3〕每个变电所的功率因数均为cosφ=0.85 ;〔4〕变电所 2 和变电所 4 分别配有两台容量为 75MVA的变压器,短路耗费414KW,短路电压〔 %〕=16.7 ;变电所 1 和变电所 3 分别配有两台容量为63MVA 的变压器,短路耗费为 245KW,短路电压〔 %〕=10.5 ;4、输电线路资料:发电厂和变电所之间的输电线路的电压等级及长度标于图中,单位长度的电阻为,单位长度的电抗为,单位长度的电纳为 2.78 * 10 -6 S 。
含风力发电机组的配电网潮流计算

含风力发电机组的配电网潮流计算一、概述随着全球能源结构的转型和可再生能源的大力发展,风电作为一种清洁、可再生的能源形式,其在电力系统中的比重日益增加。
风电场的大规模接入为电力系统带来了新的活力,但同时也带来了诸多挑战。
尤其在配电网层面,风力发电机组的接入使得配电网从一个无源网络转变为有源网络,其潮流特性、电压分布以及网损情况都发生了显著变化。
含风力发电机组的配电网潮流计算,是电力系统分析与控制领域的重要课题。
通过潮流计算,可以准确描述风力发电机组接入后配电网的运行状态,分析其对系统电压稳定性、潮流分布以及网损的影响。
这不仅有助于电力系统的规划与设计,更对于电力系统的安全稳定运行和优化调度具有重要意义。
在含风力发电机组的配电网潮流计算中,风电场的特性建模是关键环节。
由于风速的随机性、间歇性和不可预测性,风电场的出力具有极大的不确定性。
在建模过程中需要充分考虑这些因素,建立准确的风电场出力模型。
配电网的结构特点、负荷分布以及控制策略等也是影响潮流计算的重要因素。
针对含风力发电机组的配电网潮流计算已有多种方法,如前推回代法、牛顿拉夫逊法等。
这些方法各有优缺点,需要根据实际情况进行选择和优化。
随着智能电网和分布式发电技术的不断发展,配电网潮流计算也面临着新的挑战和机遇。
本文旨在深入研究含风力发电机组的配电网潮流计算方法,分析风力发电机组接入对配电网潮流分布的影响,提出相应的优化策略和建议。
通过本文的研究,可以为含风力发电机组的配电网潮流计算提供理论支持和实践指导,有助于推动可再生能源在电力系统中的广泛应用和持续发展。
1. 风力发电机组在配电网中的应用背景随着全球能源结构的转型和可再生能源的大力发展,风力发电作为一种清洁、可再生的能源形式,其在配电网中的应用愈发广泛。
风力发电机组,作为风力发电的核心设备,在配电网中发挥着举足轻重的作用。
环境问题日益严重,化石燃料燃烧导致的碳排放量不断增加,加剧了全球气候变暖的速度。
含风电场电力系统电压波动的随机潮流计算与分析

由控制器补偿 , 其数值可以保持常数 ( 通常接近于
0) . 同步发电机通过功率变换器接入系统 ,而后者通
常配有无功补偿器 , 其消耗的无功功率也可以视为
常数并接近于 0.
11 3 风力发电机出力的概率分布
风力发电机的出力可由风速的概率分布和发电
机的功率特性求出.
(1) 当 v0 ≤v < vci ∪ vco ≤v , PW = 0 时
风力发电机有功出力
图
1
Wei
bull
分布的
图
2
风力发电机功率
比较
风速曲线
0 v ≤ vci
k1 v + k2 vci < v ≤ vr
PW = Pr
vr < v ≤ vco
(2)
0
v > vco
式中 : vci 是切入风速 ; vr 是额定风速 ; vco 是切出风
速 ; k1 = Pr / ( vr - vci ) ; k2 = - k1 vci .
有功出力对应的无功功率. 因此 ,风电场出力的概率
分布最终可以表示为一组有功出力和无功功率及相
应概率的离散数据.
2 考虑风电场的随机潮流计算
21 1 随机潮流算法 本文采用的随机潮流算法[9] 不但考虑了负荷随
机波动和发电机随机停运 ,还计及了线路随机故障. 该算法将负荷波动 、发电机停运以及线路故障
(3) 当 vr ≤v < vco , PW = Pr 时
∫vco
P( PW = Pr ) = f ( v) d v = vr
exp -
vr - v0 α
β
- exp
-
vco - v0 α
风电场风速随机性及容量系数分析_牟聿强

小二乘法、矩法、极大似然法等,对于有特殊形式
的分布(双参数 Weibull 分布)还可以采用线性回归 法。矩估计的意义明确,计算相对简单,但要求处
理的样本须是完整数据;极大似然法既可处理完整
数据又可以处理不完整数据,但计算量较大。最小
二乘法鲁棒性好,应用条件广泛。下面介绍最小二
乘法以及用于估计双参数 Weibull 分布参数的矩估 计法和线性回归法。
通过对国内某风电场 2006 年实测三组平均风 速 数 据 , 分 别 用 双 参 数 Weibull 、 Rayleigh 、 LogNormal 三种分布进行最小二乘拟合,结果表明 双参数 Weibull 分布拟合效果良好,适应性也更强 一些。
以往评价 Weibull 分布参数估计效果的方法多 是从风速统计量方面进行。研究风速分布的目的是 为了确定风能分布,本文提出了一种根据风速分布 函数和风力发电机风速功率曲线求取有功功率分布 的方法。并用由此方法得出的风力发电机有功功率 累积分布与经验分布进行对比,评价双参数 Weibull 分布各种参数估计方法的优劣[8]。
本文用序列法和 Weibull 法两种方法分别计算 Growian-3MW 型风力发电机在国内某风电场 2006 年 各月的容量系数,结果表明平均风速高的月份容量 系数要相对大一些。通过对各种风力发电机的容量 系数的分析,给出了风力发电机参数对容量系数的 不同影响。
1 数学模型
1.1 常用描述风速随机性的分布函数
1.2.2 双参数 Weibull 分布的矩估计
双参数 Weibull 分布的 r 阶原点距 mr 为:
mr
=
c r Γ(1 +
r) k
(6)
其中: Γ 为 Gamma 函数。
含风电场配电网随机潮流计算及其电压安全分析

( )有 功 功 率 概 率 函 数 可 得 : 1 ,
P ) F ’P ) = ( =
式 中 : 为节 点 电压 幅 值 和 相 位 的 状 态 向量 ; z
为
} )p竿 ) ㈥ ( c[ 竿 -_ ] l( e x
同理 , 功 功 率 概 率 密 度 函 数 亦 可 得 到 。 无 至 此 .风 力 发 电 机 组 输 出 功 率 概 率 模 型 已 经 建 立 , 在 随 机 潮 流 计 算 中 的 应 用 将 在 下 一 节 中介 绍 。 其
中 风 电 机 组 节 点 被 描 述 为 P 节 点 .其 中 无 功 功 率 Q
p 可 表 示 为 : p = tn0 a ( 4)
定 性 潮 流 就 不 能 全 面 反 映 电 网 运 行 状 态 .而 基 于 统
式 中 : 0是 风 力 发 电 机 功 角 , 正 常 运 行 时 保 持 不 变 。 文 献 『 ] 入 一 种 离 散 式 风 电场 输 出 功 率 分 布 . 虑 7 引 考 到 大 多 数 风 电 场 风 速 范 围 一 般 都 满 足 风 电 机 组 运 行 要 求 , 风 速 均 分 布 在 与 V 之 间 , 以 将 其 简 化 即 可
0 kI v+k2
≤ 。 vc <v ̄ v i
算 本 文 采 用 协 方 差 矩 阵 转 换 法 , 先 确 定 节 点 注 入 首
量 协 方 差 矩 阵 的特 征 值 和 特 征 向量 ,进 而 采 用 正 交
( 2)
P
变 换 将 原 始 相 关 随 机 变 量 转 换 为 一 组 统 计 上 相 互 独 立 的 随机变 量 . 此进行 随机 潮流 分析 。 以 对 节 点 注 入 相 关 变 量 (=1 2, , ) 其 相 关 i , … m , 性 参 数 矩 阵 可 以 按 式 ( ) 化 成 协 方 差 矩 阵 6 转 , 求
含风电场的电力系统潮流计算

中图分类号:TM46
含风电场的电力系统潮流计算
吴义纯 1,2,丁 明 1,张立军 1
(1.合肥工业大学 电气与自动化工程学院,安徽省 合肥市 230009; 2.安徽电力培训中心,安徽省 合肥市 230022)
POWER FLOW ANALYSIS IN ELECTRICAL POWER NETWORKS INCLUDING WIND FARMS
j =1 n n
(14) (15) (16)
Qi = U i∑U j (Gij sin δ ij − Bij cos δ ij )
0.6 0.5 0.4 0.3 0.2 0.1 0 2 4 6 8 10 12 14 16 Cp m a x
由异步发电机原理知道, 风力异步发电机发出的 有功功率Pe与转子电流Ir、滑差s等有关,其表达式为 Pe = − I r2 Rr (1 − s) / s (3) 其中,Rr为风力异步发电机的转子电阻, Ω;s 为 滑差,计算公式为 s = (n s − nr kr ) / ns × 100% , nr 为 叶片的旋转速度; kr 为齿轮比; ns 为同步转速; ns = 60 f / p ( f 为电网频率, p 为异步电机极对 数) 。 由此可见,滑差s变化,异步发电机发出的有功 功率Pe随之变化,同时风轮机转速、尖速比Ttsr、风能 利用系数Cp与风力机机械功率也随之变化。 根据功率 守恒原理,这两个功率应相等。迭代过程中当这两个 功率不等时,滑差s需要修正,最终使风力机机械功 率与发电机电磁功率相平衡。 为此本文在采用牛顿- 拉夫逊法计算潮流时,引入了风电机组发电功率与机 械功率差∆Pem和滑差修正量∆s,修正方程式为 ∂P ∂P ∂P ∂θ ∂ ∂s ∆ θ U ∆P ∂Q ∂Q ∆Q = ∂Q ∆U (4) ∂θ ∂U ∂s ∆Pem ∂P ∆s ∂Pem ∂Pem em ∂U ∂s ∂θ 其中 {∆Pem } 为列向量,表示风电场风力机的机 械功率和电磁功率的差值,其维数表示网络中所含 风电机组的个数。 通过对雅可比矩阵的形式加以修改,使在每次 迭代过程中滑差s都得到及时的修正, 因此该方法仍 [11-12] 保留牛顿-拉夫逊法的收敛性 。 同时还应指出,在同一风电场中,可以把多台 型号和风况相同的风电机组合并成一台等值机。引 入 ∆Pem 后,其迭代过程中收敛判据为 ∆Pem / Pm ≤ ε (5) 式中 å是一预先给定的小正数。 ∆s 是滑差修正量, 用于计算下一轮迭代的滑差 值,计算公式为 si+1 = s i + ∆s (6) 根据式 (3) 及风力发电机组等值电路不难推导
含风电场的电力系统概率潮流计算

含风电场的电力系统概率潮流计算摘要:由于对环保的关注,主要收获可再生能源(RES)的分布式能源(分布式能源)得到空前上升的关注。
这种类型的能源的天生不确定性增加电力系统中的不确定性,因此,就必须对系统性能进行概率分析。
此外,除了他们的不确定性,不确定参数具有相当水平的相关性。
两点估计法(2PEM)被公认为是适当的解决小规模甚至中等规模问题概率方法。
本文通过两点估计法计算概率潮流问题。
为了证明该方法的效果,用Mathpower14节点系统验证该方法。
然后,将得到的结果与蒙特卡罗模拟(MCS)的结果相比较。
关键字:概率潮流;两点法;风力发电引言最优概率潮流是电力市场中的重要工具,通过最优潮流模拟市场竞价过程,可获得交易量和节点电价等重要指标。
传统最优潮流研究大都基于确定性模型,即市场报价、负荷分布和元件参数等条件固定不变。
从宏观上看,一定时期内发电商报价和用户消费电能具有一定的确定性,但从微观角度来看,每个时段内发电商报价和用户消费的电能又会在各种因素影响下产生变化,这将引起交易量和节点电价的不断波动。
因此采用确定性模型进行最优潮流计算得到的结果,不能全面反映不确定因素对市场交易的影响。
计及发电报价、负荷分布中存在的不确定因素,采用概率最优潮流对市场交易进行模拟,能揭示出随机性和概率性后面隐藏的规律,为市场运营提供更多信息,降低交易风险,更好地引导市场交易的开展。
2.不确定模型负荷作为最显眼的不确定变量对电力系统运行起着至关重要的作用。
它的波动与时间,天气条件和电价等有关。
对于负载一种常见的做法到通过正态分布特定平均值和STD值,从历史数据获得的模型。
在这项研究中,负荷通过正态分布函数来模拟,平均值等于基本负载并且STD等于其平均值5%。
为了模拟风力发电的不确定性,一些节点被认为具有风电场和不确定的输出功率。
风速随着时间和地点的变化而变化和它的PDF遵循weibull分布。
因此,风速用weibull分布函数建模。
考虑尾流效应的风电场建模以及随机潮流计算

Jensen 模型较好地模拟了 平坦地形的尾 流情 [ 6] 况 , 模型如图 2 所示. 设 X 是两个风电机组的距 离, 叶轮 半径和尾流半径 分别是 R 和 R W , 自然 风 速、 通过叶片 的风速 和受 尾流 影响的 风速 分别 是 v0、 vT、 vX .
图3 L issaman 模型
式中 : R G 和 R0 分别是风电机组产生的湍流和自然湍 流的均方差, 通常情况下 R 1 08 v a G = 0 R 0 = 0 1 12v a ( 18) ( 19)
假设有两个相邻的场地 , 一个地形平坦( 风机安 装的海拔高度相同 ) , 另一个地形复杂 ( 风机安装的 海拔高度不同) . 两台相同型号的风电机组分别坐落 在这两个场地的边缘 , 它 们的风速相同 v 0 , 沿着风 速方向的坐标位置都是 x = 0. 当在 x = 0 位置处没 有风电机组时 , 平坦地形 X 处风速仍为 v 0 , 而位于 海拔高度 H 处的风机的风速为
因此 , 通过调整 C , 一般取 C < min v, 由上式解 出 a 和 B, 作为 C 、 a 和 B 各自的估计值, 进而得到三 参数 Weibull 分布函数. 1 1 2 风力发电机模型 目前风力发电所采用的发电机多是异步电机, 除此以外还有双馈感应电机和同步感应电机. 但是, 就发电机出力和风速之间的关系而言, 都基本遵从 如图 1 所示的功率输出曲线. 由图 1 可以得到风机 输出有功功率 P 与风速 v 之间的关系为 P = f ( v) ( 15)
第 42 卷
第 12 期
2008 年 12 月
西 安 交 通 大 学 学 报 JOURNAL OF XIcAN JIAOT ONG U NIVERSIT Y
含风电场的电力系统潮流计算程序

%本程序的功能是用牛拉法进行含风电场的电力系统潮流计算function s1=pf(a,B1,B2)n=a(1);%节点数nl=a(2);%支路数isb=a(3);%平衡节点号pr=a(4);%误差精度for i=1:nfor j=1:nG(i,j)=0;B(i,j)=0;endend%求导纳矩阵%B1为支路参数矩阵,其每一行格式为首节点号,末节点号,支路电导,支路电纳,首节点对地电纳,末节点对地电纳for i=1:nlp=B1(i,1);q=B1(i,2)G(p,q)=G(p,q)-B1(i,3);B(p,q)=B(p,q)- B1(i,4);G(q,p)=G(p,q);B(q,p)=B(p,q);G(p,p)=G(p,p)+ B1(i,3);B(p,p)=B(p,p)+B1(i,4);G(q,q)=G(q,q)+ B1(i,3);B(q,q)=B(q,q)+B1(i,4);endfor i=1:nB(i,i)=B(i,i)+B2(i,5);end%求导纳矩阵%B2为节点参数矩阵,每一行格式为节点注入有功,注入无功,电压实部,电压虚部,对地电纳,节点类型%节点类型:1为平衡节点,2为PQ节点,3为PV节点,4为风电场节点%Bf为风电场参数,格式为:有功功率,定子电抗,转子漏抗,转子电阻,励磁电抗for i=1:nif B2(i,6)==4p(i)=Bf(1);a1=2*p(i)^2*(Bf(2)+Bf(3))^2;a2=-Bf(4)^3*Bf(5);a3=Bf(4)^2*Bf(5);a4=Bf(4)^2;a5=4*p(i)^2*(Bf(2)+Bf(3))^2*Bf(4)^2;elseP(i)=B2(i,1);Q(i)=B2(i,2);ende(i)= B2(i,3);f(i)=B2(i,4);V(i)=sqrt(e(i)^2+f(i)^2);endICT1=0;IT2=1;N0=2*n;N=N0+1;a=0;while IT2~=0IT2=0;a=a+1;for i=1:nif i~=isbC(i)=0;D(i)=0;for j1=1:nC(i)= C(i)+G(i,j1)*e(j1)-B(i,j1)*f(j1);D(i)= D(i)+G(i,j1)*f(j1)+B(i,j1)*e(j1);endP1=C(i)*e(i)+f(i)*D(i);Q1=f(i)*C(i)-D(i)*e(i);V2=e(i)^2+f(i)^2;if B2(i,6)==2DP=P(i)-P1;DQ=Q(i)-Q1;for j1=1:nif j1~=isb&j1~=iX1=-G(i,j1)*e(i)-B(i,j1)*f(i);X2=B(i,j1)*e(i)-G(i,j1)*f(i);X3=X2;X4=-X1;p=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X4;J(m,q)=X2;elseif j1==i&j1~=isbX1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i);X2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i);X3=D(i)+B(i,i)*e(i)-G(i,i)*f(i);X4=-C(i)+G(i,i)*e(i)+B(i,i)*f(i);p=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X4;J(m,q)=X2;endendelseif B2(i,6)==3DP=P(i)-P1;DV=V(i)^2-V2;for j1=1:nif j1~=isb&j1~=iX1=-G(i,j1)*e(i)-B(i,j1)*f(i);X2=B(i,j1)*e(i)-G(i,j1)*f(i);X5=0;X6=0;p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV; m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;J(m,q)=X2;elseif j1==i&j1~=isbX1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i);X2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i);X5=-2*e(i);X6=-2*f(i);p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;J(m,q)=X2;endendelseDP=P(i)-P1;for j1=1:nif j1~=isb&j1~=iX1=-G(i,j1)*e(i)-B(i,j1)*f(i);X2=B(i,j1)*e(i)-G(i,j1)*f(i);X3=X2;X4=-X1;p=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X4;J(m,q)=X2;elseif j1==i&j1~=isbX1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i);X2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i);x3=D(i)+B(i,i)*e(i)-G(i,i)*f(i);x4=-C(i)+G(i,i)*e(i)+B(i,i)*f(i);x5=2*a1*(a2+a3*a4*V2^2/(sqrt(V2^4*a4-a5)))/(a2*V2^2+a3*(sqrt(V2^4*a4-a5)))^2;X3=x3-e(i)*x5;X4=x4-f(i)*x5;p=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X4;J(m,q)=X2;endendendendend%求雅克比矩阵for k=3:N0k1=k+1;N1=N;for k2=k1:N1J(k,k2)=J(k,k2)./J(k,k);endJ(k,k)=1;if k~=3;k4=k-1;for k3=3:k4for k2=k1:N1J(k3,k2)= J(k3,k2)-J(k3,k)*J(k,k2);endJ(k3,k)=0;endif k==N0,break;endfor k3=k1:N0for k2=k1:N1J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);endJ(k3,k)=0;endelsefor k3=k1:N0for k2=k1:N1J(k3,k2)= J(k3,k2)-J(k3,k)*J(k,k2);endJ(k3,k)=0;endendendfor k=3:2:N0-1L=(k+1)./2;e(L)=e(L)-J(k,N);k1=k+1;f(L)=f(L)-J(k1,N);endfor k=3:N0DET=abs(J(k,N));if DET>=prIT2=IT2+1;endendICT2(a)=IT2;ICT1=ICT1+1;end%用高斯消去法解w=-J*Vfid1=fopen('out1.txt','wt')fprintf(fid1,‘各节点的实际电压标幺值E和电压大小V为:\n’);for k=1:nV(k)=sqrt(e(k)^2+f(k)^2);fprintf(fid1,'E(%d)=%8.5f+j%8.5f, V(%d)=%8.5f\n',k,e(k),f(k),k,V(k)); endfor p=1:nif p==isbfprintf(fid1,'平衡节点的功率S为:\n');C(p)=0;D(p)=0;for q=1:nC(p)=C(p)+G(p,q)*e(q)-B(p,q)*f(q);D(p)=D(p)-G(p,q)*f(q)-B(p,q)*e(q);endSp(p)=e(p)*C(p)-f(p)*D(p);Sq(p)=(e(p)*D(p)+f(p)*C(p));fprintf(fid1,'S=%8.5f+j%8.5f\n',Sp(p),Sq(p));endendfprintf(fid1,'各条支路的首端功率为:\n');for i=1:nlp=B1(i,1);q=B1(i,2);sip(i)=-e(p)*B1(i,5)+(e(q)-e(p))*G(p,q)-(f(q)-f(p))*B(p,q);siq(i)=(f(p)*B1(i,5)+(e(p)-e(q))*B(p,q)-(f(q)-f(p))*G(p,q));Sip(i)=e(p)*sip(i)-f(p)*siq(i);Siq(i)=e(p)*siq(i)+f(p)*sip(i);fprintf(fid1,'S(%d,%d)=%8.5f+j%8.5f\n',p,q,Sip(i),Siq(i));endfprintf(fid1,'¸各条支路的末端功率为:\n');for i=1:nlp=B1(i,1);q=B1(i,2);sjp(i)=-e(q)*B1(i,6)+(e(p)-e(q))*G(p,q)-(f(p)-f(q))*B(p,q);sjq(i)=(f(q)*B1(i,6)+(e(q)-e(p))*B(p,q)-(f(p)-f(q))*G(p,q));Sjp(i)=e(q)*sjp(i)-f(q)*sjq(i);Sjq(i)=e(q)*sjq(i)+f(q)*sjp(i);fprintf(fid1,'S(%d,%d)=%8.5f+j%8.5f\n',q,p,Sjp(i),Sjq(i));endfprintf(fid1,'各条支路的功率损耗为:\n');for i=1:nlDSp(i)=Sip(i)+Sjp(i);DSq(i)=Siq(i)+Sjq(i);fprintf(fid1,'DS(%d)=%8.5f+j%8.5f\n',i,DSp(i),DSq(i)); endfclose(fid1);。
风力发电并网系统潮流计算分析

风力发电并网系统潮流计算与分析电气工程及其自动化 09230430 张鹏飞 指导老师:张晓英 副教授 吕斌 高工摘 要随着我国能源结构的调整,风力发电日益受到重视,越来越多的风电场将会接入电力系统中,因此电力系统的潮流计算分析显得尤其重要。
首先研究的是3机9节点电力系统的潮流分布,其中以牛拉法和PQ 分解法为计算模型,运用PSASP 软件完成潮流计算及分析,其次研究的是风力发电并网系统的潮流分布,根据风力发电机组的特性,建立了风电场的Q —U 模型,通过MATLAB 编程实现潮流计算。
通过分析系统电压的稳定性得到的结论是风速越大,系统电压的稳定性越差;风电场发电量占的比例越大,系统母线电压下降越快,系统越不稳定。
关键词:潮流计算; PSASP 软件 ; 风电场模型 ; 电压稳定性AbstractThe adjustment of energy structure in our country, wind turbine generation has been paid increasing attention day by day. More and more wind farms will be connected to power system, so power flow calculation and analysis are particularly important. Firstly, the thesis studies power flow calculation analysis of the 3 machine 9-bus power system with conventional and planning operation way. The Newton Raphson method and PQ decomposition method are the power flow analysis models, the PSASP software is used to complete the flow calculation. Secondly, the power flow analysis of the system with wind farms is studied. According to the feature of the wind turbines, establishing the QU model for wind farm. The MTALAB Program is adopted to complete the flow calculation. Finally , the stability of the system is analysed. The conclusion is that the wind speed is greater, the stability of the system is worse, the proportion of wind power is greater, the voltages of the system bus drops faster , the system is more unstable .KEY WORDS :Power flow analysis ;The PSASP software; The model of wind farm; The Stability of voltage一、前言潮流是确定电力网络运行状态的基本因素,潮流问题是研究电力系统稳态问题的基础和前提。
风电场环境下的电力系统潮流算法

风电场环境下的电力系统潮流算法摘要:随着社会经济的发展,我国对电能的需求不断增加,电力系统发展迅速。
文章首先针对电力系统潮流算法的发展展开必要说明,而后进一步讨论了风电场环境下电力潮流计算的模型,对于加深该领域的理解有着积极价值。
关键词:电力:潮流计算:风电场引言风电场并网运行,当风电装机容量占总电网容量的比例较大时,风力发电的随机性将改变输电系统原有的潮流及网络损耗的分布,输电网运行的安全性会受到较大的冲击,运行的经济也会受到影响。
因此,为了研究风力发电接入电网以后对整个电力系统带来的影响,就必须计算大型风电场接入电网后的潮流。
1含风电场的电力系统最优潮流研究意义最优潮流是指当电力系统网络结构及负荷都给定时,在满足节点功率平衡及各种安全约束的条件下,通过调节系统中的控制参数使其目标函数或某一性能指标达到最优时的潮流分布。
最优潮流在电力系统的经济调度、系统规划设计及可靠性分析等方面得到了广泛应用,在节能减排、提高能源利用率和环境效益的大背景下,以风电为代表的分布式电源得到了迅速的发展,然而传统的最优潮流问题并没有考虑风电等不确定性因素,在风力发电飞速发展和追求低碳电力的影响下,大规模风电并网不可避免。
由于风能具有随机性、间歇性和不可控性的特点,使风电场输出功率具有强烈的随机性和波动性,加剧了电力系统运行中不确定因素的复杂程度,使电力系统潮流优化的难度增大,因此迫切需要研究大型风电场并网后对电力系统的影响。
包含风电场的电力系统最优潮流,在评估风电并网对电力系统运行的经济性和环境效益上起着非常重要的作用。
2电力系统潮流算法的发展对于电力系统潮流算法的研究,在很大程度上与计算机的发展保持了一种同步状态。
20世纪50年代,以节点导纳矩阵为基础的高斯赛德尔算法广泛应用,就是因为当时的计算机运算能力有限,但是算法本身较差的收敛性,又推动了算法本身的进步。
时至今日,计算机运算能力得到大幅度提升,对应的算法也呈现出新的特点。
基于实测离散数据的含风电场电力系统概率潮流计算

2. 含风电的概率潮流建模
2.1. 离散变量函数统计矩点估计法
本文采用离散实测数据实现含风电的 PLF 计算,即随机输入变量为离散型变量。不失一般性,假设 X 为一输入随机变量,Y = h(X)是以 X 为变量的非线性函数。点估计法的核心思想是通过匹配函数 h(X) 的前几阶矩, 从而用 m 个概率集合来代替 h(X)。 当随机变量 X 为 n 维随机变量时, 点估计法则采用 m × n 个概率集合来取代联合概率密度,也就是一共采用了 m × n 个点进行估计。 根据样本逼近原理可知[18],样本空间(X1, X2, , Xn)中任一样本点(x1, x2, , xn)的数学期望和各阶 中心距分别为:
i 1= j 1 =
(8)
根据同样的方法可以得出 Y 的 m 阶距,即
E Y m = ∑∑ pij h ( µ1x , xij , , µ( n −1) x , µnx )
2
韩小峰 等
但现有点估计法的应用研究都是在输入随机变量分布已知的情况下且随机变量为连续变量的情形下 实施的。而风电场输出功率实际数据采集均为离散变量,且实测数据表明,输出功率概率分布规律性不 强,难以用简单的概率密度函数描述。所以,对含风电电力系统概率潮流计算,需要对点估计方法进行 改进,使其既保持计算精度高、速度快等优点,又可以处理具备大量实测离散数据且概率分布难以用确 定数学表达式描述的随机性工程实际问题,对实现快速准确评估含风电电力系统潮流运行特性具有重要 的意义。 本文根据风电场实测离散数据,提出一种基于离散变量的函数统计矩点估计法,获得输出变量的期 望、方差和低阶原点矩。然后,利用 Gream-Charlier 展开级数算法,近似逼近输出随机变量的累积分布 函数(Cumulative Distribution Function, CDF), 得到一个更符合工程实用性的概率潮流算法。 最后应用实际 风电场实测数据并结合 IEEE39 节点仿真算例验证了所提方法的有效性和实用性。
