数字电子技术基础教材第四章答案
《数字电子技术基础》第四章习题答案
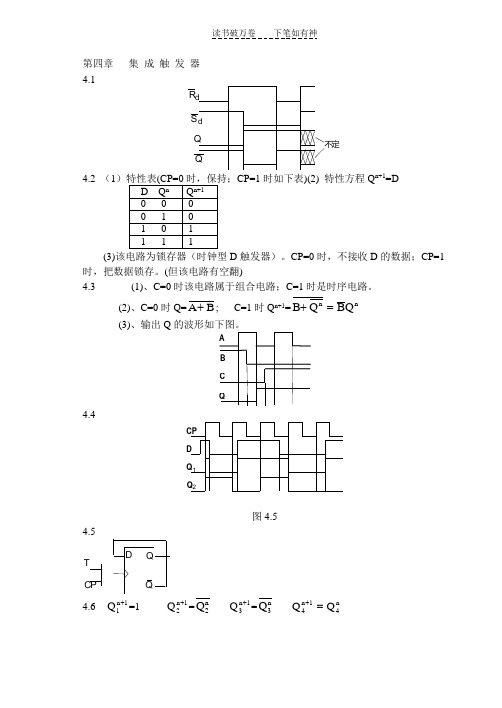
第四章 集 成 触 发 器 4.1R d S d Q Q不定4.2 (1CP=1时如下表)(2) 特性方程Q n+1=D(3)该电路为锁存器(时钟型D 触发器)。
CP=0时,不接收D 的数据;CP=1时,把数据锁存。
(但该电路有空翻)4.3 (1)、C=0时该电路属于组合电路;C=1时是时序电路。
(2)、C=0时Q=A B +; C=1时Q n+1=B Q BQ nn+= (3)、输出Q 的波形如下图。
A B C Q4.4CP D Q 1Q 2图4.54.5 DQ QCPT4.6 Q 1n 1+=1 Q 2n 1+=Q 2n Q n 13+=Q n 3 Q Q 4n 14n+=Q1CP Q2Q3Q44.7 1、CP 作用下的输出Q 1 Q 2和Z 的波形如下图; 2、Z 对CP 三分频。
DQ QCPQ1DQ QQ2ZRd CP Q1Q2Z14.8由Q D J Q KQ J Q KQ n 1n n n n +==+=⋅得D 触发器转换为J-K 触发器的逻辑图如下面的左图;而将J-K 触发器转换为D 触发器的逻辑图如下面的右图CPD Q QJKQ QDQ QJ KCP4.9CP B CA4.10CP X Q1Q2Z4.11 1、555定时器构成多谐振荡器 2、u c, u o 1, u o 2的波形u c u o 1u o 2t t t 1.67V3.33V3、u o 1的频率f 1=1074501316..H z ⨯⨯≈ u o 2的频率f 2=158H z4、如果在555定时器的第5脚接入4V 的电压源,则u o 1的频率变为1113001071501232....H z ⨯⨯+⨯⨯≈4.12 图(a)是由555定时器构成的单稳态触发电路。
1、工作原理(略);2、暂稳态维持时间t w =1.1RC=10ms(C 改为1μF);3、u c 和u o 的波形如下图:u ou ct t tu i (ms)(ms)(ms)5 10 25 30 45 503.33V4、若u i 的低电平维持时间为15m s ,要求暂稳态维持时间t w 不变,可加入微分电路4.13由555定时器构成的施密特触发器如图(a)所示 1、电路的电压传输特性曲线如左下图; 2、u o 的波形如右下图;3、为使电路能识别出u i 中的第二个尖峰,应降低555定时器5脚的电压至3V 左右。
数字电子技术基础教材第四章答案

习题44-1 分析图P4-1所示得各组合电路,写出输出函数表达式,列出真值表,说明电路得逻辑功能。
解:图(a):;;真值表如下表所示:其功能为一位比较器。
A>B时,;A=B时,;A<B时,图(b):真值表如下表所示:功能:一位半加器,为本位与,为进位。
图(c):真值表如下表所示:功能:一位全加器,为本位与,为本位向高位得进位。
图(d):;;功能:为一位比较器,A<B时,=1;A=B时,=1;A>B时,=14-2 分析图P4-2所示得组合电路,写出输出函数表达式,列出真值表,指出该电路完成得逻辑功能。
解:该电路得输出逻辑函数表达式为:因此该电路就是一个四选一数据选择器,其真值表如下表所示:,当M=1时,完成4为二进制码至格雷码得转换;当M=0时,完成4为格雷码至二进制得转换。
试分别写出,,,得逻辑函数得表达式,并列出真值表,说明该电路得工作原理。
解:该电路得输入为,输出为。
真值表如下:由此可得:完成二进制至格雷码得转换。
完成格雷码至二进制得转换。
4-4 图P4-4就是一个多功能逻辑运算电路,图中,,,为控制输入端。
试列表说明电路在,,,得各种取值组合下F与A,B得逻辑关系。
解:,功能如下表所示,两个变量有四个最小项,最多可构造种不同得组合,因此该电路就是一个能产生十六种函数得多功能逻辑运算器电路。
4-5 已知某组合电路得输出波形如图P4-5所示,试用最少得或非门实现之。
解:电路图如下:4-6 用逻辑门设计一个受光,声与触摸控制得电灯开关逻辑电路,分别用A,B,C表示光,声与触摸信号,用F表示电灯。
灯亮得条件就是:无论有无光,声信号,只要有人触摸开关,灯就亮;当无人触摸开关时,只有当无关,有声音时灯才亮。
试列出真值表,写出输出函数表达式,并画出最简逻辑电路图。
解:根据题意,列出真值表如下:由真值表可以作出卡诺图,如下图:C AB 00 10 11 100 1由卡诺图得到它得逻辑表达式为: 由此得到逻辑电路为:4-7 用逻辑门设计一个多输出逻辑电路,输入为8421BCD 码,输出为3个检测信号。
数字电子技术第四章课后习题答案(江晓安等编)

第四章组合逻辑电路1. 解: (a)(b)是相同的电路,均为同或电路。
2. 解:分析结果表明图(a)、(b)是相同的电路,均为同或电路。
同或电路的功能:输入相同输出为“1”;输入相异输出为“0”。
因此,输出为“0”(低电平)时,输入状态为AB=01或103. 由真值表可看出,该电路是一位二进制数的全加电路,A为被加数,B为加数,C为低位向本位的进位,F1为本位向高位的进位,F2为本位的和位。
4. 解:函数关系如下:SF++⊕=+ABSABS BABS将具体的S值代入,求得F 312值,填入表中。
A A FB A B A B A A F B A B A A F A A F AB AB F B B A AB F AB B A B A B A AB F B A A AB F B A B A B A F B A AB AB B A B A F B B A B A B A B A B A B A F AB BA A A B A A B A F F B A B A F B A B A F A A F S S S S =⊕==+==+⊕===+⊕===⊕===⊕===+⊕===+=+⊕===⊕==+==⊕==Θ=+=+⊕===+++=+⊕===+=⊕===⊕==+=+⊕==+=+⊕===⊕==01111111011010110001011101010011000001110110)(01010100101001110010100011000001235. (1)用异或门实现,电路图如图(a)所示。
(2) 用与或门实现,电路图如图(b)所示。
6. 解因为一天24小时,所以需要5个变量。
P变量表示上午或下午,P=0为上午,P=1为下午;ABCD表示时间数值。
真值表如表所示。
利用卡诺图化简如图(a)所示。
化简后的函数表达式为D C A P D B A P C B A P A P DC A PD B A P C B A P A P F =+++=用与非门实现的逻辑图如图(b )所示。
数字电子技术基础简明教程第三版4-6章(含答案)

第四章(选择、判断、填空共30题)一、选择题1.N个触发器可以构成能寄存位二进制数码的寄存器。
A.N-1B.NC.N+1D.2N2.在下列触发器中,有约束条件的是。
A.主从J K F/FB.主从D F/FC.同步R S F/FD.边沿D F/F3.一个触发器可记录一位二进制代码,它有个稳态。
A.0B.1C.2D.3E.44.存储8位二进制信息要个触发器。
A.2B.3C.4D.85.对于T触发器,若原态Q n=0,欲使新态Q n+1=1,应使输入T=。
A.0B.1C.QD.Q6.对于T触发器,若原态Q n=1,欲使新态Q n+1=1,应使输入T=。
A.0B.1C.QD.Q7.对于D触发器,欲使Q n+1=Q n,应使输入D=。
A.0B.1C.QD.Q8.对于J K触发器,若J=K,则可完成触发器的逻辑功能。
A.R SB.DC.TD.Tˊ9.欲使J K触发器按Q n+1=Q n工作,可使J K触发器的输入端。
A.J=K=0B.J=Q,K=QC.J=Q,K=QD.J=Q,K=0E.J=0,K=Q10.欲使J K触发器按Q n+1=Q n工作,可使J K触发器的输入端。
A.J=K=1B.J=Q,K=QC.J=Q,K=QD.J=Q,K=1E.J=1,K=Q11.欲使J K触发器按Q n+1=0工作,可使J K触发器的输入端。
A.J=K=1B.J=Q,K=QC.J=Q,K=1D.J=0,K=1E.J=K=112.欲使J K触发器按Q n+1=1工作,可使J K触发器的输入端。
A.J=K=1B.J=1,K=0C.J=K=QD.J=K=0E.J=Q,K=013.欲使D触发器按Q n+1=Q n工作,应使输入D=。
A.0B.1C.QD.Q14.下列触发器中,克服了空翻现象的有。
A.边沿D触发器B.主从R S触发器C.同步R S触发器D.主从J K触发器15.下列触发器中,没有约束条件的是。
A.基本R S触发器B.主从R S触发器C.同步R S触发器D.边沿D触发器16.描述触发器的逻辑功能的方法有。
数字电子技术基础(第4版)_课后习题答案

第一章1.1二进制到十六进制、十进制(1)(10010111)2=(97)16=(151)10 (2)(1101101)2=(6D)16=(109)10(3)(0.01011111)2=(0.5F)16=(0.37109375)10 (4)(11.001)2=(3.2)16=(3.125)10 1.2十进制到二进制、十六进制(1)(17)10=(10001)2=(11)16 (2)(127)10=(1111111)2=(7F)161621016210)3.19()1010 1(11001.101(25.7)(4))A D7030.6()0101 0000 0111 1101 0110 (0.0110(0.39)(3) B ====1.8用公式化简逻辑函数(1)Y=A+B (3)Y=1)=+(解:1A A 1)2(=+++=+++=+++=C B A C C B A C B Y CB AC B A Y ADC C B AD C B C B AD DC A ABD CD B A Y =++=++=++=)()(Y )4(解:(5)Y=0 (7)Y=A+CDE ABCD E C ABCD CE AD B BC CE AD B BC Y CE AD B BC B A D C AC Y =+=⋅+=+⋅=++++=)()()()()()6(解:CB AC B C B A A C B A C B A C B A C B C B A A C B A C B A C B A Y C B A C B A C B A Y +=++=+++=++++=++++⋅+=++++++=)())(())()(())()((8解:)(D A D A C B Y ++=)9(E BD E D BF E A AD AC Y ++++=)10(1.9 (a) C B C B A Y += (b) C B A ABC Y +=(c) ACD D C A D C A B A Y D AC B A Y +++=+=21,(d) C B A ABC C B A C B A Y BC AC AB Y +++=++=21, 1.10 求下列函数的反函数并化简为最简与或式(1)C B C A Y += (2)DC A Y++=CB C B AC C B AC B A BC AC C A B A BC AC C A B A Y BCAC C A B A Y +=++++=⋅+++=+++=+++=))((]))([())(())(()3(解: (4)C B A Y ++=DC ABD C B D C A D C B D A C A C D C B C A D A Y CD C B C A D A Y =++=+++=++++=+++=)())(())()(()5(解: (6)0=Y1.11 将函数化简为最小项之和的形式CB AC B A ABC BC A C B A C B A C B A ABC BC A CB A AC B B A BC A C B AC BC A Y CB AC BC A Y +++=++++=++++=++=++=)()()1(解:D C B A CD B A D C B A ABCD BCD A D C B A Y +++++=)(2)13()()()(3CD B A BCD A D BC A D C B A D C B A ABCD D ABC D C AB D C AB CD B A D C B A D C B A D C B A CD AB B A B A B A ACD D AC D C A D C A CD A D C A D C A D C A B BCD D BC D C B D C B CD B D C B D C B D C B A Y CDB A Y ++++++++++++=+++++++++++++++++++=++=解:)((4)CD B A D ABC D BC A D C AB D C AB CD B A ABCD BCD A Y +++++++= (5)MN L N M L N LM N M L N M L N M L Y +++++=1.12 将下列各函数式化为最大项之积的形式(1)))()((C B A C B A C B A Y ++++++= (2)))()((C B A C B A C B A Y ++++++= (3)76430M M M M M Y ⋅⋅⋅⋅= (4)13129640M M M M M M Y ⋅⋅⋅⋅⋅= (5)530M M M Y ⋅⋅=1.13 用卡诺图化简法将下列函数化为最简与或形式:(1)D A Y +=(3)1=Y (2)D C BC C A B A Y +++= (4)B AC B A Y ++=B A DC Y ++=AC B A Y +=(5)D C B Y ++= (6)C B AC B A Y ++=(7)C Y = (9)D C A C B D A D B Y +++=(8))14,11,10,9,8,6,4,3,2,1,0(),,,(m D C B A Y ∑= (10)),,(),,(741m m m C B A Y ∑=D A D C B Y ++=ABC C B A C B A Y ++=1.14化简下列逻辑函数(1)D C B A Y +++= (2)D C A D C Y += (3)C A D AB Y ++= (4)D B C B Y += (5)E D C A D A E BD CE E D B A Y +++++=1.20将下列函数化为最简与或式(1)AD D C B D C A Y ++= (2)AC D A B Y ++= (3)C B A Y ++= (4)D B A Y +=第二章2.1解:Vv v V V v T I mA I mA Vv T V v a o B o B BS B o B 10T 3.0~0(2.017.0230103.0207.101.57.05I V 5v 1021.5201.510V 0v )(i i ≈≈∴<=×≈=−≈∴−=×+−=截止,负值,悬空时,都行)饱和-=时,=当截止时,=当都行)=饱和,,-=悬空时,都行)饱和。
数电习题解答_杨志忠_第四章练习题_部分

教材:数字电子技术基础(“十五”国家级规划教材) 杨志忠 卫桦林 郭顺华 编著高等教育出版社2009年7月第2版; 2010年1月 北京 第2次印刷;第四章 组合逻辑电路(部分练习题答案)练习题P172【4.1】、试分析图P4.1所示电路的逻辑功能。
解题思路:根据逻辑图依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
(b )、Y AB AB A B =+=:;(同或功能) 真值表略; 【4.2】、试分析图P4.2所示电路的逻辑功能。
解题思路:根据逻辑图依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
(a )、Y AB AB AB AB A B =⋅=+=⊕;(异或功能) 真值表略; 【4.3】、试分析图P4.3所示电路的逻辑功能。
解题思路:根据逻辑图从输入到输出逐级依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
(a )、()Y ABC A ABC B ABC C ABC A B C ABC ABC =⋅+⋅+⋅=⋅++=+; 真值表略; 【4.4】、试分析图P4.4所示电路的逻辑功能。
解题思路:根据逻辑图从输入到输出逐级依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
解:12 Y A B C Y AB A B C AB A B C =⊕⊕=⋅⊕⋅=+⊕⋅;该逻辑电路实现一位全加运算。
Y1表示本位和数,Y2是进位输出。
mi A B C Y1 Y2 0 0 0 0 0 0 1 0 0 1 1 02 0 1 0 1 03 0 1 1 0 14 1 0 0 1 05 1 0 1 0 16 1 1 0 0 17 1 1 1 1 1【4.6】、写出图P4.6所示电路的逻辑函数表达式,并且把它化成最简与或表达式。
解题思路:变量译码器实现逻辑函数是把逻辑变量输入译码器地址码,译码器输出i i m Y =,再用与非门(输出低电平有效)变换就可以得到所需的逻辑函数,输出函数具有下列的表达形式:(,,)0356m(0,3,5,6)A B C F Y Y Y Y ==∑。
《数字电子技术基础》课后习题答案

BC A
00
01
11
10
0
0
0
0
0
1
0
1
1
1
则表达结果 Y 的表达式为:
逻辑电路如下:
技能题:
3.20:解:根据题意,A、B、C、D 变量的卡诺图如下:
CD AB
00
01
11
10
00
0
0
0
0
编辑版 word
01
0
0
0
0
11
0
1
1
1
10
0
0
0
0
电路图如下:
编辑版 word
第四章:
自测题:
一、 2、输入信号,优先级别最高的输入信号 7、用以比较两组二进制数的大小或相等的电路,A>B 二、 3、√ 4、√ 三、 5、A 7、C
第六章:
自测题:
一、 1、存储,组合逻辑,存储 3、时钟 CP,时钟 CP,时钟 CP,时钟 CP 9、4,4
二、 2、√ 9、×
三、 3、C 8、D
练习题:
6.2、
(1)输出方程
Y Q2n
(2)驱动方程
n
J0 Q2
J1 K1 Q0n
K0 1
J 2 Q1nQ0n
(3)状态方程
K2 1
Q0n1
练习题:
4.1;解:(a) (b)
,所以电路为同或门
,所以电路为与门。
4.5、解:当 M=0 时,
, 所以此时电路输出反码。
,同理可推:
当 M=1 时,
, 所以此时电路输出原码。
,同理可推:
4.7、Y ABC D ABCD ABC ABC D ABCD ABC D BD ABC BC D
《数字电子技术基础》课后习题答案

2、2: (4)解:
(8)解:
2、3:
(2)证明:左边
《数字电子技术基础》课后习题答案
=右式 所以等式成立
(4)证明:左边=
右边= 左边=右边,所以等式成立 2、4
(1) 2、5 (3) 2、6:
(1) 2、7:
(1) 卡诺图如下:
BC A
00
01
11
10
0
1
1
1
1
1
1
所以, 2、8: (2)画卡诺图如下:
(c)
(f)
3、7、解: (a)
《数字电子技术基础》课后习题答案
3、8、解:输出高电平时,带负载的个数
N OH
I OH I IH
400 20
20
G 可带 20 个同类反相器 输出低电平时,带负载的个数
N OL
I OL I IL
8 0.45
17.78
G 反相器可带 17 个同类反相器 3、12
EN=1 时,
11
10
00
0
0
0
0
01
0
0
0
0
11
0
1
1
1
10
0
0
0
0
电路图如下:
第四章:
自测题:
一、 2、输入信号,优先级别最高的输入信号 7、用以比较两组二进制数的大小或相等的电路,A>B 二、 3、√ 4、√ 三、 5、A 7、C
练习题:
4、1;解:(a) (b)
(74)10 =(0111 0100)8421BCD=(1010 0111)余 3BCD (45、36)10 =(0100 0101、0011 0110)8421BCD=(0111 1000、0110 1001 )余 3BCD (136、45)10 =(0001 0011 0110、0100 0101)8421BCD=(0100 0110 1001、0111 1000 )余 3BCD (374、51)10 =(0011 0111 0100、0101 0001)8421BCD=(0110 1010 0111、1000 0100)余 3BCD 1、8、解
数字电子技术基础(第四版)课后习题答案_第四章

第4章触发器[题4.1]画出图P4.1所示由与非门组成的根本RS触发器输出端Q、Q的电压波形,输入端S、R的电压波形如图中所示。
图P4.1[解]见图A4.1图A4.1[题4.2]画出图P4.2由或非门组成的根本R-S触发器输出端Q、Q的电压波形,输出入端S D,R D的电压波形如图中所示。
图P4.2[解]见图A4.2[题4.3]试分析图P4.3所示电路的逻辑功能,列出真值表写出逻辑函数式。
图P4.3 [解]:图P4.3所示电路的真值表S R Q n Q n+1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 0* 1 110*由真值表得逻辑函数式 01=+=+SR Q R S Q nn[题4.4] 图P4.4所示为一个防抖动输出的开关电路。
当拨动开关S 时,由于开关触点接触瞬间发生振颤,D S 和D R 的电压波形如图中所示,试画出Q 、Q 端对应的电压波形。
图P4.4[解] 见图A4.4图A4.4[题4.5] 在图P4.5电路中,假设CP 、S 、R 的电压波形如图中所示,试画出Q 和Q 端与之对应的电压波形。
假定触发器的初始状态为Q =0。
图P4.5[解]见图A4.5图A4.5[题4.6]假设将同步RS触发器的Q与R、Q与S相连如图P4.6所示,试画出在CP 信号作用下Q和Q端的电压波形。
己知CP信号的宽度t w = 4 t Pd 。
t Pd为门电路的平均传输延迟时间,假定t Pd≈t PHL≈t PLH,设触发器的初始状态为Q=0。
图P4.6图A4.6[解]见图A4.6[题4.7]假设主从结构RS触发器各输入端的电压波形如图P4.7中所给出,试画Q、Q端对应的电压波形。
设触发器的初始状态为Q=0。
图P4.7[解] 见图A4.7图A4.7[题4.8]假设主从结构RS触发器的CP、S、R、DR各输入端的电压波形如图P4.8所示,1DS。
数字电子技术第四章习题答案

4.8 用4片8线-3线优先编码器组成 线-5线优先编码器。 线优先编码器组成32线 线优先编码器 线优先编码器。 片 线 线优先编码器组成
YS'
1 0 1 0
Y’2(4) 0 1 1 1 1
' YEX
状态 不工作 工作, 工作,但无输入 工作, 工作,且有输入 不可能出现
1 1 0 0
Y’2(3) 1 0 1 1 1
C 0 1 0 1 0 1 0 1
MS 0 1 × 0 × × × 1
ML 0 0 × 1 × × × 1
MS
BC 00 A 0 1 0 x BC 00 0 x
01 1 x
11 0 1
10 x x
ML A 0 1
01 0 x
11 1 1
10 x x
MS=A+B’C ML=B
B ML
《数字电子技术基础》第五版 数字电子技术基础》
《数字电子技术基础》第五版 数字电子技术基础》
4.3
解:输入变量——水位检测结果 输入变量 水位检测结果 来表示, 用A,B,C来表示, , , 来表示 高于检测元件时为“ , 高于检测元件时为“0”, 低于检测元件时为“1”; 低于检测元件时为“ ; 输出变量——水泵工作状态 输出变量 水泵工作状态 用ML,MS分别代表两个水泵 工作为“ ,不工作为“ 。 工作为“1”,不工作为“0”。
习题答案(数电)
西安工程大学
数字电子技术基础
Q 23. 已知 D 触发器各输入端的波形如图所示,试画出 Q 、 触发器各输入端的波形如图所示, 端的波形。 端的波形。
答案: 答案:
西示为边沿 触发器构成的电路图,设触发器的初状态 如图所示为边沿D触发器构成的电路图 触发器构成的电路图, Q1Q0=00,确定 0 及Q1在时钟脉冲作用下的波形。 在时钟脉冲作用下的波形。 ,确定Q 答案: 答案: 因为 D0 = Q1
17. 试用 试用74161构成九进制计数器。(可采用异步清零法或 构成九进制计数器。( 构成九进制计数器。(可采用异步清零法或 同步预置数法) 同步预置数法) 异步清零法 同步预置数法
答案: 答案:
西安工程大学
数字电子技术基础 17.由或非门组成的触发器和输入端信号如图所示,设触发器 由或非门组成的触发器和输入端信号如图所示, 由或非门组成的触发器和输入端信号如图所示 的初始状态为1,画出输出端Q的波形 的波形。 的初始状态为 ,画出输出端 的波形。 答案: 答案:
西安工程大学
数字电子技术基础 列状态转换表 画状态转换图和时序波形图
由状态图可以看出, 由状态图可以看出, 当输入X 当输入 =0时,状态变化为: 00→01→10→11→00→… 时 状态变化为: 当X=1时,状态变化为: 00→11→10→01→00→… = 时 状态变化为: 可见,该电路既具有递增计数功能,又具有递减计数功能, 可见,该电路既具有递增计数功能,又具有递减计数功能, 是一个2位二进制同步可逆计数器 位二进制同步可逆计数器。 是一个 位二进制同步可逆计数器。 西安工程大学
数字电子技术基础 令A2=E A1=F A0=G 则
′ ′ Y0′ ~ Y7′ → m0 ~ m7
数字电子技术基础-课后习题答案第4章组合逻辑电路

第四章习题答案4-1(a)100A A F ⊕=,211A A F ⊕=,322A A F ⊕=,33A F =(b) 000B A C =,011111)()(C B A B A C ⊕+=,000B A S ⊕=,0111)(C B A S ⊕⊕= (c) B A AB F +=(同或)(d) B A AC F +=1,B A BC F +=2,C A BC F+=3, 4-2,F ,F ,F∑=)9,8,7,6,5(3m F ,∑=)9,4(2m F ,∑=)8,7,3,2(1m F ,∑=)8,6,3,1(0m F卡诺图化简D F =3,AD D C B F +=2,D A C B CD F ++=1,D B A D A F +=0,F ,F ,F∑=)9,8,7,6,5(3m Y ,∑=)9,4,3,2,1(2m Y , ∑=)8,7,4,3,0(1m Y ,∑=)8,6,4,2,0(0m Y用4-16线译码器实现987653F F F F F Y =,943212F F F F F Y =,874301F F F F F Y =,864200F F F F F Y =4-3将四片138译码器级联,ST 接高电平,ST 接低电平,ST 由译码控制3442A A ST =,3432A A ST =,3432A A ST =,3432A A ST =4-4113471347(1,3,4,7)F m m m m m F F F F ===∑ 2046046(0,4,6)F m m m m F F F ===∑4-51)一片8选1,输入A 、B 、C 分别接8选1的地址A 2,A 1,A 00,,1,17563420========D D D D D D D D D D2)两片8选1,输入A 、B 、C ,D 分别接4选1的地址012,,,A A A E1,01413121197651151084320================D D D D D D D D D D D D D D D D4-6A S SB A S S B A S S AB S S F 01010101)()(+⊕+++= A S S B A S S B A S S B S S A S S AB S S F 010*********+++++=将A S S ,,01分别接8选1的地址012,,A A A ,则输入端分别是0,1,,70635421========D D D D B D B D D D4-71) 输入A,B,C,D 分别接加法器的A 3,A 2,A 1,A 0, 加法器的B 3B 2B 1B 0=0011,CI=0 2) 输入A,B,C,D 分别接加法器的A 3,A 2,A 1,A 0, 加法器的B 3B 2B 1B 0=1101,CI=04-8假设四位被加数为ABCD ,加数为EFGH 输入A,B,C,D 分别接加法器的A 3,A 2,A 1,A 0, 加法器的B 3,B 2,B 1,B 0如下:M CI M H B M G B M F B M E B =⊕=⊕=⊕=⊕=,,,,01234-9真值表∑=)15,14,13,11,7(m F1)8选1数据选择器,将B A M ,,分别接8选1的地址012,,A A A ,则输入端分别是0,1,42107653========D D D D D C D D D2)用3-8译码器151413117151413117F F F F F m m m m m F ==4-10设三个开关分别为A,B,C ,开关的关闭为1,打开为0;灯的输出为F ,灯的亮为1,灭为0真值表C B A F =输入ABCD 分别接4-16译码器的地址段A 3,A 2,A 1,A 0 1) a 端:0158421=====D D D D D , 其余数据端接1 2) b 端:所有数据端均接1,1150=D D3) c 端:012109653======D D D D D D ,其余数据端接1 4) d 端:0158421=====D D D D D ,其余数据端接15) e 端:01514131187421=========D D D D D D D D D ,其余数据端接1 6) f 端:1150==D D ,其余数据端接07) g 端:08421====D D D D ,其余数据端接1设输出灯亮为1,灭为0真值表如下:1)4-16输入ABCD 分别接4-16译码器的地址段A 3,A 2,A 1,A 0(1) F 1端:143210=====D D D D D , 其余数据端接0 (2) F 2端:198765=====D D D D D , 其余数据端接0 (3) F3端:1151413121110======D D D D D D , 其余数据端接0 2)4位数据比较器实现用两片数据选择器,输入端ABCD 分别接两个比较器的A 3A 2A 1A 0,第一片比较器的B 3B 2B 1B 0=0101,第二片的B 3B 2B 1B 0=1001,两片的级联端0,1===<>=B A B A B A I I I ,则:B A I F <=11,B A I F >=23,212F F F =用4-16输入A 1A 0B 1B 0分别接4-16译码器的地址段A 3,A 2,A 1,A 0 (1) F 0端:1151375====D D D D , 其余数据端接0(2) F 1端:1141311976======D D D D D D , 其余数据端接0 (3) F 2端:1141110===D D D , 其余数据端接0 (4) F 3端:115=D , 其余数据端接04-141)只要把两片的B A I =直接相连就可以判断三个输入数据是否相等,假定输入为ABCD 四门课程,及格为1,不及格为0;输出F 为能否毕业,能够毕业为1,不能毕业为0。
数字电子技术基础第四章习题及参考答案

数字电子技术基础第四章习题及参考答案第四章习题1.分析图4-1中所示的同步时序逻辑电路,要求:(1)写出驱动方程、输出方程、状态方程;(2)画出状态转换图,并说出电路功能。
CPY图4-12.由D触发器组成的时序逻辑电路如图4-2所示,在图中所示的CP脉冲及D作用下,画出Q0、Q1的波形。
设触发器的初始状态为Q0=0,Q1=0。
D图4-23.试分析图4-3所示同步时序逻辑电路,要求:写出驱动方程、状态方程,列出状态真值表,画出状态图。
CP图4-34.一同步时序逻辑电路如图4-4所示,设各触发器的起始状态均为0态。
(1)作出电路的状态转换表;(2)画出电路的状态图;(3)画出CP作用下Q0、Q1、Q2的波形图;(4)说明电路的逻辑功能。
图4-45.试画出如图4-5所示电路在CP波形作用下的输出波形Q1及Q0,并说明它的功能(假设初态Q0Q1=00)。
CPQ1Q0CP图4-56.分析如图4-6所示同步时序逻辑电路的功能,写出分析过程。
Y图4-67.分析图4-7所示电路的逻辑功能。
(1)写出驱动方程、状态方程;(2)作出状态转移表、状态转移图;(3)指出电路的逻辑功能,并说明能否自启动;(4)画出在时钟作用下的各触发器输出波形。
CP图4-78.时序逻辑电路分析。
电路如图4-8所示:(1)列出方程式、状态表;(2)画出状态图、时序图。
并说明电路的功能。
1C图4-89.试分析图4-9下面时序逻辑电路:(1)写出该电路的驱动方程,状态方程和输出方程;(2)画出Q1Q0的状态转换图;(3)根据状态图分析其功能;1B图4-910.分析如图4-10所示同步时序逻辑电路,具体要求:写出它的激励方程组、状态方程组和输出方程,画出状态图并描述功能。
1Z图4-1011.已知某同步时序逻辑电路如图4-11所示,试:(1)分析电路的状态转移图,并要求给出详细分析过程。
(2)电路逻辑功能是什么,能否自启动?(3)若计数脉冲f CP频率等于700Hz,从Q2端输出时的脉冲频率是多少?CP图4-1112.分析图4-12所示同步时序逻辑电路,写出它的激励方程组、状态方程组,并画出状态转换图。
数字电子技术基本(第四版)课后知识题目解析第四章
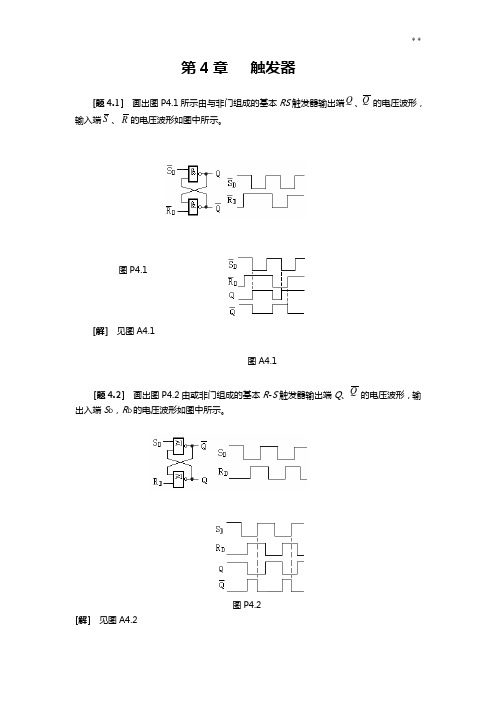
第4章触发器[题4.1]画出图P4.1所示由与非门组成的基本RS触发器输出端Q、Q的电压波形,输入端S、R的电压波形如图中所示。
图P4.1[解]见图A4.1图A4.1[题4.2]画出图P4.2由或非门组成的基本R-S触发器输出端Q、Q的电压波形,输出入端S D,R D的电压波形如图中所示。
图P4.2[解]见图A4.2[题4.3] 试分析图P4.3所示电路的逻辑功能,列出真值表写出逻辑函数式。
图P4.3[解]S R Q n Q n+1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 0* 1 110*由真值表得逻辑函数式 01=+=+SR Q R S Q nn[题4.4] 图P4.4所示为一个防抖动输出的开关电路。
当拨动开关S 时,由于开关触点接触瞬间发生振颤,D S 和D R 的电压波形如图中所示,试画出Q 、Q 端对应的电压波形。
图P4.4[解]见图A4.4图A4.4[题4.5]在图P4.5电路中,若CP、S、R的电压波形如图中所示,试画出Q和Q端与之对应的电压波形。
假定触发器的初始状态为Q=0。
图P4.5[解]见图A4.5图A4.5[题4.6]若将同步RS触发器的Q与R、Q与S相连如图P4.6所示,试画出在CP 信号作用下Q和Q端的电压波形。
己知CP信号的宽度t w = 4 t Pd 。
t Pd为门电路的平均传输延迟时间,假定t Pd≈t PHL≈t PLH,设触发器的初始状态为Q=0。
图P4.6图A4.6[解]见图A4.6[题4.7]若主从结构RS触发器各输入端的电压波形如图P4.7中所给出,试画Q、Q 端对应的电压波形。
设触发器的初始状态为Q=0。
图P4.7[解] 见图A4.7图A4.7[题4.8]若主从结构RS触发器的CP、S、R、D R各输入端的电压波形如图P4.8所S。
试画出Q、Q端对应的电压波形。
示,1D图P4.8[解] 见图A4.8图A4.8[题4.9]已知主从结构JK触发器输入端J、K和CP的电压波形如图P4.9所示,试画出Q、Q端对应的电压波形。
《数字电子技术基础》课后习题答案

《数字电路与逻辑设计》作业教材:《数字电子技术基础》(高等教育出版社,第2版,2012年第7次印刷)第一章:自测题:一、1、小规模集成电路,中规模集成电路,大规模集成电路,超大规模集成电路5、各位权系数之和,1799、01100101,01100101,01100110;11100101,10011010,10011011二、1、×8、√10、×三、1、A4、B练习题:、解:(1) 十六进制转二进制: 4 5 C0100 0101 1100二进制转八进制:010 001 011 1002 13 4十六进制转十进制:(45C)16=4*162+5*161+12*160=(1116)10(2) 十六进制转二进制: 6 D E . C 80110 1101 1110 . 1100 1000 二进制转八进制:011 011 011 110 . 110 010 0003 3 3 6 . 6 2十六进制转十进制:()16=6*162+13*161+14*160+13*16-1+8*16-2=()10所以:()16=()2=()8=()10(3) 十六进制转二进制:8 F E . F D1000 1111 1110. 1111 1101二进制转八进制:100 011 111 110 . 111 111 0104 3 7 6 . 7 7 2十六进制转十进制:(8FE.FD)16=8*162+15*161+14*160+15*16-1+13*16-2=(2302.98828125)10 (4) 十六进制转二进制:7 9 E . F D0111 1001 1110 . 1111 1101二进制转八进制:011 110 011 110 . 111 111 0103 6 3 6 . 7 7 2十六进制转十进制:(79E.FD)16=7*162+9*161+14*160+15*16-1+13*16-2=(1950. 98828125)10 所以:()16.11111101)2=(363)8=(1950.98828125)10、解:(74)10 =(0111 0100)8421BCD=(1010 0111)余3BCD(45.36)10 =(0100 0101.0011 0110)8421BCD=(0111 1000.0110 1001 )余3BCD(136.45)10 =(0001 0011 0110.0100 0101)8421BCD=(0100 0110 1001.0111 1000 )余3BCD (374.51)10 =(0011 0111 0100.0101 0001)8421BCD=(0110 1010 0111.1000 0100)余3BCD、解(1)(+35)=(0 100011)原= (0 100011)补(2)(+56 )=(0 111000)原= (0 111000)补(3)(-26)=(1 11010)原= (1 11101)补(4)(-67)=(1 1000011)原= (1 1000110)补第二章:自测题:一、1、与运算、或运算、非运算3、代入规则、反演规则、对偶规则二、2、×4、×三、1、B3、D5、C练习题:2.2:(4)解:(8)解:2.3:(2)证明:左边=右式所以等式成立(4)证明:左边=右边=左边=右边,所以等式成立(1)(3)2.6:(1)2.7:(1)卡诺图如下:BCA00 01 11 100 1 11 1 1 1所以,2.8:(2)画卡诺图如下:BC A 0001 11 100 1 1 0 11 1 1 1 12.9:如下:CDAB00 01 11 1000 1 1 1 101 1 111 ×××10 1 ××2.10:(3)解:化简最小项式:最大项式:2.13:(3)技能题:2.16 解:设三种不同火灾探测器分别为A、B、C,有信号时值为1,无信号时为0,根据题意,画卡诺图如下:BC00 01 11 10A0 0 0 1 01 0 1 1 1第三章:自测题:一、1、饱和,截止7、接高电平,和有用输入端并接,悬空;二、1、√8、√;三、1、A4、D练习题:、解:(a)Ω,开门电阻3kΩ,R>R on,相当于接入高电平1,所以(e) 因为接地电阻510ΩkΩ,R<R off,相当于接入高电平0,所以、、解:(a)(c)(f)、解: (a)、解:输出高电平时,带负载的个数2020400===IH OH OH I I N G 可带20个同类反相器输出低电平时,带负载的个数78.1745.08===IL OL OL I I NG反相器可带17个同类反相器EN=1时,EN=0时,根据题意,设A为具有否决权的股东,其余两位股东为B、C,画卡诺图如下,BC00 01 11 10A0 0 0 0 01 0 1 1 1则表达结果Y的表达式为:逻辑电路如下:技能题::解:根据题意,A、B、C、D变量的卡诺图如下:CD00 01 11 10AB00 0 0 0 001 0 0 0 0 11 0 1 1 1 10 0 0 0 0电路图如下:第四章:自测题:一、2、输入信号,优先级别最高的输入信号7、用以比较两组二进制数的大小或相等的电路,A>B 二、 3、√ 4、√ 三、 5、A 7、C练习题:4.1;解:(a),所以电路为与门。
《数字电子技术基础》课后习题答案

《数字电路与逻辑设计》作业教材:《数字电子技术基础》(高等教育出版社,第2版,2012年第7次印刷)第一章:自测题:一、1、小规模集成电路,中规模集成电路,大规模集成电路,超大规模集成电路5、各位权系数之和,1799、01100101,01100101,01100110;11100101,10011010,10011011二、1、×8、√10、×三、1、A4、B练习题:1.3、解:(1)十六进制转二进制:45 C010*********二进制转八进制:010*********2134十六进制转十进制:(45C)16=4*162+5*161+12*160=(1116)10所以:(45C)16=(10001011100)2=(2134)8=(1116)10(2)十六进制转二进制:6D E.C8011011011110.11001000二进制转八进制:011011011110.1100100003336.62十六进制转十进制:(6DE.C8)16=6*162+13*161+14*160+13*16-1+8*16-2=(1758.78125)10所以:(6DE.C8)16=(011011011110. 11001000)2=(3336.62)8=(1758.78125)10(3)十六进制转二进制:8F E.F D100011111110.11111101二进制转八进制:100011111110.1111110104376.772十六进制转十进制:(8FE.FD)16=8*162+15*161+14*160+15*16-1+13*16-2=(2302.98828125)10所以:(8FE.FD)16=(100011111110.11111101)2=(437 6.772)8=(2302.98828125)10 (4)十六进制转二进制:79E.F D011110011110.11111101二进制转八进制:011110011110.1111110103636.772十六进制转十进制:(79E.FD)16=7*162+9*161+14*160+15*16-1+13*16-2=(1950. 98828125)10所以:(8FE.FD)16=(011110011110.11111101)2=(3636.772)8=(1950.98828125)101.5、解:(74)10 =(0111 0100)8421BCD=(1010 0111)余3BCD(45.36)10 =(0100 0101.0011 0110)8421BCD=(0111 1000.0110 1001 )余3BCD(136.45)10 =(0001 0011 0110.0100 0101)8421BCD=(0100 0110 1001.0111 1000 )余3BCD (374.51)10 =(0011 0111 0100.0101 0001)8421BCD=(0110 1010 0111.1000 0100)余3BCD1.8、解(1)(+35)=(0 100011)原= (0 100011)补(2)(+56 )=(0 111000)原= (0 111000)补(3)(-26)=(1 11010)原= (1 11101)补(4)(-67)=(1 1000011)原= (1 1000110)补第二章:自测题:一、1、与运算、或运算、非运算3、代入规则、反演规则、对偶规则 二、 2、×4、× 三、 1、B 3、D5、C练习题:2.2:(4)解:Y =AB̅+BD +DCE +A D =AB̅+BD +AD +A D +DCE =AB̅+BD +D +DCE =AB̅+D (B +1+CE ) =AB̅+D (8)解:Y =(A +B ̅+C )(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅(A +B ̅+C +DE ) =[(A +B ̅+C )̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅+(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅](A +B ̅+C +DE ) =(ABC +DE )(ABC ̅̅̅̅̅̅+DE ) =DE2.3:(2)证明:左边=A +A (B +C)̅̅̅̅̅̅̅̅̅̅̅̅ =A +A +(B +C)̅̅̅̅̅̅̅̅̅̅ =A +B̅C ̅ =右式所以等式成立(4)证明:左边= (A B +AB̅)⨁C = (A B +AB ̅)C + (A B +AB̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅C = (A BC +AB ̅C )+A B ̅̅̅̅⋅AB̅̅̅̅⋅C =A BC +AB̅C +(A +B ̅)(A +B )C =A BC +AB̅C +(AB +A B ̅)C =A BC +AB̅C +ABC +A B ̅C 右边= ABC +(A +B +C )AB̅̅̅̅⋅BC ̅̅̅̅⋅CA ̅̅̅̅ =ABC +(A +B +C )[(A +B̅)(B ̅+C )(C +A )]=ABC +(A +B +C )(A B̅+A C +B ̅+B ̅C )(C +A ) =ABC +(A +B +C )(A B̅C +A C +B ̅C +A B ̅) =ABC +AB̅C +A BC +A B ̅C 左边=右边,所以等式成立 2.4(1)Y ′=(A +B̅C )(A +BC) 2.5(3)Y ̅=A B ̅̅̅̅(C +D ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅ C D ̅̅̅̅̅(A +B ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅ 2.6:(1)Y =AB +AC +BC=AB (C +C̅)+AC (B +B ̅)+BC (A +A ̅) =ABC +ABC̅+AB ̅C +A ̅BC 2.7:(1)Y =A B̅+B ̅C +AC +B ̅C 卡诺图如下:所以,Y =B2.8:(2)画卡诺图如下:Y(A,B,C)=A +B̅+C2.9:(1)画Y (A,B,C,D )=∑m (0,1,2,3,4,6,8)+∑d(10,11,12,13,14)如下:Y (A,B,C,D )=A B̅+D ̅2.10:(3)解:化简最小项式:Y =AB +(A B +C )(A B̅+C ) =AB +(A B A B̅+A BC +A B ̅C +C C ) =AB (C +C )+A BC +A B̅C =ABC +ABC ̅+A BC +A B ̅C =∑m (0,3,6,7)最大项式:Y =∏M(1,2,4,5)2.13:(3)Y =AB̅+BC +AB ̅C +ABC D ̅ =AB̅(1+C )+BC (1+AD ̅) =AB ̅+BC =AB ̅+BC ̿̿̿̿̿̿̿̿̿̿̿̿ = AB ̅̅̅∙BC ̅̅̅̅̅̅̅̅̅̅̅技能题:2.16 解:设三种不同火灾探测器分别为A 、B 、C ,有信号时值为1,无信号时为0,根据题意,画卡诺图如下:Y =AB +AC +BC =AB +AC +BC ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿ =AB ̅̅̅̅⋅AC̅̅̅̅⋅BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ =(A +B ̅)(A +C )(B ̅+C )̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ =A +B ̅̅̅̅̅̅̅̅+A +C ̅̅̅̅̅̅̅̅+B ̅+C̅̅̅̅̅̅̅̅第三章:自测题:一、1、饱和,截止7、接高电平,和有用输入端并接,悬空; 二、 1、√ 8、√; 三、 1、A 4、D练习题:3.2、解:(a)因为接地电阻4.7k Ω,开门电阻3k Ω,R>R on ,相当于接入高电平1,所以Y =A B 1̅̅̅̅̅̅=A +B +0=A +B (e) 因为接地电阻510Ω,关门电0.8k Ω,R<R off ,相当于接入高电平0,所以、 Y =A +B +0̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅⋅B ̅∙1̅̅̅̅̅̅̅̅̅̅=A +B +0=A +B3.4、解:(a) Y 1=A +B +0̅̅̅̅̅̅̅̅̅̅̅̅̅=A +B ̅̅̅̅̅̅̅(c) Y 3=A +B +1̅̅̅̅̅̅̅̅̅̅̅̅̅=1̅=0(f) Y 6=A ⋅0+B ⋅1̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=B̅3.7、解:(a) Y 1=A⨁B ⋅C =(A B +AB̅)C =A B C +AB ̅C3.8、解:输出高电平时,带负载的个数2020400===IH OH OH I I N G 可带20个同类反相器输出低电平时,带负载的个数78.1745.08===IL OL OL I I N G 反相器可带17个同类反相器3.12EN=1时,Y 1=A , Y 2=B̅ EN=0时,Y 1=A̅, Y 2=B3.17根据题意,设A 为具有否决权的股东,其余两位股东为B 、C ,画卡诺图如下,则表达结果Y 的表达式为:Y =AB +AC =AB +AC ̿̿̿̿̿̿̿̿̿̿̿=AB ̅̅̅̅⋅AC̅̅̅̅̅̅̅̅̅逻辑电路如下:技能题:3.20:解:根据题意,A 、B 、C 、D 变量的卡诺图如下:Y =ABC +ABD =ABC +ABD ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=ABC̅̅̅̅̅̅⋅ABD ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅电路图如下:第四章:自测题:一、2、输入信号,优先级别最高的输入信号7、用以比较两组二进制数的大小或相等的电路,A>B 二、 3、√ 4、√ 三、 5、A 7、C练习题:4.1;解:(a) Y =A⨁B +B ̅̅̅̅̅̅̅̅̅̅̅̅̅=A B +AB ̅+B ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A B +B ̅̅̅̅̅̅̅̅̅̅̅=A +B ̅̅̅̅̅̅̅̅=AB ,所以电路为与门。
数字电子技术基础(第4版)课后习题答案详解

(9)Y = BC + AD + AD
1.9 (a) Y = ABC + BC
(10)Y = AC + AD + AEF + BDE + BDE (b) Y = ABC + ABC
(c) Y1 = AB + AC D,Y2 = AB + AC D + ACD + ACD
(d) Y1 = AB + AC + BC,Y2 = ABC + ABC + ABC + ABC 1.10 求下列函数的反函数并化简为最简与或式
(7)Y=A+CD
(6)Y = AC(CD + AB) + BC(B + AD + CE) 解:Y = BC(B ⋅ AD + CE) = BC(B + AD) ⋅ CE = ABCD(C + E ) = ABCDE
(8)Y = A + (B + C)( A + B + C)(A + B + C) 解:Y = A + (B ⋅C)(A + B + C)(A + B + C) = A + (ABC + BC)(A + B + C) = A + BC( A + B + C) = A + ABC + BC = A + BC
(4)Y = A + B + C
(5)Y = AD + AC + BCD + C 解:Y = (A + D)(A + C)(B + C + D)C = AC(A + D)(B + C + D) = ACD(B + C + D) = ABCD
数字电子技术第4章习题解答

第4章习题解答4-1 写出图T4-1电路的输出函数式,证明a 、b 有相同的逻辑功能。
B(a)A(b)BA 图T4-1 习题4-1的图解4-1 Y 1= A B ' +A ' B ' ; Y 2=( A+B)(A ' +B ' )= AB ' +A ' B ' =Y 14-2 试写出图T4-2所示逻辑电路的输出函数式并化简,指出电路的逻辑功能。
A BMBA图T4-2习题4-2的图图T4-3习题4-3的图解4-2 由图T4-2写电路的输出函数式并化简得AB B A B A AB Y +''='''''=))()(( (JT4-2)由JT4-2式可知,电路实现的是二变量同或功能。
4-3 图T4-3是一个选通电路。
M 为控制信号,通过M 电平的高低来选择让A 还是让B 从输出端送出。
试写逻辑电路的输出函数式并化简,分析电路能否实现上述要求。
解4-3 由图T4-3写电路的输出函数式并化简得M B AM M B M A Y '+='''=)((( (JT4-3)由JT4-3式可知,电路能够实现选通要求,当M=1时,Y=A ;当M=0时,Y=B 。
4-4.用与非门设计一个四人表决逻辑电路,结果按“少数服从多数”的原则决定。
解4-4(1)列真值表设四个人的意见为变量A 、B 、C 、D ,表决结果为函数Y 。
按正逻辑给变量赋值:同意为“1”,不同意为“0”;提案通过为“1”,没通过为“0”,所列真值表如表JT4-4所示。
表JT4-4输 入输 出A B C D 0 0 0 0 0 00 0 0 1 0 1 0 1 0 10 0 0 1 1 0 1 1 0 0 0 1 1 01 1 Y000000001 0 1 0 1 0 1 01 1 1 1 1 11 1 0 0 0 1 1 0 1 1 0 00 1 1 0 1 100000000输 入输 出A B C D Y(2)写输出逻辑函数式由表JT4-4可写输出逻辑函数式ABCD D ABC D C AB CD B A BCD A Y +'+'+'+'= (JT4-4a)(3)化简填卡诺图,如图JT 4-4(a)所示合并最小项,得最简与—或式BCD ACD ABD ABC Y +++= (JT4-4b)(4)画逻辑电路图将式JT4-4(b)转换成与非—与非式)()()()(('''''=D BC ACD ABD ABC Y (JT4-4c)按式JT4-4(c)用与非门画逻辑电路图,如图JT4-4(b)所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题44-1 分析图P4-1所示的各组合电路,写出输出函数表达式,列出真值表,说明电路的逻辑功能。
解:图(a ):1F AB =;2F A B =;3F AB = 真值表如下表所示:其功能为一位比较器。
A>B 时,11F =;A=B 时,21F =;A<B 时,31F = 图(b ):12F AB AB F AB =+=; 真值表如下表所示:功能:一位半加器,1F 为本位和,2F 为进位。
图(c ):1(0,3,5,6)(1,2,4,7)F M m ==∑∏真值表如下表所示:功能:一位全加器,1F 为本位和,2F 为本位向高位的进位。
图(d ):1F AB =;2F A B =;3F AB =功能:为一位比较器,A<B 时,1F =1;A=B 时,2F =1;A>B 时,3F =14-2 分析图P4-2所示的组合电路,写出输出函数表达式,列出真值表,指出该电路完成的逻辑功能。
解:该电路的输出逻辑函数表达式为:因此该电路是一个四选一数据选择器,其真值表如下表所示:4-3 图P4-3是一个受M 控制的代码转换电路,当M =1时,完成4为二进制码至格雷码的转换;当M =0时,完成4为格雷码至二进制的转换。
试分别写出0Y ,1Y ,2Y ,3Y 的逻辑函数的表达式,并列出真值表,说明该电路的工作原理。
解:该电路的输入为3x 2x 1x 0x ,输出为3Y 2Y 1Y 0Y 。
真值表如下:由此可得:1M =当时,33232121010Y x Y x x Y x x Y x x =⎧⎪=⊕⎪⎨=⊕⎪⎪=⊕⎩ 完成二进制至格雷码的转换。
完成格雷码至二进制的转换。
4-4 图P4-4是一个多功能逻辑运算电路,图中3S ,2S ,1S ,0S 为控制输入端。
试列表说明电路在3S ,2S ,1S ,0S 的各种取值组合下F 与A,B 的逻辑关系。
解:3210()()F S AB S AB S B S B A =+⊕++,功能如下表所示,两个变量有四个最小项,最多可构造42种不同的组合,因此该电路是一个能产生十六种函数的多功能逻辑运算器电路。
4-5 已知某组合电路的输出波形如图P4-5所示,试用最少的或非门实现之。
解:()(1,3,6,7)(0)()F ABC m A C A B φ=+=+++∑∑电路图如下:4-6 用逻辑门设计一个受光,声和触摸控制的电灯开关逻辑电路,分别用A,B,C 表示光,声和触摸信号,用F 表示电灯。
灯亮的条件是:无论有无光,声信号,只要有人触摸开关,灯就亮;当无人触摸开关时,只有当无关,有声音时灯才亮。
试列出真值表,写出输出函数表达式,并画出最简逻辑电路图。
解:根据题意,列出真值表如下:由真值表可以作出卡诺图,如下图:C AB 00 10 11 10 0 1 由卡诺图得到它的逻辑表达式为:由此的到逻辑电路为:F AB C =+4-7 用逻辑门设计一个多输出逻辑电路,输入为8421BCD 码,输出为3个检测信号。
要求:(1) 当检测到输入数字能被4整除时,1F =1。
(2) 当检测到输入数字大于或等于3时,2F =1。
(3) 当检测到输入数字小于7时,3F =1。
解:1()f ABCD CD =4-8 用逻辑门设计一个两位二进制数的乘法器。
解:二进制乘法:设两个2位二进制数的乘法运算结果为:10103210()()A A A B B B P P PP ⨯= 电路图如下图所示:4-9 设计一个全加(减)器,其输入为A,B,C 和X(当X =0时,实现加法运算;当X =1时,实现减法运算),输出为S(表示和或差),P (表示进位或借位)。
列出真值表,试用3个异或门和3个与非门实现该电路,画出逻辑电路图。
解:根据全加器和全减器的原理,我们可以作出如下的真值表:1 B 3 B2 B 1 B 0由真值表可以画出卡诺图,由卡诺图得出逻辑表达式,并画出逻辑电路图:4-10 设计一个交通灯故障检测电路,要求红,黄,绿三个灯仅有一个灯亮时,输出F=0;若无灯亮或有两个以上的灯亮,则均为故障,输出F=1。
试用最少的非门和与非门实现该电路。
要求列出真值表,化简逻辑函数,并指出所有74系列器件的型号。
解:根据题意,我们可以列出真值表如下:对上述的真值表可以作出卡诺图,由卡诺图我们可以得出以下的逻辑函数:逻辑电路图如下所示:4-11试用两片8线-3线优先编码器74LS148组成16线-4线优先编码器,画出逻辑电路图,说明其逻辑功能。
解:逻辑电路图如下:逻辑功能:是一个16-4编码器。
4-12 (1)图P4-12为3个单译码逻辑门译码器,指出每个译码器的输出有效电平以及相应的输出二进制码,写出译码器的输出函数表达式。
(2)试画出与下列表达式对应的单译码器逻辑电路图。
①3210Y A A A A = ②3210Y A A A A = ③43210Y A A A A A = 解:对于(a )图来说。
3210Y A A A A = (b) 210Y A A A = (c) 3210Y A A A A = 对于(1)逻辑电路图为: (2)逻辑电路图如下图: (3)逻辑电路图如下图:4-13 试用一片3-8译码器和少量逻辑门设计下列多地址输入的译码电路。
(1) 有8根地址输入线7A ~1A ,要求当地址码为A8H,A9H ,…,AFH 时,译码器输出为0Y ~7Y 分别被译中,且地电平有效。
(2) 有10根地址输入线9A ~0A ,要求当地址码为2E0H,2E1H, …,2E7H 时,译码器输出0Y ~7Y 分别被译中,且地电平有效。
解:(1)当122100A B E E E =,即75364210111,00,A A A A A A A A ==从000~111变化时07~Y Y 分别被译中,电路如下图所示:(2)当122100A B E E E =,即97538432101111,000,A A A A A A A A A A ==从000~111变化时,07~Y Y 分别被译中。
电路如下图所示:4-14 试用一片3-8译码器74LS138和少量的逻辑门实现下列多输出函数: (1)1F AB ABC =+ (2) 2F A B C =++ (3) 3F AB AB =+1S =解:1067(0,6,7)F m Y Y Y==∑电路图如下图所示:4-15 某组合电路的输入X 和输出Y 均为三位二进制数。
当X<2时,Y=1;当25X ≤≤时,Y=X+2;当X>5时,Y=0。
试用一片3-8译码器和少量逻辑门实现该电路。
解:由题意列出真值表如下:电路图如下图所示:输入X =ABC ,输出为Y 。
4-16 由3-8译码器74LS138和逻辑门构成的组合 逻辑电路图P4-16所示。
(1) 试分别写出1F ,2F 的最简与或表达式。
(2) 试说明当输入变量A,B,C,D 为何种取值时,1F =2F =1。
解:(1)当D=1时,201F =⎧⎨=⎩1F当D=0时,0342467(,,)(,,)()()()A B C m m m ABC ABC ABCF A B C m m m A B C A B C A B C ⎧=++=++⎪⎨==++++++⎪⎩1F将1F ,2F 分别填入四变量的卡诺图后可得: (2)当ABCD=0000或0110时,1F =2F =1 4-17 已知逻辑函数(,,,)(1,3,7,9,15)F a b c d m =∑,试用一片3-8译码器74LS138和少量逻辑门实现该电路。
解:由题意的,(,,,)(1,3,7,9,15)()F a b c d m ABC ABC ABC ABC ABC D ==++++∑电路图如下图所示:4-18 某2-4译码器的逻辑符号和功能表如图P4-18所示。
试用尽量少的译码器和或门实现下列函数(允许反变量输入): (1)(,,,)F W X Y Z W X Y X YZ WZ =++ (2)(,,,)G W X Y Z WYZ X Y =+ 解:根据题意,输入分别为X,Y ,W,Z 。
对于(1)来说,我们可以作出如下的逻辑电路图: (2)由题,我们可以得出如下的逻辑电路图:4-19 由3-8译码器构成的脉冲分配器电路图如图P4-19所示。
(1) 若CP 脉冲信号加在2E 端,试画出0Y ~7Y 的波形; (2) 若CP 脉冲信号加在1E 端,试画出0Y ~7Y 的波形。
解:(1)CP=1时,i 1Y =;CP=0时07~Y Y 按210A A A 的变化分别译码。
波形如下图所示: (2)CP=1时07~Y Y 按210A A A 的变化分别译码;CP=0时,i 1Y =。
波形图如下图所示: 4-20 试用三片3-8译码器组成5-24译码器。
解:5-24译码器如下图所示,图中:43210A A A A A 为地址输入,0123Y Y Y 为译码输出。
当4300A A =时,左边第一片译码器工作,4301A A =时,中间一片译码器工作; 43A A =10时,右边一片译码器工作; 43A A =11时,三片译码器全部禁止。
4-21 用一片BCD 码十进制译码器和附加门实现8421BCD 码至余3码的转换电路。
解:3(5,6,7,8,9)E m =∑电路图如下图所示:4-22 试用一片4-16译码器组成一个5421BCD 码十进制数译码器。
解:根据四位二进制码和5421BCD 码的对应关系,可得如下图所示的电路:4-23 试用8选1数据选择器74LS151实现下列逻辑函数(允许反变量输入,但不能附加门电路):(1)F A B AC BC =⊕⊕⊕ (2) (,,)(0,2,3,6,7)F A B C m =∑(3)(,,,)(0,4,5,8,12,13,14)F A B C D m =∑ (4) (,,,)(0,2,5,7,8,10,13,15)F A B C D m =∑(5) (,,,)(0,3,5,8,11,14)(1,6,12,13)F A B C D m d =+∑∑解: (1) (2,4)()(0,0,1,0,1,0,0,0)T mF m ABC ==∑(2) ()(1,0,1,1,0,0,1,1)Tm F ABC =(3)()(1,,0,0,1,,,0)()(1,0,0,0,1,1,,0)()(,0,1,0,,0,1,)T T m m Tm F ACD B B B BCD A ABC D D D ===(4) (0)(1,0,0,1,0,0,0,0)(0)(1,0,0,0,0,0,1,0)T Tm m F BD BD ==(5)()(,1,0,,1,0,,)()(1,0,0,1,0,1,1,0)()(1,,,0,,,0,)T T m m Tm F ACD B B B B BCD ABC D D D D D ===4-24 试用16选1数据选择器和一个异或门实现一个八用逻辑电路。
