专题1:选择题专题复习1
形势与政策 专题一 专题测验与答案

形式与政策专题一中国特色社会主义道路是实现中华民族伟大复兴的必由之路——学习《习近平谈治国理政第三卷》一、单项选择题1.( B )问题是关系党的事业兴衰成败第一位的问题,( )就是党的生命。
A.制度道路B.道路道路C.制度制度D.道路制度2.党的基本路线的核心内容是( B )。
A.社会主义制度B."一个中心、两个基本点”C.改革开放D.“两个维护”3.( D )是中国特色社会主义最本质的特征,是中国特色社会主义制度的最大优势。
A.人民当家作主B.依法治国C.以德治国D.党的领导4.我国坚持走中国特色社会主义政治发展道路,这条道路的核心是坚持党的领导、人民当家作主和( A )有机统一。
A.依法治国B.社会主义制度C.以德治国D.三权分立5.改革开放以来,我们总结历史经验,不断艰辛探索,终于找到了实现中华民族伟大复兴的正确道路,取得了举世瞩目的成果。
这条道路就是( C )。
A.改革开放B.经济体制改革C.中国特色社会主义D.人民当家作主二、判断题1.中国道路的实质是中国传统文化和中国具体实践相结合。
(×)2.全党要自觉地增强道路自信、理论自信、制度自信、文化自信。
其中,制度自信位居“四个自信”之首,增强"四个自信首先要增强制度自信。
(×)3.坚持和发展中国特色社会主义,是改革开放以来包括新时代以来我们党的全部理论实践主题。
(√)4.坚持中国特色社会主义发展道路,就要坚持中国特色社会主义经济发展道路、政治发展道路、文化发展道路、社会发展道路和生态发展道路。
(√)5.中国特色社会主义道路是从中国实际出发探索出来的一条道路。
(√)。
广西中考英语考试题型专题复习-1单项选择

( C )28. —Your spoken English is much better. —Thank you. My teacher often asks us ________ English as ________ as possible. A. to speak; many B. not to speak; much C. to speak; much D. not to speak; more ( B )29. It's getting dark. Please ________ the light. A. turn off B. turn on C. turn down D. turn up
专题一┃ 单项选择
( B )26. ________ it's difficult to learn English well, ________ you should never drop it. A. Though; but B. Though; / C. Because; so D. Because; / ( B )27. The letter is ________ in French. I cannot read it. A. writing B. written C. wrote D. writes
专题一┃ 单项选择
( B )22. The father wished the twins to be doctors, but ________ of them liked to study medicine. A. both B. neither C. either D. none ( A )23. Now Helen works ________than before. A. more carefully B. more careful C. much careful D. much carefully
六年级语文选择题专题(一)

六年级语文选择题专题(一)1下面几组词语中;带点字读音都正确的一组是( )A、暂时(zàn) 魁梧(wú) 潜移默化(qiǎn)B、惩罚(chéng)勉强(qiǎng)惟妙惟肖(xiào)C、计较(jiǎo) 侮辱(wǔ) 茅塞顿开(sè)D、胆怯(qiè) 处理(chù) 扣人心弦(xián)2、下列加点字注音完全正确的一项是( )A、鸿鹄(hào)稀粥(zhōu)哆嗦(duō)军阀(fá)B、毡靴(xuē)宪兵(xiàn)涔涔(céng)潸潸(shān)C、伶俐(lì)萦绕(yíng)掺和(cān)窈窕(tiǎo)D、贮藏(zhù)梗概(gěng)烟囱(cōng)汲水(jí)3、下列带点汉字读音相同的一组是(C)A、剥花生剥落B、埋怨埋没C、夹杂夹道D、分毫分外4、下面几组词语中没有错别字的一组是( )A、穿流不息置之不理阴谋诡计兴高彩烈B、不计其数眼花缭乱郑重其事莫明其妙C、别出心裁迫不急待再接再厉出类拔萃D、德高望重不攻自破走投无路漫不经心5、下面词语中;没有错别字的一组是( )A五彩缤纷震撼天地蜿蜒曲拆 B实事求是混水摸鱼长途跋涉C不计其数含糊其词阴谋鬼计 D清澈见底处景生情面容憔悴6、下面各组没有错别字的是( )A严历畸形油光可鉴 B隐蔽虐杀咳人听闻 C菜畦弥漫再接再厉7、下列句子中加线成语运用不恰当的一项是( )A在学校的艺术节上;同学们别出心裁;自编自演了许多有趣的课本剧。
B春天的植物园;百花齐放;争奇斗艳;栩栩如生。
C我们要正确面对挫折和失败;不能怨天尤人;自暴自弃。
D他的演讲太出色了;我只好甘拜下风。
8 和“儿童急走追黄蝶”中的“走”字意思相同的一项是( )A走亲戚 B奔走相告 C走投无路 D走味儿9、下列句子没有语病的一项是(才)A、春风一阵阵吹来;树枝摇曳着;月光、树影一起晃动起来;发出沙沙的响声。
新高中地理高考专题01 地球与地图(精选练习)-备战2022年高考地理一轮复习考点帮(新高考专用)

专题01 地球与地图考点帮你练一、选择题(2021·江苏高三零模)尼泊尔拥有多条著名徒步旅行线路,是世界徒步旅行胜地。
2019年10月,小明乘机抵达加德满都,然后乘汽车前往博克拉,开始沿图示线路顺时针徒步旅行。
下图示意旅行线路及行程安排。
据此完成下面小题。
1.若汽车时速为50千米,小明从加德满都前往博克拉大约需要()A.2小时B.4小时C.6小时D.8小时2.北京时间12:00时,小明在徒步前行中发现太阳位于自己的右前方,此时小明最可能位于()A.①处B.②处C.③处D.④处【答案】1.B2.B【分析】1.从图中可知,加德满都和博克拉经度相差大约2°,两地纬度都接近30°,可以计算出两地距离为111千米×2×cos 30°,加上公路线的弯曲估算大约为200千米,汽车时速为50 千米,故大约需要4小时。
故选B。
2.根据所学知识可以计算出,当北京时间12∶00时,当地地方时在10;00 之前,正处于上午,太阳位于东南方。
由图中可以看出,当小明在②处时正向东走,太阳在其右前方,B正确。
③④处向南走,太阳位于左侧,C、D错误。
①处向西北方向走,太阳位于后方,A错误。
故选B。
(2021·北京高三一模)中国南极考察主要有三条航线:a航线(弗里曼特尔港一中山站)、b航线(霍巴特港一中山站)、c航线(利特尔顿港-长城站)。
读图,完成下面小题。
3.我国选择a航线的次数最多,主要考虑的是()A.航程最短B.沿途补给C.顺风顺水D.避开海雾4.c航线()A.跨越了南温带与南寒带B.跨越了日界线C.考察船上国旗常飘向东北D.考察船向东航行【答案】3.A4.B【分析】3.由图可知,与其他航线比较,a航线(弗里曼特尔港一中山站)航程最短,A正确;由图文材料无法推测a航线是否有沿途补给,B错误;a航线需穿越西风带和西风漂流,C错误;海雾主要是在寒暖流交汇海区或寒流经过的温暖海区或暖流经过的纬度较高的海区,与其他航线比较,a航线海雾状况不好判断,无特殊之处,D错误。
专题01 选择题83题(一)-(2020-2022)三年级数学上册江苏地区期末真题汇编(苏教版)

专题01 选择题83题(一)(2020-2022)三年级数学上册江苏地区期末真题汇编一、选择题1.(2020·江苏徐州·三年级期末)下面涂色部分可以用14表示的是()。
A.B.C.2.(2021·江苏盐城·三年级期末)有3个工人5小时生产150个零件,算式150÷5表示()。
A.每个工人1小时生产多少个零件B.这些工人1小时生产多少个零件C.每个工人5小时生产多少个零件3.(2020·江苏·摄山星城小学三年级期末)下面哪道算式的得数与90÷6得数相同?()A.90÷3÷3 B.90÷3×2 C.90÷3÷2 4.(2021·江苏盐城·三年级期末)下列算式的得数最接近于4000的是()。
A.802×5 B.889×4 C.761×55.(2021·江苏淮安·三年级期末)下面哪个数与492×8的积最接近?()。
A.4000 B.500 C.30006.(2022·江苏徐州·三年级期末)下列物品大约重1千克的是()。
A.20个鸡蛋B.一袋大米C.一筐梨7.(2022·江苏徐州·三年级期末)下面()图形是轴对称图形。
A.B.C.8.(2022·江苏徐州·三年级期末)小张同学在研究正方形的待征时,把正方形对折(如图),他是为了验证()。
A.正方形邻边相等B.正方形有4条边C.正方形对边相等9.(2022·江苏徐州·三年级期末)下面最接近1千克的物品是()。
A.3个鸡蛋B.4个苹果C.100粒花生10.(2022·江苏苏州·三年级期末)同学们研究43÷3=?,小华通过分小棒得到了答案,方方通过列竖式计算也得到了答案,图竖式中箭头所指的数相当于选项()中虚线圈出的小棒。
红楼梦专题选择题1

红楼梦专题选择题11.关于《红楼梦》中人物形象的分析,正确的一项是A.《红楼梦》中,晴雯性格温柔和顺,处事细心周到,人人称赞;袭人性情急躁直率,待人爱憎分明,受人怨谤。
二人性格迥异,却都走向悲剧结局,令人唏噓。
B.黛玉是诗社中的佼佼者,“温柔敦厚”是姐妹们对其诗风的赞誉。
C.《红楼梦》中写史湘云有金麒麟、薛宝钗有金锁,是为了说明她们有显赫的家世,从而反衬出林黛玉出身的贫寒。
D.《红楼梦》中的刘姥姥来自社会底层,农村生活孕育了她精于世故又朴实善良的复杂性格。
(正确答案)答案解析:1.【答案】D【详解】本题考查学生名著阅读的能力。
解答此类题目,考生要对大纲规定的名著名篇有熟悉程度,特别注意情节、人物、主题的把握,还要注意一些细节。
做题时要仔细。
A.“晴雯性格温柔和顺,处事细心周到,人人称赞;袭人性情急躁直率,待人爱憎分明,受人怨谤”错,二人性格正好颠倒,应是“袭人性格温柔和顺”,“晴雯性情急躁直率”。
B.“温柔敦厚”的不是黛玉,是宝钗。
C.“从而反衬出林黛玉出身的贫寒”错,不是为了反衬黛玉的贫寒,是表现她们与宝玉有着某种联系。
故选D。
2.下列有关《红楼梦》的说明,正确的一项是A.《红楼梦》中长着“两弯似蹙非蹙罥烟眉,一双似喜非喜含情目”的是王熙凤,该人最擅弄权术,例如毒设相思局、弄权铁槛寺、逼死尤二姐、破坏宝黛婚姻,最后落了个“机关算尽太聪明,反误了卿卿性命”的悲剧下场。
B.《红楼梦》中贾府的“四春”分别是:孤独的贾元春、精明的贾迎春、懦弱的贾探春、孤僻的贾惜春,取“原应叹息”之意。
C.“花谢花飞飞满天,红消香断有谁怜?……一朝春尽红颜老,花落人亡两不知!”这首诗出自《红楼梦》中人物林黛玉之手。
(正确答案)D.《红楼梦》中表明贾府收入主要书回的情节在第二十五回“乌庄头交租”一事上,表明贾府“排场费用,又不肯讲究省俭”的主要情节是“可卿丧仪”和“元春省亲”两件事。
答案解析:2.【答案】C【详解】本题考查名著阅读的能力。
专题01 选择题88题(一)-(2020-2022)六年级数学上册江苏地区期末真题汇编(苏教版)

专题01 选择题88题(一)(2020-2022)六年级数学上册江苏地区期末真题汇编一、选择题1.(2022·江苏泰州·六年级期末)一杯糖水,糖和水的比是1∶16,喝掉一半后,糖和水的比是()。
A.1∶8 B.1∶16 C.无法确定2.(2022·江苏泰州·六年级期末)在农业生产中,粮食、棉花等农作物的收成变化情况,常用“成数”来表示。
将“三成五”改写成百分数是()。
A.35% B.3.5% C.0.35% D.30.5% 3.(2022·江苏泰州·六年级期末)一件衣服打八折,就是比原价降低()。
A.2% B.20% C.8% D.80% 4.(2022·江苏·宝应县开发区国际学校六年级期末)实际节约用电15%这句话中的单位“1”的量是()。
A.节约的用电量B.实际用电量C.计划用电量5.(2022·江苏南京·六年级期末)六(1)班选举班长,规定得票超过半数的即可当选。
王小芳得票率是()时就可以当上班长。
A.50% B.0.51% C.51% D.49% 6.(2021·江苏扬州·六年级期末)树叶长和宽的比值越小,树叶就越()。
A.狭长B.宽扁C.小D.大7.(2021·江苏扬州·六年级期末)下面四幅图中的比,可以用2∶3表示的一共有()个。
A.1 B.2 C.3 D.4 8.(2021·江苏盐城·六年级期末)在900克水含100克糖,则糖占糖水的()。
A.110B.19C.18D.无法确定9.(2021·江苏盐城·六年级期末)一个百分数去掉百分号,这个数的大小()。
A.不变B.缩小1100C.扩大100倍D.不能确定10.(2021·江苏盐城·六年级期末)甲、乙两个班同时进行一次体育测试,甲班达标人数占全班人数的85%,乙班未达标人数占全班人数的15%,那么两个班的达标率()高。
新课标通用2025届高考政治一轮复习题型一选择题专题训练四引文类含解析

四、引文类【题型特点】引文类选择题一般以名人名言、成语、俗语、经典著作中的闻名论断以及党和国家领导人的重要讲话为素材,要求考生分析其中蕴含的经济学、哲学等道理。
此类试题主要包括两种形式:一类是借助名言,考查教材理论学问;另一类是依据教材理论学问,分析名言名句。
此类试题难度较大,学生获得和解读信息困难,所以称为每年高考的难点题型之一。
【技巧方法】解答此类试题一般把握三步:第一步明确名句内涵,一般结合材料背景,粗略了解名句的详细含义。
还可以通过抓取关键词,明确表达主旨。
其次步:对应教材,明确名句所体现的教材学问。
第三步:链接题干与题支,对应教材,选取答案。
【题型训练】1.《马可·波罗游记》里有这样的叙述:“纸币流通于大汗所属领域的各个地方,没有人敢冒着生命危急拒绝支付运用……用这些纸币,可以买卖任何东西,同样可以持纸币换取金条。
”这说明,在我国元代( )①纸币是由国家发行并强制运用的②黄金只具有保藏价值,不能在市场上流通③国家干脆确定货币购买力,有效防止通货膨胀④纸币在经济活动中被广泛运用,提升交易活动便利性A.①② B.③④ C.①④ D.②③答案 C解析在元代,市场上可以用纸币购买商品,这说明白纸币是由国家发行并强制运用的,而且纸币在经济活动中被广泛运用,提升交易活动便利性,①④正确;②说法错误,黄金作为货币可以在市场上流通;③说法错误,纸币的购买力是由市场来确定的。
2.(2024·江西新余联考)中国古代闻名经济学家范蠡认为,应依据市场的供求关系来推断产品价格的涨落,即“论其有余和不足,则知贵贱。
”从而提出了闻名的商业规律:“一贵一贱,极而复反。
”这一规律( )①提示生产经营者要把握好商品交易的最佳时机②说明商品价格与供求相互影响、相互制约③表明价值是价格的基础,商品价格由价值确定④揭示了价格波动在优化资源配置中的确定作用A.①② B.①④ C.②③ D.③④答案 A解析商品的价格由价值确定并受到供求关系的影响。
2023年中考道德与法治专题复习专题一 心中有法第3讲 法不可违 预防犯罪 善用法律

王某销售无标示的含有“冰墩墩”图案的台灯,被 D
罚款5 000元
违法类别 民事违法 刑事违法 行政违法
刑事违法
2.(2022·海南中考)公民权利受到侵害,要 依照法定程序维护权利。以下维权方式正确的 是( B )
A.知识产权受到侵犯,向公安机关起诉 B.发生合同纠纷,向仲裁机构申请仲裁 C.商家怀疑商品被偷,对顾客强行搜身 D.受到同学欺负,纠集他人将对方打伤
A.①② C.②④
B.①③ D.③④
5.(2022·四川遂宁中考)2022年5月5日,因侵害长津湖 战役英雄烈士名誉、荣誉,网络大V罗昌平被海南省三亚市城 郊人民法院一审判处有期徒刑七个月并承担在新浪网和《解
放军报》等媒体上公开赔礼道歉的民事责任。罗昌平的行为
(C )
①具有严重的社会危害性 ②应受到行政处罚 ③具有
轻微的社会危害性 A.①② C.①④
④应承担民事责任 B.①③ D.③④
6.下列对如图判决书内容解读正确的是 (C)
①被告人徐某某的行为属于行政违法行为 ②高空抛物的行为具有严重的社会危害性 ③判 决的依据是《中华人民共和国刑法》 ④有期徒 刑和罚金都是刑罚处罚中的主刑
A.①③ C.②③
B.①④ D.③④
法治教育 专题一 心中有法 第3讲 法不可违 预防犯罪 善用法律
一、选择题 1.(2022·江苏泰州中考)下列表格中案例与违法类别案例
A
顾某酒后多次恶意拨打110,被公安机关拘留8日
B
陈某非法贩卖濒危野生动物,被判处有期徒刑9年
孙某打球时,误伤他人眼睛,被判定民事赔偿8 500 C
法治与自由相互联系,不可分割。法治标定 了自由的界限,法治是自由的保障。我们既可以 享受数字时代带来的便利和自由,又要遵守法 律,守住法治的底线。
2021年中考物理冲刺高分必刷专题一 光现象与透镜

专题一:光现象、透镜及应用压轴题一.选择题(共 5 小题)1.为了研究光的传播规律,小明在水槽底部安装了一微型光源S,S 发出一束光照在右侧壁上形成一光斑,小明在光斑处固定了一小块橡皮泥P(如图所示)。
现往水槽内缓慢加水至水面上升到 a 位置,期间小红在左上方观察,看到右壁上一直有光斑。
在加水过程中,小红观察到光斑的移动情况正确的是()A.从P 处缓慢下移到某一位置后再缓慢上移到与橡皮泥P 重合B.从P 处缓慢下移到某一位置后再缓慢上移到橡皮泥P 上方某一位置C.从P 处迅速下移到某一位置后再缓慢上移到与橡皮泥P 重合D.从P 处迅速下移到某一位置后再缓慢上移到橡皮泥P 上方某一位置2.如图所示,甲、乙两人分别站立于一面矮墙的两边,若要在天花板上固定一平面镜使两人在图示位置彼此都能看到对方的全身,则所需的最小平面镜的位置应为()A.ae B.bc C.bd D.cd3.如图所示,一束光沿AO 射向水面,方向保持不变,反射光线在水平光屏EF 上形成光点Q,打开水阀K,水流出,水位下降,光点在光屏上移动,当光点移动了20cm 时,容器中的水位已下降了()A.0cm B.10cm C.10 cm D.54.在“探究凸透镜成像的规律”的实验中,把蜡烛和光屏固定在光具上,当移动透镜分别距光屏6cm 和34cm均可在光屏上得到清晰像。
下列判断正确的是()A.透镜距光屏34cm 时成缩小的实像B.蜡烛和光屏的距离为40cmC.透镜的焦距范围为3cm≤f≤6cmD.如将蜡烛和光屏的位置互换,透镜仍可在上述两位置成像,且像的性质不变5.如图所示,凸透镜的焦距为5 厘米,在透镜左侧10 厘米处,有一个与主光轴垂直的物体AB,在透镜右侧15 厘米处放一个平面镜,镜面与凸透镜的主光轴垂直,则该光具组中,物体AB 的成像情况是()A.一个正立实像,一个倒立实像,一个正立虚像B.一个正立实像,一个正立虚像,一个倒立虚像C.一个倒立实像,一个正立虚像,一个倒立虚像D.一个正立实像,一个倒立实像,一个倒立虚像二.实验探究题(共7 小题)6.如图甲是“探究平面镜成像特点”的情景:竖立的透明玻璃板下方放一把直尺,直尺与玻璃板垂直;两支相同的蜡烛A、B 竖立于玻璃板两侧的直尺上,以A 蜡烛为成像物体:(1)为便于观察,该实验最好在环境中进行(选填“较明亮”或“较黑暗”);(2)采用透明玻璃板代替平面镜,虽然成像不如平面镜清晰,但却能在观察到A 蜡烛像的同时,也能观察到,巧妙地解决了确定像的位置和大小的问题;(3)现有厚度分别为5mm 和2mm 的两块玻璃板,应选择mm 厚的玻璃板做实验,目的是。
2023届高考二轮总复习试题 专题一 中国特色社会主义(含解析)

专题一中国特色社会主义一、选择题(本大题共16小题,每小题3分,共48分)1.(2022·辽宁大连一模)“赤日炎炎似火烧,野田禾稻半枯焦。
农夫心内如汤煮,公子王孙把扇摇。
”与这首古代民歌所反映的社会形态相符合的是()①封建土地所有制是地主剥削农民的基础②地主通过收取地租占有农民的全部劳动成果③农民阶级和地主阶级的矛盾是社会基本矛盾④君主专制、等级森严是封建国家的显著特征A.①②B.①④C.②③D.③④2.(2022·山东聊城二模)无产阶级的运动是绝大多数人的、为绝大多数人谋利益的独立的运动,在未来社会中,“生产将以所有的人富裕为目的”。
社会主义制度以生产资料公有制和按劳分配为基本特征,社会主义制度下的社会再生产活动以全体社会成员充分参与的高水平社会化大生产为路径,以不断满足全体人民日益增长的美好生活需要为目标。
材料中() ①对“无产阶级的运动”的描述,阐明了实现共同富裕的深层次原因②对“目的”的描述,揭示了社会主义的本质要求和最终奋斗目标③对“基本特征”的描述,说明共同富裕的实现离不开经济的高质量发展④对“路径”的描述,体现了生产力决定生产关系这一马克思主义基本原理A.①②B.①④C.②③D.③④3.(2022·山东日照期末)马克思主义这一革命无产阶级的思想体系赢得了世界历史性的意义,是因为它并没有抛弃资产阶级时代最宝贵的成就,相反却吸收和改造了两千多年来人类思想和文化发展中一切有价值的东西。
这表明马克思主义()①批判地吸收了资本主义时期的有益成果②是揭示资本主义运行规律的理论之总和③是人类优秀思想和文化传统的历史延续④是无产阶级变革资本主义社会的物质力量A.①③B.①④C.②③D.②④4.(2022·北京西城区期末)“选好人,办好事”,版画中所描绘的延安居民讨论选举的场景,最适合用于说明以下主题()《延安居民讨论选举》1944年张望作A.社会主义从一国到多国的实践B.社会主义革命的伟大成就C.政治生活民主化的早期实践D.发展多层次多渠道的协商民主5.(2022·北京丰台区一模)中国共产党第八次全国代表大会是中华人民共和国成立后我们党召开的第一次全国代表大会。
2020年秋人教版数学七年级期末复习专题 :找规律之选择题专项(一)(含答案)

2020年秋人教版数学七上期末复习专题:找规律之选择题专项(一)1.下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有3颗棋子,第②个图形一共有9颗棋子,第③个图形一共有18颗棋子,…,则第⑧个图形中棋子的颗数为()A.84 B.108 C.135 D.1522.如图所示,第1个图案是由黑白两种颜色的六边形地面砖组成的,第2个,第3个图案可以看成是由第1个图案经过平移而得,那么第n个图案中有白色六边形地面砖()块.A.6+4(n+1)B.6+4n C.4n﹣2 D.4n+23.如下图所示:用火柴棍摆“金鱼”按照上面的规律,摆n个“金鱼”需用火柴棒的根数为()A.2+6n B.8+6n C.4+4n D.8n4.将一根绳子对折1次后从中间剪一刀,绳子变成3段;将一根绳子对折2次后从中间剪一刀,绳子变成5段;…将一根绳子对折n次后从中间剪一刀,绳子变成的段数是()A.n+2 B.2n+1 C.n2+1 D.2n+15.下列图形都是由同样大小的矩形按一定的规律组成,其中第①个图形中一共有6个矩形,第②个图形中一共有11个矩形,…,按此规律,第⑧个图形中矩形的个数为()A.38 B.41 C.44 D.486.下列图形都是由同样大小的圆按一定的规律组成,其中,第(1)个图形中一共有2个圆;第(2)个图形中一共有7个圆;第(3)个图形中一共有16个圆;第(4)个图形中一共有29个圆,…,则第(8)个图形中圆的个数为()A.121 B.113 C.92 D.1917.下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,…,按此规律排列下去,第⑥个图形中实心圆点的个数为()A.18 B.19 C.20 D.218.下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有()A.160 B.161 C.162 D.1639.用三个单位正方形,仅能拼出和两种不同图形(拼图时要求两个相接的单位正方形有一条边完全重合,并且各正方形不重叠).如果全等的图形算一种,那么用四个单位正方形能拼出的不同图形的种数是()A.4 B.5 C.6 D.多于610.观察下列一组图形中点的个数,其中第①个图形中共有3个点,第②个图形中共有9个点,第③个图形中共有18个点,按此规律,第⑥个图形中共有点的个数是()A.63 B.84 C.108 D.15211.观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第6个图中共有点的个数是()A.46 B.63 C.64 D.7312.如图,是由相同大小的圆点按照一定规律摆放而成,按此规律,则第n个图形中圆点的个数为()A.n+1 B.n2+n C.4n+1 D.2n﹣113.下列图形都是由同样大小〇的按一定的规律组成的,其中第1个图形一共有4个〇,第2个图形一共有9个〇,第3个图形一共有15个〇,…则第70个图形中〇的个数为()A.280 B.349 C.2485 D.269514.如图,下列图形都是由相同的花按照一定的规律摆成的,按照此规律摆下去,第n个的图形中有160朵花,则n的值是()A.40 B.41 C.42 D.4315.下列图案是用长度相同的小木棒按一定规律拼搭而成,图案①需8根小木棒,图案②需15根小木棒,…,按此规律,图案⑦需小木棒的根数是()A.49 B.50 C.55 D.5616.观察下列图形,它们是按一定规律排列的,依照此规律,第n个图形有()个太阳.A.2n B.n+2n﹣1C.n+2n D.2n17.用棋子摆出下列一组“口”字,按照这种方法摆下去,则第n个“口”字需要用棋子()A.(4n﹣4)枚B.4n枚C.(4n+4)枚D.n2枚18.如图,小正方形是按一定规律摆放的,下面四个选项中的图片,适合填补图中空白处的是()A.B.C.D.19.如图,将一张正三角形纸片剪成四个全等的正三角形,得到4个小正三角形,称为第一次操作;然后,将其中的一个正三角形再剪成四个小正三角形,共得到7个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到10个小正三角形,称为第三次操作;…,以上操作n次后,共得到49个小正三角形,则n的值为()A.n=13 B.n=14 C.n=15 D.n=1620.如图,用黑白两种颜色的平行四边形纸片,按黑色纸片数逐渐增加1的规律拼成下列图形,若第n个图案中有2020个白色纸片,则n的值为()A.674 B.673 C.672 D.671参考答案1.解:第①个图形有3颗棋子,第②个图形一共有3+6=9颗棋子,第③个图形一共有3+6+9=18颗棋子,第④个图形有3+6+9+12=30颗棋子,…,第⑧个图形一共有3+6+9+…+24=3×(1+2+3+4+…+7+8)=108颗棋子.故选:B.2.解:∵第一个图案中,有白色的是6个,后边是依次多4个.∴第n个图案中,是6+4(n﹣1)=4n+2.故选:D.3.解:由图形可知:第一个金鱼需用火柴棒的根数为:2+6=8;第二个金鱼需用火柴棒的根数为:2+2×6=14;第三个金鱼需用火柴棒的根数为:2+3×6=20;…;第n个金鱼需用火柴棒的根数为:2+n×6=2+6n.故选:A.4.解:∵对折1次从中间剪断,有21+1=3;对折2次,从中间剪断,有22+1=5.∴对折n次,从中间剪一刀全部剪断后,绳子变成2n+1段.故选:D.5.解:∵图①有矩形有6个=5×1+1,图②矩形有11个=5×2+1,图③矩形有16=5×3+1,∴第n个图形矩形的个数是5n+1当n=8时,5×8+1=41个.故选:B.6.解:第(1)个图形中最下面有1个圆,上面有1个圆共有2个;第(2)个图形中最下面有2个圆,上面有1+3+1个圆共有7个;第(3)个图形中最下面有3个圆,上面有1+3+5+3+1个圆共有16个;…第(n)个图形中共有(2n2﹣n+1)个圆;第(8)个图形中共有2×82﹣8+1=121,故选:A.7.解:∵第①个图形中实心圆点的个数5=2×1+3,第②个图形中实心圆点的个数8=2×2+4,第③个图形中实心圆点的个数11=2×3+5,……∴第⑥个图形中实心圆点的个数为2×6+8=20,故选:C.8.方法一:解:第一个图形正三角形的个数为5,第二个图形正三角形的个数为5×3+2=17,第三个图形正三角形的个数为17×3+2=53,第四个图形正三角形的个数为53×3+2=161,故选B.方法二:,,,,…,∴,⇒(a2﹣a1)+(a3﹣a2)+(a4﹣a3)+…+(a n﹣a n﹣1)=a n﹣a1,∴a n﹣a1=4×(3+32+…+3n﹣1)=4×(3+32+…+3n﹣1)=(用错位相减法可求出)∴,∵a1=5,∴.9.解:如图所示:共有如图5种不同图形.故选:B.10.解:第1个图中共有1×3=3个点,第2个图中共有1×3+2×3=9个点,第3个图中共有1×3+2×3+3×3=18个点,…第n个图有1×3+2×3+3×3+…+3n个点.所以第6个图中共有点的个数是1×3+2×3+3×3+…+6×3=63.故选:A.11.解:第1个图中共有1+1×3=4个点,第2个图中共有1+1×3+2×3=10个点,第3个图中共有1+1×3+2×3+3×3=19个点,…第n个图有1+1×3+2×3+3×3+…+3n个点.所以第6个图中共有点的个数是1+1×3+2×3+3×3+4×3+5×3+6×3=64.故选:C.12.解:观察图形的变化可知:第1个图形中圆点的个数为4+1=5;第2个图形中圆点的个数为4×2+1=9;第3个图形中圆点的个数为4×3+1=13;…发现规律,则第n个图形中圆点的个数为(4n+1).故选:C.13.解:∵第①个图形中基本图形的个数4=3×1+,第②个图形中基本图形的个数8=3×2+,第③个图形中基本图形的个数11=3×3+,…∴第n个图形中基本图形的个数为3n+当n=70时,3×70+=2695,故选:D.14.解:观察图形的变化,可知第1个图形中有花朵数:4=1×4第2个图形中有花朵数:8=2×4第3个图形中有花朵数:12=3×4…第n个图形中有花朵数:4n.所以4n=160n=40故选:A.15.解:∵图案①需火柴棒:8根;图案②需火柴棒:8+7=15根;图案③需火柴棒:8+7+7=22根;…∴图案n需火柴棒:8+7(n﹣1)=7n+1根;当n=7时,7n+1=7×7+1=50,∴图案⑦需50根火柴棒;故选:B.16.解:第一行小太阳的个数为1、2、3、4、…,第5个图形有5个太阳,第二行小太阳的个数是1、2、4、8、…、2n﹣1,第5个图形有24=16个太阳,所以第5个图形共有5+16=21个太阳,所以第n个图形共有(n+2n﹣1)个太阳.故选:B.17.解:n=1时,棋子个数为4=1×4;n=2时,棋子个数为8=2×4;n=3时,棋子个数为12=3×4;…;n=n时,棋子个数为n×4=4n.故选:B.18.解:由题意知,原图形中各行、各列中点数之和为10,符合此要求的只有故选:C.19.解:∵第一次操作后得到4个小正三角形,第二次操作后得到7个小正三角形;第三次操作后得到10个小正三角形,∴第n次操作后,正三角形的个数为3n+1.则:49=3n+1,解得:n=16,故若要得到49个小正三角形,则需要操作的次数为16次.故选:D.20.解:∵第1个图案中白色纸片有4=1+1×3张;第2个图案中白色纸片有7=1+2×3张;第3个图案中白色纸片有10=1+3×3张;…∴第n个图案中白色纸片有1+n×3=3n+1(张),根据题意得:3n+1=2020,解得:n=673,故选:B.。
中考历史复习专题一中国古代的政治与经济试题(1)

中考历史复习专题⼀中国古代的政治与经济试题(1)专题⼀中国古代的政治与经济⼀、选择题1.(2017·怀化中考)春秋时期的政治局⾯是“永乐征伐⾃诸侯出”,诸侯的出现与西周的什么政治制度有关( )A.禅让制 B.分封制C.郡县制 D.⾏省制2.(2017·泰安中考)下图是四⽅古印⽂,联系秦朝的历史,我们能够得出的结论是( )①秦朝创⽴皇帝制度②秦朝在中央设⽴丞相、御史⼤夫等职③秦朝在地⽅推⾏分封制④秦朝统⼀了⽂字A.①②③B.①②④C.①③④ D.②③④3.(2016·聊城中考)贾谊在《治安策》中提出:“欲天下之治安,莫若众建诸侯⽽少其⼒。
⼒少则易使以义,国⼩则亡邪⼼。
”汉武帝采取的下列措施体现了这⼀主张的是( )A.派张骞出使西域 B.设置“⼗三州部”C.颁布“推恩令” D.反击匈奴4.(2017·临沂四模)“⾃古男⼈掌朝纲,谁料⼥杰作俊贤。
重拳击碎贪腐吏,⽟⼿托起清廉官。
”赞扬了我国历史上唯⼀的⼥皇帝的政绩。
后世称赞她的统治是( )A.贞观之治B.政启开元,治宏贞观C.开元盛世D.康乾盛世5.(2017·黄⽯中考)2017年是我国恢复⾼考40周年,⾼考制度有利于国家⼈才的选拔。
历史学者威尔·杜兰特在《世界⽂明史》⾥评价我国古代某制度曾写道:“没有操纵的提名,没有伪君⼦卑鄙的争夺……没有混战或腐败的选举,没有仅凭巧⾔⽽能登⼊仕途的现象。
”他称赞的是中国古代的( )A.中央集权制 B.九品中正制C.郡县制 D.科举制6.(2017·青岛中考)《皇明祖训》记载:“今我朝罢丞相,设五府、六部、都察院、通政司、⼤理寺等衙门,分理天下庶务,彼此颉颃(相抗衡),不敢相压,事皆朝廷总之,所以稳当。
”明太祖这⼀做法反映的实质是( )A.扩⼤六部权⼒ B.改⾰丞相制度C.扩⼤地⽅权⼒ D.加强君主专制7.(2016·⽆锡中考)三峡⼯程是当今世界最⼤的⽔利⼯程。
【 高考物理一轮电磁学专题复习】 选择题专练1 静电场(含解析 )
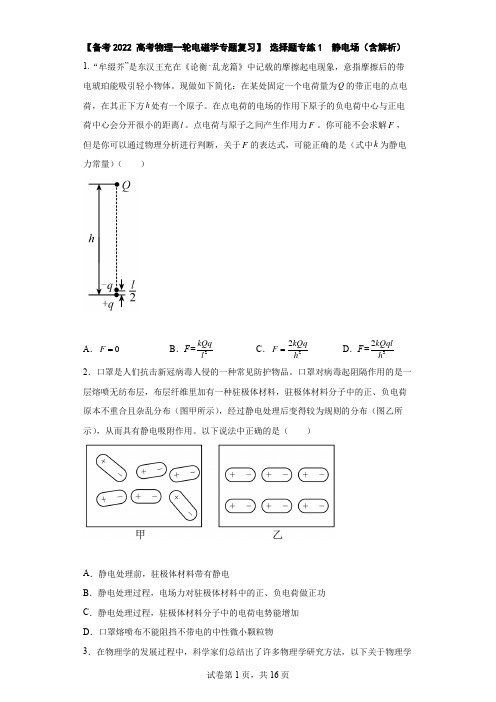
【备考2022 高考物理一轮电磁学专题复习】 选择题专练1 静电场(含解析) 1.“牟缀芥”是东汉王充在《论衡⋅乱龙篇》中记载的摩擦起电现象,意指摩擦后的带电琥珀能吸引轻小物体。
现做如下简化:在某处固定一个电荷量为Q 的带正电的点电荷,在其正下方h 处有一个原子。
在点电荷的电场的作用下原子的负电荷中心与正电荷中心会分开很小的距离l 。
点电荷与原子之间产生作用力F 。
你可能不会求解F ,但是你可以通过物理分析进行判断,关于F 的表达式,可能正确的是(式中k 为静电力常量)( )A .0F =B .F=2kQq lC .22kQq F h =D .F=32kQql h 2.口罩是人们抗击新冠病毒人侵的一种常见防护物品。
口罩对病毒起阻隔作用的是一层熔喷无纺布层,布层纤维里加有一种驻极体材料,驻极体材料分子中的正、负电荷原本不重合且杂乱分布(图甲所示),经过静电处理后变得较为规则的分布(图乙所示),从而具有静电吸附作用。
以下说法中正确的是( )A .静电处理前,驻极体材料带有静电B .静电处理过程,电场力对驻极体材料中的正、负电荷做正功C .静电处理过程,驻极体材料分子中的电荷电势能增加D .口罩熔喷布不能阻挡不带电的中性微小颗粒物3.在物理学的发展过程中,科学家们总结出了许多物理学研究方法,以下关于物理学研究方法的叙述正确的是()A.在不需要考虑带电物体本身的大小和形状时,用点电荷来代替物体的方法叫微元法B.在探究加速度、力和质量三者之间的关系时采用了假设法C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了理想模型法D.伽利略认为自由落体运动是物体在倾角为90°的斜面上的运动,再根据铜球在斜面上的运动规律得出自由落体的运动规律,这是采用了实验和逻辑推理相结合的方法4.如图,在光滑绝缘斜面上有带电小球a与b,两球同时释放瞬间,a球的加速度刚好为零,则下列关于a、b的电性及初始位置,符合要求的是()A.B.C.D.5.富兰克林为研究雷电现象,设计了如图所示的装置,避雷针线路与接地线分开,并在分开处装上帽形的金属钟A与B,两钟之间以丝线悬挂一个金属小球C,A钟下方用导线连接两个很轻的金属小球形成验电器D,避雷针上空附近的云不带电时,三个金属小球均静止下垂。
专题01 选择题92题(一)-(2020-2022)五年级数学上册江苏地区期末真题汇编(苏教版)

专题01 选择题92题(一)(2020-2022)五年级数学上册江苏地区期末真题汇编一、选择题1.(2021·江苏盐城·五年级期末)在小数8.6385中,右边的8表示( )。
A .8个千分之一B .8个0.01C .8个一D .以上都不正确2.(2021·江苏无锡·五年级期末)一根电线长30米,第一次用去4.7米,第二次用去3.55米,一共用去( )米。
A .1.15米B .4.7米C .8.25米D .21.75米3.(2022·江苏·苏州国裕外语学校五年级期末)学校运动会上,跑步比赛前三名选手的成绩分别是小明18.25秒,小华16.88秒,小军17.00秒。
( )是第一名。
A .小明B .小华C .小军4.(2022·江苏盐城·五年级期末)三名同学进行50米短跑比赛,王军用了10.01秒,李勇用了11.12秒,张林用了9.97秒。
( )获得第一名。
A .张林B .李勇C .王军D .无法确定5.(2020·江苏南京·五年级期末)六合区的占地面积大约是1500( )。
A .平方千米B .公顷C .平方米6.(2020·江苏南京·五年级期末)0.16和0.160相比,它们的( )。
A .大小相等,计数单位相同B .大小相等,计数单位不同C .大小不等,计数单位不同7.(2020·江苏·北京东路小学五年级期末)与450个0.01相等的数是( )。
A .0.045B .0.450C .450.00D .4.5008.(2020·江苏南京·五年级期末)一瓶饮料外包装上标有“净含量2005±克”,有3瓶这样的饮料,实际净含量如下,不合标准的是( )。
A .194克B .198克C .203克9.(2020·江苏·北京东路小学五年级期末)( 1.5)a b -+与 1.5a b -+两式结果相差( )。
2024年高考化学二轮复习第一部分新高考选择题突破专题1物质的组成、分类和变化专题能力提升训练(一)

专题能力提升训练(一)1. (2023·河北张家口二模)“胡服骑射”是我国古代史上的一次大变革,被历代史学家传为佳话。
下列说法正确的是( A )A.汉服和胡服的主要成分均为天然有机高分子B.竹制或木制长弓是利用了竹或木的柔韧性和延展性C.“胡服骑射”是通过改进物质的化学性质,从而增强物质性能D.弓箭上的箭羽为鹰或鹅的羽毛,其主要成分为纤维素【解析】汉服和胡服的主要成分均为天然纤维,属于天然有机高分子化合物,故A正确;该过程不涉及竹或木的延展性,故B错误;“胡服骑射”并未改变物质的化学性质,故C错误;弓箭上的箭羽为鹰或鹅的羽毛,其主要成分为蛋白质,故D错误;故选A。
2. (2023·山东省济南市统考一模)高粱酿酒过程中部分操作如图所示。
下列说法错误的是( C )“蒸粮”“拌曲”“堆酵”“馏酒”B.“拌曲”加入的酒曲在酿酒时起到催化作用C.“堆酵”时升温是因为吸收环境中的热量D.“馏酒”的原理即实验操作中的“蒸馏”【解析】“蒸粮”时可适当鼓风,增加氧气的浓度,可以加快燃烧速率,A正确;酒曲在酿酒时起到催化作用,B正确;升温是因为发酵时放出热量,C 错误;蒸馏时控制温度在酒精的沸点范围内,D正确;故选C。
3. (2023·湖北十一校联考二模)2022年我省重点建设计划超额完成任务。
下列相关说法错误的是( A )A.第6代半导体显示器件使用的半导体材料是SiO2晶体B.耐水药用玻璃(由石英砂、纯碱、方解石等原料制得)属于硅酸盐材料C.新冠灭活疫苗应冷藏保存D.电动汽车使用的锂电池属于二次电池【解析】半导体材料是晶体硅,故A说法错误;耐水药用玻璃是用石英砂、纯碱、方解石等原料制得,石英砂主要成分是SiO2,与纯碱反应生成硅酸钠,方解石成分是碳酸钙,二氧化硅与碳酸钙反应生成硅酸钙,硅酸钠、硅酸钙属于硅酸盐,故B说法正确;灭活疫苗中含有蛋白质,低温冷藏可以防止蛋白质变性失活,故C说法正确;二次电池属于可充电电池,即锂电池属于二次电池,故D说法正确;故选A。
2023 高考化学二轮专题复习 专题1 化学物质及其变化 专项训练(教师版)

专题1化学物质及其变化(一)物质的组成、分类及变化化学与传统文化(建议用时25分钟)选择题:在每小题给出的四个选项中,只有一项符合题目要求。
1.第24届冬奥会在北京市和张家口市成功举办。
下列不属于化学变化的是()A.冬奥场馆使用CO2跨临界直冷制冰(“水立方”场馆中的水冰转换)B.北京冬奥会菜单上有678道菜,工作人员对食材进行的煎、炒、烹、炸过程C.冬奥会开幕式中火炬“飞扬”中氢燃料的燃烧D.冬奥会上采用紫外线杀菌技术使蛋白质变性解析:选A。
二氧化碳跨临界直冷制冰技术,通过压力变化使二氧化碳汽化实现制冷,二氧化碳汽化属于物理变化,A正确;食材变熟,燃料的燃烧属于化学变化,B错误;氢燃料燃烧时氢气和氧气反应生成水,属于化学变化,C错误;蛋白质的变性为化学变化,D错误。
2.(2022·茂名模拟)广东省化州市的拖罗饼为省级非物质文化遗产制作技艺。
拖罗饼是以面粉、白糖为主料,用上乘的椰丝、叉烧、伍仁等作馅料,刷上油脂、蛋黄烘烤制作而成。
下列有关说法正确的是()A.面粉属于混合物B.糖类都能水解C.油脂属于高分子化合物D.烘烤拖罗饼过程发生的是物理变化解析:选A。
面粉属于高分子化合物,含聚合度不同的多种物质,属于混合物,A正确;糖类中的单糖不能水解,B错误;油脂不属于高分子化合物,C错误;烘烤拖罗饼过程将面食由生变熟,发生的是化学变化,D错误。
3.下列我国科研成果所涉及的材料中,主要成分为同主族元素形成的无机非金属材料的是()A.4.03米大口径碳化硅反射镜B.2022年冬奥会聚氨酯速滑服C.能屏蔽电磁波的碳包覆银纳米线D.“玉兔二号”钛合金筛网轮解析:选A。
碳化硅(SiC)是由碳元素和硅元素组成的无机非金属材料,且碳元素与硅元素均位于元素周期表第ⅣA族,A正确;聚氨酯为有机高分子化合物,不属于无机非金属材料,B错误;碳包覆银纳米材料属于复合材料,不属于无机非金属材料,且银不是主族元素,C错误;钛合金为含有金属钛元素的合金,其属于金属材料,不属于无机非金属材料,且钛不是主族元素,D错误。
【2022届高三数学一轮复习】专题1

专题1.8 基本不等式-重难点题型精练参考答案与试题解析一.选择题(共8小题,满分40分,每小题5分)1.(5分)(2021•三模拟)已知a >0,b >0,且a +2b =3ab ,则ab 的最小值为( ) A .1B .89C .49D .2√23【分析】利用已知条件推出1b +2a =3,然后利用基本不等式转化求解即可.【解答】解:因为a >0,b >0,且a +2b =3ab , 所以1b +2a =3,所以3=1b +2a ≥2√2ab , 所以√ab ≥2√23,即ab ≥89当且仅当{1b =2aa +2b =3ab即a =43,b =23时等号成立,故ab 的最小值89. 故选:B .【点评】本题考查基本不等式的应用,考查转化思想以及计算能力,是基础题. 2.(5分)(2021•乙卷)下列函数中最小值为4的是( ) A .y =x 2+2x +4 B .y =|sin x |+4|sinx| C .y =2x +22﹣xD .y =lnx +4lnx【分析】利用二次函数的性质求出最值,即可判断选项A ,根据基本不等式以及取最值的条件,即可判断选项B ,利用基本不等式求出最值,即可判断选项C ,利用特殊值验证,即可判断选项D . 【解答】解:对于A ,y =x 2+2x +4=(x +1)2+3≥3, 所以函数的最小值为3,故选项A 错误;对于B ,因为0<|sin x |≤1,所以y =|sin x |+4|sinx|≥2√|sinx|⋅4|sinx|=4, 当且仅当|sinx|=4|sinx|,即|sin x |=2时取等号, 因为|sin x |≤1,所以等号取不到,所以y =|sin x |+4|sinx|>4,故选项B 错误;对于C ,因为2x >0,所以y =2x +22﹣x =2x +42x ≥2√2x ⋅42x =4, 当且仅当2x =2,即x =1时取等号, 所以函数的最小值为4,故选项C 正确; 对于D ,因为当x =1e 时,y =ln 1e +4ln 1e=−1−4=−5<4, 所以函数的最小值不是4,故选项D 错误. 故选:C .【点评】本题考查了函数最值的求解,涉及了二次函数最值的求解,利用基本不等式求解最值的应用,在使用基本不等式求解最值时要满足三个条件:一正、二定、三相等,考查了转化思想,属于中档题. 3.(5分)(2021•和平区校级模拟)实数a ,b 满足a >0,b >0,a +b =4,则a 2a+1+b 2b+1的最小值是( )A .4B .6C .32D .83【分析】利用基本不等式得到ab 的范围,可解决此题. 【解答】解:∵a >0,b >0,∴4=a +b ≥2√ab ,∴0<ab ≤4. ∴a 2a+1+b 2b+1=a 2(b+1)+b 2(a+1)(a+1)(b+1)=a 2+b 2+ab(a+b)ab+a+b+1=(a+b)2−2ab+4abab+5=16+2ab ab+5=2(ab+5)+6ab+5=2+6ab+5∈[83,165).∴最小值为83. 故选:D .【点评】本题考查基本不等式应用、转化思想,考查数学运算能力,属于中档题.4.(5分)(2021•包头二模)在△ABC 中,已知C =60°,AB =4,则△ABC 周长的最大值为( ) A .8B .10C .12D .14【分析】根据余弦定理算出(a +b )2=16+3ab ,再利用基本不等式加以计算可得a +b ≤8,即可得到△ABC周长的最大值.【解答】解:∵在△ABC 中,C =60°,AB =c =4,∴由余弦定理,得c 2=a 2+b 2﹣2ab cos C ,即16=a 2+b 2﹣2ab cos60°=a 2+b 2﹣ab ≥2ab ﹣ab =ab (当且仅当a =b =4时等号成立), ∵16=a 2+b 2﹣ab =(a +b )2﹣3ab ,∴(a +b )2≤16+3ab ≤16+3×16=64,由此可得a +b ≤8(当且仅当a =b =4时等号成立),∴△ABC 周长a +b +c ≤8+4=12(当且仅当a =b =4时等号成立),即当且仅当a =b =4时,△ABC 周长的最大值为12.故选:C .【点评】本题给出三角形的一边和它的对角,求周长的最大值,着重考查了用余弦定理解三角形和基本不等式求最值等知识,属于中档题.5.(5分)(2021•南通模拟)已知x >0,y >0,且x +y =1,则下列结论中正确的是( ) A .1x+1y 有最小值4B .xy 有最小值14C .2x +2y 有最大值√2D .√x +√y 有最大值2【分析】利用“乘一法”及基本不等式的性质逐项判断即可. 【解答】解:∵x >0,y >0,且x +y =1, 对于A ,1x +1y=(1x+1y)(x +y )=2+x y +yx ≥4,故A 正确,对于B ,∵x +y ≥2√xy ,∴xy ≤(x+y 2)2=14,故B 错误,对于C ,2x +2y ≥2√2x ⋅2y =2√2,故C 错误, 对于D ,(√x +√y )2=x +y +2√xy =1+2√xy ,∵xy 有最大值14,故(√x +√y )2有最大值2,故D 错误,故选:A .【点评】本题考查基本不等式的性质,同时考查学生的运算能力.属于基础题.6.(5分)(2021•湖南模拟)数学里有一种证明方法叫做Proofswithoutwords ,也称之为无字证明,一般是指仅用图象语言而无需文字解释就能不证自明的数学命题,由于这种证明方法的特殊性,无字证明被认为比严格的数学证明更为优雅.现有如图所示图形,在等腰直角三角形△ABC 中,点O 为斜边AB 的中点,点D 为斜边AB 上异于顶点的一个动点,设AD =a ,BD =b ,则该图形可以完成的无字证明为( )A .a+b 2≥√ab (a >0,b >0)B .2aba+b ≤√ab (a >0,b >0)C .a+b 2≤√a 2+b 22(a >0,b >0)D .a 2+b 2≥2√ab (a >0,b >0)【分析】由已知图形先求出OC ,CD ,然后结合OC ≤CD 即可判断.【解答】解:由题意得AB =AD +BD =a +b ,CO =12(a +b ),OD =OB ﹣DB =12(a +b )﹣b =12(a ﹣b ),Rt △OCD 中,CD 2=OC 2+OD 2=(a+b)24+(a−b)24=a 2+b 22, 因为OC ≤CD ,所以12(a +b )≤√a 2+b 22,当且仅当a =b 时取等号, 故选:C .【点评】本题主要考查了基本不等式的应用,体现了转化思想的应用,属于基础题.7.(5分)(2021•浙江模拟)已知直线l 过第一象限的点(m ,n )和(1,5),直线l 的倾斜角为135°,则1m+4n的最小值为( )A .4B .9C .23D .32【分析】根据题意,由直线的斜率计算公式可得n−5m−1=−1,变形可得m +n =6,则有1m+4n=16×(1m+4n)(m +n )=16(5+4m n +nm),结合基本不等式的性质分析可得答案. 【解答】解:根据题意,直线l 过第一象限的点(m ,n )和(1,5),直线l 的倾斜角为135°, 则n−5m−1=−1,变形可得m +n =6,则1m+4n=16×(1m +4n)(m +n )=16(5+4m n +nm ), 又由点(m ,n )在第一象限,即m >0,n >0, 则有4m n+nm≥2√4m n ×nm =4,当且仅当n =2m 时等号成立, 故1m +4n =16(5+4m n +n m )≥32,即1m +4n 的最小值为32, 故选:D .【点评】本题考查基本不等式的性质以及应用,涉及直线的斜率,属于基础题.8.(5分)(2021•1月份模拟)已知a ,b ,c ∈[12,1],则a 2+2b 2+c 2ab+bc的取值范围是( )A .[2,3]B .[52,3]C .[2,52]D .[1,3]【分析】由a 2+2b 2+c 2=a 2+b 2+b 2+c 2,然后利用重要不等式得到a 2+2b 2+c 2ab+bc≥2,根据12≤a b≤2,12≤b a≤2,构造对勾函数,然后结合其性质可求. 【解答】解:a 2+2b 2+c 2ab+bc=a 2+b 2+b 2+c 2ab+bc≥2ab+2bc ab+bc=2,当且仅当a =b =c 时取等号, 因为12≤a ≤1,12≤b ≤1,所以12≤a b≤2,12≤b a≤2,令f (x )=x +1x ,12≤x ≤2,根据对勾函数单调性知,当x =1时,函数取得最小值2,当x =2或12时,函数取得最大值52,故2≤f(x)≤52, 所以2≤b a +a b ≤52,即a 2+b 2≤52ab , 同理b 2+c 2≤52bc ,所以a 2+2b 2+c 2≤52(ab +bc), 所以a 2+2b 2+c 2ab+bc≤52.所以2≤a 2+2b 2+c 2ab+bc ≤52.故选:C .【点评】本题主要考查了基本不等式,不等式的性质及对勾函数单调性在求解范围及最值中的应用,试题的变形比较灵活,属于中档题.二.多选题(共4小题,满分20分,每小题5分)9.(5分)(2021•二模拟)已知正数a ,b 满足ab =a +b ,则( ) A .1a−1+1b−1≥2B .1a 2+1b 2≥12C .2−a +2−b ≥12D .log 2a +log 2b ≥2【分析】由ab =a +b ,转化为(a ﹣1)(b ﹣1)=1,可判断A ; 由ab =a +b 转化为1a +1b=1,再结合2(a 2+b 2)≥(a +b )2可判断B ;取a =b =3可判断C ;由ab =a +b ≥2√ab ,得ab ≥4,可判断D .【解答】解:因为正数a ,b 满足ab =a +b ,所以(a ﹣1)(b ﹣1)=1,且a >1,b >1,所以1a−1+1b−1≥2√1(a−1)(b−1)=2,∴A 对;由ab =a +b 可得1a+1b=1,所以2(1a 2+1b 2)≥(1a +1b )2=1,即1a 2+1b 2≥12,故B 正确;当a =b =3时,2−3+2−3=14<12,故C 错误;因为ab =a +b ≥2√ab ,所以ab ≥4,所以log 2a +log 2b =log 2(ab )≥log 24=2,故D 正确. 故选:ABD .【点评】本题考查基本不等式应用,考查数学运算能力,属于中档题.10.(5分)(2021•B 卷模拟)已知a ,b ,c 为正数,且满足abc =1,则下列结论正确的是( ) A .(a +b )√c ≥2 B .1a +1b+1c≤a 2+b 2+c 2C .若0<c ≤1,则(a +1)(b +1)<4D .a 2b 2+2b 2c ≥3【分析】(a +b )√c 转化为(a +b )√1ab 可判断A ;1a+1b+1c转化为ab +bc +ac 可判断B ;由0<c ≤1可知ab ≥1,则(a +1)(b +1)=ab +a +b +1,利用基本不等式可判断C ; 2b 2c 转化为2b 2•1ab=2b a可判断D .【解答】解:∵a ,b ,c 为正数,abc =1∴(a +b )√c =(a +b )√1ab ≥2√ab •√1ab =2,∴A 对;∵a ,b ,c 为正数,abc =1,∴1a +1b +1c=ab +bc +ac ≤a 2+b 22+b 2+c 22+a 2+c 22=a 2+b 2+c 2,∴B 对;由0<c ≤1,abc =1可知ab ≥1,∵a ,b 为正数,∴(a +1)(b +1)=ab +a +b +1≥ab +2√ab +1≥4,∴C 错;∵a ,b ,c 为正数,abc =1,∴a 2b 2+2b 2c =a 2b2+2b 2•1ab=a 2b 2+b a+b a≥3√a 2b 2⋅b a ⋅ba3=3,∴D 对. 故选:ABD .【点评】本题考查基本不等式及应用,考查数学运算能力,属于中档题. 11.(5分)(2021•辽宁模拟)设x >0,y >0,则下列结论正确的是( ) A .不等式(x +y)(1x +1y )≥4恒成立B .函数f (x )=3x +3﹣x的最小值为2C .函数f(x)=xx 2+3x+1的最大值为15D .若x +y =2,则12x+1+1y+1的最小值为 56【分析】由已知结合基本不等式分别检验各选项即可判断. 【解答】解:因为x >0,y >0, (x +y )(1x+1y )=2+yx+xy ≥4,当且仅当y x =x y时取等号,A 正确; 因为3x >1,则f (x )=3x +3﹣x ≥2√3x ⋅3−x =2,当且仅当3x =3﹣x ,即x =0时取等号,但x >0,故B 错误; f(x)=xx 2+3x+1=1x+1x +3≤12+3=15,当且仅当x =1x ,即x =1时取等号,C 正确; 因为x +y =2,所以2x +2y =4, 则12x+1+1y+1=12x+1+22y+2=17(12x+1+22y+2)(2x +1+2y +2)=17(3+2y+22x+1+2x+1y+1)≥17(3+2√2), 当且仅当2y+22x+1=2x+1y+1时取等号,D 错误.故选:AC .【点评】本题主要考查了利用基本不等式求解最值,解题的关键是应用条件的检验及配凑.12.(5分)(2021•山东二模)已知实数a ,b 满足a 2﹣ab +b =0(a >1),下列结论中正确的是( ) A .b ≥4B .2a +b ≥8C .1a+1b>1 D .ab ≥274【分析】A .由验证可得:b =a 2a−1=a 2−1+1a−1=a +1+1a−1=a ﹣1+1a−1+2,利用基本不等式即可判断出正误;B .2a +b =2a +a +1+1a−1=3(a ﹣1)+1a−1+4利用基本不等式即可判断出正误; C .由a >1,可得1a∈(0,1),1a+1b=1a+a−1a 2=−1a 2+2a=−(1a−1)2+1>1,利用二次函数的单调性即可判断出正误;D .ab =a •a 2a−1=a 3a−1,令f (x )=x 3x−1,(x >1).求出f ′(x ),利用导数研究函数的单调性即可判断出正误.【解答】解:实数a ,b 满足a 2﹣ab +b =0(a >1),A .b =a 2a−1=a 2−1+1a−1=a +1+1a−1=a ﹣1+1a−1+2≥2√(a −1)⋅1a−1+2=4,当且仅当a =2时取等号,因此正确;B .2a +b =2a +a +1+1a−1=3(a ﹣1)+1a−1+4≥2√3(a −1)⋅1a−1+4=2√3+4,当且仅当a =1+√33取等号,因此不正确;C .∵a >1,∴1a∈(0,1),1a+1b=1a+a−1a 2=−1a 2+2a=−(1a−1)2+1<1,因此不正确;D .ab =a •a 2a−1=a 3a−1,令f (x )=x 3x−1,(x >1).f ′(x )=2x 2(x−32)(x−1)2, 可得x =32时,函数f (x )取得极小值,即最小值.f (32)=(32)332−1=274, ∴f (x )≥274,即ab ≥274,因此正确. 故选:AD .【点评】本题考查了基本不等式、二次函数的单调性、利用导数研究函数的单调性,考查了推理能力与计算能力,属于基础题.三.填空题(共4小题,满分20分,每小题5分)13.(5分)(2021•湖南模拟)已知a >b ,关于x 的不等式ax 2+2x +b ≥0对于一切实数x 恒成立,又存在实数x 0,使得ax 02+2x 0+b =0成立,则a 2+b 2a−b的最小值为 2√2 .【分析】不等式ax 2+2x +b ≥0对于一切实数x 恒成立,可得△≤0,存在x 0∈R ,使ax 02+2x 0+b =0成立,则△≥0,可得ab 的等式关系,利用基本不等式的性质求解a 2+b 2a−b的最小值即可.【解答】解:由题意,不等式ax 2+2x +b ≥0对于一切实数x 恒成立,可得{a >04−4ab ≤0,解得ab ≥1,存在x 0∈R ,使ax 02+2x 0+b =0成立,则△≥0,即4﹣4ab ≥0,得ab ≤1, ∴ab =1,∵a >b ,∴a >1,∴a −1a >0, 由b =1a ,a 2+b 2a−b=a 2+1a2a−1a=(a −1a )+2a−1a≥2√2,当且仅当(a−1a)2=2时取等号.故答案为:2√2.【点评】本题考查了基本不等式的性质的运用和构造思想,特别是构造分子,分母适合基本不等式,属于中档题.14.(5分)(2021•鄞州区校级模拟)若实数x,y满足2x2+xy﹣y2=1,则5x2﹣2xy+2y2的最小值为2.【分析】由已知2x2+xy﹣y2=(2x﹣y)(x+y)=1,而5x2﹣2xy+2y2=(2x﹣y)2+(x+y)2,然后利用基本不等式即可求解,【解答】解:因为2x2+xy﹣y2=(2x﹣y)(x+y)=1,令t=2x﹣y,则x+y=1 t,则5x2﹣2xy+2y2=(2x﹣y)2+(x+y)2=t2+1t2≥2√t2⋅1t2=2,当且仅当t2=1t2,即t=±1时取等号,此时5x2﹣2xy+2y2取最小值2.故答案为:2.【点评】本题主要考查了利用基本不等式求解最值,解题的关键是基本不等式的应用条件的配凑,属于基础题.15.(5分)(2021•汕头三模)函数y=a x﹣3+1(a>0且a≠1)的图象恒过定点A,若点A在直线mx+ny﹣1=0上,其中m>0,n>0,则mn的最大值为124.【分析】先利用指数函数的性质求出定点A,然后利用点在直线上,得到3m+2n=1,再利用基本不等式求解mn的最值即可.【解答】解:因为当x=3时,y=a3﹣3+1=2,所以函数y=a x﹣3+1(a>0且a≠1)的图象恒过定点A(3,2),又点A在直线mx+ny﹣1=0上,所以3m+2n﹣1=0,即3m+2n=1,因为m>0,n>0,所以mn=16⋅3m⋅2n≤16⋅(3m+2n2)2=16×14=124,当且仅当3m=2n=12,即m=16,n=14时取等号,所以mn的最大值为124.故答案为:124.【点评】本题考查了指数函数恒过定点问题,利用基本不等式求解最值问题,在使用基本不等式求解最值时要满足三个条件:一正、二定、三相等,属于中档题.16.(5分)(2021•嘉定区二模)已知正数x 、y 满足x +4y=1,则1x+y 的最小值为 9 .【分析】利用“乘1法”与基本不等式的性质即可得出. 【解答】解:因为正数x 、y 满足x +4y=1,则1x+y =(1x+y )(x +4y )=5+xy +4xy ≥5+2√xy ⋅4xy =9,当且仅当xy =4xy 且x +4y =1,即x =13,y =6时取等号,此时1x+y 的最小值9.故答案为:9.【点评】本题考查了“乘1法”与基本不等式的性质,属于基础题. 四.解答题(共6小题,满分70分)17.(10分)(2021•内江模拟)已知a >0,b >0,4a +b =2ab . (1)求a +b 的最小值;(2)若a +b ≥|2x ﹣1|+|3x +2|对满足题中条件的a ,b 恒成立,求实数x 的取值范围. 【分析】(1)由已知利用乘1法,结合基本不等式即可直接求解;(2)结合(1)中的最值,然后结合不等式恒成立与最值的相互转化关系,结合零点分段讨论即可求解. 【解答】解:(1)因为a >0,b >0,4a +b =2ab , 所以4b +1a=2,所以a +b =12(a +b )(1a+4b)=12(5+b a+4a b )≥12(5+2√b a ⋅4a b )=92, 当且仅当b a=4a b且4b+1a=2,即a =32,b =3时取等号,a +b 的最小值92;(2)若a +b ≥|2x ﹣1|+|3x +2|对满足题中条件的a ,b 恒成立,则92≥|2x ﹣1|+|3x +2|, 当x ≥12时,原不等式可化为2x ﹣1+3x +2≤92, 所以12≤x ≤710;当−23<x <12时,原不等式可化为﹣2x +1+3x +2≤92, 所以−23<x <12,当x ≤−23时,原不等式可化为﹣2x +1﹣3x ﹣2≤92,所以−1110≤x ≤−23, 综上,x 的取值范围[−1110,710].【点评】本题主要考查了乘1法及基本不等式求解最值,还考查了不等式的恒成立与最值关系的相互转化及利用零点分段求解不等式,分段讨论去绝对值是求解不等式的关键. 18.(12分)(2021春•青山湖区校级期中)已知正数a 、b 满足1a +1b=1.(1)求a +b 的最小值; (2)求4a a−1+9bb−1的最小值.【分析】(1)利用乘1法a +b =(a +b )(1a+1b),展开后结合基本不等式即可求解;(2)先对已知式子进行变形,结合已知条件可得(a ﹣1)(b ﹣1)=1,利用基本不等式可求. 【解答】解:(1)因为a 、b 是正数,所以a +b =(a +b)(1a +1b )=2+ab +ba ≥2+2√ab ×ba =4,当且仅当a =b =2时等号成立,故a +b 的最小值为4.(2)因为a >1,b >1,所以a ﹣1>0,b ﹣1>0,则4a a−1+9b b−1=4+4a−1+9+9b−1≥13+2√4a−1×9b−1=25,当且仅当a =53、b =52时等号成立,故4aa−1+9bb−1的最小值为25.【点评】本题主要考查了利用基本不等式求解最值,解题的关键是应用条件的配凑,属于中档题. 19.(12分)(2020秋•海淀区校级月考)已知x +y =1,x ,y ∈R +. (1)求x 2+y 2+xy 的最小值; (2)求√x +√y 的最大值; (3)求x (1﹣3y )的最小值.【分析】(1)x 2+y 2+xy =(x +y )2﹣xy =1﹣xy ,然后利用基本不等式即可求解; (2)(√x +√y )2=x +y +2√xy =1+2√xy ,然后利用基本不等式即可求解;(3)由x (1﹣3y )=(1﹣y )(1﹣3y )=3y 2﹣4y +1,然后结合二次函数的性质可求解. 【解答】解:(1)x 2+y 2+xy =(x +y )2﹣xy =1﹣xy ≥1﹣(x+y 2)2=34,当且仅当x =y =12时,取得最小值34;(2)因为x+y=1,x,y∈R+,所以(√x+√y)2=x+y+2√xy=1+2√xy≤1+x+y=2,当且仅当x=y时取等号,此时取得最大值2;(3)∵x,y∈R+,x+y=1,∴x(1﹣3y)=(1﹣y)(1﹣3y)=3y2﹣4y+1,结合二次函数的性质可知,当y=23时取得最小值−13.【点评】本题主要考查了基本不等式及二次函数的性质在求解最值中的应用,属于基础题.20.(12分)(2021•江西模拟)设a>0,b>0,且a+b=2ab.(1)若不等式|x+1|+2|x|≤a+b恒成立,求实数x的取值范围;(2)当实数a,b满足什么条件时,a﹣b+3ba取得最小值,并求出最小值.【分析】(1)先利用基本不等式求出a+b的最小值,从而将所求的不等式转化为|x+1|+2|x|≤2,根据绝对值的定义分别讨论,求解不等式即可;(2)利用已知的等式,将b用a表示出来,然后代入a﹣b+3ba中化简变形,由基本不等式求解最值即可.【解答】解:(1)由a>0,b>0,a+b=2ab,可得1a +1b=2,所以a+b=12(a+b)(1a+1b)=12(b a+a b+2)≥12⋅(2√b a⋅a b+2)=12×4=2.当且仅当a=b=1时取等号,不等式|x+1|+2|x|≤a+b恒成立,即|x+1|+2|x|≤2,当x<﹣1时,不等式可化为﹣x﹣1﹣2x≤2,解得x≥﹣1,此时x∈∅;当﹣1≤x≤0时,不等式可化为x+1﹣2x≤2,解得x≥﹣1,此时﹣1≤x≤0;当x>0时,不等式可化为x+1+2x≤2,解得x≤13,此时0<x≤13.综上所述,实数x的取值范围是{x|−1≤x≤13 };(2)由a>0,b>0,a+b=2ab,所以b=a2a−1,故a﹣b+3ba=a−a2a−1+32a−1=2a2−2a+32a−1=a−12+54a−2=14(4a−2)+54a−2,当4a﹣2>0,即a>12时,a﹣b+3ba=14(4a−2)+54a−2≥2√14(4a−2)⋅54a−2=√5,当且仅当a=12+√52,b=12+√510时,a﹣b+3b a有最小值√5.【点评】本题考查了不等式的求解以及基本不等式的应用,主要考查了“1”的代换的应用,在使用基本不等式求解最值时要满足三个条件:一正、二定、三相等,属于中档题.21.(12分)(2020秋•海门市校级月考)(1)已知正实数x,y满足x+2x+3y+4y=10,则xy的取值范围为多少?(2)已知a>b>0,则a2+1ab+1a(a−b)的最小值是多少?【分析】(1)令t=xy,t>0,则y=tx,然后代入后结合基本不等式即可求解,(2)由已知a2+1ab+1a(a−b)=a2−ab+ab+1ab+1a(a−b),=ab+1ab+a(a﹣b)+1a(a−b),然后结合基本不等式即可求解.【解答】解:(1)令t=xy,t>0,则y=t x,∴10=x+2x+3y+4y=x+2x+3t x+4x t=(1+4t)x+2+3tx≥2√(1+4t)x⋅2+3tx=2√(2+3t)(t+4)t,整理可得,3t2﹣11t+8≤0,解可得,1≤t≤8 3,故1≤xy≤8 3,(2)∵a>b>0,∴a﹣b>0,则a2+1ab+1a(a−b)=a2−ab+ab+1ab+1a(a−b),=ab+1ab+a(a﹣b)+1a(a−b),≥2√ab⋅1ab+2√a(a−b)⋅1a(a−b)=2+2=4,当且仅当ab=1ab且a(a﹣b)=1a(a−b)即a=√2,b=√22时取等号,此时取得最小值4.【点评】本题主要考查利用基本不等式求解最值,解题的关键是应用条件的配凑.22.(12分)(2019秋•濮阳期末)经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度υ(千米/小时)之间的函数关系为:y=920υυ2+3υ+1600(υ>0).(1)在该时段内,当汽车的平均速度υ为多少时,车流量最大?最大车流量为多少?(保留分数形式) (2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内? 【分析】(1)根据基本不等式性质可知y =920υυ2+3υ+1600=9203+(v+1600v)≤92083,进而求得y 的最大值.根据等号成立的条件求得此时的平均速度.(2)在该时间段内车流量超过10千辆/小时时,解不等式即可求出v 的范围. 【解答】解:(1)依题意,y =920υυ2+3υ+1600=9203+(v+1600v)≤92083, 当且仅当v =1600v,即v =40时,上式等号成立, ∴y max =92083(千辆/时). ∴如果要求在该时段内车流量超过10千辆/时,则汽车的平均速度应大于25km /h 且小于64km /h .当v =40km /h 时,车流量最大,最大车流量约为92083千辆/时;(2)由条件得920υυ2+3υ+1600>10,整理得v 2﹣89v +1600<0,即(v ﹣25)(v ﹣64)<0.解得25<v <64.【点评】本题主要考查了基本不等式在最值问题中的应用.要特别留意等号取得的条件.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
选择题专题复习1
1.下列有关说法和表述正确的是()
A.时间的国际单位是小时
B.空气中的声速都为340m/s
C.低于标准气压时,水的沸点可能为90℃
D.水的三种状态分别是雨、雪、霜。
2.如图所示,是我们学习物理时用到的实验仪器或工具,下列说法中不正确的是()
A.甲图中激光笔发出的红外线说明光沿直线传播
B.乙图是测量时间仪器——机械停表
C.丙图也可用来证明声可传递能量
D.丁图中三角尺在测量长度时总会有误差
3.下列有关声现象的结论或描述正确的是()
A.声的产生和传播实验都可在真空中进行
B.只要频率在20~20000Hz之间,人们都能区分回声与原声
C.声音的特性主要是指音调、音色和乐音
D.从环境保护角度讲,物理课上的睡觉鼾声是噪声
4.关于下列各幅图中物态变化的说法错误的是( )
A.甲图:空气中水蒸气遇冷的冰棒液化变成“白气”向下落
B.乙图:将装酒精的塑料袋口扎紧后放入热水中发生的是液化现象
C.丙图:清晨,蜻蜓和植物上的露珠是由水蒸气放热后形成的
D.丁图:水蒸气在寒冷的玻璃上凝华形成的花纹
5.美丽的树挂、霜是怎样形成的?如图甲所示,将冰块防御易拉罐中并加入适量的盐。
用筷子搅拌大约半分钟,用温度计测量罐中冰与盐水混合物的温度,发现低于0℃,并仔细观察会在易拉罐底部出现了霜,如图乙所示。
则下列说法正确的是()
A.白霜是空气遇冷凝华形成的
B.白霜的形成是吸热过程
C.出现白霜时,冰水混合物中冰的质量在变小
D.冰水混合物的温度低于0℃,说明含有盐的水凝固过程中温度会降低
6.图像法是利用图象这种特殊且形象的数学语言工具,来表达各种现象的过程和规律的方法,下列有关物理学习中物理量关系的图像表述正确的()
7.下列关于图片的说法不正确的是()
8.在一个空罐的底部中央打一个小孔,再用一片半透明的塑料膜蒙在空罐的口上,将小孔对着烛焰,我们就可以看到烛焰在薄膜上呈现的像。
则下列关于小孔成像说法错误的是()
A. 像与物上下颠倒,左右相反
B. 物体离得越远,像越小
C. 成像的小孔必须是圆形的
D. 将照相机底片放在光屏处可以拍摄到像
9.下列各选项中对应两幅图所包含的物理规律和原理表述都正确的是()
A.B超和清洗机都利用了声可以传递能量B.纸锅烧水和感觉冷都有水蒸汽液化吸热
C.手影和看见物体都属于光的反射D.漫反射和潜望镜看物都遵循光的反射定律
10.如图所示,太阳光与水平方向夹角为30°,小明想要利用球面镜使此时的太阳光竖直射入井中。
下列有关说法正确的是()
A.正确放置后,计算可得此时入射角为30°
B.反射光线与入射光线的夹角为150°
C.平面镜与水平方向夹角为60°
D.无论用平面镜、凸面镜还是凹面镜,放置在相同角度即可
11.下列有关光现象的说法或描述正确的是()
12.如图所示,蜡烛烛焰经凸透镜,此时光屏上能成一清晰的像,若“戴上”远视眼镜,为使光屏上的像仍然保持清晰,则下列操作可行的是()
A.靠近透镜B.远离透镜
C.靠近透镜或远离透镜都可以D.保持在原来位置
13.下列关于天平结构和使用过程描述正确的是()
A.甲图是我们实验室常用的一种电子天平
B.甲图中结构a和b在放置物体后,称量过程中可同时移动和调节直至天平平衡
C.若甲图中天平此时平衡,则被称量物体质量为10g+1.6g=11.6g
D.若调节游码如图乙位置时天平平衡,则在甲图中指针将指向分度盘的右侧
14.下列有关质量和体积的估测值正确的是()
A.教室内空气的质量约为250kg
B.容积为2.5L的饮料瓶装满水的质量约为2.5×103kg
C.一名中学生的体积约为500dm3
D.容量约3.93×1011m3的三峡水库蓄水量约为3.93×1014t
15. 下列关于眼睛和眼镜的说法正确的是()
A.人的眼球相当于一架照相机,正常眼睛的近点大约在10cm,远点大约在25cm B.近视眼只能看清近处的物体,原因是晶状体太薄,折光能力太强成像在视网膜前C.100度远视镜片的透镜焦度是1m-1,它的焦距是1m
D.+300度眼镜片是近视镜片,-200度的眼镜片是远视镜片
答案:。
