Matlab讲义5
控制系统matlab仿真讲义

matlab第五讲教案

西南科技大学本科生课程备课教案计算机技术在安全工程中的应用——Matlab入门及应用授课教师:徐中慧班级:专业:安全技术及工程第四章课型:新授课教具:多媒体教学设备,matlab教学软件一、目标与要求掌握矩阵与数组的相关运算,及matlab中矩阵运算的相关函数,包括三角分解、正交变换、奇异值分解、特征值分解、矩阵的秩的运算等。
二、教学重点与难点本堂课教学的重点在于引导学生在编写matlab程序时能够熟练运用矩阵运算的相关函数实现相应的功能。
三、教学方法本课程主要通过讲授法、演示法、练习法等相结合的方法来引导学生掌控本堂课的学习内容。
四、教学内容一、课后习题的解说。
(1)在计算器发明(约1974年)之前,人们需要用数学用表来计算正弦、余弦和对数值。
创建正弦值数学用表的步骤如下:①创建角度矢量、范围在0~3600之间,步长为180。
②计算正弦值,用角度和计算出来的正弦值创建表格。
③分别用两个disp语句给表格加上标题和表头。
④用fprintf显示数据,要求小数点后有两位有效数字。
解:angle=0:18:360; sine=sin(angle/180*pi);disp(' SINE TABLE ')disp(' Angle Sine ')fprintf(' %4.2f %4.2e\n',[angle;sine])(2)使用搜索引擎或浏览器搜索英镑、日元、欧元和人民币对美元的汇率,并把输出结果绘制成表。
要求用disp在表格中添加标题和表头,用fprintf输出格式化数据。
①创建日元和美元的汇率表,表中共有25行,从5日元开始,步长为5日元②创建人民币和美元的汇率表,表中共有30行,从5元开始,步长为5元③创建数据表格,表中有5列,第一列是美元,第二列是欧元,第三列是英镑,第四列是人民币,第五列是日元。
计算与1到10美元等价的其它货币值。
(将结果输出到.txt文件中,此步骤属选做)解:①jpy=5:5:25*5;usd1=jpy*0.01301;disp(' JPY &USD TABLE ')disp(' JPY USD ')fprintf(' %4.2f %4.2f\n',[jpy;usd1])②cny=5:5:30*5;usd2= cny *0.1567;disp(' CNY &USD TABLE ') disp(' RMB USD ') fprintf(' %4.2f %4.2f\n',[cny;usd2])③usd=1:1:10;eur=usd* 0.7323; gbp=usd* 0.6405; cny=usd* 6.3816; jpy=usd*76.358;disp(' AS Exch')disp(' USD EUR GBP RMB JPY')fprintf(' %4.2f %4.2f %4.2f %4.2f %4.2f \n',[ usd;eur;gbp;cny;jpy])二、矩阵的相关知识掌握矩阵与数组的相关运算,及matlab 中矩阵运算的相关函数,包括三角分解、正交变换、奇异值分解、特征值分解、矩阵的秩的运算等。
matlab ppt第五讲

N=4; A=magic(3); try A_N=A(N, : ); catch A_end=A(end, : ); end lasterr % 取A的第N行元素 % A为3x3矩阵
(6) 控制程序流的其他常用指令
1) v=input(‘msg’)
v=input(‘msg’, ‘s’ )
(和一维数组冒号法定义相同)
% 循环体
end
例 for循环示例
for ii=1:10
x(ii)=ii;
end
x= 1
2
3
4
5
6
7
8
9 10
说明:
● 循环不会因为在循环体内对循环变量更新设置而中 断
● 在for后面的表达式中的数组可以为任何合法的 matlab数组 ● 循环结构可以嵌套使用
● 为了得到高效率的代码,应尽量提高代码的向量化 程度,避免使用循环结构;在循环指令之前应尽量对 数组进行预定义 ● 由于i和j是预定义变量,作虚单位使用.建议不作 为循环变量使用.
(1) 函数申明行:位于函数文件的首行,以matlab关键字function开 头,函数名以及函数的输入输出宗量都在这一行定义.
(2) H1行:紧随函数申明行之后以%开头的第一注释行.包括:大写体 的函数文件名,运用关键词简要描述函数功能.该行供lookfor关键词查 询和help在线帮助使用.
(3) 在线帮助文本区:H1行及其之后的连续以%开头的所有注释行构成 的整个在线帮助文本.通常包括:函数输入输出宗量的含义,调用格式说明.
常用
常用
● 如果判决条件expression为一个空数组,认为条件为假
● 表达式由多个逻辑子表达式组成时,将尽可能少地检测子表达式的值
《MATLAB教程及实训》第五章ppt5

例5-12 根据输入参数的个数将例5-11中参数个数使用 varargin和varargout函数,绘制不同线型的曲线,绘制的 曲线与图5-6相同。 function varargout=ex5_12(varargin) x=0:10; lin=length(varargin); %取输入参数个数 在命令窗口中输入 y=lin*ones(11,1); 调用命令: hold on >> y=ex5_12('y','o') if lin==0 varargout = plot(x,y) [2] elseif lin==1 y= plot(x,y,varargin{1}) 2 else >> ex5_12('y','o') plot(x,y,[varargin{1} varargin{2}]) varargout = end [2] varargout{1}=lin ans = 2
5.3.2 函数的输入输出参数
1. 参数的传递 函数的参数传递是将主调函数中的变量值 传给被调函数的输入参数 (1)函数参数传递的是数值 (2)被调函数的输入参数是存放在函数 的工作空间中,与MATLAB的工作空间是 独立的,当调用结束时函数的工作空间被清 除,输入参数也被清除。
2. 输入输出参数的个数
例5-2 使用switch结构判断学生成绩的等级,90分以上 为优,80~90为良,70~80为中,60~70为及格,60分以 下为不及格。
>> score=98; >> s1=fix(score/10); >> switch s1 case {9,10} s='优' case 8 s='良' case 7 s='中' case 6 s='及格' otherwise s='不及格' end
MATLAB基础及应用课件(下)第5-8章

图5-5 拟合曲线
第5章 MATLAB数值计算
第5章 MATLAB数值计算
5.4.4 图形窗口的拟合和统计工具
第5章 MATLAB数值计算
在图5-6中的“绘制拟合图”中选择拟合方 法(可同时选多种);
“显示方程”复核框可以选择是否在图形上 显示拟合多项式;
“绘制残差图”复核框选中时会产生第二幅 图形,该图形显示了每一个数据点与计算出来的 拟合曲线之间的距离。
例如选择“线性”和“三次方”拟合方法, 同时选中两个复核框,产生图形如图5-7所示。
MATLAB的图形窗口中提供了简单方便的数 据拟合和基本统计工具。
数据拟合工具可以对所绘制的曲线使用多种 方法进行拟合;
基本统计工具可提供最小值、最大值、平均 值、中位值、标准差、数据范围等统计运算。
1.数据拟合工具
第5章 MATLAB数值计算
使用数据拟合工具首先需要创建一幅图形,在 命令行窗口输入以下程序:
两个矩阵x和y的相关系 数
第5章 MATLAB数值计算
5.2 数值运算 一、 多项式
名称
创建多项 式
求根
求值
多项式乘 法
多项式除 法
多项式求 导
函数格式 P=[ a0 a1 a2 …an-1
an] P=poly(A) roots(P) polyval(P,A)
polyvalm(P,m)
说明
P为多项式(以下各函数中P均为多项式),a0 a1 a2 … an-1 an为按降幂顺序排列的多项式系数 A为向量。创建以向量A中元素为根的多项式
Matlab讲义

第一章MATLAB软件的基本操作1.1矩阵的建立和基本运算一、实验的目的熟悉MATLAB软件中关于矩阵的建立以及矩阵运算的各种命令二、实验内容与要求1.启动与退出2.数、数组、矩阵的输入(1)数的输入>> a=5a =5>> b=2-5ib =2.0000 - 5.0000i>> b=[1,3,5,7,9,11]b =1 3 5 7 9 11>> c=1:2:11c =1 3 5 7 9 11>> d=linspace(1,11,6)d =1 3 5 7 9 11>> b=linspace(0,2*pi,22)b =Columns 1 through 60 0.2992 0.5984 0.8976 1.1968 1.4960 Columns 7 through 121.79522.0944 2.3936 2.6928 2.99203.2912 Columns 13 through 183.5904 3.88964.1888 4.4880 4.78725.0864 Columns 19 through 225.3856 5.6848 5.98406.2832(2)数组的输入>> A=[2,3,4;1,3,5;6,9,4]A =2 3 41 3 56 9 43.矩阵大小的测定和定位>> A=[3,5,6;2,5,8;3,5,9;3,7,9]A =3 5 62 5 83 7 9>> d=numel(A) %测定矩阵A的元素数d =12>> [n,m]=size(A) %测试A的行(n),列(m)数n =4m =3>> [i,j]=find(A>3) %找出A中大于3的元素的行列数i =12341234j =222233334.矩阵的块操作>> A(2,:) %取出A的第2行的所有元素ans =2 5 8>> A([1,3],:) %取出A的第1、3行的所有元素ans =3 5 63 5 9>> A(2:3,1:2) %取出A的2、3行与1、2列交叉的元素ans =2 53 5>> A([1,3],:)=A([3,1],:) %将A的第1行和第3行互换A =3 5 93 5 63 7 9问题:如何将A的2,3列互换?>> A(2,:)=4 %将A的第2行的所有元素用4取代A =3 5 94 4 43 5 63 7 9>> A(find(A==3))=-3 %将A中等于3的所有元素换为-3A =-3 5 94 4 4-3 5 6-3 7 9>> A(2,:)=[] %删除A的第2行A =-3 5 9-3 5 6-3 7 9>> A=[3,5,6;2,5,8;3,5,9;3,7,9]A =3 5 62 5 83 5 93 7 9>> reshape(A,2,6) %返回以A的元素重新构造的2×6维矩阵ans =3 3 5 5 6 92 3 5 7 8 9>> reshape(A,3,4)ans =3 3 5 82 5 7 93 5 6 9>> A(4,5)=3 %扩充A的维数,A成为4×5维矩阵,未定义元素为3A =3 5 6 0 02 5 8 0 03 5 9 0 03 7 9 0 3注意:“:”表示全部5.矩阵的翻转操作>> A=[3,5,6;2,5,8;3,5,9;3,7,9]A =3 5 62 5 83 5 93 7 9>> flipud(A) % A进行上下翻转ans =3 7 93 5 92 5 83 5 6>> fliplr(A) % A进行左右翻转ans =6 5 38 5 29 5 39 7 3>> rot90(A) % A逆时针旋转900ans =6 8 9 95 5 5 73 2 3 3问题:尝试操作>> rot90(A,2)和rot90(A,-2),结果有区别吗? >> rot90(A,2)ans =9 7 39 5 38 5 26 5 3>> rot90(A,-2)ans =9 7 39 5 38 5 26 5 36.特殊矩阵的产生>> A=eye(n) %产生n维单位矩阵A =1 0 0 00 1 0 00 0 1 00 0 0 1>> A=ones(n,m) %产生n×n维1矩阵A =1 1 1 11 1 1 11 1 1 11 1 1 1>> A=zeros(n,m) %产生n×n维0矩阵A =0 0 00 0 00 0 00 0 0>> A=rand(n,m) %产生n×n维随机矩阵(元素在0~1之间)A =0.9501 0.8913 0.82140.2311 0.7621 0.44470.6068 0.4565 0.61540.4860 0.0185 0.7919>> A=rand(n,m)A =0.9218 0.9355 0.05790.7382 0.9169 0.35290.1763 0.4103 0.81320.4057 0.8936 0.00997.数的运算>>4+2;>>4*2;>> 4/2; % 4右除2,等于2>> 4\2; % 4左除2,等于0.5>> 4^3; % 4的3次方>> sqrt(4); % 4的算术平方根>> exp(3); %e的三次方>> log(4); %4的自然对数>> log2(4); %4的以2为底的对数>> log10(4); %4的以10为底的对数8.矩阵的运算A=[2,3,4;1,3,5;6,9,4];B=[3,5,1;2,6,2;1,8,3];>> A'; %A的转置>> det(A); %A的行列式,A必须是方阵>> rank(A); %A的秩>> 3*A; %常数与矩阵相乘>> A+B;>> A-B;>> A*B; %(和A. *B进行比较)>> A/B; %(和A. /B 进行比较) >> A\B; %(和A. \B 进行比较)>>A^2; % A^2相当于A*A (和A.^2进行比较) 二、练习与思考(1)熟悉MATLAB 的启动和退出。
matlab讲义

第一章 Matlab 基本介绍一、数学建模常用软件简介数值计算 Matlab符号计算 Maple , Mathematica统计软件 SPSS, SAS优化软件 LINGOOFFICE 软件 Word , Excel二、matlab 界面介绍1、command window (命令窗口)2、wordspace (工作空间)3、command history (历史命令窗口)4、菜单(1)File->import data(2)View->desklayout->default(3)Help三、一些常用命令1、clc (清空命令窗口)2、clear (清空工作空间变量)3、save (保存工作空间中变量到指定文件)4、load (导入文件中数据)(注:双击数据文件也可)5、help (帮助)6、doc (查询帮助文档)第二章 数值计算一、数据类型1、主要四大类数据类型:数值型,字符串,符号型(代数式),逻辑型1⎧⎪⎧⎨⎨⎪⎩⎩、浮点数值型长整2、整型短整 字符串 name=’lisan ’a=’x ’符号型 用syms , sym 定义逻辑型 取值只能为0或1,即真或假2 常用运算符数值运算:+ , - ,* , / , \, ^,.*, ./, .^关系运算 (运算结果为逻辑型,即0或1)>,<,>=,<=,==,~=逻辑运算 (运算结果为逻辑型,即0或1)与或非,&,|,~any, all基本数学函数三角sin ,asin,cos,acos,tan,atan,cot,acot指数exp,log,log2,log10,sqrt其他abs,real,imag,sign,mod,floor,ceil2、变量命名规则(1)以字母开头,可包含字母、数字、下划线,不超过31位字符。
(2)区分大小写。
3、常量i, j 虚数单位pi , 圆周率eps,infNaN4、数字的输入输出格式format 格式参数shortlongrat5、字符串(1)字符串生成name=’lisan’a=char(‘l’,’i’)size(name) 查看字符串长度length(name) 查看字符串长度(2)字符与数组之间的转换double 字符转换为ASC码num2str 数字转化为字符str2num 字符转位数字a=’2’b=a*2b=double(a)*2b=str2num(a)*2(3)字符串操作相关函数。
MATLAB讲义

MATLAB讲义第一章 MATLAB系统概述1.1 MATLAB系统概述MATLAB(MATrix LABoratory)矩阵实验室的缩写,全部用C语言编写。
特点:(1)以复数矩阵作为基本编程单元,矩阵运算如同其它高级语言中的语言变量操作一样方便,而且矩阵无需定义即可采用。
(2)语句书写简单。
(3)语句功能强大。
(4)有丰富的图形功能。
如plot,plot3语句等。
(5)提供了许多面向应用问题求解的工具箱函数。
目前,有20多个工具箱函数,如信号处理、图像处理、控制系统、系统识别、最优化、神经网络的模糊系统等。
(6)易扩充。
1.2 MATLAB系统组成(1)MATLAB语言MATLAB语言是高级的矩阵、矢量语言,具有控制流向语句、函数、数据结构、输入输出等功能。
同时MATLAB又具有面向对象编程特色。
MATLAB语言包括运算符和特殊字符、编程语言结构、字符串、文件输入/输出、时间和日期、数据类型和结构等部分。
(2)开发环境MATLAB开发环境有一系列的工具和功能体,其中大部分具有图形用户界面,包括MATLAB桌面、命令窗口、命令历史窗口、帮助游览器、工作空间、文件和搜索路径等。
(3)图形处理图形处理包括二维、三维数据可视化,图像处理、模拟、图形表示等图形命令。
还包括低级的图形命令,供用户自由制作、控制图形特性之用。
(4)数学函数库有求和、正弦、余弦等基本函数到矩阵求逆、求矩阵特征值和特征矢量等。
MATLAB数学函数库可分为基本矩阵和操作、基本数学函数、特殊化数学函数、线性矩阵函数、数学分析和付里叶变换、多项式和二重函数等。
(5)MATLAB应用程序接口(API)MATLAB程序可以和C/C++语言及FORTRAN程序结合起来,可将以前编写的C/C++、FORTRAN语言程序移植到MATLAB中。
1.3 MATLAB的应用范围包括:MATLAB的典型应用包括:●数学计算●算法开发●建模、仿真和演算●数据分析和可视化●科学与工程绘图●应用开发(包括建立图形用户界面)以矩阵为基本对象第二章 Matlab基础2.1 MATLAB快速入门(1)搜索路径搜索路径也被看作是MATLAB的路径,其包含的文件被认为在路径上。
MATLAB学习课件第五章

4
5.1 概述
根据程序运行方式的不同,可以将MATLAB程序设计分为
两种方式:
一种是在命令窗口中逐条输入命令,另一种是将相关
的命令存储在一个M文件中。
前者称为命令行方式,又称为指令驱动模式。后者称
为M文件的程序运行方式。
命令行方式 M文件编程方式 命令逐条解释执行 自动一次执行完文件中所有命令 简单,直观 不直观 速度慢,执行过程不能保留, 速度快,可以重复执行文件 不能重复执行
25
2、while语句
while语句的一般格式为: while 表达式 循环体语句 end while语句为条件循环语句,循环次数不确定,只要循环条件
表达式的结果非零,语句体就重复执行,直到循环条件表达 式的结果为零,则跳出循环
26
5.3.4 程序流的控制
与控制程序执行过程相关的语句主要有break语句、
5.3 MATLAB程序结构
MATLAB程序的控制结构有3种:
顺序结构、选择结构和循环结构。
按照程序设计的观点, 任何算法功能都可以通过由程序模
块组成的三种基本程序结构的组合来实现。
11
5.3.1 顺序结构
顺序结构是指程序按程序语句或模块在执行流中的顺序逐
个执行,直到执行到程序的最后一个语句。
函数式M文件 接受输入参数,有返回值 文件中定义变量为局部变量, 文件执行完毕时,局部变量 清除,不保留在工作空间
要通过函数调用的方式调用 才能运行 用户需要自定义某种具体算 法时使用
5.2.3 M文件操作
对M文件常用的操作有:打开M文件、新建M文件、编辑
M文件、保存M文件和运行M文件等。
10
例5.8:判断读取矩阵是否正确。 解:程序如下 n=4; a=magic(3) try a_n=a(n,:), %取a的第n 行元素 catch a_n=a(end, : ), %如取a的第n 行出错,则改取a的最后一行 end lasterr %显示出错原因 执行结果如下; a= 8 1 6 3 5 7 4 9 2 a_n = 9 2 ans = Attempted to access a(4,:); index out of bounds because size(a)=[3,3].
MATLAB实验讲义

实验1 MATLAB环境及命令窗口的使用目的和要求(1)熟练掌握MATLAB的启动和退出。
(2)熟练MATLAB的命令窗口。
A(3)熟练常用选单和工具栏。
(4)熟悉MATLAB桌面的其他窗口。
(5)使用“帮助”查找帮助信息。
内容和步骤学习使用MATLAB必须先熟悉MATLAB的桌面环境。
MATLAB的窗口包括命令窗口(Command Window).历史命令窗口(Command History).当前目录浏览窗口(Current Directory Browser).工作空间窗口(Workspace Browser)和帮助导航/浏览窗口(Help Browser).数组编辑器窗口(Array Editor).交互界面分类目录窗口(Launch Pad).M文件编辑/调试器窗口(Editor/Debugger)和程序性能剖析窗口(Profiler).1.启动MATLAB在安装完MATLAB后,就会在Windows的桌面上出现MATLAB的图标,双击该图标,启动MATLAB;或者通过Windows的“开始”按钮,在“程序”选单中选择“MATLAB”命令来启动。
2.使用命令窗口在命令窗口中输入以下命令并查看运行结果;>> a=2.5a=2.5000>>b=[1 2;3 4]b=1 22 4>>c=’a’c=a>>d=sin(a*b*pi/180)d=0.0436 0.08720.1305 0.1736>> e=a+ce=99.5000(1)单独显示命令窗口。
选择选单”desktop”-“desktop Layout”-“Command window only”图1.1然后选择命令窗口的选单”desktop”-“desktop layout”-“default”,窗口恢复默认设置。
练习:同学们可以输入其他一些信息,查看显示结果;单击命令窗口右上角的↗钮,查看显示结果;选择菜单进行相关操作,查看显示结果。
《Matlab教案》课件

《MATLAB教案》PPT课件第一章:MATLAB概述1.1 MATLAB简介介绍MATLAB的历史和发展解释MATLAB的含义(Matrix Laboratory)强调MATLAB在工程和科学计算中的应用1.2 MATLAB界面介绍MATLAB的工作空间解释MATLAB的菜单栏和工具栏演示如何创建、打开和关闭MATLAB文件1.3 MATLAB的基本操作介绍MATLAB的数据类型演示如何进行矩阵运算解释MATLAB中的向量和矩阵运算规则第二章:MATLAB编程基础2.1 MATLAB脚本编程解释MATLAB脚本文件的结构演示如何编写和运行MATLAB脚本强调注释和代码的可读性2.2 MATLAB函数编程介绍MATLAB函数的定义和结构演示如何创建和使用MATLAB函数强调函数的重用性和模块化编程2.3 MATLAB编程技巧介绍变量和函数的命名规则演示如何进行错误处理和调试强调代码的优化和性能提升第三章:MATLAB数值计算3.1 MATLAB数值解算介绍MATLAB中的数值解算工具演示如何解线性方程组和不等式解释MATLAB中的符号解算和数值解算的区别3.2 MATLAB数值分析介绍MATLAB中的数值分析工具演示如何进行插值、拟合和数值积分解释MATLAB中的误差估计和数值稳定性3.3 MATLAB优化工具箱介绍MATLAB优化工具箱的功能演示如何使用优化工具箱进行无约束和约束优化问题解释MATLAB中的优化算法和参数设置第四章:MATLAB绘图和可视化4.1 MATLAB绘图基础介绍MATLAB中的绘图命令和函数演示如何绘制二维和三维图形解释MATLAB中的图形属性设置和自定义4.2 MATLAB数据可视化介绍MATLAB中的数据可视化工具演示如何绘制统计图表和散点图解释MATLAB中的数据过滤和转换4.3 MATLAB动画和交互式图形介绍MATLAB中的动画和交互式图形功能演示如何创建动画和交互式图形解释MATLAB中的图形交互和数据探索第五章:MATLAB应用案例5.1 MATLAB在信号处理中的应用介绍MATLAB在信号处理中的基本概念演示如何使用MATLAB进行信号处理操作解释MATLAB在信号处理中的优势和应用场景5.2 MATLAB在控制系统中的应用介绍MATLAB在控制系统中的基本概念演示如何使用MATLAB进行控制系统分析和设计解释MATLAB在控制系统中的优势和应用场景5.3 MATLAB在图像处理中的应用介绍MATLAB在图像处理中的基本概念演示如何使用MATLAB进行图像处理操作解释MATLAB在图像处理中的优势和应用场景《MATLAB教案》PPT课件第六章:MATLAB Simulink基础6.1 Simulink简介介绍Simulink作为MATLAB的一个集成组件解释Simulink的作用:模型化、仿真和分析动态系统强调Simulink在系统级设计和多领域仿真中的优势6.2 Simulink界面介绍Simulink库浏览器和模型窗口演示如何创建、编辑和运行Simulink模型解释Simulink中的块和连接的概念6.3 Simulink仿真介绍Simulink仿真的基本过程演示如何设置仿真参数和启动仿真解释Simulink仿真结果的查看和分析第七章:MATLAB Simulink高级应用7.1 Simulink设计模式介绍Simulink的设计模式,包括连续、离散、混合和事件驱动模式演示如何根据系统特性选择合适的设计模式解释不同设计模式对系统性能的影响7.2 Simulink子系统介绍Simulink子系统的概念和用途演示如何创建和管理Simulink子系统解释子系统在模块化和层次化设计中的作用7.3 Simulink Real-Time Workshop介绍Simulink Real-Time Workshop的功能演示如何使用Real-Time Workshop进行代码解释代码对于硬件在环仿真和嵌入式系统开发的重要性第八章:MATLAB Simulink库和工具箱8.1 Simulink库介绍Simulink库的结构和分类演示如何访问和使用Simulink库中的块解释Simulink库对于模型构建和功能复用的意义8.2 Simulink工具箱介绍Simulink工具箱的概念和功能演示如何安装和使用Simulink工具箱解释Simulink工具箱在特定领域仿真和分析中的作用8.3 自定义Simulink库介绍如何创建和维护自定义Simulink库演示如何将自定义块添加到库中解释自定义库对于个人和组织级模型共享的重要性第九章:MATLAB Simulink案例分析9.1 Simulink在控制系统中的应用介绍控制系统模型在Simulink中的构建演示如何使用Simulink进行控制系统设计和分析解释Simulink在控制系统教育和研究中的应用9.2 Simulink在信号处理中的应用介绍信号处理模型在Simulink中的构建演示如何使用Simulink进行信号处理仿真解释Simulink在信号处理领域中的优势和实际应用9.3 Simulink在图像处理中的应用介绍图像处理模型在Simulink中的构建演示如何使用Simulink进行图像处理仿真解释Simulink在图像处理领域中的优势和实际应用第十章:MATLAB Simulink项目实践10.1 Simulink项目实践流程介绍从需求分析到模型验证的Simulink项目实践流程演示如何使用Simulink进行项目规划和实施解释Simulink在项目管理和协作中的作用10.2 Simulink与MATLAB的交互介绍Simulink与MATLAB之间的数据交互方式演示如何在Simulink中使用MATLAB函数和脚本解释混合仿真模式对于复杂系统仿真的优势10.3 Simulink项目案例分析具体的Simulink项目案例演示如何解决实际工程问题解释Simulink在工程教育和项目开发中的应用价值《MATLAB教案》PPT课件第十一章:MATLAB App Designer入门11.1 App Designer简介介绍App Designer作为MATLAB中的应用程序开发环境解释App Designer的作用:快速创建跨平台的MATLAB应用程序强调App Designer在简化MATLAB代码部署和用户交互中的优势11.2 App Designer界面介绍App Designer的用户界面和工作流程演示如何创建新应用和编辑应用界面解释App Designer中的组件和布局的概念11.3 App Designer编程介绍App Designer中的MATLAB编程模式演示如何使用App Designer中的MATLAB代码块解释App Designer中事件处理和应用程序生命周期管理的重要性第十二章:MATLAB App Designer高级功能12.1 App Designer用户界面设计介绍App Designer中用户界面的定制方法演示如何使用样式、颜色和主题来美化应用界面解释用户界面设计对于提升用户体验的重要性12.2 App Designer数据模型介绍App Designer中的数据模型和模型视图概念演示如何创建、使用和绑定数据模型和视图解释数据模型在应用程序中的作用和重要性12.3 App Designer部署和分发介绍App Designer应用程序的部署和分发流程演示如何打包和发布应用程序解释如何为不同平台安装和运行App Designer应用程序第十三章:MATLAB App Designer案例研究13.1 图形用户界面(GUI)应用程序设计介绍使用App Designer设计的GUI应用程序案例演示如何创建交互式GUI应用程序来简化MATLAB脚本解释GUI应用程序在数据输入和结果显示中的作用13.2 数据分析和可视化应用程序设计介绍使用App Designer进行数据分析和可视化的案例演示如何创建应用程序来处理和显示大型数据集解释App Designer在数据分析和决策支持中的优势13.3 机器学习和深度学习应用程序设计介绍使用App Designer实现机器学习和深度学习模型的案例演示如何将MATLAB中的机器学习和深度学习算法集成到应用程序中解释App Designer在机器学习和深度学习应用部署中的作用第十四章:MATLAB App Designer实战项目14.1 App Designer项目规划和管理介绍App Designer项目的规划和管理方法演示如何组织和维护大型应用程序项目解释项目管理和版本控制对于团队协作的重要性14.2 App Designer与MATLAB的集成介绍App Designer与MATLAB之间的数据和功能集成演示如何在App Designer中调用MATLAB函数和脚本解释集成MATLAB强大计算和分析能力的重要性14.3 App Designer项目案例实现分析具体的App Designer项目案例实现过程演示如何解决实际工程项目中的问题解释App Designer在工程项目实践中的应用价值第十五章:MATLAB App Designer的未来趋势15.1 App Designer的新功能和技术介绍App Designer的最新功能和技术发展演示如何利用新功能和技术提升应用程序的性能和用户体验强调持续学习和适应新技术的重要性15.2 App Designer在跨平台开发中的应用介绍App Designer在跨平台应用程序开发中的优势演示如何创建适用于不同操作系统的应用程序解释跨平台开发对于扩大应用程序市场的重要性15.3 App Designer的未来趋势和展望讨论App Designer在未来的发展趋势和潜在应用领域激发学生对于应用程序开发和创新的兴趣强调持续探索和创造新应用的重要性重点和难点解析本文档为您提供了一份详尽的《MATLAB教案》PPT课件,内容涵盖了MATLAB 的基本概念、编程基础、数值计算、绘图和可视化、应用案例、Simulink的基础知识、高级应用、库和工具箱的使用、案例分析以及项目实践、App Designer 的基础知识、高级功能、案例研究、实战项目和未来趋势等方面的内容。
Matlab基本教学讲义

Matlab基本教學講義環境的基本使用方法Matlab Command Window的指令選單上有幾個選項File Edit View Window HelpFile選單上第一個指令New分有三個選項M-file →開啟一個新的檔案用來編輯matlab程式。
副檔名*.m,如同C語言程式的副檔名*.cpp或是*.c一樣。
Figure →開始一個新的圖檔。
Model →開啟一個新的simulink檔案。
Help選單上有選項可以幫助指令的查詢一些基本指令的操作運算元數學運算元加+減-乘.*除./轉置‘次方.^比較運算元小於<大於>小於等於<=大於等於>=等於==不等於~=邏輯運算元and &or |not ~矩陣矩陣的表示方法若輸入指令為A=[1 2 3;4 5 6;7 8 9]則視窗顯示出A= 1 2 34 5 67 8 9則A(1,1)=1,A(1,2)=2,A(1,3)=3A(2,1)=4,A(2,2)=5,A(2,3)=6A(3,1)=7,A(3,2)=8,A(3,3)=9特殊符號 冒號”:”繼續之前的陣列A,若輸入A( : )則會出現長數列1~9。
若輸入A( : , 3)則出現ans =369若輸入A(1:1:3,1:2)則出現ans =1 24 578其中A(X:Y:Z,P:Q) 之中若表示法為X:Y:Z 時:X 表示起始值Y 表示公差Z 表示終止值若表示法為P:Q 時P 為起始值Q 為終止值公差= 1for、if等條件式的使用forfor I = 1:n (或是1:n可改成1:x:n,其中x則為公差)運算式endifif 條件式1運算式1elseif 條件式2運算式2elseif 條件式3運算式3…………………else運算式nend副程式的設計(*.m)function 傳回值=函式名稱(引數1,引數2,…..)運算式………………例如%I am bababa.....hahahaha……………….%Matlab is easy la.....function result=summation(a,b)%.....%.....result=sum(a:b);%Oh~bye bye.....%後面的文字為註解,程式不會執行。
MATLAB实验讲义

MATLAB实验讲义目录实验大纲 (2)实验一/二 MATLAB的基础操作 (3)实验三 MATLAB运算基础(一) (3)实验四 MATLAB运算基础(二) (4)实验五循环结构程序设计(一) (5)实验六循环结构程序设计(二) (5)实验七 MATLAB的绘图操作(一) (6)实验八 MATLAB的绘图操作(二) (7)实验九函数和文件(一) (7)实验十函数和文件(二) (7)实验十一线性代数中的数值计算问题 (8)实验十二 MATLAB函数库的运用(一) (9)实验十三 MATLAB函数库的运用(二) (10)《MATLAB》课程实验教学大纲课程名称:MATLAB(MATLAB)课程编号:16072327课程性质:选修实验总学时:27实验室名称:电子设计自动化一、课程简介:本课程是电气工程及其自动化、自动化、电力工程与管理专业本科生的学科基础选修课,它在线性代数、信号分析和处理、控制系统设计和仿真等方面有着广泛的应用。
主要是学习MATLAB的语法规则、基本命令和使用环境,使学生掌握MATLAB的基本命令和基本程序设计方法,提高使用该语言的应用能力,具有使用MATLAB语言编程和调试的能力,以便为后续多门课程使用该语言奠定必要的基础。
二、课程实验目的与要求:1.基本掌握MATLAB在线帮助功能的使用、熟悉MATLAB运行环境和MATLAB语言的主要特点,掌握MATLAB语言的基本语法规则及基本操作命令的使用,学会M文件的建立和使用方法以及应用MATLAB实现二维和三维图形的绘制方法,具有使用MATLAB语言编程和调试的能力。
2.初步掌握MATLAB在电路和信号与系统中的应用。
3.能根据需要选学参考书,查阅手册,通过独立思考,深入钻研有关问题,学会自己独立分析问题、解决问题,具有一定的创新能力。
三、主要仪器设备及台(套)数:计算机50台、MATLAB软件五、主要参考书目:1.《MATLAB及在电子信息课程中的应用》陈怀琛、杨吉斌编著,电子工业出版社,2002年1版2.《MATLAB7.0编程基础》王家文、王皓、刘海等;机械工业出版社,2005年7月3.《MATLAB教程——基于6.x版本》张志涌、徐彦琴等;北京航空航天大学出版,2001年4月出版实验一/二 MATLAB的基础操作一、实验目的1、掌握MATLAB的启动和退出。
MATLAB讲义

MATLAB王春兴编物理与电子科学学院2009.9第一章MATLAB简介MA TLAB的原意为MATrix LABoratory,即矩阵实验室,是由在数值线性代数领域颇有影响的Cleve Moler博士首创的。
后来由Moler博士等一批数学家和软件专家组建了MathWorks软件公司,专门从事MATLAB的扩展与改进。
MA TLAB不仅具有强大的数值计算能力,而且具有数据图示功能和符号运算功能。
特别是大量的工具箱,扩展了应用领域,是高校学生、教师、科研人员和工程计算人员的最好选择,是数学建模必不可少的工具。
1.1MATLAB的主要特点1.功能强大MATLAB以复数矩阵作为基本编程单元,可以方便地处理诸如矩阵变换及运算、多项式运算、微积分运算、线性与非线性方程求解、常微分方程求解、偏微分方程求解、插值与拟合、特征值问题、统计及优化问题。
2.语言简单MATLAB语句书写简单,表达式的书写如同在稿纸中演算一样,允许用户以数学形式的语言编写程序,控制语句同C语言相近,并提供了强大的帮助功能。
3.扩充能力强MATLAB本身就像一个解释系统,用户可以方便地看到函数的源程序,也可以方便地开发自己的程序。
另外,MATLAB可以方便地和FORTRAN、C等语言进行接口,还和Maple有很好的接口。
4.编程易从形式上看,MATLAB程序文件是一个纯文本文件,扩展名为M,调试方便。
1.2MATLAB的窗口1.启动MATLAB2.工具栏3.命令窗口MATLAB的输入命令和输出结果的窗口,在这里输入的命令会立即执行并输出结果。
可用UP键盘将以前执行的命令调出。
1.3MATLAB的通用命令1.管理命令和函数:2.管理变量和工作空间3.控制命令窗口4.使用文件和工作环境5.启动和退出MA TLAB第二章数值计算2.1数字及运算1.数值MA TLAB中采用十进制数,并可用科学表示法,虚数用i或j 表示。
5 -39 0.0025 1.52e-20 6.9e13 3.0i -3+4i浮点数的范围大致为10-308~10308。
matlab入门教程(第五章)
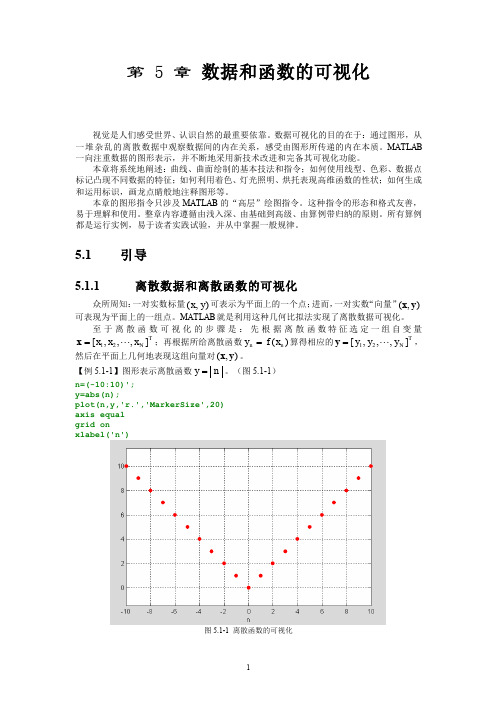
指 令 \downarrow \leftarrow \leftrightarrow \rightarrow \uparrow \circ \bullet
符
\exists \forall \in \infty \perp \prime \cdot
字符
\Nu \xi \Xi \pi \Pi \rho
6
\Delta \epsilon
\zeta 指 令 'sin\beta'
效果
\lambda \Lambd a \mu 指 令 '\zeta\omega'
\sigma \Sigma \tau
5
Normal and Grid on 4 2 0 -2 -4 -2 2
Equal 4 2 0 -2 0 -2 -4 -2
Square
0 Image and Box off 2 0 -2 -1 0 1
2
-2
0
2
0 Tight
2
Image and Fill 1 0.5 0 -0.5 -1 -1 0 1 -2 -1 0 2
一 坐标轴的控制
【例 5.2-3】观察各种轴控制指令的影响。演示采用长轴为 3.25,短轴为 1.15 的椭圆。注意: 采用多子图(图 5.2-3)表现时,图形形状不仅受“控制指令”影响,而且受整个图面“宽 高比”及“子图数目”的影响。本书这样处理,是出于篇幅考虑。读者欲想准确体会控制指 令的影响,请在全图状态下进行观察。
MATLAB基础教程(第五版)全套教学课件

02
主要应用于算法开发、数据 可视化、数据分析以及数值
计算等领域
03
在科学计算、工程设计、图 像处理、信号处理等领域有
广泛应用
MATLAB工作环境与界面介绍
01
MATLAB工作环境包括命令窗口、工作空间、编辑 器、路径管理器等
02
界面简洁直观,易于上手,支持多种操作系统
03
提供丰富的帮助文档和示例代码,方便用户学习和 使用
整数规划
对于整数规划问题,优化工具箱提供 了分支定界法、割平面法等求解方法
。
非线性规划
优化工具箱也支持非线性规划问题的 求解,如梯度下降法、牛顿法等。
多目标优化
优化工具箱还支持多目标优化问题的 求解,如遗传算法、粒子群算法等。
信号处理工具箱应用实例
信号滤波
使用信号处理工具箱可 以对信号进行滤波处理 ,如低通、高通、带通
数组与矩阵运算
介绍数值计算的定义、特点、误差分析等 基本概念。
详细讲解MATLAB中的数值类型,包括整 数、浮点数、复数等。
介绍数组和矩阵的基本概念和运算规则, 包括数组的创建、索引、操作等,以及矩 阵的加减、乘除、转置等运算。
符号运算入门
01
符号运算基本概念
介绍符号运算的定义、特点、应用领域等基本概念。
THANKS
03 支持数组元素的索引和切片操作,方便进行数据 处理
流程控制语句
01
MATLAB提供多种流程控制语句,如if语句、for循环
、while循环等
02 支持条件判断、循环控制、中断和继续等操作
03
流程控制语句的语法简洁明了,易于理解和使用
02
数值计算与符号运算
数值计算基础
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
确定自由变量示例
syms a b x X Y; k=sym('3'); z=sym('c*sqrt(delta)+y*sin(theta)'); EXPR=a*z*X+(b*x^2+k)*Y; % k为常量,z不自由 findsym(EXPR) % ans=X,Y,a,b,c,delta,theta,x,y findsym(EXPR,1) % ans=x findsym(EXPR,2) % ans=x,y findsym(EXPR,3) % ans=x,y,theta syms a b t u v x y; A=[a+b*x,sin(t)+u;x*exp(-t),log(y)+v ] findsym(A,1) % ans=x 对整个矩阵的元素判断。
f1 vm
jacobian(f)或jacobian(f,v) 注:当f是向量函数时,求得雅可比矩阵;当f是标 量函数时,求得函数梯度,等价于gradient(f)。 例: syms x1 x2; f=[x1*exp(x2);x2;cos(x1)*sin(x2)]; v=[x1 x2];fjac=jacobian(f,v)
11
置换操作示例
clear all syms a b c d W [V,D]=eig([a b;c d]); [RVD,W]=subexpr([V;D],W clear all syms a x;f=a*sin(x)+5; f1=subs(f,'sin(x)',sym('y')) f2=subs(f,{a,x},{2,sym(pi/3)}) f3=subs(f,{a,x},{2,pi/3}) f4=subs(subs(f,a,2),x,0:pi/6:pi) f5=subs(f,{a,x},{0:6,0:pi/6:pi})
7
符号表达式中自由变量的确定
MATLAB指令findsym能帮助用户了解系统对符号 表达式中的独立自变量是如何自动认定的。具体方 法如下: findsym(EXPR) 确认表达式EXPR中所有自由符号变量。 findsym(EXPR,N) 从EXPR中确认出靠x最近的N个独立自变量。 说明: EXPR可以是符号矩阵。此时指令对自由变量的确 认是对整个矩阵进行,而非元素。 按照自然科学习惯,MATLAB总是默认将x以及最 靠近x的字母表示的变量优先确认为独立的自由变 量。(小写字母总是比大写字母更靠近x)
16
d f ( x) dx n
雅可比矩阵
f v1 1 Jocbian f (v)) ( f n v1 其中 : f (v) [ f1 (v),...,
... ... ...
f n vm T f n (v)] , v (v1 ,..., vm )
9
符号表达式的操作
符号表达式常用的一些基本操作指令有: collect(EXPR [,v]) 合并同类项。 expand(EXPR) 对指定项展开。 factor(EXPR) 因式/因子分解。 horner(EXPR) 转换成嵌套形式。 [N,D]=numden(EXPR) 通分。 simplify(EXPR) 恒等式简化。 pretty(EXPR) 习惯方式显示。 simple(EXPR) 转换成最简短形式。
4
字符表达式转符号对象示例
y=sym(„2*sin(x)*cos(x)‟) %字符表达式化为符号变量。 y=simple(y) %把y表示的符号表达式化为最简形式。 syms fai1 fail2; y=simple(sin(fai1)*cos(fai2)-cos(fai1)*sin(fai2)) syms a11 a12 a21 a22; A=[a11,a12;a21,a22] DA=det(A),IA=inv(A),EA=eig(A) 注意:进行符号计算前,首先定义基本符号对象(可 以是常数、变量、表达式),然后利用这些基本符号 对象去构成新的符号表达式,进行所需的符号运算。 由符号对象构成表达式生成的衍生对象通常仍为符 号对象。
2
bab Nhomakorabeaf ( x)dx
f (u, v)dv
a
解: syms a b x; f=[a*x,b*x^2;1/x,sin(x)]; pretty(int(f)) syms x y F2=int(int(x^2+y^2,y,sqrt(x),x^2),x,1,2) 18 VF2=vpa(F2)
D:1 x 2, x y x 2
2
sym、syms的选项简要说明
f=sym(argn,flagn)中的选项flagn可取: ‘d‟ 最接近的十进制浮点数精确表示。 ‘r‟ 最接近的有理表示(缺省设置)。 所谓“有理”表示,是指用两个正整数p,q构成的: p/q,p*pi/q,sqrt(p),2^q,10^q形式之一表示。 argv=sym(„argv‟,flagv)中选项flagv可取: ‘positive‟ 限定argv为“正实数型”符号变量。 ‘real‟ 限定argv为“实数型”符号变量。 ‘unreal‟ 指定argv为“非实数型”变量(清除argv的实数属
12
基本符号微积分
求极限: limit 求导数(偏导数): diff 求雅可比矩阵: jacobian 求积分: int 级数求和: symsum 一元函数泰勒展开:taylor
13
符号微积分(续)
一般符号代数方程(组)的解: solove 符号微分方程(组)求解: dsolove 多元函数完全泰勒展开: mtaylor 求Hess矩阵: hessian Fourier变换及其反变换: fourier,ifourier Laplace变换及其反变换: laplace,ilaplace Z变换及其反变换: ztrans,iztrance
15
求导数与偏导数
(1).
1. diff(f) d (2). f ( x) n 2. diff(f,n) dx dn 3. diff(f,v,n) (3). f (u, v, w) n dv 例: clear all; syms x y z; f=x^2*sin(exp(y^(1/2)))/z; dfdx2=diff(f);pretty(dfdx2) dfdy=diff(f,y);pretty(dfdy)
14
求函数极限
(1). lim f ( x ) 1. limit(f) x 0 ( 2). lim f (u , v ) 2. limit(f,v) v 0 (3). lim f (u , v ) 3. limit(f,v,a) v a 注意:a可以为inf或-inf。 例: clear all; syms x y c; f=sin(c+2*y/x); limit(f,y),limit(f,x,inf),limit(f,c)
级数求和
(1).
f ( x)
x 0 b
x 1
symsum(f) ( 2). f ( x ) symsum(f,a,b) xa v 1 symsum(f,v) (3). f (u, v) v 0 symsum(f,v,a,b) b 例 (4). f (u, v) va syms k t; f1=[t k^3]; f2=[1/(2*k-1)^2,(-1)^k/k]; s1=simple(symsum(f1)) s2=simple(symsum(f2,1,inf))
19
一元函数泰勒展开
1. taylor(f) k 0 2. taylor(f,n) n 1 f ( k ) (a) 3. taylor(f,v) ( x a) k k! 4. taylor(f,a) k 0 5. taylor(f,n,a) n 1 f v( n ) (u , a ) 6. taylor(f,n,v,a) (v a ) k k! k 0 例 syms x y a b u v f=a*sin(x)*y^x+u*cos(v); g=exp(v)+b*v^u; Mf=taylor(f),Tf=taylor(f,3,b) Mg=taylor(g,v),Tg=taylor(g,4,v,a)
10
符号对象的置换操作
一.子表达式置换操作 为了使表达式简洁易读,MATLAB提供指令 subexpr,用符号变量替换子表达式: [RS,ssub]=subexpr(S,ssub) %用符号变量ssub置换相同的表达式,重写S为RS。 二.通用置换指令 RES=sub(ES,old,new) % 用new置换ES中old后产生RES。 RES=subs(ES,new) % 用new置换ES中自由变量产生RES。
数学软件 —— MATLAB
电子教案(五)
——符号运算与基本微积分
1
符号对象的定义
MATLAB中的Symbolic Math Toolbox工具箱对符号 对象支持数学解析式似的推演。故进行公式演算前应 将推演对象先指定为符号对象类型(sym)的数据。 定义基本符号对象的指令有sym、syms两个。它们的 基本使用方式为: f=sym(arg) 把数字/字符串/表达式转换为符号对象f。 f=sym(argn,flagn) 把数值表达式argn转换为flagn格式的符号对象f。 argv=sym(„argv‟,flagv) 按flagv要求把字符串argv定义为符号对象argv。 syms(„argv1‟,‟argv2‟,...) 把字符arg1,arg2等定义为基本符号对象。 syms argv1 argv2 ... 为syms( ... )的简洁形式。
性)。
3
符号常数与数值常数的转换
数值计算受计算机字长的限制,每次数值操作都带 截断误差,故无任采用何种算法均会产生积累误差。 但符号计算的结果是绝对准确的,因此在输出最终 结果时,再根据需要转换为指定精度的数值将减少 误差。 Symbolic Toolbox中与数值精度计算有关的指令有: double(x) 将符号常数x转为16位相对精度浮点数。 digits(n) 设置今后的数值计算以n位相对精度进行。 xs=vpa(x) 在digits指定精度下,给出x的数值型符号结果xs。 xs=vpa(x,n) 在n位相对精度下,给出x的数值型符号结果xs。
