数据库图
数据库流程图

数据库流程图数据库流程图是一种图形化的表达方式,用于表示数据库中的数据流动和处理过程。
通过数据库流程图,我们可以清晰地了解到数据在系统中的流向和处理流程,帮助我们更好地设计和调整数据库系统。
本文将介绍数据库流程图的基本概念、使用方法和注意事项。
一、数据库流程图的基本概念和作用数据库流程图是一种用来描述数据库中数据流动和处理过程的图形化表示方法。
它通常由一系列的节点和连接线组成,节点代表数据处理的各个环节,连接线表示数据的流向。
通过数据库流程图,我们可以直观地看出数据在系统中经过哪些环节、经过每个环节的处理过程以及数据的流向,帮助我们更好地理解和掌握数据库系统的整体结构。
数据库流程图的主要作用有:1. 数据库设计与优化:通过绘制数据库流程图,我们可以对数据库的整体结构和数据处理流程有一个直观的了解,从而更好地进行数据库的设计和优化工作,提高系统性能和数据处理效率;2. 故障排查与调试:当系统出现故障或数据异常时,数据库流程图可以帮助我们快速定位问题的根源,进行故障排查和调试,提高系统的可靠性和稳定性;3. 系统运维与升级:在数据库系统的运维和升级过程中,数据库流程图可以作为重要的参考依据,帮助我们快速了解系统的运行状态和升级方案,确保系统的正常运行;4. 培训与知识共享:数据库流程图可以作为培训和知识共享的工具,帮助新人快速上手数据库系统,并将经验和知识进行积累和传承。
二、数据库流程图的绘制方法数据库流程图的绘制方法较为灵活,可以根据实际情况选择合适的软件工具进行绘制。
常用的数据库流程图绘制工具有Microsoft Visio、Lucidchart等。
以下是一个基本的数据库流程图绘制步骤:1. 确定数据库的主要处理环节:首先,我们需要明确数据库系统中的主要处理环节,包括数据输入、数据检索、数据处理、数据存储等;2. 绘制节点:根据确定的处理环节,使用绘图工具绘制相应的节点。
每个节点代表着一个具体的数据处理环节,可以用矩形、圆形等形状表示,视情况而定;3. 连接节点:在节点之间使用连接线表示数据的流动。
数据库设计ER图

数据抽象(续)
聚集
第20页/共72页
数据抽象(续) ▪ 复杂的聚集,某一类型的成分仍是一个聚集
更复杂的聚集
第21页/共72页
数据抽象(续)
3. 概括(Generalization) • 定义类型之间的一种子集联系 • 抽象了类型之间的“is subset of”的语义 • 继承性
分E-R图
合并
初步E-R图
可能存在冗余的数据 和冗余的实体间联系
消除不必要的冗余
基本E-R图
第53页/共72页
消除不必要的冗余,设计基本E-R图(续)
• 冗余 • 消除冗余的方法
第54页/共72页
1.冗余
• 冗余的数据是指可由基本数据导出的数据 冗余的联系是指可由其他联系导出的联系
• 冗余数据和冗余联系容易破坏数据库的完整性,给数据库维护增加困难 • 消除不必要的冗余后的初步E-R图称为基本E-R图
该厂劳动人事管理分E-R图
图7.29 劳动人事管理的分E-R图
第66页/共72页
消除冗余,设计生成基本E-R图实例(续)
系统的基本E-R(图7.30)
某工厂管第理6信7页息/共系7统2页的基本E-R图
消除冗余,设计生成基本E-R图实例(续)
集成过程,解决了以下问题: • 异名同义,项目和产品含义相同 • 库存管理中职工与仓库的工作关系已包含在劳动人事管理的部门与职工之
联系 • 整体概念结构能满足需要分析阶段所确定的所有要求
• 概念结构设计是整个数据库设计的关键
第3页/共72页
概念结构(续)
现实世界 信息世界 机器世界
需求分析 概念结构设计
第4页/共72页
概念结构(续)
实训淘宝数据库库表图

1.E-R 图2.表设计图用户表ESHOPUSERS列名类型长度允许空主/外键描述USERID NUMBER 10 否主用户id标识用户USERNAME V ARCHAR2 16 否用户姓名USERPASSWORD V ARCHAR2 16 否用户密码USERPHONE NUMBER 16 是用户号码USERROLEID NUMBER 1 否外用户角色id角色表(roleid)USERREGDATE DA TE 否用户注册时间SHOPID NUMBER 10 是外商铺id商铺表(shopid)ACCOUNTID NUMBER 16 是外账户id账户表(accountid) IDCARD NUMBER 18 是身份证号码USERREALNAME V ARCHAR2 10 是实名EMAIL V ARCHAR2 20 否用户邮箱商铺表SHOPS列名类型长度允许空主/外键描述SHOPID NUMBER 10 否主商店idSHOPNAME V ARCHAR2 30 否商店名称SHOPDESCRIBE V ARCHAR2 200 是商店介绍USERID NUMBER 16 否外所属用户用户表(USERID)商品表goods列名类型长度允许空主/外键描述GOODSID NUMBER 12 否主商品idGOODSNAME V ARCHAR2 30 否商品名称GOODSPRICE NUMBER 9.2 否商品价格GOODSDESCRIBE V ARCHAR2 2000 是外商品描述用户表(USERID)GOODSPIC V ARCHAR2 30 否商品图片GOODSTYPE NUMBER 3 否外商品类别商品类别表(TYPEID)商铺和物品关系表SHOPSANDGOODS列名类型长度允许空主/外键描述SHOPSID NUMBER 10 否主/外商店di商铺表(SHOPID)GOODSID NUMBER 12 否主/外物品id商品表(GOODSID) GOODSNUMBER NUMBER 12 否库存GOODSSALEDNUMBER NUMBER 12 否历史卖出总数商品类别表GOODSTYPE列名类型长度允许空主/外键描述TYPEID NUMBER 3 否主商品类别id TYPENAME V ARCHAR2 20 否商品类别名称订单表ORDERFORM列名类型长度允许空主/外键描述ORDERID NUMBER 10 否主订单idGOODSID NUMBER 12 否外商品id商品表(GOODSID)USERID NUMBER 10 否外所属用户id用户表(USERID)GOODSNUMBER NUMBER 7 否订的货品数量ORDERTIME DA TE 否下单时间及交易完成时间ORDERSTATE V ARCHAR2 10 否订单状态REALPRICE NUMBER 9.2 否实际总支付价格messagestate V ARCHAR2 10 否评论状态ADDRESS V ARCHAR2 100 否收货地址购物车SHOPPINGCAR列名类型长度允许空主/外键描述CARID NUMBER 10 否主购物车idADDGOODSTIME date 否添加到购物车时间USERID NUMBER 10 否外用户id用户表(USERID) GOODSID NUMBER 12 否外商品id商品表(goodsID) GOODSNUMBER NUMBER 10 否添加到购物车的商品数量收藏表FAVORITE列名类型长度允许空主/外键描述FAVORITEID NUMBER 10 否主收藏夹idUSERID NUMBER 10 否外用户表(USERID)用户idSHOPID NUMBER 10 是外商铺表(shopid)收藏的商铺idGOODSID NUMBER 12 是外商品表(GOODSID)收藏的物品id评价内容表MESSAGE列名类型长度允许空主/外键描述MESSAGEID NUMBER 6 否主留言id唯一标识USERID NUMBER 10 否外用户表(USERID) 发表留言的用户idCONTENT V ARCHAR2 300 否留言内容SHOPID NUMBER 6 否外商铺和物品关系表(shopid)留言所属商铺EVALUATETYPE number 1 否外评价类型表(TYPEID)评价类型GOODSID NUMBER 12 否外商铺和物品关系表(GOODSID)被评价的商品评价类型表EV ALUATETYPE列名类型长度允许空主/外键描述TYPEID NUMBER 1 否主评价id唯一标识TYPENAME V ARCHAR2 8 否评价类型账户表ACCOUNTS列名类型长度允许空主/外键描述ACCOUNTID NUMBER 16 否主账户id唯一标识ACCOUNTNAME V ARCHAR2 10 否账户姓名ACCOUNTBALANCE NUMBER 10,2 否账户余额角色表USERROLE列名类型长度允许空主/外键描述ROLEID NUMBER 1 否主角色id唯一标识ROLENAME V ARCHAR2 8 否角色名称地址表useraddress列名类型长度允许空主/外键描述ADDRESSID NUMBER 10 否主地址id唯一标识USERID V ARCHAR2 10 否外用户id用户表(USERID) ADDRESS V ARCHAR2 100 否具体地址。
实验 数据库模式图
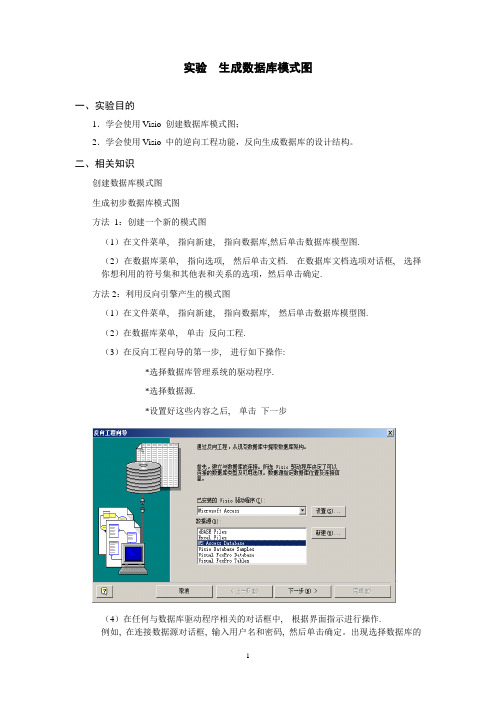
实验生成数据库模式图一、实验目的1.学会使用Visio 创建数据库模式图;2.学会使用Visio 中的逆向工程功能,反向生成数据库的设计结构。
二、相关知识创建数据库模式图生成初步数据库模式图方法1:创建一个新的模式图(1)在文件菜单, 指向新建, 指向数据库,然后单击数据库模型图.(2)在数据库菜单, 指向选项, 然后单击文档. 在数据库文档选项对话框, 选择你想利用的符号集和其他表和关系的选项,然后单击确定.方法2:利用反向引擎产生的模式图(1)在文件菜单, 指向新建, 指向数据库, 然后单击数据库模型图.(2)在数据库菜单, 单击反向工程.(3)在反向工程向导的第一步, 进行如下操作:*选择数据库管理系统的驱动程序.*选择数据源.*设置好这些内容之后, 单击下一步(4)在任何与数据库驱动程序相关的对话框中, 根据界面指示进行操作.例如, 在连接数据源对话框, 输入用户名和密码, 然后单击确定。
出现选择数据库的对话框,选择需要转换的数据库(5)选择你需要提取的信息, 然后单击下一步.(6)选择你想提取的表(或者视图),或者单击全选来抽取(extract )全部信息, 然后单击下一步.(7)在第五步, 如果你选择了存储过程检查框, 选择你想提取的过程, 或者单击全选来抽取(extract)全部信息, 然后单击下一步.(8)选择你是否需要反向工程的项的形状自动添加到当前页面.(9)检查你的选项, 确认是你需要的信息, 然后单击完成.三、实验环境1.windows9x/me/2000或windows XP;2.CPU:Pentium II 或更高级别的处理器;3.硬盘:40MB可用空间;4.显示器:256色以上,800*600或1024*768分辨率;5.Visio2003。
四、实验内容本实验将利用Visio提供的逆向工程功能,生成一个Access数据库的模式图,得到数据库中每个表的具体定义信息和表之间的关联信息。
图数据库 原理

图数据库原理图数据库是一种特殊类型的数据库,它以图的形式存储和处理数据。
图由节点(vertices)和边(edges)组成,节点表示实体,边表示实体之间的关系。
图数据库利用图结构来存储数据,并使用图遍历算法来查询和分析数据。
图数据库的原理基于图论和数据结构理论。
它使用节点和边的属性来存储数据,并使用索引和标签来支持数据的快速查询。
每个节点和边都有一个唯一的标识符,可以根据标识符来定位和访问节点和边。
节点和边之间的关系可以通过边的起始节点和结束节点的标识符来表示。
图数据库的存储方式类似于邻接表,通过节点和边的列表或表格来表示图的结构。
节点和边之间可以有多种关系,例如一对一、一对多和多对多关系。
图数据库支持属性图模型,节点和边可以有多个属性,属性可以是原子值或复杂对象。
图数据库的查询方式主要通过图遍历算法来实现。
图遍历是指通过节点和边的关系逐步遍历整个图的过程。
图数据库支持多种图遍历算法,例如深度优先搜索(DFS)、广度优先搜索(BFS)和最短路径搜索。
通过图遍历算法可以实现复杂的关系查询和分析,例如查找节点的邻居、查找共同的邻居、计算两个节点之间的距离等。
图数据库具有很多优点。
首先,它能够高效地处理复杂的关系数据,适用于大规模的关系型数据集。
其次,图数据库支持灵活的数据模型,可以动态地添加和修改节点和边的属性。
此外,图数据库能够高效地执行复杂的图遍历算法,支持更复杂的查询和分析。
总之,图数据库是一种以图的形式存储和处理数据的数据库,它基于图论和数据结构理论,利用图结构来存储数据,并使用图遍历算法来查询和分析数据。
图数据库具有高效处理关系数据、灵活的数据模型和强大的图遍历能力等优点。
数据库的表关系图

数据库的表关系图1>:one-to-one(一对一关联)主键关联:一对一关联一般可分为主键关联和外键关联主键关联的意思是说关联的两个实体共享一个主键值,但这个主键可以由两个表产生.现在的问题是:*如何让另一个表引用已经生成的主键值解决办法:*Hibernate映射文件中使用主键的foreign生成机制eg:学生表:<hibernate-mapping><class name="er" table="user" catalog="study"><id name="userid" type="ng.Integer"><column name="userid" /><generator class="native" /></id><property name="username" type="ng.String"><column name="username" length="20" /></property><one-to-one name="card" class="org.wen.beans.Card" cascade="all"></one-to-one></class></hibernate-mapping>添加:<one-to-one name="card"class="org.wen.beans.Card"fetch="join"cascade="all" /><class>元素的lazy属性为true,表示延迟加载,如果lazy设为false,则表示立即加载.以下对这二点进行说明.立即加载:表示在从数据库中取得数据组装好一个对象后,会立即再从数据库取得数据组装此对象所关联的对象延迟加载:表示在从数据库中取得数据组装好一个对象后,不会立即从数据库中取得数据组装此对象所关联的对象,而是等到需要时,才会从数据库取得数据组装此关联对象.<one-to-one>元素的fetch属性可选为select和joinjoin:连接抓取,Hibernate通过在Select语句中使用outer join(外连接)来获得对象的关联实例或者关联集合.select:查询抓取,Hibernate需要另外发送一条select语句抓取当前对象的关联实体或集合.******所以我们一般用连接抓取<join>证件表:<hibernate-mapping><class name="org.wen.beans.Card" table="card" lazy="true" catalog="study"><id name="cardid" type="ng.Integer"><column name="cardid" /><generator class="foreign"><param name="property">user</param></generator></id><!-- id使用外键(foreign)生成机制,引用代号为user的对象的主键作为card表的主键和外键。
数据库E-R图

同一类记录的集合称为文件。所有学生的记录组成了一个学 生文件。
关键字(Key)
能惟一标识文件中每个记录的字段或字段集,称为记录的关 键字 。
E-R方法
E-R方法即“实体-联系方法”。它的基本思想 是在数据库设计过程中增加一个中间步骤, 先设计一个概念性数据模型,这个概念性数 据模型在E-R方法中被称作“企业模式” (或“组织模式”)。它是现实世界的纯粹 反映,与数据库的具体实现无关,它抛开了 实现过程的具体细节,与现实世界和用户思 维很相似,能比较准确,比较自然地反映现 实世界,能为不熟悉计算机的用户所接受, 便于设计人员和用户的沟通。
相关术语: 实体
客观存在并且可以相互区别的“事物” 称为实体
实体可以是具体的人、事、物,也可 以是抽象的事件
属性
实体所具有的某一特性称为属性
实体型
学生(学号,姓名,年龄,性别,系)
具有相同属性的实体必然具有共同的特征
实体集
同型实体的集合称为实体集
键
能惟一标识一个实体的属性或属性集称为实 体的键
域
例 学生、回扣、医疗等。实体分为两级,一级为 “个体”,如“张三”、“国防科技大学”等;另 一级为“总体”,泛指某一类个体组成的集合,如 人泛指“张三”、 “李四”等。实体类型:将具 有共性的一类实体抽象为实体类型。在E-R图中, 实体这种基本成份用方框来表示。
(2)实体与联系的属性和域
属性:对实体特征的描述;域:属性的取值范 围。
“部门”(A)是一种实体,“职员”(B)也是 一种实体。这两种实体之间存在着一种联系, 设这种联系命名为“属于”,即表示某个职 员是属于某个部门的。“属于”这个联系是 1:N的,具体地说就是:一个部门可以有 多个职员,而一个职员只能属于一个部门。 在E-R图中,这两种实体间的联系可以表示 成如下图。
数据库中图数据的存储与查询优化

数据库中图数据的存储与查询优化随着大数据时代的到来,图数据的存储和查询优化成为了数据管理的重要议题。
图数据是指由节点和边组成的复杂网络结构,如社交网络、知识图谱等。
为了高效地存储和查询图数据,数据库系统在数据结构和查询算法上进行了改进和优化。
本文将讨论数据库中图数据的存储和查询优化的相关技术和方法。
一、图数据存储图数据的存储方式对数据访问的效率和系统性能起着重要影响。
常见的图数据存储方式有邻接矩阵、邻接表和属性表三种。
1. 邻接矩阵邻接矩阵是一种以二维矩阵形式来表示图数据的方法,矩阵中的每个元素代表一个节点之间的边的关系。
对于一个有n 个节点的图,邻接矩阵的大小为n*n。
邻接矩阵的存储方式简单直观,查询两个节点之间的边关系也非常高效,但是对于稀疏图(边的数量较少)来说,邻接矩阵的存储空间可能会非常浪费。
2. 邻接表邻接表是一种以链表的形式来表示图数据的方法,每个节点维护一个链表,链表中的每个元素代表当前节点和其它节点之间的边关系。
相比邻接矩阵,邻接表可以有效地解决稀疏图的存储问题,但是查询两个节点之间的边关系会比较耗时,需要遍历链表来找到匹配的边。
3. 属性表属性表是一种以属性列矩阵的形式来存储图数据的方法,每个属性都会有一个列,每一行表示一个节点,每个节点的属性值会存储在相应的列中。
属性表适用于具有大量节点和节点属性的图数据,可以跨多个属性进行高效的查询。
但是属性表在处理节点之间的边关系时相对较慢。
综上所述,邻接矩阵适用于密集图,邻接表适用于稀疏图,而属性表适用于属性丰富的图数据。
二、图数据查询优化图数据的查询通常包括按条件过滤、路径查询和子图匹配等操作。
为了高效地进行图数据查询,数据库系统采用了以下优化策略。
1. 索引加速索引是加速图数据查询的常用技术之一。
数据库系统可以根据节点和边的属性值创建索引,使得查询时可以快速定位匹配的节点和边。
索引的选择和设计需要结合具体情况来确定,以最大程度地提高查询效率。
数据库设计——ER图

数据库设计——ER图 E-R图也称实体—联系图,提供了表⽰实体类型、属性和联系的⽅法⽤来描述现实世界的概念模型。
它是描述现实世界关系概念模型的有效⽅法。
是表⽰概念关系模型的⼀种⽅式。
⽤“矩形框”表⽰实体型,矩形框内写明实体名称;⽤“椭圆图框”或圆⾓矩形表⽰实体的属性,并⽤“实⼼线段”将其与相应关系的“实体型”连接起来;⽤“菱形框”表⽰实体型之间的联系成因,在菱形框内写明联系名,并⽤“实⼼线段”分别与有关实体型连接起来,同时在“实⼼线段”旁标上联系的类型(1:1,1:n或m:n)。
构成E-R图的3个基本要素是实体型、属性和联系,其表⽰⽅法为: 实体:⼀般认为,客观上可以相互区分的事情就是实体,实体可以是具体的⼈和物,也可以是抽象的概念与联系。
关键在于⼀个实体能与另⼀个实体相区别,具有相同属性的实体具有相同的特征和性质。
⽤实体名及其属性名集合来抽象和刻画同类实体。
在E-R图中⽤矩形表⽰,矩形框内写明实体名;⽐如学⽣张三、学⽣李四都是实体。
如果是弱实体的话,在矩形外⾯再套实线矩形。
属性:实体所具有的某⼀特性,⼀个实体可由若⼲个属性来刻画。
属性不能脱离实体,属性是相对实体⽽⾔的。
在E-R图中⽤椭圆形表⽰,并⽤⽆向边将其与相应的实体连接起来;⽐如学⽣的姓名、学号、性别、都是属性。
如果是多值属性的话,在椭圆形外⾯再套实线椭圆。
如果是派⽣属性则⽤虚线椭圆表⽰。
联系:联系也称关系,信息世界中反映实体内部或实体之间的关联。
实体内部的联系通常是指组成实体的各属性之间的联系;实体之间的联系通常是指不同实体集之间的联系。
在E-R图中⽤菱形表⽰,菱形框内写明联系名,并⽤⽆向边分别与有关实体连接起来,同时在⽆向边旁标上联系的类型(1 : 1,1 : n或m : n)。
⽐如⽼师给学⽣授课存在授课关系,学⽣选课存在选课关系。
如果是弱实体的联系则在菱形外⾯再套菱形。
⼀般性约束 实体-联系数据模型中的联系型,存在3种⼀般性约束:⼀对⼀约束(联系)、⼀对多约束(联系)和多对多约束(联系),它们⽤来描述实体集之间的数量约束: (1)⼀对⼀联系(1:1):对于两个实体集A和B,若A中的每⼀个值在B中⾄多有⼀个实体值与之对应,反之亦然,则称实体集A和B 具有⼀对⼀的联系。
引用-各类数据库整体架构图汇总
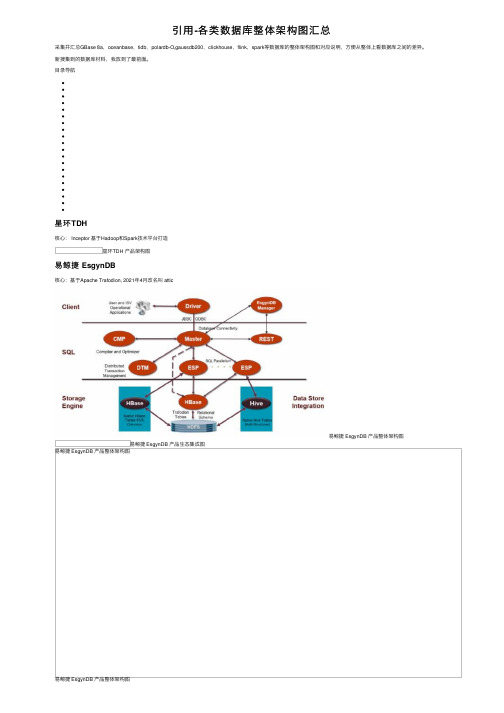
引⽤-各类数据库整体架构图汇总采集并汇总GBase 8a,oceanbase,tidb,polardb-O,gaussdb200,clickhouse,flink,spark等数据库的整体架构图和对应说明,⽅便从整体上看数据库之间的差异。
新搜集到的数据库材料,我放到了最前⾯。
⽬录导航星环TDH核⼼: Inceptor 基于Hadoop和Spark技术平台打造星环TDH 产品架构图易鲸捷 EsgynDB核⼼:基于Apache Trafodion, 2021年4⽉改名叫 attic易鲸捷 EsgynDB 产品整体架构图易鲸捷 EsgynDB 产品⽣态集成图易鲸捷 EsgynDB 产品整体架构图易鲸捷 EsgynDB 产品整体架构图中兴通讯GoldenDB中兴通讯GoldenDB产品架构图神通数据库MPP集群神通数据库MPP集群产品架构图神通数据库MPP集群产品架构图巨杉Sequoiadb巨杉Sequoiadb产品整体逻辑框架图巨杉Sequoiadb产品存储引擎框架图协调节点协调节点不存储任何⽤户数据。
作为外部访问的接⼊与请求分发节点,协调节点将⽤户请求分发⾄相应的数据节点,最终合并数据节点的结果应答对外进⾏响应。
编⽬节点编⽬节点主要存储系统的节点信息、⽤户信息、分区信息以及对象定义等元数据。
在特定操作下,协调节点与数据节点均会向编⽬节点请求元数据信息,以感知数据的分布规律和校验请求的正确性。
数据节点数据节点为⽤户数据的物理存储节点,海量数据通过分⽚切分的⽅式被分散⾄不同的数据节点。
在关系型与 JSON 数据库实例中,每⼀条记录会被完整地存放在其中⼀个或多个数据节点中;⽽在对象存储实例中,每⼀个⽂件将会依据数据页⼤⼩被拆分成多个数据块,并被分散⾄不同的数据节点进⾏存放。
阿⾥云 AnalyticDB PostgreSQL阿⾥云 AnalyticDB 产品架构图阿⾥云 AnalyticDB 产品架构图AnalyticDB PostgreSQL版采⽤MPP架构,实例由多个计算节点组成,存储磁盘类型⽀持⾼效云盘和ESSD云盘,计算和存储分离,可以独⽴增加节点或扩容,且保持查询响应时间不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V0
V2
V0
V4
V2
V4
V3
V5
V1
V3
V1
V5
无向图G3及连通分量
9
在有向图中,若任意两个顶点vi和vj都连通,则称该有向 图为强连通图。有向图的极大强连通子图称为强连通分量。
V0
V1
V1
V0
V2
图的定义和相关术语 图的存储 图的遍历 最小生成树 拓扑排序 最短路径 关键路径
2
7.1 图的基本概念 1.图的定义
图G (Graph)是由非空的顶点集合V(G)和描述顶点 之间关系的边集合E(G)构成,其形式定义为:G =(V(G),E(G))。简写为G=(V,E)。 G表示一个图,V是图G中非空顶点的集合,E是图G 中边的集合。
2.图的邻接矩阵的建立
图的邻接矩阵存储方法用一个二维数组存储顶点之间 的相邻关系,再用一个一维数组存储顶点信息,另外 还需要存储图的顶点数和边(弧)数。
12
typedef char Vextype;
typedef struct {
Vextype vexs[VEX_NUM];
int adj[MAXSIZE][MAXSIZE]; /*邻接矩阵*/
有向图:在一个图中,如果两个顶点构成的<vi, vj>∈E是序偶,则称这样的边是有向边,简称弧。用 <vi, vj>来表示。如果某图全部是由有向边构成,则称 该图为有向图。
4
无向完全图:在一个无向图中,设V是包含n个结
点的集合,且对于任意两个不相同的顶点之间都有
一条边将它们连接,则称该图为无向完全图。
13
for (i=0;i<G->n;i++) scanf("%c",&(G->vexs[i])); for (i=0;i<G->n;i++)
for (j=0;j<G->n;j++) G->adj[i][j]=0; /*初始化邻接矩阵*/
printf("输入每条边对应的两个顶点的序号:\n"); for (k=0;k<G->e;k++)
子图:设G(V,E),G’(V’,E’)是两个图,假设 V’⊆V且E’⊆E,称G’为G的子图。当满足V’=V 且E’⊆E,称G’为G的生成子图。
V0
V1 V1
V3 V0
V1 V1
V3
V2
无向图 G1
V0
V2
有向图G2
V3
V2 V0
V2
图G1和G2的子图
8
连通、强连通 若从顶点vi到顶点vj(i≠j)之间有路径 存在,则称该两个顶点是连通的。
18
假设无向图中有n 个顶点、e条边, 则它的邻接表需n个头结点和2e个边 结点。显然,在边数很少(e<<n(n1)/2)的情况下,用邻接表表示图比 邻接矩阵节省存储空间。
图的逆邻接表
V1
V3
V0
V2
有向图G2
0 V0 ∧ 1 V1 2 V2 3 V3 ∧
0 1∧
(a) 邻接表
3∧
0 V0
1 V1 2 V2 ∧ 3 V3
V3
有向图G4
V2
V3
G4的强连通分量
生成树:连通图G的生成树,是G中包含其全部n个顶点的一 个极小连通子图。即由n个顶点,n-1条边构成的连通图。 生成森林:在非连通图中,由每个连通分量都可得到一个极小 连通子图,即一棵生成树。这些连通分量的生成树就组成了一 个非连通图的生成森林。
10
7.2 图的存储表示——邻接矩阵、邻接表等
15
用邻接表表示的形式描述如下:
typedef struct node
/*边结点*/
{ int adjvex;
/*邻接点域*/
struct node * next; /*指向下一个边结点的指针域*/
}EdgeNode; typedef struct vnode
adjvex next
{ Vextype vertex;
23
1∧ 2∧
1∧
(b) 逆邻接表
19
7.3 图的遍历——从图中的某个顶点出发,对图中所 有顶点访问且只访问一次的过程。有深度优先遍历和 广度优先遍历两种方式。
7.3.1 深度优先遍历(DFS)
从图中某个顶点v出发,找一个与v相邻接且没有
被访问过的顶点w访问,然后从w开始进行深度优先
遍历。此过程依此类推,直到所有顶点全部被访问为
边结点
EdgeNode *firstedge; }VertexNode;
vertex firstedge
typedef struct
表头结点
{ VertexNode adjlist[MAXSIZE];
int n,e;
} ALGraph;
16
V0
V2
V1
3
V3
0 V0
1 V1
1∧
0
2
2 V2
1
3∧
3 V3
printf("%c",G.adjlist[i].vertex); visited[i]=1; p=G.adjlist[i].firstedge; while(p!=NULL) {if(visited[p->adjvex]==0) DFSTraverseAL(G,p->adjvex); p=p->next; } }
1
2∧
【算法7.2】建立有向图的邻接表存储 void CreateALGraph(ALGraph *G) { /*建立有向图的邻接表存储*/
int i,j,k; EdgeNode * s;
3∧
17
printf(“请输入顶点数和边数:\n”); scanf(“%d,%d”,&(G->n),&(G->e)); printf(“请输入顶点信息:\n”); for (i=0;i<G->n;i++) { scanf(“%c”,&(G->adjlist[i].vertex)); G->adjlist[i].firstedge=NULL; } printf("请输入边的信息:\n"); for (k=0;k<G->e;k++) /*建立边表*/
的边的数目,通常记为D (v)。
在有向图中,将从该顶点出发的弧的数目称为该
顶点的出度,用OD(v)表示;对应的,将以该顶点结
束的弧的数目称为该顶点的入度,用ID(v)表示;有
向图顶点的度为出度和入度之和: V0
V1
D (v)=ID (v)+OD(v)。
结论:对于具有n个顶点、e条边
的图,顶点vi的度D (vi)与边的数
int n,e;
/*顶点数和边数*/
}Mgragh;
【算法7.1】图邻接矩阵的存储实现
void CreateMGraph(Mgragh *G)
int i,j,k,w; char ch; printf("请输入顶点数和边数:\n"); scanf("%d,%d",&(G->n),&(G->e)); /*输入*/ printf("请输入顶点信息:\n");
V3
V2
目满足如下关系:
V1
V3
n
2e=( ∑ i=1
D(vi))
V0
V2
6
网络:若图的每条边(弧)都被赋予了具体含义,
这种与图的边(弧) 相关的数据称为权,称这样的图为
加权图或网络。
路径:在无向图中,若存在一个顶点序列
vi,vi1,vi2,…,vim,vj,使得(vi,vi1),(vi1,vi2),…,
{scanf("%d,%d",&i,&j); /*输入e条边*/ G->adj[i][j]=1; } /*若加入G->adj[j][i]=1;则 为无向图的邻接矩阵存储建立*/ }/*CreateMGraph*/
14
7.2.2 邻接表
邻接表是图的顺序与链式相结合的存储方法.
邻接表的存储思路:对图中的每个顶点建立一个单链表,第
止。
V0
以无向图为例,深度优先
V2
V1
遍历过程如下:
(1) 从顶点v0出发进行遍历, V3 V4 V5 V6
在访问了顶点v0之后,选择 其邻接点之一v1访问。
V7 无向图
20
(2) 从v1出发进行遍历。可选 择点有v6和v0,由于v0已经被 访问过,因此选择v6。 (3) 从v6出发进行遍历。可选 择点有v1和v5,由于v1已被访 问过,选择v5。
{ scanf("%d,%d",&i,&j); s=(EdgeNode*)malloc(sizeof(EdgeNode)); s->adjvex=j; s->next=G->adjlist[i].firstedge; G->adjlist[i].firstedge=s; } }/*CreateALGraph*/
Hale Waihona Puke DFSTraverseM(G,j); /*vj未访问,从vj开始DFS搜索*/ }/*DFSTraveseM*/
22
【算法7.4】采用邻接表存储的图的深度优先遍历 int visited[VEX_NUM]={0}; void DFSTraverseAL(ALGraph G,int i) {EdgeNode *p;
