川大版高数-物理类专用-第三册-标准答案
川大版高数_物理类专用题目

则 , , ③
有 ≤ ③≤ .又
即有
习题三
15、⑴解:对增广矩阵进行初等变换.
B=
则 无解
⑵解:对方程组的增广矩阵进行初等变换.
B=
则 无解
⑶解:对方程组的增广矩阵进行初等变换.(课本第119页题目出错,应该为
B=
则 有唯一解。即唯一解为(3,2,1,)。
由方程组 解得:
(4)、解:对方程组的增广矩阵进行初等变换.
AB=BA
充分性: AB=BA
(AB)’=B’A’=-BA
AB为反对称矩阵
综上所述:AB是反对称矩阵的充分必要条件是AB=BA。
26.解:设矩阵X为x=
则 =
Ax=o
=0
即 =0
对任意n 1矩阵都成立
A=0
27.证: : A为正交矩阵
=A
A = = =
又 正交矩阵为可逆矩阵
A =A
:
A = = =A
4.计算下列矩阵乘积
(1) = =
(2) = =
(3). (1,-1,2) =(1*2+(-1)*1+2*4,1*1+(-1)*1+2*2,1*0+(-1)*3+2*1=
(9,4,1)
(4)(x,y,1)
=(x,y,1)
=
(5)
=
=
5.设A= ,B= ,求
= =
= =
= =
= =
= =
6.
(1)A=
B=
则 <6只方程组有无穷多解。
先求它的一个特解,与阶梯形矩阵对应的方程组为
令上式中的 ,解得 。
于是得到特解:
四川大学2020年春季《高等数学(理)》在线作业3标准答案

20.
题目见图
A.有一条渐近线
B.有二条渐近线
C.有三条渐近线
D.无渐近线
正确答案:B
21.
题目见图
A.(1,-2,3)
B.(1,2,-3)
C.(-1,2,3)
D.(-1,-2,-3)
正确答案:B
22.题目见图
A.A
B.B
C.C
D.D
31.题目见图
A.A
B.B
C.C
D.D
正确答案:D
32.题目见图
A.A
B.B
C.C
D.D
正确答案:C
33.
题目见图
A.A
B.B
C.C
D.D
正确答案:A
34.题目见图
A.0
B.1
C.2
D.3
正确答案:B
35.题目见图
A.A
B.B
A.A
B.B
C.C
D.D
正确答案:A
16.题目见图
A.A
B.B
C.C
D.D
正确答案:D
17.题目见图
A.-3
B.-2
C.-1
D.0
正确答案:C
18.
题目见图
A.A
B.B
C.C
D.D
正确答案:B
19.题目见图
A.1
B.2
C.3
D.4
A.-1
B.0
C.1
D.不存在
正确答案:D
28.
川大版高数 物理类专用 第三册 答案#(精选.)

第一章 行列式1.()()[][][]23154110103631254=520010=8(1)3(1)321(1)(2)(3)2441(1)3214243(1)321012)4n n n n n n n n m n m n n n m n m n n m 1τ=++++=2τ+++++-τ-⋯=-+-+-+⋯+2+1+0===+τ-⋯=+=+τ-⋯=⋯()该数列为奇排列()该排列为偶排列() 当或时,为偶数,排列为偶排列当或时,为奇数,排列为奇排列(其中,,()[][][]12(1)13521)246(2)0123(1)244113521)246(2)424313521)246(2)012)2.(1)(2)(n n n n n n n m n m n n n m n m n n m i i i k n n n -τ⋯-⋯=++++⋯+-===+τ⋯-⋯=+=+τ⋯-⋯=⋯⋯-+-+( 当或时,(为偶数,排列为偶排列当或时,(为奇数,排列为奇排列(其中,,解:已知排列的逆序数为,这个数按从大到小排列时逆序数为()()111112(1)3)2(1)2x x x n x n x n n n n n n x i r i i i n x r i n x n n i i i i i i -+-+---+⋯+2+1+0=----τ⋯=-τ⋯个.设第数之后有个数比小,则倒排后的位置变为,其后个数比小,两者相加为故3 证明:.因为:对换改变排列的奇偶性,即一次变换后,奇排列改变为偶排列,偶排列改变为奇排列∴当n ≥2时,将所有偶排列变为奇排列,将所有奇排列变为偶排列 因为两个数列依然相等,即所有的情况不变。
∴偶排列与奇排列各占一半。
4 (1)13243341a a a a 不是行列式的项 14233142a a a a 是行列式的项 因为它的列排排列逆序列τ=(4321)=3+2+0+0=5为奇数,∴应带负号(2)5142332451a a a a a 不是行列式的项 1352413524a a a a a =1324354152a a a a a 因为它的列排排列逆序列τ(34512)=2+2+2+0+0=6 为偶数∴应带正号。
高等数学3物理类专业四川大学出版社第1章行列式习题答案详解

a
列展开 a
3a b
2a b a4 3a b
(2) 1 2 3 n -1 0 3 n -1 -2 0 n -1 -2 -3 0
解:
1 2 3
0 2 6
ci c1
原式 0 0 3 i 2,3n
0 0 0
n 2n 2n n! n
cos 2 cos 2 0 cos 2
证明:
sin2
左 边 sin2
sin2
cos2 cos2 cos2
cos2 - sin2 cos2 - sin2 cos2 - sin2
sin2
c3 c1
sin2 sin2
cos2 cos2 cos2
0 右边
cos2 cos2 cos2
(3)0 x y z 0 1 1 1
x 0 z y 1 0 z2 y2
y
z
0
x1
z2
0
x2 , ( xyz 0)
z y x 0 1 y2 x2 0
证明:
r2 x
01
1
1 r2 xyz
0 111
r3 y
左
边
r4
z
(
xyz
1 y2 x2 0
10. 计算行列式。
(1) a b
c
a ab abc
d abcd
a 2a b 3a 2b c 4a 3b 2c d
a 3a b 6a 3b c 10a 6b 3c d
解:
ab c
d
a ab
原式
ri ri1
大学物理(川大物三)答案
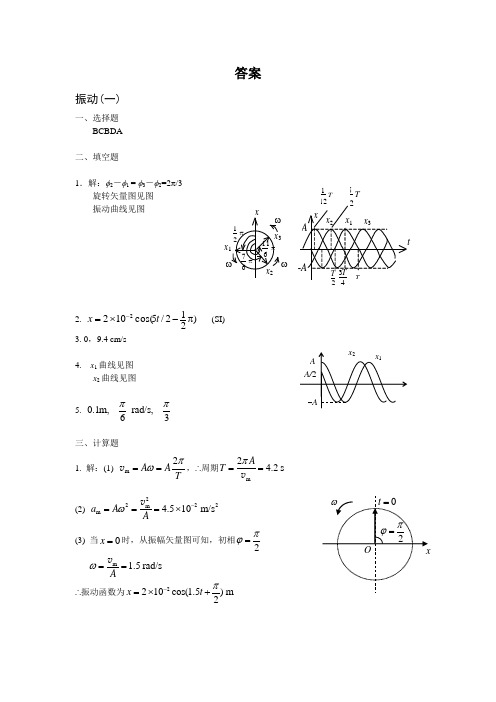
答案振动(一)一、选择题BCBDA二、填空题1.解:φ2-φ1 = φ3-φ2=2π/3旋转矢量图见图 振动曲线见图2. )212/5cos(1022π-⨯=-t x (SI)3. 0,9.4 cm/s4. x 1曲线见图x 2曲线见图5. 0.1m ,rad/s,63ππ三、计算题1. 解:(1) m 2A ATπω==v ,∴周期m2 4.2s A T π==v(2) 2222m m 4.510m/s a A Aω-===⨯v(3) 当0x =时,从振幅矢量图可知,初相2πϕ=m 1.5r a d /sAω==v ∴振动函数为2210cos(1.5)m 2x t π-=⨯+TT1T 5ω x12T 1212. 解:弹簧劲度系数 260 2.010N /m 0.3F k x===⨯ 静止时弹簧伸长量为 0249.80.196m 2.010m g x k⨯===⨯(1) 设向下为正方向,则 0ϕ= (若设向上为正方向,则 ϕπ=);0.1mA =7.07r a d /sω== 振动函数为 0.1cos(7.07)m x t =(2) 物体在平衡位置上方5cm (即0.05m ),此时弹簧的净伸长为 00.050.1960.050.146m l x =-=-=弹簧对物体的拉力 2000.14629.2N F kl ==⨯=(3) 5cm 是振幅之半,物体从平衡位置到振幅之半所需最短时间是112T ,2T πω=∴10.074s 126t T πω===3.解:(1) 容器中每滴入一油滴的前后,水平方向动量值不变,而且在容器回到O 点滴入下一油滴前, 水平方向动量的大小与刚滴入上一油滴后的瞬间后的相同。
依此,设容器第一次过O 点油滴滴入前的速度为v ,刚滴入第个油滴后的速度为v ′,则有 v v '+=)(nm M M ① 3分系统机械能守恒 2202121v M kl = ② 2分22)(2121v '+=nm M kx③ 2分由①、②、③、解出0)/(l nm M M x +=2分(2) 时间间隔( t n +1-t n )应等于第n 滴油滴入容器后振动系统周期T n 的一半.k nm M T t t t n n n n /)(211+==-=∆+π 3分4.解:由旋转矢量图和 |v A | = |v B | 可知 T /2 = 4秒, ∴ T = 8 s , ν = (1/8) s -1, ω = 2πν = (π /4) s -1 3分 (1) 以AB 的中点为坐标原点,x 轴指向右方.t = 0时, 5-=x cm φcos A =t = 2 s时, 5=x cm φφωsin )2cos(A A -=+= 由上二式解得 tg φ = 1因为在A 点质点的速度大于零,所以φ = -3π/4或5π/4(如图) 2分 25c o s/==φx A cm 1分∴ 振动方程 )434c o s (10252π-π⨯=-t x (SI) 1分 (2)速率 )434s i n (41025d d 2π-π⨯π-==-t t x v (SI) 2分 当t = 0 时,质点在A 点221093.3)43sin(10425d d --⨯=π-⨯π-==tx v m/s 1分5*.解:令θ 为杆和竖直线之间的夹角.运动方程为:θθθθc o s s i n s i n 21/d d 222kL MgL t J --= 3分θ 很小时,sin θ ≈θ ,cos θ ≈1所以:0/d d )21(222=++tJ kL MgL θθ 2分上式中231ML J =是杆绕其一端的转动惯量,所以0/d d 31)21(22=++tML Lk Mg θθ可知杆作角谐振动,并得到 )2/()2(3ML kL Mg +=ω2分)2(322/2kL Mg ML T +π=π=ω 1分振动(二)一、选择题ADDBB二、填空题 1.T /8,3T /8 2.222/2T mA π3.动能曲线见图 势能曲线见图 机械能曲线见图4.0.02 5.0三、计算题1.解:设小球的质量为m ,则弹簧的劲度系数 0/l mg k =.选平衡位置为原点,向下为正方向.小球在x 处时,根据牛顿第二定律得T220d /d )(t x m x l k mg =+- 将 0/l mg k = 代入整理后得0//d d 022=+l gx t x∴ 此振动为简谐振动,其角频率为. 3分 π===1.958.28/0l g ω 2分设振动表达式为 )c o s (φω+=t A x由题意: t = 0时,x 0 = A=2102-⨯m ,v 0 = 0,解得 φ = 0 1分∴ )1.9c o s (1022t x π⨯=- 2分2.解一:(1) 取平衡位置为原点,向下为x 正方向.设物体在平衡位置时弹簧的伸长量为∆l ,则有l k mg ∆=, 加拉力F 后弹簧又伸长x 0,则0)(0=+-+∆x l k mg F解得F = kx 02分 由题意,t = 0时v0 = 0;x = x 0 则 02020)/(x x A =+=ωv 2分又由题给物体振动周期4832=T s, 可得角频率 Tπ=2ω, 2ωm k =∴ 444.0)/4(22=π==A T m kA F N 1分 (2) 平衡位置以下1 cm 处: )()/2(2222x A T -π=v 2分 221007.121-⨯==vm E K J 2分2222)/4(2121x T m kxE p π=== 4.44³10-4J 1分解二:(1) 从静止释放,显然拉长量等于振幅A (5 cm ),kA F = 2分2224νωπ==m m k ,ν = 1.5 Hz 2分 ∴ F = 0.444 N 1分(2) 总能量 221011.12121-⨯===FA kAE J 2分当x = 1 cm 时,x = A /5,E p 占总能量的1/25,E K 占24/25. 2分∴ 21007.1)25/24(-⨯==E E K J , 41044.425/-⨯==E E p J 1分3.解:(1) 选地心为x 坐标原点,向上为x 轴正方向.质量为m 的物体在地球内部距地心为x 处受到的地心引力为232/)3/4(/x m x G x G M m F ρπ-=-=3/4x Gm ρπ-= 3分由牛顿第二定律得 xm x Gm =π-3/4ρ, 03/4=π+x G xρ 1分 令 3/420ρωG π=, 则 020=+x x ω. 显然物体作简谐振动. 2分(2) 2/10)/3(4/32/2ρρωG G T π=ππ=π=已知 G = 6.67³10-11 N ²m 2²kg -2,ρ = 5.5³103 kg/m 3代入上式 T = 5.07³103 s 2分 物体从地面落到地心的时间 t = T /4 = 1.27³103 s 2分4.解:选平板位于正最大位移处时开始计时,平板的振动方程为 t A x π=4c o s (SI)t A xπ4c o s π162-= (SI) 1分 (1) 对物体有 x m N mg =- ① 1分 t A mg xm mg N ππ+=-=4cos 162 (SI) ②物对板的压力为 t A mg N F ππ--=-=4cos 162 (SI)t ππ--=4c o s 28.16.192 ③ 2分 (2) 物体脱离平板时必须N = 0,由②式得 1分 04c o s 162=ππ+t A mg (SI) Aq t 2164cos π-=π 1分若能脱离必须 14cos ≤πt (SI) 即221021.6)16/(-⨯=π≥g A m 2分5.解:依合振动的振幅及初相公式可得 φ∆++=c o s 2212221A A A A A 22210)4143cos(65265-⨯π-π⨯⨯⨯++=m21081.7-⨯= m 2分)4/c o s (6)4/3c o s (5)4/s i n (6)4/3s i n (5a r c t g π+ππ+π=φ = 84.8°=1.48 rad 2分则所求的合成振动方程为 )48.110cos(1081.72+⨯=-t x (SI) 1分波动(一)一、选择题CBDCD 二、填空题1.φλ+π-/2Lλk L ± ( k = 1,2,3,…) λ)12(21+±k L ( k = 0, 1,2,…)2.1cos x y A t u ωϕ⎡+⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦3. ]4/)/(cos[11π+-=u L t A y ω;uL L )(21+ω4. ]2)2(2cos[π-+-π=ux t uA y λ]2)2(2c o s [π+-π=t uA y P λ5.0.2cos m 22p y t ππ⎛⎫=-⎪⎝⎭三、计算题1. 解:反射波在x 点引起的振动相位为 π+π--+π-=+21)55(4x t t φωπ-π+π+=10214x t 3分反射波表达式为)10214cos(01.0π-π+π+=x t y (SI) 2分或 )214c o s (01.0π+π+=x t y (SI)2.解: λxu t A y -π=2c o s = -0.01 m 1分1.0,2d d ===t x ty v 0)2s i n (2=-ππ-=λλxut uA 2分22d d ty a =)2c o s ()2(2λλxut uA -ππ-= = 6.17³103m/s 22分3.解:用旋转矢量解此题,如图可得A为代表P 点振动的旋转矢量. 210)cos sin 3(21-⨯-=t t y P ωω210)]cos()21cos(3(21-⨯π++π-=t t ωω)3/4c o s (1012π+⨯=-t ω (SI). 3分波的表达式为:]2/234c o s [1012λλω-π-π+⨯=-x t y )312c o s (1012π+π-⨯=-λωxt (SI) 2分4.解:从y -x 波形图中可知 40m,A λ==由振幅矢量图可知 ,2P Q πϕϕπ=-=)由20m/s u =可得 2s,rad/s T uλωπ==∴=0.2cos()m20.2cos()mP Q y t y t ππππ∴=-=+5.解:(1) 由y -x 曲线可知160m λ=。
川大版高数_物理类专用_第三册_答案

第一章 行列式1.()()[][][]23154110103631254=520010=8(1)3(1)321(1)(2)(3)2441(1)3214243(1)321012)4n n n n n n n n m n m n n n m n m n n m 1τ=++++=2τ+++++-τ-⋯=-+-+-+⋯+2+1+0===+τ-⋯=+=+τ-⋯=⋯()该数列为奇排列()该排列为偶排列() 当或时,为偶数,排列为偶排列当或时,为奇数,排列为奇排列(其中,,()[][][]12(1)13521)246(2)0123(1)244113521)246(2)424313521)246(2)012)2.(1)(2)(n n n n n n n m n m n n n m n m n n m i i i k n n n -τ⋯-⋯=++++⋯+-===+τ⋯-⋯=+=+τ⋯-⋯=⋯⋯-+-+( 当或时,(为偶数,排列为偶排列当或时,(为奇数,排列为奇排列(其中,,解:已知排列的逆序数为,这个数按从大到小排列时逆序数为()()111112(1)3)2(1)2x x x n x n x n n n n n n x i r i i i n x r i n x n n i i i i i i -+-+---+⋯+2+1+0=----τ⋯=-τ⋯个.设第数之后有个数比小,则倒排后的位置变为,其后个数比小,两者相加为故3 证明:.因为:对换改变排列的奇偶性,即一次变换后,奇排列改变为偶排列,偶排列改变为奇排列∴当n ≥2时,将所有偶排列变为奇排列,将所有奇排列变为偶排列 因为两个数列依然相等,即所有的情况不变。
∴偶排列与奇排列各占一半。
4 (1)13243341a a a a 不是行列式的项 14233142a a a a 是行列式的项 因为它的列排排列逆序列τ=(4321)=3+2+0+0=5为奇数,∴应带负号(2)5142332451a a a a a 不是行列式的项 1352413524a a a a a =1324354152a a a a a 因为它的列排排列逆序列τ(34512)=2+2+2+0+0=6 为偶数∴应带正号。
四川高等数学教材答案

四川高等数学教材答案第一章:导数与微分1. 函数的导数2. 函数的微分3. 高阶导数4. 隐函数求导5. 参数方程与导数6. 扩展应用题第二章:极限与连续1. 极限的定义与性质2. 无穷大与无穷小3. 极限存在准则4. 极限的运算法则5. 连续的定义与性质6. 连续函数的运算法则7. 中值定理第三章:一元函数微分学1. 可导函数与微分2. 微分中值定理3. 泰勒公式与高阶导数4. 函数的单调性与曲线图5. 凸函数与凹函数6. 最值问题第四章:一元函数积分学1. 原函数与不定积分2. 定积分的定义与性质3. 积分的几何应用4. 积分与微分的关系5. 牛顿-莱布尼茨公式6. 定积分的计算方法第五章:多元函数微分学1. 多元函数的极限2. 多元函数的偏导数3. 多元函数的全微分与导数4. 隐函数求导5. 多元函数的泰勒公式6. 多元函数的最值问题第六章:多元函数积分学1. 二重积分的定义与性质2. 二重积分的计算方法3. 三重积分的定义与性质4. 三重积分的计算方法5. 曲线、曲面与曲面积分6. 矢量场与曲线积分7. 散度与旋度第七章:常微分方程1. 基本概念与初值问题2. 可分离变量的方程3. 齐次方程与一阶线性方程4. 高阶线性微分方程5. 解法的存在与唯一性6. 线性方程组与矩阵法第八章:级数与传递函数1. 数项级数的概念与性质2. 正项级数的审敛法3. 幂级数与泰勒级数4. 函数项级数5. 傅立叶级数6. 傅立叶变换与拉普拉斯变换总结:以上为《四川高等数学教材》的答案内容,根据章节分节论述了每一章的主要内容和题型。
使用整洁美观的排版并确保语句通顺,全文表达流畅,无影响阅读体验的问题。
希望这些答案能够对您的学习有所帮助。
四川大学物理考试试卷III-IV06-07-h-da
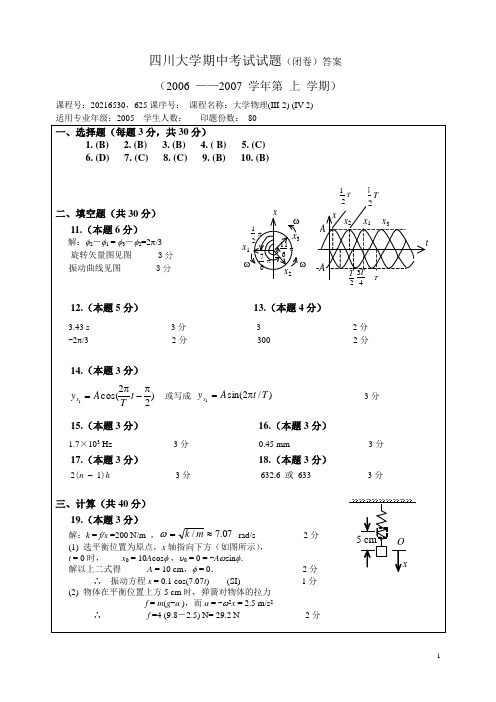
16.(本题 3 分) (
0.45 mm 3分 3分
17.(本题 3 分) (
2(n – 1)h
18.(本题 3 分) (
632.6 或 633
三、计算(共 40 分) 计算( 19.(本题 3 分) (
解:k = f/x =200 N/m , ω = k / m ≈ 7.07 rad/s (1) 选平衡位置为原点,x 轴指向下方(如图所示) , t = 0 时, x0 = 10Acosφ ,v0 = 0 = -Aωsinφ. 解以上二式得 A = 10 cm,φ = 0. ∴ 振动方程 x = 0.1 cos(7.07t) (SI) (2) 物体在平衡位置上方 5 cm 时,弹簧对物体的拉力 f = m(g-a ),而 a = -ω2x = 2.5 m/s2 ∴ f =4 (9.8-2.5) N= 29.2 N 2分
3 λ 2 θ = e4 / l = 3λ / (2l ) =4.8×10-5 rad
5分
1 1 2e4 + λ ′ ,它与波长 λ ′ 之比为 2e4 / λ ′ + = 3.0 .所以 A 处是明纹 2 2
(3) 棱边处仍是暗纹,A 处是第三条明纹,所以共有三条明纹,三条暗纹.
3分 2分
2
12.(本题 5 分) (
3.43 s -2π/3 3分 2分
13.(本题 4 分) (
3 300 2分 2分
14.(本题 3 分) (
y x1 = A cos( 2π π t− ) T 2
或写成 y x1 = A sin( 2πt / T ) 3分
15.(本题 3 分) (
1.7×103 Hz 3分 3分
四川大学期中考试试题(闭卷)答案
四川高中物理选修三第三章《热力学定律》经典测试题(答案解析)

一、选择题1.下列例子中,通过热传递改变物体内能的是()A.火炉将水壶中的水煮开B.汽车紧急刹车时轮胎发热C.压缩气体放气后温度降低D.擦火柴,火柴就燃烧2.气体膨胀对外做功100 J,同时从外界吸收了120 J的热量,它的内能的变化是A.减小20 J B.增大20 J C.减小220 J D.增大220 J3.关于元器件,下列说法错误的是()A.太阳能电池板是将光能转化为电能B.电热水壶烧水是利用电流的热效应C.电容器是用来储存电荷的装置D.微波炉加热食物是利用电磁感应原理4.一定质量的理想气体在某一过程中,气体对外界做功1.6×104J,从外界吸收热量3.8×104J,则该理想气体的()A.温度降低,密度减小B.温度降低,密度增大C.温度升高,密度减小D.温度升高,密度增大5.一定质量的理想气体,由初始状态A开始,状态变化按图中的箭头所示方向进行,最后又回到初始状态A,对于这个循环过程,以下说法正确的是()A.由A→B,气体的分子平均动能增大,放出热量B.由B→C,气体的分子数密度增大,内能减小,吸收热量C.由C→A,气体的内能减小,放出热量,外界对气体做功D.经过一个循环过程后,气体内能可能减少,也可能增加6.如图所示,带有活塞的气缸中封闭一定质量的理想气体(不考虑分子势能).将一个热敏电阻(电阻值随温度升高而减小)置于气缸中,热敏电阻与气缸外的欧姆表连接,气缸和活塞均具有良好的绝热性能,气缸和活塞间摩擦不计.则()A.若发现欧姆表示数变大,则气缸内气体压强一定减小B.若发现欧姆表示数变大,则气缸内气体内能一定减小C.若拉动活塞使气缸内气体体积增大,则欧姆表示数将变小D .若拉动活塞使气缸内气体体积增大时,则需加一定的力,这说明气体分子间有引力 7.下列改变物体内能的物理过程中,不属于对物体做功来改变物体内能的有( ) A .用锯子锯木料,锯条温度升高B .阳光照射地面,地面温度升高C .锤子敲击钉子,钉子变热D .擦火柴时,火柴头燃烧起来8.如图所示,在紫铜管内滴入乙醚,盖紧管塞.用手拉住绳子两端迅速往复拉动,管塞会被冲开.管塞被冲开前( )A .外界对管内气体做功,气体内能增大B .管内气体对外界做功,气体内能减小C .管内气体内能不变,压强变大D .管内气体内能增加,压强变大9.如图描述了一定质量的理想气体压强p 随体积V 变化的图像,O 、a 、b 在同一直线上,ac 与横轴平行,下列说法正确的是( )A .a 到b 过程,外界对气体做功B .c 到a 过程,气体向外界放出热量大于气体内能的减少量C .b 到c 过程,气体释放的热量大于气体内能的减少D .a 点时气体的内能等于b 点时气体的内能10.带有活塞的汽缸内封闭一定量的理想气体。
川大版高数第三册规范标准答案

=
=
= A
28.解:==时源自依次用V左乘和用U右乘 消去
得从而得证
29.解:(1)判断X可逆即:
因A、C可逆,
则 即
则X可逆。
(2)设 则
由
=
=E
30.证明:
31.解:(1)
原式=
(2)
(3)
第3章线性方程组
1.证:假设 线性相关,
则 不会为0,使得
整理得:
又由 ,故
由于
故由克莱默法则知:
故结论正确。
,其中 . 为任意的实数
AB=BA
充分性: AB=BA
(AB)’=B’A’=-BA
AB为反对称矩阵
综上所述:AB是反对称矩阵的充分必要条件是AB=BA。
26.解:设矩阵X为x=
则 =
Ax=o
=0
即 =0
对任意n 1矩阵都成立
A=0
27.证: : A为正交矩阵
=A
A = = =
又 正交矩阵为可逆矩阵
A =A
:
A = = =A
则
这样得到了 的另一种表出式,即表出不唯一
综上,假设成立条件下得到的结论与“ 可用 唯一表出”矛盾
故假设不成立, 线性无关
7、将A表示为 ,B表示为
若 线性无关,则必有
同理可证A
P117 T8
解:(1)
由此r=3
解:(2)
由此r=2
解:(3)
由此r=3
解:(4)
由此r=2
解:(5)
由此r=3
解:(6)
6.证:假设 线性相关,
由题意知,必存在一组使得
7.证:设
由于
6、证明:假设 线性相关,则 , 线性相关(部分相关则全体相关)
四川版高等数学第三册课后习题 八 答案

由全概率公式,
5
P(B) P(Ai )P(B| Ai ) i1
1 5
2 3
1 5
2 3
1 5
0
1 5
3 4
1 5
3 4
0.567
27. 罐中装有 n 个黑球 r 个红球,随机取出1个球观察颜色,将 球放回后,另外再装入 c 个与取出颜色相同的球,第二次再从 罐中取出1球,求下列诸事件的概率。
P(B| A) r nrc
27. 罐中装有 n 个黑球 r 个红球,随机取出1个球观察颜色,将 球放回后,另外再装入 c 个与取出颜色相同的球,第二次再从 罐中取出1球,求下列诸事件的概率。
解:设 A=“第一次取得黑球”,则 A =“第一次取得红球” 设B=“第二次取得黑球”,则 B =“第二次取得红球”
25. 三架飞机中有一架主机和两架僚机,被派出轰炸敌人阵地, 飞机缺少无线电导航设备时就达不到目的地,这种设备装置在 主机上。飞机到达目的地后,各机独立进行轰炸,每一架击中 目标的概率为0.4,在到达目的地之前,飞机需通过敌军高射炮 阵地,每机被击落的概率为0.2 。求敌军阵地被击中的概率。
解: P(敌军阵地被击中 ) 1- P(敌军阵地没有被击)中
16. 设有M只晶体管,其中有m只废品,从中任取2只,求所取 晶体管有1只正品的条件下,另1只是废品的概率。
解:令 A=(取到1只正品),B=(取到1只废品)
Hale Waihona Puke P(有一只正品的条件下另,一只是废品) P(B| A) P(AB) P( A)
CM1 mCm1
CM2
1
Cm2 CM2
CM1 mCm1 CM2 - Cm2
四川版高等数学第三册课后习题(八)答案复习课程

16. 设有M只晶体管,其中有m只废品,从中任取2只,求所取 晶体管有1只正品的条件下,另1只是废品的概率。
解:令 A=(取到1只正品),B=(取到1只废品)
P(有一只正品的条件下另,一只是废品) P(B| A) P(AB) P( A)
CM1 mCm1
CM2
1
Cm2 CM2
CM1 mCm1 CM2 - Cm2
各元件停止工作与否是相互独立的,求系统S停止工作的概率。
解: P(系统S停止工作) P(3条支路均停止工作)
P(支路1停止工作)3
E1
E2
E3
E4
P(支路1停止工)作
E5
E6
1P(E1正常工)作 P(E2正常工)作 10.70.7
0.51
P (系S 停 统止 )0 工 .531 作 0.1327
P ( A B ) P ( A B ) 1 P ( A B ) 1 p q r
12. 一个火力控制系统,包括一个雷达和一个计算机,如果这两 样中有一个操作失效,该控制系统便失灵。设雷达在100小时内 操作正常的概率为0.9,而计算机在操作100小时内失效的概率 为0.12,试求在100小时内控制系统失灵的概率。
25. 三架飞机中有一架主机和两架僚机,被派出轰炸敌人阵地, 飞机缺少无线电导航设备时就达不到目的地,这种设备装置在 主机上。飞机到达目的地后,各机独立进行轰炸,每一架击中 目标的概率为0.4,在到达目的地之前,飞机需通过敌军高射炮 阵地,每机被击落的概率为0.2 。求敌军阵地被击中的概率。
解: P(敌军阵地被击中 ) 1- P(敌军阵地没有被击)中
21. 制造某种零件可以采取两种工艺,(1)三道工序,每道工序 出废品的概率分别为0.2,0.1,0.1;(2)两道工序,每道工序出 废品的概率分别为0.2,0.15 。问哪种工艺的废品率低?(两种 工艺中,每道工序是彼此独立的。)
四川版高等数学第三册课后习题(十一)答案

习题十一1.一门高射炮向敌机连发三炮,每炮击中敌机的概率为0.9.设X 表示击中敌机的炮弹数,求EX ,DX .解:依题得:33()0.90.1,0,1,2,3k k k p x k C k -=== 所以X 的分布律为:所以:()22222200.00110.02720.24330.729 2.7()00.00110.02720.24330.729 2.70.27EX DX E X EX EX EX =⨯+⨯+⨯+⨯==-=-=⨯+⨯+⨯+⨯-=2.设随机变量X 具有分布律1{}(0,1,2,)!k P X k p k ek ==== ,求EX解:00001111111!(1)!!k k k k k k EX x p k e ek e k e k e +∞+∞+∞+∞======⋅===⋅=-∑∑∑∑ 注:从题看出,X 服从1λ=的泊松分布(P327)。
3.解:()()00.410.320.230.1100.310.520.2300.9E E =⨯+⨯+⨯+⨯==⨯+⨯+⨯+⨯=甲乙4.设随机变量X 服从下列分布,求EX ,DX .(2)Γ分布10,0,()(0,0),0()p p bx x p x b p b x e x p --≤⎧⎪=>>⎨>⎪Γ⎩均为常数解:+0++100100()()()11()()11(1)()()()()p pp bxp bx pp p p t tp EX xp x dxb b x x e dx x e dxp p b t b bx t e dt t e dt p b b b p p p p p b p b p b∞∞∞---+∞+∞--+===ΓΓ⎛⎫=⋅=⋅ ⎪ΓΓ⎝⎭=⋅Γ+=⋅Γ=ΓΓ⎰⎰⎰⎰⎰伽马函数的性质同理得:22(1)p p EX b+=所以:()222p DX EX EX b=-=5.设随机变量X 的概率密度为(),,xp x Ae x -=-∞<<+∞求:(1)系数A ;(2)EX ;(3)DX 解:0(1)()21xx xxp x dx Ae dx Ae dx Ae Ae A +∞+∞--+∞-∞-∞-∞=+=-==⎰⎰⎰所以12A =000(2)()1111(11)02222x x x x EX xp x dxx e dx x e dx xe dx xe dx +∞-∞+∞+∞---∞-∞=⎡⎤=⋅+⋅=+=-+=⎢⎥⎣⎦⎰⎰⎰⎰⎰22202220(3)()1()22x x DX EX EX EXx p x dx x e dx x e dx +∞+∞--∞-∞=-=⎡⎤==+=⎢⎥⎣⎦⎰⎰⎰ 7. 设随机变量X 服从几何分布,即分布律为:1{}(1,2,)(01,1),k k P X k p pq k p q p -====<<=-试求EX ,DX . 解:1121112222122222111(1)1111()k k k k k k k k k k p EX kp kpqp kq q pq q DX EX EX k p p k q p p p p p +∞+∞+∞--===+∞+∞-=======-+=-=-=-=-=∑∑∑∑∑8.设随机变量X 的概率密度为23,01,()0,.x x p x ⎧≤≤=⎨⎩其它 (1)4;(2)XY X Y e -==求的数学期望.解:1130(1)(4)44()433;EY E X EX xp x dx x dx =====⎰⎰1112210(2)(()33615Xxxx EY E e e p x dx x e dx x de e -----===-=-⎰⎰⎰)=10.设随机变量12X X ,的概率密度分别为1212,3,1212120,30,()()0,0,0,0.x x X X e x e x p x p x x x --⎧⎧>>==⎨⎨≤≤⎩⎩ 求21212(),(3)E X X E X X +-.解:123121211220014()3133x x E X X EX EX x e dx x e dx +∞+∞--+=+=+⋅=+=⎰⎰123222121211220(3)333211x x E X X EX EX x e dx x e dx +∞+∞---=-=-⋅=-=⎰⎰11. 设随机变量12X X ,相互独立,概率密度分别为2123211212214,01,0,()()20,0,0.x X X x x e x p x p x x -⎧⎧≤≤>⎪==⎨⎨⎩⎪≤⎩,其它求12()E X X解:21321212111220148()==42.255x E X X EX EX x x dx x e dx +∞-⋅⋅⋅=⨯=⎰⎰12.设随机向量(,)X Y 的概率密度为3,01,0,(,)0,x x y x p x y <<<<⎧=⎨⎩其它.求()E XY 解:()11240033()33210xE XY xy xdxdy x ydy dx x dx +∞+∞-∞-∞=⋅===⎰⎰⎰⎰⎰14.解:由题得,01EY DY EZ DZ σ====,,,222222242(538)5385520(538)259259EV E X Y Z EX EY EZ EX aDV D X Y Z DX DY DZ aσ∴=+-+=+-+=+=+=+-+=++=++15.设随机变量12,,n X X X 相互独立,且服从同一分布,数学期望为μ,方差为2σ,求这些变量的算术平均值11ni i X X n ==∑的数学期望及方差。
高数3,川大,物理类,第2章答案

sin cos(n 1) cos sin( 1) n
所以假设成立。
1 (2) A 0 0
1 解: A2 0 0 1 3 A 0 0 1 4 A 0 0
1 1 0
1 1 0 2 1 0 3 1 0
1 a 0 0 1 a 0 0
0 1 a 0 0 1 a 0
0 a4 0 0 0 1 a 0 0 a5 0 0 0 1 a 0
4a 3 a4 0 0 5a 4 a5 0 0
6a 2 4a 3 a4 0 10a 3 5a 4 a5 0
4 3 4
2 E ,当n为偶数 n 2 ,证明 B B ,当n为奇数 3
1 2 证明: B 0 0
4 3 4
2 1 2 0 3 0
4 3 4
2 1 2 0 3 0
0
4. 计算下列矩阵乘积。 a11 a12 b1 x (6) ( x , y ,1) a21 a22 b2 y ; (a12 a21 ) b b2 c 1 1
(a11 x a21 y b1
a12 x a22 y b2
2a a2 0 0
1 2a a2 0 3a 2 a3 0 0
0 1 2a a2 3a 3a 2 a3 0 1 3a 3a 2 a3
0 a 1 0 2a 0 2 a 0
0 a3 0 0 0 1 a 0
a3 0 4 A 0 0 a4 0 5 A 0 0
3a 2 a3 0 0 4a 3 a4 0 0
四川大学大学物理习题册解答
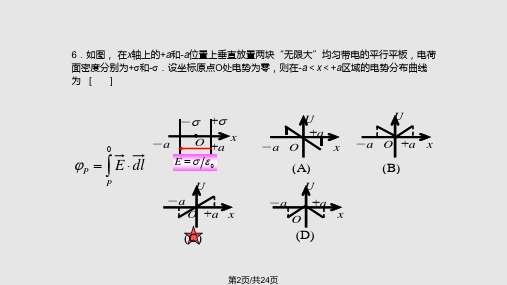
dq
1 R s 2 πrdr
x2 r 2 4 π0 0 x2 r 2
s x2 R2 x 2 0
第18页/共24页
7.如图,电荷面密度分别为+s和-s的两块无限大均匀带电平行平面,分别与x轴垂
直相交于x1=b,x2=-b两点.设坐标原点O处电势为零,试求空间的电势分布表示式 并画出其曲线.
由电势的叠加原理有,
o i i
dq Q
4 0R 4 0R
A
o
qபைடு நூலகம்
E
dl
q
o
E
dl
qo
4 0R
Q RO
第12页/共24页
11.有三个点电荷Q1、Q2、Q3沿一条直线等间距分布,已知其中任一点电荷所受合力
均为零,且Q1=Q3=Q。在固定Q1、Q3的情况下,将Q2从Q1、Q3连线中点移至无穷远
x
解: M l F M l qE sin
q
2
M max qEl
M与正方向相反
0
A Md qElsind
F
pl F q
E
2
qEl cos 0 qEl 2 第23页/共24页
谢谢您的观看!
第24页/共24页
6.如图, 在x轴上的+a和-a位置上垂直放置两块“无限大”均匀带电的平行平板,电荷 面密度分别为+s和-s.设坐标原点O处电势为零,则在-a<x<+a区域的电势分布曲线 为[ ]
-s +s
0
-a O +a x
P E dl
E s 0
P
U
-a
O +a x
U
U
川大版高数第三册答案(1)教学文案

川大版高数第三册答案(1)第一章 行列式1.()()[][][]23154110103631254=520010=8(1)3(1)321(1)(2)(3)2441(1)3214243(1)321012)4n n n n n n n n m n m n n n m n m n n m 1τ=++++=2τ+++++-τ-⋯=-+-+-+⋯+2+1+0===+τ-⋯=+=+τ-⋯=⋯()该数列为奇排列()该排列为偶排列() 当或时,为偶数,排列为偶排列当或时,为奇数,排列为奇排列(其中,,()[][][]12(1)13521)246(2)0123(1)244113521)246(2)424313521)246(2)012)2.(1)(2)(n n n n n n n m n m n n n m n m n n m i i i k n n n -τ⋯-⋯=++++⋯+-===+τ⋯-⋯=+=+τ⋯-⋯=⋯⋯-+-+( 当或时,(为偶数,排列为偶排列当或时,(为奇数,排列为奇排列(其中,,解:已知排列的逆序数为,这个数按从大到小排列时逆序数为()()111112(1)3)2(1)2x x x n x n x n n n n n n x i r i i i n x r i n x n n i i i i i i -+-+---+⋯+2+1+0=----τ⋯=-τ⋯个.设第数之后有个数比小,则倒排后的位置变为,其后个数比小,两者相加为故3 证明:.因为:对换改变排列的奇偶性,即一次变换后,奇排列改变为偶排列,偶排列改变为奇排列∴当n ≥2时,将所有偶排列变为奇排列,将所有奇排列变为偶排列 因为两个数列依然相等,即所有的情况不变。
∴偶排列与奇排列各占一半。
4 (1)13243341a a a a 不是行列式的项 14233142a a a a 是行列式的项 因为它的列排排列逆序列τ=(4321)=3+2+0+0=5为奇数,∴应带负号(2)5142332451a a a a a 不是行列式的项 1352413524a a a a a =1324354152a a a a a 因为它的列排排列逆序列τ(34512)=2+2+2+0+0=6 为偶数∴应带正号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
川大版高数-物理类专用-第三册-答案————————————————————————————————作者:————————————————————————————————日期:第一章 行列式1.()()[][][]23154110103631254=520010=8(1)3(1)321(1)(2)(3)2441(1)3214243(1)321012)4n n n n n n n n m n m n n n m n m n n m 1τ=++++=2τ+++++-τ-⋯=-+-+-+⋯+2+1+0===+τ-⋯=+=+τ-⋯=⋯()该数列为奇排列()该排列为偶排列() 当或时,为偶数,排列为偶排列当或时,为奇数,排列为奇排列(其中,,()[][][]12(1)13521)246(2)0123(1)244113521)246(2)424313521)246(2)012)2.(1)(2)(n n n n n n n m n m n n n m n m n n m i i i k n n n -τ⋯-⋯=++++⋯+-===+τ⋯-⋯=+=+τ⋯-⋯=⋯⋯-+-+( 当或时,(为偶数,排列为偶排列当或时,(为奇数,排列为奇排列(其中,,解:已知排列的逆序数为,这个数按从大到小排列时逆序数为()()111112(1)3)2(1)2x x x n x n x n n n n n n x i r i i i n x r i n x n n i i i i i i -+-+---+⋯+2+1+0=----τ⋯=-τ⋯个.设第数之后有个数比小,则倒排后的位置变为,其后个数比小,两者相加为故3 证明:.因为:对换改变排列的奇偶性,即一次变换后,奇排列改变为偶排列,偶排列改变为奇排列∴当n ≥2时,将所有偶排列变为奇排列,将所有奇排列变为偶排列 因为两个数列依然相等,即所有的情况不变。
∴偶排列与奇排列各占一半。
4 (1)13243341a a a a 不是行列式的项 14233142a a a a 是行列式的项 因为它的列排排列逆序列τ=(4321)=3+2+0+0=5为奇数,∴应带负号(2)5142332451a a a a a 不是行列式的项 1352413524a a a a a =1324354152a a a a a 因为它的列排排列逆序列τ(34512)=2+2+2+0+0=6 为偶数∴应带正号。
5 解: 112332441223344114233142a a a a a a a a a a a a 利用τ为正负数来做,一共六项,τ为正,则带正号,τ为负则带负号来做。
6 解:(1)因为它是左下三角形112122313233..........12300...00...0......n n n nna a a a a a a a a a =112131411223242233433444...............0...00 0...0000...n n n n nna a a a a a a a a a a a a a a =()()1231122331n nn a a a a τ⋅⋅⋅-⋅⋅⋅=112233nn a a a a ⋅⋅⋅(2)11123141521222324253132414251520000000a a a a a a a a a a a a a a a a =()22232425113211425200010000a a a a a a a a +-+()21`232425213112415100010000a a a a a a a a +-=()()1111112212211010a a a a ++-⋅--⋅=0(3)1200340021131751-=()1212121313451+++-⋅-=32 (4)0000000000000xy x y x y x y yx=()()01212023120000011000x y xy xy x y y x y xx yy x++++++-+-=55x y + 7.证明:11121212212............n n n n nna a a a a a a a a ⋅⋅⋅⋅⋅⋅=将行列式转化为111221200...00...0 0n n a a a a a 若 零元多于2n n -个时,行列式可变为211200...00 0...0n n a a a 故可知行列式为0.8.(1)204136113131212331---=--52041361112302331----=4310361112302331--=-54310594012302331-=-54314315945212106301231370--==-()()1122121212111212112122111112121212122112121122121.)().)1101=y mx b x y x y y y m x x y y y x b x y x x y y x y y x y x y y x b b y x x x x x x y y x y x yy x x x x x x y x y x y y y x y x =+-=--=⋅+----=⋅+⇒=-=-----=⋅+--=-- 第一章 高数 3册9.(1).经过(,,斜率代入(,则又由左边()()2122112122112120x x y x y y y x y x yy x x x x x -+-==--=⋅+--右边则问题特征:()()()()()22222222sin cos cos 2sin cos cos 2sin cos cos 2cos c 10.145os cos 2.=+=221=b cc a a b b c c a a b b c c a b a bc a c a b b c a c a b b c a c a b a b ca b c a b c αααβββγγγααα'''''''''''''''''''''''''''''''''''''''''''''+++++++++-利用性质和分成六个行列式相加其余结合为零故原式性质2()()22222222222222cos 1cos cos 2cos cos cos 22cos 1cos cos 2cos cos cos 22cos 1cos 1-2+(1)_cos 2cos 2cos cos 2cos 2cos cos 1052cos 2cos cos 2αααββββββγγγγγγαααβββγγγ---=-=--()列列性质()()()()()()22222342222222222222000013.0000401110111101010101111.12324323yz xz xzx y z xyz xyz xyz x z y x xz xy yz x y yz x y yz xz xy zyx z y z x zxyz y z y xyz xyz z x z yz xz xy y x y x a b c daa ba b ca b c d a a b a b ca b c d a a ⨯⨯⨯−−−−→←−−−−⋅⋅⨯⋅==⋅⋅+++++++++++++列列列列()()()()()()()()()()()()()()1-122+323423+43-3446310630002324320020363106300363000200b a bc a b c da b c d a b c d aa ba b ca ab a bc a a b a b ca ab a a b a bc aa ba bcda ab a b ca a ab a⋅⋅-⋅⋅-⋅++++++++++++−−−−−→−−−−−−→←−−−−−←−−−−−−+++++++++++−−−−−→=←−−−−−+列加到行行列行行行行()()()()()()()()()()()()1-2+21-3+31-+1+1112131*********23311231231000-103-12622-1-2-1032-1-2-3-1002620321-1234!004200013n n n nn nn nn n n nn nn n n n x a a a a a x x a a x x x a x x x x x ⨯⨯⨯−−−−−→←−−−−−⨯=⨯⨯⨯⨯==列列列列列列降阶()()()()()()()()3122322332312213311221331233223321-+21+131131-+11111101-111001n n n n nn n n nn n n nx n n n n x n nn n a x a a x x a x x x a x a x a x a x a x a x a x a x a x a x a x x x a x a x ⨯⨯-----------−−−−−−→-⨯⨯⨯-←−−−−−−-列列列列降阶习题一 13 (1)0000000000x y x y D x y yx= 根据“定义法”(2.3.4.5...)1(1)(1)nI n n n n n D x y x y -=+-=+-(2)123111000022000011n n D n n--=+---根据“降阶法”~n (1)n(n+1)23n-1n 2n(n+1)34n12n(n+1)12n-2n-12D −−−−−→将第2列加到第列上得-1123n-1123n-1n 011111341n(n+1)n(n+1)=01111221122101111n n nn n n n-−−−−−−→----将前一行乘以加到后一行得(2)~(n)(1)1111-n -1111-n 111-n 1-111-n 1n(n+1)(n-1)=211-n 11-11111-n 111−−−−−→将列加到列上得变为阶1111-n 111-n 1n(n+1)=-211-n 111111-1(1)(2)~(n)110110(1)-2101n n n n n ⨯--+−−−−→-列加到列2(1)(2)3222(1)2112222(1)11(1)(1)(1)(1)222n n nn n n n n n n n n n n nn ---+--+---+++=---=-=-(3)212122222111112111111a12111(1)(1)(1)(2)(1)12(2)(2)(1)(2)(1)11(1)(1)n n n n n n n n a a a a a a n a a a a a a a n a a a a a a a n a n a n a n -----------+---−−−→---+------+-+-+-+转置(1)2(-1)1!2!(1)!n n n -−−−−−→-范达蒙行列式注:根据范达蒙行列式原式=123(1)(1)(2)(1)(1)1!2!(1)!n n n ++++----+=--(1)(2)(2)n ---+-1 =(1)2(1)1!2!(1)!n n n ---(4)122111111111122122222222n n 122-111111111a nn n n n n n n n nnn n n n n n n n n n n n a a b a b a b b a a b a b a b b n a a b a b a b b --------++++++++第行提出得12211111111112122222n-11212222211111211111111n n n nn n n nn nn n n n n n n n n n n n n b a b a ba ba b b b b a a a a a a a b b b b a a a a -----+-++++-++++ =2111112111112122222n-11212222211111211111111n n n nn n n nn nn n nn n n n n n n n n n b b b b a a a a b b b b a a a a a a a b b b b a a a a ---+-++++-++++=1231()()jn n n ni n j i i j i jb b a a a a a b a b a a ππ+-=- 14 (1)证明:cossincos222cossincos 222+cossincos222αβαβαββγβγβγγαγαγα-++-++-+sincossincos2222=coscos ++22sincos sincos2222βγβγαβαβαββγγαγαγαγα++++---++sincos-22+cos++2sincos22αβαβγαβγβγ++ ++=cos(sin coscossin)cos(sincoscossin)2222222222αββγγαβγγαβγαβγααβγα-++++-++---+cos(sincoscossin)22222γααββγαββγ-++++-cossincossincossin222222αββαβγβγγααγ------=-+111sin()sin ()sin()222βαγβαγ=-+-+- []1sin()sin()sin()2βααγγβ=-+-+- (2)证明:123422221234444412341111x x x x x x x x x x x x 12341x x x x +++= (3)12(-1)(1)~()na x a a a a a a x a a an a a a a x a a aa aa+++最后一行乘以加到行得 1212123000000000000n n n x x x x x a ax x x x x aaaa a ==(4)“递推法”01211000100010n n a a x a x a x-----1n+n 112100100010100(-1)(1)01n n n a a x x xa a xx +------+--降阶11n n xD a --=+12221112011:n n n n n n D xD a D xD a D a x a x a ------=+=+∴=+++由此类推15.(1)=+=(ab+1)(cd+1)-[a(-d)]=(ab+1)(cd+1)+ad(2)==(4-6)(-1-15)=32(3)=++=-a(c-d)-a(d-b)-a(d-c)=abd= abd(c-b)(d-b)(c-d)(4) ===(==16.范达 行列式V()=31()x x -13221()())()n n n n x x x x x x x x --=---(21211111221111111n n n n n n x x x a a a a a aa ------⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦−−−→←−−−转量行列式12122111111211111n n n n n n x a a a x a x a a a ------⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=121()(n a x a x a x ----)()21(a -a )11n a a --()32(a -a )1212n n n a a ----()(a -a )(1)因为121n a a -a 为常数。
