小升初数学平面图形与立体图形综合练习知识讲解
小升初数学几何图形专题知识训练含答案解析-5篇精选

小升初数学几何图形专题知识训练含答案一、单选题1.将一块长5分米、宽3分米的长方形的木板锯成半圆形,这个半圆形的直径最长是()分米A.5B.3C.2.52.下列说法不正确的是()。
A.长方体的表面积是指6个面的总面积。
B.正方体的表面积是指前面、上面、左面的面积之和。
C.两个相同的正方体拼成一个长方体后,表面积减少了。
3.在一个长方形中剪去一个长4厘米、宽2厘米的小长方形,如下图有三种不同的方案,剩下部分的面积和周长相比,()。
A.面积相等,图①的周长最长B.面积相等,图②的周长最长C.面积相等,图③的周长最长D.面积和周长都相等4.已知两个长方形的周长相等,则这两个长方形的形状()A.完全相同B.一定不同C.不一定相同5.一根圆柱形木料从中间切开(如下图)后,表面积增加了56.52cm²,原来这根木料的体积是()cm³。
A.565.2B.282.6C.188.46.如果用表示1个小正方体,用表示2个小正方体叠加,用表示3个小正方体叠加,那么右图是由7个小正方体搭成的立体图形,从正面观察时,看到的平面图形是()。
A.B.C.D.7.工厂要装修一间长8米、宽4米的厂房,用边长是2分米的正方形地砖铺面地面,需要()块这样的地砖。
A.200B.800C.808.计算下图中三角形的面积(单位:厘米),正确的算式是()。
A.11×6÷2B.14×7÷2C.14×8÷2D.11×7÷2 9.如右图所示,在这个平行四边形中,阴影部分的面积和空白部分的面积相比较,()A.阴影部分面积大B.面积一样大C.阴影部分面积小D.无法比较10.下面问题中,不能用“42÷3”解决的是()。
A.超市运来42箱水果,3天卖完,平均每天卖出多少箱?B.一块长方形玻璃的宽是3分米,面积是42平方分米,长是多少分米?C.王林植树42棵,是张强植树棵数的3倍。
六年级下册数学试题-小升初能力训练:几何综合——立体几何(解析版)全国通用
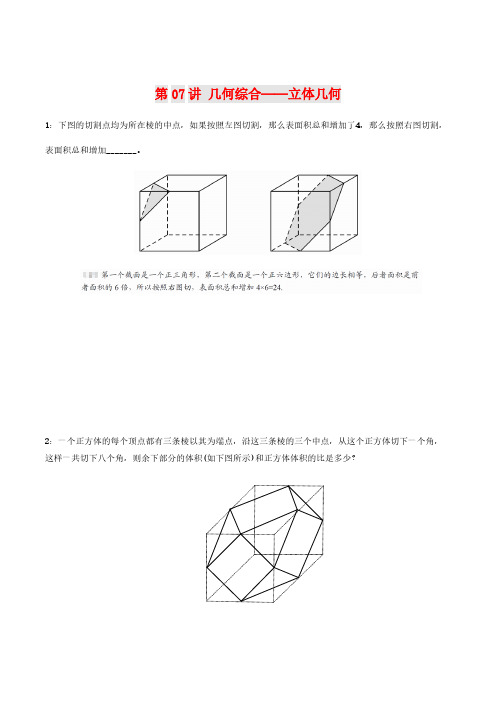
第07讲几何综合——立体几何1:下图的切割点均为所在棱的中点,如果按照左图切割,那么表面积总和增加了4,那么按照右图切割,表面积总和增加_______。
2:一个正方体的每个顶点都有三条棱以其为端点,沿这三条棱的三个中点,从这个正方体切下一个角,这样一共切下八个角,则余下部分的体积(如下图所示)和正方体体积的比是多少?假设正方体的边长为1,那么每个切去的角(三棱锥)的体积为,211111322248⎛⎫⨯⨯⨯= ⎪⎝⎭所以八个角一共切去的体积,所以余下的体积是正方体体积的,118486⨯=15166-=即余下部分的体积与正方体体积的比为.5:63:如图,原正方体的棱长为12厘米,沿图中的线将正方体切掉正面的部分,求剩下不规则立体图形的体积.倾斜于上下底面的切面,把正方体一分为二.被切掉的部分的图形和剩下的部分图形关于正方形的中心是对称的.33122864(cm )÷=4:如图,正方体的棱长为,连接正方体其中六条棱的中点形成一个正六边形,而连接其中三个顶点6cm 形成一个正三角形.正方体夹在六边形与三角形之间的立体图形有 个面,它的体积是.3cm乙9乙从图中可以看出,夹在六边形与三角形之间的立体图形有2个底面和6个侧面(六边形的每一条边对应一个侧面),所以共有个面,8由于正方体是关于它的中心成中心对称的,而根据正六边形和正三角形的连法,如果从正方体中去掉以这个正三角形为底面的三棱锥以及与它相对的三棱锥后,剩下的部分正好被六边形分成2个同样的立体图形,这就是所要求的立体图形.所以所要求的立体图形的体积是:.3111666266672(cm )232⎡⎤⎛⎫⨯⨯⨯-⨯⨯⨯⨯⨯= ⎪⎢⎥⎝⎭⎣⎦5:如图,有一个棱长为2厘米的正方体。
从正方体的上面正中间下挖一个棱长为1厘米的正方体小洞;接着在小洞的底面正中间再向下挖一个棱长为厘米的小洞;第三个小洞的挖法与前面两个相同,棱长为12厘米,最后得到的额例题图形的表面积是多少平方厘米?146:如图,把正方体用两个与它的底面平行的平面切开,分成三个长方体,这三个长方体的表面积比是3:4:5时,用最简单的整数比表示这三个长方体的体积比:::。
专题17:《平面几何的面积(一)》小升初数学专题讲练 (思维导图+知识点精讲+例题分析+变式训练
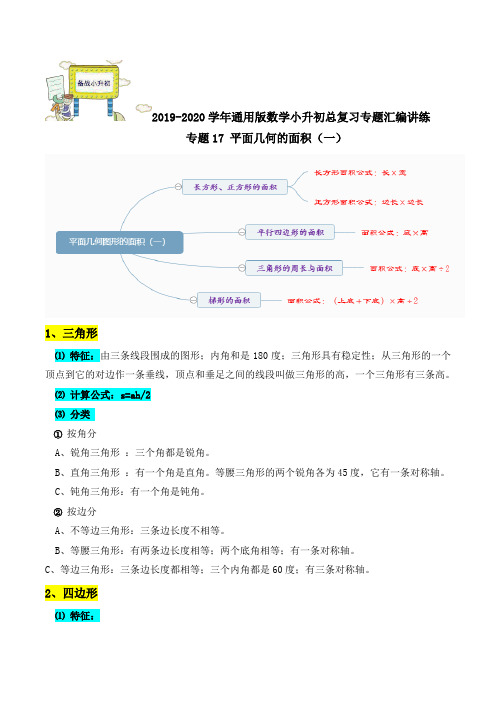
2019-2020学年通用版数学小升初总复习专题汇编讲练专题17 平面几何的面积(一)1、三角形⑴特征:由三条线段围成的图形;内角和是180度;三角形具有稳定性;从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,一个三角形有三条高。
⑵计算公式:s=ah/2⑶分类①按角分A、锐角三角形:三个角都是锐角。
B、直角三角形:有一个角是直角。
等腰三角形的两个锐角各为45度,它有一条对称轴。
C、钝角三角形:有一个角是钝角。
②按边分A、不等边三角形:三条边长度不相等。
B、等腰三角形:有两条边长度相等;两个底角相等;有一条对称轴。
C、等边三角形:三条边长度都相等;三个内角都是60度;有三条对称轴。
2、四边形⑴特征:①四边形是由四条线段围成的图形。
②任意四边形的内角和是360度。
③只有一组对边平行的四边形叫梯形。
④两组对边分别平行的四边形叫平行四边形,它简洁变形。
长方形、正方形是特殊的平行四边形;正方形是特殊的长方形。
⑵分类①长方形A、特征:对边相等,4个角都是直角的四边形。
有两条对称轴。
B、计算公式:c=2(a+b) s=ab②正方形A、特征:四条边都相等,四个角都是直角的四边形。
有4条对称轴。
B、计算公式:c=4a s=a²③平行四边形A、特征:两组对边分别平行的四边形;相对的边平行且相等;对角相等;相邻的两个角的度数之和为180度;平行四边形简洁变形。
B、计算公式:s=ah④梯形A、特征:只有一组对边平行的四边形;中位线等于上下底和的一半;等腰梯形有一条对称轴。
B、计算公式:s=(a+b)h/2=mh3、圆⑴圆的生疏圆是平面上的一种曲线图形。
圆中心的一点叫做圆心。
一般用字母o表示。
半径:连接圆心和圆上任意一点的线段叫做半径。
一般用r表示。
在同一个圆里,有很多条半径,每条半径的长度都相等。
通过圆心并且两端都在圆上的线段叫做直径。
一般用d表示。
同一个圆里有很多条直径,全部的直径都相等。
小升初数学复习第14讲立体几何综合

小升初数学复习第14讲立体几何综合在小升初的数学复习中,立体几何是一个重要的板块。
这一讲,我们将对立体几何进行综合复习,帮助同学们巩固知识,提升解题能力。
首先,让我们来回顾一下常见的立体图形。
长方体是我们非常熟悉的立体图形,它有六个面,每个面都是长方形(特殊情况下有两个相对的面是正方形),相对的面面积相等。
长方体有 12 条棱,相对的棱长度相等,有 8 个顶点。
正方体则是特殊的长方体,它的六个面都是完全相同的正方形,12 条棱长度都相等,也有 8 个顶点。
圆柱体由两个底面和一个侧面组成,底面是完全相同的圆,侧面展开是一个长方形。
圆锥体有一个底面是圆,侧面展开是一个扇形。
接下来,我们看看如何计算这些立体图形的表面积和体积。
长方体的表面积=(长×宽+长×高+宽×高)×2 ,体积=长×宽×高。
正方体的表面积=棱长×棱长×6 ,体积=棱长×棱长×棱长。
圆柱体的表面积=侧面积+两个底面积,侧面积=底面周长×高,底面积=π×半径²,体积=底面积×高。
圆锥体的体积= 1/3×底面积×高。
在解题时,我们常常会遇到一些需要灵活运用这些公式的情况。
例如,有一个长方体的盒子,长、宽、高分别是 5 厘米、4 厘米、3 厘米。
要在这个盒子的外面包一层彩纸,需要多少平方厘米的彩纸?这就是求长方体的表面积,我们按照公式(5×4 + 5×3 + 4×3)×2 来计算,就能得出答案。
再比如,有一个圆柱形的水桶,底面半径是 2 分米,高是 5 分米,这个水桶能装多少升水?这就是求圆柱体的体积,我们先算出底面积π×2² ,再乘以高 5 分米,最后将结果转换成升。
除了直接运用公式计算,还会有一些综合的题型。
比如,把一个棱长为 6 厘米的正方体木块削成一个最大的圆柱体,这个圆柱体的体积是多少?这就需要我们先分析,在正方体中削出最大的圆柱体,圆柱体的底面直径和高都等于正方体的棱长。
小升初数学知识点:数学知识点之平面图形知识点总结

小升初数学知识点:数学知识点之平面图形知识点总结为大家介绍小升初数学知识点:数学知识点之平面图形,考生们应多了解一些小升初信息,对大家会有很大帮助的。
平面图形1、长方形(1)特征对边相等,4个角都是直角的四边形。
有两条对称轴。
(2)计算公式c=2(a+b)s=ab2、正方形(1)特征:四条边都相等,四个角都是直角的四边形。
有4条对称轴。
(2)计算公式c=4as=a23、三角形(1)特征由三条线段围成的图形。
内角和是180度。
三角形具有稳定性。
三角形有三条高。
(2)计算公式s=ah/2(3)分类按角分锐角三角形:三个角都是锐角。
直角三角形:有一个角是直角。
等腰三角形的两个锐角各为45度,它有一条对称轴。
钝角三角形:有一个角是钝角。
按边分不等边三角形:三条边长度不相等。
等腰三角形:有两条边长度相等;两个底角相等;有一条对称轴。
等边三角形:三条边长度都相等;三个内角都是60度;有三条对称轴。
4、平行四边形(1)特征两组对边分别平行的四边形。
相对的边平行且相等。
对角相等,相邻的两个角的度数之和为180度。
平行四边形容易变形。
(2)计算公式s=ah5、梯形(1)特征只有一组对边平行的四边形。
中位线等于上下底和的一半。
等腰梯形有一条对称轴。
(2)公式s=(a+b)h/2=mh小升初数学知识点:数学知识点之平面图形一文就为大家整理到这儿了,小升初的同学们要好好复习。
更多精彩内容尽在。
小升初数学知识点复习之立体图形解析

(一)长方体 1、特征 六个面都是长方形(有时有两个相对的面是正方形)。 相对的面面积相等,12 条棱相对的 4 条棱长度相等。 有 8 个顶点。 相交于一个顶点的三条棱的长度分别叫做长、宽、高。 两个面相交的边叫做棱。 三条棱相交的点叫做顶点。 把长方体放在桌面上,最多只能看到三个面。 长方体或者正方体 6 个面的总面积,叫做它的外表积。 2、计算公式
本文格式为 Word 版,下载可任意编辑,页眉双击删除即可。
小升初数学知识点复习之立体图形解析
最新小升初数学学问点复习之立体图形解析 数学在人的生活中到处可见,息息相关。为大家共享的小升初数学学 问点复习之立体图形 ,供大家参考!
s=2(ab+ah+bh) V=sh V=abh (二)正方体 1、特征
s 侧=ch
都相等。
s 表=s 侧+s 底×2
通过球心并且两端都在球面上的线段,叫做球的直径,用 d 表示,每
v=sh/3
条直径都相等,直径的长度等于半径的 2 倍,即 d=2r。
(四)圆锥
2、计算公式 d=2r
1、圆锥的.认识
以上是为大家共享的小升初数学学问点复习之立体图形 ,盼望对大
圆锥的底面是个圆,圆锥的侧面是个曲面。
家有所关心!
从圆锥的顶点到底面圆心的距离是圆锥的高。
【最新小升初数学学问点复习之立体图形解析】
测量圆锥的高:先把圆锥的底面放平,用一块平板水平地放在圆锥的
顶点上面,竖直地量出平板和底面之间的距离。
把圆锥的侧面展开得到一个扇形。
第2页共2页
圆柱两个底面之间的距离叫做高。
(五)球
进一法:实际中,使用的材料都要比计算的结果多一些,因此,要保
1、认识
六年级下数学知识点讲解-小升初总复习 图形与几何第2课时立体图形的认识和测量

第2课时立体图形的认识和测量考点一表面积、体积、容积的含义及体积的单位1.表面积:物体表面面积的总和,叫做物体的表面积.表面积通常用S表示.常用面积单位是平方米、平方分米、平方厘米、平方千米、公顷.2.体积:物体所占空间的大小,叫做物体的体积.体积通常用V 表示.常用体积单位是立方米、立方分米、立方厘米.3.容积:箱子、油桶、仓库等所能容纳物体的体积,叫作它们的容积或容量.常用容积单位是升、毫升,1升=1000毫升.4.体积与容积单位之间的换算:1立方分米=1升,1立方厘米=1毫升.考点二常见立体图形的特征,侧面积、表面积和体积计算公式做一个长6分米、宽5分米、高4分米的玻璃鱼缸,至少需要多少平方分米的玻璃?【解】6×5+(6×4+5×4)×2=30+88=118(平方分米)答:至少需要118平方分米的玻璃.压路机的滚筒是一个圆柱,它的底面周长是3.14米,长是1.5米,每滚动一周能压多大面积的路面?如果它滚动20周,那么压路的面积是多少?【解】3.14×1.5=4.71(平方米)4.71×20=94.2(平方米)答:每滚动一周能压4.71平方米的路面;如果它滚动20周,那么压路的面积是94.2平方米.一个长方体,如果高减少2厘米,就成为正方体,表面积比原来减少48平方厘米,求原来长方体的体积.【解】48÷4÷2=6(厘米)6+2=8(厘米)6×6×8=288(立方厘米)答:原来长方体的体积是288立方厘米.一个高是30厘米的酒瓶中盛有酒,如果把它倒置在桌面上(如图所示),酒瓶的容积是多少?【解】3.14×(6÷2)2×[20+(30-25)]=3.14×9×25=706.5(立方厘米)答:这个酒瓶的容积是706.5立方厘米.。
小升初平面图形与立体图形专项复习

⼩升初平⾯图形与⽴体图形专项复习⼩升初平⾯图形与⽴体图形专项复习1、常⽤公式长⽅形/正⽅形的周长,⾯积公式平⾏四边形,三⾓形,梯形的⾯积公式长⽅体/正⽅体的表⾯积,体积圆,半圆,圆的⼀半的周长与⾯积公式圆柱的侧⾯积,表⾯积,体积公式圆锥的体积公式2、常见考点周长:不管求什么图形的周长,永远只算围在图形最外⾯的所有线段(直线/曲线)的总长度。
长⽅体或正⽅体的表⾯积:要分清楚算⼏个⾯,例如房间,鱼缸,抽屉,通风管圆柱的侧⾯积与展开图(正⽅形或长⽅形,长与宽和⾼与直径的对应关系)的⾯积关系3、常见技巧长⽅体,正⽅体,圆柱体的体积都可以⽤底⾯积 * ⾼来解决等底等⾼时,长⽅体,正⽅体,圆柱体的体积都是相等的。
在什么情况下,圆柱体的体积与圆锥体的体积之间的倍数对应关系利⽤体积相等来解决由⼀个⽴体图形到其他⽴体图形的转变,从⽽求出相应的⾼,或半径之类4、典型考题A、单位换算长度单位相邻进率为10,⾯积单位相邻进率为100,体积单位相邻进率为 1000,升,毫升与哪些单位的对应4.07⽴⽅⽶=()⽴⽅⽶()⽴⽅分⽶ 9.08⽴⽅分⽶=()升=()亳升B、倍数关系正⽅体的棱长扩⼤2倍,表⾯积扩⼤()倍,体积扩⼤()倍。
圆柱体的半径扩⼤3倍,体积扩⼤()倍。
圆的直径扩⼤3倍,周长扩⼤()倍,⾯积扩⼤()倍。
⼀个圆锥与⼀个圆柱的底⾯积相等,已知圆锥与圆柱的体积⽐是1:9,圆锥的⾼是4.8厘⽶,则圆柱的⾼是()厘⽶。
⼀个圆柱体和⼀个圆锥体等底等⾼,他们的体积和是72⽴⽅分⽶,圆锥的体积是()⽴⽅分⽶,圆柱体的体积是()⽴⽅分⽶。
把⼀个棱长6厘⽶的正⽅体⽊料加⼯成⼀个最⼤的圆锥体,这个圆锥体的体积是()⽴⽅厘⽶。
1C、棱长总和的计算⽤⼀根长48CM的铁丝,围成⼀个正⽅体,它的体积是(),表⾯积是()。
⽤⼀根长96CM的铁丝,围成⼀个长⽅体,与它顶点相连的三条边之和是()。
D、表⾯积的变形把⼀个长⽅体的长平均分成4段,每段长6厘⽶,表⾯积增加24平⽅厘⽶,求原来长⽅体的体积是多少⽴⽅厘⽶?⼀个长⽅体,前⾯和上⾯的⾯积之和是209平⽅厘⽶,这个长⽅体的长,宽,⾼都是以厘⽶为单位的质数,这个长⽅体的体积和表⾯积各是多少?⼀个正⽅体的表⾯积是96平⽅厘⽶,把它切成两个相等的长⽅体后,每个长⽅体的表⾯积是多少平⽅厘⽶?⼀个圆柱的侧⾯积是37.68平⽅分⽶,它的底⾯半径是3分⽶,它的⾼是多少分⽶?它的表⾯积是多少平⽅分⽶?把⼀段40厘⽶长的圆柱形⽊头沿其底⾯直径劈开,测得剖⾯⾯积是800平⽅厘⽶,求原来这段⽊头的表⾯积。
小升初立体图形数学知识点

小升初立体图形数学知识点立体图形数学知识点立体图形(一)长方体1特点立体图形数学知识点:六个面差不多上长方形(有时有两个相对的面是正方形)。
相对的面面积相等,12条棱相对的4条棱长度相等。
有8个顶点。
相交于一个顶点的三条棱的长度分别叫做长、宽、高。
两个面相交的边叫做棱。
三条棱相交的点叫做顶点。
把长方体放在桌面上,最多只能看到三个面。
长方体或者正方体6个面的总面积,叫做它的表面积。
2运算公式s=2(ab+ah+bh)V=shV=abh(二)正方体1特点六个面差不多上正方形六个面的面积相等12条棱,棱长都相等有8个顶点正方体能够看作专门的长方体2运算公式S表=6a2v=a3(三)圆柱1圆柱的认识圆柱的上下两个面叫做底面。
圆柱有一个曲面叫做侧面。
圆柱两个底面之间的距离叫做高。
进一法:实际中,使用的材料都要比运算的结果多一些,因此,要保留数的时候,省略的位上的是4或者比4小,都要向前一位进1。
这种取近似值的方法叫做进一法。
2运算公式s侧=chs表=s侧+s底2v=sh/3(四)圆锥1圆锥的认识圆锥的底面是个圆,圆锥的侧面是个曲面。
从圆锥的顶点到底面圆心的距离是圆锥的高。
测量圆锥的高:先把圆锥的底面放平,用一块平板水平地放在圆锥的顶点上面,竖直地量出平板和底面之间的距离。
把圆锥的侧面展开得到一个扇形。
2运算公式v=sh/3(五)球1认识球的表面是一个曲面,那个曲面叫做球面。
球和圆类似,也有一个球心,用O表示。
从球心到球面上任意一点的线段叫做球的半径,用r表示,每条半径都相等。
语文课本中的文章差不多上精选的比较优秀的文章,还有许多名家名篇。
假如有选择循序渐进地让学生背诵一些优秀篇目、杰出段落,对提高学生的水平会大有裨益。
现在,许多语文教师在分析课文时,把文章解体的支离破裂,总在文章的技巧方面下功夫。
结果教师费劲,学生头疼。
分析完之后,学生收效甚微,没过几天便忘的干洁净净。
造成这种事倍功半的尴尬局面的关键确实是对文章读的不熟。
小升初数学复习讲义24.立体图形的认识教案讲义及练习
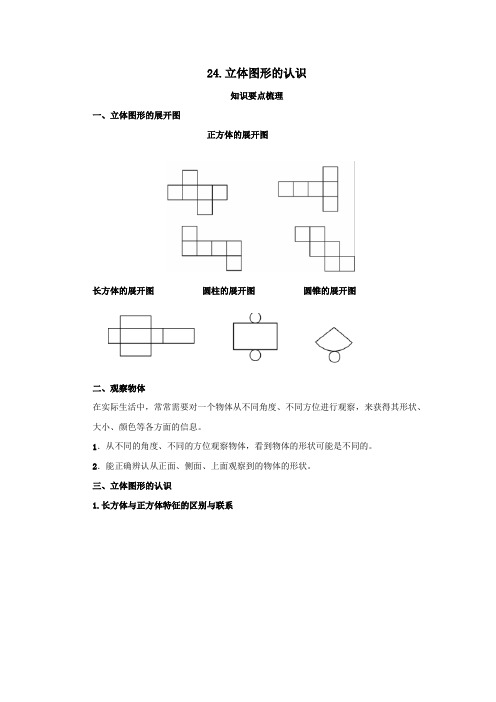
24.立体图形的认识知识要点梳理一、立体图形的展开图正方体的展开图长方体的展开图圆柱的展开图圆锥的展开图二、观察物体在实际生活中,常常需要对一个物体从不同角度、不同方位进行观察,来获得其形状、大小、颜色等各方面的信息。
1.从不同的角度、不同的方位观察物体,看到物体的形状可能是不同的。
2.能正确辨认从正面、侧面、上面观察到的物体的形状。
三、立体图形的认识1.长方体与正方体特征的区别与联系名称 图形 相同点 不同点 面 棱 顶点 面的特点 棱长长方体 6个 12条8个 6个面一般都是长方 形(也可能有两个相 对的面是正方形),相 对的面的面积相等, 相对棱长相等 每组(有3 组,分别叫 长、宽、高) 互相平行的4条棱相等 正方体6个 12条8个 6个面都是相等的正 方形 12条棱都 相等 2、圆柱、圆锥的特征考点精讲分析典例精讲考点1立体图形的认识【例1】 一个长方体的棱长总和是40厘米,其中长5厘米,宽3厘米,高是多少厘米?【精析】 根据长方体棱长总和的计算公式,计算出长方体的高。
名称 图形 特征 圆柱 由3个面围成,上、下两底面是面积 相等的圆。
侧面是一个曲面,沿高展 开是长方形或正方形。
两个底面之 间的距离叫做高,有无数条高。
圆锥 由2个面围成,底面是一个圆形。
侧 面是一个曲面,展开后是扇形。
顶点 到底面圆心的距离叫做高,只有一条高【答案】40÷4-5-3=2(厘米)答:高是2厘米。
【归纳总结】长方体的棱长总和=(长+宽+高)×4。
【例2】把一个大正方体木块表面涂上红色的漆(如图),锯成完全一样的27块小正方体木块。
小正方体中一面红色、二面红色、三面红色各有多少块?【精析】我们可以想象一下,大正方形被切割成小正方体后,一面有红色的在大正方体每个面的最中间(如A处),两面有红色的在大正方体每条棱的中间(如B处),三面有红色的在大正方体的8个角上(如C处),没有红色的在中心内部。
六年级下册数学讲义-小升初空间与图形-人教版(含答案)

空间与图形学生姓名年级学科授课教师日期时段核心内容平面图形和立体图形的拓展应用课型一对一/一对N教学目标1、能灵活运用计算公式求较复杂的平面图的周长或面积;2、能灵活运用计算公式求较复杂的立体图形的表面积或体积。
重、难点1、平面图形的特征、周长和面积公式的应用;2、立体图形的特征、表面积和体积公式的应用。
课首沟通1.回顾小学所学平面图形的特征、周长和面积公式。
2.回顾小学所学立体图形的特征、表面积和体积公式。
知识导图课首小测1.如右图,正方形的面积是5平方厘米,圆的面积是()平方厘米。
2.(黄埔区单元试题)用多种方法计算下面图形的面积。
3.下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
4.(广州市第二外国语学校面试真题)一个由27块小正方体组合而成的大正方体,表面被涂为黑色。
测量后发现,这个大正方体的棱长为2,那么所有小正方体未被涂黑部分的表面之和是多少?5.(省实天河面谈题)一个半圆里有一个小圆,求谁的面积大。
导学一:平面图形知识点讲解 1:求组合图形周长的方法。
组合图形的周长:围成组合图形的所有线段的长度和。
例 1. 如图所示,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等,图中阴影部分的周长是多少厘米?【学有所获】当发现无法用求半径或直径的方法去求阴影部分的周长时,要转换思考方向,考虑用其它方法来解答。
我爱展示1.计算下列图形的周长2.如右图为某楼梯的形状及长度(单位:米),要在楼梯表面铺地毯,地毯的长度至少需要()米.3.如图,用一根铁丝将四根直径2dm的管子紧紧捆住(接头处不计),至少需要铁丝多少分米?知识点讲解 2:求组合图形面积的常用方法。
1.平移法:将一个组合图形中的一部分平移,与另一部分组合成一个新的图形,再求出它的面积。
2.分割法:把一个组合图形分割成几个学过的规则图形,分别求出它们的面积后,再求它们的面积和。
3.割补法:把一个不规则图形的空缺部分补上一块或从其它地方割下一块补上,组成一个学过的规则图形,再求出其面积。
小升初立体图形知识点

小升初立体图形篇1、立体图形的分类:长方体、正方体、圆柱、圆锥2、棱长公式:长方体棱长之和=正方体棱长之和=3、表面积公式:长方体表面积=S=(a×b+a×c+b×c)×2正方体表面积=S=a×a×6=6a²圆柱表面积=S=πr²×2+2πr 圆柱体的侧面积=S=2πRh圆柱底面积=侧面积=4、体积公式:长方体体积=长×宽×高V=a×b×h=Sh 正方体体积=棱长×棱长×棱长V=a×a×a=a³圆柱体积=底面积×高V=Sh=πr²h 圆锥体积=31×底面积×高V=31×Sh 常见的题型:一、圆柱压路机:1.前进的路程:底面周长2.压路的面积:圆柱侧面积二、底面是正方形的长方体知识索引:画出底面是正方形的长方体的侧面展开图,写出这四个侧面的特点,写出这个长方形长、宽、高的特点。
底面是正方形的长方体,四个侧面:长方体的长=宽=正方形周长÷4三、、把一个圆柱的底面平均分成相等的若干小扇形,然后把圆柱切开,拼成一个近似的长方体(如图)特性:(1)长方体的长相当于圆柱的;(2)长方体的宽相当于圆柱的;(3)长方体的高相当于圆柱的;(4)长方体比圆柱增加了部分的表面积。
四、立体图形表面积的增加问题(1)圆柱切割后增加的面积:1刀2段:增加个面2刀3段:增加个面(2)长方体、正方体切割后增加的面积:1刀2段:增加个面2刀3段:增加个面(3)一个立体图形底面大小不变,高增加,则会跟着增加。
五、圆柱与圆锥之间的比较,可以用比的方法解决(1)底面圆:周长之比等于半径之比;面积之比等于半径的平方之比。
(2)体积之比:锥锥柱柱锥柱::h s V V 31h s =(3)高之比:)3()S V (h 锥锥柱柱锥柱::S V h ÷÷=(4)面积之比:)3()h V (S 锥锥柱柱锥柱::h V S ÷÷=六、往水中放入物体,使水面上升专题解析:抓住浸没问题的关键:水面上升(下降)的体积=物体浸没部分的体积即:容器底面积×水面上升(下降)的高度=物体底面积×高情形一:往容器里放物体(淹没或半淹没),水面上升,浸末增加V V =情形二:从容器里取出物体(淹没或半淹没),水面下降,浸末减少V V =七、展开图问题例题讲解1、将一块长方形铁皮,利用图中阴影的部分,刚好制成一个油桶,求这个油桶的体积。
小升初数学立体图形知识点详解

小升初数学立体图形知识点详解2019小升初数学立体图形知识点详解小升初数学是学习生涯的关键阶段,为了能够使同学们在数学方面有所建树,下面为大家分享小升初数学立体图形知识点,供大家参考!(一)立体图形【认识、表面积、体积】一、长方体、正方体都有6个面,12条棱,8个顶点。
正方体是特殊的长方体。
二、圆柱的特征:一个侧面、两个底面、无数条高。
三、圆锥的特征:一个侧面、一个底面、一个顶点、一条高。
四、表面积:立体图形所有面的面积的和,叫做这个立体图形的表面积。
五、体积:物体所占空间的大小叫做物体的体积。
容器所能容纳其它物体的体积叫做容器的容积。
六、圆柱和圆锥三种关系:①等底等高:体积1︰3②等底等体积:高1︰3③等高等体积:底面积1︰3七、等底等高的圆柱和圆锥:①圆锥体积是圆柱的1/3,②圆柱体积是圆锥的3倍,③圆锥体积比圆柱少2/3,④圆柱体积比圆锥多2倍。
柱里的沙子倒入圆锥中,发现三次正好倒完。
③通过实验发现:圆锥的体积等于和它等底等高的圆柱体积的三分之一;圆柱的体积等于和它等底等高的圆锥体积的三倍。
即:V=1/3Sh。
十、立体图形的棱长总和、表面积、体积计算公式:(二)图形与变换一、变换图形位置的方法有平移、旋转等,在变换位置时,每个图形的相应顶点、线段、曲线应同步平移,旋转相同的角度。
二、不改变图形的形状,只改变它的大小时,通常要使每个图形的要素,如长方形的长与宽,三角形的底与高等同时按相同比例放大或缩小。
三、对称图形是对称轴两边的图形经对折后能够完全重合,而不是完全相同。
(三)图形与位置一、当我们处在实际生活及情景中,面对教短距离时,通常用上、下、前、后来描述具体位置。
二、当我们面对地图、方位图时,通常用东、西、南、北,南偏东、北偏东……来描述方向。
再结合所示比例尺计算出具体距离,把方向与距离结合起来确定位置。
以上是为大家分享的小升初数学立体图形知识点,希望能够切实的帮助到大家,同时祝大家能够在小升初考试中取得优异的成绩!。
【小升初培优专题】六年级下册数学-立体几何综合训练(解析版)

【小升初培优专题】六年级下册数学-立体几何综合训练(解析版)知识点1、正方体表面积=棱长×棱长×6体积=棱长×棱长×棱长图形切拼:一刀两面2、长方体表面积=(长×宽+长×高+宽×高)×2体积=长×宽×高棱长和=(长+宽+高)×4切成最大的正方体:找长、宽的最大公约数展开图挖小正方体在角上挖:表面积不变在棱上挖:增加2个小正方形的面积在面上挖:增加4个小正方形的面积染色问题3面被染色:8个2面被染色:关注棱长1面被染色:关注面0面被染色:关注内部3、圆柱侧面积=Ch=2πrh表面积=2πrh +2πr ² 体积=Sh =πr ²h 4、圆锥体积=31×Sh =31πr ²h圆柱体体积是同底等高的圆锥体体积的3倍5、浸没问题完全浸没时,物体体积=水变化的体积6、三视图俯视图 标数视图主视图 左视图一、填空题。
(每道小题6分,共72分)1. 要拼成一个棱长为2厘米的正方体,需要 个棱长为1厘米的小正方体。
【解答】2×2×2=8(个)2. 一个长方体仓库从里面量约长10米,宽5米,高6米,如果放入棱长是2米的正方体木箱,至多可以放进 个。
【解答】分别从长、宽、高三个方向进行考虑:10÷2=5(个)长这个方向可以放5个;5÷2=2(个)……1(米),宽这个方向可以放2个; 6÷2=3(个),高这个方向可以放3个, 5×2×3=30(个),所以至多可以放30个。
3. 将一块长24厘米,宽18厘米,高12厘米的长方体木料,锯成尽可能大的同样大小的正方体木块,可以锯成块。
【解答】本题的关键在于正确解读"锯成尽可能大的同样大小的正方体木块"这句话,因为木块是整块整块的,所以正方体棱长必然是长、宽、高的公约数,要让木块尽可能大,那么棱长取长、宽、高的最大公约数即可。
北京小升初数学知识点复习:立体图形

2019年北京小升初数学知识点复习:立体图形北京小升初数学知识点复习:立体图形(一)长方体1特征六个面都是长方形(有时有两个相对的面是正方形)。
相对的面面积相等,12条棱相对的4条棱长度相等。
有8个顶点。
相交于一个顶点的三条棱的长度分别叫做长、宽、高。
两个面相交的边叫做棱。
三条棱相交的点叫做顶点。
把长方体放在桌面上,最多只能看到三个面。
长方体或者正方体6个面的总面积,叫做它的表面积。
2计算公式s=2(ab+ah+bh)V=shV=abh(二)正方体1特征六个面都是正方形六个面的面积相等12条棱,棱长都相等有8个顶点正方体可以看作特殊的长方体2计算公式S表=6a2v=a3(三)圆柱1圆柱的认识圆柱的上下两个面叫做底面。
圆柱有一个曲面叫做侧面。
圆柱两个底面之间的距离叫做高。
进一法:实际中,使用的材料都要比计算的结果多一些,因此,要保留数的时候,省略的位上的是4或者比4小,都要向前一位进1。
这种取近似值的方法叫做进一法。
2计算公式s侧=chs表=s侧+s底×2v=sh/3(四)圆锥1圆锥的认识圆锥的底面是个圆,圆锥的侧面是个曲面。
从圆锥的顶点到底面圆心的距离是圆锥的高。
测量圆锥的高:先把圆锥的底面放平,用一块平板水平地放在圆锥的顶点上面,竖直地量出平板和底面之间的距离。
把圆锥的侧面展开得到一个扇形。
2计算公式v=sh/3(五)球1认识球的表面是一个曲面,这个曲面叫做球面。
球和圆类似,也有一个球心,用O表示。
从球心到球面上任意一点的线段叫做球的半径,用r表示,每条半径都相等。
通过球心并且两端都在球面上的线段,叫做球的直径,用d 表示,每条直径都相等,直径的长度等于半径的2倍,即d=2r。
2计算公式家庭是幼儿语言活动的重要环境,为了与家长配合做好幼儿阅读训练工作,孩子一入园就召开家长会,给家长提出早期抓好幼儿阅读的要求。
我把幼儿在园里的阅读活动及阅读情况及时传递给家长,要求孩子回家向家长朗诵儿歌,表演故事。
小升初数学重要知识总结平面与立体形的性质与计算

小升初数学重要知识总结平面与立体形的性质与计算小升初数学重要知识总结:平面与立体形的性质与计算在小学数学中,平面与立体形是非常重要的概念。
它们不仅是基础知识,还是后续学习的基石。
本文将对平面与立体形的性质与计算进行总结。
一、平面的性质与计算1. 平面的定义:平面是一个没有厚度、无限扩展的二维几何图形。
2. 平面的要素:一个平面由无数个直线和点组成。
3. 平面的特点:- 平面上的任意两点可以用一条直线段连接。
- 平面上的任意三点不共线。
- 平面上的两条直线最多只有一个公共点。
- 平面上的两条平行直线不会相交。
4. 平面的计算:- 面积计算:平面上的图形的面积可以通过面积公式进行计算。
例如,长方形的面积等于长乘以宽。
- 周长计算:平面上的图形的周长可以通过边长或弧长进行计算。
例如,正方形的周长等于边长乘以4。
二、立体形的性质与计算1. 立体形的定义:立体形是一个有厚度、有长度和宽度的三维几何图形。
2. 立体形的要素:一个立体形由多个平面组成,可以包括表面、边和顶点。
3. 立体形的特点:- 立体形有体积,可以通过体积公式计算。
例如,长方体的体积等于长乘以宽乘以高。
- 立体形有表面积,可以通过表面积公式进行计算。
例如,正方体的表面积等于6倍的边长的平方。
- 立体形可以进行展开,展开后的平面图形称为展开图。
4. 立体形的计算:- 体积计算:立体形的体积可以通过体积公式进行计算。
例如,圆柱的体积等于底面积乘以高。
- 表面积计算:立体形的表面积可以通过表面积公式进行计算。
例如,球的表面积等于4πr的平方。
5. 不同形状的立体形:- 三棱柱:由两个平行的底面和三个连接底面对应顶点的棱所组成。
- 正四面体:由四个全等的三角形面和四个连接面对应顶点的棱所组成。
- 圆台:由一个圆形底面和连接底面和顶点的曲面所组成。
总结:小升初数学中,平面与立体形的性质与计算是基础中的基础。
掌握了平面与立体形的定义、特点和计算方法,对于后续的数学学习将有很大的帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆的应用题。
1、一座大钟的时针长30厘米,分针长40厘米。
一昼夜时针和分针的针尖经过的路程是多少厘米?2、一个半圆的周长是15.42分米,这个半圆的面积是多少平方分米?3、一个半圆的弧长为31.4cm,与这个半圆半径相等的圆的面积是多少?4、一个半圆的周长是51.4cm,与这个半圆半径相等的圆的面积是多少?5、一个边长是31.4cm的正方形内可容下多少个半径为5cm的圆?6、在一个边长是12cm的正方形内放入4个尽量大且相等的圆形,每个圆的面积是多少?7、一种压路机的前轮直径15分米,宽是2米。
如果每分钟滚动5圈,它每分钟前进多少米?每分钟压路面积是多少平方米?8、一个养鱼池周长是100.48米,中间有一个圆形小岛,半径是6米,这个养鱼池的水域面积是多少平方米?9、如果大圆半径是小圆半径的2倍,那么大圆的周长是小圆周长的()倍;面积比是()。
10、一根长31.4米的绳子,用它先围成正方形,再围成圆形,面积相差多少平方米?11、一个圆的直径是4厘米,增加到6厘米后,面积增加了多少平方厘米?12、猫和老鼠在一个半径是50米的圆周上的同一点向相反方向运动,猫每分钟走18.84米,老鼠每分钟走12.56米,当猫和老鼠相遇时,猫比老鼠多走了多少米?多边形的面积应用题1、一个梯形,下底长14厘米,高12厘米,如果下底减少6厘米,它就成为一个平行四边形。
梯形的面积是多少?2、有一块平行四边形的麦田,底275米,高60米,共收小麦19.8吨。
这块麦田有多少公顷?平均每公顷收小麦多少吨?3、一堆水泥电线杆堆成一个梯形,最上层有4根,最下层有12根,一共有5层,2堆这样的电线杆一共有多少根?4、刘店乡有一块长方形的牧地,长是宽的2倍,一辆汽车以每小时36千米的速度绕牧场一周需要0.5小时,这个牧场的面积是多少平方千米?5、一个三角形的底长3米,如果底延长1米,那么三角形的面积就增加1.2平方米,原来三角形的面积是多少平方米?6、用篱笆围成一个梯形养鸡场(如图),其中一边利用房屋墙壁。
已知篱笆长80m,求养鸡场的占地面积。
7、一个梯形的下底的长是上底的3倍,把上底延长8厘米,组成一个面积是288平方厘米的平行四边形。
原来梯形的面积是多少平方厘米?8、一块三角形地,底150m,高50m,共收油菜籽1762.5千克,平均每公顷产油菜籽多少千克?9、三角形的面积和平行四边形的面积相等,底也相等。
如果三角形的高是4米,平行四边形的高是多少米?10、求下面图形的面积(单位:m )。
11、计算下面图形中阴影部分的面积。
30dm12dm 5m3m25dm 5m组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
、③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
3、求下列图形的体积。
(单位:厘米)长方体和正方体综合练习一、基础知识1、4.07立方米=( )立方米( )立方分米 9.08立方分米=( )升=( )毫升2、一个正方体的棱长是7分米,它的表面积是()平方分米。
3、一个长方体的长是6厘米,宽和高都是4厘米,它的表面积是()平方厘米。
4、正方体的棱长扩大2倍,表面积扩大()倍。
体积扩大倍。
5、把一个棱长为6厘米的正方体分成两个大小、形状相同的长方体,每个长方体的表面积是()平方厘米。
6、用两个长4厘米、宽4厘米、高1厘米的长方体拼成一个大长方体,这个长方体的表面积最大是()平方厘米,最小是()平方厘米。
7、一个正方体的表面积是72平方分米,占地面积是( )平方分米。
8、一个长方体的体积是30立方厘米,长6厘米,宽5厘米,高( )厘米。
9、用一根长48cm的铁丝,围成一个正方体,它的体积是,表面积是。
10、用3个棱长4分米的正方体粘合成一个长方体,长方体的表面积比3个正方体的表面积少( )平方分米。
11、把一个长4分米,宽3分米,高2分米的长方体,沿着长锯成三段后,它的表面积比原来增加了平方分米。
12、一个长方体木块长6cm,宽4cm,高3cm,把它切成一个最大的正方体木块,要锯去()立方厘米。
13、把一个棱长是1分米的正方体木块切割成棱长是1cm的小正方体并把它们排起来,可排米长。
二、表面积、体积的计算1、把两个相同的正方体拼接成一个长方体,这个长方体的表面积是80平方厘米,问原来每个正方体的表面积是多少平方厘米?2、一个长方体,前面和上面的面积之和是209平方厘米,这个长方体的长、宽、高都是以厘米为单位的质数,这个长方体的体积和表面积各是多少?3、将3个表面积都是24平方厘米的正方体木块粘成一个长方体(如图),求这个长方体的表面积。
如果用6个这种正方体木块拼成一个长方体,那么长方体的表面积是多少平方厘米?4、一个正方体的表面积是96平方厘米,把它切成两个相等的长方体后,问每个长方体的表面积是多少平方厘米?5、将两个长都是8厘米,宽都是6厘米,高都是5厘米的长方体拼成一个大长方体,那么这个大长方体表面积最大是多少平方厘米?6、有一个长方体,长是8厘米,宽4厘米,高是6厘米,把它截成棱长是2厘米的若干个小正方体,这些正方体表面积之和比原来长方体的表面积增加了多少平方厘米?7、如图:正方体木块的表面积是36平方分米,把它沿虚线截成体积相等的8个正方体木块,这时表面积增加多少平方分米?8、在一个棱长是5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积。
9、一个正方体形状的木块,棱长为1米,沿着水平方向将它锯成3片,每片又按任意尺寸锯成4条,每条又按任意尺寸锯成5块,共得到大大小小的长方体60块。
问这60块长方体表面积的和是多少平方米?10、有一个底面是正方形的长方体,表面积是190平方厘米,如果用一个平行于底面的平面将它截成两个长方体,那么这两个长方体的表面积和为240平方厘米。
原来长方体的体积是多少立方厘米?三、长方体和正方体知识灵活运用1、一个正方体增高2厘米(底面不变)后,得到一个长方体,长方体的表面积比原来正方体的表面积增加96平方厘米,长方体的体积比正方体的体积增加立方厘米。
正方体的表面积是平方厘米。
2、如图:是一个由棱长为1厘米小正方体构成的,它的体积是多少?3、把一个长9厘米,宽7厘米,高3厘米的长方体铁块和一个棱长5厘米的正方体铁块熔铸成一个底面积是20平方厘米的长方体,求这个长方体的高。
4、一个长方体容器,底面是一个边长60厘米的正方形,容器里直立着一个高1米,底面边长是15厘米的长方体铁块,这时容器里的水深0.5米,现在把铁块轻轻地向上提起24厘米,那么露出水面的铁块上被水浸湿的部分长多少厘米?5、一个长方体水箱,从里面量长6分米,宽5分米,先倒入82升水,再浸入一块长2分米的正方体铁块,这时水面离水箱口1分米,这个水箱的容积是多少?6、把一个长方体的长平均分成4段,每段长6厘米,表面积增加24平方厘米,求原来长方体的体积是多少立方厘米?7、用大小相等的两个正方体拼成一个长方体,这个长方体的棱长总和是80厘米,每个正方体的体积是多少立方厘米?8、在一个棱长为3厘米的大正方体的顶部中央挖去一个棱长为1厘米的小立方体,求现在的表面积和体积。
9、棱长为1米的正方体2100个,堆成一个实心的长方体,它的高为10米,长和宽都大于高,问它的长和宽各为多少米?10、一块长方形铁皮(厚度不计),四个角剪去边长为2.8分米的正方形,焊成一个长方体铁皮盒,可以盛水546升,已知这块长方形铁皮的长是21.2分米,求长方形铁皮的面积。
11、一个长、宽、高分别是21厘米、15厘米、12厘米的长方体,现从它的上面尽可能大的切下一个正方体,然后从剩余的部分再尽可能大的切下一个正方体,最后再从第二次剩余的部分尽可能大的切下一个正方体,剩下的体积是多少立方厘米?12、在一个长15分米,宽12分米的长方体水箱中,有10分米深的水,如果在水中沉入一个棱长是30厘米的正方体铁块,那么,水箱中水深多少分米?13、有一块长方形的铁皮,长30厘米,宽20厘米,在这块铁皮的四角各剪下一个边长为2厘米的小正方形,然后制成一个无盖的长方体盒子,(1)求这个盒子的容积。
(2)做这个盒子用了多少平方厘米铁皮?14、一个长方体容器内装满水,现在有大、中、小三个铁球,第一次把小球沉入水中;第二次把小球取出,把中球沉入水中;第三次把中球取出,把小球和大球一起沉入水中,已知每次从容器中溢出的水量的情况是:第二次是第一次的3倍,第三次是第一次的2.5倍,问:大球的体积是小球的多少倍?15、将表面积分别为54平方厘米、96平方厘米、150平方厘米的三个铁质正方体熔铸成一个大正方体(不计损耗),则这个大正方体的体积是多少立方厘米?表面积是多少平方厘米?四、竞赛训练1、一个零件形状大小如下图:算一算,它的体积是多少立方厘米,表面积是多少平方厘米。
(单位:厘米)2、把一根长2米的长方形木料锯成1米长的两段,表面积增加了2平方分米,求这根木料原来的体积。
3、有一个长方体形状的零件,中间挖去一个正方形的孔(如图),你能算出它的体积和表面积吗?(单位:厘米)4、有一个棱长是4厘米的正方体,从它的一个顶点处挖去一个棱长是1厘米的正方体后,剩下物体的体积和表面积各是多少?5、一个正方体和一个长方体拼成了一个新的长方体,拼成的长方体的表面积比原来的长方体的表面积增加了50平方厘米。
原正方体的表面积是多少平方厘米?6、把4块棱长都是2分米的正方体粘成一个长方体,它们的表面积最多会减少多少平方分米?7、把11块相同的长方体砖拼成一个大长方体,已知每块砖的体积是288立方厘米,求大长方体的表面积。
8、一个长方体的体积是385立方厘米,且长、宽、高都是质数,求这个长方体的表面积。
9、一个长方体的长、宽、高是三个连续偶数,体积是960立方厘米,求它的表面积。
10、一个长方体和一个正方体的棱长之和相等,已知长方体的长、宽、高分别是6分米、4分米、5分米,求正方体的体积。
11、有两个无盖的长方体水箱,甲水箱里有水,乙水箱空着。
从里面量,甲水箱长40厘米,宽32厘米,水面高20厘米;乙水箱长30厘米,宽24厘米,深25厘米。
将甲水箱中部分水倒入乙水箱,使两箱水面高度一样,现在水面高多少厘米?12、一段钢材长15分米,横截面积是1.2平方厘米,如果把它锻造成一个横截面积是0.1平方厘米的钢筋,求这根钢筋的长。
13、有一个长方体容器,从里面量长5分米、宽4分米、高6分米,里面注有水,水深3分米。
