证明圆的切线经典例题 (1)

合集下载

中考压轴题圆的切线证明与计算(中考真题)

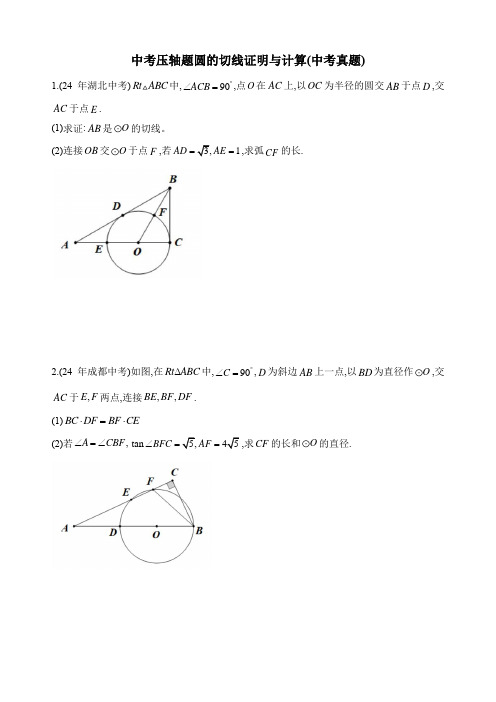
中考压轴题圆的切线证明与计算(中考真题)1.(24年湖北中考)Rt ABC 中,90ACB ︒∠=,点O 在AC 上,以OC 为半径的圆交AB 于点D ,交AC 于点E .(1)求证:AB 是O 的切线。

(2)连接OB 交O 于点F ,若1AD AE ==,求弧CF 的长.2.(24年成都中考)如图,在Rt ABC ∆中,90C ︒∠=,D 为斜边AB 上一点,以BD 为直径作O ,交AC 于,E F 两点,连接,,BE BF DF .(1)BC DF BF CE ⋅=⋅(2)若,A CBF ∠=∠tan BFC AF ∠==,求CF 的长和O 的直径.3.(24年浙江中考)如图,在圆内接四边形ABCD中,AD<AC,ADC BAD∠<∠,延长AD至点E,使AE=AC,延长BA至点F,连结EF,使AFE ADC∠=∠.(1)若60O∠的度数.∠=,CD为直径,求ABDAFE(2)求证:①EF∥BC ②EF=BD.4.(24年辽宁中考)如图,O是ABC的外接圆,AB是O的直径,点D在BC上,AC BD=,E ∠=∠．在BA的延长线上,CEA CAD(1)如图1,求证:CE是O的切线OA=,求BD的长．(2)如图2,若2CEA DAB∠=∠,85.(24年安徽中考)如图,O 是ABC ∆的外接圆,D 是直径AB 上一点,ACD ∠的平分线交AB 于点E ,交O 于另一点,.F FA FE =(1)求证:;CD AB ⊥(2)设FM AB ⊥,垂足为M ,若1OM OE ==,求AC 的长.6.(24年新疆中考)如图,在O 中,AB 是O 的直径,弦CD 交AB 于点E,AD BD =.(1)求证：△ACD ∽△ECB.(2)若AC=3,BC=1,求CE 的长.7.(24年江西中考)如图,AB 是半圆O 的直径,点D 是弦AC 延长线上一点,连接BD BC ，,60D ABC ∠=∠=︒．(1)求证:BD 是半圆O 的切线.(2)当3BC =时,求AC 的长．8.(24年呼伦贝尔中考)如图,在ABC 中,以AB 为直径的O 交BC 于点,D DE AC ⊥,垂足为E ． O 的两条弦,FB FD 相交于点,F DAE BFD ∠∠=．(1)求证:DE 是O 的切线;(2)若30,C CD ∠=︒=,求扇形OBD 的面积．9.(24年扬州中考)在综合实践活动中,“特殊到一般”是一种常用方法,我们可以先研究特殊情况,猜想结论,然后再研究一般情况,证明结论．如图,已知ABC ,CA CB =, O 是ABC 的外接圆,点D 在O 上(AD BD >),连接AD ,BD ,CD ．【特殊化感知】(1)如图1,若60ACB ∠=︒,点D 在AO 延长线上,则AD BD -与CD 的数量关系为________【一般化探究】(2)如图2,若60ACB ∠=︒,点C ,D 在AB 同侧,判断AD BD -与CD 的数量关系并说明理由【拓展性延伸】(3)若ACB α∠=,直接写出AD ,BD ,CD 满足的数量关系．(用含α的式子表示)10.(24年赤峰中考)如图,ABC中,90ACB∠=︒,AC BC=,O经过B,C两点,与斜边AB交于点E,连接CO并延长交AB于点M,交O于点D,过点E作EF CD∥,交AC于点F．(1)求证:EF是O的切线;(2)若BM=,1tan2BCD∠=,求OM的长．11.(24年绥化中考)如图1,O是正方形ABCD对角线上一点,以O为圆心,OC长为半径的O 与AD相切于点E,与AC相交于点F．(1)求证:AB与O相切．(2)若正方形ABCD1,求O的半径．(3)如图2,在(2)的条件下,若点M是半径OC上的一个动点,过点M作MN OC⊥交CE于点N．当:1:4CM FM=时,求CN的长．12.(24年河北中考)已知O的半径为3,弦MN=ABC中.∠=︒==在平面上,先将ABC和O按图1位置摆放(点B与点N重90,3,ABC AB BC合,点A在O上,点C在O内),随后移动ABC,使点B在弦MN上移动,点A始终在O上=．随之移动,设BN x(1)当点B与点N重合时,求劣弧AN的长.(2)当OA MN∥时,如图2,求点B到OA的距离,并求此时x的值.(3)设点O到BC的距离为d．①当点A在劣弧MN上,且过点A的切线与AC垂直时,求d的值.①直接写出d的最小值．13.(24年滨州中考)【教材呈现】现行人教版九年级下册数学教材85页“拓广探索”第14题: 如图,在锐角ABC 中,探究sin a A ,sin b B ,sin c C之间的关系．(提示:分别作AB 和BC 边上的高．)【得出结论】sin sin sin a b c A B C==．【基础应用】在ABC 中,75B ∠=︒,45C ∠=︒,2BC =,利用以上结论求AB 的长;【推广证明】进一步研究发现,sin sin sin a b c A B C==不仅在锐角三角形中成立,在任意三角形中均成立,并且还满足2sin sin sin a b c R A B C===(R 为ABC 外接圆的半径)．请利用图1证明:2sin sin sin a b c R A B C ===．【拓展应用】如图2,四边形ABCD 中,2AB =,3BC =,4CD =,90B C ∠=∠=︒．求过A,B,D 三点的圆的半径．14.(24年苏州中考)如图,ABC 中,AB =为AB 中点,BAC BCD ∠=∠cos ADC ∠=. O 是ACD 的外接圆．(1)求BC 的长(2)求O 的半径．15.(24年乐山中考)如图,O 是ABC 的外接圆,AB 为直径,过点C 作O 的切线CD 交BA 延长线于点D,点E 为CB 上一点,且AC CE =．(1)求证:DC AE ∥;(2)若EF 垂直平分OB ,3DA =,求阴影部分的面积．16.(24年武汉中考)如图,ABC ∆为等腰三角形,O 是底边BC 的中点,腰AC 与半圆O 相切于点D ,底边BC 与半圆O 交于E ,F 两点．(1)求证:AB 与半圆O 相切(2)连接OA ．若4CD =,2CF =,求sin OAC ∠的值．17.(24年甘肃武威中考)如图,AB 是O 的直径,BC BD =,点E 在AD 的延长线上,且ADC AEB ∠=∠．(1)求证:BE 是O 的切线;(2)当O 的半径为2,3BC =时,求tan AEB ∠的值．18.(24年深圳中考)如图,在ABD △中,AB BD =,O 为ABD △的外接圆,BE 为O 的切线,AC 为O 的直径,连接DC 并延长交BE 于点E ．(1)求证:DE BE ⊥(2)若AB =5BE =,求O 的半径．19.(24年盐城中考)如图,点C 在以AB 为直径的O 上,过点C 作O 的切线l,过点A 作AD l ⊥,垂足为D,连接AC BC 、．(1)求证:ABC ACD △△∽;(2)若5AC =,4CD =,求O 的半径．20.(24年广西中考)如图,已知O 是ABC ∆的外接圆,AB AC =．点D,E 分别是BC ,AC 的中点,连接DE 并延长至点F,使DE EF =,连接AF ．(1)求证:四边形ABDF 是平行四边形(2)求证:AF 与O 相切(3)若3tan 4BAC ∠=,12BC =,求O 的半径． 21.(24年四川广安中考)如图,点C 在以AB 为直径的O 上,点D 在BA 的延长线上,DCA CBA ∠=∠．(1)求证:DC 是O 的切线;(2)点G 是半径OB 上的点,过点G 作OB 的垂线与BC 交于点F ,与DC 的延长线交于点E ,若4sin 5D =,2DA FG ==,求CE 的长．22.(24年四川南充中考)如图,在O 中,AB 是直径,AE 是弦,点F 是AE 上一点,AF BE =,,AE BF 交于点C,点D 为BF 延长线上一点,且CAD CDA ∠=∠．(1)求证:AD 是O 的切线．(2)若4,BE AD ==求O 的半径长．23.(24年四川泸州中考)如图,ABC ∆是O 的内接三角形,AB 是O 的直径,过点B 作O 的切线与AC 的延长线交于点D,点E 在O 上,AC CE =,CE 交AB 于点F ．(1)求证:CAE D ∠=∠;(2)过点C 作CG AB ⊥于点G,若3OA =,BD =求FG 的长．24.(24年四川德阳中考)已知O 的半径为5,B C 、是O 上两定点,点A 是O 上一动点,且60,BAC BAC ∠=︒∠的平分线交O 于点D ．(1)证明:点D 为BC 上一定点;(2)过点D 作BC 的平行线交AB 的延长线于点F ．①判断DF 与O 的位置关系,并说明理由;①若ABC 为锐角三角形,求DF 的取值范围．25.(24年四川宜宾中考)如图,ABC 内接于O ,10AB AC ==,过点A 作AE BC ∥,交O 的直径BD 的延长线于点E,连接CD ．(1)求证:AE 是O 的切线;(2)若1tan 2ABE ∠=,求CD 和DE 的长．26.(24年内蒙古通辽中考)如图,ABC 中,90ACB ∠=︒,点O 为AC 边上一点,以点O 为圆心,OC 为半径作圆与AB 相切于点D ,连接CD ．(1)求证:2ABC ACD ∠=∠;(2)若8AC =,6BC =,求O 的半径．27.(24年四川达州中考)如图,BD 是O 的直径．四边形ABCD 内接于O ．连接AC ,且AB AC =,以AD 为边作DAF ACD ∠=∠交BD 的延长线于点F ．(1)求证:AF 是O 的切线;(2)过点A 作AE BD ⊥交BD 于点E ．若3CD DE =,求cos ABC ∠的值．28.(24年四川遂宁中考)如图,AB 是O 的直径,AC 是一条弦,点D 是AC 的中点,DN AB ⊥于点E ,交AC 于点F ,连结DB 交AC 于点G ．(1)求证:AF DF =;(2)延长GD 至点M ,使DM DG =,连接AM ．①求证:AM 是O 的切线;①若6DG =,5DF =,求O 的半径．29.(24年包头中考)如图,AB 是O 的直径,,BC BD 是O 的两条弦,点C 与点D 在AB 的两侧,E 是OB 上一点(OE BE >),连接,OC CE ,且2BOC BCE ∠=∠．(1)如图1,若1BE =,CE =求O 的半径;(2)如图2,若2BD OE =,求证:BD OC ∥．(请用两种证法解答)30.(24年四川自贡中考)在Rt ABC △中,90C ∠=︒,O 是ABC 的内切圆,切点分别为D,E,F ．(1)图1中三组相等的线段分别是CE CF =,AF =________,BD =________;若3AC =,4BC =,则O 半径长为________;(2)如图2,延长AC 到点M,使AM AB =,过点M 作MN AB ⊥于点N ．求证:MN 是O 的切线．31.(24年山东枣庄中考)如图,在四边形ABCD 中,AD BC ∥,60DAB ∠=︒,22AB BC AD ===．以点A 为圆心,以AD 为半径作DE 交AB 于点E ,以点B 为圆心,以BE 为半径作EF 所交BC 于点F ,连接FD 交EF 于另一点G ,连接CG ．(1)求证：CG 为EF 所在圆的切线(2)求图中阴影部分面积．(结果保留π)32.(24年青海中考) 如图,直线AB经过点C,且OA OB=．=,CA CB(1)求证:直线AB是O的切线;(2)若圆的半径为4,30∠=︒,求阴影部分的面积．B中考压轴题圆的切线证明与计算答案1.(24年湖北中考)【答案】(1)略 (2)弧CF 的长为3π2.(24年成都中考)【答案】(1)略(2)CF =;O 的直径为3.(24年浙江中考)【答案】(1)30o (2)证明略4.(24年辽宁中考)【答案】(1)见详解 (2)2π5.(24年安徽中考)【答案】(1)略 (2).6.(24年新疆中考)【答案】(1) 略 (2)CE =.7.(24年江西中考)【答案】(1)见解析 (2)2π8.(24年呼伦贝尔中考)【答案】(1)略 (2)43π 9.(24年扬州中考)【答案】(1)AD BD CD -=.(2)AD BD CD -=(3)当D 在BC 上时,2sin 2CD AD BD α⋅=-.当D 在AB 上时,2sin 2CD AD BD α⋅=+10.(24年赤峰中考)【答案】(1)略 (2)OM =11.(24年绥化中考)【答案】(1)证明略 (2)12.(24年河北中考)【答案】(1)π (2)点B 到OA 的距离为2;3 (3)①3d =2313.(24年滨州中考)【答案】教材呈现:见解析;基础应用:AB =;推广证明:见解析;拓展应用:6R =．14.(24年苏州中考)【答案】(1)4BC = (2)O 的半径为715.(24年乐山中考)【答案】(1)略 (2)3π-16.(24年武汉中考)【答案】(1)略 (2)4517.(24年甘肃武威中考)【答案】(1)略 (2)tan 3AEB ∠=18.(24年深圳中考)【答案】(1)略 (2)19.(24年盐城中考)【答案】(1)略 (2)25620.(24年广西中考)【答案】(1)略 (2)略 (3)1021.(24年四川广安中考)【答案】(1)略 (2)1422.(24年四川南充中考)【答案】(1)略 (2)23.(24年四川泸州中考)【答案】(1)证明略 (2)45 24.(24年四川德阳中考)【答案】(1)证明略(2)①DF 与O 相切,理由见解析;①DF 的取值范围为2DF <<25.(24年四川宜宾中考)【答案】(1)略 (2)CD =DE =． 26.(24年内蒙古通辽中考)【答案】(1)证明略 (2)327.(24年四川达州中考)【答案】(1)证明略 28.(24年四川遂宁中考)【答案】(1)证明略 (2)①证明略,①O 的半径为203． 29.(24年包头中考)【答案】(1)3 (2)略30.(24年四川自贡中考)【答案】(1)AD ;BE ;1 (2)略31.(24年山东枣庄中考)【答案】(1)略 3π32.(24年青海中考) 【答案】(1)详见解析 (2) 83S π=阴影。

专题证明圆的切线的常用方法(六大题型)(解析版)

（苏科版）九年级上册数学《第2章对称图形---圆》专题证明圆的切线的常用的方法★★★方法指引：证明一条直线是圆的切线的方法及辅助线作法：1、有交点：连半径、证垂直：当直线和圆有一个公共点时，把圆心和这个公共点连接起来，然后证明直线垂直于这条半径，简称：“有交点，连半径，证垂直”.2、无交点：作垂直、证半径：当直线和圆的公共点没有明确时，可以过圆心作直线的垂线，再证圆心到直线的距离等于半径，简称：“无交点，作垂直，证半径”.类型一：有公共点：连半径，证垂直●●【典例一】（2022•雁塔区校级模拟）如图，AB 是⊙O 的直径，点D 在直径AB 上（D 与A ，B 不重合），CD ⊥AB ，且CD ＝AB ，连接CB ，与⊙O 交于点F ，在CD 上取一点E ，使得EF ＝EC ．求证：EF 是⊙O 的切线；【分析】连接OF ，根据垂直定义可得∠CDB ＝90°，从而可得∠B +∠C ＝90°，然后利用等腰三角形的性质可得∠B ＝∠OFB ，∠C ＝∠EFC ，从而可得∠OFB +∠EFC ＝90°，最后利用平角定义可得∠OFE ＝90°，即可解答；【解答】证明：连接OF ，∵CD ⊥AB ，∴∠CDB ＝90°，∴∠B +∠C ＝90°，∵OB ＝OF ，EF ＝EC ，∴∠B ＝∠OFB ，∠C ＝∠EFC，∴∠OFB+∠EFC＝90°，∴∠OFE＝180°﹣（∠OFB+∠EFC）＝90°，∵OF是⊙O的半径，∴EF是⊙O的切线：【点评】本题考查了切线的判定与性质，勾股定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．【变式1-1】（2022•澄城县三模）如图，AB是△ABC外接圆⊙O的直径，过⊙O外一点D作BC的平行线分别交AC，AB于点G，E，交⊙O于点F，连接DB，CF，∠BAC＝∠D．求证：BD是⊙O的切线；【分析】证明∠ABD＝90°，根据切线的判定可得BD与⊙O相切；【解答】证明：∵AB是⊙O的直径，∴∠ACB＝90°，∵DG∥BC，∴∠AGE＝∠ACB＝90°，∴∠A+∠AEG＝90°，又∵∠A＝∠D，∠AEG＝∠DEB，∴∠D+∠DEB＝90°，∴∠DBE＝90°，∴AB⊥BD，∵AB为直径，∴BD与⊙O相切；【点评】此题考查了切线的判定，垂径定理，解答本题需要我们熟练掌握切线的判定．【变式1-2】如图，AB是⊙O的直径，点C是圆上一点，CD⊥AB于点D，点E是圆外一点，CA平分∠ECD．求证：CE是⊙O的切线．【分析】利用切线的判定定理证明∠OCE＝90°即可得出结论．【解答】证明：∵CA平分∠ECD，∴∠ECA＝∠DCA．∵CD⊥AB，∴∠CAD+∠DCA＝90°，∴∠ECA+∠CAD＝90°．∵OA＝OC，∴∠CAD＝∠ACO，∴∠ECA+∠ACO＝90°，即∠OCE＝90°，∴OC⊥EC，∵OC是⊙O的半径，∴CE是⊙O的切线．【点评】本题主要考查了圆的切线的判定，熟练应用圆的切线的判定定理是解题的关键．【变式1-3】（2022秋•阳谷县校级期末）如图，△ABC内接于半圆，AB是直径，过A作直线MN，∠MAC＝∠ABC，D是弧AC的中点，连接BD交AC于G，过D作DE⊥AB于E，交AC于F．（1）求证：MN是半圆的切线．（2）求证：FD＝FG．【分析】（1）欲证明MN是半圆的切线，只需证得∠MAB＝90°，即MA⊥AB即可；（2）根据圆周角定理推论得到∠ACB＝90°，由DE⊥AB得到∠DEB＝90°，则∠1+∠5＝90°，∠3+∠4＝90°，又D是弧AC的中点，即弧CD＝弧DA，得到∠3＝∠5，于是∠1＝∠4，利用对顶角相等易得∠1＝∠2，则有FD＝FG．【解答】证明：（1）如图，∵AB是直径，∴∠ACB＝90°，∴∠CAB+∠ABC＝90°．又∵∠MAC＝∠ABC，∴∠MAC+∠CAB＝90°，即∠MAB＝90°，∴MA⊥AB．∴MN是半圆的切线．（2）∵AB为直径，∴∠ACB＝90°，而DE⊥AB，∴∠DEB＝90°，∴∠1+∠5＝90°，∠3+∠4＝90°，∵D是弧AC的中点，即弧CD＝弧DA，∴∠3＝∠5，∴∠1＝∠4，而∠2＝∠4，∴∠1＝∠2，∴FD＝FG．【点评】本题考查了切线的判定：经过半径的外端点，并且与半径垂直的直线是圆的切线．也考查了圆周角定理及其推论、三角形外角的性质以及等腰三角形的判定．【变式1-4】如图，AB为⊙O的直径，PD切⊙O于点C，与BA的延长线交于点D，DE⊥PO交PO延长线于点E，连接OC，PB，已知PB＝6，DB＝8，∠EDB＝∠EPB．（1）求证：PB是⊙O的切线；（2）求⊙O的半径．（3）连接BE，求BE的长．【分析】（1）由已知角相等及直角三角形的性质得到∠OBP为直角，即可得证；（2）在直角三角形PBD中，由PB与DB的长，利用勾股定理求出PD的长，由切线长定理得到PC＝PB ＝6，由PD﹣PC求出CD的长，在直角三角形OCD中，设OC＝r，则有OD＝8﹣r，利用勾股定理列出关于r的方程，求出方程的解得到r的值，即为圆的半径．（3）延长PB、DE相交于点F，证明△PED≌△PEF（ASA），由全等三角形的性质得出PD＝PF＝10，DE ＝EF，求出DF的长，则可得出答案．【解答】（1）证明：∵DE⊥PE，∴∠DEO＝90°，∵∠EDB＝∠EPB，∠BOE＝∠EDB+∠DEO，∠BOE＝∠EPB+∠OBP，∴∠OBP＝∠DEO＝90°，∴OB⊥PB，∴PB为⊙O的切线；（2）解：在Rt△PBD中，PB＝6，DB＝8，根据勾股定理得：PD=10，∵PD与PB都为⊙O的切线，∴PC＝PB＝6，∴DC＝PD﹣PC＝10﹣6＝4；在Rt△CDO中，设OC＝r，则有OD＝8﹣r，根据勾股定理得：（8﹣r）2＝r2+42，解得：r＝3，则圆的半径为3．（3）延长PB、DE相交于点F，∵PD与PB都为⊙O的切线，∴OP平分∠CPB，∴∠DPE＝∠FPE，∵PE⊥DF，∴∠PED＝∠PEF＝90°，又∵PE＝PE，∴△PED ≌△PEF （ASA ），∴PD ＝PF ＝10，DE ＝EF ，∴BF ＝PF ﹣PB ＝10﹣6＝4，在Rt △DBF 中，DF==∴BE =12DF =【点评】本题考查了切线的判定和性质，勾股定理，平行线的性质，全等三角形的判定和性质，熟练掌握性质定理是解题的关键．●●【典例二】如图，△ABC 是直角三角形，点O 是线段AC 上的一点，以点O 为圆心，OA 为半径作圆．O 交线段AB 于点D ，作线段BD 的垂直平分线EF ，EF 交线段BC 于点．（1）若∠B ＝30°，求∠COD 的度数；（2）证明：ED 是⊙O 的切线．【分析】（1）根据三角形的内角和定理得到∠A ＝60°，根据等腰三角形的性质得到∠ODA ＝∠A ＝60°，于是得到∠COD ＝∠ODA +∠A ＝120°；（2）根据线段垂直平分线的性质得到∠EDB ＝∠B ＝30°，求得ED ⊥DO ，根据切线的判定定理即可得到结论．【解答】（1）解：∵∠C ＝90°，∠B ＝30°，∴∠A ＝60°，∵OD ＝OA，∴∠COD＝∠ODA+∠A＝120°；（2）证明：∵EF垂直平分BD，∴∠EDB＝∠B＝30°，∴∠EDO＝180°﹣∠EDB﹣∠ODA＝180°﹣30°﹣60°＝90°，∴ED⊥DO，∵OD是⊙O的半径，∴ED是⊙O的切线．【点评】本题考查了切线的判定，等腰三角形的性质，线段垂直平分线的性质，熟练掌握切线的判定定理是解题的关键．【变式2-1】如图，AB为⊙O的直径，点C，D在⊙O上，AC=CD=DB，DE⊥AC．求证：DE是⊙O的切线．【分析】连接OD，根据已知条件得到∠BOD=13×180°=60°，求得∠EAD=∠DAB=12∠BOD=30°，根据等腰三角形的性质得到∠ADO＝∠DAB＝30°，求得∠EDA＝60°，根据切线的判定定理即可得到结论．【解答】证明：连接OD，∵AC=CD=DB，∴∠BOD=13×180°=60°，∵CD=DB，∴∠EAD=∠DAB=12∠BOD=30°，∵OA＝OD，∴∠ADO＝∠DAB＝30°，∵DE⊥AC，∴∠E＝90°，∴∠EDA＝60°，∴∠EDO＝∠EDA+∠ADO＝90°，∴OD⊥DE，∵OD是⊙O的半径，∴DE是⊙O的切线．【点评】本题考查了切线的判定，等腰三角形的性质，正确的作出辅助线是解题的关键．【变式2-2】如图，AC是⊙O的直径，B在⊙O上，BD平分∠ABC交⊙O于点D，过点D作DE∥AC交BC的延长线于点E．求证：DE是⊙O的切线．【分析】连接OD，根据圆周角定理的推论得到∠ABC＝90°，根据角平分线的性质求出∠DBE＝45°，根据圆周角定理得到∠DOC，根据平行线的性质求出∠ODE＝90°，根据切线的判定定理证明结论；【解答】证明：连接OD，∵AC是⊙O的直径，∴∠ABC＝90°，∵BD平分∠ABC，∴∠DBE＝45°，∴∠DOC＝2∠DBE＝90°，∵DE∥AC，∴∠ODE＝∠DOC＝90°，∴DE是⊙O的切线；【点评】本题考查的是切线的判定定理、圆周角定理以及正方形的判定和性质，掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键．【变式2-3】（2023•鼓楼区校级模拟）如图，在⊙O中，AB为⊙O的直径，AC为弦，OC＝4，∠OAC＝60°．（1）求∠AOC的度数；（2）在图（1）中，P为直径BA的延长线上一点，且S△PAC=PC为⊙O的切线；【分析】（1）根据等腰三角形中有一角为60度时是等边三角形得到△ACO是等边三角形，则∠AOC＝60°；（2）由等边三角形的性质以及勾股定理得出CD的长，再利用三角形外角的性质以及等腰三角形的性质得出∠PCA＝30°，进而得出答案；【解答】（1）解：在△OAC中，∵OA＝OC＝4，∠OAC＝60°，∴△OAC是等边三角形，∴∠AOC＝60°；（2）证明：过点C作CD⊥AO于点D，∵△AOC是等边三角形，CD⊥AO，∴AD＝DO=12OA＝2，∠ACO＝60°，∴CD∵S △PAC ＝∴12PA •CD ＝∴PA ＝4，∴PA ＝AC ，∴∠P ＝∠PCA =12∠OAC ＝30°，∴∠PCO ＝∠PCA +∠ACO ＝30°+60°＝90°，∴OC ⊥PC ，∵OC 是⊙O 的半径，∴PC 为⊙O 的切线．【点评】本题考查了等边三角形的判定和性质，切线的判定，熟练掌握相关的性质和判定是解决问题的关键．【变式2-4】（2023•门头沟区二模）如图，AB 是⊙O 直径，弦CD ⊥AB 于E ，点F 在CD 上，且AF ＝DF ，连接AD ，BC ．（1）求证：∠FAD ＝∠B（2）延长FA 到P ，使FP ＝FC ，作直线CP ．如果AF ∥BC ．求证：直线CP 为⊙O 的切线．【分析】（1）根据垂径定理、圆周角定理可得∠ACD ＝∠ACD ＝∠B ，根据等腰三角形的性质可得∠FAD＝∠FDA，进而可得∠FAD＝∠B；（2）根据平行线的性质以及三角形内角和定理可得∠FAB＝∠FAD＝∠FDA＝30°，进而得到∠CFP＝60°，再利用等边三角形的性质可得∠PCO＝60°+30°＝90°，由切线的判定方法可得结论．【解答】证明：（1）如图，连接AC，∵AB是⊙O直径，弦CD⊥AB，∴AC=AD，∴∠ACD＝∠ACD＝∠B，∵AF＝FD，∴∠FAD＝∠FDA，∴∠FAD＝∠B；（2）如图，连接OC，∵AF∥BC，∴∠FAB＝∠B，∴∠FAB＝∠FAD＝∠FDA，∵∠AED＝90°，∴∠FAB＝∠FAD＝∠FDA＝30°，∴∠CFP＝60°，∵FP＝FC，∴△CFP是等边三角形，∴∠PCF＝60°，∵OB＝OC，∴∠B＝∠OCB＝30°，∴∠OCD＝30°，∴∠PCO＝60°+30°＝90°，即OC⊥PC，∵OC是半径，∴PC是⊙O的切线．【点评】本题考查切线的判定，圆周角定理、平行线的性质以及三角形内角和定理，掌握切线的判定方法，圆周角定理是正确解答的前提．●●【典例三】如图，四边形ABCD 内接于⊙O ，AB 为⊙O 的直径，过点C 作CE ⊥AD 交AD 的延长线于点E ，延长EC ，AB 交于点F ，∠ECD ＝∠BCF ．求证：CE 为⊙O 的切线；【分析】连接OC ，BD ，可推出EF ∥BD ，进而可证CD =BC ，进而得出CE 为⊙O 的切线；【解答】证明：如图1，连接OC ，BD ，∵AB 是⊙O 的直径，∴∠ADB ＝90°，∵CE ⊥AE，∴∠E＝∠ADB，∴EF∥BD，∴∠ECD＝∠CDB，∠BCF＝∠CBD，∵∠ECD＝∠BCF，∴∠CDB＝∠CBD，∴CD=BC，∴半径OC⊥EF，∴CE为⊙O的切线；【点评】本题考查了圆周角定理及其推论，圆的切线判定，解决问题的关键是作合适的辅助线．【变式3-1】（2022秋•阿瓦提县校级期末）已知：AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使AB＝AC，连结AC，过点D作DE⊥AC，垂足为E．求证：DE为⊙O的切线．【分析】连接OD，根据OA＝OB，CD＝BD，得出OD∥AC，∠ODE＝∠CED，再根据DE⊥AC，即可证出OD⊥DE，从而得出答案．【解答】证明：如图，连接OD．∵AB是⊙O的直径，∴∠ADB＝90°，∴CD＝BD，∵OA＝OB，∴OD∥AC．∴∠ODE＝∠CED．∵DE⊥AC，∴∠CED＝90°．∴∠ODE＝90°，∴OD⊥DE，∵OD是⊙O的半径，∴DE是⊙O的切线．【点评】本题考查了切线的判定与性质，解决本题的关键是掌握圆周角定理的推论、线段垂直平分线的性质以及等边三角形的判定，是一道常考题型．【变式3-2】已知，如图，在△ABC中，BC＝AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．（1）求证：点D是AB的中点；（2）判断DE与⊙O的位置关系，并证明你的结论．【分析】（1）连接CD，如图，根据圆周角定理，由BC为直径得到∠BDC＝90°，然后根据等腰三角形的性质得AD＝BD；（2）连接OD，先得到OD为△ABC的中位线，再根据三角形中位线性质得OD∥AC，而DE⊥AC，则DE⊥OD，然后根据切线的判定定理可得DE为⊙O的切线．【解答】（1）证明：连接CD，如图，∵BC为直径，∴∠BDC＝90°，∴CD⊥AB，∵AC＝BC，∴AD＝BD，即点D是AB的中点；（2）解：DE与⊙O相切．理由如下：连接OD，∵AD＝BD，OC＝OB，∴OD为△ABC的中位线，∴OD∥AC，而DE⊥AC，∴DE⊥OD，∴DE为⊙O的切线．【点评】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．【变式3-3】如图，已知点E在△ABC的边AB上，∠C＝90°，∠BAC的平分线交BC于点D，且D在以AE为直径的⊙O上．（1）求证：BC是⊙O的切线；（2）已知∠B＝30°，CD＝4，求线段AB的长．【分析】（1）连接OD，根据角平分线的定义得到∠BAD＝∠CAD，而∠OAD＝∠ODA，则∠ODA＝∠CAD，于是判断OD∥AC，由于∠C＝90°，所以∠ODB＝90°，然后根据切线的判定定理即可得到结论；（2）由∠B＝30°得到∠BAC＝60°，则∠CAD＝30°，在Rt△ADC中，根据含30度的直角三角形三边的关系得到AC＝Rt△ABC中，根据含30度的直角三角形三边的关系可得到AB＝【解答】（1）证明：连接OD，如图，∵∠BAC的平分线交BC于点D，∴∠BAD＝∠CAD，∵OA＝OD，∴∠OAD＝∠ODA，∴∠ODA＝∠CAD，∴OD∥AC，∵∠C＝90°，∴∠ODB＝90°，∴OD⊥BC，∴BC是⊙O的切线；（2）解：∵∠B＝30°，∴∠BAC＝60°，∴∠CAD＝30°，在Rt△ADC中，DC＝4，∴AC=＝在Rt△ABC中，∠B＝30°，∴AB＝2AC＝【点评】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了含30度的直角三角形三边的关系．【变式3-4】如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD，垂足为E，DA平分∠BDE．（1）求证：AE是⊙O的切线；（2）若∠DBC＝30°，DE＝1cm，求BD的长．【分析】（1）连接OA，根据角之间的互余关系可得∠OAE＝∠DEA＝90°，故AE⊥OA，即AE是⊙O的切线；（2）根据圆周角定理，可得在Rt△AED中，∠AED＝90°，∠EAD＝30°，有AD＝2DE；在Rt△ABD中，∠BAD＝90°，∠ABD＝30°，有BD＝2AD＝4DE，即可得出答案．【解答】（1）证明：连接OA，∵DA平分∠BDE，∴∠BDA＝∠EDA．∵OA＝OD，∴∠ODA＝∠OAD，∴∠OAD＝∠EDA，∴OA∥CE．∵AE⊥CE，∴AE⊥OA．∴AE是⊙O的切线．（2）解：∵BD是直径，∴∠BCD＝∠BAD＝90°．∵∠DBC＝30°，∠BDC＝60°，∴∠BDE＝120°．∵DA平分∠BDE，∴∠BDA＝∠EDA＝60°．∴∠ABD＝∠EAD＝30°．∵在Rt△AED中，∠AED＝90°，∠EAD＝30°，∴AD＝2DE．∵在Rt△ABD中，∠BAD＝90°，∠ABD＝30°，∴BD＝2AD＝4DE．∵DE的长是1cm，∴BD的长是4cm．【点评】此题主要考查了切线的判定，角平分线的性质，含30°的直角三角形的性质，勾股定理，矩形的判定和性质，构造出直角三角形是解本题的关键，是一道中等难度的中考常考题．●●【典例四】（2022•城关区一模）如图，C是⊙O上一点，点P在直径AB的延长线上，⊙O的半径为6，PB=4，PC=8．求证：PC是⊙O的切线；【分析】可以证明OC2+PC2=OP2得△OCP是直角三角形，即OC⊥PC，PC是⊙O的切线；【解答】解：如图，连接OC、BC，∵⊙O的半径为6，PB=4，PC=8．∴OC=OB=6，OP=OB+BP=6+4=10，∴OC2+PC2=62+82=100，OP2=102=100，∴OC2+PC2=OP2，∴△OCP是直角三角形，∴OC⊥PC，∴PC是⊙O的切线；【点评】本题考查圆的切线的判定和勾股定理逆定理，利用勾股定理的逆定理证明垂直是解决问题的关键．【变式4-1】如图，AD, BD是⊙O的弦，AD⊥BD，且BD=2AD=8 ,点C是BD的延长线上的一点，CD=2，求证：AC是⊙O的切线.【分析】先由勾股定理的逆定理证明垂直，再由切线的判断进行解答即可.【解答】证明:连接AB，∵AD⊥BD，且BD=2AD=8 ，∴AB为直径，AB2 =82+42 =80，∵CD=2，AD=4 ，∴AC2 =22 ＋42=20，∵CD＝2，BD=8,∴BC=102=100，∴AC2+AB2=CB2，∴∠BAC=90° ，∴AC是⊙O的切线【点评】本题考查切线的判定，圆周角定理的推论，勾股定理的逆定理，解题关键是作出辅助线构造直角三角形.【变式4-2】如图，AD，BD是⊙O的弦，AD⊥BD，且BD＝2AD＝8，点C是BD的延长线上的一点，CD＝2，求证：AC是⊙O的切线．【分析】先根据圆周角定理得到AB为⊙O的直径，再利用勾股定理计算出AB、AC，接着利用勾股定理的逆定理证明△ABC为直角三角形，∠BAC＝90°，所以AC⊥AB，然后根据切线的判定定理得到结论．【解答】证明：∵AD⊥BD，∴∠ADB＝90°，∴AB为⊙O的直径，∵BD ＝2AD ＝8，∴AD ＝4，在Rt △ADB 中，AB 2＝AD 2+BD 2＝42+82＝80，在Rt △ADC 中，AC 2＝AD 2+CD 2＝42+22＝20，∵BC 2＝（2+8）2＝10，∴AC 2+AB 2＝BC 2，∴△ABC 为直角三角形，∠BAC ＝90°，∴AC ⊥AB ，∵AB 为直径，∴AC 是⊙O 的切线．【点评】本题考查了切线的判定：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了圆周角定理、勾股定理和勾股定理的逆定理．●●【典例五】（2022•鄞州区校级开学）如图，AB 为⊙O 的直径，点C 和点D 是⊙O 上的两点，连接BC ，DC ，BC ＝CD ，CE ⊥DA 交DA 的延长线于点E ．求证：CE 是⊙O 的切线；【分析】连接OD ，OC ，证得△COD ≌△COB ，可得∠OCD ＝∠BCO ，从而得到∠ADC ＝∠DCO ，进而得到DA ∥CO ，利用切线的判定定理即可求证；【解答】证明：连接OD ，OC，如图，在△COD和△COB中，OD=OBOC=OC，CD=CB∴△COD≌△COB（SSS），∴∠OCD＝∠BCO，∵CO＝BO，∴∠B＝∠BCO，∵∠B＝∠ADC，∴∠ADC＝∠DCO．∴DA∥CO，∴∠E+∠ECO＝180°．∵CE⊥EA，∴∠E＝90°．∴∠ECO＝90°，∴EC⊥CO，∵CO是⊙O的半径，∴EC是⊙O的切线；【点评】本题主要考查了切线的判定，圆周角定理等知识，熟练掌握切线的判定，相似三角形的判定和性质，圆周角定理等知识是解题的关键．【变式5-1】如图，已知AB是⊙O的直径，BC⊥AB，连接OC，弦AD∥OC，直线CD交BA的延长线于点E．求证：CD是⊙O的切线；【分析】连接OD，利用SAS得到三角形COD与三角形COB全等，利用全等三角形的对应角相等得到∠ODC 为直角，即可得证；【解答】证明：如图，连接OD．∵AD∥OC，∴∠DAO＝∠COB，∠ADO＝∠COD，又∵OA＝OD，∴∠DAO＝∠ADO，∴∠COD＝∠COB，在△COD和△COB中，OC=OC∠COD=∠COB，OD=OB∴△COD≌△COB（SAS），∴∠CDO＝∠CBO＝90°，∵OD是⊙O的半径，∴CD是⊙O的切线；【点评】此题考查了切线的判定和性质，以及全等三角形的判定与性质，熟练掌握各自的性质是解本题的关键．【变式5-2】（2022秋•新抚区期末）如图，AB为⊙O的直径，四边形OBCD是矩形，连接AD，延长AD 交⊙O于E，连接CE．求证：CE为⊙O的切线．【分析】连接OC、BE，根据矩形性质和圆半径相等，推出∠CDE＝∠AEO，进而得到OP＝CP，然后根据OB∥CD，可以推出∠COE＝∠BOC，最后通过证明△BOC≌△EOC即可求解．【解答】证明：如图：连接OC、BE，OE，CD交于点P，∵四边形OBCD是矩形，∴OB∥CD，∠OBC＝90°，OB＝CD，∵OB∥CD，∴∠A＝∠CDE，∵在⊙O中，OA＝OB＝OE，∴OE＝CD，∵OA＝OE，∴∠A＝∠AEO，∴∠CDE＝∠AEO，∴DP＝PE，∵OE＝CD，∴OP＝CP，∴∠COE＝∠DCO，∵OB∥CD，∴∠DCO＝∠BOC，∴∠COE＝∠BOC，在△BOC和△EOC中，OB=OECO=CO，∠BOC=∠COE∴△BOC≌△EOC（SAS），∴∠CEO＝∠OBC＝90°，∴CE⊥OE，又∵OE为⊙O的半径，∴CE为⊙O的切线．【点评】本题考查圆周角定理，全等三角形的判定和性质，矩形的性质等众多知识点，熟悉掌握以上知识点是解题关键．【变式5-3】（2022•建邺区二模）如图，四边形ABCD是菱形，以AB为直径作⊙O，交CB于点F，点E在CD上，且CE＝CF，连接AE．（1）求证：AE是⊙O的切线；（2）连接AC交⊙O于点P，若AP BF＝1，求⊙O的半径．【分析】（1）连接AF，根据菱形的性质得到∠ACF＝∠ACE，根据全等三角形的性质得到∠AFC＝∠AEC，推出OA⊥AE，根据切线的判定定理即可得到结论；（2）连接BP，根据圆周角定理得到∠APB＝90°，求得AC＝2AP＝【解答】（1）证明：连接AF，∵四边形ABCD为菱形，∴∠ACF＝∠ACE，在△ACF与△ACE中，CF=CE∠ACF=∠ACEAC=AC，∴△ACF≌△ACE（SAS），∴∠AFC＝∠AEC，∵AB是⊙O的直径，∴∠AFB＝∠AFC＝90°，∴∠AEC＝90°，∵AB∥DC，∴∠BAE+∠AEC＝90°，∴∠BAE＝90°，∴OA⊥AE，∵OA是⊙O的半径，∴AE是⊙O的切线；（2）解：连接BP，∵AB是⊙O的直径，∴∠APB＝90°，∵AB＝CB，AP=∴AC＝2AP＝设⊙O的半径为R，∵AC2﹣CF2＝AF2，AB2﹣BF2＝AF2，∴2−(2R−1)2=(2R)2−12，∴R=32（负值舍去），∴⊙O的半径为3 2．【点评】本题考查了切线的判定和性质，圆周角定理，菱形的性质，三角形全等的性质和判定，勾股定理等知识，解答本题的关键是根据勾股定理列方程解决问题．类型二：无公共点：作垂直，证半径●●【典例六】如图，△ABC为等腰三角形，O是底边BC的中点，腰AB与⊙O相切于点D．求证：AC是⊙O的切线．【分析】过点O作OE⊥AC于点E，连接OD，OA，根据切线的性质得出AB⊥OD，根据等腰三角形三线合一的性质得出AO是∠BAC的平分线，根据角平分线的性质得出OE=OD，从而证得结论．【解答】证明：过点O作OE⊥AC于点E，连接OD，OA，∵AB与⊙O相切于点D，∴AB⊥OD，∵△ABC为等腰三角形，O是底边BC的中点，∴AO是∠BAC的平分线，∴OE=OD，即OE是⊙O的半径，∵圆心到直线的距离等于半径，∴AC是⊙O的切线．【点评】本题考查了切线的判定和性质，等腰三角形的性质，角平分线的性质，熟练掌握性质定理是解题的关键．【变式6-1】如图，O为正方形ABCD对角线AC上一点，以O为圆心，OA长为半径的⊙O与BC相切于点M．求证：CD与⊙O相切．【分析】利用正方形的性质得出AC平分角∠BCD，再利用角平分线的性质得出OM＝ON，即可得出答案．【解答】证明：如图所示，连接OM，过点O作ON⊥CD于点N，∵⊙O与BC相切于点M，∴OM⊥BC，又∵ON⊥CD，O为正方形ABCD对角线AC上一点，∴OM＝ON，∴ON为⊙O的半径，∴CD与⊙O相切．【点评】此题主要考查了正方形的性质以及角平分线的性质，得出OM＝ON是解题关键．【变式6-2】如图，OC平分∠AOB，D是OC上任意一点，⊙D和OA相切于点E，连接CE．（1）求证：OB与⊙D相切；（2）若OE＝4，⊙D的半径为3，求CE的长．【分析】（1）过点D作DF⊥OB于点F，先由切线的性质得DE⊥OA，则由角平分线的性质得DF＝DE，即可证得结论；（2）过E作EG⊥OD于G，先由勾股定理求出OD＝5，再由面积法求出EG=125，然后由勾股定理求出DG=95，最后由勾股定理求出CE即可．【解答】（1）证明：连接DE，过点D作DF⊥OB于点F，如图所示：∵⊙D与OA相切于点E，∴DE⊥OA，∵OC平分∠AOB，∴DF＝DE，又∵DF⊥OB，∴OB与⊙D相切；（2）解：过E作EG⊥OD于G，如图所示：由（1）得：DE⊥OA，∴∠OED＝90°，∵OE＝4，DE＝3，∴OD=5，∵EG⊥OD，∴12OD×EG=12OE×DE，∴EG=OE×DEOD=4×35=125，∴DG===9 5，∴CG＝CD+DG＝3+95=245，∴CE=【点评】此题考查了切线的判定与性质、勾股定理以及角平分线的性质等知识，解题的关键是准确作出辅助线．【变式6-3】如图，AB是⊙O的直径，AM，BN分别切⊙O于点A，B，CD交AM，BN于点D，C，DO平分∠ADC．（1）求证：CD是⊙O的切线；（2）若AD＝4，BC＝9，求⊙O的半径R．【分析】（1）过O点作OE⊥CD于点E，通过角平分线的性质得出OE＝OA即可证得结论．（2）过点D作DF⊥BC于点F，根据切线的性质可得出DC的长度，继而在Rt△DFC中利用勾股定理可得出DF的长，继而可得出半径．【解答】（1）证明：过O点作OE⊥CD于点E，∵AM切⊙O于点A，∴OA⊥AD，又∵DO平分∠ADC，∴OE＝OA，∵OA为⊙O的半径，∴OE是⊙O的半径，且OE⊥DC，∴CD是⊙O的切线．（2）解：过点D作DF⊥BC于点F，∵AM，BN分别切⊙O于点A，B，∴AB⊥AD，AB⊥BC，∴四边形ABFD是矩形，∴AD＝BF，AB＝DF，又∵AD＝4，BC＝9，∴FC＝9﹣4＝5，∵AM，BN，DC分别切⊙O于点A，B，E，∴DA＝DE，CB＝CE，∴DC＝AD+BC＝4+9＝13，在Rt△DFC中，DC2＝DF2+FC2，∴DF=12，∴AB＝12，∴⊙O的半径R是6．【点评】此题考查了切线的性质、角平分线的性质及勾股定理的知识，证明第一问关键是掌握切线的判定定理，解答第二问关键是熟练切线的性质．【变式6-4】（2022秋•清原县期末）如图，在△ABC中，∠ACB＝90°，点D是AB边的中点，点O在AC边上，⊙O 经过点C 且与AB 边相切于点E ，∠FAC =12∠BDC ．（1）求证：AF 是⊙O 的切线；（2）若BC ＝6，AB ＝10，求⊙O 的半径长．【分析】（1）作OH ⊥FA ，垂足为点H ，连接OE ，证明AC 是∠FAB 的平分线，进而根据OH ＝OE ，OE ⊥AB ，可得AF 是⊙O 的切线；（2）勾股定理得出AC ，设⊙O 的半径为r ，则OC ＝OE ＝r ，进而根据切线的性质，在Rt △OEA 中，勾股定理即可求解．【解答】（1）证明：如图，作OH ⊥FA ，垂足为点H ，连接OE ，∵∠ACB ＝90°，D 是AB 的中点，∴CD =AD =12AB ，∴∠CAD ＝∠ACD ，∵∠BDC ＝∠CAD +∠ACD ＝2∠CAD ，又∵∠FAC =12∠BDC ，∴∠FAC ＝∠CAD ，即AC 是∠FAB 的平分线，∵点O 在AC 上，⊙O 与AB 相切于点E ，∴OE ⊥AB ，且OE 是⊙O 的半径，∴OH ＝OE ，OH 是⊙O 的半径，∴AF 是⊙O 的切线；（2）解：如图，在△ABC中，∠ACB＝90°，BC＝6，AB＝10，∴AC==8，∵BE，BC是⊙O的切线，∴BC＝BE＝6，∴AE＝10﹣6＝4设⊙O的半径为r，则OC＝OE＝r，在Rt△OEA中，由勾股定理得：OE2+AE2＝OA2，∴16+r2＝（8﹣r）2，∴r＝3．∴⊙O的半径长为3．【点评】本题考查了切线的性质与判定，勾股定理，熟练掌握切线的性质与判定是解题的关键．1.如图，已知AB是⊙O的直径，AB＝BE，点P在BA的延长线上，连接AE交⊙O于点D，过点D作PC⊥BE垂足为点C．求证：PC与⊙O相切；【分析】连接OD，根据等腰三角形的性质得到∠BAE＝∠BEA，∠BAE＝∠ODA，等量代换得到∠ODA＝∠BEA，证明OD∥BE，根据平行线的性质得到PC⊥OD，根据切线的判定定理证明结论；【解答】证明：连接OD，∵AB＝BE，∴∠BAE＝∠BEA，∵OA＝OD，∴∠BAE＝∠ODA，∴∠ODA＝∠BEA，∴OD∥BE，∵PC⊥BE，∴PC⊥OD，∵OD是⊙O的半径，∴PC与⊙O相切；【点评】本题考查的是切线的判定、解直角三角形，掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键．2．如图，△ABC是⊙O的内接三角形，AC是⊙O的直径，点D是BC的中点，DE∥BC交AC的延长线于点E．（1）求证：直线DE与⊙O相切；（2）若⊙O的直径是10，∠A＝45°，求CE的长．【分析】（1）连接OD，如图，先利用垂径定理得到OD⊥BC，再根据平行线的性质得到OD⊥DE，然后根据切线的判定方法得到结论；（2）先根据圆周角定理得到∠B＝90°，则∠ACB＝45°，再根据平行线的性质得到∠E＝45°，则可判断△ODE 为等腰直角三角形，于是可求出OE，然后计算OE﹣OC即可．【解答】（1）证明：连接OD，如图，∵点D是BC的中点，∴OD⊥BC，∵DE∥BC，∴OD⊥DE，∴直线DE与⊙O相切；（2）解：∵AC是⊙O的直径，∴∠B＝90°，∵∠A＝45°，∴∠ACB＝45°，∵BC∥DE，∴∠E＝45°，而∠ODE＝90°，∴△ODE为等腰直角三角形，∴OE=＝∴CE＝OE﹣OC＝5．【点评】本题考查了切线的性质与判定：圆的切线垂直于经过切点的半径．也考查了垂径定理、圆周角定理和等腰直角三角形的性质．3．（2023•东城区校级模拟）如图，⊙O的半径OC与弦AB垂直于点D，连接BC，OB．（1）求证：2∠ABC+∠OBA＝90°；（2）分别延长BO、CO交⊙O于点E、F，连接AF，交BE于G，过点A作AM⊥BC，交BC延长线于点M，若G是AF的中点，求证：AM是⊙O的切线．【分析】（1）先根据垂径定理得到AC=BC，再根据圆周角定理得到∠BOC＝2∠ABC，然后利用互余关系得∠BOD+∠OBD＝90°，从而得到结论；（2）如图，连接OA，根据垂径定理得到BE⊥AF，再根据圆周角定理得到∠CAF＝90°，则可判断BE ∥AC，所以∠ABE＝∠BAC，接着证明∠BAO＝∠CBA得到OA∥BC，根据平行线的性质得到AM⊥OA，然后根据切线的判断方法得到结论．【解答】证明：（1）∵OD⊥AB，∴AC=BC，∠ODB＝90°，∴∠BOC＝2∠ABC，∵∠BOD+∠OBD＝90°，∴2∠ABC+∠OBA＝90°；（2）如图，连接OA，∵G是AF的中点，∴BE⊥AF，∵CF为直径，∴∠CAF＝90°，∴CA⊥AF，∴BE∥AC，∴∠ABE＝∠BAC，∴AC=BC，∴∠CAB＝∠CBA，∵OA＝OB，∴∠BAO＝∠ABO，∴∠BAO＝∠CBA，∴OA∥BC，∵AM⊥BC，∴AM⊥OA，而OA为⊙O的半径，∴AM是⊙O的切线．【点评】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了圆周角定理、垂径定理．4．（2022•思明区校级二模）如图，四边形ABCD是⊙O的内接四边形，AC是⊙O直径，BE∥AD交DC 延长线于点E，若BC平分∠ACE．（1）求证：BE是⊙O的切线；（2）若BE＝3，CD＝2，求⊙O的半径．【分析】（1）连接OB，由条件可以证明OB∥DE，从而证明OB⊥BE；（2）由垂径定理求出AD长，从而由勾股定理可求AC长．【解答】（1）证明：连接OB，∵″OB＝OC，∴∠OBC＝∠OCB，∵∠BCE＝∠OCB，∴∠OBC＝∠BCE，∴OB∥DE，∵AC是⊙O直径，∴AD⊥DE，∵BE∥AD，∴BE⊥DE，∴OB⊥BE，∵OB是⊙O半径，∴BE是⊙O切线；（2）解：延长BO交AD于F，∵∠D＝∠DEB＝∠EBF＝90°，∴四边形BEDF是矩形，∴BF⊥AD，DF＝BE＝3，∴AD＝2DF＝6，∵AC2＝AD2+CD2，∴AC2＝62+22＝40，∴AC＝∴⊙O【点评】本题考查切线的判定，矩形的判定和性质，垂径定理，勾股定理，用到的知识点较多，关键是熟练掌握知识点，并能灵活应用．5．（2023•封开县一模）如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．（1）求证：EF是⊙O的切线；（2）当AB＝5，BC＝6时，求DE的长．【分析】（1）连接OD，由AC＝AB，根据等边对等角得到一对角相等，再由OD＝OB，根据等边对等角得到又一对角相等，等量代换可得一对同位角相等，根据同位角相等两直线平行可得OD与AC平行，又EF垂直于AC，根据垂直于两平行线中的一条，与另一条也垂直，得到EF与OD也垂直，可得EF为圆O的切线；（2）连接AD，由AB为圆的直径，根据直径所对的圆周角为直角可得∠ADB＝90°，即AD与BC垂直，又AC＝AB，根据三线合一得到D为BC中点，由BC求出CD的长，再由AC的长，利用勾股定理求出AD的长，三角形ACD的面积有两种求法，AC乘以DE除以2，或CD乘以AD除以2，列出两个关系式，两关系式相等可求出DE的长．【解答】（1）证明：连接OD，∵AB＝AC，∴∠C＝∠OBD，∵OD＝OB，∴∠1＝∠OBD，∴∠1＝∠C，∴OD∥AC，∵EF⊥AC，∴EF⊥OD，∴EF是⊙O的切线；（2）连接AD，∵AB为⊙O的直径，∴∠ADB＝90°，又∵AB＝AC，且BC＝6，∴CD＝BD=12BC＝3，在Rt△ACD中，AC＝AB＝5，CD＝3，根据勾股定理得：AD=4，又S△ACD =12AC•ED=12AD•CD，即12×5×ED=12×4×3，∴ED=12 5．【点评】此题考查了等腰三角形的性质，圆周角定理，平行线的性质，勾股定理，三角形面积的求法，以及切线的判定，其中证明切线的方法为：有点连接圆心与此点，证垂直；无点过圆心作垂线，证明垂线段长等于圆的半径．本题利用的是第一种方法．6．（2023•宁德模拟）如图，OM 为⊙O 的半径，且OM ＝3，点G 为OM 的中点，过点G 作AB ⊥OM 交⊙O 于点A ，B ，点D 在优弧AB 上运动，将AB 沿AD 方向平移得到DC ；连接BD ，BC ．（1）求∠ADB 的度数；（2）如图2，当点D 在MO 延长线上时，求证：BC 是⊙O 的切线．【分析】（1）连接AO ，BO ，先根据特殊角的正弦值可得∠OAG ＝30°，再根据等腰三角形的性质可得∠OAG ＝∠OBG ＝30°，从而可得∠AOB ＝120°，然后根据圆周角定理即可得；（2）连接AO ，BO ，CO ，先证出四边形ABCD 是平行四边形，再根据等边三角形的判定与性质可得AB ＝AD ，根据菱形的判定可得四边形ABCD 是菱形，根据菱形的性质可得CB ＝CD ，然后根据SSS 定理证出△COB ≌△COD ，根据全等三角形的性质可得∠OBC ＝∠ODC ＝90°，最后根据圆的切线的判定即可得证．【解答】（1）解：如图1，连接AO ，BO ．∵点G 为OM 的中点，且OM ＝3，∴OG =12OM =32，OA ＝OB ＝OM ＝3，∵AB ⊥OM ，在Rt △AOG 中，OG =12OA ．∴∠OAG ＝30°，又∵OA ＝OB ，∴∠OAG＝∠OBG＝30°，∴∠AOB＝120°，∴∠ADB=12∠AOB=60°．（2）证明：如图2，连接AO，BO，CO，由平移得：AB＝DC，AB∥DC，∴四边形ABCD是平行四边形，∵OM⊥AB，点D在MO延长线上，∴DM⊥CD，∵OA＝OB，AB⊥OM，∴AG＝BG，∴DM垂直平分AB，∴AD＝BD，∵∠ADB＝60°，∴△ABD为等边三角形，∴AB＝AD，∴平行四边形ABCD是菱形，∴CB＝CD，在△COB和△COD中，CB=CDOB=ODOC=OC，∴△COB≌△COD（SSS），∴∠OBC＝∠ODC＝90°，又∵OB是⊙O的半径，。

24.2.2(8)---切线长定理 --3条切线(梯切圆)

24.2.2(8)---切线长定理 --梯切圆一．【知识要点】1. 圆中有多条切线时，常可考虑切线长定理，并结合等腰三角形的性质解题. 二．【经典例题】1．如图，PA 、PB 是⊙O 的切线，CD 切⊙O 于点E ，△PCD 的周长为12，∠APB ＝70°．求： PA= ；∠COD 的度数为；2.(教材P100例2变式)如图，△ABC 的内切圆⊙O 与三边分别相切于D ，E ，F 三点，AB=7，BC=12，AC=11，求AF ，BD ，CE 的长。

3．如图，⊙O 的直径AB ＝8cm ，AM 和BN 是它的两条切线，切点分别为A ，B ，DE 切⊙O 于E ，交AM 于D ，交BN 于C ，设AD ＝x ，BC ＝y ，则y 与x 的函数关系式为；4．如图所示，AB 是⊙O 的直径，AM 、BN 是⊙O 的两条切线，D 、C 分别在AM 、BN 上，DC 切⊙O 于点E ，连接OD 、OC 、BE 、AE ，BE 与OC 相交于点P ，AE 与OD 相交于点Q ，已知AD ＝4，BC ＝9．以下结论：①⊙O 的半径为；②OD ∥BE ；③PB ＝；④PECP＝．其中正确的结论是．5．如图，在梯形ABCD中，AD∥BC，∠B＝90°，以AB为直径作⊙O，恰与另一腰CD相切于点E，连接OD、OC、BE．（1）求证：OD∥BE；（2）若梯形ABCD的面积是48，设OD＝x，OC＝y，且x+y＝14，求CD的长．6.如图,正方形ABCD的边长为4,以BC为直径作圆,过A点作圆的切线,交DC于E,切点为F.(1)求△ADE的面积;(2)求BF的长.7.如图，在矩形ABCD中，AB=4，AD=5，AD，AB，BC分别与⊙O相切于E，F，G三点，过点D作⊙O的切线交BC于点M，切点为N.（1）求证：AE=BF. （2）求DM的长。

三．【题库】【A】1.如图，AD，AE，BC都是⊙O的切线，切点分别为D、E、F，若AD=6，则AE=,若CE=2，BD=3，则BC=，若AE=4，则△ABC的周长为.2．如图，AB是⊙O的直径，AD，DC，BC是切线，点A，E，B为切点（1）求证：OD⊥OC；（2）若BC＝9，AD＝4，求OB的长．3.如图，AB，BC，CD分别与⊙O相切于E、F、G三点，且AB∥CD，BO=6，CO=8，求⊙O的半径.4.如图,AD,AC,CB均为⊙O的切线,D,E,F分别是切点,若AD=8,则△ABC的周长为 .5.如图,⊙O内切于△ABC,切点分别为D,E,F,若∠C=80°,则∠EDF= .【B】1.如图,AD是☉O的直径,AB,DC,BC是☉O的三条切线,若OB=3,OC=4,则BC= ()A.3B.4C.5D.62.如图所示,P是☉O外一点,PA,PB分别和☉O切于A,B两点,C是弧AB上任意一点,过点C 作☉O的切线分别交PA,PB于点D,E.若△PDE的周长为12,则PA的长为()A.12B.6C.8D.43．如图，PA、PB分别与半径为3的⊙O相切于点A，B，直线CD分别交PA、PB于点C，D，并切⊙O于点E，当PO＝5时，△PCD的周长为（）A．4B．5 C．8 D．104.如图，AB ，BC ，CD 分别与⊙O 相切于E 、F 、、G 三点，且AB//CD. BO=6cm ，CO=8cm.求BC 的长.5.如图，AB ，BC ，CD 分别与⊙O 相切于E 、F 、G 三点，且AB ∥CD ，BE=2, ⊙O 的半径为3,求CG 的长.6.如图,⊙O 为直角梯形ABCD 的内切圆,M 、N 、F 、G 为切点，∠A=∠B=90°，AD=3，BC=6,求⊙O 的半径.7. 如图，AB 为⊙O 的直径，90ABC ∠=︒,AD ∥BC ，CD 切⊙O 于点E ，BE 交AC 于M ，若AM=CM,AB=4,求BC 的长.8.如图,AB,BC,CD 分别与⊙O 相切于E,F,G 三点,且AB ∥CD,BE=9,CG=16. (1)求证:FG ∥BO; (2)求⊙O 的半径;(3)延长BO交CD于M,求BM的长.【C】1.如图，在平行四边形ABCD中，AB＝5，AD＝6，AD、AB、BC分别与⊙O相切于E、F、G三点，过点C作⊙O的切线交AD于点N，切点为M．当CN⊥AD时，⊙O的半径为．2.如图，在矩形ABCD中，AB=4，AD=5，AD、AB、BC分别与⊙O相切于E、F、G三点，过点D作⊙O的切线交BC于点M，切点为N，则DM的长为____________.3.如图正方形ABCD，以BC为直径作半圆，边长为4，AM为⊙O的切线，M为切点，AM的延长线交直线DC于N点，求CN的长。

题型五圆的相关证明与计算类型二与切线有关的证明与计算(专题训练)(解析版)

题型五圆的相关证明与计算类型二与切线有关的证明与计算（专题训练）1.如图，ABC V 内接于O e ，AB 是O e 的直径，E 为AB 上一点，BE BC =，延长CE 交AD 于点D ，AD AC =．（1）求证：AD 是O e 的切线；（2）若1tan 3ACE Ð=，3OE =，求BC 的长．【答案】（1）见解析；（2）8【分析】（1）根据BE BC =，可得BEC BCE Ð=Ð，根据对顶角相等可得AED BEC Ð=Ð，进而可得BCE AED Ð=Ð，根据AD AC =，可得ADC ACE Ð=Ð，结合90ACB Ð=°，根据角度的转化可得90AED D Ð+Ð=°，进而即可证明AD 是O e 的切线；（2）根据ADC ACE Ð=Ð，可得1tan tan 3EA D ACE DA ==Ð=，设AE x =，则3AC AD x ==，分别求得,,AC AB BC ，进而根据勾股定理列出方程解方程可得x ，进而根据6BC x =+即可求得．【详解】（1）Q BE BC =，\BEC BCE Ð=Ð，Q AED BEC Ð=Ð，\BCE AED Ð=Ð，Q AD AC =，\ADC ACE Ð=Ð，Q AB 是直径，\90ACB Ð=°，90D AED ACD BCE ACB \Ð+Ð=Ð+Ð=Ð=°，\AD 是O e 的切线；（2）AD AC =Q ，\ADC ACE Ð=Ð，1tan tan 3EA D ACE DA \==Ð=，设AE x =，则3AC AD x ==，3,336OB OA AE OE x BC BE OE OB x x ==+=+==+=++=+，226AB OA x ==+，在Rt ABC V 中，222AC BC AB +=，即()()()2223626x x x ++=+，解得122,0x x ==（舍去），68BC x \=+=．【点睛】本题考查了切线的判定，勾股定理解直角三角形，正切的定义，利用角度相等则正切值相等将已知条件转化是解题的关键．2.如图，ABC V 内接于O e ，AB AC =，AD 是O e 的直径，交BC 于点E ，过点D 作//DF BC ，交AB 的延长线于点F ，连接BD ．（1）求证：DF 是O e 的切线；（2）已知12AC =，15AF =，求DF 的长．【答案】（1）见解析；（2）DF =【分析】（1）由题意根据圆周角定理得出90ABC CBD Ð+Ð=°，结合同弧或等弧所对的圆周角相等并利用经过半径外端并且垂直于这条半径的直线是圆的切线进行证明即可；（2）根据题意利用相似三角形的判定即两个角分别相等的两个三角形相似得出FBD FDA ~△△，继而运用相似比FB FD FD FA=即可求出DF 的长．【详解】解：（1）证明：∵AD 是O e 的直径∴90ABD Ð=°（直径所对的圆周角是直角）即90ABC CBD Ð+Ð=°∵AB AC=∴ABC C Ð=Ð（等边对等角）∵ AB AB=∴ADB C Ð=Ð（同弧或等弧所对的圆周角相等）∴ABC ADBÐ=Ð∵//BC DF ，∴CBD FDBÐ=Ð∴90ADB FDB Ð+Ð=°即90ADF Ð=°∴AD DF^又∵AD 是O e 的直径∴DF 是O e 的切线（经过半径外端并且垂直于这条半径的直线是圆的切线）．（2）解：∵12AB AC ==，15AF =∴3BF AF AB =-=∵F F Ð=Ð，90FBD FDA Ð=Ð=o∴FBD FDA ~△△（两个角分别相等的两个三角形相似）∴FB FD FD FA=，∴231545FD FB FA =×=´=∴DF =【点睛】本题主要考查圆的切线的判定、圆周角定理、相似三角形的判定与性质等知识点，熟练掌握圆周角定理和相似三角形的判定与性质是解题的关键．3.如图，AB 为O e 的直径，C 为O e 上一点，D 为AB 上一点，BD BC =，过点A 作AE AB ^交CD 的延长线于点E ，CE 交O e 于点G ，连接AC ，AG ，在EA 的延长线上取点F ，使2FCA E Ð=Ð．（1）求证：CF 是O e 的切线；（2）若6AC =，AG =，求O e 的半径．【答案】（1）见解析；（2）5【分析】（1）根据题意判定ADG DCB V V ∽，然后结合相似三角形的性质求得2AGD E ÐÐ＝，从而可得FCA AGD ÐÐ＝，然后结合等腰三角形的性质求得90FCO Ð°＝，从而判定CF 是O e 的切线；（2）由切线长定理可得AF CF ＝，从而可得2FAC E ÐÐ＝，得到AC AE ＝，然后利用勾股定理解直角三角形可求得圆的半径．【详解】（1）证明：B AGC ÐÐQ ＝，ADG CDB ÐÐ＝，ADG DCB \V V ∽，BD BC GD GA\=，BD BC Q ＝，GD GA \＝，ADG DAG \ÐÐ＝，又AE AB ^Q ，90EAD \Ð°＝，90GAE DAG E ADG \Ð+ÐÐ+Ð°＝＝，GAE E \ÐÐ＝，AG DG EG \＝＝，2AGD E ÐÐ＝，2FCA E ÐÐQ ＝，FCA AGD B \ÐÐÐ＝＝，Q AB 是O e 的直径，90CAB B \Ð+Ð°＝，又OA OC Q ＝，ACO CAB \ÐÐ＝，90FCA ACO \Ð+Ð°＝，90FCO \Ð°＝，即CF 是O e 的切线；（2）Q CF 是O e 的切线，AE AB ^，AF CF \＝，2FAC FCA E \ÐÐÐ＝＝，6AC AE \＝＝，又AG DG EG Q ＝＝，在Rt ADE △中，2AD ===，设O e 的半径为x ，则2AB x ＝，22BD BC x＝＝﹣，在Rt ABC △中，2226222x x +（﹣）＝（），解得：5x ＝，O \e 的半径为5．【点睛】本题考查了圆周角定理、切线的判定与性质、相似三角形的判定与性质、勾股定理等，熟练掌握相关定理与性质是解决本题的关键．4.如图，四边形ABCD 内接于⊙O ，AB 为⊙O 的直径，过点C 作CE ⊥AD 交AD 的延长线于点E ，延长EC ，AB 交于点F ，∠ECD ＝∠BCF ．（1）求证：CE 为⊙O 的切线；（2）若DE ＝1，CD ＝3，求⊙O 的半径．【答案】（1）见解析；（2）⊙O 的半径是4.5【分析】（1）如图1，连接OC ，先根据四边形ABCD 内接于⊙O ，得CDE OBC ÐÐ＝，再根据等量代换和直角三角形的性质可得90OCE Ð°＝，由切线的判定可得结论；（2）如图2，过点O 作OG AE ^于G ，连接OC ，OD ，则90OGE Ð°＝，先根据三个角是直角的四边形是矩形得四边形OGEC 是矩形，设⊙O 的半径为x ，根据勾股定理列方程可得结论．【详解】（1）证明：如图1，连接OC ，∵OB OC ＝，∴OCB OBC ÐÐ＝，∵四边形ABCD 内接于⊙O ，∴180CDA ABC Ð+Ð=°又180CDE CDA Ð+Ð=°∴CDE OBC ÐÐ＝，∵CE AD ^，∴90E CDE ECD ÐÐÐ°＝＋＝，∵ECD BCF ÐÐ＝，∴90OCB BCF ÐÐ°＋＝，∴90OCE Ð°＝，∵OC 是⊙O 的半径，∴CE 为⊙O 的切线；（2）解：如图2，过点O 作OG AE ^于G ，连接OC ，OD ，则90OGE Ð°＝，∵90E OCE ÐÐ°＝＝，∴四边形OGEC 是矩形，∴OC EG OG EC ＝，＝，设⊙O 的半径为x ，Rt △CDE 中，31CD DE ＝，＝，∴EC ==∴OG =1GD xOD x ＝﹣，＝，由勾股定理得222OD OG DG +：＝，∴222(1)x x =+-，解得： 4.5x ＝，∴⊙O 的半径是4.5．【点睛】本题考查的是圆的综合，涉及到圆的切线的证明、勾股定理以及矩形的性质，熟练掌握相关性质是解决问题的关键．5.如图，V ABC 内接于⊙O ，且AB ＝AC ，其外角平分线AD 与CO 的延长线交于点D ．（1）求证：直线AD 是⊙O 的切线；（2）若AD ＝，BC ＝6，求图中阴影部分面积．【答案】（1）见解析；（2）6p -【分析】（1）连接OA ，证明OA ⊥AD 即可，利用角平分线的意义以及等腰三角形的性质得以证明；（2）求出圆的半径和阴影部分所对应的圆心角度数即可，利用相似三角形求出半径，再根据特殊锐角三角函数求出∠BOC ．【详解】解：（1）如图，连接OA 并延长交BC 于E ，∵AB=AC ，△ABC 内接于⊙O ，∴AE 所在的直线是△ABC 的对称轴，也是⊙O 的对称轴，∴∠BAE=∠CAE ，又∵∠MAD=∠BAD ，∠MAD+∠BAD+∠BAE+∠CAE=180°，∴∠BAD+∠BAE=12×180°=90°，即AD ⊥OA ，∴AD 是⊙O 的切线；（2）连接OB ，∵∠OAD=∠OEC=90°，∠AOD=∠EOC ，∴△AOD ∽△EOC ，∴AD OA EC OE =，由（1）可知AO 是ABC D 的对称轴，OE \垂直平分BC ，132CE BC \==，设半径为r ，在Rt EOC D 中，由勾股定理得，，\解得6r =（取正值），经检验6r =是原方程的解，即6OB OC OA ===，又6BC =Q ，OBC \D 是等边三角形，60BOC \Ð=°，OE =BOC BOC S S S D \=-阴影部分扇形2606163602p ´=-´´6p =-【点睛】本题考查了切线的判定和性质、角平分线的性质，圆周角定理，三角形外接圆与外心，扇形面积的计算，灵活运用切线的判定方法是解题的关键．6.如图，△ABC 内接于⊙O ，AB 是⊙O 的直径，过⊙O 外一点D 作//DG BC ，DG 交线段AC 于点G ，交AB 于点E ，交⊙O 于点F ，连接DB ，CF ，∠A ＝∠D ．（1）求证：BD 与⊙O 相切；（2）若AE ＝OE ，CF 平分∠ACB ，BD ＝12，求DE 的长．【答案】（1）见解析；（2）【分析】（1）如图1，延长DB 至H ，证明90ABD Ð=°，即可根据切线的判定可得BD 与O e 相切；（2）如图2，连接OF ，先根据圆周角定理证明OF AB ^，再证明EFO EDB △∽△，列比例式可得4OF =，即O e 的半径为4，根据勾股定理可得DE 的长．【详解】（1）证明：如图1，延长DB 至H ，Q，DG BC//\Ð=Ð，CBH DQ，Ð=ÐA D\Ð=Ð，A CBHe的直径，Q是OAB\Ð=°，ACB90\Ð+Ð=°，A ABC90\Ð+Ð=°，90CBH ABC\Ð=°，90ABD∴AB⊥BD，e相切；\与OBD（2）解：如图2，连接OF，CFQ平分ACBÐ，\Ð=Ð，ACF BCF\=，AF BF∴∠AOF＝∠BOF＝90°，OF AB \^，BD AB ^Q ，//OF BD \，EFO EDB \△∽△，\OF OE BD BE=，AE OE =Q ，\13OE EB =，\1123OF =，4OF \=，4OA OB OF \===，246BE OE OB \=+=+=，DE \．【点睛】此题考查了相似三角形的判定与性质，切线的判定，圆周角定理，勾股定理等知识，解答本题需要我们熟练掌握切线的判定，第2问关键是证明EFO EDB △∽△．7.如图，在Rt △ACD 中，∠ACD ＝90°，点O 在CD 上，作⊙O ，使⊙O 与AD 相切于点B ，⊙O 与CD 交于点E ，过点D 作DF ∥AC ，交AO 的延长线于点F ，且∠OAB ＝∠F ．（1）求证：AC 是⊙O 的切线；（2）若OC ＝3，DE ＝2，求tan ∠F 的值．【答案】（1）见详解；（2）12．【分析】（1）由题意，先证明OA 是∠BAC 的角平分线，然后得到BO=CO ，即可得到结论成立；（2）由题意，先求出BD=4，OD=5，然后利用勾股定理求出6AB AC ==，10AD =，结合直角三角形ODF ，即可求出tan ∠F 的值．【详解】解：（1）∵DF ∥AC ，∴∠CAO=∠F ，∵∠OAB ＝∠F ，∴∠CAO=∠OAB ，∴OA 是∠BAC 的角平分线，∵AD 是⊙O 的切线，∴∠ABO=∠ACO=90°，∴BO=CO ，又∵AC ⊥OC ，∴AC 是⊙O 的切线；（2）由题意，∵OC ＝3，DE ＝2，∴OD=5，OB=3，CD=8，∴4BD ==，由切线长定理，则AB=AC ，设AB AC x ==，在直角三角形ACD 中，由勾股定理，则222AC CD AD +=，即2228(4)x x +=+，解得：6x =，∴6AB AC ==，6410AD =+=，∵∠OAB ＝∠F ，∴10DF AD ==，∵90FDO ACO Ð=Ð=°，∴51tan 102OD F DF Ð===．【点睛】本题考查了圆的切线的判定和性质，勾股定理，角平分线的性质，以及三角函数，解题的关键是熟练掌握所学的知识，正确的求出所需的长度，从而进行解题．8.如图，在Rt ABC V 中，90ACB °Ð=，以斜边AB 上的中线CD 为直径作O e ，与BC 交于点M ，与AB 的另一个交点为E ，过M 作MN AB ^，垂足为N ．（1）求证：MN 是O e 的切线；（2）若O e 的直径为5，3sin 5B =，求ED 的长．【答案】（1）见解析；（2）75ED =．【解析】【分析】（1）欲证明MN 为⊙O 的切线，只要证明OM ⊥MN ．（2）连接,DM CE ，分别求出BD=5，BE=325，根据ED BE BD =-求解即可．【详解】（1）证明：连接OM ，OC OM =Q ，OCM OMC \Ð=Ð．在Rt ABC V 中，CD 是斜边AB 上的中线，12CD AB BD \==，DCB DBC \Ð=Ð，OMC DBC \Ð=Ð，//OM BD \，MN BD ^Q ，MN OM \^，MN \是O e 的切线．（2）连接,DM CE ，易知,DM BC CE AB ^^，由（1）可知5BD CD ==，故M 为BC 的中点，3sin 5B =Q ，4cos 5B \=，在Rt BMD △中，cos 4BM BD B =×=，28BC BM \==．在Rt CEB V 中，32cos 5BE BC B =×=，327555ED BE BD \=-=-=．【点睛】本题考查切线的判定和性质，等腰三角形的性质，解直角三角形等知识；熟练掌握切线的判定定理是解题的关键．9.如图，AB 是半圆O 的直径，,C D 是半圆O 上不同于,A B 的两点,AD BC AC =与BD 相交于点,F BE 是半圆O 所任圆的切线，与AC 的延长线相交于点E ，()1求证：CBA DAB D D ≌；()2若,BE BF =求AC 平分DAB Ð．【答案】()1证明见解析；()2证明见解析．【解析】【分析】()1利用,AD BC =证明,ABD BAC Ð=Ð利用AB 为直径，证明90,ADB BCA Ð=Ð=°结合已知条件可得结论；()2利用等腰三角形的性质证明：,EBC FBC Ð=Ð 再证明,CBF DAF Ð=Ð 利用切线的性质与直径所对的圆周角是直角证明：,EBC CAB Ð=Ð 从而可得答案．【详解】()1证明：,AD BC =Q,AD BC\= ,ABD BAC \Ð=ÐAB Q 为直径，90,ADB BCA \Ð=Ð=°,AB BA =QCBA DAB \V V ≌．()2证明：,90,BE BF ACB =Ð=°Q,FBC EBC \Ð=Ð90,,ADC ACB DFA CFB Ð=Ð=°Ð=ÐQ,DAF FBC EBC \Ð=Ð=ÐBE Q 为半圆O 的切线，90,90,ABE ABC EBC \Ð=°Ð+Ð=°90,ACB Ð=°Q90,CAB ABC \Ð+Ð=°,CAB EBC \Ð=Ð,DAF CAB \Ð=ÐAC \平分DAB Ð．【点睛】本题考查的是圆的基本性质，弧，弦，圆心角，圆周角之间的关系，直径所对的圆周角是直角，三角形的全等的判定，切线的性质定理，三角形的内角和定理，掌握以上知识是解题的关键．10.如图，AB是⊙O的直径，点C是⊙O上一点，∠CAB的平分线AD交 BC于点D，过点D 作DE∥BC交AC的延长线于点E．（1）求证：DE是⊙O的切线；（2）过点D作DF⊥AB于点F，连接BD．若OF＝1，BF＝2，求BD的长度．【答案】（1）见解析；（2）【解析】【分析】（1）连接OD，由等腰三角形的性质及角平分线的性质得出∠ADO＝∠DAE，从而OD∥AE，由DE∥BC得∠E＝90°，由两直线平行，同旁内角互补得出∠ODE＝90°，由切线的判定定理得出答案；（2）先由直径所对的圆周角是直角得出∠ADB＝90°，再由OF＝1，BF＝2得出OB的值，进而得出AF和BA的值，然后证明△DBF∽△ABD，由相似三角形的性质得比例式，从而求得BD2的值，求算术平方根即可得出BD的值．【详解】解：（1）连接OD，如图：∵OA＝OD，∴∠OAD＝∠ADO，∵AD平分∠CAB，∴∠DAE＝∠OAD，∴∠ADO＝∠DAE，∴OD∥AE，Q AB为⊙O的直径，90,ACB\Ð=°∵DE∥BC，∴∠E＝ACB=∠ 90°，∴∠ODE＝180°﹣∠E＝90°，∴DE是⊙O的切线；（2）∵AB是⊙O的直径，∴∠ADB＝90°，∵OF＝1，BF＝2，∴OB＝3，∴AF＝4，BA＝6．∵DF⊥AB，∴∠DFB＝90°，∴∠ADB＝∠DFB，又∵∠DBF＝∠ABD，∴△DBF∽△ABD，∴BD BF BA BD=，∴BD2＝BF•BA＝2×6＝12．∴BD＝【点睛】本题考查的是圆的基本性质，圆周角定理，切线的判定，同时考查了相似三角形的判定与性质．（1）中判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”，有切线时，常常“遇到切点连圆心得半径”；（2）中能得△DBF∽△ABD是解题关键．11.如图，在⨀O中，AB为⨀O的直径，C为⨀O上一点，P是 BC的中点，过点P作AC的垂线，交AC 的延长线于点D ．（1）求证：DP 是⨀O 的切线；（2）若AC=5，5sin 13APC Ð=,求AP 的长．【答案】（1）见解析；（2）AP=．【解析】【分析】（1）根据题意连接OP ，直接利用切线的定理进行分析证明即可；（2）根据题意连接BC ，交于OP 于点G ，利用三角函数和勾股定理以及矩形的性质进行综合分析计算即可.【详解】解：（1）证明：连接OP ；∵OP=OA;∴∠1=∠2；又∵P 为 BC的中点；∴ PCPB =∴∠1=∠3；∴∠3=∠2；∴OP ∥DA ；∵∠D=90°；∴∠OPD=90°；又∵OP 为⨀O 半径；∴DP 为⨀O 的切线；（2）连接BC ，交于OP 于点G ；∵AB 是圆O 的直径；∴∠ACB 为直角；∵5sin 13APC Ð=∴sin ∠ABC=513AC=5,则AB=13,半径为132由勾股定理的12=，那么CG=6又∵四边形DCGP 为矩形；∴GP=DC=6.5-2.5=4∴AD=5+4=9;在Rt △ADP 中，==.【点睛】本题考查圆的综合问题，熟练掌握圆的切线定理和勾股定理以及三角函数和矩形的性质是解题的关键.12.如图，AB 是⊙O 的直径，C 为⊙O 上一点，连接AC ，CE ⊥AB 于点E ，D 是直径AB 延长线上一点，且∠BCE ＝∠BCD ．（1）求证：CD 是⊙O 的切线；（2）若AD ＝8，BE CE ＝12，求CD 的长．【答案】（1）见解析；（2）4【解析】【分析】（1）连接OC，根据圆周角定理得到∠ACB＝90°，根据余角的性质得到∠A＝∠ECB，求得∠A＝∠BCD，根据等腰三角形的性质得到∠A＝∠ACO，等量代换得到∠ACO＝∠BCD，求得∠DCO＝90°，于是得到结论；（2）设BC＝k，AC＝2k，根据相似三角形的性质即可得到结论．【详解】（1）证明：连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∵CE⊥AB，∴∠CEB＝90°，∴∠ECB+∠ABC＝∠ABC+∠CAB＝90°，∴∠A＝∠ECB，∵∠BCE＝∠BCD，∴∠A＝∠BCD，∵OC＝OA，∴∠A＝∠ACO，∴∠ACO＝∠BCD，∴∠ACO+∠BCO ＝∠BCO+∠BCD ＝90°，∴∠DCO ＝90°，∴CD 是⊙O 的切线；（2）解：∵∠A ＝∠BCE ，∴tanA ＝BC AC ＝tan ∠BCE ＝BE CE ＝12，设BC ＝k ，AC ＝2k ，∵∠D ＝∠D ，∠A ＝∠BCD ，∴△ACD ∽△CBD ，∴BC AC ＝CD AD ＝12，∵AD ＝8，∴CD ＝4．【点睛】本题考查了切线的判定定理，相似三角形的判定与性质以及解直角三角形的应用，熟练掌握性质定理是解题的关键．13.如图，AB 是O e 的直径，点C 是O e 上一点，CAB Ð的平分线AD 交 BC于点D ，过点D 作//DE BC 交AC 的延长线于点E ．（1）求证：DE 是O e 的切线；（2）过点D 作DF AB ^于点F ，连接BD ．若1OF =，2BF =，求BD 的长度．【答案】（1）见解析；（2）BD =【解析】【分析】（1）连接OD ，由等腰三角形的性质及角平分线的性质得出∠ADO ＝∠DAE ，从而OD ∥AE ，由DE ∥BC 得∠E ＝90°，由两直线平行，同旁内角互补得出∠ODE ＝90°，由切线的判定定理得出答案；（2）先由直径所对的圆周角是直角得出∠ADB ＝90°，再由OF ＝1，BF ＝2得出OB 的值，进而得出AF 和BA 的值，然后证明△DBF ∽△ABD ，由相似三角形的性质得比例式，从而求得BD 2的值，求算术平方根即可得出BD 的值．【详解】解：（1）连接OD ，如图：∵OA ＝OD ，∴∠OAD ＝∠ADO ，∵AD 平分∠CAB ，∴∠DAE ＝∠OAD ，∴∠ADO ＝∠DAE ，∴OD ∥AE ，∵DE ∥BC ，∴∠E ＝90°，∴∠ODE ＝180°−∠E ＝90°，∴DE 是⊙O 的切线；（2）因AB 为直径，则90ADB Ð=°∵1OF =，2BF =∴OB=3∴4AF =，6BA =∵∠ADB=∠DFB=90°, ∠B=∠B∴△DBF ∽△ABD ∴BF BD BD AB=∴22612BD BF BA =×=´=所以BD=．【点睛】本题考查了切线的判定、相似三角形的判定与性质、平行线的性质等知识点，熟练掌握圆的切线的判定及圆中的相关计算是解题的关键．。

圆的相关证明与计算--与切线有关的证明与计算(解析版)-中考数学重难点题型专题汇总

圆的相关证明与计算-中考数学重难点题型与切线有关的证明与计算（专题训练）1.如图，ABC 内接于O ，AB 是O 的直径，E 为AB 上一点，BE BC =，延长CE 交AD 于点D ，AD AC =．（1）求证：AD 是O 的切线；（2）若1tan 3ACE ∠=，3OE =，求BC 的长．【答案】（1）见解析；（2）8【分析】（1）根据BE BC =，可得BEC BCE ∠=∠，根据对顶角相等可得AED BEC ∠=∠，进而可得BCE AED ∠=∠，根据AD AC =，可得ADC ACE ∠=∠，结合90ACB ∠=︒，根据角度的转化可得90AED D ∠+∠=︒，进而即可证明AD 是O 的切线；（2）根据ADC ACE ∠=∠，可得1tan tan 3EA D ACE DA ==∠=，设AE x =，则3AC AD x ==，分别求得,,AC AB BC ，进而根据勾股定理列出方程解方程可得x ，进而根据6BC x =+即可求得．【详解】（1） BE BC =，∴BEC BCE ∠=∠，AED BEC ∠=∠，∴BCE AED ∠=∠，AD AC =，∴ADC ACE ∠=∠，AB 是直径，∴90ACB ∠=︒，90D AED ACD BCE ACB ∴∠+∠=∠+∠=∠=︒，∴AD 是O 的切线；（2）AD AC = ，∴ADC ACE ∠=∠，1tan tan 3EA D ACE DA ∴==∠=，设AE x =，则3AC AD x ==，3,336OB OA AE OE x BC BE OE OB x x ==+=+==+=++=+，226AB OA x ==+，在Rt ABC 中，222AC BC AB +=，即()()()2223626x x x ++=+，解得122,0x x ==（舍去），68BC x ∴=+=．【点睛】本题考查了切线的判定，勾股定理解直角三角形，正切的定义，利用角度相等则正切值相等将已知条件转化是解题的关键．2.如图，ABC 内接于O ，AB AC =，AD 是O 的直径，交BC 于点E，过点D 作//DF BC ，交AB 的延长线于点F，连接BD ．（1）求证：DF 是O 的切线；（2）已知12AC =，15AF =，求DF 的长．【答案】（1）见解析；（2）DF =【分析】（1）由题意根据圆周角定理得出90ABC CBD ∠+∠=︒，结合同弧或等弧所对的圆周角相等并利用经过半径外端并且垂直于这条半径的直线是圆的切线进行证明即可；（2）根据题意利用相似三角形的判定即两个角分别相等的两个三角形相似得出FBD FDA ~△△，继而运用相似比FB FD FD FA =即可求出DF 的长．【详解】解：（1）证明：∵AD 是O 的直径∴90ABD ∠=︒（直径所对的圆周角是直角）即90ABC CBD ∠+∠=︒∵AB AC=∴ABC C ∠=∠（等边对等角）∵ AB AB=∴ADB C ∠=∠（同弧或等弧所对的圆周角相等）∴ABC ADB∠=∠∵//BC DF ，∴CBD FDB∠=∠∴90ADB FDB ∠+∠=︒即90ADF ∠=︒∴AD DF⊥又∵AD 是O 的直径∴DF 是O 的切线（经过半径外端并且垂直于这条半径的直线是圆的切线）．（2）解：∵12AB AC ==，15AF =∴3BF AF AB =-=∵F F ∠=∠，90FBD FDA ∠=∠=∴FBD FDA ~△△（两个角分别相等的两个三角形相似）∴FB FD FD FA=，∴231545FD FB FA =⋅=⨯=∴DF =【点睛】本题主要考查圆的切线的判定、圆周角定理、相似三角形的判定与性质等知识点，熟练掌握圆周角定理和相似三角形的判定与性质是解题的关键．3.如图，AB 为O 的直径，C 为O 上一点，D 为AB 上一点，BD BC =，过点A 作AE AB ⊥交CD 的延长线于点E，CE 交O 于点G，连接AC，AG，在EA 的延长线上取点F，使2FCA E ∠=∠．（1）求证：CF 是O 的切线；（2）若6AC =，AG ，求O 的半径．【答案】（1）见解析；（2）5【分析】（1）根据题意判定ADG DCB ∽，然后结合相似三角形的性质求得2AGD E ∠∠＝，从而可得FCA AGD ∠∠＝，然后结合等腰三角形的性质求得90FCO ∠︒＝，从而判定CF 是O 的切线；（2）由切线长定理可得AF CF ＝，从而可得2FAC E ∠∠＝，得到AC AE ＝，然后利用勾股定理解直角三角形可求得圆的半径．【详解】（1）证明：B AGC ∠∠ ＝，ADG CDB ∠∠＝，ADG DCB ∴ ∽，BD BC GD GA∴=，BD BC ＝，GD GA ∴＝，ADG DAG ∴∠∠＝，又AE AB ⊥ ，90EAD ∴∠︒＝，90GAE DAG E ADG ∴∠+∠∠+∠︒＝＝，GAE E ∴∠∠＝，AG DG EG ∴＝＝，2AGD E ∠∠＝，2FCA E ∠∠ ＝，FCA AGD B ∴∠∠∠＝＝，AB 是O 的直径，90CAB B ∴∠+∠︒＝，又OA OC Q ＝，ACO CAB ∴∠∠＝，90FCA ACO ∴∠+∠︒＝，90FCO ∴∠︒＝，即CF 是O 的切线；（2） CF 是O 的切线，AE AB ⊥，AF CF ∴＝，2FAC FCA E ∴∠∠∠＝＝，6AC AE ∴＝＝，又AG DG EG ＝＝在Rt ADE △中，2AD ===，设O 的半径为x，则2AB x ＝，22BD BC x＝＝﹣，在Rt ABC △中，2226222x x +（﹣）＝（），解得：5x ＝，O ∴ 的半径为5．【点睛】本题考查了圆周角定理、切线的判定与性质、相似三角形的判定与性质、勾股定理等，熟练4.如图，四边形ABCD 内接于⊙O，AB 为⊙O 的直径，过点C 作CE⊥AD 交AD 的延长线于点E，延长EC，AB 交于点F，∠ECD＝∠BCF．（1）求证：CE 为⊙O 的切线；（2）若DE＝1，CD＝3，求⊙O 的半径．【答案】（1）见解析；（2）⊙O 的半径是4.5【分析】（1）如图1，连接OC，先根据四边形ABCD 内接于⊙O，得CDE OBC ∠∠＝，再根据等量代换和直角三角形的性质可得90OCE ∠︒＝，由切线的判定可得结论；（2）如图2，过点O 作OG AE ⊥于G，连接OC，OD，则90OGE ∠︒＝，先根据三个角是直角的四边形是矩形得四边形OGEC 是矩形，设⊙O 的半径为x，根据勾股定理列方程可得结论．【详解】（1）证明：如图1，连接OC，∵OB OC ＝，∴OCB OBC ∠∠＝，∵四边形ABCD 内接于⊙O，∴180CDA ABC ∠+∠=︒又180CDE CDA ∠+∠=︒∴CDE OBC ∠∠＝，∵CE AD ⊥，∴90E CDE ECD ∠∠∠︒＝＋＝，∵ECD BCF ∠∠＝，∴90OCB BCF ∠∠︒＋＝，∴90OCE ∠︒＝，∵OC 是⊙O 的半径，∴CE 为⊙O 的切线；（2）解：如图2，过点O 作OG AE ⊥于G，连接OC，OD，则90OGE ∠︒＝，∵90E OCE ∠∠︒＝＝，∴四边形OGEC 是矩形，∴OC EG OG EC ＝，＝，设⊙O 的半径为x，Rt△CDE 中，31CD DE ＝，＝，∴EC =∴OG =1GD xOD x ＝﹣，＝，由勾股定理得222OD OG DG +：＝，∴222(1)x x =+-，解得： 4.5x ＝，∴⊙O 的半径是4.5．【点睛】本题考查的是圆的综合，涉及到圆的切线的证明、勾股定理以及矩形的性质，熟练掌握相关性质是解决问题的关键．5.如图， ABC 内接于⊙O，且AB＝AC，其外角平分线AD 与CO 的延长线交于点D．（1）求证：直线AD 是⊙O（2）若【答案】（1）见解析；（2）6π-【分析】（1）连接OA，证明OA⊥AD 即可，利用角平分线的意义以及等腰三角形的性质得以证明；（2）求出圆的半径和阴影部分所对应的圆心角度数即可，利用相似三角形求出半径，再根据特殊锐角三角函数求出∠BOC．【详解】解：（1）如图，连接OA 并延长交BC 于E，∵AB=AC，△ABC 内接于⊙O，∴AE 所在的直线是△ABC 的对称轴，也是⊙O 的对称轴，∴∠BAE=∠CAE，又∵∠MAD=∠BAD，∠MAD+∠BAD+∠BAE+∠CAE=180°，∴∠BAD+∠BAE=12×180°=90°，即AD⊥OA，∴AD 是⊙O 的切线；（2）连接OB，∴△AOD∽△EOC，∴AD OA EC OE =，由（1）可知AO 是ABC ∆的对称轴，OE ∴垂直平分BC ，132CE BC ∴==，设半径为r ，在Rt EOC ∆中，由勾股定理得，OE∴，解得6r =（取正值），经检验6r =是原方程的解，即6OB OC OA ===，又6BC = ，OBC ∴∆是等边三角形，60BOC ∴∠=︒，OE ==BOC BOC S S S ∆∴=-阴影部分扇形2606163602π⨯=-⨯⨯6π=-【点睛】本题考查了切线的判定和性质、角平分线的性质，圆周角定理，三角形外接圆与外心，扇形面积的计算，灵活运用切线的判定方法是解题的关键．6.如图，△ABC 内接于⊙O，AB 是⊙O 的直径，过⊙O 外一点D 作//DG BC ，DG 交线段AC 于点G，交AB 于点E，交⊙O 于点F，连接DB，CF，∠A＝∠D．（1）求证：BD 与⊙O 相切；（2）若AE＝OE，CF 平分∠ACB，BD＝12，求DE 的长．【答案】（1）见解析；（2）【分析】（1）如图1，延长DB 至H ，证明90ABD ∠=︒，即可根据切线的判定可得BD 与O 相切；（2）如图2，连接OF ，先根据圆周角定理证明OF AB ⊥，再证明EFO EDB △∽△，列比例式可得4OF =，即O 的半径为4，根据勾股定理可得DE 的长．【详解】（1）证明：如图1，延长DB 至H ，，DG BC//∴∠=∠，CBH D，∠=∠A D∴∠=∠，A CBH的直径，Q是OAB∴∠=︒，ACB90∴∠+∠=︒，A ABC90∴∠+∠=︒，90CBH ABC∴∠=︒，90ABD∴AB⊥BD，相切；∴与OBD（2）解：如图2，连接OF，CF平分ACB∠，∴∠=∠，ACF BCF∴=，AF BF∴∠AOF＝∠BOF＝90°，OF AB ∴⊥，BD AB ⊥ ，//OF BD ∴，EFO EDB ∴△∽△，∴OF OE BD BE=，AE OE = ，∴13OE EB =，∴1123OF =，4OF ∴=，4OA OB OF ∴===，246BE OE OB ∴=+=+=，DE ∴=．【点睛】此题考查了相似三角形的判定与性质，切线的判定，圆周角定理，勾股定理等知识，解答本题需要我们熟练掌握切线的判定，第2问关键是证明EFO EDB △∽△．7.如图，在Rt△ACD 中，∠ACD＝90°，点O 在CD 上，作⊙O，使⊙O 与AD 相切于点B，⊙O 与CD 交于点E，过点D 作DF∥AC，交AO 的延长线于点F，且∠OAB＝∠F．（1）求证：AC 是⊙O 的切线；（2）若OC＝3，DE＝2，求tan∠F 的值．【答案】（1）见详解；（2）12．【分析】（1）由题意，先证明OA 是∠BAC 的角平分线，然后得到BO=CO，即可得到结论成立；（2）由题意，先求出BD=4，OD=5，然后利用勾股定理求出6AB AC ==，10AD =，结合直角三角形ODF，即可求出tan∠F 的值．【详解】解：（1）∵DF∥AC，∴∠CAO=∠F，∵∠OAB＝∠F，∴∠CAO=∠OAB，∴OA 是∠BAC 的角平分线，∵AD 是⊙O 的切线，∴∠ABO=∠ACO=90°，∴BO=CO，又∵AC⊥OC，∴AC 是⊙O 的切线；（2）由题意，∵OC＝3，DE＝2，∴OD=5，OB=3，CD=8，∴4BD ==，由切线长定理，则AB=AC，设AB AC x ==，在直角三角形ACD 222AC CD AD +=，即2228(4)x x +=+，解得：6x =，∴6AB AC ==，6410AD =+=，∵∠OAB＝∠F，∴10DF AD ==，∵90FDO ACO ∠=∠=︒，∴51tan 102OD F DF ∠===．【点睛】本题考查了圆的切线的判定和性质，勾股定理，角平分线的性质，以及三角函数，解题的关键是熟练掌握所学的知识，正确的求出所需的长度，从而进行解题．8.如图，在Rt ABC 中，90ACB ︒∠=，以斜边AB 上的中线CD 为直径作O ，与BC 交于点M ，与AB 的另一个交点为E ，过M 作MN AB ⊥，垂足为N ．（1）求证：MN 是O 的切线；（2）若O 的直径为5，3sin 5B =，求ED 的长．【答案】（1）见解析；（2）75ED =．【解析】【分析】（1）欲证明MN 为⊙O 的切线，只要证明OM⊥MN．（2）连接,DM CE ，分别求出BD=5，BE=325，根据ED BE BD =-求解即可．【详解】（1）证明：连接OM ，OC OM = ，OCM OMC ∴∠=∠．在Rt ABC 中，CD 是斜边AB 上的中线，12CD AB BD ∴==，DCB DBC ∴∠=∠，OMC DBC ∴∠=∠，//OM BD ∴，MN BD ⊥ ，MN OM ∴⊥，MN ∴是O 的切线．（2）连接,DM CE ，易知,DM BC CE AB ⊥⊥，由（1）可知5BD CD ==，故M 为BC 的中点，3sin 5B =，4cos 5B ∴=，在Rt BMD △中，cos 4BM BD B =⋅=，28BC BM ∴==．在Rt CEB 中，32cos 5BE BC B =⋅=，327555ED BE BD ∴=-=-=．【点睛】本题考查切线的判定和性质，等腰三角形的性质，解直角三角形等知识；熟练掌握切线的判定定理是解题的关键．9.如图，AB 是半圆O 的直径，,C D 是半圆O 上不同于,A B 的两点,AD BC AC =与BD 相交于点,F BE 是半圆O 所任圆的切线，与AC 的延长线相交于点E ，()1求证：CBA DAB ∆∆≌；()2若,BE BF =求AC 平分DAB ∠．【答案】()1证明见解析；()2证明见解析．【解析】【分析】()1利用,AD BC =证明,ABD BAC ∠=∠利用AB 为直径，证明90,ADB BCA ∠=∠=︒结合已知条件可得结论；()2利用等腰三角形的性质证明：,EBC FBC ∠=∠再证明,CBF DAF ∠=∠利用切线的性质与直径所对的圆周角是直角证明：,EBC CAB ∠=∠从而可得答案．【详解】()1证明：,AD BC = ,AD BC∴=,ABD BAC ∴∠=∠AB Q 为直径，90,ADB BCA ∴∠=∠=︒,AB BA = CBA DAB ∴ ≌．()2证明：,90,BE BF ACB =∠=︒ ,FBC EBC ∴∠=∠90,,ADC ACB DFA CFB ∠=∠=︒∠∠ ,DAF FBC EBC ∴∠=∠=∠BE 为半圆O 的切线，90,90,ABE ABC EBC ∴∠=︒∠+∠=︒90,ACB ∠=︒ 90,CAB ABC ∴∠+∠=︒,CAB EBC ∴∠=∠,DAF CAB ∴∠=∠AC ∴平分DAB ∠．【点睛】本题考查的是圆的基本性质，弧，弦，圆心角，圆周角之间的关系，直径所对的圆周角是直角，三角形的全等的判定，切线的性质定理，三角形的内角和定理，掌握以上知识是解题的关键．10.如图，AB是⊙O的直径，点C是⊙O上一点，∠CAB的平分线AD交 BC于点D，过点D 作DE∥BC交AC的延长线于点E．（1）求证：DE是⊙O的切线；（2）过点D作DF⊥AB于点F，连接BD．若OF＝1，BF＝2，求BD的长度．【答案】（1）见解析；（2）【解析】【分析】（1）连接OD，由等腰三角形的性质及角平分线的性质得出∠ADO＝∠DAE，从而OD∥AE，由DE∥BC得∠E＝90°，由两直线平行，同旁内角互补得出∠ODE＝90°，由切线的判定定理得出答案；（2）先由直径所对的圆周角是直角得出∠ADB＝90°，再由OF＝1，BF＝2得出OB的值，进而得出AF和BA的值，然后证明△DBF∽△ABD，由相似三角形的性质得比例式，从而求得BD2的值，求算术平方根即可得出BD的值．【详解】解：（1）连接OD，如图：∵OA＝OD，∴∠OAD＝∠ADO，∵AD平分∠CAB，∴∠DAE＝∠OAD，∴∠ADO＝∠DAE，∴OD∥AE，AB为⊙O的直径，90,ACB∴∠=︒∵DE∥BC，∴∠E＝ACB=∠90°，∴∠ODE＝180°﹣∠E＝90°，∴DE是⊙O的切线；（2）∵AB是⊙O的直径，∴∠ADB＝90°，∵OF＝1，BF＝2，∴OB＝3，∴AF＝4，BA＝6．∵DF⊥AB，∴∠DFB＝90°，∴∠ADB＝∠DFB，又∵∠DBF＝∠ABD，∴△DBF∽△ABD，∴BD BF BA BD=，∴BD2＝BF•BA＝2×6＝12．∴BD＝【点睛】本题考查的是圆的基本性质，圆周角定理，切线的判定，同时考查了相似三角形的判定与性质．（1）中判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”，有切线时，常常“遇到切点连圆心得半径”；（2）中能得△DBF∽△ABD是解题关键．11.如图，在⨀O中，AB为⨀O的直径，C为⨀O上一点，P是 BC的中点，过点P作AC的垂线，交AC 的延长线于点D．（1）求证：DP 是⨀O 的切线；（2）若AC=5，5sin 13APC ∠=,求AP 的长．【答案】（1）见解析；（2）AP=．【解析】【分析】（1）根据题意连接OP，直接利用切线的定理进行分析证明即可；（2）根据题意连接BC，交于OP 于点G，利用三角函数和勾股定理以及矩形的性质进行综合分析计算即可.【详解】解：（1）证明：连接OP；∵OP=OA;∴∠1=∠2；又∵P 为 BC的中点；∴ PCPB =∴∠1=∠3；∴∠3=∠2；∴OP∥DA；∵∠D=90°；∴∠OPD=90°；又∵OP 为⨀O 半径；∴DP 为⨀O 的切线；（2）连接BC，交于OP 于点G；∵AB 是圆O 的直径；∴∠ACB 为直角；∵5sin 13APC ∠=∴sin∠ABC=513AC=5,则AB=13,半径为132由勾股定理的12=，那么CG=6又∵四边形DCGP 为矩形；∴GP=DC=6.5-2.5=4∴AD=5+4=9;在Rt△ADP ==.【点睛】本题考查圆的综合问题，熟练掌握圆的切线定理和勾股定理以及三角函数和矩形的性质是解题的关键.12.如图，AB 是⊙O 的直径，C 为⊙O 上一点，连接AC，CE⊥AB 于点E，D 是直径AB 延长线上一点，且∠BCE＝∠BCD．（1）求证：CD 是⊙O 的切线；（2）若AD＝8，BE CE ＝12，求CD 的长．【答案】（1）见解析；（2）4【解析】【分析】（1）连接OC，根据圆周角定理得到∠ACB＝90°，根据余角的性质得到∠A＝∠ECB，求得∠A＝∠BCD，根据等腰三角形的性质得到∠A＝∠ACO，等量代换得到∠ACO＝∠BCD，求得∠DCO＝90°，于是得到结论；（2）设BC＝k，AC＝2k，根据相似三角形的性质即可得到结论．【详解】（1）证明：连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∵CE⊥AB，∴∠CEB＝90°，∴∠ECB+∠ABC＝∠ABC+∠CAB＝90°，∴∠A＝∠ECB，∵∠BCE＝∠BCD，∴∠A＝∠BCD，∵OC＝OA，∴∠A＝∠ACO，∴∠ACO＝∠BCD，∴∠ACO+∠BCO＝∠BCO+∠BCD＝90°，∴∠DCO＝90°，∴CD 是⊙O 的切线；（2）解：∵∠A＝∠BCE，∴tanA＝BC AC ＝tan∠BCE＝BE CE ＝12，设BC＝k，AC＝2k，∵∠D＝∠D，∠A＝∠BCD，∴△ACD∽△CBD，∴BC AC ＝CD AD ＝12，∵AD＝8，∴CD＝4．【点睛】本题考查了切线的判定定理，相似三角形的判定与性质以及解直角三角形的应用，熟练掌握性质定理是解题的关键．13.如图，AB 是O 的直径，点C 是O 上一点，CAB ∠的平分线AD 交 BC于点D ，过点D 作//DE BC 交AC 的延长线于点E ．（1）求证：DE 是O 的切线；（2）过点D 作DF AB ⊥于点F ，连接BD ．若1OF =，2BF =，求BD 的长度．【答案】（1）见解析；（2）BD =【解析】【分析】（1）连接OD，由等腰三角形的性质及角平分线的性质得出∠ADO＝∠DAE，从而OD∥AE，由DE∥BC 得∠E＝90°，由两直线平行，同旁内角互补得出∠ODE＝90°，由切线的判定定理得出答案；（2）先由直径所对的圆周角是直角得出∠ADB＝90°，再由OF＝1，BF＝2得出OB 的值，进而得出AF 和BA 的值，然后证明△DBF∽△ABD，由相似三角形的性质得比例式，从而求得BD 2的值，求算术平方根即可得出BD 的值．【详解】解：（1）连接OD，如图：∵OA＝OD，∴∠OAD＝∠ADO，∵AD 平分∠CAB，∴∠DAE＝∠OAD，∴∠ADO＝∠DAE，∴OD∥AE，∵DE∥BC，∴∠E＝90°，∴∠ODE＝180°−∠E＝90°，∴DE 是⊙O 的切线；（2）因AB 为直径，则90ADB ∠=︒∵1OF =，2BF =∴OB=3∴4AF =，6BA =∵∠ADB=∠DFB=90°,∠B=∠B∴△DBF∽△ABD ∴BF BD BD AB=∴22612BD BF BA =⋅=⨯=所以BD ．【点睛】本题考查了切线的判定、相似三角形的判定与性质、平行线的性质等知识点，熟练掌握圆的切线的判定及圆中的相关计算是解题的关键．。

初中数学-切线长定理典型例题

例如图，△ABC 内接于大⊙O ，∠B ＝∠C ，小⊙O 与AB 相切于点D ．求证：AC 是小圆的切线．分析 AC 与小⊙O 的公共点没有确定，故应过O 作AC 的垂线段OE ．再证明OE 等于小圆半径，用“到圆心的距离等于半径的直线是圆的切线”来判定AC 是小圆的切线．证明连结OD ，作OE ⊥AC 于E ． ∵∠B ＝∠C ，∴AB=AC ．又AB 与⊙O 小相切于D ，∴OD ⊥AB ． ∵OE ⊥AC ，∴OD=OE ．即小⊙O 的圆心O 到AC 的距离等于半径，所以AC 是小圆的切线．说明：（1）本题为证明切线的两个常见方法（①连半径证垂直；②作垂直证半径．）之一；（2）本题为基本题型，但应用到切线的性质和判定；（3）本题为教材110页例4的变形题．例（大连市，l 999）阅读：“如图△ABC 内接于⊙O ，∠CAE=∠B ．求证：AE 与⊙O 相切于点A ．证明：作直径AF ，连结FC ，则∠ACF ＝90°．∴ ∠AFC+∠CAF ＝90°． ∵∠B ＝∠AFC ． ∴ ∠B+∠CAF ＝90°．又∵ ∠CAE=∠B ，∴ ∠CAE+∠CAF ＝90°．即AE 与⊙O 相切于点A ．问题：通过阅读所得到的启示证明下题(阅读题中的结论可以直接应用)．问题：通过阅读所得到的启示证明下题(阅读题中的结论可以直接应用)．如图，已知△ABC 内接于⊙O ．P 是CB 延长线上一点，连结AP ．且PA 2＝PB ·PC ．求证：PA 是⊙O 的切线．证明：∵PA 2＝PB ·PC ，∴PAPB PC PA ．又∵ ∠P=∠P ，∴△PAB ∽△PCA ． ∠PAB=∠C ．由阅读题的结论可知，PA 是⊙O 的切线．说明：（1）此题的阅读材料来源于教材第117页B 组第1题；（2）应用“连半径证垂直”证明切线．例（西宁，1999）已知：如图，Rt △ABC 中，∠C=90°，以AB 为直径的⊙O 交斜边AB 于E ，OD ∥AB ．求证：（1）ED 是⊙O 的切线；（2）2 DE 2＝BE ·OD证明：（1）连结OE 、CE ，则CE ⊥AB ．在Rt △ABC 中，∵OA=OC ，OD ∥AB ，∴D 为BC 的中点，∴DE=CD ，又∵OC=OE ，OD=OD ，∴△COD ≌△EOD ，∴∠OED=∠OCD=90°，∴ED 是⊙O 的切线．（2）在Rt △ABC 中，CE ⊥AB ，∴△CBE ∽△ABC ，∴CB 2＝BE ·AB ， ∵OD 为△ABC 的中位线，∴AB=2OD ，BC=2ED ，∴（2ED ）2＝BE ·2OD 即2 DE 2＝BE ·OD 说明：此题为综合题，主要应用切线的性质定理、判定定理、射影定理、中位线定理等知识．C典型例题四例（北京市西城区试题，2002）已知：AB 为⊙O 的直径，P 为AB 延长线上的一个动点，过点P 作⊙O 的切线，设切点为C.（1）当点P 在AB 延长线上的位置如图1所示时，连结AC ，作APC 的平分线，交AC 于点D ，请你测量出CDP 的度数；（2）当点P 在AB 延长线上的位置如图2和图3所示时，连结AC ，请你分别在这两个图中用尺规作APC 的平分线（不写做法，保留作图痕迹），设此角平分线交AC 于点D ，然后在这两个图中分别测量出CDP 的度数；猜想：CDP 的度数是否随点P 在AB 延长线上的位置的变化而变化？请对你的猜想加以证明.解：（1）测量结果： 45CDP . （2）作图略.图2中的测量结果： 45CDP . 图3中的测量结果： 45CDP .猜想： 45CDP 为确定的值，CDP 的度数不随点P 在AB 延长线上的位置的变化而变化.证法一：连结BC .∵ AB 是⊙O 的直径， ∴ 90ACB .∵ PC 切⊙O 于点C ， ∴ A 1.∵ PD 平分APC ，.454,3,21432 CDP A CDP∴ 猜想正确. 证法二：连结OC .∵ PC 切⊙O 于点C ，.901. CPO OC PC∵ PD 平分APC ，.45)1(212.121,31.3,.212CPO A CDP A A A OC OA CPO∴ 猜想正确.典型例题五例（北京市崇文区，2002）已知：ABC ≌C B A ，3,5,90 AC AB B C A ACB ，对应边AC 与C A 重合，如图（1）.若将C B A沿CB 边按箭头所示方向平移，如图（2），使边AB 、B A 相交于点D ，边C A 交AB 于点E ，边AC 交B A 于点F ，以C C 为直径在五边形CF C DE 内作半圆O ，设C B 的长为x ，半圆O 的面积为y .1．求y 与x 的函数关系式及自变量x 的取值范围； 2．连结EF ，求EF 与半圆O 相切时的x 的值.解：1．∵ ABC ≌C B A ，3,5,90 AC AB B C A ACB ，,4,.4x C B BC C C x C B BC28)24(2122 x x x y .以C C 为直径在五边形内作半圆，依题意，在运动过程中C A 、AC 与⊙O 始终相切，故只需考虑AB 与⊙O相切的特殊位置，以确定x 的最小值.当C B A 沿CB 边按箭头所示方向平移时， ∵ ABC ≌C B A ， ∴ B B ， ∴ B DB 是等腰三角形.又∵ ,,C O OC C B BC∴ .O B BO∴ O 是B B 的中点.∴ O 到BD 、D B 的距离相等.∴ AB 与⊙O 相切时，B A 必与⊙O 相切. 设切点分别为G 、H ，连结OG ，则有,,90B B BCA BGO ∴ BOG ∽BAC ..5244324,xx BA BO AC OG解之得.1 x当1 x 或4 x 时，不合题意，∴ 自变量x 的取值范围是41 x . 2．在C BE 和FC B 中，,90,,CF B E C B C B C B B B ∴ C BE ≌FC B .,90,//.C FC FC C E FC C E∴ 四边形CF C E 为矩形. 当EF 与⊙O 相切时，C C C E21. ).4(2143,43,43tan x x x C E BC AC C B C E B解之得.58 x典型例题六例已知如图，在ABC 中，AC AB ，以AB 为直径的⊙O 交BC 于D ，过D 作⊙O 的切线交AC 于E ，求证：AC DE .分析：因为DE 是⊙O 的切线，D 是切点，所以连OD ，得DE OD ，因此本题的关键在于证明OD AC //. 证明连结AD 、OD AB 为⊙O 的直径，AC AB ， BC AD .D 是BC 中点，O 是AB 的中点， OD 为BAC 的中位线， AC OD // DE 是切线，D 为切点，OD 是⊙O 的半径 DE OD AC DE说明：连结OD 构成了“切线的性质定理”的基本图形，连结AD 构成了圆周角推论的基本图形.典型例题七例如图，已知⊙O 中，AB 为直径，过B 点作⊙O 的切线，连线CO ，若OC AD //交⊙O 于D .求证：CD 是⊙O 的切线.分析：要证AD 是⊙O 的切线，只须证AD 垂直于过切点D 的半径，由此应想到连结OD .证明连结OD OC AD // ，A COB 及ODA COD OD OA ，OAD ODA COD COBCO 为公共边，OB ODCOB ≌COD .即ODC B BC 是切线，AB 是直径， 90B ， 90ODC ， CD 是⊙C 的切线.说明：辅助线OD 构造于“切线的判定定理”与“全等三角形”两个基本图形，先用切线的性质定理，后用判定定理.典型例题八例如图，以ABC Rt 的一条直角边AB 为直径作圆斜边BC 于E ，F 是AC 的中点，求证：EF 是圆的切线.分析：连OE ，因为EF 过半径OE 的外端，要证EF 是切线，只需证 90OEF . 思路1 连OF ，证OAF ≌OEF ，则有 90OAF OEF思路2 连AE ，则 90AEC ，证 90OAE FAE OEA FEA 证明1 如图，连OF 、OE ，的中位线是中点为中点为ABC OF AB O AC FB BC OF 1//，32 又B OE OB 3，即21 ，OE OA ，OF OF 所以OAF ≌OEF有 90OAF OEF 即EF OE ， EF 过半径OE 的外端，所以EF 是⊙O 的切线.证明2 如图，连结AE 、OE AB 是⊙O 直径 90AEBFA FE AC F AEC中点为9042314321OE OAEF OE 90 FE 过半径OE 的外端所以EF 是⊙O 的切线说明：这里的辅助线OE ，仍然想着构造“切线判定定理”的基本图形的作用.典型例题九例如图，已知弦AB 等于半径，连结OB 并延长使.（1）求证AC 是⊙O 的切线；（2）请你在⊙O 上选取一点D ，使得（自己完成作图，并给出证明过程）证明：（1）即是⊙O 的切线.（2）①作BO 延长线交⊙O 于D ，连接AD ，，所以D 点为所求.②如图，在圆上取一点使得，连结，所以点也为所求.说明：证明一条直线是圆的切线，通常选择：（1）到圆心的距离等于圆的半径的直线是圆的切线；（2）经过半径的外端并且垂直于这条半径的直线是圆的切线.而涉及切线问题时，应灵活运用切线的性质，通常连结切点和圆心.题目的第（2）问是分类讨论问题，当题目中的图形未给定时，作图时，应将所有符合条件的图形作出，再分别解答.典型例题十例已知：直线AB 经过⊙O 上的点C ，并且CB CA OB OA ,.求证：直线AB 是⊙O 的切线.证明连结OC .∵CB CA OB OA ,，∴OC 是等腰三角形OAB 底边AB 上的中线. ∴.OC AB ∴AB 是⊙O 的切线.说明：本题考查切线的判定，解题关键是作出辅助线，易错点是把求证的结论“AB 是⊙O 的切线”.作为条件使用，造成推理过程中的逻辑混乱.典型例题十一例如图，AB 是⊙O 直径，弦AB CD //，连AD ，并延长交⊙O 过点B 的切线于E ，作AC EG 于G .求证：.CG AC证明连结BC 交AE 于F 点...21,32.31,//BF AF CD ABBE 为⊙O 切线，...54,21.9051,9042.EF AF EF BF BE ABAB 为直径，∴.AC BC..//,CG AC BC EG AC EG说明：本题主要考查切线的性质，解题关键是作辅助线.典型例题十二例如图，AB 是⊙O 的直径，CD 是⊙O 的切线，C 为切点，AD 交⊙O 于点E ，AC AB AD ,5,4 平分BDA .（1）求证：CD AD .（2）求AC .证明（1）连OC .CD 切⊙O 于C ，∴.CD OC..//.32,21.31,CD AD AD OC OC OA解（2）连BC .AB 是⊙O 的直径，∴ 90ACB .ABC ADC ,21,90 ∽.ACD∴.AD AC AC AB 即.52.45 AC ACAC 说明：在题目条件中若有切线，常常要作出过切点的半径.利用三角形相似的知识求出线段的长.典型例题十三例（北京朝阳区试题，2002）已知：在内角不确定的ABC 中，AC AB ，点E 、F 分别在AB 、AC 上，BC EF //，平行移动EF ，如果梯形EBCF 有内切圆，当21 AB AE 时，322sin B ；当31 AB AE 时，23sin B （提示：43223 ）；当41 AB AE ，54sin B . （1）请你根据以上所反映的规律，填空：当51AB AE 时，B sin 的值等于_________；（2）当nAB AE 1时（n 是大于1的自然数），请用含n 的代数式表示 B sin ___________，并画出图形、写出已知、求证和证明过程。

2023年中考九年级数学高频考点提升练习--切线的证明(含解析)

2023年中考九年级数学高频考点提升练习--切线的证明1．在Rt△ABC中，∠A=90°，AB=AC=4，O是BC边上的点，⊙O与AB相切，切点为D，AC与⊙O相交于点E，且AD=AE．（1）求证：AC是⊙O的切线；（2）如果F为DE弧上的一个动点（不与D、E重合），过点F作⊙O的切线分别与边AB、AC相交于G、H，连接OG、OH，有两个结论：①四边形BCHG的周长不变，②∠GOH的度数不变．已知这两个结论只有一个符合题意，找出正确的结论并证明；（3）探究：在（2）的条件下，设BG=x，CH=y，试问y与x之间满足怎样的函数关系，写出你的探究过程并确定变量x的取值范围，并说明当x=y时F点的位置．2．如图，AB是⊙O的直径，点C、D在⊙O上，且CD平分⊙ACB，过点D作DE∥AB交CB延长线于点E．（1）求证：DE是⊙O的切线；（2）若AC＝4，tan∠BAC=12，求DE的长．3．如图，以BC为直径的⊙O交⊙CFB的边CF于点A，BM平分⊙ABC交AC于点M，AD⊙BC于点D，AD交BM于点N，ME⊙BC于点E，AB2=AF·AC，cos⊙ABD=35，AD=12．（1）求证：⊙ABF⊙⊙ACB；（2）求证：FB是⊙O的切线；（3）证明四边形AMEN是菱形，并求该菱形的面积S．4．如图1，AB为⊙O直径，CB与⊙O相切于点B，D为⊙O上一点，连接AD、OC，若AD//OC.（1）求证：CD为⊙O的切线；（2）如图2，过点A作AE⊥AB交CD延长线于点E，连接BD交OC于点F，若AB=3AE=12，求BF的长.5．如图，A（-5，0），B（-3，0），点C在y轴的正半轴上，⊙CBO=45°，CD⊙AB．⊙CDA=90°．点P从点Q（4，0）出发，沿x轴向左以每秒1个单位长度的速度运动，运动时时间t秒．（1）求点C 的坐标；（2）当⊙BCP=15°时，求t 的值；（3）以点P 为圆心，PC 为半径的⊙P 随点P 的运动而变化，当⊙P 与四边形ABCD 的边（或边所在的直线）相切时，求t 的值．6．如图，A 为⊙O 外一点，AO⊙BC ，直径BC ＝12，AO ＝10，BD 的长为π，点P 是BC 上一动点，⊙DPM ＝90°，点M 在⊙O 上，且⊙DPM 在DP 的下方．（1）当sinA ＝35时，求证：AM 是⊙O 的切线；（2）求AM 的最大长度．7．如图，在平面直角坐标系中，点A 、C 的坐标分别为（0，8）、（6，0），以AC 为直径作⊙O ，交坐标轴于点B ，点D 是⊙O 上一点，且 BD =AD ，过点D 作DE⊙BC ，垂足为E.（1）求证：CD 平分⊙ACE ；（2）判断直线ED 与⊙O 的位置关系，并说明理由；（3）求线段CE 的长.8．如图，已知AB 是⊙O 的直径，AC 是弦（不是直径），OD ⊙AC 垂足为G 交⊙O 于D ，E 为⊙O 上一点（异于A 、B ），连接ED 交AC 于点F ，过点E 的直线交BA 、CA 的延长线分别于点P 、M ，且ME ＝MF ．（1）求证：PE是⊙O的切线．（2）若DF＝2，EF＝8，求AD的长．（3）若PE＝6 √2，sin⊙P＝13，求AE的长．9．如图，已知等边⊙ABC，AB＝12，以AB为直径的半圆与BC边交于点D，过点D 作DF⊙AC，垂足为F，过点F作FG⊙AB，垂足为G，连结GD．（1）求证：DF是⊙O的切线；（2）求FG的长；（3）求tan⊙FGD的值．10．如图，⊙O是⊙ABC的外接圆，圆心O在AB上，且⊙B=2⊙A，M是OA上一点，过M作AB的垂线交AC于点N，交BC的延长线于点E，直线CF交EN于点F，EF=FC．（1）求证：CF是⊙O的切线（2）设⊙O的半径为2，且AC=CE，求AM的长11．如图，⊙ O是⊙ ABC的外接圆，AC为直径，弦BD=BA，BE⊥DC交DC的延长线于点E，求证：（1）∠ECB=∠BAD；（2）BE是⊙ O的切线．12．如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，连接AD，过点D作DM⊥AC，垂足为M，AB、MD的延长线交于点N．（1）求证：MN是⊙O的切线；（2）若BC=6，cosC=35，求DN的长．13．已知，如图，AB是⊙O的直径，点C为⊙O上一点，BD⊙OF于点F，交⊙O于点D，AC与BD交于点G，点E为OC的延长线上一点，且⊙OEB=⊙ACD.（1）求证：BE是⊙O的切线；（2）若⊙O的半径为52，BG的长为154，求tan⊙CAB.14．如图，⊙ABC内接于⊙O，AB是⊙O的直径，⊙O的切线PC交BA的延长线于点P，OF⊙BC交AC于点E，交PC于点F，连接AF.（1）判断直线AF与⊙O的位置关系并说明理由；（2）若⊙O的半径为6，AF＝2√3，求AC的长；（3）在（2）的条件下，求阴影部分的面积.15．如图，在△ABC中，AB=AC，⊙O是△ABC的外接圆，连结OA、OB、OC，延长BO与AC交于点D，与⊙O交于点F，延长BA到点G，使得∠BGF=∠GBC，连接FG.备用图（1）求证：FG是⊙O的切线；（2）若⊙O的半径为4.①当OD=3，求AD的长度；②当△OCD是直角三角形时，求△ABC的面积.16．如图1，在矩形ABCD中，AB=9,BC=12，点P是线段AD上的一个动点，以点P为圆心，PD为半径作⊙P，连接CP.（1）当⊙P经过PC的中点时，PC的长为；（2）当CP平分∠ACD时，判断AC与⊙P的位置关系.说明理由，并求出PD的长；（3）如图2，当⊙P与AC交于E,F两点，且EF=9.6时，求点P到AC 的距离．答案解析部分1．【答案】（1）解：如图，连接OA，OD，OE，∵AB是⊙O的切线，点D为切点，∴⊙ADO=90°，∵AD=AE，OD=0E，AO=AO，∴⊙AOD⊙⊙AOE，∴⊙ADO=⊙AEO=90°，∴AC是⊙O的切线，点E为切点；（2）解：根据题意，四边形BCHG的周长为BC+CH+BG+HG，∵∠A=90°，AB=AC=4，∴⊙B=⊙C=45°，BC=4 √2，∵⊙ADO=⊙AEO=90°，OD=0E，∴⊙DOB=⊙EOC=45°，⊙BOD⊙⊙COE，∴OB=OC，BD=CE，∴⊙EOD=90°，⊙AOB=90°，⊙BAO=45°，∴BD=OD=DA=CE= 12AB=2，∵AB，AC，GH都是⊙O的切线，∴HF=HE，GD=GF，∴四边形BCHG的周长为BC+CE+EH+GH+BD+GD=BC+CE+BD+GH+HF+FG= BC+CE+BD+2GH=4+4 √2+2GH，∵GH是变量，∴四边形BCHG的周长不是定值，这个结论不符合题意；∵AB，AC，GH都是⊙O的切线，根据切线长定理，得GO平分⊙DOF，HO平分⊙EOF，∴⊙GOH=⊙GOF+⊙HOF= 12⊙DOF+12⊙EOF=12（⊙DOF+⊙EO）= 12⊙EOD，∵⊙EOD=90°，∴⊙GOH=45°，是个定值，故该结论符合题意（3）解：根据题意，GD=GF=x-2，HE=HF=y-2，∴GH=x+y-4，AG=4-x，AH=4-y，在直角三角形AGH中，AG2+AH2=GH2，∴(x−2)2+(y−2)2=(x+y−4）2，整理，得y= 8x，且2＜x＜4，当x=y时，∴AG=AH，∴AG：AB=AH：AC，∴GH⊙BC，∴OF⊙GH，∵BG=CH，⊙B=⊙C，BO=CO，∴⊙BOG⊙⊙COH，∴GO=HO，∴GF=FH，∴A，F，O三点一线，∴⊙DOF=⊙EOF，∴弧DF=弧EF，故点F是弧DE的中点．2．【答案】（1）解：连接OD，∵AB是⊙O的直径，∴⊙ACB＝90°，∵CD平分⊙ACB，∴⊙ACD＝45°，∴⊙AOD＝2⊙ACD＝90°，∵AB∥DE，∴⊙ODE＝⊙AOD＝90°，∵OD是⊙O的半径，∴DE是⊙O的切线；（2）解：过点B作BG⊙DE于点G，∴⊙BGD＝⊙BGE＝90°，∵⊙AOD＝90°，∴⊙DOB＝90°，∵⊙ODE=90°，∴四边形ODGB是矩形，∵OD＝OB，∴四边形ODGB是正方形，∴OB＝OD＝DG＝BG，∵AC＝4，∴tan∠BAC=1 2，∴BC＝2，∴AB=√AC2+BC2=2√5，∴BG=DG=OB=√5，∵AB∥DE，∴⊙ABC＝⊙E，∴⊙EBG＝⊙BAC，∴tan∠EBG=tan∠BAC=1 2，∴EG=12BG=√5 2，∴DE=DG+EG=3√52．3．【答案】（1）证明：∵BC为⊙O的直径∴⊙BAC=90°∴⊙BAF=⊙BAC=90°又∵AB2=AF·AC∴ABAC=AF AB∴⊙ABF⊙⊙ACB（2）证明：∵⊙ABF⊙⊙ACB∴⊙ABF=⊙C又∵⊙ABC+⊙C=90°∴⊙FBC=⊙ABC+⊙ABF=90°∴BF是⊙O的切线（3）证明：∵ME⊙BC，MA⊙AB，BM平分⊙ABC ∴MA=ME∴⊙AMN=90°－⊙ABM=90°－⊙EBM=⊙EMN∴AB=BE∵NM=NM∴⊙AMN⊙⊙EMN∴AN=NE又∵AD⊙BC，ME⊙BC，∴ME⊙AD，∴⊙ANM=⊙EMN，∴⊙ANM=⊙AMN∴AN=AM∴AN=NE=EM=MA，∴四边形AMEN是菱形．∵cos⊙ABD= 35，⊙ADB=90°∴BDAB=3 5设BD=3x，则AB=5x，AD= √(5x)2−(3x)2=4x 又∵AD=12，∴x=3，∴BD=9，AB=15，∴BE=BA=15∴DE=BE-BD=6∵ND⊙ME，∴⊙BND⊙⊙BME∴NDME=BD BE设ME=y，则ND=12-y，12−y y=9 15，解得y= 15 2∴S= ME⋅DE=152×6=454．【答案】（1）证明：连接OD∵CB与⊙O相切于点B，∴OB⊥BC∵AD//OC，∴∠A=∠COB，∠ADO=∠DOC∵OA=OD，∴∠A=∠ADO=∠COB=∠DOC，∴△DOC≌△BOC(SAS)，∴∠ODC=∠OBC=90°，∴OD⊥DC又OD为⊙O半径，∴CD为⊙O的切线（2）解：设CB=x∵AE⊥EB，∴AE为⊙O的切线，∴CD、CB为⊙O的切线，∴ED=AE= 4，CD=CB=x，∠DOC=∠BCO，∴BD⊥OC过点E作EM⊥BC于M，则EM=12，CM=x−4，∴(4+x)2=122+(x−4)2解得x=9，∴CB=9，∴OC=√62+92=3√13，∵AB是直径，且AD⊙OC∴⊙OFB=⊙ADB=⊙OBC=90°又∵⊙COB=⊙BOF∴OB BF =OC BC∴BF =OB⋅BC OC =6×93√13=1813√13 5．【答案】（1）解：∵⊙BCO=⊙CBO=45°，∴OC=OB=3，又∵点C 在y 轴的正半轴上，∴点C 的坐标为（0，3）（2）解：分两种情况考虑：①当点P 在点B 右侧时，如图2，若⊙BCP=15°，得⊙PCO=30°，故PO=CO•tan30°= √3 ，此时t=4+ √3 ；②当点P 在点B 左侧时，如图3，由⊙BCP=15°，得⊙PCO=60°，故OP=COtan60°=3 √3 ，此时，t=4+3 √3 ，∴t 的值为4+ √3 或4+3 √3（3）解：由题意知，若⊙P 与四边形ABCD 的边相切时，有以下三种情况： ①当⊙P 与BC 相切于点C 时，有⊙BCP=90°，从而⊙OCP=45°，得到OP=3，此时t=1；②当⊙P与CD相切于点C时，有PC⊙CD，即点P与点O重合，此时t=4；③当⊙P与AD相切时，由题意，得⊙DAO=90°，∴点A为切点，如图4，PC2=PA2=（9-t）2，PO2=（t-4）2，于是（9-t）2=（t-4）2+32，即81-18t+t2=t2-8t+16+9，解得：t=5.6，∴t的值为1或4或5.6．6．【答案】（1）证明：如图①，过点O作OE⊙AM于点E，∵在Rt⊙AOE 中，当sinA ＝35，OA ＝10， ∴OE ＝6∵直径BC ＝12，∴OM ＝6＝OE ，∴点E 与点M 重合，OM⊙AM ，∴AM 是⊙O 的切线．（2）解：如图②，当点P 与点B 重合时，AM 取得最大值．AM 的最大长度可以通过勾股定理求得．延长AO 交⊙O 于点F ，作MG⊙AF 于点G ，连接OD 、OM ，DM ，∵BD 的长为π，∴π＝∠BOD⋅π⋅6180， ∴⊙BOD ＝30°，∵⊙DBM ＝90°，∴DM 是⊙O 的直径，即DM 过点O ，∴⊙COM ＝30°，∵AO⊙BC ，∴⊙MOG ＝60°，在Rt⊙GOM 中，⊙MOG ＝60°，OM ＝6，∴OG＝3，GM＝3√3，在Rt⊙GAM中，AM＝√AG2+GM2＝14，∴AM的最大长度：14．7．【答案】（1）证明：∵四边形ABCD是⊙O内接四边形，∴⊙BAD+⊙BCD=180°，又∵⊙BCD+⊙DCE=180°，∴⊙DCE=⊙BAD，∵＝，∴⊙BAD=⊙ACD，∴⊙DCE=⊙ACD，∴CD平分⊙ACE.（2）解：直线ED与⊙O相切.连接OD.∵OC=OD，∴⊙ODC=⊙OCD，又∵⊙DCE=⊙ACD，∴⊙DCE=⊙ODC，∴OD⊙BE，∴⊙ODE=⊙DEC，又∵DE⊙BC，∴⊙DEC=90°，∴⊙ODE=90°∴OD⊙DE，∴ED与⊙O相切（3）解：延长DO交AB于点H.∵OD⊙BE，O是AC的中点，∴H是AB的中点，∴HO是⊙ABC的中位线，∴HO= 12BC=3，又∵AC为直径，∴⊙ADC=90°，又∵O是AC的中点∴OD= 12AC=12× √62+82=5，∴HD=3+5=8，∵⊙ABC=⊙DEC=⊙ODE=90°，∴四边形BEDH是矩形，∴BE=HD=8，∴CE=8﹣6=28．【答案】（1）证明：连接OE，∵OD⊙AC，∴⊙DGF＝90°，∴⊙D+⊙DFG＝⊙D+⊙AFE＝90°，∴⊙DFG＝⊙AFE，∵ME＝MF，∴⊙MEF＝⊙MFE，∵OE＝OD，∴⊙D＝⊙OED，∴⊙OED+⊙MEF＝90°，∴OE⊙PE，∴PE是⊙O的切线（2）解：∵OD⊙AC，∴CD=AD，∴⊙FAD＝⊙AED，∵⊙ADF＝⊙EDA，∴⊙DFA ～⊙DAE ， ∴AD DE =DF AD， ∴AD 2＝DF•DE ＝2×10＝20， ∴AD ＝2 √5（3）解：设OE ＝x ， ∵sin⊙P ＝ OE OP =13， ∴OP ＝3x ，∴x 2+（6 √2 ）2＝（3x ）2，解得：x ＝3，过E 作EH 垂直AB 于H ，sin⊙P ＝ EH PE =6√2=13 ， ∴EH ＝2 √2 ，∵OH 2+EH 2＝OE 2，∴OH ＝1，∴AH ＝2，∵AE 2＝HE 2+AH 2，∴AE ＝2 √3 ．9．【答案】（1）解：连结OD ，如图，∵⊙ABC 为等边三角形，∴⊙C ＝⊙A ＝⊙B ＝60°，而OD ＝OB ，∴⊙ODB 是等边三角形，⊙ODB ＝60°，∴⊙ODB ＝⊙C ，∴OD⊙AC ，∵DF⊙AC ，∴OD⊙DF ，∴DF 是⊙O 的切线；（2）解：∵OD⊙AC ，点O 为AB 的中点，∴OD 为⊙ABC 的中位线，∴BD ＝CD ＝6．在Rt⊙CDF中，⊙C＝60°，∴⊙CDF＝30°，∴CF＝12CD＝3，∴AF＝AC﹣CF＝12﹣3＝9，在Rt⊙AFG中，∵⊙A＝60°，∴FG＝AF×sinA＝9× √32＝9√32（3）解：过D作DH⊙AB于H．∵FG⊙AB，DH⊙AB，∴FG⊙DH，∴⊙FGD＝⊙GDH．在Rt⊙BDH中，⊙B＝60°，∴⊙BDH＝30°，∴BH＝12BD＝3，DH＝√3BH＝3√3，在Rt⊙AFG中，∵⊙AFG＝30°，∴AG＝12AF＝92，∵GH＝AB﹣AG﹣BH＝12﹣92﹣3＝92，∴tan⊙GDH＝GHDH=923√3=√32，∴tan⊙FGD＝tan⊙GDH＝√32．10．【答案】（1）证明：连接OC，如图，∵⊙O是⊙ABC的外接圆，圆心O在AB上，∴AB是⊙O的直径，∴⊙ACB=90°，又∵⊙B=2⊙A，∴⊙B=60°，⊙A=30°，∵EM⊙AB ，∴⊙EMB=90°，在Rt⊙EMB 中，⊙B=60°，∴⊙E=30°，又∵EF=FC ，∴⊙ECF=⊙E=30°，又∵⊙ECA=90°，∴⊙FCA=60°，∵OA=OC ，∴⊙OCA=⊙A=30°，∴⊙FCO=⊙FCA+⊙ACO=90°，∴OC⊙CF ，∴FC 是⊙O 的切线（2）解：在Rt⊙ABC 中，∵⊙ACB=90°，⊙A=30°，AB=4， ∴BC=12AB=2，AC=√3BC=2√3， ∵AC=CE ，∴CE=2√3，∴BE=BC+CE=2+2√3，在Rt⊙BEM 中，⊙BME=90°，⊙E=30°∴BM=12BE=1+√3， ∴AM=AB ﹣BM=4﹣1﹣√3=3﹣√311．【答案】（1）证明：∵四边形ABCD 是圆内接四边形， ∴⊙ECB=⊙BAD ．（2）证明：连结OB，OD，在⊙ABO和⊙DBO中，{AB=BD BO=BOOA=OD，∴⊙ABO⊙⊙DBO （SSS），∴⊙DBO=⊙ABO，∵⊙ABO=⊙OAB=⊙BDC，∴⊙DBO=⊙BDC，∴OB⊙ED，∵BE⊙ED，∴EB⊙BO，∴BE是⊙O的切线12．【答案】（1）证明：连接OD，∵AB是⊙O的直径，∴∠ADB=90°；又∵AB=AC，∴BD=CD，∠BAD=∠CAD，∵AO=DO，∴∠OAD=∠ODA，∴∠CAD=∠ODA，∴OD//AC；∵DM⊥AC，∴∠AMD=90°，∴∠ODN=∠AMD=90°，∴OD⊥MN；又∵OD是⊙O半径，∴MN是⊙O的切线；（2）∵BC=6，BD=CD，∴BD=CD=3；在Rt△ADC中，cosC=CD AC，∵cosC=35，∴AC=5；又∵AB=AC，∴AB=5；在Rt△ADB中，根据勾股定理AD=√AB2−BD2=4，∵∠ODN=90°，∴∠NDB+∠BDO=90°；又∵∠ADB=90°，∴∠BDO+∠ODA=90°，∠OAD=∠ODA，∴∠NDB=∠OAD；又∵∠N=∠N，∴△BDN∽△DAN，∴BNDN=DNAN=BDDA=34，∴BN=34DN，DN=34AN，∴BN=34(34AN)=916AN，∵BN+AB=AN，∴916AN+5=AN，∴AN=80 7，∴DN=34AN=607．13．【答案】（1）证明：∵∠OEB=∠ACD，∠ACD=∠ABD，∴∠OEB=∠ABD，∵OF⊥BD，∴∠BFE=90°，∴∠OEB+∠EBF=90°，∴∠ABD+∠EBF=90°，即∠OBE=90°，∴BE⊥OB，∴BE是⊙O的切线；（2）解：∵OA=OB，∴∠CAO=∠ACO，∵∠CDB =∠CAO ，∴∠ACO =∠CDB ，∵∠CFD =∠GFC ，∴△CDF ∼△GCF ，∴GF CF =CG CD， ∵∠CDB =∠CAB ， ∠DCA =∠DBA ， ∴△DCG ∼△ABG ，∴CG CD =BG AB， ∴GF CF =BG AB， ∵r =52 ， BG =154， ∴AB =2r =5 ，∴tan∠CAB =tan∠ACO =GF CF =BG AB =34. 14．【答案】（1）解：直线AF 与⊙O 相切. 理由如下：连接OC ，∵PC 为圆O 切线，∴CP⊙OC ，∴⊙OCP ＝90°，∵OF⊙BC ，∴⊙AOF ＝⊙B ，⊙COF ＝⊙OCB ，∵OC ＝OB ，∴⊙OCB ＝⊙B ，∴⊙AOF ＝⊙COF ，∵在⊙AOF 和⊙COF 中，{OA =OC ∠AOF =∠COF OF =OF，∴⊙AOF⊙⊙COF（SAS），∴⊙OAF＝⊙OCF＝90°，∴AF⊙OA，又∵OA为圆O的半径，∴AF为圆O的切线；（2）解：∵⊙AOF⊙⊙COF，∴⊙AOF＝⊙COF，∵OA＝OC，∴E为AC中点，即AE=CE=12AC，OE⊥AC，∵⊙OAF=90°，OA=6，AF=2√3，∴tan∠AOF=AFOA=2√36=√33，∴⊙AOF＝30°，∴AE=12OA=3，∴AC=2AE=6；（3）解：∵AC＝OA＝6，OC＝OA，∴⊙AOC是等边三角形，∴⊙AOC＝60°，OC＝6，∵⊙OCP＝90°，∴CP=√3OC=6√3，∴S⊙OCP＝12OC⋅CP=12×6×6√3=18√3，S扇形AOC=60⋅π×62360=6π，∴阴影部分的面积=S⊙OCP﹣S扇形AOC＝18√3−6π. 15．【答案】（1）证明：连接AF，∵BF为⊙O的直径，∴∠BAF =90° ， ∠FAG =90° ， ∴∠BGF +∠AFG =90° ，∵AB =AC ，∴∠ABC =∠ACB ， ∵∠ACB =∠AFB ， ∠BGF =∠ABC ， ∴∠BGF =∠AFB ，∴∠AFB +∠AFG =90° ，即 ∠OFG =90° . 又∵OF 为半径，∴FG 是 ⊙O 的切线.（2）解：①连接CF ，则 ∠ACF =∠ABF ，∵AB=AC ，OB=OC ，OA=OA ，∴△ABO ≅△ACO ，∴∠ABO =∠BAO =∠CAO =∠ACO ， ∴∠CAO =∠ACF ，∴AO ∥CF ，∴AD CD =OD DF. ∵半径是4， OD =3 ，∴DF =1 ， BD =7 ， ∴AD CD =3 ，即 CD =13AD ，又由相交弦定理可得： AD ⋅CD =BD ⋅DF ， ∴AD ⋅CD =7 ，即 13AD 2=7 ， ∴AD =√21 （舍负）；②∵△ODC 为直角三角形， ∠ODC =90° 不可能等于 90° . ∴（i ）当 ∠ODC =90° 时，则 AD =CD ，由于 ∠ACO =∠ACF ，∴OD =DF =2 ， BD =6 ， ∴AD ⋅CD =AD 2=6×2=12 ，∴AD=2√3，AC=4√3，∴S△ABC=12×4√3×6=12√3；（ii）当∠COD=90°时，∵OB=OC=4，∴△OBC是等腰直角三角形，∴BC=4√2，延长AO交BC于点M，∵AB=AC，∴弧AB=弧AC，∴AM⊥BC，∴MO=sin45∘⋅BO=2√2，∴AM=4+2√2，∴S△ABC=12×4√2×(4+2√2)=8√2+8.16．【答案】（1）6√3（2）⊙P与AC相切，理由如下：如图1，过点P作PH⊥AC于点H．∵CP平分∠ACD，∴PH=PD，∴⊙P与AC相切于点H．∵四边形ABCD是矩形，∴∠ADC=90∘在Rt△ADC中，CD=9,AD=12，∴AC=15，∴sin∠DAC=3 5设⊙P半径为x，则PH=PD=x，AP=12−x．在 Rt △AHP 中， sin∠PAH =PH AP =x 12−x∴x 12−x =35 ∴x =4.5 ，即 PD 的长为 4.5 ．（3）如图2，过点 P 作 PH ⊥AC 于 H ，连接 PF ．由（2）可知：在 Rt △AHP 中， sin∠PAH =PH AP =35设 ⊙P 半径为 x ，则 PF =PD =x,AP =12−x ．∴PH =35(12−x). 在 ⊙P 中， PH ⊥AC,EF =9.6∴HF =245在 Rt △PHF 中， [35(12−x)]2+(245)2=x 2 ∴x 1=6,x 2=−392 (舍)．∴PD =6 ，∴PH =35(12−x)=185 ，即点 P 到 AC 的距离为 185 ．。

圆的切线证明方法专题(基础篇)(专项练习)

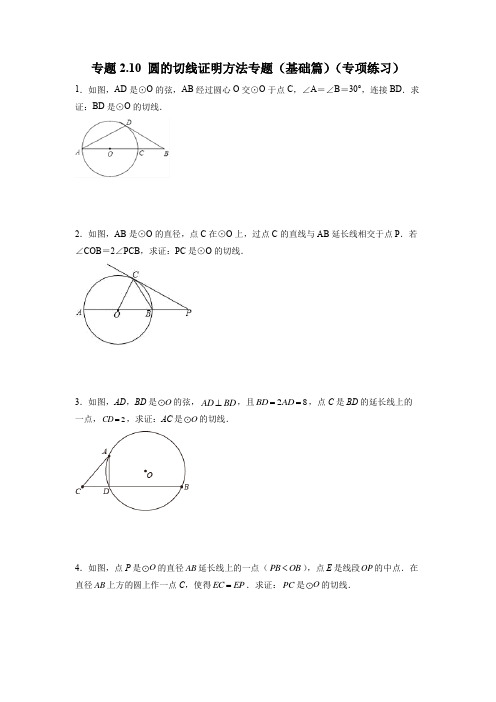
专题2.10 圆的切线证明方法专题（基础篇）（专项练习） 1．如图，AD 是⊙O 的弦，AB 经过圆心O 交⊙O 于点C ，∠A ＝∠B ＝30°，连接BD ．求证：BD 是⊙O 的切线．2．如图，AB 是⊙O 的直径，点C 在⊙O 上，过点C 的直线与AB 延长线相交于点P ．若∠COB ＝2∠PCB ，求证：PC 是⊙O 的切线．3．如图，AD ，BD 是O 的弦，AD BD ⊥，且28BD AD ==，点C 是BD 的延长线上的一点，2CD =，求证：AC 是O 的切线．4．如图，点P 是O 的直径AB 延长线上的一点（PB OB <），点E 是线段OP 的中点．在直径AB 上方的圆上作一点C ，使得EC EP =．求证：PC 是O 的切线．5．如图，在△ABC 中，∠A=45°，以AB 为直径的⊙O 交于AC 的中点D ，连接CO ，CO 的延长线交⊙O 于点E ，过点E 作EF ⊥AB ，垂足为点G ．（1）求证：BC 时⊙O 的切线；（2）若AB=2，求线段EF 的长．6．如图，AB 是O 的直径，CD 是O 的切线，切点为C ，BE CD ⊥，垂足为E ，连接,AC BC .（1）求证：BC 平分ABE ∠；（2）若60A ∠=︒，2OA =，求CE 的长.7．如图，AB是⊙O的直径，弦CD⊥AB于点E，AM是△ACD外角∠DAF的平分线.(1)求证：AM是⊙O的切线.(2)若C是优弧ABD的中点，AD＝4，射线CO与AM交于N点，求ON的长.8．如图，在△ABC中，AB＝AC，O是边AC上的点，以OC为半径的圆分别交边BC、AC 于点D、E，过点D作DF⊥AB于点F．（1）求证：直线DF是⊙O的切线；（2）若OC＝1，∠A＝45°，求劣弧DE的长．9．如图，已知△ABC内接于⊙O，点D在OC的延长线上，CD＝CB，∠D＝∠A（1）求证：BD是⊙O的切线；（2）若BC＝2，求BD的长．10．已知：如图，AB是O的直径，点C在O上，BD平分 ABC，AD＝AE，AC与BD 相交于点E．(1) 求证：AD是O的切线．(2) 若AD＝DE＝2，求BC的长．11．如图，已知AB是⊙O的直径，BD是⊙O的弦，延长BD到C，使DC=BD，连接AC，过点D作DE⊥AC，垂足为E．（1）求证：AB=AC；（2）求证：DE是⊙O的切线；（3）若⊙O的半径为6，∠BAC=60°，则DE=________．12．已知AB是⊙O的直径，点C在AB的延长线上，AB＝4，BC＝2，P是⊙O上半部分的一个动点，连接OP，CP．(1) 如图①，△OPC的最大面积是________；(2) 如图②，延长PO交⊙O于点D，连接DB，当CP＝DB时，求证：CP是⊙O的切线．13．如图，在Rt ABC △中，90ACB ∠=︒，延长CA 到点D ，以AD 为直径作O ，交BA 的延长线于点E ，延长BC 到点F ，使BF EF =．(1) 求证：EF 是O 的切线；(2) 若9OC =，4AC =，8AE =，求BE 的长．14．如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，且DC ＝AD ．过点A 作⊙O 的切线，过点C 作DA 的平行线，两直线交于点F ，FC 的延长线交AB 的延长线于点G ．(1) 求证：FG 与⊙O 相切；(2) 连接EF ，若AF ＝2，求EF 的长．15．如图，Rt △ABC ，∠ABC =90°，点O 在AB 上，AD ⊥CO 交CO 延长线于点D ，∠DAO =∠ACO ，以点O 为圆心，OB 为半径作圆．(1) 求证：AC 是⊙O 的切线；(2) 已知68CB AB ==，，求OC 的长？16．如图所示，AB 为⊙O 的直径，在△ABC 中，AB =BC ，AC 交⊙O 于点D ，过点D 作DE ⊥BC ，垂足为点E ．(1) 证明DE 是⊙O 的切线；(2) AD =8，P 为⊙O 上一点，P 到弦AD 的最大距离为8．① 尺规作图作出此时的P 点，保留作图痕迹；② 求DE 的长．17．如图，线段AB 经过O 的圆心O ，交圆O 于点A ，C ，1BC =，AD 为O 的弦，连接BD ，30BAD ABD ∠=∠=︒，连接DO 并延长交O 于点E ，连接BE 交O 于点M ．(1) 求证：直线BD 是O 的切线；(2) 求线段BM 的长．18．如图，Rt ABC △中，90C ∠=︒，点O 在AC 上，以OA 为半径的半圆O 分别交AB ，AC 于点D ，E ，过点D 作半圆O 的切线DF ，交BC 于点F ．(1) 求证：BF DF =；(2) 若4AO CE ==，1CF =，求BF 的长．19．如图，在Rt △AOB 中，∠AOB ＝90°，⊙O 与AB 相交于点C ，与AO 相交于点E ，连接CE ，已知∠AOC ＝2∠ACE ．(1) 求证：AB 为⊙O 的切线；(2) 若AO ＝20，BO ＝15，求AE 的长．20．如图，ABC 内接于O ，AC 是O 的直径，点D 是O 上一点，连接CD 、AD ，过点B 作BE AD ⊥，交DA 的延长线于点E ，AB 平分CAE ∠．(1) 求证：BE 是O 的切线；(2) 若30ACB ∠=︒，O 的半径为6，求BE 的长．21．如图，在Rt △ABC 中，∠ABC ＝90°，∠BAC 的平分线交BC 于点O ，D 为AB 上的一点，OD ＝OC ，以O 为圆心，OB 的长为半径作⊙O ．(1) 求证：AC 是⊙O 的切线；(2) 若AB ＝6，BD ＝2，求线段AC 的长．22．如图，在△ABC中，AB=AC，以AB为直径的⊙O与BC相交于点D，过点D作DE⊥AC交AC于点E．(1) 试判断直线DE与⊙O的位置关系，并说明理由；(2) 若⊙O的半径为5，BC=16，求DE的长．∠=︒，以AC为直径作O，交AB于点D，E为BC的23．如图，在Rt ABC中，ACB中点，连接DE并延长交AC的延长线于点E．(1)求证：DF是O的切线；(2)若2CF=，4DF=，求O的半径．24．如图，AB为⊙O的直径，点C在⊙O上，点P在BA的延长线上，连接BC，OC，PC．若AB＝6，AC的长为π．(1) 求∠AOC的度数；(2) 若BC＝PC，求证：直线PC与⊙O相切．参考答案1．证明见分析【分析】连接OD，求出∠ODB＝90°，根据切线的判定推出即可．解：如图，连接OD，∵OD＝OA，∴∠ODA＝∠DAB＝30°，∴∠DOB＝∠ODA+∠DAB＝60°，∴∠ODB＝180°﹣∠DOB﹣∠B＝180°﹣60°﹣30°＝90°，即OD⊥BD，∴直线BD与⊙O相切．【点拨】此题主要考查了切线的判定，三角形的内角和以及三角形的外角性质，关键是证明OD⊥BD．2．证明见分析．【分析】利用半径OA＝OC可得∠COB＝2∠A，然后利用∠COB＝2∠PCB即可证得结论，再根据圆周角定理，易得∠PCB＋∠OCB＝90°，即OC⊥CP；故PC是⊙O的切线．解：连接AC，∵OA＝OC，∴∠A＝∠ACO．∴∠COB＝2∠ACO．又∵∠COB＝2∠PCB，∴∠ACO＝∠PCB．∵AB是⊙O的直径，∴∠ACO+∠OCB＝90°．∴∠PCB+∠OCB＝90°，即OC⊥CP．∵OC是⊙O的半径，∴PC是⊙O的切线．【点拨】此题主要考查了圆的切线的判定及圆周角定理的运用，关键是利用半径OA ＝OC 可得∠COB ＝2∠A ．3．证明见分析．【分析】先由勾股定理的逆定理证明垂直，再由切线的判断进行解答即可．证明：连接AB ，∵AD BD ⊥，且28BD AD ==∴AB 为直径，AB 2=82+42=80，∵CD =2，AD =4∴AC 2=22+42=20∵CD =2，BD =8,∴BC 2=102=100∴222AC AB CB +=，∴90BAC ∠=︒∴AC 是O 的切线．【点拨】本题考查切线的判定，圆周角定理的推论，勾股定理的逆定理，解题关键是作出辅助线构造直角三角形．4．证明见分析【分析】连接OC ，根据线段中点的定义得到OE ＝EP ，求得OE ＝EC ＝EP ，得到∠COE ＝∠ECO ，∠ECP ＝∠P ，利用三角形内角和定理求出90ECO ECP ∠+∠=︒，根据切线的判定定理即可得到结论．证明：连接OC ，∵点E 是线段OP 的中点，∴OE EP =，∵EC EP =，∴OE EC EP ==，∴COE ECO ∠=∠，ECP P ∠=∠，∵180COE ECO ECP P ∠+∠+∠+∠=︒，∴90ECO ECP ∠+∠=︒，∴OC PC ⊥，∵OC 是O 的半径，∴PC 是O 的切线．【点拨】本题考查了切线的判定，等边对等角，三角形内角和定理，熟练掌握切线的判定定理是解题的关键．5．（1）证明参见分析；（2 试题分析：（1）连接BD ，由圆周角性质定理和等腰三角形的性质以及已知条件证明∠ABC=90°即可；（2）根据AB=2，则圆的直径为2，所以半径为1，即OB=OE=1，利用勾股定理求出CO 的长，再通过证明△EGO ∽△CBO 得到关于EG 的比例式可求出EG 的长，进而求出EF 的长．解：（1）如图：连接BD ，∵AB 为⊙O 的直径，∴∠ADB=90°，∴BD ⊥AC ，∵AD=CD ，∴AB=BC ，∴∠A=∠ACB=45°，∴∠ABC=90°，∴BC 是⊙O 的切线；（2）∵AB=2，∴BO=1，∵AB=BC=2，∴EF ⊥AB ，BC ⊥AB ，∴EF ∥BC ，∴△EGO ∽△CBO ，∴EG EOBC CO =，∴2EG =，∴考点：1.切线的判定；2.相似三角形的判定与性质；3.勾股定理的运用.6．（1）详见分析；（2）CE 【分析】（1）利用切线的性质得OC ⊥DE ，再证明OC ∥BE 得到∠OCB ＝∠CBE ，加上∠OCB ＝∠CBO ，所以∠OBC ＝∠CBE ；（2）利用圆周角定理得到∠ACB ＝90°，再证明△OAC 等边三角形得到AC ＝OA ＝2，再利用勾股定理可计算出BC ＝Rt △CBE 中利用含30度的直角三角形三边的关系求CE 的长．（1）证明：∵CD 是O 的切线，∴OC DE ⊥，又∵BE DE ⊥，∴OC BE ，∴OCB CBE ∠=∠，∴OBC CBE ∠=∠，即BC 平分ABE ∠；（2）解：∵AB 为O 的直径，∴90ACB ∠=︒，∵60A ∠=︒，∴OAC 是等边三角形，2AC OA ==.∴24AB OA ==，∴BC =∵1302OBC AOC ∠=∠=︒，且OBC CBE ∠=∠， ∴30CBE ∠=︒.∴12CE BC ==【点拨】本题考查了切线的性质：经过半径的外端且垂直于这条半径的直线是圆的切线；常常“遇到切点连圆心得半径”．7．(1)证明见分析；(2)ON . 【分析】(1)根据垂径定理得到AB 垂直平分CD ，根据线段垂直平分线的性质得到AC ＝AD ，得到∠BAD ＝12∠CAD ，由AM 是△ACD 的外角∠DAF 的平分线，得到∠DAM ＝12∠FAD ，于是得到结论；(2)证明△ACD 是等边三角形，得到CD ＝AD ＝4，根据直角三角形的性质即可得到结论.(1)证明：∵AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∴AB 垂直平分CD ，∴AC ＝AD ，∴∠BAD ＝12∠CAD ，∵AM 是△ACD 的外角∠DAF 的平分线，∴∠DAM ＝12∠FAD ，∴∠BAM ＝12(∠CAD+∠FAD)＝90°，∴AB ⊥AM ，∴AM 是⊙O 的切线；(2)解：∵AC ＝AD ，C 是优弧ABD 的中点，∴AC ＝AD ＝CD ，∴△ACD 是等边三角形，∴CD ＝AD ＝4，60CAD ACD ︒∠=∠=由（1）知AB 垂直平分CD ，则AB 平分CAD ∠∴CE ＝DE ＝2，1302CAE CAD ︒∠=∠= OC OA =30ACO CAE ︒∴∠=∠=30OCE ACD ACO ︒∴∠=∠-∠=在Rt OCE 中，设OC x =，则12OE x = 根据勾股定理得222OE CE OC +=，即2221()22x x +=解得x =∴OC ＝OA ∵∠ANO ＝∠OCE ＝30°，∴ON ＝2OA . 【点拨】本题是圆与三角形的综合题，涉及的知识点主要有切线的判定、垂径定理、等边三角形的判定与性质、直角三角形30度角的性质，灵活利用圆与三角形的相关性质是解题的关键.8．（1）详见分析；（2）34π．【分析】（1）连结OD ，根据等腰三角形的性质得到OD ∥AB ，根据平行线的性质得到∠ODF ＝90°，根据切线的判定定理证明；（2）根据平行线的性质得到∠AOD ＝180°﹣45°＝135°，根据弧长公式计算即可．证明：如图，连结OD ，∵AB＝AC，∴∠B＝∠ACB，∵OC＝OD，∴∠ODC＝∠ACB，∴∠B＝∠ODC，∴OD∥AB，∵DF⊥AB，∴∠ODF＝∠BFD＝90°，∵OD为半径，∴直线DF是⊙O的切线；（2）解：∵∠A＝45°，OD∥AB，∴∠AOD＝180°﹣45°＝135°，∴劣弧DE的长为1353 1804ππ⨯=．【点拨】本题主要考查了切线的判定及弧长的计算，熟练掌握切线的判定定理及弧长的计算公式是解题的关键.9．（1）见分析；（2）BD＝【分析】（1）由等腰三角形的性质得出∠CBD+∠OBC＝90°，则∠OBD＝90°，可得出结论；（2）证明△OBC为等边三角形，得出∠BOC＝60°，根据直角三角形的性质可得出答案．（1）证明：∵OB＝OC，∴∠OBC＝∠OCB，∴∠BOC+2∠OBC＝180°，∵∠BOC＝2∠A，∴∠A+∠OBC＝90°，又∵BC＝CD，∴∠D＝∠CBD，∵∠A＝∠D，∴∠CBD+∠OBC＝90°，∴∠OBD＝90°，∴OB⊥BD，∴BD是⊙O的切线；（2）解：∵∠OBD＝90°，∠D＝∠CBD，∴∠OBC＝∠BOC，∴OC＝BC，又∵OB＝OC，∴△OBC为等边三角形，∴∠BOC＝60°，∵BC＝2，∴OB＝2，∴BD＝【点拨】本题考查切线的判定，等腰三角形的性质，圆周角定理，直角三角形的性质，等边三角形的判定与性质，熟练掌握切线的判定是解题的关键．10．(1)见分析【分析】（1）根据AB是O的直径，可得∠C＝90°，由BD平分∠ABC，可得∠CBD＝∠ABD，根据AD＝AE，可得∠CEB＝∠DEA，进而可得∠BAD＝90°，即可得证；（2）连接AF，根据等腰三角形的性质可得DF＝12DE＝1，勾股定理求得AF，证明△AEF≌△BEC，即可求解．（1）∵AB是O的直径，∴∠C＝90°，∴∠CBE＋∠CEB＝90°，∵BD平分∠ABC，∴∠CBD＝∠ABD，∵AD＝AE，∴∠D＝∠AED，∵∠CEB＝∠DEA，∴∠ABD＋∠D＝∠CBE ＋∠CEB＝90°，即∠BAD＝90°，∴AD是⊙O的切线，（2）连接AF，如图，∵AB是O的直径，∴∠AFB＝90°，即AF BD⊥，∵AD＝DE＝2，∴DF＝12DE＝1，在Rt ADF∆中，AD＝2，DF＝1，∴AF＝41-＝3，∵∠DBA＋∠D＝∠EAB＋∠DAE＝90°，∠D＝∠DAE＝60°，∴∠DBA＝∠EAB，∴AE＝BE，又∠AFE＝∠C＝90°，∠AEF＝∠CEB，∴△AEF≌△BEC（AAS），∴BC＝AF【点拨】本题考查了直径所对的圆周角是直角，切线的判定，勾股定理，全等三角形的性质与判定，掌握以上知识是解题的关键．11．（1）见分析；（2）见分析；（3）【分析】（1）连接AD，由直径所对的圆周角度数及中点可证AD是BC的垂直平分线，根据线段垂直平分线的性质可得结论；（2）连接OD，由中位线的性质可得OD∥AC，由平行的性质与切线的判定可证；（3）易知ABC是等边三角形，由等边三角形的性质可得CB长及C∠度数，利用直角三角形30度角的性质及勾股定理可得结果.解：（1）连接AD．∵AB是⊙O的直径，∴∠ADB=90°．∴⊥AD BC又∵DC=BD，∴AD是BC的垂直平分线∴AB=AC．（2）连接OD．∵DE⊥AC，∴∠CED=90°．∵O为AB中点，D为BC中点，∴OD∥AC．∴∠ODE=∠CED=90°．∴DE是⊙O的切线．=（3）由（1）得AC AB60BAC ∠=︒ABC ∴是等边三角形60,2612C BC AB ︒∴∠===⨯=162DC BD BC ∴=== 在Rt CED 中，906030CDE ︒︒︒∠=-=132CE CD ∴== 根据勾股定理得222CE DE CD +=DE ∴【点拨】本题考查了圆与三角形的综合，涉及的知识点主要有圆的切线的判定、圆周角定理的推论、垂直平分线的性质、等边三角形与直角三角形的性质，灵活的将图形与已知条件相结合是解题的关键.12．(1)4(2)见分析【分析】（1）因为OC 长度确定，所以当点P 到OC 的距离最大时△OPC 的面积最大，当OP ⊥OC 时，当点P 到OC 的距离最大，等于圆O 的半径，求出此时的△OPC 的面积即可；（2）连接AP ，BP ，利用同圆中，相等的圆心角所对的弦相等，可得AP =DB ，因为CP ＝DB ，所以AP =CP ，可证△APB ≌△CPO （SAS ），得到∠OPC ＝90°，即可证明CP 是切线．(1)解：∵AB ＝4，∴OB ＝2，OC ＝OB +BC ＝4．在△OPC 中，设OC 边上的高为h ，∵S △OPC 12=OC •h ＝2h ， ∴当h 最大时，S △OPC 取得最大值．作PH ⊥OC ，如图①，则PO PH >，当OP ⊥OC 时，PO PH =，此时h 最大，如答图1所示：此时h ＝半径＝2，14242OPC S ⨯⨯＝＝．∴△OPC 的最大面积为4，故答案为：4．(2)证明：如答图②，连接AP ，BP ．∵∠AOP ＝∠BOD ，∴AP ＝BD ，∵CP ＝DB ，∴AP ＝CP ，∴∠A ＝∠C ，在△APB 与△CPO 中，AP CP A C AB CO =⎧⎪∠=∠⎨⎪=⎩，∴△APB ≌△CPO （SAS ），∴∠APB ＝∠OPC ，∵AB 是直径，∴∠APB ＝90°，∴∠OPC ＝90°，∴DP ⊥PC ，∵DP 经过圆心，∴PC 是⊙O 的切线．【点拨】本题考查了圆，熟练掌握圆的半径、切线、弦与圆心角的关系等知识是解题的关键．13．(1)见分析(2)13【分析】（1）连接OE ，根据等边对等角可得OEA OAE ∠=∠，FEB B ∠=∠，根据对顶角相等，等量代换后可得90OEA FEB ∠+∠=︒即可得证；（2）过点O 作OG BE ⊥，根据垂径定理可得4AG AC ==，由945AO OC AC =-=-=，证明AOG ≌ABC ，可得5AB =，根据BE EA AB =+即可求解．（1）如图，连接OE ，Rt ABC △中，90ACB ∠=︒，90CAB B ∴∠+∠=︒，OE OA =，OEA OAE ∴∠=∠，OAE CAB ∠=∠，90OEA B ∴∠+∠=︒，BF EF =，FEB B ∴∠=∠，90OEA FEB ∴∠+∠=︒，即90FEO ∠=︒，OE 是半径，∴EF 是O 的切线；（2）如图，过点O 作OG BE ⊥，8AE =，124EG AG AE ∴===，9OC =，4AC =，945AO OC AC ∴=-=-=，在AOG 与ABC 中，904OGA BCA AG AC GAO CAB ∠=∠=︒⎧⎪==⎨⎪∠=∠⎩∴AOG ≌ABC ，5AB AO ∴==，5813BE BA AE ∴=+=+=，【点拨】本题考查了切线的判定定理，垂径定理，掌握以上知识是解题的关键． 14．(1)见分析(2)EF =【分析】（1）连接OC ，AC ．先证明△ACD 为等边三角形．可得∠ACO =∠OAC =30°．再由FG ∥DA ，可得∠ACF =∠DAC =60°．从而得到∠OCF =90°．即可求证；（2）根据AD ∥FG ，可得∠AGF =∠DAE =30°．再根据直角三角形的性质可得FG =2AF =4，AG ADE ≌△GCE ．可得AE=GE即可求解．(1)证明：连接OC，AC．∵AB是⊙O的直径，CD⊥AB，∴CE=DE，AD=AC．∵DC=AD，∴DC=AD=AC．∴△ACD为等边三角形．∴∠D=∠DCA=∠DAC=60°．∴∠AOC=30°，∵OA=OC，∴∠ACO=∠OAC=30°．∵FG∥DA，∴∠ACF=∠DAC=60°．∴∠OCF=90°．∴OC⊥FG．∵OC为半径，∴FG与⊙O相切．(2)解：∵AD∥FG，∴∠AGF=∠DAE=30°．∵AF为⊙O的切线，∴∠F AG=90°，∴FG=2AF=4，∴AG=在△ADE和△GCE中，∵∠AGF=∠DAE=30°．∠CEG=∠AED，DE=CE，∴△ADE≌△GCE．∴AE=GE∴EF【点拨】本题主要考查了垂径定理，切线的性质和判定，直角三角形的性质，等边三角形的判定和性质，全等三角形的判定和性质，勾股定理，熟练掌握垂径定理，切线的性质和判定，直角三角形的性质，等边三角形的判定和性质，全等三角形的判定和性质是解题的关键．15．(1)见分析(2)OC=【分析】（1）证明∠BCO=∠ACO，推出OE=OB，即可证明AC是⊙O的切线；（2）证明△OBC≌△OEC，利用勾股定理求得AC=10，在Rt△AOE中，利用勾股定理列式计算可求得圆的半径，进一步求解即可．(1)证明：作OE⊥AC，垂足为E，∵AD⊥CO，∴∠ADO=90°，∴∠ADO=∠ABC=90°，∵∠AOD=∠BOC，∴∠DAO=∠BCO，∵∠DAO=∠ACO，∴∠BCO=∠ACO，∵OB⊥BC，OE⊥AC，∵OE=OB，∵OB是半径，∴AC是⊙O的切线；(2)解：∵OBC=∠OEC，∠BCO=∠ACO，OC=CO，∴△OBC≌△OEC，∴BC=EC=6，在Rt△ABC中，10AC=，∴AE=AC−EC=10−6=4，在Rt△AOE中，设半径为R，∵AE2+OE2=OA2，∴42+R2=(8−R)2，∴R=OC=3，∴在Rt△OBC中，OC==【点拨】本题考查了切线的判定和性质，勾股定理，全等三角形的判定和性质，熟练掌握切线的判定和性质是解题的关键．16．(1)见分析(2)①见分析；②DE=4.8【分析】（1）连接OD、BD，求出BD⊥AC，可得AD=DC，根据三角形的中位线得出OD∥BC，推出OD⊥DE，根据切线的判定推出即可；（2）①利用垂径定理作出AD的垂直平分线即可；②根据垂径定理以及勾股定理求得⊙O的半径和FO，再根据中位线中位线定理求得BD，然后根据三角形面积公式即可求解．(1)证明：连接OD，BD，∵AB为⊙O的直径，∴BD⊥AD，又∵AB=BC，△ABC是等腰三角形，∴BD又是AC边上的中线，∴OD是△ABC的中位线，∴OD∥BC，又DE⊥BC，∴DE⊥OD，∵OD是⊙O的半径，∴DE是⊙O的切线；(2)解：①如图，作AD的垂直平分线与☉O相交于点P，点P即为所求．②如图，AD 的垂直平分线与AD 相交于点F ，连接BD ，∵PF ⊥AD ，∴AF =12AD =4，设☉O 的半径为r ，在Rt △AFO 中，AF 2+FO 2=AO 2，即42+(8−r ) 2=r 2，解得r =5．∴FO =PF −PO =3，∵FO 是△ABD 的中位线，∴BD =2FO =6，∵AB 为⊙O 的直径，∴BD ⊥AC ，又∵AB =BC ，△ABC 是等腰三角形，∴AD =DC =8，∴BC =AB =10，在Rt △BDC 中，S △BDC =12BD ⋅CD =12BC ⋅DE ， ∴DE =4.8．【点拨】本题考查了切线的判定和性质，等腰三角形的性质，垂径定理，勾股定理，三角形中位线等知识点的综合运用．17．(1)见分析【分析】（1）根据圆周角定理可得260BOD BAD ∠=∠=︒，从而得到90ODB ∠=︒ ，即可求证；（2）连接DM ，Rt △BOD 中，根据直角三角形的性质可得 BO =2OD ，从而得到1OD OC ==，BD =DE O 为的直径，可得2DE =，90DME ∠=︒，从而得到BE =1122BDE S BD DE BE DM =⋅=⋅△，可得DM =，再由勾股定理，即可求解．(1)证明：∵∠BOD =2∠BAD ，∴260BOD BAD ∠=∠=︒，又∵30ABD ∠=︒，∴90ODB ∠=︒ ，即OD BD ⊥，又∵OD 为O 的半径，∴直线BD 是O 的切线；(2)解：如图，连接DM ，Rt △BOD 中，30DBO ∠=︒，∴2BO OD OC BC ==+，又1BC =，OD OC =，∴1OD OC ==，∴BD =∵DE O 为的直径，∴2DE =，90DME ∠=︒，在Rt △BDE 中，BE == ∵1122BDE S BD DE BE DM =⋅=⋅△，∴BD DE DM BE ⋅==在Rt △BDM 中，BM = 【点拨】本题主要考查了切线的判定，圆周角定理，直角三角形的性质，勾股定理等知识，熟练掌握切线的判定，圆周角定理，直角三角形的性质，勾股定理是解题的关键． 18．(1)见分析(2)7(1) 连接OD ，得到OAD ADO ∠=∠，利用余角的性质得到B BDF ∠=∠，得出结果；(2) 连接OF ，构造直角三角形，利用勾股定理求解．(1)证明：连接OD ，如图，∵半圆O 的切线DF ，∴90ODF ∠=︒．∴90ADO BDF ∠+∠=︒．∵90C ∠=︒，∴90OAD B ∠+∠=︒．∵OA OD =，∴OAD ADO ∠=∠．∴B BDF ∠=∠．∴BF DF =．(2)解：连接OF ．∵4AO CE ==，AO OE =，∴8OC =．∵9090C ODF ∠=︒=∠=︒，1CF =，∴2222265OF OC CF OD DF =+=+=．又∵4OD =，∴7DF BF ==．【点拨】本题考查切线的性质、等腰三角形的判定以及勾股定理，遇切线连接圆心和切点时解决问题的关键．19．(1)见分析(2)8（1）根据OC ＝OE ，得到∠OCE ＝∠OEC ，再根据∠AOC ＝2∠ACE ，得到∠OCA ＝∠OCE +∠ACE ＝12（∠OCE +∠OEC +∠AOC ）＝11802⨯＝90°，即有OC ⊥AB ，结论得证；（2）利用勾股定理求出AB ，在根据三角形的面积的不同算法可求出OC ，即AE 可求．(1)证明：∵OC ＝OE ，∴∠OCE ＝∠OEC ，∵∠AOC ＝2∠ACE ，∴∠OCA ＝∠OCE +∠ACE ＝12（∠OCE +∠OEC +∠AOC ）＝11802⨯＝90°， ∴OC ⊥AB ，∴AB 为⊙O 的切线；(2)∵AO ＝20，BO ＝15，∴25AB ， ∵1122OA OB AB OC ⨯⨯=⨯⨯，即1120152522OC ⨯⨯=⨯⨯， ∴OC ＝12，∴AE ＝OA ﹣OE ＝20﹣12＝8.【点拨】本题考查了切线的判定与性质、勾股定理以及三角形面积的知识，利用勾股定理解直角三角形是解答本题的关键．20．(1)见分析；(2)【分析】（1）根据切线的判定定理证明即可；（2）证明ABO 是等边三角形，利用30所对的直角边等于斜边的一半证明132AE AB ==，再由勾股定理，得BE (1)证明：连接BO ．∵OA OB =，∴OAB OBA ∠=∠．∵AB 平分CAE ∠，∴OAB BAE ∠=∠，∴OBA BAE ∠=∠．∴OB AE ∥，∴18090EBO E ∠=︒-∠=︒，即BE OB ⊥，又∵OB 是O 的半径，∴BE 是O 的切线．(2)解：30ACB ∠=︒，∴60AOB ∠=︒．又∵OA OB =，∴ABO 是等边三角形，∴60OBA ∠=︒，6OA OB AB ===，∴30ABE ∠=︒， ∴132AE AB ==．由勾股定理，得BE =【点拨】本题考查切线的判定定理，等边三角形的判定及性质，30所对的直角边等于斜边的一半，勾股定理，解题的关键是熟练掌握以上知识点．21．(1)见分析(2)8【分析】（1）过O 作OE ⊥AC 于E ，先证Rt △ABO ≌Rt △AEO ，OB ＝OE ，即OE 为圆的半径，即可求证；（2）利用切线的性质可得AB =AE ，再证Rt △BOD ≌Rt △COE ，即有BD ＝CE ＝2，则AC 可求．(1)证明：过O 作OE ⊥AC 于E ．∵AO 平分∠BAC ，且∠ABC ＝90°，OE ⊥AC ，∴OB ＝OE ，即OE 为圆的半径，∴AC 是⊙O 的切线；(2)∵∠ABC ＝90°，OB 为⊙O 半径，∴AB 是⊙O 的切线，又由（1）AC 是⊙O 的切线，∴AB ＝AE ＝6，在Rt △BOD 和Rt △COE 中，OB OE OD OC =⎧⎨=⎩， ∴Rt △BOD ≌Rt △COE ，∴BD ＝CE ＝2，∴AC ＝AE +CE ＝8【点拨】本题考查了切线的判定与性质，角平分线的性质定理，在OE ⊥AC 的条件下证得OE 为圆的半径是解答本题的关键．22．(1)DE 是⊙O 的切线，理由见分析；(2)DE 的长为245．【分析】（1）连接OD ，根据等边对等角性质和平行线的判定和性质证得OD ⊥DE ，从而证得DE 是⊙O 的切线；（2）由等腰三角形的性质求出BD =CD =8，由勾股定理求出AD 的长，根据三角形的面积得出答案．(1)解：DE 是⊙O 的切线，理由如下：连接OD ，∵OB =OD ，∵AB=AC，∴∠B=∠C，∴∠ODB=∠C，∴OD∥AC，∵DE⊥AC，∴OD⊥DE，∴DE是⊙O的切线；(2)解：连接AD，∵∠ADB=90°，AB=AC，∴BD=CD，∵⊙O的半径为5，BC=16，∴AC=AB=10，CD=8，∴AD= 6，∵S△ADC=12AC•DE=12AD•CD，∴DE=6824105 AD CDAC⋅⨯==．【点拨】本题考查了切线的判定与性质，圆周角定理，等腰三角形的性质和判定，三角形的内角和定理，勾股定理，三角形的面积等知识，掌握切线的判定与性质是解题的关键．23．(1)见分析(2)3【分析】（1）连接OD、CD，由AC为⊙O的直径知△BCD是直角三角形，结合E为BC的中点知∠CDE=∠DCE，由∠ODC=∠OCD且∠OCD+∠DCE=90°可得答案；（2）设⊙O的半径为r，由OD2+DF2=OF2，即r2+42=（r+2）2可得r=3，即可得出答案．(1)解：如图，连接OD、CD．∵AC为⊙O的直径，∴∠ADC=90°，∴∠CDB=90°，即△BCD是直角三角形，∵E为BC的中点，∴∠CDE =∠DCE ，∵OD =OC ，∴∠ODC =∠OCD ，∵∠ACB =90°，∴∠OCD +∠DCE =90°，∴∠ODC +∠CDE =90°，即OD ⊥DE ，∴DE 是⊙O 的切线；(2)解：设⊙O 的半径为r ，∵∠ODF =90°，∴OD 2+DF 2=OF 2，即r 2+42=（r +2）2，解得：r =3，∴⊙O 的半径为3．【点拨】本题主要考查了圆切线的判定与性质，等腰三角形的性质与判定，直角三角形斜边上的中线，勾股定理等等，熟知圆切线的性质与判定是解题的关键．24．(1)60︒(2)见分析【分析】（1）由直径为6，求得⊙O 的周长，再由AC 的长为π，求得AOC ∠的度数．（2）由（1）知60AOC ∠=︒，由于OB OC =，可得1302OBC AOC ∠=∠=︒，再由BC PC =推出30P ∠=︒，从而证得OC CP ⊥，直线PC 与⊙O 相切．(1)解：∵6AB =，∴⊙O 的周长为6π．∵AC 的长为π， ∴1360606AOC ∠=⨯︒=︒． (2)证明：∵AB 为⊙O 的直径，点C 在⊙O 上，∴OB OC =， ∴12OBC OCB AOC ∠=∠=∠．∵60AOC ∠=︒， ∴1302OBC OCB AOC ∠=∠=∠=︒． ∵BC PC =，∴30CBO P ∠=∠=︒．在COP 中，∵60COA ∠=︒，30P ∠=︒，∴180180603090OCP COA P ∠=︒-∠-∠=︒-︒-︒=︒，∴OC CP ⊥，又∵点C 在⊙O 上，∴直线PC 与⊙O 相切．【点拨】本题考查了圆的相关性质，切线的判定，综合运用圆的性质确定相关角度是解题关键．。

圆的切线证明中考数学专项训练(含答案解析)

圆的切线证明(1)求证：CD 为O 切线；(2)若1CD =，5AC =，求PB (1)求证：CD 是O 的切线；(2)若16ABCD S =正方形，求CE3．如图，在Rt ABC △中，90C ∠=︒，AD 平分BAC ∠交BC 于点D ，O 为AB 上一点，经过点A ，D 的O 分别交AB ，AC 于点E ，F 连接OF 交AD 于点G ．(1)求证：BC 是O 的切线；(2)若60OFA ∠=︒，半径为4，在圆O 上取点P ，使15PDE ∠=︒，求点P 到直线DE 的距离．4．如图，AB 是O 的直径，CD 是O 的弦，AB CD ⊥，垂足是点H ，过点C 作直线分别与AB ，AD 的延长线交于点E ，F ，且2ECD BAD ∠=∠．(1)求证：CF 是O 的切线；(2)如果20AB =，12CD =，求AE 的长．5．如图，O 是ABC 的外接圆，O 点在BC 边上，BAC ∠的平分线交O 于点D ，连接BD 、CD ，过点D 作BC 的平行线，与AB 的延长线相交于点P ．(1)求证：PD 是O 的切线；(2)若3AB =，4AC =，求线段BD 的长．6．如图，已知以Rt ABC △的直角边AB 为直径作O ，与斜边AC 交于点D ，E 为BC 边上的中点，连接DE ．(1)求证：DE 是O 的切线；(2)若AD ，AB 的长是方程210240x x -+=的两个根，求直角边BC 的长．(1)求证：DE 是O 的切线；(2)若30C ∠=︒，23CD =，求图中阴影部分的面积．(1)求证：DE 是O 的切线；(2)若2AB =，30C ∠=︒，求9．如图，AB 为O 的直径，C ，D 为O 上的两点，BAC DAC ∠=∠，过点C 作直线EF AD ⊥，交AD 的延长线于点E ，连接BC ．(1)求证：EF 是O 的切线；(2)若30CAO ∠=︒，2BC =，求CE 的长．10．如图，AB 是O 的直径，点C 是O 上一点（与点A ，B 不重合），过点C 作直线PQ ，使得ACQ ABC ∠=∠．(1)求证：直线PQ 是O 的切线．(2)过点A 作AD PQ ⊥于点D ，交O 于点E ，若O 的半径为2，30DAC ∠=︒，求图中阴影部分的面积．11．如图，等腰ABC 的顶点A ，C 在O 上， BC 边经过圆心0且与O 交于D 点，30B ∠=︒.(1)求证：AB 是O 的切线；(2)若6AB =，求阴影部分的面积12．如图，AB 是ABC 外接圆O 的直径，PA 是O 的切线，BD OP ∥，点D 在O 上．(1)求证：PD 是O 的切线．(2)若ABC 的边6cm AC =，8cm BC =，I 是ABC 的内心，求IO 的长度．13．如图，AB 是O 的直径，AC 是弦，点D 是O 上一点，OD AB ⊥，连接CD 交AB 于点E ，F 是AB 延长线上的一点，且CF EF =．(1)求证：CF 是O 的切线；(2)若8CF =，4BF =，求弧BD 的长度．14．如图所示，在Rt ABC △中，点O 在斜边AB 上，以O 为圆心，OB 为半径作圆O ，分别与BC 、AB 相交于点D 、E ，连接AD ，已知CAD B ∠=∠．(1)求证：AD 是O 的切线；(2)若23AD CD ==时，求阴影部分的面积．(1)求证：PA是O(2)若tan CAD∠=(3)延长CD，AB交于点(1)求证：DE BG=；(2)求证：BF是O的切线；(3)若23DEEG=时，AE(1)当60A ∠=︒，2AD =时，求(2)求证：DF 是O 的切线．(1)求证：DF 是O (2)若 BE DE =，tan(1)求证：直线AB 为O 的切线；(2)若4tan 3A =，O 的半径为2，求AB (1)求证：BF 是O 的切线；(2)若6EF =，cos ABC ∠①求BF 的长；②求O 的半径．参考答案：∵CD AE ⊥，∴90ADC ∠=︒，∵OC OA =，∴OCA OAC ∠=∠，∵的平分线AC 交O 于∵AB 为O 直径，∴90ACB ∠=︒，∴90ADC ACB ∠=∠=︒，∵DAC OAC ∠=∠，∴，【点睛】此题重点考查正方形的性质、等腰三角形的性质、切线的判定、平行线分线段成比例定理、锐角三角函数与解直角三角形等知识，正确地作出所需要的辅助线是解题的关键．3．(1)见解析(2)232-或423-【分析】（1）连接OD ，可得（2）①过点P 作PN DE ⊥交交于H ，可求60EOD ∠=︒，即可求解；②连接OD ，OP 60EOD ∠=︒，30POE ∠=︒，可证求解．【详解】（1）解：如图，连接∴OA OD =，∴ODA OAD ∠=∠，AD 是BAC ∠的平分线，， ∠=︒PDE15=，PE PE ∴∠=︒POE30，OA OF∠=︒60OFA=，∴∠=︒，OAF60∠的平分线， AD是BAC同理可求60EOD ∠=︒，30POE ∠=︒，1302DOL EOD ∴∠=∠=︒，30DOP EOD POE ∠=∠-∠=︒，DOP DOL ∴∠=∠，AB 是O 的直径，90ACB ∴∠=︒，AO OB =，AB CD ⊥ ，AB ∴平分弦CD ，AB 平分 CD，CH HD ∴=， CBDB =，90CHA CHE ∠=︒=∠，BAD BAC DCB ∴∠=∠=∠，∵AB 是O 的直径，∴90ADB ∠=︒，∴BDC 为直角三角形，∵E 为BC 边上的中点，∴ED EB =，∴12∠=∠，∵OB OD =，3=4∠∠∵AB AC =，∴A ABC CB =∠∠，设OB OD r ==，∴ABC ODB ∠=∠，∵AB AC =，23CD =，C ∠=∴23BD CD ==，30B C ∠=∠=∴1803030120BOD ∠=︒-︒-︒=︒OF BD ⊥==OB OD AB AC,∴∠=∠，B CB ODB∠=∠∴∠=∠．ODB C∴∥．OD AC，=OA OC∴∠=∠，OAC OCAQ，∠=∠DAC BAC∴∠=∠，DAC OCA∥，∴AD OC，EF AD⊥∴⊥，而OC为半径，EF OC的切线；∴是OEF的直径，（2）解：AB为O（1）根据题意连接OC ，可知90ACB ∠=︒，可知AOC 是等腰三角形，OAC OCA ∠=∠，继而可证90OCD ∠=︒；（2）连接OE ，过点E 作EF AB ⊥，根据题意可知60EAO ∠=︒即可得知AEO △为等边三角形，再求出扇形AOE 面积减去AEO △的面积即为阴影面积．【详解】（1）解：连接OC ，，∵OA OC =，AB 是O 的直径，∴90ACB ∠=︒，∴90CAB CBA ∠+∠=︒，∴AOC 是等腰三角形，∴OAC OCA ∠=∠，∵ACQ ABC ∠=∠，∴90ACQ OCA ∠+∠=︒，∴OC PQ ⊥，∴直线PQ 是O 的切线；（2）解：连接OE ，过点E 作EF AB ⊥，，∵AD PQ ⊥，ACQ ABC ∠=∠，∴30DAC CAB ∠=∠=︒，∴60EAO ∠=︒，∵AB 为O 的直径，∴90ADB ∠=︒，∵BD OP ∥，∴OP AD ⊥，OP 是AD 的垂直平分线，∴PD PA =，则IU IV IQ ==，∵AB 为O 的直径，∴90ACB ∠=︒，∵6cm AC =，8cm BC =，∴226810AB =+=，5OB OA ==(2)3π．【分析】本题考查了切线的判定，求弧长；（1）如图，连接OC ，OD ．证明90OCF ∠=︒即可；（2）设O 的半径为r ，在Rt COF △中，勾股定理可得6r =，再根据弧长公式可解决问题．【详解】（1）证明：连接OCCF EF= CEF ECF∴∠=∠OD AB⊥ 90DOE ∴∠=︒，90ODE OED ∴∠+∠=︒，OD OC = ，ODE OCD ∴∠=∠，CEF OED ∠=∠ ，OED ECF ∴∠=∠，90OCD ECF ∴∠+∠=︒，即90OCF ∠=︒，OC CF ∴⊥，CF ∴是O 的切线．（2）设O 的半径为r ，∵4BF =，∴4OF r =+，在Rt OCF 中，90,∠=︒ACB∴∠+∠CAD ADC=,OB OD∴∠=∠,B ODB则sin 30OH OD =⋅ODB S S S ∴=-阴影扇形∴CAD BAD ∠=∠，∴5CD BD ==，∵AB 为直径，点∴90ADB ∠=︒，∵2DOB DAB ∠=∠=∠又∵DFO CFA ∠=∠，∴DOF CAF ∽，又∵OB BF OA ==，∴23DF FO FC FA ==，∴90EHB BGF ∠=∠=︒，∵点C 为劣弧BD 中点，∴ CDBC =，∴DAC BAC DBC ∠=∠=∠∵AD 是O 的直径，∴90AED ∠=︒，∵60A ∠=︒，2AD =∴30ADE ∠=︒，则12AE =∴2222DE AD AE =-=∵AD 是直径，∴90AED ∠=︒，∴1809090DEB ∠=︒-︒=︒∵四边形ABCD 为菱形，∴DBE DBF ∠=∠，AD ∥∵BE BF =，DB DB =，∴()SAS DBE DBF ≌，∴90DFB DEB ∠=∠=︒，∵AD BC ∥，∴90ADF DFB ∠=∠=︒，∴AD DF ⊥，∵AD 为直径，∴DF 是O 的切线．【点睛】本题主要考查了直径所对的圆周角为直角，含30度角的直角三角形的性质，勾股定理，切线的判定，解题的关键是作出辅助线，熟练掌握切线的判定方法．18．(1)见解析(2)52AB 是O 的直径，90ADB ∴∠=︒，90BDC ∴∠=︒，90BDF CDF ∠∠∴+=︒，OB OD = ，OBD ODB ∴∠=∠，CDF ABD ∠∠= ，ODB CDF ∠∠∴=，90ODB BDF ∴∠+∠=︒，90ODF ∴∠=︒，DF OD ∴⊥，OD 是O 的半径，DF ∴是O 的切线；（2）如图，连接AE ，∵ BEDE =，BAE CAE ∴∠=∠，AB 是O 的直径，90AEB ∴∠=︒，90AEC ∴∠=︒，AEB AEC ∴∠=∠，∵OC OD =，∴OCD ODC ∠=∠．设OCD ODC α∠=∠=，∴22A BCD α∠=∠=．∵90ACB ∠=︒，。

中考复习专题——圆切线证明

中考复习专题--------圆的切线的判定与性质知识考点：1、掌握切线的判定及其性质的综合运用，在涉及切线问题时，常连结过切点的半径，切线的判定常用以下两种方法：一是连半径证垂直，二是作垂线证半径。

2、掌握切线长定理的灵活运用，掌握三角形和多边形的内切圆，三角形的内心。

精典例题：一、假设直线l过⊙O上某一点A，证明l是⊙O的切线，只需连OA，证明OA⊥l就行了，简称“连半径，证垂直〞，难点在于如何证明两线垂直.例1如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，交AC于E，B为切点的切线交OD延长线于F.求证：EF与⊙O相切.例2 如图，AD是∠BAC的平分线，P为BC延长线上一点，且PA=PD.求证：PA与⊙O相切.例3 如图，AB=AC，AB是⊙O的直径，⊙O交BC于D，DM⊥AC于M求证：DM与⊙O相切.例4 如图，：AB是⊙O的直径，点C在⊙O上，且∠CAB=300，BD=OB，D在AB的延长线上. 求证：DC是⊙O的切线例5 如图，AB是⊙O的直径，CD⊥AB，且OA2=OD·OP.求证：PC是⊙O的切线.例6 如图，ABCD是正方形，G是BC延长线上一点，AG交BD于E，交CD于F.求证：CE与△CFG的外接圆相切.二、假设直线l与⊙O没有的公共点，又要证明l是⊙O的切线，只需作OA⊥l，A为垂足，证明OA 是⊙O的半径就行了，简称：“作垂直；证半径〞例7 如图，AB=AC，D为BC中点，⊙D与AB切于E点.求证：AC与⊙D相切.例8 ：如图，AC，BD与⊙O切于A、B，且AC∥BD，假设∠COD=900.求证：CD是⊙O的切线.[习题练习]例1如图，AB是⊙O的弦〔非直径〕，C、D是AB上两点，并且OC=OD，求证：AC=BD．例2：如图，在△ABC中，AB=AC，以AB为直径的⊙O与BC交于点D，与AC•交于点E，求证：△DEC为等腰三角形．例3如图，AB是⊙O的直径，弦AC与AB成30°角，CD与⊙O切于C，交AB•的延长线于D，求证：AC=CD．，BF和AD交于E，例4如图20-12，BC为⊙O的直径，AD⊥BC，垂足为D，AB AF求证：AE=BE．例5如图，AB是⊙O的直径，以OA为直径的⊙O1与⊙O2的弦相交于D，DE⊥OC，垂足为E．〔1〕求证：AD=DC．〔2〕求证：DE是⊙O1的切线．AB CDEF G O例6如图，直线MN 与以AB 为直径的半圆相切于点C ，∠A=28°．〔1〕求∠ACM 的度数．〔2〕在MN 上是否存在一点D ，使AB ·CD=AC ·BC ，说明理由．例7如图，在Rt △ABC 中，∠C=90°，AC=5，BC=12，⊙O 的半径为3．〔1〕假设圆心O 与C 重合时，⊙O 与AB 有怎样的位置关系？〔2〕假设点O 沿CA 移动，当OC 等于多少时，⊙O 与AB 相切？19.如图，Rt△ABC 内接于⊙O，AC=BC ，∠BAC 的平分线AD 与⊙0交于点D ，与BC 交于点E ，延长BD ，与AC 的延长线交于点F ，连结CD ，G 是CD 的中点，连结0G ．(1)判断0G 与CD 的位置关系，写出你的结论并证明；(2)求证：AE=BF ；〔3〕假设3(22)OG DE ⋅=-，求⊙O 的面积。

圆的切线证明方法专题(巩固篇)(专项练习)

专题2.10 圆的切线证明方法专题（巩固篇）（专项练习）一、解答题1．如图，AD ，BD 是O 的弦，AD BD ⊥，且28BD AD ==，点C 是BD 的延长线上的一点，2CD =，求证：AC 是O 的切线．2．如图，四边形OAEC 是平行四边形，以O 为圆心，OC 为半径的圆交CE 于D ，延长CO 交O 于B ，连接AD 、AB ，AB 是O 的切线． (1) 求证：AD 是O 的切线． (2) 若O 的半径为4，8AB =，求平行四边形OAEC 的面积．3．如图，AB 是O 的直径，CD 是O 的一条弦，,AB CD ⊥连接,.AC OD(1) 求证：2;BOD A ∠=∠(2) 连接DB ,过点C 作,CE DB ⊥交DB 的延长线于点E ，延长,DO 交AC 于点F ，若F 为AC 的中点，求证：直线CE 为O 的切线．4．如图，△ABC中，AB＝AC，以AB为直径的⊙O与AC，BC分别交于点D和点E，过点E作EF⊥AC，垂足为F．(1) 求证：EF是⊙O的切线；(2) 若CD＝4，EF＝3，求⊙O半径．5．如图，AB是⊙O的直径，BD平分∠ABC，DE⊥BC(1) 求证：DE是⊙O的切线：(2) 若CE=2，DE=4，求⊙O的半径．6．如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．(1) 求证：CD是⊙O的切线；(2) 若AC=8，CD=12，求半径的长度．7．如图，以AB为直径作O，在O上取一点C，延长AB至点D，连接DC，⊥交DC的延长线于点E．∠=∠，过点A作AE ADDCB DAC(1) 求证：CD是O的切线；(2) 若4CD=，2DB=，求AE的长．8．如图，AB是O的直径，过点A作O的切线AC，点P是射线AC上的动点，连接OP，过点B作BD//OP，交O于点D，连接PD．(1) 求证：PD是O的切线；(2) 当APO的度数为______时，四边形POBD是平行四边形．9．如图，AB为⊙O的直径，AC是⊙O的一条弦，过点D作DE⊥AC，垂足为AC的延长线上的点E．连接DA、DB．(1) 求证：DE是⊙O的切线；(2) 延长ED交AB的延长线于F，若AD＝DF，DEO的半径．10．如图，四边形ABCD是⊙O的内接四边形，AC是⊙O直径，BE∥AD交DC延长线于点E，若BC平分∠ACE．(1) 求证：BE是⊙O的切线；(2) 若BE＝3，CD＝2，求⊙O的半径．11．如图，四边形ABCD是菱形，以AB为直径作⊙O，交CB于点F，点E在CD上，且CE＝CF，连接AE．(1) 求证：AE是⊙O的切线；(2) 连接AC交⊙O于点P，若AP=BF＝1，求⊙O的半径．12．如图，在ABC中，以AB为直径作O，交BC于点D，交AC于点E，且BD CD=，过点D作O的切线交AC于点F，过点D作AB的垂线，交AB于点G，交O于点H．⊥；(1) 求证：DF ACOG=，求AE的长．(2) 若1⊥，垂足为点E，交O于点13．如图，AB为O的切线，B为切点，过点B作BC OAC，延长CO与AB的延长线交于点D．(1) 求证：AC为O的切线；(2) 若2OC=，5OD=，求线段AD的长．14．如图，AB为⊙O的切线，B为切点，过点B作BC⊥OA，垂足为点E，交⊙O于点C，延长CO与AB的延长线交于点D．(1)求证：AC为⊙O的切线；(2)若OC＝2，OD＝5，求线段AD和AC的长．15．如图，在四边形ABCD中，AD∥BC，AD⊥CD，AC＝AB，⊙O为△ABC的外接圆．(1) 如图1，求证：AD是⊙O的切线；(2) 如图2，CD交⊙O于点E，过点A作AG⊥BE，垂足为F，交BC于点G．①求证：AG＝BG；②若AD＝2，CD＝3，求FG的长．16．如图，AB是⊙O的直径，D在AB上，C为⊙O上一点，AD＝AC，CD的延长线交⊙O于点E．(1)点F在CD延长线上，BC＝BF，求证：BF是⊙O的切线；(2)若AB＝2，CE CAE的度数．17．如图，ABC中，2∠<∠，CO平分ACBACB B∠交AB于O点，以OA为半径的圆O∠=∠．与AC相切于点A，D为AC上一点且ODA B(1) 求证：BC所在直线与圆O相切；(2) 若1CD=，2AD=，求圆O的半径．18．如图，P A为⊙O的切线，A为切点，过点A作AB⊥OP，垂足为点C，交⊙O于点B，延长BO与P A的延长线交于点D．(1) 求证：PB为⊙O的切线；(2) 若OB＝3，OD＝5，求PB和AB的长．19．如图所示，⊙O 是Rt △ABC 的外接圆，其中∠BAC ＝90°，过点A 作直线AD 交CB 的延长线于D ，且∠BAD ＝∠C ．(1) 求证：AD 为⊙O 的切线；(2) ①F 为OB 中点，OE ⊥AC 于E ，连接OA 、EF 交于G 点，探究EG 与GF 的关系并说明理由；② 延长AO 交⊙O 于H ，连接FH ，若EF ＝FH ，则∠ACB ＝______度．20．如图，半圆O 的直径是AB ，AD 、BC 是两条切线，切点分别为A 、B ，CO 平分BCD ∠．(1) 求证：CD 是半圈O 的切线．(2) 若20AD =，50CD =，求BC 和AB 的长．21．如图，PB切⊙O于点B，连接PO并延长交⊙O于点E，过点B作BA⊥PE交⊙O于点A，连接AP，AE．(1) 求证：P A是⊙O的切线；(2) 如果AB＝DE，OD＝3，求⊙O的半径．⊥，垂足为点E，交O于点22．如图，AB为O的切线，B为切点，过点B作BC OAC，延长CO与AB的延长线交于点D．(1)求证：AC为O的切线；(2)若2OC=，5OD=，求线段AD和AC的长．23．如图，AB 是⊙O 的直径，AC 是弦，P 为AB 延长线上一点，∠BCP ＝∠BAC ，∠ACB 的平分线交⊙O 于点D ，交AB 于点E ，(1) 求证：PC 是⊙O 的切线；(2) 若AC ＋BC ＝2时，求CD 的长．24．如图，点O 是矩形ABCD 中AB 边上的一点，以O 为圆心，OB 为半径作圆，O 交CD 边于点E ，且恰好过点D ，连接BD ，过点E 作EF ∥BD ，(1) 若120BOD ∠=︒，① 求CEF ∠的度数；② 求证：EF 是O 的切线．(2) 若2CF =，3FB =，求OD 的长．25．如图，在平行四边形ABCD 中，AC 是对角线，90CAB ∠=︒，以点A 为圆心，以AB 的长为半径作A ，交BC 边于点E ，交AC 于点F ，连接DE ．(1) 求证：DE与A相切；AB=，求EF的长．(2) 若30∠=︒，6ADE26．如图，AB是⊙O的直径，点C是劣弧BD中点，AC与BD相交于点E．连接BC，∠BCF＝∠BAC，CF与AB的延长线相交于点F．(1) 求证：CF是⊙O的切线；(2) 求证：∠ACD＝∠F；(3) 若AB＝10，BC＝6，求AD的长．27．已知：四边形ABCD是O的内接四边形，AC是直径，点D是AC的中点，过点D DE AC交BA的延长线于点E，四边形ABCD的面积为25作∥(1) 求证：DE是O的切线；(2) 求BD的长．28．如图，在Rt ABC 中，90ACB ∠=︒，D 为AB 边上的一点，以AD 为直径的O 交BC 于点E ，过点C 作CG AB ⊥交AB 于点G ，交AE 于点F ，过点E 作EP AB ⊥交AB 于点P ，EAD DEB ∠=∠．(1) 求证：BC 是O 的切线；(2) 求证：CE EP =；(3) 若12CG =，13AC =，求四边形CFPE 的面积．参考答案1．证明见分析．【分析】先由勾股定理的逆定理证明垂直，再由切线的判断进行解答即可．证明：连接AB ，∵AD BD ⊥，且28BD AD ==∴AB 为直径，AB 2=82+42=80，∵CD =2，AD =4∴AC 2=22+42=20∵CD =2，BD =8,∴BC 2=102=100∴222AC AB CB +=，∴90BAC ∠=︒∴AC 是O 的切线．【点拨】本题考查切线的判定，圆周角定理的推论，勾股定理的逆定理，解题关键是作出辅助线构造直角三角形．2．(1)见分析(2)32【分析】（1）连接OD ，证明AOB AOD △≌△，可得OBA ODA ∠∠=，根据切线的性质可得90OBA ∠=︒，进而可得90ODA =∠°，即可证明AD 是O 的切线；（2）根据平行四边形OAEC 2倍ADO S △即可求解．(1)证明：连接OD ．∵四边形OAEC 是平行四边形，∴AO CE ∥，,AOD ODC AOB OCD ∠∠∠∠∴==OD OC =ODC OCD ∴∠=∠AOB AOD ∴∠=∠又∵,AO AO OD OB ==，AOB AOD ∴△≌△∴OBA ODA ∠∠=，∵AB 与O 相切于点B ，OB AB ∴⊥90OBA ∴∠=︒∴90ODA =∠°，OD AD ∴⊥又∵OD 是O 的半径，∴AD 为O 的切线．(2)∵AOB AOD ≅△△8AB AD ∴==在Rt △AOD 中，84AD OD ==，∴平行四边形OABC 的面积是28432ADO S =⨯=△【点拨】本题考查了切线的性质与判定，平行四边形的性质，三角形全等的性质与判定，掌握切线的性质与判定是解题的关键．3．(1)答案见分析(2)答案见分析【分析】（1）设AB 交CD 于点H ，连接OC ，证明Rt COH Rt DOH ∆≅∆ ，故可得COH DOH ∠=∠ ，于是BC BD = ，即可得到2BOD A ∠=∠；（2）连接，解出60COB ∠=︒，根据AB 为直径得到90ADB ∠=︒，进而得到60ABD ∠=︒，即可证明//OC DB ，故可证明直线CE 为O 的切线．（1）证明：设AB 交CD 于点H ，连接OC ，由题可知，OC OD ∴=，90OHC OHD ∠=∠=︒，OH OH =，()Rt COH Rt DOH HL ∴∆≅∆，COH DOH ∴∠=∠，BC BD ∴=，COB BOD ∴∠=∠，2COB A ∠=∠，2BOD A ∴∠=∠；（2）证明：连接AD ，OA OD =，OAD ODA ∠=∠∴，同理可得：OAC OCA ∠=∠,OCD ODC ∠=∠，∵点H 是CD 的中点，点F 是AC 的中点，OAD ODA OAC OCA OCD ODC ∴∠=∠=∠=∠=∠=∠，180OAD ODA OAC OCD ODC ∠+∠+∠+∠+∠+∠=︒，30OAD ODA OAC OCA OCD ODC ∴∠=∠=∠=∠=∠=∠=︒，223060COB CAO ∴∠=∠=⨯︒=︒， AB 为O 的直径，90ADB ∴∠=︒，90903060ABD DAO ∴∠=-∠=︒-︒=︒，60ABD COB ∴∠=∠=︒，//OC DE ∴，CE BE ⊥，CE OC ∴⊥，∴直线CE 为O 的切线．【点拨】本题主要考查三角形全等的判定与性质，同弧所对的圆周角相等，圆周角定理，直线平行的判定与性质，三角形的内角和公式，证明三角形全等以及证明平行线是解题的关键．4．(1)见分析(2)⊙O半径为13 4【分析】(1)连接OE，利用等腰三角形的性质，证明OE// AC即可解答；(2)过点O作OG⊥AD，垂足为G，易证四边形OEFG是矩形，从而得出OG = EF= 3，设⊙O的半径为x，然后利用垂径定理表示出AG，最后在Rt∆OAG利用勾股定理列出关于x 的方程进行计算即可解答．(1)证明：连接OE，∵EF⊥AC，∴∠EFD=∠EFC=90°∵AB= AC，∴∠B=∠C，∵OB= OE，∴∠B=∠OEB，∴∠OEB=∠C，∴OE// AC，∴∠OEF=∠EFC = 90°，∵OE是⊙O的半径，∴EF是⊙O的切线；(2)过点O作OG⊥AD，垂足为G，∴∠OGF = 90°∵∠OEF=∠EFG=90°∴四边形OEFG是矩形，∴OG= EF= 3，设⊙O的半径为x，∴AB=AC=2x，∵CD= 4，∴AD= AC-CD= 2x- 4，∵OG⊥AD，∴AG=12AD=x-2，在Rt△OAG中，AG2 +OG2 =OA2 (x-2)2+9=x2x=13 4⊙O的半径为134．【点拨】本题考查了切线的判定与性质，等腰三角形的性质，勾股定理，垂径定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．5．(1)见分析(2)5【分析】（1）连接OD，根据等腰三角形的性质和角平分线得出OD∥BE，再根据垂线和平行线的性质得出OD⊥DE，进而得出DE是⊙O的切线；（2）根据圆周角定理和垂径定理得出AF=FC=DE=4，在Rt△OAF中，由勾股定理列方程求解即可．(1)解：如图，连接OD，∵BD平分∠ABC，∴∠ABD=∠DBC，又∵OB=OD，∴∠ABD=∠ODB，∴∠ODB=∠DBC，∵DE ⊥BE ，∴OD ⊥DE ，∴DE 是⊙O 的切线；(2)如图，连接AC ，交OD 于F ，∵AB 是⊙O 的直径，∴∠ACB =90°，又∵∠FDE =90°，∠DEC =90°，∴四边形FDEC 是矩形，∴DF =CE =2，FC =DE =4．由垂径定理可知4AF CF ==设⊙O 的半径为r ，在Rt △OAF 中，由勾股定理得，222OF AF OA +=即（r -2）2+42=r 2，解得r =5．即半径为5．【点拨】本题考查切线的判定和性质，圆周角定理、垂径定理以及勾股定理，掌握切线的判定方法，掌握圆周角定理、垂径定理以及勾股定理是正确解答的关键．6．(1)答案见分析(2)5【分析】（1）连接OD ，根据直径所对的圆周角是直角，可得∠DAB +∠DBA ＝90°，再由∠CDA ＝∠CBD 可得∠CDA +∠DAO ＝90°，然后利用OD ＝OA 证出∠DAB ＝∠ADO ，从而得∠CDO ＝90°，根据切线的判定即可得出；（2）在Rt △CDO 中利用勾股定理列出关于r 的方程即可解答．(1)证明：连接OD ，∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴∠DAB +∠DBA ＝90°，∵∠CDA ＝∠CBD ，∴∠DAB +∠CDA ＝90°，∴∠DAB＝∠ADO，∴∠CDA+∠ADO＝90°，∴∠CDO＝90°，∵OD是⊙O的半径，∴CD是⊙O的切线；(2)解：在Rt△CDO中，CD2+OD2＝OC2，∴122+r2＝（8+r）2，∴r＝5，∴半径的长度为5．【点拨】本题考查了切线的判定与性质，圆周角定理，熟练掌握切线的判定与性质是解题的关键．7．(1)见分析(2)AE＝6【分析】（1）连接OC，根据圆周角定理的推论得到∠ACB＝90°，即∠BCO＋∠ACO＝90°，求得∠ACO＝∠DCB，得到∠DCO＝90°，根据切线的判定定理得到CD是⊙O的切线；（2）根据勾股定理求出OB＝3，可得AB＝6，AD＝8，根据切线长定理得到AE＝CE，在Rt△ADE中，利用勾股定理即可得到结论．（1）证明：连接OC，如图，∵AB为直径，∴∠ACB＝90°，即∠BCO＋∠ACO＝90°，∵OC＝OA，∴∠ACO＝∠CAD，又∵∠DCB＝∠CAD，∴∠ACO＝∠DCB，∴∠DCB＋∠BCO＝90°，即∠DCO＝90°，∵OC是⊙O的半径，∴CD是⊙O的切线；（2）解：∵∠DCO＝90°，OC＝OB，∴OC2＋CD2＝OD2∴OB2＋42＝（OB＋2）2，∴OB＝3，∴AB＝6，AD＝8，∵AE⊥AD，AB是⊙O的直径，∴AE是⊙O的切线，∵CD是⊙O的切线，∴AE＝CE，∵在Rt△ADE中，AD2＋AE2＝DE2，∴82＋AE2＝（4＋AE）2，∴AE＝6．【点拨】本题考查了切线的判定与性质：过半径的外端点与半径垂直的直线是圆的切线；也考查了圆周角定理的推论、切线长定理和勾股定理，正确的作出辅助线是解题的关键．8．(1)见分析(2)45°【分析】（1）连接OD，根据切线的性质求出∠P AO=90°，根据平行线的性质和等腰三角形的性质求出∠DOP=∠AOP，根据全等三角形的判定推出△AOP≌△DOP（SAS），根据全等三角形的性质得出∠PDO=∠P AO=90°，再根据切线的判定得出即可；（2）根据全等得出P A=PD，根据平行四边形的性质得出PD=OB，求出P A=OA，再求出答案即可．（1）解：证明：连接OD，∵P A切⊙O于A，∴P A⊥AB，即∠P AO=90°，∵OP∥BD，∴∠DBO=∠AOP，∠BDO=∠DOP，∵OD=OB，∴∠BDO =∠DBO ，∴∠DOP =∠AOP ，在△AOP 和△DOP 中，AO DO AOP DOP PO PO =⎧⎪∠=∠⎨⎪=⎩，∴△AOP ≌△DOP （SAS ），∴∠PDO =∠P AO ，∵∠P AO =90°，∴∠PDO =90°，即OD ⊥PD ，∵OD 过O ，∴PD 是⊙O 的切线；（2）由（1）知：△AOP ≌△DOP ，∴PA=PD ，∵四边形POBD 是平行四边形，∴PD=OB ，∵OB=OA ，∴PA=OA ，∴∠APO=∠AOP ，∵∠PAO=90°，∴∠APO=∠AOP=45°．【点拨】本题考查了平行四边形的性质，全等三角形的性质和判定，切线的性质，平行线的性质，等腰三角形的性质，等腰直角三角形等知识点，能熟记圆的切线垂直于过切点的半径是解此题的关键．9．(1)详见分析(2)2【分析】（1）连接OD ，由圆周角定理及等腰三角形的性质可得出OD ⊥DE ，则可得出结论；（2）由等腰三角形的性质及直角三角形的性质得出∠EAD ＝∠F ＝∠DAB ＝30°，则得出答案．（1）证明：连接OD，∵D为弧BC的中点，∴∠CAD＝∠BAD，∵OA＝OD，∴∠BAD＝∠ADO，∴∠CAD＝∠ADO，∵DE⊥AC，∴∠E＝90°，∴∠CAD+∠EDA＝90°，即∠ADO+∠EDA＝90°，∴OD⊥DE，∴DE为半圆O的切线；（2）解：∵AD＝DF，∴∠DAF＝∠DF A，又∵∠EAD＝∠DAF，∴∠EAD＝∠DAF＝∠DF A，∵DE⊥AC，∴∠AEF＝90°，∴∠EAD＝∠F＝∠DAB＝30°，∴AD＝2DE＝∴BD2AD==，∴AB＝2BD＝4，∴⊙O的半径为2．【点拨】本题考查了切线的判定和性质，等腰三角形的性质，圆周角定理，直角三角形的性质，正确的作出辅助线是解题的关键．10．(1)见分析(2)r=【分析】(1）连接OB，求出OB∥DE，推出EB⊥OB，根据切线的判定得出即可；(2）根据圆周角定理得到∠ABC=∠D=90°，构造矩形BEDF，根据矩形性质、垂径定理、勾股定理即可得到结论．(1)证明：∵AC 是⊙O 直径，∴90ADC ∠=︒∵BE AD ∥，∴1801809090BED D ∠=︒-∠=︒-︒=︒连接OB ，∵OC OB =，∴13∠=∠又∵BC 平分ACE ∠，∴12∠=∠，∴23∠∠=∴OB DE ∥，∴18090OBE DEB ∠=︒-∠=︒又∵OB 为半径，∴BE 为⊙O 切线(2)延长BO 交AD 于点F ，∵90D DEB FBE ∠=∠=∠=︒∴四边形FBED 为矩形，∴90DFB ∠=︒，即OF ⊥AD ，∵OF 过圆心，3DF BE ==， ∴11×6=322DF AF AD ===Rt ADC中，AC ==r =【点拨】本题考查了切线的判定和性质，矩形的判定和性质，圆周角定理，垂径定理，直角三角形的性质，熟知这些基本知识点正确添加辅助线是解题的关键．11．(1)见分析(2)32【分析】（1）如图所示，连接AF ，先证明∠AFB =90°，然后证明△AED ≌△AFB 得到∠DAE =∠BAF ，即可证明∠BAE =90°，从而证明结论；（2）如图所示，连接BP ，根据三线合一定理求出2AC AP ==O 的半径为r ，则2AB BC r ==，21CF BC BF r =-=-，根据勾股定理可得(()2222141r r --=-，由此即可求解．(1)解：如图所示，连接AF ，∵AB 是圆O 的直径，∴∠AFB =90°，∵四边形ABCD 是菱形，∴AD =AB =CD =BC ，∠B =∠D ，AD BC ∥，∴∠DAF =∠AFB =90°，∵CE =CF ，∴CD -CE =BC -CF ，即DE =BF ，∴△AED ≌△AFB （SAS ），∴∠DAE =∠BAF ，∴∠DAE +∠EAF =90°=∠BAF +∠EAF ，∴∠BAE =90°，又∵AB 是圆O 的直径，∴AE 是圆O 的切线；(2)解：如图所示，连接BP ，∵AB 是圆O 的直径，∴∠APB =90°，∵四边形ABCD 是菱形，∴AB =CB ，∴2AC AP ==设圆O 的半径为r ，则2AB BC r ==，∴21CF BC BF r =-=-，在Rt △ACF 中，222AF AC CF =-，在Rt △ABF 中，222AF AB BF =-，∴(()2222141r r --=-，解得32r =或1r =-（舍去）， ∴圆O 的半径为32．【点拨】本题主要考查了圆切线的判定，直径所对的圆周角是直角，菱形的性质，全等三角形的性质与判定，等腰三角形的性质，勾股定理,解一元二次方程等知识，正确作出辅助线是解题的关键．12．(1)证明见分析(2)2AE =【分析】（1）根据切线，得到90ODF ∠=︒；连接OD ，通过证OD 是ABC 的中位线，证OD AC ∥，进而得到90CFD ODF ∠=∠=︒，即可证明；（2）连接DE ，分别证AC = AB =2OB ，CD =DE ，得到CF =BG ，CF =EF ，再利用222AE AC CF EF OB BG OG =--=-=，即可求解．(1)证明：∵过点D 作O 的切线交AC 于点F ，∴90ODF ∠=︒，连接OD ，∵BD CD =，OA =OB ，∴OD 是ABC 的中位线，∴OD AC ∥，∴90CFD ODF ∠=∠=︒，∴DF AC ⊥．(2)解：设圆与AC 相交于点E ，连接DE ，由（1）可知，OD AC ∥，∴ODB C ∠=∠，∵OD =OB ，∴ODB ABC ∠=∠，∴C ABC ∠=∠，∴AC = AB =2OB ，∵在Rt CFD △和Rt BGD 中，90DFC DGB C ABCCD BD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ∴()Rt CFD Rt BGD AAS ≌，∴CF =BG ，又∵四边形ABDE 是圆内接四边形，∴180AED ABC ∠+∠=︒，又∵180AED CED ∠+∠=︒，∴ABC CED ∠=∠，∴C CED ∠=∠，∴CD =DE ，又∵DF AC ⊥，∴CF =EF ，∴22AE AC CF EF OB BG =--=-，即()222AE OB BG OG =-==．【点拨】本题考查圆、全等三角形和等腰三角形的相关知识．包括圆的切线，圆内接四边形；以及全等三角形的判定和性质，等腰三角形的判定和性质，综合性强．熟练掌握圆、全等三角形和等腰三角形的判定和性质是本题解题的关键．13．(1)见分析；【分析】（1）连接OB ，证明△CAO ≌△BAO （SSS ），由全等三角形的性质得出∠OCA ＝∠OBA ．由切线的性质得出∠ABO ＝90°，则∠OCA ＝90°，可得出结论；（2）由勾股定理求出BD 的长，设AC ＝x ，则AC ＝AB ＝x，得出方程(2227x x +=，解方程可得x ，进一步得出答案． (1)证明：如图，连接OB ，∵OC OB =，∴ △OBC 是等腰三角形，∵OA BC ⊥，∴EC BE =，∴OA 是CB 的垂直平分线，∴AC AB =，在△CAO 和△BAO 中AC AB AO AO CO BO =⎧⎪=⎨⎪=⎩∴CAO BAO ≌（SSS ），∴OCA OBA ∠=∠，∵AB 为O 的切线，∴OB ⊥AB ,∴90OBA ∠=︒，∴90OCA ∠=︒，∴AC OC ⊥，∵OC 是O 的半径，∴AC 为O 的切线；(2)解：∵2OC =，5OD =，∴2OB =，7CD OC OD =+=，∵90OBD ∠=︒，∴BD设AC x =，则AC AB x ==，∵222AC CD AD +=，∴(2227x x +=，∴x =（负根已舍去），∴3 AC=∴AD AB BD AC BD=+=+==【点拨】此题考查了切线的判定与性质、全等三角形的判定与性质、等腰三角形的判定和性质、勾股定理等知识，证明△CAO≌△BAO是解题的关键．14．(1)证明见分析【分析】（1）连接OB，证明△CAO≌△BAO（SSS），由全等三角形的性质得出∠OCA＝∠OBA．由切线的性质得出∠ABO＝90°，则∠OCA＝90°，可得出结论；（2）由勾股定理求出BD的长，设AC＝x，则AC＝AB＝x，得出方程(2227x x+=，解方程可得出答案．(1)证明：连接OB，则OC＝OB，如图所示：∵OA⊥BC，∴EC＝BE，∴OA是CB的垂直平分线，∴AC＝AB，∵在△CAO和△BAO中AO AOAC ABOC OB=⎧⎪=⎨⎪=⎩，∴△CAO≌△BAO（SSS），∴∠OCA＝∠OBA．∵AB为⊙O的切线，B为切点，∴∠ABO＝90°，∴∠OCA＝90°，即AC⊥OC，∴AC是⊙O的切线．(2)解：∵OC ＝2，OD ＝5，∴OB ＝2，CD ＝OC +OD ＝7，∵∠OBD ＝90°，∴BD=设AC ＝x ，则AC ＝AB ＝x ，∵CD 2+AC 2＝AD 2，∴(2227x x +=，解得x =∴AC =∴AD ＝AB +BD ＝AC +BD =【点拨】本题主要考查了切线的性质与判定，三角形全等的性质与判定，勾股定理，切线长定理，熟练掌握切线的性质与判定是解题的关键．15．(1)AD 是OO 的切线(2)①AG BG =；②54FG =【分析】（1)连接OA ，OB ，OC ，由AC =AB ，OA =OA ，OC =OB 可证出ΔOAC ≌ΔOAB (SSS ),利用全等三角形的性质可得出∠OAC =∠OAB ,即AO 平分∠BAC ，利用垂径定理可得出AO ⊥BC ,结合AD //BC 可得出AD ⊥AO ，由此即可证出AD 是OO 的切线；（2)①连接AE ，由圆内接四边形对角互补结合∠BCE =90°可得出∠BAE =90°，由同角的余角相等可得出∠BAG =∠AEB ，结合∠ABC =∠ACB =∠AEB 可得出∠BAG =∠ABC ，再利用等角对等腰可证出AG =BG ；②由∠ADC =∠AFB =90°，∠ACD =∠ABF ，AC =AB 可证出ΔADC ≌ΔAFB (AAS )，利用全等三角形的性质可求出AF ，BF 的长，设FG =x ，在Rt ΔBFG 中，利用勾股定理可求出x 的值，此题得解．(1)证明：如图1，连接OA ，OB ，OC ．在△OAC 和△OAB 中，AC AB OA OA OC OB =⎧⎪=⎨⎪=⎩∴()OAC OAB SSS ≌，∴OAC OAB ∠=∠，∴AO 平分BAC ∠，∴AO BC ⊥，又∵AD BC ∥，∴AD AO ⊥，∴AD 是O 的切线．(2)①证明：如图2，连接AE ．∵90BCE ∠=︒，∴90BAE ∠=︒.又∵AF BE ⊥，∴90AFB ∠=︒．∵90BAG EAF AEB EAF ∠+∠=∠+∠=︒∴BAG AEB ∠=∠.∵ABC ACB AEB ∠=∠=∠，∴BAG ABC ∠=∠，∴AG BG =．②在△ADC 和△AFB 中，90ADC AFB ACD ABFAC AB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ∴()ADC AFB AAS ≌，∴2AF AD ==，3BF CD ==．设FG x =，在Rt BFG 中，FG x =，3BF =，2BG AG x ==+，∴222FG BF BG ，即()22232x x +=+， ∴54x =， ∴54FG =．【点拨】本题考查了切线的判定、全等三角形的判定与性质、垂径定理、圆周角定义、平行线的性质、圆内接四边形、等腰三角形的判定以及勾股定理，解题的关键是：（1)利用全等三角形的性质及垂径定理，找出AO ⊥BC ；(2)①利用等角的余角相等及圆周角定理，找出∠BAG =∠ABC ；②在Rt ΔBFG 中，利用勾股定理求出FG 的长。

(完整版)中考数学-圆的切线证明综合试题

专题-------圆的切线证明我们学习了直线和圆的位置关系，就出现了新的一类习题，就是证明一直线是圆的切线.在我们所学的知识范围内，证明圆的切线常用的方法有：一、若直线l 过⊙O 上某一点A ，证明l 是⊙O 的切线，只需连OA ，证明OA⊥l 就行了，简称“连半径，证垂直”，难点在于如何证明两线垂直.例1 如图，在△ABC 中，AB=AC ，以AB 为直径的⊙O 交BC 于D ，交AC 于E ，B 为切点的切线交OD 延长线于F.求证：EF 与⊙O 相切.证明：连结OE ，AD. ∵AB 是⊙O 的直径， ∴AD⊥BC. 又∵AB=BC， ∴∠3=∠4. ∴BD=DE，∠1=∠2. 又∵OB=OE，OF=OF ， ∴△BOF≌△EOF（SAS ）. ∴∠OBF=∠OEF. ∵BF 与⊙O 相切， ∴OB⊥BF. ∴∠OEF=900.∴EF 与⊙O 相切.说明：此题是通过证明三角形全等证明垂直的例2 如图，AD 是∠BAC 的平分线，P 为BC 延长线上一点，且PA=PD.求证：PA 与⊙O 相切.证明一：作直径AE ，连结EC. ∵AD 是∠BAC 的平分线， ∴∠DAB=∠DAC.⌒⌒∵PA=PD， ∴∠2=∠1+∠DAC. ∵∠2=∠B+∠DAB， ∴∠1=∠B. 又∵∠B=∠E， ∴∠1=∠E∵AE 是⊙O 的直径， ∴AC⊥EC，∠E+∠EAC=900. ∴∠1+∠EAC=900. 即OA⊥PA.∴PA 与⊙O 相切.证明二：延长AD 交⊙O 于E ，连结OA ，OE. ∵AD 是∠BAC 的平分线，∴BE=CE，∴OE⊥BC.∴∠E+∠BDE=900. ∵OA=OE， ∴∠E=∠1. ∵PA=PD， ∴∠PAD=∠PDA.又∵∠PDA=∠BDE,∴∠1+∠PAD=900即OA⊥PA.∴PA 与⊙O 相切说明：此题是通过证明两角互余，证明垂直的，解题中要注意知识的综合运用.例3 如图，AB=AC ，AB 是⊙O 的直径，⊙O 交BC 于D ，DM⊥AC 于M求证：DM 与⊙O 相切.证明一：连结OD. ∵AB=AC， ∴∠B=∠C.⌒⌒∵OB=OD，∴∠1=∠B.∴∠1=∠C. ∴OD∥AC. ∵DM⊥AC，∴DM⊥OD.∴DM 与⊙O 相切证明二：连结OD ，AD.∵AB 是⊙O 的直径，∴AD⊥BC.又∵AB=AC,∴∠1=∠2. ∵DM⊥AC，∴∠2+∠4=900∵OA=OD，∴∠1=∠3.∴∠3+∠4=900.即OD⊥DM.∴DM 是⊙O 的切线说明：证明一是通过证平行来证明垂直的.证明二是通过证两角互余证明垂直的，解题中注意充分利用已知及图上已知.例4 如图，已知：AB 是⊙O 的直径，点C 在⊙O 上，且∠CAB=300，BD=OB ，D 在AB 的延长线上.求证：DC 是⊙O 的切线证明：连结OC 、BC.∵OA=OC，∴∠A=∠1=∠300.∴∠BOC=∠A+∠1=600. 又∵OC=OB，∴△OBC 是等边三角形.∴OB=BC.∵OB=BD， ∴OB=BC=BD. ∴OC⊥CD. ∴DC 是⊙O 的切线.说明：此题是根据圆周角定理的推论3证明垂直的，此题解法颇多，但这种方法较好.例5 如图，AB 是⊙O 的直径，CD⊥AB，且OA 2=OD·OP.求证：PC 是⊙O 的切线.证明：连结OC∵OA 2=OD·OP ，OA=OC ， ∴OC 2=OD·OP ，.OCOPOD OC 又∵∠1=∠1， ∴△OCP∽△ODC. ∴∠OCP=∠ODC. ∵CD⊥AB， ∴∠OCP=900. ∴PC 是⊙O 的切线.说明：此题是通过证三角形相似证明垂直的例6 如图，ABCD 是正方形，G 是BC 延长线上一点，AG 交BD 于E ，交CD 于F.求证：CE 与△CFG 的外接圆相切.分析：此题图上没有画出△CFG 的外接圆，但△CFG 是直角三角形，圆心在斜边FG 的中点，为此我们取FG 的中点O ，连结OC ，证明CE⊥OC 即可得解.证明：取FG 中点O ，连结OC.∵ABCD 是正方形，∴BC⊥CD，△CFG 是Rt△∵O 是FG 的中点， ∴O 是Rt△CFG 的外心. ∵OC=OG， ∴∠3=∠G，∵AD∥BC，∴∠G=∠4.∵AD=CD，DE=DE，∠ADE=∠CDE=450，∴△ADE≌△CDE（SAS）∴∠4=∠1，∠1=∠3.∵∠2+∠3=900,∴∠1+∠2=900.即CE⊥OC.∴CE与△CFG的外接圆相切二、若直线l与⊙O没有已知的公共点，又要证明l是⊙O的切线，只需作OA⊥l，A为垂足，证明OA是⊙O的半径就行了，简称：“作垂直；证半径”例7 如图，AB=AC，D为BC中点，⊙D与AB切于E点.求证：AC与⊙D相切.证明一：连结DE，作DF⊥AC，F是垂足.∵AB是⊙D的切线，∴DE⊥AB.∵D F⊥AC，∴∠DEB=∠DFC=900.∵AB=AC，∴∠B=∠C.又∵BD=CD，∴△BDE≌△CDF（AAS）∴DF=DE.∴F在⊙D上.∴AC是⊙D的切线证明二：连结DE，AD，作DF⊥AC，F是垂足.∵AB与⊙D相切，∴DE⊥AB.∵AB=AC，BD=CD，∴∠1=∠2.∴DE=DF.∴F 在⊙D 上.∴AC 与⊙D 相切.说明：证明一是通过证明三角形全等证明DF=DE 的，证明二是利用角平分线的性质证明DF=DE 的，这类习题多数与角平分线有关.例8 已知：如图，AC ，BD 与⊙O 切于A 、B ，且AC∥BD，若∠COD=900.求证：CD 是⊙O 的切线.证明一：连结OA ，OB ，作OE⊥CD，E 为垂足.∵AC，BD 与⊙O 相切， ∴AC⊥OA，BD⊥OB. ∵AC∥BD，∴∠1+∠2+∠3+∠4=1800. ∵∠COD=900，∴∠2+∠3=900，∠1+∠4=900. ∵∠4+∠5=900. ∴∠1=∠5.∴Rt△AOC∽Rt△BDO.∴.ODOCOB AC = ∵OA=OB， ∴.ODOCOA AC = 又∵∠CAO=∠COD=900， ∴△AOC∽△ODC，∴∠1=∠2.又∵OA⊥AC，OE⊥CD, ∴OE=OA. ∴E 点在⊙O 上. ∴CD 是⊙O 的切线.证明二：连结OA ，OB ，作OE⊥CD 于E ，延长DO 交CA 延长线于F.∵AC，BD 与⊙O 相切，O∵AC∥BD，∴∠F=∠BDO.又∵OA=OB，∴△AOF≌△BOD（AAS ）∴OF=OD.∵∠COD=900，∴CF=CD，∠1=∠2.又∵OA⊥AC，OE⊥CD，∴OE=OA.∴E 点在⊙O 上.∴CD 是⊙O 的切线.证明三：连结AO 并延长，作OE⊥CD 于E ，取CD 中点F ，连结OF.∵AC 与⊙O 相切，∴AC⊥AO.∵A C∥BD，∴AO⊥BD.∵BD 与⊙O 相切于B ，∴AO 的延长线必经过点B.∴AB 是⊙O 的直径.∵AC∥BD，OA=OB ，CF=DF ，∴OF∥AC，∴∠1=∠COF.∵∠COD=900，CF=DF ，∴.CF CD OF ==21∴∠2=∠COF.∴∠1=∠2.∵OA⊥AC，OE⊥CD，∴OE=OA.∴E 点在⊙O 上.∴CD 是⊙O 的切线说明：证明一是利用相似三角形证明∠1=∠2，证明二是利用等腰三角形三线合一证明∠1=∠2.证明三是利用梯形的性质证明∠1=∠2，这种方法必需先证明A 、O 、B 三点共线.此题较难，需要同学们利用所学过的知识综合求解.以上介绍的是证明圆的切线常用的两种方法供同学们参考.以下是武汉市2007----2010中考题汇编：（2007中考）22．(本题8分)如图，等腰三角形ABC 中，AC ＝BC ＝10，AB ＝12。

圆的切线证明(中考)

D C A B A BCD OC A P ODCE OA DB 第二十四章圆练习1. 如图所示，OA 是圆O 的半径，弦CD ⊥OA 于点P ，已知OC=5，OP=3，则弦CD=__________。

2. 如图所示，在圆O 中，AB 、AC 为互相垂直且相等的两条弦，OD ⊥AB ，OE ⊥AC ，垂足分别为D 、E ，若AC=2cm ，则圆O 的半径为____________cm 。

3. 如图所示，AB 是圆O 的直径，弦CD ⊥AB ，E 为垂足，若AB=9，BE=1，则CD=__________。

4、如图所示，在△ABC 中，∠C ＝90°，AB ＝10，AC ＝8，以AC 为直径作圆与斜边交于点P ，则BP 的长为________________。

5. 如图所示，四边形ABCD 内接于圆O ，∠BCD=120°，则∠BOD=____________度。

6. 如图所示，圆O 的直径为10，弦AB 的长为6，M 是弦AB 上的一动点，则线段的OM 的长的取值范围是（） A. 3≤OM ≤5 B. 4≤OM ≤5 C. 3＜OM ＜5 D. 4＜OM ＜57. 如图所示，A 、B 、C 三点在圆O 上，∠AOC=100°，则∠ABC 等于（）A. 140°B. 110°C. 120°D. 130°8、如图，PA 、PB 分别与⊙O 相切于点A 、B ，⊙O 的切线EF 分别交PA 、PB 于点E 、F ，切点C 在上，若PA 长为3，则△PEF 的周长是__________9. 如图所示，已知AB 为圆O 的直径，AC 为弦，OD ∥BC 交AC 于D ，OD=cm 2，则BC=_________，∠ADO=_______.10. 如图所示，Rt △ABC 的两直角边BC=3cm ，AC=4cm ，斜边AB 上的高为CD ，若以C 为圆心，分别以r 1=2cm ，r 2=2.4cm ，r 3=3cm ，为半径作圆，试判断点D 与这三个圆的位置关系。

专题08 切线的判定与性质(解析版) -2021-2022学年九年级数学之专攻圆各种类型题

专题08 切线的判定与性质概念规律重在理解1.切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线.OA为⊙O的半径，BC ⊥OA于A。

则BC为⊙O的切线。

注意：在此定理中，“经过半径的外端”和“垂直于这条半径”，两个条件缺一不可，否则就不是圆的切线。

2.判断一条直线是一个圆的切线有三个方法：（1）定义法：直线和圆只有一个公共点时，我们说这条直线是圆的切线;（2）数量关系法：圆心到这条直线的距离等于半径(即d=r)时，直线与圆相切；（3）判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线.3.证切线时辅助线的添加方法(1) 有交点，连半径,证垂直;(2) 无交点，作垂直,证半径.4.有切线时常用辅助线添加方法见切点，连半径，得垂直.5.切线的其他重要结论(1)经过圆心且垂直于切线的直线必经过切点;(2)经过切点且垂直于切线的直线必经过圆心.6.切线的性质定理：圆的切线垂直于经过切点的半径．直线l是⊙O 的切线，A是切点，直线l ⊥OA.说明：利用切线的性质解题时，常需连接辅助线，一般连接圆心与切点，构造直角三角形，再利用直角三角形的相关性质解题.典例解析掌握方法【例题1】（2021吉林长春）如图，AB是⊙O的直径，BC是⊙O的切线，若∠BAC＝35°，则∠ACB的大小为（）A．35°B．45°C．55°D．65°【答案】C【解析】先根据切线的性质得到∠ABC＝90°，然后利用互余计算出∠ACB的度数．∵BC是⊙O的切线，AB是⊙O的直径，∴AB⊥BC，∴∠ABC＝90°，∴∠ACB＝90°﹣∠BAC＝90°﹣35°＝55°．【例题2】（2021广西玉林）如图，⊙O与等边△ABC的边AC，AB分别交于点D，E，AE是直径，过点D作DF⊥BC于点F．（1）求证：DF是⊙O的切线；（2）连接EF，当EF是⊙O的切线时，求⊙O的半径r与等边△ABC的边长a之间的数量关系．【答案】见解析。

中考数学总复习《圆的切线证明》专题训练(附带答案)

中考数学总复习《圆的切线证明》专题训练（附带答案）学校:___________班级：___________姓名：___________考号：___________⊥于点D，E是AC上一点，以BE为直径的O交1．如图，在ABC中，AB=AC，AD BC∠=︒．BC于点F，连接DE，DO，且90DOB(1)求证：AC是O的切线；(2)若1DF=，DC=3，求BE的长．、2．如图，在O中，BC为非直径弦，点D是BC的中点，CD是ABC的角平分线．∠=∠；(1)求证：ACD ABC(2)求证：AC是O的切线；(3)若1BD=，3BC=时，求弦BD与BD围城的弓形面积．是O的切线；=，且AC BD已知等腰ABC，AB=AC为直径作O交BC于点延长线于点F．是O的切线；CD=2，求O的半径．与O相离，，交O于点A是O上一点，连于点C，且PB(1)求证：PB是O的切线；(2)若25AC=，OP=5，求O的半径．6．如图，点O是ABC的边AC上一点，以点O为圆心，OA为半径作O，与BC相切于点E，连接OB，OE，O交OB于点D，连接AD并延长交CB的延长线于点F，且AOD EOD．∠=∠(1)求证：AB是O的切线；BC=，AC=8，求O的半径．(2)若107．如图，AB 是O 的直径，AC 是O 的弦．(1)尺规作图：过点C 作O 的切线，交AB 的延长线于点D （保留作图痕迹，不写作法）；(2)若2BD OB ==，求AC 的长．8．如图，ABCD 的顶点,,A B C 在O 上，AC 为对角线，DC 的延长线交O 于点E ，连接,,OC OE AE ．(1)求证：AE BC =；(2)若AD 是O 的切线6,40OC D =∠=︒，求CE 的长．9．如图，Rt ABC △中90C ∠=︒，点E 为AB 上一点，以AE 为直径的O 上一点D 在BC 上，且AD 平分BAC ∠．(1)证明：BC 是O 的切线；(2)若42BD BE ==，，求AB 的长．10．如图，已知O 的弦AB 等于半径，连接OA 、OB ，并延长OB 到点C ，使得BC OB =，连接AC ，过点A 作AE OB ⊥于点E ，延长AE 交O 于点D ．(1)求证：AC 是O 的切线；(2)若6BC =，求AD 的长．11．如图，线段AB 经过O 的圆心.O 交O 于A ，C 两点，AD 为O 的弦，连接BD ，30A ABD ∠=∠=︒连接DO 并延长交O 于点E ，连接BE 交O 于点F ．(1)求证：BD 是O 的切线；(2)若1BC =，求BF 的长．12．如图，AB 为O 的直径，C 为O 上一点,CD BD ABC CBD ⊥∠=∠．(1)求证：CD 为O 的切线．(2)当1,4BD AB ==时，求CD 的长．13．如图已知AB 是O 的直径 BC AB ⊥于B E 是OA 上的一点ED BC ∥交O 于D OC AD ∥ 连接AC 交ED 于F ．(1)求证：CD 是O 的切线；(2)若8AB = 1AE = 求ED EF 的长．14．如图 AB 是O 的直径 AC BC ，是弦点D 在AB 的延长线上且DCB DAC ∠=∠ O 的切线AE 与DC 的延长线交于点E ．(1)求证：CD 是O 的切线；(2)若O 的半径为2 30D ∠=︒ 求AE 的长．15．如图已知AB 是O 的直径点P 在BA 的延长线上弦BC 平分PBD ∠且BD PD ⊥于点D ．(1)求证：PD 是O 的切线．(2)若8cm 6cm AB BD ，求弧AC 的长．为O的直径在O上连接的延长线交于E．是O的切线；∠tan BDF为O的直径的平分线交O于点E BC的延长线于点(1)求证：DE 为O 切线；(2)若10AB = 6BC = 求DE 的长．18．如图 O 是ABC 的外接圆点D 在BC 延长线上且满足CAD B ∠=∠．(1)求证：AD 是O 的切线；(2)若AC 是BAD ∠的平分线 3sin 5B =4BC = 求O 的半径．参考答案：1．【分析】此题重点考查圆周角定理切线的判定定理勾股定理三角形的中位线定理等腰三角形的“三线合一” 线段的垂直平分线的性质等知识正确地作出辅助线是解题的关键．是O的切线；+=314是O的直径90︒则22BE=+4(22)⊥AD BC是O的半径是O的切线．）连接EFDC=DF33+=+BD DF∠OE DOBDE=．3是O的直径90︒．中EF=中BE=(3)23312π- 【分析】此题考查了解直角三角形切线的判定以及扇形的面积．注意掌握辅助线的作法．（1）点D 是BC 的中点可以得到BD CD = 即可得到DBC DCB ∠∠= 再根据角平分线的定义得到ACD BCD ∠∠= 进而得到结论；（2）连接OC OD OB 则可得到OD BC ⊥ 然后根据等边对等角可以得到90OCD ACD ∠∠+=︒ 即可得到结论（3）先求出60ODB ∠=︒ 继而利用OBD OBD S S S=-阴影部分扇形求得答案．【详解】（1）解：如图 ∵点D 是BC 的中点∵BD CD =∵DBC DCB ∠∠=又∵CD 是ABC 的角平分线∵ACD BCD ∠∠=∵ACD ABC ∠∠=；（2）证明：如图连接OC OD OB∵点D 是BC 的中点∵OD BC ⊥∵90ODC BCD ∠∠+=︒∵OD OC =∵ODC OCD ∠∠=又∵ACD BCD ∠∠=∵90OCD ACD ∠∠+=︒即OC AC ⊥∵OC 是O 的半径∵AC 是O 的切线；Rt BDE 中 ODB ∠=60ODB =︒OB OD =∵OBD 是等边三角形BOD ∠=OBD S S==阴影部分．(1)见解析(2)23进而得出BFG 是等边三角形是O 的切线；）解：如图所示∵OD AC ⊥∵AD CD =∵BD AC =∵BD AC =∵AD BC =∵AD CD BC ==；∵AB 为半圆O 的直径∵90CAB CBA ∠+∠=︒∵30DAC CAB ABD ∠=∠=∠=︒∵60GBF G ∠=∠=︒ 12GB AG =∵BFG 是等边三角形 223AB AG BG BG =-=∵3233BF BG AB ===．【点睛】本题考查了切线的判定弧与弦的关系直径所对的圆周角是直角勾股定理等边三角形的性质与判定垂径定理熟练掌握以上知识是解题的关键．4．(1)证明(2)233【分析】本题主要考查切线的性质和判定及特殊角的三角函数的应用掌握切线问题中的辅助线的作法是解题的关键．（1）连接OD 证明ODB C ∠=∠ 推出AC OD ∥ 即可证明结论成立；（2）连接AD 在Rt CED 中求得利用三角形函数的定义求得30C ∠=︒ 60AOD ∠=︒ 在Rt ADB 中利用勾股定理列式计算求得圆的半径即可．【详解】（1）证明：连接OD又OB OD=B ODB∴∠=∠ODB∴∠=∠AC OD∥DF AC⊥OD DF∴⊥DF∴是O的切线；（2）连接AD设O半径为Rt CED中3,CE CD=22ED CD∴=-又cosCE CCD ∠=30C∴∠=︒30B∴∠=︒60AOD=∠AB是O的直径．90ADB∴∠=︒12AD AB r ∴== ∵AB AC =∵2CD BD ==又222AD BD AB +=2222(2)r r ∴+=233r ∴=(负值已舍)． 5．(1)证明见解析(2)3【分析】本题考查的是勾股定理的应用等腰三角形的性质切线的判定熟练的证明圆的切线是解本题的关键；（1）连接OB 证明PCB PBC ∠=∠ OAB OBA ∠=∠ 再证明90PBC OBA ∠+∠=︒即可；（2）设O 的半径为r 表示()()22222255PC AC AP r =-=-- 222225PB OP OB r =-=- 再利用PB PC =建立方程求解即可．【详解】（1）解：连接OB∵PB PC = OA OB =∵PCB PBC ∠=∠ OAB OBA ∠=∠∵OP l ⊥ OAB PAC ∠=∠∵90BCP CAP BCP OAB ∠+∠=︒=∠+∠∵90PBC OBA ∠+∠=︒∵90OBP ∠=︒∵OB PB ⊥是O 的切线；）设O 的半径为l 2AC =2AC AP =-PB BP 2OP OB =-∵O 的半径为【点睛】．(1)见解析(2)3【分析】本题主要考查切线的判定和性质证AOB EOB ≌ 得出的半径为r 则OE OA =根据AOB EOB ≌得求得4CE = 在Rt OCE 中运用勾股定理列式求出r 的值即可．）证明：在AOB 和EOB 中∵()SAS AOB EOB ≌OAF OEF ∠=∠BC 与O 相切OE BC ⊥90OAB OEB ∠=∠=︒AF是O 的半径是O 的切线；（2）解：在Rt CAB △中 90108CAB BC AC ∠=︒==，，∵22221086AB BC AC =-=-=设圆O 的半径为r 则,OE OA r ==∵8OC r =-∵,AOB EOB ≌∵6BE AB ==∵10,BC =∵1064,CE BC BE =-=-=在Rt OCE 中 222OE CE OC +=∵()22248r r +=-解得3r =．∵O 的半径为3．7．(1)作图见解析(2)4π3【分析】本题考查了作图复杂作图切线的性质等边三角形的判定与性质弧长的计算熟练掌握切线的性质弧长公式是解答本题的关键．（1）根据题意连接OC 作OC CD ⊥ 交AB 的延长线于点D 由此得到答案．（2）根据题意得到OBC △是等边三角形求出120AOC ∠=︒ 再利用弧长公式得到答案．【详解】（1）解：如图所示 CD 即为所求．（2）如图所示连接BCBD）证明：在ABCD中AE AD ∴=∵AE BC =．（2）解：连接OA 过点O 作OF CE ⊥于点F 如图所示：AD 是O 的切线OA AD ∴⊥OA BC ∴⊥AB AC ∴=40AEC B D ︒∠=∠=∠=40ACB B ∴∠=∠=︒在ABCD 中 AD BC ∥40DAC ACB ∴∠=∠=︒又180100DAE D AEC ∠=︒-∠-∠=︒60CAE DAE CAD ∴∠=∠-∠=︒2120COE CAE ∴∠=∠=︒OC OE =30OCE ∴∠=︒OF CE ⊥22cos3063CE CF OC ∴==⋅︒=．【点睛】本题主要考查了切线的性质解直角三角形圆周角定理平行四边形的性质垂径定理等腰三角形的判定解题的关键是作出辅助线熟练掌握相关的判定和性质．9．(1)证明详见解析；(2)8．【分析】本题考查了切线的判定勾股定理等知识熟练掌握切线的判定定理勾股定理是解题的关键．（1）连接OD 根据平行线判定推出OD AC ∥ 推出OD BC ⊥ 根据切线的判定推出即可；（2）根据勾股定理求出3OD OA OE === 再根据线段的和差求解即可．【详解】（1）证明：连接OD∵OA OD =∵OAD ODA ∠=∠∵AD 平分BAC ∠∵BAD CAD ∠=∠∵ODA CAD ∠=∠∵OD AC ∥∵180C ODC ∠+∠=︒∵90C ∠=︒∵90ODC ∠=︒∵OD BC ⊥∵OD 为半径∵BC 是O 的切线；（2）解：设OD OE r ==在Rt ODB △中 42BD BE ==，∵2OB r =+由勾股定理得：()22242r r +=+ 解得：3r =∵3OD OA OE ===∵628AB =+=．10．(1)证明见解析；(2)63．【分析】（1）先证明OAB 是等边三角形再由性质得出60AOB OAB OBA ∠=∠=∠=︒ 再由BC AB =和角度和差即可求解；（2）先根据等边三角形性质求出132OE OA == 再根据勾股定理求得33AE = 最后由垂径定理即可求解；此题考查了等边三角形的判定与性质勾股定理和垂径定理解题的关键是熟练掌握以上知识点的应用．【详解】（1）证明：∵AB OA OB ==∵OAB 是等边三角形∵60AOB OAB OBA ∠=∠=∠=︒∵BC OB =∵BC AB =∵1302BAC BCA OBA ∠=∠=∠=︒ ∵90OAC OAB BAC ∠=∠+∠=︒又∵OA 为O 的半径∵AC 是O 的切线；（2）解：∵6BC =∵6AB OA OB ===∵AD OB ⊥于点E∵30OAE ∠=︒∵132OE OA == ∵2233AE OA OE =-=∵AE OB ⊥∵263AD AE ==．11．(1)见解析∠=）证明：BAD60︒6090︒-︒=OD是O的半径∴直线BD是O的切线；==（2）解：设OD OC△中sin30在Rt BDO解得：1r==+OB OCDE是O的直径∴∠=︒DFE90∠=∠即DFB BDE∠=∠DBF DBE∴△∵BDEBFD△BF BD∴=BD BE337BF ∴= 解得：377BF =．【点睛】本题考查了切线的判定和性质相似三角形的性质和判定圆周角定理勾股定理等知识点作出辅助线构造出相似三角形是解题关键．12．(1)见详解(2)3【分析】（1）连接OC 由∠=∠OCB ABC ABC CBD ∠=∠ 得OCB CBD ∠=∠ 则OC BD ∥ 所以18090OCD D ∠=︒-∠=︒ 即可证明CD 为O 的切线；（2）由AB 为的直径得90ACB ∠=︒ 则ACB D ∠=∠ 而ABC CBD ∠=∠ 所以C ABC BD ∽△△ 则AB CB CB BD = 可求得CB BD AB =⋅ 由勾股定理得22CD CB BD =-．【详解】（1）证明：连接OC 则OC OB =OCB ABC ∴∠=∠ABC CBD ∠=∠OCB CBD ∴∠=∠OC BD ∴∥CD BD ⊥90D ∴∠=︒18090OCD D ∴∠=︒-∠=︒OC 是O 的半径且CD OC ⊥CD ∴为O 的切线．（2）解：AB 为的直径ABC∠=ABC CBD ∴∽∴AB CBCB BD=1,4BD AB==1 CB BD AB∴=⋅=22CD CB BD∴=-=CD∴的长是【点睛】此题重点考查等腰三角形的性质AD OC∥ADO∴∠OA OD=ADO DAO ∴∠=∠DOC BOC ∴∠=∠OD OB OC OC ==，ODC OBC ∴≌△△∴OBC ODC ∠=∠BC AB ⊥∴90OBC ODC ∠=∠=︒OD 为经过圆心的半径∴CD 是O 的切线；（2）如图所示：作DM BC ⊥交BC 于点M8AB = 1AE =1432OA OB OD AB OE OA AE ∴=====-=， 227DE BM OD OE ==-=令=7CM x CB CD x ==+， 7BE DM ==∴在222Rt DMC CM DM CD +=△，222(7)7x x ∴+=+解得：37x =47BC ∴=DE BC ∥ADE ABC ∴△△∽是O的切线．2）在Rt△是O的切线得出Rt EAD中【详解】（1）证明：连接．是O的直径+∠OCA OCBDCB OCB+∠OCD=︒．90是半径经过O的半径外端∵CD 是O 的切线．（2）解：在Rt OCD △中∵90OCD ∠=︒ 30D ∠=︒ 2OC =∵4OD =．∵6AD AO OD =+=．∵AE 是O 的切线切点为A∵OA AE ⊥．在Rt EAD 中∵90EAD ∠=︒ 30D ∠=︒ 6AD =∵3tan 306233AE AD =⋅︒=⨯=． 15．(1)见解析(2)4π3【分析】本题考查圆与三角形的综合问题掌握与圆有关的性质正确作出辅助线是关键．（1）连接OC 根据条件证明OC BD ∥ 即可证明；（2）根据PCO PDB ∽可得PA 利用余弦值可求出COP ∠ 通过弧长公式求解即可．【详解】（1）证明：连接OC 如图∵OC OB =∵OCB OBC ∠=∠∵弦BC 平分PBD ∠∵DBC OBC ∠=∠∵OCB DBC ∠=∠．∵OC BD ∥∵BD PD ⊥∵OC PD ⊥．为O 的半径是O 的切线；）解：连接OC∵PCO PDB ∽OC PO BD PB= 8cm AB = BD =14cm 2OC AB ==4468PA PA +=+ Rt OCP 中cos COP ∠=60COP =︒AC 的长=(1)证明见解析；是O 的切线；证明FBD FDA ∽ 得到1tan tan 4BD A BDF AD ∠=∠== 进而得到164DF = 即可求解；本题考查了切线的判定相似三角形的判定与性质等腰三角形的性质余角性质根据题意正确作出辅助线是解题的关键．【详解】（1）证明：连结OD∵CO AB ⊥∵90E C ∠+∠=︒∵FE FD = OD OC =∵E FDE ∠=∠ ∠=∠C ODC∵90FDE ODC ∠+∠=︒∵90ODF ∠=︒∵OD DF ⊥∵FD 是O 的切线；（2）解：连结AD ,OD BD 如图∵AB 为O 的直径∵90ADB ∠=︒∵90∠+∠=︒A ABD∵OB OD =∵OBD ODB ∠=∠∵90A ODB ∠+∠=︒∵FBD FDA ∽DF BD AF AD= 在Rt △ABD 中 tan ∠164DF = 3DF =的平分线交O 于点E∵ED OE ⊥∵DE 为O 切线．（2）过点O 作OM BC ⊥于点M 10AB = 6BC =则132MC MB BC ===,152OB OE AB === 四边形OEDM 时矩形∵DE OM =根据勾股定理得224DE OM OB BM ==-=．18．(1)见解析(2)103【分析】（1）连接OA OC 与AB 相交于点E 如图由OA OC = 可得OAC OCA ∠=∠ 根据圆周角定理可得12B AOC ∠=∠ 由已知CAD B ∠=∠ 可得2AOC CAD ∠=∠ 根据三角形内角和定理可得180OCA CAO AOC ∠+∠+∠=︒ 等量代换可得90CAO CAD ∠+∠=︒ 即可得出答案；（2）根据角平分线的定义可得BAC DAC ∠=∠ 由已知可得BAC B =∠∠ 根据垂径定理可得 OC AB ⊥ BE AE = 在Rt BEC △中根据正弦定理可得3sin 45CE CE B BC === 即可算出CE 的长度根据勾股定理可算出22BE BC CE =-的长度设O 的半径为r 则125OE OC CE r =-=- 在Rt AOE △中 222OA OE AE =+ 代入计算即可得出答案．【详解】（1）证明：连接OA OC 与AB 相交于点E 如图OA OC =OAC ∴∠AC AC =∴12B ∠=CAD ∠=AOC ∴∠=OCA ∠+2CAO ∴∠+CAO ∴∠+OAD ∴∠OA 是O 的半径AD ∴是O 的切线；（2）解：AC 是∠BAC DAC ∴∠=∠CAD B ∠=∠BAC B ∴∠=∠OC AB ∴⊥ BE =在Rt BEC △中4BC =sin CE B BC ∴=125CE ∴=BE BC ∴=设O 的半径为r ，则125OE OC CE r =-=-在Rt AOE △中222OA OE AE =+ 222121655r r ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭ 解得：103r =．【点睛】本题主要考查了切线的性质与判定，垂径定理，勾股定理及解直角三角形，熟练掌握切线的性质与判定，垂径定理及解直角三角形的方法进行求解是解决本题的关键．。

小专题(十三) 证明切线的两种常用方法

小专题(十三)证明切线的两种常用方法类型1直线与圆有交点方法归纳：直线过圆上某一点，证明直线是圆的切线时，只需“连半径，证垂直，得切线”．“证垂直”时通常利用圆中的关系得到90°的角，如直径所对的圆周角等于90°等．【例1】(枣庄中考)如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PA，PB，AB，已知∠PBA＝∠C.求证：PB是⊙O的切线．证明：连接OB.∵AC是⊙O的直径，∴∠ABC＝90°，∠C＋∠BAC＝90°.∵OA＝OB，∴∠BAC＝∠OBA.∵∠PBA＝∠C，∴∠PBA＋∠OBA＝90°，即PB⊥OB.∴PB是⊙O的切线1．(常德中考)如图，已知⊙O是△ABC的外接圆，AD是⊙O的直径，且BD＝BC，延长AD到E，且有∠EBD ＝∠CAB.求证：BE是⊙O的切线．证明：连接OB，∵BD＝BC，∴∠CAB＝∠BAD.∵∠EBD＝∠CAB，∴∠BAD＝∠EBD.∵OA＝BO，∴∠BAD＝∠ABO.∴∠EBD＝∠ABO.∵AD是⊙O的直径，∴∠ABD＝90°.∴∠OBE＝∠EBD＋∠OBD＝∠ABO＋∠OBD＝∠ABD＝90°.∵点B在⊙O上，∴BE是⊙O的切线．2．(永州中考改编)如图，△ABC是⊙O的内接三角形，AB为直径，过点B的切线与AC的延长线交于点D，E是BD中点，连接CE.求证：CE是⊙O的切线．证明：连接CO ，OE ，∵AB 为⊙O 的直径，∴∠ACB ＝90°.∴∠BCD ＝90°.∵E 是BD 中点，∴CE ＝BE ＝12BD. 又∵OC ＝OB ，OE ＝OE ，∴△COE ≌△BOE.∴∠OCE ＝∠OBE.∵BD 为⊙O 的切线，∴∠OBE ＝90°.∴∠OCE ＝90°.∴CE 是⊙O 的切线．3．(丽水中考)如图，AB 是以BC 为直径的半圆O 的切线，D 为半圆上一点，AD ＝AB ，AD ，BC 的延长线相交于点E.(1)求证：AD 是半圆O 的切线；(2)连接CD ，求证：∠A ＝2∠CDE.证明：(1)连接OD ，BD ，∵AB 是⊙O 的切线，∴AB ⊥BC ，即∠ABO ＝90°.∵AB ＝AD ，∴∠ABD ＝∠ADB.∵OB ＝OD ，∴∠DBO ＝∠BDO.∴∠ABD ＋∠DBO ＝∠ADB ＋∠BDO.∴∠ADO ＝∠ABO ＝90°.∴AD 是半圆O 的切线．(2)由(1)知，∠ADO ＝∠ABO ＝90°，∴∠A ＝360°－∠ADO －∠ABO －∠BOD ＝180°－∠BOD ＝∠DOC.∵AD 是半圆O 的切线，∴∠ODE ＝90°.∴∠ODC ＋∠CDE ＝90°.∵BC 是⊙O 的直径，∴∠ODC ＋∠BDO ＝90°.∴∠BDO ＝∠CDE.∵∠BDO ＝∠OBD ，∴∠DOC ＝2∠BDO.∴∠DOC ＝2∠CDE.∴∠A ＝2∠CDE.类型2 不确定直线与圆是否有交点。

往年中考关于圆的证明汇总(有答案)

①求出点 C 的坐标； ②直线 BC 是否为⊙O 的切线？请作出判断，并说明理由．
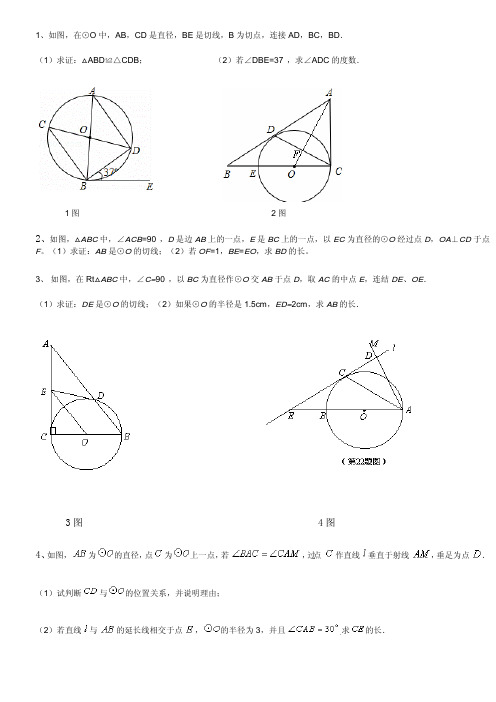
23 图
24 图
24、如图，⊙M 与 x 轴相切于点 C，与 y 轴的一个交点为 A。
（1）求证：AC 平分∠OAM；（2）如果⊙M 的半径等于 4，∠ACO=300，求 AM 所在直线的解析式．
25、如图，在直角三角形 ABC 中，∠ABC=90°．
1、如图，在⊙O 中，AB，CD 是直径，BE 是切线，B 为切点，连接 AD，BC，BD．
（1）求证：△ABD≌△CDB；
（2）若∠DBE=37°，求∠ADC 的度数．
1图
2图
2、如图，△ABC 中，∠ACB=90°，D 是边 AB 上的一点，E 是 BC 上的一点，以 EC 为直径的⊙O 经过点 D，OA⊥CD 于点
连接 AF． (1)证明：∠F＝∠CAD；(2)试判断直线 AF 与⊙O 的位置关系，并给出证明．
11 图
12 图
12、如图，AB 是半圆 O 的直径，点 C 是⊙O 上一点（不与 A，B 重合），连接 AC，BC，过点 O 作 OD∥AC 交 BC 于点 D，
在 OD 的延长线上取一点 E，连接 EB，使∠OEB=∠ABC．
那么图中两个扇形（即阴影部分）的面积之和
两等圆⊙A，⊙B外切，为．
35 图
36 图
36、如图所示，AB 是⊙O 的直径，AE 是弦，C 是劣弧 AE 的中点，过 C 作 CD⊥AB 于点 D，CD 交 AE 于点 F，过 C 作 CG
∥AE 交 BA 的延长线于点 G．
（1）求证：CG 是⊙O 的切线．（2）求证：AF=CF．（3）若∠EAB=30°，CF=2，求 GA 的长．
33 图

中考数学复习《圆的证明与计算》经典题型及测试题(含答案)

中考数学复习《圆的证明与计算》经典题型及测试题（含答案）阅读与理解圆的相关知识的考查是中考数学中的一个重要内容，圆作为一个载体，常与三角形、四边形结合，考查切线的性质及判定、相似三角形的性质与判定、解直角三角形、求阴影面积等．解题时要先分析题干中的条件，然后从图象中挖掘隐含条件，最后再解题．类型一切线的判定判定一条直线是圆的切线，首先看圆的半径是否过直线与圆的交点，有半径则证垂直；没有半径，则连接圆心与切点，构造半径证垂直．例1 (2016·黄石)如图，⊙O的直径为AB，点C在圆周上(异于A，B)，AD⊥CD.(1)若BC＝3，AB＝5，求AC的值；(2)若AC是∠DAB的平分线，求证：直线CD是⊙O的切线．【分析】（1）首先根据直径所对的圆周角为直角得到直角三角形，然后利用勾股定理求得AC的长即可；（2）连接OC，证OC⊥CD即可；利用角平分线的性质和等边对等角，可证得⊥OCA=⊥CAD，即可得到OC⊥AD，由于AD⊥CD，那么OC⊥CD，由此得证．【自主解答】（1）解：⊥AB是⊥O直径，C在⊥O上，⊥⊥ACB=90°，又⊥BC=3，AB=5，⊥由勾股定理得AC=4；（2）证明：⊥AC是⊥DAB的角平分线，⊥⊥DAC=⊥BAC，又⊥AD⊥DC，⊥⊥ADC=⊥ACB=90°，⊥⊥ADC⊥⊥ACB，⊥⊥DCA=⊥CBA，又⊥OA=OC，⊥⊥OAC=⊥OCA，⊥⊥OAC+⊥OBC=90°，⊥⊥OCA+⊥ACD=⊥OCD=90°，⊥DC是⊥O的切线．变式训练1．(2017·白银) 如图，AN是⊙M的直径，NB∥x轴，AB交⊙M于点C．（1）若点A（0，6），N（0，2），∠ABN=30°，求点B的坐标；（2）若D为线段NB的中点，求证：直线CD是⊙M的切线．解：（1）∵A的坐标为（0，6），N（0，2），∴AN=4，∵∠ABN=30°，∠ANB=90°，∴AB=2AN=8，∴由勾股定理可知：NB==，∴B（，2）．（2）连接MC，NC∵AN是⊙M的直径，∴∠ACN=90°，∴∠NCB=90°，在Rt△NCB中，D为NB的中点，∴CD=NB=ND，∴∠CND=∠NCD，∵MC=MN，∴∠MCN=∠MNC，∵∠MNC+∠CND=90°，∴∠MCN+∠NCD=90°，即MC⊥CD．∴直线CD是⊙M的切线．类型二切线的性质已知某条直线是圆的切线，当圆心与切点有线段连接时，直接利用切线的性质：圆的切线垂直于过切点的半径；当圆心与切点没有线段相连时，则作辅助线连接圆心与切点，再利用切线的性质解题．例2 (2016·资阳) 如图，在⊙O中，点C是直径AB延长线上一点，过点C作⊙O的切线，切点为D，连接BD.(1)求证：∠A＝∠BDC；(2)若CM平分∠ACD，且分别交AD，BD于点M，N，当DM＝1时，求MN的长．【分析】(1)连接OD，由切线的性质可得∠CDB＋∠ODB＝90°，由AB是直径，可得∠ADB＝90°，进而可得∠A＋∠ABD＝90°，进而求得∠A＝∠BDC；(2)由角平分线及三角形外角性质可得∠A＋∠ACM＝∠BDC＋∠DCM，即∠DMN＝∠DNM，再根据勾股定理求得MN的长．【自主解答】(1)如图，连接OD，∵CD是⊙O的切线，∴∠ODC＝90°，∴∠BDC＋∠ODB＝90°.∵AB是⊙O的直径，∴∠ADB＝90°，∴∠A＋∠ABD＝90°.∵OB＝OD，∴∠OBD＝∠ODB，∴∠A＋∠ODB＝90°，∴∠A＝∠BDC.(2)∵CM平分∠ACD，∴∠DCM＝∠ACM.∵∠A＝∠BDC，∴∠A＋∠ACM＝∠BDC＋∠DCM.即∠DMN＝∠DNM.∵∠ADB＝90°，DM＝1，∴DN＝DM＝1，∴MN＝变式训练2．(2017·长沙)如图，AB与⊙O相切于点C，OA，OB分别交⊙O于点D，E，=（1）求证：OA=OB；（2）已知AB=4，OA=4，求阴影部分的面积．解：（1）连接OC，∵AB与⊙O相切于点C∴∠ACO=90°，由于=，∴∠AOC=∠BOC，∴∠A=∠B∴OA=OB，（2）由（1）可知：△OAB是等腰三角形，∴BC=AB=2，∴sin∠COB==，∴∠COB=60°，∴∠B=30°，∴OC=OB=2，∴扇形OCE的面积为：=，△OCB的面积为：×2×2=2=2﹣π∴S阴影类型三圆与相似的综合圆与相似的综合主要体现在圆与相似三角形的综合，一般结合切线的判定与性质综合考查，求线段长或半径．一般的解题思路是利用切线的性质构造角相等，进而构造相似三角形，利用相似三角形对应边成比例求出所求线段或半径．例3 (2017·兰州) 如图，△ABC内接于⊙O，BC是⊙O的直径，弦AF交BC于点E，延长BC到点D，连接OA，AD，使得∠FAC=∠AOD，∠D=∠BAF．（1）求证：AD是⊙O的切线；（2）若⊙O的半径为5，CE=2，求EF的长．【分析】（1）由BC是⊙O的直径，得到∠BAF+∠FAC=90°，等量代换得到∠D+∠AOD=90°，于是得到结论；（2）连接BF，根据相似三角形的判定和性质即可得到结论．【自主解答】解：（1）∵BC是⊙O的直径，∴∠BAF+∠FAC=90°，∵∠D=∠BAF，∠AOD=∠FAC，∴∠D+∠AOD=90°，∴∠OAD=90°，∴AD是⊙O的切线；（2）连接BF，∴∠FAC=∠AOD，∴△ACE∽△OCA，∴，∴，∴AC=AE=，∵∠CAE=∠CBF，∴△ACE∽△BFE，∴，∴=，∴EF=．变式训练3．(2016·丹东)如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD，交AD的延长线于点E.(1)求证：∠BDC＝∠A；(2)若CE＝4，DE＝2，求AD的长．(1)证明：如图，连接OD，∵CD是⊙O的切线，∴∠ODC＝90°，即∠ODB＋∠BDC＝90°，∵AB为⊙O的直径，∴∠ADB＝90°，即∠ODB＋∠ADO＝90°. ∴∠BDC＝∠ADO.∵OA＝OD，∴∠ADO＝∠A，∴∠BDC＝∠A.(2)解：∵CE⊥AE，∴∠E＝90°，∴DB∥EC，∴∠DCE＝∠BDC.∵∠BDC＝∠A，∴∠A＝∠DCE.∵∠E＝∠E，∴△AEC∽△CED，∴∴CE2＝DE·AE，即16＝2(2＋AD)，∴AD＝6.。

初中数学专题练习：圆的切线证明(解析版)

专题07圆的切线证明1．如图，等边△ABC内接于⊙O，P是上任意一点（不与点A、B重合），连AP、BP，过点C作CM∥BP 交PA的延长线于点M．（1）求∠APC和∠BPC的度数试；（2）探究PA、PB、PM之间的关系；（3）若PA＝1，PB＝2，求四边形PBCM的面积．解：（1）∵△ABC是等边三角形，∴∠ABC＝∠BAC＝∠ACB＝60°，∵，，∴∠APC＝∠ABC＝60°，∠BPC＝∠BAC＝60°；（2）∵CM∥BP，∴∠BPM+∠M＝180°，∠PCM＝∠BPC＝60°，∴∠M＝180°﹣∠BPM＝180°﹣（∠APC+∠BPC）＝180°﹣120°＝60°，∴∠M＝∠BPC＝60°，∴∠PCM﹣∠PCA＝∠ACB﹣∠PCA，即∠ACM＝∠BCP，又∵BC＝AC，∴△ACM≌△BCP（AAS），∴AM＝BP，∵PM＝PA+AM，∴PM＝PA+PB；（3）∵△ACM≌△BCP，∴CM＝CP，又∵∠M＝60°，∴△PCM为等边三角形，∴CM＝CP＝PM＝1+2＝3，如图，过点P作PH⊥CM于H，在Rt△PMH中，∠MPH＝30°，∴PH＝，＝（PB+CM）×PH＝（2+3）×＝．∴S梯形PBCM2．如图所示，线段AC是⊙O的直径，过A点作直线BF交⊙O于A、B两点，过A点作∠FAC的角平分线交⊙O于D，过D作AF的垂线交AF于E．（1）证明DE是⊙O的切线；（2）证明AD2＝2AE•OA；（3）若⊙O的直径为10，DE+AE＝4，求AB．（1）证明：连接OD，∴DE为⊙O切线；（2）证明：连接CD．∵AC为⊙O的直径，DE⊥AF∴∠ADC＝90°，∠DEA＝90°，∴∠ADC＝∠AED，∴在△ACD和△ADE中，∠DAC＝∠EAD，∠ADC＝∠AED，∴△ACD∽△ADE，∴．∴AD2＝AE•AC．∵AC＝2OA，∴AD2＝2AE•OA；（3）解：过点O作OM⊥AB于点M，则四边形ODEM为矩形，设DE＝OM＝x，则AE＝4﹣x，∴AM＝5﹣（4﹣x）＝1+x，在Rt△AMO中，OA2＝AM2+OM2，即：（1+x）2+x2＝52解得：x1＝3，x2＝﹣4（舍去）．∴AM＝4．∵OM⊥AB，由垂径定理得：AB＝2AM＝8．3．如图1，△ABC内接于⊙O，过C作射线CP与BA的延长线交于点P，∠B＝∠ACP．（1）求证：CP是⊙O的切线；（2）若PC＝4，PA＝2，求AB的长；（3）如图2，D是BC的中点，PD与AC交于点E，求证：．（1）证明：如图1，连结OA、OC，则OA＝OC．∴∠OAC＝∠OCA．∴∠AOC+2∠OCA＝180°．由圆周角定理，得∠AOC＝2∠B．∴2∠B+2∠OCA＝180°．∴∠B+∠OCA＝90°．∵∠B＝∠ACP．∴∠ACP+∠OCA＝90°，即∠OCP＝90°．∴CP是⊙O的切线；（2）∵∠B＝∠ACP，∠ACP＝∠CPB，∴△APC∽△CPB．∴＝，∴PB＝＝＝8．∴AB＝PB﹣PA＝8﹣2＝6；（3）如图2，延长ED至F，使DF＝ED，连结BF，易得△BDF≌△CDE，∴BF＝CE，∠CED＝∠F．∴BF∥EC，∴＝＝．由（2）得，PB＝，∴＝，∴．4．定义：如果一个点能与另外两个点构成直角三角形，则称这个点为另外两个点的勾股点．如矩形OBCD 中，点C为O，B两点的勾股点，已知OD＝4，在DC上取点E，DE＝8．（1）如果点E是O，B两点的勾股点（点E不在点C），试求OB的长；（2）如果OB＝12，分别以OB，OD为坐标轴建立如图2的直角坐标系，在x轴上取点F（5，0）．在线段DC上取点P，过点P的直线l∥y轴，交x轴于点Q．设DP＝t．①当点P在DE之间，以EF为直径的圆与直线l相切，试求t的值；②当直线l上恰好有2点是E，F两点的勾股点时，试求相应t的取值范围．解：（1）如图1，连接OE，BE，若点E是O，B两点的勾股点，则∠OEB＝90°，∴∠OED+∠CEB＝90°，∵∠OED+∠DOE＝90°，∴∠DOE＝∠CEB，又∵∠C＝∠ODE，∴△BCE∽△EDO，∴＝，即＝，∴CE＝2，∴OB＝DE＝8+2＝10；（2）①如图2﹣1，设以EF为直径的圆的圆心为Q，与直线l的切点为M，直线l与OB的交点为H，连接QM，则∠FME＝90°，QM⊥PH，∴∠HMF+∠PME＝90°，∵∠PME+∠PEM＝90°，∴∠HMF＝∠PEM，又∵∠MHF＝∠EPM＝90°，∴△MHF∽△EPM，∴＝，∵QM⊥PH，l∥y轴，∴HF∥MQ∥PE，∴＝，∵FQ＝QE，∴HM＝MP＝2，又∵DP＝OH＝t，DE＝8，OF＝5，∴HF＝5﹣t，PE＝8﹣t，∴＝，解得，t1＝4，t2＝9（点P在DE之间，舍去），∴t＝4；②如图2﹣2，当直线l在⊙Q的右侧与⊙Q相切时，由①知△MHF∽△EPM，∴＝，此时，HM＝MP＝2，HF＝t﹣5，PE＝t﹣8，∴＝，解得，t1＝4，t2＝9，∴当t＝4或9时直线l与⊙Q相切，∵点E，F以及直线l上的点均可为直角三角形的直角顶点，∴当直线l上恰好有2点是E，F两点的勾股点时，相应t的取值范围为0≤t＜4或t＝5或t＝8或9＜t≤12．5．如图，AB是⊙O的直径，点P是圆上不与点A，B重合的动点，连接AP并延长到点D，使AP＝DP，点C是BD的中点，连接OP，OC，PC（1）求证：∠A＝∠D；（2）填空：①若AB＝10cm，当AP＝cm时，四边形AOCP是菱形；②当四边形OBCP是正方形时，∠DPC＝°．（1）证明：如图，连接PB，∵AB是⊙O的直径，∴BP⊥AD，∵AP＝PD，∴BP是线段AD的垂直平分线，∴BA＝BD，∴∠A＝∠D；（2）解：①∵AP＝PD，BC＝DC，∴，∵AB是⊙O的直径，∴，∴OA＝PC，∴四边形AOCP是平行四边形，∴当时，平行四边形AOCP是菱形，故答案为：5；②当四边形OBCP是正方形时，∠POB＝90°，∵OA＝OP，∴∠OPA＝∠A＝45°＝POB，∴PC∥AO，∴∠DPC＝∠A＝45°，故答案为：45．6．如图①，在矩形ABCD中，BC＝60cm．动点P以6cm/s的速度在矩形ABCD的边上沿A→D的方向匀速运动，动点Q在矩形ABCD的边上沿A→B→C的方向匀速运动．P、Q两点同时出发，当点P到达终点D时，点Q立即停止运动．设运动的时间为t（s），△PDQ的面积为S（cm2），S与t的函数图象如图②所示．（1）AB＝cm，点Q的运动速度为cm/s；（2）在点P、Q出发的同时，点O也从CD的中点出发，以4cm/s的速度沿CD的垂直平分线向左匀速运动，以点O为圆心的⊙O始终与边AD、BC相切，当点P到达终点D时，运动同时停止．①当点O在QD上时，求t的值；②当PQ与⊙O有公共点时，求t的取值范围．解：（1）设点Q的运动速度为acm/s，则由图②可看出，当运动时间为5s时，△PDQ有最大面积450，即此时点Q到达点B处，∵AP＝6t，＝（60﹣6×5）×5a＝450，∴S△PDQ∴a＝6，∴AB＝5a＝30，故答案为：30，6；（2）①如图1，设AB，CD的中点分别为E，F，当点O在QD上时，QC＝AB+BC﹣6t＝90﹣6t，OF＝4t，∵OF∥QC且点F是DC的中点，∴OF＝QC，即4t＝（90﹣6t），解得，t＝；②设AB，CD的中点分别为E，F，⊙O与AD，BC的切点分别为N，G，过点Q作QH⊥AD于H，如图2﹣1，当⊙O第一次与PQ相切于点M时，∵AP＝6t，AB+BQ＝6t，且BQ＝AH，∴HP＝QH＝AB＝30，∴△QHP是等腰直角三角形，∵CG＝DN＝OF＝4t，∴QM＝QG＝90﹣4t﹣6t＝90﹣10t，PM＝PN＝60﹣4t﹣6t＝60﹣10t，∴QP＝QM+MP＝150﹣20t，∵QP＝QH，∴150﹣20t＝30，∴t＝；如图2﹣2，当⊙O第二次与PQ相切于点M时，∵AP＝6t，AB+BQ＝6t，且BQ＝AH，∴HP＝QH＝AB＝30，∴△QHP是等腰直角三角形，∵CG＝DN＝OF＝4t，∴QM＝QG＝4t﹣（90﹣6t）＝10t﹣90，PM＝PN＝4t﹣（60﹣6t）＝10t﹣60，∴QP＝QM+MP＝20t﹣150，∵QP＝QH，∴20t﹣150＝30，∴t＝，综上所述，当PQ与⊙O有公共点时，t的取值范围为：≤t≤．7．如图，矩形ABCD中，AB＝2BC，以AB为直径作⊙O．（1）证明：CD是⊙O的切线；（2）若BC＝3，连接BD，求阴影部分的面积．（结果保留π）解：（1）过点O作OE⊥CD于E，∵四边形ABCD是矩形，∴∠A＝∠ADC＝∠OED＝90°，∴四边形ADEO是矩形，∴AD＝OE，∵AB＝2BC，∴AB＝2AD＝2OE，∴AO＝OE，∴CD是⊙O的切线；（2）∵四边形ADEO是矩形，∴∠AOE＝∠BOE＝90°，＝＝．∴阴影部分的面积＝S扇形BOE8．定义：已知点O是三角形的边上的一点（顶点除外），若它到三角形一条边的距离等于它到三角形的一个顶点的距离，则我们把点O叫做该三角形的等距点．（1）如图1，△ABC中，∠ACB＝90°，AC＝3，BC＝4，O在斜边AB上，且点O是△ABC的等距点，试求BO的长．（2）如图2，△ABC中，∠ACB＝90°，点P在边AB上，AP＝2BP，D为AC中点，且∠CPD＝90°．①求证：△CPD的外接圆圆心是△ABC的等距点；②求tan∠PDC的值．解：（1）CB＝4，AC＝3，则AB＝5，①当OH⊥BC时，只有OH＝OA一种情况，设OB＝x，则OH＝OA＝5﹣x，则sin B＝＝＝，解得：x＝；②当OH′⊥AC时，同理可得：OH′＝OB，解得：x＝，综上，OB＝或；（2）①设△CPD的外接圆圆心为点O，连接OP、OB，则OD＝OP＝OC，设圆的半径为R，AP＝2BP＝2a，则AD＝2R，OD＝R，则，故PD∥OB，故∠BOP＝∠DPO，∠COB＝∠ODP，而∠ODP＝∠OPD，∴∠POB＝∠COB，而BO＝BO，OP＝OC，∴△BCO≌△BPO（SAS），∴∠BPO＝90°，即OP⊥AB，且OP＝OC，故：△CPD的外接圆圆心是△ABC的等距点；②∵△BCO≌△BPO（SAS），∴BC＝BP＝a，而AB＝3a，AC＝4R，故（3a）2＝（4R）2+a2，解得：a＝，tan∠PDC＝tan∠COB＝＝＝＝．9．如图，AB是⊙O的直径，弦CD⊥AB于点E，G是上一动点，AG，DC的延长线交于点F，连接AC，AD，GC，GD．（1）求证：∠FGC＝∠AGD；（2）若AD＝6．①当AC⊥DG，CG＝2时，求sin∠ADG；②当四边形ADCG面积最大时，求CF的长．证明：（1）∵AB是⊙O的直径，弦CD⊥AB，∴CE＝DE，CD⊥AB，∴AC＝AD，∴∠ADC＝∠ACD，∵四边形ADCG是圆内接四边形，∴∠ADC＝∠FGC，∵∠AGD＝∠ACD，∴∠FGC＝∠ADC＝∠ACD＝∠AGD，∴∠FGC＝∠AGD；（2）如图，设AC与GD交于点M，∵，∴∠GCM＝∠ADM，又∵∠GMC＝∠AMD，∴△GMC∽△AMD，∴＝＝＝，设CM＝x，则DM＝3x，由（1）知，AC＝AD，∴AC＝6，AM＝6﹣x，在Rt△AMD中，AM2+DM2＝AD2，∴（6﹣x）2+（3x）2＝62，解得，x1＝0（舍去），x2＝，∴AM＝6﹣＝，∴sin∠ADG＝＝＝；＝S△ADC+S△ACG，（3）S四边形ADCG∵点G是上一动点，∴当点G在的中点时，△ACG的的底边AC上的高最大，此时△ACG的面积最大，四边形ADCG的面积也最大，∴GA＝GC，∴∠GAC＝∠GCA，∵∠GCD＝∠F+∠FGC，由（1）知，∠FGC＝∠ACD，且∠GCD＝∠ACD+∠GCA，∴∠F＝∠GCA，∴∠F＝∠GAC，∴FC＝AC＝6．10．如图，CD是⊙O的直径，弦AB⊥CD，垂足为H，FG是⊙O的切线，FG∥BD，DF与AB交于点E．（1）求证：BE＝BD；（2）若AB＝8，DH＝3，求EH的长．解：（1）如图，连接OF，∵FG是⊙O的切线，∴∠GFD+∠OFD＝90°，∵AB⊥CD，∴∠DEH+∠ODE＝90°，∵OF＝OD，∴∠OFD＝∠ODF．∴∠DEH＝∠GFD，∵FG∥BD，∴∠GFD＝∠BDF，∴∠DEH＝∠BDF，∴BE＝BD；（2）∵CD是⊙O的直径，弦AB⊥CD，垂足为H，∴，∵DH＝3，∴BD＝5，∵BE＝BD，∴BE＝5，∴EH＝BE﹣BH＝1，答：EH的长为1．11．如图，直线MN交⊙O于A，B两点，AC是⊙O直径，∠CAM的平分线交⊙O于点D，过点D作DE⊥MN 于点E．（1）求证：DE是⊙O的切线；（2）若DE＝6cm，AE＝3cm，求⊙O的半径．（1）证明：连接OD，如图所示：∵OA＝OD，∴∠3＝∠2，∵AD平分∠CAM，∴∠2＝∠1，∴∠1＝∠3，∴MN∥OD，∵DE⊥MN，∴DE⊥OD，∴DE是⊙O的切线；（2）解：连接CD，如图所示：∵AC是⊙O的直径，∴∠ADC＝90°，∴AD＝＝＝3（cm），∵DE⊥MN，∴∠AED＝90°，∴∠ADC＝∠AED，又∵∠2＝∠1，∴△ADC∽△AED，∴＝，即＝，∴AC＝15（cm），∴OA＝AC＝cm，即⊙O的半径为cm．12．如图，O为∠MBN角平分线上一点，⊙O与BN相切于点C，连结CO并延长交BM于点A，过点A作AD⊥BO于点D．（1）求证：AB为⊙O的切线；（2）若BC＝6，tan∠ABC＝，求AD的长．解：（1）过点O作OE⊥AB于点E，∵O为∠MBN角平分线上一点，∴∠ABD＝∠CBD，又∵BC为⊙O的切线，∴AC⊥BC，∵AD⊥BO于点D，∴∠D＝90°，∴∠BCO＝∠D＝90°，在△BOC和△BOE中，∵，∴△BOC≌△BOE（AAS），∴OE＝OC，∵OE⊥AB，∴AB是⊙O的切线；（2）∵∠ABC+∠BAC＝90°，∠EOA+∠BAC＝90°，∴∠EOA＝∠ABC，∵tan∠ABC＝、BC＝6，∴AC＝BC•tan∠ABC＝8，则AB＝10，由（1）知BE＝BC＝6，∴AE＝4，∵tan∠EOA＝tan∠ABC＝，∴，∴OE＝3，OB＝＝3，∵∠ABD＝∠OBC，∠D＝∠ACB＝90°，∴△ABD∽△OBC，∴，即＝，∴AD＝2．13．如图1是一块内置量角器的等腰直角三角板，它是一个轴对称图形．已知量角器所在的半圆O的直径DE与AB之间的距离为1，DE＝4，AB＝8，点N为半圆O上的一个动点，连结AN交半圆或直径DE 于点M．（1）当AN经过圆心O时，求AN的长；（2）如图2，若N为量角器上表示刻度为90°的点，求△MON的周长；（3）当时，求△MON的面积．解：（1）如图1中，连接FO延长FO交AB于H．则FH⊥AB，FH⊥DE．∵FA＝FB，FH⊥AB，∴AH＝HB＝4，在Rt△AOH中，∵OH＝1，AH＝4，∴OA＝＝＝，∴AN＝OA+ON＝+2．（2）如图2中，连接OM，作OJ⊥MN．在Rt△AHN中，∵AH＝4，NH＝ON+OH＝2+1＝3，∴AN＝＝＝5，由△△OJN∽△AHN，可得＝，∴＝，∴JN＝，∵OJ⊥MN，∴JM＝JN，∴MN＝2JN＝，∴△MON的周长＝2+2+＝．（3）如图3﹣1中，连接AO，延长AO交⊙O于K，作OJ⊥MN于J，连接OM，ON．设AM＝MN＝x，OJ＝y，则有，解得，∴MN＝，OJ＝，＝•MN•OJ＝××＝．∴S△MON如图3﹣2中，连接ON，作NJ⊥AB于J交DE于K．∵AM＝MN，MK∥AJ，∴NK＝JK＝OH＝1，∵NJ⊥AB，DE∥AB，∴NK⊥OE，∴sin∠NOK＝＝，∴OK＝NK＝，∵四边形OKJH是矩形，∴HJ＝OK＝，∴AJ＝4+，∴MK＝AJ＝2+，∴OM＝MK﹣OK＝2﹣，＝•OM•NK＝•（2﹣）×1＝1﹣，∴S△MON综上所述，满足条件的△MON的面积为或1﹣．14．MN是⊙O上的一条不经过圆心的弦，MN＝4，在劣弧MN和优弧MN上分别有点A，B（不与M，N 重合），且，连接AM，BM．（1）如图1，AB是直径，AB交MN于点C，∠ABM＝30°，求∠CMO的度数；（2）如图2，连接OM，AB，过点O作OD∥AB交MN于点D，求证：∠MOD+2∠DMO＝90°；（3）如图3，连接AN，BN，试猜想AM•MB+AN•NB的值是否为定值，若是，请求出这个值；若不是，请说明理由．解：（1）如图1，∵AB是⊙O的直径，∴∠AMB＝90°．∵，∴∠AMN＝∠BMN＝45°．∵OM＝OB，∴∠OMB＝∠OBM＝30°，∴∠CMO＝45°﹣30°＝15°；（2）如图2，连接OA，OB，ON．∵，∴∠AON＝∠BON．又∵OA＝OB，∴ON⊥AB．∵OD∥AB，∴∠DON＝90°．∵OM＝ON，∴∠OMN＝∠ONM．∵∠OMN+∠ONM+∠MOD+∠DON＝180°，∴∠MOD+2∠DMO＝90°；（3）如图3，延长MB至点M′，使BM′＝AM，连接NM′，作NE⊥MM′于点E．设AM＝a，BM＝b．∵四边形AMBN是圆内接四边形，∴∠A+∠MBN＝180°．∵∠NBM′+∠MBN＝180°，∴∠A＝∠NBM′．∵，∴AN＝BN，∴△AMN≌△BM′N（SAS），∴MN＝NM′，BM′＝AM＝a．∵NE⊥MM′于点E．∴．∵ME2+（BN2﹣BE2）＝MN2，∴．化简得ab+NB2＝16，∴AM•MB+AN•NB＝16．15．如图，⊙O是△ABC的外接圆，AB为⊙O的直径，在△ABC外侧作∠CAD＝∠CAB，过点C作CD⊥AD 于点D，交AB延长线于点P．（1）求证：PC是⊙O的切线；（2）若tan∠BCP＝，AD•BC＝4m2（m＞0），求⊙O的半径；（用含m的代数式表示）（3）如图2，在（2）的条件下，作弦CF平分∠ACB，交AB于点E，连接BF，且BF＝5，求线段PE的长．解：（1）如图1，连接OC，则OA＝OC，则∠OAC＝∠OCA＝α，而∠CAD＝∠CAB＝α，故∠DAC＝∠OCA＝α，∴AD∥CO，而CD⊥AD，∴CO⊥PD，故PC是⊙O的切线；（2）PC是⊙O的切线，则∠BCP＝∠CAB＝α，即tan，则sin，cos，∵∠DAC＝∠CAB＝α，∴△ADC∽△ABC，设圆的半径为R，则AC＝AB cosα＝2R×＝，CD＝AC sinα＝，故AD•BC＝AC•CD＝＝4m2，故R＝m；（3）连接OF、OC，CF平分∠ACB，则FO⊥AB，∵∠ECP＝90°﹣∠OCE，∠CEP＝90°﹣∠OFC，而∠OCE＝∠OFC，∴∠ECP＝∠CEP，∴PC＝PE，BF＝5＝R，则R＝5，AD＝AC cosα＝×＝8，同理CD＝4，∵CO∥AD，∴，即，解得：PC＝＝PE．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

证明圆的切线方法及例题
证明圆的切线常用的方法有：
一、若直线l 过⊙O 上某一点A ，证明l 是⊙O 的切线，只需连OA ，证明OA ⊥l 就行了，简称“连半径，证垂直”，难点在于如何证明两线垂直.
例1 如图，在△ABC 中，AB=AC ，以AB 为直径的⊙O 交BC 于D ，交AC 于E ，B 为切点的切线交OD 延长线于F.
求证：EF 与⊙O 相切.
证明：连结OE ，AD.
∵AB 是⊙O 的直径， ∴AD ⊥BC.
又∵AB=BC ， ∴∠3=∠4.
∴BD=DE ，∠1=∠2.
又∵OB=OE ，OF=OF ，
∴△BOF ≌△EOF （SAS ）.∴∠OBF=∠OEF.
∵BF 与⊙O 相切， ∴OB ⊥BF. ∴∠OEF=900. ∴EF 与⊙O 相切.
说明：此题是通过证明三角形全等证明垂直的
例2 如图，AD 是∠BAC 的平分线，P 为BC 延长线上一点，且PA=PD.
求证：PA 与⊙O 相切.
证明一：作直径AE ，连结EC.
∵AD 是∠BAC 的平分线，∴∠DAB=∠DAC.
∵PA=PD ， ∴∠2=∠1+∠DAC.
∵∠2=∠B+∠DAB ，∴∠1=∠B.
又∵∠B=∠E ，∴∠1=∠E
∵AE 是⊙O 的直径，
∴AC ⊥EC ，∠E+∠EAC=900.∴∠1+∠EAC=900. 即OA ⊥PA. ∴PA 与⊙O 相切.
证明二：延长AD 交⊙O 于E ，连结OA ，OE.
∵AD 是∠BAC 的平分线，∴BE=CE ，
∴OE ⊥BC.∴∠E+∠BDE=900.
∵OA=OE ，∴∠E=∠1.
⌒ ⌒ ⌒ ⌒
∵PA=PD ，∴∠PAD=∠PDA.
又∵∠PDA=∠BDE,
∴∠1+∠PAD=900
即OA ⊥PA.∴PA 与⊙O 相切
说明：此题是通过证明两角互余，证明垂直的，解题中要注意知识的综合运用. 例3 如图，AB=AC ，AB 是⊙O 的直径，⊙O 交BC 于D ，DM ⊥AC 于M
求证：DM 与⊙O 相切.
证明一：连结OD.
∵AB=AC ， ∴∠B=∠C.
∵OB=OD ∴∠1=∠B.
∴∠1=∠C.∴OD ∥AC. ∵DM ⊥AC ，∴DM ⊥OD.
∴DM 与⊙O 相切
证明二：连结OD ，AD.
∵AB 是⊙O 的直径，∴AD ⊥BC.
又∵AB=AC,∴∠1=∠2.
∵DM ⊥AC ，∴∠2+∠4=900
∵OA=OD ，∴∠1=∠3.
∴∠3+∠4=900.即OD ⊥DM. ∴DM 是⊙O 的切线
说明：证明一是通过证平行来证明垂直的.证明二是通过证两角互余证明垂直的，解题中注意充分利用已知及图上已知.
例 4 如图，已知：AB 是⊙O 的直径，点C 在⊙O 上，且∠CAB=300，BD=OB ，D 在AB 的延长线上.
求证：DC 是⊙O 的切线
证明：连结OC 、BC.
∵OA=OC ， ∴∠A=∠1=∠300.
∴∠BOC=∠A+∠1=600.
又∵OC=OB ，
∴△OBC 是等边三角形.∴OB=BC. D C
D
∵OB=BD ， ∴OB=BC=BD. ∴OC ⊥CD. ∴DC 是⊙O 的切线.
说明：此题是根据圆周角定理的推论3证明垂直的，此题解法颇多，但这种方法较好.
例5 如图，AB 是⊙O 的直径，CD ⊥AB ，且OA 2=OD ·OP.
求证：PC 是⊙O 的切线.
证明：连结OC
∵OA 2=OD·OP ，OA=OC ，∴OC 2=OD·OP ， OC OP OD OC . 又∵∠1=∠1，∴△OCP ∽△ODC.∴∠OCP=∠ODC.
∵CD ⊥AB ，∴∠OCP=900. ∴PC 是⊙O 的切线.
说明：此题是通过证三角形相似证明垂直的
例6 如图，ABCD 是正方形，G 是BC 延长线上一点，AG 交BD 于E ，交CD 于F.
求证：CE 与△CFG 的外接圆相切.
分析：此题图上没有画出△CFG 的外接圆，但△CFG 是直角三角形，圆心在斜边FG 的中点，为此我们取FG 的中点O ，连结OC ，证明CE ⊥OC 即可得解.
证明：取FG 中点O ，连结OC.
∵ABCD 是正方形，∴BC ⊥CD ，△CFG 是Rt △
∵O 是FG 的中点， ∴O 是Rt △CFG 的外心.
∵OC=OG ，∴∠3=∠G ，∵AD ∥BC ， ∴∠G=∠4.
∵AD=CD ，DE=DE ，∠ADE=∠CDE=450，
∴△ADE ≌△CDE （SAS ）∴∠4=∠1，∠1=∠3.
∵∠2+∠3=900, ∴∠1+∠2=900. 即CE ⊥OC. ∴CE 与△CFG 的外接圆相切
二、若直线l 与⊙O 没有已知的公共点，又要证明l 是⊙O 的切线，只需作OA ⊥l ，A 为垂足，证明OA 是⊙O 的半径就行了，简称：“作垂直；证半径”
例7 如图，AB=AC ，D 为BC 中点，⊙D 与AB 切于E 点.
求证：AC 与⊙D 相切.
证明一：连结DE ，作DF ⊥AC ，F 是垂足.∵AB 是⊙D 的切线，∴DE ⊥AB.
∵DF ⊥AC ，∴∠DEB=∠DFC=900. ∵AB=AC ，∴∠B=∠C.又∵BD=CD ，∴△BDE ≌△CDF （AAS ） ∴DF=DE.∴F 在⊙D 上. ∴AC 是⊙D 的切线
证明二：连结DE ，AD ，作DF ⊥AC ，F 是垂足.
∵AB 与⊙D 相切，∴DE ⊥AB.
∵AB=AC ，BD=CD ，∴∠1=∠2. ∵DE ⊥AB ，DF ⊥AC ，∴DE=DF.∴F 在⊙D 上.∴AC 与⊙D 相切. 说明：证明一是通过证明三角形全等证明DF=DE 的，证明二是利用角平分线的性质证明DF=DE 的，这类习题多数与角平分线有关.
例8 已知：如图，AC ，BD 与⊙O 切于A 、B ，且AC ∥BD ，若∠COD=900. 求证：CD 是⊙O 的切线.
证明一：连结OA ，OB ，作OE ⊥CD ，E 为垂足.
∵AC ，BD 与⊙O 相切，∴AC ⊥OA ，BD ⊥OB.
∵AC ∥BD ， ∴∠1+∠2+∠3+∠4=1800.
∵∠COD=900，
∴∠2+∠3=900，∠1+∠4=900.
∵∠4+∠5=900. ∴∠1=∠5. ∴Rt △AOC ∽Rt △BDO. ∴OD OC OB AC =.∵OA=OB ，∴OD OC OA AC =. 又∵∠CAO=∠COD=900，∴△AOC ∽△ODC ， ∴∠1=∠2.
又∵OA ⊥AC ，OE ⊥CD,∴OE=OA. ∴E 点在⊙O 上. ∴CD 是⊙O 的
切线.
证明二：连结OA ，OB ，作OE ⊥CD 于E ，延长DO 交CA 延长线于F.
∵AC ，BD 与⊙O 相切，∴AC ⊥OA ，BD ⊥OB.
∵AC ∥BD ，∴∠F=∠BDO.
又∵OA=OB ，
∴△AOF ≌△BOD （AAS ）∴OF=OD.
∵∠COD=900，∴CF=CD ，∠1=∠2.
又∵OA ⊥AC ，OE ⊥CD ，∴OE=OA. ∴E 点在⊙O 上.∴CD 是⊙O 的切线. 证明三：连结AO 并延长，作OE ⊥CD 于E ，取CD 中点F ，连结OF.
∵AC 与⊙O 相切，∴AC ⊥AO. O
∵AC ∥BD ，∴AO ⊥BD.
∵BD 与⊙O 相切于B ，
∴AO 的延长线必经过点B.
∴AB 是⊙O 的直径.
∵AC ∥BD ，OA=OB ，CF=DF ，∴OF ∥AC ，
∴∠1=∠COF.∵∠COD=900，CF=DF ， ∴CF CD OF ==2
1.
∴∠2=∠COF.∴∠1=∠2.
∵OA ⊥AC ，OE ⊥CD ， ∴OE=OA.∴E 点在⊙O 上. ∴CD 是⊙O 的切线说明：证明一是利用相似三角形证明∠1=∠2，证明二是利用等腰三角形三线合一证明∠1=∠2.证明三是利用梯形的性质证明∠1=∠2，这种方法必需先证明A 、O 、B 三点共线.。