碟簧计算方法
蝶形弹簧schnorr的选型和计算
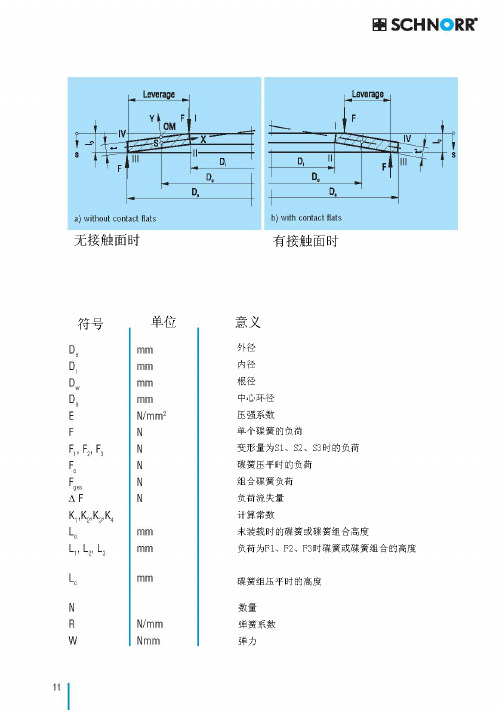
3.1单个碟簧的组合方式休诺碟簧独特的结构使得组合使用碟簧变得极为方便。
多种组合碟簧可以满足各种不同的工况。
原则上可以使用如下的组合方式(figure21):串联组合碟簧并联组合碟簧多片多组串联组合碟簧组合碟簧的特性由单个碟簧的特性和组合方式所决定3.2串联组合碟簧Figure21 中b型图即3片串联组合碟簧,此种组合形式计算公式如下:碟簧载荷量:F ges=F碟簧偏斜:S ges=i*s未装载时碟簧长度:L0=i*I03.3并联组合碟簧(并联请勿超过4片)Figure21 中c型图即双片并联组合碟簧,此种组合形式计算公式如下:碟簧载荷量:F ges=n*F碟簧组偏斜:S ges=i*s未装载时碟簧组长度:L0=I0+(n-1)*t多片并联使用时,由于摩擦起负荷变化如下图:3.4多片多组串联组合碟簧Figure21 中d型图即双片3组串联组合碟簧,此种组合形式计算公式如下:碟簧载荷量:F ges=n*F碟簧组偏斜:S ges=i*s未装载时碟簧组长度:L0=i*[I0+(n-1)*t]注:最佳排列方式为单片少量,串联外径选择越大越好由于摩擦,位移不稳定性随串联片数增加而扩大我们推荐串联总长度L0为:L0<=3*De若实际运用总长度必须超过时,请利用平垫圈均分为2-3段。
3.5碟簧的累进特性当随着碟簧偏移增加时,在许多场合对碟簧有这样一个要求,碟簧的载荷也会累进增加。
碟簧的增加特性比率(对碟簧它是典型的)会代替减少的(如图22所示)。
这样的特性曲线会通过众多方法获得。
用碟簧堆如图23.a所显示将碟簧1,2,3叠加使用,随着载荷的施加,碟簧1,2,3折叠的阶层会变平,这样的一个碟簧堆的特性是由每单个的碟簧特性导致的,如图23所示。
同样的效果也可(图23.b)由不同厚度结合性的碟簧来构成的碟簧堆来获得。
在这个事例中,根据德标2093或SCANORR工厂标准来选择,必须考虑碟簧堆1或2的折叠或薄的单个碟簧被选用在非常高的压力情况。
弹簧设计计算

D(mm)
K1
Fc(N)
100
0.686
62724.63
100
0.686
15846.15
100
0.686
9093.29
分别为959219N和15846N)均大于工作载荷F(13186.81N),所 。
F/Fc 0.210 0.832 荷F下的变形量)
4*E 824000
1-μ² 0.91
碟簧片数 5
0.384
.2-2查得)
Fσ(许用载荷)/N 48000 13100 8610
f=0.75·h0 f(变形量)/mm
1.65 2.1 2.63
σⅡ或σⅢ/Mpa
1420 1050 1240
t代替
5/32
0.15625
H0/t 1.366666667
H0/t-1 0.366666667
C2验算
(H0/t-1)²
h0(碟簧压平时
H0
变形量)/mm (自由高度)/mm
A100
100
51
6
2.2
8.2
B100
100
51
3.5
2.8
6.3
C100
100
51
2.7
3.5
6.2
由C=D/d=100/51=1.96 从表7.2-5查得系数 K1=0.686
D(外径)/mm d(内径)/mm
C
100
51
1.96
⑴ 采用A系列外径D=100mm 碟形复合组合弹簧(A100-1GB/T1972-1992)
Fc(N)
h0/t
A100
2.2
6
13186.81
碟簧压力 扭矩

碟簧压力扭矩是机械工程中一个重要的概念,它在许多机械装置的设计和运行中起着关键的作用。
本文将介绍碟簧压力扭矩的概念、计算方法以及其在工程中的应用。
1. 概念碟簧压力扭矩是指通过对碟簧施加力矩来产生弹性变形的一种装置。
碟簧由金属薄片制成,具有弹性变形特性。
当施加力矩使得碟簧弯曲时,它会产生回弹力,使其恢复到初始状态。
这种弹性特性使得碟簧可以在许多机械装置中作为一种弹性元件来使用。
2. 计算方法计算碟簧压力扭矩需要考虑到碟簧的几何形状、材料力学性质以及应用条件等因素。
下面是碟簧压力扭矩计算的基本公式:T=k⋅θ式中,T表示碟簧压力扭矩;k为碟簧的刚度系数;θ表示碟簧的变形角度。
具体的计算方法需要根据碟簧的几何形状和材料特性来确定刚度系数k。
在实际工程中,可以通过实验或者有限元分析等方法来获得。
变形角度θ则可以通过对施加的力矩和碟簧的弹性特性进行分析得到。
3. 工程应用碟簧压力扭矩在工程中有着广泛的应用。
下面列举了几个常见的应用示例:3.1 避震装置碟簧压力扭矩可以作为一种避震装置来使用。
在汽车悬挂系统中,通过将碟簧安装在减震器上,可以使得车辆在行驶过程中减少颠簸感。
碟簧的弹性特性可以有效减缓路面不平造成的冲击,提高车辆的行驶舒适性。
3.2 扭矩传感器利用碟簧的压力扭矩特性,可以设计出高精度的扭矩传感器。
通过测量碟簧的变形角度,可以间接测量出施加在碟簧上的扭矩大小。
这种传感器被广泛应用于机械测试和控制领域。
3.3 泵阀装置碟簧压力扭矩也可以用于泵阀装置中。
在某些泵阀系统中,通过调整碟簧的变形角度,可以实现对流量的控制。
当碟簧发生弹性变形时,可以改变阀门的开启程度,从而影响流体的流量。
结论碟簧压力扭矩作为一种重要的机械装置,在工程中具有广泛的应用前景。
通过对碟簧的几何形状、材料特性以及力学性质进行合理的设计和分析,可以实现对碟簧压力扭矩的有效控制和应用。
在未来的研究和设计中,我们可以进一步挖掘碟簧压力扭矩的潜力,将其应用于更多的领域,提高机械设备的性能和效率。
碟簧的选用计算1

碟簧型号选择1、碟簧选型图一碟簧基本性能图二碟簧的基本系数参数图三系数表1.1、俯仰机构根据已知的条件如下图所示:图四碟簧压力表图五碟簧受力曲线可知:碟簧预紧力7500N,压缩量92mm,压缩量在200mm时,受力16000N,刚度约为80KN/M。
根据下图初步选定外径90内径46厚度3.5的碟簧(单个碟簧在完全压平后受力为1784.69kg,大于16000N)。
下图为外径为80和90的碟簧参数。
表一 碟簧参数(一)校核计算:1、单个碟簧的负荷 17518142421032=••-=K DK h t E P C μ (1) 其中:684.0ln 2111)1(1221=--+-•=C C C c C K π 14=K25/1006.2mm N E ⨯=97.1==dD C 3.0=μt=3.5mmd=46mmD=90mmh0=2.52、单个碟簧变形量由于采用的是对合组合,所以单个碟簧的受力等于初始受力,即预紧力 KN P 5.7'1=428.0175187500'1==CP P 根据:714.05.35.20==t h 由图三可求出变形量为:04.0h f ⨯=,即15.24.0=⨯=f 0.3 0.753、碟簧组的变形量升降时的变形量:L=6000/con3°-6000=8.41mm预紧时的变形量:L=92mm4、碟簧个数计算碟簧的个数: N=L 碟/f=92/1=92弹簧个数: 92 个所以碟簧总个数为92*2=184个5、选用型号:B904635(参数见表一)6、单边整个碟簧组刚度计算:3.6972123314202024242132=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+••-⎪⎭⎫ ⎝⎛•••-=t f t f t h t h K K D K t E P t μ M KN iP P t/75== 与原系统基本一致。
根据所选型号计算碟簧的受力曲线,见下图,红色部分为碟簧的运动位移行程(压缩量),具体计算结果见附件;图六碟簧组计算曲线7、结论经计算,若保证外形尺寸,即碟簧选用外径80,内径36,厚度3的型号,压缩量符合要求时,但是单个碟簧所承受的最大压力为14092.7N,低于最大压力16000N,不能满足实际要求。
碟簧计算

计算阀座密封面积:
f ((mm))
阀座密封面外径: ϕSo ≔ 225 mm 阀座密封面内径: ϕSi ≔ 214 mm
球体直径:
ϕB ≔ 320 mm
asin ⎛⎜― ϕS― o ⎟⎞ ⎝ ϕB ⎠
则阀座密封面面积为:
As ≔
⌠ ⎮ ⎮⌡
2
π
⋅
⎛ ϕB ⎞2 ⎜⎝―2 ― ⎟⎠ ⋅
sin
((θ))
dθ
= 5214.916
mm 2
asin ⎛⎜― ϕS― i ⎞⎟ ⎝ ϕB ⎠
或者:
A's
≔
― π ⋅ 2
ϕB
⋅
⎛ ⎝
‾ϕ‾B‾2‾-‾‾ϕ‾S‾i 2‾-
假设碟簧压缩量为总变形量的0.5倍,则有:
‾ϕ‾B‾2‾-‾‾ϕ‾S‾o2‾⎞⎠ = 5214.916 mm2
f' ≔ 0.5 ⋅ h = 1.6 mm
ϕDi
杨氏模量 E ≔ 206 GPa
泊松比 λ ≔ 0.3
计算碟簧各系数:
2
⎛C-1⎞
K1
≔
― 1 ⋅ π
―⎜⎝― ―C― ―― ⎟⎠ ―=
― C +― 1 -
2 ――
0.183
C - 1 ln ((C))
K2
≔
― 6 ⋅ π
― ― lCnl((-n― ― C((1))C― -)) 1― = 0.99
⎞ K3⎟⎠
计算碟簧刚度系数:
p ((f)) ≔ ― d ― F ((f)) df
或者
ቤተ መጻሕፍቲ ባይዱ
p'
((f)) ≔ ― 14-― Eλ2 ― ⋅ ― K1 ⋅― tϕ2D― o2 ― ⋅ K4 ⋅
碟形弹簧计算

h0/t C σ σ
Ⅱa Ⅲa
P1' P2' Pf' D0 h0 h'0 t'
中 间 辅 助 变 量
中 间 辅 助 变 量
计算系数 系 计算系数 计算系数 计算系数 数 计算系数 计算系数
C1 C2 K1 K2 K3 K4
10.88846881 11.88846881 0.684054678 1.208601569 1.358877278 1
代 号 D d t H0 n i fz1 fz2 fM fR f1 f2 nz Hz Hz1 Hz2 f3 fc Hc P1 P2 Pf Pc PR1 PR2 PRf PRc PR1 PR2
A40 GB/T 1972-92
──
时 考 碟簧的最小工作负荷 ( 虑 组 碟簧的最大工作负荷 减摩 合 载擦 ) 力 碟 簧
── ── ── ── ── ──
使 用 说 明
1.本表是根据国家标准《GB/T 1972-1992 碟形弹簧》编制的。标准原件 见附件。 2.表格中黄色区域为使用者要填写数据的单元格,其它区域中的单元 格请不要随便修改。 3.对于有支撑面的弹簧,其中 H0、t 等数据要按公称数据填写。 3.本表适用于《GB/T 1972-1992 碟形弹簧》标准中的所有规格的弹簧, 非标准无支撑面的碟形弹簧也可用本表计算。
碟形弹簧的计算(附件GB/T
尺寸、参数名称 碟簧标记 外径 内径 厚度 数 入 单个碟簧的自由高度 数 每组叠合碟簧中碟簧片数 据 组合碟簧中碟簧组数 组合碟簧预压变形量 组合碟簧工作行程总变形量 碟簧锥面间的摩擦系数 承载边缘处的摩擦系数 单片碟簧预压变形量 单片碟簧工作行程总变形量 碟簧的总片数 组合碟簧的自由高度 组合碟簧预压变形时的高度 组合碟簧工作行程总变形时的高度 工作行程 压平时的碟簧组总变形 碟簧组压平时的计算高度 力不 时考 虑 摩 擦 时考 (虑 加摩 载擦 )力 碟簧的最小工作负荷 碟簧的最大工作负荷 碟簧在f=0.75h0时的负荷 压平时的碟簧负荷 碟簧的最小工作负荷 碟簧的最大工作负荷 碟簧在f=0.75h0时的负荷 压平时的碟簧负荷
碟型弹簧简介和选用尺寸标准

碟型弹簧简介简介•碟型弹簧是承受轴向负荷的碟状弹簧,可以单个使用,也可对合组合或叠合组合、复合组合成碟簧组使用,承受静负荷或变负荷。
常见组合方式单片应用:总力值=单片受力总变形=单片变形2片并联应用:总力值=单片受力*2总变形=单片变形2片串联应用:总力值=单片受力总变形=单片变形*24片并、串联组合:总力值=单片受力*2总变形=单片变形*2DIN 2093 标准DIN 2093标准将碟型弹簧分为三组:第一组(D1): 厚度(t)< 1.25mm 没有支撑座第二组(D2): 1.25mm<=厚度(t)< =6mm 没有支撑座第三组(D3): 厚度(t)> 6mm 含支撑座标准对照DIN 2093 and GB 1972 :-All requirements are identical except Raw Material and Load Tolerances除原材料和力值要求不同外, 其它技术要求均一致. DIN 2093 prefers Narrow Tolerances in Load requirements.DIN 2093 对力值公差的要求更加严格.DIN 2093 prefers to use Alloy Carbon Steel(50CrV4) instead of Plain Carbon steel (60Si2Mn or C-80)DIN 2093 首选合金钢(50CrV4), 而国标采用渗碳钢(60SiMn 或C-80)合金钢(50CrV4)想对于碳钢(60Si2Mn或C-80)优势:-合金钢比普通碳素钢拥有更高的质量, 原因是加入的Cr元素和V元素:Cr可增加材料的强度, 而V可提供更好的晶相结构.细密的晶相结构比粗糙的晶相结构使合金钢拥有更好的韧性. 由于更好的晶相结构, 合金钢在热处理后能够得到更好的性能,比如, 一致的硬度.合金元素,例如V, 的存在,使材料拥有更稳定的微观结构.球面退火结构增加了材料的延展性, 以便于冷成型加工.50CrV4 更容易成型、冲压或裁减和热处理, 因此更适合制作碟形弹簧.。
碟簧计算方法

叠合组合蝶簧组: n 片碟簧叠合后自由状态下的高度:n 片碟簧叠合后变形量与载荷的关系:变形量I s血二耳 对合组合蝶簧组: i 片碟簧对合后自由状态下的高度:i 片碟簧对合后变形量与载荷的关系:二.例主轴拉爪有三个位置,分别是拉刀位置(中间位置)内部),HMS200主轴刀柄形式为 BT50,设计拉刀力为 25000N ,拉刀位置与松刀位置间的最小距离(即打 刀距离)为5.6mm 。
根据可用安装空间、 拉刀力等因素选择碟形弹簧型号180079,两两叠合再对合的组合 形式。
变形量良列寸,回复力为不致打刀力过大(小于 30000N ),采用50对两两叠合的碟簧对合,自由状态下* = 50s所以要想得到25000N 的拉刀力,一片弹簧的回复力应为 F=12500,对应的变形量为 s=0.633最小打刀距离为 5.6,设计打刀距离为 6,松刀位置碟簧组总变形量为 31.65+6=37.65,每片碟簧变形量为 37.65/50=0.753,每片碟簧回复力为 14576N ,理论所需打刀力P 兀14576 = 29仍画;无刀状态碟簧组总变 形量为31.65-10=21.65,每片碟簧变形量为 21.65/50=0.433,每片碟簧回复力为 8847N ,所以弹簧安装时需 预压21.65,预压力为 8847匚2=17694N ,预压后碟簧高度为 477.5-21.65=455.85。
串碟簧之间最好放一个自制垫片,这个自制垫片的作用一个是凑距离,可以节省碟簧的个数;另一个就 是可以让它和拉刀杆小间隙配合把大串碟簧隔开,减小大串碟簧的离心力;还有就是这个自制垫片外径可 以做大一点,在主轴内起导向作用,避免碟簧和主轴的摩擦。
碟 簧 基 De 不带支撑面的碟簧 Di De带支撑面的碟簧s 不带支撑面的蝶簧 卜=I 。
+ 5 - 1) • t带支撑面的蝶簧= + f载荷 ___________变形量:tot 载荷區可、松刀位置(最靠主轴端部)和无刀位置(最靠主轴两片180079碟簧叠合自由状态下 卜”叫+ 2 5.3 + 3.75 = 955一、=50 x 9.55=477.5 总变形量为 , = 50 x s = 50 x 0,633 = 3 L65 ,变形后碟簧组的总高度为 477.5-31.65=445.85。
碟簧组合

一、组合碟簧变形量和载荷计算的公式叠合组合碟簧组:n片碟簧叠合后自由状态下的高度:不带支撑面的碟簧L0=l0+(n−1)∙t带支撑面的碟簧L0=l0+(n−1)∙t′n片碟簧叠合后变形量与载荷的关系:变形量stot=s 载荷Ftot=n∙F对合组合碟簧组:i片碟簧对合后自由状态下的高度:L0=i∙l0i片碟簧对合后变形量与载荷的关系:变形量:stot=i∙s载荷Ftot=F二、计算实例:主轴拉爪有三个位置,分别是拉刀位置(中间位置)、松刀位置(最靠主轴端部)和无刀位置(最靠主轴内部),HMS200主轴刀柄形式为BT50,设计拉刀力为25000N,拉刀位置与松刀位置间的最小距离(即打刀距离)为5.6mm。
根据可用安装空间、拉刀力等因素选择碟形弹簧型号180079,两两叠合再对合的组合形式。
两片180079碟簧叠合自由状态下L叠=l0+n−1∙t‘=5.8+3.75=9.55变形量s叠=s时,回复力F叠=2F为不致打刀力过大(小于30000N),采用50对两两叠合的碟簧对合,自由状态下L对=i∙L叠=50×9.55=477.5变形量s对=i∙s叠=50s时,回复力F对=F叠=2F所以要想得到25000N的拉刀力,一片弹簧的回复力应为F=12500,对应的变形量为s=0.633总变形量为s对=50×s=50×0.633=31.65,变形后碟簧组的总高度为477.5-31.65=445.85。
最小打刀距离为5.6,设计打刀距离为6,松刀位置碟簧组总变形量为31.65+6=37.65,每片碟簧变形量为37.65/50=0.753,每片碟簧回复力为14576N,理论所需打刀力2×14576=29152N;无刀状态碟簧组总变形量为31.65-10=21.65,每片碟簧变形量为21.65/50=0.433,每片碟簧回复力为8847N,所以弹簧安装时需预压21.65,预压力为8847×2=17694N,预压后碟簧高度为477.5-21.65=455.85。
碟簧计算方法

一.碟簧基本理论De Dil 0De Di t t 's不带支撑面的碟簧带支撑面的碟簧叠合组合蝶簧组:n 片碟簧叠合后自由状态下的高度:不带支撑面的蝶簧L 0=l 0+(n -1)?t带支撑面的蝶簧L 0=l 0+(n -1)?t ′n 片碟簧叠合后变形量与载荷的关系:变形量s tot =s载荷F tot =n ?F 对合组合蝶簧组:i 片碟簧对合后自由状态下的高度:L 0=i ?l 0i 片碟簧对合后变形量与载荷的关系:变形量:s tot =i ?s 载荷F tot =F 二.例主轴拉爪有三个位置,分别是拉刀位置(中间位置)、松刀位置(最靠主轴端部)和无刀位置(最靠主轴内部),HMS200主轴刀柄形式为BT50,设计拉刀力为25000N ,拉刀位置与松刀位置间的最小距离(即打刀距离)为5.6mm 。
根据可用安装空间、拉刀力等因素选择碟形弹簧型号180079,两两叠合再对合的组合形式。
两片180079碟簧叠合自由状态下L 叠=l 0+(n -1)?t ‘= 5.8+3.75=9.55变形量s 叠=s 时,回复力F 叠=2F为不致打刀力过大(小于30000N ),采用50对两两叠合的碟簧对合,自由状态下L 对=i ?L 叠=50×9.55=477.5变形量s 对=i ?s 叠=50s 时,回复力F 对=F 叠=2F所以要想得到25000N 的拉刀力,一片弹簧的回复力应为F=12500,对应的变形量为s=0.633 总变形量为s 对=50×s =50×0.633=31.65,变形后碟簧组的总高度为477.5-31.65=445.85。
最小打刀距离为 5.6,设计打刀距离为6,松刀位置碟簧组总变形量为31.65+6=37.65,每片碟簧变形量为37.65/50=0.753,每片碟簧回复力为14576N ,理论所需打刀力2×14576=29152N ;无刀状态碟簧组总变形量为31.65-10=21.65,每片碟簧变形量为21.65/50=0.433,每片碟簧回复力为8847N ,所以弹簧安装时需预压21.65,预压力为8847×2=17694N ,预压后碟簧高度为477.5-21.65=455.85。
碟簧寿命公式

碟簧寿命公式碟簧寿命公式是指用于计算碟簧(一种用于存储数据的硬件设备)的寿命的数学公式。
它可以帮助我们预测碟簧的使用寿命,并采取相应的措施来延长其寿命。
在日常生活中,我们经常使用电脑来存储和处理大量的数据。
而硬盘驱动器中的碟簧起着至关重要的作用。
然而,由于长时间的使用和频繁的读写操作,碟簧会逐渐磨损并最终失效。
因此,了解如何计算碟簧的寿命对于我们合理使用和维护硬盘驱动器至关重要。
碟簧寿命公式的计算依赖于多个因素,包括碟簧的制造材料、使用环境、读写频率等。
然而,在本文中,我们将简单介绍一种常见的碟簧寿命公式,该公式基于经验数据和统计分析。
我们需要了解碟簧的制造材料对其寿命的影响。
通常情况下,碟簧由磁性材料制成,如铁磁合金。
这种材料具有良好的磁性和机械性能,能够满足硬盘驱动器的工作需求。
然而,由于材料的特性,碟簧的寿命受到一定的限制。
使用环境也是影响碟簧寿命的重要因素之一。
硬盘驱动器通常需要在恒定的温度和湿度下运行,以确保其正常工作。
因此,过高或过低的温度、湿度都可能导致碟簧的寿命缩短。
此外,硬盘驱动器还需要避免受到冲击或振动,以免对碟簧造成额外的损伤。
读写频率也是影响碟簧寿命的重要因素之一。
硬盘驱动器中的碟簧在读写操作时会受到磁头的接触,这将引起磁头和碟簧之间的磨损。
因此,频繁的读写操作将导致碟簧的寿命减少。
为了延长碟簧的寿命,我们应尽量减少读写操作,并定期进行数据备份。
碟簧寿命公式是用于计算碟簧寿命的数学公式。
通过考虑碟簧的制造材料、使用环境和读写频率等因素,我们可以预测碟簧的寿命并采取相应的措施来延长其寿命。
然而,需要注意的是,碟簧寿命公式只是一个近似值,实际使用中还需要结合其他因素进行综合考虑。
我们应该合理使用和维护硬盘驱动器,以确保数据的安全和可靠性。
碟形弹簧的介绍及选型计算说明

压平
0.800 6747 7759
高度L
mm 2.800 2.600
2.200 2.000
载荷点 单片弹簧 变形量S
mm 0.000 0.200
0.600 0.800
载荷F
N 0 1864
5187 6747
版本 19.7.98
2012-11-9 Mubea
最大拉应力
碟形弹簧,数据表
组2
零件/图号: ##### 项目: 碟形弹簧选型计算软件
慕贝尔, 碟形弹簧和夹紧元件有限公司, 邮箱 120, 57564 达登 phone.: sales: 02743/806-184, -194, Fax.:-188; engineering: 02743/806-268, -134, -135, Fax.: -292
2.58 0.224 2076 -836 444 456 -451 2.58 0.224 2076 8809
2.54 0.256 2356 -950 512 517 -515 2.54 0.256 2356 8695
2.51 0.288 2633 2.48 0.320 2906
-1063 -1174
Mubea
phone.: sales: 02743/806-184, -194, Fax.:-188; engineering: 02743/806-268, -134, -135, Fax.: -292
载荷点
计算
载荷点
单片
应力
单片弹簧
高度L 变形量S 载荷F
sI
s II
s III s OM 高度L 变形量S 载荷F 刚度
尺寸 外径
内径
厚度 减薄碟簧厚度 弹簧高度
碟簧计算公式范文

碟簧计算公式范文
1.刚簧方程(刚性碟簧):
在刚性碟簧的计算中,忽略碟簧的变形,将其视为刚体。
碟簧的刚度(弹性系数)由下式给出:
K=(4*n*E*t^3)/(D^3)
其中,K是碟簧的刚度(N/mm),n是碟簧的盘数,E是材料的弹性模量(N/mm^2),t是碟簧的厚度(mm),D是碟簧的直径(mm)。
2.柔簧方程(变形碟簧):
在变形碟簧的计算中,考虑碟簧的变形产生的刚度。
变形碟簧的刚度(弹性系数)由下式给出:
K=(n*G*t^3)/(3*R^3)*(1-μ^2)
其中,K是碟簧的刚度(N/mm),n是碟簧的盘数,G是材料的剪切模量(N/mm^2),t是碟簧的厚度(mm),R是碟簧的平均半径(mm),μ是材料的泊松比。
3.长矩形碟簧方程:
对于长矩形碟簧,其刚度(弹性系数)由下式给出:
K=(E*b*h^3)/(12*(1-μ^2)*L^3)
其中,K是碟簧的刚度(N/mm),E是材料的弹性模量(N/mm^2),b 是碟簧的宽度(mm),h是碟簧的厚度(mm),μ是材料的泊松比,L是碟簧的长度(mm)。
这些公式提供了计算碟簧刚度的方法,可以用于确定碟簧在实际应用中的性能。
然而,实际情况还可能受到其他因素的影响,例如碟簧的几何形状、边界条件、材料非线性等。
因此,在进行碟簧设计时,需要综合考虑这些因素,并进行必要的修正和优化。
碟形弹簧计算范文

碟形弹簧计算范文碟形弹簧是一种特殊的弹簧结构,广泛应用于各种机械系统中。
它的独特设计使得其具有较大的变形能力和较高的负荷能力。
在工程实践中,我们需要对碟形弹簧进行计算,以确定其设计参数和性能。
本文将介绍碟形弹簧的计算方法及相关理论知识。
一、碟形弹簧的结构形式及基本参数碟形弹簧一般由若干个弹簧叶片组成,呈圆环形状。
其主要参数包括弹簧片数、内径、外径、高度、材料及加工工艺等。
其中,弹簧片数是一个重要的设计参数,它直接影响到碟形弹簧的刚度和负荷能力。
二、碟形弹簧的刚度计算碟形弹簧的刚度是指单位变形时的载荷增加量,通常用N/mm或N/m 表示。
碟形弹簧的刚度计算可以采用以下公式:k=3N/(2πb^3)其中,k表示碟形弹簧的刚度,N表示弹簧的负荷,b表示弹簧片的宽度。
三、碟形弹簧的变形计算碟形弹簧的变形与载荷之间存在一定的函数关系,通常采用下列公式来计算变形:δ = (N/(kb))^3 * 6(1−ν^2)/(Et^3)其中,δ表示碟形弹簧的变形,N表示弹簧的负荷,k表示碟形弹簧的刚度,b表示弹簧片的宽度,ν表示弹簧材料的泊松比,E表示弹簧材料的弹性模量,t表示弹簧片的厚度。
四、碟形弹簧的疲劳寿命计算在工程实践中,碟形弹簧一般需要承受反复变换的载荷,因此需要进行疲劳寿命计算。
碟形弹簧的疲劳寿命计算一般采用极限应力法或应力循环法。
极限应力法:碟形弹簧的疲劳寿命与应力幅值有关,可以通过应力幅值与疲劳强度系数之间的关系来计算。
具体计算公式如下:N_f=(S_a/(k_b))^b其中,N_f表示碟形弹簧的疲劳寿命,S_a表示碟形弹簧的应力幅值,k_b和b分别为疲劳强度系数和材料的强度指数。
应力循环法:碟形弹簧的疲劳寿命与应力循环次数有关,可以通过应力循环次数与应力循环寿命之间的关系来计算。
具体计算公式如下:N_f=(N_r)^b其中,N_f表示碟形弹簧的疲劳寿命,N_r表示碟形弹簧的应力循环次数,b为材料的强度指数。
碟簧的计算

序号项目名称单位代号1碟簧外径mm D碟簧内径mm d碟簧自身厚度mm t‘碟簧公称厚度mm t碟簧压平时的计算量mm h0碟簧总高度mm H0碟簧承受的静载荷N P碟簧的变形量mm fz单个碟簧的压力载荷N P单片碟簧的变形量mm f碟簧下限表面的最大应力MPaσⅡ或σⅢ弹性模量MPa E泊松比μ外径和内径的比值CC1C2无支承面K4圆周率πK1压平时的碟簧载荷N Pc复合组合,单个碟簧的载荷当P/Pc时f/h0得出单片碟簧的变形量系数mm f1复合组合碟簧的片数组i实际片数组碟簧的组合片数n未受载荷的自有高度mm Hz受90000N载荷时的高度mm H1组合碟簧接触处的摩擦因数fM单片碟簧的负荷N F1复合组合,单个碟簧的载荷修正系数当F1/Pc时h0/t得出单片碟簧的变形量修正系数mm f2复合组合碟簧的修正片数组i弹簧的刚度N/mm P'一组叠合组合碟簧的刚度N/mm PR‘复合组合碟簧的刚度N/mm PZ‘碟簧的变形能N.mm U碟簧压平时的应力MPaσOMK2K3MpaσⅠMpaσⅡ蝶形弹簧的计算示例计算公式数值160829.4103.513.5139000141390002.6313402060000.3 C=D/d 1.951219512 C1=(t‘/t)^2/(((1/4)*(H0/t)-t‘/t+3/4)*((5/8)*H0/t-t‘/t+3/8))21.49061336 C2=C1/(t‘/t)^3*(5/32*(H0/t)-1)^2+1)26.36934631 K4=(-C1/2+((C1/2)^2+C2)^(1/2))^(1/2) 1.0788761823.141592654 K1=1/π*((C-1)/C)^2/((C+1)/(C-1)-(2/lnC)))0.684054678 Pc=((4*E)/(1-μ^2))*((t^3*h0)/(K1*D^2))*K4^2210652.34对合组合P/Pc 复合组合P/2/Pc0.329927497根据h0/t和P/Pc0.351.225 i=fz/f111.42857143142 Hz=i*(H0+(n-1)*t)268.5714286 H1=Hz-i*f254.57142860.015 F1=P*(1-fm*(n-1)/n)68457.5 F1/Pc0.324978584根据h0/t和F1/Pc0.250.875 i=fz/f216 P'=4*E/(1-μ^2)*(t^3/K1/D^2)*K4^2*(K4^2*(h0/t)^2-3*(h0/t)*(f2/t)+3/2*(f2/t)^2+1)63929.7459 PR‘=P'*n/(1-fM*(n-1))129806.5907 PZ‘=PR‘/i9271.899333 U=2*E/(1-μ^2)*(t^5/K1/D^2)*K4^2*(f2/t)^2*(K4^2*((h0/t)-(f2/2/t))^2+1)25555.34187σOM==-4*E/(1-μ^2)*t^2/K1/D^2*K4^2*f/t*3/π 校验压平时(f=h0)-652.58 K2=6*π*(((C-1)/lnC)-1/lnC) 1.208601569 K3=3*π*((C-1)/lnC) 1.358877278σⅠ=(4*E/(1-μ^2))*(t^2/(K1*D^2))*K4*f/t*(k4*k2*((h0/t)-(f/2/t))+k3)2411.72479σⅡ=(4*E/(1-μ^2))*(t^2/(K1*D^2))*K4*f/t*(k4*k2*((h0/t)-(f/2/t))-k3)-1575.701093不知道碟簧承受的载荷。
碟型弹簧特性分析

03 8 . 7 0.4 5 09 .6 11 .
0 5 4 0.4 0 7 2 0 7 6 0. 0. 6 0 9l 1O .9 6 8 .0 .5 8 l 84 8 .8 11 .3 11 .4 11 .5 11 .4 1 1 1 11 .3 . 10 .9 1
系 列 3 h t1 , 06 (O9 J= .t .,) .6 6 = h=
fh /n
f
O2 .5
O2 .4
O 35
O. 5
05 .5
0. 6
0.5 6
07 .
07 0. .5 8
08 .5
1
03 6 . 3 0.8 4
0 5 0 5 6 0. 4 0 6 2 0 7 0.6 0 81 0.6 .28 . 7 62 . 7 . 2 7 8 . 6 9
F—t ×kI ×t : t 一 )h—t +】 () = x _4 [ _ (o2 1 1 1 _ ( t t f) f l D0
一
() 4
碟簧压平时 fh, -。碟簧载荷 :
F- × (Biblioteka 2 2 碟 型弹 簧 的特 性分 析
下 面 通 过 上 列 公 式 分 析 碟 型 弹 簧 的 特 性 。表 1中 为泊松 比 ,本文取 = .; 03E为弹性模 量 M a P ,本 文取 FF 值是将 f 。t 。 / / 、、 值分别带入式 ( ) h h 4 中得 出的值 。 根据 E 2 6 0 M a C为外径 和内径之 比, = /; = . ×1 P ; 0 C Dd F 为碟簧 这些数据绘出其特性曲线。本文仅绘出了具有代表性 的
最好的碟形弹簧计算公式

最好的碟形弹簧计算公式碟形弹簧是一种常用的弹簧结构,具有较大的变形能力和较小的刚度,广泛应用于各种机械装置和工艺设备中。
在设计和计算碟形弹簧时,需要考虑多个因素,如外径、内径、高度、材料的选择等。
下面将详细介绍碟形弹簧的计算公式和相关设计要点。
碟形弹簧的基本几何参数包括外径(D)、内径(d)、高度(h)和弹片数量(n)。
在开始计算之前,先需要确定碟形弹簧的设计用途和负荷条件。
根据具体应用场景和装配要求,选择合适的材料和弹性系数。
1. 计算碟形弹簧的平均直径(Mean Diameter,Dm):Dm=(D+d)/22. 计算弹片外径(Outer Diameter,Do):Do=Dm+t其中,t为弹片宽度。
3. 计算弹片平均半径(Mean Radius,Rm):Rm=Dm/24. 计算碟形弹簧的自由弹簧率(Free Spring Rate,k):k=(4*n*G*t^3)/(3*Dm*Rm^3)其中,G为剪切模量。
5. 计算碟形弹簧的弹片应力(Stress,σ):σ=(32*F*h)/(π*Dm^3*n)其中,F为负荷。
6. 计算碟形弹簧的变形(Deflection,δ):δ=(F*h^3)/(G*Dm^4*n)根据需要,可以根据碟形弹簧的设计要求和使用条件调整以上公式的系数和参数。
在实际设计和计算碟形弹簧时,还需要考虑以下几个重要因素:1.弹片数量(n):碟形弹簧的弹片数量决定了碟形弹簧的负荷能力和变形能力。
适当选择弹片数量,可以有效平衡负荷和变形需求。
2.弹片宽度(t):碟形弹簧的弹片宽度和厚度对弹簧的刚度和变形特性有重要影响。
较小的弹片宽度可以增加碟形弹簧的变形能力,但会导致刚度降低。
3.材料选择:碟形弹簧的材料选择应根据具体要求和负荷条件来确定。
一般常用的材料有合金钢、不锈钢等。
材料的选择直接影响碟形弹簧的弹性模量和刚度。
4.碟形弹簧的工作环境和使用条件也需要考虑,如温度、湿度、腐蚀等因素对材料和结构性能的影响。
碟簧计算

碟簧的设计计算(机械设计手册3)
P……单个碟簧的载荷(N)
P C……压平时的碟形弹簧载荷计算值(N)
τ……碟簧厚度(mm)
D……碟簧弹簧外径(mm)
d……碟簧弹簧内径(mm)
f……弹片碟形弹簧的变形量(mm)
h o……碟形弹簧压平时变形量的计算(mm)
E……弹性模量(Mpa)
μ……泊松比,取0.3
K 1 K 4---计算系数
注:C=D/d
弹簧外径
弹簧内径系数C K1 系数2414 1.7142857140.618453
f≠ho K1 系数K4 系数
E弹性模量(Mpa)μ泊松比t碟簧厚度(mm)f弹片弹簧变形量(mm)0.61845286212060000.30.90.45f=ho时即最大载荷
K1 系数K4 系数
E弹性模量(Mpa)μ泊松比t碟簧厚度(mm)h0压平时变形量(mm)0.6184528621
2060000.30.90.6
浮动球阀的预紧力阀座密封外圈阀座密封内圈最小预紧比压
预紧力24190.6101.265
p为在变形f下的力
h0压平时变形量(mm)P弹簧载荷(N)
0.6898.375851 P弹簧载荷(N)
1000.64037。
碟簧计算方法(可编辑修改word版)

一.碟簧基本理论叠合组合蝶簧组:不带支撑面的碟簧 带支撑面的碟簧n 片碟簧叠合后自由状态下的高度: 不带支撑面的蝶簧L 0 = l 0 + (n ‒ 1) ∙ tn 片碟簧叠合后变形量与载荷的关系:变形量s tot = s对合组合蝶簧组:i 片碟簧对合后自由状态下的高度:L 0 = i ∙ l 0i 片碟簧对合后变形量与载荷的关系:变形量:s tot = i ∙ s 二.例带支撑面的蝶簧L 0 = l 0 + (n ‒ 1) ∙ t ' 载荷F tot = n ∙ F 载荷F tot = F主轴拉爪有三个位置,分别是拉刀位置(中间位置)、松刀位置(最靠主轴端部)和无刀位置(最靠主轴内部),HMS200 主轴刀柄形式为 BT50,设计拉刀力为 25000N ,拉刀位置与松刀位置间的最小距离(即打刀距离)为 5.6mm 。
根据可用安装空间、拉刀力等因素选择碟形弹簧型号 180079,两两叠合再对合的组合形式。
两片 180079 碟簧叠合自由状态下L 叠 = l 0 + (n ‒ 1) ∙ t‘ = 5.8 + 3.75 = 9.55变形量s 叠 = s 时,回复力F 叠 = 2F为不致打刀力过大(小于 30000N ),采用 50 对两两叠合的碟簧对合,自由状态下L 对 = i ∙ L 叠 = 50 × 9.55=477.5变形量s 对 = i ∙ s 叠 = 50s 时,回复力F 对 = F 叠 = 2F所以要想得到 25000N 的拉刀力,一片弹簧的回复力应为 F=12500,对应的变形量为 s=0.633 总变形量为s 对 = 50 × s = 50 × 0.633 = 31.65,变形后碟簧组的总高度为 477.5-31.65=445.85。
最小打刀距离为 5.6,设计打刀距离为 6,松刀位置碟簧组总变形量为 31.65+6=37.65,每片碟簧变形量为37.65/50=0.753,每片碟簧回复力为 14576N ,理论所需打刀力2 × 14576 = 29152N ;无刀状态碟簧组总变形量为 31.65-10=21.65,每片碟簧变形量为 21.65/50=0.433,每片碟簧回复力为 8847N ,所以弹簧安装时需预压 21.65,预压力为 8847 × 2=17694N ,预压后碟簧高度为 477.5-21.65=455.85。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.碟簧基本理论 De Di
l 0De Di t
t
's
不带支撑面的碟簧带支撑面的碟簧
叠合组合蝶簧组:
n 片碟簧叠合后自由状态下的高度:
不带支撑面的蝶簧 带支撑面的蝶簧
n 片碟簧叠合后变形量与载荷的关系:
变形量 载荷
对合组合蝶簧组:
i 片碟簧对合后自由状态下的高度:
i 片碟簧对合后变形量与载荷的关系:
变形量: 载荷 二.例
主轴拉爪有三个位置,分别是拉刀位置(中间位置)、松刀位置(最靠主轴端部)和无刀位置(最靠主轴内部),HMS200主轴刀柄形式为BT50,设计拉刀力为25000N ,拉刀位置与松刀位置间的最小距离(即打刀距离)为5.6mm 。
根据可用安装空间、拉刀力等因素选择碟形弹簧型号180079,两两叠合再对合的组合形式。
两片180079碟簧叠合自由状态下
变形量时,回复力
为不致打刀力过大(小于30000N ),采用50对两两叠合的碟簧对合,自由状态下
=477.5
变形量时,回复力
所以要想得到25000N 的拉刀力,一片弹簧的回复力应为F=12500,对应的变形量为s=0.633
总变形量为,变形后碟簧组的总高度为477.5-31.65=445.85。
最小打刀距离为5.6,设计打刀距离为6,松刀位置碟簧组总变形量为31.65+6=37.65,每片碟簧变形量为37.65/50=0.753,每片碟簧回复力为14576N ,理论所需打刀力
;无刀状态碟簧组总变
形量为31.65-10=21.65,每片碟簧变形量为21.65/50=0.433,每片碟簧回复力为8847N,所以弹簧安装时需预压21.65,预压力为88472=17694N,预压后碟簧高度为477.5-21.65=455.85。
一串碟簧之间最好放一个自制垫片,这个自制垫片的作用一个是凑距离,可以节省碟簧的个数;另一个就是可以让它和拉刀杆小间隙配合把大串碟簧隔开,减小大串碟簧的离心力;还有就是这个自制垫片外径可以做大一点,在主轴内起导向作用,避免碟簧和主轴的摩擦。
也可以用MUBEA提供的专门计算程序进行计算,非常方便。
