七年级数学全册单元测试卷测试卷(解析版)
七年级上册数学全册单元试卷综合测试卷(word含答案)
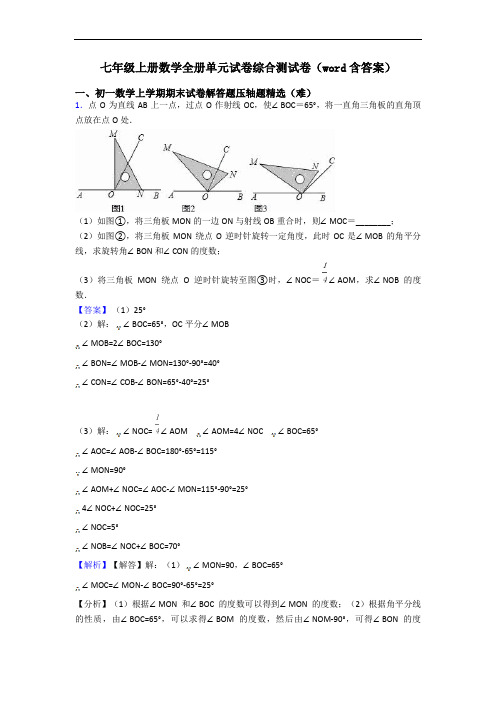
七年级上册数学全册单元试卷综合测试卷(word含答案)一、初一数学上学期期末试卷解答题压轴题精选(难)1.点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC=________;(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=∠AOM,求∠NOB的度数.【答案】(1)25°(2)解:∠BOC=65°,OC平分∠MOB∠MOB=2∠BOC=130°∠BON=∠MOB-∠MON=130°-90°=40°∠CON=∠COB-∠BON=65°-40°=25°(3)解:∠NOC= ∠AOM ∠AOM=4∠NOC ∠BOC=65°∠AOC=∠AOB-∠BOC=180°-65°=115°∠MON=90°∠AOM+∠NOC=∠AOC-∠MON=115°-90°=25°4∠NOC+∠NOC=25°∠NOC=5°∠NOB=∠NOC+∠BOC=70°【解析】【解答】解:(1)∠MON=90,∠BOC=65°∠MOC=∠MON-∠BOC=90°-65°=25°【分析】(1)根据∠MON和∠BOC的度数可以得到∠MON的度数;(2)根据角平分线的性质,由∠BOC=65°,可以求得∠BOM的度数,然后由∠NOM-90°,可得∠BON的度数,从而得解;(3)由∠BOC=65°,∠NOM=90°,∠NOC= ∠AOM,从而可求得∠NOC的度数,然后由∠BOC=65°,从而得解.2.如图,直线AB、CD相交于点O,已知,OE把分成两个角,且::3(1)求的度数;(2)过点O作射线,求的度数.【答案】(1)解:,,::3,;(2)解:,,,OF在的内部时,,,,OF在的内部时,,,,综上所述或【解析】【分析】(1)根据对顶角相等得出,然后根据::3 即可算出∠BOE的度数;(2)根据角的和差,由算出∠DOE的度数,根据垂直的定义得出∠EOF=90°;当OF在的内部时,根据,算出答案;OF在的内部时,根据,算出但,综上所述即可得出答案。
沪科版数学七年级下册全册单元测试卷含答案

沪科版数学七年级下册全册单元测试卷含答案第六章实数(2)一、选择题(每小题3分,共30分)1.下列各式中无意义的是()A.B.C.D.2.在下列说法中: 10的平方根是±; -2是4的一个平方根; 的平方根是;④0.01的算术平方根是0.1;⑤,其中正确的有()A.1个B.2个C.3个D.4个2.下列说法中正确的是()A.立方根是它本身的数只有1和0B.算数平方根是它本身的数只有1和0C.平方根是它本身的数只有1和0D.绝对值是它本身的数只有1和04.的立方根是()A.B.C.D.5.现有四个无理数,,,,其中在实数+1与+1之间的有()A.1个B.2个C.3个D.4个6.实数,-2,-3的大小关系是()A.B.C.D.7.已知=1.147,=2.472,=0.5325,则的值是()A.24.72B.53.25C.11.47D.114.78.若,则的大小关系是()A.B.C.D.9.已知是169的平方根,且,则的值是()A.11B.±11C.±15D.65或10.大于且小于的整数有()A.9个B.8个C.7个D.5个二、填空题(每小题3分,共30分)11.绝对值是,的相反数是.12.的平方根是,的平方根是,-343的立方根是,的平方根是.13.比较大小:(1);(2);(3);(4)2..14.当时,有意义。
15.已知=0,则=.16.最大的负整数是,最小的正整数是,绝对值最小的实数是,不超过的最大整数是.17.已知且,则的值为。
18.已知一个正数的两个平方根是和,则=,=.19.设是大于1的实数,若在数轴上对应的点分别记作A、B、C,则A、B、C三点在数轴上从左至右的顺序是.20.若无理数满足1,请写出两个符合条件的无理数.三、解答题(共40分)21.(8分)计算:(1);(2);(3);(4);22.(12分)求下列各式中的的值:(1);(2);(3);(4);23.(6分)已知实数、、在数轴上的对应点如图所示,化简:24.(7分)若、、是有理数,且满足等式,试计算的值。
七年级数学上册 全册单元测试卷检测题(WORD版含答案)

七年级数学上册全册单元测试卷检测题(WORD版含答案)一、初一数学上学期期末试卷解答题压轴题精选(难)1.定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角.如图1,若∠COD= ∠AOB,则∠COD是∠AOB的内半角.(1)如图1,已知∠AOB=70°,∠AOC=25°,∠COD是∠AOB的内半角,则∠BOD=________.(2)如图2,已知∠AOB=60°,将∠AOB绕点O按顺时针方向旋转一个角度口(0<a<60°)至∠COD,当旋转的角度a为何值时,∠COB是∠AOD的内半角.(3)已知∠AOB=30°,把一块含有30°角的三角板如图3叠放,将三角板绕顶点O以3度/秒的速度按顺时针方向旋转(如图4),问:在旋转一周的过程中,射线OA,OB,OC,OD 能否构成内半角,若能,请求出旋转的时间;若不能,请说明理由.【答案】(1)10°(2)解:∵∠AOB绕点O按顺时针方向旋转一个角度口(0<a<60°)至∠COD,∴∠AOB=∠COD=60°∴∠AOC=∠BOD=a∴a+∠COB=60°∵∠COB是∠AOD的内半角∴∠COB=∠AOD∴2∠COB=∠COB+2a∴∠COB=2a∴a+2a=60°解之:a=20°即当旋转的角度a为20°时,∠COB是∠AOD的内半角。
(3)解:在旋转一周的过程中,射线OA,OB,OC,OD能否构成内半角,理由:设按顺时针方向旋转一个角度α,旋转的时间为t如图1∵∠BOC是∠AOD的内半角,∠AOC=∠BOD=α∴∠AOD=30°+α,∠BOC=∠AOD=30°-α∴(30°+α)=30°-α解之:α=10°∴t=s;如图2∵∠BOC是∠AOD的内半角,∠AOC=∠BOD=α∴∠AOD=30°+α,∠BOC=∠AOD=α-30°∴(30°+α)=α-30°解之:α=90°∴t==30s;如图3∵∠AOD是∠BOC的内半角,∠AOC=∠BOD=360°-α∴∠BOC=360°+30°-α,∠AOD=∠BOC=360°-α-30°∴(360°+30°-α)=360°-α-30°解之:α=330°∴t==110s;如图4∵∠AOD是∠BOC的内半角,∠AOC=∠BOD=360°-α∴∠BOC=360°+30°-α,∴(360°+30°-α)=30°+30°-(360°+30°-α)解之:α=350°∴t=s;综上所述,当旋转的时间为s或30s或110s或s时,射线OA,OB,OC,OD能构成内半角。
人教版七年级数学上册单元测试题全套含答案

输入 x ―→ ×(-3) ―→ -2 ―→ 输出 16.太阳的半径为 696000 千米,用科学记数法表示为________千米;把 210400 精确到万位是________. 17.已知(a-3)2 与|b-1|互为相反数,则式子 a2+b2 的值为________. 18.填在下面各正方形中的四个数之间都有一定的规律,据此规律得出 a+b+c=________.
-1 A.3 个 B.4 个 C.5 个 D.6 个 7.将一把刻度尺按如图所示放在数轴上(数轴的单位长度是 1cm),刻度尺上的“0cm”和“8cm”分别对应 数轴上的-3.6 和 x,则 x 的值为( )
A.4.2 B.4.3 C.4.4 D.4.5 8.有理数 a,b 在数轴上的位置如图所示,下列各式成立的是( )
A.b>0 B.|a|>-b C.a+b>0 D.ab<0 9.若|a|=5,b=-3,则 a-b 的值为( ) A.2 或 8 B.-2 或 8 C.2 或-8 D.-2 或-8
10.观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…用你所发
5
3
___________________.
13.绝对值大于 4 而小于 7 的所有整数之和是________.
14.点 A,B 表示数轴上互为相反数的两个数,且点 A 向左平移 8 个单位到达点 B,则这两点所表示
的数分别是________和________.
15.如图是一个简单的数值运算程序.当输入 x 的值为-1 时,则输出的数值为________.
现的规律得出 22016 的末位数字是( )
A.2 B.4 C.6 D.8
二、填空题(每小题 3 分,共 24 分)
新人教版七年级数学上册第一单元测试卷(含答案)

新人教版七年级数学上册单元测试卷第一单元:有理数一、选择题(本题共10小题,每小题3分,共30分)1.如果水库的水位高于正常水位2m时,记作+2m,那么低于正常水位3m时,应记作()A.+3mB.-3mC.+13D.-132. 室内温度是150℃,室外温度是-30℃,则室外温度比室内温度低( )A .120℃ B.180℃ C.-120℃ D.-180℃3. 一个数和它的倒数相等,则这个数是()A.1B.-1C.±1 D.±1和04. 若|a|=5,b=-3,则a-b的值是()A.2或8B.-2或8C.2或-8D.-2或-85. 下列四组有理数的大小比较正确的是()A.−12>−13B.-|-1|>-|+1|C.12<13D.|−12|>|−13|6. 若三个有理数的和为0,则下列结论正确的是()A.这三个数都是0B.最少有两个数是负数C.最多有两个正数D.这三个数是互为相反数7. 下列各式中正确的是()A.a2=.(−a)2B. a3=.(−a)3C.−a2=.|−a2|D. a3=.|a|38. 若x的相反数是3,│y│=5,则x+y的值为()A.-8B.2C.-8或2D.8或-29. 两个数的差是负数,则这两个数一定是( )A.被减数是正数,减数是负数B.被减数是负数,减数是正数C.被减数是负数,减数也是负数D.被减数比减数小10. 点A在数轴上表示+2,从点A沿数轴向左平移3个单位到点B,点B表示的数是( )A. 3B.-1C.5D.-1或3二、填空题(本题共6小题,每小题3分,共18分)11. 甲潜水员所在高度为-45米,乙潜水员在甲的上方15米处,则乙潜水员的所在的高度是__________.12. 大肠杆菌每过20分便由1个分裂成2个,经过3小时后这种大肠杆菌由1个分裂成__________个。
13. 在数轴上,与表示数-1的点的距离是5的点表示的数是。
鲁教版五四制七年级上册数学全册各个单元测试卷(及答案)

鲁教版五四制七年级上册数学全册试卷(五套单元试卷+一套期末测试卷)第一章测试卷一、选择题(每题3分,共30分)1.若三角形的两个内角的和是85°,那么这个三角形是()A.钝角三角形B.直角三角形C.锐角三角形D.不能确定2.如图,AE⊥BC于点E,BF⊥AC于点F,CD⊥AB于点D,则△ABC中AC 边上的高是线段()A.AE B.CD C.BF D.AF3.如图,△ABC≌△EDF,AF=20,EC=8,则AE等于()A.6B.8C.10D.124.下列各条件中,能作出唯一的△ABC的是()A.AB=4,BC=5,AC=10B.AB=5,BC=4,∠A=30°C.∠A=90°,AB=10D.∠A=60°,∠B=50°,AB=55.如图,AB∥ED,CD=BF,若要说明△ABC≌△EDF,则还需要补充的条件可以是()A.AC=EF B.AB=ED C.∠B=∠E D.不用补充6.如图,在△ABC中,∠ABC,∠ACB的平分线分别为BE,CD,BE与CD相交于点F,∠A=60°,则∠BFC等于()A.118°B.119°C.120°D.121°7.如果某三角形的两边长分别为5和7,第三边的长为偶数,那么这个三角形的周长可以是()A.14B.17C.22D.268.如图,下列四个条件:①BC=B′C;②AC=A′C;③∠A′CA=∠B′CB;④AB =A′B′.从中任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是()A.1B.2C.3D.49.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC ,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF等于()A.1B.2C.3D.410.如图,△ABC 的三个顶点和它内部的点P 1,把△ABC 分成3个互不重叠的小三角形;△ABC 的三个顶点和它内部的点P 1,P 2,把△ABC 分成5个互不重叠的小三角形;△ABC 的三个顶点和它内部的点P 1,P 2,P 3,把△ABC 分成7个互不重叠的小三角形;△ABC 的三个顶点和它内部的点P 1,P 2,P 3,…,P n ,把△ABC 分成()个互不重叠的小三角形.A .2nB .2n +1C .2n -1D .2(n +1)二、填空题(每题3分,共24分)11.一个三角形的其中两个内角为88°,32°,则这个三角形的第三个内角的度数为________.12.要测量河两岸相对的两点A ,B 间的距离(AB 垂直于河岸BF ),先在BF 上取两点C ,D ,使CD =CB ,再作出BF 的垂线DE ,且使A ,C ,E 三点在同一条直线上,如图,可以得到△EDC ≌△ABC ,所以ED =AB .因此测得ED 的长就是AB 的长.判定△EDC ≌△ABC 的理由是____________.13.如图,E 点为△ABC 的边AC 的中点,∥AB ,若MB =6 cm ,=4 cm ,则AB=________.14.用直尺和圆规作一个角等于已知角,如图所示,则要说明∠A′O′B′=∠AOB,需要说明△C′O′D′≌△COD,则这两个三角形全等的依据是____________(写出全等的简写).15.已知△ABC的三边长分别为a,b,c,若a=3,b=4,则c的取值范围是____________;已知四边形EFMN的四边长分别为e,f,m,n,若e=3,f =4,n=10,则m的取值范围是____________.16.如图,在△ABC中,AD是BC边上的高,BE是AC边上的高,且AD,BE 交于点F,若BF=AC,CD=3,BD=8,则线段AF的长度为________.17.如图是由相同的小正方形组成的网格,点A,B,C均在格点上,连接AB,AC,则∠1+∠2=________.1(AB 18.如图,已知四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,且AE=2+AD),若∠D=115°,则∠B=________.三、解答题(19题7分,20,21题每题8分,25题13分,其余每题10分,共66分)19.如图,在△ABC中,AD是角平分线,∠B=54°,∠C=76°.(1)求∠ADB和∠ADC的度数;(2)若DE⊥AC,求∠EDC的度数.20.如图,已知线段m,n,如果以线段m,n分别为等腰三角形的底或腰作三角形,能作出几个等腰三角形?请作出.不写作法,保留作图痕迹.21.如图,在△ABC中,AB=AC,D在AC的延长线上,试说明:BD-BC<AD -AB.22.如图,是一座大楼相邻的两面墙,现需测量外墙根部两点A,B之间的距离(人不能进入墙内测量).请你按以下要求设计一个方案测量A,B的距离.(1)画出测量图案;(2)写出简要的方案步骤;(3)说明理由.23.如图,已知△ABC≌△ADE,AB与ED交于点M,BC与ED,AD分别交于点F,N.请写出图中两对全等三角形(△ABC≌△ADE除外),并选择其中的一对加以说明.24.如图,在R t△ABC中,∠ACB=90°,BC=2 cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5 cm,求线段AE的长.25.已知点P是R t△ABC斜边AB上一动点(不与点A,B重合),分别过点A,B 向直线CP作垂线,垂足分别为点E,F,点Q为斜边AB的中点.(1)如图①,当点P与点Q重合时,AE与BF的位置关系是________,QE与QF的数量关系是________;(2)如图②,当点P在线段AB上且不与点Q重合时,试判断QE与QF的数量关系,并说明理由.(温馨提示:直角三角形斜边上的中线等于斜边的一半)答案一、1.A2.C :因为BF ⊥AC 于点F ,所以△ABC 中AC 边上的高是线段BF ,故选C.3.A :因为△ABC ≌△EDF ,所以AC =EF .所以AE =CF .因为AF =20,EC =8,所以AE =CF =6.故选A.4.D5.B :由已知条件AB ∥ED 可得,∠B =∠D ,由CD =BF 可得,BC =DF ,再补充条件AB =ED ,可得△ABC ≌△EDF ,故选B.6.C 7.C 8.B119.B :易得S △ABE =3×12=4,S △ABD =2×12=6,所以S △ADF -S △BEF =S △ABD -S △ABE =2.10.B :△ABC 的三个顶点和它内部的点P 1,把△ABC 分成的互不重叠的小三角形的个数=3+2×0;△ABC 的三个顶点和它内部的点P 1,P 2,把△ABC 分成的互不重叠的小三角形的个数=3+2×1;△ABC 的三个顶点和它内部的点P 1,P 2,P 3,把△ABC 分成的互不重叠的小三角形的个数=3+2×2,所以△ABC的三个顶点和它内部的点P 1,P 2,P 3,…,P n ,把△ABC 分成的互不重叠的小三角形的个数=3+2(n -1)=2n +1.二、11.60°12.ASA :由题意可知,∠ECD =∠ACB ,∠EDC =∠ABC =90°,CD =CB ,故可用ASA 说明两个三角形全等.13.10 cm :由∥AB ,点E 为AC 的中点,可得∠EAM =∠E ,AE =CE .又因为∠AEM =∠CEN ,所以△AEM ≌△CEN .所以AM ==4 cm.所以AB =AM +MB =4+6=10(cm).14.SSS15.1<c <7;3<m <17:由三角形的三边关系得第三边的取值范围为4-3<c <4+3,即1<c <7.同理,得四边形EFMN 对角线EM 的取值范围为4-3<EM <4+3,即1<EM <7.所以10-7<m <10+7,即3<m <17.16.5:由已知可得,∠ADC =∠BDF =∠BEC =90°,所以∠DAC =∠DBF .又因为AC =BF ,所以△ADC ≌△BDF .所以AD =BD =8,DF =DC =3.所以AF =AD -DF =8-3=5.17.90°:如图,由题意可知,∠ADC =∠E =90°,AD =BE ,CD =AE ,所以△ADC ≌△BEA .所以∠CAD =∠2.所以∠1+∠2=∠1+∠CAD =90°.18.65°:过点C 作CF ⊥AD ,交AD 的延长线于点F .因为AC 平分∠BAD ,所以∠CAF =∠CAE .又因为CF ⊥AF ,CE ⊥AB ,所以∠AFC =∠AEC =90°.在⎧∠AFC =∠AEC ,△CAF 和△CAE 中,⎨∠CAF =∠CAE ,⎩AC =AC ,1所以△CAF ≌△CAE (AAS).所以FC =EC ,AF =AE .又因为AE =2(AB +AD ),1所以AF =2(AE +EB +AD ),即AF =BE +AD .又因为AF =AD +DF ,所以DF⎧CF =CE ,=BE .在△FDC 和△EBC 中,所⎨∠CFD =∠CEB ,所以△FDC ≌△EBC (SAS).⎩DF =BE ,以∠FDC =∠EBC .又因为∠ADC =115°,所以∠FDC =180°-115°=65°.所以∠B =65°.三、19.解:(1)因为∠B =54°,∠C =76°,所以∠BAC =180°-54°-76°=50°.因为AD 平分∠BAC ,所以∠BAD =∠CAD =25°.所以∠ADB =180°-54°-25°=101°.所以∠ADC =180°-101°=79°.(2)因为DE ⊥AC ,所以∠DEC =90°.所以∠EDC =180°-90°-76°=14°.20.解:能作出两个等腰三角形,如图所示.21.解:因为AB =AC ,所以AD -AB =AD -AC =CD .因为BD -BC <CD ,所以BD -BC <AD -AB .22.解:(1)如图所示.(2)延长BO 至D ,使DO =BO ,连接AD ,则AD 的长即为A ,B 间的距离.(3)因为AO =AO ,∠AOB =∠AOD =90°,BO =DO ,所以△AOB ≌△AOD .所以AD =AB .23.解:△AEM ≌△A ,△BMF ≌△DNF ,△ABN ≌△ADM .(任写其中两对即可)选择△AEM ≌△A :因为△ABC ≌△ADE ,所以AC =AE ,∠C =∠E ,∠CAB⎧∠E =∠C ,=∠EAD .所以∠EAM =∠CAN .在△AEM 和△A 中,⎨AE =AC ,所以⎩∠EAM =∠CAN ,△AEM ≌△A (ASA).选择△ABN ≌△ADM :因为△ABC ≌△ADE ,所以AB =AD ,∠B =∠D .又因为∠BAN =∠DAM ,所以△ABN ≌△ADM (ASA).选择△BMF ≌△DNF :因为△ABC ≌△ADE ,所以AB =AD ,∠B =∠D .又因为∠BAN =∠DAM ,所以△ABN ≌△ADM (ASA).所以AN =AM .所以BM =DN .又因为∠B =∠D ,∠BFM =∠DFN ,所以△BMF ≌△DNF (AAS).(任选一对进行说明即可)24.解:因为∠ACB =90°,所以∠ECF +∠BCD =90°.因为CD ⊥AB ,所以∠BCD +∠B =90°.所以∠ECF =∠B .在△ABC和△FCE中,∠B=∠ECF,BC=CE,∠ACB=∠FEC=90°,所以△ABC≌△FCE(ASA).所以AC=FE.因为EC=BC=2 cm,EF=5 cm,所以AE=AC-CE=FE-BC=5-2=3(cm).25.解:(1)AE∥BF;QE=QF(2)QE=QF.理由:如图,延长EQ交BF于点D,由题意易得AE∥BF,所以∠AEQ=∠BDQ.在△AEQ和△BDQ中,∠AQE=∠BQD,∠AEQ=∠BDQ,AQ=BQ,所以△AEQ≌△BDQ.所以EQ=DQ.因为∠DFE=90°,所以QE=QF.第二章测试卷一、选择题(每题3分,共30分)1.下面所给的图中是轴对称图形的是()2.如图,△ABC和△ADE关于直线l对称,下列结论:①△ABC≌△ADE;②l 垂直平分DB;③∠C=∠E;④BC与DE的延长线的交点一定落在直线l上.其中错误的有()A.0个B.1个C.2个D.3个3.下列说法正确的是()A.等腰三角形的一个角的平分线是它的对称轴B.有一个内角是60°的三角形是轴对称图形C.等腰直角三角形是轴对称图形,它的对称轴是斜边上的中线所在的直线D.等腰三角形有3条对称轴4.如图是小明在平面镜里看到的电子钟示数,这时的实际时间是() A.12:01B.10:51C.10:21D.15:105.如图,在△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为()A.48°B.36°C.30°D.24°6.如图,A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在()A.AC,BC两边高的交点处B.AC,BC两边中线的交点处C.AC,BC两边垂直平分线的交点处D.∠A,∠B两内角平分线的交点处7.如图,将正方形纸片三次对折后,沿图中AB线剪掉一个等腰直角三角形,展开铺平得到的图形是()8.如图,已知:AB-AC=2 cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长为14 cm,则AC的长是()A.6B.7C.8D.99.如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处,若∠B=65°,则∠BDF等于()A.65°B.50°C.60°D.57.5°10.如图,已知AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED 的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE =DF;②DB=DC;③AD⊥BC;④AC=3BF.其中正确的结论共有()A.4个B.3个C.2个D.1个二、填空题(每题3分,共24分)11.有些字母是轴对称图形,在E,H,I,M,N这5个字母中,是轴对称图形的是__________.12.我国传统的木结构房屋,窗子常用各种图案装饰,如图是一种常见的图案,这种图案有________条对称轴.13.如图是一个经过改造的台球桌面示意图(该图由相同的小正方形组成),图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入________号球袋.14.等腰三角形一腰上的高与底边所夹的角为∠α,则这个等腰三角形的顶角为________.15.如图,在△ABC中,AB=AC,AD⊥BC于点D,点E,F为AD上的两点,若△ABC的面积为12,则图中阴影部分的面积是________.16.如图,在直角三角形ABC中,∠B=90°,AD平分∠BAC,交边BC于点D,如果BD=2,AC=6,那么△ADC的面积等于________.17.如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O 恰好重合,则∠OEC=________.18.小威在计算时发现:11×11=121,111×111=12 321,1 111×1 111=1 234 321,…,他从中发现了一个规律.请根据他所发现的规律很快地写出111 111 111×111 111 111=________________________________________________________.三、解答题(19题8分,20~21题每题10分,24题14分,其余每题12分,共66分)19.如图,在正方形网格上有一个△ABC.(1)画△ABC关于直线MN的对称图形(不写画法);(2)若网格上的每个小正方形的边长为1,求△ABC的面积.20.两个城镇A,B与两条公路l1,l2的位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中用尺规作图找出所有符合条件的点C(不写已知、求法、作法,只保留作图痕迹).21.如图,在等边三角形ABC中,∠ABC,∠ACB的平分线相交于点O,作BO,CO的垂直平分线分别交BC于点E和点F.小明说:“E,F是BC的三等分点.”你同意他的说法吗?请说明理由.22.如图,在△ABC中,AB=AC,AD⊥BC于点D,CE⊥AB于点E,AE=CE.试说明:(1)△AEF≌△CEB;(2)∠ABF=2∠FBD.23.操作与探究.(1)如图,分别画出①中“”和“”关于直线l的对称图形(画出示意图即可);(2)如图,②中小冬和小亮上衣上印的字母分别是什么?(3)把字母“”和“”写在薄纸上,观察纸的背面,写出你看到的字母背影;(4)小明站在三个学生的身后,这三个学生正向前方某人用手势示意一个三位数,从小明站的地方看(如图③所示),这个三位数是235.请你判断出他们示意的真实三位数是多少?24.如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(不与点B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.(1)当∠BDA=115°时,∠BAD=________°,∠DEC=________°,点D从B向C运动时,∠BDA逐渐变________(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE?请说明理由;(3)在点D的运动过程中,是否存在△ADE是等腰三角形的情形?若存在,请直接写出此时∠BDA的度数;若不存在,请说明理由.答案一、1.A 2.A 3.C 4.B 5.A 6.C 7.A 8.A9.B :因为△DEF 是由△DEA 沿直线DE 翻折变换而来,所以AD =FD .因为D是AB 边的中点,所以AD =BD .所以BD =FD .所以∠B =∠BFD .因为∠B =65°,所以∠BDF =180°-∠B -∠BFD =180°-65°-65°=50°.故选B.10.A :因为BF ∥AC ,所以∠C =∠CBF .因为BC 平分∠ABF ,所以∠ABC =∠CBF .所以∠C =∠ABC .所以AB =AC .因为AD 是△ABC 的角平分线,所以⎧∠C =∠DBF ,BD =CD ,AD ⊥BC .故②③正确.在△CDE 与△BDF 中,⎨CD =BD ,⎩∠CDE =∠BDF ,所以△CDE ≌△BDF .所以DE =DF ,CE =BF .故①正确;因为AE =2BF ,所以AC =3BF .故④正确.故选A.二、11.E ,H ,I ,M12.213.1:如图,该球最后将落入1号球袋.14.2∠α15.6:因为AB =AC ,AD ⊥BC ,所以△ABC 关于直线AD 对称.所以S △BEF1=S △CEF .因为△ABC 的面积为12,所以图中阴影部分的面积=2S △ABC =6.16.6:过点D 作DE ⊥AC 于点E ,因为AD 平分∠BAC ,所以DE =BD =2.11所以S △ADC =2AC ·DE =2×6×2=6.17.108°18.12 345 678 987 654 321三、19.解:(1)如图,利用图中格点,可以直接确定出△ABC 中各顶点的对称点的位置,从而得到△ABC 关于直线MN 的对称图形,即为△A ′B ′C ′.111(2)S △ABC =4×6-2×4×1-2×3×6-2×2×4=9.20.解:如图.点C 1,C 2即为所求作的点.21.解:同意.理由如下:如图,连接OE ,OF .由题意知,BE =OE ,CF =OF ,∠OBC =∠OCB =30°,所以∠BOE =∠OBC =30°,∠COF =∠OCB =30°,∠BOC =120°.所以∠EOF =60°,∠OEF =60°,∠OFE =60°.所以△OEF 是等边三角形.所以OE =OF =EF =BE =CF .所以E ,F 是BC 的三等分点.22.解:(1)因为AD⊥BC,CE⊥AB,所以∠AEF=∠CEB=90°,∠AFE+∠EAF=90°,∠CFD+∠ECB=90°.又因为∠AFE=∠CFD,所以∠EAF=∠ECB.在△AEF和△CEB中,∠AEF=∠CEB,AE=CE,∠EAF=∠ECB,所以△AEF≌△CEB(ASA).(2)由△AEF≌△CEB,得EF=EB,所以∠EBF=∠EFB.在△ABC中,AB=AC,AD⊥BC,所以BD=CD.所以FB=FC.所以∠FBD=∠FCD.因为∠EFB=180°-∠BFC=∠FBD+∠FCD=2∠FBD,所以∠EBF=2∠FBD,即∠ABF=2∠FBD.23.解:(1)图略.(2)“”和“”.(3)“”和“”.(4)他们示意的真实三位数是235.24.解:(1)25;115;小(2)当DC=2时,△ABD≌△DCE.理由如下:因为DC=2,AB=2,所以DC=AB.因为AB=AC,∠B=40°,所以∠C=∠B=40°.因为∠ADB=180°-∠ADC=∠DAC+∠C,∠DEC=180°-∠AED=∠DAC+∠ADE,且∠C=40°,∠ADE=40°,所以∠ADB=∠DEC.在△ABD与△DCE中,∠ADB=∠DEC,∠B=∠C,AB=DC,所以△ABD≌△DCE(AAS).(3)存在,∠BDA=110°或∠BDA=80°.第三章测试卷一、选择题(每题3分,共30分)1.下列各组数中,能够作为直角三角形的三边长的一组是() A.1,2,3B.2,3,4C.4,5,6D.3,4,52.在Rt△ABC中,∠C=90°,若角A,B,C所对的三边分别为a,b,c,且a =7,b=24,则c的长为()A.26B.18C.25D.213.如图,阴影部分是一个正方形,此正方形的面积是()A.16B.8C.4D.24.已知四个三角形分别满足下列条件:①一个内角等于另两个内角之和;②三个内角度数之比为3∶4∶5;③三边长分别为7,24,25;④三边长之比为5∶12∶13.其中直角三角形有()A.1个B.2个C.3个D.4个5.若△ABC的三边长分别为a,b,c,且满足(a-b)(a2+b2-c2)=0,则△ABC 是()A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形6.如图,直线l上有三个正方形a,b,c,若a,b的面积分别为5和13,则c 的面积为()A.4B.8C.12D.187.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线上的D′处.若AB=3,AD=4,则ED的长为()3 A. 2B.3C.14D.38.如图,在△ABC中,AD是BC边上的中线,AC=17,BC=16,AD=15,则△ABC的面积为()A.128B.136C.120D.2409.如图是台阶的示意图,已知每个台阶的宽度都是30 cm,每个台阶的高度都是15 cm,则A,B两点之间的距离等于()A.195 cm B.200 cm C.205cm D.210 cm10.如图是一个圆柱形的饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一根到达底部的直吸管在罐内部分的长度a(罐壁的厚度和小圆孔的大小忽略不计)的范围是()A.12≤a≤13B.12≤a≤15C.5≤a≤12D.5≤a≤13二、填空题(每题3分,共24分)11.在Rt△ABC中,a,b为直角边,c为斜边,若a2+b2=16,则c=________.12.如图,在△ABC中,AB=5 cm,BC=6 cm,BC边上的中线AD=4 cm,则∠ADB=________.13.如图,一架长为4 m的梯子,一端放在离墙脚2.4 m处,另一端靠墙,则梯子顶端离墙脚的距离是________.14.飞机在空中水平飞行,某一时刻刚好飞到一个男孩正上方4 000 m处,过了10 s,飞机距离这个男孩头顶5 000 m,则飞机平均每小时飞行__________.15.已知a,b,c是△ABC的三边长,且满足关系(c2-a2-b2)2+|a-b|=0,则△ABC 的形状为____________.16.在△ABC中,AB=13 cm,AC=20 cm,BC边上的高为12 cm,则△ABC的面积为________.17.如图,在一根长90 cm的灯管上缠满了彩色丝带,已知可近似地将灯管看作圆柱体,且底面周长为4 cm,彩色丝带均匀地缠绕了30圈,则彩色丝带的总长度为________.18.如图,在Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=5,BC=12,则AD的长为________.三、解答题(19~21题每题8分,22~24题每题10分,25题12分,共66分) 19.如图,在△ABC中,AD⊥BC于D,AD=12,BD=16,CD=5.(1)求△ABC的周长;(2)判断△ABC是否是直角三角形.20.如图,在△ADC中,AD=15,AC=12,DC=9,点B是CD延长线上一点,连接AB.若AB=20,求△ABD的面积.21.如图,∠ABC=90°,AB=6 cm,AD=24 cm,BC+CD=34 cm,C是直线l 上一动点,请你探索当点C离点B多远时,△ACD是一个以CD为斜边的直角三角形.22.若△ABC的三边长a,b,c满足a2+b2+c2+50=6a+8b+10c,判断△ABC 的形状.23.如图,在△ABC中,AB:BC:CA=3:4:5,且周长为36 cm,点P从点A 开始沿AB边向点B以1 cm/s的速度移动,点Q从点B开始沿BC边向点C 以2 cm/s的速度移动,如果同时出发,过3 s时,△BPQ的面积为多少?24.如图,圆柱形玻璃容器高19 cm,底面周长为60 cm,在外侧距下底1.5 cm 的点A处有一只蜘蛛,在蜘蛛正对面的圆柱形容器的外侧,距上底1.5 cm处的点B处有一只苍蝇,蜘蛛急于捕捉苍蝇充饥,请你帮蜘蛛计算它沿容器侧面爬行的最短距离.25.如图,甲是一个直角三角形ABC,它的两条直角边长分别为a,b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b的正方形内.(1)由图乙、图丙,可知①是以________为边长的正方形,②是以________为边长的正方形,③的四条边长都是________,且每个角都是直角,所以③是以________为边长的正方形;(2)图乙中①的面积为________,②的面积为________,图丙中③的面积为________;(3)图乙中①②面积之和为________;(4)图乙中①②的面积之和与图丙中③的面积有什么关系?为什么?由此你能得到关于直角三角形三边长的关系吗?答案一、1.D 2.C 3.B 4.C 5.D 6.B 7.A 8.C9.A 10.A 二、11.412.90°13.3.2 m 14.1 080 km 15.等腰直角三角形16916.126 cm 2或66 cm 217.150 cm 18.24三、19.解:(1)因为AD ⊥BC ,所以△ABD 和△ACD 均为直角三角形.所以AB 2=AD 2+BD 2,AC 2=AD 2+CD 2.又因为AD =12,BD =16,CD =5,所以AB =20,AC =13.所以△ABC 的周长为20+13+16+5=54.(2)由(1)知AB =20,AC =13,BC =21,因为AB 2+AC 2=202+132=569,BC 2=212=441,所以AB 2+AC 2≠BC 2.所以△ABC 不是直角三角形.20.解:在△ADC 中,因为AD =15,AC =12,DC =9,所以AC 2+DC 2=122+92=152=AD 2.所以△ADC 是直角三角形,且∠C =90°.在Rt △ABC 中,AC 2+1BC 2=AB 2,所以BC =16.所以BD =BC -DC =16-9=7.所以S △ABD =2×7×12=42.21.解:设当BC =x cm 时,△ACD 是一个以CD 为斜边的直角三角形.因为BC+CD =34 cm ,所以CD =(34-x )cm.因为∠ABC =90°,AB =6 cm ,所以在Rt △ABC 中,由勾股定理得AC 2=AB 2+BC 2=36+x 2.在Rt △ACD 中,AD =24 cm ,由勾股定理得AC 2=CD 2-AD 2=(34-x )2-576,所以36+x 2=(34-x )2-576.解得x =8.所以当点C 离点B 8 cm 时,△ACD 是一个以CD 为斜边的直角三角形.22.解:因为a 2+b 2+c 2+50=6a +8b +10c ,所以a 2+b 2+c 2-6a -8b -10c +50=0,即(a -3)2+(b -4)2+(c -5)2=0.所以a =3,b =4,c =5.因为32+42=52,即a 2+b 2=c 2,所以根据勾股定理的逆定理可判定△ABC 是直角三角形.:本题利用配方法,先求出a ,b ,c 的值,再利用勾股定理的逆定理进行判断.23.解:设AB 为3x cm ,则BC 为4x cm ,AC 为5x cm.因为△ABC 的周长为36 cm ,所以AB +BC +AC =36 cm ,即3x +4x +5x =36.解得x =3.所以AB =9 cm ,BC =12 cm ,AC =15 cm.因为AB 2+BC 2=AC 2,所以△ABC 是直角三角形,且∠B =90°.过3 s 时,BP =9-3×1=6(cm),BQ =2×3=6(cm),11所以S △BPQ =2BP ·BQ =2×6×6=18(cm 2).故过3 s 时,△BPQ 的面积为18 cm 2.24.解:如图,将圆柱侧面展开成长方形MNQP ,过点B 作BC ⊥MN 于点C ,连接AB ,则线段AB 的长度即为所求的最短距离.在Rt △ACB 中,AC =MN -AN -CM =16 cm ,BC 的长等于底面周长的一半,即BC =30 cm.由勾股定理得,AB 2=AC 2+BC 2=162+302=1 156=342,所以AB =34 cm.故蜘蛛沿容器侧面爬行的最短距离为34 cm.25.解:(1)a ;b ;c ;c (2)a 2;b 2;c 2(3)a 2+b 2(4)图乙中①②的面积之和与图丙中③的面积相等.由大正方形的边长为a +b ,得大正方形的面积为(a +b )2,图乙中把大正方形分成了四部分,分别是边长为a 的正方形,边长为b 的正方形,还有两个长为a ,宽为b 的长方形.根12据面积相等得(a +b )2=a 2+b 2+2ab .由图丙可得(a +b )2=c 2+4×ab .所以a +2b 2=c 2.能得到关于直角三角形三边长的关系:两直角边的平方和等于斜边的平方.第四章测试卷一、选择题(每题3分,共30分)1.9的算术平方根是()A.±3B.3 C.-3 D.3222.下列4个数:9,7,π,(3)0,其中无理数是()A.922B.7C.πD.(3)03.下列各式中正确的是()A.497=±14412B.-3273-8=-2C.-9=-33D.(-8)2=44.已知a+2+|b-1|=0,那么(a+b)2 018的值为()A.1B.-1C.32 018D.-32 0185.若平行四边形的一边长为2,面积为45,则此边上的高介于() A.3与4之间B.4与5之间C.5与6之间D.6与7之间6.设边长为a的正方形的面积为2.下列关于a的四种结论:①a是2的算术平方根;②a是无理数;③a可以用数轴上的一个点来表示;④0<a<1.其中正确的是()A.①②C.①②③B.①③D.②③④7.实数a,b在数轴上对应点的位置如图所示,则化简a2-|a+b|的结果为() A.2a+b B.-2a+b C.b D.2a-b8.有一个数值转换器,原理如图所示,当输入x为64时,输出y的值是()A.4C.33B.43D.29.一个正方体木块的体积是343 cm3,现将它锯成8块同样大小的小正方体木块,则每个小正方体木块的表面积是()74949147A.2cm2B.4cm2C.8cm2D.2cm210.如图,数轴上A,B两点表示的实数分别为1和3,若点A关于点B的对称点为点C,则点C所表示的实数为()A.23-1B.1+3C.2+3D.22+1二、填空题(每题3分,共24分)11.6的相反数是________;绝对值等于2的数是________.12.一个数的平方根与这个数的立方根相等,那么这个数是________.313.估算比较大小:(1)-10________-3.2;(2)130________5.314.若2x+7=3,(4x+3y)3=-8,则x+y=________.15.点A在数轴上和表示1的点相距6个单位长度,则点A表示的数为________.16.若两个连续整数x,y满足x<5+1<y,则x+y的值是________.17.若x,y为实数,且|x-2|+y+3=0,则(x+y)2 017的值为________.18.任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[3]=1.现对72第一次第二次第三次进行如下操作:72――→[72]=8――→[8]=2――→[2]=1,这样对72只需进行3次操作后变为1,类似地,对81只需进行________次操作后变为1;只需进行3次操作后变为1的所有正整数中,最大的是________.三、解答题(19题16分,20题12分,24、25题每题10分,其余每题6分,共66分)19.计算:(1)(-1)2 018+16-(3)-(-2)+(-2)--82;(4)2+|3-32|-(-5)2.20.求下列各式中未知数的值:(1)|a -2|=5;(2)4x 2=25;(3)(x -0.7)3=0.0272294;(2)132+0.5-8;43|a|-|a+b|+(c-a)2 21.已知a,b,c在数轴上对应点的位置如图所示,化简:+|b-c|.322.若实数a,b互为相反数,c,d互为倒数,求2(a+b)+8c d的值.23.已知a,b,c是△ABC的三边长,化简:(a+b+c)2-(b+c-a)2+(c-b-a)2.24.我们知道a+b=0时,a3+b3=0也成立,若将a看成a3的立方根,b看成b3的立方根,我们能否得出这样的结论:若两个数的立方根互为相反数,则这两个数也互为相反数.(1)试举一个例子来判断上述猜测结论是否成立;33(2)若1-2x与3x-5互为相反数,求1-x的值.25.全球气候变暖导致一些冰川融化并消失.在冰川消失12年后,一种低等植物苔藓就开始在岩石上生长.每一个苔藓都会长成近似圆形,苔藓的直径和冰川消失后经过的时间近似地满足如下的关系式:d=7×t-12(t≥12).其中d代表苔藓的直径,单位是厘米;t代表冰川消失后经过的时间,单位是年.(1)计算冰川消失16年后苔藓的直径;(2)如果测得一些苔藓的直径是35厘米,问冰川约是在多少年前消失的?答案一、1.B 2.C3.D :A 中正确.4.A 5.B6.C:∵a 2=2,a >0,∴a =2≈1.414,即a >1,故④错误.37.C 8.B :64的立方根是4,4的立方根是 4.9.D 10.A二、11.-6;±212.013.(1)>(2)>14.-115.1-6或1+6:数轴上到某个点距离为a (a >0)的点有两个,易忽略左边的点而漏解.注意运用数形结合思想,利用数轴帮助分析.16.7:∵2<5<3,∴3<5+1<4.∵x <5+1<y ,且x ,y 为两个连续整数,∴x =3,y =4.∴x +y =3+4=7.17.-1:∵|x -2|+y +3=0,∴|x -2|=0,y +3=0,∴x =2,y =-3.∴(x +y )2 017=[2+(-3)]2 017=(-1)2 017=-1.18.3;255三、19.解:(1)(-1)2 018+16-(2)937=1+4-42=2.3497273=;B 中--144128=2;C 中-9无算术平方根;只有D1132+0.5-8=42+0.5-2=-1.3(3)-(-2)2+(-2)2--82=-4+2-(-4)=2.(4)2+|3-32|-(-5)2=2+(32-3)-5=2+32-3-5=32-6.20.解:(1)由|a -2|=5,得a -2=5或a -2=- 5.当a -2=5时,a =5+2;当a -2=-5时,a =-5+2.255(2)因为4x 2=25,所以x 2=4.所以x =±2.(3)因为(x -0.7)3=0.027,所以x -0.7=0.3.所以x =1.21.解:由数轴可知b <a <0<c ,所以a +b <0,c -a >0,b -c <0.所以原式=-a -[-(a +b )]+(c -a )+[-(b -c )]=-a +a +b +c -a -b +c =-a +2c .322.解:由已知得a +b =0,cd =1,所以原式=0+8=2.23.解:因为a ,b ,c 是△ABC 的三边长,所以a +b +c >0,b +c -a >0,c -b -a <0.所以原式=a +b +c -(b +c -a )+(a +b -c )=3a +b -c .24.解:(1)因为2+(-2)=0,而且23=8,(-2)3=-8,有8+(-8)=0,所以结论成立.所以“若两个数的立方根互为相反数,则这两个数也互为相反数”是成立的.(2)由(1)验证的结果知,1-2x +3x -5=0,所以x =4,所以1-x =1-2=-1.25.解:(1)当t =16时,d =7×16-12=7×2=14(厘米).答:冰川消失16年后苔藓的直径为14厘米.(2)当d =35时,t -12=5,即t -12=25,解得t =37.答:如果测得一些苔藓的直径是35厘米,冰川约是在37年前消失的.第五章测试卷一、选择题(每题3分,共30分)1.点P(4,3)所在的象限是()A.第一象限B.第二象限 C.第三象限 D.第四象限2.根据下列表述,能确定位置的是()A.红星电影院2排C.北偏东30°B.北京市四环路D.东经118°,北纬40°3.如图,在直角坐标系中,卡片盖住的点的坐标可能是() A.(2,3)B.(-2,1)C.(-2,-2.5)D.(3,-2)4.点P(-2,3)关于x轴对称的点的坐标是()A.(-3,2)B.(2,-3)C.(-2,-3)D.(2,3)5.已知点A(-1,-4),B(-1,3),则()A.点A,B关于x轴对称B.点A,B关于y轴对称C.直线AB平行于y轴D.直线AB垂直于y轴6.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-2,-2),“马”位于点(1,-2),则“兵”位于点()A.(-1,1)B.(-2,-1)C.(-4,1)D.(1,2)7.如图,将长为3的长方形ABCD放在平面直角坐标系中,AD∥x轴,若点D 的坐标为(6,3),则点A的坐标为()A.(5,3)B.(4,3)C.(4,2)D.(3,3)8.在平面直角坐标系xOy中,若点A的坐标为(-3,3),点B的坐标为(2,0),则三角形ABO的面积是()A.15B.7.5C.6D.39.已知点P的坐标为(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是()A.(3,3)B.(3,-3)C.(6,-6)D.(3,3)或(6,-6)10.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位长度,第2步向右走2个单位长度,第3步向上走1个单位长度,第4步向右走1个单位长度,……以此类推,第n步的走法是:当n能被3整除时,向上走1个单位长度;当n被3除,余数为1时,向右走1个单位长度;当n被3除,余数为2时,向右走2个单位长度,当走完第100步时,棋子所处位置的坐标是()A.(66,34)B.(67,33)C.(100,33)D.(99,34)二、填空题(每题3分,共24分)11.写出平面直角坐标系中第三象限内一个点的坐标:________.12.在直角坐标系中,第四象限内一点P到x轴的距离为2,到y轴的距离为5,那么点P的坐标是________.13.如图是益阳市行政区域图,图中益阳市区所在地用坐标表示为(1,0),安化县城所在地用坐标表示为(-3,-1),那么南县县城所在地用坐标表示为________.14.第二象限内的点P(x,y)满足|x|=9,y2=4,则点P的坐标是__________.15.已知点N的坐标为(a,a-1),则点N一定不在第________象限.16.如图,点A,B的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP 的面积为6,则点P的坐标为________.17.如图,长方形OABC的边OA,OC分别在x轴、y轴上,点B的坐标为(3,2).点D,E分别在AB,BC边上,BD=BE=1.沿直线DE将三角形BDE翻折,点B落在点B′处,则点B′的坐标为________.18.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每移动一个单位长度,得到点A1(0,1),A2(1,1),A 3(1,0),A4(2,0),…,那么点A4n+1(n为自然数)的坐标为______(用n表示).三、解答题(19题6分,20题8分,21,23题每题9分,22题10分,其余每题12分,共66分)19.如图,如果规定北偏东30°的方向记作30°,从O点出发沿这个方向走50 m 记作50,图中点A记作(30°,50);北偏西45°的方向记作-45°,从O点出发沿着该方向的反方向走20 m记作-20,图中点B记作(-45°,-20).(1)(-75°,-15),(10°,-25)分别表示什么意义?(2)在图中标出点(60°,-30)和(-30°,40).20.春天到了,七(1)班组织同学到人民公园春游,张明、李华对着景区示意图(如图)描述牡丹园的位置(图中小正方形的边长为100 m).张明:“牡丹园的坐标是(300,300).”李华:“牡丹园在中心广场东北方向约420m处.”实际上,他们所说的位置都是正确的.根据所学的知识解答下列问题:(1)请指出张明同学是如何在景区示意图上建立平面直角坐标系的,并在图中画出所建立的平面直角坐标系;(2)李华同学是用什么来描述牡丹园的位置的?请用张明同学所用的方法,描述出公园内其他地方的位置.。
人教版七年级上册数学单元测试试卷《第一章-有理数》(含答案解析)

人教版七年级上册数学单元测试试卷第一章《有理数》第Ⅰ卷考试时间:120分钟总分:100分得分:一、选择题(共10题,每小题2分,共20分)1.(2分)用科学记数法表示2500000000是()A.2.5×109B.0.25×10C.2.5×1010D.0.25×10102.(2分)-2022的倒数是()A.-2022B.2022C.12022-D.120223.(2分)下列各组数中,互为相反数的是()A.43和34-B.13和0.333-C.a 和a -D.14和44.(2分)温度由﹣3℃上升8℃是()A.5℃B.﹣5℃C.11℃D.﹣11℃5.(2分)下列说法错误的是()A.开启计算器使之工作的按键是ONB.输入 5.8-的按键顺序是C.输入0.58的按键顺序是58⋅D.按键6987-=能计算出6987--的结果6.(2分)小时候我们常常唱的一首歌“小燕子穿花衣,年年春天来这里”,研究表明小燕子从北方飞往南方过冬,迁徙路线长达25000千米左右,将数据25000用科学记数法表示为()A.32510⨯B.42.510⨯C.52.510⨯D.50.2510⨯7.(2分)若a 、b 为有理数,0a <,0b >,且a b >,那么a ,b ,a -,b -的大小关系是()A.b a b a -<<<-B.b b a a <-<<-C.a b b a<-<<-D.a b b a<<-<-8.(2分)a、b 两数在数轴上的位置如图所示,下列结论正确的是()A.a>b B.|a|=﹣a C.a<﹣b D.|a|>|b|9.(2分)小明家的汽车在阳光下暴晒后车内温度达到了60℃,打开车门后经过8min 降低到室外同温32℃,再启动空调关车门,若每分钟降低4℃,降到设定的20℃共用时间是()A.13minB.12minC.11minD.10min10.(2分)已知4,5x y ==,且x y >,则2x y -的值为()A.13-B.13+C.3-或13+D.3+或13-二、填空题(共10题;每题2分,共20分)11.(2分)45-的倒数是.12.(2分)比较大小:15-16-(填“>”“<”或“=”)13.(2分)如果向东走35米记作+35米,那么向西走50米记作米。
七年级数学上册全册单元测试卷测试卷(含答案解析)精选全文

精选全文完整版(可编辑修改)七年级数学上册全册单元测试卷测试卷(含答案解析)一、初一数学上学期期末试卷解答题压轴题精选(难)1.已知 (本题中的角均大于且小于 )(1)如图1,在内部作,若,求的度数;(2)如图2,在内部作,在内,在内,且,,,求的度数;(3)射线从的位置出发绕点顺时针以每秒的速度旋转,时间为秒( 且 ).射线平分,射线平分,射线平分 .若,则 ________秒.【答案】(1)解:∵∠AOD+∠BOC=∠AOC+∠COD+∠BOD+∠COD=∠AOB+∠COD又∵∠AOD+∠BOC=160°且∠AOB=120°∴(2)解:,设,则,则,(3) s或15s或30s或45s【解析】【解答】(2)解:当OI在直线OA的上方时,有∠MON=∠MOI+∠NOI= (∠AOI+∠BOI))= ∠AOB= ×120°=60°,∠PON= ×60°=30°,∵∠MOI=3∠POI,∴3t=3(30-3t)或3t=3(3t-30),解得t= 或15;当OI在直线AO的下方时,∠MON═(360°-∠AOB)═ ×240°=120°,∵∠MOI=3∠POI,∴180°-3t=3(60°- )或180°-3t=3( -60°),解得t=30或45,综上所述,满足条件的t的值为 s或15s或30s或45s【分析】(1)利用角的和差进行计算便可;(2)设,则,,通过角的和差列出方程解答便可;(3)分情况讨论,确定∠MON在不同情况下的定值,再根据角的和差确定t的不同方程进行解答便可.2.结合数轴与绝对值的知识回答下列问题:(1)探究:①数轴上表示5和2的两点之间的距离是多少.②数轴上表示﹣2和﹣6的两点之间的距离是多少.③数轴上表示﹣4和3的两点之间的距离是多少.(2)归纳:一般的,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.应用:①如果表示数a和3的两点之间的距离是7,则可记为:|a﹣3|=7,求a的值.②若数轴上表示数a的点位于﹣4与3之间,求|a+4|+|a﹣3|的值.③当a取何值时,|a+4|+|a﹣1|+|a﹣3|的值最小,最小值是多少?请说明理由.(3)拓展:某一直线沿街有2014户居民(相邻两户居民间隔相同):A1, A2, A3,A4, A5,…A2014,某餐饮公司想为这2014户居民提供早餐,决定在路旁建立一个快餐店P,点P选在什么线段上,才能使这2014户居民到点P的距离总和最小.【答案】(1)解:①数轴上表示5和2的两点之间的距离是3.②数轴上表示﹣2和﹣6的两点之间的距离是4.③数轴上表示﹣4和3的两点之间的距离是7.(2)解:①如果表示数a和3的两点之间的距离是7,则可记为:|a﹣3|=7,a=10或﹣4.②若数轴上表示数a的点位于﹣4与3之间,|a+4|+|a﹣3|=a+4+3﹣a=7;③当a=1时,|a+4|+|a﹣1|+|a﹣3|取最小值,|a+4|+|a﹣1|+|a﹣3|最小=5+0+2=7,理由是:a=1时,正好是3与﹣4两点间的距离.(3)解:点P选在A1007A1008这条线段上【解析】【分析】(1)根据两点间的距离公式:数轴上表示数m和数n的两点之间的距离等于|m﹣n|,分别计算可得出答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学全册单元测试卷测试卷(解析版)一、初一数学上学期期末试卷解答题压轴题精选(难)1.数轴上A, B, C, D四点表示的有理数分别为1, 3, -5, -8(1)计算以下各点之间的距离:①A、B两点, ②B、C两点,③C、D两点,(2)若点M、N两点所表示的有理数分别为m、n,求M、N两点之间的距离.【答案】(1)AB=3-1=2;BC=3-(-5)=8;CD=-5-(-8)=-5+8=3.(2)MN=【解析】【分析】(1)数轴上两点间的距离等于数值较大的数减去数值较小的数,据此计算即可;(2)因为m、n的大小未知,则M、N两点间的距离为它们所表示的有理数之差的绝对值.2.在数轴上、两点分别表示有理数和,我们用表示到之间的距离;例如表示7到3之间的距离.(1)当时,的值为________.(2)如何理解表示的含义?(3)若点、在0到3(含0和3)之间运动,求的最小值和最大值.【答案】(1)5或-3(2)解:∵ = ,∴表示到-2的距离(3)解:∵点、在0到3(含0和3)之间运动,∴0≤a≤3, 0≤b≤3,当时, =0+2=2,此时值最小,故最小值为2;当时, =2+5=7,此时值最大,故最大值为7【解析】【解答】(1)∵,∴a=5或-3;故答案为:5或-3;【分析】(1)此题就是求表示数a的点与表示数1的点之间的距离是4,根据表示数a的点在表示数1的点的右边与左边两种情况考虑即可得出答案;(2)此题就是求表示数b的点与表示数-2的点之间的距离;(3)此题就是求表示数a的点与表示数2的点之间的距离及表示数b的点与表示数-2的点之间的距离和,而0≤a≤3, 0≤b≤3, 借助数轴当时,的值最小;当时,的值最大.3.如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m+n=90°.(1)①若m=50,则射线OC的方向是________,②图中与∠BOE互余的角有________,与∠BOE互补的角有________.(2)若射线OA是∠BON的角平分线,则∠SOB与∠AOC是否存在确定的数量关系?如果存在,请写出你的结论以及计算过程;如果不存在,请说明理由.【答案】(1)北偏东40°;∠BOS,∠EOC;∠BOW(2)解:∠AOC= ∠SOB.理由如下:∵OA平分∠BON,∴∠NOA= ∠NOB,又∵∠BON=180°-∠SOB,∴∠NOA= ∠BON=90°- ∠SOB,∵∠NOC=90°-∠EOC,由(1)知∠BOS=∠EOC,∴∠NOC=90°-∠SOB,∠AOC=∠NOA-∠NOC=90°- ∠SOB-(90°-∠SOB),即∠AOC= ∠SOB.【解析】【解答】解:(1)①∵m+n=90°,m=50°,∴n=40°,∴射线OC的方向是北偏东40°;②∵∠BOE+∠BOS=90°,∠BOE+∠EOC=90°,∴图中与∠BOE互余的角有∠BOS,∠EOC;∠BOE+∠BOW=180°,∴图中与∠BOE互补的角有∠BOW,故答案为:①北偏东40°;②∠BOS,∠EOC;∠BOW.【分析】(1)①由m+n=90°,m=50°可求得n值,从而可得射线OC的方向.②根据余角定义可知∠BOE+∠BOS=90°,∠BOE+∠EOC=90°,从而可得图中与∠BOE互余的角;由补角定义可得∠BOE+∠BOW=180°,从而可得图中与∠BOE互补的角.(2)∠AOC=∠SOB.理由如下:由角平分线定义和领补角定义可得∠NOA= ∠BON=90°-∠SOB,结合(1)中条件可得∠NOC=90°-∠SOB;由∠AOC=∠NOA-∠NOC即可求得它们之间的数量关系.4.如图,两个形状、大小完全相同的含有30。
角的直角三角板如图1放置,PA、PB与直线MN重合,且三角板PAC和三角板PBD均可以绕点P逆时针旋转.(1)如图1.则∠DPC为多少度?(2)如图2,若三角板PAC的边PA从PN处开始绕点P逆时针旋转的角度为α,PF平分∠APD,PE平分∠CPD,求∠EPF的度数;(3)如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3。
/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2。
/秒,在两个三角板旋转过程中,当PC转到与PM重合时,两个三角板都停止转动.设两个三角板旋转时间为t秒,请问是定值吗?若是定值,请求出这个定值;若不是定值,请说明理由。
【答案】(1)解:∵∠DPC=180°-∠CPA-∠DPB,∠CPA=60°,∠DPB=30°,∴∠DPC=180゜-30゜-60゜=90゜(2)(3)解:是定值,理由如下:设运动时间为t秒,则∠NPA=3t,∠MPB=2t,∴∠BPN=1800-2t,∠CPD=3600-∠DPB-∠BPN-∠NPA-∠CPA=900-t,∴【解析】【分析】(1)利用含有30゜、60゜的三角板得出∠DPC=180°-∠CPA-∠DPB,代入计算即可;(2)根据角平分线的定义得出∠DPF=∠APD,∠DPE=∠CPD ,根据角的和差得出APD=180°−30°−α=150°−α ,∠CPD=180°−30°−60°−α=90°−α ,从而得出∠DPF及,∠DPE的度数,最后根据EPF=∠DPF−∠DPE算出结果;(3)首先得出是一个定值,设运动时间为t秒,则∠BPM=2t,∠NPA=3t ,∠BPN=1800-2t ,∠CPD=3600-∠DPB-∠BPN-∠NPA-∠CPA=900-t ,即可得出答案.5.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将有一30度角的直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(图中∠OMN=30°,∠NOM=90°)(1)将图1中的三角板绕点O逆时针旋转至图2,使OM在∠BOC的内部,且恰好平分∠BOC,问直线ON是否平分∠AOC?请说明理由;(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,求t;(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.【答案】(1)解:直线ON平分∠AOC;理由:设ON的反向延长线为OD,∵OM平分∠BOC,∴∠MOC=∠MOB=60°,又∵OM⊥ON,∴∠MON=90°,∴∠BON=30°,∴∠CON=120°+30°=150°,∴∠COD=30°,∴OD平分∠AOC,即直线ON平分∠AOC(2)解:由(1)可知∠BON=30°,∠DON=180°因此ON旋转60°或240°时直线ON平分∠AOC,由题意得,6t=60°或240°,∴t=10或40(3)解:∵∠MON=90°,∠AOC=60°,∴∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°【解析】【分析】(1)由角的平分线的定义和等角的余角相等求解;(2)由∠BOC=120°可得∠AOC=60°,则∠AON=30°或∠NOR=30°,即顺时针旋转300°或120°时ON平分∠AOC,据此求解;(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,然后作差即可.6.如图如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的一个“二倍点”.(1)一条线段的中点________这条线段的“二倍点”;(填“是”或“不是”)(2)如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.问t为何值时,点M是线段AB的“二倍点”.(3)同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.【答案】(1)是(2)解:当AM=2BM时,20﹣2t=2×2t,解得:t= ;当AB=2AM时,20=2×(20﹣2t),解得:t=5;当BM=2AM时,2t=2×(20﹣2t),解得:t= ;答:t为或5或时,点M是线段AB的“二倍点”(3)解:当AN=2MN时,t=2[t﹣(20﹣2t)],解得:t=8;当AM=2NM时,20﹣2t=2[t﹣(20﹣2t)],解得:t=7.5;当MN=2AM时,t﹣(20﹣2t)=2(20﹣2t),解得:t= ;答:t为7.5或8或时,点M是线段AN的“二倍点”.【解析】【解答】解:(1)因为线段的中点把该线段分成相等的两部分,该线段等于2倍的中点一侧的线段长.所以一条线段的中点是这条线段的“二倍点”故答案为:是【分析】(1)由中点可知,这条线段等于中点分出的线段的2倍,进而得出结论;(2)分三种情况:当AM=2BM时,当AB=2AM时,当BM=2AM时,分别列出方程解答即可;(3)分三种情况:当AN=2MN时,当AM=2NM时,当MN=2AM时,分别列出方程解答即可.7.定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角.如图1,若∠COD= ∠AOB,则∠COD是∠AOB的内半角.(1)如图1,已知∠AOB=70°,∠AOC=25°,∠COD是∠AOB的内半角,则∠BOD=________.(2)如图2,已知∠AOB=60°,将∠AOB绕点O按顺时针方向旋转一个角度口(0<a<60°)至∠COD,当旋转的角度a为何值时,∠COB是∠AOD的内半角.(3)已知∠AOB=30°,把一块含有30°角的三角板如图3叠放,将三角板绕顶点O以3度/秒的速度按顺时针方向旋转(如图4),问:在旋转一周的过程中,射线OA,OB,OC,OD 能否构成内半角,若能,请求出旋转的时间;若不能,请说明理由.【答案】(1)10°(2)解:∵∠AOB绕点O按顺时针方向旋转一个角度口(0<a<60°)至∠COD,∴∠AOB=∠COD=60°∴∠AOC=∠BOD=a∴a+∠COB=60°∵∠COB是∠AOD的内半角∴∠COB=∠AOD∴2∠COB=∠COB+2a∴∠COB=2a∴a+2a=60°解之:a=20°即当旋转的角度a为20°时,∠COB是∠AOD的内半角。
