圆锥曲线抛物线知识点归纳总结
圆锥曲线知识点总结

圆锥曲线知识点总结圆锥曲线是解析几何中非常重要的一部分,它包括直角双曲线、抛物线和椭圆。
这些曲线都是由一个平面与一个旋转椭球体相交得到的,具有广泛的应用价值。
以下是对于圆锥曲线的知识点总结:一、直角双曲线直角双曲线由于其特殊的形状和性质,在物理学、工程学和数学等方面都有应用。
直角双曲线的方程可以表示为以下形式:(x^2/a^2) - (y^2/b^2) = 1其中a和b是正实数。
在直角双曲线上,存在两个焦点以及两个称为顶点的特殊点。
双曲线还具有渐近线,与其方程的斜率相关。
二、抛物线抛物线是一种类似于开口向上或开口向下的弧线。
它的方程通常表示为:y = ax^2 + bx + c其中a、b和c是实数且a不等于零。
抛物线的焦点是它的特殊点,而直径称为准线。
抛物线具有对称性质,其形状可以用焦点和准线的位置来确定。
三、椭圆椭圆是圆锥曲线中最常见的类型,它的形状类似于椭圆形。
椭圆的方程可以表示为:(x^2/a^2) + (y^2/b^2) = 1其中a和b是正实数。
椭圆具有两个焦点,椭圆的形状和大小由焦距和长短轴决定。
椭圆还具有较为特殊的直径,它称为主轴。
四、参数方程与极坐标方程除了直角坐标系下的方程表示,圆锥曲线还可以用参数方程和极坐标方程来描述。
参数方程是将x和y表示为参数t的函数,通过参数的变化来确定曲线上的点。
极坐标方程是使用角度和极径来定义曲线上的点。
五、圆锥曲线的性质圆锥曲线具有许多重要性质和性质。
其中一些重要的性质包括:切线的斜率、焦点与直线的关系、曲率和弧长等。
这些性质在求解问题和绘图中都有重要的应用。
总结:圆锥曲线是数学中的重要概念,它包括直角双曲线、抛物线和椭圆。
每种曲线都具有独特的形状和性质,可以通过方程、参数方程或极坐标方程来描述。
了解圆锥曲线的基本知识对于解决实际问题和深入理解数学概念都是非常重要的。
掌握圆锥曲线的知识点,将有助于我们在几何学和解析几何学领域更加灵活和熟练地运用相关概念。
圆锥曲线(椭圆、双曲线、抛物线)知识点总结

双曲线知识点一、 双曲线的定义:1. 第一定义:到两个定点F 1与F 2的距离之差的绝对值等于定长(<|F 1F 2|)的点的轨迹(21212F F a PF PF <=-(a 为常数))这两个定点叫双曲线的焦点.要注意两点:(1)距离之差的绝对值.(2)2a <|F 1F 2|.当|MF 1|-|MF 2|=2a 时,曲线仅表示焦点F 2所对应的一支; 当|MF 1|-|MF 2|=-2a 时,曲线仅表示焦点F 1所对应的一支;当2a =|F 1F 2|时,轨迹是一直线上以F 1、F 2为端点向外的两条射线;当2a >|F 1F 2|时,动点轨迹不存在.2. 第二定义:动点到一定点F 的距离与它到一条定直线l 的距离之比是常数e (e >1)时,这个动点的轨迹是双曲线这定点叫做双曲线的焦点,定直线l 叫做双曲线的准线二、双曲线的标准方程:12222=-by a x (a >0,b >0)(焦点在x 轴上);12222=-bx a y (a >0,b >0)(焦点在y 轴上); 1. 如果2x 项的系数是正数,则焦点在x 轴上;如果2y 项的系数是正数,则焦点在y 轴上. a 不一定大于b.2. 与双曲线12222=-by a x 共焦点的双曲线系方程是12222=--+k b y k a x 3. 双曲线方程也可设为:221(0)x y mn m n-=> 例题:已知双曲线C 和椭圆221169x y +=有相同的焦点,且过(3,4)P 点,求双曲线C 的轨迹方程。
三、点与双曲线的位置关系,直线与双曲线的位置关系: 1 点与双曲线:点00(,)P x y 在双曲线22221(0,0)x y a b a b -=>>的内部2200221x y a b ⇔->点00(,)P x y 在双曲线22221(0,0)x y a b a b -=>>的外部2200221x y a b ⇔-<点00(,)P x y 在双曲线22221(0,0)x y a b a b -=>>上220022-=1x y a b⇔2 直线与双曲线:(代数法)设直线:l y kx m =+,双曲线)0,0(12222>>=-b a by a x 联立解得02)(222222222=----b a m a mkx a x k a b1) 0m =时,b bk a a-<<直线与双曲线交于两点(左支一个点右支一个点);b k a ≥,bk a≤-,或k 不存在时直线与双曲线没有交点;2) 0m ≠时,k 存在时,若0222=-k a ba bk ±=,直线与双曲线渐近线平行,直线与双曲线相交于一点;若2220b a k -≠,222222222(2)4()()a mk b a k a m a b ∆=-----2222224()a b m b a k =+-0∆>时,22220m b a k +->,直线与双曲线相交于两点; 0∆<时,22220m b a k +-<,直线与双曲线相离,没有交点;0∆=时22220m b a k +-=,2222m b k a +=直线与双曲线有一个交点; 若k 不存在,a m a -<<时,直线与双曲线没有交点; m a m a ><-或直线与双曲线相交于两点; 3. 过定点的直线与双曲线的位置关系:设直线:l y kx m =+过定点00(,)P x y ,双曲线)0,0(12222>>=-b a by a x1).当点00(,)P x y 在双曲线内部时:b bk a a-<<,直线与双曲线两支各有一个交点; a bk ±=,直线与双曲线渐近线平行,直线与双曲线相交于一点;b k a >或bk a<-或k 不存在时直线与双曲线的一支有两个交点;2).当点00(,)P x y 在双曲线上时:bk a =±或2020b x k a y =,直线与双曲线只交于点00(,)P x y ;b bk a a-<<直线与双曲线交于两点(左支一个点右支一个点); 2020b x k a y >(00y ≠)或2020b x b k a a y <<(00y ≠)或bk a <-或k 不存在,直线与双曲线在一支上有两个交点; 当00y ≠时,bk a =±或k 不存在,直线与双曲线只交于点00(,)P x y ;b k a >或bk a <-时直线与双曲线的一支有两个交点;b bk a a-<<直线与双曲线交于两点(左支一个点右支一个点); 3).当点00(,)P x y 在双曲线外部时:当()0,0P 时,b bk a a -<<,直线与双曲线两支各有一个交点; b k a ≥或bk a≤或k 不存在,直线与双曲线没有交点;当点0m ≠时,k =时,过点00(,)P x y 的直线与双曲线相切 bk a=±时,直线与双曲线只交于一点;几何法:直线与渐近线的位置关系例:过点(0,3)P 的直线l 和双曲线22:14y C x -=,仅有一个公共点,求直线l 的方程。
圆锥曲线知识点

圆锥曲线知识点圆锥曲线是数学中一类重要的曲线,它们是平面上所有与两个固定点(焦点)距离之和为常数的点的集合。
这些曲线包括椭圆、抛物线和双曲线。
以下是圆锥曲线的知识点总结:1. 椭圆:椭圆是平面上所有与两个焦点距离之和等于常数的点的集合。
这个常数大于两个焦点之间的距离。
椭圆的标准方程可以表示为:\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]其中,\( a \) 是椭圆的半长轴,\( b \) 是椭圆的半短轴。
2. 抛物线:抛物线是平面上所有与一个焦点和一个定点(顶点)距离相等的点的集合。
抛物线的标准方程可以表示为:\[ y^2 = 4ax \]或者\[ x^2 = 4ay \]其中,\( a \) 是抛物线的参数,表示顶点到焦点的距离。
3. 双曲线:双曲线是平面上所有与两个焦点距离之差的绝对值等于常数的点的集合。
这个常数小于两个焦点之间的距离。
双曲线的标准方程可以表示为:\[ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \]或者\[ \frac{y^2}{b^2} - \frac{x^2}{a^2} = 1 \]其中,\( a \) 是双曲线的实半轴,\( b \) 是双曲线的虚半轴。
4. 圆锥曲线的性质:- 椭圆具有两个焦点,所有点到两个焦点的距离之和是常数。
- 抛物线具有一个焦点和一个顶点,所有点到焦点的距离等于到顶点的距离。
- 双曲线具有两个焦点,所有点到两个焦点的距离之差的绝对值是常数。
- 圆锥曲线的焦点可以通过方程的参数确定。
5. 圆锥曲线的应用:- 椭圆在天文学中描述行星的轨道。
- 抛物线在光学中描述光线通过抛物面反射后的路径。
- 双曲线在工程学中用于设计某些类型的天线。
6. 圆锥曲线的参数化:- 椭圆的参数方程可以表示为:\[ x = a \cos(t) \]\[ y = b \sin(t) \]- 抛物线的参数方程可以表示为:\[ x = at^2 \]\[ y = 2at \]- 双曲线的参数方程可以表示为:\[ x = a \sec(t) \]\[ y = b \tan(t) \]7. 圆锥曲线的几何特征:- 椭圆的长轴和短轴是对称的,且椭圆是封闭的。
高二数学圆锥曲线:抛物线知识点整理和总结

【最新】高二数学圆锥曲线:抛物线知识点整理和总结高二数学圆锥曲线:抛物线知识点整理和总结专题九抛物线一.根本概念1.抛物线的定义:平面内与一个定点的距离和一条定直线的距离相等的点的轨迹.其中:定点为抛物线的焦点,定直线叫做准线.2.抛物线的标准方程.图象及几何性质:p0标准方程l焦点在_轴上,开口向右y2焦点在_轴上,开口向左y2p_2焦点在y 轴上,开口向上_2焦点在y轴上,开口向下_22p_2py2pyyP_OFPyl_FOlyPFOy轴lyOF_图形_PO(0,0)顶点对称轴焦点离心率准线二.例题分析【例1】〔河西区__高考一模〕双曲_a22_轴F(p2,0)F(p2,0)F(0,p2)F(0,p2)e1_p2_p2yp2yp2yb221a0,b0的一个顶点与抛物线y20_的焦点重合,该双曲线的离心率为252,那么该双曲线的渐近线斜率为〔〕A2B43C12D34【例2】〔南开区__年高三一模〕假设抛物线y2p_的焦点与双曲线焦重合,那么p的值为〔〕A3B-3C6D-62_26y231的左【变式1】〔河北区__年高三三模〕抛物线y245_的焦点和双曲线_a22yb221(a0,b0)的一个焦点重合,且双曲线的离心率e52,那么双曲线的方程为〔〕A【变式2】〔__年第三次六校联考〕.双曲线_a22_216y291B_29y2161C_2y241D_24y291yb221的离心率为2,它的一个焦点与抛物线y28_的焦点相同,那么双曲线的渐近线方程为--------------------------------【例3】.〔__年天津一中高三第五次月考〕抛物线y22p_p0的焦点F为双 _a22曲线yb221a0,b0的一个焦点,经过两曲线交点的直线恰好过点F,那么该双曲线的离心率为〔〕A2B【例4】〔__年天津文〕双曲线_a2221C3D31yb221(a0,b0)的左顶点与抛物线y2p_(p0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的准线的交点2坐标为〔-2,-1〕,那么双曲线的焦距为〔〕A.23B.25C.43D.45【例5】〔__年天津文〕双曲线_a22yb221(a0,b0)的一条渐近线方程是y3_,它的一个焦点与抛物线y216_的焦点相同.那么双曲线的方程为.【变式1】〔__年天津理〕双曲线_a22yb221(a0,b0)的一条渐近线方程是y=3_,它的一个焦点在抛物线y224_的准线上,那么双曲线的方程为〔〕〔A_236y21081〔B_29y2271〔C〕_2108y2361〔D〕_227y291【变式2】〔__陕西理〕设抛物线的顶点在原点,准线方程为_2,那么抛物线的方程是.【例6】〔__年福建〕双曲线_24yb221的右焦点与抛物线y212_的焦点重合,那么该双曲线的焦点到渐近线的距离为_________.【变式1】〔__年安徽〕过抛物线y4_的焦点F的直线交抛物线于A.B两点,O 为坐标原点,假设AF3,那么三角形AOB的面积为________.【例7】〔__辽宁理〕F是抛物线y2=_的焦点,A,B是该抛物线上的两点,AFBF=3,那么线段AB的中点到y轴的距离为〔〕A.34B.1C.54D.74【变式1】〔__年天津理〕抛物线的参数方程为_2pty2pt2〔t为参数,p>0〕,焦点为F,准线为l,过抛物线上一点M作l的垂线,垂足为E.假设|EF|=|MF|,点M 的横坐标是3,那么p=_________.【变式2】〔__山东文〕设M(_0,y0)为抛物线C:_28y上一点,F为抛物线C的焦点,以F为圆心.FM为半径的圆和抛物线C的准线相交,那么y0的取值范围是〔〕A.(0,2)【变式3】〔__年四川〕抛物线关于_轴对称,它的顶点在坐标原点,并且经过点 M2,y0,假设点M到抛物线焦点距离为3,那么OM长度________.B.[0,2]C.(2,+∞)D.[2,+∞)扩展阅读:抛物线题及知识点总结一.抛物线的定义及其应用[例1]设P是抛物线y2=4_上的一个动点.(1)求点P到点A(-1,1)的距离与点P到直线_=-1的距离之和的最小值;(2)假设B(3,2),求|PB|+|PF|的最小值.例2..(__山东高考)设M(_0,y0)为抛物线C:_2=8y上一点,F为抛物线C的焦点,以F为圆心.|FM|为半径的圆和抛物线C的准线相交,那么y0的取值范围是()A.(0,2)B.[0,2]C.(2,+∞)D.[2,+∞).二.抛物线的标准方程和几何性质例3.抛物线y=2p_(p>0)的焦点为F,准线为l,经过F的直线与抛物线交于A. 2B两点,交准线于C点,点A在_轴上方,AK⊥l,垂足为K,假设|BC|=2|BF|,且|AF|=4,那么△AKF的面积是()A.4B.33C.43D.8[悟一法]1.求抛物线的标准方程常采用待定系数法,未知数只有p,可利用题中条件确定p的值.注意到抛物线方程有四种标准形式,因此求抛物线方程时,需先定位,再定量.2.涉及抛物线几何性质的问题常结合图形思考,通过图形可以直观地看出抛物线的顶点.对称轴.开口方向等几何特征.例4.过抛物线y2=2p_(p>0)的焦点F的直线交抛物线于点A.B,交其准线l 于点C,假设|BC|=2|BF|,且|AF|=3那么此抛物线的方程为()39A.y2=_B.y2=9_C.y2=_D.y2=3_22三.抛物线的综合问题[例5](__江西高考)过抛物线y2=2p_(p>0)的焦点,斜率为22的直线交抛物线于A(_1,y1),B(_2,y2)(_10)上,M点到抛物线C的焦点F的1 距离为2,直线l:y=-_+b与抛物线C交于A,B两点.2(1)求抛物线C的方程;(2)假设以AB为直径的圆与_轴相切,求该圆的方程.练习题1.抛物线_2=ay的焦点恰好为双曲线y2-_2=2的上焦点,那么a等于() A.1B.4C.8D.162.抛物线y=-4_2上的一点M到焦点的距离为1,那么点M的纵坐标是() A.-1716157B.-C.16162D.15163.(__辽宁高考)F是物线y=_的焦点,A,B是该物线上的两点,|AF|+|BF|=3,那么线段AB的中点到y轴的距离为()3A.425B.1C.47D.44.抛物线y=2p_,以过焦点的弦为直径的圆与抛物线准线的位置关系是()A.相离B.相交C.相切D.不确定5.(__宜宾检测)F为抛物线y2=8_的焦点,过F且斜率为1的直线交抛物线于()A.42A.B两点,那么||FA|-|FB||的值等于D.16B.8C.826.在y=2_2上有一点P,它到A(1,3)的距离与它到焦点的距离之和最小,那么点P的坐标是()A.(-2,1)C.(2,1)B.(1,2)D.(-1,2)7.设抛物线y2=8_的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.如果直线AF的斜率为-3,那么|PF|=()A.43B.8C.83D.168.(__陕西高考)设抛物线的顶点在原点,准线方程为_=-2,那么抛物线的方程是()A.y2=-8_B.y2=8_C.y2=-4_D.y2=4_9.(__永州模拟)以抛物线_2=16y的焦点为圆心,且与抛物线的准线相切的圆的方程为________.10.抛物线的顶点在原点,对称轴为y轴,抛物线上一点Q(-3,m)到焦点的距离是5,那么抛物线的方程为________.11.抛物线y=4_与直线2_+y-4=0相交于A.B两点,抛物线的焦点为F,那么|FA|+|FB|=________.212.过抛物线y2=4_的焦点作直线交抛物线于A(_1,y1),B(_2,y2)两点,假设_1+_2=6,那么|AB|等于________13.根据以下条件求抛物线的标准方程: (1)抛物线的焦点是双曲线16_2-9y2=144的左顶点;(2)过点P(2,-4). 14.点A(-1,0),B(1,-1),抛物线C:y2=4_,O为坐标原点,过点A的动直线l交抛物线C于M,P两点,直线MB交抛物线C于另一点Q.假设向与OP的夹角为,求△POM的面积.4一.抛物线的定义及其应用[例1]设P是抛物线y2=4_上的一个动点.(1)求点P到点A(-1,1)的距离与点P到直线_=-1的距离之和的最小值;(2)假设B(3,2),求|PB|+|PF|的最小值.[自主解答](1)如图,易知抛物线的焦点为F(1,0),准线是_=-1.由抛物线的定义知:点P到直线_=-1的距离等于点P到焦点F的距离.于是,问题转化为:在曲线上求一点P,使点P到点A(-1,1)的距离与点P到F(1,0)的距离之和最小.显然,连结AF交曲线于P点,那么所求的最小值为|AF|,即为5.(2)如图,自点B作BQ垂直准线于Q,交抛物线于点P1,那么|P1Q|=|P1F|.那么有|PB|+|PF|≥|P1B|+|P1Q|=|BQ|=4.即|PB|+|PF|的最小值为 4.例2..(__山东高考)设M(_0,y0)为抛物线C:_2=8y上一点,F为抛物线C的焦点,以F为圆心.|FM|为半径的圆和抛物线C的准线相交,那么y0的取值范围是() A.(0,2)B.[0,2]C.(2,+∞)D.[2,+∞)解析:圆心到抛物线准线的距离为p,即p=4,根据只要|FM|>4即可.根据抛物线定|FM|=y0+2由y0+2>4,解得y0>2,故y0的取值范围是(2,+∞).二.抛物线的标准方程和几何性质例3.抛物线y2=2p_(p>0)的焦点为F,准线为l,经过F的直线与抛物线交于A.B两点,交准线于C点,点A在_轴上方,AK⊥l,垂足为K,假设|BC|=2|BF|,且|AF|=4,那么△AKF的面积是()A.4B.33C.43D.8设点A(_1,y1),其中y1>0.由点B作抛物线的准线的垂线,垂足为B1.那么有|BF|=|BB1|;又|CB|=2|FB|,因此有|CB|=2|BB1|,cos∠CBB1=ππCBB1=.即直线AB与_轴的夹角为.335|BB1|1=,∠|BC|pπ又|AF|=|AK|=_1+=4,因此y1=4sin=23,因此△AKF的面积等于|AK|y1=423=43.22[悟一法]1.求抛物线的标准方程常采用待定系数法,未知数只有p,可利用题中条件确定p的值.注意到抛物线方程有四种标准形式,因此求抛物线方程时,需先定位,再定量.2.涉及抛物线几何性质的问题常结合图形思考,通过图形可以直观地看出抛物线的顶点.对称轴.开口方向等几何特征.例4.过抛物线y2=2p_(p>0)的焦点F的直线交抛物线于点A.B,交其准线l 于点C,假设|BC|=2|BF|,且|AF|=3那么此抛物线的方程为()3A.y2=_B.y2=9_29C.y2=_D.y2=3_2解析:分别过点A.B作AA1.BB1垂直于l,且垂足分别为A1.B1,由条件|BC|=2|BF|得|BC|=2|BB1|,∴∠BCB1=30°,又|AA1|=|AF|=3,∴|AC|=2|AA1|=6,∴|CF|=|AC|-|AF|=6-3=3,∴F为线段AC的中点.故13点F到准线的距离为p=|AA1|=,故抛物线的方程为y2=3_.22三.抛物线的综合问题[例5](__江西高考)过抛物线y2=2p_(p>0)的焦点,斜率为22的直线交抛物线于A(_1,y1),B(_2,y2)(_1所以p=4,从而抛物线方程是y2=8_.(2)由p=4,4_2-5p_+p2=0可简化为_2-5_+4=0,从而_1=1,_2=4,y1=-22,y2=42,从而A(1,-22),B(4,42);设OC=(_,y)=(1,-2332)+λ(4,42)=(4λ+1,42λ-22).又y22(2λ-1)]2=8(4λ+1).3=8_3,即[2即(2λ-1)2=4λ+1.解得λ=0,或λ=2.例6.(__湖南高考)(13分)平面内一动点P到点F(1,0)的距离与点P到y轴的距离的差等于1.(1)求动点P的轨迹C的方程;(2)过点F作两条斜率存在且互相垂直的直线l1,l2,设l1与轨迹C相交于点A,B,l与轨迹C相交于点D,E,求ADEB的最小值2妙解](1)设动点P的坐标为(_,y),由题意有_-12+y2-|_|=1.化简得y2=2_+2|_|.当_≥0时,y2=4_;当_例7.点M(1,y)在抛物线C:y2=2p_(p>0)上,M点到抛物线C的焦点F的1距离为2,直线l:y=-_+b与抛物线C交于A,B两点.2(1)求抛物线C的方程;(2)假设以AB为直径的圆与_轴相切,求该圆的方程.解:(1)抛物线y2=2p_(p>0)的准线为_=-,由抛物线定义和条件可知2|MF|=1-(-)=1+=2,解得p=2,故所求抛物线C的方程为y=4_.22ppp2y=-1_+b,2(2)联立y=4_2消去_并化简整理得y+8y-8b=0.2依题意应有Δ=64+32b>0,解得b>-2.设A(_1,y1),B(_2,y2),那么y1+y2 =-8,y1y2=-8b,设圆心Q(_0,y0),那么应用_0=_1+_22,y0=y1+y22=-4.因为以AB为直径的圆与_轴相切,所以圆的半径为r=|y0|=4.又|AB|=5[_1-_222+y1-y22=1+4y1-y22=y1+y2-4y1y2]=564+32b64+32b所以|AB|=2r=58=8,解得b=-.548,5所以_1+_2=2b-2y1+2b-2y2=4b+16=那么圆心Q的坐标为(2424,-4).故所求圆的方程为(_-)2+(y+4)2=16.551.抛物线_2=ay的焦点恰好为双曲线y2-_2=2的上焦点,那么a等于() A.1B.4C.8D.16解析:根据抛物线方程可得其焦点坐标为(0,),双曲线的上焦点为(0,2),4依题意那么有=2解得a=8.4aa2.抛物线y=-4_2上的一点M到焦点的距离为1,那么点M的纵坐标是() A.-1716157B.-C.1616D.1516y12解析:抛物线方程可化为_=-,其准线方程为y=.设M(_0,y0),那么由416115抛物线的定义,可知-y0=1y0=-.16163.(__辽宁高考)F是物线y2=_的焦点,A,B是该物线上的两点,|AF|+|BF|=3,那么线段AB的中点到y轴的距离为()3A.45B.1C.47D.4解析:根据物线定义与梯形中位线定理,得线段AB中点到y轴的距离为:11315(|AF|+|BF|)-=-=.242444.抛物线y2=2p_,以过焦点的弦为直径的圆与抛物线准线的位置关系是() A.相离B.相交C.相切D.不确定解析:设抛物线焦点弦为AB,中点为M,准线l,A1.B1分别为A.B在直线l上的射影,那么|AA1|=|AF|,|BB1|=|BF|,于是M到l的距离d=(|AA1|+|BB1|)11=(|AF|+|BF|)=|AB|=半径,故相切.225.(__宜宾检测)F为抛物线y=8_的焦点,过F且斜率为1的直线交抛物线于()A.42B.8C.82D.16212A.B两点,那么||FA|-|FB||的值等于y=_-2,解析:依题意F(2,0),所以直线方程为y=_-2由2y=8_,消去y得_2-12_+4=0.设A(_1,y1),B(_2,y2),那么||FA|-|FB||=|(_1+2)-(_2+2)|=|_1-_2|=(_1+_2)-4_1_2=144-16=82.6.在y=2_2上有一点P,它到A(1,3)的距离与它到焦点的距离之和最小,那么点2P的坐标是()A.(-2,1)C.(2,1)B.(1,2)D.(-1,2)2解析:如下图,直线l为抛物线y=2_的准线,F为其焦点,PN⊥l,AN1⊥l,由抛物线的定义知,|PF|=|PN|,∴|AP|+|PF|=|AP|+|PN|≥|AN1|,当且仅当A.P.N三点共线时取等号.∴P点的横坐标与A点的横坐标相同即为1,那么可排除 A.C.D.答案:B7.设抛物线y2=8_的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.如果直线AF的斜率为-3,那么|PF|=()A.43B.8C.83D.168.(__陕西高考)设抛物线的顶点在原点,准线方程为_=-2,那么抛物线的方程是()A.y2=-8_B.y2=8_C.y2=-4_D.y2=4_解析:由准线方程_=-2,可知抛物线为焦点在_轴正半轴上的标准方程,同时得p=4,所以标准方程为y2=2p_=8_9.(__永州模拟)以抛物线_2=16y的焦点为圆心,且与抛物线的准线相切的圆的方程为________.解析:抛物线的焦点为F(0,4),准线为y=-4,那么圆心为(0,4),半径r=8.所以,圆的方程为_2+(y-4)2=64.10.抛物线的顶点在原点,对称轴为y轴,抛物线上一点Q(-3,m)到焦点的距离是5,那么抛物线的方程为________.解析:设抛物线方程为_2=ay(a≠0),那么准线为y=-.∵Q(-3,m)在抛4物线上,∴9=am.而点Q到焦点的距离等于点Q到准线的距离,aa99a∴|m-(-)|=5.将m=代入,得|+|=5,解得,a=±2,或a=±18,4aa4∴所求抛物线的方程为_=±2y,或_=±18y.11.抛物线y2=4_与直线2_+y-4=0相交于A.B两点,抛物线的焦点为F,那么|FA|+|FB|=________.22y2=4_解析:由2_+y-4=0,消去y,得_2-5_+4=0(_),方程(_)的两根为A.B两点的横坐标,故_1+_2=5,因为抛物线y2=4_的焦点为F(1,0),所以|FA|+|FB|=(_1+1)+(_2+1)=712.过抛物线y2=4_的焦点作直线交抛物线于A(_1,y1),B(_2,y2)两点,假设_1+_2=6,那么|AB|等于________解析:因线段AB过焦点F,那么|AB|=|AF|+|BF|.又由抛物线的定义知|AF|=_1+1,|BF|=_2+1,故|AB|=_1+_2+2=8.13.根据以下条件求抛物线的标准方程:(1)抛物线的焦点是双曲线16_2 -9y=144的左顶点;(2)过点P(2,-4).解:双曲线方程化为-=1,左顶点为(-3,0),由题意设抛物线方程为9162_2y2py2=-2p_(p>0),那么-=-3,∴p=6,∴抛物线方程为y2=-12_.2(2)由于P(2,-4)在第四象限且抛物线对称轴为坐标轴,可设抛物线方程为y2=m_或_2=ny,代入P点坐标求得m=8,n=-1,∴所求抛物线方程为y2=8_或_2=-y.14.点A(-1,0),B(1,-1),抛物线C:y2=4_,O为坐标原点,过点A的动直线l交抛物线C于M,P两点,直线MB交抛物线C于另一点Q.假设向量OMπ与OP的夹角为,求△POM的面积.4解:设点M(,y1),P(,y2),44∵P,M,A三点共线,∴kAM=kPM,即y21y22y1y21=4+1y1-y2y11=,∴y1y2=4.22,即2y1y2y1+4y1+y24-4444y2y2π12∴OMOP=+y1y2=5.∵向量OM与OP的夹角为,π1π5∴|OM||OP|cos=5.∴S△POM=|OM||OP|sin=.4242。
圆锥曲线(椭圆、双曲线、抛物线)基础知识及常用结论

圆锥曲线(椭圆、双曲线、抛物线)基础知识及常⽤结论圆锥曲线必背⼝诀(红字为⼝诀)-椭圆⼀、椭圆定义定点为焦点,定值为长轴.(定值=2a )椭圆.定点为焦点,定直线为准线,定值为离⼼率.(定值=e )定点为短轴顶点,定值为负值. (定值2k e 1=-)⼆、椭圆的性质定理长轴短轴与焦距,形似勾股弦定理①准线⽅程准焦距,a ⽅、b ⽅除以c ②通径等于 2 ep ,切线⽅程⽤代替③焦三⾓形计⾯积,半⾓正切连乘b ④注解:1长轴2a =,短轴2b =,焦距2c =,则:222a b c =+2准线⽅程:2a x c= (a ⽅除以c )3椭圆的通径d :过焦点垂直于长轴的直线与椭圆的两交点之间的距离称为椭圆的通径.(通径22c b 2b 2a c ad 2ep =??==)过椭圆上00x y (,)点的切线⽅程,⽤00x y (,)等效代替椭圆⽅程得到.等效代替后的是切线⽅程是:0022x x y y1a b+=4、焦三⾓形计⾯积,半⾓正切连乘b焦三⾓形:以椭圆的两个焦点12F F ,为顶点,另⼀个顶点P 在椭圆上的三⾓形称为焦三⾓形.半⾓是指12F PF θ=∠的⼀半.则焦三⾓形的⾯积为:2S b 2tanθ=证明:设1PF m =,2PF n =,则m n 2a +=由余弦定理:222m n 2mn 4c cos θ+-?=22224a 4b m n 4b ()=-=+-即:22mn 2mn 4b cos θ-?=-,即:22b 1mn (cos )θ=+.即:2122b mn PF PF 1||||cos θ==+故:12F PF 1S m n 2sin θ=??△2212b b 211sin sin cos cos θθθθ=?=++⼜:22221222sin cossin tan cos cosθθθθθθ==+ 所以:椭圆的焦点三⾓形的⾯积为122F PF S b 2tan θ=. 三、椭圆的相关公式切线平分焦周⾓,称为弦切⾓定理①1F2FOxyPmn切点连线求⽅程,极线定理须牢记②弦与中线斜率积,准线去除准焦距③细看中点弦⽅程,恰似弦中点轨迹④注解:1弦切⾓定理:切线平分椭圆焦周⾓的外⾓,平分双曲线的焦周⾓. 焦周⾓是焦点三⾓形中,焦距所对应的⾓.弦切⾓是指椭圆的弦与其切线相交于椭圆上时它们的夹⾓,当弦为焦点弦时(过焦点的弦),那么切线是两个焦点弦的⾓平分线.2若000P x y (,)在椭圆2222x y 1a b+=外,则过0P 作椭圆的两条切线,切点为12P P ,,则点0P 和切点弦12P P ,分别称为椭圆的极点和极线.切点弦12P P 的直线⽅程即极线⽅程是0022x xy y1a b+=(称为极线定理)3弦指椭圆内的⼀弦AB .中线指弦AB 的中点M 与原点O 的连线,即OAB ?得中线.这两条直线的斜率的乘积,等于准线距离2c a x c=-去除准焦距2bp c=,其结果是:2AB OM2c p b k k x a==- 4中点弦AB 的⽅程:在椭圆中,若弦AB 的中点为00M x y (,),弦AB 称为中点弦,则中点弦的⽅程就是2200002222x x y y x y a b a b+=+,是直线⽅程.弦中点M 的轨迹⽅程:在椭圆中,过椭圆内点000P x y (,)的弦AB ,其中点M 的⽅程就是22002222x x y y x y a b a b+=+,仍为椭圆.这两个⽅程有些相似,要擦亮眼睛,千万不要搞混了.圆锥曲线必背⼝诀(红字为⼝诀)-双曲线⼀、双曲线定义⼆、双曲线的性质定理基本同椭圆,有所区别:实轴虚轴与焦距,形似勾股弦定理①准线⽅程准焦距,a ⽅、b ⽅除以c ②通径等于 2 e p ,切线⽅程⽤代替③焦三⾓形计⾯积,半⾓余切连乘b ④注解:1实轴2a =,虚轴2b =,焦距2c =,则:222a b c +=2准线⽅程2a x c=± (a ⽅除以c )准焦距p :焦点到准线的距离:2b pc = (b ⽅除以c )3通径等于2 e p ,切线⽅程⽤代替双曲线的通径d :过焦点垂直于长轴的直线与双曲线的两交点之间的距离称为双曲线的通径.(通径22c b 2b 2a c ad 2ep =??==)过双曲线上000P x y (,)点的切线⽅程,⽤000P x y (,)等效代替双曲线⽅程得到,等效代替后的是切线⽅程是:0022x x y y1a b-=4焦三⾓形计⾯积,半⾓余切连乘b焦三⾓形:以双曲线的两个焦点12F F ,为顶点,另⼀个顶点P 在椭圆上的三⾓形称为焦三⾓形.半⾓是指12F PF γ=∠的⼀半.双曲线2222x y 1a b-=的左右焦点分别为12F F ,,点P 为双曲线上异于顶点任意⼀点12F PF γ∠=,则双曲线的焦点三⾓形满⾜:2122b PF PF 1cos γ=- 其⾯积为;122F PF S b co 2t γ=.证明:设21PF m PF n ,==,则m n 2a -=在12F PF ?中,由余弦定理得:222121212PF PF 2PF PF F F cos γ+-=,即:222m n 2mn 4c cos γ+-?=22224a 4b m n 4b ()=+=-+ 即:2222m n 2mn m n 4b cos ()γ+-?=-+即:22mn 2mn 4b cos γ-?=,即:22b mn 1(cos )γ=-即:22b mn 1cos γ=-,即:2122bPF PF 1cos γ=-那么,焦点三⾓形的⾯积为:12F PF 1S mn 2sin γ?=?212b 21sin cos γγ=?-2222b 22b 122sin cossin cos sinγγγγγ==?-2b 2cot γ= 故:122F PF S b 2cot γ= 同时:12F PF 12P P 1S F F y c y 2?=?=?,故:2p b y c 2cot γ=±? 双曲线的焦点三⾓形的⾯积为:122F PF S b co 2t γ=.三、双曲线的相关公式切线平分焦周⾓,称为弦切⾓定理①切点连线求⽅程,极线定理须牢记②弦与中线斜率积,准线去除准焦距③细看中点弦⽅程,恰似弦中点轨迹④注解:1弦切⾓定理:切线平分椭圆焦周⾓的外⾓,平分双曲线的焦周⾓.焦周⾓是焦点三⾓形中,焦距所对应的⾓. 弦切⾓是指双曲线的弦与其切线相交于双曲线上时它们的夹⾓,当弦为焦点弦时(过焦点的弦),那么切线是两个焦点弦的⾓平分线.如图,12F PF ?是焦点三⾓形,12F PF ∠为焦周⾓,PT 为双曲线的切线. 则PT 平分12F PF ∠.2若000P x y (,)在双曲线2222x y 1a b-=外,以包含焦点的区域为内,不包含焦点的区域为外,则过0P 作双曲选的两条切线,切点为1P 、2P ,则点0P 和切点弦12P P 分别称为双曲线的极点和极线,切点弦12P P 的直线⽅程即极线⽅程是0022x xy y1a b-=(称为极线定理)3弦指双曲线内的⼀弦AB .中线指弦AB 的中点M 与原点O 的连线,即OAB ?得中线.这两条直线的斜率的乘积,等于准线距离2c a x c =去除准焦距2b p c=,其结果是:2AB OM2c p b k k x a==4中点弦AB 的⽅程:在双曲线中,若弦AB 的中点为00M x y (,),称弦AB 为中点弦,则中点弦的⽅程就是:2200002222x x y y x y aba b-=-,它是直线⽅程. 弦中点M 的轨迹⽅程:在双曲线中,过双曲线外⼀点000P x y (,)的弦AB ,其AB 中点M 的⽅程就是22002222x x y y x y a b a b-=-,仍为双曲线.这两个⽅程有些相似,要擦亮眼睛,千万不要搞混了.圆锥曲线必背⼝诀(红字为⼝诀)-抛物线⼀、抛物线定义抛物线,有定义,定点定线等距离12⼆、抛物线性质焦点准线极点线①,两臂点乘积不变②焦弦切线成直⾓,切点就是两端点③端点投影在准线,连结焦点垂直线④焦弦垂直极焦线⑤,切线是⾓平分线⑥直⾓梯形对⾓线,交点就是本原点⑦焦弦三⾓计⾯积,半个p ⽅除正弦⑧注解:1抛物线的焦点和准线是⼀对极点和极线.抛物线⽅程:2y 2px =,焦点(,)p F 02,准线p p x 2=-(抛物线的顶点(,)O 00到定点(,)p F 02和定直线p p x 2=-距离相等) 焦弦:过焦点的直线与抛物线相交于两点A 和B ,则AB 称为焦弦.弦中点(,)M M M x y ,A B M x x x 2+=,A B M y yy 2+= 焦弦⽅程:()p y k x 2=-,k 为斜率. 2焦点三⾓形两边OA 和OB 的点乘积为定值,且夹⾓是钝⾓. 证明:焦弦AB 满⾜的条件()2y 2pxp y k x 2?=??=- ()22p k x 2px 2-=? ()22222k p k x k 2px 04-++=由韦达定理得:2A B px x 4=2A B py y 22p p 2==-=-?=-,即:2A B p x x 4=,2A B y y p =- ①且:2A A B B A B A B 3OA OB x y x y x x y y p 04(,)(,)?=?=+=-<. 故:焦点三⾓形两边之点乘积为定值.3即:焦弦两端点的切线互相垂直. 证明:如图,由抛物线⽅程:2y 2px =得到导数:yy p '=,即:py y'=故:AEA p k y =,BE Bp k y = 于是:2AE BEA B A Bp p p k k y y y y ?=?=将①式2A B y y p =-代⼊上式得:AE BE k k 1?=-即:AE BE ⊥,故焦弦端点在准线的投影点与焦点构成直⾓三⾓形. 4即:焦弦端点在准线的投影点与焦点构成直⾓三⾓形. 证明:坐标B p C y 2(,)-,A p D y 2(,)-则:B CF p y (,)=-,A DF p y (,)=- 于是:2A B CF DF p y y ?=+将①式2A B y y p =-代⼊上式得:CF DF 0?= 故:CF DF ⊥即:焦弦端点A B ,在准线的投影点D C ,,则CF DF ⊥,即:焦弦端点在准线的投影点与焦点构成直⾓三⾓形.5若焦弦AB 对应的极点E ,则EF 为极焦线,于是EF AB ⊥⽤向量⽅法可证.由于M 是AB 的中点,AEB ?为直⾓三⾓形,计算可得E 是DC 的中点,故:ED EF EC == 由向量法可证EF AB 0?=即:焦弦AB 与极焦线EF 互相垂直. 6即:切线平分焦弦的倾⾓(或倾⾓的外⾓) 如图:因为ADE ?和AFE ?都是直⾓三⾓形,且由定义知:AF AD =,AE AE =故ADE AFE ??≌,则对应⾓相等. 即:AE 是DAF ∠的⾓平分线同理,BE 是CBF ∠的⾓平分线 7即:直⾓梯形ABCD 对⾓线相交于原点即:A O C ,,三点共线;B O D ,,三点共线. ⽤向量法证明:OA CO //,OB DO //证明:坐标2A A y A y 2p (,),2B B y B y 2p (,),B p C y 2(,)-,A pD y 2(,)-向量:2A A y OA y 2p (,)=,B pCO y 2(,)=-各分量之⽐:2A2x A 2xy OA y 2p p p CO 2()()==,2y A AB A B y OA y y y y y CO ()()==--将①式2A B y y p =-代⼊上式得:22yA A2A By OA y y y y p CO ()()==- 故:y x xyOA OA OACO CO CO()()()()==,即:OA CO // 同理:OB DO //.直⾓梯形ABCD 对⾓线相交于原点. 8即:焦弦三⾓形的⾯积为:sin 2 AOBp S 2α= (α为焦弦的倾⾓)证明:AB AF BF =+A B A B p p x x x x p 22=+ ++=++M p2x 2()=+2EM = 如图:GF 2OF p == 则:2EF GF 1pEM sin sinsin sin αααα==?= E于是:22pAB sin α= 故:AOB1S OF AB 2sin α?=221p 2p p 222sin sin sin ααα==附:圆锥曲线必背----极坐标圆锥曲线的极坐标以准焦距p 和离⼼率e 来表⽰常量,以极径ρ和极⾓θ来表⽰变量.0ρ≥,[,)o 0360θ∈以焦点(,)F 0θ为极点(原点O ),以椭圆长轴、抛物线对称轴、双曲线的实轴为极轴的建⽴极坐标系.故准线是到极点距离为准焦距p 、且垂直于极轴的直线L . 极坐标系与直⾓坐标系的换算关系是:ρ=,arctan y xθ= 或者:cos x ρθ=,sin y ρθ= 特别注意:极坐标系中,以焦点为极点(原点),⽽直⾓坐标系中以对称点为原点得到标准⽅程. 如图,O 为极点,L 为准线,则依据定义,到定点(极点)和到定直线(准线)的距离之⽐为定值(定值e )的点的轨迹为圆锥曲线. 所以,对极坐标系,请记住:⑴极坐标系的极点O 是椭圆的左焦点、抛物线的焦点、双曲线的右焦点;⑵曲线上的点(,)Pρθ到焦点F的距离是ρ,到准线的距离是cospρθ+,根据定义:cosepρρθ=+即:cosep eρθρ+=,即:cosep eρρθ=-,即:1eρθ=-①这就是极坐标下,圆锥曲线的通式.⑶对应不同的e,呈现不同的曲线. 对双曲线,只是右边的⼀⽀;对抛物线,开⼝向右.将极轴旋转o180,α和θ分别对应变换前后的极⾓,即转⾓为o180θα=+,则极坐标⽅程变换前⽅程为:cosep1eρα=-变换后⽅程为:cosep1eρθ=+②此时的极坐标系下,此时有:⑵对应不同的e,呈现不同的曲线对双曲线,只是左边的⼀⽀;对抛物线,开⼝向左.⑴将极轴顺时针旋转o90,即:o 90θα=+,则情况如图.圆锥曲线的⽅程为:sin ep1e ρθ=- ③此时的极坐标系下:对应于直⾓坐标系下,焦点在y 轴的情况,且极点O 对应于椭圆下⽅的焦点,双曲线上⽅的焦点,抛物线的焦点.对双曲线,只是y 轴上边的⼀⽀;对抛物线,开⼝向上. ⑵如果将极轴逆时针旋转o 90,即:o 90θα=-,则情况如图. 圆锥曲线的⽅程为:sin ep1e ρα=+ ③此时的极坐标系下:对应于直⾓坐标系下,焦点在y 轴的情况,且对应于椭圆上⽅的焦点,双曲线下⽅的焦点,抛物线的焦点.对双曲线,只是y 轴下边的⼀⽀;对抛物线,开⼝向下.⑴在极坐标系中,圆锥曲线的通式为:=cos ep1e ρθ- ①即:cos e ep ρρθ-=,即:cos ep e ρρθ=+即:(cos )(cos )(cos )2222222ep e e p e 2e p ρρθρθρθ=+=++ ②将222x y ρ=+,cos x ρθ=代⼊②式得:2222222x y e p e x 2e px +=++即:()2222221e x 2e px y e p --+= ③当e 1≠时有:()[()]()()22222222222222--++=+---- 即:()()()22222 2222222e p e e p 1e x y e p 11e 1e 1e --+=+=--- 即:()()22222222222e px y 1e1e p e p1e 1e --+=-- ④⑴当e 1<时,令()22222e p a 1e =-,2222e p b 1e=-,22e p c 1e=-则:()222222222e p e p a b 1e 1e-=---[()]()()2222e p e p 11e 1e 1e =--=--⽽:()()2422222222e p e p c a b 1e 1e ===--- 代⼊④式得:()2222x c y 1ab-+= ⑤这是标准的椭圆⽅程. ⑵当e 1>时,令()222 22e p a e 1=-,2222e p b e 1=-,22e p c e 1=-则:()222222222e p e p a b e 1e 1+=+--[()]()()2242e p e p 1e 1e 1e 1=+-=-- ⽽:()()2422222222e p e p c a b e 1e 1===+-- 代⼊④式得:()2222x c y 1ab+-= ⑥这是标准的双曲线⽅程.⑶当e 1=时,由③式()2222221e x 2e px y e p --+=得:222px y p -+=即:()22p y 2px p 2p x 2=+=+ 即:()2p y 2p x 2=+ ⑦这是标准的抛物线⽅程.。
圆锥曲线方程-抛物线(知识点、典型例题、考点、练习)

抛物线 典例剖析知识点一 抛物线概念的应用已知抛物线y 2=2x 的焦点是F ,点P 是抛物线上的动点,又有点A (3,2),求|P A |+|PF |的最小值,并求出取最小值时P 点的坐标.解将x=3代入抛物线方程 y 2=2x ,得y=〒6.6>2,∴点A 在抛物线内部.设抛物线上点P 到准线l : x=21的距离为d ,由定义知|PA|+|PF|=|PA|+d , 当PA ⊥l 时,|PA|+d 最小, 最小值为27,即|PA|+|PF|的最小值为27, 此时P 点纵坐标为2,代入y 2=2x ,得x=2, ∴点P 坐标为(2,2).知识点二 求抛物线的标准方程求适合下列条件的抛物线的标准方程:(1)过点(-3,2);(2)焦点在直线x -2y -4=0上.分析 设出抛物线的标准形式,依据条件求出p 的值.解 (1)设抛物线标准方程为y 2=-2px 或x 2=2py (p >0),则将点(-3,2)代入方程得2p =43,或2p =92,故抛物线的标准方程为y 2=-43x ,或x 2=92y .(2)①令x =0,由方程x -2y -4=0,得y =-2. ∴抛物线的焦点为F (0,-2).设抛物线方程为x 2=-2py ,则由p2=2,得2p =8.∴所求的抛物线方程为x 2=-8y .②令y =0,由x -2y -4=0,得x =4. ∴抛物线的焦点为F (4,0).设抛物线方程为y 2=2px ,由p2=4,得2p =16.∴所求抛物线方程为y 2=16x .知识点三 抛物线在实际中的应用汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反射镜的轴垂直,灯泡位于抛物线焦点处,已知灯口的直径是24 cm ,灯深10 cm ,那么灯泡与反射镜的顶点(即截得抛物线顶点)距离是多少?分析 确定抛物线方程,求出抛物线的焦点到其顶点的距离解 取反射镜的轴即抛物线的对称轴为x 轴,抛物线的顶点为坐标原点,建立直角坐标系xOy ,如图所示.因灯口直径|AB|=24.灯深|OP|=10, 所以点A 的坐标是(10,12).设抛物线的方程为y 2=2px(p>0).由点A(10,12)在抛物线上,得122=2p ×10, ∴p=7.2.抛物线的焦点F 的坐标为(3.6,0).因此灯泡与反射镜顶点的距离是3.6 cm.知识点四 抛物线几何性质的简单应用抛物线的顶点在原点,对称轴重合于椭圆9x 2+4y 2=36短轴所在的直线,抛物线焦点到顶点的距离为3,求抛物线的方程.分析 先确定抛物线方程的形式,再依条件求待定参数.解 椭圆9x 2+4y 2=36可化为x 24+y 29=1,得抛物线的对称轴为x 轴.设抛物线的方程为y 2=ax (a ≠0), 又抛物线的焦点到顶点的距离为3,则有|a4|=3,∴|a |=12,即a =±12.故所求抛物线方程为y 2=12x ,或y 2=-12x .知识点五 直线与抛物线已知过抛物线y 2=2px (p >0)的焦点的直线交抛物线于A 、B 两点,且|AB |=52p ,求AB 所在的直线方程.解 焦点F (p2,0),设A (x 1,y 1)、B (x 2,y 2),若AB ⊥Ox ,则|AB |=2p <52p ,不合题意.所以直线AB 的斜率存在,设为k ,则直线AB 的方程为y =k (x -p2),k ≠0.由⎩⎪⎨⎪⎧y =k (x -p 2),y 2=2px ,消去x ,整理得ky 2-2py -kp 2=0.韦达定理得,y 1+y 2=2pk,y 1y 2=-p 2.∴|AB |=(x 1-x 2)2+(y 1-y 2)2=(1+1k 2)·(y 1-y 2)2=1+1k2·(y 1+y 2)2-4y 1y 2=2p (1+1k 2)=52p .解得k =±2.∴AB 所在直线方程为y =2(x -p 2),或y =-2(x -p 2).知识点六 抛物线的焦点弦问题AB 是过抛物线y 2=2px (p >0)焦点F 的弦,M 是AB 的中点,l 是抛物线的准线,MN ⊥l ,N 为垂足.求证:(1)AN ⊥BN ; (2)FN ⊥AB ;(3)若MN 交抛物线于Q ,则Q 平分MN .证明 (1)作AC ⊥l ,垂足为C ,作BD ⊥l ,垂足为D ,在直角梯形ABDC 中, ∵|AF|=|AC|,|BF|=|BD|, ∴|MN|=21(|AC|+|BD|) =21(|AF|+|BF|) =21|AB|, 由平面几何知识可知△ANB 是直角三角形,即AN ⊥BN. (2)∵|AM|=|NM|, ∴∠MAN=∠MNA , ∵AC ∥MN ,∴∠CAN=∠MNA ,∴∠MAN=∠CAN.在△ACN 和△AFN 中,|AN|=|AN|,|AC|=|AF|, 且∠CAN=∠FAN ,∴△ACN ≌△AFN , ∴∠NFA=∠NCA=90°, 即FN ⊥AB.(3)在Rt △MNF 中,连结QF , 由抛物线的定义及(2)的结论得 |QN|=|QF|⇒∠QNF=∠QFN ,且∠QFN=90°-∠QFM ,∠QMF=90°-∠QNF , ∴∠QFM=∠QMF ,∴|QF|=|QM|, ∴|QN|=|QM|,即Q 平分MN.知识点七 抛物线的综合问题过抛物线y 2=2px (p >0)的焦点F 作倾斜角为θ的直线交抛物线于A 、B 两点,设△AOB 的面积为S (O 为原点).(1)用θ、p 表示S ;(2)求S 的最小值;当最小值为4时,求抛物线的方程.解 (1)设直线y =k ⎝⎛⎭⎫x -p2,代入y 2=2px , 得y 2=2p ⎝⎛⎭⎫y k +p 2,即y 2-2pk y -p 2=0,∴y 1+y 2=2pk,y 1y 2=-p 2.∴|AB |= 1+1k2·(y 1+y 2)2-4y 1y 2= k 2+1k 2·4p 2k2+4p 2=(1+1k 2)2p =(1+1tan 2θ)2p=2p sin 2θ.① 当直线AB ⊥x 轴时,①也成立.∴S =12|OF ||AF |sin θ+12|OF ||BF |sin(π-θ)=12|OF ||AB |sin θ =12·p 22p sin 2θsin θ=p 22sin θ. (2)当θ=90°时,S min =12p 2.若S min =4,则12p 2=4.∴p =2 2.∴此时抛物线的方程为y 2=42x .考题赏析1.(辽宁高考)已知点P 是抛物线y 2=2x 上的一个动点,则点P 到点(0,2)的距离与点P 到该抛物线准线的距离之和的最小值为( )A.172 B .3 C. 5 D.92解析 如图所示,由抛物线的定义知,点P 到准线x =-12的距离d 等于点P 到焦点的距离|PF |.因此点P 到点(0,2)的距离与点P 到准线的距离之和可转化为点P 到点(0,2)的距离与点P到点F 的距离之和,其最小值为点M (0,2)到点F ⎝⎛⎭⎫12,0的距离,则距离之和的最小值为4+14=172.答案 A2.(全国Ⅰ高考)已知抛物线y =ax 2-1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为________.解析 ∵y =ax 2-1,∴y +1=ax 2.令y +1=y ′,x =x ′,则y ′=ax ′2,∴x ′2=2×12ay ′,∴x ′2=1a y ′的焦点坐标为⎝⎛⎭⎫0,14a ,即y +1=14a , ∴y =ax 2-1的焦点坐标为⎝⎛⎭⎫0,14a -1. 又y =ax 2-1的焦点是原点,∴14a =1,∴a =14.∴y =14x 2-1.令x =0,得y =-1,令y =0,得x =±2.故y =14x 2-1与两坐标轴的三个交点为(0,-1),(2,0),(-2,0),∴围成三角形面积为S =12×4×1=2.答案 23.(全国Ⅱ高考)已知F 是抛物线C :y 2=4x 的焦点,A 、B 是抛物线C 上的两个点,线段AB 的中点为M (2,2),则△ABF 的面积等于________.解析 设A (x 1,y 1),B (x 2,y 2),则y 21=4x 1,y 22=4x 2. ∴(y 1+y 2)(y 1-y 2)=4(x 1-x 2).∵x 1≠x 2,∴y 1-y 2x 1-x 2=4y 1+y 2=1.∴直线AB 的方程为y -2=x -2,即y =x . 将其代入y 2=4x ,得A (0,0)、B (4,4).∴|AB |=4 2.又F (1,0)到y =x 的距离为22,∴S △ABF =12×22×42=2.答案 21.抛物线y 2=ax (a ≠0)的焦点到其准线的距离是( ) A.|a |4 B.|a |2C .|a |D .-a2答案 B解析 因为y 2=ax ,所以p =|a |2,即该抛物线的焦点到其准线的距离为|a |2,故选B.2.抛物线y 2=2px (p >0)上一点M 到焦点的距离是a (a >p2),则点M 的横坐标是( )A .a +p 2B .a -p2C .a +pD .a -p 答案 B解析 由抛物线的定义知:点M 到焦点的距离a 等于点M 到抛物线的准线x =-p2的距离,所以点M 的横坐标即点M 到y 轴的距离为a -p2.3.已知抛物线的方程为标准方程,焦点在x 轴上,其上点P (-3,m )到焦点F 的距离为5,则抛物线方程为( )A .y 2=8xB .y 2=-8xC .y 2=4xD .y 2=-4x 答案 B解析 点P (-3,m )在抛物线上,焦点在x 轴上,所以抛物线的标准方程可设为y 2=-2px (p >0).由抛物线定义知|PF |=3+p2=5.所以p =4,所以抛物线的标准方程是y 2=-8x .应选B.4.抛物线y 2=ax 的焦点与双曲线x 23-y 2=1的左焦点重合,则这条抛物线的方程是( )A .y 2=4xB .y 2=-4xC .y 2=-42xD .y 2=-8x 答案 D解析 因为x 23-y 2=1的左焦点为(-2,0),所以抛物线开口向左,所以a <0,且p =|a |2=4,所以a =-8,所以抛物线方程为y 2=-8x ,故选D.5.已知F 为抛物线C :y 2=4x 的焦点,过F 且斜率为1的直线交抛物线C 于A 、B 两点.设|F A |>|FB |,则|F A |与|FB |的比值等于________.答案 3+2 2解析 ∵y 2=4x 的焦点坐标为 F (1,0),准线方程为x =-1,∴过F 且斜率为1的直线方程为y = x - 1.将其代入y 2= 4x 得 x 2 - 6x + 1=0.∴x 1, 2 =62± = 3〒22.∵|FA|>|FB|,∴x A =3+22,x B =3-22.又|FA|= x +1,|FB|= x B +1,∴|FA||FB|== 3+22. 答案 -36. 过抛物线y 2 = 4x 的焦点的直线交抛物线于A 、B 两点,O 为坐标原点,则· 的值是________.. 解析 当直线过焦点且垂直于x 轴时,直线方程为x =1,代入y 2=4x ,y 1,2=±2.A 、B 点的坐标分别为(1,2),(1,-2).∴·OB →=1-4=-3.当直线过焦点不垂直x 轴时,则直线的方程可设为y =k (x -1),设A ,B 坐标分别为(x 1,y 1)(x 2,y 2).则y 21·y 22=16x 1x 2.由⎩⎪⎨⎪⎧y 2=4x ,y =k (x -1),得k 2x 2-(2k +4)x +k 2=0, ·OB →=x 1x 2+y 1y 2=1-4=-3. 7.已知圆A :(x +2)2+y 2=1与定直线l :x =1,若动圆C 与圆A 相外切,且与直线l 相切,求动圆圆心C 的轨迹方程.解 设圆心C 到直线l 的距离为d ,则由题意知|CA |=d +1从而可知圆心C 到点(-2,0)的距离和到定直线x =2的距离相等.所以动圆圆心C 的轨迹是抛物线,其焦点为(-2,0),准线为x =2,故设动圆圆心C 的轨迹方程为y 2=-2px (p >0),由p2=2,得p =4.因此动圆圆心C 的轨迹方程为y 2=-8x .8.已知点M (-2,4)及焦点为F 的抛物线y =18x 2,在此抛物线上求一点P 使|PM |+|PF |的值最小.分析 先根据已知条件画出图形,由定义知,抛物线上的点P 到焦点F 的距离等于P 到准线l 的距离d ,所以求|PM |+|PF |的最小值问题可转化为求|PM |+d 的最小值问题,让点P 在抛物线上运动,容易发现当点P 运动到过点M 且与x 轴垂直的直线与抛物线的交点处时,|PM |+d 最小.解 如图,设MN ⊥x 轴,与准线交于N ,与抛物线交于点P ,在抛物线上任取一点P ′,连P ′M ,P ′F ,作P ′N 垂直于准线,垂足为N ′.由抛物线的定义,|PN|=|PF|,|P ′N ′|=|P ′F||P ′M|+|P ′N ′|=|P ′M|+|P ′F| |PN|+|PM|=|PM|+|PF|∵|P ′M|+|P ′N ′|≥|PN|+|PM| ∴|P ′M|+|P ′F|≥|PM|+|PF|这就是说,当P ′与P 重合时,|PM|+|PF|的值最小解方程组22,1,8x y x =-⎧⎪⎨=⎪⎩得P(-2,12). 9.已知抛物线y 2=2x ,过点Q (2,1)作一条直线交抛物线于A 、B 两点,试求弦AB 中点的轨迹方程.解 设弦AB 的中点M (x ,y ),A (x 1,y 1),B (x 2,y 2),则有y 21=2x 1,y 22=2x 2, ∴y 1-y 2x 1-x 2=2y 1+y 2,又y 1+y 2=2y ,∴y 1-y 2x 1-x 2=1y,即k AB =1y .又k MQ =y -1x -2,由题意知k MQ =k AB .∴y -1x -2=1y,整理, 得y 2-x -y +2=0.所以,弦AB 中点的轨迹方程为y 2-x -y +2=0.10.抛物线的顶点在原点,以x 轴为对称轴,经过焦点且倾斜角为135°的直线,被抛物线所截得的弦长为8,试求抛物线方程.解 如右图所示,依题意设抛物线方程为y 2=2px(p>0),则直线方程为y=-x+12p. 设直线交抛物线于A(x 1,y 1), B(x 2,y 2),则由抛物线定义得|AB|=|AF|+|FB|=|AC|+|BD| =x 1+2P + x 2 + 2P , 即x 1+x 2 +p=8.①又A (x 1,y 1)、B (x 2,y 2)是抛物线和直线的交点.由⎩⎪⎨⎪⎧y =-x +12p ,y 2=2px ,消去y 得x 2-3px +p 24=0,∴x 1+x 2=3p ,将其代入①得p =2. ∴所求抛物线方程为y 2=4x .当抛物线方程设为y 2=-2px (p >0)时,同理可求得抛物线方程为y 2=-4x . 故抛物线的方程为y 2=4x 或y 2=-4x .讲练学案部分2.4.1 抛物线及其标准方程.对点讲练知识点一 求抛物线的标准方程分别求出满足下列条件的抛物线的标准方程.(1)过点(3,-4).(2)焦点在直线x +3y +15=0上. 解 (1)∵点(3,-4)在第四象限,∴抛物线的标准方程为y 2=2px (p >0)或x 2=-2p 1y (p 1>0),把点(3,-4)的坐标分别代入得(-4)2=2p ×3,32=-2p 1×(-4)即2p =163,2p 1=94∴所求抛物线的方程为y 2=163x 或x 2=-94y .(2)令x =0得y =-5;令y =0得x =-15 ∴抛物线的焦点为(0,-5)或(-15,0)∴所求抛物线的标准方程为y 2=-60x 或x 2=-20y .【反思感悟】 求抛物线方程应首先确定焦点的位置,进而确定方程的形式,然后利用已知条件求p 的值.求满足下列条件的抛物线的方程.(1)以坐标轴为对称轴,且过点A (2,3);(2)以坐标轴为对称轴,焦点到准线的距离为52.解 (1)由题意,方程可设为y 2=mx 或x 2=ny , 将点A (2,3)的坐标代入,得32=m ·2或22=n ·3,∴m =92或n =43.∴所求的抛物线方程为y 2=92x 或x 2=43y .(2)由焦点到准线的距离为52,可知p =52.∴所求抛物线方程为y 2=5x 或y 2=-5x 或x 2=5y 或x 2=-5y .知识点二 抛物线定义的应用已知抛物线的顶点在原点,对称轴是x 轴,抛物线上的点M (-3,m )到焦点的距离等于5,求抛物线的方程和m 的值.解 设抛物线的方程为y 2=-2px (p >0),则准线方程为x =p2.∵点M (-3,m )是抛物线上的点,根据抛物线定义,M 点到焦点的距离等于M 点到准线的距离∴|-3|+p2=5 ∴p =4.∴抛物线方程为y 2=-8x .又点M (-3,m )在抛物线上故m 2=-8×(-3) ∴m =±2 6.【反思感悟】 涉及抛物线上一点与焦点的距离问题要注意用定义转化为该点到准线的距离,可简化计算.若动圆与圆(x -2)2+y 2=1相外切,又与直线x +1=0相切,则动圆圆心的轨迹是( )A .椭圆B .双曲线C .双曲线的一支D .抛物线答案 D解析 设动圆的圆心为M ,半径为r ,动圆与圆(x -2)2+y 2=1相外切,则M 到定点(2,0)的距离为r +1,动圆与直线x =-1相切,则点M 到定直线x =-1的距离为r ,所以M 到定点(2,0)和到定直线x =-2的距离相等,由抛物线定义知,答案选D.知识点三 抛物线知识在实际中的应用喷灌的喷头装在直立管柱OA 的顶点A 处,喷出水流的最高点B 高5 m ,且与OA 所在的直线相距4 m ,水流落在以O 为圆心,半径为9 m 的圆上,则管柱OA 的长是多少?解 如图所示,建立直角坐标系,设水流所形成的抛物线的方程为x 2= -2py(p>0),点C(5, -5)在抛物线上,所以25= -2p ·(-5),2p=5,所以抛物线的方程为x 2= -5y ,点A(-4,y 0)在抛物线上,所以16= -5y 0,y 0 = -165,所以OA 的长为5 - 165=1.8 (m).∴管柱OA 的长是1.8 m.【反思感悟】 根据题意,建立直角坐标系,用待定系数法求出抛物线方程,再利用抛物线方程解决实际问题.抛物线型拱桥顶距离水面2米,水面宽4米,当水下降1米后,水面宽________米.答案 2 6解析 可设抛物线方程为x 2=-2py ,则点(-2,-2)在抛物线上,则有:4=4p . ∴p =1,抛物线方程为x 2=-2y ,当y =-3时,x =±6. ∴水面宽为2 6. 课堂小结:1.四个标准方程的区分:焦点在一次项字母对应的坐标轴上,开口方向由一次项系数的符号确定.当系数为正时,开口方向为坐标轴的正方向;系数为负时,开口方向为坐标轴的负方向.2.焦点在y 轴上的抛物线的标准方程x 2=2py 通常又可以写成y=ax 2,这与以前学习的二次函数的解析式是完全一致的,但需要注意的是,由方程y=ax 2来求其焦点和准线时,必须先化成标准形式.3.经过抛物线的焦点的弦称为抛物线的焦点弦,它有以下特性:设焦点弦AB 的端点坐标分别为A (x 1 , y 1),B(x 2,y 2),则y 1y 2= - p 2, x 1x 2 = 24p ,|AB|= x 1 + x 2 + p.课时作业一、选择题1.已知抛物线的顶点在原点,对称轴为x 轴,焦点在曲线x 24-y 22=1上,则抛物线方程为( )A .y 2=8xB .y 2=4xC .y 2=2xD .y 2=±8x 答案 D解析 由题意知抛物线的焦点为双曲线x 24-y 22=1的顶点,即(-2,0)、(2,0),所以抛物线的方程为y 2=8x 或y 2=-8x .2.抛物线y =mx 2(m <0)的焦点坐标是( )A .(0,m 4)B .(0,14m )C .(0,-m 4)D .(0,-14m)答案 B解析 由于抛物线方程可化为x 2=1my (m <0),所以抛物线的焦点在y 轴的负半轴上,且2p =-1m ,所以p 2=-14m ,所以抛物线的焦点坐标是(0,14m),答案选B.3.过点M (2,4)作与抛物线y 2=8x 只有一个公共点的直线l 有( ) A .0条 B .1条 C .2条 D .3条 答案 C解析 容易发现点M (2,4)在抛物线y 2=8x 上,这样l 过M 点且与x 轴平行时,l 与抛物线有一个公共点,或者l 在M 点上与抛物线相切,故选C.4.已知P 1(x 1,y 1),P 2(x 2,y 2)是抛物线y 2=2px (p >0)上不同的两点,则y 1·y 2=-p 2是直线P 1P 2通过抛物线焦点的( )A .充分不必要条件B .充分必要条件C .必要不充分条件D .既不充分也不必要条件 答案 B解析 设直线P 1P 2的斜率为k ,在x 轴上的截距为x 0,则P 1P 2的方程为y =k (x -x 0), x =1ky +x 0(k =0时只有一个交点不合题意), 所以y 2=2p ⎝⎛⎭⎫1k y +x 0,即y 2-2pky -2px 0=0. 当直线P 1P 2过焦点时,x 0=p2,则y 1y 2=-p 2.当y 1y 2=-p 2时,即-2px 0=-p 2,则x 0=p2,直线过焦点.当斜率不存在时也可验证是充要条件.5.过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点,如果x 1+x 2=6,那么|AB |等于( )A .10B .8C .6D .4 答案 B解析 方法一 由已知得抛物线焦点为(1,0),过焦点的直线设为y =k (x -1)(由x 1+x 2=6知,此直线不平行于y 轴,因而k 存在).由⎩⎪⎨⎪⎧y =k (x -1),y 2=4x ,消去y 得k 2x 2-2(k 2+2)x +k 2=0. 由⎩⎪⎨⎪⎧x 1+x 2=2(k 2+2)k 2=6,x 1·x 2=1得k =±1.所以|AB |2=(1+k 2)(x 1-x 2)2=2(x 1-x 2)2=64,故|AB |=8.方法二 由焦半径公式|AB |=|AF |+|BF |=x 1+p 2+x 2+p2=8.二、填空题6.抛物线2y 2+5x =0的焦点坐标为____________,准线方程为______________.答案 ⎝⎛⎭⎫-58,0 x =58解析 化抛物线2y 2+5x =0为标准方程y 2=-52x,2p =52,p 2=58,所以焦点坐标为(-58,0),准线方程为x =58.7.设点M ⎝⎛⎭⎫3,103与抛物线y 2=2x 上的点P 之间的距离为d 1,P 到抛物线准线l 的距离为d 2,则当d 1+d 2取最小值时,P 点坐标为____________.答案 (2,2)解析 当P 点是M 与焦点F ⎝⎛⎭⎫12,0连线与抛物线交点时,d 1+d 2最小,MF 的方程为y =43x -23,与抛物线y 2=2x 联立得P (2,2). 三、解答题8.过点Q (4,1)作抛物线y 2=8x 的弦AB ,若弦恰被Q 平分,求AB 所在直线方程. 解 设A (x 1,y 1),B (x 2,y 2),因点Q (4,1)为A ,B 的中点则有⎩⎪⎨⎪⎧x 1+x 2=8y 1+y 2=2将A 、B 两点坐标代入y 2=8x .则有⎩⎪⎨⎪⎧y 21=8x 1 ①y 22=8x 2 ②①-②得:(y 1-y 2)(y 1+y 2)=8(x 1-x 2),由y 1+y 2=2,则有y 1-y 2x 1-x 2=4,∴k AB =4.∴所求直线方程为y -1=4(x -4),即4x -y -15=0.9.一抛物线拱桥跨度为52米,拱顶离水面6.5米,一竹排上有一宽4米、高6米的矩形大木箱,问能否安全通过?解建立坐标系如图,设抛物线方程为 x 2= -2py ,则点(26, -6.5)在抛物线上, ∴262= -2p ·(-6.5),∴p=52,抛物线的方程为x 2= -104y ,当y=-0.5时,x=〒213,则有413>4, 所以木箱能安全通过.10.已知过抛物线y 2=2px (p >0)的焦点F 的直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点. 求证:(1)x 1x 2为定值;(2)1|F A |+1|FB |为定值. 证明 (1)抛物线y 2=2px 的焦点为F ⎝⎛⎭⎫p 2,0,当AB 不垂直于x 轴时,设直线AB 的方程为y =k ⎝⎛⎭⎫x -p2 (k ≠0). 由⎩⎪⎨⎪⎧y =k ⎝⎛⎭⎫x -p 2y 2=2px消去y , 得k 2x 2-p (k 2+2)x +k 2p 24=0.由根与系数的关系得x 1x 2=p 24(定值).当AB ⊥x 轴时,x 1=x 2=p2,x 1x 2=p24也成立.(2)由抛物线的定义知,|F A |=x 1+p 2,|FB |=x 2+p2.又由(1)得x 1x 2=p24,所以1|F A |+1|FB |=1x 1+p 2+1x 2+p2=x 1+x 2+pp 2(x 1+x 2)+x 1x 2+p 24 =x 1+x 2+p p 2(x 1+x 2)+p 22=x 1+x 2+p p 2(x 1+x 2+p )=2p(定值). 2.4.2 抛物线的简单几何性质.对点讲练知识点一 由性质求方程已知抛物线的顶点为坐标原点,对称轴为x 轴,且与圆x 2+y 2=4相交的公共弦长等于23,求这条抛物线的方程.解 设所求抛物线方程为y 2=2px (p >0)或y 2=-2px (p >0),设交点A (x 1,y 1),B (x 2,y 2),(y 1>0,y 2<0),则|y 1|+|y 2|=23,即y 1-y 2=23,由对称性知,y 2=-y 1,代入上式得y 1=3,把y 1=3代入x 2+y 2=4得x =±1.所以点(1,3)在抛物线y 2=2px 上,点(-1,3)在抛物线y 2=-2px 上,所以3=2p 或3=-2p ×(-1).所以p =32,所以所求抛物线方程为y 2=3x 或y 2=-3x .【反思感悟】 (1)由已知的几何条件求抛物线方程,常用待定系数法.(2)由于抛物线是轴对称图形,所以与对称轴垂直的弦一定被对称轴平分.已知抛物线的焦点在x 轴上,直线y =2x +1被抛物线截得的线段长为15,求此抛物线的标准方程.解 ∵抛物线的焦点在x 轴上,∴设它的标准方程为y 2=2px由方程组⎩⎪⎨⎪⎧y 2=2pxy =2x +1得4x 2+(4-2p )x +1=0.∴|x 1-x 2|=(4-2p )2-164=p 2-4p2.∴1+22|x 1-x 2|=52p 2-4p .∴52p 2-4p =15.∴p =6或p =-2. ∴抛物线的方程为y 2=12x 或y 2=-4x .知识点二 与抛物线有关的证明问题过抛物线焦点F 的直线交抛物线于A ,B 两点,通过点A 和抛物线顶点的直线交抛物线的准线于点D ,求证:直线DB 平行于抛物线的对称轴.证明如图所示,以抛物线的对称轴为x 轴,它的顶点为原点,建立直角坐标系. 设抛物线的方程为y 2=2px ,①点A 的坐标为⎝⎛⎭⎫y 202p ,y 0,则直线OA 的方程为 y =2py 0x (y 0≠0),②抛物线的准线方程是x =-p2.③联立②③,可得点D 的纵坐标为y =-p 2y 0④因为点F 的坐标是⎝⎛⎭⎫p 2,0,当AB ⊥x 轴时,|y 0|=p 此时,|OA |=|OD |,∴DB ∥x 轴当AB 与x 轴不垂直时,即y 20≠p 2时,直线AF 的方程为y =2py 0y 20-p 2⎝⎛⎭⎫x -p 2,⑤ 联立①⑤,可得点B 的纵坐标为y =-p 2y 0.⑥由④⑥可知,DB ∥x 轴.【反思感悟】 因抛物线方程的独特形式,较之椭圆与双曲线,它上面的点便于用一个变量表示出来,如y 2=2px 上任一点,可表示为⎝ ⎛⎭⎪⎫y 22p ,y ,注意恰当运用.设抛物线y 2=2px (p >0)的焦点为F ,Q 是抛物线上除顶点外的任意一点,直线QO 交准线于P 点,过Q 且平行于抛物线对称轴的直线交准线于R 点,求证:PF ⊥RF .证明如图所示,设点Q ⎝⎛⎭⎫y 202p ,y 0,则R.(-2p,y 0 ) 直线OQ 的方程为y=02y p x , 当x=-2p 时,解得y=-02y p,∴P =2,20p p y ⎛⎫-- ⎪⎝⎭,又F (2p ,0),∴RF →=⎝⎛⎭⎫p ,p 2y 0,RF →=(p ,-y 0) ∴RF →·RF →=0,∴PF ⊥RF .知识点三 直线与抛物线的交点问题已知抛物线的方程为y 2=4x ,直线l 过定点P (-2,1),斜率为k .k 为何值时,直线l 与抛物线y 2=4x :只有一个公共点;有两个公共点;没有公共点?解 由题意,设直线l 的方程为y -1=k (x +2).由方程组⎩⎪⎨⎪⎧y -1=k (x +2)y 2=4x ,可得:ky 2-4y +4(2k +1)=0.① (1)当k =0时,由方程①得y =1.把y =1代入y 2=4x ,得x =14.这时,直线l 与抛物线只有一个公共点⎝⎛⎭⎫14,1. (2)当k ≠0时,方程①的判别式为 Δ=-16(2k 2+k -1). 1°由Δ=0,即2k 2+k -1=0,解得k =-1,或k =12.于是,当k =-1,或k =12时,方程①只有一个解,从而方程组(*)只有一个解.这时,直线l 与抛物线只有一个公共点.2°由Δ>0,即2k 2+k -1<0,解得-1<k <12.于是,当-1<k <12,且k ≠0时,方程①有两个解,从而方程组有两个解.这时,直线l与抛物线有两个公共点.3°由Δ<0,即2k 2+k -1>0,解得k <-1,或k >12.于是,当k <-1,或k >12时,方程①没有实数解,从而方程组(*)没有解.这时,直线l与抛物线没有公共点.综上,我们可得当k =-1,或k =12,或k =0时,直线l 与抛物线只有一个公共点;当-1<k <12,且k ≠0时,直线l 与抛物线有两个公共点;当k <-1,或k >12时,直线l 与抛物线没有公共点.【反思感悟】 当直线与抛物线的对称轴平行或重合时,抛物线和直线相交,只有一个交点.解决直线与抛物线位置关系问题时,不要忽视这一点,否则容易漏解.直线l :y =kx +1,抛物线C :y 2=4x ,当k 为何值时,l 与C 分别相切、相交、相离?解 将l 和C 的方程联立⎩⎪⎨⎪⎧y =kx +1, ①y 2=4x , ②①式代入②式,并整理,得 k 2x 2+(2k -4)x +1=0.当k ≠0时,是一元二次方程, ∴Δ=(2k -4)2-4k 2=16(1-k ).(1)当Δ=0时,即k =1时,l 与C 相切. (2)当Δ>0时,即k <1时,l 与C 相交. (3)当Δ<0时,即k >1时,l 与C 相离.当k =0时,直线l :y =1与曲线C :y 2=4x 相交.综上所述,当k =0或k <1时,l 与C 相交,当k =1时,l 与C 相切,当k >1时,l 与C 相离.课堂小结:1.在已知抛物线的顶点在坐标原点,对称轴为x 轴,求抛物线的标准方程时,为避免讨论张口的方向可设抛物线的方程为y 2=2ax (a ≠0).此时,不论a>0或a<0,焦点坐标都是(2a,0),准线方程都为x=-2a . 2.抛物线y 2= 2px (p>0)上任一点的坐标可用一个量y 1表示为21(1),2y y p;x 2 = 2py (p>0)上任一点坐标可设为(x 1 , 212x p).3.直线与抛物线的位置关系设直线l :y=kx+m ,抛物线:y 2=2px(p>0),将直线方程与抛物线方程联立整理成关于x 的方程:ax 2+bx+c=0,(1)若a ≠0,当Δ>0时,直线与抛物线相交,有两个交点; 当Δ=0时,直线与抛物线相切,有一个交点; 当Δ<0时,直线与抛物线相离,无公共点.(2)若a=0,直线与抛物线有一个交点,此时直线平行于抛物线的对称轴或与对称轴重合,因此直线与抛物线有一个交点是直线与抛物线相切的必要不充分条件.一、选择题1.P (x 0,y 0)是抛物线y 2=2px (p ≠0)上任一点,则P 到焦点的距离是( )A .|x 0-p 2|B .|x 0+p2|C .|x 0-p |D .|x 0+p | 答案 B解析 当p >0时,由抛物线定义得点P (x 0,y 0)到焦点的距离为x 0+p2,当p <0时由抛物线定义知P (x 0,y 0)到焦点的距离为-p 2-x 0,综上得所求距离为|x 0+p2|,故选B.2.过抛物线y 2=4x 的焦点作直线l 交抛物线于A 、B 两点,若线段AB 中点的横坐标为4,则|AB |等于( )A .10B .8C .6D .4 答案 A解析 设A 、B 两点的横坐标分别为x A 、x B ,则有x A +x B =8,|AB |=|AF |+|BF |=x A +p 2+x B +p2=8+p =8+2=10.3.抛物线y 2=2px 与直线ax +y -4=0的一个交点是(1,2),则抛物线的焦点到该直线的距离为( )A.32 3B.25 5C.710 5D.172 答案 B解析 由已知得抛物线方程为y 2=4x ,直线方程为2x +y -4=0,抛物线y 2=4x 的焦点坐标是F (1,0),到直线2x +y -4=0的距离d =|2+0-4|22+1=255.4.若抛物线y 2=2px (p >0)上三个点的纵坐标的平方成等差数列,那么这三个点到抛物线焦点的距离的关系是( )A .成等差数列B .既成等差数列又成等比数列C .成等比数列D .既不成等比数列也不成等差数列 答案 A解析 设三点为P 1(x 1,y 1),P 2(x 2,y 2),P 3(x 3,y 3),则y 21=2px 1,y 22=2px 2,y 23=2px 3,因为2y 22=y 21+y 23, 所以x 1+x 3=2x 2,即|P 1F |-p 2+|P 3F |-p2=2⎝⎛⎭⎫|P 2F |-p 2, 所以|P 1F |+|P 3F |=2|P 2F |. 二、填空题5.抛物线的顶点在原点,准线垂直于x 轴,且焦点到顶点的距离为4,则其方程为______________________.答案 y 2=16x 或y 2=-16x解析 焦点到顶点的距离即p2=4,p =8.6.抛物线y =x 2上的点到直线2x -y -4=0的距离最短的点的坐标是____________. 答案 (1,1)解析 设点A (x ,y )是符合题设条件的点,则由点到直线的距离公式,得d =55|2x -y -4|=55|2x -x 2-4| =55|-(x -1)2-3|≥355. 当且仅当x =1时,d 取得最小值,故所求点为(1,1).7.设抛物线y 2=8x 的准线与x 轴交于点Q ,若过点Q 的直线l 与抛物线有公共点,则直线l 的斜率的取值范围是____________.答案 [-1,1]解析 Q 点坐标为(-2,0),直线l 的斜率不存在时,不满足题意,所以可设直线l 的斜率为k ,方程为y =k (x +2).当k =0时满足.当k ≠0时,x =1ky -2,代入y 2=8x ,得y 2-8k y +16=0.Δ=64k2-64≥0,k 2≤1,即-1≤k ≤1(k ≠0).综上,-1≤k ≤1.三、解答题8.过点(-3,2)的直线与抛物线y 2=4x 只有一个公共点,求此直线方程. 解 显然,直线存在斜率k , 设其方程为y -2=k (x +3), 由⎩⎪⎨⎪⎧y -2=k (x +3)y 2=4x 消去x ,整理得ky 2-4y +8+12k =0①(1)当k =0时,方程①化为-4y +8=0,即y =2, 此时过(-3,2)的直线方程为y =2,满足条件. (2)当k ≠0时,方程①应有两个相等实根. 由⎩⎪⎨⎪⎧ k ≠0Δ=0即⎩⎪⎨⎪⎧k ≠016-4k (8+12k )=0,得k =13或k =-1.∴直线方程为y -2=13(x +3)或y -2=-(x +3),即x -3y +9=0或x +y +1=0.故所求直线有三条,其方程分别为: y =2,x -3y +9=0或x +y +1=0.9.A ,B 是抛物线y 2=2px (p >0)上两点,满足OA ⊥OB ,其中O 为抛物线顶点.求证: (1)A ,B 两点的纵坐标乘积为定值; (2)直线AB 恒过一定点. 证明(1)设A(x 1,y 1),B(x 2,y 2),x 1≠0,x 2≠0,则y 12=2px 1, y 22=2px 2. ∵OA ⊥OB ,∴x 1x 2 + y 1y 2=0.∴y 12y 22、= 4p 2 x 1x 2 = 24p -y 1y 2.∴y 1y 2 =24p -为定值, x 1x 2=-y 1y 2=4p 2也为定值.∴A 、B 两点的纵坐标乘积为定值.(2)若AB ⊥x 轴,则易知直线AB 方程为x = 2p , 过点(2p,0);若AB 与x 轴不垂直,则x 1≠x 2,y 1+y 2≠0.由y 12-y 22=2p(x 1-x 2),得1212122y y px x y y -++=. ∴直线AB 的方程是y= 122py y + (x -x 1)+y 1,即y = 211121222px px y y y y y ++-+。
圆锥曲线抛物线的基本知识点

圆锥曲线抛物线的基本知识点一、什么是抛物线?抛物线是一种特殊的圆锥曲线,它是由一个固定点(焦点)和一个固定直线(准线)确定的所有点到焦点距离等于该点到准线距离的轨迹。
二、抛物线的基本性质1. 抛物线的对称轴是准线,焦点在对称轴上;2. 抛物线上任意一点与其对称轴的距离相等;3. 焦点到抛物线上任意一点的距离与该点到准线的距离相等;4. 抛物线在对称轴上有最小值,即顶点;5. 抛物线开口方向由焦点和准线位置决定。
三、抛物线方程1. 标准式:y = ax^2 (a>0)其中 a 为常数,表示开口方向和开口大小。
2. 顶点式:y - k = a(x - h)^2其中 (h, k) 为顶点坐标。
3. 参数式:x = at^2, y = 2at其中 t 为参数。
四、抛物线应用1. 物理学中,抛物运动就是指在重力作用下,以一定初速度沿着一个确定角度投掷出去后,运动轨迹为抛物线的运动方式。
2. 工程学中,抛物线常用于设计拱形桥、天桥、高架桥等建筑结构。
3. 数学中,抛物线是圆锥曲线中最简单的一种,也是研究圆锥曲线的基础。
五、抛物线相关概念1. 焦距:焦点到顶点的距离。
2. 焦直线:过焦点且与准线垂直的直线。
3. 焦半径:从焦点到抛物线上任意一点的距离。
4. 垂直平分线:过顶点且与对称轴垂直的直线。
六、抛物线相关定理1. 抛物定理:从焦点到抛物线上任意一点的距离等于该点到准线距离的一半。
2. 切角定理:从焦点引一条切线,该切线与准线之间的夹角等于该切点处法向量与准线方向向量之间夹角(即反射角等于入射角)。
3. 两个相交抛物面交于一条直母线。
圆锥曲线知识点整理

圆锥曲线知识点整理圆锥曲线是高中数学中的重要内容,包括椭圆、双曲线和抛物线。
下面我们来详细整理一下圆锥曲线的相关知识点。
一、椭圆1、定义平面内与两个定点 F₁、F₂的距离之和等于常数(大于|F₁F₂|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
2、标准方程焦点在 x 轴上:\(\frac{x^2}{a^2} +\frac{y^2}{b^2} =1\)(\(a > b > 0\)),其中\(a\)为长半轴长,\(b\)为短半轴长,\(c\)为半焦距,满足\(c^2 = a^2 b^2\)。
焦点在y 轴上:\(\frac{y^2}{a^2} +\frac{x^2}{b^2} =1\)(\(a > b > 0\))3、椭圆的性质(1)范围:对于焦点在 x 轴上的椭圆,\(a \leq x \leq a\),\(b \leq y \leq b\);对于焦点在 y 轴上的椭圆,\(b \leq x \leq b\),\(a \leq y \leq a\)。
(2)对称性:椭圆关于 x 轴、y 轴和原点对称。
(3)顶点:椭圆有四个顶点,焦点在 x 轴上时,顶点坐标为\((\pm a, 0)\),\((0, \pm b)\);焦点在 y 轴上时,顶点坐标为\((0, \pm a)\),\((\pm b, 0)\)。
(4)离心率:椭圆的离心率\(e =\frac{c}{a}\),\(0 < e < 1\),\(e\)越接近 0,椭圆越接近于圆;\(e\)越接近 1,椭圆越扁。
二、双曲线1、定义平面内与两个定点 F₁、F₂的距离之差的绝对值等于常数(小于|F₁F₂|)的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,两焦点间的距离叫做焦距。
2、标准方程焦点在 x 轴上:\(\frac{x^2}{a^2} \frac{y^2}{b^2} = 1\),其中\(a > 0\),\(b > 0\),\(c^2 = a^2 + b^2\)。
完美版圆锥曲线知识点总结

完美版圆锥曲线知识点总结圆锥曲线是数学中的一类重要曲线,广泛应用于几何、物理、工程等领域。
由于其独特的性质和广泛的应用,掌握圆锥曲线的知识对于提高数学水平和解决实际问题具有重要意义。
本文将对圆锥曲线的基本概念、性质和常见类型进行总结和归纳。
一、圆锥曲线的基本概念圆锥曲线是由平面和一个固定点(焦点F)以及一个固定直线(准线L)共同确定的曲线。
根据焦点和准线的位置关系,圆锥曲线分为椭圆、抛物线和双曲线三类。
1. 椭圆:椭圆是焦点到准线的距离之和恒定于两倍焦半径的轨迹。
椭圆具有对称性,焦点位于椭圆的两个焦点之间。
2. 抛物线:抛物线是焦点到准线的距离等于焦半径的轨迹。
抛物线具有对称轴,焦点位于抛物线的焦点上方或下方。
3. 双曲线:双曲线是焦点到准线的距离之差恒定于两倍焦半径的轨迹。
双曲线也具有对称性,焦点位于双曲线的两个焦点之间。
二、圆锥曲线的性质圆锥曲线具有一系列重要的性质,为研究和应用圆锥曲线提供了基础。
1. 对称性:椭圆和双曲线具有两个关于准线和两个焦点的对称轴,抛物线具有一个关于准线的对称轴。
2. 焦距和半焦距:焦距是焦点到对称轴的距离,半焦距是焦距的一半。
焦距对于不同类型的圆锥曲线有不同的计算方法,但都是相对于准线和对称轴计算的。
3. 焦半径:焦半径是焦点到曲线上点的距离,焦半径对于同一曲线上不同点的值是相等的。
4. 离心率:离心率是焦半径与半焦距的比值,用e表示。
对于椭圆,离心率范围在0和1之间;对于抛物线,离心率等于1;对于双曲线,离心率大于1。
5. 焦点和准线的关系:焦点和准线的位置关系决定了曲线的类型。
当焦点在准线上时,曲线是抛物线;当焦点在准线之上时,曲线是椭圆;当焦点在准线之下时,曲线是双曲线。
三、常见类型的圆锥曲线。
(完整版)圆锥曲线知识点归纳总结

完整版)圆锥曲线知识点归纳总结1.圆锥曲线的定义和构造圆锥曲线是在平面上由一个固定点(焦点)和一个固定直线(准线)决定的点集。
三种经典的圆锥曲线分别为椭圆、抛物线和双曲线。
构造圆锥曲线需要确定焦点和准线的位置以及确定参数值。
2.椭圆的特性椭圆是圆锥曲线中最常见的一种形式,由两个焦点和一个大于等于焦距的参数决定。
椭圆的离心率小于1,且离心率等于焦点到准线的距离除以准线长度。
椭圆的焦缩比为焦点到椭圆上某一点的距离与该点到准线的距离的比值。
重要公式:椭圆的标准方程为(x^2/a^2) + (y^2/b^2) = 1;焦缩比为e = c/a,其中c^2 = a^2 – b^2.3.抛物线的特性抛物线是圆锥曲线中的一种形式,由一个焦点和一个参数决定。
抛物线的离心率为1,焦缩比为1.抛物线的轴是准线,顶点是焦点和准线的交点。
重要公式:抛物线的标准方程为(x^2/4a) = y。
4.双曲线的特性双曲线是圆锥曲线中的一种形式,由两个焦点和一个焦距决定。
双曲线的离心率大于1,离心率等于焦点到准线的距离除以准线长度。
双曲线的焦缩比为c^2 = a^2 + b^2.重要公式:双曲线的标准方程为(x^2/a^2) – (y^2/b^2) = 1.5.圆锥曲线的应用圆锥曲线在数学和物理学中都有广泛的应用。
椭圆的应用包括轨道运动、天体力学以及密码学等领域。
抛物线的应用包括抛物面反射器、人工卫星的轨道设计等。
双曲线的应用包括电磁波的传播、双曲线钟的标定等。
6.圆锥曲线的性质圆锥曲线有许多共同的性质,如对称性、切线性质和焦点性质等。
对称性:椭圆和双曲线关于x轴和y轴都有对称性,抛物线关于y轴有对称性。
切线性质:圆锥曲线上任意一点的切线与焦点到该点的连线垂直。
焦点性质:圆锥曲线上的任意一点到焦点的距离与焦缩比成正比。
此文档总结了圆锥曲线的定义、特性、应用和性质等重要知识点,并提供了相关公式和图示。
熟悉了这些知识后,我们可以更加深入地理解和应用圆锥曲线的概念。
圆锥曲线知识点整理

圆锥曲线知识点整理圆锥曲线是数学中的重要概念之一,是一个由一个动点和一个定点之间的线段所确定的曲线。
它包括椭圆、双曲线和抛物线这三种基本形式。
圆锥曲线在几何学、物理学、工程学等领域均有广泛的应用,掌握圆锥曲线的知识对于深入学习和应用这些领域的知识至关重要。
以下是圆锥曲线的一些常见知识点整理:1. 椭圆:椭圆是一个闭合的曲线,它有两个焦点和一个长轴。
定义椭圆的一个特性是到两个焦点的距离之和等于常数,这个常数被称为椭圆的短轴长度。
椭圆的方程可以表示为(x/a)² + (y/b)² = 1,其中a和b分别代表椭圆的半长轴和半短轴。
2. 双曲线:双曲线是一个开放的曲线,它有两个分离的分支。
双曲线的定义也与焦点有关,但与椭圆的定义不同,双曲线的焦点之间的距离差等于常数。
双曲线的方程可以表示为(x/a)² - (y/b)² = 1,其中a和b分别代表双曲线的半长轴和半短轴。
3. 抛物线:抛物线是一个开放的曲线,它有一个焦点和一个直线称为准线。
抛物线的定义与焦点和准线之间的距离以及焦点到曲线上任意一点的距离有关。
抛物线的方程可以表示为y = ax² + bx + c,其中a、b和c分别代表抛物线的系数。
4. 圆锥曲线的性质:圆锥曲线具有许多有趣的性质和特点。
例如,椭圆的离心率小于1,而双曲线的离心率大于1。
抛物线的离心率等于1,它在焦点上有对称性。
此外,圆锥曲线还具有切线、法线、渐近线等几何性质,这些性质在解题和实际应用中非常重要。
5. 圆锥曲线的应用:圆锥曲线在许多领域都有广泛的应用。
在天文学中,行星的轨道可以用椭圆来描述;在工程学中,双曲线常用于天线的设计和无线通信的信号传播;在物理学中,抛物线可用于描述物体在重力作。
圆锥曲线知识点总结

圆锥曲线知识点总结圆锥曲线是二维平面上的几何图形,由直角圆锥与一个平面相交而产生。
它在数学、物理、工程和计算机图形等领域具有广泛的应用。
本文将对圆锥曲线的基本概念、方程、性质和应用进行总结。
一、基本概念1. 定义:圆锥曲线可以分为三种类型,即椭圆、抛物线和双曲线。
它们的定义分别是:- 椭圆:平面上到两个定点的距离之和等于常数的点的集合。
- 抛物线:平面上到一个定点的距离等于定直线的距离的点的集合。
- 双曲线:平面上到两个定点的距离之差等于常数的点的集合。
2. 方程形式:圆锥曲线可以以各种形式的方程表示。
常见的方程形式包括标准方程、参数方程和极坐标方程。
二、椭圆1. 基本性质:椭圆是一个闭合的曲线,两个焦点之间的距离是常数,而离心率小于1。
椭圆对称于两个坐标轴,并且具有两个主轴和两个焦点。
2. 椭圆的方程:椭圆的标准方程是(x-h)²/a² + (y-k)²/b² = 1,其中(h,k)是椭圆的中心坐标,a和b分别是两个半轴的长度。
3. 参数方程:椭圆的参数方程是x = h + a*cos(t),y = k + b*sin(t),其中t是参数的角度。
4. 极坐标方程:椭圆的极坐标方程是r = (a*b) / sqrt((b*cos(t))² + (a*sin(t))²),其中r是极径,t是极角。
5. 应用:椭圆在日常生活中有多种应用,例如天体运动的轨道、水平仪和椭圆形浴缸等。
三、抛物线1. 基本性质:抛物线是一个开放的曲线,焦点和直线称为准线。
抛物线对称于准线,并且具有一个顶点。
2. 抛物线的方程:抛物线的标准方程是y = a*x² + b*x + c,其中a、b和c是常数。
3. 参数方程:抛物线的参数方程是x = t,y = a*t² + b*t + c,其中t是参数。
4. 极坐标方程:抛物线没有显式的极坐标方程。
5. 应用:抛物线在物理学、工程学和天文学中有多种应用,例如抛物线反射器、天体运动的近似模型和喷泉水流的轨迹等。
圆锥曲线知识点总结

圆锥曲线知识点总结
定义与性质:
到平面内一定点的距离r与到定直线的距离d之比是常数e=r/d 的点的轨迹叫做圆锥曲线。
其中,定点叫做该圆锥曲线的焦点,定直线叫做(该焦点相应的)准线,e叫做离心率。
当e>1时为双曲线。
当e=1时为抛物线。
当0<e<1时为椭圆。
形成方式:
用垂直于锥轴的平面去截圆锥,得到的是圆。
把平面渐渐倾斜,得到椭圆。
当平面倾斜到“和且仅和”圆锥的一条母线平行时,得到抛物线。
用平行于圆锥的轴的平面截取,可得到双曲线的一支。
应用领域:
工程:圆锥曲线被应用于各种工程设计中,如建筑、航天、船舶等。
例如,圆锥曲线被用于设计桥梁、隧道、水坝、航天器、船舶等。
光学:圆锥曲线被广泛应用于光学设计中,例如设计反射望远镜和透镜,以及光学系统中的成像和折射问题。
绘画和艺术:圆锥曲线的美学特性使其成为绘画、雕塑、建筑和设计等领域的重要元素。
物理:圆锥曲线可以用来描述粒子在空间中的运动轨迹。
以上仅为圆锥曲线部分知识点的总结,如需更全面的内容,建议查阅数学教材或咨询数学教师。
圆锥曲线知识点归纳汇总 - 抛物线
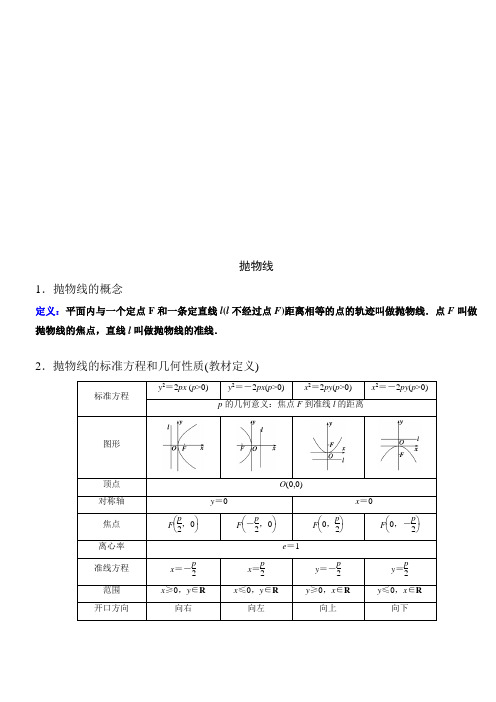
抛物线1.抛物线的概念定义:平面内与一个定点F 和一条定直线l (l 不经过点F )距离相等的点的轨迹叫做抛物线.点F 叫做抛物线的焦点,直线l 叫做抛物线的准线.2.抛物线的标准方程和几何性质(教材定义)标准方程y 2=2px (p >0)y 2=-2px (p >0)x 2=2py (p >0)x 2=-2py (p >0)p 的几何意义:焦点F 到准线l 的距离图形顶点 O (0,0)对称轴 y =0x =0焦点 F ⎝⎛⎭⎫p 2,0F ⎝⎛⎭⎫-p2,0 F ⎝⎛⎭⎫0,p 2 F ⎝⎛⎭⎫0,-p2 离心率 e =1准线方程 x =-p 2x =p 2 y =-p2y =p 2 范围 x ≥0,y ∈Rx ≤0,y ∈Ry ≥0,x ∈Ry ≤0,x ∈R开口方向向右向左向上向下学习奥数的优点1、激发学生对数学学习的兴趣,更容易让学生体验成功,树立自信。
2、训练学生良好的数学思维习惯和思维品质。
要使经过奥数训练的学生,思维更敏捷,考虑问题比别人更深层次。
3、锻炼学生优良的意志品质。
可以培养持之以恒的耐心和克服困难的信心, 以及战胜难题的勇气。
可以养成坚韧不拔的毅力4、获得扎实的数学基本功,发挥创新精神和创造力的最大空间。
3.抛物线的补充的性质及二级结论以开口向右为例:y 2=2px (p >0)1)通径:(过焦点的所有弦长中通径最短为p MN 2=) 2)准线:2px l -=:准线 3)焦半径公式:如图二θp x p AF A cos -=+=12,θpx p BF B cos +=+=12 推导:A x pAP AF +==2,AFcos θRF FT RF RT AP AF +=+=== 所以:AFcos θp AF +=即θpAF cos -=1,同理可证BF4)过焦点弦长公式:如图二θsin px x p AB B A 22=++= 推导:B A B A x x p x px p BF AF AB ++=+++=+=22θsin p cos θp cos θp BF AF AB 2211=++-=+= 5)被焦点截的线段倒数之和=p24==通径 如图二所示:pBF AF 241111==+通径 推导:由焦半径公式可知θp AF cos -=1,θpBF cos +=1所以:通径421111==++-=+p p θp θBF AF cos cos 6)一般弦长公式:直线l :y =kx +m 与抛物线C 交于A (x 1,y 1)B (x 2,y 2)则弦长AB 的计算公式为()212212212411x x x x k x x k AB -++=-+=或者()21221221241111y y y y k y y k AB -++=-+=7)sin θp 2S 2OAB=∆(如图二,直线l 过F 交抛物线与A 、B 两点) 8)42p x x B A =,2p y y B A -=(如图二,直线l 过F 交抛物线与A 、B 两点)【知识拓展】1.抛物线y 2=2px (p >0)上一点P (x 0,y 0)到焦点F ⎝⎛⎭⎫p 2,0的距离|PF |=x 0+p2,也称为抛物线的焦半径. 2.y 2=ax 的焦点坐标为⎝⎛⎭⎫a 4,0,准线方程为x =-a4. (1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点.若过抛物线的焦点,可直接使用公式|AB |=x 1+x 2+p ,若不过焦点,则必须用一般弦长公式.(3)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”、“整体代入”等解法.提醒:涉及弦的中点、斜率时一般用“点差法”求解.3.抛物线的离心率e =1,体现了抛物线上的点到焦点的距离等于到准线的距离.因此,涉及抛物线的焦半径、焦点弦问题,可以优先考虑利用抛物线的定义转化为点到准线的距离,这样就可以使问题简化. 抛物线上的点到焦点的距离根据定义转化为到准线的距离,即|PF |=|x |+p 2或|PF |=|y |+p2.。
圆锥曲线知识点 总结

圆锥曲线知识点总结1. 圆锥曲线的定义圆锥曲线是指平面内由圆锥截面形成的曲线。
圆锥曲线包括圆、椭圆、双曲线、抛物线等类型。
它们的定义方式如下:- 圆:如果平面内的一条曲线上到定点的距离恒定,那么这条曲线就是一个圆。
- 椭圆:平面内的一条曲线上到两个定点的距离之和恒定,这条曲线就是椭圆。
- 双曲线:平面内的一条曲线上到两个定点的距离之差恒定,这条曲线就是双曲线。
- 抛物线:平面内的一条曲线上到定点的距离等于到直线的距离,这条曲线就是抛物线。
2. 圆锥曲线的基本性质圆锥曲线具有一些共同的基本性质,对于不同的类型曲线具有不同的特点:- 对称性:圆锥曲线可能具有对称轴,可以对称于直线、坐标轴、原点或其他特定点。
- 过焦点性质:圆锥曲线上的任意一点到焦点的距离与到焦距的距离之和始终是一个固定值。
- 直径性质:圆锥曲线可能有两个焦点,双曲线、椭圆和抛物线有两个焦点,而圆只有一个焦点。
- 渐近线性质:双曲线和椭圆的曲线可能有渐近线,这些渐近线与曲线的某些特定方向趋近的直线。
3. 圆锥曲线的参数方程圆锥曲线可以用参数方程来表示。
参数方程是指用参数来表示一个函数或曲线的方程。
对于椭圆、双曲线等圆锥曲线,它们的参数方程可以表示为:- 椭圆:x=a*cos(t) ,y=b*sin(t) 0≤t≤2π- 双曲线:x=a*cosh(t) , y=b*sinh(t) -∞<t<+∞4. 圆锥曲线的极坐标方程圆锥曲线还可以用极坐标方程来表示。
极坐标方程是指用极坐标来表示一个函数或曲线的方程。
对于椭圆、双曲线等圆锥曲线,它们的极坐标方程可以表示为:- 椭圆:r(t)=a(1-e^2)/(1+e*cos(t))- 双曲线:r(t)=a(1+e*cos(t))5. 圆锥曲线的焦点和直径对于圆锥曲线来说,焦点和直径是它们的重要性质。
焦点是指椭圆、双曲线、抛物线曲线上的两个固定点,直径是指通过焦点的直线。
6. 圆锥曲线的渐近线部分圆锥曲线,如双曲线和椭圆,可能存在渐近线。
圆锥曲线知识点全归纳(完整精华版)

圆锥曲线知识点全归纳(精华版)圆锥曲线包括椭圆,双曲线,抛物线。
其统一定义:到定点的距离与到定直线的距离的比e 是常数的点的轨迹叫做圆锥曲线。
当0<e<1时为椭圆:当e=1时为抛物线;当e>1时为双曲线。
一、圆锥曲线的方程和性质:1)椭圆文字语言定义:平面内一个动点到一个定点与一条定直线的距离之比是一个小于1的正常数e。
定点是椭圆的焦点,定直线是椭圆的准线,常数e是椭圆的离心率。
标准方程:1.中心在原点,焦点在x轴上的椭圆标准方程:(x^2/a^2)+(y^2/b^2)=1其中a>b>0,c>0,c^2=a^2-b^2.2.中心在原点,焦点在y轴上的椭圆标准方程:(x^2/b^2)+(y^2/a^2)=1其中a>b>0,c>0,c^2=a^2-b^2.参数方程:X=acosθY=bsinθ(θ为参数,设横坐标为acosθ,是由于圆锥曲线的考虑,椭圆伸缩变换后可为圆此时c=0,圆的acosθ=r)2)双曲线文字语言定义:平面内一个动点到一个定点与一条定直线的距离之比是一个大于1的常数e。
定点是双曲线的焦点,定直线是双曲线的准线,常数e是双曲线的离心率。
标准方程:1.中心在原点,焦点在x轴上的双曲线标准方程:(x^2/a^2)-(y^2/b^2)=1其中a>0,b>0,c^2=a^2+b^2.2.中心在原点,焦点在y轴上的双曲线标准方程:(y^2/a^2)-(x^2/b^2)=1.其中a>0,b>0,c^2=a^2+b^2.参数方程:x=asecθy=btanθ(θ为参数 )3)抛物线标准方程:1.顶点在原点,焦点在x轴上开口向右的抛物线标准方程:y^2=2px 其中 p>02.顶点在原点,焦点在x轴上开口向左的抛物线标准方程:y^2=-2px 其中 p>03.顶点在原点,焦点在y轴上开口向上的抛物线标准方程:x^2=2py 其中 p>04.顶点在原点,焦点在y轴上开口向下的抛物线标准方程:x^2=-2py 其中 p>0参数方程x=2pt^2 y=2pt (t为参数) t=1/tanθ(tanθ为曲线上点与坐标原点确定直线的斜率)特别地,t 可等于0直角坐标y=ax^2+bx+c (开口方向为y轴, a<>0 ) x=ay^2+by+c (开口方向为x轴, a<>0 )圆锥曲线(二次非圆曲线)的统一极坐标方程为ρ=ep/(1-e×cosθ)其中e表示离心率,p为焦点到准线的距离。
圆锥曲线抛物线的基本知识点

圆锥曲线抛物线的基本知识点一、什么是圆锥曲线抛物线?抛物线是一种特殊的圆锥曲线,它由一个平面与一个平行于该平面的直线相交而形成。
抛物线具有独特的形状,呈现出对称性和特定的数学性质。
二、抛物线的定义与特点1.定义:抛物线是平面上到一个定点距离与到一条定直线距离相等的点的轨迹。
2.特点:–抛物线具有对称性,它关于焦点和准线对称。
–抛物线的焦点是定点,准线是定直线。
–抛物线的离心率为1,是所有圆锥曲线中离心率等于1的一种情况。
–抛物线具有无穷远点,它是一条无限延伸的曲线。
三、抛物线方程的一般形式抛物线的方程通常可以表达为一般二次方程的形式:y=ax2+bx+c,其中a、b、c为常数,且a≠0。
四、抛物线的焦点与准线1.焦点:抛物线的焦点是定义抛物线的重要元素之一,与抛物线的离心率密切相关。
焦点的坐标可通过方程求解得到。
2.准线:抛物线的准线与焦点共同决定了抛物线的形状,准线的坐标也可通过方程求解得到。
五、抛物线的性质1.对称性:抛物线关于焦点对称,对称轴为准线。
这个性质使得抛物线在很多实际应用中具有重要意义。
2.焦距公式:定义抛物线焦点到准线的距离为焦距,通过焦距公式可以计算焦点到准线的距离。
3.切线方程:抛物线上任一点处的切线方程可以通过求导得到,切线斜率即为函数的导数值。
4.弧长与曲率:抛物线上任意两点之间的弧长可以通过积分计算得到,曲率表示曲线的弯曲程度。
六、抛物线的应用抛物线在现实生活和科学研究中具有广泛的应用,以下是一些例子: 1. 物理学中的抛物线轨迹:在无空气阻力的情况下,自由落体运动的轨迹为抛物线。
2. 抛物面反射:抛物面反射是一种利用抛物面的反射特性设计的照明系统,例如汽车大灯、探照灯等。
3. 投射问题:抛体在给定初始速度和角度下的运动轨迹就是抛物线,如炮弹飞行轨迹、游泳、跳水等。
七、抛物线与其他圆锥曲线的关系抛物线与其他圆锥曲线(椭圆、双曲线)具有一些相似和不同的地方: 1. 相似之处:抛物线、椭圆和双曲线都是圆锥曲线,它们的定义都可以归纳为距离比例关系。
圆锥曲线之抛物线知识点讲解(含解析)

抛物线的概念与几何性质一、知识梳理1.抛物线的定义(1)平面内与一个定点F 和一条定直线l (F ∉l )的距离相等的点的轨迹叫做抛物线.点F 叫做抛物线的焦点,直线l 叫做抛物线的准线. (2)其数学表达式:{M ||MF |=d }(d 为点M 到准线l 的距离). 2.抛物线的标准方程与几何性质3.通径:过焦点且垂直于对称轴的弦长等于2p ,通径是过焦点最短的弦.4.焦半径:抛物线y 2=2px (p >0)上一点P (x 0,y 0)到焦点F ⎝ ⎛⎭⎪⎫p 2,0的距离|PF |=x 0+p2,也称为抛物线的焦半径.二、例题精讲 + 随堂训练1.判断下列结论正误(在括号内打“√”或“×”)(1)平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹一定是抛物线.( )(2)方程y =ax 2(a ≠0)表示的曲线是焦点在x 轴上的抛物线,且其焦点坐标是⎝ ⎛⎭⎪⎫a 4,0,准线方程是x =-a 4.( )(3)抛物线既是中心对称图形,又是轴对称图形.( )(4)过抛物线的焦点与抛物线对称轴垂直的直线被抛物线截得的线段叫做抛物线的通径,那么抛物线x 2=-2ay (a >0)的通径长为2a .( )解析 (1)当定点在定直线上时,轨迹为过定点F 与定直线l 垂直的一条直线,而非抛物线.(2)方程y =ax 2(a ≠0)可化为x 2=1a y ,是焦点在y 轴上的抛物线,且其焦点坐标是⎝ ⎛⎭⎪⎫0,14a ,准线方程是y =-14a .(3)抛物线是只有一条对称轴的轴对称图形. 答案 (1)× (2)× (3)× (4)√2.顶点在原点,且过点P (-2,3)的抛物线的标准方程是________________. 解析 设抛物线的标准方程是y 2=kx 或x 2=my ,代入点P (-2,3),解得k =-92,m =43,所以y 2=-92x 或x 2=43y .答案 y 2=-92x 或x 2=43y3. 抛物线y 2=8x 上到其焦点F 距离为5的点的个数为________.解析 设P (x 1,y 1),则|PF |=x 1+2=5,得x 1=3,y 1=±2 6.故满足条件的点的个数为2. 答案 24.(2019·黄冈联考)已知方程y 2=4x 表示抛物线,且该抛物线的焦点到直线x =m 的距离为4,则m 的值为( ) A.5B.-3或5C.-2或6D.6解析 抛物线y 2=4x 的焦点为F (1,0),它与直线x =m 的距离为d =|m -1|=4,∴m=-3或5.答案B5.(2019·北京海淀区检测)设抛物线y2=8x上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是()A.4B.6C.8D.12解析如图所示,抛物线的准线l的方程为x=-2,F是抛物线的焦点,过点P 作P A⊥y轴,垂足是A,延长P A交直线l于点B,则|AB|=2.由于点P到y轴的距离为4,则点P到准线l的距离|PB|=4+2=6,所以点P到焦点的距离|PF|=|PB|=6.故选B.答案B6.(2019·宁波调研)已知抛物线方程为y2=8x,若过点Q(-2,0)的直线l与抛物线有公共点,则直线l的斜率的取值范围是________.解析设直线l的方程为y=k(x+2),代入抛物线方程,消去y整理得k2x2+(4k2-8)x+4k2=0,当k=0时,显然满足题意;当k≠0时,Δ=(4k2-8)2-4k2·4k2=64(1-k2)≥0,解得-1≤k<0或0<k≤1,因此k的取值范围是[-1,1].答案[-1,1]考点一抛物线的定义及应用【例1】(1)(2019·厦门外国语模拟)已知抛物线x2=2y的焦点为F,其上有两点A(x1,y1),B(x2,y2)满足|AF|-|BF|=2,则y1+x21-y2-x22=()A.4B.6C.8D.10(2)若抛物线y2=4x的准线为l,P是抛物线上任意一点,则P到准线l的距离与P到直线3x+4y+7=0的距离之和的最小值是()A.2B.135 C.145 D.3解析 (1)由抛物线定义知|AF |=y 1+12,|BF |=y 2+12,∴|AF |-|BF |=y 1-y 2=2,又知x 21=2y 1,x 22=2y 2,∴x 21-x 22=2(y 1-y 2)=4,∴y 1+x 21-y 2-x 22=(y 1-y 2)+(x 21-x 22)=2+4=6.(2)由抛物线定义可知点P 到准线l 的距离等于点P 到焦点F 的距离,由抛物线y 2=4x 及直线方程3x +4y +7=0可得直线与抛物线相离,∴点P 到准线l 的距离与点P 到直线3x +4y +7=0的距离之和的最小值为点F (1,0)到直线3x +4y +7=0的距离,即|3+7|32+42=2. 答案 (1)B (2)A规律方法 应用抛物线定义的两个关键点(1)由抛物线定义,把抛物线上点到焦点距离与到准线距离相互转化.(2)注意灵活运用抛物线上一点P (x 0,y 0)到焦点F 的距离|PF |=|x 0|+p2或|PF |=|y 0|+p 2.【训练1】 (1)动圆过点(1,0),且与直线x =-1相切,则动圆的圆心的轨迹方程为__________.(2)(2017·全国Ⅱ卷)已知F 是抛物线C :y 2=8x 的焦点,M 是C 上一点,FM 的延长线交y 轴于点N .若M 为FN 的中点,则|FN |=________.解析 (1)设动圆的圆心坐标为(x ,y ),则圆心到点(1,0)的距离与到直线x =-1的距离相等,根据抛物线的定义易知动圆的圆心的轨迹方程为y 2=4x .(2)如图,不妨设点M 位于第一象限内,抛物线C 的准线交x 轴于点A ,过点M 作准线的垂线,垂足为点B ,交y 轴于点P ,∴PM ∥OF .由题意知,F (2,0),|FO |=|AO |=2. ∵点M 为FN 的中点,PM ∥OF ,∴|MP |=12|FO |=1. 又|BP |=|AO |=2, ∴|MB |=|MP |+|BP |=3.由抛物线的定义知|MF |=|MB |=3,故|FN |=2|MF |=6. 答案 (1)y 2=4x (2)6考点二 抛物线的标准方程及其性质【例2】 (1)(2018·晋城模拟)抛物线C :y 2=4x 的焦点为F ,其准线l 与x 轴交于点A ,点M 在抛物线C 上,当|MA ||MF |=2时,△AMF 的面积为( ) A.1B. 2C.2D.22(2)已知圆C 1:x 2+(y -2)2=4,抛物线C 2:y 2=2px (p >0),C 1与C 2相交于A ,B 两点,且|AB |=855,则抛物线C 2的方程为( )A.y 2=85xB.y 2=165xC.y 2=325xD.y 2=645x 解析 (1)过M 作MP 垂直于准线,垂足为P , 则|MA ||MF |=2=|MA ||MP |=1cos ∠AMP ,则cos ∠AMP =22,又0°<∠MAP <180°, 则∠AMP =45°,此时△AMP 是等腰直角三角形, 设M (m ,4m ),由|MP |=|MA |,得|m +1|=4m , 解得m =1,M (1,2),所以△AMF 的面积为12×2×2=2. (2)由题意,知直线AB 必过原点, 则设AB 的方程为y =kx (易知k >0), 圆心C 1(0,2)到直线AB 的距离d =|-2|k 2+1=22-⎝ ⎛⎭⎪⎫4552=255,解得k =2,由⎩⎨⎧y =2x ,x 2+(y -2)2=4得⎩⎨⎧x =0,y =0或⎩⎪⎨⎪⎧x =85,y =165,把⎝ ⎛⎭⎪⎫85,165代入抛物线方程, 得⎝ ⎛⎭⎪⎫1652=2p ·85,解得p =165, 所以抛物线C 2的方程为y 2=325x . 答案 (1)C (2)C规律方法 1.求抛物线标准方程的常用方法是待定系数法,其关键是判断焦点位置、开口方向,在方程的类型已经确定的前提下,由于标准方程只有一个参数p ,只需一个条件就可以确定抛物线的标准方程.2.在解决与抛物线的性质有关的问题时,要注意利用几何图形的形象、直观的特点来解题,特别是涉及焦点、顶点、准线的问题更是如此.【训练2】 (1)如图,过抛物线y 2=2px (p >0)的焦点F 的直线交抛物线于点A ,B ,交其准线l 于点C ,若|BC |=2|BF |,且|AF |=3,则此抛物线的方程为________.(2)(2019·济宁调研)已知点A (3,0),过抛物线y 2=4x 上一点P 的直线与直线x =-1垂直相交于点B ,若|PB |=|P A |,则P 的横坐标为( ) A.1B.32C.2D.52解析 (1)设A ,B 在准线上的射影分别为A 1,B 1, 由于|BC |=2|BF |=2|BB 1|,则直线的斜率为3, 故|AC |=2|AA 1|=6,从而|BF |=1,|AB |=4,故p |AA 1|=|CF ||AC |=12,即p =32,从而抛物线的方程为y 2=3x .(2)由抛物线定义知:|PB |=|PF |,又|PB |=|P A |,所以|P A |=|PF |,所以x P =x A +x F2=2(△PF A 为等腰三角形). 答案 (1)y 2=3x (2)C考点三 直线与抛物线的综合问题【例3】 (2019·武汉调研)已知抛物线C :x 2=2py (p >0)和定点M (0,1),设过点M 的动直线交抛物线C 于A ,B 两点,抛物线C 在A ,B 处的切线交点为N . (1)若N 在以AB 为直径的圆上,求p 的值; (2)若△ABN 面积的最小值为4,求抛物线C 的方程. 解 (1)可设AB :y =kx +1,A (x 1,y 1),B (x 2,y 2), 将AB 的方程代入抛物线C ,得x 2-2pkx -2p =0,显然方程有两不等实根, 则x 1+x 2=2pk ,x 1x 2=-2p .① 又x 2=2py 得y ′=xp ,则A ,B 处的切线斜率乘积为x 1x 2p 2=-2p =-1, 则有p =2.(2)设切线AN 为y =x 1p x +b ,又切点A 在抛物线y =x 22p 上,∴y 1=x 212p ,∴b =x 212p -x 21p =-x 212p ,切线AN 的方程为y AN =x 1p x -x 212p ,同理切线BN 的方程为y BN =x 2p x -x 222p . 又∵N 在y AN 和y BN 上,∴⎩⎪⎨⎪⎧y =x 1p x -x 212p ,y =x 2p x -x 222p,解得N ⎝ ⎛⎭⎪⎫x 1+x 22,x 1x 22p .∴N (pk ,-1). |AB |=1+k 2|x 2-x 1|=1+k 24p 2k 2+8p , 点N 到直线AB 的距离d =|kx N +1-y N |1+k 2=|pk 2+2|1+k 2,S △ABN =12·|AB |·d =p (pk 2+2)3≥22p , ∴22p =4,∴p =2, 故抛物线C 的方程为x 2=4y .规律方法 1.有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点.若过抛物线的焦点,可直接使用公式|AB |=x 1+x 2+p ,若不过焦点,则必须用一般弦长公式.2.涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”、“整体代入”等解法.提醒:涉及弦的中点、斜率时一般用“点差法”求解.【训练3】 (2017·全国Ⅰ卷)已知F 为抛物线C :y 2=4x 的焦点,过F 作两条互相垂直的直线l 1,l 2,直线l 1与C 交于A ,B 两点,直线l 2与C 交于D ,E 两点,则|AB |+|DE |的最小值为( ) A.16B.14C.12D.10解析 抛物线C :y 2=4x 的焦点为F (1,0),由题意可知l 1,l 2的斜率存在且不为0.不妨设直线l 1的斜率为k ,则l 2直线的斜率为-1k ,故l 1:y =k (x -1),l 2:y =-1k (x -1).由⎩⎨⎧y 2=4x ,y =k (x -1),消去y 得k 2x 2-(2k 2+4)x +k 2=0. 设A (x 1,y 1),B (x 2,y 2),∴x 1+x 2=2k 2+4k 2=2+4k 2, 由抛物线定义可知,|AB |=x 1+x 2+2=4+4k 2. 同理得|DE |=4+4k 2,∴|AB |+|DE |=8+4k 2+4k 2≥8+216=16. 当且仅当1k 2=k 2,即k =±1时取等号. 故|AB |+|DE |的最小值为16. 答案 A[思维升华]1.抛物线定义的实质可归结为“一动三定”:一个动点M ,一个定点F (抛物线的焦点),一条定直线l (抛物线的准线),一个定值1(抛物线的离心率).2.抛物线的焦点弦:设过抛物线y 2=2px (p >0)的焦点的直线与抛物线交于A (x 1,y 1),B (x 2,y 2),则:(1)y 1y 2=-p 2,x 1x 2=p 24;(2)若直线AB 的倾斜角为θ,则|AB |=2psin 2θ;|AB |=x 1+x 2+p ; (3)若F 为抛物线焦点,则有1|AF |+1|BF |=2p . [易错防范]1.认真区分四种形式的标准方程(1)区分y =ax 2(a ≠0)与y 2=2px (p >0),前者不是抛物线的标准方程.(2)求标准方程要先确定形式,必要时要进行分类讨论,标准方程有时可设为y 2=mx 或x 2=my (m ≠0).2.直线与抛物线结合的问题,不要忘记验证判别式.数学抽象——活用抛物线焦点弦的四个结论1.数学抽象素养水平表现为能够在关联的情境中抽象出一般的数学概念和规则,能够将已知数学命题推广到更一般情形.本课时中研究直线方程时常用到直线系方程就是其具体表现之一.2.设AB 是过抛物线y 2=2px (p >0)焦点F 的弦, 若A (x 1,y 1),B (x 2,y 2),则 (1)x 1·x 2=p 24. (2)y 1·y 2=-p 2.(3)|AB |=x 1+x 2+p =2psin 2α(α是直线AB 的倾斜角). (4)1|AF |+1|BF |=2p 为定值(F 是抛物线的焦点).【例1】 过抛物线y 2=4x 的焦点F 的直线l 与抛物线交于A ,B 两点,若|AF |=2|BF |,则|AB |等于( ) A.4B.92C.5D.6[一般解法]易知直线l 的斜率存在,设为k ,则其方程为y =k (x -1). 由⎩⎨⎧y =k (x -1),y 2=4x得k 2x 2-(2k 2+4)x +k 2=0,得x A ·x B =1,①因为|AF |=2|BF |,由抛物线的定义得x A +1=2(x B +1), 即x A =2x B +1,②由①②解得x A =2,x B =12, 所以|AB |=|AF |+|BF |=x A +x B +p =92.[应用结论]法一 由对称性不妨设点A 在x 轴的上方,如图设A ,B 在准线上的射影分别为D ,C ,作BE ⊥AD 于E ,设|BF |=m ,直线l 的倾斜角为θ, 则|AB |=3m ,由抛物线的定义知 |AD |=|AF |=2m ,|BC |=|BF |=m ,所以cos θ=|AE ||AB |=13,所以tan θ=2 2.则sin 2θ=8cos 2θ,∴sin 2θ=89.又y 2=4x ,知2p =4,故利用弦长公式|AB |=2p sin 2θ=92.法二 因为|AF |=2|BF |,1|AF |+1|BF |=12|BF |+1|BF |=32|BF |=2p =1, 解得|BF |=32,|AF |=3,故|AB |=|AF |+|BF |=92. 答案 B【例2】 设F 为抛物线C :y 2=3x 的焦点,过F 且倾斜角为30°的直线交C 于A ,B 两点,O 为坐标原点,则△OAB 的面积为( ) A.334B.938C.6332D.94[一般解法]由已知得焦点坐标为F ⎝ ⎛⎭⎪⎫34,0,因此直线AB 的方程为y =33⎝ ⎛⎭⎪⎫x -34,即4x -43y -3=0.与抛物线方程联立,化简得4y 2-123y -9=0, 故|y A -y B |=(y A +y B )2-4y A y B =6.因此S△OAB =12|OF||y A-y B|=12×34×6=94.[应用结论]由2p=3,及|AB|=2p sin2α得|AB|=2psin2α=3sin230°=12.原点到直线AB的距离d=|OF|·sin 30°=3 8,故S△AOB =12|AB|·d=12×12×38=94.答案D【例3】(2019·益阳、湘潭调研)如图,过抛物线y2=2px(p>0)的焦点F的直线交抛物线于点A,B,交其准线l于点C,若F是AC的中点,且|AF|=4,则线段AB的长为()A.5B.6C.163 D.203[一般解法]如图,设l与x轴交于点M,过点A作AD⊥l交l于点D,由抛物线的定义知,|AD|=|AF|=4,由F是AC的中点,知|AD|=2|MF|=2p,所以2p=4,解得p=2,所以抛物线的方程为y2=4x.设A(x1,y1),B(x2,y2),则|AF|=x1+p2=x1+1=4,所以x1=3,可得y1=23,所以A(3,23),又F(1,0),所以直线AF的斜率k=233-1=3,所以直线AF 的方程为y=3(x-1),代入抛物线方程y2=4x得3x2-10x+3=0,所以x1+x2=103,|AB |=x 1+x 2+p =163.故选C.[应用结论]法一 设A (x 1,y 1),B (x 2,y 2),则|AF |=x 1+p 2=x 1+1=4,所以x 1=3,又x 1x 2=p 24=1,所以x 2=13,所以|AB |=x 1+x 2+p =3+13+2=163.法二 因为1|AF |+1|BF |=2p ,|AF |=4,所以|BF |=43,所以|AB |=|AF |+|BF |=4+43=163.答案 C三、课后练习1.抛物线y 2=8x 的焦点为F ,设A ,B 是抛物线上的两个动点,|AF |+|BF |=233|AB |,则∠AFB 的最大值为( )A.π3B.3π4C.5π6D.2π3解析 设|AF |=m ,|BF |=n ,∵|AF |+|BF |=233|AB |,∴233|AB |≥2mn ,∴mn ≤13|AB |2,在△AFB 中,由余弦定理得cos ∠AFB =m 2+n 2-|AB |22mn =(m +n )2-2mn -|AB |22mn =13|AB |2-2mn 2mn ≥-12,∴∠AFB 的最大值为2π3. 答案 D2.(2019·武汉模拟)过点P (2,-1)作抛物线x 2=4y 的两条切线,切点分别为A ,B ,P A ,PB 分别交x 轴于E ,F 两点,O 为坐标原点,则△PEF 与△OAB 的面积之比为( )A.32B.33C.12D.34解析 设A (x 1,y 1),B (x 2,y 2),则点A ,B 处的切线方程为x 1x =2(y +y 1),x 2x =2(y +y 2),所以E ⎝ ⎛⎭⎪⎫2y 1x 1,0,F ⎝ ⎛⎭⎪⎫2y 2x 2,0,即E ⎝ ⎛⎭⎪⎫x 12,0,F ⎝ ⎛⎭⎪⎫x 22,0,因为这两条切线都过点P (2,-1),则⎩⎨⎧2x 1=2(-1+y 1),2x 2=2(-1+y 2),所以l AB :x =-1+y ,即l AB 过定点(0,1),则S △PEF S OAB=12×1×⎪⎪⎪⎪⎪⎪x 12-x 2212×1×|x 1-x 2|=12. 答案 C3.已知抛物线方程为y 2=-4x ,直线l 的方程为2x +y -4=0,在抛物线上有一动点A ,点A 到y 轴的距离为m ,到直线l 的距离为n ,则m +n 的最小值为________.解析 如图,过A 作AH ⊥l ,AN 垂直于抛物线的准线,则|AH |+|AN |=m +n +1,连接AF ,则|AF |+|AH |=m +n +1,由平面几何知识,知当A ,F ,H 三点共线时,|AF |+|AH |=m +n +1取得最小值,最小值为F 到直线l 的距离,即65=655,即m +n 的最小值为655-1.答案655-14.(2019·泉州一模)在平面直角坐标系xOy 中,抛物线C :x 2=2py (p >0)的焦点为F ,点A 在C 上,若|AO |=|AF |=32.(1)求抛物线C 的方程;(2)设直线l 与C 交于P ,Q ,若线段PQ 的中点的纵坐标为1,求△OPQ 的面积的最大值.解 (1)因为点A 在C 上,|AO |=|AF |=32,所以点A 的纵坐标为p 4,所以p 4+p 2=32,所以p =2,所以C 的方程为x 2=4y .(2)由题意知直线l 的斜率存在,设直线l 的方程为y =kx +b (b ≥0),代入抛物线方程,可得x 2-4kx-4b =0.设P (x 1,y 1),Q (x 2,y 2),则x 1+x 2=4k ,x 1x 2=-4b ,所以y 1+y 2=4k 2+2b , 因为线段PQ 的中点的纵坐标为1,所以2k 2+b =1,即2k 2=1-b ≥0,所以0<b ≤1,S △OPQ =12b |x 1-x 2|=12b (x 1+x 2)2-4x 1x 2=12b 16k 2+16b =b 2+2b =2·b 3+b 2(0<b ≤1),设y =b 3+b 2,y ′=3b 2+2b >0,函数单调递增,所以b =1时,△OPQ 的面积最大,最大值为2.5.已知点A (0,2),抛物线C :y 2=2px (p >0)的焦点为F ,射线F A 与抛物线C 相交于点M ,与其准线相交于点N ,若|FM ||MN |=55,则p 的值等于( ) A.14 B.2 C.4 D.8解析 过点M 作抛物线的准线的垂线,垂足为点M ′,则易得|MM ′|=|MF |,所以cos ∠NMM ′=|MM ′||MN |=|MF ||MN |=55,则k AM =-tan ∠NMM ′=-1-cos 2∠NMM ′cos 2∠NMM ′=-2,则直线AM 的方程为y -2=-2x ,令y =0得抛物线的焦点坐标F (1,0),则p =2×1=2,故选B.答案 B。
圆锥曲线--抛物线

【例 4】如图 7,过抛物线 y2=2px(P>0)的焦点 F 的直线与抛物线相交于 M、N 两点, 自 M、N 向准线 l 作垂线,垂足分别为 M1、N1,求证:FM1⊥FN1
★⑵
1 1 2 + =p | AF | | BF |
p2 p p 【证法一】由⑴x1x2= ,且| AF |=x1+ ,| BF |=x2+ . 4 2 2 x1+x2+p x1+x2+p 1 1 1 1 ∴ + = + = = | AF | | BF | p p p p p p2 x1+ x2+ (x1+ )·(x2+ ) x1x2+ (x1+x2)+ 2 2 2 2 2 4 x1+x2+p x1+x2+p 2 = 2 = = p p p2 p p + (x +x )+ (x +x +p) 4 2 1 2 4 2 1 2 p p p 【证法二】由| AF |=1= ,| BF |=2= = . 1-cos 1-cos(+ ) 1+cos 1 1 1 1 1-cos 1+cos 2 ∴ + = + = + = | AF | | BF | 1 2 p p p
2 2 2 2
p p 1 1 1 在直线 AB 方程 x=my+ 中令 x=0,得 y3=- ,代入上式得 + = 2 2m y1 y2 y3
p p ④【证法一】根据抛物线的定义,| AF |=| AD |=x1+ ,| BF |=| BC |=x2+ , 2 2 | AB |=| AF |+| BF |=x1+x2+p 又| AB |= (x2-x1)2+(y2-y1)2= = = 1+m2 1+m2 1+m2| y2-y1 |
【证法五】由下面证得∠DFC=90,连结 FM,则 FM=DM. 又 AD=AF,故△ADM≌△AFM,如图 4 ∴∠1=∠2,同理∠3=∠4 1 ∴∠2+∠3= ×180=90 2 ∴∠AMB=90
圆锥曲线 第3节 抛物线及其性质

第3节抛物线及其性质知识点一抛物线的定义与方程1.定义:平面内与一定点F和一条定直线l(不经过点F)距离相等的点的轨迹.2.焦点:定点F.3.准线:定直线l.思考抛物线的定义中,为什么要加条件l不经过点F?答案若点F在直线l上,点的轨迹是过点F且垂直于直线l的直线.4.抛物线的标准方程思考抛物线方程中p(p>0)的几何意义是什么?答案p的几何意义是焦点到准线的距离.一、求抛物线的标准方程例1分别求符合下列条件的抛物线的标准方程.(1)经过点(-3,-1);(2)焦点为直线3x-4y-12=0与坐标轴的交点.解(1)因为点(-3,-1)在第三象限,所以设所求抛物线的标准方程为y2=-2px(p>0)或x2=-2py (p >0).若抛物线的标准方程为y 2=-2px (p >0),则由(-1)2=-2p ×(-3),解得p =16;若抛物线的标准方程为x 2=-2py (p >0),则由(-3)2=-2p ×(-1),解得p =92.故所求抛物线的标准方程为y 2=-13x 或x 2=-9y .(2)对于直线方程3x -4y -12=0,令x =0,得y =-3;令y =0,得x =4,所以抛物线的焦点为(0,-3)或(4,0).当焦点为(0,-3)时,p2=3,所以p =6,此时抛物线的标准方程为x 2=-12y ;当焦点为(4,0)时,p2=4,所以p =8,此时抛物线的标准方程为y 2=16x .故所求抛物线的标准方程为x 2=-12y 或y 2=16x . 反思感悟 用待定系数法求抛物线标准方程的步骤注意:当抛物线的类型没有确定时,可设方程为y 2=mx (m ≠0)或x 2=ny (n ≠0),这样可以减少讨论情况的个数.跟踪训练1 (1)若抛物线y 2=2px (p >0)的焦点坐标为(1,0),则p =________,准线方程为________.解析 因为抛物线的焦点坐标为(1,0),所以p 2=1,p =2,准线方程为x =-p2=-1.(2)求焦点在y 轴上,焦点到准线的距离为5的抛物线的标准方程为____________. 解析 设方程为x 2=2my (m ≠0),由焦点到准线的距离为5,知|m |=5,m =±5,所以满足条件的抛物线有两条,它们的标准方程分别为x 2=10y 和x 2=-10y .二、抛物线定义的应用例2 (1)已知抛物线C :y 2=x 的焦点为F ,A (x 0,y 0)是C 上一点,|AF |=54x 0,则x 0等于( )A .1B .2C .4D .8 解析 ∵14+x 0=54x 0,∴x 0=1.(2)已知点P 是抛物线y 2=2x 上的一个动点,求点P 到点(0,2)的距离与P 到该抛物线准线的距离之和的最小值.解 由抛物线的定义可知,抛物线上的点到准线的距离等于它到焦点的距离.由图可知, 点P ,点(0,2)和抛物线的焦点F ⎝⎛⎭⎫12,0三点共线时距离之和最小, 所以最小距离d = ⎝⎛⎭⎫0-122+(2-0)2=172.延伸探究1.若将本例(2)中的点(0,2)改为点A (3,2),求|P A |+|PF |的最小值. 解 将x =3代入y 2=2x ,得y =± 6.所以点A 在抛物线内部.设点P 为其上一点,点P 到准线(设为l )x =-12的距离为d ,则|P A |+|PF |=|P A |+d .由图可知,当P A ⊥l 时,|P A |+d 最小,最小值是72.即|P A |+|PF |的最小值是72.2.若将本例(2)中的点(0,2)换为直线l 1:3x -4y +72=0,求点P 到直线3x -4y +72=0的距离与P 到该抛物线的准线的距离之和的最小值.解 如图,作PQ 垂直于准线l 于点Q ,|P A 1|+|PQ |=|P A 1|+|PF |≥|A 1F |min .|A 1F |的最小值为点F 到直线3x -4y +72=0的距离d =⎪⎪⎪⎪3×12+7232+(-4)2=1即所求最小值为1.反思感悟 抛物线定义的应用实现距离转化.根据抛物线的定义,抛物线上任意一点到焦点的距离等于它到准线的距离,因此,由抛物线定义可以实现点点距与点线距的相互转化,从而简化某些问题.跟踪训练2 (1)已知抛物线y 2=2px (p >0)的焦点F 1,若点A (2,-4)在抛物线上,则点A 到焦点的距离为________.解析 把点(2,-4)代入抛物线y 2=2px ,得16=4p ,即p =4,从而抛物线的焦点为(2,0).故点A 到焦点的距离为4.(2)设点A 的坐标为(1,15),点P 在抛物线y 2=8x 上移动,P 到直线x =-1的距离为d ,则d +|P A |的最小值为( ) A .1 B .2 C .3 D .4解析 由题意知抛物线y 2=8x 的焦点为F (2,0),点P 到准线x =-2的距离为d +1, 于是|PF |=d +1,所以d +|P A |=|PF |-1+|P A |的最小值为|AF |-1=4-1=3.知识点二 抛物线的简单几何性质x ≥0,y ∈Rx ≤0,y ∈Ry ≥0,x ∈Ry ≤0,x ∈R抛物线的几何性质的应用例1 (1)等腰直角三角形AOB 内接于抛物线y 2=2px (p >0),O 为抛物线的顶点,OA ⊥OB ,则△AOB 的面积是( ) A .8p 2 B .4p 2 C .2p 2 D .p 2解析 因为抛物线的对称轴为x 轴,内接△AOB 为等腰直角三角形,所以由抛物线的对称性知,直线AB 与抛物线的对称轴垂直,从而直线OA 与x 轴的夹角为45°.由方程组⎩⎪⎨⎪⎧ y =x ,y 2=2px 得⎩⎪⎨⎪⎧ x =0,y =0或⎩⎪⎨⎪⎧x =2p ,y =2p ,不妨设A ,B 两点的坐标分别为(2p ,2p )和(2p ,-2p ). 所以|AB |=4p ,所以S △AOB =12×4p ×2p =4p 2.(2)已知抛物线的顶点在坐标原点,对称轴为x 轴,且与圆x 2+y 2=4相交于A ,B 两点, |AB |=23,求抛物线方程.解 由已知,抛物线的焦点可能在x 轴正半轴上,也可能在负半轴上. 故可设抛物线方程为y 2=ax (a ≠0).设抛物线与圆x 2+y 2=4的交点A (x 1,y 1),B (x 2,y 2).∵抛物线y 2=ax (a ≠0)与圆x 2+y 2=4都关于x 轴对称,∴点A 与B 关于x 轴对称, ∴|y 1|=|y 2|且|y 1|+|y 2|=23,∴|y 1|=|y 2|=3,代入圆x 2+y 2=4,得x 2+3=4,∴x =±1,∴A (±1,3)或A (±1,-3),代入抛物线方程,得(3)2=±a ,∴a =±3. ∴所求抛物线方程是y 2=3x 或y 2=-3x .反思感悟 把握三个要点确定抛物线的简单几何性质(1)开口:由抛物线标准方程看图象开口,关键是看准二次项是x 还是y ,一次项的系数是正还是负.(2)关系:顶点位于焦点与准线中间,准线垂直于对称轴.(3)定值:焦点到准线的距离为p ;过焦点垂直于对称轴的弦(又称为通径)长为2p ;离心率恒等于1.跟踪训练1 (1)边长为1的等边三角形AOB ,O 为坐标原点,AB ⊥x 轴,以O 为顶点且过A ,B 的抛物线方程是( ) A .y 2=36x B .y 2=-33x C .y 2=±36x D .y 2=±33x 解析 设抛物线方程为y 2=ax (a ≠0). 又A ⎝⎛⎭⎫±32,12(取点A 在x 轴上方),则有14=±32a , 解得a =±36,所以抛物线方程为y 2=±36x .故选C. (2)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线与抛物线y 2=2px (p >0)的准线分别交于A ,B两点,O 为坐标原点,若双曲线的离心率为2,△AOB 的面积为3,则抛物线的焦点坐标为( ) A .(2,0) B .(1,0) C .(8,0)D .(4,0)解析 因为c a =2,所以c 2a 2=a 2+b 2a 2=4,于是b 2=3a 2,则ba=3,故双曲线的两条渐近线方程为y =±3x .而抛物线y 2=2px (p >0)的准线方程为x =-p2,不妨设A ⎝⎛⎭⎫-p 2,3p 2,B ⎝⎛⎭⎫-p 2,-3p 2,则|AB |=3p ,又三角形的高为p 2,则S △AOB =12·p2·3p =3,即p 2=4.因为p >0,所以p =2,故抛物线焦点坐标为(1,0).知识点三 直线与抛物线的位置关系直线y =kx +b 与抛物线y 2=2px (p >0)的交点个数决定于关于x 的方程组⎩⎪⎨⎪⎧y =kx +b ,y 2=2px 解的个数,即二次方程k 2x 2+2(kb -p )x +b 2=0解的个数.当k ≠0时,若Δ>0,则直线与抛物线有两个不同的公共点;若Δ=0,直线与抛物线有一个公共点;若Δ<0,直线与抛物线没有公共点.当k =0时,直线与抛物线的轴平行或重合,此时直线与抛物线有1个公共点.一、直线与抛物线位置关系的判断例1 已知直线l :y =kx +1,抛物线C :y 2=4x ,当k 为何值时,l 与C :只有一个公共点;有两个公共点;没有公共点.解 联立⎩⎪⎨⎪⎧y =kx +1,y 2=4x ,消去y ,得k 2x 2+(2k -4)x +1=0.(*)当k =0时,(*)式只有一个解x =14,∴y =1,∴直线l 与C 只有一个公共点⎝⎛⎭⎫14,1,此时直线l 平行于x 轴.当k ≠0时,(*)式是一个一元二次方程,Δ=(2k -4)2-4k 2=16(1-k ). ①当Δ>0,即k <1,且k ≠0时,l 与C 有两个公共点,此时直线l 与C 相交; ②当Δ=0,即k =1时,l 与C 有一个公共点,此时直线l 与C 相切; ③当Δ<0,即k >1时,l 与C 没有公共点,此时直线l 与C 相离.综上所述,当k =1或0时,l 与C 有一个公共点;当k <1,且k ≠0时,l 与C 有两个公共点; 当k >1时,l 与C 没有公共点. 二、直线与抛物线的相交问题例2 已知抛物线方程为y 2=2px (p >0),过此抛物线的焦点的直线与抛物线交于A ,B 两点,且|AB |=52p ,求AB 所在的直线方程.解 由题意知焦点F ⎝⎛⎭⎫p 2,0,设A (x 1,y 1),B (x 2,y 2),若AB ⊥x 轴,则|AB |=2p ≠52p ,不满足题意.所以直线AB 的斜率存在,设为k ,则直线AB 的方程为y =k ⎝⎛⎭⎫x -p 2,k ≠0.由⎩⎪⎨⎪⎧y =k ⎝⎛⎭⎫x -p 2,y 2=2px ,消去x ,整理得ky 2-2py -kp 2=0.由根与系数的关系得y 1+y 2=2pk,y 1y 2=-p 2. 所以|AB |=⎝⎛⎭⎫1+1k 2·(y 1-y 2)2=1+1k2·(y 1+y 2)2-4y 1y 2=2p ⎝⎛⎭⎫1+1k 2=52p ,解得k =±2.所以AB 所在的直线方程为2x -y -p =0或2x +y -p =0. 延伸探究本例条件不变,求弦AB 的中点M 到y 轴的距离.解 如图,过A ,B ,M 分别作准线x =-p2的垂线交准线于点C ,D ,E .由定义知|AC |+|BD |=52p ,则梯形ABDC 的中位线|ME |=54p ,∴M 点到y 轴的距离为54p -p 2=34p .反思感悟 直线与抛物线的位置关系1.设直线方程时要特别注意斜率不存在的直线应单独讨论,求解交点时不要忽略二次项系数为0的情况.2.一般弦长:(已知直线上的两点距离)设直线:l y kx m =+,l 上两点()()1122,,,A x y B x y ,所以12AB x =-或12AB y y =-(1)证明:因为()()1122,,,A x y B x y 在直线l 上,所以1122y kx my kx m=+⎧⎨=+⎩AB ∴=1122y kx m y kx m =+⎧⎨=+⎩可得:AB12x ==-同理可证得12AB y y =-(2)弦长公式的适用范围为直线上的任意两点,但如果,A B 为直线与曲线的交点(即AB 为曲线上的弦),则12x x -(或12yy -)可进行变形:12x x -==跟踪训练2 (1)过点P (0,1)与抛物线y 2=x 有且只有一个交点的直线有( ) A .4条 B .3条 C .2条D .1条解析 如图,过P 可作抛物线的两条切线,即y 轴和l 1均与抛物线只有一个公共点,过P 可作一条与x 轴平行的直线l 2与抛物线只有一个公共点.故过点P 与抛物线只有一个公共点的直线共3条,故选B.(2)设抛物线C :x 2=4y 焦点为F ,直线y =kx +2与C 交于A ,B 两点,且||AF ·||BF =25,则k 的值为( )A .±2B .-1C .±1D .-2解析 设A (x 1,y 1),B (x 2,y 2),将直线y =kx +2代入x 2=4y ,消去x 得y 2-(4+4k 2)y +4=0, 所以y 1·y 2=4,y 1+y 2=4+4k 2,抛物线C :x 2=4y 的准线方程为y =-1,因为||AF =y 1+1,||BF =y 2+1,所以||AF ·||BF =y 1·y 2+(y 1+y 2)+1=4+4+4k 2+1=25⇒k =±2.三、抛物线的综合问题例3 如图,已知抛物线y 2=4x 的焦点为F ,过点P (2,0)的直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点,直线AF ,BF 分别与抛物线交于点M ,N .(1)求y 1y 2的值;(2)连接MN ,记直线MN 的斜率为k 1,直线AB 的斜率为k 2,证明:k 1k 2为定值.(1)解 依题意,设AB 的方程为x =my +2, 代入y 2=4x ,得y 2-4my -8=0,从而y 1y 2=-8.(2)证明 设M (x 3,y 3),N (x 4,y 4),k 1k 2=y 3-y 4x 3-x 4×x 1-x 2y 1-y 2=y 3-y 4y 234-y 244×y 214-y 224y 1-y 2=y 1+y 2y 3+y 4, 设直线AM 的方程为x =ny +1,代入y 2=4x ,消去x 得y 2-4ny -4=0, 所以y 1y 3=-4,同理y 2y 4=-4,k 1k 2=y 1+y 2y 3+y 4=y 1+y 2-4y 1+-4y 2=y 1y 2-4,由(1)知y 1y 2=-8,所以k 1k 2=2为定值.反思感悟 解决抛物线综合问题的基本策略对于抛物线的综合问题,可以从直线、抛物线的方程出发,结合解一元二次方程,经过逻辑推理和数学运算,从代数法的角度推证结论.跟踪训练3 (1) 已知A (2,0),B 为抛物线y 2=x 上的一点,则|AB |的最小值为________.解析 设点B (x ,y ),则x =y 2≥0,所以|AB |=(x -2)2+y 2=(x -2)2+x =x 2-3x +4=⎝⎛⎭⎫x -322+74.所以当x =32时,|AB |取得最小值,且|AB |min =72.(2)已知动点P 在y 轴的右侧,且点P 到y 轴的距离比它到点F ()1,0的距离小1. ①求动点P 的轨迹C 的方程;②设斜率为-1且不过点M ()1,2的直线交C 于A ,B 两点,直线MA ,MB 的斜率分别为k 1,k 2,求证:k 1+k 2=0.①解 依题意动点P 的轨迹是抛物线(除原点),其焦点为F ()1,0,准线为x =-1, 设其方程为y 2=2px ()p >0,则p2=1,解得p =2,所以动点P 的轨迹C 的方程是y 2=4x ()x >0.②证明 设直线AB :y =-x +b ()b ≠3,A ()x 1,y 1,B ()x 2,y 2,由⎩⎪⎨⎪⎧y 2=4x ,y =-x +b ,得y =-y 24+b ,即y 2+4y -4b =0,Δ=16+16b >0,所以b >-1,y 1+y 2=-4,因为x 1=y 214,x 2=y 224,所以k 1+k 2=y 2-2y 224-1+y 1-2y 214-1=4()y 2-2y 22-4+4()y 1-2y 21-4=4y 2+2+4y 1+2=4()y 1+2+y 2+2()y 2+2()y 1+2=0.因此k 1+k 2=0.与抛物线有关的最值问题典例 求抛物线y =-x 2上的点到直线4x +3y -8=0的最小距离. 解 方法一 设A (t ,-t 2)为抛物线上的点, 则点A 到直线4x +3y -8=0的距离d =|4t -3t 2-8|5=|3t 2-4t +8|5=15⎪⎪⎪⎪3⎝⎛⎭⎫t -232-43+8=15⎪⎪⎪⎪3⎝⎛⎭⎫t -232+203=35⎝⎛⎭⎫t -232+43.所以当t =23时,d 取得最小值43.方法二 如图,设与直线4x +3y -8=0平行的抛物线的切线方程为4x +3y +m =0,由⎩⎪⎨⎪⎧y =-x 2,4x +3y +m =0,消去y 得3x 2-4x -m =0,∴Δ=16+12m =0,∴m =-43.故最小距离为⎪⎪⎪⎪-8+435=2035=43.[素养提升] 求距离的最值,常见的解题思路:一是利用抛物线的标准方程进行消元代换,得到有关距离的含变量的代数式,以计算函数最值来解决,体现了数学计算的核心素养;二是利用数形结合转化两平行线间距离求得,体现了逻辑推理素养,提升直观想象能力. 三圆锥曲线mx 2+ny 2=1(当m >0,n >0,m ≠n ,为椭圆方程,当mn <0,m≠n ,为双曲线,当m=n ≠0,为圆)上任意一点P(x 0,y 0)处的切线方程为mxx 0+nyy 0=1; 对比记忆抛物线y 2=2px 切线为yy 0=p(x+x 0)1.抛物线y =-14x 2的准线方程为( )A .x =116B .x =1C .y =1D .y =2答案 C解析 抛物线的标准方程为x 2=-4y ,则准线方程为y =1.2.已知抛物线y 2=2px (p >0)的准线经过点(-1,1),则该抛物线焦点坐标为( ) A .(-1,0) B .(1,0) C .(0,-1) D .(0,1) 答案 B解析 抛物线y 2=2px (p >0)的准线方程为x =-p2,由题设知-p2=-1,即p =2,故焦点坐标为()1,0.故选B.3.(多选)经过点P (4,-2)的抛物线的标准方程为( ) A .y 2=x B. y 2=8x C .y 2=-8x D .x 2=-8y答案 AD解析 当开口向右时,设抛物线方程为y 2=2p 1x (p 1>0),则(-2)2=8p 1,所以p 1=12,所以抛物线方程为y 2=x .当开口向下时,设抛物线方程为x 2=-2p 2y (p 2>0),则42=4p 2,p 2=4,所以抛物线方程为x 2=-8y .4.若抛物线y =ax 2()a >0的焦点与椭圆x 22+y 2=1的上顶点重合,则a 等于( )A.12B.14 C .2 D .4 答案 B解析 椭圆x 22+y 2=1的上顶点是()0,1 抛物线y =ax 2()a >0的焦点坐标为⎝⎛⎭⎫0,14a , 因为两点重合,所以14a =1,所以a =14.5.若抛物线y 2=2px (p >0)的焦点是椭圆x 23p +y 2p=1的一个焦点,则p 等于( ) A .2 B .3 C .4 D .8 答案 D解析 因为抛物线y 2=2px (p >0)的焦点⎝⎛⎭⎫p 2,0是椭圆x 23p +y 2p=1的一个焦点, 所以3p -p =⎝⎛⎭⎫p 22,解得p =8.6.已知双曲线x 2m -y 2=1的右焦点恰好是抛物线y 2=8x 的焦点,则m =________.答案 3解析 由题意得m +1=22,解得m =3.7.在抛物线y 2=-12x 上,与焦点的距离等于9的点的坐标是____________. 答案 (-6,62)或(-6,-62)解析 由方程y 2=-12x ,知焦点F (-3,0),准线l :x =3.设所求点为P (x ,y ), 则由定义知|PF |=3-x .又|PF |=9,所以3-x =9,x =-6,代入y 2=-12x ,得y =±6 2. 所以所求点的坐标为(-6,62)或(-6,-62).8.已知抛物线C :4x +ay 2=0恰好经过圆M :(x -1)2+(y -2)2=1的圆心,则抛物线C 的焦点坐标为________,准线方程为________. 答案 (1,0) x =-1解析 圆M 的圆心为(1,2),代入4x +ay 2=0得a =-1,将抛物线C 的方程化为标准方程得y 2=4x ,故焦点坐标为(1,0),准线方程为x =-1. 9.已知抛物线的顶点在原点,焦点在y 轴上,抛物线上一点M (m ,-3)到焦点的距离为5,求m 的值、抛物线方程和准线方程. 解 方法一 如图所示,设抛物线的方程为x 2=-2py (p >0),则焦点F ⎝⎛⎭⎫0,-p 2,准线l :y =p2,作MN ⊥l ,垂足为N , 则|MN |=|MF |=5,而|MN |=3+p2=5,即p =4.所以抛物线方程为x 2=-8y ,准线方程为y =2. 由m 2=-8×(-3)=24,得m =±2 6.方法二 设所求抛物线方程为x 2=-2py (p >0),则焦点为F ⎝⎛⎭⎫0,-p 2. ∵M (m ,-3)在抛物线上,且|MF |=5, 故⎩⎪⎨⎪⎧m 2=6p , m 2+⎝⎛⎭⎫-3+p 22=5,解得⎩⎨⎧p =4,m =±2 6. ∴抛物线方程为x 2=-8y ,m =±26,准线方程为y =2.10.花坛水池中央有一喷泉,水管O ′P =1 m ,水从喷头P 喷出后呈抛物线状,先向上至最高点后落下,若最高点距水面2 m ,点P 距抛物线的对称轴1 m ,则水池的直径至少应设计多少米?(精确到1 m)解 如图所示,建立平面直角坐标系.设抛物线方程为x 2=-2py (p >0).依题意有P (-1,-1)在抛物线上,代入得p =12.故得抛物线方程为x 2=-y .又点B 在抛物线上,将B (x ,-2)代入抛物线方程得x =2,即|AB |= 2 m , 则|O ′B |=|O ′A |+|AB |=(2+1) m ,因此所求水池的直径为2(1+2) m ,约为5 m , 即水池的直径至少应设计为5 m.11.已知抛物线y 2=4x 上一点P 到焦点F 的距离为5,则△PFO 的面积为( ) A .1 B .2 C .3 D .4答案 B解析 由题意,知抛物线的焦点坐标为F (1,0),准线方程为x =-1.因为抛物线y 2=4x 上的一点P 到焦点的距离为5,由抛物线的定义可知,点P 到准线x =-1的距离是5,则点P 到y 轴的距离是4,所以P (4,±4),所以△PFO 的面积为12×1×4=2.12.设F 为抛物线y 2=4x 的焦点,A ,B ,C 为该抛物线上三点,若F A →+FB →+FC →=0,则|F A →|+|FB →|+|FC →|=________. 答案 6解析 设A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),又F (1,0). 由F A →+FB →+FC →=0知(x 1-1)+(x 2-1)+(x 3-1)=0, 即x 1+x 2+x 3=3,|F A →|+|FB →|+|FC →|=x 1+x 2+x 3+32p =6.13.已知抛物线y 2=2px (p >0)上一点M (1,m )到其焦点的距离为5,双曲线x 2-y 2a=1的左顶点为A ,若双曲线的一条渐近线与直线AM 垂直,则实数a =________. 答案 14解析 根据抛物线的定义得1+p2=5,p =8,则m =±4,不妨取M (1,4),又A (-1,0),则直线AM 的斜率为2, 由已知得-a ×2=-1,故a =14.14.已知直线l 1:4x -3y +6=0和直线l 2:x =-1,抛物线y 2=4x 上一动点P 到直线l 1和直线l 2的距离之和的最小值是________. 答案 2解析 如图所示,动点P 到l 2:x =-1的距离可转化为到点F 的距离,由图可知,距离和的最小值,即F (1,0)到直线l 1的距离d =|4+6|(-3)2+42=2.15.对标准形式的抛物线,给出下列条件: ①焦点在y 轴上; ②焦点在x 轴上;③抛物线上横坐标为1的点到焦点的距离等于6; ④由原点向过焦点的某直线作垂线,垂足坐标为(2,1).其中满足抛物线方程为y 2=10x 的是________.(要求填写适合条件的序号) 答案 ②④解析 抛物线y 2=10x 的焦点在x 轴上,②满足,①不满足;设M (1,y 0)是y 2=10x 上一点,则|MF |=1+p 2=1+52=72≠6,所以③不满足;由于抛物线y 2=10x 的焦点为⎝⎛⎭⎫52,0,过该焦点的直线方程为y =k ⎝⎛⎭⎫x -52,若由原点向该直线作垂线,垂足为(2,1)时,则k =-2,此时存在,所以④满足.16.设P 是抛物线y 2=4x 上的一个动点,F 为抛物线的焦点. (1)若点P 到直线x =-1的距离为d ,A (-1,1),求|P A |+d 的最小值; (2)若B (3,2),求|PB |+|PF |的最小值.解 (1)依题意,抛物线的焦点为F (1,0),准线方程为x =-1. 由抛物线的定义,知|PF |=d , 于是问题转化为求|P A |+|PF |的最小值.如图,连接AF ,交抛物线于点P ,则最小值为22+12= 5.(2)把点B 的横坐标代入y 2=4x 中,得y =±12, 因为12>2,所以点B 在抛物线内部.自点B 作BQ 垂直准线于点Q ,交抛物线于点P 1(如图).由抛物线的定义,知|P 1Q |=|P 1F |, 则|PB |+|PF |≥|P 1B |+|P 1Q |=|BQ |=3+1=4. 即|PB |+|PF |的最小值为4.1.若抛物线y 2=4x 上一点P 到x 轴的距离为23,则点P 到抛物线的焦点F 的距离为( ) A .4 B .5 C .6 D .7 答案 A解析 由题意,知抛物线y 2=4x 的准线方程为x =-1, ∵抛物线y 2=4x 上一点P 到x 轴的距离为23, 则P (3,±23),∴点P 到抛物线的准线的距离为3+1=4, ∴点P 到抛物线的焦点F 的距离为4.故选A.2.过抛物线y 2=4x 的焦点作一条直线与抛物线相交于A ,B 两点,它们的横坐标之和等于5,则这样的直线( ) A .有且仅有一条 B .有且仅有两条 C .有无穷多条 D .不存在答案 B解析 当斜率不存在时,x 1+x 2=2不符合题意. 当斜率存在时,由焦点坐标为(1,0), 可设直线方程为y =k (x -1),k ≠0,由⎩⎪⎨⎪⎧y =k (x -1),y 2=4x 得k 2x 2-(2k 2+4)x +k 2=0, ∴x 1+x 2=2k 2+4k2=5,∴k 2=43,即k =±233.因而这样的直线有且仅有两条.3.设抛物线y 2=8x 的焦点为F ,准线为l ,P 为抛物线上一点,P A ⊥l ,A 为垂足.如果直线AF 的斜率为-3,那么|PF |等于( ) A .4 3 B .8 C .8 3 D .16 答案 B解析 由抛物线方程y 2=8x ,可得准线l :x =-2,焦点F (2,0),设点A (-2,n ), ∴-3=n -0-2-2, ∴n =4 3.∴P 点纵坐标为4 3. 由(43)2=8x ,得x =6, ∴P 点坐标为(6,43),∴|PF |=|P A |=|6-(-2)|=8,故选B.4.抛物线y 2=4x 与直线2x +y -4=0交于两点A 与B ,F 是抛物线的焦点,则|F A |+|FB |等于( )A .2B .3C .5D .7 答案 D解析 设A (x 1,y 1),B (x 2,y 2), 则|F A |+|FB |=x 1+x 2+2.由⎩⎪⎨⎪⎧y 2=4x ,2x +y -4=0得x 2-5x +4=0, ∴x 1+x 2=5,x 1+x 2+2=7.5.已知直线l 过抛物线C 的焦点,且与C 的对称轴垂直,l 与C 交于A ,B 两点,|AB |=12,P 为C 的准线上的一点,则△ABP 的面积为( ) A .18 B .24 C .36 D .48 答案 C解析 不妨设抛物线方程为y 2=2px (p >0), 依题意,l ⊥x 轴,且焦点F ⎝⎛⎭⎫p 2,0, ∵当x =p2时,|y |=p ,∴|AB |=2p =12,∴p =6,又点P 到直线AB 的距离为p 2+p2=p =6,故S △ABP =12|AB |·p =12×12×6=36.6.抛物线y 2=x 上到其准线和顶点距离相等的点的坐标为__________. 答案 ⎝⎛⎭⎫18,±24解析 设抛物线上点的坐标为(x ,±x ),此点到准线的距离为x +14,到顶点的距离为x 2+(x )2,由题意有x +14=x 2+(x )2,∴x =18,∴y =±24,∴此点坐标为⎝⎛⎭⎫18,±24.7.已知F 是抛物线C :y 2=8x 的焦点,M 是C 上一点,FM 的延长线交y 轴于点N .若M 是FN 的中点,则|FN |=________. 答案 6解析 如图,过点M 作MM ′⊥y 轴,垂足为M ′,|OF |=2,∵M 为FN 的中点,|MM ′|=1,∴M 到准线距离d =|MM ′|+p2=3,∴|MF |=3,∴|FN |=68.已知点A 到点F (1,0)的距离和到直线x =-1的距离相等,点A 的轨迹与过点P (-1,0)且斜率为k 的直线没有交点,则k 的取值范围是________. 解析 设点(x ,y ),依题意得点A 在以y 2=4x . 过点P (-1,0)且斜率为k 的直线方程为y =k (x +1),由⎩⎪⎨⎪⎧y 2=4x ,y =kx +k ,得ky 2-4y +4k =0,当k =0时,显然不符合题意; 当k ≠0时,依题意得Δ=(-4)2-4k ·4k <0,化简得k 2-1>0,解得k >1或k <-1, 因此k 的取值范围为(-∞,-1)∪(1,+∞).9.若抛物线的顶点在原点,开口向上,F 为焦点,M 为准线与y 轴的交点,A 为抛物线上一点,且|AM |=17,|AF |=3,求此抛物线的标准方程. 解 设所求抛物线的标准方程为x 2=2py (p >0),设A (x 0,y 0),由题意知M ⎝⎛⎭⎫0,-p 2,∵|AF |=3,∴y 0+p2=3, ∵|AM |=17,∴x 20+⎝⎛⎭⎫y 0+p 22=17,∴x 20=8,代入方程x 20=2py 0得, 8=2p ⎝⎛⎭⎫3-p2,解得p =2或p =4.∴所求抛物线的标准方程为x 2=4y 或x 2=8y . 10.已知抛物线C :y =2x 2和直线l :y =kx +1,O 为坐标原点.(1)求证:l 与C 必有两交点.(2)设l 与C 交于A ,B 两点,且直线OA 和OB 斜率之和为1,求k 的值. (1)证明 联立抛物线C :y =2x 2和直线l :y =kx +1,可得2x 2-kx -1=0, 所以Δ=k 2+8>0,所以l 与C 必有两交点. (2)解 设A (x 1,y 1),B (x 2,y 2),则y 1x 1+y 2x 2=1,①因为y 1=kx 1+1,y 2=kx 2+1,代入①,得2k +⎝⎛⎭⎫1x 1+1x 2=1,②由(1)可得x 1+x 2=12k ,x 1x 2=-12,代入②得k =1.11.若点M (1,1)是抛物线y 2=4x 的弦AB 的中点,则弦AB 的长为________. 答案15解析 设A (x 1,y 1),B (x 2,y 2),代入抛物线y 2=4x ,可得y 21=4x 1,y 22=4x 2,两式相减,可得k =y 1-y 2x 1-x 2=4y 1+y 2=2,所以直线AB 的方程为y -1=2(x -1),即y =2x -1, 代入抛物线的方程得4x 2-8x +1=0,则x 1+x 2=2,x 1x 2=14,则||AB =1+k 2·(x 1+x 2)2-4x 1x 2=5×⎝⎛⎭⎫22-4×14=15, 即弦AB 的长为15.12.已知A ,B 是抛物线y 2=2px (p >0)上两点,O 为坐标原点.若|OA |=|OB |,且△AOB 的垂心恰是此抛物线的焦点,则直线AB 的方程为________. 答案 x =5p2解析 由抛物线的性质知A ,B 关于x 轴对称.设A (x ,y ),则B (x ,-y ),焦点为F ⎝⎛⎭⎫p 2,0. 由题意知AF ⊥OB ,则有y x -p 2·-yx=-1.所以y 2=x ⎝⎛⎭⎫x -p 2,2px =x ⎝⎛⎭⎫x -p 2. 因为x ≠0.所以x =5p 2.所以直线AB 的方程为x =5p2.13.抛物线x 2=2py (p >0)的焦点为F ,其准线与双曲线x 23-y 23=1相交于A ,B 两点,若△ABF为等边三角形,则p =________.解析 抛物线的焦点坐标F ⎝⎛⎭⎫0,p 2,准线方程为y =-p 2.代入x 23-y23=1得||x = 3+p 24.要使△ABF 为等边三角形,则tan π6=|x |p=3+p 24p =33,解得p 2=36,p =6. 14.直线y =x -3与抛物线y 2=4x 交于A ,B 两点,过A ,B 两点向抛物线的准线作垂线,垂足分别为P ,Q ,则梯形APQB 的面积为________.解析 由⎩⎪⎨⎪⎧ y 2=4x ,y =x -3消去y 得x 2-10x +9=0,得x =1或9,即⎩⎪⎨⎪⎧ x =1,y =-2或⎩⎪⎨⎪⎧x =9,y =6.所以|AP |=10,|BQ |=2或|BQ |=10,|AP |=2,所以|PQ |=8, 所以梯形APQB 的面积S =10+22×8=48.15.已知抛物线C :y 2=8x 与点M (-2,2),过C 的焦点且斜率为k 的直线与C 交于A ,B 两点,若MA →·MB →=0,则k 等于( ) A.12 B.22C. 2 D .2 解析 由题意可知,抛物线的焦点为(2,0).设A (x 1,y 1),B (x 2,y 2),直线AB 的方程为y =k (x -2).由⎩⎪⎨⎪⎧y =k (x -2),y 2=8x 得k 2x 2-(4k 2+8)x +4k 2=0, 则x 1+x 2=4k 2+8k2,x 1x 2=4.y 1+y 2=k (x 1-2)+k (x 2-2)=k (x 1+x 2-4)=8k ,y 1y 2=-8x 18x 2=-16.∴MA →·MB →=(x 1+2,y 1-2)·(x 2+2,y 2-2) =(x 1+2)(x 2+2)+y 1y 2-2(y 1+y 2)+4 =x 1x 2+2(x 1+x 2)+4-16-16k+4=0, 解得k =2,故选D.16.已知直线l 经过抛物线y 2=6x 的焦点F ,且与抛物线相交于A ,B 两点. (1)若直线l 的倾斜角为60°,求|AB |的值;(2)若|AB |=9,求线段AB 的中点M 到准线的距离. 解 (1)因为直线l 的倾斜角为60°, 所以其斜率k =tan 60°=3,又F ⎝⎛⎭⎫32,0,所以直线l 的方程为y =3⎝⎛⎭⎫x -32.联立⎩⎪⎨⎪⎧y =3⎝⎛⎭⎫x -32,y 2=6x ,消去y 得4x 2-20x +9=0,解得x 1=12,x 2=92,故|AB |=1+(3)2×⎪⎪⎪⎪92-12=2×4=8. (2)设A (x 1,y 1),B (x 2,y 2),由抛物线定义,知|AB |=|AF |+|BF |=x 1+p 2+x 2+p2=x 1+x 2+p =x 1+x 2+3=9,所以x 1+x 2=6,于是线段AB 的中点M 的横坐标是3, 又准线方程是x =-32,所以M 到准线的距离等于3+32=92.1.设圆C 与圆x 2+(y -3)2=1外切,与直线y =0相切,则C 的圆心轨迹为( ) A .抛物线 B .双曲线 C .椭圆 D .圆答案 A解析 设圆C 的半径为r ,则圆心C 到直线y =0的距离为r ,由两圆外切可得,圆心C 到点(0,3)的距离为r +1,所以点C 到点(0,3)的距离和它到直线y =-1的距离相等,符合抛物线的特征,故点C 的轨迹是抛物线.2.已知抛物线y 2=2px (p >0),过其焦点且斜率为1的直线交抛物线于A ,B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为( ) A .x =1 B .x =-1 C .x =2 D .x =-2 答案 B解析 抛物线的焦点为F ⎝⎛⎭⎫p 2,0,所以过焦点且斜率为1的直线方程为y =x -p 2,即x =y +p2,代入y 2=2px 消去x ,得y 2=2py +p 2,即y 2-2py -p 2=0,由根与系数的关系得y 1+y 22=p =2(y 1,y 2分别为点A ,B 的纵坐标),所以抛物线方程为y 2=4x ,准线方程为x =-1.3.已知点(x ,y )在抛物线y 2=4x 上,则z =x 2+12y 2+3的最小值是( ) A .2 B .3 C .4 D .0答案 B解析 因为点(x ,y )在抛物线y 2=4x 上,所以x ≥0,因为z =x 2+12y 2+3=x 2+2x +3=(x +1)2+2, 所以当x =0时,z 最小,最小值为3.4.(多选)已知抛物线C :y =x 28的焦点为F ,A (x 0,y 0)是C 上一点,且|AF |=2y 0,则x 0等于( ) A .2 B .-2 C .-4 D .4答案 CD解析 ∵抛物线C :y =x 28,∴x 2=8y , ∴焦点F (0,2),准线方程为y =-2.∵A (x 0,y 0)是C 上一点,且|AF |=2y 0,由抛物线的定义,得y 0+2=2y 0,∴y 0=2,∴x 20=16,∴x 0=±4.5.已知过抛物线y 2=2px (p >0)的焦点F 且斜率为1的直线交抛物线于A ,B 两点,||AF ·||BF =16,则p 的值为( )A .2B .4C .2 2D .8答案 C解析 抛物线y 2=2px (p >0)的焦点F ⎝⎛⎭⎫p 2,0,准线方程为x =-p 2,设A (x 1,y 1),B (x 2,y 2) ∴直线AB 的方程为y =x -p 2, 代入y 2=2px 可得x 2-3px +p 24=0, ∴x 1+x 2=3p ,x 1x 2=p 24, 由抛物线的定义可知,||AF =x 1+p 2,||BF =x 2+p 2, ∴||AF ·||BF =⎝⎛⎭⎫x 1+p 2⎝⎛⎭⎫x 2+p 2 =x 1x 2+p 2(x 1+x 2)+p 24=p 24+32p 2+p 24=2p 2=16,解得p =2 2.6.若抛物线y 2=2px (p >0)的准线经过双曲线x 2-y 2=1的一个焦点,则p =________. 答案 22解析 双曲线x 2-y 2=1的左焦点为(-2,0),所以-p 2=-2,故p =2 2. 7.已知A ,B 为抛物线y 2=2x 上两点,且A 与B 的纵坐标之和为4,则直线AB 的斜率为________.答案 12解析 设A (x 1,y 1),B (x 2,y 2),∴y 1+y 2=4,∵A ,B 在抛物线上,∴⎩⎪⎨⎪⎧y 21=2x 1,y 22=2x 2,相减得 y 21-y 22=2(x 1-x 2), 即y 1-y 2x 1-x 2=2y 1+y 2=24=12. 8.已知抛物线C :y 2=2x ,直线l 的斜率为k ,过定点M (x 0,0),直线l 交抛物线C 于A ,B两点,且A ,B 位于x 轴两侧,OA →·OB →=3(O 为坐标原点),则x 0=________.答案 3解析 设直线l 的方程为y =k (x -x 0),A (x 1,y 1),B (x 2,y 2),与抛物线方程联立可得⎩⎨⎧y 2=2x ,y =k ()x -x 0,消y 并整理可得,k 2x 2-(2k 2x 0+2)x +k 2x 20=0, 由根与系数的关系可得,x 1x 2=x 20,则y 1y 2=-4x 1x 2=-2x 0,∵OA →·OB →=3,∴x 1x 2+y 1y 2=3,即x 20-2x 0=3,解得x 0=3.9.在平面直角坐标系xOy 中,曲线C 1上的点均在圆C 2:(x -5)2+y 2=9外,且对C 1上任意一点M ,M 到直线x =-2的距离等于该点与圆C 2上点的距离的最小值.求曲线C 1的方程. 解 方法一 设点M 的坐标为(x ,y ),由已知得|x +2|=(x -5)2+y 2-3.易知圆C 2上的点位于直线x =-2的右侧,于是x +2>0,所以(x -5)2+y 2=x +5. 化简得曲线C 1的方程为y 2=20x .方法二 由题设知,条件“对C 1上任意一点M ,M 到直线x =-2的距离等于该点与圆C 2上点的距离的最小值”等价于“曲线C 1上任意一点M 到圆心C 2(5,0)的距离等于它到直线x =-5的距离”.所以,曲线C 1是以点(5,0)为焦点,直线x =-5为准线的抛物线,所以曲线C 1的方程为y 2=20x .10.已知抛物线y 2=-8x 的顶点为O ,点A ,B 在抛物线上,且OA ⊥OB ,求证:直线AB 经过一个定点.证明 设直线OA 的斜率为k ,则直线OB 的斜率为-1k,则直线OA 的方程为y =kx , 由⎩⎪⎨⎪⎧y =kx ,y 2=-8x ,得A ⎝⎛⎭⎫-8k 2,-8k , 同理可得B (-8k 2,8k ),于是直线AB 的方程为y -8k =8k +8k 8k 2-8k 2(x +8k 2),整理可得y =k 1-k 2(x +8), 因此直线AB 经过定点(-8,0).11.设F 为抛物线C :y 2=3x 的焦点,过F 且倾斜角为30°的直线交C 于A ,B 两点,O 为坐标原点,则△OAB 的面积为( ) A.334 B.938 C.6332 D.94答案 D解析 由题意可知,直线AB 的方程为 y =33⎝⎛⎭⎫x -34, 代入抛物线的方程可得4y 2-123y -9=0,设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=33,y 1y 2=-94, 故所求三角形的面积为12×34×(y 1+y 2)2-4y 1y 2=94. 12.过抛物线C :y 2=4x 的焦点F ,且斜率为3的直线交C 于点M (M 在x 轴的上方),l 为C 的准线,点N 在l 上,且MN ⊥l ,则M 到直线NF 的距离为( )A. 5 B .2 2 C .2 3 D .33答案 C解析 抛物线y 2=4x 的焦点为F (1,0),准线方程为x =-1.由直线方程的点斜式可得直线MF 的方程为y =3(x -1).联立方程组⎩⎨⎧y =3(x -1),y 2=4x , 解得⎩⎨⎧ x =13,y =-233或⎩⎨⎧ x =3,y =2 3. ∵点M 在x 轴的上方,∴M (3,23).∵MN ⊥l , ∴N (-1,23).∴|NF |=(1+1)2+(0-23)2=4,|MF |=|MN |=3+1=4. ∴△MNF 是边长为4的等边三角形.∴点M 到直线NF 的距离为2 3.13.已知点A ,B 在抛物线y 2=4x 上且位于x 轴的两侧,OA →·OB →=5(其中O 为坐标原点),则直线AB 在x 轴上的截距是( )A .5 B.15 C.14D .4 答案 A解析 设A (x 1,y 1),B (x 2,y 2),因为A ,B 在抛物线上,所以y 21=4x 1,y 22=4x 2,OA →·OB →=x 1x 2+y 1y 2=y 21y 2216+y 1y 2=5,因为y 1y 2<0,所以y 1y 2=-20. 设直线AB 在x 轴上的截距为m , 若AB 斜率不存在,则y 1=-y 2,所以y 1=25,从而x 1=5,m =5,若AB 斜率存在,设直线AB 方程为y =k (x -m ),由⎩⎪⎨⎪⎧y =k (x -m ),y 2=4x , 得ky 2-4y -4km =0,y 1y 2=-4m =-20,m =5.综上,直线AB 在x 轴上的截距是5.14.过抛物线y 2=4x 的焦点F 且倾斜角为π4的直线与抛物线交于A ,B 两点,则|F A |·|FB |的值为________.答案 8解析 过抛物线y 2=4x 的焦点F 且倾斜角为π4的直线方程为y =x -1, 联立⎩⎪⎨⎪⎧y =x -1,y 2=4x 得x 2-6x +1=0, Δ=36-4=32>0,设A (x 1,y 1),B (x 2,y 2),x 1>0,x 2>0,则x 1+x 2=6,x 1x 2=1,F (1,0),|F A |·|FB |=(x 1-1)2+y 21·(x 2-1)2+y 22 =x 21-2x 1+1+4x 1·x 22-2x 2+1+4x 2=x 1x 2+(x 1+x 2)+1=8.15.已知直线l 与抛物线y 2=6x 交于不同的两点A ,B ,直线OA ,OB 的斜率分别为k 1,k 2,且k 1·k 2=3,则直线l 恒过定点( )A .(-63,0)B .(-33,0)C .(-23,0)D .(-3,0) 答案 C解析 设直线l 为x =my +n ,联立⎩⎪⎨⎪⎧x =my +n ,y 2=6x ,消去x 可得y 2-6my -6n =0, 设A (x 1,y 1),B (x 2,y 2),所以y 1y 2=-6n ,因为k 1·k 2=3,即y 1x 1·y 2x 2=3,所以y 1y 2y 216·y 226=36y 1y 2=36-6n =3, 所以n =-23,所以x =my -23,所以直线l 一定过点()-23,016.已知动圆E 经过定点D (1,0),且与直线x =-1相切,设动圆圆心E 的轨迹为曲线C .(1)求曲线C 的方程;(2)设过点P (1,2)的直线l 1,l 2分别与曲线C 交于A ,B 两点,直线l 1,l 2的斜率存在,且倾斜角互补,证明:直线AB 的斜率为定值.(1)解 由已知,动点E 到定点D (1,0)的距离等于E 到直线x =-1的距离,由抛物线的定义知E 点的轨迹是以D (1,0)为焦点,以x =-1为准线的抛物线,故曲线C 的方程为y 2=4x .(2)证明 由题意可知直线l 1,l 2的斜率存在,倾斜角互补,则斜率互为相反数,且不等于零. 设A (x 1,y 1),B (x 2,y 2),直线l 1的方程为y =k (x -1)+2,k ≠0.直线l 2的方程为y =-k (x -1)+2,由⎩⎨⎧ y =k ()x -1+2y 2=4x得k 2x 2-(2k 2-4k +4)x +(k -2)2=0,已知此方程一个根为1,∴x 1×1=()k-22k 2=k 2-4k +4k 2,即x 1=k 2-4k +4k 2,同理x 2=()-k 2-4()-k +4()-k 2=k 2+4k +4k 2,∴x 1+x 2=2k 2+8k 2,x 1-x 2=-8k k 2=-8k ,∴y 1-y 2=[k (x 1-1)+2]-[-k (x 2-1)+2]=k (x 1+x 2)-2k =k ·2k 2+8k 2-2k =8k ,∴k AB =y 1-y 2x 1-x 2=8k-8k=-1, 所以,直线AB 的斜率为定值-1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学抛物线知识点总结
1. 直线与抛物线的位置关系 直线
,抛物线
,
,消y 得:
(1)当k=0时,直线l 与抛物线的对称轴平行,有一个交点; (2)当k ≠0时,
Δ>0,直线l 与抛物线相交,有两不同交点; Δ=0, 直线l 与抛物线相切,有一个切点; Δ<0,直线l 与抛物线相离,无公共点。
(3)若直线与抛物线只有一个公共点,则直线与抛物线必相切吗?(不一定)
2. 关于直线与抛物线的位置关系问题常用处理方法
直线l :b kx y += 抛物线
,)0( p
① 联立方程法:
⎩⎨⎧=+=px
y b
kx y 22
⇒0)(2222=+-+b x p kb x k 设交点坐标为),(11y x A ,),(22y x B ,则有0 ∆,以及2121,x x x x +,还可进一步求出
b x x k b kx b kx y y 2)(212121++=+++=+,2212122121)())((b x x kb x x k b kx b kx y y +++=++=
在涉及弦长,中点,对称,面积等问题时,常用此法,比如
a. 相交弦AB 的弦长
2122122124)(11x x x x k x x k AB -++=-+=a
k ∆+=2
1 或
2122122124)(1111y y y y k
y y k AB -++=-+
=a
k ∆+=2
1 b. 中点坐标
),(00y x M , 2210x x x +=
, 2
2
10y y y += ② 点差法:
设交点坐标为),(11y x A ,),(22y x B ,代入抛物线方程,得
12
12px y = 22
22px y = 将两式相减,可得
)(2))((212121x x p y y y y -=+-
2
121212y y p
x x y y +=
--
a. 在涉及斜率问题时,2
12y y p
k AB +=
b. 在涉及中点轨迹问题时,设线段AB 的中点
为),(00y x M ,0
021*******y p
y p y y p x x y y ==+=--, 即0
y p k AB =
, 同理,对于抛物线)0(22≠=p py x ,若直线l 与抛物线相交于B A 、两点,点),(00y x M 是弦AB 的中点,则有p
x p x p x x k AB 0
021222==+=
(注意能用这个公式的条件:1)直线与抛物线有两个不同的交点,2)直线的斜率存在,且不等于零)。
