绳子支架受力分析

合集下载

模板支架的基本受力形式及受力分析

3）、从试验结果知，设扫地杆与剪刀撑后，支架仍为扣件滑移破坏，其承载力提高不多，但值得注意的是，增设扫地杆和剪刀撑后，支架立杆的有效压力明显降低了，说明支架的整体性得到提高，支架各部分参与工作的程度加深了。本试验因条件限制未进行极限承载力试验，但根据外脚手架试验临界荷载试验，设扫地杆与剪刀撑后脚手架极限承载力提高较大，因此，钢管排架支撑设置必要的扫地杆及剪刀撑有利于提高支架的整体稳定性，防止在混凝土输送管的抖动下支架的整体失稳，增加安全储备。
一、模板支架的基本受力形式（1）、轴心受压与偏心受压
示意图
1800
900
（2）、扣件钢管支模架整架受力试验
7 3
1
7
5 @333
400 6
2
4
1
44
8
12
12
5
10
10
1
4
12 9 8 12
121800Fra bibliotek1800900
900
11
1
1000 1000 1000 1000 1000 1000 1000
1--1 11
1000 1000 1000 1000 1000
用钢管扣件搭设梁模板支架的加载试验，底模下水平钢管与立杆扣接，立杆偏心受压。
扣件钢管模板支架试验用传感器在钢管底下测力。
（3）、扣件钢管支模架整架试验结论：
•1）、对模板支架而言，其承载力往往由扣件的抗滑承载力控制，而非由稳定承载力控制。设计模板支架时，应先验算扣件的抗滑承载力是否满足要求，其次复核稳定性是否满足要求。 •2）、在扭力矩为时，旧扣件的单扣件横杆在10.2~11kN时发生扣件滑移；双扣件横杆在17.5~19.3kN时发生扣件滑移。所以，单扣件抗滑设计承载力取8kN，双扣件抗滑设计承载力取12kN，是可行的。

高考物理复习受力分析之动态平衡--晾衣绳模型

高考复习微专题---动态平衡之晾衣绳模型在高考中，有一类动态平衡问题，称之为晾衣绳模型。

模型特点：非弹性绳绳长s 不变，绳子两端间水平距离L 不变，绳子上通过光滑挂钩悬挂重物G ，由几何知识可知：L =+ααsin s sin s 21，所以L =αssin ，如果只有绳子端点高度变化而距离L 不变时，则绳子形成的夹角2α不变，与绳子端点高度无关。

例1、如图所示，在竖直放置的穹形光滑支架上，一根不可伸长的轻绳通过光滑的轻质滑轮悬挂一重物 G 。

现将轻绳的一端固定于支架上的 A 点，另一端从B 点沿支架缓慢地向C 点靠近。

则绳中拉力大小变化的情况是（）A 、先变小后变大B 、先变小后不变C 、先变大后不变D 、先变大后变小例2、（2017﹒天津高考）如图所示，轻质不可伸长的晾衣绳两端分别固定在竖直杆 M 、N 上的 a 、b 两点，悬挂衣服的衣架挂钩是光滑的，挂于绳上处于静止状态。

如果只人为改变一个条件，当衣架静止时，下列说法正确的是（）A 、绳的右端上移到b'，绳子拉力不变B 、将杆N 向右移一些，绳子拉力变大C 、绳的两端高度差越小，绳子拉力越小D 、若换挂质量更大的衣服，则衣架悬挂点右移变式题：如图所示为一竖直放置的大圆环,在其水平直径上的A 、B 两端系着一根不可伸长的柔软轻绳,绳上套有一光滑小铁环.现将大圆环在竖直平面内绕O 点顺时针缓慢转过一个微小角度,则关于轻绳对A 、B 两点的拉力F A 、F B 的变化情况,下列说法正确的是 ( )A 、F A 变小,FB 变小B 、F A 变大,F B 变大C 、F A 变大,F B 变小D 、F A 变小,F B 变大例1：C例2：AB变式题：A。

高中物理相互作用(二)受力分析专题

相互作用（二）受力分析专题特殊法判断。

4．如何防止“多力”或“丢力”(1) 防止“多力”的有效途径是找出力的施力物体，若某力有施力物体则它实际存在，无施力物体则它不存在。

另外合力与分力不要重复分析。

(2) 按正确的顺序(即一重、二弹、三摩擦、四其他)进行受力分析是保证不“丢力”的有效措施。

冲上粗糙的【典例2】如图所示，A、B两个物体的1 kg，现在它们在拉力对A、B分别画出完整的受力分析。

、B之间的摩擦力大小为多少。

B．3只分析外力。

【典例5】倾角θ＝37°，质量知识点二正交分解法1. 力分解为两个相互垂直的分力的方法称为正交分解法。

例如将力F沿x和y两个方向分解，如图所示，则F x＝F cos θF y＝F sin θ多的力，也就是说需要向两坐标轴上投影分解的力少一些。

这样一来，计算也就方便一些，可以就是将物理问题的某些研究对象或某些过程、状态从系统或全过程中隔离出来进行研究的方知识点三【典例探究】【典例＝5 N，f2＝0，f3＝5 N＝5 N，f2＝5 N，f3＝0＝0，f＝5 N，f＝5 N现行高考要求，物体受到往往是三个共点力问题，利】用绳是其它-1先减小，后增大 B.F 先减小后增大(B)F1个力中其中两个力是绳的拉力，由于是同一根点位置固定，A 端缓慢左移时，答案与解析1.【答案】A2.【答案】(1) 见规范解答图 (2) 0 (3) 4 N【解析】(1) 以A 为研究对象，A 受到重力、支持力作用；以B 为研究对象，B 受到重力、支持力、压力、拉力、地面对B 的滑动摩擦力作用；如图。

(2) 对A ：由二力平衡可知A 、B 之间的摩擦力为0。

(3) 以A 、B 整体为研究对象，由于两物体一起做匀速直线运动，所以受力如图，水平方向上由二力平衡得拉力等于滑动摩擦力，即F ＝F f ＝μB 地F N B ，而F N B ＝G B ＋G A ，所以F ＝0.2×(1×10＋1×10) N＝4 N 。

热力工程中固定支架的受力状况分析

ARCHITECTURE
VDoecl . (2002) 1220028202
热力工程中固定支架的受力状况分析
夏志方
摘要 :对热力管道工程中固定支架的受力进行了分析 ,并对在不同情况下的受力状况提出了应注意的要点 ,解决了固
改变后 C 点固定支架推力 : PX3 = PK3 + P0 A =ΔX·KX + P0 A
= 5 750 + 1. 6 ×10 ×3 167 = 56 422 kg , 式中 : P0 ———管线设计压力 1. 6 MPa ;
A ———波纹补偿器的有效面积 3 167 cm2 。由此可见 ,改变前后 C 点固定支架所承受的推力与原设计固定支架的力相差 50 t 左右 ,后者相当于前者的 32 倍 ,这种分期、分阶段施工和供热的管线在实际工作中经常遇到。在这种情况下 , 采取一般的支撑和简单的对固定支架加固 ,可能满足不了要求。
P = ∑1. 2 ( qz + qw) L + ∑qyL , 式中 : P ———作用与一个支架上的总垂直荷载 ,kg ;
qz ———管道自重 ,kg/ m ; qw ———管道保温层重量 ,kg/ m ; qy ———液体重量 ,kg/ m ;
112 水平荷载
沿管道轴向的水平荷载。 1) 补偿器的弹性反力 PK 当管道膨胀时 ,补偿器被压缩变形 ,由于补偿器的刚度 (对于套筒补偿器 ,则由于填料的摩擦力作用) 将产生一个抵抗压缩的力量 ,这个力是通过管道反作用于固定支架 ,这就是补偿器的弹性反力 ,轴向型波纹补偿器的弹性反力 PK :
卷第 12 2年12
期月
SHANXI
ARCHITECTURE
VDoecl ..2 8 2N0o0.212

物体的受力分析

古典力学理论在实践中又都出现了矛盾，表现出真理的相对性。在新条件下，必须修正原有的理论，建立新的概念，才能正确指导实践，改造世界，并进一步地发展力学理论，形成新的力学分支。力学基础是一门理论性较强的技术基础课。学习理论力学的目的是: 1.直接解决工程问题。 2.是学习一系列后续课程的重要基础。
可用二个通过轴心的正交分力 Fx , Fy 表示。
(2) 、光滑圆柱铰链
约束特点：由两个各穿孔的构件及圆柱销钉组成，如剪刀。
约束力：
光滑圆柱铰链：亦为孔与轴的配合问题，与轴承一样，可用两个正交分力表示。
其中有作用反作用关系 Fcx Fcx , Fcy Fcy
一般不必分析销钉受力，当要分析时，必须把销钉单独取出。
取AB 梁，其受力图如图 (c)
CD 杆的受力图能否
画为图（d）所示？
若这样画，梁 AB的受力图又如何改动?
例1-4 不计三铰拱桥的自重与摩擦，画出左、右拱 AB, CB 的受力图与系统整体受力图。
解：
右拱 CB 为二力构件，其受力图如图（b）所示
取左拱AC ,其受力图如图（c）所示
约束力：比径向轴承多一个轴向的约束反力，亦有三个正交分力 FAx , FAy , FAz。
（1）光滑面约束——法向约束力 FN （2）柔索约束——张力 FT
（3）光滑铰链—— FAy FAx
（4）滚动支座—— FN⊥光滑面
球铰链——空间三正交分力
止推轴承——空间三正交分力
(3) 固定铰链支座
约束特点：由上面构件1或2 之一与地面或机架固定而成。
约束力：与圆柱铰链相同
以上三种约束（经向轴承、光滑圆柱铰链、固定铰链支座）其约束特性相同，均为轴与孔的配合问题，都可称作光滑圆柱铰链。

【2018新课标高考必考知识点教学计划教学安排教案设计】高三物理：绳与杆的受力分析技巧

变式训练如图所示，小车上有一支架 ABC，其中杆 AB 与斜面垂直，杆 BC 与斜面平行，在 BC 的末端有一个质量为 m 的小球。小车由静止释放后沿倾角为 α 的光滑斜面下滑，则杆对小球的弹力（）
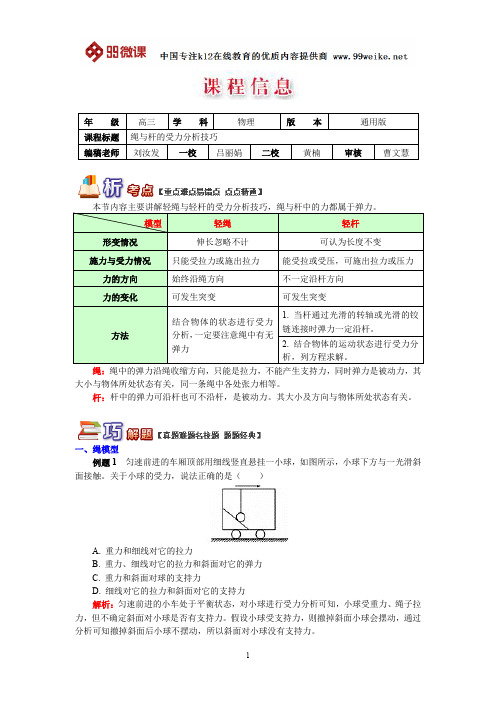
A. 竖直向上，大小为 mg B. 沿 CB 方向，大小为 mgsin α C. 垂直斜面向上，大小为 mgcos α D. 等于零解析：以整体为研究对象，由牛顿第二定律可得整体加速度 a＝gsinα，对小球进行受力分析，重力沿斜面分力为小球所受合外力，垂直斜面的分力 mgcosα 与杆对球的弹力平衡。答案：C
力二力合力为 ma，如图可得：由勾股定理可得其大小 (mg)2 (ma)2 ，方向如图所示：
答案：（1）mg、竖直向上
（2） (mg)2 (ma)2
方向：与竖直夹角的正切值 tanθ＝ a g
1. 轻绳（1）轻绳模型的特点
2
“绳”在物理学上是个绝对柔软的物体，它只产生拉力（张力），绳的拉力沿着绳的方向并指向绳的收缩方向。它不能产生支持作用。
变式一：当小车匀速运动时弹力的大小及方向？答案：大小等于重力方向，方向竖直向上变式二：当斜面有摩擦力且小车匀加速运动时弹力的方向？答案：大小介于 mgcos α—mg 之间的某个值，方向介于垂直 BC 向上到竖直向上之间。
3
1. 如图所示，细绳竖直拉紧，小球和光滑斜面接触，则小球受到的力是（）
1
答案：A 思考：若车厢向右加速运动呢？
二、杆模型例题 2 如图所示，轻杆 AB 下端通过光滑的转轴固定在竖直墙上，上端有一光滑的轻
质小滑轮，一根细绳一端 C 系在墙上，绕过滑轮另一端系一质量为 m 的物体，当 C 端在缓慢地上移过程中，则杆对滑轮的作用力将（）

支架受力分析

管道支架受力分析——曹伟选取购物中心地下室某段压力排水管道进行受力分析：系统：压力排水材质：镀锌钢管管径：DN100管道数量：两根相邻两支架间距：6米一、管道重量由三部分组成：按设计管架间距内的管道自重、满管水重及以上两项之合10%的附加重量计算（管架间距管重均未计入阀门重量，当管架中有阀门时，在阀门段应采取加强措施）。

1、管道自重：由管道重量表可查得，镀锌钢管DN100：21.64Kg/m ，支架间距按6米/个考虑,计算所得管重为：f1=21.64*6kg=129.84kg*10=1298.4N2.管道中水重f2=πr2ρ介质l=3.14*0.1062*1000*6kg=211.688kg=2116.88N3、管道重量f=f1+f2+(f1+f2)*10%=3756.81N4、受力分析根据支架详图，考虑制造、安装等因素，系数按1.35考虑，每个支架受力为：F=3756.81*1.35/2=2535.85N假设选取50*5等边角钢（材质为Q235）做受力分析试验1）应力应变关系如下：绘制成应力应变曲线图如下：从图中可以看出，应力/应变曲率变化平缓，处于弹性应力应变行为阶段，各部位均没有发生屈服现象。

由相关资料可查的50*5等边角钢的抗拉强度σb=423MPa，抗剪强度σr=σb*0.8=338.4MPa，型钢吊杆拉伸强度小于它的抗拉强度，型钢横担小于它的抗剪强度，所以50*5等边角钢可以满足使用要求。

2）危险部位应力分析图中的蓝色区域为支架应变最大的地方，也即该处最容易发生变形与开裂，在设计中应对有较大变形的地方，解决办法有两个：1、加固：可以通过增加肋板来加固，在型钢焊接的地方更应该满焊以此增大接触面，从而减小开裂的可能；2、通过选择更大规格的型钢来试验，直到满足设计要求为止。

通过上述例子，我们选择40*4的等边角钢来试验，通过计算和分析校核，发现可以满足使用要求，从而更加节省了型钢的用量。

以上分析只考虑了垂直方向的载荷，实际上对于有压管道，同时存在水平方向的受力，所以我们分开单独分析一下二、支架水平方向受力1）补偿器的弹性反力P k当管道膨胀时，补偿器被压缩变形，由于补偿器的刚度（对于套筒式补偿器，则由于填料的摩擦力作用），将产生一个抵抗压缩的力量，这个力是通过管道反作用于固定支架，这就是补偿器的弹性反力，轴向型波纹补偿器的弹性反力P k：P k=ΔX·Kx·10-1(kg)式中ΔX—管道压缩变形量（即管道的热伸长量）(mm)Kx—补偿器轴向整体刚度)(N/mm)其他各类补偿器可通过不同公式计算得出。

管道固定支架的受力分析

管道固定支架的受力分析随着资源节约型与环境友好型社会的深入发展，环保节能理念融入生活生产的方方面面，逐渐成为时代发展潮流。

一：主固定支架的受力分析
通常情况下，主固定支架设置在热力管道的端点处、各项分支点处、各型号阀门的加设点处，需要承受来自各方的力，如内压推力、各类摩擦力、波纹管膨胀节在不断位移过程中产生的力等，这就要求施工人员对其受力情况进行严格管控，全面、客观、详尽的考虑到一切可能影响其受力值的因素，并通过反复分析与比对，掌握其实际受力值及受力类型。

二：次固定支架的受力分析
次固定支架也是固定支架的重要组成部分，对热力管道的正常运转具有积极作用。

技术人员在具体安装的过程中，可选择铰链型或复式万能型波纹管膨胀节，以达到承载内压推力的作用，此后加设次固定支架，能有效分担剩余的荷载力，为热力管道安全稳定运行打下坚实的基础。

陕西雅美新材料有限公司坐落于十三朝古都西安临潼区，是一家多年专业从事HDPE、UHMW-PE、FRPP等塑料管材研发、制造、销售、安装服务于一体的高新技术企业，公司
注册资金1.01亿元，员工60余人，公司目前有三个生产基地：泰州，廊坊，西安，设有三个分公司分别为：山东分公司、山西分公司、新疆分公司，公司主要经营给水与排水系列产品，主要经营的品牌有瀚通、小管当家、真优材。

给水管产品主要有：PVC-O新型给水管、PE给水管、钢丝网骨架聚乙烯复合管、孔网钢带聚乙烯复合管、钢骨架塑料复合管等。

欢迎新老顾客前来咨询！欢迎新老顾客前来咨询！。

轻绳,轻杆模型的受力平衡问题分析

轻绳,轻杆模型的受力平衡问题分析轻绳和轻杆模型是一种简单而有用的工程分析方式，它可以帮助我们研究物理对象的运动和特征。

特别是，它是一种有效的方法，用于研究有关硬度，材料性能，静止状态，运动状态等问题的受力平衡。

本文将就轻绳和轻杆模型的受力平衡问题进行研究分析。

首先，我们来谈谈轻绳和轻杆模型。

这类模型是由一根绳索（绳索可以是弹性的，也可以是不弹性的）和几根杆组成的，可以表示物体受到拉力和扭力的情况。

轻绳模型是一种可以准确表达物体受力结构形态及变形的分析方法。

它可以有效地研究物体的固有模态以及该物体受力时的振动特性。

其次，我们来看看轻绳和轻杆模型的受力平衡问题。

受力平衡问题是指在一个结构系统中，物体受到的外力和内力是相等的，即满足力的平衡条件。

物体的受力情况的分析，可以帮助我们理解物体的静止状态，动状态以及受力时的变形等情况。

进行轻绳和轻杆模型的受力平衡分析时，一般通过物理模型分析，将由多个外力和内力组成的受力平衡条件，抽象成一个矩阵方程，然后用数学方法求解受力平衡条件。

此外，轻绳和轻杆模型的受力平衡分析还可以用来研究材料的性质。

例如，当绳索、支架或者底座等物体受到变形时，可以研究材料的弹性模量和硬度等特性，从而研究物体的受力反应情况。

最后，在针对轻绳,轻杆模型的受力平衡问题进行研究时，我们应该特别注意两个问题。

首先，我们要考虑物体受力后的稳定性，不能只考虑受力平衡的情况，还要考虑物体的受力时的振动情况等。

其次，在考虑受力平衡的情况时，应考虑物体的反作用力大小，考虑选用什么样的拉力和扭力使得物体受力过程中的位移最小。

以上就是关于轻绳和轻杆模型的受力平衡问题的分析，研究。

轻绳和轻杆模型是一种常用的工程分析方式，可以用来研究物体受力过程中的变形和受力平衡。

受力平衡问题是指，在一个结构系统中，物体受到的外力和内力要相等，满足力的平衡条件，物体的受力状况的分析，可以帮助我们理解物体的静止状态，活动状态以及受力时的变形等情况。

力学、受力分析—知识点+方法+例题

1高中物理——力学专讲学好物理要记住：最基本的知识、方法才是最重要的。

秘诀：“想”学好物理重在理解．．．．．．．．（概念、规律的确切含义，能用不同的形式进行表达，理解其适用条件） A(成功)＝X(艰苦的劳动)十Y(正确的方法)十Z(少说空话多干实事)(最基础的概念,公式,定理,定律最重要)；每一题中要弄清楚(对象、条件、状态、过程)是解题关健物理学习的核心在于思维，只要同学们在平常的复习和做题时注意思考、注意总结、善于归纳整理，对于课堂上老师所讲的例题做到触类旁通，举一反三，把老师的知识和解题能力变成自己的知识和解题能力，并养成规范答题的习惯,这样，同学们一定就能笑傲考场，考出理想的成绩！对联: 概念、公式、定理、定律。

（学习物理必备基础知识）对象、条件、状态、过程。

（解答物理题必须明确的内容）力学问题中的“过程”、“状态”的分析和建立及应用物理模型在物理学习中是至关重要的。

说明：凡矢量式中用“+”号都为合成符号，把矢量运算转化为代数运算的前提是先规定正方向。

答题技巧：“基础题，全做对；一般题，一分不浪费；尽力冲击较难题，即使做错不后悔”。

“容易题不丢分，难题不得零分。

“该得的分一分不丢，难得的分每分必争”，“会做{ EMBED Equation.3 |⇒做对不扣分”在学习物理概念和规律时不能只记结论，还须弄清其中的道理，知道物理概念和规律的由来。

Ⅰ。

力的种类:（13个性质力）这些性质力是受力分析不可少的“是受力分析的基础” 受力分析入手（即力的大小、方向、力的性质与特征，力的变化及做功情况等）。

再分析运动过程（即运动状态及形式，动量变化及能量变化等）。

最后分析做功过程及能量的转化过程；然后选择适当的力学基本规律进行定性或定量的讨论。

强调：用能量的观点、整体的方法(对象整体，过程整体)、等效的方法(如等效重力)等解决力的合成定则：○1|平行四边形定则：求共点力F 1、F 2的合力，可以把表示F 1、F 2的线段为邻边作平行四边形，它的对角线即表示合力的大小和方向，如图a 。

高中力学拉米定律(矢量圆)全反角

高中物理动态平衡①图解法②相似三角形③绳结定活杆及极限问题④晾衣绳模型⑤正弦定理（矢量圆）⑥全反力、摩擦角[飞飞老师]图解法图解法：对研究对象进行受力分析，再根据三角形定则画出不同状态下的力的矢量图（画在同一个图中），然后根据有向线段（表示力）的长度变化判断各力的变化情况。

图解法使用特征：①三个力②其中一个力为恒力③另一个力方向不变，但大小发生变化④第三个力则随外界条件的变化而变化，包括大小和方向都变化。

方法讲解：解答此类“动态型”问题时，一定要认清哪些因素保持不变，哪些因素是改变的，这是解答动态问题的关键【例1】：半圆形支架BCD上悬着两细绳OA和OB，结于圆心O，下悬重为G的物体，使OA绳固定不动，将OB绳的B端沿半圆支架从水平位置逐渐移至竖直的位置C的过程中，如图所示，分析OA绳和OB绳所受力的大小如何变化？【答案】：OA绳子拉力逐渐变小，OB绳子拉力先变小后变大。

【解析】：（1）分析力的情况，OG绳子拉力因为大小等于重力，方向始终竖直向下，属于大小方向都不变的力，OA绳子不动，OA绳子拉力属于方向不变的力，OB绳子方向变动，OB绳子拉力属于大小方向都改变的力，故符合图解法特征。

（2）对结点O受力分析如图：TA是一直变小，而TB却是先变小后增大，当OB与OA垂直时TB最小。

例题1、如图所示，一个重为G的匀质球放在光滑斜直面上，斜面倾角为α，在斜面上有一光滑的不计厚度的木板挡住球，使之处于静止状态．今使板与斜面的夹角β缓慢增大，问：在此过程中，球对挡板和球对斜面的压力大小如何变化？2、如图所示，把球夹在竖直墙AC和木板BC之间，不计摩擦，球对墙的压力为FN１，球对板的压力为FN2．在将板BC逐渐放至水平的过程中，下列说法中，正确的是（）A．FN１和FN2都增大B．FN１和FN2都减小C．FN１增大，FN2减小D．FN１减小，FN2增大3、如图所示，三段绳子悬挂一物体，开始时OA、OB绳与竖直方向夹角θ＝30，现使O点保持不动，把OB绳子的悬点移到竖直墙与O点在同一水平面的C点，在移动过程中，则关于OA、OB绳拉力的变化情况，正确的是（）A．OA绳上的拉力一直在增大B．OA绳上的拉力先增大后减小C．OB绳上拉力先减小后增大，最终比开始时拉力大D．OB绳上拉力先减小后增大，最终和开始时相等4、如图所示，小球用细绳系住放在倾角为θ的光滑斜面上，当细绳由水平方向逐渐向上偏移时，细绳上的拉力将（）A．逐渐增大B．逐渐减小C．先增大后减小D．先减小后增大5、如图所示，电灯悬挂于两壁之间，更换水平绳OA使连结点A向上移动而保持O点的位置不变，则A点向上移动时（）A．绳OA的拉力逐渐增大；B．绳OA的拉力逐渐减小；C．绳OA的拉力先增大后减小；D．绳OA的拉力先减小后增大。

受力分析大全

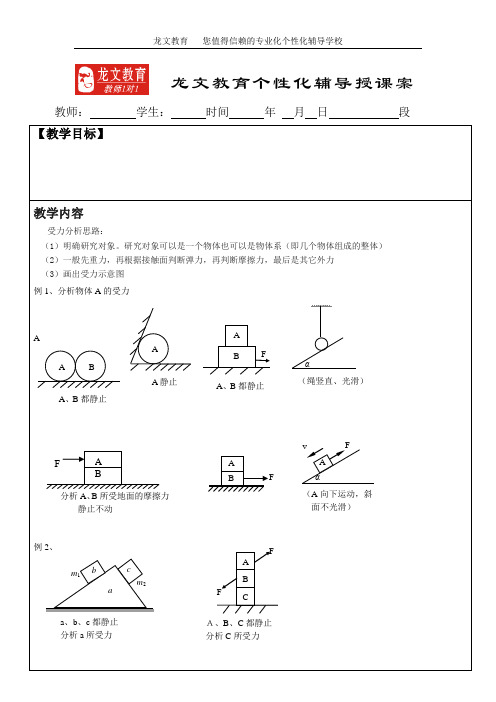
教师：学生：时间年月日段【教学目标】教学内容受力分析思路：（1）明确研究对象。

研究对象可以是一个物体也可以是物体系（即几个物体组成的整体）（2）一般先重力，再根据接触面判断弹力，再判断摩擦力，最后是其它外力（3）画出受力示意图例1、分析物体A 的受力 A 例2、龙文教育个性化辅导授课案ABA 、B 都静止 AA 静止BA FA 、B 都静止FBA 分析A 、B 所受地面的摩擦力静止不动B A CFFＡ、B 、C 都静止 c bam 1m 2a 、b 、c 都静止分析a 所受力AαF v（A 向下运动，斜面不光滑）A BFα（绳竖直、光滑）例3、如图所示，水平传送带上的物体。

（1）随传送带匀速运动（2）传送带由静止起动如图，倾斜传送带上的物体（1）向上匀速运输（2）向下匀速运输例4、如图所示，各图中，物体总重力为G ，请分析砖与墙及砖与砖的各接触面间是否有摩擦力存在？如有大小是多少？例5、分析A 、B 的受力练习：A 物体静止或匀速，分析A 物体的受力情况 A α （A 静止）α（光滑小球）A AB C（A 、B 一起匀速向右运动）AB（A 静止）ααB ABA匀速， vAv图2-1-72、分析下列杆所受的力(竖直面光滑，水平面粗糙)3.分析A 的受力（A 静止）（A 匀速下滑）例题1如图2-1-7所示，甲、乙球通过弹簧连接后用绳悬挂于天花板，丙、丁球通过细绳连接后也用绳悬挂天花板．若都在A 处剪断细绳，在剪断瞬间，关于球的受力情况，下面说法中正确的是（） A ．甲球只受重力作用 B ．乙球只受重力作用 C ．丙球受重力和绳的拉力作用 D ．丁球只受重力作用2．如图2-2-8所示，物体a 、b 和c 叠放在水平桌面上，水平力Fb=5N 、Fc=10N 分别作用于物体b 、c 上，a 、b 和c 仍保持静止．以F1、F2、F3分别表示a 与b 、b 与c 、c 与桌面间的静摩擦力的大小，则（） A ．F1=5N ，F2=0，F3=5N B ．F1=5N ，F2=5N ，F3=0C ．F1=0，F2=5N ，F3=5N ＡA 沿着墙向上运动AA 沿着水平面向右运动AA 沿着斜面向上运动FAFAＡ A 静止F cF ba b cBAABFF甲乙图2-2-212．如图12所示，将截面为三角形、底面粗糙、斜面光滑的物块P 放在粗糙的水平地面上，其右端点与竖直挡板MN 靠在一起，在P 和MN 之间放置一个光滑均匀的小圆柱体Q ，整个装置处于静止状态．若用外力使竖直挡板MN 以N 点为轴缓慢地顺时针转动至挡板MN 水平之前，物块P 始终静止不动，此过程中，下列说法正确的是( ) A ．MN 对Q 的弹力先减小后增大 B ．P 对Q 的弹力逐渐增大 C ．地面对P 的摩擦力逐渐减小 D ．Q 所受的合力逐渐增大5．如图5所示，质量为m 的物体在沿斜面向上的拉力F 作用下沿放在水平地面上的质量为M 的粗糙斜面匀速下滑，此过程中斜面体保持静止，则地面对斜面( )A ．无摩擦力B ．有水平向左的摩擦力C ．支持力为(M ＋m)gD ．支持力小于(M ＋m)g3如图2-2-1所示，A 、B 两物体叠放在水平面上，水平力F 作用在A 上，使两者一起向右作匀速直线运动，下列判断正确的是（） A ．A 、B 间无摩擦力B ．A 对B 的静摩擦力大小为F ，方向向右C ．B 对地面的动摩擦力的大小为F ，方向向右D ．B 受到了向右的静摩擦力和向左的滑动摩擦力4如图2-2-2示，物体A 、B 在力F 作用下一起以相同速率沿F 方向匀速运动，关于物体A 所受的摩擦力，下列说法中正确的是（）A ．甲、乙两图中A 均受摩擦力，且方向均与F 相同B ．甲、乙两图中A 均受摩擦力，且方向均与F 相反C ．甲、乙两图中A 均不受摩擦力D ．甲图中A 不受摩擦力，乙图中A 受摩擦力，方向均与F 相同5.如图2-2-3所示，物体A 、B 的质量mA=mB=6kg ，A 和B 、B 和水平面间的动摩擦因数都等于0.3，且最大静摩擦力等于滑动摩擦力，水平力F=30N ．那么，B 对A 的摩擦力和水平桌面对B 的摩擦力各为多大? A BF图2-2-1FA BF 2F 1F 3F 437°106°图2-3-136．如图2-2-16所示，重物A 质量为mA=5kg ，重物B 质量为mB=2kg ，A 与桌面间的最大静摩擦力为Fm=10N ．为使系统处于静止状态，试求拉力F 大小范围．（g 取10m/s2）力的分解与合成1在同一平面内共点的四个力F1、F2、F3、F4的大小依次为19N 、40N 、30N 和15N ，方向如图2-3-13所示，求它们的合力．2如图2-3-16所示，质量为m 的物体用细绳OC 悬挂在支架上的O 点，轻杆OB 可绕B 点转动，当物体静止时细绳OA 与轻杆OB 间的夹角为θ．求此时细绳OA 中张力F1的大小和轻杆OB 受力F2的大小．3如图2-3-17所示，水平横梁一端A 插在墙壁内，另一端装有小的轻质滑轮B ，一轻绳一端C 固定于墙壁上，另一端跨过滑轮后悬挂一质量为m=10kg 的重物，∠CBA=30°，则滑轮受到绳子作用力为（）A ．50NB ．503NC ．100ND ．1003N4如图2-3-19所示，物体静止于光滑水平面上，力F 作用于物体O 点，现要使物体沿着OO '方向做加速运动（F 和OO'都在水平面内）．那么，必须同时再加一个力F '，这个力的最小值是（ B ）A ．Fcos θB ．Fsin θC ．F tan θD ．Fcot θ5．用两根绳子吊起一重物，使重物保持静止，逐渐增大两绳之间的夹角，则两绳对重物的拉力的合力变化情况是图2-2-16OC mAB 图2-3-16 ACB m 图2-3-17图2-3-19图2-4-5A ．保持不变B ．逐渐增大C ．逐渐减小D ．以上说法都有可能6．如图2-3-21所示，两个完全相同的小球在挡板作用下静止在倾角为θ的光滑斜面上，求（a ）、（b ）两种情况下小球对斜面的压力之比．7．如图2-3-24所示，用跟水平方向成α角的推力F 推重量为G 的木块沿天花板向右运动，木块和天花板间的动摩擦因数为μ，求木块所受的摩擦力大小．8如图2-4-5所示，重力为 G 的物体在水平向右和跟竖直方向成θ角的斜向上绳子的拉力作用下，保持静止状态，试求两绳的拉力9如图2-4-19所示，用绳AC 和BC 吊起一重物，绳与竖直方向夹角分别为30°和60°，AC 绳能承受的最大拉力为150N ，而而BC 绳能承受的最大的拉力为100N ，求物体最大重力（a ）（b ）图2-3-21θθαF G图2-3-24 30° 6图2-4-19BCA 60030010．如图2-4-27所示，小球质量为m ，置于质量为M 的倾角为θ的光滑斜面上，悬线与竖直方向的夹角为α，系统处于静止状态．求（1）斜面对小球的支持力和悬线对小球的拉力大小．（2）地面对斜面体的水平和竖直方向的作用力大小练习题1、用轻绳AC 和BC 悬挂一重物，绳AC 和BC 与水平天花板的夹角分别为600和300，如图所示，已知悬挂重物的重力150牛顿，求AC 绳和BC 绳上承受的拉力大小？2、物体A 在水平力F 作用下，沿着倾角为 370的斜面匀速上滑，物体A 所受到的重力为G=300N ，它与斜面之间的动摩擦因数u=0.5，求：（1）物体A 所受到的支持力。

专题03 轻绳、轻杆、轻弹簧、接触面模型(1)-高考物理模型系列之对象模型(解析版)

一模型界定本模型主要讨论绳和杆的弹力以及接触面间作用力的特点、形成的挂件模型、出现的临界与极值问题，以及它们的力的作用的瞬时性即暂态过程的问题等。

二模型破解 1."轻质"的含义 (i)质量为零(ii)任何状态下所受合力为零例1.如图所示，倾角为α的等腰三角形斜面固定在水平面上，一足够长的轻质绸带跨过斜面的顶端铺放在斜面的两侧，绸带与斜面间无摩擦。

现将质量分别为M 、m(M>m)的小物块同时轻放在斜面两侧的绸带上。

两物块与绸带间的动摩擦因数相等，且最大静摩擦力与滑动摩擦力大小相等。

在α角取不同值的情况下，下列说法正确的有A ．两物块所受摩擦力的大小总是相等B ．两物块不可能同时相对绸带静止C ．M 不可能相对绸带发生滑动D ．m 不可能相对斜面向上滑动【答案】 C时还应满足m f f ≤,即当m M M +≥2μ时两物块都相对绸带静止,B 错误.当mM M+<2μ时,m 相对绸带滑动,物块所受摩擦力达到最大值:M m f mg f <=αμcos ,M 仍相对绸带静止,C 正确.当m 相对绸带滑动时,若满足ααμsin cos mg mg <即αμtan <时m 相对斜面下滑;若αμtan =时m 静止;αμtan >时m 上滑,故D 错误.模型演练1.某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力恒为f . 轻杆向右移动不超过l 时,装置可安全工作. 一质量为m 的小车若以速度v 0 撞击弹簧,将导致轻杆向右移动4l. 轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦.(1)若弹簧的劲度系数为k,求轻杆开始移动时,弹簧的压缩量x;(2)求为使装置安全工作,允许该小车撞击的最大速度v m ; (3)讨论在装置安全工作时,该小车弹回速度v ’和撞击速度v 的关系.【解析】:（1）轻杆开始移动时，弹簧的弹力kx F = ① 且f F = ② 解得kfx =③2.弹力 (I)弹力的方向（i ）绳的弹力①绷直的轻绳，其弹力方向沿着绳，与物体的运动状态无关 ②绳只能对物体施加拉力，不能对物体施加推力練1图③质量不能忽略的绳，绳中某处的张力沿该点绳的切线方向（ii）杆的弹力①轻杆的弹力不一定沿着杆，具体方向与物体的运动状态、杆与物体的连接方式有关②杆既可以对物体产生拉力，也可以对物体产生推力③满足下列条件时杆的弹力一定沿着杆:A.轻杆B.轻杆的一端由转轴或绞链固定C.除转轴或绞链对杆的作用力外,其它作用力作用于杆上同一点.（iii）弹簧的弹力①弹簧弹力的方向沿弹簧的中轴线方向,与运动状态无关②弹簧的弹力可以是拉力也可以是推力(iv)接触面的弹力①接触面的弹力一定垂直于接触面,与物体的运动状态无关②接触面只能对物体产生推力,不能对物体产生拉力③接触面间还可以存在摩擦力(II).弹力的大小①无论轻绳、轻杆还是接触面间的弹力,它们的大小具有一点相同的特征,即弹力的大小与系统所处于的运动状态有关,通常需要从平衡条件或牛顿运动定律来求解.②绕过光滑物体的同一条轻绳上各点的张力仍是相大小等的，如光滑滑轮、光滑挂钩等两侧的轻绳；系于一点的两段绳上张力大小不一定相等．③弹簧的弹力大小与运动状态无关,取决于弹簧劲度系统与形变量,遵从胡克定律.例2.重G的均匀绳两端悬于水平天花板上的A、B两点．静止时绳两端的切线方向与天花板成α角．求绳的A端所受拉力F1和绳中点C处的张力F2.例2 题图【答案】例3.如图所示，车厢里悬挂着两个质量不同的小球，上面的球比下面的球质量大，当车厢向右作匀加速运动(空气阻力不计)时，下列各图中正确的是【答案】B【解析】:由于无论系统是处于平衡状态还是处于非平衡状态,轻绳的张力总是沿着绳的.设上面一段绳与竖直方向的夹角为α，下面一段绳与竖直方向的夹角为β，先把M 、m 看做一个整体，对整体分析可知受到重力和上段绳的拉力如图所示，则由牛顿第二定律知：F 合＝(m ＋M)gtanα＝(M ＋m)a 得：a ＝gtanα.以下面的小球m 为研究对象，则有：mgtanβ＝ma′，其中a′＝a ，所以tanβ＝tanα，即α＝β，故选项B 正确．例 4.如图所示，固定在小车上的斜杆与竖直杆的夹角为θ，在斜杆的下端固定有质量为m 的小球，下列关于杆对球的作用力F 的判断中，正确的是（）A 、小车静止时，cos F mg θ=，方向沿杆向上例3答图例4题图θ例3题图B 、小车静止时，cos F mg θ=，方向垂直杆向上C 、小车向右以加速度a 运动时，一定有/cos F mg θ=D 、小车向左以加速度a 运动时，22g a m F +=，方向斜向左上方，与竖直方向的夹角为arctan(/)a g α=【答案】D根据牛顿第二定律有： sin ,F ma α= cos F mg α=可解得：/cos F mg α=，arctan(/)a g α=,可见α随a 大小而改变，不一定等于θ。

新教材2024高考物理二轮专题复习第一编专题复习攻略专题一力与运动第1讲力与物体的平衡教师用书

第1讲力与物体的平衡知识网络构建命题分类剖析命题点一静态平衡问题1．共点力平衡的常用处理方法(1)研究对象的选取：①整体法与隔离法(如图甲)；②转换研究对象法(如图乙)．(2)画受力分析图：按一定的顺序分析力，只分析研究对象受到的力．(3)验证受力的合理性：①假设法(如图丙)；②动力学分析法(如图丁)．例 1[2023·山东卷]餐厅暖盘车的储盘装置示意图如图所示，三根完全相同的弹簧等间距竖直悬挂在水平固定圆环上，下端连接托盘．托盘上叠放若干相同的盘子，取走一个盘子，稳定后余下的正好升高补平．已知单个盘子的质量为300 g，相邻两盘间距1.0 cm，重力加速度大小取10 m/s2.弹簧始终在弹性限度内，每根弹簧的劲度系数为( )A．10 N/m B．100 N/mC．200 N/m D．300 N/m例 2[2023·河北保定一模]质量为M的正方体A与质量为m的圆球B在水平向右的外力F作用下静止在墙角处，它们的截面图如图所示，截面正方形的对角线与截面圆的一条直径恰好在一条直线上，所有摩擦忽略不计，重力加速度为g.则( )A．F＝(M＋m)gB．F＝mgC．地面受到的压力为F N，F N<(M＋m)gD．地面受到的压力为F N，F N>(M＋m)g提升训练1. [2023·广东省中山市测试]如图甲为明朝《天工开物》记载测量“弓弦”张力的插图，图乙为示意图．弓的质量为m ＝5 kg ，弦的质量忽略不计，悬挂点为弦的中点．当在弓的中点悬挂质量为M ＝15 kg 的重物时，弦的张角为θ＝120°，g ＝10 m/s 2，则弦的张力为( )A ．50 NB ．150 NC ．200 ND ．200√3 N 2.[2023·浙江6月]如图所示，水平面上固定两排平行的半圆柱体，重为G 的光滑圆柱体静置其上，a 、b 为相切点，∠aOb ＝90°，半径Ob 与重力的夹角为37°.已知sin 37°＝0.6，cos 37°＝0.8，则圆柱体受到的支持力F a 、F b 大小为( )A ．F a ＝0.6G ，F b ＝0.4GB ．F a ＝0.4G ，F b ＝0.6GC ．F a ＝0.8G ，F b ＝0.6GD ．F a ＝0.6G ，F b ＝0.8G 3.[2023·河南省洛阳市模拟]如图所示，一光滑球体放在支架与竖直墙壁之间，支架的倾角θ＝60°，光滑球体的质量为m ，支架的质量为2m ，已知最大静摩擦力等于滑动摩擦力，整个装置保持静止，则支架和地面间的动摩擦因数至少为( )A ．√39B ．√34C ．√32 D ．√33命题点二动态平衡问题(含临界、极值问题)1．解决动态平衡问题的一般思路化“动”为“静”，多个状态下“静”态对比，分析各力的变化或极值． 2．“缓慢”移动的三类经典模型图例分析求力F的最小值F min＝mg sin θ，结论：sin θ＝dLF＝mg，2cosθ绳子端点上下移动，力F不变N1、N2始终减小斜面对球的支持力F1逐渐减小，挡板对球的弹力F2先减小后增大考向1 共点力作用下的动态平衡例 1[2023·四川省成都市检测](多选)某中学举行趣味运动会时，挑战用一支钢尺取出深盒子(固定不动)中的玻璃球，该游戏深受大家喜爱，参与者热情高涨．游戏中需要的器材和取球的原理分别如图甲和图乙所示．若忽略玻璃球与盒壁、钢尺间的摩擦力，在不损坏盒子的前提下，钢尺沿着盒子上边缘某处旋转拨动(钢尺在盒内的长度逐渐变短)，使玻璃球沿着盒壁缓慢上移时，下列说法正确的是( )A．钢尺对玻璃球的弹力逐渐减小B．钢尺对玻璃球的弹力先增大后减小C．盒壁对玻璃球的弹力逐渐减小D．盒壁对玻璃球的弹力先减小后增大例 2[2023·河北唐山三模]如图所示，木板B放置在粗糙水平地面上，O为光滑铰链．轻杆一端与铰链O固定连接，另一端固定连接一质量为m的小球A.现将轻绳一端拴在小球A 上，另一端通过光滑的定滑轮O′由力F牵引，定滑轮位于O的正上方，整个系统处于静止状态．现改变力F的大小使小球A和轻杆从图示位置缓慢运动到O′正下方，木板始终保持静止，则在整个过程中( )A．外力F大小不变B．轻杆对小球的作用力变小C．地面对木板的支持力逐渐变小D．地面对木板的摩擦力逐渐减小思维提升三力作用下的动态平衡考向2 平衡中的极值或临界值问题例 3[2023·山东菏泽市模拟]将三个质量均为m的小球a、b、c用细线相连后(bc间无细线相连)，再用细线悬挂于O点，如图所示．用力F拉小球c，使三个小球都处于静止状态，且细线Oa与竖直方向的夹角保持为θ＝30°，则F的最小值为( ) A．1.5mg B．1.8mgC．2.1mg D．2.4mg例 4[2023·陕西省汉中市联考]在吊运表面平整的重型板材(混凝土预制板、厚钢板)时，如因吊绳无处钩挂而遇到困难，可用一根钢丝绳将板拦腰捆起(不必捆的很紧)，用两个吊钩勾住绳圈长边的中点起吊(如图所示)，若钢丝绳与板材之间的动摩擦因数为μ，为了满足安全起吊(不考虑钢丝绳断裂)，需要满足的条件是( )A．tan α>μ B．tan α<μC．sin α>μ D．sin α<μ提升训练1.[2023·湖南张家界模拟考](多选)利用物理模型对问题进行分析，是一种重要的科学思维方法．如图甲所示为拔河比赛时一位运动员的示意图，可以认为静止的运动员处于平衡状态．该情形下运动员可简化成如图乙所示的一质量分布均匀的钢管模型．运动员在拔河时身体缓慢向后倾倒，可以认为钢管与地面的夹角θ逐渐变小，在此期间，脚与水平地面之间没有滑动，绳子的方向始终保持水平．已知当钢管受到同一平面内不平行的三个力而平衡时，三个力的作用线必交于一点．根据上述信息，当钢管与地面的夹角θ逐渐变小时，下列说法正确的有( )A．地面对钢管支持力的大小不变B．地面对钢管的摩擦力变大C．地面对钢管作用力的合力变大D．地面对钢管作用力的合力大小不变2．(多选)在如图所示的装置中，两物块A、B的质量分别为m A、m B，而且m A>m B，整个系统处于静止状态，设此时轻质动滑轮右端的轻绳与水平面之间的夹角为θ，若小车向左缓慢移动一小段距离并停下来后，整个系统再次处于静止状态，则下列说法正确的是( )A．物块A的位置将变高B．物块A的位置将变低C．轻绳与水平面的夹角θ将变大D．轻绳与水平面的夹角θ将不变3．长沙某景区挂出32个灯笼(相邻两个灯笼由轻绳连接)，依次贴上“高举中国特色社会主义旗帜，为全面建设社会主义现代化国家而团结奋斗”，从高到低依次标为1、2、3、…、32.在无风状态下，32个灯笼处于静止状态，简化图如图所示．与灯笼“斗”右侧相连的轻绳处于水平状态，已知每一个灯笼的质量m＝0.5 kg，重力加速度g＝10 m/s2，悬挂灯笼的轻绳最大承受力T m＝320 N，最左端连接的轻绳与竖直方向的夹角为θ.下列说法正确的是( )A．θ最大为53°NB．当θ最大时最右端轻绳的拉力为F2＝160√33C．当θ＝53°时第8个灯笼与第9个灯笼间轻绳与竖直方向的夹角为45°D．当θ＝37°时第8个灯笼与第9个灯笼间轻绳与竖直方向的夹角为45°命题点三电场力、磁场力作用下的平衡问题1．电场力.(1)大小：F＝Eq，F＝kq1q2r2(2)方向：正电荷所受电场力的方向与电场强度的方向相同；负电荷所受电场力的方向与电场强度的方向相反．2．磁场力(1)大小：①安培力F＝BIL；②洛伦兹力F洛＝qv B.(2)方向：用左手定则判断．3．电磁学中平衡问题的处理方法处理方法与力学中平衡问题的分析方法一样，把方法和规律进行迁移应用即可．考向1 电场中的平衡问题例 1[2023·浙江模拟预测]如图所示，A、C为带异种电荷的带电小球，B、C为带同种电荷的带电小球．A、B被固定在绝缘竖直杆上，Q AQ B ＝3√38时，C球静止于粗糙的绝缘水平天花板上．已知L ACL AB＝√3，下列说法正确的是( )A．C处的摩擦力不为零B．杆对B的弹力为零C．缓慢将C处点电荷向右移动，则其无法保持静止D．缓慢将C处点电荷向左移动，则其一定会掉下来考向2 磁场中的平衡问题例 2 如图所示，竖直平面内有三根轻质细绳，绳1水平，绳2与水平方向成60°角，O为结点，绳3的下端拴接一质量为m、长度为l的导体棒，棒垂直于纸面静止，整个空间存在竖直向上、磁感应强度大小为B的匀强磁场．现向导体棒通入方向向里、大小由零缓慢增大到I0的电流，可观察到导体棒缓慢上升到与绳1所处的水平面成30°角时保持静止．已知重力加速度为g.在此过程中，下列说法正确的是( )A．绳1受到的拉力先增大后减小B．绳2受到的拉力先增大后减小C．绳3受到的拉力的最大值为√3mgD．导体棒中电流I0的值为√3mglB提升训练1.[2024·山西省翼城中学模拟预测]如图甲所示，一通电导体棒用两根绝缘轻质细线悬挂在天花板上并静止在水平位置．当导体棒所在空间加上匀强磁场，再次静止时细线与竖直方向成θ角，如图乙所示(图甲中从左向右看)．已知导体棒长度为L、质量为m、电流为I，重力加速度大小为g.关于图乙，下列说法正确的是( )A．当磁场方向斜向右上方且与细线垂直时磁感应强度最小B．磁感应强度的最小值为mg sinθILC．磁感应强度最小时，每根细线的拉力大小为mg2cosθD．当磁场方向水平向左时，不能使导体棒在图示位置保持静止2．如图所示，一绝缘细线竖直悬挂一小球A，在水平地面上固定一根劲度系数为k′的绝缘轻质弹簧，弹簧上端与小球C相连，在小球A和C之间悬停一小球B，当系统处于静止时，小球B处在AC两小球的中间位置．已知三小球质量均为m，电荷量均为q，电性未知．则下列判断正确的是( )A.相邻两小球之间的间距为q√kmgB．弹簧的形变量为11mg8k′C．细线对小球A的拉力大小为11mg8D．小球C受到的库仑力大小为5mg8素养培优·情境命题利用平衡条件解决实际问题联系日常生活，创新试题情境化设计，渗透实验的思想，考查考生分析解决实际问题的能力，引导学生实现从“解题”到“解决问题”的转变情境1 工人推车——科学思维[典例1] [2023·四川省成都市联测]如图甲所示，工人用推车运送石球，到达目的地后，缓慢抬起把手将石球倒出(图乙)．若石球与板OB、OA之间的摩擦不计，∠AOB＝60°，图甲中BO 与水平面的夹角为30°，则在抬起把手使OA 变得水平的过程中，石球对OB 板的压力大小N 1、对OA 板的压力大小N 2的变化情况是( )A ．N 1减小、N 2先增大后减小B ．N 1减小、N 2增大C ．N 1增大、N 2减小D ．N 1增大、N 2先减小后增大情境2 悬索桥——科学态度与责任[典例2] [2023·江苏省无锡市测试]图a 是一种大跨度悬索桥梁，图b 为悬索桥模型．六对轻质吊索悬挂着质量为M 的水平桥面，吊索在桥面两侧竖直对称排列，其上端挂在两根轻质悬索上(图b 中只画了一侧分布)，悬索两端与水平方向成45°，则一根悬索水平段CD 上的张力大小是( )A ．14Mg B ．16MgC ．112Mg D ．124Mg情境3 瓜子破壳器——科学探究[典例3] [2023·福建福州4月检测]有一种瓜子破壳器如图甲所示，将瓜子放入两圆柱体所夹的凹槽之间，按压瓜子即可破开瓜子壳．破壳器截面如图乙所示，瓜子的剖面可视作顶角为θ的扇形，将其竖直放入两完全相同的水平等高圆柱体A 、B 之间，并用竖直向下的恒力F 按压瓜子且保持静止，若此时瓜子壳未破开，忽略瓜子自重，不计摩擦，则( )A ．若仅减小A 、B 距离，圆柱体A 对瓜子的压力变大 B ．若仅减小A 、B 距离，圆柱体A 对瓜子的压力变小C ．若A 、B 距离不变，顶角θ越大，圆柱体A 对瓜子的压力越大D．若A、B距离不变，顶角θ越大，圆柱体A对瓜子的压力越小第1讲力与物体的平衡命题分类剖析命题点一[例1] 解析：由题知，取走一个盘子，稳定后余下的正好升高补平，则说明一个盘子的重力使弹簧形变量为相邻两盘间距，则有mg＝3·kx，解得k＝100 N/m，故选B.答案：B[例2] 解析：对圆球B受力分析如图，β＝45°A对B的弹力T＝mg，cosβ根据牛顿第三定律，B对A的弹力T′＝T＝mg，F＝T′sin β＝mg，故A错误，B正cosβcos β＝Mg＋mg，故C、D 确；对AB整体地面受到的压力为F N＝Mg＋T′cos β＝Mg＋mgcosβ错误．故选B.答案：B[提升训练]1．解析：整体法对弓和物体受力分析如图：＝(M＋m)g竖直方向上由受力平衡可得：2F cos θ2解得：F＝(M+m)g＝200 N，故C正确，A、B、D错误．2cosθ2答案：C2．解析：对光滑圆柱体受力分析如图由题意有F a＝G sin 37°＝0.6GF b＝G cos 37°＝0.8G故选D.答案：D3．解析：对光滑球体受力分析如图所示根据平衡条件可得N2cos θ＝mg对支架受力分析如图所示根据牛顿第三定律可知N3＝N2对支架由平衡条件可得N4＝2mg＋N3cos θ，f＝N3sin θ又f＝μN4联立解得μ＝√33.故选D.可知支架和地面间的动摩擦因数至少为√33答案：D命题点二[例1] 解析：对玻璃球的受力分析如图所示，玻璃球受重力G，左侧钢尺对玻璃球的弹力F1，盒壁对玻璃球的弹力F2，玻璃球在3个力作用下处于动态平衡，玻璃球沿着纸盒壁缓慢上移时，θ角变大，利用图解法可知，F1和F2均逐渐减小，A、C项正确，B、D项错误．故选AC.答案：AC[例2] 解析：对小球A进行受力分析，三力构成矢量三角形，如图所示根据几何关系可知两三角形相似，因此mgOO′＝FO′A＝F′OA，缓慢运动过程中，O′A越来越小，则F逐渐减小，故A错误；由于OA长度不变，杆对小球的作用力F′大小不变，故B 错误；由于杆对木板的作用力大小不变，方向向右下，但杆的作用力与竖直方向的夹角越来越小，所以地面对木板的支持力逐渐增大，地面对木板的摩擦力逐渐减小，故C错误，D正确．答案：D[例3] 解析：取整体为研究对象，当F垂直于Oa时，F最小，根据几何关系可得，拉力的最小值F＝3mg sin 30°＝1.5mg，故选A.答案：A[例4] 解析：要起吊重物，只需满足绳子张力T的竖直分量小于钢丝绳与板材之间的最大静摩擦力，一般情况认为最大静摩擦力等于滑动摩擦力，如图所示即T cos αμ>T sin α，化简可得tan α<μ，故B正确，A、C、D错误．故选B.答案：B[提升训练]1．解析：对钢管受力分析，钢管受重力mg、绳子的拉力T、地面对钢管竖直向上的支持力F N、水平向右的摩擦力F f，可知F N＝mg，F f＝T＝mgtanθ即随着钢管与地面夹角的逐渐变小，地面对钢管支持力的大小不变，地面对钢管的摩擦力变大，故A、B正确；对钢管受力分析，可认为钢管受到重力mg、绳子的拉力T和地面对钢管作用力的合力F 三个力，钢管平衡，三个力的作用线必交于一点，由此可知F方向沿钢管斜向上，与水平面夹角为α(钢管与水平面的夹角为θ)，根据共点力平衡条件可知F＝mgsinα，T＝mgtanα，当钢管与地面的夹角θ逐渐变小，同时α也减小，地面对钢管作用力的合力变大，C正确，D 错误．答案：ABC2．解析：以轻质动滑轮与轻绳的接触点O为研究对象，分析O点的受力情况，作出O 点的受力分析图，如图所示设绳子的拉力大小为F，动滑轮两侧绳子的夹角为2α，由于动滑轮两侧绳子的拉力关于竖直方向对称，则有2F cos α＝m B g，又小车向左缓慢移动一小段距离后，轻绳中的拉力大小与小车移动前相同，即F＝m A g保持不变，可知α角保持不变，由几何知识得，α＋θ＝90°，则θ保持不变，当小车向左缓慢移动一小段距离后，动滑轮将下降，则物块A 的位置将变高，故选项A、D正确，B、C错误．答案：AD3．解析：当最左端连接的轻绳的拉力大小为T m＝320 N时，θ最大，此时灯笼整体受力如图所示由平衡条件T m sin θm＝F2T m cos θm＝32mg解得θm＝60°，F2＝160√3 NA、B错误；当θ＝53°时，灯笼整体受力分析如图由平衡条件知，最右端轻绳的拉力F21＝32mg tan 53°＝6403N对第9个灯笼至第32个灯笼整体，其受力情况跟灯笼整体的受力情况类似，由平衡条件tan α＝F21(32−8)mg≠1则第8个灯笼与第9个灯笼间轻绳与竖直方向的夹角α≠45°，C错误；当θ＝37°时，此时灯笼整体受力如图所示由平衡条件知，最右端轻绳的拉力F22＝32mg tan 37°＝120 N对第9个灯笼至第32个灯笼整体，其受力情况跟灯笼整体的受力情况类似，由平衡条件tan β＝F22(32−8)mg＝1则第8个灯笼与第9个灯笼间轻绳与竖直方向的夹角β＝45°，D正确．答案：D命题点三[例1] 解析：对C进行受力分析，A对C有吸引力，B对C有排斥力，及其重力，与水平天花板对C 可能有竖直向下的压力，如图所示由平衡条件，结合矢量合成法则，若不受摩擦力得F AC＝F BC cos θ由几何知识可得cos θ＝√32依据库仑定律有kQ A Q CL AC2＝√32kQ B Q CL BC2，Q AQ B＝3√38Q A Q B ＝3√38时恰好处于平衡状态；C球静止没有运动趋势，C处的摩擦力为零，故A错误；缓慢将C处点电荷向右移动，平衡状态被打破，其无法保持静止，故C正确；缓慢将C处点电荷向左移动，F BC变大，其竖直方向上的分量变大，C球一定不会掉下来，故D错误；B球如果不受杆的力，则C球给B球的排斥力在水平方向的分量无法平衡，因此杆对B 一定有弹力作用，故B错误．答案：C[例2] 解析：对整体分析，重力大小和方向不变，绳1、2弹力方向不变，根据左手定则，安培力水平向右且逐渐增大，由平衡条件得水平方向F1＝F2cos 60°＋BIl竖直方向F 2sin 60°＝mg电流逐渐变大，则F 1增大、F 2不变，故A 、B 错误；当电流增大到I 0时，安培力与重力的合力最大，即绳3的拉力最大sin 30°＝mg F 3最大值为F 3＝2mg ，故C 错误；对导体棒受力分析得tan 30°＝mg BI 0l ，得I 0＝√3mg Bl，故D 正确．答案：D [提升训练] 1．解析：对导体棒受力分析如图所示，导体棒在重力、拉力和安培力的作用下处于平衡状态．由平衡条件可知，导体棒所受拉力和安培力的合力与重力等大反向，拉力和安培力可能的方向如图所示，当安培力方向斜向右上方且与细线垂直时安培力最小，此时磁场方向沿着细线斜向左上方，A 错误；设磁感应强度大小为B ，由平衡条件得mg sin θ＝BIL ，解得B ＝mg sin θIL ，B 正确；设每条细线拉力大小为F T ，由平衡条件得mg cos θ＝2F T ，解得F T ＝12mg cos θ，C 错误；当磁场方向水平向左时，安培力竖直向上，如果安培力与重力大小相等，可以使导体棒在图示位置保持静止，D 错误．答案：B2．解析：如图甲所示，以小球B 为研究对象，小球A 和小球C 分别对小球B 的库仑力大小相等，且小球A 和小球C 对小球B 的合力与小球B 的重力等大反向，所以小球A 和小球B 带异种电荷，小球B 和小球C 带同种电荷，即小球A 和小球C 对小球B 的库仑力大小均为F A ＝F C ＝mg2，由库仑定律可得kq 2r 2＝12mg ，解得小球A 和小球B 之间距离为r ＝q √2kmg ，故A 错误；如图乙所示，以小球A 为研究对象，受到小球B 向下的库仑力为F B ＝mg 2，受到小球C向下的库仑力是受到小球B 的14，即为F C ′＝mg 8，所以小球A 受到的拉力为F T A ＝mg ＋F B ＋F ′C＝13mg 8，故C 错误；如图丙所示，以小球C 为研究对象，小球C 受到小球B 向下的库仑力为F ′B ＝mg2，受到A 向上的库仑力为F ′A ＝mg8，则小球C 对弹簧的压力为F 压＝F ′B －F ′A ＋mg＝11mg 8，小球C 受到向上的弹力为F 弹＝F 压＝11mg 8，由胡克定律得F 弹＝k ′x ，解得弹簧的形变量为x ＝11mg8k ′，故B 正确，D 错误．答案：B 素养培优·情境命题[典例1] 解析：在倒出石球的过程中，两个支持力的夹角是个确定值，为α＝120°，根据力的示意图可知N 1sin β＝N 2sin γ＝Gsin α，在转动过程中β从90°增大到180°，则sin β不断减小，N 1将不断减小；γ从150°减小到60°，其中跨过了90°，因此sin γ 先增大后减小，则N 2将先增大后减小，选项A 正确．答案：A[典例2] 解析：对整体分析，根据平衡条件，2F T AC sin 45°＝Mg ，F T AC ＝√22Mg .对悬索左边受力分析，受A 左上绳的力F T AC ，CD 上水平向右的拉力为F T ，根据平衡条件，F T ＝F T AC cos 45°＝12Mg ，一根悬索水平段CD 上的张力大小是14Mg ，故选A.答案：A[典例3] 解析：瓜子处于平衡状态，若仅减小A 、B 距离，A 、B 对瓜子的弹力方向不变，则大小也不变，A 、B 错误；若A 、B 距离不变，顶角θ越大，则A 、B 对瓜子弹力的夹角减小，合力不变，则两弹力减小，C 错误，D 正确．故选D.答案：D。

专题20：绳子有节点受力分析专练—【稳扎稳打】备战2021高考物理一轮复习微专题

【稳扎稳打】备战2021高考物理一轮复习微专题专题20: 绳子有节点受力分析专练1．如图所示，两个可视为质点的小球A、B通过固定在O点的光滑滑轮用轻绳相连，小球A 置于光滑半圆柱上，小球B用水平轻绳拉着，水平轻绳另一端系于竖直板上，两球均处于静止状态。

已知O点在半圆柱横截面圆心O1的正上方，OA与竖直方向成30°角、其长度与半圆柱横截面的半径相等，OB与竖直方向成60°角，则（）A．轻绳对球A的拉力与球A所受弹力的合力大小相等B．轻绳对球A的拉力与半网柱对球A的弹力大小不相等C．轻绳AOB对球A的拉力与对球BD．球A与球B的质量之比为1【答案】D【解析】设轻绳中拉力为T，球A受力如图A．所受弹力为绳对A的拉力和半圆对球A的弹力的合力，与重力等大反向，大于T，故A错误；B ．受力分析可得sin30sin30T N ︒=︒A cos30cos30T N m g ︒+︒=解得A 3T N g == 故B 错误；C ．细线对A 的拉力与对球B 的拉力都等于T ，故C 错误；D ．对球BB cos60T m g ︒=B 2T m g =解得A B m m = 故D 正确。

故选D 。

2．如图所示，两个轻环P 和Q 套在位于竖直面你的一固定“∧”形光滑框架上，框架两边与竖直方向的夹角均为30°，两段伸长可忽略的细绳，一端分别系在P 、Q 环上，另一端与绳套系在一起，结点为O 。

现在绳套上挂一小物块，平衡时细绳OP 所受拉力大小为F ，拉直时两段细绳长度相等，不计细绳与绳套的重力。

小物块的重力大小为（）A ．2FB ．FC ．2FD ．3F 【答案】B【解析】如图所示对P 、Q 小环分析，小环受光滑杆的支持力和绳子的拉力，根据平衡条件，这两个力是一对平衡力，支持力是垂直于杆子向上的，故绳子的拉力也是垂直于杆子的，故两细绳之间的夹角为120︒，由几何关系可知，两根绳子与竖直方向之间的夹角都是903060︒-︒=︒所以绳子OQ 的拉力也是F ，两根绳子的长度相等，对结点O 受力分析如图所示，根据平衡条件可知，由几何关系可知，三个力之间的夹角都是120︒，所以G F =故B 正确，ACD 错误。

探析杆模型受力与做功的问题

探析杆模型受力与做功的问题作者：刘扬春来源：《中学理科园地》2017年第06期摘要：杆可分为轻杆（杆的重力可忽略）和非轻杆（杆的重力不可忽略），轻杆产生的弹力可以沿杆的方向，也可以沿其它方向。

自由转动的轻杆因只能发生拉伸（或压缩）形变，产生的弹力一定沿杆的方向，对物体不做功；而一端固定的轻杆能发生不同方向的形变，产生的弹力可以不沿杆的方向，可由力的平衡或牛顿第二定律确定方向，对物体可能做功。

非轻杆由于重力作用产生的弹力也可能不沿杆的方向，对物体可能做功。

关键词：杆；受力问题；做功问题物体发生弹性形变时，由于要恢复原状，会对与它接触的物体产生力的作用，这种力叫弹力。

当杆因受外力作用而发生拉伸（或压缩）形变时会产生径向的弹力，即沿杆的方向；而当杆发生弯曲形变时产生切向的弹力，即沿垂直杆的方向；如果同时发生多种形变产生的弹力就可能沿其它任意方向。

杆可分为轻杆（杆的重力可忽略）和非轻杆（杆的重力不可忽略）。

轻杆又可分为可自由转动的轻杆和固定轻杆，可自由转动的轻杆只能发生拉伸（或压缩）形变，产生的弹力一定沿杆的方向；固定的轻杆能发生不同方向的形变，产生的弹力可沿任意方向，可由力的平衡或牛顿第二定律确定方向。

非轻杆，由于重力作用，会发生不同方向的形变，弹力可能沿任意方向。

下题是普通高中课程标准实验教科书物理1 P88作业第4题 [1 ]：如图1所示：一塔式起重机钢索与水平悬臂的夹角θ=30°。

当起重机吊着一件重G=3.0×104N的货物时，钢索和悬臂各受多大的力？（不考虑钢索和悬臂自身受到的重力）教师用书答案是 [2 ]：挂在悬臂O点的重物要对O点产生一个竖直向下的拉力作用，该拉力F的大小等于重物所受的重力G。

该力的实际作用效果有两个，一是对悬臂水平向左的压力F1，二是对钢索斜向右下的拉力F2（如图2所示）。

笔者从工地上观察到悬壁是固定在支架上而不是转轴（如图1），属于固定杆模型，因此悬壁受到的压力方向不是沿杆的方向，笔者认为仅本题的条件无法求出两个力的大小。

起重支架的受力分析

起重支架的受力分析
1、先把各个零部件受力分析,然后再做静力计算。

2、按照图示说明进行分析计算:
(1)支架的自重及其对地面产生的压力;
(2)弹簧秤拉力及其对滑轮组和钩子的作用力;
(3)吊物体时所需要的起升高度;
(4)吊物上部及下部的加速度;
(5)吊物的最大重量;
(6)地面不平引起的附加压强;
(7)吊物底部在地面上的摩擦阻力。

根据这些条件列出相应的力学公式,解方程得到结果即可。

具体情况要看你的题目中是怎么给出来的,比如你给出了起重机械的型号,那就按照它提供的数值去查找相关的公式即可!。