顺序查找和对分查找

合集下载

c语言中常用的查找

c语言中常用的查找C语言中常用的查找引言：在编程中，查找是一项非常常见且重要的操作。

无论是在数组、链表、树还是图等数据结构中，都需要进行查找操作来寻找特定的数据或者确定某个元素的存在与否。

C语言提供了多种查找算法和数据结构，本文将介绍C语言中常用的查找方法。

一、线性查找线性查找是最简单的查找方法之一，也称为顺序查找。

其基本思想是从数据集合的起始位置开始逐个比较待查找元素与集合中的元素，直到找到目标元素或者遍历完整个集合。

在C语言中，可以使用for循环或者while循环实现线性查找。

线性查找的时间复杂度为O(n)，其中n为数据集合中元素的个数。

二、二分查找二分查找又称为折半查找，是一种高效的查找算法，但要求数据集合必须是有序的。

其基本思想是将数据集合分为两部分，然后通过与目标元素的比较来确定目标元素在哪个部分中，从而缩小查找范围。

重复这个过程直到找到目标元素或者确定目标元素不存在于数据集合中。

二分查找的时间复杂度为O(logn)，其中n为数据集合中元素的个数。

三、哈希表查找哈希表是一种通过哈希函数将关键字映射到存储位置的数据结构，它能够以常数时间复杂度O(1)进行查找操作。

在C语言中，可以使用数组和链表的结合来实现哈希表。

哈希表的关键之处在于哈希函数的设计，良好的哈希函数能够将关键字均匀地映射到不同的存储位置，从而提高查找效率。

四、二叉搜索树查找二叉搜索树是一种常用的数据结构，它满足以下性质：对于任意节点，其左子树中的所有节点的值都小于该节点的值，而右子树中的所有节点的值都大于该节点的值。

在C语言中，可以使用指针和递归的方式来实现二叉搜索树。

通过比较目标值与当前节点的值，可以确定目标值位于左子树还是右子树中，从而缩小查找范围。

五、图的遍历在图的数据结构中，查找操作通常是指遍历操作。

图的遍历有两种方式：深度优先搜索（DFS）和广度优先搜索（BFS）。

深度优先搜索通过递归的方式依次访问图中的每个节点，直到找到目标节点或者遍历完整个图。

对分查找

28
35
46
58
60
i
mid
j
Key>d(mid) i=mid+1
Mid=(i+j)\2
若用一个数组d(1)到d(11)来存放升序的元素序列，查找键Key为12
1 2 3 4 5 6 7 8 9 10 11
6
12
15
18
22
25
28
35
46
58
60
j i
mid Key=d(mid) 输出：Mid=2 Mid=(i+j)\2
若用一个数组d(1)到d(11)来存放升序的元素序列，查找键Key为12
1 2 3 4 5 6 7 8 9 10 11
6
12
15
18
22
25
28
35
46
58
60
i
mid Key<d(mid)
j
j=mid-1
Mid=(i+j)\2
若用一个数组d(1)到d(11)来存放升序的元素序列，查找键Key为12
对分查找（有序数组）
• 对分查找的基本思想：首先将查找键与有序数组内处于中间位置的元素进行比较，如果中间位置上的元素数值与查找键相同，表示找到，否则根据数组元素的有序性，就可确定应该在数组的前半部分还是后半部分继续进行查找。在新确定的范围内，继续按上述方法进行查找，直到获得最终结果。
• 对分查找是一种效率很高的查找方法，但被查找的数据必须是有序的。
若用一个数组d(1)到d(11)来存放升序的元素序列，查找键Key为12
1 2 3 4 5 6 7 8 9 10
11
6

实践查找算法练习题

实践查找算法1、实践目标（1）理解顺序查找算法。

（2）初步掌握顺序查找算法的程序实现。

（3）理解对分查找算法。

（4）初步掌握对分查找算法的程序实现。

2、任务描述（1）用顺序查找算法，对数组中的数据进行查找。

在文本框中输入要查的内容，单击按钮进行顺序查找，如果找到，则在标签中显示数组下标，否则，显示在数组中没有找到。

（2）用对分查找算法，对已经排序的数组中的数据进行查找。

在文本框中输入要查的内容，单击按钮对分查找，如果找到，则在标签中显示数组下标，否则，显示在数组中没有找到。

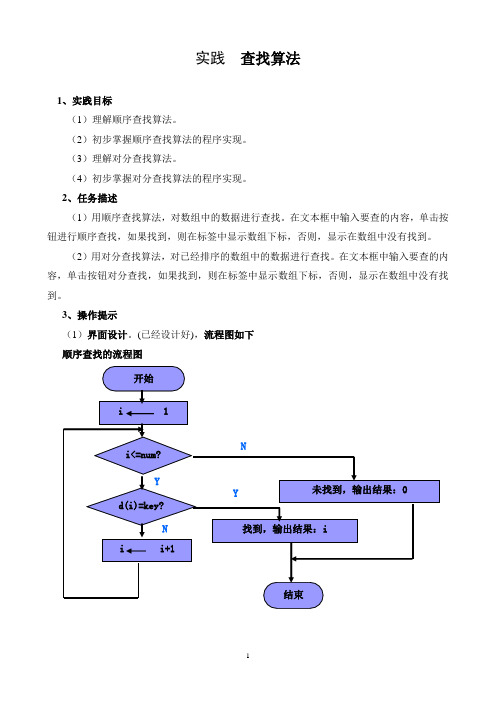
3、操作提示（1）界面设计。

(已经设计好)，流程图如下顺序查找的流程图对分查找的流程图（2）顺序查找算法。

根据顺序查找算法流程图填写完善下面的程序代码。

Private Sub Command6_Click() '顺序查找Key = Val(Text2.Text)For i = 1 ToIf __________ ThenLabel5.Caption = "在数组的" + Str(i) + " 位置中"Exit ForEnd IfNextIf i = num + 1 ThenLabel5.Caption = "在数组中没有找到" + Str(Key)End IfEnd Sub（3）对分查找算法。

根据对分查找算法流程图填写完善下面的程序代码。

Private Sub Command4_Click() '对分查找Key = Val(Text2.Text)i = 1j = numDo While i <= jM =__________If _________ ThenLabel6.Caption = "在数组的" + Str(M) + " 位置中"Exit SubEnd IfIf d(M) < Key Theni = ________Elsej =_________End IfLoopLabel6.Caption = "在数组中没有找到" + Str(Key)End Sub（4）调试运行程序。

查找算法实验报告

查找算法实验报告查找算法实验报告一、引言查找算法是计算机科学中的一个重要概念，它在数据处理和信息检索中起着关键作用。

本实验旨在探究几种常见的查找算法，并对它们的性能进行比较和分析。

二、顺序查找算法顺序查找算法是最简单直观的一种查找方法，它逐个比较待查找元素与数据集中的元素，直到找到匹配项或遍历完整个数据集。

该算法的时间复杂度为O(n)，其中n为数据集的大小。

尽管顺序查找算法的效率较低，但在小规模数据集或无序数据集中仍然具有一定的应用价值。

三、二分查找算法二分查找算法是一种高效的查找算法，它要求数据集必须是有序的。

该算法通过将待查找元素与数据集的中间元素进行比较，从而将查找范围缩小一半。

如果中间元素与待查找元素相等，则查找成功；如果中间元素大于待查找元素，则在左半部分继续查找；如果中间元素小于待查找元素，则在右半部分继续查找。

通过不断缩小查找范围，二分查找算法的时间复杂度为O(log n)，其中n为数据集的大小。

二分查找算法在大规模有序数据集中具有较高的查找效率。

四、哈希查找算法哈希查找算法是一种基于哈希表的查找方法，它通过将待查找元素映射到哈希表中的一个位置，从而快速定位到目标元素。

哈希查找算法的时间复杂度为O(1)，即常数级别。

然而，哈希查找算法对哈希函数的选择和哈希冲突的处理有一定的要求。

如果哈希函数设计不合理或哈希冲突过多，可能会导致查找效率下降。

五、比较与分析在本实验中，我们对上述三种查找算法进行了性能比较和分析。

实验结果表明，在小规模数据集或无序数据集中，顺序查找算法的效率较高；而在大规模有序数据集中，二分查找算法的效率最高。

哈希查找算法虽然具有常数级别的时间复杂度，但在哈希函数和哈希冲突处理上需要额外的开销。

因此，在实际应用中，我们需要根据具体需求选择合适的查找算法。

六、实验总结通过本次实验，我们深入了解了查找算法的原理和应用。

顺序查找算法、二分查找算法和哈希查找算法各具特点，在不同场景下有不同的优劣势。

数据结构-7顺序查找与二分查找

i=m+1=8,j=8, m=(i+j)/2=8。 r[m]>k : 在左半部分继续查找。
i=8, j=m-1=7 ,
i>j: 查找失败
存储结构
key info 0 1 k1 2 k2 3 k3
…………
n kn
typedef struct { keytype key; ………….
} elemtype;
分块有序表的结构可以分为两部分： 1、线性表本身是顺序存储结构 2、再建立一个索引表，线性表中每个子表建立一个索引节点
。索引节点包括两部分：一是数据域，一是指针域。数据域存放对应子表中的最大元素值，指针域用于指示子表第一个元素的在整个表中序号。
分块查找
template<class T> struct indnode {
key=32
d (1) 27
i=1
d (2) 36
i=2
d (3) 32i=3 Nhomakorabead (4) 18
此时d(i)=key,数组中的第3个位置
如果输入查找的元素值key=22
d (1) 27 i=1
d (2) 36 i=2
d (3) 32 i=3
d (4) 18
i=4 i=5 此时i等于5,超过数组中元素个数,找不到
T key; int k; };
上图查找过程：首先查找索引表，确定查找的子表，然后再相应的子表中应顺序表查找法查找。
• int blksearch(record r[],index idx[],keytype key)
•{
• int i=0,j;
• while(i<idxN)
•{
• if(key<=idx[i].key){

高中二年级下学期信息科技《查找》教学设计

教学重点：
1.顺序查找的基本框架
2.二分查找的基本框架
教学难点：
1.二分查找的原理
2.二分查找的优劣
教学过程
一、引入：查找的意义、顺序表
二、顺序查找：扫描仪扫描、
顺序查找的基本思想。
顺序查找的基本框架。
顺序查找的缺点。
三、二分查找
1. 二分查找的思想
2. 二分查找的基本框架。
3、二分查找的实例。
四、两种查找方式的比较：
教学设计
课程基本信息
学科
信息技术
年级
高二
学期
全学期
课题
5.2 查找
教科书
书名：选择性必修1 数据与数据结构教材
出版社：广东教育出版社
教学目标
1.知识与技能：顺序查找和二分查找的原理。
2. 过程与方法：了解二分查找Байду номын сангаас基本过程。
3. 情感态度及价值观：培养学生的计算思维，激发学生的编程兴趣。
教学内容
二分查找的高效率以排序为代价，因此适用于建立后很少修改、经常查询的线性表。
备注：教学设计应至少含教学目标、教学内容、教学过程等三个部分，如有其它内容，可自行补充增加。

常见查找算法的优缺点分析

常见查找算法的优缺点分析在计算机科学中，查找算法是一种用于在数据集合中查找特定元素的方法。

不同的查找算法在时间复杂度、空间复杂度和适用场景等方面存在差异。

下面我们就来详细分析几种常见查找算法的优缺点。

首先是顺序查找算法。

这是最简单也是最直观的一种查找方法。

它的基本思路是从数据集合的开头，依次比较每个元素，直到找到目标元素或者遍历完整个集合。

顺序查找的优点在于实现简单，理解容易，对于小型数据集或者无序数据集来说，是一种可行的选择。

而且，它不需要对数据进行预处理，如排序等操作。

然而，其缺点也很明显。

当数据量较大时，顺序查找的效率非常低，因为它的平均时间复杂度为 O(n)，其中 n 是数据集合的元素个数。

这意味着，随着数据量的增加，查找所需的时间会线性增长。

接下来是二分查找算法。

这种算法要求数据集合是有序的。

它通过不断将数据集一分为二，比较目标元素与中间元素的大小，从而缩小查找范围，逐步逼近目标元素。

二分查找的优点十分突出。

它的时间复杂度为 O(log n)，效率比顺序查找高得多。

在大型有序数据集上，能够显著减少查找时间。

但二分查找也有其局限性。

首先，它要求数据集必须是有序的，如果数据集经常变动，维护有序性的成本可能会很高。

其次，对于小型数据集，由于其实现相对复杂，可能不如顺序查找来得直接和高效。

然后是哈希查找算法。

哈希查找通过将关键码值映射到一个特定的地址，从而实现快速查找。

哈希查找的最大优点就是查找速度极快，平均时间复杂度接近O(1)，无论数据集的大小如何。

只要哈希函数设计得好，能够有效地避免冲突，就可以在常数时间内完成查找。

不过，哈希查找也并非完美。

哈希函数的设计是一个关键问题，如果设计不当，可能会导致大量的冲突，从而影响查找效率。

而且，当数据量增加时，可能需要重新调整哈希表的大小，这会带来一定的额外开销。

再说说插值查找算法。

它是二分查找的一种改进，根据要查找的关键字与查找表中最大最小关键字的比较结果，来选择合适的中间值进行比较。

几种查找算法的比较

ｗｉ（ｒｎ．ｅ！＝）ｈｌｃｒｔｙｎ｛ｅｕｅｋ
＋＋ｒ：
ｉｎｃｒｅｔｅ）ｆ＜ｕｒｎ．ｙ｛（ｋ
ｅｓ（ｃｒｎ＝ｕｒｎ．ｇｔｌｅｕｅｔｃｒｔｉｈ；ｅｒ
的结点放在前边，以提高查找效率，代码描述如下：
ｐｂｉｃａｓＣａｈｏ｛ｕｌｌｓｈｚａｃｐｂｉｔｈｎｕｉｔ，ｔ）ｕｌｉｕＸ（ｉ￣ａ｛ｃｎｓｎｎｎ
ｐｏｒｍ ’ ｏｅａｅｉｊｖｅｃｍｐｉｄＴｉｏｌｘｔｎｄｓａｅｃｍｐｅｉｏｌｏｏｅｓｍｅｄｔｒｏａｅｒｇａＳｃｄｓｂｓｄＯｌａａａｏｌ．ｈｅｔｒｅｍｅｃｍｐｅｉａｐｃｏｌｘｔｔｏｋｆｒｔａａａａｅｃｍｐｒｄ．ｙｙｈ
【ｙｗｏｄ］ｅｒｈｎ；ｇｒｈＴｍｅｃｍｌｘｔ；ｐｃｏｌｉＫｅｒｓＳａｃｉｇＡｌｉｍ；ｉｏｐｅｉＳａｅｃｍ３二叉排序树查找
数据地修改、除、入等操作都是基于查找算法的，删插因此比较查实际上就是将数据元素组织成二叉树形式，达到与二分法相同以找算法的优劣，择正确的查找算法能够极大地提高用户对数据的查的查找效率，又具有链表的插入、除操作的灵活性。二叉排序树选而删用找；而提高了计算机软件的工作效率。查找是在大量的信息中寻找实现的算法的平均时间复杂度是Ｏｎｏｎ。最佳状态的时间复杂度为从（ｌｓ）个特定的信息元素，计算机应用中，找是常用的基本运算，找１即第一次就找到数据，坏状态的时间复杂度为ｎｏｎ即未能找到在查查，最ｌｇ，

查找算法学习常用的查找算法及其时间复杂度

查找算法学习常用的查找算法及其时间复杂度查找算法是计算机科学中非常重要的一种算法，它用于在一组数据中查找指定的元素。

在实际应用中，我们经常需要对大量数据进行查找操作，因此了解不同的查找算法及其时间复杂度对于提高查找效率至关重要。

本文将介绍几种常用的查找算法，并分析它们的时间复杂度。

一、顺序查找算法顺序查找算法是最简单的一种查找算法，也被称为线性查找算法。

它的基本思想是从数据的起始位置开始，一个一个地比较待查找元素和数据中的元素，直到找到匹配的元素或者遍历完所有的元素。

顺序查找算法的时间复杂度为O(n)，其中n表示数据的规模。

由于它需要逐个比较元素，因此在数据规模较大时，效率较低。

二、二分查找算法二分查找算法，也被称为折半查找算法，是一种高效的查找算法。

它的前提是数据必须有序。

基本思想是将待查找的值与中间元素进行比较，如果相等则返回位置，如果不相等则根据大小关系决定继续在左半部分或右半部分进行查找，直到找到匹配的元素或者确定不存在。

二分查找算法的时间复杂度为O(log n)，其中n表示数据的规模。

由于每次查找都将数据规模减半，因此效率非常高。

但是它要求数据必须有序，如果数据无序，需要先进行排序操作。

三、哈希查找算法哈希查找算法是一种常用的查找算法，通过哈希函数将待查找的元素映射到一个桶中，然后在桶中进行查找操作。

它的特点是查找的速度非常快，不受数据规模的影响。

哈希查找算法的时间复杂度近似为O(1)，其中1表示常数时间。

但是它的缺点是需要额外的存储空间来构建哈希表，并且需要解决哈希冲突的问题。

四、二叉查找树算法二叉查找树算法是一种基于二叉树的查找算法，它的特点是左子树的所有节点值小于根节点的值，右子树的所有节点值大于根节点的值。

基于这个特点，可以通过比较待查找元素和当前节点的值来确定查找的方向。

二叉查找树算法的时间复杂度取决于树的高度，如果树的高度为h，则查找的时间复杂度为O(h)。

当二叉查找树退化成链表时，树的高度为n，其中n表示节点的个数，此时查找的时间复杂度为O(n)。

各种查找算法的性能比较测试(顺序查找、二分查找)

算法设计与分析各种查找算法的性能测试目录摘要 (2)第一章：简介（Introduction） (3)1.1 算法背景 (3)第二章：算法定义（Algorithm Specification） (4)2.1 数据结构 (4)2.2顺序查找法的伪代码 (4)2.3 二分查找（递归）法的伪代码 (5)2.4 二分查找（非递归）法的伪代码 (6)第三章：测试结果（Testing Results） (8)3.1 测试案例表 (8)3.2 散点图 (9)第四章：分析和讨论 (11)4.1 顺序查找 (11)4.1.1 基本原理 (11)4.2.2 时间复杂度分析 (11)4.2.3优缺点 (11)4.2.4该进的方法 (12)4.2 二分查找（递归与非递归） (12)4.2.1 基本原理 (12)4.2.2 时间复杂度分析 (13)4.2.3优缺点 (13)4.2.4 改进的方法 (13)附录：源代码（基于C语言的） (15)摘要在计算机许多应用领域中，查找操作都是十分重要的研究技术。

查找效率的好坏直接影响应用软件的性能，而查找算法又分静态查找和动态查找。

我们设置待查找表的元素为整数，用不同的测试数据做测试比较，长度取固定的三种，对象由随机数生成，无需人工干预来选择或者输入数据。

比较的指标为关键字的查找次数。

经过比较可以看到，当规模不断增加时，各种算法之间的差别是很大的。

这三种查找方法中，顺序查找是一次从序列开始从头到尾逐个检查，是最简单的查找方法，但比较次数最多，虽说二分查找的效率比顺序查找高，但二分查找只适用于有序表，且限于顺序存储结构。

关键字：顺序查找、二分查找（递归与非递归）第一章：简介（Introduction）1.1 算法背景查找问题就是在给定的集合（或者是多重集，它允许多个元素具有相同的值）中找寻一个给定的值，我们称之为查找键。

对于查找问题来说，没有一种算法在任何情况下是都是最优的。

有些算法速度比其他算法快，但是需要较多的存储空间；有些算法速度非常快，但仅适用于有序数组。

信息技术会考复习算法与程序选择题

作者联系方式
10．在事件处理过程Ok_Click()中，Click事件称为（A）窗体加载（B）鼠标单击（C）鼠标双击（D）在键盘上按键
解析：常见的事件有：单击鼠标(Click)、双击鼠标解析：常见的事件有：单击鼠标、 (DbClick)、按键盘、按键盘(KeyPress)、窗体加载、窗体加载(Load)。事件处。理过程名组成格式：对象名_事件名所以Ok_Click中Ok 事件名，理过程名组成格式：对象名事件名，所以中是对象名，是单击事件名。是对象名，Click是单击事件名。所以选。是单击事件名所以选B。
15.下列能作为赋值语句的是（A） 10 = i （B）i + j = 10 （C）t = False （D）i =10-j And j=2
解析：赋值语句格式：变量名=表达式或者对象名属性名表达式,或者对象名.属性名解析：赋值语句格式：变量名表达式或者,对象名 =表达式。赋值语句先计算右边，然后赋值给左边，左边必表达式。表达式赋值语句先计算右边，然后赋值给左边，须是一个变量。选项D是判断语句而不是赋值，是判断语句，须是一个变量。选项是判断语句，而不是赋值，所以选择 C。。
9．在Visual Basic中，设x=3216，表达式x\100 Mod 10 的值是（A） 321 （B）32 （C） 2 （D）1
解析：实数除法/，如3/2=1.5。整数除法反斜杠，如反斜杠)，解析：实数除法，。整数除法\(反斜杠 3\2=1。取余。取余Mod，如8 Mod 3=2，-8 Mod 3=-2。此，，。外乘幂^，外乘幂，如2^3=8。分析可知选。。分析可知选C。
3．在Visual Basic中，用变量p存储数值1.414，变量p的数据类型应定义为（A）Boolean（B）Integer（C）Single（D）String 解析：Integer是整数类型，Boolean是逻辑类型（True 是整数类型，是逻辑类型（解析：是整数类型是逻辑类型），Single是实数类型（带小数），是实数类型（），String是字或False），），是实数类型带小数），是字符类型（中英文、数字等）。此外，）。此外是长整数，符类型（中英文、数字等）。此外，Long是长整数，它是长整数的范围比Integer大。Double是双精度实数，它的范围比是双精度实数，的范围比大是双精度实数 Single大。所以选大所以选C

《数据结构》实验报告三：几种查找算法的实现和比较

第三次实验报告：几种查找算法的实现和比较//2019-12-4//1.随机生成5万个整数，存入一个文件；//2.算法实现：（1）顺序查找：读入文件中的数据，查找一个key，统计时间；// （2）二分查找：读入文件，排序，二分查找key，统计时间；// （3）分块查找：读入文件，分100块，每块300+数字，查找key，统计时间// （4）二分查找树：读入文件，形成BST，查找key，统计时间//二叉排序树：建立，查找#include "stdio.h"#include "time.h"#include "stdlib.h"struct JD{//定义分块查找的链表结点结构int data;JD *next;};struct INDEX_T{//定义分块查找中，索引表结构int max;//这一块中最大的数字，<maxJD *block;//每一块都是一个单向链表，这是指向块的头指针};INDEX_T myBlock[100];//这是索引表的100项struct NODE{//定义的二分查找树结点结构int data;NODE *left;NODE *right;};const int COUNT=50000;//结点个数int key=666;//待查找的关键字int m=1;//int *array2;void createData(char strFileName[]){//产生随机整数，存入文件srand((unsigned int)time(0));FILE *fp=fopen(strFileName,"w");for(int i=1;i<=COUNT;i++)fprintf(fp,"%d,",rand());fclose(fp);}void createBST(NODE* &bst){//产生5万个随机整数，创建二叉排序树FILE *fp=fopen("data.txt","r");for(int i=1;i<=COUNT;i++){int num;fscanf(fp,"%d,",&num);//从文件中读取一个随机整数//若bst是空子树，第一个结点就是根结点//若bst不是空子树，从根结点开始左小右大，查找这个数字，找到了直接返回，//找不到，就插入到正确位置//创建一个结点NODE* p=new NODE;p->data=num;p->left=0;p->right=0;if(0==bst)//空子树{bst=p;continue;}//非空子树,//在bst中，查找给结点，NODE *q=bst;//总是从根结点开始查找while(1){if(p->data == q->data)//找到了，直接退出break;if(p->data < q->data && q->left==0){//小，往左找，且左边为空，直接挂在q之左q->left=p;break;}if(p->data < q->data && q->left!=0){//小，往左找，且左边非空，继续往左边找q=q->left;continue;}if(p->data > q->data && q->right==0){//大，往右找，且右边为空，直接挂在q之右q->right=p;break;}if(p->data > q->data && q->right!=0){//大，往右找，且右边非空，继续往右边找q=q->right;continue;}}}}int BST_Search(NODE *bst,int key){//在bst中找key，if(0==bst)return -1;//非空子树,//在bst中，查找给结点，NODE *q=bst;//总是从根结点开始查找while(1){if(key == q->data)//找到了，直接退出return 1;if(key < q->data && q->left==0)//小，往左找，且左边为空，找不到return -1;if(key < q->data && q->left!=0)//小，往左找，且左边非空，继续往左边找{q=q->left;continue;}if(key > q->data && q->right==0)//大，往右找，且右边为空，找不到return -1;if(key > q->data && q->right!=0){//大，往右找，且右边非空，继续往右边找q=q->right;continue;}}}void inOrder(NODE *bst){if(bst!=0){inOrder(bst->left);array2[m]=bst->data;//反写回array数组，使数组有序// printf("%7d",array2[m]);m++;inOrder(bst->right);}}int getBSTHeight(NODE *bst){if(bst==0)return 0;else{int hl=getBSTHeight(bst->left);int hr=getBSTHeight(bst->right);int h=hl>hr?hl:hr;return h+1;}}void makeArray(int array[],char strFileName[]) {//生成5万个随机整数FILE *fp=fopen(strFileName,"r");int i=1;while(!feof(fp)){fscanf(fp,"%d,",&array[i]);// printf("%6d",array[i]);i++;}}int Seq_Search(int array[],int key){//在无序顺序数组中，找data是否存在，-1=不存在，存在返回位置下标//监视哨：把要找的那个数放到首部array[0]=key;//for(int i=COUNT;array[i]!=key;i--);if(i>0)//找到了，返回下标return i;return -1;//查找不成功，返回-1}int Bin_Search(int array[],int key){//在有序存储的数组中查找key，找到返回位置，找不到返回-1 int low=1,high=COUNT,mid;while(1){if(low>high)//找不到return -1;mid=(low+high)/2;if(key == array[mid])return mid;else if(key<array[mid])high=mid-1;elselow=mid+1;}}void makeBlock(INDEX_T myBlock[],char strFileName[]) {//从文件中读取整数，分配到块中去//1.初始化块索引表，分100块，400,800,1200，for(int i=0;i<=99;i++){myBlock[i].max=400+400*i;//400,800,1200, (40000)myBlock[i].block=0;}//2.打开文件，读取整数，把每一个整数分配到相应的块中去FILE *fp=fopen(strFileName,"r");while(!feof(fp)){int num=0;fscanf(fp,"%d,",&num);//把num分配到num/400块中，挂到该块链表第一个int blockID=num/400;//求出应该挂在的块号//生成一个新节点，把num放进去，挂上JD *p=new JD;p->data=num;p->next=myBlock[blockID].block;myBlock[blockID].block=p;}fclose(fp);}int Block_Search(INDEX_T myBlock[],int key){int blockID=key/400;//找到块号JD* p=myBlock[blockID].block;while(p!=0){if(p->data==key)return blockID;//能找到p=p->next;}return -1;//找不到}void main(){clock_t begin,end;int pos=-1;//1.生成文件，存入5万个随机整数createData("data.txt");//2.顺序查找int *array=new int[COUNT+1];makeArray(array,"data.txt");//从文件中读取数据begin=clock();for(int k=1;k<=10000;k++)pos=Seq_Search(array,key);end=clock();printf("顺序查找：%d所在的位置=%d.时间=%d毫秒\n",key,pos,end-begin);//3.二分查找树NODE *bst=0;createBST(bst);//产生5万个随机数字，建立一个二叉排序树begin=clock();for(k=1;k<=10000;k++)pos=BST_Search(bst,key);//在bst中找key，找到返回1，找不到返回-1end=clock();printf("二叉排序树查找：%d所在的位置=%d.时间=%d毫秒\n",key,pos,end-begin);array2=new int[COUNT+1];inOrder(bst);//中序输出bst// int height=getBSTHeight(bst);//求出bst的高度// printf("BST高度=%d.\n\n",height);//4.二分查找，利用前面二叉排序树产生的array2，查找key begin=clock();for(k=1;k<=10000;k++)pos=Bin_Search(array2,key);end=clock();printf("二分查找：%d所在的位置=%d.时间=%d毫秒\n",key,pos,end-begin);//5.分块查找，关键字范围[0,32767],分配到100块中去，每一块中存400个数字makeBlock(myBlock,"data.txt");//从文件中读取数据，产生块begin=clock();for(k=1;k<=10000;k++)pos=Block_Search(myBlock,key);//在block中查找key，找到返回块号，找不到返回-1end=clock();printf("分块查找：%d所在的块=%d.时间=%d毫秒\n",key,pos,end-begin);/*for(k=0;k<=99;k++){printf("\n\n\n第%d块<%d:\n",k,myBlock[k].max);JD *q=myBlock[k].block;//让q指向第k块的第一个结点while(q!=0){//输出第k块中所有数字printf("%7d ",q->data);q=q->next;}}*/}。

顺序查找与二分查找对比

顺序查找与二分查找对比近年来，随着信息技术的迅猛发展，各行各业对于数据的处理和检索需求越来越大。

其中，查找是一种常见并且重要的操作。

在众多查找算法中，顺序查找和二分查找是两种常见的方法。

本文将对这两种查找算法进行对比，并探讨它们在实际应用中的优劣势。

一、顺序查找顺序查找，又称线性查找，是一种简单直观的查找方式。

它的基本思想是逐个比对待查找元素和列表中的元素，直到找到匹配的元素或遍历完整个列表。

顺序查找的实现相对简单，只需要从列表的第一个元素开始逐个比对即可。

然而，顺序查找的缺点也是很明显的。

随着待查找元素数量的增加，顺序查找的时间复杂度由O(1)线性增长至O(n)，其中n为待查找元素的个数。

这意味着当数据量较大时，顺序查找的效率将大幅下降。

尤其是对于有序列表，顺序查找无法充分利用列表的有序性，在查找效率上存在明显的不足。

二、二分查找二分查找，又称折半查找，是一种高效的有序查找算法。

它利用了有序列表的特性，通过比较待查找元素与有序列表中间位置元素的大小关系，来确定待查找元素可能存在的区间，从而迅速缩小查找范围。

基于这个思想，二分查找可以将查找的时间复杂度从O(n)降低到O(log₂(n))，其中n为列表中元素的个数。

相比于顺序查找，二分查找的优势主要体现在高效性和适用范围上。

对于大规模有序列表，二分查找能够迅速定位目标元素，大大减少了查找的时间成本。

此外，在对近乎有序或近似有序列表进行查找时，二分查找仍能有较好的表现。

然而，二分查找也有其限制之处，它要求列表必须是有序的，这就增加了排序的前置操作，并且仅适用于静态列表，即在查找过程中列表不发生变化。

三、实际应用中的对比在实际应用中，选择合适的查找算法需要考虑到数据规模、数据的有序性以及查找的频率等因素。

下面针对不同场景进行对比：1. 对于小规模或基本有序的数据集合，顺序查找往往是一个简单而直接的选择。

顺序查找代码简单，易于实现，并且不要求待查找元素有序，适用于轻量级的查找操作。

顺序查找和二分查找的平均查找长度的范例 -回复

顺序查找和二分查找的平均查找长度的范例-回复什么是顺序查找和二分查找？顺序查找（Sequential Search）是一种简单直观的查找算法，也是最基本的查找算法之一。

它的工作原理是从待查找的数据集合的第一个元素开始，逐个比较目标值和数据集合中的每一个元素，直到找到目标值或者遍历完整个数据集合。

顺序查找适用于无序数据集合，但是在数据集合较大的情况下，它的查找效率较低。

二分查找（Binary Search）是一种高效的查找算法，使用于已排序的数据集合。

它的工作原理是将数据集合一分为二，然后分别在左右两个子集合中进行查找，以此递归地细分子集合，直到找到目标值或者确定目标值不存在。

二分查找可以大幅提高查找效率，尤其在大规模数据集合中。

顺序查找和二分查找的平均查找长度是什么？平均查找长度（Average Search Length）是用来衡量一种查找算法的效率的指标。

它表示在平均情况下，需要通过多少次关键字的比较才能找到目标值。

对于顺序查找和二分查找，它们的平均查找长度可以通过一定的计算和推导得到。

顺序查找的平均查找长度计算：设待查找的数据集合中包含n个元素，目标值出现在第i个位置（1 <= i <= n）。

因为顺序查找是逐个遍历比较的方式，所以目标值有可能在位置1到位置i之间被找到。

对于每个位置j（1 <= j <= i），找到目标值所需的比较次数为j次。

因此，顺序查找的平均查找长度为：ASL(Sequential Search) = (1 + 2 + 3 + ... + i) / i = (i+1)/2二分查找的平均查找长度计算：二分查找每次都将待查找的数据集合一分为二，每次都能将查找范围缩小一半。

设待查找的数据集合中包含n个元素，目标值出现在第i个位置（1 <= i <= n）。

在二分查找中，每次将查找范围缩小一半，直到找到目标值。

假设二分查找总共进行了k次比较，那么查找范围被缩小k次，即：(n/2^k) = 1解得k = log2(n)因此，二分查找的平均查找长度为：ASL(Binary Search) = k = log2(n)顺序查找和二分查找的平均查找长度比较：通过对比顺序查找和二分查找的平均查找长度的计算公式，我们可以发现，顺序查找的平均查找长度与目标值在数据集合中的位置直接相关，而二分查找的平均查找长度仅与数据集合的大小有关。

Java中常用的查找方法——顺序查找和二分查找

Java中常用的查找算法——顺序查找和二分查找一、顺序查找：a)原理：顺序查找就是按顺序从头到尾依次往下查找，找到数据，则提前结束查找，找不到便一直查找下去，直到数据最后一位。

b)图例说明：原始数据：int[] a={4,6,2,8,1,9,0,3};要查找数字：8代码演示：import java.util.Scanner;/** 顺序查找*/public class SequelSearch {public static void main(String[] arg) {int[] a={4,6,2,8,1,9,0,3};Scanner input=new Scanner(System.in);System.out.println("请输入你要查找的数：");//存放控制台输入的语句int num=input.nextInt();//调用searc()方法，将返回值保存在result中int result=search(a, num);if(result==-1){System.out.println("你输入的数不存在与数组中。

");}elseSystem.out.println("你输入的数字存在，在数组中的位置是第："+(result+1)+"个");}public static int search(int[] a, int num) {for(int i = 0; i < a.length; i++) {if(a[i] == num){//如果数据存在return i;//返回数据所在的下标，也就是位置}}return -1;//不存在的话返回-1}}运行截图：二、二分查找a)前提条件：已排序的数组中查找b)二分查找的基本思想是：首先确定该查找区间的中间点位置：int mid = (low+upper)/ 2；然后将待查找的值与中间点位置的值比较：若相等，则查找成功并返回此位置。

查找算法(技术)

I=9
变成d(9)~d(11)
M=fix((i+j)/2)
=12
J=16
Key=52
下标元素
1 10 2 15 3 17 4 18 5 22 6 27 7 35 8 45 9 48 10 52 11 65 12 67 13 72 14 85 15 97 16 98
第3次比较： Key=d(m) 找到了
题外话:以下三种效果是相同的 m = (i + j) \ 2 m =ｉｎｔ( (i + j) / 2) m =ｆｉｘ( (i + j) / 2)
比较
• 顺序查找是一种基本、简单的查找算法，但查找的效率往往过低；
• 对分查找时每次都把查找范围缩小一半
• 对分查找算法数据次数较少，效率较高，但它要求数组中的数据是有序的。
答案 D 本题主要考查对两种查找算法的了解。对分查找的前提条件是被查找的数据源是有序的,而顺序查找对数据源没有要求。两种查找算法,对分查找的效率较高,这是由对分查找的算法特点决定的,顺序查找平均需要比较(n+1)/2次,因此时间复杂度是O(n),而对分查找的每一次查找都将查找范围缩小一半,因此时间复杂度是O(log2n),比顺序查找的效率高。
Key = Val(Text2.Text) i=1 j = num Do While i <= j
m = (i + j) \ 2 If d(M) = Key Then
Label6.Caption = "在数组的 " + Str(M) + " 位置中" Exit Sub End If If d(M) < Key Then i=m+1 Else j=m-1 End If Loop Label6.Caption = "在数组中没有找到" + Str(Key)

信息科技应知应会

《信息科技》学业水平考试应知应会一．必修模块1、问：信息的主要特征是什么？答：传载性、共享性、可处理性、时效性。

2、问：ASCII码用几位二进制代码表示？存储时占用几个字节？共有多少种不同的组合。

答：7位，1个字节，128种不同的组合。

3、问：汉字国标码与汉字机内码的区别是什么？答：机内码是将国标码的两个字节的最高位分别置为1而得到的。

4、问：完整的计算机系统包括什么？计算机的五大逻辑部件是什么？计算机的CPU包括什么？计算机的外部设备包括什么？答：计算机系统包括硬件和软件。

五大部件是输入设备，输出设备，存储器，运算器，控制器。

CPU包括运算器和控制器。

外部设备包括：输入设备、输出设备和外存储器。

5、问：什么是计算机的指令、程序和软件？软件包括什么？答：计算机完成一步运算或判断的命令称为指令，指令的有序集合称为程序。

程序和有关的文档资料称为软件。

软件通常分为系统软件和应用软件。

6、问：请列举三类系统软件的名称。

答：操作系统，程序语言处理程序，数据库管理系统。

7、问：请叙述非裸机情况下软件的安装顺序。

答：操作系统→驱动程序→应用软件。

8、问：请叙述网络的三大功能。

其最基本的功能是什么？答：数据通信，资源共享，分布式数据处理和分布式数据库。

数据通信是最基本的功能。

9、问：请叙述网络的三要素。

答：计算机设备，通信线路及连接设备，网络协议。

10、问：有线网络中常用的传输介质有哪些？无线网络的常用传输介质有哪些？答：有线：双绞线，同轴电缆，光纤电缆。

无线：电磁波。

11、有线网络传输介质中，传输距离最短的是哪个、既可以传输数字信号又可以传输模拟信号的是哪个？传输速率最高的是哪个？答：双绞线的传输距离最短。

同轴电缆可以传输数字信号和模拟信号。

光纤的传输速率最高。

12、问：网络的无线传输有哪些技术？其应用价值体现在哪些方面？答：红外技术，蓝牙技术，无线以太网技术。

应用价值体现在：可移动性、布线容易、组网灵活、成本优势四个方面。

常用的查找算法

树表查找
树表查找
B和B+树的区别在于，B+树的非叶子结点只包含导航信息，不包含实际的值，所有的叶子结点和相连的节点使用链表相连，便于区间查找和遍历。 B+ 树的优点在于：由于B+树在内部节点上不好含数据信息，因此在内存页中能够存放更多的key。数据存放的更加紧密，具有更好的空间局部性。因此访问叶子几点上关联的数据也具有更好的缓存命中率。 B+树的叶子结点都是相链的，因此对整棵树的便利只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连，所以便于区间查找和搜索。而B 树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻，所以缓存命中性没有B+树好。B+树更适合做文件系统。但是B树也有优点，其优点在于，由于B树的每一个节点都包含key和value，因此经常访问的元素可能离根节点更近，因此访问也更迅速。
二分查找
注意事项：折半查找的前提条件是需要有序表顺序存储，对于静态查找表，一次排序后不再变化，折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说，维护有序的排序会带来不小的工作量，那就不建议使用。
插值查找
在介绍插值查找之前，首先考虑一个新问题，为什么上述算法一定要是折半，而不是折四分之一或者折更多呢？打个比方，在英文字典里面查“apple”，你下意识翻开字典是翻前面的书页还是后面的书页呢？如果再让你查“zoo”，你又怎么查？很显然，这里你绝对不会是从中间开始查起，而是有一定目的的往前或往后翻。< 同样的，比如要在取值范围1 ~ 10000 之间 100 个元素从小到大均匀分布的数组中查找5，我们自然会考虑从数组下标较小的开始查找。
查找算法

查找算法及应用时间复杂度

查找算法及应用时间复杂度查找算法是计算机科学中一类常用的算法，用于在给定的数据集中查找目标元素。

不同的查找算法有不同的时间复杂度和适用场景。

下面将介绍常见的查找算法及其应用时间复杂度。

1. 顺序查找（Sequential Search）顺序查找是一种简单直观的查找算法，它从数据集的起始位置开始逐个比较，直到找到目标元素或遍历完整个数据集。

顺序查找的时间复杂度为O(n)，其中n 是数据集中元素的个数。

顺序查找适用于数据集无序或无法利用其他特性进行查找的情况。

2. 二分查找（Binary Search）二分查找是一种常用的有序数据集查找算法。

它利用有序特性，将数据集一分为二，然后根据目标元素与中间元素的大小关系，确定目标元素在左半部分还是右半部分，再继续在相应的子集中进行查找。

二分查找的时间复杂度为O(log n)，其中n是数据集中元素的个数。

二分查找只适用于有序数据集。

3. 插值查找（Interpolation Search）插值查找是在有序数据集中进行查找的一种改进算法。

它通过根据目标元素与数据集中最大值和最小值之间的比例，推测目标元素所在的位置，然后在该位置进行查找。

这个位置的选择不再是固定的中间位置，而是根据目标元素与数据集中元素的分布情况动态变化。

插值查找的时间复杂度为O(log log n)，在数据分布均匀的情况下，插值查找的效率较高。

4. 哈希查找（Hash Search）哈希查找是一种利用哈希表进行查找的算法。

它通过将数据集中的元素映射到不同的哈希桶中，然后根据目标元素的哈希值去相应的哈希桶中查找。

哈希查找的时间复杂度为O(1)，即常量时间，但在处理哈希冲突时，可能会导致时间复杂度增加。

哈希查找适用于需要快速查找的场景，如电话号码查询、字典查询等。

5. 布隆过滤器（Bloom Filter）布隆过滤器是一种基于位数组和哈希函数实现的查找算法。

它可以判断一个元素是否在集合中，但不能确定元素具体的位置。

从顺序查找到二分查找.ppt

从顺序查找到二分查找
查找
给定一个值Key，在含有n个元素的数组中找出等于给定值Key的元素。若找到，则查找成功，返回元素的信息或该元素在表中的位置；否则查找失败，返回相关的指示信息。
顺序查找
从数组的一端开始，顺序扫描数组，依次将扫描到的元素和给定值Key相比较。若当前扫描到的元素与Key相等，则查找成功；若扫描结束后，仍未找到元素等于Key的结点，则查找失败。
程序流程图
开始
输入待查找的值给变量key
i=1
N
输出“找不到”
Y
i<＝n ？ Y
a(i)=key ?
输出“找到了”
N i=i+1
结束
顺序查找的效率
n个元素的数组：
最快：1次最慢：n次
思考
如果数组是有序的，有没有效里）
120
j=m-1 =7
125
125
125
130 j=10
130 j=10
130
Key=65
21
i=1 21
i=1
21
56
56
mid=2 56
78
78 Key > a(m) 78
98
98
101 m=5 101
106 Key < a(m) 106
110
110
120
120
125
125
130 j=10 130
1)中，故新的查找区间是左子数组a(1..m-1)中。若Key>a(m) ，则要找的Key可能在mid的右子数组
a(m+1..n)中，即新的查找区间是右子表a(m+1..n) 。 …… 找不到时结束的条件：i > j