四川省南部县第二中学2020-2021年度第一学期八年级数学上册第一次月考测试题

合集下载

2020—2021年人教版八年级数学上册第一次月考考试题及答案【1套】

2020—2021年人教版八年级数学上册第一次月考考试题及答案【1套】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．下列分解因式正确的是（）A ．24(4)x x x x -+=-+B ．2()x xy x x x y ++=+C ．2()()()x x y y y x x y -+-=-D ．244(2)(2)x x x x -+=+- 2．下列分式中，最简分式是（）A ．2211x x -+B ．211x x +-C ．2222x xy y x xy -+-D ．236212x x -+ 3．在实数|﹣3|，﹣2，0，π中，最小的数是（）A ．|﹣3|B ．﹣2C ．0D ．π4．如果1m n +=，那么代数式()22221m n m n m mn m +⎛⎫+⋅-⎪-⎝⎭的值为（） A ．-3 B ．-1 C ．1 D ．35．方程组33814x y x y -=⎧⎨-=⎩的解为（） A ．12x y =-⎧⎨=⎩ B ．12x y =⎧⎨=-⎩ C ．21x y =-⎧⎨=⎩ D ．21x y =⎧⎨=-⎩ 6．如图，∠AOB=60°，点P 是∠AOB 内的定点且OP=3，若点M 、N 分别是射线OA 、OB 上异于点O 的动点，则△PMN 周长的最小值是（）A 36B 33C ．6D ．37．已知=2{=1x y 是二元一次方程组+=8{ =1mx ny nx my -的解，则2m n -的算术平方根为（）A ．±2B ．2C ．2D ．48．体育测试中，小进和小俊进行800米跑测试，小进的速度是小俊的1.25倍，小进比小俊少用了40秒，设小俊的速度是x 米/秒，则所列方程正确的是（）A ．4 1.2540800x x ⨯-=B ．800800402.25x x -=C ．800800401.25x x -=D ．800800401.25x x -= 9．如图，在△ABC 和△DEF 中，∠B ＝∠DEF ，AB ＝DE ，若添加下列一个条件后，仍然不能证明△ABC ≌△DEF ，则这个条件是（）A ．∠A ＝∠DB ．BC ＝EF C ．∠ACB ＝∠FD ．AC ＝DF10．如图是由4个相同的小正方形组成的网格图，其中∠1+∠2等于（）A ．150°B ．180°C ．210°D ．225°二、填空题（本大题共6小题，每小题3分，共18分）1．若△ABC 三条边长为a ，b ，c ，化简：|a -b -c |-|a +c -b |=__________．2．已知三角形ABC 的三边长为a,b,c 满足a+b=10,ab=18,c=8,则此三角形为__________三角形.3．已知x 、y 满足方程组2524x y x y +=⎧⎨+=⎩，则x y -的值为________． 4．如图，ABCD 的对角线AC ，BD 相交于点O ，点E ，F 分别是线段AO ，BO 的中点，若AC+BD=24厘米，△OAB 的周长是18厘米，则EF=________厘米．5．如图，圆柱形玻璃杯高为14cm，底面周长为32cm，在杯内壁离杯底5cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿3cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到内壁B处的最短距离为___________cm（杯壁厚度不计）．6．如图，在平行四边形ABCD中，连接BD，且BD＝CD，过点A作AM⊥BD于点M，过点D作DN⊥AB于点N，且DN＝32，在DB的延长线上取一点P，满足∠ABD＝∠MAP＋∠PAB，则AP＝________.三、解答题（本大题共6小题，共72分）1．解下列方程组(1)203216x yx y-=⎧⎨+=⎩(2)410211x yx y-=⎧⎨+=⎩2．先化简，再求值：22122()121x x x xx x x x----÷+++，其中x满足x2－2x－2=0.3．已知：关于x的方程2x(k2)x2k0-++=，（1）求证：无论k取任何实数值，方程总有实数根；（2）若等腰三角形ABC的一边长a=1，两个边长b，c恰好是这个方程的两个根，求△ABC的周长．4．如图①，△ABC中，AB=AC，∠B、∠C的平分线交于O点，过O点作EF∥BC 交AB、AC于E、F.(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.(2)如图②,若AB≠AC，其他条件不变，图中还有等腰三角形吗?如果有，分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?(3)如图③，若△ABC中∠B的平分线BO与三角形外角平分线CO交于O，过O 点作OE∥BC交AB于E，交AC于F.这时图中还有等腰三角形吗?EF与BE、CF 关系又如何?说明你的理由.5．如图所示，在△ABC中，D是BC边上一点，∠1=∠2，∠3=∠4，∠BAC=63°，求∠DAC的度数．6．在“母亲节”前期，某花店购进康乃馨和玫瑰两种鲜花，销售过程中发现康乃馨比玫瑰销售量大，店主决定将玫瑰每枝降价1元促销，降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍．（1）求降价后每枝玫瑰的售价是多少元？（2）根据销售情况，店主用不多于900元的资金再次购进两种鲜花共500枝，康乃馨进价为2元/枝，玫瑰进价为1.5元/枝，问至少购进玫瑰多少枝？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、C2、A3、B4、D5、D6、D7、C8、C9、D10、B二、填空题（本大题共6小题，每小题3分，共18分）1、2b-2a2、直角3、14、35、206、6三、解答题（本大题共6小题，共72分）1、（1）42xy=⎧⎨=⎩；（2）61xy=⎧⎨=-⎩.2、1 23、（1）略；（2）△ABC的周长为5．4、（1）△AEF、△OEB、△OFC、△OBC、△ABC共5个，EF=BE+FC；（2）有，△EOB、△FOC，存在；（3）有，EF=BE-FC．5、24°．6、（1）2元；（2）至少购进玫瑰200枝.。

2020—2021年部编人教版八年级数学上册第一次月考考试及参考答案

2020—2021年部编人教版八年级数学上册第一次月考考试及参考答案班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．多项式2mx m -与多项式221x x -+的公因式是（）A ．1x -B ．1x +C ．21x -D ．()21x - 2．矩形具有而平行四边形不一定具有的性质是（）A ．对边相等B ．对角相等C ．对角线相等D ．对角线互相平分3．若关于x 的一元二次方程（k ﹣1）x 2+2x ﹣2=0有两个不相等的实数根，则k 的取值范围是（）A ．k ＞12B ．k ≥12C ．k ＞12且k ≠1D ．k ≥12且k ≠1 4．关于x 的一元一次不等式≤﹣2的解集为x ≥4，则m 的值为（） A ．14 B ．7 C ．﹣2 D ．25．已知直角三角形的两条边长分别是3和5，那么这个三角形的第三条边的长（）A ．4B ．16C ．34D ．4或346．已知a=2012x+2011，b=2012x+2012，c=2012x+2013，那么a 2+b 2+c 2—ab －bc －ca 的值等于( )A ．0B ．1C ．2D ．37．如图，函数y=2x 和y=ax+4的图象相交于A(m ，3),则不等式2x ax+4<的解集为（）A ．3x 2>B ．x 3>C ．3x 2< D ．x 3<8．某种商品的进价为800元，出售时标价为1200元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于5%，则至多可打（）A ．6折B ．7折C ．8折D ．9折9．如图,把一个矩形纸片ABCD 沿EF 折叠后,点D 、C 分别落在D ′、C ′的位置,若∠EFB=65°,则∠AED ′为（）．A ．70°B ．65°C ．50°D ．25°10．下列选项中，不能判定四边形ABCD 是平行四边形的是( )A ．AD //BC ，AB //CDB ．AB //CD ，AB CD =C ．AD //BC ，AB DC = D ．AB DC =，AD BC =二、填空题（本大题共6小题，每小题3分，共18分）1．若22(3)16x m x +-+是关于x 的完全平方式，则m =__________．2．若(x+p)与(x+5)的乘积中不含x 的一次项，则p ＝__________．3．分解因式6xy 2－9x 2y －y 3 = _____________.4．如图，AB ∥CD ，则∠1+∠3—∠2的度数等于 _________．5．如图,E 、F 分别是平行四边形ABCD 的边AB 、CD 上的点,AF 与DE 相交于点P,BF 与CE 相交于点Q,若215APD S cm ∆=，225BQC S cm ∆=，则阴影部分的面积为__________2cm ．6．如图1，点P 从△ABC 的顶点B 出发，沿B →C →A 匀速运动到点A ，图2是点P 运动时，线段BP 的长度y 随时间x 变化的关系图象，其中M 为曲线部分的最低点，则△ABC 的面积是________．三、解答题（本大题共6小题，共72分）1．解方程：（1）2(1)30x +-= （2）4(2)3(2)x x x +=+2．先化简，再求值：213(2)211a a a a a +-÷+-+-，其中a =2．3．已知关于x 的分式方程311(1)(2)x k x x x -+=++-的解为非负数，求k 的取值范围．4．如图，在平面直角坐标系中，一次函数y=kx+b 的图象经过点A （﹣2，6），且与x 轴相交于点B ，与正比例函数y=3x 的图象相交于点C ，点C 的横坐标为1．（1）求k 、b 的值；（2）若点D在y轴负半轴上，且满足S△COD =13S△BOC，求点D的坐标．5．如图所示，在△ABC中，D是BC边上一点，∠1=∠2，∠3=∠4，∠BAC=63°，求∠DAC的度数．6．班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动，基地离学校有90公里，队伍8：00从学校出发．苏老师因有事情，8：30从学校自驾小车以大巴1.5倍的速度追赶，追上大巴后继续前行，结果比队伍提前15分钟到达基地．问：（1）大巴与小车的平均速度各是多少？（2）苏老师追上大巴的地点到基地的路程有多远？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、A2、C3、C4、D5、D6、D7、C8、B9、C10、C二、填空题（本大题共6小题，每小题3分，共18分）1、7或-12、-53、－y(3x －y)24、180°5、406、12三、解答题（本大题共6小题，共72分）1、（1）11x =，21x =；（2）12x =-，243x =．2、11a -，1． 3、8k ≥-且0k ≠．4、（1）k=-1，b=4；（2）点D 的坐标为（0，-4）．5、24°．6、（1）大巴的平均速度为40公里/时，则小车的平均速度为60公里/时；（2）苏老师追上大巴的地点到基地的路程有30公里。

2020—2021年人教版八年级数学上册第一次月考考试及答案【完美版】

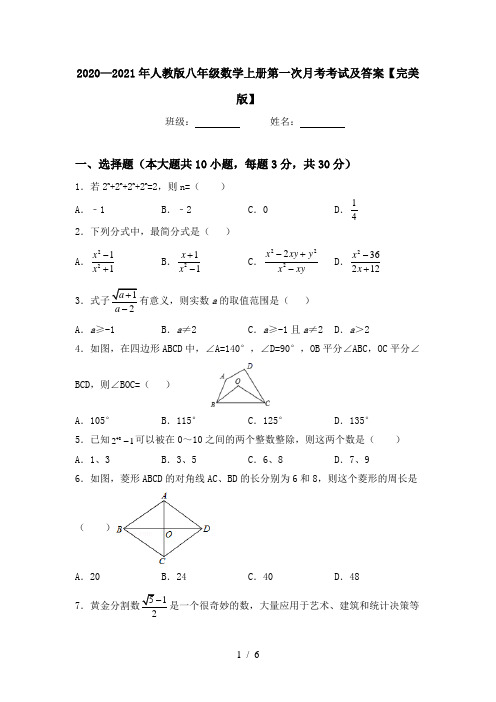
2020—2021年人教版八年级数学上册第一次月考考试及答案【完美版】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．若2n+2n+2n+2n=2，则n=（）A．﹣1 B．﹣2 C．0 D．1 42．下列分式中，最简分式是（）A．2211xx-+B．211xx+-C．2222x xy yx xy-+-D．236212xx-+3．式子12aa+-有意义，则实数a的取值范围是（）A．a≥-1 B．a≠2 C．a≥-1且a≠2 D．a＞24．如图，在四边形ABCD中，∠A=140°，∠D=90°，OB平分∠ABC，OC平分∠BCD，则∠BOC=（）A．105°B．115°C．125°D．135°5．已知4821-可以被在0～10之间的两个整数整除，则这两个数是（）A．1、3 B．3、5 C．6、8 D．7、96．如图，菱形ABCD的对角线AC、BD的长分别为6和8，则这个菱形的周长是（）A．20 B．24 C．40 D．48751-是一个很奇妙的数，大量应用于艺术、建筑和统计决策等方面，请你估算5﹣1的值（）A．在1.1和1.2之间B．在1.2和1.3之间C．在1.3和1.4之间D．在1.4和1.5之间8．如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为30海里的A处，轮船沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则此时轮船所在位置B与灯塔P之间的距离为（）A．60海里B．45海里C．203海里D．303海里9．如图，两个较大正方形的面积分别为225、289，且中间夹的三角形是直角三角形，则字母A所代表的正方形的面积为（）A．4 B．8 C．16 D．6410．如图，AD，CE分别是△ABC的中线和角平分线．若AB=AC，∠CAD=20°，则∠ACE的度数是（）A．20°B．35°C．40°D．70°二、填空题（本大题共6小题，每小题3分，共18分）1．若a，b互为相反数，则a2﹣b2=________．2．如果关于x的不等式组232x ax a>+⎧⎨<-⎩无解，则a的取值范围是__________．3．将“平行于同一条直线的两条直线平行”改写成“如果……那么……”的形式为_________.4．如图所示的网格是正方形网格，则PAB PBA ∠∠＋＝________°（点A ，B ，P 是网格线交点）.5．如图，∠1，∠2，∠3的大小关系是________．6．如图所示，在△ABC 中，∠B =90°，AB =3，AC =5，将△ABC 折叠，使点C 与点A 重合，折痕为DE ，则△ABE 的周长为________．三、解答题（本大题共6小题，共72分）1．解不等式（1）7252x x -+≥ （2）11132x x -+-<2．先化简，再求值：22169211x x x x x ⎛⎫-++-÷ ⎪+-⎝⎭，其中2x =．3．已知关于x 的一元二次方程（a+c ）x 2+2bx+（a ﹣c ）=0，其中a 、b 、c 分别为△ABC 三边的长．（1）如果x=﹣1是方程的根，试判断△ABC 的形状，并说明理由；（2）如果方程有两个相等的实数根，试判断△ABC 的形状，并说明理由；（3）如果△ABC 是等边三角形，试求这个一元二次方程的根．4．已知:在ABC ∆中,AB AC = ,D 为AC 的中点,DE AB ⊥ ,DF BC ⊥ ,垂足分别为点,E F ,且DE DF =.求证:ABC ∆是等边三角形.5．如图，在△ABC 中，AD 是BC 边上的中线，E 是AD 的中点，过点A 作BC 的平行线交BE 的延长线于点F ，连接CF ，（1）求证：AF=DC ；（2）若AB ⊥AC ，试判断四边形ADCF 的形状，并证明你的结论．6．某经销商从市场得知如下信息： A 品牌手表 B 品牌手表进价（元/块） 700 100售价（元/块） 900160 他计划用4万元资金一次性购进这两种品牌手表共100块，设该经销商购进A 品牌手表x 块，这两种品牌手表全部销售完后获得利润为y 元．（1）试写出y 与x 之间的函数关系式；（2）若要求全部销售完后获得的利润不少于1.26万元，该经销商有哪几种进货方案；（3）选择哪种进货方案，该经销商可获利最大；最大利润是多少元.参考答案一、选择题（本大题共10小题，每题3分，共30分）1、A2、A3、C4、B5、D6、A7、B8、D9、D10、B二、填空题（本大题共6小题，每小题3分，共18分）1、02、a ≤2．3、如果两条直线平行于同一条直线，那么这两条直线平行.4、45.5、∠1＜∠2＜∠36、7三、解答题（本大题共6小题，共72分）1、（1）2x ≥；（2）11x >-2、13x x -+；15．3、(1) △ABC 是等腰三角形；(2)△ABC 是直角三角形；(3) x 1=0，x 2=﹣1．4、略.5、（1）略（2）略6、（1）y=140x+6000；（2）三种，答案见解析；（3）选择方案③进货时，经销商可获利最大，最大利润是13000元．。

2020—2021年人教版八年级数学上册第一次月考考试题及答案【完整版】

2020—2021年人教版八年级数学上册第一次月考考试题及答案【完整版】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．若分式211x x -+的值为0，则x 的值为（） A ．0 B ．1 C ．﹣1 D ．±12．若点1(),6A x -，2(),2B x -，32(),C x 在反比例函数12y x =的图像上，则1x ，2x ，3x 的大小关系是（）A ．123x x x <<B ．213x x x <<C ．231x x x <<D ．321x x x <<3．已知a ，b 满足方程组51234a b a b +=⎧⎨-=⎩则a+b 的值为（） A ．﹣4 B ．4 C ．﹣2 D ．24．已知a 为实数，则代数式227122a a -+的最小值为（）A ．0B ．3C ．33D ．95．下列方程中，是关于x 的一元二次方程的是（）A ．ax 2+bx+c ＝0(a ，b ，c 为常数)B ．x 2﹣x ﹣2＝0C ．211x x +﹣2＝0D ．x 2+2x ＝x 2﹣16．如图，PA 、PB 是⊙O 切线，A 、B 为切点，点C 在⊙O 上,且∠ACB ＝55°，则∠APB 等于（）A ．55°B ．70°C ．110°D ．125°7．老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：接力中，自己负责的一步出现错误的是（）A．只有乙B．甲和丁C．乙和丙D．乙和丁8．下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（）A．B．C．D．9．如图，在正方形ABCD中，AB=9，点E在CD边上，且DE=2CE，点P是对角线AC上的一个动点，则PE+PD的最小值是（）A．310B．103C．9 D．9210．如图，已知BD是ABC的角平分线，ED是BC的垂直平分线，∠=︒，390BACAD=，则CE的长为（）A．6 B．5 C．4 D．33二、填空题（本大题共6小题，每小题3分，共18分）1．已知a、b满足（a﹣1）22b+，则a+b=________．2．正五边形的内角和等于______度．3．若关于x 的分式方程333x a x x+--=2a 无解，则a 的值为________． 4．如图，▱ABCD 中，AC 、BD 相交于点O ，若AD=6，AC+BD=16，则△BOC 的周长为________．5．如图，四边形ABCD 的对角线相交于点O ，AO=CO ，请添加一个条件________（只添一个即可），使四边形ABCD 是平行四边形．6．如图，∠AOB=60°，OC 平分∠AOB ，如果射线OA 上的点E 满足△OCE 是等腰三角形，那么∠OEC 的度数为________。

2020—2021年部编人教版八年级数学上册第一次月考测试卷及答案【完美版】

2020—2021年部编人教版八年级数学上册第一次月考测试卷及答案【完美版】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分） 1．﹣3的绝对值是（）A ．﹣3B ．3C ．-13D ．132．若点1(),6A x -，2(),2B x -，32(),C x 在反比例函数12y x=的图像上，则1x ，2x ，3x 的大小关系是（）A ．123x x x <<B ．213x x x <<C ．231x x x <<D ．321x x x << 3．已知23a b =（a ≠0，b ≠0），下列变形错误的是（） A ．23a b = B ．2a=3b C ．32b a = D ．3a=2b 4．点C 在x 轴上方，y 轴左侧，距离x 轴2个单位长度，距离y 轴3个单位长度，则点C 的坐标为（）A ．（2，3）B ．（-2，-3）C ．（-3，2）D ．（3，-2）5．为考察甲、乙、丙、丁四种小麦的长势，在同一时期分别从中随机抽取部分麦苗，获得苗高（单位：cm ）的平均数与方差为：x 甲=x 丙=13，x 乙=x 丁=15：s 甲2=s 丁2=3.6，s 乙2=s 丙2=6.3．则麦苗又高又整齐的是（）A ．甲B ．乙C ．丙D ．丁 6．如图，有一块直角三角形纸片，两直角边6cm AC =，8cm BC =．现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，则CD 等于（）A ．2cmB ．3cmC ．4cmD ．5cm7．如图，在▱ABCD中，对角线AC的垂直平分线分别交AD、BC于点E、F，连接CE，若△CED的周长为6，则▱ABCD的周长为（）A．6 B．12 C．18 D．248．一次函数y=ax+b与反比例函数a byx-=，其中ab＜0，a、b为常数，它们在同一坐标系中的图象可以是（）A． B．C． D．9．如图，AB∥CD，点E在线段BC上，CD=CE,若∠ABC=30°，则∠D为（）A．85°B．75°C．60°D．30°10．如图，将矩形ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，已知∠BDC=62°，则∠DFE的度数为（）A．31°B．28°C．62°D．56°二、填空题（本大题共6小题，每小题3分，共18分）1．9的平方根是_________．2．已知AB//y 轴，A 点的坐标为(3，2)，并且AB=5，则B 的坐标为________．3．当直线()223y k x k =-+-经过第二、三、四象限时，则k 的取值范围是________．4．如图，一次函数y=﹣x ﹣2与y=2x+m 的图象相交于点P （n ，﹣4），则关于x 的不等式组22{20x m x x +----＜＜的解集为________．5．如图，在平面直角坐标系中，△AOB ≌△COD ，则点D 的坐标是__________．6．如图一个圆柱，底圆周长10cm ，高4cm ，一只蚂蚁沿外壁爬行，要从A 点爬到B 点，则最少要爬行_______cm .三、解答题（本大题共6小题，共72分）1．解方程：2420x x +-=2．先化简，再求值[（x 2+y 2）-（x-y ）2+2y （x-y ）]÷2y ，其中x=-2，y=-12．3．已知2a﹣1的平方根为±3，3a+b﹣1的算术平方根为4，求a+2b的平方根．4．在Rt△ABC中，∠BAC=90°,D是BC的中点，E是AD的中点．过点A作AF ∥BC交BE的延长线于点F（1）求证：△AEF≌△DEB；（2）证明四边形ADCF是菱形；（3）若AC=4，AB=5，求菱形ADCF 的面积．5．如图，▱ABCD的对角线AC，BD相交于点O，点E、F在AC上，且AF=CE．求证：BE=DF．6．为支援灾区，某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件．已知B型学习用品的单价比A型学习用品的单价多10元，用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同．（1）求A、B两种学习用品的单价各是多少元？（2）若购买这批学习用品的费用不超过28000元，则最多购买B型学习用品多少件？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、B2、B3、B4、C5、D6、B7、B8、C9、B10、D二、填空题（本大题共6小题，每小题3分，共18分）1、±32、(3,7)或(3,-3)3、13k <<.4、﹣2＜x ＜25、（-2，0）6三、解答题（本大题共6小题，共72分）1、12x =-22x =-.2、2x-y ；-312．3、±34、（1）证明略；（2）证明略；（3）10．5、略.6、（1）A 型学习用品20元，B 型学习用品30元；（2）800．。

2020—2021年人教版八年级数学上册第一次月考试卷及答案【2020—2021年人教版】

2020—2021年人教版八年级数学上册第一次月考试卷及答案【2020—2021年人教版】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．已知31416181279a b c ===，，，则a b c 、、的大小关系是（）A ．a b c ＞＞B ．a c b ＞＞C ．a b c ＜＜D ．b c a ＞＞2．不等式3（x ﹣1）≤5﹣x 的非负整数解有（）A ．1个B ．2个C ．3个D ．4个3．函数2y x =-的图象不经过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．在△ABC 中，AB=10，AC=210，BC 边上的高AD=6，则另一边BC 等于（）A ．10B ．8C ．6或10D ．8或105．下列图形中，不能通过其中一个四边形平移得到的是（）A ．B ．C ．D ．6．已知1112a b -=，则ab a b-的值是（） A ．12 B ．－12 C ．2 D ．－27．如图，直线y=kx+b （k ≠0）经过点A （﹣2，4），则不等式kx+b ＞4的解集为（）A ．x ＞﹣2B ．x ＜﹣2C ．x ＞4D ．x ＜48．“凤鸣”文学社在学校举行的图书共享仪式上互赠图书，每个同学都把自己的图书向本组其他成员赠送一本，某组共互赠了210本图书，如果设该组共有x 名同学，那么依题意，可列出的方程是（）A ．x （x+1）＝210B ．x （x ﹣1）＝210C ．2x （x ﹣1）＝210D ．12x （x ﹣1）＝210 9．如图，点E 在CD 的延长线上，下列条件中不能判定AB ∥CD 的是（）A ．∠1=∠2B ．∠3=∠4C ．∠5=∠BD ．∠B +∠BDC =180°10．若关于x 的一元二次方程2210x x kb -++=有两个不相等的实数根，则一次函数y kx b =+的图象可能是:（）A ．B ．B ．C ．D ．二、填空题（本大题共6小题，每小题3分，共18分）1．已知2320x y --=，则23(10)(10)x y ÷＝_______．2．已知x ，y 满足方程组x 2y 5x 2y 3-=⎧+=-⎨⎩，则22x 4y -的值为__________． 323(1)0m n -+=，则m －n 的值为________．4．如图，▱ABCD 中，AB ＝3cm ，BC ＝5cm ，BE 平分∠ABC 交AD 于E 点，CF 平分∠BCD 交AD 于F 点，则EF 的长为________m ．5．如图，直线y =x +2与直线y =ax +c 相交于点P （m ，3），则关于x 的不等式x +2≤ax +c 的解为__________．6．已知：如图，OAD ≌OBC ，且∠O ＝70°，∠C ＝25°，则∠AEB ＝______度．三、解答题（本大题共6小题，共72分）1．解方程：2420x x +-=2．先化简，再求值[（x 2+y 2）-（x-y ）2+2y （x-y ）]÷2y ，其中x=-2，y=-12．3．已知关于x 的一元二次方程()22x 2k 1x k k 0-+++= （1）求证：方程有两个不相等的实数根；（2）若△ABC 的两边AB 、AC 的长是方程的两个实数根，第三边BC 的长为5．当△ABC 是等腰三角形时，求k 的值4．如图①，△ABC 中，AB =AC ，∠B 、∠C 的平分线交于O 点，过O 点作EF ∥BC 交AB 、AC 于E 、F .(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.(2)如图②,若AB≠AC，其他条件不变，图中还有等腰三角形吗?如果有，分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?(3)如图③，若△ABC中∠B的平分线BO与三角形外角平分线CO交于O，过O 点作OE∥BC交AB于E，交AC于F.这时图中还有等腰三角形吗?EF与BE、CF 关系又如何?说明你的理由.5．如图，直线l1：y1=﹣x+2与x轴，y轴分别交于A，B两点，点P（m，3）为直线l1上一点，另一直线l2：y2=12x+b过点P．（1）求点P坐标和b的值；（2）若点C是直线l2与x轴的交点，动点Q从点C开始以每秒1个单位的速度向x轴正方向移动．设点Q的运动时间为t秒．①请写出当点Q在运动过程中，△APQ的面积S与t的函数关系式；②求出t为多少时，△APQ的面积小于3；③是否存在t的值，使△APQ为等腰三角形？若存在，请求出t的值；若不存在，请说明理由．6．文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元，甲种图书每本的售价是乙种图书每本售价的1.4倍，若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.（1）甲乙两种图书的售价分别为每本多少元？（2）书店为了让利读者，决定甲种图书售价每本降低3元，乙种图书售价每本降低2元，问书店应如何进货才能获得最大利润？（购进的两种图书全部销售完.）参考答案一、选择题（本大题共10小题，每题3分，共30分）1、A2、C3、B4、C5、D6、D7、A8、B9、A10、B二、填空题（本大题共6小题，每小题3分，共18分）1、1002、-153、44、15、x ≤1.6、120三、解答题（本大题共6小题，共72分）1、12x =-22x =-.2、2x-y ；-312．3、（1）详见解析（2）k 4=或k 5=4、（1）△AEF 、△OEB 、△OFC 、△OBC 、△ABC 共5个，EF=BE+FC ；（2）有，△EOB 、△FOC ，存在；（3）有，EF=BE-FC ．5、（1）b=72；（2）①△APQ 的面积S 与t 的函数关系式为S=﹣32t+272或S=32t ﹣272；②7＜t ＜9或9＜t ＜11，③存在，当t 的值为3或9﹣6时，△APQ 为等腰三角形．6、（1）甲种图书售价每本28元，乙种图书售价每本20元；（2）甲种图书进货533本，乙种图书进货667本时利润最大.。

2020—2021年人教版八年级数学上册第一次月考考试及答案【可打印】

2020—2021年人教版八年级数学上册第一次月考考试及答案【可打印】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．﹣3的绝对值是（）A．﹣3 B．3 C．-13D．132．如图，若x为正整数，则表示()2221441xx x x+-+++的值的点落在（）A．段①B．段②C．段③D．段④3．成人每天维生素D的摄入量约为0.0000046克．数据“0.0000046”用科学记数法表示为（）A．74610-⨯B．74.610-⨯C．64.610-⨯D．50.4610-⨯4．若6－13的整数部分为x，小数部分为y，则(2x＋13)y的值是（）A．5－313B．3 C．313－5 D．－35．将下列多项式因式分解,结果中不含有因式(a+1)的是（）A．a2-1 B．a2+a C．a2+a-2 D．(a+2)2-2(a+2)+16．已知1112a b-=，则aba b-的值是（）A．12B．－12C．2 D．－27．如图，▱ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD=12，则△DOE的周长为（）A．15 B．18 C．21 D．248．如图，△ABC 中，AD 为△ABC 的角平分线，BE 为△ABC 的高，∠C=70°，∠ABC=48°，那么∠3是（）A ．59°B ．60°C ．56°D ．22°9．如图，点P 是∠AOB 内任意一点，且∠AOB ＝40°，点M 和点N 分别是射线OA 和射线OB 上的动点，当△PMN 周长取最小值时，则∠MPN 的度数为（）A ．140°B ．100°C ．50°D ．40°10．下列选项中，不能判定四边形ABCD 是平行四边形的是( )A ．AD //BC ，AB //CDB ．AB //CD ，AB CD =C ．AD //BC ，AB DC = D ．AB DC =，AD BC =二、填空题（本大题共6小题，每小题3分，共18分）1．若22(3)16x m x +-+是关于x 的完全平方式，则m =__________．2．计算：82-=_______．3．4的平方根是．4．如图，在高2米，坡角为30°的楼梯表面铺地毯，地毯的长至少需______米．5．如图，在平面直角坐标系中，点A 、B 的坐标分别为（1，3）、（n ，3），若直线y=2x 与线段AB 有公共点，则n 的值可以为____________．（写出一个即可）6．如图，长为8 cm 的橡皮筋放置在x 轴上，固定两端A 和B ，然后把中点C 向上拉升3 cm 到点D ，则橡皮筋被拉长了_____ cm.三、解答题（本大题共6小题，共72分）1．解分式方程：2216124x x x --=+-2．先化简，再求值：22169211x x x x x ⎛⎫-++-÷ ⎪+-⎝⎭，其中2x =．3．已知关于的方程2(2)210x k x k -++-=．（1）求证：该方程一定有两个不相等的实数根；（2）若12125x x x x +=-，求k 的值．4．（1）如图（1），已知：在△ABC 中，∠BAC ＝90°，AB=AC ，直线m 经过点A ，BD ⊥直线m, CE ⊥直线m,垂足分别为点D 、E.证明:DE=BD+CE.（2）如图（2），将（1）中的条件改为：在△ABC 中，AB=AC ，D 、A 、E 三点都在直线m 上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE 是否成立?如成立,请你给出证明;若不成立,请说明理由.（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.5．已知平行四边形ABCD，对角线AC、BD交于点O，线段EF过点O交AD于点E，交BC于点F．求证：OE=OF．6．某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件．(1)降价前商场每月销售该商品的利润是多少元？(2)要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价多少元？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、B2、B3、C4、B5、C6、D7、A8、A9、B10、C二、填空题（本大题共6小题，每小题3分，共18分）1、7或-123、±2．4、5、26、2.三、解答题（本大题共6小题，共72分）1、原方程无解2、13xx-+；15．3、（1）见解析；（2）k=84、（1）见解析（2）成立（3）△DEF为等边三角形5、略.6、(1) 4800元；(2) 降价60元.。

2020-2021学年度第一学期八年级数学月考试卷含答案共六套

2020-2021学年八年级（上）第一次月考数学试卷一、选择题（本题共10小题，每小题4分，满分40分）1．下列函数中是一次函数的是（）A．y＝B．y＝C．y＝ax+b D．y＝x22．下列各点中位于第二象限的是（）A．（﹣2，0）B．（8，﹣2）C．（0，3）D．（﹣，4）3．已知过A（﹣1，a），B（2，﹣2）两点的直线平行于x轴，则a的值为（）A．﹣1 B．1 C．2 D．﹣24．关于函数y＝﹣﹣1，下列说法错误的是（）A．当x＝2时，y＝﹣2B．y随x的增大而减小C．若x1＞x2，则y1＞y2D．图象经过第二、三、四象限5．下面四条直线，其中直线上的每一个点的坐标都是二元一次方程2x﹣3y＝6的解的是（）A．B．C．D．6．已知y﹣1与x成正比例，当x＝3时，y＝2．则当x＝﹣1时，y的值是（）A．﹣1 B．0 C．D．7．实践证明1分钟跳绳测验的最佳状态是前20秒速度匀速增加，后10秒冲刺，中间速度保持不变，则跳绳速度v（个/秒）与时间t（秒）之间的函数图象大致为（）A．B．C．D．8．一次函数y＝ax+b与y＝abx在同一个平面直角坐标系中的图象不可能是（）A．B．C．D．9．若点（﹣1，m）和（2，n）在直线y＝﹣x+b上，则m、n、b的大小关系是（）A．m＞n＞b B．m＜n＜b C．m＞b＞n D．b＜m＜n10．甲车从A地到B地，乙车从B地到A地，乙车先出发先到达，甲乙两车之间的距离y（千米）与行驶的时间x（小时）的函数关系如图所示，则下列说法中不正确的是（）A．甲车的速度是80km/hB．乙车的速度是60km/hC．甲车出发1h与乙车相遇D．乙车到达目的地时甲车离B地10km二、填空题（共4题，每题5分）11．函数中，自变量x的取值范围是．12．已知关于x的方程mx+n＝0的解是x＝﹣2，则直线y＝mx+n与x轴的交点坐标是．13．若点P的坐标是（2a+1，a﹣4），且P点到两坐标轴的距离相等，则P点的坐标是．14．直线y＝kx﹣2与直线y＝x﹣1（1≤x≤4）有交点，则k的取值范围是．三、解答题（共8题，共90分）15．已知一次函数的图象平行于y＝﹣x，且截距为1．（1）求这个函数的解析式；（2）判断点P（﹣2，）是否在这个函数的图象上．16．若函数y＝（m+1）x+m2﹣1是正比例函数．（1）求该函数的表达式．（2）将该函数图象沿y轴向上或者向下平移，使其经过（1，﹣2），求平移的方向与距离．17．如图，先将△ABC向上平移2个单位再向左平移5个单位得到△A1B1C1（1）画出△A1B1C1，并写出点A1、B1、C1的坐标．（2）求△A1B1C1的面积．18．画出函数y＝﹣x+3的图象，并利用图象解下列问题：（1）求方程﹣x+3＝0的解．（2）求不等式﹣x+3＞0的解集．（3）若﹣3≤y＜6，求x的取值范围．19．如图，大拇指与小拇指尽量张开时，两指尖的距离称为指距．人体构造学的研究成果表明，一般情况下人的指距d和身高h成如下所示的关系．指距d（cm）20 21 22 23身高h（cm）160 169 178 187 （1）直接写出身高h与指距d的函数关系式；（2）姚明的身高是226厘米，可预测他的指距约为多少？（精确到0.1厘米）20．如图，直线l1：y＝2x﹣2与x轴交于点D，直线l2：y＝kx+b与x轴交于点A，且经过点B，直线l1，l2交于点C（m，2）．（1）求m的值；（2）求直线l2的解析式；（3）根据图象，直接写出1＜kx+b＜2x﹣2的解集．（4）求△ACD的面积．21．甲、乙两个工程队完成某项工程，先由甲单独做10天，乙队再加入合作．工进度满足如图所示．（1）求工作量y与工作时间x（天）之间的函数关系式；（2）这项工程全部完成需要多少天？（3）求乙队单独完成这项工程的天数．22．甲、乙两人分别安装同一种零件40个，其中乙在安装两小时后休息了2小时，后继续按原来进度工作，他们每人安装的零件总数y（个）与安装时间x（小时）的函数关系如图1所示，两人安装零件总数之差z（件）与时间x（小时）的函数关系如图2所示．（1）a＝；b＝．（2）求出甲工作2小时后的安装的零件数y与时间x的函数关系．（3）甲、乙两人在什么时间生产的零件总数相差8个？参考答案与试题解析一．选择题（共10小题）1．下列函数中是一次函数的是（）A．y＝B．y＝C．y＝ax+b D．y＝x2【分析】根据一次函数的定义解答．【解答】解：A、是正比例函数，特殊的一次函数，故本选项符合题意；B、自变量次数不为1，不是一次函数，故本选项不符合题意；C、单a＝0时，它不是一次函数，故本选项不符合题意；D、自变量次数不为1，不是一次函数，故本选项不符合题意．故选：A．2．下列各点中位于第二象限的是（）A．（﹣2，0）B．（8，﹣2）C．（0，3）D．（﹣，4）【分析】依据位于第二象限的点的横坐标为负，纵坐标为正，即可得到结论．【解答】解：∵位于第二象限的点的横坐标为负，纵坐标为正，∴位于第二象限的是（﹣，4）故选：D．3．已知过A（﹣1，a），B（2，﹣2）两点的直线平行于x轴，则a的值为（）A．﹣1 B．1 C．2 D．﹣2【分析】根据两点所在直线平行于x轴，那么这两点的纵坐标相等解答即可．【解答】解：∵过A（﹣1，a），B（2，﹣2）两点的直线平行于x轴，∴a＝﹣2，故选：D．4．关于函数y＝﹣﹣1，下列说法错误的是（）A．当x＝2时，y＝﹣2B．y随x的增大而减小C．若x1＞x2，则y1＞y2D．图象经过第二、三、四象限【分析】根据一次函数的性质判定即可．【解答】解：关于函数y＝﹣﹣1，A、当x＝2时，y＝﹣﹣1＝﹣2，说法正确，不合题意；B、∵k＝﹣，∴y随x的增大而减小，说法正确，不合题意；C、∵k＝﹣，∴y随x的增大而减小，∴若x1＞x2，则y1＜y2，说法错误，符合题意；D、图象经过第二、三、四象限，说法正确，不合题意；故选：C．5．下面四条直线，其中直线上的每一个点的坐标都是二元一次方程2x﹣3y＝6的解的是（）A．B．C．D．【分析】根据两点确定一条直线，当x＝0，求出y的值，再利用y＝0，求出x的值，即可得出一次函数图象与坐标轴交点，即可得出图象．【解答】解：∵2x﹣3y＝6，∴y＝x﹣2，∴当x＝0，y＝﹣2；当y＝0，x＝3，∴一次函数y＝x﹣2，与y轴交于点（0，﹣2），与x轴交于点（3，0），即可得出选项D符合要求，故选：D．6．已知y﹣1与x成正比例，当x＝3时，y＝2．则当x＝﹣1时，y的值是（）A．﹣1 B．0 C．D．【分析】设y﹣1＝kx（k≠0），把x＝3，y＝2代入求出k的值，把x＝﹣1代入函数关系式即可得到相应的y的值；【解答】解：设y﹣1＝kx（k≠0），则由x＝3时，y＝2，得到：2﹣1＝3k，解得k＝．则该函数关系式为：y＝x+1；把x＝﹣1代入y＝x+1得到：y＝﹣+1＝；故选：D．7．实践证明1分钟跳绳测验的最佳状态是前20秒速度匀速增加，后10秒冲刺，中间速度保持不变，则跳绳速度v（个/秒）与时间t（秒）之间的函数图象大致为（）A．B．C．D．【分析】根据前20秒匀加速进行，20秒至50秒保持跳绳速度不变，后10秒继续匀加速进行，得出速度y随时间x的增加的变化情况，即可求出答案．【解答】解：随着时间的变化，前20秒匀加速进行，所以此时跳绳速度y随时间x的增加而增加，再根据20秒至50秒保持跳绳速度不变，所以此时跳绳速度y随时间x的增加而不变，再根据后10秒继续匀加速进行，所以此时跳绳速度y随时间x的增加而增加，故选：C．8．一次函数y＝ax+b与y＝abx在同一个平面直角坐标系中的图象不可能是（）A．B．C．D．【分析】根据a、b的取值，分别判断出两个函数图象所过的象限，要注意分类讨论．【解答】解：当ab＞0，a，b同号，y＝abx经过一、三象限，同正时，y＝ax+b过一、三、二象限；同负时过二、四、三象限，当ab＜0时，a，b异号，y＝abx经过二、四象限a＜0，b＞0时，y＝ax+b过一、三、四象限；a＞0，b＜0时，y＝ax+b过一、二、四象限．故选：D．9．若点（﹣1，m）和（2，n）在直线y＝﹣x+b上，则m、n、b的大小关系是（）A．m＞n＞b B．m＜n＜b C．m＞b＞n D．b＜m＜n【分析】根据一次函数的解析式判断出其增减性，再根据点的横坐标的特点即可得出结论．【解答】解：∵直线y＝﹣x+b中，k＝﹣1＜0，∴y随x的增大而减小．∵﹣1＜0＜2，∴m＞b＞n．故选：C．10．甲车从A地到B地，乙车从B地到A地，乙车先出发先到达，甲乙两车之间的距离y（千米）与行驶的时间x（小时）的函数关系如图所示，则下列说法中不正确的是（）A．甲车的速度是80km/hB．乙车的速度是60km/hC．甲车出发1h与乙车相遇D．乙车到达目的地时甲车离B地10km【分析】根据已知图象分别分析甲、乙两车的速度，进而分析得出答案．【解答】解：根据图象可知甲用了（3.5﹣1）小时走了200千米，所以甲的速度为：200÷2.5＝80km/h，故选项A不合题意；由图象横坐标可得，乙先出发的时间为1小时，两车相距（200﹣140）＝60km，故乙车的速度是60km/h，故选项B不符合题意；140÷（80+60）＝1（小时），即甲车出发1h与乙车相遇，故选项C不合题意；200﹣（200÷60﹣1）×80＝km，即乙车到达目的地时甲车离B地km，故选项D符合题意．故选：D．二．填空题（共4小题）11．函数中，自变量x的取值范围是x＞﹣2 ．【分析】根据二次根式的性质和分式的意义，被开方数大于或等于0，分母不等于0，就可以求解．【解答】解：根据题意得：被开方数x+2≥0，解得x≥﹣2，根据分式有意义的条件，x+2≠0，解得x≠﹣2，故x＞﹣2．故答案为x＞﹣2．12．已知关于x的方程mx+n＝0的解是x＝﹣2，则直线y＝mx+n与x轴的交点坐标是（﹣2，0）．【分析】求直线与x轴的交点坐标，需使直线y＝mx+n的y值为0，则mx+n＝0；已知此方程的解为x＝﹣2．因此可得答案．【解答】解：∵方程的解为x＝﹣2，∴当x＝﹣2时mx+n＝0；又∵直线y＝mx+n与x轴的交点的纵坐标是0，∴当y＝0时，则有mx+n＝0，∴x＝﹣2时，y＝0．∴直线y＝mx+n与x轴的交点坐标是（﹣2，0）．13．若点P的坐标是（2a+1，a﹣4），且P点到两坐标轴的距离相等，则P点的坐标是（﹣9，﹣9）或（3，﹣3）．【分析】根据点到两坐标轴的距离相等列出绝对值方程求出a的值，然后求解即可．【解答】解：∵点P（2a+1，a﹣4）到两坐标轴的距离相等，∴|2a+1|＝|a﹣4|，∴2a+1＝a﹣4或2a+1＝﹣（a﹣4），解得a＝﹣5或a＝1，当a＝﹣5时，点P的坐标为（﹣9，﹣9），当a＝1时，点P的坐标为（3，﹣3），综上所述，点P的坐标为（﹣9，﹣9）或（3，﹣3），故答案为：（﹣9，﹣9）或（3，﹣3）．14．直线y＝kx﹣2与直线y＝x﹣1（1≤x≤4）有交点，则k的取值范围是≤k≤2 ．【分析】根据已知条件得到直线y＝kx﹣2与y轴的交点坐标为C（0，﹣2），求得直线y＝x﹣1过A（1，0），B（4，3），设直线AC的解析式为y＝mx+n，得到直线AC的解析式为y＝2x﹣2，设直线BC的解析式为y＝ex+f，得到直线BC的解析式为y＝x﹣2，于是得到结论．【解答】解：令x＝0，则y＝0•k﹣2＝﹣2，所以直线y＝kx﹣2与y轴的交点坐标为C（0，﹣2），∵当x＝1时，y＝x﹣1＝0，当x＝4时，y＝x﹣1＝3，∴直线y＝x﹣1过A（1，0），B（4，3），设直线AC的解析式为y＝mx+n，则，解得．所以直线AC的解析式为y＝2x﹣2，设直线BC的解析式为y＝ex+f，则，解得．所以直线BC的解析式为y＝x﹣2，若直线y＝kx﹣2与直线y＝x﹣1（1≤x≤4）有交点，则k的取值范围是≤k≤2，故答案为≤k≤2：三．解答题（共8小题）15．已知一次函数的图象平行于y＝﹣x，且截距为1．（1）求这个函数的解析式；（2）判断点P（﹣2，）是否在这个函数的图象上．【分析】（1）根据两平行直线的解析式的k值相等求出k，然后根据截距为1求出b值，即可得解；（2）把点P（﹣2，）代入解析式，检验即可．【解答】解：（1）设这个函数的解析式为y＝kx+b，∵一次函数的图象平行于y＝﹣x，且截距为1，∴k＝﹣，b＝1，∴这个函数的解析式为y＝﹣x+1；（2）当x＝﹣2时，y＝+1＝，故点P（﹣2，）不在这个函数的图象上．16．若函数y＝（m+1）x+m2﹣1是正比例函数．（1）求该函数的表达式．（2）将该函数图象沿y轴向上或者向下平移，使其经过（1，﹣2），求平移的方向与距离．【分析】（1）根据正比例函数的定义列式计算即可得解；（2）设平移后的函数的解析式为y＝2x+b，把（1，﹣2）代入求得b的值，即可求得结论．【解答】解：（1）根据题意得，m2﹣1＝0且m+1≠0，解得m＝±1且m≠﹣1，所以m＝1．所以该函数的表达式为y＝2x；（2）设平移后的函数的解析式为y＝2x+b，∵经过（1，﹣2），∴﹣2＝2+b，∴b＝﹣4，∴函数图象沿y轴向下平移4个单位，使其经过（1，﹣2）．17．如图，先将△ABC向上平移2个单位再向左平移5个单位得到△A1B1C1（1）画出△A1B1C1，并写出点A1、B1、C1的坐标．（2）求△A1B1C1的面积．【分析】（1）直接利用平移的性质得出对应点位置进而得出答案；（2）利用△A1B1C1所在矩形面积减去周围三角形面积得出答案．【解答】解：（1）如图所示：△A1B1C1，点A1（﹣1，5），B1（﹣2，3），C1（﹣4，4）；（2）△A1B1C1的面积为：2×3﹣×1×3﹣×2×1﹣×1×2＝2.5；18．画出函数y＝﹣x+3的图象，并利用图象解下列问题：（1）求方程﹣x+3＝0的解．（2）求不等式﹣x+3＞0的解集．（3）若﹣3≤y＜6，求x的取值范围．【分析】（1）先利用描点法画出一次函数图象，然后利用直线与x轴的交点坐标确定方程﹣x+3＝0的解；（2）利用x轴上方所对应的自变量的范围确定不等式的解集；（3）利用图象确定y＝﹣3和y＝6对应的自变量的值，从而得到对应的x的取值范围．【解答】解：（1）如图，∵直线与x轴的交点坐标为（2，0），∴方程﹣x+3＝0的解为x＝2，（2）如图，∵x＜2时，y＞0，∴不等式﹣x+3＞0的解集为x＜2；（3）如图，﹣2＜x≤4时，﹣3≤y＜6．19．如图，大拇指与小拇指尽量张开时，两指尖的距离称为指距．人体构造学的研究成果表明，一般情况下人的指距d和身高h成如下所示的关系．指距d（cm）20 21 22 23身高h（cm）160 169 178 187 （1）直接写出身高h与指距d的函数关系式；（2）姚明的身高是226厘米，可预测他的指距约为多少？（精确到0.1厘米）【分析】（1）运用待定系数法求解即可；（2）把h＝226代入（1）中的结论即可．【解答】解：根据表格中数据，d每增加1，身高增加9cm，故d与h是一次函数关系，设这个一次函数的解析式是：h＝kd+b，，解得，故一次函数的解析式是：h＝9d﹣20；（2）当h＝226时，9d﹣20＝226，解得d＝27.3．即姚明的身高是226厘米，可预测他的指距约为27.3厘米．20．如图，直线l1：y＝2x﹣2与x轴交于点D，直线l2：y＝kx+b与x轴交于点A，且经过点B，直线l1，l2交于点C（m，2）．（1）求m的值；（2）求直线l2的解析式；（3）根据图象，直接写出1＜kx+b＜2x﹣2的解集．（4）求△ACD的面积．【分析】（1）把C（m，2）代入y＝2x﹣2中可求出m的值；（2）利用待定系数法求直线l2的解析式；（3）结合图象写出y＝kx+b的函数值大于2且直线l1在直线l2上方对应的自变量的范围；（4）根据两直线解析式确定A、D点的坐标，然后利用三角形面积公式计算．【解答】解：（1）把C（m，2）代入y＝2x﹣2得2m﹣2＝2，解得m＝4；（2）把C（2，2），B（3，1）代入y＝kx+b得，解得，∴直线l2的解析式为y＝﹣x+4；（3）2＜x＜3；（3）当y＝0时，2x﹣2＝0，解得x＝1，则C（1，0），当y＝0时，﹣x+4＝0，解得x＝4，则A（4，0），∴S△ACD＝×（4﹣1）×2＝3．21．甲、乙两个工程队完成某项工程，先由甲单独做10天，乙队再加入合作．工进度满足如图所示．（1）求工作量y与工作时间x（天）之间的函数关系式；（2）这项工程全部完成需要多少天？（3）求乙队单独完成这项工程的天数．【分析】（1）分段函数，运用待定系数法解答即可；（2）根据（1）的结论解答即可；（3）根据（1）可得乙队的工作效率，从而计算出乙队单独完成这项工程要60天．【解答】解：（1）当x≤10时，设y＝kx，根据题意得，解得k＝，∴y＝；当x＞10时，设y＝k1x+b，根据题意得：，解得，∴y＝．（天）∴10＜x≤28，∴；（2）由（1）得，当y＝1时，，解得x＝28．答：这项工程全部完成需要28天；（3）（1﹣）÷（28﹣10）＝（天），（天），答：乙队单独完成这项工程需要60天．22．甲、乙两人分别安装同一种零件40个，其中乙在安装两小时后休息了2小时，后继续按原来进度工作，他们每人安装的零件总数y（个）与安装时间x（小时）的函数关系如图1所示，两人安装零件总数之差z（件）与时间x（小时）的函数关系如图2所示．（1）a＝ 4 ；b＝10 ．（2）求出甲工作2小时后的安装的零件数y与时间x的函数关系．（3）甲、乙两人在什么时间生产的零件总数相差8个？【分析】（1）根据题意和图象中的数据可以求得a、b的值；（2）根据函数图象中的数据可以求得甲工作2小时后的安装的零件数y与时间x的函数关系；（3）根据函数图象，利用分类讨论的方法可以求得甲、乙两人在什么时间生产的零件总数相差8个．【解答】解：（1）由图可得，a＝10﹣6＝4，b＝4+（40﹣10）÷（10÷2）＝4+30÷5＝4+6＝10，故答案为：4，10；（2）甲后来的速度为：＝6件/小时，甲做完40个需要的时间为：2+（40﹣4）÷6＝2+36÷6＝2+6＝8，设甲工作2小时后的安装的零件数y与时间x的函数关系是y＝kx+b，∵甲工作2小时后的安装的零件数y与时间x的函数图象过点（2，4），（8，40），∴，得，即甲工作2小时后的安装的零件数y与时间x的函数关系是y＝6x﹣8（2＜x≤8）；（3）设t小时时，甲、乙两人生产的零件总数相差8个，乙的速度为：10÷2＝5件/小时，当4＜t≤8时，6+（t﹣4）×（6﹣5）＝8，解得，t＝6，当8＜t＜10时，5（10﹣t）＝8，解得，t＝8.4，答：甲、乙两人在6小时或8.4小时时生产的零件总数相差8个．2020-2021学年度第一学期第一次月考八年级数学试题卷考试方式：闭卷考试时间：100 分钟满分：120 分一．选择题（共10小题，每题3分，共30分，请把正确答案写在答案卷上.）1.下列四个图案是我国几家银行的标志，其中是轴对称图形的有（）A．1个 B．2个 C．3个 D．4个2.下列各条件不能作出唯一直角三角形的是（）A．已知两直角边 B．已知两锐角C．已知一直角边和它们所对的锐角 D．已知斜边和一直角边3．下列语句中正确的有几个（）①关于一条直线对称的两个图形一定能重合；②两个能重合的图形一定关于某条直线对称；③两个轴对称图形的对应点一定在对称轴的两侧；④一个圆有无数条对称轴．A．1 B．2 C．3 D．44.如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的（）A．CB=CD B．BAC=∠DAC C．BCA=DCA D．∠B=∠D=9005.如图，请仔细观察用直尺和圆规作一个角等于已知角AOB ∠的示意图，请你根据所学的图形的全等这一章的知识，说明画出'''A O B AOB ∠=∠的依据是（）A.SASB.ASAC.AASD.SSS6.如图，将三角形纸片ABC 折叠，使点C 与点A 重合，折痕为DE . 若∠B ＝80°，∠BAE ＝26°，则∠EAD 的度数为（）A.36°B. 37°C.38°D.45°7.如图，将一张正方形纸片对折两次，然后在上面打3个洞，则纸片展开后是( )8.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H 分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )A. A,C 两点之间B. E,G 两点之间C. B,F 两点之间D. G,H 两点之间9.如图，在△ABC 中，AD 为∠BAC 的平分线，DE ⊥AB 于E ，DF ⊥AC 于F ，△ABC 的面积是28cm 2，AB =20cm ，AC =8cm ，则DE 的长是（）A ．4cmB ．3cmC ．2cmD ．1cm10.如图，在△ABC 中，∠A=∠B ，∠ACB=90°，点D 、E 在AB 上，将△ACD 、△B CE 分别沿CD 、CE 翻折，点A 、B 分别落在点A′、B′的位置，再将△A′CD 、△B′CE 分别沿A′C 、B′C 翻折，点D 与点E 恰好重合于点O ，则∠A′OB′的度数是（） A ．90°B ．120°C ．135°D ．150°二．填空题（共8小题，每题2分，共16分，请把结果直接填在答案卷上.）11.下列图形：①角；②直角三角形；③等边三角形；④线段；⑤等腰三角形；⑥平行四边形.其中一定是轴对称图形的有个.AC OB DA'C O'B'DBAE DC第3题B CDA(第4题图) (第5题图)(第6题图)（第8题图）（第9题图）（第10题图）12.小明从平面镜子中看到镜中电子钟示数的像如图所示，这时的时刻应是．13．如图，AC=BD ，要使△ABC ≌△DCB （SAS ），只要添加一个条件．14．如图，△ABC 的周长为32，且BD=DC ，AD ⊥BC 于D ，△ACD 的周长为24，那么AD 的长为． 15．如图，已知AB ∥CF ，E 为DF 的中点，若AB ＝8 cm ，BD ＝3 cm ，则CF ＝ cm ．16．如图，点D 在边BC 上，DE ⊥AB ，DF ⊥BC ，垂足分别为点E ，D ，BD ＝CF ，BE ＝CD ．若∠AFD ＝155°，则∠EDF ＝．17．如图，方格纸中△ABC 的3个顶点分别在小正方形的顶点（格点）上，这样的三角形叫格点三角形，图中与△ABC 全等的格点三角形共有个（不含△ABC ）．18．已知在△ABC 中，AB=5，BC=7，BM 是AC 边上的中线，则BM 的取值范围为．三．解答题（共8小题，共74分. 解答需写出必要的文字说明或演算步骤.）19．（本题满分12分）如图，在3×3的正方形网格中，有一个以格点为顶点的三角形.（1）请你在图①，图②，图③中，分别画出一个与该三角形成轴对称且以格点为顶点的三角形，并将所画三角形涂上阴影．（注：所画的三幅图不能重复）．（2）格纸中所有与该三角形成轴对称且以格点为顶点的三角形共有个．20．（本题满分8分）如图，在所给正方形网格图中完成下列各题：①画出格点△ABC （顶点均在格点上）关于直线DE 对称的△A 1B 1C 1；FEDCB A(第15题图) (第16题图)(第17题图)(第12题图)(第13题图) (第14题图)②在DE上画出点Q，使QA+QC最小．（用直尺画图，保留痕迹）21.（本题满分8分）已知△ABC，按下列要求作图：（尺规作图，保留痕迹不写作法。

八年级(上)数学第一次月考试卷(附答案)

（第6小题）（第3小题）CBA2020-2021学年度（上）八年级数学第一次月考试卷一、选择题（本大题共6小题，每小题3分，共18分，每小题只有一个正确选项） 1、下列各数是无理数的是（）A 、73 B 、4 C 、5 D 、••10.2 2、下列说法错误的是（）A 、1的平方根是1B 、-1的立方根是-1C 、2是2的算术平方根D 、0是0的平方根3、如图，在Rt △ABC 中，∠B=90°，以AC 为直径的圆恰好过点B ．若AB=8，BC=6，则阴影部分的面积是（） A 、24-100πB 、48-100πC 、24-25πD 、48-25π4、如图，一圆柱高8㎝，底面半径2㎝，一只蚂蚁从A 点爬到点B 处吃食，要爬行的最短路程（π取3）是（） A 、20㎝ B 、10㎝ C 、14㎝ D 、无法确定5、已知实数086=-+-y x y x 满足、，那么以y x 、的值为两边长作直角三角形，它的第三边长为（）A 、10B 、72C 、10或72D 、以上均不对 6、如图，已知△ABC 中，∠ABC=90°，AB=BC ，三角形的顶点在相互平行的三条直线l 1、l 2、l 3上，且相邻两平行线之间的距离均为1，则AC 的长是（）A 、5B 、6C 、3D 、10二、填空题（本大题共6小题，每小题3分，共18分） 7、6的相反数是 .8、81的平方根是 .9、在Rt △ABC 中，斜边AB ＝2，则AB 2＋BC 2＋CA 2＝ . 10、若n 20是整数，则正整数n 的最小值为 .11、如图，数轴上有三点A 、B 、C,其中点A 表示的数是2-，点B 表示的数是1，且AB=BC,则点C表示的数是 .12、锐角等腰三角形的腰长为10㎝，一边上的高为8㎝，则这个锐角等腰三角形的底边长是㎝.三、（本大题共5小题，每小题6分，共30分）13、(1)计算： 331327+-(2)如图，已知Rt ∆ABC,∠ACB=90︒,AC=15和BC=20，求斜边上的高CD 的长.14、计算： 22832--15、计算：()()()2323522-+--16、求等式 ()1612=-x 中x 的值.17、如下图，正方形网格中的每个小正方形边长都是1，任意连结这些小正方形的顶点，可得到一些线段.请按要求作三角形（要求三角形各顶点落在小正方形的顶点上）：（1）在图1中作ABC Rt ∆,使三边长都为有理数；（第4小题）BAADCB0 B C-2 1 3 42•••2-A（2）在图2中作ABC ∆,使得三边边长分别是5、10、17.四、（本大题共3小题，每小题8分，共24分）18、若12+x 的平方根是±5,52-+y x 的立方根是3，求22y x +的平方根.19、已知10的整数部分是a,小数部分是b ，求31a ()310+b 的值.20、两张同样大小的长方形纸片，每张分成7个大小相同的小长方形，且每个小长方形的宽均为a（如图），如图放置，重合的顶点记作A ，顶点C 在另一张纸的其中一条分隔线DE 上，若 262=CD ，求AB 的长是多少？五、（本大题共2小题，每小题9分，共18分）21、如图，在长方形ABCD 中，AD ＝8，CD ＝6，将长方形ABCD 沿CE 折叠后，使点D 恰好落在对角线AC 上的点F 处. （1）求EF 的长；（2）求梯形ABCE 的面积.22、观察下列一组式子的变形过程，然后回答问题：①()1212121212)12)(12()12(11212-=--=--=-+-⨯=+；②()()();2323232323)23)(23(23123122-=--=--=-+-⨯=+③()()()4545454545)45)(45(45145122-=--=--=-+-⨯=+.（1）561+= ；991001+= ；（2）请你用含n （n 为正整数）的关系式表示上述各式子的变形规律；（3）利用上面的结论，求下列式子的值.99100198991341231121++++++++++六、（本大题共1小题，共12分）23.已知：如图，在Rt △ABC 中，∠C=90°，AB=5cm ，AC=3cm ，动点P 从点B 出发沿射线BC 以1cm/s 的速度移动，设运动的时间为t 秒．（1）求BC 边的长；（2）当△ABP 为直角三角形时，求t 的值；（3）当△ABP 为等腰三角形时，求t 的值.图2DEa aa a a a a图12020-2021学年度（上）八年级数学第一次月考参考答案一．选择题1.C2.A3.C4.B5.C6.D 二．填空题7. 6- 8. 3± 9. 8 10. 5 11. 22+ 12. 12或 5413.（1） ………3分（2）解：,625201522222=+=+=∆BC AC AB ABC Rt 中，在25=∴AB CD CD AB BC AC SABC2521201521,2121⨯=⨯⨯⋅=⋅=∴∆即 )(12cm CD =∴ ………6分 14. 0………6分 15. 548-………6分16. 35-==x x 或 ………6分（写对1个得3分） 17.………3分………6分18. 解：由题意得32352,)5(12=+-±=+y x x4,12==∴y x………4分1044122222±=+±=+±∴y x ………8分19. 解：由题意得310,3-==b a………4分1910)310)(310(331)310(31=-=-+⨯=+∴b a………8分 20. 解：由题意得AD=6a,AC=7a26)6(7,22222=-=-∆a a CD AD AC ACD ）即（中，在2=∴a 6分 277==∴a AB ………8分21. 解：设DE=x ，则AE=8-x ，由折叠性质得，EF=DE=x ，CF=CD=6,则AE=8-x 在Rt ACD ∆中,1006822222=+=+=CD AD AC 10=∴AC 4610=-=∴AF 在RT AEF ∆,222)8(4x x -=+ 533==∴=∴AE EF x ，………6分396)85(21=⨯+=∴ABCE S 梯形 ………9分22. (1)99100;56--………2分（2）n n nn -+=++111………5分（3）99-10098-993-42-31-2+++++=解：原式1001-+= 9101-=+= ………9分23.（1）在Rt △ABC 中，BC 2=AB 2-AC 2=52-32=16，∴BC=4（cm ）；………3分（2）由题意知BP=tcm ，①如图①，当∠APB 为直角时，点P 与点C 重合，BP=BC=4cm ，即t=4s ； ②如图②，当∠BAP 为直角时，BP=tcm ，CP=（t-4）cm ，AC=3cm ，在Rt △ACP 、Rt △BAP 中，由勾股定理得AP 2=32+（t-4）2225-=t ，解得：t=425故当△ABP 为直角三角形时，t=4s 或t=s425………7分32图1B C A图2ABC（3）①如图③，当AB=BP时，t=5s；………8分②如图④，当AB=AP时，BP=2BC=8cm， t=8s；………9分③如图⑤，当BP=AP时，AP=BP=tcm，CP=(4-t)cm，AC=3cm，在Rt△ACP中，AP2=AC2+CP2，即t2=32+（4-t）2，25解得：t=825………12分综上所述：当△ABP为等腰三角形时，t=5s或t=8s或t=s8。

2020—2021年人教版八年级数学上册第一次月考测试卷及答案【完美版】

2020—2021年人教版八年级数学上册第一次月考测试卷及答案【完美版】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．若二次根式51x-有意义，则x的取值范围是（）A．x＞15B．x≥15C．x≤15D．x≤52．在平面直角坐标系中，点P(－2，2x＋1)所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限3．成人每天维生素D的摄入量约为0.0000046克．数据“0.0000046”用科学记数法表示为（）A．74610-⨯B．74.610-⨯C．64.610-⨯D．50.4610-⨯4．在平面直角坐标系中，点A（﹣3，2），B（3，5），C（x，y），若AC∥x 轴，则线段BC的最小值及此时点C的坐标分别为（）A．6，（﹣3，5） B．10，（3，﹣5）C．1，（3，4） D．3，（3，2）5．下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．6．如图，在周长为12的菱形ABCD中，AE=1，AF=2，若P为对角线BD上一动点，则EP+FP的最小值为（）A．1 B．2 C．3 D．47．如图，快艇从P处向正北航行到A处时，向左转50°航行到B处，再向右转80°继续航行，此时的航行方向为（）A．北偏东30°B．北偏东80°C．北偏西30°D．北偏西50°8．如图，等边△ABC的边长为4，AD是边BC上的中线，F是边AD上的动点，E 是边AC上一点，若AE=2，则EF+CF取得最小值时，∠ECF的度数为（）A．15°B．22.5°C．30°D．45°9．将长方形ABCD纸片沿AE折叠，得到如图所示的图形，已知∠CED'=70°，则∠EAB的大小是（）A．60°B．50°C．75°D．55°10．尺规作图作AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA、OB于C、D，再分别以点C、D为圆心，以大于12CD长为半径画弧，两弧交于点P，作射线OP，由作法得OCP ODP≌的根据是（）A ．SASB ．ASAC ．AASD ．SSS二、填空题（本大题共6小题，每小题3分，共18分）1．若22(3)16x m x +-+是关于x 的完全平方式，则m =__________．2．若式子x 1x+有意义，则x 的取值范围是__________． 3．在△ABC 中，AB=15，AC=13，高AD=12，则ABC ∆的周长为____________．4．如图，正方形ABCD 中，点E 、F 分别是BC 、AB 边上的点，且AE ⊥DF ，垂足为点O ，△AOD 的面积为7，则图中阴影部分的面积为________．5．如图，直线AB ，CD 被BC 所截，若AB ∥CD ，∠1=45°，∠2=35°，则∠3= _________度。

2020—2021年人教版八年级数学上册第一次月考测试卷(完整版)

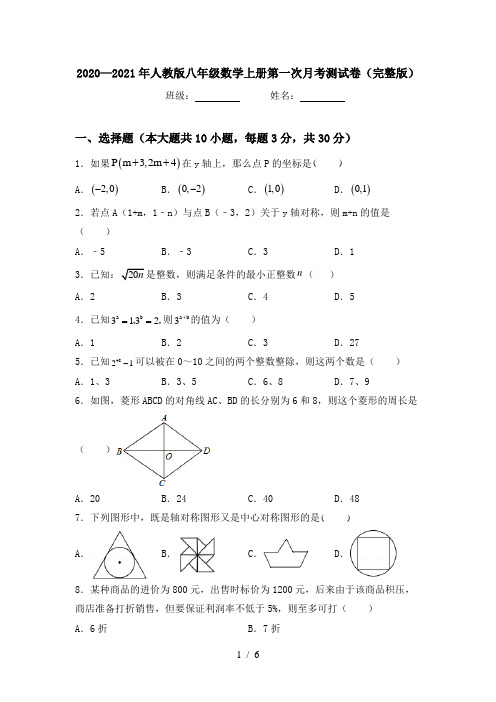
2020—2021年人教版八年级数学上册第一次月考测试卷（完整版）班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．如果()P m 3,2m 4++在y 轴上，那么点P 的坐标是( )A ．()2,0-B ．()0,2-C ．()1,0D ．()0,12．若点A （1+m ，1﹣n ）与点B （﹣3，2）关于y 轴对称，则m+n 的值是（）A ．﹣5B ．﹣3C ．3D ．13．已知：20n 是整数，则满足条件的最小正整数n （）A ．2B ．3C ．4D ．54．已知a b 3132==，，则a b 3+的值为（） A ．1 B ．2 C ．3 D ．275．已知4821-可以被在0～10之间的两个整数整除，则这两个数是（）A ．1、3B ．3、5C ．6、8D ．7、96．如图，菱形ABCD 的对角线AC 、BD 的长分别为6和8，则这个菱形的周长是（）A ．20B ．24C ．40D ．487．下列图形中，既是轴对称图形又是中心对称图形的是( )A ．B ．C ．D ．8．某种商品的进价为800元，出售时标价为1200元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于5%，则至多可打（）A ．6折B ．7折C ．8折D ．9折9．如图，∠B 的同位角可以是( )A ．∠1B ．∠2C ．∠3D ．∠410．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a ，较短直角边长为b ．若ab=8，大正方形的面积为25，则小正方形的边长为（）A ．9B ．6C ．4D ．3二、填空题（本大题共6小题，每小题3分，共18分）1．因式分解：x 3﹣4x=________．2．若二次根式x 1-有意义，则x 的取值范围是 ▲ ．3．计算：()()201820195-252+的结果是________.4．如图是一个三级台阶，它的每一级的长、宽和高分别为20 dm,3 dm,2 dm ，A 和B 是这个台阶两个相对的端点，A 点有一只蚂蚁，想到B 点去吃可口的食物，则蚂蚁沿着台阶面爬到B 点的最短路程是__________dm.5．如图，∠1+∠2+∠3+∠4=______度.6．如图，在△ABC 和△DEF 中，点B 、F 、C 、E 在同一直线上，BF = CE ，AC ∥DF ，请添加一个条件，使△ABC ≌△DEF ，这个添加的条件可以是________．（只需写一个，不添加辅助线）三、解答题（本大题共6小题，共72分）1．解方程23111x x x -=--．2．先化简，再求值：2443(1)11m m m m m -+÷----，其中22m =.3．已知11881,2y x x =--22x y x y y x y x+++-的值.4．如图，在Rt △ABC 中，∠ACB=90°，∠A=40°，△ABC 的外角∠CBD 的平分线BE 交AC 的延长线于点E ．（1）求∠CBE 的度数；（2）过点D 作DF ∥BE ，交AC 的延长线于点F ，求∠F 的度数．5．如图，在△OBC中，边BC的垂直平分线交∠BOC的平分线于点D，连接DB，DC，过点D作DF⊥OC于点F.(1)若∠BOC＝60°，求∠BDC的度数；(2)若∠BOC＝，则∠BDC＝；（直接写出结果）(3)直接写出OB，OC，OF之间的数量关系.6．某地2015年为做好“精准扶贫”，投入资金1280万元用于异地安置，并规划投入资金逐年增加，2017年在2015年的基础上增加投入资金1600万元．（1）从2015年到2017年，该地投入异地安置资金的年平均增长率为多少？（2）在2017年异地安置的具体实施中，该地计划投入资金不低于500万元用于优先搬迁租房奖励，规定前1000户（含第1000户）每户每天奖励8元，1000户以后每户每天补助5元，按租房400天计算，试求今年该地至少有多少户享受到优先搬迁租房奖励？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、B2、D3、D4、B5、D6、A7、D8、B9、D10、D二、填空题（本大题共6小题，每小题3分，共18分）1、x （x+2）（x ﹣2）2、x 1≥．324、255、2806、AC=DF （答案不唯一）三、解答题（本大题共6小题，共72分）1、2x =2、22mm -+ 1． 3、14、(1) 65°；(2) 25°．5、（1）120°；（2）180°－α；（3）OB ＋OC ＝2OF6、（1）50%；（2）今年该地至少有1900户享受到优先搬迁租房奖励．。

2020—2021年人教版八年级数学上册第一次月考考试【及参考答案】

2020—2021年人教版八年级数学上册第一次月考考试【及参考答案】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．﹣3的绝对值是（）A ．﹣3B ．3C ．-13D ．132．在平面直角坐标系中，点(3,2)关于x 轴对称的点的坐标为（）A ．(3,2)-B ．(2,3)-C ．(2,3)-D ．(3,2)-3．下列长度的三条线段，能组成三角形的是（）A ．4cm ，5cm ，9cmB ．8cm ，8cm ，15cmC ．5cm ，5cm ，10cmD ．6cm ，7cm ，14cm4．在平面直角坐标系中，点A （﹣3，2），B （3，5），C （x ，y ），若AC ∥x 轴，则线段BC 的最小值及此时点C 的坐标分别为（）A ．6，（﹣3，5）B ．10，（3，﹣5）C ．1，（3，4）D ．3，（3，2）5．一组数据：1、2、2、3，若添加一个数据2，则发生变化的统计量是（）A ．平均数B ．中位数C ．众数D ．方差6．如图，圆柱形玻璃杯高为12cm 、底面周长为18cm ，在杯内离杯底4cm 的点C 处有一些蜂蜜，此时一只蚂蚁正好也在杯外壁，离杯上沿4cm 与蜂蜜相对的点A 处，那么蚂蚁要吃到甜甜的蜂蜜所爬行的最短距离是（）A ．13B ．14C ．15D ．167．已知=2{=1x y 是二元一次方程组+=8{ =1mx ny nx my -的解，则2m n -的算术平方根为（）A ．±2B ．2C ．2D ．48．已知a ＝2018x ＋2018，b ＝2018x ＋2019，c ＝2018x ＋2020，则a 2＋b 2＋c 2－ab －ac －bc 的值是（）A ．0B ．1C ．2D ．39．如图，//DE BC ，BE 平分ABC ∠，若170∠=，则CBE ∠的度数为（）A ．20B ．35C ．55D ．7010．如图所示，圆柱的高AB=3，底面直径BC=3，现在有一只蚂蚁想要从A 处沿圆柱表面爬到对角C 处捕食，则它爬行的最短距离是（）A ．31π+B ．32C 234π+ D ．231π+二、填空题（本大题共6小题，每小题3分，共18分）1123=________．2．若不等式组130x a bx ->⎧⎨+≥⎩的解集是﹣1＜x ≤1，则a ＝_____，b ＝_____． 3．若函数y ＝(a －1)x 2－4x ＋2a 的图象与x 轴有且只有一个交点，则a 的值为________．4．如图，将三个同样的正方形的一个顶点重合放置，那么1∠的度数为__________．5．如图，已知△ABC 是等边三角形，点B 、C 、D 、E 在同一直线上，且CG=CD ，DF=DE ，则∠E=________度．6．如图，已知点E 在正方形ABCD 的边AB 上，以BE 为边向正方形ABCD 外部作正方形BEFG ，连接DF ，M 、N 分别是DC 、DF 的中点，连接MN.若AB=7，BE=5，则MN=________.三、解答题（本大题共6小题，共72分）1．解方程组：4311213x y x y -=⎧⎨+=⎩2．先化简，再求值：()22111a a a ⎛⎫ ⎪⎝⎭-+÷++，其中21a =-．3．解不等式组513(1)131722x x x x +>-⎧⎪⎨-≤-⎪⎩，并把它的解集在数轴上表示出来．4．在Rt△ABC中，∠BAC=90°,D是BC的中点，E是AD的中点．过点A作AF ∥BC交BE的延长线于点F（1）求证：△AEF≌△DEB；（2）证明四边形ADCF是菱形；（3）若AC=4，AB=5，求菱形ADCF 的面积．5．如图，在平面直角坐标系中，等腰直角三角形ABC的顶点A在x轴上，AB＝AC，∠BAC＝90°，且A（2，0）、B（3，3），BC交y轴于M，（1）求点C的坐标；（2）连接AM，求△AMB的面积；（3）在x轴上有一动点P，当PB+PM的值最小时，求此时P的坐标．6．一商店销售某种商品，平均每天可售出20件，每件盈利40元.为了扩大销售、增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.（1）若降价3元，则平均每天销售数量为________件；（2）当每件商品降价多少元时，该商店每天销售利润为1200元？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、B2、D3、B4、D5、D6、C7、C8、D9、B10、C二、填空题（本大题共6小题，每小题3分，共18分） 12、-2 -33、－1或2或14、20°.5、：略6、132三、解答题（本大题共6小题，共72分）1、53x y =⎧⎨=⎩．2、11a +，23、24x -<≤，数轴见解析.4、（1）证明略；（2）证明略；（3）10．5、（1）C 的坐标是（﹣1，1）；（2）154；（3）点P 的坐标为（1，0）．6、（1）26；（2）每件商品降价10元时，该商店每天销售利润为1200元.。