最终沉降速度对于球形颗粒
化工原理第三章习题与答案

化⼯原理第三章习题与答案第三章机械分离⼀、名词解释(每题2分)1. ⾮均相混合物物系组成不同,分布不均匀,组分之间有相界⾯2. 斯托克斯式r u d u ts r 2218)(?-=µρρ3. 球形度s ?⾮球形粒⼦体积相同的球形颗粒的⾯积与球形颗粒总⾯积的⽐值4. 离⼼分离因数离⼼加速度与重⼒加速度的⽐值5. 临界直径dc离⼼分离器分离颗粒最⼩直径6.过滤利⽤多孔性介质使悬浮液中液固得到分离的操作7. 过滤速率单位时间所产⽣的滤液量8. 过滤周期间歇过滤中过滤、洗涤、拆装、清理完成⼀次过滤所⽤时间9. 过滤机⽣产能⼒过滤机单位时间产⽣滤液体积10. 浸没度转筒过滤机浸没⾓度与圆周⾓⽐值⼆、单选择题(每题2分)1、⾃由沉降的意思是_______。
A颗粒在沉降过程中受到的流体阻⼒可忽略不计B颗粒开始的降落速度为零,没有附加⼀个初始速度C颗粒在降落的⽅向上只受重⼒作⽤,没有离⼼⼒等的作⽤D颗粒间不发⽣碰撞或接触的情况下的沉降过程D 2、颗粒的沉降速度不是指_______。
A等速运动段的颗粒降落的速度B加速运动段任⼀时刻颗粒的降落速度C加速运动段结束时颗粒的降落速度D净重⼒(重⼒减去浮⼒)与流体阻⼒平衡时颗粒的降落速度B3、对于恒压过滤_______。
A 滤液体积增⼤⼀倍则过滤时间增⼤为原来的2倍B 滤液体积增⼤⼀倍则过滤时间增⼤⾄原来的2倍C 滤液体积增⼤⼀倍则过滤时间增⼤⾄原来的4倍D 当介质阻⼒不计时,滤液体积增⼤⼀倍,则过滤时间增⼤⾄原来的4倍D4、恒压过滤时,如介质阻⼒不计,滤饼不可压缩,过滤压差增⼤⼀倍时同⼀过滤时刻所得滤液量___ 。
A增⼤⾄原来的2倍B增⼤⾄原来的4倍C增⼤⾄原来的2倍D增⼤⾄原来的1.5倍C5、以下过滤机是连续式过滤机_______。
A箱式叶滤机B真空叶滤机C回转真空过滤机D板框压滤机 C6、过滤推动⼒⼀般是指______。
A过滤介质两边的压差B过滤介质与滤饼构成的过滤层两边的压差C滤饼两⾯的压差D液体进出过滤机的压差B7、回转真空过滤机中是以下部件使过滤室在不同部位时,能⾃动地进⾏相应的不同操作:______。
化工原理-第五章-颗粒的沉降和流态化

化工原理-第五章-颗粒的沉降和流态化一、选择题1、 一密度为7800 kg/m 3 的小钢球在相对密度为1.2的某液体中的自由沉降速度为在20℃水中沉降速度的1/4000,则此溶液的粘度为 D (设沉降区为层流)。
⋅A 4000 mPa·s ; ⋅B 40 mPa·s ; ⋅C 33.82 Pa·s ; ⋅D 3382 mPa·s2、含尘气体在降尘室内按斯托克斯定律进行沉降。
理论上能完全除去30μm 的粒子,现气体处理量增大1倍,则该降尘室理论上能完全除去的最小粒径为D 。
A .m μ302⨯;B 。
m μ32/1⨯;C 。
m μ30;D 。
m μ302⨯3、降尘室的生产能力取决于 B 。
A .沉降面积和降尘室高度;B .沉降面积和能100%除去的最小颗粒的沉降速度;C .降尘室长度和能100%除去的最小颗粒的沉降速度;D .降尘室的宽度和高度。
4、降尘室的特点是 。
DA . 结构简单,流体阻力小,分离效率高,但体积庞大;B . 结构简单,分离效率高,但流体阻力大,体积庞大;C . 结构简单,分离效率高,体积小,但流体阻力大;D . 结构简单,流体阻力小,但体积庞大,分离效率低5、在降尘室中,尘粒的沉降速度与下列因素 C 无关。
A .颗粒的几何尺寸B .颗粒与流体的密度C .流体的水平流速;D .颗粒的形状6、在讨论旋风分离器分离性能时,临界粒径这一术语是指 C 。
A. 旋风分离器效率最高时的旋风分离器的直径;B. 旋风分离器允许的最小直径;C. 旋风分离器能够全部分离出来的最小颗粒的直径;D. 能保持滞流流型时的最大颗粒直径7、旋风分离器的总的分离效率是指 D 。
A. 颗粒群中具有平均直径的粒子的分离效率;B. 颗粒群中最小粒子的分离效率;C. 不同粒级(直径范围)粒子分离效率之和;D. 全部颗粒中被分离下来的部分所占的质量分率8、对标准旋风分离器系列,下述说法哪一个是正确的 C 。
《化工原理》3-4章期末考试复习题

《化工原理》3-4章期末考试复习题《化工原理》3-4章期末考试复习题一、填空题2-1 一球形石英颗粒,分别在空气和水中按斯托克斯定律沉降,若系统温度升高,则其在水中的沉降速度将,在空气中的沉降速度将。
答案:下降,增大分析:由斯托克斯定律μρρ18)(2gd u s t -=对空气系统,s ρ 》ρ,故 uu u u t t '≈'对水系统,水的密度随温度的变化可忽略,故同样有uu u u t t '≈'可见无论是气体还是液体,温度的改变主要是通过粘度变化来影响沉降速度。
气体粘度随温度升高而增加,故沉降速度下降;液体粘度随温度升高而减小,故沉降速度增大。
但要注意此结论是通过斯托克斯定律得出,其他情况还需要具体分析。
2-2若降尘室的高度增加,则沉降时间,气流速度,生产能力。
答案:增加;下降;不变分析:因沉降距离增加,故沉降时间将增加。
降尘室高度的增加使气体在降尘室内的流道截面增大,故气流速度下降。
生产能力的计算公式为: t Au Vs =可见,降尘室的生产能力只决定于沉降面积和沉降速度而与降尘室的高度无关。
2-3 选择旋风分离器型式及决定其主要尺寸的根据是;;。
答案:气体处理量,分离效率,允许压降2-4 通常,非均相物系的离心沉降是在旋风分离器中进行,悬浮物系一般可在旋液分离器或沉降离心机中进行。
答案:气固;液固2-5 沉降操作是指在某种中利用分散相和连续相之间的差异,使之发生相对运动而实现分离的操作过程。
沉降过程有沉降和沉降两种方式。
答案:力场;密度;重力;离心2-6 阶段中颗粒相对于流体的运动速度称为沉降速度,由于这个速度是阶段终了时颗粒相对于流体的速度,故又称为“终端速度”。
答案:等速;加速2-7影响沉降速度的主要因素有① ;② ;③ ;答案:颗粒的体积浓度;器壁效应;颗粒形状2-8 降尘室通常只适合用于分离粒度大于的粗颗粒,一般作为预除尘使用。
答案:50μm 2-9 旋风分离器的总效率是指,粒级效率是指。
化工原理试题库下册

第3章非均相物系分离一、选择题恒压过滤且介质阻力忽略不计时,如粘度降低20%,则在同一时刻滤液增加()。
A、11.8%;B、9.54%; C、20%; D、44%板框式压滤机由板与滤框构成,板又分为过滤板和洗涤板,为了便于区别,在板与框的边上设有小钮标志,过滤板以一钮为记号,洗涤板以三钮为记号,而滤框以二钮为记号,组装板框压滤机时,正确的钮数排列是().A、1—2—3—2—1B、1—3—2—2—1C、1—2—2—3—1D、1—3—2—1—2与沉降相比,过滤操作使悬浮液的分离更加()。
A、迅速、彻底B、缓慢、彻底C、迅速、不彻底D、缓慢、不彻底多层隔板降尘室的生产能力跟下列哪个因素无关()。
A、高度B、宽度C、长度D、沉降速度降尘室的生产能力()。
A、与沉降面积A和沉降速度ut有关B、与沉降面积A、沉降速度ut和沉降室高度H有关C、只与沉降面积A有关D、只与沉降速度ut有关现采用一降尘室处理含尘气体,颗粒沉降处于滞流区,当其它条件都相同时,比较降尘室处理200℃与20℃的含尘气体的生产能力V的大小()。
A、V200℃>V20℃B、V200℃=V20℃C、V200℃<V20℃D、无法判断有效的过滤操作是()。
A、刚开始过滤时B、过滤介质上形成滤饼层后C、过滤介质上形成比较厚的滤渣层D、加了助滤剂后当固体粒子沉降时,在层流情况下,Re=1,其ζ为()。
A、64/ReB、24/ReC、0.44D、1含尘气体通过降尘室的时间是t,最小固体颗粒的沉降时间是t 0,为使固体颗粒都能沉降下来,必须():A、t<t0B、t=t0C、t>t0颗粒作自由沉降时,Ret在()区时,颗粒的形状系数对沉降速度的影响最大。
A、斯托科斯定律区B、艾伦定律区C、牛顿定律区D、不确定(天大99)恒压过滤,单位面积累积滤液量q与时间τ的关系为()。
旋风分离器的分割粒径d50是()A、临界粒径dc的2倍B、临界粒径dc的2倍C、粒级效率ηpi=0.5的颗粒直径对不可压缩滤饼,当过滤两侧的压强差增大时,单位厚度床层的流到阻力将()。
“利用流态化原理解释颗粒终端速度(带出速度),为什么等于自由沉降速度?”论文

流态化基本原理【摘要】流态化技术是利用流动流体的作用,将固体颗粒群悬浮起来,从而使固体颗粒具有某些流体表观特征,利用这种流体与固体间的接触方式实现生产过程的操作。
自由沉降速度,又称终端速度。
指任一颗粒的沉降不因流体中存在其他颗粒而受到干扰时,在等速阶段里颗粒相对于流体的运动速度。
即加速阶段终了时颗粒相对于流体的速度。
关键词:流态化;固体;颗粒;沉降1流态化与自由沉降流态化一般指固体流态化,又称假液化,简称流化,它是利用流动流体的作用,将固体颗粒群悬浮起来,从而使固体颗粒具有某些流体表观特征,利用这种流体与固体间的接触方式实现生产过程的操作,称为流态化技术,属于粉体工程的研究范畴。
流态化技术是一种强化流体(气体或液体)与固体颗粒间相互作用的操作,如在直立的容器内间歇地或连续地加入颗粒状固体物料,控制流体以一定速度由底部通入,使其压力降等于或略大于单位截面上固体颗粒的重量,固体颗粒即呈悬浮状运动而不致被流体带走。
流态化技术在强化某些单元操作和反应过程以及开发新工艺方面,起着重要作用,广泛应用于化学、石油、冶金、原子能等工业的焙烧、干燥、吸附、气化、催化反应和催化裂化等许多过程中。
单个颗粒在流体中的沉降过程称为自由沉降。
若颗粒数量较多,相互间距离较近,则颗粒沉降时相互间会干扰,称为干扰沉降。
颗粒刚开始沉降时,速度u 为零,则曳力也为零,颗粒在净质量力(质量力与浮力之差)作用下沿质量力方向作加速运动,随着运动速度u的增加,曳力开始由零不断增大,直至与净质量力相等为止,这时,颗粒加速度减为零,速度u达到一恒定值,也是最大值,此后,颗粒等速下降,这一最终的运动速度称为沉降速度。
由此可见,单个颗粒在流体中的沉降过程分为两个阶段:加速段和等速段,对于小颗粒,加速段极短,通常可以忽略,于是,整个沉降过程都可认为是匀速沉降。
2流态化现象将一批固体颗粒堆放在多孔的分布板上形成床层,使流体自下而上通过床层。
由于流体的流动及其与颗粒表面的摩擦,造成流体通过床层的压力降。
化工原理:(含答案)第三章 非均相物系的分离

第三章 非均相物系的分离一、填空题:1.⑴一球形石英颗粒,在空气中按斯托克斯定律沉降,若空气温度由20°C 升至50°C ,则其沉降速度将 。
⑵降尘室的生产能力只与降尘室的 和 有关,而与 无关。
解⑴下降 ⑵长度 宽度 高度2.①在除去某粒径的颗粒时,若降尘室的高度增加一倍,则沉降时间 ,气流速度 ,生产能力 。
②在滞流(层流)区,颗粒的沉降速度与颗粒直径的 次方成正比;在湍流区,颗粒的沉降速度与颗粒直径的 次方成正比。
解①增加一倍 , 减少一倍 , 不变 ②2 , 1/2沉降操作是指在某种 中利用分散相和连续相之间的 差异,使之发生相对运动而实现分离的操作过程。
沉降过程有 沉降和 沉降两种方式。
答案:力场;密度;重力;离心3.已知q 为单位过滤面积所得滤液体积V/S ,e e e S V q V /,为为过滤介质的当量滤液体积(滤液体积为e V 时所形成的滤饼层的阻力等于过滤介质的阻力),在恒定过滤时,测得2003740/+=∆∆q q τ,过滤常数K = ,e q = 。
解0.000535 , 0.05354.⑴间歇过滤机的生产能力可写为Q =V/∑τ,此外V 为 ,∑τ表示一个操作循环所需的 ,∑τ等于一个操作循环中 , 和 三项之和。
一个操作循环中得到的滤液体积 ,总时间 ,过滤时间τ ,洗涤时间τw , 辅助时间τD⑵.一个过滤操作周期中,“过滤时间越长,生产能力越大”的看法是 ,“过滤时间越短,生产能力越大”的看法是 。
过滤时间有一个 值,此时过滤机生产能力为 。
不正确的 ,不正确的 , 最适宜 , 最大⑶.过滤机操作循环中,如辅助时间τ越长则最宜的过滤时间将 。
⑶ 越长(4). 实现过滤操作的外力可以是 、 或 。
答案:重力;压强差;惯性离心力5.⑴在过滤的大部分时间中, 起到了主要过滤介质的作用。
⑵最常见的间歇式过滤机有 和 连续式过滤机有 。
⑶在一套板框过滤机中,板有 种构造,框有 种构造。
一沉降速度1球形颗粒的自由沉降2阻力系数3影响沉

s g 1.2053000 1.205 9.81 6 95 10 3 K d3 2 5 2 1.81 10
4.52
2.61<K<69.1,沉降在过渡区。用艾伦公式计算沉降速度。
ut
1.6 1 1 . 4 0.154 g d 1.4
第三章
非均相物系分离
一、沉降速度
1、球形颗粒的自由沉降 2、阻力系数 3、影响沉降速度的因素 4、沉降速度的计算 5、分级沉降
第一节 重力沉降
二、降尘室
1、降尘室的结构 2、降尘室的生产能力
物系内部各处物料性质均匀而且不 均相混合物 存在相界面的混合物。 混合物 例如:互溶溶液及混合气体 物系内部有隔开两相的界面存在且 非均相混合物 界面两侧的物料性质截然不同的混 合物。 固体颗粒和气体构成的含尘气体 例如 固体颗粒和液体构成的悬浮液 不互溶液体构成的乳浊液 液体颗粒和气体构成的含雾气体
φs=0.806,查图3-3的,Ret=60,则:
Re t 60 1.005 103 ut de 998.2 8.685 104
0.0696m / s
2)纯方铅矿的尺寸范围 所得到的纯方铅矿粒尺寸最小的沉降速度应等于0.0696m/s
用摩擦数群法计算该粒子的当量直径。
Re t1
4 ( s1 ) g 3 2ut3
4 1.005 10 3 (7500 998.2) 9.81 0.2544 2 3 3 998.2 (0.0696)
φs=0.806,查图3-3的,Ret=22,则:
Re t 22 1.005 10 3 4 de 3 . 182 10 m ut 998.2 0.0696
过滤习题

一、单选题1.在滞流区颗粒的沉降速度正比于()。
D(A)(ρs-ρ)的1/2次方(B)μ的零次方(C)粒子直径的0.5次方(D)粒子直径的平方2.自由沉降的意思是()。
D(A)颗粒在沉降过程中受到的流体阻力可忽略不计(B)颗粒开始的降落速度为零,没有附加一个初始速度(C)颗粒在降落的方向上只受重力作用,没有离心力等的作用(D)颗粒间不发生碰撞或接触的情况下的沉降过程3.颗粒的沉降速度不是指()。
B(A)等速运动段的颗粒降落的速度(B)加速运动段任一时刻颗粒的降落速度(C)加速运动段结束时颗粒的降落速度(D)净重力(重力减去浮力)与流体阻力平衡时颗粒的降落速度4.对于恒压过滤()。
D(A)滤液体积增大一倍则过滤时间增大为原来的倍(B)滤液体积增大一倍则过滤时间增大至原来的2倍(C)滤液体积增大一倍则过滤时间增大至原来的4倍(D)当介质阻力不计时,滤液体积增大一倍,则过滤时间增大至原来的倍5.回转真空过滤机洗涤速率与最终过滤速率之比为()。
A(A) l (B)1/2 (C) 1/4 (D)1/36.以下说法是正确的()。
B(A)过滤速率与S(过滤面积)成正比(B)过滤速率与S2成正比(C)过滤速率与滤液体积成正比(D)过滤速率与滤布阻力成反比7.叶滤机洗涤速率与最终过滤速率的比值为()。
D(A) 1/2 (B)1/4 (C) 1/3 (D) l8.过滤介质阻力忽略不计,滤饼不可压缩进行恒速过滤,如滤液量增大一倍,则()。
C (A)操作压差增大至原来的倍(B)操作压差增大至原来的4倍(C)操作压差增大至原来的2倍(D)操作压差保持不变9.恒压过滤,如介质阻力不计,过滤压差增大一倍时,同一过滤时刻所得滤液量()。
C (A)增大至原来的2倍(B)增大至原来的4倍(C)增大至原来的倍(D)增大至原来的1.5倍10.以下过滤机是连续式过滤机()。
C(A)箱式叶滤机(B)真空叶滤机(C)回转真空过滤机(D)板框压滤机11.过滤推动力一般是指()。
化工原理简答题1

化⼯原理简答题1V 沉降1.流化床的压降与哪些因素有关?g )(A m p pρρρ-=?? 可知,流化床的压降等于单位界⾯床内固体的表观重量(即重量浮⼒),它与⽓速⽆关⽽始终保持定值。
2.因某种原因使进⼊降尘室的含尘⽓体温度升⾼,若⽓体质量及含尘情况不变,降尘室出⼝⽓体的含尘量将有何变化?原因何在?处于斯托克斯区时,含尘量升⾼;处于⽜顿定律区时,含尘量降低处于斯托克斯区时,温度改变主要通过粘度的变化⽽影响沉降速度。
因为⽓体粘度随温度升⾼⽽增加,所以温度升⾼时沉降速度减⼩;处于⽜顿定律区时,沉降速度与粘度⽆关,与ρ有⼀定关系,温度升⾼,⽓体ρ降低,沉降速度增⼤。
3.简述旋风分离器性能指标中分割直径d p c 的概念通常将经过旋风分离器后能被除下50%的颗粒直径称为分割直径d p c ,某些⾼效旋风分离器的分割直径可⼩⾄3~10m µ4.什么是颗粒的⾃由沉降速度?当⼀个⼩颗粒在静⽌⽓流中降落时,颗粒受到重⼒、浮⼒和阻⼒的作⽤。
如果重⼒⼤于浮⼒,颗粒就受到⼀个向下的合⼒(它等于重⼒与浮⼒之差)的作⽤⽽加速降落。
随着降落速度的增加,颗粒与空⽓的摩擦阻⼒相应增⼤,当阻⼒增⼤到等于重⼒与浮⼒之差时,颗粒所受的合⼒为零,因⽽加速度为零,此后颗粒即以加速度为零时的瞬时速度等速降落,这时颗粒的降落速度称为⾃由沉降速度(U t ) 5.实际流化现象有哪两种?通常,各⾃发⽣于什么系统?散式流化,发⽣于液-固系统;聚式流化,发⽣于⽓-固系统 6.何谓流化床层的内⽣不稳定性?如何抑制(提⾼流化质量的常⽤措施)?空⽳的恶性循环增加分布板阻⼒,加内部构件,⽤⼩直径宽分布颗粒,细颗粒⾼⽓速操作 7.对于⾮球形颗粒,当沉降处于斯托克斯定律区时,试写出颗粒的等沉降速度当量直径d e 的计算式 g)(18u de p t ρρµ-= 8.在考虑流体通过固定床流动的压降时,颗粒群的平均直径是按什么原则定义的?以⽐表⾯积相等作为准则流动阻⼒主要由颗粒层内固体表⾯积的⼤⼩决定,⽽颗粒的形状并不重要9.⽓体中含有1~2微⽶直径的固体颗粒,应选⽤哪⼀种⽓固分离⽅法?10.曳⼒系数是如何定义的?它与哪些因素有关?)2/u A /(F 2p D ρζ=与R e p =µρ/u d p 、ψ有关11.斯托克斯定律区的沉降速度与各物理量的关系如何?应⽤的前提是什么?颗粒的加速段在什么条件下可忽略不计?)18/(g )(d u p 2t µρρ-=R e <2颗粒p d 很⼩,t u 很⼩12.重⼒降尘室的⽓体处理量与哪些因素有关?降尘室的⾼度是否影响⽓体处理量?沉降室底⾯积和沉降速度不影响。
大气污染课后答案 6章

第六章 除尘装置66.1 在298K 的空气中NaOH 飞沫用重力沉降室收集。
沉降至大小为宽914cm ,高457cm ,长1219cm 。
空气的体积流速为1.2m 3/s 。
计算能被100%捕集的最小雾滴直径。
假设雾滴的比重为1.21。
解:计算气流水平速度s m A Q v /1087.257.414.92.120-⨯=⨯==。
设粒子处于Stokes 区域,取s Pa ⋅⨯=-51082.1μ。
按《大气污染控制工程》P162(6-4)m m gL H v d p μρμ2.17102.1719.1281.91021.157.41087.21082.1181863250min=⨯=⨯⨯⨯⨯⨯⨯⨯⨯==--- 即为能被100%捕集的最小雾滴直径。
6.2 直径为1.09m μ的单分散相气溶胶通过一重力沉降室,该沉降室宽20cm ,长50cm ,共18层,层间距0.124cm ,气体流速是8.61L/min ,并观测到其操作效率为64.9%。
问需要设置多少层可能得到80%的操作效率。
解:按层流考虑,根据《大气污染控制工程》P163(6-5)2.229.64801812122121=⨯==⇒=ηηηηn n n n ,因此需要设置23层。
6.3 有一沉降室长7.0m ,高12m ,气速30cm/s ,空气温度300K ,尘粒密度2.5g/cm 3,空气粘度0.067kg/(kg.h),求该沉降室能100%捕集的最小粒径。
解:s Pa h m kg ⋅⨯==-51086.1)./(067.0μm m m gL H v d p μμρμ10084104.8781.9105.2123.01086.118185350min<=⨯=⨯⨯⨯⨯⨯⨯⨯==--,符合层流区假设。
6.4 气溶胶含有粒径为0.63和0.83m μ的粒子(质量分数相等),以3.61L/min 的流量通过多层沉降室。
给出下列数据,运用斯托克斯定律和坎宁汉校正系数计算沉降效率。
沉降最终速度计算公式

沉降最终速度计算公式
沉降的最终速度(也称为终端速度)是颗粒在流体中沉降时的最大速度。
这个速度取决于颗粒的大小、形状、密度,以及流体的粘度、密度和重力加速度。
当颗粒接近最终速度时,阻力与重力相平衡,此时颗粒做匀速直线运动。
计算终端速度的公式有多种,以下是两个常见的公式:
1. 斯托克斯公式(Stokes' Law):适用于球形颗粒在粘性流体中的低速沉降。
公式如下:
(v_t = \frac{2\sqrt{g\Delta\rho}}{9\eta})
其中:
(v_t) 是终端速度(m/s)
(g) 是重力加速度(m/s²)
(\Delta\rho) 是颗粒与流体的密度差(kg/m³)
(\eta) 是流体的粘度(Pa·s)
2. **修正的斯托克斯公式**:考虑到非球形颗粒、非理想流体以及表面张力等因素的影响,终端速度可能会有所修正。
具体公式会因颗粒和流体的具体条件而有所不同。
这些公式主要用于研究颗粒沉降的基本原理和工程应用,例如泥水分离、颗粒过滤等。
对于具体的应用和条件,可能需要考虑更复杂或特定的模型来准确描述沉降行为。
重力沉降法

Et
沉降时间, t (min)
工
0.5m
作
1.0m
水
1.5m
深
(m)
沉降时间, t (min)
Et-t 曲线
10 20 30 40 50 60
SS等去除率曲线
§2-3 理想沉淀池
一、Hazen和Camp提出这一概念。其假设条件是:
(1)在沉淀池各过流断面上,各点处水都以流速V作水平运动。
(2)进水中SS颗粒沿水深呈均匀分布,其水平分速等于水 的水平流速,并从竖直分速u匀还下沉;
2.设计内容 ( 1 )工艺尺寸
主要确定沉砂池的池长L、池宽B、池深H等。
池容V(有效容积):V QMAXT
池长L: H V A
水流断面A: A QMAX v
池宽B: B A H
例1:曝气沉砂池:工艺尺寸
在设计计算过程中,沉砂池的长、宽、深等工艺尺寸需同 时满足有关的长宽比和宽深比,以保证沉砂池内的流 态为推流式。
污泥区
但是,为保守起见,沉降效率依然按照:
ET (1 p0 )
P0 u dp 0 u0
进行计算。
§2-4 沉砂池
一、一般说明 1.一般位于泵站之前或初沉池之前,用以分离水中较大的
无机颗粒。以使水泵、管道免受磨损和阻塞;以减轻沉 淀池的无机负荷;改善污泥的流动性,以便于排放、输运。
2.分类: 按池内水流方向的不同,可分为平流式、竖流式、离心式、 曝气式等。
u随d 而增大。
1.絮凝沉降试验
● 装置:φ140~150mm H=2.0~2.5m 4~5个取样口,间距500mm
● 取样: C0由t=0时中间取样口采集 t1、t2、…、ti、…、tn时,同时从各取样口取水样(两份, 求平均浓度),用以确定不同时间、不同水深处残留的SS 浓度C1、C2、…、Ci、…、Cn。 ● 绘图: 例如:0.5m、1.0m、1.5m处各有一取样口,按设定的 时间序列同时取样,并计算Et。
沉降法粒度测试技术与应用

一、概述沉降法粒度测试技术是指通过颗粒在液体中沉降速度来测量粒度分布的仪器和方法。
这里主要介绍重力沉降式和离心降式这两种光透沉降粒度仪的原理与使用方法。
此外移液管和沉降天平也属这类的装置,因为现在用得较少,所以这里不做介绍。
沉降粒度分析一般要将样品与液体混合制成一定浓度的悬浮液。
液体中的颗粒在重力或离心力等的作用下开始沉降,颗粒的沉降速度与颗粒的大小有关,大颗粒的沉降速度快,小颗粒的沉降速度慢,根据颗粒的沉降速度不同来测量颗粒的大小和粒度分布。
但是,在实际测量过程中,直接测量颗粒的沉降速度是很困难的。
所以通常用在液面下某一深度处测量悬浮液浓度的变化率来间接地判断颗粒的沉降速度,进而测量样品的粒度分布。
当最大颗粒没有从液面降到测量区以前,该处的浓度处在一个恒定状态;当最大颗粒降至测量区后,该处浓度开始下降,随着沉降过程的进行,浓度将进一步下降,直到所有预期要测量的颗粒都沉降到测量区以下,测量过程就结束了。
如图1所示:图1 颗粒在液体中的沉降状态示意图那么,颗粒的沉降速度与粒经之间的关系是怎样的呢?Stokes定律告诉我们,在一定条件下,颗粒在液体中的沉降速度与粒径的平方成正比,与液体的粘度成反比。
这样,对于较粗样品,我们就可以选择较大粘度的液体做介质来控制颗粒的在重力场中心沉降速度;对于较小的颗粒,在重力作用下的沉降速度很慢,加上布朗运动、温度、以及其它条件变化的影响,测量误差将增大。
为克服这些不利的因素,常用离心手段来加快细颗粒的沉降速度。
所以在目前的沉降式粒度仪中,一般都采用重力沉降和离心测降结合的方式,这样既可以利用重力沉降测量较粗的样品,也可以用离心沉降测量较细的样品。
此外也有一种采用改变测量区深度的描沉降式仪器,分动态和静态两种,属于重力沉降范筹。
新式沉降式粒度仪是一种传统理论与现代技术相结合的仪器。
它采用计算机技术、微电子技术和甚至互联网技术,在仪器智能化、自动化等方面都有很大进步。
它的种类也很多,如常见有BT-1500、SA-CP4、SG5100等。
沉降速度球形颗粒的自由沉降阻力系数影响沉
K
d3
s g
2
95 106
3
1.2053000 1.205 9.81
1.81105 2
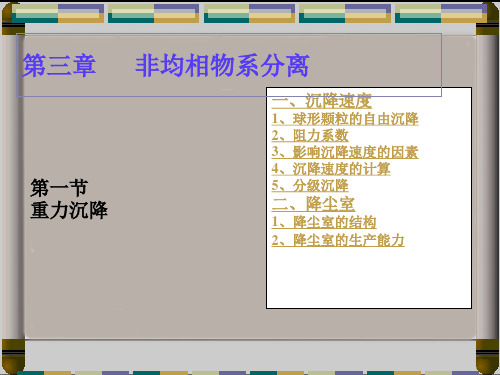
4.52
2.61<K<69.1,沉降在过渡区。用艾伦公式计算沉降速度。
ut
1 1.6
0.154g 1.4d 1.4 s
0.4 0.6
1 1.4
连续相与分散相 分离
不同的物理性质
机械 分离
分散相和连续相 发生相对运动的方式
沉降 过滤
一、重力沉降
沉降 在某种力场中利用分散相和连续相之间的密度差异 ,使之发生相对运动而实现分离的操作过程。
作用力
重力 惯性离心力
重力 沉降 离心沉降
1、沉降速度
1)球形颗粒的自由沉降
设颗粒的密度为ρs,直径为d,流体的密度为ρ,
998.2 0.0696
与此当量直径相对应的正方体的棱长为:
l de 3.182 104 2.565104 m
6
3
6
3
所得方铅矿的棱长范围为0.2565~0.7mm。
二、降尘室
1、降尘室的结构
2、降尘室的生产能力
降尘室的生产能力是指降尘室所处理的含尘气体的体积流 量,用Vs表示,m3/s。
——牛顿公式
3、影响沉降速度的因素
1)颗粒的体积浓度 在前面介绍的各种沉降速度关系式中,当颗粒的体积浓
度小于0.2%时,理论计算值的偏差在1%以内,但当颗粒浓 度较高时,由于颗粒间相互作用明显,便发生干扰沉降, 自由沉降的公式不再适用。 2)器壁效应
当器壁尺寸远远大于颗粒尺寸时,(例如在100倍以上)
空气中颗粒物沉降估算法

s ,则 ut
其它条件相同时,密度大的颗粒先沉降。
◆ 沉降速度计算
① 层流区
Rep
1,
24 Rep
斯托 (S克 to )公 k斯 e式 utsds 2 : ( 1 s 8 )g
② 过渡区
1Rep100, 01Re08..p56
阿(A 伦 l)l公 en:u 式 t 0.27ds(s )ge 0 R .6 p
沉降速度:
ur
d
2 c
su
2
18rm
沉降时间:
r
B ur
18rmB dc2su2
设:气体旋转圈数 N,则气流运行距离 2rmN
气体停留时间: 2rmN
u
颗粒分离条件: r
临界粒d径 c :N 9Bus
对常用形式的 器旋 : u1风 0~2分 5m/离 s,N3~5
将上式代入Rep中,得到:
Repdtu118ds3g(2s)
1
令: kds( s 2 )g 3
则:Rep
1k 18
令 Rep 1 则 k 2.62
层流区:k 2.62 采用斯托克斯公式 过渡区2 : .62k60.1 采用阿伦公
湍流区6: 0 .1k2364采用牛顿
(3) 离心沉降机 ▲ 分离液-固非均相混合物 ▲ 特点:转速可以根据需要调整, 适用于分离困难的体系, ▲ 常用的离心沉降机:转鼓式离心机、蝶片式离心机等。
转鼓式离心沉降机:
1-固体 2-液体
蝶片式离心机:
用 途:分离乳浊液和从液体中分离少量极细的固体颗粒, 广泛用于润滑油脱水、牛乳脱脂、饮料澄清等。
离心沉降速度ur:随颗粒旋转半径 r 变化 。
颗粒的沉降

福州大学化学化工学院
4 颗粒的沉降
均相混合物:所需分离的物质在同一相中, 均相混合物:所需分离的物质在同一相中,不能用机械 混合物 的方法分离; 的方法分离; 非均相混合物:具有一个以上的相, 非均相混合物:具有一个以上的相,可以用机械的方 法分离。相界面两侧的物质性质不同。 法分离。相界面两侧的物质性质不同。 固体——固体:固体混合物 固体: 固体 固体 固体——液体:悬浮液 液体: 固体 液体 非均相混合物 固体——气体:含尘气体 气体: 固体 气体 液体——气体:含雾气体 气体: 液体 气体 液体——液体:乳浊液 液体: 液体 液体
②过渡区(Allen区, 2< Re0 < 500) 过渡区( 区 ) 18.5 gd (ρ s − ρ ) Re0.6 0 ζ = 0.6 u0 = 0.269 Re 0 ρ ③湍流区(牛顿区, 500< Re0 < 200000 ) 湍流区(牛顿区,
ζ = 0.44
u0 = 1.74
gd (ρ s − ρ )
若Re0< 2,则假设成立 , 若Re0> 2,则用相应的公式求 0 ,则用相应的公式求u 核算Re 核算 0
4.1 重力沉降(Gravitational sedimentation) 重力沉降( )
因次分析法: 因次分析法: 通过实验整理数据得到: 通过实验整理数据得到:
阿基米德准数
Ar Re0 = 18 + 0.6 Ar
2
4
(N) )
颗粒做匀速运动,沉降速度恒定不变,该速度称为自由 颗粒做匀速运动,沉降速度恒定不变,该速度称为自由 沉降速度。达到恒定的沉降速度时,合力为: 沉降速度。达到恒定的沉降速度时,合力为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
u随d 而增大。
1.絮凝沉降试验
● 装置:φ140~150mm H=2.0~2.5m 4~5个取样口,间距500mm
● 取样: C0由t=0时中间取样口采集 t1、t2、…、ti、…、tn时,同时从各取样口取水样(两份, 求平均浓度),用以确定不同时间、不同水深处残留的SS 浓度C1、C2、…、Ci、…、Cn。 ● 绘图: 例如:0.5m、1.0m、1.5m处各有一取样口,按设定的 时间序列同时取样,并计算Et。
2.分类: 按池内水流方向的不同,可分为平流式、竖流式、离心式、 曝气式等。
3.由于曝气沉沙池和环流式(离心式)沉砂池对流量变化的适 应性较强,除砂效果好且稳定,条件许可时,建议尽量采用曝气 沉沙池和环流式沉砂池。
第二篇 不溶态污染物的分离技术
第二章 重力沉降法 §2-1 概述 §2-2 沉降的基本原理 §2-3 沉降试验和沉降曲线 §2-4 沉淀池及其设计计算
§2-1 概述
出水
排泥
进水
中心进水周边出水辐流式沉淀池示意图
§2-2 沉降的基本原理
沉降动力学 :颗粒受力情况分析
Fd
Cd
As
(s
3Cd
l l
)d
s
① 层流区(stokes区):
Cd
24 Re
Re dss l
s
g
(s 18
l
)
d
2 s
② 过渡流区(艾伦区)
③ 紊流区(牛顿区)
§2-3 沉降试验和沉降曲线
一、自由沉降试验及沉降曲线 二、絮凝沉降试验及沉降曲线
一、自由沉降试验及沉降曲线
△pi
沉降速度 u
μi
沉降速度分布曲线的图解
2.Camp图解积分法(由数据绘制沉降曲线)
E
E
沉降时间,t (min) E-t曲线
最小沉速,μ E- u曲线
小结:
1、基本概念 重力沉降
2、重点 ① 基本概念 ② 沉降试验和沉降曲线
3、难点 Camp图解积分法计算ET
二、絮凝沉降试验及沉降曲线
絮凝沉降的特点:
dp
0
对于全部μ<μ0颗粒群体,可去除部分为:
p0 dp
0 0
三.Camp图解积分法(续)
μ≥μ0部分颗粒所占百分率为1 – p0
则,总沉降效率为ET :
p0 u
ET (1 p0 )
0
dp u0
U<u0颗粒分率,p 颗粒分率,p
1-p0 p0
p0
μ0
沉降速度 μ 沉降速度分布曲线
(3)颗粒一经沉到水底再不重新浮起 (即认为沉到底部即视为被去除)
§2-3 理想沉淀池
入
出
流
流
区
区
污泥区 理想沉淀池示意图
① 沉降线为未被去除颗粒;
② 为刚好100%去除颗粒; ③ 为可部分去除颗粒; ④ 为可全部去除颗粒。
§2-3 理想沉淀池
同样地有:
ET (1 p0 )
P0 0
h H
dp
ห้องสมุดไป่ตู้
(1
p0 )
P0 u dp
0 u0
可见,静沉试验所得到的沉降规律也可适用于理想沉淀池。
§2-3 理想沉淀池
二、表面负荷q0
H H u H BV Q
u0 t
L
LB
A
① q0在数值上等于最小沉降速度; ② q0↓,ET↑; ③ 在离散型沉降中,当处理水量为定值是,处理效率ET
l
u
2 s
2
Ff l V g
Fg mg s V g
式中:As——运动方向的面积
Cd——牛顿无因次阻力系数: Cd=f(Re) μs——颗粒沉降速度 当受力平衡时,沉速变为μs(最终沉降速度)
对于球形颗粒:
Vs As
2 3 ds
1/ 2
s
4
g
对于d<d0的颗粒可被部分去除。 p0
??:对于μ<μ0的颗粒,可去除部分所占比例是多少? 去除率是多少?
H h
三.Camp图解积分法(续)
对于μ <μ0的颗粒,其中 可去除部分所占比例为:
h h/t H H / t 0
μ <μ0的颗粒中,di → di + dd范围内颗粒所占SS总量的 百分率用dp表示。 则在di → di + dd范围内能被去除部分颗粒占SS总量的百分率为:
一、试验装置 二、常规计算法及沉降曲线 三、Camp图解积分法及沉降曲线
φ100mm Δh
试验装置示意图
H0=1.5~2.0m H=H0-Δhi
二.常规计算法(数据记录与处理)
t t0
t1
t2
t3
…
ti
…
tn
H H0
H0
H0 –Δh1
…
H0 –Δhi-1
…
C C0
C1
C2
C3
…
Ci
μ H
t E E C0 Ci 100 %
Et
沉降时间, t (min)
工
0.5m
作
1.0m
水
1.5m
深
(m)
沉降时间, t (min)
Et-t 曲线
10 20 30 40 50 60
SS等去除率曲线
§2-3 理想沉淀池
一、Hazen和Camp提出这一概念。其假设条件是:
(1)在沉淀池各过流断面上,各点处水都以流速V作水平运动。
(2)进水中SS颗粒沿水深呈均匀分布,其水平分速等于水 的水平流速,并从竖直分速u匀还下沉;
其运动轨迹发生变化:
§2-3 理想沉淀池
入
出
流
流
区
区
絮凝沉降颗粒运动轨迹
污泥区
但是,为保守起见,沉降效率依然按照:
ET (1 p0 )
P0 u dp 0 u0
进行计算。
§2-4 沉砂池
一、一般说明 1.一般位于泵站之前或初沉池之前,用以分离水中较大的
无机颗粒。以使水泵、管道免受磨损和阻塞;以减轻沉 淀池的无机负荷;改善污泥的流动性,以便于排放、输运。
C0
…
Cn
二.常规计算法(由数据绘制沉降曲线)(续)
E
E
沉降时间,t (min) 图3-1 E-t曲线
最小沉速,u 图3-2 E- u曲线
三.Camp图解积分法
给定的沉降时间t内: 对于μ≥μ0的颗粒全部除去
1-p0
对于μ<μ0的颗粒可被部分去除。 p0
给定的沉降时间t内: 对于d≥d0的颗粒全部除去 1-p0
仅是沉降区表面积的函数,而与水深无关。A↑,q0↓, 则ET↑。
§2-3 理想沉淀池
三、实际沉淀池
∵ 在实际沉淀池,理想沉淀池的假设是不存在的,颗粒的 运动是不规则运动。
q
(1 1.25
1 1.75
)u
0
四、对于絮凝沉降
t (1.5 2.0)t0
颗粒之间并聚变大,或 s 变大,u也会之变大。
